Алгебра 8 клас Тарасенкова 2025 by sloven

1) 2,71 · 9,2 + 9,2 · 3,29; 4) 5223 211192; 7575 −+−

2) 15,68 · 3,1 – 13,58 · 3,1; 5) 21 624; 34

1) 6x– (x + 4)(4 – x); 3) 0,5(–y – 2)(y + 2);

2) (x + 5)2 + 21x; 4) (–a – 5)(5 – a) · 0,2a.

Укажіть степінь одержаного многочлена.

6. Розкладіть многочлен на множники:

1) 3a2 – 3b2; 9) a2 – b2 + a + b;

2) 9x3 – x; 10) z2 – 4z + 4 – 16z2;

3) y6 – y2; 11) c3 + 125;

4) 8z3 – 2z; 12) 27a3 – 8.

5) n2 + 10n + 25;

6) 4m2 – 28m + 49;

7) 0,25 + 0,81x2 – 0,9x;

8) –60xy + 45y+ 20x2y;

7. Доведіть тотожність:

1) 10a – (3a – 9b) = 7a + 9b;

2) (0,5c + d) – 2(0,5d – 0,3c) = 1,1c;

3) 9m + 1 = 4(m + n) – 5(n – m) + (n +1);

4) 10a – 2(3a –2b) = (2a + b) – (–2a – 3b).

8. У школі три

13.

14.

15.

1) значення y, якщо x = –4; –1; 1; 6; 7;

2) значення x, за якого y = –3;

3) три значення аргументу, за яких значення функції додатне; 4) три значення аргументу, за яких значення функції від’ємне. Чи належать графіку цієї функції точки

координатами: (0; 2); (2; 0); (–3; 5,5); (–5; –3)?

16. З’ясуйте, чи

1) А(3; 0); 2) В(–3; 18); 3) С(4; 1); 4) D(1,5; 2,25). 17.

1) у = –3; 2) у = x + 3; 3) у = –2x + 4; 4) у = 0,5x.

функції: 1) y = 2; 2) y = 1 3 x; 3) y = –4x + 3; 4) y = 5x – 10.

19.

у = 1 3 х + 4

3) пряма у = 0,5х– 4

31.

9x – 8x = 1 + 7; 2) 5 – 5a = –5a + 5 і 0a = 0; 3) 2(x + 1) = 3(2 – x) і 2x + 3x = 4?

4) 240, 2431. xy xy

33.

40.

42.

2; 0; 1; 3; 5; 4; 0; 5; 3; 1; 2; 2; 6; 3; 1; 5; 4; 2;

43.

44.

45.

46. Для сніданку мама купила Олі й

наповнювачами: вишневим, полуничним та абрикосовим.

1. Скільки існує способів скуштувати один йогурт на сніданок, якщо Оля й Дмитро візьмуть йогурти з різними наповнювачами?

2. Яка ймовірність того, що Олі дістанеться йогурт із полуницею?

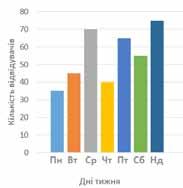
47. На стовпчастій діаграмі (мал. 2) показано кількість

48.

() 2 3:16 xyx ; 6) (5 – х2) : (25 + 10х2 + х4).

1) 23 7 bc bc ; 3) 6 (38)(26) xy xx−+ ; 2) ()2 3:(2) abab ; 4) ( ) 2 3:816 yyy−+ .

його значення, якщо: 1) x = 50 км/год; 2) x = 60 км/год; 3) x = 80 км/год; 4) x = 100 км/год.

76. Одна сторона прямокутника дорівнює 4b см, а число, що

1) x; 2) 5; 3) x2; 4) 2x3; 5) 8; 6) x + 1.

1) 6; 2) x; 3) x2; 4) 3x3; 5) 12x; 6) x – 1.

1) 6; 2) 2x; 3)

22 22 xy xyxy + ; 2)

2 36 122 cc cc + ; 3) 2 22 1025 5 ababb bab −+ . 105.

дріб: 1) 3 32 1 x xx ; 3) 232 34 abaab abb +− + ; 2) 4 32 4 222 y yyy ++ ; 4) 32 3 24 8 aaa a −+ + .

дріб: 1) 222 222 2 2 abcbc abcab +−− ; 3) 22 222 2 xxyyzz yxxzz ++− −+− ; 2) ()() ()() 2222 abcd badc ; 4) 22 2 252 525 aabb aabb++− . 107. Скоротіть дріб: 1) ()2 2 4 xyxy xxy +− ; 2) 2 22 39 233 aabb aabbab −+− −++− .

1 x

1) 3x; 2) 5x; 3) x2; 4) 2x2; 5) 5x3; 6) 6x4 .

1 2a

1) 4a; 4) 6a2; 2) 8a; 5) 10a3; 3) 2a2; 6) 14a4 . 117°. Зведіть

1 3b

1) 9b; 2) 18b; 3) 3b2; 4) 6b2; 5) 15b3; 6) 21b4 . 118°.

1) 1 ab

2 xy xy

3) 2 2mn mn

119°. Зведіть

знаменника: 4xy; 8x2y; 6xy2; –12x3y2; 8axy;

знаменника: m2n2; 2m3n; 9m3n2; –7m5n3 .

5x xy

3) 32 2() mn mn +

1) 4xy; 2)

qr.orioncentr.com.ua/wyNPt

addition and subtraction of rational fractions Addition und Subtraktion von rationalen Brüchen addition et soustraction de fractions rationnelles

23 ; 77 + 53 ; 1414 23 ; 155 + 121 . 173 2.

5) 32 ; 11 yy yy + ++ 7) 34 ; 22 aa xx + ++ 9) 22 38 . 11 xx cc + ++ 6) 4 11 cc cc + ; 8) 47 ; 11 cc yy +

140°. Знайдіть суму дробів:

1) 2 7 ab і 3 ; 7 ab 3) 2 3 2 xy ab і 2 2 ; 2 xy ab 5) 5y ac і 2 ; y ac 2) 3 9 y ac і 4 ; 9 y ac 4) 3 2 a ab + і 4 ; 2 a ab + 6) 2 3x ab + і 2 2 . x ab +

141°. Виконайте додавання дробів:

1) 25 ; 99yy + 3) 22 94 ; 33 bb aa + ++ 5) 28 ; 22 cc aa + ++

2) 24 ; 33 a aa + 4) 33 32 ; 22 acac xx + 6) 33 37 . 22 cc xx + ++

142°.

1) 123 ; 77xx 5) 49 ; 22 cc cc++

2) 117 ; 55aa 6) 314 ; 22 xx aa++

3) 135 ; 99cc 7) 417 ; 11 aa dd

4) 139 ; 11 yy yy 8) 22 1318 . 11 aa bb++

143°. Знайдіть різницю дробів: 1) 1 8ab і 11 ; 8ab 3) 2 12 5 xy ab і 2 3 ; 5 xy ab 5) 5c ac + і 12 ; c ac + 2) 4 5 y ac і 4 ; 5 y ac 4) 9a ab + і 4 ; a ab + 6) 2 8 3 x a + і 2 . 3 x a + 144°. Виконайте віднімання дробів: 1) 29 ; 55yy 3) 22 98 ; 11 bb aa 5) 68 ; 11 cc aa++

2) 23 ; 44 aa aa++ 4) 55 95 ; 44 acac xx 6) 133 . 11 aa xx++ 145°.

різницю , 99 ab cc якщо:

1) a = 5с2 , b = 4с2; 3) a = 15ас2 , b = 6ас2 .

2) a = 7с, b = –10с;

146°. Спростіть вираз: 1) 5 ; 55 x xx + ++ 3) 1112 ; 66 c cc + + ++ 5) 312 ; 11 yy yy + ++ 2) 102 ; 55 x xx 4) 22 ; 22 xx xx −+ + 6) 415 . 11 cc cc + 147°. Спростіть вираз: 1) 2 9 ; 33 x xx++ 6) 2 44 ; 22 cc cc + 2) 2 25 ; 55 x xx 7) 62 ; 33 x xx + 3) 2 36 ; 66 c cc++ 8) 2 4 ; 22 y yy + 4) 22 7 ; 4949 x xx

148°. Спростіть вираз: 1) 1 ; 11 a aa + ++ 5) 22 8 ; 6464 a aa + 2) 42 ; 22 y yy 6) −+ 2 51 ; 22 c cc 3) 314 ; 11 bb bb + 7) + 2 121 ; 333333 n nn 4) 2 16 ; 44 y yy ++ 8) −+−− 2 22 42 . 4444 yyy yyyy

149°. Спростіть вираз та знайдіть його значення: 1) 22 1 11 a aa + , якщо a = 0,9; 2) 22 2 44 y yy , якщо y = –1,8.

150°. Спростіть вираз: 1) 23 ; 510xx + 3) 57 ; 129cc + 2) 55 ; 36aa + 4) 32 ; 23(2) xx xx + ++

5) 2 ; 5(1)1 yy yy + ++ 8) 135 ; 159cc

6) 32 ; 2(1)3(1) cc cc + 9) 24 ; 25(2) aa xx++

7) 15 ; 612xx 10) 6 . 3(1)1 cc yy

151°. Знайдіть суму дробів:

1) 2 3ab і 3 ; 12ab 4) 3 5() a ab + і 6 ; 25() a ab +

2) 5 36 y ac і 4 ; 9 y ac 5) 4 3() y ac і 7 ; 15() y ac

3) 2 4 x ab і 2 3 ; 14 x ab 6) 3 8(2) x ab і 5 . 6(2) x ab 152°.

1) 1 4ab і 11 ; 8ab 3) 2 13 15 x b і 2 3 ; 25 x b 5) 5 6() c ac + і 12 ; c ac + 2) 4 5 y ac і 22 ; 35 y ac 4) 9a ab і 4 ; 5() a ab 6) () 2 9 81 x a + і () 2 . 201 x a +

153°. Спростіть вираз:

1) 13 ; 816yy + 3) () 2 2 24 ; 3 33 bb aa + + + 5) 25 ; 3(2)4(2) cc aa

2) 25 ; 14(1) aa aa + 4) 22 2 ; 721 acac xx 6) 32 . 10(1)15(1) cc xx++

154°. Спростіть вираз: 1) 2 3 131 ; 5 10 x xx + 3) 537 ; 5(5) x xxx + ++ 5) 41 ; 331 yy yy + ++ 2) 223 12 ; 46xyxy 4) 1012 ; (5)5 x xxx 6) 3 2 425 . 1 (1) cc ccc +

155°. Спростіть вираз: 1) 2 22 ; 3 9 x xx + 4) 2 510 ; 7 49 x xx + 2) 2 44 ; 5 25 x xx

3) 2 22 ; 6 36 c cc + + 5) 2 212 ; 1 1 y yy + + 6) 2 44 . 2 4 c cc

1) 2 1 1 1 a aa + + , якщо 2 ; 3 a = 2) 2 263 2 4 y yy + , якщо y = –3.

1) 2 77 3 9 a aa + + , якщо a = 2; 2) 2 82 4 16 y yy + , якщо y = –2.

158. Спростіть вираз: 1) 123 ; 333 xxx ++ 3) 2 ; 2323 xyyx xyxy 2) 23232222 ; 55 abba abab 4) 2332222 . 33 xyyx xyxy

159. Виконайте дії: 1) 33 ; ab abab + ++ 6) 3333 ; ab abab + ++ 2) 33 ; qp pqpq 7) 3333 ; cb bcbc 3) 333 2 ; xxy xyxy ++ 8) 33 11 ; 88 x xx + + ++ 4) 3 27 ; 33 x xx 9) 22 3333 ; abab abab + ++ 5) 3 8 ; 22 a aa 10) 22 3333 . cbcb bcbc + +

160. Виконайте дії: 1) 231 ; 555 yyy −+− ++ 4) 3333 ; xy xyxy + ++ 2) 33 ; ac acac 5) 22 3333 ; xyxy xyxy + ++

3) 3 64 ; 44 a aa 6) 22 3333 . yxyx xyxy + +

161.

вираз:

1) () () 22 22 2 ; abab abab + + ++ 5) () () 3 22 125 ; 55 x xx

2) () () 33 22 ; qp pqpq 6) () () ++ + ++ 2 33 341 ; 22 xx xx

3) () () 22 22 22 ; xy xyxy ++ 7) () () 22 32142612 ; 33 xx xx

4) () () 22 22 4 ; 22 xy xyyx 8) ()() () ()() + + + −+−+ 2 42 8 . 4343 xyxy xyxy

162. Спростіть вираз:

1) () () 3 22 1 ; 11 x xx 2) () () 22 22 33 . ab abab ++

163. Спростіть вираз:

1) 31223 ; 263 xxx +− 3) 22 ; 2332 xyyx xyyxyx

2) 22 2323 ; 55 abba abab 4) 223 35 . 2135 yxxy xyxy

164. Спростіть вираз:

1) 22 ; yy yxxyxx −+ 4) 22 11 ; 1 tt ttt −+

2) 222 4 ; xxy xyxyy + 5) () 2 2 ; 3 3 aa aa + 3) 3312 ; 33 aa aaa −+ −+ +− 6) ()22 121 . 1 1 1 b bbb + +− +

165. Виконайте дії: 1) 423313 ; 152535 yyy −+− ++ 3) 22 11 ; 1 tt ttt −+ 2) 22 ; yx xyxxyy + 4) 22 42 . 93 ttt −+

1) + 1 x x ; 3) + 2 1 4x x ; 5) 42 2 a a a ; 2) + 3 3x x ; 4) 2 7 y y ; 6) 9 7 b b b ; 7) 2 10 5 21 a a a ; 8) 2 21 5 c c c ; 9) −+ +− 2 1 21 xx x x .

Подайте у вигляді раціонального дробу: 1) + 1 2x x ; 2) 2 2 4 y y ; 3) + 2 6 1 9 b b ; 4) 3 3

168. Побудуйте графік функції: 1) =− ++ 32 22 22 11 xxx y xx ; 2) ++ =− 344 51036 xx y xx .

169. Побудуйте графік функції: =− 451 72126 xx y xx .

170. Знайдіть

179.

ABKAKBK

qr.orioncentr.com.ua/bMeQL

multipplying rational fractions Multiplikation rationaler Brüchen multiplication des fractions rationnelles

множення: 1) ; 85 xa ⋅ 6) 3 ; 44 xb yc ⋅ 11) 310 ; 59 ba yb ⋅ 2) 34 ; yc ⋅ 7) 32 ; 56 xa yc ⋅ 12) 2 32 . 53 xa ab ⋅ 3) ; 22 xa yc ⋅ 8) 154 ; 165 ax by ⋅ 4) 53 ; ax by ⋅ 9) 2 24 ; 35 xy yb ⋅ 5) 32 ; 75 xa yb ⋅ 10) 314 ; 75 xa yx ⋅ 184°. Виконайте множення: 1) 5 ; 3 y a ⋅ 2) 5 ; 63 xy ab ⋅ 3) 3 24 ; 3 5 xy bx ⋅ 4) 2 4 32 . 15 5 xa ab ⋅ 185°. Знайдіть

1) 1 3 x + і ()2 6 ; 1 x + 3) 21 8 a + і 16 ; 24a + 2) 55 7 y і 21 ; 1 y 4) 1 5 b і ()2 20 ;

Спростіть вираз: 1) ; 8 x x ⋅ 3) 2 3 6

3) 2244 2222 ; 2 abab abaabb ⋅

2) 22 22 . 2 yxmnxmn

205. Спростіть вираз:

206. Спростіть вираз: 1) 22 22 11 ; ababab aabbabab

2 55155 ; 511 1 5 xxxx xxx xx

2) 2 2 337414 7444 93 aaaa aaa aa

вираз: 1) () 2 2 22 1 ; yxyxyxyx xxyxy xyxyy

2) () () 33 2 224 . 2422 4 xyyxyy yyxxyxyx

⋅+

qr.orioncentr.com.ua/giG4a

dividing rational fractions Division rationalen Brücher division des fractions rationnelles

36 :; 77 25 :; 58 85 :; 258 7 :5; 15 1 4:. 2

1 1:5; 6 35 9:; 59 73 1:3. 1111

1 ; ab 2 2 ; x y (x + 1); 2 21 . 5 x x +

2 3 x і 3 2y є

1) x y ; 2) 4 9 xy ; 3) 9 4xy ; 4) y x ?

212°. Виконайте ділення:

1) 11 : ab ; 6) 15 :; 39xyx

2) 22 : xy ; 7) 12 :; 515xxy

3) 11 :; 22xy 8) 714 :; 24aba

4) 12 :; 2xy 9) 612 :; 525 xy 11) 321 :; 840 x yxy

5) 22 :; 35 xy 10) 728 :; 39ab 12) 963 :. 216abb

213°. Виконайте ділення:

1) 22 11 :; abab 3) 4834 :; 53 xx 5) 515322 :; 28 xyxy

2) 3 12 :; xyy 4) 322 39 :; 24abab 6) 42 2 416 :. 9 3 xx yy

214°. Виконайте ділення:

1) 63 :; 52 xy 3) 13 :; 535aab 5) 3322 11 :; abab 2) 15 :; 312xx 4) 714 :; 25 aa b 6) 618245 :. 735 xyxy

215°. Знайдіть частку дробів: 1) 1 3 x + і 1 ; 15 x + 5) 36 14 y і 21 ; 42 y 2) 55 7 y і 1 ; 28 y 6) 13 18 x і 93 . 42 x 3) 21 8 a + і 42 ; 16 a + 4) 1 5 b і ()2 1 ; 25 b

Знайдіть частку дробів: 1) 3 4 y + і 3 ; 36 y + 2) 31 15 x + і 39 ; 35 x + 3) 25 10 y і 156

:; 5 x x

:6;

:3;

:; 2 x x

вираз: 1) 2232 23 16123 :; 54 25 ababa xyy xy ⋅ 2) 22 22 33 22 2 :.xyxyxy xyxyxy ++− −++ 230. Спростіть

1) 33 33 :; xyxy xyxy ++ 2) 222 2244 2 :. aabaabb abab +++ +−

3) (1)(4)0; xx+−= 8) 2 5020. x −=

4) (2)(51)0; xx+−= 5) 2 60;xx−=

238°. Розв’яжіть рівняння:

1) x(6 – 2x) = 0; 3) (5 – х)(х – 4) = 0; 2) х2 + 7х = 0; 4) 2х2 – 72 = 0.

239°. Визначте ОДЗ змінної x рівняння: 1) (x – 2)(х + 3) = 0; 3) 1 0; 7 x = 5) 2 1; 2 xx xx −= 2) (х – 2)(х – 6) = 5; 4) 3 0; 1 x = 6) 25 . 34 xx x +=

240°. Визначте ОДЗ змінної x рівняння: 1) 2 1 0; 25 x = 2) 1 0; 3 x = 3) 54 2; 54xx += +− 4) ()3 1 1. 1 x x + = +

241°. Розв’яжіть рівняння: 1) 2 0; 1 x x = + 5) 2 2 0; 1 x x = + 2) 3 0; 2 x x = 6) 2 1 0; 3 x x = 3) 2 0; 2 x x = + 7) 3 3 0; 3 x x = + 4) 3 0; 3 x x + = 8) 5 0. 5 x x =

242°. Розв’яжіть рівняння: 1) 2 0; x xx = + 3) 3 32 5 0; 5 x xx = + 5) 2 4 0; 4 x xx =

2) 2 3 0; 3 x xx = 4) 2 5 0; 5 x xx + = + 6) 32 13 0. 3 x xx =

243°. Розв’яжіть рівняння: 1) 2 0; 1 x x = + 2) 4 0; 4 x x = 3) 2 0; x xx = 4) 2 3 0. 3 x xx + = +

244°. Розв’яжіть рівняння: 1) 2 1 0; 1 x x = 2) 2 2 0; 4 x x + = 3) 2 22 0; 1 x x + = 4) 2 36 0; 4 x x = 5) 2 1 0; 1 x x = 7) 2 16 0; 4 x x =

Розв’яжіть рівняння: 1) 2 3 0; 9 x x = 2) 2 9 0. 412 x x = +

246°. Чи має розв’язки рівняння: 1) 2 1 0; x x + = 3)

1) 2 2; 5 x = 3) 24 35(2)(1); xx−=−

2) 1 1; 1 x x = + 4) 117 . 5315 xx −= 251. Для кожної

1) 1,10; 33 xx =+= 3) 11 1,0; x xx == 2) 663,30; 2121 xx =−= 4) 21212 1, 0? 22 xxx xx −−+ = =

Розв’яжіть рівняння:

1) 3 1 0; 1 x x = 3) 2 4 0; 36 x x = + 5) 3 9 0; 155 xx x =

2) 3 2 0; 8 x x + = + 4) 3 22 0; 1 x x + = + 6) 3 312 0. 42 xx x =

рівняння: 1) 3 1 0; 1 x x + = + 2) 3 4 0; 64 x x = 3) 2 33 0; 44 x x = + 4) 2 218 0. 93 x x = 254. Розв’яжіть рівняння: 1) 2 2 3 2 221; 32 xx xx x + +−=− + 2) 222 6366 ; 6272212 xxx xxxxx +−− =+ −−+ 3) 2 464 ; 44 16 xx xxx + −= +− 4) 241 . 31(3)(1) x xxxx −= ++++ 255. Розв’яжіть рівняння: 1) 2 2 35 4 241; 59 xx xx x ++=+ + 3) 2 115 ; 33 9 xx xxx + += −+ 2) 2 132 ; 32 6 x xxxx −= −+ 4) 433 . 21(2)(1) x xxxx += −+−+

257.

258.

1) 0,01 · 0,0001: (–100) · 10 000 000; 2) 0,0001 : 0,01 · 10 000 : 1 000 000.

2. Обчисліть: 1) (32 + 42 + 52) : 102; 2) (21 + 22 + 23 + 24) · 25.

5 1 ; 5 10) 5 1 ; m

200 1 . r 5) 10 1 ; 20 11) 8 1 ; p 6) 3 1 ; 21

рівність: 1) 20 = 2; 2) 20 = 1; 3) 20 = 0?

14?

70 (–5)3 9–4

степеня–5100,81

1) 10; 2) 1 . 10

3: 1) 27; 2) 1; 3) 3; 4) 1 ; 3 5) 1 ; 9 6) 1 . 81

a–8: 1) 8 1 ; a 2) 8 1 ; a 3) –а8; 4) –8а?

279°. Подайте степінь як дріб: 1) 4–1; 2) 7–1; 3) 2–1; 4) 21–1; 5) 20–1; 6) 123–1.

280°. Подайте степінь як дріб: 1) 10–1; 2) 3–1; 3) 18–1; 4) 321–1.

281°. Подайте степінь як дріб: 1) 4–4; 4) 5–7; 7) 21–5; 10) 80–13; 2) 7–3; 5) 10–9; 8) 45–7; 11) 90–20; 3) 2–5; 6) 11–3; 9) 54–9; 12) 100–10.

282°. Подайте степінь як дріб: 1) 10–3; 2) 3–3; 3) 8–9; 4) 12–10; 5) 20–1; 6) 25–7.

283°. Подайте степінь як дріб: 1) а–8; 3) m–5; 5) b–11; 7) р–20; 9) z–31; 2) с–3; 4) n–8; 6) х–15; 8) у–21; 10) t–55 .

284°. Подайте степінь як дріб: 1) а–4; 3) m–12; 5) b–80; 2) с–9; 4) n–56; 6) х–100 .

285°. Знайдіть а–1, якщо а дорівнює: 1) 2; 3) 10; 5) 25; 7) 100; 2) –3; 4) 15; 6) –40; 8) –1000.

286°. Знайдіть m–1, якщо m дорівнює: 1) 4; 2) 6; 3) –5; 4) 3; 5) 20; 6) 1000.

287°. Знайдіть а–2, якщо а дорівнює: 1) 2; 3) 10; 5) 1 ; 5 7) 1 ; 10 9) 1 ; 100 2) 5; 4) 1 ; 2 6) 1 ; 6

293°. Порівняйте значення виразів: 1) 44 і 40; 3) 5–5 і 5 1 ; 5 5) 5 1 8 і 85; 2) (–4)3 і 40; 4) 3–4 і 100; 6) 3–2 і 09.

294°. Порівняйте

1) 55 і 50; 3) 3–5 і 5 1 3 ; 2) (–7)5 і 70; 4) 9–6 і 1000. 295°.

(–8)0;

6 3 ; 5 2) 100; 4) (–3)5; 6) (–4)4; 8) 

1) 2–5; 2) 80; 3) 

297. Знайдіть а–2, якщо а дорівнює: 1) 2 1; 3 3) 1 2; 5 5) 0,2; 7) 1,2; 2) 1 2; 2 4) 1 3; 8 6) 0,05; 8) –1,2.

298. Обчисліть: 1) 2–6; 4) 0,1–2; 7) (–3)–3; 10) (–1,5)–3; 2) (–1,1)–2; 5) 0,5–3; 8) 3–3; 11) 

3) (–4)–2; 6) (–2)–5; 9) (–0,2)–3; 12)

299. Обчисліть:

1) 0,4–3; 3) (–0,1) –2; 5) 

2 1 1; 3 2) 0,1–4; 4) (–0,1)–5; 6)

305*. Обчисліть: 1) 1–1 +

4,2 · 104 + 7 · 103 = = 4,2 · 104 + 0,7 · 104 = = (4,2 + 0,7)

104 = = 4,9

104.

· (104 · 103) = = 29,4 · 107 = = 2,94 · 108.

1) 125 = 1,25 · 102; 2) 0,08 = 8 · 10–2; 3) 34,6 · 105 = 3,46 · 106.

як степінь з основою 2: 1) 8 · 16; 2) 32 · 4 · 16; 3) 8 · 2 · 64.

2. Подайте як степінь: 1) х15: х4 · х3; 3) (х10х5)3 : (х10)2; 2) (х15)3 : (хх3)2; 4) (х5 х4 х6)2 : х2 .

3. Обчисліть: 1) (0,2)3 · 53; 2) (25)2 : 52; 3) 3 3 27 ; 9 4) ⋅ 5 55 32 . 82

309'. Яка з формул є правильною: 1) аn

310'.

1) аn : аm = а(n – m); 3) аn : аm = аn : m; 2) = :; nmm aa n 4) аn : аm = аn – m?

312'. Яка з формул є правильною: 1) аn – m = аn – аm; 3) аn – m = аn : аm?

2) аn – m = аn : m; 313'.

(аm)n = аmn; 3)

314'. Яка з формул є правильною: 1) аn · bn = (аb)2n; 3) аn · bn = аn + bn; 2) аn · bn = аbn; 4) аn · bn = (аb)n?

315'. Яка з формул є правильною: 1) = ; n n aa bb 2) = ; nn n aa bb 3) =−() ; n n n aab b 4)

316'. Яке із чисел записане в стандартному вигляді: 1) 1 · 102; 3) 1,09 · 113; 5) 3,1 · 10–22; 2) 2,3 · 104; 4) 2,5 · 105; 6) 51 · 108?

317°. Яка з рівностей є правильною: 1) 5–3 · 52 = 25–6; 3) 5–3 · 52 = 51; 2) 5–3 · 52 = 5–6; 4) 5–3 · 52 = 5–1?

318°. Обчисліть:

2–7

319°. Обчисліть: 1) 10–5 · 10–1; 3) 10–3 · 105; 5) 1035 · 10–9 ·

320°. Спростіть вираз: 1) а

степенів: 1) 10–1 + m; 3) 8–4 + m; 5) 5–р + 1 + (–n); 2) 9–1 + (–р); 4) 6–m + n; 6) 10–2 + 3n .

323°. Запишіть як добуток степенів: 1) 6–4 + х; 3) 12–8 + n; 2) 27 + (–х); 4) 3–р + (–n) .

324°. Яка з рівностей є правильною: 1) 3–8 : 32 = 1–6; 3) 3–8 : 32 = 3–6; 2) 3–8 : 32 = 3–4; 4) 3–8 : 32 = 3–10?

333°. Яка з рівностей є правильною: 1) (4–3)5 = 4–8; 3) (4–2)–5 = 47; 2) (4–3)5 = 4–15; 4) (4–2)–5 = 410?

334°. Запишіть як степінь: 1) (5–5)10; 7) (а–6)0; 13) (а2)–2; 2) (4–11)–4; 8) (а0)5; 14) (а–10)9; 3) (36)–7; 9) (а6)–5; 15) (а–7)–5; 4) (7–4)0; 10) (а–6)5; 16) (а11)–2; 5) ((–1)–5)–10; 11) (а–6)–5; 17) (а–5)–20; 6) (0,759)–3; 12) (а–5)5; 18) (а5)–20.

335°. Запишіть як степінь: 1) (2–1)8; 4) (10–8)0; 7) (х11)–4; 2) (3–15)–2; 5) (х–9)0; 8) (х–8)–4; 3) (315)–2; 6) (х0)9; 9) (х–3)3.

як степінь з основою 7: 1) ⋅ 74 9 77 ; 7 3) ⋅ 112 4 77 ; 7 5)

312 108 77 ; 77 6) ⋅ ⋅ 1615 98 77 . 77

85 48 77 ; 77 2) ⋅ 811 10 77 ; 7 4)

Запишіть як степінь з основою 8: 1) ⋅ 2 8 88 ; 8 3) ⋅ 412 3 88 ; 8 5) ⋅ ⋅ 82 5 88 ; 88 2) ⋅ 515 10 88 ; 8 4) ⋅ ⋅ 104 1512 88 ; 88 6) ⋅ ⋅ 613 73 88 . 88

332°. Спростіть вираз: 1) а–25 : а–12 · а–12; 2) а40 · а–30 : а10; 3) а–32 : а2 : а–14; 6) а · а–5: а–4 : а8; 4) а0 · а : а–9 · а11; 7) m6 : m–13 · m–7; 5) а : а–7 · а–1 : а5; 8) m–9 : m2 · m–2 : m9 .

336°. Запишіть як степінь: 1) 4–3 · 2–3; 8) х–5 : у–5; 2) 6–1 · 3–1; 9) 5 5 ; m n 3) 4–3 : 2–3; 10) р–6 · m–6 · n–6; 4) 6–1 : 3–1; 11) а–1 · b–1 · с–1; 5) 5–9 · 2–9 · 8–9; 12) 3–4 · m–4 · n–4; 6) 1–4 · 4–4 · 3–4; 13) 55 5 ; xy z 15) 22 22 ; xy zh 7) b–12 · а–12; 14) 1 11 3 ; ab 16)

337°. Запишіть як степінь: 1) 7–7 · 10–7; 3) 15–10 · 3–10; 5) z–3 · x–3 · y–3; 2) 7–7 : 10–7; 4) 15–10 : 3–10; 6) 77 7 . ac x 338°. Запишіть як степінь з основою 30: 1) 3–5 · 10–5; 4) 2–3 · 3–3 · 5–3; 7) 15–4 · 4–4: 2–4; 2) 6–9 · 5–9; 5) 60–1 : 2–1; 8) 40–11 : 4–11 · 3–11; 3) 2–6 · 15–6; 6) 900–2 : 30–2; 9) 120–3 : 4–3 · 170. 339°. Запишіть як степінь з основою 12: 1) 2–2 · 6–2; 3) 2–4 · 2–4 · 3–4; 5) 5–15 · 24–15 : 10–15; 2) 3–10 · 4–10; 4) 36–1 : 3–1; 6) 8–4 · 3–4 · 0,5–4.

340°. Знайдіть х:

1) (–2 · 9)–4 = х · 9–4; 4)  = 

2) (7 · 10)–3 = 7–3 · х; 5)  = 

3) (5 · 8 · 12)–1 = х · 8–1 · 12–1; 6)  = 

341°. Знайдіть х:

1) (4 · 5)–3 = х · 5–3; 3) (2 · 3 · 4)–2 = х · 2–2 · 4–2; 2) (2 · 15)–6 = 15–6 · х; 4)  =

342°. Запишіть у

1) 22; 9) 11,04; 17) 2300,02 · 10–1;

2) 31; 10) 0,333; 18) 118,8 · 1010; 3) 1008; 11) 20,407; 19) 0,32 · 102; 4) 700; 12) 0,0000012; 20) 0,00051 · 103; 5) 976; 13) 54 · 102; 21) 5072 · 106; 6) 17 000; 14) 54 · 10–2; 22) 0,0074 · 10–2; 7) 0,005; 15) 335 000 · 103; 23) 0,003 · 1010; 8) 0,45; 16) 87 500 · 10–4; 24) 0,00008 · 103.

343°. Запишіть у

1) 37; 6) 13,005; 11) 11 500 · 103; 2) 19; 7) 0,065; 12) 43 000 · 10–3; 3) 207; 8) 0,000075; 13) 0,00027 · 10–2; 4) 0,02; 9) 91 · 103; 14) 0,00011 · 103; 5) 0,38; 10) 482 · 10–5; 15) 0,305 · 10–2.

344°.

числа:

1) 8 · 10–5 і 1,1 · 10–5; 3) 3,1 · 10–2 і 1,2 · 10–2; 2) 2,5 · 108 і 3 · 108; 4) 4,1 · 1010 і 2 · 1010; 5) 1,8 · 10–15 і 1,5 · 10–15; 6) 1,25 · 109 і 4 · 109.

345°. Порівняйте числа: 1) 5

3) 10; 4) 100; 5) 1000; 6) 10 000.

1 3 : 1) 1 3 ; 2) 1 9 ; 3) 1 81 ; 4) 1; 5) 3; 6) 27.

348. Обчисліть: 1) () ( )

1235 2. 25

350. Запишіть як степінь: 1) (а–8)n : (аn)–1; 5) (

–10 а3)2; 3) (а–15: а4)–3 · (а10: а3)–2; 7) (а–2 + n)–n · аn(1– n) : (–а)–2n; 4) (а–15а4)3 : (а10а–3)–2; 8) (а –n)n ·

351. Знайдіть х, якщо: 1) а–1b24 = а5b–8 · х; 4) 1,921 = (1,9–3)–х; 2) а–1b–1 = х : аb; 5) (4,5)–20 = (4,5–х)5. 3) а–7b26 = х : b–16;

352. Знайдіть х, якщо: 1) а2b–14 = а–14b · х; 3) 3–36 = (3–х)9; 2) b–50 = а–100b100 : х; 4) 6–14 = (6х)2.

353.

вираз 5–12 як степінь з

1) 5–2; 2) 54; 3) 53; 4) 5–4.

354.

яких дорівнює: 1) а2; 2) а–6; 3) а4; 4) а–3; 5) а–4; 6) а6 .

355. Подайте

m24 як

двох степенів,

з яких дорівнює: 1) m2; 2) m–6; 3) m12; 4) m–4 .

356. Запишіть як степінь з основою 2: 1) 8–5 · 47; 3) (2–5)3 · (42)–3; 5) 0,5–25 : (4–1)3; 2) 645 · 16–2; 4) (165)9 · (8–2)7; 6) 0,25–6 : 3230.

357. Винесіть за дужки 2–5: 1) 2–6 + 27; 2) 2 – 2–5 + 210; 3) 2–3 + 23 – 2–15 + 215.

358. Винесіть за дужки 3–4: 1) 3–12 + 312; 2) 3 + 3–4 + 34; 3) 3–5 + 35 – 3–1 + 3.

359. Знайдіть х.

(0,1–8

2) (7

9)–12

(21–4)3

362.

363*. Обчисліть: 1)

https://fmf.npu.edu.ua /alumni/271- konforovitch

qr.orioncentr.com.ua/Q9gFM

expression transformation einen Ausdruck umwandeln transformation d’expression

1) 88326 : (–9) · (–13 · 2 + 26); 2) –2346 · (14 – 244 + 230) + 678; 3) 5,5 · 2,5 : 0,25 – 525 : (–5).

розв’яжіть задачі

369'. Чи правильно, що (х – 1)–1 дорівнює: 1) + 1 ;

3) () 1 33 ; ab 6)

1) (x – y)–2; 6)

2) (10 + m)–4; 7)

3) (x2 – 1)–6; 8)

1) −⋅− 22 (1)(1); yy 7) 62 83:; mm aa

2) −⋅− 53 ()(); abab 8) + + 18 2 9 22 4(1) :; (1) ac ca

3) −⋅− 46 ()(); xyxy 9) 255 73 ()() . () xyyxy yxyy ⋅⋅

4) + + 2 3 (4) ; (4) y y

5) + + 2 4 (1) ; (1) c c

6) ⋅+ +⋅ 53 5 () ; () xxy xyx

1) +⋅+33 ()(); mnmn 5) + +⋅⋅− 2 2 3 () ()(); () ab abab ab

2) +⋅+85 (5)(5); aa 6) + ⋅ + 30 01 (2) ; (1) xx yx

3) + + 1 2 () ; () pm pm 7) + ⋅ + 415 10 8 (5) ; (5) yy yy 4)

15 ; mm nn 8) ++ ⋅ + 13 10 40 (4) (4) :. (4) nmpnm pnmp

388°. Піднесіть до

394°. Спростіть вираз:

1) 2 2 1 ; y y 4) ++ + 1 7 (7); 7 nn n

2) ++ + 1 9 (10); 10 a a 5) +−+10 ()(); mnmn

3) +++11 (4)4(4); aaa 6) +−−11 (4)(4). xx

395°. Запишіть як квадрат двочлена:

1) у–2 – 4у–1 + 4;

2) х–2 – 2(ху)–1 + у–2;

3) а–4 – 10а–2 + 25;

4) 4m–2 – 12m–1n–1 + 9n–2; 5) а–2с–4 – 2а–1с–2 + 1; 6) 9а–2b–2 – 6а–1b–2c–1 + c–2b–2 .

396°. Розкладіть на множники:

1) y–2 – 4; 5) n–4 – m6;

2) x–2 – y2; 6) a–2 – (4 + a)–2;

3) a2d–2 – b–2; 7) (х–2 + y–2)2 – (х–2 – y–2)2; 4) n–4 – m–4; 8) (2 + m–2)2 – (2 – m–2)2.

397°. Розкладіть на множники:

1) x–2 – 25; 4) x–8 – (1 + x–4)2; 2) a–2 – b2; 5) (n–2 – m–2)2 – (m–2 + n–2)–2; 3) n–2 – m–2; 6) (x–2 + 2)2 – (3x–2 – 4)2.

1) а + а–1; 3) х–2 – x–3; 5) 1 1 ; 1 m

2) х + x–2; 4) y–3 + 4y–5; 6) + 1 1 . aa

414. Знайдіть m n , якщо: 1) + = 11 11 3; nm nm 2) = + 11 11 4 5. 3 mn nm

415*. Знайдіть    2 x y , якщо: 1) + = + 22 22 4 1; 5 xy xy 2) +=−22 22 23 . xy xy

416*. Обчисліть 4322 ab ab , якщо а–1b = 5.

417*. Спростіть вираз: 1) +++ ++ +++ 111 (1)(2)(3) ; 234 xxx xxx 2) ()()()() ( ) 

3) () + −+ ⋅ −+++ 2 1 33 22 1122111 1 11 :. 1 ababab abababababab

1. D (у): х — будь-яке число,

нуля, або х ≠ 0.

2. Е (у): у — будь-яке число, крім нуля, або у ≠ 0.

k < 0 (мал. 7)

1. D (у): х — будь-яке число, крім нуля, або х ≠ 0.

2. Е (у): у — будь-яке

(–8; –1), (–4; –2), (–2; –4), (–1; –8), (1; 8), (2; 4), (4; 2), (8; 1) (мал. 9).

1. Розв’яжіть рівняння:

1) (x – 10)(x + 10)= 0; 4) x2 – 5x = 0;

2) (x – 1)(x + 2)= 0; 5) x2 + 6x = 0;

3) (x – 3)(x + 4)(x – 5)(x + 6)= 0; 6) 2x2 – 6х = 0.

1) A (2; 2); 4) D (0; 4); 7) P (0; 0); 2) B (–2; –2); 5) M (4; 2); 8) R (–1; 4); 3) C (4; 4); 6) N (–8; –2); 9) S (8; 0,5)?

429°. Чи

функції = 10 y x

1) А (1; –10); 3) C (0; 0); 5) M (10; 1); 2) В (2; 5); 4) D (–1; –10); 6) N (–10; –10)?

430°. Чи

функції = 12 y x точка:

1) K (–1; 12); 2) L (1; 12); 3) M (2; 6); 4) N (–4; –8)?

431°. Яка з точок M (–2; 1), N (1; 2), P (2; –1), R (–2; 0) нале-

1) = 5 ; y x

через точку:

1) А (1; –10); 6) P (5; –10); 2) B (2; 8); 7) Н (–12; –3); 3) С (–9; –3); 8) R (–6; 3). 4) M (–2; 1); 5) N (9; 1);

ходить через точку:

1) А (–1; 1); 3) С (–4; –5); 2) B (3; 7); 4) D (7; 2).

= k y x , якщо:

1) k = 2; 3) k = 15; 5) k = 0,9; 7) k = –42; 2) k = –7; 4) k = –11; 6) k = 1,6; 8) k = –0,25? 437°.

= k y x , якщо:

1) k = 1; 3) k = 25; 5) k = –2,6; 2) k = –9; 4) k = –18; 6)

1) = 1 ; 5 y x 3) = 4 ; 9 y x 5) =− 1 ; 0,2 y x 7) 2xy = 14;

2) =− 1 ; 7 y x 4) = 5 ; 6 y x 6) xy = –8; 8) 4xy = –24? 446.

ходить через точку:

1) А (0,5; –10); 5) 2 ;15; 5 M  

2) B (0,1; 100); 6) 31;1; 42 N

3) С (–6; 0,05); 7) 1 2;35; 7 P

4) D (1,5; 0,02); 8) 1 1;1,75. 3 H

y x

1) А (2; –0,001); 2) 1 2;6; 3 B

y, якщо x = –1; 2; –4;

2) значення x, якщо y = 8; –2; 1;

3) за

451. Дано функцію:

1) = 1 ; y x 3) = 0,5 ; y x 5) = 0,01 ; y x 7) = 3 ; 7 y x

2) =− 13 ; y x 4) = 5 ; 4 y x 6) =− 1 ; 9 y x 8)

Знайдіть:

y, якщо x = –1; 1; 10;

452.

454.

5) значення x, якщо y = 1; 10;

а) є додатними; б) є від’ємними.

455. Порівняйте

1) x = 3 і х = 5; 4) x = –5 і х = –3; 2) x = 6 і х = 10; 5) x = –1 і х = –10; 3) x = 3,5 і х = 4; 6) x = –2 і х = 5.

456.

1) x = 9 і х = 10; 3) x = –5 і х = 5; 2) x = –2 і х = –4; 4) x = –12 і х = 5.

(мал.

(–3; 9), (–2; 4), (–1; 1), (0; 0), (1; 1), (2; 4), (3; 9) (мал. 28).

(мал. 29).

Мал.

1) (1515 : 15 – 11) : 15 · 21; 2) 1515 : (105 – 64:16) · 15 + 5.

2. Обчисліть: 1) 51 12; 63

472°.

через точку: 1) A (4; 2); 3) C (4; 16); 5) M (10; 100); 7) P (0; 0); 2) B (–2; 4); 4) D (0; 4); 6) N (–8; 16); 8) R (–1; 1)?

473°. Чи правильно, що графік функції y = x2 проходить через точку: 1) A (1; 1); 3) C (2; 4); 2) B (–2; –4); 4) D (4; 8)?

474°. Які з точок A (3; 9), B (–3; –9), C (9; –3), D (9; 3), M (–5; 25), N (5; 10), P (7; 49), R (6; –36) належать графіку функції y = x2?

475°. Чи належить графіку функції y = x2 точка: 1) А (1; –10); 3) C (–8; –64); 5) M (9; 81); 2) В (8; 64); 4) D (–2; 6); 6) N (–10; –10)?

476°. Чи належить графіку функції y = x2 точка: 1) K (1; –1); 3) M (–6; 12); 2) L (6; 36); 4) N (–7; 49)?

477°. На малюнку 35 зображено графік функції y = x2 . Скориставшись графіком, знайдіть:

1) значення y, якщо x = 0; –1; 3;

2) значення x, якщо y = 1; 9;

3) значення аргументу, за яких значення функції невід’ємні;

4) значення аргументу, за яких функція зростає.

478°. На малюнку 35 зображено графік функції y = x2. Скориставшись графіком, знайдіть:

1) значення y, якщо x = 1; –2; –3;

2) значення x, якщо y = 0; 4;

4) значення аргументу, за яких функція спадає.

479°.

486.

487.

488.

1) y = x2

= –2,4 і х = –2; 4) x = 0,7 і х = 1,2; 8) x = –10 і х = –8.

489.

значень аргументу: 1) x = 9 і х = 15; 3) x = –7 і х = –6; 2) x = 32 і х = 64; 4) x = –24,5 і х = –25.

490. Розв’яжіть графічно рівняння: 1) x2 = x – 5; 3) x2 = х – 2; 5) 4х – 3 = x2; 2) х–x2 = 0; 4) х – 6 = x2; 6) 2 1 . x x =−

491. Розв’яжіть графічно рівняння: 1) х2 + x = 0; 3) x2 = –х – 7; 2) –2х + 3 = x2; 4) 2 8 . x x =

5; 6; 7; 8; 9; 10.

496.

–4,6;

497.

1. 100161001610440.

2. 2252595315. =⋅=⋅=

1) 82 ⋅ ; 2) 72 2 .

1. 8282164. ⋅=⋅== 2. 7272 366. 2 2 ===

1) 32 ; 2) ()2 3 ; 3) ()2 35 .

1. 2 333. == 2. ()2 333.−=−= 3. ()2 3535. −=−

Так.

272 · 81–4; 3) (3–6)8 · (9–1)–2; 4) (81–2)3 · (27–3)–4. 2. Серед чисел 6, –11, 2 6

3) раціональні.

498'. Чи правильно, що:

502'. Чи правильно порівняли

1) 35; < 3) 65; <

2) 72; < 4) 1011? > Відповідь поясніть.

503'. Чи правильно, що для a > 0: 1) 0; a < 2) 0; a = 3) 3 0; a ≤ 4) 3 0; a > 5) 0? a ≥

504'. Чи є правильним твердження:

1) значення виразу a існує, якщо а ≥ 0;

2) значення виразу 3 a існує, якщо а > 0;

3) значення виразу a існує, якщо а < 0;

4) значення виразу 3 a існує, якщо а < 0? 505'.

509°.

1) ;aa = 3) 2 ;aa = 2) 2 ; aa = 4) 2 ? aa =

із

1) –1; 2) 2; 3) –36; 4) 40?

поясніть.

510°. Чи існує квадратний корінь із числа: 1) 3; 2) –9; 3) –16?

511°.

з числа: 1) 16; 3) 49; 5) 169; 7) 256; 2) 25; 4) 121; 6) 196; 8) 400; 9) 0,16; 13) 1,69; 17) 1 ; 16 21) 1 ; 169 10) 0,25; 14) 1,96; 18) 1 ; 25 22) 1 ; 196 11) 0,49; 15) 2,56; 19) 1 ; 49 23) 1 ; 256 12) 1,21; 16) 0,04; 20) 1 ; 121 24) 1 . 400

512°. Знайдіть усі квадратні корені з числа: 1) 81; 4) 225; 7) 1,44; 10) 1 ; 100 2) 100; 5) 0,81; 8) 2,25; 11) 1 ; 144 3) 144; 6) 0,01; 9) 1 ; 81 12) 1 . 225 513°. Якими даними потрібно

Чи

515°. Чи є правильним твердження: 1) якщо 22 = 4, то 42; = 2) якщо (–2)2 = 4, то 42; =− 3) якщо (–5)2 = 25, то 255; = 4) якщо 82 = 64, то 648? = Відповідь поясніть.

516°. Чи є правильним твердження: 1) якщо 102 = 100, то 10010; = 2) якщо (–3)2 = 9, то 93? =− Відповідь поясніть.

517°. Знайдіть арифметичний

1) 0,01; 3) 0,64; 5) 0,49; 7) 0,0001; 2) 0,04; 4) 0,36; 6) 0,0016; 8) 0,0004.

518°. Знайдіть арифметичний

1) 0,09; 3) 0,25; 5) 0,0036; 2) 0,16; 4) 0,0049; 6) 0,0169.

519°. Обчисліть: 1) 1 ; 4 3) 16 ; 25 5) 49 ; 64 7) 9 ; 16

2) 1 ; 16 4) 9 ; 100 6) 49 ; 100 8) 49 . 81

520°. Обчисліть:

1) 1 ; 9 2) 1 ; 25 3) 25 ; 49 4) 36 ; 100 5) 25 ; 64 6) 81 . 100

521°. Знайдіть значення виразу:

1) 2581; 5) 259; ⋅

2) 259; + 6) 36:464; + 3) 4909; ++ 7) 100:239; +⋅ 4) 49; ⋅ 8) 1008549. ⋅−⋅

522°. Знайдіть значення виразу:

1) 49; + 5) 1004; ⋅ 2) 464; 6) 081416; ⋅+

3) 16:42; + 7) 42316; ⋅+⋅ 4) 464; ⋅ 8) 362:9. ⋅

523°. Порівняйте числа:

1) 5 і 0; 5) 21 і 7; 9) 99 і 10; 2) 0 і 15 ; 6) 9 і 90; 10) 62 і 8; 3) 100 і –10; 7) 17 і 4; 11) 6 і 39; 4) –4 і 2; 8) 3 і 8; 12) 12 і 4.

524°. Порівняйте числа: 1) 6 і 0; 4) 35 і 37; 7) 6 і 33;

2) 0 і 0,01; 5) 74 і 9; 8) 101 і 10;

3) –5 і 26; 6) 6 і 38; 9) 101 і 99 .

Чи є

рівність: 1) ()2 816; = 2) ()2 55; = 3) ()2 1010; =− 4) ()2 93? =

526°. Обчисліть: 1) ()

4; 4) ()

9; 7) ()

0,99; 10)

2) ()2 3; 5) ()2 10; 8) ()2 1,1; 11)

528°. Обчисліть: 1) 361; ⋅ 6) 100169; ⋅⋅ 2) 94; ⋅ 7) 4100100; ⋅⋅ 3) 254; ⋅ 8) 64254; ⋅⋅ 4) 814; ⋅ 9) 164925; ⋅⋅ 5) 819; ⋅ 10) 6416100. ⋅⋅

529°. Обчисліть: 1) 41; ⋅ 3) 25100; ⋅ 5) 64364; ⋅⋅ 2) 964; ⋅ 4) 164; ⋅ 6) 100125. ⋅⋅

530°. Знайдіть значення виразу: 1) 22; ⋅ 4) 28; ⋅ 7) 5102; ⋅⋅ 2) 2020; ⋅ 5) 327; ⋅ 8) 7148; ⋅⋅ 3) 0,50,5; ⋅ 6) 0,0545; ⋅ 9) 80100,02. ⋅⋅

531°. Знайдіть значення виразу: 1) 77; ⋅ 3) 322; ⋅ 5) 5357; ⋅⋅ 2) 0,033; ⋅ 4) 312; ⋅ 6) 0,3150,5. ⋅⋅

1) 12 ; 3 3) 125 ; 5 5) 72 ; 2 7) 44 ; 11

2) 50 ; 2 4) 24 ; 6 6) 200 ; 2 8) 60 . 15

1) 18 ; 2 2) 27 ; 3 3) 45 ; 5 4) 54 ; 6 5) 99 . 11

536°. Внесіть множник під знак

1) 22; 4) 53; 7) 27; 10) 310; 2) 42; 5) 35; 8) 37; 11) 311; 3) 23; 6) 56; 9) 210; 12) 213.

537°. Внесіть

1) 32; 3) 25; 5) 710; 2) 43; 4) 36; 6) 215.

538°. Винесіть

1) 8; 9) 20; 2) 32; 10) 125; 3) 72; 11) 250; 4) 162; 12) 500; 5) 12; 13) 300; 6) 45; 14) 80; 7) 75; 15) 180; 8) 128; 16) 405.

539°. Винесіть

1) 18; 3) 98; 5) 200; 7) 48; 2) 50; 4) 28; 6) 27; 8) 108.

540°. Чи правильно

1) 5510; += 2) 55210; += 3) 5525? +=

541°. Спростіть вираз: 1) 22; + 2) 733; 3) 652535; +− 6) 8152151015; +− 4) 911211; 7) 47377; −+ 5) 321421; 8) 1010510210. +−

542°. Спростіть вираз: 1) 1010; + 3) 102320233023; 2) 77;−+ 4) 8224252. −−+

543°. Спростіть вираз: 1) () 10105; 11) () () 5656; +− 2) () 221; + 12) () () 2323; +−

3) ()1812; + 13) () () 5252; +− 4) () 323;−+ 14) () () 13151315; +−

5) () () 2223; +− 15) ()2 21; +

6) () () 5253; +− 16) ()2 521; 7) () () 3131; +− 17) ()2 31; +

8) () () 23221; +− 18) ()2 36; +

9) () () 103103; +− 19) ()2 105; 10) () () 6464; +− 20) ()2 237. +

544°. Спростіть вираз:

1) () 331; + 5) () () 5151; +−

2) () 565; + 6) () () 21112111; +−

3) () () 8122; +− 7) ()2 21;

4) () () 154154; +− 8) ()2 52.

545°. Спростіть вираз:

1) 3 27; 3) 3 64; 5) 3 1; 7) 3 27000; 2) 3 8; 4) 3 1000; 6) 3 0,008; 8) 3 0,064.

546°. Спростіть вираз:

1) 3 27; 3) 3 125; 5) 3 1;

2) 3 8; 4) 3 1000000; 6) 3 0,125.

547. Обчисліть, скориставшись таблицею

1) 16900; 6) 7840000; 11) 0,0441;

2) 409600; 7) 152100; 12) 0,3721; 3) 202500; 8) 56250000; 13) 0,009604; 4) 57600; 9) 1,44; 14) 29,16; 5) 129600; 10) 0,0144; 15) 0,000625.

548. Обчисліть, скориставшись

1) 52900; 4) 12250000; 7) 0,007396; 2) 168100; 5) 0,0196; 8) 0,00000729; 3) 688900; 6) 1,96; 9) 0,005625.

549. Обчисліть: 1) 7 2; 9 3) 21 4; 25 5) 1 2; 4 7) 1 6; 4 2) 9 1; 16 4) 13 1; 36 6) 19 1; 81 8) 1 3. 16

550. Обчисліть: 1) 1 12; 4 3) 32 1; 49 2) 4 5; 9 4) 1 7. 9

551. Порівняйте числа: 1) 43 і 7; 5) 52 і 7; 9) 20,01 і 0,09; 2) 28 і 26; 6) 23 і 32; 10) 4 9 і 0,25; 3) 35 і 7; 7) 56 і 65; 11) 9 1 16 і 2; 4) 32 і 18; 8) 142 і 87; 12) 1 0,01 і 105.

552. Порівняйте числа: 1) 52 і 7; 4) 1011 і 1110; 7) 1 4 і 0,25; 2) 45 і 9; 5) 67 і 76; 8) 1 2 4 і 5; 3) 42 і 32; 6) 40,25 і 0,49; 9) 4,5 і 23 .

553. Між якими двома послідовними цілими

1) 2; 4) 10; 7) 33; 10) 27; 2) 6; 5) 14; 8) 55; 11) 21,1; 3) 5; 6) 21; 9) 26; 12) 30,3?

554. Між якими двома послідовними

1) 3; 3) 15; 5) 36; 7) 21,2; 2) 7; 4) 23; 6) 52; 8) 50,1?

555. Обчисліть: 1) ()2 32; 3) ()2 55; 5) ()2 35; 7)

23; 4) ()

556. Обчисліть: 1) ()2 53; 2) ()2 107; 3) ()2 20,5; 4) 2 11 . 5

557. Знайдіть значення виразу:

1) 2 1412,96; 7 ⋅+ 4) 12 2231; 119 ⋅⋅

2) 7 021,44; 9 ⋅− 5) 3 10:30,01; 5 ⋅

3) 1 0356; 2 +⋅ 6) 481435 . 310 ⋅ +

558. Знайдіть значення виразу:

1) 1 0,111,820; 44 ⋅+⋅ 3) 44 30,751; 15 5 ⋅⋅

2) 1 0:53,84; 3 ⋅ 4) 2000,9 . 0,021,6 +

559. Спростіть вираз:

1) ( ) 1028,95,29; 5) 22 3712;

2) () 1 7232; 8 + 6) () () 22 101101; ++−

3) ( ) ( ) 1,30,51,30,5; +− 7) () () 22 6262; +−−

4) 22 6516; 8) () () 22 2323. ++−

560. Спростіть вираз:

1) ( ) 0,90,10,4; + 3) 22 2610; 2) ( ) 1 200,8; 5 + 4) () () 22 211211. ++−

561. Спростіть вираз:

1) ()2 23; 6) ()2 76; 2) ()2 21; 7) ()2 1523;

3) ()2 35; 8) ()2 335; 4) ()2 310; 9) () () 22 1818; −++

5) ()2 23; 10) () () 22 1737. −−+

562. Спростіть вираз: 1) ()2 523; 3) ()2 812; 2) ()2 32; 4) () () 22 1212. −++

563. Внесіть множник під знак кореня: 1) 0,13; 4) 80,2; 7) 2 2; 3 10) 21 ; 35 2) 30,1; 5) 2,42; 8) 4 0,2; 5 11) 11 ; 33 3) 1,15; 6) 1 10; 2 9) 12 ; 43 12) 21 1. 76

564. Внесіть множник під знак кореня: 1) 0,32; 3) 1 6; 2 5) 70,1; 2) 50,2; 4) 2 15; 3 6) 1 3. 2

565. Винесіть множник з-під знака кореня: 1) 0,03; 3) 1,69; 5) 8 ; 15 7) 2 2; 7 2) 0,08; 4) 22,5; 6) 45 ; 49 8) 11 1. 13

566. Винесіть множник з-під знака кореня: 1) 0,05; 3) 28,9; 5) 7 ; 36 2) 0,121; 4) 3 ; 20 6) 4 3. 15

567. Розкладіть на множники: 1) 1272; + 4) 31111; 7) 1533045; ++ 2) 45227; 5) 2714; 8) 51050200; −+ 3) 22; + 6) 366;−+ 9) 121827.

568. Розкладіть на множники: 1) 303; 3) 55; + 5) 36; + 2) 17334; + 4) 1010; 6) 1215342. −+

569. Спростіть вираз:

1) 454,5 ; 101 6) 4,4122,11 ; 12,1 −+

2) 4822 ; 61 + + 7) 1,4423,63 0,47,5; 320,3 ++ +

3) 327 ; 0,123 + 8) 22 ; 526526 + +−

4) 2252625 ; 169 + 9) 511 ; 153 +

5) 0,30,6 ; 12 10) 11 . 827827 + +−

570. Спростіть вираз:

1) 243 ; 221 3) 0,8127 ; 0,273 + +

2) 86 ; 32 + + 4) 55 . 233233 + +−

571. Спростіть вираз: 1) 228; + 4) 3104090; −+ 2) 51227; 5) 122748; ++ 3) 52045; ++ 6) 9,80,2452,45. −+

572. Спростіть вираз: 1) 728; + 2) 62454. ++

573*. Доведіть, що: 1) 23231; +⋅−= 4) 21211; −⋅+= 2) 4154151; +⋅−= 5) 5265261; +⋅−= 3) 3223221; +⋅−= 6) 7437431. +⋅−=

574*. Спростіть вираз: 1) 1465; 2) 827; 3) 223; + 4) 743.

575*. Доведіть, що: 1) 42342323; ++−= 2) 6426424. ++−=

576*. Порівняйте числа: 1) 43 і 34; 3) 25 і 43; 2) 45 і 32; 4) 12 + і 22.

577. Підлога кімнати має форму квадрата

задача 2

Серед чисел 0, 19 , 0,09, 12, 81 укажіть числа:

1) натуральні;

2) цілі;

3) раціональні;

4) ірраціональні;

5) дійсні.

розв’язання

1. Натуральними є числа 12 і 81 , оскільки 819. =

2. Цілими є числа 12, 81 і 0.

3. Раціональними є числа 0, 0,09, 12, 81 .

4. Ірраціональним є число 19 .

5. Дійсними є всі дані числа: 0, 19 , 0,09, 12, 81 .

натуральне число є і цілим числом,

числом;

= 2,333… 2,34 > 2,333… 2,34 > 2,(3).

= 1,4141…

qr.orioncentr.com.ua/JCVM4

irrational number irrationale Zahl (f) nombre irrationnel

578'.

579'.

582°.

1) 5; 3) 2 ; 5) 5,111…;

584°.

1) 5; 3) 2; 5) 5,111…;

= {1; 2; 3; 4; 5; 6; 7; 8; 9}.

1) В = {1; 5; 10}; 3) D = {10; 20}; 5) M = {6; 7; 8; 9}; 2) С = {2; 4; 6}; 4) E = {3}; 6) N = {1}?

585°. Дано множину М = {3; 6; 9; 12; 15}. Яка із

М: А = {3; 9; 27}, В = {6; 15}, С = {3; 30}?

586°. Запишіть усі підмножини множини: 1) А = {10; 20; 30}; 3) С = {–2; –1; 0; 1; 2}; 2) В = {100; 1000; 10000}; 4) M = { ; ; };

587°. Укажіть період числа: 1) 4,1111…; 6) –34; 2) 2,35; 7) 100,1; 3) 0,3535353…; 8) 99; 4) 5,7777…; 9) 9,010101…; 5) 2,123123123…; 10) 0,445566445566….

Запишіть дане число як періодичний дріб.

588°. Укажіть період числа:

1) 8; 3) 1,554444…; 2) 2,2222…; 4) 0,4235235235….

Запишіть

589°. Запишіть як нескінченний

десятковий

число: 1) 2,(8); 5) 21,88(9); 2) 19,(3); 6) 4,5(0); 3) 1,3(25); 7) 21,(0); 4) 5,9(87); 8) 5,101(12).

590°.

1) 3,(4); 2) 5,5(12); 3) 7,54(0); 4) 6,(0).

591°.

1) 1 ; 2 3) 5

1) 1

593°. Чи є

твердження: 1) 1 9 — дійсне число;

2) 5 — раціональне число; 3) –11 — дійсне число; 4) 2 7 — ірраціональне число;

5) –11 — раціональне число;

6) 5 — ціле число;

7) 2,4444… — ірраціональне число; 8) 1,55555… — дійсне число;

9) 7 — раціональне число;

10) π — ціле число;

11) π — дійсне число;

12) 121 — натуральне число?

594°. Чи є правильним твердження: 1) 2 3 — дійсне число; 2) –11 — дійсне число; 3) 5 — раціональне число; 4) 1 5 — ірраціональне число?

595°. Чи є правильним твердження: 1) 5 ∈ N; 6) –5 ∈ N; 11) 1 5 ∈ N; 16) 5 ∈ N; 2) 5 ∈ ℤ; 7) –5 ∈ ℤ; 12) 1 5 ∈ ℤ; 17) 5 ∈ ℤ; 3) 5 ∈ Q; 8) –5 ∈ Q; 13) 1 5 ∈ Q; 18) 5 ∈ Q; 4) 5 ∈ І; 9) –5 ∈ І; 14) 1 5 ∈ І; 19) 5 ∈ І; 5) 5 ∈ R; 10) –5 ∈ R; 15) 1 5 ∈ R; 20) 5 ∈ R?

596°. Чи є правильним твердження: 1) 2 ∈ N; 3) 2 ∈ Q; 5) 2 ∈ R; 2) –2 ∈ ℤ; 4) 1 8 ∈ І; 6) 16 ∈ N?

597°. Серед чисел –0,(4), 1, 9 3 , 0, 1 2 , 4, 3 5 , 1,0333…, 9,

6 , 6 оберіть числа:

1) натуральні;

2) цілі;

3) раціональні; 4) ірраціональні.

598°. Серед чисел 12 6 , –3,(9), 0, 25 , 7,8888…, –5, 2 ,

1 3 , 8 , 22, 17 2 оберіть числа: 1) натуральні;

2) цілі; 3) раціональні; 4) ірраціональні; 5) дійсні.

599°. Наведіть приклад числа, яке:

1) є дійсним, але не є раціональним;

2) є раціональним, але не є цілим; 3) є від’ємним ірраціональним.

600°. Наведіть приклад числа, яке:

1) є дійсним, але не є ірраціональним;

2) є раціональним, але не є натуральним.

601°. Визначте, скільки між числами –7 і –4 міститься чисел:

1) натуральних; 4) ірраціональних;

2) цілих; 5) дійсних.

3) раціональних;

602°. Порівняйте числа:

1) 4,105 і 5,01; 5) 10 і 9,(9); 2) 3,056 і 3,0(5); 6) 4,3(4) і 4,4(3); 3) 5,1412 і 5,(14); 7) 0,0(5) і 1,00(5); 4) 3,056 і 3,0(6); 8) 3,056 і 3,0(5).

603°. Порівняйте числа:

1) 15 і 15,(1); 2) 5,342 і 5,333…; 3) 0,165 і 0,16(5); 4) 2,999… і 2,(10).

604°.

1) А = {1; 2; 3}; 2) С = {0}; 3) D = {–1; 1}; 4) В = {х | х —

605.

множина: 1) А = {1; 2 ; 3}; 3) С = {х | х

раціональне число}; 2) В = { 3 }; 4) М = {х | х —

606. Чи є правильним твердження: 1) N ⊂ І; 2) І ⊂ Q; 3) Q ⊂ ℤ; 4) Q ⊂ R; 5) R ⊂ І; 6) Q ⊂ І?

607. Дано множини: А = {–5; –4; –3; –2; –1; 0}, В = {0; 1; 2; 3; 4; 5}, С = {–4; –2; 2; 4}, D = {0}. Запишіть множину: 1) M, для якої М ⊂ А і М ⊂ С; 2) Р, для якої А ⊂ Р і В ⊂ Р; 3) N, для якої N ⊂ А і N ⊂ В; 4) H, для якої А ⊂ Н, В ⊂ Н і D ⊂ Н.

608. Порівняйте числа: 1) 0,(8) і 3 ; 8 3) 0,(18) і 1 ; 11 5)

1) 3; aba 2) ;aab + 3) х2 – 3; 4) х – 4, якщо x > 0.

1. Винесемо за дужки a . Тоді: () 3 3.aab ba −=−

2. Скористаємося формулою ()2 aa = . Тоді: () () () 2 11. aaa ababbba aa +=+=+⋅=+

3. Скористаємося формулою ()2 aa = та формулою

1) abx , якщо а > 0, b < 0; 2) 2 . xx розв’язання

1. Якщо а > 0, то: 2 aa = . Якщо b < 0, то –b > 0 і тому: ()2 bb−=− . () () () () 22 2 2 22 . abxx xxabx ab abab =⋅−⋅=  =⋅⋅==−

Отже: якщо а > 0, b < 0, то 22 . aax bb x =

2. Якщо х ≥ 0, то: 2 xx = .

Тоді: 2 2224 2 . xxxxx xx =⋅=⋅=

Якщо х < 0, то: –х > 0 і ()2 2 . xxx = =

Тоді: () ()2 2 2 2224 . xxxxx xxxx=⋅=−⋅=−⋅=−

Отже: 4 2 4 0 якщо , якщо . , 0 , < x xx x х х  ≥ =   

задача 5

Розв’яжіть рівняння:

1) (х + 2)2 = 9; 3) 23; x += 5) ()320.xx++=

2) (х + 2)2 = 3; 4) 23; x +=−

розв’язання

1. Рівняння виду х2 = а (а ≥ 0) має два корені, які є проти-

лежними числами. Тоді: (х + 2)2 = 9, х + 2 = 3 або х + 2 = –3, х = 1 або х = –5.

Отже, коренями рівняння є числа 1 і –5.

2. Рівняння виду х2 = а (а

числами. Тоді:

1) 0; A < 2) 0; A = 3) 0; A > 4) 0? A ≥

AA−=−

620'. Чи правильно, що: 1) ;ABAB ⋅=⋅ 4) ; AA BB = 2) 22 ; ABAB ⋅=⋅ 5) 2 2 ; AA BB = 3) ; ABAB ⋅=⋅ 6) ? AA BB =

621°. Чи має зміст вираз: 1) 2 x , якщо х = 0; 10) 81 x , якщо х = 0; 2) 3 x + , якщо х = –3; 11) 72x , якщо х = 4; 3) 1 x , якщо х = 2; 12) 2 3 x ,

х =

4) 4x , якщо х = –5; 5) 2x , якщо х = 4; 6) x , якщо х = 3; 7) 9x , якщо х = –1; 8) 510 x , якщо х = 1; 9) 24 x + , якщо х = –1;

622°. Чи має зміст вираз: 1) 1 x + , якщо х = –1; 4) 6x , якщо х = 0; 2) 8 x , якщо х = 7; 5) 10x , якщо х = 2; 3) 20 x , якщо х = –21; 6) 153x , якщо х = 4?

623°. Чи має зміст вираз 1 8 x −+ , якщо: 1) х = –10; 5) х = 1; 2) х = –6; 6) х = 8; 3) х = –1,2; 7) х = 10; 4) х = 0; 8) х = 20?

624°. Чи має зміст вираз 1 3 x + , якщо: 1) х = –5; 3) х = 0; 5) х = 10; 2) х = –3; 4) х = 3; 6) х = –0,1?

626°.

1) ()2 3; x 3) ()

2) ()2 9; x + 4) ( )

628°. Спростіть вираз:

1) ()2 5; x 2) ()2 1012; x + 3) ( )

1) ()15; pp 8) () () ; aaaa +−

2) () 25;nn + 9) () () 55; mnmn +−

3) () 3; ac + 10) ()2 1; x +

4) () () 72;nn+− 11) ()2 4; a

5) () () 22; xyxy +− 12) ()2 3; m +

6) () () 11;aa+− 13) ()2 2;xy

7) () () ; xyyx +− 14) ()2 . xz +

1) ()6; nn + 5) ()2 2; y

2) () () 36;aa+− 6) ()2 1; a

3) () () 88;yy+− 7) ()2 ; yz

4) () () 3232; xyxy +− 8) ()2 10. y +

631°. Розкладіть на множники:

1) 2;aaa

2) 25; xxx + 3) 9; mnm

4) 4;xyx + 5) 615; aaa 6) 12 ; nmnnn 7) 2 2; ppppp +− 13) х – 25, якщо х ≥ 0; 8) 2; mnmpnmnn −+ 14) х – 100, якщо х ≥ 0; 9) 2; xx + 15) х2 – 5; 10) ;mm 16) х2 – 10; 11) ; nmmn 17) х – 2, якщо х ≥ 0; 12) 22; yyx 18) х – 30, якщо х ≥ 0.

632°. Розкладіть на множники: 1) 3; xxx 6) х – 36, якщо х ≥ 0; 2) ; aaca + 7) х2 – 7; 3) 2;aa + 8) х2 – 3; 4) 55; aa 9) х – 26, якщо х ≥ 0; 5) 46; pmmp 10) х – 11, якщо х ≥ 0.

633°. Спростіть вираз: 1) ; mn m 2) ; y xy 3) 5 ; 45 d d 4) . cd ad

634°. Спростіть вираз: 1) 2 ; 2 ap a 2) . mn am

635°. Спростіть вираз:

1) ; mnn mn 8) 22 ; xy xy + + 15) 2 5 ; 5 a a +

2) ; xyy xx 9) 88 ; 22 xy xy + + 16) 2 10 ; 10 m m

3) 55 ; 4545 db db + + 10) 33 ; 2727 ab ab 17) 7 ; 7 x x

4) ; cdcb adab + + 11) 1 ; 1 x x + 18) 6 ; 6 a a +

5) ; x xx 12) 4 ; 2 y y + 19) 11 ; 11 m m +

6) 5 ; aa a + 13) 5 ; 25 m m 20) ; mn nmmn +

7) 2 ; m mm 14) 2 3 ; 3 x x 21) . mn mnnmnm ++

636°. Спростіть вираз: 1) 2 ; y yy + 4) ; 1 mnm n + + 7) 2 7 ; 7 n n

2) ; 3 c cc 5) 2 ; 2 mpp maa + + 8) 19 . 19 x x +

3) 1212 ; 33 mn mn 6) 25 ; 5 y y +

637°. Внесіть множник під знак кореня: 1) 2; x 2) 5; y 3) 6; a 9) 5 mm ; 4) 2xy , якщо х > 0; 10) 2 3; yx

5) 2xy , якщо х < 0; 11) 4 2; ac

6) 3 3an , якщо а < 0; 12) mmn , якщо m > 0; 7) 3 3an , якщо а > 0; 13) mmn , якщо m < 0; 8) 2 mm , якщо m < 0; 14) 3 2xyz , якщо x < 0, y > 0.

638°. Внесіть множник

знак кореня: 1) 5; c 3) 2, mn якщо m > 0, n > 0; 2) ca , якщо с < 0; 4) 3, mn якщо m < 0, n > 0.

639°. Винесіть множник з-під знака кореня: 1) 2 2x , якщо х > 0; 7) 22 5xy , якщо х < 0, у > 0; 2) 2 3a , якщо а < 0; 8)

4) 2 ab , якщо а < 0; 10) 4 18xy ; 5) 2 ab , якщо а > 0; 11) 84 ; xyz 6) 22 5xy , якщо х > 0, у < 0; 12) 2016 . abc 640°.

2 7 y , якщо у > 0; 2) 2 7 y , якщо у < 0; 3) 22 12ab , якщо а < 0, b > 0; 4) 22 12ab , якщо а > 0, b < 0; 5) 22 12ab , якщо а > 0, b > 0; 6) 22 12ab , якщо а < 0, b < 0; 7) 8 27; mn 8) 420 32. xy 641°. Звільніться

643°. Спростіть вираз:

1) 34 ; cc 3) 21 ; 88 xx ++ 2) 52 ; pp 4) 168 . 1 11 x xx −+

644°. Спростіть вираз: 1) 21 ; aa + 2) 43 . 11xx++

645°. Розв’яжіть рівняння:

1) х2 = 1; 6) х2 = 15; 11) х2 = –1; 2) х2 = 36; 7) х2 – 64 = 0; 12) х2 = –29;

3) х2 = 0; 8) 2х2 – 42 = 0; 13) х2 = –62; 4) 3х2 = 9; 9) х2 – 81 = 0; 14) х2 = –100; 5) х2 = 11; 10) х2 – 17 = 0; 15) х2 + 13 = 0; 16) х2 + 40 = 0; 17) 0,1x2 + 1,6 = 0; 18) 2 160. 4 x −=

646°. Розв’яжіть рівняння:

1) х2 = 49; 3) 4х2 = 8; 5) х2 – 9 = 0; 7) х2 = –3; 2) х2 = 64; 4) х2 = 7; 6) х2 – 5 = 0; 8) х2 + 12 = 0.

647°. Розв’яжіть рівняння:

1) 2; x = 4) 290; x −−= 7) 340; x ++= 2) 10; x = 5) 127; x −= 8) 390; x += 3) 260; x −= 6) 213; x +=− 9) 2960. x −++=

648°. Розв’яжіть рівняння: 1) 5; x = 3) 278; x += 5) 3030; x +=−

2) 40; x −= 4) 120; x −−= 6) 0. x =

1) 2 ; x 3) ()2 7; x 5) 1 ; x 7) ; 41 x x + 2) ()2 5; x −+ 4) 2 69;xx−+

1) 2 ;

3) 1 ; 10 x + 2) ()2 1; x 4) 1 ? 1 x x + Якщо так, то

651. Спростіть вираз:

1) () () 22 33;xx++−

2) () () 22 5252;aa+−−

3) () () 22 212; yy+−−

4) () () ()2 444;xxx +−−−+

5) () () () 2 ; mnmnmn +−+−

6) () () ()2 . xyxyxy +−−−−

652. Спростіть вираз: 1) () () 22 22;aa++−

2) () () () 2 . yxyxyx −−+−

653. Спростіть вираз: 1) 11 ; 1 aa + 4) 12 ; 3322mnmn + ++

2) 11 ; 2 xx + 5) 11 ; 2222aa++

3) 11 ; xyxy +− 6) . 11 xx xx+−

654. Спростіть вираз: 1) 55 ; 55aa+− 3) 111 ; 11 11 mm

2) 1 ; 25 5 m mm 4) 5 . 5 5 pp pp + +

1) 33 ; 33 aa aa +− −+ 3) 11 ; 11 xx xx +− + −+ 2) ; mpmp mppm +− + −+ 4) 24 . 4 2 mnmn mnmn ++

1) 22 ; 22 nn nn −+ +− 2) . xyxy yxxy +− + −+

вираз: 1) 3 1 455 ; aa bb ⋅ 4) 56 27 12 ; 3 xy yx

2) 3 1 455 :; aa bb 5) 5 24 8 1; 9 17 xyxy zz ⋅⋅ 3) 56 27 12 :; 3 xy yx 6) 334 4546 . abcd cdaca ⋅⋅

вираз: 1) 33 55 32 ; 2 cc aa ⋅ 2) 33 55 32 :. 2 cc aa 659. Внесіть множник під

1) ; xx 4) 22 ; mnnm 2) 2 3; yx 5) ; nmmn +− 3) 323abab , якщо a < 0; 6) 2 34. pmp +

1) 2 8; n 3) 83 0,01; ab 5) 4

665. Розв’яжіть рівняння: 1) (х + 1)2 = 64; 6) (х – 9)2 – 3 = 0; 2) (х – 3)2 = 5; 7) (х + 5)2 – 5 = 0; 3) (х – 10)2 = 0; 8) (х – 10)2 + 320 = 0; 4) (х + 12)2 – 36 = 0; 9) (х + 8)2 + 8 = 0; 5) (х + 9)2 – 81 = 0; 10) –(x – 10)2 – 10 = 0.

666. Розв’яжіть рівняння: 1) (х + 2)2 = 4; 4) (х + 4)2 – 3 = 0; 2) (х – 9)2 = 100; 5) (х – 7)2 – 11 = 0; 3) (х – 25)2 = 0; 6) (х + 7)2 + 49 = 0.

667. Розв’яжіть рівняння: 1) (2х + 1)(х + 1) – 3х = 4х2; 2) (х + 1)(х – 1) = 2х2; 3) (5х + 1)(х + 2) – 6х2 – 11х = 0; 4) (–х + 5)(х + 4) = х (х + 1).

668. Розв’яжіть рівняння: 1) (3х + 1)(х – 3) + 8х = 2х2; 2) (х + 2)(х – 2) – 3х2 = 0; 3) (2х + 1)(х + 3) = х(х + 7).

669. Розв’яжіть рівняння: 1) 29;xx+= 4) 25160; xx−= 2) 954; xx−= 5) 35340;xx+−++= 3) 499; xx−= 6) 1318.xx+++=

670. Розв’яжіть рівняння: 1) 3210; xx+= 3) 16250; xx−= 2) 36;xx−= 4) 575120.xx+−++=

671. Розв’яжіть рівняння:

1) () () 112; xxx −+=−

2) () () 335; xxx −+=−

3) () () () () 2245;xxxx +−=−+

4) () () () () 2727465; xxxx −+=−+

5) ()2 526; xx −=+ 6) ()2 228. xx −=+

672. Розв’яжіть рівняння:

1) () () 222; xxx −+=−

2) () () () () 5576;xxxx +−=−+

3) ()2 1530.xx−−=−

673. Розв’яжіть рівняння:

1) ()120;xx+−= 5) () () 110;xx+−=

2) ()110;xx−−= 6) () () 110;xx−−=

3) 100; xx −= 7) ()100; xx −=

4) 40; xx += 8) 20. xx =

674. Розв’яжіть рівняння:

1) ()330;xx+−= 3) ()20; xx −=

2) ()330;xx−+= 4) 10. xx −=

675*. Спростіть вираз:

1) ()2 1 x , якщо х > 2; 5) 2 69xx−+ , якщо х > 9; 2) ()2 12 x + , якщо х > 20; 6) 2 21xx−+ , якщо х > 5;

3) ()2 8 x , якщо х < 0; 7) 2 816xx−+ , якщо х < 0;

4) ()2 2 8 x + ; 8) 2 44xx++ , якщо х < –4.

676*. Спростіть вираз:

1) () () 2 42;xx 2) 321025. xxx ++

677*. Спростіть

+ ++−

1) 2 :; xyxyyx xyxyxyyyx

2) ; xyxyyy xyxyy

3) 2 2 2 11 ; 11 xx x xx  ++−   +−−

4) () () () 1 33 3 . xxyyxyyy xy xyxyyxyx +− ⋅−+− + +−

678*. Обчисліть: 1) 111 ... ; 12232425 +++ +++ 2) 111 ... ; 122399100 +++ +++ 3) 111 ... ; 13352325 +++ +++ 4) 111 ... . 24467072 +++ +++

679*. Звільніться

1) 1 ; 132 +− 3) 1 ; 3710 +− 2) 1 ; 235 ++ 4) 1 . 236 ++ 680*. За яких значень а

1) (х + 24)2 = а; 3) (х – 9)2 + 7 = а; 2) (х –

1) (х + 17)2 = а; 3) (х – 9)2 = а – 5; 2) (х – 3)2 = а + 1; 4) (х + 32)2 + 4 = а2? 682*.

1) (х + 8)2 = а; 4) (х + 9)2 + 1 = а; 2) (х – 12)2 = а; 5) х2 + 4х + 4 = а; 3) (х – 25)2 = а + 4; 6) х2 + 6х + 9 = а.

qr.orioncentr.com.ua/RQYO6

English

Deutsch

Français

square rootQuadratwurzel (f) racine carrée

тренування 1. Обчисліть: 1) 0,22 – 1,22; 2) 4 · 1,52 · 160; 3) (8 + 22 · 0,25)2; 4) (3,12 – 1,92)3.

2. Знайдіть середнє

01,211,962,893,614,848,419

687°.

689°.

11,442,253,246,259,6120,25

через точку:

1) A (4; 2); 3) C (6,25; 5); 5) M (1,44; –1,2); 2) B (0; 0); 4) D (0; 4); 6) N (–9; 3)?

через точку:

1) A (16; 4); 2) B (1; 1); 3) C (2,25; –1,5); 4) D (–4; 2)?

690°.

1) А (1; 1);

2) В (81; 9); 3) C (100; 10); 4) D (25; –5); 5) M (0,01; 0,1); 6) N (0,3; 0,09)?

691°. Чи

1) K (0; 0); 3) M (49; 7); 2) L (36; –6); 4) N (0,04; 0,2)?

692°.

1) x = 1,5; 2; 5; 2) y = 1,5; 2,5; 2,7. Мал. 46

693°. На малюнку 46 зображено графік функції yx = . За графіком знайдіть: 1) значення y, якщо x = 1,5; 2; 5; 2) значення x, якщо y = 1,5; 2,5; 2,7.

694°. Чи перетинає графік функції yx = пряма: 1) х = 4; 2) х = –9; 3) x = 49; 4) у = 5; 5) y = –4; 6) y = 3? Якщо так,

695°. Чи перетинає

696°.

числа: 1) 1,3,1,5,0,8,1; 3) 1212 3,3,3,3; 3745 2) 2,5,3,2,4,8; 4) 3 10,100,102,100,5. 4

710.

1) 4,1,2,3,8,4,5; 2) 2314 2,2,2,2. 5427

711. Розв’яжіть

1) 6 і 2; 3) 5 і

1°.

2°.

3°.

В (2; 4). В. C (1; 0). Г. D (–4; 2).

3. Доповнимо ліву частину рівняння до повного квадрата двочлена. Для цього

3. Подамо другий доданок як подвоєний добуток двох

5. Згорнемо ліву частину

2 = 25; х2 = 0,625; х2 = –25; (х– 5)2 = 25.

716'. Чи правильно, що

є рівняння виду:

1) 0x2 + bx + c = 0; 3) ax2 + 0x + c = 0; 2) ax2 + bx + 0 = 0; 4) ax2 + 0x + 0 = 0?

717'. У рівнянні ax2 + bx + c = 0 назвіть:

1) перший коефіцієнт; 3) вільний член.

2) другий коефіцієнт;

718'. Чи має корені рівняння: 1) (х + m)2 = 3; 2) (х + m)2 = –4; 3) (х + m)2 = 0?

719°. Яке з даних рівнянь є квадратним:

1) 4х2 + 7х – 3 = 0; 3) 2х3 + х + 4 = 0; 5) х2 + 5х = 0; 2) х2 – 5х + 3 = 0; 4) 4х2 – 16 = 0; 6) 8х + 16 = 0?

720°.

рівняння:

1) 6х2 + 5х – 1 = 0; 3) 2х2 – 12 = 0; 5) 6х2 = 0;

2) х2 + х – 6 = 0; 4) х2 + 2х = 0; 6) 5 + х2 – 6х = 0.

721°.

1) a = 3, b = 2, с = 4;

2) a = 1, b = –3, с = 2;

3) a = 2, b = 0, с = –8;

4) a = –1, b = –2, с = 5;

5) a = 1, b = –7, с = 0;

6) a = 4, b = 8, с = 0.

722°.

1) a = 1, b = –4, с = –5; 2) a = 9, b = 6, с

724°.

729°.

(

+ 1)(х – 2) = 4; 4) 4х2 – 5 = 2х(1 + 3х); 2) 8х = (х – 4)(х + 4); 5) (х + 3)2

730°.

рівняння:

1) (х + 7)2 = 49; 4) (х + 4)2 = 1;

2) (х – 3)2 = 16; 5) (х + 2)2 = 0;

3) (х – 5)2 = 36; 6) (х – 1)2 = –25.

731°.

рівняння:

1) (х + 2)2 = 64;

2) (х – 6)2 = 0; 3) (х + 3)2 = –9.

732.

рівняння:

1) х2 + 2х – 8 = 0; 4) х2 – 8х + 15 = 0;

2) х2 – 4х + 3 = 0; 5) х2 – 6х – 16 = 0;

3) х2 + 12х + 35 = 0; 6) х2 – 10х + 25 = 0.

733.

1) х2 + 10х + 24 = 0; 2) х2 + 2х – 8 = 0; 3) х2 – 8х + 16 = 0.

734. Розв’яжіть способом

1) х2 + 3х – 4 = 0; 4) 2х2 – 9х + 10 = 0; 2) х2 – 5х + 4 = 0; 5) 3х2 – 5х + 2 = 0;

коренів квадратного рівняння: 1,2 (5)1 ; 221 bD x a −±−−±

⋅ 12 5151 3, 2. 22 xx

Отже, рівняння має 2 корені: х1 = 3, х2 = 2.

задача 2 Розв’яжіть рівняння: 2х2 – 6х – 3 = 0.

розв’язання У рівнянні 2х2 – 6х – 3 = 0: a = 2, b = –6, c = –3.

224(6)42(3)362460,Dbac=−=−−⋅⋅−=+=

D > 0 — два різні корені.

−±−−±±±± == === ⋅ bD x a 1,2 (6)6062152(315)315 ; 222442 +− = = xx 12 315315 22,.

Отже, ± = x1,2 315 . 2

задача 3 Розв’яжіть рівняння: 9х2 + 6х + 1 = 0.

розв’язання У рівнянні 9х2 + 6х + 1 = 0: a = 9, b = 6, c = 1. 224(6)49136360,Dbac=−=−⋅⋅=−=

D = 0 — два рівні корені. −±−± ===−=−=− ⋅⋅ bD x a 1,2 60661 . 22929183

Отже, =− x1,2 1 . 3

qr.orioncentr.com.ua/RogpF

English

discriminant of a quadratic equation Diskriminante der quadratischen Gleichung le discriminant d’une équation quadratique

1. Обчисліть: 152; 112; 132; 0,42; 1,62; 0,122.

2. Скільки коренів має рівняння: x2 = 25; x2 = –0,25; x2 = 5; 2x2 = 0; x2 = a2?

3. Подайте (якщо це можливо) у вигляді квадрата числа: 121; 2,25; 0,0001; 1,69; –2,56.

744'.

ax2 + bx + c = 0:

1) D = b2 + 4ac; 3) D = –b2 – 4ac; 2) D = b2 – ac; 4) D = b2 – 4ac?

ax2 + + bx + c = 0:

1) ± = bD x a 1,2 ; 2 3) −± = bD x a 1,2 ; 2 2) ± = bD x a 2 1,2 ; 2 4) 1,2 ? bD x a −± =

745'.

дорівнює: 1) 16; 2) 0; 3) –25?

746'. Які з чисел 0; 1; –1; –0,5; 0,2; 2 є коренями

рівняння: 1) х2 – х – 2 = 0; 2) 2х2 + х = 0?

747°.

значення виразу b2 – 4ac, якщо: 1) a = 1, b = 4, c = –5; 3) a = 5, b = 6, c = 1; 2) a = 1, b = –7, c = 10; 4) a = 3, b = –5, c = –2.

748°. Знайдіть значення

b2 – 4ac, якщо: 1) a = 1, b = –6, c = 8; 2) a = 2, b = 1, c = –6.

749°.

2 – 10х + 16 = 0: 1) =−⋅⋅− D 2 1041(16); 3) =− −⋅⋅− D 2 (10)41(16); 2) =−⋅⋅ D 2 104116; 4) =− −⋅⋅ D 2 (10)4116?

так: =−⋅⋅− D 2 541(6)?

1) х2 – 5х – 6 = 0; 3) х2 + 5х – 6 = 0; 2) х2 + 6х – 5 = 0; 4) х2 – 5х + 6 = 0. Скільки коренів має це рівняння?

751°.

дискримінантом: 1) =−⋅⋅ D 2 4413; 3) =−⋅⋅− D 2 841(4); 2) =−−⋅⋅ D 2 (6)433; 4) =− −⋅⋅ D 2 (3)425.

752°. Визначте

1) =−⋅⋅ D 2 6415; 3) =−⋅⋅ D 2 5426; 2) =−−⋅⋅− D 2 (3)42(5); 4) =− −⋅⋅ D 2 (6)419.

753°. Назвіть коефіцієнти

1) х2 + 5х + 6 = 0; 2) х2 + 5х – 6 = 0; 3) х2 – 3х + 4 = 0; 4) х2 – 3х – 4 = 0; 5) 2х2 + 6х – 1 = 0; 6) 2х2 – 6х + 1 = 0.

754°.

1) х2 + 4х – 5 = 0; 3) 4х2 – 4х + 1 = 0; 2) х2 + 4х + 5 = 0; 4) 4х2 – 4х – 1 = 0. Скільки коренів має рівняння?

755°. Розв’яжіть квадратне рівняння: 1) х2 + 4х – 5 = 0; 9) х2 – 7х – 8 = 0; 2) х2 – 6х – 16 = 0; 10) х2 + 6х + 3 = 0; 3) х2 + 2х – 8 = 0; 11) х2 + х – 2 = 0; 4) х2 – 8х + 16 = 0; 12) х2 + 25х + 100 = 0; 5) х2 + 8х + 7 = 0; 13) х2 – 6х – 7 = 0; 6) х2 – 4х + 8 = 0; 14) х2 + 15х + 26 = 0; 7) х2 + х – 12 = 0; 15) х2 – 3х + 2 = 0; 8) х2 – 2х – 15 = 0; 16) х2 – 10х + 25 = 0.

756°.

квадратне рівняння:

1) х2 + 4х – 12 = 0; 5) х2 – 5х + 4 = 0;

2) х2 – 3х – 10 = 0; 6) х2 + 6х + 8 = 0;

3) х2 – 6х + 9 = 0; 7) х2 – х – 6 = 0;

4) х2 + 5х + 8 = 0; 8) х2 – 7х + 10 = 0.

757°. Розв’яжіть квадратне рівняння:

1) 2х2 – х – 6 = 0; 12) –4х2 + 7х – 3 = 0;

2) 9х2 – 6х – 8 = 0; 13) 9х2 + 48х + 64 = 0;

3) 5х2 + 7х – 6 = 0; 14) –3х2 + 19х – 6 = 0;

4) 4х2 – 8х + 3 = 0; 15) 2х2 – 11х + 5 = 0;

5) –4х2 – 11х + 3 = 0; 16) –4х2 + 4х – 1 = 0.

6) 5х2 + 14х – 3 = 0;

7) –6х2 – х + 1 = 0;

8) 2х2 – 5х + 3 = 0; 9) 2х2 – 9х + 10 = 0;

10) –25х2 + 10х + 3 = 0; 11) 16х2 + 56х + 45 = 0;

758°. Розв’яжіть квадратне рівняння:

1) 2х2 + 3х – 5 = 0; 5) 5х2 + 6х + 1 = 0;

2) 9х2 – 8х – 1 = 0; 6) –4х2 + 28х – 49 = 0;

3) –2х2 + х + 10 = 0; 7) 2х2 – 5х – 3 = 0;

4) 3х2 + 5х – 2 = 0; 8) –2х2 + 3х – 1 = 0.

759. Розв’яжіть рівняння:

1) 7х = 3х2 + 4; 6) z – 3z2 = –2; 11) 13z – 3z2 = 14;

2) 6у – 1 = 5у2; 7) 4х2 = 2 – 7х; 12) 2х2 = 9х – 10; 3) z2 – 90 = z; 8) 4y2 = 33 + y; 13) 81y2 + 1 = 18y;

4) 5х2 = 8х – 3; 9) 9х2 + 25 = 30х; 14) 6z – 3 = z2; 5) 5 = 6y – y2; 10) y2 = 11y – 18; 15) 18 – y2 = 5y + 18.

760. Розв’яжіть рівняння:

1) 2х2 = 7х + 30; 3) z2 – 5 = 2z; 5) 5y = 1 – 14y2; 2) 3y = 2y2 – 5; 4) 30 – х = х2; 6) 4х2 + 7 = 7 – 12х.

761. Розв’яжіть рівняння:

1) х(х – 1) = 72; 5) 2y(y + 3) = (3 + y)2; 2) 2у(у + 2) – 3 = 9у; 6) (z + 4)2 + (z – 4)2 = 36; 3) (2z – 3)(2 – 3z) = –4; 4) (x + 5)2 = 4(x + 10); 7) (x + 2)(x + 1) = 4(x2 – 22); 8) (y + 2)2 – 10 = 6(y + 3).

762. Розв’яжіть рівняння: 1) х(х + 1) = 56; 3) 4(3 – 2z) = (z – 3)2; 2) (y – 2)(2y – 1) = 5; 4) (x + 6)(x – 2) = 2(x – 2).

763. Розв’яжіть рівняння: 1) ++ = xxx 2 37 ; 24 3) +−− −= yyyy 22 613 ; 264 2) + −= xxx 2 25 ; 536 4) −=− yyy y (7)4 4. 33

764. Розв’яжіть рівняння: 1) = xx 2 42 ; 53 2) ++ −= yyyy 2 (1)232 . 4520

765. В одноколовому

766.

767.

771*.

776'.

рівняння x2 + px + q = 0:

1) ⋅= xxp 12 ; 3) ⋅= xxq 12 ; 2) ⋅=− xxp 12 ; 4) ⋅=− xxq 12 ?

777'.

ax2 + bx + c = 0:

1) += b xx a 12 ; 3) +=− xxb 12 ;

2) += c xx a 12 ; 4) +=− b xx a 12 ?

778°.

779°. Не розв’язуючи рівняння

2) добуток

780°. Якими можуть бути

1) х2 + 3х – 4 = 0; 2) х2 – 6х – 16 = 0; 3) х2 + 7х – 30 = 0; 4) х2 – 10х + 16 = 0; 5) х2 – 12х + 11 = 0; 6) х2 – 9х + 8 = 0; 11) х2 + х – 2 = 0; 7) х2 + х – 12 = 0; 12) х2 + 25х + 100 = 0; 8) х2 – 15х + 26 = 0; 13) х2 – 9х – 10 = 0; 9) х2 + 5х + 4 = 0; 14) х2 + 8х + 7 = 0; 10) х2 + 6х + 5 = 0; 15) х2 – 3х + 2 = 0.

788°. Скориставшись теоремою

рівняння: 1) х2 + 8х – 9 = 0; 5) х2 – 5х – 14 = 0; 2) х2 – 3х – 10 = 0; 6) х2 + 6х + 8 = 0; 3) х2 – 9х + 20 = 0; 7) х2 – х – 20 = 0; 4) х2 + 9х + 8 = 0; 8) х2 – 7х + 10 = 0.

789°. Не обчислюючи коренів рівняння x2 + 13x + 22 = 0, знайдіть: 1) + xx12 ; 2) ⋅ xx12 .

790°. Не обчислюючи коренів рівняння 25x2 + 40x – 4 = 0, знайдіть: 1) + xx12 ; 2) ⋅ xx12 .

791°. Не обчислюючи коренів рівняння 9x2 – 24x + 14 = 0, знайдіть: 1) + xx12 ; 2) ⋅ xx12 .

792°. Складіть

1) 2 і 5; 4) –8 і –2; 7) 3 4 і 8; 2) –6 і 3; 5) 6 і 1 3 ; 8) –7 і 3 14 . 3) –1 і 7; 6) –3 і 2 3 ;

806.

809'.

якщо його

1) 25; 2) 0; 3) –16; 4) 20?

810°.

якщо: 1) а = 1, х1 = 4, х2 = 6; 2) а = 5, = x1 2 , 5 х2 = –5.

812°.

1) х2 – 3х – 10; 6) х2 – 6х – 7; 2)

– 2х – 15; 5) –х2 + 4х – 3;

813°.

1) х2 + 3х + 2; 3) х2 – 5х – 24; 2) –х2 – 8х + 9; 4) x2 + 6x + 9.

814. Розкладіть

1) 2х2 – 5х + 3; 5) –9х2 + 12х – 4; 2) 5х2 + 4х – 1; 6) 3

815.

816.

817. За яких значень b:

818. Скоротіть дріб: 1) +− x xx 2 31 ; 321 3) +− x xx 2 2 16 ; 12 2) xx x 2 253 ; 618

2. Зводимо рівняння до вигляду = Px Qx () 0 () . + −−= −+ x xxx 2 2 71213 0. 11 1 +−−−+() = −+ xxx xx 2 7(1)12(1)13 0. (1)(1)

3. Розв’язуємо рівняння Р(х) = 0. () +−−−+= xxx 2 7(1)12(1)130. х2 + 5х – 6 =0; x1 = –6, x2 =1.

4. Робимо

831'.

832'.

qr.orioncentr.com.ua/W6QGr

833'.

()()−+−−= xx 2 13140?

834'.

method of substitution Substitutionmethode (f) méthode de changement de variables

835'. Для

836°. Розв’яжіть рівняння: 1) −= xx(1)12; 2) +=−−xxx 9(1)1; 3) ++=+xxx 22 (4)31; 4) −++= xxx 22 (1)(1)5; 5) ++−=+ xxx 22 (3)(3)9(1); 6) −+=− xxx 2 (32)114(21).

837°. Розв’яжіть рівняння: 1) −+= xxx 2(5)5; 3) −++=+ xxx 22 (2)(2)37; 2) −+=+xxx 22 (21)537; 4) −−= xxx 2 (23)4(4).

838°. Знайдіть усі значення змінної х, за яких: 1) значення виразу (х – 5)(х + 5) на

839°.

1) = xx xx 2 56 ; 33 5) = xx xx 2 318 ; 66

2) = xx xx 2 152 ; 55 6) = xx xx 2 187 ; 22

3) + = xx xx 2 86 ; 11 7) = xx xx 2 52 ; 224 4) = xx xx 2 30 ; 55 8) + = ++ xx xx 2 53 . 881

841°. Розв’яжіть рівняння: 1) = xx xx 2 310 ; 22 2) 2 2012 . 1010 xx xx +− = 842°. Розв’яжіть рівняння: 1) +− =

2 2 56 0; 23 3) −+ =

xx 2 2 252 0; 2 2)

xx xx 2 2 32 0; 43 4) −+ = xx x 2 2 352 0. 1 843°. Розв’яжіть рівняння: 1) +− = +− xx xx 2 2 215 0; 12 2) +− = + xx xx 2 2 232 0. 2 844°. Розв’яжіть

848°. Розв’яжіть рівняння: 1) х4 – 10х2 +

2) х4 – х2 – 12 = 0; 3) х4 – 3х2 – 4 = 0; 4) х4 – 8х2 – 9 = 0; 5) х4 – 5х2 + 6 = 0; 6) х4 + 2х2 – 8 = 0; 7) х4 – 20х2 + 64 = 0;

849°.

850. Розв’яжіть рівняння: 1) 4х4 – 37х2 + 9 =

851. Розв’яжіть рівняння:

852. Розв’яжіть рівняння: 1) ()() −+−=xxxx 2 2256; 2) ++  −+=  xx xx 2 66 211150; 3) + −⋅+= + xx xx 10 1210; 10 4) −+ +=− +− xx xx 35 2. 53

853. Розв’яжіть рівняння: 1) ()()+−+=− xx 2 22112135; 2) 2 1212 5 320.xx xx ++  +−= 

854. Розв’яжіть рівняння: 1) −= xx 1081; 3 3) += +−xx 115 ; 338 2) + −= ++ x xxx 361 ; 22 4) +− += −+ xx xx 3310 . 333

3,5?

2 133 12 32 .

859. Розв’яжіть рівняння:

1) + −=− +− x xxx 2 114 ; 22 4 2) 2 314 3. 1 x xxx + += + +

860. Розв’яжіть рівняння:

1) ()−−−+= хх 4 2 15(1)40 ;

2) (х2 + х)2 – 4(х2 + х) + 4 = 0; 3) (х2 + 2х + 1)(х2 + 2х) = 12; 4) (х2 + 4х + 2)(х2 + 4х – 1) = 10.

861. Розв’яжіть рівняння:

1) ()+++−= хх 4 2 58(5)90 ;

2) (х2 – 4х + 4)(х2 – 4х) + 3 = 0.

862*.

1) ()+−++= xx 2 518130; 2) −= + xxx 2 421 . 525 10

1) () −++=xnxn 4222990; 2) 11 . xn nx +=+

864*.

865.

= –4.

4. Складаннявідповідідозадачі.

х = –4 не задовольняє

4. Задачі геометричного

розв’язання

1. Аналізтасистематиза-

ціяданих (мал. 50).

І сторона—?

ІІ сторона—?

Діагональ—13 см

Периметр—34 см

2. Побудоваматематичноїмоделі.

2х2 – 34х + 120 = 0 | : 2,

х2 – 17х + 60 = 0.

х1 = 12, х2 = 5.

4. Складаннявідповідідозадачі. Якщо х = 12, то

іншої сторони

17 – х = 17 – 12 = 5 (см). Якщо х = 5, то довжина іншої сторони становить: 17 – х = 17 – 5 = 12 (см).

довжини сторін

876°.

878°.

879°.

891°.

892°.

893°.

894°.

895.

896.

897.

898.

899.

904.

906.

907.

908.

910.

913.

922*.

914.

923*.

924*.

915.

925*.

10.

11.

12.

13.

1°.

рівняння (х – 9)2 = 0. А. ±9.

±3. Г. 9.

2°.

(

+ 5)2 = 16.

1; 9. В. 11; 21. Б. –1; –9. Г. –11; –21.

3°.

А. 3; –4. В. –1; 4 3 . Б. –3; 4. Г. 1; 4 3 .

3х2 + х

4 = 0.

х2 + 6х – 40 = 0.

А. 5; –8.

Б. –5; 8.

В. 4; –10. Г. –4; 10.

5*.

х2 + 4х + m = 0. А. ±− m 4 . В. −± m 2 .

Б. ±− m 24 . Г. −±− m 24 . № 2

1°. Розкладіть

2 + 4х – 5.

(x – 1)(x – 5). В. (x – 1)(x + 5). Б. (x + 1)(x – 5). Г. (x + 1)(x + 5).

2°. Розв’яжіть рівняння ()+=xx 28 .

А. –8; 1. Б. 8; –1. В. –2; 4. Г. 2; –4.

3°. Скоротіть дріб + +− x xx 2 5 310 . А. + x 1 5 . Б. x 1 5 . В. x 1 2 . Г. + x 1

2 6 22 . А. 2; –3. Б. –2; 3. В. 2. Г. –3.

qr.orioncentr.com.ua/Nqdq5

the concentration of a solution die Konzentration der Lösung la concentration de la solution

1) 75х + 40(30 – х) = 19; 2) 0,4х + 0,75(30 – х) = 19; 3) 0,75х + 0,4(30 – х) = 19; 4) 0,75х + 0,4(19 – х) = 30.

933°.

936°.

939°.

940°.

950°.

951.

943°.

952.

944°.

(–0,7 + 2,3) : 2 3 ;

2) (2,7 – 2,9) · (–4,5) від ⋅+−−()2 5 9,69,063,4 16 ?

953.

956.

957.

968*.

959.

969°.

961.

963.

1, 4, 2, 1, 1, 3, 0, 1, 2, 3, 2, 1, 2, 3, 0, 2, 2, 3, 2, 0.

ряд: 0, 0, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 4.

973°.

qr.orioncentr.com.ua/JHbwp

1) 18; 12; 20; 18; 2; 10; 2) 2,5; –4,3; 4,3; 6,2; 7,1; 7,1; –7,1; 3) – 2 ; 1 + 2 ; 2 ; 0; 2 + 1; 2; 5; –7.

974°.

1) 8; 12; 20; 8; 20; 12; 20; 2) – 3 ; 1 + 3 ; 3 ; 0; 1 – 3 ; 5; 0.

975°.

976°.

39, 39, 48, 62, 53, 67.

981°.

982°.

983°.

987.

988.

989.

990.

994*.

995*.

996*.

997.

1) х2 – 4 = 0; 2) х2 – 4х+ 4 = 0; 3) х2 + 3х – 4 = 0.

1) х2 = –4; 3) 5х + 1 = 5(х + 0,2);

2) += х 40 ; 4) х2 – 4х + 20 = 0.

998'.

1005°.

1006°.

1007°.

1008°. Скільки

3, 4, 5, якщо: 1) усі цифри числа різні; 2) цифри в числі

1009°. Скільки існує: 1)

1010°.

1020.

1011°.

1021.

1022.

1012°.

1023.

1013°.

1024.

1015°.

1016°.

1017. Із цифр 2, 4, 5, 6, 8 склали всі

п’ятицифрові числа без повторення цифр. Скільки серед них

таких, запис яких:

1) розпочинається цифрою 6; 2) непарних; 3) розпочинається із 46; 4) не розпочина-

1018.

1025.

1026.

1027.

1028.

1043°.

1036'.

дві кульки?

1037'. Наведіть приклад:

1) випадкової події; 2) неможливої події; 3) достовірної

1038'.

1045°.

1046°.

1047°.

1048°.

1049°.

1) «випадає 3 очки»; 2) «випадає 5 очок»; 3) «випадає парне

1056.

1057.

45;

3) число, що є квадратом іншого цілого числа?

1052. Із п’яти предметів — історія, фізика, алгебра, географія

1058.

1059.

1053. Із цифр 4, 6, 5 випадко-

вим чином утворили трицифрове число з різними цифрами. Яка ймовір-

ність того, що воно є:

1) непарним;

2) числом, у якого перша цифра 4;

3) числом, більшим за 600;

4) числом, що ділиться на 3?

1054. Із цифр 1, 2, 5 випадковим чином утворили трицифрове число з різними цифрами.

1060.

1061.

1062.

1055.

3) числом,

1) а – 10 : а – 6 · а – 5;

2) а – 10 : а 6 · а – 5;

3) а – 10 : а – 6 : а – 5;

4) а – 10 · а – 6 · а – 5;

5) а 0 : а – 8 · а – 12; 6) а 0 : (а – 8 · а – 12);

7) (а–4)– 3 : (а3)4; 9) (а–10а40)–3 : (а10а–30)0; 8) (а–4)– 3 · (а3)4; 10) (а–10а40)0 : (а10а–30)0.

16. Запишіть у вигляді степеня з основою 3: 1) 9–5 · 37; 3) (9–2)3 · (274) –1; 5) 27–20 : (9–10)3; 2) 272 · 9–7; 4) (812) –9 · (9–2) –3; 6) 81–5 : 320.

17. Запишіть як степінь: 1) 2–3 · 3–3; 3) 35–3 : 7–3; 2) 10–2 · 5–2; 4) 132–1 : 11–1.

18. Запишіть у стандартному вигляді число: 1) 90; 3) 3003; 5) 0,75; 7) 50 · 102; 9) 524 · 103; 2) 112; 4) 0,07; 6) 142,01; 8) 34 · 10 – 3; 10) 65,8 · 105.

19. Чи належить графіку функції 4 y x = точка: 1) А (1; –4); 2) В (2; 2); 3) C (0; 4); 4) M (0,1; 40)?

20.

через точку: 1) А (–2; 4); 2) B (5; 0,2); 3) С (–0,1; 6); 4) D 1 ;2,8 4

функції y = x2 точка:

1) А (1; –1); 4) D (3; 6); 2) В (2; 4); 5) M (0,5; 0,25); 3) C (–0,1; 0,01); 6) N (–1; –1)? 22.

1) y = x2 і y = 9; 2) 1 y x =− і y = x2 .

23. Оберіть серед чисел 4 2 , –1,(3), 0, 16 , 25 0,01, –100, 1,6 , 1 25,;8: 7 1) натуральні; 2) цілі; 3) раціональні; 4) ірраціональні; 5) дійсні.

24. Порівняйте числа: 1) 1 3 і 0,34; 2) 2 1 5 і 2 ; 3) 8,344 і 8,(34); 4) 3 і 1,5.

25. Запишіть у вигляді нескінченного періодичного десяткового дробу число: 1) 5 6 ; 2) 7 9 ; 3) 3 10 ; 4) 2 3 . 26.

множник під знак кореня: 1) 82 ; 3) 0,53 ; 5) 4 хх , якщо х — від’ємне;

Винесіть множник з-під знака кореня: 1) 0,4 ; 2) 2,5 ; 3) 8 а ; 4) 4 0,01у ;

1) 10 5 + 20 5 – 25 5 ; 2) ( 5 + 3 )( 5 – 3 ) + ( 3 + 5 )2; 3) ()2 32 + – (12)2 .

1) 1 7 ; 2) 1 х ; 3) 1 22 ; 4) 5 116 .

36. Розв’яжіть квадратне рівняння:

1) х2 + 8х – 9 = 0; 3) х2 – 6х + 9 = 0; 2) х2 – 6х – 7 = 0; 4) х2 + 6х + 5 = 0.

37. Знайдіть корені рівняння: 1) 10х = 3х2 + 3; 3) 9х2 + 4 = 12х; 2) 9у + 2 = 5у2; 4) 4y2 = 20y – 25.

38. Розв’яжіть квадратне рів-

1) х2 + 14х – 15 = 0; 3) х2 – 6х – 40 = 0; 2) х2 – 9х – 10 = 0; 4) х2 + 2х – 3 = 0. 39.

1) 3 і –2; 2) –4 і 1; 3) 3 і 1 3 ;

46.

47. Розв’яжіть рівняння: 1) 142 3 5 xx −= ; 3) 113 320xx += + ; 2) 108 1 3 xx −= ; 4) 111 1 34xx −=+ .

48. Розв’яжіть рівняння: 1) х4 – 26х2 + 25 = 0; 3) х4 – 40х2 + 144 = 0; 2) х4 +х2 – 2 = 0; 4) 9х4 + 8х2 – 1 = 0.

49. Розв’яжіть рівняння: 1) ()() 2 2298970xx−−−+= ; 2) (x2 – 3)2 + 5(x2 – 3) – 6 = 0.

61.

62.

54.

(Catedral Metropolitana Nossa Senhora Aparecida).

Soumaya).

Вирази. Тотожності. Одночлени і многочлени

1. 1) 55,2; 2) 6,51; 3) 34,2; 4) 8; 5) 154; 6) 2 146 3 . 2. 1) –470; 2) –640; 3) 18,5; 4) –25. 3. Павло Тичина. 4. 1) 0,8x15y3z ; 2) –12x12y29 . 5. 1) x2 + 6x – 16; 2) x2 + 31x + 25; 3) –0,5y2 – 2y – 2; 4) 0,2a3 – 0,5a. 6. 1) 3(a – b)(a + b); 2) x(3x – 1)(3x + 1); 3) y2(y2 – 1)(y2 + 1);

4) 2z(2z – 1)(2z + 1); 5) (n + 5)2; 6) (2m – 7)2; 7) (0,9x – 0,5)2; 8) 5y(2x – 3)2; 9) (a + b)(a – b + 1); 10) (–3z – 2)(5z – 2) ; 11) (c + 5) × × (c2 – 5c + 25) ; 12) (3a – 2)(9a2 + 6a + 4). 8. 1) 73 2 77 x ; 2) 17 3 70 a ;

3) 2,8375b. 9. a – 1,5; (a – 1,5)2. 10. P = 4a – 6; S = a2 – 3a. 11. 58 і 54. 12. 20. Функції

13. у = 15 + 5х. 14. у = 10 + 20х. 16. 1) так; 2) ні; 3) так; 4) так. 19. 1) 6; 2) 3; 3) 8; 4) 2. 20. (0; –4); (8; 0), прямокутний трикутник. Графік зображено на малюнку 1. 21. (0; 3); (6; 0), прямокутний трикутник. Графік

на малюнку 2. Y O 1 18 X –4 Y O 1 1 3 6 X Мал. 1 Мал. 2

22. 1) 2; 2) –5; 3) 0,2. 23. a = –0,6. 24. b = –2; a = 5.

системи 25. 1) 6; 2)

число; 3) коренів немає; 4) 15. 26. 1) так; 2) так; 3) так. 27. 1) (1; 1); 2) (–1; 2); 3) безліч розв’язків; 4) розв’язків немає. 28. 1) (2; 1); 2) (1; –2); 3) (2; –2); 4) (–4; 2).

55. 1) Так; 2) ні; 3) так; 4) так; 5) ні. 56. 3) Так. 57. 1) Ні; 2) ні; 3) так; 4) так; 5) ні; 6) так. 58. 1) x ≠ 2; 2) с ≠ 3; 3) b ≠ 1; 4) y ≠ –5; 5) b— будь-яке число. 59. 1) x ≠ –1; 2) a ≠ 2; 3) c ≠ –1; 4) y ≠ –7; 5) a— будь-яке число. 60. 1) 2; 3) 4; 4) –4; 5) 6; 6) 10. 61. 1) 3; 2) 3; 3) 9; 4) 6; 5) 15. 63. 1) Ні; 2) ні; 3) ні; 4) так. 66. 1) Ні; 2) ні; 3) ні; 4) так. 67. 1) Ні; 2) ні; 3) ні; 4) так. 68. 1) a ≠ 0, c ≠ 0; 3) х ≠ 0, y ≠ 0; 4) a ≠ 1, c ≠ –1; 5) х ≠ 3, y ≠ 4; 6) a ≠ –1, c ≠ 0; 9) b ≠ 0,25, c ≠ 0,25; 10) 12 1;1 33 dc≠≠ . 69. 1) a ≠ –2 і a ≠ 2; 2) b ≠ –3 і b

3; 3) x ≠ –4 і x ≠ 4; 4) a ≠ 1; 5) b ≠ 3; 6) x– будь-яке число. 70.

3) 2 5 . 6 a 96. 1) ; 2 xy x 3) 2 ; 2 xy y 5) ; 3 xy y + 7) 2x + 3y; 9) . 2 xy a 97. 1) 3; 3) 1,5; 5) –3; 7) ; a b 8) 2 3 a b . 98. 1)

1) 2 4 ; 1 b b

3) 4x. 102. 1) 1 ; x x 3) 3 ; 2 ab 5) () 5 . aab b + 103. 1) 1 ; x x 3) () () 4 . 4 aab bab + 104. 1) ; xy

. xz yxz + −+ 107. 1) ; xy x 2) 3 . a ab 110. 1) 5; 2) х — будь-яке число, крім –11 і 11; 3) х — будь-яке число, крім 1 6 . 111. 1) 1 ; 3 x x 3) 42 1. xx−+ 112. 1) ,0, ,0; xx y xx >  =  −<  2) 2,0,

3) 3,3, 3,3. xx y xx −<  =

−>

113. 20 30 x x ; 1) в 1 1 7

1) 9 ;

3) 8 ; 9c 5) 5 ; 2 c c + 7) 13 . 1 a d 143. 1) 5 ; 4ab 3) 2 9 ; 5 xy ab 5) 7 . c ac + 144.

2) 2 4 y y ; 0,6. 157. 1) 2 21 , 9 a 4,2. 158. 1) x – 2; 3) 1. 159. 1) 22 ; aabb −+ 3) 22 ; xxyy −+ 6)

1) 11; 2) –2;

1; 5) –9. 216. 1) 9; 2) 7 9 ; 3)

1) 3 5axy b ; 2) ()2 . xy xy + 230. 1) 4224 ; xxyy ++ 2) a(a –

). 231. 1) (x2 + y2)(x – y); 2) ()() xy xyab ++ . 232.1) 1; 2) (m – n)2.

§ 7. Раціональні рівняння

237. 1) 0 або 4; 3) –1 або 4; 5) 0 або 6; 7) –2 або 2. 238. 1) 0 або 3; 3) 4 або 5. 239. 1) x — будь-яке число; 2) x — будь-яке число; 3) x — будь-яке число; 5) x — будь-яке число, крім 0 і 2; 6) x — будь-яке число. 240. 1) x — будь-яке число; 3) x — будь-яке число, крім –5 і 4. 241. 1) 0; 2) 3; 3) 2; 4) –3; 5) 0; 6) –1 або 1; 7) 0; 8) 5. 242. 1) коренів немає; 3) коренів немає; 5) коренів немає; 6) коренів немає. 243. 1) 0; 2) 4; 3) коренів немає; 4) коренів немає. 244. 1) коренів немає; 2) коренів немає; 3) коренів немає; 4) коренів немає; 5) –1; 6) –2; 7) –4; 8) 4. 245. 1) коренів немає; 2) 3. 246. 1) Ні; 3) ні; 5) ні. 247. 1) 2,8; 3) –4,5; 5) 4; 7) 1,5; 9) 4,2; 11) 4,5; 13) 2; 15) 2 ; 3 17) 7. 248. 1) 1,75; 3) 16; 5) 11. 249. 1) Так; 3) так; 4) ні; 5) ні. 251. 1) Ні; 3) так. 252. 1) коренів немає; 3) 2; 4) коренів

немає; 5) 0; –3. 253. 1) коренів немає; 2) коренів немає; 3) 1; 4) –3. 254. 1) 2; 2) –0,5; 3) 4; 4) –3. 255. 1) –3; 2) 2,75; 3) –3,6; 4) –2,5.

256. 10 км/год, 40 км/год. 257. 5 . 3 258. 7 . 9 259. 1) (0; 0), (–3; –2,25).

260. 2 . 9 261. а ≠ 5. 262. а = –0,5 і а = –2. 263. 40 пістолів або

60 пістолів.

269. 1) 3–1; 3) 10–1; 4) 17–1; 11) с–1 . 270. 1) 4–1; 3) 345–1; 6) у–1 . 271. 1) 6–2; 3) 11–7; 4) 5–5; 7) 44–22; 9) х–4; 13) п–15; 15) с–120 . 272. 1) 5–7; 2) 18–3; 3) 22–7; 4) b–2; 5) у–9; 6) t –14 . 275. 1) 23; 2) 20; 5) 2–2; 8) 2–6.

277. 1) 33; 2) 30; 5) 3–2; 6) 3–4. 281. 3) 5 1 2 ; 5) 9 1 10 ; 7) 5 1 21 ; 12) 10 1 100 .

282. 1) 3 1 10 ; 5) 1 20 ; 6) 7 1 25 . 284. 1) 4 1 а ; 2) 9 1 c ; 3) 12 1 т ; 4) 56 1 n ; 5) 80 1 b ; 6) 100 1 х . 286. 1) 1 4 ; 3) 1 5 ; 5) 1 20 ; 6) 1 1000 . 287. 1) 1 4 ; 3) 1 100 ; 5) 25;

8) 100. 288. 1) 34; 3) 6 3 2    . 289. 1) 5; 2) 23; 3) 96; 4) 108; 5) 275.

290. 1) 1; 3) 1; 5) 1; 8) 1. 291. 1) 75; 2) 1 15 ; 3) –7; 4) 2; 5) 9; 6) 1; 7) 11,1; 8) 14. 292. 1) 2; 2) 5; 3) 7; 4) –30. 293. 1) 4440 > ; 4) 31040 < .

· 6х; 2) 27 · 2–х; 3) 12–8 · 12п; 4) 3–р · 3–п . 325. 5) 256; 7) 1; 9) 64; 10) 16. 326. 1) 32; 3) 2; 5) 1. 327. 1) а 12; 2) а–4; 3) а7; 4) а–13; 6) а2; 8) а12 . 328. 1) т 12; 2) т–8; 4) т–20 . 330. 1) 76; 2) 7–7; 3) 715; 6) 7–2. 331. 1) 87; 2) 8 20; 3) 85; 4) 8–9; 5) 8–6; 6) 83. 332. 1) а–25; 2) 1; 3) а–20; 4) а21; 5) а2; 6) а–8; 7) т12; 8) т–22 . 334. 1) 5–50; 2) 444; 4) 70; 9) а–30; 12) а–25; 16) а–22 . 335. 1) 2–8; 2) 330; 3) 3–30; 4) 100; 5) х0; 6) х0; 7) х–44; 8) х32 . 336. 1) 8–3; 2) 18–1; 3) 2–3; 4) 2–1; 5) 80–9; 6) 12–4; 7) (ba)–12; 8)

10) (pmn)–6; 11) (abc)–1; 12) (3тп)–4; 13)

4) 5–10; 5) (zху)– 3; 6)

. 339. 1) 12–2;

294. 1) 55 > 50; 2) (–7)5 < 70; 3) 5 5 1 3 3 < 4) 9–6 < 1000. 296. 1) Додатним; 4) від’ємним. 297. 1) 9 25 ; 2) 4 25 ; 5) 25; 7) 25 36 ; 8) 25 36 . 298. 1) 1 64 ; 3) 1 16 ; 4) 100; 10) 8 27 ; 11) 16 25 . 299. 1) 15,625; 2) 10 000; 3) 100; 4) –100 000; 5) 9 16 ; 6) 81. 301. 1) 2 · 9–7; 2) 6 · 8–8;

9) 9,1 · 104; 10) 4,82 · 10–3; 11) 1,15 · 107; 12) 4,3 · 101; 13) 2,7 · 10–6; 14) 1,1 · 10–1. 345. 1) 5 · 10

351. 1) 632xab = ; 4) 7. 352. 1) 1615ab ; 3) 4. 353. 1) (5)26 . 355. 1) т2 · т 22 .

356. 1) 2–1; 3) 2–27. 357. 1) 2–5(2–1 + 212); 3) 2–5(22 + 28 – 2–10+ 220). 358. 1) 3–4(3–8 + 316); 2) 3–4(35 + 1 + 38); 3) 3–4(3–1 + 39 – 33+ 35).

360. 1) 12–12; 2) 1; 4) 510; 5) 0,64; 6) 250002. 362. 1) 6 · 10–8 > 1,2 · 10–9, 6,12 · 10–8, 7,2 · 10–17, 5 · 101; 2) 0,2 · 106 > 0,16 · 104, 2,016 · 105, 3,2 · 108, 8 · 10–3; 3) 2,1 · 10–10 > 0,63 · 10–11, 2,163 · 10–10, 1,323 · 10–21, 3 · 10–2; 4) 5,5 · 1022 > 11 · 1020, 5,61 · 1022, 6,05 · 1043, 5 · 101. 363. 1) 0,25. § 10. Перетворення раціональних

376. 1) а – 2. 377. 1) 1 9 b + ; 3) 33 1 аb ; 4)

п . 386. 1) 1; 2) () 2 ab ; 3) () 10 xy ; 4) () 5 4 y + ;

xxy ⋅+ ; 9)

3 4 y xy 387. 1) 1; 2) () 3 5 a + ; 3) () 3 pm + ; 6) 2 x ; 8) (п + 4т)9. 389. 1) 2,5х–8у 3; 2) т 21п6; 4) 1518 1 8 ba . 391. 1) ()225 ab ;

2) 2,25; 3) 1; 4) 1 8 ; 5) 1; 6) х. 394. 1) 0; 2) 10 10 а + ; 3) 1; 4) 1; 6) 2 2 16 х х .

395. 1) (у–1– 2)2; 3) (а–2 – 5)2; 4) (2т–1– 3п –1)2. 397. 1) (x–1 – 5)(x–1 + 5);

2) (a –1 – b)(a –1+ b). 399. 1) 3 2 1 a a + ; 2) 2 21 x x + 402. 1) 3а3с– 2; 2) 0,25b32с14 .

403. 1) a – b; 4) –a – 2; 10) 1 1 х + . 404. 1) a – 3. 405. 1) у–2(у –6 + у –2);

4) у–2(2у 3 + 4у); 6) у–2(ху –7 + 9). 406. 1) а–4(а–8 + а–6); 2) а–4(а–3 – а7); 4) а–4(7а–10 + 6а4). 408. 1) а(а3 + а2+ а–4+ а–5); 2) а3(а +1+ а–6+ а–7);

4) а–5(а9 + а8 + а2 + а). 410. 2) 22 тп тп ; 3) х–4; 4) 2 п т    . 411. 1) 23; 2) 3; 3) 2. 412. 1) 7; 2) 83. 414. 2) 4 19 . 415. 2) 0,25. 417. 1) ()() 3 14хх++ ; 2) 22аb ab + . § 11. Функція k x y=

419. 3), 4). 423. 1) 1; 2) –4; 3) 4; 4) 10; 5) –12; 6) –25; 7) 28; 8) 100. 424. 1) 3; 2) –3. 426. 1) х — будь-яке число, крім нуля; у — будь-яке число, крім нуля. 430. 1) Ні; 2) так; 3) так; 4) ні. 431. M, P. 434. 1) –10; 2) 16; 3) 27; 4) –2; 5) 9; 6) –50; 7) 36; 8) –18.

435. 1) –1; 2) 21; 3) 20; 4) 14. 445. 1) 1 5 ; 3) 4 9 ; 5) –5; 6) –8; 7) 7.

447. 1) –0,002; 2) –14; 3) 0,9. 452. 1. Для функції 1 y x =− : 1) х — будь-яке число, крім нуля; 2) у — будь-яке число, крім нуля; 3) –1; 4) 1, –1, 0,1; 6) х < 0; 7) х > 0; 8) х < 0 і х > 0; 9) не існує таких значень аргументу. 3. Для функції 0,2 y x = : 1) х — будь-яке число,

крім нуля; 2) у — будь-яке число, крім нуля; 3) 0,2; 4) –0,2, 0,2, –0,02; 5) 0,2, 0,02, –0,1; 6) х > 0; 7) х < 0; 8) не існує таких значень аргументу; 9) х < 0 і х > 0. 457. 1) (2; 2); 2) (1; –2). 458. 2) (–2; –2), (2; 2); 3) (2; 6) і (–3; –4). 460. 4 y x = . 462. 1) –6, 1; 2) –1, 2; 3) 1, 3; 4) 1, –9. 465. 5 y x = (мал. 23); (мал. 24).

чиСла § 12. Функція y = x2

471. х –20–8–606820 у 400643603664400 473. 1) Так; 2) ні; 3) так; 4) ні. 476. 1) Ні; 2) так; 3) ні; 4) так. 477. 1) 0; 1; 9; 2) 1, –1; 3, –3; 3) х — будь-яке число; 4) х ≥ 0. 478. 1) 1; 4; 9; 2) 0; 2, –2; 3) х < 0 і х > 0; 4) х ≤ 0. 481. 1) (–3; 9) і (3; 9); 2) графіки не перетинаються; 3) (0; 0) і (1; 1). 483. 1) Не має розв’язків; 2) (2; 4) і (3; 9). 484. 1) –2 і 2; 2) –4 і 4; 3) 0; 4) не має розв’язків. 485. 1) –1 і 1; 2) не має розв’язків; 3) –3 і 3. 486. 1) (0; 0), (1; 1). 491. 1) –1 і 0; 2) 1 і –3; 3) не має розв’язків.

494. (мал. 36), (мал. 37),

(мал. 39). § 13. Арифметичний квадратний

510. 1) Так; 2) ні; 3) ні. 512. 1) –9; 9; 8) –1,5; 1,5. 518. 1) 0,3;

2) 0,4; 3) 0,5; 4) 0,07; 5) 0,06; 6) 0,13. 520. 1) 1 3 ; 3) 5 7 ; 6) 9 10 .

523. 1) 50 > ; 3)10010 >− ; 4)42 −< ; 5) 217 >− ; 12) 124 < .

524. 1) 60−< ; 2) 00,01; < 3) 526;−< 4) 3537; >−

5) 749 < ; 6) 638; < 7) 633; > 8) 10110 > . 526. 1) 4; 2) 3; 4) 9;

5) 10; 6) 0,2; 7) 0,99; 9) 2 5 ; 10) 1 8 . 527. 1) 2; 2) 2; 3) 0; 4) 0,7; 5) 5,7;

6) 1 7 . 528. 1) 6; 2) 6; 3) 10; 4) 18; 6) 120; 8) 80; 9) 140; 10) 320.

531. 1) 7; 2) 0,3; 3) 8; 4) 6; 5) 35; 6) 1,5. 533. 1) 3; 2) 3; 3) 3; 4) 3; 5) 3.

534. 1) 4; 2) 4; 3) 0; 4) 90. 535. 1) 3; 2) 3; 3) 11; 4) 5,4. 536. 1) 8 ; 2) 32 ; 3) 12 ; 4) 75 ; 8) 63 ; 9) 40 ; 10) 90 ; 11) 99 .

537. 1) 18 ; 2) 48 ; 3) 20 ; 4) 54 . 538. 1) 22 ; 2) 42 ; 3) 62 ;

§ 14. Множина та її елементи. числові множини 587. 1) 4,(1); 2) 2,35(0); 3) 0,(35); 5) 2,(123). 588. 1) 8,(0); 3) 2,(2); 3) 1,55(4); 4) 0,4(235). 589. 1) 2,888…; 2) 19,333…. ; 3) 1,3252525…; 4) 5,9878787…; 5) 21,88999…; 6) 4,5000…; 7) 21,000…; 8) 5,101121212…. 590. 1) 3,444…; 2) 5,5121212…; 3) 7,54000…. 593. 1) Так; 2) так; 3) так; 4) ні; 5) так; 6) так; 7) ні; 8) так; 12) так. 594. 1) Так; 2) так; 3) ні; 4) ні. 596. 1) Так; 2) так; 4) ні; 6) ні. 597. 1) 1, 4, 9; 2) 1, 9 3 , 0, 4, 9; 3) –0,(4), 1, 9 3 , 0, 1 2 ; 4, 3 5 ,

1,0333…, 9; 4) 6 , – 6 . 598. 3) 12 6 , –3,(9), 0, 25 , 7,8888…, –5, 1 3 , 22. 606. 1) Ні; 2) ні; 3) ні; 4) так. 609. 1) 1 0,0(6); 16 > 2) () 5 0,45; 11 = 3) 1 0,1(4); 7 > 4) () 7 0,7. 9 = § 15.

621. 1) Ні; 2) так; 3) так; 4) ні; 5) так; 6) ні; 7) так; 8) ні; 9) так. 622. 1) Так; 2) ні; 3) так. 627. 1) x – 3. 628. 1) 5x ; 2) 1012 x + .

629. 1) 15 pp ; 5) 232 xxyy ; 6) 1 a . 630. 1) 6 nn + ; 2) 318aa ; 3) 64 y ; 5) 44уy−+ ; 8) 21010yy++ .

631. 1) () 12 aa ; 3) () 9 mn ; 5) ()325aa ; 9) () 2 xx + ; 13) (5)(5) xx−+ ; 16) () ()1010xx−+ ; 17) () ()22xx−+ .

633. 3) 1 3 ; 4) c a . 634. 1) p ; 2) . n a 636. 1) 2 1 y + ; 3) 2; 7) 7 n + . 637. 1) 4x ; 3) 36a ; 4) 2 4xy ; 5) 2 4xy ; 8) 4

638. 1) 25c ; 2) 2 ac ; 3) 22 2nm ; 4) 22 3nm . 640. 1) 7 y ; 2) 7 y ; 3) 23 ab ; 4) 23 ab ; 5) 23 ab ; 6) 23 ab . 642. 1) 3 3 ; 2) 15 3 ; 4) x x ; 5) 2 2 ab b ; 6) 2 z ; 7) 2 2 y y ; 8) 81 81 x x + + . 645. 1) 1 x

4) 92 ; 5) 23 ; 6) 35 . 539. 1) 32 ; 2) 52 ; 3) 72 ; 4) 27 ; 5) 102 ; 6) 33 . 541. 1) 22 ; 2) 63 ; 3) 55 ; 5) 21 ; 6) 0; 7) 27 ; 8) 1310 . 542. 1) 210 ; 2) 0; 3) 4023 ; 4) 82 . 543. 1) 10510 ; 2) 22 + ; 6) 15 ; 7) 2; 9) 1; 10) –10; 11) –31; 14) –2; 20) 19421 + . 544. 1) 33 + ; 2) 655 + ; 4) –1; 5) 4; 6) 10. 546. 1) –3; 2) –2; 3) 5; 4) 100. 549. 1) 2 1 3 ; 5) 1 1 2 ; 8) 3 1 4 . 550. 1) 3,5; 2) 1 2 3 ; 3) 2 1 7 ; 4) 2 2 3 . 551. 1) 437 < ; 2) 2826 > ; 4) 3218 = ; 11) 9 12 16 < . 552. 1) 527 > ; 2) 459 < ; 3) 4232 = ; 1 7)0,25 4 = . 553. 1) 1 i 2; 2) –3 і –2; 3) 2 і 3. 554. 1) 1 і 2; 2) –3 і –2; 3) 3 і 4; 4) 4 і 5. 556. 1) 75; 2) 700; 3) 2; 4) 11 25 . 560. 1) 0,9; 2) 2,4; 3) 24; 4) 30. 562. 1) 523 ; 2) 23 ; 3) 128 ; 4) 22 . 564. 1) 0,18 ; 2) 5 ; 3) 1,5 . 566. 1) 0,15 ; 3) 170,1 . 568. 1) () 3101 ; 3) ()515 + ; 5) ()3123 + . 570. 1) 3 ; 2) 2 . 572. 1) 37 ; 2) 66 . 574. 1) 35 ; 2) 71 ; 3) 21 + ; 4) 23 .

7) 8 x =± ; 9) 9 x =± ; 10) 17 x =± ; 11) не

13)

розв’язків; 17) не має розв’язків. 646. 1) 7 x =± ; 2) 8 x =± ; 4) 7 x =± ; 5) 3 x =± ; 7) не має розв’язків; 8) не має розв’язків.

648. 1) х = 25; 2) х = 16; 3) х = 9; 4) х = 5; 5) не має розв’язків; 6) х = 0. 650. 1) х — будь-яке число; 2) х — будь-яке число; 3) х > –10; 4) х > –1. 651. 1) 2x + 18; 2) 202а . 652. 1) 2a + 8; 2) 22хху . 653. 1 1) aa ; 2 3) y xy . 654. 10 1) 5 a . 656. 1) 8 4 n n .

658. 1) 4. 659. 1) – 3 x ; 2) 4 9yx ; 3) 49ab ; 5) 22 nmmn−+− .

660. 1) 3 3a ; 3) ()3 ac . 661. 1) 22 п ; 3) 4 0,1abb ; 6) ()2 2 3 1 n mm + .

662. 1) 36 x ; 3) 2 6 23 7 xx y . 663. 1) 12 ; 3) 2(75) + ; 6) 52 ;

7) 2 2 2 x x + . 664. 1) 15 4 −+ ; 2) 72 + ; 6) ac ac + . 665. 1) –9, 7; 3) 10; 4) –18, 0; 8) не має розв’язків. 666. 1) –4, 0; 3) 25; 4) 34±− ; 6) не має розв’язків. 667. 1) 1 2 ± ; 2) не має розв’язків; 3) 2 ± .

668. 1) 3 ± ; 2) не має розв’язків. 669. 1) 9; 2) 1; 3) не має розв’язків; 4) 0; 5) –2; 6) 3. 670. 1) 4; 3) 0; 4) –1. 671. 1) 1,5; 2) 4; 3) 256; 6) 0. 672. 1) 2. 673. 1) 2; 2) 1; 3) 10; 4) –4; 0; 7) 0; 100. 674. 1) 3; 2) –3;

3; 3) 0; 4; 4) 1. 677. 1) у ; 4) xy xy + . 678. 1) 4; 4) 52 2 . 680. 1) a < 0;

3) a < 7. 681. 1) a = 0; 2) a = –1; 4) a = ±2. 683. 1) 0; 2) 0; 3) 1. § 16. Функція 687.

х 11,442,253,246,259,6120,25

у 11,21,51,82,53,14,5

689. 1) Так; 2) так; 3) ні; 4) ні. 691. 1) Так; 2) ні; 3) так; 4) так. 695. 1) (1; 1); 2) ні; 3) (4; 2); 4) ні. 696. 1) (1; 1); 2) (0; 0). 697. 1) (16; 4); 2) графіки не перетинаються. 699. 1) (4; 2); 2) (1; 1). 701. 1) 62 > ; 2) 2,52,7 < ; 3) 54,4 > ; 4) 39. = 710. 1) 3,8 ; 2; 4,1 ; 4,5 ; 2) 2 2 5 , 1 2 2 , 4 2 7 , 3 2 4 . 712. 1) 4; 2) 4. розДіл 4.

рівняння § 17. Квадратні рівняння

726. 1) x2 – x – 6 = 0; 2) x2 – 8x – 16 = 0; 3) x2 + x – 6 = 0; 4) 2x2 + 2x + 5 = 0; 5) x2 – 4x – 5 = 0; 6) x2 – 6x – 40 = 0. 727. 1) x2 – 4x + 3 = 0; 2) 6x2 + 11x – 4 = 0; 3) 9x2 – 12x + 2 = 0; 4) 4x2 – 7x + 3 = 0. 728. 1) 1; 2) 4; 3) 36; 4) 16; 5) 6,25; 6) 20,25. 729. 1) 9; 2) 25; 3) 12,25; 4) 2,25. 730. 1) 0 і –14; 2) 7 і –1; 3) 11 і –1; 4) –3 і –5; 5) –2 і –2; 6) коренів немає. 731. 1) 6 і –10; 2) 6 і 6; 3) коренів немає. 732. 1) 2 і –4; 2) 1 і 3; 3) –5 і –7; 4) 3 і 5; 5) –2 і 8; 6) 5 і 5. 733. 1) –6 і –4; 2) 2 і –4; 3) 4 і 4. 734. 1) 1

4; 3) 2 і –3; 4) 2 і 2,5;

747. 1) 36; 2) 9; 3) 16; 4) 49. 748. 1) 4; 2) 49. 752. 1)

755. 1) –5 і 1; 2) –2 і 8; 3) 2 і –4; 4) 4 і 4; 5) –1 і –7; 6) коренів

7) 3 і –4; 8) –3 і 5; 9) –1 і 8; 10) 36;−± 11) 1 і –2; 12) –5 і –20; 13) –1 і 7; 14) –2 і –13; 15) 1 і 2; 16) 5 і 5. 756. 1) 2 і –6; 2) –2 і 5; 3) 3 і 3; 4) коренів немає; 5) 1 і 4; 6) –2 і –4; 7) –2 і 3; 8) 2 і 5. 757. 1) 2 і –1,5; 2) 1 1 3 і 2 ; 3 3) –2 і 0,6; 4) 1,5 і 0,5; 5) –3 і 1 ; 4 6) –3 і 1 ; 5 7) 1 3 і 1 ; 2 8) 1,5 і 1; 9) 2 і 2,5; 10) 0,6 і –0,2; 11) 1 1 4 і 1 2; 4 12) 1 і 3 ; 4 13) 2 2 3 і 2 2; 3 14) 6 і 1 ; 3 15) 5 і 0,5; 16) 0,5 і 0,5. 758. 1) 1 і –2,5; 2) 1 і 1 ; 9 3) 2,5 і –2; 4) 1 3 і –2; 5) –1 і 1 ; 5 6) 3,5 і 3,5; 7) 3 і –0,5; 8) 1 і 0,5. 759. 1) 1 1 3 і 1; 2) 1 і 1 ; 5 3) 10 і –9; 4) 1 і 0,6; 5) 5 і 1; 6) 1 і 2 ; 3 7) –2 і 1 ; 4 8) 3 і 3 2; 4 9) 2 1 3 і 2 1 3 ; 10) 9 і 2; 11) 2 і 1 2; 3 12) 2,5 і 2; 13) 1 9 і 1 ; 9 14) 36; ± 15) 0 і –5. 760. 1) 6 і

–2,5; 2) –1 і 2,5; 3) 16; ± 4) 5 і –6; 5) 1 7 і 1 ; 2 6) 0 і –3. 761. 1) 9 і –8; 2) 3 і –0,5; 3) 2 і 1 ; 6 4) 326;−± 5) 3 і –3; 6) 2; ± 7) –5 і 6; 8) 6 і –4.

762. 1) 7 і –8; 2) –0,5 і 3; 3) 1 і –3; 4) 2 і –4. 763. 1) 1 і –3,5; 2) 5 і 5 ; 6 3) 3 4 і –3; 4) 8 і 1. 764. 1) 2 і 1 ; 3 2) –2 і 1 1. 3 765. 15 учасників.

766. 7 міст. 768. 2 % 769. 1) 769 5 ± ; 2) 4 і 0,6; 3) –7 і 4.

770. 1) n < 1; 2) n > 1; 3) n = 1. 772. 4. 773. Вказівка: розв’яжіть рівняння з буквеними коефіцієнтами. 774. 1) сторони ділянки 36 м і 20 м; периметр ділянки 112 м; 2) 56 секцій. § 19. Теорема Вієта

787. 1) –4 і 1; 2) –2 і 8; 3) 3 і –10; 4) 2 і 8; 5) 1 і 11; 6) 1 і 8; 7) 3

і –4; 8) 13 і 2; 9) –1 і –4; 10) –1 і –5; 11) 1 і –2; 12) –5 і –20; 13) –1 і 10; 14) –1 і –7; 15) 1 і 2. 788. 1) –9 і 1; 2) –2 і 5; 3) 4 і 5; 4) –1 і –8; 5) –2

і 7; 6) –2 і –4; 7) 5 і –4; 8) 2 і 5. 789. 1) –13; 2) 22. 790. 1) 3 1; 5 2) 4 . 25

791. 1) 2 2; 3 2) 5 1. 9 794. 11 і –14. 795. –14 і 12. 796. 13 і –39.

797. –7 і 35. 798. 6, 3 і 18. 799. 3, 6, –9 або –3, –6, 9. 800. 1) 51; 2) 3 ; 4 3) 1 4; 4 4) 1893. 801. 1) 10; 2) 2 ; 4 3) –2,5; 4) 142.

802. 13. 803. –1 804. –1 і 0,6. 805. 2. § 20. Квадратний тричлен. Розкладання квадратного тричлена на лінійні множники

812. 1) (х – 5)(х + 2); 2) (х – 6)(х – 4); 3) –(х – 1)(х – 15); 4) (х + 3) ×

× (х – 5); 5) –(х – 1)(х – 3); 6) (х + 1)(х – 7); 7) (х + 2)2; 8) –(х – 5)2. 813. 1) (х + 1)(х + 2); 2) –(х + 9)(х – 1); 3) (х + 3)(х – 8); 4) (х + 3)2. 814. 1) (2х – 3)(х – 1); 2) (5х – 1)(х + 1); 3) –(3х + 7)(х – 2); 4) (2х – 1) ×

× (3х – 1); 5) –(3х – 2)2; 6) (3х – 5)(х – 1); 7) (2х – 1)2; 8) –(2x + 1) ×

× (х – 2). 815. 1) (3х – 1)(х + 2); 2) –(2х + 5)(х – 3); 3) (3х + 1)2; 4) –(5x – 1)(х – 1). 816. 1) a = –14; 2) a = –12. 817. 1) b = 14; 2) b = –2. 818. 1) 1 1 x + ; 2) 21 6 x + ; 3) 4 3 x x ; 4) 8 x x ; 5) 2 3 x x + ; 6) 8 9 x x + . 819. 1) 4 6 x ; 2) 31 x x ; 3) 56 2 x x + + . 820. 1) мал. 3; 2) мал. 4.

1) мал. 5.

Мал. 5

822. 1) 1,8; 2) –1,75. 823. 1) 1,4; 2) 3,4. 824. 1) 1 5 х ; 2) 1 x . 825. 1 2 x + . 826. ± 10. 827. 4. 828. –6. 829. 1) (nх – 2)(х + 1); 2) (х – m – n)(х + n). 830. 1) 20; 2) 5; 3) 38. § 21. Рівняння, які

836. 1) –3 і 4; 2) –1 і 1 ; 9 3) 1,5 і –5; 4) 2 і 0,5; 5) 3 і 1,5; 6) 5 і 3. 837. 1) 5 і 0,5; 2) 2 і –3; 3) 0,5 і 1; 4) 1 і 2 1. 3 838. 1) 7; 2) 0 і –9; 3) –1 і 2 1 3 ; 4) –4 і 1. 839. 1) –7 і 3; 2) –3 і 1 3 . 840. 1) 2; 2) –3; 3) –2 і –4; 4) –6; 5) 3 і –6; 6) –9; 7) 0,5; 8) 1 і 0,6. 841. 1) –5; 2) 2.

842. 1) –6; 2) 2; 3) 0,5; 4) 2 . 3 843. 1) –5; 2) 0,5. 844. 1) 0 і 4; 2) –2 і 5; 3) 2 3 і 4 ; 5 4) 4 і –5; 5) –1 і 2,5; 6) 2. 845. 1) –1і 4; 2) 16 і 4; 3) –3.

846. 0,5. 847. 0,5. 848. 1) ±1 і ±3; 2) ±2; 3) ±2; 4) ±3; 5) 2 ± і 3; ± 6) 2; ± 7) ±2 і ±4. 849. 1) ±2; 2) ±2 і 5; ± 3) ±1 і ±2; 4) коренів не-

має. 850. 1) ±3 і 1 ; 2 ± 2) ±2 ; 3) 2 ± і 2 ; 2 ± 4) 1 2 ± . 851. 1) ±1 і 2 ; 3 ±

2) ±1 і 3 . 4 ± 852. 1) 15 2 ± ; 2) 3 і 4; 3) 5 і –2; 4) –1. 853. 1) ±2 і 6; ±

2) –20 і –6. 854. 1) 8 і –3; 2) 6; 3) 4 1; 5 4) коренів немає. 855. 1) 4;

2) ±6. 856. 1) 1 і –0,5; 2) 6 і –5. 857. 4 і –3. 858. 1) 0 і 4 ; 2) 26; ±

3) 1; 4) 1; 5) –6 ; 6) –1. 859. 1) 0; 2) 1 2 3 і –2. 860. 1) –1; 0; 2 і 3; 2) –2 і 1; 3) –3 і 1; 4) –4 і 27−± . 861. 1) –4 і –6; 2) 1; 3 і 23 ± .

862. 1) 0; 2) 20. 863. 1) ±3 і ±n; 2) n і 1 n . 864. 1) 5; 2) 3 і –2.

865. 1) 0,6 м і 1 м; 2) 0,44 м і 0,84 м; 3) ≈ 0,4 м2. § 22. Розв’язування задач за допомогою квадратних рівнянь

870. 1) 8 і 9 або –9 і –8; 2) 6 і 12 або –6 і –12. 871. 1) 8 і 6 або –6

і –8; 2) 4 і 12 або –4 і –12. 872. 1) 8 і 4; 2) 2 і 16 або –2 і –16.

873. 1) 3 і 15; 2) 5 і 9 або –5 і –9. 878. 15 і 16. 879. 11 і 12. 880. 3 4 або 5 . 8 881. 1 . 4 882. 60 км/год і 80 км/год. 883. 60 км/год і 90 км/год.

884. 5 км/год. 885. 4 км/год. 886. 10 дет. 887. 12 дет. 888. 5 год. 889. 5 год. 891. 8 см і 15 см. 892. 6 см і 8 см. 893. 5 см, 12 см і 34 см. 894. 6 см, 9 см і 30 см. 895. 12 і 13. 896. 13 і 14. 897. 12. 898. 22. 899. 4 км/год. 900. 4 км/год. 901. 30 км/год. 902. 30 км/год. 903. 40 км/год. 904. 21 год 30 хв 905. 60 км/год. 906. 15 км/год. 907. 16 км/год. 908. 2 км/год. 909. 5 км/год. 910. 25 дет. 911. 7 дет. 912. 10 л. 913. 25 л. 914. 25 м2 915. 4. 916. 75 хв. 917. 30 хв. 918. 13 см. 919. 10 см. 920. 3 м і 4 м. 921. 15 і 9. 922. 381 і 705. 923. 4 і 1. 924. 8 год. 925. У 2 рази; 4 л. 926. 56 с. 927. 1) 4; 2) 6; 3) одночасно.

935. 1740 грн. 936. 434 ст. 937. 2500 грн. 938. 20000 грн. 939. 17 м. 940. 265 кг. 941. 18 %. 942. 48 %. 943. На 25 %. 944. На 35 %. 945. 1) 12 %; 2) 130 %. 946. 1) 25 %; 2) 180 %. 947. 35%. 948. 68%. 949. 250 г. 950. 60 кг. 951. 49 %. 952. 80 000 екз. 953. 20 і 16. 954. 24 і 25. 955. 3,75 кг. 956. 1,6 кг. 957. 42 г. 958. 40 г. 959. На 28 68% 29 960. На 1 9% 11 . 961. На 60 %. 962. 120 г. 963. 300 г.

964. 3,24 кг. 965. 22 %. 966. 10,4 % 967. 1 кг і 7 кг. 968. На 20 %. § 24. Робота з даними 975. 34; 35. 976. 48; 39. 977. 20; 19. 978. 8,4; 9. 979. 12,3. 980. 6,6. 983. 300 учнів. 984. 23 %. 987. 13,4. 988. 9. 989. 6. 990. 6. 991. 1) 100; 2) 14 680 грн; 3) 16 000 грн; 4) на 8,25 %. 992. На 25 %. 993. 1) 116; 2) 19 мед., 3) 19 і 22. 994. 9. § 25.

1000. 12. 1001. 32. 1002. 1) 14; 2) 48. 1003. 1) 12; 2) 35. 1004. 1) 23; 2) 120. 1005. 35. 1006. 48. 1007. 1) 24; 2) 64. 1008. 1) 6; 2) 9. 1009. 1) 90; 2) 81; 3) 3; 4) 12. 1010. 90. 1011. 90. 1012. 336. 1013. 24. 1014. 120. 1015. 8. 1016. 16. 1017. 1) 24; 2) 24; 3) 6; 4) 96. 1018. 1) 6; 2) 6; 3) 2; 4) 18. 1019. 1) 3; 2) 3; 3) 2. 1020. 1) 4; 2) 2; 3) 2. 1021. 180. 1022. 1) 24; 2) 24; 3) 12. 1023. 1) 36; 2) 12. 1024. 1) 96; 2) 500. 1025. 1) 60; 2) 125. 1026. 10 080 с. 1027. 27; 3; 18; 6. 1028. 45. 1029. 120. Вказівка:

рових, двоцифрових, трицифрових і чотирицифрових. 1030. 90. 1031. 1) 24; 2) 47. 1032. 1) 18; 2) 48. 1033. 1) 252; 2) 648. 1034. 1) 6; 2) 9. 1035. 280. § 26.

1041. 5 9 . 1042. 3 5 . 1043. 3 7 . 1044. 1) 1 6 ; 2) 1 2 ; 3) 1 2 ; 4) 0. 1045. 1) 1 4 ; 2) 1 5 ; 3) 0. 1046. 1) 7 15 ; 2) 1; 3) 0. 1047. 1) 2 3 ; 2) 1; 3) 0. 1048. 1) 1 6 ; 2) 1 6 ; 3) 1 2 ; 4) 1 3 . 1049. 1) 1 4 ; 2) 3 4 . 1050. 1) 1 2 ; 2) 0; 3) 1 10 ; 4) 1 10 . 1051. 1) 1 2 ; 2) 4 15 ; 3) 1 15 . 1052. 1) 0,2; 2) 0,2; 3) 0,05. 1053. 1) 1 3 ; 2) 1 3 ; 3) 1 3 ; 4) 1. 1054. 1) 1 3 ; 2) 1 3 ; 3) 0; 4) 1 3 . 1055. 1) 1 3 ;

2) 1 3 ; 3) 1 2 . 1056. 1) 2 3 ; 2) 1 3 ; 3) 1 2 . 1057. 7. 1058 12. 1059. 1) 3 8 ;

2) 7 8 . 1060. 1) 1 6 ; 2) 1 18 . 1061. 1 750 . 1062. 1 15 1063. 1) 0,1; 2) 0,4;

3) 0,5; 4) 0,5. 1064. 21 120 . 1065. 1 10 .

заДачі і вПрави Для Повторення

Розділ 2. Раціональні вирази

1. 1) x — будь-яке число; 2) y — будь-яке число, крім –3 і 0; 3) a — будь-яке число, крім –2 і –1; 4) x — будь-яке число, крім –1, y — будь-яке число, крім 0,5. 5) a — будь-яке число, крім 1 3 , b — будь-яке число, крім 0,25, c — будь-яке число, крім 0; 6) x — будь-яке число, крім 0, y — будь-яке число, крім 1,5, z — будь-яке число, крім 2,6.

bc ++

10. 1) 18; 2) ± 4. 11. 3 . 4 12. 1) 4 1; 4 r p  +   2) 12 1; 4 r p  +   3) 4 1. 4 r p

13. 1) 11 2xy ; 2) 13 ; npm 3) 3322 . bdac 14. 1) 1 80 ; 2) 1,5; 3) 5; 4) 64. 15. 1) а–9; 2) а–21; 3) а; 4) а–21; 10) 1. 16. 1) 3–3; 2) 3–8; 3) 3–24. 18. 1) 9 · 101; 2) 1,12 · 102; 4) 7 · 10–2. 19. 1) Ні; 2) так; 3) ні. 20. 1) –8; 2) 1; 3) –0,6; 4) 0,625.

21. 1) Ні; 2) так; 3) так; 4) ні; 5) так; 6) ні. 25. 1) 0,8(3); 2) 0,(7); 4) 0,(6). 26. 1) 5 см; 2) 15 см; 3) 1,2 м; 5) 1 1 3 см. 27. 1) 5; 2) 1,5; 3) 6; 4) 0. 28. 1) 128 ; 2) 0,02 ; 3) 0,75 ; 4) 16х . 29. 1) 20,1 ; 2) 50,1 ; 3) 4 a . 30. 1) х = ± 9; 2) х

147

146

147

сторонній 70

151

165

166

чисел дійсних 169

168

167

множини елементи 165

модель математична 258

моделювання математичне 258

математичного етапи 259

бласть допустимих значень змінної 15 означення степеня з цілим від’ємним показником 79

0 80

– –

135

вершина 136

– додавання/віднімання раціональних дробів

однаковими знаменниками 42

– додавання/віднімання раціональних дробів із різними знаменниками 43

– зведення раціонального дробу

до нового знаменника 34

– – двох раціональних дробів

до спільного знаменника 36

– множення раціональних дробів 53

– піднесення раціонального

дробу до степеня з натуральним

показником n 54

адикал 147

рівняння біквадратне 249

– дробове раціональне 69

– квадратне 210

– – зведене 210

– – неповне 210

– – повне 210

– квадратного дискримінант 219

– коефіцієнти 210

корінь сторонній 70 – раціональне 68

рівносильні 69

Навчальневидання

ТАРАСЕНКОВА

Головна редакторка І.В.Красуцька

Редакторка І.В.Луценко

Головна художниця І.П.Медведовська Технічний редактор Е.А.Авраменко Художня редакторка К.В.Берсенєва Коректорка Ю.О.Твердохліб Комп’ютерна графіка О.І.Дядика Презентації та інтерактивні вправи І.А.Акуленко

В оформленні підручника використано фото з вільних джерел мережі «Інтернет», фотобанку Shatterstock

Бренди та ресурси зображуються лише з освітньою метою та не є закликом до їх купівлі/відвідування

Формат 60×90 1/16. Ум. друк. арк. 22 + 0,25 форзац. Обл.вид. арк. 19,8 + 0,35 форзац.

1 100121144169196225256289324361