https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html






































































4.
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
АС + ВС = 4,5 + 5,5 = 10 см = АВ.
Отже, точка С лежить на відрізку АВ.
2) ВС = 41 мм = 4,1 см
АС = 0,5 дм = 5 см
АВ = 9,6 см
Перевірка:
АС + ВС = 5 + 4,1 = 9,1 см, а АВ = 9,6 см.
Не дорівнює, отже точка С не
Відповідь:
1. Так, лежить.
2. Ні, не лежить.
6. Відстань між містами на карті становить 5 см.
туристам, якщо масштаб карти 1 : 300 000?
Масштаб 1 : 300 000 означає,
Знайдемо реальну відстань: 5 ⨯ 300000 = 1500000 см.
Переведемо в кілометри: 1500000 см : 100 = 15000 м : 1000 = 15 км.

https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
1) 6 м; 2) 5 м?
Маємо
1) Як відрізати 6 м:
Скласти
Від половини (4 м) відкласти ще
Разом: 4 м + 2 м = 6 м.
2) Як відрізати 5 м:
Скласти весь шматок навпіл → 4 м.
Залишок — теж 4 м.
Цей залишок поділити навпіл → 2 м.
Від 4 м додати половину з другого шматка (1 м із 2 м).
Отримаємо 4 м + 1 м = 5 м.
10. Зобразіть точками на площині
шматка (тобто 2 м).
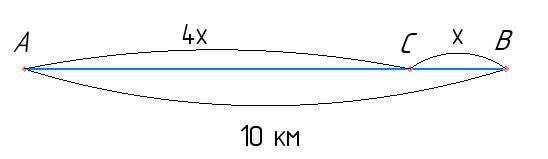
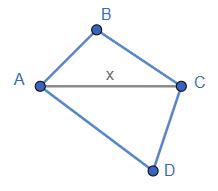
Нехай BC = x, тоді AC = 4x.
З умови:
AC + BC = AB
4x + x = 10
5x = 10.
x = 2 км,
AC = 4x = 8 км.
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
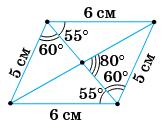
�������� = �������� + �������� = 600 + 200 = 800 м.
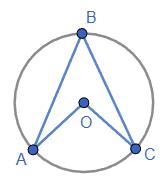
13. OC —
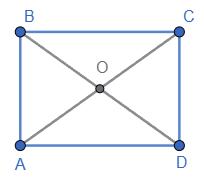
1)
Відповідь:
1) ∠АОС = 92° , ∠ВОС = 43°, ∠АОВ = 48°;
2) ∠АОС = 30°, ∠ВОС = 65°, ∠АОВ = 95°? Промінь �������� лежить
1) 1 хв; 2) 5 хв; 3) 10 хв?
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
даній прямій АВ.
Для того щоб провести пряму, паралельну
1. Намалюйте дані елементи: На
O, яка не лежить на прямій AB .
2. Перше перегинання (Побудова
означає, що ви повинні
���� + ���� = 50∘ ⟹���� = 25∘ .
інші (суміжні) = 180∘ 25∘ = 155∘ .
кути: 25∘ , 155∘ , 25∘ , 155∘ .
���� +2���� = 180∘ ⟹���� = 60∘ ,2���� = 120∘ .
1. 90∘ , 90∘ , 90∘ , 90∘ ;
2. 25∘ , 155∘ ,
1) 3 см, 5 см, 9 см; 2) 5 см, 4 см, 2 см? Для існування
1. 3+5=8 ≤ 9
2. 5+4=9>2,5+2=7>4,4+2=6>5
1) ні; 2) так
існування
1,5 см:
����4 =(����− 1.5)+(����− 1.5)+(����− 1.5)= ����− 4.5 ⟹ віднялось 4.5 см.
Відповідь:
1. ���� +9 (на 9 см більше);
2. 3���� (у 3 рази більше);
3. 2 3 ���� ;
4. ����− 4.5 (на 4,5 см менше).
34. Як зміниться довжина сторони рівностороннього
1) зменшити на 12 см;
2) збільшити в 6 разів? У рівносторонньому трикутнику
1. Якщо ���� зменшити
дорівнює: 1) 12 см; 2) 15 см?
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
1. якщо гіпотенуза = 12 см, бісектриса =6 см;
2.
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
2.
3.
1) прямим; 2) гострим; 2) тупим?
1.
2.
3.
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
1.
2.
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
позначку по відрізку �������� (або �������� ), і
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
то
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
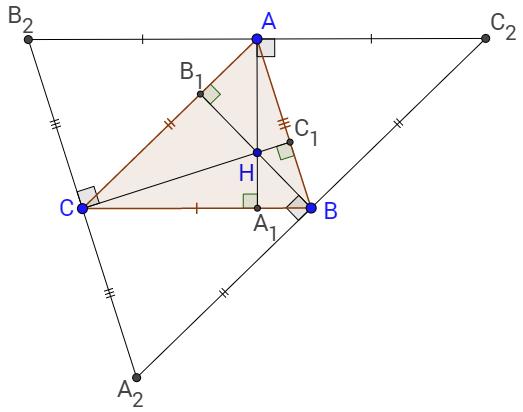
(інцентр) співпадає
трикутника, який ділить висоту у відношенні 2 ∶ 1, починаючи від вершини. Це означає, що радіус вписаного кола ���� становить одну третину висоти ℎ трикутника.
3. Обчислення радіуса вписаного кола: За умовою, висота, проведена до основи (а в рівносторонньому
висота), дорівнює 12 см. ℎ = 12 см.
1.
3.
4.
a
12 +
+
b= 115 (23 + 30 + 35)= 27(см);
a=
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
Отже сторони: 30 см, 60 см, 60 см та 60 см.
Відповідь: 30 см, 60 см, 60 см, 60 см.
81. Чи може чотирикутник мати такі сторони:
1) 1 см, 2 см, 3 см, 4 см; 2) 18 см, 6 см, 5 см, 6 см?
1. 4<1+2+3;4<6; так, можуть; 2. 18 >6+5+6; ні, не можуть.
82. Чи може чотирикутник мати такі сторони: 2 см, 3 см, 5 см, 10 см?
10 =2+3+5; ні, не може.
83. За даними

чотирикутника.
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
Нехай ���� =9; ���� =3���� = 27;
���� = ����− 8= 19;
���� = ����− 10 =9;
���� = ���� + ���� + ���� + ���� = 64.
Відповідь: 64 см
100.
сторони
Чи може периметр чотирикутника дорівнювати:
1) 90 см; 2) 72 см; 3) 115 см?
Нехай x - четверта сторона; P = 10 + 15 + 20 +x= 45 +x;
умова чотирикутника:
���� < 10 + 15 + 20 = 45
та ���� >0 ⇒ 0< ���� < 45 ⇒ 45 < ���� < 90;
���� = 90 ⇒���� = 45 - ні;
���� = 72 ⇒���� = 27 - так;
���� = 115 ⇒���� = 70 - ні.
Відповідь: 72 см.
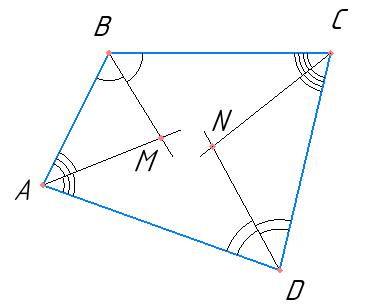
101. Доведіть, що кожна діагональ чотирикутника
Нехай ABCD — чотирикутник, P = AB + BC + CD + DA.
Для діагоналі AC:
AC < AB + BC (△ABC), AC < AD + CD (△ACD).
Додаємо:
2AC < (AB + BC) + (AD + CD) = P ⇒ AC < ���� 2 .
Аналогічно для BD:
BD < AB + AD (△ABD), BD < BC + CD (△BCD)
⇒ 2BD < P ⇒ BD < ���� 2 .
Отже,
102.

https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
Нехай ABCD — чотирикутник.
трикутника
AC < AB + BC (△ABC), BD < AD + CD (△BCD).
Додаємо почленно:
AC + BD < (AB + BC) + (AD + CD) = AB + BC + CD + DA = P.
Отже, сума діагоналей чотирикутника менша від його периметра.
103. У чотирикутнику ABCD діагональ BD ділить
кути B і D навпіл.
Доведіть, що AB = CB і DA = DC.
∆ABD = ∆CBD (за II ознакою рівності трикутників); BD — спільна стopoнa; ∠ABD = ∠CBD; ∠ADB = ∠CDB (за умовою).
З рівності трикутників маємо: AB = СВ і AD = CD.
104. Доведіть, що в чотирикутнику ABCD діагоналі AC і BD — перпендикулярні, якщо
AB = CB і DA = DC.

AB = ВС; AD = CD (за умовою). BD — спільна сторона ∆ABD і ∆CBD.
Звідси ∆ABD = ∆CBD. З рівності трикутників маємо ∠ABD = ∠CBD. АС і BD
перетинаються в т. О.
∆АВО= ∆СВО (І ознака); АВ = СВ (за умовою); ∠ABD = ∠CBO (доведено вище); ВО — спільна сторона.
З рівності ∆АВО і ∆СВО: ∠AOB = ∠COB, але ∠AOB + ∠COB = 180° (суміжні кути).
Звідси ∠AOB = 90°, ∠COB = 90°. Тобто АС ⊥ BD.
105. Знайдіть кути чотирикутника, якщо вони пропорційні числам: 1) 1, 2, 3 і 4; 2) 4, 6, 12 і 14. 1) Нехай кути чотирикутника: х; 2х; 3x; 4х, тоді x + 2x + 3x + 4x = 360°; 10x = 360°; x = 360° : 10;
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
x = 36°;
∠1 = 36°; ∠2 = 2 ∙ 36° = 72°; ∠3 = 3 ∙ 36° = 108°; ∠4 = 4 ∙ 36° = 144°;
2) ∠1 = 4х; ∠2 = 6х; ∠3 = 12х; ∠4 = 14x; 4х + 6х + 12х + 14х = 360°; 36x = 360°; x = 360° : 36; x = 10°;
∠1 = 4 ∙ 10° = 40°; ∠2 = 6 ∙ 10°= 60°; ∠3 = 12 ∙ 10° = 120°; ∠4 = 14 ∙ 10° = 140°.
106. Знайдіть кути чотирикутника, якщо вони
пропорційні числам 1, 2, 4 і 5. ∠1 = х; ∠2 = 2х; ∠3 = 4х; ∠4 = 5х; х + 2х + 4х + 5х = 360°; 12х = 360°; x = 360° : 12; х = 30°;
∠1 = 30°; ∠2 = 2 ∙ 30° = 60°; ∠3 = 4 ∙ 30° = 120°; ∠4 = 5 ∙ 30° = 150°.
107.
1) тупих; 2) прямих; 3) гострих? 1)
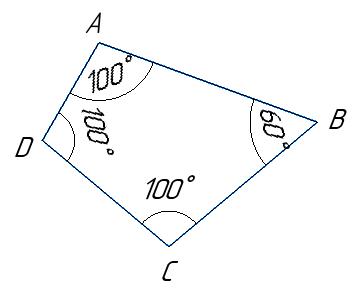
180° – 38° = 142°; 180°– 158° = 22°; 180° – 44° = 136; 180° – 120° = 60°. 2) 49°; 145°;
= 720° – 360° = 360°.
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
113. Чи існує чотирикутник,
1) 120°, 80°, 59° і 101°;
2) 49°, 98°, 68° і 125°?
1) 120° + 80° + 59° + 101° = 360°.
Отже, такий чотирикутник існує.
2) 49° + 98° + 68° + 125° = 340° ≠ 360°.
Отже, такого чотирикутника не існує.
114. Чи існує чотирикутник,
100° + 55° + 160° + 45° = 360°.
Отже, такий чотирикутник існує.
115. Знайдіть
Сума кутів чотирикутника дорівнює 360°.
Сума всіх зовнішніх кутів чотирикутника дорівнює
Отже, сума зовнішніх кутів чотирикутника
чотирикутника.
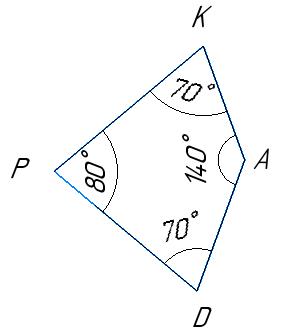
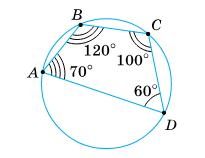
116. За
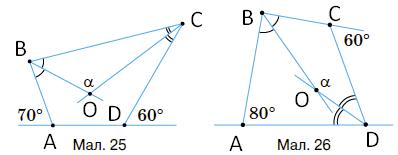
Мал. 25
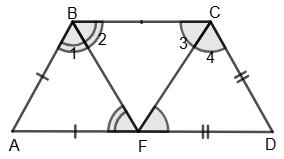
∠BAD = 180° – 70° = 110°;
∠CDA = 180° – 60° = 120°;
∠ABC + ∠DCB = 360° – (110° + 120°) = 130°;
∠NBA + ∠NAB = 1 2 ∠B + 1 2 ∠A = 1 2 (∠B + ∠A) = 1 2 ∙ 180° = 90°.
α = ∠BOC = 180° – (∠OBC + ∠OCB) = 180°– 65° = 115°. Мал. 26
∠BCD = 180° – 60° = 120°;
∠B + ∠D = 360° – (80° + 120°) = 160°;
100°, 55°, 160° і 45°?
α = 360° – (∠C + 1 2 (∠B + ∠D)) = 360° – (120° + 1 2 ∙ 160°) = 360° – 200° = 160°.
117. За
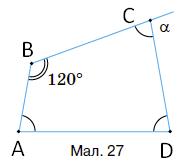
Мал. 27
∠C = (360° – 120°) : 3 = 80°;
α = 180° – 80° = 100°.
118. Діагональ
дорівнює 50 см.
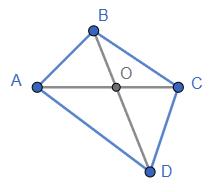
Нехай ABCD — чотирикутник, а
Позначимо AC = x.
Тоді периметри трикутників:
PABC = AB + BC + AC = 30,
PADC = AD + DC + AC = 40.
Склавши їх:
(AB + BC + AC) + (AD + DC + AC) = 30 + 40 = 70.
Але AB + BC + AD + DC
Тому P + 2AC = 70.
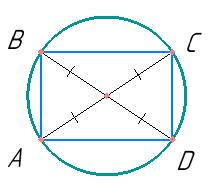
За умовою P = 50, підставимо: 50 + 2AC = 70 ⇒ 2AC = 20 ⇒ AC = 10.
Відповідь: 10 см
AB < AO + OB, CD < CO +
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
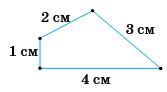
Периметр за кресленням: 1 + 2 + 3 + 4 = 10 см.
Масштаб 1 : 2000 ⇒ 1 см =20 м. Отже, реальний периметр 10 ∙ 20 = 200 м.
Стовпці через кожні 4 м: 200 4 = 50.
Оскільки довжини сторін 20, 40, 60, 80 м —
без «зсуву». Але останній стовпець співпадає
Відповідь: 49 стовпців. 123. Потрібно виготовити чотирикутну
50 – 1 = 49 стовпців.
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
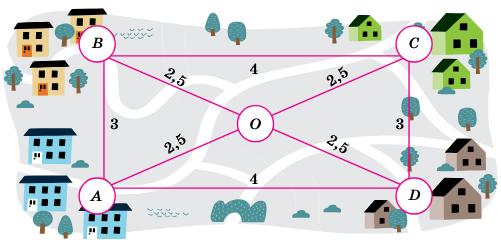
2,5 + 2,5 + 2,5 + 2,5 = 5 + 5 = 10.
3.
2,5
2,5 + 4 + 3 + 4 = 13,5.
2) Дві протилежні сторони
3) Протилежні сторони попарно
1) пряма; 2) промінь;
протилежну сторону. Визначенням
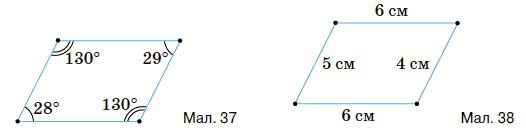
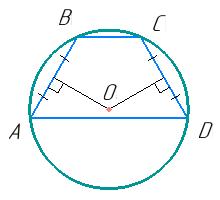
Мал. 37:
рівні, а на малюнку ∠28° ≠ ∠29°.
Мал. 38: Довжини
129. У
(х + 7х) • 2 = 48;
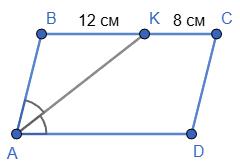
8х = 24; х = 3см; 7x = 7 • 3 = 21 (см).
Відповідь: 3 см; 21 см; 3 см; 21 см.
2) Нехай x см — одна сторона, тоді (х + 7) см —
сторона; (х + x + 7) • 2 = 8;
2х + 7 = 24;
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
2х = 17;
х = 8,5 (см);
х + 7 = 8,5 + 7 = 15,5 (см).
Відповідь: 8,5 см; 15,5 см; 8,5 см; 15,5 см.
133. Периметр
одна з його сторін на 3 см більша за іншу.
Нехай x см — одна сторона, тоді (х + 3) см — друга сторона;
Р = (х + x + 3) • 2; (2x + 3) • 2 = 32;
2х + З = 16;
2х = 13;
х = 6,5 (см);
х + 3 = 6,5 + 3 = 9,5 (см).
Відповідь: 6,5 см; 9,5 см; 6,5 см; 9,5 см.
134. За даними
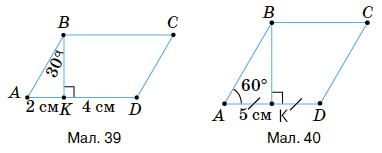
Мал. 39: З ∆АВК, за
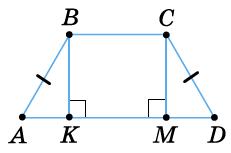
AB = 2AK = 4 см; CD = АВ = 4 см; AD = AK + КD = 2 + 4 = 6 см; ВC = AD = 6 см.
Мал. 40: З ∆ABК, у якому ∠AKB = 90°: ∠ABK
CD = AB = 10 см; AD = AK + KD = 5 + 5 = 10 cм; BC = AD
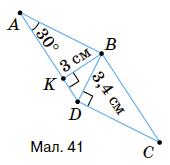
DC = AB = 6 см; ∠C = ∠A = 30°.
∆BDC: ВС = 2 • ВD = 2 •
DAB + ∠ABC = 180°.
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
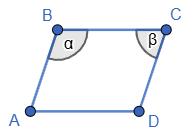
поясніть.
∠ADC = ∠ABC = α; ∠BAD = ∠BCD = β.
1) ∠ADC= 120°; ∠BAD=60°; 2) ∠ADC = ∠BAD = 90° (АВСD прямокутник).
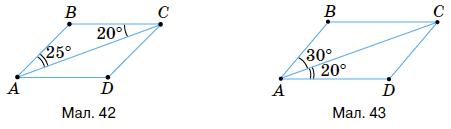
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
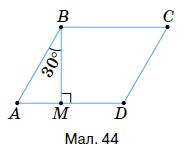
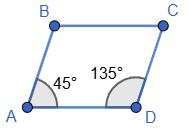
∠A = 90° – 30° = 60° (з ∆АВМ);
∠C = ∠A = 60°; ∠B = ∠D = 180° – 60° = 120° (згідно властивостей паралелограма).
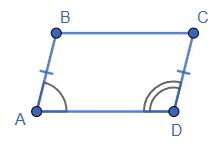
144. Знайдіть кути паралелограма, якщо:
1) один з його кутів на 50° менший від іншого;
2) сума двох його кутів дорівнює 120°.
1) Мова йде про сусідні кути. Нехай ∠1 = x, тоді ∠2 = x + 50°; Згідно властивості паралелограма про суму сусідніх кутів:
х + х + 50° = 180°;
2х = 130°;
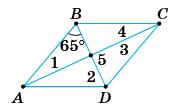
х = 65°;
∠1 = ∠3 = 65°;
∠2 = ∠4 = 65° + 50° = 115°.
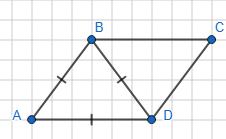
2) Дані кути не сусідні, а протилежні, бо
Тому ∠1 + ∠3 = 120°; ∠1 = ∠3 = 120° : 2 = 60°.
Тоді ∠2 = ∠4 = 180° – 60° = 120°.
145. Знайдіть кути паралелограма,
Нехай ∠1 = х, тоді ∠2 =
х + 3х = 180°; 4х = 180°; х = 45°;
∠1 = ∠3 = 45°;
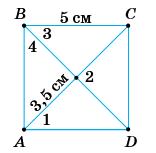
∠2 = ∠4 = 3 • 45° = 135°.
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
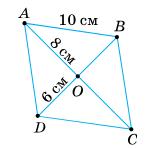
розрахунків застосуємо властивості
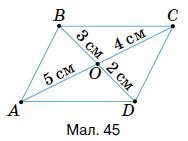
1) ОС = АО = 6 см; OD = OB = 3 cм;
2) АС = АО + ОС = 6 + 6 = 12 cм; BD = ВО + DO = 3 + 3 = 6 см;
3) AD = ВС = 8 см; DC = AB = 5 см.
149.
35°.
Згідно властивості
A = ∠C = 35°.
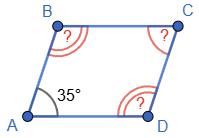
D = ∠B = 180 – 35 = 145°
= 3

= CD = 3
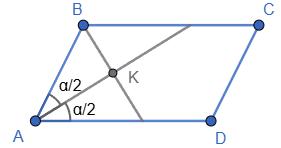
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
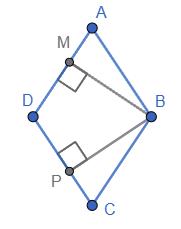
Нехай ∠A = α, тоді ∠B = 180° – α.
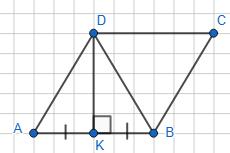
∠BAK = α 2 ; ∠ABK = 1 2 (180° – α).
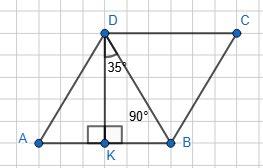
З ∆АВК:
∠AKB = 180° – (∠BAK + ∠ABK) = 180°– (α 2 + 1 2 (180° – α) = = 180° – (α 2 + 90° –α 2 ) = 90°.
Отже, ВК ⊥ АK, тобто бісектриси
перпендикулярні.
152. Доведіть, що бісектриси
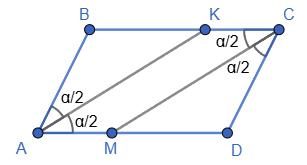
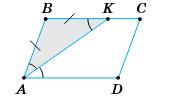
то АВ = ВК =
∠BAK = ∠BKA. Оскільки ∆АВК —
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
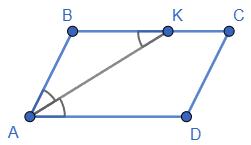
∆АВК — рівнобедрений, бо ∠BAK = ∠KAD (АК — бісектриса), а ∠KAD = ∠BKA
(внутрішні різносторонні кути
АD і січній AK)
1. AB = 6 см, AD = 9 см. Якщо AB = 6 см, то ВК = 6 см; ВС = AD (протилежні сторони
паралелограма);
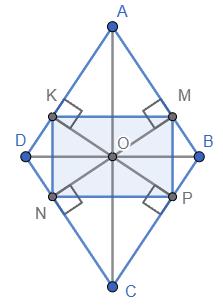
ВС = ВК + КС; 6 + КС = 9; КС = 9 – 6 = З (см).
2. AB = 4 см, тоді ВК = АВ = 4 см.
ВС = ВК + КС = 4 + 11 = 15 (см). AD = ВС (протилежні сторони паралелограма). AD = 15 (см).
155. У паралелограмі АВСD бісектриса кута
паралелограма, якщо АD = 14 см, ВK : K
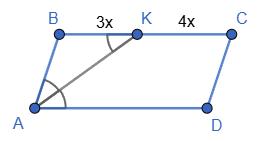
Нехай ВК = 3х; КС = 4х, тоді ВК + КС =
3х + 4х = 14;
7х = 14;
х = 2 (см).
Тоді BK = 3 · 2 = 6 (см); КС = 4 · 2 = 8 (см).
∆АВК — рівнобедрений; AB = BK = 6 (см). P = (AB + ВС) · 2 = (6 + 14) · 2 = 40 (см).
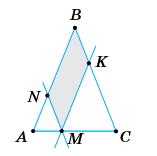
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
Оскільки ∠NМA = ∠BCA, то ∠NМA = ∠BAC.
PМNBK = МN + NB + ВК + КМ = AN + NB +
(AB = ВС, оскільки ∆АВС — рівнобедрений).
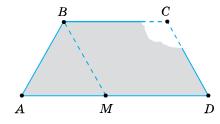
157. Із точки, узятої на основі

— рівнобедрений, тому ∠BCA = ∠BAC.
Оскільки ∠NМA = ∠BCA, то ∠NМA = ∠BAC. Звідси: ∆
PМNBK = МN + NB + ВК + КМ = AN + NB
PМNBK = 2АВ = 2 · 15 = 30 (см).
158. У паралелограмі
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
ОС = ОА (О середина діагоналі); ОЕ = OF (доведено
∠EOC = ∠FOA (вертикальні). З рівності трикутників: в) СЕ = АF.
перетинає сторони ВС і АD в точках
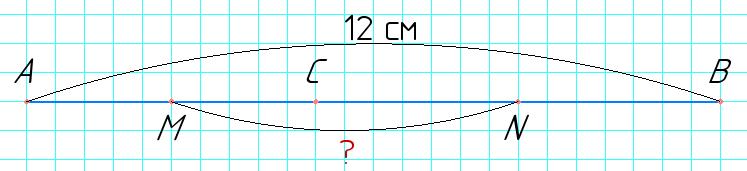
якщо ВЕ = 5 см, АF = 4 см.
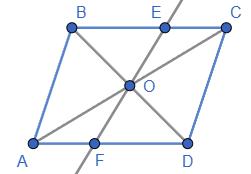
ОС = ОА (О середина діагоналі). BO = OD (О — середина діагоналі BD).
∠CОЕ = ∠AOF (як вертикальні).
∠OCE = ∠OAF (як внутрішні різносторонні при BС ∥ AD і січній AC).
Звідси ∆CОЕ = ∆AOF (II ознака рівності трикутників). Тому OE = OF, AF = EC.
BE = 5 cм; AF = 4 cм, тому EC = 4 см.
BC = BE + EC = 5 + 4 = 9 (см).
AD = ВС (протилежні сторони паралелограма).
Отже, AD = 9 см, ВС = 9 см.
160. Знайдіть кути
як: 1) 4 : 5; 2) 3 : 7.
4х + 5х = 180°; 9х = 180°; х = 20°; ∠1 = 4 · 20° = 80°;
3 —
∠1; ∠3 = 80°; ∠2 = 5 · 20° = 100°;
∠2; ∠4 = 100°.
2)
=
3х + 7x = 180°; 10х = 180°; х = 18°;
∠1 = 3 · 18° = 54°; ∠3 —
∠1; ∠3 = 54°; ∠2 = 7 · 18° = 126°;
+ 8x° = 180°, 9x° = 180°, x = 20°;
B
2 x = 1 3 (180° – x);
3x = 2(180° – x);
3х = 360° – 2x; 5x = 360°, x = 72°
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html

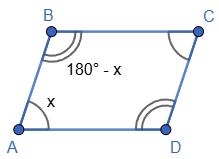
1. Нехай ∠1 = 2x, ∠2 = 3x. ∠1 і ∠2 нерівні, тому вони сусідні.
∠1 + ∠2 = 180°; 2x + 3x = 180°; 5х = 180°;
х = 180° : 5;
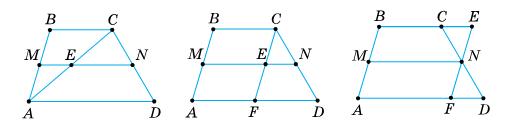
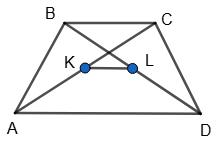
х = 36°;
∠1 = 2 · 36° = 72°;
∠2 = З · 36° = 108°;
∠3 — протилежний ∠1; ∠3 = 72°;
∠4 — протилежний ∠2; ∠4 = 108°.
2. Тупий
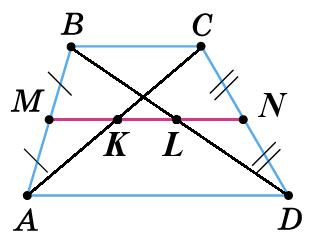
тоді 2x° — тупий кут.
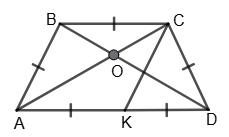
х° + 2x° = 180°, 2x = 180°, x = 60°,
∠А = ∠С = 60°,
∠B = ∠D = 60° · 2 = 120°.
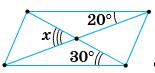
163.
Мал. 1 ∠D = 120°; ∠C = ∠A = 180° – 120° = 60°; ∠B = 120°; ∠CBK = 90° – 60° = 30°; ∠ABN = 90° – 60° = 30°; x = ∠NBK = 120° – (∠ABN + ∠CBK) = 120° – (30° + 30°) = 60°.
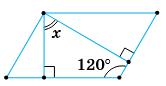
Мал. 2 ∠CBO = ∠ODA= 30° (внутрішні різносторонні
∥ AD і січній BD). З ∆ВОС; ∠BOC = 180° – (30° + 20°) = 130°. x = 180° – 130° = 50° (x і ∠BOC — суміжні).
164. На малюнку
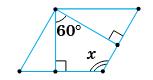
x.
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
NBKD: ∠B = 60°; ∠N = ∠K = 90°;
∠N + ∠B + ∠K + ∠D = 360°.
Тому ∠D = 360° – (∠N + ∠B + ∠K) = 360° – (90° + 60° + 90°) = 120°; x = 120°.
165. Доведіть, що кут
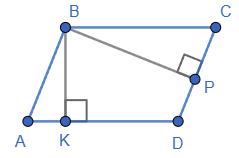
ABCD — паралелограм. BK ⊥ AD; BP ⊥ CD. ∠KBP —
Нехай ∠A = α —
У чотирикутнику BPDK:
∠K = 90°; ∠P = 90°; ∠D = 180° – α;
∠KBP = 360° – (∠K +
= 360° – (360° – α)° = 360° – 360° + α = α.
кут
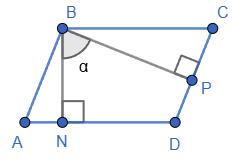
∠B = ∠D; ∠D = 84°; ∠D = ∠ADB + ∠BDC;
∠ADB = ∠D – ∠BDC = 84° – 68° = 16°;
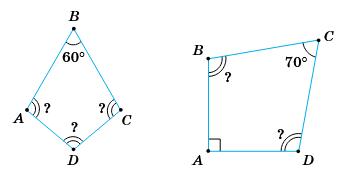
∠BCD = ∠C = 180° – ∠B = 180° – 84° = 96°.
168.
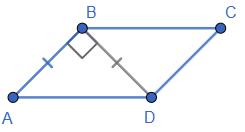
ABCD — паралелограм. BD — діагональ; BD = AB; BD ⊥ AD.
∠B = 180° – 45° = 135°.
∠C = ∠A = 45°; ∠D = ∠B = 135°.
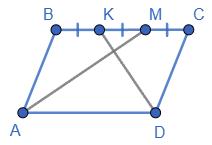
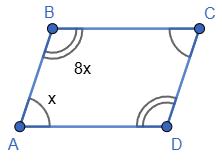
= (2х + 3х) · 2; (2х + 3х) · 2 = 48; 10х = 48; x = 4,8; AB = 2 · 4,8 = 9,6 (см);
=
· 4,8 = 14,4 (см). CD = AB = 9,6 (см); AD = ВС = 14,4 (см).
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
ABCD — паралелограм; ∠A = 60°; BK ⊥ AD; К — середина AD.
У ∆АВК висота ВК є медіаною, тому ∆ABD рівнобедрений; AB = BD; ∠BAD = ∠BDA = 60°, тоді ∠ABD = 180° – (60° + 60°) = 60°.
Отже, ∆АВD — рівносторонній. АВ = AD = BD.
У паралелограмі всі сторони рівні. Р = 4АВ; 4АВ = 24; АВ = 24 : 4 = 6 (см); BD = AB = 6 см.
171. Два кути паралелограма відносяться як 1 : 3. Знайдіть
паралелограма, проведеними з вершини:
1) тупого кута; 2) гострого кута.
Кути відносяться як 1 : 3. Отже, ці кути сусідні,
Нехай ∠A = x, ∠B = 3x.
∠A + ∠B = 180°;
х + 3 х = 180°; 4x = 180°;
х = 45°;
∠A = 45°; ∠B = 45° · 3 = 135°.
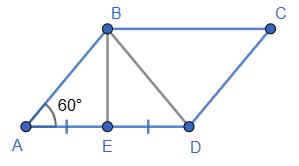
1) ВK ⊥ AD; ВD ⊥ CD; ∠KBD —
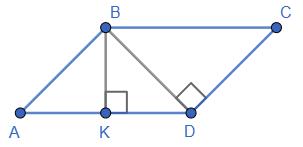
ВКА = 90°, ∠ВАК = 45°, тому ∠ABK = 45°. ∠C = ∠A = 45°.
∆СD
CBD = 45°. ∠KBD = ∠ABC – ∠ABK – ∠CBD = 135 ° – 45° – 45° = 45°.
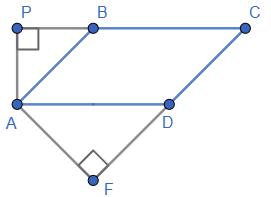
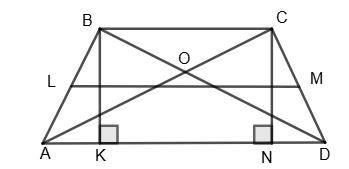
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
∠PAF — кут
∠PBA = 180° – ∠ABC = 180° – 135° = 45° (як суміжні), тоді:
∠PAB = 90° – 45° = 45° (з прямокутного ∆АРВ).
Аналогічно ∠FAD = 45° (з прямокутного ∆AFD).
∠PAF = ∠PAB + ∠BAD + ∠DAF = 45° + 45° + 45° = 135°.
172. Один із кутів паралелограма
дорівнює 5 см.
ABCD — паралелограм; PABCD = 50 см.
∆ВОС; ∆COD; ∆AOD.
= ∆COD; ∆ВОС = ∆DOA (I ознака).
Р∆BOC – P∆AOB = 5 см.
P∆BOD = ВО + ОС + BC; P∆AOB = ВO + AO + AB.
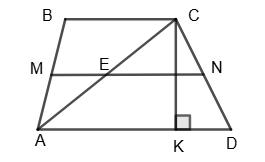
BO + OC + BC – BO – AO – AB = 5 cм.
=
ВС – АВ = 5.
+
Нехай AB = х см, тоді ВС = х + 5 (см).
РABCD = (AB + ВС) · 2, тобто (х + х + 5) · 2 = 50; 4x + 10 = 50;
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
4x = 40; x = 10;
АВ = CD = 10 (cм);
BC = AD = 10 + 5 = 15 (см).
174. За якої умови
лежить
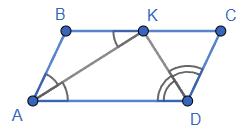
ABCD — паралелограм. AK — бісектриса ∠A. DK — бісектриса ∠D.
К ∈ ВС. ∠BAK = ∠KAD, a ∠KAD = ∠BKA (внутрішні
AK).
Тому ∠BAK = ∠BKA.
∆ABK — рівнобедрений, AB = BK.
Аналогічно ∆KCD — рівнобедрений, тому КС = CD.
Оскільки AB = CD, то BK = КС.
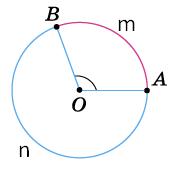
Оскільки BK = АВ, то ВС = 2ВК = 2АВ.
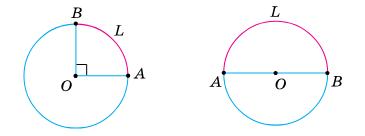
Отже, бісектриси кутів
точці, що

6x = 42; x = 42 : 6; x = 7 (см).
AB = CD = 7 cм; BC = AD = 2 · 7 = 14 (cм).
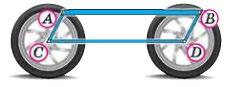
1.

1. Як виготовити?
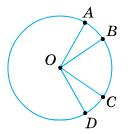
Візьміть
кінці шарнірно (наприклад, заклепками),
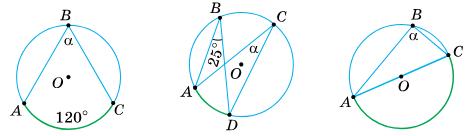
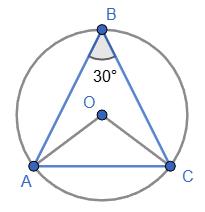
2. Як користуватися?
Покладіть одну
планку на потрібну відстань.
3. На якій властивості ґрунтується?
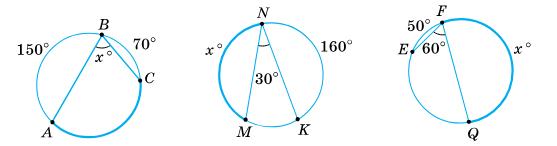
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
ABCD — не паралелограм, бо ВС = AD, але вони не паралельні.
Або: ВС = AD, але AB ≠ CD.
180. Накресліть два рівні
відрізками так,
ВС ∥ АD; BС = АD = 4 см.
правильним.
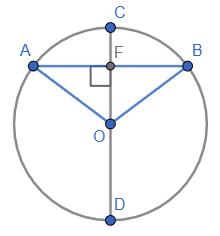
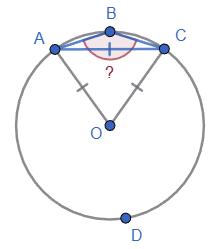
KL 4 см 5,3 дм 1,5 см 0,3 дм
LM 6 см 3 дм 25 мм 5 см
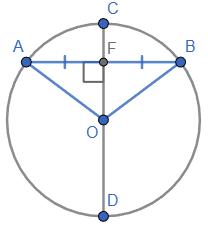
KLMN – паралелограм Доповнимо таблицю
1: МN=4 см,LМ =6 см, NK =6 см;
2: KL =5,3 дм, NK =3 дм;
стовпець 3: МN= 15 мм, NK = 25 мм;
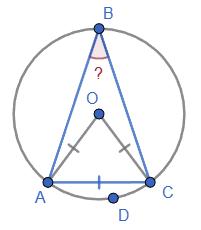
стовпець 4: KL =3 см,LМ =5 см.
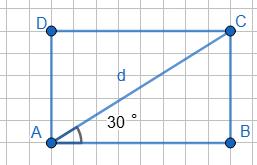
1) АВ = 3 см, АD = 2 см; 2) ВС = 2,5 см, СD = 3,7 см. Які довжини
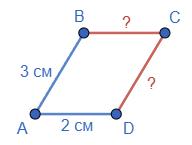
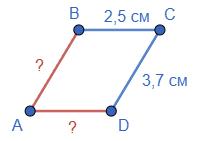
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
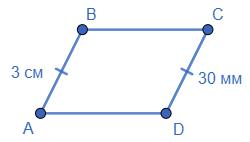
0,4дм =4см, 30мм =3см, 40мм =4см ⇒ �������� = �������� =3см, �������� = �������� =4см ⇒
паралелограм.
2) АВ + ВС = 7 см, ВС – СD = 3 см, АD = ВС = 5 см; BC = AD =5 см, CD = BC 3=2 см, AB =7 BC =2 см ⇒ AB = CD =2 см, BC = AD =5 см ⇒ ABCD – паралелограм.
3) АВ : ВС : СD : АD = 2 : 1 : 2 : 1.
AB ∶ CD =2 ∶ 2 ⇒ AB = CD, BC ∶ AD =1 ∶ 1 ⇒ BC = AD ⇒ ABCD – паралелограм.
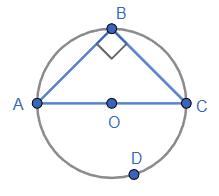
Відповідь: у всіх випадках ABCD – паралелограм.
187. Доведіть, що чотирикутник АВСD — паралелограм, якщо:
1) АВ = 0,5 дм, ВС = 2,7 см, СD = 5 см, АD = 27 мм; 0,5 дм =5 см та �������� =5 см, �������� =2,7 см та �������� = 27 мм =2,7 см ⇒ �������� = �������� , �������� = �������� ⇒ ���������������� – паралелограм.
2) АВ – АD = 3 см, СD = 2ВС, АВ = СD = 6 см. �������� = �������� =6 см i �������� =2�������� ⇒ �������� =3 см; �������� �������� =3 см
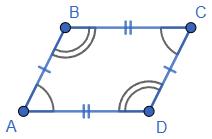

https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
1) AB ∥ CD, АВ = 3 см, СD = 30 мм;
АВ і CD — протилежні сторони чотирикутника ABCD. AB ∥ CD; АВ = 3 см; CD = 30 мм. Оскільки 3 см = 30 мм, то АВ = CD. Тоді ABCD — паралелограм, бо протилежні сторони АВ і CD паралельні і рівні.
2) AD = BC, ∠АВС = 120°, ∠ВАD = 60°.
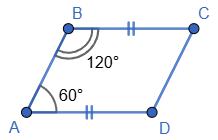
∠АВС і ∠DAB
∠ABC + ∠DAB = 120° + 60° = 180°, то AD ∥
умовою АD = ВС,
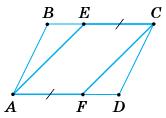
Оскільки ABCD — паралелограм, тому AB = CD.
∠B = ∠D; ∠BEA = 180° – ∠AEC; ∠DFC = 180° – ∠AFC.
Оскільки ∠AEC = ∠AFC (за умовою), то ∠BEA = ∠DFC.
∠BAE = 180° – ∠B – ∠BEA; ∠DCF = 180° – ∠D – ∠DFC.
Оскільки ∠BEA = ∠DFC, ∠B = ∠D, тo ∠BAE = ∠DCF.
∆ABE = ∆CDF (за II ознакою рівності трикутників).
3 рівності трикутників: AE = CF, BE = DF, EC = BC – BE. AF = AD – FD.
Оскільки BC = AD (протилежні сторони паралелограма), BE = FD, то EC = AF.
У чотирикутнику AECF протилежні сторони рівні (АЕ = CF, EC = AF), тому AECF — паралелограм.
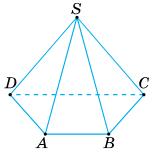
200. У піраміді SАВСD АВ = 4 см, ВС = 0,7 дм, DС = 40 мм, АD = 70 мм. Доведіть,
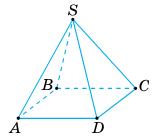
AB =4 см, CD = 40 мм =4 см;
ABCD – паралелограм. Відповідь: основа SABCD – паралелограм. 201. Доведіть, що

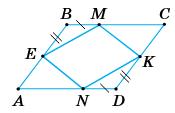
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
Звідси ∆МCK = ∠NAE. 3 рівності трикутників
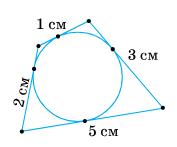
= NE.
У чотирикутнику EМKN: EМ = KN, МK = NE, тобто
Тому EМKN — паралелограм.
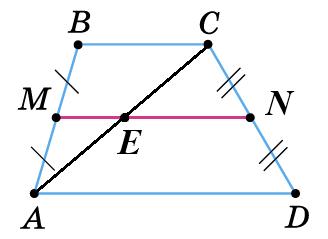
203. На сторонах паралелограма АВСD відкладено рівні відрізки AМ, DN, CP, BK, як показано на малюнку. Доведіть, що МNPK — паралелограм.
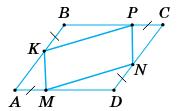
ABCD — паралелограм, тому ∠A = ∠C.
AB = CD (протилежні сторони).
BK = DN — за умовою, тому AB – BK = CD – DN або AK = CN.
∆AKМ = ∆CNP (за I ознакою рівності трикутників).
AK = CN, AМ = CO (за умовою). ∠A = ∠C.
3 рівності трикутників: KМ = PN. Аналогічно: ∆KBP = ∆NDМ. Звідси KP = МN.
У чотирикутника МNPK протилежні сторони рівні.
204. У паралелограмі
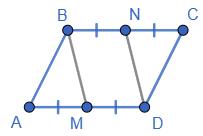
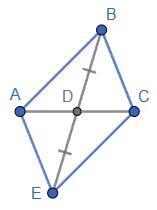
ABCD — паралелограм, тому BD = OD. ОМ = ON (за умовою).
Звідси: МBND — паралелограм, бо
207. МВND — паралелограм, ОА = ОС. Доведіть, що

МBND — паралелограм, тому ВО = OD.
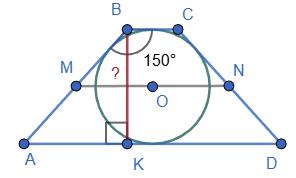
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
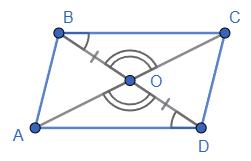
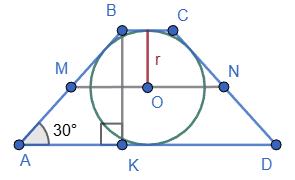
ABCD: ВС ∥ AD. Діагональ AC
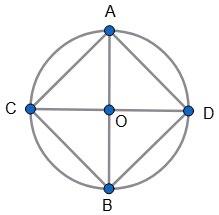
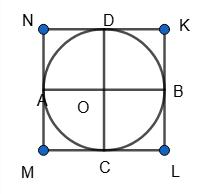
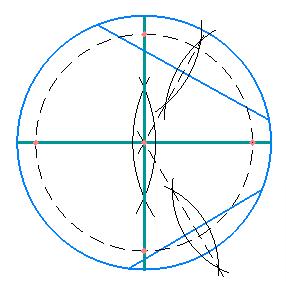
паралельних ВС, AD і січній BD. BO = OD; ∠BOC = ∠DOA (вертикальні).
Звідси ∆ВОС = ∆DOA (II ознака).
З рівності трикутників: АО = CO.
У чотирикутника ABCD діагоналі перетинаються
Отже, ABCD — паралелограм.
211. АВСD — паралелограм, АМ = KС, BN = Р
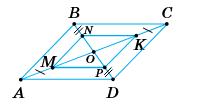
ABCD — паралелограм, тому ОА = ОС; OB = OD.
За умовою AM = КС; BN = DP.
DP, aбо ON = OP. У чотирикутнику MNKP
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
MNKP
Отже, MNKP — паралелограм.
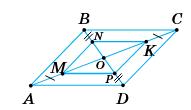
213. У чотирикутнику ABCD відомо, що AB = CD, ∠А + ∠D = 180°. Доведіть, що AD = BC.
Оскільки ∠DAB + ∠ADC = 180∘ , то прямі AB‖DC при січній AD ( як
односторонні кути).
AB = CD ⇒
Відповідь: AD = BC 214. У чотирикутнику
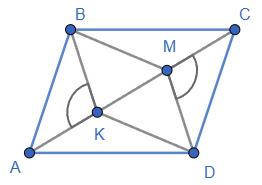
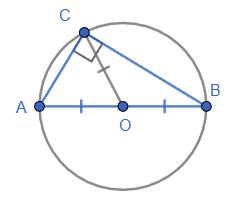
ВС ∥ AD;
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
ABCD — паралелограм. AB = CD; ВС = AD.
За умовою AK = СМ, звідси KB = МD. ВР= DE, звідси CP= EA. ∠A = ∠C, звідси ∠KAE = ∠МCP.
∠B = ∠D, звідси ∠KBP = ∠МDE. ∆KBP = ∆МDE (ДМ = KP; DE = BP; ∠EДМ = ∠KBP).
3 рівності трикутників KP = EМ. Аналогічно
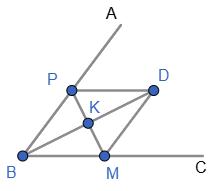
= ∆МСР, тому КЕ = PМ. У чотирикутнику КРМЕ протилежні сторони рівні, тому КРМЕ — паралелограм. 216. На діагоналі АС паралелограма АВСD позначено точки K і М так, що ∠АKВ = ∠СМD. Доведіть, що KВDМ — паралелограм.
AB ∥ CD; АС — січна, тому ∠BAK = ∠DCM, за умовою ∠BKA = ∠CMD.
У ∆АВК: ∠ABK = 180° – ∠BAK – ∠BKA. У ∆CDM: ∠CDM – 180° – ∠DCM – ∠CMD.
Оскільки ∠BAK = ∠DCM і ∠BKA = ∠CMD, то ∠ABK = ∠CDM. ∆BAK = ∆DCM, бо AB = CD; ∠BAK = ∠DCM і ∠ABK = ∠CDM.
3 рівності трикутників: BK = MD. ∠BKM = 180° – ∠BKA; ∠DMK = 180° – ∠DMC
(суміжні кути).
Оскільки ∠BKA = ∠DMC (за умовою), то ∠BKM = ∠DMK, але ∠BKM і ∠DMK —
внутрішні різносторонні
чотирикутнику KBMD ВК = MD і ВК ∥ MD, тому KBMD паралелограм.
Через точку K внутрішньої
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
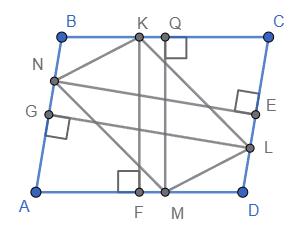
Нехай ABCD — паралелограм. Q, E, F, G — середини відповідно BC, CD, DA, AB.
Проведено перпендикуляри: NE ⟂ CD, KF ⟂ AD, LG ⟂ AB, MQ ⟂ BC. Точки перетину з
протилежними сторонами (або їх продовженнями) — N, K, L, M.
1. Оскільки AB ∥ CD, маємо NE ∥ LG і NE ⟂ AB, LG ⟂ AB. Разом з AB ∥ CD це дає, що
чотирикутник ENGL — прямокутник (сторони NE і LG паралельні, а кожна з них
перпендикулярна AB і CD). Тому EL = GN та EN = GL — протилежні сторони прямокутника рівні.
2. Аналогічно, бо BC ∥ AD і KF ⟂ AD, MQ ⟂ BC, маємо FK ∥ MQ, а FQMK —
прямокутник. Отже, FM = QK та FQ = MK.
3. Із середностей: GB = AG = 1/2·AB, DE = CE = 1/2·CD. Але AB = CD у паралелограма,
тому GB = DE.
4. З прямокутника ENGL: GN = EL. Тоді
NB = GB − GN = GB − EL = DE − EL = DL.
Отже, NB = DL.
5. З прямокутника FQMK: QK = FM. Із (3) маємо BQ = DF. Тоді
BK = BQ − QK = DF − FM = DM.
Отже, BK = DM.
6. У паралелограмі ∠B = ∠D
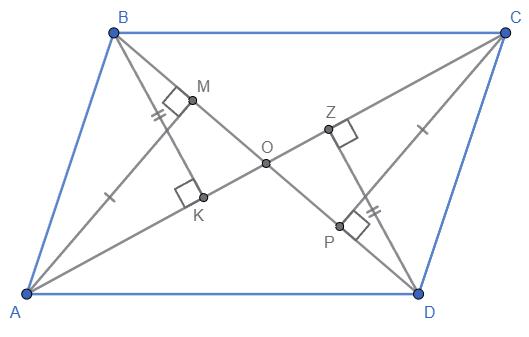
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
ABCD – чотирикутник. BD — діагональ.
AМ ⊥ BD; СР ⊥ BD; АМ = СР; ВК ⊥ AC; DZ ⊥ АС;
однієї прямої).
∥ DZ (як
BD — січна, тому ∠KBO = ∠ZDO (внутрішні різносторонні
DZ і січній BD).
∠BKO = ∠DZO = 90°; BK = DZ (за умовою). Звідси ∆ВКО = ∆DZO. З рівності трикутників: BO = OD.
Аналогічно: ∆АМО = ∆СРО. З рівності цих трикутників
чотирикутнику ABCD діагоналі точкою
Отже, ABCD — паралелограм.
220. Поясніть принцип
222.
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
2) усі кути прямі?
Так – усі кути прямі ⇒ паралелограм із прямими кутами ⇒ прямокутник.
223. Чи
поясніть.
Прямокутник – частковий випадок
навпіл.
224.
прямокутником.
1) нерівні; 2) рівні?
Діагоналі
– правильно.
Відповідь: 1) Ні; 2) Так.
226. Чи
1) нерівні;
2) рівні?
Рівні
Відповідь: 1) Ні; 2) Так.
227. ABCD —
1) AD і DC; 2) BD; 3) AO, OC, BO і OD.
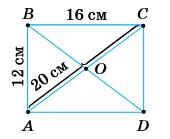
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
ABCD — прямокутник; ВС = 16 см; AB = 12 см.
1. AD = ВС; DC = AB (протилежні сторони прямокутника). AD = 16 см; СD = 12 см.
2. BD = AC = 20 см, діагоналі прямокутника рівні.
3. АО = ОС = 1 2АС = 10 см; ВО = 0D = 1 2 BD = 10 cм; діагоналі прямокутника
перетину діляться навпіл.
228. ABCD — прямокутник. За даними на малюнку знайдіть кути 1, 2 і 3.
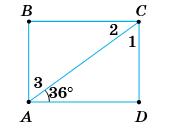
∠2 = ∠4 = 36° (внутрішні різносторонні кути);
ВС ∥ AD, АС — січна; ∠1 = ∠3 = 90° – 36° = 44°.
Відповідь: 44°; 36°; 44°.
229. Знайдіть діагоналі
1) 12 см; 2) 6 см; 3) 18 мм.
У прямокутника діагоналі рівні.
1. d1 = d2 = 12 2 = 6 (см);
2. d1 = d2 = 6 2 = 3 (см);
3. d1 = d2 = 18 2 = 9 (см).
230. ABCD — прямокутник. За
1) його діагоналі; 2) суму його діагоналей.
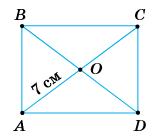
1. АО = ОМ = 7 см; АС = BD = 14 см; 2. AC + BD = 14 cм.
231. О — точка
ABCD. Доведіть:
1) трикутники AOD, BOC, AOB і DOC — рівнобедрені; 2) ∆AOB = ∆DOC, ∆BOC = ∆AOD. Нехай ABCD — прямокутник; О — точка
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
1. ∆AOD; ∆ВОС; ∆АОВ; ∆DOC — рівнобедрені; АО = OB; ОВ = ОС; ОС = OD; АО = OD, сторони цих трикутників є половинами діагоналей, а діагоналі у прямокутника рівні.
2. ∆АОВ = ∆DOC; ∆BOC = ∆AOD (за трьома сторонами); AB = CD; ВС = AD (протилежні сторони прямокутника); ВО = OD; АО = ОС (діагоналі прямокутника в точці
перетину діляться навпіл).
232. На малюнках зображено
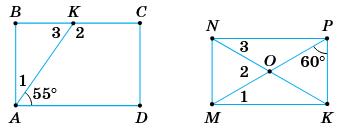
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
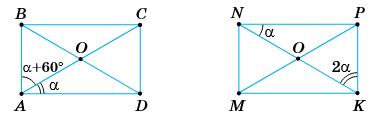
1. α + α + 60° = 90°; 2α = 30°; α = 15°;
∆AOD: ∠AOD = 180° – (α + α) = 180° – 30° = 150°;
∠AOB = 180° – 150° = 30°.
Відповідь: 30°.
2. ∆NPK: α + 2 α = 90°; 3 α = 90°; α = 30°;
∆NOP: NO = OP; ∆РОК: OP = OK; ∠P = ∠K = 60°; ∠POK = 60°.
Відповідь: 60°.
235. Знайдіть
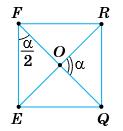
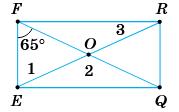
У ∆EFQ ∠F + ∠Q = 90°; α 2 + α 2 = 90°;
α = 90°; α 2 = 45°; α = 90°.
Відповідь: 90°.
236. а і b
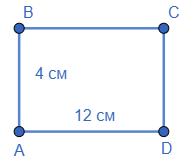
= (AB + AD) · 2 = (4 + 12) · 2 = 32 (см);
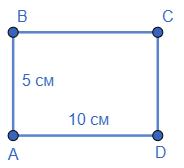
PABCD = (10 + 5) · 2 = 30 (см). Відповідь: 30 см. 238.
AB = 12 см; AD = 12 + 4 = 16 см; PABCD = (12 + 16) · 2 = 56 (см). 239.
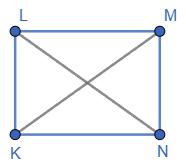
1) АС = 2 см; 2) ВD = 7 см.

діагоналей.
Отже,
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
Висновок: KLMN — прямокутник.
242. Діагоналі паралелограма АВСD утворюють рівні трикутники
що АВСD — прямокутник.
Із рівності трикутників CAB і DBA випливає
внутрішні
CBA + ∠DAB = 180°.
Оскільки ці кути рівні,
=
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
Дано: ABCD — паралелограм.
∠A = 90°; ∠D + ∠A = 180°; AB ∥ DC, тоді ∠D = 90°.
CDA = ∆BDA (за II ознакою).
AD — спільна. DC = АВ; ∠D = ∠A.
З рівності трикутників маємо: BD = АС, що й треба було довести.
245. Висота прямокутного паралелепіпеда дорівнює 8 см, ширина — у 2 рази
висоту, а довжина — на 16 см більша за ширину.
Знайдіть ширину й довжину прямокутного паралелепіпеда. Оскільки
а довжина — у 4 рази
= 18 3 =6 см
=6×4= 24 см
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
3. d = 0,44 дм; ВС = 1 2 · 0,44 = 0,22 дм.
Відповідь: 2 см; 7 см; 0,22 дм.
248. Менша сторона
перетинаються під кутом 60° і: 1) а = 10 см; 2) а = 0,25 дм; 3) а = 7 мм.
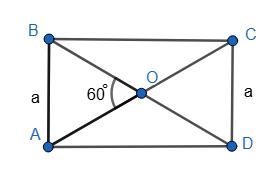
1. а = 10 см; ∆АОВ — рівносторонній. OB = OA = AB = a; d = AC = 2a; BD = 20 cм;
2. а = 0,25 дм; d = АС = 2 · 0,25 = 0,5 дм;
3. а = 7 мм; d = АС = 2 · 7 = 14 (мм).
Відповідь: 20 мм; 0,5 дм; 14 мм.
249. Доведіть, що
ними дорівнює 60°. ABCD — прямокутник.
—
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
∠DAK = 90° – 36° = 54°; ∆DKC —
∠КCD = 90° – 54° = 36°.
2. ∠ACD = ∠BDC = 36°; ∠BDK = 54° – 36° – 18°. 251. Периметр
1. AD : DC = 2 : 3; AD = ВС = 2х; AB = CD = 3х; x — спільна міра відрізків.
(2х + 3х) · 2 = 48; 10х = 48; x = 4,8; AD = ВС = 9,6 см; АВ = CD = 14,4 см.
Відповідь: 9,6 см; 14,4 см.
2. МN = 10 см; МN = АВ = CD = 10 см;
AB = CD = P–2AB 2 = 48–20 2 = 14 (см);
Відповідь: 10 см; 14 см.
3. ОК = 4 см; ВС = AD = 2ОК = 2 · 4 = 8 (см). DC = АВ = (48 – 16) : 2 = 16 (см).

Відповідь: 8 см і 16 см.
252.
1) 12 см; 2) 8,6 см.
KN + PF = 1 2PABCD = 1 2 · 12 = 6 (см).
2) KN + PF = 1 2PABCD = 1 2 · 8,6 = 4,3 (см). Відповідь: 6 см; 4,3 см.
1) 3 см і 5 см; 2) 0,2 дм і 3 см.
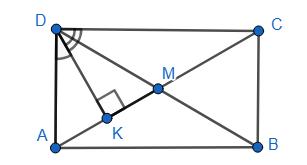
ABCD — прямокутник; AK — бісектриса ∠A.
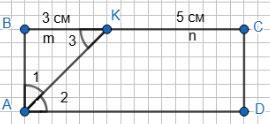
1) m = 3 cм; n = 5 cм; ∠1 = ∠2; AK — бісектриса.
∠2 = ∠3, ВС ∥ AD, A
AB = ВК = m = 3 cм; AB = CD = 3 cм; BC = AD = m + n = 8 (см).
PABCD = (3 + 8) ∙ 2 = 22 (cм).
РABCD = 5 + 5 + 8 + 8 = 26 (cм).
2) m = 0,2 дм; n = 3 см; PABCD = 14 см; PABCD = 16 см.
Відповідь: 1) 26 см або 22 см; 2) 14 або 16 см. 254. Бісектриса
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
1) 15 см; 2) 3,8 дм.
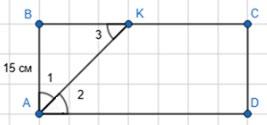
AK — бісектриса кута BAD.
1) AB = 15 cм; ∠1 = ∠2; ∠2 = ∠3 ⇒ ∠1 = ∠3.
∆АВК — рівнобедрений.
AB = BK = 15 см; ВС = 2ВК = 30 см.
РABCD = (15 + 30) · 2 = 90 (cм).
2) PABCD = (3,8 + 7,6) · 2 = 22,8 (дм).
Відповідь: 90 см; 22,8 дм.
255. У паралелограмі

цей
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html

∠A = ∠B = ∠C = ∠D.
∠A = ∠C, ∠B = ∠D ⇒ тому цей чотирикутник паралелограм.
∠A + ∠B = 180°; 2∠A = 180°; ∠A = 90°, отже ∠A = ∠B = ∠C = ∠D = 90°, тому ABCD — прямокутник, що й треба було довести.
258. Доведіть, що

ABCD — паралелограм. ∠A = ∠D;
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
цей паралелепіпед — прямокутний.
Паралелепіпед має 6 граней. Кожна грань —
паралелепіпеда). Але за умовою, усі грані мають прямі кути.
паралелограм з прямими кутами — це прямокутник. Отже, усі грані паралелепіпеда — прямокутники.
(за
З цього випливає: - Протилежні грані — прямокутники, розташовані паралельно. - Сусідні грані — прямокутники, які
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
Мал. 1 а) Нехай АВ = DC = а; AD = ВС = b; ∆ABN — рівнобедрений; AB = BN = а; NC = b – с; МN = BN – NC = a – b + a = 2a – b;
б) нехай AB = CD = b; BC = AD = a; AB = BN = b; NC = a – b; МN = BN – NC = 2b – a;
Мал. 2 B) AB = CD = b; AD = BC = a; BМ = NC = b; AD = 2b або AD = b – 2a.
264. Через середину
2.
1. ∆АВС — прямокутний, рівнобедрений,
∆МBN: ∠B = ∠N = 45°; BМ = МN;
∆NKC: ∠C = ∠N = 45°; NK = КС; МNKA — прямокутник.
AМ = NK; N = AK.
Периметр прямокутника не
2. KC = NK; AC = AK + KC = 5 cм; P = 2AK + 2NK = 10 (см).
Відповідь: 10 см.
267. Доведіть, що
прямокутником. Доведіть.
Нехай AD = ВС, DС = AB. АС = BD;
∠ACD = ∠CAB (внутрішні різносторонні
DC ∥ AB; DC = AB; ABCD — паралелограм, у
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
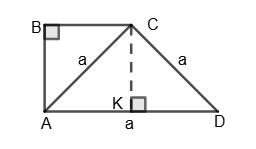
∆ABC — прямокутний; ∠BCA = 90°; CO — медіана.
Доведемо, що СО = 1 2 АВ.
Проведемо BD ∥ АС; AD ∥ ВС; ABCD — паралелограм.
∠С + ∠A = 180°; ∠A = ∠C = 90°.
ABCD — прямокутник, діагоналі
ОВ = OА = OD = ОС; ОС = 1 2АВ,
1–й спосіб.
Якщо у чотирикутнику протилежні сторони
прямокутником.
3–
то він є прямокутником.
275. На малюнку
1. Поясніть, як
2. Чому відлік
3.
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html

використати метод побудови прямокутника
дій:
точок
наприклад,
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
279. Назвіть
1) рівні;
2) взаємно перпендикулярні;
3) ділять кути ромба навпіл?
1. Ні; 2. Так; 3. Так.
281. Чи правильно, що паралелограм є ромбом, якщо його діагоналі:
1) перетинаються під гострим кутом;
2) взаємно перпендикулярні?
1. Ні; 2. Так.
282. Чи правильно, що квадратом є
1) дві сусідні сторони нерівні; 2) усі сторони рівні?
1. Ні; 2. Так.
283. Чи має квадрат
1.
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
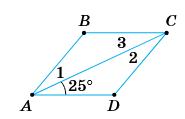
ромба всі сторони рівні.
ВС = AD = 6 см: ∠COD = 90°; СО ⊥ OD.
288. ABCD — ромб. За
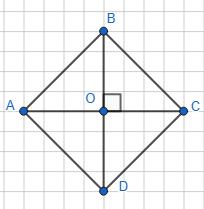
1) BC, AD, DC; 2) AC, BD.
1. ВC = AВ = 10 см; AD = 10 cм: DC = 10 cм; у
2. АС = 2АО = 16 см; BD = 2ВО = 12 см.
∠1 =
2 = ∠3 = 25°.
2,4 дм;
2) 280 мм.
Р = 4а;
1) а = 2,4 : 4 = 0,6 (дм); 2) а = 280 : 4 = 70 (мм).
∆АОВ = ∆ВОС = ∆DOC = ∆AOD (за двома катетами). Діагоналі ромба
293.
∆АВС = ∆АОС (за трьома рівними
AB = ВС = AD = DC; AC — спільна.
294. ABCD
∠1 = ∠3 = ∠4 = 25°; ∠2 = 65°; ∠5 =
Нехай ABCD — ромб, AB = ВС – AD = BD.
∆ABD — рівносторонній.
Отже, ∠A = ∠ABD = ∠ADB = 60°; ∠A = ∠C = 60°; ∠B = ∠D = 120°.
Відповідь: 60°; 60°; 120°; 120°.
298. Знайдіть
1) 30°; 2) 15°; 3) 65°.
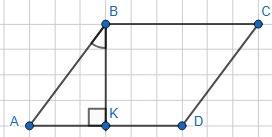
Нехай ABCD — ромб. BK ⊥ AD; BK — висота ромба.
1. ∠ABК = 30°; ∆ABK; ∠A = 60°; ∠С = ∠A = 60°; ∠B = ∠D = 120°;
2. ∠ABK = 15°; ∠A = 75°; ∠C = 75°; ∠B = ∠D = 105°;
3. ∠ABK = 65°; ∠A = ∠C = 25°; ∠В = ∠D = 155°.
Відповідь: 1) 60°; 60°; 120°; 120°; 2) 75°; 105°; 75°; 105°; 3) 25°; 155°; 25°; 155°.
299. За даними
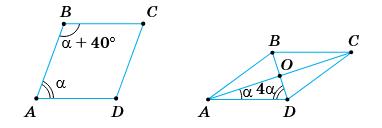
1. α + α + 40° = 180°; 2α = 140°; α = 70°.
∠A = ∠C = 70°; ∠B = ∠D = 110°.
2. α + 4α = 90°; 5 α = 90°; α = 18°;
∠A = ∠C = 36°; ∠B = ∠D = 144°.
300. За
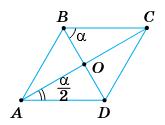
2α + α = 180°; 3α = 180°; α = 60°; ∠B = ∠D = 120°; ∠A = ∠C = 60°.
301.
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
якщо:
1) d = 3,2 дм; 2) d = 45 мм.
Нехай ABCD — ромб. ∠A = 60°; BD = d.
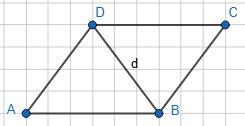
1. d = 3,2 дм; P = 4 · 3,2 = 12,8 (дм);
2. d = 45 мм; P = 4 · 45 = 180 (мм).
Відповідь: 12,8 дм; 180 мм.
302. Кут ромба
60°,

Нехай ABCD — ромб. ∠A = 60°; BD = d. d = 10 cм; ∆ABD — рівносторонній;
∠A = ∠D = ∠В = 60°; AB = BD = AD = 10 cм;
PABCD = 40 cм.
Відповідь: 40 см.
303. У чотирикутнику
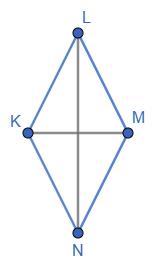
Нехай АВСD — квадрат. ОK ⊥ АВ; ОК = n.
1. n = 8 см; AD = 2n = 16 см; Ркв = 64 см; 2. n = 0,3 дм; а = 2n = 0,6 дм; Ркв = 4а = 2,4 дм.
Відповідь: 1) 64 см; 2) 2,4 дм.
307. Знайдіть периметр квадрата, якщо точка
сторони на 21 мм.

Нехай АВСD — квадрат. ОK ⊥ АВ; ОК = n.
а = 21 мм; а = 2n = 42 мм; Ркв = 4а = 42 · 4 = 168 мм.
Відповідь: 168 мм.
308. Дано паралелограм KLМN.
=
1
Відповідь: 96 см2 313.
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
Відповідь: 726 см2 . 314. Доведіть, що чотирикутник,
Нехай ABCD — чотирикутник, AB = BC = CD = AD.
Проведемо діагональ BD.
∆ABD = ∆CBD (за трьома сторонами (BD — спільна сторона)).
Тому ∠1 = ∠2. Отже, DC ∥ АВ.
ABCD — паралелограм, у якого всі сторони рівні;
ABCD — ромб, що й треба було довести.
315. Паралелограм, діагоналі якого
Нехай ABCD — паралелограм, діагоналі
∆ABD = ∆CBD — рівнобедрені:
∠4 = ∠5; ∠3 = ∠5; DC = ВС; AD = AB.
У паралелограма
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
Нехай ABCD — ромб.
PABCD = 36 см; DK ⊥ AB; DK — висота ромба; а — сторона ромба.
Р = 4а; а = 36 : 4 = 9 (см).
∆ADK : AD = 9 cм; DK = 4,5 (cм).
DK = 1 2 AD. Отже, ∠A = 30° (катет, що лежить навпроти кута 30°).
∠A = ∠C = 30°; ∠D = ∠B = 150°.
Відповідь: 30°; 30°; 150°; 150°.
317. Доведіть, що висоти ромба рівні.
Нехай ABCD — ромб. ВМ і ВР — висоти; ВМ ⊥ AD; BP ⊥ CD.
∆АВМ = ∆СВР.
∠М = ∠P = 90°; AB = ВС; ∠A = ∠C.
3 рівності трикутників
1) кути ромба; 2) периметр ромба, якщо
= ВК.
1) ∆ADB— рівнобедрений; АК = КВ; DK ⊥ AB; ∠A = 60°; ∠ADC= 120°; ∠C = ∠A = 60°; ∠D = ∠B = 120°.
2) BD = 20cм; AD = BD; PABCD = 4AD = 4 · 20 = 80 (cм).
Відповідь: 1) 60°; 60°; 120°; 120°; 2) 80 см.
319. Знайдіть
вершини, дорівнює: 1) 35°; 2) 20°.
Нехай АВСD — ромб.
∠BDK — кут між висотою і
1. ∠BDK = 35°: ∆DBK = 55°; ∠ABC = 110°; ∠ADC = ∠ABC = 110°; ∠A = ∠C = 70°;
2. ∠BDK = 20°; ∠DBK = 70°; ∠ABC = 140°; ∠B = ∠D = 140°; ∠A = ∠C = 40°.
Відповідь: 1) 70°; 110°; 70°; 110°; 2) 40°; 140°; 40°; 140°.
320. Знайдіть
40°.

Нехай АВСD — ромб. ∠
∠BDK = 40°; ∠DBA = 50°; ∠B = ∠D = 100°; ∠A = ∠C = 80°.
1 = 2х; ∠2 = 3х; 2х + 3x = 90°; 5х = 90°; х = 18°. ∠A = 4х = 72°; ∠A = ∠C; ∠B = ∠D = 6х = 108°; 2. ∠1 : ∠2 = 2 : 7; 2х + 7х = 90°; х = 10°, ∠A = ∠C = 40°; ∠B = ∠D = 140°. Відповідь: 1) 72°; 108°; 72°; 108°; 2) 40; 140°; 40°; 140°.
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
як 1 : 2.

Нехай ABCD — ромб. ∠1 : ∠2 = 1 : 2;
х + 2х = 90°; 3х = 90°; х = 30°;
∠A = ∠C = 60°; ∠B = ∠D = 120°.
Відповідь: 60°; 120°; 60°; 120°.
323. У рівносторонній трикутник
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
РAМNK = АВ + АС = 8 + 8 = 16 см.
2. PAМNK = 29 + 29 = 58 мм;
3. PAМNK = 0,41 + 0,41 = 0,82 дм.
325. Ромб, у якого один кут прямий, — квадрат. Доведіть.
Hexaй AВCD — ромб, у якого ∠A = 90°, тоді ∠C = ∠A = 90°.
∠D = ∠B = 180° – 90° = 90°.
ромба всі кути прямі, тому ABCD — квадрат, що й треба було довести.
326. AN — бісектриса прямого кута A трикутника ABC; NМ і NK — перпендикуляри
катетів. Доведіть, що AМNK — квадрат.

Нехай
- AO = BO — бо
- ∠AOB = 90° — бо
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
- AO = AC 2 , BO = BD 2 ), а оскільки AC = BD, то AO = BO. Трикутник ∆AOB
фігури однакові.
Висновок: якщо діагоналі ромба
=
що AМCN — ромб.
Нехай ABCD — квадрат, діагональ – BD. BМ = DN. ∆AND = ∆CND = ∆АМВ = ∆СМВ.
1. BМ = ND; AB = BC = CD = AD;
2. ∠1 = ∠2 = ∠3 = ∠4 = 45°.
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
Нехай ABCD — ромб.
AМ ⊥ ВС; АР ⊥ DC; ∠МAP = 30°;
∠МAP = ∠ABC = 30°; ∠ABC = ∠ADC = 30°.
∠A + ∠B = 180°; ∠BAD = ∠BCD = 180° – 30° = 150°.
Відповідь: 30°; 30°; 150°; 150°.
332. Вершини
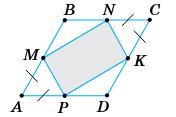
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
його сторін.
ON ⊥ DC; OP ⊥ ВС; ОМ ⊥ AB; OK ⊥ AD.
Точки К, О,
KP ⊥ ВС; МN ⊥ DC; KP ⊥ МN — висоти ромба ABCD. KP = NМ; KP і NМ — діагоналі чотирикутника KNPМ, отже, чотирикутник KNМP є
прямокутником. 335. Доведіть, що чотирикутник, вершини якого є серединами
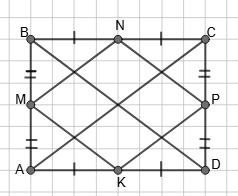
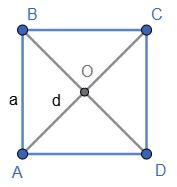
Нехай ABCD — квадрат.
P∆AOD = P∆DOC = P∆COD = P∆AOB
4P∆AOD – Pкв.ABCD = 20 см
P∆AOD = a + d, де а – сторона; d – діагональ.
4P∆AOD = 4a + 4d;
Pкв = 4а; 4a + 4d – 4a = 20 см; 4d = 20; d = 5 см
Відповідь: 5 см.
337. Чотирикутник,
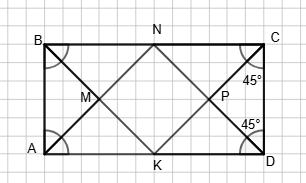
2.
1.
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html


https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
2.
3. Так. Якщо у чотирикутника
чотирикутник є квадратом.
343. Земельна
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
1. Ні; 2. Так; 3. Ні; 4. Ні; 5. Так.
1. Ні; 2. Так.
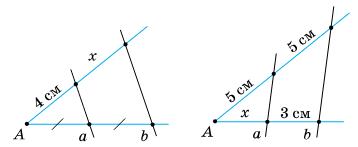
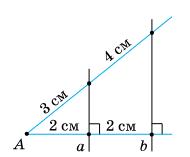

https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
2) 6.
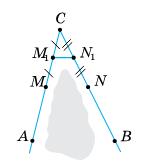
Нехай задано відрізок AB.
А6
правильно, оскільки 5 : 2 = 2,5 ≠ 2. 357. DE i EF
АВ. Знайдіть:
1) відрізок FC, якщо DE = 4 см; 2) відрізок BD, якщо EF = 7 см.
1) FC = 1 2 BC = DE = 4 см;
2) BD = 1 2 AB = EF = 7 см. 358.
1) 8 см, 5 см, 7 см; 2) 30 мм, 40 мм, 50 мм.
1)
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
трикутник ABC, у якого AB = 5 см, BC = 7 см, AC = 8 см.
FE = 1 2AB = 2,5 см; ED = 1 2BC = 3,5 см; DF = 1 2 AC = 4 см.
2) Нехай задано трикутник ABC, у якого AB = 30 мм, BC = 40 мм, AC = 50 мм.
Згідно
FE = 1
2 AB = 15 мм; ED = 1 2 BC = 20 мм; DF = 1 2 AC = 25 мм.
359. Сторони трикутника
т рикутника.

Нехай задано трикутник ABC, у якого AB = 9 см, BC = 10 см, AC =

https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
2) DE = EF = DF = P∆DEF : 3 = 48 : 3 = 16 мм.

1) 0,8 дм; 2) 100 мм.

1) P∆DEF = DE + EF + DF = 0,8 + 0,8 + 0,8 = 2,4 (дм).
P∆ABC = P∆DEF ∙ 2 = 2,4 ∙ 2 = 4,8 (дм).
2) P∆DEF = DE + EF + DF = 100 + 100 + 100 = 300 (мм).
P∆ABC = P∆DEF ∙ 2 = 300 ∙ 2 = 600 (мм).
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
MN,
1) NP = 3 cм, MP = 5 см MN = 6 см.
AB = 2NP = 2 • 3 = 6 (cм);
ВС = 2МР = 2 • 5 = 10 (см);
АС = 2MN = 2 • 6 = 12 (см);
Р∆ABC = 6 + 10 + 12 = 28 (см);
2) NP = 7 cм, MP = 9 см MN = 12 см.
AB = 2NP = 2 • 7 = 14 (cм);
ВС = 2МР = 2 • 9 = 18 (см);
АС = 2MN = 2 • 12 = 24 (см);
P∆ABC = 14 + 18 + 24 = 56 (см);
3) NP = 8 cм, MP = 10 см MN = 12 см.
AB = 2NP = 2 • 8 = 16 (cм);
ВС = 2МР = 2 • 10 = 20 (см);
АС = 2MN = 2 • 12 = 24 (см);
Р∆ABC = 16 + 20 + 24 = 60 (см).
Відповідь: 1) 28 см; 2) 56 см; 3) 60 см.
366. Визначте вид
2)
1) 0,6 дм і 0,9 дм; 2) 100 мм і 14 см. ABCD —
1) MN = 0,6 дм; MK = 0,9 дм; У ∆ADC: MN — середня
ABD:
2) MN = 100 мм; МК = 14 см; АС = 2MN = 200 мм; BD = 2МК = 28 см.
= 2MN = 1,2
BD = 2МК = 1,8 дм;
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html

Нехай ABCD — заданий паралелограм. N, M і K – середини сторін BC, AB та AD
відповідно. MN = 5 см; МК = 11 см. Знайти: діагоналі BD і AC.
У ∆ADC: MN — середня лінія; АС = 2MN = 10 см; У ∆ABD: МК — середня лінія; BD = 2МК = 22 см.
369. Точки E і F — середини ребер
якщо EF = 4 см.
завдання: знайти 6AC. Оскільки точки E
AC = 2EF = 2 ∙ 4 = 8 см.
6AC = 6 ∙ 8 = 48 см. Відповідь: 48 см.
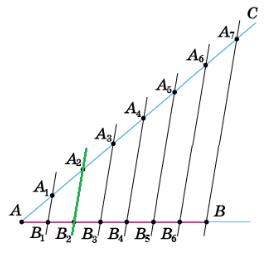
АВ1 = В1B2 = B2B3 = B3B4.
1) Якщо АB4 – B2B3 = 9 cм (довжина 3 відрізків), то AB3 = 9 cм;
2) Якщо AB4 – B1B3 = 8 см (довжина 2
B1B4 = 3 ∙ 4 = 12 см;
3) B1B4 – B1B2 = 10 cм (довжина 2 відрізків),
10 : 2 = 5
AB4 = 5 ∙ 4 = 20 cм.
374. Сторони трикутника дорівнюють а, b і c.
1) а = 8 см, b = 10 см, с = 12 см; 2) а = 0,5 дм, b = 12 см, с = 1,3 дм.

2) AB = а = 0,5 дм; BC = b = 1,2 дм; AC = с = 1,3
теореми

1)
2)
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
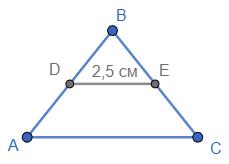
= 2,5 см. P△АВС = 25 см. Знайти AB, BC і AC. Згідно теореми про середню лінію трикутника:
AC = 2DF = 2 ∙ 2,5 = 5 см. У рівнобедреного
P
АВС = AB + BC + AC = 2BC + AC 25 = 2BC + 5 ⇒ 2BC = 20 ⇒ BC = 10 см.
Відповідь: 5 см, 10 см, 10 см. 377.
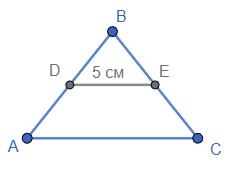
= 5 см. P
= 40 см. Знайти AB, BC і
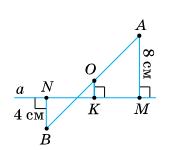
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
Нехай О — середина відрізка AB.
BL ⊥ NM; ML ∥ KP.
ML = NB = КР = 4 см.
∆ABL: OP — середня лінія.
OP ∥ AL. BO = OA, за теоремою Фалеса ВР = PL.
ОР = 1 2 AL = 1 2 (8 + 4) = 6 (cм);
ОК = ОР – КР = 6 – 4 = 2 см.
Відповідь: 2 см.
379. Сторони трикутника відносяться як 3 : 4 : 5.
середніми лініями даного
см; 2) 4,8 дм.
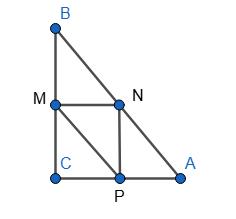
Нехай дано ∆АВС.
АВ : ВС : АС = 3 : 4 : 5. 1) Р∆ABC = 60 см; ∆MNP — трикутник, утворений
АВ = 3х; ВС = 4х; АС = 5х;
Р∆ABC = 12х; P∆MNP = 6x; 12x = 60;
х = 5;
АВ = 15 см; ВС = 20 см; АС = 25 см; МN = 1 2 AС = 12,5 см; NP = 1 2 BC = 10 см;
МР = 1 2АВ = 7,5 см.
Відповідь: 7,5 см; 12,5 см; 10 см.
2) P = 4,8 дм = 48 см; 12x = 48; x = 4 см;
AB = 12 см; ВС = 16 см; АС = 20 см; MN = 1 2 AC = 10 см;
NP = 1 2 BC = 8 см; MP = 1 2 AB = 6 см.
6 см; 8 см; 10 см. 380.
1) 48 см; 2) 2,4 дм.
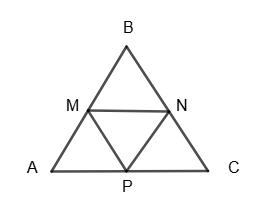
Нехай дано ∆ABC, сторони ∆ABC: AB : ВС : AC = 7 : 8 : 9.
∆MNP — трикутник, утворений середніми лініями.
1) P∆MNP = 48 cм; P∆ABC = 2P∆MNP = 96 см;
AB = 7х; ВС = 8x; АС = 9х; 7х + 8х + 9х = 96; 24х = 96; x = 4;
AB = 28 см; ВС = 32 см; AС = 36 см; 2) Р = 4,8 дм; АВ = 1,4 дм; ВС = 1,6 дм; AС = 1,8 дм. 381. Доведіть,

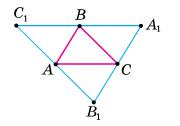
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
1) ВС ∥ B1C1; AB ∥ A1С1; AB ∥ A1В1.
AB; ВС; АС — середні
∆A1B1С1
2) А1В1 = 2АВ = 12 см; B1C1 = 2ВС = 24 см; A1С1 = 2AС = 30 см;
3) Р∆A1B1C1 = 48 см;
P∆ABC = 1 2 P∆A1B1C1 = 1 2 • 48 = 24 (см).
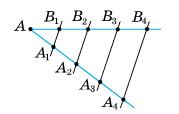
383.
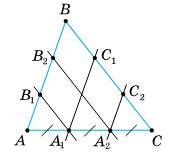
Згідно
якщо AA1 = A1A2 = A2A3,
1) AB1 = B1B2 = B2B = AB : 3 = 12 : 3 = 4 см;
BC1 = C1C2 = C2C = BC : 3 = 18 : 3 = 6 см;
2) B1A = BC = 6 см; B2A2 = BC2 = 12 см; C2A2 = BB2 = 4 см; C1A1 = BB1 = 8 см.
384. Доведіть, що
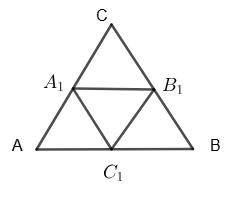
дано: ∆АВС;
A1C1 = A1A = ���� 2 ; B1C = B1B =
2 ; AC1 = C1B = ���� 2; A1B1 = 1 2c; B1C1 = 1 2b; A1C1 = 1 2 a.
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
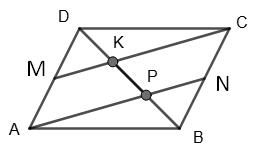
Нехай дано паралелограм ABCD.
Розглянемо кут ∠ADВ: за теоремою Фалеса АМ = MD, отже, DK = KP.
Розглянемо кут ∠CBD: за теоремою Фалеса BN = NC, тоді BP = PK.
Отже, DK = KP = PB, що й треба було довести.
386. Знайдіть периметр чотирикутника, вершинами якого є середини
чотирикутника, якщо сума діагоналей чотирикутника
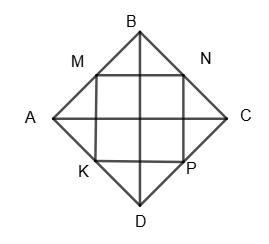
Нехай ABCD — чотирикутник,
N,
РМNРК = MN + NP + KP + KM.
∆ABC; MN — середня лінія, MN = 1 2AC;
∆ADC — середня лінія; KP = 1 2AC;
∆ABD, MK — середня лінія, MK = 1 2BD;
∆BDC; NP — середня лінія, NP = 1 2 BD.
PMNPC = 1 2 BD + 1 2 BD + 1 2 AC + 1 2 AC = BD + AC = S.
1) S = 25 см; PMNPK = 25 см; 2) S = 3,5 дм; PMNPK = 3,5 дм.
Відповідь: 1) 25 см; 2), 3,5 дм. 387. Знайдіть
1) 4 см і 6 см; 2) 24 см і 25 см.

Нехай дано чотирикутник AВСD. АС і BD — діагоналі.
1) АС = 4 см; ВD = 6 см; MNPK — чотирикутник;
М, N, Р, К — середини сторін чотирикутника ABCD.
∆АВС; MN — середня лінія ∆АВС;
MN = 1 2 AC = 2 см;
∆АDС; KP — середня лінія ∆АDС;
КР = 1 2АС = 2 см;
∆BDC: NP = 1 2 BD = 1 2 • 6 = 3 см;
∆ABD: MK = 1 2 BD = 1 2 • 6 = 3 см;
РMNPK = 2 + 3 + 2 + 3 = 10 (см).
2) АС = 24 см; ВD = 25 см;
РMNPK = 12 + 12 + 12,5 + 12,5 = 49 (см).
Відповідь: 1) 10 см; 2) 49 см.
388. Знайдіть
Нехай ABCD — квадрат. AC — діагональ; AC = d. MNKP —
MN = PK = 1 2AC;
NK = MP = 1 2BD; AC = BD = d; PMNPK = 2d.
1) Р = 16см; 2) Р = 2,6 дм.
389. Доведіть, що
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
Нехай ABCD — прямокутник; М, N, Р, К — середини його сторін.
∆ADC: MN ∥ AC; MN = 1 2AC;
∆ABC: KP ∥ AC; KP = 1 2AC (властивість середньої лінії трикуника).
Oтже, MN ∥ KP; MN = KP.
Аналогічно NP ∥ MK; NP = MK.
Якщо BD = AC, то MN = NP = PK = MK.
Отже, MNPK — ромб, що й треба було довести.
390. Доведіть, що середини сторін квадрата є вершинами квадрата.
ABCD — квадрат. М, N, Р, К — середини сторін.
MN ∥ BD; MN = 1 2BD;
PK ∥ BD; PK = 1 2BD;
MN = PK; PM ∥ AC; РМ = 1 2АС;
KN ∥ АС: KN = 1 2AC;
KN = PM; AC = BD.
Отже, PM = MN = NK = PK. PMNK – ромб. ∆PDM = ∆NCM. ∠PMD = ∠NMC = 45°; ∠PMN = 90°, отже, ромб PMNK — квадрат.
391. Доведіть, що середини сторін ромба є вершинами прямокутника.
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
Нехай ABCD — ромб. М, N, Р, К — середини
KP = MN = 1 2АС; PN = KM = 1 2BD;
KP ∥ AC; MN ∥ AC ⇒ KP ∥ MN; PN ∥ BD; KM ∥ BD ⇒ KM ∥ PN; BD ⊥ AC ⇒ PN ⊥ MN; KP ⊥ KM.
Отже, KPNM — прямокутник, що й треба
392. Як побудувати трикутник
Нехай М, N, P — середини сторін шуканого трикутника. Проведемо прямі,
393.
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
OK : OB = 1 : 2; АО : ОМ = 2 : 1; СО : ON = 2 : 1, що
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
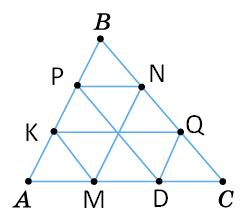
1) P∆ABC = 36 cм; АК = КР = BP; BN = NQ = QC; AM = MD = DC; AP = MN (як протилежні сторони паралелограма APMN) PB = QD (як протилежні сторони
PBQD) MN + QD = AB
Аналогічно PD + KM = BC, PN + KQ = AC
Отже, MN + QD + PD + KM + PN + KQ = AB + BC + AC = P∆ABC = 36 см.
2) аналогічно.
398. Через точку М, розміщену
який відтинають

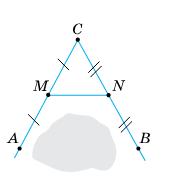
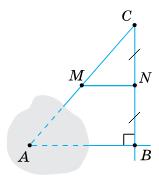
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
2.
1.
2.
3. Правильно.
трапеції.
409. Чи правильно, що
1. Неправильно.
2. Неправильно.
1. Неправильно.
2. Неправильно. 3.
4. Неправильно.
5. Правильно.
N трапеції MNKL.
1) CD = AB = З CM (за
паралельних прямих ML і NK та січній MN). Відповідь:
180°.
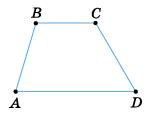
Мал. 171
∠B = 180° – ∠A = 180° – 50° = 130°; ∠D = 180° – ∠C = 180° – 140° = 40°.
Відповідь: ∠B = 130°; ∠D = 40°.
Мал. 172
∠B = 180° – ∠A = 180° – 90° = 90°;
∠C = 180° – ∠D = 180° – 46° = 134°.
Відповідь: ∠B = 90°; ∠C = 134°.
Мал. 173
∠B = 180° – ∠A = 180° – 40° = 140°;
∠C = 180° – ∠D = 180° – 36° = 144°.
Відповідь: ∠B = 140°; ∠C = 144°.
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
416. ABCD — трапеція
AD i BC.
1) ∠A i ∠C, якщо ∠B = 110°, ∠D = 30°;
2) ∠A i ∠D, якщо ∠B = 125°, ∠C = 145°.

1) ∠A = 180° – ∠B = 180° – 110° = 70°; ∠C = 180° – ∠D = 180° – 30° = 150°; 2) ∠A = 180° – ∠B = 180° – 125° = 55°; ∠D = 180° – ∠C = 180° – 145° = 35°.
Відповідь: 1) ∠A = 70°, ∠C = 150; 2) ∠A = 45°, ∠D = 35°.
417. Основою піраміди
1) ∠А = 160°; 2) ∠А = 135°; 3) ∠А = 95°.


https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
ABCD
Відповідь: ABCD — трапеція. 422. На малюнку ABCD — рівнобічна трапеція
1) чотирикутник ABCK — паралелограм; 2) трикутник KCD — рівнобедрений.
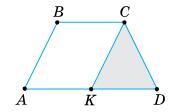
1) BC ∥ AD, бо ABCD — трапеція
Оскільки ВС ∥ AD, СК ∥ AB,
2) ∠BAD = ∠CKD — як
∠
Оскільки ∠BAD = ∠CKD і ∠BAK = ∠CDK, то ∠CKD = ∠CDK, тобто ∆KCD — рівнобедрений.
423. MNKL — трапеція з основами ML і NK, NF || KL. Знайдіть:
1) основу ML, якщо MF = 5 см, NK = 2 см; 2) основу NK, якщо ML = 10 см, MF = 7 см.
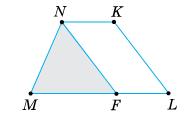
1) ML = MF + FL = MF + NK = 5 + 2 = 7 cм;
2) NK = FL = ML – MF = 10 – 7 = 3 см Відповідь: 1) 7 см; 2) 3 см.
424. BM і CK
DABM = DDCK.
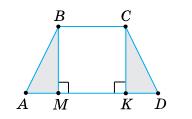
∆АВМ = ∆DCK (за
425. Знайдіть
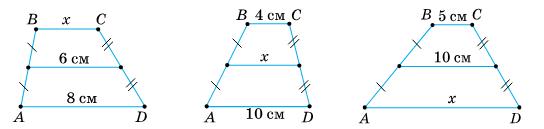
Мал.178
х+8
2 = 6;
х + 8 = 12;
х = 12 – 8;
х = 4 (см).
Відповідь: 4 см.
Мал.179
х = 4+10 2 ;
х = 7 (см).
Відповідь: 7 см.
Мал.180
х+5
5 = 10;
х + 5 = 20;
х = 20 – 5;
х = 15 (см).
Відповідь: 5 см.
426. Чи
Якщо NK = 4 см, ML = 8 см і EF —

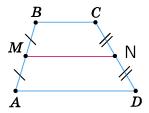
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
х = NK+ML 2 = 4+11 2 = 7,5 (см), де x — середня
Відповідь: 4 см, 11 см, 7,5 см.
432. Знайдіть
1) с = 8 см, d = 12 см, m = 10 см;
2) с = d = m = 15 см.
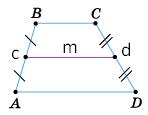
PABCD = BC + AD + AB + CD = 2 • BC+AD 2 + c + d = 2m + c + d.
1) PABCD = 2m + c + d = 2 • 10 + 8 + 12 = 40 (см);
2) PABCD = 2m + c + d = 2 • 15 + 15 + 15 = 60 (см);
Відповідь: 1) 40 см; 2) 60 см.
433. У
трапеції.

PABCD = BC + AD + AB + CD = 2 •
2 + c + d = 2m + c + d.
PABCD = 2m + c + d = 2 • 14 + 17 + 17 = 28 + 34 = 62 (см).
Відповідь: 1) 62 см.
434. Два
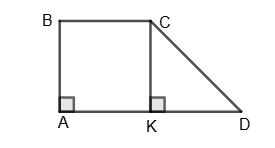
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
2) СК = 10 – 6,2 = 3,8 (см) = 38 (мм).
Відповідь: 1) 2 см; 2) 38 мм.
437. Якщо
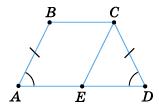
Нехай ∠A = ∠D, проведемо CE ∥ AB, тоді ∠A = ∠CKD — як
паралельних прямих AB і СE та січній АE. Оскільки ∠CED = ∠D , то ∆CED — рівнобедрений і СE = АВ. Оскільки АВСE —
то СE = AB. Враховуючи, що
AB = СE і СE = AD, то AB = CD, тобто трапеція ABCD — рівнобічна.
438.
Мал. 185
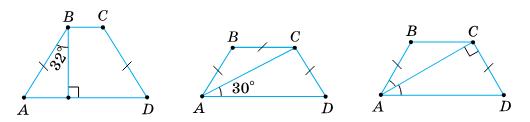
∠A = 90° – 32° = 58°,
∠B = 90° + 32° = 122°,
∠C = ∠B = 122°,
∠D = ∠A = 58°.
Відповідь: 58°, 122°, 122°, 58°.
Мал. 186
∠BCA = ∠CAD = 30° —
ВС та січній АС.
∠BAC = ∠BCA = 30° — як кути
∠BAC = ∠BAC + ∠CA = 30° + 30° = 60°.
∠D = ∠BAC = 60°;
∠B = ∠BCD = 180° – 60° = 120°.
Відповідь: 60°, 120°, 120°, 60°.
Мал. 187
∠D = ∠BAD = 2∠CAD.
Оскільки ∠D + ∠CAD = 9° і ∠D = 2∠CAD, то
∠D = 90° 2 1+2 = 60°,
∠BCD = 180° – ∠D = 180° – 60° = 120°,
∠B = ∠BCD = 120°,
∠BAD = ∠D = 60°.
Відповідь: 60°, 120°, 120°, 60°.
439. Доведіть,
∠A + ∠C = ∠A + ∠B = 180° (оскільки
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
∠B + ∠D = ∠B + ∠A = 180° (оскільки ∠D = ∠A i ∠A + ∠B = 180°).

∠С + ∠D = 180°; ∠A = ∠D; ∠C = ∠A + 40°.
Тоді ∠С + ∠А = 180°; ∠A + 40° + ∠А = 180°;
2∠А = 180° – 40°;
∠А = 70°; ∠D = 70°.
∠C = ∠A + 40°;
∠В = 180° – ∠А = 180° – 70° = 110°;
∠С = 110°.
Відповідь: ∠А = 70°, ∠В = 110°, ∠C = 110°, ∠D = 70°.
441. Протилежні кути

Нехай ∠A : ∠C = 1 : 4. Оскільки ∠A + ∠C = 180°
∠A = 180° • 1 1+4 = 36°,
∠C = 180° • 4 1+4 = 144°,
∠B = ∠C = 144°,
∠D = ∠A = 36°.
Відповідь: 36°, 144°, 144°, 36°.
442. Доведіть,
2)
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
1) ∆ABD = ∆DCA — за трьома сторонами: AD — спільна сторона, AB = DC — як
сторони рівнобічної трапеції, BD = СА (задача 307). Із рівності цих трикутників маємо ∠BDA = ∠CAD, тоді ∠ODA = ∠OAD. Отже, ∆AOD — рівнобедрений. Аналогічно ∆BOC — рівнобедрений, бо ∆ВСD = ∆СBА (ВС — спільна, CD = BA, BD = СА) і із
трикутників випливає, що ∠DBC = ∠ACB. 2) ∆AOB = ∆DOC — за трьома сторонами, о скільки AО = DO (бо ∆AOD — рівнобедрений), OB = ОС (оскільки ∆ВОС — рівнобедрений, AB = CD (як
трапеції). 444. У рівнобічній трапеції
Нехай
=
АK = 1 2 AВ = 1 2 • 4 = 2 (cм), MD = 1 2 CD = 1 2 • 4 = 2 (cм), тоді BC = KM = AD – AK – MD = 10 – 2 – 2 = 6 (см). Відповідь: 6 см.

https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
446. ABCD — рівнобічна
1) AK = MD = (AD – BC) : 2; 2) KD = AM = (AD + BC) : 2. 1) ∆ABK = ∆DCM —


1) ABCD — рівнобічна трапеція (AD ∥ BC, AB = CD),
BK ⊥ AD, CM ⊥ AD, AK = 4 см, KD = 8 см.
∆ABK = ∆DCM, тоді MD = AK = 4 см.
AD = AK + KD = 4 + 8 = 12 (см).
BC = AD – AK – MD = 12 – 4 – 4 = 4 (cм).
Відповідь: 4 см і 12 см.
2) ABCD — рівнобічна трапеція (AD ∥ BC, AB = CD),
BK ⊥ AD, CM ⊥ AD, AK = 2 см, KD = 7 см.
AD = AK + KD = 2 + 7 = 9 (cм).
∆ABK = ∆DCM, тоді BC = KM = AD – AK – MD = 9 – 2 – 2 = 5 (см).
Відповідь: 5 см, 9 см.
448. Доведіть,
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
1) 6 см і 8 см; 2) 62 мм і 10 см.
Нехай ABCD — рівнобічна трапеція, у якій AB = CD = BC, AD = b, BC = a, тоді ∆ABC —
рівнобедрений і PABCD = AB + ВС + CD + AD = a + a + a + b = 3a + b. 1) Якщо а = 6 см, b = 8 см, то PABCD = 3 • 6 + 8 = 26 (см); 2) якщо а = 62 мм = 6,2 см; b = 10 см, то PABCD = 3 • 6,2 + 10 = 18,6 + 10 = 28,6 (см).
Відповідь: 1) 26 см; 2) 28,6 см.
450. Доведіть теорему
(MN — середня лінія).
Мал.190
теоремою
МЕ = 1 2ВС, EN = 1 2AD, тодi MN =
Мал. 191
Проведемо
Мал.192
Проведемо EF ∥ AB, тоді ABEF —

https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
ABCD — трапеція (BC ∥ AD), AD : BC = 7 : 3, AD – BC = 4,8 cм, MN — середня
трапеції.
Нехай AD = 7x см, ВС = 3х см, тоді 7х – 3х = 4,8; 4x = 4,8; x = 1,2.
Отже, AD = 7 • 1,2 = 8,4 (см);
ВС = 2 • 1,2 = 3,6 (см), тоді MN = AD+BC 2 = 8,4+3,6 2 = 12 2 = 6 (см).
Відповідь: 6 см.
452. Середня лінія трапеції
ABCD — трапеція (ВС ∥ AD), MN — середня
Нехай ME = x см, тоді NE = (х + 2) см, ВС = 2МЕ = 2х см, AD = 2NE = 2(х + 2) см.
Оскільки MN = AD+BC 2 , то 10 = 2(x+2)+ 2x 2 ;
10 = x + 2 + x;
2х + 2 = 10;
2x = 10 – 2;
2х = 8; x = 4.
Отже, AD = 2(x + 2) = 2 • (4 + 2) = 12 (см); BC = 2x = 2 • 4 = 8 (см).
Відповідь: 8 см і 12 см.
453. Доведіть,
MN = 10 см, NE – ME = 2 см.
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
ABCD — трапеція, АК = КС, BL = LD, ВС = а, KL = с.
Згідно з результатами задачі 453 маємо:
KL = AD−BC 2 , тоді c = AD−a 2 ,
AD – a = 2c; AD = 2с + а.
1) Якщо а = 6 см, с = 4 см, то AD = 2с + а = 2 • 4 + 6 = 14 (см).
2) Якщо a = 50 мм = 5 см, с = 2 см, то AD = 2с + а = 2 • 2 + 5 = 9 (см).
Відповідь: 1) 14 см; 2) 9 см. 455. Якщо
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
ABCD — трапеція (AD ∥ BC), AC = BC. Проведемо BK ⊥ AD і CM ⊥ AD. ∆ACM = ∆DBK (за гіпотенузою і катетом: АС = BD, СМ = ВК), тоді ∠CAM = ∠BDK. ∆ABD= ∆DCA (за двома сторонами і кутом між ними: BD = АС — за умовою, AD — спільна, ∠ADB = ∠DAC — за доведенням), тоді AB = DC, тобто ABCD — рівнобічна трапеція. Отже, якщо
ABCD — трапеція (AD ∥ ВС), AB = CD, MN — середня лінія.
Проведемо BK ⊥ AD, CN ⊥ AD, тоді CN = AN і BK = KD (задача
і рівнобедрені,
трикутника AOD маємо ∠AOD
AС ⊥ ВD. Таким чином, якщо середня лінія рівнобічної трапеції
1) ABCD — трапеція (ВС ∥ AD), ABCK — ромб, ∆
∠COD = 60°. Відповідь: 60°.
2)
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
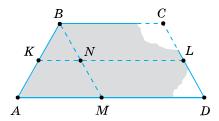
то ми зможемо визначити: BC = MD = NL; BN = CL = NM = LD. 2. Позначимо точку
AB = ME, BM = AE; CD = MF, MC = FD. 466.
1.
2.
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
2.
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
Менший ∠AOB, та більший ∠AOB (неопуклий)
Мал.221
∪ALB = 90°.
Відповідь: 90°.
Мал.222
∪ALB = 180°.
Відповідь: 180°. 476.
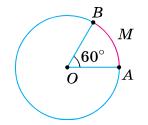
AMB = 60°. Відповідь: 60°.
477.
1) 1 2
2) 1 3
1) 1 2 • 360° = 180°; 2) 1 3 • 360° = 120°; 3) 2 3 • 360° = 240°.
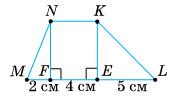
Відповідь: 1) 180°; 2) 120°; 3) 240°.
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
якщо:1) α = 30°; 2) α = 62°; 3) α = 100°?
1) Якщо α = 30°, то ∪АВ = 30° або ∪AB = 360° – 30° = 330°;
2) якщо α = 62°, то ∪AB = 62° або ∪АВ = 360° – 62° = 298°;
3) якщо α = 100°, то ∪AB = 100° або ∪АВ = 360° – 100° = 260°.
Відповідь: 1) 30° і 330°; 2) 62° і 298°; 3) 100° і 260°.
479. За даними
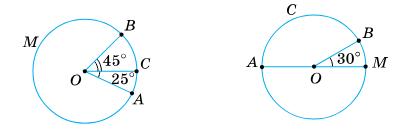
1) ∪ACB = ∪AC + ∪BC = 25° + 45° = 70°; 2) ∪AMB = ∪AM + ∪MB = 180° + 30° = 210°.
Відповідь: 1) 70°; 2) 210°.
480. На
1) 12 см; 2) 0,2 дм; 3) 39 мм.
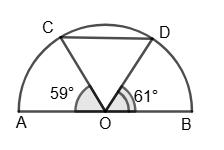
∪CD = 180° – ∪AC – ∪BD = 180° – 59° – 61° = 60°.
∆OCD — рівносторонній, тоді CD = ОС = OD = OA = OB.
1) Якщо АО = 12 cм, то CD = 12 см; 2) якщо АО = 0,2 дм, то CD = 0,2 дм; 3) якщо АО = 39 мм, то CD = 39 мм.
Відповідь: 1) 12 см; 2) 0,2 дм; 3) 39 мм.
481. У колі з центром
і CD рівні. Доведіть, що ∠АОС = ∠BOD. Оскільки ∪AB = ∪CD, тоді ∪AB + ∪ВС = ∪CD + ∪ВС.
∪AC = ∪BD, тоді ∠AOC = ∠BOD.
482. Дуги АВС і BCD кола з центром О рівні.

що ∠АОВ = ∠COD.
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
Оскільки ∪ABC = ∪BCD, тоді ∪ABC – ∪BC = ∪BCD – ∪BC.
Звідси ∪AB = ∪CD, тоді ∠AOB = ∠COD.
483. За
Мал.227
α = 1 2 ∪AC = 1 2 • 120° = 60°
Відповідь: 60°.
Мал.228
∠AD = 2∠ABD = 2 • 25° = 50°;
α = 1 2 ∪AD = 1 2 • 50° – 25°.
Відповідь: 25°.
Мал.229
α = 1 2 ∪AC = 1 2 • 180° = 90°.
Відповідь: 90°.
484. За

1) Мал.230
∪AC = 2∠ABC = 2 • 35° = 70°; 2) Мал.231
∪AC = ∠AOC = 40°;
∠ABC = 1 2 ∪AC = 1 2 • 40° = 20°.
Відповідь: 1) 70°; 2) 20°.
485. Знайдіть
1) 52°; 2) 126°; 3) 200°.
1) 1 2 • 52° = 26°;
2) 1 2 • 126° = 63°; 3) 1 2 • 200° = 100°.
Відповідь: 1) 26°; 2) 63°; 3) 100°.
486.
1) 16°; 2) 32°; 3) 110°.
1) 16° • 2 = 32°; 2) 32° • 2 = 64°; 3) 110° • 2 = 220°.
Відповідь: 1) 32°; 2) 64°; 3) 220°.
487.
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
1) ∪AC = 360° – 150° – 70° = 140°; ∠ABC = 1 2 ∪AC = 1 2 • 140° = 70°;
2) ∪MK = 30° • 2 = 60°; x° = 360° – 60° – 160° = 140°;
3) ∪EQ = 60° • 2 = 120°; x° = 360° – 50° – 120° = 190°.
Відповідь: 1) 70°; 2) 140°; 3) 190°. 488. Точки А,
міри дуг відносяться як: 1) 1 : 1 : 1; 2) 1 : 2 : 2.
∪AB; ∪BC : AC = m : n : k, тоді
∪AB = 360° • m m+n+k ; ∪BC = 360° • n m+n+k ; ∪AC = 360° • k m+n+k ;
Тоді ∠А = 1 2 ∪BC = 180° • n m+n+k ;
∠B = 1 2 ∪AC = 180° • k m+n+k ;
∠C = 1 2 ∪AB = 180° • m m+n+k .
1) ∠А = 180° • 1
1+1+1 = 60°;
∠B = 180° • 1
1+1+1 = 60°;
∠C = 180° • 1
1+1+1 = 60°;
2) ∠А = 180° • 2
1+2+2 = 72°;
∠B = 180° • 2
1+2+2 = 72°;
∠C = 180° • 1
1+2+2 = 36°;
Відповідь: 1) 60°, 60°, 60°; 2) 72°, 72°, 36°.
489. Точки
як 1 : 2 : 3.

https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
∪AB; ∪BC : AC = m : n : k, тоді
∪AB = 360° • m m+n+k ; ∪BC = 360° • n m+n+k ; ∪AC = 360° • k m+n+k ;
Тоді ∠А = 1 2 ∪BC = 180° • n m+n+k ;
∠B = 1 2 ∪AC = 180° • k m+n+k ;
∠C = 1 2 ∪AB = 180° • m m+n+k .
∠А = 180° • 3
1+2+3 = 90°;
∠B = 180° • 3
1+2+3 = 90°;
∠C = 180° • 1
1+2+3 = 30°.
Відповідь: 60°, 90°, 30°. 490. Навколо трикутника
якщо:
1) ∠А = 30°, ∠В = 90°;
2) ∠В = 110°, ∠С = 28°.
1) ∠A = 30°, тоді ∪BC = 2 • 30°= 60°;
∠B = 90°, тоді ∪AC = 2 • 90° = 180°;
∪AB = 360° – 60° – 180° = 120°;
2) ∠B = 110°, тоді ∪AC = 2 • 110° = 220°;
∠C = 28°, тоді ∪AB = 2 • 28° = 56°;
∪BC = 360° – 220° – 56° = 84°.
Відповідь: 1) 120°, 60°, 180°; 2) 56°, 84°, 220°.
491. Навколо
∠А = 65°, ∠С = 35°.
∠A = 65°, тоді ∪BC = 2 • 65° = 135°;
∠C = 35°, тоді ∪AB = 2 • 35° = 70°;
∪AC = 360° – 130° – 70° = 160°;
Відповідь: 1) 70°, 130°, 160°.
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
1) 64°; 2) 144°.
AB = BC; ∪AB = ∪BC
1) ∠A = ∠C = 1 2 ∪AB = 1 2 • 64° = 32°;
∠B = 180° – 2∠A = 180° – 64° = 116°;
2) ∠A = ∠C = 1 2 ∪AB = 1 2 • 144° = 72°;
∠B = 180° – 2∠A = 180° – 144° = 36°.
Відповідь: 1) 32°, 32°, 116°; 2) 72°, 72°, 36°.
493. Знайдіть

AB = BC; ∪AB = ∪BC
∠A = ∠C = 1 2 ∪AB = 1 2 • 120° = 60°;
∠B = 180° – 2∠A = 180° – 120° = 60°; Відповідь: 60°, 60°, 60°.
494.

Нехай АВ = СD, тоді ∆АОB = ∆COD за
радіуси, AB = CD — за умовою).
= ∪CD. Отже, у колі рівні
496. Доведіть, що діаметр, перпендикулярний
навпіл. Нехай CD ⊥ АВ, тоді ∆AOF = ∆BOF за
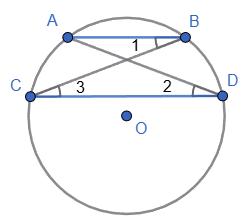
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
Дано: коло з центром O, хорди AB ∥ CD.
Довести: ∪AC = ∪BD.
Доведення:
1. ∠1 і ∠2 — вписані кути, що спираються на дугу ∪AC. ⇒ ∠1 = ∠2 (вписані кути, що спираються на одну дугу, рівні).
2. Пряма CB перетинає паралельні хорди AB ∥ CD, тому ∠1 і ∠3 — внутрішні
різносторонні ⇒ ∠1 = ∠3.
3. Із ∠1 = ∠2 та ∠1 = ∠3 маємо ⇒ ∠2 = ∠3.
4. Вписаний кут вимірюється половиною дуги, на яку спирається, тому: ∪AC = 2∠2, ∪BD = 2∠3.
5. Оскільки ∠2 = ∠3, то ∪AC = ∪BD.
Висновок: дуги, що лежать між паралельними хордами AB і CD, рівні.
499. Дуги, що лежать між дотичною та паралельною їй хордою, — рівні. Доведіть.
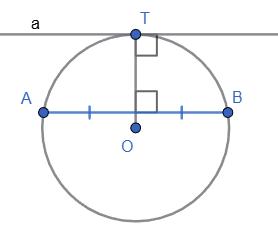
Нехай дано коло з центром O.
AB – хорда цього кола, a – дотична, проведена
дотичної OT ⟂ a. Оскільки a ∥ AB і OT ⟂ a, то
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
1) Оскільки ∪ACB : ∪ADВ = 2 : 3, то ∪ACB = 360° 2 2+3 = 144°;
∪ADB = 360° ∙ 3 2+3 = 216°, тоді ∠ACB = 1 2
∪ADB = 1 2 · 216° = 108°; ∠ADB = 1 2 ∪АСВ = 1 2 · 144° = 72°.
2) Оскільки ∪ACB : ∪ADB = 4 : 5, тo ∪ACB = 360° · 4 4+5 = 160°;
∪ADB = 360° · 4 4+5 = 200°, тоді ∠ACB = 1 2 ∪ADB = 1 2 · 200° = 100°;
∠ADB = 1 2 ∪ACB = 1 2 · 160° = 80°.
Відповідь: 1) 108° і 72°; 2) 100° і 80°. 501. Точки
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
∠ADB = 1 2 ∪ACB = 1 2 · 360° n+1 ; ∠ACB = 1 2 ∪ADB = 1 2 · 360° · n n+1 .
1) Якщо n = 3, то ∠ADB = 1 2 · 360° 3+1 = 45°. ∠ACB = 1 2 ·
2) Якщо n = 4 ,то ∠ADB = 1 2 · 360° · n 4+1 = 36°; ∠ACB = 1 2 · 360° · 4 4+1 = 144°. Відповідь: 1) 45° або 135°; 2) 36° або 144°.
180°.
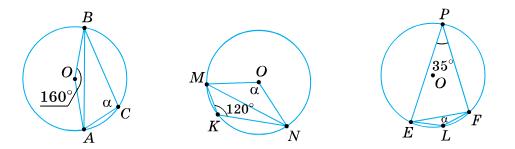
1) ∪BCA
= 290°; α = 1 2 ∪EPF = 1 2 · 290° = 145°. Відповідь: 1) 100°; 2) 120°; 3) 145°. 507.
1) n = 35°; 2) n = 45°. ∠AOC = ∠ABC + n°. Оскільки
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
1) Якщо n = 35°, то ∠ABC = 35°, ∠AOC = 2 · 35° = 70°.
2) Якщо n = 45°, то ∠ABC = 45°, ∠AOC = 2 · 45° = 90°.
Відповідь: 1) 35° і 70°; 2) 45° і 90°.
508. Доведіть, що центром кола, описаного
Якщо ∠ABC = 90°, то ∪ADC = 2∠АВС = 2 · 90° = 180°. Тоді ∠AOC = ∪AD
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
2. BA
3.
4.
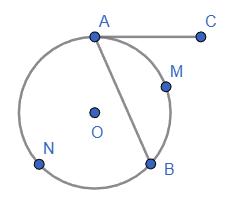
1) 45°; 2) 40°. 512. Доведіть,
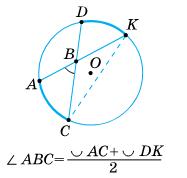
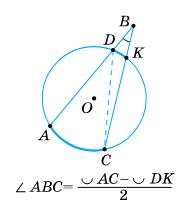
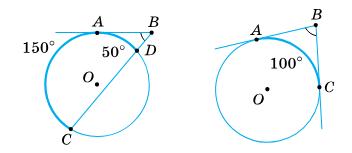
= 1 2 · (260° – 100°) = 1 2 · 160° = 80°.
Відповідь: 1) 50°, 2) 80°.
515.
∪AC : ∪AB : ∪BC = 11 : 4 : 3.
∪
= 360° ·11
= 220°; ∪АВ = 360° ·4
= 80°; ∪BC = 360° ·3
= 60°.
A ⊥ ОА, MC ⊥ ОС, NK ⊥ OB. ∠AMC = 1 2 (∪АС – ∪ABC) = 1 2 · (220° – 140°) = 1 2 · 80° = 40°; ∠ANB = 1 2(∪ВСА – ∪AB) = 1 2 · (280° – 80°) = 100°; ∠MNB = 180° – ∠ANB = 180° – 100° = 80°.
∠MKN = 180° – ∠AMC – ∠MNB = 180° – 40° – 80° = 60°.
Відповідь: 40°, 60°, 80°.
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
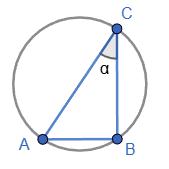
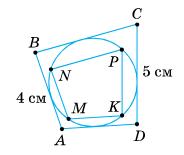
1) AD + BC = AB + CD = 4 + 5 = 9 cм;
2) ∠M + ∠P = 180° (оскільки чотирикутник MNPK — вписаний).
Відповідь: 1) 9 см; 2) 180°.
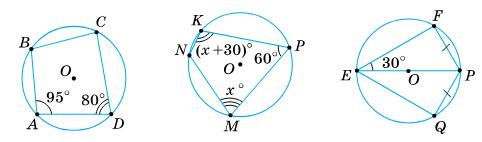
1) ∠C = 180° – ∠A = 180° – 95° = 85°; ∠B = 180° – ∠D = 180° – 80° = 100°.
2) ∠N = 180° – ∠P = 180° – 60° = 120°; x + x + 30 = 180; 2x + 30 = 180; 2x = 150; x = 75.
Отже, ∠M = 75°, ∠K = 75° + 30° = 105°.
3) ∠F = ∠Q = 90° (оскільки
∠E = 2 · 30° = 60°; ∠P = 180° – ∠E = 180° – 60° = 120°.
Відповідь: 1) 85°, 100°; 2) 120°, 75°, 105°; 3) 90°, 120°, 90°, 60°.
527.
1) 90°, 90°, 110°, 120°; 2) 70°, 130°, 110°, 50°?
1) не можна, бо 90° + 110° ≠ 180°; 2) можна, бо 70° + 110° = 130° + 50° = 180°.
Відповідь: 1) ні; 2) так.
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
528. Чи
відповідно дорівнюють:
1) 85°, 130°, 95°;
2) 60°, 100°, 119°?
Навколо чотирикутника ABCD коло описати:
1) можна, якщо ∠D = 50° і не можна, якщо ∠D ≠ 50°;
2) не можна, бо 60° + 119° ≠ 180°.
Відповідь: 1) так, якщо ∠S = 50°; 2) Hi.
Доведіть, що навколо
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
2) Навколо квадрата ABCD можна
∠A = ∠B = ∠C = ∠D = 90° і ∠A + ∠B = ∠C + ∠D = 180°.
3) Навколо ромба ABCD, відмінного
A + ∠B ≠ ∠C + ∠D ≠ 180°.
1) так; 2) так; 3) ні. 531. Доведіть,
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
ABDC — прямокутник.
2) Прямокутник ABDC буде
533.
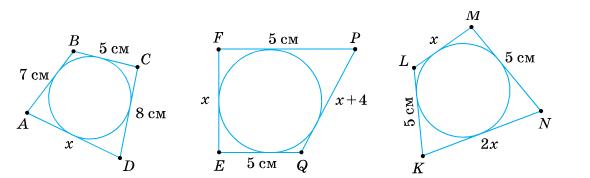
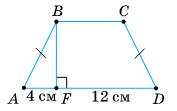
1) x = AD = (AB + CD) – BC = = (7 + 8) – 5 = 10 (cм).
2) х + x + 4 = 5 + 5; 2x + 4 = 10; 2х = 6; x = 3, тоді EF = 3 см, PQ = 3 + 4 = 7 см.
3) х + 2х = 5 + 5;
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
Зх = 10; х = 31 3,
Тоді LM = 31 3 см; KN = 31 3 · 2 = 62 3 см.
Відповідь: 1) 10 см; 2) 3 см і 7 см; 3) 31 3см, 62 3 см.
534. Чи можна вписати коло в чотирикутник, сторони якого, взяті послідовно,
дорівнюють:
1) 2 см, 3 см, 5 см, 4 см; 2) 7 см, 4 см, 3 см, 5 см?
1) Оскільки 2 см + 5 см = 3 см + 4 см, то в
2) Оскільки 7 см + 3 см ≠ 4 см + 5 см, то в
Відповідь: 1) так; 2) ні.
535. Знайдіть
1) 20 см; 2) 3,2 дм.
Оскільки
двох протилежних сторін.
1) Р = 2 · 20 см = 40 см;
2) P = 2 · 3,2 дм = 6,4 дм.
Відповідь: 1) 40 см; 2) 6,4 дм.
1) 12 см, 16 см, 28 см;
2) 10 см, 14 см, 16 см.
сторін, то:
1) P = 2 · (12 + 28) = 80 cм;
2) Р = 2 · (10 + 16) = 52 см.
Відповідь: 1) 80 см; 2) 52 см.
537. Доведіть,
1)
3) ромб?
Відповідь поясніть.

https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
Відповідь: 1) ні; 2) так; 3) так. 539. Знайдіть кут D чотирикутника ABCD,
відносяться як: 1) 2 : 3 : 4; 2) 1 : 2 : 2. Нехай
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
1) Якщо b = 10 см, то R = 10 см.
2) Якщо b = 2,3 дм, то R = 2,3 дм.
Відповідь: 1) 10 см; 2) 2,3 дм.
541. Чи можна описати коло навколо чотирикутника, кути якого, взяті послідовно,
відносяться як:
1) 2 : 4 : 5 : 3; 2) 5 : 7 : 8 : 9?
Відповідь поясніть.
1) Нехай ∠A = 2x°, ∠B = 4x°,
∠C = 5х°, ∠D = 3x°,
тоді ∠A + ∠C = 7x° = ∠B + ∠D, отже, навколо чотирикутника
2) Нехай ∠A = 5х°, ∠B = 7х°,
∠C = 8x°, ∠D = 9х°,
тоді ∠A + ∠C = 5х° + 8x° = 13x°,
∠B + ∠D = 7х° + 9х° = 16х° і ∠A + ∠C
можна описати коло.
Відповідь: 1) так; 2) ні.
542. Доведіть:
1) будь-яка трапеція, вписана в коло, рівнобічна;
2) будь-який паралелограм, вписаний у коло, — прямокутник.
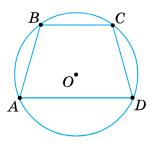
1) Нехай ABCD — трапеція, вписана в коло.
Оскільки ВС ∥ AD, то ∪AB = ∪CD, тоді AB = CD.
Отже, трапеція ABCD — рівнобічна.
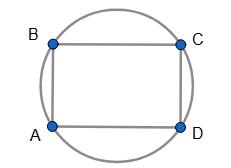
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
ABCD — паралелограм, вписаний в коло.
Оскільки ∠A + ∠C = 180° і ∠A = ∠C,
то ∠A = ∠C = 180° 2 = 90°.
Аналогічно ∠B = ∠D = 180° 2 = 90°.
Отже, ABCD — прямокутник.
543. Доведіть, що будь який ромб, вписаний у коло, — квадрат.
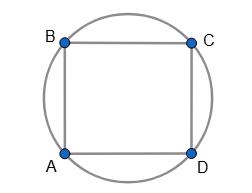
Нехай ABCD — ромб, вписаний в коло.
Оскільки ∠A + ∠C = 180° і ∠A = ∠C, то ∠A = ∠C = 180° 2 = 90°.
Аналогічно ∠B = ∠D = 180° 2 = 90°.
Отже, ABCD — квадрат.
544. Доведіть, що кут A вписаного
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
пропорційні числам:
1) 2, 2, 3, 3;
2) 2, 5, 3, 4?
1) Нехай довжини сторін, які взято послідовно,
дорівнюють 2х; 2х; 3х; 3х.
Тоді 2х + 3х = 2х + 3х.
Оскільки суми протилежних
2) Нехай
дорівнюють 2х; 5х; 3х; 4х.
Тоді 2х + 3х ≠ 5х + 4х.
Оскільки суми
Відповідь: 1) так; 3) ні.
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
Нехай ABCD — трапеція.
ВС : АВ : AD = 2 : 7 : 12,
тоді ВС = 2х, АВ = 7x, AD = 12x.
Оскільки трапеція описана,
то ВС + AD = АВ + CD,
тоді CD = ВС + AD – AB = 2х + 12х – 7х = 7х.
1) За умовою 2х + 12x + 7х + 7х = 42,
тоді 28x = 42; х = 42 28; х = 1,5.
Отже, AB = 7 · 1,5 = 10,5 (мм);
ВС = 2 · 1,5 = 3 (мм);
CD = 7 · 1,5 = 10,5 (мм);
AD = 12 · 1,5 = 18 (мм).
2) За умовою 2х + 12х + 7х + 7х = 56,
тоді 28x = 56; x = 2.
Отже, АВ = 7 · 2 = 14 (см);
BС = 2 · 2 = 4 (см);
CD = 7 · 2 = 14 (см);
AD = 12 · 2 = 24 (см).
Відповідь: 1) 10,5 мм; 3 мм; 10,5 мм; 18 мм; 2) 14 см; 4 см; 14 см; 24 см.
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
549. Складіть
дорівнює:
1) 16 см;
2) 200 мм.
ABCD — трапеція, MN — середня
PABCD = P, Р = АВ + BC + CD + AD;
AD+ BC
2 = MN, AD + BC = 2MN.
трапеції.
Оскільки трапеція описана, то AD + ВС = AB + CD, тоді
P = AD + BC + AD + ВС = 2(AD + ВС);
Р = 2 · 2MN; Р = 5МN, тоді MN = P 4 .
1) Якщо Р = 16 см, то MN = 16 4 = 4 (см);
2) Якщо Р = 200мм, то MN = 200 4 = 50 (мм).
Відповідь: 1) 4 см; 2) 50 мм.
ABC = 150°,
MN = 40 см.
BK ⊥ AD,
∠ABK = 150° – 90° = 60°,
∠BAK = 30°.
2BK = BC+ AD 2 ; 2BK = MN;
BK = MN 2 = 40 2 = 20 (см).
Відповідь: 20 см.
551.
= 30°,
MN = 20 см. Проведемо BK ⊥ AD, ∠BAK = 30°.
Оскільки трапеція рівнобедрена
2BK = BC+ AD 2 ; 2BK = MN;
BK = MN 2 = 20 2 = 10 (см).
Оскільки r = 1 2 BK i BK = 10 cм,
тo r = 1 2 · 10 = 5 (см).
Відповідь: 5 см.
552. Як побудувати квадрат: 1) вписаний у коло; 2)
AB = 2ВК.
= ВС + AD; 4ВК = ВС + AD;
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
1) Нехай дано коло з центром О.
Побудуємо довільний
Тоді ACBD — квадрат, вписаний в коло.
2) Нехай дано коло з центром О.
Побудуємо довільний
Проведемо через точки А, В, С і D прямі, які перпендикулярні
перетинаються в точках М, N, К
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
АВ = ВС, КМ ∥ АВ, АM = 1 2 KM.
Оскільки AM = 1 2КМ, тоді AM < KM, BK < AB (бо ВК — частина
Оскільки AM < KM, BK < AB, то AM + BK < KM + AB.
Оскільки
Відповідь: не можна.
558. Якщо
5.
6.
Пояснення:
1.
2.
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
сторонами.
10 : 2 = 5 см.
Відповідь: Б. 5 см.
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
Периметр ромба P = 4a (властивість ромба: усі сторони
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
Отже, ∠BAK = ∠AKB, тому △ABK рівнобедрений і AB = BK = 12 см (властивість
рівнобедреного трикутника).
Периметр паралелограма: P = 2(AB + BC) = 2(12 + 20) = 64 см.
Відповідь: Г. 64 см.
1. Знайдіть
Розв’язання:
кута). Отже, 150° : 2 = 75°.
Відповідь: Б. 75°. 2.
№ 2
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
10 + 10 = 20 см.
Відповідь: Б. 20 см.
Розв’язання:
У вписаному чотирикутнику сума протилежних
вписаного чотирикутника).
Нехай ∠A : ∠B : ∠C = 1 : 2 : 3, тоді
∠A = x, ∠B = 2x, ∠C = 3x.
Оскільки ∠A і ∠C — протилежні, маємо
∠A + ∠C = 180° ⇒ x + 3x = 180° ⇒ 4x = 180° ⇒ x = 45°.
Тоді ∠B = 2x = 90°.
Кути B і D — протилежні, тому
∠B + ∠D = 180° ⇒ 90° + ∠D = 180° ⇒ ∠D = 90°.
Відповідь: Г. 90°.
5. Діагональ рівнобічної
і 12 см. Знайдіть периметр
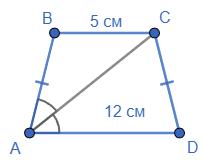
ABCD — рівнобічна
AC — бісектриса кута
BC ∥ AD, BC = 5 см, AD = 12 см, AB = CD.
1) усі кути рівні; Ні, у подібних трикутниках
2) відповідні кути рівні;
Так, відповідні кути рівні.
3) усі сторони рівні;
4) відповідні сторони
5)
Так, відповідні
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
△ABC ∼ △KLM — ні (тут A ↔ K, а має бути A ↔ M).
2) △АВС ∼ △LKM;
△ABC ∼ △LKM — ні (тут A ↔ L, а
3) △АВС ∼ △MLK?
△ABC ∼ △MLK — так (тут A ↔ M, B ↔ L, C ↔ K).
566. Чи
△ABC ∼ △KLM
сторони: AB ↔ KL, BC ↔ LM, AC ↔ KM.
1) AB KM = BC KL = AC LM;
2) AB KL = BC LM = AC KM ? Так
∼ △KLM:
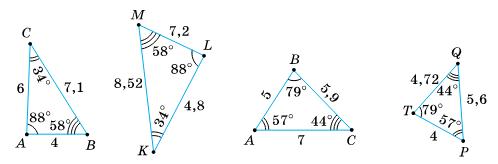
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
– ∆PTQ;
BC i TQ; AC i PQ. 569.
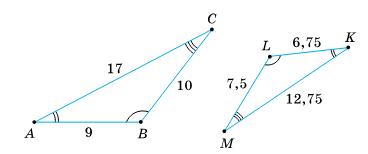
і MKC.
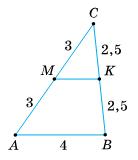
Знайдіть
Мал.1
∆ABC – ∆KLM;
AB KL = B���� LM = AC KM;
9 6,75 = 10 7,5 = 17 12,75 = k; k = 10 7,5 = 100 75 = 4 3;
Мал.2
∆ABC – ∆MKC;
AB MK = B���� KC = AC MC;
4 2 = 5 2,5 = 6 3 = k; k = 4 2 = 2; k = 2. 570.
1) K����
AB = …;
2) AC KC = …;
3) BC DC = …?
1) K����
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
∠A = 180° – (50° + 50°) = 80°; ∠A1 = ∠A = 80°.
574. Чи можуть сторони
1) 1,2 см, 1,3 см, 2,2 см і 24 мм, 26 мм, 44 мм; Так.
24 мм = 2,4 см; 26 мм = 2,6 см; 44 мм = 4,4 см.
2) 5 мм, 50 см, 50 см і 5 см, 50 мм, 50 мм?
Ні.
5 мм = 0,5 см, тому перший набір: 0,5 см, 50 см, 50 см, а другий: 5 см, 5 см, 5 см. Спільного коефіцієнта
трьох сторін немає. 575.
3
9 м = 90 дм; 12 м = 120 дм; 15 м = 150 дм.
90 3 =
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
= 4,5 дм, А1В1 = 3,9 дм.
B1C1 = 4,5 дм = 45 см, A1B1 = 3,9 дм = 39 см (переведення одиниць) За подібністю трикутників:
AB A1 B1 = BC B1 C1
AB = A1 B1 ⋅ BC B1 C1 = 39 ⋅ 13 45 = 169 15 см
Також: AC A1 C1 = BC B1 C1 A1 C1 =
⋅ B1 C1 BC = 14 ⋅ 45 13 = 630 13 см Відповідь: AB =169 15 см, A1C1 = 630 13 см.
578. Пряма, що
1C1
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
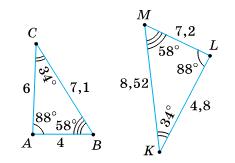
1) P∆ABC = 6 + 4 + 7,1 = 17,1;
Р∆LKM = 7,2 + 4,8 + 8,52 = 20,52;
P∆KLM : P∆ABC = 20,52 : 17,1 = 1,2.
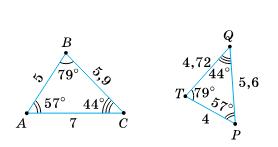
2). P∆ABC = 7 + 5 + 5,9 = 17,9;
P∆TQP = 4,72 + 5,6 + 4 = 14,32;
P∆TQP : P∆ABC = 14,32 : 17,9 = 0.8.
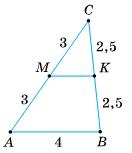
3) Р∆ABC = 4 + 5 + 6 = 15;
Р∆MKC = 2 + 2 ,5 + 3 = 7,5; Р∆ABC : Р∆MKC = 15 : 6,5 = 2.
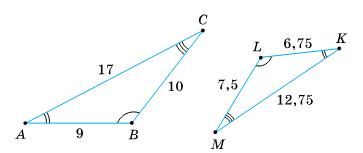
Р∆ABC = 9 + 10 + 17 = 36;
P
= 12,75 + 6,75 + 7,5 = 27;
KLM : P∆ABC = 27 : 36 = 0,75. 585. a, b,
2) 45 : 4 = 11,25 (см) — периметр
11,25 : 3 = 3,75 (см) — сторони трикутника;
3) 72 : 4 = 18 (см)
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
Найбільша сторона 4k = 12, отже k = 3. Тоді сторони: 6 см, 9 см, 12 см.
Відповідь: 6 см, 9 см, 12 см. 589.
593.
∆АВС – ∆МОР (k1 = 4);
∆МОР – ∆TEN (k2 = 1 2);
∆ABC – ∆TEH, k = k1 · k2 = 4 · 1 2 = 2.
594.
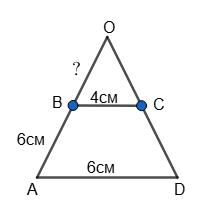
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
∆AOD – ∆BOC.
AO BO = AD BC ;
6+ x x = 6 4;
6х = 24 + 4х;
2x = 24; x = 12 (см).
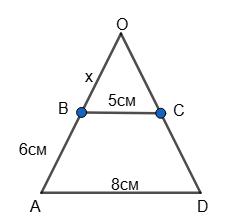
2) AO BO = AD BC ;
6+ x x = 8 5;
8x = 30 + 5х;
3х = 30;
х = 10 (см).
599.
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
∆А1В1С1 катет B1C1 —
AB = C1B1. Нехай AВ = x, тоді С1В1 = хk.
A1B1 = 2B1C1 = 2х (катет,
k= AB A1 B1 = x 2x = 1 2 . 603.
1) n = 2, Р = 50 см, k = 1,5; 2) n = 3, Р = 35 см, k = 0,75. 1) Нехай АС = x см, тоді АВ = ВС = 2х. x + 2x + 2x = 50; 5х = 50; x = 10; АС = 10 см; AB = BC = 20 см. ∆А1В1С1 – ∆АВС, k = 1,5; А1В1 = В1С1 = 20 · 1,5 = 30 (см);
A1С1 = 10 · 1,5 = 15 (см).

2)
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
AС = х см; АВ = ВС = х см. х + 3х + 3х = 35; 7х = 35; х = 5 (см).
AС = 5 см; АВ = ВС = З · 5 = 15 (см).
∆А1В1С1 – ∆АВС, k = 0,75; A1С1 = 0,75 x АС = 0,75 · 5 = 3,75 (см); А1В1 = В1С1 = 0,75 · АВ = 0,75 · 15 = 11,25 (см).
604.
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
Масштаб: 6 см : 1 500 000 см = 1 : 250 000.
2. Яка найменша
4 см · 250 000 = 1 000 000 см = 10 км.
3. Яка відстань між іншими
5 см.
5 см · 250 000 = 1 250 000 см = 12,5 км.
Відповідь: 1) 1 : 250 000; 2) 10 км; 3) 12,5 км.
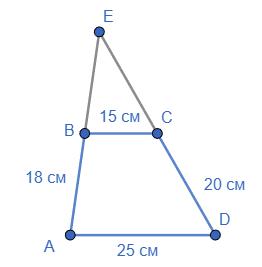
BC : AD = 15 : 25 = 3 : 5,
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
EC : ED = 3 : 5, тобто EC = 3 5ED,
тоді
CD = ED − EC = ED − 3 5 ED = 2 5ED,
звідси
ED = 5 2 CD = 5 2 ·20 = 50 см. Отже, утворений
AD = 25 см, AE = 45 см, DE = 50 см.
Відповідь: 25 см, 45 см, 50 см.
3 · 40 = 120 см.
5)
1)
Ні,
2)
3)
4)
AО : ОВ = 4 : 3.
615. Точка М
1) РМ : МН = 5 : 2;
РМ > МН.
2) РМ : МН = 3 : 7?
МН > РМ.
616.
чи НМ?
PN : NM = 4 : 3.
Оскільки 4 > 3, то
617.
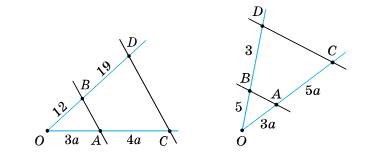
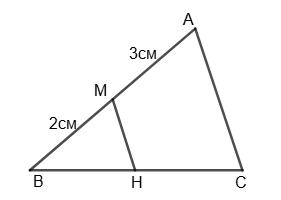
: MA = 4 : 2 = 2 :
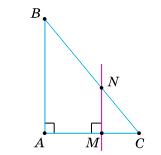
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
1) d = 10 см, m = 2, n = 3;
2) d = 16 см, m = 3, n = 1.
AB : BM = m : n; AB = d.
1) 10 : (2 + 3 )= 2 (см) — довжина 1
AM = 2 · 2 = 4 (cм);
MB = 2 · 3 = 6 (см);
2) 14 : (3 + 4) = 2 (см) — довжина 1 частини;
AM = 2 · 3 = 6 (см);
MB = 2 · 4 = 8 (см).
: (3 + 1) = 4 (см) —
CH = 3 · 4 = 12 (см); HD = 4 · 4 = 16 (см).

https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
626.
у відношенні 2 : 3.
ML = 4 клітинки; LN = 6 клітинки;
ML : LN = 2 : 3.
627. Поділіть
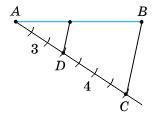
: MC = 2 : 3.
· 10 = 60
Оскільки 92,5 ≠ 60, пропорція не виконується.
Відповідь: відрізки не є пропорційними.
2) 7 см, 4 см, 2,1 см і 1,1 см.
Перевіримо пропорційність:
7 : 4 = 2,1 : 1,1
Перевірка через добутки:
7 · 1,1 = 7,7
4 · 2,1 = 8,4
Оскільки 7,7 ≠ 8,4, пропорція не виконується.
Відповідь: відрізки не є пропорційними.
631. Чи є пропорційними чотири відрізки, довжини
см?
8 24 = 3 9 .
Отже, ���� ���� = ���� ���� ;
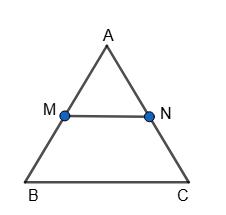
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
2) d = 50 см, а = 0,25, b = 3 4, с = 0,4.
1) 78 2 5 +0,8+3 4 · 2 5 = 78 1,95 · 0,4 = 16 (см);
78
1,95 · 0,8 = 32 (см);
78
1,95 · 0,75 = 30 (см).
Шукані відрізки 16 см; 32 см; 30 см.
2) 50 0,25+ 3 5 +0,4 = 50 0,25+0,6+0,4 = 50 1,25 = 40.
40 · 0,25 = 10 см;
40 · 3 5 = 24 см;
40 · 0,4 = 16 см.
Шукані відрізки 10 см; 24 см; 16 см.
639. На продовженні відрізка
довжини відрізків АN і ВN, якщо:
1) d = 5 см, m = 3, n = 2;
2) d = 16 см, m = 5, n = 1.
AN : BN = m : n.

m− n · m — довжина відрізка AN;
m− n · n — довжина відрізка BN.
1) 5 3− 2 · 3 = 15 см — довжина AN; 5 3− 2 · 2 = 10 см — довжина BN;
2) АN = 16 5 1 · 5 = 20 см; BN = 16 5 1 · 1= 4 см.
640. На малюнку AB || DC || KL,
AD : DK : KF = 2 : 3 : 2. Знайдіть довжини
1) AB = 70 мм, FС = 40 мм;
2) AB = 21 см, FС = 15 см.
BC, СL, LF, DС і KL, якщо:
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
1) AD : DK : KF = 2 : 3 : 2.
Тоді BC : CL : LF = 2 : 3 : 2.
BC = 2x; CL = 3x; LF = 2x;
FC = CL + LF = 3x + 2x = 5x;
FC = 40 мм; 5x = 40; x = 8 (мм).
Тоді
ВС = 2 · 8 = 16 (мм);
CL = 3 · 8 = 24 (мм);
LF = 2 · 8 = 16 (мм).
BF = 2x + 3x + 2х = 7x = 7 · 8 = 56 (мм);
CF = CL + LF = 24 + 16 = 40 (мм).
�������� �������� = �������� �������� ; 70 �������� = 56 40 ;
CD = 70 · 40 56 = 100 2 = 50 (см);
�������� �������� = �������� �������� ; 50 �������� = 40 16 ;
KL = 50 · 16 40 ; �������� = 20 (мм).
2) BC = 2x; CL = 3x; LF = 2x;
FC = 15 cм (за умовою);
FC = FL + LC = 5x;
5x = 15; x = 3 (cм).
ВC = 2 · 3 = 6 (cм);
CL = 3 · 3 = 9 (cм);
LF = 2 · 3 = 6 (cм);
ВF = 6 + 9 + 6 = 21 (cм).
�������� �������� = �������� �������� ;
DC = �������� · CF �������� = 21 · 15 21 = 15 (см);
�������� �������� = �������� �������� ;
K
= �������� · LF �������� = 15 · 6 15 = 6 (см).
641. На
1) a = 2,5 см, b = 4 см, c = 2 см, MP = 12,5 см;
2) a = 10 см, b = 16 см, c = 8 см, MP = 50 см.
1)
2) MN = ��������
= ��������
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
11x = 5x + 60; 6x = 60; x = 10; AB = 10 дм; AO = 10 + 12 = 22 (дм).
643. На стороні
паралельно МN, якщо:
1) МО = 6 см, ОN = 9 см, а = 2 см;
2) МО = 10 см, ОN = 14 см, а = 4 см.
1) Якщо AD ∥ MN,
то MA : AO = ND : DO. MO = 6 cм;
ОA = a = 2см; MAт = 6 – 2 = 4 см.
Отже, ND : DO = 4 : 2 = 2 : 1; ND = 2x; OD = x; 2x + x = 9;
3x = 9; x = 9 : 3; x = 3 (см); DN = 2 · 3 = 6 (см).
2) MA : AO = ND : DO; MO = 10 см;
AO = а = 4 cм; MA = 10 – 4 = 6 (см);
DN : DO = 6 : 4 = 3 : 2;
DN = 3x; DO = 2x;
3x + 2x = 14; 5x = 14; x = 2,8.
Тоді DN = 3 · 2,8 = 8,4 (cм); DO = 2 · 2,8 = 5,6 (см).
644.
1) АР : РВ = 5 : 6, ВС = 22 см;
2) АР : РВ = 4 : 3, ВС = 2,8 дм.
1) CO : BO = AP : PB = 5 : 6;
CO = 5x; BO = 6x;
BC = 5x + 6x = 11х;
11x = 22; x = 22 : 11; x = 2.
Тоді CO = 5 · 2 = 10 (см);
BO = 6 · 2 = 12 (см).
2) CO : BO = AP : PB = 4 : 3;
CO = 4х; ВО = 3х;
СО + ВО = СВ;
4х + 3х = 2,8; 7x = 2,8; х = 0,4;
СО = 4 · 0,4 = 1,6 (дм);
ВО = З · 0,4 = 1,2 (дм) = 12 (см).
645. Точка ділить
1)
2)
= 1, у = 2;
= 2, у = 3;
3) х = 4, у = 5.
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
1)
BD = DP = PK = КС.
Тоді BD : BP : BK : BC = FD : EP : MK : AC = 1 : 2 : 3 : 4;
1) FD = 1 4 · 1,6 = 0,4 (дм) = 4 (см); EР = 1 2 · 1,6 = 0,8 (дм) = 8 (см); MK = 3 4 · 1,6 = 1,2 (дм) = 12 (см);
2) FD = �������� 4 = 124 4 = 31 (мм) = 3,1 (см);
ЕР = �������� 2 = 124 2 = 62 (мм) = 6,2 (см);
MK = 3 4 · 124 = 93 (мм) = 9,3 (см).
AO = a a+b+c ;
OH = b a+b+c ;
HB = c a+b+c ;
A���� = a+b a+b+c ;
OB = b+c c+b+c
652. Відрізок
1) а = 6 см;
2) а = 10 см.
AM = 6 5 · 2 = 2,4 (см);
МВ = 6 5 · 3 = 3,6 (см).
1) Нехай ВТ = х (см), тоді АТ = 6 + x (см). �������� �������� = 4 3 ; 6+���� ���� = 4 3 ;
4х = 3х + 18; х = 18.
ВТ = 18 (см);
МТ = МВ + ВT = 3,6 + 18 = 21,6 (см).
2) АМ = 10 5 · 2 = 4 (см);
МВ = 10 5 · 3 = 6 (см).
ВТ = x см; АТ = 10 + x;
10+���� ���� = 4 3 ;
4x = 3x + 30; x = 30 (см);
МТ = МВ + ВТ = 6 + 30 = 36 (см).
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
1) а : с = b : d;
2) а : с = (а + b) : (с + d);
3) c : a = (b – a) : (d – c).
узагальненою теоремою Фалеса:
a : c = b : d. (відповідні відрізки)
1. a : c = b : d. (за узагальненою теоремою Фалеса)
2. (a + b) : (c + d) = a : c. (властивість пропорції: додавання відповідних членів)
3. (b − a) : (d − c) = a : c. (властивість пропорції: віднімання відповідних членів)
Отже, c : a = (d − c) : (b − a). (обернена пропорція)
Тобто з рисунка випливає пропорція c : a = (d − c)
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
1
∆АМО ∼ ∆ABA1 (за двома кутами); ∠MAO = ∠BAA1 (спільний кут);
∠AMO = ∠ABA1 (відповідні при MN ∥ ВС і січній АB). З подібності трикутників: АА1 : АО = BA1 : МО.
Аналогічно: ∆АА1С ∼ ∆AON, звідси АА1 : АО = А1С : ON. Оскільки
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
1) а = 7 см, b = 10 см;
2) а = 10 см, b = 14 см.
Проведемо PO ∥ MN. Тоді MNPO — паралелограм.
∆OPZ — трикутник;
QB = 1 3OZ; FK = 2 3OZ;
OZ = MZ – NP = b – a.
AQ = CF = a; AB = a + 1 3 (b – a); СК = а + 2 3 (b – а).
1) Якщо а = 7 см, b = 10 см, то AB = 7 + 1 3 · (10 –7) = 8 (см);
CK = 7 + 2 3 · (10 – 7) = 9 (см).
2) Якщо а = 10 см; b = 14 см, то АВ = 10 + 1 3 (14 – 10) =
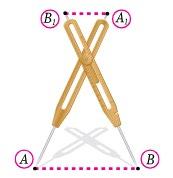
15 : t = 3 : 5 t = 15 · 5 :
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
2. △CAM ∼ △CBN (за двома кутами:
відповідні при AM ∥ BN)).
3. CA : CB = CM : CN (відповідні
ACM = ∠BCN (спільний
4. 4 : CB = 5 : 40 ⇒ CB = 4 · 40 : 5 = 32 м.
5. AB = CB − CA = 32 м − 4 м = 28 м.
Відповідь: 28 м.
має тінь
Відомо: тінь башти 24 м
висота шеста 1,2 м
шеста 80 см = 0,8 м
h : 24 = 1,2 : 0,8
h = 24 · 1,2 : 0,8 = 36 м Відповідь: 36
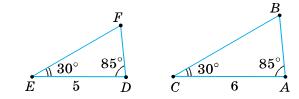
∆CRQ ∼ ∆САВ (∠C — спільний, ∠Q = ∠B).
∆CRQ ∼ ∆QPB (∠RCQ = ∠PQB; ∠CQR = ∠QBP).
∆ACB ∼ ∆PQB (∠B — спільний, ∠A = ∠P). 670.
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
672. Два кути трикутника АВС і
1) 23° і 77° та 77° і 23°;
Подібні за двома кутами;
2) 30° і 90° та 30° і 60°;
Треті кути: 180° − (30° + 90°) = 60°, 180° − (30° + 60°) = 90°.
Є кути 30° і 60° в обох трикутниках.
Подібні за двома кутами;
3) 52° і 28° та 28° і 100°;
Треті кути: 180° − (52° + 28°) = 100°, 180° − (28° + 100°) = 52°.
Є кути 52° і 28° в обох трикутниках.
Подібні за двома кутами.
4) 45° і 100° та 90° і 45°. Чи подібні ці трикутники?
Треті кути: 180° − (45° + 100°) = 35°, 180° − (90° + 45°) = 45°.
Пари двох рівних кутів немає.
Не подібні.
673.
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
Отже, ∠A = ∠B = ∠C = 60°.
Трикутники рівносторонні.
AB = ВС = AC = 2 см;
A1В1 = В1C1 = A1С1 = 6 см.
2) ∠B = ∠C = 60°, А1В1 = 2 см, АС = 4 см.
∠B = ∠C = 60°, тому ∠A = 60°.
Звідси ∠A1 = ∠B1 = ∠С1.
Трикутники рівносторонні.
А1В1 = В1С1 = А1С1 = 2 см;
AВ = ВС = АС = 4 см.
676. △АВС ∼ △А1В1С1. Знайдіть
= ∠C = 60°, ВС = 9 см, А1В1 = 3 см.
∠В = ∠C = 60°, тому ∠A = 60°.
∆АВС — рівносторонній, тому ∆A1B1C1 — рівносторонній.
AB = ВС = AC = 9 см;
A1B1 = B1C1 = A1C1 = 3 cм.
677. Рівнобедрені трикутники
1) α = 43°, β = 68°30′;
2) α = 105°, β = 38°30′?
1) У рівнобедреного трикутника
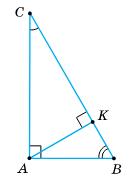
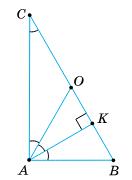
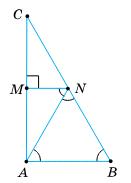
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
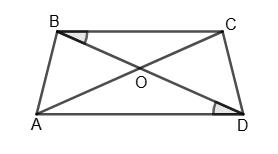
BC AD = BO DO = CO AO = a b .
Якщо BC = b; AD = a, то BO DO = CO AO = b a
687. У рівнобічній
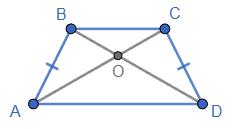
∠BOC = ∠AOD (як
△BCO ∼ △ADO (за
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
Підставимо значення: CO = 51 32 + 64 ⋅ 32 = 51 96 ⋅ 32 = 17 мм AO = 51 17 = 34 мм
P△BOC = 32 + 17 + 17 = 66 мм
P△AOD = 64 + 34 + 34 = 132 мм
Відповідь: 66 мм; 132 мм. 2)
AO = AC OC =0,8 0,3=0,5 дм
P△BOC =0,3+0,3+0,3=0,9 дм
P△AOD =0,5+0,5+0,5=1,5 дм
Відповідь: 0,9 дм; 1,5 дм.
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
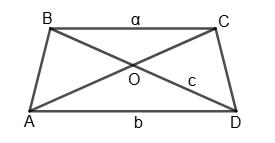
AO = BC AD = 3 8 ; CO = AC 3+8 · 3= 7 11 · 3= 21 11 =1 10 11 (см);
P∆BOC = 3 + 1 10 11 + 1 10 11 = 5 20 11 = 6 9 11 (см);
AO = AC – OC = 7 – 1 10 11 = 5 1 11 (см);
P∆AOD = 8 + 5 1 11 + 5 1 11 = 18 2 11 (см).
DO AO = CO BO = DC AB .
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
Оскільки в грані відтинається трапеція BKPC, то BK ∥ PC, а отже в трикутнику SBC
маємо KP ∥ BC.
Тоді:
∠KSP = ∠BSC (спільна вершина),
∠KPS = ∠BCS (як відповідні при KP ∥ BC і січній SC),
Отже, △BSC ∼ △KSP за двома кутами.
691. Кожне ребро піраміди SАВС дорівнює m.

2) Сторони трапеції: BK, KP, PC, CB.
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
SK=m ⋅ p 3m = p 3 ,
BK =SB SK=m p 3 .
Так само:
PC =m p 3 .
Периметр трапеції:
P = BK + KP + PC + BC = = �m − p 3� + p 3 + �m − p 3� +m= 3m − p 3 .
Звідси: p 3 = 3m −P⇒ p=3(3m −P)
Менша сторона трапеції — це KP, отже:
KP = p 3 = 3m −P.
Відповідь:
1. KP = ���� 3 ;
2. менша сторона трапеції (KP = 3m - P).
692. За даними,
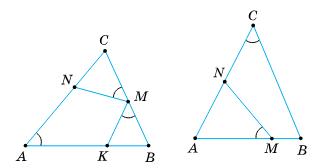
1) ∆AСВ ∼ ∆MCN (за двома кутами).
∠C — спільний, ∠A = ∠M — за умовою. ∆AСВ ∼ ∆МКВ (за двома кутами); ∠A = ∠M — за умовою; ∠B —спільний.
2) ∆AСВ ∼ ∆AMN (за двома кутами);
∠A — спільний; ∠C = ∠M — за умовою.
693. Доведіть подібність трикутників, зображених
відрізок А1D = AC.
Тоді ∆A1КD =
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
ВС = 8 см; АС = 4 см; KL = 4,5 см.
KL AB = LM BC = KM AC ; 4,5 6 = LM 8 = KM 4 .
Звідси LM = 4,5 8 6 = 6 см;
КM = 4·4,5 6 = 3 (см).
696. У трикутниках KLM і АВС: ∠K = ∠А, ∠В = ∠L, KL = m, LM = m + 2, KM = m – 2,
АВ = nm. Знайдіть сторони трикутників, якщо m = 8 см, n = 2.
∆АВС ∼ ∆KLM. KL = 8 см; LM = 10 см; KM = 6 см; AB = 16 см.
KL AB = LM BC = KM AC ; 8 16 = 10 BC = 6 AC
Звідси BC = 6 · 10 8 = 20 см;
AC = 16 · 6 8 = 12 (см).
697. Висоти АЕ і СD трикутника АВС
їхня сума дорівнює 18 см, АН = 8 см,
СН = 4 см.
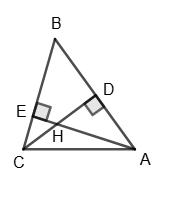
AE + CD = 18 см; АН = 8 см; СH = 4 см.
∆CEH ∼ ∆ADH (за двома кутами);
∠CEH = ∠АDH = 90°.
∠EHC = ∠DHA (вертикальнi). З
CH AH = EH HD ; 4 8 = EH HD .
Нехай EH = х, тоді HD = 2х.
ЕА = х + 8 (cм); CD = 4 + 2х (см).
За умовою ЕА + CD = 18 см.
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
Отже x + 8 + 4 + 2x = 18;
Зх = 6; х = 2. EH = 2 см;
HD = 2 · 2 = 4 см;
АE = AH + EH = 8 + 2 = 10 cм;
CD = СH + HD = 4 + 4 = 8 см.
698. Периметр
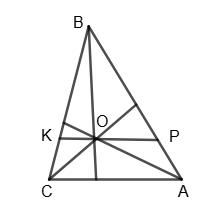
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
1) BKMC —трапеція;
KM ∥ BC, тоді ∆АКМ ∼ ∆АСВ.
AC AK = AB AM = CB KM ; 15 AK = 20 AM = 30 KM,
або 3 AK = 4 AM = 6 KM .
Нехай AK = x, тоді AM = 4AK 3 = 11 3x; KM = 2x.
Звідси CK = 15 – x; MB = 20 – 11 3 x.
PCKMB = 2x + 15 – x + 20 – 11 3x + 30, а за умовою 63 см.
Отже, 2x + 15 – x + 20 – 11 3x + 30 = 63;
1 3 x = –2; x = 6.
Тоді KM = 2 · 6 = 12 (см).
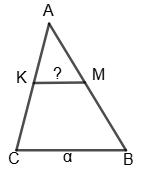
2) ∆AKM ∼ ∆ACB.
�������� �������� = �������� �������� = �������� �������� .
Оскільки AC = AB = CB, то AK = AM = KM.
Нехай AK = AM = KМ = x,
тоді CK = 18 – x; MB = 18 –x.
PCKMB = 50 см; то 18 – х + х + 18 – x + 18 = 50; –x = –4; x = 4.
Отже, KM = 4 см.
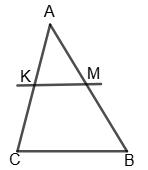
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
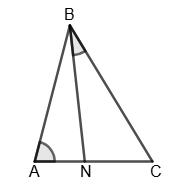
1) різносторонній;
A — спільний).
б) Проведемо MN таким чином, що ∠BMN = ∠C; N ∈ ВС.
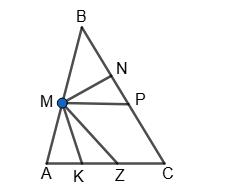
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
∆BMN ∼ ∆BAC (за двома кутами: ∠B — спільний, ∠BMN = ∠BAC).
б) Проведемо MD ∥ ВС.
∆AMD ∼ ∆АВС (за двома кутами: ∠A — спільний, ∠ADM = ∠ACB).
в) Проведемо МР таким чином, щоб ∠AMP = ∠C ( P ∈ АС).
∆АМР ∼ ∆АСВ (за двома кутами: ∠A — спільний, ∠AMP = ∠ACB).
Отже, задача має 3 розв’язки.
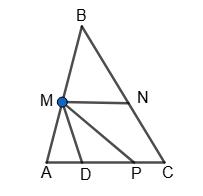
3) ∆АВС — рівносторонній. М ∈ AB.
а) Проведемо MN ∥ AC.
∆BMN ∼ ∆BAC (за двома кутами: ∠B — спільний, ∠BMN = ∠BAC).
б) Проведемо МК ∥ ВС.
∆АМК ∼ ∆AВС (за двома кутами: ∠A —
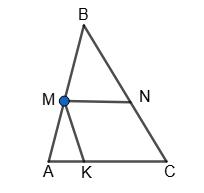
Отже, задача має 2 розв’язки. 702.
1) а = 6 см, b = 10 см;
2) а = 10 см, b = 13 см.
∠AMK = ∠ABC).
∆АВС — рівнобедрений,
ВК ⊥ AC; К — середина АС;
АК = 1 2 АС = 1 2 а.
∆АОK = ∆AOM (прямокутні); АО — спільна
одного кола).
Звідси AM = a 2,
тоді МВ = AB – AM = b –a 2 = 2b− a 2 .
ВК перетинає MN в т. Р. Р — середина MN; MN ∥ AC.
MP = d 2 ; ∆MВР ∼ ∆АВК.
AK MP = AB MB, або a 2 MP = b 2b a 2 .
Звідси MP · b =
1)
= 6 cм; b = 10 см.
d= 6·(2·10− 6) 2·10 = 6 · 14 2·10 =4,2 (см).
2) a = 10 cм; b = 13 cм.
d= 10·(2·13−10) 2·13 = 10 · 16 26 =6 2 13 (см).
703. Доведіть,
ОМ = OK — катети (як радіуси
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
1) а = 12 см, b = 10 см;
2) а = 10 см, b = 13 см.
1) ∆АВС — рівнобедрений;
АС = 12 см; AB = 10 см;
ВК ⊥ АС; К
OK = ON = r; ON ⊥ AB. ∆АВК і ∆OBN — прямокутні.
∠B – спільний, тому ∆АВК ∼ ∆OBN. AK ON = AB OB, або OB ON = AB AK = 10 6 = 5 3 . Висота
2) АС = 10 см; AB = 13 см.
Аналогічно: OB ON = AB AK = 13 5 .
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
B1 K1 = AB A1 B1 , а AB A1 C1 = AC A1 C1 .
Звідси BK B1 K1 = AC A1 C1
1М1 і CM —
СМ = С1М1 + 4; CM C1 M1 =1,5; C1 M1 +4 C1 M1 =1,5; 4 C1 M1 =0,5;
С1М1 = 4 : 0,5; С1М1 = 8 (см),
тоді CM = С1М1 + 4 = 8 + 4 = 12 см.
709. Діагоналі
ABCD — трапеція;
Отже CO AO = BC AD ;
ВС = 48 – AD; 48 – AD AD = 1 3 ; 48 AD – 1= 1 3 ; 48 AD = 4 3 ; AD = 144 4 = 36 (см);
ВС = 48 – 36 = 12 (см).
710. Діагоналі
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html

ABCD — трапеція; n — середня
BO
OD = BC AD = 3 5 ;
ВС = 48 – АD;
48− AD
AD = 3 5 ;
48 AD =1+ 3 5 ;
48 AD = 3 5 ; AD = 30 см;
ВС = 48 – 30 = 18 см.
711. У чотирикутнику
D. Доведіть,
ВС + AD = 2n = 2 · 24 = 48 см.
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
М.
O1K ⊥ MN; O2N ⊥ MN.
∆МКО1 ∼ ∆MNO2 (∠M — спільний, ∠K = ∠N = 90°).
NO2 KO2 = O2 M O2 M або R2 R1 = R2 +2R1 +AM R1 +AM ;
R1R2 + R2AM = R1R2 + 2R1 2 + R1AM;
R1AM = 2R12; AM = 2R1 2 R2 – R1 ;
O1M = R1 + AM = R1 + 2R1 2 R2 – R1 ;
O1M = R2 + 2R1 + AM = R2 + 2R1 + 2R1 2 R2 – R1 ;
R1 = 4 см; R2 = 6 см;
О1М = 4 + 2 · 42 6 – 4 = 20 (см);
О2М = 6 + 2 · 4 + 2 · 42 6 – 4 = 30 (см).
O1K ⊥ MN; O2N ⊥ MN.
1 ∼ ∆MNO2 (∠M — спільний, ∠K = ∠N = 90°).
KO2 = O2 M O2 M
R2 R1 = R2 +2R1 +AM R1 +AM ;
R1R2 + R2AM = R1R2 + 2R1 2 + R1AM;
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
R1AM = 2R12; AM = 2R1 2 R2 – R1 ;
O1M = R1 + AM = R1 + 2R1 2 R2 – R1 ;
O1M = R2 + 2R1 + AM = R2 + 2R1 + 2R1 2 R2 – R1 ;
R1 = 3 см; R2 = 6 см;
О1М = 3 + 2 · 32 6 – 3 = 9 (см);
О2М = 6 + 2 · 3 + 2 · 32 6 – 3 = 18 (см).
714. Доведіть, що трикутники з відповідно
Нехай дано два трикутники: △ABC і △A1B1C1 такі, що
AB ⟂ A1B1, AC ⟂ A1C1, BC ⟂ B1C1,
тобто відповідні
∠A утворений сторонами AB і AC.
∠A1
⟂ A1B1 і AC ⟂ A1C1,
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
OK CN = OD CD .
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
∆AOB ∼ KOL (k = 4); LK = 1 4 AB = 1 4 a.
1) a = 3 см; LK = 3 4 (см);
2) а = 4 см; LK = 1 4 · 4 = 1 (см);
3) а = 5 см; LK = 1 4 · 5 = 5 4 = 11 4 (см).
717. Доведіть, що
проведені.
AK ⊥ BC; AK = ha : BH ⊥ AC; BH = hb.
∆AKC ∼ ∆BHC (прямокутні, ∠С – спільний).
Тоді AN BK = AC BC ; ha hb = b a ,
або ha : hb = 1 a ∶ 1 b
Аналогічно: ha : hc
= 2 3 ; 3x = 2x + 20; x = 20
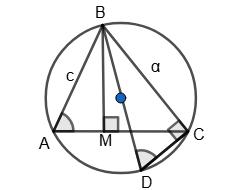
Проведемо діаметр BD.
∠ВАС = ∠BDC (вписані
∠BMA = 90° (ВМ ⊥ АС). ∠BCD = 90°
∆АВМ ∼ ∆DBC (за двома кутами).
Тоді AB BD = BM BC aбо
c 2R = hb a .
Звідси hb = ac 2R .
∠
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
= 90° (вписаний, спирається на діаметр), тоді ∠NKM = 90° (суміжний з ∠AKB).
∆АОМ ∼ ∆NKM (прямокутні трикутники, у яких ∠AMO = ∠NMK — як вертикальні).
Звідси AO NK = OM KM . (І)
∆BON ∼ ∆ВКА (прямокутні, ∠B — спільний).
Звідси BO BK = ON KA (II)
∆ВАК ∼ ∆MKN (прямокутні, ∠BAK = ∠MNK).
Звідси BK MK = KA KN . (III)
З рівності (І): ОМ = AO·KM NK .
З рівності (IІ): ОN = BO KA BK .
З рівності (IIІ): BK · KN = MK · KA.
OM · ON = AO KM NK · BO KA BK = AO · BO · KM KA NK BK .
Оскільки BK · KN = MK · KA, то KM KA NK·BK = 1.
Отже, OM · ON = AO · OB · 1 = R · R = R2.
Тобто OM · ON = R2
721. У трикутник АВС зі
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
Звідси a x = b b−x ; ab – ax = bx; bx + ax = аb; х(b + а) = аb;
х = ab a+b .
сторона
722. У трикутнику АВС з тупим
∠BDC + ∠CMB = 90° + 90° = 180°, то
∠MBD + ∠MCD = 360° – 180° = 180°.
∠BDC + ∠CMD = ∠MBD + ∠MCD.
∠BDC і ∠CMD; ∠MBD і ∠MCD
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
області з позначкою 1;
3)
4) можна провести три такі прямі.
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
На стороні AC позначаю довільну точку M.
Через M проводжу пряму MN, паралельну AB; вона перетинає BC у точці N.
Через точку N проводжу пряму NK, паралельну AC.
Через точку M проводжу пряму MK, паралельну BC.
Прямі NK і MK перетинаються в точці K.
Тоді:
MN ∥ AB, MK ∥ BC, NK ∥ AC.
Отже, у трикутників MNK і ABC
За першою ознакою подібності: △MNK ∼ △ABC.
Вимірюю сторони MN, MK, NK
(AB і MN, BC і MK, AC і NK).
MNK.
4.
Різниця позначок: 194,9 − 186,5 = 8,4 м.
1. Початок ділянки має меншу позначку: 186,5 м.
2. Кінець ділянки має більшу позначку: 194,9 м.
Підйом на 1 м шляху: 8,4 / 320 = 0,02625 м.
3. Середина ділянки: 160 м від початку. Підйом там: 160 · 0,02625 = 4,2 м.
Позначка: 186,5 + 4,2 = 190,7 м.
4. На відстані 120 м від початку підйому: підйом 120 · 0,02625 = 3,15 м.
Позначка: 186,5 + 3,15 = 189,65 м.
728. Із селища
1) південно західному;
2) південному;
3) південно східному.
Із точки P опустимо перпендикуляри: PH ⟂ OA,
PK ⟂ OC.
Із точки Q опустимо перпендикуляри:
QH1 ⟂ OA,
QK1 ⟂ OC.
Розглянемо прямокутні трикутники:
△OPH і △OQH1.
У них:
- по одному прямому куту; - ∠POA = ∠QOA (це той самий кут
променями OB і OA).
Отже, ці трикутники подібні (за двома кутами).
Тому: �������� ���� ����1 = �������� ��������
Аналогічно розглянемо прямокутні трикутники: △OPK і △OQK1.
Вони теж
2)
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
BM = BA − AM = 10 − 5 = 5 см
BP = BC − CP = 12 − 6 = 6 см
BM : BA = 5 : 10 = 1 : 2
BP : BC = 6 : 12 = 1 : 2
Отже, BM : BA = BP : BC ⇒ MP ∥ AC ⇒ △BMP ∼ △BAC.
Відповідь: так, подібні.
2) ВА = 22 см, ВС = 16 см, АМ = 11 см, СР = 10 см?
BM = BA − AM = 22 − 11 = 11 см
BP = BC − CP = 16 − 10 = 6 см
BM : BA = 11 : 22 = 1 : 2
BP : BC = 6 : 16 = 3 : 8 1 : 2 ≠ 3 : 8 ⇒ MP не ∥ AC ⇒ △BMP і △BAC не подібні. Відповідь: 1) так; 2) ні.
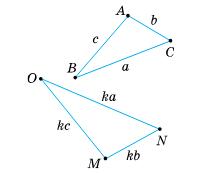
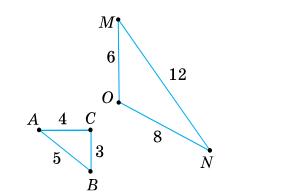
Приклади:
k = 2 → 10 см, 12 см, 18 см
k = 0,5 → 2,5 см, 3 см,
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
звідси m = 56 17 8 = 119 (см);
n = 56·15 8 = 105 (см).
746. Сторони
звідси m = 30 см; n = 45 см. 747. Чи
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
1) n –
Тоді c b = ���� a ; 6 12 = ���� 18 ; звідси n = 9 (см);
Р = 6 + 9 + 9 = 24 (см).
2) c b = ���� a ; 28 14 = ���� 25 ; n = 50 (см);
P = 50 + 50 + 28 = 128 (см).
751. Основа рівнобедреного
c b = ���� a ; 12 8 = ���� 5 ; n = 60 8 = 7,5 (см);
P = 7,5 + 7,5 + 12 = 27 (см).
752.
якщо:
1) а = 24 мм, m = 2, n = 3;
2) а = 1,5 дм, m = 5, n = 3.
b — бічна сторона
1) а : b = m : n; 24 b = 2 3 ; b = 36 (мм).
2) а : b = m : n; 1,5 b = 5 3, звідси b = 0,9 (дм).
а : b = m : n;
= 3 4 ; b = 1 (см).
ТМ ⊥ АВ; РК ⊥ АВ;
⊥ АВ ⇒ ВС ∥ ТМ ∥ РК.
1) Р∆АВС = 16 + 63 + 65 = 144 (см).
∆АКР ∼ ∆АВС:
P∆AKP = 1 3 P∆ABC = 1 3 · (16 + 63 + 65) = 48 (см).
∆АМТ ∼ ∆АВС:
P∆AMT = 2 3 P∆ABC = 2 3 · (16 + 63 + 65) = 96 (см).
2) P∆ABC = 7 + 24 + 25 = 56 (см).
P∆AKP = 1 3 P∆ABC = 1 3 · 56 = 182 3 (cм).
P∆AMT = 2 3 P∆АВС = 2 3 · 56 = 371 3 (cм).
MOP = 8 + 15 + 17 = 40 (см). P∆MBA = 1 3 P∆MOP = 1 3 · 40 = 131 3 (см). P∆MDC = 2 3 P∆MOP = 2 3 · 40 = 262 3 (см).
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
1) с = 42 мм, m = 8, n = 13;
2) с = 0,8 дм, m = 5, n = 3.
Ймовірно в умові помилка. Для того, щоб
підручника, потрібно взяти АD – ВC = 4
Розглянемо трикутники BCO і DOA.
∠BOC = ∠DOA (вертикальні).
∠BCO = ∠DAO (відповідні при AD ∥ BC).
Отже, △BCO ∼ △DOA), тому
AD BC = AO OC = DO OB .
1) З подібності:
AD BC = 13 8 .
Нехай BC = ���� , тоді AD = ���� +4. Маємо: ���� +4 ���� = 13 8 , 13���� =8���� + 32, 5���� = 32, ���� =6,4 мм
Отже,
BC = 6,4 мм, AD = 10,4 мм.
Оскільки AO : OC = 13 : 8 і AO + OC = 42,
OC = 42 13 +8 ⋅ 8= 16 мм,
AO = 42 13 +8 ⋅ 13 = 26 мм.
Аналогічно: OB = 16 мм, DO = 26 мм.
см!
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
Периметри:
P△BCO =6,4+ 16 + 16 = 38,4 мм,
P△AOD = 10,4+ 26 + 26 = 62,4 мм.
2)
AD
BC = 5 3 .
Нехай BC =3���� , AD =5���� . Тоді:
5����− 3���� =4, ���� =2.
Отже,
BC = 6 см, AD = 10 см.
AO : OC = 5 : 3, AO + OC = 8:
AO = 5 см, OC = 3 см;
DO = 5 см, OB = 3 см.
Периметри:
P△BCO =6+3+3= 12 см,
P△AOD = 10 +5+5= 20 см.
Відповідь:
1. 6,4 мм, 10,4 мм, 38,4 мм, 62,4 мм;
2. 6 см, 10 см, 12 см, 20 см.
757. У
З OT = 7:
Нехай
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
LM = ВС · 3 = 7 · 3 = 21 см;
KM = АС · 3 = 3 · 3 = 9 см.
2) АВ = 6 см; ВС = 8 см; АС = 4 см.
KL = 6 · 3 4 = 4,5 см;
LM = 8 · 3 4 = 6 см;
КМ = 4 · 3 4 = 3 см. 760. У
= 8 см;
∠A = ∠K, ∠C = ∠M.
1. Бо D — середина AC,
Отже,
AD KN = AC/2 KM/2 = AC KM =k.
2. Розглянемо трикутники ABD і KLN.
Маємо:
∠BAD = ∠K (бо D ∈ AC),
а також
AB KL =k, AD KN =k.
Отже, за
△ ABD ∼△ KLN. Звідси
BD LN = AB KL =k.
3. Аналогічно, розглянувши △ CBD і △ MLN,
BD LN = BC LM =k.
Тепер з AC KM =k та BD LN =k
BD LN = AC KM .
Отже, у
mAC
mKM = AC KM
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
Якщо KL ∥ MN, тo ∆AKL ∼ ∆AMN,
тоді AK AM = KL MN .
Нехай AK = x, тоді x x+3 = 1 5 0,25 ;
0,25x = 0,2x + 0,6;
0,05x = 0,6; x = 12.
Отже, щоб KL ∥ MN треба, щоб AK = 12 см.
764. Висота трикутника
1) m = 5, n = 9; 2) m = 3, n = 5?
1) BK ⊥ AC; AK : КС = 5 : 9; М — середина AC; MP ⊥ AC; P ∈ ВС.
∼
(за
KC MC = BC PC ; MC = 1 2 (AK + KC);
9 7 = BC PC , тоді BP : PC = 2 : 7.
2) KC MC = BC PC ;
кутами).
вертикальні). Отже, ∆МОН ∼ ∆ВОС. Нехай ∠ВСМ = ∠BHM = х, тоді ∠MBC
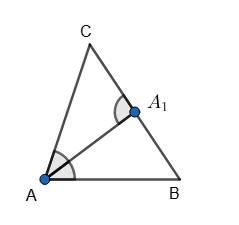
Звідси AB A1 A = BC AC = AC A1 C .
Звідси
ВС2 : АС2 = ВС2 : (1 2 BC2) = 2.
767. Точка Е — середина сторони ВС
діагональ
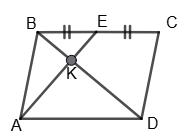
1) m = 1, n = 2;
2) m = 1, n = 1?
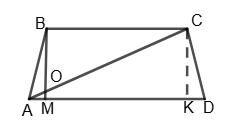
CK ⊥ AD. ∆ABM = ∆DCK.
АM = DK, ВС = МК.
AM : ВС = AО : ОС = m : n.
1) АМ : ВС = 1 : 2; AM = 1x; BC = 2x. Тоді MD = 2х + х =
AM : MD = 1x : 3x = 1 : 3.
2) АМ : ВС = 1 : 1; AM = 1x; ВС = 1x.
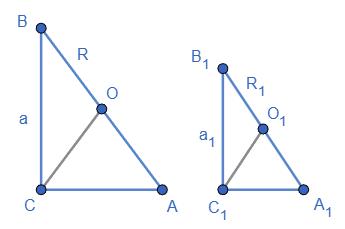
1)
Звідси ∠B = ∠B1, тоді
A1 C1 = AB A1 B1 .
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
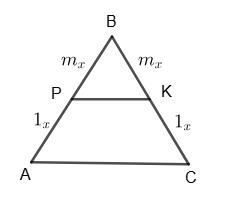
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
КN ∥ АВ; МР ∥ ВС.
Звідси МВNО — паралелограм, тому MB = NO = 1 2d (d — діагональ прямокутника).
AM ∥ KN; MN ∥ AC, тому AMNK — паралелограм.
Звідси AM = d.
AM : MB = d : 1 2 d = 2 : 1.
Аналогічно CN : NB = 2 : 1.
1) K і P — точки,
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
Нехай ВК = 1х; КА = mх. Проведемо BN ∥ CD.
BCDN — паралелограм, ОР = ND = ВС = b.
∆BKO ∼ ∆BAN; BA = mx + 1x.
KO AN = BK BA .
Звідси КО = AN· BK BA = (a− b)·1x 1x+ mx = a− b 1+
KP = KO + OP =
;
.
2) O — точка перетину діагоналей, MN ∥ AD; О ∈ MN.
∆ВОС ∼ ∆DOA (за двома кутами).
Звідси BO OD = b a = CO AO .
Нехай ВО = bx; OD = ах; BD = bx + ax; CO = bx; OA = ax.
∆BMO ∼ ∆BAD.
MO AD = BO BD ;
MO = BO· AD BD = bx· a bx+ ax = ba b+ a ;
∆CNO ∼ ∆CDA. CO CA = ON AD ;
ON = CO· AD CA = bx· a bx+ ax = ba b+ a ; MN = 2ba b+ a .
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
3) ABCD — трапеція.
а ∥ AD; О ∈ а.
Р — точка перетину а з DB; К — точка перетину а з АС.
∆ОВА ∼ ∆OAD.
OD
OC = AD BC ; OD OC = a b .
Нехай ОD = ах; OС = bх.
Тоді CD = ax – bx = (а – b)x.
∆ОСK ∼ ∆DСА.
Звідси OK AD = OC CD .
Тоді ОК = AD · OC CD = a · bx (a−b)x = ab a−b;
Аналогічно РО = ab a−b .
Тоді РК = 2ab a−b .
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
OP = AD AO OC +1 .
∆BOK ∼ ∆BDA.
Звідси AD KO = BD BO = BO+OD BO = OD BO +1;
OK = AD OD BO +1
Оскільки AO OC = OD BO (з подібності ∆AOD i ∆COB), то OP = OK.
∆OCN ∼ ∆DAN, тоді ON DN = OC DA = m 2n .
∆OMN ∼ ∆AOD, тоді MN AD = ON OD .
MN n = m 2n +m ; MN = mn 2n +m . Якщо
∆ODN ∼ ∆CBN. Тоді ON CN = n 2m .
∆OMN ∼ ∆OBC. Тоді MN BC = ON OC .
MN m = n n+ 2m ; MN = nm 2m +n .
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
звідси BC MC = HC FC ; 2= HC FC ;
HC = 2FC; HF = FC.
∆AMF ∼ ∆AKH,
звідси AK KM = AH HF ; 3 1 = AH HF ; AH = 3FH.
Звідси
AH ⊥ BC; AM = MC; AK : KH = 3 : 1.
HF ∥ BM,
AM MF = AK KH = 3 1 ; AM = 3MF. Тоді FC = 2MF. ∆CFH ∼ ∆CMB.
CH = 2BH.
Звідси BK KM = BH HG =1. 780.
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
4. Розглянемо трикутники △PBE і △PAT.
∠PBE = ∠PAT (як внутрішні
∠PEB = ∠PTA) (як внутрішні
Отже,
3)
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
= 2 3
6 ∙ 1,5 = 9 см; 10 ∙ 1,5 = 15 см; 14
i DC.
1) CD = x; AD = 20 – х; 20−x x = 10 15 ;
10x = 300 – 15х; 15х = 300; x = 12;
CD = 12 (см); AD = 20 – 12 = 8 (см).
2) AB BC = AD DC ⇒ DC = BC · AD BC = 18 · 14 21 = 12 см.
AC = AD + DC = 14 + 12 = 26 (cм).
793.
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
ВН — висота, ВН ⊥ АС.
ВA і ВС — похилі, ВС > ВА, тому СН > АН.
ВМ — медіана; т. М ділить АС навпіл. АН < АМ.
Отже, до вершини А ближче розміщена т. Н.
795. За даними на малюнках знайдіть:
1) гіпотенузу;
2) катети;
3) висоту, проведену до гіпотенузи.
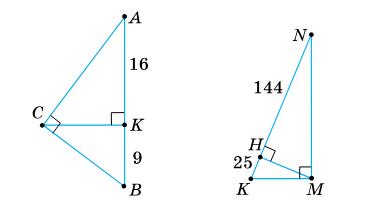
Мал.1:
1) AB = 16 + 9 = 25;
2) AC = √16 · 25 = 4 · 5 = 20; CB = √9 · 25 = 3 · 5 = 15;
3) CK = √16 · 9 = 4 · 3 = 12.
Мал.2:
1) KN = 25 + 144 = 169;
2) KM = √25 · 169 = 5 · 13 = 65; NM = √144 · 169 = 12 · 13 = 156;
3) MH = √25 · 144 = 5 · 12 = 60.
796. У трикутнику PRQ знайдіть:
1) гіпотенузу;
1) PQ = 225 + 64 = 289;
2) RP = √225 · 289 = 15 · 17 = 255; RQ = √64 · 289 = 8 · 17 = 136;
3) RT = √225 · 64 = 15 · 8 = 120.
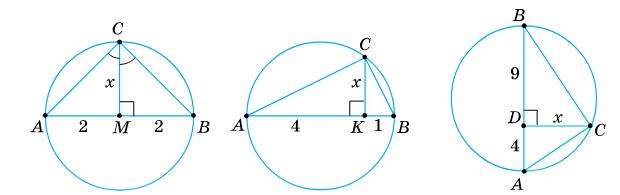
Мал. 1.
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
CK = √AK ⋅ KB = √1 ⋅ 16 =4 (см).
2) AK = 0,5 см; KB = 8 см;
CK = �0,5 ⋅ 8 =2 (см).
AB — діаметр, C — точка кола, CK ⟂ AB, AK = 4 см; KB = 9 см;

CK = √AK ⋅ KB =
4 ⋅ 9 =6 (см).
Отже:
AM : AB = 2 : 3.
Тобто M
AM : MB = 2 : 1.
Аналогічно:
AN : NC = 2 : 1. Відповідь:
801.
Розв’язання:
Нехай O — точка перетину медіан △ABC.
1. Оскільки MN — середня лінія, то:
MN ∥ AC і MN = 1 2 AC.
2. У паралелограмі MNDE маємо:
DE ∥ MN і DE = MN.
Отже, DE ∥ AC і DE = 1 2 AC.
3. Розглянемо трикутники ODE і OAC.
Вони подібні за двома кутами (бо DE ∥ AC).
Коефіцієнт подібності: k = DE AC = 1 2 .
4. З подібності маємо:
����E OA = 1 2, тобто OE = 1 2 OA.
Отже: OE —
частина, OA — дві частини.
5. Але відомо, що точка O ділить
AO : ON = 2 : 1. Оскільки OE = 1 2 OA, то точка
AE : EN = 1 : 2.
6. Аналогічно доводиться, що: CD : DM = 1 : 2.
2 : 1, рахуючи
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
803. Чи правильно, що АK є
1) АВ = 12 см, AC = 16 см, ВK = 6 см, СK = 8 см; 2) АВ = 5 см, AC =15 см, ВK = 4 см, СK = 16 см?
Розв’язання:
AK — бісектриса ⇔ BK : CK = AB : AC.
1) BK : CK = 6 : 8 = 3 : 4, а AB : AC = 12 : 16 = 3 : 4 ⇒ так, AK — бісектриса.
2) BK : CK = 4 : 16 = 1 : 4, а AB : AC = 5 : 15 = 1 : 3 ⇒ не рівні ⇒ ні, AK — не бісектриса.
Відповідь: 1) так; 2) ні.
804. Сторони трикутника дорівнюють 8 см, 12 см, 15
трикутника ділить
8 : 12 = 2 : 3. Нехай шукані
2x + 3x = 15
5x = 15 x = 3.
Отже, відрізки:
2x = 6 см, 3x = 9 см.
Відповідь: 6 см і 9 см.
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
a + b = 3x + 5x = 8x = 60 ⇒ x = 7,5.
Отже:
a = 3x = 22,5 см, b = 5x = 37,5 см.
Відповідь: 22,5 см і 37,5 см.
806. Сторони
кута прямокутника
Розв’язання:
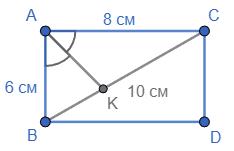
∠A = 90° (кут прямокутника),
AB = 6, AC = 8,
BC = 10 (діагональ).
Нехай AK — бісектриса ∠A
BK : KC = AB : AC = 6 : 8 = 3 : 4. Тоді діагональ BC = 10
BK = 10 · 3 3+4 = 30 7 =4
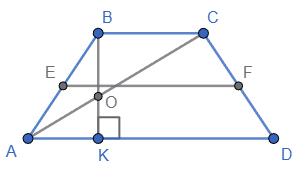
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
1. EF = (BC + AD) / 2 = (6 + 12) / 2 = 9 см. (середня лінія трапеції)
2. AB + CD = EF + 1 = 10 см, а AB = CD (рівнобічна трапеція) ⇒ AB = CD = 5 см. (рівні
бічні сторони)
3. Опустимо висоту BK на AD.
AK = (AD − BC) / 2 = (12 − 6) / 2 = 3. (рівні
4. Розглянемо трикутник ABK. Він прямокутний (BK ⟂ AD).
Промінь AC є бісектрисою ∠A трапеції, тому в △ABK відрізок AO (частина AC) є
бісектрисою ∠BAK. (за означенням)
5. За властивістю бісектриси у △ABK:
BO : OK = AB : AK = 5 : 3.
Відповідь: BO : OK = 5 : 3. 808. У рівнобедреному
висота, проведена до
— 8 см.
до його бічної сторони.
ΔABC — рівнобедрений, BK ⟂ AC.
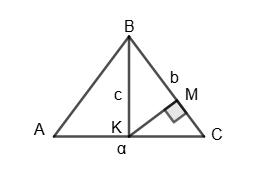
ΔBKC — прямокутний, KC
KM BK = KC BC; KM c = a 2 b ; KM = ac 2b. KM = 12 ⋅8 2⋅10 =4,8 (см).
KM = 14 ⋅24
2⋅25 =6,72 (см). 810. Діагоналі
1) а = 25 см, d1 = 30 см, d2 = 40 см;
2) а = 169 мм, d1 = 130 мм, d2 = 312 мм.
ABCD — ромб. AK — висота ромба.
ON = 1 2 MN; ON = 1 2 h; h = 2ON.
BO = OC BC ; ON = BO OC BC .
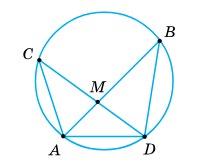
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
ΔACM ∼ ΔDBM
2) △ADM і △СВM;
3) △АBC і △АCM.
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
Дано: △ABC прямокутний,
висоти).
(ab)2 = (ch)2.
1. △ACH ∼ △ABC (за двома кутами: ∠AHC = 90° = ∠ACB, ∠CAH = ∠CAB).
AC : AB = CH : BC, тобто b : c = h : a ⇒ ah = bc.
2. △BCH ∼ △ABC (за двома кутами: ∠BHC = 90° = ∠ACB, ∠CBH = ∠CBA).
BC : AB = CH : AC, тобто a : c = h : b ⇒ bh = ac. 3.
ab = ch.
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
(ab)2 = (ch)2. Доведено. 817.
трапеції ABCD ∠A + ∠D = 90°. З т. B
BN ∥ CD.
BCDN — паралелограм.
CD = BN; ΔBKM = ΔCMD.
Тоді у ΔABM: ∠A + ∠N = 90°.
Звідси ∠ABN = 90°.
ΔABN — прямокутний, BK —
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
O1A ⟂ AC; O2B ⟂ AC; O3C ⟂ AC; O1A = r; O2B = x; O3C = R.
Проведемо O1D ⟂ O2B; O2F ⟂ O3C.
ΔO1O2D ∼ ΔO2O3F.
Тоді
O1 O2
O2 O3 = O2 D O3 F ;
r+x
R+x = x r R x ;
rR + Rx − rx − x2 = Rx − Rr + x2 − xr;
2Rr = 2x2; x2 = Rr; x = √R ⋅ r.
Отже,
3)
∠DAK = ∠CBA (за умовою).
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
4) ΔACB ∼ ΔADK, тоді AC AD = BC DK .
Звідси AC · DK = BC · AD. (I)
З
подібності ΔAKB і ΔADC: AB AC = KB DC .
Звідси AC · KB = AB · DC. (II)
Додамо почленно рівності (I) і (II). Маємо:
AC · DK + AC · KB = BC · AD + AB · DC;
AC · (DK + KB) = BC · AD + AB · DC;
AC · BD = AB · DC + BC · AD.
820. Спираючись
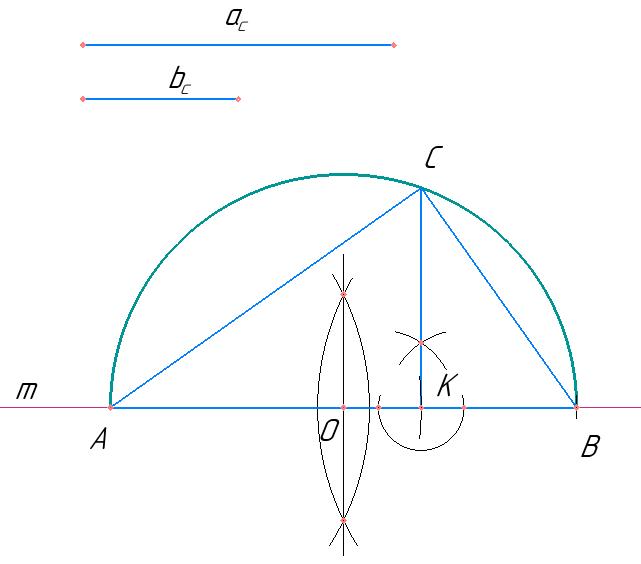
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
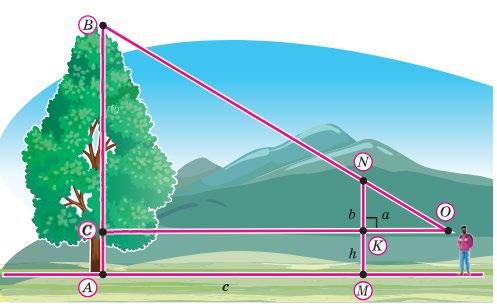
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
Знайдемо ∠C у △ABC: ∠C = 180° − (∠A + ∠B) = 180° − (60° + 40°) = 80°.
Оскільки △A1B1C1 ∼ △ABC, то
∠C1 = ∠C = 80°.
Відповідь: Б. 80°.
2. У трикутниках KLM і DEF: ∠K = ∠D = 90°, ∠M = ∠F = 30°, DF = 5KM.
DE, якщо KL = 10 см? 1.
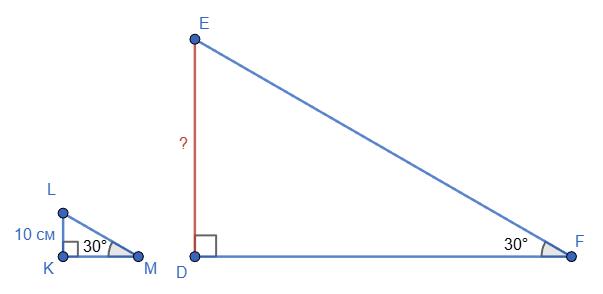
KLM ∼ △DEF
DF : KM = 5 : 1 ⇒ k = 5.
3. Тоді:
DE = k·KL = 5·10 = 50 см.
Відповідь: Г. 50 см.
3. У трикутнику зі сторонами 7 см, 15 см і
сторін.
Тобто ця
15 : 20 = 3 :
3x + 4x = 7
7x = 7 x = 1.
Отже, відрізки: 3 см і 4 см.
Відповідь: Г. 3
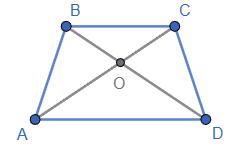
Нехай AO = 3x, OC = 2x. Тоді:
3x + 2x = 30
5x = 30
x = 6.
Отже:
AO = 18 см, OC = 12 см.
Відповідь: Г. 18 см і 12 см.
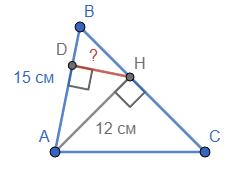
∠AHB = 90° (бо AH ⟂ BC)
∠HDB = 90° (бо HD ⟂ AB)
∠ABH = ∠HBD (спільний) Отже:
поясніть.
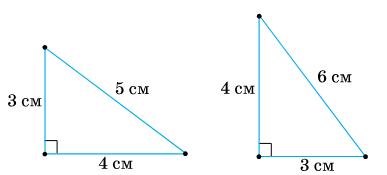
Правильно, бо 32 + 42 = 52 .
співвідношень є правильним:
1) AB = BC; — неправильно;
2) AB > BC; — неправильно;
3) AB < BC? — правильно.
827.
���� = ����� 2 + ���� 2
1. Якщо a = 12 см, b = 5 см, то
���� = √122 +52 = 13 (см).
2. Якщо a = 9 см, b = 12 см, то
���� = √92 + 122 = 15 (см).
3. Якщо a = 8 см, b = 8√3 см, то
���� = �82 +(8√3)2 = 16 (см).
828.
1. Якщо c = 13 см, b = 12 см, то ���� = √132 122 =5 (см).
2. Якщо c = 17 м, b = 15 м, то ���� = √172 152 =8 (м).
3. Якщо c = 15d, b = 9d, то ���� = �(15����)2 (9����)2 = 12����.
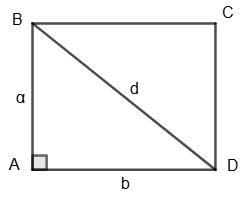
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
AC = √AB 2 + BC 2 = √2AB 2 = �2·(2√2)2 = √2·8 =4 (см)
833. Знайдіть
1) 1 см; 2) 4√2 см; 3) a.
AC = BC, тоді
AB = �AC 2 + BC 2 = �2AC 2
1. Якщо AC = 1 см, то
AB = √2·1 = √2 (см).
2. Якщо AC = 4√2 см, то
AB = �2·(4√2)2 =8 (см).
3. Якщо AC = a, то
AB = √2a2 =a√2 (см).
834. Знайдіть катети рівнобедреного
дорівнює: 1) 2 см; 2) 8 см; 3) m.
AC = BC, тоді AB2 = AC2 + BC2 або AB2 = 2AC2, тоді
AC 2 = AB 2 2 ; AC = AB √2 .
1. Якщо AB = √2 см, то
AC = √2 √2 =1 (см).
2. Якщо AB = 8 см, то
3.
(см).
2. Якщо AB = 10 см, то BD = 10√3 2 =5√3 (см).
3. Якщо AB = a, то BD = a√3 2
AB = BC, BD ⟂ AC, тоді AD = DC і з ΔABD
BD = �AB 2 AD2 = �AB 2 �AC 2 �2 .
1. Якщо AB = 26 см, AC = 20 см, то
BD = √262 102 = 24 (см).
2. Якщо AB = 17 см, AC = 16 см, то
BD = √172 82 = 15 (см).
3. Якщо AB = 13 см, AC = 10 см, то
BD = √132 52 = 12 (см).
837.
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
1. AC = 6 см, BD = 8 см,
тоді AO = 1 2· 6 = 3 (см);
BO = 1 2 · 8 = 4 (см);
AB = √AO2 +BO2 = √32 +42 =5 (см).
2. AC = 18 см, BD = 24 см, тоді
AO = 1 2 · 18 = 9 (см);
BO = 1 2 · 24 = 12 (см);
AB = √AO2 +BO2 = √92 +122 = 15 (см).
3. AC = 12 см, BD = 16 см, тоді
AO = 1 2 · 12 = 6 (см);
BO = 1 2 · 16 = 8 (см);
AB = √AO2 +BO2 = √62 +82 = 10 (см).
839.
AC = d1; BD = d2; AB = a, тоді
=
Доведення.
Розглянемо прямокутний паралелепіпед ABCDA1B1C1D1.
1.
AC2 = a2 + b2.
2.
AC). За теоремою Піфагора:
d2 = AC2 + c2 .
3. Підставляємо
Дано:діагональ d = 13 см, довжина a = 4 см, ширина b = 3 см.
Знайти: висоту c.
Розв’язання:
Для прямокутного паралелепіпеда (див. задачу 840):
d2 = a2 + b2 + c2.
Підставимо значення: 132 = 42 + 32 + c2
169 = 16 + 9 + c2
169 = 25 + c2
c2 = 144
c = 12 (см).
Відповідь: 12 см.
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
Оскільки основа — квадрат, то в грані SBC трикутник рівнобедрений:
SB = SC, а SM — висота цієї грані, отже M — середина BC.
Тоді:
BM = BC : 2 = 16 : 2 = 8 (см).
Розглянемо прямокутний трикутник SMB (∠SMB = 90°).
За теоремою Піфагора:
SB2 = SM2 + BM2
SB2 = 152 + 82
SB2 = 225 + 64
SB2 = 289
SB = 17 (см).
Відповідь: 17 см.
AB = BC = CA
Тоді:
Розглянемо
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
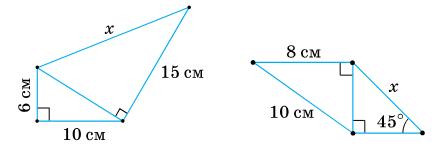
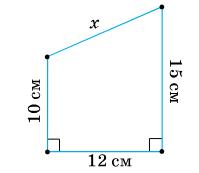
2c = b2 + 1; c = b2 +1 2
1. b = 5 см; c = 26 2 = 13 см; a = √c 2 b 2 = 12 (см).
2. b = 7 см; c = 25 см; a = 24 см.
849. Катети
гіпотенуза дорівнює: 1) 25 см; 2) 20 см.
AB = 3x; AC = 4x; BC = c.
теоремою Піфагора AB2 + AC2 = BC2; (3x)2 + (4x)2 = c2; 9x2 + 16x2 = c2; 25x2 = c2
x = � c 2 25 = c 5.
1. c = 25 см; x = 5; AB = 15 см, AC = 20 см.
2. c = 20 см, x = 4, AB = 12 см, AC = 16 см.
сторони трикутника.
AB : AC = m : n; AB = mx; AC = nx;
P = AB + BC + AC = mx + nx + ���� �(m2 +n
P = 36 см, m = 3, n = 4, 3x + 4x + 5x = 36; x = 3; AB = 9 см, AC = 12 см, BC = 15 см.
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
як 15 : 8.
a = 15x, b = 8x.
Тоді гіпотенуза:
c= �a2 +b 2 = �(15x)2 + (8x)2 = �225x 2 + 64x 2 = �289x 2 = 17x.
Периметр:
P = a + b + c = 15x + 8x + 17x = 40x.
За умовою:
40x = 80 ⇒ x = 2.
Тоді:
a = 15 ∙ 2 = 30 см,
b = 8 ∙ 2 = 16 см,
c = 17 ∙ 2 = 34 см.
Відповідь: 16 см, 30 см, 34 см.
852. Бічна сторона рівнобедреного
1) m = 5, n = 6, h = 12 см;
2) m = 17, n = 16, h = 15 см.
AB = BC;
AB : AC = m : n; BD = h; BD ⟂ AC; AB = mx; AC = nx;
AD = AC 2 = n 2 ���� .
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
m2 x 2 = n2 4 x 2 +h2 + hnx.
1. m = 5; n = 6; h = 12 см; 25x 2 = 36 4 x 2 + 144 + 72x;
x = 8; AB = 40 см; AC = 48 см.
2. m = 17; n = 16; h = 15 см; 289x2 = 64x2 + 225;
x = 1; AB = 17 см; AC = 16 см.
853. Одна
ABCD — паралелограм, AB ⟂ BD.
1. AD = 15 см, AB = 9 см;
BD = √AD2 −AB 2 = √152 −92 = 12 (см);
BO = 1 2 BD = 1 2 · 12 = 6 (см).
Із ΔABO:
AC = 2AO = 6√13 (см).
2. AD = 25 см; AB = 7 см.
ΔABD:
= √AD2 AB 2 = √252 72 = 24 (см),
BO = 1 2 BD = 1 2 · 24 = 12 (см). Із ΔABO:
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
1) а = 4 см, b = 12 см, h = 6 см;
2) а = 35 см, b = 15 см, h = 21 см.
AD ∥ BC; AB ⟂ AD; CH ⟂ AD, тоді DH = AD − BC; CK = h.
1. BC = 4 см; AD = 12 см; CK = 6 см.
Із ΔCHD:
CD = �(AD BC)2 +CH 2 = �(12 4)2 +62 = √82 +62 = 10 (см)
2. BC = 15 см; AD = 35 см; CK = 21 см.
Із ΔCHD:
CD = �(AD BC)2 +CH 2 = �(35 15)2 +212 = 29 (см)
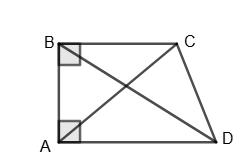
2 − AC2 = (AB2 + AD2) − (AB2 + BC2) = AB2 + AD2 − AB2 − BC2 = AD2 − BC2,
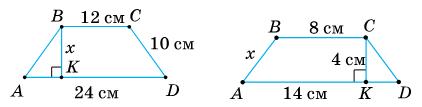
1. AB = CD = 10 см; AD = BC + 2AK =
BC = 12 см ⇒ AK = 6 см.
x= √AB 2 AK 2 = √100 36 =8 (см).
2. KD = AD BC 2 = 14 8 2 =3 (см); CK = 4 см.
x= √KC 2 +KD2 = √9+ 16 =5 (см).
857. За
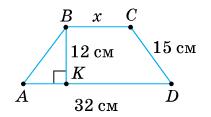
AK = √AB 2 BK 2 = √152 122 =9 (см).
x = BC = AD − 2AK = 32 – 2 · 9 = 14 (см).
858. Основи рівнобічної
якщо:
1) а = 6 см, b = 18 см, h = 16 см; 2) а = 16 см, b = 8 см, h = 5 см.
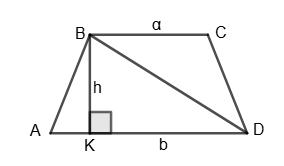
AB = CD; BC ∥ AD;
AD = BC + 2AK = q + 2AK = b; AK = b a 2 ;
AK = �h2 +KD2 = �h2 + �b b a 2 � 2 .
1. a = 6 см; b = 18 см; h = 16 см;
BD = �25 �18 18 6 2 �2 = √400 = 20 (см)
2. b = 16 см; a = 18 см; h = 5 см;
BD = �25 + �16 − 16 8 2 �2 = √25 + 144 = 13 (см)
1) а = 2 см, b = 18 см, r = 3 см; 2) а = 32 см, b = 18 см, r = 12 см.
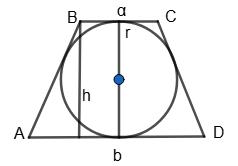
AB = CD. h = 2r = d;
1. a = 2 см; b = 18 см; r = 3 см;
AB = ��18 2 2 �2 + (2·3)2 = √64 + 36 = 10 (см)
2. b = 32 см; a = 18 см; r = 12 см;
AB = ��32 18 2 �2 + (2· 12)2 = √49 + 576 = 25 (см)
— ромб, BH ⟂ AD, AH = b, HD = c, тоді AB = b + c.
ΔABH: BH = �AB 2 AH 2 = �(b+c)2 b 2
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
1. Якщо b = 6 см, c = 4 см, то
BH = √102 62 =8 (см),
тоді r = 1 2 BH = 1 2 · 8 = 4 (см).
2. Якщо b = 5 см, c = 8 см, то
BH = √132 52 = 12 (см),
тоді r = 1 2 BH = 1 2 · 12 = 6 (см).
861. У колі радіусом r
хордами, якщо:
OB = OD = r, AB ∥ CD, KL ⟂ AB, KL ⟂ CD.
1. r = 25 см, AB = 48 см, CD = 40 см.
Із ΔOBK:
Тоді: 1 випадок — KL = OL − OK = 15 − 7 = 8 (см);
2 випадок — KL = OL + OK = 15 + 7 = 22 (см).
2. r = 65 см, AB = 120 см, CD = 32 см.
Із ΔOBK:
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
O���� = √OB 2 −KB 2 = √652 −602 = 25 (см).
Із ΔOLD:
O���� = √OD2 −LD2 = √652 −162 = 63 (см).
Тоді: 1 випадок — KL = OL − OK = 63 − 25 = 38 (см);
2 випадок — KL = OL + OK = 63 + 25 = 88 (см).
862. Два кола
їхньої
OO1 = B1B; OB1BO1 — паралелограм, OA ⟂ AB; O1B ⟂ AB; OA ∥ O1B; O1B = OB1 = 2 см; OO1 = R1 + R2 = OA + O1B = 8 + 2 =
AB1B:
= �����1 B 2 ����1 A2 = √102 62 =8 (см
1) 30°;
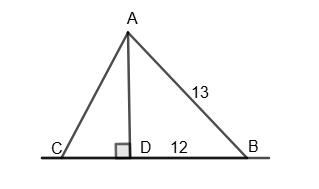
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
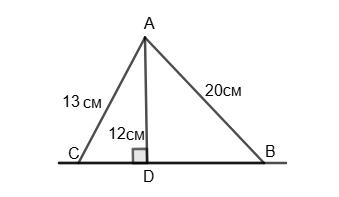
CB = √132 122 = √169 144 =5 (см)
DB = √202 122 = √200 144 = 16 (см).
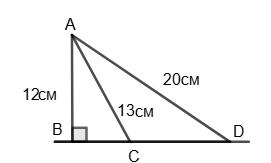
1. CD = CB + BD = 5 + 16 = 21 (см);
2. CD = BD − BC = 21 − 5 = 16 (см).
Задача має два розв’язки.
865. Із точки до прямої проведено
відносяться як 2 : 5. Знайдіть:
1) проєкції похилих;
2) відстань від точки до прямої.
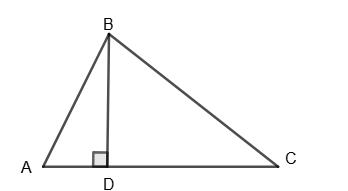
AB = 10 см, BC = 17 см, AD : DC = 2 : 5.
10 см і 17 см.
Нехай AD = 2x см; DC = 5x см, тоді 102 − (2x)2 = 172 − (5x)2; 100 − 4x2 = 289 − 25x2; 21x2 = 189; x2 = 9; x = 3.
1. Тоді AD = 2 ·3 = 6; DC = 5 · 3 = 15 (см).
2. B���� = √�������� 2 AD2 = √102 62 =8 (см).
ABD = ΔACD (AD —
BD = DC,
867.
1) m = 25 см, n = 24 см;
2) m = 17 см, n = 15 см.
∠ACB = 90°; CH ⟂ AB; AM = MB; CH = n; CM = m, тоді AB = 2CM = 2m; HM = √CM 2 CH 2 = √m2 n2 .
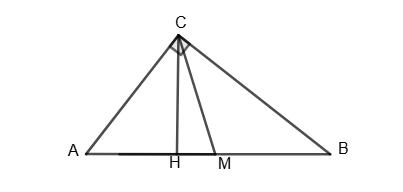
1. Якщо m = 25 см, n = 24 см, тоді AB = 2 · 25 = 50 (см); HM = √252 242 =7 (см). Із ΔACH
AC = √HC 2 + AH 2 = �242 +(25 7)2 = 30 (см)
BC = √AB 2 AC 2 = √502 302 = 40 (см).
P = 30 + 40 + 50 = 120 (см).
2. Якщо m = 17 см, n = 15 см, тоді AB = 2 17 = 34 (см);
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
HM = √172 − 152 =8 (см).
Тоді AH = 17 − 8 = 9 (см); HB = 8 + 17 = 25 (см).
Із ΔACH:
AC = √92 + 152 = √306 = 3√34 (см).
Із ΔBCH:
BC = √152 + 252 = √850 = 5√34 (см).
P = 34 + 5√34 +3√34 = 34 + 8√34 (см).
869. У
1) b = 60, n = 12;
2) b = 35, n = 14.
AC = b; AB + BC = AC + n; AB + BC = b + n.
1. Якщо b = 60, n = 12, тоді AB + BC = 72, BC = 72 − AB.
AB2 = AC2 + BC2, AB2 = 602 + (72 − AB)2;
AB2 = 3600 + 5184 − 144AB + AB2; 144AB = 8784; AB = 61.
BC = 72 − 61 = 11.
2. Якщо b = 35, n = 14, тоді AB + BC = 49, BC = 49 − AB; AB2 = AC2 + BC2, AB2 = 352 + (49 − AB)2; AB2 = 1225 + 2401 − 98AB + AB2; 98AB = 3626; AB = 37.
BC = 49 − 37 = 12.
870. Висота
інші сторони трикутника, якщо:
1) с = 60 см, h = 12 см, m = 13 см;
2) с = 42 см, h = 12 см, m = 13 см.
CH ⟂ AB, CH = h, AM = MB, CM = m, AM = MB = c 2 .
1) 10 см, 10 см, 12 см; 2) 7 см, 15 см, 20 см.
1. AB = BC = 10 см, AC = 12 см, BD ⟂ AC, AK ⟂ BC, AD = DC = 1 2 AC = 1 2 ·12 = 6 (см).
Із ΔABD:
BD = √AB 2 AD2 = √102 62 =8 (см).
Нехай BK = x, тоді 102 − x2 = 122 − (10 − x)2; 100 − x2 = 144 − 100 + 20x − x2; 20x = 56; x = 2,8.
AK = √AB 2 BK 2 = √100 7,84 = √92,16 = 9,6 (см).
CL = AK = 9,6 см.
2. BC = 7 см, AB = 15 см, AC = 20 см.
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
AK = x, KC = 20 − x, тоді AB2 − AK2 = BC2 KC2; 152 − x2 = 72 − (20 − x)2; 225 − x2 = 49 − 400 + 40x − x2; 40x = 576; x = 14,4.
BK = √AB 2 AK 2 = �152 14,42 =4,2 (см)
BH = y; тоді HC = 7 − y;
AB2 − BH2 = AC2 − HC2; 152 − y2 = 202 − (7 − y)2; 225 − y2 = 400 − 49 + 14y − y2; 14y = −126; y = −9;
AH = √AB 2 BH 2 = √152 92 = √225 81 = 12 (см)
BL = z, тоді AL = 15 − z;
BC2 − BL2 = AC2 − AL2; 72 − z2 = 202 − (15 − z)2; 49 − z2 = 400 − 225 + 30z − z2; 30z = −126; z = −4,2;
LC = √BC 2 BL2 = �72 4,22 =5,6 (см)
872. Доведіть, що сума
його сторін.
CM = BN; AN = DM.
ΔNBD: BD2 = BN2 + ND2 = BN2 + (AD − AN)2.
ΔACM: AC2 = CM2 + AM2 = BN2 + (AD + AN)2. BN2 = AB2 − AN2; AC2 + BD2 = BN2 + (AD + AN)2 + BN2 + (AD − AN)2 = = AB2 − AN2 + AD2 + 2AD AN + AN2 + AB2 − AN2 + AD2 − 2AD AN + AN2 = = AB2 + AD2 + AB2 + AD2 = 2AB2 + 2AD2, що
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
BD2 = BK2 + KD2 = (AB2 + AK2) = (AD − AK)2 + d1 2 .
ΔACL: AC2 = AL2 + CL2 = (AD − LD)2 + (CD2 − LD)2 = d2 2 .
d12 + d22 = (c2 − AK2 + b2 − 2b·AK + AK2) + ((b2 − 2b · LD + LD2 + d2 − LD2) = = c2 + b2 − 2b · AK + b2 − 2b · LD + d2 = c2 + d2 − 2b(AL + LD) + 2b2 = = c2 + d2 − 2b(b − a) + 2b2 = c2 + d2 − 2b2 + 2ab + 2b2 = c2 + d2 + 2ab.
874. Доведіть, що
1) рівні хорди рівновіддалені
⊥ AB, O1B
OC2 = OO2 1 – O1C2 , OO1 = OD + DO1 = r + R. Тоді OC2 = (r + R)2 – (R
Дано: кола K1(O; 10 см), K2(O1; 2 см); OO1 = 10 см.
Знайти: AB.
Розв’язання:
△OCA ~ △O1CB (за двома кутами);
k = OA
O1 B = 6 2 = 3.
Нехай OC = x см, тоді CO1 = (10 − x) см.
OC
CO1 = x 10 x ; x 10 x =3;
x = 30 − 3x
x + 3x = 30
4x = 30
x = 7,5
Отже, OC = 7,5 см, CO1 = 10 − 7,5 = 2,5 см.
У △OAB (∠A = 90°):
OC2 = OA2 + AC2
AC = √OC 2 OA2 = �7,52 6
AC
CB = 3, отже CB = AC : 3 = 4,5 : 3 = 1,5 (см).
AB = AC + CB = 4,5 + 1,5 = 6 (см).
Відповідь: 6 см.
877. (Задача
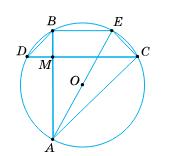
DBM: ∠DMB = 90°; DB2 = DM2 + MB2. ΔAMC: ∠AMC = 90°; AC2 = AM2 + MC2.
(см).
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
Дано: AM = 7 м, BN = 3 м, CB = 15 м.
Знайти: AB.
Розв’язання: AC = AM − CM = 7 − 3 = 4 (м).
△ABC (∠C = 90°): AB2 = AC2 + CB2
AB = �AC 2 +CB 2 = �42 + 152 =
15,5 м. 880. Діагональ
Дано: ABCD прямокутник; AC = 116 м, AD = 84 м.
Знайти: PABCD.
Розв’язання:
△ADC (∠D = 90°):
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
AC2 = AD2 + CD2
CD = �AC 2 AD2 = �1162 842 = √13456 7056 = √6400 = 80(м).
PABCD = 2(AD + CD) = 2(84 + 80) = 2 · 164 = 328 (м).
Відповідь: 328 м.
881. 1.
2,5 м?
1. AB, якщо AC = 2,5 м;
2. AC, якщо AB = 9 м.
Розв’язання:
1. △ABC (∠C = 90°):
AB 2 =BC 2 +AC 2
= �BC 2 +AC
2. △ABC (∠C = 90°):
Дано: АВ = 10 футів; ОD = ОD1; CD = 1 фут. Знайти: OC.
Розв’язання:
D1C = AO = 1 2 AB = 1 2 ∙ 10 = 5 футів.
Нехай глибина копанки OC = х футів, тоді
футів.
D1O = (x + 1) футів.
∆D1CO (∠C = 90°): D1O2 = OC2 + D1C2;
(x + 1)2 = x2 + 52;
x2 + 2x + 1 = x2 + 25;
2x = 24;
x = 12 (футів) –
Відповідь: 12 футів.
OD = OC + CD = (x + 1)
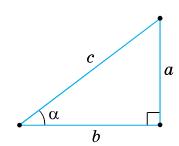
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
3. ���� ���� = sin α; ���� ���� = cos α; ���� ���� = tg α.
884. Назвіть правильну
1) tg β дорівнює: а) 5 15; б) 12 5 ; в) 5 13;
2) cos β дорівнює: а) 12 13; б) 13 5 ; в) 5 13;
3) sin β дорівнює:
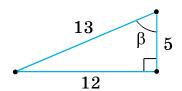
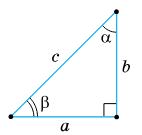
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
1) синус кута зменшується;
2) синус кута збільшується;
3) косинус кута зменшується;
4) косинус кута збільшується;
5) тангенс кута зменшується;
6) тангенс кута збільшується?
1) Ні;
2) так;
3) так;
4) ні;
5) ні;
6) так.
887. Чи є правильною рівність: 1)
1) Ні; 2) так; 3) ні;
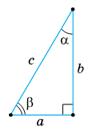
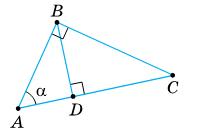
1) 1; 2) 0,9; 3) 2?
1. так; 2. так; 3. ні.
891. Чи
0,8?
1. так; 2. так; 3. так.
892. Знайдіть значення
1) 2 sin 30°; 2) 4 cos 60°; 3) √3 tg 30°; 4) 6 sin 45°; 5) 2 cos 30°; 6) 8 tg 45°.
1. 2 sin 30° = 2 · 1 2 = 1;
2. 4 cos 60° = 4 · 1 2 = 2;
3. √3 tg 30° = √3 · 1 √3 = 1.
893. Знайдіть значення
1) 1; 2) 4; 3)
1) 8 sin 30° · cos 60°; 2) √2 cos 45° − 2 sin 30°.
1) 2; 2) 0.
896. Яка
3.
897. Яка
1) 45°; 2) 30°; 3) 30°.
898. Запишіть у порядку збільшення:
1) sin 15°, sin 46°, sin 75°, sin 10°, sin 11°;
2) tg 37°, tg 87°, tg 66°, tg 17°, tg 48°.
1. sin 10°; sin 11°; sin 15°; sin 46°; sin 75°
2. tg 17°; tg 37°; tg 48°; tg 66°; tg 87°.
899. Запишіть у порядку збільшення:
cos 50°, cos 34°, cos 20°, cos 72°, cos 25°.
cos 72°; cos 50°; cos 34°; cos 25°; cos 20°; 900. За даними,
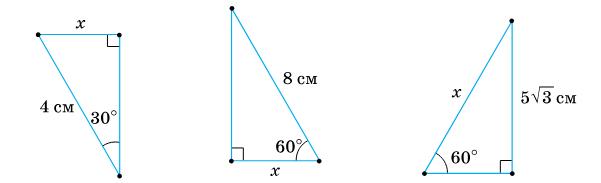
���� = 4sin 30∘ =4· 1 2 =2 (см)
���� = 8cos 60∘ =8· 1 2 =4 (см) ���� = 5√3 sin 60∘ = 5√3·2 √3 = 10 (см).
901. За
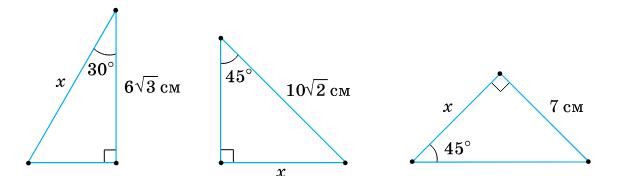
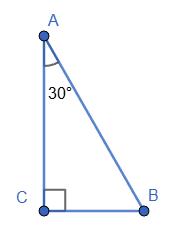
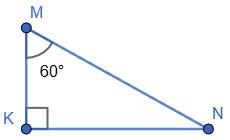
1) cos20° = sin(90° – 20°) = sin70°; cos35° = sin(90° – 35°) = sin55°; cos50° = sin(90° – 50°) = sin40°;
2) sin10° = cos(90° – 10°) = cos80°; sin65° = cos(90° – 65°) = cos25°; sin85° = cos(90° – 85°) = cos5°.
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
1) косинуси
синуси: cos 40°, cos 74°; 2) синуси
sin 55°, sin 25°.
1) cos40° = sin(90° – 40°) = sin50°; cos74° = sin(90° – 74°) = sin16°.
2) sin55° = cos(90° – 10°) = cos80°; sin25° = cos(90° – 25°) = cos35°.
907. Спростіть вираз:
1) 2 cos (90° – α) – sin α;
2) sin α + cos (90° – α);
3) 3 cos α – 2 sin (90° – α);
4) 3 sin (90° – α) – 4 cos α
1. 2 cos(90° − α) − sin α = 2 sin α − sin α = sin α;
2. sin α + cos(90° − α) = sin α + sin α = 2 sin α;
3. 3 cos α − 2 sin(90° − α) = 3 cos α − 2 cos α = cos α. 908. Спростіть вираз:
1) sin (90° – α) – cos α; 2) cos α – 2 sin (90° – α).
1) sin(90° – α) – cosα =

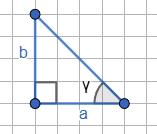
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
x = c cos α. x = c sin α. x = b tg α.
912. За
1) с = 12 см, sin A = 1 4;
2) с = 20 см, sin A = 2 5;
3) с = 18 см, sin A = 2 3;
4) с = 8 см, sin A = 3 4 .
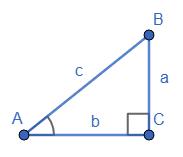
1. a = c sin ∠A = 12 · 1 4 = 3 (см);
2. a = c sin ∠A = 20 · 2 5 = 8 (см);
3. a = c sin ∠A = 18 · 2 3 = 12 (см);
4. a = c sin ∠A = 8 · 3 4 = 6 (см).
1) с = 6 см, cos A = 1 3;
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
2) с = 14 см, cos A = 2 7 .

1. b = c cos ∠A = 6 · 1 3 = 2 (см);
2. b = c cos ∠A = 14 · 2 7 = 4 (см).
915.
1) ВС = 16 см, cos B = 1 8;
2) ВС = 12 см, cos B = 3 4 ;
3) ВС = 5 см, cos B = 0,5;
4) ВС = 7 см, cos A = 0,7.
1. AB = BC cos ∠B = 16 ∶ 1 8 = 16 1 · 8 1 = 128.
2.
3. AC = BC tg ∠B = 5 ·
4. AC =
1) ВС = 24 см, sin A = 3 8;
2) ВС = 10 см, sin A = 1 5 .
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html

1. AB = BC sin ∠A = 24 ∶ 3 8 = 24·8 3 = 64 (см).
2. AB = BC sin ∠A = 10 ∶ 1 5 = 10 5 1 = 50 (см).
917. Знайдіть
1) АС = 8 см, tg A = 0,6;
2) AC = 12 см, tg A = 4;
3) AC = 11 см, tg A = 1,5.

1. BC = AC tg ∠A = 8 · 0,6 = 4,8;
2. BC = AC tg ∠A = 12 · 4 = 48;
3. BC = AC tg ∠A = 11 · 1,5 = 16,5.
918. Знайдіть
1) AB = c, ∠B = β;
2) BC = a, ∠A = α;
3) AC = b, ∠B = β.
АВС (∠C = 90°), якщо:
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
2. У ΔABC ∠C = 90°; BA = a sin α ; AC = a tg α .
3. У ΔABC ∠C = 90°; AB = b sin β ; BC = b tg β. 919. Скориставшись
1) sin α, cos α, tg α, якщо α дорівнює: 43°; 22°; 35°; 58°20′; 64°13′;
2) кут α, якщо:
sin α дорівнює: 0,642; 0,771; 0,910; 0,640; 0,712; cos α дорівнює: 0,342; 0,962; 0,087; 0,914; 0,809; tg α дорівнює: 0,178; 0,269; 0,035; 0,447; 0,532.
1. sin 43° 6′ ≈ 0,683; sin 22° 25′ ≈ 0,381;
sin 35° 48′ = 0,585; sin 58° 20′ = 0,851;
cos 43° 6′ = 0,730; cos 22° 25′ = 0,925;
cos 35° 48′ = 0,811; cos 58° 20′ ≈ 0,525;
tg 43° 6′ ≈ 0,936; tg 22° 25′ = 0,412;
tg 35° 48′ = 0,721; tg 58° 20′ ≈ 1,619;
sin 64° 13′ ≈ 0,900; sin 39° 21′ = 0,634;
sin 54° 12′ = 0,811; sin 83° 18′ ≈ 0,993;
cos 64° 13′ ≈ 0,435; cos 39° 21′ = 0,773;
cos 54° 12′ = 0,585; cos 83° 18′ = 0,117;
tg 64° 13′ = 2,069; tg 39° 21′ = 0,820;
tg 54° 12′ = 1,387; tg 83° 18′ = 8,513;
2. sin α = 0,642, α = 39,9°;
sin α = 0,771, α = 50,4°; sin α = 0,910, α = 65,5°;
sin α = 0,640, α = 39,8°;
sin α = 0,712, α = 45,4°; sin α = 0,750, α ≈ 48,6°;
sin α = 0,515, α = 31°;
sin α = 0,892, α = 63,1°;
cos α = 0,342, α = 70°;
cos α = 0,962, α = 15,8°;
cos α = 0,087, α = 85°;
cos α = 0,914, α = 23,8°;
cos α = 0,809, α = 36°;
cos α = 0,602, α = 53°;
cos α = 0,915, α = 23,8°;
cos α = 0,839, α = 33°;
tg α = 0,178, α = 10,1°;
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
tg α = 0,269, α = 15,1°;
tg α = 0,035, α = 2°;
tg α = 0,447, α ≈ 24,1°; tg α = 0,532, α = 28°;
tg α = 0,934, α = 43°;
tg α = 0,781, α = 38°; tg α = 0,578, α = 30°. 920. Скориставшись калькулятором, знайдіть:
1) sin α, cos α, tg α,
якщо a дорівнює: 39°; 54°12′;
2) кут α, якщо:
sin α дорівнює: 0,750; 0,515; cos α дорівнює: 0,602; 0,915; tg α дорівнює: 0,934; 0,781.
1) Якщо α = 39°, то:
sin α = 0,629; cos α = 0,777; tg α = 0,809;
Якщо α = 54°12′, то:
sin α = 0,811; cos α = 0,585; tg α = 1,387;
2) Якщо sin α = 0,750, то α = 48°35′;
Якщо sin α = 0,515, то α = 31°;
Якщо cos α = 0,602, то α = 52°59′;
Якщо cos α = 0,915, то α = 23°48′;
Якщо tg α = 0,934, то α = 43°3′;
Якщо tg α = 0,781, то α = 37°59′.
921. За таблицями (додатки 1, 2) знайдіть:
1) sin 20°, sin 75°, sin 33°, sin 85°; 2) cos 6°, cos 67°, cos 51°, cos 24°;
3) tg 65°, tg 1°, tg 73°, tg 19°.
1) 0,342; 0,966; 0,545; 0,996; 2) 0,994; 0,391; 0,629; 0,913; 3) 2,14; 0,017; 3,27; 0,344.
922. За таблицями (додатки 1, 2) знайдіть:
1) sin 53°, sin 2°; 2) cos 62°, cos 13°; 3) tg 10°, tg 16°.
1) 0,799; 0,035; 2) 0,469; 0,974;
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
3) 0,176; 0,287.
923. За таблицями (додатки 1, 2) знайдіть кут α, якщо:
1) sin α = 0,999; sin α = 0,017; sin α = 0,574;
2) cos α = 0,766; cos α = 0,966; cos α = 0,225;
3) tg α = 0,900; tg α = 0,344; tg α = 0,781.
1) 88°, 1°, 35°;
2) 40°, 15°, 77°; 3) 42°, 19°, 38°.
924. За таблицями (додатки 1, 2) знайдіть
1) sin α = 0,588;
2) cos α = 0,731;
3) tg α = 0,839.
1) 36°; 2) 43°; 3) 40°.
925. У прямокутному трикутнику ABC (∠C = 90°) AC
1) sin A, cos A, tg A;
2) sin B, cos B, tg B.
AC = 18 мм, BC = 24 мм, AB = √AC 2 + BC 2 = √182 + 242 = 30 (мм).
1. sin ∠A = BC AB = 24 30 =0,8; cos ∠A = AC AB = 18 30 =0,6; tg ∠A = BC AC = 24 18 =1,3;
2. sin ∠β = AC AB = 18 30 =0,6; cos ∠β = BC AB = 24 30 =0,8; tg ∠β = AC BC = 18 24 =0,75; 926.
A; 2)
B. У ΔABC ∠C = 90°.
BC = √225 81 = √144 = 12 (см).
1.
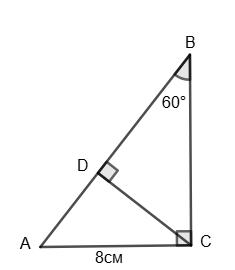
BK.
△KBC (∠C = 90°):
∠KBC = BC BK
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
1) основу трикутника;
2) висоту, проведену до основи;
3) висоту, проведену до бічної сторони.
Дано: △ABC; ∠A = 30°; AB = BC = 10 см.
Знайти: 1. AC; 2. BD; 3. DM.
=2· AD =2·5
= BD AB
3. △ADM (∠M = 90°): sinA = DM AD
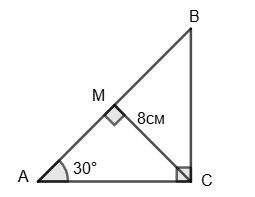
У △ABC ∠C = 90°, CM – медіана, яка
У △ABC ∠C = 90°;
AC = ABcos 30∘ = 16 · √3 2 =8√3 (см);
BC = ABsin 30∘ = 16 · 1 2 =8 (см).
934.
тому AB = 2CM, AB = 2 · 8 = 16 (см).
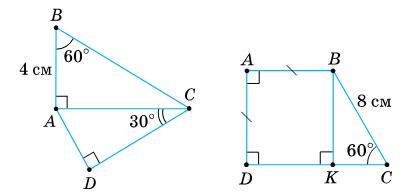
1. У △ABC ∠A = 90°;
AC = 4 tg 60° = 4√3 (см).
У △ACD ∠D = 90°;
AD = AC sin 30∘ =4√3 · 1 2 =2√3 (см);
CD = ACcos 30∘ =4√3 · √3 2 =6 (см).
AD і CD.
2. У прямокутній трапеції BK ⟂ DC, тому ABKD – прямокутник, у якого AB = DK = 6 см, BK = AD.
У △BKC ∠K = 30°; BC = 8 см, тоді
KC = BC ∙ cos60∘ =8· 1 2 =4 (см);
CD = DK + KC =6+4= 10 (см).
935. За
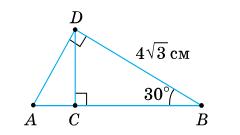
AD і CD.
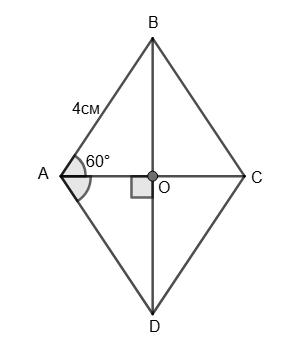
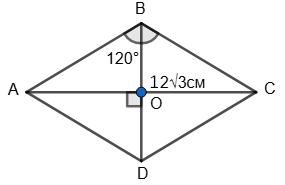
AB = AO
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
sin 60∘ = 6√3·2 √3 = 12 (см);
BO = AO
tg60∘ = 6√3 √3 =6 (см).
Оскільки BO = 1 2 BD, то BD = 2BO = 2 · 6 = 12 (см).
938. Діагональ паралелограма
сторони паралелограма, якщо
1) У △ACD ∠C = 90°, бо AC ⟂ CD за умовою.
AD = AC si n30∘ = 12 2 1 = 24 (см);
CD = AC tg30∘ = 12·3 √3 = 12(√3)2 √3 = 12√3 (см);
AB = CD = 12√3 (см)
AD = BC = 24 (см).
2) △ACD (∠C = 90°): ∠DAC = 90° ∠D = 90° 45° = 45°. ∠D = ∠CAD, тоді △ACD — рівнобедрений, AC = CD = 12 (см). AD
Відповідь: 1) 12√3
1) 30°; 2) 45°.
кут: 1) 30°; 2) 60°.
Якщо в ромб
BF ⟂ AD.
У △ABF ∠F = 90°;
1) Якщо гострий кут дорівнює 30°, то:
BF = AB sin 30° = 16 · 1 2 = 8 (см).
Якщо BF = 8 см, то діаметр
r = 8 : 2 = 4 (см).
2) Якщо гострий кут дорівнює 60°, то:
BF = AB sin 60° = 16 · √3 2 = 8√3 (см).
Якщо BF = 8√3 см, то
r = 8√3 : 2 = 4√3 (см).
Відповідь: 1) 4 см; 2) 4√3 см.
941.
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
AB ⟂ CD, AB
1) У △ABC ∠B = 90°;
AC = AB sin 45∘ = 5·2 √2 =5√2 (см);
CB = ABtg45∘ = 5 1 =5 (см).
2) У △ABD ∠B = 90°;
AD = AB sin 30∘ = 5 2 1 = 10 (см);
BD = AB tg30∘ = 5·3 √3 =5√3 (см). 943. Із
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
∠B = ∠C = 45°,
∠A = 180° − (45° + 45°) = 90°, тобто △ABC — рівнобедрений
AB = AC · sin 45° = 10 · √2 2 =5√2 (см) 944. У
1) sin A, cos A, tg A;
2) sin B, cos B, tg B.
AC = 18 мм, BC = 24 мм, AB = √AC 2 + BC 2 = √182 + 242 = 30 (мм).
1. sin ∠A = BC AB = 24 30 =0,8;
cos ∠A = AC AB = 18 30 =0,6;
tg ∠A = BC AC = 24 18 =1,3;
2. sin ∠β = AC AB = 18 30 =0,6;
cos ∠β = BC AB = 24 30 =0,8;
tg ∠β = AC BC = 18 24 =0,75;
945.
1) sin A = 0,4;
2) tg A = 1 3 .
1. sin ∠A=0,4= 2 5 .
трикутник ACB (∠C = 90°),
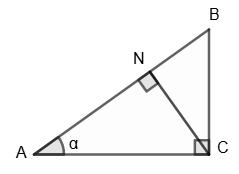
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
У ΔAMC ∠C = 90°; ∠MAC = ∠A 2 = α 2 , бо AM —
Тоді AC = AM cos ∠A 2 = l cos α 2 . 949. Бічна сторона
1) основу трикутника;
2) висоту, проведену до основи.
рівнобедреному ΔABC проведемо висоту BD,
— α. Знайдіть: 1) бічну сторону трикутника; 2) основу трикутника.
1. h sin α ; 2. 2h tg α .
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
У ΔABC AB = BC, AC = a. Проведемо
Тому AD = DC = α 2 ; ∠ABD = ∠CBD = α 2 ;
У ΔABD ∠D = 90°; BD = AD tg α 2 = a 2tgα 2 ;
AB = AD sin α 2 = a 2sin α 2 .
Відповідь: 1. a 2tgα 2 ; 2. a 2sinα 2 . 952. За даними, наведеними
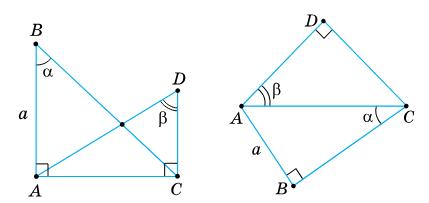
Мал. 1
У ΔABC ∠A = 90°; AC = AB + tg α = a tg α.
У ΔACD ∠C = 90°; AD = AC sin β = a tg α sin β ;
CD = AC tg β = a tg α tg β .
Мал. 2
У ΔABC ∠B = 90°;
AD = AC cos β = a cos β sin α
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
DC = AC sin β = a sin β sin α . 953. Знайдіть
AD і CD
1. ΔABC ∠C = 90°; AC = BC tg α; ∠CAB = 90° − α.
2. У ΔADC ∠D = 90°; ∠CAD = ∠A − ∠CAB; ∠CAD = 90° − (90° − α) = 90° − 90° + α = α.
Тоді AD = AC cos ∠CAD = a tg α cos α = a sin α cos α cos α = a sin α;
DC = AC sin ∠CAD = a tg α sin α. 954. Знайдіть
m, а
1) У ΔAOD ∠D = 90°, ∠OAD = α 2 , бо AO —
AD = OD �������� α 2 = R �������� α 2 і AC = 2AD = 2R �������� α 2 .
2) У ΔABD ∠D = 90°; ∠A = α; BA = AD cos α = R �������� α 2 cos α . 957. Висота
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
2) діагональ прямокутника. ΔAOD — рівнобедрений, де в прямокутнику
тобто AO = OB = OC = OD,
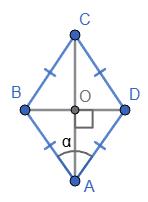
1)
2)
1.
2.
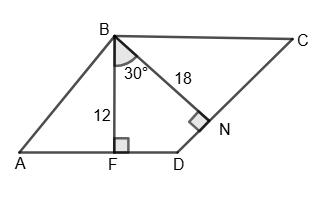
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
△BCN ∠N = 90°; BC = BN cos 60∘ ; BC = 18 2 1 = 36 (см);
AD = BC = 36 см; ∠C = 90° − 60° = 30°; У △ABF ∠F = 90°; ∠A = ∠C = 30° —
AB = BF sin 30∘ ; AB = 12·2 1 = 24(см);
AB = CD = 24 см. 964.
— 150°.
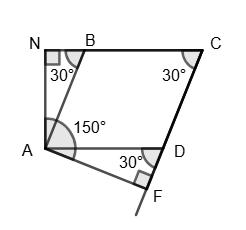
AN ⟂ BC і AD ⟂ DC. Оскільки BC =
чотирикутнику ANCF сума
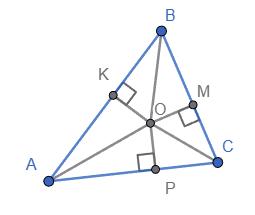
△ABC —
Знайти: AB, BC, AC.
Розв’язання:
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
△AOK (∠K = 90°): ∠OAK = 1 2 ∠A = ���� 2 .
tg∠OAK = OK AK , тому
AK = OK tg∠OAK = r tg(α/2) ; AP = AK = r tg(α/2) .
△BKO (∠K = 90°):
KB = r tg(β/2) ; BM = KB = r tg(β/2) .
△CMO (∠M = 90°):
MC = r tg(γ/2) ; PC = MC = r tg(γ/2) .
AB = AK + KB =
+
BC = BM + MC = r tg(β/2) +
AC = AP + PC = r
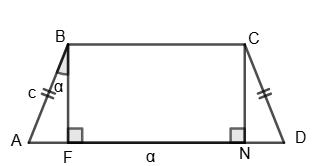
ΔABF = ΔDCN,
У ΔABF ∠F = 90°; AF = AB sin α = c sin α. Тоді AD = AF + FN + ND = FN + 2AF; AD = b + 2c sin α.
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
Проведемо
FN, і
рівні

ΔABF = ΔDCN, у яких AF = ND. У ΔABF ∠F = 90°; AF = AB sin α = c sin α.
Оскільки AD = NM = c sin α, AD = a;
FN = BC = AD − 2AF; BC = FN = a − 2c sin α. 968. У рівнобічній
b. Знайдіть:
1)
Дано: AD = 20 м; tg А = 0,8. Знайти: BC.
Розв’язання
∆ABD – рівнобедрений, тоді BC є медіаною і
АС = 1 2 AD = 1 2 ∙ 20 = 10 (м).
∆АСВ (∠C = 90°): tgA = BC AC .
BC = AC ∙ tg A = 10 ∙ 0,8 = 8 (м).
Відповідь: 8 м.
970.
рівнобічна трапеція, дорівнює 60
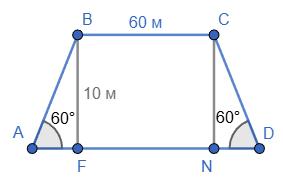

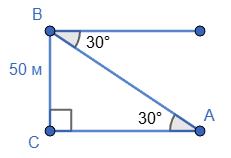
https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
1) Ні; 2) так; 3) ні; 4) ні; 5) так. 974.
трикутник:
1) за кутами;
2) за катетами;
3)
6) за гіпотенузою й гострим
1) Ні; 2) так; 3) ні; 4) так;
5) ні; 6) так; 7) ні; 8) так.
975. За
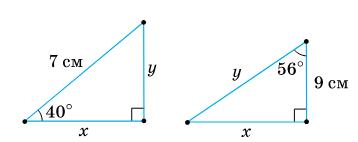
1) x = 7 cos 40° = 7 · 0,766 = 5,362 (см); y = 7 sin 40° = 7 · 0,643 = 4,501 (см).
2) x = 9 tg 56° ≈ 9 · 1,483 = 13,347 (см); ���� = 9 cos 56∘ ≈ 9 0,559 ≈ 16,1 (см).
976. За
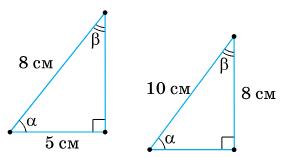
cos α = 5 8 = 0,625, α = 51°, тоді
8 10 = 0,8, β = 37°,

https://shkola.in.ua/3333-hdz-heometriia-8-klas-burda.html
BC = AB sin ∠C = 9 sin 38∘ = 9 0,616 = 14,6
2. AB = 10 см, ∠B = 54°.
BC = AB cos ∠B = 10 cos 54 ∘ = 10 0,588 = 17 (см);
AC = ABtg54∘ = 10 ·1,376 = 13,76 (см).