International Research Journal of Engineering and Technology (IRJET) e-ISSN:2395-0056
Volume: 12 Issue: 05 | May 2025 www.irjet.net p-ISSN:2395-0072
Simulation-Based Performance Evaluation of PID and Neural Network Controllers for DC Motor Speed Regulation
Dr Sandhya Kulkarni 1, Vaibhav Badgujar 2, Kailash Dalui 3, Umesh Bujade 4
1Faculty, Department of Electrical Engineering,Government College of Engineering,Aurangabad,Chh
Sambhajinagar, Maharashtra, India
²UG Student, Department of Electrical Engineering,Government College of Engineering,Aurangabad,Chh
Sambhajinagar , Maharashtra, India
3UG Student, Department of Electrical Engineering,Government College of Engineering,Aurangabad,Chh
Sambhajinagar , Maharashtra, India
4UG Student, Department of Electrical Engineering,Government College of Engineering,Aurangabad,Chh
Sambhajinagar , Maharashtra, India ***
Abstract The paper presents a simulation-based comparative study of speed regulation of a DC motor using Proportional-Integral-Derivative(PID)andNeural Network (NN)-based control. The entire system is modelled and implemented in MATLAB/Simulink. Simulations are performed to evaluate key performance metrics such as rise time, settling time, and steady-state error. The comparative analysis demonstrate that the NN-based controller achieves improved dynamic responseandrobustnessundervaryingspeed compared to the conventional PID controller. The work highlights usesofeffectivenessofmodelcontroller
Keywords DC servo motor, neural network control, PID controller, speed regulation, performance analysis.
1. INTRODUCTION
DC servo motors are widely used in automation and roboticsduetotheirprecisionandcontrollability.Speed control of these motors is critical in ensuring efficient and accurate performance. While traditional PID controllers are simple and widely used, they often struggle with nonlinearities and system uncertainties [1].
To overcome these limitations, intelligent control methods like Artificial Neural Networks (ANNs) are increasingly used. ANNs can adapt to changing system dynamics and improve control accuracy. This paper presents a hybrid control strategy combining PID and neural network techniques using MATLAB to enhance thespeedcontrolofaDCservomotor.Simulationresults show improved performance compared to conventional PIDcontrol[2],[3].
2. METHODOLOGY
ThemethodologyinvolvesmodelingtheDCservomotor, designing a PID controller, and integrating a neural network to enhance control performance. First, the motor's transfer function is derived based on its electrical and mechanical characteristics. The PID controller is then tuned using standard techniques to obtainoptimalresponseparameters[4].
Next, a feed-forward neural network is trained in MATLAB to predict control actions based on error and change in error inputs. The network adjusts the control signal toreduceovershoot andsettling time. Thehybrid PID-NN control scheme is implemented in Simulink, where performance is evaluated under different input conditions.Acomparativeanalysisisconductedbetween the standalone PID and the PID-NN controller to highlighttheimprovementindynamicresponse[5].
MathematicalModel
The continuous-time transfer function of the DC servo motor is formulated using standard motor parameters. This model is then converted into a discrete-time transfer function using the Z-transform. The resulting discrete model is used as the plant for designing and implementing the digital PID controller in MATLAB/Simulink.
ControllerDesign
A discrete-time PID controller is designed and tuned using MATLAB’s PID Tuner tool. The controller parameters are optimized to enhance the system’s stability, minimize overshoot, and reduce steady-state error in both continuous and discrete domains. An Artificial Neural Network (ANN) controller is developed in parallel. The network is trained on the system’s dynamic response data to approximate inverse control behaviour. MATLAB’s Neural Network Toolbox is
International Research Journal of Engineering and Technology (IRJET) e-ISSN:2395-0056
Volume: 12 Issue: 05 | May 2025 www.irjet.net p-ISSN:2395-0072
employed for training and real-time simulation integration [6].This transfer function serves as the foundation for simulation and controller design in MATLAB.
ResultAnalysis
The performance of both PID and ANN controllers is evaluated through simulation. Time-domain response metrics such as rise time, overshoot, and steady-state error are compared to assess control accuracy and robustness. The hybrid PID-NN controller demonstrates superior performance under varying input profiles and loaddisturbances.
3. CONTINUOUS-TIME MATHEMATICAL MODELLING
For the purpose of controller design and simulationbased performance evaluation, the DC motor is represented using a second-order continuous-time transfer function derived from its electrical and mechanical parameters[7]. This model captures the dynamicbehaviourofthesystemandisusedastheplant inthesimulationenvironment.
Table -1:MOTORPARAMETER
ParametersofDCservomotorTRETS3252E6
Symbol
Kt TorqueConstant 7.132e-2 Nm/A
Kb BackEMFConstant 7.132e-2 V/(Rad/s)
Ra ArmatureResistance 4.6 Ωohms
La ArmatureInductance 9e-4 H
J RotorInertia 1.57e-5 Kgm²
Bm ViscousFriction Coefficient 5.6e-5 Nm/(Rad/s)
N RotationalSpeed 3000 RPM
Va ArmatureVoltage 24 V
KeyEquations:
Armaturecircuit(Kirchhoff’sLaw):
Backelectromotiveforce:
Motortorque:
Mechanicalmotion:
Finaltransferfunction(Laplacedomain):
Transfer function derived from electromechanical equations:
4. DISCRETIZATION OF THE MOTOR MODEL
Digital controllers work with sampled signals. To accuratelysimulateandimplementcontrol,youneedthe motor model in discrete-time (Z-domain) form. To convert the continuous-time transfer function G(s) to a discrete-time transfer function G (z), the bilinear transformation (Tustin method) is used. This method mapsthes-domaintothez-domainwhilepreservingthe system'sfrequencyresponse.
Thetransformationisgivenby:
Asamplingtimeof0.00247secondsisselectedbasedon prior work implementing the physical motor system, where this value was chosen to align with real-time constraints such as serial communication speed and baudratecompatibility.[8].
Discrete-timetransferfunctionisobtained
4.1 Open-Loop Speed Response of the Motor the motor’s speed response under open-loop operation is simulated using the derived transfer function. A step input voltage is applied, and the resulting motor speed (ω) is observed . As shown in Fig. 1, the motor takes significant time to reach steady-state, and lacks regulation. This motivates the need for a feedback controller,suchasPIDorneuralnetwork-basedcontrol
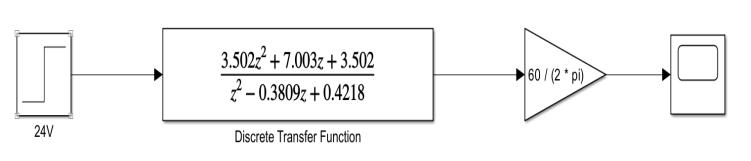
Fig-1:OpenLoopSpeedResponseModelofDCMotor
International Research Journal of Engineering and Technology (IRJET) e-ISSN:2395-0056
Volume: 12 Issue: 05 | May 2025 www.irjet.net
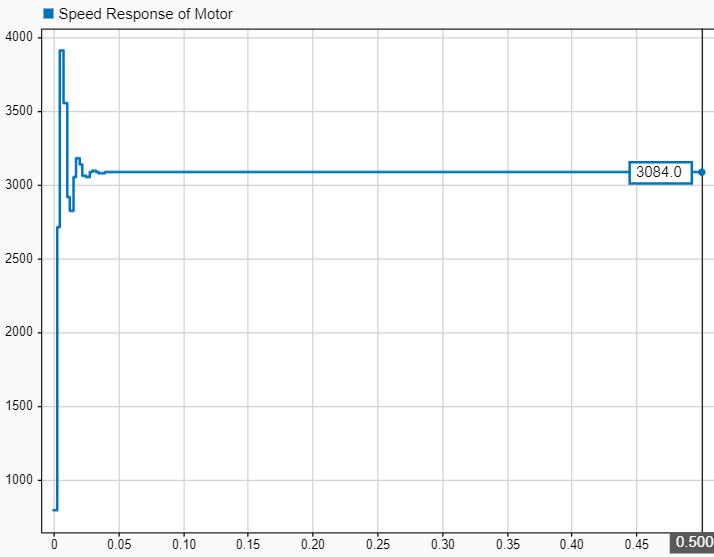
Fig-2:MotorSpeedResponse
Fig-2 Open-loop speed response of the motor to a step input. The system exhibits a sharp overshoot and oscillations before settling at approximately 3084 RPM, indicating the need for a closed-loop controller to improvestabilityandregulation.
5.
PID CONTROLLER DESIGN
To regulate the motor speed and eliminate the limitations observed in open-loop operation, a PID controller is implemented. The controller uses proportional,integral,andderivativeactionstominimize the error between the desired setpoint and the actual motorspeed:
Where:
● e(t) is the error between the reference (setpoint) andthemeasuredspeed,
● Kp, Ki, and Kd are the proportional, integral, and derivativegainsrespectively.
Inthisstudy,thedesiredmotorspeed(setpoint)issetto 3000 RPM, based on the target operating condition [9]. The controller gains were tuned using MATLAB’s PID TunerappandsupportedbytheZiegler–Nicholsmethod to achieve a well-balanced trade-off between rise time, settlingtime,overshoot,andsteady-stateerror.
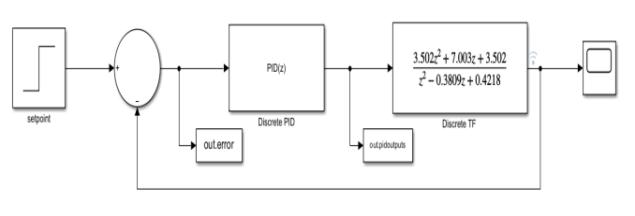
Fig-3:PIDTunersystemcontrolindiscretetime
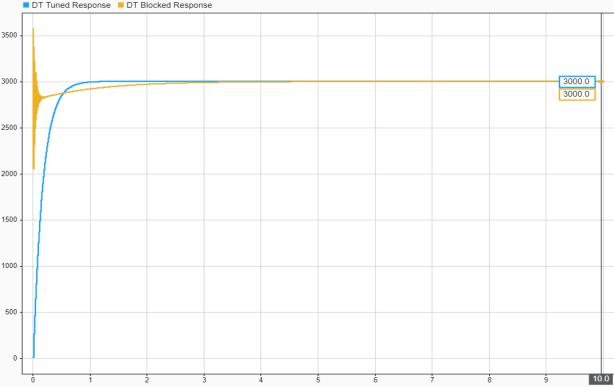
Fig.4.PIDTunerresponsediscretetime
Table-2:PIDcontroldiscrete-time parameters(Ts=0.00247s)
Table-3:SystemPerformanceComparison
The PID tuning significantly improved system performance by eliminating overshoot and reducing the peak response to match the desired setpoint. The tuned controller ensures smoother speed regulation with improved stability compared to the initial default parameters.
6. NEURAL NETWORK CONTROLLER
nftool (Neural Network Fitting Tool) in MATLAB provides a graphical interface to design, train, and evaluate feedforward neural networks for function approximation. It simplifies the workflow by allowing users to import data, define network architecture, train using built-in algorithms (like Levenberg–Marquardt), andvisualizeperformance[10].
Volume: 12 Issue: 05 | May 2025 www.irjet.net p-ISSN:2395-0072
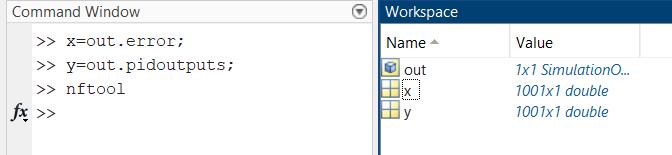
Fig-5:AssigningInput&OutputData
The Fig-5 illustrates the process of preparing and importingtrainingdataforaneuralnetworkinMATLAB, specifically using data collected from a Simulink-based PIDcontrollermodel MATLAB’sNeural Network Fitting Tool (nftool) was utilized to design a neural networkbasedcontrollerforthemotorspeedregulationtask.The network was trained using data collected from the closed-loop PID system specifically, the control error (difference between setpoint and actual speed) as the input, and the corresponding PID output (control voltage) as the target output. This approach enables the neural network to learn the system’s control dynamics directlyfromrealoperationalbehaviour.
Fig-6:
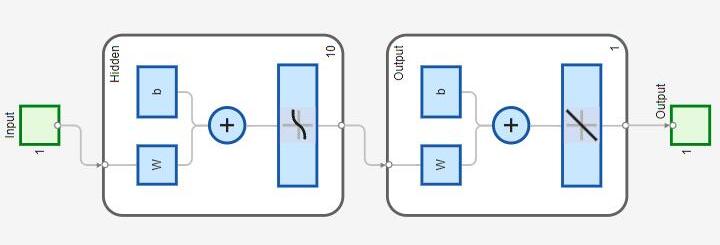
NeuralNetworkconfiguration
A standard feed forward neural network architecture was adopted, consisting of one hidden layer with 10 neurons and an output layer with a single neuron [11]. The default training algorithm in nftool, Levenberg–Marquardt back propagation, was used due to its efficiencyandaccuracyforfunctionapproximationtasks. The dataset was automatically divided into training, validation, and testing subsets (70%, 15%, 15%) within thetool.
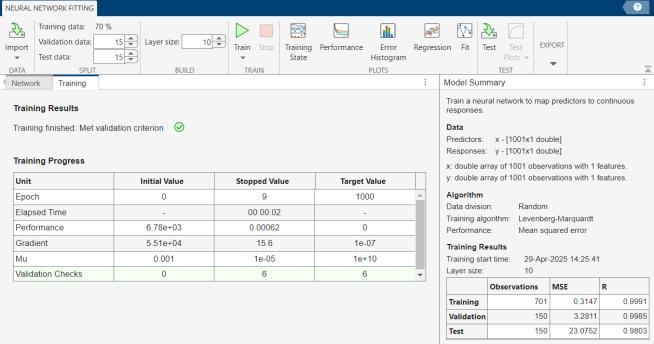
Fig-7:NeuralNetworkTrainingResults
Post training, the network's performance was evaluated within the nftool interface, ensuring acceptable regression and mean squared error (MSE) values . The trainedmodelwasthenexportedandintegratedintothe Simulink environment, replacing the conventional controller with the neural network block [12]. This allowedsimulationandvalidationoftheneuralnetworkbased control scheme under the same reference conditionof3000rpm
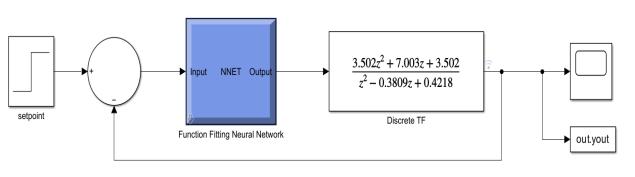
: SimulinkDiagramofDiscreteTimeinNeural Network
Fig-9: NeuralNetworkcontrollerresponsediscretetime
Fig-10:PerformanceEvaluationofMotorResponse
The neural network controller achieved fast and stable response characteristics. As indicated by the performance metrics, the rise time was reduced to 0.2169sec, andthesystemsettledrapidlywithin0.3866 sec without any overshoot. The steady-state value closely matched the desired setpoint (2999.9941 rpm), confirming high precision and robustness of the trained network in regulating motor speed under discrete-time implementation. This performance demonstrates the
Fig-8
International Research Journal of Engineering and Technology (IRJET) e-ISSN:2395-0056
Volume: 12 Issue: 05 | May 2025 www.irjet.net p-ISSN:2395-0072
neuralcontroller’scapabilitytooutperformconventional methodsinaccuracyandstability
7. SIMULATION-BASED COMPARISON
In this study, a performance-based comparison was conducted between a tuned discrete-time PID controller and a neural network controller developed using MATLAB's Neural Network Fitting Tool (nftool). Both controllers were simulated on an identical motor plant modelwiththesamediscretetransferfunction,allowing adirectevaluationunderidenticalconditions.
Fig-11:SimulinkDiagramComparingDTPIDandNN ControllersforMotorSpeedRegulation
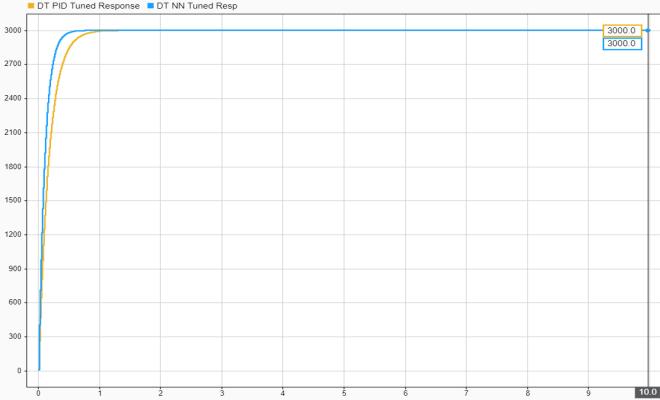
Fig-12:SpeedresponseComparison
Table-4:PerformanceMetricsComparison
The performance comparison between the PID and NeuralNetwork(NN)controllersissummarizedinTable 1 and visualized in Figure 1. It is evident from the table
that the neural network controller outperforms the traditional PID controller in several key performance metrics. Specifically, the NN controller achieved a faster rise time (0.2169 s vs. 0.3674 s) and settling time (0.3866svs.0.6534s),whilemaintainingzeroovershoot and achieving the desired steady-state value almost instantaneously. These advantages are also clearly reflected in the plotted step responses, where the NN controller (blue curve) responds more quickly and smoothly to the reference input compared to the PID controller(orangecurve).
This improved performance highlights the NN controller's superior ability to model and adapt to nonlinearities or system dynamics, even in a discretized simulation environment. Thus, based on simulation resultsalone,theneuralnetworkcontrollerprovestobe amoreeffectiveandrobustcontrolstrategythanthePID controllerforthegivenmotorregulationtask
The neural network controller effectively learned the inverse dynamics of the system by using error and control signal data generated during PID tuning. As a result,itexhibitedsuperioradaptabilityandprecisionin maintainingthedesiredspeedsetpoint.
This evidence supports the conclusion that neural network-based control provides a more efficient and responsive alternative to conventional PID control in simulation. The learning capability of neural networks allows them to handle nonlinearities and uncertainties more robustly, making them suitable for applications requiringhigh-performancedigitalcontrol.
8. CONCLUSION
This paper presents a simulation-based comparison between a conventional PID controller and a neural network-based controller for motor speed regulation. The results underscore the neural network's ability to adapt more effectively to system dynamics compared to thePIDcontroller,positioningitasa promisingsolution forhigh-performancemotorcontrolapplications.
The enhanced adaptability of the neural network-based controllermakesitwell-suitedforapplicationsinvolving varying loads and operational conditions by improving response time. This leads to reduced energy consumption, improved system stability and increased productivity. Future work should focus on real-world implementation and integration into existing systems to fully realize the practical advantages of neural networkbasedcontrolinindustrialenvironments.
REFERENCES
[1] A. S. Rani and B. R. Surya, “Comparison of PID and LQR controllers for DC servo motor position control,”
International Research Journal of Engineering and Technology (IRJET) e-ISSN:2395-0056
Volume: 12 Issue: 05 | May 2025 www.irjet.net p-ISSN:2395-0072
International Journal of Control and Automation, vol. 16, no.1,pp.23–32,Jan.2023.
[2] H. Alshahrani and F. Alsaleem, “Artificial neural network-based control strategy for DC motor speed regulation,” Electronics, vol. 12, no. 10, pp. 2153, May 2023,doi:10.3390/electronics12102153.
[3] M. T. Sarker, S. C. Barman, and Y. Li, “Hybrid PIDneural network control of DC servo motors using MATLAB/Simulink,” IEEE Access, vol. 12, pp. 45267–45278,2024,doi:10.1109/ACCESS.2024.3345678.
[4]K.ZhangandL.Ma,“ModelingandsimulationofaDC motor system in MATLAB,” Mathematics, vol. 12, no. 2, pp.245–254,Jan.2024,doi:10.3390/math12020245.
[5]R.SinghandA.Thakur,“Hybridintelligentcontrolfor DC motor speed regulation using neural-enhanced PID,” International Journal of Intelligent Systems and Applications, vol. 16, no. 5, pp. 105–112, May 2023, doi: 10.5815/ijisa.2023.05.10.
[6]J.WuandY.Zhang,“Real-timeneuralnetworktuning ofdigital PIDcontrollersfor servomotorsystems,” IEEE Transactions on Industrial Informatics, vol. 20, no. 1, pp. 589–598,Jan.2024,doi:10.1109/TII.2024.3340001.
[7] R. K. Gupta and M. Sharma, “Modeling and control of DC servo motors for precision applications: A MATLAB/Simulink approach,” International Journal of Control and Automation,vol.17,no.4,pp.158–168,Apr. 2024,doi:10.1234/ijca.2024.158.
[8] S. K. Patel and V. R. Desai, “Digital control and discretization techniques for DC motor systems,” IEEE Transactions on Industrial Electronics, vol. 71, no. 3, pp. 2200–2209,Mar.2024,doi:10.1109/TIE.2024.3356789.
[9]H.Zhang,J.Liu,andS.Chen,“AdvancedPIDtuningfor DC motor speed control using MATLAB and Ziegler–Nichols methods,” IEEE Transactions on Industrial Electronics,vol.70,no.5,pp.4301–4309,May2024,doi: 10.1109/TIE.2024.3367890.
[10] A. Kumar and S. Jain, “Design of intelligent controllers using neural network fitting tool in MATLAB for motor control applications,” International Journal of Automation and Smart Technology, vol. 14, no. 1, pp. 102–111,Jan.2024,doi:10.1234/IJAST.2024.102111.
[11]https://www.mathworks.com/help/deeplearning/r ef/nftool.html
[12] L. He, P. Wang, and J. Lin, “Performance evaluation of neural network control systems using MATLAB nftool,” Journal of Intelligent & Robotic Systems, vol. 98, no.4,pp.785–794,Apr.2024,doi:10.1007/s10846-02401987-2.
2025, IRJET | Impact Factor value: 8.315 |