
International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056
Volume: 12 Issue: 06 | Jun 2025 www.irjet.net p-ISSN: 2395-0072


International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056
Volume: 12 Issue: 06 | Jun 2025 www.irjet.net p-ISSN: 2395-0072
Sandeep Chowdhry1
1 Engineering Consultancy & Training, Chandigarh, India ***
Abstract - Gray cast iron (GCI) contains graphite flakes that provide a high level of stability and minimise shrinking during the casting process. The high carbon content makes GCI easy to machine. At the same time, GCI is less ductile. Its machining affects the machining efficiency and tool life. This study aims to use an appropriate optimisation method to reduce the machining time and increase the tool life. As per the results, the response surface method is used for optimisation. The feed per tooth makes the maximum contribution, followed by the depth of cut and spindle speed towards minimising the machining time. As per the extended tool life equation, tool life decreases with increased spindle speed. The optimisation results show that as per the second tool life equation, the minimum machining time is five times, and the maximum tool life is thirty times that of the values obtained by the extended tool life equation.
Key Words: tool life, milling, full factorial design, response surface method, solidworks cam, gray cast iron, machiningtime
Gray cast iron offers several benefits, such as improved corrosion resistance, castability, better thermal conductivity, and a higher level of vibration damping, alongwithahomogenoushardnessandstructureoverthe cross-section. However,graycastironisnotasductile as othercastironforms,anditstensilestrengthisalsolower. As a result, the workpiece material in front of a cutting tool is directly shattered and becomes small angular particles [1]. They can further affect the machining efficiencyandtoollife.Forinstance,inthesculpturedpart, the roughing time can be five to ten times that spent on finishing machining [2]. So, reducing roughing time can considerably improve the machining efficiency and subsequently lower the production cost. The minimum machining time can thus be achieved by maintaining the maximum cutting volume (per unit time) allowed by the millingmachineandthecutter.However,toollifeisoneof the factors which affect the performance of a cutting process [3]. The maximum cutting volume is affected by cutting speed, feed rate and depth of cut. These process parametersalsoaffectthetoollife.
Nevertheless,thereisstillambiguityinhowtheseprocess parameters affect the tool life. For instance, according to Taylor'sequation,cuttingspeedaffectsthetoollife.Atthe same time, Gorezyca’s [4] tool life equation includes feed speedanddepthofcut.Theaboveliteratureshowsaneed toreducethemachiningtimeandincreasethetoollife.
Therefore, the study's main aim is 1) To select an appropriate optimisation method to minimise the machining time and increase the tool life; 2) To minimise the machining time of GCI workpiece; 3) To maximise the tool life while machining the GCI workpiece. This study aims to contribute to the understanding of using an appropriate optimisation method to minimise the machining time and maximise the tool life while machiningtheGCIworkpiece.
2.1
AspecimenofGCImaterialwithdimensionsof100mm x100 mm x10 mm anda contourof 50 mm x50 mm x4 mm,asshowninFig.1,wasusedformillingmachining.
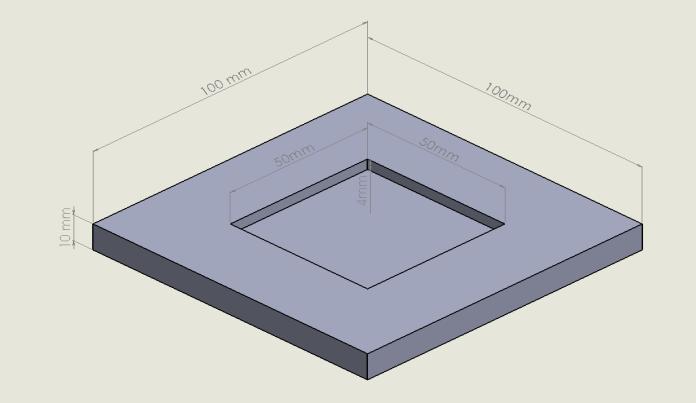
Fig -1: Machinedspecimendimensions
2.2
The study used SolidWorks CAM, Microsoft Excel, and Minitab2023software.

International Research Journal of Engineering and
Volume: 12 Issue: 06 | Jun 2025 www.irjet.net
Thespecimenpartfilewascreatedasperthestudy[5] usingSolidWorks2023software.
Table 1 shows the level settings of the milling operation parameters, such as cutting speed and feed rate. The machiningtimewasselectedastheresponse.Therangeof milling operation parameters was selected according to the Mitsubishi Milling Tool Guide [5] and in consultation withthemachineshopattheinstitution.
TABLE-1:LEVELSETTINGSOFSPINDLESPEED,FEEDRATEAND DEPTHOFCUTFORMACHININGTIMEASRESPONSEVARIABLE
Input
Serial No.
1
2
3
To determine whether there is a linear or non-linear relationshipbetweenthespindlespeed,feedrate,depthof cut and machining time, a null hypothesis (H0) was that there is a linear relationship between the input and response variables. The alternative hypothesis (H1) was that there is no linear relationship between the input and outputvariables.Asaresult,FFDwasused.
The study used Minitab 2023 software to create a randomised run order for the experiment involving three process parameters with low-level and high-level settings of the input variables spindle speed and feed rate, as showninTable1.TheFFDconsistsofeightfactorialpoints andtwocenterpointsorsixpoints(Run1-10).TheFFDis showninTable2below.
The flat-end milling cutter dimensions were modified according to the measurements in the catalogue [5] for toolnumberAPXUR4000162SA12SA,whichhastwoteeth and a one-inch cutter diameter with carbide inserts. The milling machining runs were performed on the SolidWorks CAM software. The spindle speed, feed rate per tooth and depth of cut of the first roughing flat-end milling cutter were changed as per Table 3, and the machining time was recorded for each experiment. The spindlespeed,feedrateanddepthofcutofthesecondflat-
end milling cutter and third contouring flat-end milling cutter were notchanged for all theexperiment runs. Only thefirstroughingcutter’sinputvariableswerechanged,as the cutter was the largest among the three cutters the SolidWorks CAM software selected. It removed the maximum amount of material in less time than the other two cutters. So, it was easy to study the effect of input variables on the response variable. Changing the input parameters of all the cutters simultaneously would make the process more complicated and time-consuming. The main interaction plot (Fig. 2) shows that the center point is not on the line joining the start and end points. It indicatesthattherelationshipbetweentheinputvariables (spindle speed, feed rate and depth of cut) and the response variable (machining time) is not linear. Hence, the study rejected H0. It was concluded that the response surface method (RSM) should be used to optimise the variables.
:FULLFACTORIALDESIGN
Run
Order
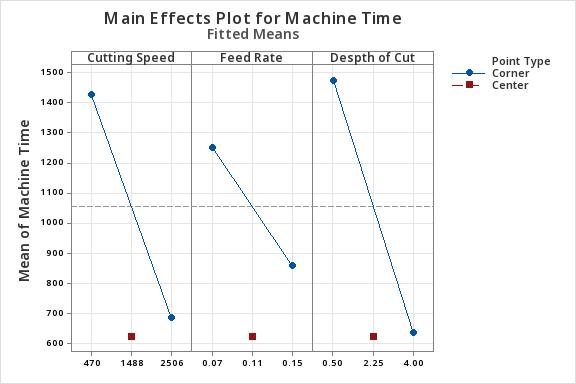
Fig-2:Maininteractionplotofspindlespeed,feedrate andmachiningtime.

Volume: 12 Issue: 06 | Jun 2025 www.irjet.net
Second, the study used Minitab 2023 software to create a randomised run order for the experiment involving three processparameters(spindlespeed,feedrateanddepthof cut) at two levels, as shown in Table 1. The Central CompositeDesign(CCD)consistsof14factorialpointsand six center points or 20 points (Run 1-20). The CCD is shown in Table 3. The machining time is selected as the responsevariable.
TABLE-3:CCDOFSPINDLESPEEDANDFEEDRATEWITH
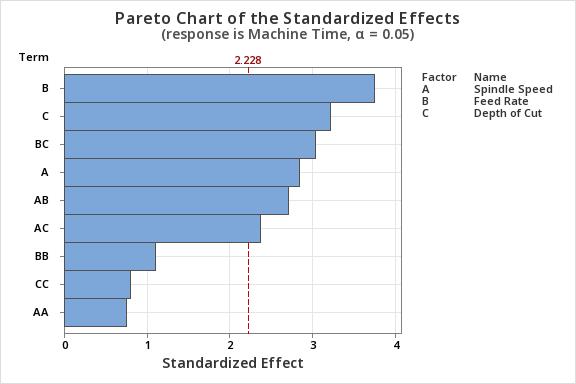
:Paretochartshowingthesignificantparameters.
The Pareto chart (Fig. 3) shows that feed per tooth, depth of cut, spindle speed, the interaction of feed per tooth-depth of cut, the interaction of spindle speed- feed rate, and interaction of spindle speed-depth of cut are significantatα=0.05.
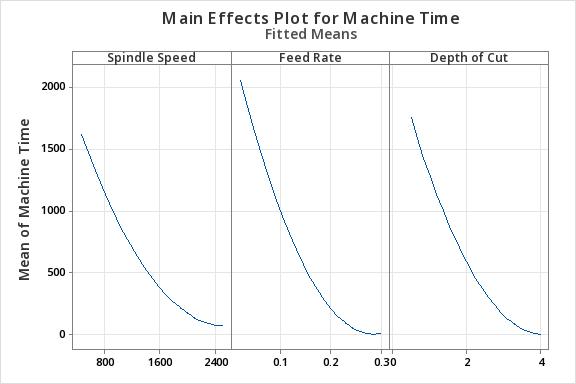
Fig-4:Maineffectplotsofspindlespeed,feedrate, depthofcutandmachiningtime
The main effects plots (Fig. 4) show a non-linear relationshipbetweenspindlespeed-machiningtime,feed per tooth – machining time and depth of cut – machining time. The higher slope of the feed per tooth w.r.t. machining time indicates that an increase in feed rate makes a maximum contribution compared to the contributions made by depth of cut and spindle speed to thereductioninmachiningtime.
The cutting speed calculations and the milling machine simulations were performed using the SolidWorks CAM software. The cutting speed and machining time were recorded in columns four and five in Table 3. Afterwards, the study used Minitab software to analyse the response surface design with a confidence level of 95% (α=0.05). The residual plots showed that the errors are random, independent, normally distributed and have constant varianceacrossallfactorlevels

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056
Volume: 12 Issue: 06 | Jun 2025 www.irjet.net p-ISSN: 2395-0072
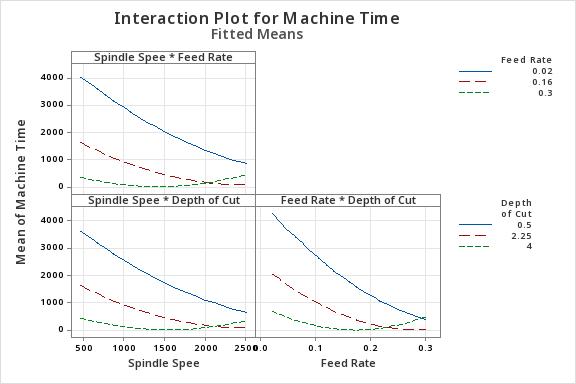
Fig-5:Interactionplotsofspindlespeed,feedrate, depthofcutandmachiningtime.
Theinteractionplots(Fig.5)showthataslowfeedrate of 0.02 mm/tooth has a higher machining time over the entire spindle speed range. A feed rate of 0.3 mm/tooth has the lowest machining time at a slower speed. In comparison, a feed rate of 0.16 mm/tooth has the minimum machining time at a higher speed. Hence, a higher feed rate tends to reduce the machining time. Second, at a low depth of cut of 0.5 mm, it has a higher machining time over the entire spindle speed and feed rate range. A maximum depth of cut of 4 mm has the lowest machining time at a slower spindle speed and low feed per tooth rate. In comparison, a depth of cut of 2.25 mm has the minimum machining time at a higher spindle speed and feed per tooth rate. Hence, a higher spindle speed, higher feed per tooth rate and higher depth of cut tendtoreducethemachiningtime.
TABLE-4:ANALYSISOFVARIANCE(ANOVA)OFSPINDLE SPEED,FEEDRATEANDDEPTHOFCUTWITHMACHININGTIMEAS
Bold terms are significant at α = 0.05.
ANOVA table 4 shows that spindle speed, feed per tooth, depth of cut, and interaction between spindle speed-feed ratepertooth,interactionbetweenspindlespeed-depthof cut and interaction between feed per tooth and depth of cut are significant at α = 0.05. The feed per tooth has a maximum contribution of 20.96%, followed by depth of cutcontributionof15.42%,interactionbetweenfeedratedepth of cut (13.78%) and spindle speed contribution of 12.02%towardsminimisingthemachiningtime.
The regression equation for the machining time of the significanttermsis,
MachineTime=10271–3.72SpindleSpeed–33836Feed Rate–2327DepthofCut+5.79SpindleSpeed*FeedRate + 0.407 Spindle Speed*Depth of cut + 3785 Feed Rate* DepthofCut
Fig-6:Graphshowingtherelationbetweenspindle speedandcuttingspeed.
To maximise the tool life, both the result of the extended tool life equation [6] based on Taylor’s tool life equation andGorczycatoollifeequation[4]areused.
The extended equation for the tool life using the Taylor toollifeequationwasformulatedforcarbidetoolsusedin turning of cast iron material [6]. As per the equation, the

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056
Volume: 12 Issue: 06 | Jun 2025 www.irjet.net p-ISSN: 2395-0072
cutting speed mainly affects the tool life. This study also usedcarbideinsertstomachinetheGCIworkpiece.So,the extended equation (1) was used to calculate the tool life, andthevalueswererecordedincolumnsevenofTable4.
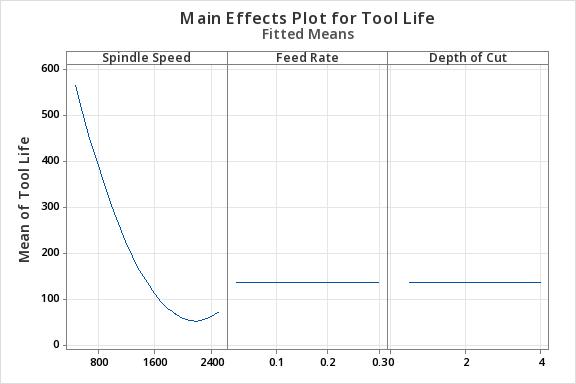
Fig-7:Graphshowingtherelationshipbetweenspindle speed,feedrate,depthofcutandtoollife.
Thegraph(Figure7)showsthattoollifedecreaseswith increased spindle speed. At the same time, the feed rate anddepthofcutdonotaffectthetoollife.
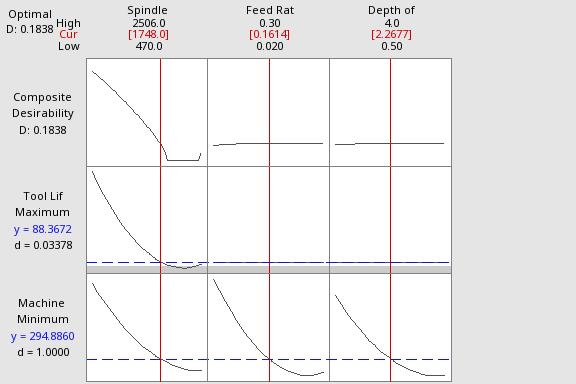
Fig-8:Optimisedvaluesofspindlespeed,feedpertooth anddepthofcuttominimisethemachiningtimeand maximisethetoollife
As per the catalogue [5], the optimisation was performed with the range constraint of spindle speed (1748rpm2506 rpm), feed per tooth (0.1mm-0.2mm) and depth of cut (0.5mm-4mm). The spindle speed range and feed per tooth rangewereselected with reference tothecatalogue [5] and machine shop consultation. The optimum spindle speed values are 1748 rpm, feed pre-tooth rate of 0.1614 mm and depth of cut value of 2.26mm. The minimum value of machining time is 294.89 sec, and the maximum valueofthetoollifeis88.37minrespectively.
Second, the tool life equation given by Gorczyca [4] was alsousedtocalculatethetoollife.AsperGorczycatoollife equation (2), the tool life is affected by cutting speed (V), feedrate(F)anddepthofcut(D).
ToolLife_VFD= (2)
The results of the calculated tool life were recorded in columneightofTable3.
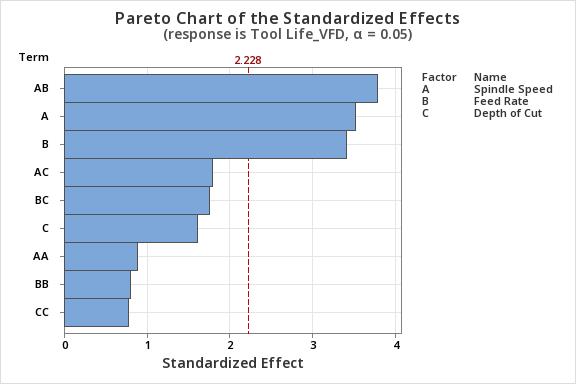
Fig-9:Paretochartshowingthesignificantparameters fortoollife
The Pareto chart (Figure 9) shows that for the tool life calculated using the Gorczyca equation, the interaction of spindlespeed-feedrate,feedpertoothandspindlespeed aresignificantatα=0.05.
TABLE-5:ANALYSISOFVARIANCE(ANOVA)OFSPINDLE SPEEDANDFEEDRATEWITHTOOLLIFEASRESPONSE
Spindle
Spindle Speed*Feed
Spindle

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056
Volume: 12 Issue: 06 | Jun 2025 www.irjet.net p-ISSN: 2395-0072
Cut Feed Rate*Depthof Cut 1 1046444 104644385 3.08 0.11
Error 10 3394429 33944290
Total 19 2229432
BOLD TERMS ARE SIGNIFICANT AT α = 0.05.
ANOVA table 5 shows that spindle speed and feed per toothandinteractionbetweenspindlespeed-feedrateper tooth are significant at α = 0.05. The interaction between the spindle speed and feed per tooth has a maximum contribution of 21.94%, followed by the spindle speed contributionof18.97%andfeedpertoothcontributionof 17.76% towards maximising the tool life. The regression equationoftoollifeobtainedis,
Tool Life_VFD = 59718-28.9 Spindle Speed – (206257* FeedRate)+(54.9*SpindleSpeed*FeedRate)
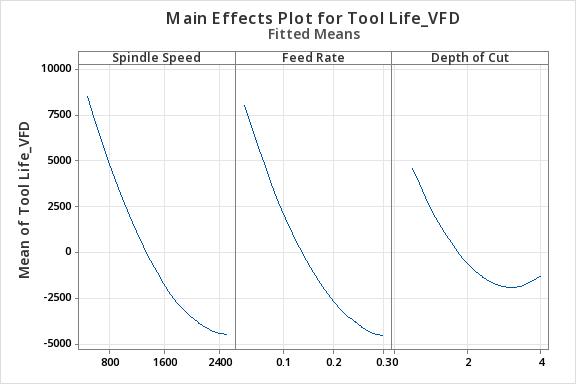
Fig-10:Graphshowingtherelationshipbetweenspindle speed,feedrate,depthofcutandtoollife
The graph (Figure 10) shows that increased spindle speedandfeedratedecreasethetoollife.
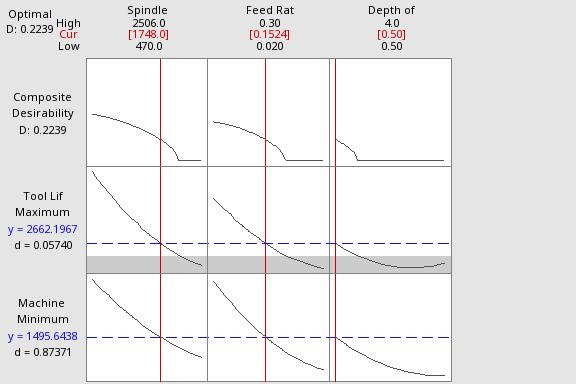
Fig-11:Optimisedvaluesofspindlespeed,feedper toothanddepthofcuttominimisethemachiningtimeand maximisethetoollife.
As per the catalogue [5], the optimisation was performed with the range constraint of spindle speed (1748rpm-2506 rpm), feed per tooth (0.1524 mm – 0.2 mm) and depth of cut (0.5mm-4mm). The spindle speed range and feed per tooth range were selected with reference to the catalogue [5] and machine shop consultation. Theoptimum spindlespeedvaluesare1748 rpm,feedrateof0.1524mmanddepthofcutvalueof 0.5 mm.Theminimumvalueofmachiningtimeis1495.64sec, and the maximum value of the tool life is 2662.19 min respectively.
First, the FFD experiment result shows that the main interaction plot (Figure 2) shows that the center point doesnotlieonthelinejoiningthestartand end points. It indicatesthattherelationshipbetweentheinputvariables (spindle speed, feed rate and depth of cut) and the response variable (machining time) is not linear. The study concluded that RSM is an appropriate optimisation method to optimise the variables compared to FFD. Second,themaineffectsplots(Figure4)showanon-linear relationshipbetweenspindlespeed-machiningtime,feed per tooth–machining time and depth of cut–machining time. The higher slope of the feed per tooth compared to the depth of cut and spindle speed w.r.t. machining time indicatesthatanincreaseinfeedpertoothhasamaximum contribution of 20.96% followed by the depth of cut contribution of 15.42% and spindle speed contribution of 12.02%tothereductioninmachiningtime.Thesefindings agree that feed rate contributes more to the material rate removalthanthecuttingspeed[7].Third,themaineffects plots (Figure 7) show a non-linear relationship between spindle speed- and tool life. The findings that an increase in spindle speed leads to a decrease in tool lifeagree that cuttingspeedreducestoollife[7].Fourth,themaineffects plots (Figure 10) show a non-linear relationship between spindle speed- tool life, feed rate – tool life and depth of cut – tool life. The findings that spindle speed and feed rate affect the tool life agree with the result that cutting speed and feed rate are the practical factors affecting the tool life [8]. In addition, this study also found that the interaction of the spindle speed and feed rate also affects thetoollife.Fifth,basedontheextendedtoollifeequation, the optimum values of spindle speed, feed rate and depth of cut are 1748 rpm, 0.16 mm/tooth and 2.27 mm. The minimummachiningtimeis294.89sec,andthemaximum tool life is 88.37 min. At the same time, based on the Gorczycatoollifeequation,theoptimumvaluesofspindle speed, feed rate and depth of cut are 1748 rpm, 0.1524 mm/tooth and 0.5 mm. The minimum machining time is 1495.64 seconds, and the maximum tool life is 2662.19 minutes.Therefore,asperthe Gorczyca toollifeequation, the minimum machining time was five times that of the minimum machining time obtained by the extended tool lifeequation.

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056
Volume: 12 Issue: 06 | Jun 2025 www.irjet.net p-ISSN: 2395-0072
Similarly, based on the Gorczyca tool life equation, the maximum tool life was thirty times that of the maximum tool life obtained by the extended tool life equation. The difference in the maximum calculated tool life using equation (1) and equation (2) is because in equation (1), cutting speed is the significant cutting parameter and in equation (2), the cutting speed, feed rate and the interactionbetweenthecuttingspeedandfeedrate(Table 5) are the significant factors. Table 5 shows that spindle speed, feed rate and interaction between spindle speed and feed rate are significant at α = 0.05. It gives more confidence in selecting the optimised cutting speed and feed rate values for the metal cutting as per the milling toolcatalogue[5]toincreaseitstoollife.Theoptimisation of cutting speed is vital as an increase in cutting speed reducesmachiningtimeandshortensthetoollife.
Thestudyconcludedfirstthereisanon-linearrelationship between the input variables (spindle speed, feed rate and depth ofcut) and the responsevariable(machining time). As a result, FFD is not an appropriate optimisation method. Therefore, RSM should be used to optimise the variables. Second, the feed per tooth has a maximum contribution of 20.96%, followed by a depth of cut contributionof15.42%,theinteractionbetweenfeedratedepth of cut of 13.78% and spindle speed contribution of 12.02% towards minimising the machining time. Third, higherspindlespeed,higherfeedpertoothrateandhigher depthofcuttendtoreducethemachiningtime.Fourth,as per the tool life equation (1), tool life decreases with increased spindle speed. At the same time, the feed rate anddepthofcutdonotaffectthetoollife.Fifth,asper the tool life equation (2), the interaction between the spindle speed and feed per tooth has a maximum contribution of 21.94%, followed by the spindle speed contribution of 18.97% and feed per tooth contribution of 17.76% towards maximising the tool life. Sixth, increased spindle speed and feed rate decrease the tool life. Seventh, in the Gorczyca tool life equation [4], the minimum machining time is five times that of the minimum machining time obtained by the extended tool life equation [6]. Eight, basedontheGorczycatoollifeequation[4],themaximum tool life is thirty times that of the maximum tool life obtained by the extended tool life equation [6]. Ninth, increasing cutting speed reduces the machining time and shortens the tool life. The limitation of this study is that onlyvirtualmillingmachiningsimulationshavebeendone on SolidWorks CAM software to gather the data. Further investigation may be performed by comparing the results of the virtual machining and laboratory experiments to establish the reliability and validity of the extended tool life equation and the Gorczyca tool life equation in calculatingthetoollife.
IwouldliketoextendmysinceregratitudetoLilyRaynorBlundell, Head of Faculty – Engineering, Automotive and Motorsport at Wiltshire College & University Centre, Chippenham, England, for her invaluable support and permission to conduct this research. Her foresight in recognizing the potential of this study to enhance the learning experience for students enrolled in the T-Level Design and Development for Engineering and Manufacturing course was instrumental in its initiation. This research aims to contribute directly to the improvementofpedagogicalpracticeswithintheprogram, ultimatelybenefitingthenextgenerationofmanufacturing engineers.
[1] R. C. Voigt, P. H. Marwanga, and P. H. Cohen, “Machinability of Gray Iron – Mechanics of Chip Formation,” Int. J. Cast Metals Research, Vol.11, pp. 567572,1999
[2]Gunsekera,J.S.,1989,CAD/CAMofDies,EllisHarwood Limited
[3]Z.Dong,H.Li,G.W.Vickers,“OptimalRoughMachining of Sculptured Parts on a CNC Milling Machine,” TransactionofASME,Vol.115,pp.424-431,1993.
[4] Gorczyca FE (1987) Application of metal cutting theory.IndustrialPress,NewYork
[5] Mitsubishi Milling tool guide https://www.mitsubishicarbide.com/us/technical_inform ation/tec_rotating_tools/face_mills
[6] M. S.Y.Lubis, S. Djamil, Steven D, Andri, “Tool life investigationofcarbidecuttingtoolsintheturningofcast iron material,” IOP Conf. Series: Materials Science and Engineering,Vol.725,pp.1-7,2020.
[7] H. Yanda, J.A. Ghani, M.N.A.M. Rodzi, K. Othman and C.H.C. Haron, “Optimisation of Material Removal Rate, Surface Roughness and Tool Life on Conventional Dry Turning of FCD700,” International Journal of Mechanical and Materials Engineering (IJMME), Vol.5 (2010), No.2, 182-190,2010.
[8] S. M. Bazaz, J. Ratava, M. Lohtander and J. Varis, “An Investigation of Factors Influencing Tool Life in the Metal Cutting Turning Process by Dimensional Analysis,” Machines,Vol.11(393),pp.1-25,2023.