Evaluation of the Performance and Stability of Dual Stator Induction Machine Using PID and H-Infinit by IRJET Journal

Evaluation of the Performance and Stability of Dual Stator Induction Machine Using PID and H-Infinity Controllers

Isidore U. Uju1 , Bariakwaadoo S. Bere2

1Department of Electrical/Electronic Engineering, Chukwuemeka Odumegwu Ojukwu University,Uli, Anambra State, Nigeria,+234-806-451-9778

2Department of Electrical/Electronic Engineering Technology, Kenule Beeson Saro-Wiwa Polytechnic, Bori, Rivers State, Nigeria, +234-806-061-5520

Abstract

Theimportanceofinductionmachineisitsreliabilityinoperationswhichhasincreaseditsusefulnessintheindustries.The requestforabetterperformanceinitsareaofapplicationcallforresearchtohandleitsdrawbackslikespeedchangewith applied load, poor trajectory tracking capabilities and low frequency vibration. The main objective of this work was to analysetheperformanceandstabilityofdualstatorinductionmachineusingbothPIDandH-infinitycontrollersinorderto ascertain the superiority of the later over the former. The implementation of the DSIM control strategy has to do with investigationofitsperformanceimprovementusngH-infinitycomparedtoPIDcontrolmethod.Theanalysisconsidered5N load condition with performance metrics like step response analysis (overshoot, rise time and settling time), bode and sigmaplotsanalysis.Theanalysisofthecomplexvector model oftheDSIMinvolvedsimulationsusingMATLAB/Simulink 2021b modelling software. From the evaluation, it was discovered that the H-infinity controller shows excellent torque stability,minimaltorqueovershootandlowcurrentripple.Thetimedomainmetricsshowsthat;PIDhadanovershoot,rise time and settling time of 4.6%, 0.213s and 0.598s respectively; H-infinity had an overshoot, rise time and settling time of 0%, 0.00227s and 0.00454s respectively. The frequency response analysis shows that PID controlled DSIM peak gain is6.02dBandH-infinitycontrolledDSIMhadagainandphasemarginsof52.5dB(atfrequencyof0.0118rad/s)and11.40(at frequencyof0.99rad/s)respectively.Insigmaplotanalysis,H-Infinitycontrollerhadaflattershapehavingsingularvalue above0dBacrosstheentirefrequencyrange.Thefindingsforcurrent,torqueandspeedresponseshowsthatefficiencyof H-infinity is the best of the two (PID and H-infinity) controllers. Time domain analysis shows that H-infinity controller is superior(overPID)intermsofovershoot,risetimeandsettlingtimeasH-infinitydeliversbettersystemresponsewithno overshoot and settles quickly after disturbance showing robustness. In sigma plot, H-infinity has flatter shape which indicateuniformpreferencesandrobustnessthanPIDespeciallyathighfrequencies.

Keywords: Performance, Stability, Dual Stator, Induction Machine, PID and H-Infinity

1.0 INTRODUCTION:

1.1Background of study

A Dual Stator Induction Motor or Machine (DSIM) is an induction machine which has two separate three-phase stator windings,sharingthesamemachinecoreandthecommonsquirrelcagerotorwinding. Thedualstatorwindinginduction machine’s two windings have input terminals which are supplied separately with drive power. The two stator windings haveadifferentnumberofpolestoessentiallyeliminatethemagneticcouplingbetweenthetwowindingsandtodecouple thetorques produced by eachsetof windings. Power is suppliedto the two windingsbytwo separatevariable frequency inverterdrivestoprovidetwoindependentlycontrollablytorquecomponents.Atlowspeed,thepowersuppliedtooneof thewindingscanproducetorquewhichopposesthetorquefromthepowerappliedtotheotherwinding,sothatverylow speedandstandstilloperationcanbeachievedwhilethefrequencyofthepowersuppliedbytheinvertersisalwaysgreater than the minimum frequency. At higher operating speeds, power is supplied to the two windings so that the torque from thewindingsadds.Thedualstatormachinecanbebuiltwithminimalmodificationstostandardwindingconfigurations.

International Research Journal of Engineering and Technology (IRJET) e-ISSN:2395-0056

Volume: 12 Issue: 10 | Oct 2025 www.irjet.net p-ISSN:2395-0072

1.2 Statement of Problem

Theproblemsexistingintheinductionmachineareasfollows:

i. The speed of the motor varies with the applied load which consequently affects the general performance of the inductionmachine,causingloworpoortrajectorytrackingcapability.

ii. From the review, it was found that the dual stator winding induction machine output still records some low frequencyvibrationswhichmeansthatthemachinesuffersfrominadequatecompensationcapabilities.

iii. The induction machineisverysensitivetodisturbances especiallythesetof disturbancesformedasa result of the variationintheload.Thus,themachinesuffersfromlowdisturbancerejectioncapabilities.

1.3 Aim and Objectives

TheaimofthestudyistoascertainthesuperiorityofH-InfinityoverPIDintheanalysisoftheperformanceandstabilityof thedualstatorwindinginductionmachine.

Theobjectivesofthestudyareasfollows:

i. Toaddressthespeedvariationproblemoftheinductionmachineusingrobustcontroltechnique.

ii. Tooptimizethe machineoutputperformanceinordertocancel thelowfrequency oscillationandtherebyimprove itsstability.

iii. ToanalyzethedualstatorinductionmachineoutputperformanceusingPIDandH-Infinitycontrollers.

iv. TocomparetheoutputperformanceoftheDSIMunderPIDandH-Infinitycontrollersinordertoascertainwhichof themhasthebestimprovementcharacteristics.

2.0 LITERATURE REVIEW

2.1 Theoretical Framework

An induction machine also known as asynchronous machine is an Alternating Current (AC) electric machine which functions in a way such that the electric current in the rotor needed to produce torque is obtained by electromagnetic induction from the magnetic field of the stator winding. This means therefore that an induction machine can be made without electrical connections to the rotor. The rotor of an induction machine can be either wound type or squirrelcage type.Aninductionmachinecanbeusedasamotorwhenitconvertselectricalenergytomechanicalenergyoragenerator whenitcovertsmechanicalenergytoelectricalenergy.Thedualstatorinductionmotorbeingarotarymachineoperateon thesameworkingprincipleasitlinearcounterpart-thelinearmotor.Inlinearmotormagneticfluxfromamover(rotor)is lockedorsynchronizedwiththatofastationarytrack(stator)convertingelectromagneticenergyintotranslationalmotion (Uju et.al, 2018 )[1]

2.2 Conceptual Framework

The analytical d- model has been developed in a general reference frame and can be used to analyze the behavior of inductionmachineinanyreferenceframe.

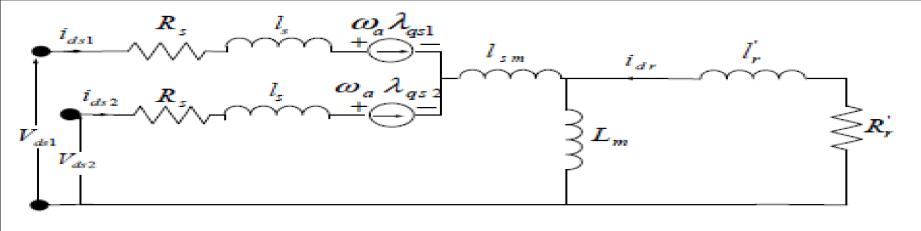
2.6: The d-axis equivalent circuit of a Dual Stator IM in arbitrary reference frame (Marwa et al, 2014)[2]

Figure

International Research Journal of Engineering and Technology (IRJET) e-ISSN:2395-0056

Thecommonmutualleakageinductanceexpressesthepointthatthetwosetsofstatorwindingsoccupythesameslotsand are,thus,theyaremutuallycoupledbyacomponentofleakageflux (Singh et al, 2003)[3].

Theelectromagnetictorqueanddynamicequationscanbeexpressedas:

Representingthemodelinstatespacemodel,thestateequationoftheformexpressedinequationwasused:

]isthestatevector ��

istheinputvector

Thefollowingequationswereobtained:

Thedualstatorinductionmachineisaphysicalsystemthatisconstantlyexperiencingchangesinoperatingconditionsdue to variations in its parameter and load patterns. Physical systems or real systems are commonly associated with uncertainties which must be considered during design and it is the purpose of robust control techniques. A parametric uncertainty in the small-signal linearized model of the system is a common attribute of physical systems (Awadallah and Soliman, 2009)[4]. In physical systems theory mathematical representation, output control is a problem of choosing the inputuofthesystemGsuchthattheoutputyor ∆��of thissystemapproachessomespecifiedreferenceinputsignal ror Vrefwithtime.Thisisachievedinthepresenceofdisturbancesignals.Inthefeedbackcontrolsystem,KorGc isafeedback controller,whichproducestheinputuofthesystemGusingthecontrolerrore.

2.3 Robust Control

Inrobustcontrol,theoutputyofthesystemGisrequiredtoconvergetothereferencesignalreveniftheparametersofthe plantexperiencesomeperturbations.Robustnessisanessentialpropertyforthecontrollersusedinpractical applications orphysicalsystems,becausethemathematicalmodelingofthephysicalsystemoftenrequiremakingapproximationsand linearization,andalsoassumptionswhich bringabout mismatchoruncertainty betweenthereal physical systemandthe model are considered. The physical systems such as the DSIM uncertainties can be in two forms: unknown disturbances affectingtheprocess,andunknownplantdynamics,i.e.,modeluncertainties.

International Research Journal of Engineering and Technology (IRJET) e-ISSN:2395-0056

Volume: 12 Issue: 10 | Oct 2025 www.irjet.net p-ISSN:2395-0072

Thefeedbackcontrolsystemcanbereformedasshowninfigure2.7.Inordertocontroltheuncertaintiesinthesystemthe natural approach is to use measurements (y) from the process, and let the manipulated variable u be a function of the measured process outputs y as well. In figure 2.7, v represents disturbance, y represents measured output, z is the final outputandKrepresentsrobustcontroller.

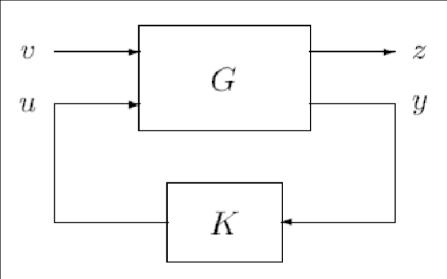
Figure 2.7: Feedback control system (Vasičkaninova and Bakošova, 2013)[5]

In (Gu at el, 2005)[6] it was stated that a control system is robust if it remains stable and achieves certain performance criteriainthepresenceofpossibleuncertainties.Therobustdesignistofindacontroller,fortheinductionmachine,such thattheclosed-loopsystemisrobust. Scherer (2001 )[7] explainedthatthemainaimofrobustcontroltechniquesistotake theuncertaintiesinasystematicfashionintoaccountwhenanalyzingacontrolsystemorwhendesigningacontrollerforit. Themajorobjectiveoftherobustcontrolforthesystemistominimizetheeffectofdisturbanceonoutput;thesensitivityS andthecomplementarysensitivityTaretobereduced (Bansal and Sharma, 2013)[8] inordertoachievearobustlystable system. Considering the functions G(s) and K(s) as the open loop transfer function of the power plant and controller transfer function respectively, this will ensure robustness and good performance of closed loop system (Bansal and Sharma, 2013)[8]

2.4 H-infinity Stabilizer Synthesis

ThedesignofacontrollerfortheDSIMsysteminvolvesgeneratingthecompensatorgainswhichcanaddressthefeedback errortoproduceacontrolsignalu,whichisusuallyfedtotheplantinordertoimprovetheperformanceofthesystemand regainequilibriumoperationquicklywhenalargedisturbanceoccurs.Inthiswork,thegoalistodesignarobustcontroller fortheDSIMsystemusingtheH-Infinitysynthesistechniqueinfrequencydomain.

Inordertoachieverobustcontrollerdesign,itisimportanttonotethatarobustcontrolsystemshouldmeetthefollowing requirementsbesidesthenominalstability (Tan et al, 1999) [9]:

• Disturbanceattenuation,

• Set-pointtracking,

• Robuststabilityand/orrobustperformance.

Thefollowingobjectivesmustbemetforthesystemtoachievefullrobustnesscharacteristics (Agbaraji et al, 2020)[10]:

i. For good set-point tracking |T(jw)| must follow the zero gain line at low frequencies. This can also be achieved if |Gc(jw)Gp(jw)|>>1i.e.,Loopgaintransferfunctionmustbeverymuchgreaterthanoneatlowfrequencies.

ii. For good disturbance rejection, S(s) or |S(jw)|<<1, i.e., sensitivity must be very much less than one. This can be achieved if |Gc(jw)Gp(jw)|>>1 i.e., Loop gain transfer function must be very much greater than one at low frequencies.

If |S(jw)|=0 yields perfect output disturbance rejection iii. For good noise suppression, |T(jw)|<<0 at frequencies of noisei.e.,T(s)mustbeverymuchlessthanzeroathighfrequencies.

H-Infinitysynthesisisafeedbackcontrollerdesignmethodthatinvolvesusingcontrolweights toaugmenttheplanttobe stabilized based on loop shaping and considering the disturbances surrounding the system (Agbaraji et al, 2020)[10].

International Research Journal of Engineering and Technology (IRJET) e-ISSN:2395-0056

Robust H-Infinity synthesis problem involves finding an output feedback control matrix K that minimizes the H-Infinity norm or maximum gain of a certain transfer function, subject to the constraint that K is stabilizing (Mammadov et al, 2005)[11]. Itwasidentifiedby (Mammadov et al, 2005)[11] thatinstabilityissueisachallengingproblemandevenfindinga stabilizerKcanbedifficult.H-InfinitysynthesisisappliedontheplantmathematicalmodeltogeneratethecompensatorK throughloopshaping.

The loop shaping technique is used to select the weight functions for the synthesis of the controller. The loop shaping techniquehelpsthedesignertofollowthetrajectoriesfortheplotofS,TandLasshowninfigure2.8,figure2.9andfigure 2.10inordertoachievethedesiredcontrollercharacteristicswhichsatisfytherobustcontrollerspecifications.

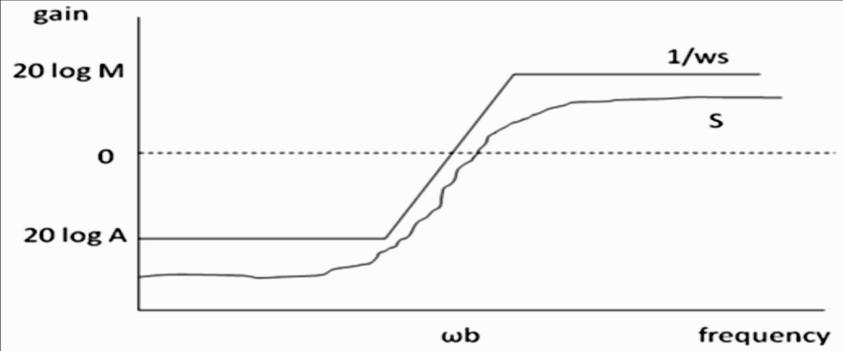
Thesensitivityfunctionplotasillustratedinfigure2.8helpstoexaminethebehaviorofthesystemsensitivityfunctionin lowandhighfrequenciesinordertodeterminetheabilityofthecontrolledsystemtorejectorcanceldisturbance.Itisstill an important control development characteristic because all physical systems encounter disturbances and must be designedtobeabletocancelthedisturbancesthatoccurinordertofunctionoptimally.

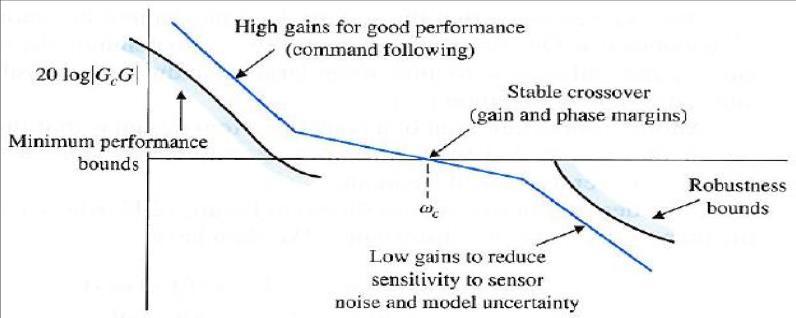
Figure 2.10: Demonstration of system behavior on Bode plot for L (Dorf and Bishop, 2008)[13]

Figure 2.8: Sensitivity graph (Nair, 2011)[12]

Figure 2.9: Complementary sensitivity graph (Nair, 2011)[12]

International Research Journal of Engineering and Technology (IRJET) e-ISSN:2395-0056

Volume: 12 Issue: 10 | Oct 2025 www.irjet.net p-ISSN:2395-0072

Loopshapingisdonetomakethefrequencyresponseoftheplantwiththeweightfunctionstocomeinthedesiredmanner. Inloopshapingtheparametersoftheweightfunctionsarechangedtomakethefrequencyresponseofthewholesystemto remainwithinlimits.Thecontrolsynthesisrequirestheplanttransferfunction,controllertransferfunctionandthevarious weightfunctionstoaugmenttogether.Thusanaugmentedplantmodelisdeveloped.ThegeneralizedplantP(s)isgivenas (Bansal and Sharma, 2013; Nair, 2011) [8] [12]:

(2.9)

ApossiblestatespacerealizationforP(s)canbewrittenas (2.10)

Earlier,theexistingnumericalmethodsfortheH-Infinitysynthesisproblemwerebasedonfirst,reformulatingtheproblem into one involving linear matrix inequalities (LMIs) and an additional nonconvex rank constraint or nonconvex equality constraint.Numericalmethodsforsuchreformulationsoftheproblemincludethosebasedonlinearization (El Ghaoui et al, 1997; Ibaraki and Tomizuka, 2001; Leibfritz, 2001)[14][15][16]; alternatingprojectionsin (Grigoriadis and Skelton, 1996; Grigoriadis and Beran, 1999; Orsi et al, 2004)[17][18]; augmented Lagrangian methods (Fares et al, 2001; Noll et al, 2004)[19][20]; and sequential semi-definite programming (Fares et al, 2002). This method was very difficult and in most cases fail to generate the robust stabilizer due to the complex computations done manually. As a result the H-Infinity synthesishasnotbeencommoninmostresearchesbutrecentlyithasattractedmanyinterestsinadvancecontroldesigns wheretheneedforarobustsystemthatcanfunctionadequatelyeveninthepresenceoflargedisturbanceisveryhigh.The dual stator inductive machine as a physical system encounter numerous forms of disturbances during design such as mistakes in its model, unmodelled or ignored parameters, etc., and operations such as friction; therefore it becomes imperativetoemployacontrolmethodthatcancancelthedisturbancesandhelpthesystemtomaintainoptimalfunction.

2.5 Proportional-Integral-Derivative (PID)

APID(Proportional-Integral-Derivative)controllerisawidelyusedcontrolloopfeedbackmechanisminindustrialcontrol systems.Itcombinesthreecontrolactions;proportional,integral,andderivativestoprovidea robustandeffectivemeans of controlling dynamic systems. The PID controller is particularly valued for its simplicity, effectiveness, and ease of implementation.

Theproportionaltermproducesanoutputthatisproportionaltothecurrenterrorvalue,whichisthedifferencebetween thedesiredsetpointandtheactualprocessvariable.Theproportionalgainkpdeterminesthereactiontothecurrenterror. A higher kp results in a larger output for a given error, leading to a faster response. However, using only proportional controlcanleadtoasteady-stateerror,asitdoesnotaccountforpasterrors.

Theintegraltermaccumulatesthepasterrorsovertime,providingacorrectiveactionbasedonthehistoryoftheerror.The integralkidetermineshowmuchinfluencetheaccumulatederrorhasontheoutput.Thistermhelpseliminatesteady-state errorbyadjustingthecontroloutputbasedonthetotalaccumulatederror.

The derivative term predicts future error based on its rate of change, providing a damping effect that helps reduce overshootandimprovesystemstability.Thederivativegainkddeterminestheinfluenceoftherateofchangeoftheerror ontheoutput.Thistermhelpstoreacttochangesintheerrorquickly.

International Research Journal of Engineering and Technology (IRJET) e-ISSN:2395-0056

Volume: 12 Issue: 10 | Oct 2025 www.irjet.net p-ISSN:2395-0072

The PID controller is a fundamental tool in control engineering, providing a simple yet effective means of managing dynamicsystems.Itsabilitytocombineproportional,integral,andderivativeactionsallowsforimprovedstability.

ThePIDcontrollawisexpressedas:

��(��) ��(��) ∫��(��)�� ( )

where��(��) ��

TheclassicalnumericalPIregulatoriswellsuitedtoregulatingthemotortorqueto thedesiredvaluesasitisabletoreach constantreference.Thetransferfunctiontakestheform (Benyoussef, 2022)[21]:

��(��) ( ) ( )

where (��) �� ( )��

2.6 Summary of Research Gaps

From the reviewed literature, the following points were identified to be the research gaps in the dual stator induction machineperformanceimprovement:

i. Therobustnessofthedualstatorinductionmachinewasnotguaranteedduetolackofproperanalysisofthesystem behaviorinfrequencydomainandlacktrackingerroranalysisdetermination.Thesemakeitdifficulttoknowexactly the ability of the system to withstand disturbances and perform optimally in the presence of significant uncertainties.

ii. The tracking performance characteristic of a controlled system determines the ability of the system to achieve optimal performance by tracking the reference input to the system with reduced error. However, the tracking performanceofthedualstatorinductionmachinewasnotanalyzed

iii. The stability of the system is required in the system design and it is used to determine the ability of the system to maintainequilibrium.However,thestabilityofthedualstatorinductionmachinewasnotanalyzed.

iv. From the results of the reviewed works, there are still ripples existing in the output of the controlled DSIM which showsthattheperformanceofthesystemneedsmoreimprovement.

v. The system sensitivity and disturbance rejection capability are not analyzed in frequency domain. Thus, there is need to carry out a thorough analysis of the system sensitivity to disturbance in frequency domain in order to ascertaintherealabilityofthecontrollerandtherobustnesscharacteristicsofthesystem.

3.0 METHODOLOGY

3.1 Controller Design

3.1.1 PID

ThePIDcontrollawisexpressedas:

TheclassicalnumericalPIregulatoriswellsuitedtoregulatingthemotortorquetothedesiredvaluesasitisabletoreach constantreference.Thetransferfunctiontakestheform (Benyoussef, 2022)[21]:

International Research Journal of Engineering and Technology (IRJET) e-ISSN:2395-0056

Volume: 12 Issue: 10 | Oct 2025 www.irjet.net p-ISSN:2395-0072

3.1.2 H-Infinity Controller Design

The objectiveis to minimize the H normofthe TFfrom w ,ensuringrobust performanceand disturbance rejection. TheloopshapingdesigninvolvesusingweightingfunctionsW1,andW2toshapetheperformanceandrobustness.

Synthesisproblem:

Thecontrollerk(s)isdesignedsuchthat:

Forareduced-orderDSIM,thecontrollermaytaketheform:

Valuesof , , , dependonsystemidentificationandH synthesis.

Thecontrollerk(s)issynthesizedusingDoyle-Gerver-Khargoneker-Francis(DGKF)algorithmviaRiccatiequation.

Where;

W1=Performanceweight

W2=controleffortweight

3.2 System Implementation

The implementation of the DSIM control strategy involves several steps. The goal is to investigate its performance improvementusingH controlsynthesiscomparedtoconventionalPIDcontrolmethod.Theevaluationconsiders5Nload condition with comprehensive performance metrics such as step response analysis (overshoot, rise time, settling time, steadystateerror),bodeplotanalysisandsigmaplotanalysis. Tovalidatethecomplexspace-vectormodeloftheDSIM,a completesetofsimulationswascarriedout.MATLAB® /Simulink2021bmodelingsoftwarewasusedforthesimulationof the proposed DSIM due to its extensive libraries and tools for control, optimization and system identification. A conceptualizedblockdiagramforthemodelingandsimulationsetupisshowninFigure3.1.

DSIM statespace model PID Controller design

Controller

Simulation/perf ormance

Thesimulationwasconductedbyreplacingthederived state-spacemodel(A,B,C,D)withtheactualDSIMandcontroller parameters to simulate responses for PID and H .The MATLAB script simulates a unit step input, which represents a disturbanceloadchange.Finallyrunningthesimulationtogenerateallcomparativeplotsforeachconditionandcontroller. AnewMATLABscript(DSIM_Control_Comparison)wascreatedusingthecontrolsystemtoolboxtogeneratePID,LQR,and H-infinityfunctions.Systemparameters(Rs,Ld,Lq,km,J,B,P)weredefinedatthebeginning.Thestate-spacematrices(A, B, C, D) were constructed based on DSIM dynamics and stored as an ss (state-space) object. After constructing the statespace, the controllers were manually selected (kp, ki, kd) for each loop and then combined into a diagonal matrix for feedback looping. The code was structured into clear sections (modeling, controllers, simulation, and plotting). The

Figure 3.1: Block diagram of the DSIM system architecture

International Research Journal of Engineering and Technology (IRJET) e-ISSN:2395-0056

Volume: 12 Issue: 10 | Oct 2025 www.irjet.net p-ISSN:2395-0072

simulation was finally executed with a time vector t=0:0.01:1, speed of 1500 RPM, and step inputs depending on load conditions.SystemparametersarespecifiedinTable(3.1).TheMATLABcodesareshowninappendix1.

Table 3.1: Dual Stator Induction Machine (DSIM) Parameters.

Parameter Value

3.4: Simulink Model of PID Controller-based DSIM

Figure

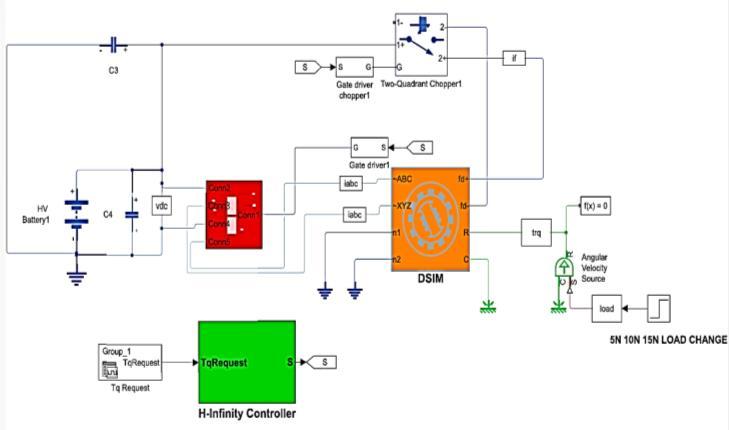
International Research Journal of Engineering and Technology (IRJET) e-ISSN:2395-0056

Volume: 12 Issue: 10 | Oct 2025 www.irjet.net p-ISSN:2395-0072

1.0 RESULTS AND DISCUSSION

4.1 Step Response Results

3.6: Simulink Model of H-Infinity Controller-based DSIM

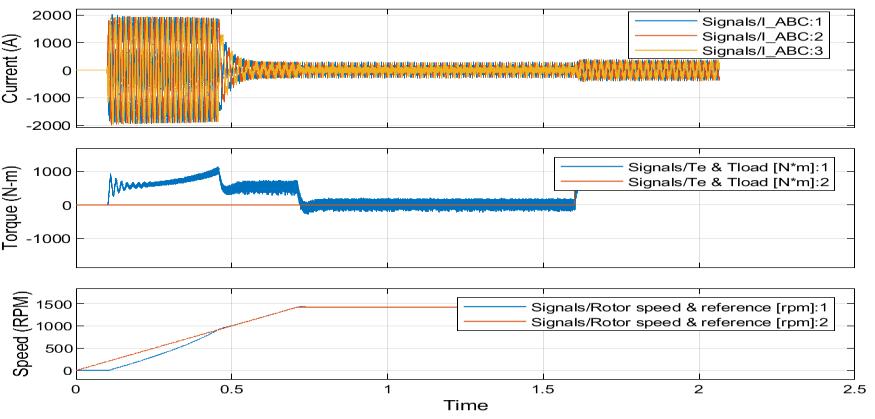
Figure 4.1: Current, Torque, and Speed Response of PID-based DSIM for 5N load

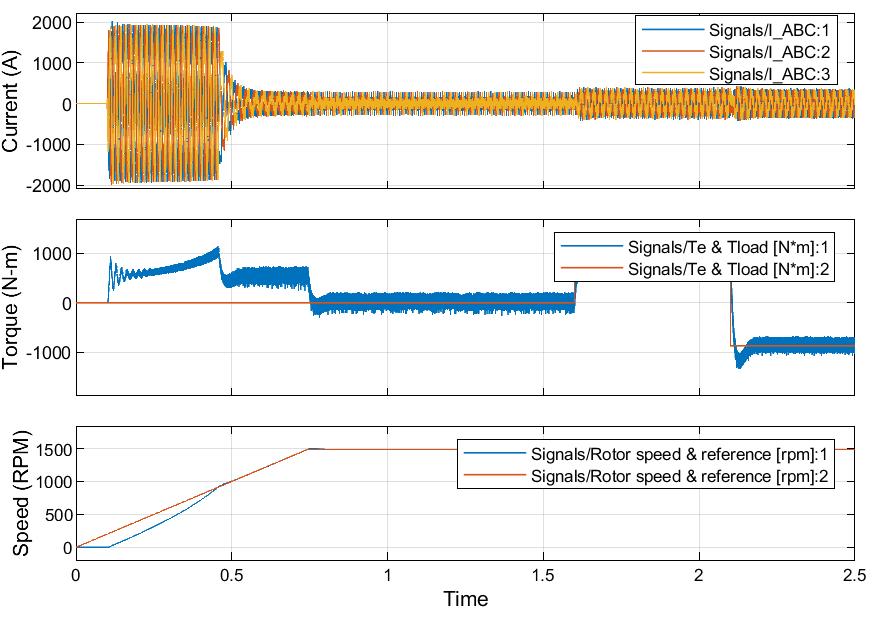
Figure 4.2: Current, Torque, and Speed Response of H-Infinity-based DSIM for 5N load

2025, IRJET | Impact Factor value: 8.315 | ISO 9001:2008 Certified Journal | Page637

Figure

International Research Journal of Engineering and Technology (IRJET) e-ISSN:2395-0056

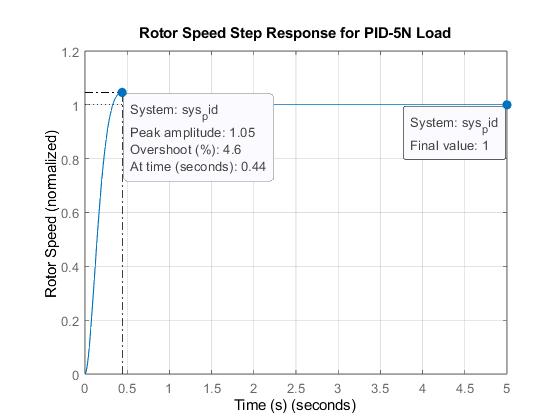
Figure 4.3: Step response of PID-based DSIM showing overshoot (5N Load)

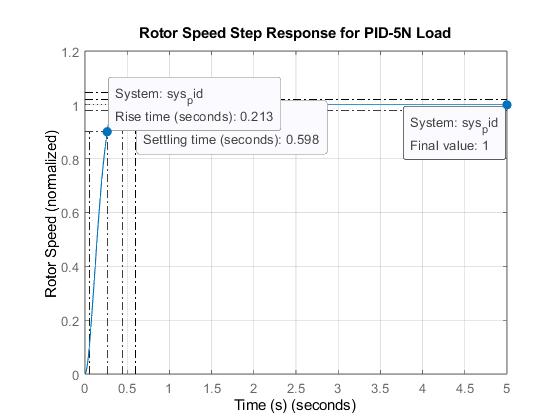
Figure 4.4: Step response of PID-based DSIM showing rise time and settling time (5N load)

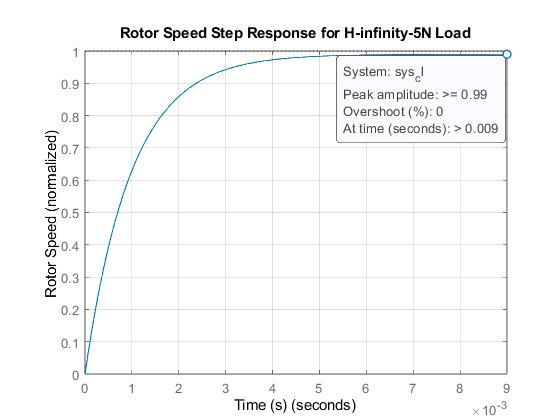
Figure 4.5: Step response of H-Infinity-based DSIM showing overshoot (5N)

International Research Journal of Engineering and Technology (IRJET) e-ISSN:2395-0056

Figure 4.6: Step response of H-Infinity-based DSIM showing settling time (5N)

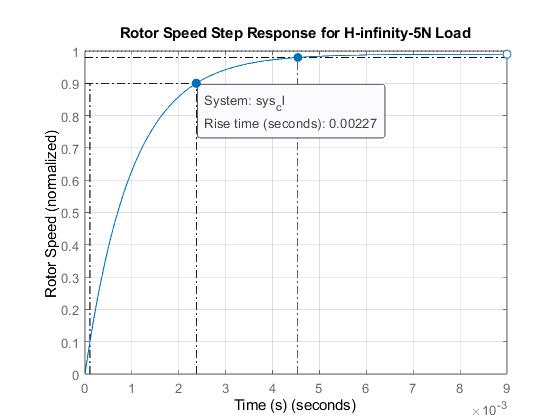
Figure 4.7: Step response of H-Infinity-based DSIM showing rise time (5N)

4.2 Frequency Response (Bode Plot) Results

Figure 4.8: Bode plot of the PID-based DSIM showing peak gain (5N)

International Research Journal of Engineering and Technology (IRJET) e-ISSN:2395-0056

Volume: 12 Issue: 10 | Oct 2025 www.irjet.net p-ISSN:2395-0072

4.3 Sigma Plots Results

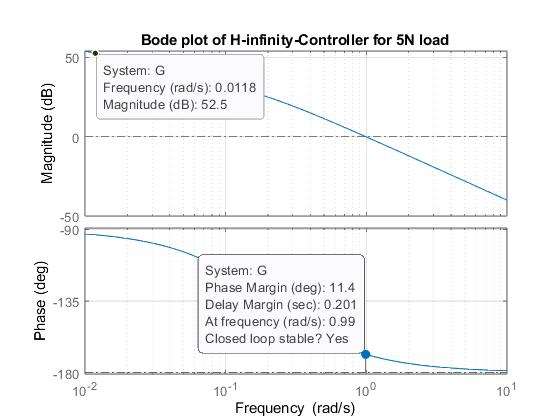
Figure 4.9: Bode plot of the H-Infinity-based DSIM under 5N load

Figure 4.10: combined sigma plot for the 3-Controllers under 5N load

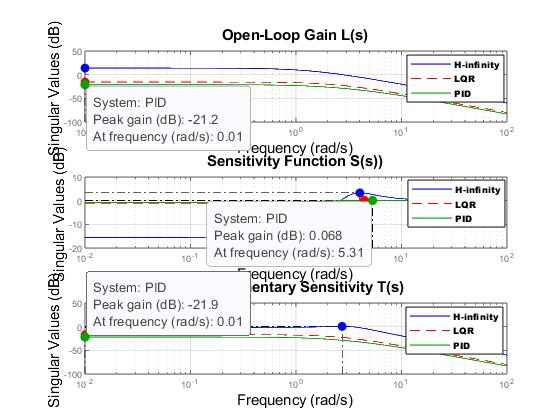
Figure 4.11: Analysis of the combined sigma plot under 5N load

4.4 Discussion of Step Response Results

Figures4.1depictsthePIDcontrollerbasedDSIMoutcomesconcerningtorque,speed,rotor,andstatorcurrentsunder5N loadchange.Thestatorcurrentsreflecthowthemachinedrawspowertomeetloaddemands.WithPIDcontrol,thecurrent response isgenerallysharp andsometimes excessive. The electromagnetic torquegenerated by the machine reflectshow thecontrollercounterstheappliedload.IncaseofPIDcontrol,torquetendstolagbehindtheloadchanges.Ascanbe seen, thereisanabruptovershootfrom0.1sto0.5sbeforeitstabilizes.Thisindicatesthecontroller’sreactivenatureandlimited abilityto handlesuddendisturbances. Figure4.2 showsthe best performance of H controller for speed responseunder 5N load disturbance, maintaining a speed within the rated speed of 1500 RPM. The currents in both stator windings increasesmoothlyandproportionallywiththeappliedloads.Thereislittleornospikes,andthetorquehasminimalripples andovershoot.

Infigure4.3,therotorspeedstepresponseofPID-basedDualStatorInductionMachinesunder5Nloaddisturbanceshows anovershootof4.6% while infigure4.5, therotorspeedstepresponseofH-infinitybasedDual StatorInductionMachine

International Research Journal of Engineering and Technology (IRJET) e-ISSN:2395-0056

Volume: 12 Issue: 10 | Oct 2025 www.irjet.net p-ISSN:2395-0072

under 5N load disturbance shows an overshoot of 0%. This establishes that H-Infinity has a better performance characteristicsthanPID.

Infigure4.4,therotorspeedstepresponseofPID-basedDualStatorInductionMachinesunder5Nloaddisturbanceshows a risetimeof 0.213second andsettlingtimeof0.598second but infigure4.6,the rotorspeedstep responseofH-infinity basedDual StatorInduction MachineunderN loaddisturbanceshowsa settling timeof0.00454secondandinfigure4.7, the rotor speed step response of H-infinity based Dual Stator Induction Machine under 5N load disturbance shows a rise time of 0.00227 second. The reduced rise time and settling time in the case of H-Infinity over PID is an indication of HInfinity’sbetterperformanceoverPID.

4.5

Discussion of Frequency Response Results

Infigure4.8,thefrequencyresponse(BodePlot)ofPID-basedDualStatorInductionMachineunder5Ndisturbanceshows apeakgainof-6.02dBatafrequencyof2.83�� rad/sandinfigure4.9,thefrequencyresponse(Bodeplot)ofH-infinity based Dual Stator Induction Machine under 5N load disturbance indicates a magnitude (gain margin) of 52.5dB at a frequencyof0.0118rad/sandaphasemarginof atafrequencyof0.99rad/s.ThehighgainintheH-Infinitycaseisa showofbetterperformanceofH-InfinityoverPID.

4.6

Discussion of Sigma Plots Results

Figures4.10and4.11,showsthesigmaplotsforthethreecontrollers(PID,LQRandH-infinity)togetherfortheDualStator InductionMachineunder5Nloaddisturbance.TheyshowthatPIDcontrollerhasanegativesingularvaluefortheload.Hinfinityshowsapeakgainof14dBat0.01rad/s.

Figure4.11,showsthesigmaplotsofallthreecontrollers(PID,LQRandH-infinity)togetherfortheDualStatorInduction Machine under 15N. For the open loop gain, L(s), PID indicates a peak gain of -21.2dB at a frequency 0.01rad/s. For the sensitivity function, S(s), PID indicates a peak gain of 0.068dB at 5.31rad/s. For the complimentary sensitivity, T(s), PID indicates peak gain of -21.9dB at frequency of 0.01rad/s. Figure 4.54, shows the sigma plots of all three controllers (PID, LQR and H-infinity) together for the Dual Stator Induction Machine under 5N. For the open loop gain, L(s), H-infinity indicatesapeakgainof10.9dBatafrequency0.01rad/s.Forthesensitivityfunction,S(s),H-infinityindicatesapeakgainof 2.53dB at 3.6rad/s. For the complimentary sensitivity, T(s), H-infinity indicates peak gain of -0.934dB at frequency of 2.11rad/s.

5.0 CONCLUSION

The performance of two control strategies (PID and H-infinity) is compared for the Dual Stator Induction Machine under 5N.Themetricsconsideredintheperformanceare;overshoot,settlingtimeandpeaktime.Also,frequencydomainanalysis viabodeandsigmaplotsareconsideredinordertoassessrobustnessandstabilitymargins.

PIDissimplertoimplement(thoughitsperformancedegradessignificantlywithincreasingload),H-infinityoffersarobust performanceanddisturbancerejectioncapability.

PID sigma plots shows higher peak, indicating poor disturbance attenuation but H-infinity controller maintains a sigma peakwellbelow0dB,validatingstrongrobustnessandminimizedgainacrossallperturbationscenarios.

FrequencydomainresultsvalidatethatH-infinityprovidessuperiorrobustnessandstabilitymargins,whichisessentialfor industrialDSIMapplication.PIDshowsreducedphasemarginandlowergaincrossoverfrequency(evenunderhighloads), indicatingreducedstabilityandincreasedsensitivitytodisturbance.

From both time domain and frequency domain, the H-infinity controller outperforms the PID in handling varying load disturbancesintheDSIMsystem.

Recommendation

International Research Journal of Engineering and Technology (IRJET) e-ISSN:2395-0056

Volume: 12 Issue: 10 | Oct 2025 www.irjet.net p-ISSN:2395-0072

The current study of H-infinity based DSIM is based on a single load condition of 5N. Future work should include a study undervaryingloadconditions.

6.0 REFERENCES

1. UjuI.U,NzeifeI.D&AsiweU.M(2018).AnalysisandApplicationofLinearMotors;anOverview. International JournalofInnovativeEngineeringTechnologyandScience.Vol.2,Issue1.

2. Marwa B.S, Larbi K.M, Mouldi B.F. and Habib R., (2014), Dual Stator Induction Motor Operation from Two PWM Voltage Source Inverters, Unit Signal, Image and Intelligent Control of Industrial Systems (SICISI)

3. SinghG.K.,PantV.,SinghY.P.,(2003).Voltagesourceinverterdrivenmulti-phaseinductionmachine, Computers andElectricalEngineering,Vol.29,no.8,pp.813–834

4. Awadallah,M.A.andSoliman,H.M.,(2009),ANeuro-fuzzyAdaptivePowerSystemStabilizerUsing Genetic Algorithms,ElectricPowerComponentsandSystems,Vol.37,pp.158–173Bansal, A. and Sharma V., (2013),DesignandAnalysisofRobustH-infinityController, Control Theory and Informatics, Vol.3, No.2, pp.7-14.

5. VasičkaninovaA.andBakošovaM.(2013),ApplicationofH2andH∞ApproachestotheRobust ControllerDesignforaHeatExchanger,ChemicalEngineeringTransactions,Vol.35,pp.463-468

6. Gu,D.W.,Petkov,P.H.andKonstantinov,M.M.,(2005),RobustControlDesignwithMatlab,Springer-Verlag LondonLimited

7. Scherer,C.,(2001),TheoryofRobustControl,DelftUniversityofTechnology,Netherlands SchwenzerM,AyM,BergsT.andAbelD.,(2021),Reviewonmodelpredictivecontrol:an engineering perspective,TheInternationalJournalofAdvancedManufacturingTechnology, Vol.117,pp.1327–1349

8. Bansal,A.andSharmaV.,(2013),DesignandAnalysisofRobustH-infinityController, Control Theory and Informatics,Vol.3,No.2,pp.7-14.

9. Tan, W., Chen T. and Marquez, H.J, (1999), Robust Controller Design and PID Tuning for Multivariable Processes,NorthChinaElectricPowerUniversity,pp.1-22

10. Agbaraji, C.E., Udeani, U.H., Inyiama, H.C. and Okezie, C.C., (2019), Robust Control for a 3DOF Articulated RoboticManipulatorJointTorqueunderUncertainties,JournalofEngineeringResearchand Reports, Vol. 9,No.4,pp.1-13.

11. Mammadov, M. A. and Orsi R. (2005), A Nonsmooth Optimization Approach to H-Infinity Synthesis, http://users.cecs.anu.edu.au/~robert/publications/cMO05.pdf

12. NairS.S.,(2011),AutomaticWeightSelectionAlgorithmforDesigningHInfinitycontrollerforActive Magnetic Bearing,InternationalJournalofEngineeringScienceandTechnology(IJEST),Vol.3,No. 1,pp.122-138

13. Dorf,R.C.andBishop,R.H.,(2008),ModernControlSystems,PearsonPrenticeHall,11thedition ElGhaoui,L.,OustryF.,andAitRamiM.,.(1997),Aconecomplementaritylinearizationalgorithm for staticoutput-feedbackandrelatedproblem, IEEE Trans. on Automatic Control,vol.42,no.8, pp.1171-1176

14. El Ghaoui, L., Oustry F., and Ait Rami M., .( 1997), A cone complementarity linearization algorithm for static output-feedbackandrelatedproblem, IEEE Trans. on Automatic Control,vol.42,no.8,pp.1171- 1176

15. Ibaraki, S. and Tomizuka, M., (2001), Rank minimization approach for solving BMI problems with random search,inProceedingsAmericanControlConference,pp.25.27

16. Leibfritz,F.,(2001),AnLMI-basedalgorithmfordesigningsuboptimalstaticH2/H-Infinityoutput feedback controllers, SIAM J. Control Optimal,Vol.39,No.6,pp.1711.1735

17. Grigoriadis,K.M.andBeran,E.B.,(1999),Alternatingprojectionalgorithmsforlinearmatrix inequalities problems withrankconstraints,InAdvancesonLinearMatrixInequality Methods in Control, L. El Ghaoui and S.I. Niculescu,Eds.SIAM,pp.251.267

18. Orsi,R.,Helmke,U.andMoore,(2004),ANewton-likemethodforsolvingrankconstrained linear matrix inequalities,In Proc. 43rd IEEE Conference on Decision and Control, ParadiseIsland, Bahamas,pp.3138.3144

19. Fares, B., Apkarian P. and Noll D., (2001), An augmented Lagrangian method for a class of LMIconstrained problemsinrobustcontroltheory,Int.J.Control,Vol.74,No.4,pp.348.360

20. Noll, D., Torki, M. and Apkarian, P., (2004), Partially augmented Lagrangian method for matrix inequality constraints, SIAM J. Optim.,Vol.15,No.1,pp.161-184

International Research Journal of Engineering and Technology (IRJET) e-ISSN:2395-0056

Volume: 12 Issue: 10 | Oct 2025 www.irjet.net p-ISSN:2395-0072

21. Benyoussef E, Barkat S (2020). Five-level Direct Torque Control with Balancing Strategy of Double Star InductionMachine.IntJSystApplEngDev.2020;14(Dci):116–23.

APPENDIX 1

MATLAB CODES

%DualStatorInductionMachineControlUsingH-Infinity

%Author:

%Date:

%Objective:ComparePIDandH-infinityControl clc; clear;

%MotorParameters

Rs=0.435; Rr=0.816; Ls=0.002; Lr=0.002; Lm=0.0693; J=0.089; B=0.005; p=4;

%Torqueconstant Kt=(3/2)*(p/2)*(Lm/Lr);

%SystemMatrices

A=zeros(7,7); Bmat=zeros(7,4);

%FillAmatrix

A(1,1)=-Rs/Ls;

A(1,5)=-Lm/(Ls*Lr)*Rr;

A(2,2)=-Rs/Ls;

A(2,6)=-Lm/(Ls*Lr)*Rr;

A(3,3)=-Rs/Ls;

A(3,5)=-Lm/(Ls*Lr)*Rr;

A(4,4)=-Rs/Ls;

A(4,6)=-Lm/(Ls*Lr)*Rr;

A(5,1)=-Lm/(Lr*Ls)*Rs;

A(5,3)=-Lm/(Lr*Ls)*Rs;

A(5,5)=-Rr/Lr;

A(6,2)=-Lm/(Lr*Ls)*Rs;

A(6,4)=-Lm/(Lr*Ls)*Rs;

A(6,6)=-Rr/Lr;

A(7,1)=Kt;

A(7,3)=Kt;

A(7,2)=-Kt;

A(7,4)=-Kt;

A(7,5)=-Kt;

A(7,6)=Kt;

A(7,7)=-B/J;

International Research Journal of Engineering and Technology (IRJET) e-ISSN:2395-0056

Volume: 12 Issue: 10 | Oct 2025 www.irjet.net p-ISSN:2395-0072

%Bmatrix(inputsarevds1,vqs1,vds2,vqs2)

Bmat(1,1)=1/Ls; Bmat(2,2)=1/Ls; Bmat(3,3)=1/Ls; Bmat(4,4)=1/Ls;

%Output:rotorspeed

C=[0000001]; D=zeros(1,4);

%Createsystem

sys=ss(A,Bmat,C,D);

%Simulationtime

t=linspace(0,5,1000); dt=t(2)-t(1);

%Displaytransferfunctionfromeachinput tf_sys=tf(sys)

%Functiontosimulateresponsewithloadtorque simulate_response=@(TL)simulate_with_load(sys,J,t,TL);

%Runsimulations [omega5]=simulate_response(5);

%Plot figure;

pl0ot(t,omega5,'r',t,'g-.','LineWidth',1.5); xlabel('Time(s)'); ylabel('RotorSpeed(rad/s)'); title('DSIMRotorSpeedResponsetoLoadTorqueDisturbances'); legend('5Nm',); gridon;

%%1.PIDControllerDesign

C_pid=pidtune(sys_siso,'PID'); T_pid=feedback(C_pid*sys_siso,1);

%%3.H-infinityController(Simpleweightingexample)

s=tf('s');

Wp=tf(10*[11],[0.11]); Wu=tf([0.11],[1]);

systemnames='sys_sisoWpWu'; inputvar='[dist;control]'; outputvar='[Wp;Wu;sys_siso]'; input_to_sys_siso='[control+dist]'; input_to_Wp='[sys_siso]'; input_to_Wu='[control]'; P=sysic;

International Research Journal of Engineering and Technology (IRJET) e-ISSN:2395-0056

Volume: 12 Issue: 10 | Oct 2025 www.irjet.net p-ISSN:2395-0072

[K_hinf,CL_hinf,~,~]=hinfsyn(P,1,1);

%%4.SimulateStepTorqueDisturbance t=0:0.01:5; dist5=-5/J*ones(size(t)); %rotordecelerationduetoload

%H-infinitysystemisalreadyconfiguredfordisturbanceasinput [y_pid5,~]=lsim(T_pid,dist5,t); [y_lqr5,~]=lsim(T_lqr,dist5,t); [y_hinf5,~]=lsim(CL_hinf,dist5,t);

[y_pid10,~]=lsim(T_pid,dist10,t); [y_lqr10,~]=lsim(T_lqr,dist10,t); [y_hinf10,~]=lsim(CL_hinf,dist10,t);

[y_pid15,~]=lsim(T_pid,dist15,t); [y_lqr15,~]=lsim(T_lqr,dist15,t); [y_hinf15,~]=lsim(CL_hinf,dist15,t);

%%5.Plotfor10NmDisturbance figure;

plot(t,y_pid10,'g',t,y_lqr10,'b ',t,y_hinf10,'r-.','LineWidth',1.5); title('RotorSpeedResponseto10NmLoadTorque'); xlabel('Time(s)');ylabel('Speed(rad/s)'); legend('PID','LQR','H-infinity');gridon;

%%6.ComparePerformance info_pid=stepinfo(y_pid10,t); info_lqr=stepinfo(y_lqr10,t); info_hinf=stepinfo(y_hinf10,t);

fprintf('\n StepResponseMetricsfor10NmDisturbance \n'); fprintf('PID |Overshoot:%.2f%%|SettlingTime:%.2fs\n',info_pid.Overshoot,info_pid.SettlingTime); fprintf('LQR |Overshoot:%.2f%%|SettlingTime:%.2fs\n',info_lqr.Overshoot,info_lqr.SettlingTime); fprintf('H-inf |Overshoot:%.2f%%|SettlingTime:%.2fs\n',info_hinf.Overshoot,info_hinf.SettlingTime);

%BodeandSigmaplot

%T_pid =closed-loopsystemwithPIDcontroller(SISO)

%T_lqr =closed-loopsystemwithLQRcontroller(canbeSISOorMIMO)

%CL_hinf =closed-loopsystemwithH-infinitycontroller(MIMO)

%Definefrequencyrange w=logspace(-1,3,500); %from0.1to1000rad/s

%%BodePlot figure;

bode(T_pid,'g',T_lqr,'b ',CL_hinf,'r-.',w); legend('PID','LQR','H-infinity'); title('BodePlotComparison'); gridon;

International Research Journal of Engineering and Technology (IRJET) e-ISSN:2395-0056

Volume: 12 Issue: 10 | Oct 2025 www.irjet.net p-ISSN:2395-0072

%%SigmaPlot(forrobustnessanalysis,onlyforMIMOsystems) figure; sigma(T_pid,'g',T_lqr,'b ',CL_hinf,'r-.',w); legend('PID','LQR','H-infinity'); title('SigmaPlot(SingularValue)Comparison'); gridon;