Norsk_start_5–7_Matematikk_7_(LK20)_blaibok by Cappelen Damm

Jan Erik Gulbrandsen

Randi Løchsen

Kristin Måleng

Vibeke Saltnes Olsen

NORSK START 5–7

MATEMATIKK 7

Bokmål

Bli kjent med boka

I denne boka blir elevene introdusert for matematikk for 7. trinn. Den bygger videre på Norsk start 5–7 Matematikk 6.

Kapitteloppslag

Hvert kapittel begynner med et samtalebilde som danner utgangspunkt for samtale og reﬂeksjon.

I Lærerveiledningen er det en liten historie til hvert bilde. Historien ender opp i en matematisk problemstilling.

Samtale

Mange sider starter med et eksempel i en ramme. Dette er et utgangspunkt for samtale med elevene om det de skal lære.

Oppgaver

Etter samtalen følger oppgaver som likner det dere har snakket om.

Samarbeidsoppgaver

Nederst på mange sider er det forslag til samarbeidsoppgaver. Snakk sammen er oppgaver hvor elevene øver på norsk sammen med læreren. Øv sammen er oppgaver hvor elevene samarbeider i læringspar eller små grupper. Utforsk sammen er oppgaver hvor elevene skal løse et litt mer krevende problem, og etterpå kan de forklare hverandre hvordan de tenkte.

Språkstopp

Underveis vises det til Språkstopp. De tar utgangspunkt i enkelte ord og uttrykk som er uthevet i teksten. Innholdet står samlet ved slutten av hvert kapittel.

Dette har jeg lært

Ved slutten av hvert kapittel får elevene vist hva de har lært. Det er oppgaver som de kjenner igjen fra kapittelet, og en liste med sentrale ord og begrep som de kan sjekke om de har forstått.

Spill

Til hvert kapittel er det et spill. Det er en morsom og annerledes måte å lære matematikk på.

Jeg heter Jojo. Triks og jeg er også venner.

Lærerressursen

Hei! Jeg heter Anna.

Jeg heter Belo. Anna og jeg er venner.

Jeg heter Pavo. Jeg er en robot som hjelper barna med matematikk.

I lærerressursen på norskstart5-7.cappelendamm.no ﬁnner du blant annet supplerende stoﬀ og oppgaver, for eksempel til regneark og GeoGebra.

Tall DU LÆRER

•om matematiske sammenhenger i hele tall og desimaltall

•hoderegningsstrategier i hele tall og desimaltall

•om partall, oddetall og primtall

•om negative tall

SNAKK SAMMEN

Hva ser du på bildet?

Hva betyr 5 moh.?

Hvor mange meter er det fra bunnen og opp til toppen?

VIKTIGE ORD

•hoderegning

•regnestrategi

•dobling

•halvering

•partall

•oddetall

•primtall

•plassverdisystemet

•siffer

•utvidet form

•negative tall

1.RESTART

Se etter sammenhenger

Sammenhenger i addisjon og subtraksjon med hele tall og desimaltall.

25 + 5 = 30

2,5 + 0,5 = 3,0

0,25 + 0,05 = 0,30 30 – 5 = 25 3,0 – 0,5 = 2,5

– 0,05 = 0,25

Regn

+ 0,6 =

+ 0,06 =

1.2 Regn ut. a) 16 – 8 = b) 24 – 8 = c) 10 – 5 = 1,6

3,6 + 5,4 = 2,9 + 4,7 = 4,8 – 3,2 =

Se etter tiervenner

Du kan bruke tiervenner når du regner med større tall og med desimaltall. 2 + 8 = 103 +7 = 10 6 + 4 = 10 0,2 + 0,8 = 1,043 + 17 = 60600 + 400 = 1000

1.4 Regn ut.

a)8 + 2 = b)66 + 4 = c)19 + 1 = 8 + 12 = 66 + 24 = 19 + 11 = 28 + 102 = 166 + 224 = 190 + 110 =

1.5 Regn ut.

a)0,3 + 0,7 = b)0,9 + 0,1 = c)1,5 + 0,5 =

d)1,2 + 1,8 = e)4,4 + 1,6 = f)5,7 + 0,3 =

1.6 Belo har fem skåler med bær og ei tom bøtte som rommer 5,0 L. Hvilke skåler kan han fylle i bøtta slik at det blir 5,0 L til sammen? Det er flere løsninger.

+ 29 = 24 + 30 – 1 =53

1.7 Regn ut.

a)32 + 19 = b)45 + 29 =

c)104 + 59 = d)16 + 79 =

e)53 + 39 = f)22 + 49 =

1.8 Regn ut.

a)54 – 39 = b)68 – 19 =

c)376 – 59 = d)188 – 79 =

e)98 – 49 = f)65 – 29 =

1.9 Isak har 123 kr og tjener 49 kr.

a)Hvor mange kroner har Isak til sammen?

Isak kjøper en is for 29 kr.

b)Hvor mange kroner har han igjen? a) b)

Du skal regne ut 1,5 + 0,9 =

+ 1

Du skal regne ut 2,4 – 1,9 = 1,5

1,5 + 0,9 = 1,5 + 1,0 – 0,1 = 2,4 2,4 – 1,9 = 2,4 – 2,0 + 0,1 = 0,5

1.10 Regn ut.

a)2,8 + 0,9 = b)4,5 + 1,9 =

c)1,2 + 3,9 = d)6,6 + 2,9 =

e)0,4 + 8,9 = f)3,2 + 4,9 =

1.11 Regn ut.

a)5,6 – 0,9 = b)8,1 – 3,9 =

c)4,7 – 1,9 = d)8,3 – 7,9 =

e)5,4 – 2,9 = f)9,5 – 3,9 =

1.12 Belo har to poser med poteter.

I den ene posen er det 1,5 kg, i den andre posen er det 3,9 kg.

a)Hvor mange kilogram poteter har han til sammen?

Belo bruker 1,9 kg poteter i en gryterett.

b)Hvor mange kilogram poteter har han igjen? a) b)

Dobling og halvering i addisjon og subtraksjon

Du kan bruke det du kan om dobling og halvering av hele tall, når du skal doble og halvere desimaltall. s. 28 1 Språkstopp

14 + 14 = 28

14 + 15 = 29

1,4 + 1,4 = 2,8

1,4 + 1,5 = 2,9

1.13 Regn ut.

– 12 = 12

a)12 + 12 = b)25 + 25 = c)15 + 15 = 1,2 + 1,2 = 2,5 + 2,5 = 1,5 + 1,5 =

1.14 Regn ut.

a)2,4 + 2,4 = b)3,5 + 3,5 = c)1,8 + 1,8 = 2,4 + 2,5 = 3,5 + 3,6 = 1,8 + 1,9 =

1.15 Håndballtreneren sjekker hvor mange liter vann spillerne drikker i løpet av en turnering.

a)Hvor mange liter vann drikker

Jon og Alex til sammen?

b)Hvor mange liter vann drikker

Petra og Anja til sammen?

1.16 Regn ut.

a)8 – 4 = b)12 – 6 = c)50 – 25 = 0,8 – 0,4 = 1,2 – 0,6 = 5,0 – 2,5 =

1.17 Regn ut.

a)5,0 – 2,5 = b)1,6 – 0,8 = c)3,0 – 1,5 =

–

1.18 Doble og halvere tallene. Halvparten Det dobbelte Halvparten Det dobbelte

1.19 Lag oppgaver med dobling og halvering der svaret blir a)8

4 + 4 = 16 - 8 = b)30c)2,4

Utforsk sammen

Belo har oppskrift på «Verdens beste vafler». Oppskriften er til 8 vafler. Belo vil lage 20 vafler.

Hjelp Belo å lage oppskrift til 20 vafler.

Verdens beste vafler

3 egg 1 dL sukker L melk 0,5 ts bakepulver 2 ts vaniljesukker 1,5 kardemomme 1 4

Dobling og halvering i multiplikasjon

I multiplikasjon kan du doble den ene faktoren og halvere den andre, og produktet blir det samme. s 28

2 Språkstopp

1.20 Regn ut.

1.22 Skriv to og to multiplikasjoner som gir samme produkt i tabellen.

12,5 · 6 4 · 7,5 1,5 · 8

2,5 · 12 0,5 · 32

2 · 15 25 · 3 3 · 4

1 · 16 5 · 6

1.23 Lag en multiplikasjon der du dobler den ene faktoren og halverer den andre. Regn ut.

a)12 · 5 = b)8 · 0,5 =

c)3 · 16 = d)2,5 · 8 =

e)4 · 3,5 = f)1,5 · 12 =

1.24 Jojo har bestilt 8 poser fuglefrø.

Det er 1,5 kg i hver pose.

Hvor mange kilogram fuglefrø har hun bestilt?

Utforsk sammen

12 : 0,25 = 36 · 0,75 = =

Hvordan kan dere bruke det dere har lært om dobling av den ene faktoren og halvering av den andre, til å løse disse oppgavene?

Multiplikasjon ved å dele opp tallene

Når du skal løse multiplikasjonsoppgaven 52 · 4 =, kan det være lurt å dele opp et av tallene.

1.25 Regn ut.

Divisjon ved å dele opp tallene

Når du skal løse divisjonsoppgaven 51 : 3 =, kan det være lurt å dele opp et av tallene.

1.26 Regn ut.

Plassverdisystemet

Alle tall i vårt tallsystem består av ett eller flere av sifrene 0, 1, 2, 3, 4, 5, 6, 7, 8 og 9. Hver plass har en verdi og et navn.

Tallet 125,783 skrevet på utvidet form:

Språkstopp

125,783 = 100 + 20 + 5 + 0,7 + 0,08 + 0,003 s. 29

1.27 Hvilket siffer står på tidelsplassen?

a)47,54 5 b)78,947 c)249,1

1.28 Hvilket siffer står på hundredelsplassen?

a)357,62 b)45,683 c)134,01

1.29 Hvilket siffer står på tusendelsplassen?

a)77,154 b)97,473 c)467,420

1.30 Hvilken verdi har sifferet 3?

a)357,62 b)1361,2 c)4713,621

d)45,683 e)13 461,9 f)30 987,11

1.31 Hvor mye øker tallets verdi når sifferet 2 endres til 6?

a)201,14 b)21,49 c)570,42 125783 ,

LÆRERTIPS La elevene øve seg på å lese de store desimaltallene på denne siden høyt for hverandre.

1.32 Bruk alle sifrene i hvert tall du lager. 4 9 7 8 1

a) Lag tre ulike tall.

b) Skriv tallene i stigende rekkefølge

c) Lag to ulike desimaltall.

1.33 Skriv tallene på utvidet form.

a) 47,178 =

b) 813,971 =

c) 607,1 =

1.34 Skriv tallene som mangler. a)

Utforsk sammen

Bruk sifrene for å lage tall. Hvert siffer kan bare brukes én gang i hver oppgave.

• Lag en addisjonsoppgave med to desimaltall hvor summen av tallene er størst mulig.

• Lag en subtraksjonsoppgave med to desimaltall hvor differansen mellom tallene er størst mulig.

1 7 8 4 3 9

Partall, oddetall og primtall

Partall er tall som slutter på sifrene 0, 2, 4, 6, 8.

Oddetall er tall som slutter på sifrene 1, 3, 5, 7, 9.

Primtall er tall som bare kan divideres med seg selv og 1, og få et helt tall til svar. De minste primtallene er 2, 3, 5, 7, 11, 13, 17,19.

13 er både oddetall og primtall.

1.35 Et tall på hver ballong er plassert feil. Skriv en X over tallet.

Partall 2, 6, 14, 29, 30, 118

Oddetall 5, 7, 13, 21, 24, 35, 99

ABC A

Primtall 2, 5, 7, 11, 25, 107

1.36 Skriv tre ulike partall som har summen 36.

+ + = 36

1.37 Skriv tre ulike oddetall som har summen 45.

+ + = 45

1.38 Regn ut og tegn ring rundt svarene som er et primtall?

a)6 + 6 + 1 = 13 b)52 – 21 = c)7 · 7 =

d)100 – 1 = e)0,5 · 4 = f)65 + 4 =

g)56 : 8 = h)12 + 6 + 5 = i)66 : 6 =

1.39 Anna tenker på et tall.

• Tallet har tre siffer.

• Sifferet på tierplassen er det minste primtallet.

• Sifferet på hundrerplassen er tre ganger så stort som sifferet på tierplassen.

• Sifferet på enerplassen er halvparten av sifferet på hundrerplassen.

Hvilket tall tenker Anna på?

1.40 Belo tenker på et tall.

• Tallet har to siffer.

• Sifferet på tierplassen er én mindre enn sifferet på enerplassen.

• Tallet er et primtall.

• Tallets verdi er mindre enn halvparten av 100.

Hvilket tall tenker Belo på?

1.41 Primtallene 3 og 5 kalles primtallstvillinger, fordi det ikke er noe annet oddetall mellom dem. Finn tre andre primtallstvillinger under 50.

Utforsk sammen

Partall og oddetall

Bruk tallene og lag mange addisjonsstykker av to og to tall. Se på svarene.

Lag en regel som sier noe om svarene når dere

• adderer to partall

• adderer to oddetall

• adderer et partall og et oddetall

LÆRERTIPS Utfordre elevene på å lage «Tenke på tall»-oppgaver til hverandre.

Negative tall

Tall som har lavere verdi enn 0, kaller vi negative tall.

tall

–5–4–3–2–1054321

1.42 Skriv tallene som skal stå der pilene peker.

1.43 Skriv tallene på riktig plass på tallinja.

1.44 Skriv tallene som skal stå der pila peker.

1.45 Skriv tallene i stigende rekkefølge.

LÆRERTIPS La elevene komme med eksempler på hvor vi bruker negative tall.

1.46 Skriv riktig tegn <, > eller =.

a)3 –1

b)–9 –10

d) -56 – 65e)–15 7

c)8 –9

1.47 I tabellen ser du temperaturen på fire ulike steder i Norge.

StedKristiansandHaugesundBodøKirkenes

Temperatur 5

a)Hvor er det lavest temperatur?

b)Hvor er det høyest temperatur?

c)Skriv temperaturene i stigende rekkefølge

1.48 Termometeret på tegningen er et termometer som viser hva slags farge på skismøring du skal bruke ved ulike temperaturer.

a)Hvilken farge på skismøring trenger du hvis det er –12°C?

b)Hvilken farge på skismøring trenger du hvis det er –2 °C?

c)Når kan du bruke rød skismøring?

LÆRERTIPS Snakk med elevene om skismøring.

Regne med negative tall

Belo sjekker temperaturen ute klokka 07.00 og klokka 14.00.

Klokka 07.00 er temperaturen –8 °C. Klokka 14.00 er temperaturen 4 °C.

Han lurer på hva temperaturforskjellen er.

Du kan finne temperaturforskjellen slik: –8 04 + 8 + 4

Temperaturforskjellen er 12 grader.

1.49 Termometerne viser temperaturen i tre byer i Norge.

a)Hvor er det høyest temperatur?

b)Hva er temperaturforskjellen mellom Oslo og Bergen?

c)Hva er temperaturforskjellen mellom Bodø og Bergen?

d)Hva er temperaturforskjellen mellom Oslo og Bodø?

1.50 I tabellen ser du temperaturen i fire ulike byer i Norge.

Sted Hamar Oslo BodøLillehammer

a)I hvilken by er det lavest temperatur?

b)Hva er temperaturforskjellen mellom byen med lavest temperatur og byen med høyest temperatur?

1.51 Markus bor i Larvik. Han skal reise til Svalbard. Han sjekker temperaturen før han pakker.

Svalbard Larvik

MandagTirsdagOnsdagMandagTirsdagOnsdag

a)Hva er temperaturforskjellen mellom Svalbard og Larvik på tirsdag?

b)Hvilken dag er det størst temperaturforskjell mellom Svalbard og Larvik?

c)Hvilken dag er det minst temperaturforskjell mellom Svalbard og Larvik?

Anna ringer til bestemor og forteller at temperaturen ute er –9 °C. «Det er 15 grader varmere hos meg», sier bestemor. Anna lurer på hva temperaturen er hos bestemor.

Du kan finne temperaturen hos bestemor slik: –9 0 6 + 9 + 6

–9 + 15 = 6

Temperaturen hos bestemor er 6 °C.

1.52 Regn ut. Du kan telle på tallinja.

a)–5 + 3 = b)–2 + 4 = c)–1 + 5 =

d)2 – 7 = e)–1 – 3 = f)1 – 5 =

1.53 Regn ut. Du kan tegne tom tallinje på et kladdeark.

a)–2 + 5 = b)–12 + 5 = c)–8 – 4 =

d)7 – 12 = e)–21 + 15 = f)25 – 31 =

1.54 En dag er det –3 °C om morgenen. Midt på dagen har temperaturen steget med 8 grader. Hva er temperaturen midt på dagen?

Hvilket regneuttrykk passer til oppgaven?

A 3 + 8 = B –3 + 8 = C 3 – 8 = 01234567 –7–6–5–4–3–2–1 uren », r

LÆRERTIPS Snakk med elevene om uttrykkene temperaturen stiger, og temperaturen synker. Bøy verbene å stige og å synke.

1.55 Et termometer viser –6 °C.

Hva viser termometeret når temperaturen

a) stiger med 2 grader?

b)stiger med 9 grader?

c) synker med 3 grader?

d)synker med 7 grader?

1.56 Esma kjøper nytt fryseskap.

Displayet viser 21 °C når hun starter fryseskapet. Etter tre timer har temperaturen sunket med 39 grader.

Hvilken temperatur viser displayet da?

1.57 Matematikeren Arkimedes ble født i år –287.

Han døde da han var 75 år.

Hvilket år døde Arkimedes?

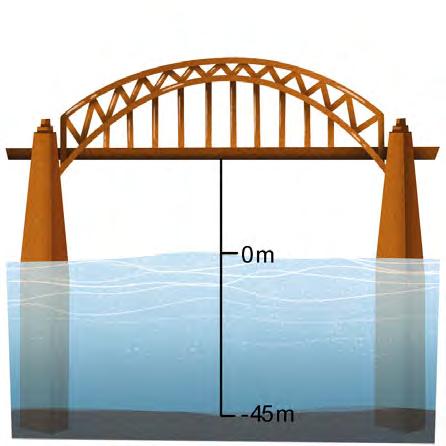
1.58 Havbunnen under Gausbroen er –45 m

på det dypeste punktet.

Fra dette punktet og opp til veien på broen er det 70 m. Havets overflate er 0 m.

Hvor mange meter over havets overflate er veien?

1 Språkstopp

Halvparten og det dobbelte

Triks har 4 klinkekuler.

Anna har halvparten så mange klinkekuler som Triks. Hun har 2 klinkekuler.

Halvparten av 4 er 2.

Å halvere er å ﬁnne halvparten.

Når vi ﬁnner halvparten av et tall gjør vi en halvering.

Belo har dobbelt så mange klinkekuler som Triks. Han har 8 klinkekuler.

Det dobbelte av 4 er 8.

Å doble er å ﬁnne det dobbelte.

Når vi ﬁnner det dobbelte av et tall gjør vi en dobling.

2 Språkstopp

I en multiplikasjon kaller vi tallene som vi multipliserer for faktor og svaret for produkt.

6 · 9 = 54

faktor · faktor = produkt

3 Språkstopp

Plassverdisystemet. Hva plassene heter.

125783 ,

Siﬀeret 3 står på tusendelsplassen og har verdien 0,003.

Siﬀeret 8 står på hundredelsplassen og har verdien 0,08.

Siﬀeret 7 står på tidelsplassen og har verdien 0,7.

Siﬀeret 5 står på enerplassen og har verdien 5.

Siﬀeret 2 står på tierplassen og har verdien 20.

Siﬀeret 1 står på hundrerplassen og har verdien 100.

4 Språkstopp

Temperatur

I Norge bruker vi celsiusskalaen når vi måler temperatur.

Vi måler temperaturen i grader celsius,°C.

Vi skriver for eksempel 15 °C. Vi leser: «Femten grader celsius.»

I dagligtale sier vi bare: «Femten grader.»

Temperaturer over 0 °C kaller vi varmegrader eller plussgrader.

Når temperaturen er under 0 .

Vi skriver –5 °C. Vi leser: «Minus fem grader celsius».

I dagligtale sier vi bare: «Minus fem grader.»

Temperaturer under 0 °C kaller vi kuldegrader eller minusgrader.

Dette har jeg lært

1.59 Regn ut. Se etter mønster.

1.60 Regn ut. Se etter tiervenner.

1.61 Regn ut. Du kan regne om ti.

53 + 19 =

1.62 Regn ut. Du kan tenke dobling og halvering. a) 13 + 13 =

1.63 Lag en multiplikasjon der du dobler den ene faktoren og halverer den andre. a) 4 · 18 = · =

1.64 Regn ut. Det kan være lurt å dele opp tallene.

63 5= 76 : 4=

1.65 Skriv tallet på utvidet form.

13 482,69 =

1.66 Hvilken verdi har sifferet 3?

1.67 Skriv et tresifret tall. Sifferet på enerplassen er et oddetall, sifferet på tierplassen er et partall, og sifferet på hundrerplassen er et primtall.

1.68 Tabellen viser temperaturen tre steder i Norge.

Sted

GjøvikFørdeKarasjok

a) Hvor er det høyest temperatur?

b) Hvor stor er temperaturforskjellen mellom Førde og Karasjok?

c) Temperaturen på Gjøvik stiger med 7 °C. Hva er temperaturen da?

en dobling en halvering

å doble

å halvere

faktor produkt

siﬀer

utvidet form

tidelsplassen

hundredelsplassen

tusendelsplassen et partall et oddetall et primtall negative tall temperaturforskjell grader celcius

Lag primtall

Antall spillere 2

Utstyr

Spillebrett, tre terninger, hver sin fargeblyant.

Spilleregler

Spillerne har et spillebrett med primtall.

Spiller A slår terningene og prøver å kombinere disse på ulike måter slik at hen får et primtall.

Eksempel:

Spilleren slår 3, 2 og 1.

Hen kan lage 32 – 1 = 31 eller 13 – 2 = 11 eller 23 · 1 = 23 eller (3 + 1) : 2 = 2 osv.

Spiller A krysser over det primtallet hen velger med sin farge. Neste spiller slår terningene og lager et primtall som hen krysser over med sin farge.

Vinner

Dersom spiller A ikke klarer å lage et ledig primtall, vinner spiller B, og omvendt.

Variant

Spillerne kan ha hvert sitt brett og for hver gang de slår, kan de lage så mange primtall som mulig og dekke over dem på sitt brett. Den som har dekket flest primtall etter for eksempel tre runder, har vunnet.