Slim leren, zeker slagen
INCLUSIEF ONLINE OMGEVING
Wil jij slim leren, zeker slagen?
Examenbundel
Oefen met echte examenopgaven per onderwerp en met complete examens. In het boek en online.
Oefenen, oefenen, oefenen
Uitleg b� de antwoorden
Oriëntatietoets geeft aan hoe je ervoor staat
Examenidioom
Speciaal voor de examens Duits, Engels en Frans.
Een grote woordenschat zorgt voor beter tekstbegrip
Duidel� ke voorbeeldzinnen
Ook voor de schoolexamens
Samengevat
De perfecte samenvatting om je voor te bereiden op je examen.
Zo leer je precies wat je moet weten.
Complete examenstof
R� tjes en defi nities
Geen lappen tekst
Zeker Slagen!
Zo leer je efficiënter leren.
J e leert hoe je moet leren
Hulp b� plannen
Je kr� gt zelfi nzicht en zelfvertrouwen
examen bundel
Natuurkunde
R. Slooten
L. van Rooyen
M.H. Overbosch
2025 2026
Colofon
Auteurs
R. Slooten
L. van Rooyen
M.H. Overbosch
Redactie
Lineke Pijnappels, Tilburg
Omslagontwerp
Studio Fabienne, Hoevelaken
Vormgeving binnenwerk
Studio Michelangela, Utrecht
Opmaak
Crius Group, Hulshout
Over ThiemeMeulenhoff
ThiemeMeulenhoff is een educatieve uitgeverij die zich inzet voor het voortgezet onderwijs en beroepsonderwijs. De mensen van ThiemeMeulenhoff zijn er voor onderwijsprofessionals met ervaring, expertise en doeltreffende leermiddelen. Ontwikkeld in doorlopende samenwerking met de mensen in het onderwijs om samen het onderwijs nog beter te maken.
We ontwikkelen lesmethodes die goed te combineren zijn met andere leermiddelen, naar eigen inzicht aan te passen en bewezen effectief zijn. En natuurlijk worden al onze lesmethodes zo duurzaam mogelijk geproduceerd.
Zo bouwen we samen met de mensen in het onderwijs aan een mooie toekomst voor de volgende generatie.
Samen leren vernieuwen.
www.thiememeulenhoff.nl
Boek ISBN 978 90 06 99455 1
Pakket ISBN 978 90 06 99230 4
Editie 1, druk 1, oplage 1, 2025
© ThiemeMeulenhoff, Amersfoort, 2025
Alle rechten voorbehouden. Tekst en datamining, AItraining en vergelijkbare technologieën niet toegestaan. Niets uit deze uitgave mag worden verveelvoudigd, opgeslagen in een geautomatiseerd gegevensbestand, of openbaar gemaakt, in enige vorm of op enige wijze, hetzij elektronisch, mechanisch, door fotokopieën, opnamen, of enig andere manier, zonder voorafgaande schriftelijke toestemming van de uitgever.
Voor zover het maken van kopieën uit deze uitgave is toegestaan op grond van artikel 16B Auteurswet 1912 j° het Besluit van 23 augustus 1985, Stbl. 471 en artikel 17 Auteurswet 1912, dient men de daarvoor wettelijk verschuldigde vergoedingen te voldoen aan Stichting Publicatie en Reproductierechten Organisatie (PRO), Postbus 3060, 2130 KB Hoofddorp (www.stichtingpro.nl). Voor het overnemen van gedeelte(n) uit deze uitgave in bloemlezingen, readers en andere compilatiewerken (artikel 16 Auteurswet) dient men zich tot de uitgever te wenden. Voor meer informatie over het gebruik van muziek, film en het maken van kopieën in het onderwijs zie www.auteursrechtenonderwijs.nl.
De uitgever heeft ernaar gestreefd de auteursrechten te regelen volgens de wettelijke bepalingen. Degenen die desondanks menen zekere rechten te kunnen doen gelden, kunnen zich alsnog tot de uitgever wenden.
Deze uitgave is volledig CO2neutraal geproduceerd. ClimatePartner
Zo werk je met deze Examenbundel
De eerste stap om vol vertrouwen je examen voor dit vak in te gaan heb je gezet! Deze Examenbundel is namelijk de beste voorbereiding, omdat je oefent met echte examenopgaven. Kijk hoe het werkt.
De indeling van het boek
Je Examenbundel bestaat uit verschillende delen:
• Deel 1 – Oriëntatietoets: krijg snel een eerste indruk hoe je scoort op de verschillende examenonderwerpen.
• Deel 2 – Oefenen op onderwerp: oefen gericht met examenopgaven over de onderwerpen die jij lastig vindt.
• Deel 3 – Examens met uitwerkingen: oefen met hele examens met heldere uitleg van onze ervaren examendocenten.
• Deel 4 – Examen 2025-I: doe de generale repetitie voor het echte examen. De antwoorden en uitwerkingen staan op mijnexamenbundel.nl.
Hints en uitwerkingen
Weet je niet hoe je een vraag moet aanpakken? Dan zijn er hints om je op weg te helpen.
Kijk de vragen na met de uitwerkingen. Daarin staat het juiste antwoord. Maar belangrijker: je krijgt duidelijke uitleg waaróm dit het juiste antwoord is en hoe je daar komt.
Zo oefen je én leer je tegelijk!
Online oefenen met Mijn Examenbundel
Bij dit boek hoort een online omgeving: mijnexamenbundel.nl. Het boek en Mijn Examenbundel werken met elkaar samen.
Boek
Maak de balans op
• oriëntatietoets maken
• hele examens maken
Mijn Examenbundel
• nakijken oriëntatietoets
• nakijken hele examens
Je scores worden bewaard!
Leren en oefenen
• examenopgaven oefenen per onderwerp
Ook handig
• onderwerpregister
• uitlegvideo’s per onderwerp
• extra examenopgaven per onderwerp
Je ziet je voortgang!
• overzicht van de examenstof
• quickscan
• examentips
Alle belangrijke info bij elkaar!
Om optimaal gebruik te maken van boek én website, verwijst het boek op handige plekken naar mijnexamenbundel.nl
Voorbeeld:
Mijn Examenbundel
Wil je weten hoe je de toets hebt gemaakt? De antwoorden staan op mijnexamenbundel.nl. Vul je punten in en bekijk je score per onderwerp. Je scores worden bewaard.
Activeer direct je code voor Mijn Examenbundel
Ga nu naar mijnexamenbundel.nl en maak meteen je account aan. Met de activatiecode die je per mail hebt ontvangen of via de ELO van je school, heb je toegang tot alle extra’s die bij je boek horen.
Gebruik ook Samengevat
Wil jij je nóg beter voorbereiden op het eindexamen? Combineer Examenbundel dan met Samengevat - alle examenstof kort en bondig in één boek.
Heel veel succes!
Namens team Examenbundel heel veel succes met je examens! #ikgazekerslagen #geenexamenstress
Heb je een vraag of opmerking over deze Examenbundel? Ga dan naar examenbundel.nl/contact.
Opmerking
De overheid stelt de regels op voor het examen. Bijvoorbeeld wat de examenonderwerpen zijn, welke hulpmiddelen je mag gebruiken en wanneer het examen is. De auteurs en uitgever hebben deze Examenbundel met grote zorg samengesteld. Soms veranderen de regels van de overheid echter of worden er nieuwe afspraken gemaakt over wat die regels betekenen. Raadpleeg daarom altijd je docent of onze website www.examenbundel.nl voor actuele informatie die voor jouw examen van belang is.
hoe maak je examenopgaven
2 OEFENEN OP ONDERWERP
1 Vaardigheden (Domein A)
2 Informatie-overdracht (Domein B1)
DEEL 3 EXAMENS MET UITWERKINGEN
Examen 2022-II
Examen 2023-I
Examen 2023-II
Examen 2024-I
Examen 2024-II
3 Medische beeldvorming (Domein B2)
4 Kracht en beweging (Domein C1)
5 Energieomzettingen (Domein C2)
6 Eigenschappen van stoffen en materialen (Domein D1)
7 Zonnestelsel en heelal (Domein E1)
8 Gebruik van elektriciteit (Domein G1)
DEEL 4 EXAMEN 2025-I
Examen 2025-I
BIJLAGEN
Cijferbepaling
Onderwerpregister
Tips: hoe maak je examenopgaven bij natuurkunde?
Bij het op de juiste manier oplossen van een probleem doorloop je in het algemeen drie stappen: de voorbereiding, de uitvoering en een controle.
Voorbereiding
• Kijk eerst vluchtig alle opgaven door en begin met de opgaven die je vertrouwd voorkomen.
• Ga na hoeveel tijd gemiddeld beschikbaar is per opgave. Probeer te voorkomen dat je te lang met een bepaalde vraag bezig blijft en daardoor weinig punten scoort bij andere vragen.
• Lees de tekst van de gekozen opgave rustig en nauwkeurig. Onderstreep of markeer hierbij aanwijzingen, begrippen, formules, getallen e.d. die van belang kunnen zijn. Deze informatie is dan bij het beantwoorden van de vragen snel terug te vinden.
• Lees elke vraag nauwkeurig en ga na welke informatie je nodig denkt te hebben om de vraag te kunnen beantwoorden. Zoek die informatie op in de tekst van de opgave, of in Binas of ScienceData.
• Bepaal welke tussenstappen je bij de beantwoording van de vraag zult moeten maken. Deze worden bepaald door het ‘gat’ dat er zit tussen de gegevens en het gevraagde. Je kunt daarbij zowel van de gegevens als van het gevraagde uitgaan.
• Begin pas aan de uitvoering, wanneer je de aanpak van het vraagstuk overziet.
Uitvoering
• Reserveer op je papier voor elke opgave voldoende ruimte. Je werk wordt daardoor overzichtelijker en je kunt je antwoord makkelijker aanvullen.
• Schrijf alle tussenstappen overzichtelijk op, zodat zichtbaar wordt hoe je tot je antwoord bent gekomen.
• Indien om uitleg wordt gevraagd, mag die niet ontbreken.
• Schrijf bij twijfel altijd iets op (behalve als je zelf al kunt beoordelen dat je antwoord nergens op slaat).
Controle
• Lees de vraag nog eens over. Is hij volledig beantwoord?
• Vind je het gevonden antwoord zinnig (klopt bv. de orde van grootte)? Zo niet, probeer je denk- of rekenfout op te sporen of maak daarover tenminste een opmerking.
• Is de juiste eenheid vermeld?
• Is de afronding van een verkregen waarde in overeenstemming met de vraagstelling?
ORIËNTATIETOETS
Hoe zou je het nu al doen op een examen?
De oriëntatietoets geeft je een eerste indruk.
Oriëntatietoets
BritNed
Sinds april 2011 ligt er op de zeebodem tussen Nederland en Engeland een 260 km lange, goed geïsoleerde, kabel. De kabel kan beide landen van stroom kan voorzien, afhankelijk van de prijs of de energiebehoefte.
Het project is gestart in 2007 en kreeg de naam BritNed.
Op een internetforum beweerde iemand over dit project: “Onderweg van Nederland naar Engeland zal een deel van de stroomsterkte verloren gaan.”
1 Ben je het met deze bewering eens of oneens? Licht je antwoord toe.
In figuur 1 staat een schematische tekening van de stroomkring die ontstaat als er 1000 MW vermogen van Nederland naar Engeland getransporteerd wordt.
In Nederland wordt een elektrische spanning opgewekt van 450,0 kV. De spanning tussen punt Q en aarde is 446,6 kV.
De 260 km lange koperen kabel wordt voorgesteld door een draad PQ.
1
Het blokje stelt de gebruikers in Engeland voor. De terugvoerkabel hoeft niet te worden aangelegd want de stroom gaat via de aarde terug naar Nederland.
De weerstand van de koperen kabel is 1,5 Ω.
2 Toon dit aan met een berekening.
De kabel heeft een diameter van 6,0 cm.
De koperen kabel is erg zwaar: de massa is 6,6 103 ton.
3 Toon dit aan met een berekening.
Het vermogensverlies in de kabel is 7,6 MW.
4 Bereken de temperatuurstijging van de kabel in de eerste minuut na inschakelen. Ga ervan uit dat alle geproduceerde warmte door de kabel wordt opgenomen.
Kangoeroesprongen
Kangoeroes staan bekend om hun enorme sprongen en sprongkracht. Die sprongkracht danken ze aan de speciale bouw van hun achterpoten. De bouw van zo’n poot is weergegeven in figuur 1.
De voet draait rondom punt D in de enkel en steunt in punt S op de grond. De voet is met een spier verbonden via pees P.
In figuur 1 staat de kangoeroe stil.
5 Leg uit of de kracht in pees P groter is dan, kleiner is dan, of even groot is als de normaalkracht op de voet in punt S. Verwaarloos hierbij de zwaartekracht op de voet.
figuur
3p
De pees bestaat uit veerkrachtig materiaal en brengt de spierkracht over naar de voet, maar dient tevens als een sterke veer. De energie die in de pees wordt opgeslagen noemen we de veerenergie.
Er is een filmpje gemaakt van een springende kangoeroe. Op de uitwerkbijlage zijn zes opeenvolgende beelden van de bewegende kangoeroe weergegeven.
6 Geef in de tabel op de uitwerkbijlage aan of voor de aangegeven situaties: – de zwaarteenergie E z van de kangoeroe toeneemt (↑), afneemt (↓) of gelijk blijft (=); – de veerenergie E veer in de pees toeneemt (↑), afneemt (↓) of gelijk blijft (=).
uitwerkbijlage bij vraag 6 en 7
foto 4 net op de gro nd
Omcirkel het juiste alternatief.
foto 5 laags t e punt foto 6 opni e u w afzet
Omcirkel het juiste alternatief.
foto 1 naar foto
foto 1 naar foto
foto 2 naar foto
foto 2 naar foto
van foto 4 naar foto 5
van foto 4 naar foto
2p
2p
Tijdens het springen werken de normaalkracht F n en de zwaartekracht F z op de kangoeroe.
7 Geef voor de foto’s 1, 3 en 5 aan of F n groter is dan Fz, kleiner is dan Fz, of gelijk is aan F z
Om het rendement van de pees (als veer) te onderzoeken is de uitrekking van de pees gemeten met toenemende kracht (1) en met afnemende kracht (2).
Het resultaat staat in figuur 2.
Om het rendement van de pees (als veer) figuur 2 te onderzoeken is de uitrekking van de pees gemeten met toenemende kracht (1 ) en met afnemende kracht ( 2 ).
Het resultaat staat in figuur 2.
De uitrekking als functie van de kracht bleek niet lineair te verlopen.
De uitrekking als functie van de kracht bleek niet lineair te verlopen.
De oppervlakte onder het (F,u)diagram geeft de arbeid aan.
De oppervlakte onder het ( F,u )-diagram geeft de arbeid aan.
8 Leg met behulp van figuur 2 uit of de pees (als veer) een hoog of een laag rendement heeft.
2p 22 Leg met behulp van figuur 2 uit of de pees (als veer) een hoog of een laag rendement heeft. F u 1 2 figuur 2
Kernafval
In een kerncentrale wordt elektrische energie opgewekt door uraniumkernen te splijten. Als een uraniumkern wordt beschoten met neutronen, splitst de uraniumkern in andere atoomkernen en neutronen.
De warmte die bij deze reactie ontstaat, wordt gebruikt om elektrische energie op de wekken.
Een voorbeeld van een splijtingsreactie is het splijten van uranium235 in barium, een andere atoomkern en neutronen. Op de uitwerkbijlage staat deze splijtingsreactie deels weergegeven.
9 Maak de reactievergelijking op de uitwerkbijlage compleet.
uitwerkbijlage bij vraag 9
235U + 1 0n → 144Ba + 90... + ... 1 0n
In een kerncentrale wordt een mengsel van de isotopen uranium235 en uranium238 gebruikt.
10 Waarin verschillen de isotopen U235 en U238?
A in aantal protonen
B in aantal neutronen
C in aantal elektronen
D in aantal protonen en aantal elektronen
Millenniumbrug
Op 10 juni 2000 werd in Londen de Millenniumbrug geopend.
Zie figuur 1.
Deze hangbrug werd al na drie dagen gesloten. Als er veel mensen op de brug liepen, begon het deel van de brug tussen de pijlers te trillen.
Eerst trilde de brug nog nauwelijks, maar doordat er steeds meer mensen in hetzelfde ritme over de brug gingen lopen als waarmee de brug trilde, werd het trillen van de brug steeds erger.
11 Hoe heet dit natuurkundig verschijnsel?
Om problemen te voorkomen werd de brug gesloten. Technici deden daarna verschillende testen. Het lukte hen om het wegdek tussen de pijlers van de brug een horizontale staande golfbeweging te laten uitvoeren. Van deze staande golfbeweging is op vijf verschillende tijdstippen een bovenaanzicht getekend. Zie figuur 2.
De trillingstijd van deze golfbeweging is 0,90 s.
De lengte van het deel van het wegdek dat trilt is 144 m. Figuur 2 is niet op schaal.
12 Bereken de golfsnelheid in het wegdek.
figuur 1
figuur 2
4p
In figuur 3 is een spankabel van de brug getekend waaraan een gedeelte van het wegdek hangt. In punt A van de spankabel werkt een kracht van 18 kN verticaal omlaag.
13 Bepaal met behulp van figuur 3 de grootte van de spankracht in de spankabel.
figuur 3
4p
Solar Impulse
De Solar Impulse is een eenpersoonsvliegtuig dat zonneenergie gebruikt om te vliegen. De ontwerpers hebben het vliegtuig in 2011 een volledige vlucht rond de wereld laten maken. Het vliegtuig vloog op een hoogte van 10 km boven de evenaar met een gemiddelde snelheid van 70 km h–1.
14 Bereken hoeveel dagen deze vlucht duurde.
Mijn Examenbundel
Wil je weten hoe je de toets hebt gemaakt? De antwoorden staan op mijnexamenbundel.nl. Vul je punten in en bekijk je score per onderwerp. Je scores worden bewaard.
OEFENEN OP ONDERWERP
Examenopgaven per onderwerp
Met hints om je op weg te helpen en uitleg bij de antwoorden.
1 Vaardigheden
Haarföhn
Feline onderzoekt een aantal eigenschappen van een haarföhn. Ze wil allereerst weten hoeveel kg lucht de föhn per seconde uitblaast. Daarvoor gebruikt ze de volgende formule:
Q = Avρ
Hierin is:
– Q de massa van de lucht die per seconde verplaatst wordt, – A de oppervlakte van de luchtopening van de föhn, – v de snelheid van de uitgeblazen lucht, – ρ de dichtheid van de lucht.
1 Laat zien dat Q dezelfde eenheid heeft als Avρ
Om Q te kunnen berekenen, meet Feline de snelheid van de uitgeblazen lucht en de diameter van de luchtopening.
De windsnelheidsmeter geeft voor de snelheid van de lucht 9,5 m s–1. Zie figuur 1.
De diameter van de luchtopening is 4,5 cm.
De dichtheid van lucht is afhankelijk van de temperatuur.
Dit is weergegeven in figuur 2.
De föhn blaast lucht van 20 °C.
figuur 2
(kg m-3)
figuur 1
Uit de metingen van Feline volgt dat Q = 1,8 10–2 kg s–1
2 Toon dit met een berekening aan.
Om deze berekening te controleren voert Feline een tweede experiment uit. Ze blaast met de föhn een plastic zak met een volume van 60 liter op.
Het opblazen duurt 3,9 s.
3 Controleer met deze gegevens dat Q = 1,8 · 10–2 kg s–1
Vloeistoffen
verwarmen
In een experiment worden gelijke massa’s van water en een andere vloeistof op twee gelijke verwarmingselementen verwarmd (zie figuur 1).
De temperatuur wordt gemeten als functie van de tijd.
Dit levert de volgende grafiek op (zie figuur 2).
figuur 1 figuur 2
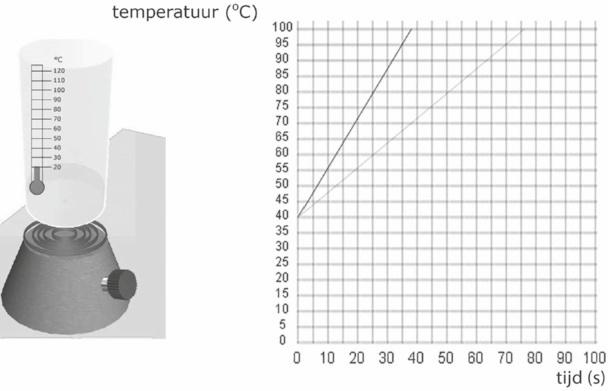
4 Leg uit welke stof, 1 of 2, de grootste soortelijke warmte heeft.
Vijftig
meter vlinderslag
In figuur 1 staat het verloop van de voortstuwingskracht (gestippelde lijn) en de snelheid van een zwemmer tijdens één zwemslag.
figuur 1
De zwemmer verricht de meeste arbeid in de eerste 0,5 s. De arbeid die hij tussen t = 0 s en t = 0,5 s verricht, is (ongeveer) gelijk aan:
a 0,09 kJ
b 0,3 kJ
c 0,9 kJ
d 3,0 kJ
5 Welke van deze antwoorden is juist? Licht je antwoord toe op basis van schattingen.
Auto
Figuur 1 toont een foto van een auto.
Door de snelheid waarmee de auto rijdt, is de afbeelding op de foto onscherp.
De onscherpte in de foto van figuur 1 is ontstaan doordat de sluiter van de fotocamera bij het nemen van de foto enige tijd open stond, in dit geval 1/30 seconde.
De wielen van de gefotografeerde auto hebben in werkelijkheid een diameter van 65 cm.
figuur 1
6 Schat de snelheid waarmee de auto reed. Licht je antwoord toe.
Ringen van Saturnus
Saturnus is de op één na grootste planeet van ons zonnestelsel. Saturnus staat bekend om zijn ringen rond de evenaar, die bestaan uit ijs en rotsdeeltjes. De diameter van deze deeltjes kan variëren van een enkele centimeter tot een meter. Zie figuur 1.
figuur 1
De ringen strekken zich uit tot een straal van 137 106 m en blijken minder dan 100 m dik te zijn. Ze worden vaak met een DVDschijfje vergeleken, wat betreft de verhouding tussen straal en dikte.
7 Laat aan de hand van een berekening zien of de Saturnusringen in verhouding veel dunner of veel dikker zijn dan een DVDschijfje.
Hints bij hoofdstuk 1
1 Vul de eenheden in van A, v en ρ.
2 Gebruik figuur 2 voor de bepaling van ρ.
3 Gebruik ρ = m V
4 Let op het verschil in temperatuurstijging als de opwarmtijd gelijk is.
5 Werk met de gemiddelde stuwkracht en snelheid om een schatting te maken.
6 Meet de hoogte en de breedte van het onscherpe achterwiel op de foto.
7 Bereken de dikte van het DVD-schijfje als de vergelijking met Saturnus juist zou zijn.
Uitwerkingen bij hoofdstuk 1
Haarföhn
1 [Q ] = kg s–1
[A v ρ ] = m2 m s–1 kg m–3 = kg s–1
Q heeft dus dezelfde eenheid als A · v · ρ
2 Q = A · v · ρ, waarin:
A = oppervlakte van de luchtopening = π r 2 = π ( 1 2 d ) 2 =
4 π d 2 (Binas 36B), met: r = straal van de cirkelvormige opening
d = diameter van de opening = 4,5 cm = 4,5 10 –2 m
zodat: A = 1 4 π ( 4,5 10 −2 ) 2 = 1,59 10 –3 m 2
v = snelheid van de lucht = 9,5 m s –1
ρ = dichtheid van de lucht bij 20 °C
Aflezen in figuur 2 geeft: ρ = 1,19 kg m –3
Invullen: Q = 1,59 · 10 –3 · 9,5 · 1,19 = 1,8 · 10 –2 kg s –1
3 methode 1
In 3,9 s wordt de plastic zak met een volume V = 60 L = 60 10 –3 m 3 gevuld met lucht.
Dat is 60 10 −3 3,9 = 1,54 10 −2 m 3 per seconde.
Voor de dichtheid ρ van de lucht geldt: ρ = m V (Binas 35C1) ⇒ m = ρ V
Voor de massa m t van de lucht die per seconde in de zak wordt geblazen, geldt dus:
m t = Q = 1,19 1,54 10 –2 = 1,8 10 –2 kg s –1 (voor ρ : zie het vorige antwoord)
methode 2
De massa m van de lucht in de zak volgt uit:
m = ρ V (Binas 35C1) = 1,19 60 10 –3 = 7,14 10 –2 kg (voor ρ : zie het vorige antwoord).
Het opblazen duurt 3,9 s, dus: Q = 7,14 10 −2 3,9 = 1,8 10 −2 kg s –1
Vloeistoffen verwarmen
4 De soortelijke warmte c vinden we uit: Q = c m ΔT (Binas 35C4), waarin:
Q = warmte-afgifte (deze is voor beide vloeistoffen in dezelfde tijd gelijk)
c = soortelijke warmte (deze is voor vloeistof 1 en vloeistof 2 niet gelijk)
m = massa van de vloeistof (deze is voor beide vloeistoffen gelijk)
ΔT = temperatuurstijging (deze is voor vloeistof 1 en vloeistof 2 niet gelijk)
Op hetzelfde tijdstip geldt: Q1 = Q2 ⇒ (c m ΔT)1 = (c m ΔT )2 ⇒ ⇒ c1 · ΔT1 = c2 · ΔT2
Uit de grafiek lezen we op hetzelfde tijdstip af: ΔT1 > ΔT2 ⇒ c2 > c1
De soortelijke warmte van stof 2 is dus het grootst.
Vijftig meter vlinderslag
5 De verrichte arbeid W in de eerste 0,5 s volgt uit:
W = Fstuw ∙ s (Binas 35A4)
Nu is de stuwkracht Fstuw niet constant tussen t = 0 s en t = 0,5 s. Om W te schatten bepalen we met tekening 1 de gemiddelde stuwkracht tussen t = 0 s en t = 0,5 s
⇒ Fstuw = 0,7 kN = 0,7 103 N
De afgelegde weg s bepalen we met tekening 2 uit:
s = v gem t (Binas 35A1), waarin:
v gem = gemiddelde snelheid in de eerste 0,5 s = = 2,5 m s–1 (zie tekening 2)
t = 0,5 s
zodat: s = 2,5 · 0,5 = 1,3 m
Invullen: W = 0,7 103 1,3 = 9 102 J = 0,9 kJ
Antwoord c is dus juist.
s is in tekening 2 ook de oppervlakte onder de grafiek van t = 0 s tot t = 0,5 s.
Auto
6
tekening 1
tekening 2
Het wiel op de foto is ongeveer 5 mm hoog en 12 mm breed. In 1 30 s heeft het wiel dus horizontaal ongeveer 7 mm = 1,4 maal zijn eigen diameter afgelegd.
Voor de snelheid v van de auto geldt: v = s t = (Binas 35A1), waarin:
s = afgelegde weg = 1,4 0,65 m
t = tijdsduur = 1 30 s = 0,033 s
Invullen: v = 1,4 0,65 0,033 = 3 · 101 m s−1
Ringen van Saturnus
7 Als een DVD-schijfje, wat betreft de verhouding tussen straal en dikte, te vergelijken zou zijn met de ringen van Saturnus, zouden we de dikte dDVD van een DVD als volgt kunnen berekenen: d DVD r DVD = d ring r ring ⇒ dDVD = dring r DVD r ring , waarin: r DVD = geschatte straal van een DVD = 6 cm = 6 10–2 m dring = maximale dikte van de ringen van Saturnus = 100 m r ring = grootste straal van de ringen van Saturnus = 137 106 m
Invullen: dDVD = 100 6 10 −2 137 10 6 = 4 10–8 m
Een DVD-schijfje is veel dikker dan 4 10–8 m, dus de Saturnus-ringen zijn in verhouding veel dunner dan een DVD-schijfje.
Mijn Examenbundel
Vind je dit onderwerp lastig? Bekijk een uitlegfilmpje op mijnexamenbundel.nl of oefen met extra examenopgaven.
2 Informatie-overdracht
Zweven op geluid
Het is mogelijk om kleine druppels te laten zweven op geluid. Zie figuur 1. De opstelling die daarvoor nodig is, bestaat uit een toongenerator met een losse luidspreker en een reflector die het geluid terugkaatst. Dit is schematisch weergegeven in figuur 2. Deze figuur is niet op schaal.
figuur 1 figuur 2
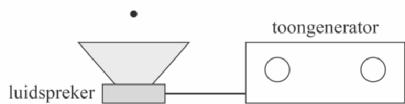
Tussen de luidspreker en de reflector wordt de lucht in trilling gebracht en er ontstaat een golfpatroon van knopen en buiken.
Op de uitwerkbijlage staan twee zinnen over de golven tussen de luidspreker en de reflector. 1 Omcirkel in iedere zin het juiste antwoord.
uitwerkbijlage bij vraag 1
De golf in de lucht tussen de luidspreker en de reflector is een transversale / longitudinale golf.
De druppels zweven op een lopende / staande golf.
In figuur 3 is een oscillogram weergegeven van het signaal van de toongenerator tijdens een experiment met de opstelling van figuur 2.
figuur 3
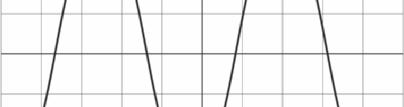
De horizontale schaalverdeling is 10 μs per hokje.
De toongenerator is ingesteld op 22 kHz.
2 Toon dat met behulp van figuur 3 aan.
Figuur 4 is een foto van zes zwevende druppels. De afbeelding is niet op ware grootte.
figuur 4
De zwevende druppels bevinden zich in opeenvolgende knopen. De toongenerator is ingesteld op 22 kHz. De temperatuur van de omgeving is 20 °C.
3 Bereken de werkelijke afstand tussen (het midden van) de eerste en de zesde druppel.
Onderzocht wordt of met deze methode druppels vloeibaar medicijn opgeslagen kunnen worden. Door het zweven is de kans op vervuiling van het medicijn namelijk kleiner. Probleem is dat de druppels niet te groot gemaakt mogen worden. Een te grote druppel wordt platgedrukt in de geluidsgolf en springt vervolgens uit elkaar. Zie figuur 5.
figuur 5
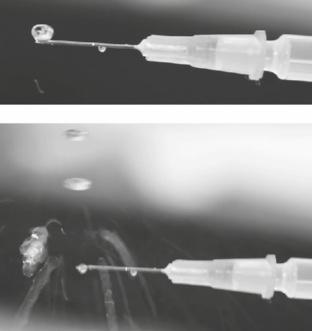
Er zijn twee mogelijke oplossingen voor dit probleem: – de geluidssterkte verlagen, – de toonhoogte verlagen.
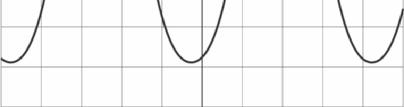
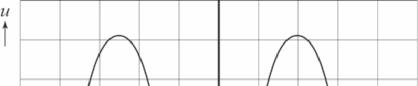
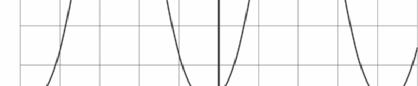
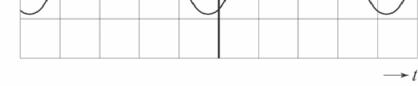
Op de uitwerkbijlage staat het (u,t )diagram van een signaal waarbij alleen een kleine druppel heel blijft.
4 Schets op de uitwerkbijlage in het (u,t )diagram een signaal waarin beide oplossingen gecombineerd zijn, zodat ook een grotere druppel heel blijft.
uitwerkbijlage bij vraag 4
Vleugel
Een vleugel is een muziekinstrument met toetsen en snaren, zie figuur 1.
Als een toets wordt ingedrukt slaat een houten hamertje (bekleed met vilt) tegen een strak gespannen snaar die vervolgens gaat trillen.
figuur 1
De klank die je hoort bestaat uit de grondtoon en enkele boventonen.
Op de uitwerkbijlage is een snaar getekend die trilt in de grondtoon.
5 Geef in de figuur op de uitwerkbijlage de plaats van de knopen en de buiken op deze snaar aan als de snaar trilt in de tweede boventoon.
uitwerkbijlage bij vraag 5 grondtoon
2-de boventoon
Afhankelijk van de plek waar het hamertje de snaar raakt, zullen de verschillende boventonen wel of niet meeklinken.
Stel dat het hamertje neerkomt op 1 8 deel van de lengte van de snaar.
De boventoon die op deze plek een knoop heeft, klinkt dan niet mee.
6 Welke boventoon klinkt dan niet mee?
A vierde boventoon
B zevende boventoon
C achtste boventoon
D negende boventoon
E zestiende boventoon
Aan de vorm van het instrument is te zien dat niet alle snaren even lang zijn. Zie figuur 1.
De snaar die de hoogste toon voortbrengt heeft een lengte van 40 cm. De hoogste toon van de vleugel heeft een frequentie van 4186 Hz, de laagste frequentie is 32,70 Hz.
Veronderstel dat alle snaren even strak gespannen zijn, even dik zijn, en van hetzelfde materiaal zijn.
7 Toon met een berekening aan dat de lengte die de langste snaar dan zou moeten hebben niet in een vleugel past.
De toonhoogte van een snaar hangt, behalve van de lengte, ook af van de spankracht in de snaar. Voor de voortplantingssnelheid v van de golven in de snaar geldt:
v = √ F s ℓ m
Hierin is:
– F s de spankracht in de snaar; – m de massa van de snaar; – ℓ de lengte van de snaar.
Om ervoor te zorgen dat de snaren die de lage tonen moeten voortbrengen toch in de vleugel passen, kun je verschillende maatregelen nemen. Op de uitwerkbijlage staan hierover twee beweringen.
8 Geef van elke bewering aan of deze bewering juist of onjuist is.
uitwerkbijlage bij vraag 8
bewering juist onjuist
1 De grondtoon van een snaar wordt lager als je de snaar strakker spant.
2 Als een snaar van roestvrij staal vervangen wordt door een snaar van koper, wordt de grondtoon lager. (De spankracht en de diameter veranderen niet.)
Eén van de snaren heeft een lengte van 90 cm en een massa van 5,7 g.
De grondtoon van deze snaar is 220 Hz.
9 Bereken de spankracht in deze snaar.
Het is belangrijk dat een vleugel goed gestemd is. Een pianostemmer kan daarvoor elke snaar precies de juiste spankracht geven. Voor de spankracht waarmee de snaar moet worden gespannen geldt:
F s = πρℓ2d 2f 2
Hierin is:
– ρ de dichtheid van het materiaal van de snaar;
– ℓ de lengte van de snaar; – d de diameter van de snaar;
– f de frequentie waarmee de snaar moet trillen.
In tabel 15C van Binas is gegeven welke frequenties horen bij welke toetsen van een vleugel.
Zo is te zien dat bij de noot a1 een frequentie hoort van 440 Hz.
Eén van de snaren is 80 cm lang, heeft een diameter van 0,94 mm en is gemaakt van roestvrij staal (zie Binas tabel 9). De spankracht in deze snaar is 949 N.
10 Ga met een berekening na welke noot van de vleugel bij deze snaar hoort.
Extra oefenen, uitlegvideo’s en podcasts
Slim leren, zeker slagen
Voortgang bijhouden
Altijd je digiboek bij de hand
Slim leren met Mijn Examenbundel
B� deze Examenbundel hoort een online omgeving: m�nexamenbundel.nl
Je vindt hier alles wat je nodig hebt om heel gericht te leren en oefenen voor je examen. Zoals de score van je oriëntatietoets, video’s, het digiboek, examentips en nog veel meer.
#ikgazekerslagen
Activeer direct je code voor Mijn Examenbundel
Ga nu naar m�nexamenbundel.nl en maak meteen je account aan. Met de activatiecode die je per mail hebt ontvangen of via de ELO van je school, heb je toegang tot alle extra’s die b� je boek horen.