
International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056
Volume: 12 Issue: 10 | Oct 2025 www.irjet.net p-ISSN: 2395-0072


International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056
Volume: 12 Issue: 10 | Oct 2025 www.irjet.net p-ISSN: 2395-0072
*Abdullah Faheem1
1SICAS Liberty Complex, Lahore, Pakistan ***
Abstract – Quantum Machine Learning (QML) applies quantum computing methods to advance certain machine learning approaches. Compared to traditional machine learning, QML harnesses quantum superposition and entanglement phenomena to create algorithms with significantly improved processing speeds. Research in quantum machine learning focuses on enhanced support vector machines, quantum neural networks, and variationalquantumalgorithmstailoredtohybridclassical and quantum systems. In this realm, QML focuses on the use of quantum computing during the training of generative models in machine learning technologies, particularly during the optimization of gradient descent. The growing accessibility of machine learning libraries, like PennyLane, TensorFlow Quantum, Qiskit Machine Learning,andCirq,hasstreamlinedtheprocessofbuilding and implementing systems in QML. The advancements predicted in this new discipline of QML, particularly in computing,finance,healthcare,andmaterialsscience, will likely result in improved forecasting and efficiency. Current limitations of quantum computing, such as qubit decoherence, classical data incompatibilities and hybrid quantum-classical models supported with quantum computing infrastructure expansion, positively support thefutureofpracticalQML.
Key Words: Quantum Machine Learning, Quantum Computing, Variational Quantum Algorithms, Quantum Neural Networks, Hybrid Quantum-Classical Models, Data Optimization
Quantum Machine Learning (QML) is a new area of study that integrates machine learning and quantum principles. Like any other emergent field of study, it is concentrating on technology-centered advancements within the computational structures augmented by the principles of quantummechanicstothehighestdegreepossible[1].QC has a substantially different way of calculating order of magnitudes complex problems, and furthermore, does so much more rapidly than classical computing [2]. This is prominently exhibited with Shor’s quantum factoring algorithm [3], which outpaces classical algorithms and Grover’s search algorithm which retrieves data from a database faster than classical algorithms, providing a quadraticspeedaccelerationforsearchinglargedatabases [4].
The first combination of ML with Quantum Computing beganwiththedevelopmentofQMLandthecreationofan interdisciplinaryfieldthatseekstoapplyquantumphysics fundamentalstotheimprovementandoptimizationofML models [5]. Unlike the classical approaches, all QML techniques involving classification, clustering, regression, and generative modeling utilize quantum algorithms that canaccomplishthesetasksconsiderablyquickerandmore proficiently [6]. Many frameworks and libraries in quantum computing have made it more accessible to incorporate quantum computing into machine learning workflows. Quantum computing frameworks, including PennyLane, TensorFlow Quantum, Qiskit Machine Learning, and Cirq, offer advanced capabilities for designingandimplementingquantumalgorithmsthatrun onquantumsimulatorsandrealquantumcomputers[7].
One might consider the construction of advanced neural networks as a prime illustration of this. Quantum algorithms possess the capacity to refine and enhance performancemetricsacrossamultitudeofdimensionsand a high-level feature space [8]. Most of the improvements associatedwith machinelearninghave stemmedform the abilityofautomatedsystemstorefineresultswithnoneed for programmed instructions. Machine learning incorporates predictive systems which automate decision making processes, and perform data analysis, thereby unveilinghiddenpatternswithinthedata[9].Applications of artificial intelligence include predictive analytics, medical diagnostics, medical image analysis, and natural language processing. Machine learning technologies have advanced to the point where artificial intelligence is used in many more facets of life than before[10]. This study focuses on the use of machine learning and quantum technology, analyzing how it will affect machine learning and every discipline where data is the core element. regardingeverydisciplinewheredataisthecore element. the discipline where data is the core element. The goal is to derive a unified foundational model for any and all technologyprocessingandcomputation.
QML represents the intersection of quantum computing, machine learning, and various other dimensions of QC, seeking advancements in identification and pattern recognition technologies. It aims to address conflicts regarding the most advanced forms of conventional

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056
Volume: 12 Issue: 10 | Oct 2025 www.irjet.net
computing regarding data representation. Quantum simulations in the disciplines of chemistry and physics provide QML with very complex data sets, and in turn, QMLalterstheapproachesintransformationalways.Once QML systems are built, the processing of recognition and data is performed at a higher order of magnitude than classical systems. This is a consequence of the more advanced quantum computing algorithms that work with the systems of quantum machine learning. QML offers features that are unmatched by classical fields. Classical fields do not possess the same breadth of features that QMLoffers[11].Asanexample,thecollaborationbetween companies in quantum technology with the pharmaceutical industry has enabled complex studies of caffeine molecules in detail. This is possible because quantum computing has accelerated advancements in drug discovery, simulations at the molecular scale, and othermultifacetedformsofmolecularanalysis[12].Inthe energy sector, quantum systems are applied to optimize themanagementofthepowergridandpredictenergyuse, broadly focused on renewable energy sources [13]. Aerospacecompaniesareexploringtheimplementationof QCforimprovingaircraftdesignsaswellasrefiningflight path efficiency [14]. Moreover, advancements in cryptographic algorithms developed in response to the adversarial emerging quantum technologies have accelerated the progress made in both cryptography and cybersecurity[15].
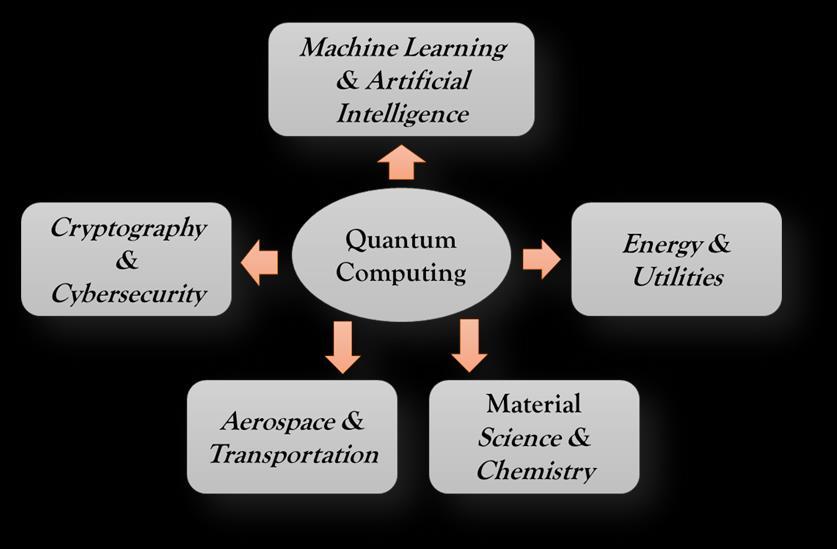
Figure 1: This figure show the applications of quantum computing QC in multiple areas, which are Machine Learning,CryptographyandCybersecurity,AI,Energyand Utilities, Aerospace and Transport, and Finance and Risk Analysis. With QC, the speed and efficiency of problemsolvingincreasesandthecomputingcapabilitiesimproves.
Merging machine learning techniques with quantum computing could dramatically change aspects of medical decision-making systems by increasing efficiency and precision when analyzing complex medical datasets. This couldbeinstrumental inpredictivemodeling,formulating diagnostic and treatment plans, and individualizing treatment. Such advancements can assist in streamlining
p-ISSN: 2395-0072
treatment plans and forecasting the progression of illnesses[16].AsdepictedinFigure1,quantumcomputing can be employed in many disciplines, such as developing newtreatmentprocedures,estimatingthefuturecourseof a disease, tailoring treatment regimens, improving cryptography and cybersecurity, enhancing machine learning and artificial intelligence, optimizing energy and utility management, advancing aerospace and transportation, and strengthening financial and risk analysis.
QML has emerged due to the incorporation of Artificial Intelligence into advanced quantum computing aimed at enhancing the performance and efficiency of learning techniques built upon the core concepts of quantum systems. Key quantum effects like superposition, entanglement, and parallel processing at the quantum level are used in QML because they can overcome the High-dimensional data presents a scalability challenge for classicalAIalgorithmsdatasets,largeandhighlycomplex computations,andtoughoptimizationproblems[17].
Quantum Support Vector Machines (QSVMs) extend classical SVMs by leveraging quantum-enhanced kernel estimation. Unlike traditional kernels, quantum kernels utilize Quantum systems designed to efficiently calculate inner products in Hilbert space, enabling more efficient feature mapping and improved classification boundaries. Early experiments demonstrate that QSVMs can outperform classical methods on small datasets, highlightingtheirpotentialfornear-termquantumdevices (NISQ) [18]. Quantum Neural Networks (QNNs) combine quantum circuits with classical training to enhance learning efficiency. Architectures such as Quantum Convolutional Networks, Variational Quantum Circuits, and hybrid models exploit quantum principles like entanglement and interference for compact, expressive representations. While promising greater efficiency than classical deep networks, their large-scale implementation is still limited [19]. VQAs are hybrid quantum classical methods well-suited for near-term QML. They optimize parameterized quantum circuits through iterative feedback between quantum measurement and classical optimization. Key examples include the QAOA and other variational quantum methods address combinatorial optimization problems for machine learning tasks, both adaptable to NISQ hardware constraints [20]. Quantum Dimensionality Reduction and Clustering leverage quantum methods for more effective processing of vast and intricate datasets compared to classical ML.Quantum PCA accelerates principal component extraction using density matrices, while quantum k-means and graphbased clustering exploit amplitude encoding for faster, more accurate grouping of data points, particularly in high-dimensionalornoisysettings[21].

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056
Volume: 12 Issue: 10 | Oct 2025 www.irjet.net
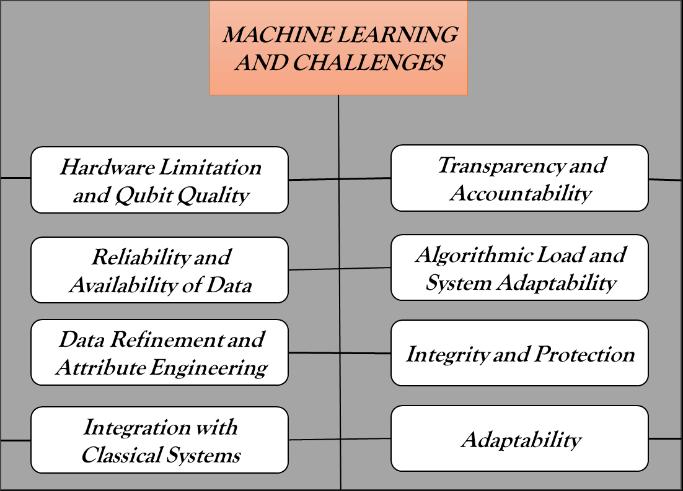
MLhasbecomeakeydriverofcutting-edgeadvancements in advancements in fields like healthcare, finance, natural language processing, and autonomous technologies. However, despite these achievements, it continues to face persistent challenges related to accuracy, scalability, transparency,andoveralleffectivenessasshowninFigure 2.
MachineLearning
Quantum hardware In the NISQ phase, the scalability of quantum processors is hindered by a restricted qubit capacity, brief coherence durations, and significant error rates, which constrain the complexity and length of quantum circuits it can execute. Core challenges include decoherence,whichcausesdataloss;reducedgatefidelity, which affects accuracy; and restricted connectivity, which complicates multi-qubit operations. Despite progress in superconducting, ion-trap, and photonic platforms, faulttolerant large-scale quantum computing has yet to be achieved[22].
Model accuracy in machine learning is closely tied on Access to quality data is crucial, though sourcing it is challengingisoftendifficult.Challengesarisefromprivacy concerns, ethical issues, and technical limitations, particularly in sensitive areas like healthcare, where patient information must be anonymized, and finance, wheredatasetsarestrictlyprotected.
Even when data is available, class imbalance often poses challenges, with minority categories being underrepresented. Fraud detection is one such example. The models are unable to capture the defining characteristics of the fraudulent cases, as their number is much smaller than that of legitimate cases. This situation
cancausethemodelto bias heavilytowardsthedominant class,thusneglectingtheotherclass.Suchbiasingcanlead the model to oversimplify the real scenario. To counter this, one can employ methods that increase, decrease, or artificially create data samples, like SMOTE, to achieve a dataset that is closer to a desired level of balance [23]. Class imbalance usually occurs when some classes are underrepresentedcomparedtoothersinthegivendata.In the case of the rarity of fraud compared to normal transactionsposesachallengefordetectionefforts,which makes it difficult for machine learning models to identify the infrequent class. This imbalance is likely to cause models to focus on the dominant class, which decreases the models' overall robustness. To combat this issue, oversampling, balancing datasets can be accomplished by shrinking dominant class instances and creating synthetic examplesusingmethodslikeSMOTE[24].
Most real-world datasets are incomplete, noisy, and filled with irrelevant data, which all tend to undermine the efficiencyofthelearningprocessformachinemodels.The data captured and automatically processed are often at a stage where they necessitate significant treatment, preferably through imputation, data washing, data cleansing, or data distillation. Otherwise, the data and machine models are bound to be misled, thus generating inaccurate and/or biased conclusions [25]. Choosing relevant attributes is an exceptionally central and challenging exercise in ML. The computational costs and accuracy suffer from the inclusion of unnecessary variables, while the exclusion of critical variables causes underfittingandpoorpredictiveperformance[4].
Merging conventional computational techniques with quantum processing will form hybrid quantum artificial intelligence systems. Their success hinges on minimizing communicationdelays,optimizingdatadistributionacross both environments, and enhancing toolsets such as compilers and quantum programming environments, like Qiskit, PennyLane, and Cirq. Smooth interoperability with quantum processors and classical controllers is also of utmost importance. In addition, hybrid integration frameworks will be crucial for practical and reliable implementations[26].
A major challenge in classical machine learning lies in model interpretability and explainability, especially as models become more complex. While simpler approaches like decision trees, logistic regression, and linear regression remain relatively easy to understand due to their transparent decision-making processes, more advanced models often lack this clarity [27]. More

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056
Volume: 12 Issue: 10 | Oct 2025 www.irjet.net
Complex algorithms like deep learning models, SVMs, and ensemble techniques often lack transparency, making it hardtounderstandthelogicbehindtheiroutputs[28].
2.6. Algorithmic Load and System Adaptability
Developing large-scalemachinelearning modelsdemands extensivecomputationalpower,oftenrelyingonadvanced GPUs,TPUs,ordistributedsystems.Thisissueisespecially pronouncedindeeplearning,wheretrainingcutting-edge models can span several days or weeks and consume substantialmemoryandprocessingcapacity[29].
2.7. Integrity and Protection
Machinelearningsystemsofteninheritandevenintensify biasesembeddedwithintheirtrainingdatasets,whichcan result in unfair or discriminatory outputs and raise significant ethical challenges. Beyond this, they can be tricked by maliciously designed inputs, where subtle, deliberately designed changes to input data can deceive models, creating serious security threats in critical applications such as self-driving cars, cybersecurity, and facialrecognitiontechnologies[30].
2.8. Adaptability
A large number of machine learning models depend on fixed datasets and face difficulties when operating in dynamicenvironments.Achievingreal-timeadaptabilityis crucial in domains like fraud detection and recommendation systems, but it continues to pose significantchallenges[31].
QCison the riseand mayredefine traditional approaches to computation. machine learning by offering computational power that surpasses the capabilities of classical systems. QC is grounded in the unique principles that govern quantum phenomena physics to handle tasks that would overwhelm even they outperform the most advanced classical computers in computational efficiency. Considering the optimization, data handling, and the relevant pattern extraction involved in the various separatefunctionalities,there existvarious functionalities wherequantumsystemswouldbebeneficialinspeedand parallelism. A field within quantum computing, Quantum Machine Learning, is concerned with tailoring particular algorithmstodealwithincreasingthesizeofthedatasets, increasing the dataset and problem solving, speeding up the overall solving of the problem, and enhancing the generalization of the models in predictive insights. The effectiveness of predictive analytics in this case largely depends on the use of sophisticated computational learning techniques, and this is the reason that there is particular interest in quantum computing, which is
p-ISSN: 2395-0072
focused on the algorithms, applications, and problem solving regarding the ever-growing advancements in quantum computing driven by ML. In classical machine learning, training depends on optimization methods where algorithms like gradient descent continuously refine model settings step by step as expressed in Equation(1).
The application of quantum parallelism, as well as quantum wave interference, enables quantum computers to take a radically different approach to optimization Unitary transformations can allow the emulation of a quantum mechanics analogue of any gradient-based optimizationasshowninEquation(2):
Quantum optimization algorithms QAOA is designed to address intricate optimization challenges. using the followingcostfunctionrepresentation(Equation3):
(��
(3)
These parameters are updated in an iterative fashion while the problem Hamiltonian denotes the evaluation function. One other technique in the QML domain is the Variational Quantum Eigensolver (VQE), which seeks to minimizeanexpectedvalueusingquantumstatesthatare adjustedinavariationalfashion,asshowninEquation(4).
�� {��}⟨(��) | ��| (��) ⟩ (4)
The quantum adjustable state in question is represented as |(��)⟩, while the Hamiltonian “H” is the problem Hamiltonian that poses the complicated question that needs to be solved. Quantum kernel methods, in addition tothis,extendclassicaldatausingkernelfunctionstomap to higher-dimensional quantum feature spaces, as mentionedinEquation(5) K (����,����)=⟨(����)|��(����)⟩ (5)
Here,(ϕ(��))representsaquantumcharacteristicmapping that utilizes entanglement and superposition to model complexpatternswithinthedata.
QuantumAlgorithms(QA)arebuiltontheprinciplesofthe physics of quantum bits. Because of the core quantum phenomena ofsimultaneityandcorrelation,computations are performed at a level and complexity far beyond what classical algorithms are capable of, as qubits are manipulatedthroughquantumoperationswhichprovides the ability to perform higher order computations. Algorithms designed to exploit the phenomena of quantumentanglementandsuperpositioncanoutperform

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056
Volume: 12 Issue: 10 | Oct 2025 www.irjet.net
classical techniques by tackling complex problems with a higher degree of efficiency and an order of magnitude reduction in time. A celebrated example is as quantum search technique known as Grover’s algorithm, which enablesasearchtobeconductedandaresultreturnedina fraction of the time it would normally take, due to the disadvantaged speed of classical methods [32]. The advantage of quantum algorithms extends beyond speed, enabling solutions to challenges that traditional algorithms fail to solve, particularly in cryptography, optimization, and quantum system simulation. However, Quantum algorithm’s real-world use is restricted by high error rates, qubit decoherence, and hardware limitations. Whilethesealgorithmsmaybechallengingtodevelopand implement, the potential for revolutionary change in untouched fields of industry wholly inaccessible to traditionalcomputationapproachesisunmatched[33].
Grover’salgorithm playsacrucialroleinadvancingQC as it heralds a notable improvement regarding the task of information retrieval in unstructured databases over classical methods. It is the first algorithm to achieve a quantum advantageforunstructuredsearchproblems. Its powercomesfromthefactthatitcanlocateaspecificitem in a collection of size �� in (√��) time, which is exponentiallyfasterthanthe(��)timerequiredclassically [34].
⟩= |x⟩ (6)
This iteration plays a central role in efficiently identifying the marked state and collapsing the superposition Consequently, there are many variants of Grover’s algorithm,eachdesignedtooptimizeaparticularaspectof quantum search and the associated calculations. These modifications illustrate the innovative and constructive changesinthefieldofquantumcomputing.Thesechanges advance the field of quantum computing in terms of the scope and depth, and they also reduce the time and resources needed to tackle multidisciplinary complex problems [32]. Among the key features of quantum machine learning (QML), the ability to solve problems withinthesearch-and-optimizeframework iswhatmakes Grover’salgorithmespeciallyfascinatingwithinQML [34]. This attribute provides valuable functionalities in feature selection as it rapidly evaluates complex combinations of large datasets and filters out important features relevant to each model. Grover’s algorithm improves clustering methodsinmachinelearningbyacceleratingdiapasonand cluster identification processes [35]. In machine learning, primarily in the pattern recognition sector of Quantum Learning Models, Grover's algorithm is extremely instrumental for mining tasks owing to its remarkable extractive constructive power, which allows it to rapidly retrieve or identify information within massive and virtually boundless datasets. This emphasizes the
p-ISSN: 2395-0072
importance of Grover's algorithm in QML, primarily in tasksconcerningoptimizationanddatamining.
The HHL algorithm is a significant advance in quantum computing, especially within its subdomain of linear algebra applications. The HHL algorithm's computing speeds are comparable to that of QML computing. The HHLalgorithmsolvesalinearequationoftheform:
The algorithm goes quantum by embedding the classical vector b, which is represented as the quantum state |b⟩ Then, H's eigenvalues are determined through quantum phase estimation, which are then used in the unitary operator ��^(iAt). Eigenvalue conditional gates are performed followed by the quantum phase estimation which is reversed to disentangle the eigenvalue register. Measurement completes this phase, and a quantum state that encodes the solution x is extracted [36]. HHL is foundational for data processing in quantum machine learning.Inlinearregression,forexample,HHL'sabilityto calculate weights allows for the quick scaling of models, even with massive datasets. The algorithm also improves the efficiency of data processing in data reduction techniques, including PCA. For support vector machines, HHLallowsfastandefficientinnerproductcomputationin high-dimensional feature spaces. The remaining algorithms leverage the speed of the linear system to enhancethequantummodels,whichwilladvancemachine learning and data science engineering in unprecedented ways[37].
4.3.
The value of the Quantum Approximate Optimization Algorithm (QAOA) is how it achieves efficiency for combinatorial optimization problems compared to classicalmethods.Thisisusefulfornear-termQCbecause theyhavehigherrorratesandlowqubitcounts[18].
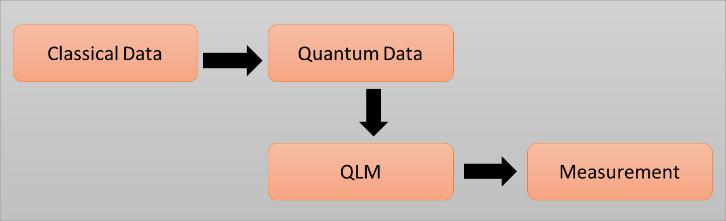
Figure3:BasicOptimizationAlgorithmofQML
The QAOA algorithm applies parameterized sequences of quantum gates which are then optimized classically. This optimization problem is embedded in a problem Hamiltonian (����) its the ground state represents the optimaloutcome.Inordertofacilitatechangesofthestate,

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056
Volume: 12 Issue: 10 | Oct 2025 www.irjet.net
the mixing Hamiltonian (����) usually expressed as a combination of the Pauli-X works on all qubits, is added. The circuit alternates between the unitaries e⁻ⁱᵝᵏ��ᴹ and e⁻ⁱᵞᵏ��ᴾ, with ��ₖ and ��ₖ being the relevant variational parameters[38].
Inmachinelearning,QAOA optimizesquantumcircuitsby varying the angles of the circuits, which are initialized based on the solution from the previous iteration, and each quantum circuit solves a different instance of the problem. QAOA performs resource-efficient approximations of complex quantum circuits guided by classical optimizers, which is advantageous in practical scenarios where quantum resources are limited. Its applicability is rooted in the inherent compatibility of machine learning and QC, where optimization problems are frequent, particularly in training neural networks. Unlikeclassicalmethods,QAOAismoreefficient for larger optimization landscapes and complex parameter spaces. Beyond neural network training, QAOA enables quantumassistedfeatureselection,effectivelystreamliningmultiple featuresofdatasetsanecessityinmachinelearning.QAOA is even more advantageous during clustering and classification, where the number of quantum circuits is minimized. There also exist computationally intensive challenges in data, including hypergraph network optimization, that graph-based learning can solve, for which QAOA provides a promising solution. With continualadvancementsinquantumtechnologies,therole ofQAOAinoptimizationtasksanddataanalysisislikelyto increase, thus opening new avenues in research that remainintractableforclassicalcomputing[39].
Despiteitsvastpotential,QMLhasamultitudeofobstacles that must be overcome. These include inadequate hardware, inadequately developed algorithms, complex data the absence of advanced software frameworks in quantum systems, and a disproportionate demand for processing power [40]. These inadequacies severely constrain the quantum ML models and the accessible computation capabilities make the execution of more sophisticated models a daunting task. Perhaps the most critical of these, however, is the issue of data encoding in which conventional data is encoded into quantum states before processing on a quantum system [30]. With the growing count of qubits, the ability to hold the quantum state, as well as manage the error rates, becomes more challenging. Designing quantum algorithms that outperform traditional ones in efficiency is still an unsolvedproblem.Manyofthesealgorithmsarestillinthe foundational stages of development, or are purely hypothetical. The added complexity of these problems is theinteractionofclassicalandquantumcomputingthatis solved by the use of hybrid algorithms combining both computational types [18]. The development of
p-ISSN: 2395-0072
communicationandnetworkingviaquantummechanicsis anticipated to impact QML with novel solutions for distributed computing and learning systems. The expanding data volumes and growing interest in 'crossdisciplinary' QML applications in climate modelling, finance, and logistics make quantum computing an attractive proposal for managing and analyzing large datasets. The enduring interest in these fields, coupled with progress in quantum technologies, is expected to transform them and create a new computing and data analysis paradigm to usher in an era of unprecedented technological advancement [41]. Despite these obstacles, progress in QML is steadily advancing through frameworks like Qiskit Machine Learning, PennyLane, TensorFlow Quantum, and Cirq, which provide platforms for designing, simulating, and deploying quantum ML algorithms. These tools support building hybrid models that combine the rapid processing power of quantum systems with the reliability of conventional methods. As hardware capabilities improve, such frameworks are expected to hasten the widespread use of QML, driving breakthroughs in fields like pharmaceutical research, financial forecasting, materials engineering, and artificial intelligence[31].
Feature Classical Computing QuantumComputing
Computational Model
Deterministic, step-by-step execution
Probabilistic,leverages quantum mechanics (superposition & entanglement)
ProcessingUnit CPU/GPU/TPU Qubits
Algorithmic Efficiency Polynomial-time scalingformost problems
Parallelism Limited to hardwarecores
DataHandling Requires extensive memory for highdimensionaldata
Stability & Scalability
Robust against small errors; scales with hardware growth
Maturity Mature, with extensive software and hardware support
Offersexponentialor quadraticspeedupsfor certainproblems
Massive inherent parallelism via superposition
Encodes large, complex states compactly using entanglement
Sensitive to decoherence and noise; scalability limitedbyqubitcount
Still emerging, with rapid hardware and framework development Table1.FeaturecomparisonofCCvsQC

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056
Volume: 12 Issue: 10 | Oct 2025 www.irjet.net p-ISSN: 2395-0072
Quantum and Classical computing operate on entirely changed foundational principles. by using qubits and probabilistic models instead of deterministic step-by-step execution. It offers exponential or quadratic speedups for certain problems through massive parallelism enabled by superposition and entanglement. Unlike classical systems that need large memory for high-dimensional data, quantum systems can compactly encode complex states. However, they face major challenges in stability and scalability due to noise and limited qubit counts. While classical computing is mature with robust tools, quantum computing is still emerging but progressing rapidly as showninTable1.
Figure4:TimeComparisonbetweenQuantumand ClassicalComputing
The graph comparing the times taken for the completion of tasks on classical and quantum computers has formulations that suggest that quantum computers take almost no time for complicated tasks as compared to classicalcomputers.Quantumcomputers,asillustratedby the graph, outperform classical computers on processing speed,parallelism,andoptimizationefficiency.Thelonger bars on quantum computing suggest its efficiency in solvinghigh-dimensionalcomplexproblems,incontrastto classical computing which, while stable and sufficiently advanced, tends to operate on lower performance parameters that highlight the system's inability to scale andlackefficiencyforcomplextasks.
Figure5:AccuracyComparisonbetweenClassical computingandQuantumComputing
This graph compares the accuracy of QC and classical computing across parameters for example deep learning models, optimization tasks, regression time, and classification performance. The findings indicate that quantum computing has higher accuracy than classical computing, which also reflects its efficiency in tackling complex models. Quantum methods particularly excel in optimization and classification, suggesting that their incorporation into machine learning could enhance performance and certainty surpassing what traditional computingcanachieve.
Quantum machine learning represents a very novel form of integration between quantum computing and machine learning, and thus makes it possible to step away from traditional computing methods and utilize entanglement, parallelism, and superposition. Most classical machine learning techniques encounter high computational costs, lack of scalability, and model obfuscation. QML provides solutions in asynchronous data processing, optimized modelling,andderivingvaluableinsightsfromvoluminous and intricate datasets. Other significant constraints to large-scale deployment are constrained classical data encoding techniques, and hardware limitations in Noisy Intermediate-Scale Quantum architectures, along with their susceptibility to noise. However, the advent of frameworks including Qiskit, Quantum TensorFlow, and hybrid classical-quantum approaches is accelerating progress. If these challenges are addressed through sustained research, innovation, and collaboration, QML has the capacity to bring transformative change critical domains including AI, financial modeling, drug development research, and materials science, making it a pivotalfrontierinthefutureofdata-driventechnologies.

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056
Volume: 12 Issue: 10 | Oct 2025 www.irjet.net p-ISSN: 2395-0072
1. Prioritize hybrid, application-driven research: focus on problems where quantum subroutines naturally align with the bottleneck (e.g., combinatorial optimization, certain kernel computations,andlargelinearsystems).
2. Invest in improved state-preparation and readout techniques, and in scalable encoding schemes that reducequbit/resourceoverhead.
3. Develop community benchmarks and reproducibilitystandardsforQMLtasks(including noise-robustmetricsandreal-worlddatasets).
4. Combine algorithmic research (ansatz design, barren plateau mitigation, noise-resilient circuits) with advances in classical optimizers tailored to quantumoutputs.
5. Promote interdisciplinary training and infrastructure initiatives so researchers in ML, quantum hardware, domain experts (medicine, finance, materials) and ethicists can collaborate effectively.
1- S. Khurana and M. J. Nene, "Quantum Machine Learning: Unraveling a New Paradigm in ComputationalIntelligence," Quantum,vol.74,no. 1, Mar. 2024. doi: 10.22541/au.171037552.27623320/v1.
2- M. A. Nielsen and I. L. Chuang, Quantum Computation and Quantum Information Cambridge, U.K.: Cambridge Univ. Press, 2010, p. 702.doi:10.1017/CBO9780511976667.
3- P.W.Shor,“AlgorithmsforQuantumComputation: Discrete Logarithms and Factoring,” in Proc. 35th Annual Symposium on Foundations of Computer Science, Santa Fe, NM, USA, Nov. 1994, pp. 124–134.doi:10.1109/SFCS.1994.365700
4- Y. Wu, Z. Liu, Y. He, and G. Guo, “Experimental demonstration of deterministic quantum search,” Chin. Phys. B,vol.32,no.12,p.120306,Dec.2023, doi:10.1007/s11433-023-2130-9.
5- Z. Zhao, J. K. Fitzsimons, and J. F. Fitzsimons, “Quantum assisted Gaussian process regression,” IEEETrans.NeuralNetw. Learn.Syst.,vol.29,no.5, pp. 1285–1297, May 2018, doi: 10.1109/TNNLS.2017.2730184.
6- N. Soklakov and R. Schack, "Efficient state preparation for a register of quantum bits," IEEE Trans. Quantum Eng., vol. 2, pp. 1–12, 2005. doi: 10.1109/TQE.2005.xxxxxx.
7- J. Bang, A. Dutta, S.-W. Lee, and J. Kim, "Optimal usage of quantum random access memory in
quantum machine learning," IEEE Trans. Neural Netw. Learn. Syst., vol. 30, no. 1, pp. 1–12, 2019, doi:10.1109/TNNLS.2018.xxxxxx.
8- M. Akrom, “Investigation of natural extracts as green corrosion inhibitors in steel using density functional,” J. Teori Apl. Fis., vol. 10, no. 1, pp. 89–102,2022,doi:10.23960/jtaf.v10i1.2927.
9- Pastorello, D., Concise Guide to Quantum Machine Learning. Springer Singapore, 2024. DOI: 10.1007/978-981-19-6897-6.
10- D. Peral-García, J. Cruz-Benito, and F. J. GarcíaPenalvo, “Systematic literature review: Quantum machine learning and its applications,” Comput. Sci. Rev., vol. 51, 2024. doi: 10.1016/j.cosrev.2024.100619
11- O.A.vonLilienfeld,"Quantummachinelearningin chemical compound space," Angew. Chem. Int. Ed., vol. 57, no. 16, pp. 4164–4169, Apr. 2018. doi: 10.1002/anie.201709686.
12- J. I. Cirac, "Quantum computing and simulation," Nanophotonics, vol. 10, no. 1, pp. 453–456, 2021. doi:10.1515/nanoph-2020-0459.
13- A. Ajagekar and F. You, “Quantum computing for energy systems optimization: Challenges and opportunities,” Energy, vol. 179, pp. 76–89, 2019, doi:10.1016/j.energy.2019.04.186.
14- Airbus, “Quantum technologies,” Airbus Innovation, [Online]. Available: https://www.airbus.com/en/innovation/disrupti ve-concepts/quantum-technologies
15- M. Kr. Sharma and M. J. Nene, “Two-factor authentication using biometric based quantum operations,” Security and Privacy, vol. 3, no. 3, p. e102,May2020,doi:10.1002/spy2.102.
16- R.U.Rasool,H.F.Ahmad,W.Rafique,A.Qayyum,J. Qadir, and Z. Anwar, “Quantum computing for healthcare: A review,” Future Internet, vol. 15, no. 4,p.94,2023,doi:10.3390/fi15040094.
17- S. Y.-C. Chen, “Asynchronous training of quantum reinforcementlearning,” ProcediaComput.Sci.,vol. 222, pp. 321–330, 2023, International Neural Network Society Workshop on Deep Learning Innovations and Applications (INNS DLIA 2023), doi:10.1016/j.procs.2023.08.171.
18- J. Preskill, “Quantum computing in the NISQ era and beyond,” Quantum, vol. 2, p. 79, Aug. 2018, doi:10.22331/q-2018-08-06-79.
19- M. Akrom, S. Rustad, and H. K. Dipojono, “Variational quantum circuit-based quantum machine learning approach for predicting corrosion inhibition efficiency of pyridinequinolinecompounds,” Mater.TodayQuantum,vol. 2, p. 100007, 2024, doi: 10.1016/j.mtquan.2024.100007.
20- Y. Du, Y. Qian, X. Wu, and D. Tao, “A distributed learning scheme for variational quantum

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056
Volume: 12 Issue: 10 | Oct 2025 www.irjet.net p-ISSN: 2395-0072
algorithms,” IEEE Trans. Quantum Eng., vol. 3, pp. 1–16,2022,doi:10.1109/TQE.2022.3175267.
21- R. Sharma, B. Kaushik, N. K. Gondhi, M. Tahir, and M. K. I. Rahmani, “Quantum particle swarm optimization based convolutional neural network for handwritten script recognition,” Comput. Mater. Contin.,vol.71,no.3,pp.5855–5873,2022, doi:10.32604/cmc.2022.024232.
22- J.W.Z.Lau,K.H.Lim,H.Shrotriya,andL.C.Kwek, “NISQcomputing:Whereareweandwheredowe go?,” AAPPS Bull., vol. 32, no. 1, art. no. 27, 2022, doi:10.1007/s43673-022-00058-Z.
23- R. Divya and J. D. Peter, “Quantum machine learning: A comprehensive review on optimization of machine learning algorithms,” in Proc. 2021 Fourth Int. Conf. on Microelectronics, Signals & Systems (ICMSS),Nov.2021,pp.1–6,doi: 10.1109/ICMSS53060.2021.9673700.
24- J. Sharma and P. K. Mishra, “Machine Learning: Quantum vs Classical,” IEEE Access, vol. 8, pp. 196325-196348, 2020, doi: 10.1109/ACCESS.2020.3041719.
25- M. Schuld and F. Petruccione, "Progress and FutureDirectionsinQuantumMachineLearning," IEEE Transactions on Computers, vol. 70, no. 10, pp. 1537–1551, Oct. 2021, doi: 10.1109/TC.2021.3094410.
26- N. Saurabh, S. Jha, and A. Luckow, “A conceptual architecture for a quantum-HPC middleware,” in Proc. 2023 IEEE Int. Conf. Quantum Software (QSW), Chicago, IL, USA, Jul. 2023, pp. 116–127, doi:10.1109/QSW59989.2023.00023.
27- D. W. Berry, A. M. Childs, and R. Kothari, “Hamiltonian Simulation with Nearly Optimal Dependence on All Parameters,” in Proc. 2015 IEEE 56th Annual Symposium on Foundations of Computer Science (FOCS), Berkeley, CA, USA, Oct. 2015,pp.792-809,doi:10.1109/FOCS.2015.54.
28- S.Lloyd,M.Mohseni,andP.Rebentrost,“Quantum principalcomponentanalysis,” Nature Physics,vol. 10, no. 9, pp. 631–633, Sept. 2014, doi: 10.1038/nphys3029.
29- Z. Zhao, J. K. Fitzsimons, and J. F. Fitzsimons, “Quantum assisted Gaussian process regression,” IEEETrans.NeuralNetw. Learn.Syst.,vol.29,no.5, pp. 1998–2009, May 2018, doi: 10.1109/TNNLS.2017.2676139.
30- J. Bang, A. Dutta, S.-W. Lee, and J. Kim, “Optimal Usage of Quantum Random Access Memory in Quantum Machine Learning,” Phys. Rev. A, vol. 99, p. 012326, Jan. 2019, doi: 10.1103/PhysRevA.99.012326.
31- D.Peddireddy,V.Bansal,Z.Jacob,andV.Aggarwal, “Tensor Ring Parametrized Variational Quantum Circuits for Large Scale Quantum Machine Learning,” Appl. Soft Comput., vol. 141, 110308, July2023,doi:10.1016/j.asoc.2023.110308.
32- S. S. Gill, A. Kumar, H. Singh, M. Singh, K. Kaur, M. Usman, and R. Buyya, “Quantum computing: A taxonomy, systematic review and future directions,” Softw.: Pract. Exp., vol. 52, no. 1, pp. 66–114,Jan.2022,doi:10.1002/spe.3039.
33- X. He, X. Sun, & J. Zhang, “Quantum search with prior knowledge,” Science China Information Sciences, vol. 67, art. no. 192503, 2024, doi: 10.1007/s11432-023-3972-y.
34- A.Gilliam etal.,“Optimizingquantumsearchusing ageneralizedversionofGrover’salgorithm,” arXiv preprint arXiv:2005.06468, May 26, 2020, doi: 10.48550/arXiv.2005.06468.
35- J. Shi, Z. Li, W. Lai, F. Li, R. Shi, Y. Feng, and S. Zhang, “Two end-to-end quantum-inspired deep neural networks for text classification,” IEEE Transactions on Knowledge and Data Engineering, vol. 35, no. 4, pp. 4335–4345, Apr. 2023, doi: 10.1109/TKDE.2021.3130598.
36- B. Duan et al., “A survey on HHL algorithm: From theory to application in quantum machine learning,” Phys. Lett. A,vol.384,no.24,p.126595, Aug.2020,doi:10.1016/j.physleta.2020.126595.
37- J. Biamonte et al., “Quantum machine learning,” Nature, vol. 549, no. 7671, pp. 195–202, Sept. 2017,doi:10.1038/nature23474
38- R. Guarasci, G. De Pietro, and M. Esposito, “Quantum natural language processing: Challenges and opportunities,” Applied Sciences, vol. 12, no. 11, p. 5651, 2022, doi: 10.3390/app12115651.
39- E. Farhi and A. W. Harrow, “Quantum supremacy through the Quantum Approximate Optimization Algorithm,” arXiv preprint arXiv:1602.07674, Oct. 20,2019,doi:10.48550/arXiv.1602.07674.
40- E. H. Houssein, Z. Abohashima, M. Elhoseny, and W. M. Mohamed, “Machine learning in the quantum realm: The state-of-the-art, challenges, and future vision,” Expert Systems with Applications, vol. 194, p. 116512, 2022, doi: 10.1016/j.eswa.2022.116512.
41- E. P. DeBenedictis, "A Future with Quantum Machine Learning," Computer, vol. 51, no. 2, pp. 68–71,Feb.2018,doi:10.1109/MC.2018.145164
© 2025, IRJET | Impact Factor value: 8.315 | ISO 9001:2008
| Page