A Comprehensive Review on Methods of Slope Stability Assessment

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 12 Issue: 10 | Oct- 2025 www.irjet.net p-ISSN: 2395-0072

A Comprehensive Review on Methods of Slope Stability Assessment

B Priyanka1 , Lovepreet Kaur2 , Kamalpreet Kaur3

1PG scholar, Dept. of Civil Engineering, SRM Global Group of Institutions, Haryana, India

2Professor, Dept. of Civil Engineering, SRM Global Group of Institutions, Haryana, India

3Professor, Dept. of Civil Engineering, SRM Global Group of Institutions, Haryana, India

Abstract - Slopestabilityassessmentcanbeconsideredone of the most complicated challenges for the geotechnical engineers. This assessment plays a very important role in the design of civil engineering structures like dams, road embankments, and slopes found in hilly areas. The factor of safety(FOS)isexpressedastheratioofshearstressdividedby the shear strength. Stable slopes are defined when driving forcesarelessthantheresistingforces,andafactorofsafetyis defined as a ratio of resistive forces divided by the driving forces.Throughoutthedecades,engineershaveanalyzedslope stability through conventional methods such as limit equilibrium methods (LEM), limit analysis methods, and numerical simulation methods like the finite element method (FEM) and finite difference method (FDM). However, recent advancementsincomputationalmethodshaveresultedinthe emergence of machine learning algorithms, consisting of artificial neural networks (ANN), support vector machines (SVM), decision trees (DT) and random forest (RF), as promising alternatives for analyzing complex slope stability problems under diverse geological and environmental conditions. This review paper will distinguish between traditional and machine learning based methods for the assessment of slope stability problems. It serves as a useful resource for researchers and practitioners, assisting in selecting the most suitable method for specific slope stability applicationsbasedonaccuracy,computationalefficiency,and complexity of the problem.

Key Words: Limit Equilibrium Method, Finite Element Method, Limit Analysis Method, Artificial Neural Network, Support Vector Machine, Decision Tree, Random Forest.

1. INTRODUCTION

Slope stability assessment is an essential element in geotechnicalengineeringbecauseitplaysasignificantrolein ensuringthesafetyofindustrialengineeringprojects[1,2]. This analysis is more complex and thorough, making it riskierandmoredifficultthanotheroperationsinvolvedin the practice of geotechnical engineering. Slope failure is a complicatednaturalphenomenonwhichresultsinserious disasters,includinglandslides,andcauseseconomicburden on several countries [3]. Consequently, it is essential to develop a safe, reliable, and effective model for analyzing, assessing, and predicting slope stability to mitigate the geological risks associated with slope failures and to safeguardpeopleandproperty[4].

Avarietyofapproachesforconductingstabilityanalysisfor finiteandinfiniteslopeshavebeendeveloped.Someofthese methods are the limit equilibrium method (LEM), finite elementmethod(FEM),finitedifferencemethod(FDM),limit analysis method, and rigid element method. Out of these methods, the limit equilibrium method is one of the most widely used. This method evaluates slope stability by calculating the factor of safety (FOS) at the critical failure surface and using assumptions regarding the shape and positionoffailuresurfaces[5].VariantsoftheLEMinclude theBishopmethod[6],Janbumethod[7],Morgenstern-Price method[8],andSarmamethod[9],whicharewidelyapplied in slope stability analysis [10-12]. Although the limit equilibriummethodisasimplemethod,itdoesnotprecisely representtheactualstresswithinthesoil;thus,assumptions for the sliding surface in terms of force and moment equilibrium need to be used. Many researchers have developed a finite element method depending on elasticplastic theory in order to reduce these limitations and describethebehaviorofsoilunderstress.Thismethodhas drawnalotofattentioninslopestabilityanalysis[13-16], but its accuracy depends on precise and accurate input parametersandtheapplicationofanadequateconstitutive model. Due tothe difficulty ofcomputing themodel along withtheseparameters,thismethodhascertainlimitations [17].

Classicaldeterministicslopestabilitymethodsmainlyfocus onthecomputationofasingleFOStoassessslopestability. However,suchanalysesdonotconsideruncertaintyinsoil properties, groundwater level, site conditions, and the quality of geotechnical investigations. Such uncertainties maydiffersignificantlyatdifferentlocationsandmayplaya majorroleindeterminingtheaccuracyoftheresults[18]. Probabilisticapproacheshavethusbecomemoreandmore prominent, taking major soil parameters as random variables and characterizing them in terms of statistical parameterslikethemean,standarddeviation,variance,and coefficient of variation. Such parameters are usually assumed to be normally or log-normally distributed. Probabilisticapproachescomputetheprobabilityoffailure (Pf)andthereliabilityindex(β),thusobtainingawiderand risk-basedslopestabilityassessment,especiallyinregionsof complex geological conditions, compared to deterministic approaches[19-21].

The latest developments in science and technology have significantlyimpactedslopestabilityanalysis,withmachine

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 12 Issue: 10 | Oct- 2025 www.irjet.net p-ISSN: 2395-0072

learning (ML) methods now widely adopted to reduce uncertaintyinfactorofsafetycalculations[22].Themethods have significantly aided in estimating the safety factor through the use of prediction modeling. Different models, suchasartificialneuralnetworks(ANN),decisiontress(DT), random forests(RF),andsupportvectormachines(SVM), are used to compute the factor of safety of soil slopes, depending on the learning rate of the algorithm and the accuracylevel.Machinelearningalgorithmsaredesignedto learn about the prevailing conditions of target data, learn from it, and then operate by using training data to make accurate predictions [23]. The algorithms are generally categorizedasshallowanddeepmachinelearningmethods, operating under different learning paradigms like supervised,unsupervised,andreinforcementlearning[24, 25]. The performance of these algorithms, though, is very muchdependentonthepropersettingofhyperparameters, andproperhyperparametersettingsimprovethepredictive accuracyofthemodels[4].

Whenassessingslopestability,thebasicinputparameters mayincludeslopegeometry,boundaryconditions,andthe mechanical properties of the soil. The output may be calculatedasafactorofSafetyoraclassificationoftheslope condition; i.e., stable or unstable. Compared to traditional probabilistic methods, machine learning methods possess several important benefits including not only greater accuracy, but that researchers do not have to make initial assumptionsoftheinput-outputrelationship,thecapacity for large data sets and the possibility for dealing with incompletedata[26].WiththeapplicationofMLmethods, geotechnical engineers will not subject themselves to the limitationsoftraditionalmethods,i.e.,forpriorassumptions or at a high computational cost, and will be able to make precisepredictionsofslopestability[27].

Thispaperoffersareviewanddiscussionofallthemethods beingutilizedcurrentlyfortheassessmentofslopestability. After reading this review paper, the researcher can determinetheoptimalmethodbasedonthesituation.

2. DISCUSSION ON SLOPE STABILITY METHODS

The slope stability assessment methods can broadly be divided into four main groups: limit equilibrium methods (LEM),numericalmodelingmethods,limitanalysismethods, andmachinelearningmethods.

2.1 Limit Equilibrium Method

The Limit Equilibrium Method (LEM) is a foundational methoddevelopedforassessingslopestability.Thismethod requirescalculatingthemobilizedshearstressalongwiththe ultimate shear strength in the slope soil mass over a trial slidesurface[5].AslopestabilityassessmentusingtheLEM method requires assuming the failure surface. With this assumption,thestabilityproblemisreducedtodetermining thecriticalpositionsofthefailuresurface.Theapproachuses stress distribution assumptions on the failure surface in

ordertoreachthetotalequilibriumequation,whichcanbe solved using the basic principles of statics, which are the summation of moments, forces in vertical and horizontal directions. As the LEM considers the static conditions in terms of slope failures, the constitutive behavior and the corresponding deformation are not considered during computation[28].Thefactorofsafetycanbecalculatedasa ratioofultimateshearstrengthofthesoilandthemobilized shearstressalongtheassumedfailuresurface[6].Incasethe plasticbehaviorofthesoilconformstotheMohr-Coulomb failurecriterion,theFOSisexpressedas:

Wherec՛istheeffectivecohesion,σ՛istheeffectivestressof soil, and φ՛ is the effective angle of internal friction. The minimum safety factor on the assumed failure surface is computedusingiterativecomputations[29].Insomecases, the 3rd dimension, in the direction perpendicular to the planeofthecross-section,isalsotakenintoconsideration andcanaffecttheoutcomeoftheslope[30].Thewell-known two-dimensionalLEMsareBishop’ssimplifiedmethodand the classical method of slices (Swedish circle method, Petterson, Fellenius, Spencer, Sarma, etc.). The methods differconsiderablyinrespecttoassumptionsmadeofintersliceforcesandwhetherequilibriumconditionshavebeen satisfied.(e.g.,forceequilibriumandmomentequilibrium). TheSpencerandSarmamethodshavesatisfiedallcriteria andarethereforecalledrigorousmethodsthatcangetthe more precise calculation than any other non-rigorous methods[18,31].

2.2 Numerical Modelling Method

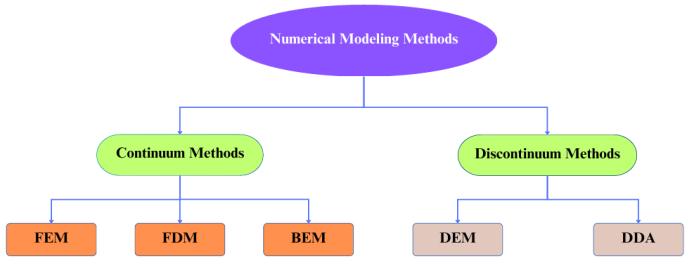
Numerical modeling techniques are much more advanced andcomplexthanlimitequilibriummethods,astheyinclude deformations(strains)inadditiontoforces(stresses),unlike themoreconventionallimitequilibriumapproaches.These methods have been utilized frequently over the last few decadesduetoadvancesincomputingpowerwithvarious numerical methods, such as the Finite Difference method (FDM), Finite Element Method (FEM), Boundary Element Method (BEM), Discrete Element Method (DEM), and DiscontinuousDeformationAnalysis(DDA),however,FEM andFDMarethemostwidelyusedinslopestabilityanalysis [32]whicharepresentedbelow:

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 12 Issue: 10 | Oct- 2025 www.irjet.net p-ISSN: 2395-0072

2.2.1 Finite Difference Method

TheFiniteDifferenceMethod(FDM)hasbeenlargelyapplied for slope stability analysis by geotechnical engineers for many years, and represents one of the oldest numerical methods used to determine factor of safety [33]. This method is used to solve systems of differential equations. Within FDM, every derivative present in the governing equation set gets substituted with an algebraic formula expressed through field variables that remain unknown within elements at specific discrete spatial locations [34]. UnliketheLimitEquilibriumMethod(LEM),notrialsurfaces or potential failure mechanisms need to be specified to computetheminimumfactorofsafetyforaslope,anddonot need to assume any function for the inter-slice force also [33].

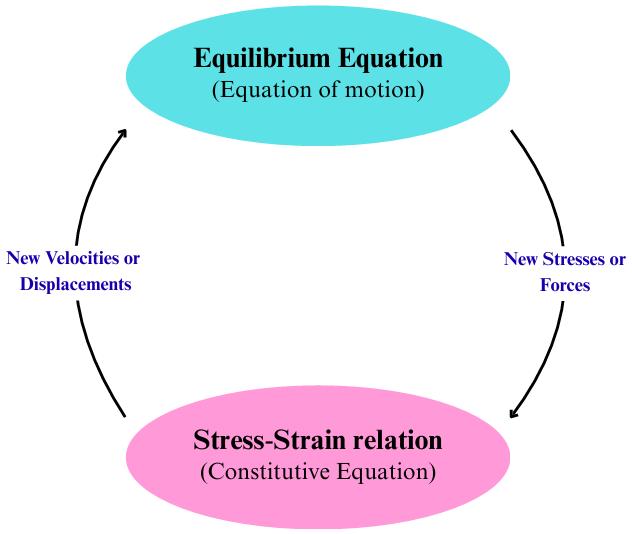
FLAC2Dor3D(FastLagrangianAnalysisofContinua)isa numerical modeling code which has a built-in strength reduction method, which uses FDM to conduct advanced geotechnical analysis of soil, rock, and structural support systems.Thistechniquefirstsolvestheequationsofmotion tofindnewdisplacementsandvelocitiesfromtheforcesand stresses.Thevelocitiesareusedtocalculatethestrainrates, and then from the strain rates, it calculates new stresses [35].FLAC/SlopeisasmallversionofFLACthatisonlyrun fromFLAC’sgraphicalInterface(theGIIC)andallowsforfast modelcreationofsoiland/orrockslopesalongwithsolving theirstabilityconditions.Itusessquareandparallelogram meshes where parallelogram meshes are used in slope direction[36].

2.2.2

Inclassicallimitequilibriumandlimitanalysistechniques, progressive failure cannot be modeled, except for the method outlined by Pan (1980). A few researchers have proposed the use of the Finite Element Method (FEM) to overcome some of the limitations found in traditional analysistechniques[37].TheFEMisamesh-basedmethod and potentially the most used numerical approach to geotechnicalproblems[38-40].Themaindifferencebetween

LEMsandFEMsisthatFEMscanincorporatetheconstitutive behaviorofthesoil,anddonothavetoassumeanyfailure surface. Two methods were introduced for slope stability alongwithFEM:theStrengthReductionMethod(SRM)and theGravityIncreasingMethod(GIM)[32,41].

In the SRM, the shear strength parameters of the soil, i.e., cohesion(c)andangleofinternalfriction(φ)aregradually reducedbyareductionfactortothepointofslopefailure. This failure condition is identified when shear strain developscontinuouslyfromthebaseoftheslopetoitstop. Theshearstrengthofaslopekeepsitstableandhowrapidly theshearstraindevelopsdeterminesthepotentialarea of slope failure. Therefore, the shear strain in the slope becomes greater as the shear strength reduces [42]. The criticalslipsurfaceisautomaticallyidentifiedasaresultof theincreaseinshearstrainwithadecreaseinshearstrength [43]. At this point, the factor of safety is calculated as the reciprocal of reduction factor by iterative calculation. The followingstudywilldemonstratetherelationshipbetween shearstrengthandstrain,andwilldepictthisrelationshipin ahyperbolicmodelofstressandstrain[44].Thehyperbolic stress-strainrelationshipisexpressedas:

Whereεistheaxialstrain,σ1andσ3arethemajorandminor principal stresses, Rf is the failure ratio, Ei is the initial tangentmodulus,cr andφr arethereducedshearstrength parameters,whicharedefinedas:

WhereRisshearstrengthreductionfactor.

Forhomogeneousslopes,theSRMandLEMoftenproduce similaroutputs,althoughtheSRMissomewhatsensitiveto nonlinearalgorithmsandflowrules[42,45].

In the case of GIM, the gravitational forces, for example weight, increases over time and thus has the potential to cause slope instability. The GIM is concerned with the limitingvalueofgravityandisbasicallyrepresentedasthe acceleration of gravity [46]. The factor of safety may be definedastheratioofthegravitationalaccelerationatthe time of failure (gf) to the actual gravitational acceleration (gi).

Thegravityincreasemethodisverysuitablefortheanalysis ofthestabilityoftheembankmentbecauseconstructionrate

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 12 Issue: 10 | Oct- 2025 www.irjet.net p-ISSN: 2395-0072

can be simulated based on increase in the rate of gravity loadingontheembankment[47].

2.3 Limit Analysis Method

Limit analysis employs the concept of an idealized stressstrainrelationship,wherebythesoilisassumedtobearigid perfectlyplasticmaterialthatobeysanassociatedflowrule. Withoutconductingadetailedelasto-plasticanalysis,limit analysis method is able to provide solutions to a vast numberofproblems.Thismethodusestwobasictheorems: (1)thelowerboundtheorem,whichstatesthatanystatically admissiblestressfieldwillgivealowerboundestimateof the true collapse load, and (2) the upper bound theorem, which states that while the energy dissipated by any kinematicallyadmissiblevelocityfieldisequaltotheenergy dissipatedbytheexternalloads,theexternalloadsprovide upper bounds on the true collapse load and the objective function will ultimately be optimized with respect to the controlvariables[48].

A statically admissible stress field satisfies equilibrium equations, boundary conditions of stress, and the yield condition.Similarly,akinematicallyadmissiblevelocityfield is characterized by its satisfaction of strain and velocity compatibilityequations,velocityboundaryconditionsand theflowrule.Thecombinationoftwotheoremsprovidesa strict bound to the actual collapse load. In lower bound methods, stress fields are often developed, without direct relationtoactualstressfields,makingitchallengingtofind lowerboundsolutionsforreal-worldgeotechnicalproblems. Ontheotherhand,collapsemechanismsinvolvedinupper boundanalysishaveaclearphysicalinterpretationthatlink torealfailuremodesandarewidelyusedinpractice[33].

In recent years, significant efforts have been directed towardsapplyingplasticlimittheoremstothelimitanalysis of slope stability. Donald and Chen (1997) introduced an energy work balance approach, also known as the upper bound approach, utilizing the associated flow rule [49]. Wang et al. (2001) further developed these methods by consideringapossiblenon-associatedflowruletodetermine the factor of safety of two-dimensional (2D) soil slopes. Similarly Chen et al. (2001a, 2001b) extended the upper boundmethodforestimatingfactorofsafetyofslopesinthe three-dimensional(3D)case[50,51].Therehavealsobeen severalnewdevelopments,asdemonstratedbySloan(1988, 1999), Sloan and Kleeman (1995), and Lyamin and Sloan (2002), who proposed various methods that utilize finite elements and linear programming (LP) or nonlinear programming(NLP)inordertoobtainrigorouslowerand upper bounds on stability for both 2D and 3D limits of stability[52-56].

2.4 Artificial Neural Network

An artificial neural network (ANN) is a type of machine learningmodelinspiredbythebiologicalneuralnetworks

oftenfoundinanimalbrains.ANNshavebeenusedtosolve numerous problems in the geotechnical field [57-59]. The structure of an ANN has three layers, an input layer, two hiddenlayers,andanoutputlayerasshowninfigure3. A neural network consists of a large number of artificial neurons, and each neuron can receive a signal, process it, andpassittotheadjacentneurons.Thesignalsthataresent from each neuron to each of its adjacent neurons are real numberswitha specific activationfunction.Aspartofthe learningprocedureandtrainingofthenetwork,theweights consisting by each neuron is adjusted. Each neuron can computeaweightedsumbymultiplyingtheincomingsignals that were sent from the neurons prior to it multiplied by theirassociatedweightsacrosseachneuron,andpassesit intoanactivationfunctionattheoutputoftheneuron[60]. Generally, more complex problems require more neurons and even layers. However, as there are very few dimensionlessparametersthatareusedinthisanalysis,a single-hidden-layer feed forward neural networks are investigated first as an option to use and the number of neurons when successful, is increased successively till a satisfactory result is acquired. In fact, for a classic ANN supportedslopestabilitypredictionmethodology,thefactor of safety would be directly treated as the output. Slope factorsresponsibleforinfluencingfactorofsafetyareinputs thattypicallyincludesoilshearstrength(e.g.,cohesionand angle of internal friction), soil unit weight, and slope geometrycommonlydescribedbyslopeheight,slopewidth, slope depth, and slope angle. Thus, around seven independentvariablesareneededasinput,whichincreases thecomplexityintermsoflearningandcomputation[61].

Training is one of the most critical stages of a neural network. The purpose of training is to find the best set of connection weights and biases that will minimize some objectivefunction,whichmayberootmeansquarederror (RMSE)orthesumofsquarederror(SSE)[62].Anartificial neuralnetworkrequiresthatthedatasetisrandomlysplit intotwodistinctsubsets:thetrainingdatasetandthetesting dataset. The ANN will use the training data for training, while the testing dataset will identify how accurate the predictiveaccuracyoftheANNisrating[61].

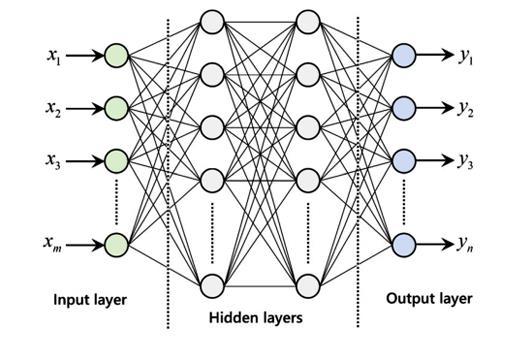
Fig -3: AnANNarchitecturewithtwohiddenlayers[Meng etal.2021(61)]

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 12 Issue: 10 | Oct- 2025 www.irjet.net p-ISSN: 2395-0072

2.5 Support Vector Machine

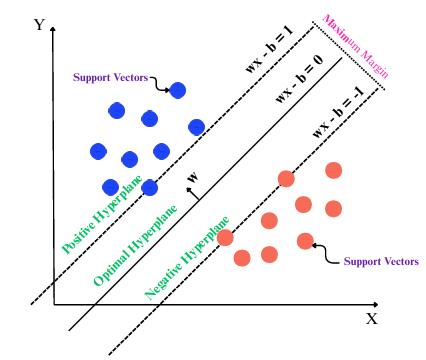
TheSupportVectorMachine(SVM)isasupervisedmachine learning technique that has been widely used for classification and regression problems [60]. SVM was initially designed for binary classification, but it is now a very powerful supervised learning algorithm [63]. The fundamental principle of SVM is the identification of an optimalhyperplane.SVMisparticularlygoodatsolvinghighdimensionaldata.Itoperatesbymappinginputpointstoa higher-dimensionalfeature spaceandthenidentifyingthe hyperplane that results in the maximum margin between differentclassesandhencemakestheclassesdistinctfrom eachother.Additionally,SVMiscapableofdealingwithnonlinear relationships by determining the data to higherdimensionalspacewherelinearseparationispossible[64].

2.6 Decision Tree

Adecisiontreeisasupervisedmachinelearningalgorithm employedforbothclassificationandregressionobjectives,in theformofatree-structuredmodelinwhicheachinternal noderepresentsadecisionrulebasedonaspecificattribute, eachbranchisanoutcomeoraresultofthatdecision,and eachleafnodesignifiesthefinaldecisionorprediction[65, 66]. The DT algorithm arrives at a prediction by learning fromsimplepowerofdecisionrulesfromthedataattributes. Decisiontreescanbegroupedintotwobroadercategories: classificationtreesandregressiontrees.Classificationtrees dividethedataintotwoclassesbasedonaclasslabel,and continue to divide the data into classes until a stopping condition is achieved. Regression trees are decision trees appliedtoregressionproblemsinmachinelearningcontexts. Incontrasttoclassificationtrees,whichmakepredictionsto beafiniteclassoutputofvalue,regressiontreespredictthe outputtobeacontinuousvariable.Regressiontreesdivide the data input using output data into two subsets, and repeatingthisprocessuntilastoppingconditionisachieved. Decision trees have multiple advantages as a method in

supervisedlearning,suchaseaseofinterpretationandease ofexplanation.Onedisadvantageoftheimplementationofa decisiontreemodelisthattheycanveryeasilybeaffectedby small fluctuations in the input data, and cause significant effectsonthetreesandfinalpredictions[67].Sincetheyare based on the greedy algorithm, decision trees sometimes mightnotyieldagloballyoptimalsolution[68].Inaddition, the decision tree algorithm has the ability to develop excessivelycomplextreesforagivenproblem,whichwould leadtopoorgeneralizationfromtrainingtodata,knownas overfitting.

2.7 Random Forest

A random forest (RF) constitutes an ensemble learning techniquewhichisusedforsolvingclassification,regression problems,andothertasks.Thefundamentalconceptbehind theRFmodelistheenhancementofthedecisiontree(DT).It worksbycreatingmultipledecisiontrees.TheRFlearnsby constructing many decision trees during training, and at prediction time uses these decision trees [69, 70]. For classification problems, the random forest produces an outputfortheclassthatreceivedthemajorityofthedecision trees, while for regression problems the random forest producesoutputbasedonthemeanoraverageprediction value of each DT. One of the main advantages of RFs is a reductionoftheoverfittingpotentialfoundwithDTs.Asthe numberoftreesinanRFincrease,thegeneralizationerror decreases and eventually stabilizes at some point. This impliesthattheperformanceofanRFbecomesindependent ofoverfitting[69].However,themaindrawbackofRFsisthe lossofinherentinterpretabilityfoundinDTs

3. CONCLUSION

This paper presents a review and classification of slope stability assessment methods, ranging from traditional methodslikeLimitEquilibriumMethod(LEM)tosomemore recentmethodsusingnumericalandmachinelearning(ML) approaches.LEMisstilloneofthemostpopularandwidely usedslopestabilityassessmentmethodsduetoitssimplicity and ease of computation, but it is less precise and not suitable for complex slope stability problems. Numerical methodssuchas,FiniteElementmethods(FEM)andfinite differencemethods(FDM)haveahigherdegreeofaccuracy andcansimulatecomplexstress-strainbehavior,butrequire enough time and knowledge. The limit analysis method providesatheoreticalbasisforboundingsolutions;however, ittoorequireseitherdepthofknowledgetoexecuteaswell as some specialized software (e.g. Optum G2). Machine learning algorithms such as, Artificial Neural Network (ANN),SupportVectorMachine(SVM),DecisionTree,and Random Forest have been very effective in predicting the slopebehaviorandfactorofsafety;buttheyusuallyrequire asignificantlylargedatasetstotrainsuccessfully,aswellas appropriateproceduretoevaluatemodelperformanceand avoidbiasedperformancemeasures.

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 12 Issue: 10 | Oct- 2025 www.irjet.net p-ISSN: 2395-0072

The utilization of machine learning for 3D slope stability analysis is of significant importance to geotechnical engineersandresearchers,especiallyduetotheinfluenceof three-dimensional spatial variability on slope stability. In ordertoincreasethereliabilityofslopestabilityassessment, itisimportanttoexploremachinelearningmethodsthatcan detectfinerfluctuationscalesandautocorrelations.Although machinelearningisrelativelynewtoslopestabilityanalysis, there is a great potential for its application. The advancement of some open-source libraries further increasestheavailabilityandflexibilityofthesemethodsto conductqualityresearch.Eventually,machinelearningwill offer accurate analysis of slope stability problems and contributetolandslide-riskmitigation.

REFERENCES

[1] Das, S.K.; Biswal, R.K.; Sivakugan, N.; Das, B. Classificationofslopesandpredictionoffactorofsafety using differential evolution neural networks. Environ. EarthSci.2011,64,201–210.

[2] Asteris,P.G.;Rizal,F.I.M.;Koopialipoor,M.;Roussis,P.C.; Ferentinou, M.; Armaghani, D.J.; Gordan, B. Slope StabilityClassificationunderSeismicConditionsUsing Several Tree-Based Intelligent Techniques. Appl. Sci. 2022,12,1753.

[3] Suman,S.;Khan,S.Z.;Das,S.K.;Chand,S.K.Slopestability analysis using artificial intelligence techniques. Nat. Hazards2016,84,727–748.

[4] Yang,Y.;Zhou,W.;Jiskani,I.M.;Xiang,L.;Wang,Z.;Luan, B.SlopeStabilityPredictionMethodBasedonIntelligent Optimization and Machine Learning Algorithms. Sustainability2023,15,1169.

[5] SamiUllah;MuhibUllahKhan;GoharRehman.ABrief Review of the Slope Stability Analysis Methods. GeologicalBehavior2020,4(2):73-77.

[6] Bishop, A.W. The use of the Slip Circle in the Stability AnalysisofSlopes.Geotechnique1955,5,7–17.

[7] Janbu, N. Slope Stability Computations. Embankment DamEngineeringCasagrandeVolume;JohnWileyand Sons:NewYork,NY,USA,1973;47–86.

[8] Spencer,E.Theanalysisofthestabilityofgeneralslip surfaces.Géotechnique1968,18,92–93.

[9] Sarma, S.K. Stability Analysis of Embankments and Slopes.J.Geotech.Eng.Div.1979,105,1511–1524.

[10] Sazzad,M.M.;Mazumder,S.;Moni,M.M.SeismicStability Analysis of Homogeneous and Layered Soil Slopes by LEM.Int.J.Comput.Appl.2015,117,12–17.

[11] Yin,Y.;Li,B.;Wang,W.;Zhan,L.;Xue,Q.;Gao,Y.;Zhang, N.;Chen,H.;Liu,T.;Li,A.MechanismoftheDecember 2015 Catastrophic Landslide at the Shenzhen Landfill and Controlling Geotechnical Risks of Urbanization. Engineering2016,2,230–249.

[12] Cho,Y.C.; Song, Y.S. Deformation measurements and a stabilityanalysisoftheslopeatacoalminewastedump. Ecol.Eng.2014,68,189–199.

[13] Clough, G.W.; Duncan, J.M. Finite Element Analyses of RetainingWallBehavior.J.SoilMech.Found.Div.1971, 97,1657–1673.

[14] Griffiths,D.V.;Lane,P.A.Slopestabilityanalysisbyfinite elements.Geotechnique1999,49,387–403.

[15] Griffiths,D.V.;Lu,N.Unsaturatedslopestabilityanalysis with steady infiltration or evaporation using elastoplastic finite elements. Int. J. Numer. Anal. Methods Geomech.2005,29,249–267.

[16] Griffiths,D.V.;Marquez,R.M.Three-dimensional slope stability analysis by elasto-plastic finite elements. Geotechnique2007,57,537–546.

[17] Zhang, H.; Luo, Y. Prediction model for slope stability basedonartificialimmunealgorithm.J.ChinaCoalSoc. 2012,37,7.

[18] Abramson,L.W.;Lee,T.S.;Sharma,S.;Boyce,G.M.Slope Stability Concepts: Slope Stability and Stabilization Methods,2nded.Wiley-Interscience:Millburn,NJ,USA, 2001.

[19] Chowdhury, R.N. Recent developments in Landslide studies:ProbabilisticMethods-StateoftheArtReport. Proceedings of the 4th International Symposium on Landslides1984,Vol.1,209-228.

[20] Chowdhury,R.N.;XuD.W.SlopeSystemReliabilitywith GeneralSlipSurfaces.SoilsandFoundations1994,Vol. 34,3,99-105.

[21] Li,K.S.;LumbP.ProbabilisticDesignofSlopes.Canadian GeotechnicalJournal1987,Vol.24,520-535.

[22] Ahangari Nanehkaran, Y.; Pusatli, T.; Chengyong, J.; Chen, J.; Cemiloglu, A.; Azarafza, M.; Derakhshani, R. Application of Machine Learning Techniques for the Estimation of the Safety Factor in Slope Stability Analysis.Water2022,14,3743.

[23] Nanehkaran, Y.A.; Licai, Z.; Chengyong, J.; Chen, J.; Anwar, S.; Azarafza, M.; Derakhshani, R. Comparative AnalysisforSlopeStabilitybyUsingMachineLearning Methods.Appl.Sci.2023,13,1555.

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 12 Issue: 10 | Oct- 2025 www.irjet.net p-ISSN: 2395-0072

[24] Müller,A.C.;Guido,S.IntroductiontoMachineLearning withPython:AGuideforDataScientists;O’ReillyMedia: Sebastopol,CA,USA,2016.

[25] Aggarwal,C.C.NeuralNetworksandDeepLearning:A Textbook;Springer:Berlin/Heidelberg,Germany,2018.

[26] Bello, O.; Holzmann, J.; Yaqoob, T.; Teodoriu, C. ApplicationofArtificialIntelligenceMethodsinDrilling SystemDesignandOperations:AReviewoftheStateof theArt. J.Artif.Intell.SoftComput.Res.2015,5,121–139.

[27] Xu, H.; He, X.; Shan, F.; Niu, G.; Sheng, D. Machine LearningintheStochasticAnalysisofSlopeStability:A State-of-the-ArtReview.Modelling2023,4,426–453.

[28] Fredlund, D.G. Analytical Methods for Slope Stability Analysis. In Proceedings of the 4th International SymposiumonLandslides,Toronto,ON,Canada,16–21 September1984;Volume250.

[29] Kalatehjari, R.; Ali, N. A Review of Three-Dimensional Slope Stability Analyses Based on Limit Equilibrium Method.Electron.J.Geotech.Eng.2013,18,119–134.

[30] Albataineh,N.Slopestabilityanalysisusing2Dand3D methods. M.Sc. thesis, Akron University, Ohio, USA, 2006,1-36.

[31] Zhu, D.Y.; Lee, C.F.; Jiang, H.D.; Lee, C.F.; Iang, H.D.J. GeneralisedFrameworkofLimitEquilibriumMethods for Slope Stability Analysis. Géotechnique 2003, 53, 377–395.

[32] Pourkhosravani, A.; Kalantari, B. A Review of Current Methods for Slope Stability Evaluation. Electron. J. Geotech.Eng.2011,16,1245–1254.

[33] Abusharar,S.W.;Han,J.Two-dimensionaldeep-seated slope stability analysis of embankments over stone columnimprovedsoftclay.EngineeringGeology2011, 120,103–110.

[34] Itasca Consulting Group Inc. FLAC – Fast Lagrangian Analysis of Continua/Slope. Version 8.0, Itasca ConsultingGroup,Minneapolis,Minnesota,2016.

[35] Reza Beyabanaki, S.A. A Comparison between Using Finite Difference and Limit Equilibrium Methods for LandslideAnalysisofSlopesContainingaWeakLayer. AmericanJournalofEngineeringResearch2020,9,6879.

[36] Zeynadin, S.M.; Kalantari, B. Traditional Methods vs. FiniteDifferenceMethodforComputingSafetyFactors of Slope Stability. Electron. J. Geotech. Eng. 2011, 16, 1120-1130.

[37] Cheng, Y.M.; Lau, C.K. Slope Stability Analysis and Stabilization:NewMethodsandInsight(2nded.).CRC Press2008.

[38] Zienkiewicz, O.C.; Taylor, R.L.; Zhu, J.Z. The Finite ElementMethod:ItsBasisandFundamentals;Elsevier: Amsterdam,TheNetherlands,2005;ISBN008047277X.

[39] Belytschko, T.; Liu, W.K.; Moran, B.; Elkhodary, K. NonlinearFiniteElementsforContinuaandStructures; John wiley & Sons: Hoboken, NJ, USA, 2014; ISBN 1118632702.

[40] Bathe, K.J. Finite Element Procedures; Klaus-Jurgen Bathe:Cambridge,MA,USA,2006;ISBN097900490X.

[41] Kaur, A.; Sharma, R.K. Slope Stability Analysis Techniques: A Review. Int. J. Eng. Appl. Sci. Technol. 2016,1,52–57.

[42] Matsui, T.; San, K. C. Finite element slope stability analysis by shear strength reduction technique. Soils andfoundations1992,32(1),59-70.

[43] Liu,S.Y.;Shao,L.T.;Li,H.J.Slopestabilityanalysisusing the limit equilibrium method and two finite element methods. Computers and Geotechnics. 2015, 63, 291298.

[44] Duncan,J.M.;Chang,C.Y.Nonlinearanalysisofstressand straininsoils.J.SoilMech.andFound.Engg.Div.1970, 96(5),1629–1653.

[45] Cheng,Y.M.;Lansivaara,T.;Wei,W.B.Two-Dimensional Slope Stability Analysis by Limit Equilibrium and Strength Reduction Methods. Comput. Geotech. 2007, 34,137–150.

[46] Sternik,K.ComparisonofSlopeStabilityPredictionsby GravityIncreaseandShearStrengthReductionMethods. Czas.Tech.Sr.2013,110,121–130.

[47] Colby, C.S.; Young, K.S. Slope stability analysis using finiteelementtechniques.13thIowaASCEGeotechnique Conference,USA,1999.

[48] Drucker, D.C.; Greenberg, W.; Prager, W. The safety factor of an elastic plastic body in plane strain, TransactionsoftheASME,JournalofAppliedMechanics 1951,73,371.

[49] Donald,I.;Chen,Z.Y.Slopestabilityanalysisbytheupper boundapproach:Fundamentalsandmethods,Canadian GeotechnicalJournal1997,34(6),853–862.

[50] Chen,Z.Y.;Wang,X.G.;Haberfield,C.;Yin,J.H.;Wang,Y.J. A three dimensional slope stability analysis method using the upper bound theorem. Part I: Theory and

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 12 Issue: 10 | Oct- 2025 www.irjet.net p-ISSN: 2395-0072

methods,InternationalJournalofRockMechanicsand MiningSciences(2001a),38(3),369–378.

[51] Chen,Z.Y.;Wang,J.;Wang,Y.J.;Yin,J.H.;Haberfield,C.A three-dimensionalslopestabilityanalysismethodusing the upper bound theorem. Part II: Numerical approaches,applicationsandextensions,International JournalofRockMechanicsandMiningSciences(2001b), 38(3),379–397.

[52] Sloan S.W. Lower bound limit analysis using finite elements and linear programming. Int J Numer Anal. MethodsGeomech.(1988a),12(1),61–77.

[53] Sloan S.W. A steepest edge active set algorithm for solving sparse linear programming problem. International Journal for Numerical Methods in Engineering(1988b),26(12),2671–2685.

[54] Sloan S.W. Upper bound limit analysis using finite elements and linear programming. Int J Numer Anal. MethodsGeomech.1989,13(3),263–282.

[55] Sloan,S.W.;Kleeman,P.W.Upperboundlimitanalysis usingdiscontinuousvelocityfields.ComputerMethods inAppliedMechanicsandEngineering1995,127(1–4), 293–314.

[56] Lyamin, A.V.; Sloan, S.W. Upper bound limit analysis using linear finite elements and non-linear programming. Int J Numer Anal. Methods Geomech. (2002b),26(2),181–216.

[57] Zhang, X.; Nguyen, H.; Bui, X-N. Evaluating and predicting the stability of roadways in tunneling and underground space using artificial neural networkbased particle swarm optimization. Tunnelling UndergroundSpaceTechnol.2020,103,517.

[58] Lee, S.; Lee, SR.; Kim, Y. An approach to estimate unsaturated shear strength using artificial neural networkandhyperbolicformulation.ComputGeotech. 2003,30(6),489-503.

[59] Gholami, V.; Sahour, H.; Amri, MAH. Soil erosion modeling using erosion pins and artificial neural networks.Catena2020,196,104902.

[60] He,X.;Xu,H.;Sabetamal,H.;Sheng,D.MachineLearning Aided Stochastic Reliability Analysis of Spatially VariableSlopes.Comput.Geotech.2020,126,103711.

[61] Meng,J.;Mattsson,H.;Laue,J.Three-dimensionalslope stabilitypredictionsusingartificialneuralnetworks.Int JNumerAnal.MethodsGeomech.2021,45,1988–2000.

[62] Khajehzadeh, M.; Taha, M.R.; Keawsawasvong, S.; Mirzaei,H.;JebeliM.R.AnEffectiveArtificialIntelligence

ApproachforSlopeStabilityEvaluation2022,10,56605671.

[63] Boser, B.E.; Guyon, I.M.; Vapnik, V.N. A Training AlgorithmforOptimalMarginClassifiers.InProceedings of the Fifth Annual Workshop on Computational LearningTheory,Pittsburgh,PA,USA,1992,144–152.

[64] Srivastava, S.; Sharma, A.K.; Nayak, S. A Comparative AnalysisofSlopeStabilitybasedonAdvancedMachine Learning Methods. Real-World Applications of AI Innovation2025,277-306.

[65] Kardani, N.;Zhou,A.; Nazem,M.; Shen, S.-L.Improved Prediction of Slope Stability Using a Hybrid Stacking EnsembleMethodBasedonFiniteElementAnalysisand FieldData.J.RockMech.Geotech.Eng.2021,13,188–201.

[66] Pekel,E.EstimationofSoilMoistureUsingDecisionTree Regression.Theor.Appl.Clim.2020,139,1111–1119.

[67] Gareth, J.; Daniela, W.; Trevor, H.; Robert, T. An IntroductiontoStatisticalLearning:WithApplicationsin R;Spinger:Berlin/Heidelberg,Germany,2013.

[68] Ben-Gal, I.; Dana, A.; Shkolnik, N.; Singer, G. Efficient ConstructionofDecisionTreesbytheDualInformation DistanceMethod.Qual.Technol.Quant.Manag.2014,11, 133–147.

[69] Breiman,L.RandomForests.Mach.Learn.2001,45,5–32.

[70] Nath,S.K.;Sengupta,A.;Srivastava,A.RemoteSensing GIS-BasedLandslideSusceptibility&RiskModelingin Darjeeling–SikkimHimalayaTogetherwithFEM-Based Slope Stability Analysis of the Terrain. Nat. Hazards 2021,108,3271–3304.

2025, IRJET | Impact Factor value: 8.315 | ISO