International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056 p-ISSN:2395-0072
Volume: 12 Issue: 10 | Oct 2025 www.irjet.net
Bridging Spectral Analysis and Clustering: A Novel Method for Identifying Hidden Patterns in Complex Data
Henil Diwan
Student, School of Computer Science and Engineering, Vellore Institute of Technology, Vellore, Tamil Nadu
Abstract - This paper introduces Data Spectroscopic Clustering (DSC), a hybrid approach that combines Fourier transformation and spectral graph theory to enhance clustering in complex, high-dimensional datasets. By analyzing data in the frequency domain, DSC suppresses noise and reveals hidden patterns that traditional distancebased methods often overlook. Experimental results on synthetic datasets show improved cluster compactness and separability, supported by strong performance metrics and visual validation. The study demonstrates DSC’s potential as arobustandinterpretableclusteringframework.
Key Words: Spectroscopic Clustering, Fourier Transform, Spectral Graph Theory, High-Dimensional Data Analysis, Unsupervised Learning, Similarity Matrix, Pattern Recognition
1. INTRODUCTION
Clustering is a fundamental technique in data science, supporting a wide range of applications such as data exploration, recommendation systems, and anomaly detection.TraditionalalgorithmslikeK-meansandDBSCAN primarilyrelyondistanceordensity-basedmetrics,which often limits their ability to detect complex or nonlinear relationshipswithindata.Thesemethodscanstrugglewhen dealingwithhigh-dimensionaldatasetswherepatternsare noteasilyseparableintheoriginalfeaturespace.
Inspiredbyspectroscopicanalysisinphysicsandchemistry, Data Spectroscopic Clustering (DSC) introduces a new perspectivebyanalyzingdatainthefrequencydomain.By decomposing data into its spectral components, this approachuncovershiddenstructuresandrelationshipsthat conventionalmethodsmayoverlook.Leveragingfrequencybased representations enhances the interpretability and accuracy of clustering, making it particularly effective for identifyingsubtlepatternsincomplexdatasets.
2. LITERATURE REVIEW
Clustering has been extensively studied, with classical algorithms such as K-means (MacQueen, 1967), DBSCAN (Ester et al., 1996), and Gaussian Mixture Models (GMMs) (Bishop, 2006) forming the foundation of unsupervised learning. While these methods perform well for linearly
separableorwell-definedclusterboundaries,theyoftenfail tocapturethecomplexrelationshipsandnonlinearpatterns presentinhigh-dimensionaldata.
Toaddresssuchlimitations,spectralclustering(Ng,Jordan,& Weiss, 2001) introduced the use of graph Laplacians and eigenvector decomposition to map data into a lowerdimensional spectral space where clusters become more distinct.Furtheradvancements,suchasNormalizedCuts(Shi &Malik,2000),improvedtheabilitytodetectclustersbased on global similarity structures rather than local distances. Parallel developments in signal processing and wavelet analysis (Mallat, 1999; Oppenheim & Schafer, 1999) have demonstratedthepowerofspectralandfrequency-domain transformations in revealing hidden structures in complex signals.
However,despitetheseadvances,mostclusteringmethods eitherrelysolelyonspatialorfeature-spacesimilarityoruse spectral information in a limited way. There is a clear research gap in integrating spectroscopic analysis techniques suchasFourierandwavelettransformations with spectral graph theory for clustering. Existing studies seldomexplorehowfrequency-domainrepresentationscan enhancetheconstructionofsimilaritymatricesorimprove clusteringindynamic,nonlinear,ornoisydatasets.
TheproposedData SpectroscopicClustering(DSC)method addresses this gap by combining Fourier transformation, spectralgraphtheory,andtraditionalclusteringtouncover hidden relationships within complex datasets. This integrationenablesamorerobust,interpretable,andnoiseresistantapproach,makingDSCparticularlysuitableforrealworlddatawithintricatestructuralpatterns.
3. EXPLANATION OF METHODS
The Spectroscopic Clustering approach integrates Fourier transformation, spectral graph theory, and traditional clustering techniques such as K-means to provide an enhancedframeworkforanalyzingcomplexdatastructures. Themethodbeginsbytransformingdataintothefrequency domain using the Fourier transform, which helps reveal significantpatternswhilereducingtheimpactofnoise.This transformation captures relationships that are often obscuredintheoriginalspatialorfeaturedomain.
Volume: 12 Issue: 10 | Oct 2025 www.irjet.net
A similarity matrix is then constructed using a Gaussian radial basis function (RBF) kernel, followed by the computation of the graph Laplacian to model intrinsic relationships between data points. Through spectral decompositionoftheLaplacianmatrix,keyeigenvaluesand eigenvectors are extracted to form a low-dimensional embedding that preserves the data’ s most meaningful structural characteristics. Clustering is subsequently performedinthisspectralspace,wheredatapointsbecome morelinearlyseparable,resultinginimprovedaccuracyand interpretability.
To evaluate the performance of this technique, clustering qualitycanbeassessedusingstandard metrics suchas the Silhouette Score, Davies–Bouldin Index, and Calinski–Harabasz Score. By combining signal processing concepts withspectralgraph-basedlearning,SpectroscopicClustering offersa robustandnoise-tolerantapproachforuncovering hiddenpatternsincomplex,high-dimensionaldatasets.
4. THEORETICAL CONCEPTS
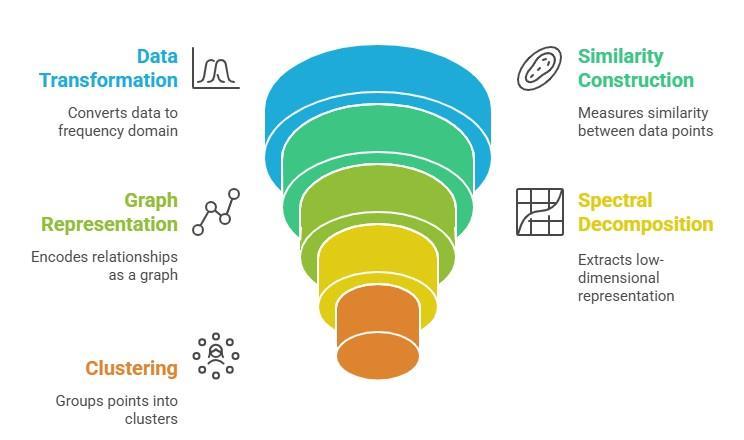
The Spectroscopic Clustering approach integrates Fourier transformation, spectral graph theory, and traditional clustering techniques such as K-means to provide an enhancedframeworkforanalyzingcomplexdatastructures. Themethodbeginsbytransformingdataintothefrequency domain using the Fourier transform, which helps reveal significantpatternswhilereducingtheimpactofnoise.This transformation captures relationships that are often obscuredintheoriginalspatialorfeaturedomain.
ByintegratingFourieranalysisandspectraldecomposition, SpectroscopicClusteringiswell-suitedforcomplexclustering tasks like image segmentation and anomaly detection, making it a powerful tool for handling both linear and nonlineardatastructures.
5. RESULTS
Preliminary experiments were conducted to evaluate the performanceoftheproposedDataSpectroscopicClustering
2395-0056 p-ISSN:2395-0072
make blobsfunction TheDSCworkflowinvolvedapplyinga Fourier transformation to each data point, extracting the dominant frequency components, and then performing spectralclusteringinthetransformedfrequencyspace
TheresultsdemonstratethatDSCiseffectiveinpartitioning the data into well-defined clusters within the spectral domain. The Fourier transformation plays a crucial role in suppressing noise and enhancing the visibility of latent structures,allowingthealgorithmtouncoverrelationships that traditional clustering methods might overlook. This is particularly important in complex or high-dimensional datasets,wherenoisecanoftenobscuremeaningfulpatterns.
Quantitativeevaluationofclusteringqualityusingstandard metricsproducedthefollowingresults:
o SilhouetteScore:0.5098
o Davies–BouldinScore:0.4657
o Calinski–HarabaszScore:1189.48
ThemoderateSilhouetteScoreindicatesthattheclustersare reasonably well-separated, while the low Davies–Bouldin ScoreandhighCalinski–HarabaszScoreconfirmstrongintraclustercompactnessandgoodinter-clusterseparation.These results suggest that DSC successfully identifies meaningful groupings in the transformed spectral space, where data pointsaremorelinearlyseparablethanintheoriginalfeature space.
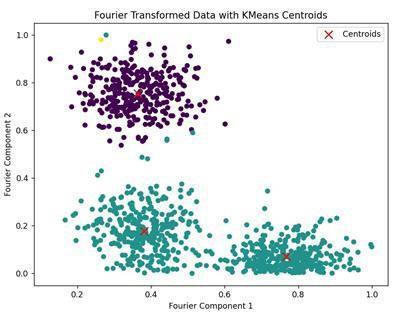
Fig -3:Fourier-transformeddataclusteredusingKMeans, withcentroidsclearlymarked (DSC)approachusingasyntheticallygenerateddatasetwith 1,000 samples and 3 cluster centers, created using the
Fig -2:Originaldatadistributionbeforepreprocessing
Fig -1:SpectralClusteringProcess
Volume: 12 Issue: 10 | Oct 2025 www.irjet.net
Visualinspectionoftheclusteringprocessfurthersupports these findings. Figure 2 presents the original data distribution prior to preprocessing, where clusters are partiallyvisiblebutstillsubjecttooverlapandnoise.Figure3 then shows the Fourier-transformed data clustered using KMeans, with centroids clearly marked. Compared to the originalspace,thetransformeddomainconfirmsthebenefit of the DSC workflow in producing compact and distinct clusters.
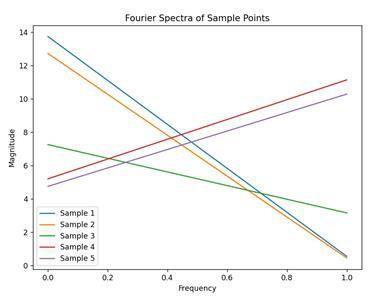
Fig -4:Fourierspectraofrepresentativesamplepoints
Figure 4 illustrates the Fourier spectra of selected sample points, showing how distinct frequency patterns emerge acrossdatainstancesanddemonstratingthediscriminative capacity of the Fourier transform in separating latent structures.
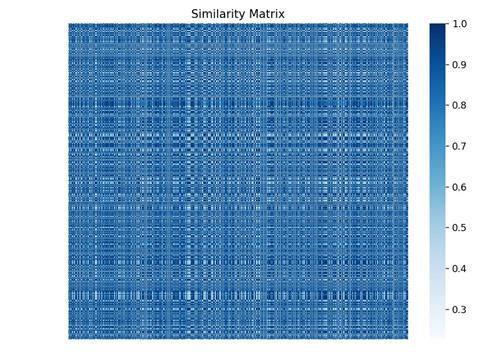
Figure 5 illustrates the similarity matrix generated usinga Gaussian RBF kernel on the Fourier-transformed features. The heatmap reveals distinct block-like structures, where sampleswithinthesameclusterexhibithighsimilarity,while samplesacrossclustersshowlowersimilarity.Thisconfirms that the Fourier transformation enhances separability by aligningdatapointsintodistinctsimilaritygroups,afeature thatiscriticalforeffectiveclustering.
2395-0056 p-ISSN:2395-0072
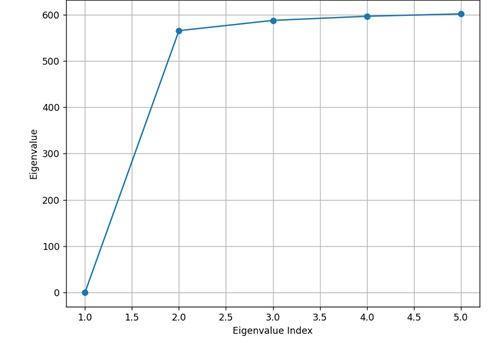
Fig -6:Eigenvaluesfromspectraldecomposition
Figure 6 presents the eigenvalue distribution from the spectraldecompositionofthegraphLaplacian.Themarked increasebetweenthefirstandsecondeigenvaluesindicatesa clearspectralgap,acharacteristicoftenassociatedwiththe optimal number of clusters. This validates the presence of three distinctclusters inthedataset,which aligns withthe groundtruthusedduringdatageneration.Thestabilization ofeigenvaluesafterthesecondcomponentfurthersupports this conclusion, suggesting that subsequent dimensions capturelessmeaningfulstructuralvariance,reinforcingthe suitabilityofthespectralembeddingforclustering.
Overall, these results provide strong preliminary evidence that DSC can outperform conventional distance-based clustering methods, particularly when applied to highdimensional or complex datasets. While the experiments wereconductedwithsyntheticdata,thefindingsunderscore the potential of DSC for real-world applications, such as image segmentation, anomaly detection, and time-series patternrecognition.Futureworkshouldfocusonscalingthe techniquetolarger,morecomplexdatasetsandexploringthe integration of adaptive Fourier features for dynamic data scenarios, to fully unlock the method's potential across differentdomains.
Together, the quantitative metrics, visualizations, and dimensionalityreductionresultssuggestthatDSCisarobust and promising clustering approach, effectively uncovering intrinsicstructuresintransformeddataspaces.
6. CONCLUSION
Spectroscopic clustering provides a robust and adaptable framework for uncovering hidden structures in highdimensional and complex datasets. By leveraging spectral properties through eigenvalues and eigenvectors of the graph Laplacian, this method enables more effective partitioning than approaches based solely on Euclidean distance. Its ability to reveal subtle patterns makes it particularly relevant in domains such as image analysis, bioinformatics,andsocialnetworkanalysis.Theintegration
Fig -5:SimilarityMatrixconstructedusingkernel
Volume: 12 Issue: 10 | Oct 2025 www.irjet.net
International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056 p-ISSN:2395-0072
of spectroscopic analysis with K-means clustering has demonstrated promising improvements in cluster quality, highlightingitspotentialasahybridapproach.Nevertheless, further research is required to enhance scalability, assess performance across a broader range of datasets, and rigorouslybenchmarkagainstexistingclusteringmethodsto establish its general applicability and long-term impact.
REFERENCES
[1] C.M.Bishop,PatternRecognitionandMachineLearning. New York: Springer, 2006.M. Young, The Technical Writer’ sHandbook.MillValley,CA:UniversityScience, 1989.
[2] A. Y. Ng, M. I. Jordan, and Y. Weiss, “On spectral clustering:Analysis andan algorithm,” inAdvances in Neural Information Processing Systems, pp. 849–856, 2001.
[3] A.K.JainandR.C.Dubes,AlgorithmsforClusteringData. EnglewoodCliffs,NJ:Prentice-Hall,1988.
[4] J.MacQueen,“K-meansclustering,”inProc.5thBerkeley Symp.MathematicalStatisticsandProbability,pp.281–297,1967.
[5] J. Shi and J. Malik, “Normalized cuts and image segmentation,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol.22, no. 8, pp. 888–905, Aug.2000.
[6] M. Ester, H.-P. Kriegel, J. Sander, and X. Xu, “A densitybasedalgorithmfordiscoveringclustersinlargespatial databaseswithnoise,”inProc.2ndInt.Conf.Knowledge DiscoveryandDataMining(KDD),pp.226–231,1996.
BIOGRAPHY
HenilDIwanisaB.Techstudentat VIT Vellore, pursuing a dualdegree in Data Science & ProgrammingfromIITMadras.