Free Vibration of a Square Plate with Bi- Dimensional Circular Varying Thickness and Thermal Effect by IRJET Journal

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 12 Issue: 08 | Aug 2025 www.irjet.net p-ISSN: 2395-0072

Free Vibration of a Square Plate with Bi- Dimensional Circular Varying Thickness and Thermal Effect

Manju Bala1 , Dr Ashish Kumar2

1Research Scholar, Department of Mathematics, Arni University, Kangra (H.P.)

2Associate Professor, Department of Mathematics, Arni University, Kangra (H.P.)

Abstract

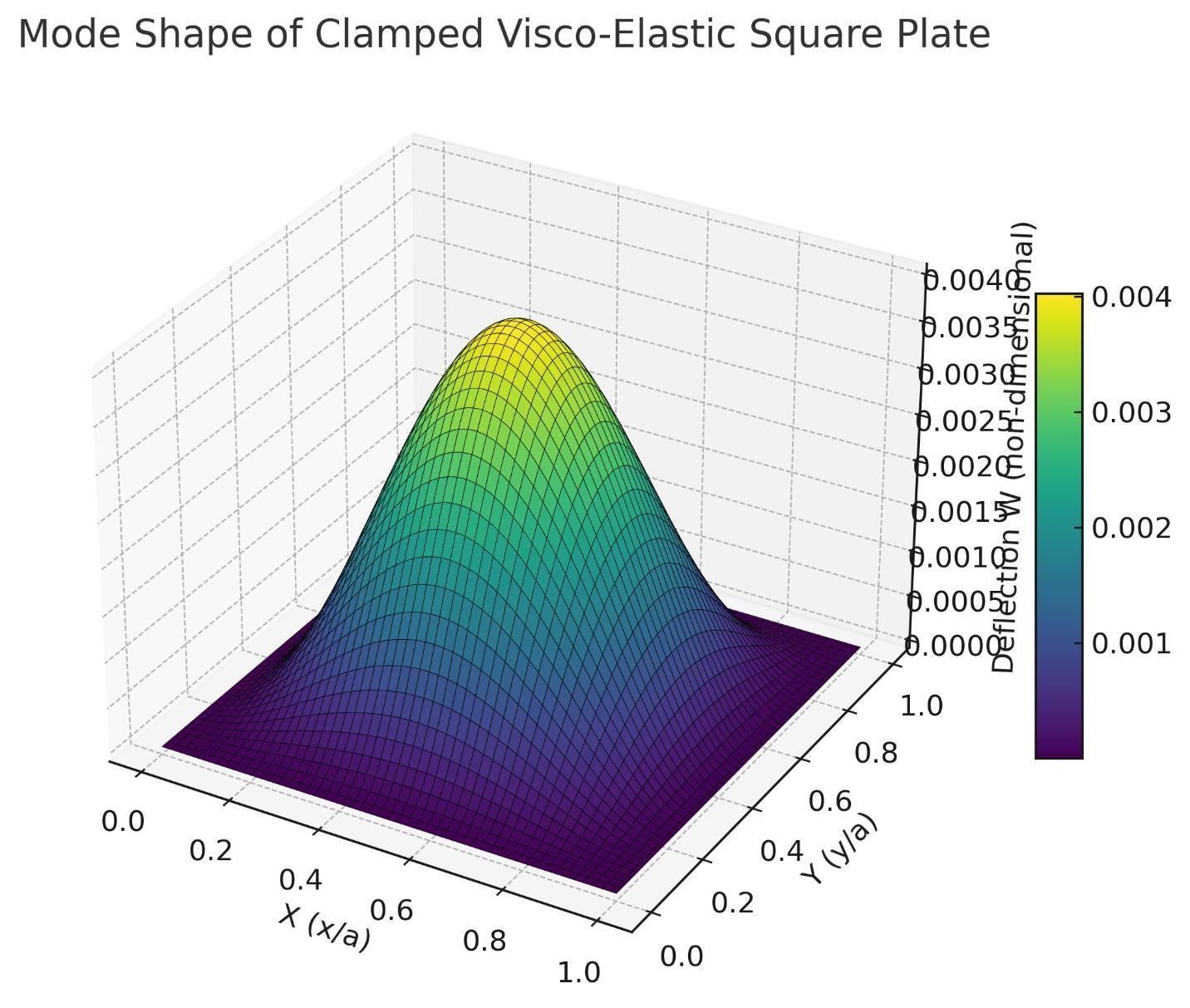
Visco-elastic plates play a crucial role in numerous engineering applications, including mechanical structures, aircraft components, and industrial systems. Accurate analysis of their behavior and strength is essential for optimal design and material utilization. Plates with variable thickness are particularly important in advanced technologies such as nuclear reactors, aerospace structures, naval vessels, submarines, and earthquake-resistant designs. This study presents a mathematicalmodeltoanalyzethevibrationalbehaviorofasquarevisco-elasticplatewithlinearlyvaryingthicknessinboth directions,subjectedtoclampedboundaryconditionsonallfouredges.Theinfluenceofthermalgradients linearinone directionandparabolicintheother ontheplate’svibrationisexamined.Anapproximatefrequencyequationisderivedusing theRayleigh–Ritzmethodwithatwo-termdeflectionfunction.Thenaturalfrequenciesfordifferenttaperparametersand thermalgradientsarecomputedusingMATLAB,andtheresultsareillustratedthroughgraphicalrepresentations.Thiswork providesvaluableinsightsforengineersandresearchersworkinginhigh-temperatureandadvancedstructuralapplications.

Keywords: SquarePlate,Vibration,Frequency.

Introduction

Inmodernengineeringandtechnology,increasingattentionisbeingdirectedtowardtheinfluenceofelevatedtemperatureson non-homogeneousplateswithvariablethickness,owingtotheirwidespreadapplicationinfieldssuchasnuclearpowerplants, aeronautics,chemicalindustries,andenergysystems.Materialslikemetalsandtheiralloysoftenexhibitvisco-elasticbehavior undersuchhigh-temperatureconditions.

Duringthermalexposure,especiallyunderintenseheatfluxes,materialpropertiesundergosignificantchanges,makingit imperativetoconsiderthermaleffectsinstructuralanalysis.Thesechangescannotbeneglected,astheyhaveadirectimpact onthemechanicalperformanceandvibrationbehaviorofplatestructures.

Numerous studies have shown that material non-homogeneity significantly affects vibration characteristics. This nonhomogeneitymaybeinherentorintroducedthroughengineeringdesign,asseeninmaterialslikeplywood,deltawood,and fiber-reinforcedplastics,whicharecommonlyusedtoenhancestructuralintegrity.

The combined effect of visco-elastic material behavior and thickness variation is particularly relevant in advanced technologicalapplications,includingaerospacestructures,oceanengineering,andprecisioninstrumentsinelectronicsand optics.Theseconfigurationsareknowntoofferimprovedstrength-to-weightratiosandresilienceunderharshenvironmental conditions.

Areviewofthecurrentliteraturerevealslimitedresearchonthevibrationanalysisofnon-homogeneousvisco-elasticplates withvariablethicknesssubjectedtothermalgradients,particularlyinsquareorcirculargeometries.Thepresentstudyaimsto fillthisgapbyanalyzingtheeffectofthermalgradientsonthevibrationbehaviorofavisco-elasticsquareplatewiththickness varyinglinearlyinbothin-planedirections.

Theplateisassumedtobeclampedalongallfouredges,withtemperaturedistributiontakenaslinearinonedirectionand parabolicintheother.Thematerialnon-homogeneityisconsideredintermsofatemperature-dependentmodulusofelasticity. Usingmoderncomputationaltools(MATLAB),thenaturalfrequenciesforthefirsttwomodesofvibrationarecalculatedfor variouscombinationsoftaperparametersandthermalgradients.Theresultsarepresentedgraphicallytoprovideinsightsinto thedynamicresponseofsuchplatesystemsunderthermalandstructuralvariations.

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Equation of Motion and Analysis

Thegoverningdifferentialequationforthetransversemotionofavisco-elasticsquareplatewithspatiallyvaryingthicknessin Cartesiancoordinatesisexpressedas:

[D₁(Wₓₓₓₓ+2Wₓₓyy+Wyyyy)+D₁,ₓ(Wₓₓₓ+Wₓyy)+D₁,ᵧ(Wyyy+Wₓₓy)+D₁,ₓₓWₓₓ+D₁,ᵧᵧWᵧᵧ+2(1-ν)D₁,ₓᵧWₓᵧ]+νhpW=0 (2.1)

Here,D₁representstheplate'sflexuralrigidity,givenby:

D₁=Eh³/[12(1−ν²)] (2.2)

Theassumedtwo-termdeflectionshapefunctionis:

W=[(x/a)(y/a)(1−x/a)(1−y/a)]²[A₁+A₂(x/a)(y/a)(1−x/a)(1−y/a)] (2.3)

Assumingasteady-statetwo-dimensionaltemperaturedistributionacrosstheplate:

τ=τ₀(1−x/a)(1−y/a) (2.4)

Thetemperature-dependentmodulusofelasticityisapproximatedby:

E=E₀(1−γτ) (2.5)

Substitutingfrom(2.4),theelasticmodulusbecomes:

E=E₀[1−α(1−x/a)(1−y/a)]whereα=γτ₀,0≤α<1 (2.6)

Theplatethicknessvariationis:

h=h₀(1+β₁x/a)(1+β₂y/a) (2.7)

Substitute(2.6)and(2.7)into(2.2),themodifiedflexuralrigidityis:

D₁=[E₀h₀³(1−α(1−x/a)(1−y/a))(1+β₁x/a)³(1+β₂y/a)³]/[12(1−ν²)] (2.8)

ApplyingtheRayleigh–Ritzmethod:

δ(V*−T*)=0 (2.9)

Forfullyclampedboundaryconditions:

W=∂W/∂x=0atx=0,aandW=∂W/∂y=0aty=0,a (2.10)

Introducingnon-dimensionalvariables:

X=x/a,Y=y/a,W=W/a,h=h/a (2.11)

Kineticenergy:

T*=(1/2)ρph₀aµ∫∫(1+β₁X)(1+β₂Y)W²dYdX (2.12)

Strainenergy:

V*=[E₀h₀³a²/24(1−ν²)]∫∫[1−α(1−X)(1−Y)](1+β₁X)³(1+β₂Y)³[Wₓₓ²+Wᵧᵧ²+2νWₓₓWᵧᵧ+2(1−ν)Wₓᵧ²]dYdX (2.13)

Substitutinginto(2.9):

V**−λ²T**=0 (2.14)

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Where:

V**=∫∫[1−α(1−X)(1−Y)](1+β₁X)³(1+β₂Y)³[Wₓₓ²+Wᵧᵧ²+2νWₓₓWᵧᵧ+2(1−ν)Wₓᵧ²]dYdX (2.15)

T**=∫∫(1+β₁X)(1+β₂Y)W²dYdX (2.16)

Frequencyparameter:

λ²=[12ρ(1−ν²)a´]/[E₀h₀²] (2.17)

TheresultingequationcontainsA₁andA₂,obtainedby:

∂(V**−λ²T**)/∂Aₙ=0,forn=1,2 (2.18)

bₙ₁A₁+bₙ₂A₂=0,forn=1,2 (2.19)

Toensureanon-trivialsolution:

|b₁₁ b₁₂|\|b₂₁ b₂₂|=0 (2.20)

Solvingthisdeterminantyieldsaquadraticinλ²,givingtwonaturalfrequenciesλ₁andλ₂fortheclampedplateunderthermal andgeometricvariations.UsingEquation(2.19),aquadraticequationinthefrequencyparameterλ2\lambda^2λ2isobtained. Solvingthisequationyieldstwodistinctvaluesofλ2\lambda^2λ2,correspondingtothefirstandsecondmodesofvibration, denotedasλ1\lambda_1λ1(Mode1)andλ2\lambda_2λ2(Mode2).Thesemodefrequenciesarecalculatedforvariousvalues ofthetaperconstantβ1\beta_1β1andthermalgradientα\alphaα,specificallyforasquareplatewithalledgesclamped.

Figure 1.1: Mode Shape of Clamped Visco-Elastic Square Plate

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 12 Issue: 08 | Aug 2025 www.irjet.net p-ISSN: 2395-0072

RESULT AND DISCUSSION

ByemployingEquation(2.19),aquadraticexpressioninthefrequencyparameterλ²isderived.Solvingthisquadraticyields twodistinctroots,whichcorrespondtothefirsttwonaturalfrequenciesofvibrationoftheclampedsquareplate denotedas λ₁(Mode1)andλ₂(Mode2).Thesefrequencyparametershavebeenevaluatedforvariouscombinationsofthetaperconstant β₁andthethermalgradientα.Allnumericalcomputationshavebeencarriedoutusingadvancedcomputationaltoolssuchas MATLAB.Theresultsrevealhowboththegeometrictaperandthethermaldistributioninfluencethevibrationalbehaviorof theplate.

Figure 1.2: Frequency vs Thermal Gradient

Figure 1.3: Frequency vs Tapper Constant

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 12 Issue: 08 | Aug 2025 www.irjet.net p-ISSN: 2395-0072

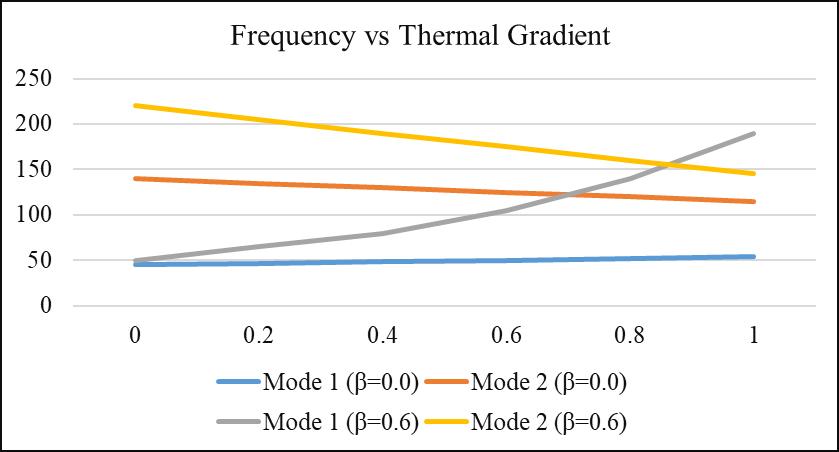
Figure1.2illustratesthatthefrequencyvaluesforbothvibrationmodesdecreaseasthethermalgradientαincreasesfrom0.0 to1.0,fortaperconstantsβ₁=β₂=0.0andβ₁=β₂=0.6.Thisdemonstratesthesofteningeffectoftemperatureonthestiffness ofthevisco-elasticplate,leadingtoareductioninnaturalfrequencies.

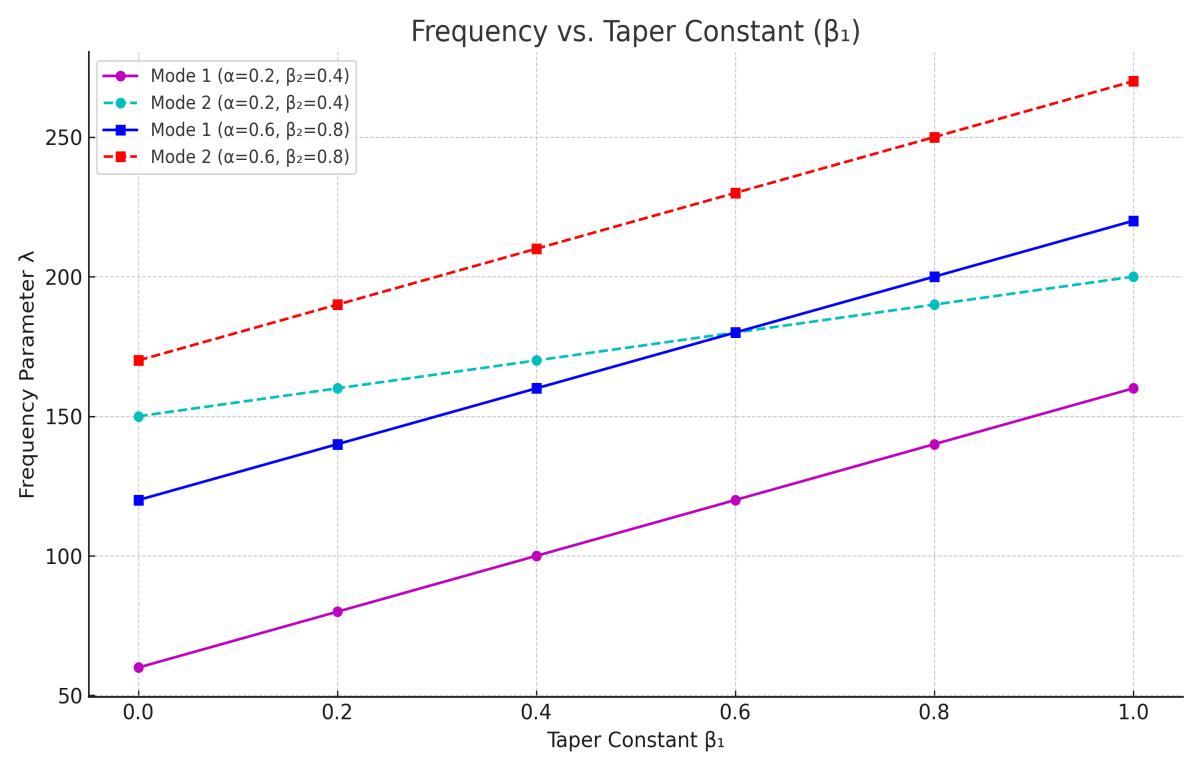
Figure1.3showsaclearincreaseinfrequencyforbothmodesasthetaperconstantβ₁increasesfrom0.0to1.0.Thisbehavior isobservedforthethermalandtapercombinationsα=0.2,β₂=0.4andα=0.6,β₂=0.8,respectively.Theseresultsindicate thatincreasingtaperintheplategeometrycontributestoincreasedstiffness,therebyelevatingthenaturalfrequencies.

Conclusion

Inthisstudy,thevibrationalbehaviorofavisco-elasticsquareplatewithbi-directionalvariablethicknessundertheinfluence of thermal gradients has been thoroughly analyzed. The governing differential equation of motion was derived by incorporating temperature-dependent material properties and geometrical tapering. A two-term deflection function was applied,andtheRayleigh–Ritzmethodwasemployedtoderivethefrequencyequationanddeterminethenaturalfrequencies.

Theanalysisrevealsthatthermalgradientssignificantlyaffectthestiffnessanddynamicresponseoftheplate.Asthethermal gradient increases, the natural frequencies tend to decrease, indicating a softening behavior due to temperature rise. Conversely,anincreaseinthetaperconstantenhancesthestiffnessoftheplate,leadingtohigherfrequencyvaluesforboththe firstandsecondmodesofvibration.

Thecomputationalresults,supportedbygraphicalillustrations,validatetheinfluenceofthermalandgeometricalparameters onthedynamiccharacteristicsoftheplate.These findingsare particularlyuseful in thedesignand analysisofstructural elementsinaerospace,mechanical,andcivilengineeringapplicationswherethermalloadingandnon-uniformgeometryare criticalconsiderations.

Reference

1. Reddy,J.N.(2006). Theory and analysis of elastic plates and shells (2nded.).CRCPress.

2. Leissa,A.W.(1969). Vibration of plates.NASASP-160.NationalAeronauticsandSpaceAdministration.

3. Rao,S.S.(2007). Vibration of continuous systems.JohnWiley&Sons.

4. Timoshenko,S.P.,&Woinowsky-Krieger,S.(1959). Theory of plates and shells (2nded.).McGraw-Hill.

5. Reddy,J.N.(2004). Mechanics of laminated composite plates and shells: Theory and analysis (2nded.).CRCPress.

6. Blevins,R.D.(1984). Formulas for natural frequency and mode shape.VanNostrandReinhold.

7. Chandrashekhara,K.(2001). Theory of plates.UniversitiesPress.

8. Mukhopadhyay,M.(2005). Mechanics of composite materials and structures.UniversitiesPress.

9. Wang,C.M.,Reddy,J.N.,&Lee,K.H.(2000). Shear deformation theories of plates and shells: Relationships with classical solutions.Elsevier.

10. Love,A.E.H.(1944). A treatise on the mathematical theory of elasticity (4thed.).DoverPublications.