Effect of Bar Diameter and Concrete Strength on GFRP RC Beam Capacity Using CSA Code-Based Analysis

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 12 Issue: 08 | August 2025 www.irjet.net p-ISSN: 2395-0072

Effect of Bar Diameter and Concrete Strength on GFRP RC Beam Capacity Using CSA Code-Based Analysis

Vallabha C D1 , Dr. Naveen R 2, Pavan3 , Veeshal Rathod V4

1PG Student (MTech) in Structural Engineering, Dr Ambedkar Institute of Technology, Bangalore, Karnataka, India

2Assistant Professor, Department of Civil Engineering, Dr Ambedkar Institute of Technology, Bangalore, Karnataka, India

3PG Student (MTech) in Structural Engineering, Dr Ambedkar Institute of Technology, Bangalore, Karnataka, India

4PG Student (MTech) in Structural Engineering, Dr Ambedkar Institute of Technology, Bangalore, Karnataka, India ***

Abstract – This paper presents a numerical investigation of the flexural behavior of a glass fiber reinforced beam by using CSA. A parametric analysis was performed by varying the GFRP bar diameter(8mm,10mm,12mm,16mm) with varying compressive strength(20MPa,40MPa,60MPa,80MPa).

The geometry of the beam was kept constant, with a width being 150 mm, 300mm, and the length of the beam is 2m. The CSA equations were used to get the load vs deflection curve, load vs crack width curve, and crack spacing for all the varying compositions of beams.

1. INTRODUCTION

The use of glass fiber–reinforced polymer (GFRP) bars in reinforced concrete structures has gained momentum in recent decades due to their non-corrosive nature, high tensilecapacity,andreducedself-weightcomparedtosteel reinforcement.TheseattributesmakeGFRPreinforcement an attractive option for structures exposed to severe environmentalconditions,suchascoastalregions,chemical processingfacilities,andinfrastructureexposedtode-icing salts. Unlike steel, GFRP remains unaffected by chlorideinduced corrosion, thereby extending the service life of structuresandreducingmaintenancedemands.Atthesame time, the lower modulus of elasticity and brittle failure characteristics of GFRP necessitate design methods that accountforitsuniquemechanicalbehaviour.

To address these requirements, the Canadian Standards Association introduced CSA S806, which provides specific design provisions for concrete members reinforced with fiber-reinforced polymer bars. The standard includes recommendations for both strength and serviceability checks,aswellasguidelinesforcrackwidthanddeflection control, enabling engineers to design GFRP-reinforced memberswithgreaterreliability.

The presentstudyfocusesona numerical investigation of the flexural response of GFRP-reinforced concrete beams usingCSAS806designprovisions.Aparametricanalysiswas performedbyvaryingreinforcementdiameters(8mm,10 mm,12mm,16mm)andconcretecompressivestrengths(20 MPa,40MPa,60MPa,and80MPa),whilekeepingthebeam

cross-section (150 mm × 300 mm) and span length (2 m) constant. The CSA-based analytical approach was used to generate load–deflection curves, load–crack width relationships, and crack spacing predictions for each configuration.Thefindingsaimtohighlighthowvariations in reinforcement size and concrete strength influence the overall flexural performance, offering insights that can support efficient and code-compliant design of GFRPreinforcedmembers.

2. LITERATURE REVIEW

Mohammedetal.(2024) [1]experimentallycompared reinforced concrete beams with traditional steel reinforcement and glass fiber–reinforced polymer (GFRP) bars under two-point loading. Their results showed that beamswithGFRPbarsexhibitedhigherdeflectionsandloadcarrying capacity compared to steel-reinforced beams, althoughthefirstcracksoccurredearlierandwerewiderin GFRP beams. The study also concluded that variations in concretecompressivestrengthhadminimalinfluenceonthe flexural properties,indicating that reinforcement typeand diameter are more significant parameters in determining beamperformance.

Belay et al. (2024) [2] tested small concrete beams reinforcedwithGFRP,BFRP,andconventionalsteelbarsto compareultimateloadcapacity,deflection,andfailuremode. They found that GFRP-reinforced specimens achieved the highestultimatecapacityamongthematerialsstudied,but bothtypesofFRPbarsproducedlargermidspandeflections than steel. Failure in FRP-reinforced beams tended to be governed by bending (with more deformation before collapse), whereas steel-reinforced beams failed more abruptly.Thestudyhighlightsthetrade-offbetweenhigher capacity and reduced stiffness for FRP reinforcement, suggesting designers must pay special attention to serviceability(deflectionandcrackcontrol)whenreplacing steelwithFRP.

Sagaya Bastina and Renganathan (2018) [3] investigatedtheflexuralperformanceofM30gradeconcrete beamsreinforcedwithGFRPbars.Fourbeamswerecast two with GFRP as main reinforcement and HYSD steel as

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 12 Issue: 08 | August 2025 www.irjet.net p-ISSN: 2395-0072

hanger bars, and two with GFRP used for both main and hangerreinforcement.TestingshowedthatGFRP-reinforced beamsexhibitedhigherductilitythantheirsteel-reinforced counterparts, along with benefits such as corrosion resistance, high tensile strength, and non-magnetic properties. Load–deflection analysis confirmed that GFRP reinforcement can achieve comparable or greater flexural strength than steel while reducing the risk of corrosionrelateddeterioration.

Goonewardena et al. (2020) [4]evaluatedtheflexural behaviorofGFRP-andCFRP-reinforcedgeopolymerconcrete beams by comparing predictions from four design approaches: ACI 440.1R-15, CSA S806-12, parabolic stress blocktheory,andequivalentrectangularstressblocktheory.

Experimentaltestingshowedthattheparabolicstressblock methodtendedtooverestimateflexuralcapacity,whileCSA S806-12 provided the most accurate and conservative predictions.Thestudy alsoanalyzed cracking,service,and ultimate moment capacities, along with deflection performance, confirming CSA S806-12 as a reliable design reference for FRP-reinforced beams in geopolymer applications.

Canadian Standards Association (2012) [5] “Design and Construction of Building Components with FibreReinforced Polymers”,whichprovidesdesignprovisionsfor FRP-reinforced and FRP-strengthened concrete members. The code includes equations for flexural capacity, shear strength, serviceability limits, and development length, calibrated for the unique properties of FRP materials, recognizingtheirlinear-elasticbehaviouruptofailureand lowermodulusofelasticitycomparedtosteel.

Bischoffetal.(2011) [6]proposedarationalmethodfor calculatingdeflectioninFRP-reinforcedconcretemembers, replacingBranson’sequation,whichoverestimatedstiffness for high Ig/Icr ratios. They introduced section-based and curvature-integration approaches, both applicable to steel andFRPreinforcementwithoutempiricalcorrectionfactors. Using 80% of the code-based cracking moment was recommended to account for shrinkage restraint, with validation against an extensive experimental database showingreliableandconservativepredictions.

3. Analytical Modelling Using CSA S806

Table -1: PropertiesofGFRPBars

TheaboveTable1showsthepropertiesoftheGFRPBar

The data were obtained from an Indian manufacturer of GFRPbars.Variationsofupto±5GPainYoung’smodulusand ±100MPaintensilestrengthmayoccurduetomanufacturing tolerances.Thesevalueshavebeen adoptedforthedesign calculationsbyCSA-S806.

Table -2: BeamTypeName/Designation

BarSize(mm) Compressive Strength BeamTypeName

8,10,12,16 20

8,10,12,16 40

8,10,12,16 60

8,10,12,16 80

8G20C,10G20C,12G20C,1 6G20C

8G40C,10G40C,12G40C,1 6G40C

8G60C,10G60C,12G60C,1 6G60C

8G80C,10G80C,12G80C,1 6G680C

Thebeamgeometryconsideredforanalyticalmodellinghas thefollowingdimensions:

Width=150mm

Depth=300mm

Length=2000mm

ShearSpan=450mm

Byusingthefollowingequationgivenbelow,usingCSAS806 code, the deflection, crack width, and crack spacing were calculated.

1.NotationsforCalculation

-Span(L),Shearspan(a)

-Beamwidth(b),Overalldepth(h),Effectivedepth(d)

-Concretecompressivestrength(f'_c)

-Modulusofelasticityofconcrete(E_c=4700×√f'c)

-ModulusofelasticityofFRP(Ef)

-AreaofGFRPreinforcement(A_f)/(A_s)

-Bardiameter(d_b),Concretecover(Cc)

2.ModularRatio

n=Ef/E_c (Eq.1)

3.NeutralAxisDepth(c)

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 12 Issue: 08 | August 2025 www.irjet.net p-ISSN: 2395-0072

The neutral axis depth is calculated by using the elastic transformed section and is used to calculate the cracked sectionmomentofinertia.

c=(√((n×A_s)×(n×A_s+2×b×d))−n×A_s)/b(Eq.2)

4.CrackedMomentofInertia(I_cr)

I_cr=(b×c³)/3+n×A_f×(d-c)² (Eq 3)

5.MomentatMidspan

M=(P×a)/2 (Eq.4)

6.Deflection

δ=(M×L²)/(8×E_c×I_cr) (Eq.5)

7.CrackWidth

Step1:f_fr=M/(A_f×j×d),wherej≈0.9 (Eq.6)

Step2:ε_f=ffr/Ef (Eq.7)

Step3:β_d=1-(ρf/ρ_fb),whereρ_f=A_f/(b×d)

(Eq.8)

Step4:ε_m=ε_f×(1-βd) (Eq.9)

Step5:z=d-c/3 (Eq.10)

Step6:w_cr=ε_m×z (Eq.11)

Where,

f_fr=stressinFRP

ε_f=straininFRP

β_d=bond-dependentcoefficient

ε_m=meanconcretestrain

z-distanceofextremecompressionfiber

w_cr-crackwidthinmm

8.CrackSpacing(CSAEmpiricalMethod)

Crackspacingcanbeestimatedusingtheempiricalformula:

S_cr=kg×Cc+kg×d_b/ρeff (Eq.12)

Where:

s_cr=crackspacing(mm)

kg = bond coefficient (often taken as 1.0 for sand-coated GFRP)

Cc=clearcovertoreinforcement(mm)

db=diameterofGFRPbar(mm)

ρ_eff=effectivereinforcementratio=A_f/(b×h_eff)

h_eff=2.5×d_b

4. RESULTS AND DISCUSSION

Figure 1 LoadVsDeflectionfor8mmGFRPBarBeam

2 LoadVsDeflectionCurve10mmGFRPBarBeam

FromFigures1,2,3,4,wecanobservethatasthediameterof the bar increases, the load carrying capacity of the beam increases[7].Asthebarsizeincreases,thedeflectionofthe beam reduces. As the compressive strength increases, the deflection values for the load also decrease. As the compressivestrengthincreasesforthesamediameterofbar inabeam,thedifferenceinthedecreaseofdeflectionalso decreases[8]

2025, IRJET | Impact Factor value: 8.315 | ISO 9001:2008 Certified

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 12 Issue: 08 | August 2025 www.irjet.net p-ISSN: 2395-0072

0.00.10.20.30.40.50.60.70.80.91.0

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 12 Issue: 08 | August 2025 www.irjet.net p-ISSN: 2395-0072

Figure5,6,7,8showthevariationofloadvscrackwidthfor all thebeamscalculatedby usingCSAS806code[5].From the graph, we can observe that as the diameter of the bar increases,crackwidthincreasesaccordingtothecalculation givenbythecode,buttheoppositehappensrealscenario, whereanincreaseinbardiametercausesadecreaseincrack width[9][10] An increase in compressive strength for the samediameterofbarinabeamdecreasesthecrackwidth,as indicatedbytheabovegraphs

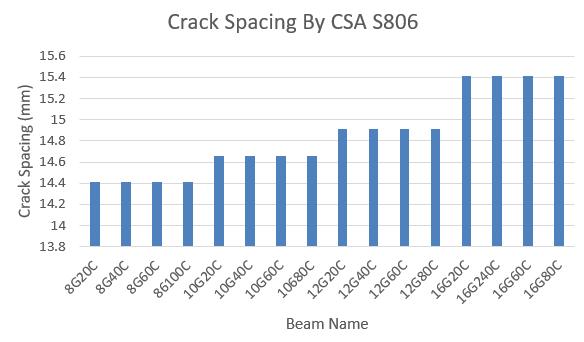
Figure 9 CrackingSpacing

Figure9showsthecrackspacingcalculatedusingCSAS806 code,whichindicatesthatcrackspacingincreaseswithan increaseinthediameterofthebar[10]

3. CONCLUSIONS

The CSA S806 code-based analytical investigation demonstrated that both reinforcement diameter and concrete compressive strength significantly influence the flexuralperformanceofGFRP-reinforcedconcretebeams.An increase in GFRP bar diameter resulted in higher loadcarrying capacity and reduced deflection, indicating improvedstiffness.Similarly,higherconcretecompressive strength decreased beam deflections for a given load; however,itsinfluencediminishedasbardiameterincreased.

Crack width predictions from CSA S806 showed an increasing trend with bar diameter, which contrasts with experimental observations where larger bar diameters typically reduce crack widths. Nevertheless, the analytical resultsconfirmedthathigherconcretestrengthsconsistently reduce crack widths for all bar sizes. Crack spacing calculationsfollowedtheexpectedpatternasperCSAS806 empiricalexpressions.

Overall,thestudyreaffirmsthatoptimalselectionofGFRP bardiameterandconcretestrengthcanleadtoserviceable andhigh-capacitystructuralmembers.TheCSAS806design approachprovidesa conservativeand reliableframework for predicting deflection, crack width, and crack spacing, thereby supporting safe and durable design of GFRPreinforcedbeamsforpracticalapplications.

REFERENCES

[1] Mohammed AD, Salih OA. An Experimental Study on Reinforced Concrete Beams with GFRP and Ordinary Steel Bars’ Flexural Strength Properties. Civil and EnvironmentalEngineering.2025Jun1;

[2] Belay AA, Krassowska J, Kosior-Kazberuk M. Comparative Performance Analysis of Small Concrete Beams Reinforced with Steel Bars and Non-Metallic Reinforcements.AppliedSciences(Switzerland).2024 May1;14(10).

[3] SagayaBastinaA,RenganathanM.FlexuralBehaviourof Concrete Beams with Glass Fiber Reinforced Polymer Rods[Internet].Availablefrom:www.ijert.org

[4] Goonewardena J, Ghabraie K, Subhani M. Flexural performance of FRP-reinforced geopolymer concrete beam.JournalofCompositesScience.2020;4(4).

[5] CanadianStandardsAssociation.CSAS806-12:Design and construction of building components with fibrereinforced polymers. Mississauga, Ontario, Canada; 2012.

[6] BischoffPH,GrossSP.DesignApproachforCalculating Deflection of FRP-Reinforced Concrete. Journal of CompositesforConstruction.2011Aug;15(4):490–9.

[7] Ahmad H, Elnemr A, Ali N, Hussain Q, Chaiyasarn K, Joyklad P. Finite element analysis of glass fiberreinforced polymer-(Gfrp) reinforced continuous concretebeams.Polymers(Basel).2021Dec1;13(24).

[8] MoawadMS,FawziA.Performanceofconcretebeams partially/fullyreinforcedwithglassfiberpolymerbars. Journal ofEngineeringand Applied Science.2021Dec 1;68(1).

[9] Ascione L, Mancusi G, Spadea S. Flexural behaviour of concretebeamsreinforcedwithGFRPbars.Strain.2010 Oct;46(5):460–9.

[10] Kara IF, Ashour AF. Flexural performance of FRP reinforced concrete beams. Compos Struct. 2012 Apr;94(5):1616–25.