Design of Cyclorotor Propeller with Out runner Ring gear Mechanism

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 12 Issue: 06 | Jun 2025 www.irjet.net p-ISSN: 2395-0072

Design of Cyclorotor Propeller with Out runner Ring gear Mechanism

Amit Patil1 , Siddhesh Pawar1 , Priyanshu Randive1, Prashil Rangari1, Sushank Sisodiya2 ,

Dr. Priya Gajjal

3

1Undergraduate Student, AISSMS College of Engineering, Pune-01, Maharashtra, India.

2Graduate Student,

3Professor, Dept. of Mechanical Engineering, AISSMS college of Engineering Pune-01, Maharashtra, India

Abstract - This abstract introduces a novel design methodology for cyclorotor propellers, focusing on the integration of an innovative outrunner ring gear mechanism. Traditional cyclorotor designs often face challenges relatedtothe complexity, weight, andefficiency of theirinternalbladepitchingandpowertransmissionsystems. This proposed design process specifically addresses these limitations by leveraging an outrunner configuration where the ring gear, typically an internal component, acts as the primary rotating element, encapsulating the blade pitching kinematics. This unique approach simplifies the mechanical linkage, potentially reducing overall mass and enhancing structural integrity. The methodology emphasizes a holistic design approach, coupling aerodynamic performance optimization with the mechanical integration of the outrunner ring gear to achieve superior thrust vectoring capabilities, improved power-to-thrust ratios, and enhanced control authority across diverse operational envelopes. The development of this new design process aims to significantly advance cyclorotor technology, paving the way for more compact, efficient, and reliable propulsion systems in various aerospace and maritime applications.

KeyWords: cyclorotorpropellers,outrunner,ringgear, Aerodynamic,performance,optimization

1.INTRODUCTION

Cyclorotorpropellersstandapartasexceptionallyversatile propulsiondevices,fundamentallygeneratingthrustthrough anarrayofbladesthatrotatearoundacentralaxis,oriented parallel to it. What makes them truly remarkable is their abilitytocyclicallyvarythepitchangleoftheseindividual bladesastheyrevolve,enablinginstantaneous360°thrust vectoring.Thisunparalleledcapabilityprovidesexceptional maneuverability, allowing for precise control and rapid changes in direction, which is critical for applications like high-performancedrones,urbanairmobilityvehicles,and agile marine vessels. Furthermore, their inherent design oftenresultsinsignificantlylowernoiseemissionscompared to conventional propellers, making them ideal for urban environments or stealth applications. Traditionally, the complex mechanical linkages required for both power transmissionandpreciseblade

pitchcontrolhasposedsignificantengineeringchallenges, often leading to increased weight and mechanical complexity. This innovative design concept directly addressesthesehurdlesbyintegratinganoutrunnerrotor mechanism,wheretheentireouterrotatingstructureofthe cyclorotor becomes the primary moving component. This outerstructureisintegralwith,ordirectlydrivenby,alarge ringgear,whichthenefficientlytransferspoweranddirectly housesoractuatestheintricatebladepitchingkinematics. This revolutionary approach profoundly simplifies the mechanicalpowertransmissionandbladecontrolsystems compared to traditional internal drives, leading to a substantial reduction in overall weight and a marked increase in efficiency due to fewer moving parts and minimizedfriction.Theresultisamorerobust,compact,and reliablepropulsionunit,poisedtounlockthefullpotentialof cyclorotor technology for a new generation of advanced aerial and marine applications demanding unparalleled agilityandperformance.

1.1

Problem Statement

The Problem statement of this paper is to provide a methodtodesignoutrunnerbasedcyclorotormechanismfor industrial, Aerospace or in marine sciences or any field requiringsmallmodularcyclorotorpropellers.

1.2 METHODOLOGY

The process of designing a cyclorotor consists of three mainfields,AerodynamicsandKinematics.So,inthispaper wewilltrytosolvethosesameandderiveothermathematic required.Inthispaperwewillnotdiscussaboutdynamics andvibrations.

2. CALCULATION

Thefollowingcalculationiswilltellusaboutdimensionsand other important information required for designing a outrunner-linkcyclorotorpropellermechanismusingring gear.

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 12 Issue: 06 | Jun 2025 www.irjet.net p-ISSN: 2395-0072

2.1 KINEMATICS

We choose to design wing and airfoil for rotating at 2000RPM,and45degpitchangleand4-wingedpropeller.So beforedesigningandchoosingairfoil,wefirstcreated4-bar linkageusingLinkage3.4open-sourcesoftware.wederived velocityofbothmovingjoints.Asthemainlinkvelocitydoes not change with respect to time, and only the velocity of secondary link changes, we choose to create a outrunner mechanismwhichwilleliminatetheneedtocreateacentral hubpoweredmechanism

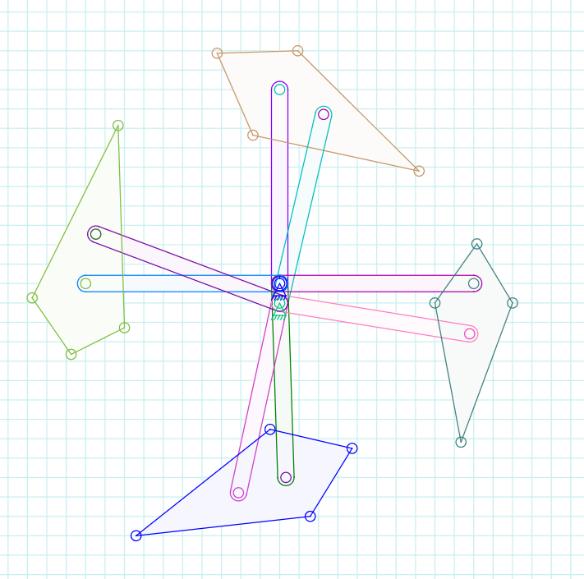
-1:4-barlinkagewith4airfoils

Themainlinkandsecondarylinklengthis28.5mm,while intermediate/connecting link (Airfoil) length is 8mm. The eccentricity between both anchors, main and supportive anchors, is 5.3mm. The following design was chosen accordingtostandardmaterialavailabilityinthemarketand FOS of kinematic interference between objects during designinginCAD.

Wealsofoundspeedvscoordinatedataforbothjoints,here asconnectorBandconnectorHinthefollowingdata.The data was directly exported as CSV file from Linkage3.4 software.

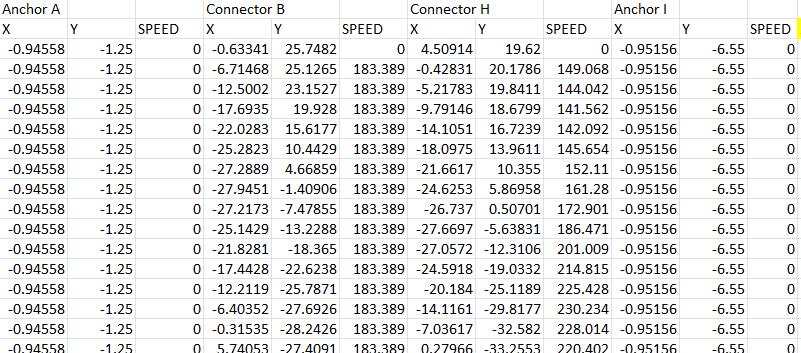
Chart -1:CSVdataofspeedvscoordinateofconnectors.

Thefollowingdata iscalculatedfor65RPM,sotocalculate linear velocity for 2000RPM or 4500RPM, we can simply divide the whole data with 65 and multiply with required RPM.WecreatedagraphtovisualizespeedvsX-coordinate and speed vs Y- coordinate and X-Y coordinate, to trace movementsofbothjointsusingDESMOSGraphingCalculator.

We used Arctan of (Speed, X-coordinate) and Arctan of (Speed,Y-coordinate)andplotteditagainstXaxis.Thisgave usthefollowinggraphs.Thegraphsgaveusindicationoflow changesinspeed,whichinturnindicateslessacceleration. Though,theaccelerationathigherRPM,willstillaffect,but ourfollowingresearchisfor 2000RPM

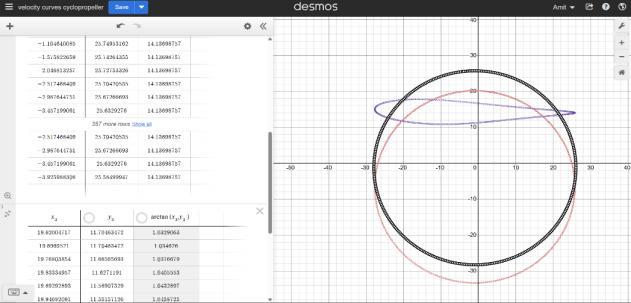
-2:SpeedofconnectorvsYcoordinate

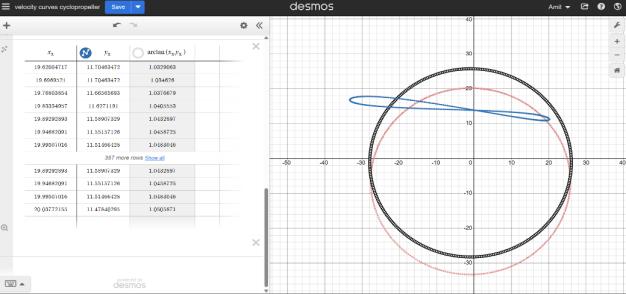
-3:SpeedofconnectorvsXcoordinate

AftercompletingourKinematics,wedesignedtheoutrunner link. We decided to create a single-stage internal-external gear train. We calculated the minimum bore radius for internalspurgear,withaccordingtoourmotor.Themotor weusedisA221212V1400KVBLDCmotor.WeChoosethe motorwithrespecttoCost,Marketavailability,specifications (RPM,Powerrequirement),andasitwaseasytostartwith.

After, calculating bore radius, as we needed 2000 RPM speed, we chose to have RPM FOS of 4 So, the maximum rated RPM of the motor is 16,800 RPM on No load. We choosea Gear ratio of 2:1 (RPM=8400).Thereasonofearly highFOSis,thecyclorotorpropellerhashigherloadcapacity ofairfoils,thatis,itcancreatehigherliftsatlowerRPM.This meanshighercurrentconsumptionbymotor.Aswecannot exceed the amperage more than 30Amps, else the motor controllerwillbedamaged.WedecidedtokeephigherGear ratio

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 12 Issue: 06 | Jun 2025 www.irjet.net p-ISSN: 2395-0072

The module is 1.5 and number of teeth on internal spur gearis 15,whileonexternalringgearis 30.Otherdatacan beseeninthefollowingtables.

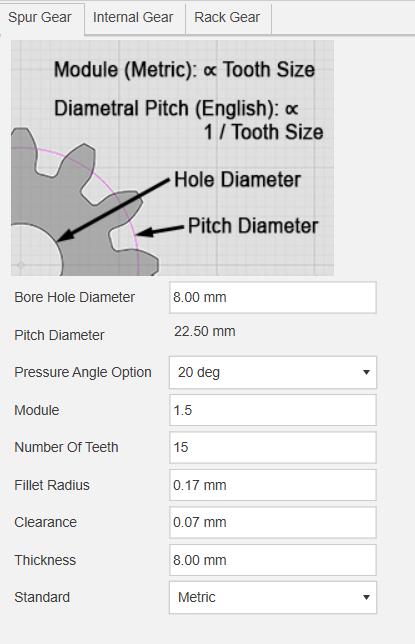
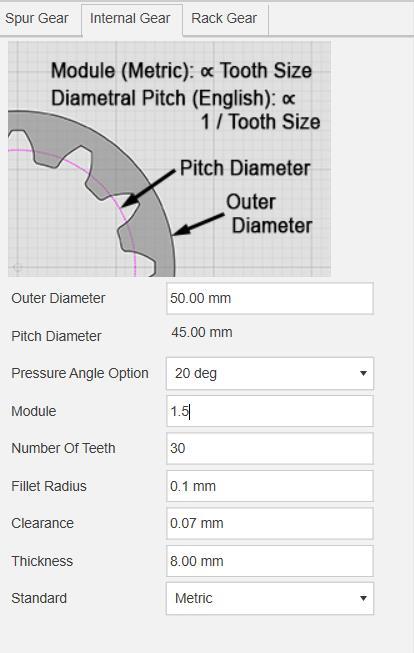
-4:FMGearlibraryinFusion360Studentversion

Fig -5:CADmodelofSpurgearandRinggear.

Wedecidedtouse3mmStainlessSteel(SS)threadedrodsas oursupportshafts,fortheremarketavailability,anddesign constrainsofavailablespaceandmotioninterference.

ForGearsandotherbodyparts,forprototyping,wedecided tousePLAPlastic(Poly-LacticAcid)whichisaeco-friendly prototypingmaterial

2.2. AERODYNAMICS

AfterBasic2DCADprofileready,wedecidedtostartwith aerodynamicsstudies.Initially,UsingGeometry,weplotted4 wings, and solved interference between wings. Then we decidedthecordlengthtobe 30mm

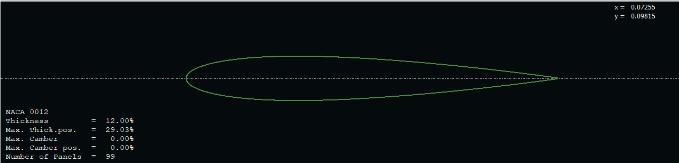
Fig -6:NACA-0012(up)andNACA-2430(down)Profile

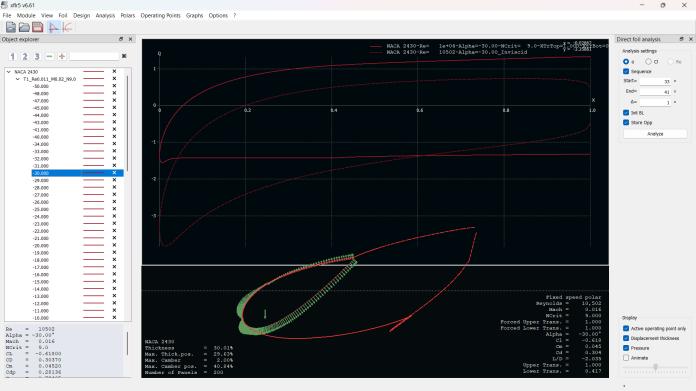
At first, we decided to use NACA0012, but due to design constrains, we opted for NACA2430. Though both have different characteristic, we found that, at lower RPM and lower Reynold’s number NACA2430 for better at higher pitchanglessuchas45degusing XFLR5 opensource airfoil and aircraft analysis software software.

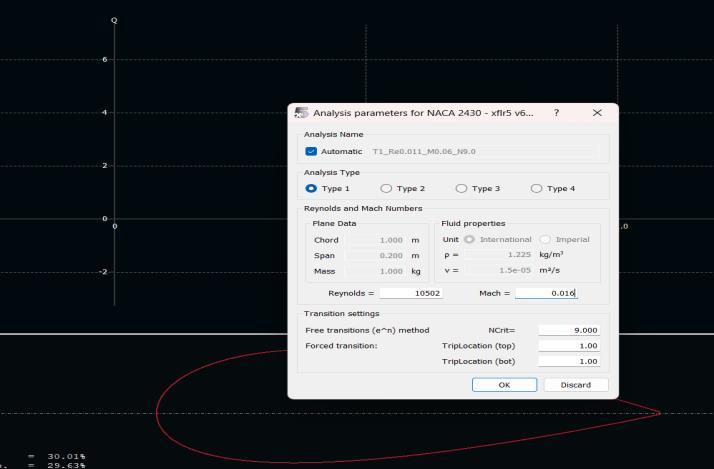
Thenweplotted CL (Coefficient of lift) and CD (Coefficient of Drag) for NACA2430 usingXFLR5

The Reynold’s number was calculated from the following formula.(formula)

Re = (ρ * V * L) / μ

ρ:(rho)isthedensityofthefluid(kg/m³).

V:isthevelocityofthefluid(m/s).

L:is a characteristic length scale (e.g., the cord length of airfoil)(m).

μ:(mu)isthedynamicviscosityofthefluid(Pa·s).

TheReynold’snumberis 10,502.Thefluidvelocityistaken tobe 5.5 m/s whichwefoundfromRPMofthemotorwhich is 2000RPM.

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 12 Issue: 06 | Jun 2025 www.irjet.net p-ISSN: 2395-0072

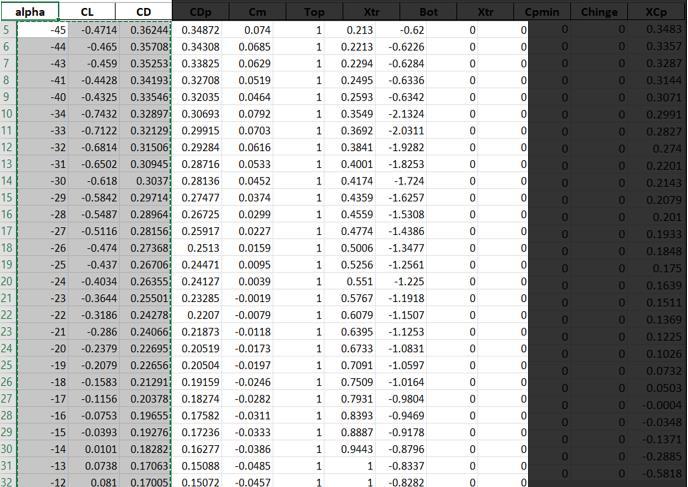
We plotted CL and CD of airfoil from positive 50deg, to negative 50 deg. Then we calculated Lift and Drag Forces usingCoefficientofLiftandDragthebelowexpression.

Lift Force = 0.5 * ρ * V² * S * Cl

where:



Liftistheliftforcegeneratedbythewing.

 ρ istheairdensity.

 V isthevelocityoftheair.

 S isthereferencearea(wingarea).

 Cl istheliftcoefficient.

Drag Force = 0.5 * ρ * S * V^2 * Cd, where:

 Fd:isthedragforce(inNewtons).

 ρ isthedensityofthefluid(inkg/m³).

 S isthereferenceareaoftheobject(inm²).

 V isthevelocityoftheobject(inm/s).

 Cd isthedragcoefficient(dimensionless).

Nowasweknow,asweknowtheairfoiltravelwillbefrom45degto+45degforthehalfrevolutionandCoefficientoflift isalwaysnormaltoairfoil.Astheairfoiltravelsfromθequal to0°to90°aroundthepivotjointofmainanchor,itwillalso rotateinternallyaroundjointBfor45°.Initiallyattheta,the angleofattack(θ),willbe45°,andtheanchorreachesφ= 90°,theθwillreach0°.(calculationofclandcdofliftand dragcoefficientofwings).Thebelowdataisforφ[-90,+90)

So,asthewingrotatesinitsprofile,thedragandliftvectors willrotateperpendiculartothelocusofrotation.So,wewill calculate lift and drag affecting the whole propeller, by projectingthevectorsinthepropeller’sreferenceplane.We computedthedatausingDESMOSgraphingcalculator.Our calculationscomparetotheabovefigurehaveachangeas our φ will be 0° at the 90°, therefore the phi in below calculationisφ’=φ+90.

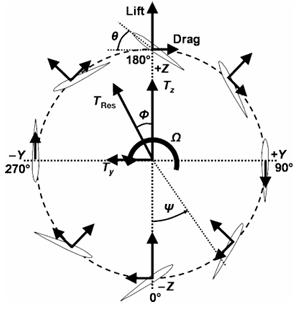
Fig -10:LiftandDragprofileonrotatingairfoil

1) Lift and Drag coefficient for Projection of Lift coefficient generated by one wing.

 CL1 = Cl * sin(φ’) = Cl * sin(2θ)

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 12 Issue: 06 | Jun 2025 www.irjet.net p-ISSN: 2395-0072

where:

CL1 isCoefficientofLiftofwinginprojectionofZ axis,asshowinthefigure.

Cl isCoefficientofLiftonnormalofwinglocus.

Θ istheangleofattackofthewing.

φ’ =Angleofanchor



Where:

CD1 = Cl * cos(φ’) *(θ /| θ |)

Cl isCoefficientofLiftonnormalofwinglocus.

Θ istheangleofattackofthewing.

φ’ =Angleofanchor.

CD1 iscoefficientofDragofwinginprojectionofz axis,asshowninfigure.

2) Lift and Force Projection of Drag induced by one wing.



where:

CL2 = - Cd * cos(φ’) &for2nd halfCd * cos(φ’)

CL2 isCoefficientofLiftofwinginprojectionofZ axis,asshowinthefigure.

Cl isCoefficientofLiftonnormalofwinglocus.

Θ istheangleofattackofthewing.



Where:

CD2= Cd * sin(φ’) &for2nd half- Cd * cos(φ’)

CD isthecoefficientofdragofwinginprojectionof Zaxis,asshowinthefigure.

Cl isCoefficientofLiftonnormalofwinglocus.

Θ istheangleofattackofthewing.

Now,Additionof CL1 and CL2 willgiveusthe overall Lift coefficient onpropeller,andadditionof CD1 and CD2 will give us overall drag coefficient on propeller by one wing whichwillbe 0 asallthevectorscanceleachotherout.We thendivideitwithnumberofsampleswetook.Thismethod willonlyworkonsymmetricangleofattackwithmirrorplane being Y axis here following above figure. Following is the computationonDESMOSfor2000RPMandsamplesizeof

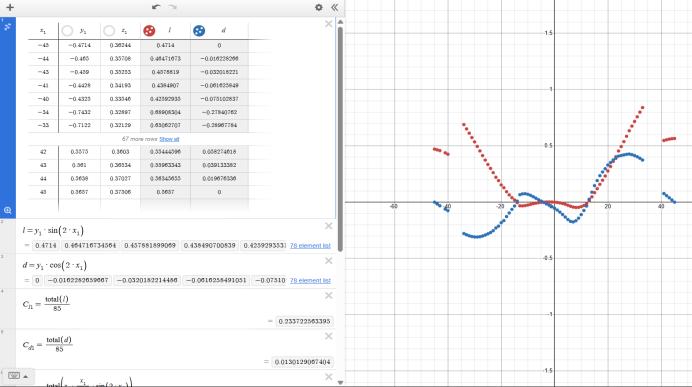
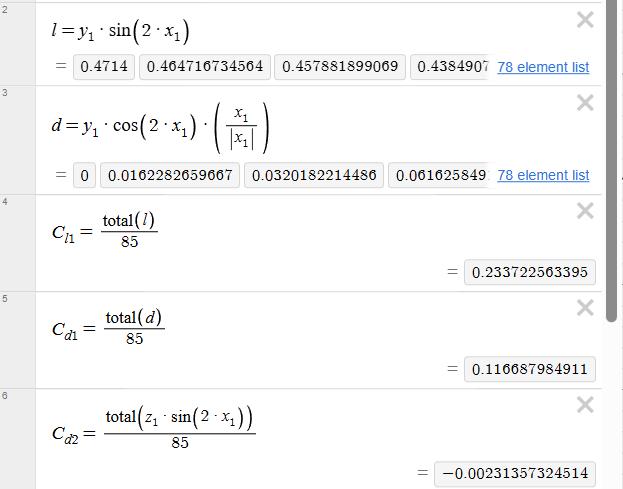
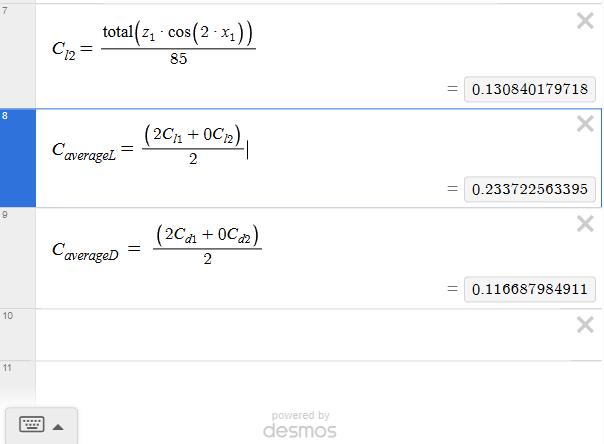
Therefore,forthewhole180°θ,wegetuniform(α)values from-50°to50°.SousingthedatawederivedfromXFLR5, asthedataofliftanddragwasnormaltothemainlinklocus, we calculated the actual lift and drag using following expressions.WesummedallthethecoefficientsCl1andCl2, andCd1andCd2,anddividedthemby85astherewere85 rowsintotal.ThisgaveustheaverageCoefficientofLiftand Drag.Thecalculationsaregivenbelow.

At2000RPMweget0.02029Nor2gthrustfromonewing. So,with4wings,thethrustwillbearound 8g.Weneedto calculate RPM required to reach 200gm thrust. Now we estimatedweightofonerotorto bearoundlessthan200, with all parts included. So, the below calculations tell us minimum RPM required for the hovering. Assuming CoefficientofLiftdoesn’tchangebyalot;

Lift = 0.5 * ρ * V² * S * CL

Lift =200g/4=50g;

ρ:1.164(densityofairat30°C)

International Research

Volume: 12 Issue: 06 | Jun 2025 www.irjet.net

S:3990mm^2(Areaofwing/airfoil) CL:0.2337;

So dividing 200g by 4, we get 50gm. One wing needs to create50gmofthrust.WithsameCL,weneedaround29.3 m/s wind speed ,9817 RPM, more than limit of our rotor speed. We will validate it with same calculation above for differentReynold’snumber,takingRPMat 4500. Thelinear velocity at 4500 RPM is 13.43 and Reynold’s number is 25,645.

At 4500 RPM,weget 10gm of thrust,whichisnotenough forourrequirementofhovering,butisenoughforpushinga body.Thisthrustforcecanbeusedwithwingstocreatelift aswecannotreallyachieveRPMhigherthan5000assuming itmaydamagethemotor.NowweupdatedourRPMto4500 asourmaxRPMtotest. The drag will be zero,werealized afterwards,astheoverallvectorprojectionofdraginliftand dragofairfoilcancelsout,exceptioninasymmetricairfoil.

@ 4500 RPM; CL = 0.25531 and CD = 0;

AfterthedeterminationofRPM,Lift,velocitiesatconnectors, weconductedstressanalysisonShafts,wingsandsecondary links,therearemanymorestressesyettobecalculated,so weskippeditinthispaper.Atthispoint,wehaddesigned ourwholeCADmodel.

2.3. DESIGN AND CAD

Ourdesignisbulkybecauseoflessweightoptimization.Our aimwastocreateastandardforoutrunner-linkcyclorotor propeller.

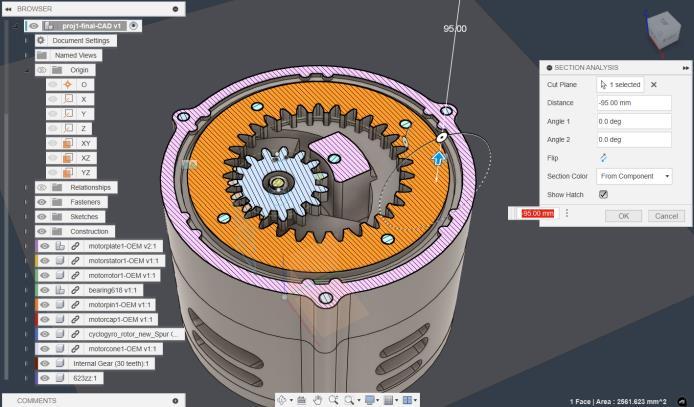
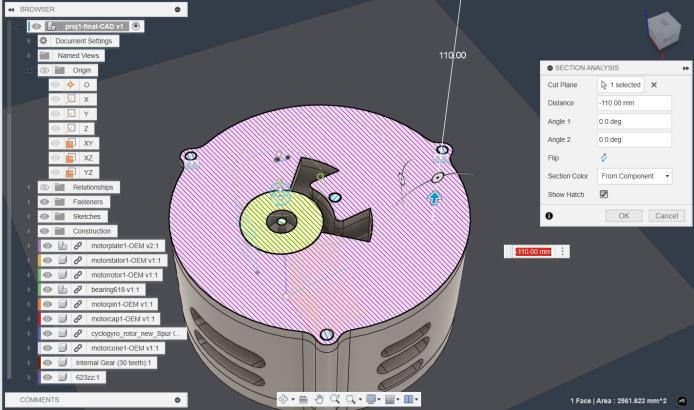
To reduce Load on motor, as the forces are radial and tangentialunlikenormalpropellers,wheretheyareaxial,we addedabearinglayer,tosupportrotorload.Also,thiswill increase the motor efficiency as the tilted motor shaft increasescurrentconsumption.

3. CONCLUSIONS

This research paper has presented a compelling novel design methodology for cyclorotor propellers, specifically integratinganinnovativeoutrunnerringgearmechanism,to fundamentally address the persistent challenges of mechanical complexity, excessive weight, and suboptimal efficiencyinherentintraditionalcyclorotorconfigurations. Byreimaginingthepowertransmissionandbladepitching kinematics within an outrunner architecture, where the primaryrotatingstructureitselfembodiestheringgear,we demonstrated a pathway to significantly streamline the mechanicaldesign.

REFERENCES

[1] M Benedict,“Performanceofacycloidalrotorconcept formicroairvehicleapplications”,April2010,Journalof theAmericanHelicopterSociety55(2):22002-1-2200214,DOI:10.4050/JAHS.55.022002

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

[2] J Páscoa,A Dumas“Anovellookattheperformanceof the cyclorotor propulsion system for air vehicles”, November2012,DOI:10.1115/IMECE2012-85544

[3] M. Benedict, Z. Adams, I. Chopra, “Design and DevelopmentofaSmall-ScaleCyclogyroUAVUtilizinga Novel Cam-BasedPassiveBladePitchingMechanism”, June 2013, International Journal of Micro Air Vehicles5(2):145-162, DOI:10.1260/17568293.5.2.145

Volume: 12 Issue: 06 | Jun 2025 www.irjet.net p-ISSN: 2395-0072 © 2025, IRJET | Impact Factor value: 8.315 | ISO 9001:2008