
Albino
Giorgio Baldisseri
Cristiano Crosera



Albino
Giorgio Baldisseri
Cristiano Crosera

Tecnologie e tecniche di rappresentazione grafica
OFFICINA
TECNOLOGIA
INTELLIGENZA
VIDEOTUTORIAL



























Gruppo
offre proposte editoriali che coprono tutti i gradi e i rami scolastici, all’insegna della qualità, del rigore e dell’innovazione.
Intelligenza Artificiale IA
Percorsi didattici con attività pratiche che mirano ad approfondire i principali strumenti di IA generativa per favorirne un utilizzo consapevole e un tool a disposizione dei docenti per personalizzare l’attività didattica.
Progetto di ricerca costante che mira a eliminare gli stereotipi di genere nei testi scolastici ponendo particolare attenzione alla scelta dei contenuti, a una valutazione iconografica ragionata e all’utilizzo di un linguaggio testuale inclusivo.

Sviluppo di una cultura dell’inclusione attraverso contenuti accessibili e adeguati ai diversi stili di apprendimento.
Approccio educativo e formativo volto a favorire la conoscenza di sé, delle proprie attitudini e delle proprie capacità, oltre a sviluppare le competenze non cognitive e trasversali necessarie per le scelte del futuro.
CIVICA secondo le NUOVE Linee guida
Aggiornamento e ampliamento dei nuclei tematici attorno ai quali si articolano le competenze e gli obiettivi di apprendimento: Costituzione, Sviluppo economico e sostenibilità, Cittadinanza digitale.

Attivazione del pensiero scientifico e computazionale, approccio interdisciplinare e laboratoriale, sviluppo della competenza multilinguistica, attraverso attività STEM, STEAM e CLIL.
Acquisizione delle competenze digitali e dell’alfabetizzazione informatica come aiuto all’inclusione sociale e alla cittadinanza attiva.
Percorsi incentrati sullo sviluppo di competenze relazionali che arricchiscono la consapevolezza del vissuto personale in relazione con la realtà circostante.
Gruppo Editoriale
ELi
TECNOGRAFICA è un corso realizzato secondo e indicazioni della didattica per competenze e della didattica inclusiva. Favorisce l’acquisizione graduale delle competenze richieste in disegno e tecnologia.





















Un percorso completo e articolato per la costruzione delle competenze





Tecnologie e tecniche di rappresentazione grafica seconda edizione













In apertura di sezione, le innovazioni e le eccellenze di Officina Italia sono argomenti di riflessione sulle realtà tecnico-scientifiche che ci circondano e sono uno stimolo per pensare al futuro mondo del lavoro.









pagine successive sono proposte assonometrie di solidi su cui indicare, come primo passo e mediante una freccia, la posizione dell’osservatore. Conseguenza di questa scelta sono le direzione dei raggi proiettanti e quindi le proiezioni sui tre piani. Normalmente la freccia viene posizionata come indicato nel caso A ➜ Fig. 17) in modo da avere in vista tre lati del solido interessati dalle successive proiezioni. Così facendo si definisce la posizione del triedro di riferimento cioè dei tre piani P.V., P.O. e P.L. ➜ Fig. 18a) con le direzioni, indicate dalle tre frecce, da cui si guarda per ottenere le relative proiezioni ortogonali ➜ Fig. 18b). La posizione dei piani tra loro, e quindi delle viste, è rigida pertanto se si decide di posizionare l’osservatore come nel caso B (➜ Fig. 19), l’orientamento del triedro di riferimento cambia ➜ Fig. 20a). Il risultato è che le proiezioni si ottengono sul P.V e sul P.O. da lati del solido in vista, mentre sul P.L., vista da sinistra, guardando il solido da un lato non in vista, come indicato dalla freccia ➜ Fig. 20a). Le proiezioni che otteniamo sono diverse dalle precedenti (➜







































nell’esporre gli argomenti con l’uso dell’assonometria, si dà per scontato che la posizione dell’osservatore sia quella A cioè come in ➜ Fig. 17 7.5.2 INDICAZIONI SULLA SEQUENZA DELLA COSTRUZIONE Collocato l’oggetto nel triedro e fissata la posizione dell’osservatore, di



























Proposta didattica a “doppio registro”







La spiegazione scritta è affiancata dalla corrispondente risoluzione grafica, indispensabile strumento per imparare a leggere gli elaborati. L’utilizzo di tre colori guida nei segni, nero, rosso e azzurro, permette di evidenziare al meglio le tre diverse fasi nella costruzione

1.1














4.6 Costruzioni di circonferenze, tangenti e raccordi

4.7 Le curve policentriche e le curve cicliche 70
4.8 Costruzioni di curve policentriche e
4.9
4.10
4.11
4.12









6.1
6.3 Assonometria isometrica
6.4
6.5
6.6 Proiezioni assonometriche a mano libera





5.1 I principali solidi geometrici 98
5.2 Metodi di rappresentazione grafica: le proiezioni 100
5.3 Proiezioni ortogonali: introduzione 101
5.4 Triedro di riferimento e sua rappresentazione sul piano Video focus 102

5.5 Convenzioni per la rappresentazione grafica Video tutorial

5.6 Proiezioni ortogonali di elementi geometrici

5.7 Proiezioni ortogonali di solidi geometrici


• Rappresentazione assonometrica di una libreria
• Rappresentazione assonometrica di una scala 169


3D 104
107
112
5.8 Approfondimenti sulle proiezioni ortogonali

119



7.5 Sezione di cono • 1 Video tutorial 182

7.6 Sezione di cono • 2 184
7.7 Sezione di cono • 3 186
7.8 Sezioni di sfera 187

VERIFICA LE CONOSCENZE Test interattivi 188
SVILUPPA LE ABILITÀ 189
COSTRUISCI LE COMPETENZE 191 RECUPERO Video tutorial Video 3D 192

8.1 Introduzione e tavola riassuntiva Video focus

8.2 Compenetrazioni tra solidi con superfici piane Video 3D 196
8.3 Compenetrazioni tra solidi con facce piane e curve Video 3D 200
8.4 Compenetrazioni tra solidi con superfici curve Video tutorial Video 3D 204

VERIFICA LE CONOSCENZE Test interattivi 206


SVILUPPA LE ABILITÀ Video tutorial 207 COSTRUISCI

CAPITOLO
9.1 Introduzione Video tutorial 212

9.2 Sviluppo dei principali solidi geometrici 213
9.3 Sviluppo di tronchi di solidi 215
9.4 Sviluppo di compenetrazioni tra solidi Video 3D 218
9.5 Sviluppo di tubature cilindriche TECNOLAB Video 3D 220

VERIFICA LE CONOSCENZE Test interattivi 226

SVILUPPA LE ABILITÀ Video tutorial


COMPITO DI REALTÀ • Costruzione di un modello di una cappa con condotto 231




Principi generali di rappresentazione
10.1 Il segno
10.2 Esempi di applicazione delle diverse tipologie di linee
10.3 Convenzioni sulle rappresentazioni UNI ISO 128-30:2006 Video focus

10.4 Convenzioni particolari di rappresentazione UNI 128-34:2006 238

Convenzioni fondamentali per tagli e sezioni
11.1 Introduzione Video tutorial

11.2 Termini, definizioni e regole generali
11.3 La rappresentazione delle parti sezionate
Casi particolari
Tavola degli errori più diffusi
CAPITOLO 14


CAPITOLO 12
Quotature: criteri di indicazione delle quote UNI EN ISO 129-1:2021
12.1 Introduzione
12.2 Elementi di una quota
12.3 Quote funzionali, non funzionali e ausiliarie
12.4 Sistemi di quotatura
12.5 Convenzioni particolari di quotatura
12.6 Quotatura della conicità
12.7 Quotatura della rastremazione
12.8 Quotatura dell’inclinazione
12.9 Rappresentazione e quotatura delle filettature
12.10 Designazione e quotatura delle parti filettate
12.11 Tavola degli errori più diffusi


Fasi





CAPITOLO 15


16
16.6 L’APE e la progettazione 327
16.7 Due modelli di economia 328
18.3 Le principali caratteristiche dei materiali 357 18.4 Proprietà chimico-strutturali 358

VERIFICA LE CONOSCENZE Test interattivi 331


18.5 Proprietà fisiche 361
18.6 Proprietà meccaniche 365


CAPITOLO 17
Indicazioni sulla sicurezza della persona e dei luoghi di lavoro
17.1 Quadro normativo: sicurezza e salute 334
17.2 Segnaletica di sicurezza e di salute sul luogo di lavoro 337
17.3 Malattie professionali 339
17.4 Dispositivi di protezione individuale (DPI) 339
17.5 Locali di lavoro e loro caratteristiche 341
17.6 Barriere architettoniche 342
17.7 Protezione dagli incendi 344
17.8 Obblighi e responsabilità nella scuola 346
17.9 Utilizzo del videoterminale 350
18.7 Proprietà tecnologiche 368
VERIFICA LE CONOSCENZE Test interattivi 371

19.1 I controlli non distruttivi





Differenza tra ghisa e acciaio
Produzione della ghisa

VERIFICA LE CONOSCENZE Test interattivi 353


18
Produzione dell’acciaio





18.1 Che cos’è la tecnologia meccanica 356
18.2 Le norme UNI 357
La colata dell’acciaio
La ghisa


































MATERIALI DIGITALI
























CAPITOLO 1 Strumenti tradizionali e loro uso
CAPITOLO 2 Strumenti attuali: il computer
CAPITOLO 3 cenni sulle norme uni




VERIFICA LE CONOSCENZE
● Gli strumenti operativi tradizionali del disegno tecnico



● Norme per la realizzazione di disegni a mano libera
● Il programma Autocad per il disegno assistito
SVILUPPA LE ABILITÀ
● Le norme UNI relative a formato e piegatura dei fogli, tabella e segno
● Eseguire correttamente la squadratura di un foglio
● Applicare le norme per l’esecuzione di disegni a mano libera
● Conoscere le funzioni del programma Autocad per eseguire disegni tecnici
● Conoscere le norme contenute nell’UNI ISO 2006





● Utilizzare correttamente gli strumenti tradizionali per il disegno

COSTRUISCI LE COMPETENZE
● Saper scegliere tra gli strumenti tradizionali quelli più adatti per realizzare un disegno tecnico



● Saper eseguire diversi tipi di disegni a mano libera seguendo le norme
● Essere consapevoli delle potenzialità del programma Autocad per realizzare disegni tecnici































As.car.i è il nome del pilota di intelligenza artificiale sviluppato dal gruppo PoliMOVE, un giovane team di ingegneri coordinato dal Professore S. Savaresi del Politecnico di Milano. La vettura è una Dallara AV-21, celebre azienda italiana produttrice di auto da competizione. La monoposto monta tre sensori LiDAR, cioè dispositivi che sfruttano la tecnologia basata sul funzionamento dei radar e che, grazie a segnali laser, riescono a rilevare dati accurati sull’ambiente circostante, restituendo informazioni tridimensionali a lunga distanza e a 360°, all’intelligenza artificiale che guida la vettura.











Dopo la partecipazione al campionato tra università di tutto il mondo, la Indy Autonomous Challenge, che ha vinto, As.car.i ha fissato un nuovo record: con i suoi 309,3 km/h sul rettilineo della pista di atterraggio dello Space Shuttle a Cape Canaveral è l’auto guidata da un’intelligenza artificiale più veloce al mondo.





VIDEO 1






1. Descrizione degli strumenti principali
2. Uso corretto degli strumenti tradizionali
L’uomo è l’unico essere vivente che sa progettare e costruire oggetti, utensili, macchine ecc. Egli ha iniziato con il vasellame, le armi, gli attrezzi, giungendo successivamente alla costruzione di manufatti più complessi, la cui realizzazione implicava la stesura preventiva di un progetto in cui fossero studiate tutte le fasi costruttive. Il disegno tecnico è stato ed è un mezzo indispensabile per la progettazione di un’opera, perché permette di rappresentare sia l’idea globale sia le caratteristiche costruttive di ogni singolo componente. Di seguito presentiamo le principali caratteristiche degli strumenti impiegati per l’esecuzione di disegni tecnici.
1.1.1
La carta è costituita principalmente da cellulosa, trattata chimicamente, ottenuta dagli alberi di legno tenero come la betulla, il pioppo, il pino. Una carta meno comune, in quanto costosa e più pregiata, è ottenuta dal cotone, il lino e la canapa. Esistono vari tipi di carta, tra cui quella per il disegno, con caratteristiche diverse a seconda dell’uso a cui è adibita.
La carta per il disegno normalmente è fornita in fogli oppure in rotoli come la carta da lucido (trasparente e usata principalmente per i disegni a china) e la carta da spolvero detta anche da scena (per usi particolari in pittura e disegno).


3. Squadratura del foglio e uso delle squadre
4. Il disegno a mano libera
permette l’esecuzione di disegni di precisione. Può essere di varia grammatura e spessore, e la scelta dell’uno o dell’altro tipo dipenderà dall’uso che se ne intende fare. Per il disegno tecnico si consiglia l’uso di una carta con grammatura di 220 gr/m2 in quanto fornisce una buona resistenza all’eventuale azione della gomma e allo strofinio delle squadrette. Per il disegno a mano libera, soprattutto nei primi tempi, conviene utilizzare carta quadrettata o anche millimetrata.
I fogli bianchi o già utilizzati conviene conservarli in cartelline rigide così da evitare piegature e arrotolamenti che ne comprometterebbero l’aspetto.
Per il disegno si usano i portamine, più adatti al disegno tecnico delle matite tradizionali di legno (➜ Fig. 1). In ogni caso l’importante è che la punta sia lunga e non tozza e, nel caso del portamine (➜ Fig. 2), sporgente almeno 10 mm in modo da poter vedere bene dove si appoggia (➜ Fig. 3).

Per il disegno tecnico la carta più indicata è la carta liscia bianca, in fogli di varie dimensioni, perché ➜ Fig. 1







Sia nella matita in legno sia nel portamine ciò che lascia il segno è la mina che è costituita principalmente da grafite con l’aggiunta di argilla. La proporzione di grafite e di argilla rende più o meno dura la mina. Ci sono mine morbide (da 9B a 2B), medie (B-HB-F), dure (da H a 9H) (➜ Fig. 4). Più le mine sono morbide più carico ne risulta il segno, ma è anche più facile sporcare il foglio. Viceversa più sono dure meno il segno risulta visibile ma è più facile incidere il foglio. Le più adatte per il disegno tecnico sono le HB, F e H e per eseguire i disegni a mano libera la B e la 2B.




















9B 8B 7B 6B 5B 4B 3B 2B B HB
9B 8B 7B 6B 5B 4B 3B 2B B HB




















F H 2H 3H 4H 5H 6H 7H 8H 9H
F H 2H 3H 4H 5H 6H 7H 8H 9H
➜ Fig. 4
Per eseguire un disegno è importante impugnare in modo corretto la matita. Pertanto nel caso in cui si avesse qualche difficoltà nel farlo, si consiglia l’uso di matite in legno a sezione triangolare oppure l’uso di opportuni correttori (➜ Fig. 5) da applicare alla matita o al portamine.
Per il disegno a matita si usano gomme bianche morbide (➜ Fig. 9); eventualmente per pulire un disegno particolarmente sporco, si usa la gommapane (➜ Fig. 10). Per il disegno a china su carta da lucido si usa una gomma specifica traslucida di colore bianco o giallo (➜ Fig. 11).


Per tracciare le linee rette si usano squadre, righe e righelli.
➜ Fig. 5
1.1.4

Per affilare le mine sono usati la carta smeriglio (➜ Fig. 6), le campane (➜ Fig. 7) e i girelli (➜ Fig. 8). Questi ultimi permettono di ottenere velocemente una corretta affilatura grazie anche a due regolatori di lunghezza, uno per ottenere una punta affilata, l’altro per ottenere una punta un po’ più grossa.



Le squadre sono a forma di triangolo rettangolo isoscele (con angoli di 45° e 90°) (➜ Fig. 12) e di triangolo rettangolo scaleno (con angoli di 30°, 60° e 90°) (➜ Fig. 13), di varie dimensioni. Si sconsiglia l’uso di squadrette troppo piccole, perché insufficienti, o troppo grandi, perché ingombranti. Nell’uso si deve fare attenzione a non spostarle trascinandole, bensì sollevandole per non sporcare il foglio.

CARTA SMERIGLIO
Foglio di tela o carta ricoperta da materiale abrasivo.
CARTA DA LUCIDO


Carta a bassa opacità che consente di vedere in trasparenza. Usata, con matita o china, per riprodurre una figura posta al di sotto di essa.
Le righe servono per tracciare linee di dimensioni tali da non poter essere eseguite con le squadrette, come ad esempio le linee della squadratura, mentre i righelli servono per rilevare misure e sono meno ingombranti delle squadrette.
Ne esistono di varie lunghezze (➜ Fig. 14). Quando si acquistano squadre, righe e righelli è bene controllare che non siano arcuate e che i bordi siano perfettamente lisci. Nel caso poi delle squadrette in plastica, è opportuno verificare che non presentino residui dovuti a uno stampaggio mal realizzato.

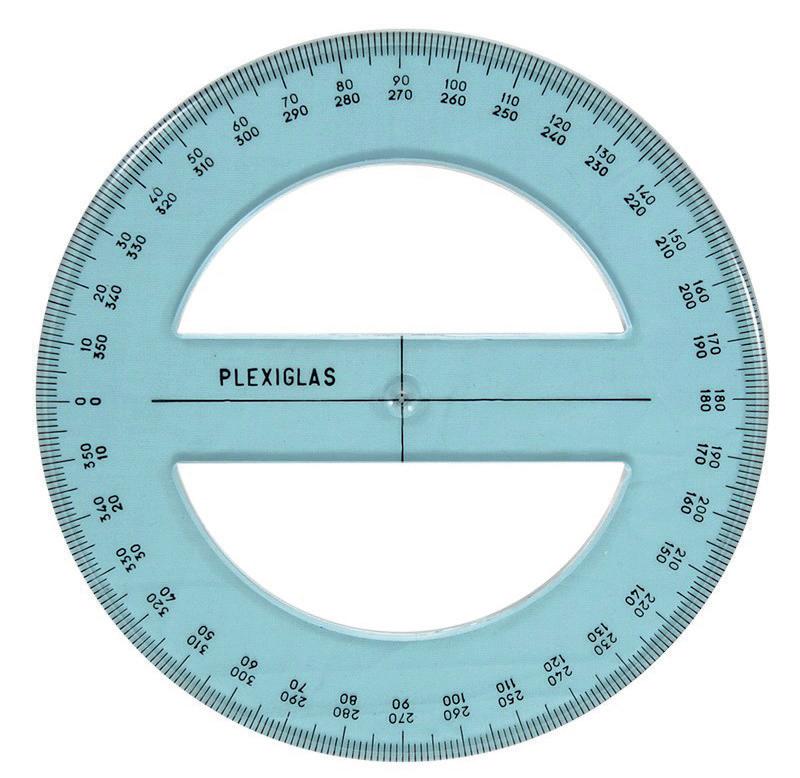
Il goniometro è uno strumento che serve per misurare l’ampiezza degli angoli. È formato da un disco graduato su cui sono riportate 360 tacche (ogni tacca corrisponde a 1°) (➜ Fig. 16), oppure da un semidisco con 180 tacche (➜ Fig. 17).
1.1.7 PARALLELOGRAFI
Il parallelografo (➜ Fig. 15) è una riga, guidata da due cavetti, che si sposta sempre parallelamente a se stessa. In commercio se ne trovano di già montati su tavolette.


Il compasso è uno strumento, formato da due aste incernierate tra loro e con una apertura regolabile, che viene usato per tracciare circonferenze o per riportare misure. In commercio ne esistono di diversi tipi, ma quelli che ci interessano sono il balaustrone (➜ Fig. 18) e il normale compasso ad aste (➜ Fig. 19).








Nell’uso del compasso è importante controllare che la punta di grafite sia sempre bene affilata e alla stessa altezza della punta metallica o un po’ più sporgente. Nel compasso tradizionale è bene controllare che l’apertura o la chiusura delle aste non sia né troppo difficoltosa nè troppo facile. Nel caso lo fossero, si deve regolare il serraggio delle viti che collegano le aste con la cerniera e che sono accessibili svitando il perno zigrinato e togliendo la copertura.
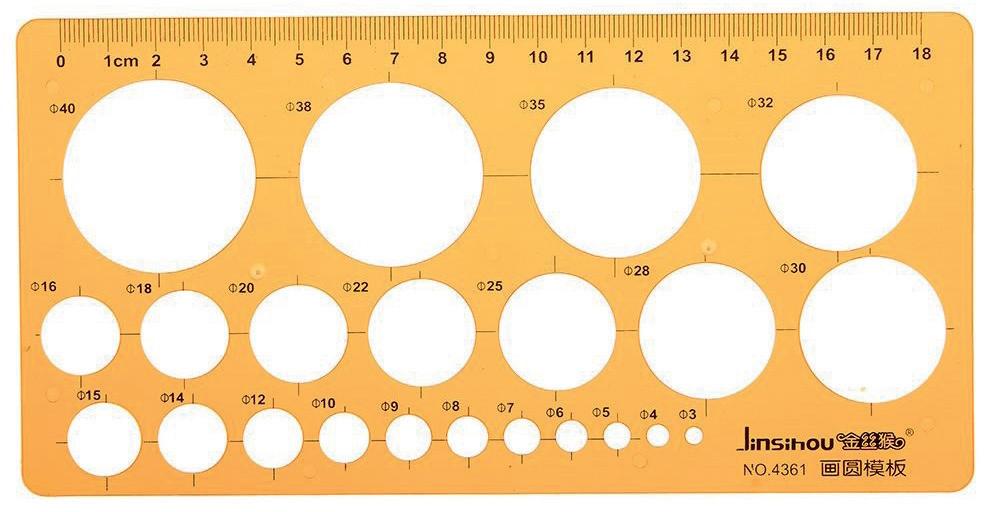
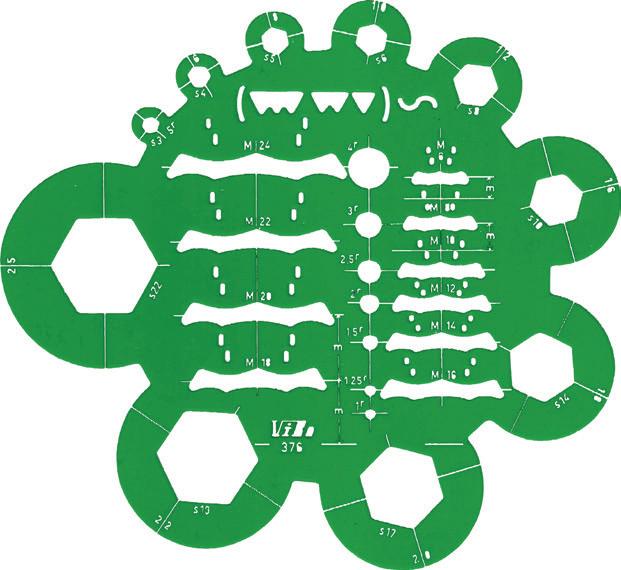
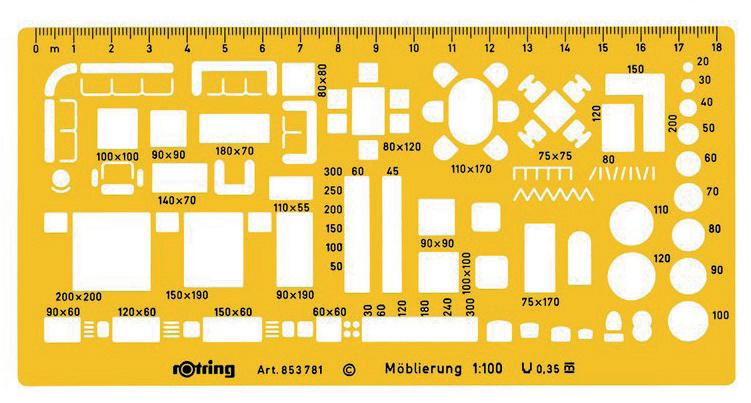
Le mascherine servono per tracciare rapidamente le principali figure geometriche (➜ Fig. 20) (cerchi, ellissi, poligoni ecc.) e i simboli ricorrenti nei disegni meccanici, come dadi esagonali (➜ Fig. 21), negli schemi elettrici, come lampade, spine ecc., o nell’arredamento, come mobili o apparecchi sanitari (➜ Fig. 22).
I curvilinei (➜ Fig. 23) sono mascherine atte al tracciamento delle curve. Col disegno a matita è consigliato l’uso di curvilinei con bordi dritti per poterli capovolgere qualora si dovessero eseguire curve simmetriche.

I normografi (➜ Fig. 24) sono mascherine usate per scrivere caratteri in stampatello. Sono dotati di supporti laterali, che li tengono sollevati dal foglio per la scrittura con penne a china, che sono rimossi quando si usano con la matita.

Perno posto sulla sommità del compasso, per poterlo ruotare agevolmente, reso rugoso mediante zigrinatura cioè per mezzo di solchi (vedi p. 382).
1.
Matita
Matita
Matita
- punta affilata, lunga e non tozza, se matite in legno, o, nel caso del portamine, sporgente almeno 10mm in modo da poter vedere bene dove si appoggia fig.1;
- impugnata in modo corretto cioè tra le punte delle dita pollice, indice e medio;
- punta affilata, lunga e non tozza, se matite in legno, o, nel caso del portamine, sporgente almeno 10mm in modo da poter vedere bene dove si appoggia fig.1;
- perpendicolare al foglio fig.2 e non inclinata nè verso la squadretta fig.3 nè contro essa fig.4;
- impugnata in modo corretto cioè tra le punte delle dita pollice, indice e medio;
- punta affilata, lunga e non tozza, se matite in legno, o, nel caso del portamine, sporgente almeno 10mm in modo da poter vedere bene dove si appoggia fig.1;
- perpendicolare al foglio fig.2 e non inclinata nè verso la squadretta fig.3 nè contro essa fig.4;
- inclinata, se vista di fronte fig.5, e trascinata nel senso dell’inclinazione roteandola, possibilmente, rispetto al suo asse fig.4.
- impugnata in modo corretto cioè tra le punte delle dita pollice, indice e medio;
- perpendicolare al foglio fig.2 e non inclinata nè verso la squadretta fig.3 nè contro essa fig.4; - inclinata, se vista di fronte fig.5, e trascinata nel senso dell’inclinazione roteandola, possibilmente, rispetto al suo asse fig.4.
- inclinata, se vista di fronte fig.5, e trascinata nel senso dell’inclinazione roteandola, possibilmente, rispetto al suo asse fig.4.
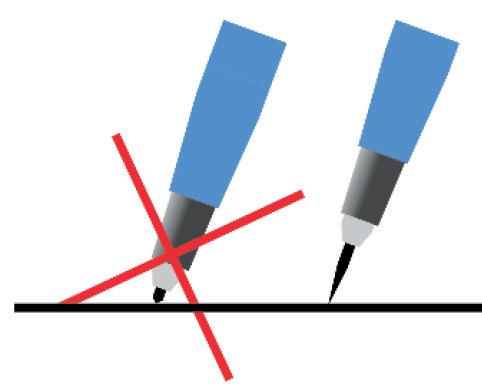
punta affilata, lunga e non tozza, se matite in legno, o, nel caso del portamine, sporgente almeno 10mm in modo da poter vedere bene dove si appoggia (➜ Fig. 25); impugnata in modo corretto cioè tra le punte delle dita pollice, indice e medio; perpendicolare al foglio (➜ Fig. 26) e non inclinata né verso la squadretta (➜ Fig. 27) né contro essa (➜ Fig. 28); inclinata, se vista di fronte (➜ Fig. 29), e trascinata nel senso dell’inclinazione roteandola, possibilmente, rispetto al suo asse (➜ Fig. 29).
SI NO SI SI NO NO NO
➜ Fig. 25 ➜ Fig. 26 ➜ Fig. 27 ➜ Fig. 28 ➜ Fig. 29
Compasso
2. COMPASSO
Compasso
Compasso - usare la punta in acciaio a spillo anziché quella conica fig.6; - punta di grafite sempre bene affilata e alla stessa altezza della punta metallica o leggermente più sporgente fig.7; - le due punte di grafite e di acciaio devono sporgere dai porta punte in modo sufficiente da permettere una facile visione del loro posizionamento sul disegno (come nel caso della punta di grafite dal portamine);
- usare la punta in acciaio a spillo anziché quella conica fig.6;
- punta di grafite sempre bene affilata e alla stessa altezza della punta metallica o leggermente più sporgente fig.7;
- usare la punta in acciaio a spillo anziché quella conica fig.6; - punta di grafite sempre bene affilata e alla stessa altezza della punta metallica o leggermente più sporgente fig.7; - le due punte di grafite e di acciaio devono sporgere dai porta punte in modo sufficiente da permettere una facile visione del loro posizionamento sul disegno (come nel caso della punta di grafite dal portamine);
- nel caso in cui la punta sia a scalpello la parte più lunga deve essere verso l’interno del compasso vicino alla punta metallica fig.8; - se l’apertura del compasso è ampia può essere utile piegare le mezze astine verso l’interno così da avere le punte quasi perpendicolari al foglio fig.9.
usare la punta in acciaio a spillo anziché quella conica (➜ Fig. 30); punta di grafite sempre bene affilata e alla stessa altezza della punta metallica o leggermente più sporgente (➜ Fig. 31); le due punte di grafite e di acciaio devono sporgere dai porta punte in modo sufficiente da permettere una facile visione del loro posizionamento sul disegno (come nel caso della punta di grafite dal portamine); nel caso in cui la punta sia a scalpello la parte più lunga deve essere verso l’interno del compasso vicino alla punta metallica (➜ Fig. 32); se l’apertura del compasso è ampia può essere utile piegare le mezze astine verso l’interno così da avere le punte quasi perpendicolari al foglio (➜ Fig. 33).
- nel caso in cui la punta sia a scalpello la parte più lunga deve essere verso l’interno del compasso vicino alla punta metallica fig.8; - se l’apertura del compasso è ampia può essere utile piegare le mezze astine verso l’interno così da avere le punte quasi perpendicolari al foglio fig.9.
- le due punte di grafite e di acciaio devono sporgere dai porta punte in modo sufficiente da permettere una facile visione del loro posizionamento sul disegno (come nel caso della punta di grafite dal portamine);
- nel caso in cui la punta sia a scalpello la parte più lunga deve essere verso l’interno del compasso vicino alla punta metallica fig.8;
- se l’apertura del compasso è ampia può essere utile piegare le mezze astine verso l’interno così da avere le punte quasi perpendicolari al foglio fig.9.






Strumenti
Uso delle squadrette per tracciare linee parallele e perpendicolari
1. USO DELLE SQUADRETTE PER TRACCIARE LINEE PARALLELE E PERPENDICOLARI
Uso delle squadrette per tracciare linee parallele e perpendicolari
Accostando due squadrette e facendole scorrere l’una sull’altra si possono tracciare linee tra loro parallele o perpendicolari.
Accostando due squadrette e facendole scorrere l’una sull’altra si possono tracciare linee tra loro parallele o perpendicolari.
Accostando due squadrette e facendole scorrere l’una sull’altra si possono tracciare linee tra loro parallele o perpendicolari.
2. USO DELLE SQUADRETTE PER COSTRUIRE ANGOLI MULTIPLI DI 15°
Uso delle squadrette per costruire angoli multipli di 15°
Appoggiando le squadrette a una riga, accostandole e ruotandole opportunamente si può ottenere una serie di angoli multipli di 15°.
Uso delle squadrette per costruire angoli multipli di 15°
Appoggiando le ssquadretta a una riga, accostandole e ruotandole opportunamente si può ottenere una serie di angoli multipli di 15°.
Appoggiando le ssquadretta a una riga, accostandole e ruotandole opportunamente si può ottenere una serie di angoli multipli di 15°.
1. CERCHIOGRAFO
Cerchiografo
Cerchiografo
Cerchiografo
- tracciare gli assi del cerchio che si vuole disegnare fig.1;
Cerchiografo
- tracciare gli assi del cerchio che si vuole disegnare fig.1;
Cerchiografo
tracciare gli assi del cerchio che si vuole disegnare (➜ Fig. 34); posizionare il cerchiografo sul foglio in modo che le quattro tacche del cerchio scelto si sovrappongano agli assi (➜ Fig. 35); tracciare la circonferenza con la matita perpendicolare al foglio (➜ Fig. 36).
- tracciare gli assi del cerchio che si vuole disegnare fig.1;
Cerchiografo
Cerchiografo
- posizionare il cerchiografo sul foglio in modo che le quattro tacche del cerchio scelto si sovrappongano agli assi fig.2;
Cerchiografo
- posizionare il cerchiografo sul foglio in modo che le quattro tacche del cerchio scelto si sovrappongano agli assi fig.2; - tracciare la circonferenza con la matita perpendicolare al foglio fig.3.
Cerchiografo
- tracciare gli assi del cerchio che si vuole disegnare fig.1;
- tracciare gli assi del cerchio che si vuole disegnare fig.1;
- posizionare il cerchiografo sul foglio in modo che le quattro tacche del cerchio scelto si sovrappongano agli assi fig.2; - tracciare la circonferenza con la matita perpendicolare al foglio fig.3.
- tracciare gli assi del cerchio che si vuole disegnare fig.1;
- tracciare la circonferenza con la matita perpendicolare al foglio fig.3.
- tracciare gli assi del cerchio che si vuole disegnare fig.1;
- tracciare gli assi del cerchio che si vuole disegnare fig.1;
- posizionare il cerchiografo sul foglio in modo che le quattro tacche del cerchio scelto si sovrappongano agli assi fig.2;
- posizionare il cerchiografo sul foglio in modo che le quattro tacche del cerchio scelto si sovrappongano agli assi fig.2;
- posizionare il cerchiografo sul foglio in modo che le quattro tacche del cerchio scelto si sovrappongano agli assi fig.2;
- posizionare il cerchiografo sul foglio in modo che le quattro tacche del cerchio scelto si sovrappongano agli assi fig.2;
- posizionare il cerchiografo sul foglio in modo che le quattro tacche del cerchio scelto si sovrappongano agli assi fig.2;
- tracciare la circonferenza con la matita perpendicolare al foglio fig.3.
- tracciare la circonferenza con la matita perpendicolare al foglio fig.3.
- tracciare la circonferenza con la matita perpendicolare al foglio fig.3.
- tracciare gli assi del cerchio che si vuole disegnare fig.1; - posizionare il cerchiografo sul foglio in modo che le quattro tacche del cerchio scelto si sovrappongano agli assi fig.2; - tracciare la circonferenza con la matita perpendicolare al foglio fig.3.
Fig. 34
- tracciare la circonferenza con la matita perpendicolare al foglio fig.3.
- tracciare la circonferenza con la matita perpendicolare al foglio fig.3.
2. CURVILINEO
Curvilineo
➜ Fig. 36 ➜ Fig. 35
determinare i punti per cui deve passare la curva fig.1;
Curvilineo determinare i punti per cui deve passare la curva fig.1; - abbozzare a mano libera e con segno appena accennato la curva per capirne l’andamento fig.2; - appoggiare il curvilineo sul foglio e orientarlo in modo da far collimare il suo bordo, possibilmente, con almeno tre punti (es. ABC); - traccia solo una parte di curva fig.3; - il tratto successivo si dovrà sovrapporre in parte a quello precedente (BCDE) fig.4 così da ottenere una linea continua e non una serie di tratti discontinui che tra l’uno e l’altro formano delle punte; - se la curva da tracciare è simmetrica rispetto a un asse orizzontale, una volta tracciato un arco, conviene ribaltare il curvilineo e tracciare il suo speculare figg.8 e 9.
- abbozzare a mano libera e con segno appena accennato la curva per capirne l’andamento fig.2;
Curvilineo determinare i punti per cui deve passare la curva fig.1;
Curvilineo determinare i punti per cui deve passare la curva fig.1; - abbozzare a mano libera e con segno appena accennato la curva per capirne l’andamento fig.2; - appoggiare il curvilineo sul foglio e orientarlo in modo da far collimare il suo bordo, possibilmente, con almeno tre punti (es. ABC);
- appoggiare il curvilineo sul foglio e orientarlo in modo da far collimare il suo bordo, possibilmente, con almeno tre punti (es. ABC);
determinare i punti per cui deve passare la curva fig.1;
Curvilineo determinare i punti per cui deve passare la curva fig.1;
- traccia solo una parte di curva fig.3;
- abbozzare a mano libera e con segno appena accennato la curva per capirne l’andamento fig.2;
- abbozzare a mano libera e con segno appena accennato la curva per capirne l’andamento fig.2;
Curvilineo determinare i punti per cui deve passare la curva fig.1; - abbozzare a mano libera e con segno appena accennato la curva per capirne l’andamento fig.2; - appoggiare il curvilineo sul foglio e orientarlo in modo da far collimare il suo bordo, possibilmente, con almeno tre punti (es. ABC); - traccia solo una parte di curva fig.3; - il tratto successivo si dovrà sovrapporre in parte a quello precedente (BCDE) fig.4 così da ottenere una linea continua e non una serie di tratti discontinui che tra l’uno e l’altro formano delle punte;
Curvilineo determinare i punti per cui deve passare la curva fig.1; - abbozzare a mano libera e con segno appena accennato la curva per capirne l’andamento fig.2; - appoggiare il curvilineo sul foglio e orientarlo in modo da far collimare il suo bordo, possibilmente, con almeno tre punti (es. ABC); - traccia solo una parte di curva fig.3; - il tratto successivo si dovrà sovrapporre in parte a quello precedente (BCDE) fig.4 così da ottenere una linea continua e non una serie di tratti discontinui che tra l’uno e l’altro formano delle punte; - se la curva da tracciare è simmetrica rispetto a un asse orizzontale, una volta tracciato un arco, conviene ribaltare il curvilineo e tracciare il suo speculare figg.8 e 9.
Curvilineo determinare i punti per cui deve passare la curva fig.1; - abbozzare a mano libera e con segno appena accennato la curva per capirne l’andamento fig.2;
- abbozzare a mano libera e con segno appena accennato la curva per capirne l’andamento fig.2;
- appoggiare il curvilineo sul foglio e orientarlo in modo da far collimare il suo bordo, possibilmente, con almeno tre punti (es. ABC);
- traccia solo una parte di curva fig.3; - il tratto successivo si dovrà sovrapporre in parte a quello precedente (BCDE) fig.4 così da ottenere una linea continua e non una serie di tratti discontinui che tra l’uno e l’altro formano delle punte; - se la curva da tracciare è simmetrica rispetto a un asse orizzontale, una volta tracciato un arco, conviene ribaltare il curvilineo e tracciare il suo speculare figg.8 e 9.
- appoggiare il curvilineo sul foglio e orientarlo in modo da far collimare il suo bordo, possibilmente, con almeno tre punti (es. ABC);
- il tratto successivo si dovrà sovrapporre in parte a quello precedente (BCDE) fig.4 così da ottenere una linea continua e non una serie di tratti discontinui che tra l’uno e l’altro formano delle punte;
- appoggiare il curvilineo sul foglio e orientarlo in modo da far collimare il suo bordo, possibilmente, con almeno tre punti (es. ABC);
- appoggiare il curvilineo sul foglio e orientarlo in modo da far collimare il suo bordo, possibilmente, con almeno tre punti (es. ABC);
- traccia solo una parte di curva fig.3;
- se la curva da tracciare è simmetrica rispetto a un asse orizzontale, una volta tracciato un arco, conviene ribaltare il curvilineo e tracciare il suo speculare figg.8 e 9.
- cominciare dalle curve più strette, più difficili, e successivamente passare a quelle più ampie;
- cominciare dalle curve più strette, più difficili, e successivamente passare a quelle più ampie; - tenere la matita perpendicolare al foglio.
- traccia solo una parte di curva fig.3; - il tratto successivo si dovrà sovrapporre in parte a quello precedente (BCDE) fig.4 così da ottenere una linea continua e non una serie di tratti discontinui che tra l’uno e l’altro formano delle punte;
- traccia solo una parte di curva fig.3; il tratto successivo si dovrà sovrapporre in parte a quello precedente (BCDE) fig.4 così da ottenere una linea continua e non una serie di tratti discontinui che tra l’uno e l’altro formano delle punte;
- cominciare dalle curve più strette, più difficili, e successivamente passare a quelle più ampie; - tenere la matita perpendicolare al foglio.
- il tratto successivo si dovrà sovrapporre in parte a quello precedente (BCDE) fig.4 così da ottenere una linea continua e non una serie di tratti discontinui che tra l’uno e l’altro formano delle punte;
- traccia solo una parte di curva fig.3; - il tratto successivo si dovrà sovrapporre in parte a quello precedente (BCDE) fig.4 così da ottenere una linea continua e non una serie di tratti discontinui che tra l’uno e l’altro formano delle punte;
- tenere la matita perpendicolare al foglio.
- se la curva da tracciare è simmetrica rispetto a un asse orizzontale, una volta tracciato un arco, conviene ribaltare il curvilineo e tracciare il suo speculare figg.8 e 9.
- se la curva da tracciare è simmetrica rispetto a un asse orizzontale, una volta tracciato un arco, conviene ribaltare il curvilineo e tracciare il suo speculare figg.8 e 9.
- se la curva da tracciare è simmetrica rispetto a un asse orizzontale, una volta tracciato un arco, conviene ribaltare il curvilineo e tracciare il suo speculare figg.8 e 9.
- se la curva da tracciare è simmetrica rispetto a un asse orizzontale, una volta tracciato un arco, conviene ribaltare il curvilineo e tracciare il suo speculare figg.8 e 9.
- se la curva da tracciare è simmetrica rispetto a un asse orizzontale, una volta tracciato un arco, conviene ribaltare il curvilineo e tracciare il suo speculare figg.8 e 9.
- cominciare dalle curve più strette, più difficili, e successivamente passare a quelle più ampie;
- cominciare dalle curve più strette, più difficili, e successivamente passare a quelle più ampie; - tenere la matita perpendicolare al foglio.
- cominciare dalle curve più strette, più difficili, e successivamente passare a quelle più ampie;
determinare i punti per cui deve passare la curva (➜ Fig. 37); abbozzare a mano libera e con segno appena accennato la curva per capirne l’andamento (➜ Fig. 38); appoggiare il curvilineo sul foglio e orientarlo in modo da far collimare il suo bordo, possibilmente, con almeno tre punti (es. ABC); tracciare solo una parte di curva (➜ Fig. 39); il tratto successivo si dovrà sovrapporre in parte a quello precedente (BCDE) (➜ Fig. 40) così da ottenere una linea continua e non una serie di tratti discontinui che tra l’uno e l’altro formano delle punte; se la curva da tracciare è simmetrica rispetto a un asse orizzontale, una volta tracciato un arco, conviene ribaltare il curvilineo e tracciare il suo speculare (➜ Figg. 41-42); cominciare dalle curve più strette, più difficili, e successivamente passare a quelle più ampie; tenere la matita perpendicolare al foglio.
- cominciare dalle curve più strette, più difficili, e successivamente passare a quelle più ampie;
- tenere la matita perpendicolare al foglio.
- cominciare dalle curve più strette, più difficili, e successivamente passare a quelle più ampie; - tenere la matita perpendicolare al foglio.
- cominciare dalle curve più strette, più difficili, e successivamente passare a quelle più ampie;
- tenere la matita perpendicolare al foglio.
➜ Fig. 37
- tenere la matita perpendicolare al foglio.
- tenere la matita perpendicolare al foglio.
Fig. 38






Si punta quindi con il compasso in A, B, C, D con una stessa apertura a piacere, si tracciano otto archetti che intersecandosi determinano i punti E, F, G, H. Si traccino quindi le linee GE e HF che passano per O, sono tra loro perpendicolari e si dicono assi del foglio.
Da O si riportano su tali assi le dimensioni del rettangolo (squadratura) determinando i punti I, L, M, N .
Da O si riportano su tali assi le dimensioni del rettangolo (squadratura) determinando i punti I, L, M, N .
Strumenti per il disegno: squadratura del foglio
1. ESEGUIRE LA SQUADRATURA DI UN FOGLIO
Eseguire la squadratura di un foglio
Per squadrare un foglio, cioè per disegnare su di esso un rettangolo che delimiti l’area per il disegno, si procede come segue:
Eseguire la squadratura di un foglio
Per squadrare un foglio, cioè per disegnare su di esso un rettangolo che delimiti l’area per il disegno, si procede come segue:
Per squadrare un foglio, cioè per disegnare su di esso un rettangolo che delimiti l’area per il disegno, si procede come segue:
Si punta quindi con il compasso in A, B, C, D con una stessa apertura a piacere, si tracciano otto archetti che intersecandosi determinano i punti E, F, G, H. Si traccino quindi le linee GE e HF che passano per O, sono tra loro perpendicolari e si dicono assi del foglio.
Tracciate le diagonali, si punta con il compasso nella loro intersezione O e, con la stessa apertura, si tracciano quattro archi, che le intersecano in A, B, C, D.
Tracciate le diagonali, si punta con il compasso nella loro intersezione O e, con la stessa apertura, si tracciano quattro archi, che le intersecano in A, B, C, D.
golo (squadratura)
Posizionando una squadra parallela all’asse orizzontale, appoggiando l’altra ad essa e facendola scorrere si tracciano le due linee orizzontali passanti per I e M.
squadratura del foglio
disegnare su di esso disegno, si
Ripetendo la stessa operazione anche per l’asse verticale si tracciano le parallele ad esso passanti per N e L completando la costruzione.
Posizionando una squadra parallela all’asse orizzontale, appoggiando l’altra ad essa e facendola scorrere si tracciano le due linee orizzontali passanti per I e M.
Strumenti per il disegno: squadratura del foglio
Posizionando una squadra parallela all’asse orizzontale, appoggiando l’altra ad essa e facendola scorrere si tracciano le due linee orizzontali passanti per I e M.
Ripetendo la stessa cale si tracciano le completando la costruzione.
Eseguire la squadratura di un foglio
Si punta quindi con il compasso in A, B, C, D con una stessa apertura a piacere, si tracciano otto archetti che intersecandosi determinano i punti E, F, G, H. Si traccino quindi le linee GE e HF che passano per O, sono tra loro perpendicolari e si dicono assi del foglio.
Tracciate le diagonali, si punta con il compasso nella loro intersezione O e, con la stessa apertura, si tracciano quattro archi, che le intersecano in A, B, C, D.
Da O si riportano su tali assi le dimensioni del rettangolo (squadratura) determinando i punti I, L, M, N .
Tracciate le diagonali, si punta con il compasso nella loro intersezione O e, con la stessa apertura, si tracciano quattro archi, che le intersecano in A, B, C, D.
Per squadrare un foglio, cioè per disegnare su di esso un rettangolo che delimiti l’area per il disegno, si procede come segue:
Si punta quindi con il compasso in A, B, C, D con una stessa apertura a piacere, si tracciano otto archetti che intersecandosi determinano i punti E, F, G, H. Si traccino quindi le linee GE e HF che passano per O, sono tra loro perpendicolari e si dicono assi del foglio.
Tracciate le diagonali, si punta con il compasso nella loro intersezione O e, con la stessa apertura, si tracciano quattro archi, che le intersecano in A, B, C, D.
Da O si riportano su tali assi le dimensioni del rettangolo (squadratura) determinando i punti I, L, M, N .
C, D con una otto archetti E, F, G, H. Si passano per O, assi del foglio.
Posizionando una squadra parallela all’asse orizzontale, appoggiando l’altra ad essa e facendola scorrere si tracciano le due linee orizzontali passanti per I e M.
Da O si riportano su tali assi le dimensioni del rettangolo (squadratura) determinando i punti I, L, M, N .
Si punta quindi con il compasso in A, B, C, D con una stessa apertura a piacere, si tracciano otto archetti che intersecandosi determinano i punti E, F, G, H. Si traccino quindi le linee GE e HF che passano per O, sono tra loro perpendicolari e si dicono assi del foglio.
Si punta quindi con il compasso in A, B, C, D con una stessa apertura a piacere, si tracciano otto archetti che intersecandosi determinano i punti E, F, G, H. Si traccino quindi le linee GE e HF che passano per O, sono tra loro perpendicolari e si dicono assi del foglio.
Posizionando una squadra parallela all’asse orizzontale, appoggiando l’altra ad essa e facendola scorrere si tracciano le due linee orizzontali passanti per I e M.
all’asse orizzonfacendola scorrere passanti per I e M.
Posizionando una squadra parallela all’asse orizzontale, appoggiando l’altra ad essa e facendola scorrere si tracciano le due linee orizzontali passanti per I e M.
Ripetendo la stessa operazione anche per l’asse verticale si tracciano le parallele ad esso passanti per N e L completando la costruzione.
Da O si riportano su tali assi le dimensioni del rettangolo (squadratura) determinando i punti I, L, M, N .
Ripetendo la stessa operazione anche per l’asse verticale si tracciano le parallele ad esso passanti per N e L completando la costruzione.
Ripetendo la stessa operazione anche per l’asse verticale si tracciano le parallele ad esso passanti per N e L completando la costruzione.
Ripetendo la stessa operazione anche per l’asse verticale si tracciano le parallele ad esso passanti per N e L completando la costruzione.
Ripetendo la stessa operazione anche per l’asse verticale si tracciano le parallele ad esso passanti per N e L completando la costruzione.
Il disegno a mano libera è certamente la più importante tra le tecniche utilizzate per eseguire un elaborato grafico. Richiede, infatti, una strumentazione molto scarna (matita, foglio di carta e gomma) e pertanto può essere utilizzato ovunque, anche nelle situazioni più disagevoli. Questa sua facoltà di utilizzo permette quindi in ogni momento di integrare spiegazioni verbali, non sempre facilmente comprensibili, con schizzi, o di apportare correzioni a un elaborato grafico, lasciando in tal modo traccia di quanto discusso. È comunque importante tenere presente che si tratta di un disegno tecnico: pertanto, nell’eseguirlo, si devono sempre rispettare le norme relative. Di seguito sono proposte alcune costruzioni geometriche, utili per acquisire dimestichezza con questa tecnica. Per eseguire un disegno a mano libera si consiglia di utilizzare una matita morbida (B o 2B) e fogli quadrettati, sia perché si possono usare le quadrettature come guide nella tracciatura di linee, sia perché i quadretti sono d’aiuto per rispettare le proporzioni.
Disegno a mano libera di quadrati e circonferenze
Il disegno a mano libera è certamente la più importante tra le tecniche utilizzate per eseguire un elaborato grafico. Richiede, infatti, una strumentazione molto scarna (matita, foglio di carta e gomma) e pertanto può essere utilizzato ovunque, anche nelle situazioni più disagevoli. Questa sua facoltà di utilizzo permette quindi in ogni momento di integrare spiegazioni verbali, non sempre facilmente comprensibili, con schizzi, o di apportare correzioni ad un elaborato grafico, lasciando in tal modo traccia di quanto discusso. E’ comunque importante tenere presente che si tratta di un disegno tecnico: pertanto, nell’eseguirlo, si devono sempre rispettare le norme relative. Di seguito sono proposte alcune costruzioni geometriche, utili per acquisire dimestichezza con questa tecnica. Per esegire un disegno a mano libera si consiglia di utilizzare una matita morbida (B o 2B) e fogli quadrettati, sia perché si possono usare le quadrettature come guide nella tracciatura di linee, sia perché i quadretti sono d’aiuto per rispettare le proporzioni.
Il disegno a mano libera è certamente la più importante tra le tecniche utilizzate per eseguire un elaborato grafico. Richiede, infatti, una strumentazione molto scarna (matita, foglio di carta e gomma) e pertanto può essere utilizzato ovunque, anche nelle situazioni più disagevoli. Questa sua facoltà di utilizzo permette quindi in ogni momento di integrare spiegazioni verbali, non sempre facilmente comprensibili, con schizzi, o di apportare correzioni ad un elaborato grafico, lasciando in tal modo traccia di quanto discusso. E’ comunque importante tenere presente che si tratta di un disegno tecnico: pertanto, nell’eseguirlo, si devono sempre rispettare le norme relative. Di seguito sono proposte alcune costruzioni geometriche, utili per acquisire dimestichezza con questa tecnica. Per esegire un disegno a mano libera si consiglia di utilizzare una matita morbida (B o 2B) e fogli quadrettati, sia perché si possono usare le quadrettature come guide nella tracciatura di linee, sia perché i quadretti sono d’aiuto per rispettare le proporzioni.
Il disegno a mano libera è certamente la più importante tra le tecniche utilizzate per eseguire un elaborato grafico. Richiede, infatti, una strumentazione molto scarna (matita, foglio di carta e gomma) e pertanto può essere utilizzato ovunque, anche nelle situazioni più disagevoli. Questa sua facoltà di utilizzo permette quindi in ogni momento di integrare spiegazioni verbali, non sempre facilmente comprensibili, con schizzi, o di apportare correzioni ad un elaborato grafico, lasciando in tal modo traccia di quanto discusso. E’ comunque importante tenere presente che si tratta di un disegno tecnico: pertanto, nell’eseguirlo, si devono sempre rispettare le norme relative. Di seguito sono proposte alcune costruzioni geometriche, utili per acquisire dimestichezza con questa tecnica. Per esegire un disegno a mano libera si consiglia di utilizzare una matita morbida (B o 2B) e fogli quadrettati, sia perché si possono usare le quadrettature come guide nella tracciatura di linee, sia perché i quadretti sono d’aiuto per rispettare le proporzioni.
Le costruzioni proposte, in tutto il testo, sono scandite da disegni che ne illustrano le fasi. Ciò che le differenzia tra loro sono i colori dei segni: il nero è utilizzato per ciò che fa parte del disegno finale, come lati, assi ecc., il rosso per ciò che si deve eseguire in quella fase e l’azzurro per ciò che è stato eseguito nella fase precedente.
Le costruzioni proposte, in tutto il testo, sono scandite da disegni che ne illustrano le fasi. Ciò che le differenzia tra loro sono i colori dei segni: il nero è utilizzato per ciò che fa parte del disegno finale, come lati assi ecc., il rosso per ciò che si deve eseguire in quella fase e l’azzurro per ciò che è stato eseguito nella fase precedente.
Le costruzioni proposte, in tutto il testo, sono scandite da disegni che ne illustrano le fasi. Ciò che le differenzia tra loro sono i colori dei segni: il nero è utilizzato per ciò che fa parte del disegno finale, come lati assi ecc., il rosso per ciò che si deve eseguire in quella fase e l’azzurro per ciò che è stato eseguito nella fase precedente.
Le costruzioni proposte, in tutto il testo, sono scandite da disegni che ne illustrano le fasi. Ciò che le differenzia tra loro sono i colori dei segni: il nero è utilizzato per ciò che fa parte del disegno finale, come lati assi ecc., il rosso per ciò che si deve eseguire in quella fase e l’azzurro per ciò che è stato eseguito nella fase precedente.
1. DISEGNARE A MANO LIBERA UN QUADRATO
Disegnare a mano libera un quadrato
Disegnare a mano libera un quadrato
Disegnare a mano libera un quadrato
1a. Si tracciano due assi tra loro perpendicolari che si intersecano nel punto O e si fissano i punti A, B, C, D equidistanti da O. Si tracciano per essi le parallele agli assi che, intersecandosi, determinano i quattro vertici del quadrato (➜ Fig. 43).
1a Si tracciano due assi tra loro perpendicolari che si intersecano nel punto O e si fissano i punti A, B, C, D equidistanti da O.
1a Si tracciano due assi tra loro perpendicolari che si intersecano nel punto O e si fissano i punti A, B, C, D equidistanti da O.
1a Si tracciano due assi tra loro perpendicolari che si intersecano nel punto O e si fissano i punti A, B, C, D equidistanti da O.
1b Si traccino per essi le parallele agli assi che, intersecandosi, determinano i quattro vertici del quadrato. Si completa la costruzione evidenziando il perimetro del quadrato.
1b. Si completa la costruzione evidenziando il perimetro del quadrato (➜ Fig. 44).
1b Si traccino per essi le parallele agli assi che, intersecandosi, determinano i quattro vertici del quadrato. Si completa la costruzione evidenziando il perimetro del quadrato.
1b Si traccino per essi le parallele agli assi che, intersecandosi, determinano i quattro vertici del quadrato. Si completa la costruzione evidenziando il perimetro del quadrato.
2. DISEGNARE A MANO LIBERA UNA CIRCONFERENZA
Primo metodo
➜ Fig. 43
Disegnare a mano libera una circonferenza
2a. Si costruisce un quadrato che abbia il lato congruente al diametro della circonferenza e siano A, B, C, D i punti di tangenza tra la circonferenza e i lati del quadrato. Con la maggior precisione possibile si traccia un quarto di circonferenza e si individuano su di esso due punti di intersezione tra la curva e la quadrettatura (➜ Fig. 45).
Disegnare a mano libera una circonferenza
Primo metodo
Disegnare a mano libera una circonferenza
Primo metodo
Primo metodo
2a Si costruisce un quadrato che abbia il lato congruente al diametro della circonferenza e siano A, B, C, D i punti di tangenza tra la circonferenza e i lati del quadrato. Con la maggior precisione possibile si tracci un quarto di circonferenza e si individuino su di esso due punti di intersezione tra la curva e la quadrettatura.
2b. Si tracciano gli altri tre quarti di circonferenza riportando simmetricamente rispetto agli assi i punti individuati precedentemente (➜ Fig. 46).
Secondo metodo
2a Si costruisce un quadrato che abbia il lato congruente al diametro della circonferenza e siano A, B, C, D i punti di tangenza tra la circonferenza e i lati del quadrato. Con la maggior precisione possibile si tracci un quarto di circonferenza e si individuino su di esso due punti di intersezione tra la curva e la quadrettatura.
2a Si costruisce un quadrato che abbia il lato congruente al diametro della circonferenza e siano A, B, C, D i punti di tangenza tra la circonferenza e i lati del quadrato. Con la maggior precisione possibile si tracci un quarto di circonferenza e si individuino su di esso due punti di intersezione tra la curva e la quadrettatura.
2b Si traccino gli altri tre quarti di circonferenza prendendo come riferimento i punti individuati precedentemente.
2b Si traccino gli altri tre quarti di circonferenza prendendo come riferimento i punti individuati precedentemente.
2b Si traccino gli altri tre quarti di circonferenza prendendo come riferimento i punti individuati precedentemente.
Secondo metodo
Secondo metodo
Secondo metodo
3a. Si costruisce un quadrato che abbia il lato congruente al diametro della circonferenza e si tracciano le sue diagonali (➜ Fig. 47).
Partendo da O, si riporta su queste ultime il raggio, valutandone la misura ad occhio con la miglior approssimazione possibile. Si determinano così i punti E, F, G, H, che appartengono alla circonferenza.
3a Si costruisce un quadrato che abbia il lato congruente al diametro della circonferenza e si tracciano le sue diagonali. Partendo da O, si riporta su queste ultime il raggio, valutandone la misura ad occhio con la miglior approssimazione possibile. Si determinano così i punti E, F, G, H, che appartengono alla circonferenza.
3a Si costruisce un quadrato che abbia il lato congruente al diametro della circonferenza e si tracciano le sue diagonali. Partendo da O, si riporta su queste ultime il raggio, valutandone la misura ad occhio con la miglior approssimazione possibile. Si determinano così i punti E, F, G, H, che appartengono alla circonferenza.
3a Si costruisce un quadrato che abbia il lato congruente al diametro della circonferenza e si tracciano le sue diagonali. Partendo da O, si riporta su queste ultime il raggio, valutandone la misura ad occhio con la miglior approssimazione possibile. Si determinano così i punti E, F, G, H, che appartengono alla circonferenza.
3b Si traccia ora la curva passante per i vari punti completando la costruzione.
3b Si traccia ora la curva passante per i vari punti completando la costruzione.
3b Si traccia ora la curva passante per i vari punti completando la costruzione.
3b. Si traccia ora la curva passante per i vari punti completando la costruzione (➜ Fig. 48).
➜ Fig. 45 ➜ Fig. 47 ➜ Fig. 44 ➜ Fig. 46
Fig. 48



Terzo metodo
Terzo metodo
4a. Si costruisce il quadrato T, U, V, Z col lato pari al diametro della circonferenza.



4a Si costruisce il quadrato T, U, V, Z col lato pari al diametro della circonferenza. Si tracciano gli assi dei lati che si intersecano in O (centro della circonferenza) e determinano i punti A, B, C, D.
Si tracciano gli assi dei lati che si intersecano in O (centro della circonferenza) e determinano i punti A, B, C, D (➜ Fig. 49).
4a Si costruisce il quadrato T, U, V, Z col lato pari al diametro della circonferenza. Si tracciano gli assi dei lati che si intersecano in O (centro della circonferenza) e determinano i punti A, B, C, D.
4b Si congiunge B con V e Z e D con T e U.
4b. Si congiunge B con V e Z allo stesso modo D con T e U (➜ Fig. 50).
4b Si congiunge B con V e Z e D con T e U.
costruisce il quadrato T, U, V, Z col diametro della circonferentracciano gli assi dei lati che si O (centro della circondeterminano i punti A, B, C,
4c Si tracciano le congiungenti di D con R e con S, punti medi di VC e AZ, che intersecano BZ in H e BV in G. Si ripete la costruzione con BP e BQ che intercettando DT e DU determinano E e F.
4c Si tracciano le congiungenti di D con R e con S, punti medi di VC e AZ, che intersecano BZ in H e BV in G. Si ripete la costruzione con BP e BQ che intercettando DT e DU determinano E e F.
4c. Si tracciano le congiungenti di D con R e con S, punti medi di VC e AZ, che intersecano BZ in H e BV in G. Si ripete la costruzione con BP e BQ che intercettando DT e DU determinano E e F (➜ Fig. 51).
congiunge B con V e Z e D con T e
4d I punti così determinati assieme a A, B, C, D permettono di tracciare la circonferenza.
4d. I punti così determinati assieme a A, B, C, D permettono di tracciare la circonferenza (➜ Fig. 52).
4d I punti così determinati assieme a A, B, C, D permettono di tracciare la circonferenza.
tracciano le congiungenti di D con punti medi di VC e AZ, che
BZ in H e BV in G. Si ripete con BP e BQ che interDU determinano E e F.
così determinati assieme a permettono di tracciare la
➜ Fig. 49
➜ Fig. 50
➜ Fig. 51
Disegnare a mano libera un triangolo equilatero
Disegnare a mano libera un triangolo equilatero
5a Si traccia una circonferenza (ad esempio tracciandone una quarto con il terzo metodo e completandola con il primo metodo) e un segmento orizzontale passante per M, punto medio di OB, che determina sulla circonferenza i punti E e F.
➜ Fig. 52
1.4.2 DISEGNO A MANO LIBERA DI UN TRIANGOLO EQUILATERO
5a Si traccia una circonferenza (ad esempio tracciandone una quarto con il terzo metodo e completandola con il primo metodo) e un segmento orizzontale passante per M, punto medio di OB, che determina sulla circonferenza i punti E e F.
1. DISEGNARE A MANO LIBERA UN TRIANGOLO EQUILATERO
5a. Si traccia una circonferenza (ad esempio tracciandone una quarto con il terzo metodo e completandola con il primo metodo) e un segmento orizzontale passante per M, punto medio di OB, che determina sulla circonferenza i punti E e F (➜ Fig. 53).
5b. Si completa la costruzione congiungendo tra loro E, F e D vertici del triangolo (➜ Fig. 54).
mano libera un triangolo equilatero
5b Si completa la costruzione congiungendo tra loro E, F e D vertici del triangolo.
una circonferenza (ad tracciandone una quarto con il e completandola con il metodo) e un segmento orizzonper M, punto medio di determina sulla circonferenza i
5b Si completa la costruzione congiungendo tra loro E, F e D vertici del triangolo.
completa la costruzione congiunE, F e D vertici del trian-
Fig. 53
Fig. 54
1. DISEGNARE A MANO LIBERA UN ESAGONO REGOLARE
6a Si traccia una circonferenza (ad esempio tracciandone una quarto con il terzo metodo e completandola con il primo metodo) e due segmenti orizzontale passanti per M e N, punti medi di DO e OB, che determinano sulla circonferenza i punti E, F, G, H.
6b Si completa la costruzione congiungendo tra loro i vertici.
6a. Si traccia una circonferenza (ad esempio tracciandone un quarto con il terzo metodo e completandola con il primo metodo) e due segmenti orizzontale passanti per M e N, punti medi di DO e OB, che determinano sulla circonferenza i punti E, F, G, H. (➜ Fig. 55).
6a Si traccia una circonferenza (ad esempio tracciandone una quarto con il terzo metodo e completandola con il primo metodo) e due segmenti orizzontale passanti per M e N, punti medi di DO e OB, che determinano sulla circonferenza i punti E, F, G, H.
6a Si traccia una circonferenza (ad esempio tracciandone una quarto con il terzo metodo e completandola con il primo metodo) e due segmenti orizzontale passanti per M e N, punti medi di DO e OB, che determinano sulla circonferenza i punti E, F, G, H.
6b. Si completa la costruzione congiungendo tra loro i vertici. (➜ Fig. 56).
6b Si completa la costruzione congiungendo tra loro i vertici.
6b Si completa la costruzione congiungendo tra loro i vertici.
7a Si traccia una circonferenza (ad esempio tracciandone una quarto con il terzo metodo e completandola con il primo metodo) e le diagonali del quadrato in cu è inscritta determinando su di essa E, F, G, H che con A, B, C, D sono i vertici dell’ottagono.
2. DISEGNARE A MANO LIBERA UN OTTAGONO REGOLARE
7a Si traccia una circonferenza (ad esempio tracciandone una quarto con il terzo metodo e completandola con il primo metodo) e le diagonali del quadrato in cu è inscritta determinando su di essa E, F, G, H che con A, B, C, D sono i vertici dell’ottagono.
7a Si traccia una circonferenza (ad esempio tracciandone una quarto con il terzo metodo e completandola con il primo metodo) e le diagonali del quadrato in cu è inscritta determinando su di essa E, F, G, H che con A, B, C, D sono i vertici dell’ottagono.
7b Si completa la costruzione congiungendo tra loro i vertici.
7b Si completa la costruzione congiungendo tra loro i vertici.
7a. Si traccia una circonferenza (ad esempio tracciandone un quarto con il terzo metodo e completandola con il primo metodo) e le diagonali del quadrato in cui è inscritta determinando su di essa E, F, G, H che con A, B, C, D sono i vertici dell’ottagono (➜ Fig. 57).
7b Si completa la costruzione congiungendo tra loro i vertici.
7b. Si completa la costruzione congiungendo tra loro i vertici (➜ Fig. 58).
8a Si traccia una circonferenza (ad esempio tracciandone una quarto con il terzo metodo e completandola con il primo metodo) e due segmenti orizzontale passanti per R e S, punti medi di DO e OB, e due verticali passanti per P e Q che determinano sulla circonferenza i otto punti che con A, B, C, D sono i vertici del dodecagono.
3. DISEGNARE A MANO LIBERA UN DODECAGONO REGOLARE
8a Si traccia una circonferenza (ad esempio tracciandone una quarto con il terzo metodo e completandola con il primo metodo) e due segmenti orizzontale passanti per R e S, punti medi di DO e OB, e due verticali passanti per P e Q che determinano sulla circonferenza i otto punti che con A, B, C, D sono i vertici del dodecagono.
8a Si traccia una circonferenza (ad esempio tracciandone una quarto con il terzo metodo e completandola con il primo metodo) e due segmenti orizzontale passanti per R e S, punti medi di DO e OB, e due verticali passanti per P e Q che determinano sulla circonferenza i otto punti che con A, B, C, D sono i vertici del dodecagono.
8b Si completa la costruzione congiungendo i tra loro i vertici.
8b Si completa la costruzione congiungendo i tra loro i vertici.
8b Si completa la costruzione congiungendo i tra loro i vertici.
8a. Si traccia una circonferenza (ad esempio tracciandone un quarto con il terzo metodo e completandola con il primo metodo) e due segmenti orizzontali passanti per R e S, punti medi di DO e OB, e due verticali passanti per P e Q che determinano sulla circonferenza gli otto punti che con A, B, C, D sono i vertici del dodecagono (➜ Fig. 59).
8b. Si completa la costruzione congiungendo tra loro i vertici (➜ Fig. 60).
57 ➜ Fig. 59






Si traccino quattro serie di linee parallele come indicato nella figura a fianco.
Si traccino quattro serie di linee parallele come indicato nella figura a fianco.
1. Traccia quattro serie di linee parallele come indicato nella figura a fianco.
Dopo aver suddiviso il foglio in quattro quadranti, si riportano nei quadranti 1, 2, 4 le tacche segnate in rosso alla distanza di 5mm. Quindi posizionando le squadrette come nelle figure e facendole scorrere nel senso indicato dalle dalle frecce si traccino le linee. Si faccia attenzione a far scorrere le squadrette non sulle linee appena tracciate in quanto raccoglirebbero la polvare di grafite che rimane sul foglio sporcandolo e sporcandosi.
Dopo aver suddiviso il foglio in quattro quadranti, si riportano nei quadranti 1, 2, 4 le tacche segnate in rosso alla distanza di 5mm. Quindi posizionando le squadrette come nelle figure e facendole scorrere nel senso indicato dalle dalle frecce si traccino le linee. Si faccia attenzione a far scorrere le squadrette non sulle linee appena tracciate in quanto raccoglirebbero la polvare di grafite che rimane sul foglio sporcandolo e sporcandosi.
Dopo aver suddiviso il foglio in quattro quadranti, si riportano nei quadranti 1, 2, 4 le tacche alla distanza di 5 mm. Quindi posizionando le squadrette come nelle figure e facendole scorrere nel senso indicato dalle frecce si tracciano le linee. Si deve fare attenzione a far scorrere le squadrette non sulle linee appena tracciate in quanto raccoglierebbero la polvere di grafite che rimane sul foglio sporcandolo e sporcandosi.
di
fatti con la punta della matita seguendo le misure indicate. Si proceda quindi secondo le indicazioni in fig.1.
Tracciare alcune serie di linee parallele e alcuni archi di circonferenza come indicato in fig. 2.
Nell’esecuzione si presti attenzione a non commettere gli errori evidenziati in fig.3, 4, 5, 6.
2. Traccia alcune serie di linee parallele e alcuni archi di circonferenza come indicato in ➜ Fig. 2
linee parcirconferenza
linee parcirconferenza
quattro traccino le sole interdeterminarne il assi. Nel 4° linee orizzontaposizioni dei punti piccoli segni seguendo le quindi secondo attenzione a non evidenziati in fig.3,
quattro traccino le sole interdeterminarne il assi. Nel 4° linee orizzontaposizioni dei punti piccoli segni seguendo le quindi secondo
attenzione a non evidenziati in fig.3,
Dopo aver squadrato e diviso in quattro quadranti un foglio UNI A4 si tracciano le diagonali nel 1° quadrante e le sole intersezioni nel 2° e 3° per determinarne il centro per cui passeranno gli assi. Nel 4° quadrante si tracciano le tre linee orizzontali. Quindi si riportano le posizioni dei punti di riferimento/partenza con piccoli segni fatti con la punta della matita seguendo le misure indicate. Si procede quindi secondo le indicazioni in ➜ Fig. 1
Tracciare alcune serie di linee parallele e alcuni archi di circonferenza come indicato in fig. 2. Dopo aver squadrato e diviso in quattro quadranti un foglio UNI A3 si traccino le diagonali nel 1° quadrante e le sole intersezioni nel 2° e 3° per determinarne il centro per cui passeranno gli assi. Nel 4° quadrante si traccino le tre linee orizzontali. Quindi si riportino le posizioni dei punti di riferimento/partenza con piccoli segni fatti con la punta della matita seguendo le misure indicate. Si proceda quindi secondo le indicazioni in fig.1.
Dopo aver squadrato e diviso in quattro quadranti un foglio UNI A3 si traccino le diagonali nel 1° quadrante e le sole intersezioni nel 2° e 3° per determinarne il centro per cui passeranno gli assi. Nel 4° quadrante si traccino le tre linee orizzontali. Quindi si riportino le posizioni dei punti di riferimento/partenza con piccoli segni fatti con la punta della matita seguendo le misure indicate. Si proceda quindi secondo le indicazioni in fig.1.
Nell’esecuzione si deve prestare attenzione a non commettere gli errori evidenziati in ➜ Figg. 3-4-5-6.
Nell’esecuzione si presti attenzione a non commettere gli errori evidenziati in fig.3, 4, 5, 6.
fig.1
➜ Fig. 1
fig.1
➜ Fig. 2
fig.2
fig.2
Nell’esecuzione si presti attenzione a non commettere gli errori evidenziati in fig.3, 4, 5, 6.






Disegno a mano libera su carta quadrettata
Disegno a mano libera: esercizi
3. Riproduci a mano libera su carta quadrettata i disegni proposti.
Riprodurre a mano libera su carta quadrettata i disegni proposti
Fase preliminare di preparazione
Disegno a mano libera: esercizi
Disegno a mano libera su carta non quadrettata
Disegno a mano libera su carta non quadrettata
4. Disegna a mano libera il supporto in Fig. 1.
Disegno a mano libera su carta non quadrettata
Disegnare a mano libera il supporto in fig.1
Disegnare a mano libera il supporto in fig.1
Disegnare a mano libera il supporto in fig.1
Disegno a mano libera su carta non quadrettata
Disegno a mano libera su carta non quadrettata
Disegno a mano libera su carta non quadrettata
Disegnare a mano libera il supporto in fig.1
La figura da riprodurre ha come contorno una serie di circonferenze raccordate tra loro con archi e tangenti. Si tracciano per primi gli assi di simmetria fissando così i centri delle circonferenze e creando inoltre un sistema di riferimento fondamentale in quanto si opera su un foglio senza la quadrettatura di supporto fig.2. Quindi per ciascun centro si costruisca il quadrato con la trama per tracciare la circonferenza corrispondente fig.3. Nel caso delle circonferenze concentriche si esegue la costruzione di quella più piccola in quanto più facile da eseguire.
Disegnare a mano libera il supporto in fig.1
La figura da riprodurre ha come contorno una serie di circonferenze raccordate tra loro con archi e tangenti. Si tracciano per primi gli assi di simmetria fissando così i centri delle circonferenze e creando inoltre un sistema di riferimento fondamentale in quanto si opera su un foglio senza la quadrettatura di supporto fig.2. Quindi per ciascun centro si costruisca il quadrato con la trama per tracciare la circonferenza corrispondente fig.3. Nel caso delle circonferenze concentriche si esegue la costruzione di quella più piccola in quanto più facile da eseguire.
Disegnare a mano libera il supporto in fig.1
La figura da riprodurre ha come contorno una serie di circonferenze raccordate tra loro con archi e tangenti. Si tracciano per primi gli assi di simmetria fissando così i centri delle circonferenze e creando inoltre un sistema di riferimento fondamentale in quanto si opera su un foglio senza la quadrettatura di supporto (➜ Fig. 2). Quindi per ciascun centro si costruisce il quadrato con la trama per tracciare la circonferenza corrispondente (➜ Fig. 3). Nel caso delle circonferenze concentriche si esegue la costruzione di quella più piccola in quanto più facile da eseguire.
La figura da riprodurre ha come contorno una serie di circonferenze raccordate tra loro con archi e tangenti. Si tracciano per primi gli assi di simmetria fissando così i centri delle circonferenze e creando inoltre un sistema di riferimento fondamentale in quanto si opera su un foglio senza la quadrettatura di supporto fig.2. Quindi per ciascun centro si costruisca il quadrato con la trama per tracciare la circonferenza corrispondente fig.3. Nel caso delle circonferenze concentriche si esegue la costruzione di quella più piccola in quanto più facile da eseguire.
La figura da riprodurre ha come contorno una serie di circonferenze raccordate tra loro con archi e tangenti. Si tracciano per primi gli assi di simmetria fissando così i centri delle circonferenze e creando inoltre un sistema di riferimento fondamentale in quanto si opera su un foglio senza la quadrettatura di supporto fig.2. Quindi per ciascun centro si costruisca il quadrato con la trama per tracciare la circonferenza corrispondente fig.3. Nel caso delle circonferenze concentriche si esegue la costruzione di quella più piccola in quanto più facile da eseguire.
La figura da riprodurre ha come contorno una serie di circonferenze raccordate tra loro con archi e tangenti. Si tracciano per primi gli assi di simmetria fissando così i centri delle circonferenze e creando inoltre un sistema di riferimento fondamentale in quanto si opera su un foglio senza la quadrettatura di supporto fig.2. Quindi per ciascun centro si costruisca il quadrato con la trama per tracciare la circonferenza corrispondente fig.3. Nel caso delle circonferenze concentriche si esegue la costruzione di quella più piccola in quanto più facile da eseguire.
La figura da riprodurre ha come contorno una serie di circonferenze raccordate tra loro con archi e tangenti. Si tracciano per primi gli assi di simmetria fissando così i centri delle circonferenze e creando inoltre un sistema di riferimento fondamentale in quanto si opera su un foglio senza la quadrettatura di supporto fig.2. Quindi per ciascun centro si costruisca il quadrato con la trama per tracciare la circonferenza corrispondente fig.3. Nel caso delle circonferenze concentriche si esegue la costruzione di quella più piccola in quanto più facile da eseguire.
➜ Fig. 1
➜ Fig. 2
➜ Fig. 3
Per le circonferenze più grandi e i raccordi è sufficiente fare riferimento a quelle già tracciate facendo cura di manternersi da esse a un distanza costante fig4. Si traccino quindi anche le tangenti e si ripassano gli archi fig.5. Si completa la figura tracciando i raccordi senza ricorrere a particolari costruzioni ma facendo attenzione a che siano archi di circonferenza e che ci sono due brevi tratti rettilinei fig.6
Per le circonferenze più grandi e i raccordi è sufficiente fare riferimento a quelle già tracciate facendo cura di manternersi da esse a un distanza costante fig4. Si traccino quindi anche le tangenti e si ripassano gli archi fig.5. Si completa la figura tracciando i raccordi senza ricorrere a particolari costruzioni ma facendo attenzione a che siano archi di circonferenza e che ci sono due brevi tratti rettilinei fig.6
Per le circonferenze più grandi e i raccordi è sufficiente fare riferimento a quelle già tracciate facendo cura di manternersi da esse a un distanza costante fig4. Si traccino quindi anche le tangenti e si ripassano gli archi fig.5. Si completa la figura tracciando i raccordi senza ricorrere a particolari costruzioni ma facendo attenzione a che siano archi di circonferenza e che ci sono due brevi tratti rettilinei fig.6
Per le circonferenze più grandi e i raccordi è sufficiente fare riferimento a quelle già tracciate avendo cura di mantenersi da esse a un distanza costante (➜ Fig. 4). Si tracciano quindi anche le tangenti e si ripassano gli archi (➜ Fig. 5). Si completa la figura tracciando i raccordi senza ricorrere a particolari costruzioni ma facendo attenzione a che siano archi di circonferenza e che ci sono due brevi tratti rettilinei (➜ Fig. 6).
Per le circonferenze più grandi e i raccordi è sufficiente fare riferimento a quelle già tracciate facendo cura di manternersi da esse a un distanza costante fig4. Si traccino quindi anche le tangenti e si ripassano gli archi fig.5. Si completa la figura tracciando i raccordi senza ricorrere a particolari costruzioni ma facendo attenzione a che siano archi di circonferenza e che ci sono due brevi tratti rettilinei fig.6
Per le circonferenze più grandi e i raccordi è sufficiente fare riferimento a quelle già tracciate facendo cura di manternersi da esse a un distanza costante fig4. Si traccino quindi anche le tangenti e si ripassano gli archi fig.5. Si completa la figura tracciando i raccordi senza ricorrere a particolari costruzioni ma facendo attenzione a che siano archi di circonferenza e che ci sono due brevi tratti rettilinei fig.6
Per le circonferenze più grandi e i raccordi è sufficiente fare riferimento a quelle già tracciate facendo cura di manternersi da esse a un distanza costante fig4. Si traccino quindi anche le tangenti e si ripassano gli archi fig.5. Si completa la figura tracciando i raccordi senza ricorrere a particolari costruzioni ma facendo attenzione a che siano archi di circonferenza e che ci sono due brevi tratti rettilinei fig.6
➜ Fig. 4
➜ Fig. 5
➜ Fig. 6






5. Riproduci a mano libera su carta quadrettata i disegni proposti. Riprodurre a mano libera su carta quadrettata i disegni proposti





1. Premessa
2. La scrivania di AutoCAD
3. L’uso del mouse in AutoCAD
4. L’uso della tastiera in AutoCAD



I layout in AutoCAD
La stampa in AutoCAD
5. I comandi di assistenza in AutoCAD
6. I layer in AutoCAD
7. Inserimenti dati
8. I comandi per disegnare

Il computer fa parte della nostra vita svolgendo funzioni che fino a poco tempo fa non avremmo mai pensato di demandare a una macchina. Anche nel disegno tecnico, con numerosi software specifici, esso ha praticamente sostituito il disegno eseguito con gli strumenti tradizionale. Per il disegno tecnico il software più diffuso è AutoCAD.
Avviato il programma, AutoCAD propone la videata Inizio (➜ Fig. 1) con le scritte Apri (per aprire un qualsiasi file dwg), Nuovo (per creare un nuovo disegno), Recenti (per aprire la lista degli disegni già realizzati), Apprendimento (visualizza i tutorial di apprendimento) (➜ Fig. 2).
Pag. 30
Pag. 30
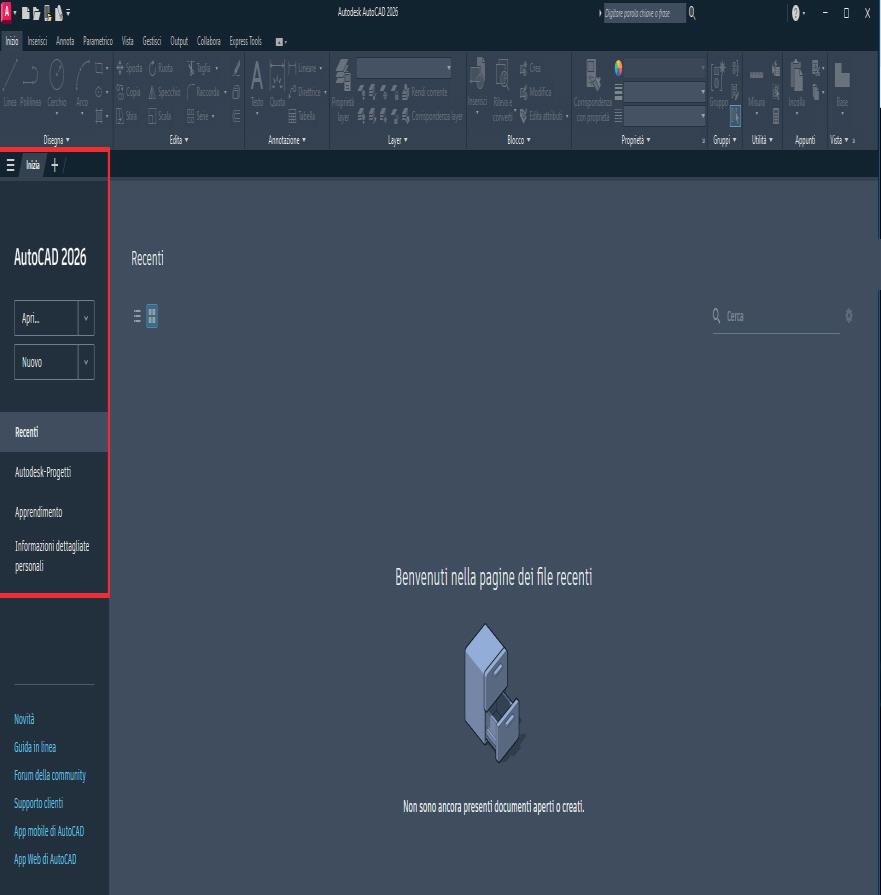
Fig. 1

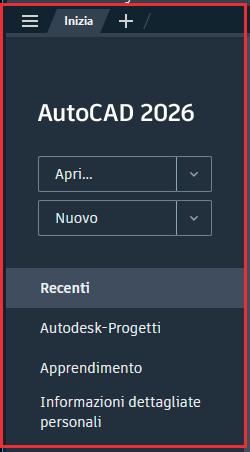

➜ Fig. 1 ➜ Fig. 2
Fig. 1
Pag. 30 aprendo così la videata di Disegno1 ( ➜ Fig. 3) e impariamo a conoscere le caratteristiche e i comandi principali di AutoCAD.
Fig. 2
Fig. 2
Cominciamo direttamente ad operare cliccando sul segno + a fianco della scritta Inizia
Pag.31
Pag.31
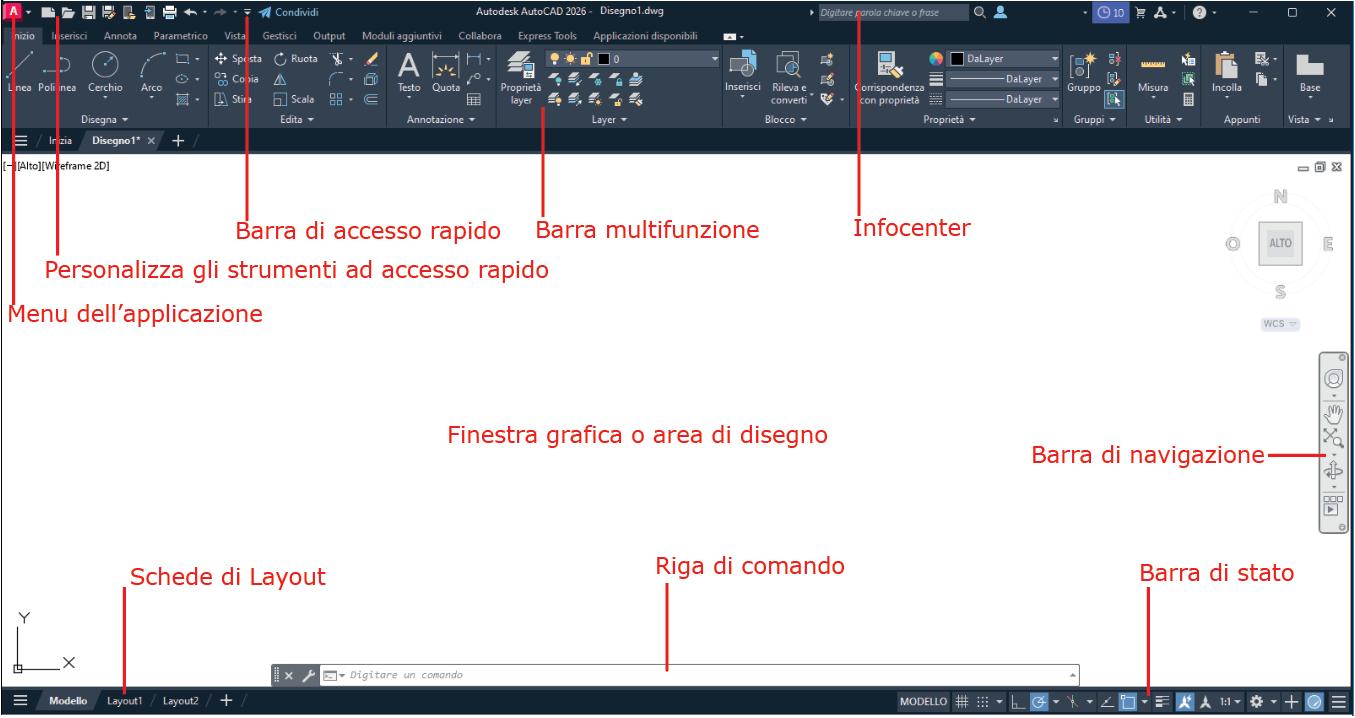













che permette di accedere alle funzioni di gestione del disegno, alla possibilità di aprire, salvare, esportare o stampare i file che compongono i vari elaborati grafici.
3

➜ Fig. 4
4
Dopo aver cliccato su
Fig. 3
Fig. 4 si apre la tendina (➜ Fig. 5) contenente le icone di Strumenti ad accesso rapido con la possibilità, cliccando sui corrispondenti triangolini, di specificare meglio il comando. Sono poi riportati i nomi degli ultimi documenti su cui si è operato e in basso il pulsante Opzioni cliccando sul quale si apre la finestra corrispondente (➜ Fig. 6). Nella parte in alto di essa ci sono alcuni pulsanti, File, Visualizza, ecc. che, una volta premuti, danno accesso a schede che permettono di impostare il funzionamento del programma se-
Pag. 32
Pag. 32
Fig. 5
condo i propri desideri. Può essere utile, nella prima fase di apprendimento, cliccare su Visualizza e spuntare la voce Mostra descrizione comandi. In questo modo, avvicinando il puntatore all’icona di un comando, dopo mezzo secondo di attesa (come impostato nel rettangolino sotto) si apre una finestra con le spiegazioni relative al comando stesso (➜ Fig. 7).
Pag. 32
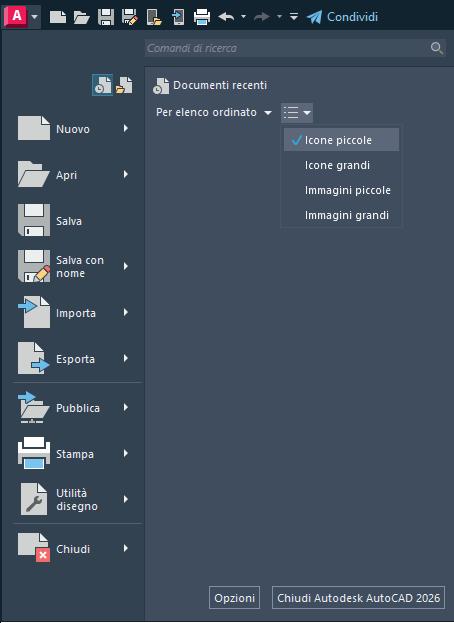
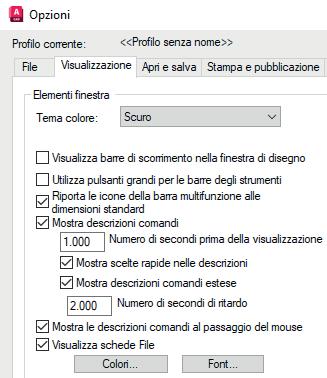
➜ Fig. 5 ➜ Fig. 6
Fig. 5
Fig. 5
2.2.2 AREA DI DISEGNO
Pag. 33
Pag. 33
Pag. 33
Fig. 10
Fig. 10
Fig. 6
Fig. 6
Fig. 6
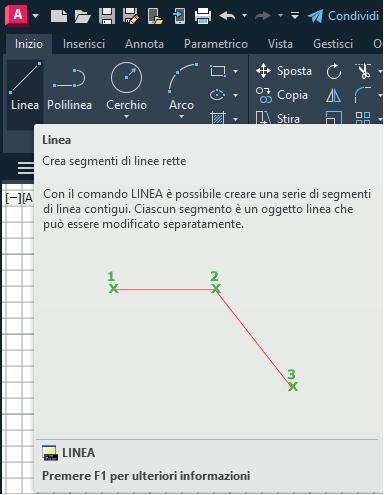
➜ Fig. 7
Fig. 7
Fig. 7
Fig. 7

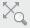
È lo spazio video in cui il disegno è visualizzato e modificato. A destra si trova la Barra di navigazione (➜ Fig. 8) con alcune icone delle quali ci interessano Pan e Zoom Estensioni . Il primo comando, una volta selezionato e tenendo premuto il tasto sinistro del mouse, ci permette di spostare il disegno a video; il secondo, che riporta il triangolino indicante l’apertura a tendina, è la raccolta dei vari Zoom di ingrandimento o riduzione disponibili.
Fig. 10
2.2.3 RIGA DI COMANDO
Fig. 11
Fig. 11
Fig. 11
È in fondo al video (➜ Fig. 9). Permette di “dialogare” col computer. È composta da una o più righe (a seconda delle impostazioni) e riporta sulla destra un triangolino cliccando sul quale si apre una finestra con la cronologia degli ultimi comandi utilizzati e operazioni eseguite. La prima scritta che appare è Digitare un comando, cioè il programma chiede quale comando si vuole utilizzare, per procedere poi con una serie di altre richieste o indicazioni che una volta immesse sono attivate premendo il tasto Invio.
Pag. 35
Pag. 35
Pag. 35
➜ Fig. 9
2.2.4 BARRA DI STATO

➜ Fig. 8
È la barra che si trova più in basso nel video (➜ Fig. 10). È divisa in due parti. A sinistra si trovano le schede di Layout che permettono di organizzare gli spazi carta di un disegno realizzato nello spazio Modello. A destra si trova una gruppo di icone che permettono di attivare o disattivare una serie di aiuti al disegno. Se sono at-



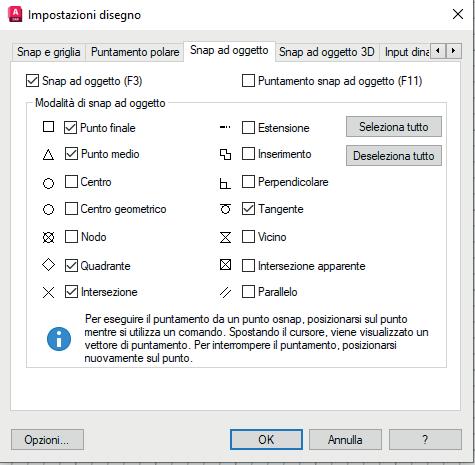

Pag. 32
Fig. 5




tivate il disegno dell’icona che le contraddistingue apparirà blu, se disattivate apparirà grigio. L’ultima icona a destra, che riporta come disegno tre lineette parallele ,se attivata, svolge una tendina in cui sono elencati tutti gli aiuti. Spuntandoli o meno li si fanno apparire o scomparire dalla barra.
Pag. 33
Fig. 6
Fig. 10
Fig. 7
Cliccando sull’icona si apre la tendina di che permette di scegliere tra tre differenti configurazioni di AutoCAD e cioè: , dedicata al disegno 2D, per il disegno 3D con funzionalità avanzate sempre nell’ambiente 3D.


Contiene dieci gruppi di comandi:Disegna, Edita, Annotazione, Layer, Blocco, Proprietà, Gruppi, Utilità, Appunti e Vista
– contiene i comandi per disegnare come: Linea, Polilinea, Cerchio ecc.


– Edita contiene i comandi per modificare disegni già realizzati con un comando Disegna.
Fig. 5
Fig. 11

Pag. 35
Pag. 33


Fig. 6
– Annotazione contiene i comandi per scrivere testi e per apporre le quote
Fig. 7
– Layer permette di scomporre un disegno e distribuirlo su fogli sovrapposti.
Proprietà permette di conoscere e assegnare alcune caratteristiche ai disegni come il colore, lo spessore delle linee ecc.



– Utilità permette, tra le altre cose, di misurare lunghezze, angoli, superfici e volumi dei disegni.
Fig. 10
11
Pag. 35

Alcune icone riportano sotto o a fianco un triangolino che una volta cliccato svolge una tendina contenete ulteriori comandi.



Nel mouse i tasti hanno funzioni distinte. Il tasto sinistro è il tasto operativo: permette di attivare i vari comandi spostare gli oggetti ecc. L’indice sul video che visualizza il suo operare è il che può assumere principalmente cinque forme:
su cornice e icone
su cornice e icone
su cornice e icone
su cornice e icone
su cornice e icone
su cornice e icone
nell’attesa di comando
nell’attesa di comando
nell’attesa di comando
nell’attesa di comando
nell’attesa di comando
nell’attesa di comando
su nestra di testo
su nestra di testo
su nestra di testo
su finestra di testo
su nestra di testo
su nestra di testo

con comando inserito


sul singolo oggetto. Quando un oggetto è selezionato, a video appare evidenziato in blu e con alcuni quadretti, detti grip, dello stesso colore (➜ Fig. 12), in corrispondenza dei suoi punti caratteristici (gli estremi e il punto medio per un segmento, il centro e i quattro punti quadrante in una circonferenza, ecc.).


➜ Fig. 12
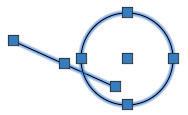
con comando inserito
con comando inserito
con comando inserito
con comando inserito
con comando inserito
con comando inserito per selezionare gli oggetti
con comando inserito per selezionare gli oggetti
a comando inserito per selezionare gli oggetti
con comando inserito per selezionare gli oggetti
con comando inserito per selezionare gli oggetti
con comando inserito per selezionare gli oggetti
Oltre alle funzioni già citate, il tasto di sinistra serve anche a selezionare gli oggetti per poterli modificare. Per eseguire questa operazione è sufficiente cliccare
Agganciando con il puntatore uno dei quadretti, cliccandolo e trascinandolo con il tasto sinistro, è possibile modificare l’oggetto o la sua posizione. Volendo selezionare un gruppo di oggetti, si clicca sul tasto sinistro e si rilascia il tasto, si trascina da sinistra verso destra creando un rettangolo che com-
prenda tutti gli oggetti desiderati e si riclicca sul tasto. In questo caso gli oggetti, perché siano selezionati, devono essere compresi per la loro interezza nel rettangolo (➜ Fig. 13).
➜ Fig. 13
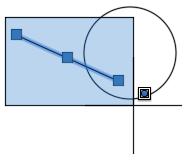
Se invece il rettangolo si ottiene trascinando da destra verso sinistra è sufficiente che gli oggetti siano toccati anche in un sol punto perché rimangano selezionati (➜ Fig. 14).
Fig. 5
Pag. 33
➜ Fig. 14
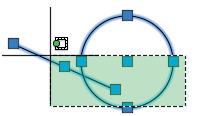
– alla richiesta di Comando, premendo INVIO si richiama l’ultimo comando utilizzato; – premendo INVIO, con un comando di modifica, si indica che si sono finiti gli elementi da selezionare; – quando è proposta un’opzione racchiusa tra < e > basta dare INVIO per accettarla.
La BARRA SPAZIATRICE assume la funzione di INVIO quando però non si sia all’interno di un comando di testo.
In alto ci sono i cosiddetti tasti funzione che permettono di richiamare alcuni aiuti o attivare alcuni supporti per i disegno. (F1= guida in linea; F2= lista comandi eseguiti; F3=puntamento snap ad oggetto; F7= griglia; F9= snap griglia; F10= puntamento polare).
Fig. 6
Fig. 7
Cliccando con il tasto destro del mouse su una delle icone nella barra di stato, in basso a destra del video (ad esempio
C’è un ulteriore modo per selezionare ed è col “lazo”.
Fig. 10
In questo caso si clicca col tasto e lo si mantiene premuto. Quindi lo si trascina inglobando o toccando gli oggetti a seconda che si operi da sinistra a destra o da destra a sinistra.
Il tasto destro può essere opportunamente impostato in Personalizza pulsante destro del mouse nella scheda Preferenze utente, in Opzioni
Fig. 11
Pag. 35
La rotellina centrale del mouse, se ruotata in avanti o indietro, ingrandisce o rimpicciolisce l’immagine a video come in Zoom tempo reale e, se tenuta premuta, permette di spostare l’immagine a schermo come si trattasse di un foglio come in Pan.
La tastiera ha in generale la stessa funzione che ha negli altri programmi, serve cioè a immettere dati, a scrivere testi e ad attivare alcuni comandi.
In particolare: il tasto INVIO permette di eseguire le seguenti operazioni:
– premuto alla fine di ogni digitazione comunica che si è terminato di scrivere e che vanno attuate le indicazioni;
), si apre una tendina in fondo alla quale c’è una scritta come impostazione griglia, impostazione Snap ad oggetto , a seconda che si sia sull’icona di griglia e quella di Snap ad oggetto (Si ricorda che il termine snap è usato nel senso di afferrare). Cliccando su tale scritta si apre la finestra di Impostazioni disegno (➜ Fig. 15) che contiene le schede Snap e griglia, Puntamento polare, Snap ad oggetto, Snap ad oggetto 3D, Input dinamico, Proprietà rapide e Selezione ciclica. Le prime tre schede si riferiscono a comandi proposti per facilitare la realizzazione di un disegno; la scheda Input dinamico invece permette di impostare e attivare alcune indicazioni a fianco del puntatore.
2.5.1 COMANDI Snap AD OGGETTO (DETTI ANCHE Osnap)
Le modalità Snap ad oggetto, dette anche Osnap, consentono di “agganciare” un punto geometricamente significativo di un oggetto, come ad esempio gli estremi di un segmento, il suo punto medio, il centro di una circonferenza, l’intersezione tra due linee ecc. Nella scheda Snap ad oggetto (➜ Fig. 15) è possibile attivare o disattivare i singoli snap selezionandoli spuntando l’apposita casella a fianco del nome. Per attivare o disattivare il comando si può cliccare sull’icona nella Barra di stato (azzurra attivata, grigia disattivata) oppure premere il tasto funzione F3.














Fig. 6
Fig. 6
35




Fig. 7 Fig. 7
Fig. 7 Tangente Fig. 6

➜ Fig. 15
Fig. 7 Fig. 7




Fig. 7
Fig. 7
Fig. 6 Fig. 7










Per attivare o disattivare Puntamento Polare basta cliccare sull’icona corrispondente nella Barra di stato oppure premere il tasto funzione F10.
7 Vicino Fig. 6 Fig. 7
alle domande rispondo sempre si cioè sono valide le figure della scorsa edizione.


Una volta attivato cliccando
A P. 37 le scritte in rosso vanno in nero.

Si devono cambiare le icone a P.35 punti: 2.5.2 2.5.3

sull’icona nella barra di stato, riporta a fianco del puntatore le indicazioni della barra di comando e le coordinate cartesiane o polari, assolute o relative, a seconda dell’impostazione data (➜ Fig. 17). Alla richiesta di un secondo punto, sono visualizzati i valori relativi alla distanza e agli angoli che cambiano in base agli spostamenti del cursore.
Quelli che seguono sono i comandi snap più comunemente usati.
























Punto medio
















Quadrante


Intersezione





Perpendicolare
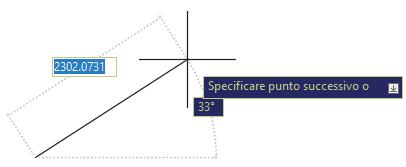
➜ Fig. 17






alle domande rispondo sempre si cioè sono valide le figure della scorsa edizione.


Mediante questo comando

Si devono cambiare le icone a P.35 punti: 2.5.2 2.5.3

A P. 37 le scritte in rosso vanno in nero. si può impostare un incremento angolare che orienta le linee durante il loro tracciamento. I valori possibili dell’Angolo invanno da 5° a 90° (➜ Fig. 16). Pertanto, nel tracciare le linee, si possono immettere direttamente le lunghezze, orientare il mouse nella direzione voluta e dare Invio.

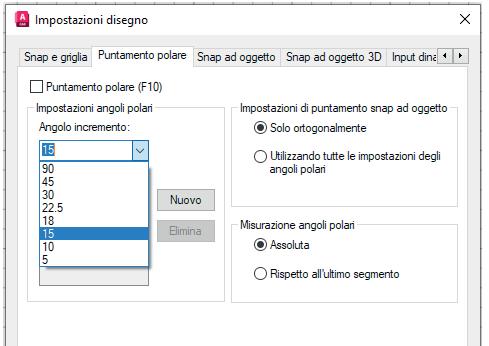
➜ Fig. 16

Il foglio di lavoro di AutoCAD si può immaginare formato da tanti fogli trasparenti sovrapposti (➜ Fig. 18)
➜ Fig. 18
Pag. 36
con la possibilità di disegnare, ad esempio, le linee in vista su un layer, quelle di costruzione su un altro, e così via. Questo modo di operare permette di escludere dalla vista e dalla stampa le parti che non interessano (ad esempio a disegno concluso si può escludere il layer delle linee di costruzione)
Pag. 36
Fig. 20
Fig. 21
Pag. 37
Piastrina
zione richiamando in tal modo la finestra Gestore proprietà layer (➜ Fig. 21).
Si clicca sull’icona Proprietà Layer ( ➜ Fig. 20) nel settore corrispondente ai layer nella Barra multifun-
Fig. 20

Fig. 22
Nella finestra è evidenziato il layer 0 che è quello di default. È creato all’avvio di ogni nuovo disegno, non si può cancellare né rinominare ed è buona norma non disegnare su di esso. La barra delle proprietà del layer è divisa in alcune colonne che contengono alcuni simboli e scritte come On, Congela, Bloccato Stampa che si riferiscono al layer stesso, e Colore, Tipo di linea, Spessore di linea che si riferiscono al disegno che sarà eseguito sul layer.

Fig. 22
Fig. 21
Pag. 37
– On

: serve per attivare e disattivare il layer.

– Congela : ha una funzione simile al comando precedente. La differenza rispetto a On consiste nella rigenerazione, che in un layer congelato non viene effettuata.
Piastrina
Fig. 22



Tampone
– Bloccato : mantiene visibili gli oggetti ma ne impedisce le modifiche.

– Stampa/Non stampare : controlla se stampare i layer selezionati.
Piastrina di base


Tampone
Sostituiamo il nome Layer1 con Spigoli visti, quindi, cliccando sul quadratino della colonna Colore, attribuiamo ad esempio il colore Bianco, lasciamo invariato il tipolinea che è Continous e attribuiamo come spessore di linea 0,40. Ripetiamo l’operazione per ulteriori layer dando loro il nome di Assi, Nascosti, Tratteggi , Quote, Testo , Foglio , attribuendo a ciascuno di essi un colore, un tipolinea e uno spessore di linea (ad esempio 0,20 o 0,40). Per passare da un layer all’altro, mentre si disegna, si utilizza il menù a tendina (➜ Fig. 22). Dopo averlo aperto, si seleziona il layer desiderato cliccando sul suo nome.


Pag. 36

– Tipo linea: serve ad assegnare al layer un tipo di linea. Cliccando prima su Continous e poi sulla scritta Carica appare la finestra Carica o ricarica tipi di linea con i tipi di linea disponibili.
Pag. 36
–Fig. 22 : serve ad attribuire un colore agli oggetti di un layer.


Piastrina di base


Fig. 20



– Spessore linea: modifica lo spessore di linea associato ai layer selezionati. Cliccando sul nome Default viene visualizzata la finestra Spessore linea con l’elenco di tutti gli spessori disponibili.
2.6.3
Ctena



Fig. 22




Fig. 20 Fig. 22


Fig. 21
Nell’iniziare un disegno è utile procedere creando un pacchetto di layer che si presume possano ser vire. Ad esempio clicchiamo in sull’icona

Pag. 37
Fig. 21 e comparirà un nuovo layer di nome Layer1.
Nell’esecuzione di un disegno si procede inserendo i dati utilizzando le coordinate cartesiane oppure le coordinate polari. Esse possono essere assolute, e cioè riferite all’origine UCS (0,0) intersezione degli assi X e Y, oppure relative e cioè riferite all’ultimo punto che si è specificato. Pertanto se si desidera procedere per:
– coordinate assolute: con l’Input dinamico disattivato si immettono direttamente i dati nella barra







1. Tipi di linee
2. Norme per il disegno tecnico: le quote
3. Formati e piegature dei fogli
4. Riquadro delle iscrizioni e archiviazione
Per il segno esiste una norma specifica che stabilisce gli spessori e i tipi di linea da usare nel disegno tecnico. La scelta dello spessore delle linee dipenderà dalla scala del disegno e dalla sua resa grafica in fase di stampa. Sotto sono riportati due estratti delle tabelle contenute nella UNI ISO 128-24:2006. Una riporta gli spessori consigliati per i vari tipi di linee (➜ Tab. 1), l’altra ne descrive le caratteristiche e la loro applicazione (➜ Tab. 2).
Gruppo di linee
Grossezza delle linee per linea n. (in mm) 01.2 01.1 – 02.1 – 04.1
0,5a 0,5 0,25
0,7a 0,7 0,35
a) Gruppi di linee preferibili
➜ Tab. 1 • Grossezza delle linee e gruppi di linee (UNI ISO 128-24:2006).
Tipo di linea
Applicazioni N. descrizione
01.1
01.2
02.1
04.1
linea continua fine
Linea continua grossa
Linea a tratti fine
Linea mista fine a punto e tratto lungo
Linee di costruzione, linee di proiezione, linee di riferimento, linee di misura, linee di griglia e tratteggi.
Spigoli in vista, contorni in vista e rappresentazioni principali in diagrammi e schemi.
Spigoli nascosti e contorni nascosti.
Assi di simmetria e tracce di simmetria.
➜ Tab. 2 • Denominazioni e applicazioni dei tipi di linee (UNI ISO 128-24:2006).
linee di costruzione 01.1
linee di riferimento 01.1 tratteggi 01.1
linee di quota 01.1
assi di simmetria 04.1
contorni in vista 01.2
contorni nascosti 02.1
spigoli nascosti 02.1
spigoli in vista 01.2
leggere le quote che li completano.
Le loro caratteristiche saranno analizzate nel modulo 7.3, per il momento è sufficiente capirne
Tale linea è sempre parallela al segmento di cui indica le dimensioni ed il numero
Le quote sono gli elementi, di un disegno tecnico, che indicano le dimensioni di ciò che è rappresentato. Le loro caratteristiche saranno analizzate nel modulo 7.3, per il momento è sufficiente capirne le indicazioni. Esse si concretizzano nella linea di quota che è una linea avente agli estremi due frecce e un numero al centro.
Per eseguire gli esercizi proposti nelle pagine seguenti, è necessario saper leggere le quote che li completano. Le quote sono gli elementi, di un disegno tecnico, che indicano le dimensioni di ciò che è rappresentato. Le loro caratteristiche saranno analizzate nel modulo 7.3, per il momento è sufficiente capirne le indicazioni.
l’apertura angolare.
Esse si concretizzano nella linea di quota che è una linea avente agli estremi due frecce e un numero al centro.
Tale linea è sempre parallela al segmento di cui indica le dimensioni ed il numero al centro esprime la lunghezza in millimetri o, nel caso degli angoli, l’apertura angolare.



Quotatura di diametri


Quotatura di segmenti Quotatura di angoli

Quotatura di segmenti e di distanze (fig.1).
Quotatura di angoli (fig.2).
Tale linea è sempre parallela al segmento di cui indica le dimensioni ed il numero al centro esprime la lunghezza millimetri o, nel caso degli angoli, l’apertura angolare.
Esse si concretizzano nella linea di quota che è una linea avente agli estremi due frecce e un numero al centro.
Quotatura di diametri
Per eseguire gli esercizi proposti nelle pagine seguenti, è necessario saper leggere le quote che li completano. Le quote sono gli elementi, di un disegno tecnico, che indicano le dimensioni di ciò che è rappresentato. Le loro caratteristiche saranno analizzate nel capitolo 16, per il momento è sufficiente capirne le indicazioni. Esse si concretizzano nella linea di quota che è una linea avente agli estremi due frecce e un numero al centro. Tale linea è sempre parallela al segmento di cui indica le dimensioni e il numero al centro esprime la lunghezza in millimetri o, nel caso degli angoli, l’apertura angolare.
fig.1
Quotatura di segmenti e di distanze (fig.1).
Quotatura di diametri
Quotatura di diametri (fig.3), con il simbolo Ø se dal disegno non risulta chiaro essere diametri (fig.4).
Quotatura di segmenti e di distanze (➜ Fig. 1).
Quotatura di angoli (fig.2).
Quotatura di diametri
Tale linea è sempre parallela al segmento di cui indica le dimensioni ed il numero al centro esprime la lunghezza in millimetri o, nel caso degli angoli, l’apertura angolare.
Quotatura di angoli (fig.2).
Quotatura di segmenti Quotatura di angoli
Quotatura di raccordi (➜ Fig. 5) dove la lettera R indica raggio.
Quotatura di raccordi (fig.5) dove la lettera R indica raggio.
Quotatura di segmenti e di distanze (fig.1).
Quotatura di diametri (fig.3), con il simbolo Ø se dal disegno non risulta chiaro essere diametri (fig.4).
Quotatura di un totale che è suddiviso in parti uguali tra loro (fig.6).
Quotatura di diametri (fig.3), con il simbolo Ø se dal disegno non risulta chiaro essere diametri (fig.4).
Quotatura di raccordi (fig.5) dove la lettera R indica raggio.
Quotatura di oggetti rappresentati in assonometria (fig.7).
Quotatura di segmenti e di distanze (fig.1).
➜ Fig. 1
Quotatura di angoli (fig.2).
Quotatura di raccordi (fig.5) dove la lettera R indica raggio.
Quotatura di un totale che è suddiviso in parti uguali tra loro (fig.6).
fig.1
Quotatura di raccordi
Quotatura di raccordi
5
Quotatura di segmenti Quotatura di angoli
Quotatura di raccordi
Quotatura di totali e
Quotatura di totali e parti uguali
Quotatura di totali e parti uguali
Quotatura di un totale che è suddiviso parti uguali tra loro (fig.6).
Quotatura di angoli (➜ Fig. 2).
Quotatura di diametri (fig.3), con il simbolo Ø se dal disegno non risulta chiaro essere diametri (fig.4).
fig.2
Quotatura di un totale che è suddiviso in parti uguali tra loro (➜ Fig. 6).
Quotatura di segmenti Quotatura di angoli
Quotatura di oggetti rappresentati in assonometria (fig.7).
Quotatura di oggetti rappresentati in assonometria (fig.7).
proposti nelle necessario saper completano. di un le rappresentato. saranno analizmomento è indicazioni. linea di agli numero al al segdimensioni ed il lunghezza angoli, distanze con il risulta (fig.4). dove la suddiviso (fig.6). rappresentati in disegno tecnico: le quote
Quotatura di diametri
Quotatura di raccordi (fig.5) dove la lettera R indica raggio.
Quotatura di un totale che è suddiviso in parti uguali tra loro (fig.6).
Quotatura di raccordi
Quotatura di assonometrie
Quotatura di totali e parti uguali
Quotatura di assonometrie
Quotatura di oggetti rappresentati in assonometria (fig.7).
proposti nelle necessario saper completano. elementi, di un indicano le rappresentato. saranno analizil momento è indicazioni. nella linea di avente agli numero al parallela al segdimensioni ed il la lunghezza degli angoli, di distanze (fig.2). (fig.3), con il non risulta (fig.4). (fig.5) dove la che è suddiviso (fig.6).
Quotatura di segmenti Quotatura di angoli
Quotatura di diametri (➜ Fig. 3), con il simbolo Ø se dal disegno non risulta chiaro essere diametri (➜ Fig. 4).
Quotatura di diametri
➜ Fig. 2 Ø20
Quotatura di diametri
Quotatura di oggetti rappresentati in assonometria (➜ Fig. 7).
Quotatura di assonometrie
fig.4
Quotatura di raccordi
Quotatura di diametri
➜ Fig. 3
fig.3 fig.5
Quotatura di assonometrie
Quotatura di totali e parti uguali
Quotatura di raccordi Quotatura di totali e parti uguali
raccordi Quotatura di totali e parti uguali
Fig. 4
rappresentati in
Quotatura di assonometrie
Le dimensioni dei fogli per il disegno sono fissate dalle tabelle EN ISO 5457/2002. La sigla A0 designa il formato base cui corrisponde una superficie di 1m2 da cui si ricavano gli altri formati mediante successivi dimezzamenti fino a giungere al formato A4 che è il formato a cui normalmente ciascun foglio di formato superiore è ridotto mediante successive piegature come indicato negli esempi sottostanti.
Le dimensioni dei fogli per il disegno sono fissate dalle tabelle EN ISO 5457/2002. La sigla A0 designa il formato base cui corrisponde una superficie di 1m2 da cui si ricavano gli altri formati mediante successivi dimezzamenti fino a giungere al formato A4 che è il formato a cui normalmente ciascun foglio di formato superiore è ridotto mediante successive piegature come indicato negli esempi sottostanti.
Le dimensioni dei fogli per il disegno sono fissate dalle tabelle UNI EN ISO 5457:2002. La sigla A0 designa il formato base cui corrisponde una superficie di 1m2 da cui si ricavano gli altri formati mediante successivi dimezzamenti fino a giungere al formato A4 che è il formato a cui normalmente ciascun foglio di formato superiore è ridotto mediante successive piegature come indicato negli esempi sottostanti.
Le dimensioni dei fogli per il disegno sono fissate dalle tabelle EN ISO 5457/2002. La sigla A0 designa il formato base cui corrisponde una superficie di 1m2 da cui si ricavano gli altri formati mediante successivi dimezzamenti fino a giungere al formato A4 che è il formato a cui normalmente ciascun foglio di formato superiore è ridotto mediante successive piegature come indicato negli esempi sottostanti.
180x277 dimensioni (mm) zona del disegno (mm)
dimensioni (mm) zona del disegno (mm)
841x1189 594x841 420x594
dimensioni (mm) zona del disegno (mm)
210x297 821x1159 574x811






delle iscrizioni o cartiglio è l’elemento identificativo del disegno poichè contiene le informazioni alla sua identificazione, interpretazione e gestione. Le sue caratteristiche sono stabilite dalla UNI EN ISO 7200:2007. La sua dimensione in larghezza è di 180 mm, occupa la parte inferiore foglio UNI A4, distante dai bordi del foglio 10 mm da destra e 20 mm da sinistra. Il suo contecomprende: i dati di identificazione (proprietario legale, numero di identificazione, indice di data di edizione, numero della parte/foglio, numero di parti/fogli, codice della lingua), i descrittivi (titolo, sottotitolo) e i dati amministrativi (reparto responsabile, riferimento autore, verificatore, tipo di documento, classificazione/parole chiave, stadio del documento, delle pagine, numero di pagine, formato dei fogli). I dati indicati in grassetto sono obbligatori. sono riportati i due esempi proposti nelle norme.
delle iscrizioni o cartiglio è l’elemento identificativo del disegno poichè contiene le informazioni alla sua identificazione, interpretazione e gestione. Le sue caratteristiche sono stabilite dalla UNI EN ISO 7200:2007. La sua dimensione in larghezza è di 180 mm, occupa la parte inferiore foglio UNI A4, distante dai bordi del foglio 10 mm da destra e 20 mm da sinistra. Il suo contecomprende: i dati di identificazione (proprietario legale, numero di identificazione, indice di data di edizione, numero della parte/foglio, numero di parti/fogli, codice della lingua), i descrittivi (titolo, sottotitolo) e i dati amministrativi (reparto responsabile, riferimento autore, verificatore, tipo di documento, classificazione/parole chiave, stadio del documento, delle pagine, numero di pagine, formato dei fogli). I dati indicati in grassetto sono obbligatori. sono riportati i due esempi proposti nelle norme.
Reparto responsabile Riferimento tecnico
Il riquadro delle iscrizioni o cartiglio è l’elemento identificativo del disegno poichè contiene le informazioni relative alla sua identificazione, interpretazione e gestione. Le sue caratteristiche sono stabilite dalla norma UNI EN ISO 7200:2007. La sua dimensione in larghezza è di 180 mm, occupa la parte inferiore destra del foglio UNI A4, distante dai bordi del foglio 10 mm da destra e 20 mm da sinistra. Il suo contenuto comprende: i dati di identificazione (proprietario legale, numero di identificazione, indice di revisione, data di edizione, numero della parte/foglio, numero di parti/fogli, codice della lingua), i dati descrittivi (titolo, sottotitolo) e i dati amministrativi (reparto responsabile, riferimento tecnico, autore, verificatore, tipo di documento, classificazione/parole chiave, stadio del documento, numero delle pagine, numero di pagine, formato dei fogli). I dati indicati in grassetto sono obbligatori. Sotto sono riportati i due esempi proposti nelle norme.
Proprietario egale
Autore
Reparto responsabile Riferimento tecnico
Proprietario egale
Verificato da Tipo di documento
Autore
Verificato da Tipo di documento
Titolo, sottotitolo AB 123 456-7
Stadio del documento
Titolo, sottotitolo AB 123 456-7
Rev. Lingua Parte Data di edizione Stadio del documento
Rev. Lingua Parte Data di edizione
— Blocco del titolo in forma compatta — Fornisce il massimo spazio per il contenuto fattuale
➜ Fig. 8 • Blocco del titolo in forma compatta — Fornisce il massimo spazio per il contenuto fattuale.
Reparto responsabile
Riferimento tecnico
Autore Verificato da
— Blocco del titolo in forma compatta — Fornisce il massimo spazio per il contenuto fattuale
Tipo di documento
Stadio del documento
Proprietario legale
Reparto responsabile
Proprietario legale
Riferimento tecnico
Autore Verificato da
Titolo, sottotitolo
Tipo di documento
AB 123 456-7
Stadio del documento
Rev. Lingua Parte Data di edizione
Titolo, sottotitolo AB 123 456-7
Rev. Lingua Parte Data di edizione
➜ Fig. 9 • Blocco del titolo con i campi dei nome delle persone sulla riga aggiuntiva — Fornisce uno spazio maggiore per gli aspetti legali.
Blocco del titolo con i campi dei nome delle persone sulla riga aggiuntiva — Fornisce uno maggiore per gli aspetti legali.
3.4.2
Blocco del titolo con i campi dei nome delle persone sulla riga aggiuntiva — Fornisce uno maggiore per gli aspetti legali.
Archiviare un documento significa conservarlo in modo ordinato in appositi contenitori come cartelline, raccoglitori, armadi, cassettiere ecc.
Ad esempio 25/23 significa: venticinquesimo documento del 2023. .....
un documento significa conservarlo in ordinato in appositi contenitori come cartelraccoglitori, armadi, cassettiere ecc. esempio semplice è la raccolta che un allievo cartellina e in ordine di data, delle tavole eseguite. Un esempio più complesso lo nell’archivio della segreteria ......del proprio
un documento significa conservarlo in ordinato in appositi contenitori come cartelraccoglitori, armadi, cassettiere ecc. esempio semplice è la raccolta che un allievo cartellina e in ordine di data, delle tavole eseguite. Un esempio più complesso lo nell’archivio della segreteria ......del proprio
Un esempio semplice di archiviazione è la raccolta che un allievo fa, in un’apposita cartellina e in ordine di realizzazione, delle tavole di disegno eseguite. Un esempio ben più complesso lo si può trovare nell’archivio della segreteria del proprio Istituto.
Un metodo di siglatura efficace può essere il seguente: immaginiamo che sia necessario archiviare dell’allievo Rossi (ROS) Alessandro (A) della classe prima A (1A) per l’anno scolastico 2023 (23) il secondo (02) compito di disegno (D). La sigla risulterà: ROS A 1A 23 D02.
Ad esempio 25/23 significa: venticinquesimo documento del 2023. .....
Nell’archiviazione di un documento ci si imbatte in due problemi: la catalogazione e il formato.
3.4.3
Nell’archiviazione di un documento ci si imbatte in problemi: la catalogazione e il formato.
Un metodo di siglatura efficace può essere il seguente: immaginiamo che sia necessario archiviare dell’allievo Rossi (ROS) Alessandro (A) della classe prima A (1A) per l’anno scolastico 2023 (23) il secondo (02) compito di disegno (D) ; la sgla risulterà: ROS A 1A 23 D02. Riassumendo, la regola è: le prime tre lettere del cognome e la prima del nome, la classe e sezione, le ultimedue cifre dell’anno, il simbolo relativo al tipo di documento (D= disegno, M= matematica ecc.) con il numero d’ordine.
La catalogazione
Nell’archiviazione di un documento ci si imbatte in problemi: la catalogazione e il formato.
Consiste nell’assegnazione di una sigla, composta da numeri e/o lettere, che identifica il documento. Essa, come una specie di targa, permette di rintracciare il documento nell’ambito dell’archivio.
nell’assegnare una sigla, composta da e/o lettere, al documento. ...Essa, come di targa, permette di rintracciare il documento nell’archivio.
La catalogazione nell’assegnare una sigla, composta da e/o lettere, al documento. ...Essa, come di targa, permette di rintracciare il documento nell’archivio.
elementare siglatura è data dalla numeraprogressiva seguita, dopo una barra separaultime due cifre dell’anno in cui viene
elementare siglatura è data dalla numeraprogressiva seguita, dopo una barra separaultime due cifre dell’anno in cui viene
Un metodo di siglatura efficace può essere il seguente: immaginiamo che sia necessario archiviare dell’allievo Rossi (ROS) Alessandro (A) della classe prima A (1A) per l’anno scolastico 2023 (23) il secondo (02) compito di disegno (D) ; la sgla risulterà: ROS A 1A 23 D02. Riassumendo, la regola è: le prime tre lettere del cognome e la prima del nome, la classe e sezione, le ultimedue cifre dell’anno, il simbolo relativo al tipo di documento (D= disegno, M= matematica ecc.) con il numero d’ordine.
Riassumendo, la regola è: le prime tre lettere del cognome e la prima del nome, la classe e sezione, le ultime due cifre dell’anno, il simbolo relativo al tipo di documento (D = disegno, M = matematica ecc.) con il numero d’ordine.
5.4.4 Il formato
Normalmente la gran parte dei documenti ha le dimensioni del foglio UNI A4 (210x297mm) e pertanto i contenitori sono realizzati in base a queste misure.
La più elementare siglatura è data dalla numerazione progressiva seguita, dopo una barra separatrice, dalle ultime due cifre dell’anno in cui viene eseguita. Ad esempio 25/23 significa: venticinquesimo documento del 2023.
Normalmente la granparte dei documenti ha le dimensioni del foglio UNI A4 (210x297mm) e pertanto i contenitori sono realizzati in base a queste misure. A volte, però, soprattutto i disegni possono avere dimensioni maggiori, per cui si deve procedere o a riporli in cassettiere, di dimensioni opportune, oppure alla loro piegatura fino a ridurli alle dimensioni UNI A4 come esemplificato nel paragrafo precedente.
A volte, però, soprattutto i disegni possono avere dimensioni maggiori, per cui si deve procedere o a riporli in cassettiere, di dimensioni opportune, oppure alla loro piegatura fino a ridurli alle dimensioni UNI A4, come esemplificato nel paragrafo precedente.
Normalmente la granparte dei documenti ha le dimensioni del foglio UNI A4 (210x297mm) e pertanto i contenitori sono realizzati in base a queste misure. A volte, però, soprattutto i disegni possono avere dimensioni maggiori, per cui si deve procedere o a riporli in cassettiere, di dimensioni opportune, oppure alla loro piegatura fino a ridurli alle dimensioni UNI A4 come esemplificato nel paragrafo precedente.









MATERIALI DIGITALI










CAPITOLO 4 costruzioni piane fondamentali




VERIFICA LE CONOSCENZE
● Enti geometrici primitivi: punto, retta, piano
● Figure geometriche
● Gli elementi di un poligono
● Triangoli: classificazione, elementi, punti notevoli


● Quadrilateri
SVILUPPA LE ABILITÀ

● Poligoni regolari






● Circonferenza, cerchio, raccordi circolari
● Curve policentriche, cicliche e meccaniche
● Coniche
● Metodi per la riproduzione dei disegni
● Scale di riduzione e di ingrandimento
● Eseguire costruzioni di rette e angoli
● Eseguire costruzioni di poligoni


● Conoscere i termini e le definizioni geometriche fondamentali per il disegno
● Eseguire costruzioni di circonferenze, tangenti e raccordi
● Eseguire costruzioni di curve policentriche e cicliche
● Eseguire costruzioni di coniche
COSTRUISCI LE COMPETENZE



● Saper cogliere la struttura geometrica di una figura
● Saper distinguere tra enti e figure geometriche
● Descrivere le caratteristiche dei diversi poligoni
● Essere in grado di seguire le indicazioni per realizzare disegni tecnici corretti


● Utilizzare le procedure apprese per riprodurre disegni complessi di oggetti reali




























Grazie alla collaborazione tra il CNR -Isof di Bologna e l’azienda italiana Medica S.P.A. è nata una nuova tecnologia per migliorare la qualità dell’acqua potabile, che si basa su filtri a base di ossido di grafene e polisulfone, un materiale termoplastico a elevata robustezza. Progettati completamente in Italia più di dieci anni fa, questi filtri riescono a catturare anche inquinanti molto resistenti come i PFAS, alcuni antibiotici e il piombo. I contaminanti dell’ambiente che rischiano di arrivare fino ai nostri rubinetti sono principalmente farmaci, pesticidi, cosmetici e perfino i filtri solari.








La novità non è solo l’efficacia: questi filtri possono essere prodotti con costi contenuti, possono essere integrati facilmente nelle linee di produzione già esistenti e utilizzano pochissimo grafene, il che rende questa tecnologia sostenibile. Questo è quindi un esempio concreto di come la scienza e le aziende, lavorando insieme, possano migliorare la vita di tutti.













sono definite figure piane è necessadette spigoli, che racchisignifica rispettandone le anche le direttamente stesso. riconducendi rappreconoscano
averso una appresentazione di più triangoli

Le forme, nel meccanismo della visione, sono definite principalmente dal loro contorno. Nelle figure piane esso è dato dal perimetro; nei solidi invece è necessa rio riprodurre anche l’insieme di linee, dette spigoli, che rappresentano le intersezioni dei piani che r udono il solido.
Le forme, nel meccanismo della visione, sono definite principalmente dal loro contorno. Nelle figure piane esso è dato dal perimetro; nei solidi invece è necessa rio riprodurre anche l’insieme di linee, dette spigoli, che rappresentano le intersezioni dei piani che r udono il solido
Le forme, nel meccanismo della visione, sono definite principalmente dal loro contorno. Nelle figure piane esso è dato dal perimetro; nei solidi invece è necessa rio riprodurre anche l’insieme di linee, dette spigoli, che rappresentano le intersezioni dei piani che r udono il solido.
Le forme, nel meccanismo della visione, sono definite principalmente dal loro contorno. Nelle figure piane esso è dato dal perimetro; nei solidi invece è necessa rio riprodurre anche l’insieme di linee, dette spigoli, appresentano le intersezioni dei piani che r
Rappresentare graficamente un oggetto significa riprodurne la forma su un foglio, rispettandone le proporzioni e riportandone eventualmente anche le

Rappresentare graficamente un oggetto significa riprodurne la forma su un foglio, rispettandone le proporzioni e riportandone eventualmente anche le
Rappresentare graficamente un oggetto significa riprodurne la forma su un foglio, rispettandone le proporzioni e riportandone eventualmente anche le
CI OCCUPEREMO

è una figura geometrica costituita da punti successivi, ha come unica dimensione la lunghezza.
è una figura geometrica costituita da punti successivi, ha come unica dimensione la lunghezza.
è una figura geometrica costituita da punti successivi, ha come unica dimensione la lunghezza.
è una figura geometrica costituita da punti successivi, ha come unica dimensione la lunghezza.
è un elemento geometrico fondamentale che indica in modo univoco una direzione nello spazio o utte le rette si indicano con una letter
è un elemento geometrico fondamentale che indica in modo univoco una direzione nello spazio o utte le rette si indicano con una lettera
è un elemento geometrico fondamentale che indica in modo univoco una direzione nello spazio o utte le rette si indicano con una lettera
aficamente un oggetto significa riprodurne la forma su un foglio, rispettandone le proporzioni e riportandone eventualmente anche le



Nel fare questo ci si imbatte in difficoltà direttamente proporzionali alla complessità dell’oggetto stesso. Queste difficoltà possono essere superate riconducenappresentazione grafica alla somma di rappresentazioni di forme semplici, delle quali si conoscano
1. Punto, retta, piano, angolo
Nel fare questo ci si imbatte in difficoltà direttamente proporzionali alla complessità dell’oggetto stesso. Queste difficoltà possono essere superate riconducenappresentazione grafica alla somma di rappresentazioni di forme semplici, delle quali si conoscano
Nel fare questo ci si imbatte in difficoltà direttamente proporzionali alla complessità dell’oggetto stesso.
Queste difficoltà possono essere superate riconducenappresentazione grafica alla somma di rappresentazioni di forme semplici, delle quali si conoscano
2. Costruzioni di rette e angoli
3. I poligoni
Nel fare questo ci si imbatte in difficoltà direttamente proporzionali alla complessità dell’oggetto stesso. Queste difficoltà possono essere superate riconducenappresentazione grafica alla somma di rappresentazioni di forme semplici, delle quali si conoscano
4. Costruzioni di poligoni
Nella fig.1 si vede come sia possibile, attraverso una serie di approssimazioni, ridurre la rappresentazione di un fiocco di neve alla sovrapposizione di più triangoli
Nella fig.1 si vede come sia possibile, attraverso una serie di approssimazioni, ridurre la rappresentazione di un fiocco di neve alla sovrapposizione di più triangoli
Nella fig.1 si vede come sia possibile, attraverso una serie di approssimazioni, ridurre la rappresentazione di un fiocco di neve alla sovrapposizione di più triangoli
6. Costruzioni di circonferenze, tangenti e raccordi
Nella fig.1 si vede come sia possibile, attraverso una serie di approssimazioni, ridurre la rappresentazione di un fiocco di neve alla sovrapposizione di più triangoli equilateri.
fig. 1
fig. 1
è un elemento geometrico fondamentale che indica in modo univoco una direzione nello spazio o nel piano. Tutte le rette si indicano con una lettera minuscola.
POSIZIONI RECIPROCHE TRA RETTE
Due rette distinte si dicono incidenti quando hanno un punto in comune.
7. Le curve policentriche e le curve cicliche
Due rette distinte si dicono incidenti quando hanno un punto in comune.
Due rette distinte si dicono incidenti quando hanno un punto in comune.
8. Costruzioni di curve policentriche e cicliche
Due rette distinte si dicono incidenti quando hanno un punto in comune.
5. La circonferenza e i raccordi circolari
9. Le coniche
10. Costruzioni di coniche
11. Metodi per la riproduzione dei disegni
12. Scale di riduzione e di ingrandimento
Due rette incidenti si dicono perpendicolari quando formano quattro angoli congruenti che, essendo la loro misura la quarta parte dell’angolo giro, risultano essere di 90°.
Due rette incidenti si dicono perpendicolari quando formano quattro angoli congruenti che, essendo la loro misura la quarta parte dell’angolo giro, risultano essere di 90°.
Due rette incidenti si dicono perpendicolari quando formano quattro angoli congruenti che, essendo la loro misura la quarta parte dell’angolo giro, risultano essere di 90°.

Due rette incidenti si dicono perpendicolari quando formano quattro angoli congruenti che, essendo la loro misura la quarta parte dell’angolo giro, risultano essere di 90°.
Questo modo di procedere ha permesso di sfruttare le forme geometriche per rappresentare l’esistente e progettare ciò che si vuole costruire.
1
Questo modo di procedere ha permesso di sfruttare le forme geometriche per rappresentare l’esistente e progettare ciò che si vuole costruire.
La geometria permette di disegnare figure anche complesse utilizzando gli elementi fondamentali, gli enti primitivi, ovvero punti, rette e piani. Con questi mattoni è possibile costruire tutto l’edificio della costruzione grafica. Una figura geometrica è un qualunque insieme di punti.
Questo modo di procedere ha permesso di sfruttare le forme geometriche per rappresentare l’esistente e progettare ciò che si vuole costruire.
Due rette incidenti sono perpendicolari quando formano quattro angoli congruenti che, essendo la loro misura la quarta parte dell’angolo giro, risultano essere di 90°.
Questo modo di procedere ha permesso di sfruttare le forme geometriche per rappresentare l’esistente e progettare ciò che si vuole costruire.
� PUNTO
Abbiamo visto come sia necessario far riferimento alla geometria come scienza che regola il rapporto tra i vari elementi di un piano o di un solido. Tutte le figure possono essere rappresentate utilizzando gli elementi geometrici fondamentali; risulta perciò utile ricordare qui quelli che sono i principi costitutivi di questa disciplina.
Abbiamo visto come sia necessario far riferimento alla geometria come scienza che regola il rapporto tra i vari elementi di un piano o di un solido. Tutte le figure possono essere rappresentate utilizzando gli elementi geometrici fondamentali; risulta perciò utile ricordare qui quelli che sono i principi costitutivi di questa disciplina.
Il punto è un ente geometrico privo di dimensioni che indica una posizione univoca nello spazio o nel piano. Ad esempio, l’intersezione tra due rette su un piano determina un punto. Il punto si indica con una lettera maiuscola.
Abbiamo visto come sia necessario far riferimento alla geometria come scienza che regola il rapporto tra i vari elementi di un piano o di un solido. Tutte le figure possono essere rappresentate utilizzando gli elementi geometrici fondamentali; risulta perciò utile ricordare qui quelli che sono i principi costitutivi di questa disciplina.
r sono definite figure piane è necessaspigoli, che racchisignifica rispettandone le anche le direttamente stesso. riconducendi rappreconoscano averso una appresentazione di triangoli
Abbiamo visto come sia necessario far riferimento alla geometria come scienza che regola il rapporto tra i vari elementi di un piano o di un solido. Tutte le figure possono essere rappresentate utilizzando gli elementi geometrici fondamentali; risulta perciò utile ricordare qui quelli che sono i principi costitutivi di questa disciplina.
Le fondamenta della geometria si basano sugli enti primitivi o elementi fondamentali, quali il punto la retta e il piano. Utilizzando questi mattoni riusciamo a costruire tutto l’edificio della costruzione grafica.
Due rette, nello stesso piano, si dicono parallele quando non hanno alcun punto in comune, coincidenti quando hanno tutti i punti in comune. fig. 1
Due rette, nello stesso piano, si dicono parallele quando non hanno alcun punto in comune, coincidenti quando hanno tutti i punti in comune.
Due rette, nello stesso piano, si dicono parallele quando non hanno alcun punto in comune, coincidenti quando hanno tutti i punti in comune.
La linea è una figura geometrica costituita da punti successivi, ha come unica dimensione la lunghezza.
Due rette, nello stesso piano, sono parallele quando non hanno alcun punto in comune, sono coincidenti quando hanno tutti i punti in comune.
La linea è una figura geometrica costituita da punti successivi, ha come unica dimensione la lunghezza.
� RETTA
Le fondamenta della geometria si basano sugli enti primitivi o elementi fondamentali, quali il punto la retta e il piano. Utilizzando questi mattoni riusciamo a costruire tutto l’edificio della costruzione grafica.
DEF: Qualunque insieme di punti si dice figura geometrica.
La retta è un ente geometrico che indica in modo univoco una direzione nello spazio o nel piano. La retta si indica con una lettera minuscola.
DEF: Qualunque insieme di punti si dice figura geometrica.
Le fondamenta della geometria si basano sugli enti primitivi o elementi fondamentali, quali il punto la retta e il piano. Utilizzando questi mattoni riusciamo a costruire tutto l’edificio della costruzione grafica. DEF: Qualunque insieme di punti si dice figura geometrica.
Le fondamenta della geometria si basano sugli enti primitivi o elementi fondamentali, quali il punto la retta e il piano. Utilizzando questi mattoni riusciamo a costruire tutto l’edificio della costruzione grafica. DEF: Qualunque insieme di punti si dice figura geometrica.
Il punto è un elemento geometrico fondamentale, privo di dimensioni e indica una posizione univoca nello spazio o nel piano. Per esempio l’intersezione di due rette determinano un punto su un piano. Tutti i punti si indicano con una lettera maiuscola dell’alfabeto latino.
Due rette, nello stesso piano, si dicono parallele quando non hanno alcun punto in comune, coincidenti quando hanno tutti i punti in comune.
La retta è un elemento geometrico fondamentale che indica in modo univoco una direzione nello spazio o nel piano. Tutte le rette si indicano con una lettera minuscola.
La retta è un elemento geometrico fondamentale che indica in modo univoco una direzione nello spazio o nel piano. Tutte le rette si indicano con una lettera minuscola.
Il punto è un elemento geometrico fondamentale, privo di dimensioni e indica una posizione univoca nello spazio o nel piano. Per esempio l’intersezione di due rette determinano un punto su un piano. Tutti i punti si indicano con una lettera maiuscola dell’alfabeto latino.
r
Elementi generati dalla retta
� SEMIRETTA
Elementi generati dalla retta
Elementi generati dalla retta
semiretta
semiretta
semiretta
Elementi generati dalla retta
semiretta
POSIZIONI RECIPROCHE TRA RETTE
Due rette possono assumere diverse posizioni reciproche nel piano. Due rette distinte sono incidenti quando hanno un punto in comune.
Il punto è un elemento geometrico fondamentale, privo di dimensioni e indica una posizione univoca nello spazio o nel piano. Per esempio l’intersezione di due rette determinano un punto su un piano. Tutti i punti si indicano con una lettera maiuscola dell’alfabeto latino.
Il punto è un elemento geometrico fondamentale, privo di dimensioni e indica una posizione univoca nello spazio o nel piano. Per esempio l’intersezione di due rette determinano un punto su un piano. Tutti i punti si indicano con una lettera maiuscola dell’alfabeto latino.
Data una retta e fissato su di essa un punto O, formano una semiretta il punto stesso e tutti i punti che lo precedono, o lo seguono. Il punto O è detto origine della semiretta. Una semiretta è il prolungamento dell’altra.
Data una retta e fissato su di essa un punto O, formano una semiretta il punto stesso e tutti i punti che lo precedono, o lo seguono. Il punto O è detto origine della semiretta.
Una semiretta è il prolungamento dell’altra
Data una retta e fissato su di essa un punto O, formano una semiretta il punto stesso e tutti i punti che lo precedono, o lo seguono. Il punto O è detto origine della semiretta. Una semiretta è il prolungamento dell’altra
Data una retta e fissato su di essa un punto O, formano una semiretta il punto stesso e tutti i punti che lo precedono, o lo seguono. Il punto O è detto origine della semiretta.
Una semiretta è il prolungamento dell’altra
Due rette distinte si dicono incidenti quando hanno un punto in comune.
Due rette distinte si dicono incidenti quando hanno un punto in comune.
�
Data una retta e fissato su di essa un punto O, formano una semiretta il punto stesso e tutti i punti che lo precedono, o lo seguono. Il punto O è detto origine della semiretta.
segmento
segmento
Due rette incidenti si dicono perpendicolari quando formano quattro angoli congruenti che, essendo la loro misura la quarta parte dell’angolo giro, risultano essere di 90°.
Due rette incidenti si dicono perpendicolari quando formano quattro angoli congruenti che, essendo la loro misura la quarta parte dell’angolo giro, risultano essere di 90°.
Una semiretta è il prolungamento dell’altra
segmento
Data una retta e fissati su di essa due punti A e B, formano un segmento i punti A e B e tutti i punti compresi tra essi. A e B sono gli estremi del segmento.
segmento
Data una retta e fissati due punti su di essa A e B, formano un segmento i punti A e B e tutti i punti compresi tra essi. A e B sono gli estremi del segmento.
Data una retta e fissati due punti su di essa A e B, formano un segmento i punti A e B e tutti i punti compresi tra essi. A e B sono gli estremi del segmento.
Data una retta e fissati due punti su di essa A e B, formano un segmento i punti A e B e tutti i punti compresi tra essi. A e B sono gli estremi del segmento.
Data una retta e fissati due punti su di essa A e B, formano un segmento i punti A e B e tutti i punti compresi tra essi. A e B sono gli estremi del segmento.
PASSO PASSO 4.2.1 ASSE DI
Problema 1: Tracciare l’asse del segmento AB
Problema 1: Tracciare l’asse del segmento AB
Problema 1: Tracciare l’asse del segmento AB
1 Consideriamo il segmento AB.
Sia dato il segmento AB
Sia dato il segmento AB
Sia dato il segmento AB

3 La retta passante per 1 e 2 è l’asse cercato.
Problema 1: Tracciare l’asse del segmento AB
Problema 1: Tracciare l’asse del segmento AB
Problema 1: Tracciare l’asse del segmento AB
Problema 1: Tracciare l’asse del segmento AB
Aperto il compasso a piacere con misura R superiore alla metà di AB, si punti in A e B e si traccino quattro archetti che si incrociano in H e in K.
2 Aperto il compasso con misura R a piacere, superiore alla metà di AB, puntiamo in A e B e tracciamo quattro archetti che si incrociano in 1 e in 2.
Aperto il compasso a piacere con misura R superiore alla metà di AB, si punti in A e B e si traccino quattro archetti che si incrociano in H e in K.
Aperto il compasso a piacere con misura R superiore alla metà di AB, si punti in A e B e si traccino quattro archetti che si incrociano in H e in K.
Tracciando una linea passante per H e K si ottiene l’asse cercato
Tracciando una linea passante per H e K si ottiene l’asse cercato
Tracciando una linea passante per H e K si ottiene l’asse cercato
Sia dato il segmento AB
Sia dato il segmento AB
Sia dato il segmento AB
Sia dato il segmento AB
Problema 1: Tracciare l’asse del segmento AB
Problema 1: Tracciare l’asse del segmento AB
Problema 1: Tracciare l’asse del segmento AB
Sia dato il segmento AB
Sia dato il segmento AB
Sia dato il segmento AB
Aperto il compasso a piacere con misura R superiore alla metà di AB, si punti in A e B e si traccino quattro archetti che si incrociano in H e in K.
Aperto il compasso a piacere con misura R superiore alla metà di AB, si punti in A e B e si traccino quattro archetti che si incrociano in H e in K.
Aperto il compasso a piacere con misura R superiore alla metà di AB, si punti in A e B e si traccino quattro archetti che si incrociano in H e in K.
Aperto il compasso a piacere con misura R superiore alla metà di AB, si punti in A e B e si traccino quattro archetti che si incrociano in H e in K.
Aperto il compasso a piacere con misura R superiore alla metà di AB, si punti in A e B e si traccino quattro archetti che si incrociano in H e in K.
Tracciando una linea passante per H e K si ottiene l’asse cercato
Aperto il compasso a piacere con misura R superiore alla metà di AB, si punti in A e B e si traccino quattro archetti che si incrociano in H e in K.
Aperto il compasso a piacere con misura R superiore alla metà di AB, si punti in A e B e si traccino quattro archetti che si incrociano in H e in K.
Tracciando una linea passante per H e K si ottiene l’asse cercato
Tracciando una linea passante per H e K si ottiene l’asse cercato
Tracciando una linea passante per H e K si ottiene l’asse cercato
Tracciando una linea passante per H e K si ottiene l’asse cercato.
Tracciando una linea passante per H e K si ottiene l’asse cercato.
Tracciando una linea passante per H e K si ottiene l’asse cercato.
con le SQUADRE
1) Allinea Sq.30/60 con AB e falla scorrere verso il basso; 2) Appoggia Sq.45 su Sq.30/60 allineata all’estremo A e traccia una linea a 45°; 3) Ripeti l’operazione in B determinando H; 4) Traccia la perpendicolare per H.
1) Allinea Sq.30/60 con AB e falla scorrere verso il basso; 2) Appoggia Sq.45 su Sq.30/60 allineata all’estremo A e traccia una linea a 45°; 3) Ripeti l’operazione in B determinando H; 4) Traccia la perpendicolare per H.
1) Allinea Sq.30/60 con AB e falla scorrere verso il basso; 2) Appoggia Sq.45 su Sq.30/60 allineata all’estremo A e traccia una linea a 45°; 3) Ripeti l’operazione in B determinando H; 4) Traccia la perpendicolare per H.
a Allinea la squadra 30/60 con AB e falla scorrere verso il basso. b Appoggia la squadra 45 sulla squadra 30/60 allineata all’estremo A e traccia una linea a 45°. c Ripeti l’operazione in B determinando 1. d Traccia la perpendicolare per 1.
1) Allinea Sq.30/60 con AB e falla scorrere verso il basso; 2) Appoggia Sq.45 su Sq.30/60 allineata all’estremo A e traccia una linea a 45°; 3) Ripeti l’operazione in B determinando H; 4) Traccia la perpendicolare per H.
1) Allinea Sq.30/60 con AB e falla scorrere verso il basso; 2) Appoggia Sq.45 su Sq.30/60 allineata all’estremo A e traccia una linea a 45°; 3) Ripeti l’operazione in B determinando H; 4) Traccia la perpendicolare per H.
1) Allinea Sq.30/60 con AB e falla scorrere verso il basso; 2) Appoggia Sq.45 su Sq.30/60 allineata all’estremo A e traccia una linea a 45°; 3) Ripeti l’operazione in B determinando H; 4) Traccia la perpendicolare per H.
1) Allinea Sq.30/60 con AB e falla scorrere verso il basso; 2) Appoggia Sq.45 su Sq.30/60 allineata all’estremo A e traccia una linea a 45°; 3) Ripeti l’operazione in B determinando H; 4) Traccia la perpendicolare per H.
1) Allinea Sq.30/60 con AB e falla scorrere verso il basso; 2) Appoggia Sq.45 su Sq.30/60 allineata all’estremo A e traccia una linea a 45°; 3) Ripeti l’operazione in B determinando H; 4) Traccia la perpendicolare per H.
1) Allinea Sq.30/60 con AB e falla scorrere verso il basso; 2) Appoggia Sq.45 su Sq.30/60 allineata all’estremo A e traccia una linea a 45°; 3) Ripeti l’operazione in B determinando H; 4) Traccia la perpendicolare per H.
1) Allinea Sq.30/60 con AB e falla scorrere verso il basso; 2) Appoggia Sq.45 su Sq.30/60 allineata all’estremo A e traccia una linea a 45°; 3) Ripeti l’operazione in B determinando H; 4) Traccia la perpendicolare per H.
Problema 2: Tracciare la perpendicolare alla retta s per un suo punto P
Problema 2: Tracciare la perpendicolare alla retta s per un suo punto P
Problema 2: Tracciare la perpendicolare alla retta s per un suo punto P
Data la retta s e il punto P si punti in P con apertura a piacere e si tracci una semicirconferenza che determina i punti A e B
Data la retta s e il punto P si punti in P con apertura a piacere e si tracci una semicirconferenza che determina i punti A e B
Data la retta s e il punto P si punti in P con apertura a piacere e si tracci una semicirconferenza che determina i punti A e B

Tracciando una linea passante per H e per P si ottiene la perpendicolare cercata
Tracciando una linea passante per H e per P si ottiene la perpendicolare cercata
Tracciando una linea passante per H e per P si ottiene la perpendicolare cercata
Problema 2: Tracciare la perpendicolare alla retta s per un suo punto P
Problema 2: Tracciare la perpendicolare alla retta s per un suo punto P
Con il compasso aperto a piacere, ma con R maggiore di AP, si punti in A e in B e si traccino due archetti che intersecandosi determinano il punto H
Con il compasso aperto a piacere, ma con R maggiore di AP, si punti in A e in B e si traccino due archetti che intersecandosi determinano il punto H
Problema 2: Tracciare la perpendicolare alla retta s per un suo punto P
Problema 2: Tracciare la perpendicolare alla retta s per un suo punto P
Con il compasso aperto a piacere, ma con R maggiore di AP, si punti in A e in B e si traccino due archetti che intersecandosi determinano il punto H
PASSO PASSO 4.2.2
Data la retta s e il punto P si punti in P con apertura a piacere e si tracci una semicirconferenza che determina i punti A e B
Data la retta s e il punto P si punti in P con apertura a piacere e si tracci una semicirconferenza che determina i punti A e B
Data la retta s e il punto P si punti in P con apertura a piacere e si tracci una semicirconferenza che determina i punti A e B
Data la retta s e il punto P si punti in P con apertura a piacere e si tracci una semicirconferenza che determina i punti A e B
Data la retta s e il punto P si punti in P con apertura a piacere e si acci una semicirconferenza che determina i punti A e B
Data la retta s e il punto P si punti in P con apertura a piacere e si tracci una semicirconferenza che determina i punti A e B
Dati la retta s e il punto P puntiamo in P con apertura a piacere e tracciamo una semicirconferenza che interseca la retta s nei punti 1 e 2.
Data la retta s e il punto P si punti in P con apertura a piacere e si tracci una semicirconferenza che determina i punti A e B
Con il compasso aperto a piacere, ma con R maggiore di AP, si punti in A e in B e si traccino due archetti che intersecandosi determinano il punto H
Problema 2: Tracciare la perpendicolare alla retta s per un suo punto P
Problema 2: Tracciare la perpendicolare alla retta s per un suo punto P
Con il compasso aperto a piacere, ma con R maggiore di AP, si punti in A e in B e si traccino due archetti che intersecandosi determinano il punto H
Con il compasso aperto a piacere, ma con R maggiore di AP, si punti in A e in B e si traccino due archetti che intersecandosi determinano il punto H
Con il compasso aperto a piacere, ma con R maggiore di AP, si punti in A e in B e si traccino due archetti che intersecandosi determinano il punto H
Problema 2: Tracciare la perpendicolare alla retta s per un suo punto P
Con il compasso aperto a piacere, ma con R maggiore di AP, si punti in A e in B e si traccino due archetti che intersecandosi determinano il punto H
Tracciando una linea passante per H e per P si ottiene la perpendicolare cercata
Con il compasso aperto a piacere, ma con R maggiore di AP, si punti in A e in B e si traccino due archetti che intersecandosi determinano il punto H
2 Con apertura a piacere, ma con R maggiore di 1P, puntiamo in 1 e in 2 e tracciamo due archetti la cui intersezione è il punto 3.
Con il compasso aperto a piacere, ma con R maggiore di AP, si punti in A e in B e si traccino due archetti che intersecandosi determinano il punto H
Tracciando una linea passante per H e per P si ottiene la perpendicolare cercata
Tracciando una linea passante per H e per P si ottiene la perpendicolare cercata
Tracciando una linea passante per H e per P si ottiene la perpendicolare cercata

Tracciando una linea passante per H e per P si ottiene la perpendicolare cercata
Tracciando una linea passante per H e per P si ottiene la perpendicolare cercata
Tracciando una linea passante per H e per P si ottiene la perpendicolare cercata
3 La retta passante per 3 e P è la perpendicolare cercata.
1) Allinea Sq.45 con s ; 2) Appoggia Sq.30/60 su Sq.45; 3) Fai scorrere Sq.45 fino ad allinearla a P; 4) Traccia la perpendicolare per P.
1) Allinea Sq.45 con s ; 2) Appoggia Sq.30/60 su Sq.45; 3) Fai scorrere Sq.45 fino ad allinearla a P; 4) Traccia la perpendicolare per P.
1) Allinea Sq.45 con s ; 2) Appoggia Sq.30/60 su Sq.45; 3) Fai scorrere Sq.45 fino ad allinearla a P; 4) Traccia la perpendicolare per P.
1) Allinea Sq.45 con s ; 2) Appoggia Sq.30/60 su Sq.45; 3) Fai scorrere Sq.45 fino ad allinearla a P; 4) Traccia la perpendicolare per P.
1) Allinea Sq.45 con s ; 2) Appoggia Sq.30/60 su Sq.45; 3) Fai scorrere Sq.45 fino ad allinearla a P; 4) Traccia la perpendicolare per P.
1) Allinea Sq.45 con s ; 2) Appoggia Sq.30/60 su Sq.45; 3) Fai scorrere Sq.45 fino ad allinearla a P; 4) Traccia la perpendicolare per P.
1) Allinea Sq.45 con s ; 2) Appoggia Sq.30/60 su Sq.45; 3) Fai scorrere Sq.45 fino ad allinearla a P; 4) Traccia la perpendicolare per P.
1) Allinea Sq.45 con s ; 2) Appoggia Sq.30/60 su Sq.45; 3) Fai scorrere Sq.45 fino ad allinearla a P; 4) Traccia la perpendicolare per P.
1) Allinea Sq.45 con s ; 2) Appoggia Sq.30/60 su Sq.45; 3) Fai scorrere Sq.45 fino ad allinearla a P; 4) Traccia la perpendicolare per P.
1) Allinea Sq.45 con s ; 2) Appoggia Sq.30/60 su Sq.45; 3) Fai scorrere Sq.45 fino ad allinearla a P; 4) Traccia la perpendicolare per P.







a Allinea la squadra 45 con s. b Appoggia la squadra 30/60 sulla squadra 45. c Fai scorrere la squadra 45 fino ad allinearla a P. d Traccia la perpendicolare per P. con le SQUADRE
1) Allinea Sq.45 con s ; 2) Appoggia Sq.30/60 su Sq.45; 3) Fai scorrere Sq.45 fino ad allinearla a P; 4) Traccia la perpendicolare per P.
1) Allinea Sq.45 con s ; 2) Appoggia Sq.30/60 su Sq.45; 3) Fai scorrere Sq.45 fino ad allinearla a P; 4) Traccia la perpendicolare per P.
1) Allinea Sq.45 con s ; 2) Appoggia Sq.30/60 su Sq.45; 3) Fai scorrere Sq.45 fino ad allinearla a P; 4) Traccia la perpendicolare per P.
1) Allinea Sq.45 con s ; 2) Appoggia Sq.30/60 su Sq.45; 3) Fai scorrere Sq.45 fino ad allinearla a P; 4) Traccia la perpendicolare per P.
1 Consideriamo la retta s e il punto P.
Problema 3: Tracciare la perpendicolare alla retta s per un punto P esterno ad essa
Problema 3: Tracciare la perpendicolare alla retta s per un punto P esterno ad essa
Problema 3: Tracciare la perpendicolare alla retta s per un punto P esterno ad essa
Sia data la retta s e il punto P Si punti in P con apertura a piacere e si tracci un arco che determina i punti A e B quindi si punti in A e in B e si traccino due archetti che intersecandosi determinano il punto H
Sia data la retta s e il punto P Si punti in P con apertura a piacere e si tracci un arco che determina i punti A e B quindi si punti in A e in B e si traccino due archetti che intersecandosi determinano il punto H
3 La retta passante per 3 e P è la perpendicolare cercata.
2 Puntiamo in P con apertura a piacere e tracciamo un arco che interseca la retta nei punti 1 e 2. Poi puntiamo in 1 e in 2 e tracciamo due archetti la cui intersezione è il punto 3.
Sia data la retta s e il punto P Si punti in P con apertura a piacere e si tracci un arco che determina i punti A e B quindi si punti in A e in B e si traccino due archetti che intersecandosi determinano il punto H
Tracciando una linea passante per H e per P si ottiene la perpendicolare cercata
Tracciando una linea passante per H e per P si ottiene la perpendicolare cercata
Tracciando una linea passante per H e per P si ottiene la perpendicolare cercata
Problema 3: Tracciare la perpendicolare alla retta s per un punto P esterno ad essa
Sia data la retta s e il punto P
Si punti in P con apertura a piacere e si tracci un arco che determina i punti A e B quindi si punti in A e in B e si traccino due archetti che intersecandosi determinano il punto H
Tracciando una linea passante per H e per P si ottiene la perpendicolare cercata
1) Allinea Sq.45 a s; 2) Appoggia Sq.30/60; 3) Fai scorrere Sq.45 fino ad allinearla a P; 4) Traccia la perpendicolare per P.
1) Allinea Sq.45 a s; 2) Appoggia Sq.30/60; 3) Fai scorrere Sq.45 fino ad allinearla a P; 4) Traccia la perpendicolare per P.
1) Allinea Sq.45 a s; 2) Appoggia Sq.30/60; 3) Fai scorrere Sq.45 fino ad allinearla a P; 4) Traccia la perpendicolare per P.
a Allinea la squadra 45 a s. b Appoggia la squadra 30/60. c Fai scorrere la squadra 45 fino ad allinearla a P. d Traccia la perpendicolare per P. con le SQUADRE
1) Allinea Sq.45 a s; 2) Appoggia Sq.30/60; 3) Fai scorrere Sq.45 fino ad allinearla a P; 4) Traccia la perpendicolare per P.
Problema 4: Tracciare la perpendicolare al segmento AB nell’estremo A
Problema 4: Tracciare la perpendicolare al segmento AB nell’estremo A
Problema 4: Tracciare la perpendicolare al segmento AB nell’estremo A
s s s s
Sia dato il segmento AB e si apra il compasso con apertura a piacere R che rimarrà fissa per tutta la costruzione
Sia dato il segmento AB e si apra il compasso con apertura a piacere R che rimarrà fissa per tutta la costruzione
Sia dato il segmento AB e si apra il compasso con apertura a piacere R che rimarrà fissa per tutta la costruzione
Si punti in A e si tracci un arco che determina il punto C quindi si punti in C e si tracci un arco che determina il punto D
Si punti in A e si tracci un arco che determina il punto C quindi si punti in C e si tracci un arco che determina il punto D
Si punti in A e si tracci un arco che determina il punto C quindi si punti in C e si tracci un arco che determina il punto D
a b c d
Problema 4: Tracciare la perpendicolare al segmento AB nell’estremo A
Sia dato il segmento AB e si apra il compasso con apertura a piacere R che rimarrà fissa per tutta la costruzione
Poi si punti in D e si tracci un arco che determina E quindi in E e si determini F. Tracciando la linea passante per A e F si ottiene la perpendicolare
Poi si punti in D e si tracci un arco che determina E quindi in E e si determini F. Tracciando la linea passante per A e F si ottiene la perpendicolare
Si punti in A e si tracci un arco che determina il punto C quindi si punti in C e si tracci un arco che determina il punto D
Poi si punti in D e si tracci un arco che determina E quindi in E e si determini F. Tracciando la linea passante per A e F si ottiene la perpendicolare
Poi si punti in D e si tracci un arco che determina E quindi in E e si determini F. Tracciando la linea passante per A e F si ottiene la perpendicolare
1) Allinea Sq.45 a s; 2) Appoggia Sq.30/60; 3) Fai scorrere Sq.45 fino ad allinearla a P; 4) Traccia la perpendicolare per P.
1) Allinea Sq.45 a s; 2) Appoggia Sq.30/60; 3) Fai scorrere Sq.45 fino ad allinearla a P; 4) Traccia la perpendicolare per P.
1) Allinea Sq.45 a s; 2) Appoggia Sq.30/60; 3) Fai scorrere Sq.45 fino ad allinearla a P; 4) Traccia la perpendicolare per P.
1) Allinea Sq.45 a s; 2) Appoggia Sq.30/60; 3) Fai scorrere Sq.45 fino ad allinearla a P; 4) Traccia la perpendicolare per P.
PASSO PASSO 4.2.4
1 Consideriamo il segmento AB e apriamo il compasso con apertura a piacere R che rimarrà fissa per tutta la costruzione.
s s
Problema 4: Tracciare la perpendicolare al segmento AB nell’estremo A
Problema 4: Tracciare la perpendicolare al segmento AB nell’estremo A
Problema 4: Tracciare la perpendicolare al segmento AB nell’estremo A
Sia dato il segmento AB e si apra il compasso con apertura a piacere R che rimarrà fissa per tutta la costruzione
Sia dato il segmento AB e si apra il compasso con apertura a piacere R che rimarrà fissa per tutta la costruzione
Sia dato il segmento AB e si apra il compasso con apertura a piacere R che rimarrà fissa per tutta la costruzione
2 Puntiamo in A e tracciamo un arco che interseca il segmento nel punto 1. Puntiamo in 1 e tracciamo un arco che interseca il primo arco nel punto 2.
Si punti in A e si tracci un arco che determina il punto C quindi si punti in C e si tracci un arco che determina il punto D
Si punti in A e si tracci un arco che determina il punto C quindi si punti in C e si tracci un arco che determina il punto D
Si punti in A e si tracci un arco che determina il punto C quindi si punti in C e si tracci un arco che determina il punto D
3 Puntiamo in 2 e tracciamo un arco che interseca in 3 il secondo arco; quindi puntiamo in 3 e tracciamo un arco che interseca in 4 il terzo arco. La retta passante per A e 4 è la perpendicolare cercata.
Problema 4: Tracciare la perpendicolare al segmento AB nell’estremo A
Problema 4: Tracciare la perpendicolare al segmento AB nell’estremo A
Problema 4: Tracciare la perpendicolare al segmento AB nell’estremo A
Problema 4: Tracciare la perpendicolare al segmento AB nell’estremo A
Sia dato il segmento AB e si apra il compasso con apertura a piacere R che rimarrà fissa per tutta la costruzione
Sia dato il segmento AB e si apra il compasso con apertura a piacere R che rimarrà fissa per tutta la costruzione
Poi si punti in D e si tracci un arco che determina E quindi in E e si determini F. Tracciando la linea passante per A e F si ottiene la perpendicolare
Poi si punti in D e si tracci un arco che determina E quindi in E e si determini F. Tracciando la linea passante per A e F si ottiene la perpendicolare
Poi si punti in D e si tracci un arco che determina E quindi in E e si determini F. Tracciando la linea passante per A e F si ottiene la perpendicolare
Sia dato il segmento AB e si apra il compasso con apertura a piacere R che rimarrà fissa per tutta la costruzione
Sia dato il segmento AB e si apra il compasso con apertura a piacere R che rimarrà fissa per tutta la costruzione
Si punti in A e si tracci un arco che determina il punto C quindi si punti in C e si tracci un arco che determina il punto D
Si punti in A e si tracci un arco che determina il punto C quindi si punti in C e si tracci un arco che determina il punto D
Si punti in A e si tracci un arco che determina il punto C quindi si punti in C e si tracci un arco che determina il punto D
Si punti in A e si tracci un arco che determina il punto C quindi si punti in C e si tracci un arco che determina il punto D
Poi si punti in D e si tracci un arco che determina E quindi in E e si determini F. Tracciando la linea passante per A e F si ottiene la perpendicolare
Poi si punti in D e si tracci un arco che determina E quindi in E e si determini F. Tracciando la linea passante per A e F si ottiene la perpendicolare
Poi si punti in D e si tracci un arco che determina E quindi in E e si determini F. Tracciando la linea passante per A e F si ottiene la perpendicolare
Poi si punti in D e si tracci un arco che determina E quindi in E e si determini F. Tracciando la linea passante per A e F si ottiene la perpendicolare
1) Allinea Sq.45 ad AB; 2) Appoggia Sq.30/60; 3) Fai scorrere Sq.45 fino ad allinearla ad A; 4) Traccia la perpendicolare per A.
1) Allinea Sq.45 ad AB; 2) Appoggia Sq.30/60; 3) Fai scorrere Sq.45 fino ad allinearla ad A; 4) Traccia la perpendicolare per A.
con le SQUADRE
1) Allinea Sq.45 ad AB; 2) Appoggia Sq.30/60; 3) Fai scorrere Sq.45 fino ad allinearla ad A; 4) Traccia la perpendicolare per A.
1) Allinea Sq.45 ad AB; 2) Appoggia Sq.30/60; 3) Fai scorrere Sq.45 fino ad allinearla ad A; 4) Traccia la perpendicolare per A.
1) Allinea Sq.45 ad AB; 2) Appoggia Sq.30/60; 3) Fai scorrere Sq.45 fino ad allinearla ad A; 4) Traccia la perpendicolare per A.
1) Allinea Sq.45 ad AB; 2) Appoggia Sq.30/60; 3) Fai scorrere Sq.45 fino ad allinearla ad A; 4) Traccia la perpendicolare per A.
a Allinea la squadra 45 ad AB. b Appoggia la squadra 30/60. c Fai scorrere la squadra 45 fino ad allinearla ad A. d Traccia la perpendicolare per A.
1) Allinea Sq.45 ad AB; 2) Appoggia Sq.30/60; 3) Fai scorrere Sq.45 fino ad allinearla ad A; 4) Traccia la perpendicolare per A.
Costruzioni piane fondamentali: parallele
Costruzioni piane fondamentali: parallele Video tutorial

PASSO PASSO 4.2.5 PARALLELA A
d

Problema 5: Tracciare una parallela alla retta s alla distanza d
Problema 5: Tracciare una parallela alla retta s alla distanza d
Problema 5: Tracciare una parallela alla retta s alla distanza d
1 Consideriamo la retta s e la distanza d.
Siano date la retta s e la distanza dPer due punti A e B di s presi a piacere si traccino le perpendicolari alla retta
Siano date la retta s e la distanza dPer due punti A e B di s presi a piacere si traccino le perpendicolari alla retta
Siano date la retta s e la distanza dPer due punti A e B di s presi a piacere si traccino le perpendicolari alla retta
2 Per due punti 1 e 2 di s presi a piacere tracciamo le perpendicolari alla retta.
Si riportino sulle perpendicolari la distanza d determinando i punti
Si riportino sulle perpendicolari la distanza d determinando i punti
H e K. Tracciando la linea passante per H e K si ottiene la parallela cercata
H e K. Tracciando la linea passante per H e K si ottiene la parallela cercata
Si riportino sulle perpendicolari la distanza d determinando i punti H e K. Tracciando la linea passante per H e K si ottiene la parallela cercata
3 Riportiamo sulle perpendicolari la distanza d e determiniamo i punti 3 e 4. Tracciando la retta passante per 3 e 4 otteniamo la parallela cercata.
1) Allinea Sq.45 con s e falla scorrere verso il basso; 2) Appoggia Sq.30/60, traccia una verticale e riporta la distanza d; 3) Allinea Sq.45 a s; 4) fai scorrere la Sq.45 fino all’estremità di d e traccia la parallela.
1) Allinea Sq.45 con s e falla scorrere verso il basso; 2) Appoggia Sq.30/60, traccia una verticale e riporta la distanza d; 3) Allinea Sq.45 a s; 4) fai scorrere la Sq.45 fino all’estremità di d e traccia la parallela.
1) Allinea Sq.45 con s e falla scorrere verso il basso; 2) Appoggia Sq.30/60, traccia una verticale e riporta la distanza d; 3) Allinea Sq.45 a s; 4) fai scorrere la Sq.45 fino all’estremità di d e traccia la parallela.
Problema 5: Tracciare una parallela alla retta s alla
Siano date la retta s e la distanza dPer due punti A e B di s presi a piacere si traccino le perpendicolari alla retta
con le SQUADRE




Si riportino sulle perpendicolari la distanza d determinando i punti H e K. Tracciando la linea passante per H e K si ottiene la parallela cercata
Si riportino sulle perpendicolari la distanza d determinando i punti H e K. Tracciando la linea passante per H e K si ottiene la parallela cercata


d
d d
a Allinea la squadra 45 con s e falla scorrere verso il basso. b Appoggia la squadra 30/60, traccia una verticale e riporta la distanza d. c Allinea la squadra 45 a s. d Fai scorrere la squadra 45 fino all’estremità di d e traccia la parallela.
1) Allinea Sq.45 con s e falla scorrere verso il basso; 2) Appoggia Sq.30/60, traccia una verticale e riporta la distanza d; 3) Allinea Sq.45 a s; 4) fai scorrere la Sq.45 fino all’estremità di d e traccia la parallela.
1) Allinea Sq.45 con s e falla scorrere verso il basso; 2) Appoggia Sq.30/60, traccia una verticale e riporta la distanza d; 3) Allinea Sq.45 a s; 4) fai scorrere la Sq.45 fino all’estremità di d e traccia la parallela.
1) Allinea Sq.45 con s e falla scorrere verso il basso; 2) Appoggia Sq.30/60, traccia una verticale e riporta la distanza d; 3) Allinea Sq.45 a s; 4) fai scorrere la Sq.45 fino all’estremità di d e traccia la parallela.
1) Allinea Sq.45 con s e falla scorrere verso il basso; 2) Appoggia Sq.30/60, traccia una verticale e riporta la distanza d; 3) Allinea Sq.45 a s; 4) fai scorrere la Sq.45 fino all’estremità di d e traccia la parallela.
1) Allinea Sq.45 con s e falla scorrere verso il basso; 2) Appoggia Sq.30/60, traccia una verticale e riporta la distanza d; 3) Allinea Sq.45 a s; 4) fai scorrere la Sq.45 fino all’estremità di d e traccia la parallela.
Problema 6: Tracciare la parallela alla retta s per un punto P esterno ad essa
Problema 6: Tracciare la parallela alla retta s per un punto P esterno ad essa
Problema 6: Tracciare la parallela alla retta s per un punto P esterno ad essa
Siano dati la retta s e il punto P.
Siano dati la retta s e il punto P. Si tracci da P la perpendicolare a s e determinando il punto H.
Si tracci da P la perpendicolare a s e determinando il punto H.
Siano dati la retta s e il punto P. Si tracci da P la perpendicolare a s e determinando il punto H.
Si scelga a piacere su s un punto Q e si tracci per esso la perpedicolare alla retta.
Si scelga a piacere su s un punto Q e si tracci per esso la perpedicolare alla retta.
Si scelga a piacere su s un punto Q e si tracci per esso la perpedicolare alla retta.
PASSO PASSO 4.2.6 PARALLELA A UNA RETTA PER UN PUNTO ESTERNO A ESSA
Problema 6: Tracciare la parallela alla retta s per un punto P esterno ad essa
1 Consideriamo la retta s e il punto P. Tracciamo da P la perpendicolare a s e determiniamo il punto 1.
Siano dati la retta s e il punto P. Si tracci da P la perpendicolare a s e determinando il punto H.
2 Scegliamo a piacere su s un punto 2 e tracciamo per esso la perpendicolare alla retta.
Si scelga a piacere su s un punto Q e si tracci per esso la perpedicolare alla retta.
Siano dati la retta s e il punto P. Si tracci da P la perpendicolare a s e determinando il punto H.
Si scelga a piacere su s un punto Q e si tracci per esso la perpedicolare alla retta.
Si riporti sulla perpendicolare in Q la distanza PH determinando il punto K. Tracciando la linea passante per P e K si ottiene la parallela cercata
Problema 6: Tracciare la parallela alla retta s per un punto P esterno ad essa
1) Allinea Sq.45 con s ; 2) Appoggia Sq.30/60 a Sq.45; 3) fai scorrere la Sq.45 fino a P e traccia la parallela. a
Si riporti sulla perpendicolare in Q la distanza PH determinando il punto K. Tracciando la linea passante per P e K si ottiene la parallela cercata
Si riporti sulla perpendicolare in Q la distanza PH determinando il punto K. Tracciando la linea passante per P e K si ottiene la parallela cercata
Si riporti sulla perpendicolare in Q la distanza PH determinando il punto K. Tracciando la linea passante per P e K si ottiene la parallela cercata
Si riporti sulla perpendicolare in Q la distanza PH determinando il punto K. Tracciando la linea passante per P e K si ottiene la parallela cercata
3 Riportiamo sulla perpendicolare in 2 la distanza P1 e determiniamo il punto 3. Tracciando la retta passante per P e 3 si ottiene la parallela cercata.
1) Allinea Sq.45 con s ; 2) Appoggia Sq.30/60 a Sq.45; 3) fai scorrere la Sq.45 fino a P e traccia la parallela.
1) Allinea Sq.45 con s ; 2) Appoggia Sq.30/60 a Sq.45; 3) fai scorrere la Sq.45 fino a P e traccia la parallela.
1) Allinea Sq.45 con s ; 2) Appoggia Sq.30/60 a Sq.45; 3) fai scorrere la Sq.45 fino a P e traccia la parallela.
a Allinea la squadra 45 con s. b Appoggia la squadra 30/60 alla squadra 45. c Fai scorrere la squadra 45 fino a P e traccia la parallela. con le SQUADRE
1) Allinea Sq.45 con s ; 2) Appoggia Sq.30/60 a Sq.45; 3) fai scorrere la Sq.45 fino a P e traccia la parallela.
Problema
Sia dato l’angolo α.
Problema 7: Dato l’angolo α se ne costruisca
Problema 7: Dato l’angolo α se ne costruisca uno di congruente
Problema 7: Dato l’angolo α se ne costruisca uno di congruente
Sia dato l’angolo α.
Problema 7: Dato l’angolo α se ne costruisca uno di congruente
Problema 7: Dato l’angolo α se ne costruisca uno di congruente
PASSO PASSO 4.2.7 COSTRUZIONE DI UN ANGOLO CONGRUENTE
Problema 7: Dato l’angolo α se ne costruisca uno di congruente
Sia dato l’angolo α.
Sia dato l’angolo α.
Sia dato l’angolo α.
Sia dato l’angolo α.
1 Consideriamo un angolo a.
Sia dato l’angolo α.
Sia dato l’angolo α.
Sia dato l’angolo α.
Sia dato l’angolo α.
Si fissi poi a piacere il punto V’ e da esso si tracci la linea s’.
Si fissi poi a piacere il punto V’ e da esso si tracci la linea s’.
Problema 7: Dato l’angolo α se ne costruisca uno di congruente
con apertura
Puntando il compasso in V con apertura R’, scelta a piacere, si tracci un arco che determina sui lati dell’angolo i punti A e B.
Puntando il compasso in V con apertura R’, scelta a piacere, si tracci un arco che determina sui lati dell’angolo i punti A e B.
Si fissi poi a piacere il punto
Si fissi poi a piacere il punto V’ e da esso si tracci la linea s’
Si fissi poi a piacere il punto V’ e da esso si tracci la linea s’.
Si fissi poi a piacere il punto V’ e da esso si tracci la linea s’.
Si fissi poi a piacere il punto V’ e da esso si tracci la linea s’
Si fissi poi a piacere il punto s’
Si fissi poi a piacere il punto V’ e da esso si tracci la linea s’
3 Fissiamo poi a piacere il punto V' fuori dall’angolo a e da esso tracciamo la semiretta s'.
Problema 7: Dato l’angolo α se ne costruisca uno di congruente
Si fissi poi a piacere il punto V’ e da esso si tracci la linea s’.
Si fissi poi a piacere il punto V’ e da esso si tracci la linea s’.
Si rilevi col compasso la distanza R”
Si rilevi col compasso la distanza R” tra A e B e puntando in A’ la si riporti sull’arco tracciato precedentemente determinando il punto B’. Tracciando da V’ una linea passante per B’ si ottiene l’angolo cercato
Si rilevi col compasso la distanza R” tra A e B e puntando in A’ la si riporti sull’arco tracciato precedentemente determinando il punto B’ Tracciando da V’ una linea passante per B’ si ottiene l’angolo cercato
Puntando il compasso in V R’, scelta a tracci un arco che
Puntando il compasso in V con apertura R’, scelta a piacere, si tracci un arco che determina sui lati dell’angolo i punti A e B.
Puntando il compasso in V con apertura R’, scelta a piacere, si tracci un arco che determina sui lati dell’angolo i punti A e B.
Puntando il compasso in V con apertura R’, scelta a piacere, si tracci un arco che determina sui lati dell’angolo i punti A e B.
Puntando il compasso in V con apertura R’, scelta a piacere, si tracci un arco che determina sui lati dell’angolo i punti A e B.
determina sui lati dell’angolo i punti A e B.
Puntando il compasso in V con apertura R’, scelta a piacere, si tracci un arco che determina sui lati dell’angolo i punti A e B.
Puntando il compasso in V con apertura R’, scelta a piacere, si tracci un arco che determina sui lati dell’angolo i punti A e B.
2 Puntando il compasso in V con apertura R', scelta a piacere, tracciamo un arco che determina sui lati dell’angolo i punti 1 e 2.
Puntando il compasso in V con apertura R’, scelta a piacere, si tracci un arco che determina sui lati dell’angolo i punti A e B.
Problema 8: Sommare due angoli dati α e ß a
Problema 8: Sommare due angoli dati α e ß a
Problema 8: Sommare due angoli dati α e ß a
Problema 8: Sommare due angoli dati α e ß a
Problema 8: Sommare due angoli dati α e ß a
Puntando il compasso in V’ con apertura R‘ si tracci un arco che determina su s’ il punto A’
Problema 8: Sommare due angoli dati α e ß a
Puntando il compasso in V’ con apertura R‘ si tracci un arco che determina su s’ il punto A’
Problema 8: Sommare due angoli dati α e ß a
Problema 8: Sommare due angoli dati α e ß a
Puntando il compasso in V’ con apertura R‘ si tracci un arco che determina su s’ il punto A’.
Puntando il compasso in V’ con apertura R‘ si tracci un arco che determina su s’ il punto A’
Puntando il compasso in V’ con apertura R‘ si tracci un arco che determina su s’ il punto A’.
Puntando il compasso in V’ con apertura R‘ si tracci un arco che determina su s’ il punto A’.
Puntando il compasso in V’ con apertura R‘ si tracci un arco che determina su s’ il punto A’.
Puntando il compasso in V’ con apertura R‘ si tracci un arco che determina su s’ il punto A’.
4 Puntando il compasso in V' con apertura R', tracciamo un arco che determina su s' il punto 1'.
Puntando il compasso in V’ con apertura R‘ si tracci un arco che determina su s’ il punto A’
Puntando il compasso in V’ con apertura R‘ si tracci un arco che determina su s’ il punto A’.
Problema 8: Sommare due angoli dati α e
PASSO PASSO 4.2.8 SOMMA DI DUE ANGOLI a E b
Siano dati gli angoli α e ß. Si fissi poi a piacere il punto V e da esso si tracci la linea s.
Siano dati gli angoli α e ß. Si fissi poi a piacere il punto V e da esso si tracci la linea s.
Siano dati gli angoli α e ß.
Siano dati gli angoli α e ß.
Siano dati gli angoli α e ß.
Siano dati gli angoli α e ß.
Problema 8: Sommare due angoli dati α e ß a
3 Fissiamo poi a piacere il punto V e da esso tracciamo la semiretta s.
1 Consideriamo gli angoli a e b. s
Si fissi poi a piacere il punto V e da esso si tracci la linea s.
Si fissi poi a piacere il punto V e da esso si tracci la linea s.
Si fissi poi a piacere il punto V e da esso si tracci la linea s.
Siano dati gli angoli α e ß. Si fissi poi a piacere il punto V e da esso si tracci la linea s.
Si fissi poi a piacere il punto V e da esso si tracci la linea s.
da esso si tracci la linea s.
Siano dati gli angoli α e ß. Si fissi poi a piacere il punto V e da esso si tracci la linea s.
Siano dati gli angoli α e ß. Si fissi poi a piacere il punto V e da esso si tracci la linea s.
2 Puntando il compasso in V' e V", con apertura R, scelta a piacere, tracciamo due archi che determinano sui lati degli angoli i punti 1, 2, 3 e 4.
Puntando il compasso in V’ e V”, con apertura R, scelta a piacere, si traccino due archi che determinano sui lati degli angoli i punti A, B, C e D.
Puntando il compasso in V’ e V”, con apertura R, scelta a piacere, si traccino due archi che determinano sui lati degli angoli i punti A, B, C e D.
Si rilevi col compasso la distanza R” tra A e B e puntando in A’ la si riporti sull’arco tracciato precedentemente determinando il punto B’. Tracciando da V’ una linea passante per B’ si ottiene l’angolo cercato
Si rilevi col compasso la distanza R” tra A e B e puntando in A’ la si riporti sull’arco tracciato precedentemente determinando il punto B’ Tracciando da V’ una linea passante per B’ si ottiene l’angolo cercato
Si rilevi col compasso la distanza R” tra A e B e puntando in A’ la si riporti sull’arco tracciato precedentemente determinando il punto B’. Tracciando da V’ una linea passante per B’ si ottiene l’angolo cercato
passante per B’ si ottiene l’angolo cercato
Si rilevi col compasso la distanza R” tra A e B e puntando in A’ la si riporti sull’arco tracciato precedentemente determinando il punto B’. Tracciando da V’ una linea passante per B’ si ottiene l’angolo cercato
tra A e B e puntando in A’ riporti sull’arco tracciato precedentemente determinando il punto B’. Tracciando da V’ una linea cercato
Si rilevi col compasso la distanza R” tra A e B e puntando in A’ la si riporti sull’arco tracciato precedentemente determinando il punto B’. Tracciando da V’ una linea passante per B’ si ottiene l’angolo cercato
Si rilevi col compasso la distanza R” tra A e B e puntando in A’ la si riporti sull’arco tracciato precedentemente determinando il punto B’ Tracciando da V’ una linea passante per B’ si ottiene l’angolo cercato
5 Rileviamo col compasso la distanza R" tra 1 e 2 e puntando in 1' la riportiamo sull’arco tracciato precedentemente determinando il punto 2'. Tracciando da V' una semiretta passante per 2' otteniamo l’angolo cercato di ampiezza a
Si rilevi col compasso la distanza R” tra A e B e puntando in A’ la si riporti sull’arco tracciato precedentemente determinando il punto B’. Tracciando da V’ una linea passante per B’ si ottiene l’angolo cercato

Si rilevino ora col compasso le distanze R’ tra A e B ed R” tra C e D e le si riportino in successione sull’arco tracciato precedentemente determinando il punto D’. Tracciando da V una linea passante per D’ si ottiene l’angolo cercato.
Si rilevino ora col compasso le distanze R’ tra A e B ed R” tra C e D e le si riportino in successione sull’arco tracciato precedentemente determinando il punto D’. Tracciando da V una linea passante per D’ si ottiene l’angolo cercato.
5 Rileviamo ora col compasso le distanze R' tra 1 e 2 e R" tra 3 e 4 e le riportiamo in successione sull’arco tracciato precedentemente, determinando il punto 4'. Tracciando da V una semiretta passante per 4' otteniamo l’angolo cercato a b. s
Si rilevino ora col compasso le distanze R’ tra A e B ed R” tra C e D e le si riportino in successione sull’arco tracciato precedentemente determinando il punto D’. Tracciando da V una linea passante per D’ si ottiene l’angolo cercato.
Si rilevino ora col compasso le distanze R’ tra A e B ed R” tra C e D e le si riportino in successione sull’arco tracciato precedentemente determinando il punto D’ Tracciando da V una linea passante per D’ si ottiene l’angolo cercato.
ora col compasso le distanze R’ tra A e B ed tra C e D e le si riportino in successione sull’arco tracciato precedentemente ottiene l’angolo cercato
Si rilevino ora col compasso le distanze R’ tra A e B ed R” tra C e D e le si riportino in successione sull’arco tracciato precedentemente determinando il punto D’. Tracciando da V una linea passante per D’ si ottiene l’angolo cercato.
Si rilevino ora col compasso le distanze R’ tra A e B ed R” tra C e D e le si riportino in successione sull’arco tracciato precedentemente determinando il punto D’. Tracciando da V una linea passante per D’ si ottiene l’angolo cercato
determinando il punto D’. ottiene l’angolo cercato
Si rilevino ora col compasso le distanze R’ tra A e B ed R” tra C e D e le si riportino in successione sull’arco tracciato precedentemente determinando il punto D’ Tracciando da V una linea passante per D’ si ottiene l’angolo cercato.
Si rilevino ora col compasso le distanze R’ tra A e B ed R” tra C e D e le si riportino in successione sull’arco tracciato precedentemente determinando il punto D’ Tracciando da V una linea passante per D’ si ottiene l’angolo cercato.
Si rilevino ora col compasso le distanze R’ tra A e B ed R” tra C e D e le si riportino in successione sull’arco tracciato precedentemente determinando il punto D’. Tracciando da V una linea passante per D’ si ottiene l’angolo cercato.
Puntando il compasso in V’ e V”, con apertura R, scelta a piacere, si traccino due archi che determinano sui lati degli angoli i punti A, B, C e D.
Puntando il compasso in V’ e V”, con apertura R, scelta a piacere, si traccino due archi che determinano sui lati degli angoli i punti A, B, C e D.
Puntando il compasso in V’ e V”, con apertura R, scelta a piacere, si traccino due archi che determinano sui lati degli angoli i punti A, B, C e D.
Puntando il compasso in V’ e V”, con apertura R, scelta a piacere, si traccino due archi che determinano sui lati degli angoli i punti A, B, C e D.
Puntando il compasso in V’ e V”, con apertura R, scelta a piacere, si traccino due archi che determinano sui lati degli angoli i punti A, B, C e D.
Puntando il compasso in V’ e V”, con apertura R, scelta a piacere, si traccino due archi che determinano sui lati degli angoli i punti A, B, C e D.
Puntando quindi il compasso in V sempre con apertura R si tracci un arco che determina su s il punto A’
Puntando il compasso in V’ e V”, Puntando quindi il compasso in V
Puntando il compasso in V’ e V”, con apertura R, scelta a piacere, si traccino due archi che determinano sui lati degli angoli i punti A, B, C e D.
Puntando quindi il compasso in V sempre con apertura R si tracci un arco che determina su s il punto A’
Puntando quindi il compasso in V sempre con apertura R si tracci un arco che determina su s il punto A’
Puntando il compasso in V’ e V”, con apertura R, scelta a piacere, si traccino due archi che determinano sui lati degli angoli i punti A, B, C e D.
4 Puntando quindi il compasso in V sempre con apertura R, tracciamo un arco che interseca s nel punto 1'. s
Puntando quindi il compasso in V sempre con apertura R si tracci un arco che determina su s il punto A’.
Puntando quindi il compasso in V sempre con apertura R si tracci un arco che determina su s il punto A’
Puntando quindi il compasso in V sempre con apertura R si tracci un arco che determina su s il punto A’
Puntando quindi il compasso in V sempre con apertura R si tracci un arco che determina su s il punto A’.
Puntando quindi il compasso in V sempre con apertura R si tracci un arco che determina su s il punto A’.
Puntando quindi il compasso in V sempre con apertura R si tracci un arco che determina su s il punto A’.
Puntando quindi il compasso in V sempre con apertura R si tracci un arco che determina su s il punto A’
PASSO PASSO 4.2.9
1 Dato il segmento AB, tracciamo da A o da B una semiretta inclinata con un angolo a piacere e, scelta una misura a piacere, la riportiamo su tale linea, partendo da A, per nove volte consecutive.
2 Congiungiamo l’estremo B con 9.
Problema 9: Dividere il segmento AB in nove parti congruenti
Dato il segmento AB, si tracci da A o da B una linea inclinata con un angolo a piacere e scelta una misura a piacere la si riporti su tale linea, partendo da A, per nove volte consecutive







3 Con le squadrette tracciamo per i punti 8, 7, 6 e così via le parallele a B9 fino a intersecare AB, che risulta così suddiviso in nove parti congruenti.
Si congiunga l’estremo B con 9 Con le squadrette si traccino per i punti 8, 7 , 6 e così via le parallele a B9 fino a intersecare AB che risulta così suddiviso in nove parti congruenti.
PASSO PASSO 4.2.10 TRISEZIONE DELL’ANGOLO RETTO
1 Sia tVs l’angolo retto da dividere in tre parti congruenti.
Problema 9: Trisezione dell’angolo retto
Sia tVs l’angolo retto da dividere in tre parti congruenti.
2 Puntiamo col compasso in V con apertura a piacere e tracciamo un arco che intersechi s e t, determinando i punti 1 e 2.
Si punti col compasso in V con apertura a piacere e si tracci un arco che intersechi s e t determinando i punti A e B.
vedi esercizio a pag. 90
3 Puntiamo col compasso in 1 e in 2 con la stessa apertura e tracciamo due archi che intersecano l’arco 1-2 in 3 e 4. Congiungendo V con 3 e 4 si ottengono gli angoli cercati.
Si punti col compasso in A e in B con la stessa apertura e si traccino due archi intersecanti s e t determinando i punti H e K. Congiungendo V con H e K si ottengono gli angolo cercati.
1) Allinea Sq.45 con s e falla scorrere varso il basso; 2) Appoggia Sq.30/60 a Sq.45 con l’angolo di 30° allineato ad A e traccia un segmento; 3)Allinea ad A l’angolo di 60° e traccia l’altro segmento.
vedi esercizio a pag. 90

a Allinea la squadra 45 con s e falla scorrere verso il basso. b Appoggia la squadra 30/60 alla squadra 45 con l’angolo di 30° allineato ad A e traccia un segmento. c Allinea ad A l’angolo di 60° e traccia l’altro segmento. con le SQUADRE
1) Allinea Sq.45 con s e falla scorrere varso il basso; 2) Appoggia Sq.30/60 a Sq.45 con l’angolo di 30° allineato ad A e traccia un segmento; 3)Allinea ad A l’angolo di 60° e traccia l’altro segmento.
Problema 11: Tracciare la bisettrice di un angolo
Problema 11: Tracciare la bisettrice di un angolo
Problema 11: Tracciare la bisettrice di un angolo
1 s s 1 3 s s t t t AA s s A
Sia dato l’angolo tVs.
Sia dato l’angolo tVs.
Sia dato l’angolo tVs.


Si punti in V col compasso aperto a piacere e si tracci un arco che intersechi s in A e t in B.
Si punti in V col compasso aperto a piacere e si tracci un arco che intersechi s in A e t in B.
Si punti in V col compasso aperto a piacere e si tracci un arco che intersechi s in A e t in B.
Problema 11: Tracciare la bisettrice di un angolo
Problema 11: Tracciare la bisettrice di un angolo
Problema 11: Tracciare la bisettrice di un angolo
Sia dato l’angolo tVs.
Sia dato l’angolo tVs.
PASSO PASSO 4.2.11 BISETTRICE DI UN ANGOLO
PASSO PASSO 4.2.12 BISETTRICE DI UN ANGOLO COL VERTICE INACCESSIBILE a b c
Si punti in A e in B con apertura superiore alla metà di AB e si traccino due archetti che, intersecandosi, determinano il punto T. Congiungendo V con T si ottiene la bisettrice cercata.
Si punti in A e in B con apertura superiore alla metà di AB e si traccino due archetti che, intersecandosi, determinano il punto T. Congiungendo V con T si ottiene la bisettrice cercata.
Si punti in A e in B con apertura superiore alla metà di AB e si traccino due archetti che, intersecandosi, determinano il punto T. Congiungendo V con T si ottiene la bisettrice cercata.
Sia dato l’angolo tVs. Si punti in V col compasso aperto a piacere e si tracci un arco che intersechi s in A e t in B.
Consideriamo l’angolo tVs.
Si punti in V col compasso aperto a piacere e si tracci un arco che intersechi s in A e t in B.
Si punti in V col compasso aperto a piacere e si tracci un arco che intersechi s in A e t in B.
2 Puntiamo in V con apertura a piacere e tracciamo un arco che interseca s in 1 e t in 2.
Si punti in A e in B con apertura superiore alla metà di AB e si traccino due archetti che, intersecandosi, determinano il punto T. Congiungendo V con T si ottiene la bisettrice cercata.

Si punti in A e in B con apertur superiore alla metà di AB e si traccino due archetti che, intersecandosi, determinano il punto T. Congiungendo V con T si ottiene la bisettrice cercata.
Si punti in A e in B con apertura superiore alla metà di AB e si traccino due archetti che, intersecandosi, determinano il punto T. Congiungendo V con T si ottiene la bisettrice cercata.
3 Puntiamo in 1 e in 2 con apertura superiore alla metà di 1-2 e tracciamo due archetti che, intersecandosi, determinano il punto 3. Congiungendo V con 3 otteniamo la bisettrice cercata.
Problema 12: Tracciare la bisettrice di un angolo col vertice inaccessibile
Problema 12: Tracciare la bisettrice di un angolo col vertice inaccessibile
Problema 12: Tracciare la bisettrice di un angolo col vertice inaccessibile
Siano date le rette s e t che si intersecano fuori dal disegno
Siano date le rette s e t che si intersecano fuori dal disegno
Siano date le rette s e t che si intersecano fuori dal disegno.
1 Consideriamo le due rette s e t che si intersecano fuori dal foglio.
Scelti su di esse due punti P e Q, si traccia il segmento PQ determinando quattro angoli α, ß, δ, ε.
Scelti su di esse due punti P e Q, si traccia il segmento PQ determinando quattro angoli α, ß, δ, ε.
Scelti su di esse due punti P e Q, si traccia il segmento PQ determinando quattro angoli α, ß, δ, ε.
Si traccino le bisettrici dei quattro angoli che intersecandosi a due a due determinano i punti A e B. Tracciando la linea passante per A e B si ottiene la bisettrice cercata.

Si traccino le bisettrici dei quattro angoli che intersecandosi a due a due determinano i punti A e B. Tracciando la linea passante per A e B si ottiene la bisettrice cercata.
Si traccino le bisettrici dei quattro angoli che intersecandosi a due a due determinano i punti A e B Tracciando la linea passante per A e B si ottiene la bisettrice cercata.
Problema 12: Tracciare la bisettrice di un angolo col vertice inaccessibile
Problema 12: Tracciare la bisettrice di un angolo col vertice inaccessibile
Problema 12: Tracciare la bisettrice di un angolo col vertice inaccessibile
Siano date le rette s e t che si intersecano fuori dal disegno
Siano date le rette s e t che si intersecano fuori dal disegno
2 Scelti su di esse due punti 1 e 2, tracciamo il segmento 1-2 che individua quattro angoli: a, b, d, g.
Siano date le rette s e t che si intersecano fuori dal disegno
Scelti su di esse due punti P e Q, si traccia il segmento PQ determinando quattro angoli α, ß, δ, ε.
Scelti su di esse due punti P e Q, si traccia il segmento PQ determinando quattro angoli α, ß, δ, ε.
Scelti su di esse due punti P e Q, si traccia il segmento PQ determinando quattro angoli α, ß, δ, ε.
Si traccino le bisettrici dei quattro angoli che intersecandosi a due a due determinano i punti A e B. Tracciando la linea passante per A e B si ottiene la bisettrice cercata.
Si traccino le bisettrici dei quattro angoli che intersecandosi a due a due determinano i punti A e B. Tracciando la linea passante per A e B si ottiene la bisettrice cercata.
3 Tracciamo le bisettrici dei quattro angoli che, intersecandosi a due a due, determinano i punti 3 e 4. La retta passante per 3 e 4 è la bisettrice cercata.
Si traccino le bisettrici dei quattro angoli che intersecandosi a due a due determinano i punti A e B. Tracciando la linea passante per A e B si ottiene la bisettrice cercata.
I Poligoni







Si definisce poligono una parte di piano delimitata da una spezzata chiusa.
Un poligono è la parte di piano delimitata da una spezzata chiusa.
Si definisce poligono una parte di piano delimitata da una spezzata chiusa.
Poligoni
Si definisce poligono una parte di piano delimitata da una spezzata chiusa.
Si definisce poligono una parte di piano delimitata da una spezzata chiusa.
Gli elementi che lo caratterizzano sono i lati, gli angoli e i vertici presenti sempre in ugual numero.
I Poligoni
Gli elementi che lo caratterizzano sono i lati, gli angoli e i vertici presenti sempre in pari quantità.
Gli elementi che lo caratterizzano sono i lati, gli angoli e i vertici presenti sempre in pari quantità.
Si definisce poligono una parte di piano delimitata da una spezzata chiusa.
Si definisce poligono una parte di piano delimitata da una spezzata chiusa.
Gli elementi che lo caratterizzano sono i lati, gli angoli e i vertici presenti sempre in pari quantità.
Gli elementi che lo caratterizzano sono i lati, gli angoli e i vertici presenti sempre in pari quantità.
Gli elementi che lo caratterizzano sono i lati, gli angoli e i vertici presenti sempre in pari quantità.
Gli elementi che lo caratterizzano sono i lati, gli angoli e i vertici presenti sempre in pari quantità.
Gli elementi che lo caratterizzano sono i lati, gli angoli e i vertici presenti sempre in pari quantità.
Gli elementi che lo caratterizzano sono i lati, gli angoli e i vertici presenti sempre in pari quantità.
Gli elementi che lo caratterizzano sono i lati, gli angoli e i vertici presenti sempre in pari quantità.
E' convesso se il segmento che ha per estremi due qualsiasi dei suoi punti appartiene interamente al poligono
Si definisce poligono una parte di piano delimitata da una spezzata chiusa.
Si definisce poligono una parte di piano delimitata da una spezzata chiusa.
Altri elementi del poligono
Altri elementi del poligono
Altri elementi del poligono
Altri elementi del poligono
Altri elementi del poligono
Altri elementi del poligono
L’angolo interno di un poligono è ciascun angolo (convesso) che ha vertice in un vertice del poligono e per lati le semirette dei lati del poligono uscenti da quel vertice.
Altri elementi del poligono
Altri elementi del poligono
Altri elementi del poligono
Angolo interno ciascun angolo (convesso) che ha vertice in un vertice del poligono e per lati le semirette dei lati del poligono uscenti da quel vertice.
Angolo interno ciascun angolo (convesso) che ha vertice in un vertice del poligono e per lati le semirette dei lati del poligono uscenti da quel vertice.
Angolo interno ciascun angolo (convesso) che ha vertice in un vertice del poligono e per lati le semirette dei lati del poligono uscenti da quel vertice.
Angolo interno ciascun angolo (convesso) che ha vertice in un vertice del poligono e per lati le semirette dei lati del poligono uscenti da quel vertice.
Angolo interno ciascun angolo (convesso) che ha vertice in un vertice del poligono e per lati le semirette dei lati del poligono uscenti da quel vertice.
Angolo interno ciascun angolo (convesso) che ha vertice in un vertice del poligono e per lati le semirette dei lati del poligono uscenti da quel vertice.
Angolo interno ciascun angolo (convesso) che ha vertice in un vertice del poligono e per lati le semirette dei lati del poligono uscenti da quel vertice.
Angolo interno ciascun angolo (convesso) che ha vertice in un vertice del poligono e per lati le semirette dei lati del poligono uscenti da quel vertice.
E' convesso se il segmento che ha per estremi due qualsiasi dei suoi punti appartiene interamente al poligono
E' convesso se il segmento che ha per estremi due qualsiasi dei suoi punti appartiene interamente al poligono
E' convesso se il segmento che ha per estremi due qualsiasi dei suoi punti appartiene interamente al poligono
Un poligono è convesso se il segmento che ha per estremi due qualsiasi dei suoi punti appartiene interamente al poligono.
E' convesso se il segmento che ha per estremi due qualsiasi dei suoi punti appartiene interamente al poligono
E' convesso se il segmento che ha per estremi due qualsiasi dei suoi punti appartiene interamente al poligono
E' convesso se il segmento che ha per estremi due qualsiasi dei suoi punti appartiene interamente al poligono
E' convesso se il segmento che ha per estremi due qualsiasi dei suoi punti appartiene interamente al poligono
E' convesso se il segmento che ha per estremi due qualsiasi dei suoi punti appartiene interamente al poligono
Si definisce poligono una parte di piano delimitata da una spezzata chiusa.
E’ concavo se esistono almeno due punti tali che il segmento che li unisce non appartiene interamente al poligono
E’ concavo se esistono almeno due punti tali che il segmento che li unisce non appartiene interamente al poligono.
E’ concavo se esistono almeno due punti tali che il segmento che li unisce non appartiene interamente al poligono.
Angolo interno ciascun angolo (convesso) che ha vertice in un vertice del poligono e per lati le semirette dei lati del poligono uscenti da quel vertice.
Angolo esterno ciascun angolo adiacente ad un angolo interno; ad ogni vertice si possono associare due angoli esterni che sono congruenti perché opposti al vertice.
I Poligoni regolari
I Poligoni regolari
I Poligoni regolari
I Poligoni regolari
I Poligoni regolari
regolari
� POLIGONI REGOLARI
I Poligoni regolari
I Poligoni regolari
I Poligoni regolari
Un poligono convesso è regolare quando è equilatero (cioè ha tutti i lati congruenti) ed equiangolo (cioè ha tutti gli angoli congruenti).
Un poligono convesso si dice regolare quando è equilatero (cioè ha tutti i lati congruenti) ed equiangolo (cioè ha tutti gli angoli congruenti).
Un poligono convesso si dice regolare quando è equilatero (cioè ha tutti i lati congruenti) ed equiangolo (cioè ha tutti gli angoli congruenti).
Un poligono convesso si dice regolare quando è equilatero (cioè ha tutti i lati congruenti) ed equiangolo (cioè ha tutti gli angoli congruenti).
Un poligono convesso si dice regolare quando è equilatero (cioè ha tutti i lati congruenti) ed equiangolo (cioè ha tutti gli angoli congruenti).
Un poligono convesso si dice regolare quando è equilatero (cioè ha tutti i lati congruenti) ed equiangolo (cioè ha tutti gli angoli congruenti).
Angolo esterno ciascun angolo adiacente ad un angolo interno; ad ogni vertice si possono associare due angoli esterni che sono congruenti perché opposti al vertice.
L’angolo esterno di un poligono è ciascun angolo adiacente a un angolo interno; a ogni vertice si possono associare due angoli esterni che sono congruenti perché opposti al vertice.
Angolo esterno ciascun angolo adiacente ad un angolo interno; ad ogni vertice si possono associare due angoli esterni che sono congruenti perché opposti al vertice.
Angolo esterno ciascun angolo adiacente ad un angolo interno; ad ogni vertice si possono associare due angoli esterni che sono congruenti perché opposti al vertice.
Angolo esterno ciascun angolo adiacente ad angolo interno; ad ogni vertice si possono associare due angoli esterni che sono congruenti perché opposti al vertice.
Un poligono convesso si dice regolare quando è equilatero (cioè ha tutti i lati congruenti) ed equiangolo (cioè ha tutti gli angoli congruenti).
Un poligono convesso si dice regolare quando è equilatero (cioè ha tutti i lati congruenti) ed equiangolo (cioè ha tutti gli angoli congruenti).
Un poligono convesso si dice regolare quando è equilatero (cioè ha tutti i lati congruenti) ed equiangolo (cioè ha tutti gli angoli congruenti).
Un poligono convesso si dice regolare quando è equilatero (cioè ha tutti i lati congruenti) ed equiangolo (cioè ha tutti gli angoli congruenti).
E’ concavo se esistono almeno due punti tali che il segmento che li unisce non appartiene interamente al poligono.
Un poligono è concavo se esistono almeno due punti tali che il segmento che li unisce non appartiene interamente al poligono.
E’ concavo se esistono almeno due punti tali che il segmento che li unisce non appartiene interamente al poligono.
E’ concavo se esistono almeno due punti tali che il segmento che li unisce non appartiene interamente al poligono
E’ concavo se esistono almeno due punti tali che il segmento che li unisce non appartiene interamente al poligono.
E’ concavo se esistono almeno due punti tali che il segmento che li unisce non appartiene interamente al poligono
E’ concavo se esistono almeno due punti tali che il segmento che li unisce non appartiene interamente al poligono
Angolo esterno ciascun angolo adiacente ad un angolo interno; ad ogni vertice si possono associare due angoli esterni che sono congruenti perché opposti al vertice.
Angolo esterno ciascun angolo adiacente ad un angolo interno; ad ogni vertice si possono associare due angoli esterni che sono congruenti perché opposti al vertice.
Angolo esterno ciascun angolo adiacente ad un angolo interno; ad ogni vertice si possono associare due angoli esterni che sono congruenti perché opposti al vertice.
Angolo esterno ciascun angolo adiacente ad un angolo interno; ad ogni vertice si possono associare due angoli esterni che sono congruenti perché opposti al vertice.
Diagonale ogni segmento che unisce due vertici non consecutivi. Corda ogni segmento che unisce due punti qualsiasi del perimetro del poligono che non appartengono allo stesso lato.
Diagonale ogni segmento che unisce due vertici non consecutivi. Corda ogni segmento che unisce due punti qualsiasi del perimetro del poligono che non appartengono allo stesso lato.
Diagonale ogni segmento che unisce due vertici non consecutivi. Corda ogni segmento che unisce due punti qualsiasi del perimetro del poligono che non appartengono allo stesso lato.
Diagonale ogni segmento che unisce due vertici non consecutivi. Corda ogni segmento che unisce due punti qualsiasi del perimetro del poligono che non appartengono allo stesso lato
Diagonale ogni segmento che unisce due vertici non consecutivi. Corda ogni segmento che unisce due punti qualsiasi del perimetro del poligono che non appartengono allo stesso lato.
In ogni poligono regolare si possono tracciare la circonferenza circoscritta (passante per i suoi vertici) e quella inscritta (tangente ai suoi lati). Il segmento a che dal centro del poligono cade perpendicolarmente al lato si dice apotema.
In ogni poligono regolare si possono tracciare la circonferenza circoscritta (passante per i suoi vertici) e quella inscritta (tangente ai suoi lati). Il segmento a che dal centro del poligono cade perpendicolarmente al lato si dice apotema
In ogni poligono regolare si possono tracciare la circonferenza circoscritta (passante per i suoi vertici) e quella inscritta (tangente ai suoi lati). Il segmento a che dal centro del poligono cade perpendicolarmente al lato si dice apotema.
In ogni poligono regolare si possono tracciare la circonferenza circoscritta (passante per i suoi vertici) e quella inscritta (tangente ai suoi lati). Il segmento a che dal centro del poligono cade perpendicolarmente al lato si dice apotema
In ogni poligono regolare si possono tracciare la circonferenza circoscritta (passante per i suoi vertici) e quella inscritta (tangente ai suoi lati). Il segmento a che dal centro del poligono cade perpendicolarmente al lato si dice apotema.
In ogni poligono regolare si possono tracciare la circonferenza circoscritta (passante per i suoi vertici) e quella inscritta (tangente ai suoi lati). Il segmento a che dal centro del poligono cade perpendicolarmente al lato si dice apotema
In ogni poligono regolare si possono tracciare la circonferenza circoscritta (passante per i suoi vertici) e quella inscritta (tangente ai suoi lati). Il segmento a che dal centro del poligono cade perpendicolarmente al lato si dice apotema.
Di ogni poligono regolare si possono tracciare la circonferenza circoscritta (passante per i suoi vertici) e quella inscritta (tangente ai suoi lati). Il segmento a che dal centro del poligono cade perpendicolarmente al lato è l’apotema.
In ogni poligono regolare si possono tracciare la circonferenza circoscritta (passante per i suoi vertici) e quella inscritta (tangente ai suoi lati). Il segmento a che dal centro del poligono cade perpendicolarmente al lato si dice apotema.
Diagonale ogni segmento che unisce due vertici non consecutivi. Corda ogni segmento che unisce due punti qualsiasi del perimetro del poligono che non appartengono allo stesso lato.
Diagonale ogni segmento che unisce due vertici non consecutivi. Corda ogni segmento che unisce due punti qualsiasi del perimetro del poligono che non appartengono allo stesso lato
La diagonale di un poligono è un segmento che unisce due vertici non consecutivi. La corda è un segmento che unisce due punti qualsiasi del contorno del poligono che non appartengono allo stesso lato.
Diagonale ogni segmento che unisce due vertici non consecutivi. Corda ogni segmento che unisce due punti qualsiasi del perimetro del poligono che non appartengono allo stesso lato.
Diagonale ogni segmento che unisce due vertici non consecutivi. Corda ogni segmento che unisce due punti qualsiasi del perimetro del poligono che non appartengono allo stesso lato
I poligoni regolari si possono suddividere in tanti triangoli isosceli (nell’esagono sono equilateri) quanti sono i lati che sono la loro base e il loro vertice è il centro del poligono.
In ogni poligono regolare si possono tracciare la circonferenza circoscritta (passante per i suoi vertici) e quella inscritta (tangente ai suoi lati). Il segmento a che dal centro del poligono cade perpendicolarmente al lato si dice apotema.
I poligoni regolari si possono suddividere in tanti triangoli isosceli (nell’esagono sono equilateri) quanti sono i lati che sono la loro base e il loro vertice è il centro del poligono.
I poligoni regolari si possono suddividere in tanti triangoli isosceli (nell’esagono sono equilateri) quanti sono i lati che sono la loro base e il loro vertice è il centro del poligono.
I poligoni regolari si possono suddividere in tanti triangoli isosceli (nell’esagono sono equilateri) quanti sono i lati che sono la loro base e il loro vertice è il centro del poligono
I poligoni regolari si possono suddividere in tanti triangoli isosceli (nell’esagono sono equilateri) quanti sono i lati che sono la loro base e il loro vertice è il centro del poligono.
I poligoni regolari si possono suddividere in tanti triangoli isosceli (nell’esagono sono equilateri) quanti sono i lati che sono la loro base e il loro vertice è il centro del poligono.
I poligoni regolari si possono suddividere in tanti triangoli isosceli (nell’esagono sono equilateri) quanti sono i lati che sono la loro base e il loro vertice è il centro del poligono
I poligoni regolari si possono suddividere in tanti triangoli isosceli (nell’esagono sono equilateri) quanti sono i lati che sono la loro base e il loro vertice è il centro del poligono
I poligoni regolari si possono suddividere in tanti triangoli isosceli (nell’esagono sono equilateri) quanti sono i lati che sono la loro base e il loro vertice è il centro del poligono.
I poligoni regolari si possono suddividere in tanti triangoli isosceli (nell’esagono sono equilateri) quanti sono i lati che sono la loro base e il loro vertice è il centro del poligono.
I Triangoli
I Triangoli
I Triangoli
I Triangoli
I Triangoli
I Triangoli
I Triangoli

Si definisce triangolo un poligono convesso di tre lati. Esso è caratterizzato da due proprietà fondamentali: la somma degli angoli interni è un angolo piatto; ogni lato è minore della somma degli altri due.
Si definisce triangolo un poligono convesso di tre lati. Esso è caratterizzato da due proprietà fondamentali: la somma degli angoli interni è un angolo piatto; ogni lato è minore della somma degli altri due.
Si definisce triangolo un poligono convesso di tre lati. Esso è caratterizzato da due proprietà fondamentali: la somma degli angoli interni è un angolo piatto; ogni lato è minore della somma degli altri due.
Si definisce triangolo un poligono convesso di tre lati. Esso è caratterizzato da due proprietà fondamentali: la somma degli angoli interni è un angolo piatto; ogni lato è minore della somma degli altri due.
Si definisce triangolo un poligono convesso di tre lati. Esso è caratterizzato da due proprietà fondamentali: la somma degli angoli interni è un angolo piatto; ogni lato è minore della somma degli altri due.
Un triangolo è un poligono convesso di tre lati. Esso è caratterizzato da due proprietà fondamentali: la somma degli angoli interni è un angolo piatto e ogni lato è minore della somma degli altri due.
Si definisce triangolo un poligono convesso di tre lati. Esso è caratterizzato da due proprietà fondamentali: la somma degli angoli interni è un angolo piatto; ogni lato è minore della somma degli altri due.
Si definisce triangolo un poligono convesso di tre lati. Esso è caratterizzato da due proprietà fondamentali: la somma degli angoli interni è un angolo piatto; ogni lato è minore della somma degli altri due.
Si definisce triangolo un poligono convesso di tre lati. Esso è caratterizzato da due proprietà fondamentali: la somma degli angoli interni è un angolo piatto; ogni lato è minore della somma degli altri due.
Si definisce triangolo un poligono convesso di tre lati. Esso è caratterizzato da due proprietà fondamentali: la somma degli angoli interni è un angolo piatto; ogni lato è minore della somma degli altri due.
Si definisce triangolo un poligono convesso di tre lati. Esso è caratterizzato da due proprietà fondamentali: la somma degli angoli interni è un angolo piatto; ogni lato è minore della somma degli altri due.
Classificazione dei triangoli rispetto ai lati
Classificazione dei triangoli rispetto ai lati
� CLASSIFICAZIONE DEI TRIANGOLI RISPETTO AI LATI
Classificazione dei triangoli rispetto ai lati
Classificazione dei triangoli rispetto ai lati
Classificazione dei triangoli rispetto ai lati
Un triangolo si dice scaleno se ha i lati non congruenti.
Classificazione dei triangoli rispetto ai lati
Un triangolo si dice scaleno se ha i lati non congruenti.
Classificazione dei triangoli rispetto ai lati
Classificazione dei triangoli rispetto ai lati
Un triangolo si dice isoscele se ha due lati congruenti.
Un triangolo si dice scaleno se ha i lati non congruenti.
Un triangolo è scaleno se ha tutti i lati non congruenti.
Un triangolo si dice scaleno se ha i lati non congruenti.
Un triangolo si dice scaleno se ha i lati non congruenti.
Un triangolo si dice isoscele se ha due lati congruenti.
Classificazione dei triangoli rispetto ai lati
Classificazione dei triangoli rispetto ai lati
Un triangolo si dice scaleno se ha i lati non congruenti.
Un triangolo si dice isoscele se ha due lati congruenti.
Un triangolo si dice scaleno se ha i lati non congruenti.
Un triangolo si dice scaleno se ha i lati non congruenti.
Un triangolo si dice scaleno se ha i lati non congruenti.
Un triangolo si dice scaleno se ha i lati non congruenti.
Un triangolo è isoscele se ha due lati congruenti.
Un triangolo si dice isoscele se ha due lati congruenti.
Un triangolo si dice isoscele se ha due lati congruenti.
Un triangolo si dice isoscele se ha due lati congruenti.
Un triangolo si dice equilatero se ha i tre lati congruenti.
Un triangolo si dice equilatero se ha i tre lati congruenti.
Un triangolo si dice equilatero se ha i tre lati congruenti.
Un triangolo si dice isoscele se ha due lati congruenti.
Un triangolo si dice isoscele se ha due lati congruenti.
Un triangolo si dice isoscele se ha due lati congruenti.
Un triangolo si dice isoscele se ha due lati congruenti.
Un triangolo si dice equilatero se ha i tre lati congruenti.
Un triangolo si dice equilatero se ha i tre lati congruenti.
Un triangolo si dice equilatero se ha i tre lati congruenti.
Un triangolo si dice equilatero se ha i tre lati congruenti.
Un triangolo si dice equilatero se ha i tre lati congruenti.
Un triangolo è equilatero se ha i tre lati congruenti.
Un triangolo si dice equilatero se ha i tre lati congruenti.
Un triangolo si dice equilatero se ha i tre lati congruenti.
Classificazione dei triangoli rispetto agli angoli
Classificazione dei triangoli rispetto agli angoli
Classificazione dei triangoli rispetto agli angoli
Classificazione dei triangoli rispetto agli angoli
Classificazione dei triangoli rispetto agli angoli
Classificazione dei triangoli rispetto agli angoli
Un triangolo è acutangolo se ha tre angoli acuti.
Un triangolo si dice acutangolo se ha tre angoli acuti.
Un triangolo si dice acutangolo se ha tre angoli acuti.
Un triangolo si dice acutangolo se ha tre angoli acuti.
Un triangolo si dice acutangolo se ha tre angoli acuti.
Un triangolo si dice acutangolo se ha tre angoli acuti.
Un triangolo si dice rettangolo se ha un angolo retto
Un triangolo si dice rettangolo se ha un angolo retto
Un triangolo si dice acutangolo se ha tre angoli acuti.
Un triangolo si dice rettangolo se ha un angolo retto
Un triangolo si dice rettangolo se ha un angolo retto
Un triangolo è rettangolo se ha un angolo retto.
Un triangolo si dice rettangolo se ha un angolo retto
Classificazione dei triangoli rispetto agli angoli
Classificazione dei triangoli rispetto agli angoli
Un triangolo si dice ottusangolo se ha un angolo ottuso
Un triangolo si dice ottusangolo se ha un angolo ottuso
Un triangolo si dice rettangolo se ha un angolo retto
Classificazione dei triangoli rispetto agli angoli
Classificazione dei triangoli rispetto agli angoli
Un triangolo si dice acutangolo se ha tre angoli acuti.
Un triangolo si dice acutangolo se ha tre angoli acuti.
Un triangolo si dice acutangolo se ha tre angoli acuti.
Un triangolo si dice acutangolo se ha tre angoli acuti.
Elementi del triangolo
Elementi del triangolo
Un triangolo si dice ottusangolo se ha un angolo ottuso
Un triangolo si dice ottusangolo se ha un angolo ottuso
Un triangolo si dice rettangolo se ha un angolo retto.
Un triangolo si dice rettangolo se ha un angolo retto.
Un triangolo si dice rettangolo se ha un angolo retto.
Un triangolo si dice rettangolo se ha un angolo retto.
Elementi del triangolo
Elementi del triangolo
Elementi del triangolo
Elementi del triangolo
Si dice mediana relativa a un lato il segmento che ha come estremi il vertice e il punto medio M del lato opposto
Si dice mediana relativa a un lato il segmento che ha come estremi il vertice e il punto medio M del lato opposto.
Si dice bisettrice relativa ad un angolo il segmento che divide in due parti congruenti l’angolo
Si dice mediana relativa a un lato il segmento che ha come estremi il vertice e il punto medio M del lato opposto
Elementi del triangolo
Elementi del triangolo
Elementi del triangolo
Elementi del triangolo
Si dice mediana relativa a un lato il segmento che ha come estremi il vertice e il punto medio M del lato opposto.
La mediana relativa a un lato è il segmento che unisce il punto medio M del lato con il vertice opposto.
Si dice mediana relativa a un lato il segmento che ha come estremi il vertice e il punto medio M del lato opposto.
Si dice mediana relativa a un lato il segmento che ha come estremi il vertice e il punto medio M del lato opposto.
Si dice mediana relativa a un lato il segmento che ha come estremi il vertice e il punto medio M del lato opposto.
Si dice mediana relativa a un lato il segmento che ha come estremi il vertice e il punto medio M del lato opposto.
Si dice bisettrice relativa ad un angolo il segmento che divide in due parti congruenti l’angolo.
Si dice mediana relativa a un lato il segmento che ha come estremi il vertice e il punto medio M del lato opposto.
Si dice mediana relativa a un lato il segmento che ha come estremi il vertice e il punto medio M del lato opposto.
Si dice bisettrice relativa ad un angolo il segmento che divide in due parti congruenti l’angolo.
Si dice bisettrice relativa ad un angolo il segmento che divide in due parti congruenti l’angolo.
La bisettrice relativa a un angolo è il segmento che divide in due parti congruenti l’angolo.
Un triangolo è ottusangolo se ha un angolo ottuso.
Un triangolo si dice ottusangolo se ha un angolo ottuso
Un triangolo si dice ottusangolo se ha un angolo ottuso
Un triangolo si dice ottusangolo se ha un angolo ottuso.
Un triangolo si dice ottusangolo se ha un angolo ottuso.
Un triangolo si dice ottusangolo se ha un angolo ottuso.
Un triangolo si dice ottusangolo se ha un angolo ottuso.
Si dice altezza il segmento che ha come estremo un vertice e cade perpendicolare sul lato opposto
Si dice bisettrice relativa ad un angolo il segmento che divide in due parti congruenti l’angolo.
Si dice bisettrice relativa ad un angolo il segmento che divide in due parti congruenti l’angolo.
Si dice altezza il segmento che ha come estremo un vertice e cade perpendicolare sul lato opposto.
Si dice altezza il segmento che ha come estremo un vertice e cade perpendicolare sul lato opposto.
Si dice altezza il segmento che ha come estremo un vertice e cade perpendicolare sul lato opposto.
Si dice altezza il segmento che ha come estremo un vertice e cade perpendicolare sul lato opposto.
Si dice altezza il segmento che ha come estremo un vertice e cade perpendicolare sul lato opposto.
H
Si dice bisettrice relativa ad un angolo il segmento che divide in due parti congruenti l’angolo
Si dice bisettrice relativa ad un angolo il segmento che divide in due parti congruenti l’angolo.
Si dice bisettrice relativa ad un angolo il segmento che divide in due parti congruenti l’angolo
Si dice bisettrice relativa ad un angolo il segmento che divide in due parti congruenti l’angolo.
Punti notevoli del triangolo
Baricentro G è il punto di incontro delle mediane
Punti notevoli del triangolo
Punti notevoli del triangolo
Punti notevoli del triangolo
Punti notevoli del triangolo
Punti notevoli del triangolo
Baricentro G è il punto di incontro delle mediane
Baricentro G è il punto di incontro delle mediane
Baricentro G è il punto di incontro delle mediane
Incentro O è il punto di incontro delle bisettrici e centro della circonferenza inscritta
Baricentro G è il punto di incontro delle mediane
Baricentro G è il punto di incontro delle mediane
Incentro O è il punto di incontro delle bisettrici e centro della circonferenza inscritta
Incentro O è il punto di incontro delle bisettrici e centro della circonferenza inscritta
Incentro O è il punto di incontro delle bisettrici e centro della circonferenza inscritta
Punti notevoli del triangolo
Punti notevoli del triangolo
Punti notevoli del triangolo
Punti notevoli del triangolo
Baricentro G è il punto di incontro delle mediane
Baricentro G è il punto di incontro delle mediane
Baricentro G è il punto di incontro delle mediane
Baricentro G è il punto di incontro delle mediane
Incentro O è il punto di incontro delle bisettrici e centro della circonferenza inscritta
Incentro O è il punto di incontro delle bisettrici e centro della circonferenza inscritta
Incentro O è il punto di incontro delle bisettrici e centro della circonferenza inscritta
Incentro O è il punto di incontro delle bisettrici e centro della circonferenza inscritta
Incentro O è il punto di incontro delle bisettrici e centro della circonferenza inscritta
Incentro O è il punto di incontro delle bisettrici e centro della circonferenza inscritta
Il baricentro G è il punto di incontro delle mediane. L’incentro O è il punto di incontro delle bisettrici e centro della circonferenza inscritta.
Si dice altezza il segmento che ha come estremo un vertice e cade perpendicolare sul lato opposto
Si dice altezza il segmento che ha come estremo un vertice e cade perpendicolare sul lato opposto
L’ altezza relativa a un lato è il segmento perpendicolare abbassato dal vertice opposto sulla retta del lato. L’asse di un lato è la perpendicolare condotta per il suo punto medio.
Circocentro O è il punto di incontro degli assi dei lati e centro della circonferenza circoscritta.
Circocentro O è il punto di incontro degli assi dei lati e centro della circonferenza circoscritta.
Circocentro O è il punto di incontro degli assi dei lati e centro della circonferenza circoscritta.
Circocentro O è il punto di incontro degli assi dei lati e centro della circonferenza circoscritta.
Ortocentro O è il punto di incontro delle altezze asse
Circocentro O è il punto di incontro degli assi dei lati e centro della circonferenza circoscritta.
Circocentro O è il punto di incontro degli assi dei lati e centro della circonferenza circoscritta.
Ortocentro O è il punto di incontro delle altezze asse
Ortocentro O è il punto di incontro delle altezze asse
Si dice altezza il segmento che ha come estremo un vertice e cade perpendicolare sul lato opposto.
Si dice altezza il segmento che ha come estremo un vertice e cade perpendicolare sul lato opposto.
Ortocentro O è il punto di incontro delle altezze asse
Ortocentro O è il punto di incontro delle altezze asse
Ortocentro O è il punto di incontro delle altezze asse
Circocentro O è il punto di incontro degli assi dei lati e centro della circonferenza circoscritta.
Circocentro O è il punto di incontro degli assi dei lati e centro della circonferenza circoscritta.
Circocentro O è il punto di incontro degli assi dei lati e centro della circonferenza circoscritta.
Circocentro O è il punto di incontro degli assi dei lati e centro della circonferenza circoscritta.
Il circocentro O è il punto di incontro degli assi dei lati e centro della circonferenza circoscritta.
Ortocentro O è il punto di incontro delle altezze
Ortocentro O è il punto di incontro delle altezze
Ortocentro O è il punto di incontro delle altezze asse
Ortocentro O è il punto di incontro delle altezze
L’ortocentro O è il punto di incontro delle altezze.
Si definisce quadrilatero un poligono convesso di quattro lati.
Si definisce quadrilatero un poligono convesso di quattro lati.
Si definisce quadrilatero un poligono convesso di quattro lati.
Trapezi
Trapezi
Trapezi






Un quadrilatero è un poligono di quattro lati.
Trapezi
Si dice trapezio un quadrilatero che ha due lati paralleli.
Si dice trapezio un quadrilatero che ha due lati paralleli.
Si dice trapezio un quadrilatero che ha due lati paralleli.
Si dice trapezio un quadrilatero che ha due lati paralleli.
Un trapezio è un quadrilatero che ha due lati paralleli.
Un trapezio si dice scaleno se i due lati obliqui non sono congruenti
Un trapezio si dice scaleno se i due lati obliqui non sono congruenti
Un trapezio si dice scaleno se i due lati obliqui non sono congruenti
Un trapezio si dice scaleno se i due lati obliqui non sono congruenti
Un trapezio è scaleno se i due lati obliqui non sono congruenti.
Un trapezio si dice isoscele se ha i due lati obliqui congruenti
Un trapezio si dice isoscele se ha i due lati obliqui congruenti
Un trapezio si dice isoscele se ha i due lati obliqui congruenti
Un trapezio è isoscele se ha i due lati obliqui congruenti.
Un trapezio si dice isoscele se ha i due lati obliqui congruenti
Un trapezio si dice rettangolo quando uno dei due lati è perpendicolare alle basi.
Un trapezio si dice rettangolo quando uno dei due lati è perpendicolare alle basi.
Un trapezio si dice rettangolo quando uno dei due lati è perpendicolare alle basi.
Un trapezio si dice rettangolo quando uno dei due lati è perpendicolare alle basi.
Un trapezio è rettangolo se uno dei due lati è perpendicolare alle basi.
Parallelogrammi
Parallelogrammi
Parallelogrammi
Parallelogrammi
Si dice parallelogramma un quadrilatero che ha i lati opposti paralleli
Si dice parallelogramma un quadrilatero che ha i lati opposti paralleli
Si dice parallelogramma un quadrilatero che ha i lati opposti paralleli
Si dice parallelogramma un quadrilatero che ha i lati opposti paralleli
Un parallelogramma è un quadrilatero che ha i lati opposti paralleli.
In un parallelogramma gli angoli opposti sono a due a due congruenti.
In un parallelogramma gli angoli opposti sono a due a due congruenti.
In un parallelogramma gli angoli opposti sono a due a due congruenti.
In un parallelogramma gli angoli opposti sono a due a due congruenti.
In un parallelogramma gli angoli opposti sono a due a due congruenti.
Il rettangolo è un parallelogramma con tutti gli angoli congruenti.
Un parallelogramma con tutti gli angoli congruenti si dice rettangolo. Nel rettangolo le diagonali sono congruenti.
Un parallelogramma con tutti gli angoli congruenti si dice rettangolo. Nel rettangolo le diagonali sono congruenti.
Nel rettangolo le diagonali sono congruenti.
Un parallelogramma con tutti gli angoli congruenti si dice rettangolo. Nel rettangolo le diagonali sono congruenti.
Un parallelogramma con tutti gli angoli congruenti si dice rettangolo. Nel rettangolo le diagonali sono congruenti.
In un parallelogramma le diagonali si bisecano vicendevolmente.
In un parallelogramma le diagonali si bisecano vicendevolmente.
In un parallelogramma le diagonali si bisecano vicendevolmente.
In un parallelogramma le diagonali si tagliano vicendevolmente a metà.
In un parallelogramma le diagonali si bisecano vicendevolmente.
Il quadrato è un parallelogramma che ha tutti i lati congruenti e gli angoli congruenti.
Un parallelogramma che ha tutti i lati congruenti e gli angoli congruenti si dice quadrato.
Un parallelogramma che ha tutti i lati congruenti e gli angoli congruenti si dice quadrato.
Un parallelogramma che ha tutti i lati congruenti e gli angoli congruenti si dice quadrato.
Il rombo è un parallelogramma con tutti i lati congruenti. Nel rombo le diagonali sono fra loro perpendicolari e bisettrici degli angoli opposti.
Un parallelogramma con tutti i lati congruenti si chiama rombo Nel rombo le diagonali sono fra loro perpendicolari e bisettrici degli angoli opposti.
Un parallelogramma con tutti i lati congruenti si chiama rombo. Nel rombo le diagonali sono fra loro perpendicolari e bisettrici degli angoli opposti.
Un parallelogramma con tutti i lati congruenti si chiama rombo. Nel rombo le diagonali sono fra loro perpendicolari e bisettrici degli angoli opposti.
Un parallelogramma con tutti i lati congruenti si chiama rombo Nel rombo le diagonali sono fra loro perpendicolari e bisettrici degli angoli opposti.
Un parallelogramma che ha tutti i lati congruenti e gli angoli congruenti si dice quadrato.
Nel quadrato le diagonali sono congruenti, sono tra loro perpendicolari e sono bisettrici degli angoli.
Nel quadrato le diagonali sono congruenti, sono tra loro perpendicolari e sono bisettrici degli angoli.
Nel quadrato le diagonali sono congruenti, sono tra loro perpendicolari e sono bisettrici degli angoli.
Nel quadrato le diagonali sono congruenti, sono tra loro perpendicolari e sono bisettrici degli angoli.
Nel quadrato le diagonali sono congruenti, sono tra loro perpendicolari e sono bisettrici degli angoli.
Problema 13: Costruire un triangolo dati i lati
Problema 13: Costruire un triangolo dati i lati
Problema 13: Costruire un triangolo dati i lati
Siano dati i lati.
Siano dati i lati.
Siano dati i lati.
Problema 13: Costruire un triangolo dati i lati
Siano dati i lati.
Si tracci ad esempio AB.
Si tracci ad esempio AB.
Si tracci ad esempio AB.
Problema 13: Costruire un triangolo dati i lati
Si punti col compasso in A con apertura AC e in B con apertura

Siano dati i lati.
1 Consideriamo tre segmenti che rappresentano i lati.
Si tracci ad esempio AB.
Si punti col compasso in A con apertura AC e in B con apertura
Si punti col compasso in A con apertura AC e in B con apertura
BC e si traccino due archetti che intersecandosi determinano C.
Tracciando i segmenti AC e BC si ottiene il triangolo cercato.
Tracciando i segmenti AC e BC si ottiene il triangolo cercato.
Tracciando i segmenti AC e BC si ottiene il triangolo cercato.
Si tracci ad esempio AB.
BC e si traccino due archetti che intersecandosi determinano C.
BC e si traccino due archetti che intersecandosi determinano C.
Si punti col compasso in A con apertura AC e in B con apertura
Si punti col compasso in A con apertura AC e in B con apertura BC e si traccino due archetti che intersecandosi determinano C.
2 Riportiamo ad esempio AB. Puntiamo il compasso in A con apertura AC e in B con apertura
BC e si traccino due archetti che intersecandosi determinano C.
BC e tracciamo due archetti la cui intersezione è C.
Tracciando i segmenti AC e BC si ottiene il triangolo cercato.
Tracciando i segmenti AC e BC si ottiene il triangolo cercato.
3 Tracciando i segmenti AC e BC otteniamo il triangolo cercato.
Problema 14: Costruire un triangolo dati un lato e gli angoli adiacenti ad esso.
Problema 14: Costruire un triangolo dati un lato e gli angoli adiacenti ad esso.
Problema 14: Costruire un triangolo dati un lato e gli angoli adiacenti ad esso.
Siano dati AB e gli angoli α e b a lui adiacenti.
Siano dati AB e gli angoli α e b a lui adiacenti.
Siano dati AB e gli angoli α e b a lui adiacenti.
Tracciato AB si costruisca nel suo estremo A l’angolo α.
Tracciato AB si costruisca nel suo estremo A l’angolo α.
Tracciato AB si costruisca nel suo estremo A l’angolo α.
Problema 14: Costruire un triangolo dati un lato e gli angoli adiacenti ad esso.
Siano dati AB e gli angoli α e b a lui adiacenti.

Problema 14: Costruire un triangolo dati un lato e gli angoli adiacenti ad esso.
Siano dati AB e gli angoli α e b a lui adiacenti.
1 Consideriamo AB e gli angoli a e b a esso adiacenti.
Tracciato AB si costruisca nel suo estremo A l’angolo α.
Si costruisca nell’estremo B l’angolo β. Le semirette che delimitano α e β si intersecano in C terzo vertice dell’angolo.
Si costruisca nell’estremo B l’angolo β. Le semirette che delimitano α e β si intersecano in C terzo vertice dell’angolo.
Si costruisca nell’estremo B l’angolo β. Le semirette che delimitano α e β si intersecano in C terzo vertice dell’angolo.
Tracciato AB si costruisca nel suo estremo A l’angolo α.
2 Tracciato AB, costruiamo nel suo estremo A l’angolo a.
Si costruisca nell’estremo B l’angolo β. Le semirette che delimitano α e β si intersecano in C terzo vertice dell’angolo
Si costruisca nell’estremo B l’angolo β. Le semirette che delimitano α e β si intersecano in C terzo vertice dell’angolo
3 Costruiamo nell’estremo B l’angolo b. Le semirette che delimitano a e b si intersecano in C, terzo vertice del triangolo.
Problema 15: Costruire un triangolo dati un lato e gli angoli adiacenti ad esso.
Problema 15: Costruire un triangolo dati un lato e gli angoli adiacenti ad esso.
Problema 15: Costruire un triangolo dati un lato e gli angoli adiacenti ad esso.
Siano dati AB e AC e l’angolo α tra loro compreso

Siano dati AB e AC e l’angolo α tra loro compreso
Siano dati AB e AC e l’angolo α tra loro compreso
PASSO PASSO 4.4.3
Tracciato AB si costruisca nel suo estremo A l’angolo α
Tracciato AB si costruisca nel suo estremo A l’angolo α
Problema 15: Costruire un triangolo dati un lato e gli angoli adiacenti ad esso.
Tracciato AB si costruisca nel suo estremo A l’angolo α
Siano dati AB e AC e l’angolo α tra loro compreso.
Siano dati AB e AC e l’angolo α tra loro compreso.
Tracciato AB si costruisca nel suo estremo A l’angolo α.
Problema 15: Costruire un triangolo dati un lato e gli angoli adiacenti ad esso.
Si riporti col compasso la misura di AC sulla semiretta che delimita l’angolo a determinando così il punto C terzo vertice del triangolo.
1 Consideriamo AB e AC e l’angolo a tra essi compreso. 2 Tracciato AB, costruiamo nel suo estremo A l’angolo a 3 Riportiamo col compasso la misura di AC sulla semiretta che delimita l’angolo a, determinando così il punto C, terzo vertice del triangolo.
Tracciato AB si costruisca nel suo estremo A l’angolo α.
Si riporti col compasso la misura di AC sulla semiretta che delimita l’angolo a determinando così il punto C terzo vertice del triangolo.
Si riporti col compasso la misura di AC sulla semiretta che delimita l’angolo a determinando così il punto C terzo vertice del triangolo.
Si riporti col compasso la misura di AC sulla semiretta che delimita l’angolo a determinando così il punto C terzo vertice del triangolo.
Si riporti col compasso la misura di AC sulla semiretta che delimita l’angolo a determinando così il punto C terzo vertice del triangolo.






Problema 16: Costruire un triangolo isoscele date la base e l’altezza
Problema 16: Costruire un triangolo isoscele date la base e l’altezza
Problema 16: Costruire un triangolo isoscele date la base e l’altezza
1 Consideriamo la base AB e l’altezza h del triangolo isoscele.
la
Problema 16: Costruire un triangolo isoscele date la base e l’altezza
Problema 16: Costruire un triangolo isoscele date la base e l’altezza
Siano date la base AB e l’altezza h. Si tracci l’asse di AB determinando H. Si riporti su di esso, partendo da H, l’altezza HC determinando C terzo vertice del triangolo
Siano date la base AB e l’altezza h. Si tracci l’asse di AB determinando H. Si riporti su di esso, partendo da H, l’altezza HC determinando C terzo vertice del triangolo
Siano date la base AB e l’altezza h. Si tracci l’asse di AB determinando H. Si riporti su di esso, partendo da H, l’altezza HC determinando C terzo vertice del triangolo
Siano date la base AB e l’altezza h. Si tracci l’asse di AB determinando H. Si riporti su di esso, partendo da H, l’altezza HC determinando C terzo vertice del triangolo
Tracciando i segmenti AC e BC si ottiene il triangolo cercato
Siano date la base AB e l’altezza h. Si tracci l’asse di AB determinando H. Si riporti su di esso, partendo da H, l’altezza HC determinando C terzo vertice del triangolo
Tracciando i segmenti AC e BC si ottiene il triangolo cercato
Siano la riporti del i
2 Tracciamo l’asse di AB determinando il punto medio H. Riportiamo sull’asse, puntando in H, l’altezza h determinando C, terzo vertice del triangolo.
3 Tracciamo i segmenti AC e BC e otteniamo il triangolo cercato.
Tracciando i segmenti AC e BC si ottiene il triangolo cercato
Tracciando i segmenti AC e BC si ottiene il triangolo cercato.
Tracciando i segmenti AC e BC si ottiene il triangolo cercato.
Problema 17: Costruire un triangolo equilatero inscritto in una circonferenza di raggio R.
Problema 17: Costruire un triangolo equilatero inscritto in una circonferenza di raggio R.
Problema 17: Costruire un triangolo equilatero inscritto in una circonferenza di raggio R.
Problema 17: Costruire un triangolo equilatero inscritto in una circonferenza di raggio R.
Problema 17: Costruire un triangolo equilatero inscritto in una circonferenza di raggio R.
Sia data la circonferenza di raggio R e centro O.
Sia data la circonferenza di raggio R e centro O.
Sia data la circonferenza di raggio R e centro O.
Sia data la circonferenza di raggio R e centro O.
Sia data la circonferenza di raggio R e centro O.
Si tracci il diametro verticale CZ.
Si tracci il diametro verticale CZ.
Si tracci il diametro verticale CZ.
Si tracci il diametro verticale CZ.
1 Consideriamo la circonferenza di raggio R e centro O. Tracciamo il diametro verticale CZ.
Si punti col compasso in Z avente apertura pari al raggio R e si tracci un arco che intersechi la circonferenza in A e B.
Si punti col compasso in Z avente apertura pari al raggio R e si tracci un arco che intersechi la circonferenza in A e B.
Si punti col compasso in Z avente apertura pari al raggio R e si tracci un arco che intersechi la circonferenza in A e B.
Si tracci il diametro verticale CZ.
R
Si punti col compasso in Z avente apertura pari al raggio R e si tracci un arco che intersechi la circonferenza in A e B.
Si punti col compasso in Z avente apertura pari al raggio R e si tracci un arco che intersechi la circonferenza in A e B.
Congiungendo A, B, C si otteniene il triangolo equilatero cercato.
Congiungendo A, B, C si otteniene il triangolo equilatero cercato.
Congiungendo A, B, C si otteniene il triangolo equilatero cercato.
circonferenza di il verticale pari circonin il cercato.
2 Puntiamo col compasso in Z con apertura pari al raggio R e tracciamo un arco che intersechi la circonferenza in A e B.
Congiungendo A, B, C si otteniene il triangolo equilatero cercato.
Congiungendo A, B, C si otteniene il triangolo equilatero cercato.
3 Congiungendo A, B e C otteniamo il triangolo equilatero cercato.
PASSO PASSO 4.4.6 QUADRATO
Problema 18: Costruire un quadrato dato il lato.
Problema 18: Costruire un quadrato dato il lato.
Problema 18: Costruire un quadrato dato il lato
Problema 18: Costruire un quadrato dato il lato.
Sia dato il lato
Sia dato il lato.
Sia dato il lato
1 Consideriamo il lato del quadrato.
Problema 18: Costruire un quadrato dato il lato.
Problema 18: Costruire un quadrato dato il lato.
Problema 18: Costruire un quadrato dato il lato.
Sia dato il lato.
Sia dato il lato Si traccino le perpendicolari al lato per gli estremi A e B e si riportino su di esse le misure del lato determinando C e D vertici del quadrato.
Sia dato il lato.
Sia dato il lato.
Si traccino le perpendicolari al lato per gli estremi A e B e si riportino su di esse le misure del lato determinando C e D vertici del quadrato.
Si traccino le perpendicolari al lato per gli estremi A e B e si riportino su di esse le misure del lato determinando C e D vertici del quadrato
Si traccino le perpendicolari al lato per gli estremi A e B e si riportino su di esse le misure del lato determinando C e D vertici del quadrato
2 Tracciamo le perpendicolari al lato per gli estremi A e B e riportiamo su di esse le misure del lato, determinando i vertici C e D.
Si traccino le perpendicolari al lato per gli estremi A e B e si riportino su di esse le misure del lato determinando C e D vertici del quadrato.
Tracciando DC si completa la costruzione del quadrato.
Tracciando DC si completa la costruzione del quadrato
Si traccino le perpendicolari al lato per gli estremi A e B e si riportino su di esse le misure del lato determinando C e D vertici del quadrato
Tracciando DC si completa la costruzione del quadrato.
Si traccino le perpendicolari al lato per gli estremi A e B e si riportino su di esse le misure del lato determinando C e D vertici del quadrato
Tracciando DC si completa la costruzione del quadrato.
Tracciando DC si completa la costruzione del quadrato.
3 Tracciando DC completiamo la costruzione del quadrato.
Tracciando DC si completa la costruzione del quadrato.
Tracciando DC si completa la costruzione del quadrato.
a Allinea la squadra 30/60 con AB e falla scorrere verso il basso. b Appoggia la squadra 45 sulla squadra 30/60 allineata all’estremo A e traccia una verticale di lunghezza pari ad AB determinando D. c Ripeti l’operazione in B. d Allinea la squadra 45 ad AB, falla scorrere fino ad allinearla a D e traccia il segmento DC.
1) Allinea Sq.30/60 con AB e falla scorrere verso il basso; 2) Appoggia Sq.45 su Sq.30/60 allineata all’estremo A e traccia una verticale pari ad AB determinando D; 3) Ripeti l’operazione in B ; 4) Allinea Sq.45 ad AB, falla scorrere fino ad allinearla a D e traccia il segmento DC.
1) Allinea Sq.30/60 con AB e falla scorrere verso il basso; 2) Appoggia Sq.45 su Sq.30/60 allineata all’estremo A e traccia una verticale pari ad AB determinando D; 3) Ripeti l’operazione in B ; 4) Allinea Sq.45 ad AB, falla scorrere fino ad allinearla a D e traccia il segmento DC.
1) Allinea Sq.30/60 con AB e falla scorrere verso il basso; 2) Appoggia Sq.45 su Sq.30/60 allineata all’estremo A e traccia una verticale pari ad AB determinando D; 3) Ripeti l’operazione in B ; 4) Allinea Sq.45 ad AB, falla scorrere fino ad allinearla a D e traccia il segmento DC.
1) Allinea Sq.30/60 con AB e falla scorrere verso il basso; 2) Appoggia Sq.45 su Sq.30/60 allineata all’estremo A e traccia una verticale pari ad AB determinando D; 3) Ripeti l’operazione in B ; 4) Allinea Sq.45 ad AB, falla scorrere fino ad allinearla a D e traccia il segmento DC.
1) Allinea Sq.30/60 con AB e falla scorrere verso il basso; 2) Appoggia Sq.45 su Sq.30/60 allineata all’estremo A e traccia una verticale pari ad AB determinando D; 3) Ripeti l’operazione in B ; 4) Allinea Sq.45 ad AB, falla scorrere fino ad allinearla a D e traccia il segmento DC.
1) Allinea Sq.30/60 con AB e falla scorrere verso il basso; 2) Appoggia Sq.45 su Sq.30/60 allineata all’estremo A e traccia una verticale pari ad AB determinando D; 3) Ripeti l’operazione in B ; 4) Allinea Sq.45 ad AB, falla scorrere fino ad allinearla D e traccia il segmento DC.
1) Allinea Sq.30/60 con AB e falla scorrere verso il basso; 2) Appoggia Sq.45 su Sq.30/60 allineata all’estremo A e traccia una verticale pari ad AB determinando D; 3) Ripeti l’operazione in B ; 4) Allinea Sq.45 ad AB, falla scorrere fino ad allinearla a D e traccia il segmento DC.
Problema 19: Costruire un quadrato data la diagonale.
Problema 19: Costruire un quadrato data la diagonale.
Problema 19: Costruire un quadrato data la diagonale.
Problema 19: Costruire un quadrato data la diagonale.
Data la diagonale d si tracci una retta e per un suo punto A preso a piacere si tracci una perpendicolare.
Data la diagonale d si tracci una retta e per un suo punto A preso a piacere si tracci una perpendicolare.

Data la diagonale d si tracci una retta e per un suo punto A preso a piacere si tracci una perpendicolare.
Data la diagonale d si tracci una retta e per un suo punto A preso a piacere si tracci una perpendicolare.
Problema 19: Costruire un quadrato data la diagonale.
PASSO PASSO 4.4.7 QUADRATO DATA LA DIAGONALE
Data la diagonale d si tracci una retta e per un suo punto A preso a piacere si tracci una perpendicolare.
1 Data la diagonale d, tracciamo una retta e per un suo punto A preso a piacere costruiamo la perpendicolare.
Data la diagonale d si tracci una retta e per un suo punto A preso a piacere si tracci una perpendicolare.
Data la diagonale d si tracci una retta e per un suo punto A preso a piacere si tracci una perpendicolare.
Si tracci la bisettrice dell’angolo in A e si riporti su di esso, partendo da A, la diagonale d determinando il vertice C.
Problema 19: Costruire un quadrato data la diagonale.
Problema 19: Costruire un quadrato data la diagonale.
Si tracci la bisettrice dell’angolo in A e si riporti su di esso, partendo da A, la diagonale d determinando il vertice C.
Si tracci la bisettrice dell’angolo in A e si riporti su di esso, partendo da A, la diagonale d determinando il vertice C.
Si tracci la bisettrice dell’angolo in A e si riporti su di esso, partendo da A, la diagonale d determinando il vertice C.
2 Tracciamo la bisettrice dell’angolo in A e riportiamo su di essa, partendo da A, la diagonale d determinando il vertice C.
Si tracci la bisettrice dell’angolo in A e si riporti su di esso, partendo da A, la diagonale d determinando il vertice C.
Si tracci la bisettrice dell’angolo in A e si riporti su di esso, partendo da A, la diagonale d determinando il vertice C.
Si tracci la bisettrice dell’angolo in A e si riporti su di esso, partendo da A, la diagonale d determinando il vertice C.
Con l’aiuto delle squadrette si traccino da C le parallele alla orizzontale e alla verticale determinando i vertici B e D.
Con l’aiuto delle squadrette si traccino da C le parallele alla orizzontale e alla verticale determinando i vertici B e D.
Con l’aiuto delle squadrette si traccino da C le parallele alla orizzontale e alla verticale determinando i vertici B e D.
Con l’aiuto delle squadrette si traccino da C le parallele alla orizzontale e alla verticale determinando i vertici B e D.
Con l’aiuto delle squadrette si traccino da C le parallele alla orizzontale e alla verticale determinando i vertici B e D.
3 Con l’aiuto delle squadrette tracciamo da C le parallele all’orizzontale e alla verticale determinando i vertici B e D.
Con l’aiuto delle squadrette si traccino da C le parallele alla orizzontale e alla verticale determinando i vertici B e D.
Con l’aiuto delle squadrette si traccino da C le parallele alla orizzontale e alla verticale determinando i vertici B e D.



Problema 20: Costruire un rettangolo date la base e la diagonale.
Problema 20: Costruire un rettangolo date la base e la diagonale.
Problema 20: Costruire un rettangolo date la base e la diagonale.




Tracciato AB si costruiscano sui suoi estremi le perpendicolari.
Tracciato AB si costruiscano sui suoi estremi le perpendicolari.
Tracciato AB si costruiscano sui suoi estremi le perpendicolari. Si punti col compasso in A con apertura AC e in B con apertura BC e si traccino due archetti che intersecandosi determinano C e D.
Tracciando i segmenti BC, CD e DA si ottiene il rettangolo cercato.
Tracciando i segmenti BC, CD e DA si ottiene il rettangolo cercato.
Tracciando i segmenti BC, CD e DA si ottiene il rettangolo cercato.
Problema 20: Costruire un rettangolo date la base e la diagonale.
1 Consideriamo AB e costruiamo le perpendicolari nei suoi estremi A e B.
Si punti col compasso in A con apertura AC e in B con apertura BC e si traccino due archetti che intersecandosi determinano C e D.
Problema 20: Costruire un rettangolo date la base e la diagonale.
Si punti col compasso in A con apertura AC e in B con apertura BC e si traccino due archetti che intersecandosi determinano C e D.
Tracciato AB si costruiscano sui suoi estremi le perpendicolari.
Tracciato AB si costruiscano sui suoi estremi le perpendicolari.
Tracciato AB si costruiscano sui suoi estremi le perpendicolari.
Tracciato AB si costruiscano sui suoi estremi le perpendicolari.
Problema 20: Costruire un rettangolo date la base e la diagonale.
Problema 20: Costruire un rettangolo date la base e la diagonale.

Tracciato AB si costruiscano sui suoi estremi le perpendicolari.
Si punti col compasso in A con apertura AC e in B con apertura BC e si traccino due archetti che intersecandosi determinano C e D.
Tracciando i segmenti BC, CD e DA si ottiene il rettangolo cercato
Tracciando i segmenti BC, CD e DA si ottiene il rettangolo cercato
Problema 20: Costruire un rettangolo date la base e la diagonale.
Tracciato AB si costruiscano sui suoi estremi le perpendicolari.
Tracciato AB si costruiscano sui suoi estremi le perpendicolari.
Si punti col compasso in A con apertura AC e in B con apertura BC e si traccino due archetti che intersecandosi determinano C e D.
2 Puntiamo col compasso in A e in B con apertura d e tracciamo due archetti che si intersecano nei punti C e D.
Si punti col compasso in A con apertura AC e in B con apertura BC e si traccino due archetti che intersecandosi determinano C e D.
Si punti col compasso in A con apertura AC e in B con apertura BC e si traccino due archetti che intersecandosi determinano C e D.
Problema 20: Costruire un rettangolo date la base e la diagonale.
Problema 20: Costruire un rettangolo date la base e la diagonale.
3 Tracciando i segmenti BC, CD e DA otteniamo il rettangolo cercato.
Tracciando i segmenti BC, CD e DA si ottiene il rettangolo cercato.
Tracciando i segmenti BC, CD e DA si ottiene il rettangolo cercato
Si punti col compasso in A con apertura AC e in B con apertura BC e si traccino due archetti che intersecandosi determinano C e D.
Si punti col compasso in A con apertura AC e in B con apertura BC e si traccino due archetti che intersecandosi determinano C e D.
Si punti col compasso in A con apertura AC e in B con apertura BC e si traccino due archetti che intersecandosi determinano C e D.
Tracciando i segmenti BC, CD e DA si ottiene il rettangolo cercato.
Problema 21: Costruire un rombo dati gli assi.
Problema 21: Costruire un rombo dati gli assi.
Problema 21: Costruire un rombo dati gli assi.
1 Consideriamo le due diagonali AB (maggiore) e DC (minore).
Problema 21: Costruire un rombo dati gli assi.
Siano dati gli assi AB e AC. Tracciato AB se ne costruisca l’asse determinando O e si riporti su di esso simmetricamente a O la metà di DC.
Siano dati gli assi AB e AC. Tracciato AB se ne costruisca l’asse determinando O e si riporti su di esso simmetricamente a O la metà di DC.
Problema 21: Costruire un rombo dati gli assi.
Siano dati gli assi AB e AC. Tracciato AB se ne costruisca l’asse determinando O e si riporti su di esso simmetricamente a O la metà di DC.
Problema 21: Costruire un rombo dati gli assi.
Problema 21: Costruire un rombo dati gli assi.
Siano dati gli assi AB e AC. Tracciato AB se ne costruisca l’asse determinando O e si riporti su di esso simmetricamente a O la metà di DC.
Siano dati gli assi AB e AC. Tracciato AB se ne costruisca l’asse determinando O e si riporti su di esso simmetricamente a O la metà di DC.
Problema 21: Costruire un rombo dati gli assi.
Problema 21: Costruire un rombo dati gli assi.
Problema 21: Costruire un rombo dati gli assi.
Siano dati gli assi AB e AC. Tracciato AB se ne costruisca l’asse determinando O e si riporti su di esso simmetricamente a O la metà di DC.
Tracciando i segmenti BC, CD e DA si ottiene il rettangolo cercato.
Tracciando i segmenti BC, CD e DA si ottiene il rettangolo cercato.
Congiungendo i vertici così determinati si ottiene il rombo
Congiungendo i vertici così determinati si ottiene il rombo
Congiungendo i vertici così determinati si ottiene il rombo
2 Costruiamo l’asse di AB e determiniamo il punto medio O di AB. Riportiamo sull’asse, simmetricamente rispetto a O la metà di DC e individuiamo C e D.
Siano dati gli assi AB e AC. Tracciato AB se ne costruisca l’asse determinando O e si riporti su di esso simmetricamente a O la metà di DC.
Congiungendo i vertici così determinati si ottiene il rombo
3 Congiungendo i quattro vertici A, B, C e D otteniamo il rombo.
Congiungendo i vertici così determinati si ottiene il rombo
Congiungendo i vertici così determinati si ottiene il rombo
Siano dati gli assi AB e AC. Tracciato AB se ne costruisca l’asse determinando O e si riporti su di esso simmetricamente a O la metà di DC.
Congiungendo i vertici così determinati si ottiene il rombo.
Siano dati gli assi AB e AC. Tracciato AB se ne costruisca l’asse determinando O e si riporti su di esso simmetricamente a O la metà di DC.
Siano dati gli assi AB e AC. Tracciato AB se ne costruisca l’asse determinando O e si riporti su di esso simmetricamente a O la metà di DC.
Congiungendo i vertici così determinati si ottiene il rombo.
Problema 22: Costruire un parallelogramma dati i lati e un angolo.
Congiungendo i vertici così determinati si ottiene il rombo.
Congiungendo i vertici così determinati si ottiene il rombo.
Problema 22: Costruire un parallelogramma dati i lati e un angolo.
Problema 22: Costruire un parallelogramma dati i lati e un angolo.
Siano dati AB e AC e l’angolo α tra loro compreso.
Siano dati AB e AC e l’angolo α tra loro compreso.
Siano dati AB e AC e l’angolo α tra loro compreso.

Si riporti sulla semiretta s la misura di AC. Puntando poi in C con misura AB e in B con misura AC si traccino due archetti determinando D.
Si traccino CD e BD completando così la costruzione.
Si traccino CD e BD completando così la costruzione.
Si traccino CD e BD completando così la costruzione.
Problema 22: Costruire un parallelogramma dati i lati e un angolo.
Problema 22: Costruire un parallelogramma dati i lati e un angolo.
Si riporti sulla semiretta s la misura di AC. Puntando poi in C con misura AB e in B con misura AC si traccino due archetti determinando D.
Si riporti sulla semiretta s la misura di AC. Puntando poi in C con misura AB e in B con misura AC si traccino due archetti determinando D.
PASSO PASSO 4.4.10 PARALLELOGRAMMA DATI I LATI E L’ANGOLO COMPRESO TRA ESSI
Siano dati AB e AC e l’angolo α tra loro compreso
Siano dati AB e AC e l’angolo α tra loro compreso
Problema 22: Costruire un parallelogramma dati i lati e un angolo
Siano dati AB e AC e l’angolo α tra loro compreso.
Siano dati AB e AC e l’angolo α tra loro compreso
1 Consideriamo AB e AC e l’angolo a tra essi compreso.
Problema 22: Costruire un parallelogramma dati i lati e un angolo.
Si traccino CD e BD completando così la costruzione.
Si traccino CD e BD completando così la costruzione.
Tracciato AB, si costruisca nel suo estremo A l’angolo α avente come altro lato la semiretta s.
Tracciato AB, si costruisca nel suo estremo A l’angolo α avente come altro lato la semiretta s.
Siano dati AB e AC e l’angolo α tra loro compreso.
Si riporti sulla semiretta s la misura di AC. Puntando poi in C con misura AB e in B con misura AC si traccino due archetti determinando D.
Si riporti sulla semiretta s la misura di AC. Puntando poi in C con misura AB e in B con misura AC si traccino due archetti determinando D.
Problema 22: Costruire un parallelogramma dati i lati e un angolo.
Siano dati AB e AC e l’angolo α tra loro compreso.
Si riporti sulla semiretta s la misura di AC. Puntando poi in C con misura AB e in B con misura AC si traccino due archetti determinando D.
Tracciato AB, si costruisca nel suo estremo A l’angolo α avente come altro lato la semiretta s.
Siano dati AB e AC e l’angolo α tra loro compreso.
Tracciato AB, si costruisca nel suo estremo A l’angolo α avente come altro lato la semiretta s.
Tracciato AB, si costruisca nel suo estremo A l’angolo α avente come altro lato la semiretta s.
Tracciato AB, si costruisca nel suo estremo A l’angolo α avente come altro lato la semiretta s.
Si riporti sulla semiretta s la misura di AC. Puntando poi in C con misura AB e in B con misura AC si traccino due archetti determinando D.
Tracciato AB, si costruisca nel suo estremo A l’angolo α avente come altro lato la semiretta s.
2 Tracciato AB, costruiamo nel suo estremo A l’angolo a avente come altro lato la semiretta s.
Tracciato AB, si costruisca nel suo estremo A l’angolo α avente come altro lato la semiretta s.
Problema 22: Costruire un parallelogramma dati i lati e un angolo.
Problema 22: Costruire un parallelogramma dati i lati e un angolo.
Si traccino CD e BD completando così la costruzione.
Si traccino CD e BD completando così la costruzione.
Si riporti sulla semiretta s la misura di AC. Puntando poi in C con misura AB e in B con misura AC si traccino due archetti determinando D.
3 Riportiamo sulla semiretta s la misura di AC. Puntando poi in C con misura AB e in B con misura AC tracciamo due archetti determinando D.
4 Tracciamo CD e BD completando così la costruzione.
Si riporti sulla semiretta s la misura di AC. Puntando poi in C con misura AB e in B con misura AC si traccino due archetti determinando D.
Si riporti sulla semiretta s la misura di AC. Puntando poi in C con misura AB e in B con misura AC si traccino due archetti determinando D.
Si traccino CD e BD completando così la costruzione.
Si traccino CD e BD completando così la costruzione.
Si traccino CD e BD completando così la costruzione.
Tracciato AB, si costruisca nel suo estremo A l’angolo α avente come altro lato la semiretta s.
Tracciato AB, si costruisca nel suo estremo A l’angolo α avente come altro lato la semiretta s.

Problema 23: Costruire un parallelogramma dati i lati e una diagonale.
1 Consideriamo i lati l' e l" e la diagonale d.
Problema 23: Costruire un parallelogramma dati i lati e una diagonale.
Problema 23: Costruire un parallelogramma dati i lati e una diagonale.
Dati i lati l’ e l”e la diagonale d.
Dati i lati l’ e l”e la diagonale d. Tracciato AB pari a l’ si punti col compasso in A con apertura d e in B con apertura BC e si traccino due archetti che intersecandosi determinano C.
Problema 23: Costruire un parallelogramma dati i lati e una diagonale.

Problema 23: Costruire un parallelogramma dati i lati e una diagonale.
Dati i lati l’ e l”e la diagonale d. Tracciato AB pari a l’ si punti col compasso in A con apertura d e in B con apertura BC e si traccino due archetti che intersecandosi determinano C.
Problema 23: Costruire un parallelogramma dati i lati e una diagonale.
Dati i lati l’ e l”e la diagonale d. Tracciato AB pari a l’ si punti col compasso in A con apertura d e in B con apertura BC e si traccino due archetti che intersecandosi determinano C.
2 Tracciato il segmento AB pari a l' puntiamo col compasso in A con apertura d e in B con apertura l" e tracciamo due archetti che si intersecano in C.
Tracciato AB pari a l’ si punti col compasso in A con apertura d e in B con apertura BC e si traccino due archetti che intersecandosi determinano C.
Si punti in C con apertura l’ e in A con apertura l” e si tracciano due archetti che determinano D. Tracciando i segmenti AD e CD si ottiene il parallelogramma cercato
Si punti in C con apertura l’ e in A con apertura l” e si tracciano due archetti che determinano D. Tracciando i segmenti AD e CD si ottiene il parallelogramma cercato
Problema 23: Costruire un parallelogramma dati i lati e una diagonale.
3 Puntiamo in C con apertura l' e in A con apertura l" e tracciamo due archetti che determinano D. Tracciando i segmenti AD e CD otteniamo il parallelogramma.
Si punti in C con apertura l’ e in A con apertura l” e si tracciano due archetti che determinano D. Tracciando i segmenti AD e CD si ottiene il parallelogramma cercato
Dati i lati l’ e l”e la diagonale d. Tracciato AB pari a l’ si punti col compasso in A con apertura d e in B con apertura BC e si traccino due archetti che intersecandosi determinano C.
Problema 23: Costruire un parallelogramma dati i lati e una diagonale.
Problema 23: Costruire un parallelogramma dati i lati e una diagonale.
Dati i lati l’ e l”e la diagonale d. Tracciato AB pari a l’ si punti col compasso in A con apertura d e in B con apertura BC e si traccino due archetti che intersecandosi determinano C.
Dati i lati l’ e l”e la diagonale d. Tracciato AB pari a l’ si punti col compasso in A con apertura d e in B con apertura BC e si traccino due archetti che intersecandosi determinano C.
Dati i lati l’ e l”e la diagonale d. Tracciato AB pari a l’ si punti col compasso in A con apertura d e in B con apertura BC e si traccino due archetti che intersecandosi determinano C.
Si punti in C con apertura l’ e in A con apertura l” e si tracciano due archetti che determinano D. Tracciando i segmenti AD e CD si ottiene il parallelogramma cercato
Dati i lati l’ e l”e la diagonale d. Tracciato AB pari a l’ si punti col compasso in A con apertura d e in B con apertura BC e si traccino due archetti che intersecandosi determinano C.
Si punti in C con apertura l’ e in A con apertura l” e si tracciano due archetti che determinano D. Tracciando i segmenti AD e CD si ottiene il parallelogramma cercato
Si punti in C con apertura l’ e in A con apertura l” e si tracciano due archetti che determinano D. Tracciando i segmenti AD e CD si ottiene il parallelogramma cercato
Si punti in C con apertura l’ e in A con apertura l” e si tracciano due archetti che determinano D. Tracciando i segmenti AD e CD si ottiene il parallelogramma cercato
Si punti in C con apertura l’ e in A con apertura l” e si tracciano due archetti che determinano D. Tracciando i segmenti AD e CD si ottiene il parallelogramma cercato
Si punti in C con apertura l’ e in A con apertura l” e si tracciano due archetti che determinano D. Tracciando i segmenti AD e CD si ottiene il parallelogramma cercato
Problema 24: Costruire un trapezio scaleno date le basi, l’altezza e una diagonale.
Problema 24: Costruire un trapezio scaleno date le basi, l’altezza e una diagonale.
Problema 24: Costruire un trapezio scaleno date le basi, l’altezza e una diagonale.
Siano date le basi AB e CD l’altezza h e la diagonale d.
Siano date le basi AB e CD l’altezza h e la diagonale d.
Siano date le basi AB e CD l’altezza h e la diagonale d.
Problema 24: Costruire un trapezio scaleno date le basi, l’altezza e una diagonale.
1 Consideriamo le basi AB e CD, l’altezza h e la diagonale d.
Siano date le basi AB e CD l’altezza h e la diagonale d.
Siano date le basi AB e CD l’altezza h e la diagonale d.
Siano date le basi AB e CD l’altezza h e la diagonale d.
Tracciato AB se ne costruisca la parallela alla distanza h, quindi si punti in A con apertura d e si tracci un arco che incontra la parallela in C.
Tracciato AB se ne costruisca la parallela alla distanza h, quindi si punti in A con apertura d e si tracci un arco che incontra la parallela in C.
Puntando in C si riporti CD sulla parallela. Conngiugendo tra loro i vertici si ottiene il trapezio
Puntando in C si riporti CD sulla parallela. Conngiugendo tra loro i vertici si ottiene il trapezio
Problema 24: Costruire un trapezio scaleno date le basi, l’altezza e una diagonale.
Puntando in C si riporti CD sulla parallela. Conngiugendo tra loro i vertici si ottiene il trapezio
PASSO PASSO 4.4.12 TRAPEZIO SCALENO DATE LE BASI, L’ALTEZZA E UNA DIAGONALE
Problema 24: Costruire un trapezio scaleno date le basi, l’altezza e una diagonale.
Tracciato AB se ne costruisca la parallela alla distanza h, quindi si punti in A con apertura d e si tracci un arco che incontra la parallela in C.
Siano date le basi AB e CD l’altezza h e la diagonale d.
Siano date le basi AB e CD l’altezza h e la diagonale d.
Siano date le basi AB e CD l’altezza h e la diagonale d.
Tracciato AB se ne costruisca la parallela alla distanza h, quindi si punti in A con apertura d e si tracci un arco che incontra la parallela in C.
Tracciato AB se ne costruisca la parallela alla distanza h, quindi si punti in A con apertura d e si tracci un arco che incontra la parallela in C.
Tracciato AB se ne costruisca la parallela alla distanza h, quindi si punti in A con apertura d e si tracci un arco che incontra la parallela in C.
Puntando in C si riporti CD sulla parallela. Conngiugendo tra loro i vertici si ottiene il trapezio
Puntando in C si riporti CD sulla parallela. Conngiugendo tra loro i vertici si ottiene il trapezio
Problema 24: Costruire un trapezio scaleno date le basi, l’altezza e una diagonale.
Problema 24: Costruire un trapezio scaleno date le basi, l’altezza e una diagonale.
2 Tracciato AB, costruiamo la parallela ad AB alla distanza h, quindi puntiamo in A con apertura d e tracciamo un arco che incontra la parallela in C.
Tracciato AB se ne costruisca la parallela alla distanza h, quindi si punti in A con apertura d e si tracci un arco che incontra la parallela in C.
Tracciato AB se ne costruisca la parallela alla distanza h, quindi si punti in A con apertura d e si tracci un arco che incontra la parallela in C.
Problema 24: Costruire un trapezio scaleno date le basi, l’altezza e una diagonale.
3 Puntando in C riportiamo CD sulla parallela. Congiungendo tra loro i vertici otteniamo il trapezio.
Tracciato AB se ne costruisca la parallela alla distanza h, quindi si punti in A con apertura d e si tracci un arco che incontra la parallela in C.
Puntando in C si riporti CD sulla parallela. Conngiugendo tra loro i vertici si ottiene il trapezio
Puntando in C si riporti CD sulla parallela. Conngiugendo tra loro i vertici si ottiene il trapezio
Puntando in C si riporti CD sulla parallela. Conngiugendo tra loro i vertici si ottiene il trapezio
Puntando in C si riporti CD sulla parallela. Conngiugendo tra loro i vertici si ottiene il trapezio
Problema 25: Costruire un trapezio isoscele date le basi e l’altezza.
Problema 25: Costruire un trapezio isoscele date le basi e l’altezza.
Problema 25: Costruire un trapezio isoscele date le basi e l’altezza.
Siano date le basi AB e CD e l’altezza h.
Siano date le basi AB e CD e l’altezza Si tracci l’asse di AB, si riporti su esso l’altezza h determinando K e si tracci per K la parallela ad AB
Problema 25: Costruire un trapezio isoscele date le basi e l’altezza.

Problema 25: Costruire un trapezio isoscele date le basi e l’altezza.
Siano date le basi AB e CD e l’altezza h. Si tracci l’asse di AB, si riporti su esso l’altezza h determinando K e si tracci per K la parallela ad AB
Problema 25: Costruire un trapezio isoscele date le basi e l’altezza.
1 Consideriamo le basi AB e CD e l’altezza h.
Si tracci l’asse di AB, si riporti su esso l’altezza h determinando K e si tracci per K la parallela ad AB
Puntando in K si riporti da entrambe le parti sulla parallela la metà di CD. Congiungendo tra loro i vertici si ottiene il trapezio
Puntando in K si riporti da entrambe le parti sulla parallela la metà di CD. Congiungendo tra loro i vertici si ottiene il trapezio
Puntando in K si riporti da entrambe le parti sulla parallela la metà di CD. Congiungendo tra loro i vertici si ottiene il trapezio
Siano date le basi AB e CD e l’altezza h. Si tracci l’asse di AB, si riporti su esso l’altezza h determinando K e si tracci per K la parallela ad AB.
Problema 25: Costruire un trapezio isoscele date le basi e l’altezza.
Siano date le basi AB e CD e l’altezza h. Si tracci l’asse di AB, si riporti su esso l’altezza h determinando K e si tracci per K la parallela ad AB.
Siano date le basi AB e CD e l’altezza h. Si tracci l’asse di AB, si riporti su esso l’altezza h determinando K e si tracci per K la parallela ad AB.
Problema 25: Costruire un trapezio isoscele date le basi e l’altezza.
Siano date le basi AB e CD e l’altezza h.
Siano date le basi AB e CD e l’altezza h. Si tracci l’asse di AB, si riporti su esso l’altezza h determinando K e si tracci per K la parallela ad AB.
Puntando in K si riporti da entrambe le parti sulla parallela la metà di CD. Congiungendo tra loro i vertici si ottiene il trapezio.
Problema 25: Costruire un trapezio isoscele date le basi e l’altezza.
Si tracci l’asse di AB, si riporti su esso l’altezza h determinando K e si tracci per K la parallela ad AB.
2 Tracciamo l’asse di AB e riportiamo su di esso l’altezza h, determinando 1. Tracciamo per 1 la parallela ad AB.
Puntando in K si riporti da entrambe le parti sulla parallela la metà di CD. Congiungendo tra loro i vertici si ottiene il trapezio.
Siano date le basi AB e CD e l’altezza h. Si tracci l’asse di AB, si riporti su esso l’altezza h determinando K e si tracci per K la parallela ad AB.
Puntando in K si riporti da entrambe le parti sulla parallela la metà di CD. Congiungendo tra loro i vertici si ottiene il trapezio.
Puntando in K si riporti da entrambe le parti sulla parallela la metà di CD. Congiungendo tra loro i vertici si ottiene il trapezio.
Puntando in K si riporti da entrambe le parti sulla parallela la metà di CD. Congiungendo tra loro i vertici si ottiene il trapezio.
Puntando in K si riporti da entrambe le parti sulla parallela la metà di CD. Congiungendo tra loro i vertici si ottiene il trapezio.
3 Puntando in 1 riportiamo sulla parallela, da entrambe le parti, la metà di CD. Congiungendo tra loro i vertici otteniamo il trapezio.






Problema 26: Costruire un poligono regolare dato il lato.
La costruzione approssimata è valida per qualsiasi poligono regolare di n lati; vediamo la costruzione per poligoni regolari da 5 a 8 lati.
Problema 26: Costruire un poligono regolare dato il lato.
Costruzione approssimata valida per qualsiasi poligono di n lati
Problema 26: Costruire un poligono regolare dato il lato.
Costruzione approssimata valida per qualsiasi poligono di n lati
Problema 26: Costruire un poligono regolare dato il lato.
Costruzione da 5 a 8 lati.
Costruzione da 5 a 8 lati.
Costruzione approssimata valida per qualsiasi poligono di n lati
Costruzione approssimata valida per qualsiasi poligono di n lati
Dato il lato AB, tracciatone l’asse si punta in B con raggio BA si tracci un arco a intersecare l’asse in O6. Si tracci AC e lo si suddivida in sei parti uguali dette u.
Costruzione da 5 a 8 lati.
Costruzione da 5 a 8 lati.
Dato il lato AB, tracciatone l’asse si punta in B con raggio BA si tracci un arco a intersecare l’asse in O6. Si tracci AC e lo si suddivida in sei parti uguali dette u.
Puntato poi in O6 con apertura u si tracci un arco a incontrare l’asse in O5 e O7 centri rispettivamente del pentagono e dell’ettagono. Aprendo poi il compasso con apertura 2a si traccino un arco a determinare O8 centro dell’ottagono.
1 Consideriamo il lato AB e costruiamone l’asse. Puntiamo in B con raggio BA e tracciamo un arco fino a intersecare l’asse in O6. Tracciamo AO6 e suddividiamolo in sei parti uguali di misura u. Puntato poi in O6 con apertura u tracciamo un arco che interseca l’asse in O5 e O7, centri rispettivamente del pentagono e dell’ettagono. Aprendo poi il compasso con apertura 2u tracciamo un arco che determina O8 centro dell’ottagono.
Dato il lato AB, tracciatone l’asse si punta in B con raggio BA si tracci un arco a intersecare l’asse in O6. Si tracci AC e lo si suddivida in sei parti uguali dette u.
Puntando il compasso con aperture O5A, O6A, O7A, O8A si tracciano le circonferenze su cui riportare, partendo da A o da B, la misura del lato determinando così i vertici dei poligoni.
Puntato poi in O6 con apertura u si tracci un arco a incontrare l’asse in O5 e O7 centri rispettivamente del pentagono e dell’ettagono. Aprendo poi il compasso con apertura 2a si traccino un arco a determinare O8 centro dell’ottagono
Puntato poi in O6 con apertura u si tracci un arco a incontrare l’asse in O5 e O7 centri rispettivamente del pentagono e dell’ettagono. Aprendo poi il compasso con apertura 2a si traccino un arco a determinare O8 centro dell’ottagono.
Puntando il compasso con aperture O5A, O6A, O7A, O8A si tracciano le circonferenze su cui riportare, partendo da A o da B, la misura del lato determinando così i vertici dei poligoni.
Dato il lato AB, tracciatone l’asse si punta in B con raggio BA si tracci un arco a intersecare l’asse in O6. Si tracci AC e lo si suddivida in sei parti uguali dette u.
Puntato poi in O6 con apertura u si tracci un arco a incontrare l’asse in O5 e O7 centri rispettivamente del pentagono e dell’ettagono. Aprendo poi il compasso con apertura 2a si traccino un arco a determinare O8 centro dell’ottagono
Puntando il compasso con aperture O5A, O6A, O7A, O8A si tracciano le circonferenze su cui riportare, partendo da A o da B, la misura del lato determinando così i vertici dei poligoni.
2 Puntando il compasso in O5, O6, O7, O8 con aperture AO5, AO6, AO7, AO8 tracciamo le circonferenze su cui riportare, partendo da A o da B, le misure dei lati, determinando così i vertici dei poligoni.
Puntando il compasso con aperture O5A, O6A, O7A, O8A si tracciano le circonferenze su cui riportare, partendo da A o da B, la misura del lato determinando così i vertici dei poligoni.
Problema 27: Costruire un poligono regolare inscritto in una circonferenza data.
PASSO PASSO 4.4.15 POLIGONO REGOLARE INSCRITTO IN UNA CIRCONFERENZA DATA
Problema 27: Costruire un poligono regolare inscritto in una circonferenza data.
Problema 27: Costruire un poligono regolare inscritto in una circonferenza data. Costruzione approssimata valida per qualsiasi poligono di n lati
Costruzione approssimata valida per qualsiasi poligono di n lati
Costruzione di un ettagono regolare.
Problema 27: Costruire un poligono regolare inscritto in una circonferenza data.
Costruzione di un ettagono regolare.
Costruzione approssimata valida per qualsiasi poligono di n lati
Dato il diametro lo si tracci in verticale e lo si divida in un numero di parti uguali pari al numero dei lati (in questo caso sette) e puntando in A e H con aprtura pari al diametro si traccino due archi che si intersecano in S e T.
Costruzione approssimata valida per qualsiasi poligono di n lati
Costruzione di un ettagono regolare.
Costruzione di un ettagono regolare.
Dato il diametro lo si tracci in verticale e lo si divida in un numero di parti uguali pari al numero dei lati (in questo caso sette) e puntando in A e H con aprtura pari al diametro si traccino due archi che si intersecano in S e T.
Si congiungano S e T con i numeri pari della suddivisione di AH e si prolunghino i segmenti a incontrare la circonferenza determinando così i vertici dell’ettagono
La costruzione approssimata è valida per qualsiasi poligono di n lati; vediamo la costruzione di un ettagono regolare.
Dato il diametro lo si tracci in verticale e lo si divida in un numero di parti uguali pari al numero dei lati (in questo caso sette) e puntando in A e H con aprtura pari al diametro si traccino due archi che si intersecano in S e T.
1 Tracciamo in verticale il diametro AH della circonferenza e dividiamolo in un numero di parti uguale al numero dei lati (in questo caso sette). Puntiamo in A e H con apertura pari al diametro e tracciamo due archi che si intersecano in S e T.
Dato il diametro lo si tracci in verticale e lo si divida in un numero di parti uguali pari al numero dei lati (in questo caso sette) e puntando in A e H con aprtura pari al diametro si traccino due archi che si intersecano in S e T.
Si congiungano S e T con i numeri pari della suddivisione di AH e si prolunghino i segmenti a incontrare la circonferenza determinando così i vertici dell’ettagono.
Si congiungano S e T con i numeri pari della suddivisione di AH e si prolunghino i segmenti a incontrare la circonferenza determinando così i vertici dell’ettagono
Questa costruzione è valida per ogni poligono e volendo ottenerlo con il lato inferiore orizzontale si congiungano i punti S e T con i numeri pari se il numero di lati è dispari e con i dispari se il numero di lati è pari.
Questa costruzione è valida per ogni poligono e volendo ottenerlo con il lato inferiore orizzontale si congiungano i punti S e T con i numeri pari se il numero di lati è dispari e con i dispari se il numero di lati è pari.
Si congiungano S e T con i numeri pari della suddivisione di AH e si prolunghino i segmenti a incontrare la circonferenza determinando così i vertici dell’ettagono
Questa costruzione è valida per ogni poligono e volendo ottenerlo con il lato inferiore orizzontale si congiungano i punti S e T con i numeri pari se il numero di lati è dispari e con i dispari se il numero di lati è pari.
Questa costruzione è valida per ogni poligono e volendo ottenerlo con il lato inferiore orizzontale si congiungano i punti S e T con i numeri pari se il numero di lati è dispari e con i dispari se il numero di lati è pari.
2 Congiungiamo S e T con i numeri pari della suddivisione di AH e prolunghiamo i segmenti fino a incontrare la circonferenza: si individuano così i vertici dell’ettagono. Questa costruzione è valida per ogni poligono e, se vogliamo ottenerlo con il lato inferiore orizzontale, congiungiamo i punti S e T con i numeri pari se il numero di lati è dispari e con i dispari se il numero di lati è pari.

Costruzioni piane fondamentali: poligoni regolari
Costruzioni piane fondamentali: poligoni regolari
1 Tracciamo AB e, con archi di raggio pari alla sua lunghezza, il suo asse determinando 1. Innalziamo da A la perpendicolare ad AB a determinare 2.
Costruzioni piane fondamentali: poligoni regolari

Costruzioni piane fondamentali: poligoni regolari
Costruzioni piane fondamentali: poligoni regolari
Costruzioni piane fondamentali: poligoni regolari
2 Tracciamo due archi: uno, puntando in 1, da 2 in 3 sul prolungamento di AB; l’altro, puntando in B, da 3 a determinare C, sul prolungamento dell’arco B2, e D sull’asse. Congiungiamo C con A e D.
3 Tracciamo quindi un arco di centro D e apertura AB a intersecare in E, quinto vertice del pentagono, il prolungamento dell’arco da A. Tracciando DE e BE si completa la costruzione.
Costruzioni piane fondamentali: poligoni regolari
Costruzioni piane fondamentali: poligoni regolari

PASSO PASSO 4.4.17
1 Tracciamo AB e sul suo prolungamento B1 pari alla sua misura tracciamo poi un arco di centro A e apertura A1 a intersecare in 2 la perpendicolare in B.
2 Costruiamo la bisettrice dell’angolo 2A1, che interseca la perpendicolare in B nel punto 3.
3 Tracciamo due archetti con centro in A e B e apertura A3 a determinare O e centrando in esso tracciamo la circonferenza circoscritta su cui riportare la lunghezza del lato.

PASSO PASSO 4.4.18 PENTAGONO REGOLARE DATA LA CIRCONFERENZA
1 Tracciamo il diametro MN, quello AF perpendicolare a MN quindi, con centro in N e raggio NO un arco a intersecare la circonferenza in 1 e 2.
2 Tracciamo 1-2 che determina 3 su MN. Con raggio A3 e centro in 3 tracciamo un arco a determinare 4.
3 Con apertura A4 e centro prima in A, tracciamo due archetti a determinare B ed E, quindi in B ed E a determinare C e D. Trovati i vertici tracciamo il pentagono.

PASSO PASSO 4.4.19 SUDDIVISIONE DI UNA CIRCONFERENZA IN SEI PARTI UGUALI E DISEGNO DI UN ESAGONO REGOLARE
1 Consideriamo un segmento AD di lunghezza pari al diametro. Individuiamo il suo punto medio O e tracciamo la circonferenza.
2 Centrando in A e D col compasso, con apertura AO, tracciamo due archi che incontrano la circonferenza in B, F, E, C.







3 Essi, con A e D, rappresentano la suddivisione della circonferenza in sei parti uguali e i vertici dell’esagono. Completiamo la costruzione tracciando i lati.

1 Consideriamo un segmento AE di lunghezza pari al diametro. Ne tracciamo l’asse determinando il centro O e disegniamo la circonferenza che intercetta l’asse in C e G.
2 Tracciamo le bisettrici degli angoli GOE e GOA che intersecano la circonferenza nei punti
B, D, F, H.

3 Essi, con A, C, E, G, rappresentano la suddivisione della circonferenza in otto parti uguali e i vertici dell’ottagono. Completiamo la costruzione tracciando i lati.

PASSO PASSO 4.4.21 SUDDIVISIONE DI UNA CIRCONFERENZA IN DODICI
1 Consideriamo un segmento AG di lunghezza pari al diametro. Tracciamo l’asse di AG determinando il centro O e disegniamo la circonferenza. Essa intercetta l’asse in L e D.
2 Centrando in A, D, G, L con apertura OA tracciamo quattro archi che intercettano la circonferenza in B, C, E, F, H, I, M, N.

3 Essi, con A, D, G, L, rappresentano la suddivisione della circonferenza in dodici parti uguali e i vertici del dodecagono. Completiamo la costruzione tracciando i lati.

PASSO
1 Tracciamo il lato AB; puntiamo in A e B con apertura AB e tracciamo due archi che si intersecano in O, centro della circonferenza circoscritta all’esagono.
2 Tracciamo la circonferenza che interseca gli archi in F e C. Quindi puntiamo in F e C con apertura AB e tracciamo due archi a determinare E e D.

3 Essi con A e B rappresentano la suddivisione della circonferenza in sei parti uguali e i vertici dell’esagono. Completiamo la costruzione tracciando i lati.

PASSO PASSO
1 Tracciamo il lato AB e il suo asse determinando 1. Puntando in 1 e apertura 1A tracciamo un arco a determinare 2 poi in 2 e apertura 2A a determinare O, centro della circonferenza circoscritta all’ottagono.
2 Tracciamo la circonferenza e col compasso, partendo da A e B, riportiamo su di essa in successione la misura del lato, determinando gli altri vertici dell’ottagno.

3 Completiamo la costruzione tracciando i lati.

1 Tracciamo il lato AB e il suo asse. Puntando in A e apertura AB tracciamo un arco a determinare 1, poi in 1 con apertura 1A tracciamo un arco a determinare O, centro della circonferenza circoscritta al dodecagono.
2 Tracciamo la circonferenza e col compasso, partendo da A e B, riportiamo su di essa in successione la misura del lato, determinando gli altri vertici del dodecagono.

3 Completiamo la costruzione tracciando i lati.

PASSO PASSO 4.6.1 CIRCONFERENZA PASSANTE PER TRE PUNTI DATI
1 Consideriamo i tre punti A, B, C non allineati.
2 Tracciamo AB e BC e costruiamo i loro assi che si intersecano in O.
3 Puntiamo in O e tracciamo la circonferenza cercata.

PASSO PASSO 4.6.2 RETTA TANGENTE A UNA CIRCONFERENZA DATA IN UN SUO PUNTO
1 Consideriamo la circonferenza di centro O e un punto P su di essa.
2 Tracciamo la semiretta s di origine O passante per P.
3 La tangente è la perpendicolare al segmento OP nell’estremo P.

PASSO PASSO 4.6.3 CIRCONFERENZA DI RAGGIO R TANGENTE A UNA RETTA DATA IN UN SUO PUNTO
1 Consideriamo la retta s, un suo punto P e il raggio R.
2 Tracciamo per P la perpendicolare a s e riportiamo da P il raggio R determinando O.
3 Puntiamo in O con raggio R e tracciamo la circonferenza cercata.







Problema 34: Tracciare le tangenti ad una circonferenza da un punto P esterno ad essa
Problema 34: Tracciare le tangenti ad una circonferenza da un punto P esterno ad essa
Problema 34: Tracciare le tangenti ad una circonferenza da un punto P esterno ad essa
PASSO
Siano dati la circonferenza di centro O e il punto P esterno ad essa.

1 Consideriamo la circonferenza di centro O e il punto P esterno a essa.
Siano dati la circonferenza di centro O e il punto P esterno ad essa.
Siano dati la circonferenza di centro O e il punto P esterno ad essa.
Si tracci il segmento OP e se ne costruisca l’asse determinando il punto C.
Si tracci il segmento OP e se ne costruisca l’asse determinando il punto C.
2 Tracciamo il segmento OP, costruiamo l’asse di OP e determiniamo il punto 1.
Si tracci il segmento OP e se ne costruisca l’asse determinando il punto C.
Si punti in C con raggio CO e si tracci una circonferenza che interseca quella data in H e K punti di tangenza. Si completi la costruzione tracciando le due tangenti
Si punti in C con raggio CO e si tracci una circonferenza che interseca quella data in H e K punti di tangenza. Si completi la costruzione tracciando le due tangenti.
3 Tracciamo una circonferenza con centro in 1 e raggio 1O che interseca in A e B quella data e quindi da P per A e B le due tangenti.
Si punti in C con raggio CO e si tracci una circonferenza che interseca quella data in H e K punti di tangenza. Si completi la costruzione tracciando le due tangenti.
Problema 34: Tracciare le tangenti ad una circonferenza da un punto P esterno ad essa
Problema 34: Tracciare le tangenti ad una circonferenza da un punto P esterno ad essa
Problema 34: Tracciare le tangenti ad una circonferenza da un punto P esterno ad essa
Siano dati la circonferenza di centro O e il punto P esterno ad essa.
Siano dati la circonferenza di centro O e il punto P esterno ad essa.
Siano dati la circonferenza di centro O e il punto P esterno ad essa.

Si tracci il segmento OP e se ne costruisca l’asse determinando il punto C.
Si tracci il segmento OP e se ne costruisca l’asse determinando il punto C.
Si tracci il segmento OP e se ne costruisca l’asse determinando il punto C.
Problema 34: Tracciare le tangenti ad una circonferenza da un punto P esterno ad essa
Problema 34: Tracciare le tangenti ad una circonferenza da un punto P esterno ad essa
Problema 34: Tracciare le tangenti ad una circonferenza da un punto P esterno ad essa
Siano dati la circonferenza di centro O e il punto P esterno ad essa.
Siano dati la circonferenza di centro O e il punto P esterno ad essa.
Siano dati la circonferenza di centro O e il punto P esterno ad essa.
Si tracci il segmento OP e se ne costruisca l’asse determinando il punto C.
Si punti in C con raggio CO e si tracci una circonferenza che interseca quella data in H e K punti di tangenza. Si completi la costruzione tracciando le due tangenti
Si punti in C con raggio CO e si tracci una circonferenza che interseca quella data in H e K punti di tangenza. Si completi la costruzione tracciando le due tangenti
Si punti in C con raggio CO e si tracci una circonferenza che interseca quella data in H e K punti di tangenza. Si completi la costruzione tracciando le due tangenti
Si tracci il segmento OP e se ne costruisca l’asse determinando il punto C.
Si tracci il segmento OP e se ne costruisca l’asse determinando il punto C.
Si punti in C con raggio CO e si tracci una circonferenza che interseca quella data in H e K punti di tangenza. Si completi la costruzione tracciando le due tangenti


Si punti in C con raggio CO e si tracci una circonferenza che interseca quella data in H e K punti di tangenza. Si completi la costruzione tracciando le due tangenti
Si punti in C con raggio CO e si tracci una circonferenza che interseca quella data in H e K punti di tangenza. Si completi la costruzione tracciando le due tangenti

vedi esercizio a pag. 91
Problema 35: Tracciare le tangenti esterne a due circonferenze date
Problema 35: Tracciare le tangenti esterne a due circonferenze date.
Problema 35: Tracciare le tangenti esterne a due circonferenze date.
Date le circonferenze si tracci OO’ e due raggi tra loro paralleli O’H e O”K. Da H si riporti su O’H il raggio O”K determinando P, quindi si tracci la circonferenza di raggio O’P
PASSO
Date le circonferenze si tracci OO’ e due raggi tra loro paralleli O’H e O”K. Da H si riporti su O’H il raggio O”K determinando P, quindi si tracci la circonferenza di raggio O’P.
4.6.5
Date le circonferenze si tracci OO’ e due raggi tra loro paralleli O’H e O”K. Da H si riporti su O’H il raggio O”K determinando P, quindi si tracci la circonferenza di raggio O’P
1 Date le circonferenze di centro O' e O'', tracciamo O'O'' e i raggi O'1 e O''2 tra loro paralleli. Da 1 riportiamo O''2 su O'1 determinando 3 e tracciamo la circonferenza di raggio O'3.
Si tracci l’asse di O’O” determinando C e puntando in esso si tracci la circonferenza di raggio CO’ che interseca la circonferenza di raggio O’P in M ed N.
Si tracci l’asse di O’O” determinando C e puntando in esso si tracci la circonferenza di raggio CO’ che interseca la circonferenza di raggio O’P in M ed N.
Si tracci l’asse di O’O” determinando C e puntando in esso si tracci la circonferenza di raggio CO’ che interseca la circonferenza di raggio O’P in M ed N.
Problema 35: Tracciare le tangenti esterne a due circonferenze date
Problema 35: Tracciare le tangenti esterne a due circonferenze date
Date le circonferenze si tracci OO’ e due raggi tra loro paralleli O’H e O”K. Da H si riporti su O’H il raggio O”K determinando P, quindi si tracci la circonferenza di raggio O’P.
Date le circonferenze si tracci OO’ e due raggi tra loro paralleli O’H e O”K. Da H si riporti su O’H il raggio O”K determinando P, quindi si tracci la circonferenza di raggio O’P.
Date le circonferenze si tracci OO’ e due raggi tra loro paralleli O’H e O”K. Da H si riporti su O’H il raggio O”K determinando P, quindi si tracci la circonferenza di raggio O’P.
Si congiunga O’ con M ed N e si prolunghino le linee determinando R e Q quindi da O” si traccino le parallele a tali linee determinando E ed F che con R e Q sono i punti di tangenza. Si traccino le tangenti.
Problema 35: Tracciare le tangenti esterne a due circonferenze date
Si tracci l’asse di O’O” determinando C e puntando in esso si tracci la circonferenza di raggio CO’ che interseca la circonferenza di raggio O’P in M ed N.
Si congiunga O’ con M ed N e si prolunghino le linee determinando R e Q quindi da O” si traccino le parallele a tali linee determinando E ed F che con R e Q sono i punti di tangenza. Si traccino le tangenti.
Si tracci l’asse di O’O” determinando C e puntando in esso si tracci la circonferenza di raggio CO’ che interseca la circonferenza di raggio O’P in M ed N.
Si tracci l’asse di O’O” determinando C e puntando in esso si tracci la circonferenza di raggio CO’ che interseca la circonferenza di raggio O’P in M ed N.
Problema 35: Tracciare le tangenti esterne a due circonferenze date
Si congiunga O’ con M ed N e si prolunghino le linee determinando R e Q quindi da O” si traccino le parallele a tali linee determinando E ed F che con R e Q sono i punti di tangenza. Si traccino le tangenti.

3 Tracciamo O'5 e O'6 che prolungati determinano A e B; da O'' tracciamo le parallele a O'A e O'B determinando C ed D. Le rette passanti per A e C e per B e D sono le tangenti.
Problema 35: Tracciare le tangenti esterne a due circonferenze date
Problema 35: Tracciare le tangenti esterne a due circonferenze date
2 Tracciamo l’asse di O'O'' e determiniamo il punto medio 4; puntiamo in 4 e tracciamo la circonferenza di raggio 4O' che interseca la circonferenza di raggio O'3 in 5 e 6.
Date le circonferenze si tracci OO’ e due raggi tra loro paralleli O’H e O”K. Da H si riporti su O’H il raggio O”K determinando P, quindi si tracci la circonferenza di raggio O’P.
Date le circonferenze si tracci OO’ e due raggi tra loro paralleli O’H e O”K. Da H si riporti su O’H il raggio O”K determinando P, quindi si tracci la circonferenza di raggio O’P.
Date le circonferenze si tracci OO’ e due raggi tra loro paralleli O’H e O”K. Da H si riporti su O’H il raggio O”K determinando P, quindi si tracci la circonferenza di raggio O’P.
Si congiunga O’ con M ed N e si prolunghino le linee determinando R e Q quindi da O” si traccino le parallele a tali linee determinando E ed F che con R e Q sono i punti di tangenza. Si traccino le tangenti.
Si congiunga O’ con M ed N e si prolunghino le linee determinando R e Q quindi da O” si traccino le parallele a tali linee determinando E ed F che con R e Q sono i punti di tangenza. Si traccino le tangenti.
Si tracci l’asse di O’O” determinando C e puntando in esso si tracci la circonferenza di raggio CO’ che interseca la circonferenza di raggio O’P in M ed N.
Si congiunga O’ con M ed N e si prolunghino le linee determinando R e Q quindi da O” si traccino le parallele a tali linee determinando E ed F che con R e Q sono i punti di tangenza. Si traccino le tangenti.
Si tracci l’asse di O’O” determinando C e puntando in esso si tracci la circonferenza di raggio CO’ che interseca la circonferenza di raggio O’P in M ed N.
Si tracci l’asse di O’O” determinando C e puntando in esso si tracci la circonferenza di raggio CO’ che interseca la circonferenza di raggio O’P in M ed N.
Problema 36:Tracciare le tangenti interne a due circonferenze date
Problema 36:Tracciare le tangenti interne a due circonferenze date.
Problema 36:Tracciare le tangenti interne a due circonferenze date.
Date le circonferenze si tracci: O’O”, aggi O’P e O”Q tra loro alleli e la congiungente PQ determinando H.
Date le circonferenze si tracci: O’O”, aggi O’P e O”Q tra loro alleli e la congiungente PQ determinando H.
Date le circonferenze si tracci: O’O”, due raggi O’P e O”Q tra loro paralleli e la congiungente PQ determinando H.
Si traccino gli assi di O’H e O”H determinando C’ e C” e si traccino le circonferenze di raggio O’C’ e O”C” che intersecano le circonferenze date in M, N, E, F punti di tangenza.
Si traccino gli assi di O’H e O”H determinando C’ e C” e si traccino le circonferenze di raggio O’C’ e O”C” che intersecano le circonferenze date in M, N, E, F punti di tangenza.
Si traccino gli assi di O’H e O”H determinando C’ e C” e si traccino le circonferenze di raggio O’C’ e O”C” che intersecano le circonferenze date in M, N, E, F punti di tangenza.
Problema 36:Tracciare le tangenti interne a due circonferenze date
Problema 36:Tracciare le tangenti interne a due circonferenze date

Si congiunga O’ con M ed N e si prolunghino le linee determinando R e Q quindi da O” si traccino le parallele a tali linee determinando E ed F che con R e Q sono i punti di tangenza. Si traccino le tangenti.
Si congiunga O’ con M ed N e si prolunghino le linee determinando R e Q quindi da O” si traccino le parallele a tali linee determinando E ed F che con R e Q sono i punti di tangenza. Si traccino le tangenti.
Si congiunga O’ con M ed N e si prolunghino le linee determinando R e Q quindi da O” si traccino le parallele a tali linee determinando E ed F che con R e Q sono i punti di tangenza. Si traccino le tangenti.
Congiungendo M con F e N con E si tracciano le due tangenti.
Congiungendo M con F e N con E si tracciano le due tangenti.
Congiungendo M con F e N con E si tracciano le due tangenti.
vedi esercizio a pag. 90
Problema 36:Tracciare le tangenti interne a due circonferenze date
Date le circonferenze si tracci: O’O”, due raggi O’P e O”Q tra loro alleli e la congiungente PQ determinando H.
Date le circonferenze si tracci: O’O”, due raggi O’P e O”Q tra loro alleli e la congiungente PQ determinando H.
Date le circonferenze si tracci: O’O”, due raggi O’P e O”Q tra loro paralleli e la congiungente PQ determinando H.
1 Date le circonferenze di centro O' e O'', tracciamo il segmento O'O'', due raggi O'1 e O''2 tra loro paralleli e la congiungente 1-2 determinando 3.
Si traccino gli assi di O’H e O”H determinando C’ e C” e si traccino le circonferenze di raggio O’C’ e O”C” che intersecano le circonferenze date in M, N, E, F punti di tangenza.
Si traccino gli assi di O’H e O”H determinando C’ e C” e si traccino le circonferenze di raggio O’C’ e O”C” che intersecano le circonferenze date in M, N, E, F punti di tangenza.
Si traccino gli assi di O’H e O”H determinando C’ e C” e si traccino le circonferenze di raggio O’C’ e O”C” che intersecano le circonferenze date in M, N, E, F punti di tangenza.
Congiungendo M con F e N con E si tracciano le due tangenti.
Congiungendo M con F e N con E si tracciano le due tangenti.
Congiungendo M con F e N con E si tracciano le due tangenti.
PASSO PASSO 4.6.6 TANGENTI INTERNE A DUE CIRCONFERENZE DATE
Problema 36:Tracciare le tangenti interne a due circonferenze date.
Problema 36:Tracciare le tangenti interne a due circonferenze date.
Problema 36:Tracciare le tangenti interne a due circonferenze date.
Date le circonferenze si tracci: O’O”, due raggi O’P e O”Q tra loro paralleli e la congiungente PQ determinando H.
Date le circonferenze si tracci: O’O”, due raggi O’P e O”Q tra loro paralleli e la congiungente PQ determinando H.
Date le circonferenze si tracci: O’O”, due raggi O’P e O”Q tra loro paralleli e la congiungente PQ determinando H.
Si traccino gli assi di O’H e O”H determinando C’ e C” e si traccino le circonferenze di raggio O’C’ e O”C” che intersecano le circonferenze date in M, N, E, F punti di tangenza.
2 Tracciamo gli assi di O'3 e O''3, determinando i punti medi 4 e 5 e le circonferenze di raggio 4O' e 5O'' che intersecano le circonferenze date in A, B, C, D.
Si traccino gli assi di O’H e O”H determinando C’ e C” e si traccino le circonferenze di raggio O’C’ e O”C” che intersecano le circonferenze date in M, N, E, F punti di tangenza.
Si traccino gli assi di O’H e O”H determinando C’ e C” e si traccino le circonferenze di raggio O’C’ e O”C” che intersecano le circonferenze date in M, N, E, F punti di tangenza.

3 Le rette passanti per A e D e per B e C sono le due tangenti.
Congiungendo M con F e N con E si tracciano le due tangenti.
Congiungendo M con F e N con E si tracciano le due tangenti.
Congiungendo M con F e N con E si tracciano le due tangenti.

PASSO PASSO 4.6.7
Problema 37: Raccordare due rette con un arco di raggio R.
Problema 37: Raccordare due rette con un arco di raggio R.
Problema 37: Raccordare due rette con un arco di raggio R.
Siano dati le rette e il raggio di raccordo.
1 Consideriamo le rette s e t e il raggio di raccordo R.

Siano dati le rette e il raggio di raccordo.
Siano dati le rette e il raggio di raccordo.
Si traccino due rette parallele a s e t distanti R che si intersecheranno in O centro del raccordo
Si traccino due rette parallele a s e t distanti R che si intersecheranno in O centro del raccordo
2 Tracciamo due rette parallele a s e t distanti R che si intersecano in C centro del raccordo.
Si traccino due rette parallele a s e t distanti R che si intersecheranno in O centro del raccordo
Problema 37: Raccordare due rette con un arco di raggio R.
Da O si traccino due perpendicolari alle rette determinando H e K punti di tangenza. Si completi tracciando l’arco.
Da O si traccino due perpendicolari alle rette determinando H e K punti di tangenza. Si completi tracciando l’arco.
Da O si traccino due perpendicolari alle rette determinando H e K punti di tangenza. Si completi tracciando l’arco.
3 Da C tracciamo le perpendicolari a s e t determinando A e B punti di tangenza ed estremi del raccordo.
Problema 37: Raccordare due rette con un arco di raggio R.
Problema 37: Raccordare due rette con un arco di raggio R.
Siano dati le rette e il raggio di raccordo.
Siano dati le rette e il raggio di raccordo.
Siano dati le rette e il raggio di raccordo.
Si traccino due rette parallele a s e t distanti R che si intersecheranno in O centro del raccordo.
Si traccino due rette parallele a s e t distanti R che si intersecheranno in O centro del raccordo.
Si traccino due rette parallele a s e t distanti R che si intersecheranno in O centro del raccordo.
Da O si traccino due perpendicolari alle rette determinando H e K punti di tangenza. completi tracciando l’arco
Da O si traccino due perpendicolari alle rette determinando H e K punti di tangenza. Si completi tracciando l’arco
Da O si traccino due perpendicolari alle rette determinando H e K punti di tangenza. Si completi tr l’arco

Problema 37: Raccordare due rette con un arco di raggio R.
Problema 37: Raccordare due rette con un arco di raggio R.
Problema 37: Raccordare due rette con un arco di raggio R.
Siano dati le rette e il raggio di raccordo.
Siano dati le rette e il raggio di raccordo.
Siano dati le rette e il raggio di raccordo. Si traccino due rette parallele a s e t distanti R che si intersecheranno in O centro del raccordo.
Si traccino due rette parallele a s e t distanti R che si intersecheranno in O centro del raccordo.
Si traccino due rette parallele a s e t distanti R che si intersecheranno in O centro del raccordo.
Da O si traccino due perpendicolari alle rette determinando H e K punti di tangenza. Si completi tracciando l’arco
Da O si traccino due perpendicolari alle rette determinando H e K punti di tangenza. Si completi tracciando l’arco
Da O si traccino due perpendicolari alle rette determinando H e K punti di tangenza. Si completi tracciando l’arco
vedi esercizio a pag. 91
Problema 38: Raccordare due circonferenze tra loro esterne con un arco di raggio R
Problema 38: Raccordare due circonferenze tra loro esterne con un arco di raggio R
Problema 38: Raccordare due circonferenze tra loro esterne con un arco di raggio R
Date le circonferenze e il raggio di raccordo R> R’+R”+O’O”/2

Date le circonferenze e il raggio di raccordo R> R’+R”+O’O”/2
Date le circonferenze e il raggio di raccordo R> R’+R”+O’O”/2
PASSO PASSO 4.6.8 RACCORDO
Poiché il centro di raccordo C disterà R-R’ da O’ e R-R” da O” si punti in O’ con raggio R-R’ e in O” con R-R” e si traccino due archi che determino C.
1 Consideriamo le circonferenze e il raggio di raccordo di lunghezza tale che R > R' R" O'O"/2.
Si congiunga C con O’ e con O”e si prolunghino le linee a determinare H e K punti di tangenza e estremi dell’arco di raccordo
TRA LORO ESTERNE CON UN ARCO DI RAGGIO R
Si congiunga C con O’ e con O”e si prolunghino le linee a determinare H e K punti di tangenza e estremi dell’arco di raccordo
Si congiunga C con O’ e con O”e si prolunghino le linee a determinare H e K punti di tangenza e estremi dell’arco di raccordo

Problema 38: Raccordare due circonferenze tra loro esterne con un arco di raggio R
Date le circonferenze e il raggio di raccordo R> R’+R”+O’O”/2
Poiché il centro di raccordo C disterà R-R’ da O’ e R-R” da O” si punti in O’ con raggio R-R’ e in O” con R-R” e si traccino due archi che determino C.
Poiché il centro di raccordo C disterà R-R’ da O’ e R-R” da O” si punti in O’ con raggio R-R’ e in O” con R-R” e si traccino due archi che determino C.
Problema 38: Raccordare due circonferenze tra loro esterne con un arco di raggio R
Problema 38: Raccordare due circonferenze tra loro esterne con un arco di raggio R
Date le circonferenze e il raggio di raccordo R> R’+R”+O’O”/2
Date le circonferenze e il raggio di raccordo R> R’+R”+O’O”/2
Poiché il centro di raccordo C disterà R-R’ da O’ e R-R” da O” si punti in O’ con raggio R-R’ e in O” con R-R” e si traccino due archi che determino C.
Poiché il centro di raccordo C disterà R-R’ da O’ e R-R” da O” si punti in O’ con raggio R-R’ e in O” con R-R” e si traccino due archi che determino C.
2 Il centro di raccordo C dista R–R' da O' e R–R'' da O''. Puntiamo in O' con raggio R–R' e in O'' con R–R'' tracciamo due archi che determinano C.
Poiché il centro di raccordo C disterà R-R’ da O’ e R-R” da O” si punti in O’ con raggio R-R’ e in O” con R-R” e si traccino due archi che determino C.
Si congiunga C con O’ e con O”e si prolunghino le linee a determinare H e K punti di tangenza e estremi dell’arco di raccordo
Si congiunga C con O’ e con O”e si prolunghino le linee a determinare H e K punti di tangenza e estremi dell’arco di raccordo
Si congiunga C con O’ e con O”e si prolunghino le linee a determinare H e K punti di tangenza e estremi dell’arco di raccordo
3 Congiungiamo C con O' e O'' e prolunghiamo le linee a determinare A e B punti di tangenza e estremi dell’arco di raccordo.
Problema 38: Raccordare due circonferenze tra loro esterne con un arco di raggio R
Problema 38: Raccordare due circonferenze tra loro esterne con un arco di raggio R
Problema 38: Raccordare due circonferenze tra loro esterne con un arco di raggio R
Date le circonferenze e il raggio di raccordo R> R’+R”+O’O”/2
Date le circonferenze e il raggio di raccordo R> R’+R”+O’O”/2
Date le circonferenze e il raggio di raccordo R> R’+R”+O’O”/2
Poiché il centro di raccordo C disterà R-R’ da O’ e R-R” da O” si punti in O’ con raggio R-R’ e in O” con R-R” e si traccino due archi che determino C.
Si congiunga C con O’ e con O”e si prolunghino le linee a determinare H e K punti di tangenza e estremi dell’arco di raccordo
Si congiunga C con O’ e con O”e si prolunghino le linee a determinare H e K punti di tangenza e estremi dell’arco di raccordo
Si congiunga C con O’ e con O”e si prolunghino le linee a determinare H e K punti di tangenza e estremi dell’arco di raccordo
Problema 39:Raccordare una circonferenza a una retta a essa esterna con un arco di raggio R
Problema 39:Raccordare una circonferenza a una retta a essa esterna con un arco di raggio R
Siano date la retta, la circonferenza e il raggio R.
Siano date la retta, la circonferenza e il raggio R.
Siano date la retta, la circonferenza e il raggio R.

Poiché il centro di raccordo C disterà R-R’ da O’ e R-R” da O” si punti in O’ con raggio R-R’ e in O” con R-R” e si traccino due archi che determino C.
Poiché il centro di raccordo C disterà R-R’ da O’ e R-R” da O” si punti in O’ con raggio R-R’ e in O” con R-R” e si traccino due archi che determino C.
Problema 39:Raccordare una circonferenza a una retta a essa esterna con un arco di raggio R
Si tracci la parallela a s alla distanza R. Si tracci un raggio OH e si aggiunga al suo prolungamento R determinando K.
Si tracci la parallela a s alla distanza R. Si tracci un raggio OH e si aggiunga al suo prolungamento R determinando K.
Si tracci la parallela a s alla distanza R. Si tracci un raggio OH e si aggiunga al suo prolungamento R determinando K.
Puntando in O con raggio OK si tracci un arco che interseca S’ in C centro del raccordo. Da C si tracci CO e la perpendicolare a s determinando P e Q punti di tangenza
Problema 39:Raccordare una circonferenza a una retta a essa esterna con un arco di raggio R
Problema 39:Raccordare una circonferenza a una retta a essa esterna con un arco di raggio R
Siano date la retta, la circonferenza e il raggio R.
Siano date la retta, la circonferenza e il raggio R.
Puntando in O con raggio OK si tracci un arco che interseca S’ in C centro del raccordo. Da C si tracci CO e la perpendicolare a s determinando P e Q punti di tangenza
Puntando in O con raggio OK si tracci un arco che interseca S’ in C centro del raccordo. Da C si tracci CO e la perpendicolare a s determinando P e Q punti di tangenza
Problema 39:Raccordare una circonferenza a una retta a essa esterna con un arco di raggio R
Siano date la retta, la circonferenza e il raggio R. Si tracci la parallela a s alla distanza R. Si tracci un raggio OH e si aggiunga al suo prolungamento R determinando K.
Si tracci la parallela a s alla distanza R. Si tracci un raggio OH e si aggiunga al suo prolungamento R determinando K.
1 Consideriamo la retta s, la circonferenza e il raggio di raccordo R.
Si tracci la parallela a s alla distanza R. Si tracci un raggio OH e si aggiunga al suo prolungamento R determinando K.
PASSO PASSO 4.6.9 RACCORDO DI UNA CIRCONFERENZA A UNA RETTA A ESSA ESTERNA CON UN ARCO DI RAGGIO R
Puntando in O con raggio OK si tracci un arco che interseca S’ in C centro del raccordo. Da C si tracci CO e la perpendicolare a s determinando P e Q punti di tangenza

Puntando in O con raggio OK si tracci un arco che interseca S’ in C centro del raccordo. Da C si tracci CO e la perpendicolare a s determinando P e Q punti di tangenza
Puntando in O con raggio OK si tracci un arco che interseca S’ in C centro del raccordo. Da C si tracci CO e la perpendicolare a s determinando P e Q punti di tangenza
Problema 39:Raccordare una circonferenza a una retta a essa esterna con un arco di raggio R
Problema 39:Raccordare una circonferenza a una retta a essa esterna con un arco di raggio R
Problema 39:Raccordare una circonferenza a una retta a essa esterna con un arco di raggio R
Siano date la retta, la circonferenza e il raggio R.
Siano date la retta, la circonferenza e il raggio R.
Siano date la retta, la circonferenza e il raggio R.
Si tracci la parallela a s alla distanza R. Si tracci un raggio OH e si aggiunga al suo prolungamento R determinando K.
2 Tracciamo la parallela a s alla distanza R e il raggio O1 cui aggiungiamo, sul suo prolungamento, R determinando 2.
Si tracci la parallela a s alla distanza R. Si tracci un raggio OH e si aggiunga al suo prolungamento R determinando K.
Si tracci la parallela a s alla distanza R. Si tracci un raggio OH e si aggiunga al suo prolungamento R determinando K.
Puntando in O con raggio OK si tracci un arco che interseca S’ in C centro del raccordo. Da C si tracci CO e la perpendicolare a s determinando P e Q punti di tangenza
3 Puntando in O e con raggio O2 tracciamo un arco che interseca s' in C, centro del raccordo. Tracciamo CO e la perpendicolare a s determinando A e B estremi dell’arco di raccordo.
Puntando in O con raggio OK si tracci un arco che interseca S’ in C centro del raccordo. Da C si tracci CO e la perpendicolare a s determinando P e Q punti di tangenza
Puntando in O con raggio OK si tracci un arco che interseca S’ in C centro del raccordo. Da C si tracci CO e la perpendicolare a s determinando P e Q punti di tangenza







Problema 40: Raccordare una circonferenza a una retta ad essa interna con un arco di raggio R.
Problema 40: Raccordare una circonferenza a una retta ad essa interna con un arco di raggio R.
Problema 40: Raccordare una circonferenza a una retta ad essa interna con un arco di raggio R.
1 Dati la circonferenza di centro O, la retta s e il raggiodi raccordo R tracciamo la parallela s' alla retta s alla distanza R e un raggio O1.
Date la circonferenza, la retta e il raggio R si tracci la parallela a s alla distanza R.
Date la circonferenza, la retta e il raggio R si tracci la parallela a s alla distanza R.
Date la circonferenza, la retta e il raggio R si tracci la parallela a s alla distanza R.
Date la circonferenza, la retta e il raggio
Date la circonferenza, la retta e il raggio
R si tracci la parallela a s alla distanza R.
Si tracci un raggio OH e si riporti da H verso O il raggio R determinando K. Puntando in O con raggio OK si tracci un arco determinando C centro del raccordo.
Si tracci un raggio OH e si riporti da H verso O il raggio R determinando K. Puntando in O con raggio OK si tracci un arco determinando C centro del raccordo.
Problema 40: Raccordare una circonferenza a una retta ad essa interna con un arco di raggio R.
R si tracci la parallela a s alla distanza R.
Date la circonferenza, la retta e il raggio R si tracci la parallela a s alla distanza R.
Si tracci un raggio OH e si riporti da H verso O il raggio R determinando K. Puntando in O con raggio OK si tracci un arco determinando C centro del raccordo.
2 Riportiamo da 1 verso O il raggio R, determinando 2. Puntando in O con raggio O2 tracciamo un arco che interseca s' determinando C centro del raccordo.
Si tracci un raggio OH e si riporti da H verso O il raggio R determinando K. Puntando in O con raggio OK si tracci un arco determinando C centro del raccordo.
Si tracci un raggio OH e si riporti da H verso O il raggio R determinando K. Puntando in O con raggio OK si tracci un arco determinando C centro del raccordo.
Si congiunga O con C e si prolunghi a incontrare la circonferenza in Q e da C si tracci la perpendicolare a s determinando P. Puntando in C si tracci il raccordo PQ.
Problema 40: Raccordare una circonferenza a una retta ad essa interna con un arco di raggio R.
Si tracci un raggio OH e si riporti da H verso O il raggio R determinando K. Puntando in O con raggio OK si tracci un arco determinando C centro del raccordo.
Si congiunga O con C e si prolunghi a incontrare la circonferenza in Q e da C si tracci la perpendicolare a s determinando P. Puntando in C si tracci il raccordo PQ.
Si congiunga O con C e si prolunghi a incontrare la circonferenza in Q e da C si tracci la perpendicolare a s determinando P. Puntando in C si tracci il raccordo PQ.
3 Congiungiamo O con C e prolunghiamo fino ad A. Tracciamo da C la perpendicolare a s determinando B. Puntando in C e apertura CA tracciamo il raccordo.
Si congiunga O con C e si prolunghi a incontrare la circonferenza in Q e da C si tracci la perpendicolare a s determinando P. Puntando in C si tracci il raccordo PQ.
Si congiunga O con C e si prolunghi a incontrare la circonferenza in Q e da C si tracci la perpendicolare a s determinando P. Puntando in C si tracci il raccordo PQ.
Problema 40: Raccordare una circonferenza a una retta ad essa interna con un arco di raggio R.
Si congiunga O con C e si prolunghi a incontrare la circonferenza in Q e da C si tracci la perpendicolare a s determinando P. Puntando in C si tracci il raccordo PQ.
Problema 40: Raccordare una circonferenza a una retta ad essa interna con un arco di raggio R.
Problema 40: Raccordare una circonferenza a una retta ad essa interna con un arco di raggio R.
Problema 40: Raccordare una circonferenza a una retta ad essa interna con un arco di raggio R.
Date la circonferenza, la retta e il raggio
R si tracci la parallela a s alla distanza R.
Date la circonferenza, la retta e il raggio R si tracci la parallela a s alla distanza R.
Date la circonferenza, la retta e il raggio R si tracci la parallela a s alla distanza R.
Si tracci un raggio OH e si riporti da H verso O il raggio R determinando K. Puntando in O con raggio OK si tracci un arco determinando C centro del raccordo
Si tracci un raggio OH e si riporti da H verso O il raggio R determinando K. Puntando in O con raggio OK si tracci un arco determinando C centro del raccordo
Si tracci un raggio OH e si riporti da H verso O il raggio R determinando K. Puntando in O con raggio OK si tracci un arco determinando C centro del raccordo
Si congiunga O con C e si prolunghi a incontrare la circonferenza in Q e da C si tracci la perpendicolare a s determinando P. Puntando in C si tracci il raccordo PQ
Si congiunga O con C e si prolunghi a incontrare la circonferenza in Q e da C si tracci la perpendicolare a s determinando P. Puntando in C si tracci il raccordo PQ
Si congiunga O con C e si prolunghi a incontrare la circonferenza in Q e da C si tracci la perpendicolare a s determinando Puntando in C si tracci il raccordo PQ
Problema 41:Raccordare una circonferenza con il segmento AB nell’estremo B.
Problema 41:Raccordare una circonferenza con il segmento AB nell’estremo B.
Problema 41:Raccordare una circonferenza con il segmento AB nell’estremo B.

Siano dati la circonferenza e il segmento AB
Siano dati la circonferenza e il segmento AB
Siano dati la circonferenza e il segmento AB
1 Consideriamo la circonferenza di raggio R e il segmento AB e tracciamo per B la perpendicolare ad AB.
Siano dati la circonferenza e il segmento AB
Siano dati la circonferenza e il segmento AB
Siano dati la circonferenza e il segmento AB
Si tracci per B la perpendicolare ad AB e si riporti su di essa da B il raggio R determinando H, si tracci HO e se ne costruisca l’asse che interseca la perpendicolare in C
Si congiunga C con O detrminando P. Si punti in C e si tracci il raccordo PB
Si congiunga C con O detrminando P. Si punti in C e si tracci il raccordo PB
Si congiunga C con O detrminando P. Si punti in C e si tracci il raccordo PB
PASSO PASSO 4.6.11 RACCORDO DI UNA CIRCONFERENZA CON IL SEGMENTO AB NELL’ESTREMO
Problema 41:Raccordare una circonferenza con il segmento AB nell’estremo B.
Si tracci per B la perpendicolare ad AB e si riporti su di essa da B il raggio R determinando H, si tracci HO e se ne costruisca l’asse che interseca la perpendicolare in C
Si tracci per B la perpendicolare ad AB e si riporti su di essa da B il raggio R determinando H, si tracci HO e se ne costruisca l’asse che interseca la perpendicolare in C
2 Da B riportiamo il raggio R e determiniamo 1. Tracciamo 1O e poi il suo asse che interseca la perpendicolare in C.
Problema 41:Raccordare una circonferenza con il segmento AB nell’estremo B.
Si tracci per B la perpendicolare ad AB e si riporti su di essa da B il raggio R determinando H, si tracci HO e se ne costruisca l’asse che interseca la perpendicolare in C
Si tracci per B la perpendicolare ad AB e si riporti su di essa da B il raggio R determinando H, si tracci HO e se ne costruisca l’asse che interseca la perpendicolare in C
Problema 41:Raccordare una circonferenza con il segmento AB nell’estremo B.
Si tracci per B la perpendicolare ad AB e si riporti su di essa da B il raggio R determinando H, si tracci HO e se ne costruisca l’asse che interseca la perpendicolare in C
Si congiunga C con O detrminando P. Si punti in C e si tracci il raccordo PB
Si congiunga C con O detrminando P. Si punti in C e si tracci il raccordo PB
Si congiunga C con O detrminando P. Si punti in C e si tracci il raccordo PB
3 Tracciamo CO determinando D. Puntiamo in C e tracciamo il raccordo DB.
Problema 41:Raccordare una circonferenza con il segmento AB nell’estremo B.
Problema 41:Raccordare una circonferenza con il segmento AB nell’estremo B.
Problema 41:Raccordare una circonferenza con il segmento AB nell’estremo B.
Siano dati la circonferenza e il segmento AB
Siano dati la circonferenza e il segmento AB
Siano dati la circonferenza e il segmento AB
Si tracci per B la perpendicolare ad AB e si riporti su di essa da B il raggio R determinando H, si tracci HO e se ne costruisca l’asse che interseca la perpendicolare in C
Si tracci per B la perpendicolare ad AB e si riporti su di essa da B il raggio R determinando H, si tracci HO e se ne costruisca l’asse che interseca la perpendicolare in C
Si tracci per B la perpendicolare ad AB e si riporti su di essa da B il raggio R determinando H, si tracci HO e se ne costruisca l’asse che interseca la perpendicolare in C
Si congiunga C con O detrminando P. Si punti in C e si tracci il raccordo PB
Si congiunga C con O detrminando P. Si punti in C e si tracci il raccordo PB
Si congiunga C con O detrminando P. Si punti in C e si tracci il raccordo PB
Problema 42:Raccordare in un suo punto P una circonferenza a una retta
Problema 42:Raccordare in un suo punto P una circonferenza a una retta
Problema 42:Raccordare in un suo punto P una circonferenza a una retta
Siano dati la circonferenza il punto P e la retta s. Si tracci il raggio OP lo si prolunghi.
Siano dati la circonferenza il punto P e la retta s.
Stracci la tangente in P che interseca la retta in H.
Stracci la tangente in P che interseca la retta in H.
Problema 42:Raccordare in un suo punto P una circonferenza a una retta

Problema 42:Raccordare in un suo punto P una circonferenza a una retta
Si tracci il raggio OP lo si prolunghi.
Problema 42:Raccordare in un suo punto P una circonferenza a una retta
Siano dati la circonferenza il punto P e la retta s. Si tracci il raggio OP lo si prolunghi.
Siano dati la circonferenza il punto P e la retta s.
Siano dati la circonferenza il punto P e la retta s.
PASSO PASSO 4.6.12 RACCORDO, A
Siano dati la circonferenza il punto P e la retta s.
Si tracci il raggio OP lo si prolunghi.
Si tracci il raggio OP lo si prolunghi.
1 Consideriamo la circonferenza di centro O, il punto P su di essa e la retta s. Tracciamo e prolunghiamo il raggio OP.
Stracci la tangente in P che interseca la retta in H.
Stracci la tangente in P che interseca la retta in H. Si tracci la bisettrice dell’angolo in H che incontra il prolungamento di OP in C. Da C si tracci la perpendicolare a s determinando T. Si punti in C e si tracci il raccordo PT
Si tracci la bisettrice dell’angolo in H che incontra il prolungamento di OP in C. Da C si tracci la perpendicolare a s determinando T. Si punti in C e si tracci il raccordo PT
Stracci la tangente in P che interseca la retta in H.
Si tracci il raggio OP lo si prolunghi.
Stracci la tangente in P che interseca la retta in H.
Si tracci la bisettrice dell’angolo in H che incontra il prolungamento di OP in C. Da C si tracci la perpendicolare a s determinando T. Si punti in C e si tracci il raccordo PT
Si tracci la bisettrice dell’angolo in H che incontra il prolungamento di OP in C. Da C si tracci la perpendicolare a s determinando T. Si punti in C e si tracci il raccordo PT
Si tracci la bisettrice dell’angolo in H che incontra il prolungamento di OP in C. Da C si tracci la perpendicolare a s determinando T. Si punti in C e si tracci il raccordo PT
RETTA, DI UNA CIRCONFERENZA IN UN SUO PUNTO P
Problema 42:Raccordare in un suo punto P una circonferenza a una retta
Si tracci la bisettrice dell’angolo in H che incontra il prolungamento di OP in C. Da C si tracci la perpendicolare a s determinando T. Si punti in C e si tracci il raccordo PT
Problema 42:Raccordare in un suo punto P una circonferenza a una retta
Siano dati la circonferenza il punto P e la retta s.
Siano dati la circonferenza il punto P e la retta s.
Siano dati la circonferenza il punto P e la retta s.
Si tracci il raggio OP lo si prolunghi.
Stracci la tangente in P che interseca la retta in H.
Si tracci il raggio OP lo si prolunghi.
Stracci la tangente in P che interseca la retta in H.
Si tracci il raggio OP lo si prolunghi.
2 Tracciamo la tangente in P, che interseca la retta in 1, e poi la bisettrice dell’angolo in 1. L’intersezione tra essa e il prolungamento di OP determina C.
Problema 42:Raccordare in un suo punto P una circonferenza a una retta
Stracci la tangente in P che interseca la retta in H.
Si tracci la bisettrice dell’angolo in H che incontra il prolungamento di OP in C. Da C si tracci la perpendicolare a s determinando T. Si punti in C e si tracci il raccordo PT
Si tracci la bisettrice dell’angolo in H che incontra il prolungamento di OP in C. Da C si tracci la perpendicolare a s determinando T. Si punti in C e si tracci il raccordo PT
3 Da C tracciamo la perpendicolare a s determinando A. Puntiamo in C e tracciamo il raccordo PA.
Si tracci la bisettrice dell’angolo in H che incontra il prolungamento di OP in C. Da C si tracci la perpendicolare a s determinando T. Si punti in C e si tracci il raccordo PT
La curve policentriche: ovali, ovoli, spirali
La curve policentriche: ovali, ovoli, spirali
La curve policentriche: ovali, ovoli, spirali
La curve policentriche: ovali, ovoli, spirali
Le curve policentriche sono le curve formate da archi di circonferenza, di centro e raggio diversi, raccordati tra loro.
La curve policentriche: ovali, ovoli, spirali
Si definiscono curve policentriche le curve formate da archi di circonferenza, di centro e raggio diversi, raccordati tra loro.
Si definiscono curve policentriche le curve formate da archi di circonferenza, di centro e raggio diversi, raccordati tra loro.
Si definiscono curve policentriche le curve formate da archi di circonferenza, di centro e raggio diversi, raccordati tra loro.
Si definiscono curve policentriche le curve formate da archi di circonferenza, di centro e raggio diversi, raccordati tra loro.
L’ ovale è la figura piana chiusa formata da quattro archi di circonferenza a due a due congruenti. Ha due assi di simmetria tra loro ortogonali, che si intersecano in O centro di simmetria.
La curve policentriche: ovali, ovoli, spirali
Si definisce ovale la figura piana chiusa formata da quattro archi di circonferenza a due a due congruenti. Ha due assi di simmetria tra loro ortogonali che si intersecano in O centro di simmetria.
Si definisce ovale la figura piana chiusa formata da quattro archi di circonferenza a due a due congruenti. Ha due assi di simmetria tra loro ortogonali che si intersecano in O centro di simmetria.
Si definiscono curve policentriche le curve formate da archi di circonferenza, di centro e raggio diversi, raccordati tra loro.
Si definisce ovale la figura piana chiusa formata da quattro archi di circonferenza a due a due congruenti. Ha due assi di simmetria tra loro ortogonali che si intersecano in O centro di simmetria.
Si definisce ovale la figura piana chiusa formata da quattro archi di circonferenza a due a due congruenti. Ha due assi di simmetria tra loro ortogonali che si intersecano in O centro di simmetria.
Si definisce ovolo la figura piana chiusa formata da una semicirconferenza e da metà ovale. Ha un solo asse di simmetria che è l’asse maggiore.
L’ ovolo è la figura piana chiusa formata da una semicirconferenza e da metà ovale. Ha un solo asse di simmetria, che è l’asse maggiore.
Si definisce ovale la figura piana chiusa formata da quattro archi di circonferenza a due a due congruenti.
Si definisce ovale la figura piana chiusa formata da quattro archi di circonferenza a due a due congruenti. Ha due assi di simmetria tra loro ortogonali che si intersecano in O centro di simmetria.
Ha due assi di simmetria tra loro ortogonali che si intersecano in O centro di simmetria.
Si definisce ovolo la figura piana chiusa formata da una semicirconferenza e da metà ovale. Ha un solo asse di simmetria che è l’asse maggiore.
Si definisce ovolo la figura piana chiusa formata da una semicirconferenza e da metà ovale. Ha un solo asse di simmetria che è l’asse maggiore.
Si definisce ovolo la figura piana chiusa formata da una semicirconferenza e da metà ovale. Ha un solo asse di simmetria che è l’asse maggiore.
Si definisce spirale una curva policentrica aperta ad andamento circolare ma con raggio progressivamente crescente.
Si definisce ovolo la figura piana chiusa formata da una semicirconferenza e da metà ovale. Ha un solo asse di simmetria che è l’asse maggiore.
Si definisce ovolo la figura piana chiusa formata da una semicirconferenza e da metà ovale.
Ha un solo asse di simmetria che è l’asse maggiore.
La spirale è una curva policentrica aperta ad andamento circolare ma con raggio progressivamente crescente.
Non ha assi di simmetria e le rette pacssnti per l’origine sono tagliate in tanti segmenti tra loro congruenti detti passo
Si definisce spirale una curva policentrica aperta ad andamento circolare ma con raggio progressivamente crescente. Non ha assi di simmetria e le rette pacssnti per l’origine sono tagliate in tanti segmenti tra loro congruenti detti passo
Si definisce spirale una curva policentrica aperta ad andamento circolare ma con raggio progressivamente crescente. Non ha assi di simmetria e le rette pacssnti per l’origine sono tagliate in tanti segmenti tra loro congruenti detti passo
Si definisce spirale una curva policentrica aperta ad andamento circolare ma con raggio progressivamente crescente. Non ha assi di simmetria e le rette pacssnti per l’origine sono tagliate in tanti segmenti tra loro congruenti detti passo.
Si definiscono curve policentriche le curve formate da archi di circonferenza, di centro e raggio diversi, raccordati tra loro.
Si definisce spirale una curva policentrica aperta ad andamento circolare ma con raggio progressivamente crescente. Non ha assi di simmetria e le rette pacssnti per l’origine sono tagliate in tanti segmenti tra loro congruenti detti passo
Si definisce spirale una curva policentrica aperta ad andamento circolare ma con raggio progressivamente crescente. Non ha assi di simmetria e le rette pacssnti per l’origine sono tagliate in tanti segmenti tra loro congruenti detti passo.
Non ha assi di simmetria e le rette passanti per l’origine sono tagliate in tanti segmenti tra loro congruenti detti passo
Curve cicliche o meccaniche: evolvente del cerchio, cicloide, epicicloide
Curve cicliche o meccaniche: evolvente del cerchio, cicloide, epicicloide
Curve cicliche o meccaniche: evolvente del cerchio, cicloide, epicicloide
Curve cicliche o meccaniche: evolvente del cerchio, cicloide, epicicloide
Curve cicliche o meccaniche: evolvente del cerchio, cicloide, epicicloide
Si definiscono curve cicliche o meccaniche le curve piane generate da un punto in movimento appartenente a una retta o a una circonferenza.
Si definiscono curve cicliche o meccaniche le curve piane generate da un punto in movimento appartenente a una retta o a una circonferenza.
Si definiscono curve cicliche o meccaniche le curve piane generate da un punto in movimento appartenente a una retta o a una circonferenza.
Si definiscono curve cicliche o meccaniche le curve piane generate da un punto in movimento appartenente a una retta o a una circonferenza.
Le curve cicliche o meccaniche sono le curve piane generate da un punto in movimento appartenente a una retta o a una circonferenza.
Si definiscono curve cicliche o meccaniche le curve piane generate da un punto in movimento appartenente a una retta o a una circonferenza.
L’evolvente del cerchio è una curva piana data dalla traccia di un punto appartenente a una retta che ruota su una circonferenza senza strisciare.
L’ evolvente del cerchio è una curva piana data dalla traccia di un punto appartenente a una retta che ruota su una circonferenza senza strisciare.
L’evolvente del cerchio è una curva piana data dalla traccia di un punto appartenente a una retta che ruota su una circonferenza senza strisciare.
L’evolvente del cerchio è una curva piana data dalla traccia di un punto appartenente a una retta che ruota su una circonferenza senza strisciare.
Curve cicliche o meccaniche: evolvente del cerchio, cicloide, epicicloide
L’evolvente del cerchio è una curva piana data dalla traccia di un punto appartenente a una retta che ruota su una circonferenza senza strisciare.
La cicloide è una curva piana generata da un punto appartenente a una circonferenza che rotola su una retta senza strisciare.
L’evolvente del cerchio è una curva piana data dalla traccia di un punto appartenente a una retta che ruota su una circonferenza senza strisciare.
La cicloide è una curva piana generata da un punto appartenente a una circonferenza che rotola su una retta senza strisciare.
La cicloide è una curva piana generata da un punto appartenente a una circonferenza che rotola su una retta senza strisciare.
La cicloide è una curva piana generata da un punto appartenente a una circonferenza che rotola su una retta senza strisciare.
La cicloide è una curva piana generata da un punto appartenente a una circonferenza che rotola su una retta senza strisciare.
La cicloide è una curva piana generata da un punto appartenente a una circonferenza che rotola su una retta senza strisciare.
Si definiscono curve cicliche o meccaniche le curve piane generate da un punto in movimento appartenente a una retta o a una circonferenza.
L’evolvente del cerchio è una curva piana data dalla traccia di un punto appartenente a una retta che ruota su una circonferenza senza strisciare.
La cicloide è una curva piana generata da un punto appartenente a una circonferenza che rotola su una retta senza strisciare.
L’epicicloide è una curva piana generata da un punto appartenente a una circonferenza che rotola sull’esterno di un’altra circonferenza senza strisciare. L’ipocicloide è una curva generata da un punto appartenente a una circonferenza che rotola all’interno di un’altra circonferenza senza strisciare. O O asse maggiore asse maggiore asse minore asse
L’epicicloide è una curva piana generata da un punto appartenente a una circonferenza che rotola sull’esterno di un’altra circonferenza senza strisciare. L’ipocicloide è una curva generata da un punto appartenente a una circonferenza che rotola all’interno di un’altra circonferenza senza strisciare.
L’epicicloide è una curva piana generata da un punto appartenente a una circonferenza che rotola sull’esterno di un’altra circonferenza senza strisciare. L’ipocicloide è una curva generata da un punto appartenente a una circonferenza che rotola all’interno di un’altra circonferenza senza strisciare.
L’epicicloide è una curva piana generata da un punto appartenente a una circonferenza che rotola sull’esterno di un’altra circonferenza senza strisciare. L’ipocicloide è una curva generata da un punto appartenente a una circonferenza che rotola all’interno di un’altra circonferenza senza strisciare.
L’epicicloide è una curva piana generata da un punto appartenente a una circonferenza che rotola sull’esterno di un’altra circonferenza senza strisciare. L’ipocicloide è una curva generata da un punto appartenente a una circonferenza che rotola all’interno di un’altra circonferenza senza strisciare.
L’epicicloide è una curva piana generata da un punto appartenente a una circonferenza che rotola sull’esterno di un’altra circonferenza senza strisciare. L’ipocicloide è una curva generata da un punto appartenente a una circonferenza che rotola all’interno di un’altra circonferenza senza strisciare.
Epicicloide
L’epicicloide è una curva piana generata da un punto appartenente a una circonferenza che rotola sull’esterno di un’altra circonferenza senza strisciare. L’ipocicloide è una curva generata da un punto appartenente a una circonferenza che rotola all’interno di un’altra circonferenza senza strisciare.
Ipocicloide



Problema 43: Costruire un ovale dati gli assi AB e CD
Problema 43: Costruire un ovale dati gli assi AB e CD



Tracciati gli assi, si congiunga C con B e da C si riporti HB, differenza tra i due semiassi, determinando K. Si tracci l’asse di KB che incontra gli assi, o i loro prolungamenti, in O1 ed O2.
Tracciati gli assi, si congiunga C con B e da C si riporti HB, differenza tra i due semiassi, determinando K. Si tracci l’asse di KB che incontra gli assi, o i loro prolungamenti, in O1 ed O2.
Problema 43: Costruire un ovale dati gli assi AB e CD
Problema 43: Costruire un ovale dati gli assi AB e CD
1 Tracciati gli assi AB e CD congiungiamo C con B e da C riportiamo 1B, differenza tra i due semiassi, determinando su CB il punto 2. Tracciamo l’asse di 2B che incontra gli assi, o i loro prolungamenti, in O1 e O2.
Tracciati gli assi, si congiunga C con B e da C si riporti HB, differenza tra i due semiassi, determinando K. Si tracci l’asse di KB che incontra gli assi, o i loro prolungamenti, in O1 ed O2.
Tracciati gli assi, si congiunga C con B e da C si riporti HB, differenza tra i due semiassi, determinando K. Si tracci l’asse di KB che incontra gli assi, o i loro prolungamenti, in O1 ed O2.
Si punti col compasso in O2 con apertura O2C e si tracci un arco che interseca l’asse di KB in G. Si punti quindi in O1 con apertura O1G e si tracci l’arco GB completando il primo quarto di ovale. Si punti quindi in O e si riporti O1 in O4 e O2 in O3.
Si punti col compasso in O2 con apertura O2C e si tracci un arco che interseca l’asse di KB in G. Si punti quindi in O1 con apertura O1G e si tracci l’arco GB completando il primo quarto di ovale. Si punti quindi in O e si riporti O1 in O4 e O2 in O3.

Si congiunga O3 con O1 e O4 con O3 e si prolunghino le linee, quindi puntando in O1, O2, O3 ed O4 si traccino gli archi come fatto per il primo quarto.
Si congiunga O3 con O1 e O4 con O3 e si prolunghino le linee, quindi puntando in O1, O2, O3 ed O4 si traccino gli archi come fatto per il primo quarto.
Si punti col compasso in O2 con apertura O2C e si tracci un arco che interseca l’asse di KB in G. Si punti quindi in O1 con apertura O1G e si tracci l’arco GB completando il primo quarto di ovale. Si punti quindi in O e si riporti O1 in O4 e O2 in O3
Si punti col compasso in O2 con apertura O2C e si tracci un arco che interseca l’asse di KB in G. Si punti quindi in O1 con apertura O1G e si tracci l’arco GB completando il primo quarto di ovale. Si punti quindi in O e si riporti O1 in O4 e O2 in O3
2 Puntiamo il compasso in O 2 con apertura O2C e tracciamo un arco che interseca l’asse di 2B in E. Puntiamo quindi in O1 con apertura O 1E e tracciamo l’arco EB completando il primo quarto di ovale. Puntiamo quindi in O e riportiamo O1 in O4 e O2 in O3.
Problema 44: Costruire un ovolo dati gli assi
Problema 44: Costruire un ovolo dati gli assi
PASSO PASSO 4.8.2 OVOLO DATI GLI ASSI AB E CD
Tracciato CD se ne costruisce l’asse determinando il centro O. Si punta in O con apertura OC e si traccia la semicirconferenza CD che determina sull’asse il punto A e da A si riporta la misura di AB.
Si congiunga O3 con O1 e O4 con O3 e si prolunghino le linee, quindi puntando in O1, O2, O3 ed O4 si traccino gli archi come fatto per il primo quarto.
3 Congiungiamo O3 con O1 e O4, O2 con O4 e prolunghiamo le linee, quindi puntando in O1, O2, O3 e O4 tracciamo gli archi come fatto per il primo quarto.
Si congiunga O3 con O1 e O4 con O3 e si prolunghino le linee, quindi puntando in O1, O2, O3 ed O4 si traccino gli archi come fatto per il primo quarto.

Tracciato CD se ne costruisce l’asse determinando il centro O. Si punta in O con apertura OC e si traccia la semicirconferenza CD che determina sull’asse il punto A e da A si riporta la misura di AB.
1 Tracciamo CD e costruiamo il suo asse, determinando il centro O. Puntiamo in O con apertura OC e tracciamo la semicirconferenza CD che interseca l’asse nel punto A e da A riportiamo la misura di AB.
Problema 44: Costruire un ovolo dati gli assi
Problema 44: Costruire un ovolo dati gli assi
Tracciato CD se ne costruisce l’asse determinando il centro O. Si punta in O con apertura OC e si traccia la semicirconferenza CD che determina sull’asse il punto A e da A si riporta la misura di AB.
Tracciato CD se ne costruisce l’asse determinando il centro O. Si punta in O con apertura OC e si traccia la semicirconferenza CD che determina sull’asse il punto A e da A si riporta la misura di AB.
Si tracci CB e da C si riporti HB, differenza tra OB e OC, determinando K. Si tracci l’asse di KB che incontra gli assi, o i loro prolungamenti, in O1 ed O2 e puntando in O si riporti O2 in O3.
Si tracci CB e da C si riporti HB, differenza tra OB e OC, determinando K. Si tracci l’asse di KB che incontra gli assi, o i loro prolungamenti, in O1 ed O2 e puntando in O si riporti O2 in O3.
2 Tracciamo CB e da C riportiamo 1B, differenza tra OB e OC, determinando 2. Tracciamo l’asse di 2B che incontra gli assi, o i loro prolungamenti, in O1 e O2 e puntando in O riportiamo O2 in O3
Si tracci CB e da C si riporti HB, differenza tra OB e OC, determinando K. Si tracci l’asse di KB che incontra gli assi, o i loro prolungamenti, in O1 ed O2 e puntando in O si riporti O2 in O3.
Si tracci CB e da C si riporti HB, differenza tra OB e OC, determinando K. Si tracci l’asse di KB che incontra gli assi, o i loro prolungamenti, in O1 ed O2 e puntando in O si riporti O2 in O3.
Si congiunga O3 con O1 e si prolunghi la linea, quindi puntando in O2 ed O3 si traccino rispettivamente gli archi CG e DI, e puntando in O1 l’arco GI.
Si congiunga O3 con O1 e si prolunghi la linea, quindi puntando in O2 ed O3 si traccino rispettivamente gli archi CG e DI, e puntando in O1 l’arco GI.
3 Congiungiamo O3 con O 1 e prolunghiamo la linea, quindi puntando in O2 e O3 tracciamo rispettivamente gli archi CE e DF, e puntando in O1 l’arco EF.
Si congiunga O3 con O1 e si prolunghi la linea, quindi puntando in O2 ed O3 si traccino rispettivamente gli archi CG e DI, e puntando in O1 l’arco GI.
Si congiunga O3 con O1 e si prolunghi la linea, quindi puntando in O2 ed O3 si traccino rispettivamente gli archi CG e DI, e puntando in O1 l’arco GI.





PASSO PASSO 4.8.3 OVALE DATO L’ASSE MAGGIORE AB
1 Tracciamo AB e il suo asse, determinando il centro O; costruiamo gli assi di OA e OB trovando O1 e O2.
2 Puntiamo in O, O 1 e O 2 e tracciamo tre circonferenze di raggio OO1 che intersecandosi danno origine ai punti 1, 2, 3, 4.

3 Tracciamo e prolunghiamo i segmenti O11, O12, O23, O24 a determinare O3 e O4 e, sulle circonferenze D, E, F, G. Puntiamo in O3 e O4 e tracciamo gli archi DG e EF.

PASSO PASSO 4.8.4 OVALE DATO L’ASSE MINORE CD
1 Tracciamo CD e il suo asse, determinando O; tracciamo la circonferenza di raggio OC trovando O1 e O2. Congiungiamo C e D con O1 e O2 e prolunghiamo.

2 Puntiamo in C e in D con raggio CD e tracciamo due archi che intersecano i segmenti precedentemente tracciati in E, F, G, L.

PASSO PASSO 4.8.5 OVOLO DATO L’ASSE MINORE
1 Consideriamo CD e il suo asse, determinando O; tracciamo la circonferenza di raggio OC trovando O1. Congiungiamo C e D con O1 e prolunghiamo i segmenti.
2 Puntiamo in C e in D con raggio CD e tracciamo due archi che intersecano i segmenti precedentemente tracciati in E, F.




3 Puntiamo in O1 e O2 con apertura O1E e tracciamo i due archi EF e GL completando la costruzione.
3 Puntiamo in O1 con apertura O1E e tracciamo l’arco EF completando la costruzione.







PASSO PASSO 4.8.6 SPIRALE DI ARCHIMEDE DATO IL PASSO p Video tutorial
1 Sia p = AB. Lo dividiamo in un numero di parti congruenti (es. otto) e dividiamo nello stesso numero di parti la circonferenza di raggio AB. Procediamo nella numerazione delle suddivisioni come indicato in figura e tracciamo i raggi B1, B2 ecc.
2 Puntiamo in B col compasso avente apertura B1', tracciamo un arco che interseca il raggio B1, con apertura B2' un arco che interseca il raggio B2 ecc.

3 Determinate tutte le intersezioni, procediamo a tracciare la curva col curvilineo.

PASSO PASSO 4.8.7
1 Consideriamo gli estremi A e B del passo. Tracciamo l’asse di AB determinando il centro O.
2 Puntiamo col compasso in O, con apertura OA, e tracciamo una semi circonferenza. Puntiamo poi in A con apertura AB e tracciamo un’altra semicirconferenza determinando C.
3 Puntiamo poi in O con apertura OC e tracciamo una semicirconferenza da C a D. Poi in A con apertura AD ecc.
vedi esercizio a pag. 90

PASSO PASSO 4.8.8
1 Costruiamo un triagolo equilatero col lato pari a 1/3 del passo e prolunghiamo i lati nello stesso verso.
2 Puntiamo col compasso in A con apertura AB e tracciamo un arco che interseca il prolungamento di CA in D. Poi in C con apertura CD a determinare E ecc.
3 Procediamo nello stesso modo fino a ottenere le spire volute. Con lo stesso metodo, partendo da poligoni regolari, si possono costruire spirali a quattro o più centri.
Problema 49: Costruire l’evolvente del cerchio dato il raggio R (vedi p.40)

Problema 49: Costruire l’evolvente del cerchio dato il raggio R (vedi p.40)
Problema 49: Costruire l’evolvente del cerchio dato il raggio R (vedi p.40)
Problema 49: Costruire l’evolvente del cerchio dato il raggio R (vedi p.40)
Sia dato il raggio R. Tracciata la circonferenza, la si divide in un numero di parti uguali (ad esempio 12) e si congiunge ogni punto della suddivisione con il centro O. Si procede nella numerazione della suddivisione come in figura. Per ogni punto si tracciano poi, nello stesso verso, le tangenti alla circonferenza (ovvero le perpendicolari ai raggi).
Sia dato il raggio R. Tracciata la circonferenza, la si divide in un numero di parti uguali (ad esempio 12) e si congiunge ogni punto della suddivisione con il centro O. Si procede nella numerazione della suddivisione come in figura. Per ogni punto si tracciano poi, nello stesso verso, le tangenti alla circonferenza (ovvero le perpendicolari ai raggi).
Sia dato il raggio R. Tracciata la circonferenza, la si divide in un numero di parti uguali (ad esempio 12) e si congiunge ogni punto della suddivisione con il centro O. Si procede nella numerazione della suddivisione come in figura. Per ogni punto si tracciano poi, nello stesso verso, le tangenti alla circonferenza (ovvero le perpendicolari ai raggi).
1 Tracciamo il cerchio e lo dividiamo in un numero di parti uguali (ad esempio 12). Numeriamo ciascun punto della suddivisione in senso orario come in figura, lo congiungiamo con il centro O e tracciamo, nello stesso verso, le tangenti alla circonferenza (cioè le perpendicolari ai raggi).
Sia dato il raggio R. Tracciata la circonferenza, la si divide in un numero di parti uguali (ad esempio 12) e si congiunge ogni punto della suddivisione con il centro O. Si procede nella numerazione della suddivisione come in figura. Per ogni punto si tracciano poi, nello stesso verso, le tangenti alla circonferenza (ovvero le perpendicolari ai raggi).

Si punta quindi in 2, con raggio 2-1, e si traccia un arco da 1 fino a incontrare la tangente in 2 nel punto a; si punta quindi in 3 con raggio 3a e si traccia un arco da a ad incontrare la tangente in 3 nel punto b; si punta in 4 con raggio 4b, e così via per tutti i punti della suddivisione. La somma dei vari archi dà l’evolvente.
Si punta quindi in 2, con raggio 2-1, e si traccia un arco da 1 fino a incontrare la tangente in 2 nel punto a; si punta quindi in 3 con raggio 3a e si traccia un arco da a ad incontrare la tangente in 3 nel punto b; si punta in 4 con raggio 4b, e così via per tutti i punti della suddivisione. La somma dei vari archi dà l’evolvente.
Si punta quindi in 2, con raggio 2-1, e si traccia un arco da 1 fino a incontrare la tangente in 2 nel punto a; si punta quindi in 3 con raggio 3a e si traccia un arco da a ad incontrare la tangente in 3 nel punto b; si punta in 4 con raggio 4b, e così via per tutti i punti della suddivisione. La somma dei vari archi dà l’evolvente.
Si punta quindi in 2, con raggio 2-1, e si traccia un arco da 1 fino a incontrare la tangente in 2 nel punto a; si punta quindi in 3 con raggio 3a e si traccia un arco da a ad incontrare la tangente in 3 nel punto b; si punta in 4 con raggio 4b, e così via per tutti i punti della suddivisione. La somma dei vari archi dà l’evolvente.
2 Puntiamo in 2, con raggio 2-1, e tracciamo un arco da 1 a incontrare la tangente in 2 nel punto A; puntiamo quindi in 3 con raggio 3A e tracciamo da A un arco a incontrare la tangente in 3 nel punto B; puntiamo in 4, ... e così via per tutti i punti della suddivisione. La somma dei vari archi dà l’evolvente.
Problema 50: Costruire una cicloide data la circonferenza (vedi p. 40)
Problema 50: Costruire una cicloide data la circonferenza (vedi p. 40)
Problema 50: Costruire una cicloide data la circonferenza (vedi p. 40)
PASSO PASSO 4.8.10 CICLOIDE
Problema 50: Costruire una cicloide data la circonferenza (vedi p. 40)
Sia data la circonferenza di raggio R. Si traccia un segmento AB di lunghezza pari a2 R pari a un giro completo e lo si suddivide in 12 parti uguali numerando con O1, O2, con apertura pari al raggio R e si tracciano 12 circonferenze.

Sia data la circonferenza di raggio R. Si traccia un segmento AB di lunghezza pari a2 R pari a un giro completo e lo si suddivide in 12 parti uguali numerando con O1, O2, con apertura pari al raggio R e si tracciano 12 circonferenze.
Sia data la circonferenza di raggio R. Si traccia un segmento AB di lunghezza pari a2 R pari a un giro completo e lo si suddivide in 12 parti uguali numerando con O1, O2, ... con apertura pari al raggio R e si tracciano 12 circonferenze.
Sia data la circonferenza di raggio R. Si traccia un segmento AB di lunghezza pari a2 R pari a un giro completo e lo si suddivide in 12 parti uguali numerando con O1, O2, con apertura pari al raggio R e si tracciano 12 circonferenze.
1 Consideriamo la circonferenza di raggio R. Tracciamo un segmento AB lungo 2πR pari a un giro completo e lo dividiamo in 12 parti uguali numerando con O1, O2, ... e tracciamo 12 circonferenze di raggio R.
Si divide la prima circonferenza in 12 parti uguali, così da ottenere la posizione del punto rispetto al piano di rotolamento a ogni dodicesimo di rotazione, e si tracciano per ogni punto le parallele ad AB. Le parallele incontrano le circonferenze nei punti P1, P2, P3, , che rappresentano l’esatta posizione del punto a ogni dodicesimo di percorso. Congiungendo col curvilineo i punti P1, P2, P3, ...,si ottiene la curva cercata.
Si divide la prima circonferenza in 12 parti uguali, così da ottenere la posizione del punto rispetto al piano di rotolamento a ogni dodicesimo di rotazione, e si tracciano per ogni punto le parallele ad AB. Le parallele incontrano le circonferenze nei punti P1, P2, P3, ..., che rappresentano l’esatta posizione del punto a ogni dodicesimo di percorso. Congiungendo col curvilineo i punti P1, P2, P3, ...,si ottiene la curva cercata.
Si divide la prima circonferenza in 12 parti uguali, così da ottenere la posizione del punto rispetto al piano di rotolamento a ogni dodicesimo di rotazione, e si tracciano per ogni punto le parallele ad AB. Le parallele incontrano le circonferenze nei punti P1, P2, P3, , che rappresentano l’esatta posizione del punto a ogni dodicesimo di percorso. Congiungendo col curvilineo i punti P1, P2, P3, ...,si ottiene la curva cercata.
Si divide la prima circonferenza in 12 parti uguali, così da ottenere la posizione del punto rispetto al piano di rotolamento a ogni dodicesimo di rotazione, e si tracciano per ogni punto le parallele ad AB. Le parallele incontrano le circonferenze nei punti P1, P2, P3, ..., che rappresentano l’esatta posizione del punto a ogni dodicesimo di percorso. Congiungendo col curvilineo i punti P1, P2, P3, ...,si ottiene la curva cercata.
2 Dividiamo la prima circonferenza in 12 parti uguali, così da ottenere la posizione del punto rispetto al piano di rotolamento a ogni dodicesimo di rotazione, e tracciamo per ciascun punto le parallele ad AB. Le intersezioni tra le parallele e le circonferenze nei punti P0, P1, P2, P3, ..., rappresentano l’esatta posizione del punto a ogni dodicesimo di percorso. Congiungendo col curvilineo i punti P0, P1, P2, P3, ..., si ottiene la curva cercata.






1 Consideriamo il punto P in rotazione all’esterno della circonferenza. Il percorso di un giro è pari a 2πR e lo dividiamo in 12 parti uguali determinando O1, ... O12. Centrando in questi punti, tracciamo 12 circonferenze di raggio OP.
2 Dividiamo la circonferenza di raggio OP in 12 parti uguali e tracciamo per ciascuna suddivisione la parallela ad AB. Le intersezioni di queste linee con le corrispondenti circonferenze ci danno i punti per cui passa la curva.
PASSO PASSO 4.8.12 CICLOIDE
1 Consideriamo il punto P in rotazione all’interno della circonferenza. Il percorso di un giro è pari a 2πR che dividiamo in 12 parti uguali determinando O 1, ... O12. Centrando in questi punti, tracciamo 12 circonferenze di raggio OP.
2 Dividiamo la circonferenza di raggio OP in 12 parti uguali e tracciamo per ciascuna suddivisione la parallela ad AB. Le intersezioni di queste linee con le corrispondenti circonferenze ci danno i punti per cui passa la curva.
Problema 51: Costruire un’epicicloide
Consideriamo r ed R, rispettivamente raggi della circonferenza su cui giace il punto e della circonferenza su cui avviene il rotolamento.
La costruzione è simile a quella della cicloide con la differenza che in questo caso il rotolamento avviene lungo un arco di circonferenza. Questo comporta che per determinare le posizioni del punto, invece di tracciare linee parallele al tratto percorso, dobbiamo tracciare archi di circonferenza concentrici con la circonferenza su cui avviene il rotolamento.
L’arco percorso sarà pari a 2pr e l’angolo b a esso sotteso è dato dalla relazione b 360°·r/R .
Siano dati r ed R, rispettivamente raggi della circonferenza su cui giace il punto e della circonferenza su cui avviene il rotolamento. La costruzione è simile a quella della cicloide con la differenza che in questo caso il rotolamento avviene lungo un arco di circonferenza. Questo comporta che per determinare le posizioni del punto, invece di tracciare linee parallele al tratto percorso, si devono tracciare archi di circonferenza concentrici con la circonferenza su cui avviene il rotolamento. L’arco percorso sarà pari a 2 r e l’angolo β ad esso sotteso è dato dalla relazione β=360° * r/R .
Problema 52: Costruire un’ipocicloide date le due circonferenze






Consideriamo r ed R, rispettivamente raggi della circonferenza su cui giace il punto e della circonferenza su cui avviene il rotolamento.
Siano dati r ed R, rispettivamente raggi della circonferenza su cui giace il punto e della circonferenza su cui avviene il rotolamento.
La costruzione è simile alla costruzione dell’epicicloide, con la differenza che in questo caso il rotolamento avviene all’interno della circonferenza.
La costruzione è simile alla costruzione dell’epicicloide, con la differenza che in questo caso il rotolamento avviene all’interno della circonferenza.
Le coniche
Le coniche
Le coniche

TECNOLAB - Eliche ed elicoidi
Si definisce conica la curva che si ottiene intersecando una superficie conica con un piano non passante per il vertice del cono.
Si definisce conica la curva che si ottiene intersecando una superficie conica con un piano non passante per il vertice del cono.
Si definisce conica la curva che si ottiene intersecando una superficie conica con un piano non passante per il vertice del cono.
Le coniche
Le coniche
Consideriamo un cono di rotazione di vertice V, asse a e angolo al vertice 2a. Sia un piano generico non passante per il vertice del cono, che forma con l’asse del cono l’angolo acuto b. Si possono considerare i seguenti casi:
Una conica è una curva che si ottiene intersecando un cono rotondo indefinito con un piano non passante per il vertice del cono. Consideriamo un cono di rotazione di vertice V, asse a e angolo al vertice 2a . Sia p un piano generico non passante per il vertice del cono, che forma con l’asse del cono l’angolo acuto b. Si verificano i seguenti casi:
Consideriamo un cono di rotazione di vertice V, asse a e angolo al vertice 2a. Sia un piano generico non passante per il vertice del cono, che forma con l’asse del cono l’angolo acuto b. Si possono considerare i seguenti casi:
se b=90° avremo un circonferenza (che è stato analizzato nelle pagine precedenti).
• se b 90° si ottiene una circonferenza, di cui abbiamo trattato nelle pagine precedenti;
Si definisce conica la curva che si ottiene intersecando una superficie conica con un piano non passante per il vertice del cono
se b=90° avremo un circonferenza (che è stato analizzato nelle pagine precedenti).
Si definisce conica la curva che si ottiene intersecando una superficie conica con un piano non passante per il vertice del cono
Si definisce conica la curva che si ottiene intersecando una superficie conica con un piano non passante per il vertice del cono.
Consideriamo un cono di rotazione di vertice V, asse a e angolo al vertice 2a. Sia un piano generico non passante per il vertice del cono, che forma con l’asse del cono l’angolo acuto b. Si possono considerare i seguenti casi: se b=90° avremo un circonferenza (che è stato analizzato nelle pagine precedenti).
se ß>α il piano taglia il cono lungo una linea chiusa detta ellisse
• se b a si ottiene una linea chiusa detta ellisse;
se ß>α il piano taglia il cono lungo una linea chiusa detta ellisse
se ß>α il piano taglia il cono lungo una linea chiusa detta ellisse
• se b a si ottiene una linea aperta detta parabola;
Consideriamo un cono di rotazione di vertice V, asse a e angolo al vertice 2a. Sia un piano generico non passante per il vertice del cono, che forma con l’asse del cono l’angolo acuto b. Si possono considerare i seguenti casi: se b=90° avremo un circonferenza (che è stato analizzato nelle pagine precedenti).
Consideriamo un cono di rotazione di vertice V, asse a e angolo al vertice 2a. Sia un piano generico non passante per il vertice del cono, che forma con l’asse del cono l’angolo acuto b. Si possono considerare i seguenti casi: se b=90° avremo un circonferenza (che è stato analizzato nelle pagine precedenti).
se ß=α il piano taglia il cono una linea aperta detta parabola
se ß=α il piano taglia il cono lungo una linea aperta detta parabola
se ß=α il piano taglia il cono lungo una linea aperta detta parabola
Consideriamo un cono di rotazione di vertice V, asse a e angolo al vertice 2a. Sia un piano generico non passante per il vertice del cono, che forma con l’asse del cono l’angolo acuto b. Si possono considerare i seguenti casi: se b=90° avremo un circonferenza (che è stato analizzato nelle pagine precedenti).
se ß>α il piano taglia il cono lungo una linea chiusa detta ellisse
se ß>α il piano taglia il cono lungo una linea chiusa detta ellisse
se ß>α il piano taglia il cono lungo una linea chiusa detta ellisse
se ß=α il piano taglia il cono lungo una linea aperta detta parabola
se ß<α il piano taglia il cono una linea aperta, costituita da due rami, detta iperbole.
se ß=α il piano taglia il cono lungo una linea aperta detta parabola
se ß<α il piano taglia il cono lungo una linea aperta, costituita da due rami, detta iperbole.
se ß=α il piano taglia il cono lungo una linea aperta detta parabola
• se b a si ottiene una linea aperta, costituita da due rami, detta iperbole
se ß<α il piano taglia il cono lungo una linea aperta, costituita da due rami, detta iperbole.
se ß<α il piano taglia il cono lungo una linea aperta, costituita da due rami, detta iperbole.
se ß<α il piano taglia il cono lungo una linea aperta, costituita da due rami, detta iperbole.
se ß<α il piano taglia il cono lungo una linea aperta, costituita da due rami, detta iperbole
Le coniche possono essere ottenute anche mediante proprietà geometriche.
Si definisce ellisse il luogo geometrico dei punti di un piano la cui somma delle distanze da due punti fissi detti fuochi è costante.
Si definisce ellisse il luogo geometrico dei punti di un piano la cui somma delle distanze da due punti fissi detti fuochi è costante.
Si definisce ellisse il luogo geometrico dei punti di un piano la cui somma delle distanze da due punti fissi detti fuochi è costante.
Essa si ottiene sezionando una superficie conica con un piano che incontri su una sola falda tutte le generatrici della superficie.
Si definisce ellisse il luogo geometrico dei punti di un piano la cui somma delle distanze da due punti fissi detti fuochi è costante.
Essa si ottiene sezionando una superficie conica con un piano che incontri su una sola falda tutte le generatrici della superficie.
Si definisce ellisse il luogo geometrico dei punti di un piano la cui somma delle distanze da due punti fissi detti fuochi è costante.
Si definisce ellisse il luogo geometrico dei punti di un piano la cui somma delle distanze da due punti fissi detti fuochi è costante.
Essa si ottiene sezionando una superficie conica con un piano che incontri su una sola falda tutte le generatrici della superficie.
Gli elementi dell’ellisse sono: gli assi di simmetria e i fuochi.
L’ellisse è il luogo geometrico dei punti di un piano la cui somma delle distanze da due punti fissi detti fuochi è costante. Gli elementi caratteristici dell’ellisse sono: gli assi di simmetria (asse maggiore e asse minore) e i fuochi.
Si definisce parabola il luogo geometrico dei punti di un piano equidistanti da un punto fisso detto fuoco e da una retta detta direttrice.
Si definisce parabola il luogo geometrico dei punti di un piano equidistanti da un punto fisso detto fuoco e da una retta detta direttrice.
Si definisce parabola il luogo geometrico dei punti di un piano equidistanti da un punto fisso detto fuoco e da una retta detta direttrice.
Essa si ottiene sezionando una superficie conica con un piano che incontri su una sola falda tutte le generatrici della superficie.
Essa si ottiene sezionando una superficie conica con un piano che incontri su una sola falda tutte le generatrici della superficie.
Gli elementi della parabola sono: l’asse di simmetria, la direttrice, il fuoco e il vertice.
Gli elementi dell’ellisse sono: gli assi di simmetria e i fuochi.
Si definisce parabola il luogo geometrico dei punti di un piano equidistanti da un punto fisso detto fuoco e da una retta detta direttrice.
Essa si ottiene sezionando una superficie conica con un piano che incontri su una sola falda tutte le generatrici della superficie.
Gli elementi dell’ellisse sono: gli assi di simmetria e i fuochi.
Gli elementi dell’ellisse sono: gli assi di simmetria e i fuochi.
Si definisce parabola il luogo geometrico dei punti di un piano equidistanti da un punto fisso detto fuoco e da una retta detta direttrice.
Gli elementi dell’ellisse sono: gli assi di simmetria e i fuochi.
La parabola è il luogo geometrico dei punti di un piano equidistanti da un punto fisso detto fuoco e da una retta detta direttrice. Gli elementi caratteristici della parabola sono l’asse di simmetria, la direttrice, il fuoco e il vertice.
Gli elementi della parabola sono: l’asse di simmetria, la direttrice, il fuoco e il vertice.
Gli elementi della parabola sono: l’asse di simmetria, la direttrice, il fuoco e il vertice.
Si definisce parabola il luogo geometrico dei punti di un piano equidistanti da un punto fisso detto fuoco e da una retta detta direttrice.
Si definisce iperbole il luogo geometrico dei punti di un piano la cui differenza delle distanze da due punti fissi detti fuochi è costante ed è uguale alla distanza tra i due vertici dell’iperbole. Gli elementi dell’iperbole sono:l’asse trasverso, l’asse non trasverso, gli asintoti, i fuochi e i vertici.
Gli elementi della parabola sono: l’asse di simmetria, la direttrice, il fuoco e il vertice.
Gli elementi dell’ellisse sono: gli assi di simmetria e i fuochi.
Gli elementi della parabola sono: l’asse di simmetria, la direttrice, il fuoco e il vertice.
Si definisce iperbole il luogo geometrico dei punti di un piano la cui differenza delle distanze da due punti fissi detti fuochi è costante ed è uguale alla distanza tra i due vertici dell’iperbole. Gli elementi dell’iperbole sono:l’asse trasverso, l’asse non trasverso, gli asintoti, i fuochi e i vertici.
Gli elementi della parabola sono: l’asse di simmetria, la direttrice, il fuoco e il vertice.
Si definisce iperbole il luogo geometrico dei punti di un piano la cui differenza delle distanze da due punti fissi detti fuochi è costante ed è uguale alla distanza tra i due vertici dell’iperbole. Gli elementi dell’iperbole sono:l’asse trasverso, l’asse non trasverso, gli asintoti, i fuochi e i vertici.
Si definisce iperbole il luogo geometrico dei punti di un piano la cui differenza delle distanze da due punti fissi detti fuochi è costante ed è uguale alla distanza tra i due vertici dell’iperbole. Gli elementi dell’iperbole sono:l’asse trasverso, l’asse non trasverso, gli asintoti, i fuochi e i vertici.
L’iperbole è il luogo geometrico dei punti di un piano la cui differenza delle distanze da due punti fissi detti fuochi è costante ed è uguale alla distanza tra i due vertici dell’iperbole. Gli elementi caratteristici dell’iperbole sono l’asse trasverso, l’asse non trasverso, gli asintoti, i fuochi e i vertici.
Si definisce iperbole il luogo geometrico dei punti di un piano la cui differenza delle distanze da due punti fissi detti fuochi è costante ed è uguale alla distanza tra i due vertici dell’iperbole. Gli elementi dell’iperbole sono:l’asse trasverso, l’asse non trasverso, gli asintoti, i fuochi e i vertici.
Si definisce iperbole il luogo geometrico dei punti di un piano la cui differenza delle distanze da due punti fissi detti fuochi è costante ed è uguale alla distanza tra i due vertici dell’iperbole. Gli elementi dell’iperbole sono:l’asse trasverso, l’asse non trasverso, gli asintoti, i fuochi e i vertici.
trasverso
di simmetria








Video tutorial
Problema 46: Costruire un’ellisse dati gli assi AB e CD
Problema 46: Costruire un’ellisse dati gli assi
Problema 46: Costruire un’ellisse dati gli assi AB e CD
1 Tracciamo i due assi AB e CD e determiniamo il centro O. Puntiamo in C con un’apertura OA e tracciamo un arco che interseca AB in F' ed F''. Fissiamo un numero di punti tra F' e O (ad esempio 5).
Problema 46: Costruire un’ellisse dati gli assi AB e CD
Date le lunghezze degli assi AB e CD li si traccino determinando il centro O. Si punti in C col compasso avente un'apertura pari a OA e si tracci un arco che interseca AB in F' ed F”. Si scelga un numero a piacere di punti tra F' e O, per esempio cinque.
Date le lunghezze degli assi AB e CD li si traccino determinando il centro O. Si punti in C col compasso avente un'apertura pari a OA e si tracci un arco che interseca AB in F' ed F”. Si scelga un numero a piacere di punti tra F' e O, per esempio cinque.
Date le lunghezze degli assi AB e CD li si traccino determinando il centro O. Si punti in C col compasso avente un'apertura pari OA e si tracci un arco che interseca AB in F' ed F”. Si scelga un numero a piacere di punti tra F' e O, per esempio cinque.
Si punti in F' col compasso avente apertura A1 e si traccino due archet -ti, uno sopra e l'altro sotto l'asse AB. Si punti in F” con apertura B1 e si traccino due archetti che intersecano i precedenti, determinando due punti P e Q appartenenti all'ellisse.
Si punti in F' col compasso avente apertura A1 e si traccino due archet -ti, uno sopra e l'altro sotto l'asse AB. Si punti in F” con apertura B1 e si traccino due archetti che intersecano i precedenti, determinando due punti P e Q appartenenti all'ellisse.
2 Puntiamo in F' con apertura A1 e in F'' con apertura B1 e tracciamo quattro archetti, sopra e sotto l’asse AB che intersecandosi determinano i punti P e Q e, invertendo i centri, i punti S e T tutti appartenenti all’ellisse.
Si punti in F' col compasso avente apertura A1 e si traccino due archet -ti, uno sopra e l'altro sotto l'asse AB. Si punti in F” con apertura B1 e si traccino due archetti che intersecano i precedenti, determinando due punti P e Q appartenenti all'ellisse.
Date le lunghezze degli assi AB e CD li si traccino determinando il centro O. Si punti in C col compasso avente un'apertura pari a OA e si tracci un arco che interseca AB in F' ed F”. Si scelga un numero a piacere di punti tra F' e O, per esempio cinque.
Date le lunghezze degli assi AB e CD li si traccino determinando il centro O. Si punti in C col compasso avente un'apertura pari a OA e si tracci un arco che interseca AB in F' ed F”. Si scelga un numero a piacere di punti tra F' e O, per esempio cinque.
Costruire un’ellisse dati gli assi AB e CD
Costruire un’ellisse dati gli assi AB e CD
Si proceda allo stesso modo anche per i punti 2, 3, 4, 5 ricavando una serie di punti che permettono, mediante il curvilineo, di tracciare mezza ellisse. Per tracciare l'altra metà si ripeta la stessa costruzione.
Si proceda allo stesso modo anche per i punti 2, 3, 4, 5 ricavando una serie di punti che permettono, mediante il curvilineo, di tracciare mezza ellisse. Per tracciare l'altra metà si ripeta la stessa costruzione.
3 Procediamo allo stesso modo anche per i punti 2, 3, 4, 5 determinando una serie di punti che permettono, mediante il curvilineo, di tracciare l’ellisse.
Si proceda allo stesso modo anche per i punti 2, 3, 4, 5 ricavando una serie di punti che permettono, mediante il curvilineo, di tracciare mezza ellisse. Per tracciare l'altra metà si ripeta la stessa costruzione.
Si punti in F' col compasso avente apertura A1 e si traccino due archet -ti, uno sopra e l'altro sotto l'asse AB. Si punti in F” con apertura B1 e si traccino due archetti che intersecano i precedenti, determinando due punti P e Q appartenenti all'ellisse.
Si punti in F' col compasso avente apertura A1 e si traccino due archet -ti, uno sopra e l'altro sotto l'asse AB. Si punti in F” con apertura B1 e si traccino due archetti che intersecano i precedenti, determinando due punti P e Q appartenenti all'ellisse.
Costruire un’ellisse dati gli assi AB e CD
Costruire un’ellisse dati gli assi AB e CD
Costruire un’ellisse dati gli assi AB e CD
Si disegnino gli assi AB e CD determinando il centro O.
Si disegnino gli assi AB e CD determinando il centro O.
Si punti poi in O con apertura OA e poi OC, si traccino due ciconferenze e le si dividano in dodici parti uguali determinando i punti E’, F’, ....M’, N’ e E”, F”, ....M”, N”.
Si punti poi in O con apertura OA e poi OC, si traccino due ciconferenze e le si dividano in dodici parti uguali determinando i punti E’, F’, ....M’, N’ e E”, F”, ....M”, N”.
Si proceda allo stesso modo anche per i punti 2, 3, 4, 5 ricavando una serie di punti che permettono, mediante il curvilineo, di tracciare mezza ellisse. Per tracciare l'altra metà si ripeta la stessa costruzione.
Si proceda allo stesso modo anche per i punti 2, 3, 4, 5 ricavando una serie di punti che permettono, mediante il curvilineo, di tracciare mezza ellisse. Per tracciare l'altra metà si ripeta la stessa costruzione.
Si disegnino gli assi AB e CD determinando il centro O.
Si disegnino gli assi AB e CD determinando il centro O.
Si traccino ora, per ciascun punto E’, F’, ....M’, N’ una linea verticale e per ciascun punto E”, F”, ....M”, N” una linea orizzontale che si incrociano determinando i punti E, F, ...M, N appartenenti all’ellisse che si può tracciare col curvilineo.
Si traccino ora, per ciascun punto E’, F’, ....M’, N’ una linea verticale e per ciascun punto E”, F”, ....M”, N” una linea orizzontale che si incrociano determinando i punti E, F, ...M, N appartenenti all’ellisse che si può tracciare col curvilineo.
Si disegnino gli assi AB e CD determinando il centro O. Si punti poi in O con apertura OA e poi OC, si traccino due ciconferenze e le si dividano in dodici parti uguali determinando i punti E’, F’, ....M’, N’ e E”, F”, ....M”, N”. Si traccino ora, per ciascun punto E’, F’, ....M’, N’ una linea verticale e per ciascun punto E”, F”, ....M”, N” una linea orizzontale che si incrociano determinando i punti E, F, ...M, N appartenenti all’ellisse che si può tracciare col curvilineo.
Si punti poi in O con apertura OA e poi OC, si traccino due ciconferenze e le si dividano in dodici parti uguali determinando i punti E’, F’, ....M’, N’ e E”, F”, ....M”, N”.
1 Disegniamo gli assi AB e CD e determiniamo il centro O. Puntiamo poi in O con apertura OA e poi OC e tracciamo due ciconferenze. Dividiamo in dodici parti uguali le due circonferenze determinando i punti E', F', ..., M', N' e E'', F'', ..., M'', N''.
Si punti poi in O con apertura OA e poi OC, si traccino due ciconferenze e le si dividano in dodici parti uguali determinando i punti E’, F’, ....M’, N’ e E”, F”, ....M”, N”.
Si traccino ora, per ciascun punto E’, F’, ....M’, N’ una linea verticale e per ciascun punto E”, F”, ....M”, N” una linea orizzontale che si incrociano determinando i punti E, F, ...M, N appartenenti all’ellisse che si può tracciare col curvilineo.
2 Tracciamo ora, per ciascun punto E', F', ..., M', N' una linea verticale e per ciascun punto E'', F'', ..., M'', N'' una linea orizzontale che si incrociano determinando i punti E, F, ..., M, N appartenenti all’ellisse.
Si traccino ora, per ciascun punto E’, F’, ....M’, N’ una linea verticale e per ciascun punto E”, F”, ....M”, N” una linea orizzontale che si incrociano determinando i punti E, F, ...M, N appartenenti all’ellisse che si può tracciare col curvilineo.
3 Completiamo la costruzione unendo i punti ottenuti col curvilineo.
Costruire una parabola dati il vertice V, l’asse s e il punto A.
Costruire una parabola dati il vertice V, l’asse s e il punto A.
Costruire una parabola dati il vertice V, l’asse s e il punto A.
Costruire una parabola dati il vertice V, l’asse s e il punto A.
Costruire una parabola dati il vertice V, l’asse s e il punto A.
Si disegni la retta s, si fissino, su di essa, il punto V ed esterna ad essa il punto A. Si tracci per A la perpendicolare ad s , determinando B e da B si riporti, sulla per-pendicolare, la misura di AB determinando il punto C.
Si disegni la retta s, si fissino, su di essa, il punto V ed esterna ad essa il punto A. Si tracci per A la perpendicolare ad s , determinando B e da B si riporti, sulla per-pendicolare, la misura di AB determinando il punto C.
Si disegni la retta s, si fissino, su di essa, il punto V ed esterna ad essa il punto A. Si tracci per A la perpendicolare ad s , determinando B e da B si riporti, sulla per-pendicolare, la misura di AB determinando il punto C.
Per V e per A e C si traccino rispettivamente la perpendicolare e le parallele all’asse s determinando D e E. Si dividano VD e DA in un numero di parti uguali (ad esempio 6), le si siglino con lettere come in figura. Quindi da V si traccino le congiungenti con F2, ...L2 e da F1, ...L1 le parallele all’asse s che intersecandosi determinano i punti F,...L appartenenti alla parabola. Si ripeta lo stesso procedimento anche per la parte inferiore e, una volta determinati tutti i punti, si tracci la
1 Disegniamo la retta s, fissiamo il punto V su di essa e il punto A esterno ad essa. Tracciamo per A la perpendicolare a s, determinando B, e da B riportiamo su di essa la misura di AB determinando il punto C. Tracciamo per V la perpendicolare e per A e C le parallele all’asse s determinando D e E.
Si disegni la retta s, si fissino, su di essa, il punto V ed esterna ad essa il punto A. Si tracci per A la perpendicolare ad s , determinando B e da B si riporti, sulla per-pendicolare, la misura di AB determinando il punto C.
Si disegni la retta s, si fissino, su di essa, il punto V ed esterna ad essa il punto A. Si tracci per A la perpendicolare ad s , determinando B e da B si riporti, sulla per-pendicolare, la misura di AB determinando il punto C.
Per V e per A e C si traccino rispettivamente la perpendicolare e le parallele all’asse s determinando D e E. Si dividano VD e DA in un numero di parti uguali (ad esempio 6), le si siglino con lettere come in figura. Quindi da V si traccino le congiungenti con F2, ...L2 e da F1, ...L1 le parallele all’asse s che intersecandosi determinano i punti F,...L appartenenti alla parabola. Si ripeta lo stesso procedimento anche per la parte inferiore e, una volta determinati tutti i punti, si tracci la
2 Dividiamo VD e DA in un numero di parti uguali (ad esempio 6) e le sigliamo con lettere come in figura.
3 Quindi da V tracciamo le congiungenti con F2, ...L2 e da F1, ..., L1 le parallele all’asse s che intersecandosi determinano i punti F, ..., L appartenenti alla parabola.
Per V e per A e C si traccino rispettivamente la perpendicolare e le parallele all’asse s determinando D e E. Si dividano e DA in un numero di parti uguali (ad esempio 6), le si siglino con lettere come in figura. Quindi da V si traccino le congiungenti con F2, ...L2 e da F1, ...L1 le parallele all’asse s che intersecandosi determinano i punti F,...L appartenenti alla parabola. Si ripeta lo stesso procedimento anche per la parte inferiore e, una volta determinati tutti i punti, si tracci la
4 Ripetiamo il procedimento anche per la parte sotto la retta s e tracciamo la parabola col curvilineo.
Per V e per A e C si traccino rispettivamente la perpendicolare e le parallele all’asse s determinando D e E. Si dividano VD e DA in un numero di parti uguali (ad esempio 6), le si siglino con lettere come in figura. Quindi da V si traccino le congiungenti con F2, ...L2 e da F1, ...L1 le parallele all’asse s che intersecandosi determinano i punti F,...L appartenenti alla parabola. Si ripeta lo stesso procedimento anche per la parte inferiore e, una volta determinati tutti i punti, si tracci la
Per V e per A e C si traccino rispettivamente la perpendicolare e le parallele all’asse s determinando D e E. Si dividano VD e DA in un numero di parti uguali (ad esempio 6), le si siglino con lettere come in figura. Quindi da V si traccino le congiungenti con F2, ...L2 e da F1, ...L1 le parallele all’asse s che intersecandosi determinano i punti F,...L appartenenti alla parabola. Si ripeta lo stesso procedimento anche per la parte inferiore e, una volta determinati tutti i punti, si tracci la

Siano dati la direttrice d, il fuoco F e l’asse di simmetria x. Si tracci l’asse di OF determinando il punto V, vertice della parabola. Si indichino sull’asse alcuni punti a piacere, per esempio A, B, C, D, E.
1 Consideriamo la direttrice d, il fuoco F e l’asse di simmetria x. Tracciamo l’asse di OF determinando V, vertice della parabola. Fissiamo sull’asse alcuni punti a piacere, per esempio 1, 2, 3, 4, 5, poi per essi e per F tracciamo la perpendicolare all’asse.
Problema 47: Costruire una parabola dati la direttrice d, il fuoco F e l’asse di simmetria x.
Problema 47: Costruire una parabola dati la direttrice d, il fuoco F e l’asse di simmetria x.

Siano dati la direttrice d, il fuoco F e l’asse di simmetria x. Si tracci l’asse di OF determinando il punto V, vertice della parabola. Si indichino sull’asse alcuni punti a piacere, per esempio A, B, C, D, E.
Siano dati la direttrice d, il fuoco F e l’asse di simmetria x. Si tracci l’asse di OF determinando il punto V, vertice della parabola. Si indichino sull’asse alcuni punti a piacere, per esempio A, B, C, D, E.
Siano dati la direttrice d, il fuoco F e l’asse di simmetria x. Si tracci l’asse di OF determinando il punto V, vertice della parabola. Si indichino sull’asse alcuni punti a piacere, per esempio A, B, C, D, E.
Siano dati la direttrice d, il fuoco F e l’asse di simmetria x. Si tracci l’asse di OF determinando il punto V, vertice della parabola. Si indichino sull’asse alcuni punti a piacere, per esempio A, B, C, D, E.
Siano dati la direttrice d, il fuoco F e l’asse di simmetria x. Si tracci l’asse di OF determinando il punto V, vertice della parabola. Si indichino sull’asse alcuni punti a piacere, per esempio A, B, C, D, E.
Per ciascuno dei punti indicati sull’asse, e per il fuoco F, si tracci la perpendicolare all’asse. Si punti il compasso in F, con apertura OF, e si traccino due archetti che intersecano la perpendicolare in F nei punti T ed S. Sempre puntando in F con apertura OA, si traccino altri due che intersecano la perpendicolare in A nei punti R e Q.
Per ciascuno dei punti indicati sull’asse, e per il fuoco F, si tracci la perpendicolare all’asse. Si punti il compasso in F, con apertura OF, e si traccino due archetti che intersecano la perpendicolare in F nei punti T ed S. Sempre puntando in F con apertura OA, si traccino altri due che intersecano la perpendicolare in A nei punti R e Q.
Si ripeta il procedimento anche per gli altri punti indicati sull’asse e si completi la costruzione tracciando la cur va col cur vilineo.
Problema 47: Costruire una parabola dati la direttrice d, il fuoco F e l’asse di simmetria x.
Problema 47: Costruire una parabola dati la direttrice d, il fuoco F e l’asse di simmetria x.
Per ciascuno dei punti indicati sull’asse, e per il fuoco F, si tracci la perpendicolare all’asse. Si punti il compasso in F, con apertura OF, e si traccino due archetti che intersecano la perpendicolare in F nei punti T ed S. Sempre puntando in F con apertura OA, si traccino altri due che intersecano la perpendicolare in A nei punti R e Q.
Si ripeta il procedimento anche per gli altri punti indicati sull’asse e si completi la costruzione tracciando la cur va col cur vilineo.
2 Puntiamo il compasso in F, con apertura OF, e tracciamo due archetti che intersecano la perpendicolare in F nei punti A e B, poi con apertura O1, tracciamo altri due archi che intersecano la perpendicolare in 1 nei punti C e D.
Problema 47: Costruire una parabola dati la direttrice d, il fuoco F e l’asse di simmetria x.
Per ciascuno dei punti indicati sull’asse, e per il fuoco F, si tracci la perpendicolare all’asse. Si punti il compasso in F, con apertura OF, e si traccino due archetti che intersecano la perpendicolare in F nei punti T ed S. Sempre puntando in F con apertura OA, si traccino altri due che intersecano la perpendicolare in A nei punti R e Q.
Per ciascuno dei punti indicati sull’asse, e per il fuoco F, si tracci la perpendicolare all’asse. Si punti il compasso in F, con apertura OF, e si traccino due archetti che intersecano la perpendicolare in F nei punti T ed S. Sempre puntando in F con apertura OA, si traccino altri due che intersecano la perpendicolare in A nei punti R e Q.
Per ciascuno dei punti indicati sull’asse, e per il fuoco F, si tracci la perpendicolare all’asse. Si punti il compasso in F, con apertura OF, e si traccino due archetti che intersecano la perpendicolare in F nei punti T ed S. Sempre puntando in F con apertura OA, si traccino altri due che intersecano la perpendicolare in A nei punti R e Q.
Si ripeta il procedimento anche per gli altri punti indicati sull’asse e si completi la costruzione tracciando la cur va col cur vilineo.
Si ripeta il procedimento anche per gli altri punti indicati sull’asse e si completi la costruzione tracciando la cur va col cur vilineo.
Si ripeta il procedimento anche per gli altri punti indicati sull’asse e si completi la costruzione tracciando la cur va col cur vilineo.
3 Ripetiamo il procedimento anche per gli altri punti indicati sull’asse e completiamo la costruzione tracciando la curva col curvilineo.
Si ripeta il procedimento anche per gli altri punti indicati sull’asse e si completi la costruzione tracciando la cur va col cur vilineo
Problema 48:
Si ripeta il procedimento anche per gli altri punti indicati sull completi la costruzione tracciando la cur va col cur vilineo Problema
Siano dati l’asse trasverso s, i fuochi F’ ed F”, i vertici V’ e V”. Nel punto medio O del segmento F’F”, si tracci l’asse non trasverso t. Si punti in O, con raggio OF, e si tracci una circonferenza.Per V’ e V” si traccino le perpendicolari all’asse trasverso che incontrano la circonferenza nei punti A, B, C, D. Si traccino due rette, una passante per A e C e l’altra passante per B e D, che rappresentano gli asintoti.
1 Consideriamo l’asse trasverso s, i fuochi F' ed F'', i vertici V' e V''. Nel punto medio O di F'F'' tracciamo l’asse non trasverso t. Con centro in O e raggio OF' tracciamo una circonferenza. Per V' e V'' tracciamo le perpendicolari all’asse trasverso che incontrano la circonferenza nei punti A, B, C, D. Per A e C e per B e D tracciamo gli asintoti.
Problema 48: Costruire un’iperbole dati i fuchi F’ ed F” e i vertici V’
Siano dati l’asse trasverso s, i fuochi F’ ed F”, i vertici V’ e V”. Nel punto medio O del segmento F’F”, si tracci l’asse non trasverso t. Si punti in O, con raggio OF, e si tracci una circonferenza.Per V’ e V” si traccino le perpendicolari all’asse trasverso che incontrano la circonferenza nei punti A, B, C, D. Si traccino due rette, una passante per A e C e l’altra passante per B e D, che rappresentano gli asintoti.
Siano dati l’asse trasverso s, i fuochi F’ ed F”, i vertici V’ e V”. Nel punto medio O del segmento F’F”, si tracci l’asse non trasverso t. Si punti in O, con raggio OF, e si tracci una circonferenza.Per V’ e V” si traccino le perpendicolari all’asse trasverso che incontrano la circonferenza nei punti A, B, C, D. Si traccino due rette, una passante per A e C e l’altra passante per B e D, che rappresentano gli asintoti.
Siano dati l’asse trasverso s, i fuochi F’ ed F”, i vertici V’ e V”. Nel punto medio O del segmento F’F”, si tracci l’asse non trasverso t. Si punti in O, con raggio OF, e si tracci una circonferenza.Per V’ e V” si traccino le perpendicolari all’asse trasverso che incontrano la circonferenza nei punti A, B, C, D. Si traccino due rette, una passante per A e C e l’altra passante per B e D, che rappresentano gli asintoti.
Siano dati l’asse trasverso s, i fuochi F’ ed F”, i vertici V’ e V”. Nel punto medio O del segmento F’F”, si tracci l’asse non trasverso t. Si punti in O, con raggio OF, e si tracci una circonferenza.Per V’ e V” si traccino le perpendicolari all’asse trasverso che incontrano la circonferenza nei punti A, B, C, D. Si traccino due rette, una passante per A e C e l’altra passante per B e D, che rappresentano gli asintoti.
Si indichino sull’asse trasverso alcuni punti a piacere, ad esempio 1, 2, 3, 4. Facendo centro in F con raggio V”1, si traccino due archi, e facendo centro in F” con raggio V”1 se ne traccino altri due che intersecano i precedenti nei punti P e Q. Invertendo la costruzione si determinino anche i punti M ed N.

Problema 48: Costruire un’iperbole dati i fuchi F’ ed F” e i vertici V’ e V”.
Siano dati l’asse trasverso s, i fuochi F’ ed F”, i vertici V’ e V”. Nel punto medio O del segmento F’F”, si tracci l’asse non trasverso t. Si punti in O, con raggio OF, e si tracci una circonferenza.Per V’ e V” si traccino le perpendicolari all’asse trasverso che incontrano la circonferenza nei punti A, B, C, D. Si traccino due rette, una passante per A e C e l’altra passante per B e D, che rappresentano gli asintoti.
Si indichino sull’asse trasverso alcuni punti a piacere, ad esempio 1, 2, 3, 4. Facendo centro in F con raggio V”1, si traccino due archi, e facendo centro in F” con raggio V”1 se ne traccino altri due che intersecano i precedenti nei punti P e Q. Invertendo la costruzione si determinino anche i punti M ed N.
Si indichino sull’asse trasverso alcuni punti a piacere, ad esempio 1, 2, 3, 4. Facendo centro in F con raggio V”1, si traccino due archi, e facendo centro in F” con raggio V”1 se ne traccino altri due che intersecano i precedenti nei punti P e Q. Invertendo la costruzione si determinino anche i punti M ed N.
Problema 48: Costruire un’iperbole dati i fuchi F’ ed F” e i vertici V’ e V”.
Problema 48: Costruire un’iperbole dati i fuchi F’ ed F” e i vertici V’ e V”.
Si indichino sull’asse trasverso alcuni punti a piacere, ad esempio 1, 2, 3, 4. Facendo centro in F con raggio V”1, si traccino due archi, e facendo centro in F” con raggio V”1 se ne traccino altri due che intersecano i precedenti nei punti P e Q. Invertendo la costruzione si determinino anche i punti M ed N.
Si ripeta il procedimento anche per gli altri punti indicati sull’asse e si completi la costruzione tracciando la cur va col cur vilineo.
Si indichino sull’asse trasverso alcuni punti a piacere, ad esempio 1, 2, 3, 4. Facendo centro in F con raggio V”1, si traccino due archi, e facendo centro in F” con raggio V”1 se ne traccino altri due che intersecano i precedenti nei punti P e Q. Invertendo la costruzione si determinino anche i punti M ed N.
2 Indichiamo sull’asse trasverso s alcuni punti a piacere, ad esempio 1, 2, 3, 4. Puntando in F' con raggio V'1, e in F'' con raggio V''1 tracciamo due coppie di archi che intersecandosi determinano i punti P e Q. Invertendo la costruzione determiniamo anche i punti M ed N.
Si ripeta il procedimento anche per gli altri punti indicati sull’a completi la costruzione tracciando la cur va col cur vilineo.
Si indichino sull’asse trasverso alcuni punti a piacere, ad esempio 1, 2, 3, 4. Facendo centro in F con raggio V”1, si traccino due archi, e facendo centro in F” con raggio V”1 se ne traccino altri due che intersecano i precedenti nei punti P e Q. Invertendo la costruzione si determinino anche i punti M ed N.
Si ripeta il procedimento anche per gli altri punti indicati sull sse e si completi la costruzione tracciando la cur va col cur vilineo.
Si ripeta il procedimento anche per gli altri punti indicati sull’asse e si completi la costruzione tracciando la cur va col cur vilineo.

Si ripeta il procedimento anche per gli altri punti indicati sull’asse e si completi la costruzione tracciando la cur va col cur vilineo.
3 Ripetiamo il procedimento anche per gli altri punti indicati sull’asse e completiamo la costruzione tracciando le curve col curvilineo.







PASSO PASSO 4.10.6 INVILUPPO DI UNA PARABOLA DATO L’ASSE Ox, UNA TANGENTE t E IL PUNTO DI CONTATTO P SU DI ESSA
1 Fissato il punto P e tracciati l’asse Ox e la tangente t, costruiamo la tangente s simmetrica a t rispetto all’asse Ox e indichiamo su di essa il punto Q simmetrico di P.
2 Dividiamo OP e OQ nello stesso numero di parti uguali e sigliamo la suddivisione con le stesse lettere ma in senso opposto.
3 Tracciando le congiungenti AA', BB', ..., otteniamo l’inviluppo cercato.
In linguaggio matematico una famiglia di rette inviluppa una curva se ogni retta della famiglia è tangente alla curva stessa.

1 Dati i due segmenti AB e CD, li prolunghiamo fino a intersecarsi in O.
2 Dividiamo BO e DO nello stesso numero di parti uguali, sigliamo i punti delle suddivisioni con le stesse lettere ma in senso opposto e li congiungiamo con B e D.
3 I punti, determinati dalle intersezioni tra le congiungenti con un estremo siglato con la stessa lettera appartengono al raccordo che va tracciato col curvilineo.

1 Tracciati gli asintoti e fissato A, tracciamo le perpendicolari agli asintoti AP e AQ.
2 Sul prolungamento di PA fissiamo un numero a piacere di punti B', ... H'. Da O tracciamo le congiungenti a tali punti che intersecano AQ in B, ..., H.
3 Tracciamo da B', ..., H' delle linee verticali e da B, ..., H delle linee orizzontali che intersecandosi determinano i punti per cui passa il ramo di iperbole.
Per eseguire la copia di un disegno, si usano tre diversi modi di riproduzione
Per eseguire la copia di un disegno, si usano tre diversi modi di riproduzione
Riproduzione per mezzo di diagonali da un angolo
Per eseguire la copia di un disegno, si usano tre diversi modi di riproduzione.
Per eseguire la copia di un disegno, si usano tre diversi modi di riproduzione.
Riproduzione per mezzo di diagonali da un angolo
Riproduzione per mezzo di diagonali da un angolo
Da un vertice del disegno da riprodurre (ad esempio B), si traccia un arco con raggio a piacere e, congiungendo B con gli altri vertici della figura, si determinano i punti A’, F’, E’, D’, C’. Fissato a piacere il punto B’, si punti esso e si tracci un arco avente lo stesso raggio del precedente. Si fissi poi un punto C” a piacere e si riportino da esso gli archi C’D’, C’E’, C’F’, C’A’, determinando così i punti D”, E”, F” e A”. Da B’ si traccino delle semirette passanti per questi punti e, su di esse, si riportino da B’ le dimensioni dei segmenti BA, BF, BE, BD, BC determinando i vertici della copia (figg. 1a e 1b)
Da un vertice (ad esempio B) (➜ Fig. 1a) del disegno da riprodurre, tracciamo un arco con raggio a piacere e, congiungendo B con gli altri vertici della figura, determiniamo i punti A', F', E', D', C'. Fissato a piacere il punto B', puntiamo in esso e tracciamo un arco avente lo stesso raggio del precedente. Fissiamo poi un punto C" a piacere e riportiamo da esso gli archi C'D', C'E', C'F', C'A', determinando così i punti D", E", F" e A". Da B' tracciamo delle semirette passanti per questi punti e, su di esse, riportiamo da B' le dimensioni dei segmenti BA, BF, BE, BD, BC determinando i vertici della copia (➜ Fig. 1b).
Da un vertice del disegno da riprodurre (ad esempio B), si traccia un arco con raggio a piacere e, congiungendo B con gli altri vertici della figura, si determinano i punti A’, F’, E’, D’, C’. Fissato a piacere il punto B’, si punti esso e si tracci un arco avente lo stesso raggio del precedente. Si fissi poi un punto C” a piacere e si riportino da esso gli archi C’D’, C’E’, C’F’, C’A’, determinando così i punti D”, E”, F” e A”. Da B’ si traccino delle semirette passanti per questi punti e, su di esse, si riportino da B’ le dimensioni dei segmenti BA, BF, BE, BD, BC determinando i vertici della copia (figg. 1a e 1b)
Da un vertice del disegno da riprodurre (ad esempio B), si traccia un arco con raggio a piacere e, congiungendo B con gli altri vertici della figura, si determinano i punti A’, F’, E’, D’, C’. Fissato a piacere il punto B’, si punti esso e si tracci un arco avente lo stesso raggio del precedente. Si fissi poi un punto C” a piacere e si riportino da esso gli archi C’D’, C’E’, C’F’, C’A’, determinando così i punti D”, E”, F” e A”. Da B’ si traccino delle semirette passanti per questi punti e, su di esse, si riportino da B’ le dimensioni dei segmenti BA, BF, BE, BD, BC determinando i vertici della copia (figg. 1a e 1b)
Fig. 1
RIPRODUZIONE
Consideriamo la figura da riprodurre (➜ Fig. 2a), tracciamo due segmenti HK e H'K' congruenti tra loro e lunghi a piacere, uno vicino alla figura e uno dove si intende riprodurla. Rilevate col compasso le distanze tra gli estremi del segmento e un vertice della figura (ad esempio D), puntando con tali misure sugli estremi dell’altro segmento tracciamo due archetti che, incrociandosi, determinano il punto D'. Ripetendo tale operazione per tutti i vertici della figura si determinano i vertici della copia (➜ Fig. 2b).
Fig. 2
Riproduzione per coordinate
Riproduzione per coordinate
Riproduzione per coordinate
Data la figura da riprodurre, dai suoi vertici si portano delle perpendicolari a una retta s tracciata a piacere, determinando su di essa i punti A’, F’, B’, E’, D’ e C’ Tracciata una nuova retta s’ e fissato su di essa il punto si riportino da A” le distanze A’F’, A’B’, A’E’, A’D’, A’C’ ecc., determinando F”, B”, E”, D”, C”; per tali punti si no quindi delle perpendicolari alla retta stessa. Su tali perpendicolari si riportino le misure AA’, BB’ ecc., minando i vertici della copia (figg. 3a e 3b).
Data la figura da riprodurre (➜ Fig. 3a), dai suoi vertici conduciamo alcune perpendicolari a una retta s tracciata a piacere, determinando su di essa i punti A', F', B', E', D' e C'. Tracciata una nuova retta s' e fissato su di essa il punto A", riportiamo da A" le distanze A'F', A'B', A'E', A'D', A'C', ..., determinando F", B", E", D", C", ...; per tali punti tracciamo quindi delle perpendicolari alla retta stessa. Su tali perpendicolari riportiamo le misure AA', BB' ecc., determinando i vertici della copia (➜ Fig. 3b).
Data la figura da riprodurre, dai suoi vertici si portano delle perpendicolari a una retta s tracciata a piacere, determinando su di essa i punti A’, F’, B’, E’, D’ e C’ Tracciata una nuova retta s’ e fissato su di essa il punto si riportino da A” le distanze A’F’, A’B’, A’E’, A’D’, A’C’ ecc., determinando F”, B”, E”, D”, C”; per tali punti si traccino quindi delle perpendicolari alla retta stessa. Su tali perpendicolari si riportino le misure AA’, BB’ ecc., determinando i vertici della copia (figg. 3a e 3b).
Data la figura da riprodurre, dai suoi vertici si portano delle perpendicolari a una retta s tracciata a piacere, determinando su di essa i punti A’, F’, B’, E’, D’ e C’. Tracciata una nuova retta s’ e fissato su di essa il punto si riportino da A” le distanze A’F’, A’B’, A’E’, A’D’, A’C’ ecc., determinando F”, B”, E”, D”, C”; per tali punti si no quindi delle perpendicolari alla retta stessa. Su tali perpendicolari si riportino le misure AA’, BB’ ecc., determinando i vertici della copia (figg. 3a e 3b).
Fig. 3






Nell’eseguire il disegno di un oggetto ci si può trovare di fronte a tre possibilità:
Nell’eseguire il disegno di un oggetto ci si può trovare di fronte a tre possibilità:
1) le sue dimensioni sono tali da poter essere riportate, così come sono, sul foglio e pertant lo si può disegnare al naturale;
1) le sue dimensioni sono tali da poter essere riportate, così come al naturale;
2) le sue dimensioni sono più grandi del foglio e pertanto è necessario ridurle tutte proporzionalmente;
2) le sue dimensioni sono più grandi del foglio e pertanto è necessario ridurle tutte proporzionalmente;
Nell’eseguire il disegno di un oggetto ci si può trovare di fronte a tre possibilità:
1) le sue dimensioni sono tali da poter essere riportate, così come sono, sul foglio e pertant lo si può disegnare al naturale; più grandi del foglio e pertanto è necessario ridurle tutte proporzionalmente; 3) le sue dimensioni sono troppo piccole per poterlo disegnare e pertanto è necessario ingrandirle tutte proporzionalmente.
3) le sue dimensioni sono troppo piccole per poterlo disegnare e pertanto è necessario ingrandirle tutte proporzionalmente.
3) le sue dimensioni sono troppo piccole per poterlo disegnare e pertanto è necessario ingrandirle tutte propor-
1) le sue dimensioni sono tali da poter essere riportate, così come sono, sul foglio e pertanto lo si può disegnare al naturale;
figura abbia come dimensioni massime 150x250 mm. In questo caso si può eseguire la rappresentazione cioè in scala 1:1.
Sia dato un foglio, ad esempio in formato UNI A4 (210x297 mm), su cui si debba rappresentare un oggetto la cui figura abbia come dimensioni massime 150x250 mm. In questo caso si può eseguire la rappresentazione riportando le misure al naturale cioè in scala 1:1.
Sia dato un foglio, ad esempio in formato UNI A4 (210x297 mm), su cui si debba rappresentare un oggetto la cui figura abbia come dimensioni massime 150x250 mm. In questo caso si può eseguire la rappresentazione riportando le misure al naturale cioè in scala 1:1.
2) le sue dimensioni sono più grandi del foglio e pertanto è necessario ridurle tutte proporzionalmente;
Se naturale, bensì è necessario ridurre proporzionalmente le dimensioni in modo che possano essere contenute nel foglio. Dividendoad esempio per 10 si ottengono le dimensioni 150x250 mm che possono essere rappresentate sul foglio. In questo caso abbiamo eseguito una riduzione in scala 1:10, cioè 1 mm sul disegno corrisponde a 10
3) le sue dimensioni sono troppo piccole per poterlo disegnare e pertanto è necessario ingrandirle tutte proporzionalmente.
Se invece l’oggetto ha come dimensioni massime 1500 2500 mm, non si può eseguire la rappresentazione al naturale, bensì è necessario ridurre proporzionalmente le dimensioni in modo che possano essere contenute nel foglio. Dividendo ad esempio per 10 si ottengono le dimensioni 150 250 mm, che possono essere rappresentate sul foglio. In questo caso abbiamo eseguito una riduzione in scala 1:10, cioè 1 mm sul disegno corrisponde a 10 mm nella realtà.
Se invece l’oggetto ha come dimensioni massime 1500x2500 mm, non si può eseguire la rappresentazione al naturale, bensì è necessario ridurre proporzionalmente le dimensioni in modo che possano essere contenute nel foglio. Dividendoad esempio per 10 si ottengono le dimensioni 150x250 mm che possono essere rappresentate sul foglio. In questo caso abbiamo eseguito una riduzione in scala 1:10, cioè 1 mm sul disegno corrisponde a 10 mm in realtà.
Se invece l’oggetto ha come dimensioni massime 1500x2500 mm, non si può eseguire la rappresentazione al naturale, bensì è necessario ridurre proporzionalmente le dimensioni in modo che possano essere contenute nel foglio. Dividendoad esempio per 10 si ottengono le dimensioni 150x250 mm che possono essere rappresentate sul foglio. In questo caso abbiamo eseguito una riduzione in scala 1:10, cioè 1 mm sul disegno corrisponde a 10 mm in realtà.
Consideriamo un foglio, ad esempio in formato UNI
Nel caso in cui si abbia un oggetto con dimensioni massime di 15x25 mm, che possono essere contenute nel tali dimensioni moltiplicandolie ad esempio per 5: si esegue cioè un ingrandimento
Nel caso in cui si abbia un oggetto con dimensioni massime di 15x25 mm, che possono essere contenute nel foglio ma la cui rappresentazione al naturale risulta difficoltosain quanto troppo piccole, si possono ingrandire tali dimensioni moltiplicandolie ad esempio per 5: si esegue cioè un ingrandimento in scala 5:1, ove a 5 mm sul disegno corrisponde 1 mm nella realtà.
Nel caso in cui si abbia un oggetto con dimensioni massime di 15x25 mm, che possono essere contenute nel foglio ma la cui rappresentazione al naturale risulta difficoltosain quanto troppo piccole, si possono ingrandire tali dimensioni moltiplicandolie ad esempio per 5: si esegue cioè un ingrandimento in scala 5:1, ove a 5 mm sul disegno corrisponde 1 mm nella realtà.
A4 (210 297 mm), su cui dobbiamo rappresentare un oggetto la cui figura abbia come dimensioni massime 150 250 mm. In questo caso si può eseguire la rappresentazione riportando le misure al naturale, cioè in scala 1:1.
Scale di ingrandimento:
Scale di ingrandimento:
Nel caso in cui si abbia un oggetto con dimensioni massime di 15 25 mm, che possono essere contenute nel foglio ma la cui rappresentazione al naturale risulta difficoltosa in quanto troppo piccole, si possono ingrandire tali dimensioni moltiplicandole ad esempio per 5: si esegue cioè un ingrandimento in scala 5:1, ove a 5 mm sul disegno corrisponde 1 mm nella realtà.
50: 1; 20 : 1; 10 :1; 5:1; 2:1
50: 1; 20 : 1; 10 :1; 5:1; 2:1
50: 1; 20 : 1; 10 :1; 5:1; 2:1
2: 1
scala 2: 1
Scala al naturale
Scala al naturale
Scala al naturale
1:1
1:1
1: 1
scala 1: 1
Scale di riduzione:
Scale di riduzione:
Scale di riduzione:
1: 2; 1: 5; 1: 10; 1: 20; 1: 50; 1: 100; 1: 200; 1: 500; 1:1 000; 1:2 000; 1:5 000; 1: 10 000
2; 5; 10; 20; 50; 100; 200; 500; 000; 000; 000;
1: 2; 1: 5; 1: 10; 1: 20; 1: 50; 1: 100; 1: 200; 1: 500; 1:1 000; 1:2 000; 1:5 000; 1: 10 000
scala 1: 2
scala 1: 2
1. Un segmento è:
a una linea con due estremi
b la parte di retta delimitata da due punti
c la parte di retta delimitata da due punti compresi i punti stessi
2. Due rette parallele:
a non si incontrano mai
b appartengono allo stesso piano e non hanno punti in comune
c non hanno punti in comune
3. Due linee secanti:
a hanno un punto in comune
b hanno almeno due punti in comune
c non hanno alcun punto in comune
4. Due rette sono perpendicolari:
a se giacciono sullo stesso piano e hanno un punto in comune
b se sono sovrapposte
c se incontrandosi formano quattro angoli retti
5. L’asse di un segmento è:
a la retta perpendicolare al segmento passante per il suo punto medio
b la linea che passa per il punto medio del segmento
c è la retta perpendicolare al segmento
6. La distanza tra due rette è:
a il segmento che unisce due punti appartenenti alle rette
b una semiretta perpendicolare alle due rette
c il segmento perpendicolare alle due rette e che unisce due punti appartenenti ad esse
7. Un angolo è:
a la parte di piano limitato da due rette
b la parte di piano compreso tra due linee rette
c la parte di piano limitato da due semirette con in comune l’origine
8. La bisettrice di un angolo è:

a la retta con origine nel vertice dell’angolo che lo divide in due parti congruenti
b la semiretta con origine nel vertice dell’angolo che lo divide in due parti congruenti
c la retta che divide in due parti un angolo
9. I triangoli sono:
a poligoni di tre lati
b figure piane delimitate da una spezzata chiusa
Costruzioni geometriche: Conoscenze
c linee spezzate formate da tre segmenti
10. Nel triangolo ABC individua:
a una bisettrice
b una mediana
c un’altezza
11. I cateti sono:
a i lati del triangolo rettangolo
b i lati di un triangolo rettangolo che non formano l’angolo retto
c i due lati di un triangolo rettangolo che formano l’angolo retto
12. Un poligono è:
a la parte di piano delimitato da una spezzata
b una figura piana formata da più linee
c la parte di piano delimitato da una spezzata chiusa
13. Un quadrilatero è:
a la parte di piano delimitata da due coppie di segmenti paralleli
b la parte di piano delimitata da coppie di segmenti paralleli
c un poligono di quattro lati
14. Indica i nomi dei seguenti quadrilateri.
b
15. Indica i nomi dei seguenti quadrilateri. a b
16. Completa la seguente frase sui poligoni regolari.
I poligoni regolari hanno tutti i uguali e gli uguali.
Possono essere suddivisi in tanti quanti sono i lati.
17. Il cerchio:
a e la circonferenza indicano la stessa figura geometrica
b è la parte di piano equidistante da un punto fisso detto centro
c è la parte di piano delimitata da una circonferenza compresi i punti della circonferenza stessa
18. Nel cerchio individua:
a un arco
b una corda
c un settore circolare






19. La tangente a una circonferenza è:
a una linea che sfiora la circonferenza senza toccarla
b una retta che passa per due punti della circonferenza
c una retta che tocca in un punto la circonferenza
20. Realizzare un raccordo circolare significa:
a collegare due linee con un cerchio
b collegare due linee con un arco di circonferenza senza soluzione di continuità
c collegare due linee con un arco di circonferenza con soluzione di continuità
21. Gli ovali sono:
a curve che hanno gli assi in comune
b curve formate da una serie di archi di circonferenza raccordati tra loro
c figure piane chiuse formate da quattro archi di circonferenza a due a due congruenti
22. L’ellisse è il luogo geometrico dei punti:
a a distanza variabile dal centro
b la cui somma delle distanze dai fuochi è costante
c la cui distanza dai fuochi è costante
23. Nella spirale l’elemento costante è:
a il senso
b il centro
c il passo
24. L’evolvente del cerchio è generata da:
a un punto che si muove liberamente su una retta ruotante
b un punto che appartiene a una retta che ruota su una circonferenza senza strisciare
c un estremo di una retta che ruota su una circonferenza senza strisciare
25. La cicloide è generata da:
a un punto che si muove nello spazio senza strisciare e ha più centri
b un punto che rotola su una circonferenza senza strisciare
c un punto appartenente a una circonferenza che rotola su una retta senza strisciare
Abilità
Riproduci su un foglio bianco le costruzioni.
Riproduci su un foglio bianco le costruzioni.
6.4-6.6-6.8 vedi i paragrafi
8. Raccordare due circonferenze con un arco di raggio R
cateti
4. Disegnare un rombo dati il lato e un angolo
dati i cateti 4. Disegnare un rombo dati il lato e un angolo
7. Disegnare una circonferenza di raggio R” tangente ad una circonferenza di raggi R’ in un suo punto P
1. Disegna un rombo dati il lato e un angolo.
7. Disegnare una circonferenza di raggio R” tangente ad una circonferenza di raggi R’ in un suo punto P
9. Disegnare una arco tangente a tre rette
9. Disegnare una arco tangente a tre rette
base 6. Disegnare un triangolo isoscele data la base e l’altezza.
data la base base.
R” tangente punto P
2. Disegna un triangolo isoscele date la base e l’altezza.
6. Disegnare un triangolo isoscele data la base e l’altezza.
11. Disegnare una spirale con quattro centri dato il passo P
11. Disegnare una spirale con quattro centri dato il passo P
3. Raccorda due circonferenze con un arco di raggio R.
8. Raccordare due circonferenze con un arco di raggio R 10. Raccordare due
4. Disegna un arco tangente a tre rette.
9. Disegnare una arco tangente a tre rette
8. Raccordare due circonferenze con un arco di raggio R
estremi
10. Raccordare due segmenti, paralleli tra loro, con gli estremi A e C allineati e B e D sfalsati
10. Raccordare due segmenti, paralleli tra loro, con gli estremi A e C allineati e B e D sfalsati
5. Raccorda due segmenti, paralleli tra loro, con gli estremi A e C allineati e B e D sfalsati.
11. Disegnare una spirale con quattro centri dato il passo P
12. Disegnare un ovale inscritto in rombo
12. Disegnare un ovale inscritto in rombo
6. Disegna un ovale inscritto in rombo.






destra della pagina seguendo le indicazioni.
destra della pagina seguendo le indicazioni.
ESERCIZIO 13. Flangia
destra della pagina seguendo le indicazioni.
Riproduci su un foglio bianco le figure seguendo le indicazioni.
ESERCIZIO 13. Flangia
ESERCIZIO 13. Flangia
ggio pari al
ggio pari al rante
ggio pari al rante
7. FLANGIA
INDICAZIONI
Riproduci su foglio bianco le figure a destra della pagina seguendo
ESERCIZIO 13. Flangia
Tracciare quattro archi di circonferenza con raggio pari al raggio maggiore e centri nei quattro punti quadrante
Riproduci su foglio bianco le figure a destra della pagina seguendo
Applica la costruzione del dodecagono sulla circonferenza maggiore e prolunga gli archi di costruzione.
ESERCIZIO 13. Flangia
Tracciare quattro archi di circonferenza con raggio pari al raggio maggiore e centri nei quattro punti quadrante
Riproduci su foglio bianco le figure a destra della pagina seguendo

ESERCIZIO 14. Piatrina
ESERCIZIO 14. Piatrina
ESERCIZIO 14. Piatrina
utilizzare
utilizzare
8. PIASTRINA
ESERCIZIO 15. Dado
ESERCIZIO 15. Dado
ESERCIZIO 15. Dado
INDICAZIONI
Applica la costruzione del pentagono e utilizza le squadrette per le parallele ai cinque assi.

ESERCIZIO 13. Flangia
Tracciare quattro archi di circonferenza con raggio pari al raggio maggiore e centri nei quattro punti quadrante
Applicare la costruzione del pentagono e utilizzare le squadrette per le parallele ai cinque assi
Applicare la costruzione del pentagono e utilizzare le squadrette per le parallele ai cinque assi
14.
24
ESERCIZIO 14.
Applicare la costruzione del pentagono e utilizzare le squadrette per le parallele ai cinque assi

Applicare la costruzione dell’esagono e utilizzare le squadrette per le parallele ai sei assi
Applicare la costruzione dell’esagono e utilizzare le squadrette per le parallele ai sei assi
24
INDICAZIONI
Applica la costruzione dell’esagono e utilizza le squadrette per le parallele ai sei assi.


24
15.
ESERCIZIO 15.
Applicare la costruzione dell’esagono e utilizzare le squadrette per le parallele ai sei assi



Video tutorial

Tracciamo l’asse orizzontale, riportiamo su di esso le distanze tra i centri e tracciamo per questi i tre assi verticali o con le squadrette oppure con la costruzione della perpendicolare per un punto.
Prima fase
Seconda fase
Centrando in O1 e O2 con le varie aperture tracciamo le tre circonferenze di cui è dato il diametro. Puntiamo in O1 e O2 con raggio= 50/2+24 e tracciamo quattro archetti a determinare O3 e O4 centri di raccordo.
Terza fase
Tracciamo le congiungenti da O3 e O4 a O1 e O2 che intersecano le circonferenze in A, B, C, D punti di contatto dei raccordi. Puntando in O3 e O4 tracciamo gli archi di raccordo.
Quarta fase
Prolunghiamo i segmenti O3O1, O3O2, O4O1, O4O2 a determinare E, F, G, H. Da questi punti riportiamo verso O1 e O2 il raggio R=9 ottenendo O5, O6, O7, O8. Puntiamo in questi ultimi con R=9 e tracciamo le quattro circonferenze e i loro diametri orizzontali.

Quinta fase
Completiamo l’esercitazione ricalcando le linee.







Utilizza le costruzioni di tangente da un punto a una circonferenza e di raccordo tra rette e rette.


Riproduci su un foglio bianco i segnali proposti.
1. MATERIALI RADIOATTIVI
bianco i segnali
Riproduci su un foglio bianco i segnali proposti.
2. IDRANTE






Oggetti dalla vita quotidiana (schede 3, 4)
Oggetti dalla vita quotidiana (schede 3, 4)
Riproduci su un foglio bianco gli oggetti qui proposti
Riproduci su un foglio bianco gli oggetti qui proposti




ESERCIZIO






Si tracciano i segmenti ad unire i punti trvati.
INDICAZIONI
Recupero
Prima Fase
INDICAZIONI
Riproduci la figure a fondo pagina seguendo le fasi indicate.
Riproduci la figure a fondo pagina seguendo le fasi indicate.
Prima Fase
Esercizio 39. Riproduci le piastrine a fondo pagina seguendo le fasi indicate.
Recupero
Costruzione col compasso
Riporta la larghezza 70; alza dai suoi estremi due perpendicolari e su entrambe riporta simmetricamente le varie altezze.
Esercizio 40. Piastrina Esercizio 41.
PRIMA FASE
Costruzione con le squadrette
Esercizio 39. Riproduci le piastrine a fondo pagina seguendo le fasi indicate.
Costruzione col compasso
Riportata la larghezza 70 si alzano dai suoi estremi due perpendicolari e su entrambe si riportano simmetricamente le varie altezze col compasso in modo che siano le stesse anche in caso di errore.
Riportata la larghezza 70 si alzano dai suoi estremi due perpendicolari e su entrambe si riportano simmetricamente le varie altezze col compasso in modo che siano le stesse anche in caso di errore.
Seconda Fase
Si tracciano le orizzontali su cui si riportano le larghezze.
Traccia le orizzontali e riporta su di esse le larghezze.
Si tracciano le orizzontali su cui si riportano le larghezze.

Si tracciano i segmenti ad unire i punti trvati.
Terza Fase
Si tracciano i segmenti ad unire i punti trvati.
Costruzione con le squadrette
PRIMA FASE
Riporta la lunghezza della piastrina, traccia ai suoi estremi le perpendicolari e suddividila in cinque parti uguali. Riporta poi le altezze simmetricamente all’asse.
Esercizio 40. Piastrina Esercizio 41.
Riportata la larghezza della piastrina si alzano dai suoi estremi con le squadrette due perpendicolari su cui si riportano le varie altezze.
Riportata la lunghezza della piastrina si tracciano ai suoi estremi le perpendicolari e la si suddivide in cinque parti uguali. Si riportano poi le altezze simmetricamente all’asse.
Riportata la larghezza della piastrina si alzano dai suoi estremi con le squadrette due perpendicolari su cui si riportano le varie altezze.
Riportata la lunghezza della piastrina si tracciano ai suoi estremi le perpendicolari e la si suddivide in cinque parti uguali. Si riportano poi le altezze simmetricamente all’asse.
Tracciato l’arco di ra colare al centro, le bisettrici degli angoli
Seconda fase
SECONDA FASE
SECONDA FASE
Si tracciano le orizzontali su cui si riportano le larghezze.
Si tracciano le linee orizzontali e, utilizzando le squdrette, le linee verticali.
Traccia le linee orizzontali e, utilizzando le squadrette, le linee verticali.
Si tracciano le linee orizzontali e, utilizzando le squdrette, le linee verticali.
Si tracciano le orizzontali su cui si riportano le larghezze.
Si traccia la spezzata, corni e con le squadrette perpendicolari agli assi
Si traccia la spezzata, corni e con le squadrette perpendicolari agli assi
Terza fase
Traccia i segmenti per unire i punti trovati.
28 28 14 14


Ricalca i contorni.







INDICAZIONI
INDICAZIONI
Prima Fase
pagina seguendo le fasi indicate.
pagina seguendo le fasi indicate.
Riproduci la figure a fondo pagina seguendo le fasi indicate. Esercizio 40. Supporto Esercizio
Riproduci la figure a fondo pagina seguendo le fasi indicate. Esercizio 40. Supporto Esercizio
Piastrina Esercizio 41. Schema di portautensili
Piastrina Esercizio 41. Schema di portautensili
Traccia una semicirconferenza di raggio
Prima Fase
PRIMA FASE
SE PRIMA FASE
SE PRIMA FASE
35 e costruisci la perpendicolare nel centro, le bisettrici degli angoli di 90° e le bisettrici degli angoli di 45°.
piastrina si tracciano ai la si suddivide in poi le altezze sim-
piastrina si tracciano ai si suddivide in poi le altezze sim-
Tracciato l’arco di raggio 35 si costruisce la perpendicolare al centro, le bisettrici degli angoli di 90° e le bisettrici degli angoli di 45°
Tracciato l’arco di raggio 35 si costruisce la perpendicolare al centro, le bisettrici degli angoli di 90° e le bisettrici degli angoli di 45°
Seconda fase
Seconda fase
SECONDA FASE
SECONDA FASE
utilizzando le Si traccia la spezzata, si riportano le larghezze dei corni e con le squadrette si tracciano le parallele e le perpendicolari agli assi a 45°
utilizzando le Si traccia la spezzata, si riportano le larghezze dei corni e con le squadrette si tracciano le parallele e le perpendicolari agli assi a 45°
Traccia la spezzata, riporta le larghezze dei corni e con le squadrette traccia le parallele e le perpendicolari agli assi a 45°.

Terza fase
Ricalca i contorni.
SECONDA FASE
16 20
16 20


Terza fase Ricalca i contorni.

Riproduci le figure seguendo le indicazioni.
5. POMELLO
PASSO PASSO
1 Disegniamo la vista laterale di un pomello date le dimensioni.
2 Tracciamo la linea di base e, perpendicolare ad essa, l’asse della figura finale.
Riportiamo le misure di elementi simmetrici con il compasso parte per parte rispetto all’asse per mantenere la simmetria.

3 Con le squadrette costruiamo il rettangolo che rappresenta il disco di base, tracciamo l’asse ortogonale passante per il centro della circonferenza e tracciamo la circonferenza che rappresenta la sfera del pomello.
4 Riportiamo le dimensioni col compasso e tracciamo le parallele all’asse che rappresentano il cilindro di collegamento tra la piastra di base e la sfera.
5 Riportiamo le misure dei raggi di raccordo, tracciamo le parallele ai segmenti da raccordare, l’arco con raggio del cerchio più raggio di raccordo determinando i centri di raccordo e i punti di contatto.
6 Ricalchiamo le linee che descrivono il pomello. La linea fina è un espediente del disegno tecnico per indicare l’intersezione tra due elementi curvi, in questo caso il cilindro con la sfera.






Ricava la “mascherina” della sagoma di uno skateborder, da utilizzare per creare il “pittogramma” al centro di un cartello segnaletico.
Riproduci perciò la figura su un foglio e poi ritagliarla lasciando il vuoto da riempire col colore pitturato ad esempio con l’aerografo. La sagoma potrà essere utilizzata per creare un segnale di divieto (➜ Fig. 1), di pista riservata a questa attività (➜ Fig. 2) oppure un segnale di pericolo (riducendo la sagoma per adattarla alla forma del segnale) (➜ Fig. 3).
I segnali in figura sono di formato piccolo in scala 1 : 10. Alla destra (➜ Fig. 4) c’è il disegno da realizzare in scala 1 : 1 per il formato piccolo, e da adattare se si volessero realizzare cartelli di formato normale o grande. Con O è indicato il centro del cartello se rotondo.
Ricavare la “mascherina”, della sagoma di uno skateborder, da utilizzare per creare il “pittogramma” al centro di un cartello segnaletico. Riprodurre perciò la figura su un foglio e poi ritagliarla lasciando il vuoto da riempire col colore pitturato ad esempio con l’aerografo. La sagoma potrà essere utilizzata per creare un segnale: di divieto Fig.1, di pista riservata a questa attività Fig.2 oppure segnale di pericolo (riducendo la sagoma per adattarla alla forma del segnale) Fig.3. I segnali in figura sono di formato piccolo in scala 1:10. Alla destra c’è il disegno da realizzare in scala 1:1 per il formato piccolo, e da adattare se si volesse realizzare cartelli di formato normale o grande. Con O è indicato il centro del cartello se rotondo.
tabella 2 - CERCHIO (divieto)
tabella 3 - CERCHIO (obbligo)