TEORIA DA COMPUTAÇÃO

TEORIADACOMPUTAÇÃO
MarcusViniciusMidenaRamos
Teoriadacomputação
©2025MarcusViniciusMidenaRamos
EditoraEdgardBlücherLtda.
Publisher EdgardBlücher
Editor EduardoBlücher
Coordenadoreditorial RafaelFulanetti
Coordenadoradeprodução AnaCristinaGarcia
Produçãoeditorial ArianaCorrêaeAndressaLira
Diagramação MarcusViniciusMidenaRamos
Revisãodetexto MaurícioKatayama
Capa LiraEditorial
Imagemdacapa iStockphoto
EditoraBlucher
RuaPedrosoAlvarenga,1245, 4o andar CEP04531-934–SãoPaulo–SP–Brasil Tel.:55113078-5366 contato@blucher.com.br www.blucher.com.br
SegundooNovoAcordoOrtográfico,conforme6.ed.do VocabulárioOrtográficodaLíngua Portuguesa,AcademiaBrasileiradeLetras,julhode2021.Éproibidaareproduçãototalou parcialporquaisquermeiossemautorizaçãoescritadaeditora.Todososdireitosreservados pelaEditoraEdgardBlücherLtda.

Sumário
1.2Máquinas....................................35
1.4Computação...................................39
1.5Funçãocomputada...............................44
1.6Equivalênciafortedeprogramas....................
1.7Equivalênciadeprogramasemumamáquina............. ....54
1.8Equivalênciademáquinas..........................
1.9Verificaçãodaequivalênciafortedeprogramas........ ........55
1.10Podercomputacional............................. .76
1.11Exercícios....................................89
2Máquinasuniversais
2.1Algoritmos...................................97
2.2Máquinasuniversais..............................
2.3HipótesedeChurch-Turing.........................
2.4TeoremaFundamentaldaAritmética..................
2.5Codificaçãodedadosestruturados................... ....102
2.6MáquinadeTuring...............................104
2.7MáquinaNorma.................................122
2.8MáquinaNormaéuniversalporevidênciasinternas..... .........123
2.9MáquinaNormaéuniversalporevidênciasexternas..... .........138
2.10MáquinadePost................................146
2.11MáquinadePostéuniversalporevidênciasexternas... ...........153
2.12MáquinacomPilhas..............................163
2.13AutômatocomDuasPilhas.......................... .175
2.14AutômatocomDuasPilhaséuniversalporevidênciasexternas........179
2.15VariaçõesdaMáquinadeTuring..................... ...190
2.16Exercícios....................................219
3Decidibilidade 231
3.1Introdução....................................232
3.2Problemasdecidíveis............................. .239
3.3CodificaçãodeMáquinasdeTuring.................... ..249
3.4MétododiagonaldeCantor.......................... .251
3.5Linguagem
3.6Complementodelinguagens.........................
3.7MáquinadeTuringUniversal........................
3.8Linguagem
3.9Redutibilidade..................................
3.10Problemadaparada...............................
3.11Linguagens
3.12TeoremadeRice................................284
3.13AutômatoLinearmenteLimitado....................
3.14Históriasdecomputação..........................
3.15Problemasindecidíveis..........................
3.16ProblemadaCorrespondênciadePost................
3.17Problemasrelacionadoscomgramáticaselinguagenslivresdecontexto...312
3.18Conclusões...................................320
3.19Exercícios....................................320
4Complexidadenotempo 327
4.6Problemas
4.8Redutibilidadeemtempopolinomial.................
4.10Reduçãode
4.11Problemas
4.12Problemas
4.14Aclasse
4.15Conclusões...................................371
4.16Exercícios....................................371
5CálculoLambdanãotipado 375
5.1Introdução....................................376
5.2Motivação....................................377
5.3Linguagemlambda...............................378
5.4Substituições..................................382
5.5Conversão-
5.6Redução-
5.7Formalnormal-
5.8NumeraisdeChurch..............................391
5.9BooleanosdeChurch..............................396
5.10Igualdade-β
5.11Interpretações.................................
5.12Pontofixo....................................404
5.13Recursão....................................405
Capítulo1 Programas,máquinase equivalências
Estecapítulotemtrêsobjetivosprincipais.Oprimeiroéintroduzir,demaneirarigorosa(com oempregodamatemática),asdiversasnoçõesempregadashabitualmenteporestudantese profissionaisdecomputação.Sãonoçõescomoprograma,máquina,computaçãoetc.,quesão normalmenteusadascomelevadograudeinformalidade,eque serãorevisitadasedefinidas demaneiraprecisa,oquepoderáinclusiverevelaraspectos poucoconhecidosacercadestas noções.
Osegundoobjetivoéapresentaralgumasnoçõesdeequivalênciadeprogramasemáquinas, emespecialanoçãodeequivalênciafortedeprogramas.Talnoção,quepoderásemostrar útilnodiaadiadoprofissionaldecomputação,éacompanhada deumalgoritmoquepermite determinarsedoisprogramassãoequivalentes(ounão).
Oterceiroobjetivoémostrarque,apesardeexistiremdiversosparadigmasdeprogramação, opodercomputacionaldeleséomesmo.Ouseja,aescolhadeum particularparadigma nãorestringeaspossibilidadescomputacionaisdecorrentesdoseuuso.Istoconstrastacom anoçãodeequivalênciafortedeprogramas,emqueosparadigmasconsideradosnãosão equivalentes.
Oconteúdodestecapítuloébaseadoem[14]e[15].
1.1Programas
Amaioriadaspessoasqueatuamnacomputação(comoestudantes,profissionaisouusuários) possuialgumafamiliaridadecomanoçãode programa.Existemcentenasdelinguagensde programação,eestenúmeronãoparadecrescer.Linguagensdeprogramaçãopermitema construçãodeprogramas,porémanoçãoqueapresentaremosaquiéumpoucodiferenteda noçãoqueamaioriadaspessoastêm.
Anoçãomaisdifundidadeprograma(decomputador)refere-seaumacoleçãodeinstruçõesquesãosequenciadasnotempo.Asinstruções,porsuavez,sãoformadasporoperações (comoadição,subtraçãoetc.)etestes(comomaior,diferenteetc.),alémdoselementosdeestruturaçãodofluxodecontrole(istoé,amaneiracomoasoperaçõesetestessãosequenciados notempo,desdeoiníciodaexecuçãodoprogramaatéoseutérmino).
Naturalmente,estamosnosreferindoaquiapenasaomodelosequencialdeexecução,ou seja,aomodelodecomputaçãoemqueasoperaçõeseostestessãoexecutadosumdecada vezeumapósooutronaordemdeterminadapeloprograma.Modelosdiversos,comoéo casodomodeloconcorrente(noqualváriasinstruçõescompartilhamummesmoprocessador, porémumadecadavez)oudomodeloparalelo(noqualasvárias instruçõessãoexecutados simultaneamenteemváriosprocessadores),nãosãodiscutidosnestetexto.
Diferentementedestanoçãomaisdifundida,noentanto,anoçãoqueestamosintroduzindo aquiéanoçãodeprogramaenquantoelementodesequencializaçãodeoperaçõesetestesno tempo.Asoperaçõeseostestespropriamenteditosnãosãodefinidospeloprograma(oupela linguagemdeprogramação),massimdefinidospelamáquinasubjacente(realouvirtual),na qualoprogramaéexecutado.Assim,oprogramanadamaisfazdoque“tomaremprestado” asoperaçõesetestesdefinidosmáquinanaqualeleexecutado,determinandoaordemde execuçãodestes.Portanto:
•Um programa éumconjuntodeinstruçõesqueestabelecemasequênciaemquecertas operaçõesetestesdevemserexecutados.
•Eletemporfinalidademanipulardadosdeentrada,produzindoassaídasdesejadas.
•A estruturadecontrole doprogramadefineamaneiracomoasoperaçõeseostestes sãosequenciadosnotempo.
Emvezdeconsiderarmosoperaçõesetestesespecíficos,como adição,subtração,maiorou igual,porexemplo,usaremosoperaçõesetestesdenotadospornomesabstratos:
•Identificadoresdeoperações: F,G,H,...
•Identificadoresdetestes: T1,T2,T3,...
•Operaçãovazia: (nãoexecutanenhumaoperação).
Quantaslinguagensdeprogramaçãoexistem?Nãosesabeaocerto,masosnúmeros variamdequase700([16])aquase9.000.Estenúmerocrescetodososanos,eébomque sejaassim.Umnúmerocrescentelinguagensdeprogramaçãocostumaindicarqueelasestão aderentesaumnúmerocadavezmaiordeáreasdeaplicação,facilitandoaconstruçãode soluçõesparaosproblemasdestasáreas.
Nadécadade1960,nãohaviamuitaslinguagensparaseescolher.Aopçãotinhaqueser entreoCOBOL(paraaplicaçõescomerciais),oFORTRAN(para aplicaçõesdeengenharia oumuméricasdeumaformageral),oALGOL(muitousadanaacademia),oBASIC(para aplicaçõesdomésticaseusuários“leigos”)ouoLisp(parapesquisaseminteligênciaartificial).Desdeentão,novaslinguagenssurgemtodososanos,voltadasparaumgrandenúmero denovasáreasdeaplicaçãodistintas.ComojádiziaoprofessorJoãoJoséNeto,emuma dassuasaulas, “quandoaúnicaferramentaqueseteméummartelo,todososproblemas separecemcomumprego”. 1 Ouseja,osurgimentodenovaslinguagensdeprogramaçãoé bem-vindonamedidaemquepermitequeosprogramadoresfaçamescolhasmaisaderentes àsáreasdeaplicaçãoemquetrabalham.Casocontrário,aspossibilidadesdoprogramador ficamlimitadaspelaspossibilidadesdalinguagemqueeleadota(ouconhece),oquepodeser desastroso.Éocaso,porexemplo,dequerercolocarumparafusonumaparedeusandoum martelo:épossível,masoresultadoseriamuitomelhorseumachavedefendafosseusada nolugardeummartelo.
Mascomoselecionar,entreumnúmerograndeecrescentedelinguagensdeprogramação, aquelasquerepresentamasmelhoresescolhasparacadacaso?Partedarespostaestáno
1OriginalmenteestafraseédeAbrahamHaroldMaslow(psicólogonorte-americano,1908-1970),tendosidopublicadapelaprimeiravezem[17].Afraseoriginalé “Isupposeitistempting,iftheonlytoolyouhaveisahammer,to treateverythingasifitwereanail”.Elaétambémconhecidacomo Maslow’sHammer (ou“MartelodeMaslow”, emtraduçãolivre).
conceitodeparadigma.Umparadigmaéumestilo,ummodelode umalinguagemdeprogramação,edescreveumcertoconjuntoderecursosquepodeserusadoparaaconstruçãode programasnestalinguagem.Emoutraspalavras,umparadigmarepresentaumacertafilosofia deprogramação,correspondendoaumadescriçãoabstratade umalinguagem.Normalmente, umalinguagemdeprogramaçãosuportaumúnicoparadigmadeprogramação,masnãoé raroencontrarlinguagensquesuportammaisdeumparadigma aomesmotempo.
Linguagensdeprogramaçãoquesuportamummesmoparadigmacostumamexibirsemelhanças(tantodopontodevistasintáticoquandosemântico),aopassoquelinguagensque suportamparadigmasdistintoscostumamexibirgrandesdiferençasentresi.
Felizmente,ediferentementedoqueacontececomonúmerode linguagensdeprogramação,onúmerodeparadigmasdelinguagensdeprogramaçãoque existeépequeno.Portanto, conhecerbemosparadigmas,esabendoaprioriquaislinguagenssuportamquaisparadigmas (umalinguagempodesuportarmaisdeumparadigmaaomesmotempo),éomelhorcaminho paraescolheralinguagemmaisindicadaparacadacaso,aindaqueseusdetalhesnãosejam conhecidos.
Nãoparecehavermuitoconsensoemrelaçãoaquaissãoosprincipaisparadigmasexistentes(ocritériovariadeautorparaautor).Entretanto,émaisoumenosconsensoqueosprincipaisparadigmassãooimperativoeodeclarativo.Noprimeiroseencontramaslinguagens quepermitemaoprogramadorexpressaraformacomoumcertoproblemadeveserresolvido. Nosegundoseencontramaslinguagensquepermitemaoprogramadorconcentrar-senoque deveserfeito,emdetrimentodocomofazê-lo.Portanto:
Paradigmas
Imperativo
Declarativo
Oparadigmaimperativocostumasersubdivididoemtrês:omonolítico(linguagensque usamdesviosarbitrários),oiterativo(linguagensestruturadas)eoorientadoaobjetos(no qualobjetosabstratosrepresentamobjetosdomundorealesecomunicamatravésdemensagens).Jáoparadigmadeclarativocostumasedividiremdois:ofuncional(noquala definiçãoechamadadefunçõeséabasedaprogramação)eológico(noqualfatoseregras deinferênciasãousadosparasechegaràsoluçãodoproblema):
Monolítico
Imperativo
Paradigmas
Declarativo
Iterativo
Orientadoaobjetos
Funcional
Lógico
Noquesegue,doscincoparadigmascitados(monolítico,iterativo,orientadoaobjetos, funcionalelógico),serãoestudadosnestelivroapenastrês:omonolítico,oiterativoeo funcional(aquichamadorecursivo).Estesparadigmasserãoconsideradosapenasnomodelo sequencialdeexecução.Osmodelosconcorrenteeparalelonãoserãolevadosemconta, tampoucoosparadigmasorientadoaobjetoselógico.
Cadaumdostrêsparadigmasconsideradosseráapresentadopormeiodeumalinguagem deprogramaçãopequena,debaixacomplexidadeequesuporta apenasoparadigmaemquestão.Aqui,oobjetivonãoéapresentarlinguagensdeprogramaçaoreais,masapenaslinguagensqueilustramosrespectivosparadigmasequesirvam aospropósitosdeestudoque serãoconduzidosmaisadiante.Cadaumdestesparadigmasofereceumaformadiferentede sequenciaroperaçõesetestesaolongodotempo,ouseja,deestruturarofluxodecontrole.
Estaformadeestruturarofluxodecontroletambéméconhecidaporestruturadecontrole dalinguagemdeprogramação.Osparadigmasdeprogramaçãoqueserãoconsideradosno presentetextosão,portanto:
•Monolítico(flowchartprograms).
•Iterativo(whileprograms).
•Recursivo(procedureprograms).
Cadaumdestesparadigmasseráestudadopormeiodeumamini-linguagemdeprogramação.Concebidacomfinalidadesexclusivamentedidáticas,estasmini-linguagenssãopequenaspornaturezaeincorporamapenasosrecursosrelevantesaoseuestudo.Nãoéoque acontececomaslinguagensdeprogramaçãocomerciais,nasquaiséfrequenteaincorporação deumoumaisparadigmasnasuadefinição,alémdeumaquantidadegrandededetalhesque sãoirrelevantesparaosnossosobjetivos.
Emtodosestesparadigmas,osquaisserãoestudadosemdetalhesmaisadiante,acomposiçãosequencialéutilizadacomoelementodeestruturação dofluxo.Eladeterminaqueas instruçõesdoprogramadevemserexecutadasemumacertasequência,detalformaquea instruçãoseguintesópodeserexecutadaapósotérminodaexecuçãodaanterior.Taltipo decomposiçãoestápresenteempraticamentetodasaslinguagensdeprogramaçãoecostuma serdenotadapelosímbolo“;”(pontoevírgula).Osdemaiselementosdeestruturaçãosão específicosdosparadigmasconsiderados.
1.1.1Programasmonolíticos
Oparadigma monolítico éaqueleemqueoselementosdeestruturaçãodofluxosão,além dacomposiçãosequencial,odesvioincondicionaleodesvio condicional(alémdealgumas variaçõesdestes).Odesvioincondicionalecondicionalcorrespondem,respectivamente,à transferênciadocontroledeumainstruçãoqualquerparaumaoutrarotuladaparaessafinalidade(deformaincondicional)eàtransferênciadocontrole deformasimilar,porémapenas seumacertacondiçãoforverificada(portanto,deformacondicional).Taisinstruçõessão normalmenteencontradasnaslinguagensdeprogramaçãocom osnomesGOTOouJUMPe servem,portanto,paratrasnferirocontroleparaumaoutra instruçãodoprograma,rompendo omodelosequencialdeexecução,noqualainstruçãoseguinteésempreexecutadaaotérmino daexecuçãodainstruçãocorrente.
Noquesegue, rótulo identificaumainstruçãoqualquerdoprogramae exp denota umaexpressãoqualquerque,aoseravaliada,retornaosvalores verdadeiro ou falso:
Desvioincondicional(paraumainstruçãoanterior):
Desvioincondicional(paraumainstruçãoposterior):
GOTO rótulo ... rótulo ...
Desviocondicional(paraumainstruçãoanterior):
rótulo ... ... IF exp GOTO rótulo
Desvioincondicional(paraumainstruçãoposterior):
IF exp GOTO rótulo
rótulo ...
Programasmonolíticos,portanto,sãoprogramasquefazemusodedesvioarbitrários(condicionaisouincondicionais)esãonormalmenteconstituídosporumúnicobloco.2
Oparadigmamonolíticoéprovavelmenteoparadigmadeprogramaçãomaisantigoque seconhece.Defato,osprimeiroscomputadoreseramprogramadospormeiodousoexclusivodedesvioscondicionaiseincondicionais,tornandoestaformadeprogramaçãobastante popularnasdécadasde1950e1960,emparticularnasprimeirasversõesdoFortranedoBasic.3,4,5 Diversosproblemasforamidentificadosnesteparadigmadeprogramação,osquais serãodiscutidosmaisadiante.
Um programamonolítico podeserrepresentadodeformagráficaoutextual:
•Gráfica,pormeiodeum fluxograma.
•Textual,pormeiodeumconjuntode instruçõesrotuladas.
Oscomponentesdeumfluxogramasãoosseguintes:
Início (únicoemcadafluxograma,eleindicaopontodeiníciodaexecuçãodofluxograma). VejaFigura1.1.
Término (podeocorreremqualquerquantidadenofluxograma,indicandoospontosdetérminodaexecuçãodofluxograma).VejaFigura1.2.
Operação (indicaolocalemqueocorre,nofluxograma,aexecuçãodeuma operação,como F , G, H etc.).VejaFigura1.3.
Desviocondicional (indicaaexecuçãodeumteste,como T1, T2 etc.,seguidodaramificaçãodofluxodecontroleconformeoseuresultado).VejaFigura1.4.
2Umblococorrespondeaumasequênciadedeclaraçõesecomandosquepodeserconsideradocomoumaabstração independentedentrodoprograma.
3SigladeFORmulaTRANslator,foiumalinguagemdeprogramaçãobastantepopularnesseperíodoequecontinua

Figura1.1 Componente“Início”deumfluxograma.

Figura1.2 Componente“Término”deumfluxograma.
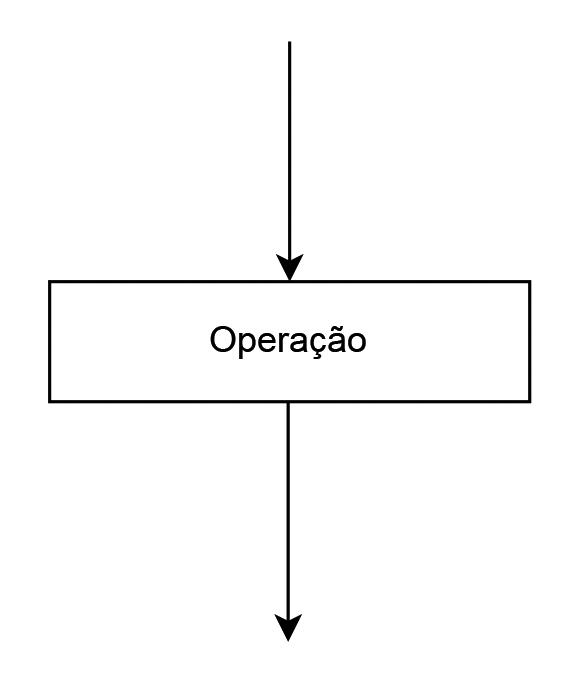
Figura1.3 Componente“Operação”deumfluxograma.
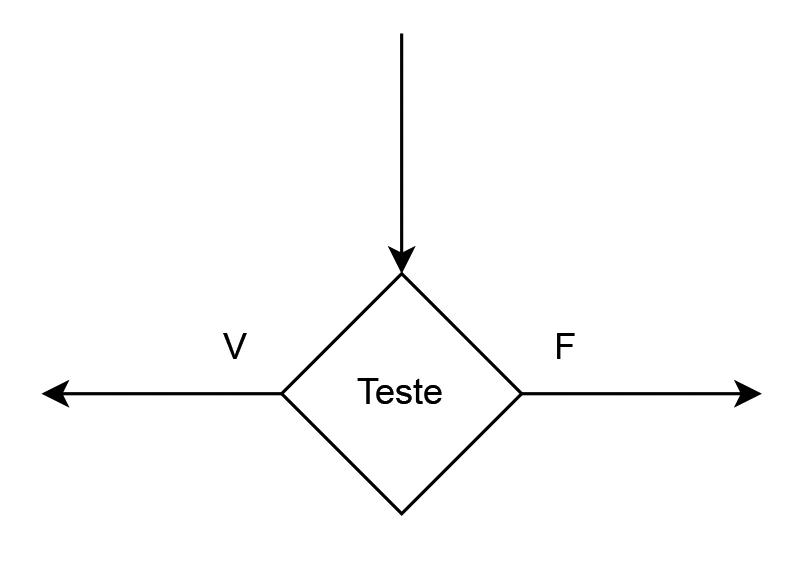
Figura1.4 Componente“Desviocondicional”deumfluxograma.
Capítulo2 Máquinasuniversais
Oobjetivodestecapítuloéapresentaredefinirasnoçõesfundamentaisdealgoritmo(Seção 2.1),MáquinaUniversal(Seção2.2),HipótesedeChurch(Seção2.3)eoTeoremaFundamentaldaAritmética(Seção2.4).NaSeção2.5émostradocomooTeoremaFundamental daAritméticapodeserusadonacodificaçãodedadosestruturados.
Emseguida,sãoapresentadasalgumasdasMáquinasUniversaismaisconhecidas,como éocasodaMáquinadeTuring(Seção2.6),daMáquinaNorma(Seção2.7),daMáquina dePost(Seção2.10),daMáquinacomPilhas(Seção2.12)edoAutômatocomDuasPilhas (Seção2.13).
Paradeterminarseumamáquinaqualqueré(ounãoé)umaMáquinaUniversal,sãoapresentadasedesenvolvidasduastécnicasdiferentes:umabaseadaemevidênciasinternase outrabaseadaemevidênciasexternas(Seção2.2).Aaplicaçãodessastécnicaséilustrada nademonstraçãodequealgumasdasmáquinascitadasanteriormentesãodefatouniversais (Seções2.8,2.9,2.11e2.14).
Porúltimo,econsiderandoarelevânciadaMáquinadeTuring paraaTeoriadaComputação,sãoapresentadaseestudadasextensõeserestriçõessobreomodelobásicodela,provando queestasnãomodificamemnadaoseupodercomputacional(Seção2.15).Aimportânciade talfatoresidenapossibilidadedeusartaisextensõeserestriçõesnasprovasseguintes,sem queissoimpliqueemqualquerressalvanosresultadosobtidos.
Oconteúdodestecapítuloébaseadoem[14],[15]e[12].
2.1Algoritmos
Anoçãodealgoritmoéfamiliarparaamaioriadaspessoas,em particularaquelesquesão daáreadacomputação.Écomumquealgoritmosejacomparadocomumareceitagastronômica,pois,decertaforma,todoalgoritmoéumaespéciedereceitasobrecomotransformar dadosdeentradaemdadosdesaída. Algoritmos,nacomputação,sãotextosquedescrevem aslinhasgeraisdefuncionamentodeumprogramadecomputador,sendopropositalmente maisresumidosemenosdetalhadosdoqueestes.Normalmente,algoritmosservemparadescrever,emalgumanotação,aestratégiaquedeveserusadana construçãodeumprograma. Representadosmuitasvezesemlinguagemnatural,emnotaçãodefluxogramaoupormeio dealgumalinguagemdebastantealtonível,ofatoéquealgoritmosprecisamsertraduzidos paraprogramasantesdepoderemserexecutados.
Tipicamente,umalgoritmoexibeasseguintescaracterísticas:
•Definidodemaneirainformal.
•Descritodeformafinitaenãoambígua.
•Constituídodepassosdiscretos,executáveismecanicamente.
•Produzrespostaemtempofinito.
Écomumquerecaiamsobreosalgoritmosalgumasrestriçõesdeordemprática,porexemplo,aquantidadedememóriaeotemponecessáriosparaasuaexecução.Dopontodevista teórico,noentanto,iremosconsiderar,pelomenosinicialmente,queumalgoritmodispõede todootempoememóriadequenecessitar.Omontantederecursosnecessáriosàexecução práticadeumalgoritmoseráobjetodeestudodaáreadaTeoriadaComputaçãoconhecida comoComplexidade.
Paraoquesegue,omaisimportanteaserconsideradoéqueumalgoritmosemprepara, fornecendoumresultado(ousaída)qualquerquesejaaentrada.Emoutraspalavras,não existeentradacapazdefazerumalgoritmoentrarem loop infinito.Seestaexistir,entãonão setratadeumalgoritmo.
2.2Máquinasuniversais
Todoalgoritmoprecisasertransformadoemumprogramaetodoprogramarequerumamáquinaparaasuaexecução.Portanto,sãocriadosmodelosdeexecução(oudecomputação) paraprogramasbaseadosemmáquinas.Estanãoé,noentanto, aúnicamaneiradesedefinir computação(vejaoCapítulo5),maséumadasmaisimportantes.Porisso,énecessário identificarascaracterísticasdasmáquinas,afimdequeelas setornemadequadasparaa representaçãodecomputações.
Taiscaracterísticassão,principalmente, simplicidade e poder.
A simplicidade garantequeapenascaracterísticasessenciais,comomissãodeoutrasnão relevantes,estarãopresentesnestasmáquinas.Issopossibilitaaobtençãodeconclusõesgeneralizadasacercadaclassedasfunçõescomputáveis,semincorreremdetalhesdesnecessários.
O poder temporobjetivogarantirqueamáquinaemquestãosejacapaz derepresentar qualquerfunçãocomputável,semrestrições.Dessaforma,elapodesimularqualqueroutra máquinarealouteórica.
Simplicidadeepodersãocaracterísticasdemáquinasqueviabilizamoestudoteóricodas funçõescomputáveisemmáquinas,osseuslimiteseassuaspropriedades.
Asmáquinasqueserãoestudadasnestecapítulo,equepossuemessascaracterísticas,são asseguintes:
•MáquinadeTuring(Seção2.6).
•MáquinaNorma(Seção2.7).
•MáquinadePost(Seção2.10).
•MáquinacomPilhas(Seção2.12).
•AutômatocomDuasPilhas(Seção2.13).
Uma MáquinaUniversal éumamáquinaque,pordefinição,permitearepresentaçãode qualqueralgoritmonaformadeumprogramaparaela.Oproblematorna-se,portanto,como caracterizarumamáquinacomosendouniversal.Existemduasformasdesefazerisso(veja [15]):
• Evidênciasinternas:quaisquerextensõesouvariaçõesdamáquinanãoaumentamo seupodercomputacional(oconjuntodefunçõescomputáveis permaneceinalterado).
• Evidênciasexternas:equivalênciacomoutrosmodelos(máquinasounão)querepresentamanoçãodealgoritmo.
Aprovadequeumamáquinaéuniversal,quandofeitapormeiodeevidênciasinternas, requerademonstraçãodequequalqueroperação,testeoutipodedadospodemserrepresentadospormeiodousoexclusivodasoperações,testesetiposprimitivosdamáquinaem questão.Comotaldemonstraçãopodesermuitolongaetrabalhosa,éusualconsiderarapenasumsubconjuntorelevantedasoperações,testesetiposdedadosmaisusadosnaprática. Normalmenteessaprovaéfeitainicialmentepormeiodaimplementaçãodenovosrecursos pormeiodeprogramasqueusamosrecursosprimitivos.Emseguida,osrecursosprimitivossãocombinadoscomosnovos,resultandonumconjuntoexpandidoderecursos,eassim pordiante.Nãoéumaprovaformal,maspodelevaraoconvencimentodequeamáquina emquestãoédefatouniversal,pormenosqueelaassimpareça numaanálisepreliminare superficial.
Aprovaporevidênciasexternasprocuraestabeleceraequivalênciadamáquinaemquestão, digamos M ,comalgumaoutramáquinaquesejaaceitacomouniversal,digamos U .Aprova envolveademonstraçãodeque M possasimular U etambémque U possasimular M .A primeiraprovajáseriasuficienteparagarantirque M éuniversal.Asduasprovasgarantem que M e U têmexatamenteomesmopodercomputacional.
Concebidaem1936,aMáquinadeTuring(Seções2.6e2.15)éodispositivodecomputaçãomaispoderosojáconcebidoatéosdiasdehoje,maisde80anosdepoisdasuaformulaçãoinicial.Todasasoutrastentativasdesedefinirmáquinasalternativasoudeincorporar extensõesnaMáquinasdeTuringmaisbásicaresultaramemmáquinascomomesmopoder computacionaldaMáquinadeTuringoriginal(veja[12]).Poressemotivo,aMáquinade Turingcostumaserusadaquandosedesejaprovarqueumamáquina M qualqueréuniversal pormeiodeevidênciasexternas.
Norestantedestecapítulo,asseguintesdemonstraçõesserãoefetuadas:
•MáquinaNormacomoMáquinaUniversal.
– Pormeiodeevidênciasinternas(Seção2.8).
– Pormeiodeevidênciasexternas(Seção2.9).
•MáquinadePostcomoMáquinaUniversal.
– Pormeiodeevidênciasexternas(Seção2.11).
•AutômatocomDuasPilhas.
– Pormeiodeevidênciasexternas(Seção2.14).
2.3HipótesedeChurch-Turing
ATeoriadaComputaçãoseocupa,principalmente,doestudodosalgoritmos:quaisproblemaspodemserresolvidos(equaisnão)equalocustoassociadoàsrespectivassoluções(em termosdetempoeespaço).Mascomoestudarosalgoritmoseas suaspropriedadessealgoritmosnãosãodefinidosformalmente(ouseja,matematicamente)?Semumadefiniçãoformal
(matemática)doquesejaumalgoritmo,qualquerabordagemquesepretendamaisprecisae rigorosaficaprejudicada.
Em1936, AlonzoChurch (matemáticonorte-americano,1903-1995)játinhapublicado oseuCálculoLambda([34])esuspeitavaquequalqueralgoritmopoderiaserrepresentando naformadeumaexpressãolambda(portanto,usandooseuCálculo).Aconfirmaçãodessa suspeitafoipublicadaem[35]eficouconhecidacomo HipótesedeChurch. Nomesmoanode1936, AlanTuring (matemáticoinglês,1912-1954)definiuasua(hoje famosa)MáquinadeTuringe,aomesmotempo,publicouquetodoalgoritmopoderiaser representadonaformadeumprogramaparaela([36]).Talafirmaçãoficouentãoconhecida como HipótesedeTuring
Em1937,TuringprovouqueoCálculoLambdaeaMáquinadeTuringeramcomputacionalmenteequivalentes([37]),ouseja,tantoumquantoaoutrapoderiamserusadascomo definiçãoformaldealgoritmo.Comoresultado,asHipóteses deChurchedeTuringforam reunidasesetornaramumasó,ficandoconhecidacomo HipótesedeChurch-Turing.Atualmente,onome TesedaComputabilidade éusadoparasereferiratalHipótese([38]).
Essencialmente,aHipótesedeChurch-TuringestabeleceaequivalênciaentreanoçãoinformaldealgoritmoeaMáquinadeTuring.Ouseja,ChurchestavapropondoqueaMáquina deTuringfosseusadacomosinônimodealgoritmo.
AaceitaçãodetalHipótese,quenuncapôdeserdemonstradapoisnãoexistedefinição formaldealgoritmo,trouxeimpactosimportantesparaaTeoriadaComputação.Apartir daquelemomento,passavaaexistirumadefiniçãoformal(portantorigorosaeprecisa)do quesejaumalgoritmo([38],[5]e[39]).Logo,jáerapossívelfazerumestudorigoroso dosalgoritmosedassuaspropriedades.EraonascimentodaTeoriadaComputaçãocomoa conhecemosnosdiasdehoje.
AHipótesedeChurch Turingéexpressadeformasdiferentesconformeoautorouafonte considerada.OpróprioChurchdizia([40]):
“Nocomputationalprocedurewillbeconsideredasanalgorithmunlessitcan berepresentedasaTuringMachine.”
ou,emtraduçãolivre:
“Nenhumprocedimentocomputacionalseráconsideradocomumalgoritmoa menosquepossaserrepresentadocomoumaMáquinadeTuring.”
AlgunsautoresformulamaHipótesedeChurchdemaneiraumpoucodiferente:
•“Qualquerpocedimentoalgorítmicoquepodeserfeitoporumserhumano,umgrupo desereshumanosouumcomputadorpodeserfeitoporumaMáquinadeTuring.”([8]).
•“Existeumprocedimentoefetivo1 pararesolverumproblemadedecisãoseesomente seexistirumaMáquinadeTuringqueparacomtodasasentradasesolucionaoproblema.”([7]).
•“AMáquinadeTuringquesempreparaemrespostaatodasasentradascorrespondeà noçãoformaleprecisadaideiaintuitivadealgoritmo.”([39]).
•“TodoprocedimentopodeserdescritonaformadeumaMáquinadeTuring.”([11]).
1AnoçãodeprocedimentoefetivocorrespondeànoçãodealgoritmoapresentadanaSeção2.1.
•“Todoalgoritmodecommputadorpodeserimplementadocomo umaMáquinadeTuring.”([41]).
Umabrevepesquisanainternetrevelaaindaoutrasformulações,porexemplo:
•“QualquerfunçãocomputávelpodeserprocessadaporalgumaMáquinadeTuring.”
•“AMáquinadeTuringéodispositivodecomputaçãomaisgenéricoqueexiste.”
•“TudoqueécomputávelécomputávelporumaMáquinadeTuring.”
•“AcapacidadedecomputaçãorepresentadapelaMáquinadeTuringéolimitemáximo quepodeseratingidoporqualquerdispositivodecomputação.”
•“Qualqueroutraformadeexpressaralgoritmosterá,nomáximo,amesmacapacidade computacionaldaMáquinadeTuring.”
Qualquerquesejaaformulação,asideiasbásicasportrásda HipótesedeChurchsãoas mesmas:opodermáximodasMáquinasdeTuring(nãosuperadopornenhumoutrodispositivodecomputação)eanoçãodequetodoalgoritmopodeser representadonaformade umprogramaparaumaMáquinadeTuring,ouseja,aaceitaçãodaMáquinadeTuringcomo representaçãoformaldanoçãodealgoritmo.
Aolongodasdécadas,desde1936eatéosdiasdehoje,evidênciasinternaseexternas apenasreforçamaHipótesedeChurch,queéaceitacomoverdadeiradeformapraticamente generalizadaenãoquestionada(veja[8]).Nenhumaoutramáquinaapresentadadesdeentão, ouqualquerextensãodaMáquinadeTuringoriginal,foicapazdeaumentaroseupoderde processamento,oqueviabilizariaoreconhecimentodeumaclassemaisampladelinguagens ou,oqueéequivalente,aresoluçãodeumaclassemaisampladeproblemas.
Devidoaoseupodereàsuasimplicidade,aMáquinadeTuringé usadacomodefinição formaldealgoritmo,atendendoaospropósitoscitadosanteriormente.TodaaTeoriadaComputação,especialmenteaDecidibilidadeeaComplexidade, estábaseadanascaracterísticas epropriedadesdaMáquinadeTuring.Seissomudarnofuturo, comaformulaçãodeum dispositivomaispoderosodoqueaMáquinadeTuring,boapartedaTeoriadaComputação precisaráserrevistaereescrita.
2.4TeoremaFundamentaldaAritmética
O TeoremaFundamentaldaAritmética,apresentadoaseguir,mostracomodecomporum númeronatural a emfatoresprimos.Alémdisso,oteoremagarantequeestadecomposição éúnica,amenosdepermutações.
Teorema2.1(TeoremaFundamentaldaAritmética) “Seja a> 1.Então:
onde(i) p1,p2,...,pk sãonúmerosprimos(nãonecessariamenteosprimeiros,nãonecessariamenteconsecutivos,porémtodosdistintos);(ii) n 1 ,n2 ,...,nk sãonúmerosinteirosmaiores ouiguaisa1e(iii)essadecomposiçãoéúnica,amenosdepermutações.2”
2
Prova:foiiniciadapor Euclides (matemáticogrego, ∼300a.C.),erecebeucontribuições posterioresde Kamalal-Dınal-Farisı (cientistapersa,1265-1318), JeanPrestet (padree matemáticofrancês,1648-1690), LeonhardEuler (matemáticosuíço,1707-1783), Adrien-MarieLegendre (matemáticofrancês,1752-1833)e CarlFriedrichGauss (matemáticoalemão,1777-1855).Maisdetalhespodemserencontradosem[42].Umaprovacompleta,que envolveaexistênciaeaunicidadedestafatoração,estádisponívelem[43].
OTeoremaFundamentaldaAritméticaestabelecequetodonúmeronaturalmaiorouigual a2podeserdecompostoemumprodutodenúmerosprimos.3 Alémdisso,queestadecomposiçãoéúnicaparaonúmeronaturalconsiderado.ÉcomoseoTeoremadividisseoconjunto dosnúmerosnaturaisemduaspartes:deumladoosprimos,ede outroaquelesquepodem serrepresentadoscomoprodutodeprimos(tambémchamadosdenúmeroscompostos).
Exemplo2.1 Aseguir,algunsexemplosdenúmerosnaturaiseasuarespectivadecomposiçãoem produtosdenúmerosprimos:
• 2=21
• 17=171
• 256=28 .
• 143=111 131
• 42.706.587=31 .76 .112 .
• 132 187 055=51 75 112 131
2.5Codificaçãodedadosestruturados
Algoritmosmanipulam,normalmente,diversostiposdedados(númerosinteiros,positivos, negativos,racionais,reais,lógicos,cadeiasdecaracteres,vetores,estruturasetc).Comoobjetivodeevitarqueosmodelosmatemáticosabstratossetornem(desnecessariamente)complexos,oescopodemanipulaçãodedadosdosalgoritmosqueserãoestudadosérestritoaos númerosnaturais.Essarestriçãonãotrazmaioresconsequências,umavezqueessesevários outrostiposdedadospodemserrepresentadosatravésdecodificaçõesapropriadasdelesno espaçodosnúmerosnaturais.ElaseráespecialmenteimportanteparaoestudodaMáquina Norma.
Seja X umconjuntodedadosestruturados.Afunçãoinjetora:
c : X → N étalque, ∀x ∈ X,c(x) representaacodificaçãododadoestruturado x.Como c éinjetora, (c(x)= c(y)) ⇒ (x = y) portantoacodificaçãorepresentadeformaunívocaodadoestruturado x naformadeum númeronatural c(x). 4
OTeoremaFundamentaldaAritmética,apresentadonaSeção2.4,éabaseparaaobtenção dafunçãodecodificaçãodesejada.Essencialmente,elemostracomomapearumelemento
3Umnúmeroprimoéaquelequesóédivisívelpor1eporelemesmo.
4Nãoénecessárioqueafunção c sejatotalesobrejetora.Mas,seesteforocaso,entãooconjunto X deveserum conjuntoenumerável(casocontrárionãohábijeçãoentre X e N).
Capítulo3
Decidibilidade
NestecapítulosãoestudadososprincipaistópicosdaTeoriadaDecidibilidade.Inicialmente (naSeção3.1)émostradocomoumalinguagem(conjuntodecadeiassobreumalfabeto, veja[1])podeserusadapararepresentarumproblemadedecisão(aquelecujasrespostassão apenasSIMouNÃO),aomesmotempoquesãodefinidostermoscomoproblemadecidível, problemaindecidíveleostermosequivalentessolucionável,nãosolucionável,insolúvele parcialmentesolucionável.
Emseguida,naSeção3.2,sãoapresentadosalgunsexemplosdeproblemasdecidíveis, juntocomasrespectivasjustificativaseexemplos.
Asseçõesseguintes(3.3e3.4)sãopreparatóriasparaademonstraçãodequealinguagem Ld,introduzidanaSeção3.5,nãoérecursivamenteenumerável.Osfatosdeque(i) ocomplementodeumalinguagemrecursivaésempreumalinguagemrecursiva,e(ii)se umalinguagemeoseucomplementosãorecursivamenteenumeráveis,entãoalinguagemé tambémrecursiva,alémderecursivamenteenumerável,sãoapresentadosedemonstradosna Seção3.6.
AMáquinadeTuringUniversaleasualinguagem(aLinguagemUniversal)sãoapresentadas,respectivamente,nasSeções3.7e3.8.
Reduções,definidasnaSeção3.9,sãoumatécnicaimportante paradeterminarseumproblemaédecidívelouindecidível.
OProblemadaParada,famosoeimportanteproblemaindecidível,éapresentadonaSeção 3.10.
Aslinguagens L e e L ne,apresentadasnaSeção3.11,sãoexemplosdeproblemasindecidíveis.OTeoremadeRice,daSeção3.12,mostraquediversas propriedadesnãotriviaisdas linguagensrecursivamenteenumeráveissãoindecidíveis. Issoinclui L e e L ne
AutômatoLinearmenteLimitado(outronomeparaMáquinadeTuringcomfitalimitada) ehistóriasdecomputação(outronomeparacomputações,conformediscutidonaSeção1.4) sãodefinidas,respectivamente,nasSeções3.13e3.14.Tudo issoéfeitoparapermitira demonstraçãodequealgunsproblemassãoindecidíveis(naSeção3.15).
Opresentecapítuloencerracomaapresentaçãodeumdosmais famososeimportantesproblemasdacomputação,oProblemadaCorrespondênciadePost,tambémconhecidocomo PCP,naSeção3.16.Apósademonstraçãodaindecidibilidade doProblemadaCorrespondênciadePost(tambémnaSeção3.16),sãomostradasalgumasaplicaçõesdelenademonstração dequediversosproblemasrelacionadoscomlinguagensegramáticaslivresdecontextotambémsãoindecidíveis(Seção3.17).
Oconteúdodestecapítuloébaseadoem[14],[12],[5],[7]e[1].
3.1Introdução
Apresenteseçãoprocuraresponderàsseguintesperguntas:
•Existeumalgoritmo1 queresolveumcertoproblema?
•Comodemonstrarqueexiste—ouquenãoexiste—talalgoritmo?
ATeoriadaDecidibilidade,ousimplesmenteDecidibilidade,correspondeaoestudodos problemascodificadoscomolinguagens.Atéestepontodonossoestudo,linguagensforam consideradasentidadesabstratas,definidascomoconjuntosdecadeiasfinitassobreumalfabetotambémfinito,semqualquersignificadoassociado.Apartirdaqui,noentanto,linguagensserãoempregadasparaarepresentaçãodeproblemas.MáquinasdeTuringserãousadas comorepresentaçãoformaldanoçãodealgoritmoeaprovadaexistência(ounão)deum algoritmoqueresolveumcertoproblemacorrespondeàdemonstraçãodaexistência(ounão) deumaMáquinadeTuringqueoresolve.
Nestaseçãotrabalharemoscomumtipoespecíficodeproblema,ochamado problemade decisão (doinglês decisionproblem).Umproblemaéditoumproblemadedecisãoquando eleétransformadoemumproblemaequivalente,cujasrespostaspossamserapenasSIMou NÃO.ProblemascujarespostasejamaiscomplexadoqueSIMou NÃOsãoconhecidoscomo functionproblems enãoserãoconsideradosnestetexto.
Exemplo3.1 Sejaaequaçãodesegundograu(tambémconhecidacomoequaçãoquadrática)cuja formageralé ax 2 + bx + c =0.Então:
•Determinarasraízesdopolinômionãoéumproblemadedecisão.
•Determinarseaequaçãopossuiraízesreaiséumproblemade decisão(bastacalcular ∆= b2 4ac.Se ∆ ≥ 0,entãoarespostaéSIM.Casocontrário,arespostaéNÃO).
•Determinarseumnúmeronaturalqualqueréprimoéumproblemadedecisão.
Pararepresentarumproblemadedecisãonaformadeumalinguagem,deve-secodificar todasasinstânciasdoproblema(sejamelasafirmativasounegativas)comocadeiassobreum certoalfabeto Σ.A linguagemquerepresentaoproblema éentãoalinguagemcomposta pelascadeiasquerepresentamasinstânciasdoproblemacujarespostaéSIM.Asinstâncias negativasnãofazempartedalinguagemquerepresentaoproblemadedecisão.Emoutras palavras,arepresentaçãodeproblemasdedecisãonaformadelinguagenssedádaseguinte forma:acoleçãodasinstânciasdeumproblemadedecisãocujasrespostassãoapenasafirmativasformaalinguagemqueorepresenta.Naturalmente,énecessárioqueasinstâncias(tanto asafirmativasquantoasnegativas)deumproblemasejamcodificadasdeformaunívocasobre Σ,deformaapermitirarecuperaçãodelas.
Notequealinguagemquerepresentaoproblemanãoprecisaserefetivamenteconstruída. Bastavisualizaralinguagemquerepresentaoproblemae,em seguida,tentarprovarquea linguagemérecursivaourecursivamenteenumerável.Aocodificarasinstânciasdeumproblemacomocadeiasdeumacertalinguagem,aspropriedadesdedecidibilidadedoproblema ficamdiretamenteassociadasàspropriedadesdedecidibilidadedalinguagem.Emoutras palavras,seumalinguagemédecidível,2 entãooproblemaqueelarepresentatambémserá decidível.Aseguinteordemdeveserobedecidaafimdedeterminaranaturezadoproblema:
1ConformedefinidonaSeção2.1,algoritmoéoprocedimentoquesempreforneceumaresposta,qualquerqueseja aentrada,jamaisentrandoem loop infinito.
2Linguagemdecidíveléaquelacujopertencimentodeumacadeiaqualqueraelasemprepodeserdecidida.
•Determinarsealinguagemquerepresentaumproblemadedecisãoérecursiva.
– Emcasoafirmativo,existeumalgoritmoqueresolveoproblema(melhorcaso).
– Emcasonegativo,investigarsealinguagemérecursivamenteenumerável.
•Determinarsealinguagemquerepresentaumproblemadedecisãoérecursivamente enumerável(vejaSeção2.6):
– Emcasoafirmativo,épossíveldeterminarasinstânciasafirmativasdoproblema, mashaverásemprepelomenosumaentrada(cujarespostaénegativa)quenunca produziráresposta.
– Emcasonegativo,haverásemprepelomenosumaentrada(afirmativa)quenunca produziráresposta(piorcaso).
Exemplo3.2 Considereoproblemadedecisão P :determinarseumnúmerobinárioépar.Então:
•Pararepresentaresteproblemanaformadeumalinguagem,bastaagruparosnúmerosbinários quesãopares(respostaafirmativaaoproblema)eformarumalinguagem L comeles.
•Umexemplodelinguagemquerepresenta P é L = {0, 10, 100, 110, 1000, 1010, 1100, 1110, }.Notequeosnúmerosímpares(1, 01, 11 etc)nãopertencema L.
• L = {w ∈{0, 1}+ | w representaumnúmerobináriopar}
•Arespostaaoproblema P —determinarseumnúmerobinárioépar—étransformadana respostaàpergunta:“onúmerobináriofornecidopertenceà linguagem L?”
•Genericamente,pretende-sedeterminarseexisteumaMáquinadeTuring M quesempreparae écapazdedecidirseumacadeiaqualquerdezeroseunspertenceàlinguagem L
•Casoexistatalmáquina,issoimplicaaexistênciadeumalgoritmoqueresolve P ediz-seque M “decide” P .Casocontrário,nãoexistetalalgoritmo.
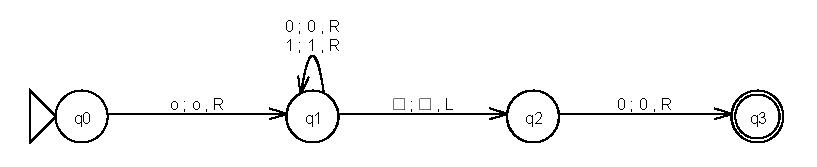
Figura3.1 MáquinadeTuringquedecideseumnúmerobinárioépar.
AFigura3.1ilustraumaMáquinadeTuringquedecide L.Aestratégiadestamáquina(algoritmo)é bastantesimples:examinarodígitomenossignificativo(maisàdireita)edeterminarseeleé0.Emcaso afirmativo,paraeaceita.Emcasonegativo,paraerejeita.Paraencontrarodígitomenossignificativo, amáquinaprocuraoprimeirobrancoàdireitaevoltaumaposição.
Exemplo3.3 Sãoexemplosderepresentaçãodeproblemasdedecisãonaformadelinguagens:
⋆⋆⋆
•Suponhaque c(X) representaumacodificaçãodoselementosdoconjunto X sobreumcerto alfabeto Σ.
•Dadasduasgramáticaslivresdecontexto([1]) G 1 e G 2 ,épossíveldeterminarse L(G 1)= L(G 2 )?3
– Codificar G 1 e G 2 sobreumcertoalfabeto Σ.
– Consideraralinguagem {c(G 1 )c(G 2 ) |L(G 1 )= L(G 2 )}
3Se G éumagramática, L(G) representaalinguagemgeradapor G,veja[1])
– Determinarseessalinguagemérecursiva.
•DadasumaMáquinadeTuring M eumaentrada w,épossíveldeterminarse M aceita w?
– Codificar M e w sobreumcertoalfabeto Σ.
– Consideraralinguagem {c(M )c(w) | M aceita w}
– Determinarseessalinguagemérecursiva.
Umproblemadedecisãoédito decidível sealinguagemquerepresentaasinstâncias afirmativasdoproblemaformaumalinguagemrecursiva.Caso contráriooproblemaédito nãodecidível (ou indecidível).ComolinguagensrecursivassãoreconhecidasporMáquinas deTuringquesempreparam,qualquerquesejaaentrada,aexistênciadeumalgoritmoque resolveumproblemadedecisãoimplicaaexistênciadepelomenosumaMáquinadeTuring quesemprepara,qualquerquesejaaentradafornecida(afirmativaounegativa).
Masoqueacontecesealinguagemquerepresentaumproblemadedecisãonãoforuma linguagemrecursiva?
•ProblemasdedecisãoqueformamlinguagensrecursivamenteenumeráveisenãorecursivassãoaceitosapenasporMáquinasdeTuringqueentramem loop parapelomenos umainstânciadoproblemadedecisãocujarespostaénegativa.
•Problemasdedecisãoqueformamlinguagensnãorecursivamenteenumeráveisnão sãoaceitospornenhumaMáquinadeTuringqueparesempreque asinstânciassão afirmativas(ouseja,todaequalquerMáquinadeTuringconstruídaparaesteproblema entraem loop infinitocompelomenosumainstânciadoproblemacujarespostaé afirmativa).
Portanto,ésempredesejávelqueproblemasdedecisãopossamserrepresentadoscomo linguagensrecursivas.Seissonãoforpossível,eoproblemadedecisãoforrepresentado comoumalinguagemrecursivamenteenumerávelnãorecursiva,entãoumobservadorexterno poderásevernasituaçãodeterqueaguardarmuitotempopelo términodoprocessamento destaentrada.Eledeveaguardarumaeventualparadadamáquinaounão?Casoamáquina tenhaentradoem loop infinito,arespostanãoviránunca.Assim,elenãosaberácomoagire, empelomenosemumcaso,oprocessamentoseráinfinitomesmo.
3.1.1Problemasolucionável × nãosolucionável
Ostermossolucionávelenãosolucionáveltambémsãousados nestecontexto.
•Umproblemaédito solucionável seforpossívelrepresentá-lopormeiodeumalinguagemrecursiva.
•Umproblemaédito nãosolucionável seelepuderserrepresentadopormeiodeuma linguagemnãorecursiva.
AFigura3.2ilustraaclassedosproblemassolucionáveis.

3.1.2Problemaparcialmentesolucionável × totalmenteinsolúvel
Ostermosparcialmentesolucionáveletotalmenteinsolúveltambémsãousadosnestecontexto.
•Umproblemaédito parcialmentesolucionável (ou computável)seépossívelrepresentá-lopormeiodeumalinguagemrecursivamenteenumerável.
•Umproblemaédito totalmenteinsolúvel (ou nãocomputável)seelepuderserrepresentadopormeiodeumalinguagemnãorecursivamenteenumerável.
AFigura3.3ilustraaclassedosproblemasparcialmentesolucionáveis.

Problemasparcialmentesolucionáveis.
3.1.3Resumo
Deacordocomasdefiniçõesanteriores:
•Todoproblemaésolucionávelounãosolucionável.
•Todoproblemasolucionáveléparcialmentesolucionável.
•Todoproblemaéparcialmentesolucionáveloutotalmenteinsolúvel.
•Umproblemanãosolucionávelpodeserparcialmentesolucionáveloutotalmente insolúvel.
•Umproblemaparcialmentesolucionávelpodesersolucionávelounão.
Naturalmente,todainvestigaçãoacercadeumproblemadenaturezadesconhecidadeve, emprimeirolugar,determinarseeleésolucionável(ouseja,seelepodeserrepresentadopor algumalinguagemrecursiva).Emcasonegativo,deve-sedeterminarseeleénãosolucionável eparcialmentesolucionável(ouseja,seelepodeserrepresentadoporalgumalinguagem recursivamenteenumerávelenãorecursiva).Casocontrário,eleéditototalmenteinsolúvel (ouseja,elenãopodeserrepresentadopornenhumalinguagemrecursivamenteenumerável).
Noquesegue,deve-seusaraFigura3.4comoreferênciaparaidentificaçãodasclassesde linguagensemdiscussão.4
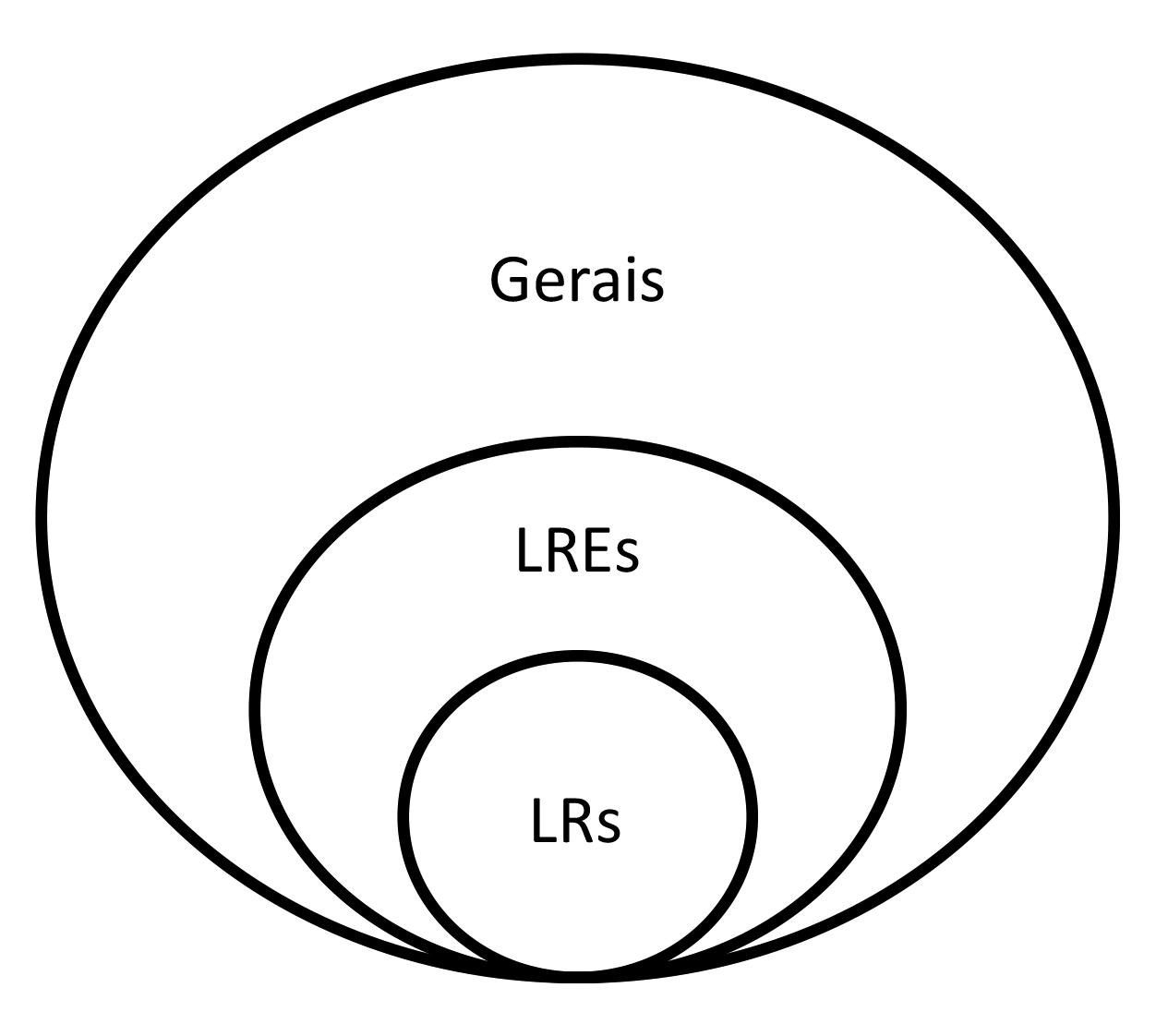
Figura3.4 Classesdelinguagens.
3.1.4Problemasolucionável
Umproblemasolucionáveléaquelequeérepresentadoporuma linguagemrecursiva.Portanto:
•Problema solucionável ⇔ linguagemrecursiva.
•ExistepelomenosumaMáquinadeTuringqueaceitaalinguagemeparacomtoda entrada.
AFigura3.5ilustraaclassedosproblemassolucionáveis.
4LREsignificalinguagemrecursivamenteenumeráveleLRsignificalinguagemrecursiva.
Capítulo4 Complexidadenotempo
Quandoumproblemaédecidível,istosignificaqueexisteumalgoritmoqueoresolve.Neste caso,cabeavaliaraquantidaderecursosnecessáriosàexecuçãodestealgoritmo.Recursos, nestecontexto,sãoprincipalmenteotempoeoespaço(ouquantidadedememória)queo algoritmodemandaparaasuaexecução.Oestudodotempoedoespaçonecessáriospara aexecuçãodeumalgoritmo(representadoporumaMáquinadeTuring)formamachamada TeoriadaComplexidade.
EstecapítuloédedicadoaoestudodosfundamentosdaTeoria daComplexidade,sendo restritoàcomplexidadedosalgoritmosnotempo.Acomplexidadenoespaçonãoseráconsideradanestetrabalho,maspodeserencontradaem[12],[7]ou[5].Umaabordagemmais completaeprofundadaTeoriadaComplexidadecomoumtodopodeserencontradaem[50].
NaSeção4.2sãoapresentadasalgumasdefiniçõesquesemostramimportantesquando setratadeavaliarotempodeexecuçãodeprogramas.Emparticular,sãoapresentadasas notações“O-grande”(big-oh)e“o-pequeno”(little-oh)ealgumasdassuasprincipaispropriedades.Aseçãoterminacomexemplosquecomparamaavaliaçãodotempodeexecuçãode diversasMáquinasdeTuringquereconhecemamesmalinguagem.
Asimportantesclasses P e NP sãodefinidas,respectivamente,nasSeções4.3e4.4,junto comexemplos.Definiçõesalternativas,baseadasnanoçãode verificadores,sãoapresentadas naSeção4.5.Doisproblemasfundamentaispertencentesàclasse NP sãodefinidosnaSeção 4.6.
Arelaçãoentreasclasses P e NP,queconstituiumproblemafundamentaldamatemática edacomputação,ecujasoluçãocontinuaemabertoaindanosdiasdehoje,édiscutidana Seção4.7.
Umatécnicaimportanteparadeterminarseumproblemapertenceàclasse P éapresentada naSeção4.8.BaseadanatécnicadefinidanaSeção3.9,elagarantequeumareduçãoeficientedeumproblema A paraumproblema B,combinadacomumasoluçãoeficienteparao problema B,geraumasoluçãoeficienteparaoproblema A
Emseguida,naSeção4.9,éapresentadooproblema 3SAT .Umareduçãoeficientedo 3SAT para CLIQUE éentãoapresentadanaSeção4.10,relacionandoassimacomplexidadedessesdoisproblemasdenaturezastãodistintas.
Problemasditos NP-completos(eanoçãode NP-completude)e NP-difíceissãoentão definidos,respectivamente,nasSeções4.11e4.12,juntocomexemplos.
Finalmente,aimportanteclasse NPC (dosproblemas NP-completos)édefinidanaSeção 4.13,juntocomumasériedeexemplos.Porúltimo,naSeção4.14,édefinidaaclasse NPH, dosproblemas NP-difíceis.
Oconteúdodestecapítuloébaseadoem[12],[5],[7],[51]e[8].
4.1Motivação
Adecidibilidadenãoimpõelimitesnosrecursosquesãonecessáriosparaseresolverum problema:
•Recursos:tempoeespaço(memória).
•Certosproblemasdecidíveispodemdemandarquantidadesexageradasdessesrecursos, inviabilizandosoluçõesquetenhaminteresseprático.
•ATeoriadaDecidibilidade(Capítulo3)classificaosproblemasemdecidíveis(ousolucionáveis)eindecidíveis(ounãosolucionáveis).
•ATeoriadaComplexidade(notempo,presentecapítulo)classificaosproblemas decidíveis em tratáveis e intratáveis.Umproblematratáveléaquelecujotempode execuçãoépolinomialcomotamanhodaentrada.Umproblemaé intratáveléaquele cujotempodeexecuçãoéexponencial(oupior,vejaSeção2.15).
Comoidentificarproblemasnessasduascategorias?AFigura 4.1ilustraofatodequeo conjuntodosproblemastratáveiséumsubconjuntodosproblemasdecidíveis.

Problemasdecidíveiseproblemastratáveis.
4.2Complexidadedetempo
Seja M umaMáquinadeTuringdeterminísticaqueparacomqualquerentrada.
•O tempodeexecução,ou complexidadenotempo,de M éafunção f : N → N, onde:
– n éocomprimentodaentrada w.
– f (n) éonúmeromáximodetransiçõesque M executaaoprocessarqualquer entradadecomprimento n
•Diz-seque M éexecutadaemtempo f (n).
•Diz-seque M éumaMáquinadeTuringdetempo f (n)
Sejaagora M umaMáquinadeTuringnãodeterminísticaqueparacomqualquerentrada.
•O tempodeexecução,ou complexidadedetempo,de M éafunção f : N → N, onde: – n éocomprimentodaentrada w – f (n) éonúmeromáximodetransiçõesque M podeexecutaremqualquerramo dasuacomputaçãoaoprocessarqualquerentradadecomprimento n
•Diz-seque M éexecutadaemtempo f (n)
•Diz-seque M éumaMáquinadeTuringdetempo f (n).
4.2.1NotaçãoO-grande
Sejam f,g : N → R+ .
•Diz-seque f (n) ∈ O(g(n)), f (n)= O(g(n)) ouainda f (n) é O(g(n)),seexistirem númerosinteirosepositivos c e n0 taisque:
∀n ≥ n0,f (n) ≤ c g(n)
•Diz-seque g(n) éum“limitantesuperiorassintótico”para f (n)
•Representaque f crescemaislentamentedoque g,amenosdefatoresconstantes suprimidos(conformeexemplosapresentadosaseguir).
4.2.2Exemplos
Exemplo4.1 Seja f (n)=5n 3 +2n 2 +22n +6.Então, f (n)= O(g(n)) com g(n)= n 3 ,ouseja, f (n)= O(n 3 )
Prova:
•Considere c =6
•Considere n 0 =6
•Então, 5n 3 +2n 2 +22n +6 ≤ 6n 3 , ∀n ≥ n 0 f tambémé O(n 4 ), O(n 5 ) etc. ⋆⋆⋆
Exemplo4.2 NográficodaFigura4.2,asseguintesfunçõesestãorepresentadas:
a. n 4
b. 6n 3
c. 5n 3 +2n 2 +22n +6
d. n 2
Exemplo4.3 Seja f (n)= n 2.Então, f (n) nãoé O(n)
⋆⋆⋆

Prova:
•Suporque n 2 é O(n)
•Então,devemexistir n 0 e c taisque ∀n ≥ n 0 ,n 2 ≤ c n.
•Escolher n 1 = máx(n 0, 2 c),ouseja, n 1 ≥ n 0 e n 1 ≥ 2 c
•Como n 1 ≥ n 0 ,então n 2 1 ≤ c n 1
•Dividirosdoisladosdainequaçãopor n 1 .
•Logo, n 1 ≤ c
•Masissoéumacontradição,pois n 1 foiescolhidoparasatisfazer n 1 ≥ n 0 e n 1 ≥ 2 · c
•Ahipóteseéfalsae n 2 nãoé O(n)
Paraprovarqueumafunção f (n) é O(g(n)) deve-se,portanto,escolhervalorespara n0 e c e,emseguida,provarque ∀n ≥ n0,f (n) ≤ c g(n).Paraprovarqueumafunção f (n) não é O(g(n)) deve-seprovarquenãoexistem n0 e c taisque ∀n ≥ n0,f (n) ≤ c · g(n).
1.Fatoresconstantesnãoimportam:
se f (n)= c g(n),então f (n) é O(g(n)) paraqualquer c> 0.
2.Termosdeordeminferiornãoimportam:
se f (n)= aknk + ak 1 nk 1 + + a2 n 2 + a1n 1 + a0n0,com ak > 0,então f (n) é O(ak nk) etambém,pelaregraanterior, O(nk ).
Exemplo4.4 Exemplosdosprincípios:
1.Fatoresconstantesnãoimportam:
2n 3 é O(0, 001n 3 ):bastaescolher n 0 =0 e c =2000.
2.Termosdeordeminferiornãoimportam:
2n + n 3 é O(2n):bastaescolher n 0 =10 e c =2
(observarque lim n→∞ n 3 2n =0) ⋆⋆⋆
4.2.3Propriedades O-grande
Aseguir,sãoapresentadasalgumasdasprincipaispropriedadesdaquiloqueédenotadopelo O-grande([51]),acompanhadasdasrespectivasprovas.
•Se f (n) é O(g(n)) e ∀n,h(n) ≥ 0,então h(n) · f (n) é O(h(n) · g(n)):
Prova:
– ∀n ≥ n0,então f (n) ≤ c · g(n).
– Adesigualdadeépreservadaaosemultiplicarambosostermospor h(n)
– h(n) · f (n) ≤ h(n) · c · g(n),ouseja, h(n) · f (n) ≤ c · h(n) · g(n).
– h(n) f (n) é O(h(n) g(n))
•Se ∀n ≥ n0,f (n) ≤ g(n),então f (n)+ g(n) é O(g(n)):
Prova:
– Como ∀n ≥ n0 ,f (n) ≤ g(n),então ∀n ≥ n0,f (n)+ g(n) ≤ g(n)+ g(n).
– Portanto, f (n)+ g(n) ≤ 2 g(n)
– f (n)+ g(n) é O(g(n)).
•Se f (n) é O(g(n)) e g(n) é O(h(n)),então f (n) é O(h(n)):
Prova:
– ∀n ≥ n1,f (n) ≤ c1 · g(n).
– ∀n ≥ n2,g(n) ≤ c2 · h(n).
– Considerar n0 = máx(n1,n2).
– Considerar c = c1 c2
– ∀n ≥ n0,então n ≥ n1 e n ≥ n2.
– Portanto, f (n) ≤ c1 g(n) e g(n) ≤ c2 h(n)
– Substituindo g(n) por c2 · h(n) em f (n) ≤ c1 · g(n),resulta f (n) ≤ c1 · c2 · h(n).
– f (n) é O(h(n))
•Se f1(n) é O(g(n)), f2(n) é O(h(n)) e g(n) é O(h(n)),então f1(n)+ f2(n) é O(h(n)):
Prova:
– ∀n ≥ n1,f1(n) ≤ c1 g(n)
– ∀n ≥ n2,f2(n) ≤ c2 · h(n).
– ∀n ≥ n3,g(n) ≤ c3 h(n)
– Considerar n0 = máx(n1,n2,n3).
– Portanto, ∀n ≥ n0,f1(n)+ f2(n) ≤ c1 · g(n)+ c2 · h(n).
– Substituindo g(n) por c3 h(n),resulta f1(n)+ f2(n) ≤ c1 c3 h(n)+ c2 h(n).
– f1(n)+ f2(n) ≤ (c1 · c3 + c2) · h(n). – f1(n)+ f2(n) é O(h(n))
Outraspropriedadessãoapresentadasaseguir(asprovassãoomitidas):
•Se f (n) e g(n) sãopolinômios,eograude g(n) émaiorouigualqueograude f (n), então f (n) é O(g(n))
•Se f (n) e g(n) sãopolinômios,eograude g(n) émenorqueograude f (n),então f (n) nãoé O(g(n))
•Se f (n) éumpolinômio,então f (n) é O(an), ∀a> 1
• an,a> 1 nãoé O(f (n)) paranenhumpolinômio f (n)
Afimdetornarousodanotaçãosimpleseintuitvo,procura-se,semprequepossível,fazer valerasseguinteregrasbásicas:
•Escolherafunção g(n) quetenhaamenordistânciaemrelaçãoa f (n),talque f (n) seja O(g(n)).
•Escolherfunções g(n) quesejamsimples,ouseja,funçõescomasseguintescaracterísticas:
– Umúnicotermo.
– Coeficiente 1
– Aseguiréapresentadaumarelaçãodasfunçõessimplesmaiscoumns.
4.2.4Funçõessimplesmaisutilizadas
UmalistadefunçõesconsideradassimpleséapresentadanaTabela4.1.
Tabela4.1 Listadefunçõessimples
Big-Oh Nome
O(1) Constante
O(log n) Logarítmica
O(n) Linear
O(n log n) n log n
O(n 2 ) Quadrática
O(n3 ) Cúbica
O(2n) Exponencial
O(n!) Fatorial
Exemplo4.5
a. 2n
b. n 2
c. n log n
d. n
e. log n
NográficodaFigura4.3estãorepresentadasasfunções:
AFigura4.4apresentaalgunsvaloresparaessasfunções. ⋆⋆⋆
Exemplo4.6
NográficodaFigura4.5estãorepresentadasasfunções:
Capítulo5
CálculoLambdanãotipado
EstecapítuloapresentaoselementosmaisimportantesdoCálculoLambdanãotipado(definidooriginalmenteem[34]),umformalismoutilizadopararepresentarcomputaçõeseque servecomoalternativaaosformalismosbaseadosemmáquinas,conformevistonoCapítulo 2.AequivalênciaentreoCálculoLambdaeaMáquinadeTuring foiprovadaporTuringem 1937([37]).
Inicialmente,nasSeções5.1e5.2,apresentamososdiversostiposdeCálculoLambdae mostramoscomooCálculoLambdapodeserusadopararepresentarfunçõescomumoumais parâmetros.
Expressõeslambda,queformamalinguagemlambda,sãoentão formalizadosnaSeção 5.3,quetambémdiscuteosconceitosdeassociatividadeeprecedência(deabstraçõeseaplicações),ousodoparênteses,comprimento,ocorrências,escopoevariáveislivreseligadas.
OconceitomaisfundamentaldoCálculoLambda,a“substituição”,éapresentadanaSeção 5.4,pormeiodeseteregras,assimcomoadefiniçãode“conversão-α”.Substituiçõespermitem,porexemplo,atransformaçãodeumaexpressãolambdaem outraexpressãolambda, supostamentemaissimples.Esteprocesso,chamadode“redução-β”,éintroduzidonaSeção5.6,juntocomanoçãode“formanormal-β”eoimportanteTeoremadeChurch-Rosser (JohnRosser,matemáticonorte-americano,1907-1989)paraaredução-β.
AlgumasaplicaçõesdoCálculoLambdanãotipadosãoapresentadasnasSeções5.8e5.9. Nestas,émostradocomonúmerosnaturais,operaçõesaritméticas,valoreslógicos,operações lógicaserelacionaispodemserdefinidasapartirdasoperaçõesprimitivasdeabstraçãoe aplicação.
A“igualdade-β”,queestabeleceaequivalênciadedoistermoslambda,éintroduzidana Seção5.10.
ASeção5.12introduzaimportantenoçãodepontofixo,quedepoiséusadanaSeção 5.13paramostrarcomosepodeconstruirfunçõesrecursivas,jáquenoCálculoLambdaas funçõessãoanônimas(istoé,nãopossuemnome).
Finalmente,algunsimportantesresultadosrelativosaoCálculoLambdanãotipadosão provadosindecidíveisnaSeção5.14.
Umaprofusãodeexemplosilustraosconceitoseasdefinições apresentadas.CarlBurch, ex-professordoDepartamentodeCiênciadaComputaçãodoHendrixCollege,nosEstados Unidos,disponibilizagratuitamenteumaferramentagráfica([63])quepermiteavaliartermoslambda.Configuráveldediversasmaneiras,estaferramentaanimadaevisualfacilitao aprendizadoeaexperimentaçãocomoassunto.
Oconteúdodestecapítuloébaseadoem[64],[65]e[66].Dois excelentestutoriaissobreo assuntosão[67]e[68].Amaioriadosexemplosdestecapítuloéformadaporsoluçõespara osexercíciosdoCapítulo1de[64].Umaseçãodeexercíciosoriginaisencerraocapítulo.
5.1Introdução
AlonzoChurch inventouoCálculoLambdanadécadade1930,comoresultadodassuas investigaçõesacercadosfundamentosdamatemática.Elepretendiaformalizaramatemática atravésdanoçãodefunçõesemvezdateoriadeconjuntos,entãopredominante.Apesarde nãoconseguiralcançaroseuobjetivo,otrabalhodeChurchtevegrandeimpactoemoutras áreas,especialmentenacomputação.
O CálculoLambda éumsistemaformalusadonarepresentaçãodecomputações.Eleé baseadonadefiniçãoechamadadefunções,querecebemonome, respectivamente,deabstraçãoeaplicação.NoCálculoLambdaasfunçõessãoanônimas,istoé,nãoestãoassociadasa identificadorescomonamaioriadaslinguagensdeprogramação.Tambémdiferentementedo queacontececomasprincipaislinguagensdeprogramação,asfunçõesnoCálculoLambda podemserpassadascomoargumentoparaoutrasfunções,eser retornadascomovalorde função(porcausadissosedizqueasfunçõessãoobjetosdeordemelevada).
OCálculoLambdaéumalinguagemmuitosimples,queusaapenasdois“comandos”ou construçõesparaaformaçãodesuassentenças:aabstração(correspondenteàdefiniçãode umafunção)eaaplicação(correspondenteàchamadadeumafunção).Tudoqueseesperaencontraremumalinguagemdeprogramaçãotípica(comotiposdedados,literais,operadores etc)podeserrepresentadonoCálculoLambdapelousoexclusivodessasduasconstruções.
Talsimplicidade,noentanto,produziuumateoriaamplaecomplexa,comodemonstraa obradediversosautores,emespecialade HenkBarendregt (lógicoholandês,nascidoem 1947).Alémdeterdedicadopraticamentetodaasuavidaaoestudodaspropriedadesdo CálculoLambda,elerecebeudiversosprêmiospeloseutrabalhoeassuaspublicaçõessão referêncianoestudodoassunto(porexemplo,[69],[70]e[71]).
OCálculoLambdaéummodeloalternativoparaarepresentaçãodecomputações(usando funçõesnolugardemáquinas,comofoivistonoCapítulo1)eé equivalenteàMáquinade Turing([37]).
Naversão pura,oCálculoLambdanãotemconstantes,tiposouoperadorespredefinidos. Aindaassim,elepermitearepresentaçãodeumaamplagamade operaçõesetiposdedados,entrenúmerosinteirosevariáveislógicas.Naversão aplicada,aocontrário,algumas operações,tiposeliteraissãoprimitivos(porexemplo,ooperadordeadição“+”ouoliteralinteiro 1),nãonecessitando,portanto,derepresentaçãousandoasconstruçõesbásicasdo CálculoLambda.
OCálculoLambdapossuitambémasversões nãotipada e tipada.Aversãotipada(originalmenteconcebidaporChurchem[72]),associatiposàssentenças,efoicriadacomo objetivodeeliminaralgumasdasinconsistênciasdoCálculoLambdanãotipado([73]).Por isso,eleémaismenospoderosodoqueoCálculoLambdanãotipado([73]).Portanto,existemasseguintesversõesdoCálculoLambda:
CálculoLambda
Nopresentecapítuloéapresentadaaversãopuraenãotipada.Asversõesaplicadaetipada nãosãoconsideradasnestetexto.
OCálculoLambdaéummodelomatemáticomuitopoderoso(pois éequivalenteàMáquina deTuring)equepodeserusadocomdiversasfinalidades.Entreelas,comofundamentação teóricaparaaespecificaçãoeimplementaçãodelinguagensdeprogramaçãobaseadasemfunções,especialmenteaslinguagensfuncionais,paraaverificaçãodeprogramasdecomputador,
paraarepresentaçãodefunçõescomputáveis,paraoestudodaTeoriadaDecidibilidade,da TeoriadeTiposedaTeoriadasProvaseparaoprojetoeaimplementaçãodeassistentesde provas(Coq,HOL,Isabelle,Agdaetc),entreoutras.OCálculoLambdatemsidousadona demonstraçãodaindecidibilidadedediversosproblemasda matemática,antesmesmodos formalismosbaseadosemmáquinas.
5.2Motivação
Considereaexpressão x y.Elapodeserformalizada,nanotaçãomatemáticausual,através defunçõescomumúnicoparâmetro:
• f (x)= x y.
• g(y)= x y
ouainda:
• f : x → x y
• g : y → x y.
Exemplo5.1 Exemplos:
• f (0)=0 y
• f (1)=1 y
• g(0)= x 0
• g(1)= x 1
NoCálculoLambdaasfunçõessãoanônimas.Abstrações(funções)sãorepresentadaspelo símbolo“λ”(daíonomeCálculoLambda),seguidopelosidentificadores querepresentamos parâmetrosdessaabstração.Osímbolo“.”éusadoparasepararosparâmetrosdocorpoda função.Ocorpo(expressãoquedefineovalorretornadopelafunção)compareceàdireitado símbolo“.”.Assim,asfunções f e g podemserrepresentadasnoCálculoLambdapormeio dassentenças:
• f = λx.x y
• g = λy.x y.
(noteque x e y denotam,respectivamente,osparâmetrosdasfunções f e g).Aaplicação deumafunçãoaumargumentoérepresentadapelajustaposiçãodaabstração(definiçãoda função)aoargumento:
• (λx.x y)(0)=0 y.
• (λx.x y)(1)=1 y
• (λy.x y)(0)= x 0.
• (λy.x y)(1)= x 1.
(notequeoparâmetrodaabstraçãoésubstituídopeloargumentonaexpressãoquedefinea função).Funçõescommúltiplosparâmetros,comoéocasodas apresentadasaseguir:
• h(x,y)= x y
• k(y,x)= x y.
podemserrepresentadasnoCálculoLambda,respectivamente,como:
• h = λxy.x y
• k = λyx.x y.
(noteousodosdoisidentificadores x e y entreossímbolos“λ”e“.”,representandoosdois parâmetrosdecadaumadestasfunções).Asfunções h e k podemtambémserrepresentadas comofunçõesqueretornamoutrasfunçõescomovalores: h∗ = λx.(λy.(x y))
Defato,paracada a temos:
h∗(a)=(λx.(λy.(x y))(a)= λy.(a y) e,paracadapar a e b,temos:
(h∗(a))(b)=((λx.(λy.(x y))(a))(b)=(λy.(a y))(b)= a b = h(a,b)
Portanto h∗ representa h e,deformageral,todasasfunçõescommúltiplosparâmetros podem serrepresentadasatravésdacombinaçãodefunçõescomumúnicoparâmetro.
NoCálculoLambda,diz-sequeumafunção F : N → N é computável seesomentese existirumasentença f talque:
∀x,y ∈ N,F (x)= y ⇔ fx = β y (= β échamada“igualdadebeta”,eserveparaestabeleceraequivalênciaentretermosdeuma equaçãoenvolvendotermoslambda,vejaSeção5.10).Emoutraspalavras,aaplicaçãoda sentença f aoargumento x deveproduziromesmoresultadoque F (x)
OCálculoLambdaéapenasumadasformaspossíveisdesedefinircomputação,comoéo casodaMáquinadeTuring,dasoutrasmáquinasvistasanteriormenteetambémdasfunções recursivas.Aequivalênciadetodosessesformalismosfoidemonstradapreviamente([36], [38]).
5.3Linguagemlambda
Estaseçãodefineformalmenteanoçãovagadesentençausadanaseçãoanterior.Um lambda termo (tambémchamadode λ-termo, termolambda, expressãolambda ousimplesmente termoouexpressão)édefinidodeformaindutivasobreumconjuntodeidentificadores {x,y, z,u,v...} querepresentamvariáveis:
•Umavariável(tambémchamada“átomo”)éum λ-termo.
•Aplicação:se M e N são λ-termos,então (MN ) éum λ-termo;representaaaplicação de M a N
•Abstração:se M éum λ-termoe x éumavariável,então (λx.M ) éum λ-termo; representaafunçãoqueretorna M comoparâmetro x.
A linguagemlambda écompostaportodosos λ-termosquepodemserconstruídossobreum dadoconjuntodeidentificadores;trata-sedeumalinguagem comapenasdoisoperadoresou “comandos”:aplicaçãodefunçãoaargumentos(chamadadefunção)eabstração(definição defunção).
Alinguagemlambdapodeserformalizadaatravésdaseguinte gramática:
Exemplo5.2 Sãoexemplosde λ-termos:
• x
• (xy)
• (λx.(xy))
• ((λy.y)(λx.(xy)))
• (x(λx.(λx.x)))
• (λx.(yz))
5.3.1Associatividadeeprecedência
Parareduziraquantidadedeparêntesesnos λ-termosgeradospelagramáticaanterior,modificamosaquelapara:
→ (T )
queassimsetornaambígua.Porexemplo,considereotermo λx.xx.Estetermorepresenta ((λx.x)x) ou (λx.(xx))?Aúltimaregraacimapermiteousoopcionaldeparênteses.Parareduziraquantidadedeparênteseseevitarambiguidades,são usadasasseguintesconvenções:
•Aplicaçõestêmprioridadesobreabstrações.
•Aplicaçõessãoassociativasàesquerda.
•Abstraçõessãoassociativasàdireita.
Exemplo5.3 Exemplos:
• λx.PQ denota (λx.(PQ)) —enão ((λx.P )Q)
• MNPQ denota (((MN )P )Q) —enão (M (N (PQ))).
• λxyz.M denota (λx.(λy.(λz.M ))).
Osímbolo“≡”éusadoparadenotaraequivalênciasintática1 de λ-termos.
Exemplo5.4 Exemplos:
• xyz(yx) ≡ (((xy)z)(yx))
• λx.(uxy) ≡ (λx.((ux)y))
• λu.u(λx.y) ≡ (λu.(u(λx.y)))
• (λu.vuu)zy ≡ (((λu.((vu)u))z)y)
• ux(yz)(λv.vy) ≡ (((ux)(yz))(λv.(vy)))
• (λxyz.xz(yz))uvw ≡ ((((λx.(λy.(λz.((xz)(yz)))))u)v)w)
5.3.2Comprimento
O comprimento deum λ-termo M lgh(M ) —éonúmerototaldeocorrênciasdeátomos em M
•Paratodoátomo a, lgh(a)=1
• lgh(MN )= lgh(M )+ lgh(N ).
• lgh(λx.M )=1+ lgh(M )
Exemplo5.5 Se M ≡ x(λy.yux),então lgh(M )=5
5.3.3Ocorrênciaeescopo
Sejam P e Q dois λ-termos.Arelação P ocorreem Q (ouainda, P estácontidoem Q, Q contém P ou P é subtermo de Q)édefinidadeformaindutiva:
• P ocorreem P .
•Se P ocorreem M ouem N ,então P ocorreem (MN ).
•Se P ocorreem M ou P ≡ x então P ocorreem (λx.M ).
Exemplo5.6
•Notermo ((xy)(λx.(xy))) existemduasocorrênciasde (xy): (( xy )(λx.( xy ))) etrêsde x: (( x y)(λx .( x y))).
•Asocorrênciasde xy em λxy.xy são λxy.xy ≡ (λx.(λy.( xy )))
•Asocorrênciasde uv em x(uv)(λu.v(uv))uv são ((((x( uv ))(λu.(v( uv ))))u)v)
•Otermo λu.u nãoocorreem λu.uv pois λu.uv ≡ (λu.(uv)).
1Doistermossãosintaticamenteequivalentesserepresentamomesmotermoamenosdeparênteses.
O estudo da Teoria da Computação permite, entre outras coisas, a percepção da computação como uma área com muitas possibilidades, mas também com muitas limitações. Conhecer essas limitações é importante para a formação de profissionais que, em suas vidas, muitas vezes, irão se deparar com problemas intratáveis ou mesmo insolúveis.
De forma introdutória, este livro apresenta os tópicos mais importantes da Teoria da Computação, como Programas, máquinas e equivalências, Máquinas universais, Decidibilidade, Complexidade no tempo e Cálculo Lambda não tipado, que podem ser estudados de forma relativamente independente uns dos outros. Além disso, o livro traz um conjunto de 230 exercícios com as suas respectivas soluções, para ajudar na fixação do conteúdo.



