Pandas e o demônio dos dados

MARCO ANTONIO LEONEL CAETANO

PANDAS E O DEMÔNIO DOS DADOS

Algoritmos em Python para Sistemas de Informação

Marco Antonio Leonel Caetano

PANDAS E O DEMÔNIO

DOS DADOS

Algoritmos em Python para

Sistemas de Informação

Pandas e o demônio dos dados: algoritmos em Python para Sistemas de Informação

© 2025 Marco Antonio Leonel Caetano

Editora Edgard Blücher Ltda.

Publisher Edgard Blücher

Editor Eduardo Blücher

Coordenador editorial Rafael Fulanetti

Coordenação editorial Ana Cristina Garcia

Produção editorial Kedma Marques

Preparação do texto Ana Lúcia dos Santos

Diagramação Roberta Pereira de Paula

Revisão de texto Ariana Corrêa

Capa Juliana Midori Horie

Imagem da capa Equipe Editora Blucher

Rua Pedroso Alvarenga, 1245, 4 o andar 04531-934 – São Paulo – SP – Brasil Tel.: 55 11 3078-5366 contato@blucher.com.br www.blucher.com.br

Segundo o Novo Acordo Ortográfico, conforme 6. ed. do Vocabulário Ortográfico da Língua Portuguesa, Academia Brasileira de Letras, julho de 2021.

É proibida a reprodução total ou parcial por quaisquer meios sem autorização escrita da editora.

Todos os direitos reservados pela Editora Edgard Blücher Ltda.

Dados Internacionais de Catalogação na Publicação (CIP) Angélica Ilacqua CRB-8/7057

Caetano, Marco Antonio Leonel

Pandas e o demônio dos dados : algoritmos em Python para Sistemas de Informação / Marco Antonio Leonel Caetano. – São Paulo : Blucher, 2025.

470 p. : il.

ISBN 978-85-212-2515-7

1. Python (Linguagem de programação de computador) I. Título

25-1039

CDD 004.68

Índice para catálogo sistemático:

1. Python (Linguagem de programação de computador)

1.9 Inserções em listas e vetores com loop

1.10 Estatísticas rápidas com array (vetores)

1.11 Gráficos básicos com matplotlib.pyplot

1.13 Customizando os gráficos pelos eixos “ax”

1.15 Definindo function (função) no Python

1.16 Exercícios para aprofundar o conhecimento

2 . Pandas

2.1 Introdução

2.2 Formas de entrada no DataFrame

2.3 Entrada e saída via Excel 81

2.4 Funções e instruções rápidas

2.5 Estatísticas básicas

2.6 Lógica condicional (and -> &, or -> |)

2.7 Tipos de indexação e reindexação 89

2.8 Apagando uma coluna (“drop”)

2.9 Exercícios 95

3 . Gráficos na Pandas

3.1 Introdução

3.2 Gráficos básicos

3.3 Customizando gráficos na Pandas

3.4 Gráficos em janelas de subplots

3.5 Subplot com layout

3.6 Gráficos de estatística

3.7 Método rolling para média móvel

3.8 Método “pct_change” para variação

3.9 Exercícios

4.1 De onde vem o diabo?

4.2 Loc e iloc no DataFrame

4.3 Groupby – Agrupamento

4.4 Groupby com datas – O diabo volta a aparecer

4.5 Exercícios

5 . Concatenação – Agrupando as diferenças

5.1 Juntando alhos com bugalhos

5.2 A função intersection( )

5.3 O diabo assombra com as datas

5.4 A função concat( ) .

5.5 O método para eliminar NaN no agrupamento

5.6 A função merge( ) .

5.7 O diabo se espreita na pressa

6 . A função lambda

6.1 A ideia inicial

6.2 A função apply

6.3 A função lambda

6.4 A função lambda para duas ou mais colunas

6.5 Exercícios

7 . Seaborn – Uma grande aliada da Pandas

7.1 Revisitando gráficos básicos

7.2 Gráficos para categorias

7.3 Gráficos de densidade (kdeplot) 217

7.4 Regressão linear com jointplot

7.5 Análise de categorias usando jointplot

7.6 Histogramas na Seaborn

7.7 Exercícios

8 . Falhas – Detalhes estatísticos

8.1 O conceito de probabilidade de falhas

8.2 A distribuição de Weibull

8.3 Análise de falhas na Pandas

8.4 Deslizamentos – Quando a natureza falha

8.5 Comparações entre base de dados

9

Dados econômicos

9.1 Banco Central do Brasil e dados econômicos

9.2 Aquisição das séries temporais

9.3 O confronto entre expectativa e realidade

10.1 Informações de ativos financeiros

10.2 Algoritmos para ativos financeiros

Mapeamento estatístico básico

10.4 Modelando o nervosismo do mercado

10.5 Comparando investimentos

10.6 A variabilidade do mercado financeiro

10.7 Estimando a tendência dos movimentos dos ativos

10.8 Indicadores de negociação para ativos

10.9 Exercícios

11 . O perigo dos asteroides

11.1 Monitoramento espacial

11.2 Fireballs – Bolas de fogo no céu noturno

11.3 Investigando asteroides

11.4 Estatísticas para asteroides

11.5 Risco de impacto dos asteroides com a Terra

12 . O ambiente Jupyter

12.1 Conhecendo o ambiente de programação

12.2 Primeiros programas em Jupyter

12.3 Alterando e editando células no Jupyter

12.4 Utilização do Kernel

12.5 Salvar e download

Referências

Solução dos exercícios

CAPÍTULO 1

Revisitando o Python

1.1 INTRODUÇÃO

A linguagem Python foi desenvolvida em dezembro de 1989 por Guido van Rossum. Conhecedor de linguagens como ALGOL e Pascal, Guido procurava por um interpretador de comandos mais fácil e poderoso do que os existentes à época. Devemos nos lembrar de que as linguagens mais populares e utilizadas na época eram BASIC, FORTRAN, COBOL e ALGOL. Apesar disso, somente em 1999, o Python estava com uma estrutura mais adaptada. Graças ao seu estilo de linguagem aberta, Guido ganhou um prêmio em 2002 por avanços em software livre.

Como toda linguagem, a premissa adotada é de que as operações básicas devem ser apoiadas por variáveis que são compostas por números reais, por estruturas unidimensionais, conhecidas como array (ou vetor), e bidimensionais (matrizes). A inovação, no caso do Python, é que bibliotecas externas aos programas (também chamados de script) podem ser importadas ou não, dependendo da natureza do problema envolvido.

Com isso, a democratização veio no sentido de que pessoas com base de programação mais simples podem atuar com essa linguagem usando conhecimento de outras linguagens. Programadores por meio de pesquisas mais avançadas também

podem usar a mesma linguagem, baixando e importando, para isso, bibliotecas específicas e direcionadas para sua área de estudo.

Uma das grandes novidades foi a construção da biblioteca NumPy (Numerical Python) para trabalhar com as estruturas de array de maneira mais rápida e amigável do que, por exemplo, o FORTRAN da época. Outra inovação veio com a biblioteca Pandas, que revolucionou o modo de resolução de problemas que envolviam grandes estruturas de dados. Isso ajudou a difundir a biblioteca e a linguagem para áreas, que foram se consolidando a partir dos anos 2000, condensando-se e integrando-se no que conhecemos hoje como ciência dos dados.

1.2 OPERAÇÕES BÁSICAS

Se tivermos duas variáveis x e y, as operações básicas são facilmente desenvolvidas, como apresentadas a seguir. Soma, subtração, multiplicação e divisão seguem o padrão de outras linguagens com os mesmos símbolos. As operações aqui apresentadas estão ocorrendo no ambiente do Spyder – Anaconda, dentro do console, e, assim, temos os símbolos In [1], In [2] etc. para as entradas; e Out [1], Out [2] etc. para os resultados das operações. Os mesmos comandos trabalham da mesma maneira em outros ambientes, como o editor de texto do Spyder (no caso da Anaconda) ou do Jupyter.

Uma operação bastante utilizada é descobrir o resto da divisão entre dois números, por exemplo, x e y. O símbolo, nesse caso, é o “%”, que não significa operação de cálculo de porcentagem, mas o acionamento do programa para se calcular o

resto da divisão entre x e y. Por exemplo, se x = 10 e y = 3, sabemos que o resto da divisão x/y será 1. Em Python, escrevemos da seguinte forma:

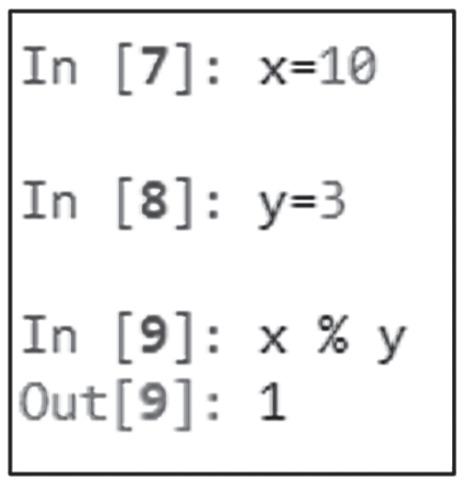
1.3 BIBLIOTECA MATEMÁTICA

Talvez a biblioteca mais simples do Python seja a Math. Ela é necessária quando desejamos utilizar expressões muito comuns, como exponencial e raiz quadrada ou expressões de logaritmos e trigonometria para números ou variáveis unidimensionais. Para se utilizar das funções existentes na biblioteca Math, é necessário antes importá-las, para então começar a utilizar os recursos existentes. Para a raiz quadrada, a função é sqrt; para a função exponencial, usamos exp; e para o logaritmo natural, usamos log. Pode-se perceber que devemos usar o nome da biblioteca antes do nome da função para termos o resultado das operações. Por isso, temos math.sqrt(4) para calcular a raiz quadrada de 4.

Claro que, além de usarmos a palavra com o nome da biblioteca, podemos colocar um apelido nela para simplificar o uso das funções. Por exemplo, se chamarmos a importação, substituindo o nome math por mt, as funções devem ser chamadas agora como mt.sqrt(4), e não como math.sqrt(4).

Para as funções trigonométricas, fazemos uso da biblioteca da mesma maneira, como demonstrado para o cálculo de seno, cosseno e tangente.

1.4 BIBLIOTECA ESTATÍSTICA

Para medidas estatísticas simples, podemos fazer uso da biblioteca estatística, cujo nome é statistics. Uma das entradas de dados para a utilização das estatísticas básicas que conhecemos, como média, desvio-padrão populacional e desvio-padrão amostral, é representar a amostra como um tupla (um conjunto de dados separados por vírgula).

CAPÍTULO 2 Pandas

2.1 INTRODUÇÃO

A biblioteca Pandas foi como uma espécie de revolução para a linguagem Python. Seguramente, foi a responsável por popularizar a linguagem Python para áreas de fora da computação. O mercado financeiro, por exemplo, foi uma das áreas que, até 2008, ainda estava muito atuante em automação de planilhas Excel. E, quando se tratava de modelos para previsões, diversas áreas utilizavam as toolboxes de Matlab. Segundo Garg (2021), a Pandas começou a ser criada em 2008 por Wes McKinney, que trabalhava no AQR Capital Management. Ele estava insatisfeito com as bibliotecas do Python e tinha dificuldades com as ferramentas existentes nelas para manipular grandes quantidades de dados financeiros. Pandas vem do termo “dados de painel”, em inglês, um conceito em economia para trabalhar com métodos que tratam de conjuntos de dados complexos multidimensionais. Duas estruturas básicas importantes são as séries e os DataFrames. Estima-se que existam 93 mil projetos open source utilizando a Pandas.

Em termos de usuários da biblioteca, em 2017, só o Stack Overflow, um website para programadores em Python atingiu o recorde de 5 milhões de visitas, procurando informações sobre a Pandas (Kopf, 2017). O que torna a Pandas tão diferente?

Pandas é uma biblioteca versátil e que economiza dezenas de linhas de programação para manipular grandes bancos de dados. É versátil e dinâmica, no mesmo sentido do recurso conhecido como “Tabela Dinâmica” ou “Pivot Table” do Excel.

2.2 FORMAS DE ENTRADA NO DATAFRAME

Um DataFrame é uma tabela com dados, com uma dinâmica própria e com comandos exclusivos para manipular grandes quantidades de dados. Tem uma notação própria e, atualmente, não precisa ser instalada, pois já vem na composição original da linguagem Python.

Vamos supor que desejamos ter a seguinte tabela com nomes dos alunos e seus desempenhos em provas e trabalhos. A Tabela 2.1 apresenta cinco linhas, incluindo o título, com três colunas. Essa formatação precisa ser mantida na biblioteca Pandas, usando a estrutura DataFrame.

Tabela 2.1 Tabela de desempenho de alunos

No Python, o primeiro passo é a importação da Pandas por meio do comando “import”, como fizemos com as outras bibliotecas no Capítulo 1. O primeiro tipo de entrada dos dados é o clássico uso do DataFrame composto por chaves, que indicam as tabelas; e os colchetes, que indicam as listas com nomes ou dados numéricos, como vistos nas linhas 3, 4 e 5. O parêntesis final indica que a função de criação do DataFrame terminou, e, na memória do Python, a Tabela 2.1 está pronta para ser usada.

1 import pandas as pd

2

3 df = pd.DataFrame({‘aluno’:[‘Mário’,’Ana’,’Carlos’,’Leila’],

4 ‘provas’:[5, 7.5, 6, 3],

5 ‘trab’:[10, 7, 5, 8]})

6 print(‘++++++++++++++++++++++++’)

7 print(df)

A impressão do DataFrame pela linha 7 do código anterior nos fornece:

O leitor observará que apareceu uma coluna extra à esquerda com os números não inseridos 0, 1, 2 e 3. Esses são índices automáticos (index) que a Pandas gera para identificação das linhas. Como veremos adiante, é possível formatar, excluir, alterar, enfim, manipular tranquilamente o índice do DataFrame “df”.

O segundo tipo de construção do DataFrame não precisa de tantos detalhes, mas podemos apenas dizer quais colunas desejamos. A linha 3, a seguir, cria o DataFrame e indica as três colunas com “columns”, apresentando os nomes das colunas por meio de uma lista de string. O preenchimento após a construção da estrutura do DataFrame ocorre logo em seguida, bastando, para isso, usar o nome do DataFrame (nesse caso, “df”) e os nomes das colunas em que estarão os dados, colocando o título dentro dos apóstrofos.

As colunas nesse segundo tipo de entrada estão em separado, nas linhas 5, 6 e 7, com listas para df[‘aluno’], df[‘provas’] e df[‘trab’].

1 import pandas as pd

2

3 df = pd.DataFrame(columns=[‘aluno’,’provas’,’trab’])

4

5 df[‘aluno’]=[‘Mário’,’Ana’,’Carlos’,’Leila’]

6 df[‘provas’]=[5, 7.5, 6, 3]

7 df[‘trab’]=[10, 7, 5, 8]

8

9 print(‘++++++++++++++++++++++++’)

10 print(df)

Uma terceira maneira mais rápida apenas cria o DataFrame “df” sem nome algum de coluna. A posteriori, à medida das necessidades, podemos colocar as listas com os nomes e dados numéricos, como apresentado a seguir. A linha 3, agora, não tem mais os nomes das colunas, apenas prepara a estrutura do DataFrame. Os nomes vêm depois, nas linhas 5, 6 e 7.

1 import pandas as pd

2

3 df = pd.DataFrame()

4

5 df[‘aluno’]=[‘Mário’,’Ana’,’Carlos’,’Leila’]

6 df[‘provas’]=[5, 7.5, 6, 3]

7 df[‘trab’]=[10, 7, 5, 8]

8

9 print(‘++++++++++++++++++++++++’)

10 print(df)

Pode-se, ainda, alimentar os dados de um DataFrame com vetores. Não necessariamente as entradas precisam ter o formato de listas. Por exemplo, como apresentado no código modificado, podemos ter um array (vetor) x na linha 6 e outro na linha 7. Ambos podem fazer parte de um DataFrame, basta inserir no nome da coluna correspondente, como feito na 10 e 11.

1 import pandas as pd

2 import numpy as np

3

CAPÍTULO 3 Gráficos na Pandas

3.1 INTRODUÇÃO

A melhor forma de visualização de dados é por meio de um gráfico. A percepção do desenrolar dos eventos, as mudanças e alterações nas variáveis, tudo fica muito mais fácil de entender quando temos um bom gráfico. E a Pandas nos proporciona uma grande evolução, não somente pela sua qualidade nos gráficos, mas também pela fácil interação com o programador e o usuário.

Muitos gráficos programados com a biblioteca Matplotlib necessitam de algumas linhas de programação para ficarem com boa representação. Na Pandas com a utilização de um ou dois comandos, obtém-se um resultado bem mais interessante e ainda melhor do que na Matplotlib. A função básica também é “plot”, mas seguida do nome do DataFrame. O importante é que temos novas e diversas estruturas para apresentar gráficos bem mais avançados e técnicos, com pouco esforço de algoritmo para isso.

3.2 GRÁFICOS BÁSICOS

Vamos supor que tenhamos a Tabela 3.1 e desejamos usá-la em um DataFrame chamado “df”, como apresentamos no Capítulo 2.

Tabela 3.1 Variáveis x, y e z

Como já apresentado, o código que transforma a Tabela em DataFrame é o que se segue, a novidade é que temos agora o comando plot na linha 10 para fazer os gráficos das três colunas (vx, vy, vz).

Primeiro criamos as colunas na linha 3; depois, colocamos no DataFrame já estruturado os valores no formato de lista para cada coluna, nas linhas 4, 5 e 6. Quando usamos apenas “df.plot( )”, sem informação adicional alguma, a Pandas constrói um gráfico básico de linhas, com cores diferentes e já pronto com legendas que identificam cada variável.

1 import pandas as pd

2

3 df = pd.DataFrame(columns=[‘vx’,’vy’,’vz’])

4 df[‘vx’] = [2, 3, 4, 3, 5, 6]

5 df[‘vy’] = [-1,-2,-1, 4, 6, 7]

6 df[‘vz’] = [0, 2, 4.5, 2.1, -2, 1]

7 print(‘++++++++++++++++++++++++++++++++’)

8 print(df)

9

10 df.plot()

O resultado é apresentado no gráfico da Figura 3.1. Assim como na Matplotlib, esse gráfico pode ser melhorado colocando informações adicionais sobre os eixos, títulos, tipos de linhas, fontes, localização da legenda, entre tantas outras modificações.

Figura 3.1 Gráfico de linhas básico com plot para as três variáveis do DataFrame.

Outro fato interessante é de que a Pandas consegue trabalhar muito bem com todas as outras bibliotecas do Python, inclusive as bibliotecas gráficas.

Se precisamos visualizar apenas uma variável, usamos a definição:

df.plot( y = ‘nome da coluna’ )

A letra y dentro do DataFrame indica qual coluna fará parte do eixo das ordenadas, o eixo vertical do gráfico feito em plot( ). Vamos supor que desejamos ver apenas o gráfico da variável “vx”:

Com o resultado seguinte:

Para mais de uma coluna no gráfico, montamos uma lista com os nomes das colunas, e, para isso, precisamos da notação com colchetes. Para as variáveis “vx” e “vz”:

Com o resultado seguinte:

CAPÍTULO 4

Agrupamento – O “diabo” aparece

4.1 DE

ONDE VEM O DIABO?

Um famoso provérbio alemão representa muito bem os problemas enfrentados todos os dias por programadores, cientistas e pessoas que trabalham com algum software. E, se estamos trabalhando com big data, o provérbio é ainda mais correto. Já o mencionei no prefácio, mas cabe repeti-lo aqui. O provérbio atribuído a Nietzsche diz que “O diabo mora nos detalhes”.

Mas podemos afirmar, sem dúvida alguma, que o “O diabo se esconde nos dados”. Todos os problemas enfrentados por pesquisadores, empresas ou máquinas que trabalham com aquisições de dados em tempo real, advêm dos próprios dados recolhidos.

Seja por filtragem e estimação erradas, oscilação não prevista, modelos com uma letra errada, matrizes com uma linha errada ou em branco, e pronto! É mais do que suficiente para transformar nossas vidas em um caldeirão do inferno. E parece que vemos o diabo rindo, atrás dos ombros, caçoando de um mero detalhe que esquecemos.

Quanto mais aberta é uma linguagem de computação, mais detalhes não previstos aparecem; o que funcionava “até ontem”, nos enche a tela de erro hoje. Quando

tomamos bases de dados diferentes e tentamos ligar essas bases e colocar em sincronia tabelas com disposições diferentes, o diabo aparece em todos os cantos e multiplica-se num completo e caloroso inferno.

Por exemplo, vamos supor que temos a seguinte planilha em Excel.

Desejamos, com essa planilha, fazer um exercício muito simples de estimativa de parâmetros. Qual é a reta de tendência que passa entre os pontos da coluna B? Esse é um problema muito antigo, resolvido por Gauss, quando ele criou o método dos mínimos quadrados. O problema possui muitos textos acadêmicos clássicos sobre as formas de estimar tendências em séries de dados temporais (por exemplo, ver Morettin, 1987; Papoulis, 1991). Esse método está implementado no Excel, ao clicar nos dados e pedir para adicionar a linha de tendência com equação.

Os pontos estão na Figura 4.1, e a linha de tendência, na Figura 4.2. A reta parece perfeita e a equação correta. Tudo parece muito bom, assim, podemos copiar para nosso relatório e entregar.

É, mas não está!

Um detalhe importante pode transformar nossa pesquisa ou relatório em um inferno e gerar problemas imprevisíveis. Um olhar mais cuidadoso pode verificar que, embora a reta passe perfeitamente nos melhores lugares entre os pontos, a equação é

yx 0 727 32915 ,

O coeficiente angular é 0.727, mas o coeficiente linear é … 32915! Só para lembrar ao leitor, o coeficiente linear é o ponto no eixo vertical y em que a reta corta e ultrapassa para o lado esquerdo do eixo x. E deveria estar (pelo menos visualmente) um pouco acima de 1. No entanto, está indicando que essa reta passa no ponto -32915?

Bem, esse é um problema atribuído à Igreja Católica na Idade Média. Em 1582, o Papa Gregório XIII resolveu corrigir problemas antigos sobre datas sagradas da Igreja, como a Páscoa, que estava ocorrendo cada vez mais tarde que o equinócio da primavera. Implementou-se uma porção de medidas, principalmente em termos de dias. Dez dias simplesmente sumiram do calendário cotidiano. O dia 4 de outubro de 1582 passou a ser 15 de outubro de 1582. Fórmulas novas para anos

bissextos foram elaboradas, e correções no número de horas dos dias são necessárias todos os anos.

E o que isso tem a ver com nosso exemplo?

É que o Excel nos mostra nas células da planilha a data que usamos, ou seja, nosso calendário gregoriano. Mas, para efeito de computação e de cálculos, todos os softwares utilizam o calendário juliano, implementado pelo imperador Júlio César, com tempo corrido, sem preocupação com meses, anos ou datas importantes.

Ao se trocar a formatação da coluna A de nossa planilha original de “data” para “geral”, outro número aparece. A data original 1/12/2023 é, na verdade, 45261 no calendário juliano, e é esse eixo x que o Excel usa para calcular a linha de tendência. E o que parece correto, é, na verdade, um enorme erro. Simples, mas enorme.

Logo, antes de sairmos usando a linha de tendência, é necessário um ajuste e a criação de um eixo sem as datas. Essas são meras representações do calendário, mas, matematicamente, não podemos usá-las para os cálculos. Pelo menos, não dessa maneira no Excel.

A Figura 4.4 apresenta a forma correta da reta e sua equação. O primeiro passo é criar uma coluna nova com os contadores dos dias observados, 0, 1, 2, … Na Figura 4.4, esse novo eixo está na coluna B e os dados originais do eixo y passaram para a coluna C. Com isso, a equação da reta ajustada torna-se:

yx 0 727 1 727 ,,

CAPÍTULO 5

Concatenação – Agrupando as diferenças

5.1 JUNTANDO ALHOS COM BUGALHOS

Um dos grandes problemas do mundo acadêmico desde os primórdios da programação de computadores foi que, ao se criarem estruturas de banco de dados, como os valores poderiam vir de fontes distintas, as informações muitas vezes não coincidiam ou, então, para os mesmos experimentos de coletas em dias diferentes, faltavam dados.

A área, criada sob o nome de processamento de dados, dividiu-se em diversas especialidades, sendo esta a mais promissora e a que se sobressaiu à área de banco de dados. Muitas empresas se interessaram por programas e algoritmos que tratam todo tipo de dados, desde dados de seguros, planos de saúde, finanças, aeroespaciais e siderurgias até dados confidenciais sob a tutela do Estado em agências de segurança. No Excel, por exemplo, existe uma função bem simples para agrupar informações separadas e coloca-las numa mesma célula, tratando de múltiplas formas de junção dos dados em colunas distintas. Por exemplo, vamos supor que tenhamos informações sobre os nomes de pessoas separadas como na Figura 5.1.

O que desejamos é ver os nomes completos, sem separação de células, para armazenarmos de alguma maneira. Num banco de dados de clientes, por exemplo, desejamos saber o histórico por nome, endereço e outras informações, mas não com separação de nomes por partes.

Esse tipo de separação é comum quando temos um formato com dados advindos de algum website que foi importado como texto (ou, no caso Excel, em “csv”).

A função do Excel que consegue agrupar e reformatar esses campos é a função concatenar. Então, poderemos colocar na coluna D do Excel, Figura 5.1, e pedir para esse programa concatenar (juntar) os dados das células que estão nas colunas A, B e C. A Figura 5.2 demonstra como colocar essa função; como é uma função, precisa do sinal “=”.

Então, dentro da função, escolhemos quais as células deverão ser agrupadas para formarem um novo dado completo na célula D1. Colocamos as células A1, B1 e C1; e usamos “ ” para separar as informações dessas células. Caso não se usem “ ”, a célula D1 ficaria com o nome completo “JoséAntoniodaSilva”. As aspas com espaço em branco separam corretamente a informação, como apresentado na Figura 5.3.

Figura 5.3 Implementação da função “concatenar” no Excel.

O resultado final nos fornecerá o nome completo, que antes estava separado em cada célula do Excel (Figura 5.4). Esse tipo de algoritmo para juntar informações foi desenvolvido ainda quando as linguagens de programação estavam no início e precisávamos criar grandes bancos de dados para interpretar experimentos distintos.

5.4 Resultado final da função “concatenar” do Excel.

No Python, essas funções de agrupamento foram diversificadas e existem muitas formas de agrupar informações que estão em bancos de dados distintos. Vamos ver as mais comuns.

5.2 A FUNÇÃO INTERSECTION( )

Em diversas ocasiões, a comparação de dados de diferentes índices tem o problema de falta de dados. Pode ocorrer de um arquivo ter mais dados do que outro, e , por isso, as medidas estatísticas ficam prejudicadas, pois é necessário que os dados estejam pareados. Ou seja, os dados devem estar em pares de ocorrência para a maioria das análises quantitativas.

Um problema muito comum é quando se deseja comparar dados ou informações sobre datas de experimentos comuns, mas que estão em datas diferentes entre países. Como cada banco de dados tem sua data de experimento, ou resultados com variáveis distintas para o mesmo problema, é comum se deparar com o problema de que, ao final da programação, um arquivo (ou banco de dados) tenha mais valores do que outro.

A resolução comum é eliminar dados em datas em que os experimentos não existem ou que não coincidam. Vamos supor que nossa intenção é parear informações com a mesma data de execução. A primeira maneira é observar as datas e, caso sejam poucas, eliminar as linhas dos dados. Outra forma é programar um algoritmo em alguma linguagem para varrer os arquivos e eliminar dados ou valores de datas não coincidentes.

No Python, uma função muito interessante é a função *.intersection( ), que elimina e coloca os dados pareados entre arquivos. Suponha que tenhamos dois arquivos [arq1, arq2], em que arq2 tem menos dados do que arq1. Então, o formato seguinte elimina dados de arq1 para que seja coincidente com arq2:

arq2.index.intersection(arq1.index)

Vamos admitir que nossos dois arquivos são como se segue:

17/1/2024

Como podemos observar os arquivos estão na forma de séries, um formato mais simples tipo DataFrame, mas não precisamos nomear as colunas. No arq1, não temos as datas 17 e 19 de janeiro; e, no arq2, não temos 12 e 13 de janeiro, que estão no arq1. As linhas a seguir demonstram como utilizar a função “intersection”.

1 # Algoritmo básico para usar intersection entre arquivos 2

3 import pandas as pd

5 arq1 = pd.Series([5, 7, 2, -8],

6  index = [‘10/1/2024’, ‘12/1/2024’, ‘13/1/2024’, ‘15/1/2024’]) 7

8 arq2 = pd.Series([30, 26, -12, 90],

9  index = [‘10/1/2024’, ‘15/1/2024’, ‘17/1/2024’, ‘19/1/2024’]) 10

11 juntos = arq2.index.intersection(arq1.index)

13 arq1_novo = arq1.loc[juntos]

14 arq2_novo = arq2.loc[juntos]

16 print(‘+++++++++++++++++’)

17 print(arq1_novo)

18 print(‘+++++++++++++++++’)

19 print(arq2_novo)

CAPÍTULO 6 A função lambda

6.1 A IDEIA INICIAL

Um dos grandes matemáticos do século XX, David Hilbert (Livio, 2009; Roque, 2012; Penrose, 2023), propôs uma lista de 23 problemas de matemática que clamavam por soluções definitivas. Essa lista foi lida no Congresso Internacional de Matemáticos, em Paris, em uma época de ouro para a ciência, com diversas invenções, descobertas e corridas para maiores desenvolvimentos tecnológicos.

Hilbert listou, por exemplo, o problema da necessidade da descrição de um processo algorítmico que sempre seria afirmativo em caso de solução de uma equação (no caso, era a equação diofantina), ou negativo, no caso de não haver solução. O que ele propunha era uma maneira de se entrar com uma função numa caixa-preta, e que na saída aparecesse “sim” ou “não” para a solução da função.

Contudo, no início da década de 1930, Alonzo Church provou (Penrose, 2023) que existem problemas que não possuem soluções por meio de algoritmos. Existirão problemas que entrarão em modo recursivo infinito e nunca fornecerão soluções, deixando em aberto se uma solução existe, mas está no infinito, ou se a solução não existe, por mais que se tente.

Kurt Gödel e Alan Turing chegaram ao mesmo resultado de forma independente e criativa, resolveram o grande problema de paradoxos que estavam deixando o formalismo matemático em desespero. Gödel provou o que se tornou conhecido como os dois teoremas da incompletude:

● em uma teoria consistente, sempre há proposições que não podem ser demonstradas nem verdadeiras, nem falsas;

● é impossível, dentro do próprio formalismo, uma teoria provar se ela é inconsistente ou consistente.

Para as questões sobre a teoria da computação, Church, Gödel e Turing usaram o conceito geral sobre funções. Eles não se preocupavam nas suas proposições com funções específicas do tipo f(x), g(x,y), h(t), ou seja, em teoria, existe um pensamento algorítmico geral (chamado de função autônoma) que independe se a função tem nome “f”, “g” ou “h”. Se provarmos que os procedimentos lógicos são sempre

válidos de forma algorítmica para uma função, eles serão válidos para qualquer função.

Daí surge o conceito de função anônima, conhecida como função lambda (λ), cujo cálculo passou a ser conhecido como Cálculo-λ. Por exemplo, vamos supor que tenhamos a função

fx x

Numa função anônima, informamos que a aplicação de toda função à variável “x” levará ao resultado da própria variável “x”. Do ponto de vista formal, escreve-se esse tipo de regra na teoria da computação como

λ xx .

A letra grega λ (lambda) representa qualquer função que é aplicada a uma variável (usando a notação de ponto [.]). Essa é a ideia para a função lambda, que nos indica que não precisamos criar uma função (uma def function no Python, por exemplo), basta, para isso, criar essa função lambda, que pode ser chamada com qualquer nome e estar em qualquer lugar do programa.

Por exemplo, a função fx x 1 indica que, numa caixa-preta, entra “x” e sai como resposta o valor de “x + 1”.

Figura 6.2 Representação da função f (x) = x + 1.

Em termos de sistema formal com função lambda, a mesma função seria escrita da seguinte forma:

xx . 1

Se quisermos saber algum valor específico para x, por exemplo, x = 5, para a função “f”, teremos:

ff 55 15 6

Para a função lambda, representamos a regra de “f” como:

xx 15 6

6.2 A FUNÇÃO APPLY

A função lambda no Python necessita do uso de uma função que vai ativá-la nos cálculos. Essa função é conhecida como função apply( ). Vamos observar seu uso, supondo que tenhamos a seguinte tabela:

Primeiramente, no Python, criamos o DataFrame desta tabela:

1 # Uso do apply

2 import pandas as pd

3 import numpy as np

4

5 df=pd.DataFrame({‘a’:[2,3,4,5],

6  ‘b’:[5,10,8,7]})

Após criarmos o DataFrame, vamos supor que desejamos criar uma coluna “c” que seja a soma de todos os elementos, separados a cada linha de “a” e “b”. Ou seja, queremos uma coluna c = a + b. A maneira de fazermos isso é usarmos a biblioteca

CAPÍTULO 7

Seaborn – Uma grande aliada da Pandas

7.1 REVISITANDO GRÁFICOS BÁSICOS

A biblioteca Pandas tem um enorme diferencial em relação às outras bibliotecas no que se refere à apresentação gráfica. Uma grande ferramenta auxiliar que trabalha muito bem com a Pandas é a biblioteca Seaborn. Essa biblioteca já foi utilizada em programas citados nos primeiros capítulos devido a sua grande facilidade em construir gráficos. Quando fazemos gráficos básicos, nem sempre conseguimos notar diferença em relação à informação. Notamos, sim, muita diferença no aspecto da estrutura e da representação, que, no caso da Seaborn, são muito interessantes. Quando precisamos de uma disposição com divulgação mais ampla, a biblioteca Seaborn consegue sanar alguns problemas que apresentam algumas disposições gráficas na Pandas. A Seaborn atua como uma grande técnica de auxílio na resolução de problemas por parte da Pandas.

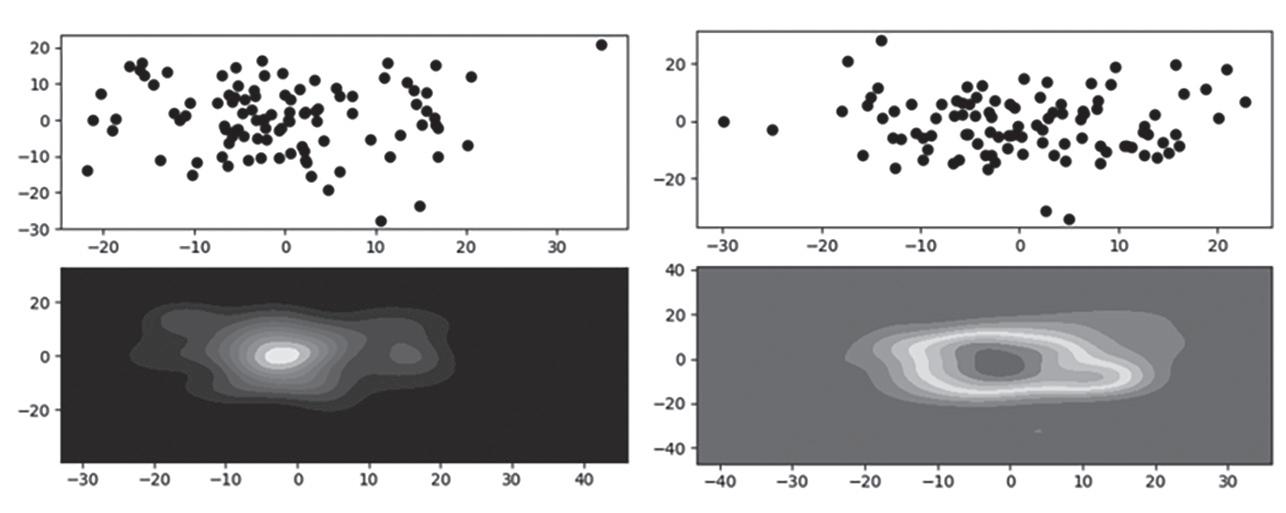
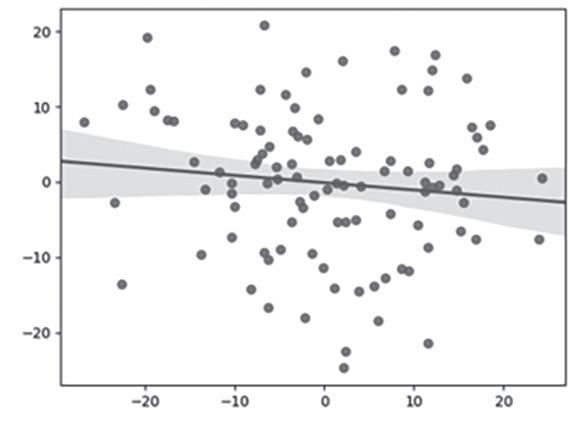
Um dos gráficos mais básicos da Seaborn é o gráfico de linhas, apresentado na Figura 7.2. O comando na Seaborn para esse tipo de gráfico é o lineplot( ), em que, dentro dos parêntesis, colocamos o DataFrame que vem da biblioteca Pandas. Vamos supor que tenhamos a seguinte tabela, entrando no Python no formato de DataFrame. Se admitirmos que importamos a biblioteca Seaborn como “sns”, então, na linha do código, esse gráfico deverá ter

sns.lineplot ( data = df ) em que “df” é o DataFrame advindo da seguinte tabela:

1 #biblioteca seaborn

2 import seaborn as sns

5 df=pd.DataFrame({‘a’:[3,4,2,3,5,8,9],

6  ‘b’:[20,25,24,30,35,40,38]})

7 sns.lineplot(data=df)

O resultado gráfico desse DataFrame é apresentado na Figura 7.2. É interessante notar que o lineplot automaticamente separa os dados das colunas “a” e “b”, coloca a legenda, usa cores diferentes e completa com tipos de linha que facilitam a leitura por parte do usuário. Em outras bibliotecas, todas essas especificações teriam de ser feitas à parte.

Figura 7.2 Gráfico lineplot para o DataFrame.

Outro formato possível que resultará no mesmo gráfico é de uso de lista para colocar as colunas do DataFrame separadamente. Isso é útil quando não queremos o gráfico com todas as colunas como na Figura 7.2, mas de algumas colunas específicas. Para tanto, escrevemos o seguinte comando na linha 7 do código anterior:

sns.lineplot(data = [ df[‘a’], df[‘b’] ])

1 #biblioteca seaborn

2 import seaborn as sns

3 import pandas as pd

4

5 df=pd.DataFrame({‘a’:[3,4,2,3,5,8,9],

6  ‘b’:[20,25,24,30,35,40,38]})

7 sns.lineplot(data=[df[‘a’],df[‘b’]])

Ainda temos uma terceira forma de representar esses dados do DataFrame, especificando quem será o eixo-x e quem será o eixo-y. Com isso, não teremos duas linhas no gráfico, mas apenas a linha da coluna escolhida. Por exemplo, se usarmos a notação de df.index para o eixo-x, nele será colocado o índice do DataFrame, como visto na linha 7 a seguir. Se forem datas, nesse índice, elas aparecerão.

CAPÍTULO 8

Falhas – Detalhes estatísticos

8.1 O CONCEITO DE PROBABILIDADE DE FALHAS

Eventos catastróficos sempre ocorrem e sempre ocorreram no Universo, seja em nosso planeta, seja em qualquer lugar de outras galáxias. Planetas são destruídos por grandes asteroides; galáxias são atingidas por outras galáxias; estrelas explodem; enfim, o que chamamos de eventos catastróficos são eventos naturais no universo desde a explosão primordial do Big Bang (segundo a cosmologia).

O fato é que associamos eventos naturais a desastres, pois o planeta onde vivemos foi concebido em nossa memória, quando crianças, de um lar perfeito e imutável. Mas, conforme crescemos, todos os dias vemos que estamos no meio do perigo em todos os momentos de nossa vida. Basta um descuido qualquer para momentos felizes se transformarem em tragédia.

Para equipamentos, esses momentos catastróficos também são declarados como “momentos finais” em suas vidas. Dizemos constantemente que um equipamento “morreu”, que o motor se “apagou”, que nosso computador “se foi” e precisamos comprar outro, que a lâmpada “queimou”, enfim, associamos equipamentos mecânicos e eletrônicos com palavras de nosso cotidiano.

A área de estatística passou, então, a medir as chances de uma catástrofe ocorrer com base em amostragens. Existe até uma teoria (teoria das falhas) que estuda as

melhores curvas de medidas de probabilidades das “vidas” dos equipamentos, as distribuições de probabilidades que conseguem captar falhas e informar-nos qual a probabilidade de algo dar errado (para estudar essa teoria: Helstrom, 1991; Meyer, 1994; e Papoulis, 1991).

Dentro da área de estatística, existem muitas distribuições de probabilidades, no entanto, nosso foco neste capítulo não é a comparação de qual método é melhor e para qual situação. Existem excelentes textos na literatura especializada que nos remetem a como podemos adaptar nossos experimentos e ajustar parâmetros para cada caso. Nosso intuito, aqui, é demonstrar como a biblioteca Pandas, junto com a SciPy (que possui um montante enorme de distribuições estatísticas), pode oferecer uma grande ajuda na prevenção e previsão de falhas.

Assim, vamos nos ater à distribuição de Ernst Hjalmar Waloddi Weibull, professor que, inicialmente, era marinheiro da Marinha da Suécia e que defendeu sua tese de doutorado em 1932, ingressando na Universidade Upsália. Foi um consultor e especialista em engenharia, sobretudo em rolamentos, ferramentas mecânicas, explosivos entre tantos outros assuntos.

Especializado em resistência de materiais, o professor Weibull desenvolveu o que conhecemos hoje como a distribuição das falhas de Weibull, usada para calcular a probabilidade de falhas em equipamentos, mas adaptada a muitas outras áreas, como tratamentos de doenças, espalhamentos de epidemias, desabamentos, terremotos, furacões, enfim, eventos que podem “falhar” com nossa normalidade aparente (Helstrom, 1991).

O conceito de falhas parte da premissa de que, antes, temos de coletar informações sobre o evento analisado, anotando os dias corridos desde a última falha. Uma vez possuindo essas informações, calculamos as probabilidades das falhas ou desastres com base no intervalo de tempo entre tragédias anteriores (ou falhas anteriores), como visto na Figura 8.1.

Com esses dias anotados, estimamos, baseados na distribuição de Weibull, parâmetros importantes que descrevem o comportamento das falhas, criando curva de probabilidade de falhas e também curvas de confiabilidade, muito utilizadas em indústrias.

8.2 A DISTRIBUIÇÃO DE WEIBULL

A função densidade de probabilidade de Weibull mais completa e clássica é definida pela seguinte função:

ft t 1 (8.1)

em que t é o intervalo de tempo entre as falhas; γ é o tempo de “vida mínima”, isto é, o tempo mínimo em que ocorreu uma falha; η é a “vida característica” e chamado de parâmetro de escala, mas que podemos associar com o tempo médio das falhas; e, finalmente, o parâmetro β, que define a forma da curva. Podemos supor, sem perda de generalidade, que, às vezes, começamos a medir um experimento e, assim que ligamos, ele falha, tornando o parâmetro γ = 0, o que nos leva à Equação (8.2) de Weibull mais simplificada:

ft t 1 (8.2)

Quando calculamos os diversos valores de f(t), podemos acumular sua soma construindo nossa curva de probabilidade cumulativa, que nos informará a probabilidade de falha grave em cada dia. Matematicamente, essa densidade de probabilidade acumulada tem a forma:

Ft t dt t 1 0 (8.3)

em que seu complemento 1-F(t) representará o que chamamos de curva de confiabilidade ou, ainda, esse complemento nos dirá qual será a probabilidade do evento não falhar até o limite em “t” dias.

Na Figura 8.2, temos uma curva de probabilidade de falhas padrão, indicando, por exemplo, que a probabilidade de um evento falhar em até dois dias é de 30%. Podemos ver que, à medida que os dias aumentam, a curva sobe, estacionando próximo dos 100% de probabilidade de falhas. Ainda nessa figura, no dia 2, a probabilidade de não falhar seria de 1-F(t) = 1-0.3 = 0.7, ou seja, 70% de não falhar em até dois dias.

Uma outra curva de análise importante é sobre o parâmetro β, que nos diz sobre o comportamento do evento, chamado de fator de forma. Ele indica um índice de padrão de falha, que pode ser dividido da seguinte forma. Valores de β muito menores do que 1.0 são também conhecidos como mortalidade infantil (do equipamento, do evento analisado etc.):

1 1 14 : : : falhamuitocedo falhaaleatória falhapor desgaste

4: falhamuito rápidapor desgaste

CAPÍTULO 9 Dados econômicos

9.1 BANCO CENTRAL DO BRASIL E DADOS ECONÔMICOS

O Banco Central do Brasil (BCB) possui uma ampla base de dados com diversas séries temporais com sensores e medidores da economia brasileira. O banco sempre manteve atualizada essa base e, com o advento da internet, disponibiliza de maneira pública dados que medem diversas variáveis ligadas a planos econômicos, independentemente do governo.

Com a introdução das linguagens voltadas para a internet, o BCB se atualizou e sempre manteve pública a base em html, java, sql, entre tantas tecnologias e linguagens de programação, para acesso livre à informação. No caso do Python, não foi diferente, e, nos últimos anos, o BCB disponibiliza uma biblioteca para aquisição de dados diretamente de scripts do Python.

A biblioteca tem o nome de python-bcb e pode ser instalada no próprio console do Spyder (Anaconda), do Jupyter ou de qualquer outro ambiente Python. No caso do console do Spyder, para instalar a biblioteca e baixar os dados do Banco Central, utiliza-se o comando “pip” da seguinte maneira:

pip install python-bcb

Caso deseje utilizar a biblioteca no Jupyter, basta usar (apenas uma vez) nas células do ambiente de programação o comando:

!pip install python-bcb

Essa biblioteca possui um sistema que gerencia os dados do BCB conhecido como Sistema Gerenciador de Séries Temporais (SGS). Esse sistema permite baixar dados diretamente do banco de dados do Banco Central. Para tanto, sempre precisaremos fazer uso da função get( ) do Python. Contudo, alguns códigos internos do SGS precisam ser conhecidos para a aquisição correta dos dados.

Esses códigos poderão ser consultados na página de referência do SGS:

https://www3.bcb.gov.br/sgspub/localizarseries/localizarSeries.do?method=prepararTelaLocalizarSeries

Atualmente, essa página tem o formato apresentado na Figura 9.1, mas isso muda com alguma frequência.

A biblioteca do BCB ainda possui conversor de moedas, expectativas divulgadas pelo boletim Focus, integração com o Odata, fornecendo dados de taxas de juros, IFdata e Mercado Imobiliário. Por exemplo, quando escolhemos “Mercados financeiros e de capitais” somos levados em outra página com vários itens, entre eles está o “Indicadores do mercado financeiro”. Abrindo esse item e, em seguida, escolhendo “Taxa de juros”, obtemos a seguinte tabela (Figura 9.2).

O número importante a saber para a coleta de dados pelo Python está na coluna “Cód”, que se refere aos diversos bancos de dados econômicos, como Selic, CDI, TR, TJLP etc.

Voltando à página principal (Figura-9.1), podemos selecionar outras bases de dados interessantes para estudos. Ao selecionar “Estatísticas monetárias” (Figura 9.3), temos disponíveis as metas de inflação, a taxa Selic com reuniões do Comitê de Política Monetária (Copom), entre tantas outras séries.

Ao selecionar a opção “Estatísticas monetárias” (Figura 9.3), depois “Política monetária” e, por fim, “Taxa SELIC”, teremos disponíveis as três séries em nova página como apresentadas na Figura 9.4. Essas três séries são indicadas com os códigos 422, 423 e 432, que podem ser escolhidos de acordo com o estudo desejado.

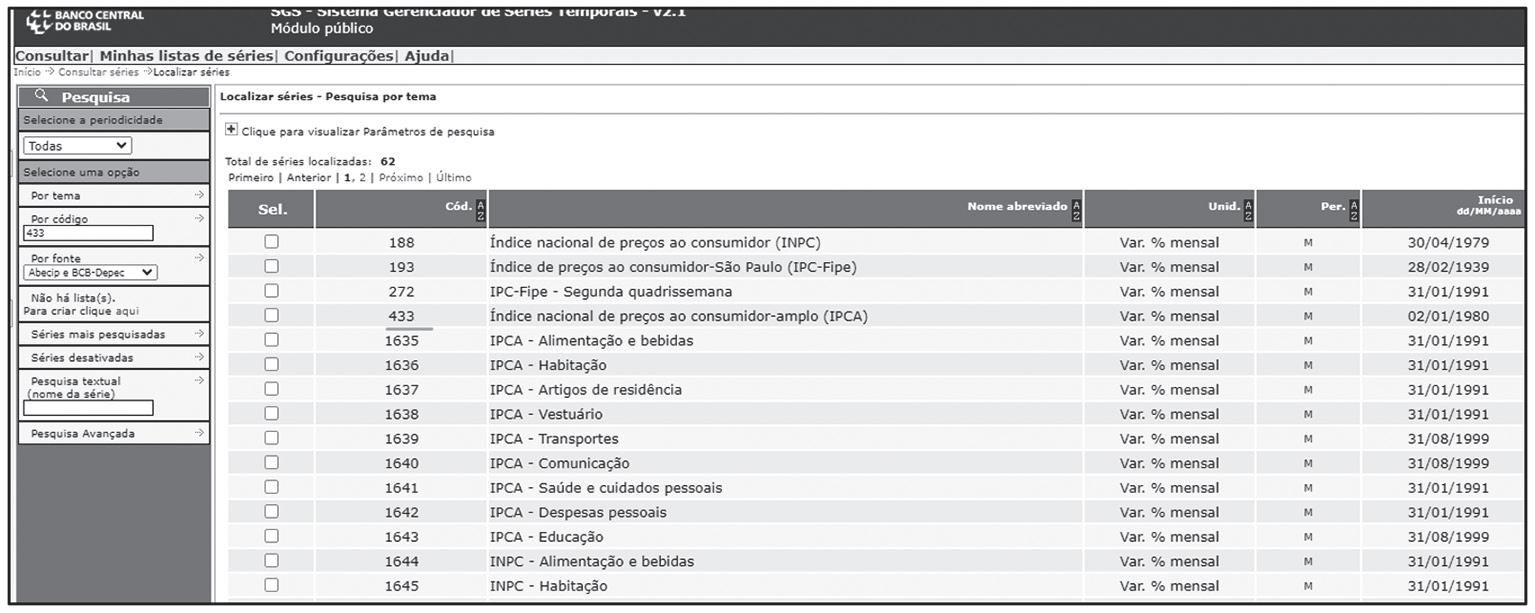
Dados da inflação estão na opção da página principal (Figura 9.1), seguindo: Atividade econômica > Preços > Índices de preços ao consumidor. Quando consultamos por esse caminho, a tabela (Figura 9.5) informa que o Índice nacional de preços ao consumidor-amplo (IPCA) tem o código 433. Podemos também consultar as séries apenas com a utilização de seus códigos, colocando o número da série na caixa à esquerda, que permite a busca, indicando o número na caixa “Por código”. Por exemplo, o IGP-M, que serve como base de preços imobiliários, tem o número de busca 189. Esse número pode ser encontrado colocando palavra-chave na busca principal e, quando aparecer a janela da página, basta ler e gravar seu número, o que torna a programação em Python mais simples do que o uso do nome da série.

CAPÍTULO 10

O nervoso mercado financeiro

10.1 INFORMAÇÕES DE ATIVOS FINANCEIROS

Quando o mercado financeiro é mencionado, as discussões e soluções de problemas giram em torno de investimentos em ativos. Esses ativos podem ser negociados em bolsas de valores ou diretamente entre cliente e bancos de investimentos. O fato é que o preço do ativo se altera conforme o ânimo é mais acirrado entre os investidores que atuam nas bolsas de valores.

Um ativo nem precisa fazer parte da bolsa de valores, mas o preço de sua negociação é baseado no sobe e desce de ações correlacionadas que são negociadas na bolsa. Por exemplo, compra e venda de apartamentos não ocorrem em sistemas ligados a bolsas de valores, mas estão amplamente relacionados com o chamado “humor” do mercado. Se a inflação está controlada, os títulos da dívida pública recuam em termos de juros, e os preços aumentam pela alta procura.

Esse recuo na taxa de juros melhora para construtoras que constroem mais edifícios para aluguéis ou vendas. Se essas empresas lograrem sucesso e possuírem ações na bolsa de valores, a procura por estas aumentam com a perspectiva de um ganho muito bom pelos dividendos. E, com o dinheiro dessas ações, as empresas colocam mais construções no mercado, mexendo com os preços de todos os apartamentos, mesmo pessoas que nada conhecem sobre bolsa de valores.

Por isso, entender e observar ativos financeiros pode ajudar a nos preparar para um “céu de brigadeiro” ou um “mar tempestivo”. O que acontece na bolsa de valores algum tempo depois, acontecerá no mercado que as pessoas conhecem, como padarias, supermercados, empórios, shoppings centers, entre tantas outras atividades do comércio de toda cidade.

O movimento dos ativos financeiros, como são chamadas as ações das empresas, os títulos de dívidas, os índices futuros, entre tantos outros, quase sempre é responsável por crises globais e generalizadas (Mandelbrot; Hudson, 2004). Por exemplo, o grande crash de 1929 quebrou o mundo todo, e, quando todos achavam que isso nunca mais ocorreria, mesmo com toda a sofisticação, em 2008, outra crise financeira global assolou o planeta (Caetano, 2013).

A Figura 10.1 ilustra dois momentos de crashes do principal e mais conhecido índice de bolsa de valores dos Estados Unidos, o Dow Jones, com sede em Nova Iorque. O eixo da esquerda apresenta os valores entre outubro de 1928 e janeiro de 1931. O gráfico mostra que o movimento não é tão errático e aleatório como se imagina, tendo muitas posições de seguidas altas para, então, aparentemente sem razão, despencar e levar todos os preços para baixo.

Ainda na Figura 10.1, à direita está o eixo com os valores do crash de 2008 com a crise das hipotecas nos Estados Unidos. Pode-se observar uma aparente estabilidade do Dow Jones em 2007, para, então, entrar em regime com tendência de queda em 2008, só voltando a recuperar-se em julho de 2009.

Essas fortes oscilações são chamadas de volatilidade, referenciando-se à variabilidade estatística medida por parâmetros como variância, desvio-padrão, amplitude, entre tantas outras existentes (Wadi et al., 2010).

Com o advento da internet e a grande velocidade dos computadores, sites especializados em mercado financeiro passaram a divulgar dados quase que instantaneamente para os investidores. Na realidade, diversas corretoras, inclusive, operam hoje em dia com fibra óptica ligada diretamente a bolsas de valores, permitindo negociações automáticas por algoritmos conhecidos como robôs traders. Essas negociações, conhecidas como “negociações de alta frequência”, operam na velocidade de 100 milissegundos (Morini, 2001; Viens et al., 2012; Yan, 2014).

Um dos sites financeiros que oferece alguns dados gratuitos e públicos é o Yahoo! Finance (Figura 10.2), que pode ser acessado em sua versão de língua inglesa pelo caminho: https://finance.yahoo.com/. Basta entrar com o código do ativo na caixa “Quote Lookup”, que uma outra página aparecerá com diversos gráficos, tabelas, histórico de dados, medidas estatísticas e notícias relacionadas ao ativo. Os programadores em Python construíram diversas bibliotecas para automatizar a busca pelos dados dos ativos financeiros. Essas bibliotecas, com o tempo, desaparecem e surgindo outras em seu lugar, deixando as antigas sem funcionamento (Caetano, 2017). Na atualidade, biblioteca que ainda está em funcionamento é a yahoo-fin.

Como toda biblioteca no Python, é necessário, pelo menos uma vez, fazer sua instalação via protocolo. No caso do ambiente Spyder, da Anaconda, basta usar o Python Installation Protocol, ou Protocolo de Instalação do Python (PIP) no console da seguinte forma:

pip install yahoo-fin

Isso permitirá que programas em Python baixem os dados do Yahoo! Finance sem a necessidade de ir até a página da web e escrever os símbolos dos ativos, nem baixar os dados em Excel. Os dados do período desejado já vêm para o Python no formato de DataFrame da biblioteca Pandas.

10.2 ALGORITMOS PARA ATIVOS FINANCEIROS

Para baixar dados do Yahoo! Finance, primeiro precisamos importar a biblioteca instalada dentro de cada novo algoritmo.

1 #################################################################

2 #

3 # ANTES DE RODAR A PRIMEIRA VEZ PRECISA INSTALAR A BIBLIOTECA #

4 # pip install yahoo-fin

5 #

6 #################################################################

7

8 import matplotlib.pyplot as fig

9 import datetime as dt

10 from yahoo_fin.stock_info import *

As linhas 8 e 9 do código anterior importam as conhecidas bibliotecas de gráfico e de formatação das datas, a matplotlib.pyplot e a datetime. Esta em especial, é necessária, pois o formato deverá ser obrigatoriamente de data para o comando baixar dados do Yahoo! Finance funcionar adequadamente. A linha 10 importa todas as funções necessárias para o funcionamento da biblioteca yahoo_fin.

Depois dessas importações, inicia-se a programação das linhas que farão o contato entre o Python e o banco de dados do Yahoo.

12 ################ importar a acao ############################

13 inicio=dt.datetime(2023,1,1)

14 fim=dt.datetime(2024,2,15)

15 df = get_data(‘PETR4.SA’, start_date=inicio, end_date=fim, headers={‘User-Agent’:Mozilla/5.0’})

CAPÍTULO 11 O perigo dos asteroides

11.1 MONITORAMENTO ESPACIAL

A Terra já foi destruída diversas vezes e ainda poderá ser outras mais, ao contrário do que o ser humano pensa. A mais recente destruição aconteceu há alguns milhões de anos e aniquilou os maiores seres que habitavam o planeta, os dinossauros. Pode ser amanhã, ano que vem, daqui a 10 anos, mas a probabilidade é bem alta de que novamente a Terra será destruída por um asteroide de grande escala. Júpiter foi atingido em 24 de março de 1993 pelo cometa Shoemaker-Levy, que media 1,8 km de diâmetro. Os astrônomos à época acompanharam em tempo real o impacto, e todos ficaram aliviados de que o Sistema Solar possui um planeta como Júpiter para atrair esses gigantes rochosos.

A Nasa mantém um sistema global de gerenciamento espacial fantástico, com dados para todos os tipos de objetos espaciais, inclusive os feitos pelo homem. Nos últimos anos, a Agência mantém uma biblioteca em Python, que ajuda a todos os interessados na obtenção, no estudo e na divulgação de dados científicos na astronomia. Para utilizar a biblioteca da Nasa, a nasapy, deve-se primeiro instalar no console, usando o comando PIP:

pip install nasapy

Como forma de apoio, a Nasa mantém uma página com documentos explicativos e exemplos de utilização de inúmeras ferramentas de monitoramento espacial que pode ser acessada em: https://nasapy.readthedocs.io/en/latest/api.html.

Com a nasapy, é possível acompanhar trajetórias de cometas, satélites, asteroides, exoplanetas, sondas espaciais e fireballs (pequenos meteoros que reentram na atmosfera terrestre). Muitos desses dados são alimentados pelo centro mundial de monitoramento de possíveis impactos de asteroides e previsão sobre energia de impacto, chamado de CNEOS. A página de acesso do CNEOS é: https://cneos.jpl.nasa.gov/.

11.2  FIREBALLS – BOLAS DE FOGO NO CÉU NOTURNO

Muitas vezes, quando éramos crianças, olhando para o céu noturno, observávamos luzes que cruzavam diante dos olhos. Rapidamente, algum adulto dizia que era uma “estrela cadente” e que as crianças deveriam fazer um pedido. Essas estrelas, na verdade, eram meteoros ou meteoritos que reentravam na atmosfera terrestre. Com a Pandas, usando a biblioteca nasapy, é possível armazenar os dados diários de impactos observados pelos astrônomos para analisarmos as estatísticas dos eventos. Para se ver a localização no mapa-múndi, pelo menos uma das muitas bibliotecas de mapas precisará ser instalada antes, assim como foi feito com a nasapy. Neste capítulo, vamos usar a biblioteca “geopandas”, que pode ser instalada no console do Spyder (ou qualquer outro ambiente de programação) usando o PIP:

pip install geopandas

Essa biblioteca fornecerá o mapa-múndi com as localizações das quedas dos fireballs. O leitor deverá ter atenção, pois essa biblioteca geopandas está em constante atualização de seus mapas de localização. Antes de rodar o script desta seção, terá que verificar se a pasta “datasets” da geopandas instalada, contempla os mapas utilizados pelos programas em Python que estarão disponíveis a seguir. Caso não tenha o cenário de mapa-múndi para os scripts a seguir, o leitor terá que adaptar o programa para a nova versão da geopandas.

Vamos buscar os fireballs que reentraram na atmosfera terrestre no período de 1/1/2021 até 31/12/2023. O primeiro passo é baixar os dados usando a nasapy:

df=nasapy.fireballs(date_min=’2021-01-01’, date_max=’2023-12-31’, return_df=True)

Quando baixamos os dados, nos deparamos de imediato um problema sério que precisa ser corrigido. As coordenadas estão separadas em Norte (N), Sul (S), Leste (E) e oeste (W). Mas, na geopandas, longitudes a oeste de Greenwich são negativas e latitudes abaixo do Equador também são negativas. Se colocarmos os dados como eles são adquiridos, os pontos ficarão sempre concentrados a leste e a norte.

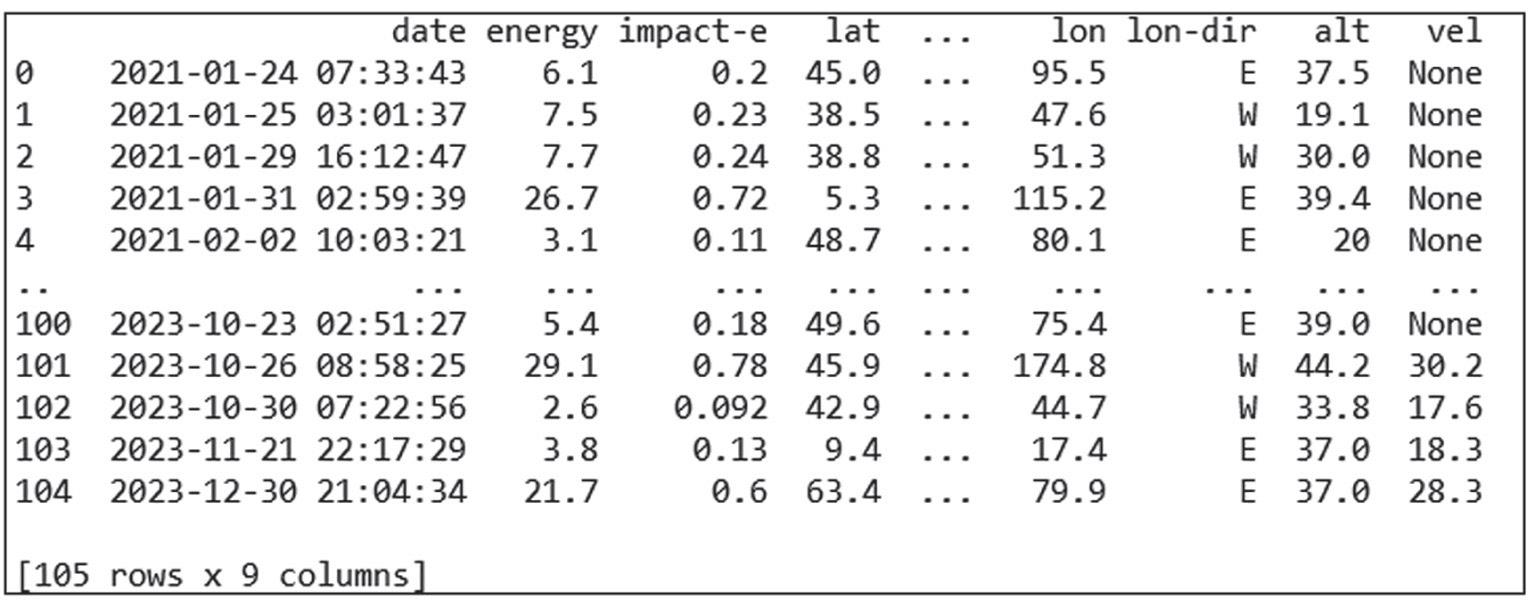
Como esses dados estão em DataFrame, podemos usar a estrutura vista anteriormente da função lambda. Ela será muito útil para separar e colocar sinais positivos e negativos, dependendo do meridiano. Antes, temos ainda outro problema. Os dados de latitude e longitude estão como texto, e precisamos transformá-los em números com ponto flutuante. Então, latitude, longitude e energia dos fireballs podem ser adaptados com função astype(float):

df[‘lat’] = df[‘lat’].astype(float)

df[‘lon’] = df[‘lon’].astype(float)

df[‘energy’] = df[‘energy’].astype(float)

Para a latitude do DataFrame, temos uma coluna “lat” e “lat-dir” (direção norte ou sul). Podemos programar a função lambda da seguinte maneira e colocar esse resultado em uma nova coluna que chamaremos de “latitude” no DataFrame:

df[‘latitude’]=df[ [‘lat’,’lat-dir’] ].apply(lambda x: -x[‘lat’] if x[‘lat-dir’]==’S’ else x[‘lat’], axis=1)

A programação pergunta para o DataFrame em duas colunas, o que torna essa forma de condução interessante. Tomando [ [‘lat’, ‘lat-dir’] ], indicamos que a função Lambda deverá olhar para as duas colunas e separar com “if” quem se tornará positivo e quem será negativo.

Ao usar o “apply”, se ‘lat-dir’ estiver com Sul (S), a coluna ‘lat’ deverá mudar de sinal e ficar negativa. Caso contrário, permanecerá como está.

Isso resolve nosso problema com a latitude. Mas e a longitude? Programamos a linha da mesma maneira na qual a coluna “lon-dir” indica a direção Leste (E) ou Oeste (W):

df[‘longitude’]=df[ [‘lon’,’lon-dir’] ].apply(lambda x: -x[‘lon’] if x[‘lon-dir’]==’W’ else x[‘lon’],axis=1)

Agora, precisamos transformar as coordenadas (latitude, longitude) em pontos do mapa da geopandas. As coordenadas são transformadas e salvas na variável “gdf”, usando o comando:

gdf = geopandas.GeoDataFrame(  df, geometry=geopandas.points_from_xy(df.longitude, df.latitude))

E, logo em seguida, criamos o mapa-múndi, importando o arquivo da biblioteca geopandas. Nesse caso, chamamos a variável que será plotada de “Mundo”.

Mundo = geopandas.read_file(geopandas.datasets.get_path(‘naturalearth_lowres’))

Para plotar o mapa e os pontos, agora, fica mais fácil, pois basta usar o comando plot da biblioteca matplotlib.pyplot:

ax = Mundo.plot(color=’white’, edgecolor=’black’)

gdf.plot(ax=ax, color=’red’)

CAPÍTULO 12 O ambiente Jupyter

12.1 CONHECENDO O AMBIENTE DE PROGRAMAÇÃO

O ambiente Jupyter de programação em Python possui muitas versões e está presente em diversas plataformas, online ou não, com uma lógica diferente de funcionamento. No Jupyter, a programação se dá em células, de forma estruturada e segmentada para cada parte do programa.

Caberá ao programador reconhecer partes importantes do programa que podem ficar juntas e outras partes que podem ser programadas separadamente. No Google, por exemplo, com uma conta particular, é possível usar um ambiente colaborativo, conhecido como Colab e que fica localizado na nuvem do Google, permitindo que os programas sejam rodados em qualquer lugar e em qualquer computador.

A Figura 12.1 apresenta a tela inicial do Colab do Google, com os retângulos representando as células nas quais partes do programa serão programadas.

Outro ambiente muito utilizado é o do Jupyter, mesmo tipo de ambiente do Colab, mas que está no software do Anaconda. Nos capítulos anteriores, desenvolvemos todos os algoritmos no editor de texto e no console do Spyder.

O Spyder é também ambiente de programação em Python, mas utiliza de maneira tradicional e clássica linhas corridas e precisa de comando print no console para se ver soluções, resultados temporários, ou mesmo apenas para acompanhar erros que estão atrapalhando a execução.

Programas no Jupyter se chamam “notebook” e podem ser importados ou iniciados em branco dentro da aba “New”, como visto na Figura 12.2.

Ao clicarmos em “New”, podemos criar um programa no formato do Jupyter, que terá como extensão *.ipynb, enquanto os programas em Python são salvos com extensão *.py. Na Figura 12.3, a tecla de início dá a possibilidade de se começar um programa em Python 3 (outras versões mais recentes terão outros nomes) em arquivo de texto (Text File), pastas novas para salvar programas (Folder), ou mesmo de se abrirem novos terminais de conexões para programações (Terminal).

Quando se clica em novo programa em Python, o nome dele aparece com “Untitled”, esperando para a programação na primeira linha, chamada de “In[ ]”. As abas File, Edit, View etc. têm as mesmas funções do Python em programação no editor de texto. Na Figura 12.4, é possível se observar a linha em branco esperando as primeiras anotações de um programa. Em versões mais recentes (por exemplo, IPython 8.25.0) a aba de abertura para novos programas aparece com o nome “notebook”, que deverá ser clicada para se abrir a mesma caixa apresentada na Figura 12.4.

Para se nomear um programa no Jupyter, ou renomear um já existente, basta clicar em cima da palavra “Untitled”, que abrirá uma tela à espera de um nome para o programa que está sendo construído, como visto na Figura 12.5. Em cima do retângulo com o nome “Untitled”, coloca-se um nome desejado e clica-se no botão “Rename”.

12.2 PRIMEIROS PROGRAMAS EM JUPYTER

Da mesma forma como fazemos no editor de texto dos programas em Python, começamos normalmente (mas isso não é uma obrigação) colocando as bibliotecas que serão importadas. Por exemplo, vamos supor que desejamos fazer um gráfico de um array no qual se tenha um vetor x e com ele se construa a função fx xx 2 2

Sabemos a partir dos capítulos introdutórios que precisaremos da biblioteca NumPy e da biblioteca matplotlib.pyplot para o gráfico. Então, na primeira célula em branco do Jupyter, colocamos nossas bibliotecas, como visto na Figura 12.6. Como passar para a próxima linha?

No ambiente Jupyter, para que ele aceite a linha e salve na memória os passos da programação, precisaremos clicar em “Shift + Enter” a fim de que o programa comece a executar os comandos. Se o usuário apenas clicar em “Enter”, as células abrirão mais espaço em branco abaixo, dentro da própria célula, não criando outra linha de programação.

“O diabo mora nos detalhes”, frase atribuída a Nietzsche, é dita sempre que algo dá errado. Quando programamos códigos no computador estamos sujeitos a erros que, a princípio, não deveriam ocorrer. Tragédias, em boa parte, ocorrem por descuido ou detalhes quase imperceptíveis.

Após anos de programação e a vivência de muitos erros em códigos, neste livro o autor buscou apresentar programas em linguagem Python que podem levar a erros quando se trabalha com dados não estruturados. Erros de programação, erros de lógica, erros de comandos e chamadas de bibliotecas que mudaram de configuração são disponibilizados no texto como alertas de erros. Soluções são apresentadas via biblioteca Pandas do Python. A obra oferece abordagens computacionais para iniciantes e amantes do assunto, com códigos em Python.