
1-fas växelströmslära
j - komplexa - metoden Mätuppgifter
Innehåll
Multimetern ........ ...................................3
Allmänt om användning och inställning
Resis ansmätning ......... ...4
Begreppet resistans, färgkod, standardvärden, potentiometern, resistansmätning
Spänning och spänningsmätning ..........5
Begreppet spänning, batterier, spänningmätning
Spänningsaggregat ...............................6
Allmänt om användning och inställning
Ledningsresistans .................................7
Ledare, isolatorer, resistivitet, temperaturberoende
Ström och strömmätning .......................9
Strömbegreppet, strömriktning, strömmätning
Ohms lag ..............................................10
Referenspilar, beteckningar, Ohms lag, enheter, I / U-grafer
Seriekretsar .........................................13
Seriekopplade resistorer, ersättningsresistans
Spänningsdelning ................................15
Delspänningar, justerbara spänningsdelare
Parallellkretsar ....................................17
Strömmar i parallellkretsar, Kirchhoffs strömlag, spänning över parallellkretsar
Resistans i parallellkretar ....................19
Ersättningsresistans, specialfall
Blandade serie och parallellkretsar.......21
Totalresistans, strömmar och delspänningar
Kirchhoffs spänningslag ......................23
Kirchhoffs spänningslag, serieslinga, parallellslinga och blandade slingor
Belastningseffekter .............................26
Allmänt om belastning, belastning vid spänningsmätning
Energi och effekt .................................28
Energi, effekt, gränsvärden
Spänningskällor ...................................30
Ideala och verkliga spänningskällor, kortslutning, inre resistans, emk, belastningens inverkan, serie- och parallellkopplade spänningskällor
Innehåll
Effektanpassning .................................33
Effektmätning, anpassning
Bryggkopplingar .................................35
Allmänt om användning, balanserad brygga, brygg-matematik-steg-för-steg
Superposition ......................................36
Superpositionssatsen och dess användning
Tvåpolssatsen .....................................37 Tvåpolssatsen, mätning av tvåpolsspänningen och tvåpolsresistansen
Magnetiska grundbegrepp ...................38 Permanentmagneter, fältlinjer, fältbilder, elektromagnetism, den magnetiska kretsen, elektriska - magnetiska likheter
Induktion ..............................................40
Inducerad emk, transformatorprincipen, induktans, motemk, generatorprincipen
Reläer och reläkopplingar ....................42 Funktion, reläsymbolen, användning av reläer, huvud- och styrkrets
Oscilloskop .........................................43 Oscilloskopets ritfunktion, X- och Y-avlänkning, oscilloskopets kontroller
Funktionsgeneratorn ............................44
Typisk funktionsgenerator, periodisk växelspänning, inställningar
Kondensatorn ......................................45 Kapacitans, märkning, RC-kretsars upp- och urladdning, tidskonstant
Växelspänning ....................................50
Generering av växelspänning, visar- och vågdiagram, polaritet och strömriktning, definitioner, växelström i resistiva kretsar, mätvärden
Vektorräkning .54 Vektorräkning - mätövning
Kapacitiv reaktans ......... ......................58
Kapacitiv reaktans, Ohms lag för växelström, mätning av XC, seriekopplade kondensatorer, kapacitiv spänningsdelning, parallellkopplade kondensatorer, kapacitiv strömgrening
Induktiv reaktans .................................61
Induktiv reaktans, lindningsresistans, impedans, mätning av XL och L , seriekopplade induktanser, parallellkopplade induktanser
Innehåll
RL - & RC - seriekretsar .......................64
Ideal och verklig induktans, spänningsdelning i RL-kretsen, visardiagram, spännings- och impedanstriangel, fasförskjutning, spänningsdelning i RC-kretsen, fasvinkeln
RC - & RL - parallellkretsar .................67
Impedans i parallell RC-krets, fasförskjutning, parallellkrets med ideal och verklig induktans
Serieresonanskretsem...........................71
Serieresonanskretsen, visardiagram, induktiv, kapacitiv och resistiv krets, resonansfrekvens
Faskompensering av induktiv last .......74
Faskompensering,
Parallellresonans ..................................77
Parallellresonans, impedans vid resonans, impedansens frekvensberoende
Effektutveckling i växelströmskretsar ..79
Effektkurvor, effekt i seriekretsar, skenbar effekt, aktiv effekt, reaktiv effekt, effektsambanden, effekttriangeln, effektfaktorn, effekt i parallellkretsar, addering av effekter
Transformatorn ....................................84
Transformatorns spännings- och strömomsättning, förluster, impedanstransformering
Facit till Testa-dig-själv-uppgifter............86
Imaginära - Komplexa -tal .....................94
Imaginära tal, allmänt om komplexa tal, trigonometrisk form, polär form, exponentiell form, addition, subtraktion, multiplikation, division, sammanfattning, testa-dig-själv-uppgifter
j Komplexa-metoden ......................98
Komplexa kretsberäkningar, impedans i serikretsar, benämningen j -metoden, ström och spänning i seriekretsar, impedans och ström i parallellkretsar, komplexa effektberäkningar, sammanfattning, testa-dig-själv-uppgifter
Facit till imaginära - komplexa - tal ....103
Facit till j Komplexa-metoden .......104
Mätövningar ........................................105
Allmänt, mätrapport, rekommenderade mätuppgifter, hur man mäter
Inledningsvis
....
Läroboken omfattar lik- och växelströmslära, komplexa tal, komplexa metoden,ochförslagtilllaborationer.
I de 6 första avsnitten introduceras ämnesbegrepp och vokabulär med ett minimum av matematik, medan det i övriga avsnitt ingår beräkningar medsteg-för-steg-löstaexempel
Viktiga satser, ord och meningar är kursiverade och ibland under struknaför att visa deras betydelse så att begreppsbildningen underlättas.
Det är t ex vanligt att man i början av elstudier blandar samman orden över och genom när man talar om spänning och ström vilket försvårar ett korrekt eltänkande.
Spänning finns över komponenter eller mellan två punkter medan ström flyter genom komponenter.
Fö fattarenrekommenderarattmanlärsigdekursivtskrivnasatsernai kombinationmednoggrannagenomgångaravvisadeberäkningsexempel.
Vidare rekommenderas att faktatexten verifieras med laborationer enligt de förslag som finns i slutet av läroboken alternativt med de mer tillrättalagda mätövningarna i Mätuppgifter Ellära grund och 1-fasväxelström
Revma Utbildning
www.revma.se
Mailkontakt: s-b@revma.se
Författare: Sven-Bertil Kronkvist
Illustratör: Sven-Bertil kronkvist
Redaktör: Agneta Kronkvist
Kopieringsförbud.
Detta verkärskyddatavupprättshovslagen! Kopieringutöverläraresrätt att kopieraförundervisningsbrukenligt BONUS-avtal,ärförbjuden.
Den som bryter mot lagen om upphovsrätt kan åtalas av allmän åklagare och dömas till böter eller fängelse i upp till två år samt bli skyldig atterläggaersättningtillupphovsman/rättsinnehavare.
Sven-Bertil Kronkvist ochRevma Utbildning
Ohms lag
Referenspilar & beteckningar
Vid analys och beräkning av mer komplicerade kretsar behöver tanken stödjas med referenspilar och storhetsbeteckningar.
Strömpilen markerar strömmen I, vars riktning alltid är från spänningskällans pluspol mot dess minuspol.
Spänningsfallspilen markerar spänningen U över resistorn. Observera att referenspilen för U har en (+) och en (-) sida och att spänningen faller från ett högre till ett lägre värde i den riktning som strömmen flyter.
Ohms lag
Med beteckningarna i kretsen skrivs Ohms lag matematiskt så här:
Enheter
För att svaret skall erhållas i grundenheten ampére skall den aktuella spänningen anges i volt och resistansen i
Vanliga under och överenheter
1A = 1000mA och 1 000000 A 1V = 1000mV och 1 000000 V 1k (1000 ) och 1M (1000000 )
Exempel på strömberäkning
Beräkna strömmen i kretsen ovan om resistansen är 150 och spänningen över resistorn är 3V.
Exempel på spänningsberäkning
I kretsen här nedan genomflyts resistorn på 100 av en ström på 0,1A. Hur stor är spänningen över resistorn?
Eftersom Ohms lag är ett matematiskt uttryck gäller de vanliga räknereglerna för sambandet mellan I, U och R. Med andra ord kan vilken som helst av de tre storheterna beräknas om värdet på de två andra är kända.
Omforma Ohms lag och gör beräkningen så här:
U I R U 0,1A 100Ω U 10V
Exempel på resistansberäkning
Nedan visas en krets där en spänning på 5V orsakar en ström på 2A genom en resistor. Hur stor resistans har resistorn?
V4,9 R I U R
I/U-grafer
47R
A2,0
I / U-grafer är ett vanligt sätt att åskådliggöra hur strömmen genom en komponent beror av spänningen över den. Nedan till vänster ser vi en elritningen som visar hur strömmen genom en resistor mäts vid olika spänningar, och till höger hur resultate "prickats" in en graf. Lägg märke till att xlar har både stor ets och enhet beteckningar inom parantes.
Beräkna de värden som saknas på strömmar, spänningar och resistanser i följande uppgifter.
Parallellkretsar
Strömmar i parallellkretsar
Från spänningskällans pluspol flyter strömmen
T till punkten A, där den delas i grenströmmarna I1, I2 och I3
Vid punkten B förenas de tre grenströmmarna åter till en ström med samma storlek som IT. Därav den gemensamma beteckningen för strömmen som flyter från respektive till spänningskällan.
Kom ihåg!
Lika stor ström som flyter från en spänningskällas pluspol flyter alltid till dess minuspol.
Eftersom strömmen från och till en spänningskälla alltid är lika stor måste IT vara lika stor som summan av grenströmmarna. Matematiskt uttrycks det så här:
Spänningen över parallellkretsar
Mellan punkterna A och B, som är direkt anslutna till spänningskällans plus- och minuspol, finns spänningen U . Eftersom alla tre resistorerna R1, R2 och R3 är anslutna mellan A och B finns samma spänning över var och en av resistorerna.
Observera att fokus är på strömmarna som flyter till och från grenpunkterna, inte vad som orsakat strömmarna eller deras storlek.
Detta är karakteristiskt för alla parallellkretsar:
Spänningen är lika stor över alla grenar i en parallellkoppling.
Exempel
Beräkna totalströmmen och respektive grenström med angivna spännings- och resistorvärden för kretsen ovan: I U R IA 1 1 1 12 1000 0012 , I U R IA 2 2 2 12 1200 0010 , I U R IA 3 3 3 12 1800 00067 ,
Totalströmmen till grenpunkt A och från grenpunkt B.
Den allmänna regel som formulerats ur detta resonemang är känd som Kirchhoffs strömlag
Summa strömmar som flyter till en grenpunkt är lika med summa ström mar som flyter från grenpunkten.
Resistans i parallellkretsar
Ersättningsresistans
De parallellkopplade resistorerna R1, R2 och R3 kan bytas mot en ersättningsresistor RP
För att spänningen U och strömmen IT ska vara exakt lika stora måste RP vara lika stor som de parallellkopplade resistorernas totala resistans mellan grenpunkterna A och B. Det finns tre bra sätt att ta reda på värdet
Resistansmätning mellan grenpunkterna A & B.
Volt-amperemetoden, dvs att strömmen IT och spänningen U mäts varefter ersättningsresistansen RP beräknas med Ohms lag.
Bryt ut U I U R U R U R T 123 IU RRR T 111 123
Dividera båda leden med U I URRR T 111 123
Eftersom R U I P T gäller också att 1 R I U P T
Därav följer att I U T kan bytas mot 1 R P
1 1 1 123 RRRR P
Vanligt specialfall: två parallella resistorer
Matematiskt. Tänk så här:
Grenströmmarna beräknas med Ohms lag I U R 1 1 I U R 2 2 I U R 3 3
Totalströmmen IT är summan av grenströmmarna I I I I T 1 2 3
Byt ut I1 , I2 och I3 mot U R 1 ; U R 2 ; U R 3 I U R U R U R T 123
Ersättningsresistansen för parallellkopplade resistorer är alltid mindre än den minsta av de ingående resistorernas värde. R U I P T U
P
Mgn i högerledet är R1 R2
Invertera och skriv talen med stigande index.
R R R RR P 12 12
Regel
Energi och effekt
Elektrisk energi
När det under en viss tid flyter en ström mellan två punkter, under inverkan av spänningen mellan punkterna, uträttas ett arbete.
Den energi som åtgår för detta arbete beräknas på följande sätt
W U I t
W = energin i Ws (wattsekund)
U = spänningen i V
I = strömmen i A
t = tiden i s (sekunder)
Exempel
Lampan i är ansluten i 2 timmar till en spänning på 15V och drar då en ström på 1,5A. Hur mycket energi åtgår för att lampan ska lysa under de två timmarna.
3600 2 1,515 W
16200Ws W
Effekt
Den takt varmed energi omsätts kallas effektförbrukning, effektuttag eller helt kort effekt. Är den totala energin som förbrukats under en viss tid känd kan effekten beräknas så här
P W t
P = effekten i W (watt)
W = totala energiförbrukning (Ws eller Wh) t = tiden för energiförbrukningen (s eller h)
Observera dubbelbetydelsen av bokstaven W, som både betecknar storheten energi och enheten watt.
Eftersom (W U I t ) kan (U I t) ersätta W i energiformeln ( t ) förkortas bort:
P W t U I t t UI
P U I
Tre sätt att beräkna effekt
En resistor som genomflyts av ström orsakar ett spänningsfall som enligt Ohms lag är:
U I R och strömmen I U R
Den energi som behövs för strömtransporten i varje ögonblick, dvs den effekt som krävs, beräknas enligt:
P U I
Eftersom U I R kan U ersättas med I R
U I R P U I P I R I
P = I2 R
På samma sätt gäller följande resonemang:
Då I U R kan (I) ersättas med U R
I U R PUIPU U R
P U R 2
Gränsvärden
Resistorer och andra komponenter tillverkas med olika effekttålighet. Överskrids den högsta tillåtna effektutvecklingen kan den aktuella komponenten gå sönder.
Spänningskällor
Ideala och verkliga spänningskällor
När du hör ordet spänningskällor tänker du säkert på batterier och spänningsaggregat, men även mikrofoner och TV-antenner är exempel på spänningskällor med emk och inre resistans.
Ideala spänningskällor
pänningskällor pol spänning UP är oberoende av belastnings strömmen IL existerar bara i teorin.
Bestämning av inre resistansen
Ri kan inte mätas genom direkt ohm mätning utan måste beräknas. et nödvändigt att veta emk:n och polspänningen vid en känd belastningsström.
Ideal spänningskälla med konstant polspänning
Verkliga spänningskällor
Verkliga spänningskällor beter sig som om de har en inre resistans Ri i serie med en emk E med konstant spänning.
Mätning av emk
Polspänningen är lika om ingen belastningsström dras från spänningskällan och nästan lika med emk:n då belastningen endast är en multimeters mätström
Verklig spänningskälla med inre resistans Ri
Den inre resistansen orsakar spänningsfall och förlusteffekt i spänningskällan.
Kortslutning, vad är det?
Kopplas en belastning på 0 eller nära 0 mellan en spänningskällas plus- och minuspoler kallas det kortslutning. Det enda som då begränsar strömmen är den inre resistansen.
Ui = IL Ri Ui = 0, 000 050 1 = 50 V UP = E-Ui UP =1,5-0, 000050 =1,49995V
Belastningens inverkan
Med större strömuttag ökar det inre spänningsfallet Ui samtidigt som polspänningen UP minskar lika mycket. Summan av Ui och polspänningen UP är alltid lika med emk:n E.
Polspänningens beroende av belastningsströmmen
Bryggkopplingar
Allmänt
Bryggkopplingar används när det krävs noggrannare resistansmätning än vad som kan göras med en multimeters ohmmeterfunktion.
I sin enklaste form består en bryggkoppling av två parallella seriekretsar med två resistorer i varje gren .
Brygg-matematik-steg-för-steg För bryggan här intill gäller följande samband:
U1 = I1 R1 U2 = I2 R2
U3 = I3 R3 UX = IX RX
Vidare ser vi att U1 + U2 = U3 + UX
Justeras R3 så att U1 = U3 följer att U2 = UX , dvs
I1 R1 = I3 R3 och I2 R2 = IX RX
vilket kan omformas till
Den resistor RX som skall mätas ansluts i grenen med den justerbara resistorn R3.
När bryggan är i balans är U2 = UX. Det finns då ingen spänning över -amperemetern och följaktligen flyter det ingen ström genom den. Det värde som den justerbara resistorn har mot svarar den undersökta resistorns ohmvärde. Försedd med en skala kan detta då avläsas.
Andra användningssätt
Kopplas en sistor i en av bryggrenarna ändrar sig spänningen mellan A och B på . Med en kalibrerad skala är bryggan då en
Eftersom ingen ström flyter mellan A och B när bryggan är balanserad gäller att I1 = I2 och I3 = IX
I3 kan därför bytas mot IX liksom I2 mot I1
Eftersom vänsterleden nu är lika i de båda ekvationerna , är också högerleden det.
Ur ovanstående likhet löser vi RX
Den sökta resistansen RX är följaktligen en konstant (k = R2 / R1) multiplicerad med värdet hos R3
RkR
Superposition
Superpositionssatsen
I krets med flera spänningskällor kan ström men i en gren erhållas som summan av de strömmar som varje emk orsaka , om övriga spänningskällornas emk:er tänkes kortslutna.
Förklaring
I kretsar med resistanser kan grenströmmarna beräknas för varje spänningskälla när de övriga spänningskällornas emk:er, men inte deras inre resistanser, tänkes kortslutna.
Är spänningskällornas inre resistanser mycket små i förhållande till kretsens övriga resistanser kan de dock försummas.
Den sökta grenströmmen är summan av de grenströmmar som varje enskild spänningskälla orsakar i kretsen. Observera att strömmarna skall summeras med sina tecken. Det innebär att om alla strömmar som flyter åt ett håll anges som positiva ska de som flyter åt motsatt håll anges som negativa.
Exempel
Vi vill beräkna den markerade strömmen som antas flyta i den angivna referensriktningen.
I nästa steg beräknas den ström som 6V-källan orsakar om 9V-källans emk tänkes kortsluten.
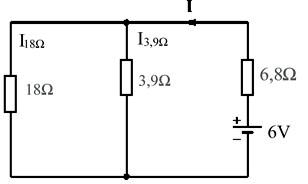
Ritar man om kretsen blir det tydligt att 3,9 och 18 är parallellkopplade och att det är I3,9 som ska beräknas.
Först beräknar vi därför strömmen I6V från 6Vbatteriet, följt av spänningen UP över parallellkombinationen 3,9 och 18 och slutligen I3,9
Börja med att beräkna den ström som 9V-källan orsakar om 6V-källans emk tänkes kortsluten.
Kretsen ser då ut som visas nedan och strömmen kan beräknas med Ohms lag.
De beräknade strömmarna summeras
Strömmen från 9V:s-källan överväger. Följaktligen flyter strömmen som antagits. Hade strömmen från 6V:s-källan övervägt hade strömriktningen varit motsatt.
Tvåpolssatsen
Tvåpolssatsen är ett mycket användbart analysverktyg inom eltekniken. Finessen består i att komplicerade linjära nätverk kan ersättas av en enkel seriekrets med en emk och en resistans.
Tvåpolssatsen
Tvåpolens ersättningsemk, är lika med spänningen som återfinns i originalkretsen mellan belastningens anslutningspunkter, då lasten är urkopplad.
Tvåpolens ersättningsresistans, är den totala resistans som kan ses i originalkretsen från belastningens anslutningspunkter, då alla emk:er tänkes kortslutna.
Exempel
Beräkna ersättningsemk:n ETP och ersättningsresistansen RTP för kretsen nedan med avseende på belastningen mellan punkterna A och B.
Resistansen i ersättningskretsen beräknas då originalkretsens emk tänkes kortsluten eller ersatts med en kopplingssladd.
Ersättningsemk:n ETP är lika med spänningen mellan belastningens anslutningspunkter A och B då belastningen RL tänkes urkopplad
TP 1001882 100 18 82 50
Den slutliga ersättningskretsen ser ut så här
TP 20 18 100 82 10010
Mätning av tvåpolsspänningen
Börja med att koppla loss belastningen RL från anslutningspunkterna A och B. Mät därefter spänningen mellan anslutningspunkterna med en multimeter. Den avlästa spänningen är den sökta ersättningsspänningen förutsatt att multimeterns mätström är liten och kan försummas.
Mätning av tvåpolsresistansen
Koppla bort alla spänningskällor och ersätt dem med en kopplingssladd. Mät därefter resistansen mellan belastningens anslutningspunkter då RL avlägsnats. Det avlästa värdet är ersättningskretsens resistans. Förutsättningen är dock att spänningskällornas inre resistanser kan försummas jämfört med övriga resistanser i kretsen.
Induktion
I en spole som omsluter ett flöde, vilket ändrar storlek, riktning eller båda, induceras (alstras) en emk, dvs en spänning.
Den inducerade emk:n har alltid en sådan riktning, att orsaken till dess uppkomst motver kas
Så länge magneten är stilla förblir voltmeterutslaget noll. Förflyttas magneten erhålls däremot ett visarutslag, det induceras en emk i spolen. Lägg märke till polaritetsändringen vid växande och avtagande flöde.
flöde
Exempel
Hur stor är den inducerade spänningen i en spole med 50 varv, om flödet som spolen omsluter ändrar sig från 2 till 4 Vs på 2s. = 4 - 2 = 2Vs t = 2s
Transformatorprincipen
Transformatorn består av två lindningar på samma järnkärna.
Växande flöde
Noggranna experiment visar att den inducerade emk:n i ett lindningsvarv är proportionell mot ändringen i det av spolen omslutna flödet.
e t e = den inducerade emk:n = flödesändring t = tiden flödesförändringen pågår t = hastigheten i flödesändringen
I en spole med N varv, seriekopplas emk:erna i varje varv med varandra.
eN t
Då primärlindningen N1 påföres en varierande spänning orsakar det en varierande ström i lindningen (här genom att R1 :s resistans ändras, annars med växelspänning) som orsakar ett va i järnkärnan.
Det varierande flödet i transformatorns järnkärna orsakar en emk i sekundärlindningen N2
Ingår N2 som en del i en sluten krets driver emk:n ström I2 som i sin tur orsakar ett flöde 2 om försöker motverka flödesändringarna.
Även N1 omsluter det flöde som förändras i järnkärnan. I spolen induceras därvid en emk med motsatt riktning mot den påtryckta spän ningen.
Storleken på den inducerade motemk:n beror på hastigheten i flödesändringen och antalet lindningsvarv
Växelspänning
Växelströmsgeneratorn
Distributionsnätets sinusformade spänning produceras med hjälp av generatorer som beskrivits i avsnittet Induktion under rubriken Generatorprincipen.
Polaritet och strömriktning
Bilden visar generatorspänningens polaritet och strömriktningen under ett rotorvarv vid positiv respektive negativ halvperiod
Visar- och vågdiagram
Storleken och polariteten på den sinusformade spänningen som induceras under ett rotorvarv kan åskådliggöras med visar- och vågdiagram. Den roterande visaren û motsvarar växelspänningens toppvärdet och u det momentana spänningsvärdet vid varje rota tionsvinkel . Förenklade visardiagram ritas i överensstämmelse med bilden till höger.
Lägg märke till hur spänning och ström ökar från noll till ett positivt toppvärde och därefter åter minskar till noll efter ett halvt rotorvarv. Här ändrar spänningen polaritet och strömmen riktning. Båda går mot ett negativt toppvärde innan de åter ökar mot noll och förloppet upprepas.
Förenklat visardiagram
Övergång mellan visar- och vågdiagram
Vektorräkning
Vid beräkningar på växelströmskretsar är det för delaktigt att k nna vektorräkning eftersom växelspänningar, växelströmmar och växelströmsmotstånd är fria vektorstorheter
Dessa kännetecknas av att de har både storlek och riktning och att de kan representeras grafiskt av en pil med lämplig längd och riktning, t ex som spännings- och strömvisare i visardiagram.
Exempel
Vågdiagrammet visar två växelspänningar, u1 med toppvärdet 3V och u2 vars toppvärde är 2,2V och ligger 60º efter u1. De representeras i visardiagrammet av var sin visare på 30 respektive 22 mm.
För att markera att det rör sig om vektorstorheter brukar de markeras med ett överliggande streck, så att man inte glömmer att de har både storlek och riktning.
Fria vektorstorheter kan flyttas om deras längd och riktning bibehålles. Det blir därför samma resultat om man flyttar ”svansen” på u2 till spetsen på u1 och därefter ritar resultanten mellan rotationspunkten och spetsen på u2 enligt följande bild.
Den stora fördelen med vektorberäkning är att den kan göras grafiskt, dvs man kan rita fram ganska komplicerade matematiska lösningar på ett enkelt sätt. Ska man t ex addera spänningars toppvärden måste det göras med hänsyn till deras faslägen (riktningar).
Exempel
Addera u1 och u2 i föregående exempel.
Rita två hjälplinjer, en från spetsen på u1 parallellt med u2 och en från spetsen av u2 parallellt med u1. Den diagonal som kan ritas i parallellogrammet är resultanten till vektoradditionen av u1 och u2. Mät resultantens längd och fasvinkeln så är den grafiska lösningen färdig.
Uppdelning av vektorer
Ibland är det nödvändigt att dela upp vektorer i horisontella och vertikala komposanter, t ex vid vektoraddering av effekter. Uppdelningen kan göras helt grafisk eller grafiskt med inslag av trigonometri.
Exempel
Gör en grafisk uppdelning av de två vektorerna S1 och S2 i vertikala och horisontala komposanter.
RL - & RC - seriekretsar
Sammanfattning
Lär sammanfattningen utantill! Den är mycket viktig för växelströmstänkande.
Resistans: spänningen över en resistor är i fas med strömmen som flyter genom resistorn.
Kapacitans: spänningen över en kapacitans ligger 90° efter strömmen.
Exempel
Beräkna UL och UR för en verklig induktansspole om L = 1,59H, R = 1000 Den pålagda växelspänning är 10V med f = 100Hz. Rita också ett visardiagram.
1.Reaktansen XL
XfLXLL221000159999 ,
2.Totala impedansen Z
ZRXZ L 22 22 10009991414
3.Strömmen genom kretsen I U Z I U RX ImA L 22 10 1414 0707 ,
4.Delspänningarnas storlek
Ideal induktans utan ledningsresistans: spänningen ligger 90° före strömmen.
Verklig induktans med ledningsresistans: spänningen är mindre än 90° före strömmen på grund av att spolen har lindningsresistans.
Uppritning av visardiagrammet
RL - & RC - seriekretsar
Spännings- & impedanstriangel
Låt oss införa U = I Z, UR = I R och UL = I XL i spänningstriangeln och ställa upp Pythagoras sats med referens till dessa likheter.
1.Reaktansen X fC C 1 2 X C 1 216000110 995 6 ,
2.Totala impedansen ZRX c 22 Z 1200 995 1559 22
ZRX L 222
ZRX L 22
De två sista utvecklingsleden visar att impedans, resistans och reaktans har ett inbördes förhållande som kan representeras med en impedanstriangel.
Spänningstriangeln: tan U U L R Impedanstriangeln: tan X R L
Fasförskjutningsvinkeln kan därmed beräknas både med utgångspunkt i spännings- och impedanstriangeln som visas ovan.
Seriekrets med R och C
ZRX C 22
Exempel
Beräkna delspänningarna UR och UC samt fasvinkeln om U=5V, f =1600Hz, R= 1200 och C=0,1 F. Rita också en spänningstriangel som visar fasförskjutningen och storleksförhållandet mellan spänningarna.
3.Strömmen genom kretsen I U Z ImA 5 1559 32 ,
4.Delspänningarna U I R U mA V UIXUmAV RR C C C 3 2 1200 3 8 3299532 , , ,,
5.Fasvinkeln 8292,0 1200 995 tan R X tan C =39,7°
6. Uppritning av visardiagrammet
Faskompensering av induktiv belastning
Faskompensering
Med faskompensering menas att matningsströmmen till en induktiv belastning minimeras och bringas i fas med matningsspänningen.
Faskompenseringen görs genom att en kondensator med lämpligt värde kopplas parallellt med den induktiva belastningen. Vid beräkning av kondensatorvärdet delas den induktiva grenströmmen upp i en vertikal- och en horisontal komposant. För fullständig faskompensering ska den kapacitiva grenströmmen vara lika stor som den induktiva grenströmmens vertikalkomposant.
Matningsströmmen I är lika med visarsumman av grenströmmarna IC och IS. För att kunna addera IC till IS delas IS upp i en horisontell komposant, ISH , och en vertikal komposant, ISV. Det går både att "rita fram" och beräkna lösningen.
De båda grenströmmarna IC och IS beräknas med Ohms lag
IC är fasförskjuten 90° före matningsspänningen medan den induktiva grenströmmen IS är fasförskjuten någonstans mellan 0° och 90° efter matningsspänningen enligt:
Antag att: IC =18mA med 90° fasförskjutning före matningsspänningen U, IS = 23mA och fasförskjuten S = 70° efter U. Ett visardiagram som motsvarar dessa förutsättningar ser ut så här:
Efter visarsubtraktionen bildas en ny triangel med kateterna (ISV-IC) och ISH . Ur denna triangel går det att beräkna den ogrenade matningsströmmen I med Pythagoras sats:
(ISV-IC ) = (21,6 - 18) = 3,6mA ISH = 7,9mA
Faskompensering av induktiv belastning
Fullständig faskompensering innebär att vid en given frekvens anpassa kondensatorvärdet så att den kapacitiva grenströmmen IC blir lika stor som ISV. Matningsströmmen IZ kommer då att ligga i fas med matningsspänningen U.
Kapacitiva grenströmmen IC beräknas ur likheten IC = ISV. När IC är känt ger Ohms lag besked om värdet på XC, ur vilket kondensatorvärdet för fullständig faskompensering kan beräknas.
Ur likheten IC = ISV kan ett uttryck härledas för beräkning av kapacitansvärdet för full faskompensering direkt ur den induktiva grenens induktans och resistansvärden.
Exempel
Beräkna kondensatorvärdet för full faskompensering av kretsen ovan. Matningsströmmen I IS nnan kondensatorn kopplats in.
Sin S beräknas ur den induktiva grenens impedanstriangel sin S L L
Inför uttrycket för (sin S ) i likheten överst:
tan S= 16,98 motsvarar vinkeln S= 86,63°
Induktiva grenströmmens vertikalkomposant ISV XC beräknas med ISV eftersom IC = ISV
Exempel
Beräkna kondensatorvärdet för full faskompensering av kretsen ovan. Beräkna också matningsströmmen efter kompenseringengen.
Matningsströmmen IZ = ISH = IS . cos S vid fullständig faskompensering
I I IA SS cos ,cos,, 03786630022
Jämför med matningsströmmen på 0,37A före kompenseringen. Skillnaden är 0,348A!
Transformatorer
Transformatorn (pedagogisk modell)
Transformatorer består av två eller flera lindningar på en järnkärna av speciell transformatorplåt.
1 som ansluts till primärlindningen N1 orsakar ett varierande magnetflöde i järnkärnan. Flödet inducerar i sin tur en strömbegränsande motemk i N1 som nästan är lika stor som den påtryckta primärspänningen U1 Även i sekundärlindningen N2 induceras en spänning U2 som kan driva ström om det finns en last R2 ansluten.
De inducerade spänningarna är lika stora räknat per varv. Det ger oss följande två likheter:
Impedanstransformering
Hur belastas en spänningskälla av en belastning om denna är ansluten via en transformator på sekundärsidan?
Vidare är tillförd primär- och avgiven sekundäreffekt lika om transformatorns förluster försummas, dvs (P1 = P2). För en sådan tänkt ideal transformator gäller:
Ohms lag
Lös ut U1
Lös ut I1
Primär Sekundär
Genom kombination av likheterna erhålls tre vanliga formler för transformatorns spännings-, varvtals- och strömförhållande.
Hyfsa
Transformatorns förluster Verkliga transformatorer har värmeförluster i lindningarna samt virvelströms-, ommagnetiserings- och magnetiska läckförluster i järnkärnan. På grund av hög verkningsgrad hos transformatorer gäller de matematiska sambanden för ideala transformatorer ändå med god approximation även för verkliga transformatorer.
Exempel
Beräkna först belastningen Z1 som spänningskällan "ser" om Z2=120 , N1=1500 och N2=100 varv och därefter primärströmmen I1 om U1=230V.
- test av transformatorn
Ohm-mäts lindningarna i en transformator indikerar oändlig resistans att det är avbrott i lindningen, medan för litet ohmvärde tyder på kortslutna varv.
Facit -Testa-dig-själv
RL & RC - parallellkretsar
1.a) 95 b) 85 c) 62 d) 37
2.a) 14,9 b) 26,1 c) 37,6 d) 44,0
3.a) IR = 0,12A, IC = 0,038A, IT = 0,13A
b) IR = 0,24A, IC = 0,075A, IT = 0,25A
c) IR = 0,48A, IC = 0,15A, IT = 0,50A
4.a) IR = 0,21A, IL = 0,16A, IT = 0,266A
b) IR = 0,43A, IL = 0,32A, IT = 0,53A
c) IR = 0,85A, IL = 0,64A, IT = 1,1A
5.a) 17,4° b) 17,4° c) 17,4°
6.a) 36,8° b) 36,8°
7.Matningsspänningens storlek har ingen inverkan på fasförskjutningen.
8.a) 17,4° b) 32,1° c) 51,5°
9.a) 71,5° b) 56,3° c) 36,8°
10.Uppgift 8 och 9 visar att fasförskjutningen varierar med frekvensen.
11.a) I220 = 0,22A, IL-grenen = 0,29A
b) IT = 0,41A c) Z = 117 d) = 42,8°
12.a) I470 = 0,051A, IL-grenen = 0,048A
b) IT = 0,093A c) Z = 258 d) = 18,52°
Serieresonans
1.a) 241,3 , b) 497,4 c) 337,6 d) -49,3º
2. Z= U I ellerZRXX 2 LC 2
3.a) 5,1V b) 10,4V c) 4,6V d) 49,3º
4.a) b)
5.fR=45994Hz
6.a) 32,3mA b) 11.2V c) 7,1V d) 11.2V e) 0º
7.
f(kHz) XL( ) XC( ) Z( ) (°) I(mA) 20,0 151
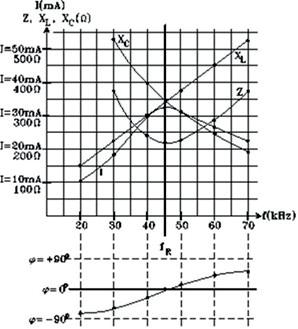
8. 253 pF
Faskompensering 1.IC = 2,6 A, IZ = 1,8 A, = 39º 2. A7,3 C I
528 227 372 53,8 19,1
Grafen finns överst i höger kolumn.
Facit -Testa-dig-själv
3.
4.IZ kan mätas i visardiagrammet till 1,4 A
Skillnaden är 3,9 -1,4 = 2,5 A
5.IZ = 2,82 A och = 66,1º
6. A 6,2º1,66 sin 8,2 C I
7.C = 36 F
8.Matningsströmmen IZ = 1,13 A, = 0º
9.Matningsströmmen blir 5 A
10.120 F
Parallellresonans
1.Parallellresonanskretsens impedans är maximal vid resonansfrekvensen.
2.Vid resonansfrekvensen.
3.Över resonansfrekvensen.
4.Vid resonansfrekvensen.
5.Fasvinkeln är 0º.
6a) fR = 45,9 kHz
b) ZR = 8 k
c) XC = 347
IC = 69,2 mA
7 a) Z S = 347
b) IS = 69,2 mA
c) 87,5º
8a) 0,01 F
b) 9,34 k
c) 2,57 mA
d) 89,4º
9a) 2,56 mA
b) 874 k
c) 0,0274 mA
11.IC och IS är nästan lika stora och motriktade varandra (89,4º 90º ).
Effektutveckling i växelströmskretsar
1) P U I R Q U I X S U I P I R 2 QIX 2 S I Z 2 P U R R 2 Q U X X 2 S U Z 2
2) cos IUP sin IUQ
3) Aktiv och reaktiv effektutveckling i växelströmskretsar är alltid lika med spänningen över de resistiva respektive reaktiva kretsdelarna, multiplicerad med strömmen genom dessa.
4.P = 0,3W, QL = 1,8VAr, QC = 4,5VAr
5.P1 = 279W, P2 = 336W, PZ = 615W
Imaginära-komplexa -tal
Detta avsnitt introducerar begreppen imaginära och komplexa tal med vilka växelströmsberäkningar kan utföras på samma sätt som i likströmsläran. Läsare som redan känner till komplexa beräkningar kan hoppa direkt till nästa avsnitt med växelströmstillämpningar.
Imaginära tal
Från matematiken vet vi att kvadratroten ur ett positivt tal (a), är ett positivt eller negativt tal (en rot) som multiplicerat med sig själv ger talet (a).
Exempel 422 och
Både (+2) och (-2) multiplicerat med sig själv blir lika med 4.
För negativa tal existerar däremot inget tal (rot) som multiplicerat med sig själv blir talet. Inget hindrar oss emellertid från att föreställa (imagin) och använda oss av sådana tal. För detta ändamål används beteckningen j för den imaginära enheten som definieras enligt: j 1
För att algebrans regler ska gälla följer att: j 1 j
Allmänt om komplexa tal
I ett koordinatsystem placeras de reella talen utmed den reella talaxeln och alla de imaginära talen utmed en imaginär talaxel Uttryck som består av ett reellt tal ( a ) och ett imaginärt tal ( jb ) i formen (a + jb) kallas ett komplext tal i rektangulär form. Ett exempel på ett sådant komplext tal är:
+ j3
Det imaginära talet (4 + j3) kan även representeras av absolutbeloppet (längden) för visaren ( Z ) tillsammans med vinkeln ( ). Beteckningen ( Z ) markerar därvid att visaren har såväl storlek som riktning. Visarens storlek betecknas med ett enkelt ( Z ) utan understrykning och beräknas med Pythagoras sats. Vinkeln ( ) är det komplexa talets vinkel eller vinkelargument och beräknas trigonometriskt.
Z 4 3 22 tan 3 4
Då visarlängden ( Z ) och vinkeln ( ) är kända kan ett komplext tal i rektangulär form skrivas i trigonometrisk form på följande sätt:
sin jZ cos Z
Exempel: Omvandla det komplexa talet (3 + j2) från rektangulär till trigonometrisk form.
6,31323Z 22 tan = 0,6667 motsvarar vinkeln 33,7º
6667,0 3 2 tan
º7,33sin6,3º7,33 cos 6,3 sinZ cos Z j j
Grafiskt kan talet åskådliggöras som en punkt P med koordinaterna 4 och j3 i det komplexa talplanet enligt följande bild.
Förkortat kan trigonometrisk form skrivas på ett sätt som kallas polär form
Z cos +j Z sin Z
j - komplexa - metoden
Komplexa kretsberäkningar
Impedans i seriekretsar
Bilden visar en induktiv seriekrets med tillhörande impedanstriangel placerad i det komplexa talplanet.
j-axeln
Re-axeln
Av ovan visade bild framgår att impedansen kan skrivas som ett komplext tal:
Z = R + jXL
På motsvarande sätt kan en kapacitiv serieimpedans tecknas:
Z = R + (- j)XC
C Re-axeln
(-j)-axeln
Benämningen j -metoden
Impedansen definieras därmed som en visare i det komplexa talplanet, med en reell komposant, R ( ), och en imaginär komposant, jXL ( ) respektive (-jXC ), där
XL = 2 f L och XC = 1 2 f C
Vinkelhastigheten ( 2 f ) brukar ofta anges med den grekiska bokstaven omega, ( = 2 f ). Införs detta skrivsätt i de komplexa reaktansuttrycken ser de ut så som följer:
Impedansformlerna får därav ett utseende som j -metoden.
Z = R + jXL Þ Z = R + j L
Z = R +(-j)XC Z = R + C jω 1
För en RCL-seriekretsen nedan tecknas den komplexa impedansen på följande sätt: C 1 L Z j jR
Ström och spänning i seriekretsar
j-axeln
Ovan är den induktiva seriekretsens spänningstriangel inlagd i det komplexa talplanet. Det är uppenbart att även sambandet mellan den pålagda spänningen U och delspänningarna UR och UL kan anges i komplex form.
U = UR + jUL
( UR = I R ) utgör realdelen med I och UR i fas.
( UL = I j L ) är den imaginära delen med UL= fasförskjutna 90º före I eftersom multiplikation med ( j ) medför 90º positiv fasvridning i det komplexa talplanet.
Facit till imaginära - komplexa - tal
Komplexa tal
1 a) j j = j2 = -1
b) j j j = j j2 = - j
c) j4 = j2 j2 = (-1) (-1) = 1
d) j5 = j2 j2 j = (-1) (-1) j = j
e)3 j3 = 3 j2 j = 3 (-1) j = - 3j
2 a)2 + j3
b)-4 + j4
c)-2 - j4
d)3 - j3
3 a)a = 3,6 ; = 56,3º
. a = 3,6 cos56,3º + j 3,6 sin56,3º
b)b = 5,7 ; = 135º
.b = 5,7 cos135º + j 5,7 sin135º
c)c = 4,5 ; = 234º
.c = 4,5 cos234º + j 4,5 sin 234º
d)d = 12,7 ; = 315º
.d = 12,7 cos315º + j 3,6 sin315º
4 a)3,6 º
b)5,7 º
c)4,5 º
d)12,7 º
5 a)3,6 e j 56,3º
b)5,7 e j 135º
c)4,5 e
d)12,7 e j 315º
6 a)Z = 3 + j
b)U = -3 + j2
c)I = -4 - j3
d)S = 2 - j4
7 a)Z = 3,2 ; = 15º
b)U = 3,6 ; = 146,3º
c)I = 5 ; = 216,9º
d)S = 4,5 ; = 296,6º
8)7 + j7
9) 11 - j3
10)9 - j9
11)-2 + j26
12)82 + j6
13) 156 55º
14)2310 53º
15) 7 77º
16) 7 39º
17) 1,4 109,4º
18)A + B = 5 + j4
19)A + B = 6,4 ; = 38,7º
20)A - B = j3
21)A - B = 3 ; = 90º
22 a)
22 b) 5 + j4) j = (-4 + j5)
22 c) Ny visare (-4 + j5)
22 d) Vinkeln blir 90º mellan visarna
22 e) 5 4 j j 4 j5
22 f) Ny visare (4 - j5)
22 g) Vinkeln blir 90º mellan visarna
Facit till j - komplexa - metoden
Komplexa metoden
1 a) j L = j 2 f L = j37,7
b) j L = j 2 f L = j75,4
b) j L = j 2 f L = j754
2 a) 1 1 2 1061 jjj CfC
b) 1 1 2 106 jjj CfC
c) 1 1 2 10 6 jjj CfC ,
3)Z = 750 + j201 ( ) eller Z = 776 15º ( )
4) Z 50 26,5 j eller Z = 50 - j26,5 ( )
UR = I R = 0,35 º 50 = 17,5V
UC=I (-jXC) = 0,35 º 26,5 º = 9,3 º (V)
U =I Z =0,35 º 56,6 - 27,9º = 19,8 - 27,9º (V)
5)Z = 4 + j3,1 ( ) eller Z = 5,1 38,1º ( )
UR = 4 0º (V)
UL = 3,1 90º (V)
U = 5,1 38,1º (V)
6 a)f = 50Hz; Z = 55 + j31,4 eller
Z = 63,3 29,7º ( ); º (A)
b)f = 500Hz; Z = 55 + j314 eller
Z = 319 80,1º ( ); I = 0,72 80,1º (A)
c)f = 5000Hz; Z = 55 + j3142 eller
Z = 3142 89,0º ( ); I = 73 89,0º (mA)
7 a)f = 50Hz; Z = 55 - j31830 eller
Z = 31830 -89,9º ( ); º (mA)
b)f = 500Hz; Z = 55 - j3183 ( eller
Z = 3184 89,0º ( ); I = 72,3 89,0º (mA)
c)f = 5000Hz; Z = 55 - j318 ( eller
Z = 323 89,0º ( ); I = 723 80,2º (mA)
8)f = 1kHzZ = R - jXC + R + jXL
9)f =2kHzZ = R - jXC + R + jXL
Z = 510 + j60 ( ) eller Z = 513,5 6,7º ( ) I = 46,7 -6,7º (mA)
10) ZRL C ZRL C j j j 1 1 Resonans inträffar då imaginärdelen är noll L C
Z = 1000 - j15915 + 1200 + j13823
Z = 2200 - j2091 ( ) eller Z = 4,6 -43,5º ( )
11)IL = 1,37 -90º (A) ; IC = 4,8 90º (A) I = 3,4 90º (A) ; Z = j14 ( )
12)IR = 2,4 0º ( ) ; IL = 1,37 -90º (A) ; IC = 4,8 90º (A) ; I = 4,2 55º (A) ; Z = 11,5 -53º ( )
13) Z j j I U Z A 152035 152035 122153 240 122153 157153 ,, ,, ,,º 14) Z j j I U Z A 35 152035 152035 46939 240 46939 05139 ,, ,, ,,º
Mätövningar
Hur man mäter
Experimentkretsarna kopplas med lösa komponenter på en kopplingsplatta (Bread Board) för lödfria anslutningar.


För direkt anslutning av mätinstrument rekommenderas ”lätta” mätkablar och testpinnar så att komponenterna inte lossnar från plattans anslutningspunkter.
För anslutning av spänningsmatning är vanliga laboratoriekablar med banankontakter kopplade till kortets labhylsor ett bra val. Labhylsorna ansluts i sin tur med enkeltråd (EKUX 0,28mm2) till kortets kopplingspunkter.
Exempel: Elritning och uppkoppling. Linjerna mellan elritningen och kompnenterna visar vilken resistor som är R1 respektive R2. Lägg märke till hur R1 och R2 förbundits med varandra i kopplingspunkt 17.

ISBN 978-91-7773-723-0
