matematik fortsättning

Attila Szabo
Niclas Larson
Daniel Dufåker
Roger Fermsjö
nivå
1c


Attila Szabo
Niclas Larson
Daniel Dufåker
Roger Fermsjö
nivå
1c
1.1 Polynom 8
Värdet av ett polynom 8 Multiplikation av polynom 11 Faktorisering av polynom 13
1.2 Polynomekvationer 15
Enkla polynomekvationer 15 Mer om polynomekvationer 18 Grafen till en polynomfunktion 22 Faktorer och nollställen 25
1.3 Rationella uttryck ....................... 30
Förkortning och förlängning av rationella uttryck 30
Addition och subtraktion av rationella uttryck 34
Multiplikation och division av rationella uttryck 36
Gränsvärden 38 Kontinuerliga funktioner 44
Symbolhanterande hjälpmedel 48
Programmering: Ekvationslösning
Historia:
2.1 Sekanter och tangenter
Räta linjens ekvation 66 Sekantens lutning 69 Tangentens lutning 73
2.2 Derivata 79
Derivatans definition 79 Att använda derivata 83
Deriverbarhet och absolutbelopp 87 Historia: Att bestämma en tangent 93
102
3.1 Deriveringsregler för potensoch polynomfunktioner 104
Derivatan av enkla potensfunktioner 104
Derivatan av polynomfunktioner 108 Mer om derivatan av potensfunktioner 110
3.2 Exponentialfunktioner och tillämpningar av derivata 114
Derivatan av ex 114 Derivatan av ekx och ax 119 Derivatans tillämpningar 123 Tillämpningar av derivata med digitalt hjälpmedel 127
Programmering: Newton-Raphsons metod 132 Uppslaget 134
Historia: Newton, Leibniz och derivatan 136
4.1 Samband mellan funktionens
graf och derivata 146
Växande eller avtagande funktion 146
Derivatans nollställen 150
4.2 Extremvärden och derivatan .......... 155
Största och minsta värde i ett intervall 155
Andraderivatan och funktionens graf 159
Andraderivatan och lokala extrempunkter 163
Extremvärdesproblem 167
Extremvärdesproblem med digitalt hjälpmedel 170
Historia:
Fermats metod för extrempunkter . 173
Uppslaget 174 Tankekarta 176
Blandade uppgifter 177
Kapiteltest 182
5.1 Primitiva funktioner 186
Vad är en primitiv funktion? 186 Primitiva funktioner till potensfunktioner och exponentialfunktioner 190
Primitiva funktioner med villkor 193
5.2 Integraler och areor 196
Arean under en kurva 196
Samband mellan derivata och integral 201
Beräkna integraler med digitalt hjälpmedel 206
5.3 Mer om integraler 212
Arean av området mellan två kurvor 212 Tillämpning av integraler i verklighetsbaserade situationer 216
Programmering: Integraler – numerisk metod 220
Historia: Integralkalkylens historia 221
6.1 Trigonometriska samband 234
Trigonometri i rätvinkliga trianglar 234
Enhetscirkeln 238 Trigonometriska ekvationer 241
6.2 Triangelsatserna 246
Areasatsen 246 Sinussatsen 249
Cosinussatsen 253
Att använda triangelsatserna 256
Programmering:

Delkapitel
1.1 Polynom
1.2 Polynomekvationer
1.3 Rationella uttryck
Förkunskaper
■ Grundläggande algebra
■ Konjugatregeln och kvadreringsreglerna
■ Andragradsekvationer
■ Potenser
■ Bråkräkning
■ Funktionsbegreppet
Centralt innehåll
■ Begreppet rationella uttryck. Hantering av rationella uttryck.
■ Begreppet polynom och egenskaper hos polynomfunktioner. Metoder för att lösa enklare polynomekvationer.
■ Begreppet gränsvärde.
■ Användning av digitala verktyg, även symbolhanterande, för att effektivisera beräkningar och komplettera metoder, till exempel vid ekvationslösning, derivering, integrering, hantering av algebraiska uttryck och problemlösning.
■ Användning av programmering som verktyg vid problemlösning, databearbetning eller tillämpning av numeriska metoder.

Algebra är ett av matematikens huvudområden. Utvecklingen av den algebra vi använder i dag har skett under lång tid. Den händelse som kommit att kallas den symboliska abstraktionen inledde i början av 1600-talet utvecklingen av det matematiska språket mot det sätt att beteckna tal med bokstäver som vi gör i dag.
I det här kapitlet får du en repetition av några grundläggande algebraiska färdigheter. Vi går sedan vidare och arbetar med egenskaper hos funktioner, polynom och rationella uttryck.
När du är klar med kapitlet ska du kunna
u förenkla och använda uttryck med polynom
u lösa polynomekvationer av högre grad med algebraiska, grafiska och digitala metoder
u använda polynomekvationer vid problemlösning
u rita grafer till polynomfunktioner för hand och med digitala verktyg
u ställa upp, förenkla och använda rationella uttryck
u bestämma definitionsmängd, värdemängd och nollställen till rationella funktioner
u bestämma gränsvärden
u känna till vad som menas med en kontinuerlig funktion
u avgöra om en funktion är kontinuerlig eller diskontinuerlig
Wingströms uthyrning erbjuder olika fordon till turisterna. Att hyra en elsparkcykel kostar 10 kr i grundavgift och 2,50 kr/minut.
u Hur mycket kostar det att hyra en elsparkcykel i en timme?
u Bestäm kostnaden per minut om man hyr elsparkcykel i 14 minuter.
u Skriv ett uttryck för den genomsnittliga hyreskostnaden K(x) kr/minut, om man hyr elsparkcykeln i x minuter.
Familjen Åkerholm har på sina ägor en äng, som är nästintill rektangulär. De vet att ängens långsida är 48 meter längre än kortsidan och att ängens area är 8 500 m2.
u Teckna en ekvation som kan användas för att bestämma ängens längd och bredd.
u Lös ekvationen.
u Bestäm ängens längd respektive bredd.
ordboken
Polynom kommer från de grekiska orden polys som betyder många och nom som betyder namn. Polynom kan sägas betyda många namn eller många termer.
En bils koldioxidutsläpp beror av farten som bilen färdas med. Om koldioxidutsläppet p mäts i gram per kilometer och bilens fart v i kilometer per timme, så kan sambandet beskrivas med uttrycket
p(v) = 0,045v2 − 6,75v + 393 för 30 ≤ v ≤ 120
Polynom
Konstantterm
2x4 + 4x3 + 5
(v)
Koefficient Variabel v km/h
Uttrycket 0,045v2 − 6,75v + 393 är ett exempel på ett polynom. Ett annat exempel på polynom är 2x4 + 4x3 + 5. Båda uttrycken innehåller ett antal termer. I uttrycket 2x4 + 4x3 + 5 är termerna 2x4 och 4x3 variabeltermer och termen 5 kallas konstantterm. Variabeltermerna består av produkter av en koefficient och en potens med variabeln x som bas och ett positivt heltal som exponent. Detta polynom är av fjärde graden eftersom 4 är den högsta exponenten. På samma sätt ser vi att polynomet 0,045v2 − 6,75v + 393 är ett andragradspolynom.
Uttrycket 2 x2 är däremot inte ett polynom, eftersom det kan skrivas 2x −2 och exponenten då inte är ett positivt heltal.
Polynomfunktion
Eftersom 0,045v2 − 6,75v + 393 är ett polynom kallas funktionen p för en polynomfunktion. Definitionsmängden 30 ≤ v ≤ 120 betyder att sambandet gäller för hastigheter från och med 30 km/h till och med 120 km/h.
Polynom
Ett polynom är en summa av konstant- och variabeltermer, där varje variabelterm är en produkt av en konstant och en variabel med positiv heltalsexponent.
Ett polynom kan allmänt skrivas i formen
anxn + an − 1xn − 1 + … + a2x2 + a1x + a0 där n är ett positivt heltal och an, an − 1, …, a2, a1, a0 är konstanter.
Om n är den högsta exponenten i polynomet, så säger man att polynomet är av grad n
Exempel: Låt p(x) = x3 + 5x2 − 7 och bestäm
a) p(3)
b) p(−2)
Lösning: a) p(3) = 33 + 5 ∙ 32 − 7 = 65
b) p(−2) = (−2)3 + 5 ∙ (−2)2 − 7 = 5
c) polynomets grad
c) Eftersom den största exponenten är 3 så är det ett tredjegradspolynom.
Exempel: Markus hyr slalomskidor. Kostnaden för att hyra skidorna beskrivs av
K(x) = 350 + 80x, där K(x) är kostnaden i kr för att hyra skidorna i x dagar.
a) Vad kostar det att hyra skidorna i 7 dagar?
b) Hur många dagar kan han hyra skidorna för 750 kr?
Lösning: a) Vi ska beräkna värdet av K(x) = 350 + 80x för x = 7.
K(7) = 350 + 80 ∙ 7 = 910
Svar: Det kostar 910 kr att hyra skidorna i 7 dagar.
b) Vi ska lösa ekvationen K(x) = 750.
350 + 80x = 750 Eftersom K(x) = 350 + 80x
80x = 400
x = 400 80
x = 5
Svar: Markus kan hyra skidorna i 5 dagar.
Nivå 1
1101 Låt p(x) = 2x2 + 3x − 7 och beräkna
a) p(0) b) p(3) c) p(−2)
1102 Beräkna värdet av polynomet x3 − 2x + 5 för
a) x = 0 b) x = 1
c) x = 5 d) x = −7
1103 Bestäm x om p(x) = 0.
a) p(x) = 40 − 10x b) p(x) = x2 − 25
1104 Ge exempel på ett polynom av tredje graden.
1105 Kostnaden för en taxiresa kan skrivas
K(x) = 55 + 22x, där K(x) är kostnaden i kr och
x är antalet kilometer som man åker.
a) Vad kostar taxiresan om man åker 1,5 mil?
b) Hur långt kan man åka för 200 kr?
1106 Vilka av alternativen A–E visar ett polynom?
A x−2 + x − 3
B x5 + x2 + 4x
C x 1 2 + x3
D x2 + 4x − 8
E 0,5x3 + 0,2x2 + 5
1107 I en rektangel är längden 3 gånger så lång som bredden.
a) Kalla rektangelns bredd för x och teckna ett uttryck för rektangelns omkrets.
b) Beräkna rektangelns omkrets om x = 1,7 cm.
c) Beräkna rektangelns längd om omkretsen är 1,6 m.
1108 Ali och Mohammad arbetar med polynom under matematiklektionen. Mohammad säger att han inte riktigt förstått vad ett polynom är. Ali bestämmer sig för att förklara genom att ge exempel på några polynom och jämföra dem med uttryck som inte är polynom. Hjälp Ali genom att ge exempel på vad han kan nämna i respektive grupp.
1109 Kurvorna visar temperaturen under en dag x timmar efter midnatt på två olika platser, A och B.
Nivå 2
1112 Låt f(x) = x2 − 4x och bestäm
a) f(5)
b) f(−1)
c) värdet av x då f(x) = 0
1113 Ge exempel på en polynomfunktion f av tredje graden, för vilken gäller att f(2) = 6.
1114 För vilka värden på x är f(x) = g(x) om
a) f(x) = 2x2 + 3x − 4 och g(x) = 2x2 − 5x + 2
b) f(x) = 2x2 + 1,5x + 1 och g(x) = 5 + 1,5x
1115 Bestäm det andragradspolynom p som ger följande värdetabell:
x 1 2 3 4
p(x) 2 5 10 17
1116 Kostnaden K kronor för att hyra en bil kan skrivas K(x) = 1 140 + 12x, där x är antalet körda mil.
Bestäm
a) fB(8)
4 2 6 8 10 12 14
b) x så att fA(x) = 20
c) x så att fA(x) = fB(x)
x Tid kl.
1110 Ett äpple faller från ett träd. Den sträcka som äpplet faller från grenen kan beskrivas med polynomet s(t) = 4,9t2, där t är tiden i sekunder och s(t) är sträckan i meter.
a) Hur långt har äpplet fallit på 0,20 s?
b) Hur länge dröjer det innan äpplet når marken om det hängde på höjden 2,7 m?
c) Hur lång sträcka faller äpplet under tidsintervallet 0,10 s ≤ t ≤ 0,20 s?
1111 Låt f(x) = x3 − 2x + 1
a) Beräkna f(3) − f(2)
b) Teckna ett uttryck för f(a) − f(b)
a) Teckna ett uttryck för genomsnittskostnaden per körd mil.
b) Med hur mycket minskar genomsnittskostnaden per mil då körsträckan ökar från 100 mil till 200 mil?


Binom
Om man multiplicerar två polynom med varandra, så blir produkten ett nytt polynom. Vi tittar på ett exempel med polynomen 3x3 + 1 och x2 − 4:
(3x3 + 1)(x2 − 4) = 3x5 − 12x3 + x2 − 4
Polynomen 3x3 + 1 och x2 − 4 kallas för binom eftersom de består av två termer. Det första binomet är av tredje graden och det andra av andra graden. Produkten är ett polynom av femte graden. Vid multiplikation av binom är konjugat- och kvadreringsreglerna bra att kunna.
Första kvadreringsregeln
Första kvadreringsregeln används när man ska kvadrera ett binom av typen
a + b.
Andra kvadreringsregeln
Andra kvadreringsregeln används när man ska kvadrera ett binom av typen
a − b. (a b)2 = (a b)(a b) = a2 2ab + b2
Konjugatregeln
Uttryck som a + b och a b kallas konjugerade binom och regeln för att multiplicera ihop sådana uttryck kallas därför konjugatregeln.
(a + b)(a b) = a2 b2 (
Exempel: a) Teckna ett polynom som beskriver skillnaden mellan de två kvadraternas areor.
b) Ange polynomets grad.
c) Beräkna polynomets värde för x = 2 och förklara vad det betyder.
a − b är det konjugerade binomet till a + b, det kallas även för konjugatet till a + b x x x + 6 x + 6 (cm)
Lösning: a) (x + 6)2 − x2 = (x2 + 12x + 36) − x2 = 12x + 36
Den större kvadratens area
Den mindre kvadratens area
b) Polynomet 12x + 36 är av första graden, eftersom exponenten i x-termen är 1. 12x = 12x1
c) Om x = 2, så är sidorna i de två kvadraterna 2 cm och 8 cm. Då blir skillnaden i area 12x + 36 = (12 ∙ 2 + 36) cm2 = 60 cm2
Eftersom polynomfunktioner är definierade, kontinuerliga och deriverbara för alla x, så är de relativt enkla att hantera.
Vi ska nu se hur man deriverar funktioner av typen f(x) = x2 − 5x + 3. Funktionen f innehåller flera termer och är ett exempel på en polynomfunktion. Vi bestämmer funktionens derivata på två olika sätt.
1. Vi använder oss av derivatans definition f’(x) = lim h → 0
(x + h) − f (x) h = lim
→ 0 ((x + h)2 − 5(x + h) + 3) − (x2 − 5x + 3) h = = lim h → 0 (x2 + 2xh + h2 − 5x − 5h + 3) − x2 + 5x − 3 h = = lim h → 0
2. Vi deriverar varje term för sig enligt deriveringsregler för potensfunktioner f’(x) = 2x2 − 1 − 5 ∙ 1 + 0 = 2x − 5
Båda metoderna ger samma resultat. Man kan visa att alla funktioner som består av flera termer kan deriveras term för term.
Derivatan av polynomfunktioner
Derivatan av en polynomfunktion får man genom att derivera varje term för sig.
Exempel: Bestäm derivatan av f(x) = x5 − 4x3 + x − 7.
Lösning: Vi deriverar varje term för sig enligt deriveringsreglerna.
(x) = 5
Svar: f’(x) =
Exempel: Bestäm y’(6) om
Lösning: Vi skriver först y som en summa av termer, så att det blir enklare att derivera. Sedan bestämmer vi y’ och beräknar y’(6).
Svar: y’(6) = 216
3114 Derivera med hjälp av deriveringsregler.
a) f(x) = x12 + 2x11
b) y = x5 + 5x + 5
c) f(x) = x + 1
d) y = 0,1 − 0,3x + 0,5x2
3115 Låt f(x) = x3 + 9x2 + 5 och bestäm f’(2) genom att
a) först derivera f(x)
b) och sedan beräkna f’(2)
3116 Låt g(t) = 2t3 + t2 − 6t.
a) Derivera g(t).
b) Bestäm g’(−5).
3117 Bestäm f’(3) med hjälp av deriveringsregler.
a) f(x) = x3 − 3x2
b) f(x) = 11 − x − 10x2 + 2x3
3118 Bestäm y’(8) med hjälp av deriveringsregler.
a) y = z − 52 b) y = πt
3119 Derivera
a) y = x4 3 + x3 4 b) V(x) = x5 5 − x4 4 + x3 3
c) z = x 3 + 1 4 d) f(y) = y5 + 5y + 5 5
3120 För vilken eller vilka av följande funktioner gäller att y’(10) = 20?
A y(x) = 10x + 10 B y(x) = 20x + x2
C y(x) = x3 3 − 80 D y(x) = x2 2 + 10x
3121 Para ihop funktionen med sin derivata.
1 y = x4 − 3 A dy dx = 2x 3 + 1 3
2 y = x3 3 + 1 3 B dy dx = x2
3 y = x4 − 3x C dy dx = 4x3 − 3
4 y = x2 3 + x 3 D dy dx = 4x3
2
3122 Bestäm D(f(x)).
a) f(x) = (x + 1)2 b) f(x) = (x − 3)(x + 3)
3123 En funktion f anges med funktionsuttrycket
f(x) = x4 − 3x3 + 101. Bestäm riktningskoefficienten för tangenten till funktionens graf i punkten där x = 3.
3124 Ge exempel på en funktion f, sådan att f’(1) = 10.
3125 För funktionen f gäller att f(x) = x2 − 4x + 3. Bestäm funktionens derivata i funktionens nollställen.
3126 Lös ekvationen f’(x) = 0.
a) f(x) = x3 − 3x + 2
b) f(x) = x3 − x2 − x − 11
3127 Anna har fått i uppgift att beräkna derivatan av f(r) = r3 − 6r i den punkt där r = 2. Hon beräknar den med följande metod:
f(2) = 23 − 6 ∙ 2 = −4
f’(2) = D(−4) = 0
a) Vilket fel gör Anna?
b) Vilket är det korrekta sättet att beräkna funktionens derivata där r = 2?
Nivå 3
3128 Ge exempel på två olika funktioner f och g som uppfyller villkoret f’(x) = g’(x) = x2 − 3x.
3129 a) Ge exempel på tre olika funktioner f, g och h som uppfyller villkoret f’(x) = g’(x) = h’(x).
b) Kan det finnas fler funktioner som har samma derivata som f, g och h? Motivera ditt svar.
3130 Tangenten till kurvan y = ax2 + bx i punkten (1, −1) har riktningskoefficienten k = 4. Bestäm talen a och b
I det här kapitlet har vi visat hur man med hjälp av areasatsen, sinussatsen och cosinussatsen kan bestämma okända sidor och vinklar i en triangel. Dessa satser kallas med ett gemensamt namn för triangelsatserna. Vilken sats man väljer att använda beror på uppgiftens förutsättningar, det vill säga vilka av triangelns sidor och vinklar som är givna och vad man vill ta reda på.
Det finns dock några riktlinjer som man kan följa.
Sinussatsen Om man vill bestämma alla sidor och vinklar i en triangel, så är det lämpligt att använda sinussatsen när
u en sida och två vinklar är kända 1
u två sidor och en av de motstående vinklarna är kända 2
Cosinussatsen Cosinussatsen är att föredra om
u två sidor och mellanliggande vinkel är kända 3
u alla tre sidor är kända 4

Areasatsen
Två lösningar
Om triangelns area är känd, så kan man använda areasatsen för att ta reda på vinklar och sidlängder hos triangeln under förutsättning att man känner till två sidor eller en sida och en vinkel som ligger vid den sidan.
Om man vill bestämma en okänd vinkel med hjälp av sinussatsen eller areasatsen, så får man en ekvation av typen sin v = k. Den ekvationen har i de flesta fall två lösningar. På liknande sätt kan man få två möjliga lösningar när man beräknar längden av en okänd sida med hjälp av cosinussatsen.
Exempel: Eva och Lars vill bestämma avståndet från ön till en mast på fastlandet. De mäter därför vinklarna till masten från två punkter på ön. Hur långt är det till masten från de två punkterna?
Lösning: Sträckan från masten till U1 antas vara a km och sträckan från masten till U2 antas vara b km. Den tredje vinkeln i triangeln är 180° − (41° + 52°) = 87°
Eftersom vi känner till en sida och samtliga vinklar i triangeln, så använder vi sinussatsen
a
sin 52° = 22 sin 87°
a = 22 ∙ sin 52° sin 87° ≈ 17
b sin 41° = 22 sin 87°
b = 22 ∙ sin 41° sin 87° ≈ 14
Svar: Avståndet till masten från U1 är 17 km och från U2 är det 14 km.
Nivå 1
6243 Hur hög är flaggstången?
6244 Området ska täckas med 15 cm matjord. Hur många kubikmeter matjord går det åt?
6245 En ledningsstolpe lutar med 7,0° från lodlinjen mot sin egen skugga. När vinkeln mellan solljuset och marken är 50° kastar stolpen en 8,0 m lång skugga. Hur hög är stolpen?
6246 Marjan vill beräkna avståndet till en bergstopp som hon är på väg till. Hon mäter avståndet mellan två närbelägna punkter och vinklarna därifrån till toppen enligt figuren. Hur långt är det till toppen?
6247 Per går till sin kompis Reza. Han går 800 m längs en rak väg och tar sedan av på en mindre väg som går i 50° vinkel till den första vägen. Längs den mindre vägen är det 1,2 km rakt fram till Reza. På vägen hem genar Per genom skogen. Hur lång blir hemvägen, om den följer en rät linje mellan Pers och Rezas hem?
6248 I en parallellogram är en vinkel 53°. Sidorna är 3,7 cm och 4,5 cm. Bestäm parallellogrammens area.
Nivå 2
6249 En klocka har en minutvisare som är 10 cm lång och en timvisare som är 7,0 cm lång. Hur långt är det mellan spetsarna på klockans visare då klockan är 7.00?

6250 En triangulär tomt har sidorna 27 m, 38 m och 50 m. Beräkna tomtens area.
6251 Bestäm tältets volym.
6252 En kraft som är 200 kN ska delas upp i två komposanter. Komposanterna ska väljas så att de bildar en parallellogram med den ursprungliga kraften som diagonal, se figuren. Bestäm komposanternas storlek.
6253 Konstruera en uppgift där en vinkel i en triangel ska beräknas. Man ska komma fram till två lösningar där den ena lösningen inte är rimlig.
6254 I en liksidig triangel är sidan 40 cm. Hur ska man välja de lika långa sidorna i en likbent triangel med toppvinkeln 100°, så att trianglarna får samma area?
6255 Artur står högst upp i ett torn, så att hans ögon befinner sig 45 meter ovanför en å som rinner 86 meter från tornet. Han mäter synvinkeln till de två stränderna och får en skillnad på 8,1°. Hur bred är ån?
6256 F markerar mittpunkten på sträckan BC. Bestäm vinkeln AEF i pyramiden som har kvadratisk basyta.
6257 Miriam funderar på att köpa grannens skogsskifte. På kartan i skala 1:20 000 mäter hon längden av skiftets gränser och storleken på två av vinklarna mellan dem. Hjälp Miriam att beräkna skiftets area. Måtten på kartan är angivna i centimeter.
6258 I triangeln ABC är vinkeln B = 25° och sidan BC är dubbelt så lång som sidan AC. Beräkna vinkeln A.
(Np Ma3c ht 2014)

6259 Hustomten som figuren visar kostar 80 kr/m2. Vad blir totalpriset för tomten?
6260 En lantmätare har mätt upp sträckan AB till 1,7 km samt alla vinklar på bilden med ett vinkelmätningsinstrument. Hjälp honom att beräkna områdets area.
6261 Armand arbetar som silversmed och hans specialitet är smycken i form av olika geometriska figurer. Han har bestämt sig för att göra ett smycke i form av en triangel. Till sitt förfogande har han en 9,0 cm lång silvertråd som han kan böja och klippa. Armand betecknar triangeln ABC och bestämmer sig för att vinkeln A ska vara 30°, sidan AB 4,2 cm och sidan BC 3,2 cm. Utred på vilket eller vilka sätt smycket kan utformas.
(Np MaD vt 2011)
6262 En fyrhörning med sidorna 5, 6, 8 och 11 cm är inskriven i en cirkel. Beräkna fyrhörningens area.
u Förklara hur man med hjälp av triangelsatserna kan uppskatta längre avstånd, som till exempel avståndet till en avlägsen bergstopp.
u Om man känner till två sidor och en motstående vinkel i en triangel, så kan det i vissa fall finnas två möjliga trianglar som uppfyller kraven. Ge ett exempel på det.
u Om man känner till alla sidor i en triangel, kan man då bestämma arean av triangeln med hjälp av triangelsatserna?
u Om man känner till alla sidor i en fyrhörning, kan man då beräkna arean av fyrhörningen med hjälp av triangelsatserna?
skriver ut text eller värden på variabler for upprepar en del av koden ett angivet antal gånger **2
betyder upphöjt till 2
def, return används för att skapa en funktion
Daryan vill bestämma ett närmevärde till ∫ 0 2 e2x 1 + ex dx genom att approximera arean under grafen med fyra parallelltrapetser.
Arean av ett parallelltrapets: A = Δx · f(xm) + f(xm + Δx) 2
För att utföra beräkningen skriver Daryan följande program i Python.
from math import e def f(x): return e**(2*x)/(1 + e**x)
a = 0 b = 2 n = 4
delta_x = (b - a)/n
trapetssumma = 0 x_m = a
for m in range(n): trapetsarea = delta_x * (f(x_m) + f(x_m + delta_x))/2 x_m = x_m + delta_x
trapetssumma = trapetssumma + trapetsarea print("Integralens värde är ca", trapetssumma)
1 Förklara vad variablerna a, b, n och delta_x står för.
2 Skriv in och kör Daryans program. Jämför hans resultat med det värde du får med ett digitalt hjälpmedel, t.ex. GeoGebra.
3 Ändra i koden så att arean under grafen i stället approximeras med 10 parallelltrapetser. Vilket värde får du?
4 Undersök hur många parallelltrapetser som behövs för att approximera arean med 3 decimalers noggrannhet?

Det var den grekiske matematikern och astronomen Eudoxos (runt 390–340 f.Kr.) som lade grunderna till den sortens integralkalkyl som vi använder i våra dagar. Han använde en metod som gick ut på att uppskatta arean eller volymen hos ett objekt genom att dela in det i många små objekt med kända areor eller volymer.
Arkimedes (287–212 f.Kr.), som var en av antikens mest framstående vetenskapsmän, utvecklade sedan Eudoxos metod. Han uppskattade cirkelns omkrets genom att rita en regelbunden månghörning såväl i cirkeln som runt cirkeln. Genom upprepad fördubbling av antalet sidor i dessa månghörningar fick han allt bättre värden på cirkelns omkrets.
Metoden ger en mycket god uppskattning av talet π. Arkimedes konstaterade att ”förhållandet mellan omkretsen av varje cirkel och dess diameter är mindre än 3 1 7 men större än 3 10 71 ”. Det var en uppskattning som placerade π mellan talen 3,141 och 3,143.
Cirkeln är omskriven av en sexhörning och i cirkeln är en annan sexhörning inskriven.
Några hundra år senare, under 300 talet i Kina, använde matematikern Liu Hui liknande metoder för att uppskatta cirkelns area. Liu Huis metoder förbättrades sedan av Zu Chongzi, som under 500 talet lyckades med att uppskatta klotets volym. Sedan dröjde det ända fram till 1100 talet tills integralkalkylen återigen utvecklades. Det var då den indiske matematikern Bhaskara (1114–1185) presenterade några idéer som anses vara grundläggande inom läran om integraler. Och det var också i Indien (under 1300talet) som matematikern och astronomen Madhava betraktade areor som integraler. Enligt Madhavas skrifter är ”integralen av pada (en variabel) hälften av varga (kvadraten på samma variabel)”. Detta skulle vi i dag uttrycka som ”integralen av x är x2 2 ”.
Uppskatta π med Arkimedes metod. Låt en cirkel med radien 1 l.e. omskriva en regelbunden sexhörning (se figuren här ovanför). Använd sedan sexhörningen för att uppskatta ett värde på π. ?
Den mest framgångsrika perioden i integralkalkylens historia har sin början i 1600 talets Europa, när italienaren Bonaventura Cavalieri vidareutvecklade Arkimedes idéer. Cavalieris arbete ledde till att de brittiska matematikerna John Wallis och Isaac Barrow samt fransmannen Pierre de Fermat kunde lägga grunderna till läran om oändligt små delar, så kallade infinitesimaler Vid slutet av 1600 talet sammanfattade Isaac Newton och Gottfried Wilhelm von Leibniz oberoende av varandra alla tidigare kända insatser inom området, vilket ledde till den moderna integralkalkylens uppkomst. Deras banbrytande upptäckt kan formuleras som att ”funktionen är integralen av derivatan”, vilket i dag även kallas för integralkalkylens fundamentalsats.
Rätt eller fel?
Differenskvoten Δy Δx beräknas med formeln x2 x1 y2 − y1
Sekantens lutning är lika med kurvans medellutning i intervallet.
En kurvas lutning i en punkt är lika med sekantens riktningskoefficient.
Derivatan i en punkt är lika med kurvans lutning i den punkten.
Derivatan definieras som gränsvärdet av ändringskvoten Δy Δx när Δx → 0.
För att beräkna derivatan numeriskt räcker det med att bestämma en enda ändringskvot om man väljer ett tillräckligt litet värde på h
Om en funktion är kontinuerlig i en punkt är den också deriverbar i punkten.
Absolutbeloppet av ett tal är alltid ett positivt tal.
Undersök
Samband funktion – derivata
u Till en funktion kan man skissa derivatans graf genom att bestämma värdet av derivatan i olika punkter på grafen till funktionen.
Uppskatta värdet av derivatan f' i minst fem punkter på kurvan y = f(x).
y x 1 1
y = f(x)
Använd de värden du fått till att skissa derivatans graf.
u Du vet följande om funktionen g
g'(−1) = g'(3) = −3, g'(0) = g'(2) = 0, g'(1) = 2, g(0) = −2 och g(2) = 2
Skissa grafen till funktionen.
u Grafen visar derivatan h' av en funktion h
Skissa en möjlig graf till funktionen h
y x 1 1
y = h'(x)
u Vilket samband tycks finnas mellan graden av en polynomfunktion och graden av dess derivata?
HB HomeSafe
Patrik och Klara har läst ämnet Ung Företagsamhet. Där fick de en inblick i hur ett företag drivs. När de nu har gått ut gymnasiet bestämmer de sig för att bilda ett handelsbolag. De kallar företaget HB HomeSafe och där ska de montera och sälja enklare hemlarm. De börjar med att ta reda på priset på de delar som behövs och får sedan hjälp med att göra en budget. Funktionen
K(q) = 1 500 + 600q − 0,02q2
beskriver kostnaden K(q) kr för att tillverka q st larm. Efter en enkel marknadsundersökning bestämmer de sig för att sätta försäljningspriset av sina larm till 995 kr/st.
För att få en uppfattning om företagets ekonomiska förutsättningar ska du hjälpa dem genom att göra följande beräkningar:
u Beräkna genomsnittskostnaden för de 25 först tillverkade larmen.
u Hur ser funktionen ut som beskriver vinsten om de tillverkar och säljer q st larm?
u Hur många larm ska de tillverka för att vinsten ska bli 15 000 kr, under förutsättning att de säljer alla larm de sätter ihop?
u Hur stor är den genomsnittliga vinstökningen per larm om försäljningen ökar från 100 till 200 larm?
Marginalkostnad är en ekonomisk term som anger den extra kostnad som tillkommer till totalkostnaden för att tillverka ytterligare en enhet av en produkt.
u Bestäm marginalkostnaden vid en produktion av 200 enheter.
u Beskriv hur marginalkostnaden förändras när produktionen ändras.
u Hur förändras vinsten om försäljningspriset ökar med 20 % och man fortfarande säljer alla larm?

Primitiva funktioner
u F är en primitiv funktion till f om F'(x) = f(x)
u samtliga primitiva funktioner till f
u primitiva funktioner med villkor
Integraler
u area under en kurva
u undre och övre integrationsgräns
u integralkalkylens fundamentalsats
∫ a b f(x) dx = [ F(x) ]a b = F(b) − F(a), där F'(x) = f(x)
u funktionen är integralen av derivatan
u värdet av en integral kan vara positivt eller negativt
u formulera integraler i enkla situationer
u arean är alltid ett positivt tal
u arean av området mellan en kurva och x-axeln
u arean av området mellan två kurvor
Formulera och beräkna
integraler i enkla situationer
u lägesändringen är integralen av hastigheten
u hastighetsändringen är integralen av accelerationen
u befolkningstillväxten är integralen av tillväxthastigheten
u Arbetet är integralen av kraften som funktion av läget
1 Ange en primitiv funktion till följande funktioner.
a) f(x) = 2x + 5x2 b) f(x) = 4 − e5x
c) f(x) = 12 d) f(x) = x3 − x2
2 Grafen y = f(x) är ritad i figuren. y x 1 1 y = f(x)
a) I vilka punkter har funktionen lokala extremvärden?
b) I vilka av punkterna har f lokala maximum?
c) I vilka av punkterna har f lokala minimum?
3 Ange samtliga primitiva funktioner till följande funktioner.
a) f (x) = 1 x 7 b) g(x) = e4x − x
c) f (x) = 0 d) g(x) = √x + π
4 Beskriv med ord vilket område i figuren som man kan bestämma arean av med följande integral.
a) ∫ 4 6 g(x) dx b) ∫ −2 3 f(x) dx
5 Derivera
a) y = ex − x b) y = e12x − 12x
c) f (x) = 3,14x + π
d) f (x) = 1 ex + 1 2x
6 Skissa grafen till f’(x) om f(x) = x2 + 1.
7 Hastigheten v(t) av en kropp ändras under en period enligt v(t) = t2 + 2t − 3, där t är tiden i sekunder räknat från periodens början. Kroppen befann sig i positionen s(0) = 7 vid periodens början. Bestäm ett funktionsuttryck s(t) som beskriver läget hos kroppen vid tiden t
8 Vilken är den största produkt som man kan få av två tal vars summa är 99?
9 Beräkna integralerna
a) ∫ 3 6 (x2 − 5x + 6) dx
b) ∫ −2 1 (ex + x + 3) dx c) ∫ −2 2 x3 dx
10 Låt f(x) = 3x4 − 6x2 + 1 och bestäm de lokala extrempunkternas koordinater i intervallet −2 ≤ x ≤ 2.
11 För en funktion vet man att y = 4 för x = 2 och y = 13 för x = −1. Beräkna ändringskvoten Δy Δx mellan dessa punkter.
12 En polynomekvation p(x) = 0 har rötterna x = −1, x = 2 och x = 4. Skissa en möjlig graf till polynomfunktionen p.
13 Hastigheten v m/s för en fyrverkeriraket, t sekunder efter uppskjutningen, beskrivs med v(t) = 50t − 30t2 .
a) Efter hur lång tid slutar raketens hastighet att öka?
b) Vilken hastighet har den då?

14 Beräkna arean av det skuggade området med hjälp av primitiva funktioner.
a) y x 1 1 y = 6 + x − x2 2
b) y x 1 1 y = x2 y = x
c) y x 1 1 y = −2 y = x + x2
15 Antalet katter K på ett katthem kan under de kommande 20 månaderna uppskattas med funktionen K(t) = 31 ∙ e0,05t, där t är tiden räknat i månader.
a) Beräkna antalet katter efter 12 månader.
b) Beräkna ökningen av antalet katter när t = 9.
16 Figuren visar grafen till funktionen f(x) = x2 + 4x . y x 1 1
a) Bestäm kurvans lutning i punkten (0, 0).
b) Bestäm kurvans lutning i punkten (−2, −4).
c) Bestäm kurvans medellutning i intervallet −1 ≤ x ≤ 1.
d) y x 1 1 y = −3
y = x2 + x − 5
17 Skissa grafen till följande funktioner, utan att använda en grafritande verktyg.
a) f(x) = x3 − 9x + 2
b) g(x) = 6 + x3
18 Bestäm med hjälp av digitalt verktyg samtliga primitiva funktioner till f(x) = ln x

19 Bestäm arean av det område som begränsas av kurvorna y = x2 − 2x och y = 2x − x2
20 Vad är skillnaden mellan begreppen funktionens största värde i ett intervall och lokalt maximum i ett intervall?
21 Bestäm en primitiv funktion F(x) till f (x) = 3 x2 + x, där grafen till F(x) går igenom punkten ( 1 2 , 0 ).
22 Bestäm de punkter på grafen y = f(x) där derivatan till f(x) = x3 − 4,5x2 + 3 har värdet −6.
23 Vid en undersökning har man registrerat när samtal tas emot i en telefonväxel. Det visar sig att förändringshastigheten av antalet samtal följer den förenklade modellen
A’(t) = 200 − 2t där A’ är antalet samtal/minut och t är tiden i minuter efter att telefonväxeln öppnat.
a) Beräkna ∫ 0 10 (200 − 2t) dt algebraiskt.
b) Beskriv med ord vad integralens värde betyder i detta sammanhang.
(Np Ma3b vt 2014)

24 Bestäm g(x) om g’’(x) = 3 − x2 , g(0) = 2 och g’(1) = 5.
25 För vilka värden på x är tangenten till kurvan parallell med x-axeln?
a) y = 5x2 + 40x − 1
b) y = x2 6 − 9 x + 1 2
26 Beräkna integralen ∫ 0 1 (1 − x)3 dx
27 Ge ett exempel på en ekvation i formen y = kx + m för en rät linje som är parallell med tangenten till f(x) = x 5 + e x 5 för x = 0.
28 Marginalkostnad är merkostnaden för att tillverka ytterligare en enhet av en produkt. För en viss produkt bestäms marginalkostnaden K’(q) av K’(q) = 230 − 0,20q där q är antalet tillverkade enheter i intervallet 0 ≤ q ≤ 750. Kostnaden för att tillverka 400 enheter är 420 000 kr. Bestäm den funktion som beskriver tillverkningskostnaden K(q).
29 Ge ett exempel på en verklig situation där Δs = ∫ t1 t2 v(t) dt = 0 för ett föremål trots att föremålet rör sig.
30 I figuren är kurvan y = 7 − x2 ritad i första kvadranten. En rektangel ritas under kurvan enligt figuren. Bestäm det största värdet som rektangelns area kan anta. y x 1 1
31 Beräkna arean av det område som begränsas av följande linjer:
{ 3x + y = 3
x = 0 y = 0

32 Beskriv vad är det som man räknar ut med följande integraler.
a) I = ∫ 3 7 v(t) dt, där v m/s är en drakflygares hastighet t sekunder efter starten.
b) I = ∫ 0 25 A(t) dt, där A invånare per år är hastigheten som befolkningen minskar med vid tiden t år.
33 Anna ska skära till rektangulära pappersark . Hon vill att skrivytan ska vara 216 cm2 och att marginalen upptill och nedtill ska vara 2 cm breda samt att båda sidomarginalerna ska vara 3 cm. Bestäm längsta sidan på det pappersark med minsta möjliga area som uppfyller dessa krav.
34 För funktionerna f och g gäller att f(x) = 5x2 + 3x och g(x) = x2 + 8x.
a) Bestäm det värde på x där grafen till f har lutningen 18.
b) Grafen till g har en tangent i den punkt där x = 6. Bestäm koordinaterna för tangentens skärningspunkt med x-axeln.
(Np Ma3c ht 2012)
37 Bestäm med hjälp av symbolhanterande verktyg värdet av integralen ∫ −∞ ∞ e x2 dx
38 Lös ekvationen x3 − x(8x − 16) = 0 (Np MaC vt 2005)
39 En rektangel ritad i den första kvadranten har ett hörn på kurvan y = −5x2 + 4x + 5 och det motsatta hörnet i origo. Beräkna rektangelns maximala area.
40 David använder sitt CAS-verktyg för att få fram alla primitiva funktioner till f(x) = 1 x . Han skriver in kommandot Integral(1/x) och får
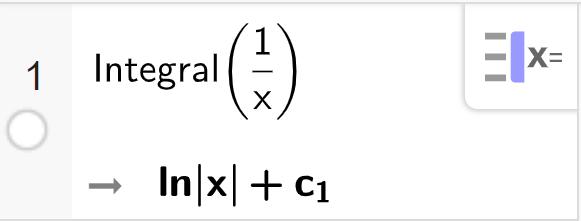
David tänker att det måste vara fel. När han deriverar ln(2x) med CAS får han ju 1 x . Hans klasskompis Flora säger dock att ln |x| + c1 betyder samtliga primitiva funktioner. Förklara hur Flora kan ha tänkt.
41 För en polynomfunktion f gäller att: u f’’(x) = −2 för alla x u f (1) = 5 u f (2) = 3
Bestäm funktionen f (Np Ma3c ht 2014)
42 Grafen till vänster hör till funktionen f. Vilken eller vilka av graferna A, B, C eller D beskriver funktionens primitiva funktion? Motivera ditt svar.
35 Lös ekvationen
x e t dt = 7
36 Kerstin och Katarina har haft matematikprov. En av uppgifterna löd: ”En funktion f har derivatan f’(x) = 3x2 + 5. Bestäm f(x).” När de får tillbaka provet ser de att båda har löst uppgiften rätt. Ändå har de inte angett riktigt samma svar. Ge en förklaring till vad som kan ha inträffat.
43 Ge exempel på en polynomfunktion av tredje graden vars derivata
a) har två nollställen
b) har ett nollställe
c) saknar nollställen
44 För vilka värden på a och b (a < b) är värdet av integralen ∫ a b (7 + 6x x2) dx som störst?
45 En glasmästare har av misstag skurit av ett hörn på ett rektangulärt spegelglas som hade måtten 12,0 dm × 10,0 dm. Den avskurna biten har formen av en rätvinklig triangel där de vinkelräta sidorna är 6,0 dm respektive 5,0 dm. Se figur.
46 Graferna visar andraderivatan till två funktioner.
Skissa hur graferna till f(x) och g(x) kan se ut.
47 Beräkna arean av det skuggade området i figuren. x 1
rektangulär spegel
Glasmästaren vill använda det kvarvarande spegelglaset till en rektangulär spegel som har sitt ena hörn på den avskurna kanten. Glasmästaren vill också att spegeln ska få så stor area som möjligt.
Beräkna det mått på bredden som ger spegelns största area.
(Np Ma3c vt 2014)
48 För en funktion f(x) gäller att f(0) = −2 och f’(x) = 0,63e0,09x. Bestäm funktionen f.
49 I en stor vattenbehållare rinner vattnet in genom ett rör. Vid tiden t min innehåller behållaren f(t) liter vatten. Vid t = 0 är behållaren tom. Figuren visar för 0 ≤ t ≤ 15 den hastighet med vilken vattnet rinner in i behållaren. Hastigheten är konstant 10 liter/min i intervallet 0 ≤ t ≤ 5 och minskar sedan linjärt till 0 då t = 15. Bestäm funktionen f.
liter/min Tid 5 10 15 min 5 10 (Cp NT3 1994)

1 Bestäm
a) sin 90° b) cos 90°
c) cos 180° d) sin 270°
2 Använd enhetscirkeln här nedanför för att lösa ekvationerna i intervallet 0° ≤ v < 360°.
a) sin v = 0,8 b) cos v = −0,2
3 Givet att sin v = √3 2 , bestäm sin (180° − v).
4 Lös ekvationerna i intervallet 0° ≤ v < 360° a) sin v = 1 2 b) cos v = √3 2
5 Avgör om påståendena är sanna eller falska, med utgångspunkt i beteckningarna i triangeln till höger.
a) a = b sin A sin B
6 Du har fått i uppgift att bestämma bredden av en flod. Till din hjälp har du ett långt måttband och ett instrument som du kan använda för att mäta vinklar. Förklara hur du med hjälp av måttbandet, vinkelinstrumentet och trigonometri kan bestämma flodens bredd utan att du behöver ta dig över den. c B b a A C
b) sin B = a2 + c2 2ac
c) b2 + c2 bc cos A = 2
7 Beräkna triangelns area.
8 Lös ekvationerna i intervallet 0° ≤ v < 360° a) sin v = 0,2 b) cos v = 0,4 c) sin v = −0,5
9 Hur långt är det mellan Pers hus och affären? 1,2 km
Evas hus
Affär
Pers hus
10 Beräkna arean av fyrhörningen.
11 I triangeln ABC här nedanför är ∧A = 37°, |AC| = 5 cm och |BC| = x cm.
u Beräkna ∧B om x = 7 cm.
u Välj ett värde på x så att det går att bestämma två värden på ∧B och därmed också bestämma två möjliga trianglar. Beräkna dessa värden på vinkeln B
u Utred hur man , beroende av längden av sidan BC, får ingen triangel, en triangel respektive två möjliga trianglar.
1.1 Polynom
1113 Tänk på att du kan välja ett tredjegradspolynom med en variabelterm och en konstantterm.
1114 Lös ekvationen f(x) = g(x) genom att sätta de båda funktionsuttrycken lika med varandra.
1115 Teckna ett allmänt andragradspolynom p(x) = ax2 + bx + c och använd tabellen för att bestämma värdet på konstanterna. Exempelvis vet du att p(1) = 2. Hur kan du uttrycka det med hjälp av ditt tecknade polynom?
1128 Tänk på att (a + b)3 = (a + b)(a + b)2 och att (a − b)3 = (a − b)(a − b)2.
1129 Undersök med exempel på p(x) och q(x) som uppfyller de givna villkoren.
1136 Kostnaden per halsduk ges av uttrycket K(q) q .
1138 Vilken gemensam faktor har uttrycken? Bryt ut den och skriv i faktoriserad form.
1140 Faktorisera A(x).
1142 Tänk på att uttrycket under rottecknet ska vara lika med summan av kvadraterna på kateterna.
1.2 Polynomekvationer
1214 Anta att kvadratens sidor är x cm. Hur långa är då rektangelns sidor? Vilken ekvation kan du ställa upp utifrån den givna informationen?
1215 Börja med att lösa ut x2. Vilket värde kan x2 ha för att lösning ska saknas? Vilket värde kan x2 ha för att lösningen ska vara unik?
1216 Rita en figur enligt den givna informationen. Hur förhåller sig sidlängderna till varandra? Vilken ekvation kan du ställa upp?
1217 Tänk på att en andragradsekvation kan ha två lösningar.
1218 Tvärsnittsarean ges här av den yttre cirkelns area subtraherat med den inre cirkelns area. Använd det för att ställa upp lämplig ekvation.
1219 Börja med att faktorisera VL med hjälp av någon av kvadreringsreglerna.
1220 Bestäm radien med hjälp av formeln för volymen av en kon.
1233 Anta att kubens sidor är x cm från början. Vilken ekvation kan du ställa upp utifrån den givna informationen?
1234 Börja med att faktorisera VL. Bryt ut största gemensamma faktor.
1236 Hur löste du uppgift 1235? Gör på samma sätt här: Ersätt x2 med t och lös först ekvationerna för t Bestäm sedan x
1237 Rita först en figur. Uttryck sedan basen med hjälp av höjden och ställ upp en ekvation utifrån den givna informationen.
1238 Lös ekvationerna så långt det är möjligt, t.ex. med pq-formeln. Fundera sedan på vad olika värden på konstanten a betyder för lösningen.
1243 Använd ett digitalt hjälpmedel för att rita några olika tredjegradsfunktioner, där du varierar tecknet på koefficienten för x3. Vilka slutsatser kan du dra?
1248 a) Fundera över hur grafen till en tredjegradsfunktion kan se ut.
1263 Tänk på att en av faktorerna ska bli 0 då x ersätts med en av lösningarna. Kan det finnas flera olika värden på A och B?
1265 a) Börja med att ta reda på polynomets nollställen genom att lösa ekvationen r(z) = 0. Faktorisera sedan genom att använda faktorsatsen på sidan 25.
1266 Vilken gemensam faktor finns i p(x)? Bryt ut den och faktorisera p(x).
1267 Vilka faktorer måste ingå i tredjegradspolynomet enligt den givna informationen?
1269 Vilket värde får faktorn x – a för x = a?
1270 b) Läs av funktionens nollställen och teckna ett ett funktionsuttryck med hjälp av dem.
1271 Vilka faktorer finns i funktionsuttrycket? Använd faktorsatsen på sidan 25 och den givna informationen för att bestämma värdet på konstanten k. (Du kan ha nytta av att titta på uppgift 1270.)
1306 Vilka faktorer måste ingå i nämnaren?
1308 Faktorisera med hjälp av t.ex. konjugat- och kvadreringsreglerna.
1310 Vilken faktor måste ingå i nämnaren? Vilka faktorer måste ingå i täljaren?
1315 b) Förenkla f(x). Vilken typ av funktion är f?
1318 Börja med att skriva uttrycket i HL med gemensam nämnare. Jämför sedan VL och HL.
1324 b) Läs exemplet på sidan 35. Multiplicera båda leden med den gemensamma nämnaren som ges av produkten av alla termers nämnare.
1333 Rita figurer av kvadraten och rektangeln utifrån den givna informationen.
1335 Bryt ut −1 ur täljaren eller nämnaren.
1337 Börja med att förenkla uttrycket.
1338 Multiplicera båda leden med bråkuttryckens gemensamma nämnare.
1340 Faktorisera täljaren i uttrycket så att en faktor i täljaren blir 1 + a + b. Du kan börja med att skriva täljaren som 1 − (a2 + 2ab + b2).
1347 Tänk på att 3 x = 1 3x
1350 Börja med att faktorisera och förenkla uttrycken så långt som möjligt. Bestäm sedan gränsvärdet.
1358 b) Faktorisera täljaren genom att ta reda på motsvarande polynoms nollställen.
1360 Tänk på att 5x + 4 2x = 5x 2x + 4 2x = 5 2 + 2 x
1361 b) Bestäm gränsvärdet för N(t) då t går mot oändligheten.
1366 Dela alla termer i uttrycket med x. Bestäm sedan gränsvärdet med A som en konstant.
1376 Kan du komma på något händelseförlopp som inte förändras lika mycket varje tidsperiod, utan där förändringshastigheten i stället ändras vid vissa enstaka tidpunkter?
1379 Börja med att identifiera för vilket värde på x som funktionen byter funktionsuttryck. Undersök sedan om vänster- och högergränsvärdet är lika i den punkten samt om gränsvärdet är lika med funktionsvärdet i den punkten. Om svaret är ja, så är funktionen kontinuerlig.
1381 Måste funktionsvärdet för x = 4 vara 7 om vänster- och högergränsvärdena är lika med 7?
1389 Vilka faktorer måste ingå i polynomet? Skriv polynomet i faktoriserad form i CAS-fönstret. Använd sedan Expandera
1392 Vad har nämnarna för nollställen?
1397 Börja med att skriva ett uttryck för polynomet i faktorform utifrån den givna informationen. Fundera sedan på hur du får grafen att gå genom punkten (1,16).
1399 c) Tänk på faktorsatsen på sidan 25. Hur många lösningar har ekvationen x2 + 1 = 0? Vad innebär det för grafen till p(x)?
2114 Börja med att rita båda linjerna i ett koordinatsystem och markera det sökta området. Hur många längdenheter är basen? Hur många längdenheter är höjden?
2115 b) Tänk på att höjden är vinkelrät mot basen. Rita ut linjen genom triangelns höjd i ett koordinatsystem.
2126 Använd sambandet (a + b)3 = a3 + 3a2b + 3ab2 + b3
2128 b) Tänk på att k1 ∙ k2 = −1 för två linjer som är vinkelräta mot varandra.
2134 Accelerationen a i en viss tidpunkt t ges av hastighetens förändring i den tidpunkten, dvs. a ges av lutningen för kurvan y = v(t) i den punkten.
2136 I vilken typ av punkter är derivatan noll?
2137 Börja med att markera de två angivna punkterna i ett koordinatsystem. I vilken typ av punkter är derivatan noll? Skissa sedan två olika förslag på hur grafen till funktionen kan se ut, som går genom dessa punkter.
2138 Vilka två punkter går Johannas sekant genom? Kan du hitta en ny punkt där x är ännu närmare 3 än 3,1?
2139 Börja med att rita kurvan y = x2 − 1. Vilken typ av punkt är (0, −1)? Vilken är lutningen i den punkten?
2140 Eftersom punkten P ligger både på kurvan och på tangenten, är y-värdet lika i den punkten. Vilken ekvation kan du då ställa upp?
2142 Välj värden på b som är närmare och närmare värdet 2.
2209 Det enklaste är att välja två linjära funktioner.
2210 e) Vilken typ av punkt är den punkten du bestämde i deluppgift c)? Vilken sorts lutning är det till vänster om den punkten? Vilken sorts lutning är det till höger om den punkten?
2211 Använd sambandet (a + b)3 = a3 + 3a2b + 3ab2 + b3 .
2212 För att den räta linjen ska vara en tangent till f, så behöver de ha en gemensam punkt och lutningen ska vara lika i den punkten. Vilka ekvationer kan du då ställa upp?
2215 Använd konjugatregeln när du förenklar kvoten.
2217 I uttrycket för derivatans definition, förläng så att täljaren får gemensam nämnare.
2228 Tangentens k-värde ges av y’(−1). Du behöver även ta reda på koordinaterna för tangeringspunkten.
2230 Bestäm y’(1) för att få k-värdet till linjen.
2232 Börja med att bestämma ekvationerna för de båda tangenterna.
2241 Tänk på att både |5| = 5 och |−5| = 5. Vilka möjliga värden på x ger det?
2.1 Sekanter och tangenter
2110 Insättning av y = 0 ger skärningen med x-axeln och insättning av x = 0 ger skärningen med y-axeln.
2112 Kalla de tre punkterna A, B och C. Bestäm lutningarna genom punkterna A och B, genom A och C samt genom B och C. Vilken slutsats kan du dra?
2113 Lös ut y
2242 Börja med att rita linjen y = x – 2. Men eftersom |x – 2| ≥ 0, så behöver du spegla linjen mot x-axeln så att y ≥ 0.
2244 a) Att |2 + x| = 6 innebär att 2 + x = 6 för x ≥ −2 och att −(2 + x) = 6 för x < −2.
b) Vilka värden är möjliga för |2x – 3|?
2245 Börja med att lösa ekvationen |x – 1| = 2. Fundera sedan på vilka värden på x som löser olikheten |x – 1| > 2.
nivå fortsättning
Matematik Origo fortsättning nivå 1c är en modern lärobok anpassad till Gy25 med utförliga förklaringar, lösta exempel och varierade övningsuppgifter
matematisk modellering, kommunikationsuppgifter och problemlösning för alla
målbeskrivningar, sammanfattning och test till varje kapitel
Till Matematik Origo fortsättning nivå 1c finns även komponenterna Lärarguide, Lärarstöd+ samt kopieringsmaterialet Prov, övningsblad och aktiviteter.
Serien Matematik Origo finns till samtliga gymnasieprogram.