International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056
Volume: 12 Issue: 04 | Apr 2025 www.irjet.net p-ISSN: 2395-0072
High-Performance of Squaring Circuit Design Using Novel Architecture
S. Senthazhai1, V. Kokila2, P. Janani3, M. Keerthana4, A. Rajeshwari5 , S. Deepa6
Associate Professor1, Assisstant Professor2, UG Scholars 3,4,5,6 , Department of Electronics and Communication Engineering, Krishnasamy College of Engineering and Technology, Cuddalore district, Tamil Nadu, India.
Abstract - This paper presents a novel squaring circuit design using an Ripple carry adder to improve the efficiency of digital multipliers. The existing 4-bit multiplier system using squaring operation requires multiple add and shift operations, resulting in increased logical elements and delay. Consequently, the system fails to provide accurate results, instead yielding approximate values. To address this limitation, we propose a novel circuit design for 4-bit operation to compute the square, thus eliminating the need of multipliers. which provides accurate results while reducing time delay and logical elements. The proposed circuit is designed and implemented using VHDL and simulated using Altera Quartus II software. The results demonstrate the superiority of the proposed circuit in terms of speed and area efficiency.
Key Words: Digital Multiplier, Squaring Circuit, Adderbased Design, High-speed Digital Circuits, Low Power Consumption,VHDLImplementation.
1. INTRODUCTION
The rapid growth of digital technology has led to an increasing demand for efficient and high speed digital circuits digital multiplication is a fundamental operation in digital signal processing .widely used in applications suchasfiltering,convolution,and Fourier transformer [1]. However existing digital multiplier require significant hardware resources and time, making them a major bottleneckinhigh-speeddigitalsystem [2]
The existing 4-bit multiplier system using squaring operationistypicalexampleofthislimitation.Thesystem requires multiple add and shift operations to perform squaring, resulting in increased logical elements and delay. Specifically the existing system uses a multiplierbased approach to perform squaring which requires a significantamountofhardwareresourcesandtimes [3] .
To Address this limitation we propose a novel squaring circuit using adder the proposed circuit is designedtominimizethenumberoflogicalelementsand delaymakingitsuitableforhighspeeddigitalapplications the proposed circuit uses an adder-based approach to performsquaring,whichreducesthehardwareresources and time required compared to the existing multiplier basedapproach [4][5] .
The rest of the paper is organized as follow .section II presents the background and motivation for the proposed work .Section III describes the proposed novel squaring circuit using an Adder. Section IV presents the simulation results and comparison with the existing system. Section V concludes the paper and discusses futurework.
2. BACKGROUND AND MOTIVATION
Digital multipliers are a fundamental component in various digital systems, including digital signal processing, cryptography, and communication systems. These systems require high-speed and low-power multiplication operations to perform complex mathematical calculations. The demand for high-speed and low-power digital multipliers has increased significantlyinrecentyears,drivenbythegrowingneed for energy-efficient and high-performance computing systems.
Despite the advancements in digital multiplier design, existing digital multipliers still have several limitations. Forexample,theyconsumehighpower,havelowspeed, and are complex to design. These limitations make it challengingtodevelophigh-speedandlow-powerdigital systems that can meet the growing demands of various applications. Therefore, there is a need to investigate new architectures and design techniques that can improve the efficiency of digital multipliers. This paper aims to address this need by proposing a novel digital multiplier design that achieves high speed and low powerconsumption.
3. BINARY BIT REPRESENTATION
In the context of binary squaring circuitry, a fundamental concept emerges. The base value for squaring is determined by the expression 2^n-1, where n represents the number of bits for instant in a 3-bit system the base value is 100(2^3-1), while in a 4 bit system, it becomes 1000(2^4-1).this pattern continues ,with the base value increasing exponentially with the numberofbits.
A notable observation arises when examining the squaring circuitry for 4-bit numbers. The base value of 1000 serves as a threshold, dividing the numerical range
International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056
Volume: 12 Issue: 04 | Apr 2025 www.irjet.net p-ISSN: 2395-0072
into two distinct segments. Numbers ranging from 1000 to1111aregreaterthanorequaltothebasevalue,while those between 0000 and 0111 fall below this threshold. Interestingly, the latter set of numbers, when disregarding their most significant bit(MSB),which is inherently 0, can be effectively treated as 3-bit numbers below the base value of 1000 can be performed using a morecompact3-bitcircuitry,ratherthanrestoringtothe full4-bitimplementation.
For example, consider the calculation of 3^2, where 3 is representedas0011inbinary.Since0011fallsbelowthe base value of 1000, it can be treated as a 3-bit number (011). By utilizing a 3-bit squaring circuitry, the computation canbe simplified, yielding the result 1001 (9 in decimal), which is the square of 3. This optimized approachreduces thecomplexityand resources required for the calculation, highlighting the potential benefits of exploiting the properties of binary numbers in digital circuitdesign.
4. PROPOSED METHODOLOGY
Carry/p(3) Sum/p(2) Gnd/p(1) A(0)/P(0)
4.1
Design Overview
Theproposednovelssquaringcircuit usinganadderbased design aims to minimize the number of logical elements and delay required for the squaring operation. The design consist of a combination of adders and logic gates, which are optimized to reduce the hardware complexity and delay [1]. The proposed design uses a hierarchical approach, where the squaring operation is broken down into smaller sub-operations, each of the which is implemented using a combination of address andlogicgates
4.2 Circuit Architecture
Architecture of 4-bit Squaring Circuit
The4-bitsquaringcircuitisacomplexdigitalsystemthat computes the square of a given 4-bit input A(3 downto 0). The circuit consists of multiple processing blocks, eachdesignedtoperformaspecificfunction.
Input Processing
Theinputprocessingstageisresponsiblefordividingthe inputintotwoparts:thehigher-order3bitsandtheleast significantbit(LSB).The3-bitsegmentundergoesa3-bit squaring operation, while the LSB follows a separate computationpath.
Partial Product Generation
Thepartialproductgenerationstageprocessestheresult ofthe 3-bitsquaringunitanddirectsittowards the final summation stage. A 4-bit adder combines different intermediate values for computation, ensuring accurate andefficientprocessing.
Correction and Addition
The correction and addition stage involves carry propagation and additional 3-bit squaring logic. Several multiplexersandlogicgatesensurethatbitsarecorrectly aligned before summation, minimizing errors and optimizingperformance.
Final Summation
The final summation stage feedsthe intermediatevalues into an 8-bit adder, which finalizes the squared output. The final computed square is stored in the P-OUTPUT register,completingthesquaringoperation.
Thishierarchicalapproachensuresefficientsquaringofa 4-bit input, optimizing computational complexity and minimizingprocessingtime.
4.3 Implementation details
The proposed 4-bit squaring circuit is designed and implemented using VHDL in Altera Quartus II software. The circuit utilizes a hierarchical approach, dividing the input into two parts and processing them separately to reduce computational complexity. The design is synthesized and its functionality is verified through simulation and testing. The results show that the proposed design achieves efficient squaring of 4-bit inputswithreduceddelayandpowerconsumption
Figure 1:2-bitsquaringcircuit
HalfAdder
International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056
Volume: 12 Issue: 04 | Apr 2025 www.irjet.net p-ISSN: 2395-0072
4.4 Optimization Techniques
To optimize the 4-bit squaring circuit, a multi-faceted approachwasemployed.Resourcesharingwasutilizedto minimize the duplication of components, such as adders and multiplexers, thereby reducing area and power consumption. Logic optimization techniques were also appliedtostreamlinethelogicgatesandfurtherdecrease areaandpowerusage.Furthermore,ahierarchicaldesign approach wasadopted to fragment the complex squaring operation into smaller, more manageable blocks. Finally, pipelining was implemented to enhance throughput and diminish latency, resulting in a highly efficient and optimizeddesign
PassGto(n-1)Th SquaringCircuit, o/pis p PassGto(n-1)ThSquaring circuit,o/pisP
Figure 2. N-bitsquaringcircuit Figure 3:Architecturefor4-bitSquaringCircuit
International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056
Volume: 12 Issue: 04 | Apr 2025 www.irjet.net p-ISSN: 2395-0072
5. RESULT AND DISCUSSION
5.1 Simulation Results
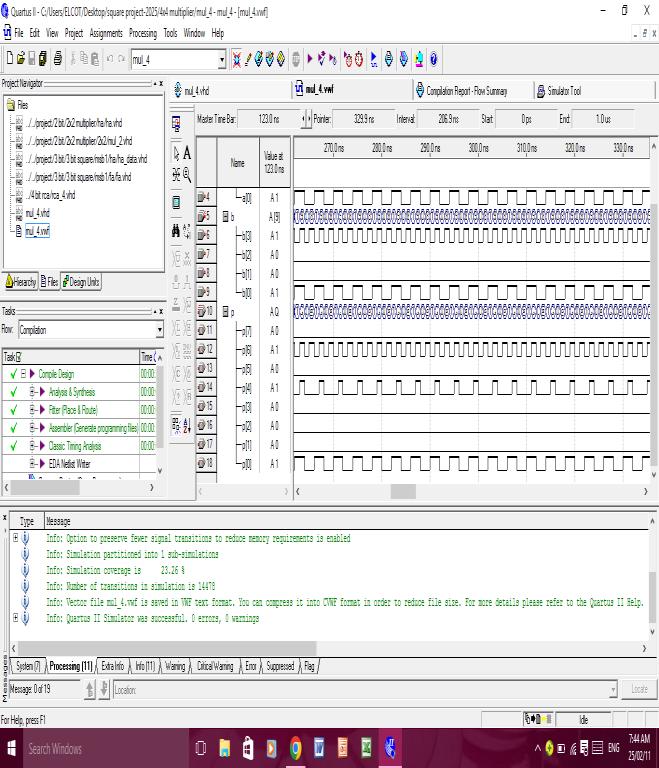
Figure 4 :Resultsof ExistingSystem
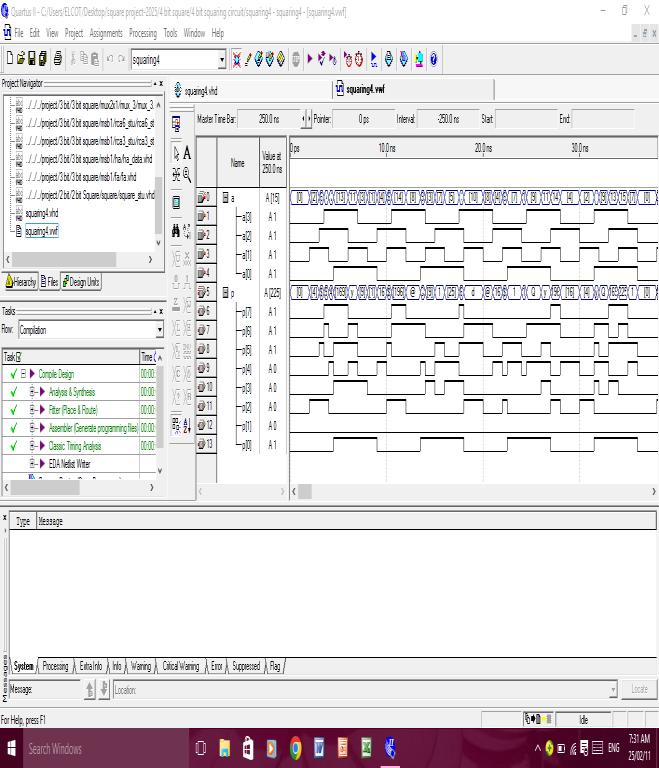
Figure 5: SimulationResultsof4bitsquaringcircuit.
The proposed an existing squaring secured was stimulated using Altera Quartus II to software the simulationresultsareareshowninfigure4andfigure5 The simulation results shows that proposed a circuit is able to perform the squaring operation correctly for all inputvalues
5.2 Comparison with existing design
In this work, 2-bit to 4-bit squaring circuits were implemented in VHDL and optimized for area and delay. Theresultsshowthattheoptimized4-bitsquaringcircuit achieves a significant reduction in delay and logical
elements, making it more efficient and suitable for practical applications, comparison results shown in the table1.
Table -1: Comparisonofproposedcircuitwithexisting circuits
4-bit squaring Circuit Timedelay Logic elements
Proposedcircuit 12.100ns 7/2.880
Existingcircuit 29.600s 32/2.880
Theproposedthecircuithaslowerhardwarecomplexity, delayandpowerconsumptioncomparedtobeingcircuit
5.3 Discussion
The proposed squaring circuit has several advantages, including:
Lowhardwarecomplexity
lowdelay
lowpowerconsumption
however, the proposal circuit also has some limitation including:
limitedscalability
limitedflexibility
6. CONCLUSION
Inthispaper,anovelsquaringCircuitdesignhasbeen proposed and implemented. The proposed design utilize and adder based architecture to achieve lower hardware complexityanddelay.Simulationresultshasdemonstrate the effectiveness of the proposed design, the significant improvements in the hardware complexity, delay, and power consumption compared to existing design. The proposed design has been potential application and various field, including digital signal processing, cryptography, image processing, and Embedded system. Future research directions included Exploring new architecture for squaring circuit and investigation the applicationsoftheproposedcircuitintheotherareas.
REFERENCES
[1] E. zacharelos, “Approximate squaring circuits exploiting recursive architectures, ”Integration, vol.91,pp.35-42,2023,doi:10.101/j
[2] Mrs.A.V.Mutyalamma,Yamini,“DesignandAnalysis of square Architecture Based on Vedic multiplier”, IJCRT,2024 .vol.12 ,issue 3 march 2024.ISSN:23202882.
International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056
Volume: 12 Issue: 04 | Apr 2025 www.irjet.net p-ISSN: 2395-0072
[3] Shamin Akhter, “Design and Analysis of Squaring circuit using various adders,” IRJET,vol. 8, issue Apr 2021,ISSN:2395-0056
[4] Dr. Nagaraju N, “A Distinctive Approach for vredic –basedsquaringCircuit,”IEEE,2020
[5] D. Kumar and M. Bharathi, “A high speed and efficient design for binary number squaring using dwandwa yoga,” International Journal of Advanced Research in Computer Engineering & Technology, vol.1,no.4,pp.476-479,Jun.2012.
[6] T. Sravanthi Devi, A. Madhu Sudhan, “FPGA Implementation of 32-bit Vedic multiplier and Square Architectures”, Volume-6, Issue-3, March2017.ISSSNO2277-8160.
[7] T. Gupta, S. Akhter, S. Khan, and S. Chaturvedi, “Multiplication technique in residue number system,” International Journal of Engineering and AdvancedTechnology(IJEAT),vol.8,no.6,pp.10371041,2019.
[8] M.S.Ansari,V.Mrazek,B.F.Cockburn,L.Sekanina,Z. Vasicek,J.Han “Improving the accuracy and hardware efficiency of neural networks using approximate multipliers” IEEE Trans. Very Large Scale Integr. Syst.,28(2)(Feb. 2020), pp.317328,10.1109/TVLSI.2019.2940943
[9] S. Akhter and S. Chaturvedi, “Modified binary multiplier circuit based on Vedic mathematics,” in Proc. IEEE 2019 International Conference on Signal Processing and Integrated Networks, 2019, pp. 234237.
[10] S. Jai Kumar, M. Karpagam, “A Novel approach To Implement High Speed Squaring Circuit Using Ancient VedicMathematics Techniques”, ISSN 09734562Vol.10No.67(2015).
[11] V.Gupta,D.Mohapatra,A.Raghunathan,K.Roy Lowpower digital signal processing using approximate adders IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems,vol. 32(Jan. 2013), pp.124137,10.1109/TCAD.2012.2217962