Chi ha paura della Matematica - Aritmetica 1

PAURA

PAURA matematica della ?

aritmetica 1

SUCCEDE CHE...

Dal problema reale alla soluzione

Educazione civica, Stem, Informatica

Storia della matematica a cura del Prof. Odifreddi

Impara dall’errore

Oltre 15000 esercizi

PAURA matematica della ?

aritmetica 1

Gruppo Editoriale ELi

Il piacere di apprendere

Il Gruppo Editoriale ELi

offre proposte editoriali che coprono tutti i gradi e i rami scolastici, all’insegna della qualità, del rigore e dell’innovazione.

INTELLIGENZA

ARTIFICIALE

Percorsi didattici con attività pratiche che mirano ad approfondire i principali strumenti di IA generativa per favorirne un utilizzo critico e il tool VELIA a disposizione dei docenti per personalizzare l’attività didattica.

EQUILIBRI

Progetto di ricerca costante che mira a eliminare gli stereotipi di genere nei testi scolastici ponendo particolare attenzione alla scelta dei contenuti, a una valutazione iconografica ragionata e all’utilizzo di un linguaggio testuale inclusivo.

INCLUSIONE

Sviluppo di una cultura dell’inclusione attraverso contenuti accessibili e adeguati ai diversi stili di apprendimento.

ORIENTAMENTO

Approccio educativo e formativo volto a favorire la conoscenza di sé, delle proprie attitudini e delle proprie capacità, oltre a sviluppare le competenze non cognitive e trasversali necessarie per le scelte del futuro.

EDUCAZIONE

CIVICA secondo le NUOVE Linee guida

Aggiornamento e ampliamento dei nuclei tematici attorno ai quali si articolano le competenze e gli obiettivi di apprendimento: Costituzione, Sviluppo economico e sostenibilità, Cittadinanza digitale

STEM/STEAM, CLIL

Attivazione del pensiero scientifico e computazionale, approccio interdisciplinare e laboratoriale, sviluppo della competenza multilinguistica, attraverso attività STEM, STEAM e CLIL.

DIGITALE

Acquisizione delle competenze digitali e dell’alfabetizzazione informatica come aiuto all’inclusione sociale e alla cittadinanza attiva.

EDUCAZIONE ALLE RELAZIONI

Percorsi incentrati sullo sviluppo di competenze relazionali che arricchiscono la consapevolezza del vissuto personale in relazione con la realtà circostante.

Gruppo Editoriale

ELi

CHI HA PAURA DELLA MATEMATICA?

Un corso pensato per accompagnare gli studenti e le studentesse alla scoperta del lato affascinante della matematica. 6 volumi dedicati ad Aritmetica , Geometria e Algebra , nei quali ogni argomento viene affrontato in modo chiaro, pratico e coinvolgente. L’obiettivo è semplice: trasformare la paura dello studio della matematica in curiosità e mostrare che le materie STEM possono essere comprese, amate e vissute con entusiasmo.

La rubrica paura matematica? Chi ha della anticipa quali sono le sensazioni che comunemente provi quando affronti gli argomenti di aritmetica, algebra e geometria, e propone come guardare la realtà con occhi diversi.

LE POTENZE

SUCCEDE CHE... e ESERCIZI Primi

Ogni lezione è introdotta da un problema reale che imparerai a risolvere autonomamente dopo aver seguito passo passo la spiegazione teorica dell’argomento. A seguire una batteria di Primi esercizi per metterti subito alla prova senza paura!

La nostra ROAD MAP per sapere in ogni momento in quale tappa del percorso didattico ti trovi insieme alla tua classe.

DIMENSIONE STORICA

Una doppia pagina che narra la dimensione storica della matematica e tante curiosità grazie alle spiegazioni del Professor Piergiorgio Odifreddi.

MAPPA CON ORGANIZZATORI GRAFICI

Non solo una semplice mappa riassuntiva dell’unità ma una mappa strutturata con organizzatori grafici, cioè forme grafiche che ancora prima del contenuto testuale, attivano un particolare processo cognitivo di apprendimento che visualizza la struttura logica del contenuto.

ESERCIZI E PROBLEMI e impara

La sezione è arricchita da esercizi di EDUCAZIONE CIVICA ed EDUCAZIONE FINANZIARIA, esercizi STEM e da esercizi riferiti a situazioni reali (MATEMATICA IN AZIONE). Ogni esercizio è contrassegnato da un livello di difficoltà e, laddove necessario, è presente un esempio con la risoluzione del problema.

COMPETENZE e SFIDA MATEMATICA

In questa sezione troverai degli esercizi per allenarti nel problem solving e nell’analisi e interpretazione dei dati, e una SFIDA MATEMATICA tratta dalle gare organizzate dal Centro PRISTEM dell’Università Bocconi di Milano.

ROAD MAP PER TUTTI

Una rubrica pensata per ripassare tutte le tappe dell’unità attraverso diagrammi di flusso ed esercizi di prima difficoltà Un doppio percorso di apprendimento in cui la forma schematica e visiva si affianca a quella testuale.

SIMULAZIONE

DI VERIFICA

Esercizi su tutti gli argomenti appresi nell’unità e finalizzata all’Esame di Stato.

GLI INSIEMI UNITÀ

1 matematica? della

Chi ha paura

In questa Unità scoprirai un concetto fondamentale, quello degli insiemi.

Non è nulla di spaventoso, anzi!

Gli insiemi sono come delle scatole, oppure dei contenitori, dove è possibile raggruppare oggetti o numeri, in base a una caratteristica comune. Pensa alla tua collezione di Manga, alla tua classe, all’assortimento di caramelle a una festa: sono categorie della realtà che si possono organizzare proprio grazie al concetto di insieme. Imparerai a rappresentare gli insiemi, a capire se un elemento appartiene o meno a una di queste scatole, e scoprirai in che modo gli insiemi possono includersi l’uno nell’altro.

Quindi, metti da parte ogni timore!

Lo studio degli insiemi sarà un’occasione per mettere ordine nei tuoi pensieri e scoprire che, se ti armi di un po’ di curiosità, ancheiconcettichesembranopiùastrattipossono diventarechiariepersinodivertenti.

ROAD MAP la nostra

FACCIAMO LA CONOSCENZA

CON GLI INSIEMI E IL CONCETTO DI APPARTENENZA

IMPARIAMO A RAPPRESENTARE GLI INSIEMI IN 3 DIVERSI MODI

CHE COSA SONO I SOTTOINSIEMI?

DEFINIAMO L’INSIEME INTERSEZIONE

DEFINIAMO L’INSIEME UNIONE

MATERIALE INTEGRATIVO MULTIMEDIALE

1

SUCCEDE CHE...

CARATTERISTICHE E APPARTENENZA

La sarta Giovanna vuole mettere ordine nel cassetto dei bottoni e chiede ai suoi

figli di aiutarla.

Pio fa tre gruppi: rettangolari, quadrati e rotondi; Emma cinque gruppi: rossi, verdi, azzurri, gialli e rosa; Lia due gruppi: con due buchi e con quattro buchi.

Chi ha svolto meglio il lavoro?

Per saperlo dobbiamo conoscere gli insiemi e il concetto di appartenenza.

Gli animali, le piante, le persone, tutto ciò che ci circonda può essere classificato secondo criteri che ne esprimono una caratteristica.

I raggruppamenti che si determinano sono gli insiemi

In matematica un insieme è un raggruppamento di elementi con una proprietà che li accomuna.

Sono insiemi: i fiumi europei, le atlete della squadra italiana di ginnastica, i mesi dell’anno, gli alunni della 1B...

Non sono insiemi: i cibi buoni, gli alunni più belli di una scuola, le bibite più dissetanti, gli abiti più eleganti...

Un insieme viene indicato con una lettera maiuscola e gli elementi che lo costituiscono vengono racchiusi da una linea curva (diagramma di Eulero-Venn).

Dato un insieme, è sempre possibile stabilire con certezza quali elementi gli appartengono.

Per indicare che un elemento appartiene a un insieme si usa il simbolo ∈.

Se un elemento non appartiene a un insieme si usa il simbolo ∉.

Un insieme che ha un numero illimitato di elementi è un insieme infinito.

Un insieme che ha un numero limitato di elementi è un insieme finito

Un insieme che non ha elementi è un insieme vuoto e si indica con i simboli ∅ oppure { }

Tutti e tre i figli della sarta Giovanna hanno lavorato bene; infatti ognuno di loro ha usato un criterio oggettivo, cioè valido per tutti, per suddividere i bottoni ed è facile stabilire con certezza se un bottone (elemento) appartiene o no a un dato gruppo (insieme). Non sarebbe stato corretto se avessero fatto dei gruppi di bottoni belli o brutti, oppure di bottoni nuovi o vecchi ecc., perchè sono criteri soggettivi.

ESERCIZI

1 Indica se le seguenti frasi rappresentano insiemi matematici.

a) I numeri pari

b) Gli animali più feroci

c) Le città più calde

d) Le poesie di Leopardi

e) I mesi dell’anno

f) I CD di Marta

g) Gli alunni più alti della tua classe

h) Le lettere dell’alfabeto inglese

i) Gli abitanti della tua città

Sì No

Sì No

Sì No

Sì No

Sì No

Sì No

Sì No

Sì No

Sì No

2 Considera l’insieme A e completa le affermazioni utilizzando i simboli ∈ (appartiene) e ∉ (non appartiene).

ESEMPIO A u e a i d o A m n r z s q

u appartiene all’insieme A → u ∈ A

d non appartiene all’insieme A → d ∉ A

3 Considera i seguenti insiemi e per ognuno di essi stabilisci se è finito (F), infinito (I), vuoto (V).

a) L’insieme dei numeri pari minori di 15 F I V

b) L’insieme dei numeri dispari maggiori di 54 F I V

c) I programmi televisivi dedicati all’ambiente F I V

d) Gli alunni della tua classe che trascorrono le vacanze sulla Luna F I V

e) L’insieme dei numeri pari F I V

4 MATEMATICA IN AZIONE Dato l’insieme

A degli oggetti presenti nel tuo astuccio, utilizza i simboli ∈ e ∉.

a) penna rossa

b) mela

c) penna verde

d) gomma pane

e) rana

f) taglierino

DI UN INSIEME 2

SUCCEDE CHE...

La mamma di Pietro, prima di andare al mercato della frutta, recupera i post-it attaccati sul frigo per ricordarsi che cosa manca in casa.

Chiede a Pietro di aiutarla a organizzare la lista della spesa.

arance cavolfiore prezzemolo cipolle insalata mele pere

Un modo è quello di usare gli insiemi. Vediamo i tre diversi metodi con cui si possono rappresentare.

Rappresentazione per elenco o tabulare

La rappresentazione per elenco si ottiene scrivendo, tra due parentesi graffe, tutti gli elementi dell’insieme → A = {.......; ........; ........; ........}

Tale rappresentazione è detta anche rappresentazione tabulare e viene usata quando gli elementi dell’insieme non sono molto numerosi o sono facilmente identificabili.

Rappresentazione per caratteristica

Nella rappresentazione per caratteristica si scrive, tra due parentesi graffe, la caratteristica che accomuna gli elementi di un insieme A = {x |x ...........}

Si legge: “l’insieme A è costituito da tutti gli elementi x tali che x appartiene ad A”.

Questo tipo di rappresentazione è utile soprattutto quando gli elementi di un insieme sono molti e non è conveniente elencarli tutti.

Rappresentazione grafica

La rappresentazione grafica utilizza il diagramma di Eulero-Venn, una linea chiusa all’interno della quale si scrivono gli elementi dell’insieme.

La lista della spesa si potrebbe rappresentare:

• con il diagramma di Venn qui a fianco

• per elenco: A = {insalata, mele, pere, arance, cavolfiore, prezzemolo, cipolle}

• per caratteristica: A = { x | x è un prodotto che la mamma di Pietro compra dal fruttivendolo}

A mele insalata prezzemolo pere cavol ore cipolle arance

Pietro si rende conto che in questo caso la rappresentazione per elenco e quella grafica sono le migliori.

1 Riconosci la rappresentazione per caratteristica esatta.

Rappresentazione per caratteristica dell’insieme S dei giorni della settimana.

S = {x|x è un giorno della settimana}

Si legge: l’insieme S è costituito da tutti gli elementi x tali che x è un giorno della settimana.

A = {ro, ma, no}:

a) {x|x è una sillaba}

b) {x|x è una sillaba della parola “mano”}

c) {x|x è una sillaba della parola “romano”}

d) {x|x è una sillaba della parola “Roma”}

Riconosci la rappresentazione per elenco esatta di ciascuno degli insiemi assegnati.

Rappresentazione per elenco dell’insieme S dei giorni della settimana.

S = {lunedì, martedì, mercoledì, giovedì, venerdì, sabato, domenica}

2 T = {x|x è una lettera della parola “topolino”}:

a) {t, o, p, o, l, i, n, o}

b) {o, o, o, i}

3 P = {x|x è una cifra pari del numero 347 297}:

a) {3, 4, 7, 2, 9, 7}

b) {4, 2}

4 Rappresenta per elenco e col diagramma di Venn l’insieme L delle lettere del tuo nome e del tuo cognome.

L = { }

c) {t, o, p, l, i, n}

d) {t, p, l, n}

c) {3, 4, 7, 2}

d) {3, 7, 9}

Nella rappresentazione per elenco gli elementi che si ripetono si scrivono una volta sola.

5 MATEMATICA IN AZIONE Scrivi per elencazione l’insieme A degli oggetti che ci sono nel tuo astuccio.

A = {

A = {x|x è ESEMPIO ESEMPIO

Scrivilo ora con la rappresentazione per caratteristica:

3 SOTTOINSIEMI E INCLUSIONE

SUCCEDE CHE...

Nella classe di Emma il professore di Scienze ha spiegato che la classe degli uccelli comprende parecchi non volatori, tra cui: pinguino, tacchino, gallo, casuario, emù, struzzo, kakapo, nandu, kiwi.

Emma si chiede in che relazione sono gli uccelli che non volano rispetto agli altri.

Per aiutare Emma occorre conoscere i sottoinsiemi.

Un insieme B è sottoinsieme di A se ogni elemento di B appartiene anche all’insieme A.

Il simbolo di sottoinsieme è ⊂. B ⊂ A

Se B è sottoinsieme di A, si scrive B ⊂ A e si legge B è incluso in A o B è un sottoinsieme di A

Per ogni insieme è possibile definire:

• sottoinsiemi propri → contengono alcuni elementi dell’insieme;

• sottoinsiemi impropri o banali → l’insieme stesso e quello vuoto.

In simboli: A ⊂ A e ∅ ⊂ A

ESEMPIO

Dato A = {U, S, A}

{U}; {S}; {A}; {U, S}; {U, A}; {S, A} → sottoinsiemi propri; {U, S, A}; {} → sottoinsiemi impropri o banali.

L’insieme B non è un sottoinsieme di A se alcuni degli elementi di B non appartengono ad A

In simboli: B ⊄ A, che si legge ‘‘l’insieme B non è incluso nell’insieme A’’ oppure ‘‘l’insieme B non è sottoinsieme dell’insieme A’’. A B

Gli uccelli che non volano, insieme N, sono un sottoinsieme della classe degli uccelli, insieme V.

1 Dato l’insieme M, individua i suoi sottoinsiemi propri (P) e quelli impropri o banali (I).

M mt ar e

B = {m, t, r} P I

D = ∅ P I

F = {a, e, r, m, t} P I

2 Osserva e completa utilizzando i simboli ⊂ e ⊄ .

ESEMPIO

A = {2, 4, 6, 8} B = {6, 8, 9}

B ⊄ A perché 9 ∉ A

N = {x|x è una lettera della parola “normanno”};

M = {x|x è una lettera della parola “mano”};

O = {x|x è una lettera della parola “orma”};

A = {x|x è una lettera della parola “anima”}.

M N O N A N

G = {a, t, e} P I

C = {a, e} P I

E = {m, t, a} P I

3 Dati A = {x|x è un vegetale} e B = {x|x è un pino marittimo}, indica quali affermazioni sono vere (V) e quali false (F).

a) pino marittimo ∈ A

b) pino marittimo ∈ B

c) B ⊂ A

4 MATEMATICA IN AZIONE Considera l’insieme A degli oggetti presenti nel tuo astuccio e determina due suoi sottoinsiemi propri, B e C .

B = {

C = {

Rappresenta gli insiemi A, B, C nel diagramma di Venn.

INSIEME INTERSEZIONE 4

SUCCEDE CHE...

Pietro vuole riordinare la sua libreria. Ha liberato uno scaffale per inserire tutti gli autori italiani e quelli della letteratura mondiale del ’900.

Dove inserirà gli autori italiani del ’900? Nel primo o nel secondo gruppo?

Per trovare una soluzione e ordinare per bene i libri useremo l’ insieme intersezione. Con gli insiemi è possibile effettuare delle operazioni i cui risultati sono altri insiemi. Con l’operazione intersezione si considerano tutti e solo gli elementi comuni tra due o più insiemi, cioè gli elementi che appartengono contemporaneamente agli insiemi dati, come vedremo per gli autori italiani del ’900.

L’intersezione di due o più insiemi è l’insieme degli elementi comuni. Il simbolo che indica l’intersezione è ∩.

Casi particolari dell’intersezione

Due insiemi che non hanno alcun elemento in comune sono insiemi disgiunti.

L’intersezione di due insiemi disgiunti è un insieme vuoto. In simboli: A ∩ B = ∅. A = {fumetti}; B = {testi scolastici}; A ∩ B = { }

Se B è sottoinsieme di A, l’insieme intersezione è il sottoinsieme B. B ⊂ A quindi A ∩ B = B

Pietro ha deciso di sistemato al centro dello scaffale i libri degli autori italiani del ’900 perché rappresentano l’intersezione tra i due insiemi autori italiani e autori del ’900.

Autori italiani

Autori italiani del ’900

Autori del ’900

ESERCIZI

1 Considera l’insieme S degli animali che saltano e quello M dei mammiferi.

a) Qual è la caratteristica degli animali dell’intersezione I = S ∩ M?

b) Scrivi il nome di qualche animale appartenente all’insieme I.

2 Determina l’intersezione delle coppie di insiemi dati.

ESEMPIO

A = {x|x lettera della parola “mare”}

B = {x|x lettera della parola “solo”}

C = {cifre indo-arabiche}

P = {cifre pari}

a) C = {x|x è una lettera della parola “canile”};

N = {x|x è una lettera della parola “scalino”};

b) V = {x|x è un vertebrato};

M = {x|x è un mammifero};

c) P = {x|x è una cifra pari};

N = {x|x è una cifra del numero 13 975}.

3 Considera le seguenti intersezioni e stabilisci se sono vere (V) o false (F).

a) A = { , , , }; B = { , , } A ∩ B = { , } V F

b) A = {x|x è un numero dispari}; B = {1, 4, 7, 13, 36} A ∩ B = {1, 4, 13} V F

c) A = {a, e, i, u, o}; B = {p, q, r, s, t} A ∩ B = { } V F

d) A = {x|x è una lettera della parola “lunatica”}

B = {x|x è una lettera della parola “luna”} A ∩ B = A V F

4 MATEMATICA IN AZIONE Dati l’insieme A = {oggetti presenti nel tuo astuccio} e l’insieme B = {penna 4 colori, forbici, gomma, evidenziatore, calcolatrice, matita, righello, block notes}, rappresenta sul quaderno gli insiemi A e B con un diagramma di Venn.

Scrivi per elencazione:

A ∩ B = {

INSIEME UNIONE 5

SUCCEDE CHE...

Ogni anno nell’Istituto Comprensivo “Grazia Deledda’’ si esegue la selezione per formare la squadra che parteciperà ai Campionati studenteschi, relativi a diverse discipline sportive. I qualificati per la gara dei cento metri sono: Mirco, Pietro, Carmine, Emiliano e Luis.

I qualificati per il salto in alto sono: Pietro, Giorgio, Omar, Luis e Vincenzo. Da quanti alunni è composta la squadra?

Con l’operazione unione si considerano tutti gli elementi di due o più insiemi. Se ci sono elementi comuni, questi si considerano una volta sola.

L’unione di due o più insiemi è l’insieme di tutti gli elementi comuni e non comuni.

Il simbolo che indica l’insieme unione è ∪

A ∪ B = C = {arancia, limone, mandarino, mapo, mela, pera, noce}

Dati un insieme A e un suo sottoinsieme B, l’unione comprende tutti gli elementi di A

L’insieme unione è quindi l’insieme A.

Se B ⊂ A allora B ∪ A = A.

Con l’operazione unione possiamo rappresentare la squadra che parteciperà ai Campionati e stabilire da quanti alunni è composta.

Squadra = A ∪ B

B A Mirco

Emiliano Carmine Luis Omar Vincenzo Giorgio Pietro

La squadra è composta da 8 alunni: Pietro, Carmine, Emiliano, Giorgio, Luis, Mirco, Omar e Vincenzo.

Determina l’insieme unione e rappresentalo nel modo che ritieni più adeguato.

ESEMPIO

A = {martello, pinza, cacciavite, lima}; B = {chiodo, lima, tenaglia, cacciavite}

A ∪ B = {martello, pinza, cacciavite, lima, chiodo, tenaglia}

1 U = {u, s, a, t, o}; M = {m, e, d, i, c, a, t, o}

2 M = {x|x è un mammifero}; C = {x|x è un cetaceo}

3 T = {x|x è una cifra del numero 34 610}; V = {x|x è una cifra del numero 27 589}

4 Considera le seguenti unioni e stabilisci se sono vere (V) o false (F).

a) A = { , , , }; B = {@, , }

A ∪ B = { , , , , @, , } V F

b) A = {x|x è una cifra dispari}; B = {x|x è una cifra pari}

A ∪ B = {x|x è una cifra del numero 10 728} V F

c) A = {x|x è una lettera della parola “calendario”};

B = {x|x è una lettera della parola “diario”}

A ∪ B = {x|x è una lettera della parola “diario”} V F

d) A = {a, e, i, o, u}; B = {x|x è una vocale della parola “cielo”}

A ∪ B = A

5 Correggi le unioni false dell’esercizio 4 e rappresentale graficamente sul quaderno.

6 Determina l’unione degli insiemi assegnati, dopo averli rappresentati per elenco.

A = {x|x è una lettera della parola “elettrico’’};

B = {x|x è una lettera della parola “menestrello’’}

A = { B = {

A ∪ B = {

7 MATEMATICA IN AZIONE Compri un insieme C di oggetti che ti serviranno per Tecnologia. Scrivilo per elenco.

C = {

Adesso li metti nel tuo astuccio e hai:

A ∪ C = {

F

MAPPA

M → {aritmetica, geometria, algebra}, { }

PER ELENCAZIONE

M → {aritmetica, geometria, algebra}

PER CARATTERISTICA

Con il diagramma di Eulero-Venn M aritmetica geometria algebra

GRAFICAMENTE

formano sottoinsiemi

SOTTOINSIEMI PROPRI

M → {aritmetica}, {geometria}, {algebra}, {aritmetica, geometria}, {aritmetica, algebra}, {algebra, geometria}

si rappresentano

GLI INSIEMI

I volumi del tuo corso di Matematica (insieme M) sono: aritmetica, geometria, algebra (elementi) che appartengono all'insieme M; aritmetica ∈ M, geometria ∈ M, geografia ∉ M

SOTTOINSIEMI IMPROPRI

M → {aritmetica}, {geometria}, {algebra}

FINITI

Insieme delle cifre dispari

Dati A = {5, 7, 9, 11, 13}; B = {1, 3, 5, 7, 9} le operazioni che si possono fare sono:

INTERSEZIONE

UNIONE

A ∪ B = = {1, 3, 5, 7, 9, 11, 13} A ∩ B = {5, 7, 9}

possono essere

INFINITI

Insieme dei numeri naturali

Insieme dei numeri pari che terminano con 5 VUOTI

ESERCIZI E PROBLEMI

LEZIONE 1

1

CARATTERISTICHE E APPARTENENZA

La frase “I giorni più caldi dell’estate 2016’’ può definire matematicamente un insieme? Perché?

●●● Il criterio per definire un insieme deve essere oggettivo.

2 La frase “I mesi del 2016 in cui non si è superata la temperatura di 10 °C” può definire matematicamente un insieme? Perché?

3 Scrivi che cosa indica ciascuno dei seguenti simboli.

4 Quanti elementi contiene un insieme infinito?

5 Quanti elementi contiene un insieme vuoto? Fai tre esempi di insiemi vuoti.

6 Quando un insieme si definisce finito? Fai qualche esempio.

7 Stabilisci quali delle seguenti espressioni sono riferibili a insiemi matematici.

a) Fiori più profumati del mondo.

b) Numeri della tabellina del 5.

c) Quadri belli di Picasso.

d) Verbi della prima coniugazione.

e) Consonanti di parole interessanti.

f) Sostanze chimiche che provocano il buco nello strato d’ozono.

g) Pietanze che hai mangiato ieri a pranzo e a cena.

h) Numeri pari di quattro cifre che terminano per 1.

i) Genitori dei tuoi compagni di classe che frequentano una palestra.

j) Piante che vivono a lungo.

k) Giocatori di una squadra di pallacanestro.

l) Città italiane più belle.

m) Alunni della tua scuola che suonano la chitarra.

8 Stabilisci se le seguenti affermazioni definiscono un insieme matematico. In caso affermativo, indica sul quaderno gli elementi che lo costituiscono.

a) I libri gialli più interessanti della biblioteca comunale.

b) Le cifre dispari del numero 89 754.

c) I mesi in cui il clima è freddo e piovoso.

d) Gli alunni della tua classe il cui nome inizia con una consonante.

Sì No

Sì No

Sì No

Sì No

e) I fiumi italiani più lunghi. Sì No

9 Scrivi tre esempi di insiemi matematici.

10 Scrivi tre esempi di raggruppamenti che non sono insiemi matematici.

11 Scrivi i nomi di almeno cinque elementi di ciascuno dei seguenti insiemi.

a) Insieme dei mammiferi

b) Insieme delle regioni italiane

c) Insieme degli Stati europei

d) Insieme delle squadre di calcio di serie A

e) Insieme dei cetacei

f) Insieme dei mesi dell’anno

g) Insieme delle materie che studi

h) Insieme delle note musicali

12 Scrivi gli elementi dell’insieme delle dita di una mano.

13 MATH List the elements of the set of all months “ending with r’’.

14 Riscrivi le frasi utilizzando i simboli ∈ e ∉.

a) Rosa non è un elemento dell’insieme R

b) Parigi appartiene all’insieme F delle città della Francia

c) 3,5 non è un elemento dell’insieme N dei numeri naturali

d) 43 non appartiene all’insieme T della tabellina del 4

e) Lo squalo appartiene all’insieme S dei selaci

f) Il limone non appartiene all’insieme C delle conifere

g) P appartiene all’insieme A delle lettere dell’alfabeto italiano

15 Considera l’insieme S delle stagioni e stabilisci quali affermazioni sono vere (V) e quali false (F).

a) Aprile ∈ S V F

b) Estate ∈ S V F

c) Autunno ∉ S V F

d) Domenica ∉ S V F

e) Inverno ∈ S V F

f) Primavera ∈ S V F

16 Completa inserendo i simboli ∈ (appartiene) e ∉ (non appartiene).

11 D 15 D

55 D 85 D

35 D 75 D

17 Completa le seguenti affermazioni inserendo i simboli ∈ (appartiene) e ∉ (non appartiene).

a) Triangolo rettangolo all’insieme dei parallelogrammi.

b) Tigre all’insieme dei felini.

c) Capodoglio all’insieme dei cetacei.

d) a all’insieme delle consonanti.

a) Rosso all’insieme dei colori dell’arcobaleno.

b) Roma all’insieme delle capitali.

c) 3 095 all’insieme dei numeri pari.

d) Il punto agli enti fondamentali della geometria.

a) Quadrato all’insieme dei quadrilateri.

b) Venere all’insieme dei pianeti del sistema solare.

c) Seppia all’insieme dei pesci.

d) Pino marittimo all’insieme dei vegetali.

20 Considera l’insieme N dei numeri naturali e completa le seguenti affermazioni utilizzando i simboli corretti (∈, ∉).

Per ciascuno dei seguenti insiemi completa utilizzando i simboli corretti (∈, ∉).

a) Quadrato verde A

b) Esagono blu A

c) Triangolo giallo A

d) Quadrilatero viola A

e) Triangolo marrone A

f) Esagono fucsia A

g) Rettangolo blu A

h) Pentagono arancione A

S = {a, u, t, n, o}

a) u S

b) p S

C = {x|x è una materia in orario oggi}

a) Storia C

a) Matematica C

b) Tecnologia C

Disegna i seguenti elementi in modo che:

c) Lettere C

d) Scienze motorie C

e) Educazione musicale C

25 MATH Draw the following elements so that:

26 Osserva il diagramma di Venn e completa. M

a) Rappresenta l’insieme M per caratteristica.

b) Rappresenta l’insieme M per elenco.

c) Inserisci i simboli ∈ e ∉

1) balena M

2) coniglio M

3) gambero M

4) granchio M

5) cavallo M

6) medusa M

27 Controlla se Salvatore ha svolto l’esercizio assegnato in modo corretto e, in caso contrario, correggi; la consegna è: “Scrivi qualche esempio di insieme finito, di insieme infinito e di insieme vuoto’’.

a) L’insieme delle dita di una mano è un insieme infinito

Falso: è un insieme finito

a) L’insieme delle specie di alberi sempreverdi è finito.

b) L’insieme dei mesi che iniziano per “a’’ è un insieme vuoto.

c) L’insieme dei numeri dispari che terminano per 0 è infinito.

d) L’insieme dei mezzi di trasporto a due ruote è finito.

e) L’insieme dei ragazzi con gli occhi azzurri è infinito.

f) L’insieme dei secondi di un anno è infinito.

g) L’insieme dei pulcini che pesano più di 5 kg è un insieme finito.

h) L’insieme delle stagioni è finito.

i) L’insieme degli animali che volano è infinito.

j) L’insieme dei punti cardinali è vuoto.

Considera i seguenti insiemi e per ognuno di essi stabilisci se è finito (F), infinito (I), vuoto (V).

a) Insieme dei numeri pari

b) Insieme dei numeri dispari maggiori di 33 e minori di 35

c) Insieme dei numeri pari maggiori di 44 e minori di 46

d) Insieme dei numeri naturali

e) Insieme dei numeri pari maggiori di 12

a) Insieme dei numeri dispari maggiori di 18 e minori di 89

b) Insieme dei numeri naturali minori di zero

c) Insieme dei numeri multipli di 7

d) Insieme dei multipli di 18 minori di 0

e) Insieme dei numeri pari minori di 10

f) Insieme dei numeri dispari di tre cifre minori di 100

Scrivi tre esempi di insieme infinito, tre esempi di insieme finito e tre esempi di insieme vuoto.

I V

I V

I V

I V

I V

I V

I V

I V

I V

I V

I V

EDUCAZIONE CIVICA Secondo il Codice della strada i cartelli stradali sono di diverso tipo: segnali di pericolo con 3 lati, segnali di prescrizione (obbligo o divieto) di forma circolare, segnali di indicazione con 4 lati, segnali con altre forme. Al fratellino di Marcella è stato regalato un gioco con dei modellini di segnali stradali e Marcella vuole aiutarlo a ordinarli a seconda della forma o del numero dei lati.

Quanti insiemi può trovare?

Marcella ordina i segnali stradali del gioco del fratellino suddividendoli tra quelli:

• di pericolo

• di indicazione

• di prescrizione

UN INSIEME

In quanti e quali modi si può rappresentare un insieme?

Il simbolo “x|x’’ significa:

La rappresentazione per elenco di un insieme è detta anche rappresentazione e si usa quando

Fai qualche esempio di insieme che è conveniente rappresentare per elenco.

Fai qualche esempio di insieme che è conveniente rappresentare per caratteristica.

37 Indica se per i seguenti insiemi è conveniente utilizzare la rappresentazione per elenco.

a) Insieme dei vertebrati

b) Insieme dei mesi di 30 giorni

c) Insieme delle dita di una mano

d) Insieme dei tuoi libri scolastici

e) Insieme dei fiumi europei

f) Insieme dei tuoi insegnanti

g) Insieme dei numeri interi maggiori di 115 e minori di 49 865

h) Insieme delle conchiglie che si trovano in una spiaggia

38 Rappresenta per elenco i seguenti insiemi.

a) A = {x|x è il nome di un mese che termina per “o’’}

b) B = {x|x è una nota musicale}

c) C = {x|x è un numero pari minore di 13}

d) D = {x|x è un tuo compagno di classe il cui nome inizia per “A’’}

e) E = {x|x è il nome di una via che percorri per andare a scuola}

f) F = {x|x è una lettera della parola “Argentina”}

g) G = {x|x è un oggetto che usi a colazione}

39 Rappresenta graficamente sul quaderno i seguenti insiemi.

a) A = {0, 2, 4, 6, 8}

b) B = {arancio, limone, cedro, bergamotto, mandarino, pompelmo}

c) C = { , , , }

d) D = {3, 6, 9, 12, 15, 18, 21}

e) E = {rosso, verde, giallo}

f) F = {a, e, i, o, u}

g) G = {F, I, R, E, N, Z}

Sì No

Sì No

Sì No

Sì No

Sì No

Sì No

Sì No

Sì No

40 Rappresenta per elenco i seguenti insiemi.

41 Scrivi tre insiemi e rappresentali tabularmente.

42 Scrivi tre insiemi che si possono rappresentare per caratteristica.

43 Scrivi tre insiemi formati da tre elementi e rappresentali graficamente con il diagramma di Venn.

44 Osserva il seguente diagramma di Eulero-Venn e stabilisci se le affermazioni a esso relative sono vere (V) o false (F).

a) f ∈ M V F

b) a ∈ M V F

c) c ∉ M V F

d) o ∉ M V F

e) i ∉ M V F

f) M = {x|x è una lettera della parola “alice’’} V F

45 Rappresenta per elenco l’insieme M dell’esercizio precedente.

46 MATH Using the roster method, write the set D of the digits in your date of birth figures and complete the following relations using the ∈ and ∉ symbols. D = {

47 Dato l’insieme S = {x|x è un numero pari di tre cifre compreso tra 90 e 105}, stabilisci quali delle seguenti affermazioni a esso relative sono vere (V) e quali false (F). a) 92 ∉ S

d) S = {100, 102, 104}

48 Osserva i seguenti insiemi e rappresentali per caratteristica. N do si mi sol re la fa

49 MATEMATICA IN AZIONE Dopo aver individuato a quali nazioni appartengono le bandiere illustrate di seguito, rappresenta per elencazione gli insiemi:

a) P = {x|x è una bandiera dell’Europa}

b) Q = {x|x è una bandiera dell’Africa}

c) R = {x|x è una bandiera dell’Asia}

d) S = {x|x è una bandiera dell’America}

e) T = {x|x è una bandiera dell’Oceania}

LEZIONE 3

SOTTOINSIEMI E INCLUSIONE

50 Completa.

a) Il simbolo che indica l’inclusione è ; quello che indica la non inclusione è

b) Se tutti gli elementi di un insieme A appartengono anche a un altro B, allora l’insieme A è in B.

c) Se l’insieme C è nell’insieme D, allora C è sottoinsieme di

51 Spiega con un esempio la differenza fra sottoinsiemi propri e sottoinsiemi impropri o banali di un insieme.

52 Dato un insieme I, quali sono i suoi sottoinsiemi impropri o banali?

53 Indica se le affermazioni relative a ciascuna delle seguenti coppie di insiemi sono vere (V) o false (F).

a) A = {x|x è un mese di 30 giorni}; B = {aprile} B ⊂ A V F

b) C = {x|x è un numero dispari}; D = {53, 68, 45} D ⊂ C V F

c) E = {do, la, si}; F = {x|x è una nota musicale} F ⊂ E V F

d) L = {x|x è un pezzo degli scacchi}; M = {re, regina, torre} L ⊂ M V F

e) P = {x|x è una città italiana}; R = {Londra, Berlino, Madrid} R ⊄ P V F

54 Completa le affermazioni relative agli insiemi dati utilizzando i simboli ⊂ e ⊄ .

a) A = {x|x è un continente};

B = {Europa, India, Africa, Oceania} A B B A

b) C = {x|x è un componente della tua famiglia};

D = {x|x è un tuo amico} C D D C

c) E = {x|x è una leguminosa};

F = {fave, piselli} E F F E

d) G = {x|x è una lettera della parola “bonifica’’};

H = {b, n, f, c} G H H G

e) M = {x|x è una lettera della parola “occasione’’};

N = {s, a, c, o} M N N M

f) P = {x|x è un numero pari};

Q = {x|x è una cifra del numero 184} P Q Q P

55 Completa inserendo ⊂ e ⊄ .

a) {2, 3, 4, 5} {6, 7, 8, 9, 10}

b) {x|x è un triangolo equilatero} {x|x è un triangolo}

c) {l, m, n, h, g} {t, m, d, l, n, h, s, a, g}

d) {x|x è un alunno di prima} {x|x è un alunno di seconda}

e) {x|x è una lettera della parola “micio’’} {x|x è una lettera della parola “amico’’}

f) {gatto, cane, rondine, delfino} {tigre, leone, pantera, elefante, giraffa}

56 Considera i due insiemi I e P:

I = {scarpe, camicia, calze, cravatta, guanti, pantaloni, maglione, orecchini};

P = {x|x si vende a paio}.

g) Stabilisci se la relazione di inclusione è vera o falsa: P ⊂ I V F

h) Rappresenta graficamente i due insiemi sul tuo quaderno.

Considerando le seguenti coppie di insiemi e le affermazioni a fianco, indica se sono vere (V) o false (F).

a) A = {soia, ceci, lenticchie, fagioli};

B = {x|x è una leguminosa} A ⊂ B V F

b) A = {Tamigi, Tevere, Nilo, Volga, Danubio, Flumendosa};

B = {x|x è un fiume europeo} A ⊂ B V F

c) A = {x|x è un mese il cui nome termina con la “e’’};

B = {x|x è un mese di trenta giorni} A ⊂ B V F

d) A = {x|x è una vocale della parola “nomade’’};

B = {x|x è una lettera dell’alfabeto italiano} A ⊂ B V F

Completa indicando a tuo piacere un insieme B tale che B ⊂ A .

a) A = {x|x è un numero naturale minore di 35}; B = {

b) A = {x|x è un verbo della 1a coniugazione}; B = {

c) A = {x|x è un animale a sangue freddo}; B = {

d) A = {x|x è una lettera della parola “inclusione’’}; B = {

e) A = {x|x è una cifra del numero 193 246}; B = {

59 Per ciascuno dei seguenti insiemi indica un possibile insieme U che lo contenga.

a) A = {x|x scanner, mouse}; U =

{x|x è un accessorio del computer}

b) A = {x|x è un quadrato}; U = {x|x

c) A = {x|x è una palma da datteri}; U = {x|x

d) A = {x|x è un numero pari}; U = {x|x

e) A = {x|x è un cardellino}; U = {x|x

60 MATEMATICA IN AZIONE Considera l’insieme degli alunni della tua classe e rappresenta con diagrammi di Venn almeno tre suoi sottoinsiemi.

Considera il diagramma di Venn e completa con ⊂ o ⊄ .

62 Completa utilizzando in modo adeguato i simboli ∈, ∉, ⊂, ⊄ .

63 Dati i seguenti insiemi, rappresenta per elenco, sul tuo quaderno, tutti i sottoinsiemi che si possono formare.

ESEMPIO ●●●

A = {x|x è un simbolo della schedina del totocalcio}

Sottoinsiemi propri: B = {1} C = {2} D = {x} E = {1, 2} F = {1, x} G = {2, x}

Sottoinsiemi impropri: A = {1, 2, x}; ⌀

a) A = {x|x è una lettera della parola “orco’’}

b) A = {quadrato, rettangolo, rombo}

c) A = {x|x è una cifra del numero 3 027}

d) A = {x, y, z}

64 Scrivi i sottoinsiemi impropri dei seguenti insiemi.

a) A = {x|x è una lettera della parola “fringuello’’}

b) A = {x|x è una cifra pari}

c) A = {x|x è un numero della tabellina del 6 minore di 33}

d) A = {x|x è un punto cardinale}

65 Indica se le seguenti relazioni sono vere (V) o false (F).

a m o r

66 MATH Given the sets R, S and T, complete the relations using the symbols ⊄, ⊂, ∈, ∉.

67 Considera gli insiemi C , M e S e completa le relazioni usando i simboli ∈, ∉, ⊂, ⊄ .

68 MATEMATICA IN AZIONE Leo e Lia vogliono sistemare la loro collezione di fumetti della Disney nella nuova cameretta. Lia vuole raggrupparli secondo l’anno di stampa, Leo invece vuole ordinarli separando i numeri più divertenti da quelli più noiosi. Quale dei due criteri è migliore per formare dei sottoinsiemi della collezione? Spiega il perché.

INSIEME INTERSEZIONE

69 Quali elementi contiene l’insieme intersezione di due o più insiemi?

70 Che cosa significa la scrittura A ∩ B = C?

71 Quando due insiemi si dicono disgiunti? Fai un esempio.

72 Qual è l’intersezione di due insiemi disgiunti?

73 Scrivi in simboli matematici che l’intersezione tra due insiemi disgiunti, R ed S, è un insieme vuoto.

74 Se C è un sottoinsieme di A , allora C ∩ A = C . È vero? Fai un esempio che illustri la tua risposta.

75 Colora l’insieme intersezione nei seguenti casi.

76 Dati i seguenti diagrammi di Venn, rappresenta per elenco l’insieme intersezione di ciascuna coppia.

Osserva i seguenti diagrammi di Venn e completa.

77 20 4 16 8 24 12 6 18 B A Rappresenta per elencazione gli insiemi:

t c x h i n s R L

Rappresenta per elencazione gli insiemi:

L = { }, R = { }, L ∩ R = { }

Considera gli insiemi dati e completa.

C = {cane, cavallo, capra, canguro}; S = {cavallo, delfino, canguro};

N = {cavallo, asino, zebra, mulo}

C ∩ S = {cavallo, canguro} ; C ∩ N = {cavallo}; N ∩ S = {cavallo}; C ∩ S ∩ C = {cavallo}

A = {x|x è una lettera della parola “mare’’};

B = {x|x è una lettera della parola “sabbia’’};

C = {x|x è una lettera della parola “burrasca’’}.

a) Scrivi le loro rappresentazioni tabulari:

A = {m, a, r, e} B = { C = {

b) Scrivi gli elementi delle loro intersezioni:

A ∩ B = { A ∩ C

c) Rappresenta l’intersezione con il diagramma di Venn:

B = {x|x è una cifra del numero 76 256};

D = {x|x è una cifra del numero 5 084};

F = {x|x è una cifra del numero 36 071}.

Rappresenta per elenco e graficamente

B ∩ D; B ∩ F;

;

MATH Insert elements 1, 5, 8, 12, 0, 16 in the graph so that:

Osserva il diagramma di Venn ed esegui le richieste contenute nei seguenti esercizi.

Completa le affermazioni.

a) Quali sono gli elementi che appartengono solo ad A?

b) Quali sono gli elementi che appartengono solo a B?

c) Quali sono gli elementi che appartengono solo a C ?

d) Quali sono gli elementi che appartengono solo ad A e a B?

e) Quali sono gli elementi che appartengono solo a B e a C ?

f) Quali sono gli elementi che appartengono solo ad A e a C ?

g) Quali sono gli elementi che appartengono a B, C e A?

Completa le rappresentazioni per elenco.

Osserva i diagrammi di Venn e rispondi.

Sport seguiti in TV dai docenti della scuola di Petralia Soprana.

a) Quanti docenti seguono solo il basket?

b) Quanti solo il calcio?

c) Che cosa rappresenta il numero 11?

d) Quanti sono in tutto i docenti della scuola?

Interrogazioni sostenute fino a oggi nelle classi prima C e prima E.

a) Quanti alunni sono stati interrogati solo in Italiano?

b) Quanti in totale in Matematica?

c) Quanti in entrambe le materie?

d) Gli alunni delle due prime in tutto sono più o meno di 40?

Predisponi dei diagrammi di Venn come quelli degli esercizi precedenti per risolvere i seguenti problemi.

MATEMATICA IN AZIONE Ada ama i fiori profumati e i fiori bianchi; sul suo terrazzo ne ha di diversi tipi. In particolare ha 30 fiori bianchi, 24 fiori profumati e 10 fiori bianchi e profumati. Ma quanti sono i fiori sul terrazzo di Ada?

a) I 10 fiori bianchi e profumati vanno nell’

b) I fiori solo bianchi sono 30 10 =

c) I fiori solo profumati

In totale i fiori sul terrazzo di Ada sono [44]

STEM Un sabato mattina di fine ottobre in un mercato rionale di Torino in una bancarella della frutta sono esposti: 80 frutti autunnali (insieme A), 60 frutti arancioni (insieme B) e 38 frutti arancioni autunnali (insieme C ).

a) Quanti sono i frutti autunnali non arancioni?

b) Quanti quelli arancioni non autunnali?

c) In quale insieme vanno inseriti i seguenti frutti: albicocca, cachi, noce, melone, uva, castagna, mapo?

Dati gli insiemi A = {1, 2, 3, 4, 6, 12}; B = {1, 2, 4, 8, 16}; C = {1, 2, 3, 5, 6, 10, 15, 30}

a) completa le rappresentazioni per elenco:

A ∩ B = A ∩ C =

B ∩ C = A ∩ B ∩ C =

b) rappresenta A, B e C con un diagramma di Venn;

c) rispondi alle domande:

1) quali elementi appartengono solo all’insieme A?

2) quali solo a B?

3) quali solo a C ?

STEM Completa il diagramma di Venn che mette in evidenza le analogie e le differenze tra un coccodrillo e una rana.

a) All’interno del diagramma scrivi i numeri che corrispondono alle caratteristiche elencate.

1) È un vertebrato

2) È un carnivoro

3) Ha i denti

4) Ha quattro zampe

5) Ha una colonna vertebrale

6) Ha due occhi

7) Depone le uova

8) È un anfibio

9) È un rettile

10) I piccoli respirano con le branchie

11) Depone le uova in acqua

12) Depone le uova in una buca

b) L’insieme intersezione rappresenta le analogie o le differenze tra i due animali?

STEM Dopo aver preparato un elenco numerato di analogie e differenze tra una mucca e un cane, come nell’esercizio precedente, scrivi nel diagramma i numeri che a esse corrispondono.

91 Scrivi degli insiemi che rispettino le seguenti richieste.

a) A e B insiemi di mezzi di trasporto con A ∩ B = ∅

b) L e M insiemi di parole con L ∩ M = {a, e, o}

c) F e G insiemi di animali con F ∩ G = G

d) P, M e R insiemi di numeri con P ∩ M ∩ R = {3, 5}

92 Considera gli insiemi:

A = {x|x è una lettera della parola “canestro’’};

B = {x|x è una lettera della parola “palestra’’};

C = {x|x è una lettera della parola “tappetino’’}.

Rappresenta per elencazione

A ∩ B, B ∩ C, A ∩ C, A ∩ B ∩ C e completa poi il diagramma di Venn.

LEZIONE 5

INSIEME UNIONE

93 Scrivi in simboli che l’insieme F è l’unione dei due insiemi C e D.

94 Quali elementi contiene l’insieme unione tra due o più insiemi?

95 Dati due insiemi disgiunti A e B che contengono rispettivamente 2 e 4 elementi, l’insieme unione contiene 6 elementi. È vero?

Illustra la tua risposta con un esempio.

96 Se L ⊂ P, allora L ∪ P = P. È vero? Fai un esempio che illustri la tua risposta.

97 Colora l’insieme unione nei seguenti casi.

98 Dati i seguenti diagrammi di Venn, rappresenta per elenco l’insieme unione di ciascuna coppia.

A ∪ B = { C ∪ D = { E ∪ F = {

99 Rappresenta per caratteristica l’unione degli insiemi dati.

a) A = {cifre pari}; B = {cifre dispari}

b) C = {vocali dell’alfabeto italiano}; D = {consonanti dell’alfabeto italiano}

c) A = {mesi di trenta giorni}; B = {mesi di trentun giorni}; C = {mesi di 28/29 giorni}

d) F = {rettangolo, parallelogramma, rombo, quadrato}; G = {trapezi}

100 Considera i seguenti insiemi:

A = {x|x è una cifra del numero 54 324};

B = {x|x è una cifra del numero 4 309};

C = {x|x è una cifra del numero 1 324}.

a) Scrivi le loro rappresentazioni per elenco:

A = {5, 4, 3, 2} B = { } C = { }

b) Scrivi gli elementi delle loro unioni:

A ∪ B = { A ∪ C = { 1, 3, 2, 4, 5 }

B ∪ C = { A ∪ B ∪ C = {

c) Rappresenta A ∪ B ∪ C con il diagramma di Venn:

102 Inserisci le seguenti cifre (attento a come sono scritte) nel diagramma, sapendo che:

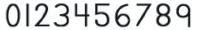
C = {x|x cifra formata da linee curve} e R = {x|x cifra formata da linee rette}.

Rappresenta poi per elenco C ∪ R e C ∩ R, sul quaderno.

103 Dati gli insiemi:

A = {x|x è un numero naturale pari e 11 < x < 21},

B = {x|x è un numero naturale dispari e 11 < x < 21}

rappresenta per elenco e graficamente A ∪ B

104 Dati gli insiemi:

⎭⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎬⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎫

L = {x|x è una lettera della parola “aprile’’},

M = {x|x è una lettera della parola “pesca’’},

N = {x|x è una lettera della parola “esca’’}

rappresenta, sul tuo quaderno, per elenco e graficamente:

L ∪ M, M ∪ N, L ∪ N, L ∪ M ∪ N

Risolvi, sul tuo quaderno, i seguenti esercizi.

Considera gli insiemi: A = {x|x è un divisore di 18} e B = {x|x è un divisore di 24}.

Rappresenta tabularmente e graficamente A ∩ B e A ∪ B

Considera gli insiemi: A = {x|x è una cifra del numero 56 290} e B = {x|x è una cifra pari}.

Rappresenta per elencazione e graficamente A ∩ B e A ∪ B

Considera gli insiemi: A = {l, m, n, o}, B = {x|x è una lettera della parola “umano’’},

C = {x|x è una lettera della parola “mano’’}.

Rappresenta per elencazione e graficamente A ∩ B ∩ C e A ∪ B ∪ C

Se A = {x |x è un mese di 31 giorni}, B = {x |x è un mese il cui nome termina con “o’’},

C = {x |x è un mese di 30 giorni}, rappresenta tabularmente A ∩ B ∩ C e A ∪ B ∪ C

109 Dati gli insiemi:

W = {x|x alunni che leggono gialli},

F = {x|x alunni che leggono fumetti},

Z = {x|x alunni che leggono fantasy}

Maria Carlo F W Z

Marta

Bea Luca Lia Lisa Piero

Emma Ugo

rappresenta per elenco:

110 MATEMATICA IN AZIONE In un centro di recupero della fauna selvatica vengono curati animali feriti.

La pulizia dello spazio dove vivono viene effettuata nei giorni pari per gli animali dell’insieme

A, nei giorni dispari per quelli dell’insieme B:

A = {lupo, orso, camoscio, muflone, capriolo, cervo};

B = {daino, muflone, capra selvatica, cinghiale, volpe, cervo}.

d) Quali animali necessitano della pulizia tutti i giorni?

A ⋂ B =

e) Scrivi i nomi di tutti gli animali ricoverati presso il centro di recupero.

A ⋃ B =

111 MATH Given the following Venn diagram, write the following sets in the roster form:

112 Dati gli insiemi:

A = {x|x ∈ N e x < 11},

B = {x|x ∈ N e x è un numero pari minore di 12},

C = {x|x ∈ N e x è numero pari minore di 5}

rappresenta per elenco e graficamente A ∩ B ∩ C e A ∪ B ∪ C

MATEMATICA IN AZIONE Al supermercato Comprabene è arrivato un carico di arance dalla Calabria per il reparto ortofrutta.

Nel seguente diagramma è rappresentata la distribuzione in cassette per qualità. Osserva e rispondi.

Arance in vendita

25 13 15 49

a) Quante cassette di tipo tarocco si vendono in tutto?

b) Quante solo del tipo tarocco?

c) Quante del tipo tarocco e/o sanguinello?

d) Quante né tarocco né sanguinello?

e) Le cassette in vendita sono più o meno di 100?

ImpArAerrOre dall'

Imparare la teoria degli insiemi è come imparare un nuovo LINGUAGGIO, e come succede per le lingue, all’inizio potresti fare dei piccoli errori.

Ecco alcuni tra i “passi falsi” più comuni: conoscerli ti aiuterà a prestare più attenzione e a non farli anche tu. Un errore frequente consiste nel confondere l’unione con l’intersezione tra due o più insiemi. Pensa all’unione come a una collezione: metti insieme tutti gli elementi che trovi nel

primo insieme e tutti quelli che trovi nel secondo, senza ripetere gli elementi, cioè senza “contarli” due volte. Pensa, invece, all’intersezione come a una specie di “caccia al tesoro” degli elementi in comune: devi cercare solo gli elementi presenti sia nel primo insieme sia nel secondo. Attenzione! Se un insieme è contenuto nell’altro, l’UNIONe è semplicemente l’insieme più grande, mentre l’INtersezIONe è rappresentata dall’insieme più piccolo. Un consiglio: usa sempre una rappresentazione grafica per evitare di confonderti.

MATEMATICA IN AZIONE Luca si diverte a classificare i suoi amici e disegna l’insieme U che li comprende tutti.

Indica poi con A il sottoinsieme degli amici che hanno i capelli castani e con B quello degli amici con gli occhi azzurri, come nel seguente diagramma di Venn. Osservalo e rispondi alle domande.

Riccardo Emma A Marta Stefano

a) Quanti sono e come si chiamano gli amici di Luca?

b) Chi tra i suoi amici ha gli occhi azzurri?

c) Chi non ha i capelli castani?

d) Chi tra i suoi amici ha i capelli castani e gli occhi azzurri?

e) Chi non ha gli occhi azzurri?

f) C’è qualche amico che non ha i capelli castani e gli occhi azzurri?

115 In ciascuno dei seguenti diagrammi di Venn inserisci degli elementi a tua scelta e scrivi le rappresentazioni tabulari richieste.

a) A

b)

c)

d)

COMPETENZE

PROBLEM SOLVING

1 Il diagramma rappresenta le rose vendute in un negozio.

19 roserosseroseconlespine 33 a) Quante rose con le spine sono state vendute?

b) E quante rose rosse con le spine?

2 Il diagramma rappresenta quale tipo di acqua bevono gli atleti di una squadra durante l’allenamento.

19 acquanaturaleacquagassata 18 8

a) Quanti bevono solo acqua gassata?

b) Quanti bevono sia l’una che l’altra?

c) Quanti sono gli atleti di questa squadra?

Risolvi i seguenti problemi utilizzando i diagrammi di Venn.

3 In una classe di 27 alunni, 11 hanno i capelli castani, 15 ricci, 6 castani e ricci. Quanti sono gli alunni né castani né ricci?

Completa il diagramma di Eulero-Venn, partendo dall'intersezione.

6 → capelli castani e ricci (intersezione)

11 − = → solo castani

15 − = → solo ricci

alunni castani e ricci

alunni castani

6 + + = → castani e/o ricci

27 − = → né castani né ricci

6

alunni ricci

alunni né castani né ricci

4 In un parco-zoo ci sono 320 animali; di questi 205 sono quadrupedi, 191 sono carnivori e 96 sono animali quadrupedi e carnivori.

Calcola quanti animali quadrupedi non sono carnivori, quanti animali carnivori non sono quadrupedi e quanti animali del parco-zoo non sono quadrupedi o carnivori.

animali del parco-zoo

quadrupedi

carnivori

[109; 95; 20]

ARGOMENTARE

5 Osserva i seguenti diagrammi di Eulero-Venn e trova gli errori motivando la risposta. a) b)

ANALIZZARE E INTERPRETARE DATI

6 Determina il più grande numero minore di 19 che sia contemporaneamente nella tabellina del 2, insieme A , e nella tabellina del 3, insieme B. a) A = {2, 4,

b) B = {3,

c) A ∩ B = d) Il numero è

7 Determina il più grande numero minore di 55 che sia nella tabellina del 2, insieme A , nella tabellina del 3, insieme B, e nella tabellina del 5, insieme C . [30]

SFIDA MATEMATICA

8 I droidi

La ditta Automati Industriali ha realizzato tre droidi: J1-M1, J2-M2, J3-M3. Ogni droide ha un numero di antenne diverse e, per sicurezza, ne ha almeno due. Ogni droide ha una vista perfetta e non mente mai. I tre droidi lavorano insieme in un dipartimento della stazione spaziale Skytop.

J1-M1 dice: “Su voi due vedo 6 antenne in totale’’.

J2-M2 dice: “Su voi due vedo 5 antenne in totale’’. Quante antenne vede J3-M3 in totale sugli altri due droidi?

(Testo tratto dalla gara Finale di Parigi, Campionati Internazionali, organizzata dal Centro PRISTEM dell’Università Bocconi di Milano)

ROAD MAP PER TUTTI

DATO IL TUO GRUPPO CLASSE

INSIEMI

Possiamo considerarlo un insieme matematico?

PAG. 4

Sì, perché è possibile stabilire con certezza quali elementi (compagni e compagne) formano il gruppo classe, cioè l'insieme.

Rispetto al numero di elementi, come può essere un insieme?

Finito: se contiene un numero limitato di elementi; Infinito: se contiene un numero illimitato di elementi; Vuoto: se non contiene elementi.

ESEMPIO

Insieme finito: il tuo gruppo classe; Insieme infinito: i numeri naturali; Insieme vuoto: i numeri pari che terminano con 3.

APPARTENENZA

Come indichiamo gli elementi che non appartengono a D?

Con il simbolo ∉ che indica non appartenenza.

DATO L'INSIEME

D = {Do, Re, Mi, Fa, Sol, La, Si} DELLE NOTE MUSICALI

Do Re Mi

Fa Sol

La Si D

Come indichiamo gli elementi che appartengono a D?

Con il simbolo ∈ che indica appartenenza.

1 Indica quali dei seguenti gruppi di oggetti determinano un insieme matematico.

ESEMPIO

I fiori più profumati Sì No

a) I giorni più belli della primavera

Sì No

b) I ragazzi della tua scuola con il nome formato da tre sillabe Sì No

c) I numeri naturali Sì No

d) Le trasmissioni televisive più noiose della domenica pomeriggio Sì No

e) Le più romantiche canzoni italiane degli anni Novanta Sì No

f) Gli oggetti presenti in un cassetto Sì No

2 Completa.

Esempio. Un gregge è un insieme di pecore. gregge pecore

Un arcipelago è un insieme di isole.

Una costellazione è un insieme di stelle.

Un frutteto è un insieme di alberi da frutta.

3 Indica se gli insiemi dati sono finiti (F), infiniti (I) o vuoti (V).

a) Mesi di 34 giorni

b) Abitanti de L’Aquila c) Numeri naturali

4 Completa utilizzando i simboli ∈ e ∉.

ESEMPIO

E maccheroni

penne rigate fusilli rigatoni

a) spaghetti E e) paccheri E

b) fusilli E f) penne rigate E

c) bucatini E g) penne lisce E

d) maccheroni E h) rigatoni E

5 Considera i seguenti insiemi e individua quelli vuoti indicandoli con il simbolo adeguato (∅).

a) N = {x | x è un numero dispari che termina con 0}

b) A = {x | x il nome di un attore comico inglese}

c) P = {x | x è il nome di una pianta grassa}

d) M = {x | x è il nome di un mese che inizia per P}

RAPPRESENTAZIONE DI UN INSIEME TEORIA PAG. 6

In quali modi si può rappresentare?

• Per elenco o tabulazione

• Per caratteristica

DATO L'INSIEME M DEI MESI DI 30 GIORNI

ESEMPIO

M = {aprile, giugno, settembre, novembre}

• Con il diagramma di Venn

M = {x | x è l'insieme dei mesi che hanno 30 giorni}

ESEMPIO

ESEMPIO aprile settembre giugno novembre

INCLUSIONE E NON INCLUSIONE TEORIA PAG. 8

DATI GLI INSIEMI:

A = {lettere della parola “sapone”}

B = {lettere della parola “pane”}

C = {lettere della parola “luci”}

Come si indica che l’insieme C non è contenuto in A?

Con il simbolo ⊄ che indica la non inclusione.

Come si indica che l’insieme B è contenuto in A?

Con il simbolo ⊂ che indica inclusione.

6 Rappresenta l’insieme D dei nomi delle dita di una mano.

a) Rappresentazione per elenco:

D = {pollice, indice, , , }

b) Rappresentazione per caratteristica:

D = {x|x è il nome }

c) Rappresentazione grafica con il diagramma di Venn.

D mignolo medio

7 Sul tuo quaderno rappresenta per elenco e col diagramma di Venn i seguenti insiemi.

ESEMPIO

B = {x|x è un colore della bandiera italiana}

B = {verde, bianco, rosso}

bianco verde rosso

P = {x | x è un punto cardinale}

S = {x|x è una lettera della parola “benvenuto’’}

A = {x|x è una cifra pari del numero 12 549}

M = {x|x è una lettera del tuo nome}

N = {x|x è una nota musicale}

8 Completa gli insiemi e utilizza i simboli ⊂ (incluso) e ⊄ (non incluso).

C = {x | x è una cifra del numero 1 379}

D = {x | x è una cifra pari}

C D D C

9 Considera gli insiemi dati e completa utilizzando ⊂ e ⊄

A = {1, 2, 9, 5, 0} B = {1, 0, 2} C = {8, 6, 7, 3} D = {7, 8, 3}

10 La mamma ha dato a Giada e Gabriel una grande scatola dove inserire tutti i loro giochi; poi ha dato loro un contenitore più piccolo per inserire i giochi di carte.

Rappresenta graficamente i giochi dati nei due insiemi.

battaglia navale • dadi • dama • domino • gioco dell’oca • memory • puzzle • scala quaranta • uno • scacchi • solo

Tuttiigiochi

Giochidicarte

DATI GLI INSIEMI A e B A B

INSIEME INTERSEZIONE

ESEMPIO

A = {x|x è un attrezzo per il disegno geometrico}; B = {riga, squadra, flauto, spalliera, colori a olio}

A ∩ B = {riga, squadra}

TEORIA PAG. 10

Che cos’è l’intersezione?

L’intersezione è un’operazione che considera solo gli elementi comuni tra gli insiemi dati.

A B

Con quale simbolo si indica?

Si indica con il simbolo ⋂

INSIEME UNIONE

DATI GLI INSIEMI A E B A B

ESEMPIO

A = {10, 20, 30, 40, 50} e B = {20, 40, 60, 80}

A ⋃ B = {10, 20, 30, 40, 50, 60, 80}

TEORIA PAG. 12

Che cos’è l’unione?

L’unione è un’operazione che considera tutti gli elementi comuni e non comuni tra gli insiemi dati.

A B A B

Con quale simbolo si indica?

L’unione si indica con il simbolo ⋃

Determina l’intersezione tra gli insiemi A e B.

11 A = {6, 9, 3, 1, 0} e B = {1, 2, 3, 4, 5, 6}; A ∩ B = {

12 A = {x|x è una lettera di “parola’’} e B = {p, r, a}; A ∩ B = {

Determina l’unione tra gli insiemi A e B

13 A = {x | x è una cifra pari} e B = {x | x è una cifra del numero 1 962 013}

A ⋃ B = {

14 A = {pentagono, triangolo, cerchio, rombo} e B = {quadrato, rettangolo, rombo}

A ⋃ B = {

15 Scrivi la rappresentazione per elenco di A e di B e poi, per ciascuna coppia di insiemi, determina l’insieme intersezione e l’insieme unione.

rosso rosa viola verde

SIMULAZIONE DI VERIFICA

1 Per ogni affermazione scegli la scrittura simbolica corretta.

a) 7 appartiene all’insieme S.

1) 7 ⋂ S 2) 7 ∈ S 3) 7 ⊂ S 4) 7 ∉ S

b) L è un sottoinsieme di M. 1) M ⊂ L 2) M Ω L 3) L ⊂ M 4) L ⊄ M

c) V è un insieme vuoto. (Più di una risposta)

1) V = ∅ 2) V = Ω 3) V = { } 4) V = ∉

d) I è l’insieme intersezione di A e B

1) A ⟳ B

2) I = A ⋃ B 3) A { } B = I 4) I = A ⋂ B

2 Stabilisci quali tra i seguenti insiemi sono finiti (F) e quali infiniti (I).

a) Insieme dei mesi di 30 giorni

b) Insieme dei numeri pari

c) Insieme dei numeri dispari

d) Insieme dei punti di una retta

e) Insieme delle lettere della parola “infinito”

f) Insieme delle specie delle orchidee F I

I

I

I

3 Dati A = {x|x è una lettera della parola “cellulare”}, B = {x|x è una lettera della parola “accendere”}, rappresenta per elenco e graficamente gli insiemi:

a) A ⋂ B b) A ⋃ B

Rappresentazione per elenco Rappresentazione grafica

a) A ⋂ B

b) A ⋃ B

4 Considera gli insiemi:

A = {agrumi, succo, marmellata, caramella}; {pomodoro, succo, passata, concentrato}; {uva, succo, marmellata} e stabilisci quali relazioni ad essi riferite sono esatte.

a) A ⋃ B ⋃ C = {succo}

b) A ⋂ B ⋂ C = {succo}

c) A ⋃ B ⋃ C comprende 9 elementi

d) A ⋂ C {marmellata}

5 Nella zona A di una serra ci sono 800 piante: 380 sono annuali, 200 aromatiche e 120 aromatiche annuali. Completa il diagramma di Venn e stabilisci:

a) quante sono le piante aromatiche non annuali:

b) quante le annuali non aromatiche:

c) quante le altre piante presenti nella zona A di quella serra:

piante della zona A

6 Dopo la merenda di Jacopo e dei suoi amici, nel sacchetto di cioccolatini ne sono rimasti solo 18 alla crema, 15 con le nocciole e 7 con la crema e le nocciole.

a) Completa il diagramma che rappresenta il sacchetto dopo la merenda.

b) Quanti cioccolatini sono rimasti nel sacchetto? Motiva la risposta. 1) 40 2) 26 3) 30 4) 36

7 Osserva il diagramma di Venn.

a) Rappresenta gli insiemi A, B e C per caratteristica.

A = {x|x }

B = {x|x }

C = A ⋂ B = {x|x }

b) Stabilisci l’appartenenza agli insiemi A, B e C degli animali seguenti:

cane, cavallo, lemure, orso polare, polpo, puma, seppia, stambecco, trota

Cane Orso polare Seppia

Cavallo Polpo Stambecco

Lemure Puma Trota

UNITÀ 2

IL SISTEMA DI NUMERAZIONE DECIMALE

Chi ha della

pAURA

MATEMATIcA?

Cominciamo a fare la conoscenza con i NUMERI NATURALI, il punto di partenza di tutta la matematica. Li usi ogni giorno, senza neanche accorgertene. Quando conti le matite nella tua cartella, le compagne e i compagni della tua classe, i giorni che mancano alle prossime vacanze o quando indichi le posizioni dei giocatori nella classifica di un videogame, stai usando i numeri naturali! Avrai sentito dire che i numeri naturali sono infiniti ed è proprio così, ma questo non deve spaventarti, significa solo che non c’è un numero naturale “più grande di tutti”. Infatti, se anche tu pensassi a un numero molto grande, basterebbe aggiungere 1 per trovarne uno ancora più grande. Così come ogni lingua ha le sue regole per formare le parole e le frasi, allo stesso modo in matematica si usa il sistema di numerazione decimale che è posizionale. Che cosa significa? Che è possibile utilizzare solo 10 cifre per riuscire a scrivere tutti i numeri che si conoscono, grazie alla magia della posizione che fa in modo che il valore delle cifre cambi a seconda del posto occupato. Continuerai con l’esplorazione dei numeri decimali, quelli con la virgola, e poi imparerai a disegnare e ordinare tutti questi numeri su una retta in modo da confrontarli tra di loro e visualizzare quanto sono grandi o piccoli.Buonlavoro!

ROAD MAP la nostra

FACCIAMO LA CONOSCENZA

CON I NUMERI NATURALI: UN ANTICO SISTEMA PER CONTARE GLI OGGETTI

SCOPRIAMO INSIEME IL SISTEMA DI NUMERAZIONE DECIMALE

2

IMPARIAMO A RICONOSCERE I NUMERI DECIMALI

3 4

RAPPRESENTIAMO I NUMERI SU UNA SEMIRETTA

MATERIALE INTEGRATIVO MULTIMEDIALE

Focus

Videolezione

Verifica interattiva

Ripasso

SUCCEDE CHE...

I NUMERI NATURALI

Cinque amici, Andrea, Dario, Giulio, Luca e Marcello, partecipano a una gara di corsa campestre.

Pino, il cronista sportivo che segue la manifestazione, raccoglie queste notizie:

Giulio arriva primo alle 15:30, Marcello arriva quinto dopo 4 minuti, Andrea arriva prima di Dario ma dopo Luca.

Aiuti Pino a stabilire l’ordine di arrivo dei cinque amici e l’ora di arrivo del quinto?

Per aiutare il cronista Pino dobbiamo utilizzare i numeri cardinali e quelli ordinali.

I numeri naturali, usati dall’uomo fin dall’antichità per indicare quantità e per contare oggetti, possono essere cardinali o ordinali

I numeri cardinali esprimono la quantità degli oggetti considerati.

I numeri ordinali indicano il posto occupato da un oggetto in una serie ordinata.

In cifre i numeri ordinali si scrivono con un esponente dopo il numero (o oppure a): 1o piano, 2a scala; in alternativa con le cifre romane: classe I B.

I numeri naturali costituiscono l’ insieme ℕ, che è una successione ordinata.

Ogni numero naturale ha:

• un successivo o consecutivo, che è il numero che lo segue;

• un precedente o antecedente, che è il numero che lo precede.

In N lo zero non ha precedente.

Dato un numero a, il successivo si ottiene aggiungendo 1; in simboli: (a + 1).

Il precedente si ottiene togliendo 1; in simboli: (a - 1).

L’insieme ℕ dei numeri naturali è infinito; infatti, per ogni numero naturale è sempre possibile, aggiungendo una unità, ottenere un successivo.

ℕ = {0, 1, 2, 3... 105, 106... 29 877, 29 878...}

I numeri pari si indicano con 2n e terminano con una cifra pari: 0, 2, 4, 6, 8.

I numeri dispari si indicano con 2n + 1 e terminano con una cifra dispari: 1, 3, 5, 7, 9.

Confrontando i numeri naturali si può stabilire se sono uguali (=) o diversi (≠), qual è il maggiore (>) e quale il minore (<). Si utilizzano anche i simboli ≥, che si legge “è maggiore o uguale a’’, e ≤, che si legge ‘‘è minore o uguale a’’.

Al cronista Pino possiamo suggerire l’ordine di arrivo: primo Giulio, secondo Luca, terzo Andrea, quarto Dario e quinto Marcello.

Il quinto amico, cioè Marcello, arriva alle 15:34.

1 Nella seguente frase individua i numeri cardinali e quelli ordinali.

a) Le pecore sono quattro. Quattro è un numero cardinale.

b) La quarta nota della scala musicale è Fa. Quarta è un numero ordinale.

In via Primo Aprile c’è un palazzo di otto piani. Al secondo piano abita una famiglia di sette persone, al terzo due pensionati con quattro gatti e un cane che si chiama Settimo, al piano terra il custode con moglie, tre figli e la suocera, quindi sei persone.

Numeri cardinali Numeri ordinali

2 Scrivi il precedente e il successivo dei seguenti numeri. 25 561 1

3 Completa la tabella suddividendo i numeri dati in numeri pari e numeri dispari.

18 36 210 sono numeri pari 47 523 499 625 sono numeri dispari

13; 56; 108; 42; 80; 95; 319; 610; 404; 903; 6 707; 3 041; 9 002; 6 993; 24 689.

4 MATEMATICA IN AZIONE Marco è un grande tifoso di calcio e ogni lunedì compra il giornale per leggere la classifica aggiornata. I suoi compagni, che lo sanno, gli si fanno intorno per porgli delle domande.

Aiuta Marco a rispondere.

a) Qual è l’ultima squadra in classifica?

b) Tra Napoli e Fiorentina quante squadre ci sono?

c) Chi è la terza in classifica?

d) Quanti punti di differenza hanno Udinese e Atalanta?

e) Il Torino è al posto mentre il Milan è al posto.

f) Quanti punti ha la squadra prima in classifica?

g) Quante sono le squadre del campionato? ESEMPIO ESEMPIO

SUCCEDE CHE...

IL SISTEMA DI NUMERAZIONE DECIMALE

Pietro osserva i cartellini dei prodotti venduti in un negozio e nota che ci sono solo le cifre 4 e 0; i prezzi, però, sono diversi e vorrebbe abbinare ogni cartellino con il corrispondente prodotto. Che cosa rende differenti i prezzi?

Per rispondere vediamo le caratteristiche del sistema di numerazione decimale.

Il sistema di numerazione decimale usa 10 simboli, le 10 cifre indo-arabiche: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

Con queste 10 cifre, unità del 1º ordine, si indicano i numeri che vanno da 0 a 9.

Per scrivere i numeri maggiori di 9 si tiene conto di quanto segue.

Dato che il sistema è decimale, le unità si raggruppano di dieci in dieci:

• dieci unità del 1º ordine formano una decina (unità del 2º ordine);

• dieci decine formano un centinaio (unità del 3º ordine);

• dieci centinaia formano un migliaio (unità del 4º ordine) e così via.

Gli ordini, a gruppi di tre, formano una classe: 1a classe (unità semplici), 2a classe (migliaia), 3a classe (milioni), 4a classe (miliardi)...

Ogni cifra ha un valore assoluto e un valore relativo, che dipende dal posto che la cifra occupa nel numero. Il valore relativo della cifra 5 è diverso nel numero 135 (unità semplici) e nel numero 531 (centinaia).

Il sistema di numerazione decimale è posizionale perché il valore di una cifra dipende dal posto che occupa nel numero.

La cifra zero indica la mancanza di elementi in un determinato ordine:

30 → zero unità semplici (u); 40 6 → zero decine (da); 8 0 91 → zero centinaia (h). Inoltre, la presenza della cifra zero permette di scrivere e distinguere numeri molto diversi tra di loro: 652 e 6 052 oppure 6 520

La scrittura polinomiale di un numero si utilizza per mettere in evidenza il valore relativo di ogni cifra in quel numero.

La scrittura polinomiale del numero 5 209 è:

5 209 = 5 × 1 000 + 2 × 100 + 0 × 10 + 9

5 migliaia, 2 centinaia, 0 decine, 9 unità semplici

I cartellini dei prezzi sono diversi per la presenza di uno o più zeri che cambiano il valore del numero. Gli abbinamenti corretti sono: colla → 4 €; zainetto → 40 €; cellulare → 400 €; ciclomotore → 4 000 €.

1 Scrivi quanto vale la cifra 7 in ciascuno dei seguenti numeri.

a) 703 → 7 517 → 7

610 → 7 b) 1 072 → 7 74 801 → 7

740 → 7

2 Aiutandoti con lo schema seguente leggi questi numeri e poi scrivili in lettere. 80 567 123 654 701 3 087 90 625 75 031 670

Terza classe

M

classe

ottantamilionicinquecentosessantasettemilacentoventitre;

3 Completa la tabella rappresentando i numeri nei due modi richiesti.

674

333

4 MATEMATICA IN AZIONE Leggi l’articolo e scrivi in cifre i numeri che trovi scritti in lettere.

Shopping all’ex Alfa di Arese

ARESE (MI) - Centoventimila metri quadrati di estensione totale e una superficie commerciale utile di novantatremila metri quadrati, di cui cinquantacinquemila al piano terra e trentottomila al primo piano. I numeri del centro sono impressionanti: aperto sette giorni su sette, dalle 9 alle 22, punta ad accogliere 13 milioni di persone all’anno, anche grazie ai 6 mila posti auto.

3 I NUMERI DECIMALI

SUCCEDE

Emma e Pietro hanno misurato la propria altezza e litigano su chi sia il più alto. “Io misuro 1,4 metri e sono più alta” dice Emma. “No, sono io il più alto, perché misuro 1,40 metri” risponde Pietro.

Chi dei due ha ragione?

Per capire come distinguere le due misure bisogna conoscere i numeri decimali e le regole per scriverli correttamente.

Con le dieci cifre indo-arabiche e con le regole viste per il sistema di numerazione decimale, oltre ai numeri naturali si possono scrivere anche i numeri decimali.

I numeri decimali si riconoscono perché la virgola separa la parte intera dalla parte decimale.

Parte intera → 1,4 ← Parte decimale

Una unità semplice è costituita da dieci unità di ordine inferiore, cioè da dieci decimi; un decimo a sua volta è costituito da dieci centesimi, un centesimo da dieci millesimi, un millesimo da dieci decimillesimi e così via.

Per ottenere un’unità equivalente di ordine inferiore occorre dividere l’unità semplice in dieci, cento, mille parti uguali; quindi: 1 decimo → d → 0,1 1 centesimo → c → 0,01 1 millesimo → m → 0,001

Decimi, centesimi, millesimi... sono le unità decimali del primo, del secondo, del terzo ordine.

Ogni numero naturale si può considerare come un numero decimale avente come cifre decimali degli zeri: 63 = 63,0 = 63,000

Un numero decimale si legge così:

• la parte intera;

• la virgola che si legge “e’’;

ESEMPIO

• la parte decimale con il nome dell’unità decimale dell’ultima cifra a destra

37,5 → trentasette e cinque decimi; 0,458 → quattrocentocinquantotto millesimi

Anche i numeri decimali si scrivono in forma polinomiale

ESEMPIO

98,301 = 9 × 10 + 8 + 3 × 0,1 + 0 × 0,01 + 1 × 0,001

Lo zero dopo l’ultima cifra decimale non fa aumentare il valore del numero: i due amici hanno la stessa altezza e possono smettere di litigare.

1 Per ciascuno dei seguenti numeri, assegna a ogni cifra il nome esatto.

a) 45,03 → , , ,

b) 7,309 →

c) 680,0603 →

4 decine 5 decimi 3

2 Riscrivi in cifre i seguenti numeri.

a) 5 unità; 4 centesimi → 5,04 4 decine; 3 unità; 7 decimi →

b) 9 decine; 2 unità; 4 centesimi → 62 unità; 7 decimi; 1 centesimo →

3 Rispondi alle seguenti domande.

a) Quanti decimi ci sono in 7 unità?

b) Quanti millesimi ci sono in 8 centesimi?

c) Quanti decimi ci sono in 43 unità?

d) Quanti millesimi ci sono in 25 decimi?

4 Sottolinea il numero minore in ognuna delle seguenti coppie.

a) 81 decimi 1 unità

b) 300 centesimi 3 decimi

c) 6 unità 660 centesimi

d) 20 decimi 2 decine

5 Tra le seguenti uguaglianze sottolinea quelle errate.

a) 107,5 = 107,500

b) 6,803 = 60,803

c) 80 = 8,0

d) 94 = 94,00

6 Per ogni scrittura in forma polinomiale scrivi il corrispondente numero.

a) 4 × 10 + 5 + 5 × 0,01 + 4 × 0,001 = 1 + 2 × 0,01 =

b) 1 × 0,1 + 2 × 0,001 = 3 × 0,1 + 5 × 0,01 =

7 MATEMATICA IN AZIONE Mattia ha i cartellini che riportano le misure, in metri, ottenute nel salto in lungo dai suoi compagni ai campionati studenteschi. Mettili in ordine per sapere quale salto ha vinto.

a) Completa: < < < < <

b) L’atleta che ha vinto ha effettuato un salto di

SUCCEDE CHE...

NUMERO SU UNA SEMIRETTA

Nel mese di febbraio Pietro ha i seguenti impegni: palestra (P) tutti i mercoledì e venerdì, bowling (B) la seconda domenica del mese, dentista (D) il giorno 7, cinema (C) il terzultimo giorno del mese, a San Valentino (SV) cena fuori, la festa di carnevale (FC) cade la prima domenica del mese.

Come puoi aiutare Pietro a organizzare meglio i suoi impegni?

Si può utilizzare la rappresentazione grafica dei numeri.

I numeri naturali, elementi dell’insieme ordinato N, possono essere rappresentati graficamente su una semiretta

Per rappresentare graficamente un numero si procede in questo modo:

• si fissa l’origine O e, alla sua destra, si disegna una semiretta; O

• si stabilisce un’unità di misura , cioè un segmento unitario che viene riportato più volte sulla semiretta identificando dei punti; l’unità di misura è detta anche unità grafica;

AB CD EF G u O

• si fa corrispondere a ogni punto un numero; ogni punto è l’ immagine del numero naturale che gli corrisponde.

AB CD EF G u =1 O

01234567

Anche i numeri decimali possono essere rappresentati graficamente su una semiretta.

L’unità di misura deve valere un’unità decimale: 1 decimo, 1 centesimo...

u

Usando la linea dei numeri Pietro può segnare gli impegni del mese di febbraio in ordine cronologico.

1 Contrassegna le risposte esatte e correggi le affermazioni false.

0 12 3456 7 HI LM NO PQ R 89 10 11 12 13 14 15

AB CD EF G

a) L’immagine del numero 15 è il punto F. V F

b) L’immagine del numero 11 è il punto N V F

c) L’immagine del numero 0 è il punto P V F

d) Il punto F è l’immagine del numero 5. V F

e) Il punto R è l’immagine del numero 15. V F

f) Il punto O è l’immagine del numero 12. V F

2 Assegna il valore 4 all’unità di misura e individua sulla semiretta i numeri dati.

8 10 16 24 30 32 34 48 0 u

3 Assegna il valore 3 all’unità di misura e individua sulla semiretta i numeri dati.

6 12 18 24 33 36 0 u =

4 Scrivi il numero che corrisponde a ogni punto sulla seguente porzione di semiretta. u AB CD EF G

7 7,5 = 0,25

5 MATEMATICA IN AZIONE La temperatura corporea oscilla intorno ai 36,5 oC. Per essere considerata febbre deve superare i 37 oC. Oggi in 3a B ci sono 5 assenti con l’influenza: Emilio ha 38,5 oC; Egidio ha la temperatura più bassa di Emilio ma non è quello che sta meglio; Eugenio è finito al Pronto Soccorso perché ha la temperatura molto alta; Ezio è in via di guarigione. Che temperatura ha Ettore? Collega ogni alunno alla temperatura corrispondente, come nell’esempio.

CURIOSITÀ STORICHE

ODIFREDDI a cura del professor

IL PRIMO STRUME NTO DI CALCOLO LE DITA ..

Gli esseri umani hanno incominciato a contare con le dita, molto tempo fa: sicuramente, prima ancora di imparare a scrivere. Agli inizi hanno usato una mano sola, e poi entrambe. Anche noi lo facciamo da bambini, ma continuiamo a farlo anche da adulti. Di solito si inizia con il pollice (1), e si prosegue con l’indice (2), il medio (3), l’anulare (4) e il mignolo (5). Ma in molti paesi, come in Germania e in Austria, fanno al contrario: incominciano dal mignolo e terminano con il pollice.

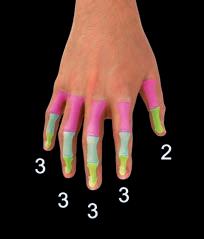
I Mesopotamici contavano sulle falangi delle quattro dita utilizzando il pollice come ‘segnaposto’.

Mettendo insieme le due mani, si arriva a contare fino a 10. Usando anche le dita dei piedi, si arriva fino a 20. Non è un caso che il nostro sistema numerico sia “decimale”: quando si conta si arriva fino a 10, poi si registra la decina, e si ricomincia. Il sistema dei Maya del Centro America era invece “vigesimale”, perché si arrivava fino a 20, prima di ricominciare.

In Mesopotamia, invece, si arrivava fino a 60: sempre contando sulle dita, ma in maniera un po’ più complicata. Usando il pollice di una mano, si possono contare le falangi delle rimanenti quattro dita: ce ne sono tre per ciascun dito, e dunque 12 in tutto. Di questa tradizione è rimasta una traccia nelle “dozzine”, che vengono ancora usate ancora oggi per comprare le bottiglie d’acqua, le uova, i servizi di posate, piatti e bicchieri ecc.

Ogni volta che, contando su una mano, si arriva a una dozzina, si può tenerne conto con le cinque dita dell’altra mano, e cinque dozzine fanno appunto 60.

Anche di questo sistema ci rimangono delle tracce: per esempio, nel modo in cui suddividiamo il tempo. Anzitutto, il giorno e la notte non vengono divisi in 10 ore ciascuno, come ci si aspetterebbe nel sistema decimale, ma in 12, per un totale di 24 ore al giorno.

I Babilonesi conoscevano il celebre teorema ben prima della nascita di Pitagora.

E poi, le ore della giornata non vengono divise in 100 minuti, come di nuovo ci si aspetterebbe, ma in 60, perché così facevano gli antichi. Analogamente, ciascun minuto viene diviso in 60 secondi. E anche i gradi vengono suddivisi in maniera “sessagesimale”: non in 100 gradi per ciascun quadrante, per un totale di 400, ma in 60 gradi per ciascun sestante, per un totale di 360, in memoria degli Assiri e Babilonesi.

Ancora oggi, utilizziamo il sistema sessagesimale mesopotamico per misurare ore, minuti e secondi.

POSIZIONALE

Il valore di una cifra dipende dal posto che occupa 8 313 3 centinaia e 3 unità

La cifra zero: indica la mancanza di elementi in un determinato ordine:

1 017 0 centinaia 450 0 unità permette di scrivere numeri diversi tra di loro: 15, 105, 1 500

Il sistema di numerazione decimale

SISTEMA DI NUMERAZIONE

DECIMALE

10 CIFRE usa

0; 1; 2; 3; 4; 5; 6; 7; 8; 9

DECIMALI

5,3; 12,03

che formano

NUMERI

che sono infiniti

che possono essere

DIVERSI

a ≠ b 62 ≠ 63 5,60 ≠ 5,06

A MINORE DI B

a < b 62 < 63

UGUALI

a = b 15 = 15 4,7 = 4,70

A MAGGIORE DI B

a > b 5,6 > 5,06

NATURALI

0; 15; 420...

38; 46; 90; 52; 78 PARI

terminano con 0; 2; 4; 6; 8

27; 35; 79; 91; 13 DISPARI

terminano con 1; 3; 5; 7; 9

ESERCIZI E PROBLEMI

LEZIONE 1

I NUMERI NATURALI

1 Rispondi alle domande con SÌ o NO.

a) Puoi scrivere il numero naturale maggiore di tutti gli altri?

b) La sequenza dei numeri cardinali inizia da 0?

c) In una serie di numeri naturali scritti in ordine decrescente, il primo numero è il minore e l’ultimo è il maggiore?

d) In una serie di numeri naturali scritti in ordine crescente, ogni numero è maggiore del precedente e minore del successivo?

2 Completa con “C’’ (cardinale) o “O’’ (ordinale).

a) Per indicare il posto che occupi nel registro di classe usi un numero

b) Per sapere quante ore ha un giorno usi un numero

c) Per esprimere quanto hai ricevuto di resto facendo la spesa usi un numero

d) Per evidenziare un corridore alla partenza di una gara usi un numero

3 Scrivi con quali simboli si traducono i seguenti termini: minore maggiore o uguale

minore o uguale diverso

4 Qual è la differenza tra numeri pari e numeri dispari?

5 In quale modo si indicano il precedente e il successivo di un numero a?

6 Individua nelle seguenti frasi i numeri cardinali e quelli ordinali e scrivili in cifre.

a) Gli angoli del quadrato sono ampi novanta gradi.

b) Alla Stramilano Antonello si è piazzato trentasettesimo e Valeria ventiquattresima.

c) Sto ascoltando il settimo CD della serie che mi hai regalato per i miei vent’anni.

d) Angela al supermercato ha ricevuto dieci buoni sconto da due euro ciascuno.

e) Caterina e Andrea festeggiano il loro venticinquesimo anniversario di matrimonio con quattro figli e tre nipoti.

f) Il centimetro è la centesima parte del metro.

Cardinali: novanta in cifre: 90;

Ordinali: trentasettesimo

in cifre: 37°;

7 Individua i numeri ordinali e cardinali e scrivili in cifre nella tabella.

a) La parola “cantante’’ è composta da otto lettere; le vocali occupano il secondo, il quinto e l’ottavo posto.

b) Il numero 340 768 503 è composto da nove cifre; lo zero occupa il terzo e l’ottavo posto.

c) Alla gara di atletica c’erano trentasette iscritti e Lucia è arrivata diciannovesima.

d) Roberta abita al numero civico dodici di piazza Venticinque aprile.

Numeri cardinali Numeri ordinali

8 Scrivi i seguenti numeri in cifre, suddividendoli anche in cardinali e ordinali.

a) ventiquattro; trentamiladuecentododici; seicentesimo; secondo; millequattrocentonovanta

b) settecentoquarantamilatrecentocinquantasei; decimillesimo; novantesimo

c) tremilioniseicentodiciassettemiladuecentoquindici; quattordicesimo; duemilasedici

Cardinali →

Ordinali →

9 Scrivi due frasi utilizzando numeri cardinali.

10 Scrivi due frasi utilizzando numeri ordinali.

Completa scrivendo i numeri mancanti.

a) 10 è il precedente di ed è il successivo di d) 31 è il precedente di ed è il successivo di

a) 76 è il successivo di ed è il precedente di a) 399 è il successivo di ed è il precedente di a) 12 è il consecutivo di ed è l’antecedente di e) 49 è il consecutivo di ed è l’antecedente di f) 80 è l’antecedente di ed è il consecutivo di g) 999 è l’antecedente di ed è il consecutivo di

13 Scrivi il precedente e il successivo dei seguenti numeri.

a) 809

14 Completa le seguenti tabelle.

15 MATH Complete the following tables.

16 Completa le seguenti successioni di numeri naturali.

a) 35; 36; ; ; ; ; ; ; ; ;

b) 101; ; ; ; ; 106; ; ; ;

c) 210; 209; ; ; ; ; ; ; ;

d) 2 647; ; ; 2 644; ; ; ; ; ;

17 Individua la regola delle seguenti successioni e completale.

a) 5; 9; 13; ; ; ; ; ; ;

(La regola e` aggiungere 4 al numero precedente → n + 4)

b) 2; 4; 8; 16; ; ; ; ; ;

c) 47; 44; 41; ; ; ; ; ;

d) 203; 193; ; 173; ; ; ; ;

e) 30; 55; ; 105; ; ; ; ;

18 Scrivi sul tuo quaderno in ordine crescente i gruppi di numeri dati.

a) 67; 15; 71; 86; 43; 39; 78; 92.

b) 8; 81; 18; 83; 38; 13; 103; 801.

c) 651; 942; 673; 759; 900; 685; 748; 926.

d) 710; 699; 789; 800; 798; 698; 700; 799.

19 Scrivi sul tuo quaderno in ordine decrescente i numeri dati.

●●●

a) 5; 49; 87; 21; 18; 36; 99; 64.

b) 78; 23; 129; 231; 96; 100; 385; 269

c) 399; 401; 390; 498; 400; 389; 499; 398.

d) 9 340; 3 490; 4 390; 9 430; 9 304; 4 903; 3 904.

20 STEM Metti in ordine crescente di altezza i seguenti monumenti:

●●●

21 MATEMATICA IN AZIONE Ordina in senso crescente le lunghezze dei seguenti fiumi. Dora Baltea 160 km; Adige 410 km; Ticino 248 km; Piave 220 km; Po 652 km; Oglio 280 km.

22 Con le cifre 3, 5, 7 scrivi tutti i possibili numeri di tre cifre e ordinali poi in senso crescente e decrescente (utilizza ciascuna cifra una volta sola). Per formare tutti i possibili numeri con le tre cifre assegnate, è utile predisporre un grafico ad albero: 57 → 357 37 → 35 → 3

Ordine crescente → 357; Ordine decrescente → 753;

23 Scrivi sul quaderno tutti i numeri di tre cifre con le cifre 1, 4, 8 e ordinali in senso decrescente (utilizza un grafico ad albero e usa ciascuna cifra una volta sola).

24 STEM Ordina in senso decrescente la durata della vita di alcuni cetacei (mammiferi marini).

Steno circa 32 anni; tursiope circa 40 anni; balenottera comune 90-100 anni; orca più di 50 anni; capodoglio può superare i 70 anni.

90-100 > > > >

25 STEM La tabella riporta le velocità massime e le lunghezze massime di alcuni animali. Dopo aver riportato tutte le lunghezze in centimetri, ordina in senso decrescente sia le velocità che le lunghezze.

Animale Velocità Lunghezza

Colibrì

Falco pellegrino

Ghepardo

Libellula

Pesce spada

Pesce vela

Squalo mako

Struzzo

Tigre siberiana

Velocità →

Lunghezza →

100 km/h 11 cm

360 km/h 58 cm

120 km/h 1,5 m =

100 km/h 5 cm

100 km/h 4,5 m =

110 km/h 2 m =

124 km/h 400 cm

70 km/h 180 cm

90 km/h 3,3 m =

26 Scrivi i numeri pari compresi tra 41 e 57.

27 Scrivi i numeri dispari compresi tra 68 e 84.

28 Scrivi i numeri pari minori di 45 e maggiori di 27.

29 Scrivi i numeri dispari maggiori di 12 e minori di 34.

30 MATH Find the even and odd numbers. 39; 46; 12; 521; 85; 741; 378; 253; 62; 44; 157; 489; 3,403; 506; 8,201; 731; 910; 658

Even numbers →

Odd numbers →

31 EDUCAZIONE CIVICA Lungo la Costiera Amalfitana, durante i mesi estivi, tutti i sabati e le domeniche le auto circoleranno a targhe alterne.

a) Il sabato circoleranno quelle che terminano con una cifra pari e la domenica quelle che terminano con una cifra dispari. Separa nella tabella le seguenti targhe a seconda del giorno in cui potranno circolare.

b) Se Aurora possiede un’auto con la targa X potrà andare a visitare Positano sabato o domenica?

32 Scrivi i numeri che rispettino le richieste.

a) Il più piccolo numero pari di tre cifre tutte diverse.

a) Il più grande numero pari di tre cifre tutte uguali.

b) Il più piccolo numero dispari di quattro cifre tutte diverse.

33 Indica se i seguenti numeri sono pari oppure dispari, sapendo che a è un numero pari qualsiasi ≠ 0 e che le scritture 2a, 3a ecc. sono forme semplificate di 2 × a, 3 × a ecc.

a) 2a =

34 Inserisci i simboli < , > o = in modo adeguato.

35 Utilizza i simboli > (maggiore) e < (minore) per completare le seguenti relazioni (le lettere indicano numeri naturali diversi da 0).

36 MATH Insert the <, > or = symbols as appropriate.

37 Utilizza i simboli = (uguale) e ≠ (diverso) per completare le seguenti relazioni (le lettere indicano numeri naturali diversi da 0). a) 7 1

38 Scrivi i numeri naturali che rendono veri gli enunciati aperti.

a) < 13 → {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12} 25 < < 31 → {26, 27, 28, 29, 30}

a) > 7 → {

b) < 8 → {

c) 13 < < 19 → {

d) 45 < < 52 → {

39 Completa i seguenti enunciati aperti scrivendo alcuni tra i numeri adatti.

a) ≥ 100 → i numeri maggiori o uguali a 100 → {100, 101, 102, 103, 104, 105, ...}

b) ≤ 5 → i numeri minori o uguali a 5 → {5, 4, 3, 2, 1, 0}

a) ≥ 52 →

b) ≥ 310 →

c) ≥ 1 001 →

d) ≤ 16 →

e) ≤ 9 →

f) ≤ 20 →

40 Sottolinea la risposta esatta.

a) x ≤ 7 A = {0, 1, 2, 3, 4, 5, 6} A = {0, 1, 2, 3, 4, 5, 6, 7}

b) x ≥ 7 B = {7, 8, 9, 10, ...} B = {8, 9, 10, 11, 12, ...}

c) 3 < x < 9 C = {4, 5, 6, 7, 8 } C = {3, 4, 5, 6, 7, 8, 9}

d) 5 ≤ x < 13 D = {5, 6, 7, 8, 9, 10, 11, 12} D = {6, 7, 8, 9, 10, 11, 12}

IL SISTEMA DI NUMERAZIONE DECIMALE

41 Rispondi con Vero (V) o Falso (F).

a) Dieci unità del 1° ordine formano una decina. V F

b) Le unità del 4° ordine sono le migliaia. V F

c) I miliardi sono le unità del 5° ordine. V F

d) 1 milione si scrive con sei zeri che seguono la cifra 1. V F

e) I numeri 2 060 e 26 hanno lo stesso valore perché lo zero non ha valore. V F

f) La prima cifra di un numero può essere 0. V F

42 Con quanti zeri si scrivono i seguenti numeri?

a) Cento Mille

b) Centomila Un milione

c) Cento milioni Un miliardo

43 Rispondi sul quaderno.

a) Quante e quali sono le cifre del sistema di numerazione decimale?

b) Da quanti ordini è formata una classe?

c) Che cosa indica la cifra zero in un numero?

d) Perché il nostro sistema di numerazione è posizionale?

e) A che cosa serve la scrittura polinomiale di un numero?

Indica sul tuo quaderno il valore delle cifre di ogni numero assegnato.

361 → 3 centinaia, 6 decine, 1 unità 44 85 39

46 Indica il valore della cifra 5.

decine

47 Indica il valore relativo della cifra 0 nei seguenti numeri.

48 Indica il valore che rappresenta la cifra 2 nei seguenti numeri.

49 MATH Indicate the value of 8 in the following numbers.

simple units

50 Per ciascun numero scrivi il valore della cifra delle decine.

51 Per ciascun numero scrivi il valore della cifra delle decine di migliaia.

52 Per ciascun numero scrivi il valore della cifra delle unità semplici.

Sposta la cifra zero per far aumentare (A) o diminuire (D) il valore del numero.

a) 7 403

b) 5 109

55 Completa le seguenti tabelle. Numero

1 345

31 987

21 086

3 918 239 10 072 536

6 421 900 435

56 MATH Complete the table.

823 4,921 192,341 2,815,104

397,612,303

Completa mettendo il numero esatto al posto dei puntini.

57 8migliaia = 80 centinaia = 800 decine = 8000 unità.

7 migliaia = centinaia = decine = unità.

3 decine di migliaia = migliaia = centinaia = decine = unità.

58 59 centinaia = decine = unità.

841 centinaia = decine = unità.

320 centinaia = decine = unità.

59 26 migliaia = centinaia = decine = unità.

517 migliaia = centinaia = decine = unità.

43 migliaia = centinaia = decine = unità.

Accanto a ogni numero scrivi la lettera che corrisponde alla sua scrittura in lettere.

60 4

a) Quattromilacinquecento

b) ottantamilaventuno

c) ottantaduemilacento

d) dodicimilaotto

e) quattromilacinque

f) ottantamiladuecentodieci

g) dodicimilaottocento

h) quattromilacinquanta

a) diciannovemila

b) settemilaventi

c) settantadue

d) diecimilanove

e) diecimilanovanta

Sul tuo quaderno scrivi in lettere i seguenti numeri.

f) settemiladue

g) settemiladuecento

h) diecimilanovecento

i) settantamila

j) duemilaventi

8 002 → ottomiladue

62 465; 873; 378; 552; 709; 790; 6 184; 1 848

63 301; 130; 3 100; 10 030; 3 010; 30 100; 103 000; 3 000 100

64 9 810; 34 629; 71 045; 39 405; 80 456; 51 070; 90 703; 1 003

65 8 165 000 000; 5 316 100 000; 2 390 165 034; 72 400 634 800; 18 003 652 000

Scrivi in cifre i numeri indicati.

8 migliaia, 3 centinaia e 6 unità → 8 306

66 9 decine e 5 unità

8 decine e 7 unità

5 centinaia e 1 decina

9 centinaia e 3 unità

67 7 decine e 4 unità

7 centinaia e 2 unità

5 centinaia, 3 decine e 0 unità

68 9 decine e 6 unità

49 centinaia e 35 unità

95 centinaia e 13 unità

69 3 centinaia, 8 decine e 5 unità

6 unità, 7 centinaia e 1 migliaio

2 unità, 64 decine e 5 migliaia

80 centinaia, 5 decine e 3 unità

70 8 migliaia e 5 decine

3 migliaia e 87 decine

36 migliaia, 9 centinaia e 5 unità

73 centinaia e 24 decine

15 decine

27 decine e 8 unità

4 unità e 13 decine

9 unità e 45 decine

7 centinaia e 3 decine

8 migliaia, 6 decine e 9 unità

3 migliaia, 5 centinaia e 7 decine

21 migliaia e 45 decine

55 decine di migliaia e 38 decine

4 milioni e 982 centinaia

3 centinaia e 76 unità

32 centinaia, 7 decine e 1 unità

8 unità e 72 decine

9 unità e 46 centinaia

6 migliaia e 9 unità

18 migliaia, 64 decine e 7 unità

2 unità, 7 decine e 92 centinaia

5 unità, 6 centinaia e 21 migliaia

Per ogni numero scritto in lettere scrivi il corrispondente numero in cifre.

71 centotrentadue

milleottocentosettantatré duecentonovantanove ottomilacentoundici cinquemiladuecento ottocentoquattordici settemilacentoundici duemilanovecentocinque

72 cinquantuno cinquemiladieci millecinquecento cinquantamilacento

73 diciottomilaseicento quarantanovemilasette novantamilaseicentotré cinquecentomiladodici novecentomilatrecentosettantadue ventimilaottocentotrentasette

diecimilacinquecento millecinque cinquecentomilauno unmilionecinquanta

74 settecentomilioniseicentomilacinquecentoquarantatré seimiliardicinquecentomilanovecentosedici seimiliarditrecentotrentamilatredici diecimiliardinovantacinquemilasettecentonove quarantamiliardiquarantaquattromilaquattrocentoquattordici

75 EDUCAZIONE FINANZIARIA

Ecco un modello di assegno compilato; leggilo e ricava i dati per rispondere.

EDUCAZIONE FINANZIARIA

1) luogo

2) data

3) importo in cifre

4) importo in lettere

5) destinatario

6) firma

Utilizza i dati forniti per compilare i fac-simile di assegni.

76 Assegno di 1 870,00 € emesso il 12 maggio 2024 da Mario Biondi per te.

Nei prezzi in euro vanno indicati sempre due zeri, anche quando non servono. 4 € si scrive sempre 4,00 €.

77 La mamma di Pippo, signora Giuseppina Sessa, il 5 novembre scorso ha pagato con un assegno una spesa di 3 780,00 € al dentista dott. Alberto Trapani per l’apparecchio del figlio.

78 EDUCAZIONE FINANZIARIA Questo è un modello di bollettino postale; osservalo e rispondi.

b) A quale associazione andrà l’importo versato?

c) Per quale anno vale il tesseramento?

d) Riscrivi l’importo in cifre e quello in lettere.

e) Che nome e indirizzo scrivi se sei tu a eseguire il pagamento?

EDUCAZIONE FINANZIARIA Compila i modelli di ricevute di bollettini postali utilizzando i dati forniti.

79 Devi versare 32,00 € per il rinnovo dell’abbonamento alla rivista Cani & Gatti del gruppo Melindori sul C/C n. 101010130, per l’anno 2024/2025.

80 La famiglia Adams (via Lungotevere 10, 00005 Renda) deve versare la rata bimestrale (novembre/ dicembre 2025) di 34,00 € per la Pay tv SecundimSede romana sul C/C n. 52535450.

81 MATEMATICA IN AZIONE Giorgia trova nel libro di geografia che l’Italia ha 60 782 668 abitanti e legge “sessantamiliardisettecentoottantaduemilaseicentosessantotto’’. Sai spiegare perché ha sbagliato?

82 Collega ciascuna scrittura polinomiale con il numero corrispondente.

2 × 10 000 + 4 × 100 + 6 × 10 + 5

7 × 1 000 + 9 × 10 + 1

a) 75 310

b) 20 465

4 × 100 000 + 6 × 10 000 + 8 × 100 + 2 c) 8 908

7 × 10 000 + 5 × 1 000 + 3 × 100 + 1 × 10 d) 460 802

8 × 1 000 + 9 × 100 + 8 e) 7 091

Sul quaderno scrivi in forma polinomiale i seguenti numeri.

1

Per ciascuna scrittura in forma polinomiale scrivi il numero corrispondente.

6 × 10 000 + 4 × 1 000 + 5 × 10 + 9 = 64 059

a) 1 × 10 000 + 3 × 1 000 + 4 × 100 + 5 × 10 + 7 b) 5 + 3 × 100 + 6 × 1 000 + 7× 100 000 c) 4 × 100 000 + 2 × 10 000 + 4 × 1 000 + 2 × 100 + 4 × 10 + 2

d) 8 + 9 × 100 + 4 × 1 000 + 6 × 10 000 + 1 × 100 000

a) 4 × 1 000 + 7 × 100 + 5

b) 3 × 1 000 + 7 × 100 + 5 × 10 + 3

c) 2 × 10 000 + 8 × 100 + 9 × 10

d) 8 × 10 000 + 7 × 1 000 + 4 × 10 + 8

a) 5 × 1 000 + 6 × 100 + 7 × 10 + 9

b) 9 × 1 000 + 7 × 10 + 4

c) 4 × 10 000 + 3 × 100 + 4 × 10 + 3

d) 1 × 10 000 + 1 × 1 000

a) 4 × 100 000 + 3 × 1 000 + 4 × 10 + 3

b) 7 × 100 000 + 5 × 10 000 + 3 × 100 + 7 × 10 + 8

c) 6 × 100 000 + 3 × 1 000 + 2 × 100 + 1 × 10 + 6

d) 9 × 100 000 + 3 × 10 000 + 6 × 100 + 9

a) 1 + 3 × 100 + 5 × 10 000 + 3 × 100 000

b) 4 × 10 + 5 × 100 + 7 × 1 000 + 3 × 100 000

c) 9 × 100 + 2 × 1 000 + 1 × 10 000 + 5 × 100 000

d) 3 × 10 + 7 × 1 000 + 6 × 10 000 + 2 × 100 000

91 Rispondi alle seguenti domande.

a) Michele ha dimenticato il suo numero di telefono: sa che è di 10 cifre, che le unità e le decine sono uguali a 5, le prime tre cifre sono uguali a tre 3, le unità di milioni e le unità di migliaia sono uguali a 7, tutte le altre cifre sono zeri. Qual è il numero?

b) Un numero è compreso tra 7 000 000 e 8 000 000. Tutte le cifre delle migliaia sono uguali. Tutte le cifre delle unità semplici sono uguali. La somma di tutte le cifre è 31. Quale può essere il numero?

LEZIONE 3

I NUMERI DECIMALI

92 Rispondi con Vero (V) o Falso (F).

a) Le unità decimali del 1° ordine sono i decimi. V F

b) 0,01 vale 1 millesimo.

c) I numeri 650,000 e 65 hanno lo stesso valore. V F

d) I numeri decimali possono essere scritti in forma polinomiale. V F

93 Rispondi alle seguenti domande sul quaderno.

a) Come si riconosce un numero decimale? Fai degli esempi.

b) Un numero naturale può essere considerato come decimale? Fai degli esempi.

c) Quanti millesimi sono contenuti in 10 centesimi?

d) Quanti decimi sono contenuti in 10 unità?

e) Quanti millesimi sono contenuti in 1 decimo?

94 Per ciascuno dei seguenti numeri indica quale cifra occupa il posto dei centesimi.

8

95 Indica il posto occupato dalla cifra 7.

→ millesimi

→

→

96 Indica il posto occupato dalla cifra 2. 2,879 →

Sul quaderno scrivi il valore delle cifre decimali dei seguenti numeri. 23,871 → 8 decimi, 7 centesimi, 1 millesimo

99 Scegli tra i seguenti numeri (438,8756 - 23,64 - 346,87 - 759,065) quello che ha 6 come: a) centesimi: b) decimi: c) decimillesimi: d) unità:

100 Sul quaderno scrivi in lettere i seguenti numeri decimali.

Rispondi alle seguenti domande.

101 A quanti decimi corrispondono i seguenti numeri? 8 = 8 × 10 = 5,1

102 A quanti centesimi corrispondono i seguenti numeri?

103 A quanti millesimi corrispondono i seguenti numeri?

104 Considera le seguenti coppie di numeri decimali e inserisci in modo adeguato i simboli = ; < ; > . (Se necessario aiutati aggiungendo lo 0 come nell’esempio.)

105 Disponi le seguenti terne di numeri nell’ordine indicato.

a) Ordine decrescente

b) Ordine crescente

106 MATEMATICA IN AZIONE George ha ottenuto i seguenti tempi negli 80 metri piani: 9,9 secondi; 9,09 secondi; 9,89 secondi; 9,99 secondi.

Metti in ordine i tempi ottenuti, dal più veloce al più lento.

107 EDUCAZIONE FINANZIARIA Un lunedì 1 dollaro ($) al cambio è stato valutato 0,7211 €. Questo significa che un dollaro vale circa 72 centesimi di euro.

Per il resto della settimana il cambio varia così: martedì 0,7122 €; mercoledì 0,7201 €; giovedì 0,7102 €; venerdì 0,7212 €.

Scrivi i cambi dal valore minore al valore maggiore.

108 In ognuno dei seguenti numeri elimina gli zeri inutili, cioè quelli che non modificano il valore del numero stesso.

109 Nei seguenti numeri elimina uno zero in modo che il numero aumenti di valore.

110 MATH Whenever possible, delete a zero to increase the value of the number.

Nei seguenti numeri decimali elimina uno zero in modo che il numero diminuisca di valore.

113 Rispondi alle seguenti domande.

a) Quanti centesimi mancano al numero 3,75 per diventare 4?

b) Quanti decimi mancano al numero 10,2 per diventare 11?

c) Quanti millesimi mancano al numero 3,408 per diventare 4?

d) Quanti centesimi mancano al numero 10,61 per diventare 11?

114 Considera i numeri dati e stabilisci quanti decimi aggiungere a ognuno di essi per ottenere l’unità.

a) 0,1 → 0,8 → b) 0,4 → 0,5 → c) 0,9 → 0,6 →

115 Considera i numeri dati e stabilisci quanti centesimi aggiungere a ognuno di essi per ottenere l’unità.

a) 0,95 → 0,64 → 0,32 →

116 Per ciascuno dei seguenti numeri indica quale valore è necessario per arrivare all’unità.

a) 0,02 → 0,41 →

b) 0,09 → 0,041 →

c) 0,90 → 0,056 → d) 0,3 → 0,065 →

Completa le seguenti tabelle.

Scrivi sul quaderno i seguenti numeri decimali in forma polinomiale.

122 Quale scrittura polinomiale corrisponde al numero 310,097?

a) 7 + 9 × 10 + 1 × 100 000 + 3 × 1 000 000

b) 3 × 100 + 1 × 10 + 9 × 0,01 + 7 × 0,001

123 Che numero corrisponde alla scrittura polinomiale 1 × 0,0001 + 3 × 0,1 + 4 × 1 000? a) 4

124 Osserva le seguenti scritture di numeri decimali in forma polinomiale e contrassegna quelle errate.

a) 7,28 = 7 + 2 × 0,1 + 8 × 0,01 109,34 = 1 × 100 + 9 × 10 + 3 + 4 × 0,01

b) 13,06 = 1 × 10 + 3 + 6 × 0,1 3,802 = 2 × 0,001 + 8 × 0,1 + 3 × 10

Per ciascuna scrittura polinomiale scrivi il numero corrispondente.

a) 5 × 0,0001 + 4 × 0,001 + 7 × 0,1 + 8

b) 7 × 10 + 3 + 6 × 0,001 + 4 × 0,0001

c) 1 × 0,0001 + 5 × 0,001 + 7 × 0,1 + 9 + 3 × 10 + 6 × 1 000

d) 3 × 100 + 2 + 3 × 0,1 + 2 × 0,0001 + 3 × 0,00001

a) 7 × 10 + 2 + 9 × 0,1

b) 8 × 100 + 4 × 10 + 8 + 2 × 0,1 + 3 × 0,01

c) 1 + 3 × 0,1 + 6 × 0,01 + 7 × 0,001

d) 3 × 0,01 + 8 × 0,1 + 5 + 7 × 10 + 9 × 100

127 STEM Rispondi alle seguenti domande.

a) Due meteoriti cadono sulla Terra: la prima pesa 26,71 Mg e la seconda pesa 26,7 Mg. Quale pesa di più?

b) Il diametro di un capello umano misura 0,000 025 m, mentre quello del filo di una ragnatela di un ragno 0,000 003 m. Qual è più sottile?

LEZIONE 4

RAPPRESENTAZIONE DI UN NUMERO SU UNA SEMIRETTA

128 Rispondi.

a) Quale ente geometrico si utilizza per rappresentare graficamente i numeri naturali e decimali?

b) In quale altro modo si può chiamare l’unità di misura fissata su una semiretta?

c) I numeri decimali possono essere rappresentati graficamente?

d) Quanto deve valere l’unità di misura da utilizzare per rappresentare graficamente un numero decimale?

129 Spiega sul quaderno come si rappresentano i numeri decimali sulla semiretta.

130 Indica quali affermazioni sono vere (V) e quali false (F).

Sulla semiretta dei numeri il numero:

a) 3 precede 3,01 V F

b) 6,4 precede 4,6 V F

c) 4,03 segue 4,30 V F

Esegui sul quaderno quanto richiesto.

d) 23,8 precede 23,89 V F

e) 35,54 segue 35,49 V F

f) 70,01 segue 70,09 V F

131 Assegna all’unità di misura il valore 2 e rappresenta su una semiretta i numeri dati.

0 2 5 8 14 16 19 20

132 Con una unità grafica adeguata rappresenta su una semiretta i numeri naturali pari compresi tra 15 e 37.

133 Utilizzando una unità grafica adeguata rappresenta su una semiretta i numeri naturali dispari compresi tra 6 e 20.

134 Individua sulla semiretta le posizioni dei seguenti numeri.

30 40 55 60 70 75

0 u = 10

135 Individua sulla semiretta le posizioni dei numeri.

15 30 45 60 75 90 105

0 u = 15

Dopo aver attribuito al segmento u un valore opportuno, individua sulla semiretta le posizioni dei numeri.

Scrivi il numero decimale che corrisponde a ogni punto.

2 Il sistema di numerazione decimale

Per ciascuna delle seguenti semirette, trova il valore che è stato assegnato al segmento u.

144 Individua il valore assegnato al segmento u e scrivi i numeri indicati dalle frecce. a) 02 1 u = .......... b) 68 7

Scrivi il numero che corrisponde a ogni punto messo in evidenza dalle frecce. 145 10 20 30 0 146 520 0

147 MATEMATICA IN AZIONE Luca legge i suoi appunti di storia sul Medioevo. Il Medioevo è il periodo storico che va dal 476, con la caduta dell’Impero romano d’Occidente, al 1492, con la scoperta dell’America. Nell’Alto Medioevo, nel 529 san Benedetto da Norcia fonda il monastero di Montecassino, nell’800 Carlo Magno diventa imperatore, nell’877, con il capitolare di Quercy, i feudi diventano ereditari. Nel Basso Medioevo, nel 1152 Federico Barbarossa diventa imperatore e nel 1176, con la battaglia di Legnano, il Barbarossa viene sconfitto. Per ricordarsi le date importanti Luca decide di scriverle sulla linea del tempo. Aiutalo a completare i cartellini.

Rappresenta i numeri dati su due semirette utilizzando un’unità grafica adeguata.

148 36 32 40 44 46 48 52 56

Individua il valore assegnato al segmento u e colloca le lettere corrispondenti ai numeri decimali dati.

Il sistema di numerazione decimale

Posizionare i numeri interi su una semiretta è abbastanza facile, ma ordinare i numeri decimali può essere più complesso.

imparaerrore dall'

Un errore piuttosto frequente è quello di confrontare i numeri decimali come se fossero interi, guardando solo la lunghezza o le cifre dopo la virgola senza tenere conto del valore posizionale. Per esempio, si può credere che 0,31 sia più grande di 0,5 perché 31 è più grande di 5, oppure che 0,325 sia più grande di 0,4 perché ha più ci-

fre. Aggiungere zeri alla fine della parte decimale non cambia il valore del numero e potrebbe essere una buona strategia da usare per non confondersi: 0,5 equivale a 0,50 e se lo confronto con 0,31, mi accorgo subito quale dei due è più grande (50 centesimi sono di più di 31 centesimi). Un altro errore molto comune è pensare che tra 0,2 e 0,3 non ci siano altri numeri. Immagina che la retta numerica sia come un righello infinito: ogni spazio tra un numero intero e l’altro può essere diviso in 10 parti più piccole (decimi), e poi ancora in 10 (centesimi).

Per ordinare i numeri guarda per prima cosa la loro parte intera: se sono diverse, il numero con la parte intera maggiore è il più grande. Solo se le parti intere sono uguali (per esempio 4,2 e 4,05) puoi passare a confrontare la parte decimale.

In ciascuna delle seguenti semirette, o porzioni di esse, colloca i numeri decimali dati.

153

155 Scrivi il numero decimale che corrisponde a ogni punto messo in evidenza sulle seguenti semirette o porzioni di esse. a) 0 1234 b) 18 19 20 21 22

Disegna 1 semiretta e, con un’unità grafica adeguata, rappresenta i numeri dati.

COMPETENZE

PROBLEM SOLVING

1 I numeri palindromi sono numeri che si possono leggere da destra verso sinistra e viceversa.

Per esempio 12 321, 2 002, 54 766 745 sono numeri palindromi.

a) Scrivi i numeri palindromi minori di 100:

Che cosa noti?

b) 02-02-2020 è una data palindroma. Trova quali sono le quattro date palindrome successive a questa.

110

c) Tra 110 anni quale sarà la nuova data palindroma?

d) Completa la piramide di numeri palindromi, proposta dal matematico statunitense G. L. Honaker.

e) Anche i numeri decimali possono essere palindromi: 41,14 è palindromo. Perché 7,67 non è palindromo? Motiva la risposta.

2 Osserva le seguenti regolarità fra numeri e completa.

a) 10 = 9 + 1 b) 1 = 1

100 = 90 + 12 = 11 + 1

1 000 = + 100 123 = 111 + 11 + 10 000 = 1 234 = 1 111 +

3 Inserisci nelle seguenti successioni i numeri mancanti.

a)

c) 6

d)

4 A Fiamma, Flavio, Frank e Fatima piace molto giocare a carte.

Sabato scorso hanno giocato con i soldi di Monopoli e, all’inizio della prima partita, avevano banconote per un totale di 40 euro. Alla fine della partita Fiamma si ritrova con: - 10 euro in più rispetto a Frank, - 5 euro in più rispetto a Flavio, - 1 euro in più rispetto a Fatima.

Quanto possiede ciascuno dei quattro amici a fine partita?

5 Irene acquista una bottiglia di olio extra vergine dal costo di 10 euro.

Se il valore dell’olio è 9 € in più di quello del vetro, quanto vale l’olio e quanto vale il vetro?

CALCOLARE

6 A ogni figura geometrica corrisponde un numero; a figure uguali corrispondono numeri uguali.

Per ogni gruppo di figure è indicata la somma dei valori. Calcola il valore complessivo del gruppo con il punto di domanda.

7 Individua il valore di ogni figura geometrica data sapendo che:

UTILIZZARE IL LINGUAGGIO MATEMATICO

8 Completa “traducendo’’ le frasi in simboli matematici o viceversa.

ESEMPIO

Numero a minore o uguale a 23 → a ≤ 23

Numeri compresi tra 17 e 27 → 17 < < 27

Numeri compresi tra 17 e 27 includendo anche 17 e 27 → 17 ≤ ≤ 27

a) Numero n maggiore o uguale a 44 →

b) 76 > 67 →

c) 89 < 98 →

d) 3 + 7 non è uguale a 37 →

e) 45 è minore di 54 →

f) 29 è maggiore di 19 →

g) x ≤ 41 →

h) 7 < ... < 12 →

i) Numeri maggiori di 8 →

l) Numeri minori o uguali a 10 →

m) Numeri compresi tra 12 e 32 →

n) Numeri compresi tra 0,4 e 1,4 →

o) Numeri compresi tra 0,75 e 4,09 →

p) Numeri compresi tra 15 e 51 includendo anche 15 e 51 →

q) 12 ≤ ≤ 17 →

r) 16,5 > ... ≥ 10,3 →

s) 18,2 ≤ ≤ 19,03 →

t) 129 > ≥ 119 →

SFIDA MATEMATICA

9 Renato si diverte con le macchinine

Renato possiede più di 100 macchinine che adesso vuole numerare. Per questo, ha comprato le cifre auto-adesive 0, 1, 2 ,3, 4, 5, 6, 7, 8 dove il 6 (capovolgendolo) può servire a rappresentare anche il 9. Di ogni cifra auto-adesiva ha comprato 20 esemplari; in tutto, 180. Se Renato numera le sue macchinine a partire dal numero 1 e prosegue nell’ordine senza saltare nessun numero, quale sarà il primo numero per il quale non ha più cifre auto-adesive a sua disposizione?

(Testo tratto dalle Semifinali italiane dei Campionati internazionali di Giochi Matematici, organizzate dal Centro PRISTEM dell’Università Bocconi di Milano)

Il sistema di numerazione decimale

ROAD MAP PER TUTTI

numeri cardinali e ordinali TEORIA

Che cosa si intende per numeri cardinali?

DATI DEI

NUMERI NATURALI 1, 2, 3 ... 1°, 2°, 3° ...

I numeri cardinali si usano per contare ed esprimere quantità.

ESEMPIO

Claudio ha 11 anni. 11 è un numero cardinale.

Che cosa si intende per numeri ordinali?

I numeri ordinali si usano per indicare un posto in un elenco, cioè rispondono alla domanda “quale posto occupa?”

ESEMPIO

Claudio è arrivato secondo alla gara di nuoto.

SUCCESSIVO E PRECEDENTE

DATO L’INSIEME N DEI NUMERI NATURALI

Che cos’è il precedente (a – 1) di un numero?

Il precedente di un numero è quello che precede il numero dato.

Lo zero non ha precedenti in N

ESEMPIO

Il precedente di 27 è 27 – 1 = 26.

TEORIA PAG. 48

Che cos’è il successivo (a + 1) di un numero?

Il successivo di un numero è quello che segue il numero dato.

ESEMPIO

Che cosa significano i simboli = , ≠, >,<? = uguale ≠ diverso > maggiore, < minore Il successivo di 27 è 27 + 1 = 28.

1 Per ogni frase stabilisci se i numeri in neretto sono ordinali (O) o cardinali (C).

a) Nella gara di salto in alto Luisa ha superato centocinque (C) cm ed è arrivata prima (O).

b) Il terzo ( ) piano di una biblioteca parigina ha più di duemilacinquecento ( ) libri.

c) Cinquanta ( ) è la quinta ( ) decina.

d) Sara abita al sesto ( ) piano di un palazzo di dieci ( ) piani.

2 Riporta, in cifre, i numeri cardinali e ordinali dell’esercizio precedente nella seguente tabella.

Numeri cardinali Numeri ordinali

RICORDA

I numeri ordinali si possono scrivere in vari modi. Per esempio: primo: 1°; seconda: 2^; terza: 3a; quarto o quarta: IV.

3 Stabilisci se le seguenti affermazioni sono vere (V) o false (F).

a) I numeri cardinali indicano la quantità degli oggetti considerati. V F

b) I numeri ordinali e i numeri cardinali sono la stessa cosa. V F

c) I numeri dispari terminano con 1, 3, 5, 7, 9. V F

d) Un numero è pari solo se termina con zero. V F

e) 35 671 è un numero pari di cinque cifre diverse. V F

f) Un numero che termina con zero non è né pari né dispari. V F

4 Scrivi il precedente e il successivo dei seguenti numeri. a) 35 1 4 b) 19

5 Completa con i simboli = e ≠ (uguale e diverso).

a) 8 2 = 6 5 + 1 7 4 + 4 8 b) 10 1 11 6 + 3 9 2 2 0

6 Completa con i simboli > e < (maggiore e minore).

a)

7 Completa utilizzando i simboli > (maggiore) e < (minore).

a)

Il sistema di numerazione decimale

SISTEMA DECIMALE E POSIZIONALE TEORIA

DATE LE DIECI CIFRE:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9

Che cosa vuol dire sistema di numerazione decimale?

Decimale significa che utilizza 10 simboli: le 10 cifre indo-arabiche.

Che cosa vuol dire sistema di numerazione posizionale?

Posizionale significa che il valore di una cifra dipende dal posto che occupa nel numero.

ESEMPIO

Nel numero 45 601, che ha cinque cifre:

il 4 vale 4 decine di migliaia

il 5 vale 5 migliaia

il 6 vale 6 centinaia

lo 0 vale 0 decine

l’1 vale 1 unità semplice

SCRITTURA POLINOMIALE

DATO IL NUMERO 5 681

Che cosa si intende per scrittura polinomiale del numero?

La scrittura polinomiale di un numero mette in evidenza il valore delle cifre rispetto al posto che occupano.

ESEMPIO

5 681 = 5 × 1 000 + 6 × 100 + 8 × 10 + 1

Analizza ogni numero dato come nell’esempio.

8 a) 729 →

b) 580 →

c) 3 064 →

d) 8 102 →

9 Completa le seguenti frasi.

a) Nel numero 359 5 rappresenta le

b) Nel numero 2 718 7 rappresenta le

c) Nel numero 8 647 8 rappresenta le

d) Nel numero 5 032 2 rappresenta le

10 Indica quale posto occupa lo zero nei seguenti numeri.

a) 50 → 309 → 1 026 →

b) 604 → 9 820 → 700 →

c) 8 048 → 2 501 → 20 345 →

11 Scrivi in forma polinomiale i seguenti numeri interi.

35 078 =

a) 4 934 =

b) 26 900 =

c) 40 821 =

d) 605 506 =

12 Trasforma le seguenti scritture in forma normale.

a) 4 × 1 000 + 3 × 10 + 8 =

7 centinaia, 2 decine, 9 unità semplici decine unità semplici 3 × 10 000 + 5 × 1 000 + 7 × 10 + 8 4 000 + 30 + 8 = 4 038

b) 6 × 1 000 + 7 × 100 + 4 × 10 + 5 =

c) 9 × 1 000 + 4 × 100 + 5 =

d) 7 × 10 000 + 8 × 1 000 + 4 × 100 + 3 × 10 + 5 =

e) 8 × 1 000 + 6 × 100 + 2 × 10 =

f) 7 × 10 000+ 2 × 100 + 3 × 10 + 4 =

NUMERI DECIMALI

DATI I NUMERI

DECIMALI 28,9 E 0,03

Perché si definiscono decimali?

Perché oltre alla parte intera hanno una parte decimale separata dalla virgola.

ESEMPIO

28,9 28 è la parte intera, 9 la parte decimale 0,03 0 è la parte intera, 03 la parte decimale

A che cosa servono i numeri decimali?

Servono per indicare parti di un intero, come nel caso dei centesimi di euro.

ESEMPIO

Se un prodotto costa 1 euro e 75 centesimi si scrive 1,75 euro, cioè un numero decimale in cui 1 è l’intero e 75 è la parte decimale.

RAPPRESENTAZIONE DI UN NUMERO SU UNA RETTA

DATA UNA SEMIRETTA

Come si rappresentano i numeri naturali e decimali?

• Si fissa l’origine O e alla sua destra si disegna una semiretta.

• Si stabilisce un’unità di misura, cioè un segmento unitario che viene riportato più volte sulla semiretta identificando dei punti; l’unità di misura è detta anche unità grafica.

• Si fa corrispondere a ogni punto un numero: ogni punto è l’immagine del numero naturale o decimale che gli corrisponde; all’origine O della semiretta si assegna il valore zero.

ESEMPIO

13 Scrivi i numeri decimali che corrispondono alle richieste. parte intera 28; parte decimale 9 → 28,9

a) parte intera 5; parte decimale 02 →

b) parte intera 0; parte decimale 21 →

c) parte intera 44; parte decimale 105 →

14 Riscrivi il prezzo dei seguenti prodotti. euro 3; centesimi 25 → 3,25 €

a) euro 2; centesimi 12 →

b) euro 0; centesimi 55 →

c) euro 1; centesimi 5 →

15 Completa le seguenti relazioni utilizzando i simboli > (maggiore), < (minore), = (uguale).

16 Scrivi i numeri che corrispondono ai punti riportati sulla semiretta.

17 Colloca i seguenti numeri sulla semiretta sotto riportata e poi scrivili in ordine crescente.

u = 0,5

18 Colloca le lettere corrispondenti ai numeri indicati sulla semiretta: si comporrà il nome di un matematico svizzero.

SIMULAZIONE DI VERIFICA

1 Scrivi il significato dei seguenti simboli scegliendoli tra quelli assegnati.

(Attenzione: non tutti i termini andranno utilizzati.)

maggiore - precedente - minore o uguale - diverso - minore costante - uguale - maggiore o uguale - compreso - dispari

2 Rispondi con Vero (V) o Falso (F).

a) I numeri ordinali esprimono la quantità degli oggetti considerati.

b) Nel numero decimale 35,38 la cifra 3 è decina e decimo.

c) Il numero 20 001 si legge ventimiladieci.

d) Il successivo di un numero si indica con a + 1.

e) Il numero 0,05 corrisponde a 50 centesimi.

f) 2n è un simbolo per rappresentare i numeri dispari.

g) La scrittura polinomiale serve anche per i numeri decimali.

F

3 Scrivi il nome del mese in cui la vocale ‘‘o’’ compare al secondo posto e la ‘‘e’’ al quarto e all’ottavo posto.

4 Scrivi il numero formato da 7 migliaia, 5 decine, 8 unità e 3 decimi.

5 Inserisci i numeri mancanti.

a) 50 è l’antecedente di che è l’antecedente di

b) 100 è il successivo di che è il successivo di

c) 1 000 è l’antecedente di ed è il successivo di

6 Scrivi in ordine crescente i numeri pari e in ordine decrescente quelli dispari.

238; 917; 719; 832; 328; 179; 3 026; 2 011; 49; 94; 2 306; 1 012; 2 101; 6 032

Ordine crescente

Ordine decrescente

7 Completa la tabella.

In cifre Scrittura polinomiale

a) 30 648

b) 5,904

c) 7 × 10 000 + 2 × 1 000 + 8 × 10 + 9

d) 1 × 100 + 8 + 6 × 0,001 + 9 × 0,0001

8 Scrivi il numero che corrisponde ad ogni punto evidenziato.

9 MATEMATICA IN AZIONE Quattro amiche misurano la loro statura e scoprono che Marika è più alta di Donatella, che Teresa è più bassa di Donatella e più alta di Sara. Elenca i nomi delle amiche secondo la loro altezza (in ordine crescente).

Amica più bassa

Amica più alta

10 MATEMATICA IN AZIONE Scrivi il valore in cifre e in lettere di ogni moneta dell’euro a partire da quella da 2 €.

In lettere In cifre

Due euro

Cinquanta centesimi di euro

11 MATEMATICA IN AZIONE Rispondi alle seguenti domande.

a) A quanti centesimi di euro equivale una moneta da 1 euro?

b) A quanti centesimi di euro equivale una moneta da 2 euro?

c) A quanti decimi di euro equivale una banconota da 5 euro?

d) A quanti centesimi di euro equivale una banconota da 5 euro?

LE QUATTRO OPERAZIONI E LE LORO PROPRIETÀ UNITÀ 3

Chi ha della

paura matematica?

In questa unità incontrerai le quattro operazioni fondamentali: addizione, sottrazione, moltiplicazione e divisione. Le hai conosciute già alla scuola primaria: sono strumenti molto utili per risolvere i problemi, sia a scuola sia nella vita di tutti i giorni.

Non aver paura di commettere errori quando fai le operazioni, e non pensare che la bravura in matematica dipenda dalla velocità con cui effettui i calcoli!

Prenditi tutto il tempo necessario per elaborare le informazioni, alcuni errori sono causati proprio dalla fretta. Ricordati che lo sforzo e la perseveranza che puoi mettere nell’eseguire le espressioni e le operazioni matematiche sono importanti quanto i risultati. Farai anche la conoscenza dell’elemento neutro, un concetto fondamentale in matematica, ma che può generare confusione o perplessità. Si tratta di un elemento che non cambia l’operazione: l’importante è non confondere mai l’elemento neutro dell’addizione, che è 0, con quello della moltiplicazione, che è 1.

DEFINIAMO L’ADDIZIONE E LE SUE PROPRIETÀ

DEFINIAMO LA DIVISIONE E LE SUE PROPRIETÀ DEFININIAMO LA SOTTRAZIONE E LE SUE PROPRIETÀ

SCOPRIAMO CHE COSA SONO LE ESPRESSIONI

RISOLVIAMO LE ESPRESSIONI CON LE 4 OPERAZIONI, USANDO LE PARENTESI

MATERIALE INTEGRATIVO MULTIMEDIALE

1 ADDIZIONE

SUCCEDE CHE...

Emma e la sorella Anna si presentano davanti a mamma e papà e, pensando di partecipare a un talent musicale, chiedono di essere votate per stabilire chi è la più brava delle due a cantare l’ultimo successo della cantante Annalisa. Osserva la tabella della “giuria’’ e spiega chi ha vinto.

Mamma Papà

Emma 10 8

Anna 8 10

La tabella si può capire meglio conoscendo l’addizione e le sue proprietà.

L’addizione è l’operazione che a due numeri fa corrispondere un terzo numero che si ottiene contando di seguito al primo le unità del secondo.

I termini dell’addizione sono gli addendi e il risultato è la somma o totale.

6 + 8 = 14 In simboli: a + b = c → somma o totale ↓ ↓ addendi

Per addizionare due o più numeri naturali o decimali è conveniente disporre gli addendi in colonna , cioè uno sotto l’altro in modo che le cifre dello stesso ordine siano nella stessa colonna.

Elemento neutro

Lo zero è l’elemento neutro dell’addizione. In simboli: a + 0 = 0 + a = a

Proprietà commutativa

Le quattro operazioni e le loro proprietà

In una addizione la somma non varia se si cambia l’ordine degli addendi. 10 + 7 + 23 = 23 + 7 + 10 In simboli: a + b + c = c + b + a

Proprietà associativa

In una addizione di più addendi la somma non cambia se ad alcuni di essi si sostituisce la loro somma.

35 + 16 + 24 = 35 + 40 = 75 In simboli: a + b + c = a + (b + c)

La proprietà si può applicare anche al contrario.

21 + 19 = 21 + 9 + 10 = 40 In simboli: a + b = a + m + n con m + n = b

Non ha vinto nessuno 10 + 8 (Emma) = 8 + 10 (Anna) = 18

La mamma e il papà, per non scontentarle, le hanno fatte pareggiare. Infatti, hanno applicato la proprietà commutativa.

1 Stabilisci se le seguenti affermazioni sono vere (V) o false (F).

a) I termini addizione e somma hanno lo stesso significato. V F

b) L’elemento neutro per l’addizione è 0. V F

c) Per l’addizione vale solo la proprietà associativa.

d) L’addendo principale è il risultato dell’addizione.

F

F

e) I termini “somma” e “totale” hanno lo stesso significato. V F

f) La somma di due numeri decimali termina sempre con 0. V F

2 Risolvi le addizioni e sottolinea quelle che hanno come somma un numero > di 1 200.

a) 653 + 205 + 384 =

b) 97 + 480 + 425 =

c) 827 + 163 + 319 =

d) 178 + 304 + 251 + 287 =

3 Indica quali proprietà sono state applicate alle seguenti uguaglianze.

a) 11 + 13 + 1 = 1 + 13 + 11

Commutativa

b) 27 + 33 + 10 = 60 + 10

c) 1,8 + 2 + 0,16 + 0,04 = 3,8 + 0,20

d) 33 + 16 + 17 = 30 + 3 + 10 + 7 + 16

Completa le seguenti uguaglianze.

6 MATEMATICA IN AZIONE Per superare un concorso bisogna totalizzare tra i 70 e i 100 punti.

Stabilisci chi ha superato la prova e fai una graduatoria dal migliore al peggiore tra i seguenti concorrenti, sommando i tre punteggi ottenuti da ognuno.

23 29 31

Pelandroni 15 18 36 Semprevolli 25 21 28

Pigroni 22 26 23

Genialoni 27 28 25

SUCCEDE CHE...

SOTTRAZIONE

Pietro e suo cugino Luca hanno messo da parte 100 € per comprare un nuovo joystick che costa 45 €. Però devono restituire 20 € avuti in prestito, spenderne 15 € per un regalo e 10 € a testa per una ricarica del cellulare. Ognuno di loro fa i calcoli, ma in modo diverso. Quale calcolo è quello giusto per sapere se rimarranno loro soldi a sufficienza per il joystick?

Conosciamo da vicino la sottrazione e le sue proprietà per capire chi ha ragione.

La sottrazione è l’operazione inversa dell’addizione. La sottrazione è l’operazione che fa corrispondere a due numeri un terzo numero, se esiste, che addizionato al secondo dà per risultato il primo.

I termini della sottrazione sono minuendo e sottraendo; differenza e resto sono il risultato.

13 - 7 = 6 In simboli: a - b = c → differenza o resto sottraendo minuendo

Per sottrarre due numeri naturali o decimali è conveniente disporli in colonna , in modo che le cifre dello stesso ordine siano nella stessa colonna.

Elemento neutro

3 5 7, 4 62 5, 3 5 =

3 3 2, 1 1

Lo zero si comporta come elemento neutro solo quando è al posto del sottraendo, ma non se è al posto del minuendo.

15 – 0 = 15 ma 0 – 15 = ?

Proprietà invariantiva

Se si addiziona o si sottrae lo stesso numero dai due termini di una sottrazione, la differenza non cambia.

In simboli: a b = (a + m) (b + m) oppure a − b = (a n) (b n) con n < a e n < b

37 25 = 12 (37 + 3 ) (25 + 3 ) = 40 28 = 12 oppure (37 - 7 ) (25 - 7 ) = 30 18 = 12

Seconda proprietà della sottrazione

Per sottrarre due o più numeri da uno stesso numero è possibile sottrarre dal primo la somma degli altri numeri. In simboli: a b c d = a (b + c + d) con a ≥ (b + c + d) 56 12 8 15 = 56 (12 + 8 + 15) = 56 35 = 21

ESEMPIO

Entrambi i calcoli sono corretti. Luca, rispetto a Pietro, ha applicato la seconda proprietà della sottrazione:

100 20 10 10 15 = 100 (20 + 10 + 10 + 15) = 100 55 = 45 Potranno sicuramente acquistare il nuovo joystick.

1 Risolvi le sottrazioni sul quaderno, dopo averle messe in colonna in modo corretto.

Risolvi le seguenti sottrazioni sul quaderno e applica la proprietà invariantiva (aggiungendo o sottraendo un numero a tuo piacere).

Calcola la differenza applicando sul quaderno la seconda proprietà.

6 MATEMATICA IN AZIONE Nella biblioteca dell’istituto comprensivo Italo Calvino a settembre risultavano in dotazione 5 304 libri. Alla fine dell’anno scolastico viene fatto l’inventario e si osserva che 17 alunni non hanno riportato i libri presi in prestito; inoltre, 45 libri vengono eliminati perché usurati. Quanti libri vi sono attualmente nella biblioteca? [5 242]

SUCCEDE CHE...

ESPRESSIONI CON ADDIZIONI E SOTTRAZIONI

Pietro non ha più soldi in tasca e ricontrolla le spese effettuate: “A inizio settimana avevo 20 € e la mamma mi ha dato la paghetta settimanale di 10 €. Mercoledì ne ho spesi 5 per un regalino di classe, venerdì la nonna me ne ha regalati 15 perché ho superato il Cambridge e sabato sono andato a comprarmi uno zainetto nuovo che mi è costato 40 €”.

Pietro riscrive tutti i conti in un’unica espressione, ma il risultato sembra impossibile. Chiede aiuto a Emma: “Che cosa sto sbagliando?’’.

Emma rivede gli appunti di Pietro e scherzando gli risponde: “Forse è il caso di ripassare le regole delle espressioni!’’

Un’espressione aritmetica è una successione di numeri collegati da segni di operazione.

Per calcolare il valore di un’espressione con addizioni e sottrazioni si risolvono le operazioni secondo l’ordine con cui si presentano

Nelle espressioni, per indicare che alcune operazioni hanno “la precedenza’’, si utilizzano le parentesi, che sono di tre tipi:

parentesi tonde parentesi quadre parentesi graffe

Le regole di “precedenza’’ stabiliscono che, per risolvere le espressioni, le operazioni vanno calcolate dalle parentesi più interne alle più esterne: tonde → quadre → graffe.

Le stesse regole valgono anche per le espressioni con numeri decimali.

ESEMPIO

2,5 + {1,5 [1,7 (3,6 3,2) 0,8] + 1,4} =

2,5 + {1,5 [1,7 0,4 0,8] + 1,4} =

2,5 + {1,5 0,5 + 1,4} = 2,5 + 2,4 = 4,9 → valore dell’espressione 20 12 + 2 - 7 + 15 = 8 + 2 - 7 + 15 = 10 7 + 15 = 3 + 15 = 18 valore dell’espressione →

Adesso Pietro ha capito che le espressioni descrivono eventi che avvengono uno dopo l’altro in successione. Quindi le operazioni si eseguono nell’ordine in cui compaiono: 20 + 10 5 + 15 40 = 30 5 + 15 40 = 25 + 15

1 Rispondi con Vero o Falso.

a) In un’espressione le addizioni hanno la precedenza sulle sottrazioni. V F

b) Le parentesi servono a indicare precedenze nelle operazioni. V F

c) Le parentesi possono essere tonde, quadre e graffe. V F

d) Per i numeri decimali le regole delle espressioni non valgono. V F

Completa lo svolgimento delle espressioni seguendo le indicazioni.

2 37 21 + 15 23 + 13 =

Svolgi le operazioni una dopo l’altra così come si presentano:

( 16 + 15 - 31 - 23 + +

3 (24 + 17 35) + (38 7 + 14) 39 =

Dai la precedenza alle operazioni nelle parentesi tonde:

( ( 6 + - 39

Risolvi le seguenti espressioni sul tuo quaderno. 4

6 40 (25 + 42 51) {2 [(79 + 46) 125]} [22]

Osserva lo svolgimento delle seguenti espressioni e sottolinea gli errori commessi. Poi, sul quaderno, esegui le espressioni correttamente.

7 48 16 ( 5 + 20 ) = 32 5 + 20 = 27 + 20 = 47

8 (53,8 1,8) (16,9 5,2 + 1,7) = 52 (16,9 6,9) = 52 10 = 42

9 MATEMATICA IN AZIONE In una gara di ballo a punti a una coppia vengono assegnati i seguenti punteggi.

Alla fine del ballo, però, vengono tolti 3 punti per ogni categoria a causa di una scorrettezza verso il pubblico. Calcola il punteggio finale con una espressione e stabilisci se sono necessarie le parentesi tonde.

4 MOLTIPLICAZIONE

SUCCEDE CHE...

Gustavo deve apparecchiare cinque tavoli per quattro persone, mettendo per ogni posto a tavola: 3 piatti, 2 bicchieri e 4 posate.

Quanti oggetti in totale deve avere a disposizione Gustavo?

Per rispondere ci tornano utili le proprietà della moltiplicazione.

La moltiplicazione è l’operazione che fa corrispondere a due numeri un terzo numero che si ottiene sommando tanti addendi uguali al primo numero quante sono le unità del secondo.

I termini della moltiplicazione sono i fattori e il risultato è il prodotto

Legge di annullamento del prodotto

In simboli: a × b = c → prodotto → → fattori 5 × 3 = 5 + 5 + 5 = 15 } 3 volte

Se un fattore è zero, anche il prodotto è zero In simboli: a × 0 = 0 × a = 0

Elemento neutro

L’elemento neutro della moltiplicazione è il numero 1. In simboli: a × 1 =

Proprietà commutativa

Il prodotto di due o più fattori non varia se si cambia il loro ordine.

In simboli: a × b × c = c × a × b

Proprietà associativa

Le quattro operazioni e le loro proprietà

Il prodotto di due o più fattori non cambia se ad alcuni di essi si sostituisce il loro prodotto.

In simboli: a × b × c = a × (b × c) a × b = a × m × n con m × n = b

Proprietà distributiva

Per moltiplicare un numero per una somma (o per una differenza) si può moltiplicare il numero per ciascun termine della somma (o della differenza) e poi sommare (o sottrarre) i prodotti ottenuti.

In simboli: (a + b c) × d = a × d + b × d c × d

Gustavo applica la proprietà distributiva della moltiplicazione: 5 × 4 × (3 + 2 + 4) = 20 × (3 + 2 + 4) = 20 × 3 + 20 × 2 + 20 × 4 = 60 (piatti) + 40 (bicchieri) + 80 (posate) = 180 oggetti

1 Indica quali proprietà sono valide per la moltiplicazione.

a) Proprietà associativa Sì No

b) Proprietà commutativa Sì No

2 Calcola.

c) Proprietà invariantiva Sì No d) Proprietà distributiva Sì No

7,3 × 1 = 0 × 45 = 1 × 4,12 = 74 × 0 = 1 × 0 =

3 Utilizza le proprietà commutativa e associativa per semplificare i calcoli.

ESEMPIO

79 × 5 × 2 → conviene “associare’’ i fattori 5 e 2 → 79 × 10 = 790

5 × 38 → conviene scrivere il numero 38 come 2 × 19 → 5 × 2 × 19 = 10 × 19 = 190

a) 2 × 36 × 5 =

b) 20 × 1,8 × 5 =

c) 54 × 5 = 2 × × 5 =

d) 75 × 4 = 25 × 3 × 4 = 25 × 4 × 3 = =

4 Per ogni uguaglianza stabilisci quale proprietà della moltiplicazione è stata applicata.

a) 15 × 61 × 38 = 38 × 61 × 15

b) 24 × 37 × 11 = 3 × 8 × 37 × 11

c) 26 × 5 × 7 × 43 = 26 × 35 × 43

d) 9 × (13 + 41) = 9 × 13 + 9 × 41

e) 17 × (59 28) = 17 × 59 17 × 28

5 MATEMATICA IN AZIONE Sapendo che un quaderno costa 1,20 €, completa la tabella.

1 2 3 4 10 15

Gino va in cartoleria e compra 12 quaderni pagandoli 15 €. Il negoziante ha fatto il conto giusto?

DIVISIONE 5

SUCCEDE CHE...

Il papà di Emma ha un televisore Full HD e lo usa in prevalenza per vedere video online, scaricando circa 1,5 GB all’ora.

Se ha un abbonamento mensile per 30 GB, quante ore al mese ha a disposizione?

Il problema si risolve con una divisione in cui il divisore è decimale.

La divisione è l’operazione che fa corrispondere a due numeri, di cui il secondo diverso da zero, un terzo numero che moltiplicato per il secondo dà come risultato il primo.

Il primo numero è il dividendo, il secondo è il divisore, il risultato della divisione è il quoto o quoziente.

28 : 7 = 4 In simboli: a : b = c → quoto o quoziente divisore dividendo

La divisione è l’operazione inversa della moltiplicazione.

Le quattro operazioni e le loro proprietà

60 : 4 = 15 infatti 15 × 4 = 60 o 4 × 15 = 60 15 60

Elemento neutro

× 4 : 4

Il numero 1 si comporta come elemento neutro solo quando è al posto del divisore, ma non se è al posto del dividendo.

15 : 1 = 15 ma 1 : 15 = 0,...

Se dividendo e divisore sono uguali il quoziente è 1.

In simboli: a : a = 1

a) 15 : 15 = 1 b) 3,6 : 3,6 = 1

Zero e la divisione

Se il dividendo è zero, anche il quoziente è zero.

In simboli: 0 : a = 0 con a ≠ 0

b) 0 : 25 = 0 perché 0 × 25 = 0 b) 0 : 4,9 = 0 perché 0 × 4,9 = 0

Se il divisore è zero, la divisione non è possibile.

In simboli: a : 0 è impossibile con a ≠ 0

37 : 0 → impossibile Non c’è alcun numero che moltiplicato per 0 dia 37 come risultato.

Se il dividendo e il divisore sono entrambi zero, il quoziente è indeterminato.

0 : 0 è indeterminato Qualunque numero moltiplicato per 0 dà come risultato 0.

Proprietà invariantiva

Se si moltiplicano o si dividono (quando è possibile) i termini di una divisione per uno stesso numero, diverso da zero, il quoziente non cambia. In simboli:

a : b = (a × m) : (b × m) oppure a : b = (a : n) : (b : n) con m ≠ 0 e n ≠ 0

La proprietà invariantiva si utilizza per eseguire le divisioni con il divisore decimale; infatti, permette di poter togliere la virgola prima di svolgere il calcolo.

ESEMPIO

80 : 2,5 = (80 × 10) : (2,5 × 10) = 800 : 25 = 32

In particolare, se il dividendo è un prodotto indicato, vale la seguente applicazione della proprietà invariantiva.

Per dividere un prodotto indicato per un numero si può dividere per quel numero uno solo dei fattori e poi moltiplicare il quoziente ottenuto per gli altri fattori.

In simboli: (a × b × c) : d = a × (b : d) × c con b divisibile per d

ESEMPIO

(10 × 28 × 6) : 7 = 10 × (28 : 7) × 6 = 10 × 4 × 6 = 240

Proprietà distributiva

Per dividere una somma (o una differenza) per un numero si può dividere ciascun termine della somma (o della differenza) per quel numero e poi sommare (o sottrarre) i quozienti ottenuti.

In simboli: (a + b) : c = a : c + b : c (a b) : c = a : c b : c

ESEMPIO

(68 36) : 4 = (68 : 4) (36 : 4) = 17 9 = 8

Con la proprietà invariantiva risolviamo la divisione:

30 : 1,5 = (30 × 10) : (1,5 × 10) = 300 : 15 = 20

Quindi il papà di Emma ha a disposizione 20 ore al mese.

1 Rispondi con Vero o Falso.

a) I termini quoto e quoziente indicano il risultato di una divisione. V F

b) I termini divisione e quoziente hanno lo stesso significato. V F

c) La divisione è l’operazione inversa della moltiplicazione.

d) La divisione non ha l’elemento neutro.

F

F

e) I termini della divisione sono il dividendo e il divisore. V F

f) L’elemento neutro della divisione è 1. V F

2 Correggi le affermazioni false dell’esercizio 1.

3 Completa le affermazioni e rispondi alle domande.

Considera la divisione 24 : 6 = 4.

a) 24 è

b) 6 è c) 4 è

d) Il resto della divisione è

4 Per ciascuna divisione indica il dividendo, il divisore e il quoziente.

a) 48 : 6 = 8 dividendo divisore quoziente

b) 7,8 : 0,2 = 39 dividendo divisore quoziente

c) 0 : 8,3 = 0 dividendo divisore quoziente

5 Rispondi con SÌ o NO alle seguenti domande.

a) Se dividendo e divisore sono entrambi 0, il quoziente è 0?

b) Se il dividendo è zero e il divisore è diverso da zero, il quoziente è zero?

c) Se il divisore è uno, il quoziente è uguale al dividendo?

Sì No

Sì No

Sì No

d) Se il quoziente è indeterminato, sia il divisore che il dividendo sono zero? Sì No

e) Aggiungendo o sottraendo uno stesso numero ai termini di una divisione, il quoziente cambia? Sì No

6 Quali proprietà ha la divisione?

7 Scrivi la moltiplicazione che è la “prova’’ di ciascuna divisione. 56 : 7 = 8 54 : 3 = 18 16,9 : 1,3 = 13 9,6 : 0,8 = 12

8 Risolvi mentalmente le seguenti divisioni.

a) 75 : 5 = 54 : 3 = 90 : 6 = 68 : 4 =

b) 96 : 8 = 99 : 11 = 126 : 7 = 189 : 9 =

9 Scrivi sul quaderno le divisioni che corrispondono alle prove e ai resti assegnati.

7 × 8 + 5 = 61 61 : 8 = 7 resto 5 oppure 61 : 7 = 8 resto 5

3 × 11 + 8 = 41 4 × 13 + 7 = 59 6 × 21 + 7 = 133 8 × 17 + 9 = 145

10 Completa scrivendo per ogni uguaglianza la proprietà applicata.

a) 364 : 14 = 182 : 7

b) (350 280) : 10 = 35 28

c) 57,2 : 0,4 = 572 : 4

d) (24 + 56 32) : 8 = 3 + 7 4

11 Indica in quali esercizi è stata applicata esattamente la proprietà invariantiva.

a) 5,4 : 1,8 = (5,4 + 10) : (1,8 + 10)

b) 96 : 1,2 = (96 × 10) : (1,2 × 10)

c) 36 : 9 = (36 9 ) : (9 9)

d) 48 : 16 = (48 : 8 ) : (16 : 8)

12 Applica la proprietà invariantiva e risolvi le seguenti divisioni.

51 : 3,4 = (51 × 10) : (3,4 × 10) = 510 : 34 = 15

:

:

:

13 Indica in quali esercizi è stata applicata esattamente la proprietà distributiva.

a) (54 30) : 6 = 54 : 6 30 : 6

b) (27 + 18) : 9 = 27 : 9 : 18 : 9

c) (36 + 24) : 15 = (36 + 15) : (24 + 15)

d) (85 20) : 5 = 85 : 5 20 : 5

14 Applica la proprietà distributiva alle seguenti divisioni.

(28 + 30 + 16) : 2 (45 18 21) : 3 (14 + 105 + 70 56 42) : 7

15 Risolvi le divisioni e poi rispondi alle domande.

a) 781 : 11 =

b) 591 : 1 =

c) 45,3 : 0,3 =

d) 84 : 0,2 =

In quali divisioni il quoziente è maggiore del dividendo?

In quale divisione il quoziente è uguale al dividendo?

16 MATEMATICA IN AZIONE Scaricare una canzone su iTunes Store costa 1,50 €.

Con 15 € quante canzoni potrai scaricare?

SUCCEDE CHE...

LE QUATTRO OPERAZIONI

Emma ha 8,50 € nel suo salvadanaio; vengono a trovarla i quattro nonni e ognuno di loro le regala 5 € perché

vorrebbe comprare la maglietta della sua band preferita. Per sapere quanti soldi ha ora, Emma fa questo calcolo:

8,50 + 5 × 4 = 13,50 × 4

ma Pietro le dice che il calcolo da fare è questo:

8,50 + 5 × 4 = 8,50 + 20

Chi ha ragione?

quattro operazioni e le loro proprietà

In un’espressione le moltiplicazioni e le divisioni vanno risolte per prime perché hanno la precedenza; poi si risolvono le addizioni e le sottrazioni rispettando l’ordine in cui sono scritte.

Se in un’espressione ci sono delle parentesi, si risolvono prima le operazioni interne alle parentesi tonde, poi quelle nelle quadre e infine quelle nelle graffe.

Anche le operazioni contenute nelle parentesi vanno risolte dando la precedenza alle moltiplicazioni e alle divisioni.

Le regole di precedenza per le operazioni e per le parentesi valgono anche per le espressioni con i numeri decimali

ESEMPIO

{[(4 + 3,1 × 2) : 2] 2 × 1,3} + 0,5 → Si risolve la moltiplicazione nella parentesi tonda

{[(4 + 6,2) : 2] 2 × 1,3} + 0,5 → Si risolve l’addizione nella parentesi tonda

{[10,2 : 2] 2 × 1,3} + 0,5 → Si risolve la divisione nella parentesi quadra

{5,1 2 × 1,3} + 0,5 → Si risolve la moltiplicazione nella parentesi graffa

{5,1 2,6} + 0,5 → Si risolve la sottrazione nella parentesi graffa

2,5 + 0,5 = 3

Emma dà la precedenza all’addizione, Pietro invece alla moltiplicazione.

Calcolo di Emma

Calcolo di Pietro

8,50 + 5 × 4 = 13,50 × 4 = 54 € 8,50 + 5 × 4 = 8,50 + 20 = 28,50 €

Errato

Esatto

Pietro con il suo calcolo ti fa capire che non devi sommare 8,50 con 5 e poi moltiplicare per 4, perché 5 × 4 ha la precedenza; quindi, il risultato 20 (euro avuti dai nonni) deve essere sommato agli 8,50 € che Emma già aveva.

1 Indica quali operazioni hanno la precedenza in un’espressione aritmetica.

a) Le addizioni e le moltiplicazioni

b) Le divisioni e le sottrazioni

2 Quali parentesi hanno la precedenza?

a) Le graffe

b) Le tonde

c) Le addizioni e le sottrazioni

d) Le moltiplicazioni e le divisioni

c) Le quadre

d) Dipende dalle operazioni che contengono

Le seguenti espressioni contengono degli errori di precedenza: correggili e risolvile.

3 30 15 : 5 + 7 4 = 15 : 5 + 3 = 3 + 3 = 6

4 56 + 24 : 4 12 + 4 × 2 = 80 : 4 12 + 8 = 20 20 = 0

Inserisci le parentesi indicate in modo da ottenere il risultato assegnato.

operazioni 4 + 5 × 3 17 parentesi: () risultato 10 espressione (4 + 5) × 3 17

5 operazioni 4 + 16 : 2 7 parentesi: () risultato 3 espressione

6 operazioni 5 + 3 × 16 11 parentesi: () () risultato 40 espressione

7 operazioni 17 12 × 8 26 parentesi: () risultato 14 espressione

Risolvi le seguenti espressioni.

8 8 × [(17 + 2 + 5) : 4 + (10 × 3 + 4) : 2 7 × 3] : 2 [8]

9 0,5 × [3,6 × 3 : 2 + (0,3 + 6,24 : 1,2) : 0,11] [27,7]

10 MATEMATICA IN AZIONE Max, l’allenatore di una squadra di basket, deve ordinare le divise per il suo team.

Ogni divisa costa 20 € e la squadra ha in cassa 143 €. Se i giocatori sono 13, qual è la quota che dovrà versare ognuno dei giocatori per acquistare la divisa? Completa l’espressione e risolvila: [( × ) ] : ESEMPIO

CURIOSITÀ STORICHE

ODIFREDDI a cura del professor

NUME RI E ALFABETO

Per indicare i numeri, gli antichi usavano i simboli più ovvi che avevano a disposizione: cioè, le lettere dell’alfabeto. I Greci, per esempio, avevano un alfabeto di 24 lettere, che potevano indicare i numeri da 1 a 24, in ordine alfabetico. Per questo motivo i grandi classici, come l’Iliade e l’Odissea, avevano 24 capitoli: uno per ciascuna lettera dell’alfabeto. Ovviamente, c’era anche bisogno di indicare numeri più grandi di 24. I Greci pensarono perciò di indicare le cifre del sistema decimale, da 1 a 9, mediante le prime nove lettere dell’alfabeto. Le decine, da 10 a 100, mediante le successive nove lettere dell’alfabeto. E le centinaia, da 100 a 900, mediante le ultime nove. Purtroppo, per fare questo c’era bisogno di 27 lettere: avendone solo 24 a disposizione, ne aggiunsero altre tre che erano cadute in disuso, e in tal modo riuscirono a indicare tutti i numeri da 1 a 999 usando soltanto triplette di lettere del loro alfabeto allargato.

Già nell’antichità, i matematici ebrei collegavano la matematica alle leggi del tempo e della vita quotidiana, oltre che allo studio del divino.

L’Iliade e l’Odissea sono divise in 24 canti, uno per ogni lettera dell’alfabeto greco, che indicava anche i numeri.

Anche gli Ebrei fecero lo stesso con il loro alfabeto di 22 lettere, opportunamente allargato con altre 5, per arrivare a 27.

Entrambi i popoli si ritrovarono così a scrivere sia le parole che i numeri con gli stessi segni. In molti casi, dunque, un gruppo di segni poteva avere un doppio significato, a seconda che lo si leggesse come una parola, o come un numero.

Quest’ambiguità diede luogo, in entrambi i popoli, a un’arte che consisteva nell’interpretare le parole come numeri, che si potevano sommare o moltiplicare. I risultati erano altri numeri che, a loro volta, si potevano reinterpretare come parole.

A volte il risultato era sorprendente. Per esempio, le lettere del nome di Jahvé, il Dio degli Ebrei, corrispondevano a numeri che, sommati fra loro, producevano un numero uguale alla somma dei numeri corrispondenti a Uno e Amore.

Nacque così l’arte della gematria, o “calcolo alfabetico”, che venne presa molto sul serio, essendo ritenuta la chiave per aprire i segreti dell’universo e dell’aldilà.

Un’arte che ormai non ha più il valore che le veniva attribuito molti anni fa. Per noi moderni può sembrare strana o bizzarra, ma viene utilizzata ancora oggi, anche se raramente e forse con meno serietà, nella cosiddetta cabala.

cabala

I sevivon mostrano il legame tra lettere e numeri: ogni faccia della trottola porta una lettera-numero ebraica.

LE QUATTRO OPERAZIONI E LE LORO PROPRIETÀ

Addizione

Le quattro operazioni e le loro proprietà

Sottrazione

Moltiplicazione

0 è l’elemento neutro 5 + 0 = 5

0 è l’elemento neutro 5 – 0 = 0

1 è l’elemento neutro

5 × 1 = 5 0 annulla il prodotto 17 × 0 = 0

Divisione 1 è l’elemento neutro

5 : 1 = 5

Proprietà commutativa 24 + 18 + 36 = = 36 + 18 + 24

Proprietà invariantiva 39 – 14 = 25 (39 + 1) – (14 + 1) (39 – 4) – (14 – 4)

Proprietà commutativa 25 × 7 × 4 = = 25 × 4 × 7

Proprietà associativa

22 + 31 + 28 = = (22 + 28) + 31

49 + 16 = = 40 + 9 + 16

Seconda proprietà 64 – 12 – 23 – 18 = = 64 – (12 + 23 + 18)

Proprietà associativa 8 × 5 × 4 = = 8 × (5 × 4) 21 × 10 = = 21 × 5 × 2

Proprietà distributiva (26 + 12) : 2 = = 26 : 2 + 12 : 2 (49 – 14) : 7 = = 49 : 7 – 14 : 7

Proprietà distributiva (5 + 3) × 7 = = 5 × 7 + 3 × 7 (18 – 7) × 3 = = 18 × 3 – 7 × 3

Proprietà invariantiva

3,5 : 0,7= (3,5 × 3,5 : 0,7 = = (3,5 × 10) : (0,7 × 10) = = 35 : 7 in particolare (7 × 15 × 9) : 5 = = 7 × (15 : 5) × 9 = = 7 × 3 × 9

ESERCIZI E PROBLEMI

LEZIONE 1

ADDIZIONE

1 Data l’addizione m + n + q = t.

a) quali lettere indicano gli addendi?

b) quale lettera rappresenta la somma?

2 Data l’addizione a + b = c:

a) quando a è uguale a c?

b) quando b è uguale a c?

c) quando c è il successivo di a?

3 Perché lo zero è l’elemento neutro per l’addizione?

4 Quale proprietà viene espressa dalla scrittura a + b + c = c + b + a?

5 Quale proprietà viene espressa dalla scrittura a + b + c = (a + b) + c?

6 A ciascuna proprietà dell’addizione abbina la frase che la espone in modo corretto.

PROPRIETÀ COMMUTATIVA

ASSOCIATIVA

a) La somma di più addendi non cambia se al posto di alcuni di essi si sostituisce la loro somma.

b) La somma di due o più addendi non cambia se si cambia il loro ordine.

7 Completa la tabella come nella prima riga.

quattro operazioni e le loro proprietà

Individua gli addendi mancanti e completa le seguenti tabelle a doppia entrata. 8 9

Risolvi le addizioni dei seguenti gruppi.

10

11 Considera delle addizioni come quelle dell’esercizio precedente e rispondi alle domande.

a) La somma di due numeri pari è sempre un numero pari?

b) La somma di due numeri dispari è sempre un numero pari?

c) La somma di due numeri dispari è sempre un numero dispari?

d) La somma di un numero pari con uno dispari è a volte pari e a volte dispari?

12 Indicando con P un numero pari e con D un numero dispari, scrivi le regole relative all’addizione di pari e dispari.

13 MATH Fill in the boxes with the missing numbers.

14 Metti al posto dei puntini un addendo affinché ogni addizione risulti esatta.

15 MATEMATICA IN AZIONE Il grafico mostra i punteggi ottenuti da tre studenti (Marco, Giorgia e Giada) in una gara musicale. Il punteggio finale è la somma dei punti ottenuti per la tecnica e per l’interpretazione. Calcola i punteggi totali dei tre ragazzi per stabilire chi ha ottenuto il punteggio maggiore.

Marco:

Giorgia:

Giada:

16 Date le seguenti uguaglianze, indica se le proprietà sono state applicate correttamente.

a) 15 + 17 = 10 + 5 + 10 + 5 + 2 Sì No

b) 48,3 + 0,7 = 40 + 0,8 + 0,3 + 7 Sì No

c) 23 + 19 + 38 = 23 + 12 + 7 + 38

d) 6,5 + 6 + 3,9 = 6 + 0,5 + 5 + 1 + 3 + 9

e) 3,5 + 18 + 4,5 + 22 = 3,5 + 4,5 + 18 + 22 = 8 + 40

Esamina le uguaglianze e per ciascuna di esse indica la proprietà che è stata applicata.

a) 30 + 50 + 8 + 2 = 30 + 50 + 10 = 90

b) 35 + 20 + 28 = 20 + 15 + 20 + 28 = 83

a) 75 + 25 + 35 + 15 = 100 + 50 = 150 b) 45 + 15 + 5 + 10 = 45 + 5 + 15 + 10 = 75

19 Applica la proprietà commutativa e risolvi.

a) 24 + 15 +

b) 1,4 + 3,2 + 5,6 + 0,8

20 Applica la proprietà associativa e risolvi.

+

+ 4,9 +

Utilizza le proprietà per eseguire più rapidamente le addizioni sul quaderno.

No

No

No

Le quattro operazioni e le loro proprietà

4,1 + 6,2 + 0,9 + 1,8 = 4 + 0,1 + 6 + 0,2 + 0,9 + 1 + 0,8 = 11 + 1 + 1 = 13

a) 1,7 + 1,6 + 5,3 + 2,4 0,5 + 3,8 + 4,7 + 1

b) 21,3 + 3,7 + 0,8 + 15,2 = 41 3,6 + 4,2 + 3,1 + 3 = 13,9

a) 6,2 + 9,8 + 7,3 + 3,7 9,1 + 1,9 + 3,4 + 5,6

b) 5,3 + 6,7 + 1,4 + 0,6 5,4 + 6,2 + 3,5 + 1,7

Sul quaderno metti in colonna gli addendi e risolvi.

a) 721 + 211 4 255 + 678

b) 4 531 + 8 927

69 001 + 3 927

a) 528 + 112 + 780 654 + 22 + 1 927

b) 25 + 23 954 + 6 714 + 505 34 + 921 + 3 784

a) 3,421 + 8,76 + 395,545

b) 857,12 + 31,2 + 729,011

7,205 + 32,82 + 7,25

544,3 + 12,73 + 461,128

a) 1,345 + 0,04 + 630,3 0,0045 + 2,503 + 130

b) 675 + 1 92,4 + 77,06 251 + 0,25 + 18,103

Continua le seguenti successioni numeriche.

a) 3; 9; 15; 21; 27; b) 1; 2; 4; 7; 11; 16;

a) 5; 4; 7; 6; 9; 8; 11; 10; b) 1; 2; 4; 8; 16;

a) 8; 6; 13; 11; 18; 16; b) 9; 19; 39; 79;

32 STEM Gli alberi monumentali sono piante di grandi dimensioni cui è riconosciuto un elevato valore paesaggistico e culturale.

In Italia nel 2021 sono stati censiti 578 esemplari di roverella (un tipo di quercia), 195 faggi e 186 lecci. Vi sono anche 159 esemplari di platano, 118 di sughere, 116 di larice e 97 di castagno; 2 216 sono di altre tipologie.

Quanti alberi monumentali c’erano in Italia nel 2021? [3 665]

33 MATEMATICA IN AZIONE Un cinema multisala ha in programmazione 4 film. Nella prima settimana di ottobre 430 spettatori hanno visto il film La Sirenetta, 210 persone Transformers, 145 Harry Potter e la pietra filosofale, 37 Inside Out

Quanti biglietti sono stati venduti quella settimana? [822]

34 MATEMATICA IN AZIONE Giulio vede che su un sito di shopping online è in vendita la maglietta della sua squadra di calcio preferita al costo di 49,90 €.

Possiede già 23,50 € e il nonno gli regala 12,50 €; inoltre, riceverà la paghetta settimanale di 15 €. Riuscirà ad acquistare la maglietta? Motiva la risposta. [Sì, perché possiede 51 €]

SOTTRAZIONE

35 Completa e rispondi.

Data la sottrazione: 53 17 = 36:

a) 53 è il , 17 è il , è la differenza.

b) se aumenti il minuendo, la differenza aumenta o diminuisce?

c) se diminuisci il minuendo, la differenza aumenta o diminuisce?

d) se aumenti il sottraendo, la differenza aumenta o diminuisce?

e) se diminuisci il sottraendo, la differenza aumenta o diminuisce

f) in quale caso la differenza resta uguale?

36 Scrivi le seguenti proposizioni sotto forma di sottrazioni.

Sedici meno tre è uguale a tredici 16 3 = 13

a) Venti meno nove è uguale a undici

b) La differenza tra dodici e cinque è sette

c) Il numero ventiquattro è la differenza tra i numeri trentasette e tredici

d) Diciannove è maggiore di dodici di sette unità

37 Considera la sottrazione a b = c, in cui a, b e c sono numeri naturali diversi da zero.

a) c è minore di a? Mai

b) c è minore di b? Mai

c) a è minore di c? Mai

d) b è minore di c? Mai

Qualche volta

Qualche volta

Qualche volta

Qualche volta

38 Scrivi al posto dei puntini i numeri o le lettere che rendono vere le uguaglianze.

a) 13 = 0 25 = 0 12 − = 12

b) 24 = 0 38 = 0 27 = 0

c) − a = 0 b = b n = 0

3,5

e)

f) 2n = 0 3a = 3a b = b

39 I seguenti schemi indicano che la sottrazione è l’operazione inversa dell’addizione. Completali. 9 + 10 – 10 15 24 + 6 13 n + 1 n

Le quattro operazioni e le loro proprietà

40 Trasforma le seguenti addizioni in sottrazioni realizzando sul quaderno degli schemi.

13,5 + 7,4 = 20,9 13,5 + 7,4 – 7,4

a) 18 + 23 = 41 9 + 37 = 46

b) 86 + 42 = 128

c) 5,6 + 0,9 = 6,5

= 209

+ 2,4 = 14,7

= 13,5

+ 26 = 51

+ 4,3 = 35,1

41 Trasforma ciascuna sottrazione nella corrispondente addizione.

35 12 = 23 → 23 + 12 = 35

a) 41 29 = 12 45 27 = 18

b) 218 95 = 123 369 135 = 234

c) 6,2 1,2 = 5 23,6 13,5 = 10,1

a) x 12 = 5 → x = 5 + 12 = 17 b) 13 x = 3 → x = 13 − 3 = 10

42 Trova il numero che sostituito alla x rende vera ciascuna uguaglianza. Segui gli esempi.

a) x 15 = 6 x 24 = 61 x 13 = 26

b) 12 x = 6 24 x = 13 65 x = 52

c) x 1,2 = 3,1 x 6,3 = 1,7 x 4,8 = 7 x + 15 = 24 → x = 24 − 15 = 9 a) x + 12 = 34

=

c) x + 4,1 = 9,4 x + 7,3 = 9,5 x + 3,5 = 8,9 d) 5,3 + x = 5,6

+ x = 24,8

+ x = 30

Continua le seguenti successioni numeriche. a) 46; 40; 34; 28; b) 200; 196; 192; 188; a) 125; ; 75; b) 27,5; 26,6; 25,7; a) 105; 103; 106; 101; 99; 102; 97; b) 9,6; 10,2; 9,4; 9,2; 9,8; 9; 8,8;

Completa le seguenti tabelle a doppia entrata.

Sul quaderno risolvi le seguenti sottrazioni mettendo in colonna ed effettuando la prova (differenza + sottraendo = minuendo).

a)

51 EDUCAZIONE CIVICA Il signor Guido Forte è un guidatore piuttosto indisciplinato.

È stato di recente sorpreso alla guida mentre parlava al cellulare. Per questo, oltre a dover pagare una multa di 160 €, gli verranno sottratti dei punti dalla patente secondo la tabella del codice della strada.

Se ne aveva 18, da quanti punti ripartirà dopo il verbale dei carabinieri?

52 MATH Fill in the boxes with the missing numbers.

degli abbaglianti ove vietato 3

Utilizza la proprietà invariantiva per eseguire in modo rapido le seguenti sottrazioni.

Aggiungi o togli un numero in modo che uno dei due termini della sottrazione risulti multiplo di 10, 100, 1 000 ecc.

349 276 = (349 − 6) (276 − 6) = 343 270 = 73

oppure

349 276 = (349 + 1) (276 + 1) = 350 277 = 73

55 MATEMATICA IN AZIONE Passeggiando lungo i sentieri del Parco Nazionale dello

Stelvio non è difficile incontrare cervi e caprioli. Ipotizziamo che vi siano 339 cervi e 127 caprioli.

Quanti cervi ci sono in più dei caprioli? [212]

56 MATEMATICA IN AZIONE Da una botte contenente 450 litri di vino se ne spillano prima 127 litri, in un secondo momento altri 149 litri e infine 89 litri.

Quanti litri di vino restano nella botte? [85 litri]

57 MATEMATICA IN AZIONE Due squadre di basket, i Gambelunghe e i Manigrandi, si contendono il primo posto in classifica.

I Gambelunghe sono in vantaggio di 2 punti. Se entrambe le squadre vincono l’ultima partita della stagione, totalizzando 2 punti a testa, quanti punti di differenza avranno alla fine? Perché? Riconosci quale proprietà è stata applicata?

Risolvi le seguenti operazioni in due modi e osserva che il risultato non cambia.

Applica la seconda proprietà per calcolare le differenze.

5 9 18 = 39 − (5 + 9 + 18) = 39 − 32 = 7

62

64 Per avvicinare i ragazzi ai contenuti dell’Agenda 2030, una scuola ligure ha organizzato alcuni giorni di attività in collaborazione con l’Acquario di Genova. Nei primi giorni viene assegnato il seguente compito agli studenti.

a) Quale operazione va utilizzata per risolvere ognuna di queste situazioni?

• Calcolare quanto varia il peso di un delfino in 6 mesi. addizione sottrazione

• Calcolare quanto pesce occorre ordinare per la vasca degli squali, conoscendo la dieta specifica di ognuno. addizione sottrazione

• Calcolare la quantità di cibo da somministrare ai piccoli di pinguino, sapendo quanto mangiano i pinguini adulti in più rispetto a loro. addizione sottrazione

• Confrontare la temperatura della vasca dei pesci tropicali e quella dell’acqua del mare di Genova. addizione sottrazione

• Calcolare la quantità totale di acqua che viene utilizzata per riempire tutte le vasche. addizione sottrazione

b) Prova a inventare un problema di aritmetica per almeno due delle situazioni precedenti, cercando informazioni su Internet (per esempio, la temperatura delle vasche dei pesci tropicali e quella del mare, oppure il peso di un delfino in crescita).

65 MATEMATICA IN AZIONE Prova a descrivere almeno due situazioni ambientate nella tua scuola in cui devi utilizzare l’addizione e due situazioni in cui devi usare la sottrazione.

ESPRESSIONI CON ADDIZIONI

E SOTTRAZIONI

66 Rispondi con Vero o Falso.

a) Una espressione con sole sottrazioni è impossibile. V F

b) Una espressione con sole addizioni non ha mai bisogno delle parentesi. V F

c) Nelle espressioni non si possono applicare le proprietà dell’addizione. V F

d) La seconda proprietà della sottrazione si può applicare alle espressioni. V F

e) In una espressione non possono esserci più di due coppie di parentesi quadre. V F

Risolvi con il 1o modo e poi verifica con il 2o.

ESEMPIO

25 16 + 23 12 17 + 31 14 1o modo 2o modo

+ 23 12 17 + 31 14 =

12 17 + 31 14 =

17 + 31 14 =

si sommano i numeri preceduti dal segno + e, dal risultato, si toglie la somma dei numeri preceduti dal segno

74 MATH Insert the round brackets where they are needed.

ESEMPIO

Risolvi i seguenti problemi impostando un’espressione.

75 MATEMATICA IN AZIONE Nella scuola di Jennifer ci sono 385 alunni in totale. Gli alunni di prima sono 128, quelli di terza 132; quanti sono gli alunni di seconda?

385 – ( + ) = [125]

76 MATEMATICA IN AZIONE Alla fermata della metropolitana di Roma Termini, in una carrozza dove c’erano 25 passeggeri, ne sono saliti 23 e ne sono scesi 8; alla fermata successiva dalla stessa carrozza scendono 35 passeggeri.

Quanti ne rimangono in carrozza? [5]

77 MATEMATICA IN AZIONE Federico parte per un viaggio con la sua auto. Guida per 250 km e arriva alla casa dei nonni. Dopo averli salutati ed essersi riposato, riprende il suo viaggio, percorre altri 150 km e arriva al mare. Se il contachilometri adesso segna 13 450 km, quanti chilometri segnava prima di partire?

Risolvi le seguenti espressioni con parentesi.

78 (7 + 28) 10 (16 2 + 9) = 35 10 − = [2]

79 18 (10 + 6) + 42 (49 16) [11]

80 (24 6) + (25 + 16 29) (12 + 18) [0]

81 30 (48 8 24) 2 + (14 8) [18]

82 15 (10 + 18 14) + (29 22) + 5 [13]

83 224 + (52 15) + (43 35) 73 (115 + 36) [45]

84 (7,2 3,6) + 3,5 2,4 + 2,6 + (5 + 9,4) [21,7]

Hanno la precedenza le operazioni interne alle ( ), poi quelle interne alle [ ] e infine quelle interne alle { }.

LEZIONE 4

MOLTIPLICAZIONE

108 A ogni affermazione fai corrispondere le uguaglianze scelte tra quelle assegnate.

a) 1 è l’elemento neutro per la moltiplicazione

b) Lo 0 annulla il prodotto

109 Osserva le moltiplicazioni e rispondi (le lettere indicano numeri naturali).

• Considera la moltiplicazione m × n × p = t.

a) Quali lettere rappresentano i fattori?

b) Quale lettera rappresenta il prodotto?

• Considera il prodotto a × b = c

c) Quando a è uguale a c?

d) Quando c è uguale a zero?

e) Quando c è uguale a b?

f) c può essere uguale a 1?

g) c è sempre un numero naturale? Perché?

110 Completa le seguenti uguaglianze.

3,5 + 3,5 + 3,5 + 3,5 = 3,5 × 4 12 × 5 = 12 + 12 + 12 + 12 + 12

a) 9,1 × 3

b) 6 + 6 + 6 + 6 + 6 + 6 + 6

c) 1,15 + 1,15 + 1,15 + 1,15

d) 18 × 5

e) 7 + 7 + 7 + 7 + 7 + 7 + 7 + 7 + 7

f) 0,2 × 6

111 Considera la moltiplicazione di numeri naturali a × b = c e rispondi alle domande

(con a ≠ 0, b ≠ 0, c ≠ 0).

a) c è maggiore di a e di b?

b) c può essere uguale a 0?

c) c può essere uguale al fattore b?

d) Se a raddoppia, anche c raddoppia?

e) Se b triplica, anche c triplica?

f) Se a aumenta di 1, anche c aumenta di 1?

Sempre Qualche volta Mai

Sempre Qualche volta Mai

Sempre Qualche volta Mai

Sempre Qualche volta Mai

Sempre Qualche volta Mai

Sempre Qualche volta Mai

112 Completa abbinando ogni scrittura alla relativa proprietà. proprietà distributiva • proprietà associativa • proprietà commutativa

a) a × b × c = c × a × b

b) (a + b) × c = a × c + b × c

c) a × b = c × d × b con c × d = a

d) a × b × c = (a × b) × c

e) (a b) × c = a × c b × c

113 Metti al posto dei puntini il numero che rende vera l’uguaglianza.

a) 13 × = 13 ma anche × 13 = 13

b) 43 × = 43 ma anche × 43 = 43

c) 11,4 × = 11,4 ma anche × 11,4 = 11,4

d) 9,5 × = 9,5 ma anche × 9,5 = 9,5

Le quattro operazioni e le loro proprietà

114 Metti al posto dei puntini il numero che rende vera l’uguaglianza.

a) 25 × = 0 ma anche × 25 = 0

b) 32 × = 0 ma anche × 32 = 0

c) × 3 × 4 × 6 × 2 = 0

d) 15 × 3 × 2 × 2 × ×

=

Completa le uguaglianze scrivendo 0 oppure 1.

119 Scrivi il numero o la lettera che renda vera ogni uguaglianza.

MATH Identify the missing factors and complete the following two way table.

122 Risolvi le moltiplicazioni dei seguenti gruppi.

123 Considera delle moltiplicazioni come quelle dell’esercizio precedente e rispondi alle domande.

a) Il prodotto di due numeri pari è sempre un numero pari?

b) Il prodotto di due numeri dispari è sempre un numero pari?

c) Il prodotto di due numeri dispari è sempre un numero dispari?

d) Il prodotto di un numero pari con uno dispari è a volte pari e a volte dispari?

124 Indicando con P un numero pari e con D un numero dispari, scrivi le regole relative alla moltiplicazione di pari e dispari.

P × P = P × D =

D × P = D × D =

Risolvi le seguenti moltiplicazioni con le regole di calcolo rapido degli esempi.

a) 32 × 10 =

c) 30 × 80 → si esegue 3 × 8 = 24 e si scrivono due zeri alla destra del prodotto ottenuto

Completa le seguenti moltiplicazioni.

130 Risolvi le seguenti moltiplicazioni.

68 × 5 59 × 7

423 × 8 52 × 48

187 × 6

265 × 14

131 Risolvi sul quaderno le moltiplicazioni mettendo in colonna i fattori; scegli poi per ciascuna di esse il risultato esatto tra quelli indicati.

a)

b)

d) 20,3 x 6,4

Risolvi sul quaderno le moltiplicazioni mettendo in colonna i fattori.

8 , 2 5 × → 2 cifre decimali 6 , 2 = → 1 cifra decimale 9 6 5 0 2 8 9 5 0 0

2 9 9 , 1 5 0 → 3 cifre decimali

136 Scrivi le cifre mancanti.

137 MATEMATICA IN AZIONE Una gallina depone in media 3 uova alla settimana. Se le galline sono 180, quante uova si raccoglieranno in una settimana (compresa la domenica)? [540]

138 MATEMATICA IN AZIONE In un sacchetto ci sono 25 caramelle da 4 g ciascuna.

In 12 sacchetti quanti grammi di caramelle ci sono? [1 200 g]

139 STEM Per far distrarre Teresa, che ha paura dei tuoni, durante un forte temporale il papà le fa calcolare a che distanza cadono i fulmini di cui si odono i tuoni. Il primo tuono si sente dopo 5 secondi dalla vista del fulmine e il secondo dopo 7 secondi.

a) A quale distanza sono avvenute le scariche elettriche, sapendo che la velocità del suono nell’aria è di circa 340 metri al secondo?

Primo tuono 5 × 340 = metri, cioè più di 1 chilometro e mezzo. Secondo tuono 7 × = metri, cioè più di due chilometri.

b) Secondo te il temporale si sta allontanando o avvicinando al luogo dove si trova Teresa?

c) Se un fulmine cade a una distanza di 1 020 m, dopo quanto tempo sentirai il tuono?

d) E se cade a una distanza di 2,72 km? [3 s; 8 s]

Risolvi le seguenti moltiplicazioni, applica la proprietà commutativa e verifica che il prodotto non cambia.

Risolvi le seguenti moltiplicazioni, applica la proprietà associativa e verifica che il prodotto non cambia.

Le quattro operazioni e le loro proprietà

Applica la proprietà distributiva alle seguenti moltiplicazioni.

a) 8 × (5 + 10) = (8 × 5) + (8 × 10) = 40 + 80 = 120 b) (7 - 3) × 5 = (7 × 5) - (3 × 5) = 35 - 15 = 20

145 7 × (6 + 9) =

8 × (9 + 7) = (12 + 13) × 5 = (14 + 9) × 6 =

146 3 × (4 + 6 + 8) = 4 × (3 + 5 + 8) = (15 + 7 + 11) × 5 = (21 + 10 + 12) × 7 =

147 5 × (26 15) = 13 × (24 6) = (37 24) × 15 = (35 18) × 12 =

Esegui le seguenti moltiplicazioni utilizzando la proprietà distributiva.

a) Per moltiplicare un numero per 11: 11 × 23 = (10 + 1) × 23 = 10 × 23 + 1 × 23 = 230 + 23 = 253

b) Per moltiplicare un numero per 9: 45 × 9 = 45 × (10 - 1) = 45 × 10 45 × 1 = 450 45 = 405

148 52 × 11 = 11 × 37 = 101 × 24 = (100 + 1) × 24 = 62 × 101 =

149 9 × 15 = 49 × 9 = 123 × 9 = 9 × 241 =

150 99 × 21 = (100 - 1) × 21 = 17 × 99 = 37 × 99 =

151 Indica la proprietà applicata al primo membro per ottenere il secondo.

a) 12 × 4 × 5 × 2 = 12 × 4 × 10

b) 15 × 9 × 10 × 7 = 7 × 10 × 9 × 15

c) 80 × 5 × 3 × 12 = 8 × 10 × 5 × 3 × 12

152 Indica quali proprietà della moltiplicazione sono state applicate e in che ordine.

a) 150 × 3 × 2 × 4 = 4 × 150 × 3 × 2 = 600 × 6 = 3 600

b) 64 × 45 = 8 × 8 × 9 × 5 = 8 × 5 × 9 × 8 = 40 × 72 = 2 880

c) 58 × 12 = 58 × (10 + 2 ) = 58 × 10 + 58 × 2 = 580 + 116 = 696

DIVISIONE LEZIONE

153 Considera le divisioni e completa.

a) 3,4 : 2 = 1,7 3,4 è il 1,7 è il 2 è il 1,7 × 2 =

b) 159 : 12 = 13 (resto 3) il dividendo è il divisore è il quoziente è 13 × 12 + = 159

154 Data la divisione a : b = c con a e b numeri naturali e b ≠ 0:

a) c è uguale a uno quando

b) c è uguale a zero quando

c) a è uguale a b × d) b è uguale a :

155 Considera la divisione a : b = c e rispondi con Vero o Falso (a ≠ 0, b ≠ 0, c ≠ 0).

a) Se c = a allora b = 1. V F

b) Se c = a allora b = 0. V F

c) a = b × c V F

d) Se b si dimezza, allora c si dimezza. V F

e) Se b triplica, allora c triplica. V F

f) Se a e b sono numeri naturali, c è sempre un numero naturale. V F

156 I seguenti schemi indicano che la divisione è l’operazione inversa della moltiplicazione; completali. 8 × 10 : 10 3 24 × 2

157 Trasforma le seguenti moltiplicazioni in divisioni sul quaderno.

42 × 14 = 588 → 588 : 14 = 42 588 : 42 = 14

a) 36 × 67 = 2 412 16 × 24 = 384 51 × 27 = 1 377

b) 18 × 28 = 504 26 × 51 = 1 326 33 × 46 = 1 518

158 Trova il numero che sostituito alla x rende vera ciascuna uguaglianza. a) x : 12 = 3 →

a) 48 : x = 12 72 : x = 8 169 : x = 13

b) 20 : x = 5 150 : x = 25 x : 20 = 15

c) x : 12 = 5 x : 12 = 12 x : 8 = 0

159 Per avvicinare i ragazzi ai contenuti dell’Agenda 2030, una scuola ligure ha organizzato alcuni giorni di attività in collaborazione con l’Acquario di Genova.

Negli ultimi giorni viene assegnato il seguente compito agli studenti. Quale operazione va utilizzata per risolvere ognuna di queste situazioni?

• Calcolare quante guide occorrono per la visita guidata di una scuola, sapendo il numero totale di alunni in visita. Ogni guida può occuparsi al massimo di un numero fissato di alunni.

moltiplicazione divisione

• Calcolare la durata del turno lavorativo giornaliero di un addestratore di delfini, sapendo il numero totale di addestratori assunti dall’acquario. In ogni momento della giornata deve esserci un addestratore in turno.

moltiplicazione divisione

• Calcolare il numero di pesci palla che saranno nati entro il 2030, se ogni anno ne nascessero tanti quanti quest’anno.

moltiplicazione divisione

• Dedurre quanti piranha possiede l’acquario, sapendo quanto pesce viene comprato per la loro vasca e quanto ne mangia un singolo piranha.

moltiplicazione divisione

160 MATEMATICA IN AZIONE Prova a descrivere almeno due situazioni ambientate nella tua scuola in cui devi utilizzare la moltiplicazione e due situazioni in cui devi usare la divisione.

Completa le seguenti uguaglianze.

161

162 0 : 4,8 = perché × 4,8 = 0 : 56 = 0 perché × 56 =

91 : → impossibile 0 : → indeterminato

Scrivi il numero o la lettera che renda vera ogni uguaglianza.

163 b : b = 2n : = 1 a : = a : 1 = m

164 : 1 = 0 : n = 0 2a : 0 →

165 Stabilisci se le seguenti divisioni hanno resto 0 o diverso da zero e completa la tabella.

= 0

≠ 0

166 Completa le seguenti tabelle, lasciando vuota la casella nel caso in cui la divisione sia con il resto.

Per ogni divisione il divisore è il numero che intesta la riga.

167 MATH Find the missing dividends and divisors and complete the tables. Leave the box empty if the division has a remainder different from 0.

Risolvi le seguenti divisioni applicando le regole di calcolo rapido come negli esempi.

Le quattro operazioni e le loro proprietà

Completa le seguenti divisioni.

Risolvi le seguenti divisioni effettuando la prova. 4 440 : 24 = 185 Prova 185 × 24 = 4 440

3 744 : 6

178 Osserva e completa.

a) 58 × 5 = 58 × 10 : 2 (infatti 5 è la metà di 10) = 580 : 2 = oppure 58 : 2 × 10 = 29 × 10 = b) 37 × 5 = 37 × 10 : 2 = 68 × 5 =

180 Stabilisci quali risultati sono errati e correggili sul tuo quaderno.

a) 125 : 25 = 5

Prova: 25 × 5 = 125 → esatto

b) 230 : 3 = 76 (resto 3)

Prova: 3 × 76 + 3 = 231 → errato; infatti 230 : 3 = 76 (resto 2)

a) 244 : 14 = 17 (resto 6)

b) 176 : 11 = 16

c) 299 : 13 = 25

d) 421 : 22 = 19 (resto 3)

e) 252 : 12 = 22

Calcola il quoziente intero e il resto.

138 : 7 = 19 (resto 5)

Calcola il quoziente con 2 cifre decimali e il resto.

123 : 8 = 15,37 (resto 4 centesimi)

f) 123 : 9 = 13 (resto 6) g) 285 : 15 = 21

h) 354 : 8 = 44 (resto 2) i) 493 : 29 = 17

j) 694 : 23 = 30 (resto 4)

3 Le quattro operazioni e le loro proprietà

Risolvi le seguenti divisioni proseguendo fino a ottenere resto 0.

171 : 6 = 28,5 189

190

193 Completa le seguenti divisioni inserendo le cifre mancanti.

: 13 = 35 (resto 8)

Risolvi le seguenti divisioni con numeri decimali. (Prosegui fino ai centesimi).

194 147,27 : 7

195 1 784,4 : 27

196

:

: 8

:

: 9

197 MATEMATICA IN AZIONE Una confezione da 6 kg di arance costa 8,04 €. Questo prezzo, al kg, è maggiore o minore del prezzo mostrato nella foto?

Applica la proprietà invariantiva in due modi diversi e verifica che il quoziente rimane lo stesso. 162 : 18 =

Per ogni divisione applica la proprietà invariantiva e calcola sul quaderno il quoziente esatto o con una cifra decimale.

↑ si moltiplicano entrambi i membri per 10

quattro operazioni e le loro proprietà

204 STEM Un corpo sulla Luna pesa circa 6 volte meno di un corpo sulla Terra: per esempio, una matita che sulla Terra pesa 6 g, sulla Luna peserà 1 g.

Quanto peserà, sulla Luna, la bandiera italiana rappresentata nel disegno? [13,67 g]

205 MATEMATICA IN AZIONE La signora Baroni, che abita al quinto piano, ha preparato 100 biscotti da dividere in parti uguali tra i 6 bimbi della sua palazzina, quando passeranno il pomeriggio del 31 ottobre per fare ‘‘dolcetto o scherzetto’’.

Quanti dolcetti avrà ciascun bambino?

Quanti ne rimarranno? [16; 4]

Risolvi applicando la proprietà distributiva della divisione.

(165 88) : 11 = (165 : 11) (88 : 11) = 15 8 = 7

206 (88 64) : 8 (56 + 84) : 7 (63 + 108) : 9 (156 108) : 6

:

:

207 (96 + 48) : 16 (180 135) : 15 (375

: 25 (144 72) : 12 (104 + 156) : 13

: 18 (312 + 192) : 24 (400 288) : 16 (154 +

: 11

208 (95 + 55 35) : 5 (48 16 + 92) : 4 (63 27 + 45) : 3 (104 56 + 32) : 8

Completa le seguenti uguaglianze utilizzando la proprietà distributiva della divisione.

a) (54 ) : 9 = (54 : 9) (18 : ) = = b) ( 44) : 11 = (99 : 11) ( ) = a) (5 + 35 + ) : 5 = ( : 5) + ( : 5) + (20 : ) = + + = b) (196 105 + ) : 7 = ( : 7) ( : 7) + (28 : ) = + =

a) (144 48 ) : 12 = ( : 12) ( : 12) (36 : ) = = b) (480 192) : 16 = ( : 16) (128 : ) ( : 16) = =

ESPRESSIONI CON LE QUATTRO OPERAZIONI

212 Considera le seguenti espressioni e stabilisci quale frase indica lo svolgimento esatto.

a) 12 + 4 × 3 24

Si esegue prima 12 + 4, si moltiplica il risultato × 3 e infine si sottrae 24.

Si esegue prima 4 × 3, si somma il risultato con 12 e infine si sottrae 24.

b) 9 × 6 30 + 18 : 3

Si risolvono prima 9 × 6 e 18 : 3, poi le altre operazioni nell’ordine in cui sono scritte.

Dal prodotto 9 × 6 si sottrae 30, poi si somma 18 e infine si divide per 3.

c) 4,9 2,4 × 0,5 + 8 : 1,6

Si risolvono le operazioni nell’ordine in cui sono scritte.

Si risolvono prima 2,4 × 0,5 e 8 : 1,6 poi le altre operazioni nell’ordine in cui sono scritte.

213 Rispondi alle seguenti domande sul quaderno.

a) In un’espressione aritmetica, quali tra le quattro operazioni hanno la precedenza e vanno risolte per prime?

b) In un’espressione aritmetica contenente parentesi, in quale ordine vanno risolte le parentesi?

c) In quale ordine vanno svolte le operazioni interne alle parentesi?

d) Nelle espressioni con numeri decimali, quali regole di precedenza si utilizzano?

Completa utilizzando i simboli = o ≠.

a) 43 + 35 (17 × 2) 43 + 35 17 × 2

b) (3 × 25) + (8 × 6) 3 × 25 + 8 × 6

a) 85 25 5 × 9 85 (25 5) × 9

b) (98 24) (13 × 4) 98 24 13 × 4

a) 12 + (64 20) 17 12 + 64 20 17

b) 247 180 : (30 : 6) 247 180 : 30 : 6

a) 4 × 240 : 5 : 2 4 × (240 : 5) : 2

b) 5 + (12 + 7) × 3 5 + 12 + 7 × 3

218 Risolvi le espressioni degli esercizi precedenti e controlla se hai inserito in modo corretto i simboli = o ≠.

Elimina le parentesi inutili nelle seguenti espressioni e risolvile.

219 42 (14 : 7) × 3 (9 × 2) + (5 + 8)

220 90 (16 + 31) + (5 × 6) (8 + 17)

221 (15 × 8) (9 × 6) + 28 : (2 × 7) + (34 : 2)

MATH Delete all the unnecessary brackets and solve the following equations.

222 {[(12 + 4 ) : 4 + (2 × 7) + 15] (2 × 8) + (13 7)}

223 3 × (5 + 6) + (4 × 9) (24 : 2)+ {[25 + (8 + 9)] 24}

224 Inserisci nei tondini i simboli delle operazioni (+, , ×, :) e, se necessario, aggiungi le parentesi, per rendere vere le uguaglianze.

a) 3 ™ 2 ™ 1 = 7

b) 2 ™ 3 ™ 1 = 5

c) 1 ™ 2 ™ 3 ™ 4 = 11

Traduci in linguaggio matematico e rispondi.

ESEMPIO

d) 4 ™ 3 ™ 2 ™ 1 = 14

e) 6 ™ 6 ™ 6 ™ 6 = 5

f) 8 ™ 2 ™ 2 ™ 3 = 10

La differenza tra 57 e 49 è maggiore della somma tra 4 e 5?

57 49 = 8 e 4 + 5 = 9 No, perché 8 < 9

225 Quanto si deve aggiungere alla somma di 12 e 28 per arrivare al numero 50?

50 (12 + 28) = = Si deve aggiungere

226 Quanto si deve aggiungere alla somma di 33 e 57 per ottenere il numero 100?

227 Quanto si deve togliere alla somma di 58 e 63 per ottenere 100?

228 La differenza tra 36 e 63 è maggiore del prodotto tra 9 e 3?

229 La differenza tra 35 e 53 è minore del prodotto tra 2 e 9?

Traduci le seguenti frasi in espressioni e risolvile.

ESEMPIO

Dal doppio della somma di 15 e 8 sottrai il prodotto di 4 e 6. 2 × (15 + 8) 4 × 6 = 2 × 23 24 = 46 24 = 22

230 Moltiplica 8 per la differenza tra 16 e 9, dividi il risultato per 4.

231 Sottrai al triplo di 8 la somma di 7 e 5, moltiplica il risultato per 3.

232 Moltiplica 4 per la somma di 5 e 6, dal risultato sottrai la somma di 9 e 5.

233 Dividi per 5 la somma di 23 e 7, aggiungi il prodotto di 9 e 3 e dividi il risultato per 11.

Risolvi i seguenti problemi impostando un’espessione.

234 MATEMATICA IN AZIONE Al supermercato le uova vengono vendute in confezioni da 4 o da 6. L’altro ieri sera sullo scaffale c’erano 5 confezioni da 4 uova e 3 confezioni da 6 uova. Quante sono le uova in totale?

a) L’espressione che risolve il problema è:

(5 × 4 + 3) × 6

(5 × (4 + 3) × 6

5 × 4 + 3 × 6

b) Il numero totale di uova sullo scaffale è: 210 38 138

235 MATEMATICA IN AZIONE Nel salone di una mensa aziendale ci sono 12 tavoli con 6 posti e 9 tavoli con 3 posti. Lunedì si sono fermati a mensa 87 dipendenti; quanti posti sono rimasti liberi? [12]

236 EDUCAZIONE CIVICA Il Consiglio di Istituto del comprensivo Don Pino Puglisi è composto dal dirigente, 6 rappresentanti dei genitori, 1 rappresentante del personale ATA e 6 docenti.

Se la composizione del Consiglio, che ha durata triennale, è completamente cambiata ogni triennio, quanti sono gli eletti che si sono succeduti in 9 anni? [42]

Costruisci delle espressioni che abbiano il risultato assegnato, usando le operazioni indicate e i numeri dati, senza ripeterli (puoi utilizzare le parentesi).

ESEMPIO

Numeri 5, 9, 2 e 4 operazioni + : risultato 3 espressione (5 + 9) : 2 – 4 = 3

237 Numeri 3, 6 e 8 operazioni + × risultato 72 espressione

238 Numeri 14, 18 e 8 operazioni + : risultato 4 espressione

239 Numeri 5,7; 2,7 e 2,1 operazioni × risultato 6,3 espressione

240 Numeri 2, 6, 9 e 10 operazioni + × : risultato 13 espressione

241 Numeri 38, 15, 19 e 17 operazioni + : risultato 0 espressione

Hanno la precedenza le moltiplicazioni e le divisioni.

262 (42 21 : 3 × 4) : 7 + 36 15 + 9 2 × (128 : 4 : 8 + 1 5) [32]

263 15 × 5 [3 × 4 + (2 × 25 + 7 + 2 × 3) : 7] [54]

264 8 × [(17 + 3 + 4) : 4 + (10 × 3 + 4) : 2 7 × 3] : 2 [8]

265 12 × 15 [13 × (8 + 10 : 5) + (9 × 3 28 : 7) × 2 6] [10]

Hanno la precedenza le operazioni interne alle ( ), poi quelle interne alle [ ] e infine quelle interne alle { }.

266 [(5 × 8) : 10 + 2 + 3 × 6 : (36 : 9 2)] : 3 + (63 : 7 5) [9]

267 [(3 × 6 2 × 5) (15 8)] + [56 : 8 (14 : 7 + 2)] + 6 × 4 21 [7]

268 42 : (6 × 4 2 × 5) + [(34 6 3 × 5 + 9 : 3) : 8 + 8] : 5 4 [1]

269 78 [56 (49 35 + 9) : (30 12 + 5)] [(65 6 × 5) : 5] [16]

270 (27 9 7) × 4 [52 : (8 7 + 12) + 36 : 6 + (21 6) : 5] [31]

271 [(63 : 7 + 1) × 2 8] : 3 + 2 × (35 : 7 27 : 9) + [(5 + 4) × 2] : 3 [14]

272 [7 + (3 × 6 + 18 : 3) : 8 4] × 6 [2 × 8 (19 3 × 3)] × 3 [18]

273 (60 : 4 + 28 : 4) + (2 × 3 + 7 × 1) [12 + 4 × 4 : (8 × 2) + 5] [17]

274 [(5 × 3 × 2 + 8 + 16 × 2) : 5 + 6 × 11 : 22 + 6] + 6 (48 : 8 + 5) [18]

275 [78 : 3 (100 : 4 4 × 5) × 1 + 2] × 3 (80 : 4 + 54 : 6) [40]

276 [(27 × 2 + 16 × 3 : 4) : (21 : 7) + 2 × 7] : (5 + 4) [4]

277 (2 × 18 × 13) : [76 : 2 (14 × 2 13 × 2)] 228 : 19 + 15 : 3 [6]

278 [(4 × 7) : (3 × 5 1) × (30 : 6) + (5 + 40 : 8)] : [(3 × 5 + 4) (45 : 3)] [5]

279 [(10 + 7) × 2 × 5 + 3 × 4] : [(107 94) × 2] + [38 : 2 + (3 + 4) × 2] [40]

280 [140 : 7 + 6 × 11 130 : 5 (4 × 8 3 × 9)] : (60 5 × 11) [11] 281 5 × 8 + 5 (7 × 5 22) 24 : 3 + 7 [30 : 6 (21 : 7 + 2)] 6 × 5 [1]

282 [(10 × 10 : 4) + 72 : (6 × 9 9 72 : 8)] : [(2 × 8 7) : 3] 2 × 3 + 7 × 6 [45]

Le quattro operazioni e le loro proprietà

283 [67 (3 × 6 + 5 × 4) + 7 × 3] : [11 × 3 (5 × 5 45 : 9) 12 × 2 : 8]

284 {[(50 : 2 + 8 × 9) 15 × 6 7] + 6 × 4 × 5} : 12

285 (9 + 5 × 5) : {2 × [14 × 2 (3 × 8 2)] + 7 × 3 16}

286 51 : {12 + 3 × [2 × 18 9 × (24 : 6 2) : 6] 60} + 4 × 0

287 {(169 + 31 6 × 30) × 6 + [(9 + 7) × 5]} × 1 : (2 × 5) : (33 : 3 1) [2]

288 18 × 30 12 × {220 [147 : 7 + 23 × 3] × 2} 3 × 4 + 27 : 3

289 3 × 13 3 × {142 [136 3 × (15 2 × 6)] 3 × 5} (10 + 3 × 6)

290 7 + {[13 + (18 + 2 × 4 3 × 8)] : [9 × (1 + 2 × 3) 5 × 6 × 2]} 13 × 0

(72 9 × 2 × 2) : {(3 × 6 + 2 × 3) + [8 × 4 (10 + 2 × 5)]}

(11 × 5 + 13) × 2 : {50 7 × 3 + (3 × 8 + 4 ×

{121 + [4 × (16 36 : 12) + (14 + 8 × 11) : 3 6 × 9]} : (17 8)

295 (40 : 8 + 2) × 4 + 27 : {5 + 35 : [24 : (4 + 50 : 25) + 1] 3}

105 : 7 {8 × 4 [29 3 × (29 4 × 5)]} : (3 × 5) + 12 × 3 : 4

(4 × 6 10) × {(3 × 8 12) [5 × (7 × 2 12) 8]} : [(2 + 5) × 10]

{[5 + (96 : 16 + 4 × 3) × 7] × (81 : 9 49 : 7 2 × 1) + 2 × 9} : 2

{[30 (24 : 6 + 72 :

304 {31 2 × [34 (42 : 3) × 2 20 : 5] 10 × 2} 2 + 35 : 7 [10]

305 {[(17 × 2 + 8 × 6 56 : 2) : 9 + 15] : 7 + 11 × 3} : 9 + (72 : 3 + 7 × 5 132 : 12) : 4 [16]

307 {[(11 × 5 4 × 8 + 1) × (3 × 3 + 35 : 7 16 : 2) + 60 : 5] : 6 + 20 : 5} : 2 5 × 2 [5]

308 {3 × 5 + 6 × [31 (36 : 12 + 2) × (56 : 7 30 : 5)] 63 : 7} : (2 × 10 6 × 3) :

+

×

{[(737 : 67 + 208 : 13) : 3 + 5 × (476 : 17 456 :

Risolvi le seguenti espressioni con numeri anche decimali.

324 [2,5 × 3 + 2,5 × (1 + 3,5)] : 1,5 4 × 1,5

325 {148 [4,2 : 0,14 (6 × 3,3 : 0,6 3) : 1,5]} : 1,2

326 {[30,3 30 × 0,4 (5,6 3,3)] : 0,5 50 × 0,4} : 0,6

327 0,3 × [1,5 × 2 : 3 + (0,6 + 0,24 : 0,3) + 1,7] + 2,3 × 0,6

328 7,2 + 5,5 : 0,11 + 0,48 : 1,2 2,4 × 3 45,4 0,4

329 9,1 0,39 : 0,3 0,56 : 0,1 + 6,3 × 2 : 0,7 10,2 + 1,5

330 (4 0,1 × 3 + 2,5) : 3,1 + (2,6 + 10 × 0,3) + 1,2 : 3 (5,2 + 0,3

(16,8 + 7,4) × 0,5 + 2,16 :

{[3 × (6 × 7 5,25 × 4 + 3) 6,3 : 0,3] : 17 + 13,5} : 3

{[(7,28 3,28) × 0,1 + 15

COMPETENZE

PROBLEM SOLVING

1 + 2 + 3 + 4 + ... + 97 + 98 + 99 + 100 = ???

1 Si racconta che Carl Friedrich Gauss, un importante matematico tedesco, fosse un bimbo turbolento e che il suo maestro lo mise in punizione affidandogli un problema difficile: calcolare la somma dei primi 100 numeri. Il bimbo tornò a scorrazzare dopo pochi minuti, dicendo che il compito lo aveva già svolto: la somma dei primi 100 numeri corrisponde esattamente a 5 050.

Come aveva fatto a calcolare una cifra del genere in così poco tempo?

a) Prova a trovare la regola osservando come si può calcolare la somma dei primi 30 numeri disponendoli in questo modo.

+ 30 = 31 2 + 29 = 31

La somma dei primi 30 numeri è:

b) Calcola la somma dei primi 40 numeri.

c) Calcola la somma dei primi 60 numeri.

d) Sai quindi spiegare come Gauss ha fatto a fare un simile calcolo in così poco tempo?

2 Inserisci in questo schema alcuni dei numeri maggiori di 4 e minori di 30, rispettando le regole seguenti: in ogni cerchietto va inserito un numero diverso; la somma di 5 numeri allineati deve essere sempre 85; nei cerchietti azzurri va inserito un numero dispari; nei cerchietti grigi va inserito un numero pari.

ANALIZZARE E INTERPRETARE DATI

Completa, senza fare calcoli, ma osservando le regolarità numeriche.

3 91 19 = 72

92 29 = 63

93 39 = 54

94 49 = 95 59 =

69 =

79 =

89 =

× 998 = 99 6004

998 × 9 998 = 99 960 004

998 × 99 998 =

998 × 999 998 =

999 998 × 9 999 998 =

999 998 × 99 999 998 =

CALCOLARE

6 Un quadrato magico è uno schema quadrato; il più semplice è quello composto da 9 caselle disposte su tre righe e tre colonne.

La particolarità di questi quadrati è che la somma dei numeri di qualsiasi riga, di qualsiasi colonna e delle due diagonali è sempre uguale.

I numeri da inserire sono sempre diversi tra loro.

Risolvi i seguenti quadrati magici.

7 Inserisci, in questi due quadrati magici, alcuni dei numeri da 1 a 16, in modo che la somma totale per riga, colonna e diagonale, sia 34 per entrambi.

ARGOMENTARE

8 Se si raddoppiano entrambi i fattori della moltiplicazione 3 × 4, che cosa accade al prodotto?

3 × 4 = 3 × 2 = 6 e 4 × 2 = 8 → 6 × 8 =

Che cosa si scopre? Il prodotto diventa quattro volte più grande, cioè il quadruplo.

Sapresti darne un’interpretazione geometrica? Osserva la figura e completa.

Osservando la figura puoi verificare che nel rettangolo

6 × 8

[(2 × 3) × (2 × 4)]

sono contenuti rettangoli congruenti al rettangolo dato 3 × 4; ecco spiegato perché il prodotto diventa il

9 Se entrambi i fattori della moltiplicazione 4 × 6 vengono moltiplicati per 3, che cosa accade al prodotto?

4 × 6 = 4 × 3 = 12 e 6 × 3 × 18 → 12 × 18 =

Che cosa scopri?

Si scopre che il prodotto diventa volte più grande

Sapresti darne un’interpretazione geometrica?

Costruisci la figura sul quaderno e spiega il risultato ottenuto.

SFIDA MATEMATICA

10 Un’addizione in maschera

Nell’addizione che figura sopra, ciascun segno rappresenta sempre la stessa cifra e due segni diversi rappresentano cifre diverse. Inoltre, nessun numero comincia mai per 0.

Quale numero è rappresentato da ◯◯?

(Testo tratto dalle Finali italiane dei Campionati internazionali di Giochi Matematici, organizzate dal Centro PRISTEM dell’Università Bocconi di Milano)

Le quattro operazioni e le loro proprietà

ROAD MAP PER TUTTI

ADDIZIONE

DATI I NUMERI 4 E 5

Che cosa significa addizionare due numeri?

Significa aggiungere al primo numero le unità del secondo.

Sì, lo 0 è l'elemento neutro dell’addizione. Ci sono casi particolari?

9 + 0 = 9

TEORIA PAG. 94

Come si chiamano i termini dell'addizione?

I termini dell’addizione sono gli addendi, il risultato è la somma o totale

PROPRIETÀ DELL’ADDIZIONE

DATA L’ADDIZIONE 25 + 18 + 12 = 55

Quali sono le sue proprietà?

PROPRIETÀ COMMUTATIVA: cambiando l’ordine degli addendi la somma non cambia.

ESEMPIO

25 + 18 + 12 = 55

ma anche 12 + 18 + 25 = 55

TEORIA PAG. 94

PROPRIETÀ ASSOCIATIVA: il risultato non cambia se al posto di due addendi si sostituisce la loro somma.

25 + 18 + 12 = 55 ma anche 25 + 30 = 55 ESEMPIO

1 Risolvi le seguenti addizioni.

a) 7 + 11 = 18 5 + 19 = 18 + 7 = 12 + 8 =

b) 5,4 + 3,1 = 8,5 6,6 + 2,1 = 15,4 + 10,6 = 16,5 + 3,2 =

2 Inserisci l’addendo corretto (la somma è sempre 10).

a) 2 + = 10 3 + = 10 4 + = 10 5 + = 10

b) 6 + = 10 9 + = 10 7 + = 10 1 + = 10

3 MATEMATICA IN AZIONE Al torneo di pallanuoto la squadra dei Pescecani, che aveva realizzato 34 reti nelle partite precedenti, nell’ultima ha segnato 5 reti.

A quante reti sono ora i Pescecani?

4 Metti in colonna e risolvi sul tuo quaderno le seguenti operazioni con numeri interi.

a) 142 + 15 + 962 =

b) 181 + 7 + 206 =

c) 124 + 374 =

5 Metti in colonna e risolvi sul tuo quaderno le seguenti operazioni con numeri decimali.

a) 62,3 + 8,6 =

b) 5,4 + 13 + 0,26 =

6 Applica la proprietà commutativa alle seguenti addizioni.

a) 25 + 12 + 15 = 43 + 6 + 7 + 14 =

b) 17 + 5 + 13 = 28 + 9 + 2 + 10 =

c) 1,8 + 0,9 + 3,2 = 7,2 + 1,4 + 0,8 =

7 Applica la proprietà associativa alle seguenti addizioni.

a) 15 + 8 + 7 = 6 + 14 + 13 + 7 = b) 13 + 37 + 8 = 41 + 9 + 24 + 36 = c) 2,1 + 3,4 + 2,6 = 2,3 + 1,7 + 4,5 =

8 Quali proprietà dell’addizione sono state applicate?

a) 31 + 12 + 9 + 48 = 31 + 9 + 12 + 48

b) 31 + 12 + 9 + 48 = 30 + 1 + 9 + 12 + 40 + 8

c) 31 + 9 + 12 + 48 = (31 + 9) + (12 + 48)

d) 31 + 12 + 9 + 40 + 8 = 31 + 9 + 40 + 12 + 8

ESEMPIO 88 + 1 035 + 907 88 + 1 035 + 907 = 2 030

ESEMPIO 0,75 + 9,8 + 31 0,75 + 9,80 + 31,00 = 41,55

Le quattro operazioni e le loro proprietà

Che cosa significa sottrarre un numero da un altro?

DATI I NUMERI 12 E 3

Significa togliere dal primo le unità del secondo.

Come si chiamano i termini della sottrazione?

Si chiamano MINUENDO e SOTTRAENDO, il risultato si chiama DIFFERENZA

12 – 3 = 12 – 1 – 1 – 1 = 9

12 è il minuendo, 3 il sottraendo e 9 la differenza.

RICORDA: la sottrazione è l’operazione inversa dell’addizione: 12 – 3 = 9 infatti 9 + 3 = 12 ESEMPIO

PROPRIETÀ DELLA SOTTRAZIONE

DATA UNA SOTTRAZIONE

Quali sono le sue proprietà?

PROPRIETÀ INVARIANTIVA:

addizionando o sottraendo lo stesso numero dai termini di una sottrazione il risultato non cambia.

48 – 23 = 25 ma anche (48 + 2) – (23 + 2) = 50 – 25 = 25 oppure (48 – 2) – (23 – 2) = 46 – 21 = 25 ESEMPIO

TEORIA

96

SECONDA PROPRIETÀ:

Per sottrarre due o più numeri da uno stesso numero è possibile sottrarre dal primo la somma degli altri due.

ESEMPIO

48 – 23 – 11 = 14 ma anche

48 – (23 + 11) = 48 – 34 = 14

9 Inserisci il numero corretto (come nell’esempio).

a) 43 = 23 54 = 50 32 = 12 76 = 36

b) 12 = 18 34 = 17 57 = 13 29 = 51

10 MATEMATICA IN AZIONE Nina e Gemma stanno misurando le loro altezze.

Gemma dice a Nina: “Io misuro 142 cm e tu misuri 135 cm; quindi, io sono più alta di te di 7 centimetri’’.

Che operazione ha fatto Gemma per scoprire di quanti centimetri è più alta?

11 Metti in colonna e risolvi sul tuo quaderno le seguenti operazioni con numeri interi.

a) 75 53 = b) 94 76 =

12 Metti in colonna e risolvi sul tuo quaderno le seguenti operazioni con numeri decimali.

a) 4,8 2,7 =

b) 13 0,5 =

c) 7,93 5,8 =

d) 29,7 14 =

13 Risolvi le sottrazioni in colonna sul quaderno.

a) 38 – 13 =

b) 236 – 105 = c) 18,7 – 10,4 =

ESEMPIO 807 45 807 45 = 762

ESEMPIO

39,4 18 56 0,32 39,4 18,0 = 56,00 0,32 = 21,4 55,68

14 Applica la proprietà invariantiva alle seguenti sottrazioni.

a) 56 18 = 28 15 = 47 24 = 39 13 = b) 37 15 = 44 13 = 63 42 = 78 26 =

15 La proprietà invariantiva della sottrazione è stata applicata correttamente?

a) 37 18 = (37 7) (18 8) Sì No

b) 29 12 = (29 2) (12 2) Sì No

c) 106 47 = (106 6) (47 5) Sì No 20 30

DATI I NUMERI 6 E 4

Che cosa significa moltiplicare due numeri?

Significa sommare il primo numero tante volte quante sono le unità del secondo numero.

Ci sono casi particolari?

1 è l’elemento neutro 0 annulla il prodotto.

I termini si chiamano fattori, il risultato si chiama prodotto

ESEMPIO

6 × 4 = 6 + 6 + 6 + 6 = 24 6 e 4 sono i fattori, 24 è il prodotto

RICORDA: la moltiplicazione è un’addizione ripetuta.

Come si chiamano i termini della moltiplicazione? 15 × 1 = 15 15 × 0 = 0

16 Risolvi le seguenti addizioni ripetute dopo averle trasformate in moltiplicazioni.

a) 9 + 9 + 9 = 9 × 3 = 27 4 + 4 + 4 + 4 + 4 = 4 × 5 =

b) 5 + 5 + 5 = 7 + 7 + 7 + 7 = c) 11 + 11 = 12 + 12 + 12 + 12 =

17 Risolvi le seguenti moltiplicazioni dopo averle trasformate in addizioni ripetute.

a) 6 × 4 = 6 + 6 + 6 + 6 = 24 13 × 3 = b) 3 × 5 = 15 × 2 = c) 8 × 4 = 7 × 6 =

18 Calcola i seguenti prodotti.

a) 12 × 3 = 21 × 5 = 17 × 8 = b) 43 × 6 = 28 × 4 = 37 × 2 =

19 MATEMATICA IN AZIONE Nonna Delia ha comprato il gelato ai suoi 5 nipotini. Se i gelati costano 2 € ciascuno, quanto ha speso in tutto?

20 Risolvi.

a) 37 × 1 = 1 ×

=

×

PROPRIETÀ DELLA MOLTIPLICAZIONE

DATA UNA MOLTIPLICAZIONE

Quali sono le sue proprietà?

PROPRIETÀ COMMUTATIVA: cambiando l’ordine dei fattori il prodotto non cambia.

PROPRIETÀ

DISTRIBUTIVA: per moltiplicare una somma o una differenza per un numero, si moltiplica ciascun termine per il numero e poi si sommano o si sottraggono i prodotti parziali ottenuti.

PROPRIETÀ

ASSOCIATIVA: il risultato non cambia se al posto di due fattori si sostituisce il loro prodotto.

5 × 7 × 2 = 70 ma anche

2 × 5 × 7 = 70 ESEMPIO

21 Completa.

5 × 8 × 3 = 120 ma anche (5 × 8) × 3 = 40 × 3 = 120 ESEMPIO (4 + 7) × 2= 11 × 2 = 22 ma anche (4 × 2) + (7 × 2) = 8 + 14 = 22 ESEMPIO

a) Le proprietà della moltiplicazione sono: , associativa e distributiva.

b) Per la proprietà commutativa → 15 × 3 × 7 = 7 ×

c) Per la proprietà associativa → 2 × 5 × 31 = ( × ) ×

d) Per la proprietà distributiva → (7 2 + 5) × 6 = 7 × 6

22 Applica la proprietà commutativa e risolvi.

2 × 7 × 2 = 4 × 9 × 5 = 6 × 7 × 10 =

23 Applica la proprietà associativa e risolvi.

9 × 2 × 4 = 25 × 4 × 3 = 18 × 2 × 10 =

24 Applica la proprietà distributiva e risolvi sul quaderno.

a) (21 + 3 + 9) × 3 (12 7) × 5 (13 3) × 4

b) (17 9 + 4) × 4 (15 + 4 8) × 6 (33 16 7) × 10

c) (4 + 7 5) × 6 (8 + 13 11) × 3 (15 9 + 2) × 5

DIVISIONE

DATI I NUMERI 20 E 5

Che cosa significa dividere 20 per 5?

Significa cercare quale numero moltiplicato per 5 dà come risultato 20.

Ci sono casi particolari nella divisione?

ESEMPIO

0 : 12 = 0

38 : 0 = impossibile, perché nessun numero moltiplicato per 0 dà 38

0 : 0 = indeterminato, perché qualsiasi numero moltiplicato per 0 dà 0.

Come si chiamano i termini della divisione?

I termini della divisione sono il dividendo e il divisore, il risultato si chiama quoziente

ESEMPIO

20 : 5 = 4

20 è il dividendo, 5 è il disisore, 4 il quoziente

RICORDA: La divisione è l’operazione inversa alla moltiplicazione, infatti: 4 × 5 = 20.

25 Risolvi le seguenti divisioni seguendo l’esempio.

18 : 9 = 2 perché 9 × 2 = 18 35 : 7 =

26 MATEMATICA IN AZIONE Per la festa di Halloween una comitiva di 16 amici ha deciso di dividersi in due gruppi uguali e girare per le strade del quartiere a fare “dolcetto o scherzetto’’.

Qual è il numero di amici in ogni gruppo?

27 Calcola dove possibile.

28 Calcola sul tuo quaderno i seguenti quozienti.

a) 120 : 5

b) 164 : 4

c) 36 : 2

d) 480 : 6

: 2

: 7

: 5

: 8

: 3

: 9

: 12

: 15

PROPRIETÀ DELLA DIVISIONE

DATA UNA DIVISIONE

Quali sono le sue proprietà?

PROPRIETÀ INVARIANTIVA: il quoziente non cambia se si moltiplicano o si dividono il dividendo e il divisore per uno stesso numero (diverso da 0).

PROPRIETÀ DISTRIBUTIVA: per dividere una somma o una differenza per un numero si divide ciascun termine per il numero e poi si sommano e si sottraggono i quozienti parziali ottenuti.

24 : 4 = 6 (24 : 2) : (4 : 2) = 12 : 2 = 6 (24 × 2) : (4 × 2) = 48 : 8 = 6

29 Esegui sul quaderno le seguenti divisioni con numeri decimali in colonna (quando necessario applica la proprietà invariantiva).

a) 45,6 : 6 103,2 : 8 600,6 : 11

b) 39,44 : 1,7 → (39,44 × 10) : (1,7 × 10) = 394,4 : 17

c) 16,64 : 1,6 → (16,64 × ) : (1,6 × )

30 Applica la proprietà invariantiva e risolvi.

a) 45 : 15 (dividi per 5) 48 : 6 (dividi per 3)

b) 35 : 5 (moltiplica per 2) 27 : 2 (moltiplica per 5)

31 Applica la proprietà distributiva e risolvi sul tuo quaderno.

a) (21 + 35) : 7 (48 36) : 6 (35 + 20 45) : 5

b) (15 + 12 21) : 3 (35 + 25 40) : 5

c) (49 42 + 28) : 7 (80 32 + 16) : 8

32 590 : 10 = 762 : 100 = 6,7 : 10 =

DATA UN’ESPRESSIONE ARITMETICA

Come si risolve un’espressione senza parentesi?

Si risolvono prima:

• le moltiplicazioni

• le divisioni nell’ordine in cui si presentano, poi:

• le addizioni

• le sottrazioni anch’esse nell’ordine in cui si presentano.

ESEMPIO

ESPRESSIONI ARITMETICHE

DATA UN’ESPRESSIONE ARITMETICA

Come si risolvono le espressioni con le parentesi?

Si risolvono prima:

• le moltiplicazioni e le divisioni, con le precedenze già viste:

• prima le operazioni nelle parentesi tonde,

• poi quelle nelle parentesi quadre,

• infine quelle parentesi graffe.

3 × (5 + 3) + 6 × (12 7) 60 : (2 × 3) =

3 × 8 + 6 × 5 60 : 6 = 24 + 30 10 = 54 10 = 44 ( ( ( ( ( ( ( ESEMPIO

Risolvi le seguenti espressioni.

10 + 15 7 2 9

3 + 4 × 5 6 : 2

12 × 2 5 + 4 : 2 + 2

104 : 4 + 13 × 2 + 20 + 6 + 78 : 3

Risolvi le seguenti espressioni con le parentesi tonde.

105 : 3 + (68 : 34 + 6 × 8) 22 + 91 : 7

59 (17 5 4) × 2 + 26 : 2 (25 3 × 5)

(5 × 8 + 4 × 17) (7 × 4 + 3 × 8) + 3 × (4 × 5 2 × 9)

Risolvi le seguenti espressioni che presentano anche le parentesi quadre. [(8 × 6 + 18) : 3 + 7 × 2] : 12 = [(48 + 18) : 3 + 14]

Risolvi le seguenti espressioni che presentano anche le parentesi graffe. {[(5 + 9) : 2] × 3 4 × 4} × 5 = {[14 : 2] × 3 16} × 5 = {7 × 3 16} × 5 = {21 16} × 5 = 5 × 5 = 25

50 6 {3 × [51 : 3 + 2 × (49 – 36 6) 18] 4} : 7 [1]

51 {(7 × 2 5) × 5 + [2 × (3 + 3 × 6)]} : 3 [29]

52 11 {[(2 × 29 9 × 4) : 2 + 46 : 2] : 17} 3 × 3 [0]

53 4 + 24 : {5 + 35 : [24 : (40 : 5 18 : 9) + 1]} [6]

54 (27 : 3 1) + {2 + [5 × (13 9 + 2)] [24 2 × (10 7)]} [22]

55 Scrivi a lato di ogni situazione la lettera che corrisponde all’espressione risolutiva.

• La somma di 7 e 18 meno la somma di 2 e 8.

• La metà della differenza tra i numeri 16 e 10.

• Il quintuplo della somma dei numeri 3 e 5.

• Il prodotto dei numeri 7 e 8 diviso 2.

• La somma tra il doppio di 20 e la terza parte di 18.

a) (3 + 5) × 5

b) 2 × 20 + 18 : 3

c) (7 + 18) (2 + 8)

d) 7 × 8 : 2

e) (16 10) : 2

56 MATEMATICA IN AZIONE Associa con una freccia ogni problema alla sua espressione risolutiva riportata in basso e calcolane il risultato.

a) Un bonsai di quercia alto 8 cm in un anno cresce di 6 cm ma con la potatura la sua altezza viene dimezzata. Quanto è alto dopo la potatura?

b) Ayub ha 8 € e chiede 2 € alla mamma per poter comprare 6 pennarelli colorati, che costano 1 € l’uno, e un compasso di 3 €. Quanto gli rimane?

c) La mamma ha 6 uova; ne compra altrettante, ne usa 8 e ne rompe uno. Quante uova le rimangono?

d) Alyson mangia 2 mele al giorno per 6 giorni e per altri 2 giorni ne mangia 3 al giorno. Quante mele mangia in tutto?

1) 6 × 2 8 1 =

2) 2 × 6 + 3 × 2 =

3) (8 + 6) : 2 =

4) 8 + 2 6 × 1 3 =

Le quattro operazioni e le loro proprietà

SIMULAZIONE DI VERIFICA

1 Scrivi i nomi dei termini di ciascuna operazione.

0,4 + 12 = 12,4 32 × 19 = 608 46 – 17,9 = 28,1 2 064 : 8 = 258

0,4 e 12 sono

32 e 19 sono

46 è

28,1 è

8 è 12,4 è 608 è 17,9 è 2 064 è 258 è

Completa.

2 La cifra zero:

a) nell’addizione è ; infatti 7 + 0 =

b) annulla il ; infatti 7 × 0 =

c) se è dividendo è anche ; infatti 0 : 7 =

d) se è divisore la divisione non ; infatti 7 : 0 =

e) se è dividendo e divisore, il quoziente è

3 La proprietà :

a) commutativa vale per

b) vale per sottrazione e divisione

c) associativa vale per

d) vale per moltiplicazione e divisione

4 La scrittura 68 – 15 – 9 – 27 = 68 – (15 + 9 + 27) esprime la

5 Nelle moltiplicazioni 54 × 1 = 54 e 1 × 0,83 = 0,83 il fattore 1 è ; quindi il è uguale all’altro fattore.

Per ciascuna delle seguenti operazioni scegli il risultato esatto tra quelli proposti.

6 9 + 4,6 + 0,74 = a)

9 29 : 0,5 =

10 Completa utilizzando i simboli = e 6 ≠. a) 5 × (7 + 19) 5 × 7 + 5 × 19 b) (36 – 28) : 4

11 Inserisci i simboli > o <.

a) 5 + 3 × 8 (5 + 3) × 8

b) 4 × 10 – 3

c) 60 : (12 – 2)

d) 35 – (10 + 18)

e) 58 – (33 – 14)

4 × (10 – 3)

60 : 12 – 2

35 – 10 + 18

58 – 33 – 14

Risolvi i seguenti problemi riferiti a situazioni presenti nella realtà.

12 Nel negozio sotto casa di Felice vendono una confezione di 6 brioche a 1,44 €, mentre nel supermercato Buonissimi una confezione da 10 delle stesse brioche costa 2,30 €.

Calcola:

a) il costo di una brioche comprata nel negozio sotto casa:

b) il costo di una brioche acquistata nel supermercato Buonissimi:

c) quanto si risparmia acquistando una brioche dove costa meno:

13 Un litro di gasolio costa 1,35 €. L’automobile di Mattias consuma un litro di gasolio ogni 10 chilometri.

a) Quanto costa il carburante necessario per percorrere un chilometro?

b) Se Mattias vuole affrontare un viaggio di 150 km, quanti euro deve prevedere per la spesa del carburante?

14 Questo è il resoconto di alcune spese effettuate da Mirella e Romeo il mese scorso.

a) Calcola se hanno speso gli stessi soldi e in caso contrario chi ha speso di più.

b) In quali casi le proprietà delle operazioni ti evitano i calcoli?

METODI PER RISOLVERE PROBLEMI UNITÀ 4

Chi ha della

paura matematica?

A che cosa pensi quando senti parlare di “problema”?

La prima cosa che probabilmente ti viene in mente è che sia una sfida difficile o qualcosa di complicato da affrontare. Potresti persino pensare che risolvere un problema di matematica sia un’abilità che solo in pochi posseggono, e non invece una competenza che tutti possono acquisire.

Davanti a un problema, specialmente se sembra complesso, la tua mente rischia di andare in “tilt”: non sai da dove iniziare, quali operazioni usare, o come interpretare il testo! I problemi di matematica non sono ostacoli invalicabili, ma sfide stimolanti, dei veri e propri enigmi da decifrare, e per farlo esistono strategie ed espedienti che ti aiuteranno a risolverli, passo dopo passo, con calma e logica. Proprio come un detective che raccoglie indizi per risolvere un caso, o un ingegnere che progetta un edificio, imparerai a leggere con attenzione le tracce, a capire quali informazioni sono utili e quali sono irrilevanti e a scegliere lastrategiamigliore.

ROAD MAP la nostra

COMPRENDIAMO COME SI RISOLVE UN PROBLEMA

CERCHIAMO I DATI NEL TESTO DI UN PROBLEMA

IMPARIAMO A SCRIVERE L’ESPRESSIONE RISOLUTIVA E IL DIAGRAMMA AD ALBERO

UTILIZZIAMO IL METODO GRAFICO

MATERIALE INTEGRATIVO MULTIMEDIALE

SUCCEDE CHE...

COME SI RISOLVE UN PROBLEMA

Emma in classe ha 24 compagni.

La professoressa di matematica, che ha 2 ore di lezione, li divide in gruppi e assegna loro il doppio degli esercizi della lezione precedente, in cui hanno svolto 2 esercizi in più di oggi.

Quanti alunni metterà in ogni gruppo?

Quanti esercizi svolgeranno oggi?

Per rispondere si deve risolvere un problema matematico.

Nel testo di un problema matematico si trovano le informazioni (dati) per rispondere alla domanda posta dal problema (richiesta) e arrivare alla soluzione. Non ci sono procedure generali sempre valide per risolvere i problemi ma, seguendo alcune regole, è possibile trovare delle strategie che ci aiutino.

È importante:

• leggere con molta attenzione il testo del problema;

• cercare le informazioni note, i dati, e le richieste, cioè le domande poste dal problema;

• individuare la sequenza delle operazioni da effettuare, cioè la risoluzione;

• formulare la risposta e controllare la sua validità.

Dalla lettura del testo si possono scoprire dati nascosti, mancanti, superflui o contradditori

Dati nascosti: termini e o parole che indicano un numero (paio, doppio, dozzina, triplo, decimo, settimana...).

Dati mancanti: informazioni numeriche che non compaiono nel testo del problema e senza le quali non è possibile pervenire alla soluzione dello stesso.

Dati superflui: informazioni numeriche che non servono per risolvere il problema.

Dati contradditori: informazioni che si contraddicono e non permettono la risoluzione del problema.

Nel problema della classe di Emma:

• manca un dato (il numero di gruppi in cui la professoressa ha diviso i ragazzi);

• ci sono dati contradditori (... assegna loro il doppio degli esercizi della lezione precedente, in cui hanno svolto 2 esercizi in più di oggi);

• c’è anche un dato superfluo (2 ore di lezione).

Il problema, quindi, non si può risolvere .

1 Scrivi le fasi di lavoro utili per risolvere un problema.

2 Completa inserendo i numeri indicati dai dati nascosti.

a) Un paio di scarpe = scarpe

b) Una settimana = giorni

c) Una decina di libri = libri

d) La terna vincente = numeri

3 Accanto a ogni parola scrivi l’operazione corrispondente (scegli tra quelle assegnate).

Quadruplo Metà Centuplo Decimo : 2 : 10 × 4 × 100

Per ogni problema leggi il testo e segna la risposta esatta.

4 Gaia ha due gatti e Marianna ne ha il quadruplo. Quanti gatti ha Marianna?

a) 4 gatti b) 8 gatti c) 12 gatti d) 16 gatti

5 Se l’abbonamento annuale a una rivista mensile costa 64,50 €, quale operazione serve per conoscere il costo di un solo numero?

a) 64,50 × 12 b) 64,50 : 12 c)

: 30 d)

+ 12

6 12 videogiochi vengono divisi tra 3 ragazzi di 10 anni: il primo ne prende 6 e il secondo 4. Se la domanda è: “Quanti videogiochi rimarranno al terzo?’’, qual è il dato superfluo?

a) 12 b) 10 c) 6 d) 4

Se possibile, risolvi i seguenti problemi.

7 MATEMATICA IN AZIONE Luca va a scuola da lunedì a venerdì: il lunedì e il mercoledì passa a prendere un compagno e allunga la strada di 120 m; gli altri giorni va direttamente a scuola.

Se si alza alle 7:00 ogni mattina, quanti metri percorre alla settimana per andare a scuola?

a) Dati contraddittori

b) Dati mancanti

8 MATEMATICA IN AZIONE Matteo, Giulia e Sara hanno in tutto 200 figurine: Matteo ne prende la metà, Giulia ne prende 80, Sara 42 e regalano a un compagno il resto delle figurine. Quante figurine avrà in regalo il compagno?

a) Dati contraddittori

b) Dati mancanti

9 MATEMATICA IN AZIONE Lo zio Alberto e la sua famiglia si sono trasferiti nel 1990 in Australia per motivi di lavoro. Sono tornati a casa in vacanza per la prima volta dopo tre lustri. Che anno era?

a) 1995 b) 2005 c) 2002 d) 2020

METODI PER RISOLVERE UN PROBLEMA 2

SUCCEDE CHE...

La mamma e la zia di Emma comprano 18 uova distribuite in contenitori tutti uguali. La mamma ha comprato il doppio delle uova della zia.

Quante uova ha comprato la mamma di Emma e quante la zia?

I problemi si possono risolvere con metodi diversi: il metodo grafico, la tabella a doppia entrata , l’espressione risolutiva e il diagramma ad albero.

Metodo grafico e tabella a doppia entrata

Per risolvere questo problema si può utilizzare il metodo grafico

Il metodo grafico utilizza disegni, segmenti o strisce, per rappresentare le relazioni tra i dati e visualizzare il ragionamento per risolvere il problema.

• Si legge il testo e si evidenziano i dati

• Si individuano le relazioni tra i dati.

• Si rappresentano graficamente le relazioni individuate.

• Si effettuano i calcoli.

Dati

uova della mamma uova della zia 18 uova totali 2 parti 1 parte 3 parti

Risoluzione

18 : 3 = 6 (1 parte → uova della zia) 6 × 2 = 12 (2 parti → uova della mamma)

Una tabella a doppia entrata è un metodo per organizzare le informazioni, per reperirle facilmente e trarre conclusioni in modo più rapido, soprattutto se i dati sono di tipo diverso.

Una tabella a doppia entrata è formata da righe e colonne.

Utilizziamo una tabella a doppia entrata per scoprire se è vero che, lanciando due dadi, il risultato più frequente è 7:

• nella colonna e nella riga che intestano la tabella riportiamo i numeri sulle facce dei dadi;

• nelle caselle degli incroci scriviamo tutti i casi possibili di somma che si possono verificare nel lancio dei due dadi.

La tabella conferma che il risultato più frequente è 7.

La mamma di Emma ha comperato 12 uova sistemate in due contenitori, la zia 6 uova in un contenitore.

Uova della mamma Uova della zia

1 Rispondi con Vero o Falso.

a) Il metodo grafico si usa solo nei problemi di geometria. V F

b) Il metodo grafico utilizza segmenti per rappresentare relazioni. V F

c) Una tabella a doppia entrata è costituita da righe e da colonne. V F

d) Le tabelle a doppia entrata si usano solo per gli orari degli autobus. V F

2 Individua la rappresentazione grafica corretta per il seguente problema. Vincenzo e Sebastiano raccolgono figurine di calciatori e in totale ne hanno 163. Vincenzo, che ha iniziato la raccolta per primo, ne ha 17 in più del doppio di quelle di Sebastiano. Quante figurine ha Sebastiano?

a) b)

Risolvi con il metodo grafico.

3 La somma di due numeri naturali è 40 e uno è il quadruplo dell’altro. Determina i due numeri. 1° numero 2° numero somma dei due numeri = 40

La somma dei due numeri, che vale 40, contiene 5 parti uguali al primo numero; quindi:

1° numero → 40 : 5 = 2° numero → × 4 =

4 MATEMATICA IN AZIONE Paolo, Emanuele e Christian ieri pomeriggio hanno giocato a biglie. Ognuno di loro ha iniziato il gioco con 20 biglie.

a) Quante biglie in totale erano presenti a inizio gioco?

Alla fine del gioco Paolo aveva 3 biglie in più di Emanuele e Christian 9 in più di Emanuele.

b) Quante biglie aveva ognuno di loro alla fine del gioco? Osserva e rispondi. [ ; 19; 25]

Emanuele Paolo Christian 3 9

5 MATEMATICA IN AZIONE Osserva la tabella del tuo orario scolastico e rispondi.

a) In quali giorni e in quali ore hai scienze motorie?

b) In quali giorni e in quali ore hai matematica?

c) In quali giorni e in quali ore hai storia e geografia?

d) Che materia hai la quarta ora di giovedì? E la prima di lunedì? E l’ultima di mercoledì?

SUCCEDE CHE...

Emma è in centro a fare acquisti con la mamma. Spendono 16 € per l’ultimo libro di Pennac, comprano due sciarpe al costo di 12 € ciascuna e un gelato da 2,50 € l’uno. A casa, la mamma, che era uscita con 50 €, si ritrova con soli 5 € in borsa ed è convinta che abbiano sbagliato a darle il resto.

In quale modo Emma può verificare se i conti sono esatti?

Espressione risolutiva e diagramma ad albero

Il problema di Emma si può risolvere con un’espressione che metta le operazioni in successione.

L’espressione che sintetizza le operazioni da svolgere per risolvere un problema si chiama espressione risolutiva e può contenere anche delle parentesi.

Un problema che prevede più soluzioni si può risolvere, invece, con un diagramma ad albero.

Il diagramma ad albero è un metodo grafico che permette di organizzare i dati con tutte le combinazioni possibili in modo da non escluderne alcuna.

ESEMPIO

Una macchina che distribuisce bevande calde offre il caffè espresso con queste modalità: normale o decaffeinato, dolce o amaro, lungo o ristretto. Con un diagramma ad albero analizziamo tutte le soluzioni possibili.

Per verificare i conti, Emma può usare il metodo dell’espressione risolutiva:

50 (16 + 12 × 2 + 2,5 × 2) = 50 (16 + 24 + 5) = 50 45 = 5 €

I conti sono giusti: nessuno ha commesso errori nel dare il resto alla mamma.

ESERCIZI Primi

Scegli l’espressione corretta per la soluzione dei seguenti problemi.

1 Un panettiere ha preparato 12 pizze da vendere a tranci e da ogni pizza ne ricava 8. Se vende 9 pizze, quanti tranci gli rimangono?

× 8 9 × 8

(12 + 9) × 8

2 Marina restituisce un prestito in tre rate: la prima è di 70 €, la seconda è di 45 € e la terza è il triplo della prima. Quanto è il totale del prestito?

70 + 45 + 3

+ 45 + 45 × 3

3 Completa i diagrammi ad albero e stabilisci quali numeri di tre cifre si possono ottenere con 1, 2 e 3, utilizzandole ciascuna solo una volta.

+ 45 + 70 × 3

Risolvi i seguenti problemi scritti in “matematichese’’ impostando un’espressione.

4 Alla differenza tra dieci e sei aggiungi il quadruplo di tre e dimezza il risultato. [8]

5 Somma il prodotto di quatto e nove al quoziente di venti e cinque e triplica il risultato. [120]

6 MATEMATICA IN AZIONE Clara si è appena trasferita in una nuova casa e fa acquisti per la sua cucina: 12 piatti piani, 6 piatti fondi, 12 bicchieri, due insalatiere e una pentola a pressione.

Spende in totale 241 €: un piatto piano costa 6,50 €, un bicchiere 6 €, la pentola a pressione 25 € e ciascuna insalatiera 7,50 €.

Calcola il costo di ogni piatto fondo.

Operazioni per la risoluzione del problema:

• costo piatti piani → 12 ×

• costo pentola a pressione → 1 ×

• costo bicchieri → 12 ×

• costo insalatiere → 2 ×

• costo 6 piatti fondi → 241 € spesa piatti piani, bicchieri, pentola a pressione e insalatiere

Espressione risolutiva: [241 − ( + + + )] : 6 =

CURIOSITÀ STORICHE

ODIFREDDI a cura del professor

LA RAPPRESE NTAZIONE E I NOMI DE I NUMERI

Quando scriviamo un numero, usiamo quelle che vengono chiamate cifre arabe, perché nel Medioevo le abbiamo imparate dagli Arabi, appunto.

Si tratta dei simboli 0, 1, 2, 3, 4, 5, 6, 7, 8 e 9, che permettono di scrivere qualunque numero nel sistema decimale.

In realtà gli Arabi chiamavano questi simboli cifre indiane, perché a loro volta le avevano imparate dagli Indiani, che le avevano inventate prima degli inizi della nostra era, un paio di migliaia di anni fa. Naturalmente, non c’è nessun legame tra un numero e le cifre che lo indicano: i simboli sono convenzionali, e infatti nel passato erano molto diversi.

Si possono seguire sulla carta geografica il percorso e i mutamenti che le cifre originali hanno fatto, partendo dall’India e arrivando fino a noi, in un viaggio durato un migliaio di anni. E ci si accorge che i simboli usati inizialmente dagli Indiani non erano affatto quelli che usiamo noi oggi. Man mano che questi simboli venivano trasmessi a popoli vicini, cambiavano un po’ la loro forma: basta andare ancora oggi in India, o nei paesi arabi, per accorgersi che le loro cifre sono rimaste molto diverse dalle nostre.

Partendo dall’India dell’impero Gupta (tra il III e il VI secolo d.C.), che era un po’ l’analogo della Grecia di Pericle (V secolo a.C.) in quanto a cultura, cioè un luogo dove fiorivano le arti, le scienze e la filosofia, le cifre sono anzitutto approdate a Bagdad, che era invece l’analogo dell’antica Roma,

ovvero una grande capitale politica e commerciale, centro dell’Impero Islamico, dove si incontravano popoli e idee provenienti da terre lontane.

Questo passaggio avvenne intorno all’VIII-IX secolo dopo Cristo, grazie agli intensi scambi commerciali e culturali lungo le vie che collegavano l’Oriente all’Occidente.

Un signore di nome Al-Khwarizmi scrisse nell’825 un famoso trattato, Sul calcolo con i numeri indù, in cui spiegava agli Arabi il sistema indiano. Il nome di questo signore è poi stato latinizzato nel termine algoritmo, che nella moderna era informatica tutti usiamo senza nemmeno sapere da dove arrivi.

Dalla Mezzaluna Fertile le cifre si trasmisero gradualmente a tutto il Nord Africa, man mano che l’Impero Islamico si allargava, e arrivarono fino alla Spagna, che all’epoca era sotto il dominio dei Mori. Raggiunsero infine l’Italia, grazie a un signore pisano di nome Fibonacci, che nel 1202 scrisse anche lui un famoso trattato, il Liber abaci, per spiegare il sistema arabo agli europei.

Ma per fare i conti la gente continuò a lungo a preferire il pallottoliere, che si chiamava abaco. Questo strumento, formato da una cornice con delle aste su cui scorrevano palline o gettoni, permetteva di calcolare in modo rapido e visivo, spostando semplicemente le palline avanti e indietro. Soltanto nel Cinquecento il sistema decimale si impose, finalmente, e la neonata stampa codificò la forma delle cifre, che da allora sono rimaste più o meno immutate fino ad oggi.

MAPPA

PROBLEMA MATEMATICO: FASI PER LA RISOLUZIONE

Leggere il testo

Leggere il testo

Leggere il testo

Step 1

Esempio

Step 2

Individuare i dati e le relazioni tra di essi

Metodo grafico

7 euro Pik 14 euro Puk

Leggere il testo

Leggere il testo

Tabella a doppia entrata

Svolgere i calcoli

Leggere il testo

Leggere il testo

Step 3 Step 4

METODI UTILI PER LA RISOLUZIONE

Verificare la validità della risposta

Leggere il testo

Leggere il testo

Diagramma ad albero

21 euro in totale (3 parti) Lu Me Ve 8:00 15:00 11:00 tisana naturale naturale con miele con miele allo zenzero ai frutti rossi

Epressione risolutiva

John compra tre quaderni da 1,50 euro l’uno, un rotolo di scotch da 2,40 euro, quattro pacchetti di figurine da 0,70 euro ciascuno e un cono gelato da 2 euro. Aveva 15 euro, quanto gli rimane? 15 – (3 × 1,50 + 2,40 + 4 × 0,70 + 2,00) = 3,30 €

ESERCIZI E PROBLEMI

LEZIONE 1

COME SI RISOLVE UN PROBLEMA

1 Ricopia sul quaderno lo schema, mettendo nel giusto ordine le fasi di lavoro per risolvere un problema.

PROBLEMA

RISPOSTA

verifica la validità del risultato e rispondi

leggi e comprendi il testo

individua le operazioni necessarie e risolvile

ricerca i dati e le relazioni tra di essi

2 Completa con una delle seguenti parole:

nascosto • superfluo • mancante • contraddittorio

a) Un dato è se afferma l’opposto di un altro dato e non permette la risoluzione del problema.

b) Un dato è se non è indicato con dei numeri ma con termini o parole che indicano un numero.

c) Un dato è se manca un’informazione utile a risolvere il problema.

d) Un dato è se non viene utilizzato per risolvere il problema.

Risolvi i seguenti problemi.

3 Andrea e Sara al mare hanno raccolto delle conchiglie:

Andrea ne ha una dozzina e Sara la metà. Quante conchiglie ha Sara?

a) 12 conchiglie

b) 6 conchiglie

4 Futura ha una decina di pesci rossi e Matteo ne ha un decimo di quelli di Futura.

Quanti pesci ha Futura e quanti ne ha Matteo?

a) Futura ha 10 pesci e Matteo 1 pesce.

b) Futura ha 1 pesce e Matteo 10 pesci.

Leggi il testo dei seguenti problemi e indica se sono o non sono risolvibili, e perché.

5 Ilenia compera alcuni DVD a 19 € ciascuno, un CD da 9,50 € e una rivista che costa 2,30 €.

Quanto spende in tutto?

Il problema risolvibile perché

6 Nicole ieri pomeriggio ha svolto i compiti scritti per un’ora e mezza, ha studiato per 2 ore ed eseguito una ricerca su Internet che l’ha impegnata per 45 minuti, poi è uscita con le amiche. Quanto tempo ha passato con le amiche?

Il problema risolvibile perché

7 Completa come negli esempi.

a) Il triplo di a aumentato di 5 = 3a + 5.

b) La quarta parte di quattordici = 14 : 4 = 3,5.

a) Il quintuplo di b =

b) Il sestuplo di 7 =

c) La decima parte di 84 =

d) Il triplo di 8 =

e) Il doppio di a aumentato di 3 =

f) La metà di b aumentata di 10 =

g) La quarta parte di due decine =

h) Il triplo di una settimana =

8 MATH John invited 15 friends to his house to celebrate his birthday by eating a hot dog, but a couple of friends didn’t come. How many hot dogs did John’s mother prepare? [14]

Per ogni problema leggi il testo e risolvilo compilando la seguente scheda sul tuo quaderno.

a) Ci sono dati superflui? SÌ NO

b) Se sì, quali sono?

c) Ci sono dati mancanti? SÌ NO

d) Se sì, quali sono?

e) Il problema è risolvibile? SÌ NO

f) Qual è la richiesta?

g) Se alla domanda e) hai risposto sì, risolvilo.

h) Se alla domanda e) hai risposto no, modifica o aggiungi i dati in modo che sia risolvibile.

9 Gisella con 23 € vuole comperare 3 quaderni a righe e due matite da 0,90 € ciascuna. Quanti quaderni può acquistare?

10 Marina si sta allenando per una gara di corsa e in una settimana ha percorso 126 chilometri, correndo ogni giorno per lo stesso numero di km. Quanti chilometri ha percorso al giorno?

11 Andrea, per andare al parco che dista da casa sua 1 350 m, ha acquistato una bicicletta da 129 € e l’ha pagata con una banconota da 200 €. Quanto ha avuto di resto?

Risolvi i seguenti problemi.

12 La nonna di Veronica è morta nel 2012 all’età di 87 anni; in che anno era nata?

13 Betta vuole regalare un braccialetto portafortuna a ciascuna delle sue 4 amiche; quanti euro spenderà, se ogni braccialetto costa 2,95 €?

14 A Franca serve un chilo e mezzo di zucchero di canna e al supermercato sono rimaste solo confezioni da 300 g; quante confezioni deve acquistare? [5]

15 Un negozio di abbigliamento ha venduto due dozzine di felpe incassando 1 008 € in totale; calcola il prezzo di vendita di ciascuna felpa. [42 €]

16 Annarita compera 4 confezioni di bagnoschiuma e spende 17,28 €; quanto costa ogni confezione? [4,32 €]

17 Un pescivendolo acquista al mercato del pesce 12 kg di seppie, che paga 6,75 € al kg. La stessa mattina, nel suo negozio, ne vende 3 kg a 9 € al kg e nel pomeriggio altri 5 kg al prezzo di 8 € al kg. L’indomani mattina riesce a vendere le seppie rimaste in frigo abbassando il prezzo a 5 € al kg.

Risolvi il problema e stabilisci se c’è stato un guadagno o una perdita. [Guadagno di 6 €]

18 Un negoziante acquista dei cestini di vimini a 1,45 € ciascuno spendendo 50,75 €. Quanto guadagna se rivende ogni cestino a 2,15 €? [24,50 €]

19 Gli organizzatori di una lotteria benefica hanno venduto 145 blocchetti, ciascuno di 25 biglietti, al prezzo di 0,80 € il biglietto. Le spese di organizzazione sono di 428 €. Qual è il guadagno della lotteria? [2 472 €]

20 Mario va al mercato e compera una cassetta di mele. Il venditore mette la cassetta piena di mele sulla bilancia e dice a Mario: “Piena pesa 9,5 kg; te la vendo a 12 €’’. Aiuta Mario a calcolare quanto ha pagato 1 kg di mele, sapendo che la cassetta pesa 1,5 kg. [1,50 €]

21 Un foglio di carta per avvolgere il prosciutto pesa, in media, 10 grammi. Hai acquistato del prosciutto e il peso totale del tuo pacchetto è 349 grammi.

Qual è il peso netto del prosciutto acquistato? [339 g]

22 Una confezione di 24 bustine di tè alla vaniglia pesa 135 g.

Se la scatola vuota pesa 15 g, quanto pesa ogni singola bustina di tè? [5 g]

23 Un vasetto contenente della conserva di pomodoro pesa 1 370 grammi; se il peso del vasetto vuoto è 175 grammi, qual è il peso netto del pomodoro contenuto nel vasetto?

Se acquisti 36 di questi vasetti di conserva di pomodoro, qual è il peso netto, in chilogrammi, del pomodoro acquistato? [1 195 g; 43,02 kg]

24 Sebastiano ha acquistato per il suo ristorante 360 scatole di grissini, ciascuna con il peso lordo di 350 grammi. Quanti sono i chilogrammi di peso lordo complessivi?

Se ogni scatola di grissini vuota pesa 42 grammi, qual è il peso netto dei grissini contenuti in ciascuna scatola?

E quale, in chilogrammi, il peso netto complessivo dei grissini? [126 kg; 308 g; 110,88 kg]

25 Un autocarro vuoto pesa 4 000 kg e su di esso vengono caricate 290 cassette di frutta. La tara di ogni cassetta è 0,5 kg e la frutta contenuta in ogni cassetta è 8 kg. Quanto peserà l’autocarro dopo aver rifornito un primo negoziante di 150 cassette e un secondo di 75 cassette? [4 552,5 kg]

26 Per un evento vengono commissionate delle composizioni floreali; al fiorista che le deve preparare servono, fra l’altro, 12 gerbere per ognuna delle 6 composizioni per i pannelli laterali e 3 gerbere per ognuno dei 9 centrotavola. Se nel negozio ha 87 gerbere, quante dovrà procurarsene per finire il lavoro? [12]

27 Due podisti partono da due località distanti tra loro 73 km e si dirigono uno verso l’altro. Dopo qualche ora il primo ha percorso 36 km e il secondo 29 km. A questo punto, a quale distanza si trovano i due podisti? [8 km]

28 Tre vicini di casa, per svolgere un lavoro comune, decidono di acquistare in società una motozappa del costo di 1 200 €; il primo versa 480 €, il secondo 50 € in meno del primo; quanto deve versare il terzo? [290 €]

29 Cecilia acquista un moderno TV color che costa 1 250 €; dà un acconto di 200 € e paga il rimanente in 8 rate. Quanto sarà il valore di ogni rata? [131,25 €]

30 Vincenzo salda un debito in tre rate: la prima volta versa 750 €, la seconda 450 € e la terza il doppio della seconda. Di quanti euro era il suo debito? [2 100 €]

31 Per la sua festa Marco compra 19 pizze da 4,85 € ciascuna; se lascia una mancia di 5 € e paga con 100 €, quanto riceve di resto? [2,85 €]

32 Zia Gabriella al mercato ha comprato 5 kg di arance e 4 kg di zucchine spendendo in totale 23 €. Se le arance costano 2 € al kg, quanto ha pagato le zucchine al chilogrammo? [3,25 €]

33 Con 14 kg di caramelle un droghiere confeziona 32 scatole da 250 grammi l’una e dei sacchetti da 120 grammi l’uno. Quanti sacchetti può confezionare? [50]

34 Giacomo per guarire da una brutta influenza ha preso per una settimana uno sciroppo. Sapendo che la dose è 1,2 mg al giorno per ogni chilogrammo di peso e che di un flacone da 600 mg ne sono avanzati 54 mg, calcola quanto pesa Giacomo. [65 kg]

35 Un gruppo di tre dozzine di amici organizza un viaggio per una spesa complessiva di 2 052 €. Il giorno della partenza 6 persone non si presentano e la loro quota va suddivisa tra gli altri partecipanti. Di quanto aumenta la quota di ogni partecipante? [11,40 €]

36 Alla proiezione di un film in un oratorio assistono 423 persone; i 285 adulti pagano il biglietto intero di 4,20 € per l’ingresso. I rimanenti sono giovani e pagano un prezzo ridotto. Sapendo che l’incasso complessivo è stato di 1 680 €, a quanto ammontava il prezzo del biglietto ridotto? [3,50 €]

37 I quattro pilastri di un ponte sono disposti nel modo seguente: il primo si trova a 25 m dall’inizio del ponte, il secondo a 28 m dal primo, il terzo a 24 m dal secondo e il quarto a 27 m dal terzo. Sapendo che il ponte è lungo 129 m, quanto dista il quarto pilastro dalla fine del ponte? [25 m]

METODI PER RISOLVERE UN PROBLEMA LEZIONE 2

metodo grafico e tabella a doppia entrata

38 Inserisci i termini mancanti. Il metodo utilizza disegni, o strisce rettangolari, per rappresentare le relazioni tra i e visualizzare il ragionamento da eseguire per il problema.

39 Elenca le fasi di lavoro da utilizzare per la risoluzione di un problema con il metodo grafico.

Per ogni problema scegli la rappresentazione grafica corretta e motiva la tua risposta.

40 MATEMATICA IN AZIONE Il papà di Silvia ha 34 anni più di sua figlia e la somma delle loro età è 116 anni. Calcola l’età di Silvia. a) 34 età del padre

età di Silvia b) 34 34 età del padre età di Silvia

116 anni = somma delle età 116 anni = somma delle età

La rappresentazione grafica corretta è la perché

41 MATEMATICA IN AZIONE Daniela al mercato acquista tre oggetti e spende 41 €; aiutala a calcolare quanto ha speso per ogni oggetto, sapendo che il primo ha un prezzo triplo del secondo e il costo del terzo è di 6 € in più del secondo. a) 6

41 € spesi in totale b) 6

41 € spesi in totale

La rappresentazione grafica corretta è la perché

Risolvi i seguenti problemi con il metodo grafico.

ESEMPIO

Trova tre numeri, sapendo che il secondo e il terzo sono rispettivamente il doppio e il triplo del primo e che la somma dei tre è 96.

1° numero

3° numero 2° numero

96

somma dei tre numeri

Come puoi notare, la somma dei tre numeri, 96, contiene sei parti congruenti al 1° numero.

Quindi:

1° numero = 96 : 6 = 16 2° numero = 16 × 2 = 32

Controlla: 16 + 32 + 48 = 96 → la soluzione del problema è corretta.

3° numero = 16 × 3 = 48

42 Un numero naturale è il triplo dell’altro e la loro somma è 56; determina i due numeri. [ ; 42]

43 La somma di un numero con il suo consecutivo è 47; quali sono i due numeri? [23; ]

44 La somma di due numeri pari consecutivi è 74; quali sono i due numeri? (Il numero maggiore supera il minore di 2.) [ ; 38]

45 La somma di un numero con il suo precedente è 399; quanto vale il numero? [200]

46 La somma di due numeri è 43,2 e il maggiore supera di 6 il doppio del minore. Quanto vale il numero maggiore? [30,8]

47 La somma di tre numeri è 31, il secondo è il doppio del primo e il terzo supera di 2,5 il secondo. Calcola il valore dei tre numeri. [5,7; ; 13,9]

48 EDUCAZIONE CIVICA La legge costituzionale del 19 ottobre 2020, che prevede la riduzione del numero dei parlamentari, è stata approvata dalla Camera dei deputati. Se i presenti erano 569 e i votanti 567, quanti sono stati gli astenuti? Considerando i votanti, la differenza tra favorevoli e contrari è stata di 539: quanti sono stati i favorevoli e quanti i contrari? [2; 553; 14]

Risolvi i seguenti problemi.

49 MATH London has 9 million inhabitants, half of which are Christian. How many Christians are there?

50 Gli alunni del corso C sono 71 e i maschi sono 7 più delle femmine; quanti sono gli alunni maschi del corso C? [39]

51 Due fratelli si dividono 12 000 € in modo che il maggiore abbia 1 500 € in più del minore; quanto avrà ogni fratello? [5 250 €; ]

52 Tommaso ha comperato due paia di pantaloni spendendo in tutto 76 €; se il primo paio costa 14 € in più del secondo, quanto costa ogni paio di pantaloni? [31 €; ]

53 Debora si è iscritta a un corso di nuoto e compera una cuffia e un paio di occhialini spendendo 7,80 €; se la cuffia costa 2 € in meno degli occhialini, quanto costa ogni oggetto?

[2,90 €;

54 Due pacchi regalo pesano complessivamente 64 kg; se quello più pesante supera di 10 kg il doppio del pacco più leggero, quanto pesa ogni pacco? [18 kg;

55 In un frutteto ci sono 160 piante di agrumi: i limoni sono 5 in più del doppio dei mandarini e gli aranci sono 15 in più dei mandarini.

Calcola quanti agrumi di ogni tipo ci sono in quell’agrumeto. [75; 50; ]

56 La somma degli anni dei tre cugini Luca, Adriano e Giorgio è 38. Calcola l’età di ciascuno di essi, sapendo che Luca, il maggiore, ha il doppio degli anni di Giorgio e che Adriano ha 2 anni in più di Giorgio. [9; 11; ]

57 Una famiglia acquista tre elettrodomestici spendendo in totale 2 240 €. Calcola il costo di ogni elettrodomestico, sapendo che il secondo costa il doppio del primo e che il terzo costa il doppio del secondo. [ ; 640 €; ]

58 Tre confezioni contengono, complessivamente, 126 caramelle. La prima ne contiene il doppio della seconda e la terza 6 in più della seconda.

Stabilisci il numero di caramelle di ciascuna confezione. [60; 30; 36]

59 Per una festa vengono acquistati 300 palloncini: i palloncini rossi superano di 40 quelli blu e quelli gialli sono inferiori di 20 rispetto a quelli rossi. Quanti sono i palloncini di ogni colore? [120; 80; 100]

60 Un supermercato promuove la vendita di un tè giapponese e di un tè inglese e Marco e Angelo approfittano dell’offerta. Osserva il disegno, interpretalo e determina il costo di una bustina di ciascun tipo di tè. [Tè giapponese: 0,60 €; tè inglese: 0,45 €]

11,40 € = tè giapponese = tè inglese

€

61 Gli alunni che frequentano una scuola secondaria di primo grado sono 314. Gli alunni di terza sono 12 in più di quelli di seconda e quelli di prima sono 8 in più di quelli di terza. Calcola quanti sono gli alunni che frequentano ciascuna classe. [114; 94; 106]

62 Una giocatrice di pallacanestro in tre partite totalizza 64 punti. Quanti punti ha realizzato in ognuna delle tre partite, sapendo che quelli della prima sono il doppio di quelli della seconda e che nella terza ha realizzato 4 punti più della prima? [24; 12; 28]

63 Un ciclista si prepara a una gara percorrendo in tre giorni 492 km. Calcola i chilometri percorsi ogni giorno, sapendo che il secondo giorno ha percorso 25 km in più rispetto al primo e il terzo 19 km in più rispetto al secondo. [141 km; 166 km; ]

64 Paolo e Marco possiedono complessivamente 196 €; se il primo cedesse al secondo 16 €, avrebbero la stessa somma di denaro. Calcola la somma posseduta da Paolo e Marco. [82 €; 114 €]

65 In un torneo di calcio giovanile disputato da quattro squadre, A, B, C, D, si sono segnate 29 reti.

La squadra A ne ha segnate 4 in più della squadra C.

La squadra B ne ha segnate 3 in meno della squadra C.

La squadra C ne ha segnate il doppio della squadra D.

Quante reti ha segnato ogni squadra? [12; 5, 8; 4]

66 Osserva la tabella a doppia entrata e completa le risposte.

a) La tabella ha colonne.

b) La tabella ha 5 .

c) Le caselle da utilizzare per gli “incroci’’ sono .

67 Fai degli esempi di uso delle tabelle a doppia entrata nella vita quotidiana.

MATEMATICA IN AZIONE Risolvi i seguenti problemi utilizzando tabelle a doppia entrata.

Tre amici si sfidano in una gara ciclistica a tappe.

Filippo percorre la prima tappa in 38 minuti e la seconda in 29 minuti.

Luca percorre la prima tappa in 41 minuti e la seconda in 27 minuti.

Carlo percorre la prima tappa in 39 minuti e la seconda in 30 minuti.

Stabilisci chi è il vincitore usando una tabella a doppia entrata.

Il vincitore è Filippo, che impiega 67 minuti.

68 Due fratelli contano i loro risparmi: Matteo ha 10 monete da 20 centesimi, 3 da 50 centesimi, 1 da 1 euro e 5 da 2 euro; Chiara ha 14 monete da 20 centesimi, 2 da 50 centesimi, 2 da 1 euro e 4 da 2 euro.

Organizza i dati con una tabella e stabilisci chi dei due fratelli ha risparmiato di più.

a) Quanti sono i fratelli? : e ; quindi la tabella deve avere 3 colonne: per i nomi dei fratelli e una per i dati variabili.

b) Quanti sono i valori delle monete? (20 centesimi, 50 centesimi, 1 euro, 2 euro); quindi nella tabella ci vogliono righe: 4 per il valore delle monete e per i dati variabili.

Totale risparmi di Matteo:

Totale risparmi di Chiara:

Ha risparmiato di più

69 Tre amici, Gigi, Andrea e Tommaso, abitano in tre città diverse, Siena, Perugia, Firenze, e si spostano con una bicicletta, una moto e uno scooter.

L’amico che abita a Siena prende la moto per fare una passeggiata e incontra Andrea che abita a Perugia. Tommaso, che va in bicicletta, ha forato una gomma.

Assegna a ciascuno la città in cui vive e il suo mezzo di locomozione.

Città Mezzo di locomozione

Gigi

Andrea Tommaso

70 Nella tabella seguente sono riportate le quantità in grammi di pasta, riso, pane e patate che hanno mangiato tre ragazzi in una settimana.

Osserva i dati e rispondi.

a) Quanti grammi di pane mangiano in tutto i tre ragazzi?

b) Federica mangia tutti i giorni la stessa quantità di pane: quanti grammi al giorno?

c) Matteo ha mangiato tre volte la stessa quantità di pasta: quanti grammi a piatto?

[1 360 g; 80 g; 100 g]

71 Fai un’indagine sul mese di nascita dei tuoi compagni e raccogli i dati in una tabella con la seguente intestazione. Rispondi poi alle domande.

Mese di nascita

a) Quante righe ha la tabella?

b) Qual è il mese in cui sono nati più compagni?

c) Qual è il mese in cui ne sono nati meno?

Nome dei compagni

d) Ci sono mesi in cui non è nato nessun compagno? Se sì, quali?

e) Ci sono mesi in cui è nato lo stesso numero di compagni? Se sì, quali?

72 MATH Rainfall in Plymouth between November and December last year. Fill in the table.

73 Carlo ha in tasca 13 €, una penna e tre biglietti da visita; Giovanni ha in tasca 21 € e tre penne; Luca ha in tasca due penne e un biglietto da visita; Alessandro 14 €, tre penne e nessun biglietto; Carola ha 4 € e una penna; Giulia due penne e due biglietti da visita. Organizza, sul quaderno, i dati in una tabella a doppia entrata e rispondi alle seguenti domande:

a) Chi ha più soldi in tasca?

b) Quanti soldi hanno i ragazzi in totale?

c) Chi non ha soldi in tasca?

d) Chi ha meno penne?

e) Quante penne hanno i ragazzi in totale?

f) Chi non ha biglietti da visita in tasca?

74 Nell’ultima tappa di una gara ciclistica sono rimasti in testa i corridori A, B e C. Nel tratto di montagna vengono fatti tre controlli che un cronista sportivo registra così nel suo tablet:

• 2° controllo " ore 8 e 50 minuti: i tre corridori passano insieme;

• 1° controllo " C era passato 30 minuti prima, seguito da A dopo 10 minuti e da B dopo altri 10;

• 3° controllo " ore 9 e 40 minuti: A e C passano insieme, mentre B ritarda 15 minuti.

Completa la tabella che riassume gli eventi e stabilisci qual è il corridore più veloce tra il 1° e il 3° controllo. ciclista 1° controllo 2° controllo 3° controllo Tempo impiegato

A → Andalù 8h 50m

B → Bicivelox 8h 50m

C → Corripiano 8h 50m

75 Per la raccolta porta a porta dei rifiuti, il comune di Beltramonto è diviso in tre zone: A, B e C. Plastica, carta, vetro e rifiuti organici il lunedì si raccolgono nella zona A, il giovedì nella zona B e il mercoledì nella zona C.

I rifiuti organici e quelli indifferenziati vengono raccolti il giovedì nella zona A, il lunedì nella zona B e il venerdì nella zona C. La casa di Maddalena si trova nella zona A; i suoi nonni materni abitano nella zona B e quelli paterni nella zona C. Compila sul tuo quaderno una tabella che organizzi la raccolta settimanale nelle tre zone e rispondi alle domande. (Ricorda che i sacchetti della raccolta differenziata vanno posizionati davanti alle abitazioni la sera precedente il giorno del ritiro.)

a) I nonni paterni possono mettere davanti alla porta di casa i sacchetti della plastica il lunedì?

b) Quando Maddalena prepara la pattumiera dei rifiuti organici per il ritiro, i nonni paterni possono fare lo stesso per i rifiuti indifferenziati?

c) In quali giorni i nonni materni possono preparare per il ritiro la pattumiera dei rifiuti organici?

d) Quando i nonni materni preparano i sacchetti della carta, la stessa sera quali sacchetti può mettere davanti alla porta di casa Maddalena?

Espressione risolutiva e diagramma ad albero

76 Inserisci i termini mancanti.

Il diagramma ad è un metodo che permette di organizzare i con tutte le combinazioni possibili in modo da non alcuna.

Risolvi i problemi utilizzando diagrammi ad albero.

ESEMPIO

Osserva il seguente diagramma ad albero: quante frasi di senso compiuto si possono formare? il cane sta

allegro aggressivo giocherellone è corre

mangiando abbaiando per strada dormendo a casa nel parco

Si possono formare 9 frasi:

• Il cane è allegro; il cane è aggressivo; il cane è giocherellone.

• Il cane sta abbaiando; il cane sta mangiando; il cane sta dormendo.

• Il cane corre a casa; il cane corre per strada; il cane corre nel parco.

77 MATEMATICA IN AZIONE Giorgio va a pranzo in un ristorante dove, come primi, servono tre formati di pasta: spaghetti, penne, fusilli.

Si può scegliere tra tre diversi condimenti: pesto, ragù di carne, vongole.

Fra quanti abbinamenti di primi piatti può scegliere Giorgio?

spaghetti ragù ................. pesto

pesto vongole

Giorgio può scegliere tra

78 MATEMATICA IN AZIONE Il seguente diagramma ad albero riporta i risultati di un torneo di ping pong tra un gruppo di amici in vacanza al mare. Le sfide sono secche e vince chi raggiunge 21 punti. Osserva il diagramma e rispondi alle domande.

Franca 21

Umberto 11

Valentina 21

Paola 13

Giacomo 8

Adriano 21

Alberto 21

Mariella 9

} → Franca 16

} → Valentina 21

} → Adriano 21

} → Alberto 14

a) Chi ha vinto il torneo?

} → Valentina 21

} → Adriano 18

b) In quale partita si ha la maggior differenza di punteggio?

c) Chi ha totalizzato il punteggio più basso in tutto il torneo? In che fase?

d) Chi sono i semifinalisti che sono stati battuti?

e) Quanti incontri si sono effettuati in tutto?

79 Predisponi un diagramma ad albero per stabilire quante parole diverse di tre lettere puoi formare con le lettere a, c, e, n senza ripeterle. [24]

80 MATH How many 4 digit even numbers can be formed using the digits 1, 3, 9, 4 only once? [6]

81 Quanti numeri dispari di tre cifre puoi formare con 5, 6, 8 utilizzando ogni cifra una volta sola all’interno di ogni numero? [2]

82 MATEMATICA IN AZIONE In una paninoteca preparano panini bianchi, integrali o di segale, con salumi, formaggi o verdure, con salse o senza salse. Quanti tipi di panini diversi è possibile ordinare? [18]

83 Giulio legge un articolo di National Geographic dove si parla del rimboschimento come possibile soluzione per l’assorbimento di carbonio, cioè piantare più alberi può aiutare a compensare le emissioni di CO2. Giulio decide quindi di far crescere un albero nel giardino di casa propria: pianta un seme e dopo 5 settimane vede spuntare il primo stelo. L’anno successivo dallo stelo sono germogliati due rami. Il terzo anno da ogni ramo sono germogliati ancora due rami, e così via per ogni anno. Quanti rami avrà l’albero di Giulio dopo 5 anni? [30, primo stelo escluso]

84 MATEMATICA IN AZIONE Quanti abbinamenti completi puoi fare con 5 magliette, 3 pantaloni e 2 giacche? [30] Disegna il diagramma ad albero.

85 Rispondi con Vero o Falso.

a) L’espressione risolutiva sintetizza le operazioni per risolvere un problema. V F

b) Le espressioni risolutive non si usano in problemi con numeri decimali. V F

c) Un’espressione risolutiva è un modo per risolvere problemi con più operazioni. V F

d) Nelle espressioni risolutive non si devono usare parentesi. V F

86 Individua l’espressione risolutiva esatta e risolvila.

Un cartolaio suddivide 180 matite in contenitori da 6 e da 12.

Se ha riempito 4 contenitori da 6 matite, quanti contenitori da 12 potranno essere riempiti?

a) (180 4 × 6) 12

b) (180 4 × 6) : 12

87 Indica il problema risolvibile con la seguente espressione e risolvi.

100 19,50 × 2 (15 + 27)

a) Paolo acquista 2 DVD da 19,50 € ciascuno e 2 confezioni di CD, una da 15 € e una da 27 €. Se aveva 100 €, quanto gli rimane dopo gli acquisti?

b) Marta esce di casa con 100 €, acquista due piantine in vaso spendendo 19,50 € e 27 caramelle da 1 € ciascuna ma ne mangia 15. Quanto le rimane?

Risolvi i seguenti problemi impostando un’espressione.

In un ristorante ci sono 15 tavoli quadrati da 4 posti e 3 tavoli rotondi da 8 posti; se ieri a mezzogiorno hanno pranzato in questo ristorante 70 persone, quanti posti sono rimasti liberi?

15 × 4 + 3 × 8 70 = 60 + 24 70 = 84 70 = 14

Sono rimasti liberi 14 posti.

88 Teresa legge in cinque giorni un giallo di 80 pagine: il primo giorno legge 15 pagine, il secondo ne legge 12, il terzo 13 e gli ultimi due giorni lo stesso numero di pagine. Quante pagine ha letto ciascuno degli ultimi due giorni? [20]

89 In una comunità che ospita 169 persone si acquistano ogni settimana 12 cassette di mele da 5 kg ciascuna, 4 cassette di pesche da 31 kg e 7 cassette di uva da 22 kg ciascuna. Quanta frutta può consumare settimanalmente ogni persona di quella comunità? [2 kg]

90 L’affrancatura per una cartolina o per una lettera costa 1,25 €. Se in un ufficio si spediscono giornalmente 13 cartoline e 35 lettere, quanto si spende in una settimana lavorativa? (Ricordati di escludere il e la domenica perché gli uffici sono chiusi.) [300 €]

91 Per sistemare un orto viene fatto questo preventivo: 30 piante di mandorli da 5 € ciascuna, 15 piante di agrumi da 8 € ciascuna, 12 piante di ulivo da 15 € ciascuna; per il concime e per il terriccio 1 150 €, per la manodopera 16 € l’ora per le 15 ore di lavoro previste. Calcola il totale del preventivo. [1 840 €]

92 La mamma manda Omar a fare la spesa. Gli chiede di comprare 4 confezioni di spaghetti da 1,50 € ciascuno, 6 litri di latte da 1,25 € al kg, due confezioni di riso a 2,50 € ciascuno e 3 kg di melograni a 2,50 € ciascuno. “Con il resto comprati un bel gelato’’ gli ha detto prima di uscire, ma si è dimenticata di dare a Omar i soldi. Quanto avrebbe dovuto dare a suo figlio, come minimo, se un cono costa 2,00 €?

93 Una famiglia, composta dai genitori e da due figli, trascorre 12 giorni di vacanza in un albergo, dove il prezzo della pensione è 55 € al giorno per persona. Per il viaggio di andata e ritorno occorrono 28 € per persona. Quanto spende quella famiglia per la vacanza? [2 752 €]

94 Per il 20º anniversario di nozze dei genitori i tre figli decidono di comperare una torta e un cesto di fiori. Nel cesto, che costa 6,50 €, dicono al fiorista di mettere 12 rose da 4,75 € l’una e 13 gigli da 4,30 € l’uno. Come decorazione aggiungono poi un nastro da 1,20 €. Quanto spende ognuno dei tre figli per il cesto di fiori? [40,20 €]

95 Un cartolaio acquista all’ingrosso 26 confezioni di pennarelli da 4,65 € ciascuna, carta per fotocopie e buste per un totale di 249 € e inoltre 50 quaderni da 2,05 € ciascuno. Quanto riceverà di resto se paga con 500 €? [27,60 €]

96 In un cinema ci sono 27 file con 18 poltrone ciascuna; se alla visione di un film partecipano 75 coppie, 23 famiglie con un bambino, 37 famiglie con 2 bambini e 7 gruppi di amici di 9 persone ciascuno, quanti posti restano liberi? [56]

97 Un supermercato ha acquistato 450 kg di arance e ne vende in media 35 kg al giorno.

Dopo 9 giorni ne deve scartare 11 kg perché sono andate a male. La rimanenza viene venduta in altri 4 giorni.

Quanti chilogrammi di agrumi si vendono in ciascuno degli ultimi 4 giorni? [31 kg]

98 STEM La famiglia Settimini prende il treno per andare a Modena a vedere una mostra sull’Impressionismo. Il papà spende 103,50 € di biglietti ferroviari.

Se i due genitori hanno pagato 18 € a testa, quanto è costato il biglietto di ciascuno dei cinque figli?

(Risolvi il problema impostando un’espressione.)

99 Angelo ha 500 €; spende 230 € dal meccanico, regala 25 € a ciascuno dei suoi due figli, compera due paia di scarpe da 45,50 € e tre camicie da 27,80 €. Dopo tutte queste spese può acquistare un regalo da 50 € per la moglie?

Qual è l’espressione che risolve il problema?

a) 500 (230 + 25 × 2 + 45,50 × 2 + 27,80 × 3)

b) 500 230 25 × 2 + 45,50 × 2 + 27,80 × 3

c) (25 × 2 + 45,50 × 2 + 27,80 × 3) 500 230

d) 500 (25 × 2 + 45,50 × 2 + 27,80 × 3)

Qual è la risposta al problema?

a) Angelo può fare il regalo.

b) Ad Angelo non restano soldi.

c) Ad Angelo restano 45,60 € e non può fare il regalo.

d) Angelo può fare il regalo perché gli restano 51,60 €.

100 STEM La professoressa di scienze ha incaricato Maia e i suoi compagni di classe di censire gli alberi di un grande parco situato vicino alla scuola. I ragazzi si dividono in gruppi e

contano:

– 23 tigli per ogni lato del viale centrale; – 10 betulle per ogni lato in due viali laterali; – 3 magnolie in ognuna delle 6 aiuole a nord; – 4 camelie in ognuna delle 5 aiuole a sud; – 3 alberi dei tulipani; – 5 platani.

a) Quanti alberi hanno trovato in totale nel parco?

b) Un forte temporale estivo sradica 4 tigli, 2 magnolie e 1 albero dei tulipani; quanti alberi ci sono ora nel parco?

c) Conosci gli alberi censiti da Maia e dai suoi compagni?

d) Nelle vicinanze della scuola che frequenti c’è un parco? Se sì, conosci i nomi degli alberi presenti? [132; ]

L'errore più comune che potresti commettere è quello di non comprendere bene il testo del problema.

imparaerrore dall'

Una lettura frettolosa e superficiale può essere il punto di partenza di molti insuccessi.

Leggi il problema più volte e lentamente, soffermarti sulle parole chiave o sulla struttura della frase, individua i dati essenziali e distingui quali numeri o informazioni sono rilevanti per la risoluzione e quali invece sono distrattori o informazioni superflue. Può capitare che il tuo ragionamento e il procedimento che ne deriva siano giusti, ma che comunque tu non riesca a centrare l’obiettivo del problema: è meglio evitare di cominciare a fare calcoli senza aver prima stabilito

una sequenza logica di passaggi. Inoltre, se il problema ti sembra complesso, prova a dividerlo in parti, in problemi più piccoli. Controlla le unità di misura, fa le conversioni, e ricordati sempre di verificare il risultato. Ogni errore è un indizio!

101 Che numero si ottiene sottraendo da 40 la somma di 5, 4 e 12? 40 (5 + 4 + ) = 40 =

102 Che numero si ottiene addizionando alla differenza tra 26 e 10 il prodotto tra 12 e 3? [52]

103 Quale risultato si ottiene moltiplicando la differenza tra 14 e 8 con la differenza tra 25 e 18? [42]

104 Che numero si ha aggiungendo al prodotto tra 3 e 7 la differenza tra 15 e 9 e dividendo il risultato per 3? [9]

105 Che numero si ottiene aggiungendo alla differenza tra 37 e 25 la differenza tra 28 e 21 e moltiplicando il risultato per 5? [95]

COMPETENZE

PROBLEM SOLVING

Risolvi sul quaderno.

1 Marta, Giulia e Carlotta hanno i capelli una corti, una lunghi e una ricci. Portano scarpe numero 36, 38 e 39. La ragazza con i capelli corti è Giulia. La ragazza con i capelli ricci porta il 36 di scarpe. Carlotta invece porta il 39. Come sono i capelli di Marta?

2 Ho comperato 3 palme e 2 pini e ho speso 115 €; Carmelo, nello stesso vivaio, ha comperato 3 palme e 4 pini spendendo in tutto 155 €. Quanto costano in quel vivaio una palma e un pino?

Dati: costo di 3 palme e 2 pini → 115 € costo di 3 palme e 4 pini → 155 €

Rappresentazione grafica:

→ 115 €

→ 155 € c) → (155 115) €

ANALIZZARE E INTERPRETARE DATI

3 Consulta la seguente tabella e rispondi alle domande successive. Autolinee: Modica - Pozzallo - Ispica - Rosolini - Noto - Avola - Aeroporto - Catania

a) Quanto tempo impiega l’autobus per andare da Modica a Catania?

b) Quante corse festive ci sono da Rosolini all’aeroporto?

c) Tra tutte le corse, feriali e festive, da Pozzallo all’aeroporto qual è la più veloce?

d) Lorena e Gabriella, che abitano a Noto, devono prendere l’aereo a Catania alle ore 19:30 di una domenica di luglio; a che ora devono prendere l’autobus per l’aeroporto? (Ricorda che bisogna essere in aeroporto almeno due ore prima del volo.)

4 I diagrammi ad albero vengono spesso utilizzati per indicare quegli elementi chiave che servono a classificare oggetti e/o organismi. Ne proponiamo due. Puoi crearne di nuove anche tu.

Osserva il seguente diagramma ad albero ed esegui le richieste.

Hanno un ciclo vitale? (nascono, crescono…)

Ricavano nutrimento da altri esseri viventi?

a) Classifica gli elementi forniti. Manciata di sabbia - pitone - rosmarino - cacciavite - abete - libro di storia - zanzara

• Non viventi:

• Animali:

• Piante:

b) A tua scelta ora scrivi almeno quattro elementi per ogni categoria.

• Non viventi:

• Animali:

• Piante:

5 Il seguente diagramma ad albero è una chiave per classificare i vertebrati. Utilizzala per classificare gli animali riportati sotto.

MAMMIFERI

Allattano la prole?

Respirano aria?

Hanno il corpo coperto di piume?

PESCI

UCCELLI Hanno il corpo coperto di scaglie?

RETTILI

ANFIBI NO NO NO NO SÌ

SFIDA MATEMATICA

6 I risparmi di Luca

Luca ha messo da parte 54,40 euro. Nel suo gruzzolo ci sono solo monete da 2 euro, da 1 euro e da 20 centesimi di euro. Il numero dei tre tipi di monete presenti nel gruzzolo di Luca è lo stesso. Quante monete da 1 euro ha Luca?

(Testo tratto dalla gara Giochi d’autunno, organizzata dal Centro PRISTEM dell’Università Bocconi di Milano)

ROAD MAP PER TUTTI

DI PROBLEMI TEORIA PAG. 164

DATO UN PROBLEMA

Come si procede per risolverlo?

Le fasi per risolvere un problema sono:

• leggere il testo con attenzione;

• scrivere i dati e le richieste;

• effettuare i calcoli per rispondere alle richieste

• formulare una risposta.

Come possono essere i dati?

NASCOSTI

cioè scritti a parole e non a numero.

Marco compra una dozzina di uova spendendo 3,60 €; quanto costa ogni uovo? Dozzina = 12 è il dato nascosto. ESEMPIO

SUPERFLUI

cioè non necessari per la soluzione.

MANCANTI

cioè non presenti, quindi impossibile risolvere il problema.

Marta, che ha 15 anni, compera 3 DVD da 23,50 €, quanto spende in tutto? 15 anni è il dato superfluo. ESEMPIO

ESEMPIO

In una bancarella del mercato ci sono 5 ceste di mele, 6 di pere, 4 di uva, 3 di prugne e le altre sono di fragole. Quante ceste ci sono in tutto?

In numero di ceste di fragole è il dato mancante.

1 Leggi con attenzione il testo del seguente problema e completa.

Ieri a Lodi il treno che doveva arrivare alle 14:05 è arrivato con 1 ora e 20 minuti di ritardo. A che ora è arrivato il treno?

Dati Richiesta

Ora prevista di arrivo del treno: Ora effettiva di arrivo del treno = ?

Ritardo: 1h e

Effettua i calcoli → + 1:20 = 15:25

Formula una risposta → Il treno è arrivato alle

2 Traduci in numero i seguenti dati nascosti.

Un paio = 2, un centesimo = 1 : 100 = 0,01

a) una settimana il quadruplo il doppio

b) il triplo una decina un decimo

3 MATEMATICA IN AZIONE Leggi il seguente problema e rispondi alle richieste.

Lo zio Carlo, che calza il numero 43 di scarpe, va in vacanza al mare con l’aereo. Parte da casa alle ore 12, l’aereo parte alle 14:50, arriva al mare nel tardo pomeriggio e dopo una decina di minuti incontra suo nipote. Quante ore impiega per arrivare al mare?

Il testo del problema:

• presenta dati superflui?

Se hai risposto SÌ, qual è il dato superfluo?

• presenta dati nascosti?

Se SÌ, qual è il dato nascosto?

• fornisce tutti i dati necessari per la soluzione?

Se hai risposto NO, quale dato manca?

In ogni problema trova il dato superfluo.

4 MATEMATICA IN AZIONE Marika lavora in pasticceria da 4 anni. Ieri ha venduto 6 kg di cioccolatini e 3 kg di gianduiotti a 25 € al chilogrammo. Quanto ha incassato?

Sì No

Sì No

Sì No

a) 4 anni b) 6 kg c) 3 kg d) 25 €

5 MATEMATICA IN AZIONE Giada ha confezionato un vestito nuovo nella sua sartoria in via Vercelli n. 42. Ha speso 12 € di bottoni e 42 € di stoffa. Se lo ha rivenduto a 106 €, quanto ha guadagnato?

a) n. 42 b) 12 € c) 42 € d) 106 €

In ogni problema trova il dato mancante.

6 MATEMATICA IN AZIONE Nonna Filippa compra una bambola e un trenino ai suoi due nipotini.

Se la bambola è costata 12 €, quanto ha speso in tutto?

a) costo della bambola

b) costo del trenino

c) costo totale

d) età dei bambini

PER RISOLVERE UN PROBLEMA

Che cos’è il metodo grafico?

Il metodo grafico è quello che utilizza dei disegni per risolvere un problema.

METODO GRAFICO

166

PER RISOLVERE UN PROBLEMA

Come è composta e a che cosa serve una tabella a doppia entrata?

Una tabella a doppia entrata è formata da righe e da colonne; serve per organizzare i dati quando sono di tipo diverso.

Metodi per risolvere problemi

Risolvi i seguenti problemi o con il metodo grafico o con una tabella a doppia entrata.

7 MATEMATICA IN AZIONE Due cugini, Pia e Mario, hanno 48 € e vogliono dividerseli in modo che Pia, che è la maggiore, abbia il triplo degli euro di Mario. Quanti euro spettano ad ognuno di loro?

parte di Mario

parte di ............................ (triplo della parte di ............................)

48 euro in totale (................. parti)

48 : 4 = € parte di Mario × 3 = € parte di [ ; 36 €]

8 MATEMATICA IN AZIONE Marco e Luca vogliono dividersi 39 figurine in modo che Luca ne abbia 7 più di Marco. Quante figurine avrà ognuno di loro?

figurine di Marco (una striscia)

figurine di Luca (una striscia + 7 figurine)

figurine totali (due strisce uguali + 7 figurine) 39

39 7 = doppio delle figurine di Marco : 2 = figurine di Marco + 7 = figurine di Luca [ ; 23]

9

10

MATEMATICA IN AZIONE Il papà paga la rata dell’automobile e quella del televisore spendendo in tutto 600 €. Qual è l’importo di ogni rata, se quella della tv è la metà di quella dell’automobile? [200 €; 400 €]

MATEMATICA IN AZIONE La tabella seguente riporta gli orari di apertura del centro benessere “Namasté”.

Lunedì Martedì Mercoledì Giovedì Venerdì Sabato Domenica

Mattina 10 - 13 10 - 13 chiuso 10 - 13 10 - 20 orario continuato 10 - 20 orario continuato 10 - 20 orario continuato

Pomeriggio 15 - 20 15 - 20 chiuso 15 – 20

a) Quante ore è aperto il centro benessere lunedì mattina?

b) E giovedì pomeriggio?

c) In quali giorni si può andare al centro nella pausa pranzo?

d) Lunedì pomeriggio Rosanna e Lamberto vogliono fare il percorso di 4 ore “Lei&Lui”. A che ora al massimo devono arrivare per essere sicuri di completarlo?

11 MATEMATICA IN AZIONE Osserva la tabella e rispondi.

Ambulatorio del dott. Cervelli - orario settimanale di apertura

Lunedì Martedì Mercoledì Giovedì Venerdì

Mattina 8 - 11 8 - 12 8 - 12

Pomeriggio 16 - 19 16 - 19 16 - 18

a) Pierino può andare dal dottore lunedì alle 11:30?

b) Se Roberta arriva in ambulatorio mercoledì alle 18, lo trova aperto o chiuso?

c) La mamma di Luisa lavora tutte le mattine e il mercoledì pomeriggio: quando può recarsi dal medico?

d) Quante ore la settimana è aperto lo studio medico?

PER RISOLVERE

UN PROBLEMA

Quando si utilizza il diagramma ad albero?

DIAGRAMMA AD ALBERO

Il diagramma ad albero si utilizza quando è necessario non escludere alcuna combinazione.

PER RISOLVERE UN PROBLEMA

ESPRESSIONE RISOLUTIVA

Si può utilizzare un'espressione?

Sì, basta mettere in successione le operazioni da svolgere per risolvere il problema, utilizzando le parentesi per stabilire le precedenze.

Esci di casa con 2 banconote da 20 € e comperi 2 CD da 13,50 € e 3 riviste da 3,75 €; quanto ti rimane?

2 × 20 (2 × 13,50 + 3 × 3,75) = = 40 (27 + 11,25) = = 40 38,25 = 1,75 €

Risolvi i seguenti problemi o con un diagramma ad albero o con un’espressione.

12 Quanti numeri diversi di tre cifre, senza ripeterle, si possono ottenere con 2, 4, 6? 2 4 6

13 MATEMATICA IN AZIONE Al torneo di scacchi della scuola si gioca per eliminazione. Ivan è risultato anche quest’anno vincitore. Osserva e completa il diagramma del torneo, poi rispondi alle domande.

1a fase Semifinali Finale Vincitore

Clelia → Clelia

Iorio

Ivan → Ivan → Ivan

Said → Said

Pietro

Vincenzo } } }

Serena

Maria } Serena

a) Quanti erano i concorrenti?

b) Quante partite ha vinto Ivan, inclusa la finale?

14 MATEMATICA IN AZIONE Nella cantina di una trattoria ci sono 640 bottiglie di vino: 170 di rosso, 240 di rosato, 230 di vino bianco. Ogni giorno se ne consumano 7 di rosso, 9 di rosato e 8 di bianco. Quante bottiglie di vino rimarranno dopo 7 giorni?

• vino consumato ogni giorno → 7 + 9 + 8 =

• vino consumato in 7 giorni → 7 × =

• espressione → 640 7 × (7 + 9 + 8) = Dopo 7 giorni nella cantina rimarranno bottiglie di vino.

15 MATEMATICA IN AZIONE Alla gita delle terze partecipano 48 alunni e 4 insegnanti. Se 16 alunni sono di terza A e 14 sono di terza B, quanti sono gli alunni della terza C? (Attenzione ai dati superflui.)

16 MATEMATICA IN AZIONE In un cesto con le offerte di un supermercato ci sono delle confezioni di pennarelli: 5 confezioni da 2 pennarelli, 13 da 12 pennarelli, 8 da 24 pennarelli e 10 da 36 pennarelli. Quanti pennarelli ci sono in totale? 5 × 2 + [718]

SIMULAZIONE DI VERIFICA

1 Per organizzare tutti i dati di un problema, senza escludere alcuna possibilità, si usa:

a) una retta orientata

b) un diagramma ad albero

c) una tabella a doppia entrata

d) un grafico

2 Quale rappresentazione grafica indica che il 1° oggetto è il quadruplo del 2°?

a)

b)

Per ogni problema indica l’espressione risolutiva.

c)

d)

3 Quattro fratelli si dividono equamente le spese sostenute per organizzare una festa e cioè l’acquisto di 7 festoni da 4 € l’uno e di 6 confezioni di fuochi artificiali da 8 € l’una.

Quanto spende ciascun fratello?

a) (7 × 4 + 6 × 8) : 4

b) 7 × 4 + 6 × 8 : 4

c) (7 × 4) + (6 × 8 : 4)

d) (7 + 6) × (4 + 8) : 4

4 Ogni 4 mesi la signora Mughetto rinnova i fiori del suo balcone comprando 5 vasi di gerani a 4 € ciascuno e 10 di garofani a 6 €.

Quanto spende in un anno?

a) 3 × (5 × 4) + (10 × 6)

b) 12 × (5 × 4 + 10 × 6)

c) 12 : 4 × (5 × 4 + 10 × 6)

d) 4 × (5 × 4 + 6 × 10)

5 Stabilisci quale rappresentazione corrisponde al seguente problema e risolvilo. In un parcheggio di Montecarlo in occasione del Gran Premio di Formula 1 sono state contate 580 autovetture; quelle con targa italiana erano 46 in più del doppio di quelle con targa straniera. a) b)

con targhe estere

auto

con targhe italiane

con targhe estere

auto 580

Quante erano le automobili di ogni tipo? straniere, italiane

Risolvi i seguenti problemi, riferiti a situazioni reali, utilizzando in modo adeguato i metodi studiati.

6 Un negoziante acquista 35 cestini di vimini alti 18 cm a 11,45 € ciascuno. Se li rivende a 15,50 € l’uno, quanto guadagna?

7 Una magliaia ha confezionato 10 maglioni lavorando 6 giorni per 8 ore al giorno ma fermandosi 10 minuti ogni 2 ore per una pausa e li ha venduti a 46,80 € ciascuno. Qual è stato il suo guadagno medio orario, se per ogni maglione ha usato 4 gomitoli che costano 4,50 € l’uno?

8 La tabella riporta i tempi di una gara di corsa tra amici.

Quale affermazione è sicuramente falsa?

a) Nicolò è arrivato ultimo.

b) Michele è arrivato prima di Davide.

c) Andrea ha impiegato 10 minuti.

d) Andrea è arrivato primo.

Quale affermazione è vera?

a) Andrea ha impiegato 11 minuti.

b) Nicolò ha impiegato 13 minuti.

Nome Ora di partenza Ora di arrivo

Nicolò 9:04 9:18

Andrea 9:04 9:13

Davide 9:04 9:17

Michele 9:04 9.15

c) Davide ha impiegato 21 minuti.

d) Michele ha impiegato 11 minuti.

9 Un depuratore domestico fornisce acqua a tre livelli di temperatura. Inoltre, l’acqua può essere naturale o gassata. In quanti modi potresti bere l’acqua fornita da quel depuratore?

(Risolvi il problema aiutandoti con un diagramma ad albero).

10 Una ditta di autotrasporti possiede 5 autocarri della portata di 32 quintali ciascuno e altri 7 della portata di 24 quintali. Sapendo che ogni autocarro può effettuare 7 viaggi in ogni giornata lavorativa, calcola quanta merce è possibile spostare in 5 giorni riempiendo completamente tutti i mezzi della ditta.

11 Un’indagine relativa alle bevande preferite effettuata tra un gruppo di ragazzi di 12 anni ha fornito i seguenti risultati:

femmine maschi

10 tè freddo 23 Coca Cola® 2 chinotto 7 aranciata 18 coca cola 4 acqua minerale 9 aranciata 5 tè freddo

Organizza i dati in una tabella e rispondi alle domande:

a) Qual è la bevanda meno gradita tra i maschi di quel gruppo?

b) Qual è la bevanda che piace meno alle femmine?

c) Qual è la bevanda che piace più ai maschi?

d) Quanti sono i maschi intervistati?

e) Quante sono le femmine intervistate?

5

I GRAFICI

Chi ha della

paura matematica?

La matematica non è fatta solamente di calcoli difficili, problemi da risolvere, formule e proprietà da conoscere, ma possiede anche degli aspetti molto pratici e interessanti, per esempio i grafici!

Non lasciarti impaurire da nomi come “ortogramma” o “aerogramma”: scoprirai ben presto che questi, come altri tipi di grafici, sono strumenti molto utili per visualizzare a colpo d’occhio le informazioni, per interpretarle, per confrontare le quantità, capire le tendenze e dedurre conclusioni importanti.

Un grafico, soprattutto quando è ricco di dati, di colori e di etichette, ti può sembrare confuso e generare in te il timore di non riuscire a coglierne il significato principale. Niente paura , usando un po’ di curiosità e osservando attentamente, grazie ai grafici, potrai vedere con chiarezza il senso di quello che prima era solo un mucchio di numeri!

ROAD MAP la nostra

IMPARIAMO A RACCOGLIERE E ORGANIZZARE I DATI

CONOSCIAMO IL CONCETTO DI FREQUENZA

RAPPRESENTIAMO GRAFICAMENTE I DATI CON UN IDEOGRAMMA

SCOPRIAMO CHE COSA SONO GLI ORTOGRAMMI, I DIAGRAMMI A SEGMENTI E GLI AEROGRAMMI

MATERIALE INTEGRATIVO MULTIMEDIALE

Focus

Videolezione

Verifica interattiva

RACCOLTA E ORGANIZZAZIONE DEI DATI 1

SUCCEDE CHE...

Nella classe di Emma hanno svolto un’indagine sui primi piatti preferiti. Il risultato è che a 5 alunni piace la pasta, a 4 piace il risotto, a 7 piacciono le lasagne, a 10 piace la pizza, a 1 il minestrone, mentre la pasta in brodo non piace a nessuno.

Come possono organizzare meglio i dati della loro indagine?

I dati di un’indagine, cioè le informazioni raccolte, per esempio tramite un questionario, si possono organizzare in una tabella riassuntiva costituita da righe e colonne, cioè una tabella a doppia entrata.

Il pregio di una tabella a doppia entrata è quello di raccogliere i dati di un’indagine in modo chiaro e in poco spazio. La prima riga e la prima colonna sono quelle che intestano la tabella, nelle caselle si riportano i dati.

Il numero delle volte con cui si presenta il dato considerato si dice frequenza. Righe

Nell’indagine della classe di Emma la frequenza è data dal numero di alunni che ha scelto un tipo di primo piatto: la frequenza della pasta è 5, quella della pasta in brodo è 0 ecc. Le informazioni raccolte possono essere quindi rappresentate con la seguente tabella.

Primo piatto preferito No alunni/e → frequenza

1 Rispondi con Vero o Falso.

a) Per raccogliere informazioni si può usare un questionario. V F

b) I dati e i questionari sono la stessa cosa. V F

c) La tabella a doppia entrata ha due righe e due colonne. V F

d) Una tabella a doppia entrata raccoglie i dati di un’indagine.

e) La frequenza è il numero di volte con cui si presenta un dato.

2 In questa tabella sono riportati i risultati di una ricerca sul mezzo di trasporto usato dagli alunni per recarsi a scuola. Osservala e rispondi.

Mezzo di trasporto No alunni/e → frequenza

a) Quanti sono in totale i casi esaminati?

b) Qual è la frequenza degli alunni che vanno a scuola in bicicletta?

c) Quale mezzo di trasporto ha la frequenza maggiore?

d) Quale mezzo di trasporto ha la frequenza minore?

e) Quanti alunni usano un mezzo totalmente ecologico per andare a scuola?

3 MATEMATICA IN AZIONE Nel gioco della morra cinese due giocatori si sfidano simulando con la mano le forbici, la carta o il sasso.

Il sasso vince sulla forbice, la forbice sulla carta e la carta sul sasso. Se escono due simboli uguali si rigioca.

F

F

Forbice Carta Sasso

Gioca con un’altra persona e riporta i risultati in una tabella come la seguente.

Nome giocatore

RAPPRESENTAZIONE GRAFICA DI DATI 2

SUCCEDE CHE...

Il nonno di Pietro sta leggendo un articolo che parla della produzione di vino nell’ultimo anno, ma non riesce a interpretare il grafico che riporta i dati, in cui ci sono una serie di bottiglie che indicano la produzione. Chiede aiuto a Pietro.

Ideogramma

Vino bianco

Vino DOC

Vino IGT

10 milioni di ettolitri

Per aiutarlo, Pietro deve conoscere un tipo particolare di rappresentazione grafica: l’ideogramma.

Le rappresentazioni grafiche servono per rendere più chiara e immediata la lettura di dati relativi a fenomeni di tipo diverso. Sono parecchi i tipi di rappresentazioni grafiche e sicuramente ne conosci e ne usi già alcuni, come il diagramma cartesiano.

Ora ne analizzeremo altri: ideogramma , ortogramma , diagramma a segmenti, poligonale delle frequenze e areogramma

Realizzare un ideogramma è semplice:

• si individua il simbolo che rappresenta l’oggetto considerato dall’indagine;

• si assegna un valore numerico al simbolo scelto (unità grafica);

• si ripete il simbolo tante volte quante servono per rappresentare i valori dei dati.

L’ideogramma ha il vantaggio di essere una rappresentazione grafica comprensibile per tutti, ma ha il limite di non essere preciso per la rappresentazione numerica dei dati, quando sono parti dell’unità grafica.

L’ideogramma è una rappresentazione grafica che utilizza come unità grafica un disegno simbolico che dà l’idea del fenomeno analizzato.

È adatto a rappresentare dati da mettere a confronto.

Pietro ha potuto aiutare il nonno a interpretare il grafico dell’articolo: una bottiglia vale 10 milioni di ettolitri; mezza bottiglia vale la metà di una, cioè 5 milioni di ettolitri. Quindi, la produzione di vino rosso supera i 20 milioni di ettolitri, ma è inferiore a quella di vino bianco, anche se non si può stabilire di quanto.

1 Rispondi con Vero o Falso.

a) Le rappresentazioni grafiche facilitano la lettura di dati. V F

b) Il diagramma cartesiano è un tipo di rappresentazione grafica. V F

c) L’ideogramma è una rappresentazione che utilizza colonne o rettangoli. V F

d) L’ideogramma è un grafico che si usa solo nelle banche. V F

e) L’ideogramma non è molto preciso nella rappresentazione dei dati numerici. V F

f) L’ideogramma è adatto per mettere dati a confronto. V F

2 Quale unità grafica utilizzeresti per rappresentare le giornate di sole del mese di luglio?

= 1 giorno = 1 giorno = 1 giorno

3 Due giorni di neve sono rappresentati dall’unità grafica .

Come indicheresti sette giorni di neve?

4 L’unità grafica di un ideogramma che rappresenta le auto vendute da una concessionaria è il simbolo: = 20 auto.

a) La vendita di 40 auto è rappresentata da:

b) La vendita di 50 auto è rappresentata da:

5 MATEMATICA IN AZIONE Due amici con la passione del bird watching si sono recati per 4 domeniche di seguito a censire le anatre presenti in un’area umida del Parco del Ticino (tra Piemonte e Lombardia).

I risultati sono riportati nell’ideogramma.

9 settembre

16 settembre

23 settembre

30 settembre

Dovranno inviare i dati alla società ornitologica insieme ad alcune informazioni. Aiutali a compilare correttamente la scheda.

a) Numero totale di avvistamenti nel mese

b) Domenica con maggior numero di avvistamenti

c) Domenica con minor numero di avvistamenti

d) Scarto minore di avvistamenti tra una domenica e un’altra = 10 anatre = 5 anatre

Ortogramma

SUCCEDE CHE...

Claudia sta terminando la sua ricerca di geografia sui più importanti monti d’Italia e vuole integrarla con un grafico che metta in evidenza le differenze di altitudine.

Quale grafico si adatta meglio alla sua ricerca?

Monte Rosa Monte Bianco Marmolada Bernina Monviso Altezza (arrotondata alle centinaia)

L’ortogramma , detto anche grafico a barre o diagramma a colonne, è sicuramente un grafico adatto allo scopo di Emma.

L’ortogramma è una rappresentazione grafica che utilizza dei rettangoli con la stessa base e l’altezza corrispondente alla frequenza. Si usa per confrontare visivamente il valore di alcuni dati.

Per realizzare un ortogramma si procede nel modo seguente:

• si tracciano due semirette che formano un angolo retto;

• si disegnano, alla stessa distanza, le basi tutte uguali di tanti rettangoli quanti sono gli elementi riportati in tabella (nel caso di Emma 5 monti);

• si stabilisce l’unità di misura sull’asse verticale (nel caso di Emma 1 000 m);

• si costruiscono le altezze dei rettangoli corrispondenti ai valori dati.

I rettangoli possono essere disposti sia in modo verticale che orizzontale: in questo secondo caso si parla di ortogramma a nastro

Anche la scelta dei colori può aiutare a rendere il grafico più adatto al tema trattato: l’ortogramma a lato parla di fiumi e si è scelto il colore azzurro. 5 000 altezza (m)

Claudia ha realizzato l’ortogramma ed è veramente soddisfatta del suo lavoro.

1 MATEMATICA IN AZIONE L’ortogramma

rappresenta il numero di gelati venduti in una sera da quattro gelaterie di una città di mare.

Scrivi il numero di gelati venduti da ogni gelateria.

2 MATEMATICA IN AZIONE Il signor Giuseppe ha segnato su una tabella la quantità di frutta presente sul proprio bancone di vendita.

Tipologia

Costruisci sul quaderno l’ortogramma che rappresenti questi dati.

3 MATEMATICA IN AZIONE Il seguente ortogramma mostra la velocità massima in km/h di alcuni animali terrestri.

Completa la tabella come nell’esempio (Per trovare il valore esatto aiutati con un righello).

Specie 1

Diagramma a segmenti

SUCCEDE CHE...

Emma per l’estate ha chiesto in regalo una bicicletta nuova. Il papà le dice che la comprerà solo se i suoi voti di matematica miglioreranno nel II quadrimestre.

Come si potrebbe rappresentare l’andamento dei suoi voti?

Questo tipo di informazioni che varia nel tempo si può rappresentare bene con il diagramma a segmenti.

Nel diagramma a segmenti la lunghezza dei segmenti corrisponde alla frequenza con cui il dato si presenta. Si usa per rappresentare dati che cambiano nel tempo.

Il diagramma a segmenti è simile all’ortogramma e si costruisce con lo stesso procedimento:

• si tracciano due semirette che formano un angolo retto;

• alla stessa distanza uno dall’altro, si tracciano tanti segmenti quanti sono i dati da rappresentare (nel caso di Emma i voti del II quadrimestre);

• si stabilisce l’unità di misura sull’asse verticale (nel caso di Emma u = 2 punti);

• si costruiscono le altezze dei segmenti corrispondenti ai valori dati.

Poligonale delle frequenze

febbraio marzo aprile maggio

La poligonale delle frequenze è la spezzata che congiunge gli estremi dei segmenti del diagramma a segmenti.

È un grafico lineare.

Partendo dal diagramma a segmenti precedente, tracciamo la poligonale delle frequenze. Questo è un grafico lineare che può essere costruito anche senza i segmenti, ma solo con i punti.

Emma rappresenta con una poligonale i suoi voti e nota che termina in salita. Il papà non ha più dubbi: la spezzata è la chiara dimostrazione che presto dovrà comprare una nuova bicicletta alla figlia.

ESERCIZI

1 Rispondi con Vero o Falso.

a) Il diagramma a segmenti è simile all’ideogramma. V F

b) Nel diagramma a segmenti la lunghezza corrisponde alla frequenza. V F

c) I diagrammi a segmenti si usano per confrontare i dati che cambiano nel tempo. V F

d) La poligonale delle frequenze è una linea spezzata. V F

e) La poligonale delle frequenze è un grafico a barre. V F

2 MATEMATICA IN AZIONE Osserva il seguente grafico lineare relativo alla quantità di frutta venduta da un minimarket e completa la tabella. frutta venduta in kg 40 30 10 0 20 lu ma me gio ve sa dom

3 MATEMATICA IN AZIONE Rappresenta sul quaderno con un grafico lineare il numero di cani dati in adozione nei canili della regione Lazio nei mesi invernali.

Mese novembre dicembre gennaio febbraio Frequenza 30 42 25 28

4 MATEMATICA IN AZIONE Osserva il grafico e determina la frequenza delle temperature massime registrate in quattro città italiane in un giorno di agosto.

Frequenze: Roma = 31 Milano = Firenze = Palermo = Giorni kg di frutta venduti → frequenza lunedì 15 martedì mercoledì

Fonte: ilmeteo.it

Areogramma circolare

SUCCEDE CHE...

Pietro ha fatto il censimento del colore dei capelli degli alunni nelle classi del tempo prolungato della sua scuola. Vuole rappresentare graficamente i dati raccolti.

Colore dei capelli castano nero biondo rosso

Totale

Numero alunni 90 45 35 10 180

Per questo tipo di indagine è molto adatto l’areogramma circolare, detto anche diagramma a torta o grafico a torta

L’areogramma circolare è una rappresentazione grafica che utilizza un cerchio suddiviso in spicchi proporzionali alle quantità da rappresentare.

È adatto per rappresentare la suddivisione in parti di un intero.

Rappresentiamo con un areogramma circolare i dati dell’indagine di Pietro.

Per trovare quanto devono essere grandi gli spicchi che corrispondono ai 4 colori di capelli si procede in questo modo:

• per calcolare quanto deve essere ampio lo spicchio relativo a ogni alunno dividiamo 360°, che è l’ampiezza dell’angolo giro, per il totale degli alunni, che è 180: 360° : 180 = 2° (ampiezza spicchio corrispondente a ogni alunno);

• si calcola ora l’ampiezza degli spicchi corrispondente a ciascun colore di capelli:

2° × 90 = 180° capelli castani

2° × 45 = 90° capelli neri

2° × 35 = 70° capelli biondi

2° × 10 = 20° capelli rossi

→ la somma deve essere sempre 360°

Un arco è la parte di circonferenza delimitata da due suoi punti (estremi dell’arco).

• per realizzare gli spicchi: si disegna una circonferenza, con il goniometro si delimitano gli archi che corrispondono alle ampiezze trovate, si congiungono gli estremi con il centro della circonferenza;

• si colorano gli spicchi in modo diverso;

• si fa corrispondere ogni colore al dato corrispondente → legenda dell’areogramma.

Il grafico a torta del censimento di Pietro evidenzia molto bene, anche con la scelta dei colori, che gli alunni con i capelli castani sono la metà di tutti gli alunni, quelli con i capelli neri sono un quarto del totale e gli alunni con i capelli biondi sommati a quelli con i capelli rossi formano un altro quarto del totale.

ESERCIZI Primi

1 Rispondi alle seguenti domande.

a) Quale figura geometrica utilizza l’areogramma circolare?

b) A che cosa corrispondono gli spicchi di un areogramma circolare?

c) Quando si utilizza un areogramma circolare?

2 Segui le indicazioni per rappresentare con un areogramma circolare i dati della tabella relativi ai fiori presenti sul terrazzo di Anna.

Fiori Rose Gerani Fresie Totale

Numero 12 15 9

Angolo corrispondente 12 × = 360°

a) Calcola il numero totale dei fiori → 12 + 15 + =

b) Dividi 360° per il totale dei fiori → 360°: = Moltiplica il risultato ottenuto per 12; 15 e 9: × 12 = × 15 = × 9 =

c) Con il goniometro delimita gli archi che corrispondono alle rose, ai e alle

d) Congiungi il centro della con gli degli archi

e) Colora con colori diversi i tre spicchi ottenuti e fai la legenda dell’ rose gerani fresie

3 MATEMATICA IN AZIONE L’areogramma in figura rappresenta le lingue utilizzate dai followers per commentare sulla pagina social di un noto influencer.

inglese tedesco italiano altre lingue francese spagnolo

Rispondi alle domande.

a) Quale lingua è stata maggiormente usata e in quale percentuale?

b) Quale è stata la terza lingua più usata e in quale percentuale?

c) Quali lingue differiscono del 5%?

d) Calcola la percentuale di francese e tedesco, sapendo che il cerchio in totale corrisponde al 100% e che le due lingue hanno la stessa percentuale. inglese tedesco italiano altre lingue francese spagnolo

MAPPA

si organizzano con tabelle di frequenza

si rappresentano graficamente con

ESERCIZI E PROBLEMI

LEZIONE 1

RACCOLTA E ORGANIZZAZIONE DEI DATI

1 Rispondi sul quaderno alle domande.

a) Che cos’è una tabella a doppia entrata?

b) Perché la tabella a doppia entrata è utile per organizzare le informazioni?

c) Che cosa si riporta nelle caselle di una tabella a doppia entrata?

d) Che cos’è la frequenza?

MATEMATICA IN AZIONE Risolvi i seguenti esercizi.

2 La seguente tabella riporta i risultati di un’indagine statistica sul consumo di bibite in un giorno nel distributore automatico di un istituto superiore.

Dopo aver letto i dati, segna con una crocetta se le affermazioni seguenti sono vere o false.

a) Le bibite consumate sono 240.

b) La frequenza delle bibite gassate è di 98.

c) La frequenza delle bibite al gusto di agrumi è 70.

d) La frequenza delle bibite al gusto di pesca è di 69.

e) La frequenza delle bibite al gusto di tè è di 27.

f) Il chinotto ha la frequenza minore.

g) Il succo di pesca ha la frequenza maggiore.

h) La frequenza dei succhi di frutta supera quella delle bibite gassate.

i) Non ci sono bibite con la stessa frequenza.

3 La tabella riporta le preferenze calcistiche in una classe di una scuola secondaria di primo grado.

Squadra Roma Lazio Juventus Milan Verona Fiorentina Totale

Frequenza 9 8 4 3 2 1

Rispondi alle seguenti domande.

a) Quanti sono gli alunni della classe?

b) Qual è la frequenza dei tifosi delle squadre della capitale?

c) Qual è la frequenza dei tifosi della squadra toscana?

d) Quanti alunni hanno dichiarato di tifare Inter?

e) Quanti alunni tifano per una squadra che non gioca in un capoluogo di regione?

f) In quale regione d’Italia è molto probabile che si sia svolta l’indagine?

4 I seguenti dati riguardano il numero di ore dedicate alla tv nell’ultimo mese di dicembre dagli alunni di una classe di scuola secondaria di primo grado: 56 65 42 31

Raccogli i dati in una tabella in modo da evidenziare il numero dei ragazzi e il numero di ore

5 MATH Take a paper cup and drop it on the floor. Do it 20 times and enter the data in the table.

6 Sono riportati di seguito i colori preferiti da 28 alunni di una classe.

arancio • verde • rosso • verde • giallo • blu • bianco • rosa • verde • blu • rosa • giallo • arancio • rosa • bianco • rosso • giallo • blu • rosso • verde • blu • bianco • verde • rosso • giallo • blu • bianco • blu

Organizza i dati in una tabella.

Colore preferito

arancio ™ ™ 2

verde

Rispondi alle seguenti domande.

a) Qual è il colore che ha la maggiore frequenza?

b) Qual è il colore che ha la minore frequenza?

c) Ci sono colori che hanno lo stesso numero di preferenze? Se la risposta è affermativa, quali sono?

7 MATEMATICA IN AZIONE È stata svolta un’indagine sul mese preferito per andare in vacanza tra gli operai di un reparto di una nota fabbrica di automobili. Ecco i risultati. aprile • giugno • luglio • agosto • luglio • agosto • giugno • luglio • settembre • agosto • aprile • luglio • maggio • agosto • maggio • dicembre • luglio • agosto • agosto • giugno • settembre

Sul quaderno registra i dati in una tabella ordinandoli dalla frequenza maggiore a quella minore e poi rispondi alle seguenti domande.

a) Quanti sono gli intervistati?

b) Quale mese ha la frequenza più alta?

c) Quale mese ha la frequenza più bassa?

d) Quali mesi hanno la stessa frequenza?

e) Qual è la frequenza dei mesi invernali?

8 Organizza con i tuoi compagni un’intervista per scoprire con quale mezzo vengono a scuola gli alunni del tuo istituto.

Sottoponete il questionario alle altre classi per avere un’indagine significativa. Raccogliete i dati ottenuti in una tabella e provate a commentarli.

9 MATEMATICA IN AZIONE Raccogli in una tabella i dati dei matrimoni celebrati nelle macroregioni italiane.

Anno 1992: Nordovest 76 321; Nordest 53 063; Centro 55 046; Sud 87 295; Isole 40 623.

Anno 2017: Nordovest 44 574; Nordest 33 287; Centro 35 833; Sud 52 611; Isole 24 982.

Fonte: ISTAT

Macroregione Nordovest

Anno 1992 76 321

Anno 2017 44 574

Segna con una crocetta se le affermazioni riguardanti la tabella sono vere o false.

a) I matrimoni totali del 1992 sono stati meno di 300 000.

b) I matrimoni totali del 2017 sono stati oltre 200 000.

c) In tutte le macroregioni c’è stato un calo dei matrimoni.

d) Il maggior calo di matrimoni è stato nelle Isole.

e) In entrambi i casi il Sud ha avuto la maggiore frequenza di matrimoni.

f) In entrambi i casi il Nordest ha superato il Nordovest.

g) La somma di Sud e Isole non ha mai superato il Centro.

10 Lancia due dadi e somma i punti ottenuti. Esegui 20 volte il lancio, completa la tabella e rispondi alle domande.

Quale somma ha la frequenza maggiore?

Quale somma ha la frequenza minore?

F

F

RAPPRESENTAZIONE GRAFICA DI DATI

Ideogramma

11 Rispondi alle domande.

a) Quali rappresentazioni grafiche dei dati conosci?

b) Che cos’è un ideogramma?

c) Per rappresentare quali dati è adatto l’ideogramma?

Risolvi i seguenti esercizi.

12 L’ideogramma seguente rappresenta gli zaini venduti da 4 cartolerie nel mese di settembre. Osservalo e rispondi alle domande.

Paperland

Carta & Co.

Colorandia

Cartoleria del Corso

a) Se Paperland ha venduto 45 zaini, quanti zaini sono rappresentati da un simbolo intero?

b) Quanti zaini indica il simbolo del mezzo zaino?

c) Qual è la differenza di zaini venduti tra la cartoleria con la maggior frequenza e quella con la minore?

13 Dopo avere scelto l’unità grafica adeguata, rappresenta sul quaderno con un ideogramma il numero di paia di scarpe vendute da un negozio in una settimana.

Giorno lunedì martedì mercoledì giovedì venerdì sabato

Frequenza 12 10 6 10 14 8

14 Scegli l’unità grafica adeguata e rappresenta sul quaderno con un ideogramma la classifica dei cannonieri del campionato provinciale di calcio a 5 tra le scuole secondarie di primo grado.

Cannoniere Tripi Bassano Pallonetti Guidi Maggi Pagani Kholki Perla

Frequenza 3 4 4 7 9 9 11 13

15 L’ideogramma rappresenta i millimetri di pioggia caduti in una settimana in una località di montagna.

= 7 mm di pioggia

lunedì martedì mercoledì giovedì venerdì sabato domenica

Predisponi sul quaderno una tabella che riporti le frequenze e rispondi alle domande.

a) Qual è stato il giorno meno piovoso?

b) E il giorno più piovoso?

c) Quanti millimetri di pioggia in più sono caduti mercoledì rispetto a martedì?

d) Quanti millimetri di pioggia in meno sono caduti lunedì rispetto a martedì?

e) Quanti millimetri di pioggia sono caduti tra giovedì e venerdì?

16 MATEMATICA IN AZIONE La tabella seguente rappresenta i dati relativi alla quantità di carburante venduto in un mese in una stazione di servizio lungo un’autostrada.

Tipo di carburante Frequenza (L)

Diesel

24 000

Diesel plus 9 000

Super

27 000

Eco super 12 000

Nell’ideogramma che rappresenta i dati della tabella ci sono due errori. Prova a correggerli, dopo avere stabilito quante migliaia di litri vale l’unità grafica.

Diesel

Diesel plus

Super

Eco super

In una situazione del genere credi che la scelta di rappresentare i dati con un ideogramma sia adeguata oppure no? Giustifica la tua risposta.

17 MATEMATICA IN AZIONE La seguente tabella riporta la spesa media mensile in euro per l’acquisto di pesce nel 2019 nelle famiglie italiane divise per macroregioni. Fonte: ISTAT

Area geografica

Nordovest Nordest Centro Sud Isole

Frequenza 37 32 42 53 47

Quale simbolo ritieni più adatto per rappresentare i dati con un ideogramma?

Utilizza il simbolo scelto per rappresentare sul quaderno i dati con un ideogramma.

18 MATEMATICA IN AZIONE Una ricerca di Eurostat, l’ufficio statistico della Comunità Europea, ha analizzato il numero di anni che trascorre uno studente europeo sui libri per completare il proprio percorso scolastico. Nella tabella seguente sono esposti i risultati di alcuni Paesi dell’Unione Europea in ordine alfabetico.

Paese UE Belgio

Danimarca Francia Italia Olanda Polonia Romania

Frequenza 20 19 16 17 18 18 17

Dopo avere scelto l’unità grafica adeguata e averle assegnato un valore, costruisci un ideogramma, mettendo i risultati in ordine decrescente.

19 MATEMATICA IN AZIONE Il seguente ideogramma rappresenta la quantità di caffè prodotto dai Paesi principali produttori. Osservalo e rispondi alle domande. (I dati sono arrotondati.)

a) Quali sono le unità grafiche di questo ideogramma?

b) Quale Paese è il maggior produttore?

c) Ci sono Paesi che producono la stessa quantità di caffè? Sì No

d) Se sì, quali?

e) Calcola la differenza tra la quantità di caffè prodotto dal Brasile e quella dal minor produttore.

Ortogramma

20 Rispondi con Vero o Falso.

a) L’ortogramma è un tipo di rappresentazione grafica. V F

b) L’ortogramma è detto anche diagramma a sbarre. V F

c) L’altezza dei rettangoli di un ortogramma corrisponde alla frequenza. V F

d) Le basi dei rettangoli di un ortogramma variano al variare della frequenza. V F

e) L’ortogramma si usa per confrontare visivamente dei dati. V F

Risolvi i seguenti esercizi.

21 MATEMATICA IN AZIONE

Nel grafico a lato ci sono i dati di un’indagine statistica effettuata dai 20 alunni di una classe sul possesso di elettrodomestici nelle loro case.

Osservalo e rispondi.

a) Quale elettrodomestico è presente nella quantità di 1 per famiglia?

b) Quale elettrodomestico ha la frequenza maggiore?

c) Quale elettrodomestico è in quantità quasi doppia rispetto al numero di famiglie?

d) Quali elettrodomestici non sono ritenuti indispensabili (ne trovi meno di 1 a famiglia)?

e) Prova a rifare la stessa indagine nella tua classe e confronta il grafico ottenuto con quello dell’esercizio.

22 MATEMATICA IN AZIONE L’ortogramma rappresenta le vendite di alcune autovetture elettriche nel mese di aprile 2023. Ricava dalla tabella i nomi dei cinque modelli di automobili e completa il grafico.

23 STEM La tabella riporta i dieci terremoti più disastrosi in Italia dal 1900 a oggi disposti in ordine cronologico. Dopo avere rifatto sul quaderno la tabella, disponendoli in ordine di magnitudo (energia sprigionata dal sisma secondo la scala Richter), rappresenta i dati con un ortogramma.

24 Nel grafico si riportano le informazioni relative alla popolazione mondiale e alla distribuzione della ricchezza per aree.

a) In quale area si concentra la maggiore parte della ricchezza mondiale?

E in quale quella minore?

b) In quale area si concentra la maggiore parte della popolazione mondiale?

E in quale quella minore?

c) Predisponi sul quaderno una tabella che riporti i dati del grafico in percentuale.

25 Erminia ha segnato i dati della raccolta differenziata di una settimana nella seguente tabella.

Costruisci sul quaderno l’ortogramma che rappresenti i dati della tabella.

26 Nel reparto di un gruppo Scout hanno fatto un sondaggio per decidere la meta della prossima route estiva. Predisponi sul quaderno una tabella per registrare i risultati e costruisci un ortogramma.

montagna mare campagna estero montagna montagna mare montagna mare estero estero campagna campagna mare estero campagna estero mare mare campagna mare montagna montagna estero

27 La seguente tabella riporta il numero di televisori venduti da 5 grandi negozi di elettronica nella settimana prima di Natale.

L’ortogramma che rappresenta i dati contiene due errori: correggili ridisegnando il grafico giusto sul quaderno.

28 MATEMATICA IN AZIONE In un sondaggio sulle macchine di lusso preferite da 100 rivenditori del settore, al primo posto ci sono le Ferrari e all’ultimo le Lamborghini, le Porsche sono meno delle Maserati, mentre le Rolls Royce occupano la posizione centrale. Completa il seguente ortogramma partendo da queste informazioni.

29 La tabella riporta le profondità delle fosse oceaniche più importanti del pianeta. Quale dei grafici seguenti rappresenta i dati nella tabella?

30 MATH Create in the notebook a bar chart with the longest rivers of the United States of America, using the data included in the table.

31 La tabella riporta la superficie in km2, approssimati all’unità, delle isole minori siciliane. Rappresenta sul quaderno i dati con un ortogramma.

32 Osserva il grafico che mostra il medagliere delle Olimpiadi di Tokyo del 2020 e rispondi.

a) Quale Paese si è classificato al primo posto nel medagliere?

E quale al sesto posto?

b) Quante medaglie ha vinto l’Italia in tutto? Quante d’oro?

c) Quante medaglie d’oro hanno vinto Paesi Bassi, Francia, Germania e Italia?

Perché i Paesi Bassi precedono in classifica le altre?

d) Quali Paesi hanno vinto lo stesso numero di medaglie di bronzo?

e) Quali Paesi hanno vinto lo stesso numero di medaglie d’argento?

f) Qual è lo scarto in medaglie d’oro tra gli Stati Uniti e l’Australia?

g) Disponi i Paesi in ordine crescente rispetto al numero di medaglie d’argento:

h) Sul tuo quaderno rappresenta i dati del grafico in una tabella a doppia entrata che riassuma il numero di medaglie d’oro, d’argento e di bronzo vinte da ciascun Paese.

Diagramma a segmenti

Poligonale delle frequenze

33 Per ogni affermazione indica se è riferita al Diagramma a segmenti (D) o alla Poligonale delle frequenze (P).

a) Si ottiene congiungendo gli estremi dei segmenti.

b) Può essere costruito solo con i punti.

D P

D P

c) Si costruisce come un ortogramma. D P

d) È un grafico lineare. D P

Risolvi i seguenti esercizi.

34 MATEMATICA IN AZIONE Gli alunni della classe 1a Z della scuola “Semprestanchi’’ sin dal primo giorno di lezione hanno cercato sul calendario i giorni di vacanza (domeniche escluse) fino a giugno e hanno realizzato il seguente diagramma a segmenti. Rispondi alle domande.

a) Quale sarà il mese con meno giorni di scuola?

b) Quale quello più faticoso?

c) Quali mesi hanno 3 giorni di festività?

settembre ottobrenovembredicembre gennaiofebbraio marzo aprile maggio giugno

d) Quanti giorni di vacanza in totale in un anno scolastico?

35 EDUCAZIONE CIVICA Nel 2022, gli articoli 9 e 41 della Costituzione Italiana sono stati modificati per includervi la tutela dell’ambiente, della biodiversità e degli ecosistemi. In questa occasione la scuola “Sempreverde” ha deciso di organizzare alcune attività che prevedano la cura del verde pubblico. Gli alunni di questa scuola hanno fatto il censimento degli alberi alla Villa comunale, ma quando hanno elaborato il grafico hanno dimenticato di mettere i nomi degli alberi.

Prova a ricostruire il grafico, sapendo che i tigli hanno la frequenza maggiore, gli ippocastani hanno la frequenza minore e gli abeti rossi sono meno degli abeti grigi.

36 STEM Rappresenta sul quaderno, con un grafico lineare, gli inanellamenti dei nuovi uccellini nati in un’oasi protetta del Sud Italia nei mesi primaverili.

Mese marzo aprile maggio giugno

Frequenza 35 55 80 65

37 STEM Saverio esegue delle prove con i suoi aerei di carta. Ecco le misure che ottiene lanciando quattro volte ciascun aereo. Rappresenta sul quaderno, con un grafico lineare, le misure della distanza in metri percorsa da ciascun aereo. (Usa colori diversi per i diversi aerei.)

38 MATEMATICA IN AZIONE Il seguente grafico lineare della figura riporta gli incassi di un piccolo supermercato da lunedì a sabato.

martedì mercoledì giovedì venerdì sabato Rispondi alle seguenti domande.

a) Quale giorno ha la maggiore frequenza?

b) Quante volte l’incasso supera i 2 000,00 €?

c) Quante volte scende sotto i 1 000,00 €?

d) Dagli incassi si può capire in quale giorno è più conveniente fare la spesa per non trovare fila?

e) Se la risposta è affermativa, in quale giorno ci andresti?

39 MATH Plot in the notebook a line graph of the data shown in the table below.

Royce cars sold in London during the first semester

40 MATEMATICA IN AZIONE Sei compagni si sfidano in una gara di velocità con l’aiuto del prof. di Scienze Motorie, che cronometra i tempi impiegati per fare il giro del giardino della scuola. Alla fine della gara il prof. trascrive i dati su una tabella e in classe viene costruito un diagramma a segmenti da appendere in aula.

Prova a farlo anche tu sul tuo quaderno.

Nome alunno Livio Federico Pietro Dario Costas Alain

Tempo in secondi 42 38 34 44 36 48

Dopo averlo realizzato rispondi alle seguenti domande.

a) Chi vince la gara?

b) Chi è il più lento?

c) Quanti secondi di differenza ci sono tra il primo e l’ultimo?

d) Quanti compagni riescono a fare il percorso in meno di 40 secondi?

41 STEM Silvia e Miranda eseguono alcune misurazioni del percorso in piano di una macchinina dopo che è scesa da un piano inclinato.

percorso

Nella tabella sono riportate le misure trovate.

Rappresenta sul quaderno con una poligonale delle frequenze i valori trovati. (Usa tre colori diversi per distinguere le tre lunghezze diverse della rampa.)

42 STEM Il seguente diagramma a segmenti riporta l’estrazione di uranio in tonnellate (Megagrammi) dei primi 6 Paesi al mondo. Fonte: Investing News Network.

Osserva il grafico e rispondi con Vero o Falso.

a) L’Australia supera di pochissimo la somma degli ultimi tre Paesi. V F

b) Il Canada estrae più della somma di Australia e Russia. V F

c) Questi dati si possono rappresentare anche con un grafico lineare. V F

d) Senza la quantità esatta segnata nel grafico avresti avuto la stessa facilità di lettura dei dati. V F

e) L’uranio estratto dal Kazakistan è più di tre volte di quello estratto dall’Australia. V F

f) Il Kazakistan produce 20 000 t meno della Russia. V F

43 STEM Il grafico mostra come diminuisce in percentuale la carica della batteria di un cellulare in un giorno. Osservalo e rispondi.

a) Di quanto diminuisce in percentuale la carica nelle prime 6 ore?

b) Che cosa accade tra le 6 e le 8?

c) In quali periodi è stato usato maggiormente il cellulare?

Da che cosa lo deduci?

d) Dopo 24 ore qual è la percentuale di carica della batteria?

e) Di quanto diminuisce in percentuale la carica dalle 12 alle 14?

Areogramma circolare

44 Rispondi con Vero o Falso.

a) L’areogramma circolare è detto anche grafico a torta. V F

b) Nell’areogramma la frequenza di un dato è rappresentata da un cerchio. V F

c) Gli spicchi in cui è diviso un areogramma circolare sono angoli la cui somma è 180° esatti. V F

d) Gli spicchi devono essere proporzionali alle quantità da rappresentare. V F

e) L’areogramma si usa per rappresentare la suddivisione in parti di un intero. V F

Risolvi i seguenti esercizi.

45 MATEMATICA IN AZIONE A casa Moneta hanno fatto il riepilogo sulle spese mensili della famiglia e hanno riportato i risultati su un grafico a torta.

Analizza l’areogramma circolare e segna con una crocetta se ogni affermazione è vera o falsa.

Alimentari

Tasse e bollette

Affitto

Trasporti

Svaghi

Salute

Abbigliamento

Risparmio

a) Alimentari e tasse assorbono la metà delle entrate. V F

b) Il risparmio è una delle spese con frequenza minore. V F

c) Affitto e trasporti hanno la stessa frequenza. V F

d) Svaghi e salute hanno la stessa frequenza. V F

e) La somma di svaghi e salute equivale alle spese di abbigliamento. V F

f) Le spese per l’affitto e i trasporti equivalgono alle spese per gli alimentari. V F

g) Le spese per tasse e bollette equivalgono alla quarta parte di tutte le spese. V F

46 La tabella e il grafico a torta rappresentano il risultato di un’intervista a 90 bambini sui loro film Disney preferiti.

Film Frequenza Ampiezza angolo

Rispondi con Vero o Falso.

a) I bambini che hanno scelto Frozen o Pinocchio sono la metà degli intervistati. V F

b) Oceania è stato scelto da 40 bambini.

c) Gli spicchi di Cars e Il re Leone hanno la stessa ampiezza.

d) L’ampiezza di Pinocchio sull’areogramma è 20 gradi.

e) Ogni bambino nel grafico corrisponde a un angolo di 4°.

47 La tabella di frequenza riporta i dati di un’indagine statistica effettuata in un cinema multisala sui quattro film più visti la domenica prima di Natale.

F

Natale sulla neve

Natale al mare

in crociera

Natale sulla Luna

Osserva gli areogrammi circolari e stabilisci qual è quello corrispondente ai valori della tabella segnandolo con una crocetta.

48 STEM Osserva il seguente areogramma circolare e rispondi alle domande.

a) I gas rappresentati inquinano l’aria, il suolo o l’acqua?

b) Quale gas è maggiormente responsabile dell’effetto serra, cioè del riscaldamento del pianeta, e in quale percentuale?

c) Gli ossidi di azoto in quale percentuale sono responsabili?

d) I clorofluorocarburi in quale percentuale sono responsabili?

e) Calcola la percentuale del metano.

49 STEM L’areogramma della figura riporta i dati del consumo di energia mondiale alla fine del `900. Dopo averlo osservato, rispondi alle domande.

a) Quale fonte di energia è stata maggiormente usata nel secolo scorso e in quale percentuale?

b) Quale fonte è stata usata di meno e in quale percentuale?

c) Quali fonti di energia hanno avuto una percentuale di utilizzo quasi uguale?

d) Calcola la percentuale di utilizzo del carbone (sapendo che il cerchio in totale corrisponde al 100%).

Rappresenta con areogrammi circolari i dati dei seguenti esercizi.

Agli insegnanti di una scuola è stato chiesto dove trascorreranno le vacanze pasquali. La tabella riporta i risultati dell’intervista da rappresentare con un grafico a torta.

Località Capitale europea Agriturismo Montagna Rimane in città

• Calcola il totale degli intervistati:

60 + 30 + 15 + 15 = 120

• Calcola l’ampiezza in gradi corrispondente a ogni singolo intervistato:

360° : 120 = 3°

• Moltiplica il risultato, 3°, per il NUMERO di insegnanti corrispondenti a ogni spicchio per trovare l’ampiezza in gradi:

3° × 60 = 180° Ampiezza corrispondente a “capitale europea’’ (spicchio viola)

3° × 30 = 90° Ampiezza corrispondente ad “agriturismo’’ (spicchio azzurro)

3° × 15 = 45° Ampiezza corrispondente a “montagna’’ (spicchio rosso)

3° × 15 = 45° Ampiezza corrispondente a “rimane in città’’ (spicchio verde)

agriturismo

50 STEM Gli alunni della 1a F fanno un esperimento con i semi di ceci e lenticchie e raccolgono i seguenti dati.

Tipo di seme

51 Un’indagine su 100 alunni che frequentano scuole a indirizzo musicale ha rilevato che metà studia la chitarra, 20 il clarinetto, 15 il violino, 10 il pianoforte e 5 la batteria. Sul quaderno rappresenta questi dati con un areogramma circolare. ESEMPIO

Numeri di semi germogliati dopo una settimana nel cotone bagnato con: solo acqua acqua salata acqua zuccherata

Rappresenta sul quaderno i dati con due areogrammi circolari, procedendo come nell’esempio del Ricorda.

52 Osserva il seguente areogramma circolare e rispondi sul quaderno.

di frumento

del Nord

Italia centrale

Italia del Sud

a) Che cosa rappresenta questo diagramma?

b) Quale zona d’Italia produce più frumento?

c) Quale zona d’Italia produce meno frumento?

d) Somma le percentuali: quale numero ottieni? Perché?

e) Conoscendo solo le percentuali dell’Italia settentrionale e centrale, potresti calcolare la percentuale dell’Italia meridionale?

53 MATH The following table shows the Trinity exam results of the pupils from a school.

Plot the results on a pie chart.

54 400 ragazzi all’uscita di una discoteca hanno risposto a un’indagine sul tipo di musica preferito. Dopo avere osservato il grafico, compila la tabella di frequenza relativa.

Esercizi riferiti ai vari tipi di grafici studiati

55 Rispondi con Vero o Falso

a) Qualsiasi indagine prevede sempre la raccolta dei dati.

b) La frequenza è il valore maggiore dell’indagine.

c) L’ideogramma è un grafico circolare.

d) L’ortogramma ha rettangoli tutti della stessa larghezza.

F

e) L’areogramma si usa per indagini che si svolgono in un arco di tempo. V F

f) La poligonale delle frequenze è un grafico lineare.

56 Abbina il tipo di indagine statistica con il grafico che meglio la rappresenta.

(Le risposte corrette possono essere più di una.)

a) Altezza dei principali monti italiani

b) Distribuzione del suolo in Italia

c) Entrate di un negozio in un arco di tempo

d) Confronto del costo dello stesso prodotto in più negozi

e) Libri letti in estate da un certo numero di ragazzi

1) grafico lineare (o poligonale)

2) ideogramma

3) ortogramma

4) areogramma

5) diagramma a segmenti

57 Scrivi in corrispondenza dei simboli il valore complessivo delle unità grafiche considerando che un’unità vale 10 ( = 10).

Risolvi i seguenti esercizi.

58 MATEMATICA IN AZIONE Un importante manager ha nell’armadio 48 vestiti: 24 sono di colore blu, 12 sono di colore grigio chiaro, 6 di colore grigio scuro e 6 gessati.

Quale dei seguenti grafici rappresenta la situazione appena descritta?

a)

b)

grigio chiaro

grigio scuro gessato

c) Blu Grigio scuro

Grigio chiaro Gessato

59 In una scuola a tempo prolungato, nel pomeriggio gli alunni si dividono nei vari laboratori per classi aperte secondo il seguente grafico.

Laboratorio di pittura

Laboratorio di danza

Laboratorio di musica

Laboratorio di giardinaggio

Laboratorio di cucina

01 35 79 11 13 15 17 19 21 23 25

Predisponi sul quaderno una tabella delle frequenze, completala e rispondi alle domande.

a) Quale laboratorio ha la maggiore frequenza?

b) Quale laboratorio ha la minore frequenza?

c) Quanti alunni frequentano un laboratorio di discipline artistiche?

d) Quanti alunni frequentano il tempo prolungato?

60 MATEMATICA IN AZIONE I risultati di un’indagine statistica rivolta a 180 edicolanti sui fumetti più venduti sono rappresentati nel grafico.

Manga

Topolino

Dylan Dog Diabolik

Quanti edicolanti hanno indicato i Manga? 20 30 40 60

Quanti edicolanti hanno indicato Diabolik? 20 30 40 60

61 MATEMATICA IN AZIONE In un bar una mattina si sono vendute le seguenti bevande. Completa la tabella con le frequenze e realizza sul quaderno un diagramma a segmenti.

Cappuccino • Caffè • Caffè • Cappuccino • Latte bianco • Cappuccino • Latte bianco • Caffè • Caffè • Caffè • Latte bianco • Caffè • Cappuccino • Cappuccino • Caffè • Caffè • Latte bianco • Cappuccino • Caffè • Cappuccino

Bevanda Frequenza

Caffè

Cappuccino

Latte bianco

62 Una nota azienda che produce occhiali da sole ha commissionato un’indagine statistica sul colore degli occhi degli italiani. I risultati sono evidenziati nell’ortogramma a fianco e si riferiscono a un campione di 100 individui per ogni area del Paese.

Occhi azzurri

Occhi verdi

Occhi castani

Dopo avere osservato il grafico, rispondi con Vero o Falso.

a) In tutte e tre le aree geografiche la somma degli intervistati fa sempre 100. V F

b) Gli occhi azzurri non superano mai la frequenza di 20.

c) In nessun caso gli occhi verdi superano in frequenza gli occhi azzurri.

d) Lo scarto maggiore tra due dati si ha nell’Italia meridionale.

e) Nell’Italia centrale la somma degli occhi azzurri e verdi supera gli occhi castani. V F

63 La seguente tabella sulle presenze/assenze in una classe di 21 alunni in una settimana contiene tre errori rispetto all’ortogramma corrispondente. Individuali e correggili.

64 Predisponi sul quaderno una tabella per registrare i dati del grafico a lato, che mostra i colori preferiti da un gruppo di bambini. Rappresenta poi i dati con un areogramma.

65 La tabella seguente riporta i risultati di una ricerca sul movimento annuo di passeggeri (espresso in milioni) dei principali aeroporti europei. Scegli il grafico più adatto e rappresentalo sul tuo quaderno.

Aeroporti

Passeggeri

milioni

Heathrow (Londra)

Francoforte (Germania)

De Gaulle (Parigi)

Schiphol (Amsterdam)

Gatwick (Londra)

66 MATEMATICA IN AZIONE Una ricerca Eurostat ha evidenziato l’uso del computer e l’accesso a Internet (per ogni 100 abitanti) in alcuni Paesi europei.

uso di PC uso di Internet

DanimarcaFranciaGermaniaGreciaIrlanda

ItaliaLituaniaSlovacchiaSpagnaRegnoUnito

Guardando attentamente il grafico, indica con una crocetta se le affermazioni che seguono sono vere o false.

a) In tutti i Paesi della ricerca l’uso del computer è superiore all’uso di Internet. V F

b) I primi tre Stati sia nell’uso di Internet sia del computer sono del nord Europa. V F

c) Il Regno Unito ha la frequenza massima sia nell’uso del computer sia di Internet. V F

d) La statistica non va mai sotto il numero di 50 utenti in entrambi gli ambiti. V F

e) La Grecia ha la frequenza minima sia nell’uso del computer sia di Internet. V F

COMPETENZE

PROBLEM SOLVING

1 Movimento naturale della popolazione

Il seguente grafico lineare pubblicato dall’Istat (Istituto di Statistica) rappresenta l’andamento di nascite e morti in Italia dal 2008 al 2022. La differenza tra i due dati in un anno è detta movimento naturale di una popolazione o anche saldo naturale. (I dati sono espressi in migliaia).

Dopo avere osservato il grafico, rispondi alle seguenti domande.

a) In quali anni ci sono state meno nascite?

b) In quale anno il saldo a sfavore delle nascite è maggiore?

c) In quale anno i decessi sono stati circa 100 000 più delle nascite?

d) Quante volte i decessi sono stati più di 650 000?

e) Questo andamento può essere definito calo demografico o incremento demografico?

Perché?

2 Un’indagine di una nota rivista di moda, che ha come oggetto le scarpe estive preferite, viene effettuata su un campione di 200 studentesse universitarie.

L’indagine ha rivelato che la metà delle intervistate preferisce le sneakers, quelle che preferiscono le ballerine sono 25 e sono tante quante quelle che preferiscono le infradito; quelle che preferiscono i sandali, poi, sono la metà di quelle che preferiscono le sneakers. Costruisci sul quaderno una tabella a doppia entrata con le frequenze e rappresenta i dati con un areogramma circolare.

ANALIZZARE E INTERPRETARE I DATI

3 Osserva i due areogrammi che rappresentano la differenza di composizione in gas tra l’aria inspirata e l’aria espirata e poi rispondi alle domande. Aria inspirata Aria espirata biossido

Nel passaggio tra inspirazione ed espirazione:

a) quale gas rimane in quantità uguale?

b) quale gas aumenta?

c) quale gas diminuisce?

Sai spiegare perché nel primo grafico non si vede lo spicchio che rappresenta il biossido di carbonio?

4 Il grafico seguente è un cartogramma, come quelli che avrai studiato in geografia. Osservalo e rispondi alle domande sul quaderno.

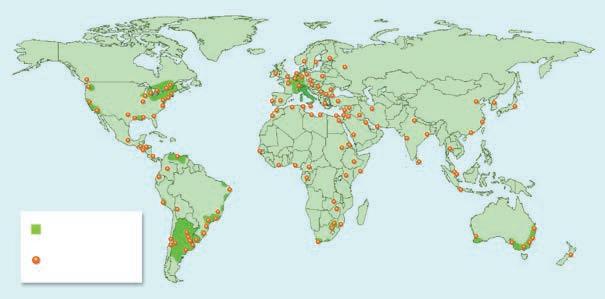
Lecomunitàitaliane nelmondo aree con consistente presenza italiana principali associazioni economiche e/o centri culturali italiani

a) Che cosa rappresenta il cartogramma?

b) In quali parti del mondo ci sono aree con consistente presenza italiana?

c) Quali motivi possono spiegare questa sistuazione?

d) Quale continente ha la minor presenza di associazioni economiche o centri culturali italiani?

e) Conosci qualcuno che ha parenti in queste zone del mondo?

SFIDA MATEMATICA

5 E che luce sia!

In figura vedete la pianta di un appartamento un po’ strano, composto da quattro stanze senza porte e separate da pareti rappresentate dalle linee più marcate.

Mettete delle lampadine nel centro di alcuni quadratini in modo che:

• ogni riga e ogni colonna del disegno abbiano una e una sola lampadina;

• ci sia una lampadina in ogni stanza;

• tutta la superficie di ogni stanza sia direttamente illuminata dalla lampadina di quella stanza.

(Testo tratto dalle Finali Nazionali dei Campionati Internazionali di Giochi Matematici, organizzata dal Centro PRISTEM dell’Università Bocconi di Milano)

ROAD MAP PER TUTTI

TABELLA DI FREQUENZA

DATA UNA TABELLA CON RIGHE E COLONNE

Colonne

Che cos'è una tabella di frequenza?

È una tabella a doppia entrata in cui si raccolgono i risultati di un'indagine

Verifiche in classe nel primo trimestre

Mese Ottobre Novembre Dicembre

Righe

IDEOGRAMMA

CHE COS’È UN IDEOGRAMMA?

È una rappresentazione grafica che utilizza dei disegni simbolici che rendono l’idea del fenomeno considerato.

Quando si usa?

È usato per rappresentare i dati da mettere a confronto

Loris = 1 goal

Luis Alex Omar

Risolvi i seguenti esercizi.

1 MATEMATICA IN AZIONE Un’indagine svolta tra un gruppo di amici sugli

sport praticati ha dato i seguenti risultati.

Giorgio nuoto

Mirella tennis

Davide calcio

Paolo nuoto

Nicolò scherma

Vincenzo tennis

Luisa nuoto

Lorena nuoto

Marta calcio

Salvatore scherma

Iacopo scherma

Giovanni nuoto

Completa la tabella di frequenza relativa all’indagine.

Sport nuoto calcio

Frequenza

Lorenzo calcio

Marco calcio

Deborah nessuno

Erika tennis

2 MATEMATICA IN AZIONE La tabella riporta i dati relativi alla lingua straniera studiata nelle scuole secondarie di primo grado di una città del centro Italia.

Lingua straniera Frequenza

Rispondi con Vero o Falso.

a) I ragazzi intervistati sono meno di 1000. V F

b) La lingua straniera meno studiata è il russo. V F

c) Inglese e tedesco hanno lo stesso numero di studenti. V F

d) I dati nella tabella sono in ordine decrescente. V F

Risolvi i seguenti esercizi.

3 Quale dei seguenti simboli useresti per rappresentare:

a) un’indagine sui trasporti pubblici?

b) un’indagine sui ristoranti preferiti?

4 Se il simbolo rappresenta 10 alunni, quanti alunni indica il seguente ideogramma?

CHE COS’È UN ORTOGRAMMA?

È una rappresentazione grafica, detta anche diagramma a colonne, che utilizza dei rettangoli aventi la stessa base; l’altezza invece corrisponde alla frequenza di ciascun dato da rappresentare.

Quando si usa?

Si usa per confrontare il valore di alcuni dati.

Rappresentazione con un ortogramma delle ore di studio di Mario in una settimana

MATEMATICA IN AZIONE Risolvi i seguenti esercizi.

5 Ricava dall’ortogramma le età di Salvo e dei suoi fratelli.

a) Anna:

b) Salvo:

c) Giada:

d) Sandro:

e) Emilio:

AREOGRAMMA CIRCOLARE TEORIA PAG. 210

CHE COS’È UN AREOGRAMMA CIRCOLARE?

È una rappresentazione grafica che utilizza un cerchio suddiviso in spicchi che hanno ampiezze corrispondenti alle frequenze dei dati considerati. È detto anche “grafico a torta’’.

Quando si usa?

È usato per rappresentare la suddivisione in parti di un intero.

Rappresentazione con un areogramma circolare delle materie preferite nella classe di Mario

6 Osserva il grafico a torta e rispondi.

a) Qual è il gusto che piace di più?

b) A quanti piace il gusto limone?

c) A quanti piace il gusto nocciola?

7 Il grafico a torta rappresenta i risultati di un’indagine sulle bevande preferite a colazione da un gruppo di ragazzi che frequentano il bar della scuola.

Rispondi con Vero o Falso.

fisica

a) Gli intervistati in totale sono 400. V F

b) Caffè e cioccolata sono scelti da metà degli intervistati. V F

c) Il latte macchiato ha avuto meno preferenze. V F

d) Il caffè è la bevanda preferita degli intervistati. V F

e) Il caffè supera la somma di tè + cioccolata + latte macchiato. V F

DIAGRAMMA

CHE COS’È UN DIAGRAMMA A SEGMENTI?

È una rappresentazione grafica che utilizza dei segmenti le cui lunghezze rappresentano le frequenze.

Quando si usa?

Si usa per rappresentare dati che cambiano nel tempo.

Fuoristrada venduti in sei mesi a Matera gennaio 2 febbraio 3 marzo 2 aprile 4 maggio 5

gennaio febbraio marzo aprile maggio giugno

CHE COS’È UNA POLIGONALE DELLE FREQUENZE?

È un grafico lineare che si ottiene congiungendo gli estremi dei segmenti del diagramma a segmenti. Si può costruire anche senza segmenti, solo con i punti.

Fuoristrada venduti in sei mesi a Matera

gennaio febbraio marzo aprile maggio giugno ESEMPIO

MATEMATICA IN AZIONE Risolvi i seguenti esercizi.

8 Ricava dal diagramma a segmenti i gelati mangiati da Piero nei primi sei mesi dell’anno. gennaio

9 Rappresenta con un diagramma a segmenti le auto elettriche vendute negli ultimi sei mesi dell’anno dal concessionario Autogreen. Luglio 3 - Agosto 1 - Settembre 4 - Ottobre 5 - Novembre 3 - Dicembre 7

10 Rappresenta con un diagramma a segmenti e con la poligonale delle frequenze i voti presi da Andrea nelle ultime due settimane di gennaio.

Voti 5 6 7 8

Frequenza 2 4 2 1

11 Rappresenta con un diagramma a segmenti e con una poligonale delle frequenze le temperature medie giornaliere di una settimana di luglio registrate nella località di Piccodelsole.

Giorno e data

Lunedì 1

Martedì 2

Mercoledì 3

Giovedì 4

Venerdì 5

Sabato 6

7

12 Rappresenta con la sola poligonale delle frequenze l’andamento delle precipitazioni in una settimana di marzo nella località di Piovesempre.

Giorno e data

di pioggia Lunedì 8

mm Martedì 9

10

11

Venerdì 12

13

14

mm

SIMULAZIONE DI VERIFICA

1 Completa con Vero o Falso.

a) L’ortogramma utilizza dei simboli a piacere. V F

b) L’ideogramma utilizza dei disegni simbolici. V F

c) L’areogramma è un cerchio diviso in spicchi. V F

d) La poligonale delle frequenze utilizza dei rettangoli. V F

e) La poligonale delle frequenze è un grafico lineare. V F

2 Contrassegna le risposte esatte.

a) Nei rettangoli di un ortogramma le basi sono uguali e le altezze:

1) sono sempre tutte diverse

2) corrispondono al numero dei dati

3) corrispondono alla frequenza

4) sono sempre uguali

b) In un ideogramma che rappresenta la corrispondenza spedita e ricevuta da un ufficio, l’unità grafica è = 10 lettere.

Per rappresentare 5 lettere occorre disegnare:

1) 5 buste

2) 2 buste e mezza

c) L’ideogramma:

1) è un grafico lineare

2) utilizza solo figure geometriche

3) una busta e mezza

4) mezza busta

3) è sempre molto preciso

4) serve per confrontare dati da rappresentare

3 MATEMATICA IN AZIONE Il seguente grafico lineare rappresenta i visitatori di un famoso museo di Londra la prima settimana di luglio dello scorso anno.

Osservalo, completa la tabella e rispondi alle domande.

Questo simbolo indica che c’è un’interruzione dei valori.

0 lu ma me gio ve sa

a) I visitatori di lunedı` sono stati più o meno di quelli di venerdı`?

b) Qual è stato il giorno con il maggior numero di visitatori?

c) In quale giorno si sono viste 140 persone?

d) Quale è stato il numero totale di visitatori?

Giorno Presenze frequenza lunedì martedì mercoledì giovedì venerdì sabato

4 MATEMATICA IN AZIONE Per prepararsi alla maratona cittadina Mario si allena, in media, 15 ore la settimana.

Se il simbolo della clessidra vale 3 ore, quale ideogramma rappresenta le ore settimanali di allenamento di Mario?

5 MATEMATICA IN AZIONE Rappresenta con un ortogramma i dati della tabella relativa al numero di fratelli degli alunni della 1ª E, classe di Alessia.

Numero fratelli 0 1 2 3 4 o più totale

Numero alunni 13 6 5 2 0 26

6 MATEMATICA IN AZIONE Osserva gli areogrammi relativi alla produzione di uva, olive e pomodori in tre regioni italiane ed esegui le richieste.

Scrivi i nomi delle tre regioni in ordine:

a) crescente per la produzione di olive:

b) decrescente per la produzione di uva:

c) Quale regione ha il primato per la produzione di pomodori?

d) Dove la produzione di olive è stata il doppio di quella del pomodori?

7 MATEMATICA IN AZIONE Abbina ogni areogramma alla frase che lo rappresenta.

a) Nella classe di Diana la metà degli alunni porta i capelli corti.

b) Solo un quarto degli intervistati da Massimo preferisce il succo d’arancia.

c) Tra gli amici che Sofia ha conosciuto al mare, un ottavo ha vinto una gara di nuoto.

LE POTENZE

Chi ha della

paura matematica?

Le potenze sono un’idea davvero “potente” in matematica! Forse anche per questo, le potenze sono fonte di diverse ansie e paure, anche quelle con basi piccole. Il motivo è che le potenze possono generare numeri molto grandi, ma non per questo devi per pensare che il calcolo sia troppo difficile o che tu possa sbagliare facilmente. Uno dei più frequenti motivi di ansia è di non saper distinguere l’elevamento a potenza (5 elevato a 3) dalla moltiplicazione tra due numeri (5 per 3): ricorda, la potenza rappresenta una moltiplicazione ripetuta del numero per sé stesso e non un’operazione tra base ed esponente. Potresti anche essere intimorito dalle proprietà delle potenze: troppe regole da memorizzare e qualche difficoltà nel riconoscerle e distinguerle. Potresti anche trovarti ad applicare le proprietà delle potenze in sequenza, ad esempio quando le potenze compaiono in espressioni più complesse, e provare la sensazione di essere imprigionato in un vero e proprio labirinto di regole! Non preoccuparti e prova a cambiare il tuo punto di vista! Considera le potenze comedeifacilitatori,comedellecomodescorciatoie perscrivereinmodocompattoeveloceicalcoliche altrimentisarebberotroppolunghidaeseguire.

ROAD MAP la nostra

CHIARIAMO IL SIGNIFICATO DI POTENZA

SCOPRIAMO COSA SONO LE ESPRESSIONI CON LE POTENZE

ESPLORIAMO LE CINQUE FONDAMENTALI PROPRIETÀ DELLE POTENZE

IMPARIAMO A USARE LA NOTAZIONE SCIENTIFICA E L’ORDINE DI GRANDEZZA DI UN NUMERO

MATERIALE INTEGRATIVO MULTIMEDIALE Focus

SUCCEDE CHE...

SIGNIFICATO DI POTENZA

Il papà di Emma deve fare un preventivo per dipingere le persiane di un grande complesso formato da sei palazzine, tutte di sei piani.

Ogni piano ha sei appartamenti, ognuno con sei finestre.

Chiede aiuto a Emma per calcolare velocemente quante finestre ci sono.

Il calcolo da fare è:

6 (palazzine) × 6 (piani) × 6 (appartamenti) × 6 (finestre)

cioè una moltiplicazione con tutti i fattori uguali.

In casi come questi la moltiplicazione si può scrivere sinteticamente usando le potenze:

6666 6 4 ### = 12 3 si legge “sei alla quarta’’

La potenza è una moltiplicazione con tutti i fattori uguali; il fattore che si ripete si chiama base mentre il numero di fattori uguali si dice esponente

In simboli: a × a × a × a × a × a = an = b

dove: a = base; n = esponente; b = valore della potenza

ESEMPIO

Dato che la potenza è una moltiplicazione “ripetuta’’ scritta in forma sintetica, si risolve svolgendo la moltiplicazione. a) 25 = 2 × 2 × 2 × 2 × 2 = 32

Nel calcolo delle potenze si presentano dei casi particolari.

• 50 = 1. Un numero (diverso da zero) elevato a 0 è sempre uguale a 1.

In simboli: a0 = 1

• 1,21 = 1,2. Un numero elevato a 1 è sempre uguale a se stesso.

In simboli: a1 = a

• 15 = 1. Una potenza con base 1 è sempre uguale a 1.

In simboli: 1n = 1

• 102 = 100. Una potenza di 10 è uguale a 1 seguito da tanti zeri quante sono le unità dell’esponente.

• 0 0 non ha significato. La potenza che ha 0 sia per base sia per esponente non ha significato. ) n

Nel caso di Emma il calcolo da fare è → 6 4 = 6 × 6 × 6 × 6 = 1 296

Le finestre del condominio sono 1 296.

1 Completa.

a) base esponente 13 4 ( base esponente 4 6 ( esponente 15 base 8 )

b) base 10 esponente3 ) esponente 0 base 11 ) base esponente 25 7 (

2 Completa come nell’esempio.

ESEMPIO

Z [ \ ] ] ] ]

quattro alla quarta → in lettere

44 44 4 4 ## #

256 → valore → sviluppo

a) Z [ \ ] ] ]

b)

La potenza con esponente 2 si legge ‘‘alla seconda’’ oppure ‘‘al quadrato’’. La potenza con esponente 3 si legge‘‘alla terza’’ oppure ‘‘al cubo’’.

dieci al quadrato × × × × × × × =

3 Calcola il valore delle seguenti potenze. Ci sono anche i casi particolari.

a) 132 = 13 × 13 = 150 = 18 = b) 33 = 121 = 104 =

c) 72 = 04 = 0 0 =

4 MATEMATICA IN AZIONE Un supermercato ha disposto su tre scaffali i succhi di frutta in brick. Ogni scaffale ha tre mensole, ogni mensola tre scomparti, in ogni scomparto ci sono tre confezioni e in ogni confezione ci sono tre brick. Quanti brick di succhi di frutta in totale può contenere il reparto, quando tutti gli scaffali sono pieni?

ESPRESSIONI

CON LE POTENZE 2

SUCCEDE CHE...

Pietro deve partire per l’Erasmus e vuole rinnovare il guardaroba. Vuole comprare cinque paia di calze a 5 € il paio, otto magliette di lana a 8 € l’una e due sciarpe a 10 € l’una, più uno zaino che costa 90 €. Ha messo da parte cento monete da 2 €.

Gli basteranno?

Impostiamo un’espressione con le potenze per risolvere il problema.

Nelle espressioni con le potenze e senza parentesi le regole di precedenza sono:

• si calcolano le potenze;

• si calcolano divisioni e moltiplicazioni nell’ordine dato;

• si calcolano addizioni e sottrazioni nell’ordine dato.

ESEMPIO

5 + 22 × 6 − 2 × 32 : 3 + 1 =

= 5 + 4 × 6 − 2 × 9 : 3 + 1 =

= 5 + 24 − 18 : 3 + 1 =

= 5 + 24 − 6 + 1 = 29 − 6 + 1 = 23 + 1 = 24

Nelle espressioni con le potenze e con le parentesi le regole di precedenza sono le stesse, ma si eseguono nell’ordine:

• prima le operazioni nelle tonde,

• poi quelle nelle quadre,

• infine quelle nelle graffe.

ESEMPIO

{122 − [33 × (25 − 15 × 2} ) – 23]} : 72 =

= {144 − [27 × (32 − 15 × 2) − 8]} : 49 =

= {144 − [27 × (32 − 30) − 8]} : 49 =

= {144 − [27 × 2 − 8]} : 49 =

= {144 − [54 − 8]} : 49 =

= {144 − 46} : 49 = 98 : 49 = 2

L’esponente può essere all’apice di una parentesi; in questo caso la potenza si risolve per ultima.

Le potenze si possono risolvere tutte subito, anche se si trovano fuori dalle parentesi.

ESEMPIO

(12 − 5 × 2)3 = (12 − 10)3 = (2)3 = 8

L’espressione che risolve il problema di Pietro è:

2 × 100 (52 + 82 + 2 × 10) 90 = 200 (25 + 64 + 20) 90 = = 200 109 90 = 1 €

Il denaro che ha messo da parte, quindi, è sufficiente per i suoi acquisti.

1 Rispondi con Vero o Falso.

a) Le potenze sono moltiplicazioni in cui si ripete lo stesso fattore. V F

b) Nelle espressioni le potenze si risolvono per prime solo dentro le parentesi. V F

c) Nelle espressioni con le potenze le regole di precedenza delle parentesi non variano. V F

d) Nelle espressioni la potenza può essere riferita a tutta la parentesi. V F

Risolvi le seguenti espressioni.

2 52 × 2 : 10 + 34 8 : 23 + 7 × 4 : 14 + 32 62

Calcola il valore delle potenze:

Esegui moltiplicazioni e divisioni nell’ordine in cui sono scritte:

Prosegui fino a trovare il risultato:

3 20 × 23 : 42 – 32 : 23 + 62

4 32 + 7 × 32 − 5 × 23 + 22 × 150

5 (17 – 24) × [34 − (52 + 7 × 23)] [0]

6 [(5 + 80) × (15 − 3 × 22)] − (3 + 22) [11]

7 (1 + 0,2 × 0,52) × [(7 + 22) : (32 + 2)] [1,05]

8 {[(102 : 4 – 24)2 − 52] : 23} + 122 : 42 [16]

9 MATEMATICA IN AZIONE Francesca apre il suo salvadanaio e trova le seguenti monete e banconote: 10 monete da 1 €; 2 da 2 €; 5 banconote da 5 €; 1 da 50 €.

Francesca vuole sapere se riuscirà a comprare 9 orsacchiotti portafortuna da 9 € l’uno, da regalare in occasione del suo compleanno alle amiche invitate.

Per verificarlo aiuta Francesca impostando e risolvendo l’espressione risolutiva.

SUCCEDE CHE...

PROPRIETÀ

DELLE POTENZE

La sorella di Emma è piuttosto vanitosa. Quando deve uscire di casa fa le prove davanti allo specchio. Può combinare vari modelli di borsa (blu o nera, coi manici o senza, di pelle o di stoffa) con numerosi modelli di scarpe (blu o nere, con i tacchi alti o no, con i lustrini o senza, di pelle o di cuoio).

Quante diverse combinazioni riesce a fare la sorella di Emma con scarpe e borse?

Questo problema, oltre che con il diagramma ad albero, si può risolvere utilizzando le proprietà delle potenze.

Quando si incontrano moltiplicazioni e divisioni di potenze, in alcuni casi è possibile applicare delle proprietà che semplificano i calcoli.

Di seguito consideriamo i casi in cui si hanno prodotti o quozienti di potenze che hanno le basi o gli esponenti uguali.

Potenze con la stessa base

1) Prodotto di potenze aventi la stessa base

Consideriamo la seguente moltiplicazione di potenze che hanno la stessa base:

Il prodotto di potenze di ugual base è una potenza che ha per base la stessa base e per esponente la somma degli esponenti.

In simboli → am × an = am + n

2) Quoziente di potenze aventi la stessa base

Consideriamo la seguente divisione di potenze che hanno la stessa base:

per la proprietà invariantiva della divisione

Il quoziente di potenze di ugual base è una potenza che ha per base la stessa base e per esponente la differenza degli esponenti.

In simboli → am : an = am − n con m ≥ n

3) Potenza di potenza

La seguente scrittura (34)3 prende il nome di potenza di potenza.

333 33 33 4 3 44 44 44 43 12 ## == == # ++ _i 12 3 più rapidamente: 33 3 4 3 43 12 == # _i

Una potenza di potenza è una potenza che ha la stessa base e per esponente il prodotto degli esponenti.

In simboli → [(am)n]p = am × n × p

Potenze con lo stesso esponente

4) Prodotto di potenze con lo stesso esponente

Consideriamo la seguente moltiplicazione di potenze che hanno lo stesso esponente:

114 × 24 =

= 11 × 11 × 11 × 11 × 2 × 2 × 2 × 2 =

= (11 × 2) × (11 × 2) × (11 × 2) × (11 × 2) =

= (11 × 2)4 = 224

Il prodotto di potenze di ugual esponente è uguale a una potenza che ha lo stesso esponente e per base il prodotto delle basi.

In simboli → am × bm = (a × b)m

5) Quoziente di potenze con lo stesso esponente

Calcoliamo la seguente divisione di potenze che hanno lo stesso esponente:

24 3 : 8 3 =

= (24 × 24 × 24) : (8 × 8 × 8) =

= (24 : 8) × (24 : 8) × (24 : 8) =

= 3 × 3 × 3 = 33

più rapidamente → 24 3 : 8 3 = (24 : 8)3 = 33

Tutte le proprietà delle potenze valgono anche per le potenze dei numeri decimali.

Il quoziente di potenze con ugual esponente è una potenza che ha lo stesso esponente e per base il quoziente delle basi.

In simboli → am : bm = (a : b)m → per la precedente proprietà delle potenze

Le combinazioni possibili per la sorella di Emma sono: 2 modelli di borsa con 3 combinazioni diverse e 2 modelli di scarpe con 4 combinazioni. Quindi:

2 3 × 2 4 = 2 3 + 4 = 2 7 = 128 combinazioni diverse Non ha che l’imbarazzo della scelta.

ESERCIZI Primi

Considera potenze con la stessa base e scegli le risposte esatte.

(Attenzione: possono essere più di una.)

1 Per calcolare il prodotto di più potenze con la stessa base gli esponenti vanno: a) sottratti b) sommati c) moltiplicati d) elevati al cubo

2 Per calcolare il quoziente di più potenze con la stessa base gli esponenti vanno:

a) sommati b) divisi c) elevati al cubo d) sottratti

3 Per calcolare la potenza di una potenza gli esponenti vanno: a) sommati b) moltiplicati c) elevati al quadrato d) divisi

4 Le proprietà delle potenze con la stessa base si applicano con:

a) le somme b) le differenze c) i prodotti d) i quozienti

Considera potenze con lo stesso esponente e scegli le risposte esatte.

(Attenzione: possono essere più di una.)

5 Il prodotto di potenze con lo stesso esponente ha:

a) per base il prodotto delle basi

b) per esponente il prodotto degli esponenti

c) per base la somma delle basi

d) per esponente la somma degli esponenti

6 Il quoziente di potenze con lo stesso esponente ha:

a) per base la differenza tra le basi

b) per base il quoziente delle basi

c) per esponente il quoziente degli esponenti

d) per esponente sempre 0

7 Le proprietà delle potenze con lo stesso esponente si applicano con: a) le differenze b) le somme c) i prodotti d) i quozienti

8 Le proprietà delle potenze con lo stesso esponente si utilizzano con i numeri:

a) solo interi

b) solo decimali

Potenze con la stessa base

c) solo pari

d) interi o decimali

9 Risolvi lasciando i risultati sotto forma di potenza.

a) 2 × 2 = 21 + 1 = 22 33 × 32 5 × 5 × 5

b) 43 × 43 × 44 × 42 62 × 64 × 6 × 62 7 × 72 × 74

10 Risolvi lasciando i risultati sotto forma di potenza.

a) 57 : 54 = 57 − 4 = 53 45 : 42 25 : 25

b) 102 : 10 38 : 33 : 32 117 : 113 : 112

11 Risolvi lasciando i risultati sotto forma di potenza.

a) (33)3 = 33 × 3 = 39 (22)5 [(102)2]2

b) [(53)2]3 (a2)3 [(a3)3]2

12 Applica le proprietà delle potenze e scrivi il risultato sotto forma di potenza.

a) 0,58 : 0,56 1,2 × 1,24 2,43 × 2,44

b) (0,24)7 (0,524)2 (10,35)3

Risolvi le seguenti espressioni.

13 [(136)4 : (138 × 137 : 1310)] × (130 × 13 × 132)

Calcola la potenza di potenza e risolvi le tonde applicando le proprietà: [13 : 13 ] × (13 ) = [1322]

14 [(88 : 85 × 83) : (84 : 82)]3 : [812 : (87 × 83 × 8)]2 [810]

Potenze con lo stesso esponente

15 Risolvi lasciando i risultati sotto forma di potenza.

a) 32 × 52 23 × 33 102 × 32 b) 22 × 32 × 42 23 × 53 × 33

× 43

16 Risolvi scrivendo il risultato come potenza.

a) 93 : 33

b) 302 : 102 c) 403 : 43 : 23 = (40 : 4 : 2)3 = d) 152 : 52 : 32

17 Applica le proprietà delle potenze alle seguenti operazioni con i numeri decimali scrivendo il risultato come potenza.

a) 3,23 × 0,53 2,45 : 0,45 0,22 × 0,32 b) 0,44 : 0,24

×

:

:

×

Risolvi le seguenti espressioni.

18 (43 × 53) : (103 : 53) 102 × 22 5 × 102 = 3 : 5 × =

19 (513 × 313) : (153) (23 × 33) : (22 × 32) × (24 × 32)0 [9]

20 0,42 × 0,52 : 0,22 + {[0,92 − (0,52 − 0,42)] : 0,8 + 0,3} : 0,6 [3]

21 STEM Dalla combinazione delle luci verde, rossa e blu si possono ottenere altri colori.

Nel pc di Luca ciascuna di queste luci si può modulare in 28 modi diversi. Quanti colori diversi si possono ottenere con le tre luci?

4 NOTAZIONE SCIENTIFICA E ORDINE DI GRANDEZZA DI UN NUMERO

SUCCEDE CHE...

Al Museo di storia naturale Emma è rimasta colpita dal fossile di un insetto preistorico simile a una libellula, grande come un gabbiano attuale, vissuto nel Carbonifero.

Nel cartellino sotto il fossile Emma legge:

Meganeura monyi

vissuta nel Carbonifero → 3 × 108 anni fa

Che cosa significa quello strano numero?

Per capirlo bisogna conoscere le potenze del numero 10 e la notazione scientifica

Ricorda che una potenza di 10 è uguale all’unità seguita da tanti zeri quante sono le unità dell’esponente.

) n

Con le potenze di dieci si possono scrivere in modo sintetico i numeri molto grandi

Dato il numero 230 000 000 000:

• si divide il numero dato per una potenza di 10 in modo che il quoziente ottenuto sia maggiore di 1 e minore di 10.

230 miliardi ha dodici cifre: si divide quindi per 1011, cioè 100 000 000 000.

230 000 000 000 : 100 000 000 000 = 2,3

• si scrive il quoziente ottenuto moltiplicato per la stessa potenza di dieci:

230 000 000 000 = 2,3 × 1011

Un numero scritto come prodotto di un numero, maggiore di uno e minore di dieci, per una potenza di dieci si dice scritto in notazione scientifica o in notazione esponenziale.

Quando non serve conoscere il valore esatto di un numero, si può utilizzare un’approssimazione del numero: l’ordine di grandezza

L’ordine di grandezza di un numero è la potenza di dieci più vicina a quel numero.

a) L’ordine di grandezza del numero 2 300 è 103 perché

2 300 = 2,3 × 103 → 2,3 è più vicino a 1.

b) L’ordine di grandezza del numero 67 000 000 è 108 perché

67 000 000 = 6,7 × 107 → 6,7 è più vicino a 10.

Lo strano numero è scritto in notazione scientifica. L’insetto gigante preistorico è vissuto 3 × 100 000 000 = 300 000 000 anni fa.

Primi

ESERCIZI

1 Scrivi il valore di ciascuna potenza di 10.

a) 104 b) 103 c) 107 d) 109 e) 10 0 f) 102

2 Scrivi in notazione scientifica i seguenti numeri naturali.

a) 65 000 000 000 = 6,5 × 10 ......

9 200 000 000 000

b) 721 000 000 000

554 000 000 000

c) 3 850 000 000 000 000

4 861 000 000 000 000 000

3 Scrivi in forma normale.

a) 4 × 1010

5,5 × 1011

b) 7,3 × 108 2,61 × 109

4 Scrivi l’ordine di grandezza dei seguenti numeri dopo averli scritti in notazione scientifica.

a) 27 000 000 000

b) 3 150 000 000

c) 86 000 000 000

2,7 × 1010

notazione scientifica ordine di grandezza

notazione scientifica ordine di grandezza

notazione scientifica ordine di grandezza

5 Trasforma in notazione scientifica i seguenti numeri e stabilisci poi l’ordine di grandezza.

Numero Notazione scientifica Ordine di grandezza

35 000 000

4 234 000 000

87 000 000 000

6 MATEMATICA IN AZIONE Alla fine del XX secolo la popolazione mondiale era di circa 6,1 miliardi di persone. Secondo fonti delle Nazioni Unite nel 2050 la popolazione si aggirerà intorno ai 9,1 miliardi di persone.

Esprimi in notazione scientifica l’incremento di popolazione mondiale nel periodo considerato.

MAPPA

si calcola

Valore

Potenza della potenza

53 = 5 × 5 × 5 = 125

a = 5 base n = 3 esponente

esprime numeri molto grandi

NOTAZIONE SCIENTIFICA

48 000 000 = 4,8 × 107

ORDINE DI GRANDEZZA

1,5 × 108 108

7,2 × 108 109

LA POTENZA an

presenta casi particolari

51 = 5

50 = 1 1n = 1 0n = 0

00 non ha significato

10n = 1 n 000000000 12 3

STESSA BASE

prodotto

75 × 7 × 72 = 75+1+2 = 78

ha queste proprietà

POTENZA DI POTENZA

[(0,62)4]3 = 0,62×4×3 = 0,624

quoziente

2,37 : 2,32 = 2,37–2 = 2,35

STESSO ESPONENTE

prodotto

48 × 0,58 = (4 × 0,5)8 = 28

159 : 39 = (15 : 3)9 = 59 quoziente

ESERCIZI E PROBLEMI

1

SIGNIFICATO DI POTENZA

1 Rispondi con Vero o Falso.

a) La potenza è una moltiplicazione di fattori ripetuti. V F

b) Il fattore che si ripete si chiama esponente.

c) 0 0 è uguale a 1.

d) Se la base della potenza è 1 il valore è sempre 1.

e) La potenza di 2 si dice “alla seconda“ o “al quadrato“.

F

F

F

F

f) La potenza di 3 si dice “alla terza“ o “al rettangolo“. V F

Segna le risposte esatte.

2 Data la potenza 64, il numero 6 è:

a) l’esponente

b) la base

3 Data la potenza 72, il numero 2 è:

a) l’esponente

b) la base

4 La potenza 53 è uguale a:

a) 5 × 3

b) 5 + 5 + 5

5 112 si legge:

a) undici al quadrato

b) undici al cubo

6 93 si legge:

a) nove al quadrato

b) nove al cubo

7 Completa.

c) il valore della potenza

d) l’indice

c) il fattore che si ripete

d) il valore della potenza

c) 3 × 3 × 3 × 3 × 3

d) 5 × 5 × 5

c) undici per due

d) due alla undicesima

c) nove per tre

d) tre alla nona

Scrivi le seguenti moltiplicazioni sotto forma di potenza.

a) 3 × 3 × 3 × 3 × 3 17 × 17 × 17 × 17

b) 25 × 25 × 25 × 25 × 25 × 25 × 25 × 25

c) 8 × 8

a) a ×

b) c ×

10 Scrivi a parole le seguenti potenze, come nell’esempio.

85 → otto alla quinta

a) 48 →

b) 152 → oppure

c) 214 →

d) 1,53 → oppure

e) 120 →

f) 110 →

Dopo averle trasformate in moltiplicazioni, trova il valore delle seguenti potenze.

seguenti potenze.

Associa ogni potenza con il suo valore (qualche valore serve per più di una potenza).

19 Valori: 81; 25; 512; 32; 441.

a) 25 b) 52 c) 83 d) 212 e) 34 f) 29

20 Valori: 256; 64; 2 197; 225. a) 133 b) 44

21 Completa la tabella.

152 d) 82 e) 28 f) 43

Calcola il valore delle seguenti potenze particolari.

40 = 1

13

Abbina ciascuna potenza con il suo valore (qualche valore serve per più di una potenza).

24 Valori: 1; 45; 0; 10. a) 101 b) 230

25 Valori: 0; 1; 39. a) 580 b) 19 c) 170 d) 010 e) 391 f) 05

26 Nel calcolare le seguenti potenze sono stati fatti degli errori. Trovali e correggili.

Eventuale correzione

Completa le seguenti uguaglianze.

29 MATH Find the missing term.

2 = 32 3 = 1 10 = 10,000 2 = 25

30 Le seguenti uguaglianze sono false; trova l’errore e scrivi la correzione adeguata.

a) 11 × 11 × 11 × 11 = 11 × 4

b) 21 × 3 = 213

c) 10 + 10 + 10 + 10 = 104

d) 81 = 1

e) 70 = 0

f) 32 = 23

g) 5,5 × 5,5 = 5,5 × 2

h) 4,010 = 4,01

31 STEM Il vibrione del colera è un batterio a forma di virgola ed è responsabile della malattia che gli dà il nome. Il colera può essere contratto in seguito all’ingestione di acqua o alimenti contaminati e, se non trattato, può essere causa di morte.

Osserva l’immagine che rappresenta la riproduzione per scissione di un vibrione, rispondi alle domande e poi completa la tabella.

a) Da un vibrione quanti se ne formano?

Esprimi il numero sotto forma di potenza di 2 → 2

b) Dopo 60 minuti quanti vibrioni ci saranno?

Esprimi il numero sotto forma di potenza di 2 → 2

c) A 0 minuti quanti vibrioni ci sono?

Esprimi il numero sotto forma di potenza di 2 → 2

32 STEM I ministri della Sanità europei hanno deliberato un testo in cui viene raccomandato di ridurre l’uso degli antibiotici per la salute umana e di quelli utilizzati per gli animali da allevamento.

L'abuso di questi farmaci, infatti, sta riducendo la loro efficacia; per esempio, sta diventando sempre più difficile curare lo streptococco, un batterio responsabile di alcune faringiti e polmoniti.

Sapendo che uno streptococco si riproduce ogni 25 minuti, rispondi alle domande utilizzando le potenze a base 2.

a) Quanti streptococchi ci saranno dopo 50 minuti?

b) Quanti ce ne saranno dopo la terza divisione?

c) Quanto tempo passerà per averne 512?

d) Quanti ce ne saranno dopo l’ottava divisione?

33 EDUCAZIONE CIVICA Chi pubblica una foto di altri sui social media senza chiedere il consenso è punito dalla legge (art. 167 D. Lgs n. 196/2003) per violazione della privacy. Una foto pubblicata sulla propria pagina social può diventare “virale”, cioè si può diffondere in modo “esponenziale” e non è più possibile controllarne l’utilizzo.

Considera una persona che manda una foto a 10 amici, che a loro volta la inviano ad altri 10, ognuno dei quali la invia ad altri 10, e così via… Quante persone verranno raggiunte al sesto invio? Completa la tabella e calcola. Numero di invi 0

di persone che ricevono la foto

Somma totale di persone che ricevono la foto

34 EDUCAZIONE CIVICA Le rondini, i loro nidi e le uova sono protetti dalla Legge n. 157/92 che ne vieta l'uccisione e la distruzione.

Le rondini sono importanti nella lotta biologica a insetti fastidiosi, per esempio le zanzare: una coppia può catturare fino a 20 000 insetti al giorno. Una rondine può fare 3 covate in un anno; se ogni volta depone 3 uova, quanti rondinotti possono nascere da 3 rondini dopo 3 anni?

Per aiutarti rispondi alle seguenti domande.

a) Quanti rondinotti possono nascere da 1 rondine in 1 anno?

b) Quanti rondinotti possono nascere da 1 rondine in 3 anni?

c) Quanti rondinotti possono nascere da 3 rondini in 3 anni? [ ; ; 34 = 81]

Completa i seguenti schemi relativi alle potenze di 10, seguendo l’esempio.

Completa le seguenti uguaglianze.

a) 105 = b) 102 = c) 108 =

a) 107 = b) 1010 = c) 1011 =

41 Per ogni numero scrivi la corrispondente potenza di dieci.

a) 1 000 =

b) 100 000 = c) 1 000 000 =

d) 1 000 000 000 = e) 1 000 000 000 000 = f) 10 000 000 000 000 =

42 Calcola le seguenti potenze di numeri decimali seguendo le istruzioni.

Potenza decimale

Calcola la potenza senza considerare la virgola

Separa tante cifre decimali quante quelle della base per le unità dell’esponente

0,34 = 0,0081 0,23 = 0, 0,52 = 0, 0,0012 = 0,

Calcola il valore delle seguenti potenze.

a)

45 Osserva le risposte dell’esercizio precedente ed elimina il termine errato.

a) Puoi concludere che le potenze dei numeri con base minore di 1 al crescere dell’esponente aumentano/diminuiscono

b) Puoi concludere che le potenze dei numeri con base maggiore di 1 al crescere dell’esponente aumentano/diminuiscono

46 Sette donne in viaggio per Roma.

(Problema col trabocchetto di Leonardo Fibonacci, 1202 )

Ci sono sette donne in viaggio per Roma. Ognuna di esse ha sette muli.

Ogni mulo porta sette sacchi. Ogni sacco contiene sette pagnotte.

In ogni pagnotta ci sono sette coltelli. Ogni coltello è in sette foderi. Donne, muli, sacchi, pagnotte, foderi: in quanti viaggiano per Roma?

2

ESPRESSIONI CON LE POTENZE

Individua le affermazioni esatte.

47 Data un’espressione con le potenze, le operazioni che hanno la precedenza, cioè che vanno risolte per prime, sono:

a) addizione e sottrazione

b) potenze

c) moltiplicazione e divisione

d) potenze al quadrato

48 Le parentesi, in un’espressione con le potenze, si risolvono in questo ordine:

a) prima le tonde, poi le graffe

b) prime le tonde, poi le quadre, poi le graffe

c) prima le quadre, poi le tonde, poi le graffe

d) prima le tonde, poi le altre a caso

Indica le risposte esatte relative alle seguenti espressioni con potenze.

49 5 × 42 23 × 5

a) Si risolvono prima 42 e 23.

b) Si risolvono prima le moltiplicazioni.

c) Dopo le potenze si risolve la sottrazione.

d) Dopo le potenze si risolvono le moltiplicazioni.

50 (2 × 32) : (22 10)

a) Si risolve prima la moltiplicazione.

b) Si risolvono prima le potenze.

c) Dopo le potenze si svolgono le operazioni nelle tonde.

d) Dopo le potenze si risolve la divisione.

51 Quale delle seguenti espressioni ha come risultato 7?

a) 23 2 + 5 3

b) (24 3) + (22 2)

c) 33 (5 + 23 + 2)

d) 24 (3 + 22) 2

52 Quali delle seguenti espressioni hanno come risultato 10?

a) 5 × 22 + 101 33 + 23

b) (23 × 7 25) : 23 + (22 × 10) : 5

c) [(30 : 5 )3 (2 × 7)2 ] : [102 : (52 × 2)]

d) (12 5)2 5 × 23 + 90

53 MATH Which of these expressions is equal to 1?

a) 52 52

b) 4 : 22 c) 62 9 × 22 d) 2 × 5 23

Esegui le seguenti espressioni seguendo le istruzioni date.

54 32 × 22 25 + 52 × 2 42 × 3 + 82 : 4 7

Calcola il valore delle potenze:

Esegui le moltiplicazioni e le divisioni:

Prosegui fino a trovare il risultato: [15]

55 12 + 3 + 4 × 22 – 16 : 22 + 15 : 3 + 72 62

Calcola il valore delle potenze:

Esegui le moltiplicazioni e le divisioni nell’ordine in cui sono scritte:

Prosegui fino a trovare il risultato: [45]

Risolvi le seguenti espressioni. 56 62 : 9 24 : 8 + 3 + 53 : 25

Le potenze hanno la precedenza.

61 7 × 52 2 × 34 + 52 32 × 22 + 102 92 [21]

62 5 × [(42 × 2 2) : 6 4]2 + 43 6

Calcola il valore delle potenze:

Esegui la moltiplicazione nelle tonde:

Esegui la sottrazione nelle tonde:

Esegui la divisione e poi la sottrazione nelle quadre:

Eleva a potenza il risultato delle quadre:

Prosegui fino a trovare il risultato: [63]

63 (53 52 4 × 5) (35 43 102) [1]

64 33 + 3 × 52 + 2 × 32 4 × (72 × 3 112 + 3) [4]

65 (42 × 5 82 : 4) : 2 (52 × 2 + 3 × 5 2) : 3 [11]

66 [2 × 52 × 2 (23 × 5)] × 350 : 10 [6] 67 [(112 32) : (21 7) 3]3 [125] 68 [2 × (7 × 5 + 33 + 20) (112 + 26 82)] + 52 23 × 3 [6] 69 [62 + 2 × 43 (92 × 3 + 7 × 8 + 46 : 2)

LEZIONE 3

PROPRIETÀ DELLE POTENZE

Potenze con la stessa base

89 Completa le frasi scegliendo tra i termini seguenti, che possono essere utilizzati più volte.

potenza • stessa • esponente/i • somma • differenza • prodotto • base

a) Il prodotto di potenze aventi la base è una potenza con la stessa e con l’esponente uguale alla degli .

b) Il quoziente di potenze aventi la stessa base è una con la base e con l’esponente uguale alla degli

c) Una di potenza è una potenza avente per base la stessa e per il degli esponenti.

90 Rispondi con Vero o Falso.

a) an × am = an + m V F

b) an : a m = an + m V F

c) an : am = an × m V F d) an × am = an : m V F e) (an)m = an + m V F f) (an)m = an × m V F

91 È possibile applicare le proprietà delle potenze?

a) 82 + 83 + 82 SÌ NO

b) 37 : 35 × 32 SÌ NO

e) 155 152 + 152 SÌ NO

f) 2,52 × 2,53 : 2,54 SÌ NO

c) 105 103 SÌ NO d) 203 × 202 × 20 SÌ NO

92 Osserva le seguenti operazioni e stabilisci quale proprietà delle potenze è stata applicata.

Esprimi sotto forma di potenza i seguenti prodotti.

Metti al posto dei puntini gli esponenti in modo che le uguaglianze siano vere.

Esprimi sotto forma di potenza i seguenti quozienti.

101

Metti al posto dei puntini gli esponenti in modo che le uguaglianze siano vere.

Esprimi sotto forma di potenza le seguenti potenze di potenze.

al

il risultato esatto.

Risolvi le seguenti espressioni lasciando il risultato sotto forma di potenza.

120 910 : 93 : 9 × 93 × (92)2

121 123 × 124 : 122 : 124

122 35 : 32 × 3 : 32

123 (54)2 : 53 × 52 : 53

124 42 × 43 × 42 : (45 × 42) × 44

125 (104 × 102)3 : (102 × 10)2

126 113 : 11 × (115 : 112) : (11 × 112) × 113 × 11 [116]

127 (33 × 32 : 3)2 × (3 × 35) : (35 : 32)3 [35]

128 (23 × 27)2 : (24 : 2)3 (23 × 2 × 25 × 27)3 : [(25 : 23)2]2 [211; 240]

129 [52 × (50 × 54)3]2 : 58 [(36)4 : (38 × 37 : 310)] × (30 × 3 × 32) [520; 322]

130 [(77 : 74) : 72]3 × [(76 : 72)2 : (77 : 75)]2 [715]

131 {(25)2 × [232 : (28 × 2 × 22)2]3}3 : [(29 : 23)2 × (23 × 25 × 20)2]4 [28]

132 {[(2 × 26 × 23)3 × (22)4]2 : [(25)3]4}5 × (24)5 [2100]

Esegui le seguenti espressioni numeriche applicando, quando è necessario, le proprietà delle potenze.

133 (58 : 56 + 35 : 33) : 2 [17]

134 (32 × 33) : 33 + (23 × 22) : 25 [10]

135 (38 × 33 : 310 27 × 211 : 217)3 [1]

(47 : 46 × 4)2 (155 : 153 : 15)2 24

(34 : 32 + 28 : 26 + 56 : 55 45 : 43)0

[(5 × 52)3 : 57 (34 : 33)2] : 23

(26 : 24 + 1) × [27 : (54 : 52 24)] 2 × 5

[106 : 106 + (22)2]3 : (22 × 5 3)2 + 2 × 3 23 + 03

Hanno la precedenza le operazioni all’interno delle ( ), poi quelle all’interno delle [ ] e infine quelle dentro le { }.

3 × {26 : 22 + [(33)3 : 36 + 1] (32 × 22 3 × 22)} : 22 (22)2 : 22

[(23 × 23 39) × (52 24) : (32 × 52 72 : 72+70)]4 × 32

143 {(73 × 74)3 : [(74)3 × (74)2]} : {[(23)3 × 23]2 : [(24)2]3} [7]

144 (32 × 2)2 : (32 × 2) + [33 × 2 : (2 × 72 : 7 + 22)]3 : 33 + 22 × 2

145 (62 × 6)4 × (5 × 4)0 : {[(40 25 : 23) : (16 + 54 : 53)]2}5 : (34 : 32)

146 [(65)4 : (64)2] : (62)2 : 68 + [(72)9 : (73)6] × (12 3 × 22) + 3 × 33 : 33

147 {[48 : (42 × 4)2]5 : [42 × (43 × 4)2 : 48]4} : 22 + (3 × 11 22 × 23) × 2

148 {[(52)4 : (53)2 + (42)4 : (43)2 (72)3 : 75] + 6} : (3 × 2 + 1 + 34 : 33)

Potenze con lo stesso esponente

149 Completa le frasi scegliendo tra i termini seguenti, che possono essere utilizzati più volte.

base/i • esponente • potenza • prodotto • quoziente • uguale

a) Il prodotto di potenze con ugual esponente è uguale a una che ha lo stesso e per base il delle basi.

b) Il di potenze con esponente è una potenza che ha lo stesso esponente e per il quoziente delle

150 Rispondi con Vero o Falso.

a) an × bn = (a + b)n V F

b) am : bm = (a : b)m V F

c) an × bn = (a × b)n V F

d) bm × cm = (b × c)m + m V F

e) an : cn = (a : c)n n V F

f) an : bn = (a b)n V F

151 È possibile applicare le proprietà delle potenze?

a) 45 + 55 SÌ NO

b) 54 × 124 × 34 SÌ NO

c) 125 : 122 SÌ NO

d) 184 34 SÌ NO

e) 155 × 35 : 55 SÌ NO

f) 0,22 × 82 : 0,42 SÌ NO

152 Osserva le seguenti operazioni e scrivi quale proprietà delle potenze è stata applicata.

Operazione Proprietà applicata

43 × 53 = 203

156 : 153 = 153

46 × 36 × 26 = 246

Esprimi sotto forma di potenza i seguenti prodotti.

153 153 × 23 (15 × 2)3 = 303 56 × 26

154 33 × 123

155 37 × 57

156

157

×

× 35

× 35

×

×

×

×

×

×

×

×

Trasforma le seguenti potenze in prodotto di potenze con lo stesso esponente.

(3 × 8)³ = 33 × 83

158 243 = 406 = (5 × ) = 363 = (3 × ) = 507 = (5 × ) =

159 484 = (6 × ) = 645 = (4 × ) =

= (3 × ) =

160 818 = (9 × ) =

= (5 × ) =

= (25 × ) =

= (7 × ) =

= (8 × ) =

Osserva l’esempio e calcola sul quaderno il valore delle seguenti potenze.

502 → si eleva a potenza il numero senza zeri e si aggiungono gli zeri necessari

quindi

= 2

= (3 x 100)2 = 32 x 1002 → 32 = e 1002 = 1

zeri, quindi 3002 = 403 = (4 × 10)3 = 43 x 103 → 43 = e 103 = 1 ha zeri, quindi 403 =

161 602 803 7003 9 0002 2 0003 […; 512 000; …; 81 000 000; …]

Esprimi sotto forma di potenza i seguenti quozienti. 164

(64 : 4)3 = 163

:

Trasforma le seguenti potenze in quoziente di potenze con lo stesso esponente.

(6 : 2)4 = 64 : 24

169 34 = 52 = (25 : ) = 33 = (60 : ) =

170 64 = (24 : ) =

171 73 = (49 : ) =

= (100 : ) = 73 = (21 : ) =

= (36 : ) =

172 Individua il procedimento corretto.

:

× 35 ×

:

= (55 : ) =

=

Calcola il valore delle seguenti espressioni lasciando il risultato sotto forma di potenza.

a) 23 × 22 × 35 b) 43 × 53 : 202

a) 405 : 55 × 82 b) 32 × 35 × 27

a) (62 × 42 ) × (83 × 33) b) (23 × 83) × 164

Anche per i numeri decimali valgono le proprietà delle potenze. Un prodotto o un quoziente di potenze può essere espresso sotto forma di un’unica potenza.

Con la stessa base

• 2,33 × 2,34 × 2,3 = 2,3(3 + 4 + 1) = 2,38

• 5,16 : 5,13 = 5,1(6 3) = 5,13

• (8,45)4 = 8,4(5 × 4) = 8,420

2,52 × 1,52

1,53 × 0,23

:

:

Con lo stesso esponente

• 3,45 × 0,25 = (3,4 × 0,2)5 = 0,685

• 1,54 : 0,34 = (1,5 : 0,3)4 = 54

:

:

:

0,22 × 0,22

: 0,73

: 1,124 0,52 × 0,5 × 0,52 × 0,55

: 0,43

: 3,64

Associa a ogni espressione il risultato esatto.

180 32 × 42 : 62 a) 24 b) 22 c) 2

181 54 × 104 : 254 a) 24 b) 1 c) 254

182 82 × 252 : 402 : 52 a) 1 b) 52 c) 82

183 (184 : 94) × (254 : 54) a) 74 b) 54 c) 104

Risolvi le seguenti espressioni lasciando il risultato sotto forma di potenza.

184 (65 : 25) × 32 : (95 : 35) [32]

185 [67 × 47 : (33 × 83)] : 84 [34]

186 26 × 36 : (184 : 34) [62]

187 (22 × 32)4 : 64 : 34 [24]

188 [(103 : 23) × 53] : (53)2 [1]

Risolvi le seguenti espressioni applicando le proprietà delle potenze.

189 103 : 53 + 162 : 82 5 × 30 [7]

190 52 × 22 42 × 32 : (22 × 32) 82 [32]

191 (3 + 1)2 (63 : 23 152 : 32) [14]

192 [(84 : 24)3 : 48 : 42 30]

Esistono degli esponenti speciali: si tratta dello 0 e dell’1.

imparaerrore dall'

Potrebbe capitarti di confondere le regole particolari che riguardano questi esponenti, che non sono intuitive e quindi anche difficili da capire.

Devi solo memorizzare questa informazione, ri cordando sempre che: a0 = 1 (se a è diverso da 0) e a1 = a Altri errori “dietro l’angolo” po trebbero derivare da una sbagliata applicazione delle proprietà delle potenze: è facile fare confusione tra la proprietà

che regola il prodotto di due potenze con la stessa base e la proprietà che ti permette di calcolare la potenza di potenza. Inoltre spesso sarai tentato di applicare queste proprietà anche a somme o sottrazioni di potenze con la stessa base. Attenzione, questi sono dei contesti NON validi, cioè sono casi in cui non ci sono proprietà da applicare. Conoscere questi schemi di errore può aiutarti notevolmente a far crescere le tue competenze: rafforza la comprensione del significato fondamentale della potenza, esercitandoti gradualmente e con attenzione nell’applicazione delle regole.

215 53 : 5 + 2 × {34 : 32 + 25 3 × [13 35 : 34 × (8 23)2]} 32 [20]

216 2 × {52 × 22 4 × [2 + 32 × (11 104 : 103) : 3] (22)3} : (27 : 24) [4]

217 (22 × 3 × 10) : {[26 : 24 × (3 × 23 2 × 7)]3 : (23 × 5)2} + 62 : 6 [9]

218 [(93 × 92)2 : 910]2 : [(32 × 38)4 : (38)5] (53)2 : 56 [0]

219 104 : 102 : {[6 + (23)2 : (26 : 24)2] : 5 + 3 × (22)2} + 33 : 3 [11]

220 {(73 × 74)3 : [(74)3 × (74)2]} : {[(23)3 × 23]2 : [(24)2]3} [7]

221 (32 × 2)2 : (32 × 2) + {33 × 2 : [2 × (72 : 7) + 22]}3 : 33 + 22 × 2 [27]

222 {(55 × 57)2 : [(53)3 × (52)7]} : {[(35)2 × 32]2 : [(33)4]2} [5]

223 {72 : [2 × (33 24)2 (22 × 32 + 23 14) : 3 50] + 27 : 24} : 3 [5]

224 (24 × 23 : 2 × 3) : {26 : 2 23 × [(52 24)3 × 52 26 : 22]2 : 33}2 +

225 {[18 : (23 : 22 + 1)2 + (23)2 : (22)2] × 3 + 3 × 23} : 7 : (23 : 22) [3]

226 {[(55 : 52 22 × 52) × 32 : 152]3 × 3 2}2 × 52 34 : 32 [16]

227 {[35 : 3 (22)2 × 2 25 : 23] : (33 3 × 23 + 2) + 26 : 82} × 23

228 {[24 : 23 + 5 × (32 7)2] : 11 + 62 : 22} : 11 + 22 × 52 3 × 7 [80]

229 [(0,42)3 × 0,44 : (0,42)4 + 0,62] : 0,4 (0,14 : 0,13) [1,2]

230 [(64)4 : (64)2] : (34)2 : 28 + [(72)9 : (73)6] × (12 – 3 × 22) + 3 × 33 : 33 [4]

231 {[68 : (62 × 6)2]5 : [62 × (63 × 6)2 : 68]4} : 32 + (22 × 11 22 × 23) × 2 [28] 232 {[(52)4 : (53)2 + (42)4 : (43)2 (72)3 : 75] + 6} : (3 × 2 + 1 + 34 : 33)

233 {[53 × 23 72 (295 : 294)2]

4

NOTAZIONE SCIENTIFICA E ORDINE DI GRANDEZZA DI UN NUMERO

238 Completa le frasi scegliendo tra i termini seguenti, che possono essere utilizzati più volte.

dieci • esponente • minore • moltiplica • potenza • prodotto • uno • vicina • zeri

a) Una potenza di dieci si ottiene scrivendo e a seguire tanti quante sono le unità dell’

b) Un numero è scritto in notazione scientifica se è espresso come di un numero compreso tra e e una potenza di

c) L’ordine di grandezza di un numero è la potenza di più a quel numero.

d) Per scrivere un numero in notazione scientifica o esponenziale:

– si divide il numero per una potenza di in modo che il quoziente sia un numero maggiore di e di 10;

– si il quoziente ottenuto per la stessa di 10.

239 Osserva i seguenti numeri e stabilisci se sono scritti in notazione scientifica.

a) 3,4 × 104 SÌ NO

b) 10,5 × 104 SÌ NO

c) 3,5 + 106 SÌ NO

d) 45 × 108 SÌ NO

e) 0,5 × 109 SÌ NO

f) 0,25 × 109 SÌ NO

Scrivi in forma normale i seguenti numeri scritti in notazione scientifica.

240 3,1 × 103 = 3,1 × 1 000 = 3 100 7,2 × 105

241 1,7 × 105 3,74 × 106

242 5,03 × 108 1,16 × 105

243 2,4 × 106 3,5 × 107

244 3,7 × 105 1,2 × 105

a) 8 × 104

× 106

b) 8,23 × 104 2,55 × 103

a) 1,02 × 107 4,2 × 108

×

× 107

× 104

b) 4,15 × 107 9 × 109 5,5 × 106

Converti le misure di grandezza usando le potenze di 10. 1 m = 1 000 mm = 103 mm

247 1 dam = mm = 10 mm

248 1 km = dm = 10 dm

249 1 hm = cm = 10 cm 250 1 dam = dm = 10 dm

Scrivi, sul quaderno, i seguenti numeri in forma polinomiale usando le potenze di 10. 2 341 = 2 × 1

Scrivi in forma normale i seguenti numeri scritti in forma polinomiale.

2 × 104 + 4 × 103 + 2 × 102 = 2 × 10 000 + 4 × 1 000 + 2 ×

Esprimi in notazione scientifica i seguenti numeri.

262 MATH Write the following numbers in scientific notation.

350,000,000 1,500,000,000

870,550 4,020,000,000

Determina l’ordine di grandezza dei seguenti numeri scritti in notazione scientifica.

2,3 × 108

7,8 × 108

2,3 è più vicino a 1

108 è l’ordine di grandezza

109 è l’ordine di grandezza

7,8 è più vicino a 10 si aumenta di 1 l’esponente

263 2,18 × 109

264 5,8 × 107

× 105

× 104

265 9,002 × 104 1,42 × 1020

× 104

× 1012

× 103

266 9,4 × 104 3,98 × 108 5,02 × 109

Determina l’ordine di grandezza dei seguenti numeri dopo averli trasformati in notazione scientifica.

ESEMPIO

23 30 0 in notazionescientifica 2,33 × 104 l‘ordinedigrandez za 104

267 2 300 in notazionescientifica

268 45 300 in notazionescientifica

269 830 000 000 in notazionescientifica

270 15 000 000 in notazionescientifica

271 16 600 000 in notazionescientifica

272 56 000 000 000 in notazionescientifica

273 2,7 miliardi in notazionescientifica

274 5,7 miliardi in notazionescientifica

Scrivi l’ordine di grandezza dei seguenti numeri.

l‘ordinedigrandez za

l‘ordinedigrandez za

l‘ordinedigrandez za

l‘ordinedigrandez za

l‘ordinedigrandez za

l‘ordinedigrandez za

l‘ordinedigrandez za

l‘ordinedigrandez za

a)

278 Raggruppa i numeri che hanno lo stesso ordine di grandezza.

a)

279 Prepara sul quaderno una tabella come quella dell’esercizio precedente e raggruppa i numeri che appartengono allo stesso ordine di grandezza.

Esegui sul quaderno i seguenti calcoli utilizzando la notazione scientifica. 12

, 10 10 10 12 32

trasformano i numeri in notazione scientifica

284 Scrivi i seguenti numeri grandi in forma esponenziale.

a) Il peso di questi due cetacei:

• Megattera: 30 000 kg

• Eubalaena glacialis: 40 000-70

b) La distanza minima Terra-Marte (31 luglio 2018): circa 57 500 000 km

285 EDUCAZIONE CIVICA L’AVIS (Associazione Volontari Italiani del Sangue)

è un’associazione nata con l’obiettivo di garantire la disponibilità di sangue a chi ne ha bisogno e vi aderiscono tutti coloro che hanno intenzione di donare volontariamente.

L’associazione gestisce i vari tipi di donazioni e il numero massimo di donazioni in un anno. Per esempio, un donatore può effettuare al massimo due donazioni di due unità di globuli rossi all’anno.

Il numero di globuli rossi in 1 mm3 di sangue è di circa 5,5 milioni.

In un uomo adulto di media corporatura ci sono circa 5 litri di sangue.

Quanti globuli rossi ci sono in totale in un uomo adulto?

(Ricorda: 1 litro = 1 dm3 = 1 000 000 mm3 )

Esprimi il numero in notazione scientifica:

286 STEM La distanza tra il Sole e la Terra è 1,496 × 108 km e la distanza tra la Luna e la Terra è 3,84 × 105 km.

Durante l’eclissi solare la Luna si trova tra la Terra e il Sole. Qual è la distanza tra la Luna e il Sole nel momento in cui c’è un’eclissi solare?

287 MATEMATICA IN AZIONE Per piastrellare un cortile di 300 m2 di superficie, un posatore ha bisogno di piastrelle dello stesso tipo. Un rivenditore gli propone delle piastrelle quadrate di 20 cm di lato (quindi di area 20 × 20 cm2). Ogni pacco contiene 20 piastrelle e i pacchi sono disposti su un bancale formato da 20 file di 20 pacchi ciascuna. Un bancale è sufficiente per il fabbisogno del posatore? [Sì, ci sono 320 m2]

288 MATEMATICA IN AZIONE La portata media di acqua del fiume Ticino al Ponte della Becca (alla confluenza tra i fiumi Ticino e Po, in provincia di Pavia) è di 350 m3 al secondo. Calcola la portata media giornaliera di acqua utilizzando la notazione scientifica. (Sapendo che al volume di 1 m3 corrisponde una capacità di 1 000 litri, calcola in notazione scientifica la portata media giornaliera espressa in litri di acqua.) [3,024 × 1010 L]

COMPETENZE

PROBLEM SOLVING

1 In astronomia come unità di misura viene utilizzata l’Unità Astronomica (UA).

L’UA è la distanza media della Terra dal Sole e vale a circa 150 milioni di km.

Completa la tabella. Terra

Pianeta Distanza in UA

Distanza in km

Venere 0,8 0,8 × 150 000 000 =

Marte 2

Terra 1

Giove 6

Saturno 10

Urano 20

Nettuno 30

Distanza in not. scient. Ordine di grandezza

2 Matt trova in un cassetto una calamita lunga e sottile. Comincia a giocarci e piegandola la spezza in due. Matt decide di continuare a spezzarle in due. Dopo 8 di queste divisioni quante piccole calamite otterrà?

= 20

= 21

= 22

Dal disegno puoi osservare che, ogni volta che Matt spezza le calamite, il numero delle piccole calamite è una potenza successiva di due.

Quindi, dopo aver spezzato per 8 volte tutte le calamite otterrà piccole calamite.

3 La fissione nucleare avviene quando una certa quantità di uranio viene bombardata con un neutrone.

Il neutrone colpisce un atomo di uranio, che si spezza in due parti liberando anche 3 neutroni; questi colpiranno a loro volta 3 atomi di uranio. Si produce così una “reazione a catena’’. Dopo quanti urti si libereranno 6 561 neutroni?

I neutroni si liberano secondo potenze di tre; quindi, completando la seguente tabella, troverai la soluzione al quesito.

Nº urti 1 2 3

31 = 3 32 = 9 33 = = = = = =

CALCOLARE

4 Dalla leggenda sugli scacchi. Il gioco degli scacchi, conosciuto in tutto il mondo, sarebbe nato in India. Secondo una leggenda, un re molto annoiato avrebbe promesso una ricca ricompensa a chi avesse inventato un nuovo gioco con cui distrarsi. Un uomo di nome Sissa, forse un matematico, gli propose un gioco inventato da lui: il gioco degli scacchi. Il re ne rimase affascinato e volle mantenere la sua promessa. Sissa come ricompensa chiese un chicco di riso per la prima casella della scacchiera, due per la seconda, quattro per la terza e così via, raddoppiando sempre il numero dei chicchi, fino alla sessantaquattresima casella. Il re fu ben contento di esaudire quella che giudicò una richiesta modesta. Ma, a conti fatti, la richiesta non era affatto modesta.

Vediamo perché.

La scacchiera ha 64 caselle:

• nella prima si mette 1 chicco 1 = 20;

• nella seconda, raddoppiando, 2 chicchi 2 = 21;

• nella terza si raddoppia ancora, quindi 2 × 2 = 22;

• nella quarta si raddoppia ancora 2 × 22 = ;

• nella quinta raddoppiando 2 × = ;

• nella sesta = ;

• nella settima = ;

• nella ventesima ;

• nella quarantesima ;

• nella cinquantaquattresima ;

• nella sessantaquattresima 2 × 262 = 263

Prova a sommare solo le prime 10 potenze trovate:

20 + 21 + 22 + 23 + + + + + + = 1 + 2 + 4 + 8 +

Come noterai, è già un bel numero e infatti il re non riuscì a pagare Sissa, in quanto i chicchi da accumulare erano ben 18 446 744 073 709 551 615.

5 Uno spago viene diviso in 4 parti e ogni parte, a sua volta, ancora in 4 parti, e così via per 4 volte. Quante parti si ottengono?

a) 4 + 4 b) 42 c) 43 d) 44

6 Trasforma le seguenti frasi in espressioni e calcola il loro valore.

a) Aggiungi al quadrato di 5 la differenza tra 10 e 3.

b) Il doppio del quadrato di 8 diminuito di 14.

c) Il cubo di 1 moltiplicato per il quadrato di 9.

d) Aggiungi al cubo di 2 il quadrato di 6.

e) Diminuisci di 7 il quadrato di 10.

f) Il triplo di 4 diminuito del quadrato di 3.

7 Dal papiro egiziano di Rhind (4 000 anni fa): “Un topo genera 7 topi, ognuno di questi ne genera altri 7; ognuno di questi altri 7 e ognuno di questi ancora altri 7”.

Quanti sono i topi in tutto? [2 401]

UTILIZZARE IL LINGUAGGIO MATEMATICO

8 Esprimi come potenze di 2:

a) il doppio di 213

b) il quadrato di 213

c) la metà di 213

9 Scrivi le seguenti operazioni sotto forma di potenze.

a) 10 × 10 + 5 × 5 × 5

b) 3 × 3 × 3 + 2 × 2 × 2 × 2

c) 2 × 2 × 7 × 7 + 3 × 3 × 3 × 4 × 4 × 4

d) 45 × 45 : 3 × 3 - 2 × 2 × 2 × 2 × 2

e) 6 × 6 × 6 × 3 × 3 × 3 - 9 × 2

SFIDA MATEMATICA

10 Metà quadrato metà cubo

Qual è il più piccolo numero (intero, positivo) che si può scrivere come somma del quadrato di un numero intero positivo e il cubo di un altro numero intero positivo, diverso dal primo?

(Giochi di Rosi, organizzati dal Centro PRISTEM dell’Università Bocconi di Milano)

ROAD MAP PER TUTTI

DATA LA SCRITTURA 35

Che cosa rappresenta?

Che cos’è una potenza? Rappresenta una potenza.

Una potenza è una moltiplicazione con un fattore che si ripete sempre uguale.

Come si calcola il valore di una potenza?

ESEMPIO

35 = 3 × 3 × 3 × 3 × 3 = 243

ESEMPIO

3 × 3 × 3 × 3 × 3

si scrive 35 e si legge “tre alla quinta’’:

3 → base: il fattore che si ripete

5 → esponente: quante volte va ripetuta la base.

Ci sono casi particolari delle potenze?

Sì, sono i seguenti:

non ha significato

1 Completa i seguenti schemi dove: = esponente = potenza = base

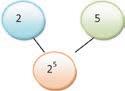
Completa e rispondi.

2 73 = 7 × ×

a) Qual è la base? Qual è l’esponente?

b) Quante volte si ripete la base?

c) Come si legge la potenza? alla o anche 7 al cubo.

3 92 = ×

a) La base è , l’esponente è

b) La base, 9, si ripete volte.

c) La potenza si legge alla seconda oppure 9 al quadrato.

4 Calcola il valore delle seguenti potenze.

a) 43 = 4 × 4 × 4 = 16 × 4 = 152 = × 15 =

b) 25 = 2 × 2 × 2 × × =

c) 33 =

5 Calcola il valore delle seguenti potenze scrivendo le moltiplicazioni necessarie (come nell’esempio).

a) 26 = 112 =

b) 72 = 53 =

c) 104 = 83 =

6 Completa la seguente tabella correggendo gli errori compiuti da uno studente distratto.

Errore 50 = 5 141 = 1 103 = 30 25 = 10 122 = 24 33 = 9 92 = 18

Correzione ⁀ 2 × 2 × 2 × 2 × 2 × 2 = 64

ESPRESSIONI CON LE POTENZE TEORIA PAG. 252

DATA L’ESPRESSIONE: 2 × 52 × 2 – (23 × 5)

Come si procede per risolverla?

Le espressioni con le potenze si risolvono tenendo presente che le potenze hanno la precedenza rispetto a tutte le altre operazioni.

2 × 52 × 2 (23 × 5) = si risolvono le potenze

= 2 × 25 × 2 (8 × 5) = si risolvono le moltiplicazioni

= 100 40 = 60

POTENZE CON LA STESSA BASE TEORIA PAG. 254

DATE LE ESPRESSIONI:

132 × 13 × 135 2812 : 289 : 28

Si può calcolare velocemente il prodotto?

Il prodotto di potenze con la stessa base ha la stessa base e per esponente la somma degli esponenti

Si può calcolare velocemente il quoziente?

Il quoziente di potenze con la stessa base ha la stessa base e per esponente la differenza tra gli esponenti.

7 Completa la risoluzione della seguente espressione con potenze.

72 3 × (52 32)

Risolvi le potenze: 49 3 × (25 )

Esegui la sottrazione nella parentesi tonda: 49

Esegui la moltiplicazione: 49

Esegui l’ultima sottrazione: [1]

Risolvi le seguenti espressioni con potenze.

8 82 (23 + 32) + 23 × 5 15 × 22 [27]

9 (92 33 × 2 + 52) : (72 + 22 × 7 43) [4]

10 (72 22 5) : 23 × 5 + 50 32 × 8 : 9 [18]

11 82 : 24 + 7 × [25 (22 × 7 + 2)]2 : 2

Calcola il valore delle potenze:

Esegui la moltiplicazione nelle tonde:

Esegui l’addizione nelle tonde:

Esegui la sottrazione nelle quadre:

Eleva alla seconda il risultato della sottrazione nelle quadre:

Esegui la prima divisione e la moltiplicazione:

Esegui l’ultima divisione:

Esegui l’addizione: [18]

12 [(22 × 7 52 + 4)2 (2 × 9 3 × 5)3 24]2 [36]

13 {[7 × 4 (28 52)2 122 : 9]2 + 3 × 22} : 3 [7]

14 Risolvi applicando la proprietà del prodotto.

a) 153 × 15 × 155 × 156 = 153 + 1 + + = 15

b) 72 × 73 × 74 =

c) 103 × 10 × 102 × 105 =

15 Risolvi applicando la proprietà del quoziente.

a) 237 : 234 : 232 = 237 − − = 231

b) 56 : 53 : 5 =

c) 710 : 74 : 72 : 7 =

Risolvi applicando le proprietà delle potenze con la stessa base.

16 94 × 95 × 9 × 97

Riscrivi la base, somma gli esponenti ed esprimi il risultato sotto forma di potenza:

17 4410 : 44 : 446

Riscrivi la base, sottrai gli esponenti ed esprimi il risultato sotto forma di potenza:

POTENZE DI POTENZA

DATA:

Come si chiama?

Come si risolve velocemente?

Si chiama potenza di una potenza [(53)2]5 = 53 × 2 × 5 = 530 ESEMPIO

Con la proprietà della potenza di potenza che dice che la potenza di una potenza ha la stessa base e per esponente il prodotto degli esponenti.

POTENZE CON LO STESSO ESPONENTE TEORIA PAG. 254

DATE LE ESPRESSIONI: 56 × 66 × 46 459 : 39 : 59

Si può calcolare velocemente il prodotto?

Sì, il prodotto di potenze con lo stesso esponente ha per base il prodotto delle basi e per esponente lo stesso esponente.

× 66 × 46 = (5 × 6 × 4)6 = 1206

Si può calcolare velocemente il quoziente?

Sì, il quoziente di potenze con lo stesso esponente ha per base il quoziente delle basi e per esponente lo stesso esponente.

18 Risolvi applicando la proprietà della potenza di una potenza.

a) [(112)4]5 = 112 × 4 × = 11

b) [(23)2}]3 =

c) [(102)4]3 =

19 {[(52)3]6}3

Riscrivi la base e moltiplica gli esponenti:

20 (103)4 = [(84)5]0 =

21 Risolvi applicando la proprietà del prodotto.

a) 73 × 33 × 23 = (7 × 3 × 2) 3 =

b) 23 × 5 3 × 33 =

c) 45 × 25 × 3 5 =

22 Risolvi applicando la proprietà del quoziente.

a) 484 : 124 = (48 : 12)4 =

b) 203 : 43 =

c) 352 : 72 =

Risolvi le seguenti espressioni, applicando le proprietà delle potenze.

23 39 × 49 : 127 : [(32)5 : 38]

Esegui la moltiplicazione di potenze di ugual esponente e la potenza di potenza:

Esegui le divisioni tra potenze con la stessa base:

Esegui la divisione tra potenze con lo stesso esponente e scrivi il risultato: [16]

24 (52)5 : 58 + (25)3 : 212 49 : 47

Esegui le potenze di potenze e la divisione di potenze di ugual base:

Esegui le due divisioni tra potenze con la stessa base:

Eleva a potenza:

Esegui le ultime operazioni così come si presentano: [17]

DATA LA SCRITTURA

7 × 105

Che cosa significa 105?

È una potenza di 10.

Osserva le potenze di 10:

101 = 10

102 = 100

103 = 1 000

104 = 10 000

105 = 100 000

Puoi notare che il numero di zeri è uguale all’esponente della potenza.

Che cosa rappresenta?

• È la notazione scientifica, detta anche notazione esponenziale, cioè un modo sintetico per scrivere numeri grandi.

• È il prodotto di un numero per una potenza di 10.

ESEMPIO

Il raggio della Terra misura circa 700 000 km, cioè 7 seguito da 5 zeri.

Con la notazione esponenziale il raggio della Terra si scrive così: 7 × 105 km

25 Esprimi con la notazione scientifica i seguenti numeri grandi.

ESEMPIO

La distanza tra la Terra e il Sole è circa 150 000 000 km.

La notazione scientifica è 1,5 × 108 km:

• 1,5 perché il numero che moltiplica la potenza di dieci deve essere maggiore di 1 e minore di 10;

• esponente 8 perché corrisponde alle 8 cifre dopo l’1 (sette 0 e il 5).

a) 9 000 000 = × 10 (conta le cifre colorate che corrispondono all’esponente della potenza di 10)

b) 50 000 000 = 4 000 000 000 =

c) 5 600 000 = 5,6 × 72 000 000 000 = 7,2 ×

Scrivi in forma normale i seguenti numeri scritti in notazione scientifica.

26 a) 5 × 106 =

b) 7,6 × 109 =

c) 1,28 × 1010 =

d) 7,5 × 108 =

27 a) 3 × 107 =

b) 9 × 108 =

c) 6,5 × 109 =

d) 1,59 × 106 =

28 Sottolinea i numeri che non sono scritti in notazione scientifica.

ESEMPIO

11,4 × 103 non è scritto in notazione scientifica perché il numero 11,4 è maggiore di 10.

a) 7,1 × 107 11,3 × 108 2,3 × 104 17 × 105

b) 2,43 × 109 5,713 × 108 0,5 × 106 9,8 × 1011

29 MATEMATICA IN AZIONE Scrivi in notazione scientifica la distanza Terra-Giove.

a) massima → circa 965 000 000 km

b) minima → circa 588 000 000 km

c) media → circa 787 000 000 km

30 MATEMATICA IN AZIONE Anna, a cui piacciono i fumetti Disney, scopre che il patrimonio di zio Paperone si aggira intorno ai 65 miliardi di dollari, rendendolo il più ricco tra tutti i personaggi dei fumetti.

Come si scrive con la notazione scientifica il valore del patrimonio di Paperon de’ Paperoni?

SIMULAZIONE DI VERIFICA

1 Completa scrivendo il nome esatto.

Data la potenza 75 = 7 × 7 × 7 × 7 × 7:

7 è la 5 è è il calcolo per risolverla.

2 Riconosci tra le seguenti potenze i quadrati e i cubi e completa la tabella.

35 52 83 a2 quadrati cubi

73 42 a3 67

Contrassegna la risposta esatta (può essere più di una).

3 Quanti zeri ha la potenza 108?

a) otto b) sette c) dieci d) zero

4 54 × 56 × 5 è uguale a:

54+6

5 68 × 48 è uguale a: a) (6 + 4)8 b) (6 × 4)8+8 c) (6 × 4)8 d) 86×4

6 [(2,73)5]6 è uguale a:

2,73+5+6

7 Calcola il valore delle seguenti potenze.

8 Riconosci la risposta esatta e risolvi lasciando il risultato sotto forma di potenza.

a) 34 × 54 1) (3 × 5)4+4 2) (3 × 5)4 b) 86 : 83 1) 86–3

(53)4

× 45

43×5 e) 452 : 92 1) (45 : 9)2

(45 : 9)2+2

9 Risolvi le seguenti espressioni (se necessario, applica le proprietà.

a) 5 × [(52 × 3 + 2) : 7 – 5 × 2]3 + (7 × 23 – 25) : 3 – 23 + 30

b) 53 : 52 + [(62)2 : 63 + (44 × 42)2 : (43)4 – 82 : 42] + 2,63 : 2,63

Risolvi i seguenti problemi riferiti a situazioni presenti nella realtà.

10 Federica, nuotatrice provetta, per allenarsi per una gara in una mattinata fa 7 vasche a dorso, 7 a rana, 7 a delfino, 7 a stile libero. Quante vasche percorre in tutto? La soluzione è una moltiplicazione o una potenza del 7?

11 Considera la massa della Terra e quella di Urano: esprimile in notazione scientifica e stabilisci quale dei due pianeti ha la massa maggiore.

– Massa della Terra → 5 970 000 000 000 000 000 000 000 kg – notazione scientifica – massa di Urano → 86 800 000 000 000 000 000 000 000 kg – notazione scientifica

Quindi

12 Da una ricerca effettuata in rete sono emersi i seguenti risultati relativi al fatturato dell’anno 2017 di alcune grandi aziende. Fonte: Reportaziende

Fatturato

Scrivi i fatturati:

a) in notazione scientifica

b) in ordine crescente rispetto alla notazione scientifica

c) in ordine di grandezza

DIVISORI E MULTIPLI DI UN NUMERO NATURALE

Chi ha della

paura matematica?

È giunto il momento di intraprendere un vero e proprio viaggio all’interno dei numeri: sei pronto per scoprire i loro segreti più nascosti? Niente paura, non si tratta di misteri incomprensibili, ma di proprietà affascinanti che balzano agli occhi mentre li studi con attenzione, sono delle regolarità che non ti aspetti e che, una volta scoperte, ti faranno dire “Wow! Non lo avrei mai pensato!”.

Hai sentito già parlare di “numeri primi” e “numeri composti”? I numeri primi sono stati definiti i “mattoni fondamentali” di tutti gli altri numeri, quelli che non possono essere costruiti se non con sé stessi e con il numero 1, mentre i numeri composti, possono essere costruiti moltiplicando tra loro i numeri primi.

Userai questi “mattoni" per costruire concetti che ti serviranno per risolvere dei problemi: il Minimo Comune Multiplo (m.c.m.) e il Massimo Comune Divisore (M.C.D.) Si sa, sono nomi lunghi e simili tra loro, e questo può generare la paura di fare confusione e di non sapere quale scegliere, ma risolvendo problemi pratici, questiconcettidiventerannofamiliari,chiari eutiliancheperte.

ROAD MAP la nostra

DEFINIAMO I MULTIPLI E I DIVISORI DI UN NUMERO

USIAMO I CRITERI DI DIVISIBILITÀ

IMPARIAMO LA SCOMPOSIZIONE DEI NUMERI COMPOSTI IN FATTORI PRIMI

CALCOLIAMO IL MCD DI PIÙ NUMERI

CALCOLIAMO IL mcm DI PIÙ NUMERI

MATERIALE INTEGRATIVO MULTIMEDIALE

MULTIPLI E DIVISORI 1

SUCCEDE CHE...

Emma vuole sistemare la sua collezione di ben 24 Rubbiz in un contenitore a scomparti. In cartoleria può scegliere tra contenitori a 3, a 4 o a 9 scomparti. Quale contenitore è adatto, visto che li vuole distribuire in parti uguali?

Per rispondere occorre conoscere i multipli e i divisori di un numero.

Il multiplo di un numero naturale n è il prodotto di n per un altro numero naturale diverso da zero.

In simboli: n × 3 = 3 n; n × 4 = 4 n e così via...

I multipli di un numero, per esempio 8, sono infiniti e si possono indicare così:

M(8) → 8, 16, 24, 32, 40, 48, ...

Un numero è divisore di un altro se il resto della loro divisione è zero.

Se dividiamo 4 per tutti i numeri che lo precedono, osserviamo che non tutte le divisioni hanno resto zero:

4 : 1 = 4 (resto 0) 4 : 3 = 1 (resto 1) 4 : 2 = 2 (resto 0) 4 : 4 = 1 (resto 0)

I numeri 1, 2, 4, risultati delle divisioni con resto 0, sono i divisori di 4

4 è multiplo dei suoi divisori; infatti → 1 × 4 = 4; 2 × 2 = 4; 4 × 1 = 4.

Quindi i divisori di un numero sono detti anche sottomultipli di quel numero.

Divisori e multipli di un numero naturale

Un numero a è divisibile per un altro numero b se a è multiplo di b.

I divisori o sottomultipli di un numero, per esempio 4, sono in numero finito e si indicano così:

D(4) → 1, 2, 4.

Ricordiamo questi casi particolari:

• Ogni numero è divisore di se stesso.

45 : 45 = 1 In simboli → a : a = 1

• L’unità è divisore di tutti i numeri.

38 : 1 = 38 In simboli → a : 1 = a

• Un divisore di un numero lo è anche di tutti i suoi multipli. Per esempio, se 5 è divisore di 10, 5 è divisore di tutti i multipli di 10, cioè di 20, 30, ... 600, ...

Emma può utilizzare solo contenitori da 3 o da 4 scomparti; infatti, 24 è multiplo di 3 e di 4, ma non di 9.

1 Osserva e completa. 3 × 5 = 15

a) 3 è divisore di 5 è di 15

b) 15 è divisibile per e per 15 è multiplo di e di

2 Scrivi i primi sette multipli dei seguenti numeri: 6; 11; 14.

3 Trova i divisori del numero 9.

9 : 1 = resto

9 : 2 = resto 9 : 3 = resto

9 : 4 = resto 9 : 5 = resto 9 : 6 = resto

9 : 7 = resto 9 : 8 = resto 9 : 9 = resto

D(9) →

4 Calcola e completa.

a) 24 = 3 × 8 da cui 24 : 3 = e 24 : = quindi: e sono divisori di 24

b) 24 = 6 × 4 da cui 24 : = e 24 : = quindi: e sono di 24

5 Scrivi tutti i divisori di 12; 14; 18; 24.

6 Calcola e completa.

a) 68 : 68 = 1 5 : 5 = 11 : = 1 13 : 13 = Ogni numero è di se stesso.

b) 35 : 1 = 35 7 : 1 = 12 : = 12 10 : 1 = L’unità è divisore di

7 Completa come negli esempi.

a) 91 = 7 × 13

b) 18 × 15 = 270

c) 65 = 13 × 5

d) 315 : 21 = 15

e) 16 : 8 = 2

8 MATEMATICA IN AZIONE Quali tra i seguenti gruppi di oggetti - 10 monete, 25 figurine e 40 biglie - sono divisibili in parti uguali tra 2 o 5 persone? multiplo → 91 divisori → 7 e 13 multiplo → 315 divisori → 21 e 15

2 CRITERI DI DIVISIBILITÀ

SUCCEDE CHE...

Un rivenditore di Ape car (a tre ruote) può acquistare con un ottimo sconto una partita di gomme da neve, scegliendo tra una composta da 140 gomme o un’altra da 150.

Per non avere avanzi, gli conviene acquistare la partita da 140 o quella da 150 gomme?

Criteri di divisibilità per 2 e 4, 3 e 9

Per rispondere velocemente ci serve conoscere i criteri di divisibilità

Tenendo conto che un numero è divisibile per un altro se il resto della loro divisione è zero, i criteri di divisibilità sono delle regole che permettono di stabilire se un numero è divisibile per un altro senza eseguire la divisione.

Criterio di divisibilità per 2

Un numero è divisibile per 2 se termina con 0, 2, 4, 6, 8.

Tutti i numeri pari sono divisibili per 2 → 80; 74; 56; 38; 12.

Criterio di divisibilità per 4

Un numero è divisibile per 4 se termina con due zeri o se le ultime due cifre a destra formano un multiplo di 4.

300 860 732 988 → sono divisibili per 4

Poiché 4 è un multiplo di 2, tutti i numeri divisibili per 4 lo sono anche per 2.

Divisori e multipli di un numero naturale

Criterio di divisibilità per 3

Osserva i multipli di 3 → ... 12, 15, 18, ... 27, 30, 33, ... 72, 75, 78, ... Sono tutti numeri nei quali la somma delle cifre è un multiplo di 3.

Un numero è divisibile per 3 se la somma delle sue cifre è un multiplo di 3.

204 è divisibile per 3 perché 2 + 0 + 4 = 6 che è un multiplo di 3.

Criterio di divisibilità per 9

Un numero è divisibile per 9 se la somma delle sue cifre è un multiplo di 9.

378 → 3 + 7 + 8 = 18 → quindi 378 è divisibile per 9.

Poiché 9 è un multiplo di 3, tutti i numeri divisibili per 9 lo sono anche per 3.

140 → (1 + 4 + 0 = 5) non è divisibile per 3; invece 150 → (1 + 5 + 0 = 6) sì.

Quindi al rivenditore conviene acquistare la partita da 150 gomme da neve.

Completa le frasi ed esegui le richieste.

1 Un numero è sempre divisibile per 2, un numero dispari mai.

2 Sottolinea i numeri divisibili per 2.

3 Un numero è divisibile per 3 se la delle sue cifre è un di 3.

4 Sottolinea i numeri divisibili per 3.

5 Un numero è per 4 se termina con due zeri o le ultime due cifre a destra formano un numero di 4.

6 Scrivi 5 numeri di due cifre divisibili per 4:

7 Un numero è divisibile per 9 se la somma delle è

8 Sottolinea i numeri divisibili per 9.

Completa con cifre a tuo piacere, in modo che i numeri siano divisibili per:

11 Scrivi 5 numeri di almeno tre cifre divisibili per 2 e anche per 4.

12 Scrivi 5 numeri di due cifre divisibili per 3 e per 9.

13 Scrivi 5 numeri di tre cifre divisibili per 2 e per 3.

14 MATEMATICA IN AZIONE Nel gioco della “Briscola’’ si usa un mazzo di 40 carte. All’inizio del gioco vengono assegnate 3 carte a ogni giocatore e poi a ogni “mano’’ ciascun giocatore gioca una carta e ne prende un’altra dal mazzo fino al loro esaurimento.

Perché a Briscola, utilizzando tutte le 40 carte del mazzo, si può giocare solo in 2 o in 4 e non in 3?

Criteri di divisibilità per 5, 25, 10, 100, 1 000

SUCCEDE CHE...

Al negozio di fiori Flowers questa mattina sono arrivati dall’Olanda i tulipani: 50 della varietà Darwin, 75 della varietà Trionfo e 90 della varietà La Belle Époque.

È possibile fare, con tutte le varietà a disposizione, mazzi da 5, 10 o 25 fiori, tutti dello stesso tipo, senza che avanzi alcun fiore?

Per rispondere alla domanda è necessario conoscere i criteri di divisibilità per 5, 10 e 25.

Criterio di divisibilità per 5

Un numero è divisibile per 5 se termina con 0 o con 5.

Se osservi i multipli di 5 → 5, 10, 15, ... 70, 75, 135, 140, ... 290, 295, ... noti che terminano tutti per 5 o per 0.

Criterio di divisibilità per 25

Un numero è divisibile per 25 se le ultime due cifre a destra formano un multiplo di 25 o sono due zeri.

Divisori e multipli di un numero naturale

25 è un multiplo di 5; quindi, tutti i numeri divisibili per 25 lo sono anche per 5.

Se osservi i multipli di 25 → 25, 50, 75, ... 250, 275, 300, ... 425, 450, 475, ... osservi che le ultime due cifre a destra formano un numero multiplo di 25 o sono due zeri.

Criterio di divisibilità per 10, 100, 1 000

Un numero è divisibile per 10, 100, 1 000 ... se termina rispettivamente con almeno 1, 2, 3 ... zeri.

M(10) → 10, 20, 30, 40, ... 90, 100, 110, ... 250, 260, 270, ... 300, 310, 320, ...

M(100) → 100, 200, ... 700, 800, 900, 1 000, ... 1 300, 1 400, 1 500, ...

M(1000) → 1 000, 2 000, 3 000, ... 9 000, 10 000, ... 14 000, 15 000, 16 000, ...

23 000 è divisibile per 10, per 100 e per 1 000

9 480 è divisibile per 10 ma non per 100 e per 1 000 perché termina con un solo zero.

No, non è possibile. Con tutte e tre le varietà si possono fare solo mazzi da 5 tulipani, perché 50, 75 e 90 sono divisibili per 5. Con le varietà Darwin e La Belle Époque anche mazzi da 10, perché 50 e 90 sono divisibili per 10. Con la varietà Trionfo anche mazzi da 25, che è un divisore di 75.

ESERCIZI

1 Rispondi con Vero o Falso.

a) Se un numero termina con 0 è divisibile per 5. V F

b) Se un numero termina con 5 è divisibile per 25. V F

c) Un numero che termina con 0 è divisibile per 10 e i suoi multipli. V F

d) Un numero che termina con due zeri è divisibile per 10 e per 100. V F

2 Completa le frasi.

a) Un numero è divisibile per 5 se termina con

b) Un numero è divisibile per 10 se termina con uno 0, è divisibile per se termina con almeno due 0, per 1 000 se termina con

3 Tra i seguenti numeri sottolinea quelli divisibili per 5. 225 340 87 1 365 5 632 96 175 503 550 515

4 Considera i numeri sottolineati nell’esercizio precedente e trascrivi quelli divisibili per 25.

5 Osserva i seguenti numeri e rispondi alle richieste.

35 85 125 6 000 190 250 700

a) Perché sono tutti divisibili per 5?

b) Quali sono divisibili per 25?

c) Quali sono divisibili per 10?

d) Quali sono divisibili per 100?

e) Quali sono divisibili per 1 000?

Scrivi 5 numeri di almeno tre cifre che rispondano alle richieste.

6 Numeri divisibili per 25 ma non per 10.

7 Numeri divisibili per 5 ma non per 100.

8 Numeri divisibili per 10 ma non per 100.

9 MATEMATICA IN AZIONE Con riferimento al gioco della “Briscola’’, in cui si utilizzano tutte le 40 carte del mazzo, è possibile giocare in 5 persone? Perché?

Criteri di divisibilità per 7 e 11

SUCCEDE CHE...

La pasticceria Dolcebontà per Pasqua ha preparato 308 ovetti di cioccolato che deve confezionare in sacchettini da 7 o da 11.

Quali sarà meglio utilizzare per non avere avanzi?

Quanti sacchettini di ogni tipo saranno necessari?

Per rispondere velocemente occorre conoscere i criteri di divisibilità per 7 e per 11.

Criterio di divisibilità per 7

Un numero è divisibile per 7 se la differenza tra il numero stesso privato delle unità e il doppio delle unità è 0 o un multiplo di 7.

Controlliamo se il numero 308 è divisibile per 7:

• prendi il numero delle unità e moltiplicalo per 2 308 → 8 × 2 = 16

• togli il risultato trovato dal numero formato dalle cifre rimanenti 30 − 16 = 14

• la differenza ottenuta è un multiplo di 7? 14 = 7 × 2

Sì, quindi il numero 308 è divisibile per 7.

Invece 827 non è divisibile per 7; infatti → 82 − (7 × 2) = 82 − 14 = 68 che non è multiplo di 7.

Criterio di divisibilità per 11

Divisori e multipli di un numero naturale

Un numero è divisibile per 11 se la differenza tra la somma delle cifre di posto pari e la somma delle cifre di posto dispari (o viceversa) è 0 o un multiplo di 11.

a) 37 51 35 71 88 3751 0

b) 16 42 14 62 58 85 1642 3

non è divisibile per 11

Controlliamo se il numero 308 è divisibile per 11.

308 → (3 + 8) 0 = 11 0 = 11; quindi 308 è divisibile per 11

La pasticceria Dolcebontà può utilizzare sia i sacchettini che contengono 7 ovetti sia quelli che ne contengono 11; infatti 308 è divisibile per 7 e anche per 11.

Serviranno 44 sacchettini da 7 ovetti oppure 28 sacchettini da 11.

ESERCIZI Primi

Completa le frasi ed esegui le richieste.

1 Un numero è divisibile per 7 se la tra il numero stesso privato delle e il delle unità è 0 o un di 7.

a) 427 è divisibile per 7; infatti 42 − 7 × 2 = che è un multiplo di 7

b) 651 è divisibile per 7; infatti 65 1 × 2 =

c) 540 non è divisibile per 7; infatti

d) 714 è divisibile per 7; infatti

e) 745 non è divisibile per 7; infatti

3 Applicando il criterio di divisibilità stabilisci quali dei seguenti numeri sono divisibili per 7.

112 154 270 357 1 894 546 623 735

Completa la frase ed esegui le richieste.

4 Un numero è divisibile per 11 se la tra la somma delle cifre di posto e la delle cifre di dispari (o viceversa) è o un multiplo di

a) 385 è divisibile per 11; infatti (3 + 5) 8 =

b) 572 è divisibile per 11; infatti (5 + 2) =

c) 1 024 non è divisibile per 11; infatti ( + ) ( + ) =

d) 2 167 è divisibile per 11; infatti

e) 3 612 non è divisibile per 11; infatti

6 Applicando il criterio di divisibilità sottolinea i numeri divisibili per 11. 242 531 616 845 2 035 891 1 650 2 288

7 Il fratellino di Giosuè è nato il 27/09/2019.

Giorno, mese e anno di nascita sono divisibili per 3?

E per 9?

8 Scrivi la tua data di nascita e, utilizzando i criteri di divisibilità, stabilisci per quali numeri è divisibile.

(Attenzione: potrebbe verificarsi che nessuno dei criteri studiati vada bene; perché?)

SUCCEDE CHE...

NUMERI PRIMI E SCOMPOSIZIONE DI NUMERI COMPOSTI IN FATTORI PRIMI

Il nonno di Pietro ha inserito la combinazione nella cassaforte e la ricorda così: “La combinazione è formata da tre numeri primi consecutivi la cui somma è 41, un altro numero primo’’.

Quali numeri ha scelto il nonno di Pietro? Che cosa intende per numeri primi?

Per rispondere dobbiamo distinguere i numeri primi dai numeri composti.

Analizziamo i divisori di alcuni numeri: 8, 11, 13 e 15.

D(8) → 1, 2, 4, 8 D(11) → 1, 11 D(13) → 1, 13 D(15) → 1, 3, 5, 15

Si può notare che 11 e 13 hanno solo due divisori, l’unità e se stessi, mentre 8 e 15 hanno più di due divisori

I numeri come 11 e 13 sono numeri primi, gli altri sono numeri composti

I numeri primi sono numeri naturali divisibili solo per 1 e per se stessi.

I numeri composti sono numeri naturali che possiedono più di due divisori.

I numeri composti si possono scrivere come prodotto di fattori primi grazie alla fattorizzazione.

La fattorizzazione, o scomposizione in fattori primi, è un procedimento che permette di scrivere un numero composto come prodotto di fattori primi.

ESEMPIO

Divisori e multipli di un numero naturale

12 = 2 × 2 × 3 = 22 × 3

18 = 3 × 6 → non è scomposto perché 6 non è fattore primo.

• Le Tavole in fondo al libro raccolgono i numeri primi minori di 5 000.

• 1 ha un solo divisore, quindi non si considera numero primo.

• Tutti i numeri primi sono dispari, tranne il 2.

Se il numero da scomporre è grande, conviene utilizzare il metodo delle divisioni successive. Scomponiamo in fattori primi il numero 210:

• dopo aver scritto il numero 210 tracciamo alla sua destra una riga verticale;

• utilizzando i criteri di divisibilità si cerca il più piccolo divisore primo di 210, cioè 2; lo scriviamo alla sua destra, eseguiamo la divisione 210 : 2 e scriviamo 105 sotto a 210;

• scriviamo a destra di 105 il più piccolo dei suoi divisori primi, 3, e sotto a 105 il risultato della divisione 105 : 3, cioè 35;

• scriviamo a destra di 35 il suo divisore primo più piccolo, cioè 5, eseguiamo la divisione 35 : 5 e scriviamo 7 sotto a 35;

• 7 è un numero primo, quindi è divisibile solo per se stesso; scriviamo 7 alla sua destra e scriviamo sotto il risultato di 7 : 7, cioè 1.

La scomposizione è finita; possiamo scrivere: 210 = 2 × 3 × 5 × 7

210 2

105 3

35 5 7 7 1 :

Pietro, facendo alcuni tentativi, ha capito che la combinazione è composta dai numeri 11, 13 e 17. Il nonno, però, gli raccomanda di non rivelarla a nessuno.

1 Rispondi con Vero o Falso.

a) I numeri primi sono divisibili solo per 1 e per se stessi. V F

b) I numeri composti devono avere almeno quattro divisori. V F

c) La fattorizzazione e la scomposizione in fattori primi sono la stessa cosa. V F

d) Il numero 2 non è un numero primo perché è pari. V F

2 Completa.

a) 13 ha come divisori 1 e 13; quindi è un numero .

b) 16 ha come divisori 1, 2, , , ; quindi è un numero

c) 17 ha come divisori ; quindi

d) 27 ha come divisori ; quindi

3 Sottolinea i numeri primi. 11

4 Scomponi in fattori primi come nell’esempio.

5 Completa le scomposizioni in fattori primi.

24

6 Scomponi in fattori primi sul tuo quaderno. 86 98 125 280 325 520

7 MATEMATICA IN AZIONE Nella classe di Anna devono fare dei lavori di gruppo. La professoressa non può formare gruppi con lo stesso numero di ragazzi. Infatti, se li divide in gruppi di 2 rimane 1 alunno; se li divide in gruppi di 3 rimangono 2 alunni; se li divide in gruppi di 4 manca 1 alunno; se li divide in gruppi di 5 mancano 2 alunni per completare l’ultimo gruppo. Scopri quanti alunni ci sono, sapendo che la classe è formata da meno di 30 alunni. (Il numero non è multiplo di 2, non è multiplo di 3, ...)

SUCCEDE CHE...

CRITERIO GENERALE DI DIVISIBILITÀ

Emma è in Umbria per le vacanze estive ed è prevista un’uscita per fare rafting vicino

alla Cascata delle Marmore con tutti i ragazzi del campo estivo.

Se i partecipanti sono 144 e si muoveranno con 24 gommoni, quanti ragazzi saliranno su ogni gommone?

È possibile sapere il risultato senza fare la divisione?

Grazie alla scomposizione in fattori primi è possibile rispondere al quesito, perché si può stabilire se un numero è divisibile per un altro e, in caso affermativo, calcolare il quoziente della divisione. Questo metodo si rivela particolarmente interessante quando i numeri da dividere sono grandi.

Un numero è divisibile per un altro se la fattorizzazione del primo contiene almeno tutti i fattori primi del secondo con esponente uguale o maggiore.

144 è divisibile per 24?

Per rispondere alla domanda scomponiamo i due numeri:

Divisori e multipli di un numero naturale

Si nota che la fattorizzazione di 144 comprende quella di 24, quindi 144 è divisibile per 24, oppure 144 è un multiplo di 24.

Stabilito che un numero è divisibile per un altro, sempre utilizzando la scomposizione in fattori primi, si può determinare il quoziente della divisione

LUZIONE

Per sapere il numero di ragazzi che salirà su ogni gommone possiamo usare la scomposizione:

144 = 2 4 × 3 2 24 = 2 3 × 3

144 è divisibile per 24

Per calcolare il quoziente si utilizzano le loro scomposizioni: (2 4 × 3 2) : (2 3 × 3)

Applichiamo la proprietà invariantiva della divisione e la proprietà di potenze con ugual base:

(2 4 : 2 3) × (3 2 : 3) = 2 × 3 = 6

Quindi 144 : 24 = 6, cioè 6 ragazzi per ogni gommone.

1 Rispondi con SÌ o NO.

a) La scomposizione in fattori primi serve per capire se un numero è primo. Sì No

b) Con la scomposizione in fattori primi si trovano i divisori comuni a due o più numeri.

c) Con la scomposizione in fattori primi si può stabilire se due numeri sono divisibili tra loro.

Sì No

Sì No

d) Con la scomposizione in fattori primi si calcola il prodotto di due numeri. Sì No

e) Con la scomposizione in fattori primi si determina il quoziente di due numeri divisibili tra loro.

2 1 260 è divisibile per 120? Osserva la scomposizione in fattori e rispondi.

1 260 = 22 × 32 × 5 × 7 120 = 23 × 3 × 5

3 Stabilisci se la fattorizzazione di b è contenuta in quella di a.

a) a = 23 × 3 × 52 b = 22 × 3 × 5

b) a = 24 × 32 × 7 b = 2 × 34 × 7

c) a = 53 × 113 × 13 b = 52 × 11

d) a = 25 × 32 × 7 b = 24 × 3 × 13

4 Stabilisci se il primo numero è divisibile per il secondo. (Svolgi le scomposizioni sul quaderno.)

a) 1 638 e 78

1 638 = 2 × 32 × 7 × 13 78 = 2 × × (i due numeri divisibili).

b) 189 e 54 c) 300 e 12 d) 392 e 21 e) 528 e 33

Sì No

5 Calcola il quoziente tra i numeri assegnati utilizzando la scomposizione in fattori primi. (Svolgi le scomposizioni sul quaderno.)

a) 4 950 e 330

4 950 = 2 × 32 × 52 × 11 330 = 2 × 3 × 5 × 11

(2 × 32 × 52 × 11) : (2 × 3 × 5 × 11) =

(2 : 2) × (32 : ) × ( : 5) × (11 : ) = 1 × × × 1 = 15

b) 224 e 32 c) 448 e 28 d) 684 e 57 e) 1 764 e 98

6 MATEMATICA IN AZIONE Una scolaresca formata da 168 tra alunni e professori deve salire in funivia sull’Etna a osservare le recenti colate laviche. Sapendo che ogni cabina contiene al massimo 12 passeggeri, di quante ne avranno bisogno per salire tutti? (Risolvi la divisione con la scomposizione in fattori primi)

CALCOLO DEL MASSIMO COMUN DIVISORE DI PIÙ NUMERI

SUCCEDE CHE...

Pietro è iscritto a un progetto PON di matematica. La tutor ha chiesto in segreteria 72 penne e 54 quaderni da distribuire equamente a tutti gli allievi del progetto.

Quanti sono gli iscritti, al massimo, compreso Pietro? Quante penne e quaderni riceverà ciascuno di loro?

Per rispondere bisogna stabilire il Massimo Comun Divisore.

Il Massimo Comun Divisore è il maggiore tra i divisori comuni a più numeri.

Cerchiamo, per esempio, i divisori comuni a 18 e 24.

D(18) → 1, 2, 3, 6, 9, 18

D(24) → 1, 2, 3, 4, 6, 8, 12, 24

I divisori comuni di 18 e 24 sono: 1, 2, 3, 6.

Il più grande tra loro è 6; quindi 6 è il Massimo Comun Divisore.

In simboli → M.C.D. (18; 24) = 6

che si legge “ il Massimo Comun Divisore di 18 e 24 è 6’’. Il procedimento precedente è poco pratico se si deve cercare il M.C.D. di numeri grandi; per questo si ricorre alla fattorizzazione applicando la seguente regola.

Il Massimo Comun Divisore (M.C.D.) di due o più numeri è il prodotto dei fattori primi comuni a tutti, ciascuno preso una sola volta con il minimo esponente con cui figura nelle fattorizzazioni.

Divisori e multipli di un numero naturale

Calcoliamo il M.C.D. di 72 e 54. 72 = 23 × 32 54 = 2 × 33

M.C.D. (72; 54) = 2 × 32 = 18

Casi particolari.

• Il M.C.D. può essere uno dei numeri assegnati.

M.C.D. (16; 64) = 16 infatti 16 è divisore di 64.

• Il M.C.D. di due o più numeri può essere 1 se non ci sono divisori comuni.

M.C.D. (9; 15; 20) = 1

infatti 9 = 32; 15 = 3 × 5; 20 = 22 × 5

I numeri che hanno 1 come M.C.D. sono numeri primi tra loro.

Gli alunni iscritti al PON sono 18 e riceveranno → 72 : 18 = 4, cioè 4 penne, e 54 : 18 = 3, cioè 3 quaderni ciascuno.

1 Rispondi sul quaderno alle seguenti domande.

a) Che cosa significa la sigla M.C.D.?

b) Che cos’è il Massimo Comun Divisore tra due o più numeri?

c) Come si calcola il M.C.D.?

d) Se due o più numeri non hanno divisori comuni, qual è il loro M.C.D.?

e) Se un numero è divisore di un altro, qual è il loro M.C.D.? Fai degli esempi.

2 Scrivi i divisori di ciascun numero, evidenzia quelli comuni e individua il M.C.D.

a) 24 e 30

D(24) → 1, 2, 3, 4, , , , 24

D(30) → 1, 2, 3, 5, , , , 30 divisori comuni , , ,

M.C.D. (24; 30) =

b) 28 e 42

D(28) → , , , , , D(42) → , , , , , , , divisori comuni , ,

M.C.D. (28; 42) =

3 Sottolinea il M.C.D. di ogni coppia di numeri.

a) 8 e 16 b) 5 e 25 c) 4 e 12 d) 100 e 200

4 Osserva le seguenti fattorizzazioni e stabilisci quali fattori devi considerare per calcolare il M.C.D.

a) 22 × 32 × 7 32 × 5 × 7 23 × 32 × 7 i fattori comuni da considerare sono 32 e

b) 23 × 52 23 × 5 × 7

c) 32 × 7 × 132 2 × 3 × 5 × 13

5 Calcola il M.C.D. dei seguenti gruppi di numeri. a) 54 = ×

M.C.D. (54; 90) = × = b) 48 e 75 c) 24; 32 e 36 d) 72; 108 e 180 e) 297 e 462

6 MATEMATICA IN AZIONE Nel negozio della signora Viola Delpensiero a fine giornata rimangono 32 rose, 65 margherite e 48 gladioli. Decide allora di confezionare dei mazzi per il mercato dell’indomani, tutti con lo stesso numero di fiori.

Quanti mazzi riesce a formare se una margherita si spezza e la deve buttare via?

SUCCEDE CHE...

CALCOLO DEL MINIMO COMUNE MULTIPLO DI PIÙ NUMERI

Emma segue una dieta che le permette di mangiare, tra i suoi cibi preferiti, il pollo con le patatine ogni 8 giorni e il gelato ogni 12 giorni.

Se il 2 marzo ha mangiato sia il pollo sia il gelato, riuscirà ad averli entrambi il 26 dello stesso mese, giorno del suo compleanno?

Per trovare la risposta Emma potrebbe contare i giorni sul calendario, ma c’è un metodo più veloce: calcolare il minimo comune multiplo.

Il minimo comune multiplo è il minore tra i multipli comuni a più numeri.

Cerchiamo i multipli comuni a 8 e 12:

M(8) → 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, ...

M(12) → 12, 24, 36, 48, 60, 72, 84, ...

I multipli comuni sono 24, 48, 72, ...

Il più piccolo tra loro è 24; quindi, 24 è il minimo comune multiplo.

In simboli → m.c.m. (8; 12) = 24 che si legge “ il minimo comune multiplo di 8 e 12 è 24’’.

Il procedimento precedente è poco pratico se si deve cercare il m.c.m. di numeri grandi; per questo si ricorre alla fattorizzazione applicando la seguente regola.

Divisori e multipli di un numero naturale

Il minimo comune multiplo (m.c.m.) di due o più numeri è il prodotto dei fattori primi comuni e non comuni, ciascuno preso una sola volta con il massimo esponente con cui figura nelle scomposizioni.

Calcoliamo il m.c.m. di 162 e 180:

162 = 2 × 34 180 = 22 × 32 × 5

m.c.m. (162; 180) = 22 × 34 × 5 = 1 620 Casi particolari.

• Il m.c.m. può essere uno dei numeri assegnati.

m.c.m. (14; 42) = 42 infatti 42 è multiplo di 14.

• Il m.c.m. di numeri primi tra loro è il loro prodotto.

m.c.m. (9; 8) = 72 infatti 9 = 32 e 8 = 23 sono primi tra loro non avendo alcun divisore in comune.

Il m.c.m. (8; 12) è 24 e 24 sono i giorni che devono trascorrere prima che Emma possa gustare di nuovo i suoi cibi preferiti; quindi il 26 marzo potrà averli a tavola.

ESERCIZI Primi

1 Rispondi sul quaderno alle seguenti domande.

a) Che cosa significa la sigla m.c.m.?

b) Che cos’è il minimo comune multiplo tra due o più numeri?

c) Come si calcola il m.c.m.?

d) Se due o più numeri sono primi tra loro, qual è il loro m.c.m.? Fai degli esempi.

2 Scrivi i primi multipli di ciascun numero, evidenzia quelli comuni e individua il m.c.m.

a) 10 e 15

M(10) → 10, 20, 30, 40, 50, 60, 70, 80, 90 ...

M(15) → 15, 30, 45, 60, 75, 90, 105 ...

multipli comuni

b) 12 e 16

M(12) →

M(16) → multipli comuni

m.c.m. (10; 15) =

m.c.m. (12; 16) =

3 Osserva le seguenti fattorizzazioni e stabilisci quali fattori devi considerare per calcolare il m.c.m.

a) 23 × 7 32 × 7 i fattori da considerare sono 23, 32 e

b) 33 × 52 3 × 5 × 7

c) 22 × 11 × 132 2 × 3 × 13

d) 24 × 32 × 113 22 × 35 × 5 × 114

4 Calcola il m.c.m. e il M.C.D. dei seguenti gruppi di numeri.

a) 48 e 84 48 = 24 × 84 = 2 × ×

m.c.m. (48; 84) = 2 × × = 336 M.C.D. (48; 84) = 2 × = 12

b) 18 e 66 c) 72 e 90 d) 16; 24 e 40 e) 594 e 231

5 MATEMATICA IN AZIONE Una chiesetta ha 3 campane che suonano rispettivamente a intervalli di 3, 4 e 5 secondi tra un colpo e l’altro.

Se battono il primo colpo insieme, dopo quanti secondi suoneranno nuovamente tutte insieme? Perché?

Divisori e multipli di un numero naturale

CRITERI DI DIVISIBILITÀ

Un numero è divisibile per:

2

14, 78, 90, 532, 946 Sì 35, 41, 87, 623, 109 No

3

513 5 + 1 + 3 = 9 Sì

102 1 + 0 + 2 = 3 Sì 47 4 + 7 = 11 No

5

65, 380, 425, 270 Sì 46, 231, 734, 509 No

7

378 37 – 2 × 8 = 21 Sì

415 41 – 2 × 5 = 31 No

11

DIVISIBILITÀ individuano

1034 (1 + 3) – (0 + 4) = 4 – 4 = 0 Sì

616 (6 + 6) –1 = 12 – 1 = 11 Sì

279 (2 + 9) –7 = 11 – 7 = 4 No

MULTIPLI

Sono infiniti

M(7) 7, 14, 21, 28, ...

m.c.m. è il più piccolo dei multipli comuni tra due o più numeri

M(18) 8, 16, 24, 32, 40, ...

M(20) 20, 40, 60, 80,...

40 è il più piccolo multiplo comune

m.c.m. (8; 20) = 40

DIVISORI

Sono limitati

D(15) 1, 3, 5, 15

M.C.D. è il più grande dei divisori comuni tra due o più numeri

D(8) 1, 2, 4, 8

D(20) 1, 2, 4, 5, 10, 20

4 è il più grandedivisore comune

M.C.D. (8; 20) = 4

NUMERI PRIMI

hanno solo due divisori: 1 e se stessi

D(13) 1 e 13

D(97) 1 e 97

NUMERI COMPOSTI

hanno più di due divisori

D(26) 1, 2, 13, 26

si scompongono con FATTORIZZAZIONE IN NUMERI PRIMI

612 = 22 × 32 × 17

ESERCIZI E PROBLEMI

LEZIONE 1

MULTIPLI E DIVISORI

1 Rispondi con Vero o Falso.

a) I divisori di un numero sono infiniti. V F

b) L’unità è divisore di ogni numero. V F

c) Zero è divisore di qualsiasi numero. V F

d) Ogni numero è divisore di se stesso. V F

2 Rispondi sul quaderno alle seguenti domande.

a) Come si ottiene il multiplo di un numero? Fai degli esempi con il numero 13.

b) Quando un numero è divisore di un altro numero? Fai degli esempi.

c) I termini divisore e sottomultiplo hanno lo stesso significato?

d) Quanti sono i multipli di un numero?

e) Che cosa indicano le scritture M(a) e D(a)?

3 Scrivi i primi 5 multipli del numero 7. 7 × 1 = 7 7 × 2 = 14 7 × 3 = 7 × = × = M(7) → 7, 14, 21, ,

4 Scrivi i primi 5 multipli di ciascuno dei seguenti numeri. 0, 4, 5, 8

a) M(0) → M(4) → 4, 8, 12, b) M(5) → M(8) →

5 Scrivi tutti i divisori dei seguenti numeri. 18, 35, 40, 60

a) D(18) → 1, 2, 3 , , 18 D(35) → b) D(40) → D(60) →

6 MATH Write down all the factors of the following numbers. 9; 12; 16; 28; 36; 48

D(9) → 1, 3, 9 D(12) → 1, 2, 3, 4, Completa.

a) 56 è multiplo di 7 secondo il numero

b) 42 è multiplo di 6 secondo il numero

c) 25 è multiplo di 5 secondo il numero

a) è multiplo di 6 secondo il numero 2.

b) è multiplo di 11 secondo il numero 9.

c) è multiplo di 12 secondo il numero 5.

a) 12 è divisore di 84 secondo il numero

b) 14 è divisore di 70 secondo il numero

c) 21 è divisore di 105 secondo il numero

10 Tra le seguenti coppie di numeri riconosci e sottolinea quelle in cui il secondo numero è multiplo del primo.

a) 2; 9 4; 16 6; 20 4; 48 9; 72 14; 46

b) 7; 42 8; 120 11; 111 10; 55 12; 60 13; 65

11 Tra le seguenti coppie di numeri riconosci e sottolinea quelle in cui il secondo numero è divisore del primo. (Aiutati eseguendo la divisione)

a) 24; 8 35; 7 42; 8 54; 3 77; 11 108; 12

b) 84; 14 75; 15 52; 13 57; 17 18; 3 42; 2

12 EDUCAZIONE CIVICA MATEMATICA IN AZIONE Per svolgere un’esperienza di laboratorio, la professoressa di scienze deve dividere una classe di 24 alunni in gruppi che abbiano esattamente lo stesso numero di persone.

Quali gruppi tra i seguenti potrebbe formare? Perché?

a) Gruppi di 4 alunni

b) Gruppi di 5 alunni

c) Gruppi di 6 alunni

Perché 24 è

Sì No

Sì No

Sì No

Prossimamente alla classe si aggiungeranno 5 alunni provenienti da altri Paesi, ospiti per il progetto Erasmus, che non conoscono bene la lingua italiana. Durante lo svolgimento degli esperimenti in laboratorio, la professoressa di scienze vorrebbe inserire uno studente ospite all’interno di ogni gruppo, in modo da favorire la collaborazione reciproca tra gli studenti.

Quale opzione deve scegliere tra le precedenti?

Verifica quanto richiesto, con esempi, sul quaderno.

13 Il numero 3, essendo divisore di 18, è divisore anche di tutti i suoi multipli.

14 Il numero 6, essendo divisore di 12, è divisore anche di tutti i suoi multipli.

15 Il numero 15, essendo divisore di 135 e di 105, è divisore anche della loro somma e della loro differenza.

105 : 15 = 135 : 15 = 105 + 135 = 240 → 240 : 15 = 135 105 = → : 15 =

16 Il numero 17, essendo divisore di 119 e di 68, è divisore anche della loro somma e della loro differenza.

17 Il numero 12, essendo divisore di 180 e di 96, è divisore anche della loro somma e della loro differenza.

18 Il numero 35, essendo divisore di 630 e di 490, è divisore anche della loro somma e della loro differenza.

19 Il numero 44, essendo divisore di 1 056 e di 616, è divisore anche della loro somma e della loro differenza.

CRITERI DI DIVISIBILITÀ LEZIONE 2

20 Rispondi con Vero o Falso.

a) Per decidere se un numero è divisibile per un altro senza effettuare la divisione si usano i criteri di divisibilità.

b) Un numero è divisibile per 3 se termina con due cifre dispari.

c) Un numero è divisibile per 4 solo se termina con due zeri.

d) Un numero nel quale la somma delle cifre è un multiplo di 3 è divisibile anche per 9.

F

F

F

F

e) Se un numero è divisibile per 25 è divisibile anche per 5. V F

f) Se un numero termina con due zeri è divisibile per 25, per 5, per 10 e per 100. V F

g) Se un numero termina con tre zeri, è divisibile per 1 000, ma non per 10 o per 100.

h) 214 è divisibile per 7 perché la somma delle sue cifre è 7.

F

F

i) 245 è divisibile per 7 perché 24 5 × 2 = 14, multiplo di 7. V F

j) 7 631 non è divisibile per 11 perché (7 + 3) (6 + 1) = 3.

F

k) 847 è un multiplo di 7 ma anche di 11, quindi è divisibile per 7 e per 11. V F

21 Applicando il criterio di divisibilità (senza eseguire la divisione), sottolinea i numeri divisibili per 2.

a) 18, 19, 20, 35, 46, 56, 73, 100, 111, 123, 145, 138, 166

b) 15, 38, 48, 62, 77, 80, 96, 119, 200, 353, 444, 467, 701

22 Applicando il criterio di divisibilità (senza eseguire la divisione), sottolinea i numeri divisibili per 4.

a) 72, 96, 100, 144, 226, 351, 402, 466, 506, 650, 773, 1 024

b) 168, 198, 285, 346, 1 122, 2 516, 2 682, 2 901, 5 300, 8 426, 9 132, 9 748

23 Applicando il criterio di divisibilità (senza eseguire la divisione), sottolinea i numeri divisibili per 3.

a) 28, 57, 84, 99, 102, 180, 211, 312, 501, 616, 753

b) 55, 71, 105, 405, 561, 642, 818, 10 341, 21 003, 50 310, 10 333

24 Applicando il criterio di divisibilità (senza eseguire la divisione), sottolinea i numeri divisibili per 9.

a) 60, 83, 108, 118, 252, 350, 513, 676, 1 017, 1 035, 3 105, 4 581

b) 81, 270, 417, 711, 919, 2 765, 3 861, 12 006, 35 793, 67 299, 123 987

25 Applicando il criterio di divisibilità (senza eseguire la divisione), sottolinea i numeri divisibili per 5.

a) 75, 95, 275, 1 004, 1 550, 3 412, 7 770, 10 032, 17 895, 100 000, 345 052

b) 19, 80, 941, 2 555, 9 405, 10 321, 77 001, 82 550, 87 555, 97 308, 1 234 005

26 Applicando il criterio di divisibilità (senza eseguire la divisione), sottolinea i numeri divisibili per 25.

a) 65, 125, 300, 555, 625, 875, 945, 2 005, 3 575, 4 000, 6 120, 9 235

b) 45, 75, 401, 605, 975, 1 235, 5 002, 32 123, 55 055, 531 135, 8 452 330

27 Predisponi sul tuo quaderno una tabella in cui suddividere, applicando il criterio di divisibilità, i numeri divisibili solo per 10, solo per 100 e solo per 1 000.

a) 40, 110, 3 000, 5 500, 6 300, 95 000, 101 000, 245 010, 356 200, 2 555 000

b) 440, 690, 8 700, 9 000, 12 020, 24 700, 78 000, 357 050, 700 000, 875 500

28 Applicando il criterio di divisibilità (senza eseguire la divisione), sottolinea i numeri divisibili per 7.

a) 84 94, 154, 223, 351, 427, 567, 708, 2 107, 3 430, 21 177

b) 91, 196, 371, 471, 807, 2 401, 2 856, 6 077, 12 021, 14 021, 301 707

29 Applicando il criterio di divisibilità (senza eseguire la divisione), sottolinea i numeri divisibili per 11.

a) 91, 121, 308, 517, 711, 8 316, 1 287, 3 784, 7 128, 21 582, 51 758, 111 011

b) 110, 111, 322, 616, 969, 9 273, 22 099, 29 192, 718 190, 800 003, 93 940

30 Applicando i criteri di divisibilità (senza eseguire la divisione), sottolinea i numeri divisibili contemporaneamente.

a) per 2 e 3: 36, 40, 72, 222, 312, 475, 432, 608, 738, 904, 972

b) per 3 e 5: 25, 90, 135, 522, 605, 735, 955, 985, 6 003, 8 015, 9 035

c) per 4 e 7: 56, 112, 147, 294, 588, 656, 784, 1 232, 1 960, 2 912, 5 336

31 Applicando i criteri di divisibilità (senza eseguire la divisione), sottolinea i numeri divisibili contemporaneamente.

a) per 3 e 4: 48, 124, 270, 432, 496, 624, 1 224, 2 574, 3 168, 5 508

b) per 5 e 9: 90, 135, 243, 375, 675, 2 610, 3 006, 6 555, 12 105, 51 120

c) per 10 e 11: 88, 110, 650, 3 410, 6 017, 8 080, 10 100, 24 915 37 070, 90 110

32 Applicando i criteri di divisibilità (senza eseguire la divisione), sottolinea i numeri divisibili contemporaneamente.

a) per 2, 3 e 5: 70, 120, 135, 350, 390, 480, 1 220, 2 214, 6 120, 9 018

b) per 3, 4 e 5: 90, 180, 815, 1 140, 2 130, 5 460, 6 180, 8 730, 13 110, 32 175

c) per 3, 5 e 7: 98, 210, 525, 840, 1 015, 3 885, 7 035, 9 450, 11 025, 29 106

Completa le seguenti tabelle con delle crocette.

MATEMATICA IN AZIONE Risolvi i seguenti problemi.

Una confezione contiene un numero di caramelle compreso tra 40 e 50. Se le dividiamo in gruppi di 2, 3 e 7 non ne resta neanche una. Quante sono le caramelle?

Tra 40 e 50 ci sono due multipli di 7 e sono il 42 e il 49.

49 è da scartare perché è divisibile solo per 7.

42 è divisibile anche per 2, perché è pari, e per 3 perché 4 + 2 = 6. Quindi, la confezione contiene 42 caramelle.

37 Quel disordinato di Jacopo ha le biglie sparse nella scatola dei giochi. Se le prende a 5 a 5 ne avanzano 3. Se invece le raccoglie a 3 a 3 non ne avanza neanche una. Sapendo che sono meno di 20, quante biglie possiede in tutto? [18]

38 Sebastiano ha un mazzo di carte napoletane. Se le divide per seme (spade, coppe, ...) fa mazzetti di 10. Se le divide per tipo (asso, due, tre, ...) fa mazzetti di 4 carte. Di quante carte è composto il mazzo? [40]

39 Le figurine dei Pokémon® di Ilaria sono più di 50 e meno di 60. Sia che le divida in 2 che in 3 mucchietti contenenti lo stesso numero di figurine, non gliene avanza neanche una. Quante sono le figurine di Ilaria? [54]

40 Lorenzo ha nel suo salvadanaio tra le 80 e le 90 monetine.

Se le divide per nazione riesce a fare 4 gruppi. Se le divide a seconda del valore (1 cent, 2 cent, 5 cent, ...) riesce a fare 7 gruppi di monetine. Calcola il numero esatto di monete contenute nel salvadanaio. [84]

LEZIONE

3

NUMERI PRIMI E

SCOMPOSIZIONE DI NUMERI COMPOSTI IN FATTORI PRIMI

41 Completa le frasi inserendo le parole mancanti.

a) Un numero naturale è primo se è solo per 1 e per

b) Un numero naturale è composto se oltre a se stesso e all’unità possiede altri

c) Il numero 1 non si può considerare perché possiede un solo invece di due.

d) I numeri primi sono sempre tranne il 2.

e) Ogni numero si può scrivere come una di due o più fattori primi. Questo procedimento è detto in fattori o

f) Qualsiasi numero naturale si può fattorizzare con il metodo delle successive.

g) Con il metodo delle divisioni successive il numero da si divide per il suo più piccolo divisore . Si procede nello stesso modo anche per il ottenuto e così via fino a ottenere come quoziente.

42 Individua i numeri primi nei seguenti gruppi di numeri. a)

43 Cerchia i numeri composti che siano il prodotto di due numeri primi. a)

44 Scrivendo il numero come prodotto di due numeri, è possibile scomporlo in fattori primi (indicati in rosso).

45 Procedendo come nell’esercizio precedente, scomponi sul quaderno in fattori primi i seguenti numeri.

46 Completa la fattorizzazione dei seguenti numeri con la tecnica delle divisioni successive.

Come nell’esercizio precedente, fattorizza sul quaderno i seguenti numeri con la tecnica delle divisioni successive.

Completa utilizzando la fattorizzazione delle potenze di 10.

Scomponi mentalmente i seguenti numeri.

62 MATH Mentally factor the following numbers.

Fattorizza sul quaderno i seguenti prodotti, come nell’esempio.

30 × 15 × 24

i fattori della moltiplicazione vengono scomposti in fattori primi:

30 × 15 × 24 = 2 × 3 × 5 × 3 × 5 × 23 × 3

si applica la proprietà del prodotto di potenze con ugual base:

30 × 15 × 24 = 24 × 33 × 52

Tutte le seguenti scomposizioni contengono errori. Evidenziali in rosso e riporta la scomposizione corretta sul quaderno.

Mediante la scomposizione in fattori primi riconosci se i numeri seguenti sono dei quadrati perfetti.

Un quadrato è perfetto se, scomposto in fattori primi, questi hanno tutti gli esponenti pari.

70 Completa le seguenti scomposizioni in modo da avere dei quadrati perfetti.

Mediante la scomposizione in fattori primi riconosci se i numeri sono dei cubi perfetti.

Un cubo è perfetto se, scomposto in fattori primi, questi hanno tutti gli esponenti multipli di 3.

= 24 × 33

Il 2 ha l’esponente che non è un multiplo di 3; quindi

non è un cubo perfetto

Gli esponenti sono multipli di 3; quindi 2 744 è un cubo perfetto

73 Completa le seguenti scomposizioni in modo da avere dei cubi perfetti. 23 × 11 73 × 11 36 × 5 11 × 23

74 MATEMATICA IN AZIONE La targa del professor Ford è EG 491 DH. 491 è un numero primo.

Quanti altri numeri primi di 2 e 3 cifre riesci a trovare con 4, 9 e 1? (Puoi utilizzare un diagramma ad albero.)

LEZIONE 4

CRITERIO GENERALE

DI DIVISIBILITÀ

75 Rispondi con Vero o Falso.

a) La fattorizzazione permette di riconoscere se un numero è multiplo di un altro. V F

b) La fattorizzazione permette di determinare un quoziente senza eseguire la divisione. V F

c) La fattorizzazione non permette di stabilire se due numeri sono primi tra loro. V F

76 Completa le frasi seguenti inserendo le parole mancanti.

a) Un numero è divisibile per un altro quando, scomposti entrambi in , il primo contiene almeno tutti i fattori primi del con esponente uguale o

b) La fattorizzazione permette di riconoscere se un numero è per un altro e di determinare il loro senza eseguire la

ESEMPIO

Utilizzando il criterio generale di divisibilità, stabilisci se il primo numero di ogni coppia è divisibile per il secondo. In caso affermativo stabilisci il quoziente senza eseguire la divisione. 1 728; 96 1

Il numero 1 728 contiene tutti i fattori di 96 con esponente maggiore; quindi 1 728 è divisibile per 96 1 728 : 96 = 26 − 5 × 33 − 1 = 2 × 32 = 18

77 64; 12 88; 22 90; 6 78; 26

78 120; 24 126; 36 196; 28 275; 15

79 648; 36 576; 48 784; 98 1 421; 29

80 1 225; 35 1 050; 42 728; 91 1 002; 32

81 1 400; 75 1 650; 66 627; 256 1 134; 126

82 825; 75 2 160; 240 1 806; 258 729; 343

83 1 240; 420 1 008; 63 755; 225 2 016; 84

84 594; 22 1 968; 164 756; 126 625; 120

85 848; 54 1 800; 108 5 200; 130 2 300; 460

86 1 680; 60 3 168; 88 3 445; 90 3 146; 402

Utilizzando il criterio generale di divisibilità, stabilisci il quoziente delle seguenti divisioni, senza eseguirle.

87 72 960 : 320 [228] 176 000 : 880 [200]

88 95 040 : 288 [330] 48 720 : 840 [58]

89 148 750 : 850 [175] 109 512 : 507 [216]

90 614 656 : 1 792 [343] 179 200 : 320 [560]

91 Utilizzando il criterio generale di divisibilità, scrivi sei numeri diversi che siano contemporaneamente divisibili per 15; 12; 20.

92 Utilizzando il criterio generale di divisibilità, verifica, con almeno tre esempi, che il prodotto di quattro numeri naturali consecutivi è sempre divisibile per 24.

93 MATEMATICA IN AZIONE I 228 alunni di una scuola hanno raccolto 7 296 € con il contributo volontario per le spese di fotocopie, cancelleria e assicurazione. Qual è stata la quota che ha versato ciascun alunno?

(Svolgi la divisione sia con la fattorizzazione sia con il metodo in colonna e stabilisci quale dei due è più semplice per risolvere il problema) [32 €]

LEZIONE

5

CALCOLO DEL MASSIMO COMUN DIVISORE DI PIÙ NUMERI

94 Rispondi con Vero o Falso.

a) Per M.C.D. si intende il maggiore tra i divisori comuni di due o più numeri. V F

b) Non sempre si può calcolare il M.C.D. V F

c) Il M.C.D. tra 36 e 48 è 6.

d) Il M.C.D. tra 7 e 4 è 1.

F

F

e) 18 e 24 hanno 3 divisori comuni se si esclude l’unità. V F

f) Nel calcolo del M.C.D. ogni fattore primo viene preso con il minor esponente. V F

g) Nel calcolo del M.C.D. si tiene conto anche dei fattori non comuni. V F

95 Completa le frasi inserendo le parole mancanti.

a) Si definisce Comun Divisore (M.C.D.) tra due o più numeri il tra i divisori

b) Due numeri si dicono tra se il loro M.C.D. è uguale a

c) Il di due o più numeri è uguale al prodotto dei primi comuni a tutti, ciascuno preso una sola volta, con il esponente con cui figura nelle

Determina sul quaderno tutti i divisori dei seguenti numeri, come nell’esempio.

ESEMPIO

D (40) → 1, 2, 4, 5, 8, 10, 20, 40

1 × 40 = 40 4 × 10 = 40 2 × 20 = 40 5 × 8 = 40

I divisori di un numero scritti in ordine crescente possiedono la seguente proprietà: il prodotto dei divisori estremi e delle coppie di divisori equidistanti dagli estremi è uguale al numero stesso.

96 18 24 32 44 50

97 20 28 36 48 64

98 50 76 66 90 105

99 52 88 75 96 120

100 Calcola mentalmente il M.C.D. tra le seguenti coppie di numeri.

a) 8; 12 15; 45 35; 30 14; 49 21; 77

b) 18; 81 20; 36 14; 6 17; 34 60; 72

c) 13; 26 36; 48 50; 70 24; 56 44; 121

Calcola il M.C.D. seguendo le indicazioni.

ESEMPIO

Per determinare il M.C.D. di 8, 12 e 20, si può procedere nel modo seguente.

1. Si trovano tutti i divisori dei numeri dati e si evidenziano quelli comuni:

D(8) → 1 , 2 , 4 , 8;

D(12) → 1 , 2 , 3 , 4 , 6, 12;

D(20) → 1 , 2 , 4 , 5, 10, 20.

2. Si evidenzia il M.C.D. → 4

101 M.C.D. (9; 24)

M.C.D. (21; 30)

D(9) → D(21) →

D(24) →

M.C.D. (9; 24) =

102 M.C.D. (28; 42)

D(28) →

D(42) →

M.C.D. (28; 42) =

D(30) →

M.C.D. (21; 30) =

M.C.D. (64; 72)

D(64) →

D(72) →

M.C.D. (64; 72) =

103 M.C.D. (20; 30; 50)

D(20) →

D(30) →

D(50) →

M.C.D. (20; 30; 50) =

104 Completa la seguente tabella.

M.C.D. (24; 36; 60)

D(24) →

D(36) →

D(60) →

M.C.D. (24; 36; 60) =

(Ricordati che due numeri primi a e b sono primi tra loro se M.C.D. (a; b) = 1)

a b a è un numero primo? b è un numero primo?

3 7

4 6 9 8 14 27

M.C.D. (a; b) a e b sono numeri primi tra loro?

105 Tra le seguenti coppie di numeri individua quelle di numeri primi tra loro.

a) 8; 10 8; 9 7; 14 10; 15 14; 15

b) 12; 13 22; 33 16; 24 18; 35 5; 22 c) 4; 9 15; 20 11; 14 26; 33 34; 51

106 MATH Identify the set of numbers that are relatively prime. a) 15; 18 b) 11; 55 c) 8; 9 d) 13; 39

107 Scrivi 5 coppie di numeri che siano primi tra loro.

108 Scrivi 5 coppie di numeri che abbiano M.C.D. = 1.

109 Verifica con alcuni esempi che:

• due numeri consecutivi sono sempre primi tra loro;

• se due numeri sono primi tra loro, sono primi tra loro anche i loro quadrati;

• se due numeri sono primi tra loro, sono primi tra loro anche i loro cubi.

a) Considera un numero naturale qualsiasi e il suo successivo. Dopo aver scritto tutti i divisori dei due numeri, determina il M.C.D.

D →

D →

M.C.D. ( ; ) =

a) Considera un altro numero naturale e il suo successivo e determina il M.C.D.

D →

D →

M.C.D. ( ; ) =

Che cosa osservi?

Calcola il M.C.D. tra i numeri dei seguenti gruppi con il metodo della scomposizione.

111 28; 40 25; 35 27; 36 45; 90 [4; 5; 9; 45]

112 48; 168 128; 208 294; 56 160; 128 [24; 16; 14; 32]

113 108; 125 266; 304 128; 168 462; 165 [1; 38; 8; 33]

114 240; 252 34; 57 540; 216 468; 594 [12; 1; 108; 18]

115 70; 105; 35 231; 147; 252 160; 256; 192 [35; 21; 32]

116 252; 396; 180 308; 352; 572 369; 693; 936 [36; 44; 9]

117 567; 189; 378; 693 378; 504; 756; 588 [63; 42]

118 540; 630; 750; 1 050 784; 441; 1 225; 1 715 [30; 49]

119 975; 546; 1 170; 1 404 840; 1 008; 720; 2 520 [39; 24]

120 1 320; 1 980; 1 815; 880 680; 3 060; 1 700; 2 448 [55; 68]

121 1 224; 1 377; 2 754; 11 016 848; 1 431; 1 272; 1 908 [153; 53]

MATEMATICA IN AZIONE Risolvi i seguenti problemi con il calcolo del M.C.D.

ESEMPIO

Melania possiede tre nastri, lunghi rispettivamente 28 m, 35 m e 21 m e li vuole dividere in pezzi tutti uguali, della massima lunghezza. Quanto dovrà essere lungo ciascun pezzo? Quanti pezzi di nastro otterrà?

Rifletti:

• ciascun nastro dovrà essere diviso in parti uguali

• i pezzi ricavati dai tre nastri devono essere tutti uguali tra loro

• i pezzi ricavati devono avere la massima lunghezza possibile

Pertanto:

D(28) → 1, 2, 4, 7 , 14, 28

→ la misura del nuovo pezzo dovrà essere un divisore della misura del nastro

→ la misura dei nuovi pezzi dovrà essere un divisore comune delle misure dei tre nastri

→ la misura dei nuovi pezzi dovrà essere il più grande dei divisori comuni delle misure dei nastri, cioè il M.C.D.

D(35) → 1, 5, 7 , 35

D(21) → 1, 3, 7 , 21

M.C.D. (28; 35; 21) = 7 → lunghezza in metri di ciascun pezzo di nastro (28 + 35 + 21) : 7 = 84 : 7 = 12 → pezzi di nastro ottenuti

122 Gli alunni della II D e della II F sono molto vivaci quando vanno nei laboratori e i loro insegnanti hanno deciso di disporli in file con il massimo numero di allievi e tutti della stessa classe. Considerando che una classe è composta da 28 alunni e l’altra da 24 alunni, quante file potranno formare i docenti e quanti alunni disporranno per ogni fila? [13; 4]

123 Per San Valentino un pasticcere ha preparato 24 cioccolatini al pistacchio, 30 alla nocciola e 42 al caffè. Li vuole confezionare in sacchettini in modo da avere sempre la stessa quantità di cioccolatini e il maggior numero di sacchetti possibile. Quanti sacchettini può confezionare? E quanti dolcetti di ciascun tipo metterà in ogni confezione?

(Per dividere i dolci in ugual numero, questo deve essere un divisore comune tra 24, 30 e 42. Il maggior numero di sacchetti possibile è dato dal M.C.D.

M.C.D. (24; 30; 42) → 24 = 2 3 × 3

30 = 2 × 3 × 5

42 = 2 × 3 × 7

6 è il numero di sacchetti che potrà confezionare. In ogni sacchetto metterà:

24 : 6 = cioccolatini al pistacchio

30 : = cioccolatini alla nocciola

42 : = cioccolatini al caffè)

M.C.D. =

124 Davide colleziona vari tipi di carte. Oggi ha comprato 72 carte di Yu-Gi-Oh!®, 63 dei Pokémon® e 45 di Dragon Ball®. Se le confezioni contengono lo stesso numero di figurine, qual è il numero massimo di carte contenute in ogni busta? E quante buste ha comprato per ogni tipo? [9; 8, 7, 5]

125 Al corso di recupero di Italiano la prof. Leopardi vuole dividere gli alunni delle due classi I A e I B in gruppi di lavoro formati dallo stesso numero di elementi, che sia il massimo possibile, e senza mischiare alunni delle due classi. Quanti gruppi forma e di quanti alunni, considerato che la I A è formata da 20 ragazzi e la I B da 16? [9; 4]

126 L’oste Maisobrio ha acquistato 72 L di pinot bianco, 60 L di pinot grigio e 90 L di pinot nero. Per trasportarli ha acquistato un certo numero di damigiane, tutte della stessa capacità. Senza mescolare i 3 tipi di vino, e considerando che vuole utilizzare il minor numero possibile di contenitori, quanti litri di vino metterà in ogni damigiana e quante gliene occorrono? [6 L; 37]

127 I cuochi devono preparare dei piattini di antipasti misti per gli invitati a una festa. Vogliono preparare il numero massimo di piattini con la stessa composizione, potendo disporre di: 95 vol-au-vent ai funghi, 190 vol-au-vent con gamberetti, 285 crostini di patè di fegato, 190 fette di salmone, 190 involtini di bresaola e 285 pizzette. Quanti piattini di antipasti misti si possono realizzare? Se gli invitati alla festa sono 80, avanza qualche piatto per i golosi che vogliono un ulteriore assaggio? Qual è la composizione di ogni piatto? [95; sì: 15 piattini; ]

128 STEM Il signor Carlo ha comprato da un falegname due tavole di legno, una di 54 cm per 120 cm e l’altra di 81 cm per 120 cm, per costruire delle mensole da mettere nel suo garage.

Quante mensole uguali può ottenere aventi la massima lunghezza possibile?

Quali sono le dimensioni delle mensole? [5 mensole; 27 cm × 120 cm]

129 STEM La veranda di Mario è lunga 4,80 m e larga 3,60 m. Le piastrelle quadrate per pavimentarla sono di 12 cm di lato. Si può piastrellare la veranda senza tagliare alcuna mattonella? Perché? [Sì, perché...]

130 Considera il rettangolo R avente larea 24 quadretti (6×4) e il quadrato Q avente larea 36 quadretti (6×6). R Q

Qual è il rettangolo di area maggiore possibile che è contenuto un numero esatto di volte sia nel rettangolo R sia nel quadrato Q? Disegnalo. Quante volte è contenuto nel rettangolo R?

E nel quadrato Q? [(2 × 3); ; ]

LEZIONE 6

CALCOLO DEL MINIMO COMUNE MULTIPLO DI PIÙ NUMERI

131 Rispondi con Vero o Falso.

a) Il m.c.m. si calcola con il metodo delle divisioni successive.

b) Il m.c.m. tiene conto solo dei fattori comuni.

c) Il m.c.m. di due numeri primi tra loro è il loro prodotto.

d) Il m.c.m. di 6 e 8 è 48.

e) Il m.c.m. di 15 e 30 è 30.

f) Il m.c.m. di 5 e 7 non si può calcolare.

132 Per ogni definizione stabilisci se è riferita al M.C.D. o al m.c.m.

a) È il maggiore tra i divisori comuni. M.C.D. m.c.m.

b) È il prodotto di fattori primi comuni e non comuni.

c) Se i numeri sono primi tra loro è 1.

d) I fattori comuni si prendono con il minimo esponente.

e) I fattori comuni si prendono con il massimo esponente.

Utilizzando la proprietà illustrata nell’esempio, determina il m.c.m. dei seguenti gruppi di numeri.

ESEMPIO

Per determinare il m.c.m. di 12 e 16, si può procedere nel seguente modo:

• si individuano i primi multipli di ciascun numero e si evidenziano quelli comuni:

M(12) → 12, 24, 36, 48 , 60, 72, 84, 96 , 108, 120, 132, 144 , 156

M(16) → 16, 32, 48 , 64, 80, 96 , 112, 128, 144 , 160

• il più piccolo tra i multipli comuni è il m.c.m.

m.c.m. (12; 16) = 48

133 m.c.m. (8; 12)

M(8) →

M(12) →

m.c.m. (8; 12) =

134 m.c.m. (7; 21)

m.c.m. (10; 30)

M(10) →

M(30) →

m.c.m. (10; 30) =

m.c.m. (15; 24)

M(7) → M(15) →

M(21) → M(24) →

m.c.m. (7; 21) =

135 m.c.m. (10; 12; 18)

M(10) →

M(12) →

M(18) →

m.c.m. (10; 12; 18) =

m.c.m. (15; 24) =

136 Sottolinea il m.c.m. (quando presente) tra le seguenti coppie di numeri.

a) 3 e 9 12 e 24 9 e 81 28 e 24 18 e 36

b) 14 e 18 25 e 75 15 e 35 36 e 72 14 e 35

137 Calcola mentalmente il m.c.m. dei seguenti gruppi di numeri.

6; 9 8; 10 15; 18 14; 21 3; 4; 5 8; 9; 24 16; 40; 8 10; 25; 4

Calcola il m.c.m. dei seguenti gruppi di numeri utilizzando il metodo della fattorizzazione.

a) 24; 48 15; 35 5; 16 [48; 105; 80]

b) 42; 63 12; 14 17; 18 [126; 84; 306]

c) 18; 30 34; 85 36; 42 [90; 170; 252]

a) 39; 52 33; 18 49; 35 [156; 198; 245]

b) 55; 70 96; 128 75; 90 [770; 384; 450]

c) 50; 90 54; 72 18; 45 [450; 216; 90]

d) 64; 80 45; 66 25; 40 [320; 990; 200]

e) 44; 36 95; 114 54; 135 [396; 570; 270]

a) 164; 205 36; 81 147; 84 [820; 324; 588]

b) 162; 198 210; 735 50; 105 [1 782; 1 470; 1 050]

c) 70; 42; 30 12; 28; 42 18; 99; 6 [210; 84; 198]

d) 15; 84; 105 36; 54; 45 14; 98; 147 [420; 540; 294]

e) 30; 24; 32 42; 70; 63 150; 85; 102 [480; 630; 2 550]

a) 35; 42; 120 63; 72; 252 42; 63; 72 [840; 504; 504]

b) 230; 138; 30 39; 65; 91 112; 224; 336 [690; 1 365; 672]

c) 60; 75; 90 90; 108; 270 [900; 540]

d) 72; 99; 264 396; 594; 891 [792; 3 564]

e) 120; 252; 630 81; 135; 216 [2 520; 3 240]

142 Il m.c.m. di due numeri si può calcolare anche utilizzando il seguente metodo:

• si moltiplicano i due numeri;

• si divide il prodotto ottenuto per il M.C.D. dei due numeri.

Verifica la validità di questo metodo facendo 5 esempi sul quaderno.

143 MATH 80 is the least common multiple of which two numbers?

a) 8; 24 b) 40; 60 c) 15; 20 d) 16; 20

EDUCAZIONE CIVICA Risolvi i seguenti problemi con il calcolo del m.c.m.

144 Per ridurre l’impatto ambientale, l’azienda GioielliPerSempre ha deciso di ripianificare gli spostamenti dei propri dipendenti con l’obiettivo di diminuire l’utilizzo dell’automobile.

Tre rappresentanti di gioielli dell’azienda devono incontrarsi per una riunione ciclicamente. Considerando che il primo passa da Milano ogni 9 giorni, il secondo ogni 12 e il terzo ogni 15, si decide che la riunione si terrà in questa città quando tutti e tre sono già presenti sul posto per incontrare i clienti. Tre giorni fa c’è stata la prima riunione; fra quanti giorni ci sarà la prossima? (Considerando il giorno dell’incontro come giorno 0, per calcolare il giorno del prossimo incontro bisognerà trovare il m.c.m. di 9, 12 e 15: m.c.m. (9; 12; 15) =

Nello scrivere il risultato ricordati che i 3 rappresentanti si sono incontrati 3 giorni fa!

3 = giorni )

145 Eugenio ha soli 6 anni ed è un enfant prodige. Riesce a palleggiare lanciando in aria una pallina ogni 10 secondi con una mano e una ogni 12 secondi con l’altra. Se comincia l’allenamento lanciandole in aria insieme, dopo quanti secondi (o se preferisci, minuti) le rilancerà in aria contemporaneamente? [60s = 1 minuto]

146 Aurelio, Attilio e Aristide ricaricano il credito del loro cellulare presso lo stesso bar. Il primo lo ricarica ogni 42 giorni, il secondo ogni 30 e il terzo ogni 35.

Se si incontrano oggi, fra quanti giorni si rincontreranno nuovamente? [210 giorni]

147 Agnese, Annalisa e Arianna vanno ad acquistare le figurine dei loro personaggi preferiti nella stessa edicola. La prima ci va ogni 3 giorni, la seconda ogni 5 e la terza una volta alla settimana. Se si incontrano in edicola il primo di marzo, quando si ritroveranno di nuovo tutte e tre insieme? (Considera che marzo e maggio sono di 31 giorni.) [13 giugno]

148 Luca, Francesco e Raul si stanno allenando al Parco degli Aironi, correndo sulla pista ciclopedonale attorno al laghetto del parco.

I tre atleti sono partiti contemporaneamente dallo stesso punto e percorrono la pista nello stesso verso: Luca compie un giro completo in 120 secondi, Francesco in 140 secondi e Raul in 150 secondi.

a) Supponendo che corrano a velocità costante, dopo quanto tempo si ritroveranno tutti e tre nel punto in cui sono partiti?

b) Quanti giri completi avrà percorso ognuno di loro?

c) Quanti chilometri avrà percorso ogni atleta, sapendo che la pista è lunga 700 metri?

149 L’orologio a pendolo di nonna Albina è vecchio e non funziona bene: resta indietro di cinque minuti ogni ora.

Se oggi, 7 febbraio ore 12, è stato regolato sull’ora esatta, in quale giorno dell’anno il ritardo accumulato sarà di 12 ore e quindi il pendolo di nonna Albina segnerà ancora l’ora esatta? [h 12 del 13 febbraio]

150 Qual è il più piccolo numero che diviso per 20, per 8 o per 12 dà sempre come resto 7? [127]

151 Qual è il rettangolo di area minore che contiene un numero esatto di volte sia il rettangolo R1 (area = 6 u2) sia il rettangolo R2 (area = 12 u2)?

Quante volte contiene il rettangolo R1? Quante volte il rettangolo R2? R1 R2 u2 u2

[rettangolo R2; 2; 1]

Utilizzando il metodo della fattorizzazione, calcola il M.C.D. e il m.c.m. dei seguenti gruppi di numeri.

152 22; 40 45; 75 36; 48 [2; 440] [15; 225] [12; 144]

153 42; 72 28; 30 44; 154 [6; 504] [2; 420] [22; 308]

154 54; 48 60; 48 84; 210 [6; 432] [12; 240] [42; 420]

155 24; 36; 90 22; 33; 132 36; 54; 90 [6; 360] [11; 132] [18; 540]

156 40; 48; 60 36; 48; 60 84; 98; 112 [4; 240] [12; 720] [14; 2 352]

157 96; 352; 144 30; 70; 150 63; 231; 154 [16; 3 168] [10; 1 050] [7; 1 386]

158 168; 105; 525 154; 220; 770 148; 111; 185 [21; 4 200] [22; 1 540] [37; 2 220]

159 90; 120; 162 68; 102; 119 54; 270; 360 [6; 3 240] [17; 1 428] [18; 1 080]

160 132; 330; 180 170; 255; 425 132; 156; 858 [6; 1 980] [85; 2 550] [6; 1 716]

161 126; 189; 147 110; 275; 165 36; 450; 180 [21; 2 646] [55; 1 650] [18; 900]

162 156; 468; 1 170 162; 189; 405 75; 275; 525 [78; 2 340] [27; 5 670] [25; 5 775]

163 210; 42; 294 560; 175; 350 252; 224; 336 [42; 1 470] [35; 2 800] [28; 2 016]

164 330; 385; 495 312; 234; 390 441; 63; 315 [55; 6 930] [78; 4 680] [63; 2 205]

165 324; 432; 1 296 378; 420; 504 154; 539; 231 [108; 1 296] [42; 7 560] [77; 3 234]

166 700; 450; 630 92; 138; 207 312; 130; 468 [10; 6 300] [23; 828] [26; 4 680]

167 234; 143; 198 480; 384; 1 440 [1; 2 574] [96; 5 760]

168 64; 288; 160; 240 405; 270; 675; 180 [16; 2 880] [45; 8 100]

169 594; 99; 132; 55 308; 588; 132; 462 [11; 5 940] [2; 6 468]

imparaerrore

Molti errori nel calcolo di m.c.m. e M.C.D. derivano da una scomposizione in fattori primi non corretta: nel fare le divisioni successive, presta sempre attenzione ai calcoli aritmetici, verificando i risultati.

Ricordati che non esiste un unico metodo per scomporre un numero nei suoi divisori, potresti trovarti meglio seguendo una procedura diversa o dei diagrammi ad albero.

Ti capiterà di fare confusione tra m.c.m. e M.C.D., è un errore molto frequente

dovuto al fatto che le regole per scegliere i fattori e gli esponenti sono opposte: ti consiglio di disegnare uno schema chiaro per evidenziare come prendere i fattori (comuni/non comuni), e gli esponenti (minimo/massimo) al variare delle richieste. E non dimenticare una cosa importante: l’1 è un fattore!

Quindi se non ci sono altri fattori primi comuni (cioè se i numeri sono “primi tra loro”), il M.C.D. è 1. Non dire che non c'è!

Calcola il M.C.D. e il m.c.m. dei seguenti gruppi di numeri lasciando i risultati sotto forma di prodotti di potenze di numeri primi.

170 2 × 32 × 5 × 7 e 22 × 3 × 52 × 7 [M.C.D. 2 × 3 × 5 × 7 m.c.m. 22 × 32 × 52 ]

23 × 32 × 5 e 2 × 3 × 52 × 11 [M.C.D. m.c.m. 23 × 32 × 52 × 11]

171 33 × 7 × 132 e 3 × 72 × 11 × 13

25 × 32 × 74 e 23 × 35 × 5 × 73

172 34 × 5 × 7 × 112 e 32 × 5 × 72 × 11

22 × 33 × 7 × 13 e 24 × 32 × 7 × 132

173 24 × 32 × 52 × 172 e 22 × 5 × 73 × 17

3 × 53 × 7 × 132 e 32 × 52 × 11 × 13

Determina il M.C.D. e il m.c.m. dei seguenti gruppi di numeri, lasciandoli indicati come prodotti di fattori primi.

174 375; 180 [3 × 5; 22 × 32 × 53] 3 600; 3 105 [32 × 5; 24 × 33 × 52 × 23]

175 3 025; 2 420 [5 × 112; 22 × 52 × 112] 552; 736 [23 × 23; 25 × 3 × 23]

176 504; 518; 296 [2; 23 × 32 × 7 × 37] 475; 325; 247 [1; 52 × 13 × 19]

177 850; 1 870; 510 [2 × 5 × 17; 2 × 3 × 52 × 11 × 17] 2 058; 2 646; 3 675 [3 × 72; 2 × 33 × 52 × 73]

Risolvi i seguenti problemi utilizzando in modo adeguato il M.C.D. o il m.c.m.

178 MATEMATICA IN AZIONE Il signor Mario, che abita a Molfetta e produce dell’ottimo olio, ne ha messo da parte 3 damigiane: una da 20 L, una da 32 L e una da 44 L. Vuole travasare l’olio in bottiglioni tutti uguali, della massima capacità possibile, senza che avanzi nemmeno un litro di olio. Di che misura saranno i bottiglioni che gli servono? [4 L]

179 EDUCAZIONE CIVICA Giacomo vuole contribuire alla cura dei beni culturali della sua città e decide di svolgere un anno di Servizio civile presso la Biblioteca comunale. I responsabili della biblioteca chiedono il suo aiuto per rinnovare gli scaffali nel reparto di scienze.

Vogliono sistemare 360 libri di biologia, 630 di geologia e 945 di astronomia in modo da avere il maggior numero di libri possibile, dello stesso tema, per ogni scaffale, riempiendoli tutti senza avere avanzi.

Quanti libri andranno in ogni scaffale? Quanti scaffali occorrono per ogni serie? [45; 8, 14, 21]

180 Due operai di Vicenza vanno al lavoro con lo stesso treno. Uno non prende il treno ogni 15 giorni, l’altro non lo prende ogni 10.

Ogni quanti giorni nessuno dei due salirà sul treno per andare a lavoro? [30 giorni]

181 I musicisti della Banda di Viggiù sfilano in fila per 3, in fila per 4 o per 5 a seconda della larghezza delle strade in cui passano. Considerando che sono meno di 100, quanti sono gli elementi della banda, compreso il direttore Bell’Arte che sta in testa al gruppo? [61]

182 Al Museo dei giocattoli hanno acquistato una collezione di 504 bambole degli anni ’30 e 990 automobiline degli anni ’70.

Le vogliono disporre nel maggior numero di vetrine possibile in modo da riempirle tutte, con lo stesso numero di pezzi, senza mischiare bambole e auto. Quante vetrine occorrono?

Quanti pezzi andranno in ogni vetrina? [18 × 2 = 36 vetrine; 28 bambole e 55 auto]

183 Da una stazione della Underground di Londra passano tre linee: la Yellow, la Red e la Green. Della prima linea passa un treno ogni 18 minuti, della seconda uno ogni 12 e della terza uno ogni 20. Quante volte al massimo, nell’arco di 24 ore, i tre treni si ritrovano contemporaneamente nella stazione? [8 volte]

184 Tre ciclisti si allenano per una gara al circuito comunale. Impiegano rispettivamente 3m 30s , 2m 20s e 4m 12s per compiere l’intero giro della pista.

Se cominciano ad allenarsi alle 14:30, a che ora si ritroveranno di nuovo tutti e tre insieme al punto di partenza? (Trasforma i minuti in secondi ) [alle ore 14:51]

185 Nello Stretto di Messina tre compagnie di traghetti fanno la spola tra la città siciliana e Villa San Giovanni in Calabria.

Il primo traghetto impiega, per completare il percorso di andata e ritorno, 196 minuti; il secondo 84 minuti e il terzo 105 minuti.

Se partono tutti e tre contemporaneamente, dopo quante ore si ritroveranno nello stesso porto? [dopo 49 h]

186 Il giardino dei signori Villoni è di forma rettangolare e i lati misurano 294 m e 54 m. Si vuole realizzare un impianto di illuminazione lungo il confine con pali a uguale distanza che sia la maggiore possibile.

Quanti pali occorrono e a che distanza saranno piazzati? [116 pali; 6 m]

187 EDUCAZIONE CIVICA La scuola di Bianca è stata coinvolta in un progetto di riqualificazione del verde urbano. A lei è stato assegnato il compito di ideare l’aiuola da mettere al centro di una rotonda. Ha a disposizione 72 bulbi di tulipano e vorrebbe interrarli in modo da formare più di 3 file con uguale numero di bulbi.

In quali modi diversi Bianca può collocare i bulbi nell’aiuola?

[4 file da 18 bulbi; 6 file da 12 bulbi; ...]

188 Il prof. di Tecnologia vuole realizzare con i suoi alunni l’illuminazione per l’albero di Natale della scuola.

Dispone di due fili elettrici lunghi 246 cm e 310 cm che vuole attrezzare con lampadine colorate alla stessa distanza tra loro che sia la maggiore possibile. Considerando uno scarto di 30 cm per filo per l’allaccio alla rete elettrica, quante lampade metterà in ogni filo e a che distanza tra loro?

(Rifletti su dove va posizionata la prima lampadina) [28 e 36; 8 cm]

189 Nella dieta di Sarah sono previsti gli spinaci ogni 7 giorni, il branzino ogni 4 e il gelato solo ogni 12. Se ha consumato queste pietanze nello stesso menù il giorno 1 febbraio 2024, in quale data le ha ritrovate di nuovo insieme?

(Ricorda: il 2024 era un anno bisestile.) [24 aprile]

190 Il primo giorno di scuola il nuovo prof. di Matematica propone il seguente indovinello:

“Ho un numero di caramelle compreso tra 300 e 310; se le raggruppo a tre a tre, oppure a quattro a quattro, oppure a cinque a cinque ne rimangono sempre 2; quante sono le caramelle?’’ [302]

191 Per riciclare alcuni vecchi vestiti inutilizzati, la nonna di Emma vuole realizzare una coperta formata da quadrati di stoffa, che abbiano i lati della massima misura possibile. La coperta sarà rettangolare e dovrà misurare 220 cm × 140 cm; il vestito più piccolo è largo 25 cm.

Quanto deve misurare il lato di ogni quadrato? Quanti quadrati dovrà avere in tutto la nonna per realizzare la coperta? [20 cm; 77]

COMPETENZE

PROBLEM SOLVING

1 13 è un numero primo particolare; infatti le sue cifre invertite danno un altro numero primo che è il 31. Lo stesso vale per il 17.

Sapresti fare un altro esempio simile?

2 Il 19 è il più piccolo numero primo che si ottiene sommando il prodotto e la somma delle sue cifre: (9 + 1) + 9 × 1 = 10 + 9 = 19.

Sapresti fare un altro esempio che finisca per 9?

3 Secondo un’ipotesi formulata nel 1742 dal matematico tedesco Goldbach, ciascun numero pari, eccetto 2, è la somma di due numeri primi.

Verifica questa ipotesi analizzando almeno 15 numeri pari a tua scelta.

4 I “numeri perfetti’’, espressione attribuita a Pitagora, sono quelli che sono uguali alla somma di tutti i loro divisori escluso il numero stesso.

ESEMPIO

496 è un numero perfetto D(496) → 1, 2, 4, 8, 16, 31, 62, 124, 248, 496 somma dei divisori 1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248 = 496

Cerca altri due numeri perfetti nella prima e nella terza decina.

5 I numeri primi che hanno come differenza 2 sono chiamati “primi gemelli’’.

Fra i primi 200 numeri naturali ci sono 15 “primi gemelli’’; elencali.

3; 5

6 Due satelliti artificiali percorrono orbite diverse intorno alla Terra.

Giannino Testainsù li vede contemporaneamente a mezzanotte. A che ora potrà rivederli, se il primo impiega 7 ore e il secondo 2 ore a percorrere la propria orbita?

7 Una veranda che misura 180 cm × 240 cm deve essere pavimentata con piastrelle quadrate che abbiano il lato più grande possibile.

Quante ne occorrono affinché non se ne tagli nemmeno una?

Quanto misurerà il lato di ogni piastrella?

CALCOLARE

8

a) Qual è il più piccolo numero di 4 cifre diverse divisibile per 3?

b) Qual è il più piccolo numero di 4 cifre diverse divisibile per 5?

c) Qual è il più piccolo numero di 4 cifre diverse divisibile per 4?

d) Qual è il più piccolo numero di 4 cifre diverse divisibile per 11?

9

a) Qual è il più grande numero di 3 cifre tutte uguali divisibile per 4?

b) Qual è il più grande numero di 3 cifre tutte uguali divisibile per 3?

c) Qual è il più grande numero di 3 cifre diverse divisibile per 3?

d) Qual è il più grande numero di 3 cifre diverse divisibile per 2?

10 Con le cifre 1-3-0-5-6 scrivi il più piccolo numero divisibile per 4 e il più piccolo divisibile per 5.

11 Considera il numero 1 001 = 103 + 1 e verifica che è divisibile per 7, 11 e 13.

Quali saranno i divisori di 2 002, 3 003, 6 006?

12 Il numero 2 520 è stato scoperto scolpito in geroglifici su una tomba egiziana: perché tanta importanza?

Forse perché è il più piccolo numero divisibile per i primi dieci numeri naturali?

Scopri se è vero.

13 Il numero 2 438 195 760 è un numero speciale perché: – è formato dalle prime dieci cifre del sistema di numerazione decimale; – ha come divisori tutti i numeri compresi tra 1 e 18, 18 incluso. Verifica sul quaderno questa sua caratteristica.

ARGOMENTARE

14 Scrivi due numeri divisibili per 4 e sommali. Il numero ottenuto è ancora divisibile per 4?

Prova con altre coppie di numeri divisibili per 4.

Sapresti spiegare perché si verifica questa situazione?

15 Considera un triangolo equilatero avente come lato un numero primo. La misura del perimetro di tale triangolo è un numero primo? Se hai risposto no, per quale numero è divisibile la misura del perimetro?

SFIDA MATEMATICA

16 Gli anni divisibili 2010 è divisibile per 10 (il numero formato dalle sue ultime due cifre); allo stesso modo 2016 è divisibile per 16.

Trovate i primi due anni, successivi al 2016, il cui numero è divisibile per quello formato dalle ultime due cifre.

(Giochi d’Autunno, organizzati dal Centro PRISTEM dell’Università Bocconi di Milano) Milano)

Divisori e multipli di un numero naturale

ROAD MAP PER TUTTI

MULTIPLI E DIVISORI

Quali sono i multipli di n?

I multipli di n si ottengono moltiplicando n per 1, 2, 3, ...

DATO UN NUMERO NATURALE n

I multipli di un numero sono infiniti.

ESEMPIO

Quali sono i multipli di 10?

10 × 1 = 10

10 × 2 = 20

10 × 3 = 30

10 × 4 = 40 e così via

TEORIA PAG.

300

Quali sono i divisori di n?

Un numero è divisore di n

se il resto della loro divisione è zero. I divisori di un numero sono finiti.

Quali sono i divisori di 10?

10 : 1 = 10 resto 0

10 : 2 = 5 resto 0

10 : 5 = 2 resto 0

10 : 10 = 1 resto 0

I divisori di 10 sono 1, 2, 5, 10

CRITERI DI DIVISIBILITÀ

DATO UN NUMERO n

come si stabilisce se:

è divisibile per 2? è divisibile per 3? è divisibile per 5? è divisibile per 10?

Un numero è divisibile per 2 se finisce con una cifra pari:

0, 2, 4, 6, 8 46; 752 sono divisibili per 2 perché terminano con una cifra pari. 67; 71 non lo sono.

Un numero è divisibile per 3 se la somma delle sue cifre è un multiplo di 3

ESEMPIO

Un numero è divisibile per 5 se finisce con 0 o 5

Un numero è divisibile per 10 se l’ultima cifra è 0

15, 410 → SÌ 53, 107 → NO

20, 30 sono divisibili per 10 23, 32 no ESEMPIO

1 Scrivi i primi otto multipli di 6. 6 × 1 = 6 × 2 = 6 × 3 = 6 × 4 =

2 Nella classe di Erika ci sono 20 alunni; quanti gruppi da 5 alunni si possono fare?

20 : 5 = gruppi; quindi e 4 sono divisori di

3 Verifica che i divisori di 18 sono 1, 2, 3, 6, 9, 18. 18 : 1 =

4 Per ciascuno dei seguenti numeri scrivi sul quaderno tutti i divisori e i primi sei multipli.

4 8 12 15 22

5 Controlla se l’ultima cifra è pari e sottolinea i numeri divisibili per 2.

6 Scrivi la data di oggi → Il giorno o il mese o l’anno sono divisibili per 2?

7 Completa.

Un numero è divisibile per 3 se la delle sue cifre è un di 3.

8 Somma le cifre dei seguenti numeri e segna quelli divisibili per 3.

a) 47 69 84 37 111 204 308 540 1 203 b) 411 152 55 702 87 279 675 734 5 741 1 683 2 475

9 MATEMATICA IN AZIONE Nico è nato il giorno di San Valentino del 2022.

Scrivi la sua data di nascita in numeri e stabilisci se giorno, mese e anno sono divisibili per 3.

10 Controlla se l’ultima cifra è 0 o 5, sottolinea i numeri divisibili per 5 e, tra questi, cerchia i numeri divisibili per 10.

36 95

11 MATEMATICA IN AZIONE Lorenzo, che ha 5 cani, vuole acquistare una scatola di biscotti da dividere tra di loro.

Al supermercato trova scatole da 48, 54 o 60 biscotti; quale deve acquistare per fare parti uguali tra i suoi 5 cani?

12 Scrivi una cifra al posto dei puntini in modo tale i numeri:

a) siano divisibili per 2:

b) siano divisibili per 3:

c) siano divisibili per 5:

d) siano divisibili per 2 e per 3:

e) siano divisibili per 2 e per 5:

NUMERI

PRIMI TEORIA PAG. 308

DATI I NUMERI NATURALI 5, 7, 11, 13, 12, 8 quali sono i numeri primi?

I numeri primi sono quelli che hanno solo due divisori: 1 e se stessi

ESEMPIO

5; 7; 11; 13 sono numeri primi perché ognuno ha solo due divisori. 12; 8 non sono numeri primi

SCOMPOSIZIONE IN FATTORI PRIMI TEORIA PAG. 310

DATO IL NUMERO NATURALE 36

che cos’è la scomposizione in fattori primi di un numero?

Un procedimento che, tramite divisioni successive, permette di trovare tutti i fattori primi che compongono un numero.

ESEMPIO

Scomponiamo in fattori primi il numero 36

Quozienti Divisori primi

• si scrive il numero 36 e alla sua destra si traccia una riga verticale

• si divide 36 per 2, che è il più piccolo dei suoi divisori primi; si scrive il quoziente 18 sotto a 36

• si divide 18 per 2, che è il più piccolo dei suoi divisori primi; si scrive il quoziente 9 sotto a 18

• si divide 9 per 3, che è il più piccolo dei suoi divisori primi; si scrive il quoziente 3 sotto a 9

• si divide 3 per se stesso perché è un numero primo e si ottiene come quoziente 1, che si scrive sotto a 3

La scomposizione è conclusa. Si scrive il prodotto dei fattori primi così come si presentano:

36 = 2 × 2 × 3 × 3 = 22 × 32

13 Consulta le tavole in fondo al volume e sottolinea i numeri primi. 3 18 23 9 19 29 33 2 57 269 371 924

14 Consultando le tavole dei numeri primi esegui le richieste.

a) Scrivi otto numeri primi che terminano per 7:

b) Scrivi dieci numeri primi che terminano per 1:

c) Scrivi dieci numeri primi che terminano per 3:

15 MATEMATICA IN AZIONE Valentina non è molto soddisfatta del voto che ha preso nell’interrogazione di Scienze. È l’unico numero primo che è compreso tra il 6 e il 10. Quale voto ha preso Valentina?

16 Segna i numeri primi corrispondenti ai giorni del mese di marzo.

17 Completa le seguenti scomposizioni seguendo le indicazioni.

a) 462 1

77 è divisibile per 7 11 è un numero primo ↷ :