VBTL 6 - Leerboek Analyse 3 Verloop van functies - inkijk & materiaal 3e graad

LEERBOEK

Analyse 3 i Verloop van functies Integraalrekening

D-finaliteit economie en wetenschappen

Philip Bogaert

Filip Geeurickx

Marc Muylaert

Roger Van Nieuwenhuyze

Erik Willockx

CARTOONS

Dave Vanroye

Hoe gebruik je VBTL ?

Dit boek bevat drie hoofdstukken. Elk hoofdstuk is opgebouwd uit verschillende paragrafen met aan het einde een handige samenvatting.

Definities vind je op een rode achtergrond. Eigenschappen vind je op een groene achtergrond. Methodes, rekenregels en formules vind je op een zachtblauwe achtergrond.

Wiskunde is een eeuwenoude wetenschap. De geschiedenis van de wiskunde en de herkomst van bepaalde begrippen worden zachtpaars afgedrukt.

1 2 *

De nummers van de oefeningen hebben een gele kleur. Een sterretje duidt op een extra uitdaging. Maak ook kennis met voorbeeldvragen uit ijkingstoetsen en toelatingsexamens.

Achteraan in dit boek vind je de oplossingen

ICT is een ideaal hulpmiddel. Bij dit boek hoort een webpagina van GeoGebra, gevuld met heel wat digitale oefeningen en applets. Die vind je terug via www.polpo.be.

Wat moet je kennen en kunnen ?

Op het einde van elk hoofdstuk zie je een handig overzicht van wat je moet kennen en kunnen

Tussen 1665 en 1685 vonden Isaac Newton (1642 – 1727) en Gottfried Wilhelm Leibniz (1646 – 1716) onafhankelijk van elkaar de differentiaalrekening uit. Hiermee konden ze raaklijnen aan krommen en grafieken van functies bepalen. Daarover leerde je al in het boek Analyse 2. Newton ontdekte kort daarna dat het omgekeerde van differentiëren kon worden toegepast op het berekenen van oppervlakten en inhouden van figuren (vlakke en ruimtelijke) die worden begrensd door krommen of gekromde oppervlakken.

Al vanaf de oudheid probeerden wiskundigen de oppervlakte onder een kromme te berekenen.

Voor de oppervlakte van een cirkelschijf werkte de geniale Griek Archimedes (3e eeuw v.Chr.) met ingeschreven regelmatige veelhoeken en leidde hij zo de formule πr2 af. In dit boek leer je zelf een methode om de oppervlakte onder een kromme te benaderen met rechthoekjes. Ook maak je kennis met een manier om de oppervlakte exact te berekenen. Daarbij ga je functies integreren. Je zult merken dat er een eenvoudig verband bestaat tussen integreren en differentiëren.

Als je ooit oppervlakten moet berekenen in Parc Güell (Barcelona), neem dan zeker dit boek mee als hulp. Maar eerst staan we in hoofdstuk 1 nog stil bij het verloop van functies.

INKIJKEXEMPLAARDIEKEURE

Inhoud

INKIJKEXEMPLAARDIEKEURE

Analyse 3 i Verloop van functies Integraalrekening

1

Verloop van functies

1.1 Verloop van algebraïsche functies   9

1.2 Verloop van exponentiële en logaritmische functies   31

1.3 Verloop van goniometrische functies   58

1.4 Differentiaal van een functie   72

2

Integraalrekening

2.1 Bepaalde integralen  81

2.2 Integratiemethoden : fundamentele integralen   132

2.3 Integratiemethoden : substitutie   140

2.4 Integratiemethoden : partiële integratie   151

3

Toepassingen van de integraalrekening

3.1 Volume van omwentelingslichamen  163

3.2 Booglengte van een vlakke kromme  171

3.3 Toepassingen in de fysica en de economie  174

Oplossingen

0

1 Verloop van functies

Hoofdstuktitel

INKIJKEXEMPLAARDIEKEURE

Hier komt het introductie tekstje. Witregels worden manueel ingegeven.

Misschien hoorde je al eens eerder volgend vrij eenvoudig maar daarom niet minder klassiek raadseltje. De waterlelies in een vijver verdubbelen dagelijks in oppervlakte. Op dag 20 is de vijver volledig bedekt met waterlelies. Na hoeveel dagen was een vierde van de vijver dan bedekt? In dit hoofdstuk leer je de afgeleide berekenen en het verloop maken van exponentiële en logaritmische functies. Een voorbeeld van exponentiële groei vind je op die vijver. De eerste dag is er één waterlelie op het oppervlak, de volgende dag zijn er twee, de dag erna vier en de dag daarna acht. Logaritmische functies zullen ontstaan als de omgekeerde bewerking van de exponentiële functies.

Verloop van functies

1.1 Verloop van algebraïsche functies

1 Limieten  9

2 Asymptoten  10

3 Afgeleiden  13

4 Eigenschappen van functies in r 15

5 Verloop van een functie  19

6 De regel van de l’Hôpital  26

7 Oefeningen  27

1.2 Verloop van exponentiële en logaritmische functies

1 Even herhalen  31

2 Afgeleide van exponentiële en logaritmische functies – getal e 33

3 Natuurlijke logaritmen  37

4 Afgeleide van een exponentiële functie 38

5 Functies waarvoor geldt dat de afgeleide recht evenredig is met de functiewaarde  39

6 Afgeleide van een logaritmische functie 40

7 Toepassingen  43

8 Verloop van een exponentiële functie  45

9 Verloop van een logaritmische functie  47

10 Verloop van een logaritmische functie met GeoGebra  49

11 Samenvatting  51

12 Oefeningen  52

1.3 Verloop van goniometrische functies

1 Elementaire goniometrische functies  58

2 Verloop van een goniometrische functie  62 3 Toepassing : harmonische en gedempte trilling  64

4 Verloop van een goniometrische functie met GeoGebra  67 5 Samenvatting  68

1.4 Differentiaal van een functie

1 Definitie  72 2 Verband tussen dy en Δy 73 3 Differentialen van hogere orde  74 4 Rekenregels  74 5 Toepassingen  75 6 Samenvatting  76 7 Oefeningen  77 Wat moet je kennen en kunnen? 78

1.1

Verloop van algebraïsche functies

1 Limieten

We herhalen enkele belangrijke begrippen in verband met limieten in

Veeltermfunctie

INKIJKEXEMPLAARDIEKEURE

Rationale functie f

= 13

Bereken de functiewaarde van de veeltermfunctie voor x = a

IsT(a ) = 0enN(a )= 0,danis

x →a f ( x )=+∞ of −∞

Hettekenonderzoekvan f ( x ) ineen omgevingvan x = a geeftuitsluitsel.

Bereken de limiet van de hoogstegraadsterm.

Is T( a ) = N( a ) = 0, deel dan T( x ) en N( x ) door x – a en bepaal de limiet van de vereenvoudigde uitdrukking.

Bereken de limiet van het quotiënt van de hoogstegraadstermen in T( x ) en N( x )

2 Asymptoten

a Verticale asymptoot

Voorbeeld :

Beschouwdefunctie f met f ( x )= x + 3 x 2

x –3 2

x + 3

x – 2 ––0 –+ –+ 0 + +

f ( x ) + 0 – | +

2 is een nulwaarde van de noemer, die geen nulwaarde is van de teller.

lim x → < 2 x + 3 x 2 = −∞ enlim x → > 2 x + 3 x 2 =+∞

x = 2 is de vergelijking van de verticale asymptoot van de grafiek van de functie f

y

INKIJKEXEMPLAARDIEKEURE

f ( x )= x + 3 x 2 x = 2

Algemeen :

• De rechte l ↔ x = c ( ∈ R) is een verticale asymptoot van de kromme k ↔ y = f ( x ) lim x → < c f (x )= ±∞ oflim x → > c f (x )= ±∞

• Eigenschap : y x O x = c y = f ( x ) l

De grafiek van een rationale functie heeft een V.A. met vergelijking x = c als c een nulwaarde is van de noemer van het functievoorschrift die geen nulwaarde is van de teller.

• Ligging van de kromme t.o.v. een V.A. : Onderzoek het teken van f ( x ) in een omgeving van c .

b Horizontale asymptoot

Voorbeeld :

Beschouwdefunctie f met f ( x )= 2 x + 4 x 2 . lim x →±∞ 2 x + 4 x 2 = 2

y = 2 is de vergelijking van de horizontale asymptoot van de grafiek van de functie f Ligging van de grafiek t.o.v. de asymptoot :

v ( x )= f ( x ) 2 = 2 x + 4 x 2 2 = 2 x + 4 2 x + 4 x 2 = 8 x 2 x 2

v ( x ) – | + grafiek onder H.A. grafiek boven H.A.

( x )= 2 x + 4 x 2 y = 2 x = 2

Algemeen :

• De rechte l ↔ y = c ( ∈ R) is een horizontale asymptoot van de kromme k ↔ y = f ( x ) lim x →+∞ f (x )= c oflim x →−∞ f (x )= c

• Eigenschap : y = f ( x ) O x y y = c l

De grafiek van een rationale functie heeft een H.A. met vergelijking y = c als in het functievoorschrift gr( T) ⩽ gr( N)

• Ligging van de kromme t.o.v. een H.A. :

Onderzoek het teken van f ( x ) – c voor x → –∞ respectievelijk x → +∞.

c Schuine asymptoot

Voorbeeld :

Beschouwdefunctie f met f ( x )= x 2 4 x + 3 x + 2

x 2 – 4x + 3 x + 2

x 2 + 2x x – 6

– 6x + 3

– 6x – 12 15

x 2 4 x + 3

x + 2 = x 6 + 15 x + 2

y = x – 6 is de vergelijking van de schuine asymptoot van de grafiek van de functie f Ligging van de grafiek t.o.v. de asymptoot :

v ( x )= f ( x ) ( x 6)

= x 2 4 x + 3 x + 2 ( x 6) = 15 x + 2

INKIJKEXEMPLAARDIEKEURE

grafiek onder S.A. grafiek boven S.A.

Algemeen :

• De rechte l ↔ y = mx + q ( m ∈ R0 en q ∈ R) is een schuine asymptoot van de kromme k ↔ y = f ( x ) lim x →+∞ [ f ( x ) (mx + q )]= 0oflim x →−∞ [ f ( x ) (mx + q )]= 0

• Eigenschap :

De grafiek van een rationale functie heeft een S.A. als in het functievoorschrift gr( T) = gr( N) + 1.

De vergelijking van deze schuine asymptoot is het quotiënt van de euclidische deling van T door N.

• Ligging van de kromme t.o.v. een S.A. :

Onderzoek het teken van f ( x ) – ( mx + q ) voor x → –∞ respectievelijk x → +∞

3 Afgeleiden

Om de helling van een grafiek van een functie f in een punt P te bepalen, laten we een willekeurig punt Q van de grafiek naderen tot het punt P via tussenliggende punten Q1, Q2

De rechte PQ zal via de tussenliggende rechten PQ1, PQ2 … naderen tot de raaklijn t aan de grafiek in het punt P. De hellingshoek van PQ nadert tot de hellingshoek van t .

INKIJKEXEMPLAARDIEKEURE

gemiddelde verandering van een functie

De gemiddelde verandering van een functie f over een interval [ a , a + ∆x ] wordt weergegeven door het differentiequotiënt

Het is de richtingscoëfficiënt van de snijlijn PQ met P( a , f ( a )) en Q( a + ∆x , f ( a + ∆x ))

– Het is de gemiddelde helling van de grafiek van f over [ a , a + ∆x ]

– Het is een benadering van de ogenblikkelijke verandering. Die benadering wordt steeds beter als ∆x → 0 ( als Q → P)

ogenblikkelijke verandering en afgeleide van een functie in een punt

Stel : a is een inwendig punt van dom f ( er bestaat een omgeving van a die volledig tot dom f behoort)

Als het differentiequotiënt een eindige limiet heeft in a , dan noemen we dat getal de afgeleide van f in a .

Notatie : f (a )= df (

– Het is de richtingscoëfficiënt van de raaklijn t in P ( a , f ( a )) aan de grafiek van f .

– Het geeft de helling weer van de grafiek van f in het punt P.

– Het is een maat voor de ogenblikkelijke verandering van f voor x = a .

– Ten opzichte van een georthonormeerd assenstelsel geldt : f (a )= tan α met α = x , t = hellingshoekvandegrafiekvan f inhetpuntP a , f (a )

Opmerkingen :

– Andere notatie voor f ′( a ):

Stel: a + ∆x = x ⟹ ∆x = x – a ∆x → 0 ⟹ x → a (1) wordt : f (a )= lim x → a

( x ) f (a ) x a (2)

– Als de afgeleide f ′( a ) bestaat, dan zeggen we dat de functie f afleidbaar of differentieerbaar is in a Het woord ‘afleiden’ betekent in het Engels ‘to differentiate’.

– Omdat a een inwendig punt van het domein moet zijn, bestaat er dus geen afgeleide in de randpunten van het domein.

Afgeleide van een functie in een punt : Beschouw de functie f met f ( x ) = x 2 f (1) (2) = lim x

2 is de richtingscoëfficiënt van de raaklijn in P( 1, 1) aan de grafiek van f De vergelijking van de raaklijn in P( 1, 1) is : y 1 = 2( x 1)

y = 2 x 1

De vergelijking van de raaklijn t in het punt P( a , f ( a )) aan de grafiek van f wordt bepaald door : y – f ( a ) = f ′( a ) · ( x – a )

afgeleide functie van een functie

De afgeleide functie van een functie f is de functie f ′ die elke x waarin f afleidbaar is, afbeeldt op de afgeleide van f in x

Notatie : f ′ met voorschrift f ( x )= lim

Voorbeeld : f ′ met f ′( x ) = 2x wordt de afgeleide functie genoemd van f met f ( x ) = x 2 .

Rekenregels voor afgeleiden :

D ( f + g )= Df + Dg

Dc = 0

Dx = 1

Dx n = n x n 1 (n

D 1 x = 1 x 2

INKIJKEXEMPLAARDIEKEURE

D √x = 1 2√x

D 3 √x = 1 3 3 x 2

D ( f g )= Df Dg

D ( f · g )= f · Dg + g · Df

D (c f )= c · Df

D f g = g Df f Dg g 2 D 1 f = Df f 2

Df m = mf m 1 Df (m ∈ Q0) dy dx = dy du du dx met u = f (x ) → kettingregel

4

Eigenschappen van functies in r

Beschouwdefunctie f met f ( x )= x 2 2 x 8 x 6 . f ( x )= x 2 12 x + 20 ( x 6)2 (controleerdit) x 2 12 x + 20 =

INKIJKEXEMPLAARDIEKEURE

f stijgt in ] –∞, 2[ en in ] 10, +∞[ f daalt in ] 2, 6[ en in ] 6, 10[

f bereikt een relatief maximum voor x = 2.

f bereikt een relatief minimum voor x = 10.

f heeft geen absolute extrema.

y = x + 4

Opdracht :

Controleer of x = 6 de vergelijking is van een V.A. en y = x + 4 de vergelijking is van een S.A. van de grafiek van de gegeven functie.

a Stijgen en dalen

Als f continu is in [ a , b ] en f ′( x ) > 0 voor elke x ∈ ] a , b [ , dan is f stijgend in [ a , b ].

Als f continu is in [ a , b ] en f ′( x ) < 0 voor elke x ∈ ] a , b [ , dan is f dalend in [ a , b ] f ′( x ) + –f ( x ) ↗ ↘

b Absolute en relatieve extrema

Definities : extrema

f bereikt een relatief maximum minimum in a ∈ dom f

f bereikt een absoluut maximum minimum in a ∈ dom f

INKIJKEXEMPLAARDIEKEURE

Ba ⊂ dom f : ∀ x ∈ Ba \{a } : f ( x ) < > f (a )

stelling 1

Als f een relatief extremum bereikt in a en afleidbaar is in a , dan is f ′( a ) = 0.

stelling 2

Als f continuisin a en ∃ Ba ⊂ dom f : ∀ x ∈ Ba : x < a =⇒ f ( x ) > < 0

> a =⇒ f ( x ) < > 0 dan bereikt f een relatief maximum minimum in a .

Om de grafiek van de functie f te construeren, is de raaklijn t in het punt P( a , f ( a )) van belang.

We doen een beroep op de resultaten die we al in het boek Analyse 2 verkregen hebben.

We geven een overzicht.

① f ′( a ) = 0 ⟺ t // x

② f iscontinuin a lim x →a f (x )= ±∞

③ f iscontinuin a linkerafgeleide = rechterafgeleide

⟹ er zijn twee verschillende raaklijnen t 1 en t 2

Je merkt dus dat in ② en ③ f ′( a ) niet bestaat.

Tweede afgeleide – test voor extrema

Als f continuisin Ba , f (a )= 0en f (a ) > < 0, dan bereikt f een relatief minimum maximum in a . f ′( x ) f ″( x ) 0 + 0 –f ( x ) minimum maximum

Definities :

hol & bol

De grafiek van f is hol in [ a, b ]

f ′ is stijgend in [ a, b ]

buigpunt

De grafiek van f is bol in [ a, b ]

f ′ is dalend in [ a, b ]

INKIJKEXEMPLAARDIEKEURE

De grafiek van f heeft een buigpunt in a ⟺

f ′ bereikt een extremum in a en er is een raaklijn aan de grafiek van f in het punt ( a , f ( a ))

eigenschappen

1 Alsvoorelke x ∈ [a , b ] f continuisen f ′′ ( x ) > < 0, dan is de grafiek van f hol bol in [ a , b ].

2 Als f continu is in a en f ″ van teken verandert in a en er bestaat een raaklijn aan de grafiek van f in het punt ( a , f ( a )), dan heeft de grafiek van f een buigpunt in a

x a

f ″( x ) + –

f ′( x ) ↗ ↘

f ( x ) ∪ hol buigpunt ( a , f ( a )) ∩ bol

De vergelijking van de buigraaklijn in het punt P( a , f ( a )) is : y – f ( a ) = f ′( a ) ( x – a )

In een tabel, die het verloop van de functie f aangeeft, gebruiken we de volgende symbolen :

f ′( x ) + + – –

f ″( x ) + – + –

f ( x ) ⤴ hol stijgend ⤵ bol stijgend ⤷ hol dalend ⤵ bol dalend

stelling van Rolle

Als een functie f continu is in [ a , b ], afleidbaar is in ]a , b [ en f ( a ) = f ( b ), dan bestaat er minstens één punt

c ∈ ]a , b [ zodat f ′( c ) = 0.

middelwaardestelling van Lagrange

Als een functie f continu is in [ a , b ] en afleidbaar is in ]a , b [ , dan bestaat er minstens één punt

c ∈ ]a , b [ zodat f ′ ( c )= f ( b ) f (a ) b a

c Holle en bolle zijde van de grafiek van een functie – buigpunten

Voorbeeld :

Beschouw de functie f met f ( x ) = x 3 – 3x + 1 f ′( x ) = 3x 2 – 3

(

Samenvattende tabel

De vergelijking van de buigraaklijn in het punt ( 0, 1) is :

1 = f (0)( x 0)

5 Verloop van een functie

Om het verloop van een functie f te bestuderen, doen we het volgende onderzoek :

1 Domein

We bepalen dom f om te weten welke x -waarden een beeld hebben.

2 Continuïteit

We onderzoeken in welke punten van dom f de functie continu is.

3 Snijpunten met de assen en tekenverloop van f ( x )

We bepalen de snijpunten van de grafiek van f met de x -as en de y -as.

We onderzoeken het tekenverloop van f ( x )

4 Symmetrie

We onderzoeken of de functie eventueel even of oneven is. (on)even functie f is even ⟺

De grafiek van f is symmetrisch om de y -as. f is oneven

De grafiek van f is symmetrisch om de oorsprong O.

INKIJKEXEMPLAARDIEKEURE

5 Asymptoten

We stellen de vergelijkingen op van eventuele verticale (V.A.), horizontale (H.A.) of schuine asymptoten (S.A.) en onderzoeken de ligging van de grafiek t.o.v. de asymptoten.

6 Eerste afgeleide

We berekenen f ′( x ) en onderzoeken het tekenverloop. Zo bepalen we het stijgen en dalen van de functie f en zo vinden we de eventuele extrema van f

7 Tweede afgeleide

We berekenen f ″( x ) en onderzoeken het tekenverloop. Zo bepalen we de holle en bolle zijde van de grafiek en de eventuele buigpunten. In de buigpunten kunnen we ook de buigraaklijn bepalen.

8 Samenvattende tabel

We brengen de gevonden informatie over in een overzichtelijke tabel. Hierin nemen we onder andere op : tekenverloop van f ′( x ) en van f ″( x ), stijgen en dalen van f, extrema, buigpunten …

9 Bereik

Hier bepalen we ber f om te weten voor welke y -waarden er een x -waarde bestaat zodat y = f ( x )

10 Grafiek

Als we de grafiek tekenen met ICT, dan moet het eindresultaat uiteraard ook overeenstemmen met alle gevonden resultaten over symmetrie, stijgen en dalen enz.

Voorbeeld 1 :

Beschouw de veeltermfunctie f met f ( x ) = 2 3 x 3 2 x 2 6 x  1 Domein

dom f = R

2 Continuïteit

f is een continue functie want elke veeltermfunctie is continu in R

3 Snijpunten met de assen en tekenverloop van f ( x )

snijpunten met de x -as :

Stel f ( x )= 0 2 3 x 3 2 x 2 6 x = 0 x 3 3 x 2 9 x = 0

( x 2 3 x 9)= 0

INKIJKEXEMPLAARDIEKEURE

snijpunten met de x -as : ( 0, 0); ( –1,85 ; 0) en ( 4,85 ; 0)

tekenverloop van f ( x ) x –∞ –1,85

4 Symmetrie

f ( x )= 2 3 x 3 2 x 2 6 x f ( x )= 2 3 ( x )3 2( x )2 6( x )= 2 3 x 3 2 x 2 + 6 x =⇒ f ( x ) = f ( x ) en f ( x ) = f ( x ) f is niet even en ook niet oneven

5 Asymptoten

V.A. : geen (dom f = R)

: lim

)=

Er zijn geen horizontale asymptoten.

S.A. : geen

snijpunten met de y -as : x = 0

f (0)= 0

snijpunt met de y -as : ( 0, 0)

6 Eerste afgeleide

f ′ ( x )= D 2 3 x 3 2 x 2 6 x = 2 x 2 4 x 6

f ( x )= 0 ⇐⇒ 2 x 2 4 x 6 = 0

⇐⇒ x 2 2 x 3 = 0

⇐⇒ x = 1 of x = 3

7 Tweede afgeleide

f ′′ ( x )= D (2 x 2 4 x 6) = 4 x 4

f ( x )= 0 ⇐⇒ 4 x 4 = 0

⇐⇒ x = 1 x –∞ 1 +∞ f ″( x ) – 0 + f ( x ) ∩ buigpunt ∪

8 Samenvattende tabel

INKIJKEXEMPLAARDIEKEURE

DevergelijkingvandebuigraaklijninP

9 Bereik

Uit punt 8 volgt : ber f = R.

10 Grafiek

Voorbeeld 2 :

Beschouw de homografische functie f met f ( x )= 2 x + 4 x 3

1 Domein

Bestaansvoorwaarde : x – 3 ≠ 0 dus x ≠ 3

dom f = R \ { 3}

2 Continuïteit

f is continu in R \ { 3}. (Elke rationale functie is continu in elk punt van haar domein.)

3 Snijpunten met de assen en tekenverloop van f ( x )

snijpunten met de x -as

f ( x )= 0 ⇐⇒ 2 x + 4 = 0

⇐⇒ x = 2

Het snijpunt met de x -as is dus ( –2, 0)

tekenverloop van f ( x )

INKIJKEXEMPLAARDIEKEURE

snijpunten met de y -as

x = 0 =⇒ f ( x )= 4 3

Hetsnijpuntmetde y -asisdus 0, 4 3

–2 3 +∞ f ( x ) + grafiek boven de x-as 0 –grafiek onder de x-as | + grafiek boven de x-as

4 Symmetrie

f ( x )= 2 x + 4 x 3 = 2 x 4 x + 3 = f ( x ) = f ( x )

De functie is dus noch even, noch oneven.

5 Asymptoten

V.A. : x = 3,wantlim x → > 3 2 x + 4 x 3 =+∞ lim x → < 3 2 x + 4 x 3 = −∞

Ligging van de kromme t.o.v. de V.A. : x = 3 x y O

H.A. : lim x →±∞ 2 x + 4 x 3 = 2 y = 2isH.A.

Liggingvandekrommet.o.v.deH.A.:

v ( x )= 2 x + 4 x 3 2 = 2 x + 4 2 x + 6 x 3 = 10 x 3 y = 2 x y O x –∞ 3 +∞ 10 x 3 –de kromme ligt onder de H.A. | + de kromme ligt boven de H.A.

S.A. : geen

6 Eerste afgeleide

f ( x )= D 2 x + 4 x 3 = ( x 3) 2 (2 x + 4) 1 ( x 3)2 = 2 x 6 2 x 4 ( x 3)2 = 10 ( x 3)2

7 Tweede afgeleide

INKIJKEXEMPLAARDIEKEURE

)=

8 Samenvattende tabel

9 Bereik

ber f = R \ { 2}

10 Grafiek

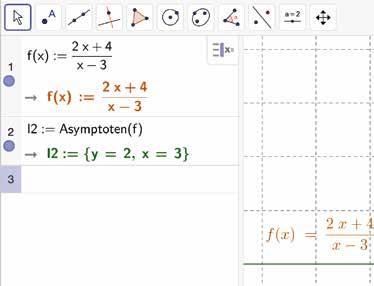
Taak : Toon aan dat M( 3, 2) het symmetriemiddelpunt is van de grafiek.

Voorbeeld 3 :

Beschouw de functie f met f ( x )= x 2 x 4

1 Domein

B.V. : x – 4 ≠ 0 dus x ≠ 4

dom f = R \ { 4}

2 Continuïteit

f is continu in R \ { 4}. (Elke rationale functie is continu in elk punt van haar domein.)

3 Snijpunten met de assen en tekenverloop van f ( x )

snijpunten met de x -as

INKIJKEXEMPLAARDIEKEURE

snijpunten met de y -as

f ( x )= 0 ⇐⇒ x 2 = 0 ⇐⇒ x = 0 x = 0 =⇒ f ( x )= 0

Het snijpunt met de x -as is dus ( 0, 0).

Het snijpunt met de y -as is dus ( 0, 0).

tekenverloop van f ( x ) x –∞ 0 4 +∞ f ( x ) –grafiek onder de x-as 0 –grafiek onder de x-as | + grafiek boven de x-as

4 Symmetrie

f ( x )= ( x )2 x 4 = x 2 x 4 = f ( x ) = f ( x )

De functie is noch even, noch oneven.

5 Asymptoten

V.A. : x = 4,wantlim x → > 4 x 2 x 4 =+∞ lim x → < 4 x 2 x 4 = −∞ Ligging van de kromme t.o.v. de V.A. : x = 4 x y O

H.A. : lim x →±∞ x 2 x 4 = lim x →±∞ x = ±∞

De grafiek van f heeft geen horizontale asymptoten. De graad van de teller is immers groter dan de graad van de noemer.

S.A. : De grafiek van f heeft een schuine asymptoot want gr T = gr N + 1

x 2 x – 4 x 2 – 4x x + 4 4x 4x – 16 16

De vergelijking van de schuine asymptoot is dus : y = x + 4 Ligging van de grafiek van f t.o.v. de S.A. : we onderzoeken het teken van v ( x )= f ( x ) x 4 = 16 x 4

INKIJKEXEMPLAARDIEKEURE

6

Eerste afgeleide

f ( x )= D x 2 x 4 = ( x 4)2 x x 2 1 ( x 4)2 = 2 x 2 8 x x 2 ( x 4)2 = x ( x 8) ( x 4)2

7

Tweede

afgeleide

( x

)4 = ( x 4)(2 x 8) 2( x 2 8 x ) ( x 4)3 = 2 x 2 8 x 8 x + 32 2 x 2 + 16 x ( x 4)3 = 32 ( x 4)3

8 Samenvattende tabel

9 Bereik ber f = R \ ] 0, 16[

6

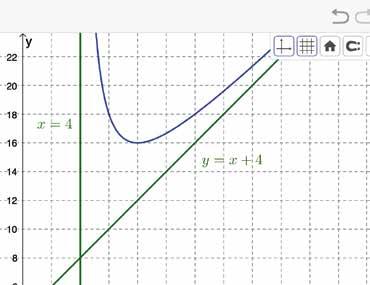
De regel van de l’Hôpital

• Islim x →a f ( x )= lim x →a g ( x )= 0,danislim x →a f ( x ) g ( x ) = 0 0 voorlopigonbepaald.

• Islim x →a f ( x )= lim x →a g ( x )= ±∞,danislim

= ∞ ∞ voorlopigonbepaald.

INKIJKEXEMPLAARDIEKEURE

De regel van de l’Hôpital zal het mogelijk maken om die onbepaaldheden op te heffen. We aanvaarden de regel zonder bewijs.

regel van de l’Hôpital

Alslim

Opmerking : de regel geldt ook als x →±∞

Voorbeelden :

betekent:toepassingvanderegelvandel’Hôpital

7 Oefeningen

Bereken de volgende limieten. alim x →2 ( x 3 2 x 2 7)

x →4 2 x 2 x 1 x 6

→−4 x 2 + 7 x + 12 x 2 + 8 x + 16

x 2 x 5 (2 x + 3)2

→3 x 2 5 x + 6 x 2 9

Bepaal de asymptoten van de grafiek van de functies f 1, f 2, f 3 en f 4 met onderstaande voorschriften.

Bepaal eveneens de ligging van de grafiek t.o.v. de asymptoten.

Teken nadien met ICT de grafiek van deze functies en ook de asymptoten.

a f 1 ( x )= x 2 x + 2 c f 3 ( x )= 2 x 2 + 1 x 2 3 x + 2

b f 2 ( x )= 2 x + 1 x 4 d f 4 ( x )= x 2 + 2 x + 5 x + 1

Bereken de afgeleide van de volgende functies als f ( x ) gelijk is aan :

a x 2 + x g x 2 + x x 1

b x 2 + 4 x + 11 h ( x 2 x 4)3

c 2 x 3 6 x 2 4 x 11

icos4 x sin3 x

d3 x 4 4 x 3 + 6 x 2 + 78 jsin2 2 x

e 2 x 4 x + 5 k (2 x 2 + x )3 (6 2 x 2 )2 f 2 x 6 4 x + 2

lsin3 (6 4 x )

Bepaal het voorschrift van de afgeleide functie f ′ van f .

Zoek de snijpunten van de grafieken van f en f ′

Zoek de x -waarden waarvoor f ( x ) > f ′( x ). Controleer dit grafisch.

a f ( x )= x 2 4 x + 5c f ( x )= x 3 2 x 2

b f ( x )= 2 x 2 4 x + 14 d f ( x )= x 3 + 3 x 2 + x + 1

6 7 8 9

Gegeven :

Defunctie f met f ( x )= x 3 3 + 2 x 2 6 x + 5

Defunctie g met g ( x )= x 3 3 + 3 x 2 18 x 15

Gevraagd :

a Zoek de snijpunten van de grafieken van f ′ en g ′ .

b Zoek de x -waarden waarvoor f ′( x ) < g ′( x )

c Zoek de x -waarden waarvoor f ″( x ) ⩾ g ″( x ).

d Controleer dit grafisch.

Gegeven :

Defunctie f met f ( x )= 2 3 x 3 + x 2 2 x 4

Defunctie g met g ( x )= x 3 + 1 2 x 2 + 5

Gevraagd :

a Zoek de x -waarden waarvoor f ′( x ) ⩾ g ′( x )

b Zoek de x -waarden waarvoor f ″( x ) = g ″( x )

c Controleer dit grafisch.

Bereken :

a D 2 ( x 2 4 x ) d D 2 (5 2 x 2 )2

b D 3 sin5 x e D 3 ( x 3 4 x 2 + 8 x 4)

c D 2 x x + 1 f D 2 (sin x cos x )

Bepaal de vergelijking van de raaklijn en de normaal aan de krommen met onderstaande vergelijking in het gegeven punt. Teken nadien met ICT de kromme, de raaklijn en de normaal in het gegeven punt.

a y = x 2 + 2 x 4 in ( 2,...)

b y = x + 2 x 2 in (4,...)

c y = sin2 x in π 4 ,...

Een steen wordt verticaal omhooggeworpen met een beginsnelheid van 20 m/s. De afgelegde weg van het voorwerp, in functie van de tijd, is gegeven door :

s ( t )= v0 t 1 2 gt 2 met v0 :debeginsnelheid

g :devalversnelling = 9,81m/s2

a Bepaal de snelheid in functie van de tijd.

b Wanneer is de snelheid gelijk aan 0 ?

c Welke hoogte bereikt het projectiel ?

d Bepaal de versnelling in functie van de tijd.

Tip: snelheid v ( t )= ds ( t ) dt versnelling a ( t )= dv ( t ) dt

Maak het volledige verloop van de volgende functies als :

a f ( x )= x 3 + 3 x 2 + 3 x 7

b f ( x )= 2 x + 2 x 5

c f ( x )= x + 4 x + 2

d f ( x )= x 2 2 x x 2

e f ( x )= x 2 x + 1

f f ( x )= 4( x 2 2 x + 1) x 2 2 x 3

Een rechthoek heeft een omtrek van 16 cm.

Op de zijden van de rechthoek staan halve cirkels, buiten de rechthoek gelegen.

Onderzoek het verloop van de totale oppervlakte (rechthoek + alle halve cirkels samen).

Wanneer is die oppervlakte minimaal ?

Los dit probleem met GeoGebra op.

INKIJKEXEMPLAARDIEKEURE

a Onderzoek het verloop van het volume van het lichaam, ontstaan door het wentelen van een rechthoek om een zijde als de omtrek van de rechthoek 2a is.

b Wanneer is het volume maximaal ?

c Wat is het maximale volume als de omtrek van de rechthoek 6 cm is ?

Gegeven :

Het volume van een cilinder is 8p.

Gevraagd :

a Onderzoek het verloop van de totale oppervlakte van de cilinder.

b Wanneer is die oppervlakte minimaal ?

Bereken de volgende limieten met de regel van de l’Hôpital.

alim x →1 x 3 1 x 3 3 x 2 + 3 x 1 blim x →0 x cos x sin x x 3 clim

INKIJKEXEMPLAARDIEKEURE

x

2 x 3 + x + 1 3 x 3 + 5 jlim x →±∞ ( x 1)2 ( x + 1)3

Waarom zijn de volgende berekeningen foutief ? Verklaar.

1.2

Verloop van exponentiële en logaritmische functies

1 Even herhalen

Het verschil tussen lineaire en exponentiële groei

Bij lineaire groei ontstaat Bij exponentiële groei de volgende waarde uit ontstaat de volgende de vorige door optelling waarde uit de vorige door met een getal. Dat getal vermenigvuldiging met is constant als de een getal. Dat getal heet tijdsintervallen even de groeifactor groot zijn.

exponentiële functie

Is a ∈ R + 0 \{1}, dan noemen we de functie f met f ( x ) = a x de exponentiële functie met grondtal of groeifactor a Eigenschappen van f met f ( x )= a x en a ∈ R + 0 \{1}:

a > 1 (positieve groei)

• Grafiek:

INKIJKEXEMPLAARDIEKEURE

0 < a < 1 (negatieve groei)

• Grafiek:

• dom f = R

• ber f = R + 0 =]0, +∞[

• f is strikt stijgend in R: x 1 < x 2 ⟹ f ( x 1) < f ( x 2)

• nulwaarden : geen

• snijpunt met de y -as : ( 0, 1)

• ( 0, 1) ∈ f en ( 1, a ) ∈ f

• lim x →−∞ a x = 0 : de x -as ( y = 0) is een horizontale asymptoot van de grafiek

• lim x →+∞ a x =+∞

• waardeverloop:

• dom f = R

• ber f = R + 0 =]0, +∞[

• f is strikt dalend in R: x 1 < x 2 ⟹ f ( x 1) > f ( x 2)

• nulwaarden : geen

• snijpunt met de y -as : ( 0, 1)

• ( 0, 1) ∈ f en ( 1, a ) ∈ f

• lim x →+∞ a x = 0 : de x -as ( y = 0) is een horizontale asymptoot van de grafiek

• lim x →−∞ a x =+∞

• waardeverloop:

logaritmen

De logaritme met grondtal a ∈ R + 0 \{1} van een strikt positief reëel getal is de exponent van de macht waartoe we a moeten verheffen om dat getal te krijgen.

Er geldt dus : ∀a ∈ R + 0 \{1}, ∀ x ∈ R + 0 : loga x = y ⟺ x = a y

Een overzicht :

1.loga x = y ⇐⇒ x = a y

2.loga a y = y ; x = a loga x

3.loga ( x · y )= loga x + loga y

4.loga x y = loga x loga y

logaritmische functie

5.loga 1 x = loga x

6.loga x n = n loga x

7.log b x = loga x loga b

hoofdeigenschap

OP : er bestaat geen eigenschap voor loga ( x ± y )

Is a ∈ R + 0 \{1}, dan noemen we de reële functie f met f ( x ) = loga x de logaritmische functie met grondtal a .

De logaritmische functie met grondtal a is de inverse functie van de exponentiële functie met grondtal a .

Eigenschappen van de logaritmische functie f met f ( x ) = loga x en a ∈ R + 0 \{1}

• Grafiek:

8.log b a = 1 loga b a > 1

• Grafiek:

(x ) = a x

• dom f = R + 0

• ber f = R

• f is strikt stijgend in R + 0

• nulwaarde : 1

• snijpunt met de y -as : geen

• ( 1, 0) ∈ f en ( a , 1) ∈ f

• lim x → > 0 loga x = −∞ : de y -as ( x = 0) is een verticale asymptoot van de grafiek

• lim x →+∞ loga x =+∞

• waardeverloop: 0 < a < 1

y x y = x

g (x ) = a x f (x ) = loga x

x 0 1 a +∞ f ( x ) –∞ 0 1 +∞ x 0 a 1 +∞ f ( x ) +∞ 1 0 –∞ 0 1 1 y x y = x

• dom f = R + 0

• ber f = R

• f is strikt dalend in R + 0

• nulwaarde : 1

• snijpunt met de y -as : geen

• ( 1, 0) ∈ f en ( a , 1) ∈ f

• lim x → > 0 loga x =+∞ : de y -as ( x = 0) is een verticale asymptoot van de grafiek

• lim x →+∞ loga x = −∞

• waardeverloop:

2 Afgeleide van exponentiële en logaritmische functies – getal e

In deze paragraaf gaat het over groeisnelheid bij exponentiële groei. We keren eerst even terug naar de lineaire groei.

– In onderstaande figuur vind je de grafieken van twee veulens die lineair groeien. a Hoe kun je aan de grafieken zien welk veulen het snelst groeit ? b Hoeveel kg komt veulen A per maand bij ? En veulen B ?

Wat is het verband met de richtingscoëfficiënt van de grafiek (helling) ?

INKIJKEXEMPLAARDIEKEURE

Bij lineaire groei is de groeisnelheid constant. Meetkundig is het de rico van de grafiek (rechte).

– Hoe kun je de helling meten van een kromme lijn ?

Kijk nog eens terug naar de groeifunctie f met f ( x ) = 2x , zoals bij de groei van waterplanten.

Het voorschrift f ( x ) = 2x wil zeggen dat de bedekte oppervlakte per tijdseenheid verdubbelt. De wekelijkse groeifactor is dus 2.

De groeisnelheid is de helling van de grafiek.

Bij exponentiële groei is de groeisnelheid niet constant. Hoe steiler de grafiek, hoe groter de groeisnelheid. In Analyse 2 heb je geleerd dat de helling in een punt van een kromme gemeten kan worden met de richtingscoëfficiënt van de raaklijn in dat punt van de kromme. Daartoe bereken je de afgeleide van de functie in dat punt.

We plotten met behulp van ICT de grafieken van y 1 = 2x en van y 2, dat is de numerieke afgeleide van y 1

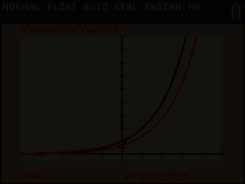
Het lijkt erop dat de grafiek van y 2 kan ontstaan uit de grafiek van y 1 door een uitrekking t.o.v. de y -as met factor c , dus dat y 2 = c y 1 De groeisnelheid lijkt evenredig met de aanwezige hoeveelheid. We gaan dit nu algebraïsch onderzoeken.

Df ( x )= definitie afgeleide

INKIJKEXEMPLAARDIEKEURE

In het bijzonder geldt : f ′ (0)= 20

Dus : f ′( x ) = 2x f ′( 0)

Om f ′( x ) te berekenen moeten we dus lim

1

kennen. Met de gewone rekenregels kunnen we die limiet niet berekenen. Die limiet bestaat omdat hij gelijk is aan de richtingscoëfficiënt van de raaklijn t aan de grafiek van f in het punt P( 0, 1) (zie ‘meetkundige betekenis van de afgeleide in een punt’ blz. 13).

Met ICT kunnen we benaderingen berekenen van de limiet in 5 decimalen.

Besluit :

Als f ( x ) = 2x, dan is f ′( x ) = c 2x met

We gaan nu aantonen dat in het algemeen geldt :

Is f ( x ) = a x met a ∈ R + 0 \{1}, dan is

In het bijzonder geldt : f ′ (0)= lim

x →0 a ∆ x 1 ∆ x = richtingscoëfficiënt van de raaklijn aan de grafiek van f in het punt P(0, 1).

Hiermee is bewezen dat bij elke functie f met f ( x ) = a x een constante c bestaat zodat f ′( x ) = c a x

De waarde van de constante c hangt af van de groeifactor a . Bij f ( x ) = 2x vonden we dat f ′( x ) = 0,693 · 2x

De volgende tabel geeft voor nog enkele andere waarden van de groeifactor a , de afgeronde waarden van c in vier decimalen nauwkeurig.

c = lim ∆x →0 a ∆x 1

– 0,6931 – 0 – 0,4055 – 0,6931 – 0,9163 – 1,0986 – 1,2528

– Alleen voor a = 1 is c = 0. Kun je dat verklaren ?

– Voor a = 0,5 is c negatief. Waarom ?

Het lijkt aannemelijk dat ‘ergens’ tussen de groeifactorwaarden 2,5 en 3 de evenredigheidsconstante c gelijk zal zijn aan 1. Dat is interessant, want dan is de afgeleide functie gelijk aan de functie zelf. De groeifactor (grondtal) waarbij c = 1 noemen we e De letter e is de eerste letter van Euler, die de notatie voor het eerst gebruikte in 1731.

Hieronder vind je de waarden voor c bij enkele groeifactoren a tussen 2,5 en 3. a c (afgerond op 4 decimalen nauwkeurig)

Het getal e ligt ergens in de buurt van 2,718.

We zoeken nu een benadering voor het getal e . Omdat

zou dus moeten gelden dat e

Of ook : e Dx – 1 ≈ Dx voor Dx ≈ 0.

e

volgt dat

We vermoeden dus (en bewijzen later)

2,70481382942 2,71692393224 2,71814592683 2,71826823717 2,71828046932 2,71828169255 2,71828181487 2,71828182832 2,71828182846

We onthouden : e = 2,718281828…

Het voorschrift van de afgeleide functie van de exponentiële functie f met f ( x ) = e x is f ′( x ) = e x of : D ( e x) = e x

Andere notatie : e x = exp( x ) Met ICT vinden we :

De functie f met f ( x ) = e x is een functie die gelijk is aan haar afgeleide, een unicum in de wiskunde ! Dat maakt het getal e zo bijzonder. Het getal speelt ook een belangrijke rol in allerlei vakgebieden waar wiskunde gebruikt wordt.

een belangrijke limiet

lim x →±∞ 1 + 1 x x = e met x ∈ R

Wekunnenbewijzendat e = lim ∆ x →0 (1 + ∆ x ) 1 ∆ x (zievermoedenblz.35).Alswe ∆ x = z stellen,danvolgthieruit:

lim z →0 (1 + z ) 1 z = e .Alswehierin z = 1 x stellen,danbekomenwelim x →±∞ 1 + 1 x x = e .

Voorbeelden :

1 Bereken lim x →−∞ 1 3 x 2 x

Stel: 3 x = 1 x =⇒ x = 3 x

Als x →−∞,dangaat x → +∞ lim x →−∞ 1 3 x 2 x = lim x →+∞ 1 + 1 x 6 x = lim x →+∞ 1 + 1 x x 6 = e 6 = 1 e 6 2 Bereken lim x →2 (2 x 3) 1 3 x 6

Stel:2 x 4 = z =⇒ x = z + 4 2

Als x → 2,dangaat z → 0 lim x →2 (2 x 3) 1 3 x 6 = lim x →2

INKIJKEXEMPLAARDIEKEURE

Het getal e

Euler bewees in 1737 dat e een irrationaal getal is. Een irrationaal getal is een getal dat niet als een breuk te schrijven is. De decimalen van zo’n getal vertonen geen enkele regelmaat. √2 , 3 √5 en p zijn ook irrationale getallen.

In 1873 bewees de Franse wiskundige Hermite (1822–1901) dat het getal e geen oplossing kan zijn van een vergelijking met rationale coëfficiënten. Zo’n getal wordt transcendent genoemd. Naar het model van zijn betoog toonde de Duitse wiskundige F. Lindemann in 1882 op zijn beurt aan dat ook p een transcendent getal is. De benaming ‘transcendent’ is afkomstig van Leibniz.

3 Natuurlijke logaritmen

Zoals alle exponentiële functies heeft ook f met f ( x ) = e x = exp( x ) een inverse : de logaritmische functie met grondtal e . Logaritmen met grondtal e worden natuurlijke of neperiaanse logaritmen genoemd.

In de notatie laten we e weg en schrijven we ln in plaats van loge loge 3 wordt dus geschreven als ln 3.

Je rekenmachine heeft er een speciale toets voor : LN . Druk LN 3 en je bekomt 1,098612289.

Verband tussen briggse logaritmen (met grondtal 10) en neperiaanse logaritmen (met grondtal e)

Uitlog b x = loga x loga b volgtlog x = ln x ln10

Dus:ln x = log x · ln10of ln x = log x · 2,302585093

enlog x = ln x ln10 of log x = ln x · 0,4342944819

In het algemeen geldt :

∀ x ∈ R0 + : y = ln x ⟺ x = e y

Hieruit volgt : e ln x = x en ln e y = y

INKIJKEXEMPLAARDIEKEURE

Met behulp van het getal e en de eigenschappen van de natuurlijke logaritmen kunnen we alle exponentiële functies afleiden.

Logaritme

Het woord ‘logaritme’ is afkomstig van de Schotse wiskundige Napier (1550 –1617). De benaming ‘natuurlijke logaritme’ (logarithmus naturalis) komt van de Duitse wiskundige Nikolaus Mercator (1620 –1687).

4 Afgeleide van een exponentiële functie

We hebben al aangetoond dat D ( e x) = e x

Met de kettingregel (zie blz. 14 : rekenregels voor afgeleiden) vinden we : D [ e f ( x )] = e f ( x ) Df ( x )

Uit e ln x = x volgt dat e ln a = a en dus kan elke a -macht als een e -macht geschreven worden :

a x = ( e ln a )x = e x ln a

INKIJKEXEMPLAARDIEKEURE

Daaruit volgt :

D ( a x ) = D ( e x ln a ) = e x ln a D ( x ln a ) = e x ln a ln a = a x ln a

Dus : D ( a x ) = a x ln a (1)

Op blz. 34 hebben we aangetoond dat de afgeleide van een exponentiële functie evenredig is met de functie zelf. Uit (1) volgt dat de evenredigheidsfactor c gelijk is aan ln a

D ( 2x ) = 2x ln 2 met ln 2 = 0,6931471806 …

Met de kettingregel vinden we : D [ a f ( x )] = a f ( x ) · ln a · Df ( x )

Voorbeelden :

D ( e x 2 +1 )= e x 2 +1 · D ( x 2 + 1)= 2 x · e x 2 +1

D (3sin √ x )= 3sin √ x ln3 D (sin √ x )= 3sin √ x ln3 cos √ x 1 2√ x = 3sin √ x ln3 cos √ x 2√ x

overzicht

D ( e x ) = e x

[ e f ( x )] = e f ( x ) · Df ( x ) D ( a x ) = a x ln a

Gevolg : Uit het voorgaande blijkt dat de afgeleide van f met f ( x ) = a x bestaat voor alle x ∈ R. Dus is f continu in R volgens de eigenschap : f is afleidbaar in a ⟹ f is continu in a

Dus : exponentiële functies f met f ( x ) = a x zijn continu in elk punt van hun domein.

5 Functies waarvoor geldt dat de afgeleide recht evenredig is met de functiewaarde

f ′ = k · f ⟺ f ( x ) = b e kx met b ∈ R

INKIJKEXEMPLAARDIEKEURE

f ( x )= b e kx

f ′ ( x )= b De kx

f ′ ( x )= b k e kx

f ( x )= k b e kx

f ′ ( x )= k f ( x )

Toepassing : bacteriën kweken

Probleemstelling :

Stel je voor dat je de groei van een cultuur bacteriën bestudeert. De groei hangt af van de tijd t in uren.

De groeisnelheid verloopt volgens de vergelijking

N ′( t ) = 0,34 N ( t ) waarbij N ( t ) het aantal bacteriën na t uren voorstelt.

Stel dat voor t = 0 het aantal bacteriën 100 bedraagt.

a Bereken N ( t ) b Bereken de verdubbelingstijd.

Oplossing :

a N ′( t ) = 0,34 · N ( t ) ⟹ N ( t ) = b · e 0,34t

Verder is N ( 0) = b = 100.

Dus is N ( t ) = 100 e 0,34t

b Dat is de tijd waarin het aantal bacteriën verdubbelt.

We hebben : 200 = 100 · e 0,34 t

2 = e 0,34 t

ln2 = 0,34 · t

t = ln2 0,34

t ≈ 2,039

De verdubbelingstijd is dus ongeveer 2 uur.

Dus: f ( x ) e kx = b (constantefunctie) of: f ( x )= b e kx met b ∈ R

6 Afgeleide van een logaritmische functie

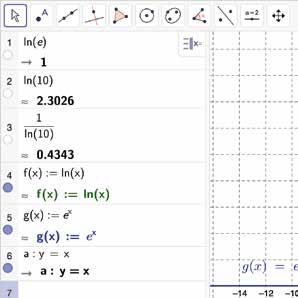
De grafieken van f met f ( x ) = ln x en g met g ( x ) = e x staan hieronder afgebeeld. De grafieken zijn elkaars spiegelbeeld om de rechte met vergelijking y = x

INKIJKEXEMPLAARDIEKEURE

De rechte t raakt aan de grafiek van g in het punt P( 1, e)

De rechte t ′ raakt aan de grafiek van f in het punt P′(e, 1).

Bereken de rico van t en leid hieruit de rico van t ′ af. Gebruik de symmetrie van de figuur. Wat kun je vermoeden voor D ( ln x )?

De afgeleide van f met f ( x ) = ln x f ( x ) = ln x met x ∈ R + 0 ⟺ x = e f ( x )

Aan deze (strikt positieve) afgeleide kun je onmiddellijk zien dat de natuurlijke logaritmische functie f met f ( x ) = ln x een stijgende functie is.

Omdat de afgeleide functie f ′ met f ′ ( x )= 1 x een dalende functie is, wordt die stijging steeds minder groot.

Het hellingsgetal blijft positief, maar wordt steeds kleiner.

INKIJKEXEMPLAARDIEKEURE

Taak : toon aan dat t.o.v. een georthonormeerd assenstelsel geldt dat de raaklijn aan de grafiek van f met f ( x ) = ln x in het punt ( 1, 0) evenwijdig is met de eerste bissectrice.

Met de kettingregel vinden we : D ln f ( x ) = Df ( x ) f ( x )

De afgeleide van f met f ( x ) = loga x

Omdat f ( x )= loga x = ln x ln a met a

Dus : D (loga x )= 1 x ln a

Met de kettingregel vinden we : D [loga f ( x )]= Df ( x ) f ( x ) ln a

Je kunt aan deze afgeleide nog eens zien dat er voor de logaritmische functie twee mogelijkheden zijn. – Als a > 1, dan is ln a > 0 en f ′( x ) > 0 op het domein van de logaritmische functie.

Zo’n logaritmische functie is daarom stijgend en continu. f ( x ) = loga x met a > 1 f ′( x ) = 1 x ln a met a > 1

Als 0 < a < 1, dan is ln a < 0 en f ′( x ) < 0 op het domein van de logaritmische functie.

Zo’n logaritmische functie is daarom dalend en continu. f ( x ) = loga x met 0 < a < 1 f ′( x ) = 1 x ln a met 0 < a < 1

Voorbeelden :

1 D [ln(kx )]= k kx = 1 x

2 D (ln x n )= D (n ln x )= n x

3 D [log(cos x )]= D cos x cos x · ln10 = sin x cos x · ln10 = tan x ln10

4 D (ln | x |)

Beschouw de functie f met f ( x ) = ln | x |. Het domein van die functie is R0 Er zijn dus voor het argument x twee mogelijkheden.

• x ∈ R + 0 : | x | = x =⇒ D ( ln | x | )= D ( ln x )= 1 x

• x ∈ R 0 : | x | = x =⇒ D ( ln | x | )= D ln( x ) = D ( x ) x = 1 x

Dus, voor de twee gevallen geldt : D (ln | x |)= 1 x

Bij het berekenen van afgeleiden maakt het geen verschil uit als we van het argument van een logaritmische functie al of niet de absolute waarde nemen.

Met de kettingregel vinden we : D (ln | f ( x ) |)= Df ( x ) f ( x )

een overzicht

D (ln x )= 1 x D ln f ( x ) = Df ( x ) f ( x )

D (loga x )= 1 x · ln a

( x ) f ( x ) · ln a D (ln | x |)= 1 x D ln | f ( x ) | = Df ( x ) f ( x )

D (ln | x + x 2 + k |)= 1 x 2 + k

INKIJKEXEMPLAARDIEKEURE

loga f ( x ) =

ln | f ( x )+ [ f ( x )]2 + k | = Df ( x ) [ f ( x )]2 + k

Uit het voorgaande volgt dat de afgeleide van f met f ( x ) = loga x bestaat voor elke x ∈ R + 0 .

Dus is f met f ( x ) = loga x continu in R + 0 = dom f

Besluit : Logaritmische functies f met f ( x ) = loga x zijn continu in elk punt van hun domein.

7 Toepassingen

1 De afgeleide van een machtsfunctie

We vonden in het boek Analyse 2 dat de regel : D ( x q ) = q x q –1 geldt voor rationale waarden van q . We tonen nu aan dat de regel ook geldt voor irrationale exponenten en dus algemeen voor reële exponenten.

Is r ∈ R en x ∈ R + 0 ,dangeldt: D (

)= D

INKIJKEXEMPLAARDIEKEURE

Metdekettingregelvindenwe: D (

2 Berekenen van limieten

• Standaardlimieten van exponentiële en logaritmische functies (zie blz. 31–32).

Voorbeelden :

• We beschikken over formules voor de afgeleiden van exponentiële en logaritmische functies.

Het wordt dus mogelijk om met de regel van de l’Hôpital limieten te bepalen van functies die nog niet eerder behandeld zijn.

Vaak blijken er dan in de opgave voorlopig onbepaalde vormen van nieuwe types voor te komen, symbolisch voorgesteld als 1∞ , ∞0, 00, …

In dit opzicht mogen we niet uit het oog verliezen dat de regel van de l’Hôpital alleen geldt voor onbepaaldheden van het type 0 0 of ∞ ∞ .

Voorbeelden

Na tekenonderzoek van e x 2 x in een omgeving van 0 vinden we : x –∞ 0 +∞ e x 2x + –

8 Verloop van een exponentiële functie

Beschouw de exponentiële functie f met f ( x )= e x 2 2

1 Domein

dom f = R

2 Snijpunten met de assen en tekenverloop van f ( x )

snijpunten met de x -as

INKIJKEXEMPLAARDIEKEURE

snijpunten met de y -as

geen, want e x 2 2 > 0 geldt voor elke x ∈ R x = 0 =⇒ f ( x )= 1.

Het snijpunt met de y -as is dus ( 0, 1).

tekenverloop van f ( x ) x –∞ +∞

f ( x ) + ↓ grafiek boven de x -as

3 Symmetrie

f ( x )= e ( x )2 2 = e x 2 2 = f ( x )

De functie is dus even en de y -as is een symmetrieas van de grafiek van f

4 Asymptoten

V.A. : geen, want er bestaat geen a zodat

H.A. : lim x →±∞ e x 2 2 = lim x →±∞ 1 e

De x -as is dus een H.A. en de grafiek van f ligt volledig boven de H.A. omdat ∀ x ∈ R : f ( x ) > 0.

S.A. : geen

5 Eerste afgeleide

f ( x )= De x 2 2 = e x 2 2 1 2 (2 x ) = x e x 2 2 f ( x )= 0 ⇐⇒ x = 0 x –∞ 0 +∞ f ′( x ) + 0 –f ( x ) ↗ max ↘

6 Tweede afgeleide

f ( x )= D x · e x 2 2 = e x 2 2 x xe x 2 2 = e x 2 2 ( x 2 1)

f ( x )= 0 ⇐⇒ x 2 1 = 0 ⇐⇒ x = ±1 x –∞ –1 1 +∞ f ″( x ) + 0 – 0 –f ( x ) ∪ buigpunt ∩ buigpunt ∪

7 Continuïteit

Uit punt 5 volgt dat f overal afleidbaar is, dus is f continu in R

8 Samenvattende tabel

INKIJKEXEMPLAARDIEKEURE

Vergelijkingen van de buigraaklijnen t en t ′ :

9 Bereik

Uit 8 volgt dat ber f = ] 0, 1]

10 Grafiek

Tip : Als je de grafiek met ICT maakt, is het aangewezen dat je regelmatig al je resultaten toetst aan de grafiek.

De grafiek van f noemen we de klokkromme van Gauss (1777–1855). Ze komt voor bij een zogenaamde ‘normale verdeling’ van grootheden in de statistiek.

Taak : In welk punt van de grafiek is de helling maximaal ? In welk punt is de helling minimaal ?

9 Verloop van een logaritmische functie

Beschouw de logaritmische functie f met f ( x ) = ln( 9 – x 2).

1 Domein

BV : 9 – x 2 > 0 ⟺ x ∈ ] –3, 3 [

dom f = ] –3, 3 [ x –∞ –3 3 +∞

9 – x 2 – 0 + 0 –

2 Snijpunten met de assen en tekenverloop van f ( x )

snijpunten met de x -as snijpunten met de y -as

f ( x )= 0 ⇐⇒ ln 9 x 2 = 0 9 x 2 = 1 x 2 = 8 x = ±2 2 x = 0 f ( x )= ln9 = 2ln3

Het snijpunt met de y -as is ( 0, 2ln 3)

INKIJKEXEMPLAARDIEKEURE

De snijpunten zijn (2√2,0) en ( 2√2,0) .

tekenverloop van f ( x )

–3

3 f ( x ) | –grafiek onder de x -as 0 + grafiek boven de x -as 0 –grafiek onder de x -as |

3 Symmetrie

f ( –x ) = ln ( 9 –( –x )2) = ln ( 9 – x 2 ) = f ( x )

De grafiek van f ligt dus symmetrisch t.o.v. de y -as.

4 Asymptoten

V.A.:lim x → < 3 ln (9 x 2 )= −∞ lim x → > 3 ln (9 x 2 )= −∞ (zieblz.43)

Degrafiekheeftdus2verticaleasymptotenmetvergelijking x = 3en x = 3.

H.A. en S.A. : geen, want dom f = ] –3, 3 [

5 Eerste afgeleide

f ′ ( x )= D (ln9 x 2 )= 2 x 9 x 2 x –3 0 3

f ′( x ) | + 0 – |

f ( x ) | ↗ max ↘ |

6 Tweede afgeleide

f ′′ ( x )= D 2 x 9 x 2 = (9 x 2 )( 2) ( 2 x )( 2 x ) (9 x 2 )2 = 18 + 2 x 2 4 x 2 (9 x 2 )2 = 18 2 x 2 (9 x 2 )2 = 2 9 + x 2 (9 x 2 )2 x –3 0 3

f ″( x ) | – |

f ( x ) | ∩ |

7 Continuïteit

Uit punt 5 volgt dat f afleidbaar is voor elke x ∈ ] –3, 3 [.

Dus : f is continu in ] –3, 3 [

8 Samenvattende tabel x –3 0 3

f ′( x ) | + 0 – | f ″( x ) | – – – |

( x ) | –∞ ⤵ 2 ln 3 ‖ max ⤵ –∞|

9 Bereik

Uit 8 volgt dat ber f = ] –∞, 2 ln 3 ].

10 Grafiek

( x )= ln (9 x 2 )

10 Verloop van een logaritmische functie met GeoGebra

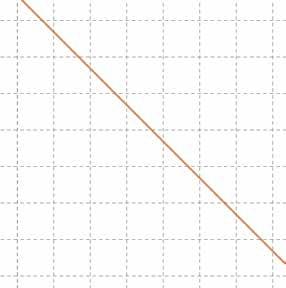
We onderzoeken het verloop van de functie f met f ( x ) = ln( 1 + x 2).

1 Domein

1 + x 2 > 0, dus dom f = R.

INKIJKEXEMPLAARDIEKEURE

2 Snijpunten met de assen en tekenverloop van f

3

Symmetrie

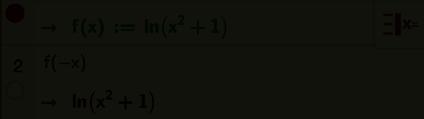
De grafiek ligt symmetrisch om de y -as.

4 Asymptoten

Er zijn geen asymptoten.

5 Eerste afgeleide

7 Bereik van f ber f = [ 0, +∞[

8 Grafiek van f

INKIJKEXEMPLAARDIEKEURE

11

Samenvatting

• Met behulp van het getal e (getal van Euler) en de eigenschappen van de natuurlijke logaritmen kun je alle exponentiële en logaritmische functies afleiden.

– e = lim x →±∞ 1 + 1 x x of e = lim z →0 (1 + z ) 1 z

e is een irrationaal en transcendent getal

e = 2,718281828…

– Logaritmen met grondtal e worden natuurlijke of neperiaanse logaritmen genoemd.

We noteren loge a als ln a

a ∈ R + 0 \{1}, ∀ x ∈ R + 0 : y = ln x ⟺ x = e y e ln x = x ln e y = y

– Afgeleiden van exponentiële functies : D ( e x ) =

( x ) D ( a x ) = a x ln a

[ a f ( x )] = a f ( x ) ln a D f ( x )

INKIJKEXEMPLAARDIEKEURE

D ( f r ) = r f r –1 D f met r ∈ R

Exponentiële functies f met f ( x ) = a x zijn continu in elk punt van R = dom f

– Afgeleiden van logaritmische functies :

D (ln x )= 1 x

D (loga x )= 1 x · ln a

ln f ( x ) = Df ( x ) f ( x )

loga f ( x ) =

( x ) f ( x ) · ln a

D (ln | x |)= 1 x D ln | f ( x ) | = Df ( x ) f ( x )

Logaritmische functies f met f ( x ) = loga x zijn continu in elk punt van R + 0 = dom f

D (ln | x + √ x 2 + k |)= 1 √ x 2 + k D ln | f ( x )+ [ f ( x )]2 + k | =

• Je kunt limieten van exponentiële en logaritmische functies bepalen met behulp van de standaardlimieten en (of) de regel van de l’Hôpital.

Regel van de l’Hôpital voor onbepaaldheden van het type 0 0 of ∞

• Je kunt het volledige verloop maken van een exponentiële en een logaritmische functie.

12 Oefeningen

Vereenvoudig.

a e 3ln2 c e 2ln 4 3 eln 1 4 e 3

bln 3 e dln( e ln e 2 ) f e ln a ln b

Verklaar.

a e ln 10 = 10 b ln e 10 = 10

Bereken volgende limieten.

x →0 (1 x ) 3 2 x

Bereken D f ( x ) als f ( x ) gegeven wordt door :

a e 4 x iln2 x

b4e 4 x 2 jlog2 x

c10 x klog (1 x 2 )

d10√ x llog3 x

e4 x 2 1 mlog5 1 x x

f e sin2 x n x 3 ln x gln | 2 x 5 | oln x x 1 hln x 2

Bereken de tweede afgeleide van y = e –3x sin 4x

Bereken y ″ + y ′ – 2y als y = 3e x – 4e –2x + x 2 – 2x + 5.

f x 2 ln x 2 lln 2 x + √4 x 2 + 1 6 * 7 8 9 10 11

Bepaal de vergelijking van de raaklijn en de normaal aan de grafiek van de functie f in het punt P als :

a f ( x ) = e 4x en P( 0, …)

b f ( x ) = ln 2x en P 1 2 ,...

c f ( x ) = 4x en P( …, 2)

d f ( x ) = ln ( 2x – 5) en P( …, 0)

INKIJKEXEMPLAARDIEKEURE

Beschouw de functie f met f ( x ) = log x

a Bepaal in 2 decimalen nauwkeurig het eerste coördinaatgetal van het punt van de grafiek van f waarin de helling gelijk is aan 0,1.

b Bepaal in 2 decimalen nauwkeurig het eerste coördinaatgetal van het punt van de grafiek van f waarin de helling gelijk is aan 1.

c Toon aan dat f ′ ( x )= log e x

Beschouw de functie f met f ( x )= x ln e + 1 x .

a Bepaal het domein van f .

b Bereken f ″( x ) en maak een tekenverloop. Leid hieruit af waar de grafiek van f hol of bol is. Controleer je antwoord met ICT.

a Zoek de vergelijking van de raaklijn en de normaal aan de grafiek van f met f ( x ) = x ln x in het snijpunt met de x -as.

b Teken de grafiek van f en de gevraagde raaklijn en normaal met behulp van ICT.

Bereken Df ( x ) als f ( x ) gegeven wordt door :

a e x (1 2 x ) g x log4 x

b e x · ln x h (lnsin x )4

c x 4 · e x i ln x 2 ln x

d10 x sin x jlog4 x log3 x

e (2 x 3) ln ( x 2 2) kln tan x 2

Bereken de volgende limieten door gebruik te maken van de standaardlimieten (zie blz. 43) en (of) de regel van de l’Hôpital. Controleer je uitkomsten met ICT.

Onderzoek telkens het verloop van de functie f als :

d f ( x )= x 2 · e x 2 i f ( x )= ln ( x 2 + 1)

e f ( x )= e 1 x x j f ( x )= ln (4 x 2 )

Voor een insectenpopulatie is de omvang N ( t )

gegeven door N ( t ) = 500 e 0,2t

met t : tijd in dagen vanaf een bepaald moment.

a Hoeveel insecten waren er op het tijdstip t = 10 ?

b Bereken hoeveel insecten er bijkomen tussen t = 10 en t = 11.

c Geef de formule voor de groeisnelheid van de insectenpopulatie.

d Wat is de groeisnelheid op het tijdstip t = 10 ?

Wat is de betekenis van dat getal ? Vergelijk met opgave b.

Een parachutespringer opent zijn valscherm op het moment ( t = 0) dat hij 700 m boven de grond is.

De valweg wordt gegeven door :

s ( t ) = 30 + 6t – 30 ( 0,223)t

met s ( t ): valweg in m na t seconden

a Geef de formule voor de snelheid van de parachutist.

b Welke snelheid (in m/s) had de parachutist op het moment dat zijn parachute openging ?

Hoeveel km/h is dit ?

c Geef de formule voor de vertraging van de parachutist.

d Wat is de vertraging (in m/s2) na 1 seconde ? En na 3 seconden ?

e Beredeneer dat de snelheid van de parachutist afneemt tot ongeveer 6 m/s.

Soms raakt drinkwater door menselijke of dierlijke afvalstoffen besmet met colibacteriën. Omdat het drinken van besmet water uiterst gevaarlijk is, zal het drinkwaterbedrijf in zo’n geval het water extra zuiveren. Als er bij het begin van de extra zuivering per liter water 1800 colibacteriën zijn, geldt de formule : N ( t ) = 1800 e –0,15t

met N ( t ): het aantal colibacteriën per liter water na t uren.

a Bereken de groeisnelheid van het aantal bacteriën op het moment dat t = 2.

b Zodra het aantal colibacteriën met 99 % is afgenomen, stopt de extra zuivering. Bereken in uren nauwkeurig hoelang de extra zuivering zal duren.

(Examen VWO A, Nederland)

De buitentemperatuur van afgelopen nacht kan benaderd worden door de functie T met

T ( t )= e 3 2 ( t 2) e 1 2 ( t 2)

met T ( t ): buitentemperatuur in graden Celsius

t : tijd in uren

t = 0 komt overeen met 11 uur ’s avonds (= 23 u.) vorige nacht.

a Schets de grafiek van de functie.

b Wanneer begon het te vriezen ?

c Wanneer begon de temperatuur weer te stijgen ?

d Wanneer steeg de temperatuur het snelst ?

e Hoe koud was het om 7 uur ’s ochtends ?

De grootte van een populatie dinosaurussen wordt gegeven door :

P ( t ) = 8000 t 3–t

met t : tijd uitgedrukt in duizenden jaren

a Teken de grafiek van P ( t ) met ICT.

b Hoe groot is de maximale populatie dinosaurussen ?

c Na verloop van tijd begint de populatie uit te sterven.

Op welk tijdstip gebeurt dat het snelst ?

De concentratie van alcohol in het bloed van een persoon op een feestje kan beschreven worden door C ( t ) = e –t – e –3t

met t : tijd in uren

C ( t ): concentratie alcohol in het bloed, uitgedrukt in promille

INKIJKEXEMPLAARDIEKEURE

Onderzoek het verloop van C ( t ) en toon aan dat de alcoholconcentratie in het bloed het snelst afneemt op het tijdstip 2t 0 met t 0 het tijdstip waarop de concentratie het grootst is.

Bij een ongeval kantelde een tankwagen. De tank scheurde en de inhoud van de tank stroomde weg volgens de formule

V = 25000 · 2 0,01t 2

met V : de resterende hoeveelheid in het vat in liter

t : de tijd in minuten

a Schets de grafiek van V

b Hoeveel liter vloeistof zat er in de tank ?

c Na hoeveel minuten was de helft van de inhoud

weggestroomd ?

d Wanneer was de uitstroomsnelheid maximaal ?

e Hoeveel tijd nadien was de uitstroomsnelheid afgenomen tot de helft van de maximale uitstroomsnelheid ?

Het verval van de radioactieve isotoop radium-228 verloopt volgens de vergelijking

m ′( t ) = –0,00043 · m ( t )

met t : tijd in jaren

m ( t ): massa in gram voor t = 0 bedraagt de massa 260 gram

a Bereken m ( t )

b Bereken de halveringstijd.

c Op welk tijdstip is nog 10 % van de beginmassa aanwezig ?

d Bereken de vervalsnelheid in gram/jaar na 10 jaar.

De relatieve toename van een kapitaal dat uitgezet wordt tegen een samengestelde intrest verloopt volgens de vergelijking

K ′( t ) = 0,0693 K ( t ) met t : de tijd in jaren

K ( t ): het kapitaal in euro

Stel dat voor t = 0 het kapitaal 5000 euro bedraagt.

a Bereken K ( t ).

b Hoelang duurt het voordat het kapitaal verdubbeld is ?

Onder bepaalde omstandigheden verloopt de afname van de luchtdruk volgens de vergelijking dp dh = λ · h

met p : luchtdruk in hectopascal h : hoogte in km boven de zeespiegel

De luchtdruk op zeeniveau is 1000 hectopascal en op 1 km boven de zeespiegel 869 hectopascal.

a Schrijf p in functie van h .

b In een luchtballon kun je echter eenvoudiger de luchtdruk meten dan de hoogte. Zoek de formule die h uitdrukt in functie van p .

c Toon aan dat de snelheid waarmee de hoogte (afhankelijk van p ) verandert, negatief is.

Zoals gebruikelijk stelt e het grondtal van de natuurlijke logaritme voor.

Gegeven is de functie f met functievoorschrift f ( x )= ln ( e x + 2). Bepaal het snijpunt van de raaklijn aan de grafiek van f in het punt met x-coördinaat ln( 2) en de rechte met vergelijking y = ln( 2). (A) ( –ln( 2), ln( 2)) (B) ( ln( 2), ln( 2)) (C) ( ln( 2), –ln( 2)) (D) ( 2ln( 2), ln( 2))

Toelatingsexamen arts 2020, vraag 8

Gegeven zijn de functies f en g met voorschrift: f ( x )= x 2 ln x en g ( x )= 2 x 2 5 x + 1.

De raaklijn in het punt P( a, g( a)) aan de grafiek van g staat loodrecht op de raaklijn in het punt Q( 1, f ( 1)) aan de grafiek van f. Bepaal g( a)

(A) –2 (B) –1 (C) 1 (D) 8

Toelatingsexamen arts 2020, vraag 9

Beschouw de functie f met functievoorschrift f ( x )= x 3ln( x 1) met x > 1.

In welk van de onderstaande intervallen is de functie f monotoon stijgend?

(A) 3 2 , 5 2

Toelatingsexamen arts 2022, vraag 7

(B) 5 2 , 7 2

Beschouw de functie f met voorschrift f ( x )= ln x 2 + x . Voor welke waarde(n) van x is de raaklijn aan de grafiek van f in het punt ( x , f ( x )) horizontaal ?

(C) 7 2 , 9 2

(A) –2 (B) 1 2 (C) –1 en 1 (D) er bestaat zo geen x

IJkingstoets basiskennis wiskunde handelsingenieur 2020, vraag 23

(D) 9 2 , 11 2 (A) 3 2 , 5 2 (B) 5 2 , 7 2 (C) 7 2 , 9 2 (D) 9 2 ,

De raaklijn aan de grafiek van de functie f met voorschrift f ( x )= e px in het punt x = 1 gaat door de oorsprong … (A) voor alle p > 0 (B) alleen voor p = 1 (C) alleen voor p = –1 (D) voor alle p < 0

IJkingstoets basiskennis wiskunde handelsingenieur 2021, vraag 26

1.3 Verloop van goniometrische functies

INKIJKEXEMPLAARDIEKEURE

Geen muziek zonder wiskunde, of die nu uit je gitaar komt of uit een speaker. Een liedje bestaat op zich enkel uit trillingen en frequenties en een geluid is een voorbeeld van een ‘harmonische trilling’ die weergegeven kan worden door een sinusfunctie. Hoe korter de gebruikte snaar (of hoe korter jij hem maakt met je vingers), hoe hoger het aantal keren dat de snaar trilt en hoe hoger ook de toon die je hoort.

1 Elementaire goniometrische functies

Sinusfunctie

Grafiek :

Eigenschappen :

domein verzameling van x -waarden die een beeld hebben

bereik verzameling van de functiewaarden [ –1, 1] periode kleinste strikt positief reële getal p zodat sin(x ) = sin ( x + p ) met x ∈ R

amplitude grootste uitwijking van de grafiek t.o.v. de evenwichtsstand 1 nulwaarden de eerste coördinaatgetallen van de snijpunten met de x -as k · p met k ∈ Z soort functie ∀x ∈ R : sin (–x ) = –sin x oneven functie symmetrie er is een symmetriemiddelpunt O tekenverloop we bekijken het tekenverloop in [ 0, 2p] x 0 p 2p

waardeverloop we bekijken het waardeverloop in [ 0, 2p]

Cosinusfunctie

Grafiek :

Eigenschappen : cosinusfunctie

domein verzameling van x -waarden die een beeld hebben R bereik verzameling van de functiewaarden [ –1, 1] periode kleinste strikt positief reële getal p zodat cos(x ) = cos ( x + p ) met x ∈ R 2p amplitude grootste uitwijking van de grafiek t.o.v. de evenwichtsstand 1 nulwaarden de eerste coördinaatgetallen van de snijpunten met de x -as

soort functie ∀x ∈ R : cos (–x ) = cos x even functie symmetrie er is een symmetrieas y -as tekenverloop we bekijken het tekenverloop in [

INKIJKEXEMPLAARDIEKEURE

waardeverloop we bekijken het waardeverloop

Tangensfunctie

Grafiek :

Eigenschappen :

domein

bereik R

periode p

nulwaarden k · p met k ∈ Z

soort functie oneven functie

∀x ∈ R : tan( –x ) = –tan x symmetrie O is een symmetriemiddelpunt

tekenverloop

INKIJKEXEMPLAARDIEKEURE

waardeverloop

asymptoten de rechten met vergelijking

zijn de verticale asymptoten van de grafiek

Cotangensfunctie

Grafiek : x y

INKIJKEXEMPLAARDIEKEURE

Eigenschappen : cotangensfunctie

domein R \{k · π | k ∈ Z}

bereik R periode p nulwaarden π 2 + k p met k ∈ Z soort functie oneven functie

∀x ∈ R : cot( –x ) = –cot x symmetrie O is een symmetriemiddelpunt tekenverloop x 0

cot x | + 0 – | waardeverloop x 0

asymptoten de rechten met vergelijking x = k p met k ∈ Z zijn de verticale asymptoten van de grafiek

Afgeleiden : D (sin x )= cos xD [sin f ( x )]= cos f ( x ) D [ f ( x )] D (cos x )= sin xD [cos f ( x )]= sin f ( x ) D [ f ( x )]

D (tan x )= 1 cos2 x

D (cot x )= 1 sin2 x

[tan f ( x )]=

[cot f ( x )]=

2 Verloop van een goniometrische functie

We onderzoeken het verloop van een goniometrische functie, bv. de functie f met f ( x ) = sin 2x + 2sin x .

1 Domein

dom f = R

De periode van f 1 met f 1 ( x )= sin2 x is 2π 2 = π

De periode van f 2 met f 2( x ) = sin x is 2p

De periode van f 1 + f 2 is dus 2p.

Het is dus voldoende de functie f te bestuderen in het interval [ 0, 2p].

2 Snijpunten met de assen en tekenverloop van f ( x )

snijpunten met de x -as :

f ( x )= 0 ⇐⇒ sin2 x + 2sin x = 0

∗ ⇐⇒ 2sin x cos x + 2sin x = 0

(*) sin2x = 2sinx cosx

INKIJKEXEMPLAARDIEKEURE

snijpunten met de y -as : x = 0 ⟹ f ( x ) = 0

Het snijpunt is dus ( 0, 0).

⇐⇒ sin x (cos x + 1)= 0

⇐⇒ sin x = 0ofcos x = 1

⇐⇒ x = k · π of x = π + k · 2π met k ∈ Z

snijpunten met de x -as in [ 0, 2p]: ( 0, 0), ( p, 0) en ( 2p, 0)

tekenverloop van f ( x ): x 0 p 2p sin x 0 + 0 – 0 cos x + 1 2 +

)

3 Symmetrie

f (–x ) = sin( –2x ) + 2sin( –x ) = –sin2x –2sinx = –f (x )

De functie is dus oneven.

De grafiek van de functie is symmetrisch om de oorsprong.

4 Asymptoten

Wegens de periodiciteit zijn er geen horizontale of schuine asymptoten. Omdat dom f = R zijn er ook geen verticale asymptoten.

5 Eerste afgeleide

f ′ ( x )= D (sin2 x + 2sin x )= 2cos2 x + 2cos x ∗ = 2(2cos2 x 1)+ 2cos x = 4cos2 x + 2cos x 2

(*) 1 + cos2x = 2cos2x

f ′ ( x )= 0 ⇐⇒ 4cos2 x + 2cos x 2 = 0

⇐⇒ cos x = 1ofcos x = 1 2

⇐⇒ x = π + k 2π of x = ± π 3 + k 2π k ∈ Z

In [0,2π] wordtdit: x = π 3 of x = π of x = 5π 3

f ′( x ) + 0 –

( x ) ↗ max ↘ ↘ min ↗

6 Tweede afgeleide

f ′′ ( x )= D (2cos2 x + 2cos x )

= 4sin2 x 2sin x = 8sin x cos x 2sin x = 2sin x (4cos x + 1)

f ′′ ( x )= 0 ⇐⇒ sin x · (4cos x + 1)= 0

⇐⇒ sin x = 0ofcos x = 1 4

⇐⇒ x = k · π of x = ±1,82 + k · 2π k ∈ Z

In [0,2π] wordtdit: x = 0of x = 1,82of x = π of x = 4,46of x = 2π

f ( x ) ∩ buigpunt ∪ buigpunt ∩ buigpunt ∪

7 Continuïteit

Omdat f afleidbaar is in R (zie 5) is f continu in R.

8 Samenvattende tabel

′( x ) + 0 –

9

t : buigraaklijn in (1,82 ; 1,46) : rico( t ) = f ′( 1,82) = –2,25

t ′ : buigraaklijn in (p, 0) : rico( t ′) = f ′( p) = 0 ⟹ t ′ valt samen met de x-as

t ″ : buigraaklijn in (4,46 ; –1,46) : rico( t ″) = f ′( 4,46) = –2,25

Bereik

Uit8blijktdatber f = 3√3 2 , 3√3 2

INKIJKEXEMPLAARDIEKEURE

3 Toepassing : harmonische en gedempte trilling

Periodieke verschijnselen – en meer bepaald trillingen – kunnen beschreven worden door algemene sinusfuncties met een voorschrift van de vorm

f ( x ) = a sin [ b ( x – c )] + d met a en b positief.

Hierbij stelt x de tijd voor en f ( x ) de uitwijking.

In VBTL 5 Analyse 1b leerden we het volgende : algemene sinusfunctie

In f ( x )= a sin [ b

is:

a de amplitude

2π b de periode met b de pulsatie

c de horizontaleverschuiving

d de verticaleverschuiving

Derechtemetvergelijking y = d geeftde evenwichtsstand weer.

HetpuntS( c , d ) noemenwehetbeginpuntvaneensinusperiode.

In het dagelijkse leven zijn er nog andere verschijnselen die door algemene sinusfuncties beschreven worden. Denk maar aan de trilling van een stemvork of een gong, de uitwijking van een slinger of een trillende snaar, de duur van de dag en nacht, de waterhoogte bij eb en vloed, het veranderen van de bloeddruk, het ritme van de hartslag, wisselstromen …

periode = 2

• De volgende grafiek is een vereenvoudigd model van de wijze waarop de bloeddruk van een mens verandert onder invloed van de hartslag. Op de x -as is de tijd uitgezet (in seconden), op de y -as staat de kwikdruk (in millimeter).

INKIJKEXEMPLAARDIEKEURE

De functiewaarden ‘schommelen’ rond de evenwichtsstand. De grootste uitwijking van de grafiek t.o.v. de evenwichtsstand is de amplitude. In de grafiek van de bloeddruk is de evenwichtsstand 110, de amplitude 20 en de periode 1.

• Trillingen zie je bij een trillende snaar, bijvoorbeeld in een piano. De hoogte van de toon hangt af van de lengte van de snaar. Hoe korter de snaar, hoe groter het aantal keer dat de snaar per seconde trilt en hoe hoger de toon.

Het aantal trillingen per seconde heet de frequentie van de toon.

Die frequentie wordt uitgedrukt in hertz (Hz).

Voor de periode p en de frequentie f geldt : f = 1 p

Een trilling ontstaat doordat de snaar heen en weer beweegt rond een bepaalde evenwichtsstand.

De uitwijking f ( x ) (in cm) van het midden van de snaar hangt af van de tijd x (in s ) die verstreken is sinds het aanslaan van de snaar. De grafiek van f ( x ) is bij benadering een sinusoïde.

Dergelijke trilling noemen we een harmonische trilling. De Fransman Jean Baptiste Fourier ontdekte dat elke trilling kan worden opgebouwd als een som van harmonische trillingen. De Fourieranalyse is daarop gebaseerd.

In realiteit werken er op een trillend systeem wrijvings- of weerstandskrachten en wordt bijvoorbeeld in een trillende veer warmte geproduceerd. Hierdoor neemt de energie van het systeem af. Het systeem voert dan een gedempte trilling uit.

Harmonische trillingen doven dus na verloop van tijd uit. Denk maar aan de trillende snaar. Na enige tijd wordt de uitwijking van de snaar kleiner, tot de toon niet langer hoorbaar is. De amplitude neemt daarbij exponentieel af omdat de uitdoving steeds langzamer gaat.

Voorbeeld 1

INKIJKEXEMPLAARDIEKEURE

factor 3

en3

komt overeen met de amplitude. Die is niet constant, maar daalt exponentieel met de tijd. Hoe sneller de amplitude afneemt, hoe sterker de demping is. De functiewaarden schommelen tussen 3 e 2 x π en3 e 2 x π

Voorbeeld 2 :

f ( x )= e x 2 cos (6 x 2) met x ⩾ 0

Type xy

Zero 0,0715

Max 0,3195 0,84942 Zero 0,5951

Min 0,8431 –0,65377

Zero 1,1187

Max 1,3667 0,50319

Zero 1,6423

Min 1,8903 –0,38728

Zero 2,1659

Max 2,4139 0,29808

Zero 2,6895

Min 2,9375 –0,22942

Zero 3,2131

Max 3,4611 0,17658

Zero 3,7367

Min 3,9847 –0,13591

Zero 4,2603

Max 4,5083 0,1046

Zero 4,7839

Min 5,0319 –0,08051

Zero 5,3075

Max 5,5555 0,06196

Zero 5,8311

Jean Baptiste Joseph Fourier (1768 – 1830)

Joseph Fourier, geboren in Auxerre (Frankrijk), had drie grote passies : zijn geloof, de politiek en natuurlijk de wiskunde. In 1787 besloot hij in te treden in een klooster om zich voor te bereiden op het priesterschap. Zijn interesse voor wiskunde deed hem echter twijfelen en uiteindelijk verliet hij het klooster. In 1793 werd hij politiek actief. Hij trad toe tot een revolutionair comité en belandde in de gevangenis. Door toedoen van o.a. Lagrange, Laplace en Monge werd hij vrijgelaten. Ten tijde van Napoleon volgde hij die naar Egypte, waar hij een belangrijke functie kreeg. Bij zijn terugkeer werd hij benoemd tot prefect in Grenoble. Fourier wordt beschouwd als de grondlegger van de mathematische fysica. Zijn belangrijkste werk was ‘Théorie analytique de la chaleur’ (1822), de theorie van de warmetegeleiding bepaald door de partiële differentiaalvergelijking ΔU = kθu θt De methoden die Fourier hierbij gebruikte, waren zo algemeen dat zijn werk het prototype is geworden voor de behandeling van de gehele theorie voor het oplossen van partiële differentiaalvergelijkingen.

4 Verloop van een goniometrische functie met GeoGebra

We onderzoeken het verloop van de functie f met f ( x ) = sin 2x + tan x .

1 Domein

dom f = R \ π 2 + k π k ∈ Z

Deperiodevan f 1 met f 1 ( x )= sin2 x is 2π 2 = π.

INKIJKEXEMPLAARDIEKEURE

Deperiodevan f 2 met f 2 ( x )= tan x is π.

Hetisdusvoldoendedefunctie f tebestuderenin [0, π]

2 Snijpunten met de assen

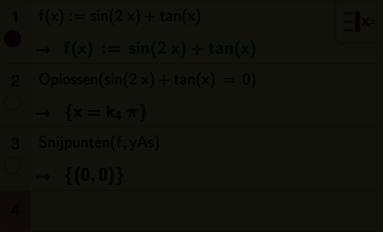
3 Symmetrie

De functie is dus oneven en de grafiek is symmetrisch om de oorsprong.

4 Asymptoten

x = π 2 + k π k ∈ Z zijnV.A.

5 Eerste en tweede afgeleide

Er zijn geen extrema want de eerste afgeleide wordt nooit nul.

Er is een buigpunt voor x = π 4 want de tweede afgeleide wordt voor x = π 4 nul.

Weziendatereenbuigpuntisvoor x =

Webepalenhetbuigpuntendevergelijkingvandebuigraaklijn:

INKIJKEXEMPLAARDIEKEURE

6 Bereik

ber f = R

7 Grafiek

5 Samenvatting

• Je kunt het verloop van een goniometrische functie bepalen door achtereenvolgens de volgende zaken te onderzoeken :

– domein ;

– snijpunten met de assen en tekenverloop van f ( x);

– symmetrie ;

– asymptoten ;

– eerste afgeleide (stijgen en dalen van de functie en bepalen van eventuele extrema) ;

– tweede afgeleide (holle en bolle zijde van de grafiek en de eventuele buigpunten) ;

– continuïteit ;

– samenvattende tabel ;

– bereik;

– grafiek.

• Je weet wat een harmonische trilling is. Voor de periode p en de frequentie f geldt : f = 1 p

• Je kent enkele voorbeelden van een gedempte trilling.

6

Oefeningen

c D 2 1 9 cos3 x + 3 2 sin2 x 38 3 cos x + 11 2 x 2 =(... + ...)3 1 2 3 *

Onderzoek het verloop van volgende goniometrische functies f met :

a f ( x )= cot x e f ( x )= sin x + cos2 x 1

b f ( x )= sin x + 2cos x f f ( x )= tan x sin x cos x

c f ( x )= sin2 x + 2cos x g f ( x )= tan x + cot x

d f ( x )= 4cos2 x 8cos x + 3h f ( x )= cos x cos3 x

Onderzoek het verloop van de volgende functies f m.b.v. ICT als :

a f ( x )= x sin x d f ( x )= 4 e x sin(10π x ) met x ⩾ 0

b f ( x )= x sin x

c f ( x )= e x · cos x

Bereken (en vereenvoudig) volgende afgeleiden :

a D 2sin x · cos3 x + 3sin x · cos x + 3 x = a · ( )4

b D sin x 3 sin2 x = a (...)3

Een slinger wordt op t = 0 in zijn uiterste stand losgelaten.

De uitwijking f ( t ) van de slinger na t seconden t.o.v. de evenwichtsstand wordt gegeven door

f ( t )= 2,5 · sin π 2 t π 4 met f ( t ) incmen t inseconden.

met f ( t ): uitwijking in cm t : tijd in seconden

a Bereken de amplitude, de periode en de frequentie van de slinger.

b Bereken de snelheid f ′( t ) en de versnelling f ″( t )

c Wanneer en waar zijn de absolute waarde van de snelheid en van de versnelling maximaal ?

Harmonische trillingen met een faseverschil. Er is sprake van faseverschil bij twee trillingen als de trillingen niet op hetzelfde moment begonnen zijn.

Voorbeeld : gegeven zijn de trillingen f 1 en f 2 met f 1( t ) = 2sint en f 2( t ) = 2sin( t – 2)

a Toon aan dat beide trillingen dezelfde amplitude en periode hebben.

Hoeveel seconden na de eerste trilling begon de tweede trilling ?

Hoe ontstaat de grafiek van f 2 uit de grafiek van f 1 ?

b Toon grafisch en algebraïsch aan dat f 3( t ) = f 1( t ) + f 2( t ) = 2 sin t + 2 sin( t – 2) opnieuw een harmonische trilling f 3 voorstelt.

Bepaal ook de amplitude, de periode, de horizontale en de verticale verschuiving van f 3.

Harmonische trillingen met verschillende amplitudes en/of evenwichtsstand.

Voorbeeld : beschouw de trillingen f 1 en f 2 met f 1( t ) f 2( t )

2 sin 2t 1 + sin 2t

cos t 1 + 2 sin t

a Toon in beide gevallen aan dat f 3 = f 1 + f 2 opnieuw een harmonische trilling oplevert.

Doe dit zowel grafisch als algebraïsch.

b Bereken telkens de amplitude, de periode, de horizontale en de verticale verschuiving van f 3.

Bij harmonische trillingen waarvan de frequenties (en dus de periodes) verschillend zijn, krijg je in het algemeen geen harmonische trilling als je ze optelt.

Voorbeeld :

Beschouw de trillingen f 1 en f 2 met f 1( t ) = sin t 2 en f 2( t ) = sin t

Na optelling bekomen we f 3 = f 1 + f 2 met f 3( t ) = sin t 2 + sin t

In de volgende figuur wordt dit grafisch weergegeven. x

Door gebruik te maken van goniometrische formules vind je : f 3 ( t )= sin t 2 + sin t = 2sin 3 t 4 cos t 4 .Gaditzelfna.

Het voorschrift van f 3 is niet van de vorm a sin( bt ) met a , b ∈ R + 0 . Hieruit volgt dat f 3 geen harmonische trilling is.

Toepassing : kerkorgel

De la-pijp van een kerkorgel veroorzaakt bij het aanblazen een harmonische trilling f 1 met f 1( t ) = sin( 56pt ) . Hierbij stelt t de tijd voor in seconden.

In een ander register van datzelfde kerkorgel zit een tweede orgelpijp die dezelfde noot aanblaast. Die pijp is echter onzuiver gestemd en veroorzaakt een harmonische trilling f 2 met f 2( t ) = sin( 54pt ) Jammer genoeg klinkt die toon iets te laag.

a Teken de grafiek van f 1 en f 2. Bereken de frequentie van beide orgelpijpen in hertz.

b Wanneer de beide la-pijpen van het kerkorgel samen aangeblazen worden, brengt dat een trilling f 3 voort met f 3( t ) = sin( 56pt ) + sin( 54pt ). Teken de grafiek van f 3 en toon aan dat f 3 niet meer harmonisch is. Muziekliefhebbers noemen zo’n klank ‘dissonant’.

c Ontbind f 3( t ) in factoren met behulp van de formules van Simpson en stel vast dat de amplitude van die trilling niet steeds even groot is. De amplitude gaat periodiek aanzwellen en afnemen. We noemen dat ook een zweving. Welke factor stelt de wisselende amplitude voor ?

d Teken de grafiek van de amplitudefunctie. Bij amplitude 0 is het geluid niet hoorbaar. Bij een maximale amplitude 2 is het geluid het best hoorbaar. Hoeveel ‘zwevingen’ hoor je per seconde ?

e Bepaal de frequentie van de dissonante toon f 3. Hoe kan die frequentie afgeleid worden uit de frequenties van de afzonderlijke pijpen ?

INKIJKEXEMPLAARDIEKEURE

1.4 Differentiaal van een functie

INKIJKEXEMPLAARDIEKEURE

1 Definitie

Als de functie f afleidbaar is in een punt a van haar domein, dan wordt de grafiek van die functie in een omgeving van P( a , f ( a )) benaderd door de raaklijn in dat punt P.

y = f ′( a ) · ( x – a ) + f ( a )

We mogen in een omgeving van a de functie f benaderen door de lineaire functie g met

g ( x ) = f ′( a ) · ( x – a ) + f ( a )

M.a.w. f ( x ) wordt benaderd door f ′( a ) · ( x – a ) + f ( a )

⟹ f ( x ) – f ( a ) wordt benaderd door f ′( a ) · ( x – a )

Het verschil x – a is een aangroeiing van het argument en noteren we als Δx Het verschil f ( x ) – f ( a ) is een aangroeiing van het beeld en noteren we als Δf ( x ) of Δy

⟹ Δf ( x ) = Δy wordt benaderd door f ′( a ) · Δx

differentiaal

Als f afleidbaar is in a en als Δx een aangroeiing is van het argument waarvoor a + Δx ∈ dom f , dan noemen we df ( a ) de differentiaal van f in a , met df ( a ): df ( a ) = f ′( a ) · Δx

Door a niet als een gegeven waarde, maar als een variabele te beschouwen, krijgen we de differentiaal van f in x . dy = df ( x ) = f ′( x ) · Δx

Gevolgen :

– Voor de functie f met f ( x ) = x geldt : f ′( x ) = 1, dus dx = 1 Δx = Δx

In bovenstaande definities mag je dus Δx door dx vervangen. Zo verkrijg je de gebruikelijke formules :

df ( a ) = f ′( a ) · dx dy = df ( x ) = f ′( x ) dx

Omdat Δx = dx ≠ 0 wordt df ( x ) dx = f ′ ( x ) (notatie van Leibniz voor afgeleiden) of nog :

Df ( x )= df ( x ) dx

2 Verband tussen dy en Dy

In het algemeen zijn dy en Δy verschillend, Δy wordt wel benaderd door dy .

Voor f ′ ( x ) = 0geldt:lim dx →0 ∆ y dy = 1

Want : lim

y dy = lim

INKIJKEXEMPLAARDIEKEURE

)= 1

Dus mogen we voor Δx → 0, Δy bij benadering vervangen door dy als f ′( x ) ≠ 0.

Meetkundige betekenis :

Op de grafiek k van de functie f nemen we de punten A( x , f ( x )) en B( x + Δx , f ( x + Δx ))

Een evenwijdige door A met de x -as snijdt een evenwijdige door B met de y -as in het punt C. Δy = Δf ( x ) is de toename van het tweede coördinaatgetal langs de kromme bij een toename dx = Δx van het eerste coördinaatgetal.

| Δy | = | BC |

De raaklijn t aan k in A snijdt de rechte BC in D. dy = df ( x ) is de toename van het tweede coördinaatgetal langs de raaklijn bij een toename dx = Δx van het eerste coördinaatgetal. | dy | = | CD |

Bewijs : Wewetendat:

rico( t )= y D y A x D x A = y D y C ∆ x (1)

rico( t )= f ′ ( x ) (2)

Uit(1)en(2)volgtdat: f ′ ( x )= y D y C ∆ x

of: y D y C = f ′ ( x ) ∆ x of: y D y C = df ( x ) y x

Dus : | CD| = df ( x ) = dy

y y = f (x ) dy

3 Differentialen van hogere orde

Uitgaand van de differentiaal df ( x ) van f in x hebben we een functie bepaald : df met df ( x ) = f ′ ( x ) dx

We noemen nu de tweede differentiaal van f in x de differentiaal van de functie df in x .

Notatie : d 2f ( x )

d 2 f ( x )= d [df ( x )]= d [ f ′ ( x ) dx ]

= f ′ ( x ) dx ′ dx = f ′′ ( x ) dx dx dx wordtconstantbeschouwd

= f ′′ ( x ) dx 2

Merk op dat we hier dx 2 schrijven voor ( dx )2.

Algemeen :

Als f n maal afleidbaar is in x , geldt : d n f ( x ) = f ( n )( x ) dx n waarbij dx n staat voor ( dx )n

4 Rekenregels

De differentiaal van een functie vinden we door de afgeleide in x te vermenigvuldigen met Δx of met dx (zie definitie). Het berekenen van differentialen verschilt niet wezenlijk van het berekenen van afgeleiden. Reken volgende formules na en onthoud ze.

INKIJKEXEMPLAARDIEKEURE

d ( c )= 0

d ( x n )= nx n 1 dx

d 1 x = dx x 2

d (√ x )= dx 2√ x

d (sin x )= cos xdx

d (cos x )= sin xdx

d (tan x )= dx cos2 x

d (cot x )= dx sin2 x

d (Bgsin x )= dx √1 x 2

d (Bgcos x )= dx √1 x 2

d (Bgtan x )= dx 1 + x 2

d (Bgcot x )= dx 1 + x 2

d (a x )= a x ln adx

d ( e x )= e x dx

d (ln x )= dx x

d (loga x )= dx x ln a

d (sinh x )= cosh xdx

d (cosh x )= sinh xdx

d ( f + g )= df + dg

d (a f )= a df (a ∈ R )

d ( f g )= g df + f dg

d 1 f = df f 2

d f g = g df f dg g 2

d ( f g )= f g ln f dg + g f g 1 df

5 Toepassingen

Differentialen zijn vooral nuttig bij het berekenen van benaderingen. df ( x ) is een benaderende waarde voor Df ( x ) als f ′( x ) ≠ 0 (zie blz. 73).

Voorbeeld 1 :

Een halfbolvormige koepel met diameter 8 meter wordt langs de buitenzijde belegd met bladgoud van 3 mm dik.

Bereken bij benadering welk volume goud hiervoor nodig is. De soortelijke massa r = 19,3 g/cm3

Oplossing :

INKIJKEXEMPLAARDIEKEURE

Het gevraagde volume is het verschil ΔV van de volumes van twee halve bollen met respectievelijke straal 4 m en 4,003 m. Omdat het verschil tussen beide stralen klein is, kunnen we ΔV benaderen door de differentiaal dV V ( r )= 1 2 4 3 π r 3 = 2 3 π r 3 =⇒ dV = V ′ ( r )∆ r = 2π r 2 ∆ r

Met r = 4 en Δr = 0,003 vinden we dV = 0,3016.

Hoeveel goud is er dan nodig ? 0,3016 m3 = 301 600 cm3

Uitgedrukt in gram : (301 600 19,3) g = 5 820 880 g = 5820,88 kg

Voorbeeld 2 :

Bereken bij benadering √401.

Oplossing :

√401 = √400 + 1

f ( x )= √ x =⇒ df ( x )= 1 2√ x ∆ x

Stelhierin x = 400en ∆ x = 1enjevindt df ( x )= 0,025.

zodat √401 ≈ 20,025.

Hoeveel procent zit je naast de feitelijke uitkomst ?

Voorbeeld 3 :

Bereken bij benadering tan 46°.

Oplossing :

tan46 ◦ = tan (45 ◦ + 1 ◦ )= tan π 4 + π 180

f ( x )= tan x =⇒ df ( x )= sec2 x ∆ x

Stelhierin x = π 4 en ∆ x = π 180 enjevindt df ( x )= π 90 zodattan46 ◦ ≈ 1,0349.

Hoeveel procent zit je naast de feitelijke uitkomst ?

Voorbeeld 4 :

Als de absolute fout op x gelijk is aan | Δx |, dan is de absolute fout | Δy | op een functie y van x bij benadering gelijk aan : | ∆ y |≈| f ′ ( x ) ∆ x | = | dy |

Bereken de absolute fout op de weerstand R als de spanning U 20 volt bedraagt en je voor de stroomsterkte I 4 ampère meet met een absolute fout van 0,2 ampère (dus I = 4 ± 0,2 ampère).

Oplossing :

De formule die het verband geeft tussen spanning, weerstand en stroomsterkte luidt : R = U I

Uit het gegeven volgt dus dat U I = R = 20 4 = 5.

De absolute fout op de weerstand bedraagt dan | ΔR |.

| dR | = | R ′ ( I ) ∆ I | = U I 2 ∆ I

Het invullen van de waarden U = 20, I = 4 en | ΔI | = 0,2 geeft | dR | = 0,25.

De absolute fout op de weerstand bedraagt dus (bij benadering) 0,25 ohm.

M.a.w. R = 5 ± 0,25 ohm.

INKIJKEXEMPLAARDIEKEURE

6 Samenvatting

• Je kent de betekenis en de definitie van het begrip differentiaal van f in a

Als f afleidbaar is in a en als Δx een aangroeiing is van het argument waarvoor a + Δx ∈ dom f , dan noemen we differentiaal van f in a : df ( a) = f ′( a ) Δx

Door a niet als een gegeven waarde, maar als een variabele te beschouwen, krijgen we de differentiaal van f (we schrijven x in plaats van a ) in x dy = df ( x ) = f ′( x ) · Δx of dy = d f( x ) = f ′( x ) · dx

• Je kent het verband tussen Δy en d y.

• Je kent de meetkundige betekenis van Δy en van d y op de grafiek van een functie.

• Je kent de betekenis van een differentiaal van hogere orde. d n f ( x ) = f ( n )( x )dx n

• Je kent de rekenregels voor het berekenen van differentialen.

• Je kunt bij het benaderingsrekenen differentialen toepassen.

7

Oefeningen

Bereken de differentiaal van f als f ( x ) gelijk is aan:

a x 2 5 x + 9

b x 2 x 2 + x

c ( x 2 1)2

d sin2 x

e e 4 x

f (2 x 4)(5 x )

g2tan2 x

hsin x · cos2 x

i x + ln ( x 2 1)

jsin2 2 x

Een cirkelvormig plaatje zet uit door een stijging van de temperatuur. Geef bij benadering de toename in oppervlakte als de straal wijzigt van 14,5 cm tot 14,6 cm.

Een staaf van 20 cm wordt vastgeklemd tussen twee punten en nadien opgewarmd. De diameter wijzigt van 16 mm tot 17 mm. Geef bij benadering de toename van het volume van de staaf.

Een vliegtuig vliegt rond de aarde langs de evenaar op 2 km hoogte. Hoeveel km legt het vliegtuig meer af dan een globetrotter die op de aarde rondtrekt langs de evenaar ?

Een halfbolvormige koepel met diameter 3 m wordt langs de binnenzijde beschilderd met een verflaag van 1 mm dik. Bereken bij benadering welk volume verf hiervoor nodig is.

Een klein frietzakje is kegelvormig, heeft een hoogte van 18 cm en de diameter van de opening bedraagt 14 cm.

Hoeveel meer bedraagt het volume van een groot frietzakje bij benadering als de hoogte 20 cm is en de diameter van de opening 14 cm is ?

Bereken bij benadering (op 0,001 nauwkeurig).

a √99 c 3 √1001 bsin31 ◦ dtan44 ◦

De snelheid van een voorwerp dat van op een hoogte h een vrije val maakt, wordt gegeven door de formule : v = 2gh g = valversnelling = 9,81 m/s2

Men meet voor de hoogte 80 meter met een absolute fout van 0,1 m (dus h = 80 ± 0,1 m).

Hoe groot bedraagt de absolute fout op de snelheid ?

De lengte van een boog wordt gegeven door de formule :

s = r α r = straal, α = hoek in radialen

Hoe groot is de fout op de lengte van een boog bij een cirkel met straal 60 cm als de absolute fout op de hoek 0,1 radiaal is ?

Ik ken de betekenis en eigenschappen van een verticale asymptoot, horizontale asymptoot en schuine asymptoot van de grafiek van een functie. 10

Ik kan de afgeleide interpreteren als limiet van een differentiequotiënt en als rico van de raaklijn aan de grafiek. 13

Ik kan het stijgen/dalen en de extrema van een algebraïsche functie bepalen aan de hand van het voorschrift van de eerste afgeleide functie. 15

Ik kan het hol/bol zijn en de buigpunten van de grafiek van een algebraïsche functie bepalen aan de hand van het voorschrift van de tweede afgeleide functie. 17

Ik ken de algemene werkwijze om het verloop van een functie te bestuderen. 19

Ik kan de grafiek van een algebraïsche functie schetsen met en zonder ICT. 21

Ik ken de regel van de l’Hôpital en kan die toepassen om limieten te berekenen.

Ik weet

Ik weet wat bedoeld wordt met een logaritmische functie en ken de hoofdeigenschap.

Ik kan een exponentiële functie gebruiken als model voor exponentiële groei.

Ik ken de formules voor de afgeleiden van een logaritmische functie.

Ik kan het stijgen/dalen en de extrema van een exponentiële functie bepalen aan de hand van het voorschrift van de eerste afgeleide functie.

Ik kan het hol/bol zijn en de buigpunten van de grafiek van een exponentiële functie bepalen aan de hand van het voorschrift van de tweede afgeleide functie.

Ik ken de algemene werkwijze om het verloop van een exponentiële functie te bestuderen.

Ik kan de grafiek van een exponentiële functie schetsen met en zonder ICT.

Ik kan het stijgen/dalen en de extrema van een logaritmische functie bepalen aan de hand van het voorschrift van de eerste afgeleide functie.

Ik kan het hol/bol zijn en de buigpunten van de grafiek van een logaritmische functie bepalen aan de hand van het voorschrift van de tweede afgeleide functie.

Ik ken de algemene werkwijze om het verloop van een logaritmische functie te bestuderen.

Ik kan de grafiek van een logaritmische functie schetsen met en zonder ICT.

Ik kan de grafiek van een elementaire goniometrische functie schetsen met en zonder ICT.

Ik kan het stijgen/dalen en de extrema van een goniometrische functie bepalen aan de hand van het voorschrift van de eerste afgeleide functie.

Ik kan het hol/bol zijn en de buigpunten van de grafiek van een goniometrische functie bepalen aan de hand van het voorschrift van de tweede afgeleide functie.

Ik ken de algemene werkwijze om het verloop van een goniometrische functie te bestuderen

Ik kan de kenmerken van de algemene sinusfunctie analyseren en kan de harmonische trilling en gedempte trilling als toepassing bespreken.

Ik ken de definitie van de differentiaal van een functie en ken de rekenregels.

39

42

45

45

45

45

47

47

47

47

58

1 Verloop van functies INKIJKEXEMPLAARDIEKEURE

62

62

62

64

72