Friettennis
INKIJKEXEMPLAARDIEKEURE
Kan je frietjes snijden met een tennisracket? De broertjes Coppens hebben dit al eens voor je uitgetest.
Bekijk het filmpje via de QR-code.
Waarom lukt het de broertjes Coppens beter met fijne ijzerdraadjes dan met gewone tennissnaren? Verklaar.
In het dagelijkse leven ben je vast en zeker al eens de grootheid ‘druk’ tegengekomen. Heel waarschijnlijk zonder er bij stil te staan dat je op dat moment bezig was met pure fysica. Van het snijden van groenten met een mes, een injectie met een injectienaald, de fundering van een huis tot zelfs sneeuwschoenen om gemakkelijk in de sneeuw te lopen. Bij elk van deze voorbeelden gebruiken we de principes van druk op vaste stoffen.
Is er ook druk in vloeistoffen en in gassen? Waarom hebben we last van onze oren als een vliegtuig opstijgt? Hoe kan een bloeddrukmeter onze bloeddruk meten?
1Druk op vaste stoffen
INKIJKEXEMPLAARDIEKEURE
In module 2 Krachten werden al een aantal krachten besproken zoals contact- en veldkrachten. We zagen ook dat krachten een statische en dynamische uitwerking hebben.
Je leerde al dat er contactkrachten en veldkrachten zijn waarbij contactkrachten rechtstreeks contact maken met het voorwerp en veldkrachten op een afstand werken. We bekeken ook het dynamisch effect. In deze module gaan we dieper in op het statisch effect van een kracht.
Een kracht kan het voorwerp tijdens het uitoefenen van de kracht zodanig vervormen dat het voorwerp blijvend vervormd is (plastische vervorming). Denk maar aan het scherm van je smartphone als je die laat vallen zonder bescherming.
In andere gevallen krijgt het voorwerp zijn oorspronkelijke vorm terug eens de kracht stopt met werken (elastische vervorming). Zoals de stressbal die je inknijpt voor je aan een examen begint of de elastiek waar je aan vasthangt bij het bungeespringen.
In sommige gevallen willen we een oppervlak net zoveel mogelijk vervormen. Uit de praktijk weten we dat die vervorming gemakkelijker gaat als we het contactoppervlak zo klein mogelijk maken.
Koksmes: het lemmet is aan één kant heel dun en heeft een zeer kleine oppervlakte. Zo dringt het mes gemakkelijk door de te snijden groente.
Sneeuwkettingen: sneeuwkettingen bestaan uit schakels met een kleine oppervlakte die veel grip hebben op de sneeuw of het ijs.
Scherpe klauwen: de klauwen van een roofvogel zijn heel scherp, zo kunnen ze gemakkelijk hun prooi vastgrijpen.
Injectienaald: een injectienaald heeft een heel dunne naald, die gemakkelijk in de huid dringt. Zo voelen we de minste pijn.
Doornen van een roos: de doornen hebben een heel scherpe punt, je bent dus niet geneigd om zomaar de bloemen te plukken. De plant beschermt op deze manier zichzelf.
INKIJKEXEMPLAARDIEKEURE
Scherpe tanden: roofdieren hebben scherpe tanden zodat ze gemakkelijk door de huid van hun prooi kunnen dringen.
Soms is het net de bedoeling dat een gegeven kracht een oppervlak zo weinig mogelijk vervormt. In dat geval moet het contactoppervlak zo groot mogelijk gemaakt worden
Poten van een olifant: de poten van de olifant hebben een grote oppervlakte, zo zakken ze niet weg in de aarde, ondanks hun grote massa.
Fakir: een fakir staat op spijkerplankjes. De fakir voelt geen pijn omdat hij ondersteund wordt door wel honderd spijkers, allemaal samen geven die een vrij groot oppervlak om de fakir te ondersteunen.
Fundering huis: bij de constructie van een huis wordt eerst een betonplaat gegoten, deze heeft een grote oppervlakte waardoor het huis niet verzakt.
Ski’s: als we skiën zakken we niet door de sneeuw omdat de ski’s een grotere oppervlakte hebben dan onze voeten.
Rupsbanden: hele zware voertuigen hebben rupsbanden, de contactoppervlakte met de grond wordt zo vergroot, waardoor het voertuig niet in de grond zakt en vast komt te zitten in de ondergrond.
Veiligheidshelm: het oppervlak van de helm zorgt voor de verdeling van de impact als er iets op valt. Daardoor is de impact veel kleiner dan wanneer je geen helm aanhebt.
Een kracht zorgt op een klein contactoppervlak voor veel vervorming, terwijl diezelfde kracht op een groot contactoppervlak voor weinig vervorming zorgt.
Blijkbaar is dus niet alleen de grootte van de kracht bepalend, maar ook de grootte van het oppervlak waarop de kracht werkt. Op basis van dit gegeven definiëren we de nieuwe grootheid druk.
De druk op een oppervlak is de verhouding van de grootte F van de kracht tot de grootte A van het oppervlak waarop die kracht werkt:
p = F A
INKIJKEXEMPLAARDIEKEURE
In deze figuur zie je de krachtvector loodrecht op het oppervlak. Op dat oppervlak werkt de krachtvector.
druk p pascal Pa
De eenheid van druk is 1Pa = 1 N m2 en noemen we pascal (Pa), genoemd naar Blaise Pascal.
1Pa = 1 N m2
De SI-eenheid van druk is de pascal (Pa) en is een kleine eenheid. Daarom gebruiken we dikwijls veelvouden van de pascal, zoals:
hPa = 102 Pa en 1 bar = 105 Pa
1 bar 100 000 Pa
1atm = 1 atmosfeer 101 325 Pa
1mmHg = 1mm kwikdruk 133,32 Pa
1cm H2O = 1cm waterdruk 98,0638 Pa
1MWK = 1 meter waterkolom 9807 Pa
1psf = 1 pound per square foot 47,880 Pa
1psi = 1 pound per square inch 6894,76 Pa
1torr 133,32 Pa
Via deze site kan je de eenheden gemakkelijk omrekenen. Scan hiervoor de QR-code.
Blaise Pascal (1623 – 1662)
Als we de formule naderbij bekijken, zien we dat er een recht evenredig verband bestaat tussen de grootte van de kracht en de druk
p = F A
Kracht en druk zijn recht evenredig.
Hoe groter de kracht is die we uitoefenen op eenzelfde oppervlakte, hoe groter de druk is.
Hoe harder we slaan op een nagel, hoe groter de druk wordt en hoe gemakkelijker de nagel door het hout gaat.
Daarnaast zien we aan de formule ook dat er een omgekeerd evenredig verband bestaat tussen de oppervlakte en de druk
p = F A
INKIJKEXEMPLAARDIEKEURE
Hoe groter de oppervlakte, hoe kleiner de druk bij eenzelfde kracht.
Hoe kleiner de oppervlakte, hoe groter de druk bij eenzelfde kracht.
Duid bij de foto’s aan of het gaat om: klein oppervlak, grote druk of groot oppervlak, kleine druk. Verklaar waarom.
2Druk in gassen
2.1De atmosferische druk
Even kijken waarom onze atmosfeer belangrijk is? Scan de QR-code.
Wie staat al eens stil bij de lucht die we inademen? Het lijkt vanzelfsprekend: adem in, adem uit … Maar we zien niet wat we inademen. De luchtlaag rondom de aarde is onzichtbaar. Ze bestaat voornamelijk uit stikstofgas (78 %) en zuurstofgas (21 %). Deze laag bepaalt ons klimaat en beschermt ons tegen de koude onherbergzame ruimte. Deze levensnoodzakelijke luchtlaag noemen we onze atmosfeer of dampkring.
Als de lucht van de atmosfeer zich verplaatst, dan ontstaat er wind. Die wind voelen we en gebruiken we in allerlei toepassingen.
De atmosfeer is een grote laag lucht rondom de aarde van kilometers dik. De zwaartekracht van de aarde zorgt ervoor dat die dikke laag lucht mooi rond de aarde blijft zitten. We leven op de bodem van een zee van lucht. Dat wil ook zeggen dat we constant de druk voelen die deze grote hoeveelheid lucht op ons uitoefent. We noemen die druk de atmosferische druk of luchtdruk.
Via de QR-code kan je nog een stukje zien over de atmosfeer.
De atmosferischedruk bedraagt 1013 hPa of 101300 Pa op zeeniveau.
INKIJKEXEMPLAARDIEKEURE
Om een idee te krijgen hoeveel dat is, moet je jezelf voorstellen dat je dezelfde druk krijgt als je tien Mini Coopers op een tafel van 1 m2 zou stapelen. Je zou denken, tien auto’s op je lijf, dat is niet niks. Hoe komt het dan dat wij dat niet voelen? De reden daarvoor zit hem in het feit dat die atmosferische druk ook op de onderkant van de tafel werkt. Beide drukken heffen elkaar zo op, waardoor we ze niet waarnemen.
Rondom de aarde is er een dikke luchtlaag, de atmosfeer. Die luchtlaag oefent een druk uit, de luchtdruk.
De atmosferische druk op zeeniveau bedraagt gemiddeld 1013 hPa. Die waarde noemen we de normdruk of standaarddruk.
Geef bij elke foto een korte uitleg.
INKIJKEXEMPLAARDIEKEURE
Lage druk
Hoge druk
2.2Verandering
van
de luchtdruk met de hoogte
We weten ondertussen dat de atmosfeer een dikke laag lucht is die ervoor zorgt dat er luchtdruk is op aarde. We kunnen stellen dat er zich boven ons een hele kolom lucht bevindt die zorgt voor de luchtdruk. Daarin wordt de lucht ijler naarmate we hoger in de atmosfeer gaan. De dichtheid van de lucht neemt dus af met de hoogte.
INKIJKEXEMPLAARDIEKEURE
de luchtdichtheid neemt af met de hoogte
De luchtkolom boven de Mount Everest.
Everest grond
De luchtkolom boven de grond.
De grafiek toont het verloop van de luchtdruk met de hoogte.
De Mount Everest (8848 m) is de hoogste berg ter wereld. Daar is de luchtdruk nog maar een derde van de atmosferische druk op zeeniveau en is de luchtdichtheid ook veel lager. De meeste klimmers maken dan ook gebruik van zuurstofflessen om de Mount Everest te beklimmen.
WIST-JE-DAT
Een hoogtemeter, de naam zegt het zelf al, gebruiken we in verschillende toestellen om de hoogte te weten. Hoogtemeters worden gebruikt in vliegtuigen, bij het deltavliegen, bij het parachutespringen, bij het bergbeklimmen … Zelfs in sport apps, zoals Strava, kan je zien hoeveel hoogtemeters bijvoorbeeld een wielrenner doet.
Eenvoudig gezien is een hoogtemeter een barometer (of drukmeter) met een schaalverdeling die de juiste hoogte aangeeft. Omdat de luchtdruk afneemt als de hoogte toeneemt, is het eenvoudig om de hoogte te bepalen. We weten dat de luchtdruk op zeeniveau met ca. 1 hPa afneemt per 8,2 meter.
INKIJKEXEMPLAARDIEKEURE
hoogteverschil in een sport app
rechts boven de hoogtemeter op het controlepaneel van een vliegtuig
hoogtemeter om de pols van een skydiver
hoogtemeter van een paraglider
De meeste hoogtemeters bevatten een elektronische luchtdruksensor en werken elektronisch.
2.3Verandering van gasdruk met de temperatuur
Niet alleen de hoogte heeft een invloed op de gasdruk, ook de temperatuur is belangrijk.
Volgens het deeltjesmodel bewegen de gasmoleculen vrij door elkaar. Als we de temperatuur van een afgesloten hoeveelheid gas laten toenemen, nemen de bewegingen van de gasmoleculen toe. Hierdoor nemen de onderlinge botsingen toe en stijgt ook de gasdruk.
Omgekeerd, als we de temperatuur laten afnemen, zal de gasdruk ook dalen.
De temperatuurschaal die we hier gebruiken, staat in graden Celsius. De temperatuur krijgt dan het symbool θ (thèta) en wordt uitgedrukt in graden Celsius.
We vermoeden dus dat er een recht evenredig verband is tussen de temperatuur en de gasdruk voor een constant aantal gasdeeltjes in een constant volume.
We kunnen dit vermoeden controleren door een labo uit te voeren.
Oriëntatie
ONDERZOEKSVRAAG
Wat is het verband tussen de temperatuur en de gasdruk voor een constant aantal gasdeeltjes in een constant volume?
Noteer je veronderstelling.
HYPOTHESE
Voorbereiding
BENODIGDHEDEN erlenmeyer thermometer manometer dop voor de erlenmeyer bunsenbrander
PROEFOPSTELLING
DOE DE TEST
WERKWIJZE
Breng een hoeveelheid gas in een erlenmeyer. Bevestig de thermometer en manometer (drukmeter) en sluit de erlenmeyer af, zodat het volume en het aantal gasdeeltjes constant blijft.
Warm de erlenmeyer op en meet de verandering van de temperatuur θ. Bepaal telkens de bijhorende druk p.
Uitvoering
MEETRESULTATEN
Het uitvoeren van het labo leverde ons volgende meetresultaten op.
INKIJKEXEMPLAARDIEKEURE
1080
1100
1170 801220 97 1280
VERWERKING
Na de verwerking van de meetresultaten krijgen we:
128013
We zien dat we geen constante krijgen voor de verhouding . Ons vermoeden dat druk en temperatuur recht evenredig zijn, lijkt dus niet correct.
Als we echter de bijhorende grafiek bekijken, zien we dat de meetresultaten wel op een rechte liggen.
INKIJKEXEMPLAARDIEKEURE
Reflectie
De p(θ)-grafiek is een schuine rechte die niet door de oorsprong gaat. We zien aan die schuine rechte wel dat: hoe hoger de temperatuur, hoe hoger de druk en daarnaast hoe lager de temperatuur, hoe lager de druk.
Als we de rechte doortrekken naar lagere temperaturen, dan zien we dat de druk bij een bepaalde temperatuur nul wordt. Die temperatuur is -273,15°C. Dat is een heel bijzondere temperatuur die we het absolute nulpunt noemen.
Bij het absolute nulpunt is de druk nul. De deeltjes zouden bij die temperatuur niet meer botsen en dus niet meer bewegen. Dat wil zeggen dat een lagere temperatuur niet meer mogelijk is. Het is immers niet meer mogelijk om de deeltjes trager te laten bewegen. Ze zijn immers al in rust. Verder afkoelen is niet meer mogelijk.
Vandaar de naam absolute nulpunt voor de temperatuur van -273,15 °C.
Op basis van dit gegeven werd een nieuwe temperatuurschaal ingevoerd, de absolute temperatuurschaal of kelvinschaal. De kelvinschaal heeft -273,15 °C als nulpunt. De schaal werd genoemd naar de Britse fysicus William Thomson, die later in de adelstand werd verheven als Lord Kelvin. GROOTHEID
(absolute) temperatuur T kelvin K temperatuur θ graden Celsius °C
De grootheid T, de (absolute) temperatuur, met zijn eenheid K (kelvin) is één van de zeven basisgrootheden die we in module 1 Grootheden meten leerden.
Lord Kelvin (1824 – 1907)
Voor een temperatuur in kelvin, gebruiken we niet het woordje ‘graden’. We zeggen bijvoorbeeld niet het is 300 graden kelvin, maar 300 kelvin. We noteren dat als 300 K
De laagst mogelijke temperatuur is – 273,15 °C. Dat is het absolute nulpunt.
De absolute temperatuur T heeft als nulpunt 0 K of – 273,15 °C
Eén schaaldeel op de kelvinschaal is even groot als één schaaldeel op de celsiusschaal.
We ronden het absolute nulpunt – 273,15 °C meestal af tot – 273 °C.
We kunnen de temperatuur in °C gemakkelijk omrekenen naar de temperatuur in K.
T = θ + 273 (in K)
θ = T – 273 (in °C)
We moeten nog een antwoord formuleren op onze onderzoeksvraag. Na reflectie over ons onderzoek, zien we dat we beter het verband bekijken tussen de absolute temperatuur in K en de gasdruk p, voor een constant aantal gasdeeltjes in een constant volume.
Na de verwerking van de meetresultaten krijgen we:
We zien dat de verhouding van de gasdruk tot de absolute temperatuur constant is en dat de p(T)-grafiek een schuine rechte door de oorsprong geeft.
Als de verhouding tussen twee grootheden constant is, dan zeggen we dat die twee grootheden recht evenredig zijn.
We kunnen besluiten dat de absolute temperatuur recht evenredig is met de gasdruk, voor een constant aantal gasdeeltjes in een constant volume.
3Druk in vloeistoffen
3.1De hydrostatische druk
INKIJKEXEMPLAARDIEKEURE
Duiken met flessen. Geen zuurstofflessen, maar plastic flessen. De zuurstofflessen heb je wel nodig om te duiken. Albert laat zien wat het effect is van druk op flessen in het water. Scan de QR-code om het filmpje van Albert te bekijken.
Als we de druk in een vloeistof meten, dan meten we een druk die hoger is dan de atmosferische druk. Het water zorgt voor een extra druk.
We merken dit onder andere als we onder water zwemmen, we voelen de druk dan in onze oren. h
Een vloeistof oefent in elk punt en op elke diepte een druk uit. Die druk noemen we de hydrostatische druk.
Met een vliesmanometer, een doosje dat afgesloten is met een elastisch vlies, meten we de hydrostatische druk op verschillende dieptes en richtingen. Onder water wordt het vlies ingeduwd door de hydrostatische druk. Hoe groter de druk, hoe meer het vlies ingeduwd wordt.
Uit metingen blijkt dat hoe dieper de vliesmanometer in een vloeistof is ondergedompeld, hoe meer het vlies ingedrukt wordt, dus hoe hoger de druk is.
Op eenzelfde diepte geeft de vliesmanometer overal dezelfde druk aan. Als we de vliesmanometer draaien, blijft de druk gelijk. De vloeistofdruk werkt dus in alle richtingen en is constant op een bepaalde diepte. Herhalen we dit experiment in een andere vloeistof, dan meten we andere waarden. De soort vloeistof heeft dus ook een impact op de druk.
INKIJKEXEMPLAARDIEKEURE
Even testen? In de applet ‘under pressure’ kan je dit zelf virtueel onderzoeken.
Scan de QR-code om te starten.
Plaats de meetlat in de vloeistof om de diepte gemakkelijk af te lezen, neem de manometer om de druk op verschillende dieptes te meten.
Om de hydrostatische druk te onderzoeken schakel je de atmosferische druk uit. Zo meet je enkel de hydrostatische druk.
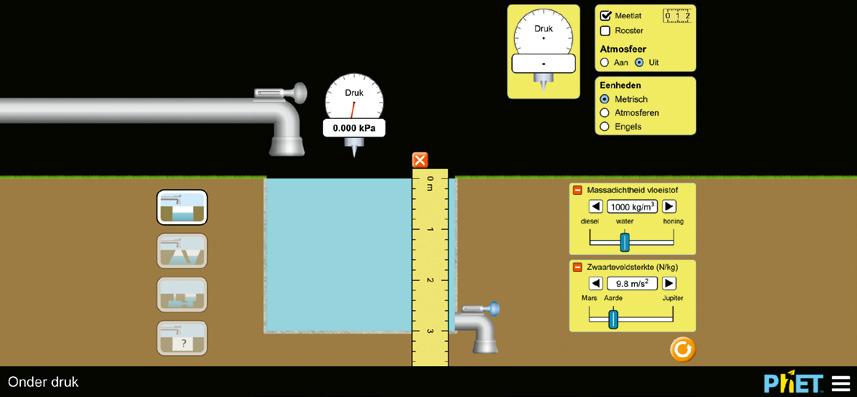
Meet de druk verschillende keren op dezelfde diepte en noteer je meetresultaten in de tabel.
INKIJKEXEMPLAARDIEKEURE
Je ziet dat in een horizontaal vlak de hydrostatische druk constant is.
Meet de druk op verschillende dieptes en noteer je meetresultaten in de tabel.
Je ziet dat de hydrostatische druk in de vloeistof recht evenredig is met de diepte h: phydro ∼ h
Meet de druk in een aantal verschillende vloeistoffen door de dichtheid van de vloeistof in de applet aan te passen. Hou hierbij de hoogte constant (h = …). Noteer je meetresultaten in de tabel.
Je ziet dat de hydrostatische druk op eenzelfde diepte recht evenredig is met de massadichtheid van de vloeistof ρvl: phydro ∼ ρvl
Dus is:
phydro ∼ ρvl · h
phydro = cte · ρvl · h
De constante blijkt bij benadering 9,81 N kg te zijn, de zwaarteveldsterkte g.
Als formule voor de hydrostatische druk vind je dus: phydro = ρvl · g · h
INKIJKEXEMPLAARDIEKEURE
De hydrostatische druk phydro op een diepte h in een vloeistof met massadichtheid
ρvl wordt gegeven door:
phydro = ρvl · g · h
Hierbij is:
ρvl = de dichtheid van de vloeistof
g = de zwaarteveldsterkte
h = de diepte
3.2Theoretische afleiding van de formule van hydrostatische druk
De hydrostatische druk wordt veroorzaakt doordat de kolom water die zich boven een bepaald punt P in de vloeistof bevindt, aangetrokken wordt door de aarde. De hydrostatische druk is dus een gevolg van de zwaartekracht.
We kunnen de zwaartekracht van die kolom vloeistof berekenen:
Fz = m ⋅ g
ρvl = m V
ρvl = m V
Fz = m ⋅ g
ρvl = m V
Fz = ρvl h A g dus Fz = m ⋅ g
Fz = ρvl h A g en Fz = m g
Fz = ρvl ⋅ h ⋅ A ⋅ g dus
m = ρvl V = ρvl h A
m = ρvl V = ρvl h A
m = ρvl V = ρvl h A
ρvl = m V m = ρvl ⋅ V = ρvl ⋅ h ⋅ A
Fz = ρvl ⋅ h ⋅ A ⋅ g
In het punt P is de hydrostatische druk gelijk aan:
p = Fz A = ρvl ⋅ h ⋅ A ⋅ g A = ρvl ⋅ h ⋅ g
Zo vinden we via een theoretische afleiding ook de formule van de hydrostatische druk.
3.3Totale druk in een vloeistof
De hydrostatische druk is de druk die enkel veroorzaakt wordt in de vloeistof. Meestal is er boven de vloeistof ook nog een gas (bijvoorbeeld lucht) aanwezig.
Als de vloeistof zich in een afgesloten vat bevindt en er zich boven de vloeistof nog een gas bevindt, dan bedraagt de totale druk in de vloeistof:
p = pgas + phydro
waarbij de hydrostatische druk op een diepte h in een vloeistof met massadichtheid ρvl wordt gegeven door:
phydro = ρvl · g · h
Dus:
p = pgas + ρvl
g · h
p = patm + phydro
waarbij de hydrostatische druk op een diepte h in een vloeistof met massadichtheid ρvl wordt gegeven door:
phydro = ρvl · g
Dus:
h
p = patm + ρvl · g · h
Als de vloeistof zich in een open vat bevindt, dan werkt boven de vloeistof de atmosferische druk:
De atmosferische druk plant zich volgens de wet van Pascal immers overal in de vloeistof onverminderd voort. Je leert daar meer over in het volgende hoofdstuk.
Wist je dat je ziek kan worden van druk? De duikersziekte of decompressieziekte is een ziekte die voorkomt bij mensen die van een omgeving met verhoogde druk naar een omgeving met verlaagde druk gaan. Het is een ziekte die vooral bij duikers voorkomt, vandaar de naam. Maar het kan ook voorkomen bij piloten van een straaljager of mensen die uit een vliegtuig stappen na een snelle decompressie. Daarom mag je ook pas vliegen 12u nadat je een duik hebt genomen.
De ziekte staat ook bekend als de caissonziekte. Caissons zijn grote duikklokken die ze vroeger gebruikten om te duiken. Duikpakken, zuurstofflessen en dergelijke bestonden eind de jaren 1890 nog niet, dus werden duikers met duikklokken in het water gelaten. Daar ervaarden de duikers een hydrostatische druk onder het wateroppervlakte. Tijdens de periode onder water kregen ze meer stikstofgas (N2) in het bloed en in hun weefsels dan normaal. Als ze terugkeerden naar de oppervlakte, en dus weer in normale druk vertoefden, kon de stikstof niet snel genoeg door de longen worden afgevoerd. Daardoor kregen de duikers belletjes in hun bloedvaten waardoor het bloed niet meer goed kon stromen en kregen ze een embolie. Bereikten die belletjes de hersenen of ontstonden ze daar, dan kon dit zelfs dodelijk zijn.
Maar hoe voorkom je dan deze ziekte? Je duikt best niet te lang en niet te diep in het water. Als je opstijgt, dan doe je dit langzaam.
En wat als je de ziekte hebt? Dan brengen ze je naar de compressiekamer. Daar voeren ze de druk weer op, om dan langzaam de druk weer te laten dalen. Op die manier kan het lichaam zich ‘reinigen’ en de stikstof via de longen afvoeren. Ze geven ook nog zuurstof bij om het proces te versnellen.
INKIJKEXEMPLAARDIEKEURE
4Beginsel van Pascal
Het beginsel van Pascal wordt ook wel de wet van Pascal genoemd en geldt voor alle ‘fluïda’, dus voor vloeistoffen en voor gassen.
Misschien is deze wet makkelijker te begrijpen als je de gravitatie wegdenkt. Als we een druk uitoefenen op een afgesloten vat dat gevuld is met een fluïdum, dan is de druk binnenin het vat in elk punt hetzelfde. De druk die uitgeoefend wordt op een deel van het fluïdum plant zich in alle richtingen onveranderd voort. Hierdoor wordt de druk in elk punt van het vat dezelfde.
Druk is een scalaire grootheid, dus geen vector. Als de druk uitgeoefend wordt op een oppervlak (bijvoorbeeld ergens in het vat), dan krijgen we natuurlijk wel weer een kracht. Die kracht staat dan altijd loodrecht op het oppervlak.
INKIJKEXEMPLAARDIEKEURE
van Pascal
De druk uitgeoefend op een ingesloten fluïdum, plant zich onverminderd voort in alle richtingen.
Dit filmpje geeft mooi weer wat Pascals wet is. Scan de QR-code hiervoor.
Een hydraulische pers bestaat uit twee met elkaar verbonden cilinders die elk met een zuiger afgesloten zijn. Zuiger 1 heeft een kleine oppervlakte en zuiger 2 heeft een groter oppervlakte. Het geheel is gevuld met een vloeistof, meestal olie.
Wet
De kracht #–F1 werkt op zuiger 1 die een oppervlakte A1 heeft. Het uitoefenen van de kracht #–F1 veroorzaakt dus een druk p1:
p1 = F1 A1
Die druk plant zich onverminderd voort in de vloeistof. Aan de andere kant van de hydraulische pers heeft die een kracht #–F2 op zuiger 2 tot gevolg:
F2 = p1 ⋅ A2 = F1 A1 ⋅ A2 = F1 ⋅ A2 A1
INKIJKEXEMPLAARDIEKEURE
Aangezien A2 groter is dan A1, is #–F2 groter dan #–F1.
Als zuiger 2 een oppervlakte heeft die 100 maal groter is dan die van zuiger 1, is de kracht op zuiger 2 ook 100 maal groter dan #–F1.
Een kracht van 200 N op zuiger 1 heeft een kracht van 200 N · 100 = 200 · 102 N tot gevolg. Met een hydraulische pers kan je een kleine kracht dus omzetten in een grote kracht.
Heel wat toepassingen die we in het dagelijkse leven gebruiken, zouden niet werken zonder het principe van de hydraulische pers. Hieronder zie je een aantal voorbeelden.
Geef bij elke foto een korte uitleg.
INKIJKEXEMPLAARDIEKEURE
5Verder oefenen?
5.1Begrijpen
Druk op vaste stoffen
Je hebt zeker al van de eenheden hPa en mbar gehoord in het weerbericht. Vergelijk beide eenheden met elkaar.
Verkiest een fakir een spijkerbed met veel of met weinig spijkers? Verklaar je antwoord.
Het symbool van druk is p. Van welk Engels woord is dit afgeleid? Noteer.
Druk in gassen
Duid het juiste antwoord aan. Op de top van een berg is: de luchtdruk gelijk aan de luchtdruk in het dal. de luchtdruk hoger dan de luchtdruk in het dal. de luchtdruk lager dan de luchtdruk in het dal. deze vraag kan niet beantwoord worden.
Druk in vloeistoffen
De hydrostatische druk op de bodem is bij A en D even groot. 1 2 3
Onderstaande vaten hebben allemaal een cirkelvormige bodem. Ze zijn gevuld met vloeistoffen met dichtheden ρ, 2ρ en 3ρ tot een hoogte h of 3 h Welke bewering is correct? Duid aan.
De hydrostatische druk op de bodem is het grootst bij C, want daar is het bodemoppervlak het grootst.
De hydrostatische druk op de bodem is het grootst bij E.
De hydrostatische druk op de bodem is bij A, B, D en E even groot.
Duid het juiste antwoord aan. Druk in een vloeistof is een: scalaire grootheid met als eenheid
scalaire grootheid met als eenheid
vectoriële grootheid met als eenheid
vectoriële grootheid met als eenheid
Duid het juiste antwoord aan. Tijdens een duikoefening stijgen luchtbellen op in het water. We zien dat tijdens het opstijgen: de dalende druk ervoor zorgt dat het volume van de luchtbel afneemt. de toenemende druk ervoor zorgt dat het volume van de luchtbel toeneemt. de dalende druk ervoor zorgt dat het volume van de luchtbel toeneemt. de toenemende druk ervoor zorgt dat het volume van de luchtbel afneemt.
Op de foto staat de watertoren van een klein Amerikaans dorp. Waarom staat het waterreservoir zo hoog? Verklaar.
Controleer de eenheden van de formule phydro = ρ · h · g.
Beide bloemvazen worden met evenveel water gevuld voor er een mooi boeket in gezet wordt. De bodem is bij beide vazen even groot.
INKIJKEXEMPLAARDIEKEURE
Duid het juiste antwoord aan. Dan weten we over de hydrostatische druk op de bodem van vaas A (pA) en van vaas B (pB) dat:
pA < pB
pA = pB
pA > pB
We hebben onvoldoende informatie om een uitspraak over pA en pB te doen.
Beginsel van Pascal
Een boot kan door een opeenvolging van sluizen op een andere hoogte gebracht worden. Waarom hebben het stuk dat de boot bevat en het gedeelte rechts ervan hetzelfde waterniveau? Verklaar.
Wat je hier ziet, zijn communicerende vaten. Verklaar waarom het niveau van de vloeistof overal hetzelfde is.
5.2Toepassen
Druk op vaste stoffen
Hoe groot is de druk die een skiër op de sneeuw uitoefent, als je weet dat zijn ski’s elk een steunvlak van 850 cm2 hebben en zijn massa 90 kg bedraagt? Reken uit.
Een verpleger duwt een injectienaald met een kracht van 75,0 N in je bil. Als je weet dat de injectienaald een doorsnede heeft van 0,200 mm2, hoe groot is dan de uitgeoefende druk? Reken uit.
Een man slaat met een kracht van 200 N op een spijker, waardoor de spijker in een stuk hout gedreven wordt met een druk van 80 · 106 Pa. Bereken de oppervlakte van de punt van de spijker.
Druk in vloeistoffen
Een waterput is 20 m diep en is volledig gevuld met water dat overal dezelfde temperatuur heeft.
Bereken de hydrostatische druk op de bodem.
Bereken de totale druk op de bodem.
Hoe diep moet een duikboot zich onder het wateroppervlak bevinden om een totale druk te ondervinden van 2,0 ⋅ 107 N m2 ? Reken uit.
Gebruik g = 10 N kg
Het is moeilijk om ons de grootte van de luchtdruk voor te stellen. Een vergelijking helpt hierbij. Duid het juiste antwoord aan. De luchtdruk komt overeen met de druk uitgeoefend door:
een kubusvormige steen van 10 kg met als zijde 10 cm. een persoon van 60 kg met een contactoppervlak van 60 cm2 een waterkolom van 0,10 m hoog. een waterkolom van 1,0 m hoog.
Tijdens het duiken ondervindt een duiker een totale druk van 3,0 bar. Duid aan op welke diepte de duiker zich bevindt.
Om deze oefening op te lossen, scan je de QR-code. De luchtdruk op zeeniveau is 1013 hPa, op de top van de Mont Blanc (h = 4808 m) is de luchtdruk zeker kleiner. Met welke formule kunnen we dit berekenen? Noteer.
Bereken de luchtdruk op de Mont Blanc. Je mag aannemen dat de massadichtheid van de lucht over de hele hoogte gelijk is aan de massadichtheid op zeeniveau 1,293 kg m3 . Is de werkelijke luchtdruk groter of kleiner dan deze waarde? Verklaar je antwoord. Waarom blijf je best niet te lang op de top van de Mount Everest? Verklaar.
Tom Waes probeerde in een zelfgebouwde duikboot het Veerse Meer over te steken. Scan de QR-code als je wilt zien of het gelukt is.
Stel dat zijn duikboot omwille van te veel ballast naar de bodem zou gezonken zijn. Bereken welke kracht hij dan nodig gehad zou hebben om het luik te openen op 15 m diepte. Het toegangsluik is vierkant met een zijde van 0,65 m
De massadichtheid van het water bedraagt 1005 kg m3 . De atmosferische druk was 1017 hPa.
Om een hoog gebouw van 40 m hoog te blussen staat een brandweerman op een 40 m hoge ladder. Het bluswater komt uit de brandslang met een druk van 6,0 bar. Hoe groot is de waterdruk aan de brandweerwagen? Omkring het juiste antwoord.
4,6 bar
9,9 bar
6,4 bar 46 bar
Beginsel van Pascal
Een U-buis is gevuld met olie. A1 = 4,0dm2 ;A2 = 5,0dm2 ; ρolie = 800 kg m3
Doordat de olie in de linker vloeistofkolom 40 cm hoger staat dan in de rechter vloeistofkolom, moet er op de rechter vloeistofkolom een extra kracht uitgeoefend worden om het systeem in evenwicht te houden.
INKIJKEXEMPLAARDIEKEURE
Omkring het juiste antwoord. Deze kracht is gelijk aan:
Om de dichtheid van een onbekende vloeistof te bepalen kan je een U-buis gebruiken. Daarbij wordt een U-buis eerst deels met water gevuld en dan wordt aan één kant een hoeveelheid onbekende vloeistof gegoten.
Eens in evenwicht worden de hoogtes van de vloeistofkolommen gemeten.
Bepaal de dichtheid van de onbekende vloeistof door middel van deze techniek.
INKIJKEXEMPLAARDIEKEURE
INKIJKEXEMPLAARDIEKEURE
INKIJKEXEMPLAARDIEKEURE
INKIJKEXEMPLAARDIEKEURE
STUDIEWIJZER
ik ken het! paginanummer
Ik kan druk definiëren. p. 4-7
Ik weet dat de grootheid druk door p wordt voorgesteld en in Pa wordt uitgedrukt. p. 4-7
INKIJKEXEMPLAARDIEKEURE
Ik weet dat druk recht evenredig is met de grootte van de uitgeoefende kracht. p. 4-7
Ik weet dat druk omgekeerd evenredig is met de grootte van het oppervlak. Ik kan dit verduidelijken met behulp van enkele voorbeelden en toepassingen. p. 4-7
Ik kan druk bij vaste stoffen verklaren. p. 4-7
Ik ken de atmosferische druk en kan die gebruiken in toepassingen. p. 8-9
Ik kan druk bij gassen verklaren. p. 8-16
Ik kan uitleggen dat de atmosferische druk daalt met de hoogte. p. 10-11
Ik kan de invloed van de temperatuur op de gasdruk bespreken. Ik kan hierbij de absolute temperatuur introduceren. p. 12-16
Ik weet dat de absolute temperatuur door T wordt voorgesteld en uitgedrukt wordt in K. p. 12-16
Ik kan een p(T)-grafiek omschrijven en interpreteren. p. 12-16
Ik kan het absolute nulpunt verklaren met behulp van het deeltjesmodel: bij die temperatuur bewegen de deeltjes niet meer. p. 12-16
Ik kan druk bij vloeistoffen verklaren p. 17-22
Ik kan het begrip hydrostatische druk definiëren. p. 17-20
Ik weet dat de totale druk in een vloeistof gelijk is aan de som van de hydrostatische druk en de atmosferische druk. p. 21-22
Ik kan het beginsel van Pascal verklaren p. 23-25
INKIJKEXEMPLAARDIEKEURE
Colofon
Auteur Freya Vermeiren
Met medewerking van Anke Van Roy
Eerste druk 2024
SO 0185/2024
Bestelnummer 90 808 0455
Module 4 van ISBN 978 90 4864 763 7
KB D/2024/0147/249
NUR 126
Thema YPMP5
Verantwoordelijke uitgever die Keure, Kleine Pathoekeweg 3, 8000 Brugge
RPR 0405 108 325 - © die Keure, Brugge
Niets uit deze uitgave mag verveelvoudigd en/of openbaar gemaakt worden door middel van druk, fotokopie, microfilm of op welke wijze ook zonder voorafgaande schriftelijke toestemming van de uitgever. No parts of this book may be reproduced in any form by print, photoprint, microfilm or any other means without written permission from the publisher. De uitgever heeft naar best vermogen getracht de publicatierechten volgens de wettelijke bepalingen te regelen. Zij die niettemin menen nog aanspraken te kunnen doen gelden, kunnen dat aan de uitgever kenbaar maken.
Die Keure wil het milieu beschermen. Daarom kiezen wij bewust voor papier dat het keurmerk van de Forest Stewardship Council® (FSC®) draagt.
Dit product is gemaakt van materiaal afkomstig uit goed beheerde, FSC®-gecertificeerde bossen en andere gecontroleerde bronnen.