BV 261 – Krämer, Harmonielehre

Krämer . Harmonielehre im Selbststudium

THOMAS KRÄMER

Harmonielehre im Selbststudium

BV 261

ISBN 978-3-7651-0261-5

9., korrigierte Auflage 2023

© 1991/2019 by Breitkopf & Härtel, Wiesbaden Alle Rechte vorbehalten

Satz: Dinges & Frick, Wiesbaden

Druck: Memminger MedienCentrum AG, Memmingen

Vorwort

Wenn an der Schwelle zum 21. Jahrhundert eine „Harmonielehre im Selbststudium“ erscheint und ihre Themenstellung aus der Musik zwischen 1600 und 1900 herleitet, so muss sich die Frage nach der Berechtigung einer solchen Publik ation aufdrängen.

Dabei gibt eine Antwort auf diese Frage unsere Zeit selbst: das g ängige Konzertrepertoire entstammt zum überwiegenden Teil dem Zeitraum zwischen 1600 und 1900, und dies hat zur Folge, dass auch die musik alische Berufs ausbildung sich an jenem Zeitraum orientiert Hinzu kommt, dass das erhaltens- und pflegenswerte Liedgut aus dem Choral- und Volksliedbereich in jenen Jahren der Musikgeschichte anzusiedeln ist und dass auch in unserem Jahrhundert Elemente der Tonsprache jener Zeit nicht verloren geg angen sind, vielmehr etwa im Bereich der „Popularmusik“ sich verstärkt wiederfinden.

Es gibt aber eine weitere Antwort auf die Frage nach der Notwendigkeit des Studiums der klassischen Harmonielehre. Diether de la Motte hat in seiner „Harmonielehre“ (1976) den Versuch unternommen, die Tonsprache unter dem Aspekt des Wandels der Zeiten neu zu ordnen Dieser Ans atz ist richtig und notwendig.

Es setzt aber voraus, dass eine Tonsprache beherrscht wird, die ich in ihrer Bedeutung mit der „Muttersprache“ gleichsetzen möchte Der Erwerb jener Muttersprache jedoch, die in der Beachtung von Regeln, Gesetzen und Verboten Komponisten wie Josquin mit Brahms, Palestrina und Mendelssohn, Bach mit Reger eint, ist Hauptgegenstand der vorliegenden Konzeption; das Aneignen von Basiswissen hat Vorrang vor einer – sicherlich notwendigen –stilistischen Differenzierung

Der Schwerpunkt der vorliegenden Harmonielehre liegt im Aspekt des Selbststudiums. Zwar ist bek annt, dass die korrigierende Hand des Lehrers durch nichts zu ersetzen ist; andererseits verfolgt der Aufbau des Buches die Absicht, schrittweise und gezielt methodisch durchdacht zur Eigenarbeit anzuleiten. Dass dabei gleichzeitig eine systematische Gliederung des Stoffes als mögliche Handreichung für den Lehrer entstanden ist, war ein von vornherein geplanter Seiteneffekt; auch k ann das Buch jederzeit im Unterricht Verwendung finden.

Da sich alle Fragestellungen im s atztechnischen Bereich am Choral und am Volkslied orientieren, wurde auf Themenbereiche wie Alteration, Medianten oder Modulation bewusst verzichtet Ein Volkslied mit tiefalterierter Quinte harmonisieren zu wollen, wäre ebenso unsinnig wie das Darstellen von Modulationstechniken mittels choralhaft empfundener Beispiele. Die Beschränkung auf das Vermitteln von Basiswissen hat den „Verzicht auf ... “ notwendigerweise zur Folge

Ein erfolgreiches Durcharbeiten der einzelnen Kapitel setzt Grundkenntnisse im Bereich der „Allgemeinen Musiklehre“ voraus Das Kapitel 1, „Grundlagen der Allgemeinen Musiklehre“, dient lediglich dazu, die für die Harmonielehre besonders wichtigen Inhalte zu bündeln und in knapper Form zus ammenzufassen Zum vertiefenden Studium sei Erich Wolfs „Allgemeine Musiklehre“ empfohlen.

Das Buch in der nun vorliegenden Form wäre ohne manchen stillen Mithelfer nicht zustande gekommen. Ihnen allen sei Dank, allen voran Herrn Dr. Gerd Sievers für seine redaktionelle Betreuung Seine ebenso unermüdlichen wie geduldigen Ratschläge haben geholfen, manche Unzulänglichkeiten zu beseitigen. Dank gebührt auch meinen ungezählten Musiktheorieschülern an der Musikschule Gütersloh und an den Musikhochschulen Detmold und Saarbrücken. Ihrer Erinnerung und einem Motto Arnold Schönbergs sei das Buch gewidmet. Schönberg stellt an den Beginn seiner „Harmonielehre“ (1911) den Satz: „Dieses Buch habe ich von meinen Schülern gelernt.“ Ich habe dem nichts hinzuzufügen.

Saarbrücken, Herbst 1990

Vorwort zur Neuausg abe

Vorwort zur 7. Auflage

Vorwort zur 9. Auflage

Nahezu 34 Jahre sind seit dem Erscheinen meiner „Harmonielehre im Selbststudium“ vergangen und anscheinend erfreut sich das Buch ungebrochener Beliebtheit. Mit der 4. Auflage wurden 2006 zahlreiche Änderungen vorgenommen. Insbesondere erhöhte sich die Anzahl der Aufgabentypen B., um die Möglichkeit der Selbstkontrolle durch den Vergleich mit dem Lösungsteil zu verbessern.

15 Jahre sind seit dem Erscheinen meiner „Harmonielehre im Selbststudium“ verg angen, wobei bis zur 3 Auflage des Buches nur marginale Änderungen vorgenommen wurden

Während dieser Jahre habe ich jedoch etliche Anregungen von Kollegen, Studierenden und insbesondere von Benutzern aus dem Umkreis der musizierenden Laien ges ammelt Die Anregungen bezogen sich vorrangig auf die Liedauswahl, aber auch auf den Aspekt der Eigenarbeit, der manchem als zu wenig akzentuiert erscheinen wollte

Es ist daher dem Verlag zu danken, dass er sich entschloss, mit der vorliegenden 4. Auflage eine stark überarbeitete Neufassung vorzulegen. Die Änderungen finden sich mit Schwerpunkt auf dem Gebiet der zu bearbeitenden Lieder, stammen diese nun noch mehr aus den Bereichen des Volksliedes, des populären Liedes und des Spirituals.

25 Jahre sind seit dem Erscheinen meiner „Harmonielehre im Selbststudium“ vergangen und anscheinend erfreut sich das Buch einer ungebrochenen Beliebtheit. Vor zehn Jahren wurden mit der 4. Auflage zahlreiche Änderungen vorgenommen; insbesondere erhöhte sich die Anzahl der Aufgabentypen B., um die Möglichkeit der Selbstkontrolle durch den Vergleich mit dem Lösungsteil nachhaltig zu verbessern. Ganz offensichtlich aber gibt es zusätzlich den dringenden Wunsch vieler Leser, nach intensiver Eigenarbeit mit meiner „Harmonielehre“ auch eine Rückmeldung zu den etwas anspruchsvolleren Aufgabentypen C. und D. zu erhalten, die ja im Buch selber nicht gelöst sind, um seine Verwendbarkeit im Unterricht zu sichern. Deshalb wird der Verlag nunmehr meine „Praktischen Harmonieübungen“ (BV 479) herausgeben, ein umfangreiches Arbeitsbuch mit Aufgaben und Lösungen, das auch Orientierungsmodelle zu allen Aufgabentypen C. und D. der vorliegenden „Harmonielehre“ enthält. Damit gehen Autor und Verlag auf vielfältige Anregungen und Wünsche ein, die von außen an sie herangetragen wurden.

Ganz offensichtlich aber gibt es den dringenden Wunsch vieler Leser, zusätzlich auch eine Rückmeldung zu den anspruchsvolleren Aufgabentypen C. und D. zu erhalten. Diese Aufgaben blieben bewusst ohne Lösungsvorschläge, um die Einsatzfähigkeit des Buches im Unterricht zu sichern. Nun hat in der Zwischenzeit der Verlag meine „Praktischen Harmonieübungen“ (BV 479) herausgegeben. Dieses umfangreiche Arbeitsbuch mit etlichen Aufgaben und Lösungen wurde als Begleitwerk zu meiner „Harmonielehre“ konzipiert und enthält jetzt auch Lösungsmodelle zu den Aufgabentypen C. und D. Damit sind Autor und Verlag auf vielfältige Anregungen und Wünsche eingegangen, die von außen an sie herangetragen wurden.

Ganz wesentlich wurde aber in der 4 Auflage auch der Aspekt des Selbststudiums erweitert So ist die Anzahl der Aufg abentypen „B“ stark angewachsen und damit die Möglichkeit der Selbstkontrolle durch den Vergleich mit dem Lösungsteil nachhaltig verbessert worden Umso mehr wird die „Harmonielehre im Selbststudium“ auch weiterhin eine erfolgreiche Verwendung als Arbeitsgrundlage im Unterricht finden können.

In der nunmehr 7. Auflage meiner „Harmonielehre“ wurden kleinere Fehler korrigiert und einige Unstimmigkeiten beseitigt, des Weiteren wurde ihre Verwendbarkeit mit den „Praktischen Harmonieübungen“ synchronisiert. Neu sind die drei Verzeichnisse und die Literaturempfehlungen im Anhang.

Keine Änderung dagegen hat das nach wie vor stimmige methodische Konzept meines Buches erfahren. Wer nun allerdings nach einer Erweiterung des Stoffes von „Harmonielehre“ sucht, ist mit meinem „Lehrbuch der harmonischen Analyse“ (BV 305) bestens für ein umfassendes Studium des Ges amtkomplexes der traditionellen Harmonielehre gerüstet. Und wer eine Ausleuchtung und Erläuterung zentraler Begriffe der Musiktheorie wünscht, dem sei das „Lexikon Musiktheorie“ (Thomas Krämer/ Manfred Dings, BV 370) empfohlen.

In der vorliegenden 9. Auflage wurden kleinere Fehler korrigiert und einige Unstimmigkeiten beseitigt. Des Weiteren wurde die Verwendbarkeit des Buches mit den „Praktischen Harmonieübungen“ synchronisiert.

Keine Änderung hat das nach wie vor stimmige methodische Konzept meines Buches erfahren. Wer dennoch nach einer vertiefenden Erweiterung des umfangreichen Stoffes von „Harmonielehre“ sucht, ist seit Jahren mit meinem „Lehrbuch der harmonischen Analyse“ (BV 305) bestens für ein umfassendes Studium gerüstet. Und wer eine anschauliche Darstellung sowie eine kurze Erläuterung zentraler Begriffe der Musiktheorie wünscht, dem sei das „Lexikon Musiktheorie“

Saarbrücken, Sommer 2006 Thomas Krämer

(Thomas Krämer/Manfred Dings, BV 370) empfohlen.

Keine Änderung hat das nach wie vor stimmige methodische Konzept des Buches erfahren. Wer nach einer vertiefenden Abrundung des umfangreichen Stoffes von „Harmonielehre“ sucht, ist seit Jahren mit meinem „Lehrbuch der harmonischen Analyse“ (BV 305) bestens für ein umfassendes Studium gerüstet. Und wer eine anschauliche Darstellung sowie eine kurze Erläuterung zentraler Begriffe der Musiktheorie wünscht, dem sei das „Lexikon Musiktheorie“ (Thomas Krämer/Manfred Dings, BV 370) empfohlen.

Saarbrücken, Herbst 2016

Saarbrücken, im Frühjahr 2023 Thomas Krämer

Arbeits anleitung

Für das erfolgreiche Durcharbeiten der einzelnen Kapitel sollten folgende Punkte beachtet werden:

1. Jedes Kapitel ist so aufgebaut, dass es als eine Lerneinheit erarbeitet werden kann.

Besonders wichtige Hinweise und markante Merks ätze sind mit gekennzeichnet

Es empfiehlt sich, diese Hinweise in einer gesonderten Übersicht zus ammenzutragen, damit bei Bedarf auf sie zurückgegriffen werden k ann.

Das Wesentliche ist am Schluss eines jeden Kapitels in besonders knapper Form zus ammen gefasst. Diese umrahmten Zus ammenfassungen sollte sich der Schüler nach Möglichkeit einprägen

2 Vom 4 Kapitel an enthält jede Lerneinheit vier Aufg abentypen

Aufg abentyp A zur Analyse gedacht: in der Regel sollen hier Funktionssymbole eingetragen werden,

Aufg abentyp B s atztechnischer Art: sollte unbedingt gelöst werden können (mit Lösung im Lösungsteil),

Aufg abentyp C s atztechnischer Art mit gesteigertem Schwierigkeitsgrad: sollte gelöst werden können (ohne Lösung im Lösungsteil),

Aufg abentyp D Zus atzaufg aben s atztechnischer Art: könnten im Unterricht Verwendung finden (ohne Lösung im Lösungsteil).

Eine wirklich erfolgreiche Arbeit ist nur dann gewährleistet, wenn die Aufg abentypen A und B (dem jeweiligen Vorschlag der Lösungsschritte folgend) zunächst völlig selbstständig gelöst werden. Erst danach empfiehlt sich ein Vergleich mit den Vorschlägen im Lösungsteil.

3. Damit der Aufg abenteil immer wieder verwendet werden k ann, ist das Abschreiben der Aufg abentypen B bis D (Notenpapier!) dringend anzuraten

Die Kontrolle der eigenen Arbeit durch Singen der einzelnen Stimme und das Hören der erzielten Ergebnisse durch Nachspielen (Tasteninstrument!) ist derart wichtig, dass es als unabdingbarer Bestandteil einer jeden Aufg abe angesehen werden muss

1. Grundlagen der Allgemeinen Musiklehre

Die heute gebräuchliche Notenschrift ist ein Versuch, die vielfältigen Klangereignisse in der Musik mit allgemein verständlichen Zeichen, Symbolen und sonstigen Anordnungen schriftlich zu fixieren

Seit Beginn der ersten Notationsbestrebungen, die bis in die griechische Antike zurückgehen, ist die Notenschrift dabei immer ein in seiner Darstellungsfähigkeit begrenzter Mittler zwischen der Klangidee des Komponisten und der praktischen Ausführung durch den Interpreten gewesen

Die Ausg angsbasis für die Notierung von musik alischen Klangfolgen ist seit ca. 1000 n. Chr. das fünflinige Notensystem.

Das gleichzeitige Erklingen mehrerer musik alischer Stimmen verlangt das Zus ammenfassen der dann benötigten Notensysteme durch die Akkolade.

Für die verschiedenen Parameter in der Musik (wie Tonhöhe, Tondauer, Tonstärke, Tempo, Ausdruck, Artikulation) werden jeweils eigenständige Symbole verwendet, die sich in teils langen geschichtlichen Prozessen herausgebildet haben.

Die Notierung der Tonhöhe stützt sich zunächst auf die Stammtöne (c d e f g a h), die mittels eines Kreuzes ( # ) um einen Halbton erhöht und mittels eines Be ( b) um einen Halbton erniedrigt werden können Auch Ganztonveränderungen der Stammtöne durch ein Doppelkreuz (‹) und Doppel-Be ( ∫) sind möglich. Diese Erhöhungen und Erniedrigungen gelten stets nur für die bezeichnete Oktavlage und für die Dauer eines Taktes.

Ein Auflösungszeichen ( n ) macht die vorgenommenen Veränderungen rückg ängig

Die Stammtöne werden unter dem Gesichtspunkt der Ordnung des gesamten Tonspektrums (tief/hoch) in Registerlagen eingeteilt, wobei sich 7 gebräuchliche Oktavlagen ergeben

Da die Verwendung zu vieler zus ätzlicher Hilfslinien die Notation unübersichtlich macht, k ann man die Oktavierung nach oben durch 8 . . . . (ottava) und nach unten durch 8va bassa (ottava bass a) fordern.

Die Festlegung der Tonhöhe und damit die Benennung der Töne geschieht durch Schlüssel am Anfang des Notensystems

Am gebräuchlichsten sind der G- oder Violinschlüssel (&), der die Note auf der zweituntersten Linie als g ´ fixiert, und der Bassschlüssel ( ? ), der die Note auf der zweitobersten Linie als f festlegt.

Die C- Schlüssel bestimmen den Ton c und werden vor allem als Altschlüssel (Viola [Bratsche], Altpos aune) und als Tenorschlüssel (Violoncello, Fagott, Tenorpos aune) eingesetzt.

Die Notation der Tondauer ist zunächst abhängig vom Grundschlag, auch Metrum genannt. Durch die Fixierung des Metrums wird das Tempo bestimmt, das für jedes Musikstück individuell festzulegen ist.

Dabei stützt man sich seit 1816 auf das „Mälzelsche Metronom“ (M M q = 60 bedeutet: 60 Schläge [Viertelnotenschläge] in der Minute, also Sekundschläge, M.M. q = 80 bedeutet demnach: 80 Viertelgrundschläge in der Minute.)

Im Gefolge der Festlegung des Metrums ergibt sich als äußere Einteilung des Grundschlags der Takt (lat. Tactus = Schlag, Berührung). Die Taktart und damit die Anzahl der Grundschläge innerhalb des Taktes sowie die Maßeinheit werden zu Beginn festgelegt (

usw )

Ein Takt als Zählzeitengruppe wird in schwere und leichte Schlagzählzeiten eingeteilt, wobei der erste Schlag nach dem Taktstrich, die Hauptzählzeit, die 1, von besonderer Betonung ist

Die konkrete Festlegung der Tondauer und damit die innerhalb des vorgegebenen Metrums zugrunde liegende Gliederung des Zeitmaßes erfolgt durch Noten- und Pausenwerte. Durch die rhythmische Gestaltung, also durch das Prinzip von Länge und Kürze der Noten und Pausen, erfährt das gleichbleibende Metrum seine Belebung.

Beispiel 1.5. – Heute gebräuchliche Noten- und Pausenwerte

Ganze Noten

Halbe Noten

Viertelnote

Achtelnote

Sechzehntelnote

Ganze Pause

Halbe Pause

Viertelpause

Achtelpause

Sechzehntelpause

Neben den in Beispiel 1.5. dargestellten rhythmischen Grundformen gibt es weitere Möglichkeiten der Tondauerbestimmung. So verlängert ein Punkt hinter einer Note oder einer Pause (Verlängerungs- oder Augmentationspunkt) diese um die Hälfte ihres Wertes.

Beispiel 1.6. – Verlängerung der Noten- und Pausenwerte durch den Punkt

Die Klangbestimmung des Tonesselber, seine Färbung und seine Intensität, wird bestimmt durch die physikalische Zusammensetzung. So erklingt neben dem Hauptton eine über diesem angeordnete Reihe von Obertönen (Partialtönen), die je nach Tonerzeuger verschieden stark mitklingen, vom Hörer jedoch nur unbewusst wahrgenommen werden. Diese Obertonreihe ist über jedem Ton angeordnet und hat den immer gleichen, rechnerisch unendlichen Aufbau: die Abstände der Obertöne zueinander werden immer kleiner.

Beispiel 1.7. – Obertonreihe auf C

4 Grundlagen der Allgemeinen Musiklehre

Zur Anpassung der Naturgegebenheit musikalischer Töne an die Erfordernisse der Musikpraxis hat es schon zur Zeit der griechischen Antike Versuche systematischer Ordnungen gegeben.

Im pythagoreischen System der Quintverwandtschaft sind alle Quinten rein gestimmt, entsprechen also den Verhältnissen, wie sie der Obertonreihe eines jeden Tones zu entnehmen sind.

Beispiel 1.8. – Reine Quinte in der Obertonreihe (2. und 3. Teilton)

Leseprobe

Würde man 12 nach dem pythagoreischen System errechnete reine Quinten aufeinander schichten, so ergäbe sich:

Beispiel 1.9. – 12 reine Quinten auf C2

12 Quinten:

Schichtet man vom gleichen Ausgangston 7 reine Oktaven aufeinander, so ergibt sich:

Beispiel 1.10. – 7 reine Oktaven auf C2

7 Oktaven:

Vergleicht man den in Beispiel 1.9. erreichten Ton his´´´mit dem in Beispiel 1.10. erreichten Ton c´´´´, so ergibt sich eine geringfügige Abweichung: der Ton his´´´des Beispiels 1.9. ist um etwa ein Viertel eines Halbtones höher als der Ton c´´´´ des Beispiels 1.10.

Der Unterschied beträgt (3: 2)12 :(2:1)7 = 129,74634:128 = 1,0136433.

Diese Differenz (z 74:73) wird pythagoreisches Komma genannt und ist die Ursache dafür, dass das pythagoreische System sich nicht schließt.

Um diesen Mangel zu beseitigen und ein für den gesamten Tonvorrat und für alle Tonarten gleichermaßen brauchbares Tonsystem zu schaffen, teilte Andreas Werckmeister 1691 in der von ihm erdachten temperierten Stimmung die reine Oktave in 12 gleiche Teile (Äquidistanz der Töne).

Dies hat zwar zur Folge, dass die Tonbeziehungen untereinander mit Ausnahme der Oktaven nicht mehr rein – im mathematischen Sinne also verstimmt – sind; doch überwiegt der Vorteil, dass aufgrund der Identität der Oktave in allen Lagen ein geschlossenes System von in allen Tonarten gleichermaßen brauchbaren Tönen entsteht.

(Das Aufkommen der temperierten Stimmung war für J. S. Bach immerhin Anlass, zwei Zyklen des „Wohltemperierten Klaviers“ in allen nun brauchbar gewordenen und damit gleichberechtigt nebeneinander stehenden Dur- und Molltonarten zu komponieren.)

Leseprobe

Intervalle

Der Begriff „Intervall“ beinhaltet nicht nur den Abstand zweier zusammen oder nacheinander klingender Töne, er umfasst auch die vielfältigen Beziehungen, die zwei Töne miteinander eingehen können.

Man unterscheidet in der Intervalllehre:

a.das Distanzprinzip

b.das Komplementärprinzip

c.das Enharmonikprinzip

d.das Klangprinzip

a. Das Distanzprinzip

Das Distanzprinzip handelt vom Abstand zweier Töne zueinander. Die in der Musik gebräuchlichen Intervallbezeichungen gehen auf lateinische Ordnungszahlen zurück und meinen grundsätzlich die Distanz zweier Stammtöne zueinander. So bedeutet Sekunde (lat. secundus = der zweite): der zweite Stammton vom Ausgangston, wenn man diesen mitzählt.

Innerhalb der Oktave werden grundsätzlich unterschieden:

Reine Intervalle – Prime, Quarte, Quinte und Oktave (diese Intervalle können nicht klein oder groß sein),

Kleine und große Intervalle – Sekunden, Terzen, Sexten und Septimen (zwischen „groß“ und „klein“ ist jeweils eine halbe Stufe, ein sogenannter Halbton, Unterschied), Übermäßige und verminderte Intervalle – alle reinen, kleinen und großen Intervalle, die durch Vorzeichen zusätzlich erhöht oder erniedrigt werden.

Beispiel 1.11. – Distanzprinzip der Intervalle bis zur Oktave

Reine Intervalle

Kleine und große Intervalle

Übermäßige Intervalle (Ü)

„Tritonus“*

* Tritonus – eigenständige Bezeichnung für die übermäßige Quarte, Abstand von 3 Ganztönen

Verminderte Intervalle (V)

Bedingt durch die in der temperierten Stimmung vorgegebenen Äquidistanz der Töne innerhalb der Oktave ergeben sich oberhalb des Oktavrahmens keine neuen Verhältnisse. Das Distanzprinzip der Intervalle oberhalb der Oktave wird nach der Formel „Oktave + …“ fortgesetzt, wobei bis zur „Oktave + Quinte“ eigenständige Bezeichnungen üblich sind:

Oktave + kleine Sekunde = kleine None

Oktave + große Sekunde = große None

Oktave + kleine Terz = kleine Dezime

Oktave + große Terz = große Dezime

Oktave + Quarte = Undezime

Oktave + Quinte = Duodezime

Leseprobe Sample

Beispiel 1.12. – Gebräuchliche Intervallbezeichnungen oberhalb der Oktave

b. Das Komplementärprinzip

Das Komplementärprinzip ordnet die Intervalle unter dem Gesichtspunkt ihrer gegenseitigen Ergänzung zur Oktave (lat.-frz. komplementär = sich gegenseitig ergänzend).

Dabei ergänzen einander:rein und rein

klein und groß

übermäßig und vermindert

Prime und Oktave

Sekunde und Septime

Terz und Sexte

Quarte und Quinte

Sexte und Terz

Septime und Sekunde

Oktave und Prime

Leseprobe

c. Das Enharmonikprinzip

Unter „Enharmonik“ wird die verschiedene Notierung und Benennung von Tönen verstanden, die aufgrund der temperierten Stimmung gleich klingen. Die notationsmäßige Umbenennung zweier gleich klingender Töne wird „enharmonische Verwechslung“ genannt.

In der Intervalllehre werden all jene Intervalle dem Enharmonikprinzip zugeordnet, die verschieden notiert werden und dennoch gleich klingen.

Beispiel 1.14.

Beispiel 1.15. – Auswahl von enharmonisch verwechselbaren Intervallen

d. Das Klangprinzip

Das Klangprinzip ordnet die Intervalle nach dem Gesichtspunkt ihrer harmonischen Stabilität bzw. Instabilität. Dabei unterscheidet man konsonante und dissonante Intervalle

Zu den konsonanten Intervallen (lat. consonare = zusammenklingen) rechnen Tonbeziehungen, die einen hohen Verschmelzungsgrad aufweisen und keiner Weiterführung bedürfen, weil sie Bestandteile eines Dur- oder Molldreiklangs sind.

Zu den konsonanten Intervallen zählen: Primen, Quinten, Oktaven, Terzen und Sexten.

Unter dissonanten Intervallen (lat. dissonare = auseinanderklingen) versteht man Tonbeziehungen, die durch Reibung und Schärfe gekennzeichnet sind und die im harmonischen Sinne als auflösungsbedürftig gelten (Auflösung der Dissonanz in eine Konsonanz).

Zu den dissonanten Intervallen zählen: Sekunden und Septimen; alle übermäßigen und verminderten Intervalle.

Eine Mittelstellung nimmt die Quarte ein, die je nach Auffassung konsonant oder dissonant sein kann (Auffassungskonsonanz).

Beispiel 1.16. – Konsonante Intervalle

Beispiel 1.17. – Dissonante Intervalle (mit Auflösung in die Konsonanz)

Beispiel 1.18. – Auffassungskonsonanz/-dissonanz Quarte

Tonleitern

Tonleitern sind ordnende Zusammenstellungen des Tonmaterials, welches ein Musikstück bestimmt.

Dabei wird der Grundton zum Ausgangs- und Endpunkt eines nach dem Prinzip der Stufenfolgen angelegten Tonsystems, das als Tonleiter lediglich die Materialzusammenstellung, als Tongeschlecht jedoch die typischen Merkmale erkennen lässt.

Grundlagen der Allgemeinen Musiklehre

Beschränkt sich der Komponist bei der Wahl der Töne auf die in der jeweiligen Tonleiter vorzufindenden, so verbleibt er im Bereich der Diatonik (gr.-lat. = durch die Tonfolge hindurch). Weicht er vom Tonleitermaterial ab und benutzt er weitere Töne, so müssen diese durch Akzidentien (Versetzungszeichen) kenntlich gemacht werden. Da diese sich im Notenbild als „Einfärbung“ äußern, wird eine solche Diatonik-Erweiterung als Chromatik (gr.-lat. Chroma = Farbe) bezeichnet.

Beispiel 1.19.

– Vergleich von C-dur-Tonleiter und C-chromatischer Halbtonleiter

Im Mittelalter unterschied man 8 Tongeschlechter, die sogenannten Kirchentonarten (Modi). Es waren – nach griechischem Vorbild (bei Übernahme-Irrtümern) – mit Namen griechischer Volksstämme (dorisch, phrygisch, lydisch, mixolydisch) belegte Tonleitermodelle, die Ausschnitten aus unserer C-dur-Tonleiter entsprechen (die authentischen von den Stufen d, e, f, und g aus, die plagalen, mit dem Zusatz „hypo“ [gr. = unter], jeweils eine Quarte darunter). Zu Beginn der Neuzeit ergänzte ein humanistischer Musikgelehrter (Glareanus) dieses System um 4 weitere Modi – die Ausschnitte von a (aeolisch) und von c (ionisch) aus als authentische nebst ihren plagalen – und gelangte so zu 12 Tonleitermodellen (Dodekachordon, 1547). Von eben diesen setzten sich im Laufe des 17. Jahrhunderts zwei mehr und mehr durch, das Ionische (c bis c) und das Aeolische (a bis a), verdrängten allmählich die anderen Modi und wurden zu unserem Dur und Moll

– 6 authentische Kirchentonarten

page

Die nach der Abspaltung von Ionisch als Dur und Aeolisch als Moll verbleibenden 4 authentischen Kirchentonarten Dorisch, Phrygisch, Lydisch und Mixolydisch weichen in jeweils einem Ton von Dur bzw. Moll ab. Diese Abweichung ist zugleich das spezifische Merkmal einer jeden Kirchentonart.

Es ist:Dorisch = Moll mit großer Sexte („dorische Sexte“)

Phrygisch = Moll mit kleiner Sekunde („phrygische Sekunde“)

Lydisch = Dur mit übermäßiger Quarte („lydische Quarte“)

Mixolydisch = Dur mit kleiner Septime, d.h. ohne Leitton („mixolydische Septime“)

Bei der Transposition der Kirchentonarten (Transposition = Übertragung in eine andere Tonart) sollte deshalb die systematische Übersicht des Beispiels 1.21. zu Hilfe genommen werden.

Beispiel 1.21. – Erkennungsmerkmale der Kirchentonarten Dorisch, Phrygisch, Lydisch und Mixolydisch

2.Hauptdreiklänge und Kadenz

Unter „Harmonielehre“ wird die Lehre von den Klangbeziehungen in der dur-moll-tonalen Epoche der Musikgeschichte zwischen etwa 1600 und 1900 verstanden. Die Harmonielehre stellt allerdings kein fest umrissenes System von dauerhaft gültigen Sätzen auf. Ihre Bedingungsfelder stehen vielmehr in Bezug zur jeweils gültigen Tonsprache der verschiedenen Epochen innerhalb dieser 300 Jahre Musikgeschichte. Dabei eint alle Epochen jedoch die Tatsache, dass das Material zur harmonischen Gestaltung aus den diatonischen, d.h. den leitereigenen Dreiklängen einer Tonleiter gewonnen wird.

Hierbei zeigt sich, dass die Dreiklänge auf der I., IV. und V. Stufe von besonderer Bedeutung sind.

Drei Gründe sind es, die diese Klänge von jeher gegenüber den anderen ausgezeichnet haben:

1.Sie sind von gleicher Intervallstruktur und somit Durdreiklänge, die einzigen im Durgeschlecht.

2.Sie weisen in ihrer Summe sämtliche Töne der Tonleiter auf.

3.Die Anordnung der Grundtöne zueinander ist die einer Quinte (vgl. Bsp. 2.2. „Quintverwandtschaft“).

Da die Dreiklänge auf der I., IV. und V. Stufe in der Lage sind, die jeweilige Tonart eindeutig zu bestimmen und festzulegen, werden sie Hauptdreiklänge genannt.

Die Klänge auf der II., III., VI. und VII. Stufe sind demgegenüber von untergeordneter Bedeutung; man nennt sie Nebendreiklänge

Um eine Tonart zu festigen und zu bekräftigen, muss man die Hauptdreiklänge in einer bestimmten Reihenfolge anordnen.

Das Prinzip dieser Anordnung ist die Geschlossenheit der Klangfolge. Sie wird mit den Hauptdreiklängen in dem Gerüst der (vielfältig erweiterungsfähigen und abwandelbaren) Kadenz erzielt.

Seit etwa einhundert Jahren werden die Hauptdreiklänge mit eigenen Namen belegt, die ihre Funktion bezeichnen:

Dreiklang auf der I. Stufe = Tonika( T)

Dreiklang auf der IV. Stufe = Subdominante( S)

Dreiklang auf der V. Stufe = Dominante( D)

Das Kadenzschema stellt sich danach wie folgt dar: T – S – D – T.

Die Bezeichnungen Tonika, Subdominante und Dominante stammen von Hugo Riemann aus dessen gegen Ende des vorigen Jahrhunderts (1893) begründeter Funktionstheorie, die auf Erkenntnissen von Jean-Philippe Rameau (Traité de l’harmonie, 1722) beruht. Damit trat an die Stelle der rein mechanisch zählenden Stufenlehre ein Konzept, das in das Wesen der Musik, in ihre inneren Zusammenhänge einführt – eine revolutionäre Entdeckung, die auch gehörpsycholgisch von eminenter Bedeutung ist. Das noch eher oberflächliche Verständnis des in Beispiel 2.4. dargestellten Kadenzschemas bedarf einer tiefergehenden Untersuchung, etwa durch Anordnung der Dreiklänge auf der Quintengeraden.

Die Quintengerade ist unendlich: steigend nach oben in den Kreuzbereich ( # ), fallend nach unten in den B-Bereich ( b).

Die häufig zu findende Anordnung der Tonarten im „Quintenzirkel“ ist insofern sachlich falsch, als die Tonarten Fis-dur und Ges-dur hier scheinbar identisch sind. In Wirklichkeit aber liegen sie – nämlich harmonisch – 12 Quinten auseinander.

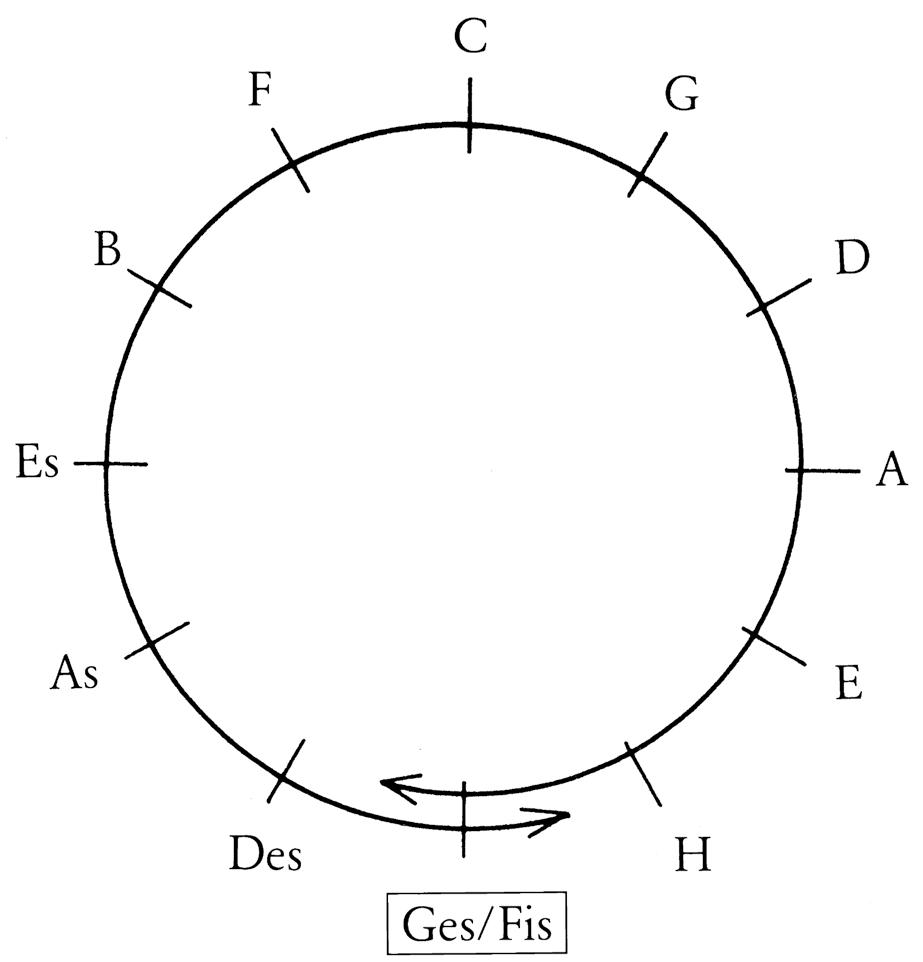
Die Ursache der akustischen Identität von Fis-dur und Ges-dur (bzw. anderen enharmonisch verwechselbaren Tonarten) liegt im Prinzip der temperierten Stimmung (vgl. Kapitel 1). Optisch veranschaulichen lässt sich dieses Quintengeschehen besser mit einer Spirale, bei der die enharmonisch gleichgesetzten Töne übereinanderliegen (vgl. Bsp. 2.6.).

Beispiel

Die Anordnung der Klänge der C-dur-Kadenz (Bsp. 2.4.) stellt sich im Ausschnitt der Quintengeraden nun folgendermaßen dar:

Beispiel 2.7. – C-dur-Kadenz in der Quintengeraden

Vom Ausgangspunkt C-dur ergibt sich zunächst ein harmonischer Abstieg um eine Quinte nach F-dur: 1; es erfolgt ein zwei Quinten umfassender Aufstieg nach G-dur: 2, von dem aus ein erneuter Quintfall abwärts (G-dur nach C-dur) zu beobachten ist: 3

In diesem zweimaligen Quintfall liegt die ursächliche Bedeutung des Begriffs Kadenz (lat. cadere = fallen)

Beispiel 2.7. veranschaulicht aber auch die Bedeutung der in der Funktionstheorie gebräuchlichen Bezeichnungen der Hauptdreiklänge:

Tonika – der „tonische“ Akkord (lat. tonus = Spannung), der Dreiklang , der im Zentrum aller harmonischen Spannungsfelder steht und dessen Grundton mit dem Grundton der Tonart identisch ist,

Dominante – (lat. dominari = herrschen), der Dreiklang, der die obere Region der Tonika harmonisch repräsentiert und dessen Kräfte von oben auf die Tonika einwirken (deshalb auch Oberdominante), Subdominante – (lat. sub = unter, unterhalb), der Dreiklang, der die untere Region der Tonika vertritt (deshalb auch Unterdominante).

ZUSAMMENFASSUNG

Die Dreiklänge auf der I., IV. und V. Stufe einer Durtonleiter werden Hauptdreiklänge genannt. Werden sie in der Reihenfolge I – IV – V – I angeordnet, so festigen und bekräftigen sie als Kadenz die jeweilige Tonart. Die Funktionstheorie weist den Hauptdreiklängen im Kadenzablauf eine spezifische „Funktion“ zu und bezeichnet den Dreiklang auf der I. Stufe als Tonika, den auf der IV. Stufe als Subdominante und den auf der V. Stufe als Dominante.

Aufgabe 2.B.1.

Die Kadenzen folgender Tonarten sind in Tonartenschrift zu notieren. Die Quintengerade (Bsp. 2.5.) mag als Orientierung hilfreich sein.

Die Qualitäten der Hauptdreiklänge

1. Die Tonika

Die Tonika ist Anfangs- und Endpunkt der harmonischen Entwicklung in einem fest umrissenen formalen Ablauf; sie hat zugleich Zentrumsfunktion, indem alle Klänge der herrschenden Tonart sich immer wieder auf sie beziehen lassen. (Ihr übermäßig gehäuftes Auftreten kann ebenso sinnvoll sein wie ihr Fehlen, etwa bei ständigem Umspieltwerden von Klängen anderer Funktionen.)

Die Tonika erscheint in der Regel am Anfang, grundsätzlich aber am Schluss des Werkes oder eines hieraus abgegrenzten Teiles. Ihr kommt dadurch die Aufgabe zu, tonal wichtige Begrenzungspunkte zu setzen.

2.Die Dominante

Die Dominante besitzt den nach dem Grundton der Tonika wichtigsten Ton einer Tonart: den Leitton, die Terz der Dominante. Dieser Leitton hat melodische Spannungskraft; seine unabdingbare Tendenz ist die Auflösung aufwärts in den Grundton der Tonika

Daraus folgt: Bei der Verwendung der Dominantfunktion überwiegt der Spannungsgehalt der Verbindung Dominante – Tonika.

Die Verbindung Dominante – Tonika als Schlussformel nennt man authentischen Schluss.

Erscheint die Subdominante nach der Dominante, so wird der Leitton in die als unbefriedigend empfundene Subdominantquinte geleitet.

Die Verbindung Dominante – Subdominante gilt (zunächst) als fehlerhaft.

Beispiel

3.Die Subdominante

nach Dominante

Im Gegensatz zur Dominante enthält die Subdominante keine Strebetöne.

Da es ihr an dem unbedingten Drang zur harmonischen Fortführung fehlt, bildet sie ein eher entspannendes Moment. Innerhalb des Kadenzvorgangs allerdings dient die Subdominante als notwendige Abrundung und Ergänzung der Tonalitätsgrundierung; hier entfaltet der Subdominantklang seine Qualitäten als „Gegenspieler“ zu den quintverwandten Klängen Tonika und Dominante.

Der Klanggehalt der Subdominante bildet den wichtigen Gegensatz zum Spannungsgehalt der Dominante.

Beispiel 2.10. – Klanggehalt der Subdominante im Volkslied „Wo bist du denn gewesen“

Die Verbindung Subdominante – Tonika als Schlussformel nennt man plagalen Schluss. Dieser gilt im Vergleich zum authentischen Schluss als „schwächer“, da ihm die Leittonspannung fehlt.

Leseprobe

(Allerdings kann die „Schwäche“ der Verbindung Subdominante – Tonika als Schlussformel eines meist größeren Satzes auch von besonderer Bedeutung sein. Plagale Wendungen werden z.B. von Händel häufig als Abschluss eines von authentischen Spannungen bestimmten oratorischen Satzes gewählt.)

ZUSAMMENFASSUNG

Die Fähigkeit der Tonika liegt in der Zentrierung des sie umgebenden Akkordmaterials. Sie ist zugleich in einem fest umrissenen formalen Ablauf Endpunkt der harmonischen Entwicklung.

Bei der Dominante überwiegt das Spannungsverhältnis zur Tonika, während die Qualitäten der Subdominante vorwiegend im klanglich entspannenden Moment liegen (Dominante = Spannungsgehalt, Subdominante = Klanggehalt).

Kadenzvorgänge im Kinder- und Volkslied

Viele Kinder- und Volkslieder beschränken sich in ihrer harmonischen Grundhaltung auf die Hauptdreiklänge.

Die Untersuchung des Liedes „Winde wehn, Schiffe gehn“ weist die Grundsätze kadenzieller Vorgänge am praktischen Beispiel auf; sie macht zugleich deutlich, dass melodische Abläufe immer in harmonische Vorgänge eingebettet sind (latente Harmonik).

Beispiel 2.12. – Lied „Winde wehn, Schiffe gehn“

Anmerkungen

Takt 1die Tonika etabliert sich

Takt 2–3 die Tonika stabilisiert sich

Leseprobe

Takt 4Öffnung zur Dominante („Halbschluss“), zur Überbrückung vermittelt der Ton a (mit Hilfe der Tonika) zwischen Dominante und Subdominante

Takt 5die „Klangergänzung“: Subdominante als Klanggehalt, gleichzeitig als melodischer Höhepunkt

Takt 6„Rückfall“ in den Ausgangspunkt der Tonika; Beginn der Schlusskadenz

Takt 7erst- und einmaliger Harmoniewechsel innerhalb eines Taktes (harmonische Verdichtung, „Beschleunigung“); dadurch besonders starke Strebefähigkeit in den Schlusstakt

Takt 8Tonika als Schlussakkord (authentischer Schluss)

Aufgabe 2.A.

Der Tonsatz zum Choral „Es ist gewisslich an der Zeit“ ist mit Funktionsbezeichnungen zu versehen.

Für die nachstehenden Aufgabentypen sind folgende Lösungsschritte zu empfehlen:

Melodie spielen und versuchen, die „latente Harmonik“ herauszuhören, – Hauptdreiklänge der jeweiligen Tonart herausfinden (aufschreiben!), – Funktionsbezeichnungen eintragen,

erneut spielen (zweistimmig: Melodie und Grundtöne der Hauptdreiklänge), eventuell korrigieren

für die Aufgaben B. Vorschläge des Lösungsteils zum Vergleich heranziehen.

Aufgabe 2.B.2. Lied „Hafermähn“

Aufgabe 2.B.3. Bänkellied „Sabinchen“

Aufgabe 2.B.4. Lied „Old Mac Donald has a farm“

Aufgabe 2.C.

Choral „Ich singe dir mit Herz und Mund“

Aufgabe 2.D.

Gospel „Hört, wen Jesus glücklich preist“

Leseprobe Sample page

3. Die Grundlagen des vierstimmigen Tonsatzes

I. Grundlagen

Zur praktischen Darstellung von harmonischen Abläufen bedient man sich seit jeher des vierstimmigen Satzes.

Die vier beteiligten Vokalstimmen Sopran (S), Alt (A), Tenor (T) und Bass (B) entsprechen den vier Lagen der menschlichen Stimme.

1. Die Umfänge der Stimmlagen

Die Umfänge der vier Stimmlagen orientieren sich an den Gegebenheiten des Chorgesangs Folgende Umfänge gelten für alle künftigen Übungen als verbindlich:

Leseprobe

Dabei ist zu beachten, dass der Abstand zweier benachbarter Stimmen die Oktave nicht überschreiten sollte; nur der Bass darf bis zu einer Duodezime (= Oktave + Quinte) vom Tenor entfernt sein. Dies gilt aus klanglichen wie aus stimmlichen Gründen.

Im Hinblick auf die ersten eigenen Satzübungen präge man sich auch die unterschiedlichen Funktionen der Stimmen im Tonsatz ein: Sopran hat als höchste Stimme des Satzes uneingeschränkte Führungsqualität und muss – als Träger der Melodie – immer erkennbar, d.h. hörbar bleiben, Alt wurde früher als hohe Männerstimme, wird heute als tiefe Frauenstimme angesehen (lat. altus = tief/hoch), Tenor wurde früher von Knaben ausgeführt und ist (u.a. deshalb) als hohe Männerstimme an den Oberstimmen Sopran und Alt zu orientieren, Bass hat als Träger des akkordischen Geschehens die Qualität einer Fundamentalstimme; der Abstand zum Tenor darf bis zu einer Duodezime reichen, ohne dass der Satz dabei an klanglichem Zusammenhalt verliert.

2. Bewegungsarten

Es werden in der Musik vier Bewegungsarten unterschieden:

Geradbewegung – zwei oder mehrere Stimmen bewegen sich in gleicher Richtung in ungleichen Intervallen (Bsp. 3.3.),

Dies ist eine Leseprobe.

Nicht alle Seiten werden angezeigt.

Haben wir

Ihr Interesse geweckt?

Bestellungen nehmen wir gern über den Musikalienund Buchhandel oder unseren Webshop entgegen.

This is an excerpt.

Not all pages are displayed.

Have we sparked your interest?

We gladly accept orders via music and book stores or through our webshop.

Thomas Krämers „Harmonielehre im Selbststudium“ bietet in erster Linie eine methodische Anleitung zur Eigenarbeit. Dieser Aspekt ist seit der Neuausgabe 2006 noch stärker betont.

Durch die systematische Gliederung und den umfangreichen Lösungsteil ist das Buch jedoch auch weiterhin für die pädagogische Arbeit hervorragend geeignet. Zahlreiche Beispiele aus der Musikliteratur aller Epochen veranschaulichen die einzelnen Fragestellungen.

Thomas Krämer (* 1952) absolvierte ein umfangreiches Studium an der Hochschule für Musik Detmold. Er war Musiklehrer, Kirchenmusiker, Privatdozent und von 1985 bis 2018 Professor für Musiktheorie an der Hochschule für Musik Saar. Zusätzlich lehrte er 27 Jahre lang Harmonielehre und Kontrapunkt an der Universität des Saarlandes.

Aus diesen vielfältigen Lehrerfahrungen heraus hat Thomas Krämer im Verlag Breitkopf & Härtel folgende Fachbücher zu Grundfragen der Musiktheorie geschrieben:

– Harmonielehre im Selbststudium

– Praktische Harmonieübungen

– Lehrbuch der harmonischen Analyse

– Lexikon Musiktheorie

(gemeinsam mit Manfred Dings)

– Musikwissen! 231 Fragen und Antworten

Als Würdigung der weiten Verbreitung und hohen Akzeptanz seiner Bücher wurde Thomas Krämer von der Hochschule für Musik Saar die Ehrendoktorwürde (Dr. h. c.) verliehen.