8-klas-geometria-burda-2025 by Орко

УДК 514*кл8(075.3) Б93

Рекомендовано Міністерством освіти і науки України (наказ Міністерства освіти і науки України від 21.02 2025 № 347)

Підручник розроблено за модельною навчальною програмою «Геометрія. 7–9 класи» для закладів загальної середньої освіти (авторський колектив програми: М. І. Бурда, Н. А. Тарасенкова, Д. В. Васильєва)

У 7 класі ви ознайомилися з

кальних кутів, паралельних та

трикутників, кола; навчилися застосовувати

ників до розв’язування задач.

Тепер ви розширите й поглибите свої

знаєтеся про властивості

трикутників, навчитеся знаходити площі трикутників і чотири

кутників, ознайомитеся з новими способами

понять. Перевірити, як засвоєно матеріал параграфа,

допоможуть

рольні

Номери

кольором.

Скориставшись

глибити й розширити свої знання.

ЕЛЕМЕНТАРНІ ГЕОМЕТРИЧНІ

1. Скільки прямих можна провести через: 1) дві точки; 2) три точки; 3) чотири точки? Зробіть малюнки.

2. Проведіть прямі АВ і СD, що перетинаються в точці О, яка лежить між точками А і

назви: 1) променів; 2) доповняльних променів.

, С і D.

3. На прямій a позначили точки K, L і M. Відомо, що точки K і M лежать по один бік від точки L, а точка K не лежить між точками L і M. Розмістіть ці точки на прямій (зробіть малюнок).

4. Три будинки А, В і С розміщені на прямолінійній вулиці. Будинки А і В розташовані по один бік

будинку С, а будинок В

розміщується між будинками А і С. Зробіть малюнок.

5. Чи лежить точка С на відрізку АВ, якщо: 1) АВ = 10 см, АС = 45 мм, ВС = 0,55 дм; 2) ВС = 41 мм, АС = 0,5 дм, АВ = 9,6 см?

6. Відстань між містами на карті становить 5 см. Скільки кілометрів потрібно пройти туристам, якщо масштаб карти 1 : 300 000?

7. Відрізок завдовжки 12 см поділено на дві нерівні частини.

йдіть відстань між серединами цих частин.

10.

12. Бібліотека, школа й кінотеатр розташовані

лою. Знайдіть відстань між бібліотекою та

якщо відстань між бібліотекою й кінотеатром дорівнює 600 м, а між кінотеатром і школою — у три рази менша.

13. OC — бісектриса кута AOB. Знайдіть: 1) ∠АОВ, якщо ∠АОC = 25°; 2) ∠BОC, якщо ∠АОB = 64° .

14. Чи проходить промінь ОС між сторонами

кута АОВ, якщо: 1) ∠АОС = 92° , ∠ВОС = 43° , ∠АОВ = 48°; 2) ∠АОС = 30° , ∠ВОС = 65° , ∠АОВ = 95°?

15. На скільки градусів повернеться

хвилинна стрілка за: 1) 1 хв; 2) 5 хв; 3) 10 хв?

ВЗАЄМНЕ

16. Знайдіть суміжні кути, якщо один із

них: 1) на 34° менший від іншого; 2) утричі більший за інший.

17. Один із суміжних кутів удвічі більший за інший. Яка градусна міра цих

кутів?

18. Дві прямі перетинаються.

23.

24.

кута.

25. Знайдіть кути при двох паралельних прямих

кута.

26. Доведіть, що бісектриси внутрішніх односторонніх

паралельних прямих і січній перетинаються.

27. Доведіть, що бісектриси двох внутрішніх

29.

третьою, якщо: 1) сума двох

у 8 разів більший за інший.

31. Чи можна утворити трикутник

різків завдовжки:

1) 3 см, 5 см, 9 см; 2) 5 см, 4 см, 2 см?

32. Чи існує трикутник зі сторонами: 1) 2 см, 2 см, 4 см; 2) 5 см, 12 см, 13 см?

33. Як зміниться периметр трикутника, якщо всі його сторони:

1) збільшити на 3 см; 2) збільшити у 3 рази;

3) зменшити в 1,5 раза; 4) зменшити на 1,5 см?

34. Як зміниться довжина сторони рівностороннього

якщо його периметр:

1) зменшити на 12 см;

2) збільшити в 6 разів?

35.

36.

37.

трикутники з периметрами 16 см і 19 см. Яка довжина медіани?

38. Периметр рівнобедреного трикутника дорівнює 16 см. Медіана, проведена до основи, поділяє його на два трикутники з периметрами по 12 см. Яка довжина висоти, проведеної до основи?

39. У рівнобедреному прямокутному трикутнику з вершини прямого

1) 12 см; 2) 15 см?

40. Знайдіть висоту даху, крокви якого

прямокутного трикутника, якщо основа цього трикутника

нює 8 м.

41. Відрізки AB і CD перетинаються в точці О так, що AO = OB, CO = OD. Знайдіть: 1) відрізок АC, якщо ВD = 10 см; 2) ∠ВАD, якщо ∠АВС = 72° .

42. Відрізки АВ і CD перетинаються в точці О так, що АО = ОВ, ∠CBO = ∠DAO. Яка довжина відрізка АС, якщо ВD = 8 см?

43. Доведіть, що в рівнобедреному трикутнику: 1) бісектриси кутів при основі — рівні; 2) висоти, проведені до бічних сторін, — рівні; 3) медіани, проведені до бічних сторін, — рівні.

44. Доведіть, що коли бісектриса зовнішнього кута

45. Знайдіть невідомі кути a, b, g трикутника АВС, якщо: 1) a = 36° , b = g; 2) b = 30° , a : g = 2 : 3.

46.

48.

49.

50.

51.

52.

53.

сторін, як у трикутнику

59. Діаметр круглої заготовки деталі дорівнює 50 мм, а діаметр виробу 46 мм. Якої товщини шар металу було знято під час виготовлення деталі?

60. Хорда кола перетинає діаметр під кутом 30° і ділиться ним на відрізки 8 см і 10 см. Знайдіть відстань від кінців хорди до діаметра.

61. Діаметр АВ перетинає хорду CD під прямим кутом, М — точка їх перетину. Чи завжди правильна рівність: 1) АМ = ВМ; 2) СМ = DМ? Відповідь поясніть.

62. На озері правильної круглої форми розташований маленький острів. Знайдіть найкоротший прямий маршрут катера, який сполучатиме дві точки берега й матиме проміжну

63. Дано коло з центром О та радіусом

всіх його радіусів?

2) Яку фігуру утворюють усі точки Х такі, що ОХ = 2R?

64.

страль так, щоб два населені пункти В і С розташовувались по різні

65.

66.

67.

про чотирикутник, його елементи та класифікацію чотирикутників;

які властивості сторін і кутів окремих видів чотирикутників: паралелограма, прямокутника, ромба, квадрата, трапеції;

як розпізнавати ці фігури;

що таке центральні та вписані

яка їхня градусна міра;

які властивості й ознаки чотирикутників,

навколо кола;

як застосовувати властивості

під час розв’язування задач.

§ 1. ЧОТИРИКУТНИК

1. Що таке чотирикутник

Ситуація. Нічна хуртовина занесла снігом подвір’я. Зранку батько з мамою та двома дітьми Ігорем і Катрусею вийшли розчистити доріжки, щоб можна було обійти подвір’я «за колом». Батько розчищав доріжку від будинку до хвіртки, мама від будинку до літньої кухні, Ігор від літньої кухні до сарайчика, а Катруся від сарайчика до хвіртки. Яка фігура утворилася на подвір’ї?

Запам’ятайте! Наприклад, на малюнку 1 точки A, B, C, D — вершини чотирикутника, відрізки AB, BC, CD, DA — його сторони. Кути DAB, ABC, BCD, CDA —

кути чотирикутника.

і однією буквою: ∠A, ∠B, ∠C, ∠D.

Записуємо: ABCD, або BCDA, або CDAB і т. д.

Чотирикутник позначають, послідовно записуючи його вершини, починаючи з будьякої.

Для чотирикутника на малюнку 1 записи, наприклад, ADBC чи CDBA — неправильні.

Чому фігури, зображені на малюнках 2 і 3, не є чотирикутниками? Поміркуємо.

У фігури на малюнку 2 відрізки AC і BD перетинаються, а у фігури на малюнку 3 точки A, D і C лежать на одній прямій.

Мал. 2

2. Елементи чотирикутника

Дві вершини, два кути або дві сторони чотирикутника можуть бути або сусідніми, або протилежними. Наприклад, у чотирикутнику ABCD (мал. 4) вершини A і D, ∠A і ∠D, сторони AD і AB — сусідні, а вершини A і C, ∠A і ∠C, сторони AD і BC — протилежні.

Мал. 3

Який елемент чотирикутника одержимо, якщо продовжити його сторону?

Зовнішній кут.

Кут, суміжний з кутом чотирикутника, називають зовнішнім кутом чотирикутника. Запам’ятайте!

На малюнку 6 ∠CDK — зовнішній кут чотирикутника ABCD при вершині D.

Щоб знайти зовнішній кут чотирикутника,

наприклад ∠CDK чотирикутника ABCD (мал. 6), застосуйте властивість суміжних кутів та обчисліть: ∠CDK = 180° – ∠ADC.

3. Опуклі та неопуклі чотирикутники

На малюнку 7 чотирикутник ABCD лежить з одного боку від

прямої, яка проходить через дві його сусідні вершини.

кожний

Наприклад, на малюнку 8 чотирикутник

Запам’ятайте!

Периметром

Поміркуйте

Задача Периметр чотирикутника дорівнює 24 см. Найменша його сторона дорівнює 3 см, а найбільша — 9 см. Одна з двох інших його сторін удвічі менша від іншої. Знайдіть невідомі сторо

ни чотирикутника.

Розв’язання Нехай ABCD — даний чотирикут

ник, у якого CD = 3 см, AD = 9 см, РABCD = 24 см (мал. 9). Нехай AB = х. Тоді, за умовою, BC = 2х.

Оскільки Р = 24 см, то х + 2х + 3 + 9 = 24. Звідси х = 4. Отже, AB = 4 см, BC = 8 см.

Відповідь: 4 см, 8 см.

5. Властивість сторін чотирикутника

Чи може чотирикутник

такі сторони: 1 см, 2 см, 3 см, 6 см? Не може. Справді, найбільший

6. Властивість кутів чотирикутника

Дослід. Накресліть довільний чотирикутник і виміряйте транспортиром

кути. Чому дорівнює їх сума?

Запам’ятайте!

Теорема (про суму кутів чотирикутника)

Сума кутів чотирикутника дорівнює 360° .

Дано: чотирикутник ABCD (мал. 10).

Довести: ∠A + ∠B + ∠C + ∠D = 360° .

Доведення. У даному чотирикутнику ABCD проведемо діагональ AC (мал. 11). Одер

жали два трикутники — DABC і DACD. Тоді ∠A = ∠BAC + ∠CAD, ∠С =∠BCA + ∠ACD. Звідси: ∠A + ∠B + ∠C + ∠D = = ∠BAC +∠CAD +∠B + ∠BCA + ∠ACD + ∠D = = (∠BAC + ∠B + ∠BCA) + (∠ACD + ∠D+ ∠CAD) = = 180° + 180° = 360° .

Чи можуть усі кути чотирикутника бути гострими?

Ні.

Справді, сума чотирьох гострих

Так.

1. У вас може виникнути запитання: Які відмінні властивості мають опуклі й неопуклі чотирикутники? Діагоналі опуклого чотирикутника ABCD (мал. 5) перетинаються, і кожна з них розбиває його на два трикутники. А діагоналі неопуклого чотирикутника MNKP (мал. 13) не перетинаються, і лише одна з них розбиває його на два трикутники. Кожний кут опуклого чотирикутника менший від 180° Якщо чотирикутник неопуклий, то один з його кутів більший за 180° .

2. На відміну від трикутника, чотирикутник фігура нежорстка. Якщо взяти чотири планки та з’єднати їх за допомогою шарнірів, то форму одержаного чотирикутника можна змінювати (мал. 14).

3. Термін «діагональ» походить від грецького слова diagonios, що означає «той, що йде від кута до кута». Цей термін став загальноприйнятим лише у XVIII ст.

4. Для стародавніх греків математика була насамперед геометрією. Значний внесок у розвиток геометрії зробив давньогрецький вчений Платон (428 р. до н. е. 348 р. до н. е.).

Словничок

УкраїнськаАнглійська/ English Німецька/ Deutsch Французька/ Français чотирикутникquadrangleViereck (n)quadrilatère

qr.orioncentr.com.ua/8lZcl Пригадайте головне

1. Що таке чотирикутник?

2. Як позначають чотирикутник?

3. Що таке діагональ чотирикутника?

4. Що таке зовнішній кут чотирикутника?

5. Що таке периметр чотирикутника?

6. Як

72'. Чи правильно, що в чотирикутнику: 1) три вершини лежать на одній прямій; 2) жодні три вершини не

73'. Яка з фігур, зображених на малюнках 15–17, є чотирикутником ABCD?

74'. Чи правильно, що зовнішній кут чотирикутника:

1) не суміжний із кутом чотирикутника;

2) суміжний із кутом чотирикутника;

3) вертикальний із кутом чотирикутника?

75'. Яке з наведених тверджень правильне?

Периметр чотирикутника — це сума довжин:

1) трьох його сторін;

2) чотирьох сторін;

3) усіх сторін і діагоналей.

76'. Чи правильно вказано градусну

ABCD на малюнках 18 і 19? Відповідь поясніть.

77'. Назвіть зображені

MNPK при вершині:

1) N;

2) М; 3) K.

78°.

79°.

80°. Периметр чотирикутника дорівнює 210 см, а

сторони чотирикутника.

81°. Чи може чотирикутник мати такі сторони: 1) 1 см, 2 см, 3 см, 4 см; 2) 18 см, 6 см, 5 см, 6 см?

82°. Чи може чотирикутник мати такі сторони: 2 см, 3 см, 5 см, 10 см?

83°. За даними на

84°.

87°. Чи можуть кути чотирикутника дорівнювати: 1) 55°, 75°, 100°, 80°; 2) 145°, 85°, 70°, 65°?

88°. Чи можуть кути чотирикутника

89°. За даними таблиці

90°. Чи

91°.

92°. Якщо

93°.

кут — прямий.

94°. Знайдіть зовнішній

якщо:

95°. Знайдіть зовнішній кут при вершині А чотирикутника ABCD, якщо: 1) ∠А = 80°; 2) ∠А = 120° .

96°. Піраміда має п’ять граней, чотири з яких

97°.

98.

100. Три сторони чотирикутника дорівнюють 10 см, 15 см і 20 см. Чи може периметр чотирикутника дорівнювати: 1) 90 см; 2) 72 см; 3) 115 см?

101. Доведіть, що кожна діагональ чотирикутника менша від його півпериметра.

102. Доведіть, що сума діагоналей чотирикутника менша від

периметра.

103. У чотирикутнику ABCD діагональ BD ділить

кути B і D навпіл (мал. 24).

Доведіть, що AB = CB і DA = DC.

104. Доведіть, що в чотирикутнику ABCD (мал. 24)

діагоналі AC і BD — перпендикулярні, якщо AB = CB і DA = DC.

105. Знайдіть кути чотирикутника, якщо вони пропорційні числам: 1) 1, 2, 3 і 4; 2) 4, 6, 12 і 14.

106. Знайдіть кути чотирикутника, якщо вони пропорційні числам 1, 2, 4 і 5.

107. Якою в чотирикутнику може бути найбільша кількість кутів: 1) тупих; 2) прямих; 3) гострих?

108. Чи можна накреслити чотирикутник, у якому: 1) три кути прямі, а четвертий — тупий; 2) один із кутів дорівнює сумі трьох інших?

109. Сума двох кутів чотирикутника, прилеглих до

110.

111.

зовнішні кути.

112. Доведіть, що сума

117.

118*.

119*.

що сума двох протилежних сторін

ша від суми його діагоналей.

120*. У чотирикутнику ABCD бісектриси кутів А і В перетинаються в точці M, а бісектриси кутів C і D — у точці N. Доведіть, що сума кутів AMB і CND дорівнює 180° .

121*. Бісектриси зовнішніх кутів чотирикутника ABCD, перетинаючись, утворюють чотирикутник MNKP (мал. 28). Доведіть, що сума протилежних кутів чотирикутника MNKP дорівнює 180° .

122. На малюнку 29 зображено земельну ділянку в масштабі 1 : 2000. Межі ділянки потрібно обгородити парканом. Скільки стовпців необхідно для огорожі, якщо відстань між ними має бути 4 м?

123. Потрібно виготовити

4. Розробіть найкоротший маршрут заводського

найменшою?

з території заводу, у кожному населеному пункті забирає

зупинці та привозить усіх разом на завод. 5. Розробіть найкоротший маршрут заводського автобуса після робочого дня, якщо він вирушає з території заводу, у кожному населеному пункті висаджує робітників

Запам’ятайте!

Чотирикутник, у якому

Паралелограм.

попарно паралельні, називається паралелограмом.

Наприклад, у чотирикутнику АВСD (мал. 31) AD || BC і АВ || DС, тому цей чотирикутник — паралелограм.

Який елемент паралелограма одержимо, якщо з

ни проведемо перпендикуляр до протилежної сторони?

Висоту.

Висотою паралелограма називають перпендикуляр, проведений із будь-якої точки однієї сторони до паралельної їй сторони (або до її продовження).

Запам’ятайте! На малюнку 32 відрізки ВМ і ВN — висоти паралелограма АВСD. Висоту паралелограма можна провести з будьякої точки його сторони.

2. Властивості паралелограма

Теорема (властивість

Доведемо, що

АО = СО, DО = ВО. Розглянемо DАОD і DСОВ. У них ВС = АD як протилежні сторони паралелограма, ∠СВО = ∠АDО як внутрішні різносто

ронні кути при паралельних прямих ВС і АD та

січній ВD, ∠ВСО = ∠DАО (ВС || АD, АС — січна).

Отже, DАОD = DСОВ за стороною та прилеглими до неї кутами. З рівності трикутників АОD і СОВ випливає: АО = СО, DО = ВО.

Щоб довести рівність відрізків

рівність трикутників,

3. Паралелограм як основа піраміди

Якщо основою піраміди SАВСD є паралелограм АВСD (мал. 36 ), то:

1) АВ || DС і АD || ВС;

2) АВ = DС і АD = ВС;

3) ∠А = ∠С і ∠B = ∠D.

Дізнайтеся більше

1. Назва «паралелограм» (parallelogrammon) походить від поєднання грецькиx слів: «паралелос» той, що йде поряд, і «грамма» лінія.

Цей термін уперше трапляється в «Началах» Евкліда (ІІІ ст. до н. е.). Хоча замість терміна «паралелограм» давньогрецький учений спочатку вживав словосполучення «утворена паралельними лініями площа» (мається на увазі частина площини, обмежена двома парами паралельних прямих).

2. Ада Августа Лавлейс (Байрон) (10.12.1815–27.11.1852) відома англійська математикиня, яку називали «Королева паралелограмів». Вперше зро-

qr.orioncentr.com.ua/Uq1Ln

1. Який чотирикутник

2. Що таке висота паралелограма?

125'. Чи правильно, що паралелограмом є чотирикутник, у якому:

1) сусідні сторони паралельні;

2) дві протилежні сторони паралельні;

3) протилежні сторони попарно паралельні?

126'. Чи правильно, що висотою паралелограма є:

1) пряма; 2) промінь; 3) відрізок?

127'. Чи правильно, що в будьякому паралелограмі:

1) сусідні сторони рівні;

2) протилежні сторони попарно рівні;

3) сусідні кути рівні;

4) протилежні кути попарно рівні?

128'. Чи правильно вказано градусні міри кутів паралелограма

129°. У паралелограмі МNРK МN = 1,2

NР = 0,4 дм.

дорівнюють сторони РK і МK? Відповідь поясніть.

130°. У паралелограмі АВСD АВ = 5 см, ВС = 10 см. Чому дорівнюють сторони АD і DС? Відповідь поясніть.

131°. За даними таблиці 4 знайдіть

134°.

135°.

136°.

137°.

кути АDС і ВАD, якщо: 1) a = 120° , b = 60°;

138°.

поясніть.

139°. А, В, С, D — кути паралелограма АВСD. Накресліть

таблицю 5 і заповніть її. Таблиця

1) лише

143°. За даними на малюнку 44 знайдіть кути

паралелограма АВСD.

144°. Знайдіть кути паралелограма, якщо:

1) один з його кутів на 50° менший від іншого;

2) сума двох його кутів дорівнює 120° .

145°. Знайдіть кути паралелограма, якщо один з його кутів у 3 рази більший за інший.

146°. Доведіть, що діагональ паралелограма ділить його на два рівні трикутники.

147°. Чи правильно вказано довжини відрізків діагоналей паралелограма на малюнку 45?

Відповідь поясніть.

148°. АВСD — паралелограм (мал. 46).

За даними на малюнку знайдіть:

1) відрізки ОС і ОD; 2) діагоналі АС і ВD; 3) сторони АD і DС.

149°. Основа піраміди — паралелограм АВСD (мал. 47). Знайдіть кути паралелограма, якщо ∠А = 35° .

150°. Основа піраміди — паралелограм АВСD (мал. 47). Знайдіть усі сторони паралелограма, якщо АВ = 3 см, ВС = 0,6 дм.

151. Доведіть, що бісектриси кутів, прилеглих до однієї сторони паралелограма, взаємно перпендикулярні.

152. Доведіть, що бісектриси двох протилежних кутів паралелограма паралельні.

Якщо в задачі дано бісектрису кута паралелограма, то утворений трикутник (DАВK на малюнку 48) — рівнобедрений. Скористайтеся його властивостями.

153. Бісектриса

154. У паралелограмі АВСD бісектриса кута А перетинає сторону ВС в точці K. Знайдіть: 1) ВK і KС, якщо АВ = 6 см, АD = 9 см; 2) АD, якщо АВ = 4 см, KС = 11 см.

155. У паралелограмі АВСD бісектриса кута А перетинає сторону ВС в точці K. Знайдіть периметр паралелограма, якщо АD = 14 см, ВK : KС = 3 : 4.

156. Із точки М, узятої на основі АС рівнобедреного трикутника АВС, проведено прямі, паралельні бічним сторонам (мал. 49). Доведіть, що периметр утвореного паралелограма МNВK не залежить від положення точки М.

157. Із точки, узятої на основі АС рівнобедреного

трикутника АВС, проведено прямі, паралельні бічним сторонам (мал. 49). Знайдіть периметр паралелограма МNВK, якщо АВ = 15 см.

158. У паралелограмі АВСD через точку О перетину

діть, що: а) OE = OF; б) BE = DF; в) CE = AF.

159.

сторони ВС та АD паралелограма, якщо ВЕ = 5 см, АF = 4 см.

160. Знайдіть кути паралелограма, якщо два його кути відносяться як: 1) 4 : 5; 2) 3 : 7.

161. Знайдіть кути паралелограма, якщо:

1) один із них у 4 рази більший за суму двох інших; 2) половина одного кута дорівнює третині іншого.

162. Знайдіть кути паралелограма, якщо: 1) два його кути відносяться як 2 : 3; 2) один з його кутів дорівнює

166.

167.

170*. У паралелограмі гострий кут

24 см.

171*.

висотами паралелограма, проведеними з

1) тупого кута; 2) гострого кута.

172*. Один із кутів паралелограма в три рази

два відрізки, які

1. Яким може бути взаємне розміщення стрижня АВ та лінії центрів CD?

А. АВ ⊥ CD.

Б. АВ || CD.

В. АВ і CD лежать на прямих, що не перетинаються.

Г. Не можна визначити.

2. Уявіть, що стрижень АВ зламався. Як його відновити?

Запропонуйте власний план дій.

177. Для проведення паралельних прямих використовують паралельні лінійки (мал. 54).

1. Поясніть, як виготовити такий прилад.

2. Поясніть, як користуватися цим приладом.

3. На якій властивості ґрунтується будова приладу?

Мал. 54

§ 3. ОЗНАКИ ПАРАЛЕЛОГРАМА

1. Ознака паралелограма за попарною рівністю протилежних сторін

Ситуація. Батько лагодив огородження сходів і попросив Юлю з’ясувати, чи паралельні нові перила і лінія підйому сходів. Юля виміряла довжини двох балясин та відстані між їхніми верхніми й нижніми кінцями і встановила, що ці довжини відповідно рівні. Вона стверджує, що кожна пара балясин

Дано: ABCD — чотирикутник (мал. 55), AB = DC, BC = AD.

Довести: ABCD — паралелограм.

Доведення. У даному чотирикутнику ABCD проведемо діагональ BD (мал. 56).

Розглянемо DBCD і DDAB. У них BD — спіль

на сторона, DC = AB і BC = AD за умовою.

Отже, DBCD = DDAB за трьома сторонами. Із рівності трикутників випливає: ∠CBD = ∠ADB

і ∠CDB = ∠ABD. Кути CBD і ADB — внутріш

ні різносторонні при прямих BC і AD та січній

BD. Тому BC || AD. Так само кути CDB і ABD — внутрішні різносторонні при прямих AB і DC та січній BD. Тому AB || DC. Оскільки в чотирикут

нику ABCD BC || AD і AB || DC, то, за означенням, цей чотирикутник — паралелограм.

паралельні?

Мал. 57 Чи можна вважати чотирикутник паралелограмом, якщо в ньому

Не можна.

На малюнку 57 AB = CD, BC || AD, але чотирикутник ABCD — не паралелограм. 2.

Запам’ятайте!

Теорема (ознака паралелограма)

Якщо в чотирикутнику дві протилежні сторони рівні й паралельні, то такий чотирикутник — паралелограм.

Дано: ABCD — чотирикутник (мал. 58), AB = DC, AB || DC.

Довести: ABCD — паралелограм.

Доведення. У даному чотирикутнику ABCD проведемо діагональ АС (мал. 59). Розглянемо DABC і DСDА. У них АС — спільна сторона, AB = DC за умовою, ∠BAС = ∠DCА як внутрішні різносторонні кути при пара

лельних прямих AB і DC та січній АС. Отже, DABC = DСDА за двома сторонами та кутом між ними. Із рівності трикутників випливає: ∠DАC = ∠BСА. Але кути DАC і BСА — внутрішні різносторонні при прямих BC і AD та січній АС. Тому BC || AD.

Оскільки в чотирикутнику ABCD BC || AD (за доведеним) і AB || DC (за умовою), то, за означенням, цей чотирикутник — паралелограм.

3. Ознака паралелограма за діагоналями

Задача (ознака паралелограма) Якщо діагоналі чотирикутника точ-

кою їх перетину діляться навпіл, то такий чотирикутник — паралелограм. Доведіть.

Розв’язання

Нехай ABCD — даний чотирикутник, О — точка перетину його діагоналей і ВО = DО, АО = СО (мал. 60).

Доведемо, що ABCD — паралелограм.

Розглянемо DBОC і DDОА. У них ВО = DО, АО = CО за умовою, ∠ВОC = = ∠DОА як вертикальні. Отже, DBОC = DDОА за двома сторонами

4. Як переконатись, що основою чотирикутної піраміди є паралелограм

Щоб установити, що основою чотирикут-

ної піраміди є паралелограм, доведіть, що в чотирикутнику основи:

або АВ || DС і АD || ВС,

або АВ = DС і АD = ВС,

або AB = DC і AB || DC,

або ВО = DО і АО = СО (мал. 61).

Дізнайтеся більше

Мал. 61

Вам доводилося стикатись із поняттями «необхідно», «достатньо», «необхідно й достатньо». За таблицею 6 розгляньте

цих понять.

Чотирикутник є

паралелограмом

паралелограмом Протилежні сторони чотирикутника попарно рівні

Чотирикутник є

що

є взаємно оберненими. Їх можна об’єднати і сформулювати так: Для того щоб чотирикутник був паралелограмом,

ньо, щоб його протилежні сторони були попарно рівними. Замість того щоб говорити «необхідна й достатня умова», іноді кажуть «необхідна й достатня ознака», або, частіше, просто «ознака». Тому

паралелограма sign of the parallelogram Anzeichen eines Parallelogramms propriétés du parallélogramme

qr.orioncentr.com.ua/fxreo

1. Доведіть, що коли протилежні сторони

2. Доведіть, що коли в чотирикутнику дві

сторони рівні й паралельні, то він є паралелограмом.

3. Доведіть, що коли діагоналі чотирикутника точкою їх перетину діляться навпіл, то такий чотирикутник паралелограм.

4. Поясніть, як переконатися, що даний чотирикутник є паралелограмом.

Усне тренування

1. Запишіть у дециметрах: 6 мм, 6 см, 6 м, 6 км; 2. Запишіть у метрах: 10 мм, 10 см, 10 дм, 10 км.

Розв’яжіть задачі

178'. Чи є паралелограмом чотирикутник, у якому дві протилежні сторони: 1) рівні; 2) паралельні; 3) паралельні й рівні? Відповідь поясніть.

179'. Чому чотирикутник на малюнку 62 не є паралелограмом?

180'. Накресліть два рівні й паралельні відрізки завдовжки 4 см. Їхні кінці сполучіть відрізками так, щоб вони не перетиналися. Чому утворений чотирикутник є паралелограмом?

181'. Який із чотирикутників, зображених

лелограмом? Відповідь

184°. Дано чотирикутник KLMN. Доповніть дані в таблиці 7 так, щоб наведений висновок був правильним.

см

3 дм25 мм

дм

6 см

Висновок KLMN — паралелограм

185°. Відомі довжини двох сторін чотирикутника АВСD: 1) АВ = 3 см, АD = 2 см; 2) ВС = 2,5 см, СD = 3,7 см. Які довжини мають бути в інших сторін цього чотирикутника, щоб був правильним висновок: АВСD — паралелограм?

186°. Доведіть, що чотирикутник АВСD — паралелограм, якщо:

1) АВ = 3 см, ВС = 0,4 дм, СD = 30 мм, АD = 40 мм;

2) АВ + ВС = 7 см, ВС – СD = 3 см, АD = ВС = 5 см; 3) АВ : ВС : СD : АD = 2 : 1 : 2 : 1.

187°. Доведіть, що чотирикутник АВСD — паралелограм, якщо:

1) АВ = 0,5 дм, ВС = 2,7 см, СD = 5 см, АD = 27 мм;

2) АВ – АD = 3 см, СD = 2ВС, АВ = СD = 6 см.

188°. У чотирикутнику АВСD АВ = СD, ВС = АD. Знайдіть:

1) AB, якщо CD = 4 см;

2) BC, якщо AD = 2 см;

3) ∠В, якщо ∠D = 120°;

4) ∠А, якщо ∠С = 60° .

Щоб довести рівність (паралельність) двох відрізків:

1) виділіть на малюнку чотирикутник, протилежними сторонами якого є ці відрізки;

2) доведіть, що чотирикутник — паралелограм;

3) зробіть висновок: відрізки рівні (паралельні) як протилежні сторони паралелограма.

Висновок KLMN — паралелограм

191°. Відомі довжини двох сторін чотирикутника АВСD:

1) АВ = СD = 2 см; 2) ВС = АD = 7 см.

Які сторони цього чотирикутника мають бути паралельними, щоб був правильним висновок: АВСD — паралелограм?

192°. Доведіть, що чотирикутник АВСD — паралелограм, якщо:

1) AD || BC, АD = 0,5 дм, ВС = 50 мм;

2) AB || CD, АВ = 2 см, СD = 0,02 м;

3) AB = CD, ∠ВАD = 45° , ∠АDС = 135° .

193°. Доведіть, що чотирикутник АВСD — паралелограм, якщо:

1) AB || CD, АВ = 3 см, СD = 30 мм; 2) AD = BC, ∠АВС = 120° , ∠ВАD = 60° .

194°. У чотирикутнику АВСD діагоналі

Доповніть дані таблиці 9 так, щоб

правильним.

см

см Висновок АВСD — паралелограм

195°. Діагоналі чотирикутника KLMN перетинаються

довжини їхніх частин: 1) KO = 2 см, NО = 3 см; 2) LО = 3,5 см, МО = 1,9 см. Які довжини мають бути

199°. На сторонах ВС і АD паралелограма АВСD

позначено точки Е і F так, що ЕС = АF (мал. 67). Доведіть, що чотирикутник АЕСF — паралелограм.

200°. У піраміді SАВСD (мал. 68) АВ = 4 см, ВС = 0,7 дм, DС = 40 мм, АD = 70 мм. Доведіть, що основа піраміди — паралелограм.

201°. Доведіть, що основою піраміди SАВСD (мал. 68) є паралелограм, якщо АВ || DС, АВ = 65 мм, DС = 6,5 см.

202. На сторонах АВ, ВС, СD і АD паралелограма АВСD позначено точки E, M, K і N відповідно і так, що BM = DN, BE = DK (мал. 69). Доведіть, що EMKN — паралелограм.

Мал. 67

Мал. 68

203. На сторонах паралелограма АВСD відкладено рівні відрізки AM, DN, CP, BK, як показано на малюнку 70. Доведіть, що MNPK — паралелограм.

Мал. 69

204. У паралелограмі АВСD точка М — середина сторони АD, а N — середина сторони ВС. Доведіть, що ВNDМ — паралелограм.

205. АВСD — паралелограм (мал. 71), AE = CF. Доведіть, що відрізки CE і AF рівні й паралельні.

206. АВСD — паралелограм (мал. 72), ОМ = ОN. Доведіть, що МВND — паралелограм.

Мал. 72

207. МВND — паралелограм (мал. 72), ОА = ОС. Доведіть, що АВСD — паралелограм.

208. Медіану ВD трикутника

209. Бісектриса кута А паралелограма АВСD перетинає сторону

N. Доведіть, що АМСN — паралелограм.

210. Якщо дві протилежні сторони чотирикутника паралельні, а одна з діагоналей ділить іншу навпіл, то такий чотирикутник — паралелограм. Доведіть.

211. АВСD — паралелограм (мал. 73), АМ = KС, BN = РD. Доведіть, що MР = NK і МР || NK.

212. Діагоналі паралелограма АВСD перетинаються в точці О. Доведіть, що чотирикутник MNPK, вершинами якого є середини відрізків ОА, ОВ, ОС і ОD, — паралелограм.

213. У чотирикутнику ABCD відомо, що AB = CD, ∠А + ∠D = 180° . Доведіть, що AD = BC.

214. У чотирикутнику АВСD ∠А + ∠В = 180° і

діть, що протилежні сторони чотирикутника рівні.

215*. На продовженнях сторін АВ, ВС, СD і DА паралелограма АВСD позначено відповідно точки K, P, M і E так, що AK = BP = CM = DE. Доведіть, що чотирикутник KPME — паралелограм.

216*.

218*.

220.

Чи має рацію Денис?

Так.

шафи – форму прямокутника. Така невідповідність не дозволить зібрати шафу правильно. Денис вирішив перевірити за допомогою шкільного косинця, чи є кути каркаса прямими.

Прямокутник — один із видів паралелограма. На малюнку 78 ви бачите паралелограм ABCD, що є прямокутником. Дайте означення прямокутника та порівняйте його з наведеним у підручнику. Паралелограм, у якого

ється прямокутником. Запам’ятайте!

Так.

Оскільки прямокутник — окремий вид паралелограма, то він має всі властивості паралелограма:

1) протилежні сторони рівні;

2) протилежні кути рівні;

3) діагоналі точкою їх перетину діляться навпіл.

Крім цих властивостей, прямокутник має ще особливу властивість.

Запам’ятайте!

Теорема (властивість діагоналей прямокутника)

Діагоналі прямокутника рівні.

Дано: ABCD — прямокутник (мал. 79).

Довести: AC = DB.

Доведення. Розглянемо прямокутні трикут

ники ACD і DBA. У них AD — спільний катет, а катети AB і DC рівні як протилежні сторони парале

лограма. Отже, DAСD = DDВA за двома катетами.

З рівностей трикутників випливає: AC = DB. Властивості

паралелограма

1. AB = DC, AD = BC

2. ∠A = ∠C, ∠B =∠D

3. AО = CО, BО = DО особлива

4. AC = DB

У них AD — спільна сторона, AC = DB за умовою, AB = DC як протилежні сторони паралелограма.

Отже, DABD = DDCA за трьома сторонами. Звідси випливає, що ∠A = ∠D. Але ∠A = ∠C і ∠D = ∠B як протилежні кути паралелограма, тому ∠A = = ∠C = ∠D = ∠B. За властивістю кутів чотирикутника, ∠A + ∠C + ∠D + ∠B = 360°. Отже, ∠A = = ∠C = ∠D = ∠B = 360° : 4 = 90°, тобто паралелограм ABCD — прямокутник. Щоб установити, що даний паралелограм — прямокутник, доведіть, що в ньому: або всі кути прямі (означення прямокутника), або діагоналі рівні (ознака прямокутника).

Чи можна стверджувати, що чотирикутник, у якому діагоналі рівні, є прямокутником? Не можна (мал. 81).

Мал. 81

Потрібно ще перевірити, чи виконується одна з ознак паралелограма. Наприклад, чи діляться діагоналі точкою їх перетину навпіл.

4. Прямокутник як грань паралелепіпеда і піраміди

Ви вже знаєте, що прямокутник — окремий вид паралелограма. Можливі такі види паралелепіпеда:

1) прямокутний паралелепіпед (мал. 82), у нього всі грані є прямокутниками;

2) прямий паралелепіпед (мал. 83), у нього бічні

ники, а основи — паралелограми;

3) похилий паралелепіпед (мал. 84), у

Виникає запитання: Чи можна дати інші означення прямокутника? Поміркуємо. У молодших класах прямокутник визначали як чотирикутник, усі кути якого прямі. Тепер ми визначили прямокутник як

паралелограма. Можна сказати, що прямокутник це: паралелограм, у якого всі кути рівні

становить 360

, тоді

із них дорівнює 90°); паралелограм, який має прямий кут (справді, у паралелограма сусідні кути в сумі становлять 180° , а протилежні кути рівні. Тому, якщо один із кутів паралелограма прямий, то і три

(n)rectangle

qr.orioncentr.com.ua/11bYy Пригадайте головне

1. Що таке прямокутник?

2. Сформулюйте та доведіть властивість діагоналей прямокутника.

3. Поясніть, як установити, що даний паралелограм є прямокутником.

Усне тренування

Обчисліть: 1) 5,86 + 4,14; 0,79 + 9,21; 8,62 + 1,38; 2) 3,56 + 6,44; 4,25 + 5,75; 1,13 + 8,87.

Розв’яжіть задачі

222'. Чи правильно, що прямокутником

у якому: 1) усі сторони рівні; 2) усі

223'.

224'.

226'. Чи правильно, що паралелограм є прямокутником, якщо

гоналі: 1) нерівні; 2) рівні?

227°. ABCD — прямокутник (мал. 85). За

1) AD і DC; 2) BD; 3) AO, OC, BO і

на

228°. ABCD — прямокутник (мал. 86). За

кути 1, 2 і 3.

229°. Знайдіть діагоналі прямокутника, якщо їх сума дорівнює: 1) 12 см; 2) 6 см; 3) 18 мм.

230°. ABCD — прямокутник (мал. 87).

За даними на малюнку знайдіть: 1) його діагоналі; 2) суму його діагоналей.

231°. О — точка перетину діагоналей прямокутника ABCD. Доведіть: 1) трикутники AOD, BOC, AOB і DOC — рівнобедрені; 2) DAOB = DDOC, DBOC = DAOD.

232°. На малюнках 88, 89

234°.

(мал. 91, 92).

235°.

(мал. 93).

236°.

237°. Знайдіть периметр прямокутника, якщо: 1) одна його сторона дорівнює 4 см, а інша — утричі більша; 2) одна його сторона дорівнює 10 см, а інша — удвічі менша.

238°. Одна сторона прямокутника дорівнює 12 см, а інша — на 4 см більша. Знайдіть периметр прямокутника.

239°. Чотирикутник KLMN

240°.

242°. Діагоналі паралелограма АВСD утворюють рівні трикутники САВ і DВА. Доведіть, що АВСD — прямокутник.

243°. Доведіть, що коли в паралелограмі хоча б один кут прямий, то він є прямокутником.

244°. Якщо в паралелограмі хоча б один кут прямий, то його діагоналі рівні. Доведіть.

245°. Висота прямокутного паралелепіпеда дорівнює 8 см, ширина — у 2 рази менша за висоту, а довжина — на 16 см більша за ширину. Знайдіть ширину й довжину прямокутного паралелепіпеда.

246°. Висота прямокутного паралелепіпеда дорівнює 18 см, ширина — у 3 рази менша за висоту, а довжина — у 4 рази більша за ширину. Знайдіть ширину й довжину прямокутного паралелепіпеда.

247. Діагональ прямокутника дорівнює d й утворює зі стороною кут 30° . Знайдіть меншу сторону прямокутника, якщо: 1) d = 4 см; 2) d = 14 мм; 3) d = 0,44 дм.

248. Менша сторона прямокутника дорівнює

прямокутника, якщо вони перетинаються під кутом 60° і: 1) а = 10 см; 2) а = 0,25 дм; 3) а = 7 мм.

249. Доведіть, що коли в прямокутнику сторона

діагоналі, то кут між ними дорівнює 60° .

250. Перпендикуляр, проведений із вершини кута прямокутника до діагоналі, ділить цей кут у

2 : 3. Знайдіть:

1) кути, утворені діагоналями зі сторонами прямокутника;

2) кут між проведеним перпендикуляром та іншою діагоналлю.

251. Периметр прямокутника дорівнює 48 см. Знайдіть сторони прямокутника, якщо:

1) дві його сторони відносяться як 2 : 3;

2) відстань

252.

254.

1) 15 см; 2) 3,8 дм.

255.

паралелограм — прямокутник.

256. Якщо в паралелограмі сума двох протилежних кутів

180°, то він є прямокутником. Доведіть.

257. Якщо всі кути чотирикутника рівні, то він є прямокутником. Доведіть.

258. Доведіть, що коли в паралелограмі кути, прилеглі

ни, рівні, то він є прямокутником.

259. Діагоналі паралелограма утворюють рівні кути

стороною. Доведіть, що цей паралелограм є прямокутником.

260. У основи паралелепіпеда всі кути рівні. Доведіть, що

лепіпед — прямокутний.

261. У паралелепіпеда гранями є чотирикутники, у яких усі

є прямими. Доведіть, що цей паралелепіпед — прямокутний.

262*. Діагоналі прямокутника ABCD перетинаються в точці

метр трикутника ABD більший

трикутника AOB на 12 см, а периметр прямокутника дорівнює 50,2 см. Знайдіть сторони прямокутника.

263*. У прямокутнику ABCD зі сторонами AB = a і BC = b проведено бісектриси кутів A і D, які перетинають сторону BC

(мал. 94, 95). Знайдіть довжину відрізка MN.

264*.

266*. У рівнобедрений прямокутний трикутник

вписано прямокутник так, що вони мають спільний кут (мал. 96).

1. Доведіть, що периметр прямокутника не залежить від положення його вершини на гіпотенузі.

2. Знайдіть периметр прямокутника, якщо катет трикутника дорівнює 5 см. 267*. Доведіть, що коли в чотирикутнику діагоналі рівні й у точці перетину діляться навпіл, то такий чотирикутник є прямокутником.

Щоб довести, що чотирикутник є прямокутником, покажіть, що: або цей чотирикутник є паралелограмом, а паралелограм — прямокутником, або три кути чотирикутника — прямі.

268*. У чотирикутнику діагоналі точкою їх перетину діляться навпіл, а один кут — прямий. Доведіть, що цей чотирикутник є прямокутником.

269*. Чотирикутник, у якому протилежні сторони попарно рівні й діагоналі рівні, є прямокутником. Доведіть.

270*. Доведіть, що чотирикутник, у якому діагоналі рівні і дві проти

сторони рівні

271*. Доведіть, що в прямокутному трикутнику медіана, проведена з вершини прямого кута, дорівнює половині гіпотенузи.

Щоб довести рівність двох відрізків, покажіть, що вони є:

або протилежними сторонами прямокутника (паралелограма);

або діагоналями прямокутника;

або частинами діагоналі прямокутника (паралелограма), на які вона ділиться точкою

273. Учень виготовляв рамку прямокутної форми.

Щоб перевірити правильність виготовлення рамки, він перевірив рівність її діагоналей. Чи достатньо такої перевірки? Чому?

274. Якими способами можна перевірити, що даний чотирикутний предмет має форму прямокутника? Відповідь поясніть.

275. На малюнку 98 зображено прилад для вимірювання діаметра колод.

1. Поясніть, як користуватися цим приладом.

2. Чому відлік на горизонтальній лінійці приладу відповідає діаметру колоди?

3. Якщо відлік на горизонтальній лінійці приладу дорівнює 20 см, то який діаметр колоди?

4. Поясніть, як виготовити такий прилад.

276. Провішена на місцевості пряма упирається в будівлю (мал. 99).

Поясніть, як продовжити пряму за будівлю.

1. Що таке ромб

Ситуація. Учні й учениці 8-А класу розробляли емблему своєї спортивної команди для участі в шкільному етапі всеукраїнського змагання «Плічо-пліч. Всеукраїнські шкільні ліги». Футбольні фани Іван та Оля запропонували взяти форму емблеми легендарного футбольного клубу «Динамо» (Київ), бо в ній використано «гармонійний»

Паралелограм, у якого всі сторони рівні, називається ромбом. Запам’ятайте! Чи можна стверджувати, що паралелограм є ромбом, якщо в нього дві сусідні сторони рівні?

Так. Справді, рівність усіх сторін

2. Властивості ромба

Оскільки ромб є окремим видом

властивості паралелограма:

1) протилежні сторони рівні;

2) протилежні кути рівні;

3) діагоналі точкою їх перетину діляться навпіл.

Крім того, ромб має ще особливі властивості.

Запам’ятайте!

Так.

Теорема (властивості діагоналей ромба)

Діагоналі ромба взаємно перпендикулярні.

Діагоналі ромба ділять його кути навпіл.

Дано: ABCD — ромб (мал. 101), О — точка перетину діагоналей.

Довести: AC ⊥ BD; ∠ABD = ∠CBD = ∠ADB = ∠CDB; ∠BAC = ∠DAC = ∠BCA = ∠DCA.

Доведення. За означенням ромба, AB = BC, тому трикутник ABC — рівнобедрений. Оскільки ромб

A C B D O

1. AB = DC, AD = BC

2. ∠A = ∠C, ∠B =∠D

3. AО = ОC, BО = ОD особливі

4. AC ⊥ BD

5. AC і BD — бісектриси

Чи можна встановити не за означенням, що даний паралелограм — ромб?

Так.

Задача (ознака ромба) Паралелограм, діагоналі якого взаємно перпендикулярні, є ромбом. Доведіть.

Розв’язання Нехай ABCD — даний паралелограм, у якому AC ⊥ BD (мал. 102). Доведемо, що ABCD — ромб. Розглянемо DAOB і DAOD. У них AO — спільна сторона, OB = OD за властивістю діагоналей паралелограма, ∠AOB = ∠AOD = 90° за умовою. Отже, DAOB = DAOD за двома сторонами й кутом між ними. Із рівності трикутників

випливає: AB = AD. Тоді AB = CD і AD = BC за властивістю

4. Квадрат і його властивості

Запам’ятайте!

Так.

Прямокутник, у якого всі сторони рівні, називається квадратом.

На малюнку 103 ви бачите квадрат ABCD. Можна дати різні означення квадрата: ромб, у якого всі кути прямі, називається квадратом;

прямокутник, у якого всі сторони рівні, називається квадратом;

паралелограм, у якого всі сторони рівні й усі кути прямі, називається квадратом.

Квадрат має всі властивості паралелограма, прямокутника та ромба.

Основні властивості квадрата подано в таблиці 14. Таблиця 14

ABCD — квадрат

Властивість A B D C O

паралелограма

1. AB = DC, AD = BC

2. ∠A = ∠C, ∠B =∠D

3. AО = ОC, BО = ОD прямокутника ромба

4. AC = BD

5. AC ⊥ BD 6. AC і BD —

7. AB = BC = СD = DА 8. ∠A = ∠B = ∠C =∠D = 90° 5.

Словничок

УкраїнськаАнглійська/ English

Deutsch

Français ромбrhombusRhombus (m) losange квадратsquareQuadrat (n)carré

qr.orioncentr.com.ua/bNAbg

Пригадайте головне

1. Що таке ромб?

2. Сформулюйте та доведіть властивості

3. Доведіть, що паралелограм, діагоналі якого

4. Що таке квадрат?

5. Назвіть властивості квадрата.

тренування

Обчисліть:

1) (15 : 0,5 + 7 : 0,1 – 50) · 0,1; 2) 100 : (0,5 · 40 + 8 : 0,1) – 1.

Розв’яжіть задачі

277'. Чи правильно, що ромбом є паралелограм, у якому: 1) протилежні сторони попарно рівні; 2) усі сторони рівні?

278'. Чи має ромб усі властивості паралелограма? Відповідь поясніть.

279'. Назвіть властивості, які має ромб, але яких не має паралелограм, що не є ромбом.

280'. Чи є ромбом будьякий паралелограм, у якого діагоналі:

1) рівні; 2) взаємно перпендикулярні; 3) ділять кути ромба навпіл?

281'.

2) взаємно перпендикулярні?

282'.

283'. Чи має квадрат усі властивості прямокутника? Відповідь поясніть.

284'. Чи має квадрат усі властивості ромба? Відповідь поясніть.

285'. Чи правильно, що у квадраті:

1) протилежні сторони рівні й паралельні;

2) сусідні сторони рівні та взаємно перпендикулярні;

3) протилежні кути рівні;

4) усі кути рівні?

286'. Чи правильно, що діагоналі квадрата:

1) рівні;

2) взаємно перпендикулярні;

3) ділять кути навпіл;

4) точкою перетину діляться навпіл?

287°. Чи правильно вказано довжини сторін і градусні

на малюнку 106? Відповідь поясніть.

288°. ABCD — ромб (мал. 107). За даними на малюнку знайдіть:

1) BC, AD, DC; 2) AC, BD.

108

289°. ABCD — ромб (мал. 108). За даними на малюнку знайдіть кути 1, 2 і 3.

290°. Знайдіть сторону ромба, якщо його периметр дорівнює: 1) 2,4 дм; 2) 280 мм.

291°. Периметр ромба дорівнює 12 см. Знайдіть сторону ромба.

292°. Доведіть, що діагоналі

293°.

294°.

295°.

296°.

297°.

298°.

299°.

300°.

1) d = 3,2 дм; 2) d = 45 мм.

302°.

304°. Відомі довжини двох паралельних сторін чотирикутника АВСD: 1) АВ = СD = 3 см; 2) ВС = АD = 4 см.

Які елементи цього чотирикутника мають бути перпендикулярними, щоб був правильним висновок: АВСD — ромб?

305°. За даними на малюнку 113 знайдіть: 1) інші сторони квадрата; 2) діагоналі квадрата; 3) кути 1, 2, 3 і 4.

306°. Знайдіть периметр квадрата, якщо точка перетину його діагоналей віддалена від сторони на: 1) 8 см; 2) 0,3 дм.

307°. Знайдіть периметр квадрата, якщо точка перетину його діагоналей віддалена

21 мм.

308°. Дано паралелограм KLMN. Доповніть дані в таблиці 17 так, щоб наведений висновок

вильним.

309°. Доведіть, що паралелограм ABCD

малюнку 114 — квадрат.

310°. Накресліть у

18 (продовження)

3.Усі сторони рівні

4.Усі кути прямі

5. Діагоналі точкою їх перетину діляться навпіл

6.Діагоналі рівні

7. Діагоналі взаємно перпендикулярні

8. Діагоналі ділять кути навпіл

311°. Чи може лише одна грань прямокутного паралелепіпеда

форму квадрата?

312°. Знайдіть суму площ

однієї грані дорівнює 16 см.

313°. Знайдіть суму площ усіх

ребер дорівнює 132 см.

314. Доведіть, що чотирикутник, усі сторони якого рівні, є

315. Паралелограм,

316. Знайдіть кути ромба, якщо його

та — 4,5 см.

317. Доведіть, що висоти ромба рівні.

318. Висота ромба, проведена з вершини

319. Знайдіть

323. У рівносторонній трикутник вписано ромб, який має з ним спільний кут (мал. 115).

1. Знайдіть периметр ромба, якщо периметр трикутника дорівнює 24 см.

2. Доведіть, що сторона ромба дорівнює половині сторони трикутника.

3. Знайдіть довжини відрізків, на які вершини ромба ділять сторони трикутника.

324. У рівнобедрений прямокутний трикутник вписано квадрат, який має з ним спільний кут. Знайдіть периметр квадрата, якщо катет трикутника дорівнює: 1) 8 см; 2) 29 мм; 3) 0,41 дм.

325. Ромб, у якого один кут прямий, — квадрат. Доведіть.

326. AN — бісектриса прямого кута A трикутника ABC (мал. 116); NM і NK — перпендикуляри до катетів. Доведіть, що AMNK — квадрат.

327. Доведіть, що ромб, діагоналі якого рівні, — квадрат.

Мал. 116

Мал. 117

328. На діагоналі BD квадрата ABCD відкладено рівні відрізки BM = DN (мал. 117). Доведіть, що AMCN — ромб.

329. Чи правильні твердження:

1) паралелограм, діагоналі якого взаємно перпендикулярні

рівні, — квадрат;

2) чотирикутник, усі сторони

квадрат;

3) чотирикутник, діагоналі

332*. Вершини протилежних кутів ромба сполучено із серединами його сторін так, як показано на малюнку 118. Доведіть, що утворений чотирикутник MNKL — паралелограм.

333*. Від двох протилежних вершин ромба на його сторонах відкладено рівні відрізки (мал. 119). Доведіть, що утворений чотирикутник PMNK — прямокутник.

334*. Із точки перетину діагоналей ромба проведено перпендикуляри до його сторін. Доведіть, що основи цих перпендикулярів є вершинами прямокутника.

335*. Доведіть, що чотирикутник, вершини якого є серединами сторін прямокутника, — ромб.

336*. Сума периметрів чотирьох трикутників, на які квадрат

ється діагоналями, більша

йдіть діагональ квадрата.

337*. Чотирикутник, діагоналі

тів,

340.

бом. Щоб

переконалася, що краї тканини суміщаються. Чи є

342. Щоб перевірити, чи має стільниця форму квадрата, столяр виміряв її сторони й переконався, що вони рівні.

1. Чи є правильною така перевірка?

2. Чи достатньо виміряти діагоналі стільниці й переконатися, що вони рівні?

3. Чи матиме стільниця форму квадрата, якщо її сторони рівні й діагоналі рівні?

343. Земельна ділянка, яка має форму квадрата, була обнесена парканом. Із часом

лишилося два стовпці у протилежних вершинах квадрата. Як відновити межу ділянки?

344. Наталка вирішила перевірити, чи має серветка

обох половинок серветки сумістилися. Але їй зауважили, що така перевірка є недостатньою. Потрібно перегнути серветку

містяться, то вона має форму квадрата.

1. Чи правильно діяла учениця?

2. Чи правильно їй порадили?

Відповідь поясніть.

1. Теорема Фалеса Ситуація. Учні й учениці 8-А класу на

вони накреслили кут АСВ та відклали на його стороні СА

Запам’ятайте!

лельні ВС (мал. 124).

умовою,

Мал. 126

Відкладемо на промені АС

А3А4, А4А5. Проведемо пряму А5В. Через точки А1, А2, А3, А4

А5В.

частин.

теоремою

Мал. 127

2. Що таке середня лінія трикутника Ситуація. Учні й учениці 8-А класу вирішили продовжити своє мінідослідження, але вже в трикутнику. Вони точно знали, що тут можна застосувати теорему Фалеса. Можливо, це дозволить виявити нові властивості трикутника? У довільному трикутнику АВС через середину М сторони АВ вони провели пряму, паралельну стороні АС (мал. 128). На стороні ВС утворилися рівні відрізки BN і NC. Цей висновок учні підтвердили і вимірюванням, і аналітично. А от відрізок МN цієї прямої примусив їх замислитися. Якщо діяти навпаки, тобто спочатку сполучити середини двох сторін трикутника, то виявляється, що цей відрізок не лише паралельний третій стороні трикутника.

Цей відрізок має довжину,

Середньою лінією трикутника

трикутника Чи можна встановити аналітично властивості середньої лінії трикутника? Так.

Запам’ятайте!

Теорема (властивості середньої лінії трикутника)

Середня лінія трикутника паралельна третій його стороні й дорівнює її половині.

Дано: DАВС (мал. 129), DE — середня лінія.

Довести: 1) DE || AC; 2) 1 . 2 DEAC =

Доведення. 1. Оскільки DE — середня лінія

трикутника АВС, то точка D є серединою відрізка

АВ, а точка Е — серединою відрізка ВС. Проведемо

через точку D пряму, паралельну AC. За теоремою

Фалеса, вона перетинає відрізок ВС в його середині, тобто в точці Е. Тому побудована пряма містить середню лінію DE даного трикутника. Отже, DE || AC. 2. Проведемо пряму EF || AB (мал. 130). За теоремою Фалеса, пряма EF ділить відрізок АС

Задача Доведіть, що середини сторін чотирикут

ника є вершинами паралелограма.

Розв’язання Нехай АВСD — даний чотирикут

ник і M, N, P і K — середини його сторін (мал. 131).

Доведемо, що MNPK — паралелограм.

Проведемо діагональ АС (мал. 132). MN — серед

ня лінія трикутника АВС. Тому MN || AC i 1 . 2 MNAC = KP — середня лінія трикутника ADC. Тому

KP || AC i 1 . 2 KPAC =

Одержали: MN || AC i KP || AC, звідси MN || KP; 1 2 MNAC = i 1 , 2 KPAC = звідси MN = KP.

Отже, протилежні сторони MN i KP чотирикут

ника MNPK рівні й паралельні, тому він — парале

лограм (за ознакою).

Якщо в умові

лінії трикутника. Дізнайтеся більше Давньогрецького вченого Фалеса з Мілета (625–548 рр. до н. е.) вважають одним із семи мудреців

знайшов

людської діяльності. Він займався інженерною справою, був державним діячем, математиком, астрономом. Особливою заслугою Фалеса вважають те, що він увів у математику ідею доведення. Учений довів, що кути при основі рівнобедреного трикутника рівні, що діаметр ділить круг на дві рівні частини, що прямий кут можна вписати в півколо та ін. Як вважають історики, саме Фалес почав застосовувати основні геометричні інструменти циркуль і лінійку. Учений

пірамід

1. Чи існує трикутник, у якого сторони дорівнюють: 4,56, 5,44 і 10; 2,39, 3,61 і 5; 7,65, 1,35 і 6,3?

2. Чи існує трикутник, у якого кути дорівнюють: 20°, 80°, 90°; 55°, 35°, 80°; 18°, 62°, 100°? Розв’яжіть задачі

345'. Чи правильно, що в теоремі Фалеса йдеться про те, що:

1) сторони кута перетинають будьякі прямі;

2) сторони кута перетинають паралельні прямі;

3) усі утворені відрізки дорівнюють один одному;

4) дорівнюють один одному лише відрізки, утворені на одній стороні кута;

5) дорівнюють один одному відрізки, утворені на

стороні кута, але два відрізки

таку саму довжину?

346'.

середини: 1) усіх сторін трикутника; 2) двох сторін трикутника?

347'. Чи правильно, що середня лінія трикутника:

1) перетинає третю сторону трикутника;

2) паралельна третій стороні трикутника; 3) дорівнює половині будьякої сторони трикутника; 4) дорівнює

348°.

349°.

350°. На малюнку 136 АА1 = А1А2 = А2А3 і А1В1 || A2B2 || A3B3. Знайдіть: 1) АВ1, якщо В2В3 = 6 см; 2) В2В3, якщо АВ3 = 12 см.

351°. На малюнку 136 АА1 = А1А2 = А2А3 і А1В1 || A2B2 || A3B3. Знайдіть АВ3, якщо В1В2 = 5 см.

352°. За даними на малюнку 137 доведіть, що АВ1 = В1В2 = В2В3.

353°. Поділіть даний відрізок на вказану кількість рівних частин: 1) 4; 2) 6.

354°. Поділіть даний відрізок на три рівні частини.

355°. За даними на малюнках 138, 139 знайдіть х.

Мал. 136

356. Чи правильно вказано довжини відрізків на малюнку 140? Відповідь поясніть.

357°. DE i EF — середні лінії трикутника АВС, які відповідно паралельні сторонам ВС і АВ. Знайдіть: 1) відрізок FC, якщо DE = 4 см; 2) відрізок BD, якщо EF = 7 см.

358°. Знайдіть середні лінії трикутника, якщо його сторони дорівнюють: 1) 8 см, 5 см, 7 см; 2) 30 мм, 40 мм, 50 мм.

359°. Сторони трикутника дорівнюють 9 см, 10 см і 14

360°.

Мал. 140

361°. Знайдіть середні лінії рівностороннього трикутника, якщо його периметр дорівнює: 1) 24 дм; 2) 48 мм.

362°. Периметр рівностороннього трикутника дорівнює 12 см. Знайдіть його середні лінії.

363°. Знайдіть периметр рівностороннього трикутника, якщо його середні лінії дорівнюють: 1) 0,8 дм; 2) 100 мм.

364°. Середні лінії рівностороннього трикутника дорівнюють 4 см. Знайдіть його периметр.

365°. Знайдіть периметр трикутника, якщо його середні

ють: 1) 3 см, 5 см, 6 см; 2) 7 см, 9 см, 12 см; 3) 8 см, 10 см, 12 см.

366°. Визначте вид трикутника, якщо: 1) усі його середні лінії рівні; 2) дві його середні лінії рівні.

367°. Знайдіть діагоналі паралелограма, якщо два відрізки, що сполучають середини його сусідніх сторін, дорівнюють: 1) 0,6 дм і 0,9 дм; 2) 100 мм і 14 см.

368°. Знайдіть діагоналі паралелограма, якщо два відрізки, які сполучають середини його сусідніх сторін, дорівнюють 5 см і 11 см.

369°. Точки E і F — середини ребер куба

373. На малюнку 143 АА1 = А1А2 = А2А3 = А3А4 і

А1В1 || A2B2 || A3B3 || A4B4. Знайдіть:

1) АВ3, якщо різниця довжин відрізків АВ4 і В2В3 дорівнює 9 см;

2) В1В4, якщо різниця довжин відрізків АВ4 і В1В3 дорівнює 8 см;

3) АВ4, якщо різниця довжин відрізків В1В4 і В1В2 дорівнює 10 см.

374. Сторони трикутника дорівнюють а, b і c. Знайдіть сторони іншого трикутника, вершини якого є серединами сторін даного трикутника, якщо:

1) а = 8 см, b = 10 см, с = 12 см; 2) а = 0,5 дм, b = 12 см, с = 1,3 дм.

375. Складіть формулу та обчисліть периметр трикутника АВС, якщо периметр трикутника, утвореного середніми лініями трикутника АВС, дорівнює:

1) 18 см;

2) 2,4 дм; 3) 300 мм.

376. Середня лінія рівнобедреного трикутника, що паралельна основі, дорівнює 2,5 см, а його периметр — 2,5 дм. Знайдіть сторони трикутника.

377. Знайдіть сторони рівнобедреного трикутника з периметром 40 см, якщо його середня лінія, паралельна основі, дорівнює 5 см.

378. Точки А і В лежать по різні боки від прямої а на відстані 8 см і 4 см від неї (мал. 144). Знайдіть відстань від середини О відрізка АВ до прямої а.

379. Сторони трикутника відносяться як 3 : 4 : 5. Знайдіть сторони трикутника, утвореного середніми лініями даного трикутника, якщо периметр даного трикутника дорівнює: 1) 60 см; 2) 4,8 дм.

380. Сторони трикутника відносяться як 7 : 8 : 9. Знайдіть

381.

382. Прямі, проведені через вершини А, В і С трикутника АВС паралельно протилежним сторонам, утворюють трикутник А1В1С1 (мал. 145).

1. Доведіть, що сторони трикутника А1В1С1 точками А, В і С діляться навпіл.

2. Знайдіть сторони трикутника А1В1С1, якщо АВ = 6 см, ВС = 12 см, АС = 15 см.

3. Знайдіть периметр трикутника АВС, якщо периметр трикутника А1В1С1 дорівнює 48 см.

383. У трикутнику АВС (мал. 146) АВ = 12 см, ВС = 18 см. Сторону АС поділено на три рівні частини й через точки поділу проведено

прямі, паралельні АВ і ВС. Знайдіть:

1) довжини відрізків, утворених на сторонах АВ і ВС; 2) довжини відрізків паралельних прямих, що містяться між сторонами трикутника.

384. Доведіть, що середні лінії трикутника ділять

385. Точки M і N — середини сторін AD i BC паралелограма ABCD. Доведіть, що прямі AN i CM ділять діагональ BD

386. Знайдіть периметр чотирикутника, вершинами якого є середини сторін даного чотирикутника, якщо сума діагоналей чотирикутника дорівнює: 1) 25 см; 2) 3,5 дм.

387. Знайдіть периметр чотирикутника, вершинами якого є середини сторін даного чотирикутника, якщо діагоналі чотирикутника дорівнюють: 1) 4 см і 6 см; 2) 24 см і 25 см.

388. Знайдіть периметр чотирикутника, вершинами якого є середини сторін квадрата, якщо діагональ квадрата дорівнює: 1) 8 см; 2) 1,3 дм.

389. Доведіть, що середини

392.

Побудова (мал. 147). Проводимо MN || AB; відкладаємо на стороні ВС кута відрізок NK = BN; проводимо через точки K і М шукану пряму. Доведіть, що наведена побудова є правильною.

394*. Точка K — середина медіани АМ трикутника АВС. Пряма ВK перетинає сторону АС в точці D. Доведіть, що AC = 3AD.

395*. Доведіть, що точка перетину медіан трикутника ділить кожну медіану у відношенні 2 : 1, починаючи від вершини трикутника.

396*. Доведіть, що три висоти трикутника перетинаються в

397*. Кожну зі сторін трикутника АВС поділено на три рівні частини й точки поділу сполучено відрізками (мал. 148).

1. Знайдіть суму довжин усіх відрізків, які сполучають точки поділу, якщо периметр трикутника АВС дорівнює 36 см.

2. Розв’яжіть задачу за умови, що кожну сторону трикутника поділено на чотири рівні частини.

398*. Через точку М, розміщену всередині кута АВС, проведіть пряму так, щоб її відрізок, який відтинають сторони кута, точкою М ділився у відношенні 1 : 2.

399. Потрібно поділити прямокутну смугу (дошку, кусок жерсті, картону) на п’ять смужок однакової ширини. За малюнком 149 поясніть, як це можна зробити. Чому смуга поділилася прямими на п’ять рівних частин?

400.

цього аркуша.

401. На малюнку 151 показано, як

точки M i N — середини відрізків АС і ВС — та виміряли відстань між точками M i N. Поясніть, чому шукана відстань АВ = 2MN.

402. Може трапитися так, що провісити пряму між точками M i N, як у задачі 401, неможливо (мал. 152).

1. За малюнком поясніть, як виміряти відстань АВ в цьому випадку.

2. Чому шукана відстань АВ = 4M1N1?

Мал. 151 Мал. 152 Мал. 153

403. На малюнку 153 показано, як виміряти відстань між пунктами А і В, якщо до пункту А підійти не можна.

1. Поясніть вимірювання.

2. Чи обов’язково кут В має бути прямим?

404. Три населені пункти А, В і С розташовані на рівнині й не лежать на одній прямій. Потрібно прокласти дорогу, щоб вона пройшла на однаковій

відстані від цих пунктів.

1. Як це зробити? Покажіть на малюнку.

2. Скільки таких доріг можна прокласти?

1. Що таке трапеція

Ситуація. Учні й учениці 8 класу готувалися до шкільного благодійного ярмарку. Для всіх продавчинь вони вирішили пошити нарядні фартухи без нагрудника. Дівчата знайшли кілька залишків тканини трикутної форми й розрізали їх так, як показано на малюнку 154. Для пошиття фартухів взяли нижні частини.

Яку форму мали фартухи? Форму трапеції.

Запам’ятайте!

Трапецією називається чотирикутник, у якому

сторони паралельні, а дві інші — непаралельні.

На малюнку 155 зображено трапецію

ABCD. У ній дві сторони AD і BC паралельні, а дві інші — AB і CD — непаралельні.

Паралельні сторони трапеції називають її

основами, а непаралельні — бічними сторонами. На малюнку 156 AD і BC — основи трапеції, AB і CD — бічні сторони.

Висотою трапеції називають перпенди

куляр, проведений з будьякої точки однієї основи до іншої

(мал. 156).

Трапецію, один із кутів якої прямий, називають прямокутною. Трапеція ABCD (мал. 157) — прямокутна, оскільки ∠A = 90° .

Трапецію, у якої бічні сторони рівні, називають рівнобічною. На

люнку 158 трапеція MNKP — рівнобічна, оскільки MN = KP.

Мал. 157 Мал. 158

Задача (властивість рівнобічної трапеції) У рівнобічній трапеції

Розв’язання Нехай у трапеції ABCD (мал. 159) AB = CD. Доведемо, що кути при основі AD рівні. Проведемо CE || AB. Утворений чотирикутник ABCE — паралелограм, бо його протилежні сторони попарно паралельні. За властивістю парале

лограма, AB = CE, а за умовою, AB = CD. Отже, CE = CD i DCDE — рівнобедрений. Тому ∠CDE = = ∠CED. Але ∠CED = ∠BAD як відповідні кути при паралельних прямих CE і AB та січній АЕ. Звідси ∠CDE = ∠BAE.

Якщо в умові задачі дано трапецію, то корисною буде така допоміжна побудова: проведіть через вершину трапеції пряму, паралельну бічній стороні (мал.

мал. 160), і використайте

На малюнку 161 відрізок MK — середня лінія трапеції ABCD, бо точки M і K — середини бічних сторін AB і CD відповідно.

Які властивості має середня

лінія трапеції?

Запам’ятайте!

Поміркуємо.

Теорема (властивості середньої лінії трапеції) Середня лінія трапеції паралельна основам і дорівнює їх півсумі.

Дано: ABCD — трапеція з основами AD і BC (мал. 162), EF — середня лінія.

Довести: 1) EF || AD, EF || BC, 2) . 2 ADBC EF + =

Доведення. Оскільки EF — середня лінія трапеції ABCD, то AE = BE, DF = CF. Через точ

ки B i F проведемо пряму, яка перетне продов

ження основи AD в точці Q (мал. 163). Розглянемо DBCF і DQDF. У них CF = DF за умовою, ∠BFC = ∠QFD як вертикальні, ∠BCF = ∠QDF

як внутрішні різносторонні кути при паралельних прямих BC i AQ та січній CD. Отже, DBCF = DQDF за стороною та прилеглими до неї кутами. З рівності трикутників випливає: BF = QF, тобто середня лінія EF трапеції є середньою лінією трикутника ABQ.

1) За властивістю середньої лінії трикутни

ка, EF || AQ, тому EF || AD. Оскільки AD || BC, то EF || BC.

Чи є зв’язок між різними видами чотирикутників?

Так.

Подивіться на малюнок 165, на якому зображено вивчені

чотирикутники. Ви бачите, що серед чотирикутників

лелограми (протилежні сторони попарно паралельні) і трапеції (тільки дві протилежні сторони паралельні). Серед трапецій, своєю чергою, — рівнобічні й прямокутні. Якщо в паралелограмі всі сторони рівні

кути прямі, то одержимо ромби або прямокутники. Нарешті, квадрат є окремим видом і ромба (усі сторони рівні), і прямокутника (усі кути прямі), і паралелограма (усі

Мал. 165

midline of a trapezoid Mittellinie eines Trapezes médiane du trapèze

qr.orioncentr.com.ua/KZpew

1. Що таке трапеція?

2. Які сторони трапеції називають основами?

3. Які сторони трапеції називають бічними сторонами?

4. Яку трапецію називають рівнобічною?

5. Яку трапецію називають прямокутною?

7. Сформулюйте та

407'. Чи правильно, що в рівнобічній трапеції (мал. 166):

1) основи рівні; 2) усі сторони рівні;

3) бічні сторони рівні?

408'. Які з наведених тверджень правильні?

У прямокутній трапеції (мал. 167):

1) основи перпендикулярні; 2) один із кутів — прямий; 3) бічна сторона перпендикулярна до основи.

409'.

Чи правильно, що середньою лінією трапеції є: 1) пряма; 2) промінь; 3) відрізок?

410'.

Чи правильно, що середня лінія трапеції:

1) сполучає її вершини;

2) сполучає середини її сусідніх сторін;

3) сполучає середини її бічніх сторін;

4) паралельна бічним сторонам;

5) паралельна основам?

411'. Які з наведених тверджень правильні?

Щоб знайти середню лінію трапеції, потрібно:

1) суму бічних сторін поділити на 2;

2) суму основ поділити на 2;

3) різницю основ поділити на 2.

Мал. 166

Мал. 167

412°. На малюнку 168 зображено трапецію ABCD, у якій AD || BC. Назвіть:

1) основи трапеції; 3) кути, прилеглі до основи;

2) бічні сторони трапеції; 4) кути, прилеглі до бічної сторони.

413°. За малюнками 169, 170 знайдіть:

1) сторону CD рівнобічної трапеції ABCD (мал. 169); 2) кут N трапеції MNKL (мал. 170).

Мал. 168 Мал. 169 Мал. 170

414°. Доведіть,

415°. За даними на малюнках 171–173 знайдіть невідомі кути трапеції ABCD.

Мал. 171 Мал. 172 Мал. 173

416°. ABCD — трапеція з основами AD i BC. Знайдіть: 1) ∠A i ∠C, якщо ∠B = 110° , ∠D = 30°; 2) ∠A i ∠D, якщо ∠B = 125° , ∠C = 145° .

417°. Основою піраміди (мал. 174) є трапеція АВСD (АВ || СD). Знайдіть ∠D цієї трапеції, якщо: 1) ∠А = 160°; 2) ∠А = 135°; 3) ∠А = 95° .

418°. Трапеція АВСD (АВ || СD) є основою піраміди (мал. 174).

якщо ∠В = 120° , ∠D = 40° .

419°.

420°. Накресліть гострокутний трикутник KLМ. Проведіть

що перетинають сторони кута. Позначте точки перетину прямих

423°. MNKL — трапеція з основами ML і NK, NF || KL (мал. 176). Знайдіть: 1) основу ML, якщо MF = 5 см, NK = 2 см; 2) основу NK, якщо ML = 10 см, MF = 7 см. Мал. 177 Мал. 176

424°. BM і CK — висоти рівнобічної трапеції ABCD з основами AD і BC (мал. 177). Доведіть, що DABM = DDCK.

425°. Знайдіть х за даними на малюнках 178–180.

Мал. 178

Мал. 179

426°. Чи правильно вказано довжину середньої лінії трапеції на малюнку 181? Відповідь поясніть.

427°. Основою піраміди SАВСD є трапеція із середньою лінією МK (мал. 182). Знайдіть сторону АD основи піраміди, якщо:

1) МK = 3 см, ВС = 2 см; 2) МK = 11 см, ВС = 7 см; 3) МK = 14,5 см, ВС = 12 см.

428°. Трапеція АВСD (АD || BC) — основа піраміди (мал. 182). Точки М і K — середини сторін АВ і СD основи піраміди. Знайдіть МK, якщо АD = 10 см, ВС = 4 см.

Мал. 180

Мал. 181

Мал. 182

429°. AD i BC — основи трапеції, MN — її середня лінія. Заповніть таблицю 21. Таблиця 21

AD 10 см7 см 11 см9 см

BC 6 см 5 см 15 см MN 8 см9 см10 см

430°. За даними на малюнку 183 знайдіть основи й середню лінію трапеції.

431°. Яка довжина основ і середньої лінії трапеції MNKL (мал. 184)?

432°. Знайдіть периметр трапеції з бічними сторонами с і d та середньою лінією m, якщо: 1) с = 8 см, d = 12 см, m = 10 см; 2) с = d = m = 15 см.

433°. У рівнобічній трапеції бічна сторона дорівнює 17 см, а середня лінія — 14 см. Знайдіть периметр трапеції.

434. Два кути трапеції дорівнюють: 1)

436.

440. Знайдіть кути рівнобічної трапеції, якщо різниця

кутів дорівнює 40° .

441. Протилежні кути рівнобічної трапеції відносяться як 1 : 4.

йдіть кути трапеції.

442. Доведіть, що діагоналі рівнобічної трапеції — рівні.

443. ABCD — рівнобічна трапеція, AD || BC, AC i BD — діагоналі, О — точка їх перетину (мал. 188). Доведіть: 1) DBOC i DAOD — рівнобедрені; 2) DAOB = DDOC.

444. У рівнобічній трапеції більша основа дорівнює 10 см, бічна сторона — 4 см, а кут між ними — 60°. Знайдіть меншу

445. Гострий кут рівнобічної трапеції дорівнює 60°, а основи — 15 см і 49 см. Знайдіть бічну сторону трапеції.

446. ABCD — рівнобічна трапеція, AD || BC, BK i CM — висоти (мал. 189). Доведіть: 1) AK = MD = (AD – BC) : 2; 2) KD = AM = (AD + BC) : 2.

447. Знайдіть основи рівнобічної трапеції, якщо її висота, проведена з вершини тупого кута, ділить основу на відрізки: 1) 4 см і 8 см; 2) 2 см і 7 см.

448. Доведіть, що

449. У рівнобічній трапеції

450.

452.

453.

454.

якщо: 1) а = 6 см, с = 4 см; 2) а = 50 мм, с = 2 см.

455*. Якщо бісектриси

на

трапеції. Доведіть.

456*. Знайдіть кути

461*.

дорівнює 18 см.

462*. Прямокутна трапеція ділиться діагоналлю

463.

464.

465. Плитка для даху має форму трапеції (трапеція не рівнобічна).

Знайдіть розміри її сторін, якщо:

1) обламано один ріжок плитки (мал. 194); 2) обламано два ріжки плитки (мал. 195, 196).

Поясніть, як це зробити.

Мал. 194 Мал. 195

Мал. 196

466. Знайдіть відстань від кінця транспортера до поверхні землі (яку безпосередньо виміряти не можна), якщо інший

кінець і середина віддалені від поверхні землі

на 0,5 м і 2 м (мал. 197).

467. Розгляньте малюнок 198. Будівельникам потрібно виміряти відстань між серединами

(точки А і В). Їм запропонували такий спосіб: із верхньої вершини покрівлі умовно провісити пряму, перпендикулярну

ви покрівлі, орієнтуючись, наприклад, на відповідні краї покриття; позначити точку С перетину цих прямих і виміряти відстань CD. Тоді шукана відстань АВ дорівнюватиме CD. Чи є правильним цей спосіб? Чому?

(мал. 199).

Мал. 199

Мал. 200

Мал. 203

Записують: ALB ∪ i AFB ∪ (мал. 201). Дугу можна позначити й без проміжної точки, наприклад AB ∪ , якщо зрозуміло, про яку з двох дуг ідеться. Чи можна виміряти дугу кола? Так.

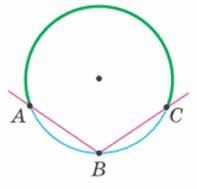
Мал. 206, а Мал. 206, б

Довести: 1 . 2 ABCAC∠=∪

із центром O (мал. 207–209).

Мал. 207

Мал. 208 Мал. 209

Доведення. Розглянемо три випадки розміщення центра кола відносно сторін даного вписаного кута. 1. Центр кола лежить на стороні вписаного кута (мал. 207). Проведемо відрізок ОА (мал. 210). Тоді центральний кут АОС є зовнішнім кутом трикутника АОВ. За властивістю зовнішнього кута трикутника, ∠АОС = ∠ОВА + ∠ОАВ. Але

AD і DC, тобто

Наслідок 1. Вписані кути,

рівні (мал. 213).

Мал. 213 Мал. 212 Мал. 214

Справді, кожний

Наслідок

(мал. 214).

Справді,

a (наслідок 1 з теореми про вписаний кут). Оскільки точку

нує ще одна дуга, наприклад ANB (мал. 219), з

1) провести

Мал. 217Мал. 218

2. Значний внесок у шкільну

Мал. 219

Мал. 220

УкраїнськаАнглійська/ English

Deutsch

Français дуга колаcircular arcKreisbogen (m)arc de cercle

qr.orioncentr.com.ua/bXroE

Пригадайте головне

1. Який кут називається центральним?

2. Що вважають градусною мірою дуги кола?

4. Доведіть, що вписаний кут

задачі

468°. Чи правильно, що центральний

вершину, що лежить: 1) на колі; 2) поза колом; 3) у центрі кола?

469°. Чи правильно, що сторони центрального кута:

1) не перетинають коло; 2) перетинають коло?

470°. Чи правильно, що центральному куту АОВ:

1) не відповідає жодна дуга даного кола із центром О; 2) відповідає лише одна дуга кола з кінцями в точках А і В;

471°.

3) відповідають дві дуги кола з кінцями в точках А і В?

472°. Чи правильно, що сторони

кута: 1) не перетинають коло; 2) перетинають коло?

473°. Чи правильно, що вписаний кут вимірюється: 1) дугою, на яку він спирається; 2) половиною дуги, на яку він спирається?

474°.

1) 1 2 кола; 2) 1 3 кола; 3) 2 3 кола? Яка градусна міра відповідного центрального кута?

478°. Один із двох центральних кутів АОВ дорівнює a. Скільки градусів мають

відповідні

якщо: 1) a = 30°; 2) a = 62°; 3) a = 100°?

479°.

224

480°.

482°.

483°.

484°.

485°.

489°.

491°.

492°.

493°.

якого стягує дугу 120° .

494. У колі рівні дуги стягуються рівними хордами. Доведіть.

495. У колі рівні хорди стягують рівні дуги. Доведіть.

496. Доведіть, що діаметр, перпендикулярний до хорди, ділить дуги, які вона стягує, навпіл.

497. Доведіть, що діаметр, проведений через середину хорди, яка не проходить через центр

хорда.

498. Дуги, що лежать між паралельними хордами, — рівні. Доведіть.

499. Дуги, що лежать

ні. Доведіть.

500. Кінці хорди АВ ділять коло

ні в це коло кути ACB i ADB, якщо: 1) :2:3;ACBADB ∪∪= 2) ∪∪= ACBADB:4:5.

501. Точки Р і

як: 1) 3 : 5; 2) 2 :

502.

503.

505. Доведіть, що

506.

507.

1) n = 35°; 2) n = 45° .

508. Доведіть, що центром кола, описаного

трикутника, є середина гіпотенузи.

509. Доведіть, що медіана прямокутного трикутника, проведена до гіпотенузи, розбиває його на два рівнобедрені трикутники.

510. Кут між дотичною та хордою, що проходить через точку дотику, вимірюється половиною дуги, яка лежить між його сторонами (мал. 238). Доведіть.

511. Через кінець хорди проведено дотичну. Знайдіть гострий кут між хордою та дотичною, якщо хорда ділить коло у відношенні: 1) 1 : 3; 2) 2 : 7.

512*. Доведіть, що кут із вершиною всередині кола вимірюється півсумою дуг, на які спирається даний кут і кут, вертикальний із ним. (Скористайтеся малюнком 239.)

513*. Доведіть, що кут, вершина якого

515*.

516*.

517*.

519. Правильність

1. Що таке вписаний та описаний чотирикутник

Ситуація. Дівчата й хлопці 8-А класу аналізували старі назви «хордіальний чотирикутник» і «дотичний чотирикутник» і намагалися пояснити, яким сучасним термінам вони відповідають.

Дівчата Хлопці

Позначили на колі чотири точки, сполучили їх хордами.

Позначили на колі чотири точки, провели через них дотичні.

Мал. 244 Отримали:

хордіальний

Мал. 245 Отримали:

дотичний чотирикутник. ВПИСАНИЙ ОПИСАНИЙ

чотирикутник.

Як визначити вписаний чотирикутник і описаний чотирикутник?

Аналогічно до вписаного трикутника й описаного трикутника відповідно.

Теорема (властивість

Дано: чотирикутник ABCD, вписаний у коло (мал. 246).

Довести: ∠A + ∠C = 180° , ∠B + ∠D = 180° .

Доведення. Кути A, B, C і D — вписані в коло. За теоремою про вписаний

Мал. 246

Тоді ( ) 11 360180. 22 ACDCBDAB ∠+∠=∪+∪=⋅°=°

Сума всіх кутів чотирикутника дорівнює

На відміну від трикутника, не кожний чотирикутник

Наприклад, ромб, що не є

не є вписаним чотирикутником. Наведемо ознаку вписаного чотирикутника без доведення.

Теорема (ознака вписаного чотирикутника)

дорівнює 180°, то навколо такого чотирикутника можна описати

Отже, ∠A + ∠В = 180° . За властивістю рівнобічної трапеції,

=∠D.

∠B + ∠D = 180° і, за ознакою вписаного чотирикутника, навколо трапеції ABCD можна описати коло.

3. Властивість і ознака описаного чотирикутника

описаного чотирикутника?

його сторонами.

Запам’ятайте!

Теорема (властивість сторін

протилежних

Дано: чотирикутник ABCD, описаний навколо кола (мал. 248), E, F, K і P — точки дотику.

Довести: AB + CD = BC + AD.

Доведення. За властивістю дотичних, проведених

точки, маємо (мал. 249):

AE = AP, BE = BF, CK = CF, DK = DP.

Додавши почленно ці рівності, одержимо:

AE + BE + CK + DK = AP + BF + CF + DP, тобто AB + CD = BC + AD.

На відміну від трикутника, не будь-який чотирикутник може

описаним.

Наприклад, прямокутник, що не є квадратом, не є описаним чотирикутником.

Наведемо ознаку описаного чотирикутника без доведення.

Запам’ятайте!

Теорема (ознака описаного чотирикутника)

Якщо в чотирикутнику суми протилежних сторін рівні, то в цей чотирикутник можна вписати коло.

Щоб довести, що чотирикутник MNKP (мал. 250) є вписаним у коло, покажіть, що:

або ∠М + ∠K = 180°, або ∠N + ∠P = 180° .

Щоб довести, що чотирикутник ABCD (мал. 250) є описаним навколо кола, покажіть, що: AB + CD = AD + BC.

Дізнайтеся більше

1. Крім кіл, вписаного в чотирикутник й описаного навколо нього, є ще зовнівписані кола.

Проведемо в довільному чотирикутнику

ABCD бісектриси зовнішніх кутів при вершинах A, B, С і D (мал. 251). Точки їх перетину О, О1, О2 і О3 є центрами чотирьох зовнівписаних кіл. Кожне з них дотикається до однієї сторони чотирикутника та до продовжень двох інших його сторін. 2. Давньогрецькі вчені відкрили, крім уже відомих вам, інші цікаві властивості вписаних й описаних чотирикутників. Наприклад, добуток діагоналей вписаного чотирикутника дорівнює сумі добутків його протилежних сторін.

3. Значний внесок у розвиток шкільної математичної освіти, виховання талановитої молоді в галузі математики, популяризації математичної науки зробив відомий український

а потім використовуємо

хорд,

вписаних кутів, кутів з вершиною всередині кола та ін. Задача З довільної точки М катета ВС прямокутного трикутника АВС проведено перпендикуляр МD до гіпотенузи АВ (мал. 252). Доведіть, що ∠МАD = ∠МСD.

Розв’язання Навколо чотирикутника АDМС можна описати коло, оскільки ∠АСМ + ∠АDМ = 180° Тоді ∠МАD = ∠МСD як вписані кути, що спираються на одну й ту саму дугу МD. Мал. 252

УкраїнськаАнглійська/ English

Deutsch

Français

описане коло circumscribed circle umschriebene Kreis (m) cercle circonscrit

вписане коло inscribed circle einbeschriebener Kreis (m) cercle inscrit

qr.orioncentr.com.ua/MsmPa

Пригадайте головне

1. Який чотирикутник називається вписаним у коло?

2. Який чотирикутник називається описаним навколо кола?

3. Сформулюйте та доведіть теорему про властивість кутів вписаного чотирикутника.

4. Сформулюйте ознаку вписаного чотирикутника.

5. Сформулюйте та доведіть

521'. На якому з малюнків 253–255

ний у коло?

253

254

255

522'. На якому з малюнків 256–258 зображено чотирикутник,

ний навколо кола?

256

257

523'. Чи правильно вказано градусні

люнку 259? Відповідь поясніть.

258

кутів чотирикутника

524'. Чи правильно вказано довжини сторін чотирикутника на малюнку 260? Відповідь поясніть.

525'.

526°.

кутників.

Мал. 262 Мал. 263 Мал. 264

527°.

чотирикутника ABCD, якщо

A, B, C і D відповідно дорівнюють:

1) 90°, 90°, 110°, 120°; 2) 70°, 130°, 110°, 50°?

528°.

A, B і C відповідно дорівнюють:

1) 85°, 130°, 95°; 2) 60°, 100°, 119°?

529°. У трикутнику ABC проведено висоти ВВ1

і СС1, що перетинаються в точці K (мал. 265).

Доведіть, що навколо чотирикутника АВ1KС1 можна описати коло. Знайдіть кут В1KС1, якщо кут A дорівнює: 1) 55°; 2) 72°; 3) 60° .

530°. Чи можна описати коло навколо довільного: 1) прямокутника; 2) квадрата; 3) ромба?

Відповідь поясніть.

Мал. 265

531°. Доведіть, що центр кола, описаного навколо прямокутника, є точкою перетину

532°. АD і ВC — діаметри кола.

1. Доведіть,

533°.

Мал. 266

267

268

534°. Чи можна вписати коло в чотирикутник, сторони якого, взяті

слідовно, дорівнюють:

1) 2 см, 3 см, 5 см, 4 см; 2) 7 см, 4 см, 3 см, 5 см?

535°. Знайдіть периметр чотирикутника, описаного навколо кола, якщо сума двох протилежних його сторін дорівнює:

1) 20 см; 2) 3,2 дм.

536°. Знайдіть периметр описаного чотирикутника, три сторони якого, взяті послідовно, дорівнюють: 1) 12 см, 16 см, 28 см; 2) 10 см, 14 см, 16 см.

537°. Доведіть, що центром кола, вписаного в ромб, є точка перетину його діагоналей (мал. 269).

538°. Чи можна вписати коло в довільний: 1) прямокутник; 2) квадрат; 3) ромб?

Відповідь поясніть.

539. Знайдіть кут D чотирикутника ABCD, вписаного в коло, якщо його

як: 1) 2 : 3 : 4; 2) 1 : 2 : 2.

540. Кут між

541.

542. Доведіть:

1) будь-яка трапеція, вписана в коло, — рівнобічна (мал. 270); 2) будь-який паралелограм, вписаний у коло, — прямокутник.

543. Доведіть, що будьякий ромб, вписаний у коло, — квадрат.

544. Доведіть, що кут A вписаного чотирикутника ABCD дорівнює зовнішньому куту при вершині С.

545. Чи можна вписати коло в чотирикутник, сторони якого,

послідовно, пропорційні числам:

1) 2, 2, 3, 3; 2) 2, 5, 3, 4?

546. Два рівнобедрені трикутники

ни лежать по різні

чотирикутник вписати коло?

547. Як потрібно розмістити

548.

1) 42 мм; 2) 56 см.

549. Складіть формулу

1) 16 см; 2) 200 мм.

550.

551.

552.

553*.

554*. Доведіть, що бісектриси

ABCD, перетинаючись, утворюють чотирикутник MNKL, навколо якого можна описати коло (мал. 272).

555*. Доведіть, що у вписаному чотирикутнику

ABCD бісектриса кута А перетинається з бісектрисою зовнішнього кута при верши

ні С в точці, що лежить на колі, описаному навколо чотирикутника.

Мал. 272

556*. Із точки Р перетину взаємно перпендикулярних діагоналей чотирикутника ABCD провели перпендикуляри РK, PL, PM і PN до сторін, причому точки K, L, M і N лежать на сторонах АВ, ВС, CD, DA відповідно. Доведіть, що чотирикутник KLMN —

у коло.

557*. Пряма, паралельна бічній

559.

560. Поясніть,

561.

562.

1. Доведіть теорему про суму кутів чотирикутника.

2. Який чотирикутник називається паралелограмом?

3. Назвіть властивості паралелограма.

4. Які ознаки паралелограма?

5. Що таке прямокутник; ромб; квадрат; трапеція; рівнобічна трапеція?

6. Сформулюйте та доведіть теореми про властивості діагоналей прямокутника; ромба.

7. Які властивості квадрата?

8. Доведіть теореми про властивості середньої лінії трикутника; трапеції.

9. Який кут називається центральним?

10. Який кут називається вписаним у коло?

11. Доведіть, що вписаний кут вимірюється половиною

12. Який чотирикутник називається вписаним у коло; описаним навколо кола?

13. Які властивості вписаного чотирикутника; описаного чотирикутника?

14. Яка ознака вписаного чотирикутника; описаного чотирикутника?

№ 1

1°.

Б.

В.

2°.

A. 15 см.

Б. 5 см.

В. 20 см.

Г. 6 см.

A. 60° .

Б. 90° .

В. 30° .

Г. 45° .

5*.

Бісектриса кута

KС = 8 см.

А. 20 см.

Б. 40 см.

В. 44 см.

Г. 64 см. № 2

1°. Знайдіть вписаний кут, якщо дуга, на яку

нює 150° .

А. 150° . В. 90° .

Б. 75° . Г. 85° .

2°. Точки М і N — середини сторін АВ і ВС трикутника АВС

А. 8 см.

Б. 12 см.

В. 2 см.

Г. 6 см.

3°. Сума двох протилежних сторін описаного

нює 10 см. Знайдіть

А. 10 см.

Б. 20 см.

В. 30 см.

Г. 40 см.

4. Кути А, В і

А. 30° .

Б. 60° .

В. 120° .

Г. 90° .

А. 17 см.

Б. 22 см.

їхні

про властивості медіани і бісектриси трикутника;

що таке пропорційні відрізки, як їх знаходити;

які середні пропорційні

Для подібних трикутників, як

чення порядок запису вершин.

трикутників

неправильний.

Задача 1 Два трикутники на малюнку

, 5

1) визначте відповідно рівні

трикутників та

цих трикутників; 2) з’ясуйте, які їхні сторони є відповідними; 3) запишіть рівність трьох дробів, у чисельниках яких — сторони одного з трикутників, а в знаменниках — відповідні сторони іншого.

2. Коефіцієнт подібності трикутників

Число, якому дорівнює відношення

називають

буквою k.

Подивіться на малюнок 273. Сторони трикутника А1В1С1 удвічі довші за відповідні сторони подібного йому трикутни

ка АВС. Тобто:

Отже, коефіцієнт подібності трикутників А1В1С1 і

АВС дорівнює 2.

Коротко записуємо: DА1В1С1  DАВС (k = 2).

Якщо розглядати дані трикутники

подібності буде іншим, а саме: 1 . 2 k =

записуємо:

цьому

сторони,

Рівність

Задача

ників дорівнює відношенню їхніх відповідних сторін.

Доведіть.

Розв’язання

рентійський

(Італія, 1471–1528), Альбрехт Дюрер (Німеччина, 1471–1528) та

трія. Її започаткував французький геометр,

та інженер Жерар

Обчисліть:

100 : 25; 25 : 100; 63 : 7; 7 : 63; 36 : 18; 18 : 36; 72 : 9; 9 : 72.

Розв’яжіть задачі

563'. Чи правильно, що в подібних трикутниках:

1) усі кути рівні;

2) відповідні кути рівні;

3) усі сторони рівні;

4) відповідні сторони рівні;

5) відповідні сторони пропорційні?

564'. Чи правильно зроблено висновок із

1) ∠А = ∠M; 4) ∠С = ∠K;

2) ∠А = ∠K; 5) ∠С = ∠M?

3) ∠В = ∠L;

565'.

1) DАВС  DKLM;

2) DАВС  DLKM;

3) DАВС  DMLK?

566'. Чи правильно зроблено

1) ; ABBCAC KMKLLM == 2) ? ABBCAC KLLMKM ==

567'. Чи може коефіцієнт подібності

1) –2; 2) 0; 3) 3; 4) 1; 5) 1 ; 5 6) 6 ? 5

568°.

 DKLM:

569°. Дано подібні трикутники:

1) АВС і KLM (мал. 282); 2) АВС і MKC (мал. 283).

Знайдіть відношення їхніх відповідних сторін.

Мал. 282 Мал. 283

570°. На малюнку 284 DАВС  DKDС. Доберіть пари відрізків так, щоб

1) ...; KD AB = 2) ...; AC KC = 3) .... BC DC =

Скільки таких

571°. Чи можуть бути подібними трикутники:

1) гострокутний і тупокутний; 2) прямокутний і тупокутний; 3) рівнобедрений і рівносторонній?

572°. DАВС  DА1В1С1. Знайдіть невідомі

Мал. 284

трикутників, якщо: 1) ∠А = 30° , ∠В1 = 60°; 2) ∠В = 110° , ∠С1 = 25° .

573°. DАВС  DА1В1С1. Знайдіть невідомі

трикутників, якщо ∠С = ∠В1 = 50° .

574°. Чи можуть сторони двох подібних трикутників мати довжину:

1) 1,2 см, 1,3 см, 2,2 см і 24 мм, 26 мм, 44 мм; 2) 5 мм, 50 см, 50 см і 5 см, 50 мм, 50 мм?

575°. Чи можуть сторони двох подібних трикутників мати довжину: 3 дм, 4 дм, 5 дм і 9 м, 12 м, 15 м?

576°. DАВС  DА1В1С1. Знайдіть сторони АС і В1С1, якщо:

1) АВ = 8 см, ВС = 10 см, А1В1 = 56 мм, А1С1 = 42 мм; 2) АВ = 40 мм, ВС = 37 мм, А1В1 = 20 см, А1С1 = 6,5 см.

577°. DАВС  DА1

578°.

579°. Пряма перетинає дві сторони трикутника АВС в точках

тинає від нього подібний трикутник. Назвіть паралельні прямі, які утворилися при цьому, якщо: 1) М ∈ АВ і N ∈ ВС; 2) М ∈ АС і N ∈ ВС.

580°. Пряма перетинає дві сторони трикутника

тинає від нього подібний трикутник. Назвіть паралельні прямі, які утворилися при цьому, якщо М ∈ АС і N ∈ АВ.

581°. Побудуйте за клітинками спочатку трикутник KLM (мал. 285), а потім DKВС  DKLM, якщо:

1) k = 2; 2) 2 . 3 k =

582°. Побудуйте за клітинками спочатку трикут

ник KLM (мал. 285), а потім DKВС  DKLM, якщо 1 . 2 k =

583°. Обчисліть периметри подібних трикутників, зображених

люнках: 1) 280; 2) 281; 3) 283. Знайдіть відношення периметрів подібних трикутників.

584°. Обчисліть периметри подібних трикутників, зображених на малюнку 282. Чому дорівнює відношення

ків?

585°.

586°.

587.

588.

589.

590. Кожну сторону

Чи може він бути подібним даному?

591. Кожну сторону трикутника

на: 1) третину її довжини; 2) 25 % її довжини. Чи можна з утворених

побудувати трикутник?

Чи може він бути подібним даному?

592. DАВС  DМОР (k1 = 3) і DАВС  D

(k2 = 2). Чи подібні трикутники МОР

593. DАВС  DМОР (k1 = 4) і D

ники АВС і ТЕН? З яким коефіцієнтом подібності?

594. Два рівнобедрені трикутники подібні з коефіцієнтом k = 0,5.

ного з них дві сторони дорівнюють 12 см і 5 см. Знайдіть третю сторону іншого трикутника.

595. Два рівнобедрені трикутники подібні з коефіцієнтом k = 2,5. В одного з них дві сторони дорівнюють 6 см і 15 см. Знайдіть третю сторону іншого трикутника.

596. Визначте периметри

ників, якщо їхні відповідні сторони відносяться як 7 : 4, а різниця

597.

598.

сторону, якщо: 1) a = 4 см, b = 6 см, c = 6 см; 2) a = 8 см, b = 5 см, c = 6 см?

599*.

подібний цей трикутник даним трикутникам?

600*. Чи існують подібні трикутники, у яких відношення

601*.

602*.

коефіцієнт подібності цих трикутників.

603*. У рівнобедреному трикутнику

трикутника з коефіцієнтом k, якщо:

1) n = 2, Р = 50 см, k = 1,5; 2) n = 3, Р = 35 см, k = 0,75.

604*.

608. На географічній карті три населені

одного на 6 см, 5 см і 4 см. На місцевості найбільша відстань між ними дорівнює 15 км.

1. Який масштаб цієї карти?

2. Яка найменша відстань між населеними пунктами?

3. Яка відстань між іншими населеними пунктами?

609. Якщо до листа сталі, що має форму трапеції з основами 15 см і 25 см та бічними сторонами 18 см і 20 см, прикладемо сталевий лист у формі трикутника з основою 15 см, то одержимо сталевий лист трикутної форми. Які розміри утвореного листа?

610. Триярусну ялинку з тасьми утворюють три подібні рівносторонні трикутники. У них відповідні сторони паралельні, а висоти до горизонтальних сторін лежать на одній прямій.

1. Чи вистачить 2,5 м тасьми для такої ялинки, якщо її основа дорівнює 40 см, а трикутники

1 ? 2

2. Проведіть необхідні вимірювання та з’ясуйте, скільки метрів тасьми знадобиться, щоб

штори

Ситуація. Учні та учениці 8-А класу на уроці геометрії виконували мінідослідження. Вони накреслили кут MАN Відклали на його стороні AM пропорційні відрізки АВ і ВМ, такі, що АВ : ВМ = 1 : 2. Через точки В і М провели паралельні прямі, що перетинають сторону АN цього кута в точках С і N (мал. 287). А потім порівняли довжини відрізків АС і СN та зробили висновок.

Узагальнену теорему Фалеса інакше називають теоремою

Щоб довести подібність трикутників:

1) доведіть рівність відповідних

3) зробіть висновок: трикутники

1. Може виникнути запитання: Як довести узагальнену теорему Фалеса? Поділимо відрізок АВ на n рівних

(мал. 289). Нехай довжина кожного з них дорівнює d. Тоді AB = dn. Відкладемо від точки В на промені ВМ відрізки завдовжки d Через усі точки поділу проведемо прямі, паралельні ВС За теоремою Фалеса, ці прямі відтинають рівні відрізки й на стороні АС даного кута.

Позначимо їхні довжини d 1 На відрізку АС їх буде та сама кількість n, тому AC = d1n

Нехай на відрізку ВМ уміщується ціла кількість m таких відрізків (мал. 289). На відрізку СN їх теж буде m Тоді BM = dm, а CN = d1m

Знайдемо відношення відрізків на двох сторонах кута: ABnACn BMmCNm == ,.

Бачимо, що два відношення дорівнюють тому самому числу , n m отже, можемо їх прирівняти: . = ABAC BMCN

Мал.

Мал. 290

Нехай на відрізку ВМ уміщується m відрізків завдовжки d і залишається остача відрізок меншої довжини, ніж d (мал. 290). Це означає, що відрізок з m частин завдовжки d менший від відрізка ВМ, а відрізок з m + 1 частин завдовжки d більший за цей відрізок.

Одержали нерівність: dm < BM < d(m + 1).

Оскільки , = AB d n то

qr.orioncentr.com.ua/0YY23

1. Як формулюється узагальнена теорема Фалеса?

2. Сформулюйте наслідок

3) відрізки, утворені на

4) відрізки, утворені

5) відрізки, утворені

612'. Чи правильно, що від даного трикутника

тинає:

1) будьяка пряма; 2) пряма, що проходить через вершину трикутника;

3) пряма, що перетинає дві сторони трикутника;

4) пряма, що перетинає дві сторони трикутника й паралельна третій його стороні?

613°. У якому відношенні точка О ділить відрізок АВ (мал. 292, 293)?

614°. Запишіть відношення, у якому

відрізок АВ (мал. 294).

615°. Точка М ділить відрізок РН у

ношенні. Який із

чи МН, якщо: 1) РМ : МН = 5 : 2; 2) РМ : МН = 3 : 7?

616°. Точка

4 : 3.

чи НМ?

617°.

619°.

620°.

621°.

622°. Чи подібні трикутники

поясніть. Мал. 297 Мал. 298

623°.

йдіть довжини відрізків

298?

і ВМ, якщо: 1) d = 10 см, m = 2, n = 3; 2) d = 16 см, m = 3, n = 1.

624°. Відрізок СD завдовжки 14 см точка

625°. Побудуйте відрізок АВ завдовжки 12 клітинок зошита. Поділіть його за клітинками у відношенні: 1) 1 : 2; 2) 5 : 7.

626°. Побудуйте відрізок МN

його за клітинками у відношенні 2 : 3.

627°. Поділіть даний відрізок AB у відношенні 3 : 4. За малюнком 299 складіть план побудови.

628°.

шенні: 1) 2 : 3; 2) 1 : 4.

629°. Побудуйте відрізок

630°.

1) 5 см, 6 см, 10 см і 18,5 см; 2) 7 см, 4 см, 2,1 см і 1,1 см.

631°. Чи є пропорційними чотири відрізки,

8 см, 3 см, 24 см і 9 см?

632°. До

ни відповідно:

1) 1, 2, 3; 2) 6, 3, 4; 3) 3, 5, 7.

Скільки розв’язків має задача?

633°. На сторонах кута АВС розміщено чотири точки: P і Q — на стороні ВА, E і F — на стороні ВС. Чи паралельні прямі PE і QF, якщо:

1) ВР = РQ і ВЕ = ЕF; 3) ВР = РQ і ВF = FЕ; 2) ВQ = QР і ВF = FЕ; 4) ВQ = QР і ВЕ = ЕF? Зробіть малюнки та поясніть відповідь.

634°. Чи подібні трикутники ABC і AMN, якщо MN — середня лінія трикутника ABC?

635°. Як найпростіше побудувати трикутник,

636°. Паралельно стороні АВ

639. На продовженні відрізка АВ завдовжки d взято точку N так, що АN : ВN = m : n. Знайдіть довжини відрізків АN і ВN, якщо:

1) d = 5 см, m = 3, n = 2; 2) d = 16 см, m = 5, n = 1.

640. На малюнку 300 AB || DC || KL, AD : DK : : KF = 2 : 3 : 2. Знайдіть довжини відрізків BC, СL, LF, DС і KL, якщо:

1) AB = 70 мм, FС = 40 мм; 2) AB = 21 см, FС = 15 см.

641. На малюнку 301 AМ || BN || CK || DP. Знайдіть довжини відрізків MN, NK і KP, якщо:

1) a = 2,5 см, b = 4 см, c = 2 см, MP = 12,5 см; 2) a = 10 см, b = 16 см, c = 8 см, MP = 50 см.

642. Сторони кута А перетинають дві паралельні прямі ВС і ОН, причому точка В лежить

між точками А і О. Знайдіть:

1) АН, якщо АВ = 8 см, АО = 12 см, АС = 10 см; 2) АО, якщо 3 ::0,6, 11 ACAH = ВО = 12 дм.

643. На стороні МО трикутника МОN позначено точку А

відстані а від вершини О. Знайдіть довжини відрізків, на які ділить сторону ОN пряма, що проходить через точку А паралельно МN, якщо:

1) МО = 6 см, ОN = 9 см, а = 2 см; 2) МО = 10 см, ОN = 14 см, а = 4 см.

644. Через точку Р на стороні АВ трикутника АВС паралельно стороні АС проведено пряму. Вона перетинає сторону ВС в точці О. Знайдіть довжину відрізка ВО, якщо: 1) АР : РВ = 5 : 6, ВС = 22 см; 2) АР : РВ = 4 : 3, ВС = 2,8 дм.

645. Точка ділить сторону трикутника у

ношення кожного з утворених

сторони, якщо: 1) х = 1, у = 2; 2) х = 2, у = 3; 3) х = 4, у = 5.

646. У трикутнику АВС три точки

647.

1) 1 ; 2 2) 2 ? 3

648.

1) АD = 5, ВN : МN = 3 : 2; 2) АD = 3, ВN : МN = 0,2 : 0,3.

649.

відносяться як 2 : 3.

650. Побудуйте два кола, що дотикаються внутрішньо, якщо їхні радіуси відносяться як 3 : 4.

651*. На відрізку АВ позначено дві точки О і Н (АО < АН). Утворені три частини відрізка АВ, починаючи від точки А, мають довжини а, b і с. Знайдіть, які частини відрізка АВ становлять відрізки АО, ОН, НВ, АН і ОВ.

652*. Відрізок АВ має довжину а. Точки М і Т розміщені на прямій АВ так, що точка М лежить на відрізку АВ і АМ : МВ = 2 : 3, точка Т не належить відрізку АВ і АТ : ТВ = 4 : 3. Знайдіть відстань між точками М і Т, якщо: 1) а = 6 см; 2) а = 10 см.

653*. За даними на малюнку 302 доведіть: 1) а : с = b : d; 2) а : с = (а + b) : (с + d); 3) c : a = (b – a) : (d – c).

654*. На малюнку 303 AB || CD.

1. Застосувавши теорему про пропорційні відрізки, доведіть, що AO : OD = OB : OC.

2. Знайдіть АО і ОD, якщо АD = 10 см, ОВ = 5 см, ОС = 3 см.

655*. Відрізок MN має кінці на сторонах AB і AC трикутника ABC і паралельний стороні ВС. Доведіть, що медіана АА1 ділить цей відрізок навпіл.

656*. Пряма, паралельна основам трапеції АВСD (мал. 304), перетинає її

трапеції, якщо: 1) n = 2; 2) n = 3.

659. Для зменшення або

660. Вулиці

661.

їх А і В), які розташовані на протилежних берегах річки (мал. 306), якщо АМ || ВN і СА = 4 м, СМ = 5 м, МN = 35 м.

662.

1. Навіщо потрібні ознаки подібності

Ситуація. Іван і Дарина з’ясовували, чи подібні два трикутники, і пригадали означення: Два трикутники називаються подібними, якщо їхні відповідні кути рівні, а відповідні сторони пропорційні.

Як за означенням встановити, чи подібні два трикутники?

Довести рівність їхніх відповідних кутів та пропорційність їхніх відповідних сторін.

Це не раціонально, бо відповідних

користуються ознаками

Запам’ятайте!

Теорема (ознака подібності трикутників

двома кутами) Якщо два кути одного трикутника відповідно дорівнюють двом кутам іншого трикутника, то такі трикутники подібні.

Дано: DАВС і DА1В1С1 (мал. 307), ∠А = ∠А1, ∠В = ∠В1.

Довести: DАВС  DА1В1С1.

Доведення. Накладемо

Наслідок. Рівносторонні трикутники подібні.

Справді, у рівносторонніх трикутниках усі кути дорівнюють по 60° .

Тому ці трикутники подібні за двома кутами.

Задача У трапеції АВСD діагоналі АС і ВD пе

ретинаються в точці О (мал. 309). Доведіть, що

DАОВ  DСОD.

Розв’язання Розглянемо трикутники АОВ і

СОD. У них: ∠АОВ = ∠СОD як вертикальні,

∠ОАВ = ∠ОСD як внутрішні різносторонні при

паралельних прямих АВ і СD та січній АС. Отже,

DАОВ  DСОD за двома кутами.

Щоб довести подібність двох трикутників:

1) виділіть їх на малюнку;

2) доведіть рівність двох пар відповідних кутів;

3) зробіть висновок: трикутники

На властивостях подібних трикутників ґрунтується принцип побудови номограми спеціального креслення, за допомогою якого можна, не виконуючи обчислень, одержувати розв’язки певного рівняння. Розглянемо задачу. Задача До даного відрізка АВ в його кінцях і по один бік від нього проведено два перпендикуляри АМ = а і ВN = b, а також відрізки МВ і NA, які перетинаються в точці О. Відстань від О до АВ дорівнює х. Знайдіть залежність х від а і b. Розв’язання Нехай точка K (мал. 311) є основою перпендикуляра, проведеного з точки О до прямої АВ За умовою задачі, АМ ⊥ АВ, ВN ⊥ АВ.

Тоді одержимо:

Мал. 311

1) у прямокутному трикутнику АВN ОK || ВN, звідси ; = xAK bAB

2) у прямокутному трикутнику ВАМ ОK || АМ, звідси = xKB aAB .

Додавши одержані рівності, маємо: 1, + +=== xxAKKBAB baABAB тобто 1. += xx ba

Звідси 111 . += bax

Одержали рівняння, що виражає шукану залежність.

Для знаходження його наближеного розв’язку можна на аркуші в клітинку або на міліметровому папері побудувати (як на мал. 311) відрізки

signs

similarity of

Zeichen der Ähnlichkeit von Dreiecken conditions de similitudes des triangles

1) 20°, 80°, 90°; 55°, 35°, 80°; 18°, 62°, 100°;

2) 120°, 30°, 40°; 125°, 35°, 10°; 108°, 51°, 21°?

Розв’яжіть задачі

663'. Чи правильно, що в першій

про:

1) сторони даних трикутників;

2) кути даних трикутників;

3) рівність двох кутів трикутника;

4) рівність двох кутів даних трикутників;

5) рівність двох відповідних кутів даних трикутників?

664'. Чи правильно, що рівносторонні трикутники: 1) рівні; 2) подібні?

665°. За даними на малюнку 312 назвіть дві пари відповідно рівних кутів трикутників. Чи подібні дані трикутники? За якою ознакою? Зробіть

666°.

DFE

667°. Накресліть

313

670°.

671°.

675°. D

676°.

677°.

якщо ∠B = ∠C = 60° , ВС = 9 см, А1В1 = 3 см.

678°.

679°.

нює 64°?

680°. Прямокутні трикутники з рівним

діть.

681°. Доведіть, що вказані прямокутні трикутники подібні: 1) DАВС і DKВА (мал. 316); 2) DОKА і DВАС (мал. 317).

682°. Доведіть подібність прямокутних трикутників

(мал. 318).

Мал. 316 Мал. 317 Мал. 318

683°. Чи подібні прямокутні трикутники, в одному з яких гострий

дорівнює a, а в іншому — b, якщо: 1) a = 42° , b = 48°; 2) a

684°.

685°.

686°.

1) а = 32 мм, b = 64 мм, с = 51 мм; 2) а = 0,3 дм, b = 0,5 дм, с = 0,8 дм.

688°.

689°.

ADBCAB

точці О. Доведіть, що ==

AOBODC .

690°. Пряма KP перетинає ребра SB і SС піраміди й відтинає від грані трапецію BKPC (мал. 319). Обґрунтуйте подібність трикутників BSС і KSP.

691°. Кожне ребро піраміди SАВС дорівнює m. Відрізок KP грані BSС відтинає від неї трапецію BKPC (мал. 319). Знайдіть:

Мал. 319

1) сторону KP трикутника KSP, якщо його периметр дорівнює р; 2) меншу сторону трапеції BKPC, якщо її периметр дорівнює Р.

692. За даними, наведеними на малюнках 320, 321, доведіть подібність зображених трикутників.

693. Доведіть подібність трикутників, зображених на малюнку 322.

Мал. 320 Мал. 321 Мал. 322

694. Доведіть, що трикутники з відповідно паралельними сторонами — подібні.

695. У трикутниках АВС і KLM: ∠А = ∠K, ∠В = ∠L, АВ = c, ВС = c + 2, АС = c – 2, KL = nс. Знайдіть сторони

якщо: 1) с = 5 см, n = 3; 2) с = 6 см, = n 3 . 4

696. У трикутниках KLM і

, KL = m, LM = m + 2, KM = m – 2,

= nm.

m = 8 см, n = 2.

697.

698.

за формулою: = P d 2 . 9

699. У трикутнику зі сторонами а, b і

трапеції, якщо: 1) а = 30 см, b = 20 см, c = 15 см, Р = 63 см; 2) а = b = c = 18 см, Р = 50 см.

700. Доведіть, що через вершину

кутника завжди

від даного трикутника подібний йому трикутник.

701. Через точку М на стороні трикутника АВС проведено

1) різносторонній; 2) рівнобедрений; 3) рівносторонній.

702. У рівнобедрений трикутник

сано коло. Знайдіть

сторін трикутника, якщо: 1) а = 6 см, b = 10 см; 2) а = 10 см, b = 13 см.

703.

= aba d b 2 . 2

704. У рівнобедрений трикутник

1) а = 12 см, b = 10 см; 2) а = 10 см, b = 13 см.

705.

706.

708.

709.

710.

711.

712.

713.

714*.

715*.

716*. У рівнобедреному трикутнику

СD проведено прямі АK і ВL (K ∈ ВС, L ∈ АС). Знайдіть довжину відрізка KL, якщо: 1) АВ = 3 см; 2) АВ = 4 см; 3) АВ = 5 см.

717*. Доведіть, що висоти трикутника

пропорційні сторонам, до яких вони проведені (мал. 323).

718*. Знайдіть відповідні

720*.

можна обчислити за формулою: = + ab x ab .

722*. У трикутнику АВС з тупим кутом В проведено висоти ВD і СM. Доведіть, що трикутники АВС і АDM подібні.

723*. Основи трапеції АВСD дорівнюють a і b (a > b), ∠АDC — тупий. Знайдіть квадрат довжини діагоналі AC, яка ділить трапецію на два подібні трикутники.

724*. Проведемо три прямі через сторони трикутника та ще три прямі — через його вершини паралельно протилежним сторонам. Цими прямими площина трикутника розбивається на 16 областей (мал. 324). Пряма, яка перетинає

дві сторони трикутника й пара

лельна третій його стороні, відти

нає від нього подібний трикутник.

Дослідіть, якій з областей нале

жать точки, через які: 1) не мож

на провести жодної такої прямої; 2) можна провести тільки одну таку пряму; 3) можна провести тільки дві такі прямі; 4) можна

провести три такі прямі.

725. Триповерховий будинок на світлині має висоту 8 мм. Знаючи, що його справжня висота дорівнює 13 м,

726.

1. Яка позначка відповідає початку ділянки?

2. Яка позначка стоїть наприкінці ділянки?

3. Якою має бути позначка, що відповідає середині ділянки?

4. Яка позначка має бути на відстані 120 м від початку підйому?

728. Із селища виходять три дороги в напрямках: 1) південнозахідному; 2) південному; 3) південносхідному. Якою б дорогою не йшов пішохід із селища, відношення його відстаней до двох інших доріг залишається сталим. Поясніть, чому це так.

трьома сторонами.

подібності трикутників?

Так.

Але тут потрібно виявити не рівність, а пропорційність відповідних сторін двох трикутників.

2. Друга ознака подібності трикутників

Теорема (ознака подібності трикутників за двома сторонами й кутом між ними)

Якщо дві сторони одного трикутника пропорційні двом сторонам іншого трикутника й кути, утворені цими

Відкладемо на стороні А1B1 трикутника А1В1С1 відрізок А1В2 = АВ = с (мал. 327). Через точку В2 проведемо пряму В2С2 || В1С1. Утворився трикутник А1В2С2, який, за наслідком з узагальненої теореми Фалеса, подібний трикутнику А1В1С1.

Отже, == ABACBC ABACBC 121222 111111 .

Звідси = ABAC ABAC 1212 1111 .

Підставимо в цю пропорцію відомі довжини сторін і скоротимо одержані дроби.

Тоді маємо: = AC c kckb 12 , = AC b 12 1. Звідси А1С2 = b.

Розглянемо DА1В2С2 і D

доведеним.

Отже, DА1В2С2 = DАВС за двома

пропорційними катетами подібні за двома сторонами й

3. Третя ознака подібності трикутників

Запам’ятайте!

Теорема (ознака подібності трикутників за трьома сторонами) Якщо сторони одного трикутника пропорційні сторонам іншого трикутника, то такі трикутники подібні.

Дано: DАВС і DА1В1С1 (мал. 328), == ABACBC ABACBC 111111 .

Мал. 328

Мал. 327

Відкладемо на стороні А1B1 трикутника А1В1С1

відрізок А1В2 = АВ = с (мал. 329). Через точку В2

проведемо пряму В2С2 || В1С1. Утворився трикутник А1В2С2, який, за наслідком із узагальненої теореми Фалеса, подібний трикутнику А1В1С1.

Отже, == ABACBC ABACBC 121222 111111 .

Далі одержимо: == ACBC c kckbka 1222 , або == ACBC ba 1222 1.

Звідси А1С2 = b, В2C2 = а.

Отже, А1С2 = АС і В2C2 = ВС.

Розглянемо DА1В2С2 і DАВС.

У них А1В2 = АВ = с за побудовою,

А1С2 = АС = b і В2C2 = ВС = а за доведеним.

Отже, DА1В2С2 = DАВС за трьома сторонами.

Із рівності трикутників АВС і А1В2С2 та подібності трикутника

трикутнику А1В1С1 випливає, що DАВС  DА1В1С1.

Задача У кожному з трикутників АВС і RST (мал. 330) медіана, проведена до більшої сторони, дорівнює половині цієї сторони. Чи подібні дані три

кутники, якщо АС = 9, AK = 7,5, TR = 6, MR = 5?

Розв’язання Медіани СK і TМ відтинають від даних

трикутників АВС і RST відповідно DАСK і DRTМ.

У кожному з них відомі три сторони:

АС = 9, AK = KС = 7,5; RT = 6, RM = MT = 5.

З’ясуємо, чи пропорційні відповідні сторони цих

трикутників: ==== AC AK RT RM 937,53 ,. 6252

Отже, DАСK  DRTМ за трьома сторонами. Із по

дібності цих трикутників

DАВС і DRST. У них:

трикутника Н, точка перетину його медіан М і центр описаного

жать на одній прямій (мал. 331). Цю пряму називають прямою

найвидатнішого математика ХVІІІ ст. Леонарда

(1707–1783).

народився в Базелі (Швейцарія).

ім’ям, Л.

пряма Ейлера Euler line ['s] Eulersche Gerade (f) la droite d’Euler Словничок

УкраїнськаАнглійська/ English

qr.orioncentr.com.ua/IfC08

1. Сформулюйте ознаку

Deutsch

1) 1, 2, 3; 2, 3, 4; 3, 4, 5; 4, 5, 10; 2) 4,56, 5,44 і 10; 2,39, 3,61 і 5; 7,65, 1,35 і 6,3?

Розв’яжіть задачі

729'. Чи правильно, що в другій

про:

1) дві сторони та два кути даних трикутників;

2) дві сторони й кут даних трикутників;

3) рівність двох відповідних сторін даних трикутників;

4) рівність відповідних кутів даних трикутників;

5) рівність двох відповідних сторін і кутів між ними даних трикутників;

6) пропорційність двох відповідних

ними даних трикутників?

730'.

731'.

732°. За даними на малюнку 332 назвіть

відповідно рівні кути та відповідно

пропорційні сторони трикутників. Чи

подібні дані трикутники? За якою ознакою? Зробіть відповідні записи.

733°. На малюнку 333 задано елементи три

кутників DEF i ACB. Чи подібні дані трикутники?

734°. Трикутник має сторони 5 см і 8 см. Кут між ними дорівнює 50°. Які виміри може мати подібний йому трикутник?

735°. На малюнку 334 знайдіть подібні трикутники. Поясніть, чому вони подібні.

736°. На малюнку 335 знайдіть подібні трикутники. Поясніть, чому вони подібні.

Мал. 335 Мал. 333 Мал. 334

737°. У трикутниках KLM і РОН один із

ни в них мають бути

739°. У трикутнику АВС на сторонах АВ і АС взято точки

ні трикутники АВС і АDЕ, якщо:

1) АВ = 12 см, АС = 15 см, ВD = 2 см, СЕ = 7 см;

2) АВ = 15 см, АС = 18 см, ВD = 3 см, СЕ = 8 см;

3) АВ = 20 см, АС = 21 см, ВD = 10 см, СЕ = 10,5 см?

740°. У трикутнику ВАС на сторонах ВА і ВС взято точки М і

ні трикутники ВАС і ВМР, якщо:

1) ВА = 10 см, ВС = 12 см, АМ = 5 см, СР = 6 см; 2) ВА = 22 см, ВС = 16 см, АМ = 11 см, СР = 10 см?

741°. За даними на малюнку 336 назвіть відповідно пропорційні сторони трикутників. Чи подібні

742°.

трикутники? За якою ознакою?

Мал. 337 Мал. 336

малюнку 337

дані трикутники?

743°. Трикутник має сторони 5 см, 6 см і 9 см. Які сторони

мати подібний йому трикутник?

744°. Які з трьох трикутників подібні, якщо їхні сторони дорівнюють: 8 см, 10 см, 14 см; 12 см, 15 см, 21 см; 16 см, 20 см, 30 см?

745°. Сторони одного трикутника дорівнюють а, b і с. У подібному трикутнику найменша сторона дорівнює d. Знайдіть його сторони, якщо: 1) а = 7 см, b = 9 см, с = 12 см, d = 21 см; 2) а = 17 см, b = 8 см, с = 15 см, d = 56 см.

746°.

748°. Які з трьох

дорівнюють: 3 см і 4 см; 5 см і 12 см; 45 мм і 6 см?

749°. Які з трьох прямокутних

дорівнюють: 1 см і 24 см; 5 см і 12 см; 25 мм і 0,6 дм?

750°. Основа рівнобедреного трикутника

сторона — а. У подібному трикутнику основа дорівнює с. Знайдіть

метр, якщо: 1) а = 18 см, b = 12 см, с = 6 см; 2) а = 25 см, b = 14 см, с = 28 см.

751°. Основа рівнобедреного трикутника дорівнює 8 см,

на — 5 см. Знайдіть периметр подібного йому трикутника, якщо його основа дорівнює 12 см.

752°. Периметри двох тупокутних трикутників відносяться як m : n. У першому трикутнику більша сторона дорівнює а. Знайдіть

шу сторону другого трикутника, якщо: 1) а = 24 мм, m = 2, n = 3; 2) а = 1,5 дм, m = 5, n = 3.

753°. Периметри двох тупокутних

більшу сторону другого трикутника.

754°. У прямокутнику АВСD точки

му утворилися, якщо:

1) АВ = 16 см, ВС = 63 см, АС = 65 см; 2) АВ = 7 см, ВС = 24 см, АС = 25 см.

755°.

рівні частини. Із цих точок проведено

цьому утворилися, якщо

759. У трикутниках АВС і KLM: ∠А = ∠K, АВ = c, ВС = c + 2, АС = c – 2, KL = nс, KM = nс – 2n. Знайдіть сторони трикутників, якщо: 1) с = 5 см, n = 3; 2) с = 6 см, = n 3 . 4

760. У трикутниках ТОМ і ВСЕ: ∠Т = ∠В, ТО = 8 см, ОМ = а + 2, ТМ = а – 2, ВС = ра, ВЕ = ра – 2р. Знайдіть сторони трикутників, якщо р = 2.

761. Доведіть, що в подібних трикутниках відповідні медіани відносяться як сторони, до яких вони проведені (мал. 338).

762. Два подібні трикутники мають по медіані, що дорівнюють одна одній. Чому не можна стверджувати, що дані трикутники рівні?

763. Сторони кута А одна пряма перетинає в точках K i L, а інша — в точках M i N відповід

но, причому = KLMN 1 ::0,25, 5 KМ = 3 см.

Якої довжини повинен бути

764. Висота трикутника ділить

відношенні

сторону, якщо: 1) m = 5, n = 9; 2) m = 3, n = 5?

765. У гострокутному

766. Медіана АА1 трикутника

767. Точка

768.

770*.

771*.

772*. У рівнобедрений трикутник вписано прямокутник так, що його діагоналі

Знайдіть відношення, у якому

прямокутника ділять бічні сторони трикутника, починаючи від вершин основи.

773*. З вершини тупого кута ромба проведено дві висоти. Відстань між кінцями висот дорівнює половині більшої діагоналі. Знайдіть кути ромба.

774*. За основами а і b трапеції (а > b) визначте:

1) відстань між точками, які ділять

1 : m, починаючи від меншої основи;

2) довжину відрізка, що проходить паралельно

ку перетину діагоналей;

3) довжину

775*.

776*.

779*. Медіана ВМ ділить висоту АН трикутника АВС у відношенні 3 : 1, починаючи від вершини. У якому відношенні ця висота ділить медіану ВМ?

780. На малюнку 339 ви бачите дачний столик у поперечному розрізі.

АD і ВС — дві з чотирьох його ніжок. АО = ВО = 52 см, ОС = ОD = 88 см, ЕF — розріз горизонтальної поверхні стола, GH — лінія підлоги. Поясніть, чому за такої будови столика прямі

ЕF і GH — паралельні.

781. Як знайти відстань між двома пунктами А і В, між якими не можна пройти?

Мал. 339

782. У певний момент часу тінь від двометрової віхи мала довжину 1,4 м, а тінь від дерева (якщо міряти від стовбура) — 6,3 м. Визначте висоту дерева, знаючи, що діаметр стовбура біля землі дорівнює 1,2 м.

783. Чому вдень за тінню можна визначити висоту дерева, а вночі за тінню від ліхтаря — ні?

784. Щоб поділити відрізок АВ на три рівні частини, діяли так. На промені АD, що не збігається з АВ, відклали рівні відрізки АЕ і ЕK. Потім на промені KВ побудували точку Т так, щоб KВ = ВТ. Пряма ТЕ поділила відрізок АВ у відношенні 2 : 1. Отже, одержали, що

1. Про суть застосувань подібності трикутників

Ситуація. Дмитро і Наталка міркували про те, якими можуть бути застосування подібності трикутників. Наталка стверджувала, що тільки практичними. А Дмитро що не лише практичними, а й теоретичними, коли застосування відомих фактів дозволяє встановити нові математичні факти.

Хто має рацію — Дмитро чи Наталка? Дмитро.

Справді, практичне застосування очевидне. Однак у попередніх

раграфах як задачітеореми були доведені, наприклад, ознаки

ності рівнобедрених трикутників, прямокутних трикутників тощо. А це нові математичні факти, якими можна користуватися в подальшому. Розглянемо деякі нові факти, встановлені шляхом

подібності трикутників.

2. Властивості медіан трикутника

Запам’ятайте!

Теорема (властивість медіан трикутника)

Точка перетину двох будь-яких

трикутника ділить кожну з них у відношенні 2 : 1.

Дано: DАВС, АА1, ВВ1 — медіани, О — точка перетину медіан.

Довести: AO : OA1 = BO : OB1 = 2 : 1.

Доведення.

Сполучимо відрізком точки A1 і B1 (мал. 340).

Одержали середню лінію A1B1 трикутника АВС. Трикутники AOB і A1OB1 подібні за двома кутами: ∠AOB = ∠A1OB1 як вертикальні, ∠OAB = = ∠OA1B1 як внутрішні різносторонні при паралельних прямих AB і A1B1 та січній AA1.

точку.

3. Властивість бісектриси трикутника

Запам’ятайте!

Теорема (властивість бісектриси трикутника)

Бісектриса кута трикутника ділить протилежну сторону на відрізки, пропорційні до прилеглих сторін.

Дано: DАВС (мал. 341), CL — бісектриса.

Довести: AL : BL = АC : ВC.

Доведення.

Із точок А і В проведемо перпендикуляри

AM і BN до прямої СL (мал. 342).

Розглянемо DАMC і DBNC.

У них: ∠АMC = ∠ВNС = 90° , ∠АCM = ∠ВСN,

оскільки СL — бісектриса кута C.

Отже, DАMC  DBNC за двома кутами.

Звідси = ACAM BCBN . (1)

Розглянемо DАLM і DВLN. У них: ∠АML = = ∠ВNL = 90° , ∠АLM = ∠ВLN як вертикальні. Отже, DАML  DBNL за двома кутами.

Звідси = AMAL BNBL . (2)

Із рівностей (1) і (2) одержимо: = ALAC BLBC .

Якщо сторони трикутника позначено маленькими буквами, то

проєкції катетів а і b на гіпотену

зу c позначають відповідно: а с і b с .

Запам’ятайте!

Відрізок х називається середнім

пропорційним між відрізками а і b, якщо виконується рівність а : х = х : b.

Задача (Властивості середніх пропорційних у прямокутному трикутнику)

У прямокутному трикутнику:

1) висота, проведена до гіпотенузи, є середнім пропорційним між проєкціями катетів на гіпотенузу;

2) катет є середнім пропорційним між гіпотенузою та

єю на гіпотенузу;

3) проєкції катетів на гіпотенузу відносяться як квадрати катетів. Доведіть.

Розв’язання 1. Розглянемо DАHС і DСHВ (мал. 344).

Вони прямокутні, оскільки CH — висота. ∠АСН = = ∠СВН, оскільки доповнюють до 90° відповідно кути А і В даного трикутника АСВ. Отже, DАНС  DСНВ за

двома кутами.

Із подібності трикутників випливає: = AHCH CHBH .

Звідси CH2 = АH · ВH.

2. Кожний із трикутників АНС і СНВ подібний даному трикутнику АСВ. Це випливає з рівності їхніх відповідних кутів.

Тоді одержимо:

а) DАНС  DАСВ, тому = AHAC ACAB .

Звідси АС2 = АН · АВ.

б) DСНВ  DАСВ, тому = BHCB BCAB .

Звідси ВC2

У прямокутному трикутнику (мал. 345): Дізнайтеся

більше

1. Подібність трикутників застосовують не лише в задачах на доведення чи обчислення, але й у задачах на побудову. Задача Побудуйте трикутник за двома кутами А і С та бісектрисою l кута В. Розв’язання

у трикутнику А1ВС1: ∠А1 = = ∠А, ∠С1 = ∠С, BL1 бісектриса кута В і BL1 = l Отже, DА1ВС1 шуканий.

2. Значний внесок у розвиток теорії геометричних побудов вніс відомий український математик Олександр Степанович Смогоржевський (1896–1969), який народився в с. Лісові Берлінці на Вінниччині. У своїх працях, адресованих учням і вчителям, учений розкриває особливості розв’язування задач на побудову різними засобами: циркулем і лінійкою; одним циркулем; однією

досі не втратила цінності його

на побудову» (1961 р.).

«Дослідження

1) х : 12 = 3 : 4; 12 : х = 4 : 3; 3 : 4 = х : 12; 4 : 3 = 12 : х; 2) х : 35 = 7 : 5; 35 : х = 5 : 7; 7 : 5 = х : 35; 5 : 7 = 35 : х.

785'.

787'. Чи правильно записано співвідношення для трикутника АСВ (мал. 348): 1) CH = АС · ВС; 6) АC2 = АH · АВ; 2) CH2 = АВ · ВH; 7) ВC = ВА · АH; 3) CH2 = АH · ВH; 8) ВC2 = АС · ВА; 4) АC = АH · ВH; 9) ВC2 = ВH · ВА? 5) АC2 = ВС · АВ;

788°. Медіани трикутника дорівнюють:

1) 9 см, 12 см і 15 см; 2) 6 см, 6 см і 3 см; 3) 45 см, 45 см і 45 см.

790°. Знайдіть

1) 12 см, 16 см і 24 см; 2) 4 см, 4 см і 6 см; 3) 8 см, 8 см і 8 см.

791°. Знайдіть

794°.

шини А? Висновок поясніть.

795°. За даними на малюнках 349, 350 знайдіть:

1) гіпотенузу;

2) катети;

3) висоту, проведену до гіпотенузи.

796°. У трикутнику PRQ (мал. 351) знайдіть:

1) гіпотенузу;

2) катети;

3) висоту, проведену до гіпотенузи.

797°. За даними на малюнках 352–354

відрізка х (АВ — діаметр кола).

Мал. 352 Мал. 353 Мал. 354

798°. Із точки кола проведено перпендикуляр до діаметра.

стань від цієї точки до діаметра, якщо одержані відрізки діаметра дорівнюють: 1) 16 см і 1 см; 2) 0,5 см і 8 см.

799°. Перпендикуляр, проведений

діаметра.

800. Через точку перетину медіан трикутника

сторони трикутника?

801.

трикутника. У якому відношенні ці вершини паралелограма ділять медіани трикутника, рахуючи від відповідних вершин трикутника?

803. Чи правильно, що АK є бісектрисою трикутника АВС, якщо: 1) АВ = 12 см, AC = 16 см, ВK = 6 см, СK = 8 см; 2) АВ = 5 см, AC =15 см, ВK = 4 см, СK = 16 см?

804. Сторони трикутника дорівнюють 8 см, 12 см, 15 см. Знайдіть відрізки, на які

сторону.

805.

807.

809.

трикутника до його бічної сторони, якщо його основа дорівнює 14 см, бічна сторона — 25 см, а висота, проведена до основи, — 24 см?

810. Діагоналі ромба зі стороною а дорівнюють d1 і d2. Визначте висоту ромба, якщо: 1) а = 25 см, d1 = 30 см, d2 = 40 см; 2) а = 169 мм, d1 = 130 мм, d2 = 312 мм.

811. За даними на малюнках 355–357 доведіть, що вказані трикутники — подібні: 1) DАСM і DDВM (мал. 355); 2) DADM і DСВM (мал. 356); 3) DАBC і DАCM (мал. 357).

Мал.

812. Якщо хорди АВ і СD кола перетинаються

= СМ · DМ. Доведіть.

813. Якщо з точки М поза колом проведено дві січні, що перетинають коло

точках А, В, С і D, то АМ ·

814.

DМ

816*. Доведіть, що

817*. Сума

є середнім пропорційним між проєкціями її бічних сторін на основу.

818*. У гострий кут вписано три кола, причому середнє коло дотикається до двох інших. Доведіть, що радіус середнього кола є середнім пропорційним між радіусами крайніх кіл.

819*. Спираючись на малюнок 360, доведіть, що:

1) DАDВ  DАСВ; 2) DВАС  DВDС;

3) DАDK  DАСВ; 4) АС · ВD = АВ · DС + АD · ВС.

820. Спираючись

821.

823. На малюнку 362 показано, як можна виміряти висоту дерева, користуючись однією віхою. Поясніть вимірювання.

Мал. 362

3 КОНТРОЛЬНІ ЗАПИТАННЯ

1. Які трикутники називаються подібними?

2. Як записати, що два трикутники подібні з коефіцієнтом k?

3. Поясніть, як скласти відношення відповідних сторін двох подібних трикутників.

4. Чому дорівнює коефіцієнт подібності рівних трикутників?

5. Що можна сказати про відношення периметрів подібних трикутників?

6. Як формулюється узагальнена теорема Фалеса?

7. Сформулюйте наслідок з узагальненої теореми Фалеса.

8. Поясніть, як довести подібність трикутників за означенням.

9. Сформулюйте та доведіть ознаку подібності

17.

18.

19.

1°. DА1В1С1  DАВС. Кут А дорівнює 60°, а кут В на 20° менший від

A. 40° .

Б. 80° .

В. 100° .

Г. 120° .

2°. У трикутниках

, DF = 5KM. Чому дорівнює DE, якщо KL = 10 см?

А. 2 см.

Б. 15 см.

В. 25 см.

Г. 50 см.

3°. У трикутнику зі сторонами

меншого

сторону?

А. 1,5 см і 2 см.

Б. 3,5 см і 3,5 см.

В. 2 см і 5 см.

Г. 3 см і 4 см.

АD : ВС = 3 : 2, АС = 30 см.

А. 10 см і 15 см.

Б. 6 см і 9,5 см.

В. 12 см і 18 см.

Г. 18 см і 12 см.

5*.

А. 5,4 см.

Б. 7,2 см.

В. 9,6 см.

Г. 12 см.

та про співвідношення

1. Теорема Піфагора

Ситуація. Учні й учениці 8-А

проводили мінідослідження. Спочатку вони побудували два прямокутні трикутники з катетами 3 см і 4 см та 5 см і 12 см, а потім виміряли їхні гіпотенузи. Марія Іванівна сказала, що може назвати

Тому: АС2 = АВ · АD і ВС2 = АВ · DВ.

Додавши рівності почленно та врахувавши, що AD + DB = АВ, одержимо:

АС2 + ВС2 = АВ · АD + АВ · DВ = АВ (АD + DВ) = АВ · АВ = AB2 .

Отже, АВ2 = АС2 + ВС2 .

гіпотенуза, то з формули с2 = а2 + b2 одержимо такі формули: =+ cab22 ; а2 = с2 – b2, або =− acb22 ; b2 = с2 – a2, або =− bca22 .

Скориставшись цими формулами,

Наприклад:

1) якщо а = 6 см, b = 8 см, то =+=+=cab22226810 (см);

2) якщо с = 13 см, а = 5 см, то =−=−=bca222213512 (см).

Правильною є і теорема, обернена

Піфагора: якщо квадрат сторони трикутника дорівнює сумі квадратів двох інших його сторін, то цей трикутник — прямокутний.

За теоремою, оберненою до теореми Піфагора, трикутник зі сторонами 3 см, 4 см і 5 см — прямокутний, оскільки 32 + 42 = 52. Такий трикут

16 см. Знайдіть

=−=−==ODADAO2222108366 (см).

Тоді ВD = 2 · ОD = 2 · 6 = 12 (см).

Щоб знайти деякий елемент фігури (сторону, висоту, діагональ), виділіть на малюнку прямокутний трикутник, стороною якого є шуканий елемент, і застосуйте теорему Піфагора.

2. Перпендикуляр і похила

Нехай ВС — перпендикуляр, проведе

ний із точки В до прямої а (мал. 365). Ві

зьмемо довільну точку А на прямій а, відмінну від точки С, і сполучимо точки А і В.

Відрізок АВ називають похилою, проведе

ною з точки В до прямої а. Точку А

1) будь-яка похила більша

2) рівні похилі мають

Мал. 366 Мал. 367 Мал. 368

Задача Із точки до прямої проведено дві похилі, проєкції яких

нюють 5 см і 9 см. Знайдіть похилі, якщо

за іншу.

Розв’язання Нехай АD = 5 см, DC = 9 см (мал. 369). Оскільки АD < DC, то, за властивістю похилих, АВ < BC. Позначимо АВ через х, тоді ВС = х + 2. Із прямокутних трикутників АВD і СВD знаходимо ВD2 .

Із DАВD : ВD2 = АВ2 – АD2 = х2 – 52 = х2 – 25.

Із DСВD : ВD2 = ВС2 – DС2 = (х + 2)2 – 92 = = х2 + 4х – 77.

Прирівнявши праві частини рівностей, одержимо: х2 + 4х – 77 = х2 – 25.

Звідси 4х = 52, х = 13 см. Отже, АВ = 13 см, ВС = 13 + 2 = 15 (см). Якщо

прямої.

3. Прямокутні трикутники

ває її на два прямокутні трикутники

трикутник (наприклад, прямокутний трикут

ник А1АС на малюнку 370).

У зображеній на малюнку 371 чотирикутній піраміді АС і BD — діагоналі основи, SО — висота піраміди, SМ — перпендикуляр, проведений до сторони ВС. Ці відрізки утворюють прямокутні трикутники (наприклад, трикутники SМС, SМВ, SОС, SОВ).

Дізнайтеся більше

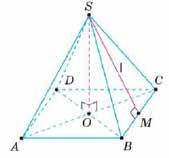
Теорема Піфагора одна з визначних теорем математики. Протягом багатьох століть вона була поштовхом до важливих математичних досліджень.

Піфагор (570–496 рр. до н. е.) народився на острові Самосі (на півдні Егейського моря). Довгий час вивчав математику в Єгипті та Вавилоні. У м. Кротон, на півдні Італії, заснував наукову школу так званий піфагорійський союз. Піфагор та його учні займалися математикою, філософією, астрономією й теорією музики. Серед досягнень піфагорійців найвагомішим вважають теорему, названу Піфагоровою, та її

доведення. (Нині встановлено, що цю теорему застосовували за 1500 років до Піфагора в Давньому Вавилоні.)

Теорема була сформульована так: площа квадрата, побудованого на гіпотенузі прямокутного трикутника, дорівнює сумі площ квадратів, побудованих на катетах (мал. 372).

Доведенням теореми Піфагора займалось багато математиків протягом кількох століть. Нині є понад 150 різних доведень цієї теореми. Так, індійський математик Бхаскара (ХІІ ст.) запропонував таку фігуру, як на малюнку 373, без жодних пояснень. Під малюнком стоїть лише одне слово «дивись». Спробуйте пояснити справедливість теореми за цим малюнком. Із теоремою Піфагора пов’язані учнівські жарти: малюнок до теореми для випадку рівнобедреного прямокутного трикутника називали «піфагоровими штанами» (мал. 374). Іноді цей малюнок зображали у вигляді різних смішних фігурок (мал. 375 і 376).

Словничок qr.orioncentr.com.ua/fPUx0 Пригадайте

УкраїнськаАнглійська/ English

Deutsch

Français

теорема Піфагора Pythagorean theorem Satz des Pythagoras Théorème de Pythagore

1. Сформулюйте та доведіть теорему Піфагора.

2. Поясніть, як за двома сторонами прямокутного трикутника

сторону.

3. Що таке похила; основа похилої; проєкція похилої?

4. Сформулюйте властивості похилих.

Усне тренування

Обчисліть:

1) 32 + 42; 52 + 122; 72 + 242; 82 + 152; 2) 92 + 402; 112 + 602; 122 + 352; 202 + 212.

Розв’яжіть задачі

824'. Яке з наведених тверджень є правильним?

У прямокутному трикутнику:

1) квадрат гіпотенузи дорівнює різниці квадратів катетів;

2) гіпотенуза дорівнює сумі квадратів катетів;

3) квадрат гіпотенузи дорівнює сумі квадратів катетів.

825'. Чи правильно вказано довжини сторін прямокутних

826'. На малюнку 379 AD і DC

AD < DC. Яке із співвідношень є правильним: 1) AB = BC; 2) AB > BC; 3) AB < BC?

827°.

нюють: 1) 12 см і 5 см; 2) 9 м і 12 м; 3) 8 см і 83 см.

828°.

1) 13 см і 12 см; 2) 17 м і 15 м; 3)

831°.

832°. Знайдіть діагональ квадрата, якщо

833°. Знайдіть гіпотенузу рівнобедреного

трикутника, якщо його катет дорівнює: 1) 1 см; 2) 42 см; 3) a.

834°. Знайдіть катети рівнобедреного прямокутного трикутника, якщо його гіпотенуза дорівнює: 1) 2 см; 2) 8 см; 3) m.

835°.

дорівнює: 1) 3 см; 2) 10 см; 3) a.

836°.

1) 26 см і 20 см; 2) 17 см і 16 см; 3) 13 см і 10 см.

837°. Через точку A до кола з центром О проведено дотичну AB, де B — точка дотику (мал. 380). Знайдіть:

1) радіус кола, якщо відрізок дотичної AB дорівнює 8 см, а відстань від точки A до центра кола — 17 см; 2) відстань від точки A до центра кола, якщо радіус кола дорівнює 12 см, а відрізок дотичної AB — 16 см.

Мал. 380

838°. Знайдіть сторону ромба, якщо його діагоналі дорівнюють:

1) 6 см і 8 см; 2) 18 см і 24 см; 3) 12 см і 16 см.

839°. Доведіть, що коли a — сторона ромба, d1 і d2 — його діагоналі, то =+ add 222 12 4.

840°. Доведіть, що квадрат діагоналі прямокутного паралелепіпеда дорівнює сумі квадратів трьох його вимірів: d2 = а2 + b2 + с2 (мал. 381).

841°. Діагональ прямокутного паралелепіпеда дорівнює 13 см, а його довжина і ширина — відповідно 4 см і 3 см. Знайдіть висоту прямокутного паралелепіпеда.

842°. Основою піраміди SАВСD, бічні ребра якої рівні, є квадрат зі стороною 16 см (мал. 382). Знайдіть бічне ребро піраміди, якщо висота SМ її грані дорівнює 15 см.

843°. Кожне ребро трикутної піраміди дорівнює m. Знайдіть висоту грані піраміди.

844°. Із точки A до прямої проведено перпендикуляр AB і похилу AC. Знайдіть: 1) похилу AC, якщо її проєкція BC дорівнює 24 см, a перпендикуляр AB — 10 см;

2) проєкцію BC похилої, якщо пер

пендикуляр AB дорівнює 83 см, а похила AC — 16 см;

3) перпендикуляр AB, якщо похила AC дорівнює 17 см, а її проєкція BC — 8 см.

Мал. 381

Мал. 382

845°. Із точки О до прямої проведено перпендикуляр ОB і похилу ОC. Знайдіть:

1) похилу ОC, якщо її проєкція BC дорівнює 4 см, a перпендикуляр ОB — 3 см;

2) проєкцію BC похилої, якщо перпендикуляр ОB дорівнює 12 см, а похила ОC — 13 см;

3) перпендикуляр ОB, якщо похила ОC дорівнює 25 см, а її проєкція BC — 7 см.

846.

847.

848. Один із катетів прямокутного трикутника

1) b = 5 см; 2) b = 7 см.

849. Катети прямокутного трикутника відносяться як 3 : 4. Знайдіть катети трикутника, якщо його гіпотенуза дорівнює: 1) 25 см; 2) 20 см.

850. Периметр прямокутного трикутника дорівнює

як

851. Знайдіть сторони прямокутного трикутника, якщо його периметр дорівнює 80 см, а катети відносяться як 15 : 8.

852.

853.

1) 15 см і 9 см; 2) 7 см і 25 см.

854.

1) а = 4 см, b = 12 см, h = 6 см; 2) а = 35 см, b = 15 см, h = 21 см.

855. Доведіть, що

856. За даними на малюнках 386, 387

рівнобічної

857. За

трапеції ABCD.

386 Мал. 387

388

858.

1) а = 6 см, b = 18 см, h = 16 см; 2) а = 16 см, b = 8 см, h = 5 см.

859.

трапецію

1) а = 2 см, b = 18 см, r = 3 см; 2) а = 32 см, b = 18 см, r = 12 см.

860. Висота ромба, проведена

відрізки b і с, рахуючи від вершини гострого кута. Знайдіть радіус кола, вписаного в ромб, якщо: 1) b = 6 см, с = 4 см; 2) b = 5 см, с = 8 см.

861. У колі радіусом r проведено паралельні хорди завдовжки

і b. Знайдіть відстань між хордами, якщо: 1) r = 25 см, а = 40 см, b = 48 см; 2) r = 65 см, а = 120 см, b = 32 см.

862. Два кола радіусами 2 см і 8 см

864.

865. Із

проєкції відносяться як 2 : 5. Знайдіть: 1) проєкції похилих;

866. Якщо

проведені до прямої з однієї точки, мають рівні проєкції, то вони рівні між собою. Доведіть.

867. Якщо з однієї точки до прямої проведено дві похилі, то

має

Доведіть.

868*. У прямокутному трикутнику медіана й висота,

периметр трикутника, якщо: 1) m = 25 см, n = 24 см; 2) m = 17 см, n = 15 см.

869*. У прямокутному трикутнику один катет дорівнює b см, а сума гіпотенузи та іншого

Знайдіть гіпотенузу й інший катет, якщо: 1) b = 60, n = 12; 2) b = 35, n = 14.

870*. Висота й медіана, проведені до сторони с трикутника, дорівнюють h і m. Знайдіть дві інші сторони трикутника, якщо: 1) с = 60 см, h = 12 см, m = 13 см; 2) с = 42 см, h = 12 см, m = 13 см.

871*. Знайдіть висоти трикутника, якщо його сторони дорівнюють: 1) 10 см, 10 см, 12 см; 2) 7 см, 15 см, 20 см.

872*. Доведіть, що сума квадратів

сумі квадратів усіх його сторін.

873*. Доведіть, що коли d1 і d2 —

трапеції, а і b

її основи, c і d — бічні сторони, то 2222 12 2.ddcdab +=++

874*. Доведіть, що в колі:

1) рівні хорди рівновіддалені від центра; 2) із двох нерівних хорд більша хорда ближча до центра.

875*. Два кола дотикаються зовнішньо. Доведіть, що відрізок їхньої зовнішньої спільної дотичної, що лежить між точками дотику,

876*.

877*. (Задача Архімеда) Дві хорди, які перетинаються, — взаємно перпендикулярні. Доведіть, що сума квадратів відрізків цих хорд дорівнює квадрату діаметра (мал. 391).

878. На малюнку 392 показано, як застосували теорему Піфагора, щоб виміряти відстань між пунктами A і B, розділеними перешкодою. Поясніть вимірювання.

879. Між двома фабричними будівлями потрібно побудувати похилий жолоб для транспортування матеріалів. Кінці жолоба мають бути розташовані на висоті 7 м і 3 м над землею. Якою має бути довжина жолоба, якщо відстань між будівлями дорівнює 15 м?

880. Діагональ прямокутної ділянки землі дорівнює 116 м, а одна зі сторін — 84 м. Який периметр цієї ділянки?

881. 1. Якої довжини має бути драбина (мал. 393), щоб її можна було приста

вити до вікна, розташованого на висоті 6 м, якщо відстань від нижнього кінця драбини до будинку має дорівнювати 2,5 м?

2. На яку відстань від стіни будинку потрібно відсунути нижній кінець драбини завдовжки 9 м, щоб верхній її кінець був на висоті 6 м?

882. (Задача давньокитайського

1. Синус, косинус і тангенс гострого кута прямокутного трикутника

Ситуація. Учні й учениці 8-А класу продовжу-

вали досліджувати властивості прямокутних трикутників. Вони побудували прямокутний трикутник зі сторонами 6, 8, 10 і його середню лінію та отримали подібний прямокутний трикутник зі сторонами 3, 4, 5. Спільний гострий кут цих трикутників позначили a (мал. 395). Учнівство помітило таку закономірність відношення обох катетів до гіпотенузи, а також катета до катета у кожному з цих трикутників відповідно рівні: = 63 105 , 84 105 = , 63 84 =

Виникла гіпотеза,

нусом гострого

дорівнювати йому.

Звідси випливають

1. Для кута 45° .

Нехай АВС — прямокутний

(мал. 396).

ничним відрізкам (мал. 398). З точки В, як із центра, радіусом, що дорівнює трьом таким самим одиничним відрізкам, опишемо дугу, яка перетне іншу сторону прямого кута. Точку перетину позначимо буквою А. З’єднавши точки А і В, одержимо прямокутний трикутник АВС. ∠

— шуканий, оскільки == BC A AB 2 sin . 3

3. Залежності між сторонами

Так.

синуса,

го трикутника

(мал. 399),

1) — 6) (табл. 33)

2. Катет,

Задача

трикутник із бічною стороною

му трикутнику DВС катет DС, прилеглий до кута a, дорівнює добутку гіпотенузи а на cos a: DС = а cos a.

Оскільки висота рівнобедреного трикутника, яку проведено до основи, є медіаною, то DС = АD. Тоді основа АС = 2 · DС = 2а cos a.

4. Знаходження синуса,

й «синуси».

Верхні назви «синуси» й «косинуси» стосуються кутів, менших від

45°, а нижні — кутів, більших за 45° .

Наприклад, за таблицею знаходимо: sin 34° ≈ 0,559, cos 67° ≈ 0,391, sin 85° ≈ 0,996 і т. д.

За таблицею можна знайти кут a за даним значенням sin a або cos a. Наприклад, треба знайти кут a, якщо sin a ≈ 0,615. У стовпцях синусів знаходимо число, близьке до 0,615. Таким числом є 0,616. Отже, a ≈ 38° .

Таблиця тангенсів (див. додаток 2) складається із двох стовпців: в одному вміщено градусну міру кутів від 0° до 89°, а в іншому — значення тангенсів цих кутів. Наприклад, tg 19° ≈ 0,344. Якщо tg a ≈ 0,869, то a ≈ 41° .

Дізнайтеся більше

1. Крім синуса, косинуса й тангенса кута a, є ще одне відношення сторін прямокутного трикутника, яке має особливу назву котангенс Це відношення катета b, прилеглого до кута a, до протилежного катета a (мал. 401). Позначають: ctg a. Отже, ctg. α= b a

2. Індійський математик Аріабхата (V ст.) відношення протилежного катета до гіпотенузи назвав ardhajya ардхажіа (півхорда). У ХІІ ст. європейські вчені переклали цю назву на латинську як sinus синус. Слово cosinus косинус складається із двох слів: complementi доповнення і sinus синус, тобто доповняльний синус. Утворенню цієї назви послужила рівність cos a = sin (90° – a). Арабські астрономи-математики ал-Баттані (858–929) і Абу-ль-Вефа (940–998) визначили поняття тангенса, вимірюючи кутову висоту Сонця за тінню від жердини. Тому відношення катета, протилежного куту a, до прилеглого катета вони називали словом «тінь». Пізніше, у ХVІ ст., це відношення одержало назву «тангенс».

3. Знаки «sin», «cos», «tg» увів Леонард Ейлер у ХVІІІ ст.

4. Дубинчук Олена Степанівна (1919–1994) одна з визначних педагогинь-математикинь України. Народилася на Вінниччині, у м. Ямполі, закінчила механіко-математичний факультет Київського державного університету ім. Тараса Шевченка. З 1951 р. й

Deutsch

Français синусsineSinus (m)sinus

косинусcosineKosinus (m)cosinus тангенсtangentTangens (m)tangente

qr.orioncentr.com.ua/7af0l

2. Поясніть, чому синус,

3. Поясніть, чому sin a < 1, cos a < 1 для

4. Яких значень може набувати tg a?

5. Сформулюйте

6. Назвіть значення синуса,

7. Поясніть, як знайти

1. Обчисліть:

гострого кута a.

884'. Назвіть правильну відповідь (мал. 403).

1) tg b дорівнює:

а) 5 ; 15 б) 12 ; 5 в) 5 ; 13

2) cos b дорівнює:

а) 12 ; 13 б) 13 ; 5 в) 5 ; 13

3) sin b дорівнює:

а) 5 ; 12 б) 12 ; 13 в) 13 . 5

885'. За малюнком 404 назвіть правильну відповідь:

1) для кута a відношення a c є:

а) sin a; б) cos a; в) tg a;

2) для кута b відношення a c є:

а) sin b; б) cos b; в) tg b;

3) для кута b відношення b a є:

а) sin b; б) cos b; в) tg b.

886'. Чи правильно, що при збільшенні гострого кута (мал. 405):

1) синус кута зменшується;

2) синус кута збільшується;

3) косинус кута зменшується;

4) косинус кута збільшується;

5) тангенс кута зменшується;

6) тангенс кута збільшується?

887'. Чи є правильною рівність:

1) 3 sin30; 2 °= 4) 2 sin45; 2 °= 7) 1 sin60; 2 °= 2) 3 cos30; 2 °= 5) 2 cos45; 2 °= 8)

cos60; 2 °= 3) 3 tg30; 2 °= 6)

tg45; 2 °= 9)

tg60? 2 °=

Мал. 403

Мал. 404

Мал. 405

888°.

889°.

890°.

строго кута прямокутного трикутника дорівнювати: 1) 1; 2) 0,9; 3) 2? Відповідь поясніть.

891°. Чи може тангенс гострого кута прямокутного трикутника дорівнювати: 1) 1; 2) 4; 3) 0,8?

892°. Знайдіть значення виразу: 1) 2 sin 30°; 3) 3tg30; ° 5) 2 cos 30°; 2) 4 cos 60°; 4) 6 sin 45°; 6) 8 tg 45° .

893°. Знайдіть значення виразу: 1) 4 sin 60°; 2) 2 cos 45°; 3) 3tg60. °

894°. Знайдіть значення виразу: 1) tg 30° · tg 60°; 2) 2cos45tg45; °⋅°

3) 2sin303cos30; °+°

4) 6cos603tg30. °−°

895°. Знайдіть значення виразу: 1) 8 sin 30° · cos 60°; 2) 2cos452sin30. °−°

Мал. 406

896°. Яка градусна міра кута a, якщо:

1) α= 1 sin; 2 3) tg3; α= 5) α= 1 cos; 2 2) α= 2 cos; 2 4) α= 3 sin; 2 6) tg a = 1?

897°. Яка градусна міра кута a, якщо: 1) α= 2 sin; 2 2) α= 3 cos; 2 3) 3 tg? 3 α=

898°. Запишіть у порядку збільшення: 1) sin 15°, sin 46°, sin 75°, sin 10°, sin 11°; 2) tg 37°, tg 87°, tg 66°, tg 17°, tg 48° .

899°. Запишіть у порядку збільшення: cos 50°, cos 34°, cos 20°, cos 72°, cos 25° .

900°.

407–409, знайдіть х. Мал. 407

1) ВС, якщо АВ = 4 см; 2) АС, якщо = BC 23 см; 3) АВ, якщо = AC 43 см.

903°. У трикутнику MNK (∠K = 90°) кут M дорівнює 60°. Знайдіть:

1) MN, якщо MK = 3 см; 3) MK, якщо = NK 73 см.

2) NK, якщо = MK 23 см; 904°. Кут А трикутника АВС (∠C = 90°) дорівнює 45°. Знайдіть:

1) АВ, якщо = AC 2 см; 3) АС, якщо ВС = 9 см.

2) ВС, якщо = AB 52 см; 905°. Скориставшись формулами cos a = sin (90° – a), sin a = cos (90° – a), замініть:

1) косинуси даних кутів на синуси: cos 20°, cos 35°, cos 50°;

2) синуси даних кутів на косинуси: sin 10°, sin 65°, sin 85° .

906°. Скориставшись формулами cos a = sin (90° – a), sin a = cos (90° – a), замініть:

1) косинуси даних кутів на синуси: cos 40°, cos 74°;

2) синуси даних кутів на косинуси: sin 55°, sin 25° .

907°. Спростіть вираз:

1) 2 cos (90° – a) – sin a; 3) 3 cos a – 2 sin (90° – a); 2) sin a + cos (90° – a); 4) 3 sin (90° – a) – 4 cos a.

908°. Спростіть вираз: 1) sin (90° – a) – cos a; 2) cos a – 2 sin (90° – a).

909°. Побудуйте кут:

1) синус якого дорівнює: а) 3 ; 5 б) 0,3;

2) косинус якого дорівнює: а) 5 ; 6 б) 0,6;

3) тангенс якого дорівнює: а) 2; б) 4 . 7

910°. Побудуйте кут: 1) синус якого дорівнює 0,5;

2) косинус якого дорівнює 5 12 ; 3) тангенс якого дорівнює 1.

911°. За даними, наведеними на малюнках 413–415, знайдіть x.

413

912°.

913°.

1) с = 12 см, = A 1 sin; 4 3) с = 18 см, 2 sin; 3 A =

2) с = 20 см, = A 2 sin; 5 4) с = 8 см, 3 sin. 4 A = 914°. Знайдіть катет b прямокутного трикутника, якщо гіпотенуза с і косинус прилеглого до нього кута А дорівнюють:

1) с = 6 см, = A 1 cos; 3 2) с = 14 см, 2 cos. 7 A = 915°. Знайдіть

(∠C = 90°), якщо:

1) ВС = 16 см, = B 1 cos; 8 3) ВС = 5 см, cos В = 0,5;

2) ВС = 12 см, = B 3 cos; 4 4) ВС = 7 см, cos A = 0,7.

916°. Знайдіть гіпотенузу

(∠C = 90

), якщо:

1) ВС = 24 см, = A 3 sin; 8 2) ВС = 10 см, 1 sin. 5 A = 917°. Знайдіть

АВС (∠C = 90°), якщо:

1) АС = 8 см, tg A = 0,6; 3) AC = 11 см, tg A = 1,5. 2) AC = 12 см, tg A = 4; 918°. Знайдіть невідомі сторони прямокутного трикутника АВС (∠C = = 90°), якщо: 1) AB = c, ∠B = b; 2) BC = a, ∠A = a; 3) AC = b, ∠B = b. 919°. Скориставшись калькулятором, знайдіть: 1) sin a, cos a, tg a, якщо a дорівнює: 43°; 22°; 35°; 58°20′; 64°13′; 2) кут a, якщо: sin a дорівнює: 0,642; 0,771; 0,910; 0,640; 0,712; cos a дорівнює: 0,342; 0,962; 0,087; 0,914; 0,809; tg a дорівнює: 0,178; 0,269; 0,035; 0,447; 0,532.

920°. Скориставшись калькулятором, знайдіть:

1) sin a, cos a, tg a, якщо a дорівнює: 39°; 54°12′; 2) кут a, якщо: sin a дорівнює: 0,750; 0,515; cos a дорівнює: 0,602; 0,915; tg a дорівнює: 0,934; 0,781.

921°. За таблицями (додатки 1, 2) знайдіть: 1) sin 20°, sin 75°, sin 33°, sin 85°; 2) cos 6°, cos 67°, cos 51°, cos 24°; 3) tg 65°, tg 1°, tg 73°, tg 19° .

922°. За таблицями (додатки 1, 2) знайдіть: 1) sin 53°, sin 2°; 2) cos 62°, cos 13°; 3) tg 10°, tg 16° .

923°. За таблицями (додатки 1, 2) знайдіть кут a, якщо: 1) sin a = 0,999; sin a = 0,017; sin a = 0,574; 2) cos a = 0,766; cos a = 0,966; cos a = 0,225; 3) tg a = 0,900; tg a = 0,344; tg a = 0,781.

924°. За таблицями (додатки 1, 2) знайдіть кут a, якщо: 1) sin a = 0,588; 2) cos a = 0,731; 3) tg a = 0,839.

925. У прямокутному трикутнику ABC (∠C = 90°) AC = 18 мм, BC = 24 мм. Знайдіть: 1) sin A, cos A, tg A; 2) sin B, cos B, tg B.

926. Із точки A до прямої проведено похилу AB = 15 см і перпендикуляр AC = 9 см. Знайдіть синус і косинус: 1) кута A; 2) кута B.

927. У прямокутному трикутнику катети дорівнюють 24 см і 7 см.

Знайдіть:

1) косинус гострого кута, який лежить проти

2) синус

3) тангенс

928.

929.

932. Бічна сторона рівнобедреного трикутника дорівнює 10 см, а кут при основі — 30° (мал. 419). Знайдіть:

1) основу трикутника; 2) висоту, проведену до основи; 3) висоту, проведену до бічної сторони.

Мал. 419

933. Знайдіть катети прямокутного трикутника, якщо медіана, проведена до гіпотенузи, дорівнює 8 см, а кут трикутника: 1) 30°; 2) 45° .

934. За даними, наведеними на малюнках 420, 421, знайдіть довжини відрізків AD і CD.

935. За даними, наведеними на малюнку 422, знайдіть довжини відрізків AD і CD.

936. Сторона ромба дорівнює 4

діагоналі ромба.

937. Більша діагональ ромба

938. Діагональ паралелограма дорівнює 12 см і перпендикулярна

939.

940.

943.

944. У прямокутному трикутнику ABC (∠C = 90°) AC = 18 мм, BC = 24 мм. Знайдіть: 1) sin A, cos A, tg A; 2) sin B, cos B, tg B.

945. Побудуйте

ACB (∠C = 90°), у якому: 1) sin A = 0,4; 2) 1 tg. 3 A =

946. Побудуйте

947.

948.

949.

основі — a. Знайдіть:

1) основу трикутника; 2) висоту, проведену до основи.

950. Висота рівнобедреного трикутника, проведена до основи, дорівнює h, а кут при основі — a. Знайдіть: 1) бічну сторону трикутника; 2) основу трикутника.

951. Основа рівнобедреного трикутника дорівнює

сторонами — a. Знайдіть: 1) висоту, проведену до основи; 2) бічну сторону трикутника.

952. За даними, наведеними на малюнках 423, 424, знайдіть відрізки AD і CD.

953. Знайдіть відрізки AD і CD за даними на малюнку 425.

423

424

425

954.

955.

956.

1) основу трикутника; 2) бічну сторону трикутника.

957. Висота рівнобедреного трикутника, проведена до

нює h, а кут при основі

кутник.

958. Сторона АD прямокутника ABCD дорівнює а й утворює

кутника.

959. Гострий кут між діагоналями прямокутника

на, що лежить проти цього кута, — а. Знайдіть: 1) іншу сторону прямокутника; 2) діагональ прямокутника.

960. Більша діагональ ромба дорівнює d, а його гострий кут — a. Знайдіть: 1) сторону ромба; 2) меншу діагональ ромба.

961. Визначте знак різниці: 1) tg 64° – tg 58°; 2) sin 21° – sin 36° .

962. Визначте знак різниці: cos 51° – cos 41° .

963*. Дві висоти паралелограма, проведені з вершини тупого кута, дорівнюють 12 см і 18 см, а кут між ними — 30°. Знайдіть

паралелограма.

964*. Дві висоти паралелограма, проведені

рівнюють 5 см і 12 см,

шосейної дороги, поперечний

різ якого — рівнобічна трапеція, дорівнює 60 м (мал. 427). Яка ширина основи

971.

запитання:

далеку давнину

спочатку вимірювали безпосередньо інструментами. Так, транспортиром вавилоняни користувалися ще за 2000 років до н. е. Проте на практиці безпосередньо виміряти відстані й кути не завжди можливо. Як виміряти відстань між двома пунктами, розділеними перешкодою (річкою, озером, лісом), відстань до Сонця, Місяця? Як виміряти висоту дерева, гори? Як знайти кут підйому дороги або кут, під яким спускаємося з гори? Були відкриті прийоми опосередкованого вимірювання відстаней і

допоміжний

сторонами

сторони й гострі кути.

Можливі такі види задач, у яких

ний трикутник:

1) за катетами;

2) за гіпотенузою й катетом;

3) за гіпотенузою й гострим кутом;

4) за катетом і гострим кутом.

Алгоритми розв’язування цих чотирьох

лиці 35.

Дано: АС = b,

ВС = а.

Знайти: AB, ∠A, ∠B

Дано: AB = c,

BC = a.

Знайти: AC, ∠A, ∠B

Дано: AB = c,

∠A = a.

Знайти: AC, BC, ∠B

Дано: BC = a,

∠A = a.

Знайти: AB, AC, ∠B

a = 76° (мал. 431).

1) =+ ABab22 ,

2) tg, a A b =

3) ∠B = 90° – ∠A

1) =− ACca22 ,

2) = a A c sin,

3) ∠B = 90° – ∠A

1) ∠B = 90° – a,

2) AC = c · cos a,

3) BC = c · sin a

1) ∠B = 90° – a,

2) = α a AB , sin

3) tg a AC = α

Розв’язання Це задача третього виду. Алгоритм її розв’язування наведено в таблиці 35.

1) ∠B = 90° – a = 90° – 76° = 14°;

2) AC = c · cos a = 16 · cos 76° ≈ 16 · 0,242 ≈ 3,9;

3) BC = c · sin a = 16 · sin 76° ≈ 16 · 0,970 ≈ 15,5.

Розглянемо кілька видів прикладних задач.

2. Задачі на знаходження висоти предмета, основа якого є доступною

Задача 2 Знайдіть висоту дерева (мал. 432).

Розв’язання На деякій відстані MN = a від дерева встановлюємо кутомірний прилад AM (наприклад, теодоліт) і знаходимо кут a між горизонтальним напрямком AC і напрямком на верхню точку B дерева. Тоді з прямокутного трикутника ABC одержимо: BC = a · tg a. Урахувавши висоту кутомірного приладу AM = h, одержимо формулу для обчислення висоти дерева: BN = a · tg a + h.

Нехай результати вимірювання такі: a = 40 м, h = 1,5 м і a = 31° .

Тоді BN = 1,5 + 40 · tg 31° ≈ 1,5 + 40 · 0,601 ≈ 25,5 (м).

3. Задачі на знаходження висоти предмета, основа якого недоступна

Задача 3 Знайдіть висоту вежі, яка відокремлена від вас водною перешкодою (мал. 433).

Розв’язання На горизонтальній

Мал. 431

Почленно віднімемо знайдені рівності й отримаємо: tgtg DCDC ACBC−=− αβ , tgtg tgtg ABDC β−α = α⋅β , ⋅α⋅β = β−α a DC tgtg . tgtg

Додавши до DC висоту приладу AM = h, яким вимірювали кути, одержимо формулу для обчислення висоти вежі: ⋅α⋅β = + β−α a DK h tgtg . tgtg

Нехай результати вимірювання такі: a = 10 м, h = 1,5 м і a = 35° , b = 40° .

Тоді ⋅°⋅°⋅⋅ = +≈ +≈ °−° DK 10tg35tg40100,7000,839 1,5 1,543,8 tg40tg350,8390,700 (м).

4. Задачі на знаходження відстані між двома пунктами, що розділені перешкодою

Задача 4 Знайдіть відстань між пунктами A і B, розділеними річкою (мал. 434).

Розв’язання Провішуємо пряму AD ⊥ AB та позначаємо на ній деяку точку C. Вимірюємо відстань AC = a і кут a. Із прямокут

ного трикутника ABC одержимо формулу

AB = a · tg a для знаходження відстані між

пунктами A і B.

Нехай результати вимірювання такі: a = 50 м, a = 72° .

Тоді AB = 50 · tg 72° ≈ 50 · 3,08 ≈ 154 (м).

5. Задачі на знаходження кутів (кута підйому

434

Тоді a ≈ 2° .

Дізнайтеся більше

1. Накопичення обчислювальних прийомів розв’язування задач привело до створення нового розділу математики, який у ХVІ ст. назвали тригонометрією Слово «тригонометрія» походить від грецьких слів trigonon трикутник і metreo вимірюю. Грецьких математиків Гіппарха (ІІ ст. до н. е.) і Птолемея (ІІ ст.) вважають першими, хто використав тригонометричні прийоми для розв’язування різних задач. Подальше їх удосконалення було зроблено індійським математиком Брахмагуптою (VІ ст.), а потім узбецькими математиками аль-Каші й Улугбеком (ХІІ ст.). У працях академіка Леонарда Ейлера (ХVІІІ ст.) тригонометрія набула того вигляду, який в основному вона має й нині.

2. У вас могло виникнути запитання: Чому

ляють саме прямокутному трикутнику, хоча

на предмети такої форми? Давайте поміркуємо. Як у хімії вивчають

а в біології одноклітинні, а потім багатоклітинні організми, так і в геометрії вивчають спочатку простіші геометричні фігури точки, відрізки і трикутники, з яких складаються інші геометричні фігури. Серед цих фігур прямокутний трикутник відіграє особливу роль. Справді, будь-який многокутник можна розбити на трикутники (мал. 436). Уміючи знаходити кутові й лінійні елементи цих трикутників, можна знайти й усі елементи многокутника. Своєю чергою будь-який трикутник можна розбити однією з його висот на два прямокутні трикутники, елементи яких зв’язані простішою залежністю (мал. 437). Знайти елементи трикутника можна, звівши їх до розв’язування цих двох прямокутних трикутників. Наведемо приклад.

Задача 6 У DABC АС = 50 см, АВ = 35 см і ∠A = 76° (мал. 438). Знайдіть ∠B, ∠C і сторону ВС Розв’язання Проведемо висоту BD Точка D ле-

Звідси ∠C ≈ 44° . ∠B = 180° – (∠A + ∠C) ≈ 180° – (76° + 44°) ≈ 180° – 120° ≈ 60°

Із прямокутного трикутника BDC: 4040 57,6 sin 0,695 sin44 ==≈≈ BD BC C  (см).

Словничок

Отже, ВС ≈ 57,6 см, ∠B ≈ 60° , ∠C ≈ 44° УкраїнськаАнглійська/ English Німецька/ Deutsch Французька/ Français

прикладна задача applied problem angewandte Übungsaufgabe (f) problème appliqué

qr.orioncentr.com.ua/NlVgA

Пригадайте головне

1. Що означає «розв’язати прямокутний трикутник»?

2. Назвіть види задач, у яких вимагається розв’язати прямокутний трикутник.

3. Запишіть алгоритм

1. Обчисліть: 23° + 37°;

2. Знайдіть х, якщо:

достатньо знати:

1) одну сторону; 4)

2) дві сторони; 5) одну сторону і

прямокутний трикутник: 1) за кутами; 2) за катетами; 3) за гіпотенузою; 4) за гіпотенузою і катетом;

5) за гіпотенузою та прямим кутом; 6) за гіпотенузою й гострим кутом;

7) за катетом і прямим кутом; 8) за катетом і гострим кутом?

975°. За даними, наведеними на малюнках 439, 440, знайдіть х і y.

976°. За даними, наведеними на малюнках 441, 442, знайдіть кути a і

Мал. 439 Мал. 440 Мал. 441 Мал. 442

977°. У прямокутному трикутнику АВС (∠С = 90°) знайдіть:

1) ВС, якщо АВ = 5 см, ∠А = 55°;

2) АВ, якщо АC = 7 см, ∠В = 41°;

3) АС, якщо ВС = 6 см, ∠В = 38° .

978°. Знайдіть невідомі сторони прямокутного трикутника, якщо:

1) катет дорівнює 9 см, а протилежний йому кут — 38°;

2) катет дорівнює 10 см, а прилеглий до нього кут — 54° .

979°. У прямокутному трикутнику з гіпотенузою 14 см і

65° знайдіть:

1) катет, прилеглий до цього кута;

2) катет, протилежний цьому куту.

980°. Знайдіть кут А прямокутного

1) АВ = 12 см, ВС = 9 см;

2) АВ = 10 см, АС = 6 см; 3) АС = 8 см, ВС = 16 см.

981°. У прямокутному

984°. Сторони прямокутника дорівнюють 7 см і 14 см. Знайдіть кут між його діагоналлю й більшою стороною.

985°. Через точку А до кола радіусом 45 см проведено дотичні АВ і АС (мал. 443). Знайдіть кут, утворений дотичними, якщо: 1) АВ = 60 см; 2) АВ = 50 см.

986°. Через точку В до кола радіусом 30 см проведено дотичні ВМ і ВС (мал. 444). Зна

йдіть кут, утворений дотичними, якщо

ВМ = 30 см.

987. Знайдіть невідомі сторони й гострі кути прямокутного трикутника за такими да

ними:

1) за двома катетами:

а) а = 20, b = 21; в) а = 24, b = 18; б) а = 9, b = 12; г) а = 23,5, b = 40,2;

2) за гіпотенузою та катетом:

а) с = 17, а = 15; в) с = 65, а = 56; б) с = 20, а = 16; г) с = 2,93, b = 2,85.

988. Знайдіть невідомі сторони й гострі кути

прямокутного трикутника за такими да

ними:

1) за гіпотенузою та гострим кутом:

а) с = 8, ∠А = 70°; в) с = 18,2, ∠А = 32°; б) с = 82, ∠А = 42°; г) с = 4,67, ∠А = 65°; 2) за катетом і прилеглим кутом:

а) а = 12, ∠А = 32°; в) а = 12, ∠А = 53°; б) а = 18, ∠А = 17°; г) а = 3,71, ∠А = 19° .

989. Діагональ прямокутника дорівнює 25 см й утворює зі стороною кут 36°. Знайдіть сторони прямокутника.

990. Бічна сторона рівнобедреного трикутника дорівнює 12 см, а кут при основі — 75°. Знайдіть: 1) основу трикутника; 2) висоту, проведену

991.

992.

993. У прямокутному трикутнику ABC (

Знайдіть: 1) невідомий катет; 3) проєкцію кожного катета на гіпотенузу. 2) гіпотенузу;

994. Із точки, що розміщена на

похилі, які утворюють із прямою кути 24° і 61°. Знайдіть: 1) довжину похилих; 2) проєкції похилих на пряму.

995. Знайдіть висоту ромба, якщо його сторона дорівнює 7,5 см, а гострий кут — 22° .

996. Сторони паралелограма дорівнюють 5 см і 8 см, а гострий кут — 36°. Знайдіть висоти паралелограма.

997. Сторона ромба дорівнює 64,5 см, а гострий кут — 28°. Знайдіть діагоналі ромба.

998*. У трапеції

трапеції — 24 см, а менша основа — 18 см.

трапеції.

999*. Основи трапеції

1000*.

1002.

1003. Гірська залізниця на одному з перегонів підіймається

дороги на цій ділянці.

1004. На яку висоту h піднявся

1005. Вертикальний промінь прожектора перетинає хмару. Яка висота нижньої межі хмари, якщо спостерігач, який стоїть на відстані 600 м від прожектора, бачить місце перетину променя прожектора і хмари під кутом 75°?

1006. Знайдіть відстань між пунктами A і B (до пункту B підійти не можна), якщо AC = 60 м, ∠BAC = 41° , ∠ACB = 90° (мал. 445).

1007. Санаторій розташований на вершині гори. Пряма дорога до санаторію завдовжки 1500 м має кут підйому 5°. На якій висоті від підніжжя гори розташований санаторій?

1008. Щогла закріплена трьома однаковими тросами, що нахилені до землі під кутом 64

. Нижні

тросів віддалені від щогли на 35 м. На якій висоті закріплені на щоглі верхні кінці тросів?

1009. За вісімсот метрів від

h приладів, визначили шукану висоту CK. Поясніть спосіб знаходження висоти. Знайдіть висоту, на якій перебував літак, якщо результати вимірювання такі: а = 80 м, h = 1,5 м, a = 39° , b = 44° .

1012. З башти маяка заввишки 75 м над рівнем моря видно корабель під кутом зниження 2° (мал. 448). Знайдіть відстань від маяка до корабля.

1013. На малюнку 449 схематично зображено спосіб вимірювання недоступної відстані АВ. Поясніть вимірювання. Знайдіть відстань АВ, якщо СD = 200 м, ∠KCB = 28° , ∠KCA = 39° .

Мал. 448

Мал. 449

2. Назвіть властивості похилих.

3. Дайте

кутника.

5. Як за двома сторонами прямокутного трикутника знайти

1°. Знайдіть бічну сторону рівнобедреного трикутника, якщо його

А. 22 см.

2°.

В. 13 см.

Б. 14 см. Г. 15 см.

Знайдіть гіпотенузу прямокутного трикутника,

8 см, а прилеглий

кут — 60° .

А. 10 см. В. 14 см.

Б. 48 см. Г. 16 см.

3°. Діагональ прямокутника

кут 30°. Знайдіть сторони прямокутника.

А. 1 см і 3 см. В. 2 см і 3 см.

Б. 2 см і 1 см.

до основи, дорівнює h,

А. 12 см.

Б. 13 см.

В. 22 см.

Г. 20 см.

У розділі дізнаєтесь:

про многокутник та його елементи;

про суму кутів опуклого многокутника;

які властивості многокутників, вписаних у коло та описаних навколо кола;

що таке площа та які її властивості;

як обчислити площу трикутника й окремих видів чотирикутників;

як застосувати вивчене на практиці

1. Що таке многокутник Ситуація. Батько будував садову альтанку. Для її основи він з’єднав кілька брусів. Марина сказала, що він побудував многокутник.

Чи мала рацію Марина?

Так.

На малюнку 450 ви бачите многокутник ABCDEF. Він складається з відрізків AB, BC, CD, DE, ЕF, FA, розміщених так, що суміжні відрізки не лежать на одній прямій, а несуміжні — не мають спільних точок. Відрізки, з яких складається многокутник, називають його сторонами, кути, утворені суміжними сторонами, — його кутами, а вершини цих кутів — вершинами многокутника. Залежно від кількості вершин (кутів або сторін) многокутник називають трикутником, чотирикутником, п’ятикутником і т. д. Многокутник, що має n вершин, називають nкутником. Многокутник позначають назвами

(мал. 451).

Мал. 452

Жодна з прямих, що проходять через сторони

інших його сторін. Він лежить

прямих. Такий многокутник називають опуклим

опуклим.

Так.

Чотирикутник є окремим видом nкутника, коли n = 4.

кутник і чотирикутник мають

Суму довжин усіх сторін n-кутника називають його периметром.

Наприклад, у шестикутника ABCDEF (мал. 450):

РABCDEF = AB + BC + СD + DE + EF + FА.

Відрізок, що сполучає

шини n-кутника, називають його діагоналлю.

Наприклад, у шестикутнику ABCDEF (мал. 453) відрізки AC, AD, AE — його діагоналі. Теорема (про суму

(мал. 454).

453

454

Доведення. З вершини A1 у даному nкутнику проведемо діагоналі А1А3, А1А4, А1А5… А1А n–1 (мал. 455). Вони розбивають nкутник на n – 2 трикутники. Сума всіх кутів утворених трикутників дорівнює сумі кутів

ного nкутника. Оскільки в кожному трикутнику сума кутів дорівнює 180°, то сума кутів дано

го nкутника дорівнює 180° · (n – 2).

Кут, суміжний із кутом многокутника, називають зовнішнім кутом много-

кутника. Наприклад, у п’ятикутнику ABCDМ (мал. 456) кут МАN є його зовнішнім кутом.

3. Вписані й описані многокутники

Чи може nкутник бути вписа

ним чи описаним, як чотирикутник?

Так. Многокутник

налі — січними (мал. 460).

Дізнайтеся

Мал. 459 Мал. 460

(див. мал. 453).

коло не є простою фігурою (мал. 461). Навіть вписавши в коло

периметр і площу многокутника.

2. У вас могло виникнути запитання: Чи

випливає

3. Кованцов Микола Іванович (1924–1988) відомий український математик-геометр, доктор фізико-математичних наук, професор. Багато років обіймав посаду завідувача кафедри геометрії Київського державного університету імені Тараса Шевченка. Перу М. І. Кованцова належать наукові та науково-популярні праці в галузі геометрії, методики навчання математики, історії математики, філософських проблем природознавства. Серед них особливе місце займають навчальні посібники для студентів університетів: «Проективна геометрія» (1985), «Диференціальна геометрія» (1973), «Математика і романтика» (1980).

вписане коло inscribed circle einbeschriebene Kreis (m) cercle inscrit Словничок

УкраїнськаАнглійська/ English

Deutsch

описане коло circumscribed circle umschriebene Kreis (m) cercle circonscrit

qr.orioncentr.com.ua/Q2oYD

Пригадайте головне

1. Що таке многокутник; n-кутник? Як його позначають?

2. Який многокутник називають опуклим? А неопуклим?

3. Який відрізок називають діагоналлю многокутника?

4. Що таке периметр многокутника?

5. Сформулюйте теорему про суму кутів многокутника.

6. Що таке зовнішній кут многокутника?

7. Який многокутник називається вписаним у коло;

Мал. 464 Мал. 465

1015'. Чи правильно, що на малюнку 466 зображено опуклий многокутник? Відповідь поясніть.

1016'. Чи правильно, що периметр многокутника — це сума його: 1) кутів; 2) сторін?

1017'. Чи правильно, що діагональ многокутника сполучає: 1) дві сусідні його вершини; 2) дві несусідні його вершини?

1018'. Чи правильно записано формулу для обчислення суми кутів nкутника: 1) 90°(n – 1); 2) 180°(n + 2); 3) 180°(n – 2)?

1019'. Назвіть зображені на малюнку 467 зовнішні кути п’ятикутника KLMNP при вершині: 1) L; 2) P; 3) K.

1020'. Чи правильно, що у многокутника, вписаного в коло, на колі лежать: 1) середини всіх його сторін; 2) усі вершини?

1021'. Чи правильно, що у многокутника, описаного навколо кола, до кола дотикаються: 1) усі його діагоналі; 2) усі його сторони?

1022°. Знайдіть периметр nкутника, якщо в ньому всі сторони дорівнюють по 2 см і: 1) n = 7; 2) n = 10; 3) n = 9.

1023°. Які

1) A; 2)

1026°.

1027°. Скільки вершин у n

1) 1440°; 2) 1080°?

1028°. Скільки вершин у nкутника, якщо

1620°?

1029°. Скільки вершин у nкутника, якщо кожний

1) 90°; 2) 144°?

1030°. Скільки вершин у n

156°?

1031°. За даними

1032°.

1033°.

1034°.

Послідовно сполучіть

1036°.

1039. Периметр п’ятикутника дорівнює 136,4 см.

сторін відносяться як 6 : 7 : 8 : 11. Знайдіть

рони п’ятикутника, якщо вона на 15,6

з чотирьох інших сторін.

1040. Доведіть, що кожна сторона многокутника менша від його півпериметра.

1041. Скільки діагоналей у n-кутнику?

1042. Знайдіть кількість діагоналей у:

1) десятикутнику (мал. 468); 2) сімнадцятикутнику (мал. 469).

1043. Чи існує п’ятикутник, у якого кути

нюють:

1) 100°, 90°, 120°, 116°, 113°; 2) 110°, 100°, 118°, 112°, 101°?

1044. Чи можна побудувати многокутник, крім трикутника, у якому всі кути гострі?

1045. Три кути многокутника дорівнюють: 1) по 80°; 2) по 90° .

Усі інші кути дорівнюють по 150° .

Яка кількість вершин у многокутнику?

1046. Три кути многокутника дорівнюють по 100°. Усі інші кути дорівнюють по 120° . Яка кількість вершин у многокутнику?

1047. Зовнішні кути

Мал. 468

1052*.

1053*.

1054*. Доведіть, що вписаний многокутник, у якому всі сторони рівні, має: 1) рівні кути; 2) рівні зовнішні кути.

1055*. Скільки вершин у вписаному многокутнику з рівними сторонами, якщо його кут: 1) дорівнює зовнішньому куту; 2) удвічі більший за зовнішній кут;

3) відноситься до зовнішнього кута як 5 : 2?

1056*. Доведіть, що у вписаному nкутнику з рівними

1057*.

1. Поняття площі

Ситуація. Мама облаштовувала сучасну європейську фотостіну й запитала Дениса: «Як визначити, яка з рамок займає більше місця на стіні?» Денис відповів: «Порівняти фоторамки за площею.»

А що таке площа?

Поміркуємо.

Будьякий опуклий многокутник розбиває площину на дві області — внутрішню і зовнішню (мал. 472). Многокутник разом з його внутрішньою областю називають плоским многокутником. Наприклад, рамка разом з фотографією є плоским многокутником.

Кожний плоский многокутник (наприклад, многокутник F на мал. 473) займає частину площини. Якщо міру цієї властивості (займати частину

площини) виразити деяким числом, то одержимо площу многокутника.

Далі будемо говорити «площа многокутни

ка», маючи на увазі, що многокутник — плоский. Це стосується й інших плоских фігур. Площа — геометрична величина.

472

Площу позначають буквою S. Іноді вказують назву фігури, наприклад SF, а для кількох фігур використовують індекси, наприклад S1, S2 і т. д.

2. Властивості площі

На малюнку 474 фігури F1 і F2 рівні, бо суміщаються накладанням. Зрозуміло, що вони мають рівні площі. Рівні фігури

ниці вимірювання довжини. Площа квадрата зі стороною 1 см

це одиниця вимірювання площі у квадратних сантиметрах, зі стороною 1 м — у квадратних метрах і т. д.

Одиницею вимірювання площі є площа квадрата зі стороною, що

дорівнює одиниці довжини.

Коротко записують так: 1 см2, але говорять: «один квадратний сантиметр».

Говорити «сантиметр у квадраті» — неправильно!

Деякі одиниці вимірювання площі мають спеціаль

ні назви: ар (площа квадрата зі стороною 10 м), гектар (площа квадрата зі стороною 100 м) та ін.

На малюнку 475 ви бачите квадрат

стороною 2 см. Він складається із чотирьох

Записують: SАВСD = 4 см2.

Площу будь-якої фігури

додатним числом. Чи зміниться площа квадрата АВСD, якщо за одиницю вимірювання візьмемо 1 мм2? Ні, площа квадрата не зміниться, але буде виражена інакше: SАВСD = 400 мм2.

На малюнку 476 довжина сторони квадрата KLMN дорівнює 2,5 см. Він уміщує 4 квадрати площею 1 см2 і ще 9 маленьких квадратів площею 0,25 см2. Тому SKLMN = 4 + 9 · 0,25 = 6,25 (см2).

і вертикальних прямих із кроком, що дорівнює деякій одиниці довжини. Палетку накладають на

фігуру F і підраховують кількість n «цілих» квадратів, розміщених усередині неї. Потім підраховують кількість m квадратів, у яких лише частина розміщена всередині фігури. Після того до числа n

додають половину числа m.

Два многокутники називають рівноскладеними, якщо їх можна розкласти на одне й те саме число попарно рівних многокутників. Такими є, наприклад, фігури F1 і F2 на малюнку 478, бо кож

на з цих фігур складається з однакової кількості

квадратів.

3. Площа прямокутника

Із попередніх класів ви знаєте, що площу квадрата зі стороною а можна обчислити поіншому — за формулою площі квадрата: S = а2 .

Для квадратів АВСD (див. мал. 475) і KLMN (див. мал. 476) одержимо: SАВСD = 22 = 4 (см2), SKLMN = 2,52 = 6,25 (см2).

Оскільки 4 см2 < 6,25 см2, можемо

вважати

чись на основні властивості площі.

Щоб вивести

Доведення. Добудуємо даний прямокутник ABCD до квадрата AMKN зі стороною а + b (мал. 479). Тоді:

SAMKN = (а + b)2.

З іншого боку, квадрат AMKN складається з двох прямокутників ABCD і OKLC та двох квадратів BMOC і DNLC. Тому, за властивостями площі:

SAMKN = SАВСD + SOKLC + SBMOC + SDNLC. Прямокутники ABCD і OKLC — рівні, бо мають рівні суміжні сторони а і b. Тому, за властивостями площі, SАВСD = SOKLC.

Квадрати BMOC і DNLC мають сторони b і а відповідно, тому SBMOC = b2 , SDNLC = а2. Отже:

SAMKN = 2SАВСD + а2 + b2 .

Далі одержуємо: (а

Наслідок. Площа прямокутного трикутника з катетами а і b

добутку катетів. Справді, діагональ АС розбиває

ник ABCD зі сторонами а і b (мал. 480) на

а і b, тому:

них прямокутних трикутників дорівнює квадрату їх коефіцієнта

1. У вас могло виникнути запитання: Як довести, що площа квадрата дорівнює квадрату його сторони? Нехай сторона квадрата ABCD дорівнює а Можливі два випадки: сторону АВ можна розбити на n одиничних відрізків, де n натуральне число (мал. 484); на стороні АВ можна розмістити n одиничних відрізків, але залишається остача відрізок, коротший від одиничного відрізка (мал. 485). Перший випадок (мал. 484). Розіб’ємо

шим

відрізка АВ, а відрізок АМ із n + 1 одиничних відрізків більшим за цей відрізок.

Одержали нерівність: n < a < n + 1.

Щоб точніше оцінити площу даного квадрата, поділимо одиничний відрізок на m рівних частин.

Тоді довжина кожної частини дорівнюватиме 1 . m

Нехай на відрізку АK їх

Мал. 485

3. Що таке рівновеликі фігури?

трикутників?

8. Як знайти площу поверхні прямокутного паралелепіпеда? А куба?

Усне тренування

Обчисліть: (2 + 3)2; (4 + 6)2; (2 + 3)2 : (4 + 6)2; (4 + 6)2 : (2 + 3)2.

Розв’яжіть задачі

1059'. Чи правильно, що площа — це: 1) фігура; 2) величина, що характеризує фігуру?

1060'. Чи правильно, що фігури на малюнках 486 і 487: 1) рівновеликі; 2) рівноскладені? Відповідь поясніть.

1061'. Чи правильно записано формулу площі квадрата зі стороною а: 1) S = 2а; 2) S = а + 2; 3) S = а : 2; 4) S = а2?

1062'. Чи правильно записано формулу площі прямокутника зі сторонами а і b:

1) S = 2(а + b); 3) S = а2b2; 2) S = 2аb; 4) S = аb?

1063'. Чи правильно записано формулу

кутного трикутника з катетами а і b:

1) S = а + b; 3) = Sab22 1 ; 2 2) S = аb; 4) 1 ? 2 Sab =

1064°.

ку: 1) 488; 2) 489 (одиниця площі — 1 клітинка).

Мал. 486

Мал. 487

Мал. 488

Мал. 489

1065°. Знайдіть наближені значення площ фігур, зображених на малюнку 490 (одиниця площі — 1 клітинка).

1066°. Доведіть, що висота рівнобедреного трикутника, проведена до основи, ділить його на рівновеликі трикутники.

1067°. Доведіть, що діагональ прямокутника ділить його на рівновеликі трикутники.

1068°. Точку всередині трикутника сполучено відрізками з його вершинами. Знайдіть площу трикутника, якщо утворені частини мають площу 12 см2, 39 см2 і 45 см2.

1069°. Точку всередині трикутника сполучено відрізками з його вершинами. Утворені частини трикутника мають площу 90 см2, 25 см2 і 45 см2. Знайдіть площу трикутника.

Мал. 490

1070°. Знайдіть сторону квадрата, якщо його площа дорівнює: 1) 16 см2; 2) 9 см2; 3) 121 см2.

1071°. Яка довжина сторони квадрата, площа якого дорівнює: 1) 25 см2; 2) 49 см2?

1072°. За даними на малюнках 491, 492 обчисліть площу прямокутника АВСD.

Мал. 491 Мал. 492

1073°. Яку площу має прямокутник АВСD на малюнку 493?

1074°. Як зміниться площа прямокутника, якщо одну

з його сторін:

1) збільшити у 3 рази; 3) збільшити на 50 %?

2) зменшити в 4 рази; 1075°.

його сторін:

1) збільшити у 3 рази; 3) збільшити на 50 %?

2) зменшити в 4 рази;

Мал. 493

, якщо вони

як: 1) 2 : 3; 2) 3 : 8; 3) 0,3 : 0,5.

ку KLMN сторони дорівнюють 2 см і 9 см. Знайдіть сторони прямо

1) 3 см і 5 см;

1081°. Знайдіть площу прямокутного

1082°. Знайдіть площу

6 см.

з катетами 4 см і 9 см?

1083°. Квадрат зі стороною а та прямокутник зі сторонами

якщо: 1) а = 6 см, b = 9 см; 2) а = 6 см, с = 2 см. Який

1084°. Квадрат

1085°.

1) а = 4 см, b = 3 см, d =13 см; 2) а = 8 см, b = 6 см, d = 15 см.

1086°.

1) d = 9 см; 2) d = 6 см.

1087.

1088.

частини й одержані точки спо

лучено так, як показано на малюнку 495. Зна

йдіть площу зафарбованої фігури.

1089. Різниця периметрів двох квадратів дорівнює с, а різниця їхніх площ — d. Знайдіть площі квадратів, якщо: 1) с = 16 см, d = 56 см2; 2) с = 12 см, d = 105 см2.

1090. Ширина прямокутної рамки дорівнює с, а її площа — S. Знайдіть периметри зовнішнього та внутрішнього контура рамки, якщо: 1) с = 2 см, S = 96 см2; 2) с = 3 см, S = 564 см2.

1091. Площа прямокутника дорівнює S. Складіть

Мал. 494

Мал. 495

дження сторін прямокутника, якщо сторони відносяться як m : n. 1092. Периметр прямокутника дорівнює

дження сторін прямокутника, якщо

1093. Який

1) (a + b)c = ac + bc; 2) (a – b)c = ac – bc; 3) (a + b)(c + d) = ac + bc + ad + bd?

1094. Катети прямокутного трикутника

міщена на відстані d від кожного катета. Знайдіть відстань від цієї точки до гіпотенузи, якщо:

1) а = 3 см, b = 4 см, d = 1 см; 2) а = 6 см, b = 8 см, d = 2 см.

1095*. Будь-які два рівноскладені

1096*. Точка

1099*.

1100*.

1101*. Доведіть, що площі трикутників, на які розбиває прямокутний трикутник висота, проведена до гіпотенузи, відносяться як проєкції катетів на гіпотенузу.

1102. За картою України (див. QRкод) з’ясуйте: з яких частин складається площа України; яка частина має найменшу площу, найбільшу площу. Яку частину площі України становить площа області, у якій ви мешкаєте?

1103. Побудуйте: 1) коло радіусом 2 см; 2) будьякий многокутник. Із прозорої плівки виготовте палетку та визначте наближені значення площ зображених фігур.

1104. Площа ділянки дорівнює 6

1105. Ділянка прямокутної форми

ділянки?

1106. Прямокутний шматок лінолеуму має розмір 9 × 4 м. Чи вистачить його для покриття підлоги у двох кімнатах розмірами 2 × 8 м і 4 × 5 м?

1107. Проведіть необхідні вимірювання та розрахуйте, яку кількість рулонів шпалер (без підгонки малюнка) необхідно придбати для ремонту кімнати у вас удома, якщо рулон має довжину 10,5 м і ширину 0,6 м.

1108.

порівнюють масу обох фігур. Поясніть, на чому ґрунтується такий спосіб. Мал. 496

1. Формула площі паралелограма

Ситуація. Іван і Марійка виготовляли шарнірний пристрій для проведення паралельних прямих. Прямокутну конструкцію вони стиснули так, що утворився паралелограм із тими самими сторонами, що й прямокутник.

Ні.

Щоб переконатися в цьому, виведемо формулу площі паралелограма.

Запам’ятайте!

Теорема (про площу паралелограма)

Площа паралелограма дорівнює добутку його сторони на висоту, проведену

сторони: S = аh а .

Дано: ABCD — паралелограм (мал. 497), DН — висота, AB = а, DН = h а .

Довести: SАВСD = аh а .

Доведення. Проведемо з вершини C висоту СМ = DН = h а (мал. 498). Одержали трапецію АМCD. Розглянемо

497

1) SАМСD = SАВСD + SDВМC;

2) SАМСD = SНМСD + SDАНD.

Тому SАВСD + SDВМC = SНМСD + SDАНD.

Розглянемо DВМС і DAНD.

У них: СМ = DН як висоти, проведені до однієї сторони AB паралелограма, AD = ВС як протилежні сторони паралелограма.

Отже, DВМС = DAНD за катетом і гіпотенузою.

Тому, за властивостями площі, SDВМC = SDАНD.

Отже, SАВСD = SНМСD. Для прямокутника НМCD маємо:

SНМСD = CD · DН = AВ · DН = аh а .

Оскільки, за доведеним, площа даного паралелограма ABCD дорівнює площі прямокутника НМCD, то: SАВСD = аh а .

Задача У паралелограмі сторони дорівнюють 8 см і 6,4 см, а висота, проведена до більшої сторони, — 6 см. Знайдіть висоту паралелограма, проведену до меншої його сторони.

Розв’язання Нехай ABCD — даний паралелограм (мал. 499), у якому AB = 6,4 см, BС = 8 см, DМ = 6 см.

Потрібно знайти висоту DН.

Площу паралелограма ABCD можна виразити двома способами: як добуток сторони ВС на висо

ту DМ і як добуток сторони АВ на висоту DН.

Звідси:

SАВСD = ВС · DМ = 8 · 6 = 48 (см2), (1)

SАВСD = АВ · DН. (2)

Із рівностей (1) і (2) одержуємо:

DН = SАВСD : АВ = 48 : 6,4 = 7,5 (см).

Щоб знайти

Справді, ромб (мал. 500) — окремий вид паралелограма, тому: S = аh а .

Ви знаєте, як знаходити площу прямокутного трикутника за його катетами. Скористаємося цим, щоб вивести ще одну формулу площі ромба.

Запам’ятайте!

Теорема (про площу ромба за його діагоналями)

Площа ромба дорівнює половині добутку його діагоналей: 12 1 . 2 ABCD Sdd =

Дано: ABCD — ромб (мал. 501), АС і ВD

діагоналі, AС = d1, ВD = d2.

Довести: = ABCD Sdd12 1 . 2

Доведення. У ромбі ABCD всі сторони рівні. Його діагоналі АС і ВD взаємно перпендикулярні й у точці перетину діляться навпіл. Тому вони розбивають ромб на чотири рівні

кутники АВО, СВО, СDО і АDО

English

Deutsch

Français площа паралелограма area of the parallelogram Flächeninhalt des Parallelogramms aire du parallélogram

qr.orioncentr.com.ua/HilBu

Мал. 504 Мал.

1) S = d1 + d2; 2) S = d1d2; 3) S = 2d1d2; 4) = Sdd12 1 ? 2

1114'.

1) S = 2d; 3) S = 2d2; 2) S = d2; 4) = Sd 2 1 ? 2

1117°. У паралелограмі ABCD проведено ви

соту ВН до сторони CD. Знайдіть пло

щу паралелограма, якщо: 1) CD = 60 см, ВН = 50 см; 2) CD = 25 см, ВН = 40 см.

1118°. У паралелограмі ABCD проведено ви

соту СМ до сторони AB. Знайдіть пло

щу паралелограма, якщо AB = 25 см, СМ = 100 см.

1119°. До сторони a паралелограма проведено висоту h а. Знайдіть його площу, якщо: 1) a = 10 см, h а = 0,8a; 2) a = 2 дм, h а = 0,75a.

1120°. Знайдіть площу паралелограма, у якому проведено висоту hb = 5 см до сторони b = 1,2hb.

1121°. Площа паралелограма дорівнює S, а одна з його сторін — a. Знайдіть висоту, проведену до цієї сторони, якщо: 1) S = 60 см2, a = 15 см; 3) S = 75 см2, a = 25 см; 2) S = 175 см2, a = 35 см; 4) S = 96 см2, a = 12 см.

1122°. Площа паралелограма дорівнює 180 см2, а одна з його сторін 15 см. Знайдіть висоту, проведену до цієї сторони.

1123°. Знайдіть висоти паралелограма зі сторонами a і b та

S за таблицею 38.

5 см8,5 см14 см16 см b 10 см17

1124°. Площа

1) S = 56 см2, n = 7 см; 2) S = 90 см2, n = 18 см.

1125°. Площа паралелограма дорівнює 24 см2. Знайдіть відстань

1126°. Сторони паралелограма

1) a = 6 см, b = 3,6 см, h а = 2,4 см; 2) a = 18 мм, b = 9 мм, h а = 6 мм.

1127°.

1128°.

1129°. Через точку перетину діагоналей

Мал. 508

1132°. Знайдіть

дорівнюють: 1) 12 см і 16 см; 2) 1,6 дм і 3 дм. 1133°. Знайдіть площу ромба, якщо його діагоналі дорівнюють 40 мм і 42 мм. 1134°. Доведіть, що діагоналі ромба розбивають його на чотири прямокутні

Мал. 509

1140. Паралелограм має гострий кут 30°. Знайдіть площу

ма, якщо його сторони дорівнюють:

1) 15 см і 10 см; 2) 25 см і 20 см.

1141. Дві смуги завширшки m і n, перетинаючись, утворюють паралелограм із площею S. Знайдіть сторони паралелограма, якщо:

1) m = 9 см, n = 24 см, S = 72 см2; 2) m = 4 дм, n = 1 дм, S = 6 дм2.

1142. Площа паралелограма дорівнює S.

точки перетину його діагоналей

периметр паралелограма, якщо:

1) S = 56 см2, m = 4 см, n = 3,5 см; 2) S = 36 см2, m = 2 см, n = 3 см.

1143. У

далена від його сторін на відстань

грама, якщо: 1) Р = 64 см, m = n = 4 см; 2) Р = 63 см, m = 4 см, n = 5 см.

1144.

сторонам.

1) 1 дм; 2) 2,6 см.

1146. Площа ромба дорівнює

як: 1) 3 : 4; 2) 2 : 3; 3) 1 : 1.

1147. Площа ромба удвічі

1148. Два квадрати мають

1149. У скільки разів площа квадрата,

1153*.

1154*.

1155*. Радіус

якщо: 1) m = 1,8 см, n = 3,2 см; 2) m = 4 см, n = 9 см.

1156*. Знайдіть геометричне місце вершин паралелограмів зі спільною стороною, у яких площа дорівнює

1157*. На кожній стороні паралелограма взято

точці. Площа чотирикутника

ходить путівець завширшки 5 м, який перетинає краї

завдовжки

1159. Ділянку, що має форму паралелограма, потрібно поділити на 3 частини однакової площі. Як провести межі?

1160. Проведіть необхідні вимірювання та розрахуйте, скільки кахельної плитки розміром 33 × 33 см потрібно придбати,

SDABH = 1 34 2 = 6, SDCBH = 1 44 2 = 8, SDАBС = 6 + 8 = 14.

Наталка помітила, що площу DАВС можна

знайти інакше, якщо одразу помножити 1 2 на

всю сторону АС та висоту ВН. Такий висновок вона отримала, спростивши вираз для знаходження площі трикутника АВС за його частинами: SDABС

Запам’ятайте!

Теорема (про площу трикутника)

Площа трикутника дорівнює половині добутку його сторони на висоту, проведену до цієї сторони: 1 . 2 ABC a Sah ∆ =

Дано: DABC (мал. 512), АН — висота, BС = а,

АН = h а .

Довести: ∆ = ABC a Sah 1 . 2

Доведення. На стороні АВ даного три

кутника АВС побудуємо рівний йому три

кутник ВАD (мал. 513). Утворений чотири

кутник ADBC — паралелограм, оскільки, за

побудовою, АD = BС, ВD = АC. У ньому

511

Щоб знайти площу фігури, можна скористатися способом доповнення її до такої фігури, формула площі якої відома. Для трикутника такою допоміжною фігурою є паралелограм.

Задача Виведіть формулу площі рівностороннього трикутника.

Розв’язання Нехай ABC — даний трикутник зі сто

роною а (мал. 514). Оскільки трикутник є рівностороннім, то всі його висоти — рівні. Проведемо висоту h до сторони АС. Утворилися рівні прямокутні трикутники ABН і СBН.

Розглянемо DABН. У ньому AB = а, AН = a 2 .

За теоремою Піфагора знаходимо

були відомі ще в Стародавньому Єгипті. Відомості про це дійшли до нас у папірусах. Найбільш відомі з них папірус Рінда (близько 1800 р. до н. е.), який містить 84 задачі з розв’язаннями (сторінку

званий московський папірус (близько 1600 р. до н. е.), який містить 25 задач із розв’язаннями. Щоб знайти площу трикутника, стародавні єгиптяни основу трикутника ділили навпіл і множили на висоту.

Мал. 517 Мал. 518

2. Геометричні розрахунки за точними формулами проводились і в Стародавньому Вавилоні. Відомості збереглися на клинописних табличках (мал. 518). Тексти, які дійшли до нас, свідчать, що вавилоняни знали й використовували у практичних задачах пропорційність паралельних відрізків. Наприклад, вони вміли знаходити довжину відрізків MN, СМ і ВМ (мал. 519) у трикутнику АВС за його стороною АС = 30, різницею S1 – S2 = 42 площ трапеції і трикутника, на які даний трикутник розбивається паралельною прямою MN, та різницею BМ – CМ = 20. Зараз для розв’язування цієї задачі нам

520 Мал. 521 Мал. 522

1) ∆ =⋅ ABC SABAM 1 2 (мал. 520); 4) SD

= AB · CL (мал. 521);

2) ∆ =⋅ ABC SACBK 1 2 (мал. 520); 5) SDАВС = AB · AC (мал. 522);

ABC SBMAK 1 2 (мал. 521); 6)

SBCAC 1 2 (мал. 522)?

Мал. 523

Мал. 524

1165°. У трикутнику ABC проведено висоту ВН (мал. 526). Знайдіть площу три

кутника, якщо:

1) АC = 6 см, ВН = 5 cм; 2) АC = 25 см, ВН = 100 см.

1166°. У трикутнику ABC проведено висоту ВН завдовжки 4 дм. Знайдіть площу трикутника, якщо АC = 2,5 дм.

1167°. До сторони a трикутника проведено висо

ту h а. Знайдіть його площу, якщо:

1) a = 10 см, h а = 0,8a; 2) h а = 12 мм, a = 1,5h а .

1168°. До сторони a = 2 дм трикутника проведено висоту h а = 0,75a. Знайдіть площу трикутника.

Мал. 525

1169°. Площа трикутника дорівнює S, а одна з його висот — h. Знайдіть сторону, до якої проведено цю висоту, якщо: 1) S = 72 см2, h = 12 см; 3) S = 75 см2, h = 7,5 см. 2) S = 155 см2, h = 10 см;

1170°. Площа трикутника

Знайдіть

Таблиця 39 (продовження) hb h c

1172°. Як зміниться площа даного трикутника, якщо: 1) одну з його сторін збільшити у 2 рази, а висоту, проведену до цієї сторони, зменшити у 2 рази; 2) одну з його сторін зменшити у 2 рази, а висоту, проведену

цієї сторони, збільшити в 4 рази?

1173°. Як зміниться площа даного трикутника, якщо одну з його сторін збільшити в 4 рази, а висоту, проведену до цієї сторони, зменшити у 2 рази?

1174°. Знайдіть площу рівностороннього трикутника (мал. 527), якщо його сторона дорівнює: 1) 8 см; 2) 1,2 дм; 3) 2 м; 4) 23 см; 5) 6 дм.

1175°. Знайдіть площу рівностороннього трикутника, якщо його сторона дорівнює: 1) 10 см; 2) 3 дм.

1176°. Знайдіть площу рівнобедреного трикутника, якщо його бічна сторона та основа відповідно дорівнюють: 1) 26 см і 20 см; 2) 17 см і 16 см.

1177°. Знайдіть площу рівнобедреного трикутника, якщо його бічна сторона та основа відповідно дорівнюють 13 см і 10 см.

1178°. За даними на малюнках 528, 529 доведіть,

1179°.

1180°.

1) S = 52,5 см2; 2) S = 105 см2?

1183°.

1184°.

1185°.

1186°.

1187°. Основа піраміди

хонь піраміди.

1188°.

1189. Бічна сторона рівнобедреного

як m : n, а висота, проведена

щу трикутника, якщо: 1) m = 5, n = 6, h = 12 см; 2) m = 17, n = 16, h = 15 см.

дорівнює h.

1190. У рівнобедреному трикутнику основа відноситься до бічної сторони, як 10 : 13, а висота, проведена до основи, дорівнює 24 см. Знайдіть площу трикутника.

1191. Середня лінія трикутника дорівнює q, а висота, перпендикулярна до неї, дорівнює h. Знайдіть площу трикутника, якщо:

1) q + h = 12,5 см, q – h = 0,5 см; 2) q + h = 23 см, h – q = 17 см.

1192. Доведіть, що два трикутники мають рівні

відповідні середні лінії та висоти, які перпендикулярні до

ніх ліній.

1193. Знайдіть площу прямокутного трикутника за

відношенням катетів: 1) 25 см, 3 : 4; 3) 25,5 см, 8 : 15; 2) 5 см, 7 : 24; 4) 82 см, 9 : 40.

1194. Катети прямокутного трикутника відносяться як 5 : 12. Знайдіть площу трикутника, якщо його

1) 39 см; 2) 26 см.

1195. Площа прямокутного трикутника дорівнює S,

носяться як m : n

1) S = 720 см2, m = 9, n = 40; 2) S = 1320 см2, m = 11, n = 9,6.

1196. Знайдіть площу прямокутного трикутника,

1) 4 см і 9 см; 2) 1 см і 16 см.

1197. Знайдіть площу прямокутного трикутника

1) 8 см; 2) 12 см.

1198. Знайдіть площу прямокутного трикутника

1) t = 7 см, r = 2 см, R = 5 см; 2) t = 17 см, r = 4 см, R = 13 см.

1199. Трикутник

1200. Доведіть, що площа трикутника з вершиною в точці перетину медіан

трикутника та спільною

становить третину площі даного трикутника (мал. 533).

1201. Відома площа одного з двох подібних трикутників. Які вимірювання та обчислення треба виконати, щоб знайти площу іншого трикутника?

Мал. 533

1202. У паралелограмі АВСD вершина D розміщується на відстані 4 см від діагоналі АС, що дорівнює 16 см. АВ = 12 см. Знайдіть відстань:

1) від точки D до прямої АВ;

2) між прямими АВ і СD;

3) від середини діагоналі до сторони СD паралелограма.

1203*. Доведіть, що площу прямокутного трикутника АВС (∠C = 90°) обчислюють за формулою: =⋅⋅=⋅⋅ SbcAacB 11 sinsin 22 (мал. 534).

1204*. Доведіть, що площу гострокутного трикутника

формулою:

SbcAacBabC 111 sinsinsin 222 (мал. 535).

534

1205*.

1206*.

535

1208*.

1209*.

1210*.

бічну сторону трикутника

основі, щоб площа трикутника була поділена на три рівні частини?

1211*. Висота трикутника дорівнює 4 см. На якій відстані від вершини трикутника потрібно провести пряму, що перетинає ці дві сторони та паралельна третій його стороні, щоб площа трикутника

лась у відношенні m : n, рахуючи від вершини?

1212*. Доведіть, що коло, вписане

1213.

1214. Площу трикутника можна визначити

1217.

1218. На

трикутної форми потрібно провести межу так, щоб одержати дві частини з рівними площами. Як це зробити за допомогою віх і польового циркуля?

Ситуація. Марія Іванівна поставила 8-А класу запитання: «Як знайти площу трапеції AMNC на малюнку 537?» Юля запропонувала скористатися аркушем в клітинку як палеткою. Вона порахувала всередині трапеції кількість повних квадратиків n (їх виявилося 6), кількість неповних квадратиків n1 (їх виявилося теж 6) та скористалася формулою:

S ≈ n + 0,5 n1. Після обчислень Юля отримала, що S ≈ 9 кв. од. Оксана запропонувала інший спосіб знайти площу двох трикутників АВС і MBN, а потім знайти різницю цих площ. Оксана отримала:

∆ =⋅⋅= ABC S 1 4612 2 (кв. од.), ∆ =⋅⋅= MBN S 1 233 2 (кв. од.),

∆∆ =−=−= AMNCABCMBN SSS 1239 (кв. од.).

Максим же висунув гіпотезу, що площу даної трапеції можна обчислити ще

відну формулу.

Дано: ABCD — трапеція (мал. 538),

AB і CD — основи, СН — висота,

AB = а, CD = b, СН = h.

Довести: + =⋅ ABCD ab Sh. 2

Доведення. Проведемо в трапеції діагональ АС (мал. 539). Вона розбиває трапецію на два трикутники АВС і АDС. Висота h трапеції є висотою трикутника АВС, проведеною до сторони

AB = а, і дорівнює висоті трикутника АDС, про

веденій до сторони CD = b. Площа трапеції дорівнює сумі

кутників, тому:

дорівнює

лінії даної трапеції та її висоти h.

Задача Діагоналі АС і BD трапеції ABCD

перетинаються в точці О (мал. 540). Доведіть, що трикутники AOD і BOС мають рівні площі.

Розв’язання Розглянемо трикутники ABD і ABС. У них сторона AB — спільна, а висоти, проведені до цієї сторони, дорівнюють висоті трапеції.

Тому: SDАBD = SDABC.

Трикутник ABD складений із трикутників AOB і AOD, а трикутник ABC — із трикутників AOB і BOC. Звідси одержуємо: SDАОD = SDАBD – SDAOB

являється найлегшим.

який підтверджує існування деякого математичного об’єкта, вчені витрачали багато років. Щоб спростити пошук, проводять попередні аналітичні розрахунки.

Нехай дана трапеція ABCD (мал. 541) має основи а і b та висоту h. Середня лінія MN розбиває

пеції, які мають рівні висоти, що дорівнюють

Мал. 541

Знайдемо відношення площ S1 і

площ S1 і S2 можлива лише тоді, коли 3b + a = 3a + b, тобто якщо а = b.

А такої трапеції не існує.

Цікавим є той факт, що відрізок, який з’єднує середини основ трапеції, ділить площу трапеції навпіл. Доведіть цей факт самостійно, спираючись на малюнок 542.

2. Вивчаючи чотирикутники, ви ознайомилися з дельтоїдом (мал. 543). Цей чотирикутник, як і ромб, має взаємно перпендикулярні діагоналі. Існують трапеції із

Мал. 542

взаємно перпендикулярними діагоналями (мал. 544), а також довільні чотирикутники з такою самою властивістю (мал. 545). І ромб, і дельтоїд, і названа трапеція є окремими видами чотирикутників із взаємно перпендикулярними діагоналями. Доведіть самостійно, що площа чотирикутника із взаємно перпендикулярними діагоналями дорівнює половині добутку цих діагоналей. Мал. 543

544 Мал. 545

УкраїнськаАнглійська/ English

Deutsch

площа трапеції area of the trapezoid Flächeninhalt des Trapezes aire du trapèze

qr.orioncentr.com.ua/v71c7

рівність: 25 – 8 = 8 + 9; 7 + 9 = 21 – 5; 18 – 12 = 10 + 6; 24 + 5 = 36 – 7?

1) =⋅ ABCD SABDH 1 2 (мал. 546);

2) =+() ABCD SABDH 1 2 (мал. 546);

3) () =+⋅ KLMN SKLNMTL 1 2 (мал. 547);

4) () =+⋅ KLMN MH SKLLM 2 (мал. 547);

5) SPQНT = PQ · PT (мал. 548);

6) + =⋅ PQHT HTPQ S PT 2 (мал. 548)?

546

547

548

1220°. За даними на малюнках 549, 550 знайдіть площу трапеції ABCD.

1221°. За

Мал. 549 Мал. 550

551

трапеції ABCD.

1222°. У трапеції ABCD з основами AB і CD проведено висоту

якщо: 1) АВ = 60 см, CD = 36 см, СН = 50 см; 2) АВ = 25 см, CD = 55 см, СН = 100 см.

1223°. У трапеції ABCD з основами AB = 25 см і CD = 45 см

висоту СН = 40 см. Знайдіть

1224°. Основи трапеції дорівнюють a і b, а висота

трапеції, якщо:

1) a = 10 см, b = 0,8a, h = a; 2) a = 2 дм, b = 0,75a, h = 0,5a.

1225°. Основи трапеції дорівнюють

трапеції, якщо b = 5 см, a = 1,2b, h = a.

1226°. Площа трапеції дорівнює S,

трапеції, якщо:

1) S = 60 см2, h = 12 см; 2) S = 150 см2, h = 25 см.

1227°. Площа трапеції

основ трапеції.

1228°.

1) S = 60 см2, q = 15 см;

2) S = 175 см2, q = 35 см.

1229°.

1230°.

1231°. Як зміниться площа трапеції, якщо: 1) обидві її основи зменшити у 2 рази, а висоту — збільшити у 2 рази; 2) середню лінію збільшити у 2 рази?

1232°. Як зміниться площа трапеції, якщо обидві її основи збільшити у 2 рази, а висоту — зменшити у 2 рази?

1233°. Площа трапеції дорівнює S, висота — h, а її основи відносяться як m : n. Знайдіть основи трапеції, якщо: 1) S = 36 см2, h = 2 см, m = 4, n = 5; 2) S = 150 см2, h = 5 см, m = 2, n = 3.

1234°. Площа трапеції дорівнює 90 см2, висота

сяться як 1 : 2. Знайдіть основи трапеції.

1235°. У трапеції з основами a і b проведено діагоналі (мал. 553). Чому дорівнює відношення площ трикутників, що прилягають до основ?

1236. За даними основами a і b та бічною стороною с рівнобічної трапеції знайдіть її площу, якщо:

1) а = 24 см, b = 12 см, с = 10 см; 2) а = 14 см, b = 8 см, с = 5 см.

1237. У рівнобічній

1238.

1240.

1) a = 2 см, b = 5 см; 2) a = 5 см, b = 3 см.

1241.

якщо: 1) a = 2 см; 2) a = 3 см.

1242. Основи рівнобічної трапеції дорівнюють a і 3a, а площа — 2a2 . Чому дорівнює гострий кут трапеції?

1243. У трапеції менша діагональ d перпендикулярна до її основ a і b. Знайдіть площу трапеції, якщо: 1) a + 2b = 3,3 см, a – b = 1,8 см, d = 4 см; 2) 3a + 2b = 44 см, a – 2b = 4 см, d = 12 см.

1244. Відрізок, проведений з вершини тупого кута трапеції

її бічній стороні, ділить

1245. Менша

на паралелограм і трикутник з рівними площами. Знайдіть більшу основу трапеції.

1246. Доведіть, що площа трапеції, описаної навколо кола, дорівнює добутку півсуми її бічних сторін на висоту (мал. 554).

1247. Трапеція, описана навколо кола, має периметр Р і площу S. Знайдіть радіус кола.

1248. Діагоналі трапеції взаємно перпендикулярні. Одна з діагоналей дорівнює 8 см, а площа трапеції — 40 см2. Знайдіть іншу діагональ.

1249*. Основи трапеції дорівнюють 15 см і 20 см, а бічна

1250*.

1253*.

1254*.

1257*.

1258*.

1259*.

1261.

1263.

1. Що таке многокутник; n-кутник? Як

2. Які елементи многокутника?

3. Що таке зовнішній кут многокутника; діагональ; периметр?

4. Сформулюйте та доведіть теорему про суму кутів многокутника.

5. Який многокутник називається вписаним у коло; описаним навколо кола?

6. Поясніть,

1°. Знайдіть суму кутів шестикутника.

А. 60° .

Б. 120° .

В. 540° .

Г. 720° .

2°. Квадрат і прямокутник мають

рівнює 24 см, а одна зі сторін прямокутника — 4 см. Знайдіть іншу сторону прямокутника.

А. 6 см.

Б. 9 см.

В. 20 см.

Г. 36 см.

3°. Площа рівнобедреного трикутника АВС з

якщо АВ = 100 см.

А. 24 см і 48 см.

Б. 48 см і 48 см.

В. 48 см і 96 см.

Г. 96 см і 96 см.

4. У трапеції АВСD

7 см і 8 см.

дорівнює 60 см2.

А. 45 см2.

Б. 56 см2.

В. 75 см2.

Г. 88 см2.

5*.

А. 90 см2.

Б. 135 см2.

В. 180 см2.

Г. 54 см2.

ПОВТОРЕННЯ

ЧОТИРИКУТНИКИ

ЧОТИРИКУТНИК

Паралелограм

АD || BC, АB || DC

Види паралелограмів

Прямокутник

∠А = ∠В = ∠С = ∠D = 90°

Ромб

АВ = ВС = CD = DA

А + ∠В + ∠С + ∠D = 360°

Властивості

1. АВ = DC, AD = ВС

2. ∠А = ∠С, ∠B = ∠D

3. АО = ОС, ВО = OD

Властивості

Властивості паралелограма

1. АВ = DC, AD = ВС

2. ∠A = ∠С, ∠В = ∠D

3. АО = ОС, ВО = OD

Особлива властивість

4. АС = BD

Властивості паралелограма

1. АВ = DC, AD = ВС

2. ∠А = ∠С, ∠В = ∠D

3. АО = ОС, ВО = OD

Особливі властивості

4. АС ⊥ BD

5. ∠ABD = ∠CBD, ∠ВАС = ∠DAC Квадрат

c 2 = a 2 + b 2

c = + 22ab

= 22cb b = 22ca

Дано: a, b

Знайти: с, A, B

= sin a

= cos a

= tg a

Дано: a, с

Знайти: b, A, B

Дано: c, a

Знайти: a, b, B

Дано: a, a

Знайти: c, b, B

AC перпендикуляр

AB похила

AB > AC, AB > BC

B =

° – A 1) B = 90° – a, 2) a = c · sin a, 3) b = c · cos a 1) B = 90° – a, 2) c = α sin a ,3) b = α tg a

1283. Точки E і F — середини протилежних сторін AB і CD паралелограма — сполучено з вершинами B і D. Дове

діть, що:

1) DADE = DCBF; 2) DE || FB.

1284. Якщо сполучити точки E і F

лограм розіб’ється на чотири рівні трикутники. Доведіть.

1285. Сторони

1286.

1288. Через середини

прямими?

1289. Сторони паралелограма відносяться як 7 : 11, а діагоналі дорівнюють

1290.

1291.

1295.

15 см більша за периметр ромба.

1296.

драт його діагоналями, більша

Чому дорівнює діагональ квадрата?

1297. Доведіть, що в рівнобічній трапеції квадрат діагоналі дорівнює квадрату бічної сторони, доданому до добутку основ.

1298. Менша основа рівнобічної трапеції дорівнює бічній стороні, а діагональ перпендикулярна до бічної сторони. Знайдіть кути трапеції.

1299. У трапеції ABCD з основами AD і BC кут A гострий,

пий. Доведіть, що різниця проєкцій бічних сторін трапеції

основу дорівнює різниці основ. Подібність трикутників

1300. Поділ відрізка на два відрізки, більший з яких відноситься до меншого як

частини, має назву золотий переріз. Це відношення наближено дорівнює 1,62.

відрізка АВ, побудуйте на ньому, як на катеті, прямокутний трикутник АВС (ВС < АВ). На гіпотенузі

відрізок СМ = ВС, а на катеті АВ від

вершини А — відрізок АО

1303.

1304.

довно перпендикулярні до кожної

сторони. Від перетину цих прямих утворився трикутник. Чи подібний він даному трикутнику? Відповідь поясніть.

1305. Бісектриси зовнішніх кутів трикутника утворюють трикутник. Чи подібний він даному трикутнику? Відповідь поясніть.

1306. ABCK і MKTP — рівні квадрати зі спільною вершиною K. Сторони СK і KТ взаємно перпендикулярні. Знайдіть площу чотирикутника АСТМ, якщо АВ = 6 см.

1307. З вершин гострих кутів паралелограма проведено висоти. Чи

бні утворені при цьому трикутники? Відповідь поясніть.

1308. Теорема Птолемея. Доведіть, що у вписаному чотирикутнику

буток діагоналей

1309.

1310.

вжено до перетину з колом,

на колі точку сполучено з вершиною А. Знайдіть усі подібні

1311.

1312.

1314. Знайдіть значення синуса й косинуса

ного трикутника, якщо:

1) a – b = 17 см, c = 25 см; 2) c – a = 1 см, c – b = 50 см; 3) c + a = 49 см, c + b = 50 см.

1315. Точка A лежить на відстані 2 см від кола радіусом 3 см. Знайдіть косинус кута між дотичними, проведеними з точки A

1316. Радіус кола дорівнює R

Многокутники.

Площі многокутників

1322. Раніше циркуль називали «шестернею». Така назва

пов’язана з тим, що коли розхил циркуля дорівнює ра

діусу кола, то це коло можна поділити на 6 рівних частин. Перевірте це практично.

1323. У шестикутнику є три пари рівних кутів. Відомо, що один кут дорівнює

120°, а два інші відносяться як 7 : 9.

Знайдіть кути шестикутника.

1324. Сторони прямокутника відносяться як 8 : 15, а його діагональ дорівнює

34 см. Знайдіть площу прямокутника.

1325. У паралелограмі одна зі сторін дорівнює 10 см, а один із кутів — 30°. Знайдіть площу паралелограма, якщо його периметр дорівнює 56 см.

1326. Знайдіть площу ромба зі стороною 4 см,

кола дорівнює 1,5 см.

1327. Висота трикутника дорівнює 4 см. Вона ділить сторону, до

проведена, у відношенні 1 : 8.

цями на сторонах трикутника, який паралельний

1328.

1329.

1330. У трапеції

За

допомогою лінійки можна

провести:

• довільну пряму;

• пряму, що проходить через

дану точку;

• пряму, що проходить через дві

дані точки

За допомогою циркуля можна:

• провести коло з даного центра

даним радіусом;

• відкласти відрізок заданої

довжини на промені від його

початку

Ніяких інших операцій виконувати циркулем і лінійкою не можна

Дано:

Побудувати

∆ABC так, щоб

AB = BC = b,

AD = mb , (D — середина BC)

1) виконуємо малюнокескіз; 2) ∆ABD — допоміжний (AB = b, BD = 2 b , AD = mb);

3) BC = b

Будуємо: 1) ∆ABD за трьома сторонами

AB = b, BD = 2 b , AD = mb; 2) відрізок BC = b на промені BD; 3) відрізок AC; ∆ABC — шуканий

У ∆ABC

AB = BC = b,

AD = mb, (D — середина BC) за

Дано:

Задача Аналіз

Точка X:

1) рівновіддалена від сторін кута

ABC;

2) рівновіддалена від точок M і N

ГМТ, що задовольняє: • умову 1 — бісектриса кута

Побудувати

точку X, рівновіддалену від сторін кута

ABC і точок M, N

Будуємо:

ABC; • умову 2 — серединний перпендикуляр до відрізка MN

X — точка перетину цих ГМТ Побудова Доведення

1) бісектрису BD кута ABC; 2) серединний перпендикуляр a до відрізка MN; 3) X — точку перетину BD і a

X ∈ BD, тому X рівновіддалена від сторін кута ABC

X ∈ a, тому MX = NX

1332. На малюнку 536 побудовано чотирикутник ABCD за чотирма

1333. Побудуйте чотирикутник за чотирма його сторонами a, b, c, d і

том a.

1334. Побудуйте чотирикутник за його сторонами a, b, c та діагоналями d1 і d2.

1335. Складіть план побудови паралелограма:

1) за сторонами а, b і кутом a (мал. 558); 2) за стороною а та діагоналями d1 і d2 (мал. 559).

Щоб побудувати паралелограм (ромб), спочатку побудуйте допоміжний трикутник (DАDС на мал. 558 або DАОD на мал. 559). Потім добудуйте цей трикутник до паралелограма (ромба), спираючись на властивості паралелограма (ромба).

1336. Побудуйте паралелограм:

1) за сторонами а і b та діагоналлю d;

2) за діагоналями d1 і d2 та кутом a між ними;

Мал. 558

Мал. 559

3) за стороною а, діагоналлю d і кутом a, який лежить проти цієї

діагоналі;

4) за стороною а, діагоналлю d і кутом a між ними.

1337. Побудуйте ромб:

1) за діагоналями d1 і d2;

2) за стороною a й діагоналлю d;

3) за стороною a й кутом a.

1338. Побудуйте ромб за гострим кутом a й діагоналлю d, яка виходить із вершини цього кута.

1339. Побудуйте паралелограм

Мал.

1342. Побудуйте прямокутник:

1) за діагоналлю d і кутом a між діагоналлю та

стороною;

2) за діагоналлю d і кутом a між діагоналями.

1343. Побудуйте квадрат:

1) за стороною а;

2) за діагоналлю d.

1344. Побудуйте прямокутник:

1) за діагоналлю d і сумою s двох нерівних сторін;

2) за діагоналлю d і різницею m двох сторін.

1345. Побудуйте квадрат:

1) за сумою s діагоналі та сторони;

2) за різницею m діагоналі та сторони.

1346. За малюнком 541 складіть план побудови трапеції ABCD за основами a i b (a > b) та бічними сторонами c i d.

Щоб побудувати трапецію, як і паралелограм, спочатку побудуйте допоміжний трикутник (наприклад, DKCD на мал. 562), а потім добудуйте

1347. Побудуйте трапецію

міжного трикутника АВС.

Побудова.

1. Будуємо допоміжний DАВС за

2. Проводимо бісектрису BL кута В.

3. На промені BL відкладаємо відрізок

4. Через точку L1 проводимо

Доведення.

За побудовою, у трикутнику

1351. Побудуйте трикутник за

1352. Побудуйте трикутник за його периметром

тами a і b.

1353. Побудуйте трикутник за відношенням сторін та:

1) найбільшою медіаною; 2) найменшою висотою.

1354. Побудуйте рівнобедрений трикутник за:

1) кутом при вершині та сумою основи й висоти;

2) відношенням двох нерівних сторін та висотою, проведеною до бічної сторони.

1355. У дане коло впишіть трикутник:

1) подібний даному трикутнику;

2) сторони якого паралельні сторонам даного трикутника.

1356. Побудуйте трикутник за двома кутами та найбільшою висотою.

1357. Побудуйте трикутник за двома кутами та найменшою медіаною.

1358. Побудуйте трикутник за відношенням двох сторін, кутом між ними та бісектрисою цього кута.

1359. Побудуйте трикутник за серединами

з вершинами.

1360. Як побудувати відрізок, що є середнім

1361. Побудуйте прямокутний трикутник за

ношенням проєкцій катетів на гіпотенузу.

1362. Впишіть у трикутник ABC квадрат так, щоб дві його вершини лежали на більшій стороні трикутника, а дві інші вершини

1363. Впишіть у трикутник ABC такий трикутник, сторони якого

Додаток 3

Елементарні геометричні фігури та їхні властивості

1. 1) Одну; 2) дві або три; 2) одну, чотири або шість. 5. 1) Так; 2) ні. 6. 15 км. 7. 6 см. 8. 36 см. 9. Вказівка: 2) перегніть шматок тканини навпіл, потім одну з половинок перегніть ще раз навпіл. Четвертину, яка ближче до середини, знову перегніть навпіл. 10. 8 км. 11. 1 км або 3 км. 12. 800 м. 13. 8 см. 14. 1) Ні; 2) так. 15. 1) 6°; 2) 30°; 3) 60° . Взаємне розміщення прямих на

16. 1) 73°, 107°; 2) 45°, 135° . 17. 60°, 120° . 18. 1) 42°, 42°, 138°, 138°; 2) 111° , 111°, 69°, 69° . 19. 45°, 45°, 135°, 135° . 20. Вказівка: спочатку

паперу по даній прямій АВ так, щоб дана точка О була на

21. Ні. 22. 1) 4 см або 20 см; 2) 10 см або 2 см. 23. 1) 4; 2) 4; 3) 8. 24. 60°, 60°, 60°, 60°, 120°, 120°, 120° , 120° . 25. 45°, 45°, 45°, 45°, 135°, 135°, 135°, 135° . 26. Вказівка: позначте внутрішні односторонні кути a і b. Доведіть, що 2 α + 2 β ≠ 180° . 27. Вказівка: скористайтеся наслідком з теореми про

ка: за допомогою

побудованої прямої. Остання пряма

паралельною даній. 29. 1) Усі по 90°; 2) 25°, 25°,155°, 155°; 3) 60°, 60°, 120°, 120° . 30. 1) 70° і 110°; 2) 20° і 160° .

Трикутники

31. 1) Ні; 2) так. 32. 1) Ні; 2) так. 33. 1) Збільшиться на 9 см; 2) збільшиться у 3 рази; 3) зменшиться в 1,5 раза; 4) зменшиться на 4,5 см. 34. 1) Зменшиться на 4 см; 2) збільшиться в 6 разів. 35. 36 см. 36. 9 см. 37. 5 см. 38. 4 см. 39. 1) 6 см; 2) 7,5 см. 40. 4 м. 41. 1) АC = 10 см; 2) ∠ВAD = 72° . 42. 8 см. Вказівка: доведіть рівність ОС = ОD. 43. Вказівка: 1) скористайтеся властивістю рівнобедреного трикутника та другою ознакою

55. 1) 24 см; 2) 14 см. 56. 8 см. 57. 6 см і 2 см. 58. 2 mn або 2 mn + . 59. 2 мм.

60. 4 см і 5 см. 61. 1) Ні; 2) так. 62. Вказівка: найкоротший

збігається з хордою, перпендикулярною

довжину. 63. 1) Коло

65. Вказівка

сторону магістралі,

72. 1) Ні; 2) так. 73. Мал. 16. 74. 1) Ні; 2) так; 3) ні. 75. 2). 76. Ні (мал. 18); так (мал. 19). 77. 1) ∠ENM, ∠FNP; 2) ∠AMN, ∠CMK; 3) ∠DKM, ∠BKP.

79. 5 см, 45 см, 45 см, 45 см. 80. 30 см, 60 см, 60 см, 60 см. 81. 1) Так; 2) ні. 82. Ні. 83. 100°, 100°, 100° (мал. 21); 100°, 100° (мал. 22). 84. 60° . 85. 1) 60°; 2) 70° . 86. 150° . 87. 1) Ні; 2) ні. 88. Так. 90. Ні. 91. 90°, 90°, 90°, 90° . 92. 180° . 93. Вказівка: знайдіть градусну міру четвертого кута. 94. 1) 105°; 2) 90° . 95. 1) 100°; 2) 60° . 96. Чотирикутником. 97. 5 граней і 8 ребер. 98. 15 см, 7 см, 23 см, 21 см. 99. 64 см. 100. 1) Ні; 2) так; 3) ні. 101. Вказівка: скористайтеся нерівністю трикутника. 102. Вказівка: скористайтеся нерівністю трикутника. 103. Вказівка: скористайтеся ознакою рівності трикутників за стороною і прилеглими кутами. 104. Вказівка: скористайтеся ознакою рівності трикутників за трьома сторонами і властивістю рівнобедреного трикутника ABC. 105. 1) 36° , 72°, 108°, 144°; 2) 40°, 60°, 120°, 140° . 106. 30°, 60°, 120°, 150° . 107. 1) 2; 2) 4; 3) 2. 108. 1) Ні; 2) ні. 109. 90° . 110. 1) 142°, 22°, 136°, 60°; 2) 131°, 35°, 89°, 105° . 111. 130°, 30°, 115°, 85° . 112. Вказівка: сума зовнішніх кутів чотирикутника дорівнює сумі кутів, суміжних із кутами цього чотирикутника. 113. 1) Так; 2) ні. 114. Так. 115. Вказівка: сума зовнішніх кутів чотирикутника вдвічі більша за суму його кутів. 116. 115° (мал.

§ 2. Паралелограм та його властивості

125. 1) Ні; 2) ні; 3) так. 126. 1) Ні; 2) ні; 3) так. 127. 1) Ні; 2) так; 3) ні; 4) так. 128. Ні (мал. 37); ні (мал. 38). 129. 1,2 дм, 0,4 дм. 130. 10 см, 5 см. 132. 1) 3 см, 21 см, 3 см, 21 см; 2) 15,5 см, 8,5 см, 15,5 см, 8,5 см. 133. 6,5 см, 9,5 см, 6,5 см, 9,5 см. 134. AB = CD = 4 см, AD = BC = 6 см (мал. 39); AB = CD = 10 см, AD = BC = = 10 см (мал. 40). 135. AB = CD = 6 см, AD = BC = 6,8 см. 136. Вказівка: скористайтеся властивістю внутрішніх односторонніх кутів. 137. 1) 120°, 60°; 2) 90°, 90° . 138. 45°, 135° . 139. 35°, 145°, 35°, 145°; 40°, 140°, 40°, 140°; 75° , 105°, 75°, 105°; 116°, 64°, 116°, 64° . 140. 1) Ні; 2) ні. 141. Ні. 142. ∠A = ∠C = = 45° , ∠B =∠D = 135° (мал. 42); ∠A = ∠C = 50° , ∠B = ∠D = 130° (мал. 43). 143. ∠A = ∠C = 60° , ∠B = ∠D = 120° . 144. 1) 65°, 115°, 65°, 115°; 2) 60°, 120° , 60°, 120° . 145. 135°, 45°, 135°, 45° . 146. Вказівка: скористайтесь ознакою рівності трикутників за трьома сторонами. 147. Ні. 148. 1) OC = 6 см, OD = 3 см; 2) AC = 12 см, BD = 6 см; 3) AD = 8 см, DC = 5 см. 149. Вказівка: врахуйте, що протилежні кути паралелограма попарно рівні. 150. Вказівка: врахуйте, що протилежні сторони паралелограма попарно рівні. 151. Вказівка: доведіть, що трикутник, який утворюють бісектриси зі стороною паралелограма, прямокутний. 152. Вказівка: скористайтесь ознакою паралельності прямих. 153. 1) 70 см; 2) 14 см. 154. 1) 6 см, 3 см; 2) 15 см. 155. 40 см. 156. Вказівка: скористайтесь ознакою рівнобедреного трикутника. 157. 30 см. 158. Вказівка: доведіть рівність відповідних трикутників. 159. По 9 см. 160. 1) 80°, 100° , 80°, 100°; 2) 54°, 126°, 54°, 126° . 161. 1) 160°, 20°, 160°, 20°; 2) 72°, 108°, 72° , 108° . 162. 1) 72°, 108°, 72°, 108°; 2) 120°, 60°, 120°, 60° . 163. 60° (мал. 50); 50° (мал. 51). 164. 120° . 165. Вказівка: проведіть висоти з вершини тупого кута паралелограма й розгляньте утворені прямокутні трикутники. 166. 1) 35°, 145° , 35°, 145°; 2) 45°, 135°, 45°, 135°; 3) 89°, 91°, 89°, 91° . 167. 16°, 96° . 168. 45°, 135° , 45°, 135° . 169. 9,6 см, 14,4 см, 9,6 см, 14,4 см. 170. 6 см. 171. 1) 45°; 2) 135° . 172. 2 см або 4 см. 173. 10 см, 15 см, 10 см, 15 см. 174. Сторони відносяться як 1 : 2. 175. 7 см, 14 см, 7 см, 14 см. 176. 1) АВ || CD. § 3. Ознаки паралелограма

178. 1) Ні; 2) ні; 3) так. 180. За ознакою паралелограма. 181. На мал. 64. 184. 1) MN = 4 см, LM = 6 см; 2) KL = 5,3 дм, NK = 3 дм; 3) MN = 1,5 см, NK = = 25 мм; 4) KL = 0,3 дм, LM = 5 см. 185. 1) СD = 3 см, ВС = 2 см; 2) АD = 2,5 см, АВ = 3,7 см. 186. Вказівка: скористайтесь ознакою паралелограма. 187. Вказівка: скористайтесь ознакою паралелограма. 188. 1) 4 см; 2) 2 см; 3) 120°; 4) 60° . 189. 1) 35°; 2) 5 см. 190. 1) KL || MN; 2) LM || NK; 3) KL || MN; 4) LM || NK. 191. 1) АВ і СD; 2) АD і ВС. 192. Вказівка: скористайтесь ознакою паралелограма. 193. Вказівка: скористайтесь ознакою паралелограма. 195. 1) LO = 3 см, MO = 2 см; 2) KO = 1,9 см, NO = 3,5 см. 196. Вказівка: кожний кут однієї пари рівних кутів позначте a, а іншої — b. Скористайтеся властивістю

197. 1) Ні; 2) так. 198. Так. 199.

паралелограм. 202. Вказівка: спочатку доведіть рівність трикутників EBM і KDN. 203. Вказівка: спочатку доведіть, що DAKM = DCNP і DBPK = DDMN. 204. Вказівка: скористайтесь ознакою паралелограма. 205. Вказівка: спочатку доведіть, що AECF — паралелограм. 206. Вказівка: скористайтесь ознакою паралелограма. 207. Вказівка: скористайтесь ознакою паралелограма. 208. Вказівка: скористайтесь ознакою паралелограма. 210. Вказівка: спочатку доведіть рівність трикутників, а потім скористайтесь ознакою паралелограма. 211. Вказівка: спочатку доведіть, що MNKP — паралелограм, а потім скористайтеся властивістю паралелограма. 212. Вказівка: скористайтесь ознакою паралелограма. 213. Вказівка: скористайтесь ознакою паралельності прямих та ознакою паралелограма, а потім — властивістю паралелограма. 214. Вказівка: доведіть, що чотирикутник — паралелограм та скористайтеся властивістю сторін паралелограма. 216. Вказівка: спочатку доведіть рівність трикутників, а потім скористайтесь ознакою паралелограма. 217. Вказівка: скористайтеся властивістю діагоналей паралелограма. 218. Вказівка: скористайтесь ознакою паралельності прямих, а потім — ознакою паралелограма. 219. Вказівка: скористайтесь ознакою паралелограма.

§ 4. Прямокутник

222. 1) Ні; 2) так. 223. Так. 224. Властивість діагоналей паралелограма. 225. 1) Ні; 2) так. 226. 1) Ні; 2) так. 227. 1) АD = 16 см, DС = 12 см; 2) ВD = 20 см; 3) АО = ОС = ВО = ОD = 10 см. 228. 54°, 36°, 54° . 229. 1) по 6 см; 2) по 3 см; 3) по 9 мм. 230. 1) 14 см і 14 см; 2) 28 см. 231. Вказівка: скористайтеся властивостями діагоналей прямокутника. 232. 35°, 125°, 55° (мал. 88); 30°, 60° , 30° (мал. 89). 233. 65°, 130°, 25° . 234. 30° (мал. 91); 60°(мал. 92). 235. 90° . 237. 1) 32 см; 2) 30 см. 238. 56 см. 239. 1) LN = 4 см; 2) KM = 3 дм; 3) LN = 1,5 дм; 4) KL = 2,7 см. 240. 1) ВD = 2 см; 2) АС = 7 см. 241. Вказівка: доведіть рівність діагоналей KM і LN. 242. Вказівка: доведіть рівність діагоналей АС і ВD. 243. Вказівка: доведіть, що всі кути даного паралелограма — прямі. 244. Вказівка: доведіть, що паралелограм є прямокутником. 245. 4 см і 20 см. 246. 6 см і 24 см. 247. 1) 2 см; 2) 7 мм; 3) 0,22 дм. 248. 1) 20 см; 2) 0,5 дм; 3) 14 мм. 249. Вказівка: скористайтеся тим, що кути рівностороннього трикутника дорівнюють по 60° . 250. 1) 54°, 36°; 2) 18° . 251. 1) 9,6 см, 14,4 см; 2) 10 см, 14 см; 3) 8 см, 16 см. 252. 1) 6 см; 2) 4,3 см. 253. 1) 26 см або 22 см; 2) 14 см або 16 см. 254. 1) 90 см; 2) 22,8 дм. 258. Вказівка: обчисліть кути чотирикутника. 259. Вказівка: нехай a — кут між діагоналлю та стороною паралелограма; знайдіть кути паралелограма. 260. Вказівка: врахуйте, що сума кутів чотирикутника дорівнює 360° . 261. Вказівка: врахуйте, що сума кутів чотирикутника дорівнює 360° . 262. 12 см, 12 см, 13,1 см, 13,1 см. 263. 2а – b (мал. 94); b – 2a (мал. 95). 264. 3 см, 3 см. 265. Вказівка: через дану точку

пряму, паралельну бічній

§ 5. Ромб. Квадрат

277. 1) Ні; 2) так. 278. Так. 279. Наприклад, взаємна перпендикулярність діагоналей. 280. 1) Ні; 2) так; 3) так. 281. 1) Ні; 2) так. 282. 1) Ні; 2) так. 283. Так. 284. Так. 285. 1) Так; 2) так; 3) так; 4) так. 286. 1) Так; 2) так; 3) так; 4) так. 287. Ні. 288. 1) ВС = АD = DС = 10 см; 2) АС = 16 см, ВD = 12 см. 289. ∠1 =∠2 = ∠3 = 25° . 290. 1) 0,6 дм; 2) 70 мм. 291. 3 см. 292. Вказівка: скористайтеся тим, що діагоналі ромба перпендикулярні й точкою перетину діляться навпіл. 293. Вказівка: скористайтесь

рівності трикутників за трьома сторонами. 294. ∠1 = ∠3 = ∠4 = 25° , ∠

. 295. 1) 18°, 72°; 2) 27°, 63° . 296. 30°, 60° . 297. 60

ка: діагональ даного ромба розбиває

рівносторонні трикутники. 298. 1) 60°, 120°, 60°, 120°; 2) 75°, 105°, 75°, 105°; 3) 25°, 155°, 25°, 155° .

299. 70°, 110°, 70°, 110° (мал. 110); 36°, 144°, 36°, 144° (мал. 111). 300. 60°, 120° , 60°, 120° . 301. 1) 12,8 дм; 2) 180 мм. 302. 40 см. 303. 1) KM ⊥ LN; 2) KM ⊥ LN; 3) KM ⊥ LN; 4) KM ⊥ LN. 304. 1) АС і ВD; 2) АС і ВD. 305. 1) по 5 см; 2) по 7 см; 3) ∠1 = ∠3 = ∠4 = 45° , ∠2 = 90° . 306. 1) 64 см; 2) 2,4 дм. 307. 168 мм. 308. 1) KL ⊥ LM; 2) LM ⊥ MN; 3) MN ⊥ NK; 4) KL ⊥ NK. 309. Вказівка: обчисліть кути чотирикутника. 311. Не може. 312. 96 см2. 313. 726 см2. 314. Вказівка: скористайтесь означеннями паралелограма та ромба. 315. Вказівка: покажіть, що сторони даного паралелограма рівні. 316. 30°, 150°, 30°, 150° . 317. Вказівка: нехай АВСD — ромб, АМ і АР — його висоти, проведені відповідно до сторін ВС і СD; доведіть, що DАВМ = DАDР. 318. 1) 60°, 120°, 60°, 120°; 2) 80 см. 319. 1) 70° , 110°, 70°, 110°; 2) 40°, 140°, 40°, 140° . 320. 80°, 100°, 80°, 100° . 321. 1) 72°, 108° , 72°, 108°; 2) 40°, 140°, 40°, 140° . 322. 60°, 120°, 60°, 120° . 323. 1) 16 см; 3) всі по 4 см. 324. 1) 16 см; 2) 58 мм; 3) 0,82 дм. 325. Вказівка: обчисліть кути ромба. 328. Вказівка: доведіть, що DAND = DCND = DAMB = DCMB. 329. 1) Так; 2) так; 3) ні. 330. Вказівка: нехай АВСD — ромб, АМ, АР — його висоти, проведені відповідно до сторін ВС і СD; доведіть, що DАСМ = DАСР; див. задачу 317. 331. 30° , 150°, 30°, 150° . 332. Вказівка: проведіть діагоналі ромба та покажіть, що кути АCN і САL та кути ВDK і DBM відповідно рівні. 333. Вказівка: обчисліть кути чотирикутника MPKN. 334. Вказівка: покажіть спочатку, що точка перетину діагоналей та основи перпендикулярів, проведених до протилежних сторін ромба, лежать на одній прямій; потім покажіть, що діагоналі чотирикутника з вершинами в основах побудованих перпендикулярів є рівними. 335. Вказів

ка: доведіть, що сторони чотирикутника паралельні діагоналям прямокутника й дорівнюють їх половині. 336. 5 см. 338. Вказівка: покажіть спочатку, що бісектриси двох пар сусідніх кутів прямокутника перетинаються під прямим кутом; потім доведіть, що одержаний прямокутник є квадратом. 339. Вказівка: якщо перегнути тканину за діагоналями, то краї тканини мають суміститися. 340. 1) Вказівка: покажіть, що промені ВА і ВС є доповняльними. 341. Два. 342. 1) Ні, бо може бути ромб. 343. Вказівка: позначте стовпці

пряму через

§ 6. Теорема Фалеса. Середня лінія трикутника

345. 1) Ні; 2) так; 3) ні; 4) ні; 5) так. 346. 1) Ні; 2) так. 347. 1) Ні; 2) так; 3) ні; 4) так. 348. 4 см (мал. 133); 3 см (мал. 134). 349. Ні. 350. 1) 6 см; 2) 4 см. 351. 15 см. 355. 4 см (мал. 138); 12 см (мал. 139). 356. Ні. 357. 1) 4 см; 2) 7 см. 358. 1) 4 см, 2,5 см, 3,5 см; 2) 15 мм, 20 мм, 25 мм. 359. 4,5 см; 5 см; 7 см. 360. Вказівка: виразіть середні лінії трикутника через його сторони. 361. 1) По 4 дм; 2) по 8 мм. 362. По 2 см. 363. 1) 4,8 дм; 2) 600 мм. 364. 24 см. 365. 1) 28 см; 2) 56 см; 3) 60 см. 366. 1) Рівносторонній; 2) рівнобедрений. 367. 1) 1,2 дм і 1,8 дм; 2) 200 мм і 28 см. 368. 10 см і 22 см. 369. 96 см. 370. 36 см. 373. 1) 9 см; 2) 12 см; 3) 20 см. 374. 1) 4 см, 5 см, 6 см; 2) 0,25 дм, 6 см, 6,5 см. 375. 1) 36 см; 2) 4,8 дм; 3) 600 мм. 376. 10 см; 10 см; 5 см. 377. 15 см; 15 см; 10 см. 378. 2 см. Вказівка: продовжте відрізок АМ на 4 см за точку М, одержите точку Р; продовжте відрізок ОK за точку K на 4 см, одержите точку D; розгляньте трикутник ВАР. 379. 1) 7,5 см, 10 см, 12,5 см; 2) 6 см, 8 см, 10 см. 380. 1) 28 см, 32 см, 36 см; 2) 1,4 дм, 1,6 дм, 1,8 дм. 381. Вказівка: виразіть периметри трикутників через сторони одного з них. 382. 2) 12 см, 24 см, 30 см; 3) 24 см. 383. 1) По 4 см і по 6 см; 2) 6 см і 12 см; 4 см і 8 см. 384. Вказівка: виразіть сторони кожного з чотирьох трикутників через сторони даного трикутника. 385. Вказівка: скористайтеся теоремою Фалеса для кутів АDВ і DВС та прямих МС і АN. 386. 1) 25 см; 2) 3,5 дм. 387. 1) 10 см; 2) 49 см. 388. 1) 16 см; 2) 2,6 дм. 391. Вказівка: проведіть прямі, що проходять через дані точки паралельно середнім лініям трикутника. 392. Вказівка: через точку М проведіть пряму паралельно ВD; скористайтеся теоремою Фалеса. 394. Вказівка: через основу медіани трикутника проведіть пряму паралельно іншій його медіані; скористайтеся теоремою Фалеса. 397. 1) 36 см. 398. Вказівка: через точку М проведіть пряму, паралельну ВС; скористайтеся теоремою Фалеса. 400. 2) Вказівка: відкладіть відрізок АВ так, щоб точка B лежала на першій лінії аркуша, а точка A — на п’ятій лінії. 401. Вказівка: MN — середня лінія трикутника АВС. 404. 2) Таких доріг є три. Вони є середніми лініями трикутника ABC.

§ 7. Трапеція

405. 1) Ні; 2) так. 406. 1) Ні; 2) так. 407. 1) Ні; 2) ні; 3) так. 408. 1) Ні; 2) так; 3) так. 409. 1) Ні; 2) ні; 3) так. 410. 1) Ні; 2) ні; 3) так; 4) ні; 5) так. 411. 1) Ні; 2) так; 3) ні. 412. 1) BC і AD; 2) AB і CD; 3) ∠A і ∠D — прилеглі до основи AD, ∠B і ∠C — прилеглі до основи BC; 4) ∠A і ∠B — прилеглі до бічної сторони AB, ∠C і ∠D — прилеглі до бічної сторони CD. 413. 1) 3 см (мал. 169); 2) 90° (мал. 170). 414. Вказівка: скористайтеся властивістю паралельних прямих. 415. ∠B = 130° , ∠D = 40° (мал. 171); ∠B = 90° , ∠C = 134° (мал. 172); ∠B = 140° , ∠C = 144° (мал. 173). 416. 1) ∠A = 70° , ∠C = 150°; 2) ∠A = 55° , ∠D = 35° . 417. 1) 20°; 2) 45°; 3) 85° . 418. 1) ∠A = 140° , ∠C = 60°; 420. KCDМ — трапеція. 421. ABCD — трапеція. 422. Вказівка: 1) скористайтесь означенням трапеції і паралелограма. 423. 1) 7 см; 2) 3 см. 424. Вказівка: скористайтесь ознакою рівності прямокутних трикутників за гіпотенузою та гострим кутом. 425. 4 см (мал. 178); 7 см (мал. 179); 15 см (мал. 180). 426. Ні. 427. 1) 4 см; 2) 15 см; 3) 17 см; 428. 7 см. 429. 1) 8 см; 2) 9 см; 3) 13 см; 4) 9 см; 5) 12 см. 430. 8 см, 16 см, 12 см. 431. 4 см, 11 см, 7,5 см. 432. 1) 40 см; 2) 62 см. 433. 62 см. 434. 1) 134° і 36°; 2) 145° і 25° . 435. 128° і 56° . 436. 1) 2 см; 2) 38 мм. 437. Вказівка: нехай ABCD —

дана трапеція з основами BC і AD (BC < AD). Проведіть CE || AB і доведіть, що трикутник CED — рівнобедрений. 438. ∠A = ∠D = 58° , ∠B = ∠C = 122° (мал. 185); ∠A = ∠D = 60° , ∠B = ∠C = 120° (мал. 186); ∠A = ∠D = 60° , ∠B = ∠C = = 120° (мал. 187). 439. Вказівка: скористайтеся властивістю рівнобічної трапеції та властивістю паралельних прямих. 440. 70°, 110°, 110°, 70° . 441. 36°, 144° , 144°, 36° . 442. Вказівка: скористайтесь ознакою рівності трикутників за стороною і прилеглими кутами. 443. Вказівка: доведіть рівність трикутників ABD і DCA. 444. 6 см. 445. 34 см. 446. 1) Вказівка: доведіть, що DABK = DDCM. 447. 1) 4 см і 12 см; 2) 5 см і 9 см. 448. Вказівка: скористайтеся властивістю рівнобедреного трикутника і властивістю паралельних прямих. 449. 1) 26 см; 2) 286 мм. 451. 6 см. 452. 8 см і 12 см. 453. Вказівка: продовжте відрізок до перетину з бічними сторонами трапеції та скористайтеся теоремою Фалеса;

скористайтеся властивостями середньої лінії трапеції та середньої лінії трикутника. 454. 1) 14 см; 2) 9 см. 455. Вказівка: скористайтеся властивостями паралельних прямих. 456. 120°, 60°, 120°, 60° . 457. Вказівка:

має основи АВ і СD, а її

перетинаються в точці О; доведіть рівність трикутників АВС і ВАD. 458. Вказівка: скористайтеся властивістю паралельних прямих. 459. Вказівка: з вершини тупого

тайтеся властивістю висоти рівнобедреного трикутника. 460. Вказівка:

ції та доведіть,

і 24 см. 462. 3 . 4 a 464. EF — середня лінія трапеції, EF = 3 см. 466. 3,5 м. 467. Так.

8. Центральні та

468. 1) Ні; 2) ні; 3) так. 469. 1) Ні; 2) так. 470.1) Ні; 2) ні; 3) так. 471. 1) Так; 2) ні; 3) ні. 472. 1) Ні; 2) так. 473. 1) Ні; 2) так. 475. 90° (мал. 221); 180° (мал. 222). 476. 60° . 477. 1) 180°; 2) 120°; 3) 240° . 478. 1) 30° і 330°; 2) 62° і 298°; 3) 100° і 260° . 479. 1) 70°; 2) 210° . 480. 1) 12 см; 2) 0,2 дм; 3) 39 мм. 481. Вказівка: доведіть рівність дуг АC і ВD. 482. Вказівка: скористайтеся тим, що дуга BC є спільною. 483. 60° (мал. 227); 25° (мал. 228); 90° (мал. 229). 484. 70° (мал. 230); 20° (мал. 231). 485. 1) 26°; 2) 63°; 3) 100° . 486. 1) 32°; 2) 64°; 3) 220° . 487. 70° (мал. 232); 140° (мал. 233); 190° (мал. 234). 488. 1) 60°, 60°, 60°; 2) 36°, 72° , 72° . 489. 30°, 60°, 90° . 490. 1) 120°, 60°, 180°; 2) 56°, 84°, 220° . 491. 70°, 130° , 160° . 492. 1) 32°, 32°, 116°; 2) 72°, 72°, 36° . 493. 60°, 60°, 60° . 494. Вказівка: скористайтеся наслідком 1

кут. 495. Вказівка: нехай AB і CD — хорди кола і AB = CD; сполучіть точки A, B, C і D із центром O

доведіть, що DAOB = DCOD. 496. Вказівка: нехай хорда AC і діаметр BD кола із центром O

трикутників AKO і CKO. 497. Вказівка:

ристайтеся наслідком 2 з теореми про вписаний кут. 509. Вказівка: див. задачу 508. 511.1) 45°; 2) 40° . 512. Вказівка: скористайтеся теоремою про зовнішній кут трикутника і знайдіть кут ABC. 513. Вказівка: скористайтеся теоремою про суму кутів трикутника і теоремою про суміжні кути; знайдіть кут DBC трикутника DBC. 514. 50° (мал. 241); 80° (мал. 242). 515. 40°, 60°, 80° . 318. 1) Коло, радіус якого дорівнює половині відрізка, що сполучає дані точки; 2)

описаного навколо трикутника зі стороною AB і протилежним гострим кутом a. 519. Вказівка: скористайтеся наслідком 2

520. Вказівка: прикладіть вершину прямого

будьяких двох точок кола, що є зовнішнім контуром диска, та проведіть два діаметри кола. § 9. Вписані й описані чотирикутники

521. Мал. 255. 522. Мал. 258. 523. Ні. 524. Ні. 525. 1) 9 см; 2) 180° . 526. ∠B = 100° , ∠C = 85° (мал. 262); ∠M = 75° , ∠N = 120° , ∠K = 105° (мал. 263); ∠F = 90° , ∠E = 60° , ∠Q = 90° , ∠P = 120° (мал. 264). 527. а) Ні; б) так. 528. а) Так; б) ні. 529. 1) 125°; 2) 108°; 3) 120° . 530. 1) Так; 2) так; 3) ні. 531. Вказівка: скористайтеся наслідком 2 з теореми про вписаний кут. 532. 1) Вказівка: скористайтеся наслідком 2 з теореми про вписаний кут; 2) за умови, що AD ⊥ BC.

533. 10 см (мал. 266); 3 см і 7 см (мал. 267); 1 3 3 см і 2 6 3 см (мал. 268).

534. 1) Так; 2) ні. 635. 1) 40 см; 2) 6,4 дм. 636. 1) 80 см; 2) 52 см. 538. 1) Ні; 2) так; 3) так. 539. 1) 90°; 2) 60° . 540. 1) 10 см; 2) 2,3 дм. 541. 1) Так; 2) ні. 545. 1) Так; 2) ні. 546. Так. 547. Вказівка: в утвореному чотирикутнику сусідні сторони мають бути рівними. 548. 1) 3 мм, 10,5 мм, 18 мм, 10,5 мм; 2) 4 см, 14 см, 24 см, 14 см. 549. Середня лінія трапеції дорівнює 1 4 P , тому: 1) 4 см; 2) 50 мм.

550. 20 см. 552. 1) Вказівка: побудуйте коло радіусом R та проведіть у ньому два перпендикулярні діаметри; послідовно сполучіть точки перетину діаметрів з колом. 557. Так. Вказівка: скористайтесь ознакою описаного чотирикутника. 560. Вказівка: діаметр круга дорівнює меншій стороні прямокутника. 561. Вказівка: проведіть у даному крузі два перпендикулярні діаметри. 562. 2) Вказівка: криниця має бути розміщена в центрі кола, описаного навколо трапеції.

§ 10. Подібні трикутники 563. 1) Ні; 2) так; 3) ні; 4) ні; 5) так. 564. 1) Ні; 2) так; 3) так; 4) ні; 5) так. 565. 1) Ні; 2) ні; 3) так. 566. 1) Ні; 2) так. 567. 1) Ні; 2) ні; 3) так; 4) так; 5) так; 6) так. 568. DАВС і DLMK (мал. 280): 1) ∠А і ∠L, ∠В і ∠М, ∠С і ∠K; 2) АВ і LM, ВС і МK, АС і LK; DАВС і DPTQ (мал. 281): 1) ∠

Q; 2) АВ і PT, ВС і TQ, АС і PQ. 569. 1) 1 1; 3 2) 2. 570. 1) KC AC і ; DC BC 2) AB KD і ; BC DC

3) AB KD і . AC KC 571. 1) Ні; 2) ні; 3) ні. 572. 1) ∠A1 = 30

; 2) ∠A = ∠A1 = 45° ,

B1 = 110° ,

C = 25° . 573.

574. 1) Так; 2) ні. 575. Так. 576. 1) 6 см, 7 см; 2) 13 см, 18,5 мм. 577. 169 15 AB = см; 11 630 13 AC = см. 578. Вказівка: скористайтеся

трикутників. 579. 1) DABC  DMBC; 2) DABC  DAMN. 580. MN || BC. 583. 1) 17,1 од.; 20,52 од.; 5 6 ; 2) 17,9 од.; 14,32 од.; 5 4 ; 3) 15 од.; 7,5 од.; 2. 584. 36 од.; 27 од.; 4 3 . 586. 1) 3 см; 2) 3,75 см; 3) 6 см. 587. 1) 5 см, 1 8 3 см, 2 11 3 см. 588. 6 см, 9 см, 12 см. 589. Вказівка: скористайтеся тим, що в подібних трикутниках відповідні

кути рівні. 590. 1) Ні; 2) ні. 591. 1) Так; 2) так. 592. Так, 2 . 3 k = 593. Так, k = 2. 594. 6 см. 595. 37,5 см. 596. 112 см, 64 см. 597. 30 см, 45 см. 598. 1) 12 см; 2) 10 см. 599. Так. 600. Так. 601. Так, k = 1. 602. 1 . 2 k = 603. 1) 15 см, 30 см, 30 см; 2) 3,75 см, 11,25 см, 11,25 см. 604. Вказівка: скористайтеся властивістю периметрів подібних трикутників. 605. Вказівка: скористайтеся властивістю периметрів подібних трикутників. 606. Вказівка: під мікроскопом градусні міри кутів не змінюються. 608. 1) Масштаб 1 : 250 000; 2) 10 км; 3) 12,5 км. 609. 45 см, 50 см, 25 см. 610. 1) Так. § 11. Узагальнена теорема Фалеса

611. 1) Ні; 2) так; 3) ні; 4) ні; 5) так. 612. 1) Ні; 2) ні; 3) ні; 4) так. 613. 3 : 5 (мал. 292); 4 : 2 (мал. 293). 614. 4 : 3. 615. 1) PM; 2) MH. 616. РH. 617. 1) Ні; 2) ні. 618. 1) 2 : 3; 2) 5 : 1. 619. 2 : 1. 620. 4. 621. Так. 622. Так. 623. 1) 4 см, 6 см; 2) 12 см, 4 см. 624. 6 см, 8 см. 630. 1) Ні; 2) ні. 631. Так. 632. 1) 6 або 1,5; 2) 8 або 4,5; 3) 2 11 3 або 4,2. 633. 1) Так; 2) так; 3) ні; 4) ні. 634. Так. 635. Вказівка: ско

ристайтеся наслідком з узагальненої теореми Фалеса. 637. ; am AC mn = + . an CB mn = + 638. 1) 16 см, 32 см, 30 см; 2) 10 см, 24 см, 16 см. 639. 1) 15 см, 10 см; 2) 20 см, 4 см. 640. 1) BC = 16 мм, CL = 24 мм, LF = 16 мм, DC = 50 мм, KL = 20 мм; 2) BC = 6 см, CL = 9 см, LF = 6 см, DC = 15 см, KL = 6 см. 641. 1) 125 34 см, 100 17 см, 50 17 см, 2) 250 17 см, 400 17 см, 200 17 см. 642. 1) 15 см; 2) 22 см. 643. 1) 3 см, 6 см; 2) 5,6 см, 8,4 см. 644. 1) 12 см; 2) 1,2 дм. 645. 1) 1 , 3 2 ; 3

2) 2 , 5 3 ; 5 3) 4 , 9 5 . 9 646. 1) 4 см, 8 см, 12 см; 2) 3,1 см, 6,2 см, 9,3 см. 647. Вказів

ка: скористайтеся

трикутників. 648. 1) 10 ; 3

2) 4,5. 651. ; a abc ++ ; b abc ++ ; c abc ++ ; ab abc + ++ . bc abc + ++ 652. 1) 21,6 см;

2) 36 см. 653. Вказівка: скористайтесь узагальненою теоремою Фалеса. 654. 1) Вказівка: спочатку доведіть, що DAOB  DDOC; 2) 6,25 і 3,75. 655. Вказівка: нехай AA1 перетинає MN в точці O; доведіть, що DAMO  DABA1 і DANO  DACA1. 656. 1) Так; 2) лише для рівнобічної трапеції. 657. 1) 8 см, 9 см; 2) 1 11 3 см, 2 12 3 см. 658. 1) 12 , 33 ab + 21 ; 33 ab + 2) 13 , 44 ab + 11 , 22 ab + 31 . 44 ab + 660. 10 хв. 661. 28 м. 662. 36 м.

§ 12. Перша ознака подібності трикутників 663. 1) Ні; 2) ні; 3) ні; 4) ні; 5) так. 664. 1) Ні; 2) так. 666. Так. 669. DABС  DPBQ, DABС  DRQC, DPBQ  DRQC. 670. DABС і DМNС. 672. 1) Так; 2) так; 3) так; 4) ні. 673. Так. 674. Тому, що з рівності даних відношень не випливає рівність відповідних кутів трикутників. 675. 1) ∠A = ∠B = ∠C = 60° , AB = BC = AC = 2 см, ∠A1 = ∠B1 = ∠C1 = 60° , AB1 = BC1 = AC1 = 6 см; 2) ∠A = = ∠B = ∠C = 60° , AB = BC = AC = 4 см, ∠A1 = ∠B1 = ∠C1 = 60° , AB1 = BC1 = AC1 = = 2 см. 676. ∠A = ∠B = ∠C= 60° , AB = BC = AC = 9 см, ∠A1= ∠B1= ∠C1= 60° , AB1= BC1= AC1= 3 см. 677. Вказівка: скористайтесь ознакою рівнобедреного трикутника та ознакою подібності трикутників за двома кутами. 678. 1) Так; 2) ні. 679. Так. 680. Вказівка: скористайтесь ознакою подібності трикутників за двома кутами. 681. Вказівка: скористайтесь ознакою подібності трикутників за двома кутами. 683. 1) Так; 2) так. 684. Ні. 685. Вказівка: знайдіть гострі кути трикутників та скористайтесь ознакою

кутами. 686. a : b або b : a. 687. 1) 66 мм, 132 мм; 2) 0,9 дм, 1,5 дм. 688. 9 6 11 см, 2 18 11

см. 689. Вказівка: скористайтесь

кутами. 690. Вказівка: скористайтесь

відрізків МK і АС. 691. 1) 3 p ; 2) 3m – Р. 592. Вказівка: скористайтесь ознакою подібності трикут

ників за двома кутами. 693. Вказівка: скористайтесь ознакою подібності трикутників за двома кутами. 694. Вказівка: скористайтесь ознакою паралельності прямих та ознакою подібності трикутників за двома кутами. 695. 1) 5 см, 7 см, 3 см; 15 см, 21 см, 9 см; 2) 6 см, 8 см, 4 см; 4,5 см, 6 см, 3 см. 696. 8 см, 10 см, 6 см; 16 см, 20 см, 12 см. 697. 10 см, 8 см. 698. Вказівка: скористайтеся тим, що медіани трикутника точкою їх перетину діляться у відношенні 2 : 1, рахуючи від вершини, та розгляньте подібні трикутники, що утворилися. 699. 1) 12 см; 2) 4 см. 700. Вказівка: один із кутів, що утворює дана пряма з найбільшою стороною даного трикутника, має дорівнювати найбільшому його куту. 701. 1) 4; 2) 3; 3) 2. 702. 1) 4,2 см; 2) 6 см. 703. Вказівка: див. задачу 702. 704. 1) 5 : 3; 2) 13 : 5. 705. Вказівка: скористайтесь ознакою

706. Вказівка: рівні

ми. 707. Вказівка: скористайтесь

тами. 708. 8 см, 12 см. 709. 12 см, 36 см. 710. 18 см, 30 см. 711.

712. 20 см, 30 см. 713. 9 см,

що спираються на хорду BC. 720. Вказівка: доведіть подібність спочатку трикутників AOM і NKM та BON і BKA, а потім трикутників BKA і MKN. 721. Вказівка: доведіть подібність DABC і, наприклад, DALK. 722. Вказівка: скористайтеся тим, що навколо чотирикутника BDCM можна описати коло, а вписані кути BCD і BMD спираються на одну хорду. 723. ab. 725. 195 м. 726. Вказівка: побудуйте подібний трикутник, сторони якого відповідно паралельні сторонам даного трикутника. 727. 4) 189,65 м. 728. Вказівка: на одному з трьох променів візьміть дві точки і проведіть із них перпендикуляри до двох інших променів; розгляньте дві пари подібних прямокутних трикутників, які при цьому утворилися.

729. 1) Ні; 2) ні; 3) ні; 4) ні; 5) ні; 6) так. 730. 1) Ні; 2) так. 731. 1) Ні; 2) ні; 3) ні; 4) так. 732. DABС  DKLМ. 733. Ні. 734. Наприклад, 10 см і 16 см та кут 50° між ними. 736. DABС і DМNС. 738. Перший і третій. 739. 1) Ні; 2) ні; 3) так. 740. 1) Так; 2) ні. 741. Так. 742. Ні. 743. Наприклад, 10 см, 12 см, 18 см. 744. Перший і другий. 745. 1) 27 см, 36 см; 2) 119 см, 105 см. 746. 30 см, 45 см. 747. Так. 748. Перший і третій. 749. Другий і третій. 750. 1) 24 см; 2) 128 см. 751. 27 см. 752. 1) 36 мм; 2) 0,9 дм. 753. 16 см. 754. 1) 144 см, 96 см, 48 см; 2) 56 см, 1 37 3 см, 2 18 3 см. 755. 40 см, 2 26 3 см, 1 13 3 см. 756. 1) 6,4 мм, 10,4 мм,

38,4 мм, 62,4 мм; 2) 6 см, 10 см, 12 см, 20 см. 757. 2 2 3 см, 2 6 3 см, 2 6 3 см, 2 16 3 см. 758. Вказівка: перетворіть дану рівність добутків у пропорцію.

759. 1) AB = 5 см, BC = 7 см, AC = 3 см, KL = 15 см, LM = 21 см, KM = 9 см; 2) AB = 6 см, BC = 8 см, AC = 4 см, KL = 4,5 см, LM = 6 см, KM = 3 см. 760. TO = 8 см, OM = 10 см, TM = 6 см, BC = 16 см, CE = 20 см, BE = 12 см. 761. Вказівка: скористайтесь ознакою подібності трикутників за двома сторонами й кутом між ними. 762. Рівні медіани можуть не бути відповідними. 763. 12 см. 764. 1) 2 : 7; 2) 1 : 4. 765. Вказівка: нехай O — точка перетину висот BH і CM; спочатку на стороні BC як на діаметрі побудуйте допоміжне коло та доведіть подібність трикутників BOC і MOH. 766. 2. 767. 1) 2 : 1; 2) 1 : 2. 768. 1) 1 : 3; 2) 1 : 2. 769. 1) Ні; 2) так; 3) так. 770. Вказівка: скористайтеся

сторонами. 771. . 1 ma m + 772. 2 : 1. 773. 60°, 120°, 60°, 120° . 774. 1) ; 1 amb m + + 2) 2 ; ab ab + 3) 2 . ab ab

776. 1) 4 ; 9 2) 3 . 7

3 : 2. 779. 1 : 1. 780. Вказівка:

ма сторонами і кутом між ними. 781. Вказівка: скористайтесь ознакою подібності трикутників за двома кутами. 782. 9,8 м. 784. Вказівка: у трикутнику AKB проведіть допоміжну середню лінію, паралельну AB, та розгляньте дві пари подібних трикутників, які при цьому утворилися. § 14. Застосування подібності трикутників

785. 1) Так; 2) ні; 3) так. 787. 1) Ні; 2) ні; 3) так; 4) ні; 5) ні; 6) так; 7) ні; 8) ні; 9) так. 788. 1) 6 см і 3 см, 8 см і 4 см, 10 см і 5 см; 2) 4 см і 2 см, 4 см і 2 см, 2 см і 1 см; 3) 30 см і 15 см, 30 см і 15 см, 30 см і 15 см. 789. 12 см і 6 см, 12 см і 6 см, 18 см і 9 см. 790. 1) 18 см, 24 см, 36 см; 2) 6 см, 6 см, 9 см; 3) 12 см, 12 см, 12 см. 791. 9 см, 15 см, 21 см. 792. 1) АD = 8 см, DС = 12 см; 2) AC = 26 см, DC = 12 см; 3) АD = 1,5 см, BC = 5 см; 4) АC = 12 см, DС = 9 см. 793. L. Вказівка: скористайтеся властивістю бісектриси і властивістю медіани трикутника. 794. Н. 795. Мал. 338: 1) 25 од.; 2) 15 од. і 20 од.; 3) 12 од.; мал. 339: 1) 169 од.; 2) 65 од. і 156 од.; 3) 60 од. 796. 1) 289 од.; 2) 136 од. і 255 од.; 3) 120 од. 797. 2 од. (мал. 341); 2 од. (мал. 342); 6 од. (мал. 343). 798. 1) 4 см; 2) 2 см. 799. 6 см. 801. 8 см, 12 см, 16 см. 802. 1 : 2. 803. 1)Так; 2) Ні. 804. 6 см, 9 см. 805. 22,5 см, 37,5 см. 806. 62 см, 32 см. 807. 1) 3 4 ; 2) 1 6 . 808. 4,8 см. 809. 6,72 см. 810. 1) 24 см; 2) 120 мм. 811. Вказівка: скористайтесь ознакою подібності трикутників за двома сторонами та кутом між ними. 812. Вказівка: див. задачу 811 (1). 813. Вказівка: див. задачу 811 (2). 814. Вказівка: див. задачу 811 (3). 817. Вказівка: через вершину тупого кута проведіть пряму, паралельну бічній стороні; розгляньте утворений прямокутний трикутник та скористайтеся властивістю висоти, проведеної до гіпотенузи. 818. Вказівка: доведіть, що трикутник з вершинами в центрі середнього

однієї зі сторін даного кута є прямокутним. 819. Вказівка: скористайтеся

тивістю вписаних кутів, що спираються на

хорду. 821. Вказівка: щоб побудувати точки, які не є кінцями двох перпендикулярних діаметрів, поділіть діаметр у відношенні 1 : 9 та скористайтеся властивістю висоти, проведеної до гіпотенузи прямокутного трикутника. 823. Вказівка: три точки — око, верхівка віхи й верхівка дерева

§ 15. Теорема Піфагора. Перпендикуляр і похила

824. 3). 825. Так (мал. 366); ні (мал. 367). 826. 3). 827. 1) 13 см; 2) 15 м; 3) 16 см. 828. 1) 5 см; 2) 8 м; 3) 12a. 829. 1) a = 12 см; 2) b = 16 см; 3) c = 10a. 830. 1) d = 25 см; 2) b = 24 см; 3) b = 9a. 831. Вказівка: у даному прямокутнику проведіть

кутному трикутнику. 832. 4 см. 833. 1) 2 см; 2) 8 см; 3) 2. a 834. 1) 1 см; 2) 42 см; 3) 2 . 2 m 835. 1) 1,5 см; 2) 53 см; 3) 3 . 2 a 836. 1) 24 см; 2) 15 см; 3) 12 см. 837. 1) 15 см; 2) 20 см. 838. 1) 5 см; 2) 15 см; 3) 10 см. 839. Вказівка:

стосуйте теорему

842. 17 см. 843. 3 2 m . 844. 1) 26 см; 2) 8 см; 3) 15 см. 845. 1) 5 см; 2) 5 см; 3) 24 см.

846. 19 см (мал. 382); 62 см (мал. 383). 847. 13 см. 848. 1) 5 см, 12 см, 13 см; 2) 7 см, 24 см, 25 см. 849. 1) 15 см, 20 см; 2) 12 см, 16 см. 850. 9 см, 12 см, 15 см. 851. 30 см, 16 см, 34 см. 852. 1) 15 см, 18 см; 2) 16 см, 17 см. 853. 1) 12 см, 211721,6 ≈ см; 2) 24 см, 219327,8 ≈ см. 854. 1) 10 см; 2) 29 см. 855. Вказівка: розгляньте два прямокутні трикутники, одним із катетів яких є менша бічна сторона трапеції. 856. 8 см (мал. 385); 5 см (мал. 386). 857. 14 см. 858. 1) 20 см; 2) 13 см. 859. 1) 10 см; 2) 25 см. 860. 1) 4 см; 2) 6 см. 861. 1) 8 см або 22 см; 2) 38 см або 88 см. 862. 8 см. 863. 1) 10 см; 2) 52 см. 864. 21 см або 11 см. 865. 1) 6 см, 15 см; 2) 8 см. 866. Вказівка: скористайтесь ознакою рівності прямокутних трикутників за двома катетами. 867. Вказівка: скористайтеся теоремою Піфагора. 868. 1) 120 см; 2) ≈ 80,7 см. 869. 1) 61 см, 11 см; 2) 37 см, 12 см. 870. 1) 37 см, 76927,7 ≈ см; 2) 20 см, 220528,6 ≈ см. 871. 1) 8 см, 9,6 см, 9,6 см; 2) 12 см, 5,6 см, 4,2 см. 872. Вказівка: нехай ABCD — даний паралелограм, O — точка перетину його діагоналей. Проведіть перпендикуляри з вершин B і C до прямої AD; розгляньте прямокутні трикутники, що утворилися, та скористайтеся теоремою Піфагора. 873. Вказівка: див. задачу 872. 874. Вказівка: скористайтеся теоремою Піфагора. 876. 6 см. 877. Вказівка: проведіть BE || CD та обґрунтуйте, що AE — діаметр і CE = DB. 879. 24115,5 ≈ м. 880. 328 м. 881. 1) 6,5 м; 2) ≈ 6,7 м. 882. 12 футів.

§ 16. Співвідношення між сторонами і кутами прямокутного трикутника 884. 1) б; 2) в; 3) б. 885. 1) а; 2) б; 3) в. 886. 1) Ні; 2) так; 3) так; 4) ні; 5) ні; 6) так. 887. 1) Ні; 2) так; 3) ні; 4) так; 5) так; 6) ні. 889. sin, BD AB α= cos, AD AB α= () tg , BD BDA AD α=∆ sin, BC AC α= cos, AB AC α= () tg . BC ABC AB α=∆ 890. 1) Ні; 2) так; 3) ні. 891. 1) Так; 2) так; 3) так. 892. 1) 1; 2) 2; 3) 1; 4) 32; 5) 3; 6) 8. 893. 1) 23; 2) 2; 3) 3. 894. 1) 1; 2) 1; 3) 2,5; 4) 2. 895. 1) 2; 2) 0. 896. 1) 30°; 2) 45°; 3) 60°; 4) 60°; 5) 60°; 6) 45° . 897. 1) 45°; 2) 30°; 3) 30° . 898. 1) sin 10° , sin 11°, sin 15°, sin 46°, sin 75°; 2) tg 17°, tg 37°, tg 48°, tg 66°, tg 87° . 899. cos 72° , cos 50°, cos 34°, cos 25°, cos 20° . 900. 2 см (мал. 407); 4 см (мал. 408); 10 см (мал. 409). 901. 12 см (мал. 410); 10 см (мал. 411); 7 см (мал. 412). 902. 1) 2 см; 2) 6 см; 3) 8 см. 903. 1) 6 см; 2) 6 см; 3) 7 см. 904. 1) 2 см; 2) 5 см; 3) 9 см. 905. 1) sin 70°; sin 55°; sin 40°; 2) cos 80°; cos 25°; cos 5° . 906. 1) sin 50°, sin 16°; 2) cos 35°, cos 65° . 907. 1) sina; 2) 2 sina; 3) cosa; 4) –cosa. 908. 1) 0; 2) –cosa.

911. c · cos a (мал. 413); c · sin a (мал. 414); b · tg a (мал. 415). 912. tg a α (мал. 416); sin a α (мал. 417); cos b α (мал. 418). 913. 1) 3 см; 2) 8 см; 3) 12 см; 4) 6 см. 914. 1) 2 см; 2) 4 см. 915. 1) 128 см; 2) 16 см; 3) 10 см; 4) 10 см. 916. 1) 64 см; 2) 50 см. 917. 1) 4,8 см; 2) 48 см; 3) 16,5 см. 918. 1) BC = c · cosb, AC = c · sinb; 2) , sin a AB = α ; tg a AC = α 3) , sin b AB = β . tg b AC = β 919. 1) ≈ 0,682; ≈ 0,731; ≈ 0,933. 920. 1) a = 39°: 0,629; 0,777; 0,809; a = 54°12′ : 0,811; 0,585; 1,387; 2) 48°35′; 31°; 52°59′; 23°48′; 43°3′; 37°59′ . 921. 1) 0,342; 0,966; 0,545; 0,996; 2) 0,994; 0,391; 0,629; 0,913; 3) 2,14; 0,017; 3,27; 0,344. 922. 1) 0, 799; 0,035; 2) 0,469; 0,974; 3) 0,176; 0,287. 923. 1) 88°, 1°, 35°; 2) 40°, 15°, 77°; 3) 42°, 19°, 38° . 924. 1) 36°; 2) 43°; 3) 40° . 925. 1) sin A = 0,8; cos A = 0,6; 4 tg; 3 A = 2) sin B = 0,6; cos B = 0,8; 3 tg. 4 B = 926. 1) sin A = 0,8; cos A = 0,6; 2) sin B = 0,6; cos B = 0,8. 927. 1) 0,96; 2) 0,96; 3) 24 . 7 928. 1) 3; 2) 6. 929. 2. 930. 4 см. 931. 18 см. 932. 1) 103 см; 2) 5 см; 3) 53 см. 933. 1) 8 см і 83 см; 2) 82 см і 82 см. 934. 23 см і 6 см (мал. 420); 33 см і 9 см (мал. 421). 935. 4 см і 23 см. 936. 4 см, 43 см. 937. 12 см і 12 см. 938. 1) 123 см і 24 см; 2) 12 см і 123 см. 939. 3 , 6 a r = 3 . 3 a R = 940. 1) 4 см; 2) 43 см. 941. 1:2. 942. 1) 52 см і 10 см;

2) 5 см і 53 см. 943. 53 см. 944. 1) sin A = 0,8; cos A = 0,6; 4 tg; 3 A = 2) sin B = 0,6; cos B = 0,8; 3 tg. 4 B = 947. b · sina. 948. cos. 2 l α 949. 1) 2b · cosa; 2) b · sina. 950. 1) ; sin h α 2) 2 . tg h α 951. 1) ; 2tg 2 a α 2) . 2sin 2 a α 952. tg sin a α β і tg tg a α β (мал. 423); cos sin a β α і sin sin a β α (мал. 424). 953. a · sina і a · sina · tga. 954. 2m · cosa,

2m · sina. 955. . 2cos b α 956. 1) 2 ; tg 2 r α 2) . costg 2 r α α 957. tg 2 . tg h α α 958. . 2cos a α 959. 1) ; tg 2 a α 2) . sin 2 a α 960. 1) ; 2sin 2 d α 2) tg. 2 d α 962. «–». 963. 24 см і 36 см. 964. 10 см і 24 см. 965. 11 , tgtg22 r

966. b + 2c · cos a. 967. a – 2c · · sin a. 968. 1) ; cos h α 2) b + 2h · tga. 969. 8 м. 970. 203 6071,5 3 +≈ м. 971. 1) tg a = 0,8. 972. 100 м. Вказівка: скористайтеся властивістю прямокутного трикутника з кутом 30° . § 17. Розв’язування прямокутних трикутників

973. 1) Ні; 2) так; 3) ні; 4) ні; 5) так. 974. 1) Ні; 2) так; 3) ні; 4) так; 5) ні; 6) так; 7) ні; 8) так. 975. y ≈ 4,5 см і x ≈ 5,36 см (мал. 439); x ≈ 13,37 см і y ≈ 16, 09 см (мал. 440). 976. a ≈ 51° і b ≈ 38° (мал. 441); a ≈ 53° і b ≈ 36° (мал. 442). 977. 1) ≈ 4,1 см; 2) ≈ 10,67 см; 3) ≈ 4,69 см. 978. 1) ≈ 11,52 см і ≈ 14,62 см; 2) ≈ 13,76 см і ≈ 17,01 см. 979. 1) ≈ 5,92 см; 2) ≈ 12,64 см. 980. 1) ≈ 48°36′; 2) ≈ 53°6′; 3) ≈ 63°24′ . 981. 1) ≈ 45°34′; 2) ≈ 44°26′ . 982. ≈ 78°28′ , ≈ 11°32′ . 983. 1) ≈ 36°54′; 2) ≈ 41°59′ . 984. ≈ 26°36′ . 985. 1) ≈ 73°44′; 2) ≈ 83°58′ . 986. 90° . 987. 1) а) c = 29, a ≈ 43°36′ , b ≈ 46°24′; б) c = 15, a ≈ 36°52′ , b ≈ 53°8′; в) c = 30, a ≈ 36°56′ , b ≈ 53°4′; г) c ≈ 46,56; a ≈ 30°19′; b ≈ 59°41′; 2) а) b = 8, a ≈ 61°56′ , b ≈ 28°4′; б) b = 12, a ≈ 53°8′ , b ≈ 36°52′; в) b = 33, a ≈ 59°29′ , b ≈ 30°31′; г) a ≈ 0,68; a ≈ 13°25′; b ≈ 76°35′ . 988. 1) а) a ≈ 7,52; b ≈ 2,74; ∠B = 20°; б) a ≈ 54,87; b ≈ 60,94; ∠B = 48°; в) a ≈ 9,64; b ≈ 15,43; ∠B = 58°; г) a ≈ 4,23; b ≈ 1,97; ∠B = 25°; 2) а) b ≈ 7,5, c ≈ 14,15, ∠B = 58°; б) b ≈ 5,5, c ≈ 18,82, ∠B = 73°; в) b ≈ 15,92, c ≈ 19,4, ∠B = 37°; г) b ≈ 1,71, c ≈ 3,92, ∠B = 71° . 989. ≈ 14,69 см і ≈ 20,22 см. 990. 1) ≈ 6,21 см; 2) ≈ 11,59 см. 991. 1) ≈ 6,71 см; 2) ≈ 8,19 см. 992. 1) ≈ 23,04 см; 2) ≈ 65°44′ . 993. 1) ≈ 41,22 см; 2) ≈ 46,26 см; 3) ≈ 36,72 см і ≈ 9,53 см. 994. 1) ≈ 17,15 см і ≈ 36,88 см; 2) ≈ 8,31 см і ≈ 33,69 см. 995. 2,81 см. 996. ≈ 2,94 см і ≈ 4,70 см. 997. ≈ 31,25 см і ≈ 125,16 см. 998. ≈ 119,14 см. 999. ≈ 7,43 см. 1000. ≈ 3,4 см. 1001. ≈ 73,1 см. 1002. ≈ 61° . 1003. ≈ 0°57′ . 1004. 1) ≈ 0,118 км; 2) ≈ 0,438 км. 1005. ≈ 2239,2 м. 1006. ≈ 79,5 м. 1007. ≈ 130,8 м. 1008. ≈ 71,76 м. 1009. ≈ 1°26′ . 1010. ≈ 1°17′ . 1011. ≈ 403 м. 1012. ≈ 2149 м. 1013. ≈ 129,1 м.

5. МНОГОКУТНИКИ. ПЛОЩІ МНОГОКУТНИКІВ § 18. Многокутник та його властивості

1015. Ні. 1016. 1) Ні; 2) так. 1017. 1) Ні; 2) так. 1018. 1) Ні; 2) ні; 3) так. 1020. 1) Ні; 2) так. 1021. 1) Ні; 2) так. 1022. 1) 14 см; 2) 20 см; 3) 18 см. 1024. 1) 5; 2) 5. 1025. 1) 540°; 2) 1260° . 1026. 2700° . 1027. 1) 10; 2) 8. 1028. 11. 1029. 1) 4; 2) 10. 1030. 15. 1031. 1) 30°, 60°, 120°, 150°, 180°; 2) 80° , 100°, 110°, 110°, 140°; 3) 100°, 110°, 120°, 90°, 120°; 4) 20°, 100°, 140°, 180° , 100° . 1032. 1) 90°; 2) 24° . 1033. 36° . 1034. Восьмикутник. 1035. Семикутник. 1036. Семикутник. 1039. 8,4 см. 1040. Вказівка: скористайтеся

трикутника. 1041. () 3 . 2 nn 1042. 1) 35; 2) 119. 1043. 1) Ні; 2) ні. 1044. Ні. 1045. 1) 5; 2) 6. 1046. 5. 1047. 1) 6 : 5 : 4 : 2 : 1; 2) 8 : 7 : 5 : 4 : 3. 1048. Вказівка: сума

180° . 1049. 1) 6; 2) 9. 1050. 360 . n ° 1051. 23. 1052. Вказівка:

ням опуклого многокутника. 1053. 1) 3 і 6; 2) 6 і 3; 4 і 4. 1054. 1) Вказівка: проведіть радіуси до вершин многокутника та розгляньте утворені трикутники.

1055. 1) 4; 2) 6; 3) 7. 1056. Вказівка: розгляньте трикутник, сторона якого є стороною даного многокутника, а протилежна вершина лежить у центрі описаного кола. 1058. 62 см, ≈ 4,6 см, 32 см. Вказівка: нехай О — центр кола; доведіть, що DВОD — прямокутний. § 19. Поняття площі. Площа прямокутника

1059. 1) Ні; так. 1060. 1) Ні; 2) ні. 1061. 1) Ні; 2) ні; 3) ні; 4) так. 1062. 1) Ні; 2) ні; 3) ні; 4) так. 1063. 1) Ні; 2) ні; 3) ні; 4) так. 1064. 1) S1 ≈ 6 кв. од. 1065. SKLM ≈ 22,5 кв. од. 1068. 96 см2. 1069. 160 см2. 1070. 1) 4 см; 2) 3 см; 3) 11 см. 1071. 1) 5 см; 2) 7 см. 1072. 4 см2 (мал. 491); 8 см2 (мал. 492). 1073. 2 см2. 1074. 1) Збільшиться у 3 рази; 2) зменшиться в 4 рази; 3) збільшиться на 50 %. 1075. 1) Збільшиться в 9 разів; 2) зменшиться в 16 разів; 3) збільшиться на 125 %. 1076. 1) b = 1,5 см; S = 6 см2; 2) a = 0,5 см; P = 25 см; 3) a = 3,5 см; S = 24,5 см2; 4) b = 0,5 см; P = 17 см. 1077. 1) 20 і 30; 2) 15 і 40; 3) 610 і 1010. 1078. 3 см і 6 см. 1079. 1) 7,5 см2; 2) 5 см2; 3) 22,5 см2. 1080. 18 см2. 1081. 1) 2 см2; 2) 4,5 см2; 3) 25 2 см2. 1082. 18 см2. 1083. 1) 24 см, 26 см; 2) 24 см, 40 см. Квадрат. 1084. 40 см, 50 см. Квадрат. 1085. 1) 192 см2; 2) () 248705 + см2. 1086. 1) 162 см2; 2) 72 см2. 1087. 2 7 . 9 a 1088. 2 5 . 9 a 1089. 1) 81 см2, 25 см2; 2) 19 см2, 16 см2. 1090. 1) 56 см, 40 см; 2) 200 см, 176 см. 1091.) ; mS n . nS m 1092. () ; 2 nP mn + () . 2 nP mn + 1093. 1) Площа прямокутника зі сторонами b + а і

нами а – b і с дорівнює різниці площ

зі сторонами а і

та b і с. 1094. 1) 1 см; 2) 2 см. 1095. Вказівка: скористайтеся означенням рівноскладених фігур. 1096. Вказівка: скористайтеся властивостями площі. 1097. 9 см2, 1 см2, 7 см2, 7 см2. 1098. ≈ 15,21 см і ≈ 35,83 см. 1099. Так. Вказівка: покажіть, що сума площ квадратів зі сторонами відповідно АВ і ВC дорівнює площі квадрата зі стороною АС без подвоєної площі

1100. Вказівка: площа

трикутника дорівнює сумі площ прямокутних трикутників, на які його розбиває

1101. Вказівка: скористайтеся властивостями середніх пропорційних у прямокутному трикутнику. 1104. 600 м2, 0,06 га. 1105. 250 м2. 1106. Так. § 20. Площа паралелограма 1112. Ні (мал. 504); так (мал. 505). 1113. 1) Ні; 2) ні; 3) ні; 4) так. 1114. 1) Ні; 2) ні; 3) ні; 4) так. 1115. 45 кв. од. 1116. 42 кв. од. 1117. 1) 3000 см2; 2) 1000 см2. 1118. 2500 см2. 1119. 1) 80 см2; 2) 300 см2. 1120. 30 см2. 1121. 1) 4 см; 2) 5 см; 3) 3 см; 4) 8 см. 1122. 12 см. 1123. 1) h a = 8,2 см; hb = 4,1 см; 2) h a = 4 см; hb = 2 см; 3) h a = 4,5 см; hb = 3 см; 4) h a = 4 см; hb = 6,4 см. 1124. 1) 8 см; 2) 5 см. 1125. 4 см. 1126. 1) 4 см; 2) 12 мм. 1127. 15 см. 1128. Вказівка:

даного паралелограма. 1129. Так. 1130. 24 кв. од. 1131. 96 кв. од. 1132. 1) 96 см2; 2) 2,4 дм2. 1133. 840 мм2. 1134.

що

перетину діляться навпіл. 1135. 1) 100 см2; 2) 120 см2. 1136. 72 см2. 1137. 1) 8 см2; 2) 0,45 см2. 1138. 0,72 м2. 1139. 1) 753 мм2; 2) 2503 мм2. 1140. 1) 75 см2; 2) 250 см2. 1141. 1) 8 см, 3 см; 2) 1,5 дм, 6 дм. 1142. 1) 30 см; 2) 30 см. 1143. 1) 128 см2; 2) 140 см2. 1144. Вказівка: якщо від трикутників, що мають рівні площі, відрізати трикутники з рівними площами, то дістанемо фігури з рівними площами. 1145. 1) 0,5 дм2; 2) 3,38 см2. 1146. 1) 36 см; 46 см; 2) 43 см; 63 см; 3) 62 см; 62 см. 1147. 30° . 1148. 4 см. 1149. У 2 рази. 1150. 48 см2. 1151. Вказівка: спочатку покажіть, що діагональ ромба розбиває його на два рівносторонні трикутники, а потім виразіть площу ромба і площу трикутника, утвореного висотами, через сторону й висоту ромба. 1153. Вказівка: трикутники

сотами, проведеними з вершини М, на прямокутні трикутники та покажіть, що сума їхніх площ дорівнює

паралелограма. 1154. Діагональ дорівнює стороні, до якої ця діагональ перпендикулярна. 1155. 1) 24 см2; 2) 156 см2. 1156. Дві прямі, які паралельні даній стороні паралелограма й

далені від неї на відстань . S h 1158. 23 750 м2. § 21. Площа трикутника 1162. 1) Ні; 2) так; 3) ні; 4) ні; 5) ні; 6) ні. 1163. 10 кв. од. (мал. 523); 210 кв. од. (мал. 524). 1164. 42,5 кв. од. 1165. 1) 15 см2; 2) 1250 см2. 1166. 5 дм2. 1167. 1) 40 см2; 2) 108 мм2. 1168. 1,5 дм2. 1169. 1) 12 см; 2) 31 см; 3) 20 см. 1170. 12 см. 1171. 1) 168 13 a h = см, 12 hb = см, 168 15 c h = см; 2) 252 13 a h = см, hb = 12,6 см, h c = 12 см; 3) h а = 12 см, 42 15 hb = см, h c = 2,1 см; 4) h а = 8 см, hb = 7,2 см, 72 17 c h = см. 1172. 1) Не зміниться; 2) збільшиться у 2 рази. 1173. Збільшиться у 2 рази. 1174. 1) 163 см2; 2) 0,363 дм2; 3) 3 м2; 4) 33 см2; 5) 33 2 дм2. 1175. 1) 253 см2; 2) 33 4 дм2. 1176. 1) 240 см2; 2) 120 см2. 1177. 60 см2. 1178. Вказівка: порівняйте основи та висоти трикутників. 1179. Вказівка: порівняйте основи та висоти трикутників. 1180. Навпіл. 1181. 0,25. 1182. 1) 210 см2; 2) 420 см2. 1183. 84 см2. 1184. Вказівка: проведіть у трикутнику відрізки, що з’єднують центр

трикутника. Площу трикутника

трьох утворених трикутників. 1185. 1) р = 42 см, S = 210 см2; 2) р = 27 см, S = 126 см2; 3) р = 21 см, S = 42 см2; 4) р = 45 см, S = 240 см2. 1186. 1 см. 1187. 432 см2; 756 см2. 1188. 3 см2; 144 3 см2. 1189. 1) 108 см2; 2) 136 см2. 1190. 260 см2. 1191. 1) 39 см2; 2) 60 см2. 1192. Вказівка: скористайтеся

1193. 1) 150 см2; 2) 3,36 см2; 3) 135 см2; 4) 720 см2. 1194. 1) 270 см2; 2) 120 см2. 1195. 1) 18 см, 80 см; 2) 48 см, 55 см. 1196. 1) 39 см2; 2) 34 см2. 1197. 1) 83 см2;

2) 183 см2. 1198. 1) 24 см2; 2) 120 см2. 1199. h c < hb < h а . 1200. Вказівка: скористайтеся тим, що медіани трикутника точкою

2 : 1, рахуючи від вершини. 1201. Вказівка: виміряйте відповідні

трикутників. 1202. 1) 16 3 см; 2) 16 3 см; 3) 8 3 см. 1203. Вказівка: скористайтеся формулою площі прямокутного трикутника й

із катетів

формулами 1 і 2 таблиці 33 (с. 175). 1205. Вказівка: спочатку з’єднайте дану точку з вершинами трикутника, потім знайдіть площу трикутника як

жаних трьох трикутників. 1206. Вказівка: скористайтеся означенням рівноскладених фігур. 1208. Вказівка: скористайтеся двома формулами площі трикутника. 1209. 7S, де S — площа даного трикутника. 1210. () () 1:21:32. 1211. 4. m mn + 1214. Вказівка: трикутники АВС і АСМ мають рівні площі, тому

площа трикутника АВС дорівнює половині добутку

ширину лінійки. 1217. 0,927 кг. § 22. Площа

1219. 1) Ні; 2) так; 3) так; 4) ні; 5) ні; 6) так. 1220. 300 кв. од. (мал. 549); 150 кв. од. (мал. 550). 1221. 44 кв. од. 1222. 1) 2400 см2; 2) 4000 см2. 1223. 1400 см2. 1224. 1) 90 см2; 2) 1,75 дм2. 1225. 33 см2. 1226. 1) 10 см; 2) 12 см. 1227. 12 см. 1228. 1) 4 см; 2) 5 см. 1229. 3 см. 1230. 1) q = 12 см, S = 84 см2; 2) b = 27 см, h = 5 см; 3) a = 20 см, q = 21 см; 4) a = 23 см, h = 11 см. 1231. 1) Не зміниться; 2) збільшиться у 2 рази. 1232. Не зміниться. 1233. 1) 20 см, 16 см; 2) 36 см, 24 см. 1234. 20 см, 10 см. 1235. 2 . a



1236. 1) 144 см2; 2) 44 см2. 1237. 276 см2. 1238. 1) 645 см2; 2) 180 см2. 1239. ()1833 + см2. 1240. 1) 10,5 см2; 2) 8 см2. 1241. 1) 6 см2; 2) 13,5 см2. 1242. 45° . 1243. 1) 5,6 см2; 2) 96 см2. 1244. Розгляньте два випадки: 8 см і 12 см або 2 см і 6 см. 1245. 12 см. 1246. Вказівка: якщо трапеція є описаною навколо кола, то сума її основ дорівнює сумі бічних сторін. 1247. 2 . S P 1248. 10 см. 1249. ≈ 130,03 см2. 1250. 963 см2. 1251. Вказівка: скористайтеся властивістю середньої лінії трапеції. 1252. Від 16 см до 32 см. 1253. 2 . ab ab + 1254. Вказівка: доведіть, що площі трикутників ВОС і COD та площі трикутників АОВ і

Висота трапеції 73

Відрізок четвертий пропорційний 119

Властивість бісектриси трикутника 150

—

діагоналей паралелограма 24

кутів вписаного чотирикутника 97

— рівнобічної трапеції 74

— сторін описаного

чотирикутника 98

— діагоналей прямокутника 41

Властивості діагоналей ромба 50

—

медіан трикутника 149

— середніх пропорційних

у прямокутному трикутнику 151

—

середньої лінії трапеції 75

— трикутника 64

—

площі 212

похилих 162

Дельтоїд 53

Діагональ nкутника 204

— чотирикутника 12

Дуга кола 85

Квадрат 52

Косинус гострого кута

прямокутного трикутника 172

Кут вписаний 86

— зовнішній многокутника 205

— чотирикутника 12

— центральний 85

— що спирається на дугу кола 87

Метод подібності 264

Многокутник 203

— вписаний у коло 205

— неопуклий 204

— описаний навколо кола 206

— опуклий 204

— плоский 212

Многокутника вершини 203

— діагоналі 204

— кути 203

— периметр 204

— сторони 203

кутник 203

Ознака вписаного чотирикутника 97

— описаного чотирикутника 99

— паралелограма 31

— подібності трикутників

за двома кутами 128

— сторонами й кутом

між ними 138

— трьома сторонами 139

— прямокутника 41

— ромба 51

Паралелограм 23

Паралелограма висота 23

Проєкції катетів

гіпотенузу 150 Прямокутник 40 Подібності коефіцієнт 110

Похила 162

Похилої основа 162 — проєкція 162

Предметний

Площа 212

Розв’язати прямокутний

трикутник 192

Ромб 50

Середня лінія трапеції 74

— трикутника 63

Середнє пропорційне

двох відрізків 151

Синус гострого кута прямокутного

трикутника 172

Співвідношення між сторонами

та кутами прямокутного

трикутника 176

Сторін відношення 108

Сторони пропорційні 108

Тангенс гострого кута

прямокутного трикутника 172

Теорема Піфагора 160

— про вписаний кут 87

— про відношення площ подібних трикутників 215

—

властивість бісектриси трикутника 150

— властивості медіан трикутника 149

—

площу паралелограма 222

— прямокутника 214

— ромба за його діагоналями 224

— трапеції 240

— трикутника 231

— пропорційні відрізки 119

— суму кутів nкутника 204

— чотирикутника 15

— Фалеса 62

— узагальнена 119

Трапеції бічні сторони 73

Трапеція 73

— рівнобічна 74

— прямокутна 74

Трикутники подібні 109

Умова достатня 34

— необхідна 34

Фігура проста 206

— що не є простою 206

Фігури рівновеликі 212

— рівноскладені 212

Формула площі квадрата 214

– – паралелограма 222

–

– прямокутника 214

— трапеції 240

— трикутника 231

Чотирикутник 11

— вписаний у коло 96

— неопуклий 13

— описаний навколо кола 96

— опуклий 13

Чотирикутника вершини 11

— сусідні 12

— протилежні 12

— елементи 12

— кути 11

— зовнішні 13

— сусідні 12

— протилежні 12

— периметр 14

— сторони 11

— сусідні 12

— протилежні 12

Головна редакторка І. В. Красуцька Редакторка І. В. Луценко

художниця І. П. Медведовська Художня редакторка К. В. Берсенєва Технічний редактор Е. А. Авраменко Коректорка Ю. О. Твердохліб Комп’ютерна графіка О. І. Дядика Презентації та інтерактивні вправи Л. М. Шабанової В оформленні підручника використано фото з вільних джерел мережі «Інтернет», фотобанку Shatterstock

Бренди та ресурси зображуються лише