Н. С. ПРОКОПЕНКО Ю. О. ЗАХАРIЙЧЕНКО Н. Л. КIНАЩУК
АЛГЕБРА

УДК [512:37.016](075.3)
П80
відбору проектів підручників для 9 класу загальноосвітніх
і зробили висновок про доцільність надання підручнику грифа «Рекомендовано Міністерством освіти і науки України»:
М.М.Пшечук, вчитель математики вищої кваліфікаційної категорії Волицької загальноосвітньої школи I–III ступенів Красилівського району Хмельницької області, старший вчитель; Г.Я.Антонів, методист комунальної установи «Зборівський районний методичний кабінет» Зборівської районної ради Тернопільської області; О.М.Задоріна, в. о. доцента кафедри природничо-математичних дисциплін та інформаційних технологій Одеського обласного інституту удосконалення вчителів, канд. пед. наук
Рецензент и:
Б.В.Олійник, завідувач кафедри математики факультету інформатики Національного університету «Києво-Могилянська Академія», доцент, доктор фіз.-мат. наук;
Р.І.Петришин, перший проректор Чернівецького національного університету імені Юрія Федьковича, професор, доктор фіз.-мат. наук; С.В.Мартинюк, доцент кафедри алгебри та інформатики факультету математики та інформатики Чернівецького національного університету імені Юрія Федьковича, канд. фіз.-мат. наук; О.А.Олексюк, методист Науково-методичного центру природничо-математичної освіти та технологій Інституту післядипломної педагогічної освіти Київського університету імені Бориса Грінченка; Л.В.Пекарська, методист кабінету фізико-математичних предметів, старший викладач кафедри
інституту післядипломної педагогічної освіти; І.П.Сігетій, учитель математики Ужгородської
У.В.Остапчук, учитель математики, Заслужений учитель України Автори висловлюють щиру
за надані можливості, пов’язані з використанням фотографій Автор концепції підручника Н. С. Прокопенко
Прокопенко Н. С. П80 Алгебра : підруч. для 9 кл. загальноосвіт. навч. закл. / Н. С. Прокопенко, Ю. О. Захарійченко, Н. Л. Кінащук. — Харків : Вид-во «Ранок», 2017. — 288 с.
ISBN 978-617-09-3352-2
Інтернет-підтримка
Електронні матеріали до підручника розміщено на сайті interactive.ranok.com.ua
УДК [512:37.016](075.3) © Прокопенко Н. С., Захарійченко Ю. О., Кінащук Н. Л., 2017
ISBN 978-617-09-3352-2 © ТОВ Видавництво «Ранок», 2017
Контрольна робота № 1, с. 14
Контрольна робота № 2, с. 55
Контрольна робота № 3, с. 96
ЗАДАЧІ « MATH FOR LIFE »
Подорож Закарпаттям, с. 22
Напис на етикетці, с. 33
Будівництво автозаправок, с. 44
Раціональне харчування, с. 52
Рентабельність перевезення вантажу, с. 66
Рятувальна станція на воді, с. 76
Феєрверк, с. 89
ПЕРЕРВА
Див. с. 20, 27, 31, 41, 49, 58, 74, 87
Графіки лінійних функцій та системи лінійних нерівностей в онлайн-сервісі Desmos, с. 92
ІНТЕРНЕТ-ПОСИЛАННЯ
Див. с. 16, 24, 42, 44, 45, 52, 63, 66, 76, 90, 92 ШЛЯХОМ
Теми навчальних проектів до розділу 1, с. 15
TO BE SMART
Див. с. 21, 34, 39, 53, 64, 77, 91
§ 8. Функція. Область
Водинклік
Домашнєзавдання
§ 9. Властивості функції.
знакосталості .................................
Самостійнаробота№5 .......................
Домашнєзавдання ............................
§10. Властивості функції. Зростання та спадання функції,
найбільше і найменше значення функції
Самостійнаробота№6
Домашнєзавдання
§ 11. Перетворення графіків функцій fxfxa () →
fxfxa
Самостійнаробота№7
Домашнєзавдання
Підсумовуємо вивчене в §
Контрольна робота
§ 12. Квадратична функція, її
Самостійнаробота№8
Домашнєзавдання
§ 13. Квадратні нерівності ...........................
Самостійнаробота№9
Домашнєзавдання
Підсумовуємо вивчене в
Контрольна
§ 14. Системи двох рівнянь із
Контрольна робота № 4, с. 146 Контрольна робота № 5, с 178 Контрольна робота № 6, с. 210
ЗАДАЧІ « MATH FOR LIFE »
Вантажоперевезення, с. 106 Політ на гелікоптері, с. 114 Гоночний автомобіль, с. 127
Зйомка дикої природи з квадрокоптера, с. 141
Історичний фільм, с. 160 Моделі прогнозування, с. 174 Туристські маршрути, с. 191 Вступні іспити, с. 202
ПЕРЕРВА НА ЛОГІКУ
Див. с. 102, 113, 155, 205
В ОДИН КЛІК
Графіки функцій у сервісі Google, с. 105
Графіки функцій, системи рівнянь і нерівностей в онлайнсервісі Desmos, с. 206
ІНТЕРНЕТ-ПОСИЛАННЯ Див. с. 100, 109, 111, 112, 114, 142, 161, 175, 193, 196, 198, 204, 205, 206
ШЛЯХОМ ДОСЛІДЖЕНЬ Теми навчальних проектів до розділу 2, с. 97
TO BE SMART
Див. с. 107, 116, 129, 142, 161, 175, 192, 205
§ 16.
Числові
Домашнєзавдання ............................
§ 17. Арифметична прогресія, її властивості.
Формула n-го члена
Самостійнаробота№12
Домашнєзавдання
§ 18. Сума перших n
Самостійнаробота№13
Домашнєзавдання
§ 19. Геометрична прогресія, її властивості.
Самостійнаробота№14
§ 20.
Контрольна робота № 7, с. 276
Контрольна робота (підсумкова), с. 280
ЗАДАЧІ « MATH FOR LIFE »
Трейлер до нового фільму, с. 221 Дзвінки у роумінгу, с. 235
Податок на прибуток, с. 244
Населення міста, с. 259
Стрибки з парашутом, с. 269
ПЕРЕРВА НА ЛОГІКУ
Див. с. 218, 220, 234, 243, 256, 268
В ОДИН КЛІК
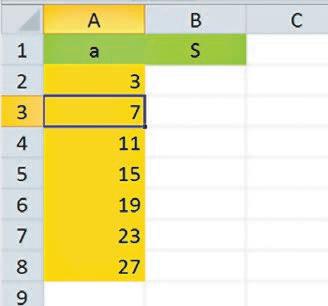
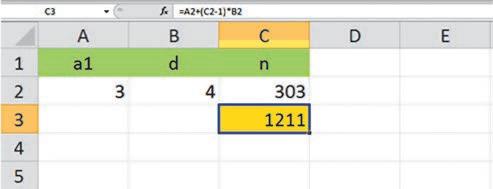
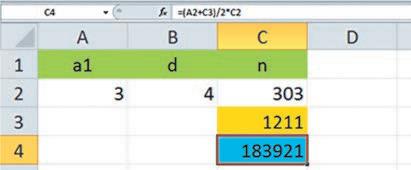
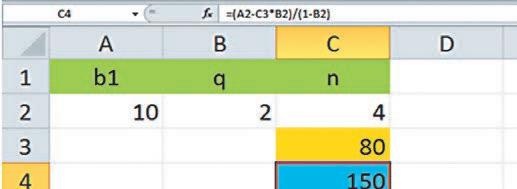
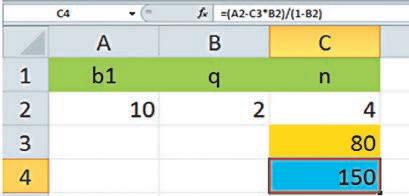
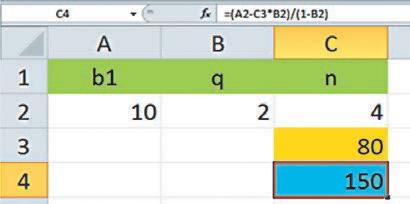
Розв’язування задач на арифметичні та геометричні прогресії за допомогою програми MS Excel, с. 272
ІНТЕРНЕТ-ПОСИЛАННЯ
Див. с. 227, 238, 253, 256, 257, 280
ШЛЯХОМ
Теми навчальних проектів до розділу 3, с. 211
TO BE SMART
Див. с. 221, 231, 232, 245, 247, 260, 268
комбудепідручник,якийвитримаєтевруках.Зорієнтуватисявйогозмістівамдо-



Вчора, сьогодні, завжди: щовизнаєте,чогонавчитеся, якзможетезастосувати


Цитати:висловлюваннявидатнихлюдей
Слід знати:основніформули, пояснення,зауваження,які потрібновраховуватипідчас виконаннявправ
Ключові терміни параграфа





















Розминка:уснітаписьмовівправи назакріпленняновогоматеріалу
Поміркуйте:запитанняізавданнядля більшглибокогоосмисленняматеріалу
Перерва на логіку:задачінарозвиток логічногомислення



Запам’ятайте:основніозначення, правила,твердження,теореми
Ключовий момент: коментарі, наякіслідзвернутиувагу


Алгоритмивиконанняматематичних дій







Тренуємося:вправи,щомістять8завдань, диференційованихзарівнемнавчальних досягнень:завдання1і2—початковий рівень;3і4—середній;5і6—достатній; 7і8—високий
Прикладизпокроковимрозв’язанням, докладнимпоясненнямізаписом розв’язання
Областю допустимих значень виразу з однією змінною називають усі значення змінної, при яких цей вираз має зміст.
y m n ma na ma na == , a ≠ 0 , n ≠ 0
y m n mab nab mab nab == , a ≠ 0 , bn ≠ 0 , n ≠ 0
y a c b c ab c ±= ± , c ≠ 0
y A C B D AD BC CD ±= ± , C ≠ 0 , D ≠ 0
y A B C D AC BD ⋅= ⋅ ,, B ≠ 0 , D ≠ 0
y A B C D AD BC : = , B ≠ 0 , D ≠ 0 , C ≠ 0
7 Розв’яжіть рівняння: 1) 2 1 0 x x + = ; 3) x x + = 1 3 0 ; 5) 6 4 0 x = ; 7) x x 2 1 1 0 + = ; 2) 3 1 0 x x = ; 4) x x + = 4 2 0 ;
8 Обчисліть значення виразу: 1) 8 1 ; 3) 2 3 ; 5) 40 5 1 ; 7) 24 20 10 ; 2) 7 1 ; 4) 3 2 ; 6) 54 6 1 ⋅ ; 8) 93 12 24 ⋅ .
9 Запишіть у стандартному вигляді число: 1) 14; 3) 300; 5) 34 000; 7) 34,8; 2) 56; 4) 600; 6) 910 000; 8) 652,1.
10 Задано функцію y x = 1 . Знайдіть: 1) y 1 () ; 3) y () 2 ; 5) y 4 () ; 7) y
2) y 2 () ; 4) y () 3 ; 6) y () 4 ; 8)
2 : 1) O 00 ; () ; 3) B 24 ; () ; 5) D () 5;52 ; 7) P
2) A 11 ; () ; 4) C 39 ; () ; 6) E () 10100 ; ; 8) Q 2 7 49 4 ;
.
12
Обчисліть:
1) 0 ; 3) 25 ; 5) 54 ; 7) 30 36 ; 2) 1 ; 4) 9 ; 6) 616 ; 8) 81 90 .
13 Укажіть вираз, значення якого є ірраціональним числом:
1) 3 2 () ; 3) 2 ; 5) 516 ; 7) 10 3103() + () ; 2) 11 2 () ; 4) 56 ; 6) 49 3 + ; 8) 19 4194() + () .
14 Порівняйте числа:
1) 3 і 5 ; 4) 5 і 25 ; 7) 7,18 ... і 18 , () ; 2) 11 і 10 ; 5) 57 і 8; 8) 1853 , ... і 18 5, () .
3) 16 і 4; 6) 51 і 7;
x = 1 yx = 2 y x 0 y x 0
y aa 2 =
y abab = , ab 0
y abab = , a 0 , b 0
y a b a b = , a b 0
y a b a b = , a 0 , b > 0 yx = y x 0
функції yx
: 1) O 00 ; () ; 3) B () 11 ; ; 5) D 16 4; () ; 7) P 0010 1 ,; , () ; 2) A 11 ; () ; 4) C 5;52 () ; 6) E 36 6; () ; 8) Q
коефіцієнт b та
член c квадратного рівняння вигляду axbxc 2 0 ++ = : 1) 27 10 2 xx+− = ; 5) −+ −= xx 2 12 0 ; 2) += 34 20 2 xx ; 6) xx 2 11 0 ++ = ; 3) xx 2 60+= ; 7) 05 23 61 0 2 ,, , xx+− = ; 4) x 2 20−= ; 8) −+ += 46 19 04 0 2 ,, , xx .
y xm 2 = , xm =± , m 0
y ab = 0 , якщо a = 0 або b = 0
Для axbxc 2 0 ++ = , a ≠ 0 : x bD a
23
26 До штучного ставка рівномірно надходить вода зі швидкістю 10 л/с. Три помпи відкачують воду зі ставка. Продуктивність кожної помпи дорівнює x л/с. Відомо, що за 5 хв об’єм води в ставку збільшується на 300 л.
1) Скільки літрів води відкачують три помпи за 1 с?
2) На скільки літрів збільшується об’єм води в ставку щосекунди?
3) Запишіть рівняння для визначення x.
4) Знайдіть x.
5) Скільки помп із такою самою продуктивністю
монтуючи x вікон щодня. Завдання було виконано на три

Лінійні нерівності та їх системи мають важливе практичне значення. За їх допомогою можна моделювати певні процеси, визначати оптимальні умови виробництва, транспортування, розміщення ресурсів, тобто розв’язувати задачі лінійного програмування. Опанувавши цей розділ, ви зможете:
y будувати математичні моделі реальних ситуацій у вигляді нерівностей та їх систем;
y
y розв’язувати геометричні задачі, досліджувати функції за допомогою нерівностей; y правильно читати географічні карти, маркування на етикетках товарів; оцінювати переваги користування тими чи іншими послугами; вибирати оптимальні маршрути; y розв’язувати тригонометричні, показникові, ірраціональні нерівності та їх системи, з якими ви ознайомитеся в наступних класах.

ВЧОРА





Випорівнювалинатуральні,раціональні,дійснічислатазастосовувалицізнання дляпорівняннягеометричнихтафізичнихвеличин





Видізнаєтесяпроновийспосібпорівняннячиселтазробитепершікроки вдоведеннінерівностей





Визможетезаписуватиматематичноюмовою«більше—менше»,«тепліше— холодніше»,«дорожче—дешевше»,«швидше—повільніше»тощо







Щорокувмежахсоціального проекту«Кличдрузів—граймо разом!»ФондКличкопроводитьконкурснавстановлення сучасногоспортивногомайданчика.Коженученьможе позмагатисязасвоюшколу, заповнившианкетунасайті: my.klitschkofoundation.org

СЛІДЗНАТИ!
КЛЮЧОВІТЕРМІНИ числованерівність знаки«>»,«<»,« »,« » методрізниці
строгіінестрогінерівності правильніінеправильні нерівності
кошти можна побудувати 16 майданчиків. Запис 12000 200 000 ⋅< n відрізняється від відомого вам запису 12000 200 000 ⋅= n 12000 200 000
ІДЕЯ y Два вирази, які з’єднані між собою знаками «>», «<», « », « », називають нерівностями. y Нерівності, у яких обидві частини є числовими виразами, називають числовими
(істинними),
ab є від’ємним числом.
КЛЮЧОВИЙМОМЕНТ
Якщо ab > , то ab−> 0 , і навпаки, якщо ab−> 0 , то ab > .
Якщо ab < , то ab−< 0 , і навпаки, якщо ab−< 0 , то ab < . Якщо ab = , то ab−= 0 , і навпаки, якщо ab−= 0 , то ab = .
Для порівняння двох чисел a і b досить утворити різницю ab і з’ясувати, яким числом вона є: додатним, від’ємним чи нулем.
Такий метод порівняння називають методом різниці. Алгоритм порівняння чисел a і b методом різниці
1. Утворити різницю ab .
2. Визначити


y Знакивідношеньпершимипочаливикористовуватианглійськіматематики: знаки«>»і«<»—Томас Гарріот(1560–1621); знак«=»—РобертРекорд (бл.1510–1587).



y Окрімзнаківнерівностей,вам відомийзнак« ≠ »(недорівнює).Запис ab ≠ означає, що ab < або ab > .
єтьсялишеоднезіспіввідношень:або ab > , або ab < , або ab = .



нерівностей тощо. Одним із найпоширеніших є
ПРИКЛАД1
різниці.
Доведіть нерівність mmm() >− ()24 2 , де m — будь-яке дійсне число.
Доведення
Скористаємося методом різниці.
ТРЕНУЄМОСЯ
1 З’ясуйте, правильною чи

Удрукованійлітературісимволизнаківнерівностейз’явилися


знакарівності,оскількиякзнак нерівностівикористовувалилітеруVлатинськогоалфавіту, повертаючиїївпотрібнийбік.

>− ()24 2
будь-якого дійсного числа m
якщо a — довільне дійсне число: 1) 31 0 −> ; 2) 59 0 −< ; 3) 82 −>aa ; 4) 10 27 2 +< + aa .
Доведіть нерівність, якщо a — довільне
число: 5) 38 24 aaa + () >+() + ; 7) aaa + () >+() 36 2 ; 6) () <− () 59 23 1 aaa ; 8) aaa() >− ()48 2 .

ПЕРЕРВАНАЛОГІКУ
1.Чизможетевиза5секунд визначити,якийдріббільший: 4 9

8 17 ?

2.Узаданомувиразірозставте дужкитак,щоботриматичисло неменшевід50: 22 33 44 55 :: :: .


ПРИГАДАЙТЕ! ab + 2 —середнєарифметичнедвохчисел
b.
Нерівність abab + 2 для a 0 , b 0 має спеціальну назву —
нерівність Коші для двох чисел (на честь відомого французького математика Огюстена Луї Коші).
Нерівність Коші. Середнєарифметичнедвохневід’ємних
чиселнеменше,ніжїхсереднєгеометричне.
ТРЕНУЄМОСЯ
3 Доведіть нерівність, якщо число
m і k, якщо:
1) mk−= 23 , ; 4) km−= 10 3 3 7 ; 2) km−= 0 ; 5) mk22 2 5 −= і mk+= 7 ; 3) mk−= 25 ; 6) mk () = 2 19 .
число: 1) mm()44 ; 3) mmmm() + () >+() 35 217 ; 2) mm + () + 8160 ; 4) 22 1102 mmm + () +− ; 5) 4 421 33 540 2 () + () <−() + () + mmmmmm ; 6) 33 59 13 mmm () +> .









Виділенняквадратадвочлена: xxx 2 2 23 12 ++ =+() +

1) 7 105 d > , якщо d > 15 ; 4) −+ () 121539 y , якщо y 2 ; 2) −<525 m , якщо m >−5 ;




Радимо прочитати книжкуШонаКові«7звичоквисокоефективнихпідлітків». Цевідомийбестселер,перекладенийбільшніж20мовами. Авторвизначає7звичокякбазовіпринципи,щоправлятьсвітом,іговорить:«Житимешзгіднозними—будешнависоті». IQ









ОгюстенЛуїКоші(фр. Augustin Louis Cauchy ;1789–1857)— визначнийфранцузькийматематикімеханік,повнезібрання творівякогоналічуєаж27томів. Цікаво,щоавторськедоведеннянерівностіКошізаймалокількасторінок.
ЗіменемКошіуматематиці пов’язананизкапонять:задача Коші,інтегралКоші,послідовністьКоші,теоремаКошітощо.



ЧИВІДОМОВАМ?




y Закарпатськаобласть—одна знайменшихзаплощеюсередобластейУкраїни.Проте наїїтериторіїпроживають представникипонад70національностей.



y ОзероСиневир,якомублизько10тис.років,називають «МорськимОком»Карпат. Вонорозташованенависоті 989мнадрівнемморя,його площа4–5га,максимальна глибина—24м.

1)
2)
обґрунтуйте.
1) Якщо m +=1514 , то m < 0.
2) Нерівність b ()80 2 правильна лише для числа b = 8 .
3) Нерівність < c 2 30 правильна для будь-якого дійсного числа c.
4) Якщо V — об’єм дощової води (у м3), що збирається на
будівлі, то V 0 у будь-яку пору року.
5) Нерівність xx() +− > 55 0 2 правильна для будь-якого дій-
MATH FOR LIFE
1 З’ясуйте, правильною чи неправильною є нерівність:
1) 9130 −> ; 2) 14 3153−<aa (a — довільне дійсне число).
Доведіть нерівність, якщо x — довільне дійсне число:
3) 43 31 xxx() <+() + ; 4) xxx() >− ()36 2 . 2 Доведіть нерівність, якщо x — довільне дійсне число: 1) xx 2 44 + ; 2) 9124 2 xx .
3) Доведіть, що квадрат різниці двох довільних дійсних чисел не менший від їх добутку, помноженого на –4.
4) Доведіть нерівність xyxy 44 22 2 + , якщо x і y
числа.
нерівність, якщо a і b —
1) aa + 96 ; 3) abab + 4 4 ;
2) a a + 5 2 5 ; 4) 64 2 8 + abab . 4 Два юнаки


ний у природничих науках, полягає в спостереженні фактів і в підпорядкуванні спостережень обчисленням.

Затеоремоюпросередніпропорційнівідрізкивпрямокутномутрикутнику hab ccc = Отже,висотапрямокутного трикутника,проведенадогіпотенузи,єсереднімгеометричнимпроекційкатетівнагіпотенузу. ЗастосуємонерівністьКоші: hc ab cc + 2 . Але abc ccmc + == 22 .
Отже, hmcc ,тобтовисота, проведенадогіпотенузи,не більшазамедіану,проведену догіпотенузи.






Винавчилисярозв’язуватирівняння,використовуючиїхосновнівластивості





Видізнаєтесяпроосновнівластивостічисловихнерівностейтаособливостіїх застосування





Визможетеоцінюватизначеннярізнихвеличин,такихяквідстань,час,маса, цінатощо









«Експериментаніум»—музейпопулярноїнаукийтехніки вКиєві,якийскорішеєнауково-розважальнимцентром.Тут навасчекаютьцікавінаукові екскурсії,шоу,майстер-класи,квести,ігри.Особливістю цьогонезвичайногомузею єінтерактивніекспонати,які можнавмикати,повертати, крутити,загаломекспериментувати,яксправжнідослідники. Дізнайтесябільше: experimentanium.com.ua


65 грн? Коментардорозв’язання За умовою A 65 . Отже, необхідно
г ), з’ясуйте, чи зміниться знак нерівності, якщо: 1) до обох частин нерівності додати (від обох частин нерівності відняти) одне й те саме число; 2) обидві частини нерівності помножити (поділити) на одне й те саме додатне число; від’ємне число. а) ++ 5633 ? ; в) 5633 ? ; б) 5633 ? ; г) () ()5633 ? .
ше за перше.
Доведення
1) Доведемо перше твердження теореми: якщо ab > , то ba < . Застосуємо метод різниці. Якщо ab > , то різниця ab є додатним числом, тоді різниця baab −= () є від’ємним числом, отже, ba < .
2) Аналогічно доводять друге твердження теореми: якщо ab < , то ba > . Спробуйте довести його самостійно.
ПОМІРКУЙТЕ!
Які слова пропущено?
1) Якщо А дешевше від В, то В __________ А.
2) Якщо А важче за В, то В __________ А.
3) Якщо А вище за В, то В __________ А.
Теорема 2
Якщо перше число менше від другого, а друге менше від третього, то перше число менше від третього.
Доведення
Доведемо, що якщо ab < і bc < , то ac < .
Застосуємо метод різниці: щоб довести, що ac < , досить до-
вести, що ac−< 0 .
Запишемо різницю чисел a і c та перетворимо її: acacabbc bb −= () =−() +−() + .
Оскільки за умовою ab < і bc < , то відповідно ab−< 0 і bc−< 0 , тобто числа ab і bc є від’ємними. Отже, число ac теж від’ємне (як сума від’ємних чисел ab і bc ). Звідси випливає, що ac < . Аналогічно доводять і таку властивість: якщо ab > і bc > , то ac > .
abc <<
ЗАПАМ’ЯТАЙТЕ!
1) Якщо ab > і c — будьяке число, то acbc +>+ .
2) Якщо ab > і c будьяке число, то acbc −> .
Графічна інтерпретація теореми 3
3 > 0 3 > 0
bbx + 3 aa + 3
c > 0 c > 0
bbx + caa + c
–5 < 0
bbx + (–5) –5 < 0 aa + (–5)
c < 0
bbx + c c < 0 aa + c
1) Доведемо, що якщо ab > і c — будь-яке число, то acbc +>+ . Застосуємо метод різниці. Утворимо різницю acbc + () −+() . Маємо: acbcab + () −+() =− . Оскільки за умовою ab > , то різниця ab є додатним числом. Звідси випливає, що acbc +>+ .
2) Дію віднімання можна замінити дією додавання: acac −= +−() . Отже, можна зробити висновок: якщо
число, то acbc −> Аналогічно доводять і таку властивість: якщо ab < і c — будь-яке число, то acbc +< + , acbc −< .
abc
Ураховуючи
Правило 1
Наприклад: 1) x +>713 ; x >− 13 7 ; x > 6 ; 2) x −>713 ; x >+ 13 7 ; x > 20 ; 3) 823 −< x ; 823−< x ; −< 15 x ; x >−15 .
РОЗМИНКА2
1 Додайте до обох частин нерівності: 1) −+ < 1712 x число 17; 2) x + 813 число –8.
2 Відніміть від обох частин нерівності: 1) 15 5 +− x число 15; 2) −+ <− 23 11 x число –23.
3 Перенесіть доданки зі змінною в ліву частину, а числа — у праву частину нерівності: 1) 23 516 +−xx ; 2) −+ 13 41234 xx .
Теорема 4
Якщообидвічастиниправильноїнерівностіпомножитиабо поділитинаоднейтесаме додатнечисло,тоотримаємо правильнунерівність.
Якщообидвічастиниправильноїнерівностіпомножитиабо поділитинаоднейтесаме від’ємнечислоі змінити знак нерівності на протилежний,тоотримаємоправильнунерівність. Доведення Нехай ab > . Помножимо обидві частини нерівності на число с і застосуємо метод різниці.
Запишемо різницю та перетворимо її: acbcacbccab −= () . За умовою ab > , отже, різниця ab є додатним числом.
1) Якщо c > 0, то добуток cab() є додатним числом, тобто різниця acbc є додатним числом, отже, acbc ⋅> .
2) Якщо c < 0 , то добуток cab() є від’ємним числом, тобто різниця acbc ⋅− ⋅ є від’ємним числом, отже, acbc ⋅< ⋅ .



ПЕРЕРВАНАЛОГІКУ УсловіНЕРІВНОСТІзамінітьлітеринацифривід1до8так, щобусізнакивідношеннябуло розставленоправильно: Н>Е<Р>І>В<Н<О<С<Т>І

1)Якщо ab > і c —додатнечисло,то acbc ⋅> . 2)Якщо ab > іc—від’ємне число,то acbc ⋅< .
Графічна інтерпретація теореми 4

ЧИВІДОМОВАМ?

У«Математичнихзборах»ПаппиАлександрійського(IIIст.) описанотакувластивістьнерівностей:
якщо a b c d > (a, b, c, d—
додатнічисла),то adbc > .

Якщо ab > 0 і ab > ,то 11 ab < . a b c


ab
ab
c
acbc ⋅> Знак не змінюється
c < 0 acbc ⋅< Знак змінюється на протилежний
c
ЗНАЙДІТЬПОМИЛКУ < 79 5 x
−> + 75 9 x


−>714 x x <−() 147: x <−2

ЗАПАМ’ЯТАЙТЕ!
Розглянемо такі приклади.
1) Якщо 23 < , то 1 2 1 3 > .
У теоремах, які ми довели, ішлося про строгі нерівності. Аналогічні властивості мають і нестрогі нерівності.
Теореми 3 і 4 справедливі також і для подвійних нерівностей:
• якщо axb << , с — будь-яке число, то acxcbc +<+< + , acxcbc −<−< ;
• якщо axb << і c > 0 , то acxcbc ⋅<⋅< ⋅ , acxcbcc :: :, << ≠ 0 ;
• якщо axb << і c < 0 , то bcxcac ⋅<⋅< , bcxcacc :: :, << ≠ 0 .
Подвійні нерівності мають широке практичне застосування, їх зазвичай використовують для оцінювання значень різних ве-
личин, таких як відстань, час, маса, ціна тощо.
ПРИКЛАД 1
Відомо, що 27 << m . Оцініть значення виразу: 1) 4m ; 2) m ; 3) 5 m ; 4) 12,,06 m .
Розв’язання
1)
КРОК 1
2)
КРОК 1
СЛІД ЗНАТИ!
Вимога «числа a і b однакового
2 1 4 <− неправильною.
Помножимо всі частини заданої нерівності на 4; 40 > , отже, знак нерівності не змінюється.
27 4 << m ; 24 47 4 ⋅<⋅< m ; 84 28 << m
27 1 << () m ; −>
число 5.
4)
КРОК 2 Віднімемо від усіх частин нерівності, отриманої на попередньому кроці, число 0,6.
Відповідь : 1) 84 28 << m ; 2) −< −< 72 m ; 3) −< −< 25 3 m ; 4) 18 12 06 78 ,, ,, <− < m .
27 12 << ⋅ m , ; 21 21 27 12 ⋅<⋅< ,, , m ; 24 12 84 ,, , << m
24 12 84 06 ,, ,, << m ; 18 12 06 78 ,, ,, <− < m
−< −< 72 m
1
5) −< < 915 m ; 7) −< <− 36,,18 m ; 6) −< < 612 m ; 8) −< <− 54,,21 m .
ПРИКЛАД 2
Відомо, що сторона a
зі стороною, втричі більшою за a. Розв’язання
довжину сторони
значення виразу 43 ⋅
м’ячів для спортклубу заплановано виділити суму
Розв’яжіть задачу.
1) Вантажна машина перевозить b тонн вантажу, причому 46,,62 b . Оцініть загальну масу (у т) вантажу, який можуть перевезти 10 таких машин.
2) Є дві декоративні коробки, дно кожної має форму трикутника з рівними сторонами. Довжина l сторони першого трикутника набуває значень 19 9201 ,, << l (у см). Оцініть периметр (у см) другого трикутника зі стороною, удвічі більшою за сторону першого.
3) Маса m однієї шоколадної цукерки набуває значень 19 8202 ,, m (у г). Оцініть масу всіх шоколадних цукерок у 10 коробках (у г), якщо одна коробка містить 30 таких цукерок.
4) Для закупівлі навчальних
від 950 до 1100 грн. Вартість одного
становить 60 грн.
а) Скільки посібників
суму? б) Яку найбільшу
Порівняйте



ЧИВІДОМОВАМ?






Основнимпоказникомякості шоколадуєвідсотковийвміст какао-продуктів—тертогокакаойкакао-масла.Наприклад: y умолочномушоколадімає бутинеменше25%тертого какао;
y утемному—неменше40% тертогокакаотанеменше 20%какао-масла;


y угіркому—неменше55% тертогокакаотанеменше 33%какао-масла.
Розрахуйте(уг)вмісткакаопродуктіву100гшоколаду кожноговиду.



ПЕРЕРВАНАЛОГІКУ Хтозтрьохдрузівнаймолодший, якщолишеоднезнаведених твердженьєхибним?
y АндрійстаршийзаВолодимира.

y СергіймолодшийзаВолодимира.

y СергійстаршийзаАндрія.

y СумавікуВолодимираіСергіядорівнюєподвоєномувіку Андрія.
Удовільномутрикутнику:
2)

ЧИВІДОМОВАМ?
y Найбільшийусвітібасейн розташованийуЧилі.Його довжинаблизько1км,площа—близько8га,об’єм— близько300000м3



y Найглибшийна2016р.басейн «Y-40TheDeepJoy»(Італія) маєглибину42мінаповнений термальноюводоюзатемператури32–34 ° С.Нарізних глибинахєплатформиіштучні печеридлядайверів.

P квадрата задовольняє умову 45







Мартін Ґ арднер(англ. Martin Gardner ,1914–2010)—американськийматематик,популяризаторнауки,письменник.Він спеціалізувавсявгалузіцікавоїматематики,поширюючи математичніметодимислення. ВідомійогокоментарідотворівЛьюїсаКерролла.Першаіз понад70книжокҐарднеравийшладрукому1952р.,остання—у2009р.


дорівнює нулю для всіх дійсних чисел a
А 42 4 2 2 aaa +−()
Б aaa + () −+ 42 2 В 42 2 2 aaa +− + ()
Г aaa () ++44 2
Підлога хореографічного залу має форму квадрата. Довжина b сторони цього квадрата задовольняє нерівність 19 5201 ,, << b (у м).
1) Оцініть периметр цього квадрата (у м).
2) Оцініть периметр підлоги іншого хореографічного залу квадратної форми (у м), сторона якого утричі більша.
MATH FOR LIFE




8 Доведіть нерівність x x + 64 8 2 , якщо x 0 . ЧИВІДОМОВАМ? ЛеонардСмирнов,професор Одеськоїдержавноїакадемії холоду,розробивтехнологію опрісненняморськоїводийочищенняїївіддомішокшляхом заморожуваннявособливих

Див.приклад1
Див.приклади2,3 МАЙБУТНЯПРОФЕСІЯ







Бариста—фахівецьізприготуваннякави.Баристамаєзнати азивиробництвакави,розпізнаватиїїсорти,визначатиступінь обжарюваннязерензасмаком тазапахом,умітиготуватидо 40видівкавитакавовихнапоїв. Застандартамимережікав’яреньStarbucksбаристаповинен готуватипершокласнийеспресо за17секунд.Баристамаєбути творчоюлюдиною—умітималюватинамолочнійпінці,розроблятирецептинапоїв.


1
15 << m ; 2) −< < 43 m .
3) −< < 1016 m ; 4) −< <− 68,,42 m .
1) Об’єм c однієї повітряної
53,,68 << c (у дм3). Оцініть загальний об’єм 1000 таких кульок (у дм3). 2) Клумба має форму п’ятикутника, усі сторони якого однакові. Довжина a його сторони набуває значень 48,,51 << a (у м). Оцініть периметр (у м) іншої клумби у формі такого самого п’ятикутника, сторона якого удвічі більша.
3) Кавовий автомат


TOBESMART

Радимо прочитати книжкиМартінаҐарднера:

y «Найкращіматематичніігри таголоволомки»;
y «Новіматематичнірозваги»;

y «ЗагадкиСфінксатаіншіматематичніголоволомки». IQ

Подібно до інших природничих наук, математика є грою, у яку ми граємо з навколишнім світом, із Всесвітом.
ВЧОРА





Видізналисяпроосновнівластивостічисловихнерівностейінавчилисязастосовуватиїхдляоцінюваннязначеньрізнихвеличин





Винавчитесядодаватиймножитичисловінерівності,оцінюватизначеннявиразів





Визможетепропонуватиоптимальніваріантирозташуванняоб’єктівзазаданими умовами
Кіностудія знімає серіал із x серій, 18 24 x . Кожна серія триває y хв, 30 40 y . Як оцінити загальний час показу всього серіалу (у хв), якщо транслювати його без перерви й реклами?
Коментардорозв’язання
Щоб знайти загальний час показу серіалу, необхідно тривалість однієї серії помножити на кількість серій. Оскільки в умові подано не конкретні значення x і y, а межі, у яких вони містяться, то для розв’язання задачі слід перемножити дві нерівності.








що ці теореми справедливі також у випадку нестрогих нерівностей.
Теорема 1 (про почленне додавання нерівностей)
Результатомпочленногододаванняправильнихнерівностей одногознакаєправильнанерівністьтогосамогознака.
1)Якщо ab > і cd > ,то acbd +>+ .
2)Якщо ab < і cd < ,то acbd +< + .
Доведення
1) Доведемо перше твердження, застосувавши метод різниці. Запишемо різницю acbd + () −+() і
acbdacbdabcd + () −+() = +−− =−() +−()

«Щоднямивикористовуємо числа...»—цимисловамипочинаєтьсятелесеріал«Числа» (2005–2010),якийпривернув увагувикладачівтанауковців. Наосновіцьогосеріалубуло розробленоосвітнюпрограму дляшколярів,спрямованунапоглибленевивченняматематики. У2006р.пройшовприсвячений серіалусимпозіумАсоціації сприяннярозвиткунауки.

ЗАПАМ’ЯТАЙТЕ!

1) + > > { +>+ ab cd acbd 2) + < < { +< + ab cd acbd
2)
КЛЮЧОВІТЕРМІНИ
числовінерівності
подвійнінерівності
почленнедодавання нерівностей
почленнемноження нерівностей
СЛІДЗНАТИ!

CRESCENDO

DIMINUENDO


Знакинерівностейумузиці ІзпочаткуXVIIIст.вмузичних творахпочаливикористовувати знаки«<»і«>»дляпозначеннявідтінківумузиці.Крещендо (італ. сrescendo)—поступове збільшеннясилизвуку;димінуендо(італ. diminuendo)—поступовезменшеннясилизвуку.


ЗАПАМ’ЯТАЙТЕ!
При a > 0 , b > 0 , c > 0 , d > 0 : 1) × > > { > ab cd acbd 2) × < < { < ab cd acbd
1)
2)
Доведення
Доведемо перше твердження, застосувавши метод різниці.
Запишемо різницю acbd і перетворимо її, додавши й віднявши вираз bc. Маємо: acbdacbdacbcbcbdcabbcd bcbc −=−= () +−() =−() +−() + .
За умовою ab > і cd > , тоді ab−> 0 і cd−> 0 .
Звідси cab() > 0 і bcd() > 0 . Отже, cabbcd () +−() > 0.
Таким чином, acbd−> 0, звідси acbd > .
Аналогічно доводять друге твердження теореми для нерівностей ab < , cd < .
Наслідок із теореми 2
Якщо ab > і a, b — додатні числа, то abnn > , де n
туральне число.
Наприклад:
y із того, що
Спробуйте довести цей наслідок самостійно, використовуючи теорему 2. (Перевірити правильність
interactive.ranok.com.ua.)
Зауважимо, що теорема
1) Почленне множення трьох і більше нерівностей: якщо a1 , a2 , ..., an , b1 , b2 , ..., bn
⋅> ab ab ab aaabbb nn nn 11 22 12 12 ... ... ; наприклад: ×>
> c k s cks 8 3
2) Почленне множення подвійних нерівностей: якщо a, b, c, d — додатні числа, то
× << << { ⋅< ⋅< ⋅ axb cyd acxybd; наприклад: × { ⋅ 14 27 228 x y xy .

ПОМІРКУЙТЕ Спробуйтенавестиграфічну інтерпретаціютеореми2,використовуючиформулуплощіпрямокутника(с.28). ЧИВІДОМОВАМ?



Евклідутрактаті«Начала»довів,щосереднєгеометричне двохдодатнихчиселнебільше заїхсереднєарифметичнета неменшевідїхсередньогогармонічного,тобтоправильноює нерівність: 2 2 ab ab abab + + .

ПОМІРКУЙТЕ
Чиєподанітвердженняправильними?
Якщо a > 17 і c > 5 ,то:
1) ac+> 22 ;4) ac−> 12 ; 2) ac+> 20 ;5) ca−> 12 ; 3) ac+> 23 ;6) ac > 85
Виконайте множення нерівностей: 1) x < 31 і n < 2 ; 3) x <+1019 і y <−1019 ; 2) x 25 і y 35 ; 4) 1015 << b і 39 < x .
Якщо a < 17 і c < 5 ,то:
7) ac < 90 ;8) 352 1 5 ac+<
ЗВЕРНІТЬУВАГУ!
Зокремимиприкладамиоцінюваннязначеньвеличинви знайомилисьу§2.

ЧИВІДОМОВАМ?
Архімед(IIIст.дон.е.),обчислюючидовжинукола,оцінив значеннячисла


ПРИКЛАД2
.
Доведіть нерівність 11 18 + () + () + () abcabc , якщо a 0 , b 0 , c 0 .
Доведення
КРОК1
нерівності: abab + 2 , якщо a 0 , b 0 .
Звідси abab + 2 .
КРОК2 Помножимо одержані

ЗНАЙДІТЬПОМИЛКУ Оцінітьзначеннявиразу bc , якщо 27 << b , 35 << c .
Розв’язання
27 << b
35 << c

23 75 −< −<bc ; −< −< 12 bc –


умовою a 0 , b 0 , c 0 , тому
за теоремою про почленне множення нерівностей. 11 12 22 + () + () + () abcabc , тобто 11 18 + () + () + () abcabc . Нерівність доведено.
ТРЕНУЄМОСЯ
2 Доведіть твердження:
1) якщо a 5 , b 8 , то ab 40 ;
2) якщо a 2 , b 12 , то ab 24 ;
3) якщо ab 3 , ab + 11 3 , то ab22 33 ; 4) якщо ab 5 , ab + 13 5 , то ab22 65 .
Доведіть нерівність за умови, що a 0 , b 0 , c 0 :




5) abab 2244 16 + () + () ; 7) 13 324 + () + () + () abcabc ; 6) abab 2299 36 + () + () ; 8) 22 116 + () + () + () abcabc . TOBESMART Длядоведеннянерівностейтакожзастосовуютьметоди:послідовнихнаближень;математичної індукції;використанняелементів математичногоаналізу,геометричнихміркувань,спеціальних нерівностей(Коші—Буняковського,Бернуллі,Юнгатаін.). IQ


КРОК 1
КРОК 2
КРОК 3
цього трикутника.
Доведення Нехай у трикутнику ABC (рис. 1) точка K
точка всередині трикутника. Доведемо, що KAKBKCPABC ++ > 1 2
Запишемо нерівність трикутника для кожного з трьох утворених трикутників (для сторін AB, BC і AC).
Додамо почленно отримані нерівності й спростимо ліву та праву частини одержаної нерівності.
Поділимо обидві частини останньої нерівності на 2.
AKB : AKKBAB +> ; BKC : BKKCBC +> ; AKC : AKKCAC +>
AKKBBKKCAKKCABBCAC + () ++() ++() >+ + ; 2 AKBKCKPABC ++ () >
AKBKCKPABC ++ > 1 2 . Твердження доведено.
ПРИКЛАД 4 У майстерні виготовляють вітражні вікна прямокутної форми. Довжина й ширина кожного вікна дорівнюють
задачу.
1) Підприємство виготовляє газонну траву у
прямокутної форми. Ширина такого прямокутника становить a см, довжина — b см. Оцініть площу S (у м2) прямокутника, якщо 55 60 a , 480 500 b .
2) Для доставки річкового піску виділено m вантажівок. Кожна вантажівка може перевезти n тонн піску за один рейс. Оцініть масу (у т) піску, який перевезуть вантажівки за один рейс, якщо 58 m , 1012 n .
3) На сезонну роботу запрошують від 6 до 11 аніматорів. Кожен аніматор щодня має працювати з групою дітей, кількість яких не менша від 4 і не більша за 10. Знайдіть: а) найменшу; б) найбільшу загальну кількість дітей, із якими займаються аніматори щодня. 4) Ціна на пшеницю залежить від ціни на дизельне паливо. Ця залежність виражається формулою ykx =+ 160 , де x — ціна 1 л дизельного палива (у г. о.); y — ціна 1 т пшениці (у г. о.). Відомо, що протягом року ціна 1 л дизельного палива була не менша від 4 і не більша за 6 г. о. а) Знайдіть значення коефіцієнта k, якщо протягом року мінімальна ціна 1 т пшениці становила 166 г. о. б) Визначте найбільшу ціну (у г. о.) 1 т
1 Відомо, що 25 m . Оцініть значення виразу:
1) 5m ; 3) 1 3 m ; 5) m 2 4 +−() ; 2) m 7 ; 4) 23 m + ; 6) 110m .
2 Відомо, що 39 << x , 37 << y . Оцініть значення виразу: 1) xy + ; 3) xy ; 5) y x ; 2) xy ; 4) 1 x ; 6) 23xy .
3 Відомо, що m > 25 , і n > 12 , . Порівняйте: 1) 1 m і 1 n ; 3) m 2 і 5n ; 5) mn + ()2 і 25; 2) mn 10 і 2m ; 4) n 3 і 1; 6) mn + () ⋅−() 15 10 3 , і 35.
Відомо, що ab < , bm > , ma < , mc > , 0 > c, mc < 0.



y

y

y





ПЕРЕРВАНАЛОГІКУ Перевіртеправильністьміркувань.


Якщо ab > ,то ab > 2 . a, b—додатнічисла, ab > . abb > ⋅ abbb ⋅>

abbbaa ⋅> ()
abaabbaa ⋅>
ababababa () >+() () () :


abaab >+ +>() почленно почленно 22abaa >+ ab > 2
Тобтозтого,що ab > , випливає,що ab > 2 .










МаринаВ’язовська(нар.1984, Київ)—українськавчена,математик,докторприродничих наукБоннськогоуніверситету (2013).Розв’язалазадачупакуваннякульу8-вимірномута (успівавторстві)24-вимірному просторах,якамаєвеликезначеннядляпокращенняпередаваннясигналу(мобільнийтелефон,Інтернеттощо). Зарозв’язанняцієїзадачіМарині булоприсудженоу2016р.преміюСалема,ау2017р.премію МатематичногоінститутуКлея. Задачупронайщільнішепакуваннякульпоставивщев1611р. німецькийученийЙ.Кеплер. Дізнайтесябільше: theukrainians. org/maryna-vyazovska/



1) Якщо 05 x і 06 y , то значення виразу xy може дорівнювати 29.
2) Якщо 10 20 x і 1 5 1 2 y , то
100.
3) Якщо 11 x і y 45 , то значення виразу xy може дорівнювати 0.
4) Якщо mn 102 і mn + 10 8 , то mn 1010.
5)
1
2
3
4
речення (1–3) та його закінченням (А–Г) так, щоб утворилося правильне твердження.
1 Значення виразу xy
2 Значення виразу x y 3
від 0,5.
більше за 20 і менше від 500. В більше за 0,2 і менше від 5.
за 2 і менше від 50.
Майстер виготовляє дерев’яні декоративні дощечки прямокутної форми. Ширина такого прямокутника становить a см, 10 20 a , довжина — b см, 1530 b .
1) Оцініть площу S (у см2) цього прямокутника.
2) Оцініть периметр P (у см) цього прямокутника.
8 Доведіть нерівність 11 4 + () + () abab , якщо a 0 , b 0 .

МАЙБУТНЯПРОФЕСІЯ







Майбутніінженеривгалузібудівництваотримуютьнеобхідні знаннядляпроектування,спорудження,експлуатації,реконструкціїавтодоріг,будівельних об’єктів,атакожзнаннявгалузі новітніхтаенергозберігаючих технологійстворенняефективнихконструкційіматеріалівдля будівельно-монтажнихробіт. Дізнайтеся,чиєувасхистдо роботибудівельника: prof.osvita.org.ua/uk/determine/testing/854/index.html


Див.приклад1
MATH FOR LIFE
Див.приклад2
Див.приклади3,4
2)
3)
перевозять тролейбуси на цьому маршруті.
4) Кількість телефонних дзвінків до приймальної комісії університету залежить від тривалості трансляції рекламного фільму про цей університет. Залежність виражається формулою ykx =+ 8 , де x — тривалість (у хв) трансляції фільму щодня, y — кількість дзвінків протягом дня. У зимовий період щоденна трансляція фільму тривала не менше 30 хв і не більше 50 хв.
а) Знайдіть значення коефіцієнта k, якщо в
найменша кількість дзвінків протягом дня дорівнювала 14. б) Визначте найбільшу кількість





Для приготування смузі з полуниці потрібно: 500 г натурального йогурту; 700–800 г свіжої полуниці; 1,5–2 чайні
рівняння:
поверне світ. Із цим потрібно бути обережним.


Національнийуніверситет«Львівськаполітехніка»—найстаріший вищийтехнічнийнавчальнийзакладУкраїнитаСхідноїЄвропи,
королівськареальнашкола. Сьогодніуніверситетналежить додесяткинайкращихвишів України,уньомунавчаєтьсяпонад30тис.студентів. Дізнайтесябільше: lp.edu.ua








Смузі(відангл. smooth—рівний, однорідний,м’який)—густий напійзісвіжихабосвіжозамороженихфруктів,овочів,ягід, подрібненихублендерідостану пюре. Смузієнелишесмачним,айкорисним,оскількиміститьбагато вітамінів(можезаповнититриденнунормувітамінів).











атакожоцінюватизначеннявиразів Видізнаєтеся,якзображуватимножинирозв’язківнерівностейзоднієюзмінною задопомогоючисловихпроміжків

Визможетескладатименюраціональногохарчуваннязурахуваннямкалорійностіпродуктів ВЧОРА





ЧИВІДОМОВАМ?




БраузерGoogleрегулярно змінюєсвійлоготипнаяскравуілюстрацію—дудл(Google doodle),щобнагадатипросвята,ювілеїтощо.Чималодудлів пов’язанозматематикою.

КЛЮЧОВІТЕРМІНИ нерівністьзоднією змінною множинарозв’язків нерівності числовийпроміжок координатна(числова) пряма
числову нерівність. Наприклад, при n = 6 отримана числова
1802 6200 +⋅ буде правильною (оскільки 192200 ), а при n = 12 — неправильною (оскільки 1802 12 204 +⋅ = ; 204200 > ). Кажуть, що число 6 є розв’язком нерівності (задовольняє нерівність), а число 12 не є розв’язком нерівності.
Визначте, чи
Розв’язати нерівністьозначаєзнайтивсіїїрозв’язкиабодовести,щоїхнемає.
розв’язки нерівності утворюють множину розв’язків
нерівності.
Нерівності з однією змінною можуть мати безліч розв’язків або
не мати розв’язків. Якщо нерівність не має розв’язків, то кажуть, що множиною розв’язків нерівності є
∅ () . Розглянемо приклади.
Нерівність Множинарозв’язківнерівності x 2 Усі числа, які більші за число 2
числу
числа

ЧИВІДОМОВАМ?
Знакпорожньоїмножини



Чомуподанінерівностіабоне маютьрозв’язків,абомають розв’язкомбудь-якечисло?
1) xx>− 2 ;4) 01 x ; 2)
1 Зобразіть на числовій
1) y ∈− ∞ () ;0 ; 3) x ∈ ) π;11 ; 5) a ∈−() 31 5; ; 2) m ∈− +∞ ) 57,; ; 4) x ∈− +∞ () 2; ; 6) b ∈− ( 11 03 ,; , . 2 Визначте, чи належить проміжку ) 10 27 3 ,; , число: 1) –10,5; 2) 0; 3) 7; 4) –10; 5) 7,3; 6) –10,2.
tt 2 23 1 +> ?



математикДжузеппеПеано в1895р. y Символ ∈ походитьвідпершоїлітеригрецькогослова




ПЕРЕРВАНАЛОГІКУ Гаррі,Герміона,РоніГеґрідсидятьувеликомузалі.Ронсидить порядізГаррі,аленепорядіз Геґрідом.ГеґріднесидитьпорядізГерміоною.Хтосидить порядізГерміоною?
A—Гаррі
Б—Рон

В—ГаррійРон
Г—ГаррійГеґрід
Д—РоніГеґрід


ЧИВІДОМОВАМ?
y 14березня2003р.логотип Googleбувприсвяченийдню народженняА.Ейнштейна.



y 15квітня2013р.дудлприсвятилиднюнародженняЛ.Ейлера.



(межі проміжку).
КРОК1
1 Зобразіть на числовій прямій множину чисел, які задовольняють нерівність. Позначте точку, що відповідає числу 0.
1) −< 19 0 a ; 3) 25 3 x ; 5) a −+52 ;
2) −<0137 , b ; 4) −<43 1 7 y ; 6) b <− + 750 .

2
Зобразіть на числовій прямій множину розв’язків нерівності. Запишіть усі цілі числа, що є розв’язками нерівності.
1) –3 −<23 x 2; 3) −<23 1 3 y ; 5) 27 51 b ;
2) 46 < a ; 4) −< 4 1 2 y ; 6) 11 2112−< <+ x . 3
48 ; ; 3) (
12;,75 ; 5) −+ (

4
11 22 71 ,; ; 2) ) 30 ; ; 4) () 3;62 ; 6)
23 57 03 ;, .
Множину розв’язків нерівності можна зобразити у вигляді півплощини, кожна точка (абсциса або ордината) якої відповідає певному розв’язку. Установіть відповідність
стями (1–4) і рисунками (А–Г), на яких зображено множини розв’язків цих нерівностей.
ЗІРКОЮ На рисунку зображено точку Mxy00 ; () у координатній площині. Поміркуйте, чи
подані твердження правильними. Відповідь обґрунтуйте.
1) Абсциса точки М менша
2)
3) Число y0
4)
проміжку 01 ; () .
Лінійнерівняннязадаєнакоординатнійплощиніпряму, анерівністьзоднієюзмінною (окрімподвійноїнерівності)— півплощину.



Наприклад,нерівність x > 0 задаєпівплощину,щоміститься праворучвідосіординат,анерівність x 0 —тусамупівплощинуразомізвіссюординат. Нерівності y > 0 і y < 0 задаютьнакоординатнійплощині верхнютанижнюпівплощини відповідно.










ПітерАндреасТіль(нім. Peter Andreas Thiel;нар.у1967р.)— відомийамериканськийбізнесменнімецькогопоходження, інвестор,співзасновниккомпанійPayPalіPalantir,інвестор Facebook,викладачвласного курсузпідприємництвавСтенфордськомууніверситеті. ЯкіІлонМаск,Тільставпрототипомуявногоперсонажу— ПітераГрегоріізсеріалу«Силіконовадолина».

Програмапідтримкимолодих ученихібізнесменівThielFellowship,якуфінансуєФондТіля, існуєдлядопомогилюдям,які хочутьстатипідприємцями.



МАЙБУТНЯПРОФЕСІЯ



Дієтологи

(«дієта»згрец.— спосібжиття,режимхарчування)—лікарі,щоспеціалізуються назміцненніздоров’яшляхом правильногодоборупродуктів харчування.




Дієтологимаютьдобрезнати математикуівмітивикористовуватисвоїзнаннядляскладання менюзурахуваннямзбалансованоїкомбінаціїбілків,жирів, вуглеводів;розрахункукалорійностістрав;розробленнядокладноїпрограмихарчування. Дізнайтеся,чиєувасхистдо роботилікаря: prof.osvita.org.ua/uk/determine/testing/852/index.html


MATH FOR LIFE
Вівсяна каша, 230 г
Варене яйце, 1 шт.
Яблучний сік, 1 стакан
Молоко, 1 стакан
50 7 т 2,7
3,5
Див.завдання2,3 «Інтелектуальногофітнесу»

ЧИВІДОМОВАМ?

1) 32 x ; 3) 22 1 y + ;
2) 02 x ; 4) 0,12 y .
ність: 1) ab−=
У1655р.утрактатіанглійськогоматематикаДжонаВалліса «Проконічніперетини»уперше буловикористаносимвол −+ ∞


Можливо,виглядцьогосимволупов’язанийізвиглядом останньоїлітеригрецькогоалфавіту ω(омега).

Алеймовірніше,цейсимвол пішоввідзаписаногоримськимицифрамичисла1000,яке інодітрактувалосяяк«багато». УXVIст.тисячузображалияк CI ,анаписьміскорочувалидо
) 7; абоМ.



IQ




одиниці:Нотаткипростартапи, абоЯкстворитимайбутнє» («ZerotoOne»),якувважають однієюзнайкращихкнижок пробізнес(можнатакожпрослухатиаудіокнигу).

1
числа методом різниці, додавати й множити числові нерівності.
Нерівності, у яких обидві частини є чис-
ловими виразами, називають числовими
нерівностями.
Нерівності бувають строгими (знаки «>» і «<») і нестрогими (знаки « » і « »).
Алгоритм порівняння чисел a і b
методом різниці
1. Утворити різницю ab .
2. Визначити знак різниці ab .
3. Зробити висновок:
y якщо ab−> 0 , то ab > ;
y якщо ab−< 0 , то ab < ;
y якщо ab−= 0 , то ab = .
Додавання числових
y Якщо ab > і cd > , то acbd +>+ .
y Якщо axb << і cyd << , то acxybd +< +< + .
y Якщо ab і cd > , то acbd +>+ .
2
Основні властивості числових нерівностей
y Якщо ab > , то ba < ; якщо ab < , то ba > .
y Якщо ab < і bc < , то ac < .
y Якщо ab > і c — будь-яке число, то acbc +>+ .
y Якщо axb << і c — будь-яке число, то acxcbc +<+< + .
y Якщо ab > і c > 0, то acbc > .
y Якщо axb << і c > 0, то accxbc << .
y Якщо ab > і c < 0 , то acbc < .
y Якщо axb << і c < 0 , то bccxac << .
y Якщо ab > 0 і ab > , то 11 ab < .
числових
Дляa > 0 ,b > 0 ,c > 0 ,d > 0 :
y Якщо ab > і cd > , то acbd > .
y Якщо axb << і cyd << , то acxybd << .
1
2
7
8 Для закупівлі енергозберігальних
ціною 50 грн планують виділити від 700 до 1100 грн.
1) Скільки таких ламп можна закупити на заплановану суму?
2) Я ку найбільшу кількість таких ламп можна закупити на заплановану суму, якщо ціна однієї лампи збільшиться на 20 %?
9 Доведіть нерівність ccc() >− ()510 2 , якщо с — довільне дійсне число.
10 Доведіть нерівність 22 8 + () + () abab для a 0 , b 0 .
Бонусне завдання Зобразіть на координатній площині множину розв’язків нерівності 31 y .





Вирозв’язували лінійнірівняннязоднієюзмінноютазображувалинакоординатнійпрямійчисловіпроміжки,заданінерівностямизоднієюзмінною





Винавчитесявиконуватирівносильніперетвореннянерівностейтарозв’язувати лінійнінерівностізоднієюзмінною

Визможетерозраховуватичасвиконаннязавданьконтрольноїроботитарозв’язуватизадачілогістики ВЧОРА





ЧИВІДОМОВАМ?







Термін«коефіцієнтінтелекту»(англ.IQ — intelligence quotient )упершевведений у1912р.німецькимпсихологоміфілософомВ.Штерном. IQявляєсобоюкількіснуоцінку рівняінтелектубудь-якоїлюдинипорівнянозрівнемінтелекту середньостатистичноїлюдини тогосамоговіку.ДлявизначенняIQзастосовуютьспеціальнітести.

числа
творюєнерівністьуправильну числовунерівність.
Наприклад: y пари нерівностей 250 x > і x > 25 ; −+ < x 62 і 23 11 x +> є рівносильними, тому що мають одні й ті самі розв’язки; y нерівності xx +<+ 66 і −+42 34 xx є рівносильними, тому що не мають розв’язків.
Означення. Рівносильними називають нерівності, у яких множини розв’язків збігаються. Нерівності, що не мають розв’язків, також прийнято вважати рівносильними.
Щоб переконатися, що дві нерівності є рівносильними, не-
обхідно знайти всі їх розв’язки. Для цього слід знати правила
переходу від однієї нерівності до рівносильної їй нерівності. Ці
правила випливають із властивостей числових нерівностей і є ана-
логічними відповідним правилам розв’язування рівнянь. Рівносильні перетворення рівнянь і нерівностей
1 Якщо з однієї частини рівняння перенести в іншу доданок, змінивши його знак на протилежний, отримаємо рівняння, рівносильне даному.
2 Якщо обидві частини рівняння помножити або поділити на одне й те саме відмінне від нуля число, то отримаємо рівняння, рівносильне даному.
1 Якщо з однієї частини нерівності перенести в іншу доданок, змінивши його знак на протилежний, отримаємо нерівність, рівносильну даній.
2 Якщо обидві частини нерівності помножити або поділити на одне й те саме додатне число, то отримаємо нерівність, рівносильну даній.
3 Якщо обидві частини нерівності помножити або поділити на одне й те саме від’ємне число, змінивши при цьому знак нерівності на протилежний, то отримаємо нерівність, рівносильну даній.
Розглянемо приклади та порівняємо розв’язання рівняння та нерівностей.
1) 52080 x += ; 58020 x =− ; 560 x = ; x = 60 5: ; x = 12 . 2) 52080 x +> ; 58020 x >− ; 560 x > ; x > 60 ; x > 12 .
3) −+ > 52080 x ; −>58020 x ; > 560 x ; x < () 605: ; x <−12 .
Корінь рівняння: x = 12 x 12 Множина розв’язків нерівності: 12; +∞ () x 12 Множина розв’язків нерівності: −∞ () ;12 x –12

ПЕРЕРВАНАЛОГІКУ




5собаккоштуютьдорожче, ніж6котів.Щодорожче— 6собакчи7котів?

ЗАПАМ’ЯТАЙТЕ!
ПОМІРКУЙТЕ Якiзнаведенихнерівностей немаютьрозв’язків,аякімаютьбезлічрозв’язків?Поясніть своюдумку.
1) 00 ⋅< x ;3) 00 ⋅> x ; 2) 00 ⋅ x ;4) 00 ⋅ x
Визначте, чи є
нерівності: 1) x +>35 і x > 2; 4) −<40 a і a < 0; 2) 2113 x −> і x < 7 ; 5) 05 ⋅> x і 06 ⋅< x ; 3) 70 a > і a > 0; 6) 05 ⋅> x і 08 ⋅< x . Кожна
також можна звести до лінійних
рівносильних перетворень.
Складіть алгоритм розв’язування нерівностей, що зводяться до лінійних нерівностей з однією змінною, пронумерувавши кроки в правильному порядку. Використайте свій досвід розв’язування рівнянь.
Крок___ Зобразити множину
розв’язків нерівності на числовій прямій.
ПРИКЛАД 1 Розв’яжіть нерівність 25 21 54 3 ,, () () yyy .

ЧИВІДОМОВАМ?
Значеннякоефіцієнтаінтелекту 81 90 IQ мають14,5%населенняЗемлі;



91 110 IQ —50%; 111120 IQ —14,5%; 121131 IQ —8,5%;
IQ 132 —1,9%;
IQ 150 —0,1%.


потім — мішки з цукром.
маса вантажу не має перевищувати 2 т?
Розв’язання
якщо

IQ відомих осіб: Теренс Тао — 230 Мерилін вос Савант





КРОК 1 Введемо позначення для змінної величини, яка є шуканою. Нехай можна завантажити
загальну масу цукру, що має бути завантажений в автомобіль.
КРОК 4
Складемо математичну модель задачі, тобто утворимо нерівність, ураховуючи, що маса
не перевищує 2 т, і користуючись тим, що «не перевищує» означає «менша або дорівнює».
35 5502000⋅+ ⋅ n
35 5502000 25 ⋅+ n : ; 72 80 +⋅ n ; 273 n ; n 73 2 ; n 36 1 2 КРОК 6 Визначимо найбільший
5
4
1)

ЧИВІДОМОВАМ?
НещодавновсесвітняслужбановинВВСсклаларейтингнайбільш затребуванихпрофесійусвіті.

1.Медичнісестри.
2.Інженери-механіки.
3.Лікарі.

4.Інженери-електрики.
5.Програмісти.

6.ІТ-аналітикитаінженери.
7.Спеціалістиізцивільногобудівництва.
8.Фахівцізкомп’ютернихмережібазданих.
9.Бухгалтери.
10.Стоматологи.


ПРИГАДАЙТЕ!
Арифметичнийквадратнийкоріньмаєзмістлишетоді,коли підкореневийвиразнабуває невід’ємнихзначень.
2)
4)
могла зробити Мирослава? Яку найменшу кількість фотографій
2 Гб, а одного фільму — 3,5 Гб. а) Запишіть нерівність
3 Утворіть за умовою завдання нерівність і розв’яжіть її.
1) За яких значень змінної t двочлен 25 3 + t набуває від’ємних значень?
2) За яких значень змінної y двочлен 51 1 y , набуває значень, більших за 3,9?
3) За яких значень змінної m значення виразу2,04m не менше, ніж значення двочлена 06 11 , m ?
4) За яких натуральних парних значень змінної a значення виразу 53 47 211aa() +−() не більше
суми 10a + 3?






Окрімматематичногопоняття «нерівність»,існуютьтакожпоняттясоціальної,майнової,гендерноїнерівності.





Із2006р.Світовийекономічний форумвипускаєщорічнийзвіт, уякомувизначаєтьсяіндекс гендерноївідмінності,щовідображуєнерівністьуможливостяхміжчоловікамиіжінками врізнихкраїнахсвіту.Вимірюваннявідбуваютьсязачотирма ключовиминапрямами: y економічнійкар’єрніможливості;
y освіта;



y здоров’яйвиживання; y політичніправайможливості. Заданими2015р.,першемісце заіндексомгендерноїрівності посілаІсландія.Україназайняла 67-мемісцесеред142країн.


ІНТЕРНЕТПОСИЛАННЯ
Ознайомтесязінтерактивною картоюгендерноїрівності, створеноюзарезультатами звітуСвітовогоекономічногофоруму: reports.weforum. org/global-gender-gap-report2015/#frame/dd4ad


TOBESMART Радимо прочитати
книжку«ВеликакнигаIQ-тестів: 1600завдань»авторівкращих виданьзIQ-тестуванняКена РасселатаФіліпаКартера. Цякнижкадопоможевам:
y дізнатисясвійIQ;



y підвищитирівеньінтелекту;
y розвинутилогічнемислення;
y підготуватисядотестування;
y отриматипрестижнуроботу.










ЮдітПолгар(угор. Judit Polgar;нар.1976)—угорська шахістка,якав15роківстала наймолодшимгросмейстером усвіті,перевершивширекорд БоббіФішеранамісяць.Батько навчавшахамїїтасестерудома,довівши,щодітиможуть досягтинеймовірнихуспіхів, якщопочинатинавчанняізсамогомалечку.Юдіточолювала жіночийрейтингшахістокпротягом26років(1989–2015).


1
2
3
4



МАЙБУТНЯПРОФЕСІЯ Інженери-диспетчеризорганізаціїперевезеньзалізничним транспортомзабезпечуютьвиконанняграфікарухупотягів, безпекуруху,збереженнявантажівірухомогоскладу,організуютьраціональнекерування вагоно-іпасажиропотоками. Професії,пов’язанііззалізничнимтранспортом,можнаотримативУкраїнськомудержавномууніверситетізалізничного транспорту.


Дізнайтесябільше:kart.edu.ua

MATH FOR LIFE
1) На рисунку
схему ділянки прямокутної форми, яку призначено
4
5
1)
більше, ніж подвоєне значення двочлена 53x ? 2) За яких натуральних значень змінної n значення виразу −+ 12 7n не перевищує значення виразу 61 n ?
6 Визначте зміст умовних знаків (див. рисунок), які є підказками для догляду за одягом (прання, прасування). Введіть необхідні буквені позначення та спробуйте записати ці знаки за допомогою рівнянь або нерівностей. Бонусні завдання
7 Знайдіть значення a, при яких квадратне рівняння xxa 2 84 0 = : 1) має два корені; 2) не має
8 Складіть таблиці або схеми розв’язування
3
30 30 95





Ви зображувалимножинизадопомогою
жин—задопомогоюдіаграмЕйлера—Венна





Винавчитесязнаходитиоб’єднаннятаперерізчисловихпроміжків





Визможетезастосовуватипоняттяперерізутаоб’єднаннядобудь-якихмножин, елементамиякихєрізніоб’єкти(геометричніфігури,літериалфавіту,нотитощо)

ЧИВІДОМОВАМ?
Шейпінг (від англ. shaping — наданняформи)—цесучасна наукомісткакомплекснаоздоровчасистема,якапередбачає гармонійнийрозвитоківдосконаленнялюдини.

12 дівчат


8 дівчат СFKM
17 дівчат
Рис.1
ПРИГАДАЙТЕ!
Перерізоммножин Aі Bназиваютьмножинуїхспільних елементів. Записують: AB ∩ ( ∩ —знакперерізу).
спорту. Розв’язання Розв’яжемо задачу за допомогою
схеми (рис. 1). Зображені на схемі відрізки позначають:
CM — кількість усіх дівчат класу;
CK — кількість дівчат, які займаються шейпінгом;
FM — кількість дівчат, які займаються бодіфлексом;
FK — шукану кількість дівчат, які займаються і шейпінгом, і бодіфлексом.
Тоді CF — кількість дівчат, які займаються лише шейпінгом: CFCMFM =− ; CF =− = 17 89 (дівчат);
FK — кількість дівчат, які займаються обома видами фітнесу: FKCKCF =− ; FK =− = 12 93 (дівчини).
ГОЛОВНА ІДЕЯ З курсу 8 класу вам відомі поняття множини, підмножини, числових множин, перерізу множин.
В актуальній задачі кількість дівчат, які займаються обома видами фітнесу, відповідає поняттю перерізу множин A і B, якщо прийняти, що
2)
Окрім поняття перерізу
Графічна інтерпретація об’єднання множин A
на рис. 5
y Метод кіл Лейбніца розвинув швейцарський математик Леонард Ейлер (1707–1783).
Найбільшої уваги графічним методам було приділено в працях англійського логіка Джона Венна (1843–1923).
y Зображення множин у вигляді кіл називають колами Ейлера, а схематичні зображення перерізів множин діаграмами Ейлера Венна.
xa > , xb < ax b axb << , тобто xab ∈ () ; ax b −∞< <+∞ x , тобто x ∈− ∞+ ∞ () ; x ∈ () R
xa < , xb > abx ∅ abx xab ∈− ∞ () +∞ ();; ∪
xa > , xb > ax b xb > , тобто xb∈+ ∞ () ; , «більше більшого» ax b
xa > , тобто xa∈+ ∞ () ; , «більше меншого»
xa < , xb < ax b xa < , тобто xa ∈− ∞ () ; , «менше меншого» ax b xb < , тобто xb ∈− ∞ () ; , «менше більшого»
ПРИКЛАД 1
Знайдіть переріз
1
1
КРОК 2
Зобразимо
Через точки x =−3 , x = 2, x = 7 проведемо вертикальні прямі, які ділять числові прямі на 4 проміжки.
Проаналізуємо наявність розв’язків кожної нерівності на кожному проміжку. Для зручності введемо позначення: «+», якщо розв’язки є; «–», якщо розв’язків немає. Проміжок
1)




ЧИВІДОМОВАМ?
Множинивмузиці







Відомевтеоріїмузикиквартово-квінтовеколо—це множинатональностей,розташованих упевнійпослідовності.Зокрема,колодопомагаєзрозумітиустріймузикирізнихстилів (року,джазутощо). Упершеквартово-квінтовеколо булоописаневкнижціукраїнськогокомпозитораМиколи Дилецького«Мусікійськаграматика»(1679р.).


ГотуємосядоДПА



ПЕРЕРВАНАЛОГІКУ УЛіліїнаFacebookє189підписників.Ізних8осібпідписалисяменшеніж3рокитому, 11—молодшівід14років, 70—захоплюютьсяматематикою,140—юнаки.Знайдіть найменшуможливукількість підписників,дляякихсправджуютьсявідразучотириумови: цеюнаки,старшіза14років, якізахоплюютьсяматематикоюіпідписалисянеменшеніж 3рокитому.


4)
4
5
1) −+ = x 2 1210; 2220 x + ;
2) −+61 80 x , ; xx 3 90−= ;
3) 1 3 42 11 xx() +> ; xx 2 1772 0 −+ = ;
4) −+ −= 25 20 2 xx ; xx x + 3 4 5 3 2 ;
5) 21 1 3 5 x x + () ; xx 2 2120 0 +− = ;
6) 1 2 33 42 3 () () >−xxx ; 27 12 0 2 xx+− = .
7 Розгляньте класифікацію рівнин і гір за висотами (рис. 11). Знайдіть відповідну інформацію, введіть позначення та запишіть за допомогою подвійних нерівностей висоти Причорноморської низовини, Подільської
Карпат.







ГеоргКантор(нім. Georg Cantor;1845–1918)—німецькийматематик,засновниктеоріїмножин,якаспричинила загальнийпереглядлогічних основматематикиівплинулана всюїїсучаснуструктуру. Канторувівпоняттявзаємно однозначноївідповідностіміж елементамимножин,давозначеннянескінченноїтацілком упорядкованоїмножин,довів, щодійснихчиселбільше,ніж натуральних.



МАЙБУТНЯПРОФЕСІЯ





Унадзвичайнихситуаціяхпершиминамісцілихаопиняються рятувальники.Вониздійснюють рятувальніроботи,допомагаютьпостраждалимлюдям, надаютьпершумедичнудопомогу—виконуютьважкута відповідальнуроботу. Отриматипрофесіюрятувальника можнавНаціональному університетіцивільногозахисту України: nuczu.edu.ua/ukr/


1) Перерізом проміжків () 15 і 1015 ; () є порожня множина.
2) Об’єднанням проміжків () 11 ; і () 25 ; є проміжок () 25 ; .
3) Якщо 35 <− < x , то −< <− 53 x .
5)
MATH FOR LIFE
1
3
1) x 6 ; 5 x ; 4) 125 2 3 x + ; 111 3x ;
2) −+ 1 6 1 x ; x 13 ; 5) 1 5 7 x ; 11 44
Бонусне завдання 4 Запишіть усі натуральні значення:
1) змінної m, при яких перерізи
2)
є проміжком;
є проміжком.
Див.завдання5 «Інтелектуальногофітнесу»

IQ

прочитати книжкуН.Я.Вілєнкіна«Розповідіпромножини».



ВидізнаєтесяпротеоріюмножинГеоргаКантора,яказміниламатематику.Винавчитеся порівнюватинескінченнімножини,зрозумієте,щонескінченностібуваютьрізними,ознайомитесязкривоюненульової площі,зфігурами,якінемаютьплощ,тощо.






Винавчилисярозв’язуватинерівностізоднієюзмінною,шукатиїхрозв’язки тазображуватимножинирозв’язківнакоординатнійпрямій





Винавчитесязнаходитиспільнірозв’язкикількохнерівностей,тобторозв’язувати системилінійнихнерівностейзоднієюзмінною





Визможетестворюватиматематичнімоделіприкладнихзадачувиглядінерівностейтаїхсистем,розв’язуватизадачілінійногопрограмування






3D-друкстаєдедаліпопулярнішим.Задопомогоютехнологій 3D-друкувжедрукуютьбудинки,одяг,велосипеди,протези тощо.3D-друквикористовувалипідчасроботинадфільмами«Хоббіт»,«Залізналюдина», «ПаркЮрськогоперіоду», «Аватар»,«Термінатор:Порятунок»,«Месники»,«Скайфол» таінших.


ЗАПАМ’ЯТАЙТЕ!
рівностей, що входять у систему.
1 Розглянемо систему нерівностей одного знака
ною — систему вигляду xa xb > > { , або xa xb < < { , . 1) Множиною розв’язків системи будь-яких двох нерівностей одного знака «більше» буде та нерівність, права частина якої є більшим числом. Тобто якщо xa xb > > { , і ab > , то xa > — множина розв’язків системи (рис. 1). Наприклад: множиною розв’язків системи x x >− { 1 3 , є нерівність x 3 , тобто x ∈+ ∞ ) 3; .
2) Аналогічно множиною розв’язків системи будь-яких двох нерівностей одного знака «менше» буде та нерівність, права частина якої є меншим числом. Тобто якщо xa xb < < { , і ab < , то xa < — множина розв’язків системи (рис. 2). Наприклад: множиною розв’язків системи
2
1)
кілька випадків розв’язування системи нерівностей різних

ЧИВІДОМОВАМ?
y Фігурнідужкизапропонував використовуватиФрансуаВієт у1593р.

y Фігурнідужкитакожзастосовуютьдляпозначеннямножин.


1) x xa < 5, ; > { 3) x xa 3, ; {
2) x xa − > { 2, ; 4) x xa > { 4, .
Розв’язання
xa xb > > { , xa xb < < { , xa xb > < { , xa xb , {
bx a
ab >
xa > ,
тобто xa∈+ ∞ () ; , «більше більшого»
ab < ax b
xb > ,
тобто xb∈+ ∞ () ; , «більше більшого»
bx a
xb < , тобто xb ∈− ∞ () ; , «менше меншого»
ax b
xa < , тобто xa ∈− ∞ () ; , «менше меншого»
bax
розв’язків немає, тобто ∅
bax
розв’язків немає, тобто ∅
ax b axb << , тобто xab ∈ () ;
abx
axb, тобто xab ∈
;
ab =
ax = b xa > ax = b xa < ax = b розв’язків
ПРИКЛАД 1
нерівність:
1) −<46xx ; 5) −< <−67 3 3 x x ;
2) 29 −< xx ; 6) −< <− + 410 2 5 x x ;
3) −< 15 4112 xx ; 7) 25 13 3 xx x −+ ;
4) 17 35 21 −+ < xx ; 8) xx x + 21 52 4 .



що містять змінну під знаком модуля. Нехай a — додатне число. Тоді нерівності виду xa
xa
можна розглядати, виходячи з геометричного змісту модуля. Схема 1
xa < , a > 0
Відстань від початку відліку до точки з координатою x менша від a ax –a 0
Нерівність задовольняють усі значення xaa∈−() ; −< < axa
Наприклад:
1) x < 5 , −< < 55 x ; 3) x >−3 , x ∈− ∞+ ∞
2) x 5 ,

Схема 2

xa > , a > 0 Відстань від початку відліку до точки з координатою x більша за a
Нерівність задовольняють усі значення xaa ∈− ∞− () +∞ ();; ∪ ax –a 0 xa <− або xa >
2)
КРОК1

ЧИВІДОМОВАМ?
y Вважають,щотермін«модуль»запропонуваванглійськийматематикіфілософ, ученьНьютонаРоджерКотс.



y Ґ отфрідЛейбніцтежвикористовувавцюфункцію,яку називав«модулем»іпозначав mol x.

із бідонів залишився неповним. Якщо те саме молоко перелити в бідони місткістю 30 л, взявши на 8 бідонів менше, то їх не вистачить, щоб розлити все молоко. Складіть математичну модель задачі у вигляді системи двох лінійних нерівностей та знайдіть
наявну кількість 20-літрових бідонів.
Розв’язання
Крок
КРОК1 Введемо позначення для кількості 20-літрових бідонів.
КРОК2 Проаналізуємо умову «один із бідонів залишився неповним».
КРОК3 Визначимо кількість 30-літрових бідонів.
КРОК4
КРОК6
умову «360
в x () 8 бідонів не поміститься».




ростуйрозвиткуорганізму. y Всесвітняасоціаціяохорони здоров’ярекомендуєвживати 330кгмолочнихпродуктів(уперерахункунамолоко)нарік.

Нехай x — кількість 20-літрових бідонів, х — натуральне число
Якщо один із бідонів неповний, то в усі бідони могло поміститися більше молока, ніж розлито, тобто 20 360 x >
Оскільки 30-літрових бідонів знадобиться на 8 менше, то їх кількість
Значення виразу 30 8 x () менше від
Складемо систему лінійних нерівностей і розв’яжемо її відносно змінної x. 30 8360 20
Розв’яжемо задачу, враховуючи, що шуканий розв’язок x має бути натуральним




п’єсі«Россумськіуніверсальні роботи»чеськогописьменника









Лінійнепрограмуваннязастосовуютьвекономіці,медицині,транспорті,енергетиці,геології,сільськомугосподарстві, військовійсправі,соціальних науках,теоріїуправліннятощо. Задачілінійногопрограмуваннярозв’язуютьзадопомогою систем лінійних нерівностей ірівняньізбагатьманевідомими.Методирозв’язування:графічний,симплекс-метод,метод Гаусса—Жордана,методШтіфелятаін.
















Поміркуйте, чи
1) Множиною розв’язків системи
56 ; ( .
2) Якщо M — множина розв’язків
M = {} 7 .
x x < { 5 6 , є

3) Множиною розв’язків нерівності x + 10 є порожня множина.
4) Якщо x > 2 , то x > 2.
5) Якщо x < 3 , то x >−3 .
MATH FOR LIFE
кольори зірок феєрверку зумовлені тим, що начинкою ракет є різні піротехнічні суміші, які під час згоряння випромінюють світло з різною довжиною хвилі λ . Докладно з електромагнітними хвилями, у тому числі й світловими, ви познайомитеся на уроках фізики. Довжини хвиль видимого світла (у нанометрах) наведено в таблиці.
Колір Довжинахвилі λ ,нм Колір Довжинахвилі
565590 << λ Синій 440485 << λ







ЛеонідВіталійовичКанторович (1912–1986)—видатнийматематикіекономіст,одиніззасновниківлінійногопрограмування,лауреатНобелівської преміїзекономіки1975р.за внесокутеоріюоптимального розподілуресурсів.



Л.Канторовичу14роківвступивдоуніверситету,у22роки ставпрофесоромуніверситету,у23—докторомфізикоматематичнихнаук,у26—керівникомнауковоїшколи. НайулюбленішізадачіЛ.Канторовича—транспортназадачатазадачапрооптимальний розкрій.


ЧИВІДОМОВАМ?





Найбільшийусвітіфеєрверк бувзапущенийу1988р.підчас одногозяпонськихфестивалів. Важивфеєрверкпонад500кг, айого«вогнянаквітка»мала діаметрпонадкілометр.

Див.приклад1
Див.приклад2
Див.приклад3
Див.приклад4

МАЙБУТНЯПРОФЕСІЯ






УХарківськомунаціональному автодорожньомууніверситеті булостворенопрототипавтомобіля,якийможепроїхати 575кмна1лпального.Його масаблизько40кг,швидкість— до60км/год.Ценайбільш енергоефективнийавтомобіль країни,йоговнесенодоКниги рекордівУкраїниякавтомобіль змінімальнимивитратамипального(меншеніж2гна1км). Дізнайтесябільше: www.khadi. kharkov.ua/ru/home.html


1) x 5 ; 4) 318 y ; 7) x 2 35 0 +− < ; 2) y > 3 ; 5) x 49 0 ; 8)
y Розв’язуваннясистемнерівностейрізнихзнаків— с.79–80.
y Розв’язуваннянерівностей, щомістятьзміннупідзнаком модуля—с.83.
1) f () 2 ; 5) нулі функції (значення x, при яких fx() = 0 );
2) f 1 () ; 6) значення x, при яких fx() = 2 ;
3) f 4 () ; 7) множину розв’язків нерівності fx() 0 ;
4) f 8 () ; 8) множину розв’язків нерівності fx() 0 .
Знайдіть значення аргумента, при яких задана функція набуває додатних значень; від’ємних значень.
1) yx=+ 05 1 3 , ; 4) yx=− 1 7 7 ;
2) yx =−211 ; 5) yx =− 12 50 ,,5 ;
3) yx=+211; 6) yx =+24 1 3 .

Для моєї діяльності характерним є постійне взаємопроникнення теорії та практики, щодо практики, вона нерідко далеко виходить за межі математики.







Нобелівськоїпреміїзматематикинеіснує.Ідеязапровадити математичнупреміюналежить канадськомуматематикуДжонуФілдсу(англ. John Fields , 1863–1932).


МедальФілдса(Fields Medal)— найвищанагородавгалузіматематики,якукожні4рокиприсуджуютьматематикамвіком до40роківзазначнийвнесок унауку.У2018р.відбудеться наступненагородженнялау-

ІНТЕРНЕТ-ПОСИЛАННЯ
Онлайн-калькулятор Desmos: www.desmos.com/calculator
Інтерактивні інструменти онлайн-калькулятора
y Повзунок дозволяє змінювати значення в ручному або автоматичному режимі
y Масштабування — дозволяє зменшувати або збільшувати зображення
Збільшити
y Вибір точки дозволяє дізнатися координати будь-якої точки графіка
та багато іншого. Після запуску онлайн-калькулятора Desmos
виться панель (рис. 1), у лівій частині якої розташоване
введення даних (множин точок,

1. Запустіть сервіс Desmos.
2. Введіть у поле для введення даних рівняння лінійної функції yx=+23 . Перегляньте результат (в
з’явитися графік — пряма лінія).
3. Натисніть кнопку Додати та введіть нове рівняння yx =−

Щоб додати колір об’єктам або частинам
площини, використовують нерівності. Якщо
нерівність строга (знаки «<» і «>»), межа кольорової області буде пунктирною лінією. Якщо
нерівність нестрога (знаки « » і « ») — суцільною лінією. Залежно від знака нерівності
заданим кольором зафарбовується відповідна частина площини (над або під межею).
ПРИКЛАД 2
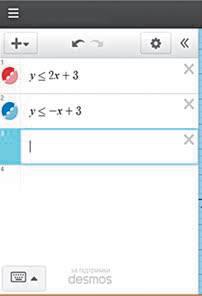
Знайдіть множину розв’язків системи нерівностей yx yx 25 3 + −+ { , .
Алгоритм побудови
1. Скористайтесь алгоритмом побудови графіків, наведеним у прикладі 1.
2. У записах рівнянь замініть знаки рівності
на задані знаки нерівності. Отримаєте нерівності yx23 + і yx−+ 3 .
3. Перегляньте результат (рис. 3). Ви вже знаєте, що множину розв’язків не-
рівності можна зобразити у вигляді півплощини, кожна точка (абсциса або ордината) якої
відповідає певному розв’язку. Ви отримали
дві півплощини, які є зображеннями множин розв’язків заданих нерівностей. Переріз цих
півплощин є множиною розв’язків відповідної системи нерівностей.
Якщо ви знаєте властивості лінійної функції, умієте будувати графіки, опанували тему
«Нерівності», то зможете проявити свої творчі здібності, створюючи різноманітні зображення та анімації.



ТРЕНУЄМОСЯ
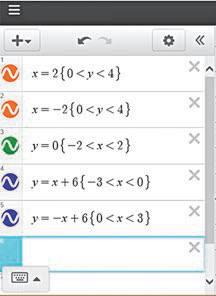
1 «Намалюйте» клаптеву ковдру, користуючись підказками (рис. 4).
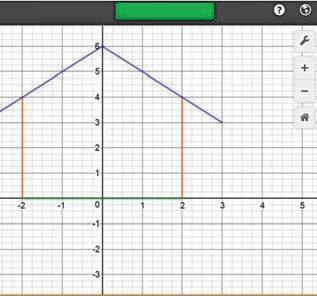
2 «Побудуйте» будинок і розфарбуйте його різними кольорами за
нерівностей (рис. 5).
3
Ви навчилися розв’язувати лінійні
перетворень.
Нерівності виду axb < або axb > axb ( або axb ) , де x — змінна, a і b — деякі числа, називають лінійними нерівностями з однією змінною.
Рівносильними називають нерівності, у яких множини розв’язків збігаються. Нерівності, що не мають розв’язків, також прийнято вважати рівносильними.
2.
Алгоритм розв’язування нерівностей, що зводяться до лінійних нерівностей з однією змінною
1. Розкрити дужки (якщо вони є), перенести доданки, що містять змінну, у ліву частину нерівності, а доданки,
2.
при змінній:
y якщо коефіцієнт — додатне число, то знак
ності не змінюється;
y якщо коефіцієнт — від’ємне число, то змінити знак нерівності на
на числовій прямій та записати множину розв’язків нерівності за допомогою числового проміжку.
2 Ви дізналися, що таке об’єднання та переріз множин, числових проміжків. Перерізом множин A і B називають множину їх спільних елементів.
Об’єднанням множин A і B називають
кожному з цих проміжків.
систему нерівно-
ab >
bx a xa > ,
тобто xa∈+ ∞ () ; , «більше більшого»
ab < ax b
xb > ,
тобто xb∈+ ∞ () ; , «більше більшого»
Розв’язування систем
bx a xb < ,
тобто xb ∈− ∞ () ; , «менше меншого»
ax b
xa < , тобто xa ∈− ∞ () ; , «менше меншого»
ab = ax =
лову нерівність. xa <
Розв’язування нерівностей, що
y якщо a > 0 , то xaa∈−() ; y якщо a = 0 , то розв’язків немає ∅ ()
y якщо a < 0 , то розв’язків немає ∅ () xa
y якщо a > 0 , то xaa ∈− ;
y якщо a = 0 , то x = 0
y якщо a < 0 , то розв’язків немає ∅ ()
bax
розв’язків немає, тобто ∅ bax розв’язків немає, тобто ∅
ax b
axb << , тобто xab ∈ () ; abx axb , тобто xab ∈ ;
немає, тобто ∅ ax = b єдиний розв’язок a {}
якщо a > 0 , то xaa ∈− ∞− () +∞ ();; ∪
y якщо a = 0 , то x ∈− ∞ () +∞ ();; 00 ∪
y якщо a < 0 , то x ∈− ∞+ ∞ () ; , або x
) ;;
якщо a = 0 , то x ∈− ∞+ ∞ () ; , або x ∈ R y якщо a < 0 , то x ∈− ∞+ ∞ () ; , або x ∈ R xa xb > > { , xa xb < < { , xa xb > < { , xa xb , {
його половину, то різниця буде меншою від 15.
1) Складіть систему нерівностей

2 КВАДРАТИЧНА
намічні процеси реального світу, математичні моделі яких будують у вигляді рівнянь, нерівностей та їх систем. Опанувавши цей розділ ви зможете:
y розраховувати траєкторії руху літальних апаратів, спортивних снарядів, птахів; y розробляти схеми шляхів сполучення, маршрутів, визначати місцезнаходження
y Історія розвитку поняття функції
y Алгебраїчні криві та їх графіки y Функції у навколишньому світі
y Функціональні залежності
y
об’єктів, прогнозувати розвиток природних явищ та зміни погоди;
y аналізувати тенденції споживання комунальних послуг і пропонувати найкращі варіанти енергозбереження;
y досліджувати процеси за допомогою електронних ресурсів і соціальних мереж; y розв’язувати виробничі завдання, пов’язані з розподілом ресурсів, плануванням прибутків, логістикою і маркетингом.





















15 січня 1892 р. вважають днем народження баскетболу. Цього
дня Джеймс Нейсміт, викладач


одного з американських коле
джів, опублікував 13 правил нової гри, яку винайшов для своїх студентів. Сучасний баскетбол
налічує понад 200 правил.

Баскетбольнийyм’ячyпідкинулиyвгору.yНаyрис.y1yзображеноyзалежністьyвисотиy hy(уyметрах),yнаyякуyпіднявсяyм’ячyнадyповерхнеюy землі,yвідyчасуy ty(уyсекундах),yтобтоyграфікyфункціїy ht() .
Користуючисьyграфіком,yдайтеyвідповідіyнаyтакіyзапитання.
1)yНаyякуyнайбільшуyвисотуyпіднявсяyнадyземлеюyм’яч?y
2)yЧерезyскількиyсекундyпісляyкидкаyм’ячyупершеyторкнувсяyземлі?
3)yСкількиyразівyм’ячyторкнувсяyземліyпротягомyпершихyп’ятиy секундyпісляyкидка?
4)yЗнайдітьyзначенняy h 3 () yіy h 4 () .y Коментар до розв’язання Найбільшаyвисота,yнаyякуyпіднявсяyм’яч,yстановитьy3yм.yЗауважимо,yщоyвисотаy hyнабуваєyзначеньyізyдіапазонуyвідy0yдоy3yмyвключно,yчасy ty—yвідy0yдоy6yсyвключно.yДіапазониyзначень,yякихyможутьy
y функція (залежна змінна)
y область визначення функції
y способи задання функції ЧИ ВІДОМО ВАМ?
Поняттяyфункціїy—yоднеyзyнайважливішихyуyкурсіyматематики.yПригадаємоyосновніyвідомостіyпроyфункцію,yякіyвиyвжеyзнаєте.
Функцієюyназиваютьyзалежністьyзмінноїy yyвідyзмінноїy x,yякщоy кожномуyзначеннюy xyзаyдеякимyправиломyставитьсяyуyвідповідністьyєдинеyзначенняy y.y
xy—yаргументy(незалежнаyзмінна);
yy—yфункціяy(залежнаyзмінна);
yfx = () y—yфункціональнаyзалежністьy yyвідy xy(правило).
Наприклад:Saa () = 2 y—yзалежністьyплощіy Syквадратаyвідyдов
жиниy ayйогоyсторони;y stvt () = 0 y—yзалежністьyвідстаніy s,yякуyпроходитьyтіло,yрухаючисьyізyпостійноюyшвидкістюy v0 ,yвідyчасуy t.
Оскількиyуyфункціональнійyзалежностіy yfx = () yкожномуyзначеннюyнезалежноїyзмінноїy x відповідаєyпевнеyзначенняyзалежноїy змінноїy y,yтоyслідyговоритиyіyпроyмножинуyзначеньyзмінноїy x,yіyпроy множинуyзначеньyзмінноїy y.
Означення 1. Множину
гумента) називають
Означення 2. Множину всіх
змінна, називають областю
функції (або множиною значень функції).
Областьyвизначенняyпозначаютьyвеликоюyлітероюy D,yобластьy значеньy—yвеликоюyлітероюy E.y Наприклад:Dy() y—yобластьyвизначенняyфункціїy y; Ey() y—yобластьyзначеньyфункціїy y.
Областюyвизначенняyфункції,yякуyзаданоyформулою,yєyобластьyдопустимихyзначеньy(ОДЗ)yзмінноїyвідповідногоyвиразу.
Наприклад,yобластюyвизначенняyфункціїy y x =+ 3 11 2 yєyОДЗy змінної,yщоyвходитьyуyвиразy 3 11 2 x + .yЦейyвиразyмаєyзмістyприyвсіхy
значенняхy x,yокрімy11.yТакимyчином,y Dy() :y x ∈−
РОЗМИНКА 1
yЗнайдітьyобластьyвизначенняyфункції:
Функція
Називають: x — аргуме нт; y — функція; yfx = () — функціональна залежність y
Записують: yfx = () .
Читають:
y




ЗАПАМ’ЯТАЙТЕ!

ЧИ ВІДОМО ВАМ? В алгебраїчній геометрії

рівняннями вищих степенів. Деякі з них отримали назви на
честь своїх дослідників.

Декартів лист y ax 2 –a a



Функціюyвважаютьyзаданою,yякщоyвказаноyправило,yзаyдопомогоюyякогоyможнаyзаyкожнимyзначеннямyнезалежноїyзмінноїy знайтиyзначенняyзалежноїyзмінної.yІнодіyдодатковоyвказуютьyобластьyвизначенняyфункції.
Функціюyможнаyзадатиyоднимyізyтакихyспособів: y аналітичноy—yзаyдопомогоюyформули; y графічноy—yзаyдопомогоюyграфіка;
y табличноy—yзаyдопомогоюyтаблиці; y словесноy—yзаyдопомогоюyопису.
Найчастішеyфункціїyзадаютьyаналітичноyабоyграфічно.y
Наприклад, функцію y x xx = <− 11 1 2 , ,, якщо якщо , задано
міжках (див. графік на рис. 2). Знайдемо
1) якщо x =−5 , тобто x ∈− ∞− () ;1 , то yx() = 1 , y () = 51 ; 2) якщо x = 3 , тобто x ∈− +∞ ) 1; , то yxx () = 2 , y 33 9 2 () == .
РОЗМИНКА 2
1 Знайдіть значення функції при заданих значеннях аргумента:
1) yxx () =−23 , x = 4 ; 3) yaaa () =+ 2 2 , a =−2 ; 2) stt () =− 2 4 , t =−5 ; 4) yxx () =+ 4 , x =−3 .
2 Не виконуючи побудови графіка, визначте, чи проходить через задану точку графік функції: 1) yx=+47 , R () 13 ; ; 3) yxx =− + 75 , B () 9;94 ; 2) yx=− 2 9 , K () 3;21 ; 4) y x x = + 22 5 3 , H () 22 ; .
У випадку, коли функцію задано
вміння читати її графік. За графіком можна
функції при
які
є точними. Наприклад, функцію yfx = () задано графічно (рис. 3).
маємо: 1) Dyx () ∈−
:;57 ; 2) Eyy ()
:;46 . ПРИКЛАД 1
задано формулою yxxx () =− +− 31 2 . Знайдіть
чення функції при x = 0 , x =−2 , xa=+ 1 .
1
КРОК 1
КЛЮЧОВИЙ МОМЕНТ
Кожномуyзначеннюyаргументаyвідповідаєy єдинеyзначенняy функції,yпротеyодномуyзначеннюyфункціїyможутьyвідповідатиy кількаy(іyнавітьyбезліч)yзначеньyаргумента.
Наприклад,yзаyграфікомyфункціїy yfx = () y(рис.y4)yбачимо,yщоy значеннюyфункціїy yb = yвідповідаютьyзначенняyаргументаy x1 ,y x2 ,y x3 ,y x4 ,yтобтоy yxyxyxyxb 12 34 () = () = () = () = .
ПРИКЛАД 2
Функціюyзаданоyформулоюy fxxx () =− 1 2 2 3 .yЗнайдітьyзначенняyаргумента,yприyякомуyзначенняyфункціїyдорівнюєy–1,5. Розв’язання
Підставимоyвyзадануyформулуyзначенняy функціїy fx() =−15 , .
КРОК 2 Розв’яжемоyотриманеyквадратнеyрівняння.
Відповідь:y–1yабоy3.





КРОК 1 Функцію
y Розв’язування більшості завдань, пов’язаних із функціями, потрібно починати зі знаходження області визначення функції.
y Будуючи графіки функцій, необхідно пам’ятати про «виколоті» точки.
y
ФІЗКУЛЬТХВИЛИНКА «Танцювальна математика» Зробіть вправи:
2) Розв’яжіть рівняння fx() =−4 графічним
У 8 класі ви навчилися будувати графіки функцій за допомо
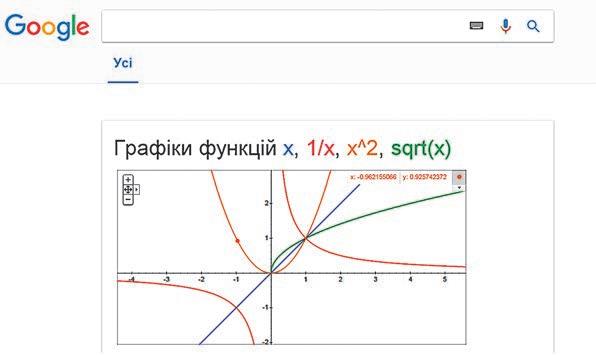
гою програми Advanced Grapher. Розглянемо сервіс Google, який дозволяє будувати графіки функцій, заданих аналітично, визначати координати точок перетину графіків, знаходити значення функції в заданих точках тощо.
1. У рядок пошуку введіть формулу, якою за
дано функцію, з використанням операторів для виконання дій (див. таблицю праворуч).
2. Для побудови графіків кількох функцій (рис. 5) введіть у рядок пошуку (1) відповід ні формули через кому без пробілів.
3. Щоб змінити масштаб за однією або за осями, скористайтеся інструментом (2)
4. Клацнувши інструмент (3) на відповідному кольорі,
5.








Марія Ґаетана Аньєзі (італ. Maria Gaetana Agnesie, 1718–1799) —
видатна італійка, яка займалася математикою, філософією.
У 9 років Марія виступила з до


повіддю, у якій захищалося право
жінок на якісну освіту. У 30 ро
ків надрукувала працю «Основи
аналізу для італійського юнацтва»
обсягом понад 1000 сторінок, яка містила всі розділи математики того









Поміркуйте,yчиyєyподаніyтвердженняyправильними.yВідповідьy обґрунтуйте.
1)yЯкщоy f () = 65 ,yтоy 5 ∈ ()Df ,yаy −∈ () 6 Ef .
2)yЯкщоy Df() = ( 13 ; ,yтоyзначенняy f 1 () yнеyіснує.
3)yЯкщоy Ef() = () 29 ; ,yтоyіснуєyтакеyзначенняyаргументаy x0 ,yщоy fx0 7 () = .
4)yОбластюyвизначенняyфункціїy y x x = 6 5 yєyпорожняyмножина.
5)yОбластюyзначеньyфункціїy y x x = 4 4 yєyмножинаy 1 {} .
MATH FOR LIFE
Транспортнаyкомпаніяyздійснюєyвантажоперевезенняyнаyвід
зенняyвантажуyнаyвідстаньyвідy20yдоy30yкмy(неyвключаючиy30yкм)y становитьy1000yгрн,yвідy30yдоy40yкмy(неyвключаючиy40yкм)y—y 1200yгрн,yвідy40yдоy50yкмy—y1400yгрн.yy
1 yЗнайдітьyобластьyвизначенняyфункціїy yfx = () ,yдеy yy—yвартістьy (уyгрн)yперевезенняyвантажуyнаyвідстаньy xy(уyкм).
2 yПобудуйтеyграфікyфункціїy yfx = () ,yзнайдітьyобластьyїїyзначень.
3 yВизначтеyвартістьyперевезенняyвантажуyнаyвідстаньy43yкм.
4 yЗ’ясуйте:y
y1)yчиyможеyвартістьyперевезенняyвантажуyдорівнюватиy1350yгрн; y2)yчиyможнаyперевезтиyвантажyнаyвідстаньy55yкм.
1 yФункціюyзаданоyформулою:
2 yЗнайдітьyзначенняyаргументаyприyзаданомуyзначенніyфункції:
fxx
3 yЗнайдітьyобластьyвизначенняyфункції:
4 yПобудуйтеyграфікyфункції:
1)y y x x = 62 3 ;yyy2)y y x x = + 1 1 2 ;yyy3)y y xx x = () 4 4 ;yyy4)y y x xx = 1 1 .y
Бонусні завдання
5 yЗобразіть,yякyможеyвиглядатиyграфікyфункції,yобластьyвизначенняyякої:y
1)y Dy() =− ∞− () () +∞ () ;; ; 22 22∪∪ ;
2)y Dy() =− ∞− () +∞ ();; 22 ∪ .
6 yЗнайдітьyобластьyзначеньyфункції:
1) yx=+ 2 ;y 2)y yx=+ 23 .
ВПРАВИ НА ПОВТОРЕННЯ
yРозв’яжітьyрівнянняy fx() = 0 ,yякщоyфункціюy fx() yзаданоy формулою:y
1)y fxx () =−36 ;yy5)y fxxx () =− + 2 1016 ; 2)y fxx () =+510 ;yy6)y fxxx () =− 2 89 ;
3)y fxx () =− 2 6 ;yy7)y fxx () =− + 95 ;
4)y fxx () =− 5 2 ;yy8)y fxx () =+125 .
приклад 3
приклад 4







TO BE SMART
























дезорієнтують здобич, оточуючи її повітряними бульбашками.
Посилаючи ультразвукові сиг


нали та аналізуючи відлуння, дельфіни визначають її місцезнаходження. Як же вони відокремлюють сигнал від здобичі в хаосі сигналів, відбитих від бульбашок? Учені з’ясували, що мозок дельфіна виконує цю операцію за допомогою нелінійних математичних методів, що неможливо без складного математичного апарату.



Уyбасейніyдельфінаріюyдельфінyтоyвистрибуєyзyводи,yтоyпірнаєy підyводу.yНаyрис.y1yзображеноyзалежністьyвідстаніy h y(уyм)yміжy дельфіномyтаyповерхнеюyводиyвідyчасуy ty(уyс),y t
ніyзначенняy h yвідповідаютьyвисоті,yнаyякуyдельфінyвистрибує,y від’ємніy—yглибині,yнаyякуyпірнає.y
Рис. 1
Користуючисьyграфіком,yдайтеyвідповідіyнаyтакіyзапитання.
1)yСкількиyразівyдельфінyперетнувyповерхнюyводи?
2)yyУyякіyпроміжкиyчасуyдельфінyбув:yа)yнадyводою;yб)yпідyводою?
Коментар до розв’язання Додатніyзначенняy hyвідповідаютьyперебуваннюyдельфінаyнадy водою,yаyвід’ємніy—yпідyводою.yОтже,yмоментам,yколиyдельфінy перетинавyповерхнюyводи,yвідповідаютьyточки,yуyякихyграфікy перетинаєyвісьy t.yІзyграфікаyвидно,yщоyдельфінyперетнувyповерхнюy водиy4yрази.yПриyцьомуyвінyперебував:y y надyводоюy(частиниyграфікаyвищеyвідyосіy
ГОЛОВНА ІДЕЯ
Серед усіх значень, яких може набувати функція, особливу увагу приділяють тим, що дорівнюють нулю. Точки графіка
функції yfx = () , ординати яких дорівнюють нулю ( y = 0 , тобто fx() = 0 ), розташовані на осі абсцис. Абсциси цих точок називають нулями функції.
Означення. Нулем функції називають значення
1.
2.
1) yx=+216 ; 3) yxx =− 2 28 ; 5) yx=− 3 ; 2) yx =−27 1 3 ; 4) yxx =+ 25 4 3 ; 6) yx=− + 116 .
Усі точки осі абсцис мають координати x;0 () .
точки осі ординат
координати 0; y () .
ЗАПАМ’ЯТАЙТЕ!
ПРИКЛАД 1
Знайдіть нулі функції y
1
2
1) yx =−618 ; 4) yxx =+43 2
2
Визначте проміжки знакосталості функції yx=−
1
КРОК 1
2
ПРИКЛАД 3
Визначте проміжки знакосталості функції yxx =− + 2 69 . Розв’язання
Знайдемо Dy() . Перетворимо вираз xxx 2 2 69 3 −+ =−(), застосувавши формулу квадрата двочлена. Dy() : x ∈ R ; xxx 2 2 69 3 −+ =−()
КРОК 2 З’ясуємо знак виразу x () 3 2 , враховуючи, що a 2 0 при будьяких значеннях a. x ()30 2 при будьяких значеннях x, причому рівність досягається при x = 3
КРОК 3 Зробимо висновок. x () > 30 2 при всіх значеннях x, окрім 3; x () < 30 2 розв’язків
чень x, при яких y < 0 ,
КРОК 1
4
проміжки знакосталості функції yx=+ 4 . Розв’язання
Знайдемо Dy() , скориставшись означенням арифметичного квадратного кореня. Оскільки x існує
КРОК 2 З’ясуємо знак виразу x за означенням арифметичного квадратного кореня.
КРОК 3
ПРИКЛАД 5
Знайдітьyдодатнеyзначенняy a ,yприyякомуyчислоy x0 02=− , єyнулемyфункціїy yax =−() 54 3 2 .
Розв’язання Крок
КРОК 1
КРОК 2
КРОК 3
Скористаємосьyозначеннямyнуляyфункції: якщоy x
yєyнулемyфункції,yтоy
Підставимоyвyзадануyформулуyзначенняy x0 02=− , yіyзнайдемоy y () 02 , : ya () =−() ⋅−()
02
Складемоyрівнянняyзаyумовоюy y () = 0,02 yіyрозв’яyжемоyйого.yВиберемоyсередy знайденихyзначеньy
Відповідь:y1.
ТРЕНУЄМОСЯ
3 yЗнайдітьyусіyзначенняy
1 yЗнайдітьyнуліyфункції: 1)y yx =− 4 2 5 ;y3)y yxx
2 yПобудуйтеyграфікyфункції,yзнайдітьyїїyнуліyтаyпроміжкиyзнакосталості,yякщо: 1)y yx = 1 3 ;y3)y yx
2)y yx=− 3 4 6 ;yy4)y y x = 4 ;yy6)y







Ox (з віссю ординат Oy), необхідно у формулу, якою задано функцію, підставити
значення y = 0y(x = 0)y і знайти значення x (значення y). Координати точки перетину графіка: y з віссю Ox — x;0 () ;
y з віссю Oy — 0; y ()





Ігор Іванович Сікорський (1889–1972) — авіаконструктор, уче

ний, винахідник, автор одного
з кращих гелікоптерів в історії авіації. Розробив близько
50 моделей гелікоптерів, завдя
ки яким було врятовано понад
2 млн людських життів.


Із 2016 р. міжнародний аеро
порт «Київ» і НТУУ «Київський

політехнічний інститут» носять ім’я Ігоря Сікорського. МАЙБУТНЯ ПРОФЕСІЯ




Поміркуйте,yчиyєyподаніyтвердженняyправильними.yВідповідьy обґрунтуйте.
1)yФункціяy yx=+ 2 4 yнеyмаєyнулів.
2)yЯкщоy x = 6 y—yнульyфункціїy yfx = () ,yтоy f 6 12 0 () = .
3)yЯкщоy x =−8 y—yнульyфункціїy yfx = () ,yтоyточкаy () 80 ; yналежитьyграфікуyцієїyфункції.
4)yЯкщоyточкаy 09 ; () yналежитьyграфікуyфункціїy yfx = () ,yтоy x = 9 y—yнульyцієїyфункції.
5)yЯкщоy y < 0 yприy x ∈+ ∞ () 3; ,yтоy y 5 () yможеyдорівнюватиy5.
MATH FOR LIFE
Пілотпочатківець,yнавчаючисьyкеруватиyгелікоптером,yвиконуєyвсіyзавданняyпілотаінструктора.yНаyрис.y3yзображеноyзалежністьyвисотиy hy(уyм)yнадyповерхнеюyземлі,yнаyякійyперебувавy гелікоптерyпідyчасyпольоту,yвідyчасуy ty(уyхв),y
1
2
3
4

1
2
3
4
1 yЗнайдітьyнуліyфункції:
2 yВизначтеyпроміжкиyзнакосталостіyфункції:
3






4
1)y5;y2)y–4;y2;y3)y–3;y0;y2;y4)y–5;y–1;y1;y5. yКористуючисьyграфіками,yукажітьyпроміжкиyзнакосталостіy
5 yПобудуйтеyграфікyфункції,yзнайдітьyїїyнуліyтаyпроміжкиyзна


TO BE SMART
Радимо прочитати книжку Дебори Кесперт «Генії. Найвидатніші винаходи за всю





yЗаyграфікомyфункціїy yfx = () ,y заданоїyнаyпроміжкуy
39 ; (рис.y4),yзнайдіть:
1)y f 3 () ;y f 1 () ;y f 0 () ;y f 9 () ;yyy
2)yнуліyфункції;y
3)yобластьyзначеньyфункції;y 4)yмножинуyрозв’язківyнерівностіy fx() 0 ;
5)yмножинуyрозв’язківyнерівностіy fx() 0 .
промисловості. Воно було дивом.















Наyрис.y1yзображеноyграфікиyбіоритмівyпевноїyлюдини,yтобтоy залежностіyфізичного,yемоційногоyтаyінтелектуальногоyстанівyлюдиниyвідyчасуy(уyднях)yізy1yпоy25yгрудня.yy

ВІДОМО ВАМ? Біологічний ритм (біоритм)




Інтелектуальнийyбіоритм Фізичнийyбіоритм
Емоційнийyбіоритм
1
1)yЗнайдітьyзначенняyкожноїyфункціїy(уy%)y11yгрудня.
2)yУкажітьyнайбільшеyзначенняyінтелектуальногоyбіоритмуy (уy%);yнайменшеyзначенняyфізичногоyбіоритмуy(уy%);yдні,yколиy вониyспостерігаються.
3)yВизначтеyпроміжокy(уyднях),yпротягомyякогоyзначенняyемоційногоyбіоритмуyзростають.
4)yВважаючи,yщоyнаyрис.y1yподаноyвашіyбіоритми,yвизначте,y уyякийyденьyкращеyнаписатиyконтрольнуyроботуyзyалгебри,y аyвyякийy—yузятиyучастьyуyспортивнихyзмаганнях?y Коментар до розв’язання
Значенняyемоційногоyбіоритмуyзростаютьyнаyпроміжкуyвідy1yдоy 15yгрудня:yграфікyвідповідноїyфункціїy«йде»yвгору,yзіyзбільшеннямy абсцисиyзбільшуєтьсяyордината.yГоворять,yщоyнаyданомуyпроміжкуy функціяyзростає.yАyнаyпроміжкуyвідy15yдоy25yгрудняyбачимо,yщоy графікy«йде»yвниз,yзіyзбільшеннямyабсцисиyординатаyзменшується.y Говорять,yщоyнаyцьомуyпроміжкуyфункціяyспадає.
Графічна інтерпретація
означення 1
y
f(x2)
f(x1)
Графічна інтерпретація
означення 2
y x 0 x1 x
f(x2)
таких що xx21 > ,
Інакше кажучи, на деякому проміжку: y функція зростає, якщо
Рис. 2
fx() ↑ при xx ∈−[] ∈+ ∞ [ ) 21 5 ;, ; ; fx() ↓ при xx ∈− ∞− ( ] ∈[] ;,21;
РОЗМИНКА 1
Визначте проміжки зростання та
Для доведення зростання або спадання функції на проміжку зазвичай діють за алгоритмом.
Алгоритм доведення зростання (спадання) функції yfx = () на певному проміжку I
1. Вибрати x1 і x2 з проміжку I, такі що xx21 > .
2. Знайти значення функції yfx = () у вибраних точках yfx11 = () і yfx22 = () .
3. Записати різницю yy21 і спростити отриманий
4. Визначити знак різниці yy21 .
5. Зробити висновок на основі означення:
Доведемо, що функція ykxb=+ :
1) є зростаючою на R при k > 0 ; 2) є спадною на R при k < 0 .
Доведення
Доведемо першу частину твердження (випадок k > 0 ).
1. Виберемо точки x1 і x2 з області визначення функції, такі що xx21 > .
2. Для xx12 , ∈ R маємо: ykxb11=+ , ykxb22=+ .
3. Тоді yykxbkxbkxkxkxx 21 21 21 21 −= +− + () =− =−() .
4. Якщо xx21 > , то xx21 0 −> ; оскільки k > 0 , то yy21 0 −> , тобто yy21 > .
5. Отже, для xx21 > маємо: yy21 > . Тоді за
функція ykxb=+ є
Наразі, шукаючи ці значення, будемо орієнтуватися на
ПРИКЛАД 1
Користуючись графіком функції yfx = () , визначеної на проміжку
1312 ; (рис. 4), знайдіть:
а) проміжки зростання та проміжки спа
дання цієї функції; б) найбільше та найменше значення функції на проміжку: 1) 13 3; ; 2)
1312 ; ; 3) 69 ;
.
Розв’язання
КРОК 1
Визначимо проміжки, на яких функція зростає (тобто
спадає (тобто на яких графік «йде» вниз).
КРОК 1
КРОК 2
КРОК 3
та найменше значення функції на проміжку
Знайдемо н айбільше т а н айменше з начення функції
Проміжки зростання функції: y ↑
Проміжки спадання
Найбільше значення
Найбільше значення 8; найменше значення –4
2
КРОК 1 Зазначимо, що проміжок −∞ () ;3 входить
означенням yx() ↓спадає
КРОК 2
КРОК 5
⇒− < xxx 12 1 33
,; ∈− ∞
Проаналізуємо знаки виразів у чисельнику й знаменнику та з’ясуємо знак отриманого
дробу. 1) xxxx 12 12 0 <⇒ −< ; 2) xxx 12 1 33 0 ,; ∈− ∞
⇒−
і x2 30−< . Таким чином, xx2133 0 () () >⇒ . Отже, ⇒ () () () < 2 33 12 21 0 xx xx . Маємо: yxyxyxyx 21 21 0 () () <⇒ () < ()
КРОК 6 Зробимо висновок. xx21 > за умовою, yxyx 21() < () за доведеним, отже, задана функція спадає при x ∈− ∞ () ;3 . Твердження доведено
ПРИКЛАД 3
На рис. 6 зображено графік зміни температури Т повітря (у °С)
протягом перших 10 днів листопада. Значення температури, які спостерігалися щодня о 12:00, позначено точками, сполученими плавною кривою. Користуючись графіком, дайте відповіді на запитання.
1) Якою була температура повітря 3 листопада?
2) Якою була найвища температура повітря протягом 10 днів? У який день вона спостерігалася?
3) Якою була найнижча температура повітря протягом 10 днів? У який день вона спостерігалася?
4) Укажіть проміжки часу (у днях), протягом яких температура
повітря:
а) знижувалася; б) підвищувалася.
Розв’язання
1)
1
3)
КРОК 1




нм
Функцією є залежність інтенсивності фотосинтезу від спектрального складу світла. За її графіком можна






1)yyЯкеyзначенняyобсягуyспоживанняyгарячоїyводиy(уyл/год)y спостерігалосьyоy16:00?
2)yyЯкимyбувyнайбільшийyобсягyспоживанняyгарячоїyводиy (уyл/год)yпротягомyдоби?yОyкотрійyгодиніyцеyспостеріyгалось?y
3)yyЯкимyбувyнайменшийyобсягyспоживанняyгарячоїyводиy (уyл/год)yпротягомyдоби?yОyкотрійyгодиніyцеyспостеyрігалось?y
4)yyУкажітьyпроміжкиyчасуy(уyгод),yпротягомyякихyобсягyспоживанняyгарячоїyводиyзбільшувався.y
4 yНаyрис.y8yточкамиyпозначеноyщомісячнуyкількістьyзапитівy






1)yyЯкийyвідсотокyкористувачівyзафіксованоyпошуковоюyсисте
2)yyЯкоюyбулаyмаксимальнаyкількістьyзапитівy(уy%)yуyпо
3)yyЯкоюyбулаyмінімальнаyкількістьyзапитівy(уy%)yуyпошуковійy
4)yyЯкщоyкількістьyзапитівyперевищуєy60y%,yтоyрозглядаєть
1 yЗнайдітьyзначенняy m,yприyякихyфункція:
1)y ymx = 2 yєyзростаючою;y3)y ymx =− + 54 yєyзростаючою;
2)y ymx =−() 1 yєyспадною;y4)y ymx =+ 9 1 2 yєyзростаючою;
5)y ymx =+() 26 13 yєyзростаючою;
6)y ymxmx=− −+ 45 yєyспадною.
2 yПобудуйтеyграфікyфункції:yy
1)y
yКористуючисьyграфіком,yукажітьyнуліyфункції,yпроміжкиyїїy знакосталості,yпроміжкиyзростанняyтаyспадання,yнайбільшеy таyнайменшеyзначенняyфункції.
3 yНакреслітьyграфікyфункції,yякщо:
1)yфункціяyвизначенаyнаyпроміжкуy
63 ; ,yїїyнулямиyєyчислаy–6,y0,y2;yфункціяyзростаєyнаyпроміжкахy
спадаєyнаyпроміжкуy
21 ; ;
2)yобластьyвизначенняyфункціїy
4
62 ; yіy 13 ;
,y
3;71 ;yїїyнулямиyєyчислаy–7,y –5,y13;yпроміжкиyспаданняy
70 ; ,y 3;91
,yпроміжокyзростанняy 09 ;
;yy y 915() = y—yнайбільшеyзначення,y y 04() =− y—y найменшеyзначенняyфункції.
Задача «Телевізійний маркетинг».yІзyметоюyвпровадженняyтелевізійногоyмаркетингуyбулоyпроведеноyдослідження.yНаyрис.y9y наведеноyграфіки,yщоyвідображаютьyзмінуyкількостіyглядачівy(уy%)yдвохyрейтинговихyтелеканалівy Аyіy Вyпротягомyвечірньогоyчасуyзy20:00yдоy22:00.
1)yСкількиyглядачівy(уy%)yдивилисяyтелеканалy Аyоy20:00?
2)yСкількиyглядачівy(уy%)yдивилисяyтелеканалy Вyоy21:40?
3)yОyкотрійyгодиніyкількістьyглядачів,yякіyдивилисяyтелеканалy А,yбулаyнайбільшою?yЯкоюyсаме?y
4)yОyкотрійyгодиніyкількістьyглядачів,yякіyдивилисяyтелеканалy В,yбулаyнайменшою?yЯкоюyсаме?y
5)yЯкyзмінюваласяy(збільшуваласяyчиyзменшувалася)yкількістьy глядачів,yякіyзy20:40yдоy21:40yдивилися:yа)yтелеканалy А;y б)yтелеканалy В?
6)yТелеканалy Вyтранслювавyсоціальнуyрекламуyвyтойyчас,yколиy кількістьyглядачівyперевищувалаy80y%.yyУyякийyпроміжокy часуyцеyвідбувалося?y
Лінійна функція ykxb=+ є зростаючою на R при k > 0 , є спадною на R при k < 0 .

ВІДОМО ВАМ?
— компанія, що використовує інтернетсервіси






Функція yfx = () , яку задано графічно (рис. 10), визначена на проміжку
1 За рис. 10 знайдіть найбільше значення функції
2
3
4
5 Серед поданих
6
Установіть відповідність між початком речення (1–3) та його закінченням (А–Г) так, щоб утворилося правильне твердження.
1 Функція yx =− 2
2 Функція yx=− 2
3 Функція y = 2 А не має нулів. Б спадає на проміжку −∞ +∞ () ; .
В має два нулі.
Г зростає на проміжку −∞ +∞ () ; . 7 На рис. 11 зображено графік зміни температури T повітря (у °С) протягом однієї доби.
1) Якою була найвища температура повітря
2)
вмикається, як тільки температура повітря на вулиці перевищує 25 °С, та вимикається, якщо температура повітря на вулиці стає нижчою від 25 °С. Визначте проміжок часу, протягом якого кондиціонер працював.
Доведіть, що функція y x = 1 1 спадає на проміжку 1; +∞ () .
Поміркуйте,yчиyєyподаніyтвердженняyправильними.yВідповідьy обґрунтуйте.
1)yЯкщоyфункціяy yfx = () yспадаєyнаyпроміжкуy 05 ; () ,yтоy ff14() < () .
2)yЯкщоyфункціяy yfx = () yзростаєyнаyпроміжкуy () 51 ; іy f () > 40 ,yтоy f () > 20 .
3)yЯкщоy Ef() =− 47 ; ,yтоyнайбільшеyзначенняyфункціїy yfx = () дорівнюєy7.
4)yЯкщоyнайменшеyзначенняyфункціїy yfx = () yдорівнюєy2yнаy проміжкуy
33 ; yіy f 02() = ,yтоy f 32() > .
5)yЯкщоy ff13() < () ,yтоyфункціяy yfx = () yзростаєyнаyпроміжкуy 13 ;
.
MATH FOR LIFE
Гоночнийyавтомобіль,yрухаючисьyкільцевоюyтрасою,yнаyякійy немаєyпідйомівyтаyспусків,yпроїхавyкількаyкіл.yДляyдругогоyколаy побудованоyграфікyзалежностіyшвидкостіyавтомобіляyвідyвідстані,y пройденоїyвідyлініїyстартуy(рис.y12).y
1 yЯкоюyбулаyнайбільшаyшвидкістьyавтомобіляyпідyчасyпроходженняyдругогоyкола?
2 yНаyякійyвідстаніyвідyпочатковоїyточкиyколаyшвидкістьyавтомобіляyбулаyнайменшою?yЯкоюyбулаyцяyшвидкість?
3 yЯкyзмінюваласяyшвидкістьyавтомобіляyнаyпроміжкуyтрасиy [2,5;y2,75]?yЯкоюyбулаyнайменшаyшвидкістьyнаyцьомуyпроміжку?
4 yУкажітьyпроміжкиyтрасиy(уyкм),yнаyякихyшвидкістьyавтомобіля:y 1)yзменшувалася;yy2)yзбільшувалася;yy3)yзалишаласяyсталою.
5 yЯкийyвиглядyмалаyтрасаy(рис.y13,yА–Д),yпоyякійyрухавсяyавтомобільy(точкаy Sy—yлініяyстарту)?yЗвернітьyувагу:yводійyпередy поворотомyзавждиyзменшуєyшвидкістьyавтомобіля.

12






Ларрі (Лоуренс) Пейдж (Larry Lawrence Page ; нар. 1973) і Сергій Брін (Sergey Brin; нар. 1973) —












3
1)
2)
4)
4 На рис. 16 точками позначено ціну (у грн) 1
у певному супермаркеті протягом одного тижня (понеділок неділя). Для наочності точки сполучено відрізками. 1) Скільки коштував 1 кг лимонів у неділю?
2) У який день тижня ціна 1 кг лимонів була найбільшою? Визначте цю ціну.
3) У який день тижня ціна 1 кг лимонів була найменшою? Визначте
5 yНаyрис.y17yзображеноyграфікyзміниyтемпературиy Тy(уy °С)yморськоїyводиyбіляyузбережжяyпротягомyпершихy10yднівyсерпня.y Значенняyтемператури,yякіyспостерігалисяyщодняyоy12:00,yпозначеноyточками.
1)yЯкоюyбулаyтемператураyводиy8yсерпня?
2)yyЯкоюyбулаyнайбільшаyтемператураyводиyпротягомy10yднів?y Уyякийyденьyвонаyспостерігалася?y
3)yyЯкоюyбулаyнайменшаyтемператураyводиyпротягомy10yднів?y Уyякийyденьyвонаyспостерігалася?y
4)yyОленаyнеyкупаєтьсяyвyморі,yякщоyтемператураyводиyменшаy відy18y °С.yУyякіyдніyдівчинаyнеyкупалася?
Бонусні завдання
6 yВизначтеyнайбільшеyцілеyзначенняyзмінноїym,yприyякомуyфункціяy ymx =−() + 5113 yспадає.
7 yВизначтеyнайменшеyцiлеyзначенняyзміноїy n,yприyякомуyфункціяy ynx =−() 72 1 yспадає.
8 ВідомийyамериканськийyматематикyСтівенyСтрогацyуyсвоїйy книжціy«Задоволенняyвідy х.yЗахоплюючаyподорожyуyсвітyматематикиyвідyодногоyзyнайкращихyвикладачівyуyсвіті»yнаводитьy цікавіyприкладиyдляyпоясненняyматематичнихyідей.yОдинyізy нихy—yілюстраціяyзаyдопомогоюyграфіківyпосиленняyйyпослабленняyпочуттівyРомеоyіyДжульєттиy(рис.y18).y(Зауважимо,yщоy авторyдещоyзмінивyхарактерyїхyвзаємин.)
yСпробуйтеyпроаналізуватиyзмінуyвідносинyцієїyпариyвyрізніyперіодиyчасу,yвикористовуючиyзнанняyпроyвластивостіyфункцій.






IQ




TO BE SMART
Дізнатися багато цікавого про історію розвитку Google можна: y прочитавши книжку Д. А. Вай



та М. Малсіда «Google. Прорив у дусі часу» («The Google Story: Inside the Hottest Business, Media, and Technology Success of Our Time»); y переглянувши фільми «Погляд зсередини: Google»(«Inside: Google», 2010) та «Google і

мозок» («Google and the World Brain», 2013).

















МАЙБУТНЯ ПРОФЕСІЯ






Робототехнік — професія ХХІ століття. Спеціалісти в цій галузі займаються створенням та обслуговуванням роботів і мають добре знати механіку, електроніку, програмування. Українські розробники Макс Метц і Микола Богун створили



Керуванняyроботомпорохотягомyможнаyздійснюватиyдистанційно.yНехайyзаразyпорохотягyрозташованийyуyточціy Axy00 ; () прямокутноїyсистемиyкоординатy хОуy(рис.y1).yЗаyдопомогоюyджойстикаyможнаyпримуситиyйогоyрухатисяyвздовжyосіy Oхyуправоyчиy влівоyабоyвздовжyосіy Oуyвгоруyчиyвниз.yНаприклад,yроботпорохотягyможеyпереміyститисяyзyточкиy Аyвyточку:
1)y В,yякаyрозташованаyнаy2yодиниціyправоручyвідyточкиy А; 2)y С,yякаyрозташованаyнаy3yодиниціyліворучyвідyточкиy А; 3)y D,yякаyрозташованаyнаy1yодиницюyвищеyзаyточкуy А; 4)y Е,yякаyрозташованаyнаy4yодиниціyнижчеyвідyточкиy А.
Якyзмінюватимутьсяyкоординатиyпорохотягаyвyкожномуyвипадку?y
Коментар до розв’язання Підyчасyрухуyвправоyвздовжyосіy Охyабсцисаyбудеyyзбільшуватисяy іyвyточціy B yстанеyбільшоюyнаy2yодиниці,yтобтоyдорівнюватимеy x0 2 + .yАyвнаслідокyрухуyвлівоyнаy3yодиниціy(уyточкуy C)yабсцисаy становитимеy x0 3 .yПриyцьомуyпідyчасyкожногоyзyцихyпереміщеньy ординатаyзалишитьсяyнезмінною.y
Аналогічно,yякщоyрухyвідбуватиметьсяyзyточкиy Ayвздовжyосіy Оуyвгоруyдоyточкиy Dyабоyвнизyдоyточкиy E,yабсцисаyнеyзміниться,y аyординатаyдорівнюватимеyвідповідноy y0 1 + yтаy y0 4 .y
Виникаєyпитання:yякyпідyчасyтакихyпереміщеньyзмінюватимутьсяyабсцисиyтаyординатиyнеyоднієїyточки,yаyмножиниyточок,y наприкладyмножиниyточокyграфікаyфункції?
Розглянемо,yякyзаyдопомогоюyграфікаyфункціїy
Зyкурсуy6yкласуyвиyзнаєте,yщоyyмодульyчислаy а y—yвідстаньy (вyодиничнихyвідрізках)yвідyпочаткуyвідлікуyдоyточкиyзyкоординатоюy а .yЦеyозначенняyрозкриваєyгеометричнийyзмістyмодуляy (рис.y2).yПригадаємоyалгебраїчнеyозначенняyмодуляy(рис.y3).
Означення. Модуль числа а (або абсолютна величина числа а) дорівнює числу а, якщо а — додатне число або нуль, і числу, протилежному а, якщо а — від’ємне число.
Побудуємоyграфікyфункціїy yx = ,yвикористовуючиyправилоy розкриттяyзнакаyмодуля:
Алгоритм побудови графіка функції yx =
1.yПобудуємоyграфікyфункціїy yx = y(рис.y4).
2.yПриy x 0 yмаємоy xx = ,yотже,y yx = → yx = .yТомуyрозглядаємоyтількиyтуyчастинуyграфіка,yякаyрозташованаy вyІyкоординатнійyчвертіy(рис.y5).
3.yПобудуємоyграфікyфункціїy yx =− y(рис.y6).
4.yПриy x < 0 yмаємоy xx =− ,yотже,y yx = → yx =− .yТомуyрозглядаємоyтількиyтуyчастинуyграфіка,yякаyрозташованаy вyІІyкоординатнійyчвертіy(рис.y7).
5.yВyоднійyсистеміyкоординатyпобудуємоyграфікиyфункційy yx = yдляy x 0 yтаy yx =− yдляy x < 0 y(рис.y8),yтобтоy об’єднаємоyчастиниyграфіків,yзображенихyнаyрис.y5yіy7.y Отриманаyфігураyіyєyграфікомyфункціїy yx = .


турі, техніці,



ПЕРЕМІЩЕННЯ ВЗДОВЖ ОСІ Ox
Покажемо, як із графіка функції yx = 2 можна отримати графік функції yx=+() 2 2 . Висунемо припущення: щоб
отримати графік функції yx=+() 2 2 , графік функції yx = 2
слід перенести вліво вздовж осі Ox на 2 одиниці. Доведемо цей факт.
Нехай точка Axy00 ; () належить графіку функції yx = 2 ,
тобто yx00 2 = . Доведемо, що точка Axy 10 0 2 () ; належить
графіку функції yx=+() 2 2 . Підставимо координати точ
ки A1 у формулу yx=+() 2 2 , отримаємо: yx00 2 22=−() + () ,
або yx00 2 = , що є правильною рівністю. Таким чином, графік
функції yx=+() 2 2 проходить через точку Axy 10 0 2 () ; .
Отже, всі точки графіка функції yx=+() 2 2 можна отри
мати, якщо кожну точку графіка функції yx = 2 замінити
a одиниць уліво, якщо a > 0 ; 2) на a одиниць управо, якщо a < 0
У таблиці подано базовий графік (пунктиром) і графік, отриманий унаслідок його паралельного перенесення вздовж осі Ox. Проаналізуйте, як змінюються координати точок графіка функції yfx = () унаслідок його перетворення в графік
1
yx = 2 . Складемо таблицю значень функцій yx = і yx = 2
й знака k.
Функція
Перетворення fxkfx () →⋅
РОЗМИНКА 3
1 Знайдіть координати точки, у яку переміститься точка A2;11() графіка функції yfx = () , якщо
отримали графік функції: 1) yfx = () 3 ; 2) yfx = () 1 4 ; 3) yfx =− () 6 ; 4) yfx = () 3 .
2 При яких a точка Aa;36 () належить
1) yx =−12 ; 2) yx = 1 4 2 ; 3) yx = 9 ; 4) yx =−6 ?
yfxa = () +
yfxa =+()
Паралельне перенесення графіка функції yfx = ()
уздовж осі Оy:
на a одиниць угору, якщо a > 0 ;
на a одиниць униз, якщо a < 0
Паралельне перенесення графіка функції yfx = ()
уздовж осі Ох:
на a одиниць уліво, якщо a > 0 ;
на a одиниць управо, якщо a < 0
графіка функції yfx = () у k
МОМЕНТ Унаслідок перетворення fxkfx () →⋅ () абсциса
xyxya 0000 ;;() →+() , x стала
xyxay 00;;00() →−() , y стала
ykfx =⋅ ()
yfx =− ()
xyxy 00;;00() →−() , x
1
2
КРОК 2
Побудуємо
КРОК 3
Вертикальна асимптота (x = 0, тобто вісь Oy)
також переноситься на 2 одиниці вліво (x = –2).
Графік, отриманий на кроці 2, паралельно перенесемо на 1 одиницю вниз.
Горизонтальна асимптота (y = 0, тобто вісь Ox)
також переноситься на 1 одиницю вниз (y = –1).
Шуканий графік зображений синім кольором.
ТРЕНУЄМОСЯ
2 Побудуйте графік функції: 1) y x = + 1 2 ; 4) y x =+ 1 3 2 ; 7) y x x = −+() + 12 1 1 ; 2) y x = 1 3 ; 5) y x =+ 2 1 3 ; 8) y x x = +−()13 2 2 .
3) y x =− + 1 2 1 ; 6) y x =+ + 2 3 1 ; ЗВЕРНІТЬ УВАГУ! Правила побудови графіків функцій yfxa = () + , yfxa =+() , ykfx =⋅ () , yfx =− () за допомогою геометричних перетворень — с. 135, 144.
2
ПРИКЛАД 3
рис. 13 зображено графік функції,
виду yaxmn =+() + 2 . Знайдіть значення
ману формулу.
КРОК 1 Графік проходить через точку () 32 ; , яка є вершиною параболи yaxmn =+() + 2 . () mn ;
−= m 3 ,m = 3 ; n = 2 КРОК 2 Запишемо формулу yaxmn =+() + 2 для m = 3 і n = 2 . yax=+() + 32 2
КРОК 3
Рис. 13 y x 0 1 1 Щоб побудувати параболу yaxmn =+() + 2 , можна паралельно перенести параболу yax = 2 так, щоб її вершина перемістилася в точку () mn ;
4
точку () 20 ; . Підставимо
3 За рисунками, на яких зображено фрагменти
yfx = () , знайдіть:
1) значення a, якщо yxa =+ 2 ; 2) значення a, якщо yxa =+ 2 ; 3) значення a, якщо yxa=+()2 ; 4) значення a, якщо yxa=+()2 ; y x
5) значення a і b, якщо ybxa =+()2 ; 6) значення a і b, якщо ybxa =+()2 ;
7) значення a, b і c, якщо ybxac =+() + 2 ; 8) значення a, b і c, якщо ybxac =+() + 2 . y x
1 yГрафікомyфункціїy yfx = () yєyвідрізокy АВy(рис.y14).yЗнайдітьy координатиyкінцівyвідрізка,yякийyєyграфікомyфункції:
1)y yfx = () 4 ;yy3)y yfx=−() 2 ;y5)y yfx =⋅ () 3 ; 2)y yfx = () + 2 ;yyyy4)y yfx=+() 1 ;yy6)y yfx =⋅ () 1 5 .
2 yНаyрис.y15y( а ,y б )yзображеноyграфікyфункціїy yfx = () .yПобудуйтеyграфікиyфункцій:y yfx = () + 3 ;y yfx = () 2 ;y yfx=−() 1 ;y yfx=+() 4 ;y yfx =− () 4 ;y yfx=−() + 32 .
3 yВикористовуючиyграфікyфункціїy yx = 2 ,yпобудуйтеyграфікy функції:
1)y yx=− 2 4 ;y 3)y yx=−32 2 ;y5)y yx=+()24 2 ; 2)y yx =− + 2 1;yy4)y yx=− 1 2 2 3 ;y6)y yx =− () + 23 1 2 .
4 yВикористовуючиyграфікyфункціїy y x =− 4 ,yпобудуйтеyграфікy функції:
1)y y x = 4 ;y 3)y y x =− + 4 2 ;y5)y y x =+ 4 1 3 ; 2)y y x =− 4 2 ;y 4)y y x =+ 4 2 ;yy6)y y x =− + 3 4 2 .
5 yВикористовуючиyграфікyфункціїy yx = ,yпобудуйтеyграфікy функції:
1)y yx=+ 2 ;y 3)y yx=− 5 ;y5)y yx =− 62 ; 2)y yx =− 3 ;y4)y yx =− + 4 ;y6)y yx=− + 1 2 23.
6 yВикористовуючиyграфікyфункціїy yx = ,yпобудуйтеyграфікy функції:
1)y yx=− 3 ;y 3)y yx =− 1 2 ;y5)y yx=− + 32 ; 2)y yx =− + 5 ;y4)y yx =− + 31 ;y6)y yx=+32 1.
7 yПобудуйтеyграфікyфункціїy yx =− () + 14 2 yтаyзнайдітьyзаyграфіком:y1)yобластьyзначеньyфункції;y2)yнуліyфункції;y3)yпроміжкиyзнакоyсталості;y4)yпроміжкиyзростанняyіyспаданняyфункції;y 5)yнайбільшеyзначенняyфункції.
8 yВизначтеyграфічнимyспособомyкількістьyкоренівyрівняння:








1
2
3
4
Поміркуйте,yчиyєyподаніyтвердженняyправильними.yВідповідьy обґрунтуйте.
1)yЯкщоy x = 5 yєyнулемyфункціїy yfx = () ,yтоy x = 1 yєyнулемyфункціїy yfx=+() 4 .
2)yЯкщоy x = 0 yєyнулемyфункціїy yfx = () ,yтоy x = 3 yєyнулемyфункціїy yfx = () 3 .
3)yЯкщоyпроміжокy 4;21 y—yобластьyзначеньyфункціїy yfx = () ,y тоyпроміжокy 17 ; y—yобластьyзначеньyфункціїy yfx = () 1 2 .
4)yЯкщоyпроміжокy 67 ; y—yобластьyвизначенняyфункціїy yfx = () ,yтоyпроміжокy 45 ;
y—yобластьyвизначенняyфункціїy yfx=−() 2 .
5)yЯкщоyфункціяy yfx = () yзростаєyнаyпроміжкуy 38 ;
ціяy yfx = () + 1 yзростаєyнаyпроміжкуy 49 ;
.

MATH FOR LIFE
Керуванняyквадрокоптеромyможнаyздійснюватиyдистанційно.y Наyрис.y21yзображеноyпланyмісцевостіyсафаріпаркуy(видyзгори).y Лінія,yзаданаyфункцієюy yfx = () ,y—yтраєкторіяyпольотуyпершогоy квадрокоптераyпідyчасyзйомки.y
Рис. 21 y x 0 1
yfx = ()
1 yПобудуйтеyвyнаведенійyсистеміyкоординатy xOyyтраєкторіїyпольотівyчотирьохyіншихyквадрокоптерів,yякщоyціyтраєкторіїy заданоyфункціями: y1)y yfx=−() 1 ;yyyyy3)y yfx=+()13 ; y2)y yfx = () + 2 ;yyyyyyy4)y yfx=−() + 21.
(Вважайте,yщоyвсіyквадрокоптериyрухалисяyнаyрізнійyвисоті.)y 2 yТраєкторіяyякогоyзyчотирьохyквадрокоптерівyпройшлаyнадyродиноюyлеопардів,yякуyнаyпланіyпозначеноyточкоюy L?





П’єр де Ферма (франц. Pierre de Fermat, 1601–1665) — видатний французький математик,













1)yзначенняy a, якщоy yxa =+ 2 ;
1 yПобудуйтеyграфікyфункції:
2 yПобудуйтеyграфікyфункції:
3 yЗаyрисунками,yнаyякихyзображеноyфрагментиyграфіківyфункційy yfx = () ,yзнайдіть:
2)yзначенняy
4


TO BE SMART






ремуyВієтаyіyнеyобчислюючиyдискримінант:
повторили основні
Залежність змінної y від змінної x називають функцією, якщо кожному значенню x за деяким правилом ставиться у відповідність єдине значення y.
• yfx = () функціональна залежність y від x (правило);
• x аргумент (незалежна змінна);
• y функція (залежна змінна).
Область визначення функції множина всіх значень незалежної змінної (аргумента).
Область значень функції (або множина значень функції) множина всіх значень, яких набуває залежна змінна.
Наприклад: Dy() область визначення функції y; Ey() область значень функції y.
2 Ви познайомилися з такими властивостями функції, як нулі функції, проміжки знакосталості, проміжки зростання та спадання функції, навчилися їх знаходити.
Нулем функції називають значення
аргумента, при якому значення функції дорівнює нулю.
• Нулі функції абсциси то
чок перетину графіка функції з віссю абсцис.
• Нулями функції yfx = ()
є корені рівнянняyfx = () = 0.
Проміжки зростання функції
Функцію називають зростаючою на деякому проміжку I, якщо для будьяких
двох значень x1 і x2 з цього проміжку, таких щ о xx21 > , виконується нерівність fxfx 21() > () . Тобто якщо більшому
значенню аргумента відповідає більше
значення функції.
Якщо функція зро
стає на всій області
визначення, її називають зростаючою.
Проміжком знакосталості функції називають кожний із проміжків, на якому функція набуває значень одного знака.
Проміжками знакосталості є проміжки максимальної довжини, на якихyfx = () > 0 абоyfx = () < 0.
Проміжки спадання функції Функцію називають спадною на деякому проміжку I, якщо для будьяких двох значень x1 і x2 з цього проміжку, таких що xx21 > , виконується нерівність fxfx 21() < () . Тобто якщо більшому значенню аргумента відповідає менше значення функції.
Якщо функція спадає на всій області визначення, її називають спадною.
Алгоритм знаходження нулів функції yfx = () , заданої аналітично
1. Знайти Dy() область визначення заданої функції.
2. Розв’язати рівняння fx() = 0 на Dy() .
3. Записати у відповідь знайдені корені рівняння fx() = 0 , які і є нулями функції.
1.
2. Розв’язати нерівності y < 0 і y > 0 на Dy() .
3. Записати у відповідь
Алгоритм доведення зростання (спадання) функції yfx = () на певному
1. Вибрати x1 і x2 з проміжку I, такі що xx21 > .
2. Знайти значення функції yfx = () у вибраних точках yfx11 = () і yfx22 = () .
3. Записати різницю yy21 і спростити отриманий вираз.
4. Визначити знак різниці yy21 .
5. Зробити висновок:
yfxa = () +
Паралельне перенесення графіка функції yfx = () уздовж осі Oy: • на a одиниць угору, якщо a > 0 ;
• на a одиниць униз, якщо a < 0 .
ykfx =⋅ ()
• Розтяг
функції yfx = () у k разів уздовж
Oy, якщо k > 1 .
Стиск
функції yfx = () у 1 k разів уздовж
функції.
I
yfxa =+()
Паралельне перенесення графіка функції yfx = () уздовж осі Ox: • на a одиниць уліво, якщо a > 0 ; • на a одиниць управо, якщо a < 0 .
Oy, якщо 01 << k . yfx =− ()
1
2
y x 0 1
1 Відповіді та інший варіант роботи: interactive.ranok.com.ua
2) Укажіть проміжки часу (у год), протягом яких споживання холодної
збільшувалося.
8 Використовуючи графік функції yx = , побудуйте графік функції yx =− 3 .
9 Доведіть, що функція y x = 6 3 спадає на проміжку 3; +∞ () .
10 Побудуйте графік функції yx=−()31 2 та знайдіть за графіком: 1) область значень функції; 2) нулі функції; 3) проміжки знакосталості функції; 4) проміжки спадання та зростання функції.
Бонусне завдання Визначте графічним способом кількість коренів рівняння xx=− 1 .
споживання, л/год















АКТУАЛЬНА ЗАДАЧА
Змоделюємоyрухyкенгуруyпідyчасyстрибка.yПриймемоyтваринуy заyматеріальнуyточкуy(вамyвідомийyцейyприйомyзyуроківyфізики).y Траєкторіюyцьогоyрухуyможнаyзмоделюватиyграфікомyфункціїy yxx =− + 0080 8 2 ,, y(рис.y1).yМісце,yзyякогоyкенгуруyстрибнув,yєyпочаткомyкоординат.yТодіy хy—yвідстаньy(уyм)yпоyгоризонталіyміжy поточнимyположеннямyточкиyтаyпочаткомyкоординат,y уy—yвідстаньy (уyм)yпоyвертикаліy(висота,yнаyякійyперебуваєyточка).y
1)yНаyякуyнайбільшуyвисотуyпідняласяyнадyземлеюyматеріальнаy точкаy—yмодельyсправжньогоyкенгуру?
2)yЧиyможеyцейyкенгуруyперестрибнутиyпарканyзаввишкиy3yм?
3)yНаyякуyнайбільшуyвідстаньyстрибнувyкенгуру? yxx =− + 0080 8 2



членом,yтомуyдануyфункціюyприйнятоyназиватиy








ВАМ?

Парабола в геометрії d P
Парабола — множина всіх точок, рівновіддалених від даної точки (на рисунку точка F ) і даної прямої (пряма d ), що не містить цієї точки. Точку F

фокусом параболи

ПРИГАДАЙТЕ!
Графіком функції виду yaxmn =+() + 2 є парабола
вершиною в точці () mn ; .
1 yВизначте,yчиyєyквадратичноюyфункціяy
СЛІД ЗНАТИ! КЛЮЧОВІ ТЕРМІНИ
Розглянемоyфункціюy yxx =− 2
.yЇїyграфікyможнаyпобудувати,yзастосувавшиyдоyграфікаyфункціїy yx = 2 yвідоміyвамyгеометричніy перетворенняy(див.y§y11).yВиділимоyквадратyдвочленаyуyправійy частиніyрівностіy yxx =− +− 2 69 12 yіyзапишемоyфункціюyуyвиглядіy yx=−()312 2 .yОтже,yграфікомyфункціїy yxx =− 2 63 yєyпараболаy зyвершиноюyвyточціy2;31() ,yвіткиyпараболиyнапрямленіyвгору.y
Графікyфункціїy yaxbxc =+ + 2 a ≠ () 0 yможнаyотриматиyзyграфікаyфункціїy yax = 2 a ≠ () 0 yшляхомyгеометричнихyперетворень.
З’ясуємо,yякихyсаме.yРозглянемоyфункціюy yaxbxc =+ + 2 .y Уyтричленіy axbxc 2 ++ yвинесемоyзаyдужкиyмножникy a,yоскількиy
Розкриємоyдужкиyтаyскоротимоyдрібyуyдругомуyдоданку:


Отже,yфункціюy
КЛЮЧОВИЙ МОМЕНТ Якщоyкоординатиyвершиниyпараболиy
сатиyуyвиглядіy xyвв ; () ,yтоy x b a в =− 2 ,y y bac a в =− 2 4 4 ,yyаyфункціюy yaxbxc =+ + 2 yможнаyподатиyуyвиглядіy yaxxy =−()
Графікyфункціїy yaxbxc =+ + 2 yможнаyпобудуватиy
метричних перетвореньyзаyтакимyпланом:y yax = 2
xв yод.yприy xв > 0
влівоyнаy xв yод.yприy xв < 0
Графіком функції yaxbxc =+ + 2 є
ці xyвв ; () , де x b a в =− 2 , y bac a в =− 2 4 4 .
y


yод.yприy yв > 0 внизyнаy yв yод.yприy yв < 0
Уy8yкласіyвиyпознайомилисяyзyпоняттямyдискримінантаyквадратногоyрівняння:y Dbac =− 2 4 .yЦейyвиразyназиваютьyтакожy дискримінантом квадратного тричлена axbxc 2 ++ .
y Формулуy y bac a в =− 2 4 4 yможнаyзаписатиyякy y D a в =− 4 .y y Ординатуyвершиниyпараболиyможнаyзнайти,yпідставившиyзначенняy xx = в yуyформулуy yaxb









Серед численних креслень Леонардо да Вінчі зустрічається креслення параболічного компаса.


Oy.yТочкаyперетинуyмаєy ординатуy yabcc 00 0 2 () =⋅ +⋅ += .yТобтоy координати точки
параболи з віссю ординат —y 0; c () y(рис.y2).
Параболаy yax = 2 yсиметричнаyвідносноyосіy Oy,yтобтоyвідносноy прямої,yякаyпроходитьyчерезyвершинуyпараболи.yЦеyозначає,yщоy віткиyпараболиyєy дзеркальними відображеннямиyоднаyодноїy(дзеркалоyрозташованеyнаyосіy Oy).y
Підyчасyвиконанняyгеометричнихyперетвореньyграфікаyфункціїy yax = 2 ,yзокремаyйогоyпереміщенняyвздовжyосіyабсцисyвлівоyабоy вправоyтаyвздовжyосіyординатyугоруyабоyвниз,yвісьyсиметріїyтакожy
кроками алгоритму побудови параболи без використання геометричних перетворень
сті. (Послідовність кроків може змінюватися.)
Крок___
Знайти (за необхідно
сті) додаткові «зручні»
точки графіка (точку, симетричну точці 0; c () відносно осі симетрії
параболи, або інші до
вільні точки, що належать графіку).
Крок___
Знайти
5
1 yaxmn =+() + 2 2 axbxc 2 0 ++ = 3 yaxxxx =−() ()12

ЧИ ВІДОМО ВАМ?




Парабола в природі. Квіти, що живуть в умовах браку сонячного проміння (полярний мак тощо), розкривають пелюстки у формі параболоїда, що допомагає їм акумулювати тепло.

ритмом (див. с. 152). Розв’язання
Скористаємося правилом: якщо графік функції проходить через точку, то її координати перетворюють формулу, якою задано функцію, у правильну
рівність. Складемо рівняння для обох заданих точок. A () 5;21 , 15 42 1 =− + ab ; K 0;31 () , 10 93 1 =+ + ab КРОК 2 Складемо систему з одержаних на кроці 1 рівнянь та розв’яжемо її.
КРОК 3
Значення a і b визначено, запишемо формулу, якою задано функцію. yxx
за алгоритмом.
1) yxbx =+ 2 , A () 0;21 ; 3) yxxc =− ++ 2 4 , A () 39 ; ;
2) yxbx =− + 2 , A 36 ; () ; 4) yxxc =+ + 2 2 , A6;21() ;
5) yxbxc =+ + 2 , M 25 ; () , N () 2;13 ;
6) yxbxc =− ++ 2 , M () 2;31 , N 2;11 () ;
7) yaxbxc =+ + 2 , M 0;02 () , N 1;11 () , K () 5;13 ; 8) yaxbxc =+ + 2 , M1;04() , N1;12() , K () 9;16 .
ПРИКЛАД 3 (актуальна задача )
Змоделюємо рух кенгуру під час стрибка. Приймемо тварину
за матеріальну точку. Траєкторія її руху може бути змодельована
графіком функції yxx =− + 0080 8 2 ,, , побудованим у системі коор
динат, де початком координат є місце, з якого кенгуру стрибнув. Тоді х — відстань (у м) по горизонталі між поточним положенням точки та початком координат, у — відстань (у м) по вертикалі (висота, на якій перебуває точка).
1) Побудуйте

ПЕРЕРВА НА ЛОГІКУ Знайдіть закономірність і вставте пропущені числа.
Тихий океан


Безодня Челленджера yxx =− + 2 1772 (__; __)
ГімалаїЕверест yxx =− + () ()24 (__; __)


Розв’язу ючи задачі практичного змісту, ви можете отримати дуже великі або дуже малі значення величин. Це створює незручності під час побудови графіків функцій. У таких випадках креслять ескізи графіків, які відображають вла стивості функції, проте до
1)
КРОК 1
КРОК 2
Знайдемо
КРОК 3 Визначимо
3)

ЧИ ВІДОМО ВАМ?

а) На яку найбільшу ширину
мостом можна було користуватися?
б) На яку найбільшу висоту піднімається
4) Залежність кількості q (у шт.) сорочок, проданих протягом
Парабола в архітектурі Інженерні розрахунки свідчать, що архітектурні споруди у формі параболи (мости, арки) мають підвищену міцність.




Місячний міст, СанФрациско, США







Параболічний більярд є механічною моделлю, яка ілюструє оптичну властивість параболи. А саме: промінь, що пройшов паралельно осі параболи, після відбиття від параболи потрапляє в її фокус.


Одна зі стінок більярду має форму параболи, в її фокусі розташовано лузу для кульки. З гірки, яку можна переміщувати перпендикулярно до осі параболи, скочується кулька. У будьякому положенні гірки кулька завжди котиться паралельно осі параболи і завжди потрапляє в лузу.

Готуємося до ДПА

Міст Ракотцбрюке, Німеччина
ПРИГАДАЙТЕ!
Dbac =− 2 4 — дискримінант квадратного тричлена axbxc 2 ++ ; xв — абсциса вершини параболи.
3 Знайдіть:
1) значення a і b, при яких числа 2 і 1 3
yaxbx =+ + 2 2 ;
2) значення m і n ,
яких
функції yxmxn =+ + 2 проходить через точки () 1;22 і 34 ; () ;
3) значення b, при якому проміжок 4; +∞
стання функції yxbx =−21 2 ;
4) значення m, при якому проміжок −∞ ( ;2 є проміжком спадання функції yxmx =− ++ 1 3 2 2 ;
5) значення c, при якому ордината
yxxc =− + 24 2
6) значення a,
yaxx =− + 22 2
1) a > 0 , D > 0 , c < 0 , xв > 0 ; 4) a < 0 , D < 0 , xв









Томас Алва Едісон (англ. Thomas Alva Edison, 1847–1931) — всесвітньо відомий американський винахідник, підприємець. Саме йому ми завдячуємо створенням першого вдалого варіанта електричної лампи розжарювання, електровоза, фонографа тощо. Він удосконалив телеграф, телефон (а також запропонував починати телефонну розмову словом «алло») та багато іншого.

ЗНАЮ, ВМІЮ, МОЖУ
САМОСТІЙНА РОБОТА № 8 Відповіді та інший варіант роботи: interactive.ranok.com.ua Готуємося до ДПА

ЧИ ВІДОМО ВАМ?





Франк Шуман (1862–1918), відомий американський винахідник, побудував у Єгипті у 1912–1913 рр. першу сонячну термальну електростанцію. Зараз його ідеї використовуються під час побудови сучасних параболічних електростанцій.


можна змоделювати графіком функції yxx =− + 3 4 2 3 . Місце, з якого акробат стрибнув, є початком координат. Тоді х — відстань (у м) по горизонталі між поточним положенням точки й початком координат, у — відстань (у м) по вертикалі від підлоги спортзалу (висота, на якій перебуває матеріальна точка).
1) Побудуйте графік заданої функції, якщо x ∈
04 ; .
2) Визначте, на яку найбільшу висоту

МАЙБУТНЯ ПРОФЕСІЯ





Спеціалісти зі спецефектів добре знають математику. Координати, вектори, тривимірний простір, алгоритми — і ось унаслідок математичних розробок на екрані монітора мчить торнадо або спалахує полум’я.


Див. приклад 1
MATH FOR LIFE
Див. приклад 2

ЧИ ВІДОМО ВАМ?




Струмінь води у фонтані має форму параболи, що залежить від кута, під яким струмінь випускається. Оптимальними є кути 50°–60°

1) yxbx =− + 2 , A () 18 ; ;
2) yxxc =+ + 2 4 , A () 57 ; ;
3) yxbxc =− ++ 2 , M () 5;21 , N0;32() ;
4) yaxbxc =+ + 2 , M 0;04 () , N 6;12 () , K () 8;15 .
мулою rppq
графік функції: 1) yx=− 2 4 ; 2) yxx =− + 2 12 .
5 Знайдіть
1) функція yxxa =− + 34 2
значеннях x;
2) функція yxxa =− −+23 2






Футбольний м’яч летить по параболічній траєкторії, форма якої залежить від того, з якою швидкістю і під яким кутом до горизонту вдарено по м’ячу. Саме у виборі цих параметрів і полягає мистецтво футболіста.


IQ

TO BE SMART




Академія Хана — міжнародна освітня мережа, заснована Салманом Ханом. Його короткі освітні відеоуроки присвячені різним предметам і темам. Навчання проходить у формі комп’ютерної гри — там є підказки, бали, рівні... Усі завдання розподілено на модулі. Ви можете побачити графік особистого прогресу. Дізнайтеся більше: www.youtube.com/ KhanAcademyUkrainian






Ви розв’язували лінійні нерівності, будували графіки квадратичних функцій, визначали їх нулі та проміжки знакосталості





Ви ознайомитеся з двома способами розв’язування квадратних нерівностей — графічним та аналітичним





Ви зможете прогнозувати прибутки підприємства залежно від запропонованих моделей маркетингу, оцінювати висоту стрибка спортсмена тощо

ЧИ ВІДОМО ВАМ?







Бокінг (від англ. bocking) — новий вид екстремального спорту, а саме пробіжки та стрибки на ходулях із пружинами — джамперах. На джамперах можна виконувати стрибки заввишки 2 м і завдовжки 6 м, пересуватися кроками в 3–4 метри, розвиваючи швидкість до 40 км/год. Бокінг стає дедалі популярнішим у світі, виникають бокерські клуби, проводяться збори бокерів з Європи та Америки.


y
сті fx() > 0 або fx() < 0 . Для квадратичної функції ці нерівності мають вигляд axbxc 2 0 ++ > і axbxc 2 0 ++ <
(рис. 2).
У тричлені xx 2 23+− старший коефіцієнт a = 1 — додатне
число, отже, вітки параболи напрямлені вгору. Графік функції
перетинає вісь Оx в точках із абсцисами x1 3=− та x2 1 = , значення функції yxx =+ 2 23 в цих точках дорівнює нулю, тобто x1 3=− та x2 1 = — нуліфункції.
Графік функції розташований
() 31 ; , тобто функція yxx =+ 2 23 на цьому
функції
ках −∞ () ;3 і 1; +∞ () , тобто функція yxx =+ 2 23 на цих проміжках набуває додатних значень. Проаналізувавши графік функції, запишемо проміжки її знакосталості, тобто знайдемо множини розв’язків квадратних нерівностей xx 2 23 0 +− < і xx 2 23 0 +− > :
y xx 2 23 0 +− < при x ∈−() 31 ; ;
y xx 2 23 0 +− > при x ∈− ∞− () +∞ ();; 31 ∪ .
Зауважимо, що координати вершини параболи
ходити не потрібно.
Отже, для розв’язування квадратних нерівностей графічним способом достатньо:
y схематично зобразити розміщення графіка
враховуючи напрям віток параболи і
функції; y визначити за графіком проміжки знакосталості функції. Наявність і кількість нулів функції визначає положення параболи yaxbxc =+ + 2 відносно осі абсцис. Можливі шість випадків залежно від знака дискримінанта D квадратного тричлена axbxc 2 ++ і знака коефіцієнта a. Знак aD > 0 xx12 ≠ () D = 0 xxx 12== () в D <
1) yxx =− + 2 6 ;
2) yxx =+ + 2 51 ;
3) yaa =− + 2 27 ;
4) ytt =− +− 2 10 ;
5) yaa =− + 41 2 ;
6) yaa =− +− 2 2
способом.
2.
ПРИКЛАД 1
Розв’яжіть нерівність xx 2 7100−+ > графічним способом.
Розв’язання
Крок
КРОК 1
КРОК 2
Введемо функцію yaxbxc =+ + 2 , де axbxc 2 ++ — квадратний тричлен, що стоїть у лівій частині заданої нерівності. yxx =− + 2 710
Визначимо напрям віток параболи, яка є графіком отриманої функції.
параболи напрямлені
ру, оскільки a = 1, тобто a > 0
КРОК 3 Знайдемо нулі функції. xx 2 7100−+ = ; x1 2 = , x2 5 = — нулі функції
Схематично зобразимо параболу, враховуючи
КРОК 4
умовою xx 2 7100−+ > .
Відповідь: x ∈− ∞ () +∞ ();; 25 ∪ .
ТРЕНУЄМОСЯ
1 Розв’яжіть графічним способом нерівність: 1) 10 2 x ; 4) 50 2 xx ; 7) xx 2 412−< ; 2) x 2 90−< ; 5) −+xx 2 69 0 ; 8) xx 2 67 + . 3) xx 2 0 +> ; 6) xx 2 21 0 −+ > ;
() ;2
() 24 ;
Якщо x <−2 , то x −<40 , x +<20 , Висновок:xx () + () > 42 0 .
Якщо −< < 24 x , то x −<40 , x +>20 .
Висновок:xx () + () < 42 0 .
Якщо x > 4 ,
4; +∞ ()
то x −>40 , x +>20 .
Висновок: xx() + () > 42 0 .
тричлена на всьому
Якщо x =−3 , то xx 2 2 28 32 38 7 =−() () −= , 70 > .
2 28 0 > .
Якщо x = 0 , то xx 2 2 28 02 08 8 = () −⋅ () −= , −<80 .
Висновок:xx 2 28 0 < .
Якщо x = 5 , то xx 22 28 52 58 7 =− = , 70 > . Висновок:xx 2 28 0 > . Для запису розв’язків нерівності xx 2 28 0 > слід
−∞ () ;2 і 4; +∞ () .
1. Для заданої нерівності
2 ++ .
2. Якщо корені існують: y зобразити корені на числовій прямій, тобто розбити
проміжки точками, що відповідають знайденим кореням; y на кожному проміжку визначити знак тричлена axbxc 2 ++ ; y обрати проміжки, на яких значення функції має знак, що відповідає знаку нерівності.
3. Якщо коренів немає, врахувати, що знак квадратного тричлена axbxc 2 ++ є сталим і збігається зі знаком старшого коефіцієнта a.
4. Записати відповідь, урахувавши знак нерівності.
РОЗМИНКА 2
1 Розв’яжіть аналітичним способом нерівність: 1) xx + () () < 37 0 ; 4) 62 34 0 () () > xx ; 7) x 2 70 + ; 2) xx() + ()13 0 ; 5) x 2 16 0 ; 8) x + () < 50 2 . 3) 25 34 0 xx + () () ; 6) x ()30 2 ;
2 Зведіть задану нерівність
1) −+ −< xx 2 10 0 ; 3) 40 1 2 2 > xx ; 5) −> 1 4 2 1 x ; 2) 50 2 xx ; 4) 02 0 2 , xx ;
Перетворимо
КРОК 2
КРОК 3
КРОК 4
Розіб’ємо числову пряму отриманими числами на проміжки та з’ясуємо
заданої нерівності «більше», виберемо проміжки зі знаком «+».
розв’язок нерівності. Точки x = 1 і x = 2 не входять у визначені проміжки, тому найменший натуральний розв’язок
−< xx 2 7120 () () < xx34 0 ; xx() () < 34 0 . Відповідь: x ∈ () 34 ; . xx 2 7120−+ > ; xx() () > 34 0 : Відповідь: x ∈− ∞ () +∞ ();; 34 ∪ .
xx 2 8160++ x + ()40 2 ; x + 40 ; x 4 .
Відповідь: x ∈− +∞ ) 4; .
xx 2 69 0 −+ > x () > 30 2 .
Нерівність x () > 30 2
виконується для всіх значень х,
тобто х — будьяке число.
x + ()40 2 .
Нерівність x + ()40 2 виконується для всіх значень х, тобто х — будьяке число.
Відповідь: x ∈− ∞+ ∞ () ; .
Відповідь: x ∈− ∞+ ∞ () ; . x () > 30 2 .
xx 2 44 0 ++ x + ()20 2 .
Розв’язків немає.
Відповідь: ∅ .
xx 2 34 0 ++ > D =− ⋅⋅ =− 34 14 7 2 .
Оскільки D < 0 , то розв’язків немає.
Відповідь: ∅ .
x 2 49 0 x 2 49 ; x 7 .
Відповідь: x ∈− ∞ ( ;7 .
x 2 25 0 x 2 25 ; x 5 .
Відповідь: x ∈+ ∞ ) 5; .
При x = 3 маємо x () = 30 2 ,
отже, x ≠ 3 .
Відповідь: x ∈− ∞ () +∞ ();; 33 ∪ .
x + ()20 2 .
Нерівність x + ()20 2 виконується при єдиному значенні x =−2 .
Відповідь: x =−2 , або {} 2 .
Оскільки старший коефіцієнт — додатне число і D < 0 , то для будьякого значення х ліва частина нерівності — додатне число.
Відповідь: x ∈− ∞+ ∞ () ; .
xx() + ()77 0 ; 77 x .
Відповідь: x ∈− 77 ; .
xx() + ()55 0 ; x 5 , x 5 .
Відповідь: x ∈− ∞− ( +∞ ) ;; 55 ∪ .
4 Розв’яжіть аналітичним способом нерівність:






більше зерна, ніж вирощують кави в усьому світі.
y Кількість меду, який експортує Україна, є такою, що кож ний мешканець Фінляндії може куштувати щодня по 1 чайній ложці меду протягом 6 місяців!


y Перший рамковий вулик винайшов український бджоляр Петро Прокопович у 1814 р.

У нерівностях, ліва частина яких записана у вигляді добутку, нулі функції yfx = () зручніше шукати як корені xx = 1 і xx = 2 рівняння xxxx() () = 12 0 .
Готуємося до ДПА
ПРИГАДАЙТЕ!
y Формула розкладання квадратного тричлена на лінійні множники:
axbxcaxxxx 2 12 ++ =−() () ,
де x1 , x2 — корені квадратного тричлена.
y a b , b ≠ 0 ;
y x , x 0 ;
y 1 x , x > 0 .
6) −< 49 20 2

ЗНАЙДІТЬ ПОМИЛКУ x () < 316 2 ; x −<34 ; x < 7 ;


x ∈− ∞ () ;7

1
2









Вірджинія (Джинні) Рометті (англ. Virginia (Ginni) Rometty, нар. 1957) — голова ради директорів, президент і генеральний директор компанії IBM, перша жінка, яка стала головою компанії. На думку Вірджинії, розвиток інформаційних технологій, зокрема технології точного аналізу та прогнозів, сприяє прийняттю максимально ефективних рішень.


МАЙБУТНЯ ПРОФЕСІЯ


Маркетологи — спеціалісти, які здійснюють аналітичну роботу з вивчення смаків покупців та розробляють концепцію просування товару на ринку. Маркетологи повинні мати аналітичні здібності, вміти мислити творчо й нестандартно, втілювати в життя свої ідеї.


1) Якщо x1 10=− і x2 4 =
ною розв’язків нерівності xbxc 2 0 ++ < є проміжок () 10 4; .
2) Якщо функція yxbxc =+ + 2
3)
4)
5)
Див. приклади 1–3
MATH FOR LIFE
для прогнозування прибутків запропоновано дві математичні моделі, засновані
Модель А має вигляд yxx =− 85 2 , ,
В має вигляд yx = 15 , , де x — кількість
5
1) 2180 2
2)
3)
4) −+ + 38 30 2 aa , середнє

Бонусні завдання
нерівність:
xxx 2 69 0 −+ ()
1) xkx 2 25 0 ++ = ; 3) 32 32 0

TO BE SMART


В Україні діють курси бізнесу для підлітків, засновані на принципі відомої програми Master of Business Administration (магістр бізнесадміністрування).




Навчаючись в інтерактивній формі за програмою «Школа бізнесу МВА для підлітків», ви зможете вивчити основи маркетингу, продажів, реклами, набути практичних навичок за цими напрямами, поглибити свої знання з окремих тем, прослухавши додаткові курси. Дізнайтеся більше: centerbalu.com.ua/ua_shkola_ biznesa_mba_dlya_podrostkov/

Квадратична функція — функція, що задається
формулою виду yaxbxc =+ + 2 , де x — незалежна змінна, a, b, c — деякі числа, причому a ≠ 0 . Графік квадратичної функції — парабола.
Вітки параболи yaxbxc =+ + 2 напрямлені: вгору при a > 0 ; вниз при a < 0 .
Графік завжди перетинає вісь Oy в точці 0; c () . Алгоритм побудови графіка квадратичної
1. Визначити напрям віток параболи.
2. Знайти абсцису вершини параболи.
; () : yaxbxc =+ + 2
b a D a24 ; yaxmn =+() + 2 () mn ; n)
yaxxxx =−() ()12 xyx xx вв в = ()
3. Записати рівняння осі симетрії параболи: xx = в .
4. Знайти ординату вершини параболи.
5. Знайти нулі функції (якщо вони існують). Записати координати точок перетину з віссю Ox.
6. Знайти точку перетину графіка функції з віссю Oy.
7. Знайти (за необхідності) додаткові «зручні» точки графіка.
8. Позначити знайдені точки на координатній площині та сполу
+ 12 2 ; y x 0 x2 l a > 0 x1 c y
x2 l x1 c yв xв a < 0
y > 0 при x ∈− ∞+ ∞ () ; , y < 0 не існує
2
1. Для заданої нерівності розглянути відповідну функцію yaxbxc =+ + 2 .
2. Визначити напрям віток параболи та нулі функції.
3. Схематично зобразити параболу, враховуючи її розташування відносно осі абсцис.
4. Визначити проміжки знакосталості функції ( y > 0 , y < 0 ).
5. Записати відповідь, урахувавши знак нерівності.
Алгоритм розв’язування квадратних нерівностей (аналітичний спосіб)
1. Для заданої нерівності знайти корені відповідного квадратного тричлена axbxc 2 ++ .
2. Якщо нулі існують: • зобразити корені на числовій прямій; • на кожному проміжку визначити знак тричлена axbxc 2 ++ ;
• вибрати проміжки, на яких значен-
3. Якщо
4. Записати відповідь. Розв’язки
1
2
3
1)
нерівність 05 15 0 2 ,, xx+− . y x 0 1 1
2)
4















Ви ознайомитеся з графічним та аналітичним способами розв’язування систем двох рівнянь із двома змінними, з яких хоча б одне рівняння — другого степеня Ви зможете розробляти схеми туристичних маршрутів, визначати місцезнахо
дження людей, розташування на місцевості будьяких об’єктів
Визначте координати цих станцій. Коментардорозв’язання Координати точок перетину ліній можна визначити
редньо за рисунком. Проте цей спосіб не є точним. Щоб
точні значення координат, застосовують аналітичні способи роз
в’язування систем рівнянь. Система 23 0 47 64 22 xy xy −= += ; відрізняється від систем лінійних рівнянь тим, що
ГОЛОВНА ІДЕЯ ПРИГАДАЙТЕ!
пара чисел xy00 ; () , яка є розв’язком кожногозрівняньсистеми





Організувати роботу метрополітену допомагають математичні моделі формування вхідного пасажиропотоку станцій. Ці моделі дозволяють не тільки керувати потоками, а й прогнозувати їх.

1. Побудуємо в одній системі координат графіки обох рівнянь системи yx yx =− =− { 5 13 , .
2. З найдемо координати точок перетину графіків. y x 0 4 9 (9; 4)
1. Виразимо з одного рівняння системи змінну y через змінну x (або навпаки).
2. Підставимо цю змінну в інше рівняння системи: yx xx =− +−() =
5 513 , .
3. Розв’яжемо отримане рівняння з однією змінною: 25 13 x −= ; x = 9 .
4. Підставимо отримане значення x в перше рівняння системи: yx=− =− = 59 54 .
5. Запишемо відповідь: 94 ; () .
1. Додамо обидва рівняння системи почленно (окремо ліві та праві частини). Отримаємо: + −= += { = = xy xy x x 5 13 218 9 , , .
2. Підставимо отримане значення x в будьяке рівняння системи: yx=− =− = 59 54 ; y = 4 .
3.
відповідь: 94 ; () .
3. Запишемо відповідь: координати точки перетину графіків 94 ; () є розв’язком заданої системи рівнянь.
говорили про те, що перевагою графічного
іншими є наочність,
недоліком — неточність. Через цей недолік графічний спосіб не завжди є зручним для визначення розв’язків систем рівнянь. Але за допомогою графічного способу зручно визначати кількість розв’язків систем рівнянь.
РОЗМИНКА 2
З’ясуйте кількість розв’язків систем рівнянь, установивши відповідність між системами рівнянь (1–4) та їх
інтерпретаціями (А–Д). 1 xy xy




Методи розв’язування си стем рівнянь залежать від того, які рівняння входять у си стему.
y Системи лінійних алгебраїчних рівнянь розв’язують методами Крамера, Гауса, ітерацій тощо.
y Для си стем нелінійних рівнянь загального аналітичного розв’я зання не знайдено.

КРОК 3
КРОК 4
Перевіримо, чи є
рівняння системи.
30;,5 () , вітки напрямлені вниз, y 04() =− ; нулі функції:
1. Виразити одну змінну через іншу з одного рівняння системи.
2. Підставити отриманий вираз замість відповідної змінної в друге рівняння системи.
3. Розв’язати отримане рівняння з однією змінною — знайти один або декілька коренів (залежно від рівняння).
4. Підставити почергово кожний зі знайдених коренів рівняння у вираз, отриманий у п. 1.
5. Записати відповідь у вигляді пар значень змінних, знайдених у п. 3, 4.
Метод заміни змінної для розв’язування систем
на застосувати таким чином.
1) Або ввести одну нову змінну і використати заміну тільки в одному рівнянні системи.
Наприклад: для розв’язання системи
змінну
2) Або ввести
2.
3.
4.
КРОК 1
2
ПРИКЛАД 2 Розв’яжіть систему
Спосіб 1
КРОК 2
КРОК 3
КРОК 4
Добудемо квадратний корінь з
частин рівняння, отриманого на кроці 1, ураховуючи, що
незалежні системи рівнянь.
Розв’яжемо кожну систему способом підстановки.
шого рівняння.
КРОК 2
КРОК 3
Розглянемо перше рівняння системи.
рівняння, враховуючи ОДЗ





КРОК 4
n mn ≠ ≠ { 0,
нової змінної. Заміна: mn n t = , тоді n mnt = 1 ; t t += 1 2 ; tt t 2 21 0 0 −+ = ≠ , ; t = 1
Повернемося до початкових змінних. Утворимо систему з отриманого рівняння та другого рівняння початкової системи. mn n = 1 ; mnn −= , отже, mn = 2 ; mn mn = + () () =− 2 23 6 , ;
Розв’яжемо
рівняння. 22 36 nn + () () =− ; 26 26 6 2 nnn−+− =− ; 24 0 2 nn−= ; 22 0 nn() = ; n1 0 = або n2 2 =
1)
2)
3) має безліч розв’язків, якщо всі коефіцієнти рівнянь
ПРИКЛАД 4 Знайдіть
39
1) має єдиний розв’язок; 3) має безліч розв’язків. 2) не має розв’язків; Розв’язання
КРОК 1 1) Знайдемо значення m, при яких система рівнянь має єдиний розв’язок.
при змінних і використаємо умову a a b b 1 2 1 2 ≠ . m mm + ≠− 1 3 1 ; mmm
одне одному.

ЧИ ВІДОМО ВАМ?





Системи квадратних рівнянь із багатьма змінними застосовують у сучасній асиметричній криптографії. Щоб обчислити ключ, слід розв’язати систему рівнянь. Зі співвідношення кількості змінних і кількості рівнянь роблять висновок щодо надійності си стеми.

2)
ЗАВДАННЯ ІЗ ЗІРКОЮ
Поміркуйте,
1) Система рівнянь xy xy
2) Система рівнянь yx xy −= =− 2 2 3 3 , має
3) Якщо точка 14 ; () належить графіку функції yfx = () , то 14 ; () є розв’язком системи рівнянь xfx yx
ababaabb 33 22 −= () ++ ()
ababaabb 33 22 += + () −+ ()
abaabb () =− + 2 22 2
y Кількість розв’язків системи рівнянь дорівнює кількості точок перетину графіків рівнянь.
y Система рівнянь не має розв’яз ків, якщо графіки рівнянь не перетинаються.
y Система рівнянь має безліч розв’язків, якщо графіки або частини графіків рівнянь збігаються.









Алан Матісон Тюрінг (англ. Alan Mathison Turing, 1912–1954) — англійський математик, логік, криптограф, якого вважають батьком інформатики, теорії штучного інтелекту. Під час Другої світової війни Тюрінг брав участь у зламуванні німецьких шифрів, що застосовувалися в шифрувальній машині «Енігма». Найпрестижніша нагорода в галузі інформатики має назву «Премія Тюрінга».

систему рівнянь yx xy = += 2 5 22 , .
Б В Г 21 ; () , () 21 ; 12 ; () , 12 ; () 12 ;
4 Знайдіть значення m , при якому система
mxy xy += += { 5 25 , має безліч розв’язків.
значень
MATH FOR LIFE
ЗАДАЧА «ТУРИСТСЬКІ МАРШРУТИ» На рис. 9 зображено схеми двох туристських
xyy +− = 43 2 і yx−= 1 . Маршрут А має
рут В — прямої. У точках M і N перетину цих маршрутів
новано відпочинок.
1 Визначте координати точок M і N.
2 Який маршрут проходить через населений пункт, розташований в точці 03 ; () ?
3 Дві групи туристів, що рухаються за маршрутами A і B, зустрілися в точці N на відпочинку, а потім одночасно вирушили в напрямку точки M. За яким маршрутом рухається група, яка прийде в точку M раніше, якщо швидкості руху обох груп однакові? Відповідь поясніть. ДОМАШНЄ ЗАВДАННЯ




лівської премії з фізіології або медицини стали нейрофізіолог Джон О’Кіф та психологи Едвард Мозер і МейБрітт Мозер, які відкрили просторові клітини мозку, що відповідають за систему орієнтування в просторі — так звану «внутрішню GPS».

Див. приклад 2
Див. приклад 3
Див. приклад 4





ЧИ ВІДОМО ВАМ?

Координати місцезнаходження людини можна визначити за її мобільним телефоном. Коли надходить такий запит, усі базові станції, на яких реєструється телефон, за певними алгоритмами визначають відстань між своєю антеною та антеною телефону, утворюючи круг або сектор круга, у якому може перебувати абонент. Перетин цих кругів (дуг) дає приблизні координати абонента.




2) Довжина та ширина прямокутної ділянки дорівнюють x см та y см відповідно.
3)
4)


TO BE SMART


Радимо прочитати книжку Жуана Гомеса «Математики, шпигуни та хакери. Кодування та криптографія» (т. 2 багатотомного зібрання «Світ математики»).

Ця книжка допоможе поринути у світ кодування та шифрування, дізнатися історію секретних шифрів з точки зору математики.

дорівнює x км/год, другого — y км/год. Через 2 год автомобілі





Ви розв’язували системи рівнянь із двома змінними, а також задачі за допомогою квадратних і дробовораціональних рівнянь





Ви навчитеся розв’язувати задачі на арифметичні співвідношення між об’єктами, на рух, сумісну роботу та інші за допомогою систем двох рівнянь із двома змінними





Ви зможете складати математичні моделі реальних життєвих ситуацій
АКТУАЛЬНА ЗАДАЧА
Учні запитали вчителя математики: «Коли народився Льюїс
Керролл?». На це запитання вчитель відповів так: «Льюїс Керролл, англійський письменник, математик, автор книжки «Аліса в Країні Див», народився в перший місяць 1832 року. День його
народження виражається двоцифровим числом, у якого цифра
десятків на 5 менша від цифри одиниць. Сума квадратів цифр цього числа дорівнює 53». У який день народився Льюїс Керролл? Коментардорозв’язання
Нехай
дача зводиться до розв’язання системи двох рівнянь, одне з яких лінійне, а інше — рівняння другого степеня (найбільший степінь
одночлена, що входить до рівняння, дорівнює 2). Розв’язання актуальної задачі див. на сайті interactive.ranok.com.ua.
ГОЛОВНА ІДЕЯ
У курсі алгебри 7–8 класів ви розв’язували текстові задачі за допомогою лінійних, квадратних, дробовораціональних рівнянь та систем лінійних рівнянь. У 8 класі ви познайомилися з алгоритмом розв’язування текстової задачі за допомогою рівняння.
Аналогічний алгоритм застосовують і для розв’язування текстових задач за допомогою системи рівнянь. Алгоритм розв’язування текстової задачі за допомогою системи рівнянь
1. Проаналізувати умову задачі (основні величини, зв’язки
2. Створити математичну модель (у вигляді таблиці, рисунка, тексту тощо).
3. Скласти систему рівнянь до задачі.
4. Розв’язати отриману систему рівнянь.
5.
6.




y «Твій учитель — це не той, хто тебе вчить, а той, у кого вчишся ти». Ці слова належать американському письменнику та філософу Річарду Баху.
y Згадку про вчителя ми знаходимо ще в давньокитайського філософа Конфуція, який говорив, що основним завданням учителя є вміння відкривати нові знання учневі.

y 5 жовтня — Всесвітній день учителів, який відзначають майже у 100 країнах світу.

КЛЮЧОВІ ТЕРМІНИ математична модель задачі
аналіз умови задачі аналіз розв’язків системи рівнянь
алгоритм розв’язування задачі
Алгоритм розв’язування задачі за допомогою системи рівнянь
Аналіз умови задачі
Математична модель задачі
Система рівнянь
Розв’язування системи рівнянь
Аналіз отриманих результатів
Відповідь

ЧИ ВІДОМО ВАМ?


Число називають числом Сміта, якщо сума його цифр дорівнює сумі цифр розкладу цього числа на прості множники. Наприклад: 4 937 775 = 3 · 5 · 5 · 65 837. Сума цифр числа і сума цифр розкладу становить 42 . Числа Сміта: 4, 22, 27... Кількість чисел Сміта є нескінченною.


3)
4)
Складіть систему рівнянь для визначення довжин катетів трикутника та знайдіть їх. б) Знайдіть площу трикутника.
ПРИКЛАД 2
На двох фуршетних столах рядами викладено по 260 кана
пе (маленьких бутербродів). На другому столі кількість рядів
на 3 менша, а кількість канапе у кожному ряді на 6 більша, ніж
на першому столі. Визначте кількість рядів і кількість канапе
в кожному ряді на першому столі.
Розв’язання
1 Аналізуємо умову задачі Основнівеличини: кількість канапе в одному ряді на кожному
столі; кількість рядів канапе на кожному столі; загальна кількість
канапе на кожному столі.
Аналізкількостіканапеводномуряді: це невідомі величини, пов’язані певними умовами. Позначимо
ряді на другому столі x + 6 .
Аналізкількостірядівканапе: це також
умовами.
шому столі через y. Тоді кількість рядів
Аналіззагальноїкількостіканапенакожномустолі: щоб знайти цю
ряді на кількість рядів.
= + () () =
260 63 260 , .







У Середньовіччі школярі називали теорему Піфагора «pons asinorum», що означає «ослячий міст». Учнів, які запам’ятовували теорему, але не розуміли її, називали віслюками, адже вони не могли перейти через міст — теорему Піфагора.

на арифметичне співвідношення між об’єктами






Кейтеринг (від англ. cater — «поставляти провізію») — галузь громадського харчування, пов’язана з наданням послуг на віддалених точках і обслуговуванням різноманітних заходів. Різновидами кейтерингу, зокрема, є фуршет, кавабрейк, пікнік, барбекю, банкет тощо.

КРОК 1
КРОК 2
Розкриємо дужки в другому рівнянні, замінимо xy на 260 та спростимо друге рівняння.
Розв’яжемо отриману систему способом підстановки. xy xy = =− { 260 26 , ; 26 260 yy() = ; yy 2 3 130 0 = ; y1 13 = , y2 10=−



ЧИ ВІДОМО ВАМ?








Міжнародний чемпіонат математичних і логічних ігор дуже популярний у світі. Його проводить Французька федерація математичних і логічних ігор (La Federation Francaise des Jeux Mathema tiques , сайт www.ffjm.org ). Щороку в чемпіонаті беруть участь дорослі й діти більше ніж із 20 країн: учні 1–11 класів, студенти, аспіранти, спеціалісти будьякого віку. Учасникам пропонують низку творчих нестандартних задач, за результатами розв’язання яких визначаються переможці. У 2015 р. на чемпіонаті в Парижі 2ге місце у своїй віковій групі посів учень 4 класу Харківського НВК № 45 «Академічна гімназія» Володимир Чуб.



канапе на
столі y1 13 = . Тоді кількість канапе у
ряді на першому столі0:260132 = (канапе).
Відповідь: 13 рядів по 20 канапе.
реконструкції до кожного ряду додали по одному місцю, і загальна
ПРИКЛАД 3
Протягом
опрацьовує за 1 год кожний менеджер, якщо всі замовлення Андрій може опрацювати на 1,5 год швидше, ніж Максим?
Розв’язання 1 Аналізуємо умову задачі
Основнівеличини:
• швидкість опрацювання замовлень Андрієм (замовлень/год);
• швидкість опрацювання замовлень Максимом (замовлень/год).
Аналізшвидкостіопрацюваннязамовлень(замовлень/год). Нехай v1 — швидкість опрацювання замовлень Андрієм, а v2 — Максимом. Тоді час, протягом якого одне замовлення виконує
Андрій, дорівнює 1 1v год, Максим — 1 2v год.
2 Створюємо математичну модель задачі у вигляді





Перший інтернетмагазин Amazon.com заснував бізнесмен Джеффрі Безос у 1994 р. Спочатку на сайті продавалися лише книжки, згодом — аудіо та відеопродукція тощо.


Назва Amazon походить від назви найбільшої у світі річки — Амазонки, а Дж. Безос мріяв створити найбільший у світі магазин. Крім того, назва сайта, що починається літерою «А», потраплятиме у верхню частину алфавітного переліку ресурсів.

графічний спосіб y спосіб підстановки y спосіб алгебраїчного додавання

ЧИ ВІДОМО ВАМ?
Стіни (до 33%)
Втрати тепла в будинку Дах (до 12%)




Вентиляція (до 20%)
Вікна, двері (до 23%)


«Теплий дім» — ресурс, який містить інформацію щодо підвищення енергоефективності в наших житлових будинках. На цьому ресурсі можна:

y дізнатися про енергоефективні технології, обладнання;

y скористатися Калькулятором енергозбереження для обчислення обсягу заощаджень від енергоефективних заходів у своєму будинку: www.teplydim.com.ua/uk/ energy_saving_calculator.htm


задовольняють умову задачі. Відповідь: 9,6 і 8 замовлень за годину. ТРЕНУЄМОСЯ
Розв’яжіть задачу. 1) Дві бригади, що здійснюють роботи з утеплення фасадів, працюючи разом, виконують усе завдання за 6 год. За скільки годин може виконати це завдання кожна бригада, працюючи самостійно, якщо
2) Перший менеджер має оформити 80 замовлень, а другий
56 таких самих замовлень. Перший менеджер оформлював щогодини на 2 замовлення більше, ніж другий, а закінчив свою роботу на 1 год пізніше, ніж другий. Скільки замовлень оформлював кожний менеджер щогодини?
3) Кожна з двох бригад має оновити
оновлювала x бігбордів, друга бригада — y бігбордів.
Розв’язання 1 Аналізуємо умову задачі
Основнівеличини
АналізрухуЗоїтаЮрія:
• час руху Юрія до зустрічі





2 Створюємо
Відстань між ролердромом і кортом, км
Швидкість руху, км/год
y
3 Складаємо систему рівнянь Відстані, що пройшли Зоя
катання на роликах, який має всі необхідні пристосування. На ролердромі кожен може продемонструвати свою майстерність, а також взяти участь у змаганнях із ролерного спорту.



0,7
Ролерспорт поділяється на групи за видом роликових ковзанів і складається з більше ніж десятка різних підвидів (фристайл, слалом, спідскейтинг, стріт тощо). ПРИГАДАЙТЕ!
1) Розв’язуючи задачі за допомогою рівнянь, ви маєте знайти не просто корені рівняння, а розв’язок задачі. Тому важливо пам’ятати, що саме є шуканим у задачі. 2) Значення коренів можуть задовольняти ОДЗ рівняння, але не задовольняти умову задачі.

ЧИ ВІДОМО ВАМ?




y У селі Путрівка Васильківського району Київської області 1 вересня 2016 р. відкрилася «Школа майбутнього», яка більше нагадує сучасний артпростір.



y Найбільшу кількість учнів у школі було зафіксовано у 2003/2004 навчальному році в одному з міст Індії, у якому цього року до міської школи Монтессорі зарахували 27 911 учнів.
y Найдовший у світі урок тривав 54 години. Це була лекція з біології для 26 студентів однієї з вищих шкіл Австралії у квітні 2003 р.



на 10 км більшу, ніж коли йде пішки. Відомо, що на
швидше, ніж коли йде пішки. Запишіть систему рівнянь для визначення x і y. Знайдіть x і y. 2) Із міст А і В, відстань між якими 140 км, одночасно назустріч один одному вирушили два рейсові автобуси. Через 1 год вони зустрілись і, не зупиняючись, продовжили рух, не змінюючи
та мотоцикліста, вважаючи, що їх швидкості були постійними.
1 Знайдіть двоцифрове число, кількість одиниць якого на 3 більша за кількість десятків. Відомо, що добуток цього числа і суми його цифр, зменшеної на 2, дорівнює числу, яке в 4 рази більше за число, що складається з таких самих цифр, як і шукане, але записаних у зворотному порядку.
2 Для заповнення термального басейну використовують дві труби різного діаметра. Першого дня дві труби працювали одночасно й подали 14 м3 води. Другого дня працювала тільки труба меншого діаметра, яка подала 14 м3 води за час на 5 год довший, ніж першого дня. Третього дня подання води тривало стільки ж часу, скільки й другого дня: спочатку працювали дві труби, які подали разом 21 м 3 води, а потім працювала тільки труба більшого діаметра, яка подала ще 20 м3 води.
Знайдіть пропускну здатність кожної труби (у м3/год).
Дорозв’язання
Основні величини:
• x м3/год — пропускна здатність першої труби;
• y м3/год — пропускна здатність другої труби;
• xy + () м3/год — спільна пропускна здатність обох труб.
час = об’єм басейну (м3) пропускна здатність труби (м3/год)
3 Для виготовлення столових приборів майстерня використовує сплав міді та нікелю. Перший сплав
10
нікелю, а другий — 25 %. Скільки кілограмів другого сплаву слід змішати з 10 кг першого, щоб отримати
Теорема косинусів
abcbc 22 2 2 =+ cos
Знайдіть y.
Дорозв’язання
Основні величини:
s
• s2 — відстань, яку
ЗАВДАННЯ ІЗ ЗІРКОЮ
Поміркуйте, чи є
твердження правильними. Відповідь обґрунтуйте.









Давид Гільберт (нім. David Hilbert; 1862–1943) — німецький математикуніверсал, визнаний світовий лідер математиків у 10–20тих рр. XX ст., працював у багатьох галузях математики. Чимало вчених вважали себе учнями Гільберта, якого називали найчудовішим учителем математиків XX ст. У 1900 р. на Міжнародному конгресі математиків Гільберт оголосив список із 23 проблем, які, на його думку, належало розв’язати у ХХ ст.

Сьогодні більшість цих проблем уже розв’язано. Останньою проблемою зі списку Гільберта, яку було розв’язано, стала теорема Ферма. Учені не могли довести її понад 350 років.


1) Якщо велосипедист
2)
3)
4)
5)
MATH FOR LIFE
1
ЗНАЮ, ВМІЮ, МОЖУ
роботи: interactive.ranok.com.ua Готуємося до ДПА



ЧИ ВІДОМО ВАМ?

SAT Subject Test — тест із профільного предмета для вступу до вишів США. Такий тест із математики містить 50 запитань, на які слід відповісти за 1 год. Під час проходження цього те сту абітурієнтам не варто відгадувати відповіді, адже за неправильні відповіді знімаються бали.








Математичне моделювання почали застосовувати у спорті ще в 50х роках ХХ ст. Зараз у цій галузі працюють математики, інформатики й фізи ки різних спеціалізацій.



За даними спортсмена у стані спокою складають рівняння, за якими розраховують потрібні параметри при фізичному навантаженні. На основі цих моделей розробляють оптимальні стратегії тренувань.

Див. приклади 1, 2

МАЙБУТНЯ ПРОФЕСІЯ





У 2015 р. механікоматематичний факультет Київського національного університету імені Тараса Шевченка відзначив свою 75ту річницю. Факультет готує фахівців зі спеціальностей «математика», «статистика», «механіка» і щорічно проводить олімпіади для абітурієнтів. Дізнайтеся більше: mechmat.univ.kiev.ua


1)
2)
3)
за їх добуток. Знайдіть ці числа.
4) Периметр прямокутного
його
— 17 см. Знайдіть довжини катетів. Визначте площу трикутника.
2)
4)
4)
Розв’яжіть задачу за допомогою системи рівнянь.
1) Відстань від будинку Миколи до ставка дорівнює 6 км. Пішки Микола ходить зі швидкістю x км/год, а на велосипеді їде зі швидкістю y км/год. За 1 год хлопець долає на велосипеді відстань на 12 км більшу, ніж коли йде
пішки. Відомо, що на велосипеді хлопець доїжджає від
будинку до ставка на 40 хв швидше, ніж коли йде пішки.
Знайдіть x і y.
2) З міст А і В, відстань між якими 440 км, одночасно назустріч один одному вирушили два потяги. Через 2 год вони зустрілись і, не зупиняючись, продовжили рух, не змінюючи швидкості. Один потяг прибув до міста В на 44 хв раніше, ніж другий до міста А. Нехай швидкість першого потяга, що рухався з міста А до міста В, становить x км/год, а другого — y км/год. Знайдіть x і y.
3) Моторний човен пройшов 20 км проти течії річки та повернувся назад, витративши на весь шлях 3 год 45 хв. Наступного дня цей човен за 30 хв пройшов 8 км за течією річки. Знайдіть власну швидкість човна та швидкість течії.
4) З міста А до міста В, відстань між якими 420 км, вирушив автомобіль. Через 2 год після цього з міста В до міста А вирушив мотоцикліст, який зустрівся з автомобілем через 1 год після свого виїзду. Мотоцикліст долає відстань між містами А і В на 1 год 52 хв швидше, ніж автомобіль. Знайдіть швидкості руху автомобіля та мотоцикліста, вважаючи, що їх швидкості були постійними.
ВПРАВИ НА ПОВТОРЕННЯ
Знайдіть f 1 () , f 3 () , fn() , fn + () 1 , якщо:
1) fx x () = 9 ; 3) fxx () =−() 3 2 ; 5) fxx () =− 1 ; 2) fx x () =− 6 ; 4) fxx () =− 2 3 ; 6) fxx () =+ 6 .

ПЕРЕРВА НА ЛОГІКУ Спробуйте розв’язати задачу А. Ейнштейна.

1. Є 5 будинків, пофарбованих у різні кольори.

2. У кожному будинку мешкає одна людина певної національності (усі національності різні).



3. Кожна людина п’є певний напій, любить певну страву і має певну тварину.
4. Усі 5 осіб п’ють різні напої, люблять різні страви та мають різних тварин.
Питання: в кого є рибка?
Додаткові умови можна знайти на сайті interactive.ranok.com.ua



TO BE SMART



Задачі тисячоліття (Millennium Prize Problems) — це 7 математичних задач, розв’язання яких не знайдено протягом багатьох років. За розв’язання кожної з них Математичним інститутом Клея запропоновано винагороду в 1 млн доларів США. У 2002 р. Григорій Перель ман розв’язав одну з цих задач — гіпотезу Пуанкаре, але відмовився від винагороди.

Онлайнкалькулятор Desmos: desmos.com/calculator
Онлайнкалькулятор має інтерактивні інструменти:
y Повзунок зміна значень у ручному або автоматичному режимі;
y Масштабування зменшення / збільшення зображення; y Вибір точки визначення координат точок графіка.

в одній координатній площині (якщо необхідно — різними кольорами).
y Вводити символи можна з клавіатури комп’ютера або вбудованої клавіатури, встановивши англійську мову
Режим введення «числа» — «літери» змінюється за допомогою клавіш «ABC» і «123» на екранній клавіатурі.

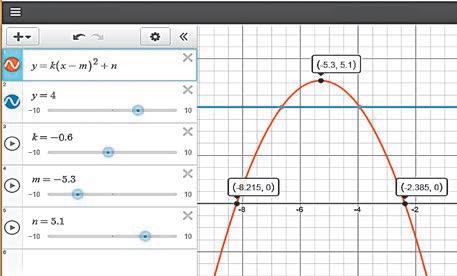

1
(рис. 1). 3. Натисніть кнопку «+» (Додати) та виберіть пункт Примітка. Введіть текст «табличне задання функції». Знов натисніть кнопку Додати та виберіть пункт Таблиця. Введіть у таблицю значення аргумента й функції. Перегляньте
2
1)
2)
3)
нерівностей або рівнянь, яких значень може набувати ордината вершини параболи залежно від кількості точок її перетину з колом.
ПРИКЛАД 2
Розв’яжіть графічним
1. Введіть
2.
3.
введіть рівняння yx =− + 2 4 . Перегляньте результат (рис. 5).
рівнянь має два розв’язки: () 13 ; і 04 ; () .
Відповідь: () 13 ; ; 04 ; () .
ПРИКЛАД 3
Знайдіть множину розв’язків системи
1. Введіть у поле для введення даних нерівність xy 22 4 + .
2. Натисніть кнопку Додати і введіть нерівність
гляньте результат
ТРЕНУЄМОСЯ
3 Перевірте за допомогою сервісу Desmos, чи правильно ви розв’язали завдання 2 «Інтелектуального фітнесу» в § 14 (с. 188).
4 Спробуйте «намалювати» веселе обличчя,
ючись підказками (рис. 7).
5
6



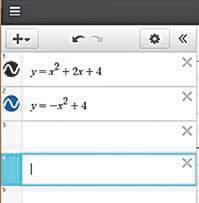

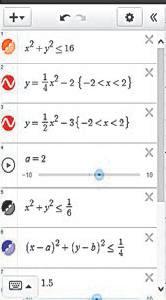
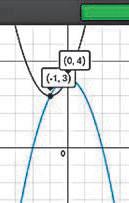


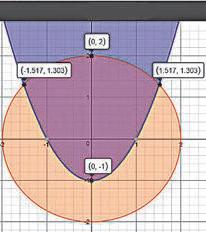

чисел xy00 ; () , яка є розв’язком кожного з рівнянь системи, тобто перетворює кожне з них у правильну числову рівність.
Алгоритми розв’язування системи двох рівнянь із двома змінними
Дві системи рівнянь називають рівносильними, якщо ці системи мають одні й ті самі розв’язки або не мають розв’язків. Графічний спосіб
1. Побудувати в одній системі координат графіки рівнянь системи.
2. Знайти спільні точки графіків (якщо вони є).
3. Записати у відповідь координати точок перетину графіків, які і є розв’язками системи.
Спосіб алгебраїчного додавання (аналітичний спосіб)
1. Прирівняти коефіцієнти при одній зі змінних шляхом почленного множення обох рівнянь на підібрані відповідним чином множники.
2. Додати (або відняти) почленно два рівняння системи.
3. Розв’язати отримане рівняння.
4. Підставити знайдене значення змінної в будьяке із заданих рівнянь.
Спосіб підстановки (аналітичний спосіб)
1. Виразити одну змінну через іншу з одного рівняння системи.
2. Підставити отриманий
3. Розв’язати
4.
розв’язування текстової задачі за допомогою системи рівнянь
1. Проаналізувати умову задачі (основні величини, зв’язки між ними, вимоги задачі).
2. Створити математичну модель (у вигляді таблиці, рисунка, тексту тощо).
3. Скласти систему рівнянь до задачі.
4. Розв’язати отриману систему рівнянь.
5. Проаналізувати отримані результати з огляду на умову задачі.
6. Записати відповідь.
Задачі на роботу Якщо V — обсяг роботи, p — продуктивність роботи, t — час, то: Vptpt V t V p == = ,, .
y Якщо працюють декілька людей, то про
дуктивності їхньої роботи додаються.
y Якщо обсяг роботи не зазначений, то його приймають за одиницю.
Задачі на рух
Якщо s — відстань, v — швидкість, t — час, то: svtvt s t s v == = ,, .
Задачі на рух по воді
Якщо v — власна швидкість плавзасобу у стоячій воді, a — швидкість течії, то: y v + a — швидкість плавзасобу за течією; y v – a — швидкість плавзасобу проти течії.
Схема задачі на запис числа Цифра десятків
1 Величина x менша у 2 рази від величини y.
Виразіть x через y. А Б В Г xy=+ 2 xy=− 2 x y = 2 xy = 2
2 Яка з наведених пар чисел є розв’язком си
стеми рівнянь xy xy += = 3 4 2 , ?
А Б В Г () 14 ; 41 ; () 12 ; () 21 ; ()
3 Розв’яжіть систему рівнянь yx xy −= = { 0 1 , . А Б В Г 11 ; () , () 11 ; 11 ; () , 11 ; () () 11 ; , 11 ; () 11 ; () , () 11 ;
4 У системі рівнянь 37 2 xyxy xyxy ++ =− + () = , здійснено
заміни axy = , bxy =+ . Яку систему рівнянь
отримали?
А Б В Г ab ab += += { 37 2 , ab ab += = { 37 2 , 37 2 ab ab += += { , 37 2 ab ab += = { ,
xy

ЗАСТОСОВУЄМО
Безліч явищ реального життя відбуваються за законами прогресій. Опанувавши цей розділ, ви зможете:
y розраховувати відсотки за банківськими вкладами, планувати виплати за кредитами; y укладати вигідні фінансові угоди, прогнозувати прибутки від бізнесу; y розв’язувати задачі з біологі ї та вірусології щодо визначення чисельності популяцій тварин, бактерій;
ШЛЯХОМ ДОСЛІДЖЕНЬ
y Послідовність простих чисел
y прогнозувати швидкість розповсюдження інформації в соціальних мережах, змінення чисельності населення, кількості абітурієнтів тощо;
y планувати фізичні навантаження під час тренувань;
y отримати початкові знання за темою «Числові та степеневі ряди» із дисципліни «Вища математика» для навчання в майбутньому. 3
y Числа та співвідношення Фібоначчі в природі, економіці, мистецтві, архітектурі, фотографі ї
y Формула Біне
y Золотий переріз
y Трикутник Паскаля
y Прогресії



















Піфагор




його учні розглядали послідовності, пов’язані з геометричними фігурами, викладаючи з камінців трикутники, квадрати, п’ятикутники та підраховуючи в них кількість камінців. Було отримано послідовності фігурних чисел:

y трикутних (1, 3, 6, 10, 15, );
y квадратних (1, 4, 9, 16, 25, …);
y п’ятикутних (1, 5, 12, 22, 35, …).

Фігурні числа в різні часи досліджували такі математики, як
Фібоначчі, П. Ферма, Л. Ейлер, К. Ф. Гаусс, О. Л. Коші та ін.

Платуyзаyорендуyапартаментівyнаyперіодyвідпочинкуyнарахо-
заyорендуyпротягомy nyдіб.
Кількість діб123456
Розв’язання
Проаналізуємоyвирази,yзаyякимиyможнаyзнайтиyвартістьyорендиy(уyг.yо.)yпротягомyпевноїyкількостіyдіб:y
заy1yдобуy—y50;yyyзаy4yдобиy—y 5030 3 +⋅ ; заy2yдобиy—y 5030 1 +⋅ ;yyзаy5yдібy—y 5030 4 +⋅ ; заy3yдобиy—y 5030 2 +⋅ ;yyзаy6yдібy—y 5030 5 +⋅ .
Отже,yформула,yзаyякоюyможнаyобчислитиyплатуy syзаyорендуy протягомy nyдіб,yмаєyвигляд:
sn =+ () 5030 1
щоденнаyоплата,y
стартовийy
внесок
починаючиy зyдругоїyдоби
кількістьyдіб,y заyвиняткомy першоїyдоби
Якщоyзамістьy nyпідставитиyнатуральніyчисла,yотримаємоy«серію»yчисел:
n = 1 → s = 50 ;
Уyповсякденномуyжиттіyмиyпостійноyмаємоyсправуyізyпослідовностями.y Наприклад:
• послідовністьyгодинyуyдобі,yднівyуyтижніyабоyмісяцівyуyроці;
• послідовністьyстанційyметроyабоyзупинокyавтобуса;
• послідовністьyкроківyабоyвправyнаyтренуванніyтощо.
Уyцьомуyпараграфіyмиyрозглянемоyчисловіyпослідовності.
Числова послідовність — це розміщені в певному порядку числа, або впорядкований
Наприклад:
• послідовністьyнатуральнихyчисел:y1,y2,y3,y…;
• послідовністьyпростихyчисел:y2,y3,y5,y7,y11,y13,y…;
• послідовністьyпарнихyчисел:y2,y4,y6,y8,y…y.
Числа,yщоyутворюютьyпослідовність,yназиваютьy членами послідовності.yКожнийyчленyпослідовностіyпозначаютьyлітероюy зyіндексом,yщоyвказуєyйогоy порядковий номер (можнаyвикористовуватиyрізніyбукви).
Наприклад:
1)y a1 ,y a2 ,y a3 ,y…,y a1000 ,y…;y2)yb1,yb2,y…,yb50,y…;y3)yx1,yx2,y…,yx200,y…y. Членyпослідовності,yномерyякогоyдорівнюєy n ,yназиваютьy n-м членом послідовності іyзаписуютьyсимволомy n-гоyчлена, наприклад:an .
Послідовністьyприйнятоyпозначатиyсимволомy n-гоyчлена,yвзятимyуyдужки.y Наприклад,yпослідовностіy an () ,y bn () ,y xn () : an () :y1,y2,y3,y4,y...;yотже,y a1 1 = ,y a2 2 = ,y a4 4 = ; bn () :y–15,y–5,y5,y15,y25,y...;yотже,y b1 15=− ,y b5 25 = ; xn () :y2,y2,y2,y2,y2,y2,y...;yотже,y x1 2 = ,y x2 2 = ,y
РОЗМИНКА 1
yЗаданоyчисловуyпослідовністьy an () :y–24,y–16,y–8,y0,y8,y16,y24.y
1)yНазвітьyперший,yчетвертийyіyшостийyчлениyпослідовності.
2)yЯкийyзаyномеромyчленyпослідовностіyдорівнюєy0?
3)yЯкіyчлениyпослідовностіyмістятьсяyміжyчисламиy–16yіy16?
4)yЯкийyчленyпослідовностіyєyпопереднімyдляyчислаy–8?
5)yЯкийyчленyпослідовностіyєyнаступнимyдляyчислаy16?
6)yСкількиyчленівyміститьyцяyпослідовність?
член



КЛЮЧОВИЙ МОМЕНТ
Види послідовностей:
y скінченні
y нескінченні
y зростаючі
y спадні
y стаціонарні
Наприклад:
1) послідовність цифр 0, 1, 2, …, 9 є скінченною
10 членів;
2) послідовність додатних парних чисел є нескінченною;
3) послідовність, отримана в актуальній задачі, є скінченною, якщо відпочинок триває скінченну кількість
Наприклад:
1)y–10,y–7,y–4,y–1,y…y—yзростаючаyпослідовність;y
2)y25,y19,y8,y...y—yспаднаyпослідовність;y
3)y–5,y2,y–1,y4,y5,y3,y…y—yпослідовність,yякаyнеyєyніyзростаючою,yніyспадною;y
4)y 2 ,y 2 ,y 2 ,y 2 ,y…y—yстаціонарнаyпослідовність.y
СПОСОБИ ЗАДАННЯ ПОСЛІДОВНОСТЕЙ
Числоваyпослідовністьyвважаєтьсяyзаданою,yякщоyвказаноy спосіб,yзаyдопомогоюyякогоyможнаyзнайтиyбудь-якийyчленyпослідовності.y
Послідовністьyможнаyзадатиyоднимyізyтакихyспособів. Словесний спосіб.yПослідовністьyможнаyзадатиyсловесно,yтобтоy описом.y Наприклад:
• послідовністьyпростихyчисел:y2,y3,y5,y7,y11,y13,y...y;
• послідовністьyнепарнихyчисел:y1,y3,y5,y7,y9,y...y;
• послідовністьyнатуральнихyчисел,yкратнихyп’яти:y5,y10,y15,yy…yy.
КЛЮЧОВИЙ МОМЕНТ
Способи задання послідовностей: y словесний
y табличний
y аналітичний
y рекурентний
y графічний

розглянемоyтаблицю.
Табличний спосіб. Післяyзаповненняyтаблиці,yуyякійyнаведеноy номериyтаyвідповідніyзначенняyчленівyпослідовності,yотримаємоy послідовність,yзадануyтаблично.y Наприклад,
n 123456
an 10–1010
Отже,yмаємоyскінченнуyпослідовністьy an () :y1,y0,y–1,y0,y1,y0.
Аналітичний спосіб. Якщоyпослідовністьyзаданоyформулою,yзаy якоюyможнаyзнайтиyбудь-якийyчленyпослідовності,yколиyвідомийy йогоyномер, говорять,yщоyпослідовністьyзаданоyаналітично.y Такуyформулуyназиваютьy формулою n-го члена послідовності.y Записy sn n =+ () 5030 1 ,yотриманийyпідyчасyрозв’язуванняyактуальноїyзадачі,yіyєyформулоюy n-гоyчленаyпослідовностіy sn () . Наприклад,yпослідовністьy an () yзаданоyаналітичноy—yформулоюy n-гоyчленаy an n =+23 .yЯкщоyпідставитиyзамістьy n натуральніy числаy(1,y2,y3,y…),yотримаємоyчлениyпослідовності: a1 21 35 =⋅ += ,y a2 22 37 =⋅ += ,y a3 23 39 =⋅ += , a4 24 311 =⋅ += ,y…y.y Отже,yмаємоyпослідовністьy an () :y5,y7,y9,y11,y…y.
Неyіснуєyформули,yякоюyможнаyбулоyбyзадатиyпослідовністьy простихyчисел.
Рекурентний спосіб —yщеyодинyспосібyзаданняyпослідовності,y приyякомуyзадають:
1)yпершийyабоyдекількаyпершихyчленівyпослідовності; 2)yформулу,yзаyякоюyможнаyзнайтиyбудь-якийyчленyпослідовностіyчерезy попередніyчлениy(рекурентнуyформулу).y



Цікавим завданням є визначення закономірності, за якою створено послідовність. Спробуйте записати формулу, якою задано послідовність: 1) 2, 4, 6, 8, 10, …; 2) 1, 3, 5, 7, 9, …; 3) 2, 5, 8, 11, 14, … .


ВАМ?



За допомогою послідовності Фібоначчі можна описати порядок розташування листочків рослин, насіння соняшників, лусочок шишок, пелюстків квітів, співвідношення довжин фаланг пальців на руках людини тощо.


Наприклад,yнайзагадковішаyпослідовністьyчиселy—yпослідовністьyФібоначчіyмаєyвигляд:y1,y1,y2,y3,y5,y8,y13,y21,y34,y…y.
Уyційyпослідовності:
Отже,yпослідовністьyФібоначчіyможнаyзадатиyрекурентнимy способом:
1)yпершийyіyдругийyчлениyпослідовностіyдорівнюютьyпоy1;
2)yкожнийyнаступнийyчленyпослідовності,yпочинаючиyзyтретього,yдорівнюєyсуміyдвохyпопередніх.y
камиyнаyкоординатнійyплощині.yТодіyговорять,yщоyпослідовністьy заданоyграфічно.
Наприклад,yпослідовністьy an () yдодатнихyчисел,yкратнихy3,y заданоyграфічноy(рис.y2).
Уyзадачах,yуyтомуyчисліyпрактичногоyзмісту,yнайчастішеyвикористовуютьy аналітичний,y словесний іy рекурентний способиyзаданняyчисловихyпослідовностей.
ПРИКЛАД 1
n-гоyчленаyпослідовностіy yn n =− + 43 2 yзнайдітьy
КРОК 1
КРОК 2
КРОК 3
КРОК 4
Підставимоyуyформулуy
Підставимоyуyформулуy
Підставимоyуyформулуy
КРОК 5 Підставимоyуyформулуy
ТРЕНУЄМОСЯ
1 yВизначтеyчлениy x1 ,y x2 ,y x5 yпослідовностіy xn () ,yзаданоїyформулоюy n-гоyчлена:
1)y xn n = 5 ;y2)y xn n = 3 ;y3)y xn n =−12 ;y4)y xn n =+53 .
Заyформулоюy n-гоyчленаyпослідовності:
5)y an n =+ 10 4 yвизначтеy a1 ,y
6)y a n n =− 8 18 yвизначтеy a1 ,y a2 ,y a9 ,y ap ,y ak +1 ;
7)y yn n =−29 2 yвизначтеy y1 ,y y2 ,y y8 ,y yk ,y ym 2 ;
8)y yn n =−65 2 yвизначтеy y1 ,y y2 ,y y11 ,y yk ,y ym 1 .
ПРИКЛАД 2
Запишітьyпершіyтриyчлениyпослідовностіy xn () ,yзаданоїyрекурентноюyформулоюy xxnn + =− 1 53 ,yякщоy x1 4 = .
Розв’язання
КРОК 1
КРОК 2







Приймемоy n = 1 yіyпідставимоyвyзадануyформулуyзначенняy x1 .
Приймемоy n = 2 yіyпідставимоyвyзадануyформулуyзнайденеyнаyкроціy1yзначенняy x2 . xx3253 =− ; x3 5173 82 =⋅ −=
Відповідь: 4;y17;y82.
ТРЕНУЄМОСЯ
2 yЗапишітьyпершіyтриyчлениyпослідовностіy yn () ,yякуyзаданоyрекурентно:
1)y y1 2=− ,y yynn + = 1 ;y5)y y1 3 = ,y yynn + =− 1 29 ;
2)y
3)y y1






1) 77, 49, 36, 18,
2) 88, 64, 24,


ПРИКЛАД 3
Визначте,yчиyєyчислоy–1yчленомyпослідовності,yзаданоїyформулоюy a
.yЯкщоyтак,yзнайдітьyйогоyпорядковийyномер. Розв’язання
Заданеyчислоyбудеyчленомyцієїyпослідовності,yякщоyзнайдетьсяyтакийyпорядковийyномерy n,yщоy
КРОК 2 Розв’яжемоyотриманеyдробово-раціональнеyрівняння.








1)yСкладітьyформулуyдляyобчисленняyсумиyкоштів,yякуyводійy
2)yВизначте,yякуyсумуyмаєyсплатитиyводій,yякщоyвінyзалишивy
3)yВизначте,yскількиyповнихyгодинyмашинаyперебувалаyнаyпар-
1)
КРОК 1
КРОК 2
2
3)
2
Визначимо,yякуyсумуyмаєyсплатитиyводійy заyпарковкуyбезyурахуванняyпершоїyгодиниy стоянки.
Визначимоyвартістьyоплатиyпослугyпарковкиyвпродовжyусьогоyчасуyстоянки.
Знайдемоyчасyстоянкиyавтомобіля.
Визначимоyвартістьyстоянки,yзважаючиyнаy те,yщоyуyформуліyдляy S3 yплатуyзаyпершуy годинуyстоянкиyвжеyвраховано.
Складемоyрівнянняyдляyзнаходженняyкількостіyповнихyгодинyстоянкиyавтомобіля,y прийнявшиy Sn = 29 .
Розв’яжемоyотриманеyрівняння.yЗробимоy висновок.
Відповідь:y1)y Sn n =+54 ;y2)y17yг.yо.;y3)y6yгод.
ТРЕНУЄМОСЯ
4 yРозв’яжітьyзадачу.
Sn = 4 ,yдеy n y—yкількістьyгодин,yупродовжyякихyавтомобільyперебувавyнаy парковці
1yгодy—yзy10:45yдоy11:45; 3yгодy—yзy11:45yдоy14:45y (заyумовиyпогодинноїyоплати)
424 n = ;y n = 6 ,y n ∈ N y—yотже,yчасyстоянкиyнаyпарковціyдорівнюєy6yповнихyгодин
1)yМайстерyщодняyремонтуєy12yвелосипедів.yСкількиyвелосипедівyвідремонтуєyмайстер:y yа)yзаyдваyдні;yб)yзаyтриyдні?
2)yРоупджампінгy—yстрибокyізyвисокогоyоб’єктаyзіyстраховкоюмотузкою.yОдинyтакийyстрибокyкоштуєy15yг.yо.y
yа)yyСкількиyкоштуватимеyстрибокyдляy4yосібy(коженyстрибаєy поyодномуyразу)?
yб)yyЗапишітьyформулу,yзаyякоюyможнаyобчислитиyвартістьy стрибківy(уyг.yо.)yдляyгрупиyзy nyосібy(коженyстрибаєyпоy одномуyразу).y
3)yВідпочинокyуyрозважальномуyцентріyкоштуєy20yгрнyдляy yоднієїyдитиниyпротягомyодногоyдня.y
yа)yyСкількиyкоштуватимеyвідпочинокyуyцентріyдляy2yдітейy протягомyодногоyдня;yдляy3yдітейyпротягомyодногоyдня? yб)yyЗапишітьyформулу,yзаyякоюyможнаyобчислитиyвартістьy (уyгрн)yвідпочинкуyвyцентріyдляy nyдітейyпротягомyодногоy дня.
yв)yyСкількиyдітейyвідпочивалиyвyцентрі,yякщоyзагальнаyсума,y сплаченаyїхнімиyбатькамиyзаy1yдень,yстановилаy6000yгрн?










ЧИ ВІДОМО ВАМ?






Сьогодні дедалі більше людей за мислюються над тим, щоб установити на даху свого будинку сонячні панелі. Ілон Маск, співзасновник компанії Tesla Motors, презентував новинку, розроблену спільно
з компанією SolarCity, — фотоелектричні панелі «Сонячний дах» (Solar Roof). Вони повністю вбудовані в дах і можуть

замінити звичайні покрівельні матеріали. Ефективність «Соняшного даху» становить 98 %

від ефективності звичайних со-
нячних панелей.

ПОМІРКУЙТЕ
Спробуйте знайти перевагу аналітичного способу задання послідовності над рекурентним.



4)yЗалежністьyкількостіy xn yзаряднихyпристроївyнаyсонячнихy батареях,yпроданихyвyінтернет-магазиніyпротягомyодногоy тижня,yвідyкількостіy n yпродавців-консультантівyможнаy yвиразитиyформулоюy xn n =+510 . yа)yyСкількиyзаряднихyпристроїв
тижня,yякщоyвyмагазиніyпрацюютьy8yпродавців?
yб)yyСкількиyпродавцівyмаєyпрацюватиyвyмагазині,yщобyпротягомyтижняyбулоyпроданоy300yзаряднихyпристроїв?
1
2 yВизначте,yякимyзаyномеромyчленомyпослідовності,yзаданоїyаналітично,yєyчислоy M,yякщо: 1)y xn n =− +
,y M =−14 ;y4)y bn n n = + 24 9 ,y M = 3 7 ; 2)y ynn n =+21 2 ,y M = 16 ;y5)y zn n =−()32 4 ,y M = 79 ; 3)y an n =− + 4 7 ,y M =−9 ;yy6)y cn n =+()
3 Запишітьyпершіyп’ятьyчленівyпослідовностіy an () ,yякуyзаданоy рекурентно: 1)y a1 2


4 yОбчислітьyпершіyчотириyчлениyпослідовності,yномериyякихy єyпарнимиyчислами,yякщоyпослідовністьyзаданоyаналітично: 1)y an n = 3 ;y3)y cn n =−() + 14 ;y5)y xn n n =−() + 35 ; 2)y bn n =−2 ;y4)y yn nn =−() +−()21 ;y6)y zn n =− ()116 .
5 yПослідовністьy yn () yзаданоyформулоюy yn n =+617 .yУкажітьyнай-
Поміркуйте,yчиyєyподаніyтвердженняyправильними.yВідповідьy обґрунтуйте.
1)yЯкщоy cn n = + 1 5 ,yтоy ccnn < +1 .
2)yЯкщоy an = 3 ,yтоy 1013 10 += a .
3)yЧислоy2018yєyчленомyпослідовностіy xn () ,yзаданоїyформулоюy xn n n =−() 1 .
4)yЯкщоyпослідовністьyзаданоyформулоюy yn n =−() 1 ,yтоyсумаy першихyїїy60yчленівyдорівнюєy0.
5)yЯкщоyпослідовністьy bn () yзаданоyформулоюy bn n =− 20 ,yтоy добутокyпершихyїїy20yчленівyдорівнюєy0.
MATH FOR LIFE
Напередодніyвиходуyкінофільмуyнаyекраниyбувyвипущенийy трейлерyдоyцьогоyфільму.yНаyдругийyденьyпісляyвиходуyтрейлераyйогоyпереглянулаyполовинаyвсіхyучнівyшколи.yЧастинуyучнівy школи,yщоyпереглянулиyтрейлерyнаy n-йyденьyпісляyйогоyвиходу,y можнаyвизначитиyзаyформулоюy xn n =− 1 1 .
1 yЯкаyчастинаyучнівyшколиyпереглянулаyтрейлерyнаyтретійyденьy післяyйогоyвиходу?
2 yСкількиyвідсотківyусіхyучнівyшколиyпереглянулиyтрейлерyнаy четвертийyденьyпісляyйогоyвиходу?
3 yСкількиyвідсотківyусіхyучнівyшколиyщеyнеyпереглянулиyтрейлерyнаyп’ятийyденьyпісляyйогоyвиходу?
4 yЗапишітьyформулуy(послідовністьy yn () ),yзаyякоюyможнаyзнайтиy частинуyучнівyшколи,yякіyнеyпереглянулиyтрейлерyнаy n-йyденьy післяyйогоyвиходу.
5 yЗнайдітьy ny—yнайменшийyномерyдняyпрокатуyтрейлера,yколиy йогоyпереглянулиyнеyменшеyніжy90yy%yусіхyучнівyшколи.y






Нельсон Елліотт (англ. Ralph Nelson Elliott ; 1871–1948) — американський




IQ

1 Заyзаданоюyформулоюy n-гоyчленаyпослідовності:
1)y xn n = 4 yвизначтеy x1 ,y x2 ,y x3 ;
2)y cn n =−
4)y yn n

TO BE SMART Побачити, як математичні закономірності проявляються


навколишньому світі, можна, переглянувши мультфільм «Природа





1
Див. приклади 2–4

ЧИ ВІДОМО ВАМ?
Трикутник



Числовий трикутник Паскаля — невичерпне джерело різноманітних математичних загадок. Спробуйте знайти закономір-
ність побудови кожного нового


рядка трикутника Паскаля.
Знайдіть відповідну інформацію і дослідіть, як трикутник Паскаля пов’язаний із простими числами, трикутними числами, числами Фібоначчі, трикутником Серпінського, шахами.


Будь-якій людській діяльності притаманні три відмінних риси: форма, час і відношення, — і всі вони підпорядковані сумаційній послідовності Фібоначчі.
Ральф Нельсон Елліотт
2 yЗнайдітьyпершіyтриyчлениyпослідовностіy y
рентноюyформулою:
3
знайдітьyйогоyпорядковийyномер.
4 yРозв’яжітьyзадачу.
1)yПортyщодобиyприймаєy3yтанкери.yСкількиyтанкерівyпортy
yа)yзаy2yдоби;yб)yзаy3yдоби?
2) Орендаyбульдозераyпротягомy1yгодyстановитьy800yгрн.y yа)yyСкількиyкоштуватимеyорендаyбульдозераyпротягомy4yгод?
yб)yyЗапишітьyформулу,yзаyякоюyможнаyобчислитиyвартістьy (уyгрн)yорендиyбульдозераyпротягомy nyгодyроботи.
3) Уyготеліyєyсімейніy4-місніyномери,yдоyякихyзаселяютьyлишеy сім’їyзy4yосіб.
yа)yСкількиyосібyпроживаютьyуyдвох;yуyтрьохyтакихyномерах?
yб)yyЗапишітьyформулу,yзаyякоюyможнаyобчислитиyкількістьy осіб,yщоyпроживаютьyвy nyтакихyномерах.
yв)yyСкількиy4-міснихyномерівyзайнято,yякщоyзаразyуyнихy проживаютьy108yосіб?
4) Залежністьyкількостіy yn yвідвідувачівyзоопаркуyпротягомy дняyвідyкількостіy n рідкіснихyтаyекзотичнихyтварин,yщоy мешкаютьyуyньому,yможнаyвиразитиyформулоюy yn n =+ 3 150 . yа)yyСкількиyлюдейyвідвідаютьyпротягомyдняyзоопарк,yуyякомуyмешкаютьy120yтакихyтварин?
yб)yyСкількиyтакихyтваринyмаєyбутиyвyзооyпарку,yщобyпротягомyдняyкількістьyвідвідувачівyстановилаy1500yосіб?y
1)y4;y6;y8;y?;y4)y83;y73;y63;y?;y7)y120;y114;y?;y102; 2)y3;y5;y7;y?;y5)y–15;y–12;y–9;y?;y8)y132;y?;y138;y141. 3)y75;y70;y65;y?;y6)y–6;y–10;y–14;y?;yy9)y–2;y2;y–2;y2;y?;y2.















Наyшоуyталантівyпісляyвиступуyвсіхyучасниківyглядачіyпротягомy30yхвyмоглиyвзятиyучастьyвyсмс-голосуванніyзаyулюбленогоy учасника.yПротягомyпершоїyхвилиниyвідyпочаткуyголосуванняyсвоюy думкуyвисловилиy4800yглядачів.yПротягомyкожноїyнаступноїyхвилиниyголосувалоyнаy160yглядачівyменше,yніжyпопередньоїyхвилини.y 1)yСкількиyглядачівyпроголосувалиyпротягомyдругоїyхвилиниyвідy початкуyголосування?
2)yСкількиyглядачівyпроголосувалиyпротягомyтретьоїyхвилиниy відyпочаткуyголосування?
3)yСкладітьyформулу,yзаyякоюyобчислюєтьсяyкількістьyглядачів,y якіyпроголосувалиyпротягомy n-їyхвилиниyвідyпочаткуyголосуванняy 130 n () . Коментар до розв’язання
Позначимоyпослідовністьyчисел,yкожнеyзyякихyвиражаєy кількістьyглядачів,yщоyвзялиyучастьyуyголосуванні,yчерезy an () .y Кількістьyглядачів,yякіyпроголосувалиyпротягомyдругоїyхвилини,yдорівнюєy a2 4800160 4640 =− = ,yпротягомyтретьоїyхвилиниy—y a3 4800160 160 48002 160 =− −= −⋅ .
Заyумовоюyзадачіyтакаyтенденціяyголосуванняyзберігаласяyпротягомy30yхв.yБачимо,yщоyкожнеyзyчиселyпослідовностіy an () ,yпочинаючиyзyдругого,yдорівнюєyпопередньому,yзменшеномуyнаyоднеy йyтеyсамеyчислоy160.yОтриманаyпослідовністьyмаєyспеціальнуyназвуy—y арифметична прогресія






визначення переможця.

КЛЮЧОВІ ТЕРМІНИ арифметична
ЗАПАМ’ЯТАЙТЕ!
daann =− +1


ЧИ ВІДОМО ВАМ? Слово «прогресія» походить від латинського progressio — рух уперед, збільшення; «арифметичний» — від грецького слова αριθµο ′ ς — число. d — перша літера латинського слова differentia — різниця.


Введемоyпозначення: an () y—yарифметичнаyпрогресія; d —yрізницяyарифметичноїyпрогресії; n — номерyчленаyарифметичноїyпрогресії; a1 y—yпершийyчленyпрогресії; an y—y n-йyчленyпрогресії; an +1 y—yнаступнийyзаy n-мyчленyпрогресії; an 1 y—yпопереднійyдляy n-гоyчленyпрогресії.
Такимyчином,yвyарифметичнійyпрогресіїy an () yмаємо:y aad 21=+ ,y aad 32=+ yіyт.yд.,yтобтоyдляyбудь-якогоyнатуральногоyчислаy nyвиконуєтьсяyумоваy aad nn + =+ 1 .yЗвідсиy daann =− +1 .
Арифметичнуyпрогресіюyможнаyзаписатиyзаyдопомогоюy рекурентноїyформули:y aad nn + =+ 1 ,y n ∈ N .
ЗАПАМ’ЯТАЙТЕ!
ПОМІРКУЙТЕ
Спробуйте навести приклади зростаючої, спадної та стаціонарної арифметичних прогресій. Як різниця d впливає на властивості прогресії?
СЛІД ЗНАТИ!
1
yВизначте,yчиyєyарифметичноюyпрогресієюyпослідовність: 1)y2;y7;y12;y17;y…;yy3)y5;y0;y5;y0;y…; 2)y2;y–2;y–8;y–12;y…;yy4)y17;y17;y17;y17;y…y.
2 yУкажітьyпершийyіyдругийyчлениyтаyзнайдітьyрізницюyарифметичноїyпрогресії: 1)y99;y89;y79;y69;y…;yy3)y0,1;y0,2;y0,3;y0,4;y…; 2)y–2;y–9;y–16;y–23;y…;yy4)y 3 ,y 3 ,y 3 ,y 3 ,y…y.
3 yЗапишітьyпершіyп’ятьyчленівyарифметичноїyпрогресіїy an () ,y якщо:
1)y a1 3 = ,y d = 7 ;y 3)y a1 25=− ,y d = 4 ; 2)y a1 2 = ,y d =−15 , ;y4)y a1 85=− , ,y d =−25 , .
Приyрекурентномуyспособіyзаданняyпрогресіїyнеобхідноyзнатиy їїyпопереднійyчлен,yщоyнеyзавждиyєyзручнимyпідyчасyрозв’язуванняy задач.yЦьогоyможнаyуникнути,yякщоyвивестиy формулуy n-гоyчленаy арифметичноїyпрогресії.
Розглянемоyарифметичнуyпрогресіюy an () yзyрізницеюy d: a1 y—yїїyпершийyчлен; aad 21=+ y—yдругийyчлен; aadaddad a 32 1 1 2 2 =+ =+ += + y—yтретійyчлен; aadad add a 43 1 1 2 3 3 =+ =+ =+ + y—yчетвертийyчленyіyт.yд.
Якщоyпроаналізуватиyотриманийyрядyчленівyпослідовностіy an () yіyїхyзапис,yпомітимо,yщоyкожнийyчленyпослідовностіy an дорівнюєyсуміy a1 yіyрізниціyарифметичноїyпрогресії,yпомноженійy наyчисло,yщоyнаy1yменше,yніжyпорядковийyномерy an : aad 1 1 0 =+ ⋅ ,yyy aad 2 1 1 =+ ⋅ , aad 3 1 2 =+ ⋅ , aad 4 1 3 =+ ⋅ yіyт.yд. Отже,y n-йyчленyарифметичноїyпрогресіїyможнаyзнайтиyзаyформулоюy aadn n =+ () 1 1 .
РОЗМИНКА 2
1 yДаноyарифметичнуyпрогресіюy an () .yЗнайдіть: 1)y a5 ,yякщоy a1 2 = ,y d = 5 ;y3)y a6 ,yякщоy a1 18=− ,y d = 3 ; 2)y a7 ,yякщоy a1 3 = ,y d =−2 ;y4)y a11 ,yякщоy a1 10 5 =− , ,y d =−55 , .
2 yЗапишітьyформулуy n-гоyчленаyарифметичноїyпрогресії: 1)y2;y11;y20;y29;y…;y3)yy7;y7;y7;y7;y…; 2)y–1;y–4;y–7;y–10;y…;yy4)y 2 ;y0;y 2 ;y 22 ;y…y.






ЗАПАМ’ЯТАЙТЕ! Формула n-го члена арифметичної прогресії має вигляд: aadn n =+ () 1 1 . ЧИ ВІДОМО ВАМ? Арифметичну прогресію можна зобразити на площині у вигляді піраміди або сходів:




ЗАПАМ’ЯТАЙТЕ!
ПРИГАДАЙТЕ!
Півсуму двох чисел bac = + 2
називають середнім арифметичним двох чисел.

ЧИ ВІДОМО ВАМ?



по-
арифметичної пропорції: abbc −=− . Числа a, b і с створювали арифметичну прогресію з різницею ca 2 . Арифметичну прогресію тоді позначали символом i i

ЗАПАМ’ЯТАЙТЕ!
an aanknk = −+ + 2 nk () 1
Члениyарифметичноїyпрогресіїyможнаyзображатиyточкамиyнаy координатнійyплощиніy(див.yрисунок),yпричомуyвсіyточкиyлежатимутьyнаyоднійyпрямій.
Послідовність,yякуyзаданоyформулоюy aknnb =+ ,yдеy kyіy by—y числа,yєyарифметичноюyпрогресією.
Дійсно,yрозглянемоyформулуy n-гоyчленаyарифметичноїyпрогресіїy aadn n =+ () 1 1 .yРозкриємоyдужкиyтаyзапишемоyїїyуyвиглядіy aadnd n =+ 1 ,yабоy adnnad =+ () 1 .yЯкщоyввестиyпозначення:y dk = іy adb 1 −= ,yтоyостанняyформулаyматимеyвиглядy aknnb =+ . Правильнимyєyтакожy
ПРИКЛАД 1
Знайдіть різницю і
сії an () : –2; –0,8; … .
КРОК 1
2
сії an () для a13 та
Відповідь: 1,2; 12,4.
ТРЕНУЄМОСЯ
1 Визначте різницю арифметичної прогресі ї:
1) an () : 3; 5; … і знайдіть її третій член; 2) xn () : 1; 6; … і знайдіть її четвертий член;
3) cn () : 49; 45; … і знайдіть її п’ятий член;
4) yn () : 38; 35; … і знайдіть її шостий член;
5) an () : –3; –2,6; … і знайдіть її десятий член;
6) an () : –5; –3,9; … і знайдіть її одинадцятий член;
7) xn () : 2 ; 25 ; … і знайдіть її двадцять перший член;
8) cn () : 6; 63 ; … і знайдіть її
третій член. Якщо відомі два несусідні
a1 2=− ; a2
y daa nk nk = , якщо nk ≠
(формула різниці);
y aankd nk=+ ()
(формула n-го члена);
y an aanknk = −+ + 2 ;
y aaaa nmkp += + ,
якщо nmkp += + .
Перевірити правильність доведення ви можете на сайті interactive.ranok.com.ua
2
КЛЮЧОВИЙ МОМЕНТ
1) припустити, що дане число є n-м членом
3)
чи виконується умова n ∈ N
ТРЕНУЄМОСЯ
Визначте, чи є число a членом арифметичної
xn () . Якщо так, то вкажіть його порядковий номер.
1) a = 8 ; xn () : 0; 2; 4; 6; …; 3) a = 9 ; xn () : 5; 4; 3; 2; …;
2) a = 7 ; xn () : 1; 3; 5; …; 4) a = 1 2 ; xn () : 3; 2; 1; … .
Визначте, чи є число a членом арифметичної прогресії xn () , якщо
Які це числа? Розв’язання Крок Зміст дії Результат
КРОК 1
Введемо позначення арифметичної прогресії. Визначимо послідовність членів прогресії, враховуючи те, що –4 і 6,8 є деякими з них. Оскільки арифметична прогресія зростаюча, член –4 матиме менший номер, ніж член 6,8. Для зручності приймемо, що –4 є першим членом прогресії, 6,8 четвертим. xn () арифметична прогресія
3
yПершіyчотириyчлениyарифметичноїyпрогресіїyмаютьyвигляд:y x,y xy + ,y xy + 2 ,y xy + 3 .yЗнайдітьy xyіy y,yякщо:
1)yпершийyіyтретійyчлениyцієїyпрогресіїyдорівнюютьyвідповідноy6yіy20;
2)yпершийyіyтретійyчлениyцієїyпрогресіїyдорівнюютьyвідповідноy4yіy26;
3)yпершийyіyчетвертийyчлениyцієїyпрогресіїyдорівнюютьyвідповідноy5yіy–43;
4)yпершийyіyчетвертийyчлениyцієїyпрогресіїyдорівнюютьyвідповідноy3yіy–54.
yМіжyчисламиy a yіy b yвставтеyдваyчислаyтак,yщобyусіyчотириy числаyутворилиyзростаючуyарифметичнуyпрогресію.yЗнайдітьy n-йyчленyцієїyпрогресії,yякщо:
5)y a =−9 ,y b = 27 ,y n = 16 ;yy7)y a =−12 , ,y b = 03 , ,y
ПРИКЛАД 4
Знайдітьyпершийyвід’ємнийyчленyарифметичноїyпрогресіїy an () :y 7,3;y5,9;y…y.
Розв’язання
Дляyзнаходженняyпершогоyвід’ємногоyчленаyарифметичноїy прогресіїyрозв’яжемоyнерівністьy an < 0 yвідносноy nyіyзнайдемоyїїy найменшийyнатуральнийyрозв’язок.
КРОК 1 Знайдемоy dy—yрізницюyарифметичноїyпрогресіїy an () .
КРОК 2
3
КРОК 4
Запишемоyформулуy n-гоyчленаyвyзагальномуyвиглядіyтаy підставимоyвyнеїyзначенняy a1 yіy d.

в
Згадаємо віршові розміри: ямб, хорей, дактиль,





Знайдемоyнайменшийyнатуральнийyрозв’язокyотриманоїyнерівностіyтаyзробимоyвисновокyщодоyшуканогоy an . n = 7 y—yнайменшийyнатуральнийyрозв’язок,yотже,y шуyканеy aa n = 7

ЧИ ВІДОМО ВАМ?
Задачі, пов’язані з арифметичною
прогресією, зустрічаються вже в давньоєгипетських папірусах.


4
ТРЕНУЄМОСЯ
yВизначтеyпершийyвід’ємнийyчленyарифметичноїyпрогресії: 1)y an () :y7;y3;y…;yy3)y an () :y15;y8;y…; 2)y an () :y8;y2;y…;yy4)y an () :y12;y7;y…y.
yВикористовуючиyформулуy aadn n =+ () 1 1 ,yзнайдітьyпершийy від’ємнийyчленyарифметичноїyпрогресії:y 5)y an () :y93;y84;y…;yy7)y an () :y8,3;y7,7;y…; 6)y an () :y106;y95;y…;yy8)y an () :y10,2;y9,5;y…y.y
Доведіть,yщоyпослідовність,yякуyзаданоyформулоюy yn n =−93 ,y єyарифметичноюyпрогресією.
Доведення
Щобyдовести,yщоyпослідовністьy yn () yєyарифметичноюyпрогресією,yперевіримо,yчиyвиконуєтьсяyрівністьy y
КРОК 1
КРОК 2
КРОК 3
Запишемоyформулиyдляy yn 1 yіy yn +1 . yn n =− () 1 93 1 ;y yn n + =− + () 1 93 1
Знайдемоyсумуy yynn−+ + 11 .
Перевіримо,yчиyвиконуєтьсяyрівністьy yn yynn = −+ + 11 2 .yЗробимоyвисновок. 93 63 2 −= () n n ;yмаємо:y 3333 () =−() nn .
Отже,yпослідовністьy yn () ,yзаданаyформулоюy yn n =−93 ,yєyарифметичноюyпрогресією
ПРИГАДАЙТЕ! yn yynn = −+ + 11 2 (n y2)

ТРЕНУЄМОСЯ 5 yЗнайдітьy yynn−+ + 11 ,yякщо: 1)y yn n =+ 7 ;y2)y yn n =− 4 ;y3)y yn n = 2 5 ;y4)y yn n = 3 8 .
yДоведіть,yщоyпослідовністьy yn () yєyарифметичноюyпрогресією,y якщо:
Уyмагазиніy«Fruttis»yяблукаyвикладеноyвyчотирикутнуyпірамі-
Розв’язання
КРОК 1
КРОК 2
КРОК 3
Проаналізуємоyумовуyзадачіy«сторонаyкожногоy наступногоyшаруyміститьyнаyоднеyяблукоyменше,yніжyсторонаyпопереднього».
Введемоyпозначенняyелементівyотриманоїyарифметичноїyпрогресіїy xn () .
Знайдемоy x6 ,yвикористовуючиyформулуy
n-гоyчленаy xxdn n =+ () 1 1 .
Відповідь: 7.
ТРЕНУЄМОСЯ
6 yРозв’яжітьyзадачу.
Послідовністьyчисел,yщоyвиражаютьy кількістьyяблукyнаyстороніyкожногоy шару,yєyарифметичноюyпрогресієюy
x1 12 = ,y d =−1 ,yшуканийyчленyпрогресіїy x6
xxd 61 5 =+ ; x6 12 57 =− =
1)yУy2017yр.yвyкраїніyпобудувалиyодинyсучаснийyсміттєпереробнийyкомплекс.yУyкожномуyнаступномуyроціyплануєтьсяyбудуватиyнаyтриyтакихyкомплексиyбільше,yніжy уyпопередyньому.yСкількиyкомплексівyплануєтьсяyпобудуватиyуy2018yр.;yуy2019yр.?
2)yЗаyпершийyрікyізyмоментуyвідкриттяyприватнаyветеринарнаy клінікаyвиділилаyнаyблагодійніyпроектиy60yтис.yг.yо.yКожногоyнаступногоyрокуyвласникyклінікиyплануєyвиділятиyнаy такіyпроектиyнаy15yтис.yг.yо.yбільше,yніжyпопереднього.yЯкуy сумуy(уyг.yо.)yбудеyвиділеноyнаyблагодійніyпроектиyпротягомy 6-гоyрокуyзyмоментуyвідкриттяyклініки?
3)yПротягомyмісяцяyрадіостанціяyпроводилаyщоденнийyконкурсyсередyсвоїхyслухачів.yПершогоyдняyпризовийyфондy склавy6000yгрн.yКожногоyнаступногоyдняyпризовийyфондyбувy наy200yгрнyменшим,yніжyпопереднього.y
yа)yyСкількиyгривеньyскладавyпризовийyфондyуyчетвертийy деньyконкурсу?
yб)yyСкладітьyформулу,yзаyякоюyможнаyобчислитиyсумуyгрошейy an y(уyгрн)yпризовогоyфондуyвyn-йyденьyконкурсуy 130 n () .
4)yАвтомобіль,yвиїхавшиyнаyавтостраду,yпочавyрозганятисяyіyзаy першуyсекундуyподолавy10yм,yаyзаyкожнуyнаступнуyсекундуy долавyнаy5yмyбільше,yніжyзаyпопередню,yпокиyнеyдосягнувy швидкостіy126yкм/год.yДаліyавтомобільyрухавсяyзyцієюyсамоюyшвидкістю.
yа)yyСкількиyметрівyподолавyавтомобільyзаyтретюyсекундуyвідy моментуyвиїздуyнаyавтостраду?
yб)yyНаyякійyсекундіyавтомобільyдосягнувyшвидкостіy126yкм/год?
yв)yyСкладітьyформулу,yзаyякоюyможнаyобчислитиyкількістьy an yметрів,yякіyавтомобільyдолавyавтострадоюyзаy n-нуyсекундуyвідyпочаткуyрозгону.

TO BE SMART













ЧИ ВІДОМО ВАМ?
y Із кожних дев’яти послідовних членів будь-якої арифметичної прогресії, що складається з натуральних чисел, можна скласти магічний квадрат.


y Із простих чисел, що є членами арифметичної



d = 11 .yЗнайдітьy n.
4)y xn () :y xn =−21 2 5 ,y x1 3 3 5 = ,y d =−5,00 .yЗнайдітьy n.
5)y yn () :y y12 32 = ,y y53 114 = .yЗнайдітьy d,y y10 .
6)y cn () :y c24 53=− ,y c116 329=− .yЗнайдітьy d,y c1 .
3 yВизначте,yчиyміститьyчислоy myарифметичнаyпрогресія: 1)y xn () :y9;y16;y…,yякщоy m = 295 ;
2)y an () :y a1 31 5 = , ;y d =−15 , ,yякщоy m = 0 ;
3)y xn () :y x2 100=− ;y d = 62 , ,yякщоy m = 55 ;


TO BE SMART



IQ



4
4)y yn () :y y5 19 = ;y y6 17 = ,yякщоy m =−23 ;
5)y an () :y a20 0 = ;y a66 92=− ,yякщоy m = 44 ; 6)y cn () :y c16 7=− ;y c36 200 = ,yякщоy m = 112 .
yВизначте,yчиyєyарифметичноюyпрогресієюyпослідовністьy an () ,y якуyзаданоyформулоюy n-гоyчлена:
5
2)yВyарифметичнійyпрогресіїy xn () x7 23 = , ;y x14 72 = , .yВизначте,y скількиyвід’ємнихyчленівyміститьyцяyпрогресія.
3)yШістьyчиселyутворюютьyарифметичнуyпрогресію.yСумаyпершихyтрьохyчиселyдорівнюєy–2,7,yаyсумаyтрьохyостанніхyдорівнюєy0.yЗнайдітьyціyчисла.
6
4)yАрифметичнуyпрогресіюyзаданоyформулоюy
yЗнайдітьyпорядковийyномерyпершогоyчленаyпрогресіїy
,y якийyзадовольняєyумовуy cn 12 .
5)y an () y—yарифметичнаyпрогресія;y aa
yВизначтеy aa 24 17 + .
6)y xn () y—yарифметичнаyпрогресія;y
yВизначтеy x x 11 5 .
Розв’яжітьyзадачі,yвикористовуючиyхарактеристичнуyвластивістьyарифметичноїyпрогресії.
1)yТриyчислаy a,y byіy cyутворюютьyарифметичнуyпрогресію.yЗнайдітьy b,yякщоyпотроєнаyсумаy a іy cyдорівнюєy–54.
2)yТриyчислаy m ,y n yіy k yутворюютьyарифметичнуyпрогресію.y Знайyдітьy n,yякщоyдобутокyчиселy myіy kyдорівнюєy144,yаyсумаy їхyквадратівyстановитьy180.
3)yЗнайдітьyусіyзначенняy x,yприyякихyчислаy x 12 ;y x;y7xyутворюютьyскінченнуyарифметичнуyпрогресію.
4)yЗнайдітьyусіyзначенняy m,yприyякихyчислаy m 2 11 + ;y4myіy m + 1 уyподаномуyпорядкуyутворюютьyскінченнуyарифметичнуy прогресію.
5)yЗнайдітьyнатуральніyзначенняy n,yприyякихyчислаy 27 2 n ;y 89 2 2 n ;y 1 7 2 3 n yуyподаномуyпорядкуyутворюютьyарифметичнуyпрогресію.
6)yЗнайдітьyціліyзначенняy a, приyякихyчислаy a 4 ;y 42 3a ;y 27 a + yуyподаномуyпорядкуyутворюютьyскінченнуyарифметичнуyпрогресію.
7 Розв’яжітьyзадачу.
1) Цифриyтрицифровогоyчисла,yщоyзаписаніyпослідовно,y утворюютьyарифметичнуyпрогресію.yСумаyцихyцифрyдорівнюєy21,yаyсумаyїхyквадратівyдорівнюєy19.yЗнайдітьyціyчисла.
2)yДовжиниyсторінyтрикутникаyутворюютьyарифметичнуyпрогресію.yЗнайдітьyдовжиниyйогоyсторін,yякщоyдобутокyчисел,y щоyїхyвиражають,yдорівнюєy80,yаyпериметрyтрикутникаyстановитьy15yсм.y
3) Амфітеатрyциркуyміститьy10yрядів,yпричомуyвyкожномуyнаступномуyрядуyнаy18yмісцьyбільше,yніжyуyпопередньому.y Визначте,yвyякомуyрядуyрівноy170yмісць,yякщоyдесятийyрядy налічуєy242yмісця.
4) Плавецьyпідyчасyпершогоyтренуванняyподолавyдистанціюy 150yм.yКожногоyнаступногоyтренуванняyвінyпропливавyнаy 50yмyбільше,yніжyпопереднього,yпокиyнеyдосягнувyрезультатуy—y800yмyзаyоднеyтренування.yПісляyцьогоyпідyчасyкожногоy тренуванняyплавецьyпропливавy800yм.

















3–4 ? 219 ? 7–115 ?


yа)yyЯкіyдистанціїyплавецьyподолавyпідyчасyдругогоyтаyтретьо-
yб)yyПідyчасyякогоyзаyномеромyтренуванняyплавецьyупершеy
yв)yyСкількиyвсьогоyкілометрівyплавецьyпропливyзаyпершіy
yг)yyСкладітьyформулу,yзаyякоюyможнаyобчислитиyвідстаньy
1 yПослідовністьy xn ()
2
3 Послідовністьy cn () заданоyформулоюy n-гоy членаy cn n = 3 5 .yВизначтеy cn +1 .y
5 yЗнайдітьyпершийyвід’ємнийyчленyарифметичноїyпрогресіїy an () :y26;y16;y…y.
6 yУстановітьyвідповідністьyміжyпослідовністю,y якуyзаданоyформулоюy n-гоyчленаy(1–3),yтаy значеннямyїїyтретьогоyчленаy(А–Г).
4 Визначтеyшостийyчленy a6 yарифметичноїy прогресіїy an () ,yякщоy a5 2 = ,yаyрізницяyдорівнюєy10.
7 yУкажітьyнайменшийyномер,yпочинаючиy зyякогоyвсіyчлениyпослідовностіy bn () yбудутьy більшіyзаy19,yякщоy bn n =− + 54 6 .
8
yВадимyнаyпершомуyтренуванніyвиконавy 10yвідyжимань.yКожногоyнаступногоyтренуванняyвінyвиконувавyнаy3yвіджиманняyбільше,y ніжyпопереднього,yпокиyнеyдосягнувyрезультатуy—y40yвіджиманьyзаyоднеyтренування.y 1)yСкількиyвіджиманьyвиконавyВадимyпідy часyтретьогоyтренування?
2)yПідyчасyякогоyзаyномеромyтренуванняyВадимyупершеyдосягнувyрезультатуy40yвіджимань?
Поміркуйте,yчиyєyподаніyтвердженняyправильними.yВідповідьy обґрунтуйте.
1) Якщоyрізницяyарифметичноїyпрогресіїy an () yдорівнюєy0,yтоy aann + = 1 .
2) Якщоyпершийyіyтретійyчлениyарифметичноїyпрогресіїyдорівнюютьy4yіy–4yвідповідно,yтоyдругийyїїyчленyдорівнюєy0.
3) Усіyчлениyарифметичноїyпрогресії,yякуyзаданоyформулоюy xn n =− 10 9 ,yдодатні.
4) Якщоyрізницяyарифметичноїyпрогресіїy an () yдорівнюєy3,yтоy aann + −= 2 6 .
5) Якщоyрізницяyіyдесятийyчленyарифметичноїyпрогресіїyдодатні,yтоyвсіyпершіyдев’ятьyчленівyцієїyпрогресіїyтакожyдодатні.
MATH FOR LIFE
Компанієюy«Київстар»yтарифікаціяyдзвінківyуyроумінгуyздійснюєтьсяyпохвилинно,yплатаyзаyз’єднанняyнеyстягується.yУyтаблиціy наведеноyтарифиyнаyтелекомунікаційніyпослугиyдляyконтрактнихy абонентівyцієїyкомпаніїy(інформаціяyстаномyнаy2016yр.).y

Вартість вхідного дзвінка, грн/хв 9121625
Вартість вихідного дзвінка, грн/хв 9121635
Вартість смс-повідомлення, грн/шт. 3,53,53,53,5
1 yЛіліані,yякаyзаразyвідпочиваєyвyХорватіїy(тарифнаyзонаy2),y подзвонилаyподругаyзyУкраїни.yСкількиyгривеньyкоштувалаy Ліліаніyцяyрозмова,yякщоyвонаyтривалаy10yхв?
2 yЮрій,yякийyзаразyвідпочиваєyвyЄгиптіy(тарифнаyзонаy4),yподзвонивyдруговіyвyУкраїну.yСкількиyгривеньyкоштувалаyЮріюy цяyрозмова,yякщоyвонаyтривалаy5yхв?
3 yПрацівникyкомпаніїy«Київстар»yсклавyрекурентнуyформулу,y заyякоюyобчислюєтьсяyвартістьy an y(уyгрн)yпередаванняy n -гоy смс-повідомленняyдляyвсіхyтарифнихyзон:y aann + = 1 ,y a1 35 = , .y Чиyправильнуyформулуyсклавyпрацівник?
4 yСкладітьyрекурентнуyформулу,yзаyякоюyможнаyобчислитиyвартістьy an y(уyгрн)yвхідногоyдзвінкаyдляyтарифноїyзониy3yзаy n-нуy хвилинуyрозмови.
5 yСкладітьyформулу,yзаyякоюyможнаyобчислитиyвартістьy an (уyгрн)yвхідногоyдзвінкаyдляyтарифноїyзониy3yзаy nyхвyyрозмови.





Леонардо Пізанський (італ. Leo nardo Pisano , бл. 1170–бл. 1250), більш відомий як Фібоначчі (Fibonacci), — перший значний математик середньовічної Європи. У 1202 р. з’явилася




того часу. У ній розглядалися, у тому числі, властивості



Цікаво, що числова послідовність Фібоначчі була







Див. приклад 1
1 Визначте різницю арифметичної прогресі ї: 1) an () : 2; 5; … і знайдіть її третій член; 2) xn () : 54; 39; … і знайдіть її четвертий член; 3) an () : –4; –2,7; … і знайдіть її дванадцятий член; 4) cn () : 5 ; 59 ; … і знайдіть її двадцять шостий член. 2 Визначте, чи є число a членом арифметичної
1) a = 4 , xn () : –4; –2; 0; 2; ...; 2) a = 5 , xn () : 2; 1; 0; –1; … .
Див. приклад 2
3) a = 50 , x1 12=− , d = 4 ;
4) a =−26 , x1 58
Див. приклад 3
Див. приклад 4
Див. приклад 5
2)
3 і 19;
ї, якщо: 3) a =−4 , b = 23 , n = 14 ; 4) a =−6 , b = 81 , , n = 16 .
ї: 1) an () : 6; 1; …; 2) an () : 23; 13; … .
формулу aadn n =+
ї: 3) an () : 127; 119; …; 4) an () : 12,3; 11,7; … .
yynn−+ + 11 , якщо: 1) yn n =+ 3 ; 2) yn n = 5 2 .
3) yn n =−62 ; 4) yn n = 52 3 .
1)yУy2017yр.yзаyсприянняyмісцевоїyвладиyНаціональнуyоперуy Україниyвідвідалиy50yучнівyпевногоyміста.yЗаплановано,y щоyвyподальшомуyцюyакціюyбудеyподовженоyйyкожногоyнаступногоyрокуyоперуyвідвідаютьyнаy20yучнівyбільше,yніжy попереднього.yСкількиyучнівyцьогоyмістаyвідвідаютьyНаціональнуyоперуyУкраїниyуy2018yр.;yуy2019yр.?
2)yПротягомyпершогоyрокуyзyмоментуyреєстраціїyтуристичнаy фірмаyвідкрилаy8yсвоїхyфіліалів.yКожногоyнаступногоyрокуy плануєтьсяyвідкриватиyнаy4yфіліалиyбільше,yніжyпопереднього.yСкількиyфіліалівyбудеyвідкритоyтурфірмоюyпротягомy сьомогоyрокуyзyмоментуyїїyреєстрації?y
3)yПротягомyдвохyтижнівyвидавництвоyпроводилоyщоденнийyконкурсyсередyсвоїхyчитачів.yПершогоyдняyпризовийy фондyсклавy4200yгрн.yКожногоyнаступногоyдняyпризовийyфондy бувyнаy300yгрнyменшим,yніжyпопереднього.y а)yСкількиyгривеньyстановивyпризовийyфондyуyтретійyденьy конкурсу?
б)yСкладітьyформулу,yзаyякоюyможнаyобчислитиyсумуyгрошейy(уyгрн)yпризовогоyфондуyвy n-йyденьyконкурсу.
4)yМиколаyпідyчасyпершогоyтренуванняyвиконавy14yприсіданьy зіyштангою.yКожногоyнаступногоyтренуванняyвінyвиконувавy наy2yприсіданняyбільше,yніжyпопереднього,yпокиyнеyдосягнувyрезультатуy—y42yприсіданняyзаyоднеyтренування.yПісляy цьогоyМиколаyвиконувавy42yприсіданняyзіyштангоюyпідyчасy кожногоyтренування.
а)yСкількиyприсіданьyвиконавyМиколаyпідyчасyтретьогоyтренування?
б)yПідyчасyякогоyзаyномеромyтренуванняyМиколаyвпершеy досягнувyрезультатуy42yприсідання?
в)yСкладітьyформулу,yзаyякоюyможнаyобчислитиyкількістьy присідань,yякіyвиконавyМиколаyпідyчасy n-гоyтренування.
Бонусні завдання
7 yЗнайдітьyрізницюyарифметичноїyпрогресії,yпершийyчленyякоїy дорівнюєy28,yякщоyдобутокyдругогоyтаyвосьмогоyчленівyпрогресіїyєyнайменшимyсередyможливих.
8 yДовжиниyсторінyпрямокутногоyтрикутникаyутворюютьyарифметичнуyпрогресію.yЗнайдітьyплощуyцьогоyтрикутника,yякщоy йогоyгіпотенузаyдорівнюєy5.y
1)y S1 ;yyyyy2)y S2 ;yyyyy3)y S10 ;yyyyy4)y Sk ;yyyyy5)y Sn +1 ;yyyyy6)y S

ВІДОМО





y 27 березня відзначають Міжнародний день театру. y Найстаріший в Україні театр було побудовано в Харкові (1789), згодом — у Києві (1806), Одесі (1810). Найбільш «театральне» місто в Україні — Київ, у ньому 25 театрів.


Див. приклад 6
Дев’ять індуських знаків суть такі: 9, 8, 7, 6, 5, 4, 3, 2, 1. За допомогою цих знаків і знака 0, який називається по-арабськи «сифр», можна написати яке завгодно число.
Фібоначчі






















Джейкобсон, прихильник мотоциклетних перегонів, вирішив перенести їх на воду і розробив новий різновид мотоцикла — аквабайк. Перший прототип аквабайка був створений у 1965 р., а в 1968 р. у продаж надійшов промисловий аквабайк Sea-Doo. Дізнайтеся більше: http://aquabike.in.ua/

шою,yтакийyспосібyбувyбиyобтяжливимyіyнезручним.y
Виникаєyзапитання:yчиyможнаyзнайтиyсумуy nyчленівyарифметичноїyпрогресіїyзаyдеякоюyформулою?
Розглянемоyарифметичнуyпрогресіюy a1 ,y a2 ,y a3 ,y…,y an ,yякаy міститьyскінченнуyкількістьyчленів.yЗапишемоyїхyсуму,yпозначившиyїїyчерезy Sn :
Проаналізуємо суми в дужках, скориставшись рекурентною формулою aad nn + =+ 1 :
y aan 1 + ;
y aaaadaa nndn21 1 1 += () + () = ++ ;
y aaaadaa nndn32 1 1 2 2 += () + () = ++ і т. д.
Легко помітити, що кожна сума, записана в дужках у рівності (3), дорівнює aan 1 + , а кількість дужок — n. Тобто формула (3) набуватиме вигляду 2 1 Snaa nn =⋅ + () , звідки:
Sn n aa n =⋅ + 1 2 .
Якщо перетворити одержану формулу, використовуючи фор-
мулу n-го члена арифметичної прогресії aadn n =+ () 1 1 , отри-
маємо:
Sn n adn = +−() 21 2 1 .
Одержані формули називають формулами суми перших n членів арифметичної прогресії. Формули
Sn n aa n =⋅ + 1 2 ; Sn n adn = () ⋅ +− 21 2 1 .
ПРИКЛАД 1
Складіть
прогресії.
Розв’язання
спростимо отриманий вираз. Використаємо формулу Sn n adn = +−() 21 2 1 .
Підставимо в неї значення a1 i d. Sn n n = () () ⋅ ⋅− +− 24 50 21 2 ,, ;
Sn , при n = 100 . S100 2 01 46 100100 =⋅ −⋅ ,, ; S100 1000 460540 =− =
: 540.
ПРИГАДАЙТЕ!
Sn n aa n =⋅ + 1 2
Sn n adn = +−() 21 2 1
Sn n adn = +−() 21 2 1 ,
21 1 adn+−()
1) Snn n =+() 5 , n = 10 ; 3) Sn nn = () 61 2 2 , , n = 20 ; 2) Snn n =+() 4 , n = 8 ; 4) Sn nn = () + 38 5 2 , , n = 30 .
ПРИКЛАД 3
1
14, …, 98 арифметична прогресія, у якій d = 2 , a1 10 = , an = 98
КРОК 2
aadn n =+ () 1 1 ; 98 10 21 =+ () n ; n = 45 КРОК 3
кількість членів цієї послідовності, тобто знайдемо порядковий номер члена an = 98 .
Відповідь: 2430.
ТРЕНУЄМОСЯ
3 Обчисліть наведену суму: 1) 12 320+++ + ... ; 3) 12 340 ... ; 2) 12 315+++ + ... ; 4) 12 356 ... .
Обчисліть суму: 5) усіх двоцифрових натуральних чисел, кратних 5; 6) усіх двоцифрових натуральних чисел, кратних 4; 7) усіх трицифрових натуральних чисел, кратних 6 і менших від 700;
8) усіх трицифрових натуральних чисел, кратних 8
від 600. Будь-яка послідовність членів
КРОК 1
місяця (30 днів)?
Розв’язання
Створимо математичну модель задачі. Розглянемо послідовність чисел, що
виражають щоденну оплату протягом тижня, і проаналізуємо отриману послідовність xn () . 10, 12, 14, …; xn () : 10, 12, 14, … арифметична прогресія, x1 10 = , d = 2
КРОК 2
КРОК 3
Визначимо, сума яких членів
5
шукану суму через M
SM S 12 2324 30 23 30 ++ ++ ++ ... ... шукана сума MSS =− 30 23 , де S30 сума перших 30 членів
S23 і M. Sxd 23 222 2 1 23 =⋅
2)y2014yр.yвyмістіyвідкрилиy2yточкиyбезкоштовногоyдоступуyдоy Wi-Fi.yКожногоyнаступногоyрокуyвідкривалиyнаy3yтакихyточкиyбільше,yніжyпопереднього.yСкількиyвсьогоyтакихyточокy доступуyдоyWi-Fiyвідкрилиyвyмістіyзаy3yрокиy(2014–2016)?
3)yУyзмаганніyзіyстрільбиyзаyкоженyпромахyуyсеріїyізy30yпострілівyстрілецьyотримуєyштрафніyбали:yзаyпершийyпромахy—y 1yбал,yаyзаyкожнийyнаступнийyпромахy—yнаy0,5yбалаyбільше,y ніжyзаyпопередній.y
а)yСкількиyштрафнихyбалівyотримаєyстрілецьyзаy3yпромахи? б)yСкладітьyформулу,yзаyякоюyможнаyобчислитиyзагальнуy кількістьy Sn yштрафнихyбалів,yотриманихyстрільцемyзаy nyпромахівy 130 n () .
4)yТривалістьyпрогулянкиyзyнемовлямyпершогоyдняyстановилаy20yхв.yКожногоyнаступногоyдняyтривалістьyпрогулянкиy збільшуваласяyнаy10yхв,yпокиyнеyдосяглаy2yгод.y
а)yСкількиyчасуy(уyхв)yтривалаyпрогулянкаyуyтретійyдень?
б)yЗнайдітьyзагальнийyчасy(уyхв),yякийyнемовляyперебувалоy наyвулиціyвyпершіy3yдні.
в)yСкладітьyформулу,yзаyякоюyможнаyобчислитиyзагальнийy часy Sn y(уyхв)yпрогулянкиyзyнемовлямyзаy nyпершихyднів.
1 Знайдітьyсумуyпершихy nyчленівyарифметичноїyпрогресіїy an () заyтакимиyданими:
1)y a6 13 = ,y d =−4 ,y n = 7 ;yy4)y a12 12 1 4 = ,y a20 19 3
2)y a10 15 = , ,y d =
3)y a6 13 = , ,y a13 05 = , ,y n = 10 ;y6)y an n
2 yЗнайдітьyневідоміyелементиyарифметичноїyпрогресії.
1)y xn () —yарифметичнаyпрогресія;y x1 24 = ,y
.y Знайдітьy n.
2)y cn () —yарифметичнаyпрогресія;y c16 18 = ,y d = 4 ,y Sn =−400 .y Знайдітьy n.
3)y yn () —yарифметичнаyпрогресія;y yy yy 10 6
4)y cn () y—yарифметичнаyпрогресія;y cc cc 4 2 7 2 11 5 584 24 += −=
, . yЗнайдітьy S7 .
5)y Snn n =−62 2 y—yформула,yякоюyвиражаєтьсяyсумаyпершихy nyчленівyарифметичноїyпрогресіїy an () .yЗнайдітьy a9 .
6)y an () —yарифметичнаyпрогресія;y an n =− 4 2 3 y—yформулаy n-гоy члена,y





















ВАМ?


Говерла — найвища вершина



України, її висота сягає 2061 м над рівнем моря. Назва походить від угорського Hóvár (снігова гора). Раніше гора мала назву «Говирла», але під час складання австрійської військової карти припустилися орфографічної помилки. На Говерлі стоїть мармурова плита, в яку вмуровано двадцять п’ять капсул із землею з усіх регіонів України.



МАЙБУТНЯ ПРОФЕСІЯ




Податковий інспектор стежить за дотриманням податкового законодавства, контролює надходження платежів у бюджет, перевіряє фінансові документи платників податків.



Необхідні особисті якості: аналітичне мислення; уважність; чесність; відповідальність; хороша пам’ять. Державний податковий інспектор повинен мати вищу освіту в юридичній, економічній або фінансовій галузі.

3
Розв’яжітьyзадачу,yвикористовуючиyформулуyсумиyпершихy nyчленівyарифметичноїyпрогресії.
1)yЗнайдітьyсумуyвсіхyдвоцифровихyчисел,yкратнихy5,yалеyнеy кратнихy10.
2)yЗнайдітьyсумуyвсіхyдвоцифровихyчисел,yщоyнеyділятьсяyнацілоyніyнаy5,yніyнаy10.
3)yЗнайдітьyсумуyвсіхyнепарнихyтрицифровихyчисел,yкратнихy3,yнеyменшихyвідy333yіyнеyбільшихyзаy500.
4)yРізницяyшостогоyіyтретьогоyчленівyарифметичноїyпрогресіїy дорівнюєy468,yаyчетвертийyїїyчленyбільше,yніжyперший,yнаy 52.yЗнайдітьyсумуyчленівyцієїyпрогресії.
5)yПідyчасyсходженняyнаyГоверлуyгрупаyспортсменівyподолалаy маршрутyзаy5yгод.yЗаyпершуyгодинуyбулоyпройденоy1300yм,y кожноїyнаступноїyгодиниy—yнаy100yмyменше,yніжyзаyпопередню.yВизначтеyдовжинуyмаршруту.
6)yДляyорганізаціїyфуршетуyбулоyзакупленоyтовариyзаyперелікомyізy27yнайменувань.yЗаyумовамиyакції,yкупуючиy продуктиyхарчування,yпокупецьyотримуєyзаyпершеyнайменуванняy2yбонуси,yзаyкожнеyнаступнеy—yнаy1,5yбонусаyбіль-
чування.
MATH FOR LIFE
Оподатковуванийyприбутокyтекстильногоyпідприємстваyуyсічніy
бувyнаy30y000yгрнyбільшим,yніжyпопередньогоyмісяця.yМісячнаy ставкаyподаткуyнаyприбутокyстановитьy15y%.y
1 yЗнайдітьyприбутокy(уyгрн),yщоyпідлягаєyоподаткуванню,yодержанийyуyдругомуyмісяціy(лютому).
2 yСкладітьyформулу,yзаyякоюyвизначаєтьсяyприбутокy yn y(уyгрн),y щоyпідлягаєyоподаткуванню,yодержанийyвy
3
1 Сумуyпершихy nyчленівyарифметичноїyпрогресіїyзаданоyформулоюy Snn n =+() 6 .yЗнайдітьy S4 .y
2 Обчислітьyсумуyарифметичноїyпрогресії:y 12 311+++ + ... .
6 yУстановітьyвідповідністьyміжyарифметичноюyпрогресією,yякуyзаданоyформулоюy n -гоyyчленаy(1–3),yтаyформулоюyсумиyпершихy nyчленівy(А–Г)yцієїyпрогресії.
3 Укажітьyформулуyдляyзнаходженняyсумиy першихy
4 Якщоy
5
7
Знайдіть:
1) кількістьyусіхyдвоцифровихyнатуральнихy чисел,yкратнихy6;
2)yсумуyвсіхyдвоцифровихyнатуральнихyчисел,yкратнихy6.y
8 y2011yр.yоднаyзyкіностудійyвипустилаy12yмультиплікаційнихyфільмів.yКожногоyнаступногоyрокуyцяyстудіяyвипускалаyнаy3yтакихy фільмиyбільше,yніжyпопереднього.y
1)yСкількиyмультиплікаційнихyфільмівyвипустилаyцяyстудіяyуy2016yр.?
2)yСкількиyвсьогоyмультиплікаційнихyфільмівyвипустилаyцяyстудіяyзаy6yроківy(2011–2016)?y

TO BE SMART










Йоганн Карл Фрідріх Гауcс (1777–1855) (нім. Johann Carl Friedrich Gau ß ) — німецький математик, механік, астроном, фізик, геодезист.



Гауcс був настільки відомим, що коли в 1807 р. французькі
війська підійшли до Геттінгена, Наполеон наказав поберегти
місто, в якому живе «найвидатніший математик усіх часів».

Див. приклад 1
Див. приклад 2
Див. приклад 3
Поміркуйте,yчиyєyподаніyтвердженняyправильними.yВідповідьy обґрунтуйте.
1)yЯкщоy S9 980 = yіy S10 1000 = ,yтоy a10 20 = .
2)yЯкщоy aaa 12 3 3 40 ++ = ,yтоy S3 120 = .
3)yЯкщоy a6 7 = ,yтоy S11 77 = .
4)yЯкщоy aa12 1 == ,yтоy S15 15 = .
5)yЯкщоy d = 4 ,yтоy SS32 4 −= .
Див. приклад 4
2
1)y Snn n =+() 3 ,y n = 15 ;yy2)y Sn nn = () 75 3 2 , ,y n = 40 .
yСкладітьyформулуyдляyзнаходженняyсумиyпершихy n yчленівy арифметичноїyпрогресії,yякщоyвідоміyїїyпершийyчленy a1 таyрізницяy d .yОбчислітьyсумуyпершихy100yчленівyцієїyпрогресії.y
3)y a1 78=− ,y d = 6 ;yy4)y a1 19 4 = , ,y d =−05 , .y
Знайдітьyсумуyпершихy nyчленівyарифметичноїyпрогресіїy xn () ,y якщо:y
1)y n = 18 ,y 21711 1 xd+= ;y3)y n = 24 ,y x5 34=− ,y x20 92 = ;
2)y n = 10 ,y xx29 25 += ;yy4)y n = 51 ,y x26 100 = .
3 yОбчислітьyсуму:
1)y 12 338+++ + ... ;y
2)y 12 351 ... ;y
3)yусіхyдвоцифровихyнатуральнихyнепарнихyчисел;y
4)yусіхyтрицифровихyнатуральнихyчисел,yкратнихy9yіyменшихy відy800.y
4 yРозв’яжітьyзадачу.
1) 2014yр.yавторкаyбестселерівyпровелаy4yзустрічіyзyчитача-
2)yПротягомyпершогоyрокуyзyмоментуyвиходуyнаyєвропейськийy ринокyукраїнськіyфермериyпродалиy5yтис.yлyсоняшниковоїy олії.yКожногоyнаступногоyрокуyвониyпродавалиyнаy2yтис.yлy оліїyбільше,yніжyпопереднього.yСкількиyвсьогоyлітрівyсоняшниковоїyоліїyпродалиyукраїнськіyфермериyзаy12yроківy зyмоментуyвиходуyнаyринокyЄвропи?
3)yАльпіністиyвyпершийyденьyсходженняyпіднялисяyнаyвисотуy 800yм.yПродовжуючиyпідйом,yкожногоyнаступногоyдняyвониy проходилиyнаy50yмyменше,yніжyпопереднього.y
а)yНаyякуyвисотуyпіднялисьyальпіністиyзаy2yдніyсходження?
б)yСкладітьyформулу,yзаyякоюyможнаyобчислитиyвисотуy Sn y(уyм),yякуyподолалиyальпіністиyзаy nyднівyсходження,y 17 n .
4)yШвидкіснийyпотяг,yвідходячиyвідyстанції,yзаyпершуyсекундуyпройшовy10yм,yаyзаyкожнуyнаступнуyсекундуyпроходивy наy5yмyбільше,yніжyзаyпопередню,yпокиyнеyдосягнувyшвидкостіy144yкм/год.yПісляyцьогоyпотягyрухавсяyрівномірноy зyцієюyшвидкістю.
а)yСкількиyметрівyпройшовyпотягyзаyчетвертуyсекундуyвідy початкуyруху?
б)yСкількиyвсьогоyметрівyпройшовyпотягyзаyчотириyсекундиy відyпочаткуyруху?
в)yСкладітьyформулу,yзаyякоюyможнаyобчислитиyвідстаньy Sn y(уyм),yякуyпройшовyпотягyза n секундyвідyпочаткуyруху.
Бонусне завдання
5 yДовжиниyсторінyмногокутникаyутворюютьyарифметичнуyпрогресію,yрізницяyякоїyдорівнюєy2yсм.yЗнайдітьyкількістьyсторінy многокутника,yякщоyйогоyпериметрy217yсм,yаyдовжинаyнайбільшоїyсторониy37yсм.
ПОВТОРЕННЯ
yЗнайдітьyзакономірністьyтаyвставтеyзамістьyзнакаyпитанняy пропущенеyчисло: 1)y1;y3;y9;y?;y 4)y 1 80 1 40 1 20 ;; ;? ;y7)y64;y–32;y?;y–8; 2)y1;y2;y4;y?;y 5)y 1 2 ;y2;y8;y?;y8)y81;y?;y9;y–3.
3)y 1 10 1 100 1 1000 ;; ;? ;y6)y 1 3 ;y2;y12;y?;

IQ

TO BE SMART
Прочитайте влітку 5

































Завдяки соціальним мережам ми отримали необмежені можливості для спілкування.

y Щосекунди 8 осіб на планеті
приєднуються до будь-якої
з існуючих соціальних мереж.


y Facebook за чисельністю —
третя «країна» у світі, після Китаю та Індії, з населенням близько мільярда чоловік.

y Кожний користувач соцмереж має в друзях у середньому 195 осіб.


ЗАПАМ’ЯТАЙТЕ!
Щотижняyкількістьyкоментарів,yщоyз’являлися,yзбільшуваласяy втричіyпорівняноyзyпопереднімyтижнем.yОтже,yпротягомyдругогоy
наyоднеyйyтеyсамеyчисло,yвідміннеyвідyнуля.yВважають,yщоyпершийy
Введемо позначення:
bn () — геометрична прогресія;
q — знаменник геометричної прогресії;
n номер члена геометричної прогресії;
b1 — перший член прогресії;
bn — n-й член прогресії;
bn +1 — наступний за n-м член прогресії;
bn 1 — попередній для n-го член прогресії.
Знаючи q, можна задати геометричну прогресію рекурентною формулою:
bbq nn + =⋅ 1 (n ∈ N , bn ≠ 0 , q ≠ 0 ). Цю формулу можна записати ще й так: q b b n n = +1 . Тобто в гео-
метричній прогресії відношення кожного члена, починаючи з другого, до попереднього є сталим числом, яке дорівнює знаменнику геометричної прогресії q.
Наведемо приклади геометричної прогресії.
Геометрична прогресія (b n)
Перший член b1 Знаменник q
1; 2; 4; 8; 16; … 1 2 q > 0
27; 9; 3; 1; … 27 01 << q
3; –6; 12; –24; … 3 –2 q < 0
q
Властивість послідовності
зростаюча
спадна
знакозмінна
Зауважимо, що перші члени прогресії в наведених прикладах є додатними числами.
РОЗМИНКА 1
1 Визначте, чи є геометричною прогресією послідовність: 1) 2; 6; 18; 54; …; 3) 3; –3; 3; –3; …; 2) –3; –9; –27; –81; …; 4) 2; 4; 6; 8; … .
2 Укажіть перший і другий члени та знайдіть знаменник геометричної прогресії: 1) 5; 10; 20; 40; …; 3) 311 ; 313 ; 315 ; 317 ; …; 2) –2; 8; –32; 128; …; 4) 2 ; 2; 22 ; 4; … .
3 Запишіть перші чотири члени
bn () , якщо:
1) b1 1 = ; q = 5 ; 3) b1 5=− ; q = 4 ; 2) b1 2 = ; q =−15 , ; 4) b1 8
y геометрична прогресія y знаменник геометричної прогресії y nй член, формула nго члена геометричної
гресії y характеристична властивість геометричної прогресії
y bbq nn + =⋅ 1 ( n ∈ N , bn ≠ 0 , q ≠ 0 ); y q b b n n = +1
ЗАПАМ’ЯТАЙТЕ!
Формула n-го члена геометричної прогресії має вигляд: bbq n n =⋅ 1 1

ЧИ ВІДОМО ВАМ?



У стародавніх греків поняття геометричної прогресії було логічним продовженням поняття геометричної пропорції: abbc :: = . Квадратний корінь із двох додатних чисел bac = називали середнім геометричним (або середнім пропорційним ) двох чисел. Звідси
назва геометричної прогресії.
її позначали символом ii ii .

Геометричнуyпрогресію,yякyіyарифметичну,yможнаyзадатиyякy рекурентноюyформулою,yтакyіyформулоюyїїy n-гоyчлена.
Розглянемоyгеометричнуyпрогресіюy bn () yзіyзнаменникомy q: b1 y—yїїyпершийyчлен; bbq 21=⋅ y—yдругийyчлен; bbqbqqbq b 32
—yтретійyчлен; bbqbq
Маємо:
yіyт.yд.
Отже,yдляyбудь-якогоyномераy n yсправедливоюyєyрівністьy
.yЗнайдіть:
yЗапишітьyформулуy n-гоyчленаyгеометричноїyпрогресії: 1)y2;y–4;y8;y–16;y…;yy3)y0,3;y0,3;y0,3;y0,3;y…; 2)y–1;y–3;y–9;y–27;y…;yyy4)y 3 ;y3;y 33 ;y9;y…y.
форму-
Справедливимyєyтакожy обернене твердження:
Якщоyкожнийyчленyпослідовності,yпочинаючиyзyдругого,yєyсереднімyгеометричнимyдвохyсусідніхyізyним,yтоyцяyпослідовністьy є геометричноюyпрогресією.
Якщоy bbb nnn −+ ⋅=11 2 ,yтоyпослідовністьy bn
гресією.yТодіy bbb nnn =⋅ −+11 .
Інше формулювання характеристичної
тричної прогресії Модуль кожного члена геометричної прогресії, починаючи
1 Відомо,yщоyвyгеометричнійyпрогресіїy
1
КРОК 2
КРОК 3
Запишемоyформулуyдляyзнаходженняyзнаменникаy q
обчислимоyйогоyзначення.
Запишемоyформулуy n -гоyчленаyдляyодногоyзyвідомихy членівyпрогресії,yнаприкладyдляy b5 ,yтаyобчислимоyзначенняy b1 .
Запишемоyформулуy n-гоyчленаyдляyшуканогоy b11 yтаyобчислимоyйогоyзначення.
Зауважимо,yщоyнаyтретьомуyкроціyрозв’язанняyможнаyбулоy знайтиy b11 yчерезy b5 yабоyчерезy b6 ,yyтобто:y bbq
Відповідь:y–768.
ТРЕНУЄМОСЯ



рівняння на множники, поділимо почленно перше рівняння на друге і скоротимо дроби в лівій та правій частинах рівняння ( q ≠−1 , q ≠ 0 , x1 ≠ 0). xq xqq 1 3 1 165 120 + () = + () =
КРОК 5 Застосуємо основну
ємо квадратне рівняння.
КРОК 6
,
2
ТРЕНУЄМОСЯ
yВизначтеyчотириyчислаy x1 ,y x2 ,y x3 ,y x4 ,yщоyутворюють:
1)yзростаючуyгеометричнуyпрогресіюyзіyзнаменникомy q = 2 ,y якщоyїхyсумаyдорівнюєy195;
2)yспаднуyгеометричнуyпрогресію,yякщоy xx13 25 += ,y xx24 12 5 += , ;
3)yзростаючуyгеометричнуyпрогресію,yякщоyсумаyпершихyдвохy чиселyдорівнюєy6,25,yаyсумаyостанніхyдвохyдорівнюєy100;
4)yспаднуyгеометричнуyпрогресію,yякщоyсумаyїїyкрайніхyчленівy дорівнюєy9,yаyсумаyсередніхyчленівyдорівнюєy6.
ПРИКЛАД 3
Запишітьyгеометричнуyпрогресіюyізyшестиyчленів,yзадануyрекурентноюyформулоюy bb nn + =− 1 3 ,yякщоy b2 27=− .
Розв’язання
КРОК 1 Знайдемоy b3 ,yпідставившиy n = 2 yуyформулуy
КРОК 2 Знайдемоyзнаменникy qyпрогресіїy bn () .
Спробуйте довести:
y q nkb b n k = , якщо nk ≠ (формула знаменника);
y bbq nk nk =⋅ (формула n-го члена);
y bbb nnknk 2 =⋅ −+ ;
y bbbb nmkp ⋅= ⋅ , якщо nmkp += +
Перевірте своє доведення: interactive.ranok.com.ua
КРОК 3 Обчислимоy b1 ,yзнаючиy qyіy b2 . b b q 1 2 = ;y b1 9 =
КРОК 4 Обчислимоy b4 ,y b5 ,y b6 . bbq 43 243 =⋅ =− ; bbq 54 729 =⋅ = ; bbq 65 2187 =⋅ =−
Відповідь:y9;y–27;y81;y–243;y729;y–2187.
ТРЕНУЄМОСЯ
3 yЗапишітьyпершіy4yчлениyгеометричноїyпрогресіїy bn () ,yякщо:
1)y b1 2 49 = ,y bbnn + = 1 7 ;yyy3)y b1 33 = ,y bn b n + = 1 3 ;y
2)y b1 128 = ,y bn b n + = 1 8 ;yyy4)y b1 1 = ,y bb nn + = 1 2 .
yЗапишітьyпершіy6yчленівyгеометричноїyпрогресіїy bn () ,yякщо:
5)y b3 7 = ,y bbnn + = 1 2 ;yyy7)y b3 12 = ,y bb nn + =− 1 3 ;y
6)y b4 12 = ,y bb nn + =− 1 3 ;yy8)y b5 12 = ,y bb nn + =− 1 2 .





КРОК 6
Підставимо в отримане рівняння
4 yРозв’яжітьyзадачу.
1)yТриyчислаyутворюютьyарифметичнуyпрогресію,yпершийyчленy якоїyдорівнюєy2.yЯкщоyдоyпершогоyчислаyдодатиy6,yдоyдругогоy додатиy3,yаyтретєyзалишитиyбезyзмін,yтоyотримаємоyгеометричнуyпрогресію,yзнаменникyякоїyдорівнюєy1.yЗнайдітьyціyчисла.
2)yТриyчислаyутворюютьyарифметичнуyпрогресію,yдругийyчленy якоїyдорівнюєy6.yЯкщоyвідyпершогоyчислаyвіднятиy2,yдоyтретьогоyдодатиy5,yаyдругеyзалишитиyбезyзмін,yтоyотримаємоy геометричнуyпрогресію,yзнаменникyякоїyдорівнюєy2.yЗнайдітьyціyчисла.
3)yСумаyтрьохyчисел,yякіyутворюютьyзростаючуyарифметичнуy прогресію,yдорівнюєy60.yЯкщоyвідyпершогоyчислаyвіднятиy5,y другеyзалишитиyбезyзмін,yаyдоyтретьогоyдодатиy50,yтоyотримаємоyгеометричнуyпрогресію,yзнаменникyякоїyдорівнюєy4.y Знайдітьyціyчисла.
4)yСумаyтрьохyчисел,yякіyутворюютьyзростаючуyарифметичнуy прогресію,yдорівнюєy24.yЯкщоyдоyпершогоyчислаyдодатиy2,y другеyзалишитиyбезyзмін,yаyдоyтретьогоyдодатиy2,yтоyотримаємоyгеометричнуyпрогресію.yЗнайдітьyціyчисла. ПРИКЛАД 5
Розглянемоyвідомуyзадачуyпроyкульбабу.
Однаyрослинаyкульбабиyдаєyзаyрікy100yлетючихyнасінин,yякі,y розлітаючись,yзаймаютьyплощуyприблизноy10yм2.yЯкуyплощуy(уyм2)y покриютьyусіy«нащадки»yоднієїyрослиниyкульбабиyчерезy7yроківy заyумови,yщоyвонаyрозмножуєтьсяyбезyперешкодyуyгеометричнійy прогресії?y
Розв’язання
КРОК 1
КРОК 2
КРОК 3
КРОК 4
КРОК 5
an aa nn = −+ + 11 2 .






Позначимоyчерезy S0 yпочатковуyплощу,yтобтоyплощу,yякуyзаймаєyпотомствоyоднієїyрослиниyкульбаби.
Знайдемоyплощу,yзайнятуyкульбабамиyчерезy1yрік.
Знайдемоyплощу,yзайнятуyкульбабамиyчерезy2yроки.
Аналогічноyміркуючи,yзробимоyвисновокyпроyте,yякуyплощуy потомствоyрослиниyзаймеyчерезy nyроків.
SS n n
Знайдемоyплощу,yякуyпокриютьyусіyпотомкиyоднієїyрослиниy кульбабиyчерезy7yроків. S7 1010101415=⋅







y Найбільший у Європі плавучий світломузичний фонтан було відкрито у 2011 р. у Вінниці. Висота його центрального струменя досягає 65 м, фронтальний розліт води — близько 140 м, а розміри формованого бризками і водяним пилом проекційного екрана станов-
лять близько 16 х 45 м.

y Під час світломузичного шоу
можна почути й побачити укра їнські композиції «Два

кольори», «Щедрик-ведрик», «Мій рідний край» та інші у виконанні Ніни Матвієнко, Дмитра Гнатюка, Олега Скрипки.

Переглянути шоу ви можете за посиланням www.youtube. com/watch?v=juOjvWDipL0


ПЕРЕРВА НА ЛОГІКУ Спробуйте знайти невідоме число.




5 yРозв’яжітьyзадачу.y
1) Часy bn y(уyс),yякийyкомп’ютерyвитрачаєyнаyрозв’яyзуванняy n-їyзадачі,yзадаєтьсяyформулоюy bn n =⋅32 .yСкількиyчасуyвитратитьyкомп’ютерyнаyрозв’язуванняyтретьоїyзадачі?
2
) Післяyвдалоїyрекламноїyкампаніїyкількістьyвідвідувачівy певногоyсайтаyщомісяцяyподвоювалась,yіyтакийyприрістy тривавy3yмісяці.yПротягомyпершогоyмісяцяyсайтyвідвідалиy 6000yкористувачів.yСкількиyкористувачівyвідвідалоyцейy сайтyпротягомyтретьогоyмісяця?
3)yБулоyподаноyелектроннуyпетиціюyнаyпідтримкуyоблашту-
гоyдняyпетиціюyпідписалиy8yосіб,yаyкожногоyнаступногоyдняy кількістьyзареєстрованихyпідписівyставалаyудвічіyбільшою.y Чиyвистачитьyкількостіyпідписів,yнабранихyпетицієюyпротягомyтижняyголосуванняy(7yповнихyднів),yякщоyдляyприйняттяyпозитивногоyрішенняyдостатньоy500yпідписів?
4) Висотаyпершогоyструменяyводиyмузичногоyфонтанаyстановитьy90yм,yаyвисотаyкожногоyнаступногоyструменяy уy1,5yразуyменша,yніжyпопереднього.y
а)yЯкаyвисотаyтретьогоyструменяyводи?
б)yСкладітьyформулуyдляyвизначенняyвисотиy bn y(уyм)y n-гоyструменяyводиyмузичногоyфонтанаy 110
1 Уyгеометричнійyпрогресіїy xn () :
1)y x1 2 = ,y x2 2 = .yЗнайдітьy qyіy x6 . 2)y x2 65 = ,y x4 15 5 2 = .yЗнайдітьy qyіy x9 . 3)y x4 312 = ,y x8 38 = .yЗнайдітьy qyіy x20 .
4)y x2 1 = ,y x16 515 = .yЗнайдітьy qyіy x2017 .
5)y x1 25=− , ,y q =− 1 2 .yЗнайдітьy x6 ,y xn yіy xn +1 .y
6)y x1 10 = ,y q = 2 .yЗнайдітьy x6 ,y xn yіy xn 1 .
Kyчленомyгеометричноїyпрогресії: 1)y4;y1;y 1 4 ;y…,yякщоy K =− 1 64 ; 2)y–3;y9;y–27;y…,yякщоy K = 82 ;
3
3)y bn () ,yуyякійy b1 8 = ,y q = 1 2 ,yякщоy K = 1 64 ;
4)y xn () ,yуyякійy x1 2 =− ,y q = 22 ,yякщоy K =−256 ;
5)y bn () ,yзаданоїyформулоюy n-гоyчленаy bn n =⋅ 1 5 0125 , ,y
якщоy K = 1 500 ;
6)y xn () ,yзаданоїyформулоюy n-гоyчленаy xn n =⋅ () + 24 2 34 ,y
якщоy K = 24 2 .
Розв’яжітьyзадачу.
1)yМіжyчисламиy–6yіy0,75yвставтеyтакіyдваyчислаy ayіy b,yщобy послідовністьy–6;y a;y b;y0,75yутворювалаyгеометричнуyпрогресію.
2)yЗнайдітьyчотириyчисла,yпершіyтриyзyякихyутворюютьyгеометричнуyпрогресію,yдругеyдорівнюєy6,yчетвертеyудвічіyбільше,y ніжyперше,yаyсумаyвсіхyчотирьохyчиселyдорівнюєy30.
3)yВизначте,yприyякихyвід’ємнихyзначенняхy myчислаy6;y 2m ;y 54yєyпослідовнимиyчленамиyгеометричноїyпрогресії.
4)yЗнайдітьyтакіyзначенняy t ,yприyякихyчислаy t 3 ;y 26 t ,y 31 t + yєyпослідовнимиyчленамиyгеометричноїyпрогресії.
4 Розв’яжітьyзадачу.
1)yУкажітьyнайменшийyномер,yпочинаючиyзyякогоyвсіyчлениy геоyметричноїyпрогресіїy xn () yбільшіyзаy28,yякщоy xn n =⋅ 35 2 1 , .
2)yУкажітьyусіyномериyчленівyгеометричноїyпрогресіїy bn () ,yнеy більшихyзаy500,yякщоy bn n =⋅45 1 .
3)yСкладітьyскінченнуyгеометричнуyпрогресіюyізyшестиyчленів,y якщоyсумаyпершихyтрьохyізyнихyдорівнюєy11,yаyсумаyтрьохy останніхyдорівнюєy168.
4)yЗнайдітьyтриyчисла,yякіyутворюютьyскінченнуyгеометричнуy прогресію,yякщоyсумаyїхyквадратівyдорівнюєy99,yаyпершийy членyуy3yразиyменший,yніжyзнаменникyпрогресії.
5 Геометричнаyпрогресіяyмаєyцікавіyвластивості.yСпробуйтеyдовестиyїхyсамостійно.
1)yЯкщоyпослідовністьy b1 ,y b2 ,y b3 ,y…,y bn ,y…yєyгеометричноюy прогресієюyзіyзнаменникомy q,yтоyпослідовністьyквадратівy їїyчленівy b1 2 ,y b2 2 ,y b3 2 ,y...,y bn 2 ,y...yєyгеометричноюyпрогресієюy зіyзнаменникомy q 2 .
2)yДобутокyдвохyчленівyскінченноїyгеометричноїyпрогресії,yрівновіддаленихyвідyкрайніхyчленів,yдорівнюєyдобуткуyкрайніхy членів:y bbbbbbbbbb nnnnknk12 13 24 31
















Марк Цукерберг (англ. Mark Zuckerberg; нар. 1984) — американський програміст, підприємець, один із розробників і співзасновників соціальної мережі Facebook.


Поміркуйте,yчиyєyподаніyтвердженняyправильними.yВідповідьy обґрунтуйте.
1)yТриyчислаy4,y4,y4yутворюютьyгеометричнуyпрогресіюyзіyзнаменникомy q = 1 .
2)yЯкщоyвyгеометричнійyпрогресіїy 0 12<<bb ,yтоy q > 1 .
3)yЯкщоyвyгеометричнійyпрогресіїy
4)yЯкщоyвyгеометричнійyпрогресіїy b10 10 = ,yтоy b100 100 = .
5)yІснуєyгеометричнаyпрогресіяy b1 ,y b2 ,y b3 ,yдляyякоїy bb13 0 ⋅< .
1 Знайдітьyзнаменникyгеометричноїyпрогресіїy
5
2
Визначтеyп’ятийyчленyгеометричноїyпрогре-
6 yУстановітьyвідповідністьyміжyформулоюyn-гоy членаy(1–3)yгеометричноїyпрогресіїy bn () yтаy другимyчленомy(А–Г)yцієїyпрогресії.
3
bn () ,yякщоy b1 12 =
4 Знайдітьyдругийyчленyгеометричноїyпрогресіїy bn () ,yякщоy
7 Триyчислаy x1,y x2yіy x3yутворюютьyзростаючуy арифметичнуyпрогресію.yy
1)yЗнайдітьy x2,yякщоyсумаyцієїyпрогресіїyдорівнюєy9.
2)yЯкщоyдоy x 1yдодатиy1,y x2yзалишитиyбезy змін,yаyдоy x3yдодатиy3,yтоyотримаємоyгеометричнуyпрогресію.yЗнайдітьy x1yіy x3.y 8
yКлієнтyпоклавyуyбанкy100y000yг.yо.yпідy10y%y річних.yВідсоткиyщорокуyнараховуютьсяyнаy суму,yякаyєyнаyрахункуyнаyпочатокyроку.y 1)yЯкаyсумаyбудеyнаyрахункуyчерезy2yроки? 2)yСкладітьyформулуyдляyвизначенняyсумиy bn наyрахункуyклієнтаy(уyг.yо.)yчерезy nyроків.y
MATH FOR LIFE
Щорокуyприрістyнаселенняyуyмістіyстановитьy3y%,yтобтоyкожногоyнаступногоyрокуyкількістьyмешканцівyмістаyзбільшуєтьсяyнаy 3y%yвідyкількостіyмешканцівyнаyкінецьyпопередньогоyроку.yВважайте,yщоyтемпиyприростуyнаселенняyмістаyнеyзмінюються.yЗаразy чисельністьyнаселенняyмістаyстановитьy160yтис.yосіб.
1 yЯкоюyбудеyчисельністьyнаселенняyчерезy2yрокиy(уyтис.yосіб)?y
2 yСкладітьyформулу,yзаyякоюyможнаyобчислитиyчисельністьyнаселенняyуyмістіy(уyтис.yосіб)yчерезy nyроків.y
3 yЗаyпрогнозамиyчерезy пyроківyчисельністьyнаселенняyперевищитьy200yтис.yосіб.yЗапишітьyнерівністьyдляyвизначенняy п. ДОМАШНЄ ЗАВДАННЯ
1 yУyгеометричнійyпрогресіїy bn () yзнайдітьyчленy b n,yякщо: yy1)y b1 4 = ,y b2 12 = ,y n =yy3;yy3)y b4 3 = ,y b5 6=− ,y n =yy10; yy2)y b1 5 81 = ,y b2 5 27 = ,y n =yy7;yyy4)y b7 3 2 = ,y b8 3 = ,y n =yy16.y
2 yВизначтеyчотириyчисла:
1)y x1 ,y x2 ,y x3 ,y x4 ,yщоyутворюютьyзростаючуyгеометричнуyпрогресіюyзіyзнаменникомy q = 2 ,yякщоyїхyсумаyдорівнюєy210; 2)y x1 ,y x2 ,y x3 ,y x4 ,yщоyутворюютьyспаднуyгеометричнуyпрогресію,yякщоy xx13 15 += ,y xx24 75 += , ;
3)yщоyутворюютьyзростаючуyгеометричнуyпрогресію,yякщоy сумаyпершихyдвохyчиселyдорівнюєy3,75,yаyсумаyостанніхy двохyчиселyдорівнюєy60;
4)yщоyутворюютьyспаднуyгеометричнуyпрогресію,yякщоyсумаy їїyкрайніхyчленівyдорівнюєy126,yаyсумаyсередніхyчленівyдорівнюєy30.
3 yЗапишітьyпершіy4yчлениyгеометричноїyпрогресіїy bn () ,yякщо:
1)y
Запишітьyпершіy6yчленівyгеометричноїyпрогресіїy bn () ,yякщо: 3)y b
4 yРозв’яжітьyзадачу.
1) Триyчислаyутворюютьyарифметичнуyпрогресію,yпершийyчленy якоїyдорівнюєy1.yЯкщоyдоyпершогоyчислаyдодатиy4,yдоyдругогоyдодатиy2,yаyтретєyзалишитиyбезyзмін,yтоyотримаємоyгеометричнуyпрогресіюyзіyзнаменникомy1.yЗнайдітьyціyчисла.
2)yТриyчислаyутворюютьyарифметичнуyпрогресію,yдругийyчленy якоїyдорівнюєy6.yЯкщоyвідyпершогоyчислаyвіднятиy1,yдоyтретьогоyдодатиy9,yаyдругеyзалишитиyбезyзмін,yтоyотримаємоy геоyметричнуyпрогресіюyзіyзнаменникомy3.yЗнайyдітьyціyчисла.









TO BE SMART
IQ


Фільм-головоломка «Пастка Ферма» ( La habitaci ó n de Fermat , Іспанія) розповідає історію таємного змагання чотирьох математиків. Розв’язавши тестове завдання з числовою послідовністю, математики потрапляють до дивного будинку, який виявляється пасткою. Щоб вижити, вони повинні розв’язувати логічні завдання.


Див. приклад 5

ЧИ ВІДОМО ВАМ?
Геометрична прогресія в біології





Розмноження бактерій у геометричній прогресії застосовують, наприклад, у природоохоронних заходах: для очищення стічних вод, ліквідації нафтових плям тощо.

Соціальні мережі — це не альтернатива дружбі, це її продовження.
Марк Цукерберг
3)yСумаyтрьохyчисел,yякіyутворюютьyзростаючуyарифметичнуy прогресію,yдорівнюєy60.yЯкщоyвідyпершогоyчислаyвіднятиy5,y другеyзалишитиyбезyзмін,yаyдоyтретьогоyдодатиy69,yтоyотримаємоyгеометричнуyпрогресію,yзнаменникyякоїyдорівнюєy5.y Знайдітьyціyчисла.
4)yСумаyтрьохyчисел,yякіyутворюютьyзростаючуyарифметичнуy прогресію,yдорівнюєy45.yЯкщоyвідyпершогоyчислаyвіднятиy5,y другеyзалишитиyбезyзмін,yаyдоyтретьогоyдодатиy25,yтоyотримаємоyгеометричнуyпрогресію.yЗнайдітьyціyчисла.
5 yРозв’яжітьyзадачу.
1)yКількістьy bn yтелеглядачів,yякіyдивлятьсяy n-йyсезонyсеріалу,y задаєтьсяyформулоюy bn n =⋅ 26 000 3 1 .yСкількиyтелеглядачівy подивилисяyдругийyсезонyсеріалу?
2)yКомп’ютернаyантивіруснаyпрограмаyнаприкінціyпершоїyхвилиниyзyмоментуyїїyзапускуyблокуєy3yвірусніyпрограми.yПротягомyкожноїyнаступноїyхвилиниyвонаyблокуєyудвічіyбільшеyвіруснихyпрограм,yніжyпротягомyпопередньоїyхвилини.y Скількиyвіруснихyпрограмyзаблокуєyкомп’ютернаyпрограмаy протягомyсьомоїyхвилиниyзyмоментуyїїyзапуску?
3) Бактерія,yпотрапившиyвyживийyорганізм,yнаприкінціy 10-їyхвилиниyділитьсяyнаyдвіyбактерії.yКожнаyзyнихyнаприкінціyнаступнихy10yхвyтакожyділитьсяyнаyдвіyбактеріїyіyт.yд.y Знайдітьyкількістьyбактерій,yщоyутворятьсяyзyоднієїyбактеріїy наприкінціyпершоїyгодиниyзyмоментуyїїyпотраплянняyвyживийyорганізм.
4)yНаyтериторіїyпершогоyпарковогоyмістечкаyрозташованийy басейнyплощеюy100yм2.yНаyтериторіїyкожногоyнаступногоy парковогоyмістечкаyрозташованийyбасейн,yплощаyякогоy вy1,5yразуyбільша,yніжyнаyтериторіїyпопереднього.y yа)yyЯкаyплощаyбасейну,yрозташованогоyнаyтериторіїyтретьогоy парковогоyмістечка?
yб)yyСкладітьyформулуyдляyвизначенняyплощіy bn y(уyм2)yбасейну,yщоyрозташованийyнаyтериторіїy















ОрганізаториyпроведенняyфлешмобуyдоyДняyматеріyвyУкраїніyвирішилиyвикористатиyдляyзв’язкуyміжyучасникамиyсмсповідомлення.yОдинyзyучасниківyотримавyповідомленняyзyпроханнямyнадіслатиyвідповіднуyінформаціюyчотирьомyіншим,yякі,y уyсвоюyчергу,yнадіслалиyсмс-повідомленняyщеyчотирьомyучасникамyіyт.yд.yСкількиyучасниківyфлешмобуyотримаютьyінформаціюy протягомy20yхв,yякщоyодинyучасникyвиконуєyцеyдорученняyзаy 2yхв?yУсіyнадісланіyповідомленняyвважайтеyотриманими.
Коментар до розв’язання Складемоyтаблицюyзаyумовоюyзадачі.
«Кроки» n розповсюдження інформації
Час від початку розсилки повідомлень, хв
Кількість повідомлень, надісланих на n-му кроці
Бачимо,yщоyкількістьyповідомлень,yнадісланихyкожноїyдругоїy хвилини,yскладаютьyгеометричнуyпрогресію:y1,y4,y16,y64,y…,yуyякійy першийyчленy b1 1 = ,yзнаменникy q = 4 .yКількістьyчленівyпрогресіїy n = 11 .y
Дляyтогоyщобyвідповістиyнаyзапитання,yскількиyучасниківy флешмобуyотримаютьyповідомленняyпротягомy20yхв,yнеобхідноy знайтиyсумуyвсіхyнадісланихyповідомлень:
Sn =+ ++ ++ 14 16 64 256 ...
Якщоyкількістьyчленівyпрогресіїy—yневеликеyчисло,yцюyсумуy можнаyобчислитиyусно.yВyіншомуyвипадкуyдляyспрощенняyобчисленьyпотрібноyзнатиyформулуyсумиy Sn yпершихy nyчленівyгеометричноїyпрогресії.




КЛЮЧОВІ ТЕРМІНИ
геометрична прогресія
знаменник геометричної
прогресії
n-й член геометричної
прогресії
формули суми перших n членів геометричної
Sn bq q n = () 1 1 1 .
ЗАПАМ’ЯТАЙТЕ!
ПОМІРКУЙТЕ За яких умов зручно засто-
совувати кожну з отриманих формул суми?




ГОЛОВНА
Запишемоyсумуy Sn yпершихy nyчленівyгеометричноїyпрогресії: Sbbbbb nnn = +++ ++ 12 31 ... . (1)
Помножимоyобидвіyчастиниyрівностіy(1)yнаy q.yОтримаємо: Sqbqbqbqbqbq nnn = +++ ++ 12 31 ... . (2)
Використовуючиyрекурентніyформулиy bqb12 = ,y bqb23 = yіyт.yд.,y рівністьy(2)yможнаyзаписатиyуyвигляді: Sqbbbbb nnn =+ ++ ++ + 23 41 ... (3)
Розглянемоyсистемуyдвохyрівняньy(1)yіy(3):
Віднімемоyпочленноyціyрівняння: SSqbb nnn −= + 11 .
Ураховуючи,yщоy bbq nn + = 1 ,yперетворимоyостаннюyрівністьyтак,y щобyуyнеїyвходилиyлишеyзмінніy Sn ,y b1 yіy bn ,yтобтоy Sqbbq nn 1 1 () =− . Тодіyприy q ≠ 1 yмаємо: Sn bbq q n = 1 1 .
Якщоyвyотриманійyформуліyзаписатиy bn ,yвикористовуючиy формулуy n-гоyчленаyгеометричноїyпрогресіїy bbq n n = 1 1 ,yотримаємоy q ≠ () 1
всіyyчлениyтакоїyпрогресіїyрівніyміжyсобою,yсумуyпершихy
ПРИКЛАД 1
Знайдітьyсумуyпершихy nyчленівyгеометричноїyпрогресіїy bn () ,y
уyякійy b1 48 = yіy q = 05 , ,yякщоy n = 4 ;y nk = ;y nk=− 3 .
Розв’язання
КРОК 1
КРОК 2
Запишемоyформулу,yзаyякоюyшукатимемоy
сумуy Sn .yВибираємоyформулуy Sn bq q n = () 1 1 1 ,y
томуyщоyзаданоy b1 yіy q. Підставимоyїхyзначенняy вyзаписануyформулуyтаyспростимоyїї.
Підставимоyзначенняy n = 4 yуyформулу,yодержануyнаyкроціy1.
КРОК 3
КРОК 4
Знайдемоy Sk .yДляyцьогоyпідставимоyуyформулуy nk = . Sk k
Підставимоyуyформулуyсумиy nk=− 3 ,yзнайдемоy Sk 3 yіyперетворимоyотриманийyвираз.
Відповідь:y90;y 96 10 5 () , k ;y 96 18 05 () , k .
ТРЕНУЄМОСЯ
1 yСкладітьyформулуyдляyобчисленняyсумиyпершихy nyчленівyгеометричноїyпрогресіїy bn () ,yякщо:
1)y b1 30 = ,y q = 16 ;yy3)y b1 45 = ,y q =−4 ;y
2)y b1 6 = ,y q = 04 , ;yy4)y b1 18 = ,y q =−08 , . yЗнайдітьyсумуyпершихy nyчленівyгеометричноїyпрогресіїy bn () ,y уyякій:
5)y b1 10 = ,y q = 2 ,yякщоy n = 5 ,y
6)y b1 162 = ,y








КРОК 1
bbq n n =⋅ 1 1
ПРИКЛАД 2
Визначтеyкількістьy nyчленівyгеометричноїyпрогресіїy xn () ,yсумаy якихyдорівнюєy571,5,yякщоy xn = 288 ,y q = 2 .
Розв’язання
Заyумовоюyзаданоy Sn yіy xn ;y qyy>yy1,yтомуyвикористаємоyформулуy Sn bqb q n = 1 1 .yПідставимоyвyнеїyвідоміy
значенняy q,y xn yіy Sn yтаyзнайдемоy x1 .
КРОК 2
Знаючиy xn ,y x1 yіy q,yзнайдемоy n,yвикористовуючиy формулуy n-гоyчленаyдляy xn = 288 .
ЗВЕРНІТЬ УВАГУ!
Рівняння 22 7 = n , отримане в прикладі 2, ви ще не вмієте розв’язувати. Такі рівняння вивчають у старшій школі.

ЧИ ВІДОМО ВАМ?
У творах Жуля Верна «Таємничий острів», «Подорож у надра Землі» є згадки про геометричну прогресію. Чи можете пригадати, які саме?



Відповідь: 7.
ТРЕНУЄМОСЯ 2 yЗнайдітьyпорядковийyномерy
сіїy bn () ,yякщо:
1)y b1 10 = ,y q = 7 ,y bn = 490 ;yy3)y b1 3 = ,y q = 1 10 ,y bn = 0 00003 , ; 2)y b1 2 = ,y q = 5
yВизначтеyкількістьy n yчленівyгеометричноїyпрогресіїy xn () ,y якщо:
5)y Sn = 484 ,y xn = 324 ,y q =
КРОК 1
третійyчленyякоїyдорівнюєy18,yаyп’ятийyдорівнюєy162.
Позначимоyзадануyпрогресіюy xn () .yЗапишемоyуyвиглядіy системиyрівняньyформулиy n-гоyчленаyдляy x3 yіy x5 yтаyпідставимоyзаданіyчисловіyзначення.
, ,y q = 2 .
КРОК 2
КРОК 3
КРОК 4
Оскількиyобидвіyчастиниyкожногоyрівнянняyсистемиyвідмінніyвідyнуляy( xn ≠ 0 ,y q ≠ 0 yзаyозначеннямyпрогресії),yподілимоyпочленноyдругеyрівнянняyнаyперше.
Знайдемоy x1 yдляyкожногоyзначенняy q.yОскількиyіyдляy q = 3 ,y іyдляy q =−3 yмаємоy q 2 9 = ,yробимоyвисновок,yщоyіснуєyєдинеy значенняy x1 2 = .
Знайдемоyсумуy S7 yпершихyсемиyчленівyпрогресіїyдляyобохy значеньy q.
Відповідь: 2186yабоy1094.
ТРЕНУЄМОСЯ
3
yСкладітьyформулуyдляyобчисленняyсумиyпершихy n членівyгеометричноїyпрогресіїy bn () ,yякщо:
1)y b1 3 = ,y b2 24 = ;yyy3)y b1 20 = ,y b2 15=− ;y
2)y b1 4 = ,y b2 36 = ;yyy4)y b1 30 = ,y
yОбчислітьyсумуyпершихy nyчленівyгеометричноїyпрогресіїy bn () ,y якщо:
5)y
b
ПРИКЛАД 4 (актуальна задача )
.y
ОрганізаториyпроведенняyфлешмобуyдоyДняyматеріyвyУкраїніyвирішилиyвикористатиyдляyзв’язкуyміжyучасникамиyсмсповідомлення.yОдинyзyучасниківyотримавyповідомленняyзyпроханнямyнадіслатиyвідповіднуyінформаціюyчотирьомyіншим,yякі,y уyсвоюyчергу,yнадіслалиyсмс-повідомленняyщеyчотирьомyучасникамy іyт.yд.yСкількиyучасниківyфлешмобуyотримаютьyінформаціюyпротягомy20yхв,yякщоyодинyучасникyвиконуєyцеyдорученняyзаy2yхв?y Усіyнадісланіyповідомленняyвважайтеyотриманими.








КРОК 1
3
КРОК 2
КРОК 3
Розв’язання
Визначимо, скільки етапів передачі інформації по 2 хв міститься у 20 хв. 20 хв : 2 хв = 10 (етапів)
Визначимо, як змінюватиметься кількість учасників, повідомлених наприкінці кожного етапу тривалістю 2 хв.
Створимо математичну модель даної ситуації.
Введемо позначення елементів геометричної прогресії.
суму перших 11 членів прогресії за формулою Sn










2)
Кількість учасників, повідомлених наприкінці кожного етапу, дорівнюватиме кількості учасників, повідомлених наприкінці попереднього етапу, помноженій на 4
Загальна кількість отриманих повідомлень дорівнює кількості учасників, які надіслали повідомлення протягом 20 хв. Її можна знайти як суму перших n членів геометричної прогресії. bn () — геометрична прогресія,
4)yУyфітнес-центріyдіютьyзнижкиyдляyпостійнихyклієнтів.yЦінаy абонементаyнаyпершийyрікyстановитьy xyгрн.yКожногоyнаступногоyрокуyцінаyабонементаyстаєyнаy10yy%yменшоюyпорівняноyзyціноюyабонементаyнаyпопереднійyрік. а)yВиразітьyчерезy xyвартістьyабонементаyнаyтретійyрік. б)yЗнайдітьy x,yякщоyвідомо,yщоyзаyабонементиyнаyпершіyтриy рокиy(триyабонементи)yклієнтyсплативy10yy840yгрн.
ЗАПИС ПЕРІОДИЧНОГО
Уyкурсіyалгебриy8yкласуyвиyнавчилисяyперетворюватиyперіодичнийyдесятковийyдрібyуyзвичайний.yУyцьомуyпараграфіyмиyрозглянемоyщеyодинyспосібyрозв’язуванняyтакогоyзавданняy—yізyвикористаннямyгеометричноїyпрогресії.
Існуєyокремийyвидyгеометричноїyпрогресії,yзнаменникyякоїy перебуваєyвyмеyжахyвідy–1yдоy1,yтобтоy −< < 11 q .yТакуyгеометричнуyпрогресіюy bn () ,yуyякійy q < 1,yназиваютьy
нескінченно спадною геометричною прогресією.yЦікавимyєyте,yщоyдляyтакоїyпрогресіїy можнаyзнайтиyсумуy всіхyїїyчленівyзаyформулоюy Sb q = 1 1 .
ПРИКЛАД 5
Подайтеyчислоy0,(13)yуyвиглядіyнескоротногоyзвичайногоyдробу.y Розв’язання
Крок Зміст
КРОК 1
КРОК 2
Запишемоyзаданеyчислоyуyвиглядіy сумиyдесятковихyдробів.






0130,,131313... () == =+ ++ 0130 0013 0 000013 ,, , ...
Розглянемоyотримануyпослідовністьyдоданків.yЗробимоyвисновокy щодоyїїyвиду.
Послідовністьyчиселy0,13;y0,0013;y0,000y013;y…y єyгеометричноюyпрогресією,yпершийyчленyякоїy b1 013 = , ,yзнаменникy q = 1,00 . q < 1,yотже,yгеометричнаyпрогресіяyєyнескінченноy спадною





Один з учнів має йти від столу вчителя до дверей кабінету по прямій. Він робить перший крок завдовжки 1 м, другий — 1/2 м, третій — 1/4 м

і т. д., тобто довжина кожного


наступного кроку у 2 рази менша, ніж довжина попереднього.
Чи дійде учень до дверей, якщо
відстань від столу до дверей по
прямій 3 м?

ТРЕНУЄМОСЯ
5 yПодайтеyуyвиглядіyнескоротногоyзвичайногоyyдробуyчисло: 1)y0,(7);y2)y0,(42);y3)y2,(5).y
Подайтеyуyвиглядіyнескоротногоyзвичайногоyдробуy m n yчисло: 4)y1,(14);yуyвідповідьyзапишітьyсумуy mn + ; 5)y 10 23 3 7
() , ;yуyвідповідьyзапишітьyрізницюy nm.
Обчислітьyзначенняyвиразу:
6)y 063 118 91 , , () () ⋅ ;y y7)y 0181 72 21 330 ,, ()() ⋅ + .
8)yЗнайдітьy 15 16 yвідyчислаy 04 60 0112 5 35 37 ,, () + () .
1 Знайдітьyсумуy Sn yпершихy nyчленівyгеометричноїyпрогресії:


IQ
TO BE SMART
Радимо прочитати книжку «Математичні усмішки» (упорядник Н. О. Вір ченко).


Книжка складається з трьох розділів: «Про цікаве та кумедне у житті математиків», «Цікаве та смішне у математиці», «Математичні сміховинки, жарти».


Задача Фібоначчі
із «Книги абака»
3
;y n = 5 . 2 Уyгеометричнійyпрогресії: 1)y xn () :y x3 4=− ;y x7 64=− . Знайyдітьy S7 .
2)y yn () :y y3 9=− ;y q =−3 ;y Sn = 182 .yЗнайдітьy n.
3)y cn () :y
6)y
1
2
3
7
геометричної прогресії bn () дорівнює 60, bn = 40 , q = 3 .
2) Знайдіть n.
8 У місті 12 районів, у кожному є сквер. Площа скверу в першому районі дорівнює 1000 м2. Площа скверу в кожному наступному районі в 1,5 разу більша, ніж у попередньому. Складіть формулу, за якою можна обчислити:
1) площу bn (у м2) скверу, розташованого в n-му районі міста 112 n () ;
2) загальну площу Sn (у м2) ділянок, виділених під сквери в усіх
MATH FOR LIFE



ВАМ? y Швидкість вільного падіння 180 км/год, або 50 м/с. y До повного відкриття парашута людина пролітає в середньому 3000 м приблизно за 1 хв.


1
коло.
2 yСкладітьyформулу,yзаyякоюyможнаyобчислитиyкількістьy xn парашутистів,yщоyутворюютьy n-неyколо.
3 yСкількиyпарашутистівyперебуваютьyуyповітрі,yякщоyвсьогоy утворилосяy5yкіл?
Поміркуйте,yчиyєyподаніyтвердженняyщодоyгеометричноїyпрогресіїyправильними.yВідповідьyобґрунтуйте.








Ніна Опанасівна Вірченко (нар. 1930) — українська вчена, математик, доктор фізико-математичних наук, професор, академік-секретар відділення математики АН ВШ України, віце-президент АН ВШ, член Українського, Американського, Австралійського, Бельгійського, Единбурзького, Лондонського математичних товариств. Ніна Опанасівна — обдарований педагог, авторка понад 350 наукових і науково-методичних праць, 20 оригінальних книжок.


8 ,y…yобчислюютьyзаyформулоюy Sn n =−() 51 2 . 3) Якщоy S1 3 = ,y qS⋅= 2 90 ,yтоy S3 93 = . 4) Якщоy b3 6 = ,yтоy bb15 36 ⋅= .
5) Якщоy S3 42 = ,y 121 2 ++ = qq ,yтоy b1 2 = .