TESTY pro devá áky
K JEDNOTNÝM PŘIJÍMACÍM ZKOUŠKÁM
515 úloh
Vypočtěte: 1 bod
Zapište ve tvaru zlomku: 2 body pětinu z dvojnásobku výrazu 2x – 3 zvětšenou o 1
Vypočtěte a výsledek zapište zlomkem v základním tvaru: max. 4 body
a)
Doplňte výrazy tak, aby platila rovnost: max. 4 body a)
b)

Tři ocelové tyče o délkách 12 dm, 2 m a 160 cm mají být rozřezány max. 4 body na stejné, co možná nejdelší části.
a) Určete délku jedné části v decimetrech.
b) Určete počet částí.
c) Určete celkový počet řezů, kterými budou dané tyče rozřezány.
d) Určete cenu řezů, jestliže víte, že tři řezy stojí 10 Kč.
Řešte rovnici:
3 body
Dva chlapci vyběhli ve stejný okamžik ze stejného místa. 2 body První z nich běžel přímo na sever průměrnou rychlostí 3 m/s, druhý pak přímo na západ průměrnou rychlostí 4 m/s.
Jak daleko budou od sebe po minutě běhu?
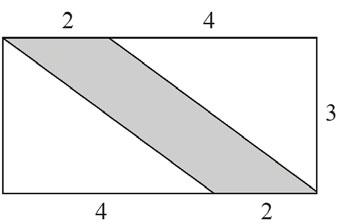
Na obrázku je obdélník (údaje jsou v centimetrech) max. 3 body a v něm šedě vybarvený geometrický útvar.
a) Vypočtěte obsah šedě vybarveného geometrického útvaru.
b) Vypočtěte obvod šedě vybarveného geometrického útvaru.
Plechová nádrž je zcela naplněna vodou. Kolik ze 180 litrů z ní vyteče, 2 body jestliže do ní ponoříme žulový kvádr o rozměrech 20 cm, 30 cm a 40 cm?
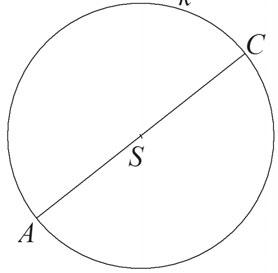
Na obrázku je kružnice k se středem S a úsečka .
a) Sestrojte čtverec ABCD.
b) Sestrojte obraz čtverce ABCD ve středové souměrnosti se středem S.
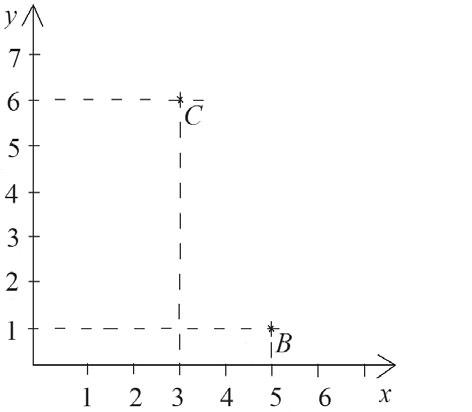
V pravoúhlé soustavě souřadnic s jednotkou délky 1 cm jsou
3 body
3 body vyznačeny body B a C.
a) Vyznačte v ní bod A tak, aby byly body A, B a C vrcholy rovnoramenného trojúhelníku se základnou AB. Souřadnice bodu A zapište.
b) Zjistěte délku výšky k základně v trojúhelníku ABC.
c) Vypočtěte obsah trojúhelníku ABC.
Vnitřní úhel kosočtverce ABCD α = 65°.
Rozhodněte o každém z následujících tvrzení, jestli je pravdivé, nebo nepravdivé:
a) Velikost úhlu β je 115°. ANO – NE
b) Úhlopříčka BD je delší než úhlopříčka AC. ANO – NE
c) Úhlopříčky svírají úhel 65°. ANO – NE
Eliška složila ze šestnácti tyček o délce 4 cm čtverec.
Bára jej rozebrala a z tyček složila obdélník s maximálním obsahem.
Rozhodněte o každém z následujících tvrzení, jestli je pravdivé:
a) Délky stran tohoto obdélníku jsou 20 cm a 12 cm. ANO – NE
b) Obsah tohoto obdélníku je 252 cm2. ANO – NE
c) Obvod obdélníku je roven obvodu původního čtverce. ANO – NE
3 body
Vypočtěte poloměr kružnice opsané pravoúhlému trojúhelníku
2 body s odvěsnami délek 6 cm a 8 cm.
Na obrázku je trojúhelník XCD. Sestrojte pravoúhlý lichoběžník ABCD
3 body s pravým úhlem při vrcholu A tak, aby bod X byl středem jeho delší základny.
Na obrázku je úsečka AB. max.
3 body

a) Nad touto úsečkou sestrojte Thaletovu kružnici.
b) Sestrojte množinu všech středů těchto Thaletových kružnic za předpokladu, že délka úsečky AB se nezmění a z jejích krajních bodů budete posunovat pouze bod B.
Rovnostranný trojúhelník má délku strany 6 cm. max. 3 body
Rozhodněte, zda jsou následující tvrzení o zadaném trojúhelníku pravdivá, nebo nepravdivá:
a) Každá z jeho těžnic má jinou délku. ANO – NE
b) Jeho výška měří ANO – NE
c) Jeho obsah je ANO – NE
Rozhodněte o každém z následujících tvrzení, zda je pravdivé, max. 3 body nebo nepravdivé:
a) ANO – NE
b) ANO – NE
c) ANO – NE
17
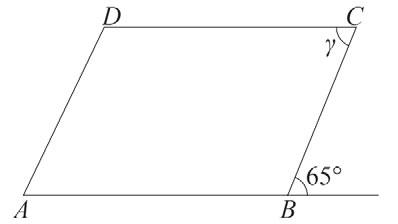
Na obrázku je kosodélník ABCD
Určete velikost úhlu γ.
Vyberte jednu z nabízených možností:
a) 25°
b) 45°
c) 65°
d) 105°
e) 115°
2 body
Spotřeba nákladního auta je x litrů na y kilometrů. 3 body Podle jakého vzorce správně určíme, kolik litrů nafty spotřebuje na 120 km? Vyberte jednu z nabízených možností:
a)
b)
c)
d)
e) podle jiného vzorce
Přiřaďte ke každé úloze (a–c) odpovídající výsledek (A–F): max. 6 bodů
a) Běžec uběhl za 45 min 9 km. Kolik kilometrů by stejným tempem uběhl za 1 h a 15 min?
b) Na mapě s měřítkem 1 : 250 000 je přímá vzdálenost dvou míst 5 cm. Jaká je jejich přímá vzdálenost ve skutečnosti?
c) Rozsáhlý pozemek tvaru obdélníku má výměru 400 ha. Jakou má pozemek délku, když jeho šířka je 500 m?
A) 800 m
B) 8 km
C) 10 km
D) 12,5 km
E) 13,5 km
F) 15 km
Lesní dělník sází stromky. Kdyby jich každou hodinu místo 8 zasadil 12, max. 3 body byl by s prací hotový o 2 hodiny dříve.
a) Kolik stromků má vysadit?
b) Jak dlouho by tato práce trvala sehrané trojici lesních dělníků, kteří dokáží zasadit 36 stromků za hodinu?
Matěj měl 9 bonbónů, Dan jich měl 6. Matěj dal Danovi 2 bonbóny. 1 bod
Který z nich má teď víc bonbónů a o kolik?
Vypočtěte:
2 body
Přímá vzdálenost dvou míst je ve skutečnosti 30 m. Jaká bude jejich
2 body vzdálenost na plánu s měřítkem 1 : 200?
Jsou dány zlomky O kolik je větší jejich součet než jejich součin?
2 body
Zadané výrazy upravte na součin. V případě, že použijete vytýkání, max.
4 body tak zvolte jeho maximální možnou míru.
a)
b)
a) Kolik gramů modré skalice je potřeba na přípravu 5% vodného max.
3 body roztoku modré skalice, jestliže hmotnost roztoku má být 200 g?
b) Hmotnost konve s vodou je 10,5 kg. Jestliže z ní odlijeme 75 % vody, bude mít konev s vodou hmotnost 4,5 kg. Jaká je hmotnost prázdné konve?
Která kladná celá čísla vyhovují následující nerovnici?
3 body
Na záhon s bramborami tvaru obdélníku s rozměry 10 m a 4 m
3 body napršelo 10 mm srážek. Kolik plných desetilitrových konví bychom tímto množstvím vody naplnili?
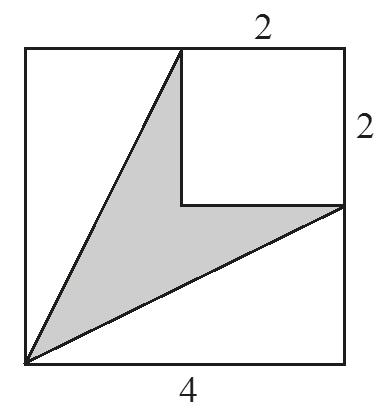
Jakou část čtverce se stranou délky 4 cm
3 body zabírá šedě vybarvený obrazec (údaje na obrázku jsou v centimetrech)?
Výsledek uveďte jako zlomek v základním tvaru.
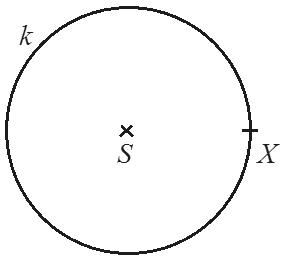
Na obrázku je kružnice k se středem S a bod X,
a) Sestrojte obraz kružnice k ve středové souměrnosti se středem X.
b) Kolik společných tečen mají kružnice k a k' ?
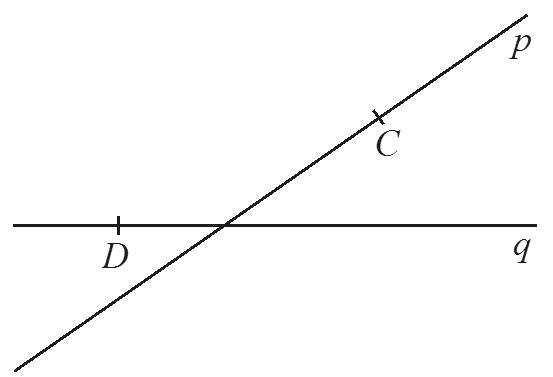
Na obrázku jsou přímky p, q, na nichž leží úhlopříčky kosodélníku ABCD.
Dále platí:
a) Sestrojte kosodélník ABCD.
b) Kolik má kosodélník os souměrnosti?
3 body
3 body
Větší zavařovací sklenice má tvar válce s podstavou o obsahu 2 dm2 max.
3 body a výškou 25 cm.
Rozhodněte o každém z následujících tvrzení, jestli je pravdivé, nebo nepravdivé:
a) Do prázdné sklenice se vejde 5 litrů vody. ANO – NE
b) Pokud 85 % objemu sklenice tvoří okurky, pak nálevu je ve sklenici 2,5 decilitru. ANO – NE
c) Pokud nálev vyplňuje sklenice, pak okurky v ní zabírají 90 % objemu. ANO – NE
V 7.A měla na konci školního roku třetina žáků vyznamenání, max.
3 body 60 % žáků prospělo a dva žáci neprospěli.
Rozhodněte o každém z následujících tvrzení, jestli je pravdivé, nebo nepravdivé:
a) Vysvědčení na konci školního roku dostalo v 7.A 20 žáků. ANO – NE
b) Vyznamenání mělo 10 žáků. ANO – NE
c) Prospělo 18 žáků. ANO – NE
V rovině je dána přímka p a mimo ní bod S. max. 3 body
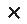
a) Sestrojte přímku q tak, aby platilo: .
b) Sestrojte obraz přímky q v osové souměrnosti s osou p.
V rovině je dána úsečka AB. Sestrojte rovnoramenný trojúhelník ABC tak, 2 body aby výška k základně a základna měly stejné délky.
Na obrázku je kružnice k se středem S. max. 3 body
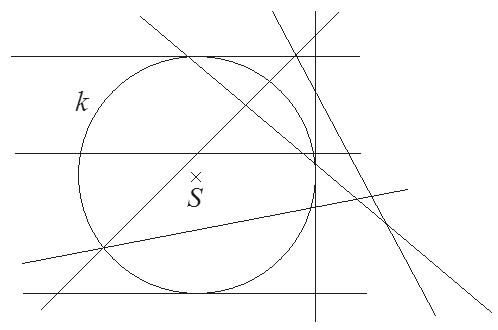
Rozhodněte o každém z následujících tvrzení, jestli je pravdivé, nebo nepravdivé:
a) Na obrázku jsou 3 tětivy kružnice k. ANO – NE
b) Na obrázku jsou 3 tečny kružnice k.
ANO – NE
c) Na obrázku jsou dvě vnější přímky kružnice k. ANO – NE
Plánovaná cena jednodenního výletu 300 Kč na žáka byla zvýšena o 15 %. max. 3 body Žáci dohromady zaplatili o 990 Kč navíc.
Rozhodněte o každém z následujících tvrzení, jestli je pravdivé, nebo nepravdivé:
a) Každý žák nakonec zaplatil 375 Kč. ANO – NE
b) Počet žáků této třídy je 24. ANO – NE
c) Pokud by se někdo ze žáků výletu nezúčastnil, ANO – NE dostal by zpět 80 % ze zaplacené částky, tedy 276 Kč.
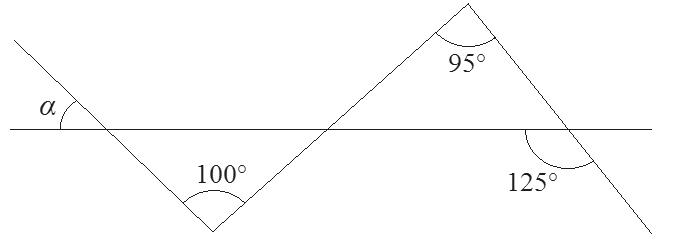
Vypočtěte velikost úhlu α na obrázku. 2 body
Vyberte jednu z nabízených možností:
a) α = 20°
b) α = 30°
c) α = 50°
d) α = 60°
e) α = 80°
Obsahy dvou kruhů jsou v poměru 16 : 9. V jakém poměru jsou jejich obvody? 2 body
Uveďte ho v základním tvaru. Vyberte jednu z nabízených možností:
a) 2 : 1
b) 3 : 4
c) 16 : 9
d) 4 : 3
e) 3 : 2
f) jiný poměr
Přiřaďte ke každé úloze (a–c) odpovídající výsledek (A–F): max. 6 bodů
a)
b)
c)
A) –2
B) 1
C) –1
D) E) F)
Místo hvězdičky doplňte číslici tak, aby vzniklé číslo bylo dělitelné patnácti. 2 body 17 22*
Nádrž na vodu má tvar kvádru s rozměry dna 2 m a 3 m. Její největší 3 body stěna má obsah 18 m2. Kolik hektolitrů vody je v nádrži, pokud je naplněna ze ?
Na obrázku je kružnice k se středem S a body A, C, pro které platí: max. 3 body
a) Sestrojte rovnoramenný trojúhelník ABC se základnou AB tak, aby
b) Sestrojte obraz trojúhelníku ABC v osové souměrnosti s osou, kterou je přímka BC.
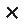
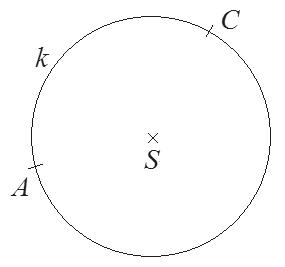
Na obrázku je trojúhelník SCD. Sestrojte kosočtverec ABCD tak, 2 body aby bod S byl středem souměrnosti tohoto kosočtverce.
Na obrázku je rovnoramenný lichoběžník ABCD s vyznačenými max. 3 body vnitřními úhly. Dále platí, že základny a = 12 cm, c = 6 cm a výška lichoběžníku je v = 4 cm.
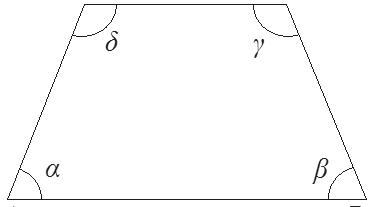
Rozhodněte o každém z následujících tvrzení, jestli je pravdivé, nebo nepravdivé:
a) α + β < γ + δ ANO – NE b) a + c > b + d ANO – NE c) ANO – NE
představujíkuchařky a zbylých 6 zaměstnanců jsou
takzvaní správní zaměstnanci (školník a uklízečky).
Rozhodněte o každém z následujících tvrzení, jestli je pravdivé, nebo nepravdivé: a) Správních zaměstnanců je více než kuchařek. ANO – NE
b) Kuchařek a správních zaměstnanců je dohromady méně než čtvrtina všech zaměstnanců školy. ANO – NE
c) Pedagogických pracovníků je sedmkrát víc než správních zaměstnanců. ANO – NE
Nepřímá úměrnost je dána rovnicí . Doplňte souřadnici bodu 2 body
A[x; 30] tak, aby tento bod ležel na grafu zadané nepřímé úměrnosti.
Vyberte jednu z nabízených možností:
a)
b) 5
c)
d) 6
e)
f) 4
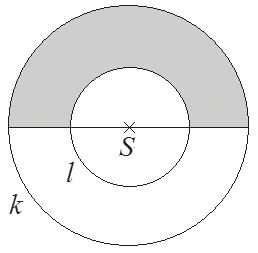
Na obrázku jsou dvě soustředné kružnice k a l se společným středem S. 3 body
Poloměr kružnice k je 6 cm, kružnice l 3 cm. Vypočtěte obsah šedě vybarveného útvaru.
Vyberte jednu z nabízených možností:
a) 11,5π cm2
b) 13,5π cm2
c) 16π cm2
d) 27π cm2
e) 36π cm2
f) jiný obsah
S l k
TESTY pro devá áky K JEDNOTNÝM PŘIJÍMACÍM ZKOUŠKÁM
Ve sbírce je 30 testů, které obsahují veškeré učivo základní školy. Jsou obdobou testů, které se řeší v rámci jednotných přijímacích zkoušek na střední školy. Sbírka poskytuje jedinečnou možnost vyzkoušet si různé typy úloh a prověřit si své znalosti. Testy jsou bodované stejně jako u přijímacích zkoušek, maximum je také stejné – 50 bodů. Sbírka obsahuje i výsledky testů s podrobným rozpisem, jak jednotlivé úlohy obodovat.
