9789152368763

matematik

Daniel Dufåker

Roger Fermsjö

nivå

2b

1

Innehåll

Räta linjer och ekvationssystem 6

1.1 Räta linjens ekvation 8

Räta linjens ekvation i k-form 8

Räta linjens ekvation i allmän form 13

1.2 Ekvationssystem 17

Grafisk lösning av linjära ekvationssystem 17

Substitutionsmetoden 23 Additionsmetoden 29

Problemlösning med hjälp av ekvationssystem 34

Historia: Att lösa ekvationssystem 37

Uppslaget 38

Blandade uppgifter 41

2 Algebra och andragradsekvationer

46

2.1 Algebraiska uttryck 48

Multiplicera och faktorisera algebraiska uttryck 48

Kvadreringsreglerna och konjugatregeln 53

Faktorisering av uttryck 57

2.2 Enkla andragradsekvationer 60

Ekvationer av typen x2 = a 60

Att lösa andragradsekvationer med faktorisering 63

2.3 Fullständiga andragradsekvationer 66

Kvadratkomplettering 66

Lösningsformel för andragradsekvationer 70

Antal lösningar till en andragradsekvation 75

Problemlösning med andragradsekvationer 77

Historia: Ekvationer av högre grad 81

3 Andragradsfunktioner 90

3.1 Andragradsfunktioner 92

Funktioner 92 Grafen till en andragradsfunktion 97

Andragradsekvationer och andragradsfunktioner 104

Andragradsfunktioner och modellering 110

3.2 Andragradsfunktioner och grafritande hjälpmedel 117

Andragradsekvationer och olikheter 117

Problemlösning med grafritande hjälpmedel 122 Uppslaget

Geometri och bevis 140

4.1 Matematisk bevisföring 142

Olika slags vinklar 142 Vinklar i trianglar och månghörningar 146 Implikation och ekvivalens 150

Satser och bevis 155 Pythagoras sats 161

Koordinatgeometri 164

4.2 Klassiska satser om trianglar 167

Likformiga månghörningar 167

Likformiga trianglar 169 Topptriangelsatsen, transversalsatsen och bisektrissatsen 173

Satser om kongruens 178

4.3 Klassiska satser om cirkeln 183

Satser om vinklar i cirkeln 183 Kordasatsen och vinklar i inskrivna fyrhörningar 189

Historia:

6.1 Sammanställa och bearbeta

Lägesmått 244 Spridningsmått 249

Statistik med digitala verktyg 255

Standardavvikelse 260 Normalfördelning 265

6.2 Statistiska samband

Linjär regression 273

Olika regressionsmodeller 280

Normalfördelning

Ledtrådar

5

Logaritmer

5.1 Exponentialekvationer

Exponential- och potensekvationer 206

Tiologaritmer 212

Exponentialekvationer och tiologaritmer 217

5.2 Logaritmlagar

Räkneregler för logaritmer 221

Tillämpningar av logaritmer 225

1

Räta linjer och ekvationssystem

Delkapitel

1.1 Räta linjens ekvation

1.2 Ekvationssystem

Förkunskaper

■ Ekvationslösning

■ Räta linjens ekvation

■ Begreppet linjärt ekvationssystem. Metoder för att lösa linjära ekvationssystem. Centralt innehåll

Ibland kommer rapporter om att en asteroid riskerar att kollidera med jorden. Forskare kan finna modeller för jordens och asteroidens rörelsebanor genom att beskriva dem med ekvationer. Varje punkt i respektive bana är en lösning till den ekvationen och om det finns någon punkt som löser båda ekvationerna, skär banorna varandra i den punkten. Om banorna dessutom skär varandra vid samma tidpunkt är katastrofen ett faktum.

Att hitta en gemensam lösning till två ekvationer kallas att lösa ett ekvationssystem. Ett exempel från vardagen kan uppkomma vid val av elavtal. Ett sätt att jämföra två olika avtal är att ställa upp ekvationer som beskriver kostnaden vid förbrukning av ett visst antal kilowattimmar. För att se vid vilken förbrukning de båda avtalen ger samma kostnad, kan man lösa ekvationssystemet där de tillhörande ekvationerna ingår och därefter avgöra vilket avtal som är bäst.

När du är klar med kapitlet ska du kunna u bestämma en rät linjes ekvation i k-form och i allmän form u lösa ekvationssystem med grafiska och algebraiska metoder u lösa problem med hjälp av ekvationssystem

Att hyra bil

Ekvationerna y = 15x + 300 och y = 11x + 400 beskriver kostnaden att hyra en bil i ett dygn hos biluthyrarna Alfa respektive Beta. Den totala kostnaden y kr beror i båda fallen av antalet körda mil x.

u Vilken av biluthyrarna Alfa eller Beta bör man välja om man ska köra ca 15 mil på ett dygn?

u Vilken av biluthyrarna Alfa eller Beta bör man välja om man ska köra ca 40 mil på ett dygn?

u Red ut för vilka körsträckor per dygn som de olika biluthyrarna är billigast.

Nog med information?

Miriam och Samuel är syskon. Vilken information behöver du som minst känna till för att kunna avgöra hur gamla de är? Välj bland påståendena här nedanför.

A Miriam och Samuel är tillsammans 21 år.

B Miriam är sju år äldre än Samuel.

C Samuel är sju år yngre än Miriam.

D Miriam är dubbelt så gammal som Samuel.

1.1 Räta linjens ekvation

Räta linjens ekvation i k-form

Räta linjer behandlade vi utförligt redan i Matematik nivå 1b. Vi visade då att varje ekvation i formen y = kx + m motsvarar en rät linje i ett koordinatsystem. Ett exempel på en sådan ekvation är y = 3x + 4, där k = 3 och m = 4.

När x = 0 är y = k ∙ 0 + m = m

Från ekvation till graf Om vi vill rita linjen y = 3x + 4 i ett koordinatsystem, räcker det att vi känner till två punkter på linjen. Sätter vi in x = 0 i ekvationen, får vi y = 3 ∙ 0 + 4 = 4

Linjen skär alltså y-axeln vid y = 4, dvs. i punkten med koordinaterna (0, 4).

För att bestämma ytterligare en punkt som ligger på linjen väljer vi ett annat x-värde än 0 och räknar ut motsvarande y-värde. För x = 2 får vi y = 3 ∙ 2 + 4 = 10

Linjen går alltså även genom punkten med koordinaterna (2, 10).

Talparen (0, 4) och (2, 10) utgör alltså var sin lösning y x 1 1 till ekvationen y = 3x + 4. Vi markerar punkterna med koordinaterna (0, 4) och (2, 10) i ett koordinatsystem och drar en rät linje genom dem. Den räta linjen består av oändligt många talpar (x, y), som alla är lösningar till ekvationen y = 3x + 4.

Från graf till ekvation Om vi i stället har en rät linje i ett koordinatsystem och vill bestämma linjens ekvation, kan vi börja med att markera två punkter på linjen. I exemplet till höger väljer vi (x1, y1) = (3, 5) och (x2 , y2) = (9, 1).

Linjens konstantterm m anger alltså alltid skärningen med y-axeln. y x 1 1

Med hjälp av punkternas koordinater bestämmer vi linjens riktningskoefficient, k. k

− 2 3 Om x-värdet ökar med 3, så minskar y-värdet med 2

I grafen kan vi avläsa att den räta linjen skär y-axeln i punkten med koordinaterna (0, 7). Det ger att m = 7. Ekvationen för den räta linjen blir alltså y = − 2 3 x + 7

k-form Ekvationerna y = 3x + 4 och y = − 2 3 x + 7 är skrivna i formen y = kx + m, så kallad k-form. Det är ett vanligt sätt att ange ekvationen för en linje.

Räta linjens ekvation i k-form

u Ekvationen y = kx + m, där k och m är konstanter, kallas räta linjens ekvation i k-form.

u Riktningskoefficienten k anger linjens lutning (riktning) i förhållande till x-axeln. Värdet av m anger y-koordinaten för linjens skärningspunkt med y-axeln.

u Riktningskoefficienten för en linje genom två olika punkter med koordinaterna (x1, y1) och (x2, y2) är

Exempel: I figuren är en rät linje ritad. Bestäm linjens ekvation.

Lösning: Linjen skär y-axeln för y = 5. Det ger att m = 5 i ekvationen y = kx + m

Vi bestämmer riktningskoefficienten k genom att välja två punkter på linjen, t.ex. skärningspunkten med y-axeln (0, 5) och punkten med koordinaterna (3, −1), och beräkna

k = ∆y ∆x = y2 − y1

= −2

Svar: Ekvationen för linjen är y = −2x + 5.

Exempel: Bestäm ekvationen för den räta linje som går genom punkterna med koordinaterna (1; 3,5) och (4; 12,5).

Lösning: Linjen går genom punkterna (1; 3,5) och (4; 12,5). Vi använder punkternas koordinater för att bestämma linjens riktningskoefficient.

k = ∆y ∆x = y2 − y1 x2 − x1 = 12,5 − 3,5 4 − 1 = 9 3 = 3

Vi sätter in värdet på riktningskoefficienten tillsammans med koordinaterna för en av de givna punkterna i räta linjens ekvation.

3,5 = 3 ∙ 1 + m

m = 3,5 − 3 = 0,5

Vi sätter in koordinaterna x = 1 och y = 3,5

Svar: Ekvationen för den räta linjen är y = 3x + 0,5.

Exempel: Rita linjen y = − 4 3 x − 1 i ett koordinatsystem.

Lösning: Metod 1: Utan värdetabell

Av ekvationen ser vi att m = −1. Alltså skär linjen y-axeln i punkten med koordinaterna (0, −1).

Vi markerar den punkten i koordinatsystemet.

Riktningskoefficienten ges av

Nivå 1

1101 I koordinatsystemet är en rät linje ritad.

Den räta linjen kan beskrivas

med en ekvation i formen y = kx + m.

a) Bestäm värdet av konstanten m

b) Bestäm riktningskoefficienten k.

c) Ange linjens ekvation.

Det betyder att om vi utgår från (0, −1) och tar tre steg åt höger i x-led (∆x = 3), så behöver vi gå fyra steg nedåt (∆y = −4) för att åter nå en punkt på linjen. Vi markerar den punkten. Nu kan vi rita den räta linjen med hjälp av de två punkterna.

Metod 2: Med värdetabell

Vi gör en värdetabell:

= 0 ger y = − 4

=

− 1 = −1

Vi markerar punkterna i ett koordinatsystem och drar en rät linje genom dem.

b)

1102 Bestäm ekvationen för den räta linjen. a) y x 1

1103 Rita följande linjer för hand i ett koordinatsystem.

a) y = x + 2

b) y = −2x + 3

c) y = 1 2 x − 3

1104 Ge exempel på ett talpar x och y som är en lösning till ekvationen y = 3x − 4.

1105 Ligger punkten med koordinaterna (−2, 6) på den räta linje som beskrivs av ekvationen y = −3x + 1?

1106 En rät linje med riktningskoefficienten k = 3 går genom punkten med koordinaterna (1, 4). Bestäm linjens ekvation.

1107 Bestäm ekvationen för den räta linje som går genom punkterna med koordinaterna a) (1, 3) och (3, 7) b) (−1, −2) och (1, 3)

1108 Den räta linjen y = x 2 + 3 går genom punkten med koordinaterna (2, 4). Ange ekvationen för en annan rät linje som går genom samma punkt.

1109 Punkten med koordinaterna (2, b) ligger på linjen med ekvationen y = 2x + 7. Bestäm b.

1110 Vi har ekvationen y = −2x + 5.

a) Bestäm det värde på x som löser ekvationen om y = −3.

b) Bestäm ytterligare en lösning till ekvationen.

1111 Tabellen visar vilken skostorlek som passar respektive fotlängd.

Fotlängd (cm) Skostorlek

22,8 36

23,6 37

24,4 38

25,2 39

26,0 40

26,8 41

27,6 42

a) Ange en ekvation y = kx + m som beskriver hur skostorleken y beror av fotlängden x cm.

b) Använd din ekvation och bestäm skostorleken för en person som fotlängden 20,4 cm.

c) Använd din ekvation och bestäm fotlängden för en person som har storlek 47.

1112 Givet ekvationen y + 2 3 x = 6

a) Bestäm värdet på x som löser ekvationen om y = 1 4

b) Bestäm ytterligare en lösning till ekvationen där ett av talen är ett bråk.

1113 En ekvation i formen y = kx + m har en lösning x = 3 och y = −2.

a) Bestäm en ekvation som har dessa värden som en lösning.

b) Bestäm ytterligare en ekvation som har dessa värden som en lösning.

1114 Bestäm ekvationen för den räta linje som går genom punkterna med koordinaterna

a) (−2, −1) och (1, −2)

b) (1; 2,5) och (5; 6,5)

c) ( 1, 1 3 ) och ( 4, 1 2 )

Problemlösning med grafritande hjälpmedel

En nyårsrakets höjd över marken kan beskrivas med funktionsuttrycket

h(t) = −4,9t2 + 23t + 0,3

där h(t) är höjden i meter t sekunder efter att raketen skjutits upp. För att bestämma raketens högsta höjd över marken ritar vi grafen till funktionen i GeoGebra.

Bestämma extrempunkt Vi skriver sedan Extrempunkt(h) i inmatningsfältet för att bestämma funktionens största värde.

Du kan också välja verktyget Extrempunkt

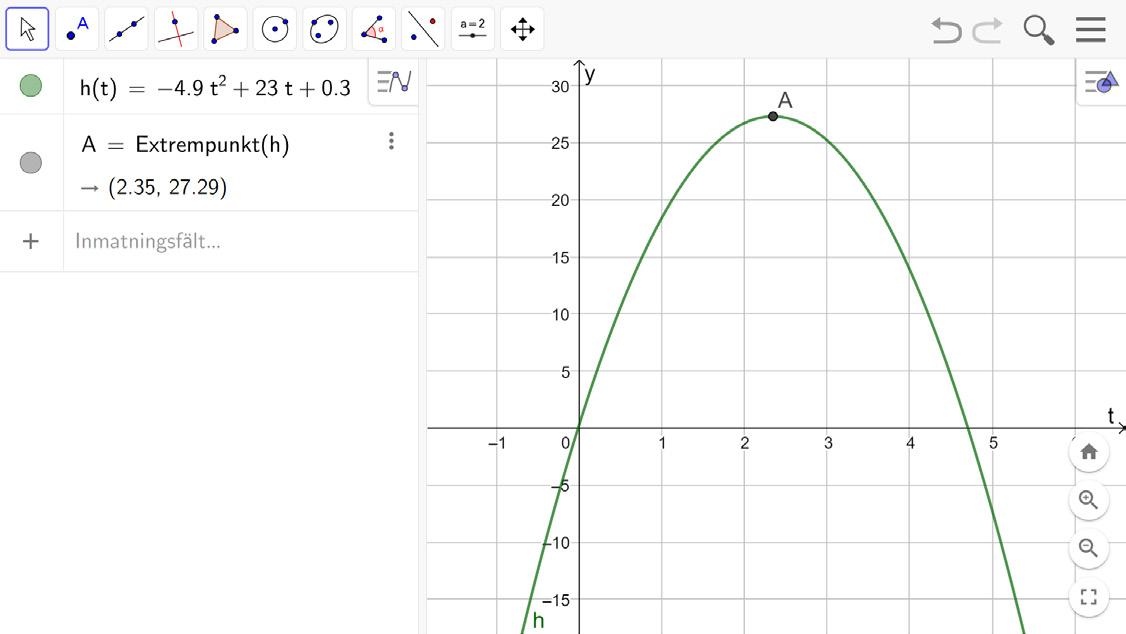
Extrempunktens koordinater är ca (2,3; 27). Vi tolkar detta som att raketen når sin högsta höjd, 27 m, efter 2,3 sekunder.

Välj metod Om det krävs en exakt lösning på ett matematiskt problem bör man lösa det algebraiskt, t.ex. med någon av de metoder som du fick lära dig i förra delkapitlet. För praktiska problem räcker det oftast med ett närmevärde. Då kan man nöja sig med en numerisk lösning från sitt grafritande hjälpmedel.

Exempel: Låt f(x) = −0,5x2 − x + 2. Bestäm symmetrilinjens ekvation samt koordinaterna för extrempunkten och extrempunktens karaktär.

Du kan också skriva Extrempunkt(f) direkt i inmatningsfältet

Lösning: Vi ritar grafen till f(x) = −0,5x2 − x + 2 i GeoGebra. Vi väljer verktyget Extrempunkt och klickar på grafen till funktionen. Då markeras extrempunkten i grafen och koordinaterna visas i algebrafönstret.

Vi ser att extrempunktens koordinater är (−1; 2,5). Av grafens form framgår att det är en maximipunkt. Eftersom extrempunkten ligger på symmetrilinjen är symmetrilinjens ekvation x = −1.

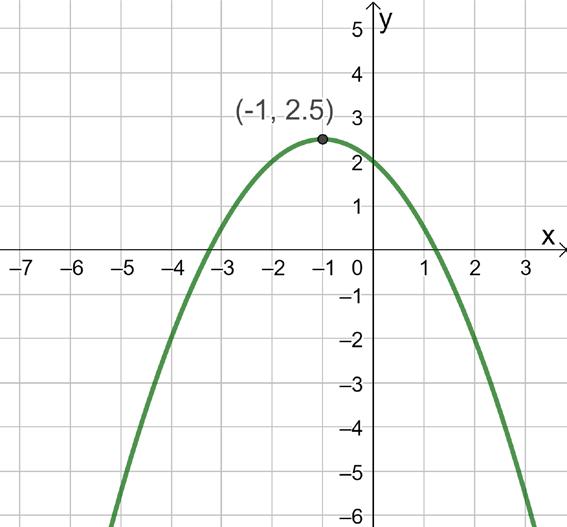
Svar: Symmetrilinjens ekvation är x = −1. Koordinaterna för extrempunkten är (−1; 2,5) och det är en maximipunkt.

Exempel: Höjden för nyårsraketen på föregående sida beskrivs med funktionsuttrycket h(t) = 4,9t2 + 23t + 0,3, där h(t) är höjden i meter t sekunder efter att raketen skjutits upp. Hur länge befinner sig raketen på minst 15 meters höjd över marken?

Lösning: Vi ritar grafen till funktionen h(t) = −4,9t2 + 23t + 0,3 i GeoGebra. Vi ritar även in linjen y = 15.

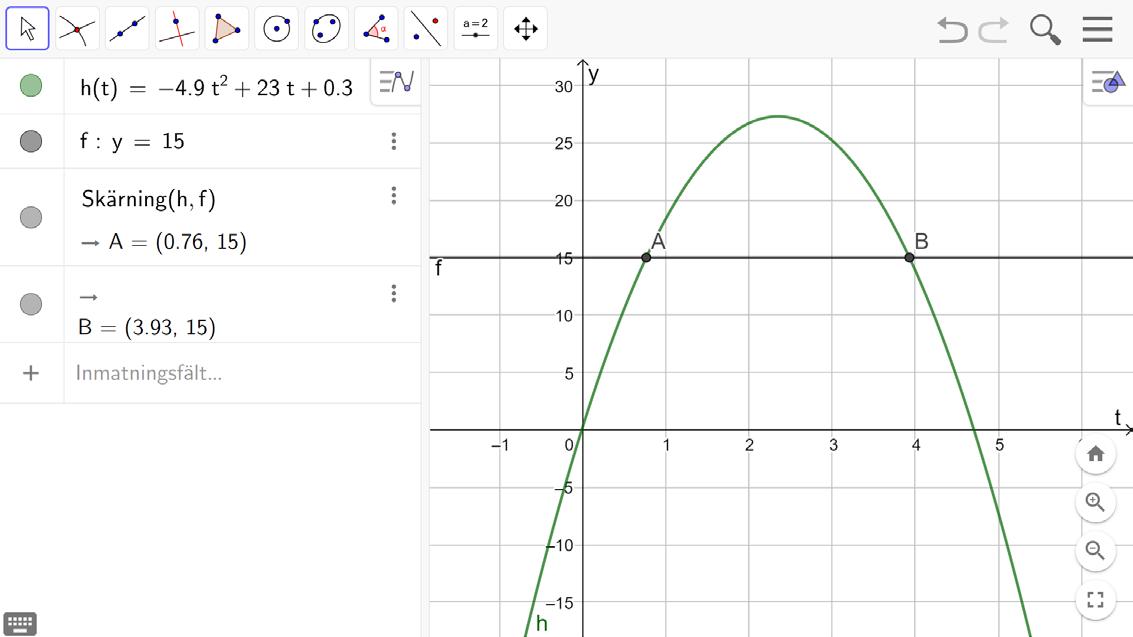
Vi bestämmer skärningspunkterna mellan andragradskurvan och linjen med verktyget Skärning mellan objekt och får t1 ≈ 0,76 och t2 ≈ 3,93 t2 − t1 ≈ 3,93 − 0,76 = 3,17 ≈ 3,2

Svar: Nyårsraketen befinner sig på minst 15 meters höjd under ca 3,2 sekunder.

Exempel: En av bågarna på Sydney Harbour Bridge kan enligt en matematisk modell beskrivas med funktionen

f(x) = −0,001834x2 + 0,9225x

där x är avståndet i meter från den vänstra bropelaren och f(x) är bågens höjd i meter över vattnet.

a) Hur högt över vattnet är bågens högsta punkt enligt modellen?

b) Hur långt är det mellan bropelarna enligt modellen?

Lösning: a) Vi ritar grafen till f(x) = −0,001834x2 + 0,9225x i GeoGebra och skriver sedan Extrempunkt(f) i inmatningsfältet.

Du kan också välja verktyget och klicka på grafen

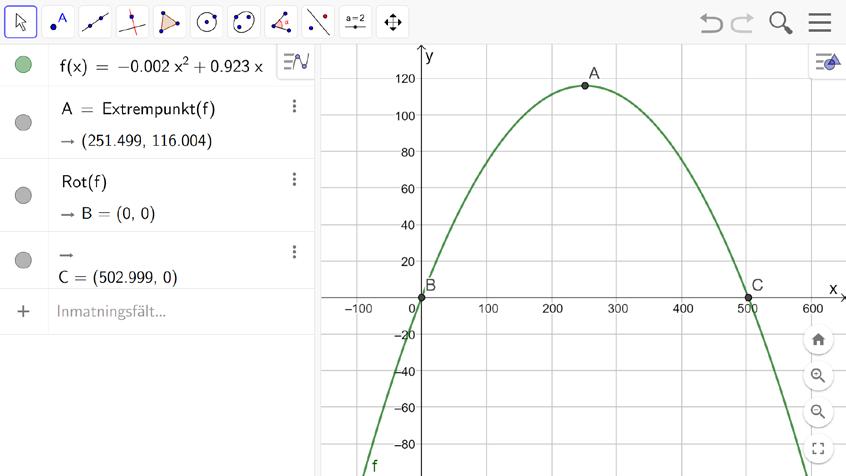
I detta exempel har vi valt att ändra inställningen till tre decimalers noggrannhet

Funktionens största värde är ca 116 m, vilket motsvarar bågens höjd över vattenytan.

Svar: Bågens höjd över vattnet är cirka 116 meter.

b) Differensen mellan nollställena motsvarar avståndet mellan bropelarna. Vi bestämmer därför funktionens nollställen med hjälp av verktyget

Rot(f) och får resultatet (0, 0) och ca (503, 0). Nollställena är alltså x = 0 och x = 503.

Svar: Avståndet mellan bropelarna är cirka 503 meter.

Lös uppgifterna med grafritande hjälpmedel.

Nivå 1

3219 Ange koordinaterna för grafens extrempunkt.

a) f(x) = 2x2 − 11x − 21

b) g(x) = −(3x − 2)(7x + 11)

3220 Låt f(x) = x2 + 2x − 3.

a) Bestäm funktionens nollställen.

b) Ange symmetrilinjens ekvation.

c) Bestäm funktionens största eller minsta värde.

3221 Låt f(x) = −x2 + 2x − 249 250

a) Bestäm funktionens största eller minsta värde. Svara med tre decimaler.

b) Ange symmetrilinjens ekvation .

c) Bestäm funktionens nollställen. Svara med tre decimaler.

3222 Diskuskastaren Ricky får i väg en diskus som befinner sig h(s) meter över marken, då den flugit s meter horisontellt. Diskusens bana kan förenklat beskrivas av funktionen

h(s) = −0,01s2 + 0,52s + 1,94

a) Rita funktionens graf.

b) Hur högt över marken når diskusen som högst?

c) Hur långt blev kastet?

3224 Vid ett växtodlingsförsök undersökte man avkastningen av korn som funktion av mängden kväve som tillfördes på en försöksyta. Den funktion f man fann kunde skrivas

f(x) = 3 270 + 18,9x − 0,058x2

där f(x) är avkastningen av korn i ton och x är tillsatsen av kväve i kg. Hur stor var den maximala avkastningen?

3225 Martin ska tillverka och sälja fågelholkar. Han vet att försäljningspriset påverkar hur många holkar han kan sälja och därmed också vinsten. För att kunna sätta ett rimligt pris använder han en funktion V för att beskriva vinsten:

V(x) = 70x − 0,25x2 − 3 150

där x är priset per holk och V(x) kr är den vinst han kan beräknas göra om han kan sälja alla holkar han tillverkar.

a) Vilket pris ska han sätta på holkarna för att få maximal vinst?

b) Hur stor blir den maximala vinsten?

3226 En traktors bränsleförbrukning beror bland annat på traktorns hastighet.

Under vissa förhållanden kan en traktors bränsleförbrukning beskrivas med modellen

B(v) = 0,0010v2 − 0,040v + 0,92 v > 0

3223 Kristina har forskat på hur ett visst ämne bryts ner i laboratoriemiljö. Hon fann att nedbrytningen enligt en enkel modell kan beskrivas med

y = 10 − 2x + 0,1x2

där y är massan av ämnet i gram och x är antalet månader efter försökets start.

a) Rita funktionens graf.

b) Hur länge dröjde det enligt modellen innan ämnet var helt nedbrutet?

där B (liter/km) är bränsleförbrukningen och v (km/h) är traktorns hastighet.

a) Beräkna traktorns bränsleförbrukning vid hastigheten 10 km/h.

b) Bestäm den lägsta bränsleförbrukning traktorn kan ha enligt modellen.

(Np ma2b ht 2013)

3227 Sandöbron är en bro över Ångermanälven.

Bron byggdes 1943 och var fram till 1964 världens största betongbro med endast ett brospann.

Brospann y x

Ångermanälvens bredd

Formen på brospannet kan beskrivas med andragradsfunktionen h där

h(x) = −0,0023x2 + 40

h(x) är höjden i meter över vattnet.

x är avståndet i meter längs vattenytan från mitten av bron.

a) Hur högt över vattnet kör bilarna när de passerar brons högsta punkt?

b) Beräkna bredden på Ångermanälven under bron.

(Np ma2b ht 2012)

3228 Låt f(x) = x2 − 3,2x + 12 . Funktionen f är definierad i intervallet −3,5 ≤ x ≤ 12. Bestäm funktionens största värde.

3229 Ett företags vinst, y miljoner kronor, varierar med antalet sålda enheter av en produkt. Om företaget säljer x tusen enheter ges vinsten av

y = −0,05x2 + 0,55x − 0,5 för 0 ≤ x ≤ 11

a) Bestäm extrempunktens koordinater och tolka ditt svar.

b) Ange funktionens värdemängd.

3230 En bils bensinförbrukning B(v) liter/mil, beror på hastigheten v km/h enligt

B(v) = 1,5 v 50 + v2 8 000 för 70 ≤ v ≤ 180

a) Vid vilken hastighet förbrukar bilen 1,0 liter/mil?

b) Vid vilken hastighet förbrukar bilen minst bensin?

c) Mellan vilka värden varierar bensinförbrukningen?

3231 Antalet sumatraelefanter har minskat i antal de senaste 75 åren. År 2020 beräknades beståndet vara bara 2 600 individer. Två forskare har beskrivit elefantbeståndet med var sin matematisk modell , där P(t) är antalet elefanter t år efter 1945.

Modell 1: P(t) = 0,1t2 − 200t + 17 000

Modell 2: P(t) = 17 000 − 200t

a) Beskriv två likheter mellan de båda modellerna.

b) Båda modellerna har begränsningar. Ge exempel.

3232 Åsa vill göra ett inhägnat trädgårdsland mot en betongmur. Landet ska vara rektangulärt och Åsa har ett 16 meter långt staket att sätta upp. Hur stor kan arean bli maximalt?

Nivå 3

3233 En kula skjuts uppåt från en 80 meter hög byggnad. Kulan når maxhöjden 144 meter efter 2 sekunder. Under hur många sekunder befinner sig kulan över 130 meter?

3234 Ragnar ska kasta in en fil till Sickan, som är på andra sidan av en 5 meter hög mur. Ragnars bästa kast beskrivs av modellen

h(s) = 2,0 + 3,3s − 0,75s2

där h meter är kastets höjd efter s meter horisontell rörelse.

a) Bestäm definitionsmängd och värdemängd för Ragnars bästa kast.

b) Hur långt från staketet ska Ragnar stå för att lyckas kasta över filen till Sickan?

3235 Marit ska dela upp ett område i tre lika stora fårhagar enligt figuren. Hon har 1 500 m stängsel att tillgå y y y y x x x x x x

a) Beskriv hagarnas totala area med ett funktionsuttryck i en variabel.

b) Bestäm funktionens definitionsmängd.

c) Bestäm hagarnas maximala totala area.

3236 Kristin ska sälja glass vid stranden. Inköpspriset är 4 kr per glass. Hon räknar med att sälja x stycken glassar per dag, där x beror av försäljningspriset a kr enligt formeln

x = 310 − 12a.

a) Skriv ett funktionsuttryck för hur vinsten V(a) beror av försäljningspriset a.

b) Vilket pris ska Kristin sätta på glassarna för att maximera sin vinst?

Resonemang och begrepp

 är maximipunkt och maximivärde samma sak för en andragradsfunktion?

 Vilka fördelar finns det med att lösa en ekvation grafiskt respektive algebraiskt?

 Nämn två olika sätt att bestämma symmetrilinjens ekvation med ett grafritande hjälpmedel

 hur gör man för att grafiskt lösa en olikhet av typen f(x) > g(x)?

 Beskriv hur man gör för att bestämma en andragradsfunktions största värde grafiskt respektive algebraiskt.

Rätt eller fel?

En andragradsfunktion har alltid ett största värde.

En andragradsfunktion kan sakna nollställen

Funktionen f som bestäms av f(x) = 5x + 32 är ett exempel på en andragradsfunktion

Alla andragradsfunktioner som har ett största värde har två nollställen

En andragradsfunktion skär alltid y-axeln.

Om en extrempunkts y-koordinat är negativ, så vet man att det är en minimipunkt

Om en andragradsfunktion saknar nollställen, så kan man inte bestämma ekvationen för grafens symmetrilinje.

Om man känner till nollställena till en andragradsfunktion, så kan funktionsuttrycket bestämmas

Undersök

Grafen till en andragradsfunktion

Din uppgift är ett ta reda på hur grafen till en andragradsfunktion f påverkas av faktorn b i funktionsuttrycket f(x) = x2 + bx

 Rita graferna y = x2 , y = x2 + x och y = x2 − x med ett digitalt verktyg.

 Gissa hur grafen y = x2 + 2x ser ut. Rita därefter grafen med hjälp av det digitala verktyget.

 Rita grafen till y = x2 + bx för några olika värden på b. Fundera varje gång på hur grafen kommer att se ut innan du ritar grafen. Vilken betydelse har faktorn b för grafens utseende?

 Förklara med hjälp av algebra hur faktorn b påverkar grafens utseende. Ta till exempel hjälp av funktionens nollställen.

Symmetrilinje och extrempunkt

 Rita graferna till y = (x − 1)2 + 2 y = (x + 1)2 + 2

y = (x − 3)2 + 2 y = ( x + 1 2 )2 − 3

 Bestäm symmetrilinjen och minimivärdet för var och en av graferna

 Rita sedan grafen till y = (x − a)2 + b för ytterligare några värden på a och b

 Vad kan du säga om symmetrilinjen och minimivärdet? Förklara.

 Förklara hur man kan gå till väga för att hitta en funktion med maximipunkten i (2, 3).

Problemlösning och modellering

Profit i solsken

Anders och Berit gör ett projektarbete i företagsekonomi, där de undersöker omsättningen hos två företag. Företagen laerol och Sevy tillverkar lyxig solkräm och säljer den vidare till butiker. Tillverkningskostnaden per liter solkräm under ett kvartal är olika för de båda företagen och beskrivs av två andragradsfunktioner.

Kostnad per liter vid tillverkning av x liter solkräm är

laerol: K(x) = 0,000 001 25x2 − 0,045x + 420

Sevy: K(x) = 0,000 002x2 − 0,092x + 1 070

Vid försäljning till butikerna är intäkten per liter solkräm densamma för de båda företagen. Intäkterna är 45 kr/l.

 hur stor är tillverkningskostnaden per liter för företagen, om de tillverkar 20 000 liter under ett kvartal?

 hur många liter solkräm ska respektive företag tillverka för att tillverkningskostnaden per liter ska bli så låg som möjligt? Vilken blir då literkostnaden?

 hur många liter solkräm ska företagen tillverka och sälja, för att intäkterna per liter precis ska motsvara kostnaderna per liter?

 hur stor är vinsten per liter för laerol, om de tillverkar och säljer 20 000 liter under ett kvartal?

 Teckna ett förenklat uttryck för de båda företagens vinst per liter solkräm.

Räknehjälpmedel

Abakus

Kulramen, eller abakus som den också kallas, är det äldsta kända räknehjälpmedlet. I dag använder vi kulramen endast i de lägre klasserna i skolan, för att öka förståelsen för beräkningar. Men i många andra delar av världen är den fortfarande ett effektivt hjälpmedel för att utföra beräkningar.

En abakus kan vara uppbyggd på många olika sätt. Den japanska modellen, som du ser här till vänster, kallas soroban. Längs varje stav finns det två uppsättningar av kulor, där den ena uppsättningen har fyra kulor och den andra har en. På det viset kan man med varje stav representera talen 0−9. Den ensamma kulan används för att markera ett femtal och de fyra kulorna markerar ental.

Här beskriver en soroban talet 45 810. De röda kulorna markerar ental och de blå ett femtal.

Skickliga användare av abakus sägs kunna utföra beräkningar med de fyra räknesätten snabbare än vad en van användare av ett digitalt hjälpmedel klarar av att göra.

Räknesnurran

En räknesnurra är en mekanisk räknemaskin. Den utvecklades under 1800talet och användes långt in på 1900 ­ talet. Vill man till exempel utföra multiplikationen 6 ∙ 7, så ställer man in talet 7 på snurran och vevar därefter 6 varv. Varje varv hoppar då värdet fram 7 steg och man landar på produkten 42. Produkten 9 ∙ 31 kan på samma sätt beräknas genom att man ställer in 31 och vevar 9 varv. Det är förstås också möjligt att ställa in 9 och veva 31 varv, men det tar längre tid. Men det finns genvägar att gå. En sådan genväg är att man först ställer in 9 och vevar 1 varv. Sedan ställer man in 90 och vevar 3 varv. Man har då beräknat 1 ∙ 9 + 3 ∙ 90 = 31 ∙ 9 som var vad vi ville beräkna. På detta sätt räcker alltså fyra varv för att utföra beräkningen. Ytterligare ett sätt att genomföra beräkningen är att först ställa in 310 och veva 1 varv, därefter ställer man in 31 och vevar 1 varv bakåt. Då har man också beräknat produkten 31 ∙ 9.

Tidig räknare med LED-display

Miniräknaren

Miniräknaren har funnits sedan omkring år 1970. De tidiga miniräknarna hade displayer med lysdioder, så kallad LED ­ display. De var energikrävande och det var därför inte ovanligt att man använde elnätet i stället för batterier. Det gjorde miniräknaren mindre flexibel.

Med tiden blev miniräknarna mer energisnåla och det blev möjligt att enbart använda batterier. Samtidigt som storleken på räknarna blev mindre, så blev också priset lägre och de blev allt vanligare som hjälpmedel i skolor, på arbetsplatser och i hemmen.

Grafritande räknare och CAS-räknare

Vilket tal visar abakusen? ?

Förklara varför multiplikationen 31 9 kan utföras på räknesnurra genom att veva talet 310 ett varv framåt och därefter talet 31 ett varv bakåt. ?

hur många varv måste man minst veva för att utföra multiplikationen 43 21 på en räknesnurra? ?

Den första grafritande räknaren tillverkades i mitten av 1980 ­ talet. Grafritande räknare erbjuder stora möjligheter till att snabbt lösa problem, men kan även användas som stöd för att förstå matematiken. En vanlig grafritande räknare kan t.ex. hitta numeriska lösningar till ekvationer och finna största eller minsta värdet till en funktion.

En grafritande räknare kan däremot inte förenkla algebraiska uttryck. Men det kan en symbolhanterande räknare. En sådan klarar av både att förenkla algebraiska uttryck och att hitta exakta lösningar till många ekvationer. Den här typen av räknare kallas också CAS ­räknare, där CAS står för Computer Algebra System.

Matematikprogram och webbsidor

Om man har tillgång till en dator, så finns det i dag flera olika program som kan hjälpa oss med matematiken. Några exempel är Excel, Maple, Mathematica och GeoGebra. Många matematikprogram går att ladda ner gratis från internet. På internet finns också webbsidor där man direkt kan få hjälp för att lösa problem. Ett sådant exempel är Wolfram Alpha, som du finner på www.wolframalpha.com.

Vi har alltså väldigt goda möjligheter till stöd för att förstå matematiken och för att genomföra beräkningar, men vi får inte glömma bort att den viktigaste kunskapen och uppfinningsrikedomen finns hos oss själva.

Geometri och bevis

Vinklar

u spetsig vinkel

u trubbig vinkel

u rät vinkel

u rak vinkel

u sidovinklar

u likbelägna vinklar

u vertikalvinklar

u alternatvinklar

u bisektis

Matematiskt resonemang

u utsagor

u implikation ⇒

u motexempel

u ekvivalens ⇔

Likformighet

u ABCD ~ A'B'C'D'

u motsvarande vinklar är lika

u förhållandet mellan motsvarande sidor är lika

Kongruens

u ABCD ≅ A'B'C'D'

u motsvarande vinklar är lika och motsvarande sidor är lika

u tre kongruensfall för trianglar

Cirkeln

u korda

u tangent

u randvinkel

u medelpunktsvinkel

Satser om cirkeln

u randvinkelsatsen

u följdsatser till randvinkelsatsen

u kordasatsen

u motstående vinklar i inskrivna fyrhörningar

Matematisk bevisföring

u logiska resonemang utan luckor

u ej mätningar eller gissningar

u utgår från definitioner och axiom

u tidigare bevisade satser

u motivera varje steg

Satser om triangeln

u triangelns vinkelsumma

u transversalsatsen

u topptriangelsatsen

u bisektrissatsen

u basvinkelsatsen

u Pythagoras sats

Beräkningar i koordinatsystem

u avståndsformeln

u mittpunktsformeln

1 Mia såg följande bild med text i sin bok:

Mät vinkeln med hjälp av en gradskiva.

Mia räckte upp handen och undrade vilken vinkel hon skulle mäta, eftersom hon såg två vinklar vid A. Förklara hur Mia kan ha tänkt.

2 Vi har en funktion f, där f(x) = x2. Bestäm

a) f(2)

b) f(−2)

c) lösningen till ekvationen f(x) = 9

3 Beräkna vinklarna x, y och z. a) x 49° b) y 92° x z

4 Lös ekvationerna

a) x2 + 2x − 35 = 0

b) x(x + 3) = 0

5 Beräkna vinklarna x, y och z a)

x b)

c)

6 Bestäm avståndet mellan punkterna med koordinaterna (1, 2) och (4, 5). Svara exakt.

7 Beräkna längden av sträckan markerad med x. a) (cm) x 3,0 7,0 b) 6,0 5,0 x (cm)

8 Lös ekvationssystemet med en algebraisk metod.

{ x + 2y = 4,5 3x + y = 4,5

9 Visa, med hjälp av motexempel, att följande implikationer inte gäller.

a) man promenerar mycket ⇒ man mår bättre

b) xy = −1 ⇒ x < 0 och y > 0

10 Förenkla så långt som möjligt.

a) x2 + 36 − (x + 6)2

b) (x − 3)(x + 3) + 9

c) (x − 5)2 − (x + 25)

11 Mellan de två lika stora kvadraterna i figuren bildas en triangel. Hur stor är vinkeln u?

62° u

12 Visa att de rödmarkerade vinklarna är lika stora.

z

13 Slobodans vedstapel har formen av ett rätblock. Stapelns längd är lika lång som dess bredd och höjden är 2,1 meter. Bestäm stapelns mått, om den innehåller 17,4 m3 ved.

14 Skyttelokalens väggar är parallella. Med vilken vinkel u kommer skytten att träffa målet?

20 Femhörningarna här nedanför är likformiga. Beräkna vinklarna v och w samt sidorna x och y.

15 Vi har funktionerna f och g, där f(x) = (x + 5)(x − 5) och g(x) = 25. Bestäm f(x) g(x).

16 Bestäm vinkeln AOB i figuren.

17 Vinkeln u = 50° är dubbelt så stor som vinkeln v. Bestäm vinkeln w. u v

21 Lika stora vinklar och sidor är markerade på samma sätt i figuren. Bestäm de okända vinklarna.

85° 60° y z x

22 I funktionsuttrycket f(x) = x2 + 2x + C är C en konstant. Kurvan y = f(x) går genom punkten med koordinaterna (−2, 8). Bestäm koordinaterna för ytterligare en punkt som ligger på kurvan.

23 Sträckorna MN och PQ är parallella. Visa att trianglarna MNO och QPO är likformiga.

18 Beräkna vinkeln v

19 Talen x = 1 och y = 4 är en lösning till ekvationen y = 3x + 1.

a) Ange ytterligare en lösning till ekvationen. b) Hur många lösningar har ekvationen?

24 Sträckan PQ är parallell med sidan BC. Beräkna längden av sträckan markerad med x. a) 14 19 P Q x 11 A B C (cm) b) 4 2 7 x 3 A C B P Q (cm)

25 När Tina multiplicerar två på varandra följande positiva heltal med varandra får hon produkten 992. Vilka tal har hon multiplicerat?

26 Ge exempel på ett ekvationssystem som har lösningen

{ x = 2 y = 5

27 Beräkna vinkeln α 3x 5x α

28 I figuren är de räta linjerna tangenter till cirkeln. Beräkna vinkeln α. 63° α

32 Bilden visar en romersk metod för att bestämma en flods bredd med hjälp av likformiga trianglar. Avstånden kunde mätas utan att de romerska trupperna behövde korsa floden. Hur bred är floden mellan punkterna P och Q? 9 m

2

29 Lös ekvationerna a) (2x − 10)2 = 400 b) (7 + 3x)2 = 1

30 Sträckan CD är en bisektris. Bestäm längden av sträckan AD. A

B D C 18 (cm) 5 15

31 Läget för en ort A kan i ett rätvinkligt koordinatsystem anges med koordinaterna (0, 4) och för en annan ort B med (6, 7). Hur långt är det fågelvägen mellan orterna om 1 längdenhet i koordinatsystemet motsvarar 1 kilometer i verkligheten?

33 I en likbent triangel är en av vinklarna 15° större än en annan vinkel. Beräkna triangelns alla vinklar.

34 Lös ekvationssystemet med grafritande hjälpmedel. Svara med två decimalers noggrannhet.

{ x + 2y = 8 x2 + y = −4

35 Hypotenusan i en rätvinklig triangel är 17 cm. Den ena kateten är dubbelt så lång som den andra. Bestäm kateternas längder.

36 Under Europamästerskapen i fotboll gjorde en av backarna ett inkast. Bollen följde en bana som kan beskrivas med modellen

h(x) = −0,042x2 + 0,58x + 2,2

där h(x) meter är bollens höjd över marken och x är avståndet i meter längs marken från den plats där inkastet gjordes.

a) Bestäm h(0) och tolka resultatet.

b) Bestäm längden på inkastet om vi antar att bollen landade på marken.

c) Bestäm bollens högsta höjd över marken.

Del 1 Utan digitalt hjälpmedel

1 I en påse ligger fem apelsiner. Apelsinernas vikt är 234 g, 219 g, 258 g, 210 g och 248 g. Hur ändras medianvikten och medelvikten om man byter ut den apelsin som väger 210 g mot en som väger 260 g?

2 Lönerna i ett företag med sju anställda är 24 000 kr, 22 000 kr, 27 000 kr, 25 000 kr, 68 000 kr, 24 000 kr och 27 000 kr. Vilket lägesmått beskriver lönerna bäst? Motivera ditt svar.

3 Lådagrammet visar resultatet av ett lopp på skidor. 60 70 80 90 100 110 120 130 140 Minuter

a) Vilken tid hade segraren?

b) Efter hur lång tid hade hälften av deltagarna kommit i mål?

c) Bestäm kvartilavståndet.

4 Avgör om det finns någon korrelation mellan variablerna x och y och ange i så fall om korrelationen är positiv eller negativ.

5 I en djuraffär paketerar man hundgodis i påsar för att sälja på en hundutställning. En eftermiddag visar det sig att vågen man använt inte har nollställts på morgonen. Vågen har därför visat 150 g för mycket. Hur ändras medelvärde, median, kvartilavstånd och variationsbredd på de redan vägda påsarna?

6 Tolka begreppet percentil i följande exempel.

a) Lenas lön ligger ovanför 90:e percentilen i företagets lönejämförelse.

b) Ett sängföretag använder den 95:e percentilen av vuxnas längd som ett mått på sängens längd.

c) I en affär finns jeans från 5:e till 95:e percentilen av alla storlekar som tillverkas av ett visst märke.

d) En students resultat ligger på den 82:a percentilen.

7 En maskin som fyller mjölkförpackningar är inställd så att medelvolymen är µ = 1 040 ml och standardavvikelsen σ = 20 ml. Hur stor är risken att du får mindre än 1 liter mjölk när du köper en förpackning som den maskinen har fyllt på?

Del 2 Med digitalt hjälpmedel

8 Amanda hade plockat äpplen. Histogrammet visar äpplenas vikt.

Uppskatta äpplenas medelvikt.

9 På ett dagis ville man köpa in stövlar som barnen kunde låna. Därför antecknade man barnens skostorlek. Resultatet ser du i frekvenstabellen. Rita ett lådagram som visar spridningen av stövlarnas storlek.

Skostorlek 21 22 23 24 25 26 27 28 29 30 31 32

Frekvens 2 0 4 6 2 0 6 2 4 1 4 5

10 Beräkna kvartilavstånd, standardavvikelse och variationsbredd för följande serier. Diskutera spridningen.

A: 5, 7, 4, 4, 5, 6, 3, 5, 5, 4 B: 4, 6, 15, 3, 3, 4, 3, 3, 4, 3

11 Använd ett digitalt hjälpmedel och för in följande mätvärden som punkter i ett diagram.

x 2 4 5 7 11 y 23 50 65 100 178

a) Anpassa en rät linje till mätpunkterna och ange linjens ekvation.

b) Hitta en annan regressionsmodell som passar mätpunkterna bättre än den linjära. Ange funktionsuttrycket till den anpassade funktionen.

12 För att söka till en elitutbildning i USA, fick Ebbe göra ett prov i tre delar. Resultatet anses vara normalfördelat. Medelvärde och standardavvikelse beräknades för varje delprov.

Muntlig del Matematisk del Logiska resonemang

Medelvärde 84 118 14

Standardavvikelse 10 18 4

a) Ebbes resultat var 90 på den muntliga delen, 133 på den matematiska och 18 på delen med logiska resonemang. På vilken del lyckades Ebbe bäst?

b) 16 % av alla sökande kom in. Vilka poänggränser borde de olika delproven haft? Kom Ebbe in? Motivera ditt svar.

Ledtrådar

1 Räta linjer och ekvationssystem

1.1 Räta linjens ekvation

1104 Välj ett värde på x och räkna ut vilket värde på y som gör att likheten stämmer. Då har du funnit en lösning till ekvationen.

1108 Rita en rät linje som går genom punkten (2, 4). Bestäm den räta linjens ekvation.

1111 Vi kan tolka varje par av värden i tabellen som koordinater: Fotlängden 22,8 cm och skostorleken 36 motsvarar t.ex. punkten (22,8; 36). Välj ut två av punkterna i tabellen och använd dem för att bestämma k och m i ekvationen y = kx + m

1113 Att bestämma en ekvation y = kx + m som har lösningen x = 3 och y = −2 är detsamma som att bestämma ekvationen för en valfri rät linje som går genom punkten (3, −2).

1116 Anta att linjens ekvation är y = kx + m. Vad kan du säga om linjens m-värde? Använd Pythagoras sats för att skriva ett uttryck för avståndet från origo till B. Vad vet du om det avståndet?

1117 Ställ upp en ekvation med a som obekant genom att sätta in de givna värdena i formeln k = y2 – y1 x2 – x1

1118 Vilken är triangelns höjd? Använd formeln för triangelns area för att ställa upp en andragradsekvation med a som obekant.

1119 Använd sambandet k = ∆y ∆x = y2 – y1 x2 – x1 . Låt en av punkterna vara obestämd, dvs. ha koordinaterna (x, y).

1122 b) Inled med att multiplicera båda leden i ekvationen med 3.

1126 I vilka punkter skär den röda och blå linjen y- respektive x-axeln? Dessa två punkter ligger på den tredje linjen.

1127 b) Börja med att skriva ekvationen i k-form. Då kan du avläsa linjens k-värde (lutning).

1129 Skriv om 2x + 3y + 6 = 0 och ekvation D i k-form.

1132 Börja med att skriva ax + 2y +4 = 0 i k-form.

1134 Eftersom skärningspunkten ligger på linjen y = 3x kan du ersätta y med 3x i båda ekvationerna.

1137 Den gemensamma lösningen till ekvationerna ges av koordinaterna för den punkt där linjerna skär varandra.

1139 Börja med att finna riktningskoefficienten för respektive linje.

1.2 Ekvationssystem

1213 Jämför linjernas riktningskoefficienter. Vad ska gälla för linjernas k-värden om ekvationssystemet ska ha noll, en eller ett oändligt antal lösningar?

1215 Skriv om alla ekvationer i k-form och jämför linjernas riktningskoefficienter. Vad ska gälla för linjernas k-värden om ekvationssystemet ska ha noll, en eller ett oändligt antal lösningar?

1218 Skriv om den nedre ekvationen i k-form och jämför sedan linjernas riktningskoefficienter.

1219 Ställ upp två ekvationer, som representerar kostnaderna för hyrbilsalternativen. Undersök sedan vilken körsträcka som ger lika kostnad för båda alternativen.

1220 Skriv ekvationerna i k-form och jämför sedan riktningskoefficienterna.

1222 Lös ekvationssystemet grafiskt t.ex. genom att skriva ekvationerna i inmatningsfältet i GeoGebra, en i taget.

1236 Rita båda linjerna i ett koordinatsystem. Vilka två punkter passar bäst för att bestämma triangelns bas? Vilken punkt kan då användas för att bestämma triangelns höjd?

1237 Vilken sorts linje representerar hastigheten? Vad betyder i så fall a i linjens ekvation?

1242 Hur kan man uttrycka Andres fart om den adderas med strömmens fart, respektive om den minskas med strömmens fart?

1251 Hur anges lösningen till ett linjärt ekvationssystem med två obekanta?

1255 Ställ upp ett linjärt ekvationssystem där den ena ekvationen visar hur intäkten beror av antalet hamburgare och antalet läsk, och den andra ekvationen visar hur vinsten beror av antalet hamburgare och antalet läsk.

1257 Förenkla först den övre ekvationen. Samla sedan x- och y-termerna i VL och konstanttermerna i HL för båda ekvationerna.

1258 Lösningen till ekvationssystemet är den punkt där linjerna skär varandra. Vilka linjer går genom punkten (12, −7)?

1259 Börja med att skriva ekvationerna i k-form. Vad ska gälla för ekvationernas k- och m-värden för att ekvationssystemet ska ha oändligt många lösningar?

1260 Anta att antalet barn i morfars by var x och antalet barn i grannbyn var y. Hur kan du nu uttrycka att det sammanlagt fanns 127 barn? Hur kan du uttrycka att det fanns 19 fler barn i morfars by?

1261 Kalla de två övriga vinklarna för x och y. Hur kan du uttrycka att skillnaden mellan dem är 32°? Hur kan du uttrycka att vinkelsumman i en triangel är 180°?

1262 Kalla kostnaden för mjukglassen för x kr och kostnaden för toppingen för y kr. Hur kan du nu uttrycka informationen i uppgiften?

1264 Börja med att bestämma den första linjens ekvation. Koordinaterna för linjernas skärningspunkt är ekvationssystemets lösning.

1265 Anta att det finns x ankor och y får på gården. Hur kan du då uttrycka att

• det finns totalt 28 djur

• djuren har totalt 78 ben

1268 Räkna insekternas ben i bilden.

1270 Anta att chokladkakan kostar p kr. Hur kan du då uttrycka hur mycket Maria respektive Peter har i kronor? Vilka samband kan du sedan ställa upp utifrån den givna informationen?

1271 Börja med att rita linjerna för hand i ett koordinatsystem.

1272 Börja med att ta reda på vad en läsk kostar.

1275 Att lösa ekvationssystemet betyder i det här fallet att du uttrycker lösningarna x och y i variabeln a.

1276 Vi vet att s = v ∙ t. Att Pontus cyklade totalt 23 km kan vi uttrycka med ekvationen 2 3 ∙ v + 1 2 ∙ w = 23, där talet 2 3 anger att han cyklade i två tredjedels timme med hastigheten v km/h. Hur kan du på liknande sätt uttrycka att Kristina cyklade i totalt 3,5 timme?

2 Algebra och andragradsekvationer

2.1 Algebraiska uttryck

2116 Det sökta området kan tecknas som en subtraktion.

2118 c) Multiplicera två av faktorerna först, t.ex. (y + 2)(y2 – 2). Multiplicera sedan resultatet med den tredje faktorn 2y

2119 Bryt först ut x i nämnaren innan du ersätter x med (a – 1).

2120 a) Börja med att skriva uttrycken med gemensam nämnare.

(En gemensam nämnare är (x − 1)(x + 1).) b) Bryt ut −1 i täljaren eller nämnaren.

2125 För att visa att VL = HL förenklar du vänsterledet (VL) till ett uttryck som är lika med högerledet (HL).

2126 a) (x − )(x + ) = x2 – 3x – 18 b) (x )(x + ) = x2 + x – 6

2138 b) Tänk på att potenser beräknas före multiplikation.

2143 För att visa att VL = HL förenklar du vänsterledet (VL) till ett uttryck som är lika med högerledet (HL).

2144 Pussla ihop de fyra bitarna till en kvadratisk hage. Hur stor blir den kvadratiska hagens sida?

2150 Använd att 1002 = 10 000 och att 32 = 9.

2151 Använd att x2 – 6x + 10 = x2 – 6x + 9 + 1.

2166 a) Tänk på att 4 9 = 22 32 = ( 2 3 ) 2 .

2170 Titta på exemplet på sidan 58.

2172 a) Tänk på att xa ∙ xb = xa + b .

2174 Börja med att skriva termerna i täljaren respektive termerna i nämnaren med samma nämnare.

2175 a) Börja med att bryta ut gemensamma faktorer. b) Börja med att skriva x2 + 12x + 36 som en kvadrat. Använd sedan konjugatregeln.

2.2 Enkla andragradsekvationer

2213 Kvadraten på kateterna är (3x)2 och (4x)2.

2216 a) Ersätt (x – 2) med y.

2217 Tänk på att √ a b = √a √b .

2218 Rita en figur och inför beteckningar för sidlängderna.

2219 Rita en figur. Hur kan du uttrycka sidlängderna?

2228 Vilket värde har h(t) då raketen slår ner i vattnet?

2231 Att x = 1 är en lösning till den givna ekvationen innebär att (a + 2)(b – 5) = 0. Vilka värden på a och b är då möjliga? Vilka värden på a och b är möjliga då x = 5 är en lösning?

2.3 Fullständiga andragradsekvationer

2324 a) Vilket värde har x när Fanny stöter i väg kulan?

b) Vilket värde har y där kulan landar?

2327 Ekvationen (x – r)(x – s) = 0 har rötterna x1 = r och x2 = s.

2329 Lös först ekvationen t2 – 20t + 19 = 0 och bestäm sedan x.

2330 Dividera båda leden i ekvationen ax2 + bx + c = 0 med a och sätt sedan in i pq-formeln.

2331 Uttryck x1 och x2 med hjälp av pq-formeln.

2332 Jämför √ ( p 2 ) 2 – q med p 2 om q < 0.

2336 a) Ange en ekvation i formen (x – a)(x – b) = 0.

2346 a) Bestäm h(0).

c) Vilken höjd har bollen när den landar?

2349 Vilket värde ska diskriminanten ha för att ekvationen ska få exakt en lösning?

2350 Ett inverterat tal är det tal som multiplicerat med det givna talet ger 1, dvs. b a är det inverterade talet till a b

2351 Sätt in x = −6 i ekvationen och bestäm konstanten a 2352 Använd konjugatregeln.

2353 Två på varandra följande positiva heltal kan t.ex. skrivas som x och x + 1.

2354 Faktorisera först och bestäm en rot. Bestäm sedan de övriga rötterna.

2355 Anta att familjen köpte x liter mjölk under första månaden.

2b nivå

Matematik Origo nivå 2b är en modern lärobok anpassad till Gy25 med

utförliga förklaringar, lösta exempel och varierade övningsuppgifter

matematisk modellering, kommunikationsuppgifter och problemlösning för alla

målbeskrivningar, sammanfattning och test till varje kapitel

Till Matematik Origo nivå 2b finns även komponenterna Lärarguide, Lärarstöd+ samt kopieringsmaterialet Prov, övningsblad och aktiviteter.

Serien Matematik Origo finns till samtliga gymnasieprogram.