Lärarpaketet
I lärarpaketet ingår den tryckta och den digitala lärarhandledningen med facit, digitala resurser och elevens digitala läromedel.
LÄRARHANDLEDNINGENS UPPBYGGNAD
Det innehållsrika lärarpaketet gör att du enkelt kan ge dina elever en inspirerande, varierad och lustfylld undervisning.
Din lärarhandledning ger dig stöd i att planera din undervisning på termins, kapitel och lektionsnivå.
Förutom huvudräkningsuppgifter, aktiviteter, lekar och matematikdidaktiska tankar till varje lektion innehåller din tryckta lärarhandledning facit till alla sidor i elevboken och Kommer du ihåg?. Till Snilleblixtar (svårare uppgifter) finns det även förklaringar och tips för passande problemlösningsstrategier.
Förslag på terminsplanering
TERMINSPLANERING
Terminsplaneringen är ett förslag på hur bokens 34 lektioner kan fördelas på vårterminens 20 skolveckor. En lektion i boken är inte tänkt att undervisas på ett mattepass på 45 minuter, utan en lektion kan ta mer tid än så.
Du har alltså gott om utrymme för att kunna ge eleverna tid för ett varierat arbete med varje lektion i elevboken.
Ge eleverna tid att börja med ett nytt område (kapitel).
Ge dem tid för att se kapitel och lektionsfilmerna, lära sig nya begrepp, föra samtal, arbeta i par, spela spel, repetera och genomföra laborationer i kombination med arbetet i elevboken.
LÄRARENS DIGITALA RESURS
Här får du en översikt över några delar som du har tillgång till i din digitala resurs. Den digitala resursen ingår i lärarpaketet.
Klura tillsammans (gemensam problemlösning)
I din digitala lärarresurs hittar du en gemensam problemlösningsuppgift till varje lektion. Uppgifterna handlar om lektionens innehåll och är ett bra sätt för eleverna att träna på att resonera och motivera samt att använda sig av matematiska begrepp.
Huvudräkning
Till varje lektion har du tre huvudräkningsuppgifter. Huvudräkningsuppgifterna inleds av en faktatext kallad för Visste du? som bäddar in uppgifterna i en meningsfull kontext. Starta en ny lektion genom att anknyta till det ni har gått igenom tidigare. Eleverna skriver sina svar i svarsrutor på s. 156–157 i elevboken.
Kapitelfilmer (Introduktionsfilmer)
Du har tillgång till 5 filmer som inleder varje nytt kapitel. Kapitelfilmerna är filmade med barn som möter matematiskt innehåll i vardagen. Filmerna inspirerar till samtal kring matematiken i våra liv och meningen med att lära sig visa saker.
Att ladda ner
Lektionsfilmer
Du har tillgång till 45 lektionsfilmer som är korta men tydliga genomgånger av lektionernas matematiska innehåll. I filmerna förklaras nya begrepp och det visas hur vissa övningar kan lösas.
Eleverna har själva tillgång till alla filmer i sitt digitala läromedel.
Digital tavla
I din digitala lärarresurs har du tillgång till en tavla som smidigt verktyg i dina genomgångar och gemensamma övningar.
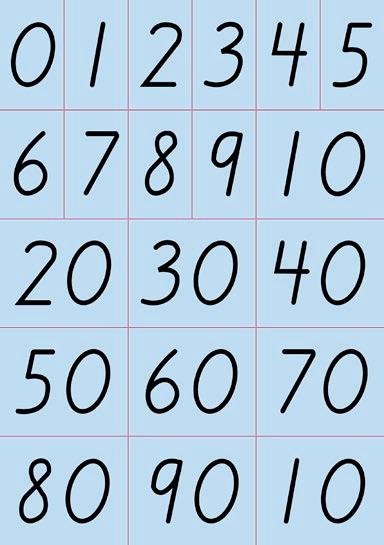
Här kan du använda tallinjer, talkort, färgcirklar, mynt, geometriska figurer, bråkdelar och mycket mer för att visualisera och förklara matematiskt innehåll för dina elever.
Tomoyo
Tomoyo är ett spelifierat, digitalt läromedel där arbetet med de matematiska momenten varvas med fantasifulla berättelser.
Elevens motivation och engagemang höjs när hen får snabb återkoppling och samlar poäng och märken.
Svårighetsnivån regleras automatiskt. Övningarna anpassas så att eleven får dem på samma, enklare eller svårare nivå, beroende på hens tidigare svar.
I Tomoyo är all text inläst och till varje övning finns det skräddarsydd hjälp i form av filmer, tips och begreppsförklaringar.
Som lärare kan du skapa ett digitalt klassrum och på så sätt följa dina elevers arbete och skicka uppdrag.
Läs mer
Vid texten ”Läs mer” hittar du en länk. Följ länken i din digitala lärarhandledning för att läsa mer om ämnet.
Klura tillsammans från Matteblixt 3a
Kapitelfilm från Matteblixt 3a
KAPITELÖVERSIKT
I kapitelöversikten hittar du allt du behöver för att sätta igång med ett nytt område, från kapitlets innehåll, vilka förkunskaper eleverna bör ha, till vilket material du hittar i din digitala resurs.
1 Introduktionsfilm
Inled kapitlet med att visa introduktionsfilmen, som handlar om ett barn i en vardaglig situation med matematisk anknytning.
2 Klura tillsammans
Få igång elevernas tankar med en gemensam problemlösningsuppgift. Du kan visa den digitalt.
3 Pedagogiska tankar inför kapitlet
Varje kapitel inleds med specifika pedagogiska tips inför kapitlet. Tipsen ger konkreta förslag på hur du stödjer lärandet.
4 Ämnesövergripande aktiviteter
Här får du tips på hur du kan integrera matematiskt innehåll från kapitlet i andra ämnen.
5 Samtalsbilden
Bilden visar innehåll ur kapitlet. Men den visar mycket annat också. Speciellt om du har elever med annat modersmål än svenska kan bilderna stödja och befästa inlärningen av ord som är nya för dem och som kan förekomma i kapitlet.
Börja med att låta eleverna själva titta på bilden och upptäcka den. Be dem att hitta en sak de tycker om som de berättar om för klasskompisen bredvid. Sedan riktar du uppmärksamheten åt det matematiska innehållet i bilden genom att ställa frågor. Använd några av exempelfrågorna eller egna frågor.
6 Arbeta med begrepp
Du hittar hela begreppslistan med tillhörande förklaringar i din digitala lärarresurs.
Du kan skriva ut listan med bilder och förklaringar och hänga upp den i klassrummet så att eleverna har tillgång till den.
Det är viktigt att lägga tid på att arbeta med begreppen. Gå tillsammans igenom begreppen till kapitlet. Påminn eleverna att de kommer att kunna titta på listan med förklaringar när de stöter på ett begrepp de är osäkra på. En del begrepp finns även förklarade i sammanfattningen i slutet av kapitel 1, 2, 4 och 5.
Börja med att läsa upp begreppen och fråga om någon elev känner igen något av dem. Berätta att eleverna kommer att arbeta med dessa begrepp i kapitlet och att de kommer att kunna titta på listan med förklaringar när de stöter på ett begrepp de är osäkra på.
Elevernas förståelse för begreppen kommer att utvecklas under arbetet med dem i ett meningsfullt sammanhang. Skapa gott om tillfällen för dem att använda begreppen.
Se hur du kan arbeta med begrepp under ”Kooperativt lärande” (s. 16).
LEKTIONSÖVERSIKT
I lektionsöversikten hittar du allt du behöver till lektionen. I översiktsrutan ser du lektionens innehåll, viktiga begrepp, vilket material som behövs, vilka kopieringsunderlag som finns till lektionen, hänvisningar till Kommer du ihåg? samt vad du hittar i din digitala resurs.
INTRODUKTION
Välj mellan att starta lektionen med huvudräkningsuppgifter för att repetera eller få igång elevernas tankar med en gemensam problemlösningsuppgift, Klura tillsammans.
1 Huvudräkning
Till varje lektion finns det 3 huvudräkningsuppgifter som du hittar i din lärarhandledning. Huvudräkningsuppgifterna inleds med en faktatext kallad för Visste du? som bäddar in uppgifterna i en meningsfull kontext. Svaren antecknar eleverna i svarsrutor (elevbok s. 156–157).
Du kan läsa uppgifterna högt för eleverna eller visa dem digitalt och läsa dem gemensamt. Du kan också läsa upp texten och enbart skriva talen på tavlan. Det kan vara svårt för eleverna att hålla talen i huvudet, så det är bra att träna på den här färdigheten. Till vissa huvudräkningsuppgifter finns det bilder som du antingen ritar på tavlan eller visar digitalt. Du når huvudräkningsuppgifterna via länken i din digitala lärarresurs.
2 Klura tillsammans
Till varje lektion finns det en gemensam problemlösningsuppgift som fungerar bra att starta lektionen med. Eleverna arbetar i grupp och får tillfällen att träna på matematiska resonemang och matematiska begrepp.
3
Gå igenom lektionens viktiga begrepp och därefter lektionens innehåll genom att titta på lektionsfilmen.
Aktiviteterna som finns till varje lektion i din lärarhandledning är anpassade till lektionens innehåll. Du hittar aktiviteter av olika karaktärer som aktiverar elevernas olika sinnen. Aktiviteterna utförs individuellt, i par eller i små grupper. I aktiviteterna används ofta laborativt material och många aktiviteter ger eleverna möjlighet att röra på sig samtidigt som de tränar på matematiskt innehåll.
4 Tillämpande aktivitet
I tillämpande aktiviteter använder eleverna det nyinlärda innehållet på olika sätt. Dessa aktiviteter förutsätter elevernas förståelse för det nya innehållet.
5 Ur pedagogisk synvinkel
Under Ur pedagogisk synvinkel lyfts viktiga matematiska moment, hur du kan möta elever i behov av stöd samt konkreta tips för din undervisning. Här hittar du även matematikdidaktiska tankar, som till exempel möjliga missuppfattningar och annat du bör tänka på när du undervisar matematik.
6 Facit
Till alla sidor i elevboken och Kommer du ihåg? finns facit. Facit finns även att ladda ner.
7 Kopieringsunderlag
Till både kapitlen och lektionerna finns det kopieringsunderlag att ladda ner. Kopieringsunderlagen till lektionerna finns på tre olika nivåer (a: ordinarie nivå, som i boken, b: utmanande nivå och c: lägre nivå). Dessutom hittar du kopieringsunderlag till specifika aktiviteter samt klassrumsbilder. Till arbetet i klassrummet används
bilderna som visar olika arbetssätt på matematiklektioner som bildstöd. Många elever mår bra av att veta vad som kommer att hända under lektionen. Tryck ut korten från din digitala lärarresurs (under Kopieringsunderlag) och sätt upp bilderna som visar det eleverna ska göra under dagens mattepass.
Kooperativt lärande (KL)
Använd dig av kooperativt lärande för att stärka elevernas delaktighet i undervisningen och för att skapa förståelse. Med olika kooperativa arbetssätt (strukturer) stärks elevernas färdighet i att sätta ord på sina tankar, diskutera matematiska resonemang och att samspela med andra elever i klassen. I samtal berikar eleverna varandras förståelse för begrepp, sätt att tänka och lösa matematiska problem. Eleverna stöttar varandra i kunskapsutvecklingen när du till exempel använder EPA (Ensam, Par, Alla), där
Självständigt arbete
eleverna först funderar själva över ett matematiskt problem (E=ensam) för att sedan föra ett samtal i par där eleverna resonerar tillsammans (P=par). Slutligen samlas allas tankar, funderingar och lösningsförslag i klassen (A=alla).
Läraren har den viktiga rollen i att leda eleverna genom arbetssättet och lära ut, inte bara matematik utan även det sociala samspelet.
Läs mer
Använd kooperativa strukturer för begreppsträning
Material för begreppsträning med kooperativa övningar finns i din lärarresurs
Spel
KOMMER DU IHÅG?
Boken Kommer du ihåg? ingår i elevpaketet. I den finns det uppgifter till varje lektion och de kan användas som repetition eller som läxa. Uppgifterna är alltid på tre olika nivåer; den första är lite enklare, den andra är på medelnivå och den tredje är en kugghjulsuppgift som är lite svårare. I Kommer du ihåg? finns även spel med innehåll anpassat till olika matematiska moment.
Spelen
Spelen i Matteblixt ger eleverna en utmärkt möjlighet att träna och befästa matematiskt innehåll på ett roligt och lekfullt sätt. Eftersom spelen finns i boken Kommer du ihåg? kan du enkelt använda något spel som läxa.
Spelen i Matteblixt är anpassade till det matematiska innehållet i lektionerna. Oftast behövs enbart tärningar, ibland även spelpjäser eller färgpennor. Vissa spel går att spela själv men det finns en vinst med att låta eleverna spela i par. Eleverna kan hjälpas åt och berika varandras sätt att tänka samt träna på det sociala samspelet. Lär eleverna att vara schyssta, till exempel genom att tacka varandra efter spelet, att peppa varandra och att trösta den som har förlorat.
Ska eleverna spela spelen i flera omgångar men redan har fyllt i spelplanen i sina böcker kan du trycka ut flera spelunderlag från din digitala lärarresurs.
Till de olika matematiska områden finns det övningsbanor där eleverna löser uppgifter i par. Övningsbanan finns på baksidan av boken Kommer du ihåg?. Instruktioner till övningsbanan finns på s. 120 och uppgifterna finns i din digitala lärarresurs. Ge eleverna flera tillfällen att repetera innehåll av de olika matematiska områdena.
REPETITION
Det kan finnas olika anledningar till varför eleverna vid något tillfälle inte får grepp om något moment i matematikundervisningen. Att låta eleverna göra flera övningar och repetera på samma sätt saker de inte har förstått är sällan en bra lösning. Speciellt när det introduceras nya begrepp och koncept är det en bra tumregel att ”först reparera, sen repetera”. Det är viktigt att säkerställa elevens förståelse innan hen är redo att repetera. Presentera matematiska begrepp på flera olika sätt så att eleven har möjlighet att reparera eventuella missuppfattningar. Säkerställ först förståelsen och befäst den sen med hjälp av varierad repetition.
Repetitionslektion
Repetitionslektionen kan användas på olika sätt. Utöver repetition kan den bland annat fungera som en slags diagnos på innehållet i kapitlet. Om uppgifterna på repetitionssidorna är utmanande för eleven (om hen till exempel räknar långsamt, är osäker eller gör många fel) behöver ni gå tillbaka och befästa innehåll från tidigare kapitel.
Använd gärna kopieringsunderlagen till kapitlet då eleven repeterar. Det finns även övningsbanor med repetitionsuppgifter, se sid. 120. Dessutom ingår Tomoyo, ett digitalt, spelifierat läromedel som ger eleven färdighetsträning på rätt nivå.
Sammanfattning
I slutet av kapitel 1, 2, 4 och 5 finns en sammanfattning av kapitlets matematiska innehåll och begrepp. Räknesätten och andra matematiska koncept med tillhörande begrepp blir förklarade med hjälp av tydliga illustrationer och exempel.
Påminn eleverna om att slå upp sammanfattningen som hjälpsida ifall de är osäkra över något innehåll.
Självbedömning – Matematiken och jag
Låt eleverna med hjälp av Matematiken och jag utvärdera arbetet med kapitlet.
Eleverna utvärderar dels sin studieteknik dels styrkorna de har använt under arbetet med kapitlet.
Reflektion om det egna lärandet och bekräftelse av positiva beteenden möjliggör medvetna val och en hållbar och långsiktig inlärningsstrategi.
Matematiken och jag består av tre delar.
Den första delen handlar om elevernas agerande under lektionerna. Ge konkreta exempel för de olika punkterna som
”... deltar aktivt under lektionerna” innebär att man räcker upp handen, lyssnar på genomgången, ställer frågor;
”... bidrar till en positiv stämning i klassen” innebär att man uppmuntrar andra, delar med sig, inte skrattar när någon säger fel.
I den andra delen i Matematiken och jag utvärderar eleverna vilka superkrafter de har använt under kapitlets gång. Superkrafterna lyfter en positiv inställning till inlärningen. Känslan av att lyckas gör att elevens självförtroende och den positiva inställningen till matematiken växer. Förklara för eleverna vad de olika superkrafterna handlar om.
Den tredje delen i Matematiken och jag ger eleverna möjlighet att fundera över och utvärdera sin egen studieteknik. Påminn eleverna om att alla lär sig på olika sätt och att det inte finns något rätt eller fel här.
”Jag vill satsa på…”
Du kan även låta eleverna träna på att formulera egna mål och arbeta med dem. Låt eleverna fundera över vad de vill bli bättre på. De kan välja en sak de vill tänka på under matematiklektionerna. Eleverna kan i par berätta för varandra vad de vill satsa på. De kan rita eller skriva en komihåglapp som de sedan tar fram till lektionerna.
Karaktärsstyrkor är elevernas superkrafter
I Matteblixt har du möjlighet att låta eleverna lyfta och bekräfta sina egna styrkor för att ge dem de bästa förutsättningarna att älska matematik.
I årskurs 3 arbetar eleverna med sex karaktärsstyrkor som blir elevernas superkrafter; uthållighet, samarbetsförmåga, engagemang, kreativitet, mod och ansvar.
Genom att fokusera på det positiva och synliggöra användandet av superkrafterna kan elevernas tilltro och självkänsla utvecklas och blomma. Elever som mår bra och tror på sina egna styrkor lär sig bättre.
Läs mer
UTHÅLLIGHET
Du har tålamod och orkar jobba.
Du stannar upp och funderar.
Du ger inte upp om något är svårt.
Du vill göra klart uppgifter även om de känns svåra.
SAMARBETSFÖRMÅGA
Du lyssnar på andra.
Du respekterar andras tankar och idéer.
Du är schysst när du spelar och jobbar med andra.
Du hjälper andra samt tar emot hjälp av andra.
ENGAGEMANG
Du är aktiv och nyfiken på nya uppgifter.
Du berättar om dina tankar och lösningar.
Du gör en bra insats.
Du blir glad när du lär dig och lyckas.
KREATIVITET
Du använder din fantasi.
Du prövar olika sätt att lösa svåra uppgifter.
Du förklarar på olika sätt hur du tänker.
Om en lösning inte fungerar provar du en annan.
MOD
Du är inte rädd för att göra fel ibland.
Du vågar berätta dina förslag och lösningar.
Du vågar modigt prova något nytt.
Du är modig och säger till när det är något du inte kan.
ANSVAR
Du tar ansvar för att göra klart dina uppgifter.
Du har med dina saker till lektionen.
Du koncentrerar dig på det du ska göra.
Du anstränger dig och gör ditt bästa.
BEDÖMNING
Bedömningen i serien Matteblixt är mångsidig och en viktig del av lärandet.
Matteblixt digitala material för läraren innehåller bedömningsmaterial i form av:
Prov
Proven till kapitel 1, 2, 4 och 5 är tänkta som diagnoser för att kontrollera om alla elever kan följa med i matematikundervisningen. Proven a1 och a2 är på samma nivå och uppgifterna liknar dem som finns i elevboken. Att proven finns i två versioner ger dig möjlighet att följa upp någon elevs utveckling utan att behöva återanvända samma uppgifter. Dessutom finns prov c där uppgifterna är på en något enklare nivå. Elever som visar svårigheter i matematikundervisningen har bättre möjlighet att lyckas och bekräftas med de här proven. Nivån i cproven motsvarar baskunskapsnivån i årskurs 3.
Parprov
Till kapitel 3 är det ett parprov till respektive lektion. Parproven fokuserar både på det matematiska innehållet i kapitlet och elevernas styrkor och färdigheter. Parproven går att använda på olika sätt som ett verktyg för inlärning. Passa på att gå runt och lyssna på elevernas samtal och sätt att resonera. I parproven är det sättet hur eleverna löser uppgifterna på som är underlag för bedömningen av elevernas kunskaper, inte det de skriver som svar på sina papper. Samtidigt tränar eleverna på kamratbedömning. De kan behöva hjälp när de ska identifiera superkraften som klasskompisen har använt under provet.
Alla prov kan genomföras i delar, det vill säga att du kan dela upp proven och låta eleverna göra delarna vid olika tillfällen.
3
Prov från Matteblixt 1b
Prov Matteblixt 3b
Kapitel 1 prov a1, prov a2, förenklat prov c
Kapitel 2 prov a1, prov a2, förenklat prov c
Kapitel 3 parprov lektion 19–22
Kapitel 4 prov a1, prov a2, förenklat prov c
Kapitel 5 prov a1, prov a2, förenklat prov c
2 Addera först tiokompisarna. Addera sedan resten.
Räkneflyt
I Matteblixt åk 1 och åk 2 finns det Räkneflytsövningar inom olika talområden för addition och subtraktion och senare även för multiplikation. Här i Matteblixt 3b är fokus på att träna på addition och subtraktion samt division. Vid behov kan eleverna även arbeta med Räkneflytsövningarna från tidigare årskurser.
Varje Räkneflytavsnitt består av ett antal uttryck. Räkneflytsövningarna är tänkta att användas för att träna räknefärdigheter, det vill säga att automatisera multiplikationer inom kända talområden. Tanken är att eleverna kan lösa varje uttryck på ungefär 3 sekunder. Elever som har svårt och behöver lång tid för att forma siffrorna kan göra testen muntligt eller digitalt.
För att få upp räknehastigheten ska eleverna göra varje avsnitt vid upprepade tillfällen.
Elevens utveckling kan synliggöras med hjälp av underlaget Mitt räkneflyt som finns i din digitala lärarresurs. Att eleven får se sina framsteg har ofta en positiv inverkan bland annat på elevens motivation och självbild i matematiken.
Läs mer
Mitt räkneflyt
DIFFERENTIERING
Uppgifterna i elevboken är uppbyggda för att systematiskt träna nya färdigheter. På lektionens första två sidor kan eleven använda sig av den inledande rutan, tillhörande lektionsfilm och ett konkret bildstöd. På den tredje sidan möter eleverna mer tillämpande uppgifter. Det finns även andra delar i Matteblixt som ger eleverna möjlighet att få uppgifter på sin nivå.
Kopieringsunderlag på olika nivåer
Det finns kopieringsunderlag till varje lektion i Matteblixt. De kan användas för att befästa ny förståelse genom repetition. Kopieringsunderlagen är på olika svårighetsnivåer vilket ger dig möjlighet att anpassa övningarna till olika elevers behov.
Kopieringsunderlagen a är på ordinarie nivå. De fungerar utmärkt som repetition då de innehåller uppgifter på en liknande nivå som i elevboken.
Kopieringsunderlagen b är på en lite högre nivå och fungerar för elever som är säkra på innehållet i elevboken och är redo att ta nästa steg eller behöver lite mer utmaning.
Kopieringsunderlagen c är på en något lägre nivå än kopieringsunderlagen a. Uppgifterna är lite enklare utformade och är tänkta att kunna användas av elever i behov av stöd med något moment i matematikundervisningen.
De olika svårighetsnivåerna går att välja emellan helt fritt. Elever som behöver utmaning i ett område behöver kanske stöd i ett annat. Låt eleverna använda laborativt material i kombination med arbetsuppgifter på papper för att stödja kopplingen mellan det konkreta och det abstrakta.
2
1
4
1 Ringa först in tiokompisarna. Räkna ut summan.
2 Skriv först tiokompisen. Addera sedan resten.
3 Hitta på och fortsätt instruktionen. Be någon att lösa uppgiften.
Exempel från Matteblixt 1b: Kopieringsunderlagen a: ordinarie nivå, b: högre nivå och c: lägre nivå
Namn 21c Fyll upp tiotalet
1 Måla tiokompisarna. Använd två olika färger. 2 Skriv termen som saknas.
45537_kopunderlag_kap4.indd 3
10:44
Symboler som stöd för eleverna
För att tydliggöra olika moment och aktiviteter finns det i elevboken och i boken Kommer du ihåg? förklarande symboler. En symbol är den omålade pennan. Elever med svårigheter i sitt färgseende kan ha svårt att arbeta med uppgifter som bygger på att kunna skilja på färgerna, till exempel med mönster där enbart färgen ändras.
I Matteblixt används i dessa fall färger med stark kontrast.
I de fall eleverna ska använda färger får de ofta själva välja vilka färger de använder så att de kan styra och välja färger de kan skilja på.
Var uppmärksam på elever som visar svårigheter med att lära sig färgerna eller att lösa uppgifter där färger ingår. Andra symboler är hänvisningar till spelen eller om uppgiften kräver till exempel en räknare.
Spel: Ser du den här symbolen finns det ett spel i slutet av boken .
Till det här spelet behöver du en tärning
Till det här spelet behöver du spelpjäser .
Kugghjul: Det här är ett matematiskt problem, lättast att lösa i par
Idébox: Här får du tips
Använd en räknare
Här väljer du själv vilken färg du ska använda
12 16 18 20
Använd kontrollrutan för att kontrollera uppgiften
Kugghjul = problemlösning i par Kugghjulsuppgifterna i elevboken är tänkta att lösas av alla elever.
Eftersom uppgifterna är på en utmanande nivå då de kräver uthållighet och ett kreativt tänkande, är det viktigt att alla elever ges möjlighet att arbeta med dem för att lära sig och träna på sin problemlösningsförmåga.
Det kan vara frustrerande att sitta själv framför en uppgift som överstiger ens kompetens. Det underlättar om du låter eleverna arbeta i par med kugghjulsuppgifterna. De flesta eleverna känner större tilltro och säkerhet när de arbetar i par. Uthålligheten är bättre och eleverna berikar varandras sätt att se på uppgiften.
Titta på filmen!
Två personer: du spelar med någon annan
Uppsnapparen: förklarar och hjälper dig med knep och tips .
Ta hjälp av papper och penna .
Rita med linjal .
Pi: peppar och hejar på
Paruppgift: arbeta med någon annan .
Snilleblixtar
I slutet av boken hittar du fler problemlösningsuppgifter
Dessutom ger arbetet med kugghjulsuppgifter i par välkomna tillfällen för matematiska samtal. Dessa samtal är mycket viktiga för såväl användning av begrepp som för att träna på att sätta ord på sina tankar och lösningar.
Kugghjulsuppgifter finns även som utmaning i Kommer du ihåg? där det alltid finns tre uppgifter på tre nivåer.
Dessutom finns det en samling med fler kugghjulsuppgifter till varje kapitel i Snilleblixtar som finns i slutet av elevboken.
Låt inte eleverna välja vem de ska arbeta med utan dela in dem i par. Byt efter en tid. Det kan finnas elever som föredrar att arbeta ensamma. Det är du som lärare som får avgöra hur inlärningen för eleverna fungerar bäst.
MATEMATIKDIDAKTISKA TANKAR
Från konkret till abstrakt
Introducera nytt innehåll med laborativt material. Inlärning av nytt matematiskt innehåll, speciellt till yngre elever, görs bäst genom att introduceras laborativt, med konkret material (t.ex. makaroner eller tiobasmaterial). Arbetet med konkret material aktiverar elevernas olika sinnen. Eleverna hanterar materialet fysiskt, tar i det, ser det och känner det med händerna när de arbetar. Här bygger eleverna upp en förståelse för matematiska begrepp och koncept.
Nästa steg i förståelsen för nytt matematiskt innehåll kan vara att det konkreta materialet visas på bild. Det kan t.ex. vara en film där bekant material (t.ex. tiobasmaterial, klossar eller rektanglar) visas och flyttas. Eleverna känner igen materialet och fortsätter skapa inre bilder.
Så småningom kopplas det konkreta materialet till det abstrakta, till exempel på en tallinje eller skrivna med siffror. I början kan detta ske bredvid det konkreta, till exempel genom att skriva motsvarande tal under tiobasmaterial eller ritade rektanglar. Det är av stor vikt att eleverna kopplar det konkreta materialet till symbolerna, dvs. att de förstår vad symbolerna står för.
Slutligen ska det matematiska innehållet enbart hanteras på en abstrakt nivå. Eleverna använder siffrorna och förstår att dessa representerar tal.
Samma inlärningsprocess från konkret till abstrakt används för andra matematiska koncept som till exempel ”addition”, ”hundratal”, ”tiotal” och ”ental” eller ”multiplikation” och ”division”.
TALUPPFATTNING
Tiobasmaterial och tiobasunderlag
Arbetet med tiobasmaterial underlättar förståelsen för vårt talsystem då tio entalskuber tillsammans är lika med en tiotalsstav och tvärtom, en tiostav är lika med 10 entalskuber, vilket stödjer addition och subtraktion med tiotalsövergång. Likaså är tio tiostavar lika med en hundraplatta, och tio hundraplattor är lika med en tusenkub.
Tiobasmaterial kan användas för att bygga och visa tal med olika antal hundratal, tiotal och ental som visas med hjälp av olika många hundraplattor, tiostavar och entalskuber. Sätt ihop eller dela upp tal i talsorterna (se lektion 1).
Använd talsortsunderlaget för uppställning som finns på s. 160 i slutet av elevboken.
2 4 5 3 0 + 3 2
Visa addition och subtraktion med uppställning genom att lägga talkort och räknetecknen i motsvarande kolumner för de olika talsorterna.
Speciellt när det kommer till växlingar är det viktigt att eleverna får möjlighet att modellera räkneprocessen med laborativt material. På så sätt har de möjlighet att förstå växlingsproceduren som de utför när de använder sig av algoritmen (uppställningar).
Läs mer
Tallinjen
Att använda tallinjen hjälper dina elever att förstå och befästa talens relation till varandra. Börja med att använda kortare tallinjer, till exempel 0 till 20 som visar alla tal (finns som kopieringsunderlag).
Ograderade tallinjer
Ett bra sätt för att stödja och befästa elevernas uppfattning om talens relation till varandra är att arbeta med ograderade tallinjer. Det är tallinjer med eller utan streck och med enbart två utplacerade tal. Visa eller rita tallinjen på tavlan eller häng upp ett långt snöre med talen 0 och 1 000.
Genom att placera ut olika tal på tallinjen och resonera tillsammans ges eleverna tillfälle att sätta ord på talens position med hjälp av begrepp som ”större än” och ”mindre än” eller ”hälften” och ”dubbelt”.
Läs mer
Pre-algebra, öppna utsagor och likhetstecknet
Prealgebra förbereder det senare arbetet med algebraisk ekvationslösning. Prealgebra handlar till exempel om att räkna med okända tal utan att använda sig av bokstäver. Förståelsen för jämvikt i ekvationen är basen till arbetet med ekvationer (i åk 3 additioner, subtraktioner, multiplikationer och divisioner) där något eller några tal ersätts med en symbol. I Matteblixt förekommer uppgifter med symboler i kugghjulsuppgifterna.
Sådana prealgebraiska uppgifter liknar öppna utsagor där det saknas ett tal i uttrycket. Arbetet med öppna utsagor stärker förståelsen om likhetstecknets betydelse: både sidorna måste vara lika stora.
Även additioner och subtraktioner där summan eller differensen står i vänstra ledet eller består av ett uttryck, stärker förståelsen av likhetstecknet.
Räkna inte bara 29 + 14 = ____ utan även ____ = 20 – 4, och 3 · ____ = 15 eller 10 – 3 = ___ + 2
Använd vågen från den digitala tavlan för att illustrera olika ekvationer. Lägg tal eller uttryck med tal och symbolkorten på vågens sidor för att träna och befästa förståelsen för likhetstecknets betydelse.
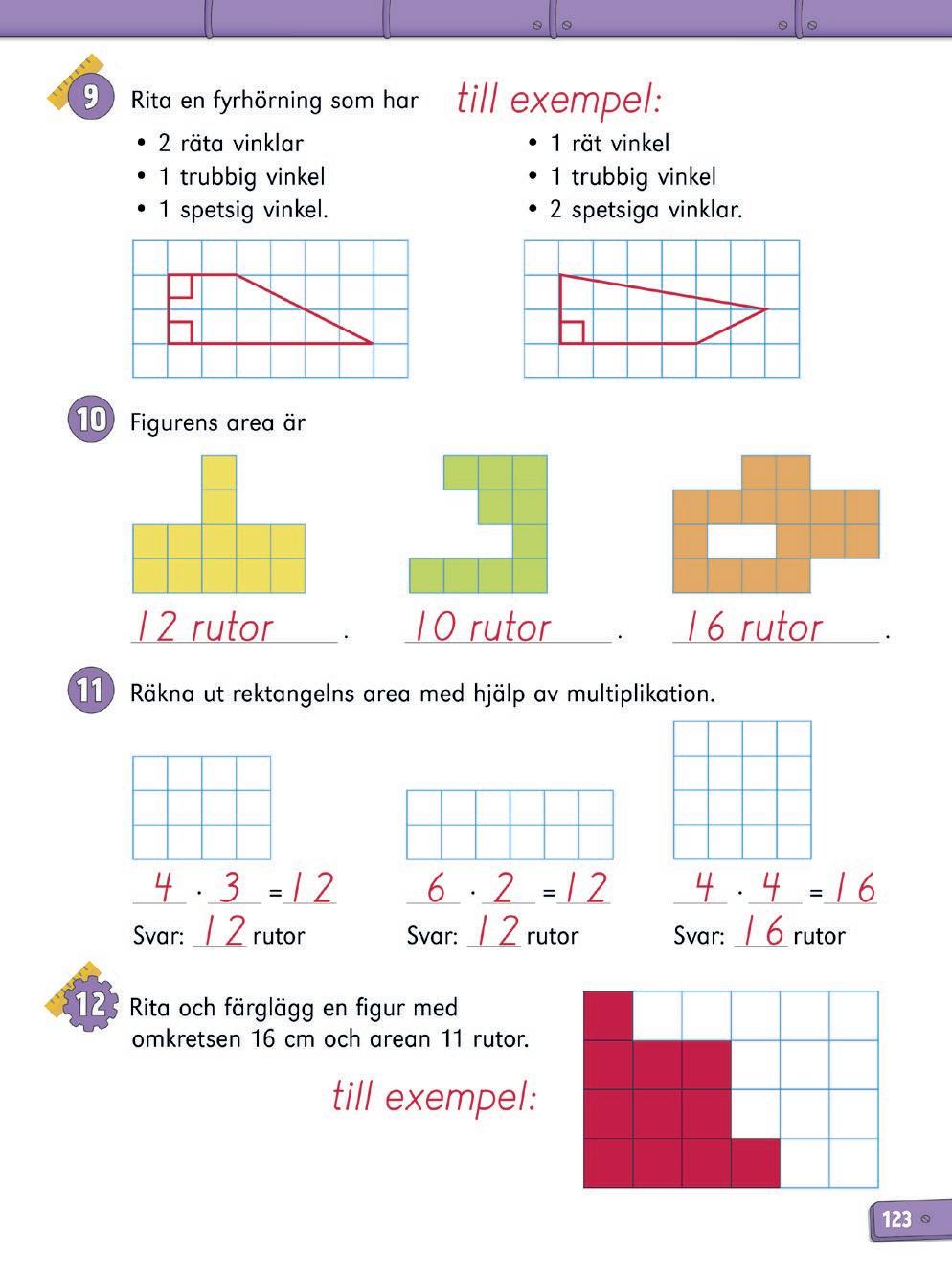
Multiplikation och area
Ett smidigt sätt att illustrera multiplikationer är att visa dem som rektanglar. Antal rutor i rektangeln kan beräknas genom att multiplicera antalet kolumner (t.ex. 3) med antalet rutor i kolumnen (t.ex. 5).
Tal i bråkform
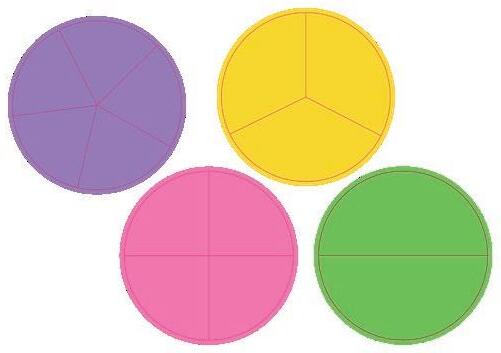
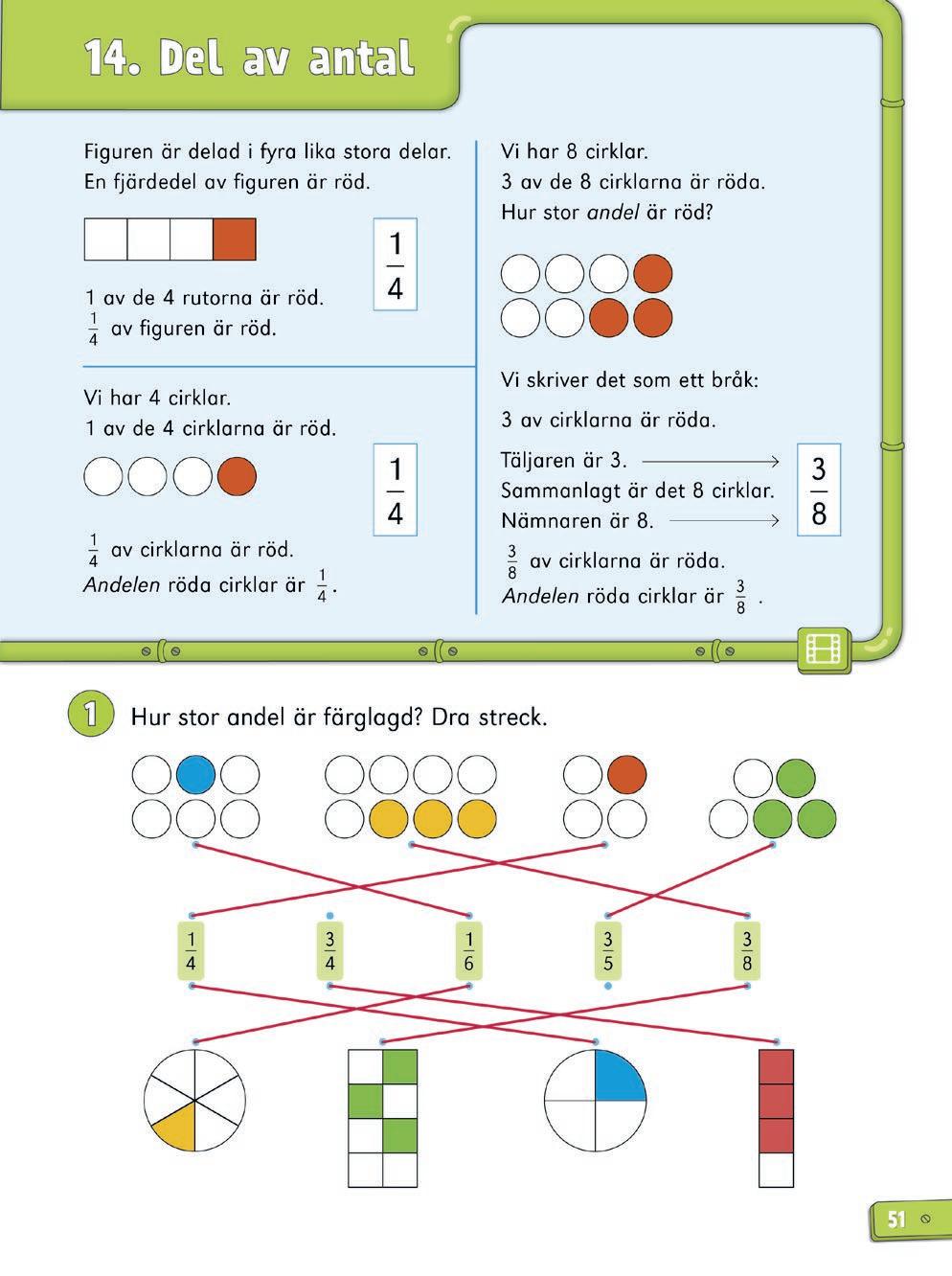
Tal i bråkform introduceras ofta genom att visa lika stora cirklar som är uppdelade i olika många delar (se bråkcirklar). Cirklarna är tacksamma modeller eftersom de senare kan utvecklas till cirkeldiagram där hela cirkeln är 100 %. När man jämför de olika delarna syns det tydligt att en tredjedel är större än en fjärdedel. Det är dock svårare att jämföra storlek på olika delar när eleverna själva ska rita bråkcirklar. Ge eleverna möjlighet att bekanta sig med olika modeller när tal i bråkform visas.
Eleverna kan till exempel använda rutat papper så att de kan rita tal i bråkform med hjälp av rektanglar där en del av rutorna färgläggs. Det är viktigt att eleverna förstår att de måste utgå från lika stora rektanglar när de ska jämföra tal i bråkform med varandra.
1/3 1/4
Använd även tallinjer när ni arbetar med tal i bråkform. En ograderad tallinje med talen 0 och 1 kan användas för att låta eleverna placera olika tal i bråkform på tallinjen.
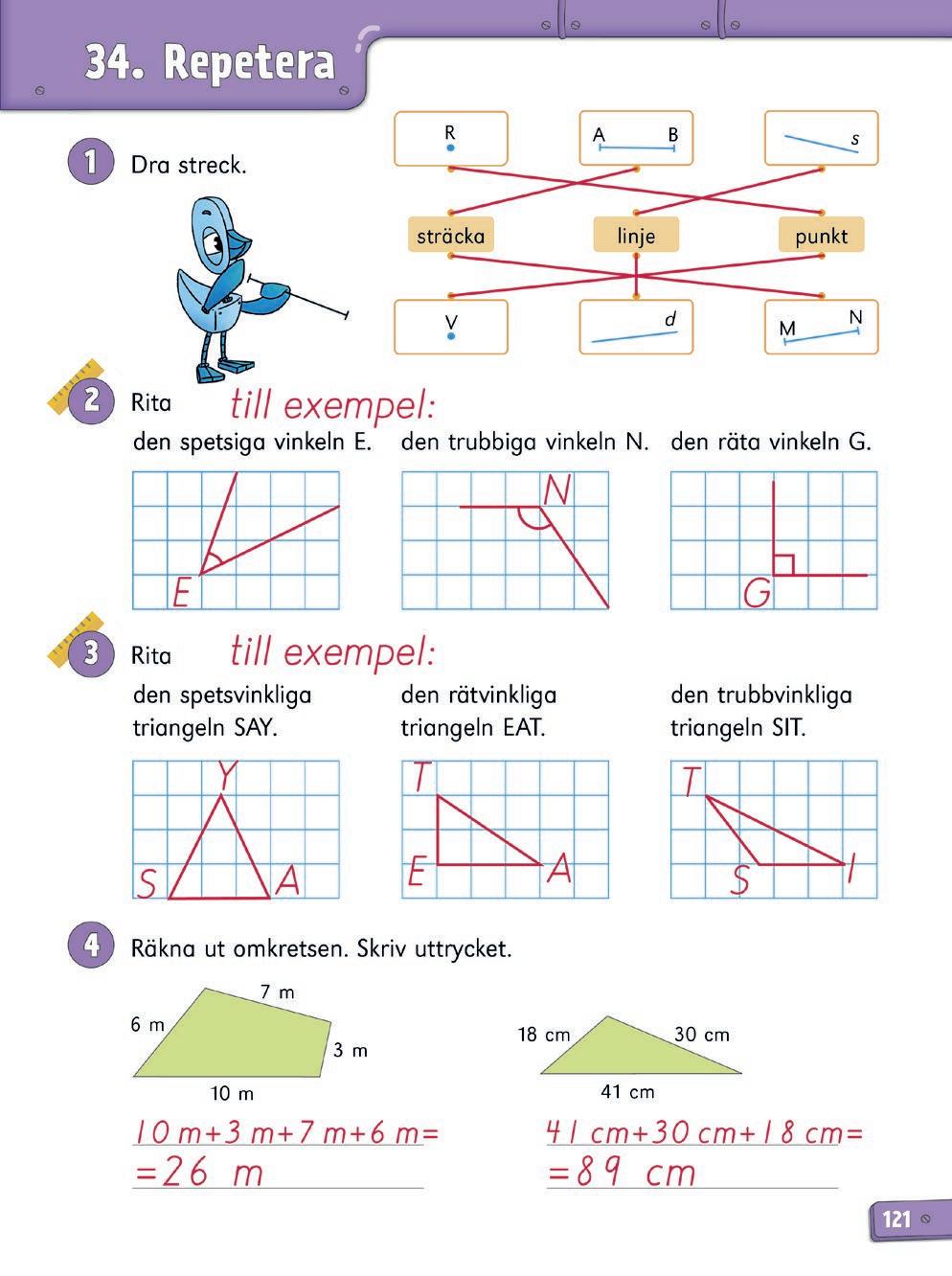
Antalet rutor i rektangeln är även rektangelns area, räknat i antal rutor. Låt eleverna arbeta med cmrutat papper för att underlätta jämförelsen av olika figurers area (och även omkrets).
Att multiplicera antalet kolumner med antalet rutor i varje kolumn lägger grunden för senare areaberäkning i rektanglar, där basen multipliceras med höjden.
När det kommer till flera hela är det värdefullt att uppmärksamma eleverna på att värdet på tal i bråkform kan räknas ut med hjälp av division. Tolv fjärdedelar är samma som tre hela och tolv dividerat med fyra är också tre (hela). Förståelsen för sambandet mellan tal i bråkform och division ger eleverna värdefulla insikter när de senare ska arbeta med decimaltal.
Elevbok s. 6–7
KAPITLETS INNEHÅLL
• uppdelning av tal i talsorterna: ental, tiotal, hundratal och tusental
• jämförelse av talen 0–10 000 med jämförelsetecken
• addition och subtraktion med uppställning och växling – flera växlingar
FÖRKUNSKAPER
• talen 0–1 000
• addition och subtraktion med uppställning och växling
MATERIAL
• A3-papper
• färgpennor
DIGITALT INNEHÅLL
Introduktionsfilm 1: Räkna med uppställning
Lektionsfilmer 1a till 9b
Digital tavla
Klura tillsammans: Mattestaty
KOPIERINGSUNDERLAG
Begreppslista 1
Visste du? Lektion 1–10
Instruktioner för övningsbanan
Svarskort till övningsbanan
Djurkort till övningsbanan
Mitt räkneflyt
Räkneflyt – addition och subtraktion med talsorter
Räkneflyt – addition och subtraktion med tiotalsövergång
SNILLEBLIXTAR
• Elevbok, s 126–131
BEDÖMNING
Prov 1: Räkna med uppställning
Prov 1a1
Prov 1a2
Prov 1c
KAPITEL 1: Räkna med uppställning
PEDAGOGISKA TANKAR INFÖR KAPITEL 1
I kapitlet delar vi upp tal från 0 till 10 000 i talsorter. Vi jämför också talen och använder oss av jämförelsetecknen mindre än <, lika med = och större än >. Vi jämför en talsort i taget och det är viktigt att eleverna förstår positionssystemet, att en siffras värde beror på dess plats i talet.
Vi repeterar uppställningar i addition och subtraktion med växling och minnessiffra. Därefter går vi vidare med uppgifter som innehåller flera växlingar och minnessiffror, samt i subtraktion även växling över noll.
Visa uppställningarna i både addition och subtraktion med tiobasmaterial.
Låt eleverna använda materialet som stöd när de räknar. Det hjälper eleverna att förstå additionen respektive subtraktionen av de olika talsorterna samt hur växlingen sker mellan talsorterna, till exempel när ental växlas till ett tiotal, tiotal växlas till ett hundratal, och tvärtom.
INLEDANDE UPPGIFT
Backhoppningstävling
Fem domare ger poäng i en backhoppningstävling. Varje domare kan ge mellan 0 och 20 poäng (hela poäng). Den lägsta och den högsta poängen tas bort.
Backhopparen får sammanlagt 48 poäng. Hur många poäng kan domarna ge? Försök att hitta fem olika förslag.
ÄMNESÖVERGRIPANDE
Fem fakta om vintersport
Ni behöver: A3papper och färgpennor
1. Gör en affisch om en vintersport tillsammans i par.
2. Rita eller hitta passande bilder till affischen.
3. Hitta och skriv fem fakta om sporten. Faktauppgifterna ska innehålla tal (t.ex. antal medaljer, rekord, lag, storlek …).
4. Presentera er affisch för klassen.
FAKTARUTA
Hur långt är hoppet?
Titta på faktarutan på s. 7 i elevboken och hitta svar på följande frågor.
1. Hur långt är hoppet i hoppbacken? (250 m)
2. Hur många bussar får plats i hoppet (cirka 7 · 3 = 21 st)
3. Vilka egenskaper, styrkor och färdigheter tror du att en backhoppare behöver? (noggrannhet, mod, skicklighet – Visste du?)
ÖVNINGSBANAN
Till några lektioner finns det en övningsbana med repetitionsuppgifter inom området ni har arbetat med. Du kan använda övningsbanan som finns på baksidan av elevernas Kommer-du-ihåg?bok eller trycka ut djurkorten och göra en övningsbana i klassrummet.
I det här kapitlet finns det uppgifter till övningsbanan efter lektion 5 och 9. Läs mer i instruktionerna för övningsbanan, digitalt eller på s. 120.
SAMTALSBILDEN
Bilden visar innehåll ur kapitlet. Men den visar mycket annat också. Speciellt om du har elever med annat modersmål än svenska kan bilderna stödja och befästa inlärningen av ord som är nya för dem och som kan förekomma i kapitlet.
Börja med att låta eleverna själva titta på bilden och upptäcka den. Be dem att hitta en sak de tycker om som de berättar om för klasskompisen bredvid.
Sedan riktar du uppmärksamheten åt det matematiska innehållet i bilden genom att ställa frågor. Använd några av exempelfrågorna eller egna frågor.
För att säkerställa elevernas delaktighet i klassrumssamtalet, gå gärna igenom frågorna genom att använda någon kooperativ struktur som aktiverar många elever, till exempel EPA.
1. Vilken/vilka pister är längst? (Svängen och Ormen)
2. Vilken/vilka pister är kortast? (Puckeln)
3. Hur mycket längre är Blixten än Väggen? (400 m eller dubbelt så lång)
4. Hur mycket kortare är Puckeln än Ormen? (750 m)
Du kan använda samtalsbilden även i slutet av kapitlet, då för att utvärdera elevernas förståelse för olika begrepp som ”jämförelsetecken” eller ”summa/differens”.
Fråga då till exempel:
5. Mellan vilka två pister är differensen mellan längderna 300 meter? (Väggen och Puckeln)
6. Vilka två pister har en sammanlagd längd – en summa – på 1 200 meter? (Blixten och Väggen)
7. Storleksordna pisterna från kortast till längst med hjälp av jämförelsetecken. (Puckeln < Väggen < Blixten < Svängen/Ormen)
ARBETA MED BEGREPP
Du hittar hela begreppslistan med tillhörande förklaringar i din digitala lärarhandledning. Du kan trycka ut listan och hänga upp den i klassrummet så att eleverna har tillgång till den.
Tänk på att det är många nya och delvis svåra begrepp som eleverna möter i det här kapitlet. Det är viktigt att lägga tid på att arbeta med begreppen. Elevernas förståelse för begreppen kommer att utvecklas under arbetet med dem i ett meningsfullt sammanhang.
Börja med att läsa upp begreppen och fråga om någon elev känner igen något av dem. Berätta att eleverna kommer att arbeta med dessa begrepp i kapitlet och att de kommer att kunna titta på listan med förklaringar när de stöter på begrepp de är osäkra på.
AKTIVITETER FÖR BEGREPPSTRÄNING
Skriv ut elevernas begreppslista och klipp isär begrepp och förklaringar. Använd kooperativa strukturer för att träna på begreppen. Lämpliga strukturer är ”Frågafrågabyt” (använd bara begreppen) eller ”Hör vi ihop?” (använd begrepp och förklaring).
LEKTIONENS INNEHÅLL
• talsorterna: ental, tiotal, hundratal, tusental, tiotusental
• att dela upp tal i talsorter
• att jämföra talen 0–10 000
VIKTIGA BEGREPP
• talsorter: ental, tiotal, hundratal, tusental, tiotusental
• talföljd
• jämförelsetecken <, = och >
• udda – jämnt
MATERIAL
• tiobasmaterial
KOPIERINGSUNDERLAG
Talen 0–10 000: 1a 1b 1c
Talkort 0 till 9
Små talkort och tecken
KOMMER DU IHÅG?
• Lektion 1, s 6
DIGITALT MATERIAL
Klura tillsammans: Den hemliga koden
Lektionsfilm 1a: Talen 0–10 000
– Talsorter
Lektionsfilm 1b: Talen 0–10 000
– Uppdelning i talsorter
HUVUDRÄKNING
Visste du? – Vilken vintersport?
1 250 + 100 (350)
2 Anna åker 13 kilometer skidor på måndagen och 17 kilometer på onsdagen Hur många kilometer åker hon sammanlagt under veckan? (30 km)
3 Omar har som mål att åka 45 kilometer skidor under en vecka Han har redan åkt 25 kilometer Hur många kilometer har Omar kvar att åka för att nå sitt mål? (20 km)
1. Talen 0–10 000
GENOMGÅNG OCH
AKTIVITETER
Att bilda tal
Ni behöver (analogt eller digitalt): tiobasmaterial eller Talkort 0 till 9
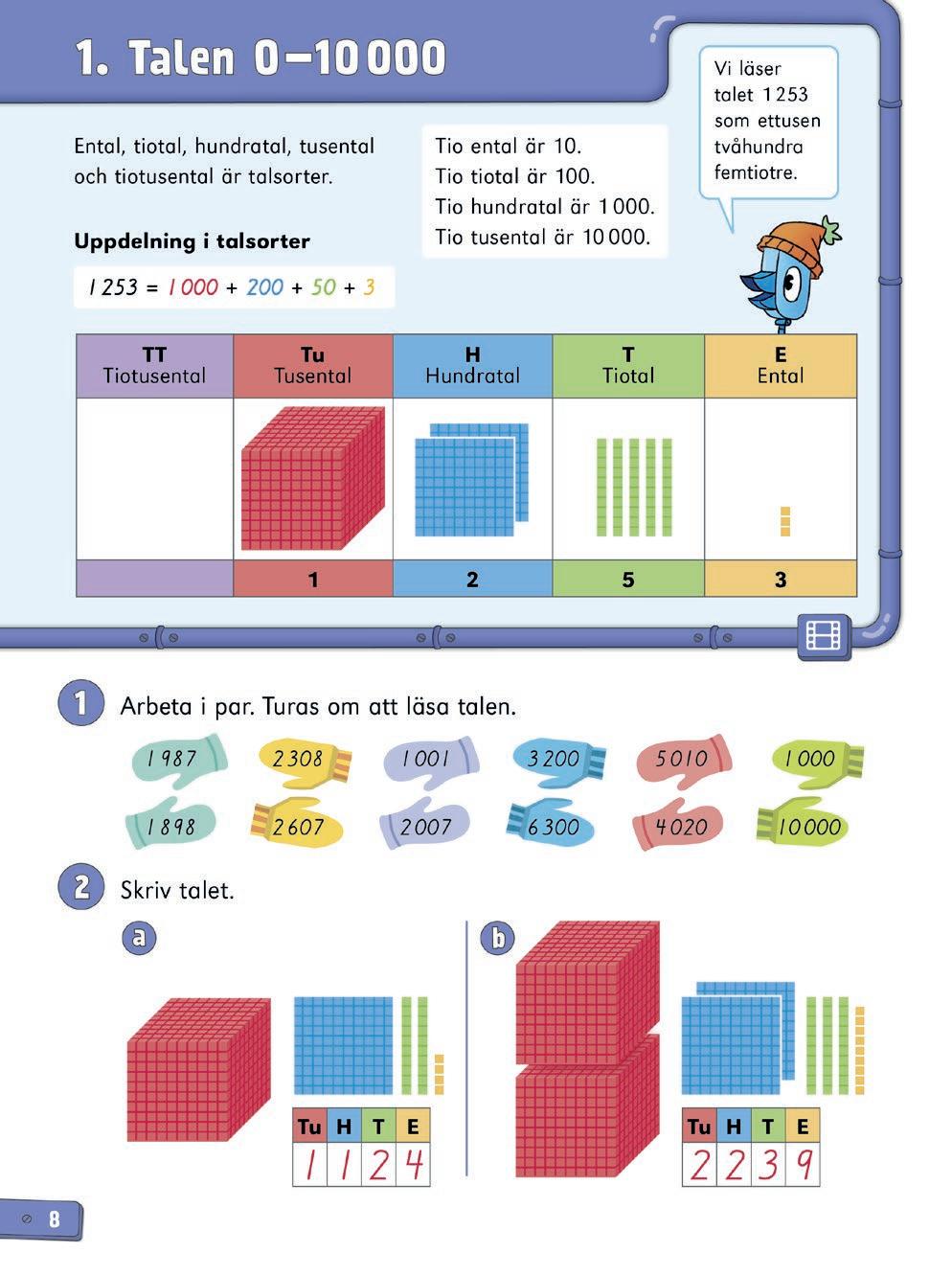
Bilda talet 1 243 med hjälp av talkort eller tiobasmaterial. Gå igenom talsorterna i talet och titta på deras antal: tusental (1), hundratal (2), tiotal (4) och ental (3). Skriv talet 1 243 uppdelat i talsorter: 1 243 = 1 000 + 200 + 40 + 3.
Andra lämpliga tal är 1 352, 1 074, 1 205 och 1 430.
Tal med talkort
Ni behöver (analogt eller digitalt): Små talkort och tecken
Använd talkorten för att bilda ett tal som uppfyller villkoren.
a. Talet består av tre siffror. Tiotalen är färre än entalen.
b. Talet består av fyra siffror. Alla siffror är udda.
c. Talet består av fyra siffror. Siffran på hundratalens plats är jämn.
d. Talet består av fyra siffror. Tusentalen är fler än entalen.
e. Talet består av tre siffror. Summan av siffrorna är 20.
f. Talet består av fyra siffror. Summan av siffrorna är mindre än 12.
TILLÄMPANDE AKTIVITET
Placera talen rätt
Ni behöver: Talkort 0 till 9
Dela in eleverna i lag med fem personer i varje och ge varje spelare två talkort var.
1. Lekledaren säger ett fyrsiffrigt tal som går att bilda av talkorten.
2. De spelare som har rätt siffror ska ställa sig bredvid varandra så att de bildar rätt tal.
3. Det lag som först bildat talet får en poäng.
4. Det lag som först får 3 poäng vinner.
Lämpliga tal är 2 541, 5 896, 7 032, 3 128, 4 607 och 8 230.
UR PEDAGOGISK SYNVINKEL
I Matteblixt 3a bekantade vi oss med talområdet 0–1 000. I det här kapitlet introducerar vi den nya talsorten tiotusental. Det går att visa hur man bildar, delar upp och jämför tal med hjälp av tiobasmaterial. Använd tiobasmaterial till exempel tillsammans med talsortsunderlaget för uppställning som finns på sidan 160 i elevboken. Ett centralt mål är att befästa elevens förståelse för positionssystemet. En siffras värde beror på dess plats i talet.
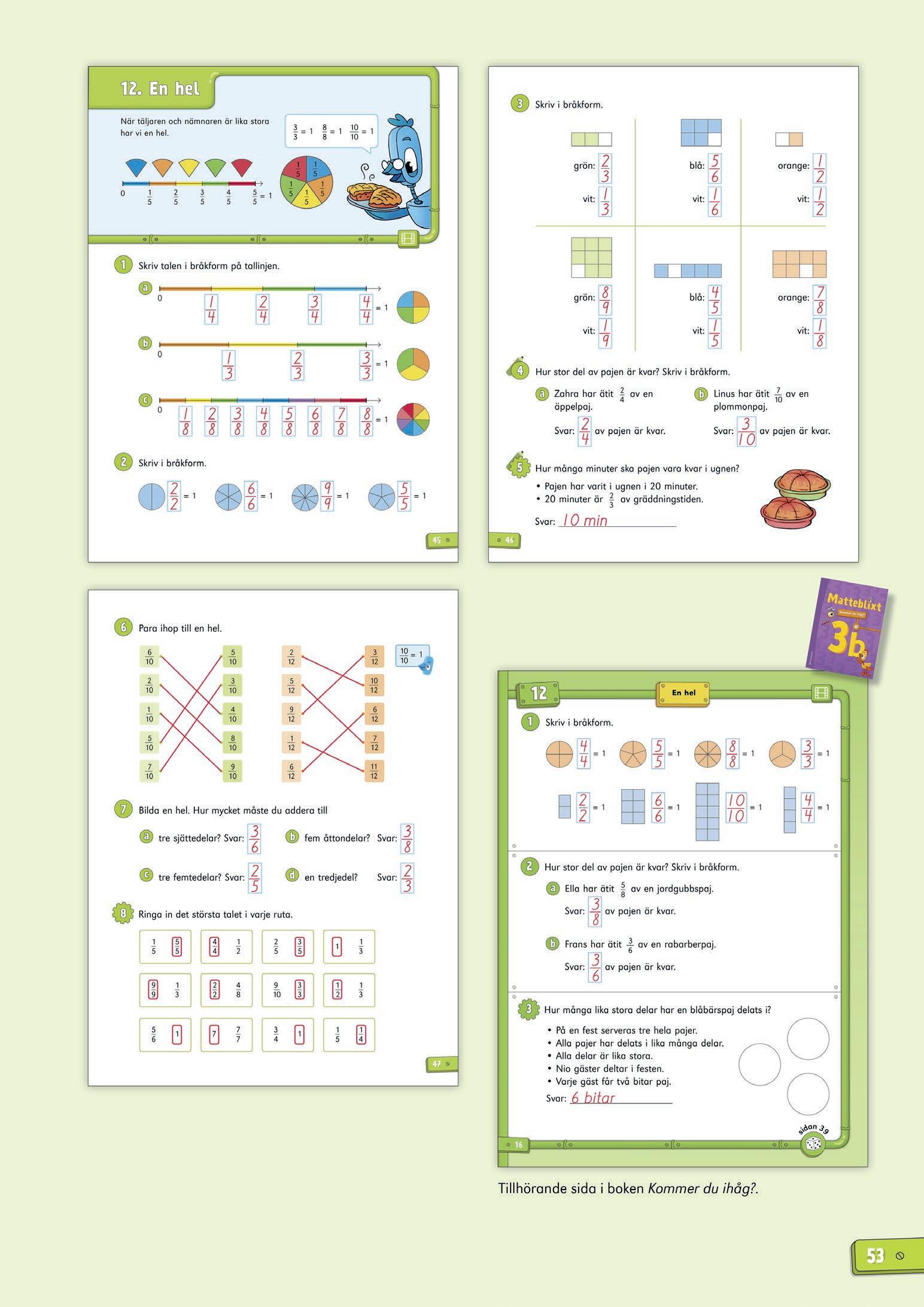
Tillhörande sida i boken Kommer du ihåg?
Elevbok s. 20–22
LEKTIONENS INNEHÅLL
• addition med uppställning
• flera växlingar
VIKTIGA BEGREPP
• talsorter: ental, tiotal, hundratal, tusental
• addition – addera – summa
• växling – minnessiffra
MATERIAL
• talsortsunderlag för uppställning (s 160 i elevboken)
• färgcirklar (t ex från kuvertet i Matteblixt 1a, 1b)
• färgpennor
• papper och penna
• tärningar
KOPIERINGSUNDERLAG
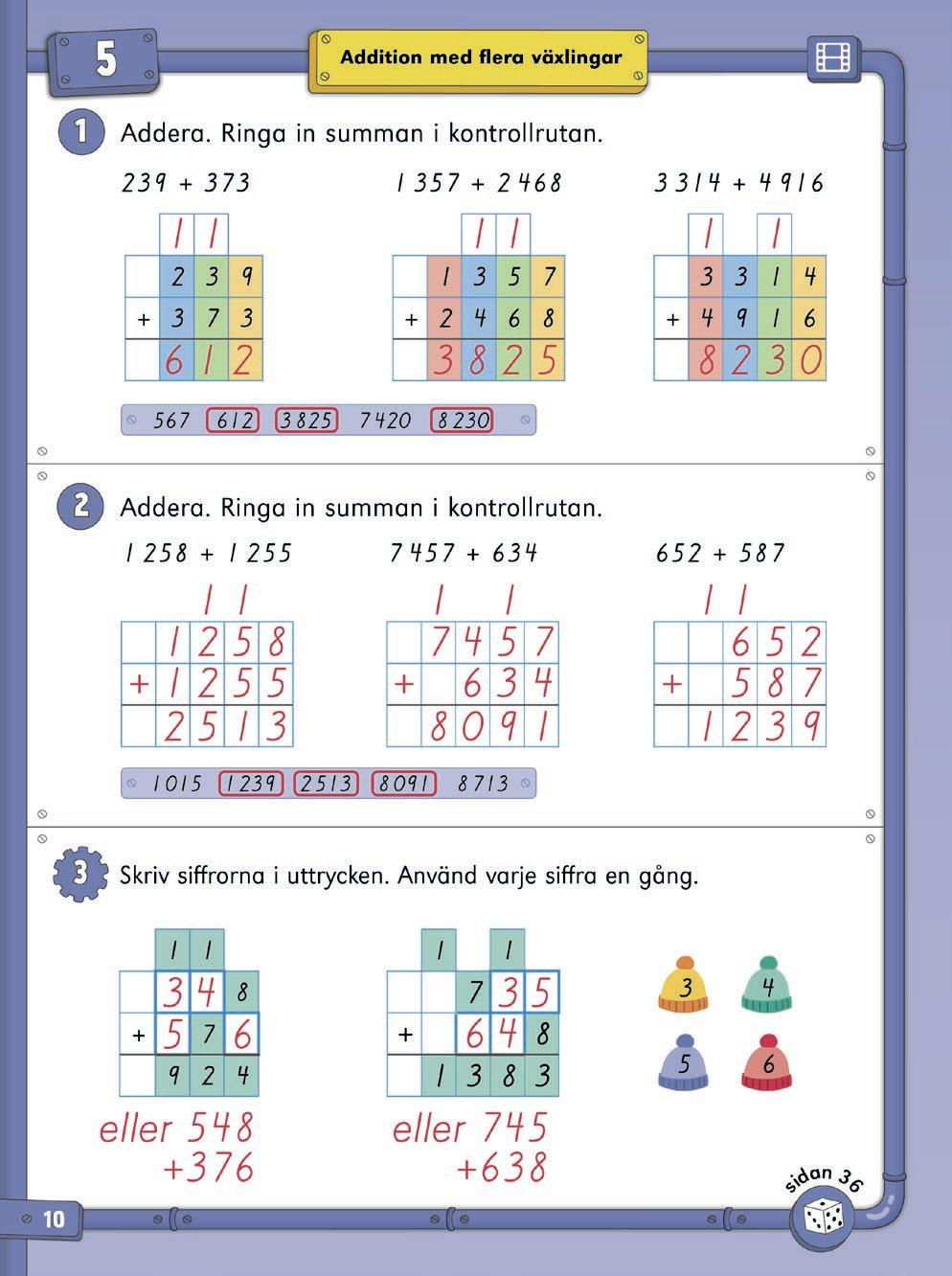
Addition med flera växlingar: 5a 5b 5c
Färgcirklar
Talsortsunderlag för uppställning
Lektion 5: Uppgiftskort och facit till övningsbanan
Små talkort och tecken
Underlag för uppställning (fyr- och femsiffriga tal)
KOMMER DU IHÅG?
• Lektion 5, s 10
• Spel: Additionsmästaren, s 36
DIGITALT MATERIAL
Klura tillsammans: Isflaket
Lektionsfilm 5: Addition med flera växlingar
HUVUDRÄKNING
Visste du? – Spännande snöskor
1 180 + 120 (300)
2 På den översta hyllan i ett förråd står 70 snöskor och på den nedersta hyllan 60 snöskor Hur många snöskor står det sammanlagt på hyllorna? (130)
3 Anton går 820 steg med snöskor på måndagen och 450 steg på tisdagen Hur många steg går Anton sammanlagt under de här två dagarna? (1 270)
5. Addition med flera växlingar
GENOMGÅNG OCH AKTIVITETER
Addition på talsortsunderlag för uppställning
Ni behöver (analogt eller digitalt): talsortsunderlag för uppställning, färgcirklar (eller andra små föremål) och Små talkort och tecken
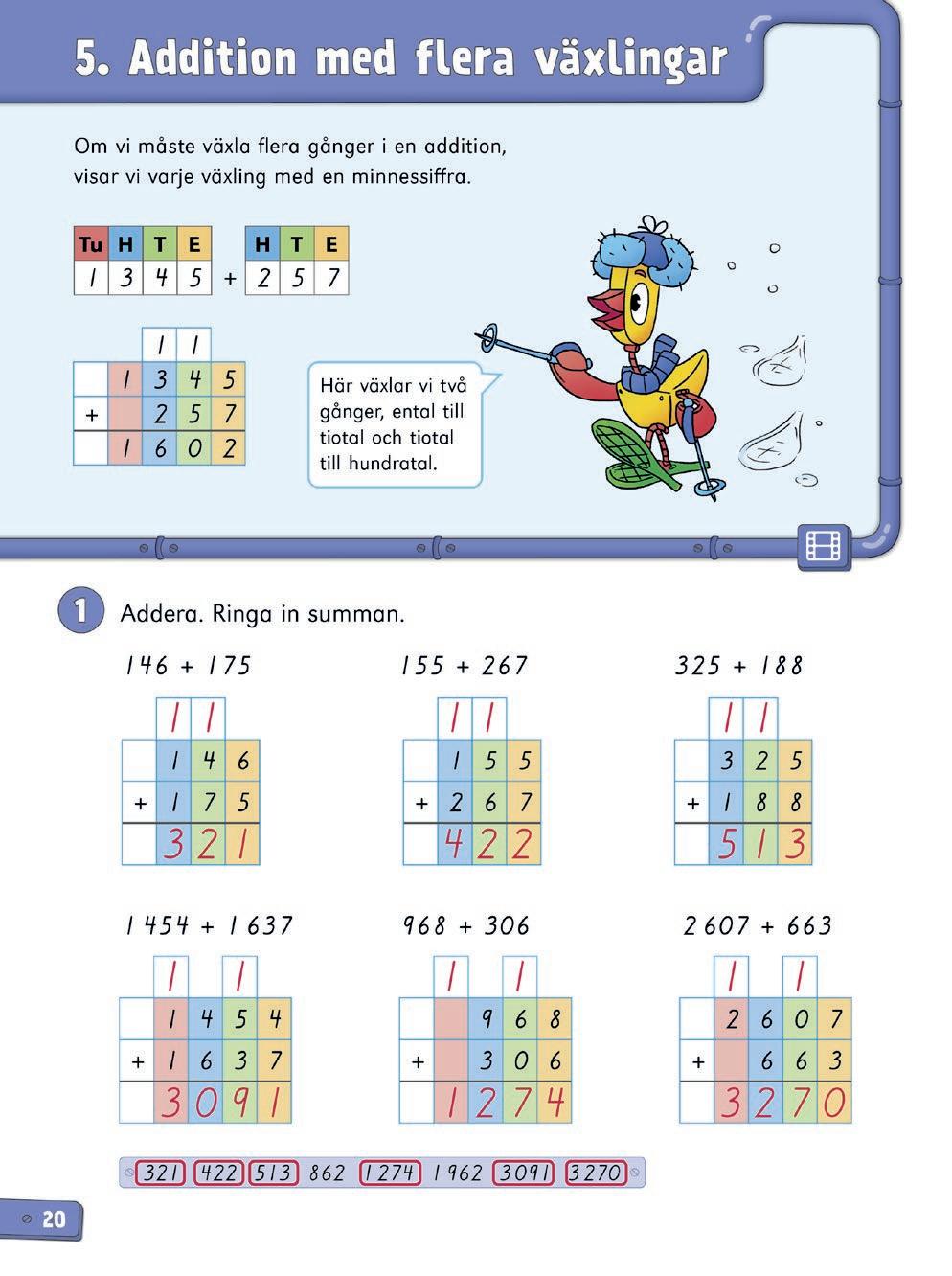
Skriv additionen 366 + 475 så att eleverna ser den. Bilda termerna med färgcirklar på tiobasunderlaget. Addera entalen. Ta bort och växla 10 färgcirklar från entalen och lägg till en cirkel till tiotalen. Visa summan med ett talkort. Addera tiotalen. Ta bort och växla 10 färgcirklar från tiotalen och lägg till en cirkel till hundratalen. Visa summan med ett talkort. Addera hundratalen. Visa summan med ett talkort. Lämpliga uttryck är 156 + 257 (413), 1 365 + 246 (1 611), 1 526 + 1 645 (3 171) och 1 947 + 1 235 (3 182).
TIPS: Det går också att utföra övningen med tiobasmaterial, knappar, pärlor eller makaroner.
Känn igen växling
Ni behöver: färgpennor och Underlag för uppställning (fyr- och femsiffriga tal)
Skriv upp uttrycken 1 454 + 367, 546 + 432, 1 850 + 1 324 och 1 258 + 605. Lös uttrycken med uppställning och ringa in
a. additionen där man inte behöver växla – med rött. (546 + 432)
b. additionen med en växling mellan entalen och tiotalen – med blått. (1 258 + 605)
c. additionen med en växling mellan hundratalen och tusentalen – med gult. (1 850 + 1 324)
d. additionen med flera växlingar – med grönt. (1 454 + 367)
TILLÄMPANDE AKTIVITET
Additionskamp
Ni behöver: papper, penna och 3 tärningar
1. Eleverna arbetar i par och turas om att slå tre tärningar var.
2. Varje elev bildar två så stora tal som möjligt av sina tärningar, t.ex. 543 och 664.
3. Eleven ställer upp talen och adderar dem för att räkna ut sin summa.
4. Den som får den största summan vinner omgången.
5. Paren spelar tre omgångar. Flest vinster vinner spelet!
ÖVNINGSBANA
Ni behöver: Lektion 5: Uppgiftskort och facit till övningsbanan
Läs mer i instruktionerna för övningsbanan, digitalt eller på s. 120.
UR PEDAGOGISK SYNVINKEL
I alla lektioner med additionsuppställning, med eller utan tiotalsövergång, med en eller flera växlingar, kan arbetet visas med hjälp av tiobasmaterial.
Låt eleverna använda materialet som stöd när de räknar med uppställning.
Tillhörande sida i boken Kommer du ihåg?
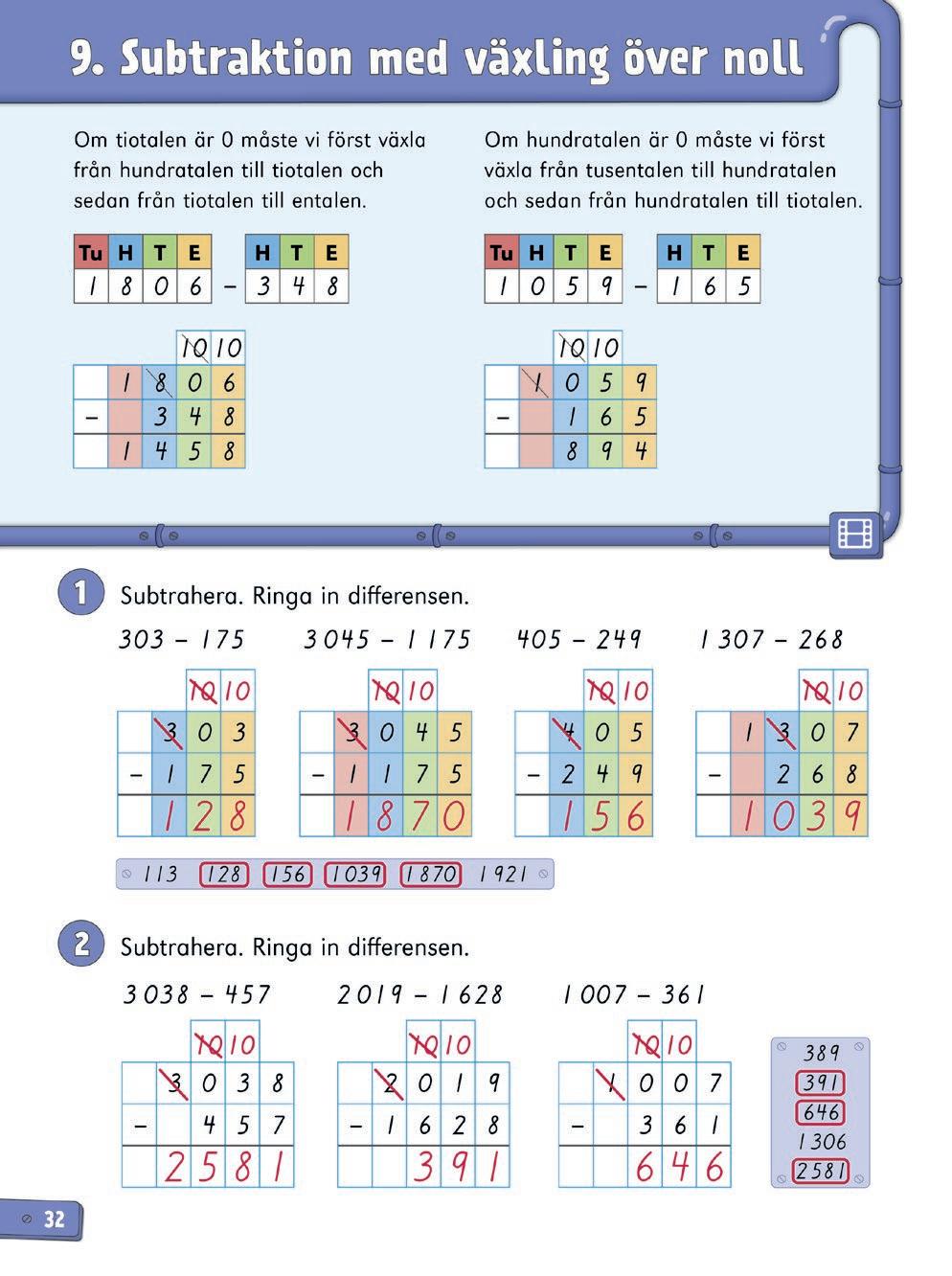
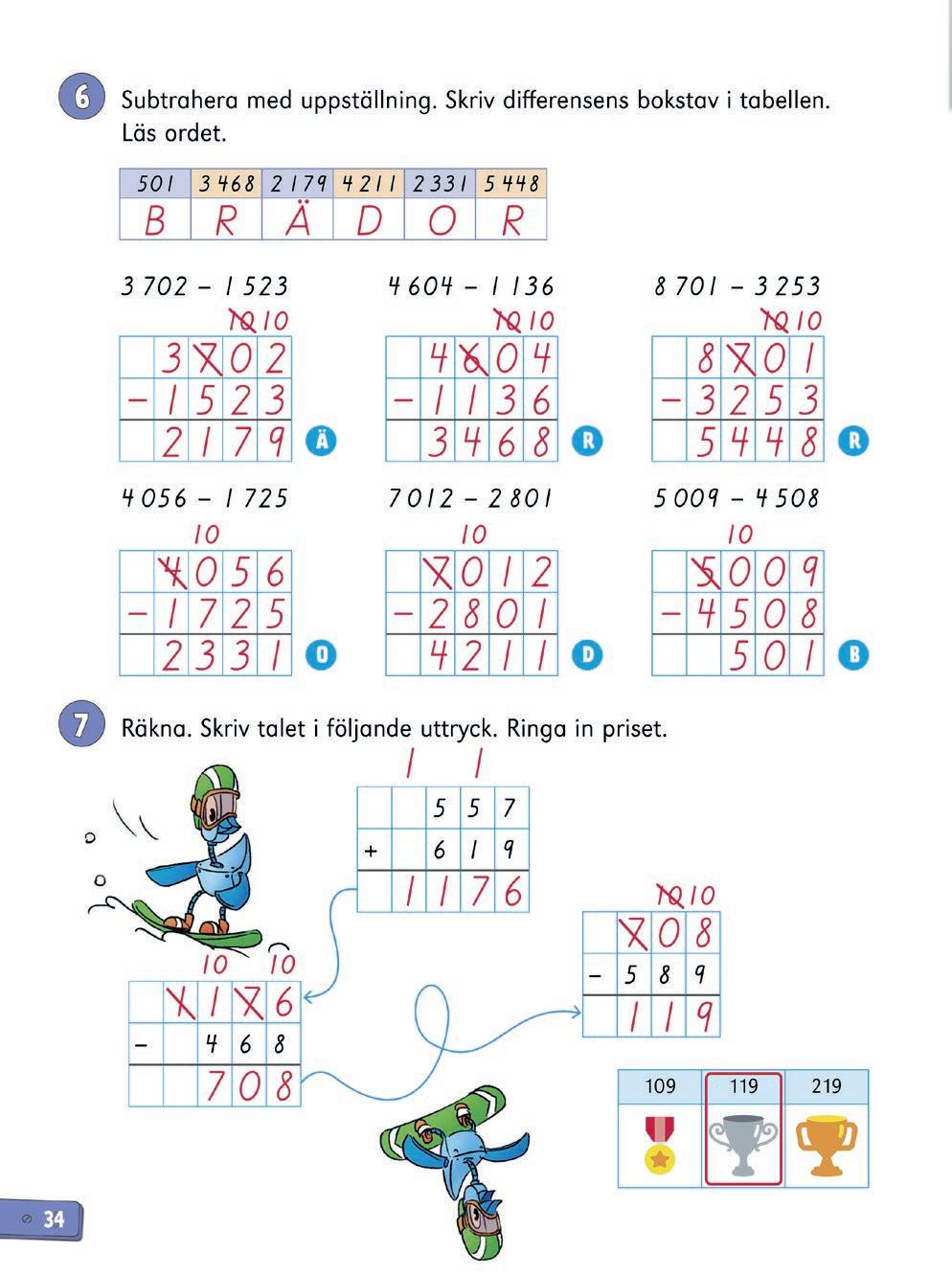
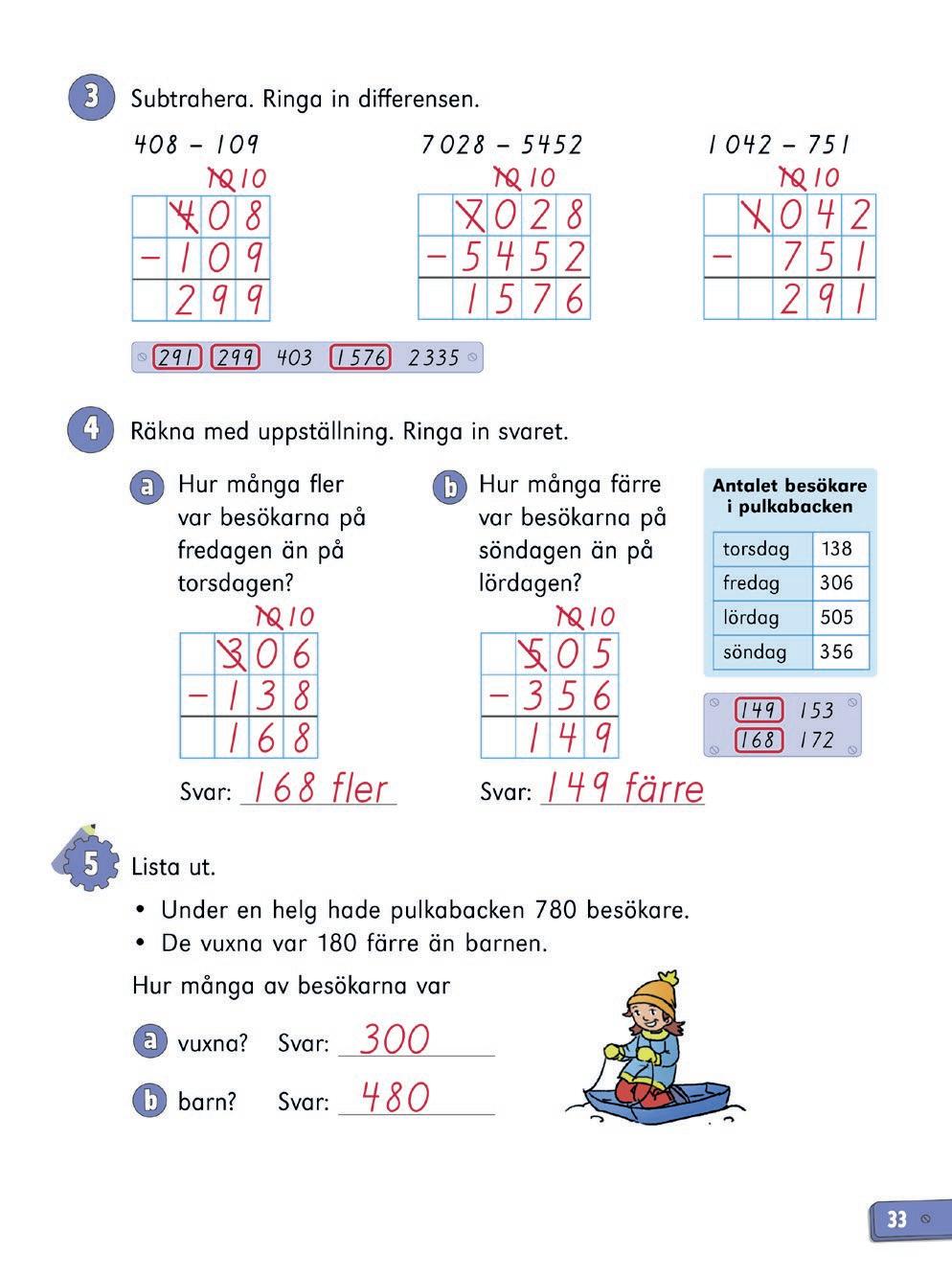
Elevbok s. 32–34
LEKTIONENS INNEHÅLL
• subtraktion med uppställning
• växling över noll
VIKTIGA BEGREPP
• talsorter: ental, tiotal, hundratal, tusental
• subtraktion – subtrahera – differens
• växling – minnessiffra
MATERIAL
• talsortsunderlag för uppställning (s 160 i elevboken)
• färgcirklar (t ex från kuvertet i Matteblixt 1a, 1b)
• färgpennor
• tärningar
KOPIERINGSUNDERLAG
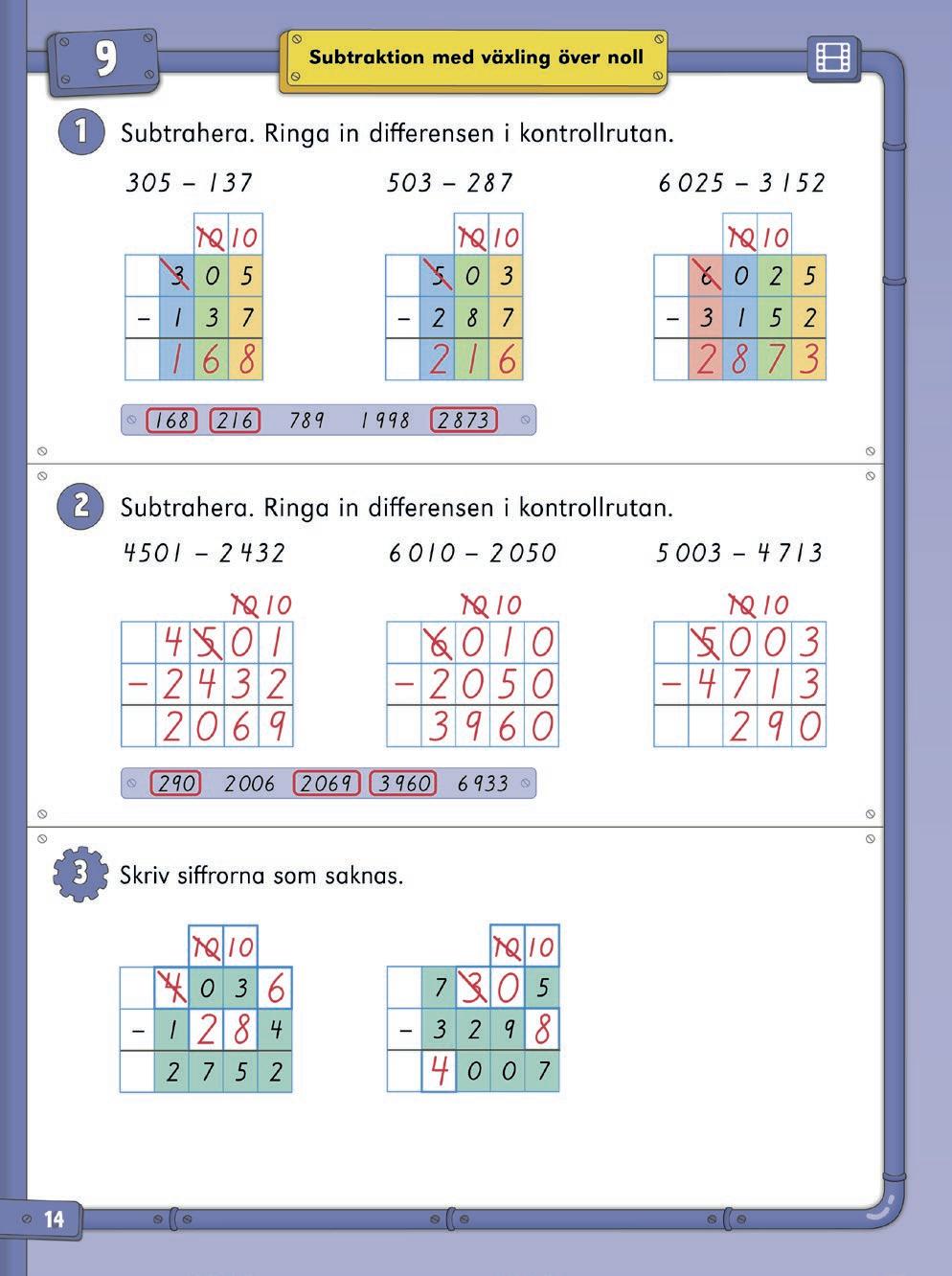
Subtraktion med växling över noll: 9a 9b 9c
Färgcirklar
Talsortsunderlag för uppställning
Lektion 9: Uppgiftskort och facit till övningsbanan Kampen över nollan, spelplaner Små talkort och tecken Underlag för uppställning (fyr- och femsiffriga tal)
KOMMER DU IHÅG?
• Lektion 9, s . 14
DIGITALT MATERIAL
Klura tillsammans: Vilket tal passar inte in?
Lektionsfilm 9a: Subtraktion med växling över noll – Om tiotalen är noll
Lektionsfilm 9b: Subtraktion med växling över noll – Om hundratalen är noll
HUVUDRÄKNING
Visste du? – Var finns de längsta slalombackarna?
1 . 230 – 40 (190)
2 1 300 m – 700 m (600 m)
3 Blå blixten är 450 meter lång och Skogsbanan 800 meter Hur stor är skillnaden i längd mellan slalombackarna? (350 m)
9.
KAPITEL 2: Tal i bråkform
PEDAGOGISKA TANKAR INFÖR KAPITEL 2
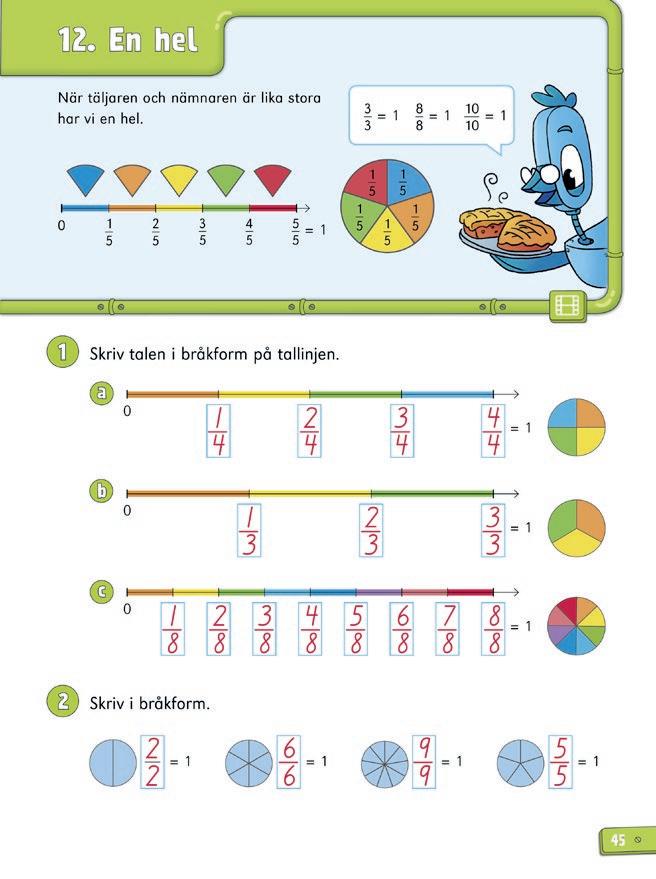
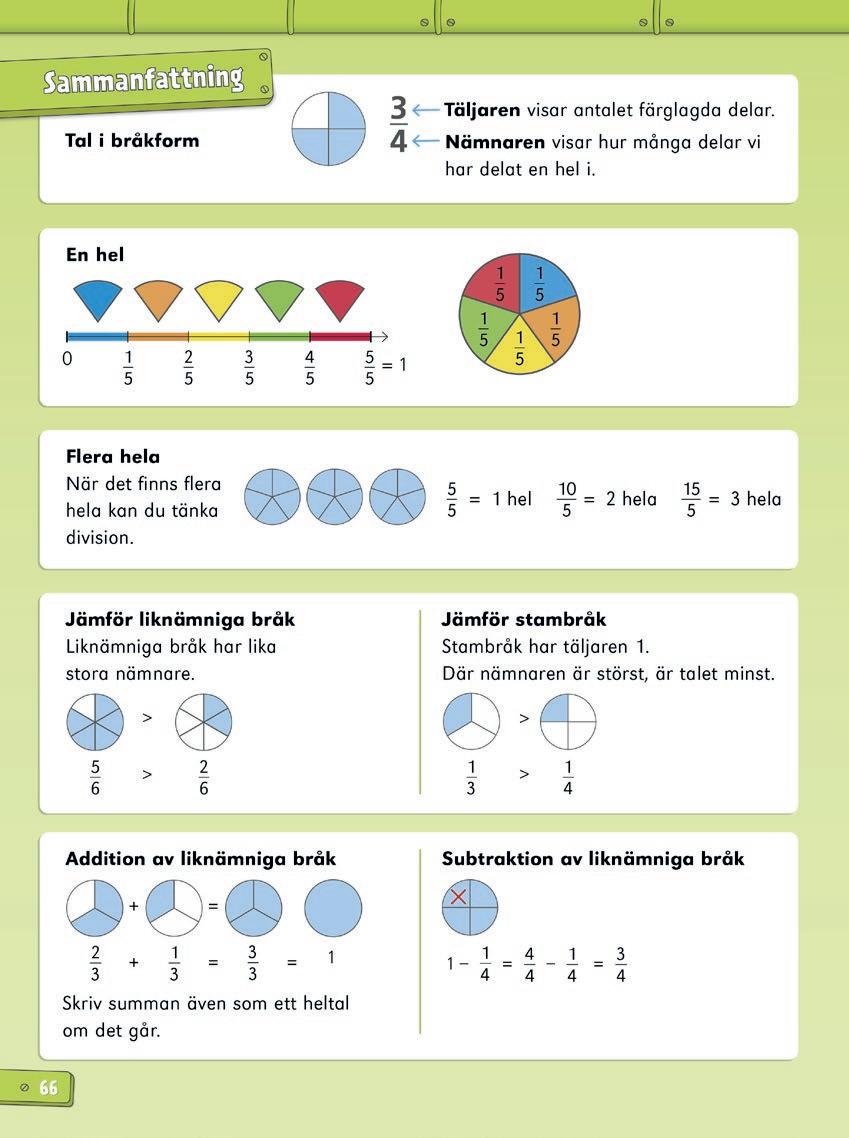
I Matteblixt 2b fick eleverna bekanta sig med begreppet tal i bråkform. De behövde då ännu inte kunna skriva tal i bråkform, utan fick lära sig att ta delar av en hel figur eller en hel grupp och uttrycka detta muntligt och skriftligt, exempelvis ”tre fjärdedelar”, men utan att använda bråknotation 3/4.
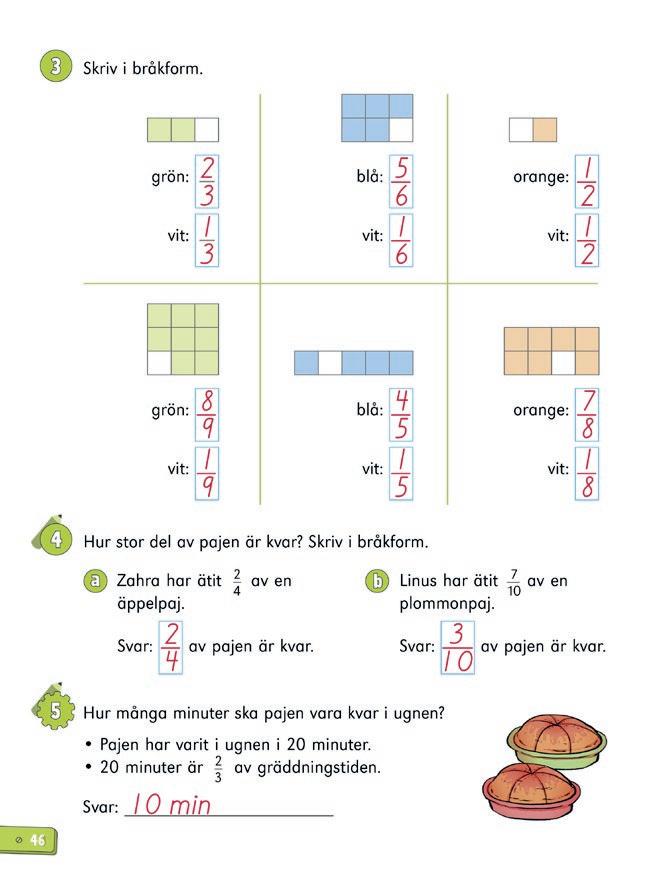
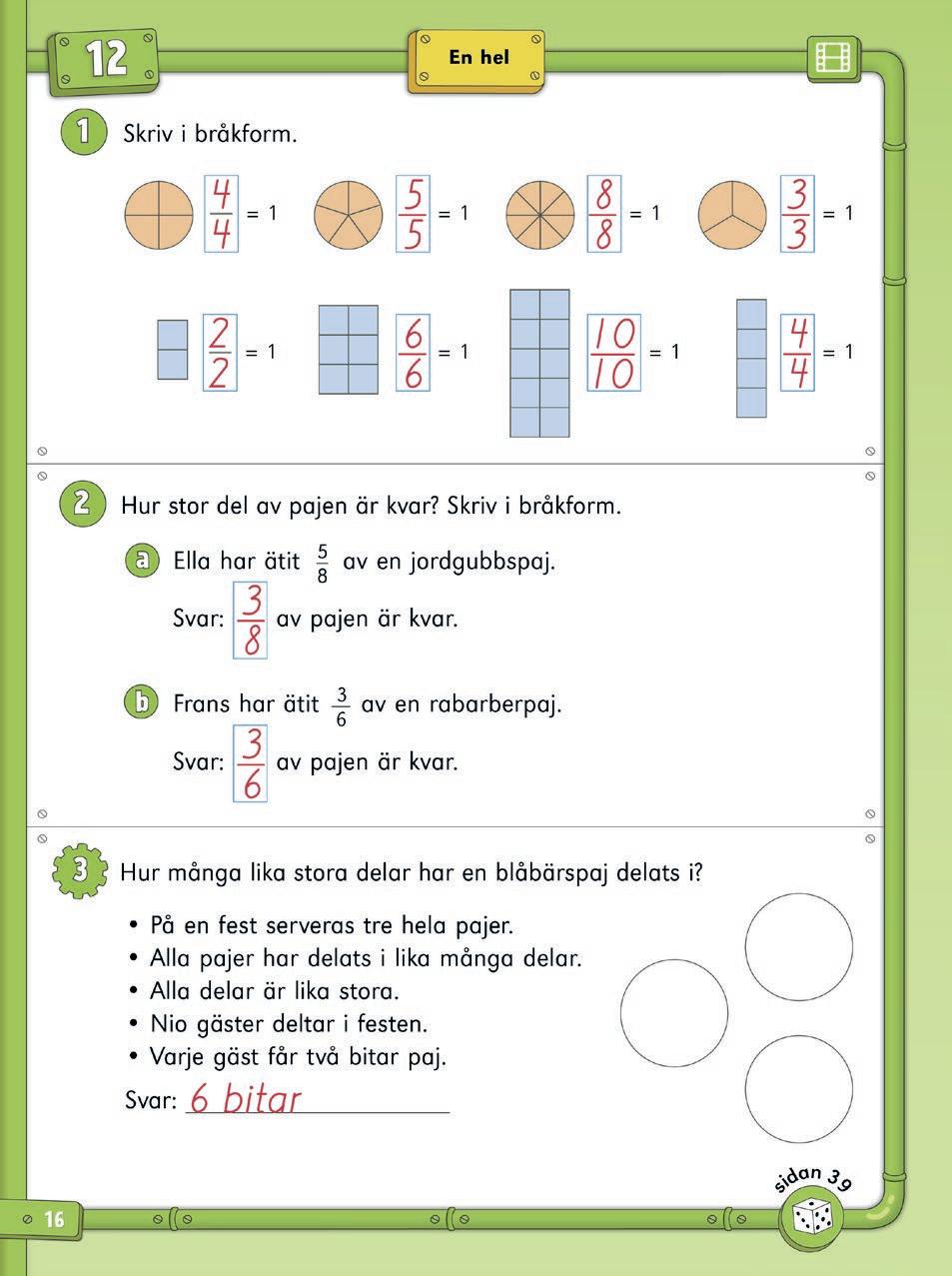
I detta kapitel får eleverna lära sig hur man använder tal i bråkform för att skriva delar av helheter och delar av antal. De får även öva på att skriva tal i bråkform som heltal som till exempel 8/4 = 2 . En viktig strategi som lyfts är att man kan tänka på tal i bråkform som divisioner. Här går divisionen jämnt ut, vilket innebär att kvoten blir en eller flera hela.
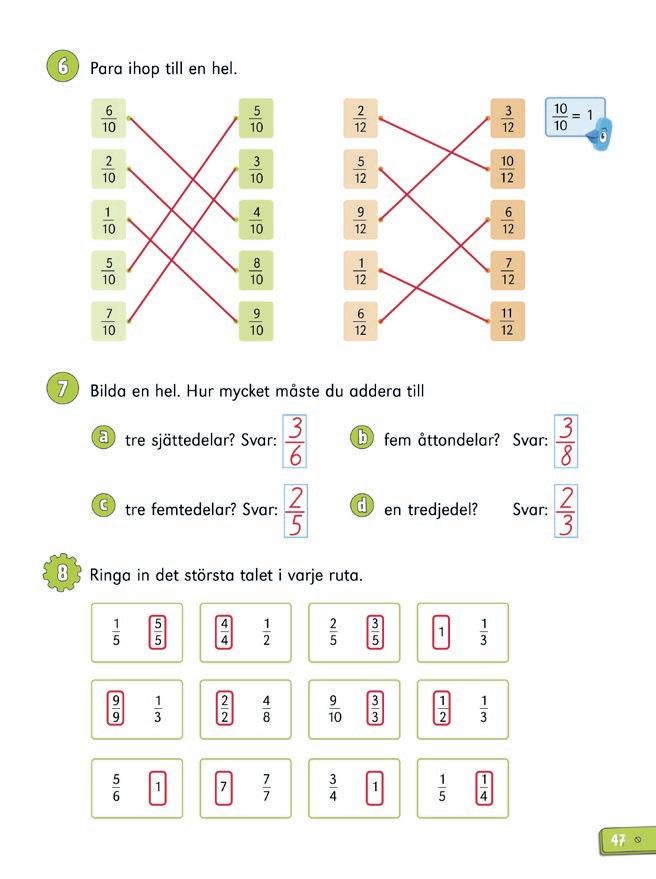
Eleverna får också lära sig hur man jämför liknämniga bråk eller stambråk samt hur man adderar och subtraherar liknämniga bråk.
INLEDANDE UPPGIFT
Chokladkakan
En chokladkaka består av 10 lika stora bitar. Fyra kompisar, Emi, Leo, Sam och Amir, ska dela på kakan. Hur kan de dela rättvist, så att ingen bit blir över?
Kom på minst tre olika kreativa sätt att dela kakan.
ÄMNESÖVERGRIPANDE
Baka sockerkaka
Ingredienser:
1 msk smör eller margarin – till formen
2 msk ströbröd – till formen
3 ägg
3 dl socker
3 ½ dl vetemjöl
2 tsk bakpulver
1 ½ dl mjölk
50 g smör eller margarin
Smaksättning:
2 tsk vaniljsocker eller
1 tsk kardemumma eller rivet skal av apelsin/citron
FAKTARUTA
dl = deciliter msk = matsked tsk = tesked
Gör så här:
• Sätt ugnen på 175 °C.
• Smörj och bröa en bakform.
• Vispa ägg och socker pösigt.
• Blanda mjöl, bakpulver, och någon smaksättning, och rör ner i äggsmeten.
• Värm upp mjölken med matfettet och rör ner i smeten. Häll smeten i formen.
• Grädda kakan i nedre delen av ugnen i 35–40 minuter.
• Känn efter med sticka om kakan är klar. Då ska stickan vara torr.
Tallriksmodellen hjälper dig att sätta ihop en näringsrik måltid
Titta på faktarutan på sid. 41 och hitta svar på följande frågor:
1. Hur mycket grönsaker bör du äta vid varje måltid? (en halv tallrik)
2. Hur mycket potatis, pasta, ris eller bröd bör du äta vid varje måltid?
(en fjärdedels tallrik, det vill säga hälften av en halv tallrik)
3. Hur mycket baljväxter, fisk eller kött bör du äta vid varje måltid?
(en fjärdedels tallrik, det vill säga hälften av en halv tallrik)
ÖVNINGSBANAN
Till några lektioner finns det övningsbanan med repetitionsuppgifter inom området ni har arbetat med. Läs mer i instruktionerna för övningsbanan.
SAMTALSBILDEN
Bilden visar innehåll ur kapitlet. Men den visar mycket annat också. Speciellt om du har elever med annat modersmål än svenska kan bilderna stödja och befästa inlärningen av ord som är nya för dem och som kan förekomma i kapitlet.
Börja med att låta eleverna själva titta på bilden och upptäcka den. Be dem att hitta en sak de tycker om som de berättar om för klasskompisen bredvid.
Sedan riktar du uppmärksamheten åt det matematiska innehållet i bilden genom att ställa frågor. Använd några av exempelfrågorna eller egna frågor.
För att säkerställa elevernas delaktighet i klassrumssamtalet, gå gärna igenom frågorna genom att använda någon kooperativ struktur som aktiverar många elever, till exempel EPA.
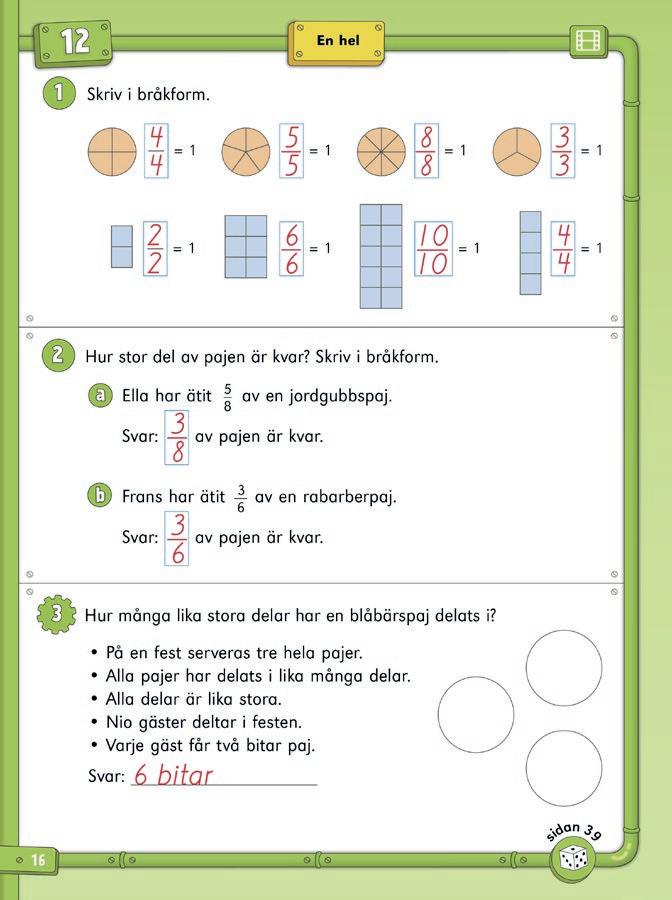
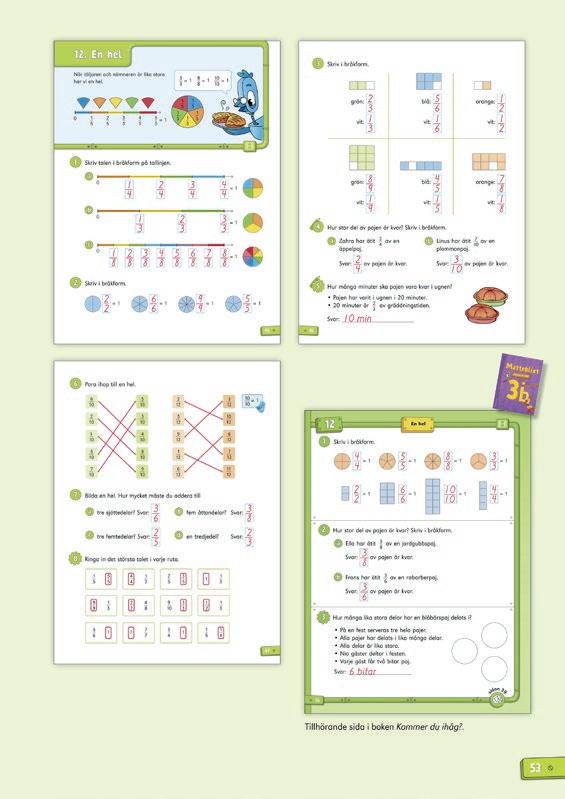
1. Hur stor del av jordgubbstårtan tar flickan på bilden? (en fjärdedel – 1/4)
2. Hur många lika stora bitar är pizzan delad i?
(6 delar – sjättedelar)
3. Tre kompisar ska dela på pizzan. Hur stor del får var och en? (två sjättedelar – 2/6, eller en tredjedel)
4. Hur många lika stora bitar är varje sockerkaka delad i? (6 delar – sjättedelar)
5. Hur många sjättedelar finns det sammanlagt i två sockerkakor? (tolv sjättedelar – 12/6)
Du kan använda samtalsbilden även i slutet av kapitlet, då för att utvärdera elevernas förståelse för olika begrepp som ”liknämniga bråk” eller ”stambråk”. Fråga då till exempel:
6. Hur många hela sockerkakor är 18 sjättedelar? (18/6 = 3)
7. Hälften (1/2) av Leos tallrik består av pasta och hälften (1/2) av köttfärssås. Har du något tips till Leo? (byt ut 1/2 av pastan och 1/2 av köttfärssåsen mot grönsaker)
ARBETA MED BEGREPP
Du hittar hela begreppslistan med tillhörande förklaringar i din digitala lärarhandledning. Du kan skriva ut listan och hänga upp den i klassrummet så att eleverna har tillgång till den.
Börja med att läsa upp begreppen och fråga om någon elev känner igen något av dem. Berätta att eleverna kommer att arbeta med dessa begrepp i kapitlet och att de kommer att kunna titta på listan med förklaringar när de stöter på ett begrepp de är osäkra på.
AKTIVITETER FÖR BEGREPPSTRÄNING
Skriv ut elevernas begreppslista och klipp isär begrepp och förklaringar. Använd kooperativa strukturer för att träna på begreppen. Lämpliga strukturer är ”Frågafrågabyt” (använd bara begreppen) eller ”Hör vi ihop?” (använd begrepp och förklaring).
LEKTIONENS INNEHÅLL
• att skriva en del av ett antal som ett tal i bråkform
VIKTIGA BEGREPP
• andel
• täljare
• nämnare
MATERIAL
• små föremål – pärlor, knappar, byggstenar
KOPIERINGSUNDERLAG
Del av antal: 14a 14b 14c
Lektion 14: Uppgiftskort och facit till övningsbanan
Instruktioner för övningsbanan
Djurkort till övningsbanan
Svarskort till övningsbanan
KOMMER DU IHÅG?
• Lektion 14, s 18
DIGITALT MATERIAL
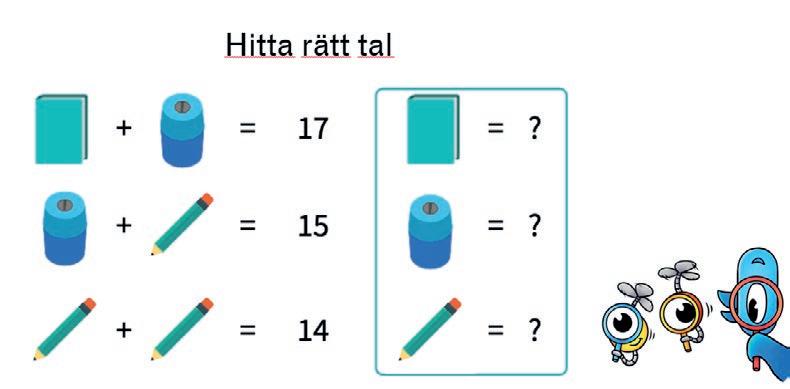
Klura tillsammans: Hitta rätt tal Lektionsfilm 14: Del av antal
HUVUDRÄKNING
Visste du? – Hurra för gratis skolmat!
1 Skriv 20/4 som ett heltal (5)
2 Skriv 9/3 som ett heltal (3)
3 Maxi har 2 hela pannkakor Hon delar varje pannkaka i 4 lika stora delar Hur många fjärdedelar blir det? (8)
14. Del av antal
GENOMGÅNG OCH AKTIVITETER
Del av antal - med elever
Be några elever att komma fram och ställa sig på rad längst fram i klassrummet (till exempel fem elever). Undersök först hur många elever det finns i hela gruppen (5). Fråga sedan hur många av eleverna som har en viss egenskap, till exempel röda strumpor (t.ex. två). Konstatera tillsammans att om det i en grupp med fem elever finns två elever med röda strumpor, så har två femtedelar av eleverna röda strumpor. Skriv svaret som tal i bråkform så att eleverna ser det: 2/5. Fortsätt aktiviteten med olika antal elever (2–6) och olika egenskaper, till exempel hårfärg, ögonfärg eller färg på tröjorna.
Del av antal - med små föremål
Ni behöver: små föremål – pärlor, knappar, byggstenar
Eleverna bildar en hel grupp med exempelvis 7 föremål, till exempel 3 röda, 2 blå och 2 gröna. Först undersöker de hur många föremål som finns i hela gruppen (7). Därefter väljer de en färg, till exempel blå, och räknar hur många föremål som finns av den färgen (2). Sedan skriver de andelen som ett tal i bråkform (2/7). De fortsätter sedan med de andra färgerna och skriver alla andelar i bråkform. Övningen kan upprepas med olika antal föremål och olika kombinationer av färger
TILLÄMPANDE
AKTIVITET
Övningsbanan
Ni behöver: Lektion 14: Uppgiftskort och facit till övningsbanan
Till den här lektionen finns det en övningsbana med repetitionsuppgifter om del av antal.
Du kan använda övningsbanan som finns på baksidan av elevernas Kommerdu-ihåg?bok eller använda de stora djurkorten och göra en övningsbana i klassrummet. Placera uppgiftskorten och facit tillgängligt för eleverna.
Eleverna arbetar i par. De startar vid det djuret de fick i utlottningen (använd djurkort). De löser uppgiften och antecknar på sitt svarskort. Eleverna går sedan till facit och kontrollerar sitt svar. Vid behov gör de om uppgiften. Sedan fortsätter de med uppgiften för nästa djur på övningsbanan.
UR PEDAGOGISK SYNVINKEL
Det är viktigt att introducera begreppet del av antal med hjälp av konkreta föremål. På så sätt blir det tydligt att en del inte alltid handlar om delar av en figur, utan kan vara en del av en hel grupp.
En hel kan bestå av flera delar, till exempel en grupp knappar, olikfärgade pärlor eller byggstenar. Börja med att undersöka hur många delar gruppen består av. Fortsätt sedan med att ta reda på hur många av delarna som har en viss egenskap, till exempel färg eller form. Delar av en grupp kan skrivas med olika tal i bråkform. 3 av 6 kan både skrivas som 3/6 (tre sjättedelar) men också som 1/2 (en halv – hälften).
Tillhörande sida i boken Kommer du ihåg?
Elevbok s. 73-75
LEKTIONENS INNEHÅLL
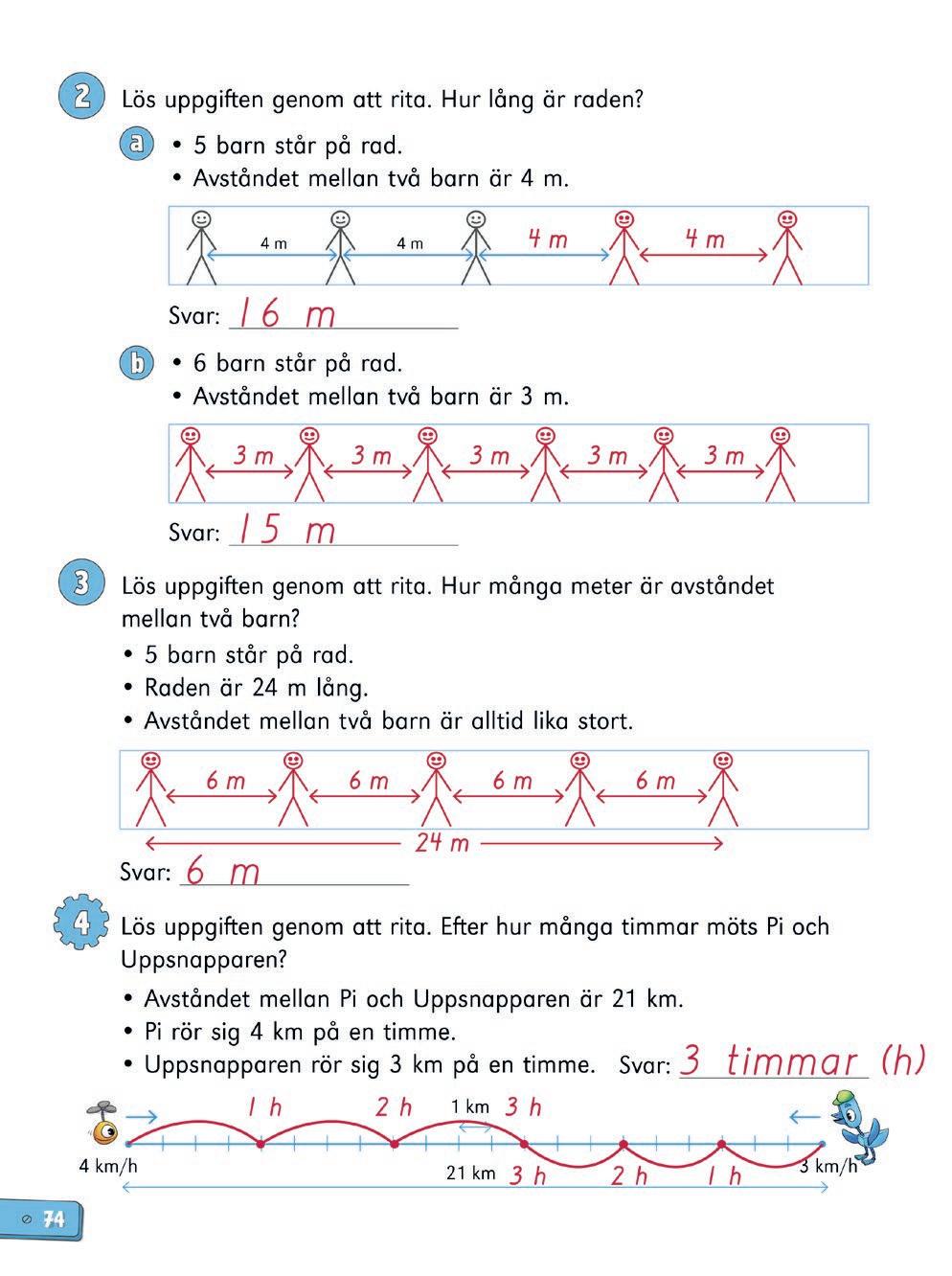
• att rita och använda bilder som en strategi vid problemlösning
VIKTIGA BEGREPP
• problemlösning
MATERIAL
• tärningar
• papper och penna
KOPIERINGSUNDERLAG
Problemlösning genom att rita: 20a
20b
20c
Lös uppgiften genom att rita
KOMMER DU IHÅG?
• Lektion 20, s . 23
• Spel: Kvartetten, s 42
DIGITALT MATERIAL
Klura tillsammans: Pi och Uppsnapparen möts
Lektionsfilm 20: Problemlösning genom att rita
HUVUDRÄKNING
Visste du? – Gamlingar i skogen
1 . 38 + 26 (64)
2 En låda innehåller 39 trädplantor och en annan 34 plantor Hur många plantor innehåller lådorna sammanlagt? (73)
3 Amos har som mål att plantera 85 trädplantor Just nu har han planerat 66 plantor Hur många plantor har han kvar att plantera? (19)