© MATEpristem, 2018
Esame di Stato 2018 – Prova di Matematica Problema 1
1) La funzione y=f(x) è data da y=‐x+1 e la curva chiusa Γ si rappresenta con |y|+|x|=1 essendo ‐1 1. In dettaglio la curva Γ si può rappresentare con le quattro funzioni: y=‐x+1 e y=x‐1 per 0 1. y=x+1 e y=‐x‐1 per ‐1 0. 2) Una funzione polinomiale di secondo grado y=ax2+bx+c che soddisfi le condizioni richieste deve essere tale che c=1 (passaggio per (0,1)) b=0 (f’(0)=0) a=‐1(passaggio per (1,0)). Dunque y=‐x2+1. L’area della zona colorata è data da
1
2/3,
quantità maggiore di 0,55. Le condizioni richieste per una funzione polinomiale di terzo grado y=ax3+bx2+cx+d danno d=1, c=0, a+b+1=0. Quindi la funzione ha la forma y=ax3‐(a+1)x2+1. L’area della zona colorata è data da 1
1
. Posto questo valore uguale a 0,55, si ricava a=7/5.
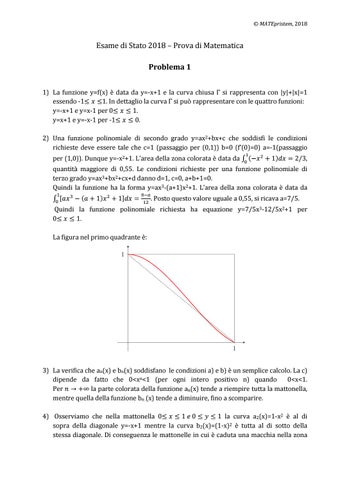
Quindi la funzione polinomiale richiesta ha equazione y=7/5x3‐12/5x2+1 per 0 1. La figura nel primo quadrante è:
3) La verifica che an(x) e bn(x) soddisfano le condizioni a) e b) è un semplice calcolo. La c) dipende da fatto che 0<xn<1 (per ogni intero positivo n) quando 0<x<1. Per → ∞ la parte colorata della funzione an(x) tende a riempire tutta la mattonella, mentre quella della funzione bn (x) tende a diminuire, fino a scomparire. 4) Osserviamo che nella mattonella 0 1 0 1 la curva a2(x)=1‐x2 è al di sopra della diagonale y=‐x+1 mentre la curva b2(x)=(1‐x)2 è tutta al di sotto della stessa diagonale. Di conseguenza le mattonelle in cui è caduta una macchia nella zona