1. La funzione g(x) è continua in tutto R per qualsiasi valore di a e b. Per a 6= 0 si ha lim g(x) = 0 x→±∞
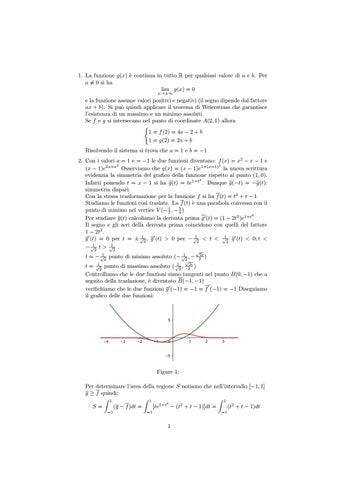
e la funzione assume valori positivi e negativi (il segno dipende dal fattore ax + b). Si può quindi applicare il teorema di Weierstrass che garantisce l’esistenza di un massimo e un minimo assoluti. Se f e g si intersecano nel punto di coordinate A(2, 1) allora ( 1 = f (2) = 4a − 2 + b 1 = g(2) = 2a + b Risolvendo il sistema si trova che a = 1 e b = −1 2. Con i valori a = 1 e = −1 le due funzioni diventano: f (x) = x2 − x − 1 e 2 2 (x − 1)e2x−x Osserviamo che g(x) = (x − 1)e1−(x−1) la nuova scrittura evidenzia la simmetria del grafico della funzione rispetto al punto (1, 0). 2 Infatti ponendo t = x − 1 si ha g(t) = te1−t . Dunque g(−t) = −g(t): simmetria dispari. Con la stessa trasformazione per la funzione f si ha f (t) = t2 + t − 1 Studiamo le funzioni cosı̀ traslate. La f (t) è una parabola convessa con il punto di minimo nel vertice V (− 12 , − 54 ) 2 Per studiare g(t) calcoliamo la derivata prima g 0 (t) = (1 − 2t2 )e1−t Il segno e gli zeri della derivata prima coincidono con quelli del fattore 1 − 2t2 . g 0 (t) = 0 per t = ± √12 , g 0 (t) > 0 per − √12 < t < √12 g 0 (t) < 0; t < − √12 t > √12 . t = − √12 punto di minimo assoluto (− √12 , − √
√
2e 2 )
t = √12 punto di massimo assoluto ( √12 , 22e ) Controlliamo che le due funzioni siano tangenti nel punto B(0, −1) che a seguito della traslazione, è diventato B(−1, −1) 0 verifichiamo che le due funzioni g 0 (−1) = −1 = f (−1) = −1 Disegniamo il grafico delle due funzioni:
Figure 1: Per determinare l’area della regione S notiamo che nell’intervallo [−1, 1] g ≥ f quindi: Z 1 Z 1 Z 1 1−t2 2 S= (g − f )dt = [te − (t + t − 1)]dt = (t2 + t − 1)dt −1
−1
−1
1