Issuu

BUTLLETÍ

DE LA SOCIETAT CATALANA DE MATEMÀTIQUES

Institut d’Estudis Catalans

Volum 39 • Número 1-2 • Desembre 2024

BARCELONA 2024

Editat per la Societat Catalana de Matemàtiques filial de l’Institut d’Estudis Catalans

Carrer del Carme, 47 08001 Barcelona

Text original revisat lingüísticament per la Unitat d’Edició del Servei Editorial de l’IEC

Compost per Rosa M. Rodríguez

Imprès a Ediciones Gráficas Rey, SL

ISSN: 0214-316-X

Dipòsit Legal: B 19272-1987

Els continguts del butlletí de la societat catalana de matemàtiques estan subjectes —llevat que s’indiqui el contrari en el text o en el material gràfic— a una llicència Reconeixement - No comercial - Sense obres derivades 3.0 Espanya de Creative Commons, el text complet de la qual es pot consultar a https://creativecommons.org/licenses/by-nc-nd/3.0/es/deed.ca. Així, doncs, s’autoritza el públic en general a reproduir, distribuir i comunicar l’obra sempre que se’n reconegui l’autoria i l’entitat que la publica i no se’n faci un ús comercial ni cap obra derivada.

ButlletídelaSocietatCatalanadeMatemàtiques Vol.39,núm.1-2,2024

Índex

JaumeAguadé

Unrepàsalesrotacionsenbaixadimensió.........................................5

JaumeCollGuerrero

Políedresipapiroflèxiamodular....................................................37

XavierGuitartiMarcMasdeu

Puntsracionalsencorbesel.líptiques..............................................73

JaumedeHaro

LesequacionsdeFriedmann:mecànicanewtoniana versus relativitatgeneral..103

LuisSierra,MartaCasanellasiPiotrZwiernik Tensorsenestadísticaalgebraica.................................................131

Englishsummaries.....................................................................171

ButlletídelaSocietatCatalanadeMatemàtiques Vol.39,núm.1-2,2024.Pàg.5–36. DOI:10.2436/20.2002.01.113

Unrepàsalesrotacionsenbaixadimensió

JaumeAguadé

Resum: Comencemamblesrotacionsdelageometriaelementalilesmatriusortogonalsiacabemconstruintdemaneraexplícita,elementaliautocontingudaels isomorfismesclàssicsentreelsgrupsd’espinorsendimensió < 7icertsgrupsunitaris osimplèctics.Laintenciódeltreballésessencialmentdidàcticaiespotllegircomuna introduccióalateoriadelsgrupsdeLiecompactes.

Paraulesclau: rotació,espinor,grupdeLie,quaternions.

ClassificacióMSC2020: 22-01,20G20,22E15.

1Presentació

Enaquesttreballdecaràcterelemental—iintencióclaramentdidàctica—,estudiaremambdetalllesrotacionsielsespinorsendimensionsmenorsque set,ielsgrupsqueformen.Abansdecomençar,potserútilincloureunscomentarisadreçatsalslectorsquejaconeguinlateoriabàsicadelsgrupsdeLie compactes.Aquestslectorsjasabenque,peravalorsmoltpetitsdelrang n hi hacoincidènciesentreelsdiagramesdeDynkindelesfamílies An, Bn, Cn, Dn. Aquestescoincidències,juntamentambelteoremaquerelacionaelsgrupsde LiecompactesconnexossimplesambelsdiagramesdeDynkinatravésdels seussistemesd’arrels,impliquenquehihaisomorfismesentreelsrepresentantssimplementconnexosd’algunsgrupsclàssicsderangpetit.Aquests isomorfismess’anomenen isogèniesesporàdiques.Ambaquestesisogènies,els grupsd’espinors Spin(3), Spin(4), Spin(5), Spin(6) —inomésaquests—són isomorfsacertsgrupssimplècticsounitaris.

L’existènciad’aquestesisogèniesesporàdiquesésunaconseqüènciad’un teoremadegrandíssimaenvergaduracoméselqueensdonalaclassificaciódelsgrupsdeLiecompactesconnexossimples,peròaquestesisogènies tambéespodenconstruirexplícitamentpermètodesquepodríemqualificar

d’elementals. 1 Sónunesconstruccionsqueduensovintl’eufemísticqualificatiu de«benconegudes»però,mésenllàdelcasde Spin(3),noésfàciltrobar-ne unaexposicióelementalicompleta.

Elprimerobjectiud’aquesttreballvaserconstruirexplícitamentaquestes isogèniesesporàdiquesi,almateixtemps,repassarcertsresultatsclàssics sobrelageometriadelesrotacionsenbaixadimensió,peròràpidamentens vamadonarque,sibéaquestesisogènieserenlanostra Ítaca —«senseella nohauríempartit»—,totselspaisatgesqueanàvemtrobantfentcamíeren potsermésinteressantsquel’objectiufinal.Eltextvaanaradquirintunfort componentdidàctic,italcomelpresentemarapotserespotllegircomuna introduccióalateoriadelsgrupsdeLiecompactes,basadaenl’estudiconcret deles rotacions enbaixadimensióilasevarelacióambelsespinors.2

2Preliminars:parlemderotacions

Euclides,probablementperevitarlesfamoses aporiesdelmoviment (Zenó, Aquil.les...),intentadesenvolupartotalasevageometriasenseutilitzarmaiel moviment.Tanmateix,nopotdeixardefer-ho(dissimuladament)enalgunpunt concret,elmésescandalósdelsqualsésnimésnimenysquelaproposició quartadelllibreprimer:el criteriCAC decongruènciadetriangles.Defet, aquestcriteriésindemostrableapartirdelsaxiomesd’Euclides:calincloure’la lallistad’axiomes—comvaferHilbert—obédisposard’ungrupprougran demoviments,ésadir,delesrotacionsilestranslacions.Enqualsevolcas, d’unamaneraod’unaaltra,elconceptede rotació ésinherentalageometria euclidianaielpodemdefinircom qualsevoltransformaciódelplaquedeixiun puntfix,conserviladistànciaiconservil’orientació.

Unaconseqüènciasignificativadelsaxiomesdelageometriaeuclidianaés quepodemidentificarelspuntsilesrectesd’Euclidesambelspuntsilesrectes del’espaiafídedimensió2o3sobreuncosordenatarquimediàpitagòric. Si,amés,volemdisposardetotselsangles,detotselspolígonsregulars,del nombre π i,engeneral,sivolempoderutilitzarconceptescom continuïtat, connexió i completesa,aleshoresaquestcospitagòrichadeserelcosreali hemd’identificarlageometriad’Euclidesplanaalageometriaafíeuclidiana ordinàriade R2.Enaquestcontext,noésdifícildemostrarqueunarotaciónoés altracosaqueunaaplicaciólineal R : R2 → R2 queconservaelproducteescalar ordinariiconserval’orientació.Si MR éslamatriude R enlabasecanònica, R ésunarotaciósiinoméssi MR M t R = I (ésadir,silescolumnesde MR (iles files)sónvectorsortonormals)idet(MR) = 1.

Ambaixòquehemdit,elconceptede rotació admetunageneralitzacióòbvia al’espaieuclidià Rn enqualsevoldimensió n.Lesmatriusreals M quecompleixen MM t = I s’anomenen matriusortogonals i,necessàriament,tenendetermi-

1 SenseàlgebresdeClifford,àlgebresdeLie,sistemesd’arrels,teoriaderepresentacions,geometriadiferencial,grupsdeCoxeter,grupsdeWeylni,evidentment,elteoremadeclassificació.

2 QuanheimpartitcursossobregrupsdeLiehededicatméstempsatreballar«amà»ambels grupsclàssicsquenopasaferteoriageneral.Aquesttreballsegueixlesmateixesidees.

nant ±1.Formenungrupqueesdesigna O(n):el gruportogonal endimensió n. Lesrotacionss’identificaranalselementsde O(n) dedeterminant1iformenun subgrupnormalde O(n) queesdenotaamb SO(n):elgrup especial ortogonal. Siincloem Rn ⊂ R1+n coml’hiperplà x1 = 0,tindremunacadenadesubgrups

{I}= SO(1) ⊂ SO(2) ⊂ SO(3) ⊂ SO(4) ⊂ SO(5) ⊂ SO(6) ⊂···

L’objectiud’aquesttreballésestudiard’unamaneraminuciosaels sis primers grupsd’aquestacadenairelacionar-losambels espinors,unconceptequeja explicaremquanarribielmoment.

Lageometriaafísobreelsespaisvectorialscomplexos Cn ésforçadiferent delageometriaeuclidiana,peròtambéésextraordinàriamentimportant.Quan passemde Rn a Cn elproducteescalarestàndard—queésl’einabàsicadela geometriad’Euclides—s’hadereemplaçarpel productehermític: ⟨(u1,...,un),(v1,...,vn)⟩ := u1v 1 +···+ unv n ∈ C.

Enaquestnoucontext,lesmatriusqueconservenelproductehermíticde Cn sónlesquecompleixen MM∗ = I on M∗ := M t .S’anomenen matriusunitàries i formenungrup:el grupunitari U(n).Igualqueabans,lesmatriusunitàries dedeterminant1formenunsubgrupnormal SU(n) de U(n) itenimuna cadenadesubgrups {I}= SU(1) ⊂ SU(2)

Rotacionsdelpla

Lateoriadelesrotacionsdelplaéstanconegudaquepotsernoensadonemde toteslesmatemàtiquesquehihaalseudarrere,delaquantitatdematemàtica quenecessitemperfonamentar-larigorosament.Caldriaparlar,comamínim, delateoriageomètricadelsangles,delaquadraturadelacircumferència —i,pertant,delnombre π —,delesfuncionstrigonomètriques,delcosdels nombrescomplexos,delafuncióexponencialcomplexaidelafórmulad’Euler.3 Aquínotocarepetirtotaaquestateoria,peròsíqueenfaremunresumràpid:

• Podemidentificarelspuntsdelacircumferènciaunitatambels angles, quesónelselementsde R/2πZ.Elsanglesformenungrupabeliàambla suma.

• Si A ∈ SO(2),existeixunangle θ únictalque A = cos θ sin θ sin θ cos θ .Elproducte derotacionsplanesescorresponambla suma d’angles.

• Elsvectorsdelpla R2 espodenidentificarambelsnombrescomplexos C,demaneraquelacircumferènciaunitat S 1 de R2 coincideixambel conjuntdelsnombrescomplexosdemòdul1: S 1 ={z ∈ C : zz = 1}

3 Podeullegir,perexemple,eldarrercapítoldelllibre Matemàtiques:comenceuperaquí (2024, accéslliureambllicènciaCreativeCommons),delmateixautorqueaquesttreball.

• Elsnombrescomplexosdemòdul1formenungrupamblamultiplicació: éselgrup U(1).Pertant,lacircumferència S 1 adquireixunaestructura degrup(abelià)deduesmaneres(quesónlamateixa):siidentifiquemla circumferènciaalsangles,podemconsiderarlasumad’angles;siidentifiquemlacircumferènciaalscomplexosdemòdul1,tenimelproductede complexos:

• Si z ésunnombrecomplexdemòdul1,latransformació w zw és unarotaciódelpla R2 (identificata C).L’angled’aquestarotacióésl’únic angle θ talque z = (cos θ, sin θ) = eiθ .Elsnombrescomplexosens permetendonarunaformamoltméscompactaal’expressiód’unarotació: unarotaciódelplaéslamultiplicacióperunnombrecomplexunitari.

Rotacionsenqualsevoldimensió

Alavistadetotaixò,podríempensarqueunarotacióa Rn deuserunacosa bencomplicada,iencaramésamesuraque n esfagran.Noésaixí:totarotació a Rn éssimplementunacomposicióderotacionsplanesenplansortogonals.4 Mésacuradament,escompleixaquestresultatnotable:

Si R ésunarotacióde Rn,existeixunadescomposicióortogonal

Rn = P0 ⊥ P1 ⊥···⊥ Pk, dim(P0) ≤ 1, dim Pi = 2,i = 1,...,k,

talque R éslaidentitatsobre P0 i R ésunarotacióplanasobrecada Pi, i = 1,...,k.(Observemque P0 = 0 si n ésparelli P0 ≊ R si n éssenar.)

Podemdemostraraixòd’aquestamanera.Definim S := R + Rt ,queésuna matriusimètricai,pertant,seràdiagonalitzable.Sigui w unvectorpropi de S devalorpropi λ iconsideremelsubespai W :=⟨w,R(w)⟩⊆ Rn.Si W tédimensió1,aleshores R(w) ∈ W i W ésestableper R.Si W tédimensió2, aleshores λw = S(w) = R(w) + Rt (w) i,pertant, R2(w) = λR(w) w,ambla qualcosa W ésestableper R.Hemdemostratque R téunsubespaiestable W dedimensió1o2.

Escrivimara Rn = W ⊥ W ⊥ iprocedimperinducció:arribemalaconclusió quehihaunabaseortonormalde Rn enlaquallamatriude R s’expressaen formadiagonal R = Diag(λ1,...,λk,B1,...,Br ),oncada Bi ésunamatriu2 × 2. Comque R ésortogonal, λi =±1icada Bi éstambéortogonal.Fentuncanvi debaseortonormal,podemaconseguirque det(Bi) = 1.Agrupantperparelles els 1tambéobtenimblocsquesónrotacionsde180graus.Quedarà,coma màxim,un λi desparellati,comque R tédeterminant1,serà λi = 1. ✷

4 Estemdientquecadarotacióde Rn és,geomètricament,unobjectebensenzillperquè esredueixaunproductederotacionsplanes;perònoestemdient,nimoltmenys,queels grups SO(n) esredueixinaunproductedegrups SO(2)!

Unamicadetopologia

L’estudidelatopologiadelsgrups U(n) i O(n) téuninterèsimmens,peròaquí noméspodemesbossarbreumentalgunespropietatselementals.Enprimer lloc,totsaquestsgrupssón,perdefinició,grupsdematrius(realsocomplexes) i,comquepodemidentificarl’espaivectorialreal Mn×m a Rnm il’espaivectorialcomplex Mn×m a R2nm,totselsgrupsdematriusheretenunatopologia Hausdorff.Amés,comquelesoperacionsdemultiplicacióipasal’inverses podenescriureapartirdefuncionsalgebraiquesi,pertant,contínues,podem parlarde grupstopològics. 5

Tambéésimmediatobservarqueelsgrups O(n), SO(n), U(n) i SU(n) són compactes:6 sónclaramenttancatsperquèestandefinitsperl’anul lacióde certesfuncionsalgebraiques,isónacotatsperquèlescolumnesdelesmatrius d’aquestsgrupssónvectorsunitaris.

Observemque,comaespaitopològic, U(n) espotdescompondrecom a S 1 × SU(n),utilitzantlafuncióquetransformacadaparella (z,A) enla matriuques’obtémultiplicantper z laprimerafiladelamatriu A.Ésuna funciócontínuaibijectivaque,comqueelsespaisinvolucratssóncompactes Hausdorff,seràunhomeomorfisme.Calremarcarqueaquestadescomposició no éscompatibleambl’estructuradegrupde U(n):els grups U(n) i S 1 × SU(n) sóndiferents,peròels espaistopològics U(n) i S 1 × SU(n) sónhomeomorfs.

Unaeinaútilperal’estudid’aquestsgrupséslaidentificaciódelsespaisde classeslaterals SO(n)/ SO(n 1) i SU(n)/ SU(n 1) ambesferes.Concretament, siassignemacadamatriuortogonal/unitàriaelvectorunitariformatperla sevaprimeracolumna,tenimaplicacionscontínuesexhaustives SO(n) → Sn 1 i SU(n) → S 2n 1 quefactoritzenperhomeomorfismes

SO(n)/ SO(n 1) ≊ Sn 1 , SU(n)/ SU(n 1) ≊ S 2n 1

Aquestshomeomorfismesespodenexplotarperdemostrarinductivament propietatstopològiquesdelsgrups SO(n) i SU(n).Perexemple:

Pera n ≥ 1 escompleixque SO(n), U(n), SU(n) sónconnexos, O(n) tédos componentsconnexosi SU(n) éssimplementconnex.

Laprimerapartd’aquestteoremaesdemostraperinducciósobre n,començantpelfetque SO(1) = SU(1) ={I} i U(1) = S 1.Fem-hoambdetallperalcas delgrupderotacions SO(n), n> 1.Comhemditabans,tenimunaaplicació contínuaexhaustiva

f : SO(n) → Sn 1

que,comqueelsespaisinvolucratssóncompactesHausdorff,seràtambé tancada.Sipoguéssimescriure SO(n) comunauniódisjunta A ∪ B detancats

5 Defet,elsgrups O(n), SO(n), U(n) i SU(n) sónmoltmésquegrupstopològics:sónvarietats diferenciablesilesoperacionsdemultiplicacióipasal’inverssóndiferenciables.Diremquesón grupsdeLie.Peròenaquesttextelementalnovolemaprofundirenaquestadirecció.

6 Comquetenimunaestimacióespecialpelsgrupscompactes,elsdistingimusantlletra negreta

nobuits,tindríem Sn 1 = f(A) ∪ f(B) i,comque Sn 1 ésunespaiconnex, aquestauniónopotserdisjunta.Si x ∈ f(A) ∩ f(B),considerem X := f 1(x) iescrivim X = (X ∩ A) ∪ (X ∩ B),queésunauniódisjuntadetancatsde X. Observemaraque X estàformatpertoteslesmatriusortogonalsquetenen comaprimeracolumnaelvector x iaquestsubespaiésclaramenthomeomorf a SO(n 1),que,perhipòtesid’inducció,ésconnex.Arribem,doncs,auna contradicciói SO(n) tambéhadeserconnex.Pelquefaa O(n),elresultat ésclarperquè O(n) ésuniódisjuntadedostancats: SO(n) ielsubespaide lesmatriusortogonalsde det =−1.Comqueaquestsubespaiéshomeomorf a SO(n),tenimjaelsdoscomponentsconnexosde O(n).Finalment,una induccióutilitzantlesidentificacions SU(n)/ SU(n 1) ≊ S 2n 1 iunsteoremes (senzills)detopologiaquearanopodementraradiscutirensdemostrenque totselsgrups SU(n) sónsimplementconnexos. ✷

3Rotacionsendimensió3iespinors

Ladescripciógeneraldelesrotacionsenqualsevoldimensióquehemvist abansensdiuquetotarotaciónotrivialentresdimensionstindràuneixde rotacióbendefinitiescomportaràcomunarotacióenelplaperpendicular aaquesteix.Ésadir,perdeterminarunarotació R a R3 prendremunvector unitari ⃗ u ∈ R3 —queensindicaràl’eix—iunangle θ —queseràl’anglede rotacióenelplaortogonalal’eix.Aleshores,larotació R,quepodemdesignar coma Rθ, ⃗ u,deixaràfixostotselspuntsdelarecta ⟨ ⃗ u⟩ irotaràunangle θ els puntsdelpla H :=⟨ ⃗ u⟩⊥,entenentqueunabasepositivade H seràqualsevol baseortonormal ⃗ e1, ⃗ e2 talque ⟨⃗ e1 × ⃗ e2, ⃗ u⟩ > 0.Ambunamicadetrigonometria elementalpodemtrobarfàcilmentunaexpressióde Rθ, ⃗ u( ⃗ v) queesconeixcom a fórmulad’OlindeRodrigues: Rθ, ⃗ u( ⃗ v) = cos θ ⃗ v + sin θ( ⃗ u × ⃗ v) + (1 cos θ)⟨ ⃗ u, ⃗ v⟩ ⃗ u.

Tenim,doncs,unabonadescripciódecadarotació—tinguemencompteque ⃗ u i θ noestanunívocamentdeterminats—,peròencaraestemllunyd’entendre elconjuntde totes lesrotacionsdel’espai,ésadir,latopologiade SO(3) ilasevaestructuracomagrup—enparticular,elproductededuesrotacions Rθ,u Rθ′,u′ .Perdonarrespostaaaquestesqüestionshemdeparlard’uns objectesanomenats espinors.

Espinors

Unespinorésunaparelladenombrescomplexos (ζ1,ζ2) talsque

Siescrivimaquestaequacióencoordenadesreals,obtenim a2 +b2 +c2 +d2 = 1, quedefineixl’esferaunitatde R4,ésadir,l’esfera S 3.Enconclusió,elsespinors estanencorrespondènciabijectivaambelspuntsdel’esfera S 3

Elsespinorsespodenmultiplicard’unamaneracuriosa:

Aquestaestranyamultiplicacióilessevespropietatss’entenenmoltmillorsi escrivimelsespinorsenaquestaformamatricial: (ζ1,ζ2)

Aleshores,lamultiplicaciódelsespinorséslamultiplicaciódematriusipodem comprovarqueelsespinorsformenungrup:eldesignarem Spin(3)

Quèpodemdirdelesmatriuscomplexes2 × 2anteriors?Noésdifícilveure quesónmatriusunitàriesdedeterminant1,ésadir,pertanyenalgrup SU(2)

Amés,totamatriude SU(2) ésdelaforma

peralgunespinor (ζ1,ζ2)

Aixòésconseqüènciadelaidentificació SU(2) = SU(2)/ SU(1) ≊ S 3 quehem esmentatabans,peròtambéadmetunademostracióelementaldirecta.En conclusió:

Un espinor éslaprimeracolumnad’unamatriuespecialunitària 2 × 2.Els espinorsformenungrupdesignat Spin(3) queésisomorfalgrup SU(2). Aquestsdosgrupsisomorfss’identifiquen,topològicament,al’esfera S 3 . 7

Espinorsirotacionsdel’espai

Hemintroduïtelsespinorsielgrup Spin(3) amblaintenciód’entendremillor lesrotacionsde R3,ésadir,elgrup SO(3).Percomprendrelarelacióentreels espinorsilesrotacionsdel’espai,consideremles matriusantihermítiques de traçazero:

H ′ 0 :={H ∈M2×2(C) : H + H∗ = 0, tr(H) = 0}.

H ′ 0 ésun R-espaivectorialipodemprendreaquestabaseortonormal: σx = i 0 0 i ,σy = 0 1 10 ,σz = 0 i i 0

demaneraquecadavectorde R3 s’identificaalamatriuhermítica

⃗ u = (x,y,z) → Hu := xi y zi y zi xi

Aquestespropietatsdelesmatrius H ⃗ u sónsenzillesdedemostrar:

• SU(2) normalitza H ′ 0,enelsentitque,si U ∈ SU(2),aleshores U H ′ 0 U ∗ = H ′ 0.

• H ⃗ u H ⃗ v =−⟨ ⃗ u, ⃗ v⟩I + H ⃗ u× ⃗ v i H ⃗ v H ⃗ u H ⃗ u H ⃗ v =−2H ⃗ u× ⃗ v .

• H ⃗ u H ⃗ v H ⃗ u =−⟨ ⃗ u, ⃗ v⟩H ⃗ u +H( ⃗ u× ⃗ v)× ⃗ u.Sirecordemlaidentitat ( ⃗ u× ⃗ v)× ⃗ w = ⟨ ⃗ u, ⃗ w⟩ ⃗ v −⟨ ⃗ u, ⃗ v⟩ ⃗ w,obtenimque,si ⃗ u ésunitari, H ⃗ u H ⃗ v H ⃗ u =−2⟨ ⃗ u, ⃗ v⟩H ⃗ u + H ⃗ v .

7 Potsemblarestranyquedonemunnomcom Spin(3) aungrupquenoésaltracosaqueel grup SU(2).Quanpassemadimensionssuperiorsentendremmillorelmotiudetotaixò.

• Si U ∈ SU(2),existeixunvectorunitari ⃗ u ∈ R3 iunangle α ∈ [0,π]

talsque U = cos αI + sin αH ⃗ u.Percomprovaraixò,observemquela primeracolumnade U ésunespinor (a + bi,c + di) amb a2 + b2 + c2 + d2 = 1.Aleshores,laidentitatanterioréscertaamb cos α = a i ⃗ u = (sin α) 1(b,c, d)

Laprimerapropietatdelallistaanteriorensdiuquecadamatriude SU(2) i, pertant,cadaespinorde Spin(3) donalloc,perconjugació,aunaaplicació lineal R3 → R3.Calculemaquestaaplicació.Sigui U ∈ SU(2),iexpressem U en laforma U = cos αI + sin αH ⃗ u,on ⃗ u ésunitari.Volemcalcular (cos αI + sin αH ⃗ u)H ⃗ v (cos αI + sin α H ⃗ u)t .

Tenim,aplicantlespropietatsqueacabemd’explicar:

UH ⃗ v U 1 = (cos αI + sin αH ⃗ u)H ⃗ v (cos αI + sin α H ⃗ u)t = = cos2 αH ⃗ v + sin2αH ⃗ u× ⃗ v sin2 αH ⃗ u H ⃗ v H ⃗ u = = cos2αH ⃗ v + sin2αH ⃗ u× ⃗ v + 2sin2 α⟨ ⃗ u, ⃗ v⟩H ⃗ u = H ⃗ w

Comparantamblafórmulad’OlindeRodrigues,obtenim ⃗ w = R2α, ⃗ u( ⃗ v).En conclusió:

Hihaunepimorfisme π3 : Spin(3) → SO(3) segonselquall’espinor [cos α + ix sin α,y sin α iz sin α]

donalarotaciód’angle 2α ambvectordirector ⃗ u = (x,y,z)

Clarament,elnuclide π3 téordre2iestàformatperlesmatrius ±I ∈ SU(2).Aquesthomomorfismeensdonaunaexcel lentdescripciótopològica de SO(3).Recordemque Spin(3) ≊ SU(2) ≊ S 3.Pertant,hihaunhomeomorfisme SO(3) ≊ S 3/{±1}= RP(3) entreelgrupdelesrotacionsdel’espaidedimensió3il’espaiprojectiurealdedimensió3.Deduïmque SO(3) noés simplement connex:elseugrupfonamentaltédoselementsielseurecobrimentuniversal ésl’esfera S 3.Amés,araqueconeixemelgrupfonamentalde SO(3),podem demostrarperinducció—utilitzantlaidentificació SO(n)/ SO(n 1) ≊ Sn 1 queelgrupfonamentalde tots elsgrups SO(n) per n> 2éselgrupdedos elements.

Noésdifícildemostrarqueelrecobrimentuniversald’ungruptopològic admetunaestructuracanònicadegruptopològiccompatibleambl’aplicació derecobriment.Aixòenspermet definir elgrupdelsespinors Spin(n) comel recobrimentuniversaldelgrupdelesrotacions SO(n).Arabé,aquestadefinició ensdiubenpocsobrel’estructurad’aquestsnousgrups:convéseguirllegint aquesttreball.

Desprésdetotaixòquehemvist,podempensarelsespinors—d’unamanera moltinformal—comsifossin«rotacionsambsigne».Percadarotacióhiha dosespinorsqueladefineixen,iaquestsdosespinorsdifereixenenunsigne.

Digressió#1:elcinturódeConway

Comqueelgrupfonamentalde SO(3) tédoselements,had’existiralgun camí ω de SO(3) quecomenciiacabia I talque2ω ∼∗ però ω ̸∼∗. 8 L’existènciad’aquestcamíespotvisualitzarmoltbéambelqueesconeixcom a cinturódeConway (vegeulafigura1):

Imaginemunacintallargaiestreta—comuncinturó—demaneraque undelsseusextremsestàfixatal’origende R3 il’altreextrempotestar situataqualsevolpuntde R3.Suposem,perexemple,quelacintaéscomel rectangle [0, 2] × [0, 100].Encadainstantdetemps t ∈ [0, 100],considerem unabaseortonormalpositivade R3 situadaalpunt (1,t) delacintatalque elprimervectorapuntasegonsl’eixdelacinta,enladirecciódel’extrem lliure,elsegonvectorapuntacapalpunt (0,t) ieltercervectorésnormal alacinta.Cadascunad’aquestesbasesortonormalsdefineixunívocament unarotacióde R3 ilafamíliauniparamètricadebasesalllargdelacinta defineixuncamíde SO(3) quecomençaalaidentitat.

Comencemamblacintaplanasobreelplahoritzontaligireml’extrem lliure 360 grausensentitpositiurespectedel’eixcentraldelacinta.La cintaquedaràentortolligada.Aixòdefiniràuncamí ω de I a I a SO(3).Si ara,sensecanviarl’orientaciódel’extremlliure,intentemdesentortolligar lacinta,nopodremfer-ho:elcamíquehemconstruïtnoéstrivial,noespot deformarcapalcamíconstant.Acontinuació,tornemagirarl’extremlliure 360 grausenelmateixsentitd’abans:hauremconstruïtelcamí 2ω.Arala cintaestaràmoltmésentortolligada,perònomésaparentment:fàcilment podremaconseguir,sensecanviarl’orientaciódel’extremlliuredelacinta, retornarlacintaalasevaposicióoriginal.Elcamí 2ω éstrivial.

Figura 1: ElcinturódeConway.

8 Ambelsímbol ∼ indiquemuna homotopia,ésadir, α0 ∼ α1 voldirquehihaunafamíliade camins αt , t ∈ [0, 1],quedepèncontínuamentdelparàmetre t.

Digressió#2:elsespinorsil’electró

L’electróté momentangular comunpetitplanetaenrotacióalvoltantd’un eix.Enmòdul,elmomentangulardetotselselectronstésempreelmateixvalor: ℏ/2.Peròelmomentangularésunamagnitudvectorial—comlesrotacions del’espai—i,peracadaelectróconcret,enuninstantconcret,vindràdonat perunvector ⃗ m entresdimensions: ⃗ m = mx ⃗ x + my ⃗ y + mz ⃗ z.Pelprincipi d’incertesa,nopodemmesurarsimultàniamentelstresvalors mx , my , mz Suposem,doncs,quemesurem mx .Pelfenomendelaquantització,quanmesurem mx obtindremund’aquestsdosvalors ±ℏ/2.Segonselvalorobtingut, diemquel’electróté spin ±1/2.

Segonselformalismeestàndarddelafísicaquàntica,l’estatinicialdelparàmetre mx esdescriuperunafunciód’ona Ψ queéscombinaciólinealdels dospossiblesresultatsdelamesura: Ψ = ζ1Ψ+ + ζ2Ψ ,on ζ1, ζ2 sónnombres complexosi ||ζ1||2 , ||ζ2||2 sónlesprobabilitatsdecadascundelsdosresultats. Enparticular, ||ζ1||2 +||ζ2||2 = 1i,pertant, (ζ1,ζ2) ésun espinor.Ésen aquestsentitquediemqueelmomentangulardel’electrónoésunvector(una rotació),sinóqueésunespinor(una«rotacióambsigne»).

4Rotacionsendimensió3iquaternions

Recordemquel’existènciadelsnombrescomplexosenspermetdonaruna versióméscompactadelesrotacionsdelpla, sensesinusnicosinus:elsnombres complexosensvanpermetrepassardeladescripciórealdelesrotacionscoma

Rθ (a,b) = (cos θa sin θb, sin θa + cos θb) aladescripciódelesrotacionscoma multiplicarperunnombrecomplexde mòdul 1.Éspossiblequehihagiunaestructura mésenllàdelscomplexos que tinguiunrolsimilaralesrotacionsdel’espai?Larespostaéssíil’estructuraés l’anelldedivisió9 dels quaternions,quediscutiremara.

Probablement,lamillormaneradedefinirelcosdelsnombrescomplexosés

C := a b ba : a,b ∈ R ⊂M2×2(R),

demaneraque i ∈ C s’identificaalamatriu 0 1 10 ,cadanombrereal a ∈ R s’identificaalamatriu a 0 0 a i,aleshores, a + ib ∈ C éslamatriu a b ba .Amb aquestadefinicióde C,lespropietatsdecossónimmediates.Enparticular,el fetquetotelement z ≠ 0tinguiinversesdedueixdelfetqueeldeterminantde lamatriucorresponenta z és a2 + b2 =||z||2.Aleshores, ||zz′||=||z||||z′||.

9 Unanelldedivisióésunanellambunitat1 ≠ 0enelqualtotelementnonultéinvers bilateral.Ditinformalment,unanelldedivisióésun cosnocommutatiu

Siararepetimaquestaestratagemaamb a,b ∈ C,observemquel’existència d’inversosesperd.Sivolemobteniruncosqueampliïelcosdelscomplexos, calferunapetitamodificacióutilitzantlaconjugacióde C.Ambladefinició següentsíqueobtenimuna R-àlgebradedivisiódedimensió4:

H := z w w z : z,w ∈ C ⊂M2×2(C).

Elselementsde H s’anomenen quaternions icompleixenaquestespropietats senzillesdedemostrar:

• Siidentifiquem z ∈ C amb z 0 0 z ,tenimque C ésunsubcòsde H.Si definim j := 0 1 10 ∈ H,veiemque j2 =−1ique k := ij =−ji,amb laqualcosaenelpasde C a H hemperdutlacommutativitatdela multiplicació.Cada q ∈ H s’escriucoma q = z + jw amb z,w ∈ C i tambécoma q = a + ib + jc + kd amb a,b,c,d ∈ R H és,doncs,una R-àlgebraassociativaambunitat,dedimensió4,nocommutativa.

• H tambéestàdotatd’unaconjugació q q queés R-lineal,generalitzala conjugacióde C icompleix pq = q p —ésadir,ésun antiautomorfisme de H.Elconjugatde a + ib + jc + kd és a ib jc kd.Interpretant —comhemfet—elsquaternionscomamatriuscomplexes2 × 2,si q ésla matriu H,aleshores q éslamatriu H∗

• L’existènciad’inversosperacada q ≠ 0esgaranteixpelfetquelamatriu corresponenta q tédeterminant ||q||2,iaquestainterpretacióensdona lamultiplicativitatdelanormaa H: ||pq||=||p||||q||.Tenim,doncs, que H ésunanelldedivisióiuna R-àlgebranormada.

• Unaaltramanerad’escriureunquaternió q ésenlaforma q = λ + ⃗ u, on λ = (q + q)/2 ∈ R s’anomena partreal o partescalar de q i ⃗ u = (q q)/2 ∈⟨i,j,k⟩R esdenomina partvectorial de q.Elsquaternions ambpartescalarzerodiremquesón quaternionspurs.Si ||q||= 1,podem escriure

q = cos α + sin α ⃗ u, on α ∈ [0,π] i ⃗ u ∈H éspurdenorma1,unívocamentdeterminatsi q ∉R

• Si u, v sónquaternionspurs,escompleix

uv =−⟨u,v⟩+ u × v, enquè u × v s’enténmirant u, v comavectorsenlabaseortonormal i, j, k.

• Fórmulad’anticommutació. Unaidentitattrivialmoltútilés

p q + q p = 2⟨p,q⟩, quetécomaconseqüènciaquedosquaternions p, q sónortogonals(com avectorsde R4)sicompleixen p q =−q p.D’altrabanda,si q ∈ H∗ i

consideremlaconjugació cq : H → H comunisomorfisme R-linealde R4 , lafórmulaanteriorenspermetcomprovarque cq conservaelproducte escalarde R4 iés,pertant,unaaplicació ortogonal.

• Si λ ∈ R éslapartescalarde q,escompleixaquestaidentitat: q2 2λq +||q||2 = 0.

Enparticular,lessolucionsde x2 =−1sóntotselsquaternionsunitaris purs,ésadir,elspuntsdel’esferaunitatde ⟨i,j,k⟩R ≊ R3 . 10

• Trivialment,elcentredel’anelldedivisió H és R.Aixòenspermetrà determinarfàcilmentelgrupd’automorfismesde H (pàgina21).

Àlgebralinealsobreelsquaternions

Lateoriabàsicadelsespaisvectorialss’esténsenseproblemesalcasqueels escalarsnoforminuncos,sinóunanelldedivisió.Pertant,podemferàlgebra linealambelsquaternionscomaescalarsi,perabúsdellenguatge,parlarem de H-espaisvectorials.Calnoméstenirpresentsalgunspetitsdetalls:

• Lanocommutativitatde H donaimportànciaaladistincióentre H-espais vectorialsperladretai H-espaisvectorialsperl’esquerra,segonsqueel producted’unescalar q ∈ H iunvector ⃗ e s’escrigui ⃗ eq o q ⃗ e.Enelnostre cas,consideraremquetotsels H-espaisvectorialssónperl’esquerra.

• Si ϕ : Hn → Hn ésunaaplicació H-linealbijectiva,l’aplicació ϕ 1 també és H-linealipodemparlar,pertant,delgruplinealGL(n, H).

• Si A ésunamatriu n × n ambcoeficientsa H,l’aplicació ⃗ v A ⃗ v amb ⃗ v ∈ Hn no és H-lineal,però ⃗ v ⃗ vA síquehoés.Enconseqüència,enun Hespaivectorialperl’esquerra,lesmatriusactuenperladretasobrevectors fila.Sihofemaixí,tenimisomorfismeentrelesmatrius n × n iles aplicacions H-linealsde Hn a Hn (queformenun H-espaivectorial per ladreta)ielsisomorfismeslineals Hn → Hn s’identifiquenalesmatrius invertibles n × n

• Comquelamultiplicacióde H noéscommutativa,lateoriaclàssica deldeterminantdeixadeservàlida.Perexemple, M = ij ji ésclaramentinvertible(M 2 =−2I)però,siintentemcalcular-neeldeterminant (multiplicantelsfactorsenqualsevolordre),sempreobtenimzero.11

• Quantreballemambmatriusquaterniòniques,nilatransposiciónila conjugaciónorespectenelproductedematrius.Encanvi,laconjugació seguidadelatransposiciósíqueésunantiautomorfisme: (AB)∗ = B∗A∗

10 Veiem,doncs,queelconegutfetqueelnombred’arrelsd’unpolinominopotsuperarelgrau delpolinomideixadesercertsilamultiplicaciónoéscommutativa.

11 Peraunadiscussiómésafonssobrel’extensiódeldeterminantcomplexaundeterminant quaterniònic,vegeuN.Cohen,S.deLeo,«Thequaternionicdeterminant», Electron.J.Linear Algebra,7(2000),100–111.

• Quanelscoeficientsdelesmatriuspertanyenaundomininocommutatiupotpassarqueunamatriutinguiinversaperuncostatinoper l’altre,oqueentinguipelsdoscostats,peròsiguindiferents.Aquests fetspatològicsnopassenenelcasdelesmatriusquaterniòniques,precisamentperquèpodemidentificarlesmatriusamblesaplicacionslinealsi unaaplicaciólineal Hn → Hn exhaustivaoinjectivaésautomàticament bijectiva.

• Perdecidirsiunamatriuquaterniònicaésinvertibleipercalcular-nela inversa,podemmirarl’àlgebra Mn×n(H) comasubàlgebrade M2n×2n(C) delamanerasegüent:si A ∈Mn×n(H), A defineixunaaplicació Hlineal A : Hn →Hn,queenspodemmirarcomaaplicació C-lineal AC : C2n → C2n.Aleshores, A ésinvertiblesiinoméssi det AC ≠ 0.Evidentment,si A 1 existeix,tambéexisteix A 1 C i,pertant, det(AC) ≠ 0.Recíprocament, sidet AC ≠ 0,aleshores AC ésbijectivai A també.Pertant, A téinversa.

Decaraalquefaremmésendavant,ensconvéexplicitarclaramentla inclusiódelesmatriusquaterniòniquesenlesmatriuscomplexesdemida doble.Denotemamb ⃗ e1,..., ⃗ en labasecanònicade Hn iconsideremaquesta C-basede Hn

e1,..., ⃗ en,j⃗ e1,...,j⃗ en.

Recordemquemirem Hn coma H-mòdulperl’esquerrai,pertant,lesmatrius actuenperladreta.Percoherència,tambélesmatriuscomplexesactuaranper ladreta.Sigui A ∈Mn×n(H) iescrivim A = A1 + A2j amb A1,A2 ∈Mn×n(C). Aleshores,uncàlculsenzillmostraquel’aplicació H-linealdonadaper A ésla mateixaquel’aplicació C-linealdonadaperlamatriu

Ésfàcilcomprovarqueaquestaaplicació Mn×n(H) →M2n×2n(C) ésunhomomorfismed’anellsirespectal’operació A A∗ .

Elproductehermíticde Cn espotgeneralitzaralsvectorsde Hn,peròara calferatencióal’ordredelsfactorsialfetquelesmatriusactuenperladreta:12

• ⟨ ⃗ u + ⃗ u′ , ⃗ v⟩=⟨ ⃗ u, ⃗ v⟩+⟨ ⃗ u′ , ⃗ v⟩, ⟨ ⃗ u, ⃗ v + ⃗ v′⟩=⟨ ⃗ u, ⃗ v⟩+⟨ ⃗ u, ⃗ v′⟩, ⟨p ⃗ u,q ⃗ v⟩= p ⟨ ⃗ u, ⃗ v⟩q;

• ⟨ ⃗ u, ⃗ v⟩= ⟨ ⃗ v, ⃗ u⟩;

• ⟨ ⃗ u, ⃗ u⟩=|| ⃗ u||2 on || ⃗ u|| éselmòdulde ⃗ u comavectorde R4n;

• (nodegenerat) ⟨ ⃗ u, ⃗ v⟩= 0peratot ⃗ v siinoméssi ⃗ u = 0;

• ⟨ ⃗ uA, ⃗ v⟩=⟨ ⃗ u, ⃗ vA∗⟩.

12 Enelcas n = 1,lanotació ⟨ ⃗ u, ⃗ v⟩ ésambiguaperquèpotferreferènciaalproducteescalar delsquaternions ⃗ u, ⃗ v comavectorsde R4 oalproductehermíticde ⃗ u, ⃗ v comavectorsde H1

Elsgrupssimplèctics

Lamentablement,hihaduesfamíliesdegrupsquerebenelmateixnomde grupssimplèctics,comaconseqüènciadelfetquehihadosconceptesdiferents de matriusimplèctica.Hauremdededuirdelcontextdequinadelesdues famíliesestemparlant.Perdistingir-los,utilitzaremnotacionsdiferentsi,a més,comqueelsgrupsd’unadelesfamíliessóncompactesielsdel’altrano hosón,encasdedubtediremqueparlemdelgrupsimplècticcompacteodel grupsimplècticnocompacte.

Elsgrupssimplècticsnocompactes. Elpasdelageometriaeuclidiana ala geometriasimplèctica —importantalamecànicahamiltoniana,l’òptica geomètricailamecànicaquàntica,entrealtrescamps—començasubstituintel producteescalar(simètric)perunproducteantisimètric.Mésconcretament, suposemque V ésunespaivectorialdedimensiófinitasobreuncos k de característicazero.Unaestructurasimplècticasobre V vedonadaperuna 2-formabilineal ω quecompleixi

1. ω( ⃗ v, ⃗ v) = 0peratot ⃗ v ∈ V

2. Si ω( ⃗ u, ⃗ v) = 0peratot ⃗ v ∈ V ,aleshores ⃗ u = 0.

Lamatriude ω ésantisimètricaiinvertibleiaixòimplicaimmediatament queladimensióde V hadeserparella2n.Amés,podemtrobarunabase de V enlaquallamatriude ω tinguilaforma Ω = 0 I I 0 ,on I éslamatriu identitat n × n.

Delamateixamaneraquealageometriaeuclidianaensinteressenels automorfismesqueconservenlaformaquadràticaestàndardde Rn —les transformacionsortogonals—,enlageometriasimplècticaensinteressenels automorfismesqueconservenlaformasimplècticaestàndard Ω —endirem, naturalment, transformacionssimplèctiques

Éssenzilldeveurequeunamatriu M éssimplècticasicompleix M t ΩM = Ω. Aquestesmatriusformenunsubgrupde GL2n(k) quedenotaremamb Sp2n(k). Aquestsgrupss’anomenen grupssimplèctics iobtenimunacadenadesubgrups Sp2(k) ⊂ Sp4(k) ⊂ Sp6(k) ⊂··· completantcadamatriusimplècticaambunamatriuidentitat.Comqueles matrius λ 0 0 λ 1 sónsimplèctiquesperatot λ ≠ 0,veiemqueelsgrups Sp2n(R), Sp2n(C) nosóncompactes.

Enelcasparticular n = 1ésimmediatque Sp2(k) = SL2(k).Laigualtat deixadesercertaendimensionssuperiors,peròsíqueéscertengeneral que Sp2n(k) ésunsubgrupde SL2n(k).Aquestfetqueeldeterminantdetota matriusimplècticaésiguala1noésevidentapartirdelacondició M t ΩM = Ω, peròespotdemostrarambaquestraonament:

Comencemrecordantquetotaaplicaciólineal φ : V → V indueixaplicacions lineals φi : i V → i V enelsproductesexteriors.Enparticular,si V ésde dimensió m,l’espaivectorial m V ésdedimensió1il’aplicació φm : m V → m V éslamultiplicaciópeldeterminantde f .Siguiara V unespaivectorial

simplècticamb2-forma ω ∈ V ∗ ∧ V ∗.Prenemunabase ⃗ u1,..., ⃗ un, ⃗ v1,..., ⃗ vn de V enlaquallamatriude ω sigui Ω,ésadir,

, on ⃗ u ∗ 1 ,..., ⃗ u ∗ n , ⃗ v ∗ 1 ,..., ⃗ v ∗ n éslabasedualde V ∗.Sigui M unamatriusimplècticaisigui φ : V → V l’aplicaciólinealinduïdaper M enlabaseanterior.Elfet que M siguisimplècticaestraduiràenelfetque φ∗ 2 (ω) = ω,on φ∗ : V ∗ → V ∗ ésl’aplicaciódual.Considerem ωn := ω ∧···∧ ω ∈ 2n(V ∗).Aleshores, det(φ)ωn = φ ∗ 2n(ωn) = ωn itotesredueixademostrarque ωn ≠ 0.Siobservemque,peratot i, j,elselements

j ∈ 2(V

) commuten, veuremimmediatamentque

Elsgrupssimplècticscompactes. Elproductehermíticde Hn enspermet estendreelsconceptesdematriuortogonal(real)imatriuunitària(complexa)al casquaterniònic.Endirem matriussimplèctiques (perònoleshemdeconfondre amblesmatriussimplèctiquesdel’apartatanterior):unamatriu A ∈Mn×n(H) éssimplèctica(enaquestnoucontext)siconservaelproductehermític:

Vegemalgunesprimerespropietatsdelesmatriussimplèctiques.

• Claramentunamatriusimplècticarepresentaunaaplicacióbijectivai,per tant,ésunamatriuinvertible,ilainversatambééssimplèctica.Pertant, lesmatriussimplèctiquesformenungrupquedesignarem Sp(n)

• Elgrup Sp(1) s’identificaalgrupmultiplicatiudelsquaternionsdemòdul1i,perlamateixadefinicióde H,aquestgrupés SU(2).Topològicament,estractade S 3,l’esferadedimensió3.

• Si A ∈ Sp(n), A conservalanormade Hn,irecíprocament.

• Igualqueenelcasdelgrupunitari U(n),lesmatriussimplèctiquesestan caracteritzadesperlapropietat AA∗ = I,queésequivalenta A∗ = A 1 i ésequivalenta A∗A = I.

• L’aplicació Mn×n(H) →M2n×2n(C) quehemconstruïtanteriormentdona unainclusiódegrups Sp(n) ⊂ U(2n).Enparticular,elsgrups Sp(n) són compactes:jasabemque U(2n) éscompacteiésclarque Sp(n) éstancat (espotdefinirapartird’equacionsalgebraiques).

• Elsgrups Sp(n) sónconnexosisimplementconnexos.Lademostracióés lamateixaquehemindicatalapàgina9iutilitza Sp(n)/ Sp(n 1) ≊ S 4n 1 .

Enresum:

Elmateixconceptede matriuqueconservaelproducteintern,aplicatales tresàlgebresdedivisió R, C i H,ensproporcionatresfamíliesinfinitesde grupscompactes: O(n), U(n), Sp(n), n ≥ 1.

Relacióentrelesduesfamíliesdegrupssimplèctics. Entreelgrupsimplècticnocompacte Sp2n(C) delesmatrius M ∈M2n×2n(C) talsque M t ΩM = Ω i elgrupsimplècticcompacte Sp(n) ⊂ U(2n) delesmatrius M ∈Mn×n(H) tals que MM∗ = I hihaaquestarelació:

Sp(n) = Sp2n(C) ∩ U(2n) = Sp2n(C) ∩ SU(2n).

Demostremaquestaidentitat.Sitenimlamatriu A = A1 +A2j ∈ Sp(n),consideremlamatriu AC ∈ U(2n) quehemdefinitalapàgina17Aleshores, At C AC = I ensdona

D’altrabanda,

C Ω AC =

ihemdemostratque AC ∈ Sp2n(C).Recíprocament,si M ∈ Sp2n(C) ∩ U(2n), tenim M t ΩM = Ω i,almateixtemps, M 1 = M∗.Deduïmque Ωt M = M Ωt i aixòimplicaque M ésdelaforma AC peraalgunamatriu A ∈ Sp(n). ✷

Enconclusió:

Sivolemprescindirdelsquaternions,podemdefinirelgrupsimplèctic Sp(n) comelgrupformatperlesmatriuscomplexes 2n × 2n queconserven, simultàniament,laformahermíticailaformasimplèctica.

Elsquaternionsilesrotacionsde R3

Abanshemvistqueelsespinors—quehemidentificatambelselementsdel grup SU(2)—ensdonenlesrotacionsdel’espaidedimensió3.Arahempogut identificarelsespinorsambelsquaternionsdenorma1.Enaquestapartatintegraremaquestsdosfetsiveuremcomelgrupmultiplicatiudelsquaternions H∗ ensdonaunaexcel.lentdescripciódelgrupdelesrotacions SO(3).

Al’apartat Espinorsirotacionsdel’espai,delapàgina11,hemvist,d’unamaneramoltexplícita,comelselementsde SU(2) actuenperconjugaciósobre H ′ 0, un R-espaivectorialdedimensió3.D’altrabanda,comque R éselcentre de H,isabem(pàgina16)quelaconjugacióperunquaternió q ≠ 0conserva elproducteescalarde R4,tindremque cq donaunautomorfismeortogonal de ⟨i,j,k⟩R ⊂ H,elsubespai(real)delsquaternionspurs.Observemqueaquest subespaide H,sielmiremdinsde M2×2(C),comhemfetquanhemdefinitels quaternions,coincideixamb H ′ 0.D’aquestamanera,l’acciódelsquaternionsde norma1perconjugaciósobre ⟨i,j,k⟩R ésexactamentlamateixaquel’acció de SU(2) sobre H ′ 0 quehemestudiatdetalladamental’apartat3.

Endefinitiva,delamateixamaneraqueelsnombrescomplexosensvan proporcionarunamaneramoltméssimplededescriurelesrotacionsdelpla z → zz0 vs. cos α sin α sin α cos α ,

tambéelsquaternionsensdonenunadescripciómoltméssimpledelesrotacionsdel’espaidetresdimensions: h → p0hp 1 0 vs. Rθ, ⃗ u( ⃗ v) = cos θ ⃗ v + sin θ( ⃗ u × ⃗ v) + (1 cos θ)⟨ ⃗ u, ⃗ v⟩ ⃗ u.

Femaraexplícitalarelacióentreunquaternióunitari q ∈ H iunarotació descritageomètricamentenlaforma Rθ, ⃗ u: q = cos α + sin α(xi + yj + zk) R2α, → (x,y,z), entenent,però,queacadarotacióde SO(3) licorresponendosquaternions (odosespinors) ±q.Observemtambéquel’eixdelarotacióassociadaaun quaternió p éssimplementelvector p p ∈⟨i,j,k⟩R ⊂ H perquè p(p p)p 1 = p p.

Digressió#3:automorfismesde H

Arapodemdescriurefàcilmentelsautomorfismesde H.Curiosament,elcomportamentpatològicde C respectedelsautomorfismes—recordemquel’axioma del’eleccióenspermetdemostrarl’existènciad’unainfinitatnonumerable d’automorfismesde C—noesgeneralitzaalcasdelsquaternions.Elmotiu rauenelfetque R ésel centre de H iqualsevolautomorfisme(itambéqualsevolantiautomorfisme)haderespectarelcentre.Pertant,si φ : H → H ésun (anti)automorfisme,aleshores φ és R-lineali,enconseqüència,éscontinui vedonatperunamatriureal4 × 4.Perestudiarelsautomorfismesde H ens convéconsiderarsimultàniamentelsautomorfismesielsantiautomorfismes. Observemque,entotcas, φ hadeconservarlessolucionsdel’equació q2 =−1 iaquestessolucions(pàgina16)formenl’esferaunitatdinsde ⟨i,j,k⟩R ⊂ H = R4.Pertant, φ donaràunisomorfismelinealde R3 queconservaràlanormai, pertant,vindràdonatperunamatriuortogonal.Si φ tédeterminant1,seràuna rotaciói,segonshemvist, φ seràlaconjugacióperunquaterniódenorma1.Si φ tédeterminant 1,tindremque cφ seràlaconjugacióperunquaternióde norma1,on c ésl’antiautomorfismede H donatperlaconjugació.Enconclusió, totselsautomorfismesde H sóninternsitotselsantiautomorfismesseran producted’unautomorfismeinternperlaconjugació c.Pelquehemvistabans, deduïmqueelsautomorfismesde H formenelgrup SO(3).

Rotacionsendimensió3:conclusió

L’estudidelesrotacionsde R3 enshadutatresdescripcionsd’unmateix objecte

SU(2) ≊ Spin(3) ≊ Sp(1),

elrecobrimentuniversalde SO(3),ungrupambunsubgrupnormal {±I} ambquocient SO(3),demaneraque,topològicament,obtenimelrecobriment universal

S 3 → RP 3 .

Comhemditabans,donartresnomsdiferentsaunmateixgrupquedarà justificatquanvegem,mésendavant,quelestresfamílies SU(n), Spin(n) —quehemdefinitcomelrecobrimentuniversalde SO(n)—i Sp(n) divergeixen quan n creix.

Digressió#4:l’aplicaciódeHopf

Elgrup Sp(1) estàformatpelsquaternionsdemòdul1i,pertant,admet comasubgrupelgrup U(1),formatpelscomplexosdemòdul1.Aixòens permetconsiderarl’espaidelesclasseslaterals Sp(1)/ U(2).Topològicament, Sp(1) s’identificaal’esfera S 3 i U(1) s’identificaalacircumferència S 1,queactuaperladretasobre S 3.Aleshores, Sp(1)/ U(2) ésunespaitopològicquepodemidentificarfàcilmentdelamanerasegüent.Pensem S 2 coml’esferaunitat dinsdelsquaternionspursiescollimcomapuntbaseelpunt i ∈ S 2 ⊂⟨i,j,k⟩R. Aleshores,larepresentació S 3 = Spin(3) → SO(3) ensdonaunaaccióortogonal de S 3 sobre R3 i,enconseqüència,unaaccióde S 3 sobrel’esfera S 2 ⊂ R3.Aleshores,si q ∈ S 3,podemconsiderar qiq ∈ S 2.Enconclusió,tenimunaaplicació contínua

η : S 3 → S 2 ,

queesconeixcoma aplicaciódeHopf itépropietatsremarcablescomaquestes:

• Enspermetidentificar Sp(1)/ U(2) ambl’esfera S 2.Enparticular,l’aplicació η ésun fibratprincipal iuna fibració i,localment,escomporta comunproductede S 2 per S 1,queésla fibra.Geomètricament,podem descompondrel’esferatridimensionalcomauniódisjuntadecircumferències,unaperacadapuntdel’esfera2-dimensional.AInternet13 hi podeutrobarmoltesrepresentacionsgràfiquesmagnífiquesd’aquesta descomposició.

• η vaserelprimerexempled’unaaplicacióhomotòpicamentnotrivial entreesferesdedimensionsdiferents.HeinzHopfvapoderdemostrar quetotaaplicaciócontínuade S 3 a S 2 éshomotòpicamentequivalenta un múltiple enterde η,enunsentitquearanoexplicitarem,i,d’aquesta manera,vademostrarque π3(S 2) = Zη,elprimercàlculd’ungrupd’homotopiad’esferes πk(Sn) amb k>n.S’haafirmatqueaquestresultatde Hopfrepresentaelmomentfundacionaldela teoriad’homotopia.

Hihaunasenzillarelacióentrel’aplicaciódeHopfila geometriaprojectiva Recordemque,si V ≠ 0ésun k-espaivectorial—encaraque k siguinomésun anelldedivisió—,podemdefinirelseuespaiprojectiu P(V) comel conjunt

13Vegeu,perexemple,aquesta figura del’entrada«Hopffibration»delaWikipedia.

delssubespaisdedimensió1de V ,iaquestespai P(V) ésl’àmbitnaturaldela geometrialineal.Si k = R, C,obtenimelsespaisprojectiusrealsicomplexos

i,si k = H,obtenimelsespaisprojectiusquaterniònics ∗= HP 0 ⊂ HP 1 ⊂ HP 2 ⊂ HP 3 ⊂ HP 4 ⊂··· ,

enelsqualslageometrialinealescomportapràcticamentigualqueenels casosclàssicsrealsicomplexosllevatque,degutalanocommutativitatde lamultiplicacióa H,noescompleixel teoremadePapos.Enelstrescasos anteriors,podemidentificarlarectaprojectivaamblacompactificacióper unpuntdelarectaafí,ésadir,ambl’esferadeladimensiócorresponent:

Enelstrescasosreal,complexiquaterniònic,cadasubespaidedimensió1 de kn+1 estàdeterminatperunvectorunitari,idosvectorsunitarisdefineixen elmateixsubespaisiuns’obtédel’altremultiplicantperunescalardemòdul1. Aixòenspermetidentificar kP n ambelquocient(topològic)del’esferaunitat de kn+1 perl’acciódel’esferaunitatde k:

Pera n = 1obtenim

Enelcasrealobtenim S 1 → S 1,queésl’aplicació z z2 queesdenotaper2ι Enelcascomplexobteniml’aplicaciódeHopf η ienelcasquaterniònicobtenim unageneralitzaciódel’aplicaciódeHopf

ν : S 7 → S 4 , quetambéésunaaplicaciónohomotòpicamenttrivialsignificativa.

PrecisamentlarelacióquehemcomentatentrelesaplicacionsdeHopf2ι, η i ν ilageometriaprojectivaensdonalaclaudelasevanotrivialitathomotòpica. Considerem,perexemple,elcasde η : S 3 → S 2.Noésdifícilveurequeelpla projectiu CP 2 s’obtéadjuntantalarectaprojectiva CP 1 = S 2 unabolade dimensió4atravésdel’aplicació η.Aleshores,si η foshomotòpicaal’aplicació constant,tindríemque CP 2 seriahomotòpicamentequivalenta S 2 ∨ S 4.Això ésimpossibleperquèlacohomologiade CP 2 ilacohomologiade S 2 ∨ S 4 són diferents.

Laimportànciaquel’aplicaciódeHopfvatenireneldesenvolupamentde lateoriad’homotopiavaferqueesbusquessingeneralitzacionsadimensions superiors,deltipus S 2n+1 → Sn+1 ambfibra Sn.Pera n = 0, 1, 3elsplans projectiusreal,complexiquaterniònicensdonenaplicacionscomaquestai

lapreguntavasersiespodiaanarmésenllà.Resultaqueperconstruiruna aplicaciódetipusHopf S 2n+1 → Sn+1 n’hihaprouquelapresumptafibra Sn tinguiuna multiplicaciócontínuaambunitat ilaconstruccióéstansenzilla comaixò:

• Consideremaquestesduesconstruccionstopològiqueselementals:

La suspensió.Si X ésunespai,lasevasuspensióésl’espai

ΣX := (X × [0, 1]) {(x, 0) ∼ (x′ , 0),(x, 1) ∼ (x′ , 1) : x,x ′ ∈ X}

La juntura.Si X, Y sónespais,lasevajunturaésl’espai

X ∗ Y := (X × Y × [0, 1]) R;

R :={(x,y, 0) ∼ (x,y ′ , 0),(x,y, 1) ∼ (x′ ,y, 1) : x,x ′ ∈ X,y,y ′ ∈ Y }.

Si Y ésl’espaiambunúnicpunt,aleshores X ∗ Y esconeixcomel con de X,iesdenota CX.

La cofibrahomotòpica.Si f : X → Y ésunaaplicaciócontínua,la cofibrahomotòpicade f ésl’espaiquocient

(Y ∪f CX) := (X ∪ CY) {(x, 0) ∼ f(x) : x ∈ X}.

Elcasmésinteressantésquan X ésunaesfera Sn i CX ésuna bolatancada en+1.Enaquestcas,diemquelacofibrahomotòpica de f : Sn → Y ésl’espaiques’obté adjuntant a Y una cel·la de dimensió n + 1.

• Noésdifícilcomprovarquelesduesoperacionsanteriorstransformen esferesenesferes(llevatd’homeomorfisme): ΣSn ≊ Sn+1 , Sn ∗ Sm ≊ Sn+m+1 .

• Si Sn admetunamultiplicacióambunitat,podemconsiderarl’aplicació f : S 2n+1 ≊ Sn ∗ Sn → ΣSn ≊ Sn+1,f([x,y,t]) := [xy,t],

que,pera n = 0, 1, 3,és,llevatd’homotopia,l’aplicaciódeHopf.Amés,si utilitzem f peradjuntara Sn+1 unacel.la e2n+2,obtenimunespai Sn+1 ∪f e2n+2,quepodeminterpretarcomel plaprojectiu associata Sn

Enparticular,si Sn ésungrup—comhosón S 0 ={±1}, S 1 = U(1) i S 3 = Sp(1)—,jateniml’aplicaciódeHopf S 2n+1 → Sn+1 quevolíem,perònocal que Sn compleixitotselsaxiomesdegrup,noméselqueafirmal’existènciade l’elementneutre!ElcasésqueunteoremaclàssicdeFrankAdams—moltdifícil, sibés’hantrobatdemostracionsforçaméssenzillesquel’originald’Adams— afirmaquelesúniquesesferesquepodentenirunamultiplicaciócontínua ambunitatsón S 0 , S 1 , S 3 i S 7 i,enconseqüència,lesúniquesaplicacions detipusHopfquepodenexistirsónlestresquejaconeixem:2ι, η, ν iuna hipotètica σ : S 15 → S 8 ambfibra S 7,siésquerealment S 7 —quenosembla quepuguemidentificarambcapgrupconegut—admetcomamínimuna multiplicaciócontínuaambunitat.14

14 S7 síqueadmetaquestamultiplicació,peròaquestfet—deconseqüènciesimmenses—el discutiremenalgunaltrelloc.

5Rotacionsendimensió4

Volemestudiararalesrotacionsdel’espaieuclidià R4 amblaintencióde trobar,potser,algunarelacióentreelgrup Spin(4) —quehemdefinitdemanera abstractacomelrecobrimentuniversalde SO(4)—ialgungrupconegut.Com veurem,l’estudidelgrup SO(4) ésmoltbonic,itambéésbensingularperquè Spin(4) ésl’únic grupd’espinorsquetéunadescomposiciónotrivialcoma productecartesià.

Considereml’aplicació

π4 : Sp(1) × Sp(1) → SO(4)

definidad’aquestamanera:identifiquem R4 amb H idefinim π4(p,q) com l’aplicació R-lineal H → H donadaper

h → ph q.

Alllargd’aquestapartat,persimplificar,escriurem π enllocde π4.Lafórmulad’anticommutacióensdiuque π(p,q) conservaelproducteescalar,és adir, π(p,q) ∈ O(3) i,comque Sp(1) × Sp(1) ésunespaiconnex,tenim que π(p,q) ∈ SO(3).Que π ésunhomomorfismedegrupsésevident.Les rotacions π(p, 1) i π(1,p) per p ∈ Sp(1) rebenelnomd’isoclíniques. Vegemprimerque π ésunaaplicacióexhaustiva.Sigui A ∈ SO(4) isigui (a,b,c,d) laprimeracolumnade A.Aleshores,si p := a + bi + cj + dk ∈ H, observemque B := π(p, 1)A deixafixelprimervectordelabasecanònica de R4 = H,amblaqualcosa B ∈ SO(3) —entèscomelsubgrupde SO(4) deles matriusambprimerafilaiprimeracolumnaiguala (1, 0,..., 0)—i,comhem vistenl’estudidelesrotacionsde R3,existeixunquaternióunitari q talque φ = π(q,q).Enconclusió, A = π(pq,q) ihemcomprovatque π ésexhaustiva. D’altrabanda,ésclarqueelnuclide π éselsubgrupdiagonal {(1, 1),( 1, 1)}. Pertotaixò,podemafirmarqueelrecobridoruniversalde SO(4) és Sp(1) × Sp(1) iaixòensduuaidentificar

Spin(4) = Sp(1) × Sp(1),

demaneraquecadarotaciódel’espaieuclidiàdequatredimensionsvedeterminadaperunaparelladequaternionsunitaris,únicallevatdelsigne.

Observemque,comjahavíemanunciat,sibé Spin(3) ≊ SU(2) ≊ Sp(1), aquestsisomorfismesjanoesmantenensiaugmentemladimensióenuna unitat.Tanmateix, Spin(4) noensaportacapgrupnoumésenllàdelesfamílies SU(n) i Sp(n). 15 Amblesdefinicionsquehemdonat,lacompatibilitatentre

15 Espòiler:Calarribaraladimensió7perquèelsgrups Spin(n) esmostrincomunafamília independentdelesfamílies SU(n) i Sp(n)

lesdescripcionsquetenimdelesrotacionsde R3 ilesde R4 ésimmediata: tenimundiagramacommutatiu

Sp(1) ≊ Spin(3)

Spin(4) ≊ Sp(1) × Sp(1) SO(3) SO(4)

on ι vedonadaperlainclusióde R3 =⟨i,j,k⟩R en R4 = H, ∆ ésl’aplicació diagonali π3, π4 sónlesrepresentacionsquehemexplicatenaquesttext.

L’epimorfisme π tambéenspermetobtenirunabonadescripciódel’estructuradegrupde SO(4).Consideremaqueststressubgrupsde SO(4)

Hl ={π(p, 1) : p ∈ Sp(1)}≊ Sp(1),

Hr ={π(1,p) : p ∈ Sp(1)}≊ Sp(1),

H∆ ={π(p,p) : p ∈ Sp(1)}≊ SO(3).

Observemque

Hl i Hr sónnormalsa SO(4),commutenentreellsitenen intersecció {±I}.Entotsdoscasos,elgrupquocientés SO(3).Elgrup H∆ no ésnormalilesclasseslateralss’identifiquena Sp(1) comaespaistopològics.

L’epimorfisme π tambéenspermetobtenirunabonadescripciódela topologia del’espai SO(4).D’entrada, SO(4) s’identificaal’espaiquocient de S 3 × S 3 perl’acciódiagonaldel’aplicacióantipodal τ,però,d’altrabanda, l’aplicació f(p,q) = (p,pq) de S 3 × S 3 ensdonaunhomeomorfisme (S 3 × S 3) τ ≊ (S 3/τ) × S 3 ,

onl’accióde τ sobrel’espaidel’esquerraésdiagonal.Enconclusió,topològicament—nocomagrup!— SO(4) s’identificaalproducte RP 3 × S 3 = SO(3) × Sp(1).

Finalment,voldríemrelacionarladescripcióde SO(4) anteriorambla geometria delesrotacionsenquatredimensions.Recordemquetotamatriude SO(4) espotescriure,prenentunabaseortonormaladient,enlaforma cos α sin α sin α cos α ⊕ cos β sin β sin β cos β

Ésadir,hihadosplansinvariantsortogonalsisobrecadaplatenimuna rotaciód’angle α i β,respectivament.Compodemllegirelsplansinvariantsi elsanglesderotaciódelarotació π(p,q)?D’ençàqueCayleyvadescriureper primeravegada(1855)lesrotacionsenquatredimensionscomaproductes dequaternions x pxq,diversosautorscomKlein,HurwitzoCoxetervan completaraquestateoriaquedesenvoluparemacontinuació.

Rotacionsnoisoclíniques. Consideremdosquaternionsunitaris p,q ≠ ±1i escrivim-losenlaforma

p = cos α + sin αu, q = cos β + sin βv, on α,β ∈ (0,π) i u, v sónquaternionsunitarispurs.Suposem,enprimerlloc, que u ≠ ±v idefinim

x+ 1 = 1 + uv,x+ 2 = u v, x1 = 1 uv,x2 = u + v.

Unscàlculselementalsdemostrenaquestespropietatsde x+ 1 , x+ 2 , x1 , x2 (tingueuencomptelesfórmulesdelapàgina16):

• ||x+ 1 ||2 =||x+ 2 ||2 = 2 2⟨u,v⟩; ||x1 ||

, x1 , x2 sónortogonalsdosados.

• Comqueestemsuposant u ≠ ±v,normalitzantelsquaternions x+ 1 , x+ 2 , x1 , x2 ,obtenimunabaseortonormalde H coma R-espaivectorial.Amés, podemafirmarqueaquestabaseés positiva.Aixòesdedueixd’aquest resultat:

Si u, v sónquaternionspurs,aleshores,perladesigualtatdeCauchySchwarz, det(1,u,v,uv) =||u||2 ||v||2 −⟨u,v⟩2 ≥ 0.

Percomprovar-ho,recordemlafórmuladelproductevectorialtriple ⃗ a × ( ⃗ b× ⃗ c) =⟨ ⃗ a, ⃗ c⟩ ⃗ b−⟨ ⃗ a, ⃗ b⟩⃗ c irecordemtambéqueendimensió3tenimaquestarelacióentreeldeterminantielproductevectorial: det(⃗ e1, ⃗ e2, ⃗ e3) = ⟨⃗ e1, ⃗ e2 × ⃗ e3⟩.Aleshores: det(1,u,v,uv) = det(1,u,v, −⟨u,v⟩+ u × v) = = det(u,v,u × v) =⟨u,v × (u × v)⟩= =⟨u, ||v||2u−⟨u,v⟩ v⟩=||u||2 ||v||2 −⟨u,v⟩2 ≥ 0. ✷

Enelcasdelabase x+ 1 , x+ 2 , x1 , x2 ésfàcilveurequeelseudeterminant ésiguala4det(1,u,v,uv)> 0.

• L’accióde π(p,q) compleixaquestesfórmules:

px+ 1 q = cos(α + β)x+ 1 + sin(α + β)x+ 2 , px+ 2 q =− sin(α + β)x+ 1 + cos(α + β)x+ 2 , px1 q =− cos(α β)x1 + sin(α β)x2 , px2 q =− sin(α β)x1 + cos(α β)x2 .

• Lesfórmulesanteriorsdemostrenque H+ :=⟨x+ 1 ,x+ 2 ⟩ i H :=⟨x1 ,x2 ⟩ sónplansortogonalsinvariantsper π(p,q) ique π(p,q) éslarotació planad’angle α + β enelpla H+ ilarotacióplanad’angle α β enel pla H .

Elcas u =±v escomportapràcticamentigual.Perexemple,si u = v, seguimtenintelplainvariant H =⟨1,u⟩ sobreelqual π(p,q) éslarotació planad’angle α β.Escollimaraunquaterniópurunitari w ortogonala u i definim H+ :=⟨w,uw⟩.Aleshores, H+ i H sóndosplansinvariantsortogonalsiunscàlculscomelsanteriorsensmostrenque π(p,q) actuasobre H+ comlarotacióplanad’angle α + β.Observemque,pelresultatanteriorsobre eldeterminant,labasequehempreséspositiva.Elcas u =−v ésexactament igual,exceptequeara H :=⟨w,uw⟩ i H+ =⟨1,u⟩.

Estudiemaral’existènciad’altres plansinvariants enlarotació π(p,q) amb p,q ≠ ±1.Sidescartemelcas α = β = π/2—enelqual π(p,q) té, evidentment,infinitsplansinvariants—,demostraremqueelsplans H+ i H anteriorssónelsúnicsplansinvariantsde ρ := π(p,q).

Suposemque H ≠ H+,H ésunplainvariantisigui h ∈ H talque h = h+ + h amb h+ ∈ H+ , h ∈ H i h+,h ≠ 0.Leshipòtesisquehemfet sobre α, β impliquenque ρ(h) ≠ ±h iquecomamínimunadelesdues parellesdevectors (h+,ρ(h+)) i (h ,ρ(h )) éslinealmentindependent.En particular, h i ρ(h) formenunabasede H.Pelquehemvistmésamuntsobre larotació ρ,elpolinomianul ladorde ρ sobre H+ és x2 2 cos(α + β)x + 1i elpolinomianul.ladorde ρ sobre H és x2 2 cos(α β)x + 1.Calculemara ρ2(h):

ρ2(h) = 2cos(α + β)ρ(h+) h+ + 2cos(α β)ρ(h ) h .

Comqueestemsuposantque H ésunplainvariant,tindrem ρ2(h) h = λh + µρ(h) i,comque H+ ∩ H ={0},obtenimaquestesduesigualtats:

(2cos(α + β) µ)ρ(h+) = λh+ , (2cos(α β) µ)ρ(h ) = λh , queimpliquen(recordemquecomamínimunadelesduesparelles (h+,ρ(h+)) i (h ,ρ(h )) éslinealmentindependent) λ = 0i cos(α + β) = cos(α β),que escontradiuamblahipòtesi p,q ≠ ±1.

Rotacionsisoclíniques. Restanomésestudiarelcasdelesrotacions isoclíniques,ésadir,elcasenquè p = 1o q = 1.Enaquestcas,hihainfinitsplans invariantsicadaquaternió h ≠ 0pertanyaund’aquestsplans.Concretament, sigui p unquaternióunitari p = cos α + sin αu ≠ ±1isigui h ∈ H −{0}.Siapliquemlaidentitat p2 = 2 cos αp 1,veiemque p2h = 2 cos αph h ∈⟨h,ph⟩ i ⟨h,ph⟩ ésunplainvariantper π(p, 1) i,anàlogament, ⟨h,hp⟩ ésunpla invariantper π(1,p).

Si w ésunquaternióunitaripurortogonala u,podemprendrelabase ortonormalpositiva(pàgina27)de H formadaper1, u, w, uw iobservem

que π(p, 1) éslarotaciód’angle α encadascundelsplansinvariantsortogonals ⟨1,u⟩ i ⟨w,uw⟩.Encanvi, π(1,p) éslarotaciód’angle α a ⟨1,u⟩ ila rotaciód’angle α a ⟨w,uw⟩.Veiem,doncs,quelesrotacionsisoclíniqueses classifiquenendostipus:lesquegirenanglesigualsendosplansinvariants ortogonalsilesquegirenanglesoposatsendosplansinvariantsortogonals (±I pertanyalsdostipus).Lesprimeress’obtenenpermultiplicacióperl’esquerraperunquaternióunitarii,lessegones,permultiplicacióperladretaper unquaternióunitari.Aquestadistincióescorresponalsdossubgrupsnormals de SO(4) —noconjugats,ésclar— Hl i Hr quehemconsideratabans.

Digressió#5:rotacionsdel’espaitemps

L’espaitempsdelateoriadelarelativitat(especial,ésadir,sensegravetat)no ésl’espaieuclidià R4 perquèlacoordenada temps (t) escomportademanera diferentdelestrescoordenades espacials (x,y,z) i,pertant,elconceptede rotació requeriràunadefiniciódiferentdelaquehemutilitzatenlageometria euclidianade Rn,ésadir,enelsaltresapartatsd’aquesttext.Expliquem demaneramoltsuccinta—quevoldirquehoexplicaremnecessàriament malament—16 quinaésla distància quehemd’utilitzara R4 quanl’identifiquem al’espaitempsdelateoriadelarelativitat.

Consideremunsistemadereferènciainercial S ambunsistemadecoordenadesortonormal x, y, z iunrellotgequemesuraeltemps t, 17 iunaltresistema inercial S′ ambcoordenades x′ , y ′ , z′ iunrellotgequemesuraeltemps t′.Acadaesdevenimentelsistema S liassignaràunescoordenades (x,y,z,t) ∈ R4 ielsistema S′ liassignaràunesaltrescoordenades (x′,y ′,z′,t′) ∈ R4.Suposemque,quan t = 0,també t′ = 0ielsorígensde S i S′ coincideixen.Suposem queenl’instant t = t′ = 0unfotósurtdel’origenitenimunobservadora S iunaltrea S′ quevolencalcularlavelocitatdelfotó.Suposemqueaquest fotópassaperunpunt P .Aleshores, S detectaràelfotóenelpunt P amb coordenades (x,y,z) enl’instant t i S′ detectaràelfotóenelmateixpunt P ambcoordenades (x′,y ′,z′) enl’instant t′.Ésadir, S observaràqueelfotó harecorregutunadistància x2 + y 2 + z2 enuntemps t i S′ observaràqueel fotóharecorregutunadistància x′2 + y ′2 + z′2 enuntemps t′.Perl’axioma fonamentaldelateoriadelarelativitat, S i S′ hand’arribaralmateixvalorper alavelocitatdelfotó.Pertant, x2 + y 2 + z2 t = c = x′2 + y ′2 + z′2 t′

Aquestraonamentensdiuqueelpuntsenquès’anul lalaformaquadràtica

Q(X,Y,Z,T) = X2 + Y 2 + Z 2 c2T 2

16 Sivoleumésdetallssobretotelqueexplicaremara,llegiuelllibreimprescindible Geometria diferencialirelativitat,deJoanGirbau,enelqualtrobareumoltbenexplicattotelqueaquíhem deresumirexcessivament.

17Defet,unrellotgeacadapuntdel’espai,totssincronitzats.

segonsl’observadorde S sónelsmateixospuntsenquès’anul.lasegonsl’observadorde S′.Ditambmésexactitud:sigui A elcanvidecoordenades(queno coneixem)entre (x,y,z,t) i (x′,y ′,z′,t′),isigui QA laquàdricatransformada de Q per A;aleshores, Q(⃗e) = 0 ⇐⇒ QA(⃗e) = 0

Aixòimplica18 quelesduesquàdriquesdifereixenenunaconstantnonul la.A partird’aquí,fentunscàlculsmésomenysllargs,19 podemdeduir:

• LesclàssiquesfórmulesdeLorentzqueexpressenelcanvidecoordenades (x,y,z,t) (x′,y ′,z′,t′) enfunciódelavelocitat v de S′ respecte de S (sempreque |v| <c).

• λ = 1ielcanvidecoordenades conservalaformaquadràtica Q

Elqueensinteressadetotaixòésaquestdarrerpunt:al’espaitemps,els movimentshanderespectarlaforma Q,que,pertant,faelpaperquefala formaquadràtica X2 + Y 2 + Z 2 + T 2 al’espaieuclidià.Enconclusió,deixant debandalestranslacions,elgrupdelsmovimentsrígidsdel’espaitemps estaràformatperlesmatriusrealsinvertibles4 × 4queconservinlaforma quadràtica Q = X2 + Y 2 + Z 2 c2T 2,unaformaquadràticanosingularde rang4iíndex1equivalentalaforma X2 + Y 2 + Z 2 T 2.Aquestesmatrius formenelqueesconeixcoma grupdeLorentz.Eldenotaremamb O(3, 1) iés elgrupdelqualvolemdiralgunacosaenaquestadigressió.

Si Γ éslamatriudiagonal (1, 1, 1, 1) —ésadir,lamatriudelaforma quadràtica Q anterior—,aleshores

(3, 1) ={

ésclaramentunsubgrupde GL4(R).Podemconsiderarelsubgrup O(3)×O(1) ⊂ O(3, 1) tenintencomptelestransformacionsortogonalsdelestresprimeres coordenadesielcanvidesignedel’últimacoordenada.

O(3, 1) noéscompacte:peracada λ ∈ R podemconsiderarlamatriu

O(3, 2)

18 Éscuriósquemoltsllibresdeteoriadelarelativitatometenaquestpunt(unaexcepcióésel llibredeBernardSchutz),ésadir,delaigualtatdelsconjuntsdepuntsenquèlesquàdriques s’anul lenpassenalaigualtatdelesformes,sensecapcomentari.Matemàticament,elproblema esplantejaenaqueststermes:siguin f i g dospolinomisirreductiblesen n variablestalsqueel conjuntdezerosde f siguielmateixqueelconjuntdezerosde g,ésadir, V(⟨f ⟩) = V(⟨g⟩), enelllenguatgedelageometriaalgebraica;podemdeduirque ⟨f ⟩=⟨g⟩?Sielcosbaseés algebraicamenttancat,larespostaéssíiesdedueiximmediatamentdelNullstellensatz,però, sielcosés R,comenelnostrecas,larespostaésno: x2 + y 2 i x2 + 2y 2 tenenelsmateixos zerosa R2 inodifereixenenunaconstant.Calalgunahipòtesiaddicional.Afortunadament,el llibre Afinitats,movimentsiquàdriques,d’AgustíReventós,síquetractaeltema(apèndixD)i demostraque,si f i g sóndegraudossobre R,ambelsmateixosconjuntsdezeros,iund’ells compleixquetéunzero regular (ésadir,ambgradientnonul),aleshores f i g difereixenen unaconstantnonul la.Comqueenelcasdelaformaquadràtica Q lacondicióderegularitates compleix,podemafirmarque Q = λQA 19HopodeutrobarmoltbenexplicatalllibrecitatdeJoanGirbau.

amb µ = √1 + λ2.Usualment,aquestesmatriuss’escriuenutilitzantlesfuncionstrigonomètriqueshiperbòliques:

10 01 ⊕ cosh x sinh x sinh x cosh x ,x ∈ R,

querecordal’expressiódelesrotacionsambsinusicosinus.Espotdemostrarqueelsubgrup O(3) × O(1) ésunsubgrupcompactemaximaldeO(3, 1) Ésclarquelesmatriusde O(3, 1) tenendeterminant ±1itenim,pertant, unhomomorfismedegrups det:O(3, 1) → Z/2queésexhaustiui,enparticular,ensdiuqueelgrupdeLorentznoésconnex.Talcomfemambelgrup ortogonal,definim SO(3, 1) comelsubgrupnormalde O(3, 1) delesmatrius dedeterminant1.

Araapareixunfenomenquenotenimenelcasdelsgrupsortogonals clàssics.Hihaencaraunaltrehomomorfismeexhaustiu θ :O(3, 1) → Z/2que esdefineixd’aquestamanera:si A ∈ O(3, 1),escrivim A = Mv wt µ amb µ ∈ R

Delacondició At Γ A = Γ esdedueix µ2 = v t v + 1 =||v||2 + 1 ≥ 1.Per tant, µ ≠ 0ipodemdefinir θ(A) := µ/|µ|∈{±1}= Z/2.Resultaque θ és unhomomorfisme,perònoconeccapdemostracióelementald’aquestfet. Resultaque θ s’identificaambunconceptegeneraldeformesquadràtiques ques’anomena normaespinorial ique,perlasevamateixadefinició,ésun homomorfisme.Endefinitiva,tenimunepimorfisme

O(3, 1) → Z/2 × Z/2

queensdiuque O(3, 1) té,comamínim,quatrecomponentsconnexes—són exactamentquatre—ienspermetdefiniraquestsubgrupnormal connex

SO+(3, 1) :={A ∈ O(3, 1) :det(A) = θ(A) = 1}

Arapodríemcomençaraestudiarungrup Spin(3, 1) quefosunrecobriment doblede SO+(3, 1),identificar-loaalgunaltregrupconegut(coincideixamb elgrupsimplècticnocompacte Sp2(C)),etc.,peròseràmillorquehodeixem aquí.

6Rotacionsendimensió5

Enaquestapartatestudiaremlesrotacionsdel’espaieuclidià R5,ambla mateixaintenciódelscasosanteriors:veuresipodemidentificarelsespinors endimensió5ambalgungrupconegut.Avancemquelarespostaquetrobarem seràque Spin(5) s’identificaa Sp(2).Perveure-ho,consideremaquest R-espai vectorialdedimensió5: V := λq q λ ∈M2×2(H) : λ ∈ R,q ∈ H .

Observem:

• V estàformatperlesmatriushermítiquesquaterniòniquesdetraçazero: V ={M ∈M2×2(H) : M∗ = M, tr(M) = 0}.Escriuremelsvectorsde V en laforma [λ,q] iprendremcomabaseortonormalde V laformadaper lesmatrius [1, 0], [0, 1], [0,i], [0,j], [0,k].

• Sp(2) actuasobre V perconjugació.Aixòésevidentpelpuntanteriori pelfetque,perdefinició,lesmatriusde Sp(2) compleixen Q 1 = Q∗

• Uncàlculimmediatmostraque,si M ∈ V ,aleshores M 2 =||M||2I,onla normal’entenemambelproducteescalareuclidiàde V coma R-espaivectorial.Comaconseqüènciad’això,laconjugacióperunamatriude Sp(2) conservalanormade V = R5 i,pertant,ésunatransformacióortogonal.

• Tenim,pertant,unhomomorfisme Sp(2) → O(5) i,comque Sp(2) és connex,laimatgeestaràcontingudaenelcomponentdelaidentitat:

π5 : Sp(2) → SO(5).

Recordeml’epimorfisme Sp(1) × Sp(1) → SO(4) delaseccióanterior.Ésevidentque,siidentifiquem R4 = H ambl’hiperplà λ = 0de V iidentifiquem Sp(1) × Sp(1) amblesmatriusdiagonalsde Sp(2),aleshoresl’homomorfisme π5 : Sp(2) → SO(5) ésunaextensiódelarepresentaciódelesrotacionsen dimensió4itenimundiagramacommutatiu

Sp(1) × Sp(1) Sp(2) SO(4) SO(5)

Calculemelnuclide π5,ésadir,lesmatrius Q ∈ Sp(2) quecommutenamb toteslesmatriusde V .Lacommutativitatamb [1, 0] implicaque Q ésdiagonal. Lacommutativitatamb [0, 1] implicaque Q ésdelaforma pI amb ||p||= 1. Finalment,lacommutativitatambtoteslesmatrius [0,q] peratot q implica que p éscentrala H i,pertant, Q =±I.

Finalment,demostremque π5 ésexhaustiva.Sigui A ∈ SO(5) isigui [λ,q] ∈ V uneixde A.Noésrestrictiusuposarque ||[λ,q]||= 1i λ ≥ 0.Siguiara µ := 1 + λ 2 ,p := q 2µ ,Q := µ p pµ .

Escompleixque Q ∈ Sp(2) ique Q[1, 0]Q∗ = [λ,q] ∈ V .Aleshores B := π5(Q) 1Aπ5(Q) ∈ SO(4) perquèfixal’eix [1, 0].Pertant, B pertanyalaimatge de π5 i A també.

Observemqueelsdossubgrupsnormals Hl, Hr delesrotacionsisoclíniques de SO(4) passenaserconjugatsa SO(5).Notincconstànciaques’hagifetun estudidelseixosielsplansinvariantscomelquehemexplicatal’apartatde lesrotacionsendimensió4.

Enconclusió, Sp(2) éselrecobrimentuniversalde SO(2) ipodemidentificar

Spin(5) = Sp(2).

Unavegadamés,tampocnoenshacalgutdescobrircapgrupnouperdescriure elsespinorsendimensió5.

7Rotacionsendimensió6

Estemarribantallímitdelqueconsiderem baixadimensió enaquesttreball: estudiaremlesrotacionsendimensió6iveuremcomtambélespodemdescriureutilitzantunsespinorsapropiatsque,novament,identificaremambalgun delsgrupsquejaconeixem.Recordemquehemidentificat Spin(5) amb Sp(2) irecordemtambéquehemvist(pàgina20)que Sp(2) ésunsubgrupde SU(4), concretament, Sp(2) = SU(4) ∩ Sp4(C).Aixòenspotduraintuirquepotser podremidentificarelgrup Spin(6) amb SU(4) i,efectivament,aquestaintuïció éscorrecta,peròalgunsdetallsseranméscomplicatsqueenlesdimensions inferiors.20 Percomençar,enscaldràrepassaralgunsconceptesd’àlgebramultilineal.

Sigui V = Cn ambelproductehermíticordinariilabasecanònica e1,...,en. Ensinteressaconsideraraquestesrepresentacionsde GLn(C):l’acciónatural sobre V ,l’acciósobre V ∗ donadaper

(A ω)(e) = ω(At e) = ω(A∗e)

ilesaccionsnaturalsqueesdesprenend’aquestesduessobreelsproductes exteriors k V i k V ∗,per k = 1,...,n.Apartird’aquí,observem:

• Hihaunisomorfisme GLn(C)-equivariant α : k V ∗ → ( k V)∗ donatpel determinant: α(ω1 ∧···∧ ωk)(u1 ∧···∧ uk) := det(ωi(uj ))

• Tenimuna dualitat d : V → V ∗ definidaaixí:

d(e)(u) :=⟨u,e⟩

d ésbijectivai semilineal enelsentitque d(λe) = λd(e).Diremque d és unc-isomorfisme.Observemque d és U(n)-equivariant.Tambépodem considerarelc-isomorfisme k d : k V → k V ∗ .

• Si n = 2k,podemconsideraraquesta formabilinealsimètrica B sobre k V : B(u1 ∧···∧ uk,v1 ∧···∧ vk) := det(u1,...,uk,v1,...,vk).

Aquestaformabilinealdonalloc,demaneranatural,aunisomorfisme b : k V → ( k V)∗ iéssenzillcomprovarque b és SU(n)-equivariant.

20SeguiremelcamíindicatperPaulGarreta Sporadicisogeniestoorthogonalgroups (2015).

• Combinantlesaplicacionsanteriors

(

obtenimunc-isomorfisme J : k V → k V queés SU(n)-equivariant.

• Sigui W := Fix(J) elconjuntdels ρ ∈ k V fixosper J.Observemque W no ésunsubespaivectorialde k V —perquè J noéslineal—,peròsí queésun R-subespaivectorial.D’altrabanda,ésclarque W éstancatper l’accióde SU(n) —perquè J ésequivariant.

Peral’estudidelgrup Spin(6) ensinteressal’aplicació J enelcas n = 4 J : 2 C4 → 2 C4 , quenoésdifícildecalculardemaneraexplícita.Consideremlabasecanònica eij := ei ∧ ej , i<j,de 2 C4.Uncàlculsenzillensdona J(e12) = e34,J(e34) = e12,J(e13) =−e24, J(e24) =−e13,J(e23) = e14,J(e14) = e23

Ésadir,lamatriude J comaaplicació R-linealenlabase

{e12,e34,ie12,ie34,e13,e24,ie13,ie24,e23,e14,ie23,ie14}

és

Apartird’aquíobtenimaquestabasede W coma R-espaivectorial: w0 := ie13 + ie24,w1 := e24 e13,w2 :=−e14 e23, w3 := ie23 ie14,w4 := e12 + e34,w5 := ie12 ie34

Recordemquesobre 2 C4 —i,pertant,sobre W —hitenimunaformabilineal simètrica B.Sicalculemelsvalorsquepren B sobrela R-basede W ,observem queobtenimunamatriudiagonalamb2aladiagonal.Ésadir, B ésunproducte escalar(real)definitpositiusobre W i {wi/√2 : i = 0,..., 5} ésunabase ortonormalrespectede B.D’altrabanda,l’accióde SU(4) conservalaforma bilineal B.Enconclusió,hemobtingutunhomomorfismedegrups SU(4) → O(6).

Comqueelsgrups SU(n) sónconnexos,tenim

π6 : SU(4) → SO(6).

Acontinuació,demostremqueelnuclide π6 és {±I}.Suposemque A = (aij ) ∈ SU(4) éstalquedeixafixoselselementsdelabasede W .Apartird’aquí ésfàcilveureque A actuatrivialmentsobre 2 C4:peracada i<j tindrem Aei ∧ Aej = ei ∧ ej ;prenem k ≠ i,j i,considerantelscoeficientsde eik, ejk i eij alaigualtatanterior,arribema

aiiakj = akiaij ,ajiakj = akiajj ,aiiajj ajiaij = 1

Deduïmque A hadeserdiagonalielproductededoselementsqualssevolde ladiagonalhadeseriguala1,quenoméséspossiblesi A =±I.

Relacionemara π6 : SU(4) → SO(6) ambl’epimorfisme π5 : Sp(2) → SO(5) del’apartatanterior.Recordemquehavíemvistque Sp(2) s’identificaalsubgrupde SU(4) formatperlesmatriusqueconservenlaformaalternadano degeneradasobre V donadaper Ω = 0 I I 0 enlabasecanònica e1, e2, e3, e4 (pàgina20).Aquestaformadonaunaaplicaciólineal ω : 2 V → C que compleix

ω(e12) = ω(e14) = ω(e23) = ω(e34) = 0,ω(e13) = ω(e24) = 1

i,pertant, ω(w0) = 2i i ω(wi) = 0per i ≠ 0.Aixòensdiuqueunelement de SU(4) conserva ω siinoméssideixafix w0.Enconclusió, π6 : SU(4) → SO(6) envia Spin(5) = Sp(2) a SO(⟨w0⟩⊥) = SO(5).Aracaldràrelacionar aquestepimorfismede Spin(5) a SO(5) amb π5:escompleixqueaquestdiagramaéscommutatiu: Sp(2)

(4)

(5)

(6)

Lamaneraelementaldedemostrarlacommutativitatd’aquestdiagramaés fentuncàlculdirecte:prenemunamatriuarbitrària A ∈ Sp(2),calculem explícitamentlamatriu π6(AC) ilacomparemamblamatriu π5(A). 21 Finalment,demostraremque π6 ésexhaustiva.Considerem,doncs,una matriu R ∈ SO(6) peralaqualvolemtrobar P ∈ SU(4) talque π6(P) = R. Escrivim

R(w0) = λw0 + µw,w ∈⟨w0⟩⊥ , ||w||2 =||w0||2 = 2,λ2 + µ2 = 1.

Sigui S ∈ SO(⟨w0⟩⊥) unarotacióqualsevoltalque S(w) = w1,demanera que SR(w0) = λw0 + µw1.Jasabemqueexistirà A ∈ Sp(2) ⊂ SU(4) talque S = π6(A).Consideremlamatriucomplexadiagonal M := Diag(λi µ,λi + µ, i, i).

21 Perferaquestcàlculitrobarlabase w0,...,w5 quefaqueeldiagramasiguicommutatiu vaigutilitzar sagemath,enparticular,aquest script (accessibledesdelaversióelectrònicade l’article).Seriabonictrobarunademostracióbreuinocomputacionaldelacommutativitatdel diagrama,peròlaveritatésqueferaquestcàlculamb sagemath tambétéelseuencant.

Tenimque M∈ SU(4) i π6(M)(w0)=λw0 +µw1.Aleshores π6(M 1)π6(A)R(w0)= w0,amblaqualcosaexistirà B ∈ Sp(2) talque π6(M 1)π6(A)R = π6(B) i deduïmque R ésalaimatgede π6.

8Conclusió

Hemcompletatelnostreobjectiudedonardescripcionsexplícites,detallades icoherentsdeles isogèniesesporàdiques entreelsgrupsd’espinors Spin(k) per k< 7igrupsdelesfamílies SU(n) i Sp(n),ihemobtingutaquestdiagrama commutatiu:

Esperemque,mésenllàdel’interèsqueaquestesisogèniesclàssiquespuguin tenir,elcamíquehemseguit—ilesdigressionsquehemfet—puguinserútils periniciar-seenl’estudidels grupsdeLiecompactes ilessevesapassionants propietatsgeomètriquesitopològiques.22

Catedràticdetopologiajubilat UniversitatAutònomadeBarcelona Jaume.Aguade@uab.cat

22 Siushaagradataquestestudidelesrotacionsendimensió < 7,nousperdeuelsfets extraordinarisquesucceeixenendimensió8.

ButlletídelaSocietatCatalanadeMatemàtiques Vol.39,núm.1-2,2024.Pàg.37–71. DOI:10.2436/20.2002.01.114

Políedresipapiroflèxiamodular

JaumeCollGuerrero

Lapapiroflèxiaéslamaneramésfàcil deconèixerlageometria.

JoanBascuñana,artistadelavidaolotí

Resum: Enaquesttreballs’expliquentècniquesdepapiroflèxiamodularqueens permetenferambpaperunagranvarietatdepolíedres:elscincsòlidsplatònics,els tretzepolíedresarquimedians,elsvuitdeltaedresconvexosilessevesestelacions, prismes,antiprismes,piràmidesicúpulesgeodèsiquesfullerianes,entred’altres.

Paraulesclau: papiroflèxiamodular,políedres,sòlidsplatònics,políedresarquimedians,tècniquesdepapiroflèxia,tessel.lacions.

ClassificacióMSC2020: 00A08,00A66,05B45,51M20,52B05,52B10.

Introducció

Arafacinquantaanysesvapublicarambelnomde caixadecolors uncubdepaperqueactualmentésmoltpopulariqueesconeixcoma cubdeSonobe.Aquestafiguradepaperesconstrueixapartirdesismòdulsbàsicsques’uneixen mitjançantpestanyesibutxaques,senseutilitzarcola,performaruncub.El cubdeSonobevadonarllocalnaixementdetotaunanovabrancadelapapiroflèxia:lapapiroflèxiamodular.Desd’aleshoress’hancreataltresmòduls perferpolíedresmodularsenpaper,comeltetràedreil’octàedredeKunihikoKasahara(OmnibusOrigami,1988),l’icosàedredeTomokoFuse(BOS Convention,1987),eldodecàedredeLewisSimon(Pajarita núm.26,1989),el cubooctàedredeLewisSimon(PajaritaExtra,1988),elcubtruncatd’OriolBach (Pajarita núm.29,1989),elrombicuboctàedredeNataleFietta(CDO,1986)oel dodecàedreròmbicdeDavidBrill(BOSConvention,1986).

Totsaquestsmòdulss’uneixendelamateixamaneraqueelcubdeSonobei l’essènciadelamajoriad’aquestsmòdulsésaconseguirunanglemoltconcret perferelspolígonsqueformaranelpolíedre.

Caldestacarunmòduldetipusarestamoltversàtil,flexibleiresistent, elKantenmodul(2002),del’alemanyaCarmenSprung;ambaquestmòdules podenconstruirunagranvarietatdepolíedres,comperexemplequatredels cincsòlidsplatònics,lafamíliadelsvuitdeltaedresconvexos,moltsdeltaedres còncaus,prismes,antiprismes,piràmides,cúpulesfullerianes,triangulacions desòlidsplatònicsiarquimedians,etc.

Tambécaldestacarelsmòdulsarestade120graus(1987),135graus(1987) i144graus(2013)del’origamistadeSingapurFrancisOw(1949–2018),que permetenferelstretzepolíedresarquimedians.Lacol lecciódelstretzepolíedresarquimediansfetsamborigamimodularfouexposadaperDirkEisner l’any2011aFriburgdeBrisgòviaenla6InternationaleTagunzZurFaltikdidaktik,convenciódepapiroflèxiaorganitzadaperNickRobinsonielbadaloníJoan Sallas.Elsmòdulsutilitzatsenaquestesfiguresidissenyatsl’any2007conjuntamentperTomokoFuse,DirkEisnerielmateixFrancisOwerenvariantsdels mòdulsdeFrancisOw.

Acabemlaintroduccióexplicantl’estructurad’aquestarticle.Alaprimera partdeltreballesfanalgunesobservacionssobrel’origendelspolíedresi esdemostraquetansolsexisteixencincsòlidsplatònicsoregularsitretze políedresarquimediansosemiregulars.

AlasegonapartdeltreballesdescriuenelsmòdulsarestadeFrancisOwiel mòdularestaKantenmoduldeCarmenSprungiesveuenalgunesdelesseves possibilitats.Enaquestapartdeltreballdescriuremunageneralitzaciódels mòdulsarestade120i135grausdeFrancisOw.Aquestageneralitzaciódescriu unprocedimentqueenspermetcanviarl’anglegeneralperunaltredeconcret, obtenircasosparticularsdemòdulsarestaiconstruiraltrestipusdepolíedres. Elsmòdulsarestade120i135grausdeFrancisOwsóncasosparticulars d’aquestmètodemésgeneral.

AlatercerapartdeltreballesdescriuelmòduldeSonobeitambéesveuen algunesdelessevespossibilitats,enparticularlaconstrucciódefractals,com l’esponjadeMenger.Enaquestapartatescalculaiesdemostraquinéselgènere delasuperfícieques’obtéenl’enèsimaiteracióperdefiniraquestfractal.

Ladarrerapartdeltreballestàdedicadaalaconstruccióambpapiroflèxia modulardemosaicsplans.Veuremquealgunsmotiusdel’AlhambradeGranadatambépodentessel.laruncubienfaremefectiusdos:l’aviónassaritail’os nassarita.Eltreballfinalitzaamblaconstrucciód’unafiguranomodularmultiformeinspiradaenuntercermotiudelsmosaicsdel’AlhambradeGranada:un tetràedrenomodularconstruïtapartird’unocelletnassaritatridimensional.

1Políedres

1.1Elshumansielspolíedres

Familersd’anysqueelshumansconeixenelspolíedres.Undelsexemplesmés antics,enigmàticiemotiuéslagranpiràmidedeKheops,segonfaraódela iv dinastiaegípcia.Aquestaconstrucciófaraònicaestàsituadaalaplanurade Guiza,avuidiaalcostatdelaciutatdelCaireoAl-Qahira(laVictoriosa).Essent

lamésgrandetoteslespiràmidesegípcies,téunaalçàriadeh = 146.6m ielcostatdelabasefab = 230.4mdelongitud,delaqualcosapodem deduirquelasevainclinaciótéunvalornumèricqueespotaproximarper l’arrelquadradadelnombreauri m = tan(α) ≈ φ,ambunerrorrelatiu del0 04 %,otambéunvaloraproximatde m = tan(α) ≈ 12√18,ambunerror relatiudel0.01 %.Enlarestadelespiràmidesdel’anticEgiptenoesdonen aquestesaproximacionsnumèriquesi,pertant,calesperarqueaquestesi d’altresaproximacionsexpressadesambfuncionssenzillessiguincasualitats numèriques.

AltrespolíedresforçaenigmàticsespodenveureenelMuseuGaloromà LugdunumdelaciutatfrancesadeLió.Amésdedausicompassosdel’època romana,aquestmuseutédosdodecàedresdebronzedatatsalvoltantdelssegles ii i iii delanostraera.Enlessevesdotzecaresforadadespercerclesde diferentsmidesespodenveurealgunesmarquescirculars,iencadascun delsseusvintvèrtexsqueconnectenlestrentaaresteshihaunespetitesesferes.Avuidiaesconeixenmésdecentd’aquestsdodecàedres,lamajoria trobatsaFrança,iunúnicicosàedrealLVR-LandesmuseumdeBonn.Encara noesconeixquinaeralautilitatd’aquestsobjectesperquènosen’hantrobat referèncieshistòriquesdocumentades.

Comhanarribatelshumansaconèixerfiguresgeomètriquestanregulars? Unapartdelarespostaésqueobservessinaquestesformesgeomètriquesala natura.Moltsmineralscristal.litzenmacroscòpicamentendiferentstipusde políedresforçaregulars.Aquestprocésnaturalesprodueixal’escorçadela terradesdemilionsd’anysabansdel’apariciódelshumans.Així,tenimque lapiritacristal.litzaencubs,octàedresidodecàedres,ilafluoritailamagnetita, enoctàedresgairebéperfectesperal’ullhumà.Aquestssóntresexemplesde políedresenquètoteslescaressónpolígonsregularsigualsientotselsvèrtexs conflueixelmateixnombredecares.Aquestspolíedress’anomenen políedres regulars o sòlidsplatònics enhonordePlató,queelsmencionaenel Timeu [10]: «Elfocestàformatpertetràedres;l’aire,d’octàedres;l’aigua,d’icosàedres;laterra, decubs;comqueencaraéspossibleunacinquenaforma,Déuhautilitzataquesta,el dodecàedrepentagonal,perquèserveixidelímitalmón».

Lapiritatambépotcristal litzarenformadecubooctàedre,queésun políedresemiregularformatpersisquadratsivuithexàgonsregulars.Un darrerexempleéselgranat,quepotcristal.litzarcomadodecàedreròmbic, queésundelstretzepolíedresdeCatalan.

Elspolíedressemiregularstambés’anomenen políedres o sòlidsarquimedians enhonord’ArquimedesdeSiracusa(segle iii aC).Totiquenoesconserventraduccionsdel’obraoriginald’Arquimedesqueparlind’aquestspolíedres, hihareferènciesd’autorsgrecs,comPaposd’Alexandria(segle iv dC),queenel llibre v secció xix delaseva Collecciómatemàtica,dedicadaalscossossòlids, descriuelscincpolíedresplatònicsitretzepolíedresformatsperdiferents polígonsequilàtersiequianglesqueatribueixaArquimedes[19].

1.2Políedresplatònicsiarquimedians

Elspolíedresestanformatsperelementsdedimensió2(lescares C),dedimensió1(lesarestes A)idedimensiózero(elsvèrtexs V ).Peraqualsevolpolíedre homeomorfal’esfera,aquestselementsestanrelacionatsperlafórmulad’Euler:

C + V = A + 2 (1)

LeonhardEuler(Basilea,1707-SantPetersburg,1783)vaproposaraquesta igualtatenunacartaescritaaBerlínambdata14denovembrede1750i dirigidaalseuamicChristianGoldbach,queviviaaSantPetersburg.Laprimera demostraciórigorosadelafórmulad’Eulernofoudonadafinsal1847perKarl vonStaudt[16].Aquestaequaciódiofànticalineal (1) téinfinitessolucions,però nototeslessolucionsescorresponenaunpolíedre;perexemple,noexisteix cappolíedreambelsvalors C = V = A = 2,totiqueaquestsvalorscompleixen larelaciód’Euler2 + 2 = 2 + 2.

Acontinuacióenscentraremenelspolíedresconvexos,quetenencerta regularitatenlescaresienelsvèrtexs.

Definició 1. Diremqueunpolíedreconvexésregularoplatònicsitotesles sevescaressónpolígonsregularsd’unúnictipusiencadavèrtexconflueixel mateixnombredecares.

Altrespolíedresforçaregularssónelsprismesregularsielsantiprismes regulars.Aquestspolíedresestanformatsperdospolígonsregularsparal lels de n costatsunitsper n quadratsiper2n trianglesequilàters,respectivament. Existeixeninfinitsprismesregularsiinfinitsantiprismesregulars,unpercada polígonregular.Elprismaregularambbaseunquadratéselcubil’antiprisma regularambbaseuntriangleequilàterésl’octàedre.

Definició 2 Diremqueunpolíedreconvex,quenosiguiunprismaoantiprisma,éssemiregularoarquimediàsitoteslessevescaressónpolígons regularsdedosoméstipusiencadavèrtexconflueixelmateixtipusdecaresi enelmateixordre.

Perdemostrarquetansolsexisteixencincpolíedresplatònicsitretze políedresarquimedians,imposaremlesrespectivescondicionsderegularitata lafórmulad’Euler.

Teorema 3 Tansolsexisteixencincpolíedresregularsoplatònics.

Prova. Cadaarestaestàlimitadaperdosvèrtexs.Acadaarestaconflueixenduescares,iduescarescomparteixencomamàximunaúnicaaresta.

Comqueelpolíedreésregular,toteslescaresqueelformensónpolígons regularsamb n arestesi n vèrtexs;amés,acadavèrtexdelpolíedreconflueixen m caresi m arestes.Evidentment, n ≥ 3i m ≥ 3.Aquestainformacióens permetobtenirrelacionsentreelnombredecares C,elnombred’arestes A iel nombredevèrtexs V :

Substituintaquestesexpressionsenlafórmulad’Euler (1),obtenimelsvalors C,A,V ∈ N enfunciódelsparàmetresnaturals n,m ∈ N:

(2)

Aracalresoldreaquestestresnovesequacionsdiofàntiquesalgebraiques. Primerdetotveuremqueundelsparàmetresval3: n = 3obé m = 3.Enefecte, ésevidentqueeldenominadord’aquestesexpressionséspositiu: 2n + 2m nm> 0 ⇒ 1 n + 1 m > 1 2 (3)

Sielsdosparàmetressóndiferentsde3,aleshores n ≥ 4i m ≥ 4,iobtenimla contradicciósegüent: 1 2 = 1 4 + 1 4 ≥ 1 n + 1 m > 1 2

Si n = 3,deladesigualtat (3) deduïmque m ≤ 5,ipersimetriadelesvariables n, m enlamateixadesigualtat (3),tenimque n ≤ 5si m = 3.Aixídoncs, tenimcincpossibilitats,iamblesexpressions (2) podemdeduirelnombrede cares,arestesivèrtexs.

nmCAV

35203012Icosàedre 348126Octàedre 33464Tetràedre 436128Cub 53123020Dodecàedre

Observemqueelnombred’arestessempreésunmúltiplede6iqueel nombredecaresidevèrtexsésparell.

Canviantlacondiciódeconvexpercòncau,s’obtéunafamíliadequatre políedresregularscòncaus,conegutsambelnomde políedresdeKepler-Poinsot. Seguintelspassosdelademostracióanterioriambunargumentmés elaborat,espotdemostrarquetansolsexisteixentretzepolíedresarquimedians osemiregulars[2].

Prèviamentveuremtreslemesqueenspermetrandescartarmoltspossibles casos.Definim s comelnombredetipusdepolígonsregularsdiferentsqueté elpolíedrearquimedià.

Lema 4. Encadavèrtexd’unpolíedresemiregularoarquimediànopodenconfluirquatreoméstipusdepolígonsdiferents.Ésadir, s ≤ 3

Prova. Suposemelcontrari;aleshoreselsanglesinteriorsdelspolígonsregularsqueforminelpolíedrearquimediàseransuperiorsoigualsa π 3 rad (60graus,triangleequilàter), π 2 rad(90graus,quadrat), 3π 5 rad(108graus, pentàgonregular)i 2π 3 rad(120graus,hexàgonregular).D’aquíobtenimla contradicciósegüent:

perquèlasumadelsanglesinteriorsdelspolígonsregularsqueconflueixenen unmateixvèrtexhadeserinferiora2π rad,jaqueelpolíedreésconvex. ✷

Lema 5 Siacadavèrtexd’unpolíedresemiregularoarquimediàhiconflueixen trespolígonsiund’ellstéunnombresenardecares,aleshoreselsaltresdos polígonshandetenirelmateixnombredecares.

Prova. Suposemelcontrari,ésadir,existeixunaconfiguraciódeltipus (a,b,c)

a senari b ≠ c;

aleshoresundelsvèrtexsdelpolígonambunnombresenardecostatsno tindràlamateixaconfiguració,degutal’alternançadelsvalors b, c alvoltant delpolígonambunnombresenardecostats.Hoil lustremambunpentàgon.

Lema 6. Siacadavèrtexd’unpolíedresemiregularoarquimediàhiconflueixen quatrepolígonsicomamínimund’ellsésuntriangleequilàter,aleshoresles úniquesconfiguracionsdevèrtexssón (3, 3, 3,a) i (3,a,b,a) amb a ≠ 3,ésadir, podemaconseguirunaconfiguraciódevèrtexsonundelstrianglesequilàtersté elsdospolígonsadjacentsambelmateixnombredecares.

(3, 3, 3,a)(3,a,b,a)

Prova. Siacadavèrtexconflueixenquatretrianglesequilàters,aleshorestenim unpolíedreregular.

Siacadavèrtexconflueixenexactamenttrestrianglesequilàters,aleshores obtenimlaconfiguraciódevèrtexsdelsantiprismes (3, 3, 3,n)

Siacadavèrtexconflueixenexactamentdostrianglesequilàters,aleshores tenimduespossibilitats (3, 3,a,b) (trianglesequilàtersadjacents)i (3,a, 3,b) (trianglesequilàtersoposats).Elsdoscasosnosónpossiblescoms’il.lustraen eldibuixsegüent:

Siacadavèrtexconflueixexactamentuntriangleequilàter,aleshoresenla configuració (3,a,b,c) lacarade b costatssempreestàoposadaaltriangle equilàter,delaqualcosaesdedueixque a = c

(3,a,b,c)(3,a,b,a)

Teorema 7. Tansolsexisteixentretzepolíedressemiregularsoarquimedians.

Prova. Lademostraciód’aquestteoremaesdivideixenl’anàlisidediferents casos.Observemqueenunmateixvèrtexnopodenconfluirmésdecinc polígons,perquèaleshoreslasumadelsanglesseriasuperiorals2π rad. Utilitzemlanotaciósegüent: n(c) voldir n polígonsde c costats, {≥ n}(c) vol dirunnombresuperioroiguala n polígonsde c costats, n(2m ≥ c) voldir n polígonsamb c oméscostatsquecompleixenlacondició m ≥ c/2.

1. Políedresformatstansolspertrianglesequilàtersiquadrats.

(4, 3, 3) encontradiccióambellema5 (4, 3, 3, 3) antiprismaquadrangular

(4, 3, 3, 3, 3)s = 2, m3 = 4, m4 = 1, m = 5 (i) cubxato

1(4)+{≥ 5}(3) Lasumad’anglessupera2π

(4, 4, 3) prismatriangular

(4, 4, 3, 3) encontradiccióambellema6

(4, 3, 4, 3)s = 2, m3 = 2, m4 = 2, m = 4 (ii) cubooctàedre

2(4) +{≥ 3}(3) Lasumad’anglesval ≥ 2π

(4, 4, 4, 3)s = 2, m3 = 1, m4 = 3, m = 5 (iii) rombicuboctàedre

3(4) +{≥ 2}(3) Lasumad’anglessupera2π {≥ 4}(4) +{≥ 1}(3) Lasumad’anglessupera2π

2. Políedresformatstansolspertrianglesequilàtersipentàgons.

(5, 3, 3) encontradiccióambellema5

(5, 3, 3, 3) antiprismapentagonal

(5, 3, 3, 3, 3)s = 2, m3 = 4, m5 = 1, m = 5 (iv) dodecàedrexato

1(5) +{≥ 5}(3) Lasumad’anglessupera2π

(5, 5, 3) encontradiccióambellema5

(5, 5, 3, 3) encontradiccióambellema6

(5, 3, 5, 3)s = 2, m3 = 2, m5 = 2, m = 4 (v) icosidodecàedre

2(5) +{≥ 3}(3) Lasumad’anglessupera2π

{≥ 3}(5) +{≥ 1}(3) Lasumad’anglessupera2π

3. Políedresformatstansolspertrianglesequilàtersihexàgons.

(6, 3, 3) encontradiccióambellema5

(6, 3, 3, 3) antiprismahexagonal

1(6) +{≥ 4}(3) Lasumad’anglesval ≥ 2π

(6, 6, 3)s = 2, m3 = 1, m6 = 2, m = 3 (vi) tetràedretruncat

2(6) +{≥ 2}(3) Lasumad’anglesval ≥ 2π

{≥ 3}(6) +{≥ 1}(3) Lasumad’anglesval ≥ 2π

4. Políedresformatstansolspertrianglesequilàtersi n-àgons, n ≥ 7.

(n, 3, 3) encontradiccióambellema5

(n, 3, 3, 3) antiprisma n-gonal

1(n) +{≥ 4}(3)

Lasumad’anglessupera2π

(8, 8, 3)s = 2, m3 = 1, m8 = 2, m = 3 (vii) cubtruncat

(10, 10, 3)s = 2, m3 = 1, m10 = 2, m = 3 (viii) dodecàedretruncat

(2n + 1, 2n + 1, 3) encontradiccióambellema5

2(2m ≥ 12)+{≥ 1}(3) Lasumad’anglessupera2π

2(n) +{≥ 2}(3) Lasumad’anglessupera2π {≥ 3}(n) +{≥ 1}(3) Lasumad’anglessupera2π

5. Políedresformatstansolsperquadratsi n-àgons, n ≥ 5.

(n, 4, 4) prisma n-gonal

1(n) +{≥ 3}(4) Lasumad’anglessupera2π

(2n + 1, 2n + 1, 4) encontradiccióambellema5

(6, 6, 4)s = 2, m4 = 1, m6 = 2, m = 3 (ix) octàedretruncat

(6, 6, 4, 4) Lasumad’anglessupera2π

2(2m ≥ 8) +{≥ 1}(4) Lasumad’anglessupera2π

{≥ 3}(n) +{≥ 1}(4) Lasumad’anglessupera2π

6. Políedresformatstansolsperpentàgonsi n-àgons, n ≥ 6.

(n, 5, 5) encontradiccióambellema5

1(n) +{≥ 3}(5) Lasumad’anglessupera2π

(6, 6, 5)s = 2, m5 = 1, m6 = 2, m = 3 (x) icosàedretruncat

2(2m ≥ 7) +{≥ 1}(5) Lasumad’anglessupera2π {≥ 3}(n) +{≥ 1}(5) Lasumad’anglessupera2π

7. Políedresformatstansolsperdostipusdiferentsde n-àgons, n ≥ 6. Aquestcasésimpossibleperquèlasumadelsanglesinternssempreés superiora2π

8. Políedresformatstansolspertrianglesequilàters,quadratsi n-àgons, n ≥ 5.

(n, 4, 3) encontradiccióambellema5 (n, 4, 3, 3) encontradiccióambellema6 (n, 3, 4, 3) encontradiccióambellema6 (n, 3, 3, 4) encontradiccióambellema6 (5, 4, 4, 3) encontradiccióambellema6

(5, 4, 3, 4)s = 3, m3 = 1, m4 = 2, m5 = 1, m = 4 (xi) petitrombicosidodecàedre

(5, 3, 4, 4) encontradiccióambellema6

1(n) + 1(4) +{≥ 3}(3)

1(n ≥ 6) +{≥ 1}(4) +{≥ 1}(3)

{≥ 2}(n) +{≥ 1}(4) +{≥ 1}(3)

Lasumad’anglessupera2π

9. Políedresformatstansolspertrestipusdepolígonsquenosiguintriangles.

Enaquestdarrercaslasumadequatreanglesinternsdiferentssempre éssuperiora2π :

Pertant,encadavèrtexconflueixentrespolígonsregularsdiferentsque, degutallema5,tindranunnombreparelldecostats;enaquestasituació lesúniquescombinacionsquenosuperenels2π radianssón:

(8, 6, 4)s = 3, m4 = 1, m6 = 1, m8 = 1, m = 3 (xii) granrombicuboctàedre

(10, 6, 4)s = 3, m4 = 1, m6 = 1, m10 = 1, m = 3 (xiii) granrombicosidodecàedre

Elsargumentsanteriorssóndetipuslocalinohemutilitzatlacaracterísticad’Euler-Poincarédelpolíedre.Percalcularelnombreexactedecares, vèrtexsiarestesd’aquestspolíedres,definim Cn comelnombrede n-àgonsde n arestesi n vèrtexsd’unpolíedrearquimedià, m comelnombredecares oarestesqueconflueixenenunvèrtexi mi comelnombredecares ni-gonals queconflueixenenunvèrtex.

Teorema 8. Elnombredevèrtexs,caresiarestesdelspolíedresarquimedians vedonatperlatauladevalorssegüent.

PolíedreVèrtexsArestesCares

(I)cubxato 246038

(II)cubooctàedre 122414

(III)petitrombicuboctàedre 244826

(IV)dodecàedrexato 6015092

(V)icosidodecàedre 306032

(VI)tetràedretruncat 12188

(VII)cubtruncat 243614

(VIII)dodecàedretruncat 609032

(IX)octàedretruncat 243614

(X)icosàedretruncat 609032

(XI)petitrombicosidodecàedre 6012062

(XII)granrombicuboctàedre 487226

(XIII)granrombicosidodecàedre 12018062

Prova. Utilitzantelmateixargumentqueenelcasplatònicdeduïm:

Enaquestcaselnombredevèrtexstambécompleixlesigualtatssegüents:

Aleshorespodemdeduirelsvalorsde Cni resolentelsistemade s equacions linealsen Cni formatperlarelaciódonadaperlafórmulad’Euleri s 1deles equacionsanteriors:

Concretament,siacadavèrtexconflueixendostipusdepolígons(s = 2),cal resoldreunsistemadeduesequacionsiduesincògnites:

i,enelcasqueencadavèrtexconflueixintrestipusdepolígons(s = 3),cal resoldreunsistemadetresequacionsitresincògnites:

Elsvalors m i ni, mi, ∀i = 1,...,s,elshemdeterminatenlademostració delteorema7,cosaquepermetcalcularelsvalors Cni , ∀i = 1,...,s,itambélaternadevalors (C,V,A) peracadatipusdepolíedremitjançantles igualtats(4). ✷

Elcubxatoieldodecàedrexatoexisteixenenduesvariantsquesónisomètriques:laformalevogirailaformadextrogira.Elrombicuboctàedreestàformat perduescúpulesiunprismaoctogonalcentral;girant45grausunad’aquestes cúpules,s’obtél’anomenat pseudorombicuboctàedre,tambéanomenat sòlidde Sommerville [14]o sòliddeMiller [7].Aquestpolíedretélesmateixespropietats deregularitatenelsvèrtexsqueelrombicuboctàedre,peròtémenyssimetries axialsiespeculars.Elrombicuboctàedreielpseudorombicuboctàedrenosón figuresisomètriques.

2Papiroflèxiad’algunsmòdulsaresta

2.1Quèéslapapiroflèxia?

Aquestamateixapreguntaesdevienferelnovembrede1936elslectorsdeldiari LaPrensadeBuenosAires,enelqual,enunaentrevistadeCarlosA.Leumann al’odontòlegburgalèsVicenteSolórzanoSagredo,apareixperprimercopla paraula papiroflèxia.Defet,enaquestarticlesurtenduesparaulescreadespel docorSolórzano(vegeutambé[12,13]):

• «papirola:todaslasproduccionescientífico-artísticasrealizadasconpapel.»

• «papiroflexia:Elartededoblargeométricamenteelpapel.»

Aquestesduesparaules,aixícomlaparaula papirofléxico,novanserincloses aldiccionaridelaRAEfinsl’any1986,totiquesíqueapareixienenaltres diccionaris.EldoctorSolórzanotambévafundarl’any1954elMuseude PapiroflèxiaalaciutatdeBuenosAires.Posteriorment,l’any1961,aquesta col leccióesvatraslladaraValladolid,onundelsseuscompanysd’estudis, NemesioMonteroPérez,lavadipositarenelMuseudeCiènciesNaturals d’aquestaciutat.Ambelsanys,idesprésd’algunesgestionsamblesgermanes deldoctorMontero,lesfiguresd’aquestacol.leccióvansercedidesal’Asociación EspañoladePapiroflexia(AEP),onesconservenactualmentendosgransbaguls, queestanpendentsd’estudiicatalogació.

Trenta-sisanysabansdelapublicaciódelllibredeldoctorSolórzano,quan encaranoexistialaparaula papiroflèxia,l’escriptorifilòsofMigueldeUnamuno vapublicarunapèndixalllibre Amorypedagogía ambeltítol Apuntesparaun tratadodecocotología;enaquestapèndixpodemllegirelsegüent[18]:

Lapalabra cocotología secomponededos,delafrancesa cocotte,pajaritade papel,ydelagriega logia,de logos,tratado.Lapalabrafrancesa cocotte esuna palabrainfantilyqueseaplicaensusentidoprimitivoyrectoalospollosy porextensiónalasaves.Ensentidotraslaticio,alaspajaritasdepapelyalas mozasdevidaalegre.

Poquesllengüesdelmóntenenunaparaulapròpiaequivalenta papiroflèxia Trobemlaparaula paperfolding enanglès, Papierfalten enalemany, zhézhˇ ı en xinèsi origami enjaponès(de oru,«plegar»,i kami,«paper»).Aquestadarrera paraulaéslaques’utilitzaenlamajoriadellengüesdelmónperdesignar aquestartdeplegarelpaper.

Avuidianoestàclarquelapapiroflèxias’originésalJapó.D’aquestpaís,a mésd’imposar-selaparaula origami enlesaltresllengüesdelmón,esconeix elllibremésanticdedicatíntegramentalapapiroflèxia.Ésunanònimde1797 queportapertítol HidenSenbazuruOrikata,iquepodríemtraduirper Elsecret delplegatgedeles1000grues,onesdescriuenlesconstruccionsdediferents tipusdegruesdepaper.DelJapótambéesconeixdocumentalmentuncubde paperanomenat Tamatebako ocofredeltresor,publicatl’any1734perHayato Ohokaenelllibre RanmaZushiki.

AOccidentlafigurad’origamidocumentadamésantigaqueesconeixésla caixadel Llibred’hores,deCaterinadeClèveris(segle xv).Uns500anysmés

tardpodemtrobarladescripciódelasevaconstruccióenlafiguranúmero6del llibreanònim Unahojadepapel,publicatperl’EditorialSalvatella[1].Vicente PalaciosGarrido,expresidentdel’AEP,vaesbrinarqueaquestllibrefouescrit perLorenzoHerreroSáiz.MoltprobablementLorenzoHerreronoconeixiael Llibred’hores,deCaterinadeClèverisi,pertant,calesperarqueaquestacaixa id’altresfigurestradicionalsimoltpopularsqueapareixenenelmateixllibre, coml’ocellet (pajarita encastellà, cocotte enfrancès),s’hagintransmèsper tradicióoralalllargdelssegles.

Amésdelapapiroflèxiaclàssica,enquèesconstrueixunafiguraapartir d’unúnicpaper,quenormalmentésunfulldinA4ounpaperquadrat,avuidia existeixendiferentsbranquesdelapapiroflèxia,comlapapiroflèxiamodular,en quèesconstrueixenfiguresdepaperunintdiversescòpiesd’unmateixmòdul (odediferentsmòduls,papiroflèxiamultimodular),lapapiroflèxiacinètica, enquèesconstrueixenfiguresdepaperambmoviment,olapapiroflèxia multiforme,onapareixendiferentsfiguresenunasuccessiódeplecs.

Enelmaterialsuplementari1 veuremcompodemconstruirambpaperels cincsòlidsplatònicsielstretzepolíedresarquimediansambtècniquesde papiroflèxiamodular.

3ElcubdeSonobe

ElcubdeSonobeéselcubdepaperméspopular.Aquestcubésmodulariestà formatpersismòdulsiguals,unpercadacaradelcub.ElmòduldeSonobees construeixfentunsdeterminatsplecsenunfullquadratdepaper.

Pas1Pas2Pas3

ComenceuambPlegueuidesplegueuPlegueuidesplegueu unfullquadratenvallperlameitatenvallperlaquartapart

Pas4Pas5Pas6Pas7

PlegueuenvallPlegueuenvallPlegueuPlegueu envallenmuntanya

1 Vegeuelmaterialsuplementarial’ediciódigitald’aquestvolum, ButlletídelaSocietatCatalana deMatemàtiques (enlínia)(2024),vol.39(1-2), https://revistes.iec.cat/index.php/BSCM.

ObservemquelaconstrucciódelmòduldeSonobeésasimètrica;en efecte,enelpas4hemfetelsplecsendosvèrtexsoposatsdelquadrat. Tambéespodenferelsplecstriantelsaltresdosvèrtexsoposatsdelquadratirepetirelspassos4a7;d’aquestamaneraobtenimunmòdulsimètric.

Pas4’Pas5’Pas6’Pas7’

PlegueuenvallPlegueuenvallPlegueuPlegueu envallenmuntanya

ElmòduldeSonobetéformaderomboideambanglesde45i135graus, ilasevabaseéseldobledelasevaalçària.Podeucomprovarquecadapunt delromboidetéquatrecapesdepaperi,pertant,lasevasuperfícieésla quartapartdelquadratinicial.Perunirelssismòdulsromboidalsiformar elcubnocalutilitzarcola;s’uneixenperquècadamòdultéduesbutxaques iduespestanyes.Lesduesbutxaquesestansituadesaladiagonalmenordel romboide,quetambéésunadiagonaldelquadratcentral,ilespestanyessón elsdostrianglesrectanglesisòsceleslaterals.

MòduldeSonobe:

Perunirdosmòduls,engiremun90grausiintroduïmunapestanyadel primermòdulenunabutxacadelsegon.Larestadelsmòdulss’uneixendela mateixamanera.Elmòdulobtingutenelpas7noespotencaixardemanera naturalambelmòduldelpas7’.Perconstruiruncubcalfersismòdulsidèntics comenelpas7osismòdulsidènticscomelpas7’;enelsdoscasosl’efecte visualéselmateix.Sienelpas7o7’femunplecenvallenllocdemuntanya, aleshores,quanunimsismòduls,obtenimuncubamblescaresllises,no divididesentriangles.

b = 2h

butxaca

3.1LajoiadeTakahama

FentunnouplecenelmòduldeSonobes’obtéunavariantqueenaquesta seccióanomenaré mòduldeTakahama.

Plegueuenmuntanya

UninttresmòdulsdeTakahamaobtenimunaltrehexàedre:labipiràmide triangular.LauniódedosmòdulsdeTakahamaesfacomenelcasdelmòdul deSonobe.LesaltrespropietatsdelmòduldeTakahamasónsemblantsalesdel mòduldeSonobe.Elmòdulobtingutenelpas8noespotencaixardemanera naturalambelmòduldelpas8’.Perconstruirunabipiràmidetriangularcalfer tresmòdulsidènticscomenelpas8,otresmòdulsidènticscomenelpas8’; enelsdoscasosl’efectevisualéselmateix.Sienelspassos7–8o7’–8’fem plecsenvallenllocdemuntanya,aleshores,quanunimtresmòduls,obtenim unabipiràmidetriangularamblescaresllisesnodivididesentriangles.

UniódedosmòdulsUniódetresmòdulsdelsUniódetresmòdulsdels deTakahamapassos7–8o7’–8’passos7–8o7’–8’ enmuntanyaenvall

Notahistòrica: segonsl’historiadordel’origamiDavidLister(Grimsby, 1930–2013),lajoiadeTakahamafoupublicadaperprimercopl’any1974 enelllibre Vidacreativaamborigamicreatiu [17],escritenjaponèsperl’origamistaniponaToshieTakahama(Tòquio,1910–1999).Elnomde joia ésdegutal fetqueToshieTakahamafeiacollaretsunintunsquantsd’aquestshexaedres ambunacorda.Afinalsdeladècadadelsanysseixanta,ToshieTakahamava fundarelSosakuOrigamiGroup67(grupdecreacióod’estudidel’origami), delqualformavenpart,entred’altres,MitsunobuSonobeiKunihikoKasahara. Aquestpetitgrupdeplegadorsesreuniaperiòdicamental’escolaTamagawa Gakuen,al’oestdeTòquio.

DavidListertambéafirmaqueelcubdeSonobefoupublicatperprimercop l’any1968alespàgines10i11delasegonadelessetrevisteseditadespel SosakuOrigamiGroup67.

AmblespublicacionsdeToshieTakahamaesvadonaraconèixerelmòdul deSonobe.Així,elcubdeSonobeilajoiadeTakahamavanserlesfigures modularsquevandonarllocal’actualespecialitatdel’origamimodular.El cubdeSonobeesvapublicarposteriormentendiversesrevistesillibresde papiroflèxiaambelnomde caixadecolors,comperexempleenlapàgina19 delnúmero0,volum3,delbutlletídelaNOA(NipponOrigamiAssociation),de l’any1974,delqualeradirectoraToshieTakahama.

CubsdeSonobeijoiesdeTakahamaToshieTakahamaiMitsunobuSonobe

MitsunobuSonobe( 薗部光伸 )vanéixerl’any1937.Enelllibre Atarashii OrigamiNyumon [15],editatpelSosakuOrigamiGroup67l’any1970,en elqualapareixpublicadalacaixadecolors,podemllegirqueteniasisanys d’experiènciaenelplegatgedepaperiqueviviaalbarrid’Ikebukuro,enel districtedeToshima-kudelaciutatdeTòquio.Treballavaenungrupdeteatrei elquemésliagradavaeralacreaciódetottipusdeflorsdepaper.Enelmateix llibreesfanpetitsapuntsbiogràficsdelsaltresmembresdelSosakuOrigami Group67.

Alsanyssetanta,ToshieTakahamaeramésconegudaqueMitsunobuSonobe idurantalgunesdècadeselmòduldeSonobevaserconegutaOccidentcom a mòduldeTakahama,peròésclarquel’autord’aquestmòdulésMitsunobu Sonobe,comapareixenelllibre Papiroflexiaparaexpertos [6],delsmestres d’origamiKunihikoKasahara( 笠原邦彦 )iToshieTakahama( 高濱利恵 ), contemporanisdeMitsunobuSonobe.

CaldestacarlasemblançaentreelcubdeSonobeielcubdepaperanomenat tamatebako o cofredeltresor,queapareixenunail.lustraciódelllibre Ranma Zushiki,publicatl’any1734perHayatoOhoka.

PodeutrobarunaltrecubdepaperforçadiferentdeldeSonobeenelllibre Guíaprácticadelartemanual [3],publicatl’any1977,totiquelesinstruccions delasevaconstrucciónosóngaireclares.

3.2Deltaedresestelats

Elsdeltaedressónpolíedrestoteslescaresdelsqualssóntrianglesequilàters. Existeixeninfinitsdeltaedrescòncausitansolsvuitdeltaedresconvexosde4, 6,8,10,12,14,16i20cares,comvandemostrarl’any1947FreudenthaliVan derWaerden[4].Elsvalorsmínimimàximdelnombredecaresd’undeltaedre

convexés4i20,respectivament,queescorresponenalssòlidsplatònicso regularsambelsvalorsmínimimàximdecares:eltetràedreil’icosàedre. Existeixuntercerpolíedre,l’octàedre,queésdeltaedreisòlidplatònicalhora. L’octàedretambéespotinterpretarcomunabipiràmidequadrangular.Elsaltres cincdeltaedres(lesbipiràmidestriangularipentagonal,eldodecadeltaedre, eltetracaidecadeltaedreil’hexacaidecadeltaedre)nosónregularsenelsseus vèrtexs.Caldestacarquenoexisteixendeltaedresconvexosde18caresod’un nombredecaressuperiora20.

ElmòduldeSonobetémoltesméspossibilitats.Sienelpas7femelplecen muntanyaienelpas8femelplecenvall,aleshoresobtenimunnoumòdul ambquèespodenconstruirdeltaedresestelats. Pas7Pas8

PlecenmuntanyaPlecenvallMòdulfinalUniódetresmòduls

Uninttresd’aquestsmòdulsobtenimunapiràmidetriangularobertaen quèlabaseésuntriangleequilàterielstrescostatslateralssóntriangles rectanglesisòsceles.Ambaquestesnovesconfiguracionsdesegonnivellpodem ferestelacionsdedeltaedres.Ambvuitpiràmidesobtenimunoctàedreestelat, iambvint,unicosàedreestelat.Comquecadamòdulformapartdedues piràmidesadjuntes,observemqueesnecessitendotzemòdulsperferl’octàedre estelatitrentamòdulsperferl’icosàedreestelat.Engeneral,sitenimun deltaedrede C caresivolemferundeltaedreestelat,enscalen 3C 2

mòduls;d’aquestraonamentorigàmicdeduïmquequalsevoldeltaedretésempreunnombreparelldecares.

Observemque,sifeml’estelaciódeltetràedreambaquesttipusdeconfiguraciódesegonnivell,obtenimelcubdeSonobe.Aixòésaixíperquèespot inscriureuntetràedredinsd’uncub;lessisarestesdeltetràedrecoincideixen ambsisdelesdotzediagonalsdelcub.AquestfetjafouobservatperKepler enl’HarmonicesMundi (1619).

Delail.lustraciódelllibredeKeplerdeduïmquelalongituddel’arestadel cub l coincideixambladistànciaentreduesarestesoposadesdeltetràedre,i lalongituddel’arestadeltetràedreregularinscritval √2l.Amés,ladescomposiciódelcubencinctetràedresenspermetcalcularelvolumdeltetràedre regular.

l3 = Vcub = Vtetràedreregular + 4 · Vtetràedresnoregulars, l3 = Vtetràedreregular + 4 1 6 l3 , Vtetràedreregular = l3 3 .

Observemqueelvolumdeltetràedreregularéseldoblequeelvolumdel tetràedrerectangle.

L’estelaciódel’octàedreapareixenunsegellqueesvaemetrealJapóper commemorarlacelebracióaKyoto,l’any1990,delXXICongrésInternacional deMatemàtiques.

Elsdeltaedresestelatsconstruïtsambaquestmòdultenenlescarestriangulades.Siinvertimeltipusdeplecsenelpas7(vallenllocdemuntanya)iel pas8(muntanyaenllocdevall),aleshoresobtindremelsdeltaedresestelats amblescaresllises.

Pas7 Pas8 Políedre

Plecenmuntanya CubdeSonobeambcarestriangulades

Plecenvall CubdeSonobeambcaresllises

Plecenmuntanya Plecenmuntanya JoiadeTakahamaambcarestriangulades

Plecenvall Plecenvall JoiadeTakahamaambcaresllises

Plecenmuntanya Plecenvall Deltaedresestelatsambcarestriangulades Plecenvall Plecenmuntanya Deltaedresestelatsambcaresllises

3.3ElcubdeSonobeielsfractals

L’esponjadeMengerésunfractaldescritperprimercoppelmatemàticaustríacKarlMenger(1902–1985).Ladescripciód’aquestfractal,quedenotarem amb M∞,començaambuncub M0 decostat L.Dividimaquestcubenvint-isetcubsigualsdecostat L/3ieliminemelcubcentralielssiscubscentralsde cadacara.Aquestanovafigura M1 tévintdelsvint-i-setcubsinicials.Araiterem infinitamentelprocéspercadascundelscubs.Observemqueencadaiteració cadacubestransformaenvintcubsi,pertant,l’enèsimaiteració Mn està formadaperlaunióconnexade Kn = 20n cubsdecostat L/3n.D’aquesta maneratenimunasuccessiódevarietatstopològiques.Definiml’esponjade Menger,quedenotaremamb M∞,comlaintersecciódetotesaquestesvarietats topològiques.

Defet,l’esponjadeMengerésunageneralitzacióa R3 delacatifade Sierpinski (R2)

idelconjuntopolsdeCantor (R1),

Aquestsid’altresfractalsvanserestudiatsambprofunditatalsegle xx;per exemple,lessevesdimensionsdeHausdorffsón,respectivament:

log20/ log3 ≈ 2.727, log8/ log3 ≈ 1.8927, log2/ log3 ≈ 0.631.

ElmòduldeSonobeenspermetconstruirientendrealgunespropietats d’aquestasuccessiódesuperfícies.Elcubinicial M0 espotferamb C0 = 6mòdulsdeSonobe;aquestcubté V0 = 8vèrtexsi A0 = 12arestes,laseva característicad’Euler-Poincaréval χ0 = C0 V0 + A0 = 6 8 + 12 = 2ielseu gènereés g0 = (2 χ0)/2 = 0.

AcontinuacióveuremquantsmòdulsdeSonobesónnecessarisperconstruir laiteracióenèsimadel’esponjadeMenger Mn.

Inicialmenttenim K0 = 1cubdecostat L.Enferlaprimeraiteracióde l’esponjadeMengerdividimcadaarestaentrespartsiguals,aixícadaaresta aportaràdosnousvèrtexs.

Enlaprimeraiteraciódel’esponjadeMengerobservemquecadacara quadradadecostat L delcubinicialestransformaenvuitnovescaresquadradesdelongitud L/3;aaquestesnovescarescalafegirquatrecarescentrals interiorspercadacaradelcubinicial.Aixídoncs,laprimeraiteraciódel’esponjadeMenger M1 espotferamb C1 = 24 + 8C0 = 72mòdulsdeSonobe. Elnombred’aresteséseldobledelnombredecares A1 = 4C1/2 = 144. Percalcularelnombredevèrtexs V1 observemquecadaaresta A0 esdivideixentrespartsigualsi,pertant,cadaarestaaportaràdosvèrtexsen laiteració,alsqualscalafegirelsvèrtexs V0 delcubinicial,aixícomels nousvèrtexsqueapareixenalapartcentraldelcub,quatrepercadacarainicialivuitmésalcentredelcub V1 = V0 + 2A0 + 4C0 + 8 = 64;així doncs, χ1 = C1 A1 + V1 = 72 144 + 64 =−8i,pertant,elseugènere és g1 = (2 χ)/2 = 5.

Defet,aquestargumentésvàlidperaqualsevoliteracióiensproporciona fórmulesrecursivespercalcularelsvalorsdelnombredecares,arestes,vèrtexs, característicad’Eulerigèneredelasuperfíciedecadaiteració Mn

Nombredecares

Nombred’arestes An = 2Cn

Nombredevèrtexs

Característicad’Euler χn = Vn An + Cn

Gèneredelasuperfície gn = (2 χn)/2

Utilitzantlesrecurrènciesanteriors,iavaluantpolinomisciclotòmicsen duesvariables,espodemdemostrarperinducciólessegüentsfórmulesque donenelsvalorsexactesenfuncióde n:

Nombredecares Cn = 4 · 8n + 2 · 20n

Pertant,elsvalorsdelnombredemòdulsdeSonobenecessarisperconstruir l’enèsimaiteraciódel’esponjadeMengerielgèneredelasuperfícievenen donatsperlessuccessions {Cn}n∈N ={6, 72, 1056, 18048, 336384, 6531072,..., ∞}, {gn}n∈N ={0, 5, 81, 1409, 26433, 514625,..., ∞}

Prenentlímitquan n tendeixa ∞,deduïmquel’esponjadeMenger M∞ té unasuperfícied’àreainfinitaambvolum0.

AplicantelteoremadeRingel-Youngs[11],veiemqueelnombremínimde colors(nombrecromàtic)necessarisperacolorirlasuperfíciedonadaperl’enèsimaiteraciódel’esponjadeMengersensequeduescaresadjacentstinguinel

mateixcolorvedonatperlafórmulasegüent,conjecturadaperHeawood el1891,quetansolsdepèndelgèneredelasuperfície

H(gn) = 7 + 1 + 48gn 2 =

Elsprimersvalorsd’aquestasuccessiódenombrescromàticssón:

{H(gn)}n∈N ={4, 11, 34, 133, 566, 2488, 11056, 49323, 220373, 985176,...,∞}.

3.4Cubsdepapericubsaritmètics

JuanManuelGimenoViguera,eruditdelapapiroflèxia,vaproposarl’any1992 untrencaclosquesgeomètric-papiroflècticinspiratenlaigualtat 63 = 53 + 43 + 33 .

Aquestjocconsistiaenlaconstrucciódevuitpecesfetesambelmòdulde Sonobe-Takahama,quecaliareordenarperaconseguirelsquatrecubs.

Unasegonaigualtatambcubsbenconegudaésl’exempledeSrinivasa Ramanujan,queexpressaelnombre1729deduesformesdiferentscomala sumadedoscubs

1729 = 13 + 123 = 93 + 103 .

AquestaigualtatielTaxiCabquelavainspirarapareixenenlapel lícula biogràfica L’homequeconeixial’infinit,2015.

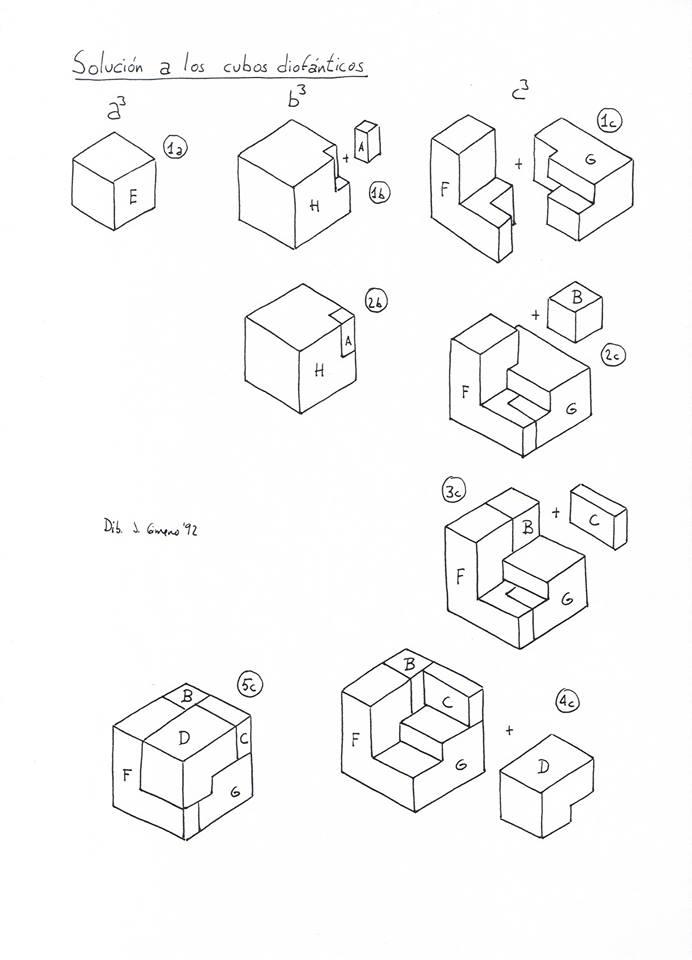
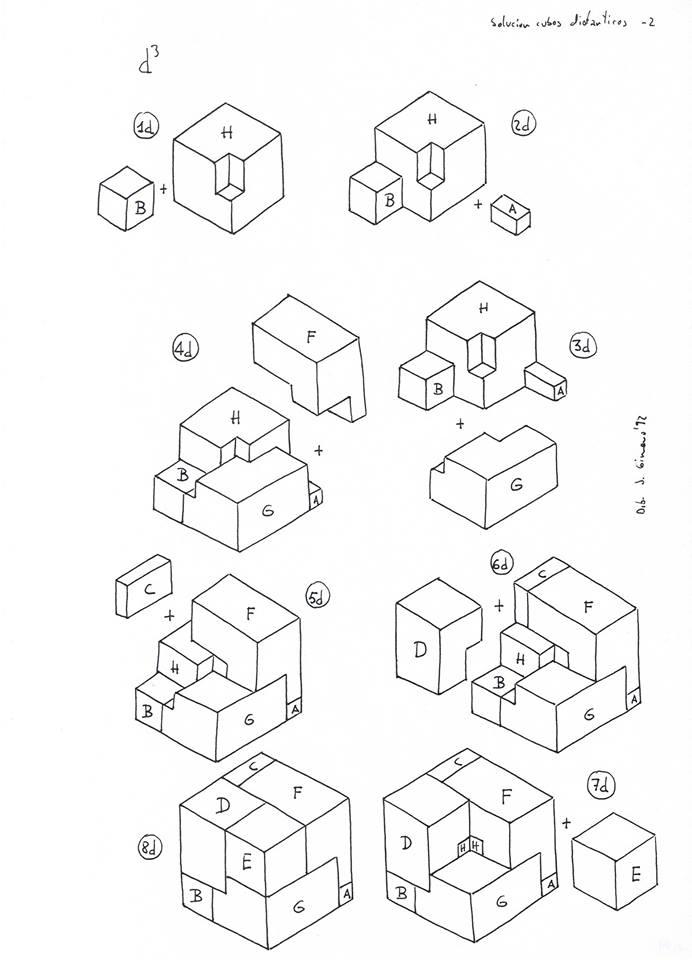
Peròcomespodendeduiraquestesoaltresigualtatsambnombresnaturals?

Observemquelesigualtatsnumèriquesanteriorssónsolucionsenteresdela superfíciecúbica

(5)

L’estudiprofunddelessuperfíciescúbiquescomençal’any1849,quan ArthurCayleydemostraquetotasuperfíciecúbicallisasobreelcos C téun nombrefinitderectesielmateixanyGeorgeSalmonprecisaqueelnombrede rectesésexactament27.Caldestacartambéelstreballsd’AlfredClebsch,que el1871descobreixunasuperfíciecúbicaqueconté27rectesreals.Aquesta superfíciecúbicaespotexpressarambl’equació

Observemqueles27rectesdelasuperfície (5) venendonadesperlesequacions

Li,j ={x + ξiy = 0,z + ξj w = 0}, L′ i,j ={x + ξiz = 0,y + ξj w = 0}, L′′ i,j ={x + ξiw = 0,y + ξj z = 0}, (6) on ξ ésunaarrelprimitivacúbicadelaunitatielsíndexs {i,j} prenenels valors {0, 1, 2}.Tresd’aquestesrectes (i = j = 0) tenencoeficientsenelcos delsnombresracionals Q ilesaltres24rectes(i ≠ 0o j ≠ 0)tenencoeficients enelcos Q(√ 3).Espodenobtenirparametritzacionsdelasuperfície (5) triant duesrectesquenoestallind’aquestacol leccióde27rectes(6).

NoamElkiesiIrenePolo-Blancovantrobar,respectivament,lesparametritzacionssegüents:

Φ : P2 → F

(r : s : t) → ( (s +

Ψ : P2 → F

(r : s : t) → (

Defet,existeixentransformacionslineals f , g quefanqueaquestesdues parametritzacionssiguinequivalents:

f =

, on f : P2 → P2 (r : s : t)

Donantvalorsalsparàmetres (r : s : t) en (7),podemobtenirnovesrelacions numèriquesentrecubsdenombresnaturals: r = 1 s = 1 t = 1:63 = 53 + 43 + 33 , r = 1 s =−1 t = 1:93 = 83 + 63 +

L’exempledeRamanujanespotobtenirambelssegüentsvalorsdelsparàmetres

Eneljardímatemàtic,ubicatentreelsedificisTorretamaritiTorrepinet delcampusdelaUniversitatMiguelHernándezd’Elx,podeuveureunaesculturade3metresd’alturafetaambpedranaturaldelasuperfíciecúbica w(x + y + z)2 + xyz = 0.Aquestasuperfícietéquinzerectesiunúnicpunt

singular (0:0:0:1).L’esculturafourealitzadal’any2009perl’escultormurcià CayetanoRamírezLópeziésconegudapopularmentcoma Damatemàtica per lasevasemblançaamblaDamad’Elx.Aquestescultorvarestaurarl’any2005la col.lecciódesuperfíciescúbiquesdelaUniversitatdeGroningen;enparticular, vaferambescaiolaiambresinalasuperfíciecúbicadeCayleydefinidaper l’equació xyz + yzw + zwx + wxy = 0.LacúbicadeCayleyténourectesi quatrepuntssingulars,queéselmàximnombredepuntssingularsquepot tenirunasuperfíciecúbica.TambévaferunsmodelsenpolièsterdelasuperfíciedeClebsch,onespodenveureclaramentles27rectesreals,id’altres superfíciescúbiquesquevanserexposadesenelXXVCongrésInternacional deMatemàtiques,celebrataMadridl’any2006,elmateixcongrésenquèel matemàticrusGrigoriPerelmanvarebutjarlamedallaFields.Posteriorment esvaferunaexposicióitinerantsotaeltítol Artimatemàtiques ambaquestes esculturessobresuperfíciescúbiquesialtresescultures,comunaampollade Klein,unnàutilbasatenlaproporcióàuria,algunscargolsambformesespirals iunromanescoperil.lustrarelconceptedefractal.

DuesesculturesdeCayetanoRamírez

ActualmentlesesculturesdelessuperfíciescúbiquesdeCayetanoRamírez estrobenenelMuseuDidàcticiInteractiudeCiènciesdelBaixSegura(MUDIC, http://www.mudic.es)ubicatal’EscolaPolitècnicaSuperiord’Orioladela UniversitatMiguelHernández(Elx)idirigitperlamatemàticaCarmenPerea. Finsarahemvistqueexisteixeninfinitscubsnaturalsqueespodendescompondrecomasumadetrescubsnaturalsnonuls.Aquestaafirmaciós’il.lustrava ambuntrencaclosquesqueutilitzavaelmòduldeSonobe.Encanvi,nopodem feruntrencaclosquessemblantambaquestmòdulperdescompondreuncub comasumadedoscubs.Enefecte,comvadirPierredeFermatel1635:

Cubumauteminduoscubos,autquadrato-quadratuminduosquadratoquadratos,etgeneraliternullamininfinitumultraquadratumpotestatemin duoseiusdemnominisfasestdividerecuiusreidemonstrationemmirabilem sanedetexi.Hancmarginisexiguitasnoncaperet.

DamatemàticaCúbicadeClebsch

Aquestaéspossiblementlafrasemésfamosadelesmatemàtiquesiactualmentesconeixcoma darrerteoremadeFermat. Durant359anyselsmatemàticsvanintentardemostrarsenseèxitaquesta afirmacióquePierredeFermat(BèumontdeLomanha,1601-Castres,1665)va ferel1635.Elcas n = 4espotdemostraramblatècnicadeldescensinfinit; aixídoncs,perdemostrareldarrerteoremadeFermatéssuficientestudiarel cas n = p nombreprimeri,amés,podemsuposarque x, y, z sónnombres naturals,nonulsidosadoscoprimersentresi. ∀x,y,z ∈ N −{0},xp + y p ≠ zp,p ≥ 3

Delsnombrososarticlesdedicatsaaquestteorema,caldestacareltreball delamatemàticafrancesaSophieGermain,queenunacartadirigidaaGaussi ambdata12demaigde1819intentaferunademostraciógeneralperatots elsexponentsdeldarrerteoremadeFermat.LestècniquesdeSophieGermain vanpermetredemostrarelteoremaperatotselsnombresprimers p< 100 idividireldarrerteoremadeFermatendoscasos: p ∤ xyz (cas1)i p | xyz (cas2).

Aprincipisdelsegle xx elstreballsdeDmitriMirimànov(1905)id’Arthur Wieferich(1909)redueixenelcas1atrobarlessolucionsdelacongruència: 2p ≡ 2 (mod p2).

Defet,tansolsesconeixenduessolucions p = 1093(Meisner,1913)i p = 3511(Beeger,1921)delacongruènciadeWieferichpera p< 4·1012.Pertant,el cas1deldarrerteoremadeFermatéscertperagairebétotprimer p< 4 1012

PeròlademostraciódefinitivadeldarrerteoremadeFermatcomença l’any1986ambeltreballdeGerhardFrey,queassociaaunapossiblesolució ap + bp = cp ambnombresentersnonulsdel’equaciódeFermat,la corbael.líptica y 2 = x(x ap)(x + bp).

Estudiantlessevespropietats,Freydemostraqueaquestacorbael.líptica nopotsermodular,encontradelaconjecturadeShimura-Taniyama-Weil:tota corbael.lípticaésmodular.ElcercleesvatancareldiadelarevetlladeSant Joandel’any1993enelSirIsaacNewtonInstitutedelaCambridgeUniversity, quanAndrewWilesvafinalitzartresconferènciesendiesconsecutiussotael títol Modularforms,ellipticcurvesandGaloisrepresentations afirmanthaver demostratlaconjecturadeShimura-Taniyama-Weili,comacorol.lari,eldarrer teoremadeFermat.Alcapdepoctempselsexpertsvantrobarunforaten lademostració,quevaserresoltapelmateixWilesielseudeixebleRichard Taylor.Finalment,lademostraciórigorosafoupublicadapelsdosautorsel maigde1995enels AnnalsofMathematics.EltreballdeWilesesredueixa estudiarelspuntsde3-torsióide5-torsiód’unacorbael líptica.Posteriorment, NoamElkiesvaferunasimplificaciódelademostracióivaprovarquepel darrerteoremadeFermatnocaliaestudiarelspuntsde5-torsió.

Acontinuacióveuremunademostracióelementaldeldarrerteoremade Fermatperalcas1del’exponent p = 3.

Proposició 9 Siguin x,y,z ∈ N nonulstalsque x3 + y 3 = z3.Aleshores, 3 | xyz.

Prova. Siguin x, y, z tresnombresnaturals,nonuls,2a2coprimersino divisiblesper3quecompleixenl’equaciódeFermatpera p = 3.

x3 + y 3 = z3,x,y,z ∈ N −{0}, 3 ∤ xyz. (8)

Lasumadedoscubs x3 + y 3 espotdescompondrecomelproducte (x + y)(x2 xy + y 2) dedosfactors.Aquestsfactorsnosóndivisiblesper3 perquèelseuproducteval z3,quenoésdivisibleper3.Amés,tambésón coprimers,enefecte, mcd(x + y,x2 xy + y 2) = mcd(x + y, 3xy) = 1;per tant,espodenexpressarcomapotènciescúbiques.Unraonamentanàleges potaplicarperalesdiferènciesdedoscubs z3 x3 i z3 y 3 . x + y = z3 1 ,x2 xy + y 2 = z3 2 ,z1z2 = z, z x = y 3 1 ,z2 + zx + x2 = y 3 2 ,y1y2 = y, z y = x3 1 ,z2 + zy + y 2 = x3 2 ,x1x2 = x.

Aratenimsisnousvalorsnonuls (x1,y1,z1,x2,y2,z2) quesón2a2coprimersinodivisiblesper3.Defet,elsvalors (x2,y2,z2) nointervenenenla restadelademostració.

Delestresprimeresequacionslinealspodemaïllarelsvalors x, y, z en funcióde x1, y1, z1 x = z3 1 y 3

Substituïmaquestescombinacionslinealsdecubsenl’expressió (8) imultipliquemper8,

Desenvolupantelscubsobtenim:

D’aquestadarreraigualtatesdedueixlacontradiccióque3ésuncubperfecte alconjuntdelsnombresracionals:

AlalocalitatoccitanadeBèumontdeLomanhapodeuvisitarlacasanatal deFermat,avuiconvertidaenmuseu,aixícomunmonumentdel’il.lustre matemàticalcostatd’unpreciósmercatcobertdefustadelsegle xv.Aquesta petitapoblacióestàsituadaauns60kmalnord-oestdeTolosadeLlenguadoc, onFermattreballavacomaadvocat.

4Mosaicsdepaper

Elsdiferentsmotiusdelsmosaicsdel’AlhambradeGranadasóndesdefa tempsunafontd’inspiracióperalacreacióartísticaimatemàtica.Enaquest palaudeladinastianassarita,construïtentreelssegles xiii i xv,espoden contemplardiferentsmotiusgeomètrics.Algunsd’aquestsmotiusesconeixen ambunnompropi:ocelletnassarita,osnassarita,aviónassaritaoratpenat nassarita.

Peròquèésunmosaic?Lasevaetimologiaensdiuqueaquestaparaula provédelllatí mosaicumopus,ésadir,unaobradelesmuses.Antiguescivilitzacionscomlagregaolaromanajafeienaquestescomposicionsdecoratives ambpetitespecesdediferentscolorsimaterialsanomenades tessel.les.Molts d’aquestsanticsmosaicsialtresdemésmoderns,comelsqueespodenveure enlesobresmodernistesd’AntoniGaudí,totilasevabellesa,notenencap tipusdesimetria.Tambéexisteixenmosaicsquemostrensimetries,comels mosaicsdelesvoreresdelpasseigdeGràciadeBarcelona,fetsambrajoles hexagonals,oelsmosaicsdelpatid’entradadel’Institutd’EstudisCatalans, elaboratsambrajolescatalanes.Desd’unpuntdevistamatemàtic,definirem unmosaicotessel laciócomunadivisiódelplasenseencavalcamentsnibuits mitjançantunaomésformesgeomètriques,tambéanomenades tessel.les.Per estudiarelsmosaicsrespondremlespreguntessegüents:Quinssónelsmosaics méssimples?Compodemcrearnousmosaics?Quantsmosaicsessencialment diferentsexisteixen?Compodemclassificarelsmosaics?

Elsmosaicsméssimples,queanomenarem regulars,s’aconsegueixenprenentcomatessel.labàsicatrestipusdepolígonsregulars:eltriangleequilàter, elquadratil’hexàgonregular.Elsmosaicsregularstenensimetriescentralso rotacionalsde60,90i120graus,respectivament,aixícomdiferentstipusde simetriesaxials,enquèelseixosdesimetriaformenentresianglesde30,45i 60graus,respectivament.

Mosaicsregulars

Espodenfernousmosaicsmodificantelsmosaicsregulars.Aquestaobservacióvaserdesenvolupadaenlesobresdel’artistaneerlandèsMauritsCornelius Escherenquedarimpressionatenlasevavisitaal’Alhambra,l’any1936,pels motiusdecoratiusdelsmosaicsnassarites.

Latessel.laosnassaritaespotaconseguirapartird’unquadrat.Endos costatsoposatsd’unquadratseccionemuntrapeziquetinguiperbasemajor elcostatdelquadrat,peralçàrialaquartapartdelalongituddelcostatdel quadratianglesinternsde45,135,135i45graus.Unimperlapartexterior delquadratlabasemajord’aqueststrapezisalsaltresdoscostatsdelquadrat, comesmostraenlafiguraanterior.

ElteoremadeFedorov(1891)ensdiuquetansolsexisteixendissettipus demosaicsessencialmentdiferents[5].Elsdiferentstipusdemosaicsvenen descritsperdissetgrupsdesimetries.Aquestsgrupstambéesconeixenamb elnomde grupscristallogràficsplans,perquèFedorovelsvatrobarestudiant laformaenquècristal.litzenalanaturaelsminerals.Existeixendiferentsnotacionsequivalentsperclassificarelsgrupscristal logràficsplans:Pólya,Conway, FejesThót-Cadwell,Niggli,Speiser,Shubinov-Koptsik,Wells-Bell,internacional llarga,etc.Enlataulasegüents’utilitzalanotacióinternacionalcurta.

Anglemínim

Existeixalgunareflexió? derotació

Sí No

360◦/6 = 60◦ p6m p6

360◦/4 = 900

360◦/3 = 120◦

360◦/2 = 180◦

360◦/1 = 0◦

Totselscentresderotacióestan p4 sobreelseixosdereflexió?

Sí:p4m No:p4g

Totselscentresderotacióestan p3 sobreelseixosdereflexió?

Sí:p31m No:p3m1

Existeixenreflexionsamb Existeixalgunareflexió eixosperpendiculars? amblliscament?

Sí No

Totselscentresderotacióestan pmg sobreelseixosdereflexió?

Sí:cmm No:pmm

Sí:pgg No:p2

Existeixalgunareflexióamblliscament Existeixalgunareflexió ambeixdiferentd’uneixdereflexió? amblliscament?

Sí:cm No:pm

Sí:pg No:p1

Al’AlhambradeGranadahihacatorzedelsdissettipusdemosaicssi estenenencompteelscolors[9]itotsdissetsinoestenenencompteels colors[8].

Acontinuacióesdescriuunmòduldepaperquepermetfermosaics.Aquest mòdulilessevesvariantsesconeixenambelnomde variacionsFroebel,pel fetquevaserutilitzatalsegle xix passatpelpedagogalemanyFredericFröbel enlesescolesKindergarten(jardinsd’infància).

Pas1Pas2Pas3Pas4Pas5

PlecsenvallPlecsenvallPlecsenmuntanyaMòdulfinal

Peraconseguirdiferentstipusdemotiusésnecessariutilitzarunpaperbicolor,comperexempleelpaperdetipuskami(blanc/color).Enelpas1 comencemamblacaradecoloraldavantiladecolorblancaldarrere;enel pas2pleguemverticalmentenvallelpaperperlameitatiperlaquartapart; enelpas3femelmateixqueenelpas2peròhoritzontalment;enelpas4 pleguemenmuntanyaelsquatrevèrtexsdelquadratcapalcentre,ienel pas5obtenimelmòdulfinalcol.lapsantelsquatrecostatsdelquadratcapa l’interior.

Uniódecincmòduls

Peraconseguirelsmotiusosnassaritaiaviónassaritacalferelssegüents plecsenelmòdulfinal.

Combinantelscolorsenelsmosaicsfetsamblatessel.ladel’osnassaritaes podenaconseguironzedelesdissetconfiguracionsdelsgrupscristal logràfics.

Ésclarqueeldesenvolupamentpladelcubtésisquadrats.Vistal’inrevés espotpensarqueelcubésunmosaictridimensionalformatpersistessel.les quadrades.D’aquestamanerapodemconstruirdiferentstipusdemosaics

cúbicsfentmodificacionsenelquadratllisinicial.Perexemple,siconsiderem sistessel.lesdel’osnassaritaodel’aviónassarita,espotferunmosaiccúbic tridimensionalambcadascund’aquestsmotius.

DesenvolupamentdelcubDesenvolupamentdelcubDesenvolupamentdelcub osnassaritaaviónassarita

Espodenconstruircubsambelstresmotiusanteriorsambsismòduls idènticsfentdeterminatsplecs.Elprimermotiu,unquadratllis,escorrespon alcubdeSonobe.Elcubaviónassaritaespotferambelsplecssegüents:

Pas1Pas2Pas3Pas4

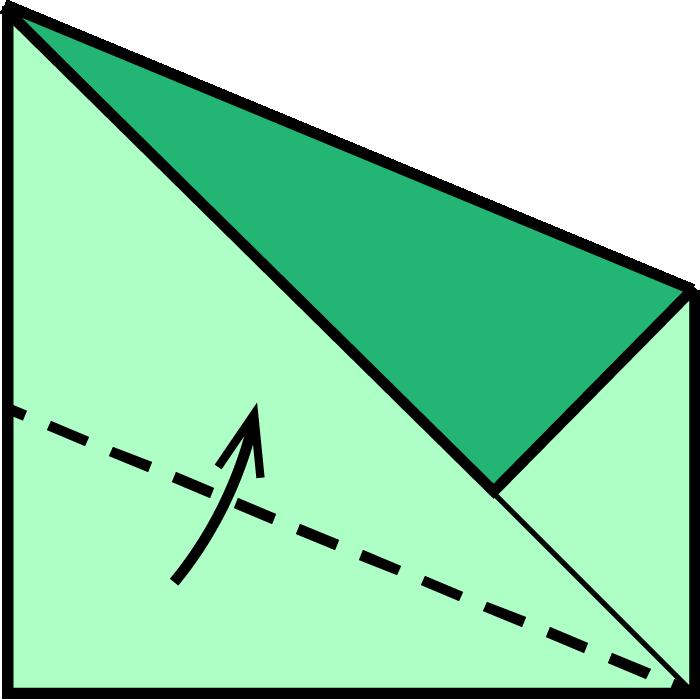
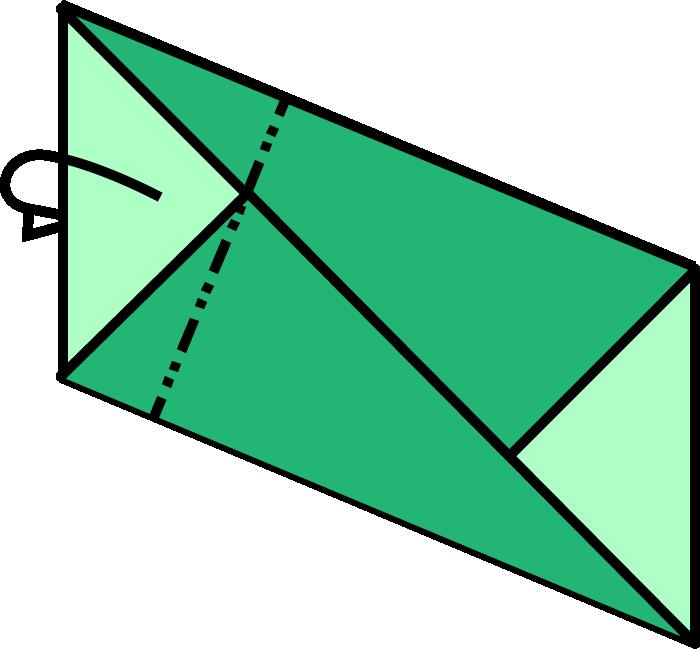
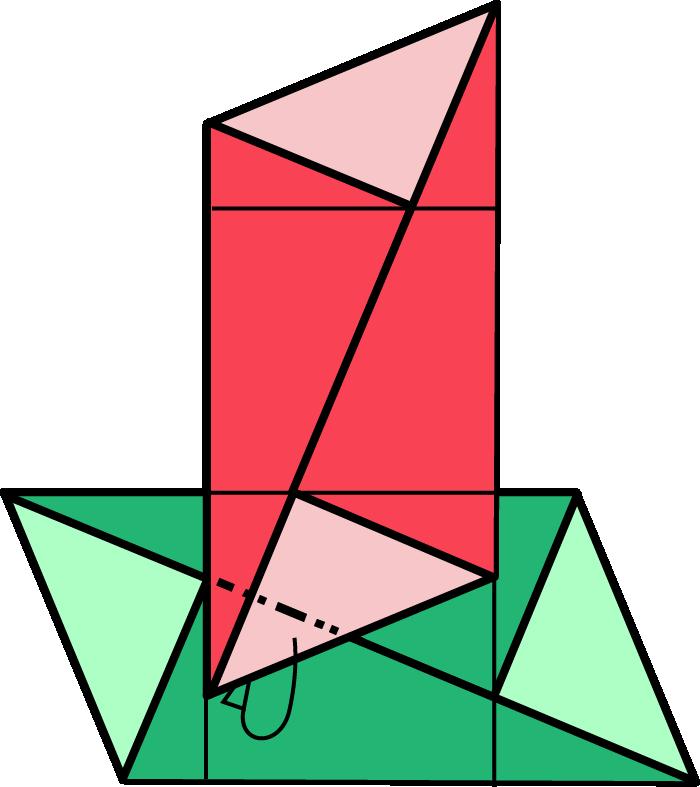
Pas5Pas6Pas7 MòdulfinalUniódeUnióde dosmòdulssismòduls

Sialaconstruccióanterior,enllocdeladiagonal,prenemunsegmentque passipelcentredelquadratambpendentaleatori m ∈ R,aleshoresobtenim unainfinitudnonumerabledemotius.

Pas1Pas2Pas3Pas4

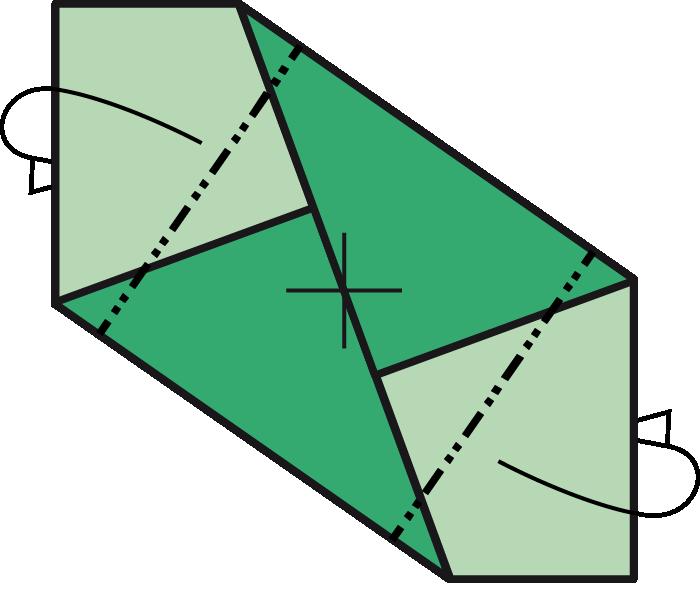
Pas5Pas6Pas7

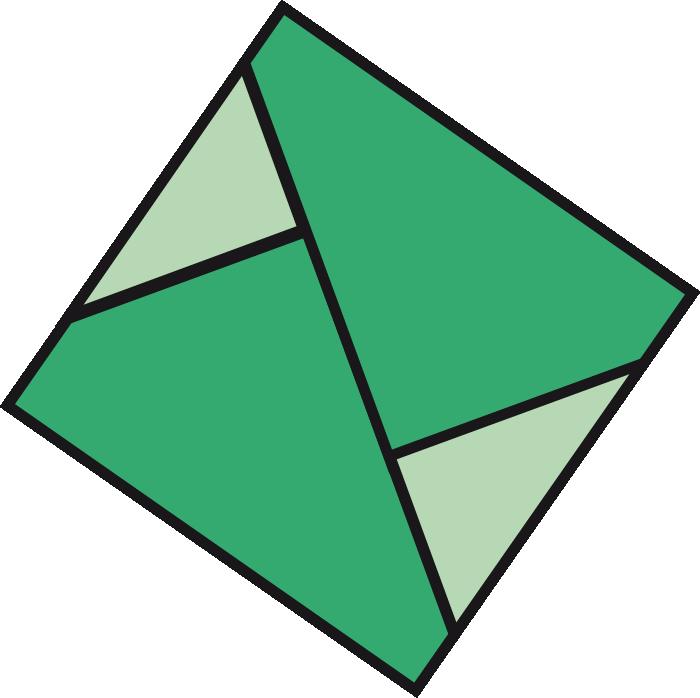
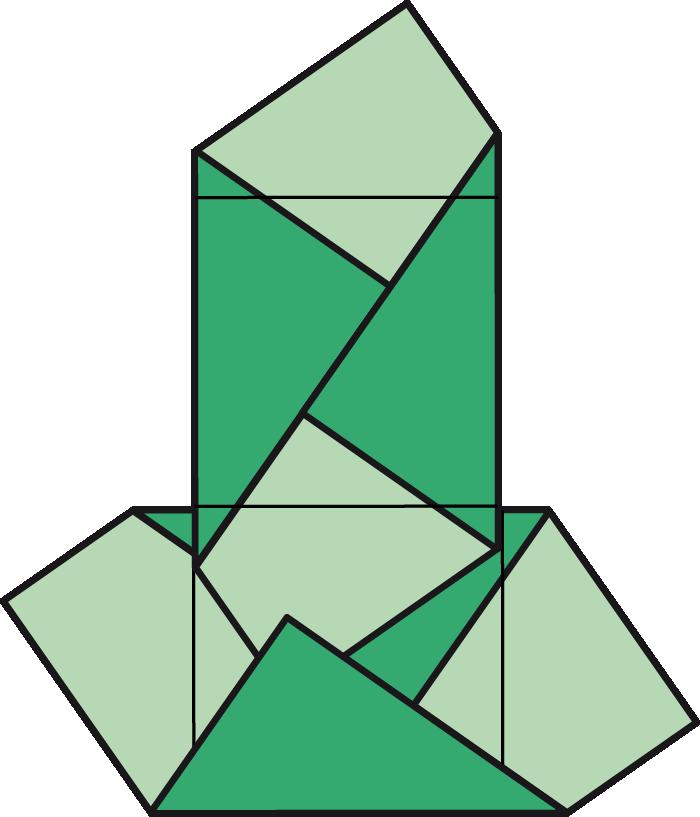
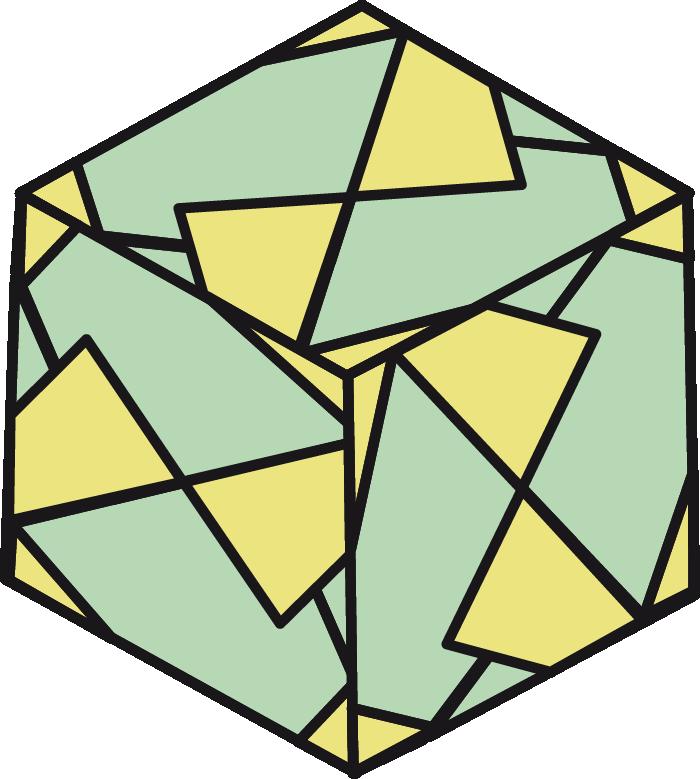
MòdulfinalUniódeUniódeCubmodular dosmòdulssismòdulsmosaicaleatori Latessel.laciódelcubambelmotiuosnassaritaespotferambelsplecs següents:

Pas1Pas2Pas3Pas4

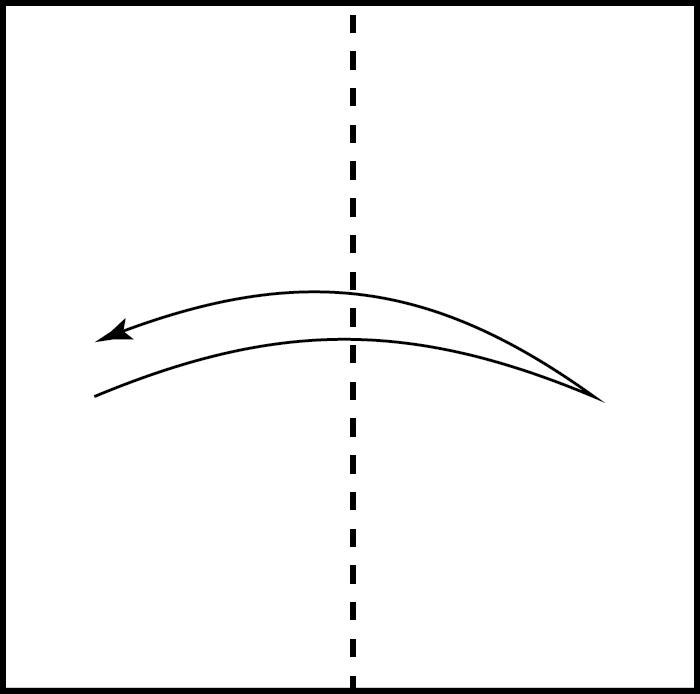
Pas5Pas6Pas7Pas8

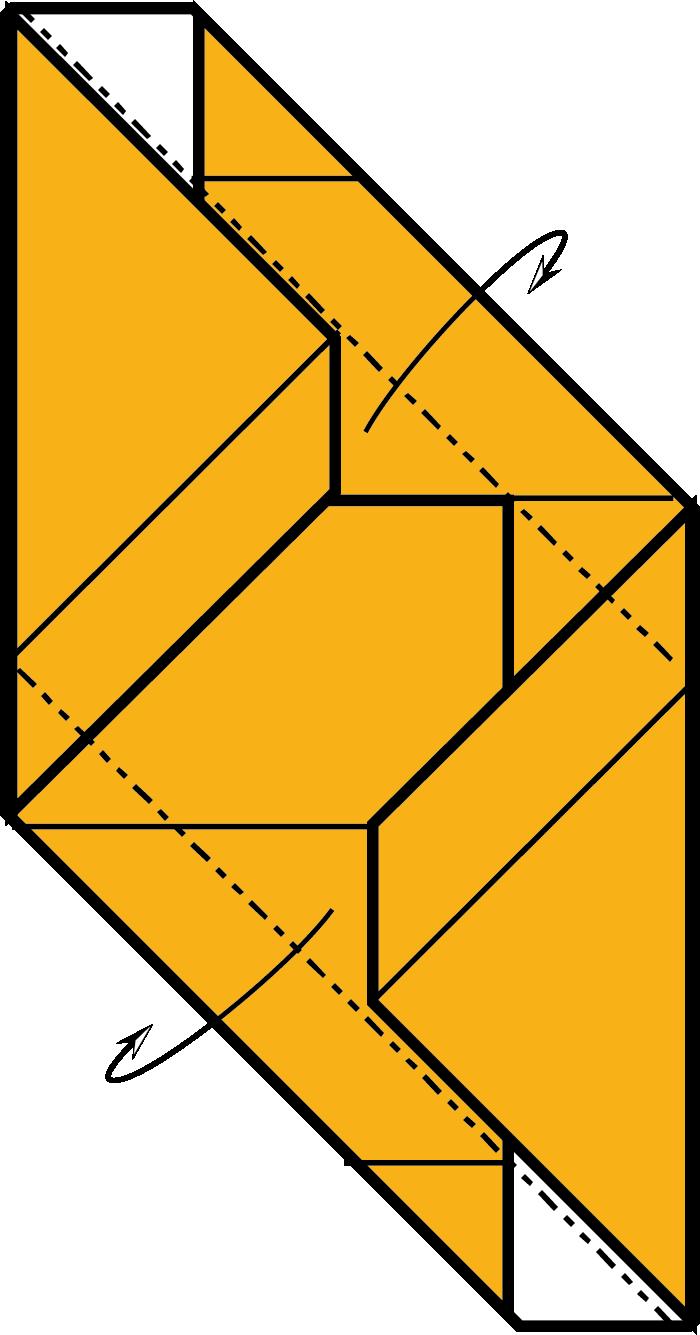
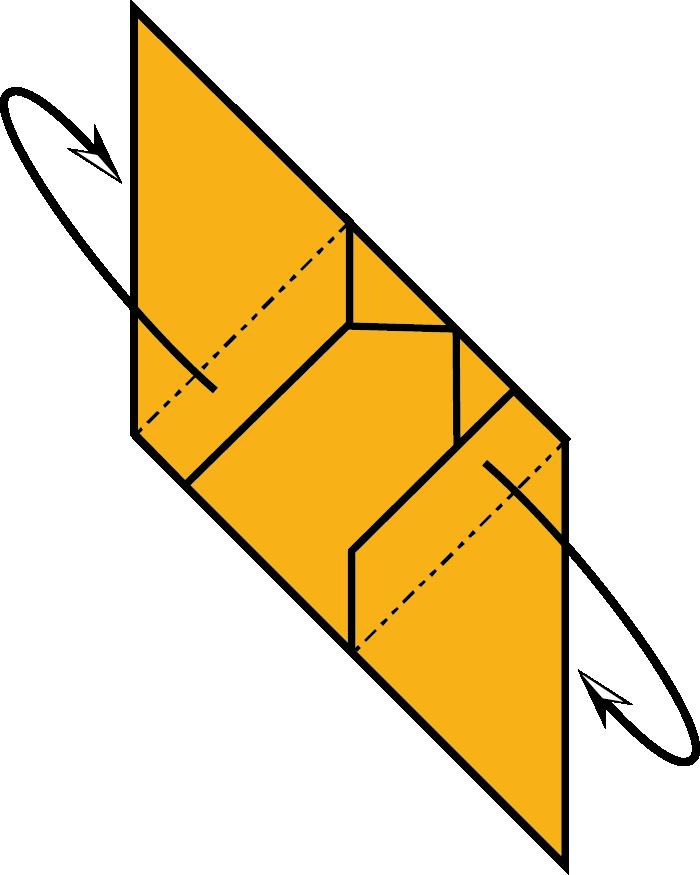
Pas9Pas10

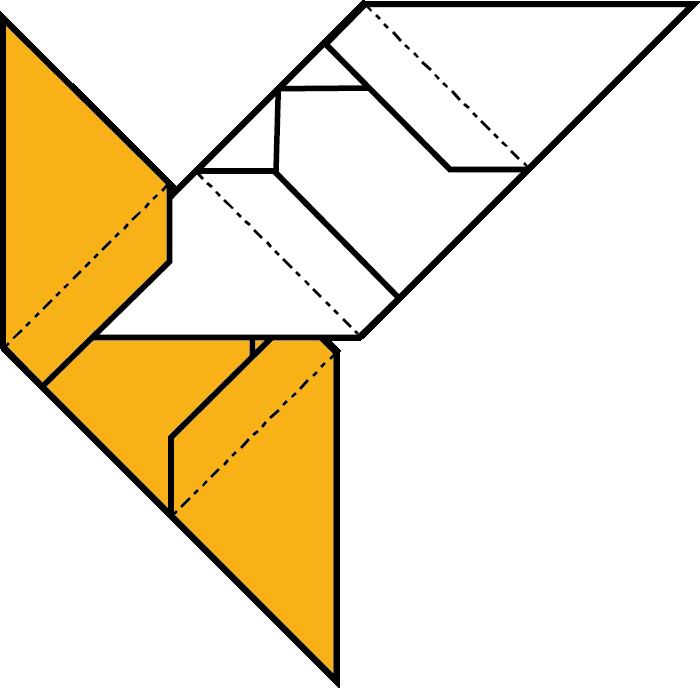
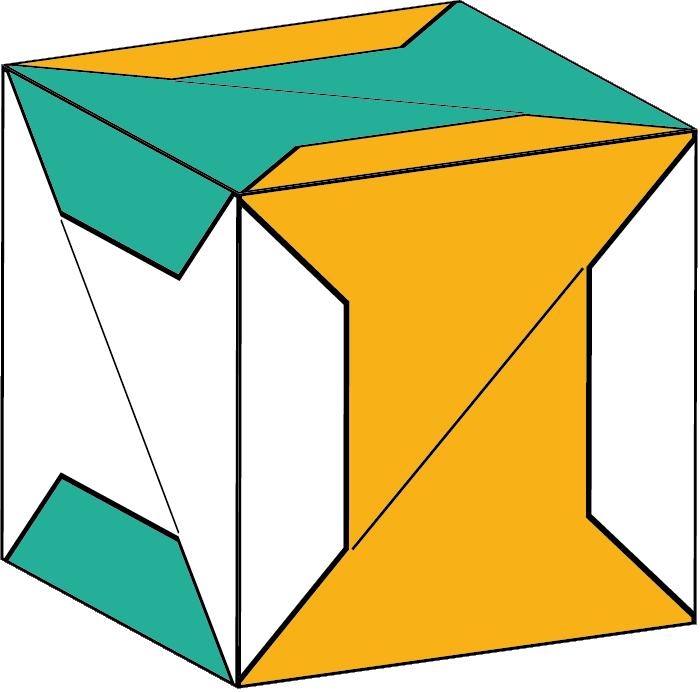
Finalitzemaquestadissertacióambunafiguranomodularmultiforme:la construcciód’untetràedreobtingutmitjançantelcol.lapsed’unocelletnassarita tridimensional.

Pas1Pas2Pas3Pas4

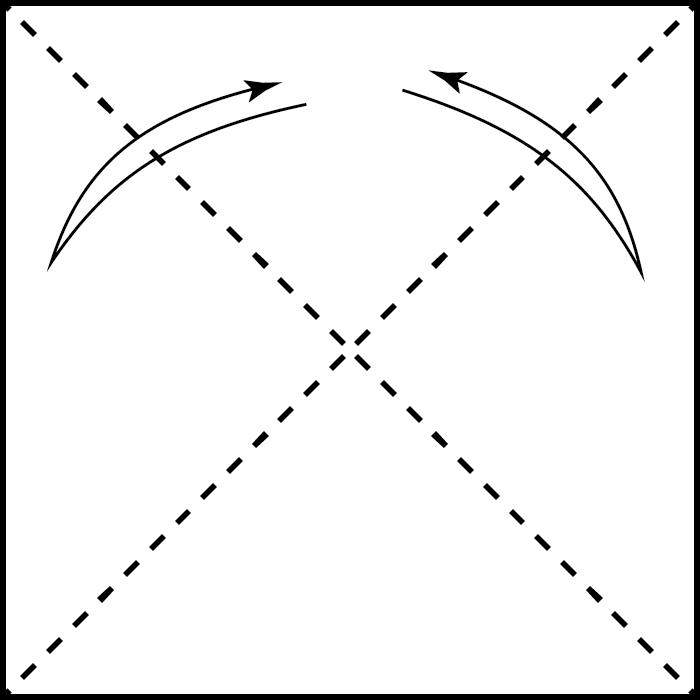
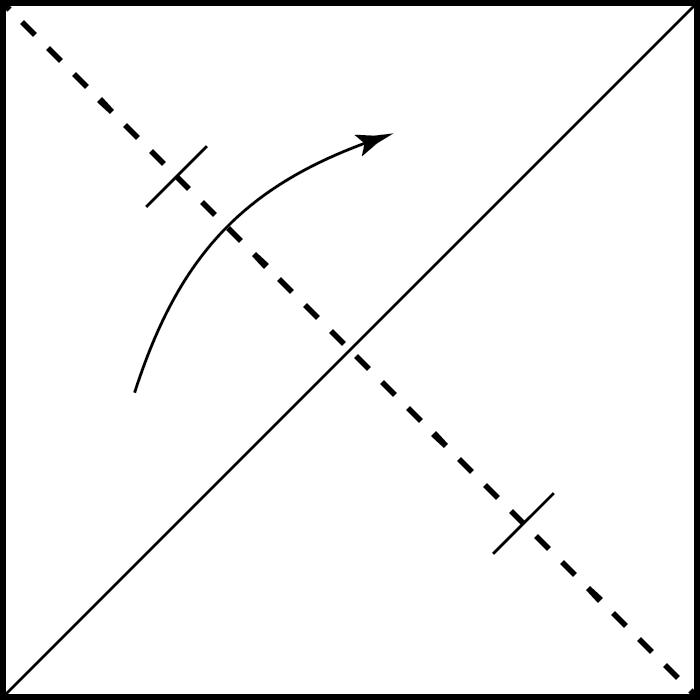
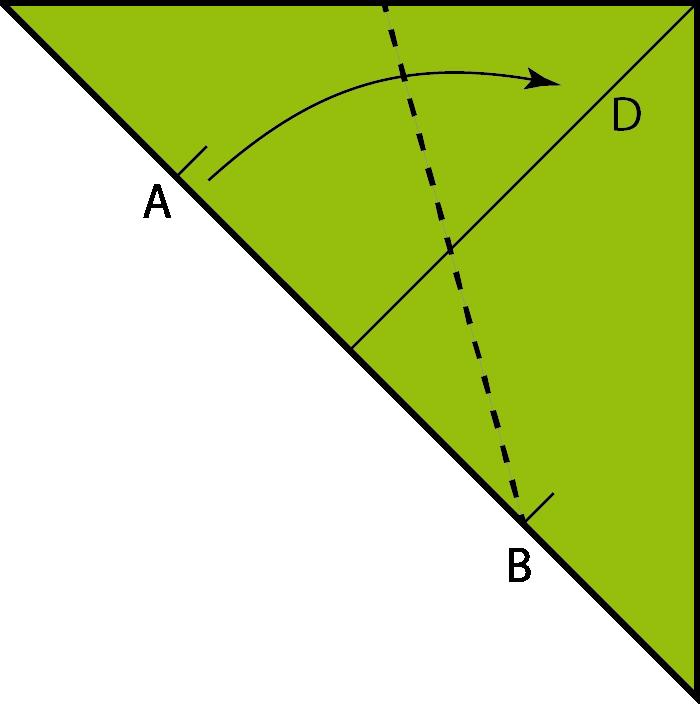
Pas5Pas6Pas7Pas8

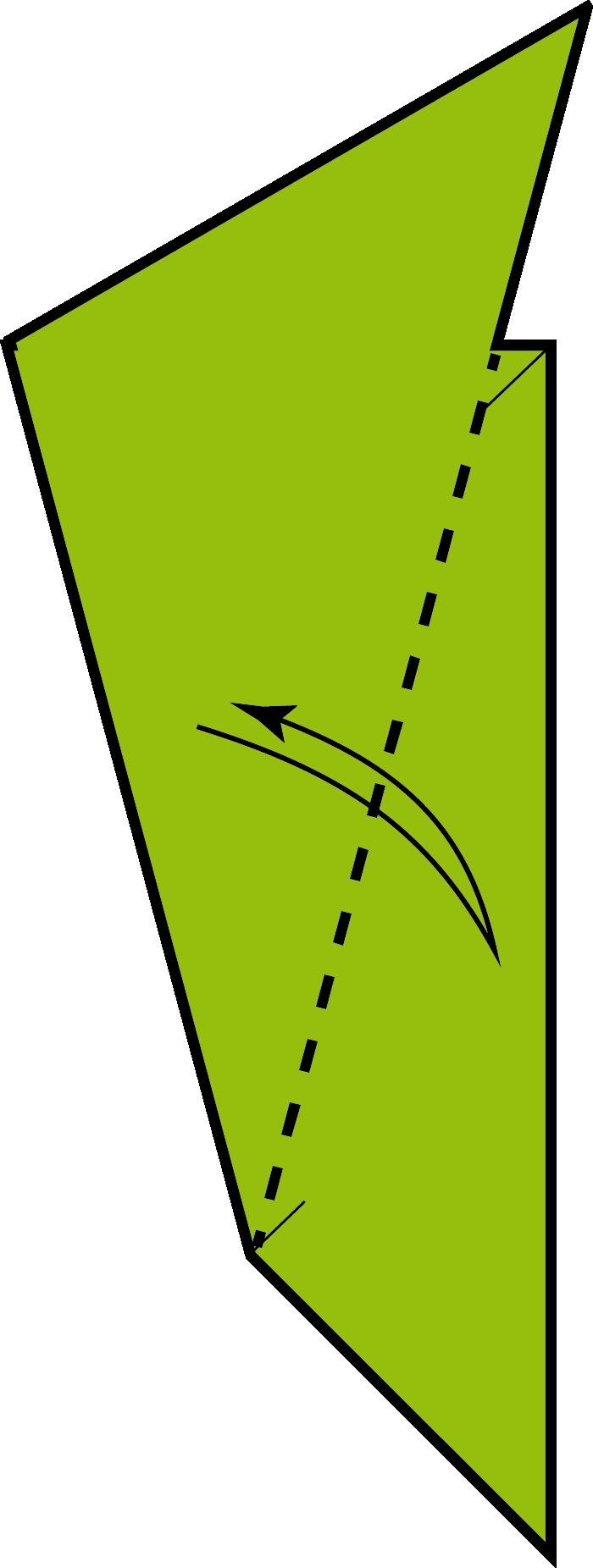
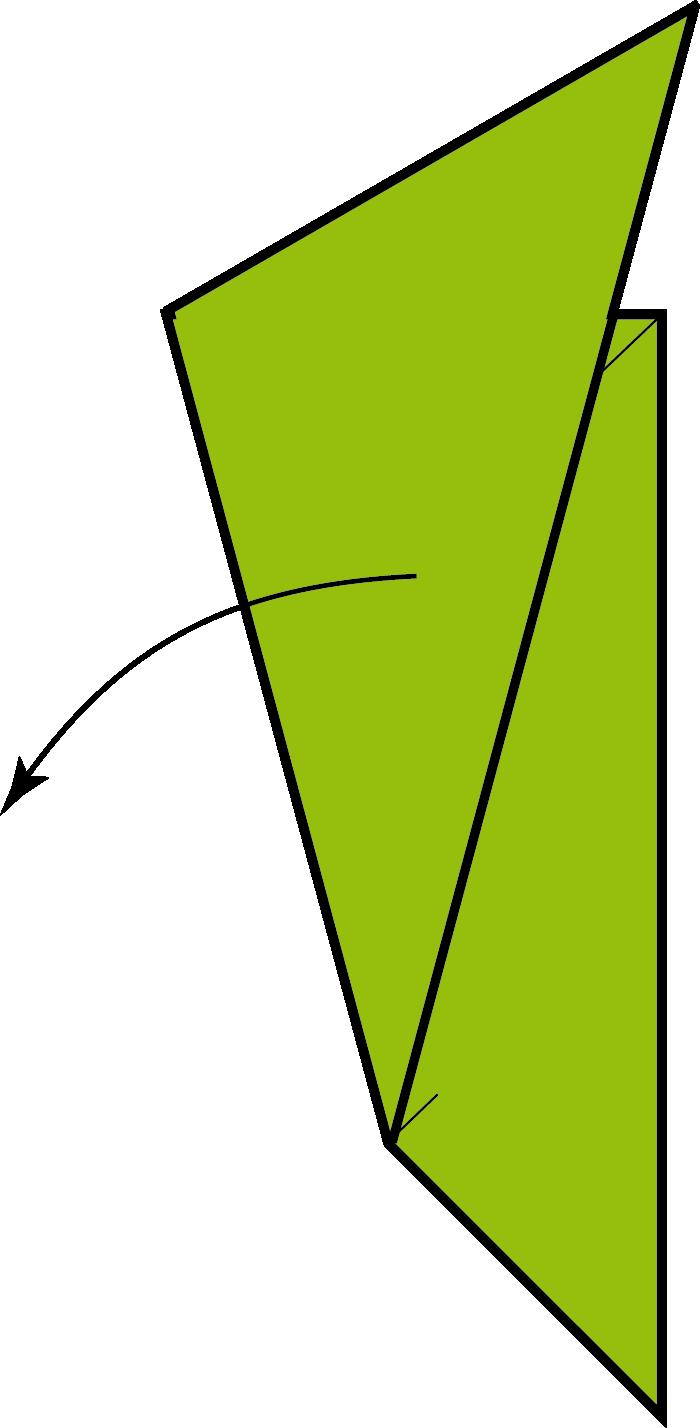
Pas9Pas10Pas11Pas12

Pas13Pas14Pas15Pas16

Pas17Pas18Pas19Pas20

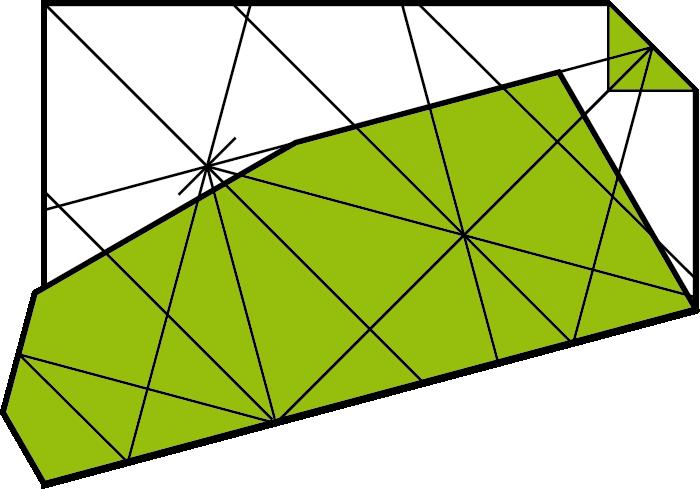
Pas21Pas22Pas23Pas24

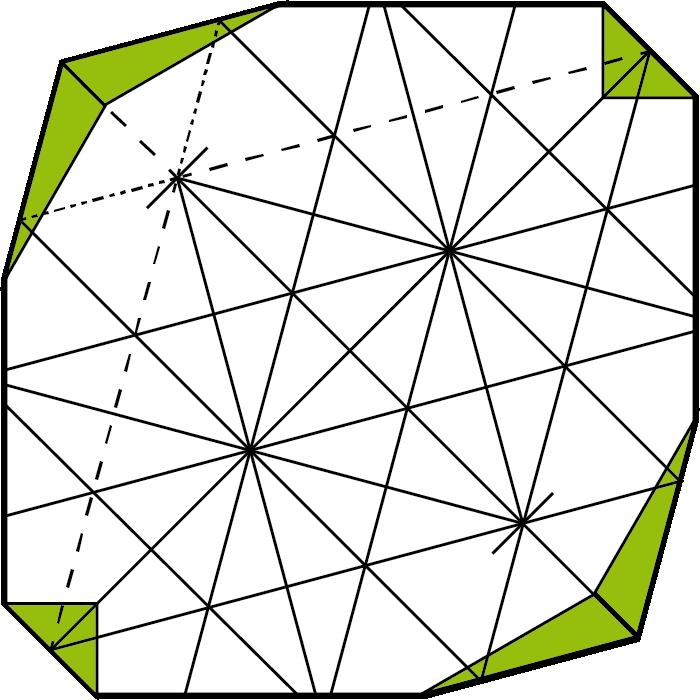
Pas25Pas26Pas27

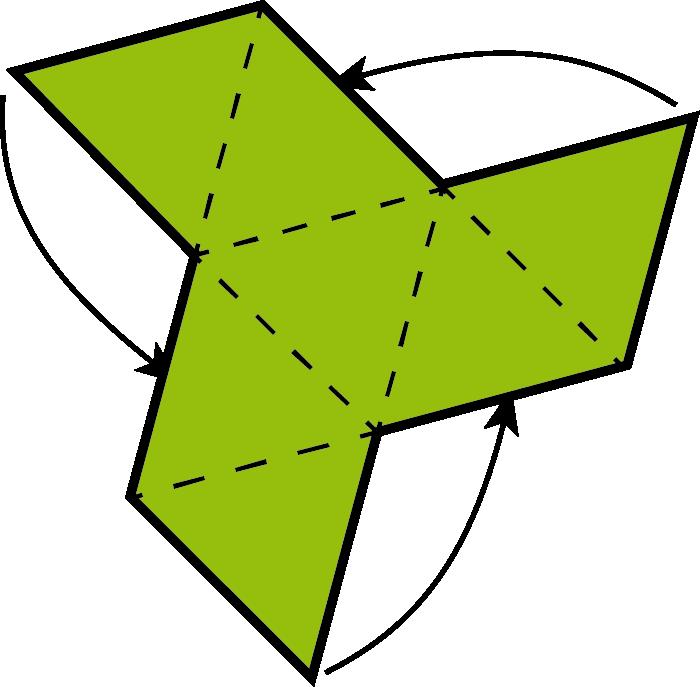
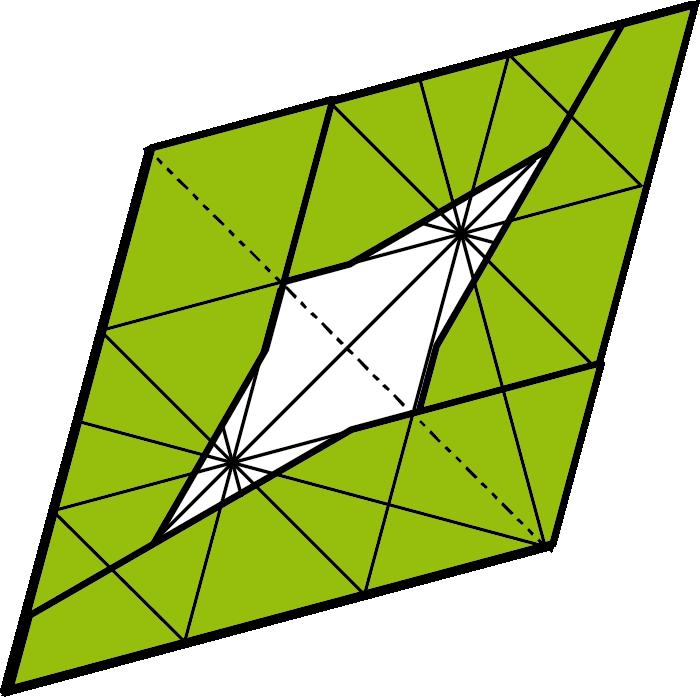
OcelletnassaritaTetràedre

Agraïments

AMinervaCiruelaperintroduir-meenelmóndelapapiroflèxia;aJuanGimeno perlessevesconversessobreeltema;aJoanSallasperconvidar-meaexperimentaridesenvoluparaquestesideesenlesjornadesFALTIKaFriburgde BrisgòviaienlesjornadesAPLECaBadalona;aCarmenSprungperdeixar-me publicarelsseusdiagrames,iaDavidBrillperfacilitar-melaimatged’una sessiódelSosakuOrigamiGroup67enquèapareixenToshieTakahamai MitsunobuSonobe.

Referències

[1] Anònim. Unahojadepapel.2aed.Barcelona:MiguelA.Salvatella,1964.

[2] Cromwell,P.R. Polyhedra.Cambridge:CambridgeUniversityPress,1997.

[3] Diferentsautors Guíaprácticadelartemanual.Barcelona:Kairós,1977.

[4] Freudenthal,H.;VanderWaerden,B.L. «OvereenbeweringvanEuclides». SimonStevin,25(1947),115–128.

[5] Fyodorov,Y. «Simmetrijanaploskosti». ZapiskiImperatorskogoSantPetersburgskogoMineralogicheskogoObshchestva,s.2,28(1891),245–291.

[6] Kasahara,K.;Takahama,T. Papiroflexiaparaexpertos.Madrid:EDAF, 2011.

[7] MillerJ.C.P. Polyhedron.11aed.EncyclopædiaBritannica.NovaYork: UniversityPress,1910.

[8] Montesinos,J.M. ClassicalTessellationsandThree-Manifolds.Berlín: Springer-Verlag,1987.(Universitext)

[9] Müller,E. «Elestudiodeornamentoscomoaplicacióndelateoríade gruposdeordenfinito». Euclides(Madrid),6(1946),42–52.

[10] Plató. TimeuCrítias.Barcelona:Edicions62,2010.

[11] Ringel,G.;Youngs,J.W.T. «SolutionoftheHeawoodmap-coloring problem». Proc.Nat.Acad.Sci.U.S.A.,60(1968),438–445.

[12] Solórzano,V. Papirolas.Tratadodepapiroflexia.Figurasgeoméricasde papeldoblado.BuenosAires:LibreríadelaSalud,1939.

[13] Solórzano,V. Tratadodepapiroflexiasuperior.BuenosAires,1945.

[14] Sommerville,D.M.Y. «Semi-regularnetworksoftheplaneinabsolute geometry». TransactionsoftheRoyalSocietyofEdinburgh,41,part iii,29, 725–747.

[15] SosakuOrigamiGroup’67. AtarashiiOrigamiNyumon.Tòquio:Nihon Bungeisha,1970.

[16] vonStaudt,K. Geometriederlage.Nuremberg:VerlagvonBauerund Raspe,1847.

[17] Takahama,T. CreativeLifewithCreativeOrigami1.1974.[Enjaponès]

[18] deUnamuno,M. Amorypedadogía.Apuntesparauntratadodecocotología.Barcelona:EspasaCalpe,1964.(Austral;141)

[19] VerEecke,P. Pappusd’Alexandrie.Lacollectionmathématique.París: Blanchard,1982.

CentredeformaciódePersonesAdultesRafaelFarré(MolinsdeRei)

DepartamentdeMatemàtiques

UniversitatAutònomadeBarcelona jaume.coll.guerrero@uab.cat

ButlletídelaSocietatCatalanadeMatemàtiques Vol.39,núm.1-2,2024.Pàg.73–102. DOI:10.2436/20.2002.01.115

Puntsracionalsencorbesel.líptiques

XavierGuitartiMarcMasdeu

Resum: Lescorbesel.líptiquessónundelsobjectesmésestudiatsenteoriade nombresactualment.Esdescriuenperequacionscúbiquesiallòquelesdistingeixdela restadecorbes—ilesfatanfascinants—ésl’estructuraalgebraicatanricaquepresenta elconjuntdelessevessolucions.Aquestarticletécomaobjectiuexplicarquèsónles corbesel líptiquesiexploraralgunesdelessevespropietatsmésimportants,quesovint estrobenentreelsresultatsmésrellevantsdelesmatemàtiquesdelssegles xx i xxi, aixícomalgunesdelesconjecturesencaraobertesiqueguiengranpartdelarecerca actual.Persituar-lesenuncontexthistòriciconceptualmésampli,lespresentemcom uncasparticulard’equacionsdiofàntiques,untemafonamentalitransversaldinsla teoriadenombres.

Paraulesclau: equacionsdiofàntiques,corbesel.líptiques,puntsdeHeegner,integració p-àdica,puntsdeStark-Heegner.

ClassificacióMSC2020: 14H52,11G05.

1Equacionsdiofàntiques

Undelstemescentralsenteoriadenombresésl’estudideles equacions diofàntiques,enquèhomestàinteressatenlessolucionsenteresoracionals d’equacionspolinòmiquesambcoeficientsenters.Demaneramésprecisa,una equaciódiofànticaésunaequaciódelaforma

F(x1,...,xn) = 0, (1.1)

on F ésunpolinomiambcoeficientsenters,ivolemdeterminarlessolucions enquètoteslescomponentsviuena Z o,alternativament,a Q.Perexemple, ( 1, 0) ésunasolucióenteradel’equaciódiofàntica

x2 + y 2 1 = 0, (1.2)

i ( 3/5, 4/5) n’ésunasolucióracional.Defet,iaixòhoveuremmésendavant, aquestaequaciódiofànticatéinfinitessolucionsracionals.

Elterme diofàntic fareferènciaalmatemàticDiofantd’Alexandria,quevisquédurantelsegle iii ifeu,entrealtres,untractatd’aritmèticaenquèestudià problemesqueesresolenambaquestesequacions.Veiem,doncs,quel’interès perlesequacionsdiofàntiquesvedemoltlluny.Alllargdelssegles,matemàtics il lustres,comaraFermat,EuleroGauss,n’hantractatcasosconcretsi,defet, sovinthanestatlamotivaciód’algunesnocionsalgebraiquesquehanacabat formantpartdelcosteòricdelamatemàticaactual.Undelscasosmésfamosos éseldel’equaciódeFermat

on n ésunnaturalfixat.Fermatdeixàanotatenunmarged’undelsseusllibres d’estudi,justamentunvolumdel’Aritmètica deDiofant(vegeufigura1),que, si n ≥ 3,aleshoresl’equació (1.3) notésolucionsenteresnotrivials;ésadir, notésolucions (x,y,z) amb x,y,z ∈ Z totstresnonuls.Aquestenunciat, d’aparençainnocent,romanguésensedemostrardurantmésde300anys,i moltesdelesnocionsitècniquesmatemàtiquesactualsprovenendelsintents d’aquellsquevansucceirFermatenlatascadeprovarl’enunciat.1

Figura 1: Edicióposteriordel’Aritmètica deDiofant,ambl’observaciódeFermat.(Font: https://en.wikipedia.org/wiki/Fermat%27s_ Last_Theorem.)

1 Fermatafirmàquen’haviatrobatunademostració,peròqueelmargeonescriviaeramassa petitperaencabir-la-hi.Aquestasuposadaprovanoesvatrobarmai,iaquestés,enpart,el motiupelqualtantsmatemàticsprovarendedemostrarl’anomenat darrerteoremadeFermat.

Perexemple,lateoriagenerald’idealsenanellssorgídel’estratègiaideadaperKummerperaatacarelproblema;o,mésrecentment,elstreballs deWiles[37]iTayloriWiles[35]sobrelaconjecturademodularitat,dela qualparlaremmésendavant,forenelpasdefinitiuqueresolguéelproblema l’any1994.

Noespotdirquehihagihagutsemprealllargdelahistòriauninterèsper unateoriageneraldelesequacionsdiofàntiques,sinóquemésaviatestractaven demanerafragmentada,caspercas.Undelsprimersaplantejarlanecessitatde sistematitzar-nel’estudifouHilbert,quealasevallistade23problemesque presentàalcongrésinternacionaldematemàtiquesdeParísl’any1900,inclogué comaproblemanúmero10elsegüent:

Donadaunaequaciódiofànticaambqualsevolnombredequantitatsdesconegudesiambcoeficientsnumèricsenters:Idearunprocéssegonselquales puguideterminar,enunnombrefinitd’operacions,sil’equacióésresolubleen nombresenters.

AquestprocésenunnombrefinitdepassosdequèparlavaHilbertés elqueavuiendiaconeixemcoma algoritme.Elproblema,talicomelva plantejarHilbertambsolucionsenteres,resultaquenotésolució.El1970 Matiyasevich([25])donàunafamíliad’equacionsdiofàntiquesperalesquals nopotexistircapalgoritmequepuguidecidirsitenensolucionsenteresono. Aixònoobstant,elproblemaanàlegperasolucionsracionalssegueixobert.De fet,apartird’araenscentraremensolucionsracionals,demaneraque,quan parlemd’equacionsdiofàntiques,enshireferiremenelsentitdesolucions racionals.

Malgratsermésgeneralsquelesenteres,lessolucionsracionalssolen presentarmésestructura,laqualcosan’acostumaafacilitarl’estudi.Unprimer exempled’aixòéselfetqueunaequaciócom (1.1) donallocaunavarietat algebraica,ipodememprarleseinesprovinentsdelageometriaalgebraica. Unaconseqüènciaterminològicad’aquestpuntdevistaésquepensemles solucions (x1,...,xn) comapuntsdel’espaiafí(odel’espaiprojectiu,siel polinomiquedefineixl’equacióéshomogeni).Aixídoncs,sovintensreferirem aunasolucióde (1.1) comaunpunt,entenentqueensreferimaunpunt delavarietatdefinidaperl’equació.Perexemple,l’equació (1.2) defineixuna circumferènciaalplaafí,ilessolucionsracionalsescorresponenalspuntsde lacircumferènciaamblesduescomponentsracionals.

Seguintambl’esperitdelproblemadeHilbert,algunesdelespreguntesmés generalsquepodemplantejarperaequacionsdiofàntiquessón:

1. Existeixalgunalgoritmeque,donadaunaequaciódiofàntica,decideixisi aquestatéalgunasolucióracional?

2. Sil’equaciótésolucions,hihaalgunalgoritmeperacalcular-lestotes?O, enqualsevolcas,peracalcular-nealguna?

3. Podemdiralgunacosasobreelnombredesolucions?Perexemple,decidir siésfinitoinfinitidonar-neunafitaenelcasfinit?

Aquestsproblemessegueixenoberts,nonomésperalcasgeneral,sinó,finsi tot,peralcasparticular,moltrestringitperò,totiaixò,moltinteressant,de corbesplanes,queseràenelqueenscentraremapartird’ara.

Una corbaplana2 vedonadaperunpolinomienduesvariables f(x,y) = 0 enelcasafí,operunpolinomihomogenientresvariables F(X,Y,Z) = 0enel casprojectiu.3 Defet,l’exemple (1.2) ésunacorbaplanaafíi (1.3) ésunacorba planaprojectiva.

L’invariantmésimportantd’unacorbaéselseu gènere,quepodempensar enprimerainstànciacomunanociótopològica.Consideremunacorba C donadaperunaequaciódelaforma

C : f(x,y) = 0.

Comaequaciódiofàntica,esteminteressatsenlessolucionsracionalso,dit d’unaaltramanera,enelconjuntdepuntsracionalsde C,quedenotarem amb C(Q).Mésconcretament,

C(Q) ={(x,y) ∈ Q × Q : f(x,y) = 0}.

Peròtambétésentitconsiderarelconjuntdepuntsde C ambcomponents complexes;ésadir,

C(C) ={(x,y) ∈ C × C : f(x,y) = 0}.

Clarament C(Q) ⊆ C(C) i C(C) admetunaestructuratopològicaquegovernadeterminatsaspectesaritmèticsde C(Q).Percomençar,vistcomasubespai de C × C,resultaque C(C) ésunasuperfície.Unamaneradepensar-hoésescrivintlesvariablescomplexes x i y com x = a+bi i y = c +di amb a,b,c,d ∈ R, iobservantquel’equació f(x,y) = 0donallocaduesequacionsdenombres reals(unaperalapartrealiunaperalapartimaginària)enlesquatrevariablesreals a, b, c, d;duesequacionsenquatrevariablesrealsdefineixenuna superfície.Lacompactificaciód’aquestasuperfícieésunasuperfícieorientable compactaqueés,doncs,homeomorfaauntoramb g foratsperaalgun g ≥ 0; aquest g ésel gènere delacorba.Perexemple,silacorba C(C) éshomeomorfa al’esfera,aleshores g = 0;isiéshomeomorfaaltorestàndard, g = 1.

Enelcasdecorbesplanes,elgènereestàrelacionatambunaltreinvariant important,queéselgrau:silacorbaésnosingular4 degrau d,elgèneredela

2 Ensrestringiremalcasdecorbesplanespersimplicitat,peròtotelquediremenaquesta secciótambééscertperacorbesalgebraiquesmésgenerals,nonecessàriamentplanes(ésa dir,quenoestiguincontingudesnecessàriamentalplaafíoalplaprojectiu,sinóenespaisde dimensiósuperior).

3 Enelcasprojectiu,comqueelpolinomi F(X,Y,Z) éshomogeni,si (X0,Y0,Z0) ≠ (0, 0, 0) és solució,aleshorestambéhoés (λX0,λY0,λZ0) peratot λ ∈ Q nonul;totesaquestessolucions s’identifiquenambunúnicpuntdel’espaiprojectiu.

4 Unacorbaésnosingularsitotpunttéunaúnicarectatangent.Lafórmulaperalgènereque donemnomésvalperacorbesplanesquesegueixenessentnosingularsquanlespensemalpla projectiu.

corbaés (d 1)(d 2)/2.Perexemple,lacorbadeFermat Fn tégènere (n 1) (n 2)/2;enparticular, F2 tégènere0i F3 tégènere1.

Doncsbé,aquestinvarianttopològicpermetdistingirtrescomportaments aritmèticsmoltdiferenciatsenlescorbes,iésquedonainformaciómolt importantsobreelconjuntdepuntsracionals.

Enprimerlloc,lescorbesdegènere0sóncòniquesplanes;ésadir,venen donadesper f(x,y) = 0,on f ésunpolinomidegrau2.Peraaquestescorbes, existeixunalgoritmequepermetdecidirsihihaalgunpuntracional.Encas quen’hihagialgun,aleshoresn’hihainfinitsiespodentrobartotsapartir d’und’ells.Perexemple,enelcasdel’equació (1.2),quetégènere0,podem partirdelpuntracional ( 1, 0).Aleshores,larectaquepassaperaquestpunti tépendent t vedescritaperl’equació

y = t(x + 1). (1.4)

Aquestarectatallalacorbaenunaltrepunt Pt (vegi’slafigura2).Substituint(1.4)a(1.2),obtenimque Pt = 1 t2 1 + t2 , 2t 1 + t2 y y = t(x + 1) x2 + y 2 1 = 0

( 1, 0) pendent = t x

Figura 2: Apartirdelpuntracional ( 1, 0) delcercle,podemtrobar totselsaltresambrectesdependentracional.

D’aquíespotveureque Pt técoordenadesracionalssiinoméssi t és racional,iquesi P ′ ésunpuntracionaldelacorba,aleshoresescorrespona unpuntdelaforma Pt peralgunvalor t ∈ Q.Hemvist,doncs,quelacorbaté infinitspuntsracionalsiqueelspodemcalcularexplícitamentsienconeixem un.Elmateixprocedimentfuncionaperaqualsevolcorbadegènere0.

Elcassegüentserienlescorbesdegènere1,peròaquesteldeixaremper alfinaliaraparlaremdequèsucceeixamblescorbesdegèneremésgrano igualque2.Mordellvaconjecturarl’any1922que,siunacorbatégènere g ≥ 2, aleshorestéunnombrefinitdepuntsracionals.Aquestaconjecturavaser demostradaperFaltingsel1983[12],enunresultatquelivavalerunamedalla Fieldsl’any1986.Tambéhiharesultatsquedonenunafitapelnombrede punts.Undelsmésrecents,deDimitrov-Gao-Habegger[11],ensdiuque

#C(Q) ≤ c1+r(C) g ,

on cg ésunaconstantquenomésdepènde g i r(C) ésuninvariantde C (elrangdelgrupdepuntsracionalsdelasevajacobiana).Totiqueaquests resultatsensdonenmoltainformaciósobreelconjuntdepuntsd’unacorbade gènere ≥ 2,avuidiaencaranoesconeixcapalgoritmeperadeterminarsiuna corbadegènere ≥ 2téalgunpuntracionalono,niperacalcular-lostotsen casqueentingui.

Ensqueda,doncs,veurequinaéslasituacióenelcasdecorbesdegènere1. Hemvistqueunacorbadegènere0obénotépuntsobéentéinfinits,ique unacorbadegènere ≥ 2téunnombrefinitdepunts.Lescorbesdegènere1exhibeixenuncomportamentencaradiferent.Enprimerlloc,demanerasemblant alcasdegènere ≥ 2,noesconeixcapalgoritmeperadeterminarsiunacorba degènere1tépuntsracionalsono.Però,adiferènciadelscasosdegènere0o gènere ≥ 2,sienté,tantenpottenirunnombrefinitcomunnombreinfinit. Defet,unacorbadegènere1ambalgunpuntracionalés,justament,elque esconeixambelnomde corbaellíptica,ielconjuntdelsseuspuntsracionals admetunaestructuramoltespecialqueliconfereixunseguitdepropietats moltnotables.Aquestessónlescorbeso,siesvol,lesequacionsdiofàntiques, aquèdedicaremlarestadel’article.

2Corbesel.líptiques

Una corbael.lípticasobre Q ésunacorbaprojectivanosingulardegènere1amb unpuntracionaldistingit.Aquestadefiniciópotsemblarunamicaabstracta, peròespotveurequetotacorbael.lípticaespotdescriure,defet,peruna equacióafídelaforma5

E : y 2 = x3 + ax + b, amb a,b ∈ Q i4a3 + 27b2 ≠ 0. (2.1)

5 Totiqueelnompuguiduraconfusió,lescorbesel líptiquesnosónel lipses,comesveu d’aquestadescripció:l’equaciód’unael lipseésdegrau2,mentrequelad’unacorbael líptica ésdegrau3.Desdelpuntdevistahistòricsíquehiha,però,unacertarelació,atravésdeles funcionsel líptiques,queapareixenenelcàlculdelalongituddel’arcdelesel lipsesiquees trobenal’origendelterme corbaellíptica

Lacorbaprojectivaassociadavedonadaperl’equació

Y 2Z = X3 + aXZ 2 + bZ 3 .

Lacondició4a3 + 27b2 ≠ 0ésequivalentalfetquelacorbasiguinosingular, ilaquantitat ∆E =−16(4a3 + 27b2) s’anomena discriminant delacorba.De l’equacióprojectivaveiemqueelpunt O = [0:1:0] ésunpuntracionalde E; s’anomena puntdel’infinit,jaqueésl’únicpuntdelacorbaalarectadel’infinit enelplaprojectiu(ésadir,ésl’únicpuntdelacorbaprojectivaquenoveiem almodelafí(2.1)).

L’equació (2.1) s’anomena equaciódeWeierstrass delacorbael.líptica.Sovint ésconvenienttreballarambequacionsunamicamésgenerals,delaforma y 2 + a1xy + a

ques’anomenen equacionsgeneralitzadesdeWeierstrass.Sitreballemsobre Q, coméselnostrecas,totaequaciódelaforma (2.2) espottransformarmitjançantuncanvidevariablesenunadelaforma (2.1).Peròencossosde característica2o3nosempreéspossible,peraixòcaladmetretambéequacionsgeneralitzades.

Seguintambelplantejamentdelasecció1,esteminteressatsen E coma equaciódiofàntica;ésadir,ensinteressenelspuntsracionalsde E:

E(Q) ={(x,y) ∈ Q × Q : y 2 = x3 + ax + b}∪{O}.

Comquehemdefinitelspuntsracionalsfentservirl’equacióafí,enscalafegirhielpunt O,quenoveiemalmodelafí.Alternativament,podríemhaverdefinit elspuntsracionalsdirectamentcomelspuntsdel’espaiprojectiuquesatisfan l’equacióprojectivadelacorba.

Jaenshemtrobatambunexempledecorbael.líptica.Recordemqueala secció1hemvistquelacúbicadeFermat

F3 : X3 + Y 3 = Z 3

tégènere1.Comquetépuntsracionals(perexemple,elpunt [1: 1:0]),és unacorbael líptica.Defet,elcanvidevariables x = 12Z X + Y ,y = 36(X Y) X + Y

transformal’equació F3 en

E3 : y 2 = x3 432,

queésdelaforma (2.1).Fixem-nosqueelcanvidevariablesinvolucrafuncions racionalsambcoeficientsa Q;pertant,transformapuntsracionalsde E3 en puntsracionalsde F3 iestableix,defet,unabijeccióentreelspuntsracionals delesduescorbes.

Lapropietatmésimportantdelescorbesel.líptiquesésque,apartirdedos puntsracionals,podemfabricar-neunaltreambunprocedimentgeomètric. Hoexplicaremambunexemple.Suposemquetenimlacorbael líptica E : y 2 = x3 16x + 16. (2.3)

Perajudar-nosavisualitzarelprocés,ésútildibuixarelspuntsrealsdelacorba, demanerasemblantacomhemfetambl’exempledelcercleanteriorment. Podemveureelresultatalafigura3.Remarquemqued’aquestspuntsamb coordenadesreals,lessolucionsracionalsdel’equaciódiofàntica y 2 = x3 16x 16escorresponenambelspuntsdelagràficaamblesduescomponents racionals.Perexemple,elsdospunts

P = (0, 4),Q = (4, 4)

sónpuntsracionalsdelacorba,ésadir, P,Q ∈ E(Q),jaquetenencomponents racionalsisatisfanl’equació.

Figura 3: Elspuntsrealsdelacorba y 2 = x3 16x 16.

Resultaquelarectaquepassaper P i Q tallalacorba E enuntercerpunt. Escrivintl’equaciódelarecta PQ isubstituint-laal’equacióde E,podem calcularqueaquesttercerpunt(vegeulafigura4)ésel ( 4, 4),quetambété coordenadesracionalsiqueanomenarem P⋆Q

Aquestprocedimentfuncionaperatotacorbael.líptica E iperatotparell depuntsracionals P i Q:larecta PQ vedonadaperunaequaciódegrau1,i E perunadegrau3,demaneraquelarectailacorbaestallenentrespunts.A més,uncàlculexplícitpermetveureque,si P i Q tenencoordenadesracionals, elnoupunt P⋆Q també.

Figura 4: Apartirdelspuntsracionals P = (0, 4) i Q = (4, 4) podem trobarelpunt ( 4, 4),prenentlaintersecciódelacorba E amblarecta quepassaper P i Q

Pertant,donatsdoselementsde E(Q),podemfabricarunaltreelement de E(Q) ambaquestprocedimentgeomètric,iaixòdonallocaunalleide composició;ésadir,aunaaplicació

E(Q) × E(Q) → E(Q) (P,Q) → P⋆Q.

Bé,hihaunparelldedetallspendentsquenohemtractat.Elprimerésquè passasiprenem P = Q,jaqueenaquestcasnotésentitparlardelarecta queuneix P i Q.Però,comquelacorbaésnosingular,podemprendrelacorba tangenta E quepassaper P (silacorbafossingularen P ,hihauriamésd’una rectatangentiaixònotindriasentit).Podemrepetirl’argumentanterioramb aquestarectatangent:lasevainterseccióamb E ensdonaunpunt P⋆P ,que tambéésunpuntracional.

Elsegondetallpendentésquèpassasiundelspuntsquesumemésel punt O,quenoveiemalmodelafí.Larespostaésqueaquestpuntelpodempensarcom«ladireccióvertical»;perexemple,sivolemcalcular P⋆O, prendremcomarecta PO larectaverticalquepassaper P .

Aaquestprocedimentperaconstruirnouspuntsapartirdepuntsconeguts se’lconeixcoma mètodedelasecantilatangent,peròlalleidecomposició quehemdescritcalmodificar-launamicapertalquetinguimillorspropietats

algebraiques.Encomptesde P⋆Q,prenemunaltrepuntdefinitdelamanera següent:femlarectaverticalquepassaper P⋆Q iconsideremelpuntd’intersecciód’aquestarectaamb queanomenarem novalleidecomposició

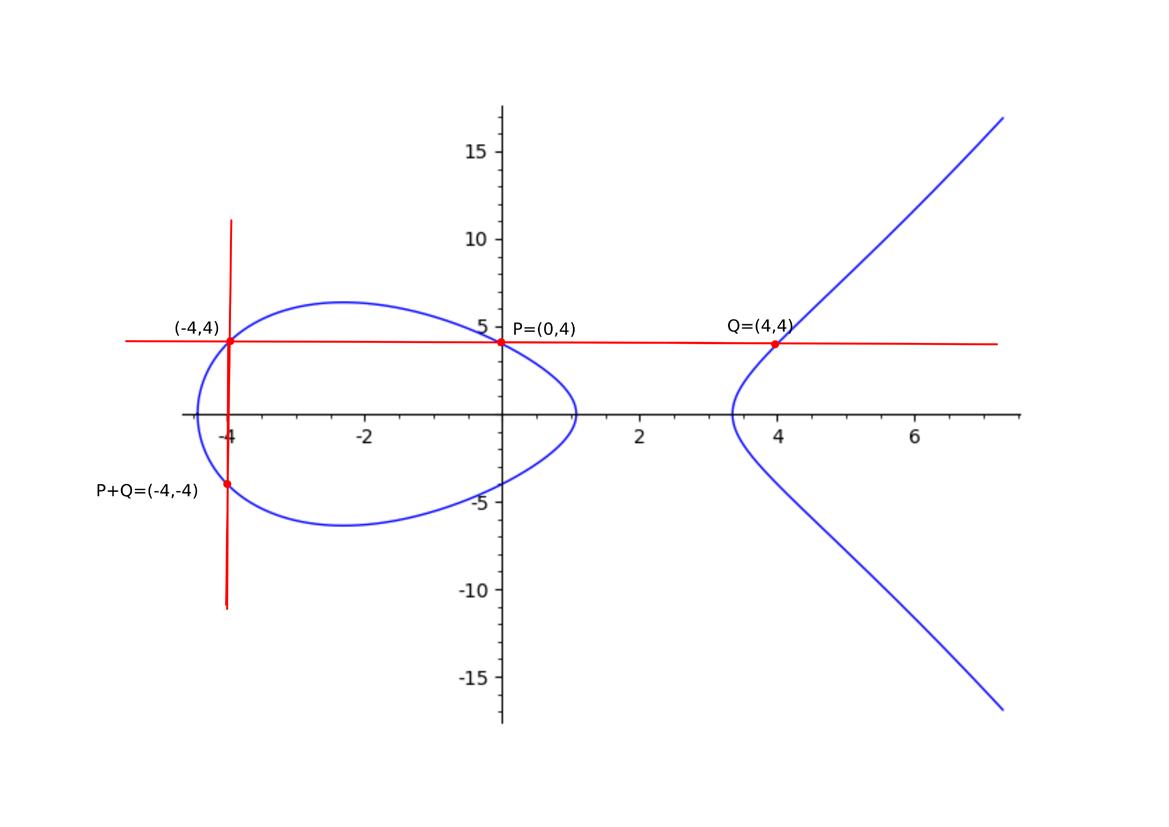
Figura 5: Apartirdelpunt P⋆Q = ( 4, 4),trobemunnoupuntracional fentlarectaverticalquepassaper P⋆Q itallantamb E.Aquestnou punt,enaquestcasel ( 4, 4),éselqueanomenem P + Q

Poincarévademostrarqueaquestaoperació + satisfàunseguitdepropietatsmoltrellevants:

1. Peratot P ∈ E(Q) sesatisfàque P + O = O.Ésadir, O ésunelement neutreperal’operació.

2. Totelementtéuninvers:peratot P ∈ E(Q),existeixunúnicpunt Q tal que P + Q = O.Aquestpuntl’anomenarem P

3. L’operacióésassociativa: (P + Q) + R = P + (Q + R)

4. L’operacióéscommutativa: P + Q = Q + P . Veiem,doncs,que E(Q) ambl’operació + satisfàelsaxiomesdegrupabelià.6 Aquestéselprimerresultatclaudelateoriadecorbesel.líptiques[30].

Teorema 2.1 (Poincaré, 1901). L’operació P,Q P + Q donaunaestructura degrupabeliàalconjunt E(Q).

6 Encanvi,l’operació P,Q P⋆Q nocompleixelsaxiomesd’unalleidegrup,jaquenoés associativa.

Poincarétambévaconjecturaralmateixarticle7 quesemprepodemtrobar unconjuntfinitdepuntsracionalsapartirdelsqualsespotconstruirqualsevol altrepuntracionalaplicantrepetidamentelmètodedelasecantilatangent. Ditambterminologiamodernadeteoriadegrups,Poincaréconjecturàque E(Q) ésungrupfinitamentgenerat.AixòfoudemostratperMordell[28]un quartdesegledesprés.

Teorema 2.2 (Mordell, 1922). E(Q) ésungrupfinitamentgenerat.

Aquestresultatjaensproporcionamoltainformaciósobrel’estructura de E(Q).Elteoremadeclassificaciódegrupsabeliansfinitamentgeneratsens diuqueestéunisomorfismedelaforma

E(Q) ≃ Zr ⊕ T,

on T ésungrupfiniti r ∈ Z≥0.Elgrup T escorresponambelspuntsracionals de E d’ordrefinit,opuntsdetorsió;ésadir,punts P ∈ E(Q) talsquepera algun n ∈ Z>0 estéque8 nP = O.L’enter r denotaelnombremàximdepunts d’ordreinfinitlinealmentindependents,iesconeixcoma rang de E

Exemple 2.3. Perlacorba E3 corresponentalacúbicadeFermat,resultaque

E(Q) ≃ Z/3Z.

Ésadir, T = Z/3Z (hihatrespuntsracionals)ielrangés0(nohihacappunt d’ordreinfinit).Defet,

E3(Q) ={(12, 36),(12, 36)}∪{O}.

Elpunt (12, 36) téordre3,iescompleixque2(12, 36) = (12, 36) i3(12, 36) = O

Exemple 2 4 Lacorba E de(2.3)satisfàque

E(Q) ≃ Z.

Ésadir,l’únicpuntdetorsióés O,ihihaunpuntd’ordreinfinitapartirdel qualespodenobtenirtoteselsaltrespuntsracionals.Elpunt P = (0, 4) ésun generador;algunsdelsseusmúltiplessón:

2P = (4, 4), 3P = ( 4, 4), 4P = (8, 20), 5P = (1, 1), 6P = (24, 116).

Podriasemblarquesempreobtindrempuntsambcoordenadesenteres.Però aixònoéscert;jaalsegüentmúltiplede P veiemque7P = ( 20/9, 172/27) ia partird’aquítotselsaltresmúltiplestenencoordenadesracionalsnoenteres.

7 PeraunavisióméscompletadelescontribucionsdePoincaréal’aritmètica,podeuconsultar[1].

8Coméshabitualenelsgrupsabelians, nP denota P + P + n) ···+ P

Exemple 2.5. Podemconsiderararalacorba

E : y 2 = x3 15058251x + 21601366470, quesatisfàque E(Q) ≃ Z2 ⊕ Z/2Z ⊕ Z/4Z.Elsgeneradorssón

(51, 27),(45, 153),( 124, 62),(9, 594).

Elsdosprimerspuntstenenordreinfinit,eltercertéordre2ieldarrerté ordre4.

Veiem,doncs,unapropietatquehavíemavançatalasecció1:unacorba el lípticatantpottenirunnombrefinitdepuntsracionalscomunnombre infinit.Però,gràciesal’estructuraalgebraicadelconjuntdepunts,arapodem precisarmoltmésaquestaqüestió:podempreguntar-nosquinaésl’estructura degrupde E(Q).Demaneranatural,elproblemaespotdesglossarendos, corresponentsalapartdetorsióialapartlliure:

1. Quinaésl’estructuradelgrupdepuntsdetorsió?

2. Quinéselrangde E?

Tambéenspodempreguntar,ésclar,sobrecomcalcularelsgeneradorsde E(Q). Novament,enaquestproblemapodemdistingirelsgeneradorsd’ordrefiniti elsd’ordreinfinit.

Relacionatambelpunt1hihalaqüestiósobrequinspossiblesgrupsapareixencomagrupsdetorsiódecorbesel.líptiques.Aixòvaquedarcompletament resoltgràciesaunresultatdeMazur[26]quehaviaestatconjecturatel1908 perLevi.

Teorema 2 6 (Mazur, 1977). Sigui E unacorbael·lípticasobre Q.Aleshores E(Q) ésisomorfaalgundelsgrupssegüents:

• Z/NZ amb 1 ≤ N ≤ 10 o N = 12.

• Z/2Z ⊕ Z/2NZ amb 1 ≤ N ≤ 4.

Amés,sesapquecadascund’aquests15grupsapareixcomagrupdetorsió d’infinitescorbesel líptiques.

Encanvi,elrangésuninvariantdelescorbesel.líptiquesdelqualsabemmolt menys.Perexemple,nosesapsihihacorbesel.líptiquesderangarbitràriament gran.Abanshemmostratexemplesdecorbesderang1i2.Lacorbael líptica derangmésgranqueesconeix9 vasertrobadaperElkies-Klagsbrunel2024 itérang ≥ 29.Elrècordanterioreraunacorbaderang ≥ 28,ihaviaestat trobadaperElkiesel2006.

9Éslacorbad’equació:

y2 x3 35000013481153675195091309180305500105059398789899919909339650987x + 2578119979771429916851971456123315357665330364495541948135763833876310204081495487106234897116966

Nosesapsihihacorbesderangmésgran.UnargumentheurísticdeParkPoonen-Voight-Wood[29]suggereixqueelspossiblesrangshauriend’estar fitatsi,demaneramésprecisa,quenoméshihaunnombrefinitdecorbes el.líptiquesderangmésgranque21.

Undelsproblemesobertsmésimportantsenteoriadenombresés,doncs, eldedeterminarelrangdelescorbesel.líptiques,jasiguidesd’unpuntde vistaalgorítmicomitjançantalgunafórmulaquepermetientendremillorla naturalesad’aquestinvariant.Aquestsegonpuntdevistaés,precisament,el quepersegueixlaconjecturadeBirchiSwinnerton-Dyer,queformapartdela llistadesetproblemesdelmil lennipresentatsperlaFundacióClayl’any2000. Abansdeparlard’aquestaconjectura,però,hemdeferunpetitparèntesienel nostreestudidelessolucionsa Q iparlar,breument,delessolucionsencossos finits.

3Puntssobrecossosfinits

Suposemquetenimunacorbael.lípticacomara,perexemple,

Si p ésunnombreprimer,podempensaratrobarsolucionsdel’equació (3.1) mòdul p.Perexemple,pera p = 3resultaqueelpunt (2, 1) ésunasoluciómòdul3.Enefecte,sisubstituïm x = 2i y = 1al’equaciódelacorba,noobtenim unaigualtatdenombresenters,peròsíunacongruènciamòdul3:

Elcostatesquerrede (3.2) val1ielcostatdretval7,i7 ≡ 1(mod3)o,elqueés elmateix,7 1ésmúltiplede3.Fixem-nosque (2, 1) noésunpuntracionalde lacorba,jaque,comhemdit,quansubstituïm x = 2i y = 1al’equaciódela corbanoobtenimunaigualtatdenombresracionals.Peròsíqueobtenimuna congruènciamòdul3;equivalentment,obtenimunaigualtatdeclassesa Z/3Z Diemque (2, 1) ésunpuntde E a Z/3Z.Defet,ésfàciltrobartotselspunts de E a Z/3Z,jaquelesúniquesclassesderesidusmòdul3quecalconsiderar pera x i y són0,1i2,ipodemprovartoteslespossibilitatsiquedar-nosamb aquellesqueproporcioninpuntsmòdul3.Fentunacercaexhaustivaveiemque E(Z/3Z) ={(0, 1),(0, 2),(1, 1),(2, 1),(2, 2)}∪{O}.

Elcos Z/pZ esdenotahabitualmentamb Fp,iésl’úniccosfinitdecardinal p,llevatd’isomorfisme.Peracadanombreprimer p,podemconsiderar laquantitat Np depuntsmòdul p;ésadir, Np = #E(Fp).Peral’exemple (3.1) hemcalculat Np peralsprimersvalorsde p:

p 23571113171923293137

Np 378121019142223373536

Podemobservarque Np creixaproximadamentalmateixritmeque p.Defet,un argumentheurísticensmostraquepodemesperarqueelvalorde Np estiguial voltantde p + 1.Perveuresi (x0,y0) ∈ Fp × Fp pertanya E(Fp),substituïm x0 alapartdeladretadel’equació (3.1).Sielvalor x3 0 x0 + 1és0a Fp,aleshores (x0, 0) seràunpunt;siésdiferentde0,aleshorestrobaremdospuntssiaquest valorésunquadrata Fp inotrobaremcappuntsinoésunquadrat.Comque lameitatdelsvalorsnonulsde Fp sónquadratsilameitatsónnoquadrats,per acadascundels p valorspossiblesde x0 esperemtrobarunpunt,enmitjana. Aixòensdona p puntsentotal,que,sihisumemelpunt O,ensdona p + 1com avaloresperatde Np.Aquestargumentésheurísticperquènosabemquina ésladistribuciódelsvalorsde x3 0 x0 + 1quan x0 recorre Fp.Enqualsevol cas,podemesperarquelaquantitat ap = ap(E) = p + 1 Np,quemesurala diferènciaentreelnombredepuntsrealil’esperat,seràpetita.Alafigura6 veiemrepresentadalaquantitat p + 1 #E(Fp) respectealsprimers p en l’interval2 ≤ p ≤ 105,iveiemquenonomésaquestvaloréspetitrespectea p, sinóquesemblasempreconfinataunaparàbola.Aixòéscert,iéselcontingut d’aquestresultatconjecturatperArtinalasevatesiidemostratperHasse.

Teorema 3 1 (Hasse, 1936). Sigui E unacorbael.lípticasobre Q, p unprimeri posem ap = p + 1 #E(Fp).Aleshores, |ap|≤ 2√p.

p + 1 #E(Fp )

y = 2√x

Figura 6: Il lustraciódelteoremadeHasse.

Noesconeixunafórmulatancadaque,donadaunacorba E,calculilaquantitat ap.Encertamanera,lafunció p ap escomportademaneraaleatòria, ielquesíqueconeixemésladistribuciódeprobabilitatquesegueix.Per

formalitzaraquestfet,comencemobservantqueperlafitadeHassedelteorema3.1laquantitat ap = ap/√p ésunnombrerealquecaual’interval [ 2, 2]. Podempreguntar-nosperla«distribuciódeprobabilitat»delaquantitat ap, quanpensem p comunaquantitataleatòria.Ditd’unaaltramanera,donatun subinterval [α,β] del’interval [ 2, 2],quinaéslaprobabilitatque,siprenem unprimer p al’atzar,elcorresponent ap caiguial’interval [α,β]?

Figura 7: Il.lustraciódelaconjecturadeSato-Tate.Font:[33].

Observemalafigura7unhistograma(perlacorba y 2 = x3 + x + 1)ons’han repartitelsvalors ap entre151subintervalsde [ 2, 2] pera2 ≤ p ≤ 218 . L’any1960SatoiTate,demaneraindependent,vanconjecturarqueladistribuciódeprobabilitatveniadonadaperunsemicercled’entre 2i2;ésadir, eralafunció 4 π √4 x2.LaconjecturadeSato-Tatefoufinalmentdemostradaa finalsdelaprimeradècadadelsegle xxi [34,20].

Teorema 3 2 (Clozel-Harris-Shepherd-Barron-Taylor, 2008). Si E és«genèrica»,aleshores

Elterme genèrica fareferènciaalfetquelacorbanotinguimultiplicació complexa.Pernoallargar-nosexcessivamentnoendonaremladefinicióprecisa (ellectorinteressatpotconsultar[8,§3.1]),però,enelcasenquèlacorbano siguigenèrica,tambésesapquinaésladistribuciódeprobabilitati,defet,el resultatésanterioraldelcasgenèric.

4LaconjecturadeBirchiSwinnerton-Dyer

LaintuïciódarrerelaconjecturadeBirchiSwinnerton-Dyer(d’araenendavant, BSD)ésqueunranggrande E hauriadedonarllocamoltspuntsmòdul p;ésa dir,esperaríemque Np fossistemàticamentmésgranqueelnombredepunts esperatengeneral,queés p + 1.Pertaldequantificaraquestaidea,afinalsde ladècadadels1950BirchiSwinnerton-Dyervanestudiarexperimentalmentla funció

onperacadavalorrealde x elproducterecorretotselsnombresprimers p menorsoigualsque x.

Emprantundelsprimersordinadorselectrònicsdelahistòria,l’EDSAC, delaUniversitatdeCambridge,vancomprovarqueperacorbesderang0la funció CE (x) semblavacomportar-seasimptòticamentcomunaconstant.En canvi,peracorbesderang r> 0lafunciósemblavatendirainfinitquan x →∞, il’observacióclaufouquehofeiaproporcionalmentalafunció (log x)r ,com podemveurealafigura8,ons’il lustraambcorbesderangfinsatres.10 Ésa dir,semblavaqueelrangde E esmanifestavaenl’ordredecreixementdela funció CE (x).Aixòvadonarllocaunaprimeraversiódelaconjectura[4].

Figura 8: Il.lustraciódelaconjecturaBSD,perlescorbes11.a1,37.a1, 389.a1i5077.a1,derangs0,1,2i3,respectivament.

10 Lescorbesanomenades 11.a1, 37.a1, 389.a1 i 5077.a1 espodentrobara https://www. lmfdb.org,isónles«primeres»quetenenrangs0,1,2i3,respectivament.

Al’enunciatsegüent,elsímbol ∼ denotaqueelquocientdelesduesfuncions tendeixa1quan x →∞.

Conjectura 4.1 (BirchiSwinnerton-Dyer). Si E ésunacorbael·lípticasobre Q derang r ,aleshoresexisteixunaconstant αE talque

E (x) ∼ αE (log x)r

Laformulaciód’aquestaconjecturaésunexempledecomlesmatemàtiques tambépodentenirunacomponentexperimentalessencial,iésqueelcàlcul computacionalil’observaciódelesdadesobtingudesfouelquerevelàlarelació precisaentreelnombredepuntssobrecossosfinitsielrang.Defet,unaeina fonamentalenl’estudidelescorbesel.líptiquessónlestaulesquerecullen exemplesconcretsdecorbesialgunsdelsseusinvariantsmésnotables(rang, puntsdetorsió,etc.),comaralestaulesd’Anvers[3],lestaulesdeCremona[6] olabasededadesonlineLMFDB[22],accessiblea https://www.lmfdb.org/ Lafunció CE (x) resultasercomplicadadecontrolardesdelpuntdevista analític.Peraixò,habitualmentlaconjecturaBSDs’enunciaentermesd’una altrafuncióambmillorspropietatsanalítiques,ques’anomena funció L de E i és,defet,unafunciódevariablecomplexa.11 Aquestafuncióesdefineixcomun producteinfinitdefuncionsanalítiquesdevariablecomplexa,indexadespels nombresprimersienquèlacontribuciócorresponentaunprimer p incorpora lainformaciósobreelnombredepuntsmòdul p,vialaquantitat ap(E).De maneramésprecisa,si E vedonadaperunaequació

E : y 2 = x3 + ax + b,

lafunció L incompletade E esdefineixcoma

on s ∈ C éslavariabledelafunciói p recorretotselsprimerssenarsqueno divideixen4a3 + 27b2.EspotveurequelafitadeHasse |ap(E)|≤ 2√p implica queaquestproducteinfinitconvergeixaunafuncióanalíticaenelsemiplà delplacomplexformatpelsnombresdepartrealmésgranque3/2.Defet, Hassetambévaconjecturarque L(E,s) admetcontinuacióanalíticaatotelpla complex.Aixòestàdemostratavuiendia,comaconseqüènciadelteorema demodularitat,demostratperBreuil-Conrad-Diamond-Taylorel2001[5]amb lestècniquesintroduïdesperWilesiTayloriWilesenlasevademostraciódel darrerteoremadeFermat.

Enparticular,tésentitavaluar L(E,s) en s = 1.Nopodemfer-hodirectament alafórmula (4.2),jaqueelproducteinfinitnomésconvergeixperapartreal 11 Unaaltrafunciódevariablecomplexaqueapareixdemaneranotableenaritmèticaésla funció ζ deRiemann[31].Defet,hihaunaconstrucciógeneralquepermetassociarfuncions L aobjectesgeomètricsiobtenir ζ(s) i L(E,s) comacasosparticulars,aixíquepodempensar en L(E,s) comunadeterminadageneralitzacióde ζ(s)

de s mésgranque3/2.Però,siensoblidemperunmomentdelproblemaamb laconvergènciaisubstituïmformalment s = 1alproducteinfinit,multiplicant idividintelterme p-èsimper p obtenimque

1)«

Lescometesalssignesd’igualtatindiquenquel’argumentésheurísticinosón igualtatsrigoroses.Però,tolerantaquestinconvenient,sicomparemamb (4.1), veiemqueaixòhauriadecorrespondreal’inversdelvalor limx→∞ cE (x).Per tant,semblaqueelcomportamentde L(E,s) en s = 1hauriadereflectirel comportamentasimptòticde cE (x),i,comqueunésl’inversdel’altre,com mésgransiguielrang r ,mésràpidhauriadetendira0lafuncióen s = 1. Aixòés,justament,elquediulaversióméshabitualdelaconjecturaBSD;per exemple,laqueapareixenladescripcióoficialdelproblemadelmil lennidela FundacióClay[38].

Conjectura 4 2 (BSD). Si E térang r ,aleshores L(E,s) téunzerod’ordre r en s = 1.Ésadir,

L(E,s) = c(s 1)r + termesd’ordresuperior, peradeterminadaconstant c ≠ 0

Malgratqueaprimercopd’ullpuguisemblarelcontrari,aquestaconjectura noensajudagaireenelproblemaalgorítmicdelcàlculdelrang,jaqueno esconeixenalgoritmesperacalcularl’ordred’anul.lacióde L(E,s) en s = 1 quanaquestordreésmésgranque3.Defet,avuidianoconeixemcapcorba el.líptica E perlaqualpuguemdemostrarquel’ordred’anul.lacióde L(E,s) és4.

Hihauna«versióforta»delaconjectura,queinvolucralafunció L completa (enquès’incorporentambétermescorresponentsa p | 2(4a3 + 27b2),que sónunamicaméscomplicatsdedefinir).Enaquestcaslaconjecturaprediu elvalordelaconstant c enelprimertermedeldesenvolupamentdeTaylor enfunciódecertsinvariantsaritmèticsigeomètricsde E.Siaquestaversió fortafoscerta,aixòsíquedonariallocaunalgoritmeperacalcularelrangi unconjuntdegeneradorsde E(Q).

LaconjecturaBSD,finsitotenlaseva«versiódèbil»quehemenunciat, encaraestàobertaencompletageneralitat.Aixònoobstant,se’nconeixen algunsresultatsparcials.Elmésimportantdesdelpuntdevistadelpresent articleés,sensdubte,elqueesderivadelstreballsdeGross,ZagieriKolyvagin definalsdeladècadadel1980[16,21].

Teorema 4 3 (Gross-Zagier 1986,Kolyvagin 1988). Sil’ordred’anul·lacióde lafunció L(E,s) en s = 1 és 0 o 1,aleshoreslaconjecturaBSDpera E éscerta.

Ditd’unaaltramanera:si L(E, 1) ≠ 0,elrangés0;isi L(E, 1) = 0i L′(E, 1) ≠ 0,elrangés1.Enparticular,si L(E, 1) = 0i L′(E, 1) ≠ 0,aleshoreshihaun puntd’ordreinfinita E.AquestaéslapartdelresultatquevanprovarGross iZagier,iperalaqualvanresoldreelproblemaclau:donadaunacorbaellípticaamb L(E, 1) = 0i L′(E, 1) ≠ 0,comconstruirunpuntracionald’ordre infinit?L’einafonamentalquevanemprarsónelsanomenats puntsdeHeegner, introduïtsunsanysabansperBirchique,encertamanera,jahavienestat descobertsperHeegnerenuncontextlleugeramentdiferent.

5PuntsdeHeegneriexemples

Comjahemavançatmésamunt,elspuntsdeHeegnersónpuntsdefinits alacorbael.líptica E quesónd’ordreinfinitquanl’ordred’anul.laciódela funció L(E,s) ésexactament1,i,pertant,enaquestaseccióassumiremque aquestéselcas.Amés,enscalutilitzarelfetque E és modular,aixíqueprimer veuremquèvoldirqueunacorbael.lípticasiguimodular.Defet,unamanera ràpidadedir-hoésdirquelacorba E estàassociadaaunaformamodular.Però aleshoresenscalexplicarquèésunaformamodular,iquèvoldirque E hi estiguiassociada.

Considerem,doncs,elsemiplàsuperiordePoincaré H,quesimplementés conjuntdecomplexosambpartimaginàriapositiva:

H ={z ∈ C | Im(z)> 0}.

Aquestespai,quetambés’anomena semiplàhiperbòlic,téunamètricaassociada donadaper

ds = dxdy y 2 ,z = x + iy.

Lesisometriesde H venendonadesjustamentpelgrup

PSL2(R) ={γ ∈ M2(R) | det γ = 1}/{±1}, onl’acciód’unamatriu γ = ab cc ésperunatransformaciófraccionàrialineal z → az + b cz + d

Enparticular,elgrup SL2(R) actuaa H,iensinteressaestudiarfuncions queescomportendemaneramoltsimètricarespecteadeterminatssubgrups. Concretament,enelcasdelescorbesel líptiquesfixaremunenterpositiu N i consideraremelgrup

Γ0(N) = ab cc ∈ M2(Z) | ad bc = 1,N | c , ésadir,enelgrupdematriusdosperdosacoeficientsenters,determinant1i ambl’entradainferioresquerradivisibleper N.

Definició 5.1. Unaformamodulardenivell N (cuspidalidepes2)ésuna funcióholomorfa f : H → C talque:

1. f(γz) = (cz + d)2f(z) peratota γ = ab cc ∈ Γ0(N),i

2. limz→i∞(cz + d) 2f(γz) = 0peratota γ = ab cc ∈ SL2(Z)

Comquelamatriu 11 01 pertanya Γ0(N) siguiquinsigui N,totaforma modular f és1-periòdica,i,pertant,téunasèriedeFourier.Defet,comque f ésholomorfa,podemescriure f(z) = ∞ n=1 an(f)e2πinz,an(f) ∈ C.

Sovints’abreuja q = e2πiz is’anomena ∞ n=1 an(f)qn la q-expansióde f . EvidentmentéstemptadorconsiderarlasèriedeDirichletassociadaaaquests coeficients,quenoésmésquelafunció L(f,s) =

n=1 an(f)n s

UnteoremadeHeckeensasseguraqueperatotprimer p esté |ap(f)|= O(p), i,comaconseqüènciadelsresultatsdeDelignesobrelesconjecturesdeWeil, sabemque,defet, |ap(f)|≤ 2√p.Entotcas,lasèrie L(f,s) convergeix per Re(s) suficientmentgran.Amés,lasimetriade f enspermetcontinuar analíticament L(f,s) aunafuncióholomorfaatot C

Teorema 5 2 (Taylor-Wiles,Wiles,Breuil-Conrad-Diamond-Taylor). Donadaunacorbael líptica E,hihaunenterpositiu NE iunaformamodular fE denivell NE ,demaneraqueperatotprimer p esté

ap(fE ) = p + 1 #E(Fp).

Laquantitat NE s’anomena conductor delacorba,ihihaalgoritmesque elcalculendemanerasenzillaapartirdel’equaciódeWeierstrass.Amés,els primersquedivideixen NE sónessencialmentelsmateixosquedivideixenel discriminantde E.Ésmés,lafunció L(E,s) espotdefinirdemaneraquetambé incorporielsprimersquedivideixeneldiscriminant,ialeshoreselteoremade modularitatensdiuquehihaunaformamodular fE talque L(fE ,s) = L(E,s). Talcoml’hemenunciat,noestàclarcomespotaprofitaraquestteoremaper aconstruirpuntsalacorbael líptica,querecordemqueéselnostreobjectiu.

Peraentendrecoml’existènciadelaformamodular fE enspermettrobar puntsa E enscaldriaentendrel’estructuraalgebraicaquehihaaldarreredel quocientanalític Y0(N) = Γ0(N)\H.Enaquestanota,però,ensconformarem amblasegüentconseqüència.

Talcomhemvistalasecció1,elspuntscomplexos,quedenotemamb E(C), formenunasuperfícieal’espaidedimensió(real)4queés C×C,ques’anomena

superfíciedeRiemann,jaquefouRiemannquiprimerestudiàaquesttipusde superfícies.Enelcasqueensocupa,espotcalcularunreticle

ΛE ={m + nτE | m,n ∈ Z}⊂ C

peraundeterminatelement τE ∈ H,iestéunisomorfismeanalític12 C/ΛE ≊ → E(C).

L’aplicació

πifE (z)dz

envia Y0(N) a C/Λ,on Λ éshomotètica ΛE .Aixòfaque,reescalantlaintegral anterior,puguemconsiderarunaaplicacióanalítica

ΦN : Y0(N) → E(C),

queanomenarem parametritzaciómodular.Valadirqueaquestafunció(o unaaproximacióarbitràriamentbona)espotcalcularapartirdela q-expansió de fE ,iques’hafetmoltarecercaperaaconseguirqueaquestcàlculsiguimolt eficient.

L’últimingredientqueensfalta,doncs,peraobtenirpuntsa E(Q) ⊂ E(C) éstrobarpuntsadequatsa Y0(N).Lafunció ΦN ésaltamenttranscendent, i,pertant,enprincipinoesperaríemquepuntsalgebraicsa H doninlloca puntsalgebraicsa E(C),cosaquegairebénopassamai.Totiaixí,lateoria demultiplicaciócomplexagaranteixque,si τ ∈ H ésunquadràticimaginari (ésadir,satisfàunaequaciódelaforma Aτ 2 + Bτ + C = 0amb A,B,C ∈ Z i B2 4AC< 0),aleshores ΦN (τ) ∈ E(C) técoordenadesdefinides13 enuna extensióalgebraicade Q(τ).Lasituacióéssemblantalquepassaambles funcionstrigonomètriques:lafunció x sin(2πx) éstranscendent,però resultaque,si x ésracional,aleshoressin(2πx) ésunnombrealgebraic.14 Vegemunexemplequeensajudaràaclarificarlaconstruccióquehemfet. Consideremlacorbael líptica15

E : y 2 + y = x3 x, queéslacorbael.líptica«méssimple»derang1.Laformamodular fE associada a E permodularitatté q-expansió fE (q) = q 2q2 3q3 + 2q4 2q5 + 6q6 q7 + 6q9 +···

12 Unisomorfismeanalíticésaquellquevedonatperfuncionsholomorfesambinversaholomorfa.

13 Pertalqueaixòsiguicertenscalassumirunacondiciótècnica,conegudacomla«hipòteside Heegner»:elsprimersdivisorsde N nopodenser inerts a Q(τ)

14 Defet,lateoriadeGaloisenspermetpredirenquinaextensióde Q estàdefinit sin(2πx) en aquestcas.

15 https://www.lmfdb.org/EllipticCurve/Q/37/a/1

Consideremara

τ = 21 + √ 3 74 ∈ H

Calculemdemaneraaproximada ΦN (τ) iobtenim

ΦN (τ) ≃ 1.000000, 1.11 · 10 16 ∈ E(C).

Podemcomprovarque ( 1, 0) = 3(0, 1) + (0, 1),ique E(Q) ={O,(0, 1)}×

⟨(0, 1)⟩.Aixídoncs,laconstrucciódelspuntsdeHeegnerenshadonatlloc alpuntd’ordreinfinitl’existènciadelqualhauríempogutpredir(gràciesala conjecturaBSD)delfetquelaL-sèrie L(E,s) tinguésunzero(simple)a s = 1.

Observemqueenaquestcaselpuntquehemobtinguttécoordenades racionals,peròaixòprovédelfetquerang E(Q) = rang E(Q(√ 3)) = 1.

VegemperacabarunaltreexemplequemostracomelspuntsdeHeegnertenencoordenadesaextensions(potsertrivials)decossosquadràticsimaginaris. Enaquestcas,consideremlacorba16 donadaperl’equació E : y 2 + y = x3

quetéconductor11iformamodularassociada

Enaquestcasprenem τ = 9 + √ 7 22 , quegeneraelcosquadràticimaginari Q(√ 7),icalculem

Elpuntobtingutésmoltpropera

queespotescriurecoma

Espotveureque E(Q(√ 7)) ésisomorf(comagrupabelià)a Z/5Z ⊕ Z, ambgeneradorde Z/5Z donatper (5, 5) igeneradordelapartlliuredonat per 6, 1 11√ 7 2

16 https://www.lmfdb.org/EllipticCurve/Q/11/a/2

6Corbesel.líptiquessobreels p-àdics

Afinalsdelseglepassat,Darmonproposàa[7]unaconstruccióanàlogaala delspuntsdeHeegner,enelcasquel’extensióquadràticaqueconsiderem siguireal.Enaquestaseccióilaproperaintentaremdonarunaidead’aquesta construcció,que,adiferènciadelaconstrucciódepuntsdeHeegner,donalloc apuntsque—avuidia—encaranosabemdemostrarquesiguinalgebraics.

Jad’entradaensadonemfàcilmentquelaconstrucciódeHeegnernofuncionaràenaquestasituació,jaque,si τ ésreal,aleshoressegurquenopertanya H (recordemque H estàformatpercomplexosambpartimaginària estrictament positiva).LaideabrillantdeDarmonvaserconsiderarunaltretipusdesemiplà quesíquecontindriaaquestspuntsreals.Així,substituí H perunpla p-àdic, on p ésunprimerdivisordelconductordelacorba.Pertaldesimplificar l’exposiciósuposaremqueelconductordelacorbael.lípticaqueconsiderem ésprimer.

Elsnombres p-àdics,quehabitualments’escriuencoma Qp,s’obtenena partirdelsracionalsdemaneraanàlogaacomsen’obtenenelsnombresreals, ésadir,prenentunacompleciódelsracionalsrespected’unvalorabsolut.Si prenemelvalorabsolutusual,obtenimelsreals R,però,siprenemelvalor absolut p-àdic(queveuremseguidament),aleshoresobtindremelsnombres p-àdics.

Elvalorabsolut p-àdic,quedenotaremamb |·|p,esdefineixenelsenters coma

|a|p = p vp (a),vp(a) = max{k | pk divideix a}.

Perexemple,comque32 divideix18i33 no,tenim |18|3 = 1/9.Així,sipensem 3-àdicament,elnombre18és méspetitque elnombre1(peraqualsevol p,es té |1|p = 1).Demanerasemblant,elsnombres3, 9, 27,..., 3n ,... tendeixena zero3-àdicament,encaraqueambelvalorabsolutusualenssembliqueesfan grans.

Elvalorabsolut p-àdicespotestendredemaneradirectaalsracionals, definint

iaixíobtenimunvalorabsolutquerespectalamultiplicació:peratot x,y ∈ Q, tenim |xy|p =|x|p|y|p

Delamateixamaneraquepodemaproximarqualsevolrealnonulmitjançantunentermultiplicatperunapotènciade10,tambépodemaproximar qualsevol p-àdicnonulmitjançantunentermultiplicatperunapotènciade p. Enaquestcas,dosentersseranmoltpropers(p-àdicament)silasevadiferència ésdivisibleperunapotènciamoltgrande p.Perexemple,elsnombres14i500 sónbastantpropersa Q3,jaquelasevadiferènciaés486 = 2 · 35,quetévalor absolut3-àdiciguala3 5 ≃ 0 004115.D’altrabanda,14estàadistància1de2, jaque |14 2|3 =|13|3 = 1.

DelamateixamaneraqueperadefinirelspuntsdeHeegnernon’hem tingutprouambelsrealsihemhagutdeconsiderarelsnombrescomplexos,en

elcas p-àdictambéenscaldràconsideraruncosmésgranque Qp.Recordem queperconstruirelscomplexosadjuntemunaarreldelpolinomi x2 + 1,que ésirreductiblesielpensemenelsreals.Així,consideraremunaextensió Cp de grau2de Qp,queespotobtenir,perexemple,adjuntantl’arreld’unpolinomi mònicdegrau2ambcoeficientsa Z quesiguiirreductiblemòdul p 17

Hihaunateoriadecorbesel.líptiquessobre Qp,iresultaquetambédonenllocators(enaquestcas,tors p-àdics),peròenaquestasituacióenscal unaversiómultiplicativa.Fixem-nosque,enelcascomplex,lafuncióexponencial z e2πiz donallocaunisomorfisme C/ΛE ≊ C×/qZ E ,on qE = e2πiτE i

Z E ={qn E

Enelcas p-àdic,estéunisomorfismeanalític(donatpersèriesdepotències ambcoeficients p-àdics)

Cp),

on qE ∈ Q× p ,ques’anomena períodedeTate,s’obtétambédemanerasenzillaa partirdel’equacióde E.

Finsaquíhemintentatconvèncerellectordesubstituirelspuntscomplexos delacorbael.líptica E(C) pelspunts p-àdics E(Cp).Enshemdepreguntar, doncs,perquinsobjectesanàlegssubstituiremelsemiplàdePoincaré H iel grup Γ0(p).D’entrada,podempensarque H = (C \ R)+,onelsímbol + fa referènciaalacomponentconnexaformadapelscomplexosambpartimaginàriapositiva.Així,noenssorprendràquedefinimel semiplà p-àdic Hp com a Cp \ Qp (enaquestcas,notésentitconsiderarunacomponent«positiva»).El grup PSL2(Qp) actuaa Hp pertransformacionsfraccionàrieslineals,ielgrup anàlega Γ0(p) queconsideràDarmon,seguintIhara,éselgrup Γ = SL2(Z[1/p]) = γ = ab cd ∈ M2(Z[1/p])) | det γ = 1 .

Lanotació Z[1/p] significal’anellformatpelsracionals a/b,on b ésuna potènciade p.Arajatenimdefinitsobjectes p-àdics Γ \Hp i E(Cp),iensresta perveure:

1. Quinésl’anàleg p-àdicdel’aplicació ΦN delaseccióanterior,i

2. Quinspuntsinteressantsespodendefinira Γ \Hp quedoninllocapunts algebraicsa E(Cp)?

Enlasecciósegüentveuremqueelcamínoéstandirecte,iensveurem obligatsacombinarlateoria p-àdicaamblacomplexaperdefinirelspuntsque cerquema E(Cp)

17 Alaliteraturasovints’escriu Cp perareferir-sealacompleciódelaclausuraalgebraica de Qp ,queaquínofaremservir.

ηTate : C× p /qZ E → E(

7PuntsdeStark-Heegneriexemples

Recordemqueelteoremademodularitatenspermetassociaraunacorba el.líptica E unacertaformamodular fE .Defet,elqueacabemintegrantés una1-formadiferencial ωE = 2πif(z)dz.Lapropietatdesimetriaperal grup Γ0(p) (recordemqueestemassumintqueelconductor NE = p ésprimer) faque ωE siguiinvariantperaaquestgrupi,pertant,laformadiferencial ωE ésunaformaa Y0(p).

UndelspuntsclaudelaconstrucciódeDarmonconsisteixaconsiderarel producte Hp × H,onactuaelgrup Γ demaneradiagonal,iaassociara E una (1, 1)-formadiferencial ΩE a XΓ = Γ \(Hp × H).Valadirqueelllenguatgeque estemfentservirnoésgaireprecís,jaque Hp éstotalmentdisconnexambla topologia p-àdicailadiferenciabilitatnofuncionacomambelscomplexos.Per fer-hoprecíshauríemderecórreralageometriarigidoanalítica,peròenaquest articlel’analogiaensservirà.

Demaneraanàlogaacomenlaseccióanteriorhemintegratuna1-formadiferencialalllargd’uncamícomplex i∞ ❀ τ,aquestanova (1, 1)-formadiferencial l’hauremd’integrarsobreuna2-cadena.Fixem-nosqueelcamícomplex i∞ ❀ τ técomavorala0-cadenatancada (τ) (i∞).Així,sivolemseguirl’analogia,hauríemdetrobarun1-cicleexacte,ésadir,quesiguilavorad’una 2-cadena.Heusacícompodemprocedir:donatunpunt τ ∈ Hp quesatisfaci unaequació Aτ 2 + Bτ + C = 0amb B2 4AC> 0,espotconsiderarelsubgrup estabilitzador

queresultaestargeneratperunamatriu γ.Tambéespotveurequeunacerta potència18 de γ espotescriurecomaproductedecommutadors:

ElciclequeconsideraDarmonés

= (γe∞

) ×{τ}∈

\(H × Hp).

Aquestcicleéstancat,i,defet,espotveurequeésexacte,ésadir,que hihauna2-cadena ∆ talque ∂∆ = Θ.Perfer-hosuposem,pertaldesimplificarlanotació,quenomésapareixuncommutadorenladescomposició de γe,aixíque γe = aba 1b 1.Eldiagramasegüentmostrala2-cadenacorresponent:

18 Engeneral,calmodificar γ fentservirunsoperadorsdeterminatsconegutscoma operadors deHecke,peròpodemobviaraquestdetallenaquestaprimeraaproximació.

Observemquemoltsdelstermesescancel.len.D’altrabanda,lapartque apareixenquadradaespotreescriurecoma

Però,comque

aquesta1-cadenaésnul la.Enconclusió,totselstermesexcepteunescancel len i,pertant,

Podemdefinirlaintegral

Perexemple,consideremlacorbael lípticadel’apartatanterior E : y 2 + y = x3 x2 10x 20,

deconductor p = 11.Comque x2 13notéarrelsmòdul11,podemescollir τ = 3 √13 2 ∈ H11

Calculemunaaproximaciódelaintegralanterior,quedonallocalpunt

Jτ = 275514415488849148207τ+302729526018381608293 (mod1120).

Aplicantl’isomorfismea E(C11),obtenim

ηTate(Jτ ) ≃ 645077502996 + 732103938720τ + O(1120), 4172141459976479 + 4172141459976479τ + O(1120) ,

queésproperalpuntalgebraicd’ordreinfinit

2 8071272/139129τ + 52783800/139129, 109494875952/51895117τ 329723275860/51895117 ∈ E(Q( 13)).

Comhemremarcatalaseccióanterior,unadiferènciaimportantentre lateoriadepuntsdeHeegnerdelasecció5ilateoriadepuntsdeStarkHeegnerquehemvistenaquestaseccióésqueaquestadarreraésunateoria encaramajoritàriamentconjectural.Aixòesdeualfetquelaconstrucció quehemexplicatdepuntsdeHeegneréslavessantanalíticad’unateoria geomètricadepuntsdeHeegner,quepermetdemostrarqueelspuntsobtinguts nonoméssónpuntsambcomponentscomplexes,sinóque,defet,sónpunts ambcomponentsalgebraiques.LaconstrucciódepuntsdeStark-Heegneres potveurecomunanàleganalític p-àdicdelaconstrucciócomplexadepuntsde Heegner,peròenelcasdeStark-Heegnernoesconeixl’anàlegdelaconstrucció geomètrica.

Totiaixí,alllargdelsanyshanaparegutmoltsresultatsquedonenevidència delavalidesad’aquestaconjectura,tantdecairecomputacionaliexperimental([9, 17]),enquèescomprovaennombrososexemplesqueelspuntsde Stark-Heegnersónmoltpropersapuntsracionalsd’ordreinfinit,comdecaireteòric([27, 23, 2, 24, 10]),enquèesdemostrencasosparticularsdela conjectura.

8Epíleg

LaconstruccióoriginaldeDarmons’hageneralitzatenmúltiplesdireccionsen lesmésdeduesdècadesquehanpassatdesdel’articlefundacional[7].LahipòtesideHeegner(sobreelcomportamentenelcosquadràticdelsdivisorsdel conductor)espotrelaxaracanvideconsiderarsubgrupsde SL2(R) o SL2(Qp) donatsperàlgebresdequaternionsencomptesdelsgrups Γ0(N) ([15]),iespodenconsiderarcorbesel líptiquessobrecossosdenombresdiferentsde Q,com aracossosquadràticsimaginaris([36]).Avuiendia,disposemdeconstruccions conjecturalsdepuntsalgebraicssemprequeelsignedel’equaciófuncional de L(E/K,s) siguisenar,ilesconjecturesprediuenqueaquestesconstruccions donenllocapuntsalgebraicsd’ordreinfinitsemprequel’ordred’anul.lació de L(E/K,s) a s = 1siguiexactament1.Peramésdetalls,convidemellectora consultar[19]i[18],enquèlaconstruccióespresentadesdelpuntdevista mésgeneral.

Tambécalmencionarl’existènciadegeneralitzacionsquevanmésenllà delasituaciódecorbesel.líptiquesderang1tractadaenaquestarticle.Per

exemple,elsciclesdeStark-Heegner([32])o,mésrecentment,elsanomenats puntsplèctics,que,inspiratsperlesconstruccionsdeDarmon,proporcionen invariants p-àdicsencertessituacionsderang > 1([13,14]).

Enaquestarticlehemvolgutferuntastd’algunesconjecturessobrecorbes el líptiquesilescorresponentsrespostesparcialsquesabemdonar.Concretament,laconjecturadeBirchiSwinnerton-Dyersegueixessentunafont d’inspiracióperalateoriadenombresdelsegle xxi,ilesconstruccionsexplícitesquevaintroduirHeegnerihageneralitzatDarmonialtrescontemporanis ensproveeixend’unapetitaajudaal’horad’entendreaquestamisteriosarelació entrel’anàlisidelesL-sèriesil’aritmèticadelspuntsracionals.Segurament caldranaltresideesfonamentalmentnovesperapoderdemostrarlaconjectura encasosderangssuperiorsa1,onfinsavuitenimbenpocsresultatsteòrics.

Referències

[1] Bayer,P. «LescontribucionsdePoincaréal’aritmètica». Butlletídela SocietatCatalanadeMatemàtiques,21(1)(2006),5–38.

[2] Bertolini,M.;Darmon,H. «TherationalityofStark-Heegnerpointsover genusfieldsofrealquadraticfields». Ann.ofMath.(2),170(1)(2009), 343–370.

[3] Birch,B.J.;Kuyk,W.(ed.). ModularFunctionsofOneVariable.IV. ProceedingsoftheInternationalSummerSchool,UniversityofAntwerp, July17–August3,1972.Berlín;NovaYork:Springer-Verlag,1975.(Lecture NotesinMath.;476)

[4] Birch,B.J.;Swinnerton-Dyer,H.P.F. «Notesonellipticcurves.II». J. ReineAngew.Math.,218(1965),79–108.

[5] Breuil,C.;Conrad,B.;Diamond,F.;Taylor,R. «Onthemodularityof ellipticcurvesover Q:wild3-adicexercises». J.Amer.Math.Soc.,14(4) (2001),843–939.

[6] Cremona,J.E. AlgorithmsforModularEllipticCurves.2aed.Cambridge: CambridgeUniversityPress,1997.

[7] Darmon,H. «Integrationon Hp ×H andarithmeticapplications». Ann. ofMath.(2),154(3)(2001),589–639.

[8] Darmon,H. RationalPointsonModularEllipticCurves.Washington,DC: ConferenceBoardoftheMathematicalSciences;Providence,RI:American MathematicalSociety,2004.(CBMSReg.Conf.Ser.Math.;101)

[9] Darmon,H.;Pollack,R. «EfficientcalculationofStark-Heegnerpointsvia overconvergentmodularsymbols». IsraelJ.Math.,153(2006),319–354.

[10] Darmon,H.;Rotger,V. «Stark-Heegnerpointsanddiagonalclasses».A: HeegnerPoints,Stark-HeegnerPoints,andDiagonalClasses. Astérisque, 434(2022),1–28.

[11] Dimitrov,V.;Gao,Z.;Habegger,P. «UniformityinMordell-Langfor curves». Ann.ofMath.(2),194(1)(2021),237–298.

[12] Faltings,G. «EndlichkeitssätzefürabelscheVarietätenüberZahlkörpern». Invent.Math.,73(3)(1983),349–366.

[13] Fornea,M.;Gehrmann,L. «PlecticStark-Heegnerpoints». Adv.Math.,414 (2023),articlenúm.108861,42p.

[14] Fornea,M.;Guitart,X.;Masdeu,M. «Plectic p-adicinvariants». Adv. Math.,406(2022),articlenúm.108484,26p.

[15] Greenberg,M. «Stark-Heegnerpointsandthecohomologyofquaternionic Shimuravarieties». DukeMath.J.,147(3)(2009),541–575.

[16] Gross,B.H.;Zagier,D.B. «Heegnerpointsandderivativesof L-series». Invent.Math.,84(2)(1986),225–320.

[17] Guitart,X.;Masdeu,M. «Elementarymatrixdecompositionandthe computationofDarmonpointswithhigherconductor». Math.Comp., 84(292)(2015),875–893.

[18] Guitart,X.;Masdeu,M.;Molina,S. «AnautomorphicapproachtoDarmonpoints». IndianaUniv.Math.J.,69(4)(2020),1251–1274.

[19] Guitart,X.;Masdeu,M.;¸Sengün,M.H. «Darmonpointsonellipticcurves overnumberfieldsofarbitrarysignature». Proc.Lond.Math.Soc.(3), 111(2)(2015),484–518.

[20] Harris,M.;Shepherd-Barron,N.;Taylor,R. «AfamilyofCalabi-Yau varietiesandpotentialautomorphy». Ann.ofMath.(2),171(2)(2010), 779–813.

[21] Kolyvagin,V.A. «Eulersystems».A: TheGrothendieckFestschrift,Vol.II. Boston,MA:BirkhäuserBoston,Inc.,1990,435–483.(Progr.Math.;87)

[22] LMFDB,«TheL-functionsandmodularformsdatabase(LMFDB)».Publicat enlínia(2024). https://www.lmfdb.org.

[23] Longo,M.;Martin,K.;Hu,Y. «RationalityofDarmonpointsovergenus fieldsofnon-maximalorders». Ann.Math.Qué.,44(1)(2020),173–195.

[24] Longo,M.;Vigni,S. «TherationalityofquaternionicDarmonpointsover genusfieldsofrealquadraticfields». Int.Math.Res.Not.IMRN,2014(13) (2014),3632–3691.

[25] Matiyasevich,Ju.V. «TheDiophantinenessofenumerablesets». Dokl. Akad.NaukSSSR,191(2)(1970),279–282.[Enrus]

[26] Mazur,B. «ModularcurvesandtheEisensteinideal».Ambunapèndix deB.MazuriM.Rapoport. Inst.HautesÉtudesSci.Publ.Math.,47(1977), 33–186.

[27] Mok,C.P. «OnatheoremofBertolini-DarmonontherationalityofStarkHeegnerpointsovergenusfieldsofrealquadraticfields». Trans.Amer. Math.Soc.,374(2)(2021),1391–1419.

[28] Mordell,L.J. «Ontherationalsolutionsoftheindeterminateequationsof thethirdandfourthdegrees». Proc.CambridgePhilos.Soc.,21(1922/23), 179–192.

[29] Park,J.;Poonen,B.;Voight,J.;Wood,M.M. «Aheuristicforboundednessofranksofellipticcurves». J.Eur.Math.Soc.(JEMS),21(9)(2019), 2859–2903.

[30] Poincaré,H. «Surlespropriétésarithmétiquesdescourbesalgébriques». J.Math.PuresAppl.,7(3)(1901),161–233.

[31] Quer,J. «Lafunció ζ deRiemann». ButlletídelaSocietatCatalanade Matemàtiques,22(2)(2007),197–228.

[32] Rotger,V.;Seveso,M.A. «L-invariantsandDarmoncyclesattachedto modularforms». J.Eur.Math.Soc.(JEMS),14(6)(2012),1955–1999.

[33] Sutherland,A.V. «Sato-Tatedistributionsingenus1». https://math. mit.edu/~drew/g1SatoTateDistributions.html.[Consulta:10setembre 2024].

[34] Taylor,R. «Automorphyforsome l-adicliftsofautomorphicmod l Galoisrepresentations.II». Publ.Math.Inst.HautesÉtudesSci.,108(2008), 183–239.

[35] Taylor,R.;Wiles,A. «Ring-theoreticpropertiesofcertainHeckealgebras». Ann.ofMath.(2),141(3)(1995),553–572.

[36] Trifkovi´c,M. «Stark-Heegnerpointsonellipticcurvesdefinedoverimaginaryquadraticfields». DukeMath.J.,135(3)(2006),415–453.

[37] Wiles,A. «ModularellipticcurvesandFermat’slasttheorem». Ann.of Math.(2),141(3)(1995),443–551.

[38] Wiles,A. «TheBirchandSwinnerton-Dyerconjecture».A: TheMillennium PrizeProblems.Cambridge,MA;ClayMathematicsInstitute,2006,31–41.

XavierGuitart

DepartamentdeMatemàtiquesiInformàtica UniversitatdeBarcelona xevi.guitart@gmail.com

MarcMasdeu

DepartamentdeMatemàtiques UniversitatAutònomadeBarcelona marc.masdeu@uab.cat

ButlletídelaSocietatCatalanadeMatemàtiques Vol.39,núm.1-2,2024.Pàg.103–129. DOI:10.2436/20.2002.01.116

LesequacionsdeFriedmann:mecànicanewtoniana versus relativitatgeneral

JaumedeHaro

Compotserquelesmatemàtiques,essent alcapialafiunproductedelpensament humàindependentdel’experiència,siguin tanadmirablementadequadesalsobjectes delarealitat?Ésquelaraóhumana,aleshores,senseexperiència,nomésambel pensament,potcomprendrelespropietats delescosesreals?Enlamevaopinió:la respostaaaquestapreguntaés,breument, aquesta:enlamesuraquelesproposicions delesmatemàtiquesesrefereixenalarealitat,nosóncertes;ienlamesuraquesón certes,noesrefereixenalarealitat.

AlbertEinstein(1879–1955)

Resum: Enaquestassaig,presentemunaderivacióheurísticadelesequacionsde Friedmannpertorbadesbasadaenlamecànicanewtoniana,oferintunaperspectiva intuïtivasobreaquestesrelacionscosmològiques.Aquestenfocamentressaltal’acord notableentrelesdescripcionsnewtonianesirelativistesdinsdecertslímits,actuant tantcomunnexeconceptualifinsitotfilosòficicomunaeinapedagògicaper aprofundirenelsprincipisfísicsquegovernenl’evoluciódel’univers.

Simplificantelcomplexmarcmatemàticdelateoriadelarelativitatgeneral,aquest mètodeproporcionaunaviaaccessibleperexplorarladinàmicadel’univers.Subratlla comlamecànicaclàssica,quans’aplicaambcura,potoferirperspectivesques’alineen ambelsresultatsrelativistesenl’aproximaciólineal.Aquestaconnexiónonomés aprofundeixlanostracomprensiódelauniversalitatdeleslleisfísiques,sinóque tambéreforçalaideaqueelsfenòmensrelativistessovintespodenentendreatravés d’anàlegsclàssicsfamiliars.

Paraulesclau: equacionsdeFriedmann,pertorbacionscosmològiques,mecànica newtoniana,relativitatgeneral.

ClassificacióMSC2020: 83C05,83C99,70F99,83F05.

1Introducció

Enelpresentestudi,enscentremenlesequacionsdeFriedmann,formulades perprimeravegadaperAleksandrFriedmannaprincipisdeladècadadels anysvintdelseglepassat.Aquestesequacions,sotacerteshipòtesis,representenlaformaqueadoptenlesequacionsdecampd’Einsteinenelmarcdela relativitatgeneral(RG)quans’apliquenalacosmologia.Constitueixenlapedra angulardelacosmologiamoderna,jaquedescriuenladinàmicaagranescala del’universsotaleshipòtesisd’homogeneïtatiisotropia,tenintencomptela curvaturaielcontingutd’energiaimatèriadel’univers.Proporcionenunmarc matemàticperexplorarcoml’universevolucionaalllargdeltemps,abastant tantescenarisd’expansiócomdecontracció.

L’innovadortreballdeFriedmann[10, 11]inicialmentvatenirdificultatsper obtenirreconeixement.Durantanys,lessolucionsdelessevesequacions,que revelavenlapossibilitatd’universosenexpansióicontracció,vanserengran partignoradesperlacomunitatcientífica[20].FinsitotEinstein,malgratelseu paperfonamentaleneldesenvolupamentdelaRG,vadesestimarinicialment elsresultatsdeFriedmann,considerant-losinconsistentsamblessevespròpies equacions.Benaviat,però,ainstànciesdelmateixFriedmann,Einsteinva reconèixer-nelavalidesadesprésd’unexamenmésdetallat,totiquedurant deuanysvaseguirsentescèpticsobrelaidead’ununiversenexpansió.No vaserfinsalaformulaciódelalleideHubble-Lemaître,quevaestabliruna relaciódirectaentreeldesplaçamentcapalvermelldelallumdelesgalàxies ilessevesdistàncies,queeltreballdeFriedmannvaserplenamentapreciat. Aquestavençvaconnectarlacosmologiaobservacionalamblafísicateòrica,i vaconsolidarlarellevànciadelessolucionsdelesequacionsdeFriedmannper entendrel’evoluciódel’univers.

PartintdelescontribucionspioneresdeFriedmann,l’estudiquepresentem derivalesequacionsdeFriedmannpertorbadesatravésd’unenfocament alternatiu.Inspirant-nosentreballsanteriors,comelsdeMcCreaiMilne[25]i posteriormentelsdeCallan,DickeiPeebles[4],utilitzaremunmètodeheurístic basatenlamecànicanewtoniana.Aquestaperspectivaalternativanonomés serveixcomaeinapedagògicapercomprendrelesequacionsdeFriedmann, sinóquetambésubratllalacoherènciaentreelsmarcsnewtoniansirelativistes sotacondicionsespecífiques.Atravésd’aquestenfocament,espreténil.luminar elsprincipisfísicssubjacentsal’evoluciócòsmicaioferirperspectivesque complementinlavisiórelativista.

Lesimplicacionsd’aquesttreballvanmésenllàdel’aspectepedagògic.La derivacióposademanifestelpaperdelesinhomogeneïtatsdelfactord’escala ilataxad’expansiódeHubble(lamesuradelavelocitatenquès’expandeix l’univers),unfetambprofundesconseqüènciesobservacionals.Enparticular, suggereixquelesvariacionslocalsenlataxad’expansiódeHubblepodriensorgiracausadediferènciesenelsentornsfísicsdelsobjectescòsmicsutilitzats permesurar-la.Aquestaperspectivapodriaoferirunanovavisiósobrela tensió deHubble,lapersistentdiscrepànciaentreelvaloractualdelataxad’expansiódeHubblemesuradalocalmentielseuvalorinferitdelfonsdemicroones còsmic,iproporcionariaaixíunmarcperinterpretaraquestesvariacions.

Amésamés,aquestenfocamentposaèmfasienlaimportànciadel’anàlisi pertorbativaperconnectarlateoriaambl’observació.Obrelaportaauna exploraciómésprofundadecomlesestructuresidinàmiqueslocalsinflueixen enelsparàmetrescosmològicsagranescala,connectantlafísicaapetitaescala ambelrelatmésamplidel’evoluciócòsmica.Aquestenfocamentdual—que ofereixtantunaintroducciópedagògicacomperspectivessobreproblemes avançats—subratllalaversatilitatdeltreballquepresentem.

Eltreballestàestructuratdelamanerasegüent:Alasecció2,ipartintde laconsideracióquel’universpresentahomogeneïtatiisotropiaagranescala, asumiremqueestàpled’unfluidperfectehomogeni,elselementsdelquales podenidentificaramblesgalàxiesqueelcomponen.Enaquestcontext,derivaremlesequacionsdeFriedmannenlasevaformahomogènia,lessolucions delesqualsdescriuentantl’evoluciód’aquestfluxcoml’expansiódel’univers, basant-nosenelmarcteòricdelarelativitatgeneral.Alasecció3s’exposa comaquestesequacionsespodenderivarnovamentfentúsexclusivament deconceptespropisdelamecànicanewtoniana.Lasecció4,queconstitueix l’apartatmésrellevantd’aquestestudi,estàdedicadaaladeterminació,de maneraheurística,delesequacionsdeFriedmannpertorbadesenprimera aproximació.Somconscientsquel’universnoéscompletamenthomogenia granescala,iaquestesinhomogeneïtatsensproporcioneninformacióessencialsobrelasevaestructura.Peraquestmotiu,ésfonamentaldeterminarles equacionspertorbades,jaquepermetendescriureientendrel’evoluciód’aquestesinhomogeneïtats.Alasecció5,deduiremlesequacionsdeconservaciói d’Eulerrelativistes,lesquals,juntamentamblesequacionspertorbadesde Friedmann,constitueixenelsistemaquedescriudemaneracompletal’evolució delesinhomogeneïtats.Alasecció6establiremlarelacióentrelamètricade Schwarzschild—unadelesprimeressolucionsdelesequacionsd’Einstein—i lamecànicanewtoniana.Tambéanalitzaremlasevaconnexióambelsforats negresidiscutiremcom,apartird’aquestamètrica,espotreproduircorrectamentlaprecessiódelperihelideMercuri.Finalment,alasecció7,debatrem elsignificatfísicdelessingularitatsmatemàtiquesque,sovint,apareixenen cosmologia.

2 LesequacionsdeFriedmannapartirdelarelativitatgeneral

EnaquestaseccióobtindremlesequacionshomogèniesdeFriedmannapartirdelarelativitatgeneral.Perpoderfer-ho,primerdetothemd’assumir l’homogeneïtatilaisotropiadel’universagranescala,cosaqueensportaa descriure’lgeomètricamentcomunavarietatdeLorentz(unavarietatpseudoriemannianaambsignatura (1, 3),queéslageneralitzacióambcurvaturade l’espaitempsdeMinkowskiqueapareixenlarelativitatespecial)amblamètrica deFriedmann-Lemaître-Robertson-Walker(FLRW) ds2 =−N 2(t)dt2 + a2(t) dr 1 kr 2 + r 2 dΩ ,

on dΩ = dθ2 + sin2 θdφ2 , N(t) denotalafunciólapse,querepresentala llibertatdereparametritzareltemps, k representalacurvaturadel’espai,i a(t) indicaelfactord’escala:perentendre’ns,unamenade«radidel’univers», almenysenelcasquel’espaitinguicurvaturapositiva.

Peraaquestamètrica,l’invariantgeomètricmésimportantésl’escalarde Ricciocurvaturaescalar,ques’expressacoma

R = 6 1 aN d dt ˙ a N + H2 N + k a2 ,

on,enaquestasecció,el«punt»indicaladerivadarespecteal tempscòsmic t,i H = a a representalataxad’expansiódeHubble,tambéanomenada paràmetre deHubble,jaquedepèndeltempscòsmic.Pertant,nosemblagaireapropiat anomenar-la constantdeHubble,comesfahabitualment.

Quanconsideremununivershomogeniiisòtropagranescala,pled’unfluid perfecteenquèlapressiódepènúnicamentdeladensitatd’energia,elmodel deFLRWenspermetdescriurediferentsetapesevolutives.Inicialment,elfluid estariacompostperradiació(dominantenlasevaetapaprimitiva),seguitd’una distribucióhomogèniadominadapermatèriabariònicai,sobretot,matèria fosca.Enl’èpocaactual,elcomponentpredominantseriaelques’anomena energiafosca,enquèlapressióésaproximadamentigualaladensitatd’energia canviadadesigne.

Enaquestcontext,ellagrangiàd’Einstein-Hilbert([18])espotexpressarcom unafunciódel’escalardeRicci,lamesuraespaitempsielcontingutmaterial,i prenlaformasegüent:

on ρ0 representaladensitatd’energiahomogènia, G éslaconstantdela gravitacióuniversal,i √ g = Na3 actuacomamesuraquadridimensionalper alamètricadeFLRW.

Caldestacarqueaquestlagrangiàespotreformularcoma

Pertant,tenintencomptequeelprimertermeésunaderivadatotal,aquest lagrangiàésequivalentalsegüent:

Noti’squelavariaciórespectedelafunciólapsecondueixalaconeguda restriccióhamiltoniana

on,desprésd’escollir N(t) = 1(recordemquelafunciólapsenomésrepresenta lallibertatdereparametritzareltemps.Entriar-laiguala1,elqueestemfent ésseleccionareltempspropid’unobservadorqueestrobaenrepòsrespecte alfluidqueomplel’univers),s’arribaalaprimeraequaciódeFriedmann:

quenoésaltracosaqueunarestricció,jaquenoméscontéladerivadaprimera delfactord’escala.

Perderivarl’equaciódinàmica,realitzemunavariaciórespectedelfactor d’escala.Desprésdefixar N = 1,l’equaciód’Euler-Lagrange

6aa + 3 ˙ a2 = 8πG d da (ρ0a3) 3ka, on,degutaladependènciadeladensitatd’energiaúnicamentrespectedel factord’escala,substituïm ∂ ∂a per d da

Acontinuació,assumimunaevolucióadiabàticaenquèl’entropiatotal esconserva,iutilitzemlaprimeralleidelatermodinàmica dE =−pdV (la variaciódel’energiaésigualamenyslapressióperlavariaciódelvolum).Enel nostrecas, E = a3ρ0, V = a3 i p = p0,essent p0 lapressióhomogènia,obtenim d(ρ0a3) =−p0da3 ⇒ d da (ρ0a3) =−3p0a2 , i,pertant:

Finalment,apartirdelaprimeraequaciódeFriedmann (1),arribema l’equaciódel’acceleració,osegonaequaciódeFriedmann a a =− 4πG 3 (3p0 + ρ0) =− 4πG 3 (1 + 3w0)ρ0, (2)

onhemintroduïtel paràmetredel’equaciód’estat w0 ≡ p0 ρ0 .

Observemqueaquestaúltimaequacióensdiuque,quan w0 > 1/3,l’universs’expandeixdemaneradesaccelerada,i,quan w0 < 1/3,hofademanera accelerada.

Aquestfetésimportant,jaque,segonselmodelactualmésutilitzat,l’anomenat ΛCDM-model (model Λ dematèriafoscafreda,on Λ ésla constant cosmològica d’Einstein),l’universvaexperimentarinicialment,comexplicarem alasecció7,unafased’expansióacceleradamoltràpidaconegudacoma inflació [13].Actualment,comsabemgràciesalesobservacionsdesupernovesde

tipusIafetespelsgrupslideratspelsastrònomsguardonatsambelPremiNobel Perlmutter,RiessiSchmidtafinalsdelseglepassat,l’universestrobadenou enunafased’expansióaccelerada.Perexplicaraquestasegonafase,elscosmòlegspostulenqueelcomponentdominantdel’universresponsabled’aquesta acceleraciós’anomena energiafosca.Curiosament,comjahemcomentat,el candidatmésutilitzatpermodelar-laéslafamosaconstantcosmològica,la qualdonallocaunaforçarepulsiva,iqueEinsteinjahaviaintroduïtl’any1917 percompensarl’atracciógravitatòriaenelseumodelestàtic.

Posteriorment,Einsteinvahaverderenunciar-hiuncopesvareconèixer quel’universs’estavaexpandint,gràciesalesobservacionsdeHubbleialtres astrònoms.Totiaixí,jaabansd’aquestdescobriment,cosmòlegsdeprestigi, comaraWillemdeSitter,havienidentificatqueelmodelestàticd’Einsteinera dinàmicamentinestableiquepetitespertorbacionspodriendesencadenarel col.lapseol’expansiódel’univers.Aquestainestabilitatinherentvaserundels primersindicisqueelmodelestàticnoerasostenible.

Comesdiuambcertaironia,«sis’esternudaenelmodeld’Einstein,l’univers col lapsa»,unaexpressióque,enelfons,subratllaquefinsitotunapetita pertorbacióseriasuficientperalterarl’equilibriprecariqueplantejava.Avui dia,sihoanalitzemdesdelpuntdevistadelssistemesdinàmics,diríem que,qualitativament,elpuntd’equilibriquerepresentamatemàticamentla soluciód’Einsteinésinestable;defet,corresponaunpuntdesella(vegeu, perexemple,[16]).Tanmateix,calrecordarque,enaquellaèpoca,lateoria qualitativadelssistemesdinàmicsencaranoestavaproudesenvolupadaper proporcionarunaanàlisiformalidetalladad’aquestainestabilitat.

3LesequacionsdeFriedmannapartirdelamecànica newtoniana

AratornaremaderivarlesduesequacionsdeFriedmannhomogènies,peròdes d’unaperspectivanewtoniana.Considerem,encoordenadescomòbils(sónles coordenadesadoptadesperunobservadorqueesmouambelfluidhomogeni queomplel’univers),unabolahomogèniademidagranambunradi R en l’espaieuclidià(tambépodemconsiderar R =∞,però,peraunradifinit,la massatotaldinsdelabolaésfinita: M = 4π 3 ϱ0R3,on ϱ0 ésladensitatdemassa homogènia).

Suposemquelabolas’expandeixradialment.Aixòvoldirque,si O és elcentredelabola,unpunt P dinsdelabolaal’instant t0 estransformaenel punt Pt al’instant t,iladistànciadesde O finsa Pt vedonadaper dOPt ≡ dOP (t) = a(t)dOP = a(t)| → OP |,on a(t),amb a(t0) = 1,éselfactord’escala queenshaaparegutalaseccióanterior.

Amésamés,al’instant t0,consideremeltriangle POQ,queestransforma eneltriangleequivalent Pt OQt al’instant t.Pertant,comque dOPt = a(t)dOP i dOQt = a(t)dOQ,utilitzantelteoremadeTales,trobemque,peraqualsevol parelldepunts P i Q dinsdelabola, dPt Qt = a(t)dPQ.

Larelaciómostraquequalsevolbola,al’instant t0,centradaenunpunt P ambradi R ≪ R s’expandeixradialmentamblamateixataxaquelabola granoriginal.Amésamés,lavelocitatrelativaentre Pt i Qt segueixlalleide Hubble-Lemaître d dt (dPt Qt ) = a(t)dPQ = H(t)dPt Qt .

L’equaciódemovimentperalfactord’escalaenlamecànicanewtoniana esderivaconsiderantunabolacentradaenunpuntdonat P iambunradi inicial R al’instant t0.Al’instant t,laforçaradialenunpuntdonat Qt ,situat alavoradelabola,escalculacoma F(Qt ) = f(a(t)R) → Pt Qt a(t)R .Perdeterminarla funció f ,escalculaelfluxqueentraalabola

Ψ = F · n dS = 4πa2(t)R2f(a(t)R), on n éslanormalexterioral’esferaqueenvoltalabolai dS éslamesurade l’àreadel’esfera.

D’altrabanda,apartirdel’equacióclàssicadePoisson ∇· F =−4πGϱ0,iel teoremadeladivergènciadeGauss,elfluxtambévedonatper Ψ = ∇· F dV =− 16π 2G 3 ϱ0a3(t)R3 ,

laqualcosacondueixalasegüentexpressióde f : f(a(t)R) =− 4πG 3 ϱ0a(t)R ⇒ F(Qt ) =− 4πG 3 ϱ0 → Pt Qt .

Pertant,l’acceleracióqueexperimentaunapartículadeprovademassa m alpunt Q acausadelabolaesdeterminamitjançantlasegonalleideNewton coma

ϱ0, onhemusatque → Pt Qt = a(t) → PQ,iensproporcionalasegonaequacióde Friedmannperaunfluiddepols,ésadir,ambpressiónul.la.

Aquestaequacióespotderivarapartirdellagrangià

N = R2 ˙ a2 2 + GM aR = R2 ˙ a2 2 + 4πG 3 R2a2ϱ0, on M = 4π 3 a3R3ϱ0 representalamassadinsdelabola. Defet,utilitzantl’equaciód’Euler-Lagranges’obté d dt

onhemusatlaconservaciódelamassa

∂a (a3ϱ0) = 0 ⇒ ∂ ∂a (a2ϱ0) =−aϱ0

Observemqueelradi R delabolatriadanoafectalesequacionsdinàmiques. Pertant,fixem R = 1.

PerderivarlasegonaequaciódeFriedmannperaunfluidqualsevol,ara hemdetenirencomptel’energiadelmovimentmicroscòpicdelespartícules queconstituexenelfluid,aixícomlainteraccióentreelles;pertant,substituïm ladensitatdemassaperladensitatd’energia,diem-n’hi ρ0,enellagrangià newtoniàamb R = 1,delaqualcosaresulta

Utilitzantl’equaciód’Euler-Lagrangeilaprimeralleidelatermodinàmica,

derivemfàcilment(2).

ElpassegüentésobtenirlaprimeraequaciódeFriedmann.Aixòespotaconseguircombinantlasegonaequacióamblaprimeralleidelatermodinàmica, expressadadelamanerasegüent:

Primer,reescrivim(2)coma

icalculem

Inserint(3)enaquestaúltimaequació,obtenim

Lasoluciód’aquestaequacióvedonadaper H2

πG 3 ρ

= C a2 , iestablintlaconstantd’integració C iguala k,obtenimlaprimeraequacióde Friedmann.

I,finalment,considerantquel’energiad’unabolahomogèniaderadi a és E = 4π 3 a3ρ0,ellagrangiànewtoniàapareixcoma LN = Ecin V ,on Ecin = a2 2 ésl’energiacinèticaperunitatdemassai V =− GE a éselpotencialgravitatori generatperlabolaambmassaenrepòs E.

4LesequacionsdeFriedmannpertorbades

Aquestaseccióestàbasadaenelsrecentsresultatsobtingutsa[17],enquètindremencomptelespetitesinhomogeneïtatsquetél’universagranescala,ique considerarempertorbacions.Comencemamblamètricasegüent,anomenada g, enl’aproximaciódelcampfebleperunpotencialnewtoniàestàtic |ΦN|≪ 1, queéslapertorbaciódelamètricadeFLRW ds2 = (1 + 2ΦN(x))dt2 (1 2ΦN(x))dx2 . (4)

Aquestaexpressióésunasoluciónotrivialdelesequacionspertorbades d’Einsteinquanesconsiderauncampnewtoniàfebleiestàtic.Espottrobara lafórmula(106.3)de[21]itambése’nfareferènciaenelllibred’Einstein The MeaningofRelativity [7].Enlaterminologiamoderna,s’anomenahabitualment calibraciónewtoniana.Aquí, x representalescoordenadesfísiques.Teninten comptel’expansiódel’univers,descritapelfactord’escala,ilavariabilitat delpotencialnewtonià,lamètrica (4) encoordenadescomòbils q,on x = aq, adoptalaformadinàmicad’unamètrica conformestàtic ([31]),ésadir,d’una mètricaambpartespacialconformementplanaiestàtica ds2 = a2 a2 N(q,t) dt2 a2 N(q,t)dq2 , (5)

on aN(q,t) ≊ a(t)(1 ΦN(q,t)) representaelfactord’escalapertorbat,queté unpapervitalenlacomprensiódeladinàmicadel’univers.

AraexpressemlaprimeraequaciódeFriedmannenununiversFLRWpla espacialmentiutilitzanteltempsconforme dt = adη,comellligamsegüent:

H ((a2)′ −H a2) = 8πGa4 3 ρ0, onusemladerivadarespectealtempsconformei H= a′/a éselparàmetre deHubbleconforme.

D’altrabanda,escrivint ρ = ρ0 + δρ, p = p0 + δp,l’equacióclàssicade Poissonvedonadaper ∆xΦN = 4πGδρ, que,utilitzantlescoordenadescomòbils,télaforma 1 3 ∆q( 2a2ΦN ) = 8πGa4 3 δρ.

Perreconciliarambduesequacions,iconsiderantlalinealitat,s’assumeix quelaprimeraequaciódeFriedmannpertorbadaés

H (∂η(a2 N) −H a2 N)

qa2 N = 8πGa4 3 ρ.

Acontinuació,ensocupemdelasegonaequaciódeFriedmannnopertorbada,ésadir,ladinàmica,queespotescriurecoma

on T0 = ρ0 3p0 éslatraçanopertorbadadeltensord’energia-impuls T = (ρ + p)u ⊗ u pg,essent u laformadualdelavelocitatdelfluidqueomple l’univers,i ⊗ elproductedeKronecker.

Enl’esperitdelesprimeresteoriesescalarsdelagravetat[1, 2, 27, 28],la generalitzaciónaturaldel’equacióclàssicadePoissonés

onpodemveureque,enaquestmarc,elpotencialnewtonià ΦN éscomunaona sonoraqueviatjaambvelocitat1/√3,impulsadaperlapertorbaciódela font δT .

Unavegadatenimaquest,lesequacions (6) i (7),l’equaciódinàmicamés senzillaquelescontéés

Pertant,enaquestenfocament,lesequacionsdeFriedmannpertorbades són

Ésimportantdestacarqueaquestesequacionscorresponenalesequacions linealitzadesdelarelativitatgeneral.Concretament,lesequacionspertorbades delaRGsón([26])

lesquals,desprésdecombinar-se,condueixen,enl’aproximaciólineal,ales equacionsdeFriedmannpertorbades(8)i(9).

PertrobarunaformamésfamiliardelesequacionsdeFriedmannpertorbades,ésimportantreconèixerque,enaquestenfocament,igualqueen l’espaitempsdeFLRW,emergeixunsistemadereferènciaprivilegiat:elsistema dereferènciacomòbil,queesdesplaçaambelfluidqueomplel’univers.De fet,comqueestemtractantambunproblemad’evolució,procedimcomenel formalismed’Arnowitt-Deser-Misner(ADM)[3],enquèlavarietatdeLorentzté

unafoliacióprivilegiadaperasuperfíciesespacials Σt ,iadoptemcoordenades comòbils.Enaquestmarc,definimper ∂t elvectornormaldetipustemps,la taxad’expansiódeHubbleescalaren«tempscòsmic» HN ≡ ∂t aN aN ielvector tridimensionaldeHubble HN = 1 aN ∇qaN.Llavors,utilitzantaquestesdefinicions,lesequacionsdeFriedmannpertorbadesadquireixenlaformahabitual del’espaitempshomogeni

amblapeculiaritatqueensapareixladivergènciadelvectordeHubble.

Tambéconsideremelvectorgradientquadridimensionald’unafunció f , definitengeometriadiferencialcoma gradg f = gµν ∂µ f∂ν .Llavors,enla mètrica(5),tenim

Delamateixamanera,ladivergènciaquadridimensionald’unquadrivector és divg w = 1 √ g ∂µ (√ gwµ ).Llavors,l’equaciódinàmicadeFriedmanns’expressacomlarelacióentrelageometriadelavarietatdeLorentzilamatèria queomplel’univers divg Hg,N = 4πG(ρ p), (12)

onhemintroduïtelquadrivectordeHubble Hg,N ≡ 1 aN gradg aN

Lesaltresequacionsdinàmiquesprovenendelaconservaciódeltensor d’energia-impuls,ésadir,de divg T = 0,que,enl’aproximaciólineal,condueix a

, (13) ∂t(a2 N(ρ + p)v) + (ρ + p)[3HNa2 Nv HN] +∇qp = 0, on v ≡ dq ds éslavelocitatespacial.

Enconclusió,lesequacionsdinàmiquesquegovernenl’evoluciódel’univers prenenunaformageomètricaforçasenzilla

divg Hg,N = 4πG(ρ p), divg T = 0. Peracabarlasecció,faremquatreobservacionsrellevants:

1. PodemescriurelaprimeraequaciódeFriedmannenunaformamés geomètricasiesconsideralacurvaturaintrínseca,diem-n’hi R,dela varietatdeLorentz.Comquealprimerordredepertorbacionstenim R= 4 a2 N ∇q · HN i H2 N = g(Hg,N, Hg,N),podemescriure g(Hg,N, Hg,N) 1 6 R= 8πG 3 ρ.

2. LacombinaciódelesduesequacionsdeFriedmann (10) i (11) juntamentambl’equaciódeconservació(13)condueixalarestricció

(14)

i,combinantlesduesequacionsdeFriedmann,obtenim

itambé

3. Multiplicant (15) per HN,combinantambl’equaciódeconservacióila restricció(14),s’obtélaprimeraequaciódeFriedmann.

4. Definintles coordenadesespacialsfísiques coma xN = aNq,prenentla derivadarespectealtempspropi s iutilitzantque

= aN a

t ,s’obté dxN ds = dt ds ∂t aN + v ·∇

i,tenintencompteque

HN xN + aNv, que,enl’aproximaciólineal,condueixalalleideHubble-Lemaîtrepertorbada dxN ds = HNxN + aN

Així,hemaconseguitreobtenir,demaneraheurística,lesequacionsque descriuenl’evoluciódelesinhomogeneïtatsdel’univers,lesqualsenspermeten comprendreambmésprofunditatlaformaciód’estructurescomplexescom lesgalàxiesielscúmulsdegalàxies.Amésamés,aquestesequacionstambé ofereixenlapossibilitatdeconfrontarelsresultatsteòricsamblesobservacions actuals,cosaquefacilitaunavalidacióempíricadelmodelcosmològic.En particular,enspermetenveurecomelmodelactualdelainflacióexplica adequadamentlafasemésprimitivadel’univers,icontribuiraixíalanostra comprensiódelseuorigenidelasevaevolució.Aquestesconnexionsentre teoriaidadesobservacionalssónfonamentalsperconsolidarlesnostresidees sobrel’universilessevescaracterístiquesagranescala.

5Lesequacionsdeconservacióid’Eulerrelativistes

UncopobtingudeslesequacionsdeFriedmannpertorbades,podemtrobar lesequacionsd’evolucióperaladensitatd’energiailavelocitatdelespertorbacions,apartirdel’equaciódeconservació divg T = 0.Noobstantaixò,

volemtrobar-lesapartirdelprimerprincipidelatermodinàmicaidel’equació clàssicad’Eulerdelsfluids.

Primerdetot,volemobtenirl’equaciódeconservaciódelarelativitatgeneral. Perfer-ho,necessitemelresultatsegüent:Sigui ϕη : R3 → R3 elfluxd’un fluidperfecte,amb ϕη sentlatransformacióidentitat.Definimlavelocitat tridimensionalentempsconforme u(ϕη(q),η) = dϕη(q) dη .Aleshores,arribem alresultatfonamental(trobareumésdetallsenelmoltrecomanablellibredel professorGirbau[12])

Ara,consideremunvolumcomòbilinfinitesimal δV ,onsuposaremque,dins d’aquestelementdevolum,lapressióéslamateixaentotselspunts.Aleshores, aplicantaquestresultatalaprimeralleidelatermodinàmica,obtenim([14])

dη ϕη(δV) ρ(q,η)dV η=η =−p(q,η) d dη ϕη(δV) 1 dV η=η , onl’elementdevolumespacialés dV = a3 N dq1 dq2 dq3.Aquestaformulació integralésequivalental’equaciódiferencial Dη

onhemutilitzatladerivadatotal D

ihemintroduïtlataxa d’expansiódeHubble HN ≡ ∂ηaN aN entempsconforme. Mantenintnoméselstermeslineals,s’obté

∂ηδρ + 3H (δρ + δp) + (ρ0 + p

)[∇q u 3

ΦN] = 0, elqualcoincideix,finsalprimerordre,amblesequacionsdelarelativitatgeneral,ial’ordrezeros’obtéòbviamentl’equaciódeconservacióenl’espaitemps deFLRWpla,ésadir, ρ0 =−3H(ρ0 + p0)

Finalment,necessiteml’equaciód’evoluciódelavelocitat u.Enprimerlloc, recordemqueperaunfluiddepols,ésadir,amb |p|≪ ρ,prenentl’elementde línia ds2 = dt2 dq2 enl’espaitempsdeMinkowski,l’equaciód’Eulerclàssica espotescriurecoma d dt ϕt (V) ϱv dV t=t = ∂V T(n)dS V ϱ∇qΦN dV,

on ϱ ésladensitatdemassa, T : R3 → R3 ésel tensord’esforç, v = dq dt , dS és l’elementd’àrea,i n éslanormalexterioralafrontera.Tenintencompteque

peraunfluidperfecteestéque T(n) =−pn,i,apartirdelteoremadela divergènciadeGauss,l’equaciód’Eulerespotescriurecoma

laformadiferencialdelaqualés

obé

onhemutilitzatlaprimeralleidelatermodinàmicaperaunfluiddepols,ésa dir,l’equaciódecontinuïtat ∂t ϱ +∇q · (ϱv) = 0.

Calassenyalarquel’equació (17) ésincompatibleamblarelativitatespecial. Peraquestmotiu,lacompararemamblalleideconservaciódeltensorenergiaimpuls,divg T = 0,enl’espaitempsdeFLRWpla.

Hemdetenirencompteque,usantcoordenades,l’equaciódeconservació s’escriu ∇µ T µ ν = 0,onamb ∇µ esdenotaladerivadacovariant.Apliquemla fórmula(86.11)de[21]

µ T µ ν =

alamètricadeFLRW ds2 = a2(dη2 dq2),on uµ = dη ds , dq

Atèsquesuposemquelavelocitatdelfluidésmoltmenorquelavelocitat delallum,aleshores, ∇µ T µ k = 0,queésequivalenta ∂µ (a4T µ k ) = 0,perquè,pel fetd’estarenunespaitempshomogeni, ∂kgµν = 0condueixa

∂η((ρ + p)u) + 4H (ρ + p)u +∇q · ((ρ + p)u)u + (ρ + p)u ·∇qu +∇qp = 0

Pertant,l’equacióclàssicad’Euler (16) enununiversenexpansióéscompatibleamblarelativitatespecialil’expansiódel’universquansubstituïm ladensitatdemassa ϱ perlafuncióde calorperunitatdevolum (ρ + p) i v per au.

Així,tenintencompteaquestasubstitució,quans’incloulagravetat,la formaintegraldel’equaciód’Euleresconverteixen([14]) d aN dη ϕη(V) aN(ρ + p)u dV η=η =− V

amb dV = a3 N dq1 dq2 dq3 (l’elementdevolumtridimensional)ionhemfet lasubstitució ∇qΦN →− 1 aN ∇qaN.I,enformadiferencial,l’equaciód’Euler relativistaesdevé

que,utilitzantladerivadatotalidesconsiderantalgunstermesdesegonordre, espotescriurecoma

Finalment,tinguemencompteque,alprimerordredepertorbacions,l’equacióesdevé

quecoincideixamblalinearitzaciódel’equaciódeconservaciódeltensor energia-impuls,divg T = 0.

6LamètricadeSchwarzschildapartirdelamecànica newtoniana

Unaaltraaplicaciód’aquestaanalogiaentrelamecànicanewtonianailarelativitatgeneralésl’obtenció,sensenecessitatderesoldrelesequacionsde campdelaRG,delafamosamètricadeSchwarzschild,unadelesprimeres solucionsdelesequacionsd’Einstein,quedescriulamètricaproduïdaperuna partículapuntualdemassa M situadaal’origendecoordenades.1 Enlaseva formamésconeguda,lamètricadeSchwarzschildéslaquevanobtenirde maneraindependentelsmatemàticsDavidHilbertiJohannesDroste[18,6]:

ds2 = (1 + 2ΦN(r))dt2 (1 + 2ΦN(r)) 1 dr 2 r 2 dΩ, (18) on dΩ = dθ2 + sin2 θdϕ2 , r representaladistànciaeuclidiana,i ΦN(r) = MG r éselpotencialnewtoniàcreatperunapartículapuntualdemassa M.

Notemqueaquestamètricaéssingularal’anomenat radideSchwarzschild r = 2MG,i,amésamés,noésestàticapera r< 2MG (elvector ∂r estornatemporal),totiqueelfísicKarlSchwarzschildvaobtenirunafamíliade solucionsquedepeniend’unparàmetre,ivatriarintencionadamentaquest

1 RecordemlafamosafraseatribuïdaaJohnArchibaldWheeler:«Lamatèrialidiual’espaitemps coms’hadecorbar,il’espaitempslidiualespartículesdeprovacoms’handemoure»,que, d’algunamanera,podríemdirqueéslarealització,asegonordre(unordremésdelamecànica newtoniana),delpensamentd’ErnstMachsobrelainèrcia.

paràmetredemaneraquelamètricanomésfossingularal’origendecoordenades,onestavasituadalapartícula([30]).Detfet,lasolucióqueellvatrobarva ser

ds2 = 1

, (19)

amb α = 2MG ion σ eraunparàmetrelliure,que,pertraslladarlasingularitatal’origen(mireuelcoeficientquemultiplicaa dt2 enl’equació (19)), Schwarzschildvatriariguala σ = α3.Noteuque,sitriem σ = 0,obtenimla soluciótrobadaperHilbertiDroste.

Defet,Schwarzschild,usantcoordenadesesfèriques,escriulamètrica, estacionàriaambsimetriaesfèrica,mésgeneralpossiblecoma

ds2 = F(r)dt2 H(r)dr 2 G(r)dΩ, i,resolentlesequacionsd’Einsteinalbuit,trobaelsvalorsde F , H i R enla formaqueesveua(19).

LadiferènciaambelstreballsdeHilbertiDrosteésque,degutalacovariànciadelesequacionsdelcampgravitatori,vantriarlanovavariable r ∗ = G(r), amblaqualcosalamètricaquedadelaforma

ds2 = W(r ∗)dt2 Z(r ∗)dr ∗2 r ∗2 dΩ

enlesnovescoordenades.I,comvaescriureHilbertenelseuarticle[18]:«estem igualmentjustificatsainterpretar r ∗ , θ i ϕ comacoordenadesesfèriques». Desafortunadament,Schwarzschildmoríl’any1916,durantlaPrimera GuerraMundial,encontraurepèmfigmentreerasoldat(vaserenelfrontde guerraonvaobtenirlasevasolució),imainovaconèixerlasolucióobtinguda perHilbertiDroste.Detotesmaneres,veuremquelamecànicanewtonianaens condueixalaversiódeHilbertiDroste.Amésamés,enmecànicanewtoniana, lavelocitatd’escapamentvedonadaper ve = 2MG r ,laqualcosaimplicaquela llum,ambvelocitatiguala1enunitatsnaturals,nopotescapardel’interiordel radideSchwarzschild.Això,enrelativitat,nomésescompleixsiestria σ = 0. Caldestacarque,basant-seenlaversiódeHilbertiDroste,l’any1939OppenheimeriSnydervanpublicarelseutreballsobreelcol.lapsegravitatori,en elqualvanconsiderarunmodelsimplificat,específicamentunaestrellasense rotació,sensepressióiambsimetriaesfèrica[29].Enaquesttreball,elsautors vanestablirlarelacióentrelescoordenadesd’unobservadorestàticilesd’un observadorqueesmouconjuntamentamblamatèria.Elfetcruciald’aquest treballésque,peraunobservadorextern,eltempsquetrigalasuperfíciede l’estrellaaentrardinsdelradideSchwarzschildésinfinit,encontrastamb eltempsexperimentatperunobservadorqueesmouconjuntamentambla matèria.Aquestfenomenesvaentendreinicialmentcomlaformaciód’un «estelcongelat»(cadavegadaalentiaméslasevacontraccióimainoarribavaaentrardinsdelradideSchwarzschild)finsamitjansdelsanysseixanta.

Posteriormentvaserrebatejatcomlaformaciód’un«foratnegre»,primerper J.A.Wheeler,peròdesd’unaperspectivadiferent:lad’unobservadorquees mouconjuntamentamblamatèriaqueescontreu.Desd’aquestpuntdevista, unforatnegreesformaenuntempsfinit,cosaquehadonatllocaunaàmplia literaturadedicadaaexplorar-nel’estructura.

Arribatsaaquestpunt,unespodriapreguntar:quèéselqueobserven elsastrònoms,estelscongelatsoforatsnegres?Defet,elsastrònomsno tenenaccésdirectealesobservacionsdesdelpuntdevistad’unobservador comòbil.Elquerealmentdetectensónfenòmensassociatsauncampgravitatori extrem,comaralaradiacióemesapermatèriaqueorbitaapropdelradide Schwarzschild.Així,éstemptadordirqueelques’observasónelsefectesdela formaciód’unforatnegre,talcomespercepdesd’unaperspectivaexterna. Unaspecteclauenaquestadiscussióéslaformaciódelqueesconeixcoma horitzód’esdeveniments.Tanmateix,unaanàlisidetalladad’aquestfenomen implicariaendinsar-nosenconsideracionsdediversaíndolequeensallunyarien del’objectiuprincipald’aquestasecció.

Fetaquestbreuresumhistòric,vegemcomobtenirlamètrica (18) utilitzant nomésconceptesnewtoniansiunamicaderelativitatespecial,i,pertant,sense haverderesoldrelescomplicadesequacionsdelaRGd’Einstein.Comencem perlaforçad’inèrciaintroduïdaperNewtonalsseus Principia,ésadir,aquella resistènciaquetenenelscossosaromandreenrepòsoenmovimentrectilini respected’unsuposat«espaiabsolut».Aquestas’expressacoma Fi =−miac , on mi éslamassainercialdelcosi ac lasevaacceleració.

D’altrabanda,laforçad’atracciódelaTerrasobreuncosés Fg =−gmg , on mg éslamassagravitatòriadelcos.Arribatsaaquestpunt,caldestacar quetotselsexperiments,desdeGalileufinsal’actualitat,ensindiquenqueel valornumèricdelamassainercialilamassagravitatòriaéselmateix.Aquesta igualtatesconeixcoma principid’equivalènciafeble,elqualpodemexpressar atravésdelasegonalleideNewtoncom ac =−g o,equivalentment,coma

Fi + Fg = 0amb mi = mg , (20) queensdiuquelasumadeforces—aquínocomptemamblafricció—que actuensobreunapartículaencaigudalliureészero;laforçad’inèrciacompensa lagravetat.Dit«al’estild’Einstein»,unapersonaencaigudalliure,iqualsevol objectequecaiguiambell,nosentenelseupes.Aquestfet,queenssemblatan natural,éselquevaguiarEinsteinenlaformulaciódelasevateoriarelativista delagravetat,ialqualellmateixvareferir-secom«laideamésfeliçdelameva vida».

Seguintaquestaidea,consideremlacaigudalliure,endireccióradial,d’un objectepuntualdinsuncampambsimetriaradial ΦN(r),on r tornaaserla distànciaeuclidianaal’origen.Llavors,lallei(20)s’escriucoma

ac =−∂r ΦN,

on ac ésl’acceleraciódel’objecteencaigudalliure.Arabé,comcalculem l’acceleració ac ?

Recordemquelarelativitatespecialjaensensenyaqueeltempsnoés absolut.Pertant,enquinsistemadereferènciahemd’aplicarlasegonalleide Newton?Perfer-nos-enunaidea,tornemaEinstein:l’objectenosentelseupes, ésadir,lesforcesqueactuensobreell,lagravetatilainercial,s’anul.len.

Peròquinahadeserlaforçad’inèrciaquesentl’objecteiquecompensala gravetat?Semblariaquelamésnaturalhadeseraquellaqueescalculaapartir deltempspropidel’objecte Fi =−m d2r ds2 ,jaqueésl’objecteelquelasent,i,per tant,l’acceleracióquehemd’agafarenlasegonalleideNewtonésl’acceleració pròpia,l’obtingudaenelsistemadereferènciadel’objecteencaigudalliure. Unavegadafetaaquestahipòtesi,lasegonalleideNewtons’escriucoma d2r ds2

Elpassegüentésaratrobarlamètrica,lesgeodèsiquesradialsdelaqual (recordemquel’objecteesmoulliurement,jaquenoactuacapforçasobre ell)ensdonenlalleideNewton (21).Persimetria,labusquem,encoordenades esfèriques,delaforma ds2 = A(r)dt2 B(r)dr 2 r 2 dΩ, i,enferlavariaciódel’acciórelativista S = ds respectede r ,s’obtél’equació delageodèsicaradial

d2r ds2 1 2 ∂r A = 0amblacondició A(r)B(r) = 1,

i,imposantquelamètricasiguiladeMinkowskial’infinit,jaqueelpotencial gravitatoris’anul.laal’infinit,juntamentambelfetqueescompleixilasegona lleideNewton(21),obtenim

A(r) = 1 + 2ΦN(r) i B(r) = (1 + 2ΦN(r)) 1 .

Veiem,doncs,que,apartirdelamecànicanewtonianaiimposantquela forçad’inèrciavedonadaperl’acceleraciópròpiadelcos,estrobalaversióde HilbertiDrostedelamètricadeSchwarzschild,enquèlescoordenadesque s’utilitzens’hand’interpretar,segonsensacabadedirlamecànicanewtoniana, comaesfèriques,talcomjavasuggerirHilbert.Observem,doncs,queésla físicalaqueensproporcionalainterpretacióadequadadelescoordenades. Ditd’unaaltramanera:lescoordenadesnotenenunsignificatindependent, desvinculatdelasoluciódelamètrica.Cadaunadelesmúltiplessolucions delamètricaportaassociadalasevapròpiainterpretaciófísicadelesseves coordenadeslocals,comensil lustraiensajudaacomprendrel’exempledela mètricadeSchwarzschild(vegi’sladiscussióqueesfaa[19]).

6.1SobrelaprecessiódelperihelideMercuri

LalleidelagravitacióuniversaldeNewtonhaviaestatunaeinaextraordinàriamentprecisaperdescriureelmovimentdelsplanetesdurantmésdedos

segles.Noobstantaixò,afinalsdelsegle xix,elsastrònomsvanidentificaruna discrepànciapersistentenelmovimentdelperiheli(elpuntdemàximaproximitatalSol)del’òrbitadeMercuri,quenopodiaserexplicadacompletament amblateoriadeNewton.

Segonselscàlculsbasatsenlamecànicanewtoniana,elperihelideMercuri haviadeprecessionarenpartacausadelesinteraccionsgravitacionalsamb elsaltresplanetesdelsistemasolar.Totiaixò,lesobservacionsmostravenun excésd’aproximadament43segonsd’arcperseglequenoespodiajustificar ambleslleisconegudes.

Durantdècadesesvanproposardiverseshipòtesisperexplicaraquestadiscrepància,incloent-hil’existènciad’unnouplaneta(anomenathipotèticament Vulcà)ocorreccionsalalleideNewton.Capd’aquestesteories,però,noesva demostrarquefosconcloent.

Afortunadament,pocdesprésdetrobarlessevesequacions,iusantpertorbacionsdesegonordredelessevesequacions,Einsteinvatrobarqueel termeaddicionalassociatalacurvaturadel’espaitempsexplicavaexactament els43segonsd’arcpersegleobservatsexperimentalment.Aixòvaserunèxit espectacular,quevaconvèncerEinsteinquelasevateoriaeracorrecta(anys abansdeltanfamóseclipsi),ivamarcarunafitaenlahistòriadelaciència. Defet,aquestcàlculbasatenaproximacionsdesegonordredelesequacions delaRG,iqueaportavanovescorreccionsalamecànicanewtoniana,vaser elquevamotivarSchwarzschildabuscarunasolucióexactadelesequacions gravitatòriesdelaRG,laqualpermetiadescriurecorrectamentelmoviment d’unplanetaalvoltantdelSol.

Aquínomésfaremunabreumenciódecomespottrobarlaprecessiódel perihelideMercuriatravésdelacalibraciónewtoniana.Comencemambles anomenades coordenadesharmòniques ([32]) X1 = R sin θ cos ϕ,X2 = R sin θ sin ϕ, X3 = R cos θ,t = t, on R = r MG.Enaquestescoordenades,lamètricadeSchwarzschildesdevé ds2 = 1 MG/R 1 + MG/R dt2

(

· dX)2 , laqual,enl’aproximació MG ≪ R,iretenintnoméstermeslinealsen MG/R, s’escriucoma

queéslacalibraciónewtonianaperaunapartículapuntual,iquetambédona lamateixaprecessiódelperihelideMercuriquelamètricadeSchwarzschild,ja

queambduesmètriques,enl’aproximació MG/r ≪ 1,donenllocalamateixa equacióclau([32,24])

dϕ du 2 = 1 + 2MG(u + u+ + u ) (u u+)(u u) , (22)

onhemintroduïtlanotació u = 1/r , u+ = 1/r+ i u = 1/r ,essent r la distànciadelperihelii r+ ladel’afeli.Laintegraciódel’equació (22) permet calcularlaprecessiódelperihelideMercuri.(Podeutrobartotselscàlculs detallatsenelllibredeWeinberg[32].)

Elmateixocorresifemservirlesanomenades coordenadesisotròpiques,en lesqualslamètricadeSchwarzschilds’expressadelamanerasegüent:

amb r = r 1 + MG 2r 2,i,pertant,per MG/r ≪ 1,tornemaobtenirlarelació r = r MG,araentrecoordenadesesfèriquesiisotròpiques.

Perconcloure,convédestacarunaobservaciórellevant:Siconsideremla primeraequaciódeFriedmann (10) albuitibusquemsolucionsestacionàries ambsimetriaesfèrica,obtindrem

∇q · HN = 0 ⇒

on q =|q| éselmòdulde q.Lasoluciód’aquestaequació,que,alineant-seamb lamètricadeMinkowski,al’infinitval1,és: aN = eC/q.Peravalorsgransde q, tindrem aN ≊ 1 + C q ,i,pertant,sivolemobtenirlamètricacreadaperuna partículapuntualdemassa M,hemdetriar C = MG.

Finalment,pertrobarlarelacióamblescoordenadesesfèriquesqueapareixenenlamètricadeHilbertiDroste,ésadir,entre q iladistànciaeuclidiana r , sicomparemlapartangular—laquemultiplicaa dΩ—per q ≥ MG,s’obté: r = qeMG/q ⇒ q ≊ r MG

per MG/q ≪ 1.Aixídoncs,peravalorsgransde r ,larelacióéslamateixa quehihaentrelescoordenadesesfèriquesiharmòniquesoisotròpiques,i,per tant,amblamètricaques’obtéapartirdelaprimeraequaciódeFriedmann, tambéestrobalaprecessiódelperihelideMercuri.

Efectivament,consideremunmovimentenelpla θ = π/2,llavorslamètrica deHilbert-Drostes’escriucoma

ds2 = a 2 N (r)dt2 a2 N(r)dr 2 r 2 dϕ2 , on a2 N(r) = 1 1+2ΦN(r) .D’altrabanda,l’acciórelativistaespotescriurecom a S = ds = ds2 ds2 ds,i,pertant,ellagrangiàés

L= a 2 N (r) ˙ t2 a2 N(r)r 2 r 2ϕ2 , amb L= 1.

Comqueellagrangiànodepènnide t nide ϕ,tenimduesquantitatsque esconserven a 2 N (r)t = 2E + 1i r 2ϕ = L, amblaqualcosalacondició L= 1ensportaa

Siaraconsideremlamètricaconformestàtica ds2 = a 2 N (q)dt2 a2 N(q)dq2 , amb a2 N(q) = e2MG/q ≊ 1 2ΦN(q), obtindrem

i,usantlarelació r 2 = a2 Nq2,s’arriba,enl’aproximació MG/q ≪ 1,a(23).

7Algunesreflexionssobreelsignificatfísicdeles singularitatsmatemàtiquesqueemergeixenencosmologia

Elbig-bang,totiserunasingularitatmatemàticadelesequacionsd’Einstein (noméscalresoldrelesequacionshomogèniesdeFriedmannambunaequació d’estatlineal: p0 = wρ0 on w> 1),sovints’harepresentatdemanera inexactacomunaexplosióliteralalcomençamentdel’univers.Perexemple,en elreconegutprogramatelevisiu Cosmos,emèsalsanysvuitantaipresentatper l’astrònomCarlSagan,l’inicidel’universespresentavasovintcomunacolossal explosió.Tanmateix,aquestarepresentaciómancadefonamentcientíficquan s’examinadesdelaperspectivadelarelativitatgeneral.Recordemqueelmateix AlbertEinsteinvaremarcarque,peradensitatsd’energiaelevades,lesseves equacionsperdenelseusignificat[7].Enlessevesparaules:

Elsdubtesteòricsesbasenenelfetque,enelmomentinicialdel’expansió,la mètricaesdevésingulariladensitatd’energia, ρ,estornainfinita.Enaquest sentit,caltenirencompteelsegüent:lateoriaactualdelarelativitatesbasaen unadivisiódelarealitatfísicaenuncampmètric(gravetat),d’unabanda,ienun campelectromagnèticimatèria,del’altra.Enrealitat,l’espaiprobablement tindràuncaràcteruniforme,ilateoriaactualnomésseràvàlidacomuncas límit.Peradensitatselevadesdelcampidelamatèria,lesequacionsdecamp, ifinsitotlesvariablesdecampquehiintervenen,notindrancapsignificatreal. Pertant,noespotassumirlavalidesadelesequacionsperadensitatsmolt altesdecampimatèria,niconclourequeelcomençamentdel’expansióimplica necessàriamentunasingularitatenelsentitmatemàtic.Elquecalentendre ésquelesequacionsnoespodencontinuarenaquestesregions.Aquesta consideració,però,noalteraelfetqueelprincipidelmónconstitueixrealment uninicidesdelpuntdevistadeldesenvolupamentdelsestelsisistemesd’estels actuals,momentenquèaquestsestelsisistemesencaranoexistiencoma entitatsindividuals.

Pertant,elqueaquestasingularitatmatemàticaindicaésque,peraun tempscòsmicmoltpropera t = 0,onhemtraslladatlasingularitatal’instant t = 0,lesequacionsdelarelativitatgeneralnosónvàlidesperdescriure clàssicamentl’univers.Enaquestsentit,s’assumeixgeneralmentquelarelativitatgeneraldescriul’universnomésperaescalesd’energiaotemperaturaper sotadeladePlanck.Aquestaideal’expressàclaramentAlanGuth,l’inventor delparadigmainflacionari,a[13]quanvaescriure:

Elmodelestàndardpresentaunasingularitatqueconvencionalmentesconsidera eneltemps t = 0.Quan t → 0,latemperaturadel’universtendeixal’infinit. Aixòimplicaquenoespotdefinirunproblemadevalorsinicialsen t = 0.No obstantaixò,quanlatemperaturadel’universésdel’ordredelamassade Planck(mpl ∼ 1 22 × 1019 GeV)osuperior,lesequacionsdelmodelestàndard sónindubtablementinoperants,jaques’esperaqueelsefectesgravitacionals quànticsesdevinguinessencials.

Pertant,dinsdelslímitsdelnostreconeixement,ésraonableiniciarl’escenari delbig-bangcalentaunatemperaturaquesiguicòmodamentinferiorala massadePlanck.Enaquestmoment,espotprendreladescripciódel’univers comunconjuntdecondicionsinicials,ilesequacionsdemovimentdescriuen llavorsl’evolucióposterior.Perdescomptat,l’equaciód’estatdelamatèria aaquestestemperaturesnoesconeixrealment,peròespodenferdiverses hipòtesisiexplorar-nelesconseqüències.

Ampliantaquestaconcepcióprofundamentarreladad’unacreaciódel’univers—possiblementheretada,almenysaOccident,d’unatradiciópaulina—,la representaciódelbig-bangcomunaexplosiódramàticaprovémésdeldesig detransmetreunanarrativacaptivadoraqued’unarepresentacióprecisadels principisqueregeixenlanatura.Defet,elterme big-bang vaserencunyat inicialmentdurantunaemissióderàdiodelaBBCl’any1949comunaetiqueta unamicadespectivaperl’astrònomFredHoyle,quepreferiaelseumodel d’estatestacionaridavantdel’universenevolucióproposatpelfísicteòric isacerdotbelgaGeorgesLemaître.Lemaîtrevasuggerirquel’universesva expandirdesd’un àtomprimigeni [22].Defet,comDiracvaexplicara[5],la propostadeLemaîtreeraquel’universesvaoriginarapartird’unúnicàtom superradioactiuambunamassaextremadamentgran,queesvadesintegrar demaneramoltabrupta,iesvatrencarenfragments,iaquestsfragmentsen pecesencaraméspetites.EnparaulesdelmateixLemaître:

Necessitemunateoriadel’evolucióenformadefocsartificials.Elsdarrers dosmilmilionsd’anyssónunaevoluciólenta:sóncendresifumd’unsfocs artificialsbrillantsimoltràpids.

Ésimportantdestacarque,enaquestafrase,l’úsfiguratiudelterme focs artificials hageneratmalentesospersistents,perpetuatsfinsavuipernarratives popularsquepresentenl’inicidel’universcomunaexplosiódematèrialocalitzadaenl’espaiexterior.Tanmateix,d’unamaneramésaclaridora,Lemaîtreva escriurea[23]:

Sielmónhacomençatambunsolquàntum,lesnocionsd’espaiitempsno tindriencapsentitalprincipiinoméscomençarienaadquiriralgunsignificat quanelquàntumoriginals’haguésdividitenunnombresuficientdequàntums. Siaquestapropostaéscorrecta,l’inicidelmónvasucceirunamicaabansde l’inicidel’espaiieltemps.Uninicidelmónd’aquesttipusestàprouallunyat del’ordreactualdelanatura,inoésenabsolutrepugnant.

Ésevidentquelacomprensióactualdel big-bang haevolucionatsignificativament,especialmentamblaintroducciódelparadigmainflacionari[13].La majoriadelscosmòlegsacceptenavuiqueunadescripcióclàssicadel’univers nomésésfactiblealesescalesdelagranteoriaunificada(GTU),momenten quèunaexpansióacceleradaésimpulsadaperuncampescalarconegutcom a inflató.Desprésdelainflació,l’universexperimentaunprocésdereescalfament,jasiguiatravésdel’energiaalliberadaperl’inflatóomitjançantla producciógravitacional(aquíentralamecànicaquàntica,nopasenlaseva totalitatquantitzantlagravetat,perosí,demanerasemiclàssica,introduint uncampquànticinteraccionantamblagravetat,laquallicedeixpartdela sevaenergiaperproduirpartículessupermassivesquefinalmentdecauranen lesdel modelestàndard [15])departícules,pertald’alinear-seambl’univers calentdeFriedmann.

Defet,notenimcapexperimentaescalesproperesaladePlanck,en quèprobablementelsefectesquànticstinguinunaimportànciafonamental, opotseraaquestesescalesl’acciód’Einstein-Hilbertpresentano-linealitats enl’escalardeRicci,i,pertant,lesequacionsd’Einsteinpresentaranfortes correccionsosimplements’haurandecanviarenaquestaescala.Totaixòsón especulacionsivanmésenllàdelafísicaqueconeixem,iésclarquepodem ferteoriesaaquestaescala,comperexemplelateoriaquànticadellaços,la desupercordesitantesmés,iobtenirresultatssorprenents,peròaixòvamés enllàdelqueentenemperfísica,i,defet,espodriaqualificarcomunamena demetafísicaquefaúsd’unimmensaparellmatemàtic.Sovint,aquestaparell resultatancomplexquelaricaiintricadaestructuradelesmatemàtiques, ambtoteslessevesmúltiplesramificacions,dificulta,especialmentenaquestes teoriesalternativesqueaspirenatranscendirelslímitsdelarelativitatgeneral, l’obtenciód’unavisióclarainítidadelarealitatfísica.Aquestaperspectivaestà àmpliamentdesenvolupadaalllibre[8].

Així,adoptantunaactitudpositivista,sempreespotargumentarquenocal preocupar-seperlessingularitatsmatemàtiquesqueapareixenenfísica,car lamateixafísicalesresoldrà.Unexempleclareltrobemenl’electrodinàmica quàntica,enquèelstreballsdeFeymann,SchwingeriTomonaga,guardonats ambelPremiNobell’any1965,vandemostrarcomeliminarelsinfinits:primer regularitzantlateoriaidesprésrenormalitzant-la,laqualcosapermetobtenir resultatsfinitsid’acordamblesobservacionsexperimentals.

Aquestprecedentensconvidaapensarquelessingularitatsmatemàtiques quepodenaparèixerenaltresàmbits,comaraenlacosmologia,nosónmésque indicadorsdeleslimitacionsdelesteoriesactuals.Perexemple,lessingularitats

associadesalbig-bangoalsforatsnegresreflecteixenelfetquelarelativitat generalnoésaplicableaescalesextremes,onelsefectesdelagravetatquàntica hauriendetenirunpaperpredominant.Aixídoncs,aquestessingularitatsno s’hand’interpretarcomunafallidafonamentaldelafísica,sinócomunsenyal delanecessitatd’unateoriaméscompleta.

Enaltresparaules,lessingularitatsmatemàtiquesnosónmésqueunsímptomadelainaplicabilitatdelesteoriesfísiquesactualsacertesescaleso condicions(vegi’s[9],peraunadiscussiómésdetallada).Aquestessituacions, comlesassociadesalbig-bangol’interiordelsforatsnegres,plantegendesafiamentsperalsfísicsteòrics,jaqueelsexperimentsdirectesenaquestes escalesnosónaccessibles.Tanmateix,lahistòriadelafísicaensmostraqueles limitacionsd’unateoriasovintcondueixenalnaixementdenousparadigmes científics,obrintlaportaaunacomprensiómésprofundaiobjectivadela realitat.

8Conclusionsiunareflexiófinal

Enaquestassaig,s’hapresentatunaderivacióheurísticadelesequacionsde Friedmannrelativistesalprimerordredepertorbacions,partintdelsprincipis fonamentalsdelamecànicanewtoniana.Aquestenfocamentconnectalamecànicaclàssicaamblacosmologiarelativista,iofereixunaperspectivaintuïtiva sobreaquestesequacionsfonamentals.

Unresultatespecialmentsorprenentd’aquestaformulacióésqueelfactor d’escala,ienconseqüènciaelparàmetredeHubble,nosónestrictamenthomogenis.Aquestainhomogeneïtatsuggereixquelesdesviacionsenelsvalors mesuratsdelataxadeHubblepodensorgirenfunciódelsobjectescòsmics utilitzatscomareferènciaperaaquestesmesures.Diferentstipusd’objectes,comsupernoves,galàxiesoquàsars,podensondejarregionsdel’univers ambpropietatslocalsdiferents,cosaquecondueixadiscrepànciesenlataxa d’expansióinferida.

Aquestfetpottenirimplicacionssignificativesenl’anomenada tensióde Hubble,eldesacordobservatentreelvaloractualdelparàmetredeHubble mesuratlocalmentielseuvalorinferitdelfonsdemicroonescòsmic.Les inhomogeneïtatspreditesperaquestmarcpodrienproporcionarunaexplicació parcialperaaquestesvariacions,totmotivantunaexploraciómésprofunda delpaperdelesestructurescòsmiqueslocalsenlaconfiguraciódelanostra comprensiódel’expansiódel’univers.

D’altrabanda,aquestenfocamentpermetalleugerarlabretxaentrelamecànicaclàssicailarelativitatgeneral,vinculantelsfonamentsintuïtiusdela físicanewtonianaambelsprofundsconeixementsdelacosmologiamodernamitjançantlasenzillarelacióentregeometriaimatèriarepresentadaen l’equació (12).Aquestatascanonomésenriqueixlanostracomprensióteòrica del’evoluciódinàmicadel’univers,sinóquetambéofereixunaperspectiva unificadasobrecomlesdescripcionsclàssiquesirelativistesconvergeixenen l’estudidelsfenòmenscosmològics.

Voldriaacabarambunareflexióqueemsemblaadient.Aprimercopd’ull, ellectorpodriaestartemptatapensarqueenaquestassaigesticprioritzantla mecànicanewtonianasobrelarelativitatgeneral.Ansalcontrari,lamevaguia semprehanestatlesequacionslinealitzadesdelarelativitat,inomésbuscant unesequacionsque,enl’aproximaciólineal,coincidissinamblesd’Einstein éscoms’hanpoguttrobarlesequacionsdeFriedmannpertorbades.Ésaixí comfuncionenlesciènciesnaturals:primeresbusquenunesequacionsque, enunacertaaproximació,coincideixinamblesconegudes,idesprés,sical,ja estrobaràunprincipivariacionalquelesjustifiqui.Aquestvaserelpuntde vistad’Einsteinpertrobarlessevesequacionsperalcampgravitatori.Volia aconseguirunesequacionstensorials,i,pertant,covariantsperdifeomorfismes passius(canvisdecoordenades),que,enprimeraaproximació,s’alineessin amblesdeNewtoniPoisson,ivasernoméspocsdies—defet,setmanes— desprésdepresentar-lesal’AcadèmiaPrussianadeCiències,elnovembre de1915,quanHilbertlesvareobtenirapartird’unprincipivariacional,ja coneixent-lesprèviament.

Agraïments

AquesttreballcomptaambelsuportdelasubvencióespanyolaPID2021123903NB-I00finançadaperMCIN/AEI/10.13039/501100011033iper«FEDER UnamaneradehacerEuropa».

Referències

[1] Abraham,M. «ZurTheoriederGravitation». Physik.Zs.,13(1912),1–5.

[2] Abraham,M. «NeuereGravitationstheorien». JahrbuchderRadioaktivitat undElektronik (1915),470–520.

[3] Arnowitt,R.;Deser,S.;Misner,C.W. «Republicationof:Thedynamics ofgeneralrelativity». Gen.RelativityGravitation,40(2008),1997–2027.

[4] Callan,C.;Dicke,R.H.;Peebles,P.J.E. «CosmologyandNewtonian Mechanics». Amer.J.Phys.,33(2)(1965),105–108.

[5] Dirac,P.A.M. «ThescientificworkofGeorgesLemaître». Comment. PontificiaAcad.Sci.,2(11)(1968),1–20.

[6] Droste,J. «ThefieldofasinglecentreinEinstein’stheoryofgravitation, andthemotionofaparticleinthatfield». Nederl.Akad.Wetensch.Proc., 19(1917),197–215.

[7] Einstein,A. TheMeaningofRelativity.4aed.Princeton:PrincetonUniversityPress,1953.

[8] Elizalde,E. TheTrueStoryofModernCosmology:Origins,Protagonists andBreakthroughs.Berlín:Springer,2021.

[9] Elizalde,E. «Mathematicalsingularitiesinthefarthestconfinesofthe Universe–andafriefreportonitsevolutionaryhistory». Universe,9,33 (2023),1–24.

[10] Friedmann,A. «Onthecurvatureofspace». Z.Physik,10(1922),377–386.

[11] Friedmann,A. «ÜberdieMöglichkeiteinerWeltmitkonstanternegativer KrümmungdesRaumes». Z.Physik,21(1924),326–332.[Traduïta:«On thepossibilityofaworldwithconstantnegativecurvatureofspace». Gen. RelativityGravitation,31(12)(1999),2001–2008]

[12] Girbau,J. GeometriaDiferencialiRelativitat.Bellaterra:Manualsdela UniversitatAutònomadeBarcelona,1993.

[13] Guth,A.H. «Inflationaryuniverse:apossiblesolutiontothehorizonand flatnessproblems». Phys.Rev.D(3),23(2)(1981),347–356.

[14] deHaro,J. «RelationsbetweenNewtonianandRelativisticCosmology». Universe,10,263(2024).

[15] deHaro,J.;ArestéSaló,L.;Pan,S. «Gravitationalreheatingformulas andboundsinoscillatingbackgrounds». Phys.Rev.D,110(12)(2024), 123504.

[16] deHaro,J.;Elizalde,E. «Topicsincosmology—Clearlyexplainedby meansofsimpleexamples». Universe,8(3),166(2022).

[17] deHaro,J.;Elizalde,E.;Pan,S. «OntheperturbedFriedmannequations inNewtonianGauge».Preprint(2024).[Disponibleenlíniaa: https:// arxiv.org/abs/2412.15139]

[18] Hilbert,D. «DieGrundlagenderPhysik.(ZweiteMitteilung)». NachrichtenvonderGesellschaftderWissenschaftenzuGöttingen,MathematischPhysikalischeKlasse,1917(1917),53–76.

[19] Johns,O.D. «ValidityoftheEinsteinholeargument». Stud.Hist.Philos. Sci.BStud.Hist.Philos.ModernPhys.,68(2019),62–70.

[20] Klimchitskaya,G.L.;Mostepanenko,V.M. «CentenaryofAlexander Friedmann’spredictionoftheuniverseexpansionandthequantumvacuum». Physics,4(3)(2022),981–994.

[21] Landau,L.D.;Lifshitz,E.M. TheClassicalTheoryofFields.3aedició enanglèsrevisada.Oxford:PergamonPress,1971.(CourseofTheoretical Physics;2)

[22] Lemaître,A. «ContributionstoaBritishAssociationDiscussiononthe EvolutionoftheUniverse». Nature,128(1931),704–706.

[23] Lemaître,G. «Thebeginningoftheworldfromthepointofviewof quantumtheory». Nature,127(1)(1931),706.[ReproduïtcomaGolden OldieEditoriala: Luminet,J.-P. «Editorialnoteto:GeorgesLemaître,The beginningoftheworldfromthepointofviewofquantumtheory». Gen. RelativityGravitation,43(10)(2011),2911–2928]

[24] Magnan,C. «CompletecalculationsoftheperihelionprecessionofMercuryandthedeflectionoflightbytheSuninGeneralRelativity».Preprint (2007).[Disponibleenlíniaa: https://arxiv.org/abs/0712.3709]

[25] McCrea,W.H.;Milne,E.A. «Newtonianuniversesandthecurvatureof space». Q.J.Math.,5(1)(1934),73–80.

[26] Mukhanov,V. PhysicalFoundationsofCosmology.Ambunpròlegd’Andrei Linde.NovaYork:CambridgeUniversityPress,2005.

[27] Nordström,G. «Theprincipleofrelativityandgravitation». Phys.Zeit., 13(1912),1126–1129.

[28] Nordström,G. «ZurTheoriederGravitationvomStandpunktdesRelativitätsprinzips». Ann.Phys.,347(13)(1913),533–554.

[29] Oppenheimer,J.R.;Snyder,H. «Oncontinuedgravitationalcontraction». Phys.Rev.(2),56(5)(1939),455–459.

[30] Schwarzschild,K. «Onthegravitationalfieldofamasspointaccording toEinstein’stheory». Gen.RelativityGravitation,35(5)(2003),951–959. [Traduïtdel’articleoriginalalemany«ÜberdasGravitationsfeldeinesMassenpunktesnachderEinsteinschenTheorie». Sitzungsber.Königl.Preussich.Akad.Wiss.BerlinPhys.Math.Kl. (1916),189–196perS.Antocii A.Loinger]

[31] Synge,J.L. Relativity:TheGeneralTheory. Amsterdam:North-Holland PublishingCo.;NovaYork:IntersciencePublishers,Inc.,1960.(Seriesin Physics)

[32] Weinberg,S. GravitationandCosmology:PrinciplesandApplicationsof theGeneralTheoryofRelativity.NovaYork:JohnWiley&Sons,1972.

DepartamentdeMatemàtiques UniversitatPolitècnicadeCatalunya C.Colom, 11, 08222 Terrassa jaime.haro@upc.edu

ButlletídelaSocietatCatalanadeMatemàtiques Vol.39,núm.1-2,2024.Pàg.131–169. DOI:10.2436/20.2002.01.117

Tensorsenestadísticaalgebraica

LuisSierra,MartaCasanellasiPiotrZwiernik

Resum: Enestadísticaianàlisidedadestrobemtensorscontínuament.Elsobjectes centralsquevinculenlaciènciadedadesamblateoriadetensorsil’àlgebrasónels modelsambvariableslatents.Enaquestarticleproporcionemunavisiógeneralde lateoriadetensors,posantèmfasiespecialenlessevesaplicacionsenestadística algebraica.Reforcemaquestenfocamentambnombrososexemplesambl’objectiu d’il lustrarelsconceptesclau.Amés,s’inclouunarevisióextensadelaliteraturaper guiarelslectorscapaestudismésdetallatssobrelamatèria.

Paraulesclau: tensors,estadísticaalgebraica,modelsgràfics,descomposiciótensorial. ClassificacióMSC2020: 14M99,15A69,62H22,62R01,62R07.

1Introducció

Elstensors,comaconceptequegeneralitzalesmatriusadimensionssuperiors, vanserintroduïtsafinalsdelsegle xix perautorscomWilliamRowanHamilton, WoldemarVoigtoGregorioRicci-Curbastro,iesvanferpopularsambel treball[69].Totiqueelstensorsvanserdesenvolupatsperalcàlculdiferencial ilageometria,avuiendiatenenunpapercrucialenestadísticaiciènciade dades,jaqueofereixenunmarcmatemàticpotentperentendrefenòmens complexos,capturarrelacionsintricadesiextreureintuïcionsvaluosesde conjuntsdedadesd’altadimensió(vegeuelresum[46],perexemple).En aquestarticlevolemmostrarlaimportànciadelstensorsenestadísticaiciència dedades,centrant-nosenelsseusfonamentsmatemàticsilesconnexionsamb l’estadísticaalgebraica.

Aplicacionsbàsiques. Elstensorstenenaplicacionsextensesendiversos àmbits,incloent-hil’aprenentatgeautomàtic,laneurociènciailagenòmica. Enl’aprenentatgeautomàtic,elstensorsfacilitenl’anàlisidedadesmultidimensionalsipermetentasquescomelreconeixementd’imatges,elresum automàticdevídeosielprocessamentdelllenguatgenatural.Perexemple,en

elreconeixementd’imatgess’utilitzentensorsperrepresentarimatgesd’altaresolució,capturarrelacionsespacialsipermetreeldesenvolupamentde modelssofisticatsd’aprenentatgeprofund(vegeu[42,9]).

Enneurociència,elstensorstenenunpapercrucialperdesxifrarelspatronsdeconnectivitatcerebralicomprendrel’organitzaciófuncionaldelcervell (vegeu,perexemple,[28]).Lesxarxescerebrals,representadescomatensors d’ordresuperior,capturenlesinteraccionsentrediversesregionscerebralsi proporcioneninformaciósobreprocessoscognitius,trastornsneurològics iplasticitatcerebral.Elstensorspermetenl’extracciódecaracterístiquessignificativesdelesdadesd’imatgesperressonànciamagnèticafuncional,cosaque ajudaelsinvestigadorsaidentificarlesregionscerebralsassociadesatasques ocondicionsespecífiques;vegeu[16].

Lagenòmicaésunaltreàmbitenquèelstensorsofereixenunmarcpotentperanalitzardadesbiològiquesd’altadimensió.Enelcampdelesdades òmiques,s’emprentensorsperintegrardiversescaracterístiquesmoleculars comaral’expressiógènica,lametilaciódel’ADNilesmodificacionsd’histones(vegeu,perexemple,[94, 60, 74]).Mitjançantlamodelitzaciód’aquestes relacionscomplexesambtensors,elsinvestigadorssóncapaçosd’identificar signaturesmolecularsassociadesamalalties,predirresultatsdepacientsi orientarestratègiesdetractamentpersonalitzades.

Modelitzaciótensorial. Lacomplexitatgeomètricadelstensorsplantejareptesenlasevaanàlisiiinterpretació.Persuperar-loss’handesenvolupatmètodes queaprofitenestructuresdetensorsméssimples.Moltsdelsmodelsaplicats esbasenenaltresdemésbàsics:tensorsdiagonalsitensorsderanguodebaix rang.Aquestasimplificaciómilloralainterpretabilitatifacilitalacomputació eficientilainferènciaenaltesdimensions.

Comveurem,tantelstensorsdiagonalscomelsderanguapareixendemaneranaturalenelcontextd’independènciadevariablesaleatòries.Engeneral, moltsdelsmodelsestadísticsquefanservirindependènciadevariables(per exemple,l’anàlisidecomponentsindependents,olaindependènciacondicionada)esbasenatrobarunadescomposiciótensorialentermesdetensorsde ranginferior.

Elcampdel’estadísticaalgebraica s’erigeixcomelmarcadequatperestudiarelstensorsdinsdelsmodelsestadístics(labibliografiasobreestadística algebraicainclouelsllibres[66, 61, 34, 85, 99]).Aprofitantconceptesalgebraics, aquestanovadisciplinaproporcionanouspuntsdevistasobrelespropietats ielcomportamentdelstensorsencontextsestadísticsdiversos.Leseines algebraiquess’hanaplicatambèxitperabordarreptesrelacionatsamblaidentificabilitatdemodelsdevariableslatents,l’estimaciódeparàmetres,l’ajustde models,eldissenyd’experimentsialtresproblemesestadísticsfonamentals. Variableslatentsimodelsgràfics. Enciènciadedades,lainclusiódevariables latents (o ocultes,noobservades)ésunametodologiahabitualperamillorar l’expressivitatd’unmodelsenseincrementardràsticamentlasevacomplexitat

computacional.Malgratelseuimmenspotencial,lapresènciadevariables latentsintrodueixreptesimportantsenl’estimacióiinterpretaciódelmodel.Per abordaraquestsreptessovintesrequereixenalgorismessofisticatsitècniques estadístiquescomplexes.Aixòhaconstituïtunamotivacióimportantperal desenvolupamentdelateoriad’aprenentatgesingular(vegeu[92])iunagran partdelsavençosrecentsenestadísticaalgebraicasecentraenproblemes relacionats.

Aprofitantl’estructuraalgebraicadelstensors,s’haaconseguitunacomprensiómésprofundadelsmodelsestadísticsambvariableslatentsis’han desenvolupatalgorismesd’estimacióeficients.Lamodelitzaciódeladependènciaentrelesvariablesaleatòries(tantlesobservadescomleslatents)se solfermitjançantun modelgràfic.Enunmodelgràfic,elsvèrtexsd’ungraf representenvariablesaleatòriesilessevesarestescodifiquenlesrelacionsde dependènciacondicionada.Quanaquestarepresentacióutilitzaarestesdirigidesenungrafacíclic,elmodeltambéésconegutcoma xarxabayesiana o graf acíclicdirigit.

Elsarbreslatentsformenlafamíliamésmanejabledexarxesbayesianesamb variableslatentsipodenutilitzar-sepermodelitzarestructuresdedependència quans’esperenvariablesdeconfusió(confounders)noobservades(vegeu,per exemple,[62,secció2].Noobstantaixò,hihadiversesaltresraonsperlesquals elsmodelsd’arbreslatentshanesdevingutpopularsenciències.Enprimer lloc,elsmodelsd’arbreslatentsenglobenunrangmésamplidedistribucions deprobabilitatqueelsmodelsd’arbrestotalmentobservats,peròmantenen avantatgescomputacionals,especialmentenescenarisd’altadimensió.Amés, l’algorisme max-product permetunainferènciaeficientd’estatsnoobservats. Ensegonlloc,elsarbrespodenrepresentarprocessosevolutiusis’utilitzen comatalsenanàlisifilogenètica(vegeu,perexemple,[80]ilasecció6.1),en lingüística,modelitzantl’evoluciódelllenguatge(vegeu[70, 76]),ientomografiadexarxesperinferirestructuresd’Internet([19, 36]).Elsmodelsd’arbres latentsgaussians(perexemple,elsmodelsd’arbresdemovimentbrownià) capturencorrelacionsdeformanaturalperalatomografiadexarxesgràciesa ladisminuciódecorrelacionsambladistànciaenl’arbre;vegeulasecció4.3. Entercerlloc,elsmodelsd’arbreslatentscapturenl’estructurajeràrquicaen conjuntsdedadescomplexesiestanestretamentrelacionatsambmètodesde clusteritzaciójeràrquics([10, 50, 96, 59]).Aquestmarctambétrobaaplicació envisiópercomputador;vegeu[93]i[24].

Elsmodelsd’arbreslatentsgeneralitzenelsmodelsdeMarkovocults(HMM), coincidintambaquestsenarbreseruga([68]).Elsmodelsd’arbresdeMarkov ocults(HMTM;vegeu[29])relaxenlesrestriccionsdelsHMMipermetenqualsevolestructurad’arbrelatent.Lesaplicacionsinclouenelprocessamentdel senyal([23, 72]),labiomedicina([52, 65])ilalingüística([95]).Aquestsmodels inclouenmodelsfilogenètics,modelsdeBayesprimaris,modelsd’arbresde movimentbrowniàiunmodeld’anàlisifactorial,fetquecondueixaunmarc unificatperadiversesclassesdemodels([90]).

Unaltreexempleimportantdemodeldevariableslatentsésl’anàlisifactorial,queesfaservirpopularmentenl’estudidedadesmultivariadesper

identificarfactorslatentsqueinflueixenenlesvariablesobservades.Aquest camptéaplicacionsenfinances,psicologiaiciènciessocials,entred’altres.Una classedemodelsrelacionatsésl’anàlisidecomponentsprincipals (PCA),una tècnicaàmpliamentutilitzadaperalareducciódeladimensionalitatilacompressiódedades.Laversióprobabilística,conegudacoma PCAprobabilístic, introdueixvariableslatentspertenirencompteelsorolldelesdades,ielfa mésflexibleenaplicacionsreals(vegeulasecció6.3).

Unaaltraclasseimportantdemodelsgràficsésladeles màquinesdeBoltzmannrestringides (RBM;vegi’slasecció6.2),quesóncomponentsessencialsen l’aprenentatgeprofund,particularmentenl’entrenamentdexarxesdecreença profundes(deepbeliefnetworks)ialtresmodelsgeneratius.LesRBMinvolucren variableslatentsquecapturenpatronsocultsenlesdadesiespodenestendre amodelsgràficsprobabilísticsambmúltiplescapesdevariableslatents.Han revolucionatcampscomlavisiópercomputadorielreconeixementdeveui, desdelaperspectivaalgebraica,aquestaclassedemodelshaestatàmpliament estudiadaperMontúfaricol.laboradorsen[58,57].

Enaquestarticleexpositiuexpliquemelpaperquetenenelstensorsen l’estadísticaalgebraicaienmostremdiversosexemples.Alasecció2presentem tensorsqueapareixendemaneranaturalenestadísticaiproporcionemels primersresultatsquedonenrespostaapreguntesestadístiquesentermesde propietatsalgebraiquesdelstensors.Alasecció3aprofundimenelsmodels gràficsipresentemexemplesdemodelsgràficsdirigitsinodirigits,amb variablesdiscretesocontínues,fentèmfasiespecialenelsmodelsd’arbres latents.Lasecció4ladediquemalcasdevariablesgaussianes,querequereix untractamentespecífic.Basant-nosenelsexemplesanteriors,alasecció5illustremelsconceptesderangtensorialidescomposiciótensorialtotexplorant elmètodedelsmomentsenaquestcontext.Finalment,lasecció6estàdedicada aaplicacionsaddicionalsdelstensorsenestadísticaalgebraica,enquèens centremenl’anàlisifilogenètica,lesmàquinesdeBoltzmannrestringides,i l’anàlisidecomponentsindependents.

2Primersexemplesidefinicions

Enaquestaseccióintroduïmbreumentelsprincipalsobjectesd’estudi:tensors, tensorssimètrics,tensorsdiagonals,tensorsderangu,ielsseusnomscorresponentsenestadística.Enscentremsobretotenelcasdetensorsdiscrets peraaquestasecció,peròalgunsresultatstambévalenperalcasgeneral.Les referènciesbàsiquesperaaquestsconceptesinclouen[48,99,13,56].

Unamatriureal r1 × r2 ésunatauladosdimensional, A = (ai1,i2 ),on i1 ∈ {0,...,r1 1}, i2 ∈{0,...,r2 1},i ai1,i2 ∈ R.Donats m ∈ N ienters r1,...,rm ≥ 1,una matriu r1 ×···× rm -dimensional ésunacol.lecciódenombresreals ai1,...,im on ij ∈{0,...,rj 1} pera j = 1,...,m.Comexplicaremacontinuació, aquestesmatriusmultidimensionalss’identifiquendemaneranaturalambels tensors.

Començantpelcasdelesmatriususuals2-dimensionals,sigui {ej i }i=0,...,rj 1 labasecanònicaa Rrj , j = 1,...,m.Unamatriu A espotidentificarambuna

aplicacióbilinealde Rr1 ×Rr2 en R, (x,y) x⊤Ay (onl’element (e1 i ,e2 j ) s’envia a ai,j ).Si Ei,j denotalamatriuformadaperzerosexcepteun1enl’entrada enlaposició (i,j),lasevaaplicacióbilinealcorresponentesdenotaambel tensor e1 i ⊗ e2 j .D’aquestamanera,unamatriu A comlad’abansescorrespon ambeltensor ai,j e1 i ⊗ e2 j enl’espaivectorialdetensors Rr1 ⊗ Rr2 (pensat comal’espaideformesbilinealsen Rr1 × Rr2 ).

Donatsdosvectors v 1 = (v 1 0 ,...,v 1 r1 1) ∈ Rr1 i v 2 = (v 2

,...,v 2 r2 1) ∈ Rr2 , elseu productetensorial esdefineixcomeltensor v 1 ⊗ v 2 =

⊗ e2 i2 ∈ Rr1 ⊗ Rr2 Perexemple,si v 1 = (2, 0) ∈ R2 i v 2 = (1, 1) ∈ R2,aleshores v 1 ⊗v 2 = 2e1 0 ⊗e2 0 +2e1 0 ⊗e2 1 ésuntensordiferentde v 2 ⊗v 1 = 2e1 0 ⊗

Mésgeneralment,un tensor r1 ×···× rm sovintesdefineixcoml’aplicació multilineal Rr1 ×···× Rrm → R:eltensor e1 i1 ⊗···⊗ em im escorresponamb l’aplicaciómultilineal Rr1 ×···× Rrm → R (e1 j1 ,...,em jm ) → 1si (j1,...,jm) = (i1,...,im), 0altrament

iaqueststensorsformenunabasenaturaldel’espaivectorial Rr1 ⊗···⊗ Rrm delstensors r1 ×···× rm.Enaquestsentit,eltensor t = ii,...,im ai1,...,im e1 i1 ⊗

···⊗ em im enaquestespaiescorresponamblamatriumultidimensional A = [ai1,...,im ]ij =0,...,rj 1 dedimensions r1 ×···× rm.Quanparlemdecoordenades d’untensor,ensreferimalessevescoordenadesenlabasenatural.

Comabans,donats m vectors

v 1 = (v 1 0 ,...,v 1 r1 1) ∈ Rr1 ,...,v m = (v m 0 ,...,v 2 rm 1) ∈ Rrm ,

elseu productetensorial éseltensor v 1 ⊗···⊗v m = i1,...,im v 1 i1 v 2 i2 v m im e1 i1 ⊗

···⊗ em im .

Diemqueuntensor T de ⊗r Rn = Rn ⊗ r ···⊗ Rn és simètric si Ti1 ir = Tj1 jr peratotapermutació (j1,...,jr ) de (i1,...,ir ).L’espaidetensors simètricsde ⊗r Rn esdenotaper Sr (Rn).Ladimensióde Sr (Rn) és n+r 1 r , donatqueuntensor T ∈ Sr (Rn) espotcodificaramblesentrades Ti1 ir ,on 1 ≤ i1 ≤···≤ ir ≤ n.

2.1Mesuresdiscretescomatensors

Consideremunacol.leccióde m variablesaleatòriesdiscretes,cadascunaamb ri possiblesestats, Xi ∈Xi ={0,...,ri 1} amb i = 1,...,m.Elvector aleatori X = (X1,...,Xm) prenvalorsa X=X1 ×···×Xm iunadistribució deprobabilitat p = (p(x))x∈X de X espotidentificarambunpunta

RX := RX1 ⊗···⊗ RXm ,

on RXi ésunacòpiade Rri ambcoordenadesindexadesper Xi.Lescoordenades del’espaitensorial RX esdenotenamb px , x ∈X.Perexemple,si m = 2,

r1 = r2 = 2,aleshorescada Xi ésbinàriailescoordenadesde p ∈ RX són p00, p01, p10, p11, p = p00e0 ⊗ e0 + p01e0 ⊗ e1 + p10e1 ⊗ e0 + p11e1 ⊗ e1 (ometemels superíndexsperquèenaquestcaselsdosespaissónelmateix).

Perdefinició,toteslesdistribucionsdeprobabilitatdiscretesespoden representaralsímplex ∆X ⊆ RX ,on

X :=

Qualsevolmodelestadísticpera X és,perdefinició,unafamíliadedistribucionsdeprobabilitati,pertant,unafamíliadepuntsde ∆X .Aixòdonauna identificacióbàsicadelsmodelsestadísticsdiscretsambsubconjuntsdel’espai tensorial RX .

Quanesfanconsideracionsgeomètriquesreferentsalstensors,solser mésconvenienttreballarsobrel’espaiprojectiu.Denotemamb Proj(V) la projectivitzaciód’unespaivectorial V isigui PX R := Proj(RX ).Perdefinició, aquestéselconjuntdepunts RX \{0},identificantaquellsqueestroben sobrelamateixarectaquepassaperl’origen.Observemqueelsímplexde probabilitat ∆X estàencorrespondènciaamblapartnonegativade PX R .En efecte,labijeccióenviaunpunt q ∈ PX R ambcoordenades qx nonegatives a p = (px )x∈X ∈ ∆X ,on px = qx / y∈X qy

Laimmersióenelprojectiuéssovintconvenientperquèmoltsmodelsde dependènciescomplexessovintestandefinitsmòdulunaconstantdenormalització(vegeu,perexemple,elsmodelsdefinitsa(2)).

2.2Modeld’independènciaitensorsderangu

Donadaunacol lecciódevariablesdiscretes X = (X1,...,Xm) ∈X,diemqueles componentsde X sónindependents(oque X pertanyal modeld’independència total)sieltensor p ∈ ∆X corresponentaladistribucióde X espotescriure comelproductetensorialdelesdistribucionsindividuals pi ∈ RXi , p = p1 ⊗···⊗ pm Enaltresparaules, pi1i2 im = p1 i1 p2 i2 ··· pm im , pertot x = (i1,...,im) ∈X. (1)

Pertenirunequivalentgeomètricd’aquestaconstrucció,diemque p ∈ RX ésun tensorderangu (oun tensorpurodescomponible)siéselproducte tensoriald’una m-tupladevectors pi ∈ RXi pera i = 1,...,m.Elmodel d’independènciaperalvector X estàcontingutenelconjuntdetensorsde rangu.Quan m = 2,elstensorsderanguescorresponenamblesmatrius derangu.Enefecte, p = p1 ⊗ p2 éseltensor i,j p1 i p2 j e1 i ⊗ e2 j ,que,ambla correspondènciaintroduïdaadalt,espotidentificaramblamatriuderangu

Enelcontextdelageometriaalgebraicaprojectiva,elconjuntdetensorsde ranguescorresponamblavarietatdeSegrereal

Seg(PX1 R ×···× PXm R ) ⊂ PX R = Proj(RX1 ⊗···⊗ RXm );

vegeu[13,10.5.12].Perexemple, Seg(P1 R × P1 R) éslaimmersióde P1 R × P1 R a P3 R = Proj(R2 ⊗ R2) donadaperl’aplicació

P1 R × P1 R → P3 R

([p1 0 : p1 1 ],[p2 0 : p2 1 ]) → [p1 0 p2 0 : p1 0 p2 1 : p1 1 p2 0 : p1 1 p2 1 ].

Aquestavarietatestàformadapelspunts [p00 : p01 : p10 : p11] a P3 R que satisfanl’equació p00p11 p01p10 = 0iescorresponambelstensorsderangu, p1 ⊗ p2,omatrius p00 p01 p10 p11

derangu.Anàlogament,sipensemelselementsde RX1 ⊗ RX2 comamatrius,

Seg(PX1 R ⊗ PX2 R ) éselconjuntdematrius r1 × r2 derangu(definidespels menors2 × 2nuls).Defet,espotprovarfàcilmentquelapartnonegativade

Seg(PX1 R ×···× PXm R ) ésisomorfaalmodeld’independènciatotal.

2.3Tensorsdemoments-casdiscret

Consideremlesmesuresdiscretesdelasecció2.1.Donats u = (u1,...,um) ∈ Nm iunvector x = (x1,...,xm) ∈X,definimelmonomi

xu := x u1 1 x um m ,

onfemservirlaconvenció00 = 1.Si X tédistribució p,aleshoresel moment corresponentés

µu = E[Xu] = x∈X px xu

iesdiuqueésun momentd’ordre k si k = u1 +···+ um.Enparticular, µ0 0 = 1.

Exemple 1. Considerantelcasbinari (X1,X2) ∈{0, 1}2,esté µ00 = 1, µ10 = p10 + p11, µ01 = p01 + p11, µ11 = p11.

Proposició 1. L’aplicació RX → RX definidacoma

µu = E[Xu], peratot u ∈X,

ésunabijecciólinealqueenviaelconjunt x∈X px = 1 alconjunt {µ0 0 = 1}.

Hihaaltresmaneresdecodificarunadistribuciódeprobabilitatdiscreta quenosiguinomésambelsseusmoments.Unexempleimportantéseldels cumulants.Desdelpuntdevistageomètric,tractarambcumulantscorrespona feruncanvidevariables(nolineal)quepotsermésadientperestudiarlageometriadesegonsquinsmodels;vegeu[83, 98, 25].Siconsidereml’exemple1, podememprarlatransformacióencumulants: κ00 = 0, κ10 = µ10, κ01 = µ01, i κ11 = µ11 µ10µ01.Enaquestcaslaimatgedelmodeld’independènciapera aquestaaplicacióéselsubespailinealdonatper κ11 = 0.

3Modelsgràfics

Moltsmodelsenestadísticaiaprenentatgeautomàticinvolucrenmodelitzarla dependènciaentrediversescomponentsd’unvectoraleatori.Entreelsmúltiples exemplestrobeml’anàlisifactorial,lesmàquinesdeBoltzmannrestringides, oelmodeldeBayesprimari.Elsmodelsgràficsconstitueixenelllenguatge naturalperaaquestestasquesdemodelitzaciómultivariant,jaquerepresenten lesrelacionsdedependènciamitjançantgrafs.Enaquestcontext,elsvèrtexs d’ungrafrepresentenvariablesaleatòriesilesarestescodifiquenlesrelacions dedependènciacondicionadaentreelles.Segonseltipusd’arestes,podem distingirdostipusprincipalsdemodelsgràfics:elsquetenenarestesdirigides ielsqueno,cadascunadientperadiferentstasques.

Peraambdóstipusdemodelsgràficsésconvenientcomençarperlanoció de distribuciófactoritzada.Donatunvectoraleatori X = (X1,...,Xm) quepren valorsa X comabansidonat F unconjuntdesubconjuntsde [m],podem considerarelconjuntdedistribucionssobre X quesatisfan

p(x) =

on φF sónfuncionsnonegativessobre RXF (anomenades potencials)i Z ésla constantnormalitzadora.

Unexempletrivialéselde (1),onladistribuciófactoritzaencomponents individuals.Enaquestcas,elsfactorsescorresponenambdistribucionsmarginals,peròaquestapropietatnoéscertaengeneral.

Exemple(Modeld’Ising). Elmodeld’Isingconsideradistribucionsa X= {0, 1}m definidesper p(x) = 1 Z

on h = [hi] ∈ Rm , J = [Jij ] ∈ Rm×m,éssimètricaambzerosaladiagonal,i Z éslaconstantnormalitzadora Z = x∈{0,1}n eh⊤x+ 1 2 x⊤Jx .

Estracta,pertant,d’unadistribuciófactoritzada.Enmoltesaplicacions d’aquestmodel, J tésuportenungraf G (ienaquestcas, Jij = 0,sempre quenohihagiunaarestaconnectant i amb j a G).Desdelpuntdevista algebraic,aquestmodelesconeixcoma modelgràficbinari ihaestatestudiat a[31].

Si X ésfinitcomalasecció2.1,estàclarque (2) imposarestriccions algebraiquessobreeltensordeprobabilitat p ∈ RX .Mésendavantestudiarem algunesdelesformesquepodenprendreaquestesrestriccions.Enaquest puntnomésvallapenaassenyalarqueaquestespropietatsdefactorització sónequivalentsalsmodelsdexarxadetensors,àmpliamentconsideratsen aplicacionsindustrialsdiverses.L’article[71]exploraaquestaconnexióamb mésdetall.

3.1Grafsacíclicsdirigits

Sigui G= (V,E) ungrafdirigit.Si (a,b) ∈ E ésunaarestadelgraf,també designadaper {a → b},diemque a ésun predecessor de b,i b un successor de a.Ungrafdirigit G ésacíclic(breumentDAG)sinocontéciclesdirigits. Si v ∈ V ésunvèrtexd’unDAG G,esdenotaamb pa(v) elconjuntdels predecessors de v iamb de(v) elconjuntde descendents de v formatpels vèrtexs w talsqueexisteixuncamídirigit {v → w}⊆G.Contràriament,també podemdefinir nd(v) comelconjuntde nodescendents V \ ({v}∪ de(v)). DonatunDAG G= (V,E) amb V ={1,...,m},assignemunavariable aleatòria Xv acadanode v ∈ V .Elmodelprobabilísticassociatalvector aleatori X = (X1,...,Xm) ialDAG G,tambéanomenat xarxabayesiana,pren valorsa X= m i=1 Xi icontétoteslesdistribucionssobre X quesatisfanla factoritzaciórecursivasegüent:

p(x) = m i=1 p(xi|pa(xi)), (3) on,pera XC = pa(Xi),tenimque p(xi|xC ) denotalafunciódedensitatdela probabilitatcondicionadade Xi donat XC = xC ,especificadaper

p(xi|pa(xi)) = p(xi, pa(xi)) p(pa(xi)) , si p(pa(xi))> 0.

Nota 1 Persimplificarlanotació,utilitzemlamateixalletraperdenotar toteslesdensitatscondicionades.Perevitarconfusions,unestatdenotaten minúsculaambelmateixnomqueunavariablealeatòria(enmajúscula)es refereixatalobservaciódelavariablealeatòria.

Enaquestarticleenscentremenlasituacióenquèelvectoraleatori X és exclusivamentobédiscret,obécontinu,peròtambésónd’interèslessituacions mixtes;vegi’s[49].

Donadestresvariablesaleatòries X, Y , Z,diemque X ésindependent de Y donada Z (denotatamb X ⊥⊥ Y |Z),siladistribuciócondicionadasatisfà p(x,y|z) = p(x|z)p(y|z) peratot x, y, z (o,equivalentment, p(x|y,z) = p(x|z)).Lafactorització (3) permetunainterpretacióimportantentermes d’independènciacondicionadaconegudacoma propietatdeMarkovdirigida local:

Exemple 2. Considereml’estructurad’una cadenadeMarkov,enquèlesvariablesaleatòries X1,...,Xm satisfanlapropietat p(xk|xk 1,...,x1) = p(xk|xk 1) peratot k = 2,...,m (col.loquialmentl’interpretemcomqueelfuturnoméses veuafectatpelpresentimmediat,perònopelpassat).Degutaaquestapropietat d’independènciacondicionada,unacadenadeMarkovespotrepresentarcom unmodelprobabilísticsobreungraflíniaenquècadanoderepresentaunestat (modelitzatcomunavariablealeatòria) Xk i Xk 1 éselseuúnicpredecessor directe,donatque Xk ésindependentdel«passat»quanconeixem Xk 1.Si m = 3,elgrafassociatéselqueil lustremalafigura1(a).

L’anàlisidemodelsDAGpotportaraobservacionsinesperades.Perexemple, elgraf(a)delafigura1defineixexactamentelmateixmodelqueelsgrafs(b) i(c).Enparticular,sensehipòtesisaddicionals,noexisteixunabijeccióentre modelsenDAGielsseusgrafscorresponents[89,21].

Exemple(Col·lisionadors). Consideremunvectoraleatoriformatpertresvariablesaleatòriesdiscretes X1, X2, X3,enquèelgrafdedependènciaestàdonat perlafigura1(d).Enaquestmodel,lafunciódedensitatespotfactoritzarcom a p(x1,x2,x3) = p(x2|x1,x3)p(x1)p(x3).Observeuqueladistribuciómarginalde (X1,X3) esfactoritzacoma p(x1,x3) = p(x1)p(x3) i,pertant,aquestes duesvariablessónindependents.Noobstantaixò,encondicionar X1, X3 respectede X2 = x2,podemobservarqueestrencalapropietatd’independència, jaque

p(x1,x3|x2) = p(x2|x1,x3)p(x1)p(x3) p(x2)

Aixídoncs,totique X1 ⊥⊥ X3,tenimque X1 ̸⊥⊥ X3|X2 = x2.Intuïtivament,el fenomenescorresponamblaideaque,malgratquedosprogenitorssiguin (genèticament)independents,siobservemunfillencomú,totelquenovingui explicatperundelsprogenitorshauràdeserexplicatperl’altre,i,pertant,

Figura 1: Diversosgrafssobretresnodes.

deixendeserindependents.Aquestaconfiguraciós’anomena col lisionador (collider enanglès)iésunaconegudafontdeconfusióeninferènciacausal, tambéconegudacoma paradoxadeBerkson.

Exemple(DAGestrella). ConsideremunDAGsenzillsobrequatrenodesamb arestesdirigides (0, 1), (0, 2) i (0, 3) comeldelafigura2.Elmodelprobabilístic associatcorresponalafactorització p(x) = p(x0)p(x1|x0)p(x2|x0)p(x3|x0), peratot x ∈X

Figura 2: Modelgràficsobrequatrenodesambunpredecessoritres descendents.

Suposemque X={0, 1}4.Cadadistribuciócondicionada p(xi|x0), i = 1, 2, 3,espotrepresentarperuna matriuestocàstica 2 × 2(unamatriuno negativaenquètoteslesfilessumen1)

Ai = p(xi = 0|x0 = 0)p(xi = 1|x0 = 0) p(xi = 0|x0 = 1)p(xi = 1|x0 = 1)

Denotantamb πx = p(X0 = x) i ai x,y l’entrada (x,y)-èsimadelamatriu Ai, veiemqueelmodelestàparametritzatper

(5)

Observemqueladimensiódel’espaidelscatorzeparàmetres πx , ai x,y ésset perquèlessumesdelesfilesde Ai ésui π0 + π1 = 1.Del’equació (5) éssenzill veureque,fixantl’estata X0 iguala i,lesmatrius

pi000 pi001 pi010 pi011 pi100 pi101 pi110 pi111

pi000 pi010 pi001 pi011 pi100 pi110 pi101 pi111

pi000 pi100 pi001 pi101 pi010 pi110 pi011 pi111

sónderangu.D’aquí,podemverificarfàcilmentlescondicions pijklpij′k′l′ = pijkl′ pij′k′l = pijk′lpij′kl′ = pij′klpijk′l′ , pera i,j,j′,k,k′ ∈{0, 1}.

D’aquestamanera,lescondicionsd’independènciaestradueixenenrelacions polinomialsentrelesentradesdelvectordeprobabilitats p.Entermesdegeometriaalgebraica,podempensarenlafactorització (5) coml’aplicaciópolinomial

queenviacadaconjuntdesetparàmetreslliuresaladistribució p.Tantdesdel puntdevistaestadísticcomdegeometriaalgebraica,ésd’interèsconèixerun conjuntgeneradorminimald’equacionspolinomialsquedefineixenelmodel(és adir,ques’anul linprecisamentenlaimatgede ϕ).Enaquestcas,ésconegut quel’idealdepolinomisques’anul.lena Im(ϕ) ésgeneratminimalmentper divuitequacionsquadràtiquesdelesquehemllistatadalt;vegeu[40].

Aquestssóneltipusdepreguntesqueestrobenenelcentredel’estadísticaalgebraica:permodelsd’estadísticaalgebraica,utilitzartècniquesde geometriaalgebraicaiàlgebracommutativapertrobarequacionsenpolinomis irestriccionssemialgebraiquesquedefineixinelmodel.Conèixer-lespotser útilperesbrinarsielsparàmetressónidentificablesono,perestimarels paràmetres,perinferènciadeversemblançaiperajustarelmodel.

3.2Modelsgràficsnodirigits

Sigui G ungrafnodirigitisigui C elconjuntdecliques(subgrafscomplets) maximalsde G.Un modelgràficnodirigit ésunconjuntdedistribucionsde probabilitatdetipus

f(x) = 1 Z C∈C

C (xC ),

(6)

i ψC : XC → [0, ∞) esconeixencoma funcionspotencials degutalaseva interpretacióenelcampdelafísicaestadística.Aquestésuncasparticularde l’expressióa(2)prenentcoma F elconjunt C decliquesde G.

Aquestadefiniciópotsemblarunamicaallunyadadelesnocionsd’independènciacondicionadaquehemdescritperalsgrafsdirigits,peròel1971,enun articlenopublicat,JohnHammersleyiPeterCliffordvarendemostrarque,sota lacondició p(x)> 0peratot x ∈X,lafactorització (6) enungrafnodirigit G ésequivalentales propietatsglobalsdeMarkov:peraqualssevolsubconjunts A,B,C ⊂ V esté XA ⊥⊥ XB |XC sempreque C separi A, B en G (ésadir,quetots elscaminsentre A i B passinper C).

Reprenemelcasdevariablesdiscretesdelasecció2.1.Sigui iC := (ij )j∈C ∈ XC unestatdelvector XC perunaclica C ⊆ V .Llavors,lafunciópotencial ψC : XC → [0, ∞) espotveurecomunvector θ(C) ambentrades θ(C) iC = ψC (iC ) ∈ [0, ∞).Talcomvamveureal’exempleDAGestrella,aixòensdonala parametrització

pi1i2 in = 1

Z(θ) C∈C

θ(C) iC (7)

D’aquestamanera,aconseguimdenouunmodelparamètricambunaestructura semialgebraica.Podríemrepresentarunadistribucióquesatisfés (7) comun punta PX R (ignorantlaconstantnormalitzadora).Veiemquelafamíliadetots aquestspuntsadmetunaparametritzaciómonomialicomatalformauna varietattòricaenterminologiadegeometriaalgebraica;vegi’s[85]peramés detalls.

3.3Modelsgràficslatents

Elsmodelsgràficslatentsestandissenyatspergestionarsituacionsenquè determinadesvariables Z noespodenobservardemaneradirectaperòtenen unpapercrucialal’horad’explicarpatronsirelacionsenlesdadesobservades X.Defet,l’úsdevariableslatentspermet,fentservirunmenornombre devariables,assolirunamajorexpressibilitatdelmodel,ésadir,capturaruna majorcomplexitativariabilitatdelesdades.Ésperaixòqueaquestesvariables latents,tambéconegudescomavariables ocultes,estanpresentsenmoltes àreesisónessencialspermodelitzarfenòmenscomplexos.Malgrataixò,com jahemesmentatanteriorment,aquestsmodelspresentendificultatsal’hora deferinferència.

Exemple(modelBayesprimari). Consideremunproblemadeclassificació sobreunesdadesdevariablesdiscretes X = (X1,X2,...,Xm) ambunaaltra variablediscreta Z codificantaquinadeles k classes C={c1,c2,...,ck} pertanyunaobservació.Silaclasseésdesconegudaperanovesobservacions, lapodemmodelitzarcomunavariablelatent.Lahipòtesiqueesfaserviren elmodelBayesprimari(tambéanomenat classificadorbayesiànaïf )ésque elsatributssóncondicionalmentindependentssiesconeixlaclasse,ésadir, Xi ⊥⊥ Xj | Z.Aquestapropietatespotrepresentarcomunmodelgràficacíclic dirigit(DAG)enelgrafsegüent:

Figura 3: Modelgràficambunavariablelatent Z ivariablesobservables X1,...,Xm condicionalmentindependentsdonat Z = z

Pertaldepredirlaclasse z ∈C perunaobservacióconcretadelesdades x = (x1,...,xm),podemferservirlaregladeBayespercalcularlaprobabilitat a posteriori decadaclasse:

i,segonsaquestaprobabilitat,laclasse z ∈C s’escullsegonslaregladedecisió bayesiana,laqualmaximitzaaquestaprobabilitat aposteriori:

Aquestaestratègias’utilitzaàmpliamentenelprocessamentdellenguatge naturaliperatasquesdeclassificaciódetexts.Totiserunmodeltansimple, elmodelBayesprimariobtéresultatssorprenentmentbonsalapràctica, especialmentperatasquesdedetecciódecorreubrossa,anàlisid’opinionsi classificaciótemàtica.

Exemple(modelevolutiuenuntrípode). Coms’hamencionatanteriorment,elsmodelsd’arbreslatentsformenunexempleimportantdemodels devariableslatentsihanestataplicatsambèxitalabiologia.Alasecció5, consideremprocessosdeMarkovenarbresfilogenètics,peròaquíconsiderem uncassenzillmitjançantelmodelBayesprimariamb m = 3,enquètotesles variablesaleatòries X1, X2, X3 i Z sóndiscretesiprenenvalorsa S ={0, 1, 2, 3} Aquestconjuntd’estatsrepresentaelsquatrenucleòtids(adenina,citosina, timinaiguanina)queestrobenenlesseqüènciesd’ADN.Enaquestcas,les variablesaleatòries X1, X2, X3 corresponenaobservacionsdenucleòtidsen seqüènciesd’ADNassociadesaespèciesbiològiquesactuals(perexemple,humà,ximpanzéigoril la),mentrequelavariablelatent Z codificanucleòtidsen unaseqüènciad’ADNd’unancestrecomúaaquestesespècies.Lapropietatde MarkovlocalenaquestDAGdona

p(x1,x2,x3,z) = p(z)p(x1|z)p(x2|z)p(x3|z) (cf.exempleDAGestrella),i,marginalitzantsobrelavariablelatent,obtenim que

p(x1,x2,x3) = z∈S

p(z)p(x1|z)p(x2|z)p(x3|z),

peraqualssevol (x1,x2,x3) ∈ S 3.Aquestesprobabilitats p(x1,x2,x3) representenlaprobabilitatd’observarelsnucleòtids x1, x2, x3 alesfullesdel’arbre iespodenestimarapartirdelesobservacionsdelesdadesalesespècies actuals,mentreque p(z) i p(xi|z) sónparàmetres(desconeguts)delmodel. Enfilogenètica,l’estimaciód’aquestsparàmetresésrellevantperquèmesuren laquantitatdesubstitucionsdenucleòtidstranscorregudesdesdel’ancestre comúfinsacadaespècieactual,quedonaunanocióde distànciaevolutiva entre unaespècieancestralielsseusdescendents.Alasecció5exploremmètodes basatsenmomentsperestimaraquestsparàmetres,ialasecció6comentem aquestsmodelsambmésdetall.

Exemple(bossadeparaules). ConsideremaraunaversiórestringidadelmodelBayesprimarienquèles Xi condicionadesrespectedelavariablelatent Z sónidènticamentdistribuïdes.Comaexemplepràctic,consideremelmodel

delabossadeparaules(bag-of-words enanglès),enquèundocumentformat per m parauleshadeserclassificatenundels k temes ocults.Suposemque elvocabularitéunamida d iquecadatema ch ∈C téelseupropivectorde probabilitat µh ∈ ∆d peremetreparaulesdelvocabulari:primers’escullun tema ch ∈C ambprobabilitat p(z = ch),idesprésesmostregen m paraules (x1,...,xm) demaneraindependentambvectordeprobabilitat µh.

Enaquestexemple,l’ordredelesparaulesencadadocumentésirrellevant, nomésestéencomptesihisónpresentsono,i,pertant,elsmotsesconsiderencomavariablesaleatòries intercanviables.Aixòsignificaquelaseva distribucióconjunta p(x1,...,xm) ésinvariantperpermutacionsdelsíndexsi, enconseqüència,eltensor p corresponentésuntensorsimètric.

L’estimaciódeparàmetresenunmodellatentnoésunatascafàcil.A l’exemple mètodedelsmomentsperalabossadeparaules explicaremun mètodeespecíficperalmodeldebossadeparaulesbasatenelmètodedels moments.Unaaltraaproximacióésoptimitzarlaversemblança.

Nota 2 Comhemapuntatenseccionsanteriors,unadistribució p(x,z| θ) ambvariableslatentson z denotaunestatlatent,lainferènciadeparàmetres potsercomplicadadonatque z noésconegut.L’aproximaciómésclàssica éslademirardemaximitzarlaversemblançamarginalsobrelesvariables observades

p(x|θ) = z p(x,z| θ), onpodemsubstituirlasumaperunaintegralsi Z tambéinclouvariables contínues.Calremarcarquetotalainformacióconegudasobrelesvariableslatents Z estrobaatravésdelasevadistribució aposteriori p(·| x,θ).Enno disposardelaversemblançaperalconjuntdedadescomplet,comaalternativa esprocedeixaestimar-laprenentelvaloresperatdeladistribució aposteriori (pasE),iseguidamentaquestaversemblançaestimadaesmaximitzarespecte alsparàmetres θ (pasM).Aquestprocedimentrellevantpertractarlesdades incompletesqueprovenendevariableslatentsesconeixcoma algorismeEM (expectationmaximization enanglès);vegeu[30].

4Elcasgaussià

Enaquestaseccióposemelfocusenvariablesaleatòriescontínuesi,enparticular,envariablesnormalsmultivariants.Generalitzemprimerelstensorsde momentsintroduïtsabansenelcasdiscret.

4.1Tensorsdemoments-casgeneral

Elstensorssimètricsapareixendemaneranaturalcomaderivadesd’ordre superiordefuncionsdiferenciables f : Rn → R:lesderivadesparcialsd’ordre r de f espodenorganitzarcomuntensor T ∈ Sr (Rn) ambcoordenades

Enrelacióambl’estadísticail’aprenentatgeautomàtic,hihadostipus concretsdefuncionsilessevesderivadesparcialsquesónparticularment rellevants.Consideremunvectoraleatori X = (X1,...,Xm) enquèarapermetemqueelsespaisd’estats Xi siguinsubconjuntsarbitrarisde R.Siguin MX (s) = E[es⊤X ] i KX (s) = log E[es⊤X ] lesfuncionsgeneratriusdemoments idecumulants,respectivament(vegeu[54]).El tensordemoment d’ordre r esdenotaamb µr (X) iéslamultitauladedimensions m × r ···× m,l’entrada (i1,...,ir ) delaqualés

i1 ir (X) = E[Xi1 ··· Xir ] =

i1 ··· ∂sir MX (s) s=0 .

Demanerasimilar,el tensorcumulant κr (X) esdefineixencoordenadescoma

κi1 ir (X) = cum(Xi1 ,...,Xir ) = ∂r ∂si1 ··· ∂sir KX (s) s=0

Larelacióentre µr (X) i κr (X) perauna r qualsevolésrebuscadaperòestà moltbenentesa;vegi’s[79, 54].Directament,perconstrucció, µr (X) i κr (X) sóntensorssimètricsdel’espai Sr (Rm).

Nota 3. Aquíestemfentservirunanotacióestàndardperatensordemoments icumulants.Enaquestaconvenciótenim,perexemple,que µ1(X) = E[X1], µ13(X) = E[X1X3], κ12(X) = E[X1X2] E[X1]E[X2].Aixòcontrastaambla notacióqueempremenlasecció2.3,quetambéesfaservirregularmenten l’estudialgebraicdemodelsdiscrets.

Comaexemple,noteuque,si X = (X1,X2) sónduesvariablesaleatòries independents,aleshores µ12 = µ1µ2 i κ12 = 0.

Noobstantaixò,elsmomentsicumulantsd’ordrebaixnosónsuficients peral’estudid’unmodelestadístic,engeneral.Unaexcepcióimportantés elcasdedistribucionsnormalsmultivariants(vegi’slasubsecciósegüent), queesparametritzenpelvectordemitjanes µ iperlamatriudevariànciesi covariàncies Σ,quesónmoments/cumulantsd’ordre1i2,respectivament.

4.2Distribuciónormalmultivariant

Ladistribuciónormalogaussianamultivariadaésladistribuciómésimportant enl’estadísticamultivariantienciènciadedadesengeneral.Tambétéunpaper importantenmoltestècniquesdereducciódedimensionalitatperatensors queesmentaremenaquestdocument.

Denotantamb S 2 +(Rn) elconjuntdematriussimètriques n × n definides positives,ladistribuciógaussiana n-variadaambmitjana µ ∈ Rn imatriude covariància Σ ∈ S 2 +(Rn) ésunadistribuciósobre Rn ambfunciódedensitat f(x) = det(2π Σ) 1/2 exp 1 2 (x µ)⊤Σ 1(x µ) (8)

Lesfuncionsgeneradoresdemomentsicumulantsd’unvectoraleatorinormal X són MX (s) = eµ⊤s+ 1 2 s⊤Σs ,KX (s) = µ⊤s + 1 2 s⊤Σs

Observemquelafunciógeneratriudecumulantsésunpolinomiquadràtic i,pertant,totselscumulantsd’ordretresosuperior,comaral’asimetriao lacurtosi,quesónelscumulantsd’ordretresiquatre,respectivament,són nuls.PerunresultatclàssicdeJózefMarcinkiewicz,ladistribuciónormalés l’única distribuciótalquelasevafunciógeneratriudecumulantséspolinomial[53, 51].Elfetqueaquestafunciósiguiunpolinomitéconseqüències importantsenprobabilitatiestadística(vegeu,perexemple,[44])ielfetquecap altradistribuciónotinguiaquestapropietattambéésrellevantperjustificarel resultatd’identificabilitatde[26]queapareixeràenlasecció6.3.

Unadelespropietatsfonamentalsdeladistribuciónormalésqueéstancada perlaconsideraciódemarginalsicondicionades.Demaneramésprecisa,pera unvectoraleatori X ambdistribuciónormal n-variantdemitjana µ imatriu decovariància Σ,considerantunadivisióarbitràriaendosblocs (XA,XB ),la distribuciódelsubvector XA éstambénormalambmitjana µA = (µi)i∈A i matriudecovariància ΣA,A = [Σij ]i,j∈A.Aixímateix,ladistribuciócondicionada de XA donat XB = xB ésnormalambmitjana µA + ΣA,B Σ 1 B,B (xB µB ) icovariància ΣA,A + ΣA,B Σ 1 B,B ΣB,A.Pertant,treballarambdistribucionsmarginalsi condicionadesd’unanormalmultivariantimplicaunatransformaciópurament algebraicaentermesdelsparàmetres.

4.3Modelsgràficsgaussians

Lesrestriccionsdelsmodelsgràficstantperalcasdirigitcomnodirigitpermetenunadescripcióalgebraicasenzillaquanelvector X segueixunadistribució normalmultivariant.

Suposemque G= (V,E) ésungrafnodirigitambvèrtexs V ={1,...,m} i que X = (X1,...,Xm) segueixunadistribuciónormalmultivariant.Aleshores, desenvolupant (8),ésfàcilveurequeladistribuciófactoritzacomunmodel (6) en G semprequelamatriudecovariància Σ satisfaci

(Σ 1)ij = 0, pertot (i,j) ∉ E,i ≠ j.

Pertant,parametritzarelmodelentermesdelainversadelamatriudecovariància K = Σ 1 enspermetdefinirelmodelapartirdesenzillesrestriccions lineals.Aquestaobservacióhamotivatunadireccióderecercaenestadísticaalgebraicaperentendreelssubespaislinealsdematriussimètriques,per exemple,[87,81,82,100].

LesdistribucionsgaussianesdefinidesperDAG G tambétenenunadescripciósimple,laqualésequivalentalmodeld’equacionslinealsestructurals(vegeu lasecció6.3)abasedeconsiderarelsistemad’equacionslinealsestocàstiques Xi = j∈pa(Xi) λij Xj + εi, per i ∈ V, (9)

onels εi pera i ∈ V sesuposenindependentsentresiiindependentsdels pa(Xi) corresponents.Suposemqueels εi sónvariablesnormalsdemitjana

zero,ielscoefficients λij prenenvalorsrealsarbitraris.Enformamatricial podemescriure-hocoma X = ΛX +ε,on Λ éstriangularsuperior(reordenant X, sical).Comque G ésacíclic, Im Λ ésinvertibleitenimque X = (Im Λ) 1ε. D’aquísegueixquelainversadelamatriudecovariància K = Σ 1 satisfà

K = (Im Λ)⊤Ω 1(Im Λ), on Ω éslamatriudiagonalamblesvariànciesdels εi comaentrades.Per tant,aquestmodelespotdescriuredemaneraequivalentambcondicions d’anul.laciósobrelafactoritzaciódeCholeskyde K.Aquestsmodelshanestat estudiatsdesd’unaperspectivaalgebraicaa[84].

Exemple(anàlisifactorial). Peraunconjuntde m variablesobservables X= (X1,...,Xm) ambdistribucióconjuntanormalmultivariant X ∼Nm(µ, Σ),ens potinteressarreduiraquestesvariablesenunespaide d<m dimensionsmitjançantunaprojecciólineal.Equivalentment,busquemmodelitzar m variables observadesgaussianesquedepenenlinealmentde d variablesgaussianeslatentsindependents Z = (Z1,...,Zd).Podemescriure,doncs,que X = µ+WZ +ε on µ ∈ Rd , W ésunamatriu m × d,ieltermedesoroll ε podemsuposarque técovariància Ω := Cov(ε) diagonal.Lamatriudecovariància Σ enaquestcas vedonadaper

E[(WZ + ε)(WZ + ε)⊤] = WW ⊤ + Cov(ε).

Aixídoncs, Σ viualconjunt

Fm,d ={Ω + WW ⊤ ∈ Rm×m : Ω ≻ 0diagonal,W ∈ Rm×d},

onfemservir ≻ 0perdirquelamatriuésdefinidapositiva.Observi’sque Fm,d ésunconjuntsemialgebraic,jaqueespotveurecomlaimatgede Rm >0 × Rm×d sotaunaaplicacióracional.Pertant,elmodeld’anàlisifactorialformatper lesdistribucionsnormalsmultivariants X ambmatriudecovariància Σ ∈ Fm,d ésunexempledemodelestadísticsemialgebraic.Entendrequinessónles equacionsalgebraiquesisemialgebraiquesquedefineixenelconjunt Fm,d és claupersaberquinesdistribucionspodenencaixarenaquestmodel.

5Descomposiciótensorialenestadísticaalgebraica

Demaneraanàlogaaladescomposiciódematrius,ladescomposiciódetensors técomaobjectiurepresentaruntensord’altesdimensionscomunasèrie d’operacionselementalsentensorsméssimples.Lesdescomposicionsdetensorss’hanutilitzatendiferentscamps,comaraenlavisiópercomputador,la neurociènciacomputacional,lafilogenèticaolapsicometria.S’utilitzenperobtenirseparaciócegadefonts(blindsourceseparation),l’anàlisidecomponents independentsiperproporcionarestimadorsenmodelsdevariableslatents. Remetemellectora[46]i[45],ontrobaràexcel.lentscompilacionssobrela descomposiciódetensorsilessevesaplicacionsenaprenentatgeautomàtic.

5.1Rangd’untensor

Unexercicisenzilld’àlgebralineal(usantladescomposicióenvalorssingulars, perexemple)consisteixaveurequeunamatriu M dedimensions n1 × n2 té rang k siinoméssiespotescriurecoma

M = u1 ⊗ v 1 +···+ uk ⊗ v k

peradeterminatsvectors ui ∈ Rn1 , v i ∈ Rn2 ,inoéspossibleescriureaquesta descomposicióambmenyssumands(aquí ui ⊗ vi s’hadepensarcomala matriuderangucorresponent).

Unamaneradegeneralitzaraquestconceptedelrangpertensorsésla següent.

Definició 2 El rang d’untensor T ∈ Rr1 ⊗···⊗ Rrm éselmenorenter k tal que T espotescriurecoma k j=1 u1,j ⊗ u2,j ⊗···⊗ um,j (10)

peradeterminats ui,j ∈ Rri , i ∈ [m], j ∈ [k].Ditd’unaaltramanera,untensor térang k siespotescriurecomunacombinaciólinealde k tensorsderangu (purs),perònocomasumad’unnombremenorde k tensorspurs.

El rangsimètric d’untensorsimètric T ∈ Sr (Rm) esdefineixcoml’enter k méspetittalque T = k j=1 uj ⊗uj ⊗···⊗uj peradeterminats uj ∈ Rm , j ∈ [k]

Jahemvistqueelstensorsqueapareixenenelmodeld’independència totalsóntensorsderangu.Acontinuaciódonemexemplesdetensorsderang superior.Entermesdegeometriaalgebraica,donatquelavarietat Seg(PX1 R × ···× PXm R ) estàformadapelstensorsderangu,elconjuntdetensorsderang k estrobaalaseva k-èsimavarietatsecant(defet,lavarietatsecantéslaclausura enlatopologiadeZariskid’aquestconjuntdetensors).

Exemple(rangtensorial). Enelstensorsquecodifiquenladistribucióde X enelmodeldel’exemple modelBayesprimari ambunavariablelatent Z que prenvalorsenunconjunt C decardinal k,elrangéscomamàxim k.En efecte,lapropietatdeMarkovdonalafactoritzaciódeladistribucióconjunta, i,marginalitzantsobrelavariablelatent Z,obtenim p(x1,...,xm) = z∈C p(z) m i=1 p(xi|z)

peraqualsevolconjuntd’observacions x = (x1,...,xm) ∈X.Llavors,considerantelsvectors ui,z = (p(xi = 0|z),...,p(xi = ri 1|z)) ∈ RXi , on z ∈C,i = 1,...,m, podemescriureladistribució p = (p(x))x∈X ∈ RX de X = (X1,...,Xm) coma p = z∈C p(z)u1,z ⊗···⊗ um,z (11)

Pertant, p térangtensorialmenoroigualque k.Enparticular,ladistribució conjunta p alesfullesdelmodelevolutiusobreeltrípodedel’exemple model evolutiuenuntrípode ésuntensorderangmenoroigualaquatre.

Exemple 3. Consideremelmodelintroduïtalabossadeparaules.Enaquest cas,elsvectors ui,z coincideixenamb µh si z éseltema ch (inodepènde i). Llavors,l’expressió(11)esdevé p = k h=1 p(z = ch)µh ⊗···⊗ µh iobtenimque p ésuntensorsimètricderangcomamàxim k.

5.2Descomposiciótensorial

Unadescomposiciócomlade (10) haestatintroduïdaendiversosàmbits.Es coneixcoma descomposicióderangtensorial ocomadescomposició poliàdica canònica (CPenanglès)otambé factorparal·lel (PARAFAC);vegeu[43,41].

Aquestadescomposiciónoésúnicaengeneral:espodenreescalarels vectors ui,j opermutarelssumandsperobtenirunaaltradescomposició. Aquestessónambigüitatsinherentsquesolenpoderresoldre’speracada aplicacióparticularenquètreballem.Restringint-nosadescomposicionsespecials,podemobtenirlaunicitatmòdulaquestesambigüitats.Comenelcas delteoremaespectralperamatriussimètriques,l’ortogonalitatésunrequisit comúperdescompondretensorssimètrics,perònototselstensorssimètrics tenenunadescomposicióortogonal.LaunicitatenladescomposicióCP(mòdul permutacionsireescalatge)espotobtenirperatensorsdebaixrang,com veuremacontinuació.

Exemple 4. ConsideremelmodelBayesprimaridel’exemple modelBayesprimari amb m = 3ideixemque k siguielcardinaldelconjuntd’estatsdela variablelatent.A[47],l’autorvadonarcondicionsexplícitesperalaidentificabilitatdelssumands(mòdulpermutacionsiescalars)enladescomposicióde rangdeltensordistribucióconjunta.Aquestacondicióexplícitaescompleix peratensors genèrics delmodelsi k ésmenorqueelnombre ri d’estatsde cadavariableobservada,icontrastafortamentamblanounicitatdedescomposicionsdematriusderang k comasumesdematriusderangu.A[1],els autorsmostrencomaquestresultatbàsicespotusardemanerapotentper establirlaidentificabilitatd’unagranclassedemodelsdevariableslatents.

Enelcontextdelsarbresfilogenèticscomal’exemple modelevolutiuen untrípode,aquestresultatesvaredescobrira[20].Enaquestcas,elresultat diuqueelsparàmetresdelmodel(ladistribuciódenucleòtidsenlavariable latentilesprobabilitatscondicionades)espodenrecuperardemaneraúnica (mòdulpermutacions)apartirdeladistribucióconjuntadelesvariablesobservadesiesdonaunaconstruccióexplícitaperalasevarecuperacióutilitzant descomposicionsespectralsdedeterminadesmatriusextretesdeladistribució conjunta.

5.3Rangtensorialnonegatiu

Elstensorsqueprovenendedistribucionsdeprobabilitat,jasiguidiscretao contínua,formenunsubconjuntespecialdinsdelaclassedetotselstensors.

Peraquestaraó,iespecialmentperalcasdiscret,sovintésútilparlarnodel seurangcomen (10),sinód’unavariantconegudacoma rangnonegatiu:diem queuntensor T té rangnonegatiucomamàxim k siespotescriurecomla sumade k tensorsderangucomabans

onararequerimquetotselsvectors ui,j tinguinentradesnonegatives.El rangnonegatiu denotatamb rank+ éselmenorenter k talqueexisteixuna expressiócomlade (12).Elrangnonegatiunohadecoincidirnecessàriament ambelrangusuald’untensor,iperdefinicióesté rank T ≤ rank+ T .Peramés generalitzacionsivariantsdelrangdetensors,vegeu[48].

Nota 4 Ésunexercicisenzillcomprovarquelamatriusegüentésderangtres, peròelseurangnonegatiuésquatre.

Aquestésunexemplesenzillsobrecomelrangclàssicielrangnonegatiu podendiferir.

Determinarsielsrangsclàssicinonegatiucoincideixenésunproblema NP-difícil.Defet,lafactoritzaciónonegativadematriuséspersimateixaun problemaNP-difícil,totiquemitjançantheurístiquesdecercalocal[88]espot aconseguirunrendimentpolinomial.Afortunadament,hihacondicionssota lesqualsaquestesdescomposicionsderangnonegatiusónúniques,iaquestes estanestretamentlligadeslaidentificabilitatdelmodelsubjacent[67].

Ladescomposiciónonegativadetensorshaestatestudiadaenelcontext PARAFACincloent-hirestriccionsdenonegativitatenquimiometria[14, 15],ies potinterpretartambécomunadescomposiciódeBayesprimaridedistribucions deprobabilitatrespecteacondicionalscomesfaa[40].

Tenintencomptel’expressióa (1),elmodeld’independènciatotalésun exempled’untensorderangnonegatiu ≤ 1.Perexemple,elsubconjunt dematrius r1 × r2 amb rank+ ≤ 1éslapartnonegativadelavarietatde Segre PX1 × PX2 .Lesdistribucionsdelmodeld’independènciadeduesvariables discretescorresponenamatriusenlainterseccióde ∆X ambelconjuntde matriusderank+ ≤ 1.

Elsmodelsdemixturaodebarreja(mixturemodel enanglès)fanúsimplícit delrangtensorialnonegatiu.Peraunmodelestadístic P⊂ ∆X ,el k-èsim modeldemixtura Mixtk(P) vedonatper

Estàformatpertoteslesdistribucionsdeprobabilitatderangnonegatiumenor oigualque k iéstambéunmodelgràficambvariablesocultes.Untractament completsobreaquestarelacióespottrobara[34].

Uncasimportantéseldelstensorsderangnonegatiu ≤ 2,quesónclauen l’estudidemodelsdeMarkovenarbresfilogenèticsambestatsbinaris.Elmodel Bayesprimarien4ambvariablesobservadesbinàriesiduesclasseslatentses potrepresentarpertensorsdedimensions2 × 2 ×···× 2derangnonegatiu comamàxim2icorresponenamixturesdeduesdistribucions.Vegeu[3]pera unacaracteritzaciód’aqueststensorsambrank+ ≤ 2ilasevageometria.

Exemple(modelstemàtics). Elmodeldescritabossadeparaulesésunclassificadorbasatenelcontingutdeldocument,perònoésunmodelgeneratiui elseupotencialrepresentatiuéslimitat.Elsmodelstemàtics(topicmodels en anglès),[11],s’utilitzenquanelsdocumentspodenexhibirmésd’unatemàtica ilaclassificaciódelmodel bossadeparaules seriaunaaproximaciómassa restrictiva.Unexempled’aquesttipusdemodeléseldel’assignaciólatentde Dirichlet(LDA)[12],queésunmodelgeneratiuquefuncionacomunaxarxa bayesiana(secció3.1),onestéunacol leccióde n documentsi k temes,amb lapropietatqueelselementspodenpertànyeradiversesclasses(ésadir,un documentpottractarsobremésd’untema).

Cada topic otemaesrepresentencomadistribucionsdeprobabilitatsobre lesparaules,ielsdocumentsesrepresenten,alseutorn,comadistribucions sobretemeslatents.Peracadadocument,s’assignaunescalar θij ∈ [0, 1] a cadatema j ∈{1, 2,...,k} segonslasevaadequacióaldocument,ésadir,la probabilitatqueeltema j apareguieneldocument i,comunmodeldemixtura enquèassumimqueelnombretotaldetemes k ésconegut.Elspesosassociats alstemesdeldocumentsegueixenunadistribuciódeDirichlet Dir(α),ambuna funciódedensitatdefinidacoma

p(θi; α) = f(θi1,...,θik; α1,...,αk) = 1 B(α) k j=1 θαj 1 ij ,

on B éslafuncióBetaquenormalitzaladistribució.Elspesos θi = (θi1,...,θik) ∈ ∆k 1 sumenui,pertant,formenunamesuradiscretacomteníemalasecció2.1. D’altrabanda,unaparaula i téunaprobabilitat ϕij depertànyeraltema j,on ϕij segueixunadistribuciódeDirichlet Dir(β).Elstresconjuntsdevariables aleatòriesquerepresentenparaules,temesidocumentsespodeninterpretar comunmodelgràfic.Concatenantaqueststresconjuntsdevariables,obtenim demaneranaturalunaxarxabayesianaambcapesdevariablesenl’ordre esmentatdepredecessorsadescendents.

5.4Mètodedelsmoments

Feraprenentatgeenelstipusdemodelsdiscutitsalasecció3.3generamolts problemes.Elsmètodesdeversemblança,quesónunaopciópopularpera moltsmodelssimples,ràpidamentestornenintractablesenpresènciade variableslatents.Ambpoquesalternativesbones,elmètodedelsmoments[64] aras’utilitzarutinàriamentenmixturesgaussianes[5]ienmodelsd’arbres latents[7],[6],[73].Comqueaquestmètodeésintrínsecamentalgebraic,el descrivimambmésdetallenaquestmanuscrit.

Laideadelmètodeéssenzilla.Suposemquelaparametritzaciódelmodel indueixunaparametritzacióexplícitad’algunsmoments µ = f(θ) deladistribuciósubjacent.Unestimadorpelmètodedelsmomentsprocedeixendues etapes:primer,estrobaunbonestimador ˆ µ delsmomentsapartirdelamostra idesprésesdefineix ˆ θ comunasolucióde ˆ µ = f(θ)

Unproblemaevidentd’aquestmètodeésque,peraun ˆ µ donat,notenim garantiesquel’equació ˆ µ = f(θ) tinguisolució.Encertamesura,aixòespot solucionarescollintadequadamentunsmomentsdeterminatsperal’anàlisi. Però,finsitotsiexisteixunasolució,potserquenocompleixialgunesde lesrestriccionsnecessàries.Peraquestmotiu,elmètodedelsmomentsnormalments’aplicacaspercasirequereixunabonacomprensiódelaclassede modelsqueestemtenintencompte.

Atalld’exemple,eneltreballclàssic[63],esvautilitzarunamixturade duesvariablesgaussianespermodelitzarlesmidesdelespartsdelcosd’una poblaciódecrancs.Perfer-ho,Pearsonvaproposarunsistemad’equacions queinvolucravaelsprimerscincmomentsdeladistribució,iseguidamentva aconseguireliminarlesvariablesivaobtenirunpolinomidegraunouenuna únicavariable.Resolentelpolinomidegraunouresultant,vapoderobtenir elsparàmetresdeladistribuciódemixtura.Peramésdetallsd’aquestprimer exemplebàsicdelmètodedelsmoments,consulteu[4].

Exemple(mètodedelsmomentsperalabossadeparaules). Considerem labossadeparaulesdel’exemple bossadeparaules isuposemqueelnombre m deparauleseneldocumentésalmenys3.Anandkumar etal. ([7])vanmostrar que,fentservirmomentsd’ordrecomamàximtres,hompotrecuperarelsparàmetresdelmodel(ésadir,elsvectorsdelesdistribucionscondicionades µh i lesprobabilitats wh = p(z = ch) pera h = 1,...,k).Aquíexpliquembreument aquestmètodedelsmomentsseguint[6,apèndixD].

Podemrepresentarlesparaulesdelvocabulariambelsvectorsdelabase canònica e1,...,ed ∈ Rd,iconsiderem X talquel’espaid’estatsde Xi sigui D={e1,...,ed}.Consideremlesvariables Xi comaindicadorsdelamanera següent:

Xi = ej ⇐⇒ la i-èsimaparauladeldocumentés j.

Aleshoreselsmomentscreuatsd’aquestsvectorsaleatorisescorresponenamb lesprobabilitatsconjuntes:

E[X1 ⊗ X2] = i,j p(x1 = ei,x2 = ej )ei ⊗ ej

iobtenim

E[X1 ⊗ X2] = k h=1 i,j p(z = ch)p(x1

Amblanotacióintroduïdaespotescriurecoma E[X1 ⊗ X2] = k h=1 whµh ⊗ µh (13)

Demaneraanàlogaobtenim

E[X1 ⊗ X2 ⊗ X3] = k h=1

⊗ µh

Siprenem V = (µ1| |µk) i D = diag(w1,...,wk),aleshores,considerant M2 = E[X1 ⊗ X2] comunamatriu,podemexpressar(13)coma

M2 = VDV ⊤ (14)

Noestractad’unadiagonalitzacióde E[X1 ⊗X2] (llevatdequan V ésortogonal), peròpodememprartècniquesespectralsincorporantelsmomentsdetercer ordre.Defet,considerem M3 = E[X1 ⊗X2 ⊗X3] iperaqualsevol η ∈ Rd definim el2-tensor M3 • η coma

(M3 • η)i,j = l (M3)i,j,l ηl.

Llavors,comamatriustenim M3•η = VDd(η)V ⊤,on d(η) = diag(µ⊤ 1 η,...,µ⊤ k η), isi M = (M3 • η)M 1 2 ,obtenim M = Vd(η)V 1.Prenent η ambentradesno repetides,lescolumnesde V estandeterminadespelsvectorspropisde M (llevatdepermutacionsimultiplicacióperescalars).Uncopesrecupera V , w1 ...,wk sónfàcilmentrecuperablesmitjançantl’expressió(14).

Existeixenenfocamentsmésrobustsperal’estimaciódeparàmetresutilitzantmoments,peròvanmésenllàdel’abastd’aquestestudi.Vallapena assenyalarqueelsparàmetresestimatspelmètodedelsmomentstambées podenutilitzarcomapasiniciald’unalgorismeEM(vegeulanota2);enaquest cas,l’EMsovintconvergeixaunmàximlocaldesprésd’unsolpas;vegeu[97].

6Aplicacionsdel’estadísticaalgebraica

6.1Anàlisifilogenètica

Un arbrefilogenètic T sobreunconjunt L d’espècies(oaltresentitatsbiològiques)ésunarbreamblesfullesetiquetadespelselementsde L.Lafigura4 mostratalarbreambfulles L = {humà,ximpanzé,goril la,orangutan}.

L’objectiuprincipaldelafilogenèticaésreconstruirlahistòriaevolutivadel conjunt L d’espèciesactualsapartirdelainformacióproporcionadaperunacollecciódemolèculesd’ADNassociadesaelles.Degutal’estructuradedoblehèlix del’ADN,aquestesmolèculesespodeninterpretarcomaparaulesoseqüències enl’alfabetquerepresentenelsquatrenucleòtids, {A,C,G,T}.Sotacertes hipòtesisbiològiquesespotsuposarquecadaposiciód’aquestesseqüències evolucionaindependentmentdelesaltresposicionsiquelesposicionsestan idènticamentdistribuïdes.

humà ximpanzé goril.la orangutan

Figura 4: Unarbrefilogenèticambconjuntdefullesdonatper L = {humà,ximpanzé,goril la,orangutan},nodearrel r ,imatriusestocàstiquesperfilesassociadesalprocésdeMarkov.

Si T ésunarbrefilogenètic,modelemlasubstituciódenucleòtidsen T seleccionantprimerunnodeinterior r quefacielpaperd’arreldel’arbre (quepodriarepresentarl’ancestrecomúatoteslesespèciesde L)idirigint toteslesarestesdesde r perveure T = (V,E) comunDAG.Acada v ∈ V liassociemunavariablealeatòria Xv prenentvalorsa S ={0, 1, 2, 3} (en representaciódelsquatrenucleòtids)iconsideremlapropietatdeMarkov localsobreelDAG.Aquestapropietatésequivalentalfetquecadavariable aleatòriasiguiindependentdelessevesvariablesnodescendentsdonades lesobservacionsalseunodepareimmediat,coms’expressàa (4).Ésconegut que,perobtenirlaidentificabilitatdelsparàmetres,calquel’arbrenotingui nodesdegrau2.Peraunarbredetresfulles,aquestmodeléselqueesdonaa l’exemple modelevolutiuenuntrípode.

Perescriurelafactoritzaciódeladistribucióconjunta (1) sotaaquestmodel deMarkov,codifiquemlesdistribucionscondicionadesenmatriusestocàstiquesperfiles:acadaaresta e ={u → v}∈ E associem M e,unamatriu4 × 4 ambentrades M e x,y = p(Xv = y|Xu = x),laprobabilitatcondicionadaqueun estat x enelnodeancestral u esvegisubstituïtperl’estat y eneldescendent v

Aleshores,laprobabilitatconjuntad’observarestats(nucleòtids) xv ales variables Xv ,pera v ∈ V ,és

Enfilogenèticanoméstenimobservacionsperalesvariablesaleatòries trobadesalesfullesdel’arbre,demaneraquelesvariablesaleatòriesalsnodes interiorssónlatents(jaquerepresentenespèciesextintes).Així,sielconjunt defulles L és [n],laprobabilitat pi1 in d’observarelnucleòtid ij alafulla j per j ∈ [n] espotobtenirmarginalitzant(15)sobreelsnodesinteriors:

Percadaarbrefilogenètic T sobre L = [n] definimcoma p⊤ ∈ RX = R4 ⊗ n) ···⊗R4 eltensordeladistribucióconjunta (p0 0,p0 1,...,p3 3) obtingutd’aquesta manera.Aquestmodels’anomena procésdeMarkovgeneralsobrel’arbre filogenètic

Sil’arbrefilogenèticqueexplicalahistòriaevolutivadelconjunt L ésconegut itenimunesseqüènciesd’ADNobservadessobreelconjunt L,elsparàmetres delprocésdeMarkovcorresponentsesolenestimarmitjançantunmètodede màximaversemblança.Noobstantaixò,undelsproblemesprincipalsenfilogenèticaésobtenirl’arbre T ques’ajustimilloralesdades:comqueelnombre d’arbresfilogenèticscreixsuperexponencialmentenelnombredefulles,no éspossiblebuscarexhaustivamentpertotl’espaid’arbres.Aquíl’estadística algebraicatéunpaperimportant,talcomexpliquemacontinuació(consulteu també[17]).

Afinalsdelsanysvuitanta,elsbiòlegsCavender,FelsensteiniLakeesvan adonarquealgunesequacionspolinomialssatisfetesperlescoordenadesde p⊤ permetendistingirentreelsdiferentsarbresquedonenllocaladistribució. Ésadir,hihaequacionspolinomialssobrelescoordenadesd’untensor p ∈ R4 ⊗ n ···⊗ R4 queescompleixensi p = p⊤ peraalgunsarbres T perònopera altres.Unexempled’aquestesequacionsprovédel’aplanament (flattening en anglès)deltensor,comdetallemacontinuació.

Consideremunabipartició A|B de L = [n]:unsubconjunt A ielseucomplement B = L \ A.Comteníemalasecció2.2,aquestadivisióindueixun isomorfismedel’espaidetensorsal’espaidematrius RX ≊ RXA ⊗ RXB →M|XA|×|XB |(R) p = (px1 xn ) → flattA|B (p), (16) onl’entrada (xA,xB ) de flattA|B (p) éslacoordenadade p queescorresponamb laprobabilitatd’observarestats xA ={xl}l∈A alesfullesde A i xB ={xl}l∈B alesfullesde B.Perexemple,al’arbrefilogenèticdelafigura4,silesfulles

humà,ximpanzé,goril.laiorangutanesdenotenamb1,2,3,4,respectivament, tenimque flatt12|34(p) =

p0000 p0001 p0002 ...p0033 p0100 p0101 p0102 ...p0133 p0200 p0201 p0202 ...p0233

p3300 p3301 p3302 ...p3333

Suposemque p = p⊤ peraalgunarbrefilogenètic T ,iconsideremuna bipartició A|B delconjuntdefullesinduïdaperlasupressiód’unaaresta e de T , queanomenarem biparticiód’aresta.Llavors flattA|B (p⊤) espotconsiderarcom unatauladeprobabilitatconjuntadelesvariablesaleatòries XA = (Xl)l∈A i XB = (Xl)l∈B .PerlapropietatdeMarkoven T sabemque XA ⊥⊥ XB |Xu,on Xu éslavariableocultacorresponentaundelsvèrtexsde e.Aquestésunmodel deBayesprimariambduesvariablesaleatòriesobservades XA, XB (m = 2)i unadelatent.Pertant, p⊤ ésuntensorderangcomamàximquatresegons l’exemplerangtensorial.Enparticular, flattA|B (p⊤) ésunamatriuderangcom amàximquatreperquè (16) enviaunasumadetensorsderanguaunasumade matriusderangu.Aixídoncs,hemobtingutlaprimeraafirmaciódelsegüent teorema:

Teorema 3 ([2]). Sigui T unarbrefilogenètici A|B unadivisiódelseuconjuntde fulles L.Sigui p⊤ untensordedistribucióobtingutperunprocésdeMarkoven T . Aleshores,si A|B ésunabiparticiód’arestaen T , flattA|B (p⊤) térangmenor oigualaquatre.Amés,si A|B noésunabiparticiód’arestaen T ,elrang de flattA|B (p⊤) ésmésgranquequatre(sempreque p⊤ compleixideterminades condicionsgenèriques).

Aixídoncs,l’anul.laciódelsmenors5 × 5de flattA|B (p) defineixequacions polinomialsqueescompleixenperadistribucionsqueprovenend’arbres quetenen A|B comabiparticiód’aresta,peròquenoescompleixenpera distribucionsenaltresarbres.Enllocd’utilitzardirectamentaquestesequacions algebraiques,ésmésnaturalcalcularladistànciaentrematriusderangquatre directamentutilitzantvalorssingulars.Aquestaestratègias’haaprofitatper proporcionardiversosmètodesperalareconstrucciófilogenètica;consulteu, perexemple,[22,37,18].

6.2MàquinesdeBoltzmannrestringides

Consideremunconjuntdevariablesaleatòriesbinàries V ={X1,...,Xn,Y1,... , Ym} enelsvèrtexsd’unmodelgràficnodirigit,on X = (X1,...,Xn) sónles variablesobservadesi Y = (Y1,...,Ym) sónlesvariablesocultes.Aquests modelsgràfics,conegutscoma màquinesdeBoltzmannrestringides (restricted Boltzmannmachines oRBMenanglès)venendotatsd’unaestructuradegraf bipartitdemaneraqueúnicamenthihaarestesentrevariablesobservadesi

variableslatents;vegeulafigura5.L’energia d’unaconfiguraciódonadade variablesaleatòriesambelsseusparàmetresenaquestgrafesdefineixcomla funció

E(x,y; θ) =− n

on θ = (W,b,c) sónelsparàmetresdelmodel.Lanotacióqueusemperals paràmetresestàinfluenciadaperlanotacióenlaliteraturadeperceptronsi xarxesneuronals.Apartirdel’energia,podemdefinirlaprobabilitatd’una realitzaciódelvectoraleatoricoma

p(x,y; θ) = 1 Z(θ) exp( E(x,y; θ)),(x,y) ∈{0, 1}n+m , (17)

on Z(θ) éslaconstantnormalitzadora.Compodemveureperlaconnectivitat delgraf,lesvariablesobservadessónindependentsentreellescondicionades sobreleslatents,iviceversa.Ladistribuciómarginalde X espotobtenirde l’equació (17) sumantsobreelsestatsdelesvariableslatents y ∈{0, 1}m,i després,mitjançantlesmanipulacionsadients,obtindremelproductesegüent (vegeu[57]peramésdetallssobreladerivacióilesmàquinesdeBoltzmannen general):

p(x; θ) = 1 Z(θ) exp (b⊤x) m j=1 (1 + exp (wj x + cj )) = 1 Z(θ) m j=

(18)

pera λj entrezeroiu,on wj éslafila j-èsimade W i p ′ ji,p ′′ ji sóndistribucions quedepenenexclusivamentde xi.D’aquestamaneratrobemunaexpressióque ensrecordaunadistribucióproducte q(x1,...,xn) = qi(xi) quelligaamb unproductetensorial.Concretament,l’expressiódel’equació (18) mostrauna estructuradeproductetensorialderangnonegatiudos,deltipusquehem esmentatalasecció5.3.Hoveiemenl’equaciósegüent,quefaexplícitaaquesta connexiófentservirnotaciótensorial:

q ′′ jn),

peradeterminats q ′ ji, q ′′ ji.Aixídoncs,lesRBMsónunexempled’unproducte de m factorstensorialsderangnonegatiucomamàximdos.

Aquestsmodelshanestatexploratsiutilitzatsenprocessamentdelainformacióa[78]ia[39]comaprecursordelesxarxesneuronalsdeduescapes,de maneraquelessevespropietatscomaaproximadorsdefuncionssónespecialmentrellevantsenaplicacionsd’aprenentatgeautomàtic.Elstensorsderang nonegatiudoshanestatdescritsentermesderestriccionsdesubmodularitat a[3].

Figura 5: DiagramaquemostraunamàquinadeBoltzmannrestrictiva comunmodelgràficambcincvariableslatentsicincvariablesobservades.

Nota 5. L’anàlisidelesdistribucionsquesorgeixend’aqueststensorsde rangdosésremarcadamentdifícil.Noobstantaixò,peralcasenquèelmodel éslasumadedostensors2 × 2 × 2,SeigaliMontúfar([75])handemostratque elmodeldedistribucionsnodegenerades(ésadir,lesquecauenal’interiordel símplex)sónequivalentsaunmodelgràficenunarbreambunaúnicavariable ocultadetresestats.

6.3Componentsindependentsimodelsd’equacionsestructurals

Consideremelmodelsegüentperaunvectoraleatori X, X = Aε, (19)

on A ∈ Rm×m i ε ésunvectoraleatori(latent)ambunaestructuradedependènciasenzilla.Elsmodelsd’aquestaformas’utilitzenextensamentenaplicacions. Depenentdelcontext,podemimposarrestriccionsaddicionalsalamatriu A oalvectoraleatori(latent) ε.Perexemple,enseparaciócegadefontséshabitualsuposarque A ésinvertibleique ε técomponentsindependents,[27].La proposicióensajudaràenaquestadiscussió:

Proposició 4. Lescomponentsde X sónindependentssiinoméssieltensor cumulant κr (X) ésdiagonalperatot r ≥ 2

Elresultatanteriortéconseqüènciesimportantsenciènciadedades.En l’anàlisidecomponentsindependents (ICA),espostulaqueelvectoraleatori observat X = (X1,...,Xm) espotescriurecomunatransformaciólineal Aε, on ε = (ε1,...,εm) técomponentsindependentsi A ∈ Rm×m ésinvertible. Sotacondicionsfeblessobreladistribuciódelvectornoobservat ε,podem recuperarlamatriu A apartirdelesobservacions X (llevatdepermutacions defilesicanvisenelsseussignes),[26].Alapràcticaaquestarecuperacióes realitzaambelscumulantsd’ordrebaix κ3(Y) i κ4(Y),aprofitantelfetque aquestssóntensorsdiagonals.

Donatqueelvector ε nos’observadirectament,lapreguntaprincipaléssi lamatriu A espotrecuperarúnicamentapartirdelesobservacionsde X.Sense pèrduadegeneralitat,suposemque ε témitjanazeroimatriudecovariància identitat.Sotaaquestahipòtesi,lacovariànciade X satisfà Cov(X) = AA⊤ , cosaqueenspermetidentificar A mòdull’acciódelgruportogonalsobre l’espaidelescolumnesde A (AA⊤ = (AQ)(AQ)⊤ peraqualsevolmatriu ortogonal Q).Aquestresultatd’identificabilitatespotmillorarsi ε ésno gaussià.Concretament,enuntreballclau,Comon([26])vademostrarque A es potrecuperarllevatdepermutacionsireescalamentsdelescolumnespera ±1, semprequecomamàximunacomponentde ε siguinormal.Sotacondicions genèriquesfebles, A espotrecuperarapartirdelsmomentsdeterceroquart ordrede X.Alapràctica,moltsmètodesutilitzenaquestsmomentsd’ordre inferior.

Perconnectarelmodel (19) alanostradiscussiósobretensors,considerem µr (X),µr (ε) ∈ Sr (Rm) comelsmomentstensorialsde X i ε,respectivament, talcomhemintroduïtalasecció4.1.Suposemque ε técomponentsindependentsi,pertant,perlaproposició4, µr (ε) ésuntensordiagonal.Aixímateix, perlapropietatmultilinealdelsmoments,tenimque

µr (X) = µr (Aε) = A • µr (ε), onlanotació A • µr (ε) ∈ Sr (Rm) ésl’acciómultilinealde A ∈ Rm×m sobre Sr (Rm): (A • µr (ε))i1,...,ir = j1,...,jr Ai1j1 ··· Air jr (µr (ε))j1,...,jr .

Enaltresparaules,l’equació (19) estableixque,peratot r ≥ 2,eltensormoment r -èsimde X ésdelaforma A • D,pera A ∈ Rm×m iuntensordiagonal D ∈ Sr (Rm).Lapreguntaesconverteix,doncs,en:enquinscasospermet aquestacondició,pera r fixada,identificarlamatriu A?Comquelamatriu decovariànciajaenspermetiaidentificar A mòdull’acciódelgruportogonal, podemreformular-hodelamanerasegüent.Suposem A • D = (AQ) • D′ per a A invertiblei Q ortogonal,on D, D′ sóntensorsdiagonals;equivalentment, Q • D′ ésdiagonal.Llavors,podemconcloureque Q hadeserunamatriu depermutacióllevatdesignes?Peramésdetallssobreaquestenfocament, vegeu[55].

Exemple 5. Consideremelcas r = 3, m = 2.Lacondicióque Q • D′ sigui diagonalperauntensordiagonal D′ espotexpressarpelsistemad’equacions cúbicenlesentradesde Q:

(Q • D′)112 = Q2 11Q21D′ 111 + Q2 12Q22D′ 222 = 0, (Q • D′)122 = Q11Q2 21D′ 111 + Q12Q2 22D′ 222 = 0.

Enformamatricialaixòés

Comque Q ésortogonal,cadascunadelesmatriusdiagonalsanteriorshan deserobélamatriudezeros,obéinvertibles.Sialgunadelesduesés idènticamentzero,aleshores Q hadeserunamatriudepermutacióllevatde signes,il’equaciósesatisfàtrivialment.Siambduesmatriussóninvertibles, l’equaciónomésespotsatisfersi D′ 111 = D′ 222 = 0,ienaquestcas D′ es corresponambeltensoridènticamentzero.Aixòensmostraque,mentre D′ siguiuntensordiagonaldiferentdezero, Q • D′ ésdiagonalnoméssi Q ésuna matriudepermutaciósignada.

Enlamajoriad’aplicacionssuposemque ε técomponentsindependents, peròtambééspossiblerelaxaraquestescondicions(perexemple,enelmodel devariànciacomuna).Peramésmotivacióiresultatsbàsics,vegeu[55].Addicionalment,elcassobredeterminaton A ésunamatriurectangularésaltament rellevantalapràctica;vegeu[91]peralsdetalls.

Elsmodelsdelaforma (19) tambés’hanestudiatextensivamentenelcontext d’anàlisidelacausalitat,i,enaquestàmbit,lamatriu A prenunaestructura especial.Pearl([62])consideraelmodelsegüentd’equacionsestructurals definit sobreungrafdirigit:

Xi = fi(pa(i),εi),i = 1,...,m,

ésadirquecadavariabledelsistemaespotexpressarcomunafunciódels seusnodespredecessorsiuntermed’error εi.Aquestsistemaésnolineali noparamètric,perògeneralitzalaversiólinealàmpliamentutilitzadaenels campsdel’economiailesciènciessocialsquehempresentata (9).Peralcas delmodellineal,espotescriuredeformacompactacoma

X = ΛX + ε,

on Λij = 0tretque j → i siguiunaarestade G.Prenent A = (Im Λ) 1 , recuperemelmodelqueteníema(19).

Donatque,enaquestcontext,lamatriu A téunaestructuraparticular, podríemaspiraraidentificar-ladirectamentamblamatriudecovariàncies de X.Peraresultatsenaquestadirecció,vegeu[33, 35, 38].L’exemplesegüent haestatadaptatde[32].

Exemple 6. Fumardurantl’embaràsafectaelpesennéixerdelnadó?Per respondreaquestapregunta,suposemqueunestudiregistraelnivelldetabaquismematerndurantl’embaràs(X1)ielpesennéixerd’unnadó(X2).Suposant queexisteixunefectecausaldeltabaquismesobreelpesennéixer,pretenem quantificaraquestefecte.Alapràctica,secentrenlesdadesiesfaservirun modellineal:

X1 = ε1,X2 = λ12X1 + ε2; l’objectiuésinferirl’efecte λ12.Si ε1, ε2 sónvariablesnocorrelacionadesde mitjana0,podemferservirque Cov(X1,X2) = λ12 Var(X1) perrecuperar λ12 a partirdeladistribucióobservada.

Unaaltrageneralitzacióimportantéslad’inclourevariableslatentsa (9) per modelitzarpotencialsvariablesdeconfusió.Aquestespodendistorsionarles relacionsdecausalitatobservadesentrelescomponentsde X;vegeu[8, 86]. L’exempleacontinuacióhaestatadaptattambéde[32].

Exemple 7. L’efecte λ12 del’exempleanteriorpotnoserdirecteipotveure’s distorsionatperaltresvariablesdeconfusiólatents.Perexemple,factorsde predisposiciógenèticaosocioeconòmicspodenafectartantl’hàbitdefumar comelpesennéixerdelsnadons.Enaquestasituació,lainferènciasobre elquocient Cov(X1,X2)/ Var(X1) noseriavàlida.Unapossiblesolucióésla d’introduiruna«variableinstrumental»queinfluenciïdirectamentelnivellde tabaquismeperònoelpesennéixer,iquenoestiguiinfluenciadaperlavariable latent.Seguintlabibliografia,espotemprarunavariableinstrumental X3 que mesurielsimpostossobreeltabac.Lesequacionslinealsquedefineixenel modelamblavariablelatent H vindriendonadesper: X1 = λ01 + λ31X3 + λH

onelserrors {ε1,ε2,ε3,εH } sónindependentsdosados.D’aquísesegueix quel’equació Cov(X2,X3) = λ12 Cov(X1,X3) sesatisfàperaaquestmodeli, sempreque Cov(X1,X3) ≠ 0,podremdeduirpropietatsde λ12 apartirdel quocientCov(X2,X3)/ Cov(X1,X3).

Unaltreproblemaconegutenl’anàlisidecausalitatéssil’estructuradel grafespotrecuperarapartirdelesobservacionsde X.Unaltrecop,això requereixmomentsd’ordresuperiordelesdades,lanogaussianitat,iels resultatsd’identificabilitatcomelsquehempresentatperICA;vegeu[77].

Referències

[1] Allman,E.S.;Matias,C.;Rhodes,J.A. «Identifiabilityofparameters inlatentstructuremodelswithmanyobservedvariables». Ann.Statist., 37(6A)(2009),3099–3132.

[2] Allman,E.S.;Rhodes,J.A. «Phylogeneticidealsandvarietiesforthe generalMarkovmodel». Adv.inAppl.Math.,40(2)(2008),127–148.

[3] Allman,E.S.;Rhodes,J.A.;Sturmfels,B.;Zwiernik,P. «Tensorsof nonnegativeranktwo». LinearAlgebraAppl.,473(2015),37–53.

[4] Améndola,C.;Casanellas,M.;GarcíaPuente,L.D. «Tapasofalgebraic statistics». NoticesAmer.Math.Soc.,65(8)(2018),936–938.

[5] Améndola,C.;Faugère,J.-C.;Sturmfels,B. «MomentvarietiesofGaussianmixtures». J.Algebr.Stat.,7(1)(2016),14–28.

[6] Anandkumar,A.;Ge,R.;Hsu,D.;Kakade,S.M.;Telgarsky,M. «Tensor decompositionsforlearninglatentvariablemodels». J.Mach.Learn.Res., 15(2014),2773–2832.

[7] Anandkumar,A.;Hsu,D.;Kakade,S.M. «Amethodofmomentsfor mixturemodelsandhiddenMarkovmodels».A: Proceedingsofthe25th AnnualConferenceonLearningTheory.Vol.23(2012),33.1–33.34.

[8] Barber,R.F.;Drton,M.;Sturma,N.;Weihs,L. «Half-trekcriterion foridentifiabilityoflatentvariablemodels». Ann.Statist.,50(6)(2022), 3174–3196.

[9] Bertolini,M.;Turrini,C. «Problemsandrelatedresultsinalgebraic visionandmultiviewgeometry». Rend.Circ.Mat.Palermo(2),73(6) (2024),2205–2231.

[10] Bishop,C.M.;Tipping,M.E. «Ahierarchicallatentvariablemodelfor datavisualization». IEEETrans.PatternAnal.Mach.Intell.,20(3)(1998), 281–293.

[11] Blei,D.M. «Probabilistictopicmodels». Comm.ACM,55(4)(2012), 77–84.

[12] Blei,D.M.;Ng,A.Y.;Jordan,M.I. «LatentDirichletallocation». J.Mach. Learn.Res.,3(2003),993–1022.

[13] Bocci,C.;Chiantini,L. AnIntroductiontoAlgebraicStatisticswithTensors.LaMatematicaperil3+2.Cham:Springer,2019.(Unitext;118)

[14] Bro,R.;deJong,S. «Afastnon-negativity-constrainedleastsquares algorithm». JournalofChemometrics,11(5)(1997),393–3401.

[15] Bro,R.;Sidiropoulos,N.D. «Leastsquaresalgorithmsunderunimodalityandnon-negativityconstraints». JournalofChemometrics,12(4) (1998),223–247.

[16] Calamante,F.;Mørup,M.;Hansen,L.K. «Definingalocalarterialinput functionforperfusionMRIusingindependentcomponentanalysis». MagneticResonanceinMedicine,52(4)(2004),789–797.

[17] Casanellas,M. «PhylogeneticreconstructionbasedonAlgebra».A: Cutting-EdgeMathematics.Cham:Springer,2024,26–44.(RSMESpringer Ser.;13)

[18] Casanellas,M.;Fernández-Sánchez,J.;Garrote-López,M. «SAQ:semialgebraicquartetreconstruction». IIEEE/ACMTrans.Comput.Biol.Bioinform.,18(6)(2021),2855–2861.

[19] Castro,R.;Coates,M.;Liang,G.;Nowak,R.;Yu,B. «Networktomography:recentdevelopments». Statist.Sci.,19(3)(2004),499–517.

[20] Chang,J.T. «FullreconstructionofMarkovmodelsonevolutionarytrees: identifiabilityandconsistency». Math.Biosci.,137(1)(1996),51–73.

[21] Chickering,D.M. «Atransformationalcharacterizationofequivalent Bayesiannetworkstructures».A: UncertaintyinArtificialIntelligence (Montreal,PQ,1995).SanFrancisco,CA:MorganKaufmann,1995,87–98.

[22] Chifman,J.;Kubatko,L. «QuartetinferencefromSNPdataunderthe coalescentmodel». Bioinformatics,30(23)(2014),3317–3324.

[23] Choi,H.;Baraniuk,R.G. «MultiscaleimagesegmentationusingwaveletdomainhiddenMarkovmodels». IEEETrans.ImageProcess.,10(9)(2001), 1309–1321.

[24] Choi,M.J.;Lim,J.J.;Torralba,A.;Willsky,A.S. «Exploitinghierarchical contextonalargedatabaseofobjectcategories».A: IEEEComputer SocietyConferenceonComputerVisionandPatternRecognition.San Francisco,CA:IEEE,2010,129–136.

[25] Ciliberto,C.;Cueto,M.A.;Mella,M.;Ranestad,K.;Zwiernik,P. «Cremonalinearizationsofsomeclassicalvarieties».A: FromClassicalto ModernAlgebraicGeometry.Cham:Birkhäuser/Springer,2016,375–407. (TrendsHist.Sci.)

[26] Comon,P. «Independentcomponentanalysis,anewconcept?». Signal Process.,36(3)(1994),287–314.

[27] Comon,P.;Jutten,C.(ed.). HandbookofBlindSourceSeparation.IndependentComponentAnalysisandApplications.AcademicPress,2010.

[28] Cong,F.;Lin,Q.-H.;Kuang,L.-D.;Gong,X.-F.;Astikainen,P.;Ristaniemi,T. «TensordecompositionofEEGsignals:Abriefreview». Journalof NeuroscienceMethods,248(2015),59–69.

[29] Crouse,M.S.;Nowak,R.D.;Baraniuk,R.G. «Wavelet-basedstatisticalsignalprocessingusinghiddenMarkovmodels». IEEETrans.Signal Process.,46(4)(1998),886–902.

[30] Dempster,A.P.;Laird,N.M.;Rubin,D.B. «Maximumlikelihoodfrom incompletedataviatheEMalgorithm».Ambdiscussió. J.Roy.Statist.Soc. Ser.B,39(1)(1977),1–38.

[31] Develin,M.;Sullivant,S. «Markovbasesofbinarygraphmodels». Ann. Comb.,7(4)(2003),441–466.

[32] Drton,M. «Algebraicproblemsinstructuralequationmodeling».A: The50thAnniversaryofGröbnerBases.Tòquio:MathematicalSocietyof Japan,2018,35–86.(Adv.Stud.PureMath.;77)

[33] Drton,M.;Foygel,R.;Sullivant,S. «Globalidentifiabilityoflinear structuralequationmodels». Ann.Statist.,39(2)(2011),865–886.

[34] Drton,M.;Sturmfels,B.;Sullivant,S. LecturesonAlgebraicStatistics Basilea:BirkhäuserVerlag,2009.(OberwolfachSemin.;39)

[35] Drton,M.;Weihs,L. «Genericidentifiabilityoflinearstructuralequationmodelsbyancestordecomposition». Scand.J.Stat.,43(4)(2016), 1035–1045.

[36] Eriksson,B.;Dasarathy,G.;Barford,P.;Nowak,R. «Towardthe practicaluseofnetworktomographyforinternettopologydiscovery».A: ProceedingsIEEEINFOCOM.SanDiego,CA:IEEE,2010,1–9.

[37] Fernández-Sánchez,J.;Casanellas,M. «Invariantversusclassicalquartetinferencewhenevolutionisheterogeneousacrosssitesandlineages». SystematicBiology,65(2)(2016),280–291.

[38] Foygel,R.;Draisma,J.;Drton,M. «Half-trekcriterionforgenericidentifiabilityoflinearstructuralequationmodels». Ann.Statist.,40(3)(2012), 1682–1713.

[39] Freund,Y.;Haussler,D. «Unsupervisedlearningofdistributionson binaryvectorsusingtwolayernetworks».A: AdvancesinNeuralInformationProcessingSystems.Vol.4.Morgan-Kaufmann,1991,912–919.

[40] Garcia,L.D.;Stillman,M.;Sturmfels,B. «AlgebraicgeometryofBayesiannetworks». J.SymbolicComput.,39(3-4)(2005),331–355.

[41] Harshman,R.A.;Lundy,M.E. «PARAFAC:Parallelfactoranalysis». Comput.Statist.DataAnal.,18(1)(1994),39–72.

[42] Hartley,R.;Zisserman,A. MultipleViewGeometryinComputerVision.2aed.Ambunpròlegd’OlivierFaugeras.Cambridge:Cambridge UniversityPress,2003.

[43] Hitchcock,F.L. «Theexpressionofatensororapolyadicasasumof products». J.Math.andPhys.,6(1-4)(1927),164–189.

[44] Janson,S. «Normalconvergencebyhighersemi-invariantswithapplicationstosumsofdependentrandomvariablesandrandomgraphs». Ann. Probab.,16(1)(1988),305–312.

[45] Janzamin,M.;Ge,R.;Kossaifi,J.;Anandkumar,A. «Spectrallearning onmatricesandtensors». FoundationsandTrends® inMachineLearning, 12(5-6)(2019),393–536.

[46] Ji,Y.;Wang,Q.;Li,X.;Liu,J. «Asurveyontensortechniquesandapplicationsinmachinelearning». IEEEAccess,7(2019),162950–162990.

[47] Kruskal,J.B. «Three-wayarrays:rankanduniquenessoftrilineardecompositions,withapplicationtoarithmeticcomplexityandstatistics». LinearAlgebraAppl.,18(2)(1977),95–138.

[48] Landsberg,J.M. Tensors:GeometryandApplications.Providence,RI: AmericanMathematicalSociety,2012.(Grad.Stud.Math.;128)

[49] Lauritzen,S.L. GraphicalModels.OxfordSci.Publ.NovaYork:The ClarendonPress,OxfordUniversityPress,1996.(OxfordStatist.Sci.Ser.; 17)

[50] Lawrence,N.D. «Gaussianprocesslatentvariablemodelsforvisualisationofhighdimensionaldata».A: NIPS’03:Proceedingsofthe16th InternationalConferenceonNeuralInformationProcessingSystems.Cambridge,MA:MITPress,2004,329–336.

[51] Lukacs,E. «SomeextensionsofatheoremofMarcinkiewicz». PacificJ. Math.,8(1958),487–501.

[52] Makhijani,M.K.;Balu,N.;Yamada,K.;Yuan,C.;Nayak,K.S. «Accelerated3DMERGEcarotidimagingusingcompressedsensingwith ahiddenMarkovtreemodel». JournalofMagneticResonanceImaging, 36(5)(2012),1194–1202.

[53] Marcinkiewicz,J. «SurunepropriétédelaloideGauß». Math.Z.,44(1) (1939),612–618.

[54] McCullagh,P. TensorMethodsinStatistics.MonographsonStatisticsand AppliedProbability.ChapmanandHall/CRC,2018.

[55] Mesters,G.;Zwiernik,P. «Nonndependentcomponentsanalysis». Ann. Statist.,52(6)(2024),2506–2528.

[56] Michałek,M.;Sturmfels,B. InvitationtoNonlinearAlgebra.Providence, RI:AmericanMathematicalSociety,2021.(Grad.Stud.Math.;211)

[57] Montúfar,G. «RestrictedBoltzmannmachines:introductionandreview».A: InformationGeometryanditsApplications.Cham:Springer, 2018,75–115.(SpringerProc.Math.Stat.;252)

[58] Montúfar,G.;Morton,J. «DiscreterestrictedBoltzmannmachines». J. Mach.Learn.Res.,16(2015),653–672.

[59] Mourad,R.;Sinoquet,C.;Zhang,N.L.;Liu,T.;Leray,P. «Asurvey onlatenttreemodelsandapplications». J.ArtificialIntelligenceRes.,47 (2013),157–203.

[60] Nafees,S.;Rice,S.H.;Wakeman,C.A. «Analyzinggenomicdata usingtensor-basedorthogonalpolynomialswithapplicationtosynthetic RNAs». NARGenomicsandBioinformatics,2(4)(2020),lqaa101.

[61] Pachter,L.;Sturmfels,B.(ed.). AlgebraicStatisticsforComputational Biology.NovaYork:CambridgeUniversityPress,2005.

[62] Pearl,J. Causality.Models,Reasoning,andInference.Cambridge:CambridgeUniversityPress,2000.

[63] Pearson,K. «Contributionstothemathematicaltheoryofevolution». Philos.Trans.Roy.Soc.LondonSer.A,185(1894),71–110.

[64] Pearson,K. «Methodofmomentsandmethodofmaximumlikelihood». Biometrika,28(1/2)(1936),34–59.

[65] Pfeiffer,M.;Betizeau,M.;Waltispurger,J.;Pfister,S.S.;Douglas, R.J.;Kennedy,H.;Dehay,C. «Unsupervisedlineage-basedcharacterizationofprimateprecursorsrevealshighproliferativeandmorphological diversityintheOSVZ». JournalofComparativeNeurology,524(3)(2016), 535–563.

[66] Pistone,G.;Riccomagno,E.;Wynn,H.P. AlgebraicStatistics.ComputationalCommutativeAlgebrainStatistics.BocaRaton,FL:Chapman& Hall/CRC,2001.(Monogr.Statist.Appl.Probab.;89)

[67] Qi,Y.;Comon,P.;Lim,L.-H. «Semialgebraicgeometryofnonnegative tensorrank». SIAMJ.MatrixAnal.Appl.,37(4)(2016),1556–1580.

[68] Rabiner,L.R. «AtutorialonhiddenMarkovmodelsandselectedapplicationsinspeechrecognition».A: ProceedingsoftheIEEE,77(2)(1989), 257–286.

[69] Ricci,M.M.G.;Levi-Civita,T. «Méthodesdecalculdifférentielabsoluet leursapplications». Math.Ann.,54(1-2)(1900),125–201.

[70] Ringe,D.;Warnow,T.;Taylor,A. «Indo-Europeanandcomputational cladistics». TransactionsofthePhilologicalSociety,100(1)(2002),59–129.

[71] Robeva,E.;Seigal,A. «Dualityofgraphicalmodelsandtensornetworks». Inf.Inference,8(2)(2019),273–288.

[72] Romberg,J.K.;Choi,H.;Baraniuk,R.G. «Bayesiantree-structured imagemodelingusingwavelet-domainhiddenMarkovmodels». IEEE Trans.ImageProcess.,10(7)(2001),1056–1068.

[73] Ruffini,M.;Casanellas,M.;Gavaldà,R. «Anewmethodofmoments forlatentvariablemodels». Mach.Learn.,107(8-10)(2018),1431–1455.

[74] Schreiber,J.;Durham,T.;Bilmes,J.;Noble,W.S. «Avocado:amultiscaledeeptensorfactorizationmethodlearnsalatentrepresentationof thehumanepigenome». GenomeBiology,21,articlenúm.81(2020).

[75] Seigal,A.;Montúfar,G. «Mixturesandproductsintwographicalmodels». J.Algebr.Stat.,9(1)(2018),1–20.

[76] Shiers,N.;Aston,J.A.D.;Smith,J.Q.;Coleman,J.S. «Gaussiantree constraintsappliedtoacousticlinguisticfunctionaldata». J.Multivariate Anal.,154(2017),199–215.

[77] Shimizu,S.;Inazumi,T.;Sogawa,Y.;Hyvärinen,A.;Kawahara,Y.; Washio,T.;Hoyer,P.O.;Bollen,K. «DirectLiNGAM:adirectmethod forlearningalinearnon-Gaussianstructuralequationmodel». J.Mach. Learn.Res.,12(2011),1225–1248.

[78] Smolensky,P. «Informationprocessingindynamicalsystems:Foundationsofharmonytheory». ParallelDistributedProcess,1(1986).

[79] Speed,T.P. «Cumulantsandpartitionlattices». Austral.J.Statist.,25(2) (1983),378–388.

[80] Steel,M. Phylogeny—DiscreteandRandomProcessesinEvolution.Filadèlfia,PA:SocietyforIndustrialandAppliedMathematics(SIAM),2016. (CBMS-NSFRegionalConf.Ser.inAppl.Math.;89)

[81] Sturmfels,B.;Timme,S.;Zwiernik,P. «Estimatinglinearcovariance modelswithnumericalnonlinearalgebra». Algebr.Stat.,11(1)(2020), 31–52.

[82] Sturmfels,B.;Uhler,C. «MultivariateGaussian,semidefinitematrix completion,andconvexalgebraicgeometry». Ann.Inst.Statist.Math., 62(4)(2010),603–638.

[83] Sturmfels,B.;Zwiernik,P. «Binarycumulantvarieties». Ann.Comb., 17(1)(2013),229–250.

[84] Sullivant,S. «AlgebraicgeometryofGaussianBayesiannetworks». Adv. inAppl.Math.,40(4)(2008),482–513.

[85] Sullivant,S. AlgebraicStatistics.Providence,RI:AmericanMathematical Society,2018.(Grad.Stud.Math.;194)

[86] Tramontano,D.;Drton,M.;Etesami,J. «Parameteridentificationin linearnon-Gaussiancausalmodelsundergeneralconfounding».Preprint (2024).[Disponibleenlíniaa: https://arxiv.org/abs/2405.20856]

[87] Uhler,C. «GeometryofmaximumlikelihoodestimationinGaussian graphicalmodels». Ann.Statist.,40(1)(2012),238–261.

[88] Vavasis,S.A. «Onthecomplexityofnonnegativematrixfactorization». SIAMJ.Optim.,20(3)(2009),1364–1377.

[89] Verma,T.;Pearl,J. «Equivalenceandsynthesisofcausalmodels».A: ProceedingsoftheSixthConferenceonUncertaintyinArtificialIntelligence NovaYork:ElsevierScienceInc.,1990,220–227.

[90] Wainwright,M.J.;Jordan,M.I. «Graphicalmodels,exponentialfamilies, andvariationalinference». FoundationsandTrends® inMachineLearning, 1(1-2)(2008),1–305.

[91] Wang,K.;Seigal,A. «Identifiabilityofovercompleteindependentcomponentanalysis».Preprint(2024).[Disponibleenlíniaa: https://arxiv. org/abs/2401.14709]

[92] Watanabe,S. AlgebraicGeometryandStatisticalLearningTheory.Cambridge:CambridgeUniversityPress,2009.(CambridgeMonogr.Appl. Comput.Math.;25)

[93] Willsky,A.S. «MultiresolutionMarkovmodelsforsignalandimage processing».A: ProceedingsoftheIEEE,90(8)(2002),1396–1458.

[94] Yang,K.D.;Katcoff,A.;Uhler,C. «CharacterizingandlearningequivalenceclassesofcausalDAGsunderinterventions». Proceedingsof MachineLearningResearch,80(2018),5537–5546.

[95] Žabokrtsk`y,Z.;Popel,M. «HiddenMarkovtreemodelindependencybasedmachinetranslation».A: ProceedingsoftheACL-IJCNLP2009 ConferenceShortPapers,2009,145–148.

[96] Zhang,N.L. «Hierarchicallatentclassmodelsforclusteranalysis». J. Mach.Learn.Res.,5(2003/04),697–723.

[97] Zhang,Y.;Chen,X.;Zhou,D.;Jordan,M.I. «SpectralmethodsmeetEM: aprovablyoptimalalgorithmforcrowdsourcing». J.Mach.Learn.Res., 17(2016),articlenúm.102,44p.

[98] Zwiernik,P. «L-cumulants, L-cumulantembeddingsandalgebraicstatistics». J.Algebr.Stat.,3(1)(2012),11–43.

[99] Zwiernik,P. SemialgebraicStatisticsandLatentTreeModels.BocaRaton, FL:Chapman&Hall/CRC,2016.(Monogr.Statist.Appl.Probab.;146)

[100] Zwiernik,P.;Uhler,C.;Richards,D. «MaximumlikelihoodestimationforlinearGaussiancovariancemodels». J.R.Stat.Soc.Ser.B.Stat. Methodol.,79(4)(2017),1269–1292.

LuisSierra DepartmentofStatisticalSciences UniversityofToronto luis.sierra@mail.utoronto.ca

MartaCasanellas DepartamentdeMatemàtiques UniversitatPolitècnicadeCatalunya marta.casanellas@upc.edu

PiotrZwiernik DepartmentofEconomicsandBusiness UniversitatPompeuFabra piotr.zwiernik@upf.edu

ButlletídelaSocietatCatalanadeMatemàtiques Vol.39,núm.1-2,2024.Pàg.171–173

Englishsummaries

JaumeAguadé

Areviewofrotationsinlowdimensions

Webeginbydiscussingrotationsinlineargeometryandorthogonalmatrices, andgoontopresentexplicit,elementaryandself-containedconstructions oftheclassicalisomorphismsbetweenspinorgroupsindimensions < 7and certainunitaryorsymplecticgroups.Thepaperisintendedtoserveaslecture notesforanintroductorycourseoncompactLiegroups.

Keywords: rotation,spinor,Liegroup,quaternions.

MSC2020SubjectClassification: 22-01,20G20,22E15.

JaumeCollGuerrero

Polyhedraandmodularorigami

Thispaperpresentsmodularorigamitechniquesthatallowustocreatea widevarietyofpolyhedrafrompaper:thefivePlatonicsolids,thethirteen Archimedeanpolyhedra,theeightconvexdeltahedraandtheirstellations, prisms,antiprisms,pyramidsandFulleriangeodesicdomes,amongothers.

Keywords: modularorigami,polyhedra,Platonicsolids,Archimedeanpolyhedra, origamitechniques,tessellations.

MSC2020SubjectClassification: 00A08,00A66,05B45,51M20,52B05,52B10.

XavierGuitartandMarcMasdeu

Rationalpointsonellipticcurves

Ellipticcurvesarecurrentlyamongthemostextensivelystudiedobjectsin numbertheory.Theycanbedescribedbycubicequationsintwovariables, butwhatsetsthemapart–andmakesthemfascinating–istherichalgebraic structureexhibitedbytheirsolutions.Theaimofthisarticleistoexplain whatellipticcurvesareandtoexploretheirmostsignificantproperties,some ofwhichrankamongthemostimportantresultsin20th-and21st-century mathematics.Wewillalsodiscussseveralopenconjecturesthatcontinueto shapecurrentresearch.Toplaceellipticcurveswithinabroaderhistorical andconceptualcontext,wepresentthemasaspecificclassofDiophantine equations–arecurrentandcentralthemeinnumbertheory.

Keywords: Diophantineequations,ellipticcurves,Heegnerpoints, p-adicintegration,Stark-Heegnerpoints.

MSC2020SubjectClassification: 14H52,11G05.

JaumedeHaro

TheFriedmannequations:Newtonianmechanicsvs.generalrelativity

Inthispaper,wepresentaheuristicderivationoftheperturbedFriedmann equationsbasedonNewtonianmechanics,offeringanintuitiveperspectiveon thesecosmologicalrelations.ThisapproachhighlightstheremarkableagreementbetweenNewtonianandrelativisticdescriptionswithincertainlimits, servingbothasaconceptual–andevenphilosophical–bridge,andasapedagogicaltooltodeepenunderstandingofthephysicalprinciplesgoverningthe evolutionoftheuniverse.Bysimplifyingthecomplexmathematicalframework ofgeneralrelativity,thismethodprovidesanaccessiblemeansofexploring thedynamicsoftheuniverse.Itunderscoreshowclassicalmechanics,when appliedcarefully,canofferinsightsthatalignwithrelativisticresultsinthe linearapproximation.Thisconnectionnotonlyenhancesourunderstandingof theuniversalityofphysicallawsbutalsoreinforcestheideathatrelativistic phenomenacanoftenbeinterpretedthroughfamiliarclassicalanalogues.

Keywords: Friedmannequations,cosmologicalperturbations,Newtonianmechanics,generalrelativity.

MSC2020SubjectClassification: 83C05,83C99,70F99,83F05.

LuisSierra,MartaCasanellasandPiotrZwiernik

Tensorsinalgebraicstatistics

Tensorsareubiquitousinstatisticsanddataanalysis.Thecentralobjectthat linksdatasciencetotensortheoryandalgebraisthatofamodelwithlatent variables.Weprovideanoverviewoftensortheory,withparticularemphasison itsapplicationsinalgebraicstatistics.Thishigh-leveloverviewisaccompanied bynumerousexamplestoillustratekeyconcepts.Additionally,anextensive literaturereviewisincludedtoguidereaderstowardsmoredetailedstudieson thesubject.

Keywords: tensors,algebraicstatistics,graphicalmodels,tensordecomposition.

MSC2020SubjectClassification: 14M99,15A69,62H22,62R01,62R07.

Instruccionsperalsautors

Elsarticlessotmesosapublicaciós’hand’enviaralseditorsoaqualsevol membredelcomitèeditorialpercorreuelectrònic,preferentmentenformat PDF.Elsoriginalshandecontenirlaversióanglesadeltítol,unresumbreuen catalàienanglès,paraulesclauencatalàienanglèsielscodisdelaclassificació permatèriesMSC2020.

Lesversionsdefinitivesdelsarticlesacceptatss’handepresentarencodiTEX, preferentmentenl’estilLATEXpropidel butlletí.Aquestestilespotobtenira lespàgineswebdelaSocietatCatalanadeMatemàtiques(SCM).Esrecomana unaextensiód’entre15i35pàgines.Femnotarqueenaquestapublicació s’utilitzapreferentmentelpuntperaseparardecimals,enllocdelacoma recomanadaperl’IEC,perapoderfacilitarlacomprensiódelesexpressions matemàtiques.Pertald’accelerarelprocésdeproducció,espregaalsautors quesegueixinlesindicacionscontingudeseneldocumentd’exemple.

Laversióenpaperdel butlletí s’imprimeixenblancinegre.Quanunarticle continguifiguresencoloriesconsidericonvenient,l’autorproporcionaràuna versiódelsgràficssubstituintelcolorpertonsdegrisosilíniesdegruix variable.Aixímateix,modificaràelscomentarisquefacinreferènciaalcolorde lesfigures.Enqualsevolcas,el butlletí publicaràl’originalencolorenelseu formatelectrònic.

Lapropietatintel.lectualdelsarticlesésdelsrespectiusautors.

Elsautors,enelmomentdelliurarelsarticlesal butlletí perasol licitar-ne lapublicació,acceptenelstermessegüents:

—ElsautorscedeixenalaSCM(filialdel’Institutd’EstudisCatalans)els dretsdereproducció,comunicaciópúblicaidistribuciódelsarticlespresentats peraserpublicatsal butlletí

—ElsautorsresponendavantlaSCMdel’autoriail’originalitatdelsarticles presentats.

—Ésresponsabilitatdelsautorsl’obtenciódelspermisosperalareproducciódetotelmaterialgràficinclòsenelsarticles.

—LaSCMestàexemptadetotaresponsabilitatderivadadel’eventual vulneraciódedretsdepropietatintel lectualperpartdelsautors.

CadaautorrebràunacòpiaenPDFd’altaqualitatdelaversiódigitaldelseu articleiunexemplarimprèsdelnúmerodel butlletí enelqualespubliqui.

Lacorrespondènciaadministrativarelacionadaambel butlletí s’had’adreçaralaSCM.

Pelquefaalaprotecciódedadespersonals,l’Institutd’EstudisCatalans(IEC) compleixelqueestableixelReglamentgeneraldeprotecciódedadesdelaUnió Europea(Reglament2016/679,del27d’abrilde2016).Deconformitatamb aquestanorma,s’informaque,ambl’acceptaciódelesnormesdepublicació, elsautorsautoritzenquelessevesdadespersonals(nomicognoms,dadesde contacteidadesdefiliació)puguinserpublicadesenelcorresponentvolum del butlletí

Aquestesdadesseranincorporadesauntractamentqueésresponsabilitat del’IECamblafinalitatdegestionaraquestapublicació.Únicaments’utilitzaranlesdadesdelsautorsperagestionarlapublicaciódel butlletí ino serancedidesatercers,niesproduirantransferènciesatercerspaïsosoorganitzacionsinternacionals.Uncoppublicatel butlletí,aquestesdadeses conservarancomapartdelregistrehistòricd’autors.Elsautorspodenexercir elsdretsd’accés,rectificació,supressió,oposició,limitacióeneltractament iportabilitat,adreçant-seperescrital’Institutd’EstudisCatalans(carrerdel Carme,47,08001Barcelona),obéenviantuncorreuelectrònical’adreça dades.personals@iec.cat,enquès’especifiquidequinapublicacióestracta.

Comitèeditorial

AntoniGuillamon(editorencap)

DepartamentdeMatemàtiques UniversitatPolitècnicadeCatalunya antoni.guillamon@upc.edu

CarmeCascante

Dep.deMatemàtiquesiInformàtica UniversitatdeBarcelona cascante@ub.edu

BartomeuColl

Dep.deMatemàtiquesiInformàtica UniversitatdelesIllesBalears tomeu.coll@uib.cat

NúriaFagella

Dep.deMatemàtiquesiInformàtica UniversitatdeBarcelona fagella@maia.ub.es

ArmengolGasull

DepartamentdeMatemàtiques UniversitatAutònomadeBarcelona armengol.gasull@uab.cat

GáborLugosi

ICREAiDepartamentd’Economia UniversitatPompeuFabra gabor.lugosi@upf.edu

RosaCamps(editoraadjunta)

DepartamentdeMatemàtiques UniversitatAutònomadeBarcelona rosa.camps@uab.cat

MarcNoy

DepartamentdeMatemàtiques UniversitatPolitècnicadeCatalunya marc.noy@upc.edu

FrancescPlanas

DepartamentdeMatemàtiques UniversitatPolitècnicadeCatalunya francesc.planas@upc.edu

JoanSaldaña

Dep.d’Informàtica,Mat.AplicadaiEstadística UniversitatdeGirona joan.saldana@udg.edu

MartaSanz-Solé

Dep.deMatemàtiquesiInformàtica UniversitatdeBarcelona marta.sanz@ub.edu

GilSolanes

DepartamentdeMatemàtiques UniversitatAutònomadeBarcelona gil.solanes@uab.cat

SocietatCatalanadeMatemàtiques

La SocietatCatalanadeMatemàtiques(SCM) ésunasocietatfilialdel’Institutd’EstudisCatalansquecontinualesactivitatsdelaSecciódeMatemàtiques delaSocietatCatalanadeCiències,quefoufundadaperl’Institutl’any1931. Lesfinalitatsdela SCM són:elconreudelesciènciesmatemàtiques,l’extensió delseuconeixementenlasocietatcatalana,elfomentdelseuensenyament idelasevainvestigacióteòricaiaplicada,aixícomlapublicaciódetotamena detreballsques’adeqüinaaquestsobjectius.La SCM desenvolupalesseves activitatsenlesterresdellenguaiculturacatalanes.Elcatalàés,doncs,la llenguapròpiadela SCM ilaqueésusadanormalmententotselsseusactesi publicacions.

La SCM editalespublicacionsperiòdiques SCM/Notícies, ButlletídelaSocietatCatalanadeMatemàtiques, NouBiaix (encol.laboracióamblaFEEMCAT)i Reports@SCM.Elssocisdela SCM reben,gratuïtament,aquestespublicacions.

La SCM téconvenisdereciprocitatambdiversessocietatsmatemàtiques d’arreudelmón,mitjançantelsqualselssocisdela SCM obtenenunareduccióenlaquotadesocid’aquestessocietats.Aixímateix,elssocisdela SCM podenfer-sesocisdelaSocietatMatemàticaEuropeapagantunaquota complementària.

LaJuntaDirectivadela SCM estàconstituïdaperlespersonessegüents:

Presidenta:MontserratAlsinaiAubach

Vicepresident:JosepVivesiSanta-Eulàlia

Secretària:MargaridaMitjanaiRiera

Tresorer:AlbertGranadosiCorsellas

Vocals:ClaraMateoCampo,AinoaMurilloLópez,AlbertRuizCirera, DavidVirgiliCorreas

Delegatdel’IEC:JoaquimBrunaiFloris

L’adreçadela SCM éscarrerdelCarme,47,08001Barcelona.Telèfon: 933248583.Fax:932701180.Correuelectrònic: scm@iec.cat.Adreçaweb: https://scm.iec.cat.