IMPARIAMO METODO MATEMATICA
12 Che cosa ci insegna la MATEMATICA
NUMERI
14 I primi numeri
6 Parole per… CONOSCERE Numeri e Armonia
18 Il nostro sistema di numerazione
19 Esercizi
10 I grandi numeri
11 Esercizi
12 Dossier problemi
Le tappe del problema
14 Dalla testa ai piedi
16 L’addizione
17 Le proprietà dell’addizione
18 Esercizi
20 La sottrazione
21 La proprietà della sottrazione
22 Esercizi
24 Problem solving In partenza per…
26 La moltiplicazione
27 Le proprietà della moltiplicazione
29 Esercizi
30 La divisione
31 La proprietà della divisione
32 La divisione in colonna
34 Esercizi
36 Dossier problemi
I dati del problema
38 Le domande del problema
40 I multipli
41 I divisori
42 Dal più facile...
43 ... al più difficile
44 Dossier problemi Il procedimento risolutivo
46 Diversi procedimenti
47 Diversi modi per rappresentare il procedimento risolutivo
48 Problem solving A spasso per il mercato
50 La frazione
51 Esercizi
52 Le frazioni complementari
53 Le frazioni proprie e improprie
54 Confrontare le frazioni
56 Le frazioni equivalenti
57 Esercizi
58 La frazione di un numero
59 Esercizi
60 Dal più facile...
61 ... al più difficile
62 per imparare Le frazioni nell’arte
164 Problem solving Un giro in libreria
166 Le frazioni decimali
167 Esercizi
168 Le frazioni decimali e i numeri decimali
169 I centesimi e i millesimi
170 I numeri decimali
171 Esercizi
172 Confrontare i numeri decimali
173 Esercizi
174 Addizioni e sottrazioni con i decimali
175 Esercizi
176 Moltiplicazioni e divisioni per 10 • 100 • 1 000
177 Moltiplicazioni con i numeri decimali
178 Divisioni con i numeri decimali
179 Problem solving Pausa in viaggio
180 Dal più facile...
181 ... al più difficile
MISURE
182 Le prime misurazioni
184 Parole per… CONOSCERE Eureka!
186 Le misure di lunghezza
187 Le equivalenze
188 Le misure di capacità
189 Esercizi
190 Le misure di massa-peso
191 Peso lordo • Peso netto • Tara
192 Dal più facile...
193 ... al più difficile
113 Retta • Semiretta • Segmento
114 L’angolo
115 Vari tipi di angolo
116 Simmetria e traslazione
117 La rotazione
118 I poligoni
119 Classificare i poligoni
120 I triangoli
121 Esercizi
122 I quadrilateri
123 Esercizi
124 I parallelogrammi
125 Esercizi
126 I trapezi
127 Esercizi
128 per imparare Linee e forme geometriche nell’arte
130 Il perimetro
131 L’area
132 Isoperimetria ed equiestensione
133 Comporre e scomporre figure
134 Le misure di superficie
135 Esercizi
136 L’area del rettangolo e del quadrato
137 Esercizi
138 L’area del parallelogramma
139 L’area del rombo
140 Esercizi
141 Problem solving Il parco divertimenti
142 L’area del trapezio
143 Esercizi
144 L’area del triangolo
145 Problem solving
Tra i resti antichi
194 Problem solving Comprare online: ordini e consegne
196 Le misure di valore
197 Costo unitario e costo complessivo
198 Spesa • Guadagno • Ricavo
189 Esercizi
100 Educazione finanziaria Tu e il denaro
102 Le misure di tempo
103 Esercizi
104 Dal più facile...
105 ... al più difficile
GEOMETRIA
106 Le forme nella realtà
108 Parole per… CONOSCERE La coppa di Pitagora
110 Linee • Figure piane • Solidi
111 Esercizi
112 Le Linee
146 Dal più facile...
147 ... al più difficile
148 Educazione civica L’informazione consapevole
RELAZIONI, DATI e PREVISIONI
150 Le relazioni
151 Gli schemi
152 Le classificazioni e i diagrammi
154 La statistica
155 La moda e la media
156 I grafici
157 Esercizi
158 Certo • Possibile • Impossibile
159 Il calcolo delle probabilità
160 Dal più facile...
161 al più difficile
162 Compito di realtà
Indagine sulla raccolta differenziata
MATEMATICA
Che cosa ci insegna la MATEMATICA
Che cos’è la Matematica
La Matematica non è solo numeri. È una scienza che studia e rappresenta la realtà.
Per capire le quantità, lo spazio, la misura, le relazioni tra i fatti, la probabilità, abbiamo bisogno della Matematica.
La Matematica non è solo sui libri
Ti piace giocare con i videogiochi? Usi il computer per giocare o fare delle ricerche? Videogiochi e computer non esisterebbero senza la Matematica. La vita di ogni giorno è piena di “Matematica”, anche se non ce ne accorgiamo. È proprio questo il bello della Matematica: ci è utile e riusciamo a usarla anche senza conoscerla a fondo, perché il suo utilizzo ci risulta naturale.
Come si “fa” Matematica
• Cercando di immaginare le situazioni.
• Applicando le tecniche di calcolo.
• Trovando strategie di soluzione.
Come “parla” la Matematica
La Matematica ha un suo linguaggio particolare semplice ed efficace.
Con pochi segni riesce a rappresentare situazioni complesse. Pensa a un problema: segni che indicano numeri e operazioni che rappresentano una situazione. Di quante parole avresti bisogno per spiegarlo?
Non c’è una sola Matematica
Quante facce ha la Matematica?
Se, per esempio, entri in una pasticceria, ne incontri molte:
• l’aritmetica, cioè i numeri delle paste, delle torte, dei clienti…
• la geometria, cioè la forma delle torte, lo spazio occupato dal bancone…
• la misura, cioè il peso dei dolci, il loro costo…
• la statistica, cioè l’indagine sui dolci più venduti, le previsioni di vendita…
I PRIMI NUMERI
Anche i numeri hanno una storia?
Certo! La loro storia inizia nel lontano passato e possiamo vederla rappresentata su una linea del tempo e su una carta geostorica.
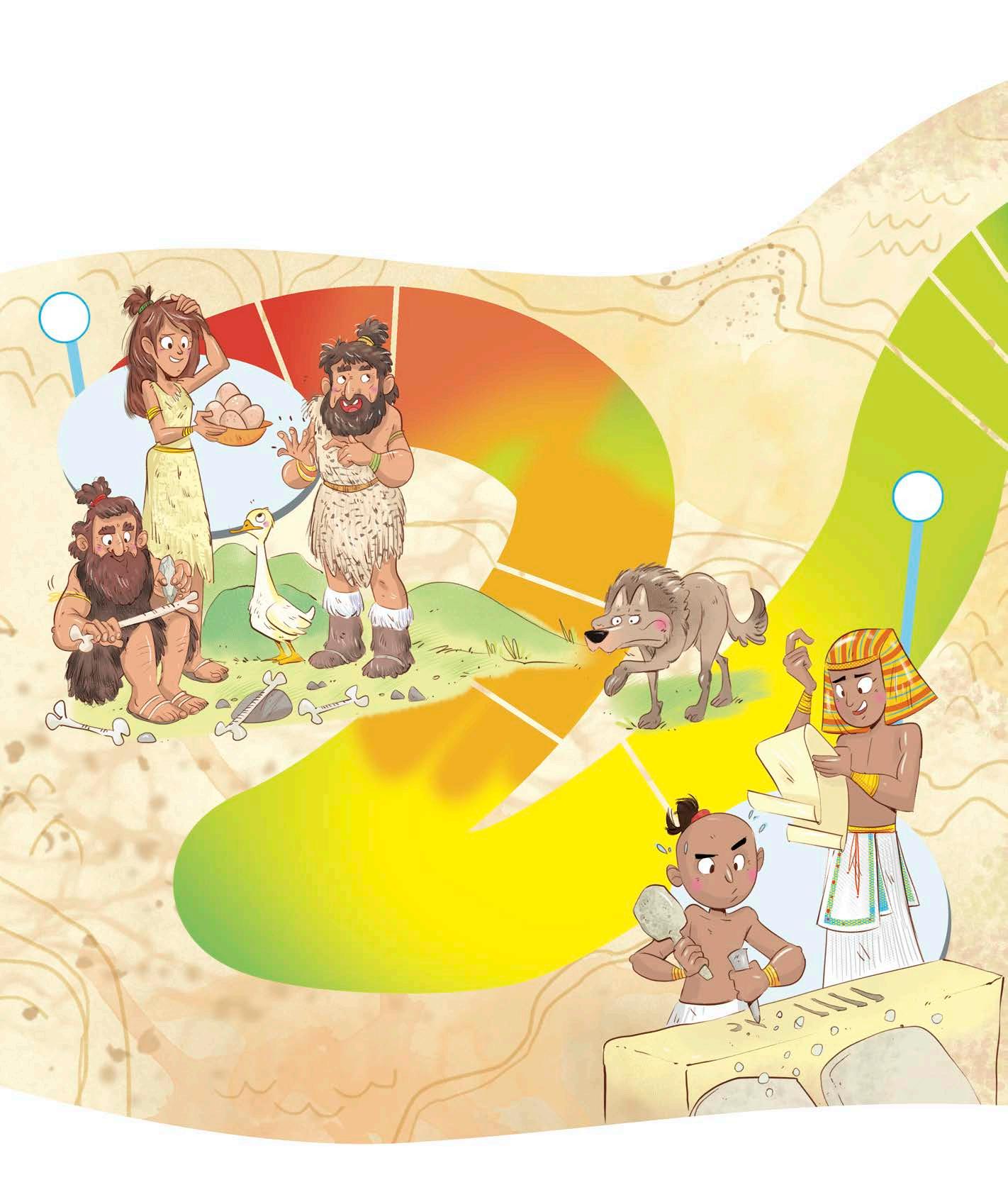
L’osso di Ishango
È un osso di babbuino trovato nell’Africa
Centrale. Risale a circa
Vi è incisa una serie di tacche suddivise in tre righe.
L’osso di Vestonice
In Repubblica Ceca è stato ritrovato l’osso di una zampa di lupo che risale a 32 000 anni fa. Vi sono incise una serie di tacche raggruppate per 5. Questo fa pensare che i nostri antenati utilizzassero le mani per contare.
I numeri babilonesi
I popoli mesopotamici incidevano le loro cifre sui gettoni e sulle tavolette di argilla con segni cuneiformi. Furono i Babilonesi a semplificare questi segni.
Un solo segno veniva ripetuto per indicare le quantità fino a 9. Un segno diverso indicava il 10, che si ripeteva proseguendo fino a 60, numero che veniva scritto come l’1, ma più grande.
Per i numeri maggiori si utilizzavano altri simboli: per esempio, il 600 era indicato come un 10 con sopra 60.
I numeri egizi
Gli Egizi utilizzavano disegni semplici per rappresentare i numeri. Ogni simbolo aveva un valore fisso e per indicare i numeri occorreva fare un’addizione: per esempio, un fiore di loto (1 000) e una corda (100) indicavano il numero 1100.
Da allora i numeri ne hanno percorsa di strada… una strada fatta di conoscenza e di scambio tra i popoli, per migliorare sempre di più il sapere e la vita di tutti e tutte.
Parole per... CONOSCERE di CRISTINA DELL’ACQUA
Benvenute e benvenuti nella biblioteca della mitica maestra Margherita! Guardate: è una biblioteca con il tetto trasparente! Margherita ha un superpotere: lei conosce tantissimi racconti, che ama narrare ai suoi alunni e alle sue alunne.
Durante tutto l’anno, la maestra Margherita condurrà la classe in un percorso in cui, grazie a storie del passato, si potrà avere uno sguardo nuovo sul presente.
Oggi ci racconterà che i numeri sono intorno a noi, più di quanto ci immaginiamo. E dove ci sono numeri c’è armonia, una parola che impareremo a conoscere.
numeri e armonia
Aritmetica, arte e armonia hanno in comune la radice ar-, che in tante parole greche dà l’idea di connettere tra di loro parti diverse che insieme formano qualcosa di bellissimo, in armonia! Non ci credete? Eppure, i Greci la pensavano così: il bello non è solo questione di gusto, ma di un insieme di armonia.
Una statua greca è bella se il piede è lungo un sesto dell’altezza, la testa un ottavo e il volto un decimo.
Regole numeriche: arte e aritmetica.
Un giorno studierete la sezione aurea, che è il simbolo dell’armonia tra le misure numeriche. Se non ne avete mai sentito parlare, sicuramente l’avete già vista, senza saperlo, nelle forme a spirale di alcune conchiglie, delle galassie, dei cicloni e dei petali di una rosa.
I numeri sono così, danno forma e bellezza a ciò che ci circonda.
LIFE
SKILLS
PAROLE per CONOSCERE
• Galileo Galilei, un famoso scienziato, diceva che il libro della natura è scritto usando il linguaggio matematico.
Per leggere la natura occorre conoscere la Matematica. Tu che cosa ne pensi? Parlane con l’insegnante e con la classe.
Quando volete fare una bella fotografia è importante scegliere il formato e l’inquadratura. Dare armonia alle vostre fotografie è questione di numeri. Anche gli schermi non sono tutti uguali. I più belli hanno un formato che rende l’immagine più simile alla percezione dei vostri occhi. L’armonia colpisce sempre!
Parole
IL NOSTRO SISTEMA DI NUMERAZIONE
Ti spiego
ARGOMENTO
I numeri e il valore delle cifre.
REGOLA
Le cifre sono i simboli che usiamo per scrivere i numeri. Sono 10. Con esse formiamo qualsiasi numero. La cifra 0 serve anche a indicare una posizione vuota nella composizione del numero.
Il nostro sistema di numerazione è:
• decimale, perché raggruppa in base 10: 10 u = 1 da 10 da = 1 h 10 h = 1 k
• posizionale, perché ogni cifra ha un valore differente in base al posto che occupa all’interno del numero:
546 6 vale 6 u, cioè 6
465 6 vale 6 da, cioè 60
654 6 vale 6 h, cioè 600
Capisco
• Utilizzando le cifre 5 • 2 • 8, scrivi tutti i numeri possibili.
• Scrivi in ordine crescente i numeri che hai trovato.
Esercizi
1 Rappresenta ciascuna quantità sull’abaco e scrivi il numero. 3 h 2 da 6 u
Direzione Invalsi
Io ho 12 biglie.
Alice
Io abito in via Roma, 12.
• Chi esprime una quantità? .................................
• Chi indica un ordine?
Leo
1 Scomponi i numeri. Segui l’esempio.
5 304 = 5 k (5 000) 3 h (300) 0 da (0) 4 u (4)
7 845 = ...... k (..................) ...... h (..................) ...... da (...............) ...... u (......)
4 338 = k ( ) h ( ) da ( ) u ( )
2 015 = k ( ) h ( ) da ( ) u ( )
3 665 = k ( ) h ( ) da ( ) u ( )
2 Componi i numeri. Segui l’esempio.
7 k • 3 h • 6 u = 7 000 + 300 + 6 = 7 306
3 k • 1 h • 4 da • 6 u = + + + =
4 k • 2 h • 1 da • 5 u = .................. + .................. + .................. + .................. = ..................
1 k • 6 da • 8 u = + + =
4 k • 9 h • 4 u = + + =
3 Metti in ordine le cifre da quella con maggior valore a quella con minor valore, poi scrivi il numero.
Segui l’esempio.
9 da 3 u 5 h 4 k = 4 k 5 h 9 da 3 u = 4 593
3 da 7 h 8 u 1 k = k h da u =
6 h 2 k 6 u 8 da = k h da u =
5 k 2 da 1 u 4 h = k h da u =
5 Che valore ha la cifra evidenziata? Indicalo. Segui l’esempio.
3 8 04
8 h 800
6 Trova nel numero la cifra indicata e colorala. Segui l’esempio.
4 Colora nello stesso modo i riquadri che hanno lo stesso valore.
7 Leggi i numeri scritti in lettere e scrivili in cifre.
Settemilatrecentosei .....................
Novemilaundici Quattromilasettecentouno ..................... Tremilaottocentotrenta
Ti spiego
ARGOMENTO
I GRANDI NUMERI
Scrivere e leggere numeri che indicano
grandi quantità.
REGOLA
Le classi possono essere delle:
• unità semplici;
• migliaia.
Ogni classe è composta da tre ordini: centinaia, decine, unità.
Tra una classe e l’altra si lascia un piccolo spazio.
classe delle migliaia classe delle unità semplici
centinaia decine unità centinaia decine unità hk dak uk h da u 100 000 10 000 1 000 100 10 1
Capisco
• Leggi il numero.
hk dak uk h da u
6 3 2 9 4 5
Seicentotrentaduemilanovecentoquarantacinque
• Leggi e scrivi il numero.
Cinquecentoquarantaduemilaottocentonovantasei
hk dak uk h da u
Pienone!
125 376 persone!
Intelligenza visiva
Centoventicinque MILA trecentoset tantasei
Direzione Invalsi
Ho pensato un numero. Ho aggiunto una decina di migliaia e ho ottenuto 145 910. Che numero avevo pensato?
• Alice aveva pensato al numero: 135910 155910 145900
1 Scrivi il numero rappresentato su ciascun abaco.
2 Leggi i numeri scritti in lettere e scrivili in cifre.
Duecentotrentamilacentododici ................................................
Trentaseimilanovecentonovantaquattro
3 Scrivi i numeri in lettere.
Settecentocinquantaduemilatrecentoventisei
Ottocentosessantatremiladuecentoventuno
140 250 mila 507 300 ................................................................................................................................................................................................................. 100 654
4 Confronta i numeri inserendo i simboli > (maggiore) o < (minore).
5 Trova e scrivi un numero compreso tra i due numeri indicati.
10 000 < <
6 Scrivi il numero precedente e il numero successivo.
7 A quanto corrisponde 1 uk? E 1 dak? E 1 hk? Rifletti, poi completa le tabelle.
Le tappe del problema
Problemi Nel linguaggio comune “avere un problema” indica una situazione spiacevole, da superare trovando una soluzione. Anche in Matematica è così, con la sola differenza che non sempre le situazioni problematiche sono spiacevoli, anzi molte volte è divertente cercare di risolverle.
Partenza
Quando devi risolvere un problema non devi farti prendere dalla fretta di raggiungere il risultato. Devi seguire un percorso a tappe.
Tappa 1
Leggi il problema con attenzione per capire bene il testo.
Andrea ha bisogno di un nuovo astuccio e di un quaderno.
In cartoleria gli astucci costano tutti 15 euro e ogni quaderno costa 2 euro. Ha a disposizione 20 euro.
Quanto spenderà in tutto? Quanto avrà di resto?
Tappa 2
Immagina la situazione e rappresentala con un semplice disegno.
Tappa 3
Leggi le domande per capire che cosa ti chiede il problema. Sottolinea le domande con colori diversi.
Tappa 4
Individua le informazioni, cioè i dati Evidenzia i dati. Scrivili.
Tappa 5
Individua il procedimento, cioè trova le operazioni. Scrivile e calcola.
Tappa 6
Rileggi le domande e scrivi le risposte.
Dalla testa ai piedi
1 Ricordi le tappe fondamentali per risolvere i problemi?
Mettile in pratica.
Tappa 1
Leggi con attenzione.
Emma ha messo in vendita a prezzo scontato 7 berretti rossi, 6 blu, 8 gialli. Emma ha venduto tutti i berretti a 12 euro l’uno.
Quanti berretti ha venduto?
Quanto ha incassato dalla vendita?
Tappa 3
Leggi le domande.
Sottolinea le domande. Scrivile qui e pensa a che cosa devi trovare.
• • Tappa 5
Trova le operazioni. Scrivile e calcola.
Tappa 2
Immagina la situazione.
Tappa 4
Individua i dati Evidenzia i dati e scrivili.
7 = berretti
6 = berretti
8 = berretti .................
12 euro = costo
Tappa 6
Scrivi le risposte
• Emma ha venduto .................................................................................
• Emma ha incassato
2 Leggi con attenzione il problema e indica con X la rappresentazione grafica giusta.
Poi risolvi sul quaderno.
Emma, all’ingrosso, ha acquistato 6 buste di magliette. In ogni busta ce ne sono 3.
Le magliette sono blu oppure rosse. Quelle blu sono 5.
Quante magliette ha acquistato? Quante sono le magliette rosse?
3 Leggi con attenzione il problema.
Carlo, nel negozio di Emma, ha comperato 2 paia di calze per ciascuno dei suoi 3 figli.
Ogni paio costa 4 euro.
Quante paia di calze ha comperato Carlo?
Quanto ha speso?
• Ecco come tre bambini hanno scritto i dati. Indica con X quelli scritti nel modo giusto.
2 = paia di calze in tutto
3 = numero dei figli
4 = costo di un paio di calze in euro
2 = paia di calze per figlio
3 = numero dei figli
4 = costo di un paio di calze in euro
2 = paia di calze per figlio
3 = numero dei figli
4 = costo totale in euro
• Ecco come tre bambini hanno risolto il problema. Indica con X il procedimento giusto.
Ti spiego
ARGOMENTO
L’operazione che unisce, aggiunge, aumenta quantità.
REGOLA
addendo 243 + addendo 502 = somma o totale 747
• L’addizione può sempre essere eseguita.
• Nell’addizione lo zero è l’elemento neutro perché non modifica la somma.
3 + 11 = 14
3 + 11 + 0 = 14
• Nelle addizioni in colonna devi rispettare il valore posizionale delle cifre. Poni attenzione ai cambi.
Esercizi
1 Esegui sul quaderno.
Senza cambio
L’ADDIZIONE
Capisco
• A che cosa serve l’addizione? Indica con X.
Lia ha 5 figurine. Teo ne ha 7. Quante figurine hanno insieme?
5 + 7 = 12
Unire.
Aggiungere. Aumentare.
Tea ha 4 magneti. Ne compera altri 2. Quanti magneti ha ora?
4 + 2 = 6
Unire.
Aggiungere.
Aumentare.
Alba ha 10 anni. Gaia ha 6 anni in più. Quanti anni ha Gaia?
10 + 6 = 16
Unire.
Aggiungere. Aumentare.
Con il cambio
85 + 113 + 701 =
23 451 + 16 348 =
30 705 + 125 093 =
a. 234 + 125 = 306 + 471 = 942 + 57 = 32 + 811 = b. 105 + 324 + 570 =
Direzione Invalsi
c. 548 + 247 = 589 + 312 =
605 + 197 =
286 + 814 = d. 333 + 241 + 118 =
505 + 273 + 136 =
88 099 + 10 122 =
68 547 + 422 343 =
• Formula la domanda del problema in modo che si risolva con un’addizione. Lucia aveva nel portafogli 50 euro. Ha comperato un giornale da 4 euro, un quaderno da 2 euro e, facendo colazione al bar, ha speso 4 euro.
ti guido • È necessario utilizzare tutti i dati?
Ti spiego
ARGOMENTO
LE PROPRIETÀ DELL’ADDIZIONE
Modi per facilitare i calcoli
nelle addizioni.
REGOLA
Proprietà commutativa dell’addizione
• Se cambi l’ordine degli addendi, il totale non cambia.
La proprietà commutativa si utilizza per fare la prova dell’addizione.
3 + 75 = 78
75 + 3 = 78
Proprietà associativa dell’addizione
• Se sostituisci due o più addendi con la loro somma, il totale non cambia.
99 + 1 + 20 = 120
100 + 20 = 120
Per facilitare il calcolo, si può scomporre un addendo in due numeri e poi applicare la proprietà associativa.
105 + 15 =
100 + 5 + 15 =
100 + 20 = 120
Intelligenza visiva
4 pizzette con le olive, 5 con i funghi.
5 pizzette con i funghi, 4 con le olive.
Capisco
• Esegui a mente e completa.
25 + 5 = 5 + 25 =
8 + 18 = 18 + 8 =
Hai cambiato l’ordine degli
La somma non è 15 + 5 + 50 = + 50 = 10 + 18 + 2 = 10 + =
Per facilitare il calcolo dell’addizione hai unito prima due
47 + 23 =
40 + + 23 =
40 + ........... = .................
Hai scomposto un addendo in ............... numeri e poi hai unito uno dei due numeri al
1 Esegui le addizioni sul quaderno. Fai la prova applicando la proprietà commutativa.
a. 235 + 146 = 674 + 189 =
564 + 237 =
b. 236 + 108 + 320 = 48 + 306 + 231 =
480 + 34 + 96 =
2 Evidenzia i due addendi che ti conviene associare per semplificare il calcolo.
Es. 7 + 98 + 2 = 100 + 7 = 107
10 + 92 + 8 = + =
25 + 15 + 4 = + =
100 + 100 + 3 = + =
1 + 9 + 5 000 =
+
=
c. 1 342 + 2 677 = 3 406 + 2 835 = 16 456 + 22 634 = d. 3 742 + 1 540 + 2 004 = 12 435 + 43 001 + 29 122 =
+ 223
+ 76 011 =
3 Applica la proprietà commutativa e quella associativa per semplificare il calcolo.
Es. 12 + 11 + 8 + 9 = 12 + 8 + 11 + 9 = 20 + 20 = 40
7 + 5 + 5 + 13 =
90 + 80 + 10 + 20 =
200 + 10 + 30 + 100 = 18 + 4 + 12 + 6 =
4 Indica con X i problemi che si risolvono con un’addizione. Poi risolvi sul quaderno.
Giada sta leggendo un libro di 144 pagine. Il libro del suo amico Peter ha 24 pagine in più. Quante pagine ha il libro di Peter?
Giada e Peter contano i loro libri: in tutto ne hanno 84. Ne regalano 15 alla biblioteca della scuola.
Quanti libri hanno in tutto ora?
Giada ha una libreria con tre scaffali. Dispone 24 libri sul primo scaffale, 18 sul secondo, 14 sul terzo. Quanti libri ci sono nella libreria di Giada?
Giada ha letto 167 pagine di un libro di avventura. Le mancano 36 pagine a finirlo. Quante pagine ha il libro?
Direzione Invalsi
• Stima il risultato. Indica con X. 302 + 495 = Circa… 700 800 3 900 + 1 143 = Circa… 4 000 5 000 13 005 + 454 = Circa… 13 500 17 000
• Ora esegui le operazioni e scrivi i risultati sui puntini. Quante stime erano corrette? su 3.
ti guido • Non ti viene chiesto il risultato esatto, ma una stima quindi… arrotonda gli addendi!
Calcolo mentale
• Per eseguire velocemente le addizioni a mente puoi utilizzare questi piccoli “trucchi”.
Scomponi il secondo addendo in modo da raggiungere la decina successiva al primo addendo. Poi aggiungi ciò che è rimasto.
28 + 18 = (28 + 2) + 16 = 30 + 16 = 46
Arrivo alla decina.
5 Utilizza la strategia che hai imparato per eseguire a mente queste addizioni. Fai “ tappa al 10”.
+ 15 = ....................
Calcolo mentale
+ 19 = ....................
Aggiungo 9, 99, 999
se devi aggiungere che cosa fai? esempio 9 aggiungi 10 e togli 1 72 + 9 = (72 + 10) – 1 = 81 99 aggiungi 100 e togli 1 325 + 99 = (325 + 100) – 1 = 424 999 aggiungi 1 000 e togli 1 1 876 + 999 = (1 876 + 1 000) – 1 = 2 875
6 Completa le tabelle.
Competenze
Addizionare vuol dire aggiungere.
• La somma può essere minore di ciascun addendo? Sì No
• Quando la somma è uguale a uno degli addendi?
7 Non c’è un solo modo per eseguire i calcoli a mente. Tra questi sistemi, tu quale sceglieresti?
LA SOTTRAZIONE
ARGOMENTO
L’operazione che calcola:
• il resto;
• la differenza tra due quantità;
• quanto manca a completare una quantità.
REGOLA
minuendo 345 –sottraendo 103 = resto o differenza 242
• Con i numeri naturali la sottrazione può essere eseguita solo se il sottraendo è minore o uguale al minuendo 147 – 148 = con i numeri naturali non è possibile
• Sottraendo 0 a un numero si ottiene il numero dato. 11 – 0 = 11
• Nelle sottrazioni in colonna devi rispettare il valore posizionale delle cifre. Poni attenzione ai cambi.
OPERAZIONI INVERSE
La sottrazione è l’operazione inversa dell’addizione. – 8 20 12 + 8
Perciò l’addizione può essere usata come prova della sottrazione.
Capisco
• A che cosa serve la sottrazione? Indica con X.
Sul tavolo del ristorante c’erano
7 bicchieri. 2 si sono rotti. Quanti bicchieri sono ancora interi?
7 – 2 = 5
Calcolare il resto.
Trovare la differenza.
Calcolare quanto manca.
Sul tavolo A ci sono 3 piatti, sul tavolo B ce ne sono 5.
Quanti piatti in più ci sono sul tavolo B? Quanti piatti in meno ci sono sul tavolo A?
5 – 3 = 2
Calcolare il resto.
Trovare la differenza.
Calcolare quanto manca.
A un tavolo ci sono sedute 8 persone. I tovaglioli sono 5.
Quanti tovaglioli bisogna aggiungere?
8 – 5 = 3
Calcolare il resto.
Trovare la differenza.
Calcolare quanto manca.
• Formula la domanda del problema in modo che si risolva con una sottrazione. Poi risolvi.
Stella è all’aeroporto. Ha con sé una valigia che pesa 25 kg (che metterà nella stiva) e un bagaglio a mano che pesa 7 kg. Può portare a bordo un bagaglio a mano del peso massimo di 5 kg.
Direzione Invalsi
LA PROPRIETÀ DELLA SOTTRAZIONE
spiego
ARGOMENTO
Un modo per facilitare i calcoli nelle sottrazioni.
REGOLA
Proprietà invariantiva della sottrazione
• Aggiungendo o togliendo a entrambi i termini della sottrazione lo stesso numero, il risultato non cambia.
35 – 15 = 20
40 – 20 = 20 + 5 + 5
35 – 15 = 20
30 – 10 = 20 – 5 – 5
Proprietà invariantiva e il calcolo rapido
• 1253 – 29 = 1224
Capisco
• Leggi e completa.
• Tiago ha 10 anni e Sara ha 6 anni. La differenza tra le loro età è di 4 anni.
• L’anno scorso avevano 9 e 5 anni: la differenza tra le loro età era diversa? Sì No
• Tra 10 anni avranno 20 e 16 anni: la differenza tra le loro età sarà diversa? Sì No
• Osserva e calcola.
– 8 =
Esercizi
1254 – 30 = 1224
• 1251 – 11 = 1240
+ 1 + 1 – 1 – 1
1250 – 10 = 1240
Per facilitare il calcolo mentale applica la proprietà invariantiva arrotondando il sottraendo.
1 Applica la proprietà invariantiva. Per facilitare il calcolo, arrotonda il sottraendo. 460 – 19 = + 1 + 1
– 20 =
2 Esegui a mente.
4 150 – 19 =
– 29 =
– 39 =
– 23 =
– 41 = 3 184
=
Calcolo mentale
• Per eseguire velocemente le sottrazioni a mente puoi
utilizzare questi piccoli “trucchi”.
Scomponi il sottraendo in modo da raggiungere la decina precedente al minuendo. Poi togli ciò che è rimasto.
45 – 9 = (45 – 5) – 4 = 40 – 4 = 36
1 Fai tappa alla decina precedente ed esegui.
Faccio tappa alla decina precedente.
49 – 13 = 33 – 12 = 23 – 7 = 47 – 14 = 58 – 11 = 41 – 8 = 35 – 14 = 76 – 16 =
Calcolo mentale
se devi togliere che cosa fai? esempio
Tolgo 9, 99, 999
9 togli ............. e aggiungi ............. 98 – 9 = (98 – 10) + 1 = 89 99 togli ............. e aggiungi ............. 205 – 99 = (205 – 100) + 1 = 106 999 togli e aggiungi 2 306 – 999 = (2 306 – 1 000) + 1 = 1
2 Esegui a mente.
150 – 9 = .................... 756 – 9 = 150 – 99 = .................... 756 – 99 = 1 500 – 999 = .................... 7 560 – 999 = 1 500 – 99 = .................... 7 560 – 9 =
3 Esegui le sottrazioni sul quaderno. Fai la prova applicando l’operazione inversa.
a. 389 – 258 = 984 – 562 = b. 782 – 491 = 805 – 472 = c. 17 654 – 11 368 = 31 520 – 10 817 = d. 46 500 – 13 608 = 70 000 – 54 600 =
Direzione Invalsi
• Con quale operazione risolvi il problema?
a. Giulio ha 20 €, 15 € in meno di quanto gli occorre per comprare il casco della bicicletta.
Quanto costa il casco? 20 + 15 = 35 20 – 15 = 5
b. Valeria ha nel portafogli 45 €, 12 € in più del casco della bicicletta che desidera.
Quanto costa il casco? 45 + 12 = 57 45 – 12 = 33
ti guido • Per non sbagliare, immagina la situazione. Le parole “meno” e “più” potrebbero ingannarti.
4 Quale operazione devi fare? + 12 ? 25 – 12
25 + 12 = 37 25 – 12 = 13
5 Scrivi i segni delle operazioni e i numeri che mancano.
Ho pensato un numero. Ho aggiunto 12 e ho ottenuto 25. Quale numero avevo pensato?
6
+ 11 = 22 + 5 = 9
+ 20 = 27
7 Completa le operazioni usando l’operazione inversa. Esegui i calcoli sul quaderno.
6 Completa le operazioni calcolando a mente. a. 880 + = 1 000 1 000 – 880 =
8 Completa le sottrazioni. In questo caso non puoi usare l’operazione inversa, ma devi calcolare la differenza tra il minuendo e il resto.
a. 175 – = 75 175 – 75 = b. 510 – = 10 – = 500 – = 300 500 – 300 = 140 – = 100 – =
9 Leggi e risolvi sul quaderno.
a. Alla prima fermata dello scuolabus scendono 18 bambini e bambine, alla seconda 27 e lo scuolabus si svuota. Quanti bambini e bambine hanno utilizzato lo scuolabus?
b. Con lo scuolabus sono arrivati a scuola 53 bambini e bambine. Alla prima fermata sono saliti 15 bambini e bambine. Quanti ne sono saliti nelle fermate successive?
• Quale problema si risolve con un’addizione?
• Quale con una sottrazione?