Chi ha paura della matematica_GEOMETRIA_1

PAURA matematica della ?

PAURA

geometria

Dal problema reale alla soluzione

Educazione civica, Stem, Informatica

Storia della matematica a cura del Prof. Odifreddi

Impara dall’errore

Oltre 15000 esercizi

Costruire il futuro insieme

Il Gruppo Editoriale ELi

offre proposte editoriali che coprono tutti i gradi e i rami scolastici, all’insegna della qualità, del rigore e dell’innovazione.

INTELLIGENZA

ARTIFICIALE

Percorsi didattici con attività pratiche che mirano ad approfondire i principali strumenti di IA generativa per favorirne un utilizzo critico e il tool VELIA a disposizione dei docenti per personalizzare l’attività didattica.

EQUILIBRI

Progetto di ricerca costante che mira a eliminare gli stereotipi di genere nei testi scolastici ponendo particolare attenzione alla scelta dei contenuti, a una valutazione iconografica ragionata e all’utilizzo di un linguaggio testuale inclusivo.

INCLUSIONE

Sviluppo di una cultura dell’inclusione attraverso contenuti accessibili e adeguati ai diversi stili di apprendimento.

ORIENTAMENTO

Approccio educativo e formativo volto a favorire la conoscenza di sé, delle proprie attitudini e delle proprie capacità, oltre a sviluppare le competenze non cognitive e trasversali necessarie per le scelte del futuro.

EDUCAZIONE

CIVICA secondo le NUOVE Linee guida

Aggiornamento e ampliamento dei nuclei tematici attorno ai quali si articolano le competenze e gli obiettivi di apprendimento: Costituzione, Sviluppo economico e sostenibilità, Cittadinanza digitale.

STEM/STEAM, CLIL

Attivazione del pensiero scientifico e computazionale, approccio interdisciplinare e laboratoriale, sviluppo della competenza multilinguistica, attraverso attività STEM, STEAM e CLIL.

DIGITALE

Acquisizione delle competenze digitali e dell’alfabetizzazione informatica come aiuto all’inclusione sociale e alla cittadinanza attiva.

EDUCAZIONE ALLE RELAZIONI

Percorsi incentrati sullo sviluppo di competenze relazionali che arricchiscono la consapevolezza del vissuto personale in relazione con la realtà circostante.

Gruppo

Gruppo

Editoriale

Editoriale

ELi

ELi

I QUADRILATERI

1

MISURA DI GRANDEZZE

Chi ha della

paura matematica?

Con questa unità inizia il tuo viaggio nel mondo della geometria, partendo dalle grandezze e dalle loro unità di misura. Ora so che vorresti gridare: “Fermate tutto! Voglio scendere! A cosa mi serve calcolare il volume di un solido? Quando mai userò nella mia vita le equivalenze per trasformare i kilogrammi in decigrammi?”. Niente paura: troverai numerosi riferimenti al modo con cui misuri le cose ogni giorno e scoprirai che la geometria è un utile strumento per capire più a fondo la realtà che ti circonda. Nel trattare le grandezze e le misure, potresti avere la sensazione di muoverti in un labirinto intricato, fatto di formule e popolato da dubbi come: “Che differenza c’è tra lunghezza e superficie? Perché misuriamo la superficie in metri quadrati e il volume in metri cubi? Che differenza c’è tra volume e capacità? E tra massa e peso?”. Per riuscire a orientarti non sarà necessario memorizzare tante informazioni, l’importante sarà capirne il senso: solo così avrai tra le mani un “filo conduttore”, che ti aiuterà a segnare la strada percorsa nel labirinto e uscirne con facilità!

ROAD MAP la nostra

CHIARIAMO COS’È UNA GRANDEZZA E COME SI PUÒ MISURARE

SCOPRIAMO COME MISURARE LE LUNGHEZZE

MISURIAMO LE SUPERFICI E I VOLUMI

INTRODUCIAMO LA MISURA DELLA CAPACITÀ E LA MISURA DELLA MASSA

RIPASSIAMO LE UNITÀ DI MISURA DEL TEMPO

MATERIALE INTEGRATIVO MULTIMEDIALE Focus

LEZIONE GRANDEZZE E MISURE 1

SUCCEDE CHE...

Emma iscrive il suo cane a una gara di agility dog, uno sport cinofilo in cui il cane deve eseguire un percorso a ostacoli nel minor tempo possibile. Pietro invece iscrive il suo cane a un concorso di bellezza in cui i cani partecipanti vengono giudicati in base a dei requisiti di bellezza che, per ciascuna razza, sono definiti dalla Federazione Cinofila Internazionale. In quale dei due concorsi si stabilisce il vincitore misurando una grandezza?

Per rispondere alla domanda occorre sapere che cos’è una grandezza e come si misura.

Una grandezza è tutto ciò che si può misurare.

Per misurare una grandezza occorre stabilire un’unità di misura.

Per esempio, per misurare quanto zucchero ho in un barattolo (grandezza da misurare), prendo un bicchiere (unità di misura) e, riempiendolo e svuotandolo più volte, trovo che il barattolo contiene 4 bicchieri di zucchero (valore numerico che esprime la grandezza).

4 = valore numerico che esprime la grandezza =

unità di misura grandezza da misurare

Si possono sempre confrontare due grandezze per stabilire qual è la maggiore o la minore? No; per esempio la capacità di una bottiglia e la larghezza di una finestra non sono confrontabili perché le unità con cui si misura la prima non sono uguali a quelle con cui si misura la seconda.

Per poter confrontare due grandezze occorre che siano della stessa natura, cioè che la grandezza di riferimento sia la stessa.

Le grandezze che sono della stessa natura e che si possono confrontare tra loro si dicono omogenee.

Nella gara di agility dog il tempo impiegato per effettuare il percorso è una grandezza, perché per classificare i concorrenti si effettua una misurazione. La bellezza di un cane, invece, non è una grandezza, perché non vi è un’unità di misura di riferimento.

In passato non esisteva un sistema unico di unità di misura e questo rendeva più difficoltosi gli scambi commerciali e i calcoli da effettuare nelle compravendite. Per questo alla fine del ’700 si decise di unificare le unità di misura e si arrivò al Sistema Metrico Decimale, che fu adottato in molti Paesi. Nel 1960 venne introdotto il Sistema Internazionale di Unità di Misura (SI) formato da sette grandezze fondamentali o primitive, come la lunghezza e la massa, e da grandezze derivate, come la capacità, la superficie e il volume.

1 Riconosci quali tra le seguenti caratteristiche si possono misurare e sono quindi delle grandezze.

a) La pulizia del bucato SÌ NO

b) Il peso di una sedia SÌ NO

c) La trasparenza di un bicchiere SÌ NO

2 Completa.

a) Una grandezza è

d) La capienza di un bidone SÌ NO

e) La durata di una partita SÌ NO

f) La memoria di un hard disk SÌ NO

b) Per essere confrontate due grandezze devono essere

c) Le grandezze sono o

d) La lunghezza è una grandezza

e) Il volume è una grandezza

f) La massa è una grandezza

3 STEM Contrassegna le caratteristiche di una balenottera che sono grandezze.

a) Indole: curiosa, spesso si avvicina alle imbarcazioni.

b) Gestazione: circa 10 mesi.

c) Nascite: nei mesi estivi.

d) Lunghezza di un piccolo: circa 2,5 m.

e) Allattamento: meno di 1 anno.

f) Durata della vita: 30-50 anni.

g) Alimentazione: pesci o crostacei.

Misura della lunghezza 2

SUCCEDE CHE...

Gli addetti alla manutenzione del Parco degli Aironi devono sostituire alcuni pali della staccionata che delimita il laghetto del parco. Per poter preparare i nuovi pali, di quale misura hanno bisogno? Quale strumento possono utilizzare?

Per rispondere alle domande è necessario saper individuare correttamente la grandezza da misurare e scegliere l’unità di misura adeguata.

Come detto nella lezione precedente, la lunghezza è una grandezza fondamentale del sistema metrico decimale e del SI; la sua unità di misura è il metro (m), con i suoi multipli e sottomultipli.

I multipli sono: decametro, ettometro, kilometro.

I sottomultipli sono: decimetro, centimetro, millimetro.

La definizione di metro negli anni è cambiata: prima era la lunghezza del campione di platino e iridio conservato nel Museo dei pesi e delle misure di Sèvres; poi il metro fu definito come la quarantamilionesima parte del meridiano terrestre; infine oggi la definizione di metro è stata riferita alla lunghezza d’onda di una radiazione.

Il metro è uguale a 1 650 763,73 volte la lunghezza d’onda della radiazione emessa dall’atomo di Cripto 86.

Questa definizione piuttosto complicata presenta due vantaggi:

• ha un elevato livello di precisione;

• è sempre riproducibile.

Nel seguente schema sono indicate le operazioni che devi eseguire per ottenere la misura equivalente espressa in un’unità di ordine superiore o inferiore.

Gli addetti devono misurare la lunghezza dei pali e come strumento possono usare un metro a nastro o una rotella metrica in cui sono indicati sia i metri sia i centimetri.

1 Sottolinea i completamenti corretti.

a) La lunghezza è una misura / grandezza fondamentale / grandezza derivata del sistema metrico binario / decimale

b) L’unità di misura della lunghezza è il decimetro / metro; i suoi sottomultipli sono il millimetro / decametro / centimetro / decimetro e i suoi multipli sono l’ettometro / il decametro / il kilometro

c) Il centimetro è un centesimo del / cento volte il metro.

d) Il kilometro è un millesimo del / mille volte il metro

2 Completa le seguenti equivalenze.

ESEMPIO

5 200 dm = 5,2 hm (nello schema di pagina 6 si va verso sinistra di tre posti)

0,0006 km = 0,06 dam (nello schema si va verso destra di due posti)

914 000 mm = 9,14 hm (nello schema si va verso sinistra di cinque posti)

a) 15 dm = mm 13 hm = cm 0,008 km = dm

b) 46 cm = dam 150 mm = dm 3,5 cm = mm

c) 8,5 m = cm 2,25 dam = dm 75,8 dm = hm

d) 0,47 km = dam 5,2 m = mm 1,45 km = m

e) 22 m = km 150 000 cm = hm 180 hm = dm

3 EDUCAZIONE CIVICA Risolvi il seguente problema.

Nelle contrade Petrarca e Pozzi del comune di Pietrasecca hanno da poco sistemato l’illuminazione stradale con dei lampioni alimentati a energia eolica e fotovoltaica, posti a 26 m l’uno dall’altro. Contrada Petrarca è lunga 5,2 km, contrada Pozzi 78 hm. Calcola quanti lampioni sono stati piazzati in ogni contrada e quanti in totale, sapendo che anche all’inizio della contrada va messo un lampione.

Risoluzione

5,2 km = m (lunghezza contrada Petrarca) 78 hm = m : 26 = n° lampioni contrada Petrarca n° lampioni contrada Pozzi numero totale dei lampioni : 1 000 × 100 : 10 000 × 100 : 1 000 × 100 × 100

Misura della superficie e misura del volume 3

Misura della superficie

SUCCEDE CHE... OS LUZIONE

Alla ditta Greengrass, specializzata nella semina e manutenzione di prati erbosi, è stato richiesto un preventivo per il rifacimento di un campo da calcio di un centro sportivo. Di quale misura la ditta avrà bisogno per preparare il preventivo?

La superficie è una grandezza derivata dalla lunghezza; infatti, è una lunghezza per una lunghezza. La sua unità di misura è il metro quadrato (m2), con i suoi multipli e sottomultipli.

Nelle unità di superficie ogni unità è 100 volte più grande dell’unità immediatamente inferiore ed è 100 volte più piccola dell’unità immediatamente superiore. Nel seguente schema sono indicate le operazioni che devi eseguire per ottenere la misura equivalente espressa in un’unità di ordine superiore o inferiore.

ettometro quadrato hm2

Per preparare il preventivo la ditta Greengrass deve conoscere la misura della superficie del campo da calcio.

Misura del volume

SUCCEDE

La ditta Moviterra ha ricevuto l’incarico di effettuare lo scavo di un terreno in cui verrà costruito un nuovo centro commerciale. Per calcolare il costo del lavoro di quale misura avrà bisogno?

Il volume è anch’esso una grandezza derivata dalla lunghezza; infatti, è una superficie per una lunghezza. La sua unità di misura è il metro cubo (m3), con i suoi multipli e sottomultipli.

Nelle unità di volume ogni unità è 1 000 volte più grande dell’unità immediatamente inferiore ed è 1 000 volte più piccola dell’unità immediatamente superiore.

Nel seguente schema sono indicate le operazioni che devi eseguire per ottenere la misura equivalente espressa in un’unità di ordine superiore o inferiore.

OS LUZIONE

Per calcolare il costo del lavoro la ditta Moviterra deve conoscere il volume dello scavo da effettuare nel terreno.

Primi

ESERCIZI

1 Completa le seguenti equivalenze.

a)

e) 0,5432 dm3 = cm3 g) 1 209 m3 = hm3

f) 7,5148 dam3 = dm3 h) 6 250,7 cm3 = m3

2 MATEMATICA IN AZIONE Risolvi il seguente problema.

La cooperativa Tuttinsieme possiede un terreno con la forma e le misure indicate in figura.

a) Quanti ettari misura?

b) Il possedimento contiene 11 × 7 – 3 × 3 = = = 68 quadratini.

c) Ogni quadratino vale 4 are, quindi 68 × 4 = a = ha.

d) Il frutteto contiene 6 × 4 = quadratini, quindi × 4 = are = ha.

e) La zona a foraggio contiene

L’ettaro, l’ara e la centiara sono unità di superficie che si utilizzano per misurare i terreni; il loro valore è: 1 ettaro (ha) = 10 000 m2 1 ettaro = 100 are.

Misura della capacità e misura della massa 4

Misura della capacità

SUCCEDE CHE...

Pietro ha comprato un acquario il cui volume è 70 dm

Per un pesce rosso servono almeno 10 litri d’acqua. Quanti pesci potrà mettere nel suo acquario?

Pietro deve mettere in relazione il volume con la capacità. Per farlo gli occorre sapere che cos’è la capacità.

La capacità è la quantità di liquido che un recipiente può contenere.

La capacità è una grandezza derivata, la sua unità di misura è il litro (L), con i suoi multipli e sottomultipli. Capacità e volume sono due grandezze che si equivalgono, infatti:

un litro di un liquido equivale a un volume di 1 dm3

Nel seguente schema sono indicate le operazioni che devi eseguire per ottenere la capacità equivalente espressa in un’unità di ordine superiore o inferiore.

Per il litro usiamo il simbolo L e non l per evitare confusione con il numero 1.

Misura della massa

Emma, navigando su internet, trova questo grafico e vuole calcolare l’acqua presente nel suo corpo rispetto alla massa corporea. Il peso di Emma è 56 kg, ma qual è la sua massa?

La massa è una grandezza primitiva e la sua unità di misura fondamentale è il kilogrammo (kg). : 10 × 10 : 10 × 10 : 10 × 10 : 10 × 10 : 10 × 10 litro L decilitro dL centilitro cL millilitro mL ettolitro hL decalitro daL

Poiché 70 dm3 = 70 L, 70 : 10 = 7. Quindi Pietro può mettere nel suo acquario al massimo sette pesci rossi.

La massa di un corpo è la quantità di materia che lo compone.

Nel seguente schema sono indicate le operazioni che devi eseguire per ottenere la massa equivalente espressa in unità di ordine superiore o inferiore.

Nel linguaggio comune si parla di peso anche quando si tratta della massa. In realtà queste due grandezze sono diverse: il peso è la forza di gravità con cui un corpo viene attirato dalla Terra, è una grandezza derivata la cui unità di misura è il newton (N). In varie parti della Terra o su altri pianeti il peso di un corpo cambia mentre la quantità di materia (massa) non varia. In questo testo useremo sempre la parola “peso” anche quando si dovrebbe parlare di massa.

Il mio peso sulla Terra è di circa 560 N Il mio peso sulla Luna è di circa 90 N La mia massa è sempre di 56 kg

In realtà 56 kg è la sua massa. Emma ha fatto confusione tra massa e peso.

1 Completa.

a) La capacità di 1 L di acqua distillata equivale al volume di 1

b) 1 dL corrisponde a L. c) 1 hL corrisponde a L. d) 1 cL corrisponde a L.

2 Completa le seguenti equivalenze.

12 L = 1 200 cL 23,4

3 STEM Risolvi il seguente problema.

Nel laboratorio di chimica di un istituto tecnico gli alunni di terza hanno preparato

2 L di una soluzione salina di cloruro di potassio (KCl) da suddividere in provette da 0,5 dL. Quante provette riempiranno?

2 L = dL (soluzione salina di KCl) : 0,5 = n° provette necessarie

Misura del tempo 5

SUCCEDE CHE...

Pietro deve prendere l’aereo alle 14:05 e legge sul biglietto che l’imbarco chiude alle 13:35. Guarda l’orologio, sono le 12:20 e per arrivare all’aeroporto di Malpensa gli occorrono 50 minuti. Se parte subito, quanti minuti prima della chiusura del gate arriverà?

Vediamo quali sono le unità di misura del tempo che, a differenza di quelle che hai incontrato nei paragrafi precedenti, appartengono a un sistema misto perché formato da:

• una parte non decimale (anno, mese, giorno);

• una parte sessagesimale ( ora , minuto , secondo ), cioè da multipli o sottomultipli di 60;

• una parte decimale (i sottomultipli del secondo).

L’unità fondamentale per misurare il tempo è il secondo

Nel seguente schema sono indicate le operazioni che devi eseguire per ottenere il tempo equivalente espresso in un’unità di ordine superiore o inferiore.

: 10 × 10 : 10 × 10

anno a mese ms giorno g ora h minuto m secondo s decimo di secondo d centesimo di secondo c

Poiché i mesi non hanno la stessa durata, ma ci sono mesi di 31 giorni, mesi di 30 giorni (Aprile, Giugno, Settembre e Novembre), un mese di 28 giorni, Febbraio, che però ogni quattro anni ne ha 29, per convenzione si utilizza il mese commerciale di 30 giorni.

Anche gli anni hanno una durata variabile: 365 giorni o 366 giorni (anno bisestile); per questo si utilizza l’anno commerciale di 360 giorni Tra i multipli delle misure del tempo ricordiamo la settimana (7 giorni), il lustro (5 anni) e il secolo (100 anni).

Riduzione in forma normale

Una misura di tempo si dice ridotta in forma normale quando:

• il valore numerico dei minuti e dei secondi non supera 59;

• il valore numerico delle ore non supera 23.

Per ridurre in forma normale una misura di tempo occorre trasformarla in unità di ordine superiore.

Pietro fa i calcoli: 12 h 20 m + 50 m = 12 h 70 m

Deve ridurre in forma normale perché i minuti superano i 59:

70 m = 60 m + 10 m = 1 h + 10 m 12 h 70 m = 13 h 10 m

Quindi Pietro arriverà 25 minuti prima della chiusura del gate.

1 Completa.

a) 60 minuti (m) = ora (h)

b) 120 minuti (m) = ore (h)

c) 24 ore (h) = giorno (g)

d) 30 giorni (g) = mese (ms)

e) 60 giorni (g) = mesi (ms)

f) 360 giorni (g) = anno (a)

2 Riduci in forma normale le seguenti misure di tempo.

ESEMPIO

13h 97m 68s

Trasforma in forma normale i secondi 68s = 60s + 8s = 1m + 8s

Aggiungi i minuti trovati a quelli dati 97m + 1m = 98m

Trasforma in forma normale i minuti 98m = 60 m + 38m = 1h + 38m

Aggiungi le ore a quelle date 13h + 1h = 14h

La misura ridotta in forma normale è: 14h 38m 8s

a) 7h 150m 124s

Trasforma in forma normale i secondi 124s = 120s + 4s = m + 4s

Aggiungi i minuti trovati a quelli dati 150m + m = m

Trasforma in forma normale i minuti 152m = 120m + 32m = h + m

Aggiungi le ore a quelle date

La misura ridotta in forma normale è: [9h 32m 4s]

b) 15h 103m 98s

Trasforma in forma normale i secondi

Aggiungi i minuti trovati a quelli dati

Trasforma in forma normale i minuti

Aggiungi le ore a quelle date

La misura ridotta in forma normale è:

3 MATEMATICA IN AZIONE Risolvi il seguente problema.

In una gara a cronometro Marta ha registrato un tempo di 5m 35s.

Se la gara è iniziata alle 15:30, stabilisci l’ora di arrivo di Marta.

[16h 44m 38s]

ODIFREDDI a cura del professor

L’Egitto, la culla della geometria

Leggendo i nostri libri di storia antica, siamo portati a pensare che la Grecia sia stata la culla della cultura occidentale, e che il pensiero filosofico e scientifico sia incominciato con i Greci. Leggendo i loro antichi libri di storia, si scopre invece che i Greci erano ben consapevoli di discendere culturalmente dagli Egizi, e riconoscevano questo loro debito in maniera molto esplicita. Numerosi miti raccontano che i grandi pensatori greci, da Talete a Pitagora, da Solone a Platone, fossero andati in Egitto a “risciacquare i loro panni nel Nilo”, per attingere alla sapienza millenaria degli antichi che erano vissuti sulle sponde di quel fiume.

Secondo il grande storico greco Erodoto, la geometria nacque in Egitto per un motivo molto pratico: misurare i campi coltivati. Lo dice la parola stessa, che si compone di due parti: “geo” e “metria”. La prima parte deriva da Gea, che era il nome greco della dea Terra. La troviamo anche nella parola “geografia”, che significa “descrizione della

Il Nilo, il grande fiume lungo il quale fioriva l’agricoltura degli antichi Egizi.

Scene di agricoltura egizie

terra”. La seconda parte significava “misura” in greco, e da essa deriva anche la parola “metro”, l’unità di misura che utilizziamo tutti i giorni per misurare lunghezze e distanze.

Erodoto racconta anche il motivo per cui gli Egizi erano interessati a misurare la Terra. La loro agricoltura dipendeva in modo essenziale dalle periodiche piene del Nilo, che due volte l’anno inondavano i terreni vicini al fiume, e li rendevano fertili. Quando il Nilo rientrava negli argini, i confini dei campi erano stati distrutti dalle acque, e bisognava ripristinarli con precisione, per restituirli ai proprietari terrieri. Di qui il bisogno di saper ricostruire con precisione geometrica i perimetri dei campi, e calcolarne le aree.

I due strumenti che i Greci usavano nella geometria erano la riga, per disegnare le rette, e il compasso, per disegnare i cerchi. Gli Egizi usavano invece le corde, e per questo chiamavano i matematici “tenditori di corde”. La corda può infatti funzionare sia come riga, che come compasso. Nel primo caso, basta tenderla fra due punti, in modo da farla diventare rettilinea. E nel secondo caso, basta fissarla in un punto e girarci attorno tenendo la corda tesa, in modo da disegnare un cerchio attorno a un centro. Oltre all’agrimensura, ovvero questa misurazione dei campi coltivati, da cui prendeva il nome, la geometria serviva agli Egizi anche per l’architettura. In particolare per la costruzione delle loro famose piramidi, delle quali bisognava saper calcolare i volumi per sapere, per esempio, quanti mattoni usare.

Le piene del Nilo, che si verificavano due volte l’anno, inondavano le coltivazioni vicine distruggendone i confini.

MAPPA

FONDAMENTALI

Sono 7 e costituiscono il Sistema Internazionale di Unità di Misura (sigla SI)

alcune sono

LUNGHEZZA

L’unità di misura fondamentale

è il metro (m).

Strumento: il metro a nastro (flessometro), il righello...

GRANDEZZE

Una grandezza è tutto ciò che si può misurare

possono essere

DERIVATE

Si ottengono da quelle fondamentali

alcune sono

L’unità di misura fondamentale è il kilogrammo (kg).

Strumento: la bilancia a bracci uguali

L’unità di misura fondamentale è il secondo (s).

Strumento: l’orologio

SUPERFICIE

Deriva dalla lunghezza: superficie = = lunghezza × lunghezza

L’unità fondamentale è il metro quadrato (m2).

metro quadrato

1 m 1 m

VOLUME E CAPACITÀ

Il volume deriva dalla lunghezza: volume = = superficie × lunghezza L’unità fondamentale

è il metro cubo (m3).

La capacità si usa per i liquidi. L’unità fondamentale della capacità è il litro (L). 1 L 1 dm3

1 ESERCIZI E PROBLEMI

GRANDEZZE

E

MISURE LEZIONE

1 Rispondi alle seguenti domande.

a) Che cos’è una grandezza?

b) Che cosa occorre per misurare una grandezza?

c) Quando due grandezze sono omogenee?

d) Che cos’è il Sistema Internazionale di Misura? Qual è la sua sigla?

e) Come si chiamano i due gruppi in cui vengono divise le grandezze nel Sistema Internazionale?

2 Completa la tabella.

Prima grandezza

Seconda grandezza

a) temperatura di una giornata invernale peso di un cioccolatino

b) lunghezza di un’automobile altezza di un albero

c) profondità di un lago lunghezza di un’autostrada

d) superficie di un campo da calcio

e) peso di un tuo compagno

f) durata della ricreazione

volume di una piscina

peso di un fustino di detersivo

velocità di una lumaca

Sono omogenee Non sono omogenee

2

MISURA DELLA LUNGHEZZA

3 Completa il seguente schema scrivendo il nome di ogni simbolo.

PUNTI FERMI

Moltiplicazioni e divisioni per 10, 100, 1000, …

REGOLA

× 10, 100, 1 000… si aggiungono degli zeri al numero e/o si sposta la virgola verso destra. : 10, 100, 1 000… si tolgono degli zeri al numero e/o si sposta la virgola verso sinistra.

ESEMPIO

=

ESERCIZI

Calcola:

4 Scegli la misura che ritieni esatta tra quelle di seguito elencate e completa le frasi (non tutte le misure verranno utilizzate).

a) Lunghezza di una matita colorata ………………….

b) Altezza di un condominio di 4 piani ………………….

c) Distanza tra Torino e Bologna ………………….

d) Lunghezza del fiume Po ………………….

e) Larghezza della cattedra

f) Lunghezza di uno spillo

5 Scegli la misura adatta.

a) Altezza di un gradino 1) 20 cm 2) 90 mm

b) Lunghezza di un garage 1) 300 dm 2) 400 cm

c) Larghezza di una strada 1) 5 m 2) 50 cm

d) Altezza di una finestra 1) 110 dm 2) 110 cm

6 Prendi un righello, misura il tuo libro di geometria ed esprimi le misure effettuate in centimetri.

Larghezza lunghezza spessore

Confronta i tuoi valori con quelli dei tuoi compagni. Che cosa osservi?

7 MATH Convert the following measurements into metres.

a) 1 cm = 1 dm = b) 1 km =

1 hm =

c) 1 dam = 1 mm =

8 Collega con una freccia le misure equivalenti a 1 m.

1 000 mm 0,0001 km

10 hm 1 m 100 cm

0,01 mm 0,1 dam

10 dm 0,001 km

Scrivi sul quaderno le seguenti misure di lunghezza sotto forma di numeri decimali.

ESEMPIO

4 m e 8 cm = 4, 0

dm e 4 mm

Completa le seguenti equivalenze.

13 a) 23 dm = mm c) 425 m = dam b) 72 cm = hm d) 44 km = m

14 a) 156 cm = dam c) 63,2 m = cm b) 81 cm = m d) 624 mm = dm

15 a) 7,25 km = dam c) 1 430 cm = hm b) 8,02 m = mm d) 0,02 dm = mm

16 a) 2 400 mm = hm c) 0,4 km = m

b) 6,23 dam = cm d) 0,36 mm = dam

17 a) 777 hm = dm c) 0,45 hm = km

b) 32,45 dam = km d) 325,3 mm = dam

Completa le seguenti catene di equivalenze.

18 4 526 dm = ................ m = .................. mm = .................... km = dam

19 75,3 m = ................ dam = ................... dm = ................... hm = cm

20 2,46 km = m = cm = dam = hm

21 0,24 dam = km = dm = cm = m

22 Riconosci la risposta corretta.

a) Un centimetro vale:

c) Un decametro vale: 1)

Mezzo metro vale:

23 Utilizza i simboli <, =, > per completare le seguenti relazioni.

a) 3

24 Calcola le seguenti addizioni effettuando a mente le equivalenze necessarie.

a) 6 dam + 52 m = dm c) 95 hm + 2 km = hm

b) 85 m + 27 dm = m d) 7 dam + 85 m = cm

25 Calcola le seguenti sottrazioni effettuando a mente le equivalenze necessarie.

a) 92 km – 23 hm = hm c) 293 cm – 2 m = dm

b) 243 cm – 17 dm = dm d) 34 hm – 3 km = dam

26 Calcola le seguenti moltiplicazioni e completa le uguaglianze.

a) 25 dm × 4 = m

c) 27 m × 5 = dam

b) 7 dam × 9 = hm d) 750 dm × 8 = m

27 Esegui le seguenti divisioni e completa le uguaglianze.

a) 6 300 dm : 9 = dam

b) 840 mm : 6 = dm

c) 1 600 dm : 5 = hm

d) 1 200 km : 12 = m

MATEMATICA IN AZIONE Risolvi i seguenti problemi riferiti a situazioni presenti nella realtà.

28 Se hai un righello di 20 cm (doppio decimetro), quanti te ne servirebbero (identici) per formare un metro? E quanti per formare un decametro?

29 EDUCAZIONE CIVICA Matteo deve sistemare dei coni stradali a 3 m di distanza l’uno dall’altro lungo una strada di 2,7 km. Quanti birilli gli serviranno se mette il primo all’inizio della strada?

30 Il percorso casa-scuola di Luigi è lungo 0,2 km e 73 m.

Quanti m di strada percorre Luigi per andare a scuola? [273 m]

31 Se da una pezza di stoffa lunga 80 m se ne tolgono 450 dm, quanti dm di stoffa restano? [350 dm]

32 Silvia per allenarsi percorre ogni giorno una pista lunga 450 m per 13 volte. Quanti km percorre quotidianamente? E quanti in una settimana? [....................; 40,95 km]

33 In una corsa di mezzofondo di 1 km, i partecipanti percorrono 2 giri completi di pista e metà del terzo giro. Quanti metri è lunga la pista? [400 m]

34 Massimo sta viaggiando con il furgone della ditta e si deve fermare per fare rifornimento.

Un cartello indica che la prossima stazione di servizio è a 12 500 m.

Se il suo contachilometri segna 87 960 km, quanti ne segnerà quando si fermerà per il rifornimento? [87 972,5 km]

35 Una pista ciclabile è lunga 0,7 km.

Quanti giri devo fare per percorrere 84 hm? [12 giri]

36 Una staffetta composta da 4 persone deve compiere un percorso di 32 hm. Quanti metri percorrerà ciascun componente? [800 m]

37 Carlo ha comprato 700 cm di filo per una canna da pesca. Luigi ha comprato 11 dm dello stesso filo e ha speso 4,40 €. Quanto ha speso Carlo per il suo filo da pesca? [28 €]

38 Gli schermi dei televisori, dei monitor, dei tablet e dei telefoni cellulari si misurano in pollici. Il pollice (inch) è una misura inglese (1 inch = 2,54 cm).

La misura in pollici indica la lunghezza della diagonale dello schermo.

a) A casa di Donatella c’è un televisore da 40 pollici e un monitor del portatile da 15,6 pollici. La figlia possiede uno smartphone con lo schermo da 2,3 pollici. Calcola le dimensioni degli schermi di ciascun oggetto in centimetri.

b) La distanza minima che bisogna tenere dal televisore per evitare disturbi visivi è il doppio della dimensione dell’apparecchio in pollici. Calcola la distanza minima, in metri, per un televisore da 14 pollici, uno da 27 e uno da 32.

c) Trova ora la misura in pollici dello schermo del televisore che normalmente utilizzi in casa. Calcola la distanza minima, in cm, in cui dovresti metterti per guardarlo e… rispetta la distanza! [a) 101,6 cm; 39,62 cm; 5,84 cm; b) 71,12 cm; 137,16 cm; 162,56 cm]

3

MISURA DELLA SUPERFICIE E MISURA DEL VOLUME

Misura della superficie

39 Completa le caselle scrivendo il nome di ogni simbolo.

40 Scrivi il simbolo dell’unità di misura che useresti per esprimere le seguenti grandezze.

a) La superficie dell’ala di una farfalla

b) La superficie della Lombardia

c) La superficie del foglio del tuo quaderno

d) La superficie della copertina del tuo libro di geometria

e) La superficie di un campo da tennis

f) La superficie di un poster

g) La superficie di un campo di mais

41 Scegli la misura adatta.

a) Superficie di un’aula scolastica

b) Estensione di un campo da calcio

c) Superficie di una pagina di un libro di testo

d) Superficie della vetrina di un negozio 1) 4 000 dm2

Completa le seguenti equivalenze.

ESEMPIO

a) 43,6 dam2 = m2 " 43,6 dam2 = 4 360 m2 b) 81,52 cm2 = dm2 " 81,52 cm2 = 0,8152 dm2

42 a) 5 m2 = mm2 c) 25 m2 = cm2

b) 73 km2 = dam2 d) 356 dm2 = dam2

43 a) 7,9 m2 = cm2 c) 38 871 dm2 = hm2

b) 588 hm2 = km2 d) 741 dam2 = cm2

44 MATH Complete the following equivalences.

a) 0.046 km2 = dam2 c) 0.09 dm2 = mm2

b) 736 cm2 = m2 d) 0.0099 hm2 = m2

45 Completa inserendo i simboli <, =, >.

a)

46 Calcola le aree delle seguenti figure con l’unità di misura assegnata. a) c)

47 Disponi in ordine crescente le seguenti misure.

a)

48 Disponi in ordine decrescente le seguenti misure.

a) 6,43 dam2

b) 76 m2 7 654,3 mm2

49 MATEMATICA IN AZIONE Nella vetrina di un’agenzia immobiliare sono esposti i seguenti cartelli.

AFFARE A ORTONA

Vendita terreno di 5,65 ha in collina, con uliveto e vista mare. Costo: 13 € al m2

OCCASIONE IRRIPETIBILE

A SILAMONTANA area edificabile di 0,45 ha a soli 252 000 € 1 ettaro (ha) = 10 000 m2

a) Paolo ed Elena sono interessati all’acquisto del terreno. Se hanno a disposizione 500 000 €, quanto dovranno chiedere in prestito alla banca?

b) Filippo, il presidente della cooperativa BEISOCI, vuole sapere il costo al m2 dell’area edificabile. Lo vuoi aiutare a fare i conti? [a) 234 500 €; b) 56 €/m2]

Misura del volume

50 Completa le caselle scrivendo il significato di ogni simbolo.

51 Scegli l’unità di misura più appropriata per le seguenti situazioni.

a) La capienza di un cucchiaino da tè

b) Lo spazio occupato da una piscina

c) Lo spazio occupato da una scatola di scarpe

d) La capienza di una zuccheriera

e) La capienza del silo per il grano

f) La capienza della betoniera per la malta

g) Lo spazio occupato dal cubo di Rubik

52 Scegli la misura adatta.

a)

b)

c)

d)

di un acquario

della vasca di un depuratore

Completa le seguenti equivalenze.

ESEMPIO

a) 316 dm3 = 316 000 cm3

b) 769,5 dm3 = 0,7695 m3

53 a) 5 784 m3 = dam3

b) 931 dm3 = m3

c) 2 143 m3 = ....... dm3

d) 312 099 m3 = ....... hm3

54 a) 7 842,9 cm3 = m3

b) 9 dm3 = m3

c) 0,54 km3 = dam3

d) 21,43 hm3 = km3

55 MATH Complete the following equivalences.

a) 4,562 dm3 = m3

b) 854.9 dm3 = dam3

c) 215.43 km3 = hm3

d) 0.021 dm3 = cm3

56 Calcola i volumi dei seguenti solidi con l’unità di misura assegnata. a) d)

57 Disponi in ordine crescente le seguenti misure.

58 Disponi in ordine decrescente le seguenti misure.

MISURA DELLA CAPACITÀ E MISURA DELLA MASSA

Misura della capacità

59 Rispondi alle seguenti domande.

a) Che cos’è la capacità?

b) Qual è l’unità di misura fondamentale della capacità?

c) Quali sono i suoi sottomultipli?

d) Quali sono i suoi multipli?

60 Completa il seguente schema scrivendo il nome di ogni simbolo.

imparaerrore dall'

Passare da un’unità di misura all’altra (da kilogrammi a grammi, o da litri a decilitri) potrebbe rappresentare un ostacolo. Le regole per spostare la virgola o aggiungere zeri possono sembrarti senza senso e spesso potrebbe capitare di saltare qualche unità intermedia.

Per evitare questo, puoi utilizzare una tabella che ti aiuta a visualizzare il percorso tra le unità di misura: quando ti sposti verso destra devi moltiplicare, quando lo

61 Sottolinea il completamento esatto.

fai verso sinistra, devi fare la divisione. Un altro errore molto comune riguarda le unità di misura al quadrato e al cubo: il fattore di conversione non è lo stesso! Per esempio, per convertire 1 m² in dm², non devi moltiplicare per 10, ma per 10 al quadrato, cioè 100. Allo stesso modo, se si tratta di unità di volume, il fattore per cui moltiplicare o dividere a ogni passaggio di unità è 1 000.Un suggerimento: memorizzare i prefissi “kilo”, “centi”, “deca” ti può aiutare a trovare le analogie tra le unità di misura delle diverse grandezze.

a) Il volume di un corpo è la superficie / lo spazio occupato da un cubo / dal corpo stesso

b) La capacità di un corpo è la quantità / la misura di liquido che il corpo / il contenitore può contenere.

c) Volume e capacità misurano / non misurano la stessa grandezza; infatti, la capacità di 1 L equivale a un volume di 1 m3 / 1 dm3

62 Riconosci la risposta corretta.

a) Un litro vale:

b) Mezzo litro vale:

c) Un quarto di litro vale: 1)

d) Tre quarti di litro valgono: 1) 75 mL 2)

63 MATH Choose the appropriate measurement.

a) The capacity of a can. 1) 33 cL 2) 66 dL

b) The capacity of a refrigerator. 1) 280 dL 2) 250 L

c) The capacity of a bottle of syrup. 1)

d) The capacity of a hot tub.

Completa le seguenti equivalenze.

64

9

Completa le seguenti catene di equivalenze.

66

Completa le seguenti uguaglianze aggiungendo l’unità di misura appropriata.

68 a)

Indica il valore di ciascuna cifra delle seguenti misure di capacità come da esempio.

ESEMPIO

a) 75,32 L 7 daL, 5 L, 3 dL, 2 cL b) 0,032 hL 0 hL, 0 daL, 3 L, 2 dL

70 a) 4,78 hL 87,32 dL

b) 98,41 daL 0,076 L

71 a) 7,432 hL 76,532 daL

b) 7 600 mL 27 427 L

Completa le seguenti uguaglianze utilizzando l’unità di misura assegnata.

72 a) 7 hL, 4 daL = daL

b) 7 dL, 5 cL = dL

c) 5 L, 4 dL, 1 cL = ……..…..…… cL

73 a) 9 daL, 4 L, 6 dL = ……..…..…… L

b) 8 dL, 7 cL, 1 mL = ……..…..…… mL

c) 1 dL, 3 cL, 0 mL = ……..…..…… mL

Esegui i calcoli ed esprimi il risultato nell’unità di misura indicata.

74 58 daL + 27 mL – 370 cL + 56 mL = L

75 3,5 L + 84 dL – 4,4 L + 0,01 daL = ……………… dL

76 6,3 daL + 92 L – 240 dL + 1 543 cL – 400 mL = cL

MATEMATICA IN AZIONE Risolvi i seguenti problemi riferiti a situazioni reali.

77 Una borsa termica può contenere fino a 18 lattine da 33 cL. Quanti litri può contenere in tutto?

78 Una confezione in offerta propone 4 docciaschiuma di tipo diverso, ognuno da 275 mL. In tutto la confezione contiene più o meno di un litro di prodotto?

79 5,8 daL di aceto vengono travasati in bottiglie della capacità di 40 cL ciascuna. Quante bottiglie sono state riempite? [145]

80 Sapendo che un’automobile percorre in media 12 km con 1 litro di benzina, quanti kilometri percorre con 25 litri? Dovendo effettuare un viaggio di 624 km, quanti litri di benzina saranno necessari? [300 km; 52 L]

81 Per riempire il serbatoio della propria macchina Marco deve versare 40 litri di gas GPL. Per effettuare un viaggio deve riempire il serbatoio 3 volte. Quanto spenderà per il gas, sapendo che il suo costo è di 0,72 € il litro? [86,4 €]

82 In una cantina sociale di Pachino ci sono 140 bottiglie da 75 cL, 4 damigiane da 0,8 daL, 2 silos da 3 hL ciascuno di vino Nero d’Avola. Calcola quanti litri di vino ci sono in tutto nella cantina. Se il vino sfuso costa 1,4 € al litro, vendendo tutto il vino la cantina ricava più o meno di 1 000 €? [ ; di più]

83 Un flacone di sgrassatore universale liquido da 750 mL costa 2,50 €, un altro tipo da 10 dL costa invece 3,25 €. Quale dei due sgrassatori è il più conveniente? [Il secondo]

84 Clara deve prendere uno sciroppo e legge le istruzioni: 4 mL di sciroppo ogni 10 kg di peso.

Clara pesa 50 kg; quanti millilitri deve prenderne? Se ha a disposizione un cucchiaino da 5 mL, quanti cucchiaini deve prenderne?

Misura della massa

85 Rispondi alle seguenti domande.

●●●

a) Qual è l’unità fondamentale di misura della massa?

b) Che cos’è la massa? .

c) Che cos’è il peso?

d) Quali sono i sottomultipli del kilogrammi? .

e) Qual è il multiplo del kilogrammi?

86 Inserisci il termine esatto (La massa/Il peso).

a) è la quantità di materia presente in un corpo.

b) è la forza di gravità con cui un corpo viene attirato dalla Terra.

c) è una grandezza primitiva.

d) varia al variare della posizione del corpo sulla Terra.

e) non varia mai.

87 Completa il seguente schema scrivendo il nome di ogni simbolo.

88 Scegli la misura adatta.

a)

Completa le seguenti equivalenze.

89 a) 1 hg = dag 1 g = dg b) 1 dg = mg 1 dag = cg

90 a) 1 cg = mg 1 hg = g b) 1 cg = g 1 dag = kg

91 MATH Identify the correct answer.

92 MATEMATICA IN AZIONE Il cuoco Salomone vuole preparare come secondo un polpettone e ha trovato una ricetta per 4 persone. Per 6 persone che cosa gli occorre?

Ingredienti Dose per 1

Carne di maiale

Carne di pollo

Pancarrè

Latte 0,5 : 4 =

Parmigiano

Prosciutto cotto

Formaggio

Burro

Dose per 6

3 4 di bicchiere

Ingredienti per 4 persone:

200 g di carne di maiale macinata

200 g di carne di pollo macinata

4 fette di pancarrè

1 2 bicchiere di latte

1 uovo

20 g di parmigiano

100 g di prosciutto cotto

100 g di formaggio

20 g di burro

sale pepe

93 MATEMATICA IN AZIONE Salomone, il cuoco, utilizza una bilancia di questo tipo:

– ogni linea grande rappresenta 100 g; – ogni linea piccola rappresenta 10 g.

a) Qual è il peso indicato dalla bilancia?

b) Qual è la portata massima della bilancia?

Completa le seguenti equivalenze.

94 a) 85 Mg (t) = kg 8 g = mg

b) 2 400 g = hg 3 100 hg = kg

c) 73 hg = g 1 700 dag = Mg (t)

95 a) 2 457 hg = dg 765 dag = cg b) 16 Mg (t) = hg 985 kg = g

96 a) 5,78 q = dag 9,3 hg = g b) 6,519 kg = dg 586 dag = kg

97 a) 4 532 mg = dag 657 g = hg

b) 46 758 cg = kg 547 dg = q

Completa le seguenti catene di equivalenze.

[a) 240 g; b) 1 200 g]

1 quintale (q) = 100 kg

98 a) 8,3 hg = dg = dag = kg

b) 76,5 g = hg = cg = dag

99 a) 453,2 dag = q = cg = mg b) 0,0678 Mg = dag = g = hg

Inserisci l’unità di misura appropriata nelle seguenti equivalenze.

100 73 mg = 0,073 ……… 8 476 dg = 8,476 ………

101 65,4 dag = 0,654 0,0065 kg = 65

102 64 392 cg = 6,4392 ………

657,4 g = 6,574 ………

103 54 320 g = 54,32 ……… 34 Mg = 340 000 ………

Risolvi le seguenti operazioni ed esprimi il risultato in hg.

104 87 mg + 658 cg + 479 g 47,9 hg + 845 dg – 3 250 g

105 2,46 dag + 9,35 kg + 9547 mg 7 q + 42,7 dag – 659,7 dg

106 Completa in modo che il risultato di ogni operazione sia 7 kg. 7 kg

0,4 hg + 300 dag + 9 500 g –140 hg –

Esegui i calcoli ed esprimi il risultato nell’unità di misura indicata.

107 43,5 kg + 420 dag – 77 hg + 720 dag + 3 000 dg = hg

108 0,04 Mg + 400 kg + 2 430 hg – 40 hg – 4 500 dag = kg

109 0,3 dag + 0,75 hg – 42 g – 200 dg + 2 020 cg = ………………… dg

110 0,068 kg + 0,8 dag + 4 g – 30 000 mg + 2 250 g = g

MATEMATICA IN AZIONE Risolvi i seguenti problemi riferiti a situazioni reali.

111 Da un sacchetto di farina di frumento che pesa 3 kg vengono tolti prima 450 g e poi ancora 630 g. Quanti kilogrammi di farina rimangono?

112 Sopra uno scaffale di un supermercato ci sono 245 vasetti di confettura di diverso tipo. Se ogni vasetto pesa 340 g, quanti kilogrammi peseranno in tutto?

113 Con 300 kg di patate quanti sacchetti da 750 g si possono confezionare? [400]

114 Benedetto, il fruttivendolo di via dei Fruttaroli, acquista all’ingrosso 210 kg di mele Golden e, per rivenderle nel suo market, prepara delle cassette con 7 kg di mele ciascuna. Quante cassette riempirà? Se ogni cassetta vuota (tara) pesa 600 g, quale sarà il suo peso lordo? [30; 7,6 kg]

MISURA DEL TEMPO

115 Completa il seguente schema scrivendo il nome di ogni simbolo.

a ms g h m s d c

116 Rispondi alle seguenti domande.

a) Qual è l’unità di misura fondamentale del tempo?

b) Quali sono i suoi sottomultipli?

c) Quali sono i suoi multipli?

d) Quanti anni vale un lustro?

e) Quanti anni vale un secolo?

117 Completa.

La misura del tempo è un sistema di misura misto, infatti:

a) le ore, i si misurano con un sistema sessagesimale;

b) .................................................................................. si misurano con un sistema decimale;

c) non si misurano né con un sistema decimale né sessagesimale.

Usando la simbologia appropriata, scrivi quanto richiesto in modo abbreviato.

118 a) Otto ore, quindici minuti e venticinque secondi 8 h 15 m 25 s

b) Sette mesi e dodici giorni

119 a) Dodici mesi, nove giorni e ventitré secondi

b) Sette anni, dieci giorni e trentasette secondi

120 a) Sette giorni, ventiquattro mesi, cinque ore e quattro secondi

b) Dieci giorni e dieci secondi

121 a) Otto mesi, dodici giorni, cinque ore e nove minuti

b) Otto anni, tre mesi, quindici giorni e otto ore

122 MATH Choose the appropriate measurement.

a) The length of a TV commercial. 1) 6m 15s 2) 25s

b) The length of a film.

c) Record for the women’s 200 m freestyle.

d) Duration of a basketball game.

123 Riconosci la risposta corretta.

a) Mezz’ora vale: 1) 30s 2) 3 600s 3) 900s 4) 30m

b) La metà di mezz’ora vale: 1) 15s 2) 90s 3) 1 quarto d’ora 4) 540s

c) Novanta minuti valgono: 1) 9 000s

d) La metà di novanta minuti vale: 1) 45s 2) 35m 3) 45m 4) 270s

Completa le seguenti relazioni.

124 a) 3 giorni = ore b) 7 giorni = ore c) 3 ore = minuti

125 a) 8 ore = minuti b) 6 minuti = secondi c) 15 minuti = secondi

126 a) 5 anni = giorni b) 11 anni = giorni c) 20 anni = giorni

127 a) 1 anno e 6 mesi = ore b) 1 anno e 5 mesi = ore

128 a) 3 mesi e 10 giorni = ore b) 8 mesi e 15 giorni = ore

129 MATEMATICA IN AZIONE Osserva la linea del tempo con le date di alcune Olimpiadi e rispondi. Corea invernali Pechino estive Rio estive

Nagano invernali

invernali

Atene estive Torino invernali Vancouver invernali Londra estive

a) Quanti anni vale un segmento ?

b) Che cosa è successo tra il 1995 e il 2001? ……………………………………………………………

c) Le Olimpiadi avvengono ogni 4 anni; quando sono avvenute le Olimpiadi invernali di Torino? ………..………………

d) Tra Atene e Rio sono avvenute altre Olimpiadi estive? Se sì, in quali anni?

Riduci in forma normale, come nell’esempio.

57 380 s Poiché 60 s formano 1m , dividiamo 57 380 s per 60.

57 380 s : 60 = 956 m resto 20 s Poi dividiamo 956 m per 60.

956 m : 60 = 15h resto 56 m

Quindi 57 380 s = 15h 56 m 20 s

Risolvi le seguenti addizioni con misure di tempo.

Risolvi le seguenti sottrazioni con misure di tempo.

si trasforma 1g in 24 h

4 g 11h 45 m – 2g 15 h 42m

3g 35 h 45 m –

2g 15 h 42m = 1g 20 h 3m –

137 22h 45m 54s – 8h 38m 48s [14h 7m 6s]

138 2g 7h 30 m – 11h 50 m 36 s [1g 19h 39m 24s]

139 12g – 4 g 43m 24s [7g 23 h 16 m 36 s]

140 12g 1m – 7g 15 h 12 s [4 g 9h 48 s]

Risolvi le seguenti moltiplicazioni con misure di tempo.

(3 h 15 m 42 s) × 4 3 h 15 m 42 s × 4s = — si trasforma in forma normale 12h 60 m 168 s 13 h 2m 48 s

141 (2g 24h 23 s) × 5 [15g 1m 55 s]

142 (24 g 14h) × 15 [1a 8g 18 h]

143 (4 g 8 m 23 s) × 16 [2ms 4 g 2h 14m 8 s]

144 (2ms 19g 8 h) × 9 [1a 11ms 24 g ]

145 (2h 17m 25 s) × 12 [1g 3 h 29m]

146 (23 h 50 s) × 48 [1ms 16 g 40 m]

Esegui le seguenti divisioni con misure di tempo. 24h 41m : 5 24h 41m 0 s 5 4h = (4 × 60)m = 240 m 4h 56 m 12 s

1m = (1 × 60)s = 60 s

147 (18h 24m 54s) : 6 [3h 4m 9s]

148 (8g 4h) : 32 [6 h 7m 30 s]

149 (24g 36h 48m) : 12 [2g 3h 4m]

150 (8 h 50 s) : 25 [19m 14s]

151 (5ms 25g 15h) : 5 [1ms 5g 3h]

152 (5g 6 m 8 s) : 8 [15 h 46 s]

MATEMATICA IN AZIONE Risolvi i seguenti problemi riferiti a situazioni presenti nella realtà.

153 La torta di mele ha un tempo di cottura pari a 45 minuti. Se la tortiera viene messa in forno alle 20 h 45 m, a che ora si deve spegnere il forno? [21h 30 m]

154 Un orologio ritarda di 14 secondi ogni ora. Se alle 14h 20 m è esatto, dopo 8 ore che orario darà? [22h 18 m 8 s]

155 Un pullman di linea parte da Milano alle 6h 30 m, si ferma a Bologna dopo 2h 20 m, arriva a Firenze alle 10 h 45m e infine si ferma a Roma alle 13h 20 m . Calcola la durata del viaggio completo e il tempo necessario per andare da Bologna a Firenze e da Firenze a Roma.

[6 h 50 m; 1h 55 m; ................]]

COMPETENZE

CONFRONTARE

1 Utilizza i numeri nei riquadri e assegna a ogni isola la sua superficie sapendo che:

• Sicilia e Sardegna misurano più di 20 000 km2

• La Maddalena è l’isola meno estesa

• l’Asinara è più estesa di Ischia

• la Sicilia è l’isola più estesa

RISOLVERE PROBLEMI

2 Caterina vuole fare un dolce e mette gli ingredienti “secchi” in un recipiente: un quarto di kg di farina e mezzo kilo di zucchero.

Deve aggiungere 4 mL di latte per ogni grammo di secco.

Quanto latte deve aggiungere?

(Un quarto di chilo si ottiene dividendo ……… per 4; mezzo chilo si ottiene dividendo un chilo per .)

3 Inserisci la lancetta in modo da segnare le misure indicate.

a) 520 g

b) 860 g

4 Una caraffa contiene 1 L d’acqua.

a) Se ne vengono versati 150 mL, quanta acqua rimane?

b) Se hai a disposizione un bicchiere da 200 mL, quanti bicchieri d’acqua potrai riempire con una caraffa piena?

5 Si devono somministrare a un paziente 0,12 litri di un farmaco in 4 dosi.

Se 1,5 g di farmaco corrispondono a 1 cm3, quanti grammi di farmaco occorre somministrare in ogni dose?

a) 1 L = dm3 allora 0,12 L = dm3

b) Trasforma i dm3 trovati in cm3 → dm3 = cm3

c) Calcola la quantità di farmaco in cm3 di ogni dose → : 4 = cm3

d) Calcola i g di farmaco per ogni dose → × = g

6 Quanti centilitri di sciroppo ci sono in 4 cucchiai da 15 mL?

7 Con un litro di acqua distillata, quante fiale da 0,5 cL si possono riempire?

8 La mamma di Marco prepara il tè per 6 amiche. In ogni tazza mette una bustina di zucchero dal peso netto di 5 g. Sulla confezione che contiene tutte le bustine c’è scritto che il peso lordo è 20 hg. La tara della confezione è di 2 hg. Trova il numero di bustine di zucchero in essa contenute.

CALCOLARE

Peso lordo → peso netto + tara

9 La tabella rappresenta la distanza in miglia da alcune città. Sapendo che un miglio è circa 1,8 km, calcola tutte le distanze delle città in km.

a) Marina Gioiosa - Marittima = 19 miglia = ……… km

b) Marina Gioiosa - Maremontuosa = ……… miglia = ……… km

19 27 11 18 20 9 Marittima

Marina Gioiosa Maremontuosa Marisacca

c) Marina Gioiosa -

d) Marittima -

e) Marittima -

f) Maremontuosa -

10 Calcola la durata di ogni ora di lezione.

Inizio 8:05 9:52 10:44 11:30 12:23

Fine 9:37 10:35 11:19 12:19 13:52

Durata

SFIDA MATEMATICA

11 Tutto casa, scuola e palestra

Pietro abita a un’estremità di una lunga strada, in piano, e la sua scuola si trova all’altra estremità della stessa strada. La palestra, dove si reca con una certa frequenza, è a metà cammino (tra casa e scuola). Quando lascia la scuola a mezzogiorno, riesce a essere a casa per le 12:30. Se riparte da casa alle 15:00, a che ora arriverà in palestra?

(Testo tratto dalla gara Giochi di Rosi del 2014, organizzata dal Centro PRISTEM dell’Università Bocconi di Milano)

ROAD MAP PER TUTTI

la lunghezza

DATI UN TEMPERINO E UN RIGHELLO

Quale grandezza misura il righello?

Con il righello si misura la lunghezza di un oggetto

• Il temperino misura 2,5 cm

PAG. 6

• Una libreria è alta 3 m

• Un moscerino è lungo 4 mm

Qual è l'unità di misura della lunghezza?

Il metro (m)

I suoi sottomultipli sono il decimetro (dm), il centimetro (cm) e il millimetro (mm); i suoi multipli sono il decametro (dam), l'ettometro (hm) e il kilometro (km)

equivalenze

DATE DUE MISURE: 34 m E 7 cm

Come si chiama il passaggio da un'unità di misura a un'altra?

Si chiama EQUIVALENZA

Come si passa a un'altra unità di misura?

Utilizzando il seguente schema

10, 100, 1 000…

10, 100, 1 000…

PAG. 6

• 34 m = …………… cm

Nello schema ci si sposta di due posti a destra, quindi: 34 m = (34 x 100) cm = 3 400 cm × 100 m dm cm

• 7 cm = …………… dam

Nello schema ci si sposta di tre posti a sinistra, quindi 7 cm = (7 : 1 000) dam = 0,007 dam : 1 000 dam m dm cm

1 Calcola la lunghezza dei rettangoli rossi e trova la misura tra quelle proposte.

1,5 cm; 2 cm; 5 cm; 11 cm; 4,5 cm; 10,5 cm.

2 Scomponi le seguenti misure completando la tabella. Riconosci prima le unità di ciascun numero.

a) 34,56 m le unità rappresentano i quindi

b) 245,1 dm le unità rappresentano i quindi

c) 3,4756 km le unità rappresentano i …………… quindi

d) 54,768 hm le unità rappresentano i quindi

e) 91,565 m le unità rappresentano i quindi

3 Completa le seguenti equivalenze.

a) 18 m = cm

b) 23 mm = … … ….. cm

c) 3,4 dm = cm

d) 7 hm = … … ….. cm

e) 5,12 dam = cm

f) 6,31 m = … …….. cm g) 12 cm = m

h) 0,32 dam = …… … .. m

i) 327 mm = m

l) 0,0005 km = … ….. m

m) 82 dm = m

n) 3 hm = …… .. m

4 MATEMATICA IN AZIONE Risolvi il seguente problema.

Una pista ciclabile è lunga 5 km.

a) Quanto è lunga in metri? Quanto è lunga la sua metà? 5 km = m; : 2 = 2 500 m

b) Se Luisa ha percorso 2750 m della pista, quanti metri le mancano per completarla? – 2 750 m = m

c) Giorgio ha fatto 4 giri; quanti kilometri ha percorso? 4 × km =

d) Miriam invece ha percorso 30 km; quanti giri di pista ha fatto?

30 km : = Miriam ha fatto giri di pista.

DATE LE MISURE DI UN LIBRO:

(lunghezza = 20 cm, altezza = 30 cm, profondità = 2 cm)

Qual è l'unità di misura della superficie della copertina?

Il metro quadrato (m²)

I suoi sottomultipli sono il decimetro quadrato (dm²), il centimetro quadrato (cm²), il millimetro quadrato (mm²).

I suoi multipli sono il decametro quadrato (dam²), l'ettometro quadrato (hm²), il kilometro quadrato (km²)

ESEMPIO

• La superficie della copertina è di 600 cm²

Qual è l'unità di misura del suo volume?

Il metro cubo (m³)

Un suo sottomultiplo è il decimetro cubo (dm³)

ESEMPIO

• Il volume del libro è 1 200 cm³

la capacità

DATO UN BICCHIERE VUOTO

Qual è l'unità di misura della capacità?

Il litro (L)

I suoi sottomultipli sono il decilitro (dL), il centilitro (cL) e il millilitro (mL).

I suoi multipli sono il decalitro (daL) e l'ettolitro (hL)

Qual è la grandezza equivalente della capacità?

Il volume è la grandezza equivalente della capacità

Perchè?

1 dm³ = 1 L

• Un bicchiere ha la capacità equivalente di 200 mL, equivalente a 0,2 dm³

10

5 Completa le seguenti equivalenze.

a) 1,2 m2 = dm2

b) 1,2 dm2 = m2

c) 34 mm2 = cm2

d) 8 cm2 = ……………… mm2

e) 2 km2 = dam2

f) 0,6 m2 = cm2

g) 15,7 dam2 = dm2

h) 7,85 hm2 = …………………… cm2

6 MATEMATICA IN AZIONE Quale di queste piastrelle ha la superficie maggiore?

7 Completa le seguenti equivalenze.

3,50 dm2 3,50 cm2 × 10, 100, 1 000… : 10, 100, 1 000… hL daL L dL cL mL

a) 32 daL = dL d) 18 L = mL

b) 4 hL = dL e) 6,5 dL = mL

c) 702 cL = ………………………. L f) 3 692 mL = ………………………. L

8 MATEMATICA IN AZIONE Risolvi il seguente problema.

Milena deve prendere tre misurini di sciroppo per la tosse quattro volte al giorno.

a) Se un misurino è da 10 mL, quanti millilitri di sciroppo prende in una volta?

3 × 10 mL = mL

b) Quanti millilitri di sciroppo beve al giorno?

4 × = mL

c) Il terzo giorno ogni volta deve bere 0,08 cL in meno: quanti millilitri di sciroppo deve bere ogni volta?

0,08 cL = mL

30 mL – mL = mL

9 MATEMATICA IN AZIONE Rispondi alle seguenti domande.

a) Qual è la capacità in litri di una bottiglia che ha un volume di 75 cm3?

b) Qual è la capacità in litri di una bottiglia che ha un volume di 80 cm3?

c) Se un flacone contiene 1,5 L di detersivo, qual è il suo volume in dm3?

d) Se una bottiglietta contiene 30 mL di profumo, qual è il suo volume in cm3?

DATA UNA PENNA MASSA

Qual è l'unità di misura della massa?

Il kilogrammo (kg)

Quali sono le altre unità di misura della massa?

Il megagrammo (Mg), che nel linguaggio comune prende il nome di tonnellata (t), l'ettogrammo (hg), il decagrammo (dag), il grammo (g), il decigrammo (dg), il centigrammo (cg), il milligrammo (mg)

Come si passa da un'unità di misura all'altra?

Utilizzando il seguente schema

× 1 000

× 10, 100, 1 000…

Mg (t) kg hg dag g dg cg mg

: 1 000 : 10, 100, 1 000…

• Si moltiplica per 10, 100, 1000... se nello

schema si va verso destra di uno, due, tre... posti, per 1000 da Mg a kg

• Si divide per 10, 100, 1000... se nello

schema si va verso sinistra di uno, due, tre... posti, per 1000 da kg a Mg

• Una penna ha una massa di 5,8 g = 580 cg

TEMPO

DATO UN OROLOGIO DIGITALE

Qual è l'unità di misura del tempo?

L'unità di misura del tempo è il secondo (s)

I suoi sottomultipli sono il decimo di secondo (d) e il centesimo di secondo (c).

I suoi multipli sono i minuti (m), le ore (h), i giorni (g), i mesi (ms) e gli anni (a)

ESEMPIO

• I primi due numeri indicano le ore, i due numeri centrali i minuti e gli ultimi due i secondi: 12:14:25

ESEMPIO 12:14:25 12:14:25

10 Completa le seguenti equivalenze.

a) 2 g = cg

b) 3 dag = dg

c) 6 kg = g

d) 45 dg = g

e) 56 mg = dg

f) 0,97 kg = dag

11 MATEMATICA IN AZIONE Risolvi il seguente problema.

Un trolley pesa 42 hg.

a) Quanto pesa in chilogrammi? 42 hg = kg

b) Quanto pesano tre trolley in chilogrammi? 3 × kg = kg

c) Una valigia pesa 10 kg. Quanto pesa in più del trolley? 10 kg – kg = kg

12 Calcola quanti grammi mancano alle seguenti misure per arrivare a 1 kg.

a) 385 g 123 g 546 g

b) 31 dag 5,7 dag 0,92 dag

c) 5 hg 9 hg 6 hg

Risolvi i seguenti problemi.

13

a) Quanti secondi ci sono in un minuto? 1m = s

b) Quanti minuti ci sono in un’ora?

c) Quanti secondi ci sono in un’ora?

Poiché da ore a secondi ci sono due posti, bisogna moltiplicare due volte per 60, cioè 60 × 60 = ………………… Quindi 1h = ………… …

14 MATEMATICA IN AZIONE

a) Il nonno di Elena è nato nel 1942 ed è morto nel 2015. Quanti anni è vissuto? [73]

b) Claudia oggi compie 18 anni; in che anno è nata?

c) Alex va da Milano a Firenze in treno. Se è partito alle 8:15 e il tragitto dura 1h 55m, a che ora arriverà a Firenze? [10:10]

SIMULAZIONE DI VERIFICA

15 Rispondi con Vero o Falso ed effettua la correzione di ogni falso.

a) Una grandezza è tutto ciò che si può misurare.

b) Le grandezze omogenee sono della stessa natura ma non sempre sono confrontabili.

c) Il volume è una grandezza derivata.

d) La massa è una grandezza derivata.

e) SI è la sigla che indica il Sistema Metrico Decimale.

f) La definizione di metro è riferita alla lunghezza d’onda della radiazione emessa dall’atomo di Cripto 86.

g) La superficie è una grandezza derivata dalla lunghezza; infatti è una lunghezza per una lunghezza.

h) Il peso di un corpo è la quantità di materia che lo compone.

16 Completa le seguenti tabelle.

Unità di misura Grandezza misurata dm cm2 ... h

17 Scrivi le parti mancanti nei seguenti schemi con le sigle delle unità di misura appropriate. a) b) c)

F

F

F

F

F

F

F

Unità di misura Grandezza misurata cL Mg dm3 dam2

18 Di seguito sono riportate alcune attività che Gianpaolo svolge durante la giornata. Completa scegliendo la misura appropriata tra quelle proposte.

Ora Attività

7:00 Si sveglia e si fa una doccia con 5 (L, secondi, cL) di acqua.

7:30 Fa colazione con 100 (kg, g, mg) di biscotti, 150 (m, mL, L) di latte e 2 (g, kg, mm) di zucchero.

8:10 Esce per andare in ufficio e prende l’autobus che si ferma a 100 (m, km, mm) da casa.

17:30 Al rientro trova la strada allagata per la rottura di una tubazione: ci sono (mL, km, L) di acqua che zampillano.

18:15 Si allena per una corsa da 1 500 (km, m, mm) in 6 (minuti, ore, secondi). .

21:30 Va al cinema; lo spettacolo dura 105 (ore, minuti, secondi).

Alla fine dello spettacolo rientra a casa.

19 Completa le equivalenze riferite a tutte le misure studiate.

a) 2,5 km = . m g) 579 dL = . . . daL

b) 628 cm = hm h) 3,2 cm2 = mm2

c) 14,4 Mg = . hg i) 9 603 m2 = . hm2

d) 345 mg = dag l) 8,5 dm3 = cm3

e) 7,03 L = cL m) 2 468 dm3 = dam3

f) 3 h = s n) 180 s = minuti

20 Confronta e completa utilizzando i simboli <, =, >.

a) 40 cm 390 mm d) 2g 36 h

b) 2 000 cm2 2 m2 e) 500 g 0,5 kg

c) 86 mL 9 dL f) 31 L 31 dm3

21 MATEMATICA IN AZIONE Lucia e sua mamma vogliono preparare un po’ di polenta per pranzo. Per la quantità di farina che hanno deciso di utilizzare sono necessari 2,5 litri di acqua. Per versare nella pentola la quantità giusta di acqua hanno a disposizione un dosatore di liquidi come quello in figura. La mamma sostiene che sia necessario riempire tre volte il dosatore fino a 750 mL e una volta fino a 250 mL. Lucia invece sostiene che occorra riempire per cinque volte il dosatore fino a 500 mL. Chi ha ragione? Motiva la risposta.

700600500400300200100

Chi ha della

paura matematica?

I PRIMI ELEMENTI DELLA GEOMETRIA UNITÀ 2

In molti ritengono che la geometria sia troppo astratta. Anche a te capita di domandarti come sia possibile che persinounpunto, una retta, un segmento, possano avere delle regole e delle proprietà? Per rendere la geometria meno astratta, ti invito a usare l’immaginazione: ti aiuterà a intuire persino gli enti geometrici privi di spessore, cioè quelli che non si possono “toccare con mano”. Ti sarà di grande aiuto l’osservazione della realtà fisica che ti circonda: non dimenticare che i concetti geometrici sono collegati a situazioni e oggetti di cui fai esperienza nella vita quotidiana!

Imparerai a fare le operazioni con alcuni enti geometrici. Ti starai chiedendo: “Ma come si fa con delle linee?”. Sarai, invece, stupito nel vedere quanto sarà semplice sommare due segmenti o trovare la differenza tra di loro.

Le parole della geometria non devono spaventarti: termini come “semiretta” o “congruenti” sembrano difficili, ma sono solo specifici e dovrai imparare a usarli opportunamente.

ROAD MAP la nostra

ENTRIAMO NEL MONDO DELLA GEOMETRIA

SCOPRIAMO GLI ENTI GEOMETRICI FONDAMENTALI E LE LORO PROPRIETÀ

DEFINIAMO LE SEMIRETTE E I SEGMENTI

RAPPRESENTIAMO GLI ENTI GEOMETRICI NEL PIANO CARTESIANO

MATERIALE INTEGRATIVO MULTIMEDIALE

LA GEOMETRIA: DALLA REALTÀ AL MODELLO 1

SUCCEDE CHE...

Nel golfo di Napoli gli aliscafi effettuano i collegamenti: Napoli-Capri-Pozzuoli e Napoli-Sorrento-Pozzuoli. Emma vuole rappresentarli sul quaderno in modo semplice ma comprensibile. Come può fare?

Da sempre l’uomo, osservando la natura, ha trasformato ciò che vedeva in segni e in forme, schematizzando la realtà: così invece di un vulcano ha disegnato un cono, una stella è diventata un punto, un tronco un cilindro, il sole un cerchio…

Si pensa che la geometria sia stata “inventata” dagli antichi Egizi: presso questo popolo la terra apparteneva, per la maggior parte, al faraone; il resto era di proprietà dei templi o dei ricchi. Le piene del Nilo cancellavano spesso i confini e l’estensione dei vari appezzamenti era da rimisurare ogni anno per attribuirli ai vari contadini, sottoposti a un tributo annuale.

Da qui il termine geometria: “misura della terra” (dal greco antico geo = “terra” e metro = “misura”).

Inizialmente, quindi, la geometria fu utilizzata per misurare campi o progettare edifici ma, ancora oggi, molte scienze si basano sullo studio della geometria: basti pensare all’astronomia, all’architettura, all’ingegneria. La geometria, infatti, interpreta la realtà e costruisce dei modelli che mettono in luce le loro caratteristiche: così una cornice, un campo da calcio, un libro, una finestra… possono essere rappresentati da un rettangolo e, studiando le proprietà del “modello” rettangolo, si studiano le proprietà di tutti gli oggetti rettangolari.

Anche un oggetto in movimento può essere rappresentato con un modello geometrico, per esempio una porta che gira ha come “modello” un cilindro.

La geometria è la scienza che si occupa della forma e della grandezza dei corpi geometrici e delle proprietà delle trasformazioni cui tali corpi sono sottoposti.

Emma può rappresentare i percorsi degli aliscafi come il modello geometrico qui a fianco. Questo modello è una spezzata.

Gli enti geometrici fondamentali

Che cos’è una spezzata? Per descriverla occorre introdurre gli enti geometrici fondamentali: il punto, la retta e il piano, le loro caratteristiche e proprietà.

Il punto geometrico è privo di dimensioni e indica una posizione nello spazio.

Per dare l’idea del punto basta pensare al segno lasciato dalla punta di un compasso. Il punto si indica con una lettera in stampatello maiuscolo: A, B, C

La linea è un insieme continuo e infinito di punti. Ha una sola dimensione: la lunghezza

La traccia lasciata su un foglio da una matita ci dà l’idea di una linea. La linea si indica con una lettera in stampatello minuscolo: a, b,… r, s, t Essendo un insieme infinito di punti, si mettono dei tratteggi all’inizio e alla fine della linea disegnata.

Il simbolo  indica che S e B sono coincidenti, cioè occupano la stessa posizione. A C S B S  B

linea a

linea b

La linea retta è una linea particolare perché mantiene sempre la stessa direzione.

Le linee possono essere aperte o chiuse, intrecciate o semplici

linea intrecciata chiusa

linea semplice aperta

linea semplice chiusa

linea intrecciata aperta

Il piano è un insieme continuo e infinito di rette. Si estende in due dimensioni: la lunghezza e la larghezza

Il piano della lavagna o il vetro di una finestra sono rappresentazioni di superfici piane. Il piano si indica con una lettera minuscola dell’alfabeto greco: α (alfa), β (beta), γ (gamma), δ (delta) …

In geometria quando si parla di punti, rette o piani si utilizzano le seguenti frasi.

“Il punto S non appartiene alla retta r ”.

Ecco come diventa il modello che rappresenta il percorso degli aliscafi utilizzando gli enti geometrici fondamentali: puoi notare quattro punti (N, S, P, C) che indicano le città e quattro linee che indicano i percorsi (a, b, c, d).

“La retta t appartiene al piano α”. α t C P S N a b d c P S r “Il punto P appartiene alla retta r ”.

“La retta t giace sul piano α” oppure

1 Osserva le seguenti figure reali e associale al loro modello.

2 Completa le seguenti frasi.

a) Il punto è privo di

b) Il punto si indica con le lettere in maiuscolo.

c) La retta ha dimensione.

d) La retta è un insieme infinito di

e) La retta si indica con le lettere in stampatello

f) Il piano è un insieme infinito di

g) Il piano ha dimensioni.

h) Il piano si indica con le lettere dell’alfabeto

3 Osserva i disegni e assegna il nome esatto a ciascuna linea (aperta, chiusa, semplice, intrecciata).

4

Osserva il disegno e completa le frasi.

a) A, C, S, P, T, U sono

b) r e m sono

c) k è una

d) C appartiene alla retta

e) Il punto S a k

f) U non appartiene alla retta

5 In base alle lettere stabilisci se si tratta di un piano, di una retta o di un punto e poi disegnali in modo

tale che la retta appartenga al piano e il punto no.

a) b

b) β c) B

6 MATEMATICA IN AZIONE Per ciascun oggetto segna con una crocetta le caratteristiche di cui si occupa la geometria. a) c)

1) ha la forma di un parallelepipedo

2) è fragile

3) ha vari ingredienti

4) è alta 19 cm

5) è lunga 32 cm

1) ha forma circolare

2) è di legno trattato per esterni

3) il suo diametro misura 180 cm

4) è allungabile e diventa di forma ovale

5) vi prendono posto 4 persone

b) d)

1) contiene 40 g di colla

2) è senza solventi

3) è alto 12 cm

4) ha forma cilindrica

5) è prodotto in Italia

1) ha la forma di una mezza sfera

2) è di cioccolato fondente al 90%

3) pesa 120 g

4) è su un piattino di forma quadrata

5) fornisce più di 700 calorie

SUCCEDE CHE... LEZIONE

PROPRIETà DEGLI ENTI

GEOMETRICI FONDAMENTALI

Pietro vede quest’immagine e capisce che è un’illusione ottica. Perché?

Per rispondere bisogna aver presente quali sono le proprietà legate agli enti geometrici alla base della geometriaalla base della geometria.

La geometria presentata nella maggior parte delle unità di questo libro si chiama euclidea e prende origine dai libri intitolati Elementi scritti dal matematico greco Euclide (III sec. a.C.). In questi libri Euclide organizza ed espone i concetti geometrici già usati dagli antichi Egizi e Babilonesi.

Punto, retta e piano sono gli enti geometrici fondamentali poichè sono la base della geometria euclidea.

Vediamo di seguito alcune loro proprietà.

• Per due punti distinti passa una e una sola retta.

• Per un punto passano infinite rette.

• Per tre punti distinti, non allineati, passa uno e un solo piano.

• Per una retta e un punto non appartenente ad essa passa uno e un solo piano.

• Per tre punti allineati o per una retta passano infiniti piani.

Pietro capisce che è un’illusione ottica per la prima proprietà: se B appartiene alla retta passante per A e D, non può appartenere alla retta passante per A e C.

1 Completa i seguenti assiomi.

a) Per due punti distinti passa retta.

b) Per tre punti allineati passano piani.

c) Per tre punti allineati passa retta.

d) Per tre punti non allineati passa piano.

e) Per una retta e un punto non ad essa passa piano.

f) Per un punto passano rette.

2 Disegna tre punti allineati L, M, N.

Quante rette passanti per essi puoi disegnare?

3 Disegna tre punti non allineati S, T, V.

a) Puoi disegnare una sola retta passante per essi?

b) Quanti piani passanti per essi puoi disegnare?

4 MATEMATICA IN AZIONE Gianni vuole costruire un tavolo. Qual è il numero minimo di gambe che deve mettere in modo che il tavolo non traballi?

a) 4

b) 3

c) 2

d) 1

Quale proprietà deve sapere per rispondere alla domanda?

Semirette e segmenti 3

SUCCEDE CHE...

La mappa a lato mostra in colore rosso il percorso del sentiero che da Saint Jacques (valle d’Ayas) porta al rifugio Mezzalama. La linea in colore verde invece che cosa indica?

Per rispondere alla domanda è necessario conoscere le diverse linee che si usano in geometria. Un punto su una retta individua due semirette opposte Il punto è l’origine delle semirette.

Una semiretta è ognuna delle due parti in cui una retta viene divisa da uno dei suoi punti, detto origine della semiretta.

Le semirette si indicano con lettere minuscole dell’alfabeto.

Due punti su una retta individuano un segmento e vengono detti estremi del segmento. Poiché il segmento è la linea più breve che congiunge due punti, il segmento esprime la distanza tra due punti

semiretta t

semiretta r O = origine

segmento AB la distanza tra i punti A e B è il segmento AB

Un segmento è la parte di retta compresa tra due punti detti estremi del segmento.

Due segmenti, in base alla loro posizione, hanno nomi diversi:

Consecutivi se hanno solo un estremo in comune.

Adiacenti se hanno solo un estremo in comune e appartengono alla stessa retta.

Incidenti se hanno in comune un punto diverso dagli estremi.

AB e BC sono consecutivi perché hanno solo l’estremo B in comune.

RS e ST sono adiacenti perché hanno l’estremo S in comune e appartengono entrambi alla retta r

ON e LM sono incidenti perché hanno il punto P in comune diverso dagli estremi.

Sovrapposti se hanno un estremo in comune e tutti i punti di uno appartengono all’altro.

Coincidenti se sono sovrapposti e hanno entrambi gli estremi in comune.

OS LUZIONE

DE e DF sono sovrapposti perché hanno l’estremo D in comune e tutti i punti di DE sono anche punti di DF

I segmenti AB e CD sono coincidenti AB  CD.

Rispondiamo alla domanda posta all’inizio del paragrafo: la linea verde è un segmento e indica la distanza in linea d’aria tra le due località della mappa.

Primi

ESERCIZI

1 Riconosci la posizione delle seguenti coppie di segmenti (consecutivi, adiacenti, incidenti, sovrapposti) e completa le frasi.

AB e BC sono e sono e sono e sono

2 Disegna un segmento consecutivo al segmento LM e un segmento adiacente al segmento ST.

3 MATEMATICA IN AZIONE Nella figura a lato è rappresentato un trabattello, impalcatura mobile di tubi metallici e tavole usata per l’esecuzione di lavori (intonacatura e imbiancatura di pareti ecc.). Prendendo come riferimento le lettere scritte in colore rosso, che rappresentano i punti, individua:

a) una coppia di segmenti incidenti:

b) due coppie di segmenti consecutivi:

c) due coppie di segmenti adiacenti:

d) due coppie di segmenti sovrapposti:

con i segmenti 4

SUCCEDE CHE...

I tre segmenti AB, BC e CD tracciati sulla mappa indicano il percorso fatto da Emma per recarsi in un negozio. Senza conoscere le loro misure, come fai a stabilire quale dei tre segmenti rappresenta il tratto di percorso più lungo?

Per rispondere occorre sapere come si confrontano le lunghezze di due segmenti.

Vediamo prima il significato di alcuni simboli che incontrerai in questo testo.

2 cm B A B

2 cm D C D

AB = CD

AB  CD

AB = CD = 2 cm

• I trattini sui segmenti AB e CD indicano che i due segmenti hanno la stessa lunghezza;

• AB = CD significa che AB e CD hanno la stessa lunghezza;

• AB ≅ CD significa che AB e CD sono congruenti, cioè, pur occupando posizioni diverse, sono sovrapponibili e tutti i loro punti coincidono;

• AB = CD = 2 cm significa che AB e CD sono lunghi 2 cm.

Vediamo adesso quali operazioni sono possibili con i segmenti.

Confronto

EF > AB oppure AB < EF

EF è maggiore di AB oppure AB è minore di EF

AB + DE + GH = AH AH è il segmento somma

Per confrontare i segmenti AB e EF, li si sovrappone facendo coincidere A con E. In questo modo si vede quale dei due è maggiore.

Addizione

Per ottenere il segmento somma si disegnano i segmenti AB, DE e GH uno dopo l’altro in modo che diventino a due a due adiacenti.

Sottrazione

Per ottenere il segmento differenza si sovrappongono i segmenti UV e ST facendo coincidere gli estremi U e S:

AB = 8 × EF

EF = 1 8 × AB

FM = MG

Multipli e sottomultipli

AB è 8 volte EF; quindi AB è multiplo di EF

EF è l’ottava parte di AB; quindi EF è sottomultiplo di AB

Punto medio

M è il punto medio di FG, infatti lo divide in due parti che hanno la stessa lunghezza.

Per capire quale dei tre segmenti è il più lungo, si confrontano a due a due i tre segmenti e si stabilisce quale di questi rappresenta il tratto di percorso più lungo.

ESERCIZI

1 Osserva e completa le frasi.

Il segmento EF è del segmento In simboli EF = Il segmento CD è del segmento In simboli CD =

2 La differenza tra i segmenti AB e CD è il segmento nullo. Quindi:

a) AB > CD b) AB < CD c) AB = CD

3 MATEMATICA IN AZIONE Confronta, utilizzando il righello o il compasso, la lunghezza di questi segmenti. Che cosa noti? a) c)

Appare più lungo il segmento orizzontale o quello verticale? Come sono le loro misure?

Appare più lungo il segmento orizzontale a sinistra o quello a destra? Come sono le loro misure? b) d) A B C

Appare più lungo il segmento nel disegno in alto o quello nel disegno in basso? Come sono le loro misure?

Appare più lungo il segmento AB o il segmento AC ? Come sono le loro misure?

LEZIONE Il piano cartesiano 5

SUCCEDE CHE...

Quali posizioni occupano sulla scacchiera il cavallo nero, il re nero e il re bianco?

Per rispondere alla domanda occorre conoscere il metodo delle coordinate.

Per rappresentare elementi geometrici su un piano, nel XVII secolo il filosofo matematico René Descartes, detto Cartesio, per primo usò un sistema di riferimento

Come si costruisce il sistema di riferimento di un piano cartesiano?

• Si disegnano due semirette, x e y, che hanno la stessa origine e formano un angolo retto.

• Si stabilisce un’unità di misura u e la si riporta sulle semirette.

• Si fissa su ciascuna semiretta la punta di una freccia.

Le due semirette perpendicolari x e y si chiamano assi:

• l’asse orizzontale si chiama asse delle ascisse o asse delle x;

asse delle ascisse o delle x origine asse delle ordinate o delle y

• l’asse verticale si chiama asse delle ordinate o asse delle y. Il punto in comune degli assi si chiama origine degli assi e si indica con la lettera O.

Per individuare un punto A:

• si determina la sua posizione rispetto all’asse delle x, si trova cioè l’ascissa del punto: xA;

• si determina la sua posizione rispetto all’asse delle y, cioè l’ordinata del punto: yA

L’ascissa e l’ordinata di un punto P sono le sue coordinate cartesiane P (ascissa; ordinata) o P(xP; yP)

Per convenzione, nell’indicare le coordinate di un punto si scrive prima il valore dell’ascissa e poi quello dell’ordinata.

Nella figura:

• le coordinate del punto A sono 2 e 3 e si scrive A(2; 3);

• le coordinate del punto B sono 5 e 2 e si scrive B(5; 2).

In particolare si ha:

• il punto corrispondente all’origine ha entrambe le coordinate nulle: O(0; 0);

• i punti con ascissa nulla appartengono all’asse delle ordinate: P(0; yP);

• i punti con ordinata nulla appartengono all’asse delle ascisse: P(xP; 0).

OS LUZIONE

Anche nel gioco degli scacchi si utilizza il metodo delle coordinate. Ogni quadrato della scacchiera è individuato da una coppia formata da una lettera e da un numero, quindi: cavallo nero (D5), re nero (G7) e re bianco (A2).

Primi

ESERCIZI

1 Rispondi alle seguenti domande.

In un piano cartesiano:

a) come si chiama l’asse orizzontale?

b) come si chiama l’asse verticale?

c) come si chiama il punto in comune degli assi?

d) come si chiama la prima coordinata di un punto?

e) come si chiama la seconda coordinata di un punto?

2 Scrivi i termini corretti negli spazi.

3 MATEMATICA IN AZIONE Osserva la mappa e indica le coordinate richieste.

Negozio di alimentari

Fast food (6; )

Negozio di animali

Negozio di alimentari

Negozio di giocattoli

Ambulatorio

Negozio di souvenir

MAPPA

che si può rappresentare con un

semirette segmenti a

le cui parti si dicono r

ENTI GEOMETRICI FONDAMENTALI

s A B incidenti sovrapposti consecutivi adiacenti

Per due punti distinti passa una e una sola retta.

PROPRIETÀ

Per tre punti distinti, non allineati, passa uno e un solo piano.

Per un punto passano infinite rette.

Per una retta e un punto non appartenente a essa passa uno e un solo piano.

Per tre punti allineati o per una retta passano infiniti piani.

LEZIONE

1 ESERCIZI E PROBLEMI

LA GEOMETRIA: DALLA REALTÀ AL MODELLO

1 Contrassegna le affermazioni che ti fanno pensare a dei punti.

a) Le stelle nel cielo

b) Un pallone gonfiabile

c) Il filo del telefono

d) La luce di un faro nella notte

e) Una pagina di libro

f) Un granello di sale fino

g) La punta di una penna vista dall’alto

h) Un dado da gioco

2 Quali tra i seguenti “oggetti” rappresentano una linea? Contrassegnali con una crocetta.

a) Un cavo elettrico

b) Una carta da gioco

c) La scia di un aereo

d) Un filo da ricamo

e) Un elastico

f) Una moneta

g) Una lenza da pesca

h) Una circonferenza

3 Fra i seguenti oggetti quali hanno una superficie piana e quali una superficie curva?

Completa la tabella.

a) Il soffitto di un’aula

f) Un vaso da fiori

b) La buccia di un agrume g) La superficie di una lampadina

c) Un campo da tennis h) Le facciate di un palazzo

d) La cialda di un cono gelato i) Un tappeto steso

e) Lo schermo di un tablet l) Il vetro di un bicchiere

Superfici piane

Superfici curve

4 MATEMATICA IN AZIONE Completa la tabella inserendo accanto alle figure rappresentate i corrispondenti modelli geometrici.

nella realtà modello

1 costellazione punti, linee

2 città

3 campi coltivati

4 curve di livello (isoipse)

5 strade

6 abitazioni

5 Stabilisci, per ogni oggetto, di quale caratteristica si occupa la geometria.

a) Un laghetto artificiale 1) contiene 10 000 hL di acqua

b) Il cellulare di Mary 1) è prodotto in Italia

c) La palla da tennis 1) ha una forma sferica

d) Un albero di susine 1) produce frutti giallo-dorato

e) Il gazebo di Arturo 1) è aperto sui quattro lati

2) contiene pesci rossi

2) pesa 180 g

2) è prodotta in Malesia

2) produce in media 60 kg di frutti

2) è più grande di quello di Elvis

6 Collega con una freccia i nomi degli enti geometrici fondamentali ai simboli che li rappresentano.

a) Piano

b) Punto

c) Retta

1) r, lettera in stampatello minuscolo

2) α, lettera minuscola dell’alfabeto greco

3) L, lettera in stampatello maiuscolo

7 Quale dei seguenti simboli utilizzeresti per indicare:

a) una superficie piana o un piano? 1) P 2) a 3) α 4) Z 5) γ 6) s

b) una linea? 1) A 2) a 3) β 4) B

c) un punto?

8 Osserva il disegno e completa le frasi.

a) I piani sono

b) Le rette sono

c) I punti sono

d) Il punto C appartiene alla retta

e Il punto L al piano

f) Il punto A alle rette

g) La retta r sul piano

9 MATH Mark with any letter all the points you can find in the following figures.

10 Nella seguente figura indica con β il piano, con r e s le due rette

e con D, E, F i tre punti, in modo che il punto E appartenga alla retta r e il punto F appartenga a s.

11 Osserva il disegno e stabilisci se le seguenti affermazioni sono Vere o False.

a) S, P, R sono punti. V F

b) a è una linea chiusa. V F

c) P e R appartengono ad a. V F

d) R non è una linea. V F

e) a non è una linea intrecciata. V F

f) S appartiene ad a V F S P R a

12 Dopo aver osservato la figura, completa utilizzando i termini appartiene o non appartiene.

a) A

b) B

c) C

d) D

E

f) F

g) G

13 Assegna il nome esatto alle seguenti linee. a) b) c) d) e) f)

14 Osserva le seguenti cifre del sistema decimale e individua se sono linee aperte (A) o chiuse (C), semplici (S) o intrecciate (I). 1 2 3 4 5 6 7 8 9 0

15 Osserva il disegno e completa le richieste.

a) Quali linee congiungono i punti P e M ?

b) Potresti disegnarne altre?

c) Qual è la più breve?

d) Come si chiama questa linea?

16 Osserva il disegno e completa le frasi e la tabella.

a) n è una

b) m è una

Punti appartenenti

17 Stabilisci se le terne di punti assegnate appartengono alla stessa retta e, in caso affermativo, indica il nome della retta.

a) A, D, E SÌ NO

b) B, C, D SÌ NO

c) B, C, F SÌ NO

d) A, E, C SÌ NO

18 Stabilisci se le terne di punti assegnate appartengono alla stessa retta e, in caso affermativo, indica il nome della retta.

a) E, B, D SÌ NO

b) F, A, E SÌ NO

c) G, F, C SÌ NO

d) A, G, C SÌ NO

19 Disegna seguendo le istruzioni.

a) Retta r passante per A e B.

b) Linea aperta semplice m passante per M e T.

c) Rette t e s aventi il punto F in comune.

d) Linea chiusa intrecciata p non passante per C. A

PROPRIETÀ DEGLI ENTI GEOMETRICI FONDAMENTALI

20 Rispondi con Vero o Falso.

a) Per due punti distinti passano tantissime rette.

b) Per un punto passano infinite rette.

c) Per tre punti distinti non allineati passa una sola retta.

d) Una retta che ha due punti in comune con un piano giace su di esso.

e) Per tre punti allineati passano solo 1 000 piani.

f) Per una retta passano infiniti piani.

g) Per tre punti non allineati non passa alcun piano.

h) Per una retta e un punto che non gli appartiene passa un solo piano.

i) Per due rette che si intersecano in un punto passano infiniti piani.

21 Completa gli assiomi.

a) Per due punti distinti passa sola retta.

b) Per tre punti allineati passa retta.

c) Per una retta passano piani.

d) Per due rette incidenti passa piano.

Disegna e rispondi.

22 Dato un punto P, disegna una retta passante per il punto P

Quante ne puoi disegnare?

a) 1 b) 10 c) infinite P

23 Dati due punti R e S, disegna una retta passante per essi.

Quante ne puoi disegnare?

a) 1 b) 10 c) infinite

24 Disegna tre punti, L, M, N, e una retta passante per essi.

È sempre possibile?

Come devono essere i tre punti?

F

25 Dati due punti A e B, disegna una retta passante per essi e un piano che li contiene.

Quanti piani puoi disegnare?

a) 1

b) 10

c) infiniti

26 Disegna un piano che contenga i tre punti A, B e C

Quanti piani puoi disegnare?

a) 1

b) 10

c) infiniti

Disegna tutte le rette che passano per due dei tre punti assegnati.

27 Data una retta r e un punto T che non appartiene a r, quanti piani passanti per essi puoi disegnare?

a) 1

b) 10

c) infiniti

28 Date due rette r e s, disegna tutti i piani passanti per entrambe.

Quanti piani puoi disegnare?

a) 1

b) 10

c) infiniti

29 Disegna tre punti A , B e C allineati.

Quante rette passanti per essi puoi disegnare?

a) 1

b) 10

c) infinite

Quanti piani?

a) 1

b) 10

c) infiniti

SEMIRETTE E SEGMENTI

30 Completa scegliendo tra questi termini, che si possono ripetere più volte

congruenti • due • estremi • maiuscole • medio • minuscola • origine • punti • punto • retta • semiretta • una

a) Una è ciascuna delle parti in cui una retta viene divisa da un suo , detto della

b) Un segmento è la parte di compresa tra due suoi che sono gli del segmento.

c) Una semiretta si indica con lettera dell’alfabeto italiano.

d) Un segmento si indica con ………… lettere ……………………………… dell’alfabeto italiano che indicano gli ………………………………… del segmento.

e) Il punto ……………… è il punto che divide un segmento in due parti

31 Osserva i seguenti disegni e completa le frasi.

a) I due segmenti DE e sono perché hanno l’estremo in comune e appartengono alla stessa ………………………………………………

b) I due segmenti e sono perché hanno l’estremo …… in comune.

c) I segmenti e sono perché hanno il punto …… in comune che non coincide con uno degli

32 Scrivi se le seguenti scritture simboliche indicano un punto, una semiretta o un segmento.

Scrittura Punto/Semiretta/Segmento

33 Associa a ogni frase il disegno corretto. (Non tutti i disegni verranno utilizzati.)

a) - Il segmento ST:

b) La semiretta n:

c) Il segmento di estremi R e T:

d) La semiretta di origine G:

e) Le semirette opposte m e n:

34 Osserva il disegno e rispondi.

a) - Quante semirette riesci a individuare? …….… …

b) - Quali semirette hanno origine in O ?

c) - Quali semirette hanno origine in P ?

d) - Ci sono semirette opposte?

35 Indica i segmenti che osservi nella figura e rispondi.

, , , , , , ,

a) Ci sono segmenti incidenti? Quali?

b) - Ci sono segmenti consecutivi?

Quali?

c) - Ci sono segmenti adiacenti? Quali?

36 Disegna due segmenti consecutivi al segmento AB e indicali con lettere a tua scelta.

37 Disegna due segmenti adiacenti al segmento CD e indicali con lettere a tua scelta.

38 Nella seguente retta segna due punti, E e F, poi rispondi alle domande.

a) Quante semirette individui? Indica l’origine di ogni semiretta:

b) Quanti segmenti individui? Quali sono? v

39 Nella seguente retta segna tre punti, L, M, N, e poi rispondi alle domande.

a) Quante semirette individui? ………… Indica l’origine di ogni semiretta: …………………

b) Quanti segmenti individui? Quali sono?

40 Osserva le seguenti coppie di segmenti e scrivi il nome rispetto alla loro posizione.

41 MATH Draw on your notebook:

a) three different line segments; b) two non adjacent line segments with one point in common; c) two adjacent line segments; d) two incident line segments.

42 Disegna sul tuo quaderno:

a) tre segmenti, a due a due consecutivi;

b) due segmenti consecutivi e uno incidente a tutti e due;

c) un segmento e una semiretta aventi la stessa origine;

d) due segmenti coincidenti.

43 Disegna sul tuo quaderno:

a) due segmenti incidenti e un terzo segmento consecutivo al primo;

b) tre segmenti incidenti in un unico punto;

c) quattro segmenti a due a due consecutivi;

d) i segmenti AB e BC adiacenti e il segmento CD consecutivo, ma non adiacente, a BC

44 MATEMATICA IN AZIONE In questa immagine sono disegnati tre tralicci. Individua in essi gli enti geometrici e indicali specificando il nome.

45 MATEMATICA IN AZIONE Il disegno riporta un tavolo da biliardo con le traiettorie di alcune palline. Riconosci e indica in modo appropriato:

a) semirette

b) segmenti

c) segmenti consecutivi

d) segmenti adiacenti

OPERAZIONI CON I SEGMENTI

46 Collega con una freccia ogni simbolo al relativo significato.

a) = 1) congruente

b)  2) coincidente

c)  3) stessa lunghezza

47 Rispondi con Vero o Falso.

a) Il confronto tra due segmenti stabilisce quale ha lunghezza maggiore e quale minore.

b) Il segmento somma si ottiene disegnando consecutivamente sulla stessa retta i segmenti da sommare.

c) Per ottenere il segmento differenza si cercano i sottomultipli del segmento maggiore.

d) Il punto medio di un segmento lo divide in tante parti congruenti.

e) Un segmento è multiplo di un altro se lo contiene un numero esatto di volte.

Confronto tra segmenti

F

F

F

F

F

48 Osserva i seguenti segmenti e, utilizzando il righello o il compasso, stabilisci quali sono tra loro congruenti.

a)  b) ……………………… ………………………

49 Dato il segmento MN, confrontalo con gli altri segmenti e scrivi le relazioni di uguaglianza (=) o diseguaglianza (∙).

50 MATH Draw a line segment that is longer than, a line segment that is shorter than, and a line segment that is congruent with the given segment.

51 Confronta i segmenti disegnati e completa le affermazioni utilizzando i simboli di maggiore, minore o congruente (>, <, ).

52 Confronta i seguenti segmenti e completa la scrittura.

Addizione e sottrazione di segmenti

53 Considera i segmenti AB e CD e costruisci il segmento somma e il segmento differenza.

a) Segmento somma: disegna una retta r e riporta su di essa i segmenti, prima AB e poi CD, in modo che gli estremi B e C corrispondano.

Quindi AB + CD = …………………

b) Segmento differenza: ridisegna il segmento maggiore (CD) e sovrapponi ad esso l’altro segmento.

Quindi CD – ……… = ………

54 Dati i tre segmenti FG, HI, LM, costruisci il segmento somma. L I H G F M

55 Dati i segmenti MN e PS, costruisci il segmento differenza. P N M S

56 MATH Observe the figure and determine whether the statements are true or false.

a) DE + EF = DF T F c) DE + FG = DG T F b) EF + FG = EG T F d) DE + EF + FG = DG T F

57 Osserva la figura e completa. A B C D

a) AD – AC = c) BD – BC = b) AC – AB = d) AD – AB =

58 Calcola la misura del segmento somma RT con le misure seguenti: a) RS = 15 cm e ST = 8 cm

59 Calcola la misura del segmento differenza con i seguenti dati:

a) PM = 20 cm e GH = 13 cm = P M

b) PM = 26 cm e GH = 7 cm = G H

Risolvi i seguenti problemi.

60 Considera i segmenti FG = 10 cm e CD = 4 cm. Costruisci il segmento differenza e determina la sua misura. [6 cm]

61 Dati i segmenti GH = 13,5 cm e UV = 3,4 cm, costruisci i segmenti somma e differenza e determina le loro misure. [16,9 cm; 10,1 cm]

62 MATEMATICA IN AZIONE Marta vuole fare una passeggiata in montagna. Studia la cartina dei sentieri e si accorge che a Collelungo c’è un bivio. Quale strada deve percorrere per fare meno kilometri?

Per la strada a sinistra riporta il segmento P1P6 sulla prima retta.

La strada a destra presenta invece varie curve; puoi utilizzare una spezzata (una linea ottenuta con più segmenti consecutivi), riportando ciascun segmento

(P1P2, P2P3 , ) in modo che tutti siano adiacenti sulla seconda retta. Confronta i segmenti ottenuti e stabilisci qual è la strada che Marta deve prendere per camminare di meno.

63 MATEMATICA IN AZIONE Il servizio traghetti delle Isole Eolie parte dall’Isola di Vulcano.

Indica qual è il percorso più breve tra:

a) Vulcano-Alicudi-FilicudiVulcano

b) Vulcano-Alicudi-SalinaVulcano

(Usa un procedimento analogo a quello dell’esercizio precedente.)

Multipli e sottomultipli di un segmento

64 Osserva i disegni e completa come nell’esempio.

a) A B C D

b) S X T Y

c) H I F G

AB è multiplo di CD CD è sottomultiplo di AB …………………………………… AB = 4 × CD CD = 1 4 × AB

65 Disegna i segmenti secondo le indicazioni.

a) AB è il doppio di CD.

b) MN è la metà di ST.

c) LM è un terzo di XY C S X D T Y

66 Calcola le misure dei multipli dei seguenti segmenti dopo averli disegnati.

a) AB = 13 cm LM = 3 × AB LM =

b) DE = 8 m ST = 4 × DE

c) GH = 17 cm VZ = 2 × GH

67 Riconosci la risposta corretta.

68 MATH Identify the correct answer. a)

Risolvi i seguenti problemi.

69 Disegna sul tuo quaderno un segmento di 12 cm. Dividilo, poi, in tre parti tra loro congruenti. Quanto misura ognuna di esse? [4 cm]

70 Disegna sul tuo quaderno un segmento AB di 4 cm e i multipli e sottomultipli indicati:

CD = 3 × AB EF = 1 4 × AB GH = 1 2 × AB IL = 4 × AB

71 Disegna sul tuo quaderno due segmenti, LM e RS, in modo che LM = 2 × RS

a) Disegna il segmento ST = LM – RS.

b) Com’è ST rispetto al segmento LM? E rispetto a RS?

c) Calcola la misura di LM e di RS, sapendo che la differenza tra loro è 15 dm.

Punto medio di un segmento

72 Trova il punto medio dei seguenti segmenti e indicalo con la lettera X. (Il punto medio divide a metà…)

73 Disegna sul quaderno i seguenti segmenti e per ciascuno di essi individua e segna il punto medio M. AB = 10 cm CD = 64 mm EF = 14 cm RS = 90 mm

74 Facendo riferimento al disegno, completa la tabella. AM  BM perché M è punto medio

75 Considera due segmenti adiacenti AB e BC e i loro punti medi M e M '. Sapendo che AB = 4 cm e BC = 2 × AB, determina la misura del segmento MM '. [6 cm]

76 Considera due segmenti adiacenti EF e FG e i loro punti medi M e M '. Determina la misura del segmento MM ', sapendo che EF = 14 cm e FG = 1 2 × EF. [10,5 cm]

Problemi con i segmenti

77 Completa trasformando in descrizioni a parole le indicazioni date nei disegni (procedi come nell’esempio).

78 Per ogni disegno scrivi la lettera che corrisponde alla sua descrizione.

a) Il segmento minore è la terza parte del maggiore.

b) Un segmento è il quadruplo di un altro.

c) Un segmento supera un altro di 1,5 cm.

d) Un segmento è la metà di un altro.

Risolvi i seguenti problemi.

ESEMPIO

1,5 cm

La somma di due segmenti è 40 cm e uno di essi è il triplo dell’altro. Calcola le misure dei due segmenti.

Dati

Le informazioni contenute nel testo del problema si scrivono: “la somma di due segmenti è 40 cm’’

AB + CD = 40 cm “uno di essi è il triplo dell’altro’’

CD = 3 × AB la richiesta è:

AB = ? CD = ? la rappresentazione grafica è:

Risoluzione

Si evidenzia che la somma, 40 cm, comprende 4 parti congruenti al segmento AB; quindi:

AB = 40 : 4 = 10 cm

CD = 10 × 3 = 30 cm oppure CD = 40 – 10 = 30 cm

AB misura 10 cm e CD misura 30 cm.

79 La somma di due segmenti è 64 mm e il maggiore è il triplo del minore. Calcola le lunghezze dei due segmenti. [16 mm; 48 mm]

80 Determina le misure di due segmenti, sapendo che la loro somma è 200 cm e che uno è il quadruplo dell’altro. [40 cm; 160 cm]

81 Sapendo che la somma di due segmenti misura 24,6 dm e che uno è la metà dell’altro, trova le loro misure. [8,2 dm; 16,4 dm]

82 Un segmento è il doppio dell’altro e la loro somma è 147 m. Calcola le lunghezze dei due segmenti. [49 m; 98 m]

83 MATEMATICA IN AZIONE Giovanni, per sostenere le piante del suo orto, acquista delle canne di bambù lunghe 2,4 m e da ognuna di esse ne ricava due.

Quanto misurano le due parti se la prima è metà della seconda? [0,8 m; 1,6 m]

84 Calcola la lunghezza di due segmenti, sapendo che la loro somma è 37,5 m e il minore è 1 4 del maggiore. [7,5 m; 30 m]

Dopo aver osservato disegni e dati, risolvi i seguenti problemi.

85 C E F D

CD = 144 cm

EF = 2 × CE

FD = 3 × CE

CE = ?

EF = ?

FD = ? [24 cm; 48 cm; 72 cm]

86 E F C D A B

AB + CD + EF = 162 dm

CD = 2 × AB

EF = 3 × CD

Risolvi i seguenti problemi.

ESEMPIO

AB = ?

CD = ?

EF = ?

[18 dm; 36 dm; 108 dm]

La differenza tra due segmenti è di 16 cm e il segmento maggiore è il triplo del minore.

La frase “la differenza tra due segmenti è di 16 cm’’ si scrive: AB – CD = 16 cm.

Dati

AB – CD = 16 cm

AB = 3 × CD

AB = ?

CD = ?

Risoluzione

Il segmento differenza è il doppio del segmento minore CD. Quindi:

CD = 16 : 2 = 8 cm

AB = CD × 3 = 8 × 3 = 24 cm

Il segmento CD misura 8 cm e AB misura 24 cm.

87 Calcola le lunghezze di due segmenti, sapendo che uno è il triplo dell’altro e che la loro differenza misura 64 cm. [32 cm; 96 cm]

88 La differenza tra due segmenti misura 33 cm. Calcola le loro lunghezze, sapendo che uno è il quadruplo dell’altro. [11 cm; 44 cm]

89 MATEMATICA IN AZIONE Determina le misure di due gessetti, sapendo che uno è la metà dell’altro e che la loro differenza è 59 mm.

[ ; 118 mm]

Dopo aver osservato disegni e dati, risolvi i seguenti problemi.

90 A C B D

8,4 m

6444444447444444448

AB – CD = 8,4 m AB = ?

AB = 5 × CD CD = ?

91

20,5 dm A C B D

6444444444447444444444448

AB – CD = 20,5 dm CD = ?

CD = 1 6 × AB AB = ?

Risolvi i seguenti problemi.

ESEMPIO

La somma di due segmenti misura 47 m e uno supera l’altro di 5 m. Calcola le misure dei due segmenti.

La frase “uno supera l’altro di 5 m’’ si scrive: AB = CD + 5 m.

Dati

[10,5 m; 2,1 m]

[4,1 dm; 24,6 dm]

AB + CD = 47 m AB = ? C D A B 5 m 47 m

Risoluzione

AB = CD + 5 m CD = ?

Se non ci fosse la parte rossa di 5 m, i due segmenti sarebbero congruenti e la somma sarebbe il doppio di ciascuno di loro.

Se si toglie la parte rossa (5 m) dalla somma, si ottiene il doppio del segmento CD. Quindi:

CD = (47 – 5) : 2 = 42 : 2 = 21 m AB = CD + 5 m = 21 + 5 = 26 m

Il segmento CD misura 21 m e il segmento AB misura 26 m.

92 Un segmento supera un altro di 49 mm; calcola la lunghezza di ciascuno dei due segmenti, sapendo che la loro somma è 107 mm.

[29 mm; 78 mm]

93 Sapendo che la somma di due segmenti è 41,8 dm e che uno supera l’altro di 11,8 dm, trova le lunghezze dei due segmenti. [15 dm; 26,8 dm]

94 La somma di due segmenti è 258 m e il maggiore supera il minore di 48 m.

Calcola le misure dei due segmenti.

ESEMPIO

[105 m; 153 m]

La differenza tra due segmenti è 7 cm e il maggiore è 15 cm. Calcola la misura del minore.

Dati

CD = 15 cm AB = ?

CD – AB = 7 cm

Risoluzione

AB = CD – B'D = 15 – 7 = 8 cm Il segmento AB misura 8 cm.

95 La differenza tra due segmenti è 6,7 cm e il minore misura 18 cm.

Determina la lunghezza del segmento maggiore. [24,7 cm]

96 Dati due segmenti, il maggiore misura 45 m e la loro differenza è di 17 m.

Calcola la misura del segmento minore. [28 m]

97 Un segmento lungo 25 dm supera un altro di 8,3 dm.

Calcola la misura del secondo segmento. [16,7 dm]

98 La differenza tra due segmenti è 10,9 cm. Il maggiore è lungo 18 cm.

Calcola la lunghezza del segmento minore.

ESEMPIO

[7,1 cm]

La somma di due segmenti misura 78 dm e la loro differenza 24 dm. Determina le misure dei due segmenti.

Dati

RS + TU = 78 dm RS = ?

RS – TU = 24 dm TU = ?

Risoluzione

Togliendo dalla somma dei due segmenti la parte rossa (24 dm), rimangono due segmenti congruenti al minore TU. Quindi:

TU = (78 – 24) : 2 = 54 : 2 = 27 dm

RS = (27 + 24) = 51 dm

Il segmento TU misura 27 dm e il segmento RS misura 51 dm.

99 La somma di due segmenti CD e FG misura 48 cm. Sapendo che la loro differenza è 22 cm, determina le lunghezze dei due segmenti. [13 cm; 35 cm]

100 Di due segmenti conosci la somma che misura 520 dm e la differenza che misura 90 dm. Determina la misura dei due segmenti. [215 dm; 305 dm]

101 La somma di due segmenti è 162 m, la loro differenza è 31 m. Determina la lunghezza di ciascuno dei due segmenti. [65,5 m; 96,5 m]

102 Calcola le lunghezze di due segmenti, sapendo che la loro differenza è 23,7 cm e la loro somma 85,9 cm. [31,1 cm; 54,8 cm]

103 MATEMATICA IN AZIONE Leonardo acquista un tubo in polietilene lungo 60 m.

Per predisporre un impianto di irrigazione nel suo orto deve tagliare il tubo in due parti in modo che la prima sia 10 m più corta della seconda. Quanto misurano le due parti?

[25 m; 35 m]

I problemi con i segmenti ti sembrano degli scioglilingua incomprensibili e non sai mai da dove partire per risolverli? Provo a suggerirti qualche strategia per rimuovere gli ostacoli.

Così come fai quando traduci una frase dall’inglese all’italiano, allo stesso modo devi prima comprendere il linguaggio usato nel problema e poi tradurlo in uno schema di calcolo, cioè in un’espressione matematica. Per evitare gli errori di comprensione del testo, quando affronti un problema sui segmenti, leggi il testo con attenzione, ma soprattutto impara a

scomporre il problema, cioè a spezzettarlo in più parti, per poi visualizzarlo.

Un problema del tipo: “La somma di due segmenti è 16 cm e uno è 3 volte l’altro. Determina la lunghezza dei due segmenti” può essere trasformata in una sequenza di informazioni distinte: “disegna il segmento A; disegna il segmento B in modo che sia 3 volte più grande di A e scrivici accanto B = 3 × A; disegna il segmento somma e scrivici accanto A + B= 16”. Ora hai 4 pezzi uguali la cui somma è 16...: il gioco è fatto!

Esercizi di riepilogo

Risolvi i seguenti problemi.

104 La somma di due segmenti è 12,9 cm e uno è il doppio dell’altro. Determina le lunghezze dei due segmenti. [4,3 cm; 8,6 cm]

105 STEM Elisabetta acquista un listello lungo 280 cm.

Con questo listello costruisce una cornice in cui il lato maggiore è lungo 20 cm in più di quello minore. Quanto misurano i lati della cornice? [60 cm; 80 cm]

107 STEM Per costruire una staccionata Marco deve piantare nel terreno dei pali in modo che la parte fuori terra sia il doppio di quella interrata. Se la lunghezza di un palo è 180 cm, quanto misurano le due parti? [60 cm; 120 cm]

106 Due segmenti sono uno il triplo dell’altro. Sapendo che la loro differenza è 12,8 dm, trova la misura di ciascun segmento. [6,4 dm; 19,2 dm]

108 La differenza tra i segmenti LM e NO è 17,6 dm e LM è il quintuplo di NO. Trova le lunghezze di LM e NO [22 dm; 4,4 dm]

109 Il segmento AB supera di 10 cm il segmento CD. Sapendo che la loro somma è 228 cm, trova le lunghezze di AB e CD. [119 cm; 109 cm]

110 La somma di due segmenti misura 68,6 cm e la loro differenza 32,8 cm. Quanto è lungo ciascun segmento? [17,9 cm; 50,7 cm]

111 Sapendo che la somma e la differenza tra due segmenti sono rispettivamente 96,5 cm e 40,5 cm, determina le lunghezze dei due segmenti. [28 cm; 68,5 cm]

112 MATH Find the lengths of two line segments whose sum is 120 cm and whose ratio is 3 5 . [45 cm; 75 cm]

113 Un segmento è i 7 3 di un altro e la loro somma è 180 dm. Trova le misure dei due segmenti. [126 dm; 54 dm]

114 Il segmento AB è 5 3 del segmento CD Sapendo che la loro differenza misura 26 cm, calcola le misure di AB e CD [65 cm; 39 cm]

115 Calcola le misure di due segmenti, sapendo che il segmento maggiore è 7 4 del minore e che la loro differenza è 75 dm. [100 dm; 175 dm]

116 STEM Pietro deve costruire

il telaio in legno per la porta d’ingresso della casetta in cui deposita gli attrezzi da giardino.

Ha a disposizione un listello da telaio lungo 480 cm da cui deve ottenere tre pezzi ( AB, BC e CD nell’immagine) in modo

che la lunghezza di BC sia 2 5 di CD e che

CD sia uguale ad AB. Calcola la lunghezza dei tre pezzi del telaio della porta.

[80 cm; 200 cm; 200 cm]

117 Considera tre segmenti, AB, CD ed EF, la cui somma è 170 mm. Sapendo che AB supera CD di 17 mm e CD supera EF di 33 mm, quanto misurano AB, CD ed EF ? [79 mm; 62 mm; 29 mm]

118 Di tre segmenti LM, NO, PR si sa che:

LM = NO + 12 cm

NO = PR + 16 cm

LM + NO + PR = 428 cm

Determina le lunghezze di LM, NO e PR . [156 cm; 144 cm; 128 cm]

119 MATEMATICA IN AZIONE Si divide una fune lunga un metro e mezzo in parti tali che la prima superi la seconda di 35 cm e la seconda a sua volta superi la terza di 20 cm.

Determina la lunghezza delle tre parti in cui viene divisa la fune. [25 cm; 45 cm; 80 cm]

120 La misura della somma di tre segmenti è 632 dm. Sapendo che il primo segmento supera il secondo di 124 dm e che il secondo supera il terzo di 86 dm, trova le lunghezze dei tre segmenti. [112 dm; 198 dm; 322 dm]

121 Dividi un segmento di 101 cm in tre parti tali che la prima sia 1 3 della seconda e che la seconda superi la terza di 4 cm. [15 cm; 45 cm; 41 cm]

122 La differenza tra due segmenti è 18,6 mm e uno è 8 5 dell’altro. Quanto misura il segmento minore? [31 mm]

IL PIANO CARTESIANO

123 Completa le seguenti frasi.

a) Il piano cartesiano è determinato da due aventi la stessa e che formano un angolo e da un’ di

b) L’asse orizzontale si chiama asse delle ……… o delle ………………………………

c) L’asse verticale si chiama asse delle o delle

d) Ogni punto del piano cartesiano è individuato da due : il primo valore si chiama ; il secondo valore si chiama

e) I punti che hanno ascissa uguale a zero appartengono all’asse delle …………………

f) I punti che hanno ordinata uguale a zero appartengono all’asse delle

124 Nel seguente piano cartesiano evidenzia:

• l’origine con un punto rosso;

• l’asse delle ascisse con il colore blu;

• l’asse delle ordinate con il colore verde;

• l’unità di misura con il colore rosso;

• le punte delle due frecce con il colore rosso.

Riferendoti ai piani cartesiani, stabilisci le coordinate dei punti rappresentati.

Riporta sul piano cartesiano i punti di cui ti sono date le coordinate.

A (3; 6) B (2; 1) D (3; 2) E (4; 5) F (5; 5) G (1,5; 3,5) I (5,5; 2,5) L (0; 5,5) M (4; 0) N (0; 4,5) P (1,5; 4,5) R (3; 0,5) S (3,5; 5) T (5; 3,5) V (5,5; 0) Z (7; 2)

129 Osservando i due esercizi precedenti, rispondi alle seguenti domande.

a) I punti S e T hanno le stesse coordinate? Sono punti coincidenti? Perché?

b) Il punto M appartiene all’asse delle Perché?

c) Il punto N appartiene all’asse delle Perché?

d) I punti L e V hanno le stesse coordinate? Sono punti coincidenti? Perché?

e) Quali sono i punti allineati?

Rappresenta sul piano cartesiano i seguenti punti.

130 A (3; 8) B (9; 11) F (9,5; 7,5) G (8,5; 3,5) I (1; 0) H (0; 6)

131 C (2; 1) I (7; 0) H (0; 9) D (1,5; 7) P (6; 11) L (10; 0)

132 L (9; 0) M (0; 7) R (1,5; 10) S (1; 3) T (5; 5) N (0; 13)

Risolvi i seguenti problemi.

133 Scrivi sul tuo quaderno le coordinate di tre punti allineati al punto P (7; 3). Predisponi poi un piano cartesiano e verifica l’esattezza di ciò che hai scritto.

134 Dove si trovano i punti A (0; 7), B (0; 12), C (0; 2)? Perché? Se incontri difficoltà a rispondere, rappresenta i punti su un piano cartesiano.

135 Dove si trovano i punti E (5; 0), F (8,5; 0), G (12,5; 0)? Perché?

136 Scrivi le coordinate di tre punti che appartengono all’asse delle ordinate.

137 Scrivi le coordinate di tre punti che appartengono all’asse delle ascisse.

138 Scrivi, sul tuo quaderno, le coordinate di sei punti allineati al punto M (3; 6), in modo che tre punti appartengano a una retta e altri tre, invece, si trovino su un’altra retta.

139 Considera i seguenti segmenti nel piano cartesiano, individua le coordinate dei loro estremi ed effettua le considerazioni del caso.

ESEMPIO

Trova le coordinate degli estremi dei segmenti FD e DE. Che cosa noti?

DE ha come estremi i punti D ed E, le cui coordinate

sono DE: [D (3; 1) E (3; 5)]

DF ha come estremi i punti D e F, le cui coordinate

sono DF: [D (3; 1) F (1; 4)]

I segmenti DE e DF hanno l’estremo D in comune e quindi sono consecutivi.

FG: [F (……; ……) G (……; ……)]

GH: [G ( ; ) H ( ; )]

CD : [C ( ; ) D ( ; )]

DE: [D ( ; ) E ( ; )]

FG e GH sono

CD e DE sono

Le seguenti coppie di punti sono estremi di segmenti; rappresentale nel piano cartesiano.

140 a) AB: [A (3; 7) B (11; 7)]

b) FG: [F (3; 3) G (9; 10)]

141 a) AB: [A (1; 2) B (5; 2)]

b) DE: [D (2; 2) E (4; 2)]

c) CD : [C (6; 3) D (6; 9)]

d) IL : [I (2; 5) L(7; 5)]

c) CD : [C (2; 6) D (0; 4)]

d) EF: [E (4; 2) F (6; 4)]

142 MATH Draw the line segments in the coordinate plane. Describe the resulting shape.

AB: [A (5; 0) B (10; 5)]

CD : [C (5; 10) D (0; 5)]

AM : [A (5; 0) M (5; 5)]

CM : [C (5; 10) M (5; 5)]

BM : [B (10; 5) M (5; 5)]

DM : [D (0; 5) M (5; 5)].

143 Rappresenta i segmenti AB, EF e CD, evidenzia il punto medio di ciascun segmento e indicalo con una lettera a tuo piacere. Infine, scrivi le coordinate di ogni punto medio.

AB: [A (3; 1) B (9; 1)]

EF: [E (3; 10) F (3; 2)]

CD : [C (2; 2) D (8; 8)]

144 STEM Un marinaio deve rientrare in porto ma ha perso l’orientamento e non ha una bussola. È sera, il cielo è limpido e osserva l’Orsa Maggiore. Come può fare per orientarsi?

Il marinaio si orienta con la Stella Polare.

Riconosci la costellazione dell’Orsa

Maggiore o Grande Carro, rappresentata anche nel piano cartesiano, e immagina di disegnare un prolungamento dalla parte di FG, pari a 5 volte la distanza tra le due stelle indicate con F e G: la stella che si trova alla fine del prolungamento è proprio la Stella Polare che indica sempre il Nord.

Trovala anche tu: parti dal segmento FG e segui le indicazioni precedenti.

P ( ; )

145 STEM In questa immagine sono evidenziate alcune costellazioni. Sul quaderno traccia un piano cartesiano, individua i seguenti punti e congiungili nell’ordine:

A (3,5; 1) B (4; 2)

C (2,5; 4) D (4; 5,5)

E (3; 6,5) F (4; 7,5)

G (3; 8,5) H (4; 9,5)

Quale costellazione dell’immagine corrisponde alla figura ottenuta?

ANALIZZARE E INTERPRETARE DATI

Vi è un tipo di grafico che si rappresenta con segmenti consecutivi: la poligonale delle frequenze. Impariamo a leggerlo.

1 a) Che cosa rappresenta l’asse delle x?

b) Che cosa rappresenta l’asse delle y ?

c) Quali sono le coordinate del punto A?

d) Quali sono le coordinate del punto B ?

e) Quali sono le coordinate del punto C ?

f) Quali sono le coordinate del punto D ?

g) Quali sono le coordinate dell’origine?

2 Osserva il grafico e rispondi alle seguenti domande. Le linee grigie rappresentano le strade.

a) Indica le coordinate del punto in cui si trova il fioraio:

b) Per andare dal fioraio al fabbro quanti metri bisogna percorrere?

c) Per andare dal fast food al laboratorio di analisi quanti metri bisogna percorrere?

d) Che cosa si trova sulla stessa strada del fast food?

e) Che cosa si trova sulla stessa strada del teatro?

f) Che cosa si trova sulla stessa strada del negozio di animali?

di analisi

3 Costruisci un grafico lineare a partire dai seguenti dati. Manuela colleziona statuette etniche in legno pregiato e durante le vacanze ne acquista di ogni tipo.

Statuette acquistate da Manuela

Anno Numero statuette

2017 2

2018 3

2019 6

2020 5

a) Osserva la tabella e completa il grafico.

b) Inserisci gli anni nell’asse orizzontale.

c) Inserisci i numeri nell’asse verticale.

d) Trova i punti e collegali.

RISOLVERE PROBLEMI

4 Per confezionare dei costumi di Carnevale per un gruppo di ballo, la sarta dispone di una pezza di stoffa lunga 15 m. Deve confezionare:

• 4 corpetti, per ognuno dei quali servono 150 cm di stoffa;

• 4 gonne, per ognuna delle quali serve 1 m di stoffa in più di quella usata per i corpetti.

Le basta la stoffa? Se no, quanta gliene manca? [No; 1 m]

5 Giovanni sta costruendo la struttura di un deposito per gli attrezzi e ha ancora bisogno di tre pali lunghi più di 10 m. Nella segheria di fiducia ne hanno tre, la cui somma è 77 m, la differenza tra il primo e il secondo è 10 m e la differenza tra il secondo e il terzo è 12,5 m.

Vanno bene per Giovanni? Qual è la misura di ogni palo? [Sì; 14 m; 26,5 m; 36,5 m]

SFIDA MATEMATICA

6 Sulla retta

Sei punti, A , B, C , D, E, F, sono marcati su una retta, non necessariamente in questo ordine.

Sappiamo che AB = 2 cm, BC = 3 cm, CD = 5 cm, DE = 7 cm, EF = 8 cm, FA = 9 cm.

Qual è (in centimetri) la distanza fra i punti più lontani?

(Testo tratto dalla gara Finale di Parigi, Campionati Internazionali del 2008, ≠organizzata dal Centro PRISTEM dell’Università Bocconi di Milano)

ROAD MAP PER TUTTI

enti geometrici

DATI UN PUNTO, UNA RETTA E UN PIANO

Come si definiscono?

Sono gli enti geometrici fondamentali

Punto: lettera maiuscola A

Come si indicano in geometria?

PAG. 50

parti di una retta

DATA UNA RETTA

Che cos'è una semiretta?

Una semiretta è una parte di una retta che ha un inizio (origine) ma non ha una fine

Come si indica?

Con una lettera minuscola

Linea retta: lettera minuscola r O a

Che cos'è un segmento?

Piano: lettera greca a origine

Segmento EF: due lettere maiuscole estremo estremo ESEMPIO

PAG. 56

Un segmento è una parte di una retta che ha un inizio e una fine: gli estremi

Come si indica?

Con due lettere maiuscole

Semiretta a: lettera minuscola E F

1 Scrivi il nome dei seguenti enti geometrici, come nell’esempio.

a) L b) t c) β d) S punto L

2 Scrivi il nome dei seguenti enti geometrici.

a) Q R c) b b) c d) N O

3

Disegna:

a) un punto P

b) una retta f

c) un segmento DG

d) una semiretta s

4 Stabilisci se i seguenti punti appartengono o non appartengono alla retta s.

a) Il punto A ……………………………… alla retta s.

b) Il punto B …………………………… …

c) Il punto C …………………………… …

d) Il punto D …………………………… …

e) Il punto F …………………………… …

f) Il punto M ……………………………

Consecutivi

coppie di segmenti

DATI DUE SEGMENTI

Come possono essere rispetto alla loro posizione?

PAG. 56

Sovrapposti

hanno un estremo in comune e tutti i punti di uno appartengono all'altro

punto medio

DATO IL SEGMENTO AB DI 6 cm

Che cos'è il punto medio?

Il punto medio è il punto che divide un segmento in due parti congruenti

58

5 Stabilisci se i seguenti segmenti sono consecutivi o adiacenti.

GF e FE sono ...................................... ........

PL e LM sono ..............................................

XY e YZ sono

AB e BC sono ..............................................

LS e ST sono ......................................... .....

HN e QR sono ...................................... ......

LT e LS sono

6 Osserva il disegno e completa le frasi.

AC e CB sono segmenti

AC e sono segmenti consecutivi, l’ in comune è C.

Il segmento CD è consecutivo anche di , l’estremo in comune è sempre

AB e AC sono segmenti , l’estremo in comune è

7 Disegna sul quaderno.

a) due segmenti incidenti,

b) due segmenti sovrapposti,

c) tre segmenti a due a due consecutivi ma non adiacenti.

8 Traccia i punti medi dei seguenti segmenti, indicali con M e determina poi le misure delle due parti congruenti.

= MB = cm

9 Considera il segmento LN di 47 cm e il suo punto medio M; quanto misurano LM e MN? [23,5 cm]

10 Dato un segmento RS e il suo punto medio K, se RK misura 8,9 cm quanto misura RS?

8,9 × 2

: 2

si può stabilire

ADDIZIONI E SOTTRAZIONI DI SEGMENTI

DATI DUE SEGMENTI AB

e CD

Come si determina il segmento somma? Come si determina il segmento differenza?

• Addizionano le misure dei segmenti

• Sottraendo le misure dei due segmenti

11 Calcola la misura del segmento somma.

12 Calcola la misura del segmento differenza.

Risolvi i seguenti problemi.

13 Dati due segmenti di 6 cm e 4 cm, disegna il segmento somma e il segmento differenza e calcola le loro misure. [10 cm; 2 cm]

14 Due segmenti misurano 34 cm e 27 cm. Dopo aver disegnato il segmento somma e il segmento differenza, calcola le loro misure. [61 cm; 7 cm]

MULTIPLI E SOTTOMULTIPLI DI segmenti

DATO UN SEGMENTO AB

Come si indicano i suoi sottomultipli?

ESEMPIO

CD è un mezzo di AB CD = 1 2 × AB

FG è un terzo di AB FG = 1 3 × AB

RS è un quarto di AB RS = 1 4 × AB

Come si disegnano?

TEORIA PAG. 58

Come si indicano i suoi multipli?

ESEMPIO ESEMPIO

CD è il doppio di AB CD = 2 × AB

EF è il triplo di AB EF = 3 × AB

LM è il quadruplo di AB LM = 4 × AB

Come si disegnano?

15 Traduci in simboli le seguenti frasi.

a) EF è il triplo di FG : c) ST è il doppio di YZ:

b) MN è il triplo di RS : d) PQ è il quadruplo di NH:

16 Disegna i segmenti indicati rispettando le consegne.

a) CD = 3 × AB

b) GH = 2 × EF

c) ST = 4 × LM

Risolvi i seguenti problemi.

(Ti suggeriamo di scrivere i dati e la richiesta, fare un disegno rispondente ai dati, evidenziando le misure conosciute, e infine risolvere il problema.)

17 Il segmento AB misura 34 cm. Quanto misura il segmento EF che è il suo doppio?

Disegno Dati

34 cm A

AB = 34 cm

EF = 2 × …

EF = ? Risoluzione

Bisogna calcolare il doppio di AB, cioè il doppio di 34:

= 2 ×

= 2 ×

18 Il segmento GH misura 18 mm e il segmento LM è il suo triplo. Calcola la misura del segmento LM [54 mm]

19 Traduci in simboli le seguenti frasi.

a) LM è un quarto di YZ:

b) PT è un terzo di AB:

20 Un segmento è un terzo di un altro segmento; se la loro somma è 60 cm, quanto è lungo ciascuno di essi?

Disegno

60 cm A C B D

Dati

AB = 1 3 × CD

AB + CD = 60 cm

AB = ?

CD = ?

Risoluzione

Quanti segmenti uguali a AB ci sono nella somma? ………

Si trova prima il segmento più corto:

AB = 60 : ……… = ………………

Poi si trova CD che è tre volte AB:

CD =

[15 cm; 45 cm]

21 La differenza di due segmenti è di 42 cm e uno è 1 4 dell’altro. Calcola le misure dei due segmenti.

Disegno B D A C

64748

42 cm

Dati

AB – CD = …………

CD = ………… × AB

AB = ?

CD = ?

Risoluzione

La differenza è divisa in …… segmentini uguali a CD

Trova la lunghezza di CD:

CD = 42 : ……… = ………… cm

AB è quattro volte CD; quindi:

AB = 4 × CD = [14 cm; .....]

prima canalina

22 MATEMATICA IN AZIONE Per predisporre un impianto elettrico, l’elettricista acquista 3 canaline passacavi di cui due di uguale lunghezza e l’altra più lunga. Se la canalina maggiore è il doppio delle altre due e la somma delle loro lunghezze è 10 m, quanto misura ognuna delle tre canaline? [2,5 m; 2,5 m; 5 m]

23 La somma di due segmenti è 98 m e la loro differenza è 14 m; quanto misura ciascun segmento?

AB + CD = 98

AB – CD = 14 m

seconda canalina

terza canalina

10 m

AB = ?

CD = ? [42 m; 56 m]

Misura del segmento più corto somma, 98, meno differenza, 14, e poi diviso 2. Misura del segmento più lungo misura del più corto più la differenza

24 Dei segmenti FG e MN conosci la somma, 64 cm, e la differenza, 12 cm. Calcola la lunghezza di FG e quella di MN [FG = 38 cm; MN = 26 cm]

piano cartesiano

DATO UN PUNTO

Scrivendo le sue coordinate (x; y) Come si stabilisce la sua posizione in un piano cartesiano?

• Immagina che il punto O sia l’entrata di un supermercato in cui si cammina solo lungo i lati dei quadretti.

Per andare al bar, fai 4 passi a destra e poi 5 verso l’alto.

Le coordinate del bar sono (4; 5).

Allo stesso modo si individuano le coordinate di un punto (lo spostamento verso destra si chiama ascissa, lo spostamento verso l’alto si chiama ordinata).

Quindi: (4; 5) (ascissa; ordinata)

25 Scrivi le coordinate dei seguenti punti, rappresentati su un piano cartesiano. (Ricorda di considerare prima l’ascissa e poi l’ordinata.)

SIMULAZIONE DI VERIFICA

1 Completa la tabella.

Definizione

Disegno Ente geometrico definito

a) segmento AB

b) È privo di dimensioni e indica una posizione nello spazio.

c) d) retta r e)

2 Rispondi con Vero o Falso.

a) Il punto ha una dimensione. V F

b) Un assioma è una proprietà che non si dimostra. V F

c) Per due punti distinti passa una e una sola retta. V F

d) Per tre punti non allineati passano infiniti piani. V F

e) La scrittura AB ≡ CD indica che i due segmenti sono coincidenti. V F

f) Due segmenti che hanno un solo estremo in comune e appartengono alla stessa retta si dicono sovrapposti. V F

3 Classifica le seguenti linee.

4 Se AB ≅ CD, CD = 9 cm, AD = 53 cm, quanto misura BC?

5 Risolvi i seguenti problemi.

a) La differenza tra due segmenti è 90 cm. Se un segmento è 3 5 dell’altro, quanto misura ciascuno di essi?

b) 10,6 dm e 4,2 dm sono le misure della somma e della differenza di due segmenti EF e GH. Calcola le loro lunghezze.

6 Scrivi le coordinate dei punti rappresentati sul piano cartesiano e poi rispondi ai quesiti.

a) Ci sono punti sugli assi? . . ..

Se sì, quali? . ................................................

b) Ci sono punti allineati?

Se sì, quali?

7 Nel piano cartesiano con unità di misura u:

a) trova l’ascissa del punto B( ; 4) sapendo che il segmento AB misura 6 u e A (5; 4);

b) sapendo che C(1; 2) e che CD = 3 u, trova l’ordinata del punto D (1; );

c) disegna poi i segmenti AB e CD

8 MATEMATICA IN AZIONE Federico per costruire un’altalena doppia utilizza 5 pali di legno di cui quattro di uguale lunghezza e il quinto lungo 1,2 m più degli altri. Se la somma delle lunghezze dei 5 pali è 11,2 m, quanto misurano i pali?

9 MATEMATICA IN AZIONE Secondo le disposizioni del regolamento governativo, le grandezze ordinarie della bandiera italiana sono tre, ma in tutti e tre i casi il lato più corto è sempre 2 3 di quello più lungo (in figura lati AB e BC ).

• Nella bandiera più grande la somma delle misure dei due lati è 7,5 m;

• in quella di grandezza media la somma è 5 m;

• in quella più piccola la somma è 2,5 m.

In ognuno dei tre casi quanto misurano i lati AB e BC ?

GLI ANGOLI UNITÀ 3

Chi ha della

paura matematica?

Non dirmi che anche gli angoli ti fanno paura! Eppure, hai a che fare con loro quotidianamente: quando apri una porta, quando giochi a calcio o a biliardo, persino quando inclini lo schermo del tuo cellulare o del tablet. Imparare a riconoscerli, misurarli e combinarli tra loro ti sarà utile, perché il tuo sguardo attento e curioso avrà uno strumento in più per osservare espiegarelarealtà! In questo momento le tue domande saranno: “Come farò a ricordarmi tutti i tipi di angoli?”, “E se sbaglio a usare il goniometro?”, “Come farò a sommare e sottrarre gli angoli, soprattutto perché sono espressi in gradi, primi e secondi?”.

Come avrai capito, sono qui a rassicurati e a liberarti da queste e da altre paure! Imparerai facilmente a riconoscere ogni tipo di angolo grazie a trucchi e associazioni che aiutano la memorizzazione e ben presto riuscirai a fare le operazioni in modo automatico. E quando tutto accadrà… andrai alla ricerca di un “angolo nel mondo” dove rifugiarti per pensare alla MATEMATICA!

ROAD MAP la nostra

DEFINIAMO I SEMIPIANI E GLI ANGOLI

CERCHIAMO LE RELAZIONI TRA GLI ANGOLI

3

MISURIAMO L’AMPIEZZA DI UN ANGOLO CON UN GONIOMETRO

2

5

INDIVIDUIAMO GLI ANGOLI PARTICOLARI

ESEGUIAMO LE OPERAZIONI TRA LE MISURE ANGOLARI

4

MATERIALE INTEGRATIVO MULTIMEDIALE

Focus

LEZIONE Semipiani e angoli 1 α

SUCCEDE CHE...

A scuola di Emma si deve comprare un supporto inclinato per esporre la bandiera italiana all’entrata dell’edificio. Nello schema a fianco è segnata in rosso l’inclinazione del supporto. Che cosa indica il simbolo α?

Il simbolo α indica sicuramente una parte di piano. Per individuarla occorre conoscere la differenza tra semipiano e angolo.

Una retta disegnata su un piano lo divide in due parti: ciascuna di esse si chiama semipiano ed è indicata con una lettera minuscola dell’alfabeto greco.

semipiano

semipiano

Un semipiano è ciascuna delle parti in cui un piano viene diviso da una retta giacente sul piano stesso.

Se su un piano disegniamo due semirette con la stessa origine, il piano viene diviso in due parti, ciascuna delle quali prende il nome di angolo

Le semirette sono i lati dell’angolo, l’origine in comune è il vertice dell’angolo e l’unica dimensione dell’angolo è la sua ampiezza

angolo concavo lato lato

vertice angolo convesso

Un angolo è ciascuna delle due parti in cui il piano viene diviso da due semirette che hanno la stessa origine e che appartengono allo stesso piano.

Osservando i due angoli ottenuti disegnando due semirette con la stessa origine, si nota che un angolo (angolo verde) contiene il prolungamento dei lati e viene detto concavo, mentre l’altro (angolo azzurro) non li contiene e viene detto convesso

Attenzione. L’angolo senza alcuna specificazione è l’angolo convesso. Vediamo come si indicano gli angoli.

Con il vertice:

• angolo convesso: O

• angolo concavo: O

Con tre punti, il punto in mezzo è il vertice:

• angolo convesso: AOB

• angolo concavo: AOB

Con una lettera minuscola greca:

• angolo convesso: α

• angolo concavo: β

L’inclinazione della bandiera della scuola non è altro che un angolo e quindi viene indicato con la lettera greca α.

1 Scrivi il termine indicato dalle seguenti definizioni.

a) Angolo che contiene i prolungamenti dei suoi lati.

b) Ciascuna delle parti in cui un piano viene diviso da due semirette aventi la stessa origine.

c) Angolo che non contiene i prolungamenti dei suoi lati.

d) Ciascuna delle due parti in cui il piano viene diviso da una retta.

2 Osserva e completa le affermazioni.

L’angolo è convesso perché

L’angolo è concavo perché

3 Osserva il seguente angolo e completa.

R T p r α

a) I lati dell’angolo sono le semirette e

b) Il vertice è il punto

c) Utilizzando il vertice, l’angolo della figura si indica con:

d) Utilizzando tre lettere, l’angolo della figura si indica con:

e) Utilizzando la lettera greca, l’angolo della figura si indica con:

4 MATEMATICA IN AZIONE Stabilisci il tipo di angolo descritto dalla lancetta delle ore negli intervalli di tempo richiesti.

a) Dalle 4 alle 9 1) concavo 2) convesso

b) Dalle 23 alle 4 1) concavo 2) convesso

c) Dalle 5 alle 13 1) concavo 2) convesso

d) Dalle 12 alle 22 1) concavo 2) convesso

Relazioni tra angoli 2

F G D LEZIONE

angolo di entrata α

SUCCEDE CHE...

di uscita

Pietro sta studiando le regole del biliardo e legge che in un tavolo regolare, colpendo la palla senza effetti, l’angolo di entrata ( α) è uguale all’angolo di uscita ( β), cioè α ≅ β. Quando la palla è colpita sulla sua parte destra, come cambia l'angolo di uscita ( γ)?

traiettoria senza effetto

Vediamo come possono essere due angoli in base alla loro posizione:

• consecutivi se hanno un lato e il vertice in comune;

vertice V in comune lato VB in comune

AVB e BVC sono consecutivi

• adiacenti se sono consecutivi e i lati non comuni sono semirette opposte;

i lati OP e OR sono semirette opposte lato OS in comune

O R

POS e SOR sono adiacenti

• opposti al vertice se i loro lati sono uno il prolungamento dell’altro e sono congruenti;

i lati in verde sono il prolungamento dei lati in nero e viceversa

≅ β' sono angoli opposti al vertice

• sovrapposti se hanno il vertice e un lato in comune e tutti i punti di un angolo appartengono anche all’altro.

vertice E in comune lato DE in comune i punti dell’angolo verde appartengono all’angolo rosso

DEF e DEG sono sovrapposti

Per effettuare il confronto di due angoli occorre sovrapporre i due angoli, per esempio confrontando i due angoli della figura si ha: DEF > DEG.

Confrontando i due angoli Pietro nota che quando la palla viene colpita sulla destra l’angolo di uscita “diminuisce”:

Primi

ESERCIZI

1 Completa le frasi relative alle figure seguenti.

a) COB e sono angoli perché hanno un lato in comune.

b) FGE e sono angoli perché hanno il lato in comune e FG e sono semirette opposte.

c) α e sono angoli al perché i lati di uno sono il dei lati dell’altro.

Gli angoli α e sono congruenti, cioè hanno la stessa

2 Disegna un angolo consecutivo a CDE e un angolo adiacente a LM ˆ N.

3 MATEMATICA IN AZIONE Osserva e rispondi.

Questo è un segnale stradale di pericolo che puoi trovare nei passaggi a livello incustoditi; si chiama Croce di Sant’Andrea.

a) Come si chiamano gli angoli che formano la croce?

b) Come sono tra di loro?

SUCCEDE CHE... LEZIONE

Ampiezza di un angolo e goniometro 3

Emma vuole disegnare un fiocco di neve. Partendo da un segmento verticale (in azzurro nella figura) deve disegnare altri due segmenti formando due angoli consecutivi ampi 60°. Come deve fare?

La dimensione dell’angolo è l’ampiezza e la sua unità di misura è il grado (°) che è l’ampiezza dell’angolo ottenuto dividendo un cerchio in 360 parti uguali La scelta di dividere il cerchio in 360 parti non è casuale perché 360 corrisponde all’incirca al numero dei giorni di un anno solare.

I sottomultipli del grado sono i primi (') e i secondi ('') e il sistema di misura che si utilizza è il sistema sessagesimale, perché i primi si ottengono dividendo il grado in 60 parti e i secondi si ottengono dividendo in 60 parti i primi

• un grado = 60 primi = 3 600 secondi in simboli 1°= 60' = 3 600''

• un primo = un 60esimo di grado = 1°: 60 in simboli 1' = 1° : 60

• un secondo = un 60esimo di primo = 1': 60 in simboli 1'' = 1' : 60

ESEMPIO

a) L’ampiezza 34° 23' 56'' si legge: 34 gradi 23 primi e 56 secondi.

b) F = 45° 12' 38'' si legge: l’angolo F è ampio 45 gradi 12 primi e 38 secondi.

Il sistema di numerazione sessagesimale veniva già usato dai Babilonesi; noi lo abbiamo conservato solo per misurare gli angoli e, in parte, il tempo.

Per misurare l’ampiezza di un angolo si utilizza il goniometro o rapportatore.

Riduzione in forma normale

L’ampiezza di un angolo si dice ridotta in forma normale quando il valore numerico dei primi e dei secondi non supera 59.

ESEMPIO

a) 23° 45' 34'' è in forma normale.

b) 45° 98' non è in forma normale perché i primi, 98, superano 59.

Per ridurre in forma normale l’ampiezza di un angolo si tolgono i 60 “in più”, si trasformano e si aggiungono all’unità di ordine superiore.

45° 98' +1° ! – 60' Si tolgono 60' da 98' e, visto che 60' = 1°, si aggiunge 1° a 45°.

46° 38'

Per disegnare il fiocco di neve, Emma deve quindi misurare gli angoli con un goniometro.

ESERCIZI Primi

1 Esegui le seguenti trasformazioni di unità di misura.

a) 1° = ' c) 1' = '' e) 240' = ° (moltiplica per 60) (moltiplica per 60) (dividi per 60)

b) 3° = ' d) 2' = '' f) 180'' = '

2 Contrassegna le misure angolari da ridurre in forma normale.

a) 56° 77' 120'' c) 15° 72' 18'' e) 33° 18' 9''

b) 22° 86' 99'' d) 47° 47' 16'' f) 83° 18' 84''

3 Riduci in forma normale le misure segnate in b) e c) nell’esercizio precedente.

ESEMPIO

56° 77' 120''

+2' ! – 120''

56° 79' 0''

+1° ! – 60'

57° 19' a) b) b)

4 MATEMATICA IN AZIONE Osserva l’areogramma che rappresenta la distribuzione dei negozi di alimentari in una città.

Angolo dei supermercati

a) Misura con il goniometro gli angoli dei tre spicchi.

Angolo dei fruttivendoli

Angolo delle gastronomie

b) Com’è l’ampiezza dell’angolo dei fruttivendoli rispetto a quella dell’angolo delle gastronomie?

c) E rispetto a quella dell’angolo dei supermercati?

ESERCIZI PAG. 126

LEZIONE Angoli particolari 4

SUCCEDE CHE...

Emma è in barca a vela e il suo istruttore le dà istruzioni. Deve effettuare un’andatura “al traverso” cioè mettere la barca in modo che il vento sia perpendicolare all’asse longitudinale dell’imbarcazione. Qual è l’ampiezza dell’angolo che la barca deve formare con la direzione del vento?

Gli angoli vengono definiti a seconda della loro ampiezza.

• Angolo nullo: 0° nullo 0°

• Angolo acuto: 0° < α < 90°

• Angolo retto: 90°

• Angolo ottuso: 90° < β < 180°

• Angolo piatto: 180°

• Angolo concavo: 180° < γ < 360°

TRAVERSO asse longitudinale

Un angolo è nullo se è ampio 0°.

I lati dell’angolo nullo sono coincidenti.

Un angolo è acuto quando la sua ampiezza è minore di 90°.

I lati dell’angolo acuto sono consecutivi.

Un angolo è retto se è ampio 90°.

I lati dell’angolo retto sono consecutivi e si dicono perpendicolari. Per indicare l’angolo retto si utilizza uno dei seguenti simboli: o

Un angolo è ottuso quando la sua ampiezza è maggiore di un angolo di 90° e minore di un angolo di 180°.

I lati dell’angolo ottuso sono consecutivi.

Un angolo è piatto se è ampio 180°.

I lati di un angolo piatto sono adiacenti.

Un angolo è concavo quando la sua ampiezza supera i 180° ed è minore di 360°.

I lati di un angolo concavo sono consecutivi.

• Angolo giro: 360°

Un angolo è giro quando è ampio 360°.

I lati di un angolo giro sono sovrapposti.

La barca deve formare con la direzione del vento un angolo ampio 90°.

1 Riconosci i seguenti angoli: acuto, retto, ottuso, piatto.

2 Completa le seguenti definizioni.

a) Un angolo di 90° è

b) Un angolo minore di un angolo retto è

c) Un angolo è ottuso se è maggiore di e minore di

d) Un angolo di 360° è

e) Un angolo che ha ampiezza uguale a zero è

f) Un angolo concavo è maggiore di e minore di

3 MATEMATICA IN AZIONE In commercio esistono soluzioni diverse per irrigare i giardini in modo tale da risparmiare tempo, fatica e soprattutto acqua, che è un bene prezioso.

I disegni illustrano il getto di alcuni tipi di irrigatore.

Irrigatore a 90°

Irrigatore a 180°

ADDIZIONI E SOTTRAZIONI DI ANGOLI 5

SUCCEDE

CHE...

Osservando un’altalena che dondola si nota come essa forma con il perno centrale due angoli, α e β, che variano con il movimento.

Ma c’è una misura che rimane sempre uguale: quale?

Per rispondere alla domanda occorre conoscere i casi particolari dell’addizione.

Addizione

• Per disegnare l’angolo somma basta disporre i due angoli in modo che siano consecutivi.

• Per sommare due misure angolari, si mettono in colonna in modo da addizionare separatamente i secondi con i secondi, i primi con i primi, i gradi con i gradi. Se necessario, si riduce il risultato in forma normale.

ESEMPIO

8° 29’ 45’’ + 38° 52’ 49’’

Si dispongono in colonna le unità dei vari ordini (gradi, primi, secondi) e si eseguono le addizioni separatamente:

8° 3 29' 45'' +

38° 52' 49'' =

46° 81' 94''

In questo caso il risultato si deve ridurre in forma normale:

46° 81' 94'' – si tolgono 60’’ che si trasformano in 1' 1' 60'' =

46° 82' 34'' si tolgono 60’ che si trasformano in 1°

1° 60' =

47° 22' 34'

Quindi:

8° 29' 45'' + 38° 52' 49' = 47° 22' 34''

Sottrazione

• Per disegnare l’angolo differenza occorre sovrapporre i due angoli.

Anche per sottrarre due misure angolari occorre metterle in colonna e sottrarre separatamente i secondi, i primi e i gradi.

Se, però, nei primi o nei secondi il minuendo è minore del sottraendo, è necessario che un’unità di ordine superiore venga trasformata in un’unità di ordine inferiore (1° si trasforma in 60', 1' si trasforma in 60''): è il cosiddetto “prestito” della sottrazione.

ESEMPIO

121° 56' 12'' – 14° 32' 34''

Si dispongono in colonna le unità dei vari ordini (gradi, primi, secondi).

La sottrazione dei secondi non si può fare; si trasforma 1' in 60''. (i primi prestano 60’’ ai secondi)

55’ 72’’

121° 56' 12'' – a 56' si toglie 1' = 60''; a 12'' si aggiunge 60''

14° 32' 34'' =

107° 23' 38''

Quindi:

121° 56' 12'' – 14° 32' 34'' = 107° 23' 38''

Casi particolari dell’addizione

Due angoli sono complementari se la loro somma è uguale a un angolo retto.

α = 70° e β = 20° sono complementari; infatti α + β = 70° + 20° = 90°.

Due angoli sono supplementari se la loro somma è uguale a un angolo piatto.

α = 145° e β = 35° sono supplementari; infatti α + β = 145° + 35° = 180°.

Due angoli sono esplementari se la loro somma è uguale a un angolo giro.

α = 30° e β = 330° sono esplementari; infatti α + β = 30° + 330° = 360°.

+ β = 90°

+ β = 180°

I due angoli, α e β , che l'altalena forma mentre dondola sono supplementari: la loro somma è sempre 180°.

1 Scegli l’incolonnamento esatto e risolvi le seguenti operazioni.

a) 45° 12' 26'' + 32' 31''

45° 12' 26'' + 45° 12' 26'' +

12' 26'' + 32' 31'' = 32' 31'' = 32' 31'' =

b) 61° 24' 58'' – 27° 38''

24' 58''

38'' =

=

=

2 Contrassegna le sottrazioni che richiedono il “prestito”, poi metti in colonna ed eseguile.

ESEMPIO

Senza “prestiti”

92° 54' 31'' – 64° 42' 11''

• Si dispongono in colonna

• Si eseguono le sottrazioni separatamente

92° 54' 31'' –64° 42' 11'' = 28° 12' 20''

a) 105° 37' 43'' – 67° 30' 40''

Con “prestiti”

34° 44' 12'' – 24° 20' 32''

• Si dispongono in colonna

• A 44' si toglie 1' e si aggiungono 60'' a 12'' 43' 72''

34° 44' 12'' –

24° 20' 32'' = 10° 23' 40''

c) 56° 55' 54'' – 18° 58' 55''

b) 92° 38' 24'' – 90° 15' 21'' d) 34° 43' 7'' – 30° 49' 11''

3 Osserva le figure e completa con le parole: complementare, esplementare, supplementare.

a) L’angolo β è dell’angolo α b) L’angolo β è dell’angolo α c) L’angolo β è dell’angolo α

4 Facendo riferimento all’esercizio precedente, completa le frasi.

a) Due angoli sono complementari se la loro

è uguale a un angolo in gradi

b) Due angoli sono esplementari se la loro

è uguale a un angolo in gradi

c) Due angoli sono supplementari se la loro

è uguale a un angolo in gradi

5 MATEMATICA IN AZIONE Riconosci le coppie di angoli complementari e supplementari.

SUCCEDE CHE...

Pietro osserva una ruota panoramica. Rispetto all’angolo AOB, che cosa può dire del braccio OP?

Dati due angoli, il maggiore è multiplo del minore se lo contiene un numero esatto di volte. Per esempio, l’angolo γ è multiplo dell’angolo α secondo il numero 5 e si scrive γ = 5 × α.

Il sottomultiplo di un angolo, invece, è contenuto un numero esatto di volte nell’angolo dato. Nell’esempio precedente α è un sottomultiplo di γ e si scrive α = 1 5 × γ

Per trovare l’ampiezza di multipli o sottomultipli di angoli occorre eseguire delle moltiplicazioni o delle divisioni.

Moltiplicazione

Per moltiplicare una misura angolare per un numero occorre moltiplicare separatamente per quel numero i gradi, i primi e i secondi e, se necessario, ridurre in forma normale il risultato ottenuto.

Divisione

Per dividere una misura angolare per un numero, si dividono separatamente per quel numero i gradi, i primi e i secondi. Se vi sono gradi o primi di resto, vanno trasformati nell’unità di misura immediatamente inferiore e aggiunti a quelli del dividendo, prima di eseguire la divisione successiva.

ESEMPIO (21° 34' 23'') × 3 21° 34' 23'' × 3 = 63° 102' 69 '' Il risultato va ridotto in forma normale, quindi: (21° 34' 23'') × 3 = 64° 43' 9''

La bisettrice

65° 14' 16'' : 8 65° 14' + 16'' + : 8 = 8° 9' 17'' 1° $ 60' = 120'' = 74' 136'' 2'

Quindi (65° 14' 16'') : 8 = 8° 9' 17''

La bisettrice di un angolo è una semiretta che ha l’origine nel vertice dell’angolo e lo divide in due parti congruenti. La bisettrice di un angolo è il suo asse di simmetria.

Pietro può dire che il braccio OP è la bisettrice dell’angolo AOB.

1 Esegui le seguenti moltiplicazioni riducendo in forma normale quando è necessario.

a) 32° 3' 45'' × 4 = ridotto in forma normale b) 34' 49'' × 3 = ridotto in forma normale

2 Esegui le seguenti divisioni.

ESEMPIO

(23° 13' 32'') : 4

23° 13' + 32'' + : 4 = 5° 48' 23''

3° $ 180' = 60'' = 193' 92'' 1'

Quindi (23° 13' 32'') : 4 = 5° 48' 23''

a) (49° 21' 63'') : 7

Esegui tre divisioni 49 : ; 21 : e 63 : ; sono tutti multipli di 7 quindi:

(49° 21' 63'') : 7 = ° ' ''

b) (28° 15') : 3 = ° '

c) (113° 17' 14'') : 2 = ° ' ''

3

STEM Esegui le seguenti divisioni “naturali”.

Giglio di mare è il nome dato a un echinoderma (Comatula, un animale marino simile alla stella marina) e al fiore di una pianta (Pancratium maritimum) dei litorali sabbiosi.

L’echinoderma Giglio di mare ha 10 braccia che partono dal corpo centrale. Se lo immagini appoggiato immobile su un angolo giro, questo viene diviso in 10 parti.

Quanto è ampio l’angolo delimitato da due braccia consecutive?

° : 10 =

Il fiore del Giglio di mare, bianco e molto profumato, ha 6 tepali lunghi (lacinie) alla base di una corona con 12 piccoli denti.

Se lo immagini appoggiato immobile su un angolo giro, questo viene diviso in 6 e in 12 parti. Calcola le ampiezze di queste parti.

° : 6 =

° : =

Convesso simbolo

MAPPA

Concavo simbolo 1° = 60'

può essere

Giro (360°)

Primo (')

Secondo ('') 1' = 60''

Grado (°) 3 600'' = 1°

le unità di misura sono

AMPIEZZA

la grandezza che si misura si chiama

ANGOLO

in base all’ampiezza un angolo può essere

Piatto (180°)

Retto (90°)

due angoli possono essere

Opposti al vertice b b'

Consecutivi

Acuto <90°

rispetto all’angolo retto un angolo può essere

Ottuso >90°

Adiacenti

Complementari (la somma è 90°)

Supplementari (la somma è 180°)

Esplementari (la somma è 180°)

LEZIONE

1 ESERCIZI E PROBLEMI

SEMIPIANI E ANGOLI

1 Rispondi con Vero o Falso.

a) Il semipiano è delimitato da una retta.

b) I lati di un angolo sono rette.

c) Un angolo si può indicare con una lettera greca.

d) Il vertice di un angolo è un punto.

e) Un angolo si può indicare anche con tre lettere minuscole.

f) Un angolo convesso contiene i prolungamenti dei suoi lati.

g) Un angolo concavo è delimitato da due semirette.

h) Un angolo ha due dimensioni.

2 Osserva il disegno e completa.

a) α indica un: 1) piano 2) semiretta 3) angolo

b) r indica una: 1) retta 2) semiretta 3) linea curva

c) β indica un: 1) piano 2) semipiano 3) angolo

3 Osserva i seguenti angoli e completa la tabella.

4 Indica con delle lettere a tuo piacere i lati e il vertice dei seguenti angoli.

5 Prolunga i lati dei seguenti angoli e identifica quelli concavi e quelli convessi.

6 MATH Observe the drawing and complete the following statements.

a) The sides of the AOC angle are

b) The sides of the AOB angle are

c) The sides of the BOC angle are

d) The vertex of the AOC angle is

e) The AOB angle is marked with the Greek letter

f) The BOC angle is marked with the Greek letter

7 Nelle seguenti figure segna gli angoli con degli archetti in modo che le scritture siano vere.

a) SVT = concavo b) AOB e COD = convessi c) MPR = convesso, MPR = concavo

RELAZIONI TRA ANGOLI LEZIONE 2

8 Rispondi con Vero o Falso.

a) α e β sono sovrapposti.

b) γ e δ sono adiacenti.

c) γ e δ sono sovrapposti.

d) AOC e COB sono consecutivi.

e) Le semirette OA e OB sono opposte.

f) Le semirette PR e PM sono opposte.

g) SOR ≅ POT

h) TOR ≅ POT

i) Le semirette OS e OR sono opposte.

l) POS e TOR sono opposti al vertice.

9 Osserva la figura e completa le seguenti affermazioni.

a) α e β sono

b) α e δ sono

c) β e γ sono

d) γ e δ sono

10 MATH Consider the following figure and indicate whether the statements are true or false.

F

F

F

F

F

F

F

F

a) The angles γ and β are vertical angles. T F

b) The angles δ and γ are vertically opposite angles. T F

c) α ≅ β T F

d) γ = 148° and α = 148°. T F

e) α = 29° and β = 29°. T F

11 Quali fra le seguenti sono coppie di angoli consecutivi? Gli angoli sono segnati in rosso. a) b) c) d)

12 Quali fra le seguenti sono coppie di angoli adiacenti? Gli angoli sono segnati in rosso. a) b) c) d)

13 Osserva il seguente disegno e individua:

a) tutte le coppie di angoli opposti al vertice;

b) tutte le coppie di angoli adiacenti.

a) b)

14 Per ogni coppia di angoli indica la relazione esistente. a) b) c)

15 MATEMATICA IN AZIONE Osserva le coppie di angoli evidenziati in colore e indica la relazione che c'è tra essi.

Disegna rispettando le richieste.

16 Disegna due angoli consecutivi e indicali con i simboli che ritieni opportuni.

17 Disegna due angoli aventi lo stesso vertice ma non consecutivi.

18 Disegna due angoli consecutivi ma non adiacenti.

19 Disegna tre angoli tali che il primo e il secondo siano consecutivi e il terzo sia adiacente al secondo.

20 Disegna tre angoli in modo che il primo e il secondo siano consecutivi e il terzo abbia il vertice comune ai primi due, ma non sia consecutivo né al primo né al secondo.

AMPIEZZA DI UN ANGOLO E GONIOMETRO

21 Completa le seguenti affermazioni.

a) Un grado corrisponde a …………… primi e a …………… secondi.

b) Un primo corrisponde a di grado.

c) Un secondo corrisponde a di primo e a di grado.

d) Le ampiezze degli si misurano con un sistema che si chiama perché per trasformare i gradi in primi o in e viceversa si deve o dividere per

e) Per misurare lampiezza di un si utilizza il

22 MATH Complete the following diagram.

degrees (symbol

minutes (symbol

seconds (symbol

23 Completa le frasi inserendo i termini mancanti.

a) Lampiezza di un angolo si dice ridotta in forma normale quando il valore numerico dei

e dei

non supera

b) Per ridurre in forma normale lampiezza di un angolo si tolgono i “in più”, si trasformano e si aggiungono allunità

24 Scrivi in lettere le seguenti misure angolari, come nell’esempio.

a) 34° 21' 46''

b) 145° 26''

c) 56' 31''

d) 27° 75' 17''

e) 348° 57'

trentaquattro gradi; ventuno primi; quarantasei secondi

Completa le seguenti uguaglianze riferite a misure angolari.

ESEMPIO

a) 7° = (7 × 60) primi = 420 primi c) 240' = (240 : 60) gradi = 4 gradi b) 7 200'' = (7 200 : 3 600) gradi = 2 gradi

25 a) 21° = primi b) 300 ' = gradi

26 a) 37° = primi b) 154 800'' = gradi

27 a) 7' = secondi b) 42° = primi

28 a) 1 140' = secondi b) 3 600' = gradi

29 a) 100 800'' = gradi b) 180° = primi

30 a) 1 200' = secondi b) 720'' = primi

(21 × 60' = 1 260'; 1 260' + 5' = ………)

31 a) 21° 5' = primi b) 5° 31' = primi c) 13° 44' = …………………………………………………………… primi

32 a) 8' 13'' = ………………… secondi c) 14' 25'' = ………………… secondi b) 10' 31'' = secondi d) 7° 36'' = secondi

PUNTI FERMI

MISURARE ANGOLI CON IL GONIOMETRO

Per misurare lampiezza di un angolo si fa coincidere il centro del goniometro con il vertice dellangolo e si fa in modo che un lato dellangolo passi per la tacca del goniometro che indica lo zero. Si legge lampiezza dellangolo in corrispondenza dellaltro lato. Langolo COA della figura è ampio 75°.

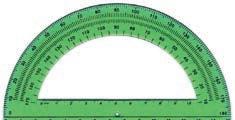
Misura con il goniometro l’ampiezza di ognuno dei seguenti angoli e riportala sotto.

35 Misura con il goniometro le ampiezze di tutti gli angoli convessi della seguente figura.

AOB = BOC =

COD = AOD =

AOC = BOD =

36 Misura i due angoli e completa utilizzando il simbolo adeguato (> o <).

a) α

37 Misura le ampiezze degli angoli dell’illustrazione e completa le affermazioni con i simboli adeguati (<; >).

a)

b)

38 STEM I venti vengono classificati secondo la direzione da cui provengono e vengono rappresentati dalla rosa dei venti. Nell’area mediterranea prendono nomi particolari.

a) Segna il Nord (N) a 360°, il Sud (S) a 180°, lEst (E) e lOvest (O) rispettivamente a 90° e a 270°.

b) Colloca i venti rispetto allangolo formato e scrivi il punto cardinale corrispondente.

• Grecale a 45°

• Levante a 90°

• Scirocco a 135°

• Mezzogiorno a 180°

• Libeccio a 225°

• Ponente a 270°

• Maestrale a 315°

• Tramontana a 360°

Costruisci sul tuo quaderno gli angoli proposti utilizzando il goniometro.

PUNTI FERMI

DISEGNARE ANGOLI UTILIZZANDO IL GONIOMETRO

Lillustrazione ti spiega come utilizzare il goniometro per costruire angoli di ampiezza data. Per realizzare un angolo di 100°:

1) Si traccia una retta a e si segnano il vertice O e il punto D.

2) Si posiziona il goniometro in modo che il suo centro coincida con O e OD passi dallo zero.

3) Si segna C in corrispondenza di 100° e, tolto il goniometro, si congiunge C con O.

39 α = 65° β = 25° γ = 70° LMN = 90°

40 EFG = 110° O = 210° P = 245° S = 105°

41 Disegna sul tuo quaderno un angolo A di ampiezza 60°. Costruisci, poi, il suo opposto al vertice e misura le ampiezze di tutti gli angoli che si sono originati sul piano.

42 Dopo aver misurato i seguenti angoli, per ognuno di essi disegna un angolo congruente.

Riduci in forma normale le seguenti misure angolari.

ESEMPIO

a) 97' " 97' : 60 = 1° resto 37' " 97' = 1° 37' oppure 97'" 97' − 60' = 37' e poiché 60' = 1° " 97' = 1° 37' b) 138'' " 138'' : 60 = 2' resto 18'' " 138'' = 2' 18'' oppure 138'' " 138'' − 120'' = 18'' e poiché 120'' = 2' " 138'' = 2' 18’’

43

46 a) 73° 37' 73''

47 a) 18° 75' 26'' b) 78° 112' 44''

48

49

51

52 a) 128° 63' 60'' b) 12° 60' 3 600''

24 048'' Si dividono i secondi per 60

048'' : 60 = 400' resto 48'' Si dividono per 60 i primi trovati 400' : 60 = 6° resto 40' Quindi: 24 048’’ = 6° 40' 48''

LEZIONE 4

ANGOLI PARTICOLARI

59 Indica quale dei seguenti angoli è acuto, quale ottuso, quale retto e quale piatto.

60 MATH Find the correct size of the angle.

a) Right angle 1) 0°

b) Null (or zero) angle

c) Straight angle

d) Full angle

e) Acute angle

90°

> 90°

> 180° 3) < 90°

f) Obtuse angle 1) > 360° 2) > 90° 3) < 90°

61 Rispondi alle seguenti domande.

a) Come sono i lati di un angolo nullo?

b) Come sono i lati di un angolo ottuso?

c) Come sono i lati di un angolo piatto?

d) Come sono i lati di un angolo giro?

e) Con quali simboli si indica un angolo retto?

62 Completa la seguente tabella, segnando con una crocetta la casella che ritieni esatta.

63 Dopo aver indicato i seguenti angoli con le tre lettere, classificali rispetto alla loro ampiezza.

64 MATEMATICA IN AZIONE Classifica gli angoli evidenziati nelle immagini rispetto alla loro ampiezza.

65 EDUCAZIONE CIVICA Osserva e rispondi.

Giorgio prova la sua nuova automobile. Quello in figura è il tachimetro che ne misura la velocità in km/h.

a) Da fermo la lancetta punta sullo 0, a quale velocità andrà quando la lancetta avrà percorso un angolo retto?

b) La velocità massima in autostrada è 130 km/h: se la lancetta disegna un angolo piatto, Giorgio prenderà la multa?

c) Ammesso che Giorgio vada alla velocità massima, che angolo disegnerà la lancetta?

66 MATEMATICA IN AZIONE Per ogni situazione indica il valore toccato dalla lancetta quando percorre un angolo retto e un angolo piatto. a) b)

1) Angolo retto:

1) Angolo retto: 2) Angolo piatto: 2) Angolo piatto:

67 Disegna la lancetta dei minuti in modo che l’angolo sia quello indicato.

Calcola l’ampiezza degli angoli incogniti e classificali.

ESEMPIO

Gli angoli opposti al vertice sono congruenti!

angolo acuto

ADDIZIONI E SOTTRAZIONI DI ANGOLI

70 Completa le frasi mettendo i termini mancanti scelti tra i seguenti.

colonna • consecutivi • inferiore • primi • separatamente • sottraendo • sovrapporli • superiore

a) Per sommare due misure angolari si dispongono in le unità dei vari ordini (gradi, e secondi) e si eseguono le addizioni Se in una sottrazione i primi e/o i secondi del minuendo sono minori di quelli del …………………………. occorre che ununità di ordine ………………………….. venga trasformata in ununità di ordine

b) Per ottenere graficamente langolo somma occorre disporre i due angoli in modo che siano

c) Per sottrarre graficamente due angoli occorre

71 Completa le seguenti affermazioni.

a) Due angoli sono complementari se

b) Due angoli sono supplementari se

c) Due angoli sono esplementari se

72 Osserva la figura e riconosci gli angoli complementari, supplementari, esplementari.

a) DOC e COA •

b) COB e BOA

c) DOE e EOF

d) DOF e FOD

e) COA e AOF

f) FOD e DOC

g) COB e BOC

h) DOB e BOA

73 Esegui le addizioni e riconosci la risposta corretta. a)

13° 15'' + 24° 18' 52''

15'' +

Esegui le seguenti addizioni.

74

75 a) 73° 54' 40'' + 4° 23' 37'' c) 115° 57' 52'' + 48° 63'' b) 5° 38'' + 40° 30' d) 70° 28' 17'' + 45° 58''

76 a) 7° 44' 59'' + 82° 47' 52'' c) 32° 59'' + 132° 32' 14'' b) 52° 18' 12'' + 43° 56' d) 43° 43' + 17' 46''

77 Esegui le sottrazioni e riconosci la risposta corretta.

25° 33'' – 15° 47''

24° 59 ' 93''

25° 33'' –

15° 47'' = 9° 59' 46''

a) 46' 54'' – 56' 44'' = 1) impossibile 1) 10' 10'' 3) 10''

b) 58° 35'' – 18° 35' = 1) 40° 2) 39° 25' 35'' 3) impossibile

c) 103° 54'' – 24' 44'' = 1) 36' 10'' 2) 79° 10'' 3) 102° 36' 10'' d) 59° 59' 59'' – 10° 20' 30'' = 1) impossibile 2) 49° 39' 29'' 3) 39° 29' 19''

Esegui le seguenti sottrazioni.

78 a) 75° 46' 25'' – 39° 28' 22''

●●●

c) 57° 56' 51'' – 48° 46' 48''

b) 83° 35' 43'' – 60° 31' 43'' d) 79° 58' 29'' – 17° 42' 16''

79 a) 45° 37' 25'' – 24° 8' 35'' c) 106° 24' 22'' – 72° 25' 22'' b) 63° 44' 53'' – 31° 45' 57'' d) 65° 43' – 41° 43''

80 a) 143° 11'' – 75° 16' 32'' c) 5° 30' – 55' 45''

b) 126° – 100° 35' 53''

d) 7° – 37' 50''

81 Calcola le ampiezze degli angoli AOC , BOD e AOD utilizzando le misure indicate nel disegno.

AOC =

BOD =

AOD =

Le operazioni con gli angoli sono un punto critico: gli angoli richiedono di lavorare con il sistema sessagesimale (gradi, primi e secondi) e di fare calcoli in base 60, una base insolita, diversa dalla base 10 (60 primi = 1 grado, 60 secondi = 1 primo).

Se ci pensi bene, però, questo tipo di calcolo non ti è del tutto estraneo. Il sistema sessagesimale, infatti, è usato anche per misurare il tempo: come ben sai, 60 secondi formano un minuto e 60 minuti formano

un’ora. Questa analogia con le unità di misura degli angoli potrebbe aiutarti a ridurre gli errori di distrazione. L’errore più comune nelle operazioni di addizione e sottrazione è quello di dimenticare i “riporti” e i “prestiti”. Fai pratica usando un approccio passo dopo passo: inizia sempre da destra, cominciando dai secondi, passando poi ai primi e infine ai gradi; e non dimenticare i “riporti” e i “presiti” in base 60, segnandoli con una matita.

82 Calcola le ampiezze degli angoli BOD , BOC e AOC utilizzando le misure indicate.

AOD = 116° 43' AOB = 29° 50' COD = 37° 30'

BOD =

BOC = ……………………………………………………

AOC =

83 Indica l’angolo somma degli angoli assegnati.

a) ABC + CBD = AOB + BOC + COA =

b) EFG + GFE = ………………………… AOB + BOC + COD =

84 Utilizzando il goniometro, costruisci sul tuo quaderno l’angolo somma e l’angolo differenza.

85 Osserva il disegno, conferma le affermazioni esatte e correggi quelle errate.

a) α e β sono supplementari. V F

b) β , γ e δ sommati danno 180°. V F

c) α , β e γ sommati danno 180°. V F

d) γ e δ sono complementari. V F

e) β e δ sono consecutivi. V F

f) β è ottuso. V F

g) δ è acuto. V F

Disegna gli angoli e rispondi.

86 Disegna sul tuo quaderno due angoli, uno retto e uno acuto, e determina il loro langolo somma. Langolo ottenuto è convesso o concavo?

87 Disegna sul tuo quaderno due angoli, uno retto e uno acuto. Langolo differenza è acuto o ottuso?

88 Disegna sul tuo quaderno due angoli ottusi e determina il loro angolo somma. Langolo ottenuto è convesso o concavo?

89 Disegna sul tuo quaderno due angoli, uno retto e uno ottuso, e determina il loro langolo somma. Langolo ottenuto è convesso o concavo?

Esegui le richieste e rispondi.

90 Disegna langolo complementare allangolo dato.

91 Disegna langolo supplementare allangolo dato.

92 Disegna langolo esplementare allangolo dato.

93 Disegna sul tuo quaderno un angolo di 40°. Quanto misura il suo complementare? E il suo supplementare? Disegna e classifica tali angoli.

94 Disegna sul tuo quaderno un angolo B di 45°, calcola lampiezza del suo complementare, del suo supplementare e classifica gli angoli ottenuti.

95 Disegna sul tuo quaderno un angolo di 110°. Esiste il suo complementare? E il suo supplementare? In caso affermativo, illustra le risposte.

96 Esegui la somma delle seguenti coppie di misure e individua quali rappresentano angoli complementari, supplementari o esplementari.

a) 36° + 54°

b) 245° + 115°

c) 123° + 57°

d) 45° + 45°

97 Fra le seguenti coppie di angoli individua quelli complementari.

98 Determina l’ampiezza del complementare di ognuno dei seguenti angoli.

Determina l’ampiezza del complementare di ognuno dei seguenti angoli.

99 Se α e β sono angoli complementari, completa le richieste.

Angolo α Complementare di α Angolo α Complementare di α

a) α = β × 2

= β × 4

× 3

= 90° : 3 =

100 MATEMATICA IN AZIONE Nell’orologio a lato gli angoli formati dalla lancetta delle ore con quella dei secondi e dalla lancetta dei minuti con quella dei secondi sono complementari.

Se a e b sono angoli complementari, completa le richieste. a)

× 2 allora

= 90° : 3

=

=

× 4

Individua le ampiezze dei due angoli.

101 Individua le coppie di angoli supplementari.

Individua le coppie di angoli supplementari.

102 Determina l’ampiezza del supplementare di ognuno dei seguenti angoli.

Determina l’ampiezza del supplementare di ognuno dei seguenti angoli.

103 Se α e β sono angoli supplementari, completa le richieste.

Se a e b sono angoli supplementari, completa le richieste.

a)

=

× 5 allora

× 5

× 3

= β × 7

= 180° : 6 =

Traccia la bisettrice di ognuno dei seguenti angoli.

104 MATEMATICA IN AZIONE L’immagine mostra il ponte progettato dall’architetto Santiago Calatrava, inaugurato nel 2018 a Cosenza. Il pilone di acciaio, alto 104 metri, è inclinato di 51° rispetto al piano stradale. Quanto misura langolo supplementare?

105 MATEMATICA IN AZIONE La barca raffigurata proviene dal corso d’acqua laterale e per immettersi in quello in cui sta navigando ha effettuato una “virata”. Tenendo conto del disegno e del dato indicato, calcola ampiezza della “virata” (x°).

MOLTIPLICAZIONI

E

DIVISIONI

DI ANGOLI

106 Completa le seguenti frasi scrivendo i termini mancanti scelti tra quelli indicati.

dividendo • esatto • gradi • moltiplicano • multiplo • secondi • sottomultiplo • trasformano • 60

a) Dati due angoli, il maggiore è del minore se lo contiene un numero di volte.

b) Il di un angolo è contenuto un numero esatto di volte nellangolo dato.

c) Per moltiplicare una misura angolare per un numero si separatamente per quel numero i , i primi e i

d) Se in una divisione di una misura angolare per un numero vi sono gradi o primi di resto, si nellunità di misura immediatamente inferiore, moltiplicandoli per , e si aggiungono a quelli del

107 Come si chiama la semiretta a della figura?

Scrivi la definizione.

13° 30' 13° 30' a

Ricopia la figura su un foglio e piegalo lungo la semiretta. Che proprietà hai verificato?

Rispondi con Vero o Falso. 108 a)

ESEMPIO

(15° 31') × 4

(15° 31' × 4 =

(60° 124' " 62° 4'

Esegui le seguenti moltiplicazioni.

112

114 MATH Calculate what is required.

3

115 Individua la risposta corretta.

116 MATEMATICA IN AZIONE Nei seguenti modelli di fiocco di neve, l’angolo giro è diviso in 8 o 6 parti. Calcola l’ampiezza di ogni parte.

117 Esegui le divisioni e riconosci la risposta corretta.

118 STEM Calcola ciò che è richiesto.

a) I quattro angoli raffigurati sono congruenti e hanno il vertice A in comune.

Calcola la loro ampiezza.

b) I sei angoli raffigurati sono congruenti e hanno il vertice P in comune.

Calcola la loro ampiezza.

c) I tre angoli raffigurati sono congruenti e hanno il vertice R in comune.

Calcola la loro ampiezza.

Esegui le seguenti divisioni.

119 a) (28° 46' 34'') : 2 b) (102° 84' 96'') : 4 c) (93° 45' 33'') : 3 d) (95° 45' 40'') : 5

120 a) (38° 12' 20'') : 4 b) (100° 6' 55'') : 11 c) (145° 24'') : 3 d) (212° 17'') : 7

121 a) (49° 22' 40'') : 8 b) (76° 16' 10'') : 5 c) (47° 15')

●●● ESEMPIO 3 5 di 162° 42 ’ 20 ’’ (162° 42 ’ 20 ’’) : 5 × 3 = (32° 32 ’ 28’’) × 3 = 97° 37’ 24’’

4 di 21° 18' 24'' c) 3 8 di 26° 2' 8''

Esegui le seguenti espressioni con misure angolari.

ESEMPIO

Usa le regole di precedenza delle espressioni con i numeri naturali. (68° 27' + 5° 58' 48'') : 4 × 5 = = (73° 85' 48'') : 4 × 5 = = (18° 36' 27'') × 5 = = 90° 180' 135'' in forma normale: 93° 2' 15''

124 a) (180° – 89° 13' 45'') : 3 b) (24° 36' 9'') × 2 + 6° 24'

●●●

125 36° 17' 28'' – [6° 14' 50'' + 2 × (72° 12' 15'' – 70° 24' 10'')] × 2 3 [29° 43' 28'']

126 (5° 10' 22'' + 45° 28' 12'') × 2 – 98° 30' 20''] : 2 + 10° 40' 50'' [12° 4' 14'']

Risolvi i seguenti quesiti.

ESEMPIO

L’angolo α misura 34°; quanto è ampio un angolo che è il suo triplo?

Indicando con β l’angolo incognito, si ha:

β = α × 3 e quindi β = 34° × 3 = 102°

127 Il quadruplo di un angolo di 34° è un angolo acuto o ottuso? Perché?

128 Quanto misura un angolo γ se il suo triplo è un angolo retto?

129 Quanto misura il sottomultiplo secondo il numero 4 di un angolo piatto? È un angolo acuto o ottuso? Perché?

130 Come si chiama e quanto misura un quarto di angolo giro?

131 Come si chiama e quanto misura la metà di un angolo piatto?

132 Un angolo misura 69°; quanto misura un angolo che è il suo doppio?

PUNTI FERMI

DISEGNARE LA BISETTRICE DI UN ANGOLO

Per tracciare la bisettrice dellangolo MON si procede nel modo seguente:

1) Con apertura a piacere del compasso si punta nel vertice O dellangolo e si traccia un arco in modo da intersecare i lati OM e ON nei punti A e B

2) Con la stessa apertura si punta il compasso in A e si traccia un piccolo arco nella parte centrale dellangolo. Si ripete la stessa procedura puntando il compasso in B e tracciando un secondo arco che interseca il primo. Si indica con P lintersezione tra i due archi.

3) Si traccia la semiretta che ha origine in O e passa per il punto P. Tale semiretta è la bisettrice dellangolo.

133 Utilizza il compasso per tracciare la bisettrice dei seguenti angoli.

134 Considera l’angolo α , gli angoli β e γ ottenuti tracciando la sua bisettrice f e completa la tabella.

Risolvi i seguenti quesiti.

135 Un angolo misura 49°; quanto misurano gli angoli in cui è diviso dalla bisettrice?

136 Disegna le bisettrici degli angoli AOB e AOB (convesso e concavo), raffigurati nel disegno ed effettua le osservazioni del caso.

137 La bisettrice divide un angolo β in due angoli ampi 59° 30'. Quanto misura langolo β? È un angolo acuto o ottuso?

Proprietà dei punti della bisettrice Fissati due punti A e B sui lati di un angolo in modo che abbiano la stessa distanza dal vertice, tutti i punti della bisettrice hanno la stessa distanza da A e da B, cioè: se AO  BO allora PA  PB; SA  SB ...

138 Osserva la figura, in cui la semiretta t è la bisettrice dell’angolo PAR , e rispondi alle domande.

Come sono tra loro i segmenti BP e BR, CP e CR, DP e DR, EP ed ER ? Per quale motivo?

Risolvi i seguenti problemi.

139 MATEMATICA IN AZIONE La lancetta delle ore, partendo dalla posizione 12, ha descritto un angolo come quello rappresentato nella figura.

Quanto è ampio langolo?

Quanto misura la sua metà?

140 Due angoli misurano rispettivamente 46° e 134°. Quanto misura la loro somma? Come sono gli angoli?

141 Quanto misura la differenza tra due angoli di 357° e 240°?

142 Un angolo è ampio 79°; calcola lampiezza di un angolo che è il suo doppio. Quanto misura la loro somma? E la loro differenza?

143 La somma di due angoli è 92° 56'. Sapendo che il primo è ampio 48° 16', calcola lampiezza del secondo angolo. [44° 40']

144 Sapendo che la differenza tra due angoli è 45° 27' 33'' e che langolo maggiore è ampio 88° 33' 45'', calcola lampiezza dellangolo minore. [43° 6' 12'']

145 Langolo C misura 49° 27'. Calcola lampiezza degli angoli formati dalla bisettrice. [24° 43' 30'']

ESEMPIO

Due angoli supplementari sono uno il doppio dell’altro. Calcola le loro ampiezze.

Chiamiamo α e β i due angoli:

• essendo supplementari α + β = 180°

• essendo uno il doppio dell’altro β = 2 × α

Per illustrare graficamente i due angoli puoi usare la rappresentazione con i segmenti già utilizzata nell’unità precedente.

Rappresentazione grafica

Risoluzione

Poiché la somma è divisa in tre parti congruenti ad α:

α = 180° : 3 = 60°

β = 60° × 2 = 120°

Un angolo misura 60° e l’altro 120°.

146 Calcola lampiezza di un angolo che è la quarta parte del suo supplementare. [36°]

147 I due angoli rappresentati nella figura a lato sono supplementari. Se uno è il triplo dellaltro, quanto misurano i due angoli? [45°; 135°]

148 EDUCAZIONE CIVICA Un gruppo di scout si è perso nel bosco. Per trovare il Sud usano un orologio con le lancette. Si posiziona il quadrante dellorologio in orizzontale in modo che la lancetta delle ore punti verso il Sole; la bisettrice dellangolo che la lancetta forma con la linea delle ore 12 (ruotando in senso antiorario) è lasse che indica il Nord-Sud. Quindi il Sud si trova a ore

a) A che ora si trova il Nord, se lorologio segna le 14:00?

b) A che ora si trova il Sud quando lorologio segna le 17:00?

149 Trova lampiezza di due angoli supplementari, sapendo che uno è il quintuplo dellaltro. [30°; 150°]

150 MATEMATICA IN AZIONE Gli angoli rappresentati nella figura a lato sono complementari. Se uno è la metà dellaltro, quanto misurano i due angoli?

[30°; 60°]

151 Due angoli sono complementari e il primo è sottomultiplo dellaltro secondo il numero 8. Calcola le loro ampiezze. [10°; 80°]

152 Due angoli complementari sono uno la quinta parte dellaltro. Trova le ampiezze dei due angoli. [15°; 75°]

ESEMPIO

Un angolo misura 32° 8’ 4’’ e un altro è i suoi 3 2 ; calcola l’ampiezza del secondo angolo.

Rappresentazione grafica

α = 32° 8' 4'' Dati

β

α = 32° 8' 4''

β = 3 2 × α

β = ?

Risoluzione

β = α : 2 × 3 = (32° 8' 4'') : 2 × 3 = = (16° 4' 2'') × 3 = 48° 12' 6''

153 Calcola lampiezza dei due angoli, sapendo che la loro somma è 168° e che uno è i 4 3 dell’altro. [96°; 72°]

154 Langolo α è ampio 120°. Calcola lampiezza dellangolo β che è i 2 3 di α [80°]

155 Calcola le misure del supplementare e del complementare di un angolo che è i 2 5 di un angolo retto. [144°; 54°]

156 Un angolo piatto è diviso in tre parti. La prima misura 62° e la seconda è 3 2 della prima. Determina lampiezza del terzo angolo. [25°]

157 Due angoli sono uno i 7 2 dell altro e la loro somma è 135°. Calcola le loro ampiezze. [30°; 105°]

158 Due angoli complementari sono uno i 7 8 dell’altro. Calcola la misura dei due angoli. [42°; 48°]

159 Langolo α è più ampio dellangolo β di 45°. Sapendo che β è i 2 5 di α, calcola le misure dei due angoli. [30°; 75°]

160 La differenza di due angoli è 27° e uno è il quadruplo dellaltro; quanto misurano i due angoli? [9°; 36°]

161 La somma di due angoli è un angolo piatto e la loro differenza è un angolo retto. Calcola lampiezza dei due angoli.

Rappresentazione grafica

90° 678 6447448

Dati

162 MATEMATICA IN AZIONE Un raggio di luce colpisce uno specchio e forma con la perpendicolare allo specchio un angolo detto di incidenza. La differenza tra l’angolo di incidenza e il suo complementare è di 12°.

Calcola le ampiezze dei due angoli.

specchio angolo di incidenza

163 Un angolo è più ampio di un altro di 17°. Sapendo che i due angoli sono complementari, determina le loro ampiezze. [53° 30'; 36° 30']

164 La somma di due angoli è 260° e la loro differenza è 90°.

Calcola le ampiezze dei due angoli. [85°; 175°]

165 Due angoli adiacenti sono uno gli 11 7 dellaltro; calcola le loro ampiezze. [110°; 70°]

166 Un angolo è i 5 9 di un angolo retto. Determina la misura del suo supplementare e del suo complementare.

[130°; 40°]

167 Tre semirette aventi l origine in comune dividono il piano in tre angoli; sapendo che il primo misura 136° e che il secondo è i 5 3 del terzo, quanto sono ampi il secondo e il terzo angolo?

[84°; 140°]

168 Calcola lampiezza di due angoli, sapendo che sono complementari e che uno supera laltro di 48° 36' 54''. [20° 41' 33''; 69° 18' 27'']

169 La somma di tre angoli misura 140°. Il primo angolo supera il secondo di 19° 8' e il secondo angolo è il triplo del terzo. Calcola le ampiezze dei tre angoli. [70° 56'; 51° 48'; 17° 16']

170 Un angolo piatto è diviso in quattro parti: la prima misura 30°, la seconda è 2 3 della terza e la terza è 3 5 della quarta. Determina le ampiezze degli altri angoli. [30°; 45°; 75°]

171 Un angolo giro è formato da quattro angoli tali che ognuno sia il triplo del successivo. Trova le ampiezze dei quattro angoli. [9°; 27°; 81°; 243°]

COMPETENZE

ANALIZZARE E INTERPRETARE DATI

1 a) Completa la tabella che rappresenta le misure di coppie di angoli complementari: x + y = 90°.

x 20° 30° 40° 70°

y 80° 45° 60° 40°

b) Traccia nel piano cartesiano i punti che hanno come coordinate le ampiezze trovate.

Congiungi i punti.

Che linea ottieni?

2 a) Completa la tabella che rappresenta le misure di coppie di angoli supplementari: x + y = 180°.

x 20° 60° 90° 140°

y 150° 90° 50° 30°

b) Traccia nel piano cartesiano i punti che hanno come coordinate le ampiezze trovate.

Congiungi i punti.

Che linea ottieni?

Misura angolo y (in gradi) u

Misura angolo y (in gradi)

Misura angolo x (in gradi) x

Misura angolo x (in gradi) x

3 Osservando le tabelle degli esercizi precedenti, completa utilizzando i termini sempre, a volte, mai .

a) Se x e y sono angoli complementari, allora sia x sia y sono acuti

b) Se x e y sono angoli supplementari, allora x è acuto

c) Se x e y sono angoli complementari, allora sia x sia y sono ottusi

d) Se x è un angolo retto, allora y è acuto

e) Se x e y sono angoli complementari, allora x e y sono adiacenti

f) Se x e y sono angoli supplementari, allora x è ottuso

ARGOMENTARE

4 BOC è un angolo ottuso; è possibile che la bisettrice lo divida in due angoli ottusi? Perché?

5 Riconosci l’illustrazione che corrisponde alla seguente descrizione.

“Disegna un angolo ottuso AOB . Dal vertice O conduci la perpendicolare al lato AO Fissa su questa perpendicolare un punto P a tuo piacere e da esso conduci la parallela al lato OB.”

a)

b)

RISOLVERE PROBLEMI

6 Dario si mette a contare gli oggetti che ha sulla sua scrivania e costruisce il relativo areogramma. Sapendo che le buste sono 10, rispondi alle seguenti domande.

a) Qual è l’ampiezza dell’angolo relativo ai libri?

b) Qual è l’ampiezza dell’angolo relativo alle buste?

c) Qual è l’ampiezza dell’angolo relativo ai giocattoli?

d) Qual è l’ampiezza dell’angolo relativo alle puntine?

e) Qual è il numero dei libri, dei giocattoli e delle puntine?

SFIDA MATEMATICA

7 I quattro orologi

Siamo in una delle aule dove si svolge la finale nazionale dei “Campionati di Giochi

Matematici”, tra le due e le tre di pomeriggio. Il disegno mostra, in questo istante, i quattro orologi che sono presenti nell’aula. Uno è fermo. Dei tre che funzionano, uno è indietro (di meno di un’ora); un altro indica l’ora esatta e un altro ancora è avanti (di meno di un’ora). Che ore sono in questo momento?

(Testo tratto dalla gara Finale Nazionale Campionati Internazionali del 2010, organizzata dal Centro PRISTEM dell’Università Bocconi di Milano)

ROAD MAP PER TUTTI

ANGOLI

DATE DUE SEMIRETTE AVENTI LA STESSA ORIGINE

TEORIA PAG. 106

Cosa individuiamo?

Due parti di piano chiamate angoli

Come si possono distinguere?

• l'angolo che non contiene i prolungamenti delle semirette è l'angolo convesso

• l'angolo che contiene i prolungamenti delle semirette è l'angolo concavo

a b angolo concavo

DATO UN ANGOLO vertice O lato lato r s ampiezza

angolo concavo angolo convesso a b angolo convesso a b

parti di un ANGOLO

Come si chiamano le parti dell'angolo?

• le semirette r e s sono i lati dell'angolo

• l'origine comune è il vertice dell'angolo

• l'ampiezza è la grandezza dell'angolo da misurare

vertice O lato lato r s ampiezza

PAG. 106

Come si indica?

Un angolo si può indicare in tre modi:

• solo con il vertice: O ; D

• con tre lettere, quella centrale deve essere il vertice: AOB; MNP …

• con una lettera greca: α, β …

1 Individua i lati e il vertice dei seguenti angoli e colorane l’ampiezza.

Lati: a e

Vertice: ……

Lati: Vertice: ……

Lati: VR e

Vertice: ……

2 Indica i seguenti angoli in tre modi diversi.

Lati: Vertice: ……

3 Dopo aver assegnato tre lettere a ogni angolo, indicalo correttamente.

4 Prolungando i lati dei seguenti angoli, stabilisci se sono convessi o concavi.

Consecutivi, se hanno anche un lato in comune

DATI DUE ANGOLI CON UN VERTICE IN COMUNE

Come possono essere?

Adiacenti, se sono consecutivi e i due lati non comuni sono semirette opposte

Opposti al vertice, se i lati di uno sono i prolungamenti dei lati dell'altro

ESEMPIO

O a b c

angoli consecutivi O c a b

angoli adiacenti

ESEMPIO

Sovrapposti, se hanno un lato in comune e tutti i punti di uno appartengono anche all'altro

angoli opposti al vertice sono congruenti: a ≅ b O

angoli sovrapposti O b a c

ampiezza di un angolo

DATO UN ANGOLO O a

Cosa misura un goniometro?

Quale unità di misura utilizza?

Un goniometro misura l'ampiezza di un angolo, l'unità di misura è il grado (°) con i suoi sottomultipli, i primi (') e i secondi (''): 60' = 1°; 60'' = 1'

Ampiezza Nome Rappresentazione grafica

0° nullo

0° < α < 90° acuto

90° retto

90° < α < 180° ottuso

180° piatto

180° < α < 360° concavo

360° giro

nullo 0° piatto 180° acuto retto 90° ottuso concavo giro 360°

Quando l'ampiezza di un angolo si deve ridurre in forma normale?

L'ampiezza di un angolo si deve ridurre in forma normale quando i primi e/o i secondi superano 59; per farlo si tolgono i 60' in più' e, trasformati, si aggiungono all'unità superiore

30° 12' 89''

+1' – 60'' si tolgono 60'' da 89'' e, poiché 60'' = 1', si aggiunge 1' a 12'

30° 13' 29''

5 Individua gli angoli consecutivi, adiacenti, sovrapposti e opposti al vertice.

a) b) c) d) e)

6 Quanto sono ampi gli angoli colorati nei tre orologi? Verifica l’esattezza delle tue risposte misurandoli con il goniometro.

7 Riduci in forma normale le seguenti misure angolari. (È evidenziata in grassetto la misura da ridurre.)

a) 134° 75' 23'' b) 162° 35' 63'' +1° –60'

Riduci sul quaderno in forma normale le misure angolari.

8 34° 77' 9

12 Classifica i seguenti angoli rispetto all’ampiezza.

a)

13 MATEMATICA IN AZIONE Per ogni immagine classifica l’angolo in base alla sua ampiezza.

somma di misure angolari

DATE DUE MISURE ANGOLARI α E β

Come si sommano?

La somma di misure angolari si ottiene sommando separatamente i gradi con i gradi, i primi con i primi, i secondi con i secondi e, se necessario, riducendo in forma normale il risultato

23° 13' 25'' + 23° 23' 11''

23° 13' 25'' + 23° 23' 11'' = 46° 36' 36''

Quali sono i casi particolari?

Se α + β = 90° sono complementari

Se α – β = 180° sono supplementari

Se α + β =360° sono esplementari

14 Esegui sul tuo quaderno le seguenti addizioni e, se necessario, riduci in forma normale il risultato. a) 212° 31' + 34° 12' b) 47° 17' + 3° 39'

43'; 50° 56'] c) 46° 28' + 76° 45' d) 3° 35' + 111° 42'

15 Esegui le seguenti addizioni utilizzando i dati del disegno a lato. a) α + β =

13'; 115° 17']

misure angolari

DATE DUE MISURE ANGOLARI α E β differenza di

Come si sottraggono?

La differenza di misure angolari si ottiene sottraendo separatamente i gradi, i primi e i secondi. Se occorre si effettua “un prestito”

ESEMPIO

i primi prestano 1' = 60'' ai secondi 54' 83''

Completa la seguente sottrazione.

16 158° 25' – 96° 37' = a 158° tolgo 1° = 60' e a 25' aggiungo 60'

Esegui le sottrazioni in colonna, sul quaderno.

17 a) 174° 59' – 95° 47' b) 34° 45' – 12° 58' c)

18 Esegui le seguenti sottrazioni utilizzando i dati del disegno. a) α – β = b) α – δ = ………………………………………. c) γ = α – β – δ =

19 Completa la seguente tabella.

PAG. 114

prodotto e quoziente di misure angolari

DATE DUE MISURE ANGOLARI α E β

Come si moltiplicano?

Per moltiplicare una misura angolare per un numero si moltiplicano gradi, primi e secondi separatamente per quel numero

ESEMPIO

(12° 34' 7'') × 4

12° 34' 7 '' × 4 =

48° 136' 28 '' ridotto in forma normale, 50° 16' 28 ''

Come si dividono?

Per dividere una misura angolare per un numero, si dividono separatamente i gradi, i primi e i secondi per quel numero. Se dividendo i gradi o i primi vi è un resto, questo si trasforma nell'unità di ordine inferiore

46° 32' 20'' : 5 = 9° 18' 28'' + + 1° 60 ' 120'' • 1° di resto sono 60' che si sommano ai 32' 92' 140'' • 2' di resto si trasformano in 120'' che si sommano ai 20''

bisettrice di un angolo

DATO UN ANGOLO O 60°

Che cos'è la bisettrice di un angolo?

La bisettrice di un angolo è la semiretta che divide l'angolo in due parti congruenti

bisettrice

Esegui le seguenti moltiplicazioni, riducendo in forma normale il risultato.

20 (52° 14') × 5

Moltiplica per 5 il valore dei gradi e quello dei primi:

Riduci in forma normale:

21 (36° 41') × 4

Moltiplica per 4 il valore dei gradi e quello dei primi:

Riduci in forma normale:

22 Calcola utilizzando le misure indicate nei disegni.

a) β = α × = b) β = α × =

23 Risolvi sul quaderno le seguenti divisioni. a) (12° 48') : 3 b) (240° 53') : 4 c) (356° 46') : 5 [4° 16'; 60° 14'; 71° 21']

24 Completa utilizzando le misure indicate nei disegni. a) b) …

L’angolo β è formato da 4 angoli che hanno la stessa ampiezza di α quindi:

= β : =

L’angolo β è formato da 7 angoli che hanno la stessa ampiezza di α quindi:

= β : =

25 Completa la seguente tabella facendo riferimento al disegno.

SIMULAZIONE DI VERIFICA

1 Rispondi con Vero o Falso e nel caso effettua la correzione.

a) Due angoli adiacenti sono complementari.

b) Il secondo è un sottomultiplo del grado.

c) Due angoli opposti al vertice sono supplementari.

d) Un angolo convesso non contiene il prolungamento dei suoi lati.

e) La bisettrice divide l’angolo in due parti congruenti.

f) L’angolo acuto è maggiore di 90°.

g) Due angoli sono complementari se la loro somma è 180°.

2 Rispetto alla loro ampiezza, classifica i seguenti angoli.

F

F

F

F

F

F

3 Osserva la figura e classifica le coppie di angoli indicate scegliendo tra i seguenti termini: acuti • adiacenti • complementari • consecutivi • opposti al vertice • ottusi • supplementari

a) 1 e 2 sono e

b) 9 e 11 sono e

c) 10 e 11 sono e

d) 7 e 8 sono

e) 10 e 12

4 Esegui le seguenti operazioni con le misure angolari.

a) 18° 35' 53'' + 41° 41' 41'' =

b) 56° 52' 25'' – 38° 48' 28'' =

c) (13° 23' 33'') × 4 =

d) (49° 35' 42'') : 3 =

5 Stabilisci in quali casi la semiretta r è la bisettrice dell’angolo.

a)

6 Risolvi i seguenti problemi.

a) Dato un angolo di 45°, calcola il suo doppio e il suo triplo e classifica gli angoli trovati.

b) La differenza tra due angoli complementari è 28°. Quanto è ampio ciascun angolo?

c) Considera due angoli supplementari che siano uno i 5 13 dell’altro. Calcola le loro ampiezze.

d) α + β + γ = 180° β = ?

α = 75° γ = ?

β = γ × 1 5

7 MATEMATICA IN AZIONE Un robot deve percorrere tutta la strada disegnata qui a fianco con il minor numero di passi possibile. Sai che ogni quadretto vale un passo e che le istruzioni che può ricevere sono:

• avanti di n passi: - n

• girare a destra: " 90°

• girare a sinistra: ! 90°

Quali sono le istruzioni da dare per completare il percorso?

RETTE NEL PIANO

Chi ha della

paura matematica?

È giunto il momento di spiccare un salto. Niente panico! Non si tratta di fare un salto nel buio e neanche un salto nel vuoto: grazie alla geometria che studierai, da questo momento in poi farai un vero e proprio salto di qualità nel mondo della matematica.

Conoscerai in maniera più approfondita le rette nel piano e le loro proprietà e scoprirai tanti termini nuovi. Non farti intimorire dai nomi strani: per ciascuno di loro potrai trovare degli opportuni riferimenti a elementi che già conosci. L'asse di un segmento, per esempio, è semplicemente la linea perfetta che lo taglia a metà in modo dritto; le rette parallele non si incontrano mai, come i binari di un treno; le rette perpendicolari. che formano angoli perfetti di 90°, le potrai riconoscere nell'incrocio di due strade.

Anche “distanza” e“proiezioni” sono concetti che usi ogni giorno: la distanza di un punto da una retta, per esempio, non è altro che la linea più corta che li unisce. Proprio come un elicottero che atterra seguendo la linea più diretta per raggiungere la pista!

ROAD MAP la nostra

CLASSIFICHIAMO LE POSIZIONI RECIPROCHE DI DUE RETTE NEL PIANO

TRACCIAMO L’ASSE DI UN SEGMENTO

OSSERVIAMO LE PROPRIETÀ DELLA DISTANZA DI UN PUNTO DA UNA RETTA

VERIFICHIAMO IL PARALLELISMO TRA DUE RETTE

INTEGRATIVO MULTIMEDIALE

Posizione reciproca di due rette nel piano 1

SUCCEDE CHE...

Emma si trova a Ortigia in via XX Settembre e chiede a un passante come fare ad andare all’hotel Ancora.

Il passante le dice di prendere la perpendicolare e poi la parallela sempre a via XX Settembre e camminare fino al punto d’intersezione con Corso Giacomo Matteotti.

Dove si trova l’hotel?

Via XX Settembre

Nelle mappe stradali alcune strade si possono paragonare a delle linee rette complanari cioè che appartengono allo stesso piano.

In base ai punti che hanno in comune, due rette complanari possono essere:

• parallele se non hanno alcun punto in comune; il simbolo di parallelismo è //.

• sovrapposte se hanno tutti i punti in comune; il simbolo di sovrapposte è =.

• incidenti se hanno un punto in comune che viene detto punto di intersezione.

• perpendicolari se sono incidenti e dividono il piano in quattro angoli retti; il simbolo di perpendicolarità è ⊥.

Seguendo le indicazioni del passante, tracciate in rosso in figura, Emma arriva a destinazione.

Via XX Settembre

1 Completa le seguenti affermazioni.

a) Due rette che hanno un punto in comune sono

b) Due rette che hanno un punto in comune e formano quattro angoli sono ; il simbolo di è

c) Due rette che non hanno punti in comune sono ; il simbolo di è

d) Due rette che hanno tutti i punti in comune sono

2 Trova alcune delle coppie di rette incidenti indicando il loro punto in comune, come nell’esempio.

a) b) c) d) e) f) P Q S n s r t p R

3 Rappresenta con un disegno le seguenti situazioni.

a // b s ⊥ t r e s incidenti O in comune

4 MATEMATICA IN AZIONE La mappa accanto mostra alcune vie (carrer) di Barcellona.

Individua:

a) due vie parallele

c) due vie incidenti n e r, P in comune

b) due vie perpendicolari

Asse di un segmento e distanze 2

SUCCEDE CHE...

Pietro, attraversando sulle strisce pedonali, nota che sono state disegnate in diagonale e si chiede perché di solito vengano disegnate perpendicolarmente all’attraversamento. Come mai, secondo te?

Sia EF un segmento e M il suo punto medio, il punto cioè che divide a metà EF

La perpendicolare a passante per il punto medio M prende il nome di asse del segmento EF.

L’asse di un segmento è la retta perpendicolare passante per il punto medio del segmento stesso.

Se si misurano le coppie di segmenti ottenuti congiungendo un punto qualsiasi dell’asse (A, B, C …) con gli estremi del segmento, si scopre che i segmenti sono a due a due congruenti. Inoltre se, disegnandolo su un foglio, si piega il segmento lungo il suo asse, le due parti coincidono, quindi:

l’asse di un segmento è l’asse di simmetria del segmento.

Consideriamo una retta r e un punto M che non appartiene alla retta r

Da M tracciamo la retta p perpendicolare a r; la retta p incontra la retta r nel punto H.

Il segmento MH così individuato si chiama distanza del punto M dalla retta r, mentre il punto H è il piede della perpendicolare

Il segmento che congiunge un punto con una retta formando angoli retti è la distanza del punto da una retta.

Si può osservare che la distanza di un punto da una retta è minore di qualsiasi segmento obliquo condotto dal punto alla retta.

a asse del segmento EF

= punto medio di EF

MH distanza del punto M dalla retta r H piede della perpendicolare M H r p p ⊥ r

Date due rette parallele si ha che:

il segmento perpendicolare che congiunge due rette parallele è la distanza tra le rette parallele.

Poiché tutti i segmenti perpendicolari alle due rette sono congruenti, si può affermare che le due rette parallele sono equidistanti

distanza

Quindi nelle strisce pedonali disegnare segmenti perpendicolari richiede meno vernice che disegnarli in diagonale, poiché il segmento perpendicolare ha una misura minore di quello obliquo.

1 Osserva il disegno e completa.

a) La distanza del punto P dalla retta a è il segmento , perché è alla retta a; il punto L è il della

b) I segmenti e sono del segmento distanza.

2 Disegna seguendo le istruzioni.

La distanza del punto F dalla retta s

La distanza tra le due rette parallele a e b

L’asse del segmento XY

3 MATEMATICA IN AZIONE

Traccia sul disegno la distanza tra il centro dell’aquilone e la linea di terra. Misurala in cm.

Proiezioni su una retta 3

SUCCEDE CHE...

Sondine 1040 m s.l.m.

Ponteille 1690 m s.l.m.

Emma si è iscritta alla corsa in montagna con partenza da Aosta e arrivo nella località Comboé. Ha una mappa come quella rappresentata a lato. In che modo può stabilire le distanze che hanno le località Sondine, Ponteille e Comboé dalla partenza?

Partenza

Aosta 525 m s.l.m.

Per rispondere alla domanda occorre sapere che cosa sono le proiezioni.

Proiezione di un punto su una retta

Dato un punto P, per “proiettarlo” su una retta r occorre tracciare la distanza di P da r. Il piede della perpendicolare H è la proiezione del punto P sulla retta.

La proiezione di un punto su una retta è il piede della distanza del punto dalla retta.

Proiezione di un segmento su una retta

proiezione di P su r H

La proiezione di un segmento su una retta è il segmento che ha per estremi le proiezioni degli estremi del segmento dato.

Rispetto alla posizione del segmento, si hanno le seguenti situazioni. 1) 2) 3) 4)

1) Il segmento è parallelo alla retta r: la proiezione A'B' ha la stessa lunghezza del segmento AB (A'B' = AB).

2) e 3) I segmenti non sono paralleli alla retta r: le proiezioni C'D' e E'F' sono minori dei segmenti CD e EF (C'D' < CD e E'F' < EF).

4) Il segmento è perpendicolare alla retta r: la proiezione del segmento GH

è il punto H'

Emma può individuare le distanze delle tre località dalla partenza, proiettando sulla linea che indica i km i punti che le rappresentano.

Primi

ESERCIZI

1 Sottolinea il completamento esatto.

a) La proiezione di un punto P su una retta / un piano è la distanza / un punto che si ottiene tracciando la distanza / la parallela del punto P dalla retta.

b) La proiezione di un segmento ST su una retta si ottiene congiungendo / segnando i punti ottenuti proiettando i vertici / gli estremi del segmento stesso sulla retta.

c) Se il segmento è parallelo / perpendicolare alla retta, la sua proiezione è un segmento maggiore del / uguale al segmento stesso.

2 Stabilisci quali proiezioni sono state disegnate correttamente e contrassegnale.

a) b) c) d) e)

3 Traccia le proiezioni dei seguenti punti e segmenti sulle rette.

4 MATEMATICA IN AZIONE Una tettoia a casa di Gianni è inclinata come nella figura. Se i raggi del sole cadono perpendicolari, come sarà la lunghezza dell’ombra (cioè la sua proiezione sull’asfalto) rispetto alla lunghezza della tettoia?

a) Maggiore

b)

c)

LEZIONE

Rette tagliate da una trasversale 4

SUCCEDE CHE...

Pietro osserva l’asse da stiro che suo papà ha appena acquistato e gli sembra che il ripiano inferiore non sia parallelo a quello superiore. Come può verificare il parallelismo dei due ripiani?

Per rispondere alla domanda occorre conoscere le proprietà degli angoli formati da due rette parallele tagliate da una trasversale.

Una retta si dice trasversale quando incontra due o più rette. Nella figura puoi osservare la retta t che interseca le rette r e d: si dice che le rette r e d sono tagliate dalla trasversale t.

La trasversale alle due rette individua 8 angoli:

4 sono esterni, cioè si trovano “fuori” dalle due rette (7, 8, 5, 6), e 4 sono interni, cioè si trovano “dentro” le rette r e d, (1, 2, 3, 4).

Gli 8 angoli, a coppie, prendono nomi diversi a seconda della loro posizione:

• 1 e 4 oppure 2 e 3 sono alterni interni;

• 7 e 6 oppure 8 e 5 sono alterni esterni;

• 7 e 3 oppure 1 e 5 oppure 8 e 4 oppure 2 e 6 sono corrispondenti;

• 1 e 3 oppure 2 e 4 sono coniugati interni;

• 7 e 5 oppure 8 e 6 sono coniugati esterni

Gli otto angoli che formano le coppie sopra scritte sono di diversa ampiezza, come puoi notare dalla figura.

Rette parallele

Un caso particolare di rette tagliate da una trasversale si ha quando le rette sono parallele. In questo caso le ampiezze delle coppie di angoli analizzati precedentemente possiedono le seguenti proprietà.

Gli angoli alterni interni e alterni esterni sono congruenti

4 ≅ ; 3 ≅ 2

6 ≅ 7; 8 ≅ 5

Gli angoli coniugati interni e coniugati esterni sono supplementari, cioè la loro somma

è uguale a 180°.

1 + 3 = 180°; 2 + 4 = 180°

5 + 7 = 180°; 6 + 8 = 180°

Gli angoli corrispondenti sono congruenti.

3 ≅ 7; 2 ≅ 6

5 ≅ 1; 4 ≅ 8

Pietro può verificare che i due ripiani sono paralleli se gli angoli corrispondenti hanno uguale ampiezza.

Primi

ESERCIZI

1 Osserva i disegni e scrivi il nome delle coppie di angoli segnate.

2 Sottolinea il completamento esatto.

Date due rette parallele tagliate da una trasversale:

a) gli angoli alterni interni sono congruenti / supplementari.

b) gli angoli corrispondenti sono congruenti / supplementari.

c) gli angoli coniugati interni sono congruenti / supplementari.

d) gli angoli alterni esterni sono congruenti / supplementari.

3 Date due rette parallele tagliate da una trasversale, calcola le ampiezze degli angoli incogniti.

4 MATEMATICA IN AZIONE La metropolitana di Futurama ha quattro linee che corrono parallele e una che le incrocia tutte in maniera trasversale.

Prova a disegnare la mappa sul tuo quaderno e individua:

a) quanti angoli acuti forma la linea trasversale con le altre 4 linee.

b) quanti angoli ottusi.

CURIOSITÀ STORICHE

ODIFREDDI a cura del professor

LA GEOMETRIA

DEGLI ANIMALI

La geometria non è solo una materia scolastica, ma è il modo in cui il nostro cervello interpreta lo spazio che ci circonda, tramite le informazioni che ci forniscono i sensi. Per esempio, ogni volta che guardiamo qualcosa, calcoliamo automaticamente, senza neppure accorgercene, quanto è lontano quell’oggetto, attraverso un “trucco” geometrico. Immaginiamo un triangolo. La base di questo triangolo è lo spazio fra i nostri occhi. I due lati del triangolo sono come due linee immaginarie che partono dai nostri occhi e arrivano all’oggetto che stiamo guardando. L’altezza di questo triangolo corrisponde proprio alla distanza dell’oggetto da noi.

Il fatto che un triangolo sia completamente determinato dalla base e dai due angoli che si trovano ai suoi estremi, è un teorema che scoprirono i Greci: si chiama “criterio di uguaglianza ALA (Angolo-Lato-Angolo)”. Questo criterio si trova nel grande libro degli Elementi di Euclide. Da sempre tutti gli uomini lo hanno usato intuitivamente, anche senza conoscerlo. Per poter applicare questo teorema alla valutazione delle distanze, sia pure senza pensarci, dobbiamo però avere due occhi mobili e posti sul davanti, in modo da poter convergere su un oggetto. Gli angoli tra la linea dei nostri occhi e le linee immaginarie tra i nostri occhi e l’oggetto sono proprio gli elementi sufficienti alla determinazione di quel triangolo. Inoltre, gli occhi

Distanza degli occhi come linea.

devono essere a una distanza fissa, così da dover calcolare soltanto gli angoli. I predatori, come i felini, i rapaci e i serpenti, hanno in genere occhi come i nostri, per percepire con precisione le distanze delle prede, e poter saltar loro addosso. Le prede, invece, come gli erbivori, gli uccellini e i pesci, hanno in genere occhi laterali: possono controllare bene la presenza dei pericoli, avendo un campo visivo più ampio, ma male la sua distanza. Dunque, devono poter scappare appena avvistano qualcosa di sospetto.

Anche il nostro senso dell’udito ci permette di valutare le distanze. Il cervello valuta la distanza di un rumore misurando il tempo che passa fra il momento in cui il suono arriva a un orecchio e il momento in cui arriva all’altro. Poiché la velocità del suono è alta, la distanza delle orecchie deve essere la massima possibile per rendere percepibile questa differenza: per questo sono posizionate ai lati della testa. Ma non serve che siano mobili, perché per noi il suono è solo complementare. Per molti altri animali, sia predatori che prede, è invece fondamentale, e le loro orecchie sono dunque orientabili. Le persone non vedenti riescono a percepire gli ostacoli schioccando la lingua, e stimando il tempo di rimbalzo del suono sugli ostacoli. I pipistrelli e i delfini usano questo metodo sistematicamente, mentre le api percepiscono il campo magnetico, come una bussola. Sicuramente, dunque, avranno un’idea della matematica molto differente dalla nostra!

MAPPA

Perpendicolari

Incidenti

RETTE NEL PIANO

a ⊥ b b a r s r s r s determinano

Parallele r // s

Distanze

Proiezioni

Angoli alterni

con una trasversale determinano

Sovrapposte r ≡ s

Angoli corrispondenti

interni interni esterni esterni (congruenti) (supplementari) (congruenti)

Angoli coniugati

LEZIONE

1 ESERCIZI E PROBLEMI

POSIZIONE RECIPROCA DI DUE RETTE NEL PIANO

1 Rispondi alle seguenti domande.

a) Quando due rette sono parallele? Qual è il simbolo per indicarle?

b) Quando due rette sono incidenti?

c) Quando due rette sono perpendicolari? Qual è il simbolo per indicarle?

2 Nelle seguenti bandiere indica se le rette evidenziate in colore sono incidenti, parallele o perpendicolari.

a) a e b sono c e d sono

b) e e f sono f e g sono

3 MATH The given line marking shows how the roads are related to one another.

a) Name a pair of parallel lines.

b) Name a pair of perpendicular lines.

c) Is FE ∕∕ AC ?

4 Leggi le seguenti frasi e correggi gli errori.

a) Due rette sono sovrapposte quando si incontrano in un punto.

b) Due rette perpendicolari non hanno alcun punto in comune.

c) Due rette parallele formano quattro angoli retti.

d) Due rette incidenti non hanno punti in comune.

5 Rispondi con Vero o Falso.

a) Due rette parallele sono sempre complanari.

b) Due rette incidenti hanno due punti in comune.

c) Due rette incidenti dividono il piano in quattro angoli.

d) Due rette perpendicolari non sono mai complanari.

e) Si dicono sovrapposte le rette di due piani diversi.

6 Osserva il disegno e classifica le seguenti coppie di rette.

a) a e b sono

b) a e c sono

c) d e b sono …………………………………………………

d) c e d sono

e) c e b sono

PUNTI FERMI

Angoli opposti al vertice

ESEMPIO

ESERCIZI

Calcola le ampiezze degli angoli richiesti facendo riferimento al disegno precedente.

1) α = 36° " β = ; α1 = ; β1=

2) β = 104° " α = ; α1 = ; β1=

3) α = 28° " β = ;

4) β = 114° "

1=

7 Osserva il seguente disegno e, utilizzando squadra e righello, individua tutte le coppie di rette incidenti, di rette parallele e di rette perpendicolari che riconosci.

a) Rette incidenti

b) Rette parallele

c) Rette perpendicolari

8 Prolunga le seguenti coppie di rette e indica quali sono incidenti e quali parallele.

ESEMPIO

DISEGNARE RETTE PARALLELE CON RIGA E SQUADRA

Per disegnare delle rette parallele basta posizionare riga e squadra come vedi in figura.

Tieni ferma la riga con una mano e fai scorrere lateralmente la squadra con l’altra mano, fermandoti ogni volta che vuoi tracciare una riga.

9 Disegna seguendo le indicazioni:

a) due rette perpendicolari s e t con G punto in comune

b) due rette r e s incidenti in K

c) tre rette parallele g, h e f

d) tre rette m, n e p in modo tale che:

m // n;

p ⊥ m;

A punto in comune di m e p;

B punto in comune di n e p.

10 Calcola le misure degli angoli acuti e ottusi formati da due rette incidenti.

Risolvi i seguenti problemi.

11 Due rette incidenti formano un angolo ottuso di 137°. Quanto misurano gli altri tre angoli? [43°; …]

12 Calcola la misura degli angoli formati da due rette incidenti, sapendo che l’ampiezza dell’angolo ottuso è il doppio di quella dell’angolo acuto. [60°; 120°; …]

13 L’angolo acuto formato da due rette incidenti è 1 5 dell’angolo piatto. Quale frazione rappresenta l’angolo ottuso? Quanto misurano i due angoli? [ 4 5 ; 36°; 144°]

14 Considera i due angoli adiacenti AOB e BOC della figura e le loro bisettrici m e n Come sono fra di loro le due bisettrici? Misura l’angolo formato e giustifica la risposta.

15 MATEMATICA IN AZIONE Pietro si trova nel punto indicato con Qui . Deve raggiungere la scuola Pieve di Cadore ma prima deve riportare un libro in biblioteca e fare un prelievo in banca.

Colora il percorso che può fare nella mappa; indica poi se le strade che percorre sono parallele, perpendicolari o incidenti a Via Padova.

Viale Laguna Veneta

Disegna e rispondi.

16 Disegna sul quaderno un angolo di 45° e il suo adiacente; traccia poi le bisettrici dei due angoli. Come sono tra loro le bisettrici? Misura l’angolo formato e giustifica la risposta.

17 Disegna sul quaderno due rette incidenti t e d. Traccia poi le perpendicolari alle due rette passanti nel loro punto di intersezione.

18 Disegna sul quaderno tre rette m, n, p in modo che m sia parallela a n e n sia parallela a p. Come sono tra loro le rette m e p?

19 Disegna sul quaderno due rette perpendicolari c e d, la retta m parallela a c e la retta n parallela a d. Come sono tra loro le rette m e n?

20 MATEMATICA IN AZIONE Le linee del grafico rappresentano le auto a marchio Fiat e Alfa Romeo che una concessionaria ha venduto nei primi mesi dell’anno.

a) In quale mese le linee sono incidenti? Che cosa puoi dedurre?

b) In quali mesi la concessionaria ha venduto il maggior numero di auto Fiat e Alfa Romeo?

c) In quali mesi è stato venduto il minor numero di auto Fiat e Alfa Romeo?

21 MATEMATICA IN AZIONE Il grafico rappresenta il numero di pizze e di primi piatti consumati in una settimana in un ristorante. Rispondi alle domande.

a) Qual è il giorno di chiusura del ristorante?

b) Nell’arco della settimana sono state ordinate più pizze o più primi piatti?

c) In quale giorno i grafici sono incidenti?

Che cosa puoi dedurre?

d) Il segmento che unisce mercoledì a giovedì dei primi piatti è parallelo all’asse orizzontale. Perché?

Completa la tabella dei dati.

sabato

domenica

2

ASSE DI UN SEGMENTO E DISTANZE

22 Rispondi con Vero Falso.

a) Se una retta è perpendicolare a un segmento, è detta asse.

b) Il punto medio di un segmento è esterno al segmento stesso.

c) La distanza di un punto da una retta è un segmento perpendicolare.

d) Due rette parallele sono equidistanti.

e) L'asse di un segmento è l'asse di simmetria del segmento.

f) Un segmento perpendicolare a due rette parallele è la loro distanza.

23 Osserva il disegno e completa.

a) AH è un segmento …………………………………… alla retta r perché forma 2 angoli

b) Il punto H viene detto della

c) Il segmento AH è la del punto dalla retta

24 Osserva il disegno sotto e completa usando simboli e termini che ritieni opportuni.

a) M è il del segmento

b) a è del segmento ; quindi a è a CD

c) PD ≅ PC perché ………………………………………………………………………………………

d) P 'D ……… P 'C

e) PM e P 'M sono ………………………………………… a CD

F

F

PUNTI FERMI

Punto medio di un segmento

A M b M B

ESEMPIO

AM = 12 cm " AB = 12 × 2 = 24 cm

AB = 20 cm " MB = 20 : 2 = 10 cm

ESERCIZI

Individua con il righello il punto medio dei primi due segmenti e calcola quanto richiesto utilizzando le misure indicate.

1)

3)

AM = ? PQ = ?

2)

AM = ?

ESEMPIO

COSTRUIRE L’ASSE DI UN SEGMENTO CON RIGA E COMPASSO

1) Punta il compasso in A

Apri il compasso con un’apertura maggiore della metà della lunghezza di AB e traccia un arco.

2) Punta il compasso in B. Con la stessa apertura traccia un altro arco. I due archi si intersecheranno in due punti.

3) Con il righello traccia la retta passante per i due punti di intersezione; questa retta è l’asse del segmento e il punto M in cui l’asse incontra il segmento è il punto medio di AB

25 Dopo aver individuato il punto medio dei seguenti segmenti, traccia il rispettivo asse.

Disegna e rispondi.

27 Disegna sul tuo quaderno due segmenti consecutivi e traccia i loro assi. Si incontrano in un punto?

28 Dopo aver disegnato sul tuo quaderno due segmenti adiacenti, traccia i loro assi. Si incontrano in un punto? Sapresti spiegare perché?

29 Considera i due segmenti adiacenti PS e SR con i punti medi M e M' Traccia l’asse di ciascuno dei due segmenti. Spiega la relazione esistente tra gli assi e la distanza tra i punti medi (M e M' ).

30 Disegna due segmenti adiacenti e i loro assi. Traccia una retta parallela ai due segmenti e passante per i due assi. A quale dei due assi sarà perpendicolare?

ESEMPIO

LA DISTANZA DI UN PUNTO DA UNA RETTA CON RIGA E COMPASSO

1) Punta il compasso su P e traccia un arco che interseca la retta in A e B

2) Punta il compasso in A e traccia un arco; con la stessa apertura punta il compasso in B e trova il punto di intersezione Q

3) La retta che passa per P e Q è perpendicolare a m: PS è la distanza di P da m

31 Traccia la distanza dei punti dalle rette assegnate e misurale in millimetri.

32 MATEMATICA IN AZIONE Emma vuole attraversare il ruscello e decide che il punto più facile da raggiungere è il punto segnato con C . Perché i punti segnati con B, D, E non le convengono?

Disegna e rispondi.

33 Disegna sul tuo quaderno una retta r e un punto T che dista da esso 5 cm. Puoi tracciare altri punti che sono alla stessa distanza dalla retta r ?

34 Disegna sul tuo quaderno una retta r e due punti P e H equidistanti da essa.

35 Disegna sul tuo quaderno due rette parallele che distano tra loro 4 cm.

3

PROIEZIONI SU UNA RETTA

36 Rispondi alle domande.

a) Se un segmento è parallelo alla retta, la sua proiezione è maggiore, minore o uguale al segmento stesso?

b) Se un segmento è perpendicolare alla retta, la sua proiezione è un segmento o un punto?

c) Se un segmento non è parallelo alla retta, la sua proiezione è maggiore, minore o uguale al segmento stesso?

d) Se un segmento ha gli estremi su una retta, la sua proiezione è maggiore, minore o uguale al segmento stesso?

37 Evidenzia con un colore e indica con delle lettere le proiezioni dei segmenti AB , PR , ST e CD.

PUNTI FERMI

Segmenti consecutivi e adiacenti

Segmenti consecutivi

ESERCIZI

Segmenti adiacenti

Classifica le coppie di segmenti indicate osservando il disegno.

1) AB e BC

2) AH e HB

3) GF e GH

4) GH e HD

ESEMPIO

PROIETTARE UN PUNTO SU UNA RETTA UTILIZZANDO RIGA E SQUADRA

Per proiettare il punto P sulla retta r basta posizionare riga e squadra come vedi in figura.

1) Fai coincidere il bordo superiore della riga con la retta r.

2) Tenendo la riga ferma con una mano, fai scorrere lateralmente la squadra con l’altra mano fino a incontrare il punto P

3) Traccia ora il segmento perpendicolare fino a intersecare la retta r nel punto P’

38 Traccia le proiezioni dei seguenti punti sulla retta r.

39 MATH Draw the projection lines for the following line segments onto the straight line r.

40 Disegna sul quaderno una retta t e tre segmenti congruenti AB, CD ed EF le cui proiezioni sulla retta abbiano diversa lunghezza.

41 Disegna tre segmenti consecutivi AB, BC e CD e sotto ad essi una retta r. Traccia le proiezioni dei tre segmenti sulla retta r; come risultano essere le proiezioni?

42 Trova le proiezioni dei seguenti segmenti sull’asse delle x e determina le coordinate degli estremi della proiezione di ciascun segmento.

43 Sul tuo quaderno ricopia i segmenti degli esercizi precedenti e trova le loro proiezioni sull’asse delle y, determinando le coordinate degli estremi della proiezione di ciascun segmento.

4

RETTE TAGLIATE DA UNA TRASVERSALE

44 Considera le rette a, b, c e completa.

• La retta c è la delle rette a e

• Gli angoli alterni interni sono ( ; ) ( ; )

• Gli angoli alterni esterni sono ( ; ) ( ; )

• Gli angoli coniugati interni sono ( ; ) ( ; )

• Gli angoli coniugati esterni sono ( ; ) ( ; )

• Gli angoli corrispondenti sono ( ; ) ( ; ) ( ; ) ( ; )

Poiché le rette a e b non sono parallele, che cosa puoi dire su queste coppie di angoli?

45 MATH Write down the name of the following pairs of angles. a) 1 and 8 are b) 4 and 5 are c) 2 and 8 are …………………………

d) 1 and 7 are e) 2 and 6 are f) 3 and 6 are ………………………… …………………………

46 Classifica le seguenti coppie di angoli indicate con 1 e 2.

47 Osserva l’illustrazione e stabilisci se le seguenti affermazioni sono vere o false.

a) L’angolo 2 è corrispondente dell’angolo 7

b) L’angolo 4 è coniugato interno dell’angolo 5

c) L’angolo 6 è alterno interno dell’angolo 3

d) L’angolo 7 è coniugato esterno dell’angolo 2

48 Osserva l’illustrazione e completa.

a) Gli angoli α e α ' sono congruenti perché

b) Gli angoli α ' e δ sono congruenti perché

c) Gli angoli δ e δ ' sono congruenti perché

d) Gli angoli β e γ ' sono congruenti perché

e) Gli angoli δ e β ' sono supplementari perché

f) Gli angoli α e γ ' sono

F

F

49 Date due coppie di rette parallele e una trasversale t, classifica le coppie di angoli indicate.

a) 2 e 3

b) 1 e 4

c) SPT e PTR

d) 5 e PSR

Rette parallele tagliate da una trasversale: questo è l’argomento più insidioso del capitolo.Glli errori sono in agguato e riguardano sia la difficoltà nel memorizzare i nomi degli angoli accoppiati (nomenclatura), sia la possibile confusione tra le loro proprietà. Quello che accade quando due rette parallele (come due binari) vengono attraversate da una terza retta, è veramente magico: gli 8 angoli che si formano non sono casuali, ma sono tra di loro in relazione.

imparaerrore

Per non sbagliare, usa delle strategie per ricordare i nomi degli angoli e per visualizzare il modo con cui essi sono in relazione; uno schema che associ le loro posizioni ad alcune immagini può esserti utile. Per esempio, gli angoli alterni interni possono essere rappresentati con una x piccola, quelli alterni esterni con una X più grande, e così via. Cerca altre analogie con le lettere dell’alfabeto e non preoccuparti: l’unico errore che puoi fare è quello di non provarci!

50 MATEMATICA IN AZIONE In colore rosso sono evidenziate due rette parallele tagliate da due trasversali. Scrivi tutte le seguenti coppie di angoli che individui nella figura:

alterni interni:

alterni esterni:

coniugati interni:

coniugati esterni:

corrispondenti:

PUNTI FERMI

Angoli complementari e supplementari

ANGOLI COMPLEMENTARI: α + β =90° ANGOLI SUPPLEMENTARI: α + β =180°

ESEMPIO

α + β =90° se α =24° " β =90°– 24°=66°

α + β =180° se α =103° " β =180°–103°=77°

ESERCIZI

Completa e calcola quanto richiesto.

51 Avendo come riferimento il disegno, calcola le ampiezze degli angoli incogniti nei seguenti casi.

(Poiché le rette a e b non sono parallele…)

a) α = 47°; β' = 124°

b) γ = 146°; δ' = 28° α

c) β = 132°; γ ' = 16°

Determina l’ampiezza degli angoli indicati e giustifica la risposta. (Le rette in nero sono parallele.)

1 = 180° – 32° = 148° perché coniugato esterno con l’angolo di 32° 2 = 32° perché alterno esterno con l’angolo di 32°

54 EDUCAZIONE CIVICA Osserva la figura a lato in cui sono raffigurate due linee parallele di un parcheggio tagliate da una trasversale. Quanto sono ampi gli angoli colorati in rosso e in giallo? Perché?

55 STEM Per misurare il raggio terrestre Eratostene, un grande matematico greco, utilizzò le ombre solari.

Eratostene aveva osservato che a Siene (oggi Assuan) nel giorno del solstizio estivo, a mezzogiorno, anche i pozzi più profondi erano illuminati, perché i raggi del Sole erano perfettamente perpendicolari.

Nello stesso giorno e alla stessa ora, ad Alessandria d’Egitto (che noi oggi sappiamo essere quasi sullo stesso meridiano di Siene) un bastone piantato verticalmente gettava invece un’ombra.

Egli usò l’ampiezza degli angoli 1 e 2 per le sue misurazioni. Che cosa puoi dire degli angoli 1 e 2? Perché Eratostene sosteneva che erano uguali?

56 Considera due rette parallele tagliate da una trasversale e, sapendo che l’angolo 2 = 31°, calcola la misura degli angoli indicati. Giustifica le risposte.

a) 8 = perché con 2

b) 6 = perché

c) 7 = perché

2

57 L’ampiezza di uno degli otto angoli formati da due rette parallele tagliate da una trasversale è 124° 43'; calcola le ampiezze degli altri sette.

58 Calcola la misura degli angoli numerati, sapendo che m e n, f e g sono due coppie di rette parallele e che un angolo è di 128°.

Risolvi i seguenti problemi.

59 STEM Gli operai di Lucegas devono installare delle tubazioni sotto una strada. Per farlo si dividono in due squadre che lavorano dai lati della strada verso il centro.

a) Se una squadra posa la tubazione con un angolo di 125°, quanto deve essere ampio l’angolo 1 che forma l’altra tubazione dall’altro lato della strada affinché le tubazioni si incontrino?

b) Come sono i due angoli?

60 Due angoli coniugati interni formati da due rette parallele tagliate da una trasversale sono tali che uno è il triplo dell’altro. Determina l’ampiezza degli altri angoli formati dalle tre rette. [45°; 135°; .....]

3 × β β

Due angoli coniugati interni sono supplementari; quindi la loro somma è

61 MATEMATICA IN AZIONE Con riferimento alle linee tracciate sulla mappa e alle ampiezze degli angoli indicate, spiega il motivo per cui Corso Cosenza e Corso Luigi Settembrini non sono paralleli.

Corso Luigi Settembrini

Corso Cosenza

62 Se due rette tagliate da una trasversale formano due angoli corrispondenti di 46° e 134°, si può dire che le due rette sono parallele? Motiva la risposta.

63 Calcola le ampiezze di due angoli coniugati esterni formati da due rette parallele tagliate da una trasversale, sapendo che un angolo è il doppio dell’altro. [60°; 120°]

64 Due rette parallele tagliate da una trasversale formano una coppia di angoli interni

tali che uno dei due misura 2 9 dell’angolo piatto. Qual è la frazione che indica l’altro angolo? Quanto misurano i due angoli? [ 7 9 ; 40°; 140°]

65 L’ampiezza di uno degli otto angoli formati da due rette parallele tagliate da una trasversale è 28° 45'. Determina l’ampiezza:

• del suo alterno interno;

• del suo corrispondente;

• del suo coniugato esterno. [28° 45'; 28° 45'; 151° 15']

66 Due angoli coniugati interni formati da due rette parallele tagliate da una trasversale sono uno i 7 8 dell’altro. Calcola le ampiezze degli altri angoli. [84°; 96°; .....]

67 Due angoli coniugati esterni formati da due rette parallele tagliate da una trasversale sono uno i 4 5 dell’altro. Calcola le ampiezze degli altri angoli. [80°; 100°; .....]

68 Quando una trasversale taglia due rette parallele si formano due angoli adiacenti, tali che il maggiore supera il doppio del minore di 45°. Determina le ampiezze di tutti gli angoli che si sono originati. [45°; 135°; .....]

69 I due angoli coniugati interni che si formano quando una trasversale taglia due rette parallele sono uno i 7 11 dell’altro. Trova le ampiezze di tutti gli angoli che si sono originati sul piano. [70°; .....]

70 Due rette parallele tagliate da una trasversale formano due angoli coniugati esterni uno maggiore dell’altro di 36° 43'. Quanto misurano i due angoli? [108 ° 21' 30''; 71° 38' 30'']

71 Uno dei due angoli adiacenti che si formano quando una trasversale taglia due rette parallele è maggiore del triplo dell’altro di 14° 18'. Trova le ampiezze dei due angoli. [41° 25' 30''; 138° 34' 30'']

COMPETENZE

ARGOMENTARE

1 Due rette r e s , tagliate da una trasversale, formano una coppia di angoli alterni esterni, uno dei quali ha un’ampiezza di 137° 15' .

Quale ampiezza dovrà avere l’altro angolo della coppia affinché le due rette siano parallele? Giustifica la risposta, aiutandoti con il disegno.

2 STEM L’arcobaleno è un fenomeno che si ha dopo un temporale quando le gocce d’acqua rimangono in sospensione nell’aria. Un raggio solare che entra in una goccia d’acqua viene scomposto nelle radiazioni che lo compongono (colori). Queste radiazioni escono dalla goccia con angoli diversi, da 40° a 42°. Per esempio la luce blu esce con un angolo a = 40° rispetto al raggio solare che è entrato nella goccia (vedi figura). Quanto è ampio l’angolo b evidenziato nella stessa figura? Perché? (I raggi solari sono tra loro paralleli.)

raggio solare

gocce d’acqua α = 40°

raggio solare

tagliate da una trasversale t formano i seguenti angoli:

• a con t forma angoli adiacenti di cui uno è 8 17 dell’altro;

• b con t forma angoli adiacenti di cui uno supera il doppio dell’altro di 8° 12’.

Dopo aver determinato le ampiezze degli angoli formati dalle rette a e b con t, spiega se le rette sono parallele. (Autati con il disegno.)

4 Due rette tagliate da una trasversale formano una coppia di angoli corrispondenti di cui uno è i 9 16 dell’angolo retto e l’altro è complementare dell’angolo di 57° 36' .

Determina l’ampiezza di ciascuno degli altri angoli e spiega se le due rette sono parallele.

SPIEGARE PROCEDIMENTI

5 Due rette parallele a e b sono tagliate da una trasversale t .

Due semirette r e s sono le bisettrici di due angoli corrispondenti, come in figura. Spiega, con una breve dimostrazione, la relazione che intercorre tra le due bisettrici.

6 Dati i segmenti AD e BC paralleli e AB e DC segmenti trasv ersali non paralleli, spiega come calcolare le ampiezze degli angoli 1 e 2, conoscendo le misure degli angoli A e D .

Dati

AD BC 1 = ?

A ; D 2 = ?

Risoluzione

a) Se AB è trasversale dei segmenti paralleli e …………, allora A e 1 sono ; quindi l’ampiezza di 1 è uguale a

b) Se DC è trasversale dei segmenti paralleli e , allora D e 2 sono

SFIDA MATEMATICA

7 La figura a lato mostra una “illusione ottica”. Una serie di rette parallele che apparentemente non lo sono.

Quale spiegazione geometrica puoi dare per dimostrare che sono parallele?

ROAD MAP PER TUTTI

Quando si definiscono parallele?

Due rette sono parallele quando non hanno punti in comune

Con quale simbolo si indicano?

rette nel piano

DATE DUE RETTE NEL PIANO

Quando si definiscono perpendicolari?

Quando sono incidenti e formano quattro angoli retti

Con quale simbolo si indicano?

Quando si definiscono incidenti?

Il simbolo di parallelismo è indicato da due trattini paralleli // ESEMPIO ESEMPIO ESEMPIO

Il simbolo di perpendicolarità è indicato da due trattini che si incontrano a formare una T rovesciata ⊥

Due rette sono incidenti quando hanno un punto in comune

W punto di intersezione

asse di un segmento

DATO UN SEGMENTO FG

Che cos'è l'asse del segmento?

L'asse di un segmento è la retta perpendicolare al segmento stesso che passa per il suo punto medio

Che cos'è il punto medio?

Il punto medio è il punto che divide a metà un segmento

ESEMPIO

F a M G

asse del segmento punto medio

1 Indica le seguenti coppie di rette parallele utilizzando i simboli (per esempio f  g). a c b d

e f

2 Riconosci le coppie di rette perpendicolari e indicale con i simboli (per esempio, f ⊥ g). p q

s t l m

3 Individua la coppia di rette parallele, quella di rette incidenti, quella di rette perpendicolari e, quando possibile, scrivi in simboli le relazioni.

rette a b a b l m …….…,,..............…… r s r s

4 MATEMATICA IN AZIONE Osserva la seguente immagine, che rappresenta un campo di baseball, e completa le affermazioni utilizzando termini e simboli adegu

a) a e b sono rette incidenti

b) b e d sono rette

c) c e d sono rette

d) a e c sono

e) a e d sono rette

f) b e c sono rette

b ⊥ d c  d b c

DATI UN PUNTO E UNA RETTA

Che cos'è la distanza del punto dalla retta?

DATE DUE RETTE PARALLELE

Che cos'è la distanza delle due rette?

distanze

ESEMPIO

La distanza di un punto da una retta è il segmento perpendicolare alla retta che ha come estremo il punto stesso

ESEMPIO

La distanza di due rette parallele è il segmento perpendicolare che congiunge le due rette

r PQ distanza di P da r

Che cos'è la proiezione di un punto su di essa?

proiezioni

UNA RETTA r

Che cos'è la proiezione di un segmento su di essa?

ESEMPIO ESEMPIO

La proiezione di un punto su una retta è il piede della perpendicolare alla retta passante per quel punto

Il punto P' è il piede della perpendicolare.

proiezione di P su

La proiezione di un segmento su una retta è il segmento che si ottiene unendo le proiezioni degli estremi del segmento sulla retta

DATA UNA COPPIA DI RETTE retta trasversale

Che cos'è una retta trasversale?

proiezione di FG su r

ESEMPIO

Una retta viene detta trasversale quando incontra due o più rette

trasversale

5 Trova il punto medio dei seguenti segmenti e tracciane l’asse.

6 Traccia la distanza dei seguenti punti dalla retta r e indicala.

a) Distanza di A da r :

b) Distanza di B da r : ………………

c) Distanza di C da r :

d) Distanza di D da r :

e) Distanza di E da r : ………………

f) Distanza di F da r : ………………

7 Considera la retta r e i punti indicati; disegna le proiezioni di ciascuno di essi sulla retta r. Procedi come indicato per il punto L.

8 Considera i seguenti disegni e in ognuno di essi individua la trasversale e le rette parallele.

La trasversale è

Le rette parallele sono ………………

La trasversale è

Le rette parallele sono

Gli angoli alterni interni sono la coppia 1 e 3 e la coppia 2 e 4; i due angoli di ogni coppia sono tra loro congruenti

RETTE PARALLELE TAGLIATE DA UNA TRASVERSALE

DATE DUE RETTE PARALLELE TAGLIATE DA UNA TRASVERSALE

Quali coppie di angoli si formano?

Gli angoli alterni esterni sono la coppia 6 e 8 e la coppia 5 e 7; i due angoli di ogni coppia sono tra loro congruenti

Gli angoli coniugati interni sono la coppia 3 e 2 e la coppia 4 e 1; i due angoli di ogni coppia sono supplementari (la loro somma è 180°)

Corrispondenti

Gli angoli coniugati esterni sono la coppia 6 e 7 e la coppia 5 e 8; i due angoli di ogni coppia sono supplementari (la loro somma è 180°)

Gli angoli corrispondenti sono le coppie 6 e 2, 4 e 8, 3 e 7, 1 e 5; i due angoli di ogni coppia sono congruenti

9 MATEMATICA IN AZIONE Individua le coppie di angoli alterni interni.

10 MATEMATICA IN AZIONE Individua le coppie di angoli coniugati interni.

11 Osserva la seguente illustrazione e, in base ai dati forniti, completa le richieste.

108° corrispondente di a

a’ = ………… perché ...............................................................................................................

g ’ = ………… perché ............................................................................................................... 108° coniugato esterno di a d’ = ………… – ………… = …......… perché ......................................................................... 108° d = – = perché

b’ = perché di a .

12 MATEMATICA IN AZIONE Le finestre di una stalla hanno due assi di legno parallele fermate da un’asse trasversale.

a) Come si chiamano gli angoli 1 e 2 ?

b) Che cosa puoi dire sulla loro ampiezza?

c) Se l’angolo 1 misura 48°, quanto misurerà l’angolo 2 ?

SIMULAZIONE DI VERIFICA

1 Rispondi con Vero o Falso ed effettua la correzione di ogni falso.

a) La distanza di un punto da una retta è un segmento parallelo alla retta data. V F

b) Due rette parallele hanno sempre la stessa distanza. V F

c) Due rette incidenti hanno un estremo in comune.

d) Due rette sovrapposte hanno tutti i punti coincidenti.

e) Due rette perpendicolari formano solo due angoli retti. V F

f) Gli angoli formati da due rette incidenti sono a due a due congruenti. V F

g) Il simbolo di parallelismo è =.

h) Il simbolo di perpendicolarità è ⊥

2 Osserva il disegno e completa.

a) La retta passante per M e H è alla retta r.

b) MH è la del punto dalla retta .

c) H è il della perpendicolare.

d) H è la del punto M sulla retta r

3 Identifica le coppie di angoli indicati con lo stesso colore.

a)

b) c)

4 Date due rette parallele tagliate da una trasversale:

a) gli angoli di quali coppie sono congruenti?

b) gli angoli di quali coppie sono supplementari?

F

5 Traccia sulla retta r le proiezioni dei segmenti assegnati (usa una matita colorata). In quale dei casi considerati la proiezione del segmento sulla retta ha la stessa lunghezza del segmento?

Risposta: A

6 Calcola le ampiezze degli angoli incogniti.

7 Date due rette parallele tagliate da una trasversale, due angoli coniugati esterni sono tali che la loro differenza è 38°. Determina la misura degli otto angoli formati dalle rette.

8 Date due rette tagliate da una trasversale, sai che due angoli coniugati interni misurano 54° e 125°; puoi stabilire se le due rette sono parallele? Motiva la risposta.

9 MATEMATICA IN AZIONE Osserva la scatola degli attrezzi chiusa e aperta e rispondi alle domande.

a) Sapendo che l’ampiezza dell’angolo 1 = 70°, calcola le ampiezze degli angoli 2 e 3

b) Aprendo la scatola, qual è l’ampiezza dell’angolo ABC ?

c) Se l’ampiezza dell’angolo 1 fosse 60°, la pendenza ( 3 ) della scatola aperta sarebbe minore o maggiore rispetto alla scatola chiusa?

I POLIGONI UNITÀ 5

Chi ha della

paura matematica?

Non ci crederai, ma anche i poligoni possono essere classificati! Ovviamente non si tratta di stabilire la loro posizione in una graduatoria, né di proclamare il poligono vincitore; più semplicemente classificarli vuol dire distribuirli in raggruppamenti, in base ad alcune caratteristiche, come il numero dei lati e le relazioni tra gli angoli, o rispetto ad alcune misure.

Con un po’ di attenzione riuscirai a non confonderti: i prefissi “tri”, “quadri”, “penta” possono aiutarti a collegare i nomi dei poligoni con i numeri dei lati e degli angoli. Scoprirai che alcuni di questi prefissi derivano dal greco antico e, una volta memorizzato il loro significato, comprenderai meglio le proprietà delle relative figure.

Quando avrai a che fare con le regole che permettono di stabilire quanto vale la somma degli angoli esterni di un poligono (ti “spoilero” il risultato: è sempre 360 gradi!) e quella degli angoli interni, un sottile brivido di paura potrebbe correrti lungo la schiena, ma a quel punto saprai come ricordarle, perché i poligoni avranno già dato una formaaituoi pensierigeometrici!

ROAD MAP

DISTINGUIAMO LE SPEZZATE DAI POLIGONI

CLASSIFICHIAMO I POLIGONI

INDIVIDUIAMO LE RELAZIONI TRA I LATI DI UN POLIGONO

CALCOLIAMO IL NUMERO DI DIAGONALI IN UN POLIGONO

INDIVIDUIAMO LE RELAZIONI TRA GLI ANGOLI DI UN POLIGONO

MATERIALE INTEGRATIVO MULTIMEDIALE

Spezzate e poligoni 1

SUCCEDE CHE...

Pietro, sfogliando un libro di geografia, ha scoperto che sia Palmanova (Udine) sia Grammichele (Catania) hanno la piazza principale a forma esagonale. Vorrebbe sapere quale delle due ha il contorno più lungo. Che cosa deve calcolare?

Per rispondere alla domanda è necessario conoscere le caratteristiche dei poligoni.

Una spezzata è una linea formata da tre o più segmenti a due a due consecutivi ma non adiacenti.

Come le linee, le spezzate possono essere classificate in spezzate aperte semplici o intrecciate e spezzate chiuse semplici o intrecciate.

spezzata aperta semplice

spezzata aperta intrecciata

spezzata chiusa semplice

Le spezzate chiuse delimitano parti di piano.

spezzata chiusa intrecciata

Un poligono è la parte di piano delimitata da una spezzata chiusa semplice.

Osservando il poligono ABCDE si ha:

• la spezzata che lo delimita è detta contorno;

• i segmenti che costituiscono la spezzata (AB, BC, CD...) sono i lati del poligono;

• gli estremi dei lati sono i vertici;

• due lati che hanno un vertice in comune si dicono consecutivi (BC e CD, …);

• due vertici che appartengono allo stesso lato si dicono consecutivi (A e B, …);

• gli angoli della spezzata formati da due lati consecutivi si dicono angoli interni;

• gli angoli formati da un lato e dal prolungamento del lato consecutivo si dicono angoli esterni;

• due angoli che hanno un lato in comune si dicono adiacenti allo stesso lato (A e B , …);

• i segmenti che congiungono due vertici non consecutivi si dicono diagonali.

Il perimetro di un poligono è la misura del suo contorno e viene indicata con 2p.

La metà del perimetro è il semiperimetro e si indica con p. Se due poligoni A e B hanno lo stesso perimetro, sono isoperimetrici e si scrive 2pA = 2pB.

OS LUZIONE

Pietro deve calcolare i perimetri dei due esagoni e confrontarli.

Ogni lato della piazza di Palmanova è lungo circa 90 m e ogni lato della piazza di Grammichele è lungo circa 55 m; i perimetri delle due piazze rispettivamente misurano:

2 p = 90 m × 6 = 540 m 2 p = 55 m × 6 = 330 m

La piazza di Palmanova ha il contorno più lungo.

1 Classifica le seguenti spezzate.

2 Osserva il poligono ABCD e completa le seguenti frasi.

a) C è un

b) AB è un

c) Quanti vertici ha ABCD?

d) Quanti lati ha ABCD?

e) ABC è un

f) Quanti angoli interni ha ABCD?

3 MATEMATICA IN AZIONE Quali tra le seguenti linee rappresentano dei poligoni?

Classificazione dei poligoni 2

SUCCEDE CHE...

Partendo da piazza Cavour, Pietro e Emma percorrono in senso orario tutto il marciapiede intorno ai giardini pubblici Indro Montanelli a Milano. Durante il percorso, ogni volta che cambiano direzione voltano a destra. Arrivati in via Palestro, però, si accorgono che per due volte cambiano direzione voltando a sinistra. Come mai?

Per rispondere alla domanda è necessario saper classificare i poligoni.

Rispetto al numero dei lati

I poligoni prendono il nome dal numero dei lati e degli angoli; quando non esiste un nome particolare si specifica il numero dei lati, per esempio: poligono di 15 lati, poligono di 20 lati…

triangolo quadrilatero pentagono esagono ettagono ottagono ennagono (9 lati), decagono (10 lati), endecagono (11 lati), dodecagono (12 lati).

Rispetto agli angoli

Un poligono è convesso se tutti i suoi angoli sono minori di 180°. Un poligono è concavo se almeno un angolo è maggiore di 180°.

Rispetto alla misura dei lati e/o degli angoli

Un poligono è equilatero se tutti i suoi lati sono congruenti.

I lati e gli angoli indicati con lo stesso simbolo sono congruenti.

Un poligono è equiangolo se tutti i suoi angoli sono congruenti.

Un poligono regolare ha sia i lati che gli angoli congruenti.

Un poligono regolare è equilatero ed equiangolo.

OS LUZIONE

Riprendi la mappa: Pietro e Emma svoltano due volte a sinistra perché il percorso effettuato delimita un poligono concavo con due angoli interni maggiori di 180° (angoli colorati in giallo), proprio nella parte adiacente a via Palestro.

Primi

ESERCIZI

1 Stabilisci se i poligoni sono concavi o convessi.

2 Segna con un colore l’angolo concavo dell’esercizio precedente.

3 Calcola il perimetro dei seguenti poligoni regolari, dove con , si indica la misura del lato e con n il numero dei lati.

a) 24 cm b) 16 cm c) 18 cm

Il poligono ha lati;

è un

2p = , × n = 24 × =

Il poligono ha lati; è un

2p = , × n = × =

Il poligono ha lati; è un

2p = , × n = × =

4 MATEMATICA IN AZIONE La figura rappresenta la vista dall’alto di una piazza in cui, attorno alla fontana, ci sono 4 aiuole.

Osservala e stabilisci se le seguenti affermazioni sono vere o false.

a) La fontana è a forma di ottagono. V F

b) La fontana è a forma di poligono regolare. V F

c) Le aiuole sono tutti pentagoni. V F

d) Le aiuole sono a forma di poligono convesso. V F

LEZIONE

Relazione tra i lati di un poligono. Diagonali di un poligono 3

I nonni di Emma vogliono costruire nel loro giardino un recinto in cui tenere una capretta. Hanno a disposizione quattro moduli metallici rigidi. Tre misurano ciascuno 2 m e il quarto 7 m, ma si accorgono che non riescono a chiudere il recinto utilizzando per intero le lunghezze dei quattro moduli. Perché?

Per rispondere alla domanda occorre aver presente le condizioni necessarie per costruire un poligono.

Relazione tra i lati

Non sempre è possibile costruire dei modelli di poligoni con listelli di legno o metallo.

Se prendiamo, per esempio, quattro listelli rispettivamente di 2 cm, 3 cm, 7 cm e 15 cm non è possibile costruire un quadrilatero: il lato di 15 cm è troppo lungo.

Se al posto del listello di 15 cm ne usiamo uno lungo 9 cm, la spezzata si potrà chiudere formando un poligono.

Questo perché la somma dei tre lati minori, 2 + 3 + 7 = 12, è maggiore del listello più lungo, cioè quello di 9 cm.

In ogni poligono il lato maggiore è sempre minore della somma degli altri lati.

Diagonali

Esiste una formula che ci permette di stabilire quante diagonali escono da ogni vertice di un poligono. Indicando con dv il numero di diagonali uscenti da un vertice e con n il numero dei lati si ha:

dv = n – 3, cioè il numero di diagonali uscenti da un vertice è uguale al numero dei lati meno 3.

Esiste anche una formula che ci permette di stabilire il numero totale di diagonali (d) di un poligono con n lati:

d = n × (n – 3) 2

Per costruire il recinto i nonni di Emma non possono utilizzare per intero le lunghezze dei quattro moduli perché il modulo più lungo è maggiore della somma dei tre moduli più corti: (2 + 2 + 2) m = 6 m " 7 m > 6 m

Primi

ESERCIZI

1 Completa la seguente frase.

In un poligono il lato maggiore è sempre della degli altri

2 Osserva il disegno e completa.

a) AC e BD sono del poligono ABCD che ha lati.

b) Calcola il numero delle diagonali uscenti da un vertice del poligono ABCD: dv =

c) Calcola il numero totale delle diagonali del poligono

ABCD: d =

3 Date le seguenti misure (in centimetri), stabilisci se è possibile costruire un quadrilatero. Quanto misura il lato maggiore?

3 13 16 2

Somma gli altri tre lati: + + =

Confronta la misura trovata con il lato maggiore: è possibile costruire il quadrilatero?

4 Applica le formule per calcolare il numero di diagonali uscenti da ogni vertice e il numero totale delle diagonali del poligono a fianco. Verifica l’esattezza dei tuoi calcoli tracciando nel disegno tutte le diagonali.

dv =

d =

5 EDUCAZIONE CIVICA Il cartello stradale di stop indica l’obbligo di fermarsi e di dare la precedenza.

a) Che tipo di poligono è?

b) Quante sono le diagonali uscenti da ogni vertice?

c) Quante sono in tutto le diagonali?

Relazioni tra gli angoli di un poligono 4

SUCCEDE CHE...

Pietro vuole costruire in giardino un’aiuola a forma di esagono regolare, delimitata da mattoni di tufo. A tale scopo comincia a tracciare sul terreno due lati uguali che formano un angolo di 100°, ma suo papà le dice che l’ampiezza dell’angolo non va bene. Perché?

Per rispondere alla domanda occorre sapere quale relazione intercorre tra il numero dei lati e la somma degli angoli interni di un poligono.

Relazione tra gli angoli esterni

Ritagliamo gli angoli esterni di un pentagono e sistemiamoli in modo che abbiano un vertice in comune: notiamo che la loro somma è un angolo giro 360°.

Si può provare che la somma degli angoli esterni di qualunque poligono misura 360°.

La somma degli angoli esterni di un poligono è un angolo giro e misura 360°.

Relazione tra gli angoli interni

Osserva il poligono disegnato a lato e i suoi angoli interni.

Puoi notare che ogni angolo interno con il suo corrispondente esterno forma un angolo piatto. Poiché il poligono ha cinque lati, la somma degli angoli interni (Si) e dei suoi angoli esterni (Se) è uguale a 5 angoli piatti:

Si + Se = 5 × 180°

a f g b h c i d j e

Essendo la somma degli angoli esterni uguale a 360° = 2 ×180° si ha:

Si = 5 × 180° – 2 × 180° = (5 – 2) × 180°

Quindi la somma degli angoli interni di un pentagono è uguale a tanti angoli piatti quanti sono i lati meno due. Il ragionamento appena fatto vale per tutti i poligoni convessi e concavi. In generale si ha che:

Si = (n – 2) × 180° dove n = numero dei lati

La somma delle ampiezze degli angoli interni di un poligono qualsiasi è uguale a tanti angoli piatti quanti sono i lati meno due.

OS LUZIONE

In un esagono Si = (6 – 2) × 180° = 720°.

Essendo i suoi angoli interni congruenti ognuno misura

720° : 6 = 120°, mentre Pietro ha formato un angolo di 100°.

Primi

ESERCIZI

1 Completa le seguenti frasi.

La somma degli angoli interni varia al variare del numero dei lati del poligono. La somma degli angoli esterni, invece, è sempre uguale a 360°.

a) In un poligono la somma degli angoli esterni è uguale a un angolo che è ampio

b) La somma degli angoli interni di un poligono qualsiasi è uguale a tanti angoli quanti sono i lati due. In simboli: Si =

2 Calcola la somma degli angoli interni di un quadrilatero.

3 Dopo aver disegnato gli angoli esterni del quadrilatero, calcola le loro ampiezze.

b

1 = 180° – a =

MATEMATICA IN AZIONE Il centro storico di Avola, in provincia di Siracusa, ha la forma di un esagono pressoché regolare. Tutti i lati misurano mediamente 270 m.

a) Quanto misura l’angolo (in bianco nella figura) formato dalle strade del perimetro a ogni incrocio?

b) La strada che prosegue da un lato dell’esagono forma un angolo esterno acuto (in rosso). Quanto misura?

c) Trova la misura approssimativa del perimetro dell’esagono ed esprimila in kilometri.

MAPPA

PERIMETRO

2p = somma delle misure dei lati

la cui lunghezza complessiva si chiama

spezzate chiuse semplici

sono delimitati da

ANGOLI ESTERNI

ANGOLI INTERNI

la cui somma è la cui somma è 360° 180° × (numero dei lati – 2)

I POLIGONI

i loro elementi

sono possono essere hanno

CONVESSI

CONCAVI

VERTICI

vertice diagonale lato

Il lato maggiore è minore della somma degli altri.

–

SPEZZATE E POLIGONI

1 Rispondi alle seguenti domande.

a) Che cos’è una spezzata?

b) Come può essere una spezzata?

2 Seguendo le indicazioni date, disegna all’interno della tabella le spezzate.

Spezzata aperta chiusa semplice intrecciata

3 Osserva la figura e completa.

a) La spezzata ABCDEF delimita un poligono perché

b) Il contorno del poligono è

c) I vertici sono A,

d) I lati sono AB,

e) Gli angoli interni sono 6: FAB ,

f) Il segmento FB è una

g) BCM è un angolo

4 Contrassegna i poligoni.

5 Indica quali sono i vertici e i lati dei seguenti poligoni.

Poligono 1: • vertici .................................................

• lati

Poligono 2: • vertici

• lati

Poligono 3: • vertici

• lati

Poligono 4: • vertici

• lati

6 Osserva il poligono e completa le frasi.

a) D e C sono vertici consecutivi

b) A e B sono vertici

c) I vertici consecutivi di F sono e

d) AB e BC sono lati consecutivi

e) I lati consecutivi di CD sono e

f) I lati AF e FE sono

g) L’angolo A e l’angolo B sono adiacenti al lato

h) L’angolo C e l’angolo D sono adiacenti al lato

i) Gli angoli e sono adiacenti al lato EF.

7 Completa le seguenti frasi.

a) Una spezzata è una formata da tre o più segmenti non

b) Un poligono è la di piano delimitata da una spezzata

c) I segmenti che costituiscono la spezzata sono

d) Due lati sono consecutivi se hanno un in comune.

e) Un vertice è un di un

f) Gli angoli formati da due lati consecutivi sono

g) Gli angoli esterni sono formati da un e dal prolungamento di uno dei due consecutivi.

h) Due angoli adiacenti hanno un in

8 Disegna, sul tuo quaderno, una spezzata:

a) aperta intrecciata di 5 lati c) chiusa intrecciata di 7 lati

b) aperta intrecciata i cui lati d) chiusa semplice di 6 lati misurino 2,5 cm, 3 cm, 4 cm e 6 cm e) aperta semplice con 7 lati congruenti

9 Indica i vertici della spezzata con le lettere A , B, C , D, E, F, scrivendole in senso antiorario a partire dalla lettera già segnata. Classifica poi la spezzata.

Nei piani cartesiani sotto riportati sono segnati dei punti. Congiungili in modo tale da ottenere per ognuno di essi: (Usa colori diversi per evidenziarle e indica in sequenza le lettere dei vertici.)

10 a) una spezzata semplice aperta

a) una spezzata semplice chiusa

b) una spezzata intrecciata aperta b) una spezzata intrecciata chiusa

12 Rappresenta sul quaderno i seguenti gruppi di punti in un piano cartesiano. Congiungili seguendo l’ordine alfa betico e definisci la spezzata che ottieni.

a) A (2; 7) B (1; 2) C (4; 3) D (7; 1)

b) A (3; 8) B (4; 4) C (7; 8) D (2; 3)

c) A (15; 8) B (5; 4) C (11; 4) D (13; 10) E (9; 8)

Calcola il perimetro dei seguenti poligoni, scrivendo prima le misure dei lati nel disegno.

ESEMPIO

Dati

NO = 13 cm

PO = 12 cm NP = 10 cm

Richiesta

2p (PNO) = ?

13

14

15

16

Risoluzione

Il perimetro è la somma dei lati, quindi:

2p = NO + PO + NP = 13 + 12 + 10 = 35 cm

AB = 2,4 cm |

BC = 1,3 cm

CA = 1,6 cm

2p ( ABC ) = ?

LM = 9,5 cm

MN = 8,4 cm

NO = 6,2 cm

OL = 2,4 cm

2p (LMNO) = ?

ST = 8,6 cm

TU = 12,2 cm

UV = 4,8 cm

VS = 6,2 cm

2p (STUV ) = ?

AB = 2 cm

BC = 1,8 cm

CD = 3,2 cm

DE = 2,2 cm

EF = 3,6 cm

AF = 4,1 cm

2p ( ABCDEF ) = ?

Con il righello, misura in millimetri la lunghezza dei lati del poligono e calcola il suo perimetro.

Dati

AB

Determina il perimetro delle seguenti figure.

25 Completa i dati e calcola il perimetro del poligono dato.

Dati

BC = 4 3 × AB

AB = 15 cm

CD = 24 cm

AD = 16 cm

A B

Richiesta

2p ( ABCD) = ?

AB = BC = 3 5 × AB

CA = …………

2p ( ABC ) = ?

Risoluzione

CB = 1 4 × CD

AB = 3 4 × AD

2

) = ?

Bisogna trovare la misura del lato BC:

BC = 15 : 3 × 4 = 20 cm

2p ( ABCD) = 15 + 20 + 24 + 16 = 75 cm

26 Indica i vertici nel disegno, scrivi i dati e calcola il perimetro del poligono.

Risolvi i seguenti problemi.

27

28

CD = 48 cm

BC = 2 × CD

AE = 29,6 dm

DE = 1 2 × AE

AB = 1,22 m

2p ( ABCDE ) = ?

OP = ON = 77 dm

ML = 3 11 × ON LP = 7 4 × MN

= 1,2 m

2p (LMNOP ) = ?

29 I lati di un quadrilatero ABCD misurano rispettivamente:

AB = 34 cm

BC = 25 cm

AD = 36 cm

CD = 5 2 × AD

Calcola il perimetro di ABCD. [185 cm]

30 Dato il quadrilatero LMNO, calcola il suo perimetro sapendo che:

LM = MN + 3 dm ON = OL × 2 − 6 dm MN = 24 dm

= 1 3 × LM + 5 dm [87 dm]

31 Il quadrilatero CDEF ha il perimetro che misura 198 dam.

Calcola la misura del lato ED sapendo che:

= 7 4 × FC + 6

= 3 ×

32 Dato il triangolo ABC , calcola il suo perimetro sapendo che:

AB misura 48 mm;

CA è tre quinti di BC aumentato di 14 mm;

BC è il doppio di AB diminuito di 26 mm. [174 mm]

2

CLASSIFICAZIONE DEI POLIGONI

33 Rispondi con Vero o Falso.

a) Un poligono non può avere meno di 4 lati.

b) Un poligono con 7 lati si chiama ennagono.

c) Un poligono è concavo se ha almeno un angolo maggiore di 180°.

d) Un poligono che ha solo i lati uguali si dice regolare.

e) Un poligono che ha tutti gli angoli uguali si dice equiangolo.

34 Osserva i seguenti poligoni, scrivi il nome e classificali rispetto agli angoli (concavo o convesso). a)

F

35 STEM Osserva le seguenti fotografie e distingui i poligoni concavi da quelli convessi.

b) c) d)

36 Determine which of the following polygons are concave and which are convex. concave convex

37 Tra i seguenti poligoni riconosci quelli regolari e quelli irregolari.

38 Disegna tre poligoni concavi: uno di 4, uno di 5 e uno di 6 lati.

39 Completa i disegni in modo che siano rispettate le classificazioni scritte sotto.

a) quadrilatero solo equiangolo b) quadrilatero regolare c) quadrilatero solo equilatero

Risolvi i seguenti quesiti.

40 Rappresenta i seguenti punti nel piano carte siano.

F (2; 3) P (3; 11)

G (5; 1) Q (10; 12)

H (9; 2) R (15; 13)

I (8; 7) S (13; 5)

L(6; 9) T (4; 6)

M (4; 14) U (15; 3)

N (13; 10) V (11; 13)

a) Considera ora i punti F, G, H, I, L e stabilisci le coordinate di un punto Z tale che, congiungendo i sei punti, si ottenga un poligono convesso.

b) Determina poi le coordinate di un punto Z ' tale che, unito con i cinque precedenti, dia un poligono concavo.

41 Rappresenta su un piano cartesiano il poligono RSTUV i cui vertici hanno coordinate:

R (2; 0) S (4; 0) T (5,5; 2,5) U (3,5; 1,5) V (1; 3,5)

a) Modifica le coordinate di un punto del poligono RSTUV in modo da ottenere un poligono convesso che disegnerai in un altro piano cartesiano.

b) Ripartendo dal poligono RSTUV inserisci un altro vertice in modo da ottenere un nuovo poligono con 2 angoli concavi.

Poligoni regolari

Risolvi i seguenti problemi.

42 Calcola il perimetro dei seguenti poligoni regolari.

43 Calcola il perimetro di un pentagono regolare, sapendo che il lato misura 36 cm.

44 Il perimetro di un esagono regolare misura 138 cm; quanto misura il suo lato?

45 Calcola il perimetro di un quadrato, sapendo che il lato misura 12,5 cm.

46 Il perimetro di un triangolo misura 45 cm. Trova la misura del suo lato, sapendo che è regolare.

47 Il lato di un pentagono è uguale a quello di un esagono che ha il perimetro di 60 cm.

Calcola il perimetro del pentagono.

48 Date le seguenti coppie di poligoni regolari, in base ai dati forniti, calcola quanto è richiesto.

RELAZIONE TRA I LATI DI UN POLIGONO. DIAGONALI DI UN POLIGONO

49 Scrivi quale relazione deve esserci tra i lati di un poligono.

50 Quali dei seguenti gruppi di misure possono indicare le lunghezze dei lati di un pentagono? Motiva le tue scelte.

a) 56 cm; 38 cm; 14 cm; 8 cm; 64 cm.

• La misura maggiore è 64 cm

?

• Si sommano le altre misure: 56 + 38 + 14 + 8 = 116 cm

• Si confronta il risultato con la misura maggiore: 116 cm è maggiore di 64 cm (116 cm > 64 cm)?

Sì, quindi è possibile costruire il pentagono.

b) 14 cm; 20 cm; 3 cm; 124 cm; 12 cm.

14 + 20 + 3 + 12 = 49 cm

Non è possibile costruire il pentagono poiché

49 cm < 124 cm.

a)

b) 4,6

c) 27 dam 93 dam 39 dam 17 dam 9 dam

d)

Risolvi i seguenti esercizi.

51 Con la terna di misure 24 dm, 48 dm, 78 dm, si può costruire un triangolo?

Motiva la risposta.

52 Esiste un pentagono con tre lati congruenti di 16 cm e gli altri due di 96 cm e 6 cm?

Motiva la risposta.

53 STEM Leo ha 5 pezzi di una staccionata lunghi 120 cm, 80 cm, 190 cm, 160 cm, 130 cm.

Vuole fare il bordo di un’aiuola; riesce a chiudere il recinto? Motiva la risposta.

54 STEM Giulia vuole realizzare una casetta con dei bastoncini.

Riesce a costruirla se ha due pezzi lunghi 10 cm, due pezzi 15 cm e un pezzo lungo 20 cm? Motiva la risposta.

55 Completa in modo che le quaterne che ogni volta si formano siano le misure in metri dei lati di quadrilateri (motiva i valori inseriti).

a) a = 7 b = 9 c = 10 d =

b) a = 25 b = 32 c = 27 d =

c) a = 11 b = 13 c = 14 d =

d) a = 22 b = 22 c = 17 d =

Rispondi ai seguenti quesiti.

56 Una spezzata di quattro lati lunga 49 cm ha tre lati che misurano 8,5 cm, 6 cm e 7,5 cm. Questa spezzata può essere il contorno di un quadrilatero? Perché?

57 Una spezzata di cinque lati è lunga 98 cm; sapendo che quattro dei suoi lati sono lunghi 12 cm, 8 cm, 19 cm, 16 cm, la spezzata può essere un pentagono? Motiva la risposta.

58 Quattro lati di un pentagono misurano 18 cm, 28 cm, 9 cm, 35 cm e il suo perimetro è di 252 cm. Esiste questo pentagono? Perché?

Diagonali di un poligono

59 Rispondi alle seguenti domande.

a) In un poligono come si definisce un vertice?

b) Qual è la definizione di diagonale di un poligono?

c) Qual è il poligono che non ha diagonali?

d) Qual è la formula per determinare il numero di diagonali uscenti da un vertice?

e) Qual è la formula per determinare il numero di diagonali di un poligono?

60 Osserva il disegno e completa le frasi.

a) EC è la diagonale uscente dal vertice e dal vertice

b) Le diagonali uscenti dal vertice A sono e

c) La diagonale uscente dal vertice B è ……………… ; qual è l’altra diagonale che non è stata tracciata? ………………

61 Dati i quadrilateri ABCD riconosci quali segmenti sono diagonali. a)

62 In the following polygons, draw the diagonals from the vertex A . a) b) c) d) e)

63 STEM Questa conchiglia si può considerare come un poligono con 16 lati.

Calcola il numero di diagonali uscenti dal vertice A utilizzando la formula dv = n − 3.

64 EDUCAZIONE CIVICA Ale, Marco, Ciro, Daniela, Elisa e Francy hanno organizzato una serie di partite a tennis.

a) Nello schema si può contare il numero di partite che dovrà affrontare Ale, che corrisponde al numero di diagonali uscenti dal vertice A più i due lati consecutivi. Quante partite giocherà Ale?

b) Traccia ora tutte le diagonali e sommale al numero dei lati: troverai quante partite giocheranno in tutto i sei tennisti. Quante sono?

65 MATEMATICA IN AZIONE A un torneo di pallavolo sono presenti 9 squadre. Quante partite si giocheranno in tutto se ogni squadra dovrà scontrarsi solo una volta con ciascuna delle altre? (Utilizza uno schema come quello dell’esercizio precedente.) [36]

Rispondi ai seguenti quesiti.

66 Qual è il numero di diagonali uscenti da un vertice di un ottagono?

67 Qual è il numero di diagonali uscenti da un vertice di un poligono di 18 lati?

68 Qual è il numero totale di diagonali di un triangolo?

69 Qual è il numero totale di diagonali di un decagono?

70 Quale poligono ha in totale 14 diagonali?

71 Quale poligono ha in totale 27 diagonali?

Esegui i disegni sul quaderno e rispondi alle domande.

72 Disegna un quadrilatero e un pentagono; traccia poi tutte le diagonali pos sibili per ognuno dei due poligoni e verifica l’esattezza del tuo disegno utilizzando le formule studiate.

73 Disegna un esagono. Quanti triangoli ottieni tracciando le diagonali uscenti da un solo vertice?

74 Disegna un decagono. Quanti triangoli ottieni tracciando le diagonali uscenti da un solo vertice?

RELAZIONI TRA GLI ANGOLI DI UN POLIGONO

75 Considera il seguente poligono e completa le frasi.

a) α e β sono adiacenti al lato

b) Il lato BC è consecutivo a e

c) γ e δ sono adiacenti al lato

d) E e F sono adiacenti al lato

e) A e F sono adiacenti al lato

f) L’angolo esterno evidenziato in azzurro

è adiacente all’angolo

76 Considera i poligoni qui sotto e calcola le ampiezze degli angoli evidenziati in rosso. a) b) c) d)

? ?

77 Rispondi alle seguenti domande.

?

a) Se l’angolo interno di un poligono regolare misura 60°, possiamo sapere quanti lati ha il poligono? Se sì, quanti sono? ……………….

b) Se l’angolo esterno di un poligono regolare misura 90°, potrebbe trattarsi di un quadrilatero? Se sì, quale?

c) Se un poligono ha un angolo esterno che misura 35° 30’, possiamo calcolare il suo angolo interno? Se sì, quanto misura?

Risolvi i seguenti problemi.

ESEMPIO

Calcola la misura della somma degli angoli interni di un ettagono.

L’ettagono ha 7 lati, quindi n = 7. Applicando la formula si ha:

Si = (n − 2) × 180° = (7 − 2) × 180° = 5 × 180° = 900°

78 Determina l’ampiezza della somma degli angoli interni di un esagono.

79 Determina l’ampiezza della somma degli angoli interni di un ennagono.

80 Un triangolo ha un angolo di 90°; calcola l’ampiezza degli altri due, sapendo che sono tra loro congruenti.

81 MATEMATICA IN AZIONE Questa scatola di dolci esternamente ha la forma quadrata e internamente ottagonale regolare.

Dopo aver classificato gli angoli delle parti triangolari, calcola le loro ampiezze.

Dopo aver determinato la somma degli angoli interni di ciascun poligono, calcola l’ampiezza degli angoli indicati con le lettere.

88 STEM In una macchina fotografica il diaframma è un sistema di lamelle posto all’interno dell’obiettivo che permette di regolare la quantità di luce che viene lasciata passare.

a) Le lamelle formano un poligono regolare, nel caso della figura un decagono; qual è la misura dell’angolo CBD ?

b) Calcola l’ampiezza dell’angolo nel caso in cui il diaframma abbia 12 lamelle, 15 lamelle, 18 lamelle o 20 lamelle.

Determina il numero dei lati di ciascuno dei poligoni di cui conosci la somma degli angoli interni.

ESEMPIO

La somma degli angoli interni di un poligono è 1 260°; determina il numero dei lati del poligono.

In questo caso dobbiamo usare la formula inversa di Si = (n − 2) × 180°, ovvero: n = Si

+ 2

che ci indica di dividere la somma degli angoli interni per 180° e di aggiungere 2 al risultato.

Quindi: n = 1 260° 180° + 2 = 7 + 2 = 9. Il poligono ha 9 lati.

COMPETENZE

ARGOMENTARE

La tassellatura

Si ha una tassellatura soltanto quando le varie “tessere” che la compongono non si sovrappongono né lasciano spazi vuoti, come le piastrelle di un pavimento. Vale la seguente proprietà: se la somma degli angoli attorno a un vertice comune è di 360°, le tessere permettono una tassellatura.

A + B + C + D = 360°

1 Spiega sul tuo quaderno, aiutandoti con i disegni, perché con delle piastrelle di forma esagonale regolare o di forma quadrata o con dei triangoli equilateri, è possibile pavimentare una stanza.

2 Puoi ricoprire con dei pentagoni equilateri una superficie piana senza sovrapporli o lasciare spazi vuoti?

Giustifica la risposta.

3 È possibile tassellare con una combinazione di due esagoni regolari e due triangoli equilateri?

Giustifica la risposta.

4 È possibile tassellare con una combinazione di un esagono regolare, due quadrati e un triangolo equilatero?

Giustifica la risposta.

5 È possibile tassellare con tessere tutte uguali a forma di triangolo scaleno?

Giustifica la risposta.

6 Dato un poligono regolare di n lati, con la formula 360° : n che cosa trovi?

Spiega come puoi trovare la misura di ciascun angolo interno. D A B C

RISOLVERE PROBLEMI

7 Calcola il perimetro della seguente figura.

8 Un cerchio è stato diviso in dodici parti congruenti usando un goniometro.

a) Unendo i punti trovati che figura si ottiene?

b) Quali punti devi unire per ottenere un triangolo regolare?

c) Quali punti devi unire per ottenere un quadrato?

d) Quali punti devi unire per ottenere un esagono regolare?

e) È possibile ottenere un ottagono regolare?

f) Spiega per ogni risposta il procedimento che hai utilizzato.

9 Riccardo utilizza questo metodo per calcolare la somma degli angoli interni di un poligono.

Segna un punto interno al poligono e lo unisce ai suoi vertici. Conta il numero dei triangoli ottenuti, moltiplica per 180° e poi sottrae 360°. Il suo metodo è accettabile? Motiva la risposta.

10 I triangoli

Quanti triangoli riesci a vedere in figura?

(Testo tratto dalla gara Giochi di Rosi del 2015, organizzata dal Centro PRISTEM dell’Università Bocconi di Milano)

ROAD MAP PER TUTTI

Da che cosa è delimitato?

Da una spezzata semplice chiusa

DATO UN POLIGONO

Che cos'è un vertice?

Il vertice di un poligono è il punto comune di due lati

Che cos'è un lato?

Il lato di un poligono è ciascun segmento della spezzata

Che cos'è la diagonale?

La diagonale è un segmento che unisce due vertici non consecutivi.

AD e AC sono le due diagonali uscenti dal vertice A

Che cos'è il perimetro di un poligono?

Il perimetro di un poligono è la misura del suo contorno, cioè la somma delle misure dei lati del poligono

Come si indica?

Il perimetro si indica con 2p

Il perimetro di un poligono di lati 18 dm, 14 dm, 6 dm e 4 dm è: 2p = 18 + 14 + 6 + 4 = 42 dm

1 MATEMATICA IN AZIONE Osserva le figure ed esegui le richieste. a) Per ogni riga cerca l’intruso, cioè la figura che non è un poligono.

b) Segna in rosso i lati delle figure che sono poligoni.

2 Calcola il perimetro dei seguenti poligoni.

3 Traccia tutte le diagonali dei seguenti poligoni.

Come si classificano rispetto agli angoli?

DATI DEI POLIGONI

Se un poligono ha almeno un angolo maggiore di 180° si dice concavo, se ha tutti gli angoli minori di 180° è convesso

Come si classificano rispetto ai lati?

In base al numero dei lati

convesso

concavo

Quando è equiangolo?

3 lati triangolo 4 lati quadrilatero 5 lati pentagono 6 lati esagono

Quando ha tutti gli angoli congruenti

DATO UN POLIGONO

Quando è regolare?

Quando ha tutti gli angoli e tutti i lati congruenti

Quando è equilatero?

Quando ha tutti i lati congruenti

4 Scrivi il nome di ognuno dei seguenti poligoni e stabilisci se è concavo o convesso. a) b) c)

5 EDUCAZIONE CIVICA Scrivi i nomi dei seguenti poligoni.

6 Stabilisci quali dei seguenti poligoni sono equiangoli, quali equilateri e quali regolari. (A simbolo uguale corrisponde elemento congruente) a) b) c)

7 Dati i seguenti poligoni regolari, calcola il loro perimetro. [42 cm; 6 cm]

8 dm 15 dm 11 dm C F 1,5 m

8 Considera un ettagono regolare avente il perimetro di 26,25 dm; quanto misura il suo lato? a) 375 cm b) 37,5 cm c) 3,75 cm

9 Considera un decagono regolare con il perimetro di 85 m; quanto misura il suo lato? a) 0,85 dm b) 8,5 dm c) 85 dm

poligoni e angoli

Cosa si intende per angolo esterno?

Un angolo esterno è l'angolo formato da un lato e dal prolungamento del suo consecutivo

ESEMPIO

DATO UN POLIGONO angolo esterno

Cosa si intende per angolo interno?

Un angolo interno è l'angolo formato da due lati consecutivi

angolo interno E

Quale relazione esiste tra angolo interno e corrispondente esterno?

La somma di un angolo interno più il corrispondente angolo esterno è uguale a un angolo piatto: angolo interno + angolo esterno = 180°

somma angoli interni e esterni

Da cosa dipende la somma degli angoli interni?

DATO UN POLIGONO

La somma degli angoli interni di un poligono Si dipende dal numero di lati n ed è uguale a tanti angoli piatti quanti sono i lati meno due

Come si calcola?

Si = (n – 2) × 180°

Quanto misura la somma degli angoli esterni?

La somma degli angoli esterni misura sempre 360°

10 Nei seguenti poligoni evidenzia con un archetto gli angoli interni e con due archetti quelli esterni, come nell’esempio. a) b)

11 Calcola le ampiezze degli angoli interni dei seguenti poligoni. a)

12 Calcola le ampiezze degli angoli interni del seguente quadrilatero.

–

13 Calcola la somma degli angoli interni dei poligoni, come nell’esempio.

Poligono n = numero dei lati Si = somma degli angoli interni quadrilatero 4 (4 – 2) × 180° = pentagono esagono ettagono ottagono decagono

SIMULAZIONE DI VERIFICA

1 Osserva il disegno e completa.

a) ABCDE è un poligono

b) B è un

c) AB è un

d) AC è una

e) AED è un

f) α è un

2 Classifica i seguenti poligoni rispetto ai lati e rispetto agli angoli.

Poligono 1 Poligono 2 Poligono 3 Poligono 4

Rispetto ai lati

Rispetto agli angoli

3 Rispondi con Vero o Falso ed effettua la correzione di ogni falso.

a) Un poligono è una parte di piano delimitata da una spezzata chiusa intrecciata. V F

b) Il perimetro di un poligono è la misura del suo contorno. V F

c) Un poligono regolare è equilatero ed equiangolo.

d) Per calcolare la somma degli angoli interni di un poligono si usa la formula Si = (n – 3) × 180°. V F

e) La somma degli angoli esterni di un poligono è un angolo piatto. V F

f) In ogni poligono il lato maggiore è sempre minore della somma degli altri lati. V F

g) La formula per calcolare il numero delle diagonali uscenti da un vertice è

= n – 2.

4 Calcola la misura degli angoli incogniti.

a) ? ? ? ? 73° 73° b) ? ? ? ? ?

Risolvi i seguenti problemi.

5 Se un quadrilatero ha i lati che misurano 13 cm, 21 cm, 54 cm, quanto potrà essere lungo il quarto lato?

a) 2 cm

b) 12 cm

c) 18 cm

d) 32 cm

6 Un pentagono ha gli angoli interni di 133°; 85°; 112°; 124°. Quanto è ampio il quinto angolo?

a) 123° b) 86° c) 73° d) 145°

7 Un poligono ABCD ha due angoli ampi 49° e 107°; sapendo che gli altri due sono uno il doppio dell’altro, quanto è ampio il minore?

a) 24°

b) 68°

c) 102°

d) 136°

8 Calcola il perimetro di un quadrilatero, sapendo che due lati sono congruenti e ciascuno misura 46 cm, il terzo lato misura 65 cm e il quarto è i suoi 3 5

9 Quanti lati ha un poligono nel quale da ogni vertice escono 7 diagonali?

10 STEM Nell’immagine a lato è raffigurato un pavimento costituito da tre tipi diversi di piastrelle a forma di poligoni regolari. Quali sono questi poligoni?

Per ciascun poligono qual è l’ampiezza di ogni angolo interno? Qual è la somma delle ampiezze di quattro angoli che hanno il vertice in comune?

11 MATEMATICA IN AZIONE Calcola il perimetro del prospetto laterale della scala (poligono rosso), utilizzando le due misure indicate.

I TRIANGOLI UNITÀ

Chi ha della

paura matematica?

La forma del triangolo e le sue numerose proprietà hanno avuto un ruolo cruciale non solo nella matematica, ma anche nella storia, nell’arte e in tante altre situazioni umane. Vuoi vedere che affascineranno anche te? Perché questo accada, devi liberarti dalle paure della matematica e indossare gli “occhiali della curiosità” scoprire i numerosi misteri che si celano in un poligono così comune. Non lasciarti confondere dalle diverse classificazioni dei triangoli: queste possono essere fatte in base ai lati (triangolo scaleno, isoscele, equilatero) o in base agli angoli (triangolo retto, acuto, ottuso). Gli elementi notevoli dei triangoli – altezze, mediane e bisettrici, assi – possono sembrare complicati in apparenza, ma sono solo delle linee! Alcune partono dai vertici e hanno una finalità specifica: per esempio, lamediana, lo dice la parola stessa, è la linea del punto medio; la bisettrice linea che taglia l’angolo in due parti uguali come una forbice; l’altezza è la linea che segue la direzione perpendicolare. I punti d’incontro di queste linee hanno nomi un po’ strani e molto simili tra di loro (ortocentro, baricentro, incentro), ma sono solo i loro“puntidiritrovo”.

CONOSCIAMO LE CARATTERISTICHE DEI TRIANGOLI

CLASSIFICHIAMO I TRIANGOLI

2

CERCHIAMO I PUNTI D’INCONTRO DI ALTEZZE, BISETTRICI, MEDIANE E DEGLI ASSI

CONOSCIAMO I DIVERSI TIPI DI TRIANGOLI E LE LORO PROPRIETÀ 1

4

IMPARIAMO I CRITERI DI CONGRUENZA DEI TRIANGOLI

MATERIALE INTEGRATIVO MULTIMEDIALE

Focus Videolezione

Verifica interattiva

LEZIONE Le caratteristiche dei triangoli 1

SUCCEDE CHE...

Emma osserva una foto del grattacielo della Banca di Cina a Hong Kong in cui la struttura portante è costituita da triangoli. Si ricorda di aver visto altre immagini di costruzioni con struttura triangolare e si chiede: per quale motivo viene usato proprio il triangolo?

Per rispondere alla domanda occorre conoscere le caratteristiche dei triangoli.

Un triangolo è un poligono con tre lati (AB, CB, CA) e tre angoli interni (a, b, g).

Nel triangolo non esistono diagonali. Il triangolo è una struttura rigida e indeformabile: non cambia forma se si esercita una pressione su un vertice o un lato. In un triangolo:

è opposto al lato CA CA è adiacente agli angoli γ e α CA è opposto all’angolo β

è compreso tra i lati CB a AB

• ogni lato è minore della somma degli altri due, ciò comporta che ogni lato è maggiore della differenza degli altri due;

• il perimetro è la somma dei tre lati;

• la somma degli angoli esterni (Se) è 360°;

• la somma degli angoli interni è Si = (3 – 2) × 180° = 180°; quindi a + b + g = 180°.

La somma degli angoli interni di un triangolo corrisponde a un angolo piatto e vale 180°.

Un angolo esterno è sempre congruente alla somma dei due angoli interni non adiacenti ad esso.

Infatti, se consideriamo il triangolo ABC della figura:

• l’angolo B è esterno al triangolo;

• i due angoli interni non adiacenti a B sono a e g;

poiché a + b + g = 180° a + g = 180°– b

poiché b + B = 180° B = 180°– b

ma allora a + g = B

α + γ = B = angolo esterno

Negli edifici viene usata la struttura triangolare perché è rigida e indeformabile.

Primi

1 Osserva la figura e inserisci i termini corretti.

a) Il poligono RST è un

b) R, S e T sono i ………………………………………….……

c) I lati sono , ,

d) R, S , T sono gli ………………………………………………

e) R + S + T =

f) L’angolo R è ……………..……………… al lato ……………

g) Il lato SR è adiacente agli angoli e

h) L’angolo T è tra i lati RT e TS

2 Date le seguenti misure (espresse in cm) stabilisci quando è possibile costruire un triangolo.

a) b) c)

a = 22

b = 13

c = 20

a

= 46

= 8

= 3

3 Calcola le ampiezze degli angoli incogniti.

2,5

4 MATEMATICA IN AZIONE Le misure del triangolo, strumento musicale, sono 10 cm × 10 cm × 10 cm.

Carlo vede che è aperto e si chiede se il triangolo sia stato appositamente lasciato aperto oppure se con le misure dei suoi lati non sia possibile chiuderlo. Quale delle due ipotesi è quella valida? Motiva la risposta.

Classificazione dei triangoli 2

SUCCEDE CHE...

Emma osserva un pannello decorativo, di cui l’immagine mostra una parte. I poligoni raffigurati sono tutti triangoli con caratteristiche diverse. È possibile raggruppare i triangoli del pannello in base a proprietà comuni?

Per rispondere alla domanda occorre sapere come vengono classificati i triangoli sia rispetto ai lati sia rispetto agli angoli. I triangoli si possono suddividere in gruppi diversi e, a seconda delle lunghezze dei lati e delle ampiezze degli angoli, vengono denominati nei seguenti modi.

Classificazione rispetto ai lati

Triangolo scaleno

Triangolo isoscele

Triangolo equilatero

Ha tutti i lati di lunghezza diversa.

Ha almeno due lati congruenti.

Classificazione rispetto agli angoli

Triangolo acutangolo

B C A, B, C < 90°

Ha tre angoli acuti, cioè minori di 90°.

Triangolo rettangolo

F G cateti ipotenusa

Ha un angolo retto. I lati che formano l’angolo retto sono i cateti, il lato opposto all’angolo retto è l’ipotenusa

Ha tutti e tre i lati congruenti.

Triangolo ottusangolo

S T

> 90°

Ha un angolo ottuso, cioè maggiore di 90°.

Poiché la somma degli angoli interni di un triangolo è 180°, è evidente che un triangolo non può avere due angoli retti o due angoli ottusi.

I triangoli del pannello si possono classificare sia rispetto ai lati sia rispetto agli angoli, quindi:

• rispetto ai lati: blu equilatero, rosso isoscele, verde scaleno;

• rispetto agli angoli: viola ottusangolo, rosa rettangolo, azzurro acutangolo.

Primi

ESERCIZI

1 Scrivi a quale tipo di triangolo si riferiscono le seguenti affermazioni.

a) Ha almeno due lati congruenti:

b) Ha tre lati congruenti:

c) Ha un angolo retto:

2 Osserva i seguenti triangoli e le loro misure espresse in centimetri. Classificali rispetto ai lati e rispetto agli angoli. (Se lo ritieni necessario, utilizza il goniometro)

Rispetto ai lati

Rispetto agli angoli

3 Calcola l’ampiezza dell’angolo indicato con x e classifica il triangolo rispetto agli angoli. a) b) c)

La somma degli angoli interni di un triangolo è di ………......…

Per trovare il 3° angolo si sottrae da 180° a) x = …… – (…… + ……) = …… b) x = ……………………c) x =

4 MATEMATICA IN AZIONE Osserva e rispondi.

La Sicilia e il suo simbolo hanno forma triangolare, ma si tratta di due triangoli diversi.

a) Unendo le estremità dell’isola (in blu), che tipo di triangolo ottieni rispetto ai lati?

b) Unendo le estremità del simbolo (in nero), che tipo di triangolo ottieni?

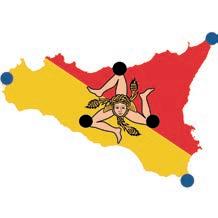
Altezze e ortocentro 3

SUCCEDE CHE...

Pietro deve raggiungere Emma al Museo di Storia Naturale. Dalla mappa si nota che le due strade laterali formano con il lato di ingresso del Museo un triangolo. Deve scegliere la strada più breve.

Museo di storia naturale

Per scegliere la strada Pietro deve sapere che cos’è l’altezza di un triangolo. Osserva i seguenti triangoli.

Nel 1° caso è stato tracciato il segmento CH che congiunge perpendicolarmente il vertice C con il lato opposto AB. Il segmento CH è l’altezza relativa alla base AB Puoi notare che l’altezza è interna al triangolo e rappresenta la distanza del vertice C da AB

Nel 2° caso il segmento CH “cade” esternamente al triangolo. Per tracciarlo devi prolungare il lato AB e poi tracciare il segmento perpendicolare condotto da C. Anche in questo caso CH si dice altezza relativa alla base AB e H è il piede dell’altezza.

CH è l’altezza relativa alla base AB

prolungamento del lato AB

In un triangolo il segmento perpendicolare che congiunge un vertice con il lato opposto (o il suo prolungamento) si dice altezza.

Poiché ogni lato può essere considerato una base, il triangolo ha tre altezze che si incontrano in un punto di intersezione detto ortocentro (nel triangolo ottusangolo per trovare l’ortocentro occorre prolungare le altezze). A seconda del triangolo l’ortocentro può essere interno, coincidente con un vertice o esterno al triangolo.

Nel triangolo acutangolo

l’ortocentro O è interno al triangolo.

Nel triangolo rettangolo

l’ortocentro O coincide con il vertice dell’angolo retto

Q A

=

Le altezze di un triangolo si incontrano in un unico punto detto ortocentro. L’ortocentro è un punto interno, esterno o coincidente con un vertice.

Nel triangolo ottusangolo

l’ortocentro O è esterno al triangolo.

Pietro, per far presto, deve prendere la strada centrale perché l'ingresso del Museo coincide con il piede dell’altezza del triangolo, come si vede nella mappa, ed è quindi la distanza minore dal Museo.

1 Rispondi con Vero o Falso. In un triangolo:

a) l’altezza è una retta perpendicolare. V F

b) l’altezza è un segmento perpendicolare. V F

c) ci sono due altezze. V F

d) l’altezza è la distanza di un vertice dal lato opposto. V F

e) il punto di incontro delle altezze si chiama ortocentro. V F

2 Completa le frasi.

a) Nel triangolo ……………………….. l’ortocentro è interno al triangolo.

b) Nel triangolo l’ortocentro è esterno al triangolo.

c) Nel triangolo ……………………….. l’ortocentro coincide con il ……………………….. dell’angolo

3 Nei seguenti triangoli traccia l’altezza relativa alla base AB.

4 Osserva i tre triangoli e classificali rispetto ai lati e agli angoli. Di ciascuno traccia, poi, le tre altezze e individua l’ortocentro.

5 MATEMATICA IN AZIONE Guardando la facciata di questa casa, calcola la misura dell’altezza del tetto indicata con h.

Bisettrici e incentro 4

SUCCEDE CHE...

Nella sua cameretta Emma ha una cornice vuota di forma triangolare. Al suo interno vuole inserire un orologio da parete rotondo così da avere ben chiara l’ora e cercare di essere più puntuale. Ma quanto grande può essere l’orologio?

La risposta alla domanda risulterebbe semplice se Emma conoscesse l’incentro. Vediamo che cos’è.

Anche nel triangolo la bisettrice è una semiretta che ha origine in un suo vertice e divide l’angolo in due parti congruenti.

bisettrice dell’angolo B

Poiché un triangolo ha tre angoli, possiede tre bisettrici che si incontrano sempre in un punto detto incentro

In un triangolo le bisettrici degli angoli si incontrano in un punto detto incentro L’incentro è sempre interno al triangolo.

Si può provare che l’incentro è equidistante dai lati: le distanze (IK, IG e IS) dell’incentro I dai lati sono congruenti.

Emma deve trovare l’incentro della cornice e misurarne la distanza dal bordo (OK).

Per inserire l’orologio nella cornice, la distanza del centro dell’orologio dal suo bordo esterno non può essere maggiore della misura di OK.

1 Rispondi con Vero o Falso. In un triangolo:

a) la bisettrice è un segmento che divide in due un angolo. V F

b) la bisettrice divide in due parti uguali un angolo. V F

c) ci sono tre bisettrici. V F

d) il punto di intersezione delle bisettrici si chiama incentro. V F

e) l’incentro è esterno se il triangolo è ottusangolo. V F

f) l’incentro è equidistante dai vertici. V F

2 Traccia le tre bisettrici dei triangoli assegnati e determina l’incentro di ognuno di essi. a)

3 Dato il triangolo ABC e le bisettrici AH, BK e CL , completa la tabella utilizzando le misure indicate.

4 MATEMATICA IN AZIONE Il cerchietto rosso indica dove è situata la piazza di una piccola cittadina e i segmenti verdi sono i viali che collegano la piazza alle strade laterali. Sai spiegare che cosa rappresenta geometricamente la piazza e perché è stata collocata in quella posizione?

LEZIONE Mediane e baricentro 5

Pietro vuole costruire una giostrina da regalare alla sorella appena nata. Ha già costruito la struttura dove appendere vari animali, ma vuole aggiungere anche dei triangoli di colori diversi, e vuole che questi triangoli rimangano orizzontali rispetto al pavimento. In che punto dovrà forarli?

Per rispondere alla domanda, Pietro deve conoscere che cos’è il baricentro di un triangolo.

Dato un triangolo, se segniamo il punto medio di un lato e lo congiungiamo al vertice opposto, otteniamo un segmento che è la mediana del triangolo.

Le mediane di un triangolo, sono tre e si incontrano in un unico punto detto baricentro; esso è sempre interno al triangolo.

Il baricentro è il punto di equilibrio di un triangolo, infatti il termine significa “centro del peso”.

Per le mediane vale la seguente proprietà

In ogni triangolo il baricentro divide ciascuna mediana in due parti di cui quella contenente il vertice è il doppio dell’altra.

ESEMPIO

AC = mediana

B = baricentro

BC = 2 × AB

BC = 12 cm

AB = ?

Per la proprietà del baricentro: AB = BC : 2 quindi AB = 12 : 2 = 6 cm

Per far stare in equilibrio i triangoli, Pietro deve appenderli nel loro baricentro.

1 Rispondi con Vero o Falso. In un triangolo:

a) la mediana è un segmento. V F

b) la mediana divide l’angolo in due parti congruenti. V F

c) le mediane sono tre. V F

d) il punto di incontro delle mediane è interno solo nel triangolo acutangolo. V F

2 Disegna la mediana relativa al lato AB nei triangoli dell’illustrazione.

3 Traccia le tre mediane di ciascuno dei triangoli assegnati e individua, in ogni triangolo, il baricentro.

a) b) c)

4 Riferendoti al triangolo PQR dell’esercizio precedente e alla proprietà delle mediane, calcola:

a) PB = 2 × se PB = 14 cm, BM ' = PB : =

b) BM = …………… BR se BM = 20 cm, BR =

c) BM ' = 16 cm PM ' =

5 MATEMATICA IN AZIONE Osserva e rispondi.

Gianni ha costruito dei triangoli di plexiglass nell’ora di laboratorio e vuole stupire i compagni: “sono capace di tenerli fermi in aria poggiandoli su un solo dito”. Noi sappiamo che ciò è possibile, basta trovare il punto giusto.

Qual è il punto che Gianni dovrà trovare per tenere i triangoli in equilibrio?

Assi e circocentro 6

SUCCEDE CHE...

Il papà di Emma vuole posizionare un irrigatore in giardino per innaffiare i suoi tre ulivi. Ma non sa dove metterlo. Emma, osservando che gli alberi formano un triangolo acutangolo, ha un’idea. Quale?

Per rispondere alla domanda bisogna sapere che cos’è l’asse di un lato.

L’asse di un lato è una retta perpendicolare passante per il suo punto medio.

Nel triangolo DEF, M è il punto medio del lato DE e r è l’asse del lato.

r D E M r ⊥ DE asse di DE punto medio

Anche gli assi di un triangolo sono tre e si incontrano in un unico punto detto circocentro.

= circocentro

C = circocentro

r asse di RS s asse di ST t asse di TR

Nel triangolo acutangolo il circocentro C

è interno al triangolo.

C = circocentro

r asse di RS s asse di TR t asse di TS

Nel triangolo rettangolo il circocentro C coincide con il punto medio dell’ipotenusa

S t C r s

r asse di RT s asse di ST t asse di RS

Nel triangolo ottusangolo il circocentro C

è esterno al triangolo.

Gli assi di un triangolo si incontrano in un punto detto circocentro che può essere interno, esterno o può coincidere con il punto medio dell’ipotenusa. Il circocentro è sempre equidistante dai vertici del triangolo. Emma suggerisce al papà di posizionare l’irrigatore nel circocentro del triangolo formato dai tre alberi, così sarà equidistante da ciascuno di loro.

Ortocentro, incentro, baricentro e circocentro sono i punti notevoli di un triangolo.

In particolare, nel triangolo isoscele i punti notevoli appartengono all’altezza relativa alla base, invece nel triangolo equilatero coincidono in un punto che è il centro del triangolo equilatero.

Primi

ESERCIZI

1 Rispondi con Vero o Falso.

In un triangolo:

triangolo isoscele

triangolo equilatero C = circocentro I = incentro

= baricentro

= ortocentro

centro del triangolo equilatero

a) l’asse di un lato è la perpendicolare al lato passante per il vertice.

b) l’asse è una retta.

c) il punto di incontro degli assi è l’incentro.

d) il circocentro è esterno al triangolo se è rettangolo.

2 Disegna gli assi relativi ai cateti dei seguenti triangoli rettangoli e completa la frase.

Indica il punto di incontro dei due assi con K: K è il ………………………. dei triangoli; in particolare K è il punto dell’

3 Facendo riferimento ai triangoli precedenti e indicando con K il circocentro, applica la proprietà del circocentro per rispondere alle richieste.

a) Se CB = 28 cm " CK = KB = …… : 2 = …… cm e AK = ……......….

b) Se NK = 26 cm " MN = ……… × 2 = ……… cm e LK = ……......….

c) Se QP = 30 cm " QK = …………………………. e SK = ……......….

4 MATEMATICA IN AZIONE Se la casetta si trova nell’ortocentro del triangolo ABC e dista 40 km da Old Town, quanto dista da New City? Old Town New City

SUCCEDE CHE...

Triangoli isoscele ed equilatero e loro proprietà

Pietro vuole costruire una casetta per il suo gatto. A tale scopo deve predisporre con dei listelli di legno una struttura come quella illustrata a lato. I listelli obliqui su cui appoggerà il tetto hanno tutti la stessa lunghezza e formano un angolo di 80°. Quanto devono essere ampi gli angoli che i listelli obliqui formano con quello di base?

Per rispondere alla domanda occorre conoscere le proprietà dei triangoli isosceli.

Triangolo isoscele

Un triangolo isoscele ha due lati congruenti e le sue caratteristiche sono:

• i lati congruenti si dicono lati obliqui;

• il lato non congruente si chiama base;

• l’angolo opposto alla base si dice angolo al vertice;

• gli angoli adiacenti alla base sono congruenti e si dicono angoli alla base

S T angolo al vertice angoli alla base R ≅ S lato obliquo lato obliquo

Indicando con b la base e con , i due lati congruenti, il perimetro è:

2p = b + , × 2 da cui b = 2p – , × 2

Triangolo equilatero

Il triangolo equilatero ha tre lati congruenti e quindi è un caso particolare del triangolo isoscele. Nel triangolo equilatero anche i tre angoli sono congruenti; infatti, essendo isoscele, i due angoli alla base sono congruenti. Inoltre ogni lato può essere considerato come base e quindi i tre angoli possono essere considerati sia alla base che al vertice.

Poiché la somma degli angoli interni di un triangolo è 180°, nel triangolo equilatero ogni angolo misura 60°:

A ≅ B ≅ C = 180° : 3 = 60°

Nel triangolo equilatero le altezze, le mediane, le bisettrici e gli assi coincidono tra loro.

Indicando con , ciascuno dei tre lati congruenti, il perimetro del triangolo equilatero è:

2p = , × 3 da cui , = 2p : 3

Primi

Il tetto è un triangolo isoscele e gli angoli alla base sono congruenti; quindi ognuno misura (180° – 80°) : 2 = 50°.

ESERCIZI

1 In un triangolo isoscele il perimetro è di 105 dm e ciascun lato obliquo misura 32,4 dm.

Completa e calcola la misura della base.

ESEMPIO

Un triangolo isoscele ha l’angolo al vertice di 48°. Calcola le ampiezze degli angoli alla base. C = 48° A ≅ B = ?

2 In un triangolo isoscele un angolo alla base misura 28°; quanto misura l’angolo al vertice? A ≅ B = = C = ?

Poiché A + B + C = ° allora C = =

3 Un triangolo equilatero ha il perimetro che misura 135 cm.

Calcola la misura del lato.

2p = , = ? , = 2p : 3 = ……………………………………

4 MATEMATICA IN AZIONE Osserva e completa.

La capriata semplice di un tetto è un triangolo isoscele; ogni suo elemento ha una terminologia.

Prova a individuarlo sulla figura:

• catena = base

• puntone = lato obliquo

• monaco = altezza

Il monaco, oltre all’altezza, quali altri elementi del triangolo può rappresentare?

Perché?

Triangolo rettangolo e sue proprietà 8

Pietro vuole costruire una casetta per gli uccellini come quella raffigurata a lato.

Da un foglio di compensato quadrato potrà ottenere i due triangoli della facciata?

Vediamo le proprietà del triangolo rettangolo.

Il triangolo rettangolo ha un angolo retto e le sue caratteristiche sono:

• i lati che formano l’angolo retto sono i cateti;

• il lato opposto all’angolo retto è l’ipotenusa;

• gli angoli acuti sono complementari;

• due altezze coincidono con i cateti;

• la terza altezza è l’altezza relativa all’ipotenusa.

OH = altezza relativa all’ipotenusa c = cateto minore

C = cateto maggiore i = ipotenusa

Tra i triangoli rettangoli ne esistono due con particolari caratteristiche.

Triangolo rettangolo isoscele

Ha gli angoli acuti di 45° ed è la metà di un quadrato.

Triangolo rettangolo

scaleno con gli angoli di 30° e 60°

Il triangolo rettangolo ABC

è la metà del triangolo equilatero EBC e quindi il cateto minore, c, è la metà dell’ipotenusa i: c = i : 2

Sì, perché i due triangoli della casetta sono rettangoli isosceli.

Il quadrato va tagliato lungo la sua diagonale, ottenendo così due triangoli rettangoli isosceli congruenti.

1 Osserva la figura e completa.

a) I cateti sono i segmenti ……… e ………

b) L’ipotenusa è il segmento ………

c) AH è l’ relativa all’

d) AC è l’altezza relativa al lato ………

e) AB è l’altezza relativa al lato ………

f) A =

g) C + B = ; quindi, i due angoli sono

2 In base ai dati ricavati dalla figura, calcola il perimetro del triangolo rettangolo.

VW = …………… 2p = ?

VX =

Poiché VWX ha gli angoli acuti di 30° e 60°, il cateto minore

………… è la metà dell’ipotenusa; quindi:

WX = × 2 =

2p =

3 MATEMATICA IN AZIONE Osserva e rispondi.

Elisa e Gioele vogliono costruire una capanna per giocare sul prato. Fissano un palo con due tiranti, come in figura, formando un triangolo isoscele. Per ottenere un triangolo che sia anche rettangolo, quanti gradi deve formare l’angolo compreso tra ogni tirante e il terreno?

a) 30° b) 45° c) 60° d) 90°

Criteri di congruenza dei triangoli 9

SUCCEDE CHE...

Pietro osserva la facciata del grattacielo e gli sembra che tutti i triangoli siano congruenti.

S’informa e scopre che tutti i triangoli hanno i lati ordinatamente congruenti.

È sufficiente questo dato per stabilire la congruenza dei triangoli?

Per rispondere alla domanda deve conoscere i criteri di congruenza dei triangoli.

Due triangoli sono congruenti quando, sovrapponendoli, lati e angoli combaciano perfettamente.

Due triangoli congruenti hanno i tre lati e i tre angoli congruenti.

Il simbolo di congruenza è ≅; quindi, per scrivere che i triangoli ABC e DEF della figura sono congruenti, si scrive: ABC ≅ DEF

Vi sono dei criteri che permettono di stabilire se due triangoli sono congruenti senza verificare che tutti i lati e tutti gli angoli siano congruenti.

1° criterio di congruenza

Due triangoli sono congruenti se hanno due lati e l’angolo da essi formato ordinatamente congruenti.

2° criterio di congruenza

Due triangoli sono congruenti se hanno un lato e i due angoli ad esso adiacenti congruenti.

3° criterio di congruenza

Due triangoli sono congruenti se hanno i tre lati ordinatamente congruenti.

I triangoli che formano la facciata del grattacielo sono congruenti per il 3° criterio, infatti hanno i tre lati ordinatamente congruenti.

1 Segna con una crocetta la risposta esatta.

a) Per il 1° criterio due triangoli sono congruenti se hanno ordinatamente congruenti:

1) tre lati 3) due lati e l’angolo tra essi compreso

2) tre angoli 4) un lato e due angoli ad esso adiacenti

b) Per il 2° criterio due triangoli sono congruenti se hanno ordinatamente congruenti:

1) tre lati 3) due lati e l’angolo tra essi compreso

2) tre angoli 4) un lato e due angoli ad esso adiacenti

c) Per il 3° criterio due triangoli sono congruenti se hanno ordinatamente congruenti:

1) tre lati 3) due lati e l’angolo tra essi compreso

2) tre angoli 4) un lato e due angoli ad esso adiacenti

2 In base alle informazioni date nell’illustrazione dimostra che i triangoli ABC e LMN sono congruenti (simboli uguali indicano elementi uguali).

• In ogni triangolo la somma delle ampiezze degli angoli interni è sempre

• Calcola l’ampiezza degli angoli B e M: B ≅ M = 180° – ( + ) =

• I triangoli ABC e LMN hanno congruente un lato, ≅ , e gli angoli ad esso adiacenti, ......... ≅ ......... e ......... ≅ .........; quindi, per il criterio di congruenza, sono

3 MATEMATICA IN AZIONE Per calcolare la larghezza di una grossa buca un geologo utilizza un metodo indiretto eseguendo le misurazioni che vedi in figura. Quanto è larga la buca?

Completa il seguente procedimento.

I triangoli ABC e DCE hanno: AC  …… e BC  …… e ACB  perché opposti al vertice quindi ABC  DCE per il criterio. I due triangoli, essendo congruenti, hanno anche tutti gli altri elementi ordinatamente congruenti, quindi:

AB  = m

MAPPA

I TRIANGOLI

hanno come elementi hanno come elementi hanno come elementi

ANGOLI VERTICI LATI

e si classificano

rispetto agli ANGOLI acutangoli

e si classificano

rispetto ai LATI

ottusangoli isosceli rettangoli equilateri scaleni

C = circocentro T R S C

R S C T

I PUNTI NOTEVOLI SONO

Circocentro

individuato dagli assi

Baricentro

individuato dalle mediane

baricentro

= ortocentro

Ortocentro

individuato dalle altezze

Incentro

individuato dalle bisettrici

LEZIONE

1 ESERCIZI E PROBLEMI

LE CARATTERISTICHE DEI TRIANGOLI

1 Rispondi con Vero o Falso.

a) È un poligono con tre lati.

b) Ha tre angoli e tre diagonali.

c) Ogni vertice è opposto a un angolo.

d) Ogni lato è minore della somma degli altri due.

e) L’angolo esterno e il suo interno corrispondente sono complementari.

f) Il perimetro si trova sempre moltiplicando un lato qualsiasi per tre.

2 Osserva le seguenti figure e completa le frasi.

a) • I lati del triangolo sono ; ;

• Gli angoli interni del triangolo sono ; ;

• Il lato TS è opposto all’angolo

• L’angolo S è opposto al lato

• Il lato è opposto all’angolo T

b) • I lati del triangolo sono ; ;

• Gli angoli interni del triangolo sono ; ;

• Il lato è opposto all’angolo

• Il lato è opposto all’angolo

• Il lato è opposto all’angolo

• Gli angoli γ e β sono adiacenti al lato

3 Esegui le richieste.

• Indica i vertici del triangolo a con A , B, C e i vertici del triangolo b con K , L, M.

• Colora di rosso i lati del triangolo a e di blu i lati del triangolo b

• Segna gli angoli interni dei due triangoli.

a)

b)

4 Con a, b, c, sono indicate le misure di tre segmenti; stabilisci se con essi è possibile costruire un triangolo.

ESEMPIO

a) a = 57 cm; b = 68 cm; c = 72 cm

La misura maggiore deve essere minore della somma delle altre due. Si calcola la somma dei segmenti minori: a + b = 57 + 68 = 125 cm e si confronta con il segmento maggiore: 125 > 72; quindi è possibile costruire il triangolo.

b) a = 11 cm; b = 8 cm; c = 30 cm

Si calcola la somma dei segmenti minori: a + b = 11 + 8 = 19 cm e si confronta con il segmento maggiore: 19 < 30; quindi non è possibile costruire il triangolo.

a) a = 14 cm b = 32 cm c = 58 cm

b) a = 23 cm b = 21 cm c = 30 cm

c) a = 4,5 mm b = 3,6 mm c = 14,3 mm

d) a = 34,7 cm b = 76,1 cm c = 11,9 cm

5 MATH Is it possible to build a triangle with the following sets of line segments?

Calcola il perimetro dei seguenti triangoli.

ESEMPIO

2p = 11 + 13 + 8 = 32 cm 11 cm 8 cm 13 cm

6 a) b)

Il perimetro è la somma delle misure dei lati, quindi:

10 MATEMATICA IN AZIONE Nella mappa a lato sono indicate le distanze tra le isole Pianosa, Giglio e Montecristo. Una barca effettua il percorso Giglio-Montecristo-Pianosa-Giglio come indicato nella figura.

All’incirca quanti km percorre?

a) Meno di 100.

b) Più di 150 e meno di 200.

c) Più di 200 e meno di 250.

d) Più di 100 e meno di 150.

11 MATEMATICA IN AZIONE Osserva e rispondi. La Brianza è un’area geografica della Lombardia che si estende tra la pianura monzese e le Prealpi. È compresa all’interno del triangolo disegnato dalle città di Como, Lecco e Monza. Quale di queste misure potrebbe essere il perimetro del triangolo brianzolo?

(Aiutati con una cartina o con Google Earth)

a) 180 km c) 38 km

b) 88 km d) 18 km

Osserva le figure e, in base ai dati forniti, calcola quanto richiesto.

12 a) b)

13 a) b)

14 a) b)

Risolvi i seguenti problemi.

ESEMPIO

In un triangolo il perimetro misura 37 cm, un lato 10 cm e gli altri due sono uno i 4 5 dell’altro. Calcola le misure di questi due lati.

Dati

2p = 37 cm

CB = 10 cm

= ? AC = 4 5 × AB

Risoluzione

Si calcola la somma dei due lati non conosciuti:

AB + AC = 2p − CB = 37 − 10 = 27 cm

La somma di AB e AC è composta da 9 segmentini.

Si trova la misura del segmentino unità e quindi le misure dei due lati.

u = ( AB + AC ) : 9 = 27 : 9 = 3 cm

AB = u × 5 = 3 × 5 = 15 cm

= u × 4 = 3 × 4 = 12 cm

15 Il perimetro di un triangolo misura 67 cm e un lato è di 28 cm. Calcola le misure degli

altri due lati, sapendo che uno è i 5 8 dell’altro. [15 cm; 24 cm]

16 La base di un triangolo scaleno misura 59 dm. Determina la misura del perimetro, sapendo che i due lati obliqui sono uno i 2 7 dell’altro e la loro differenza è 45 dm. [140 dm]

17 EDUCAZIONE CIVICA Un’aiuola è di forma triangolare e la si vuole irrigare con un impianto a goccia posto lungo il suo perimetro.

Se un lato misura 185 cm, un altro 135 cm e il terzo 124 cm, basteranno 450 cm di tubo per costruire l’impianto di irrigazione?

18 In un triangolo con il perimetro lungo 86 m, un lato è lungo 24 m e la differenza tra gli altri due lati misura 16 m. Calcola le lunghezze degli altri due lati. [23 m; 39 m]

19 Esiste un triangolo con il perimetro di 175 cm e i lati uno il doppio dell’altro? Motiva la risposta.

20 Il primo lato di un triangolo misura 96 cm, il secondo è 5 6 del primo e il terzo è più corto del secondo di 15 cm. Calcola il perimetro. [80 cm; 65 cm; 241 cm]

21 Può esistere un triangolo che abbia il perimetro di 224 dm e i lati ciascuno la metà dell’altro? Motiva la risposta.

22 MATEMATICA IN AZIONE La sarta deve abbellire un telo di stoffa a forma di triangolo isoscele con un bordino colorato lungo 2,5 m. Sapendo che le misure di due dei tre lati del telo sono 77 cm e 96 cm, quale sarà la lunghezza della base e quale quella del lato obliquo? [96 cm; 77 cm] VERIFICA CHE LA SOMMA DEGLI ANGOLI INTERNI È 180°

ESEMPIO

Disegna un triangolo scegliendo casualmente le misure dei suoi lati.

Colora gli angoli come nella prima figura e poi taglialo in tre parti, ognuna delle quali contenga un vertice.

A C B

Sul tuo quaderno incolla, affiancandoli, i tre vertici del triangolo come nella seconda figura. La somma dei tre angoli sarà un angolo di 180°, ossia un angolo piatto.

23 In base alle ampiezze indicate nelle figure calcola quelle incognite. a) c) b) d)

24 Le seguenti terne rappresentano gli angoli interni di triangoli. Calcola l’ampiezza degli angoli incogniti.

α = 34° β = α + 20°

γ =

= β = 35°

= β + 10°

25 MATEMATICA IN AZIONE Il papà di Emma ha costruito su una grossa quercia una casetta per sua figlia.

Per sostenere il pavimento che fa da supporto alla casetta ha utilizzato due travi di legno fissate al tronco dell’albero e inclinate nel modo indicato nella figura. Quanto è ampio l’angolo formato dalle due travi?

AOB = 40°

EOF = 3 × AOB

COD =

Risolvi i seguenti problemi.

ESEMPIO

Un angolo interno di un triangolo misura 39° e gli altri due sono uno il doppio dell’altro. Quanto misurano questi due angoli?

Dati

C = 39° A = ?

A e= 2 × B B = ?

Risoluzione

A + B = 180° − 39° = 141°

B = 141° : 3 = 47°

A = 2 × B = 2 × 47° = 94°

26 In un triangolo CDE l’angolo C supera l’angolo D di 14° e la loro somma misura 100°. Determina le ampiezze dei tre angoli del triangolo. [43°; 57°; 80°]

27 Nel triangolo ABC la somma degli angoli A e B è di 124° e un angolo è 1 3 dell’altro. Trova le ampiezze dei tre angoli di ABC [31°; 93°; 56°]

28 L’angolo A di un triangolo è la metà della somma degli angoli B e C . Sapendo che B = 5 7 di C , calcola le ampiezze degli angoli. [60°; ; 70°]

29 Sapendo che l’angolo di un triangolo è ampio 98° 24' e che gli altri due sono uno il doppio dell’altro, calcola le ampiezze degli angoli del triangolo. [27° 12'; 54° 24']

30 Il triangolo ADC ha l’angolo A ampio 71° 24' e l’angolo B è i 5 4 dell’angolo C . Calcola le ampiezze degli angoli B e C . [48° 16'; 60° 20']

31 L’angolo di un triangolo è ampio 80° 27' 52''. Sapendo che la differenza tra gli altri due è di 22° 17' 36'', calcola le ampiezze di questi angoli. [38° 37' 16''; 60° 54' 52'']

32 Facendo riferimento alla figura, calcola gli angoli incogniti.

a) A = 44°; C = 56° α =

b) A = 27°; C = 89° α =

c) C = 19°; α = 56° A =

d) A = 94°; α = 136° C =

e) A = 25°; C = 105° α =

f) C = 23° 34'; α = 127° A =

g) A = 78° 27'; C = 45° 15' α =

h) C = 84° 37'; α = 159° 52' A =

33 Sapendo che l’angolo BAC misura 124° e l’angolo ABC = 35°, completa le richieste.

34 Completa le misure degli angoli interni e calcola le ampiezze di quelli esterni.

35 Calcola la misura degli angoli indicati con “?”. a) c) b) d)

Risolvi i seguenti problemi.

36 MATEMATICA IN AZIONE Un cuneo fermaporta ha la parte inclinata che forma un angolo di 165° con il pavimento. Quanto misura l’angolo A C B ?

37 In un triangolo ABC , l’angolo esterno all’angolo A è di 80°. Calcola le ampiezze degli angoli interni, sapendo che B e C sono congruenti. [100°; 40°; ............]

38 Un angolo esterno di un triangolo misura 87°. Sapendo che gli angoli interni non adiacenti a quello esterno sono uno il doppio dell’altro, calcola le ampiezze degli angoli del triangolo. [29°; 58°; 93°]

39 L’angolo esterno all’angolo A di un triangolo misura 110°. Calcola le ampiezze di B e C sapendo che sono uno i 3 8 dell’altro. [30°; 80°]

40 Sapendo che i due angoli esterni di un triangolo sono ampi 106° e 98°, calcola le ampiezze degli angoli interni. [74°; 82°; 24°]

41 Due degli angoli interni di un triangolo sono ampi 74° e 26°. Calcola l’ampiezza del terzo angolo e le ampiezze di quelli esterni. [80°; 100°; 106°; 154°]

42 L’angolo C e l’angolo D del triangolo CDE misurano rispettivamente 96° e 36°. Calcola le ampiezze degli angoli esterni del triangolo. [84°; 144°; 132°]

CLASSIFICAZIONE DEI TRIANGOLI

43 Completa il seguente schema.

Rispetto agli angoli un triangolo può essere scaleno se ha isoscele se ha equilatero se ha Rispetto ai lati un triangolo può essere

acutangolo se ha ottusangolo se ha rettangolo se ha

44 Osserva i seguenti triangoli e classificali rispetto ai lati (a simboli uguali corrispondono misure uguali).

45 MATH Classify the triangles by measuring the size of their angles.

46 Classifica i seguenti triangoli rispetto ai lati e rispetto agli angoli. (A simboli uguali corrispondono misure uguali). a) d) g)

Risolvi e classifica i triangoli rispetto ai lati.

47 AB ≅ BC = 49 cm; AC = 88 cm

2p = tipo di triangolo:

48 AB = 32 cm; BC = 42 cm; AC = 28 cm

2p = tipo di triangolo:

49 BC = 37 cm; AC ≅ BC; AB = 64 cm

2p = ............................... tipo di triangolo:

50 AB = 25 cm; AC = AB + 15 cm; 2p = 90 cm

AC = .........................; BC = .........................; tipo di triangolo:

51 CA = 96 cm; AB = 3 4 × CA ; 2p = 320 cm

AB = ; CB = ; tipo di triangolo:

52 CB = 45 cm; AC = 4 5 × AB; 2p = 153 cm

AC = ; AB = ; tipo di triangolo:

Risolvi e classifica i triangoli rispetto agli angoli.

53 A = 67°; B = 23°; C = tipo di triangolo:

54 A = 27°; B = 11 9 × A; C = tipo di triangolo:

55 A = 16°; B = C = tipo di triangolo:

Risolvi i seguenti problemi.

56 MATEMATICA IN AZIONE Nella mappa sono indicate le principali città del Portogallo.

Tra esse ci sono: Lisbona, la capitale (in portoghese Lisboa), Portalegre (a circa 160 km da Lisbona) vicino al confine con la Spagna, e Faro (a circa 210 km da Lisbona) sulla costa atlantica meridionale.

Rispondi alle domande.

a) Unendo con dei segmenti, nell’ordine: Lisbona, Portalegre, Faro e Lisbona che triangolo ottieni? ………………………

b) Antonio da Portalegre vuol raggiungere Faro: percorrerà più o meno kilometri se va a Faro in linea retta o se prima passa da Lisbona? Motiva la risposta.

c) La distanza in linea d’aria tra le città di Faro e Portalegre è:

1) circa 370 km

2) circa 50 km

3) sicuramente minore di 370 km e maggiore di 50 km 4) sicuramente maggiore di 370 km e minore di 500 km

57 La somma di due angoli di un triangolo è di 80° e uno è i 7 3 dell’altro. Calcola le ampiezze dei tre angoli e classifica il triangolo. [24°; 56°; 100°; ........ .. ]

58 Che tipo di triangolo è quello che ha un angolo di 88° e gli altri due che sono uno il triplo dell’altro?

59 Un triangolo ha gli angoli tali che il secondo è il doppio del primo e il terzo è il triplo del primo. Calcola le ampiezze dei tre angoli e classifica il triangolo. [30°; 60°; 90°; ..............................]

60 Un triangolo ha un angolo di 80°. Qual è la massima differenza che possono avere gli altri due angoli affinché sia un triangolo acutangolo (senza tenere conto dei sottomultipli del grado)? [78°]

61 MATEMATICA IN AZIONE Il perimetro di una finestrella di forma triangolare è 180 cm. Se un lato misura 55 cm e uno 70 cm, quale dei due deve essere necessariamente la base della finestra? Prova a disegnare la figura sul tuo quaderno in scala 1 : 5 (1 cm = 5 cm).

62 Un angolo di un triangolo misura 58° e un altro è il triplo di questo diminuito di 70°. Calcola le misure degli angoli e classifica il triangolo. [104°; 18°; 58°; ]

63 Calcola le misure degli angoli interni di un triangolo, sapendo che un angolo esterno misura 150° e che gli angoli interni non adiacenti ad esso sono uno i 3 2 dell’altro. Classifica poi il triangolo. [90°; 60°; 30°; ]

64 STEM Il frontone di un tempio greco ha i lati obliqui che misurano 12 m ciascuno e la base che misura 20 m.

Dopo averne calcolato il perimetro, disegnalo sul tuo quaderno (1 cm = 2 m) e, utilizzando il goniometro, classificalo in base agli angoli.

Risolvi i seguenti quesiti sul piano cartesiano.

65 Individua le coordinate dei vertici del seguente triangolo e classificalo.

A ( ; )

B ( ; ) C (………; ………)

Il triangolo è:

66 Disegna sul tuo quaderno un sistema di assi cartesiani e, dopo aver scelto l’unità di misura appropriata, individua le seguenti terne di punti dalla cui unione si originano quattro triangoli. Disegnali e classificali (usa un colore diverso per ogni terna).

a) A (1; 1) B (6; 1) C (6; 4)

b) A (2; 0) B (4; 2) C (1; 4)

c) A (3; 1) B (9; 1) C (6; 7)

d) A (4; 5) B (10; 3) C (2; 10)

67 Date le coordinate di A (4;3) e di B (4;9), fissa le coordinate di un punto C tale che si ottenga:

a) un triangolo isoscele acutangolo;

b) un triangolo ottusangolo; c) un triangolo rettangolo isoscele.

68 Date le coordinate di A (1; 3) e B (7; 3), stabilisci le coordinate del punto C in modo da ottenere un triangolo rettangolo isoscele. C’è un solo modo per fissare C ? Perché?

3

ALTEZZE E ORTOCENTRO

69 Completa le affermazioni.

a) Il segmento che unisce il vertice di un triangolo con il lato opposto formando due angoli retti si chiama

b) In ogni triangolo ci sono ................. altezze, una per ogni .......................................

c) Il punto di incontro delle tre altezze si chiama del triangolo.

70 Completa lo schema.

ortocentro

punto in comune delle

interno nel triangolo

vertice dell’angolo retto nel triangolo

esterno nel triangolo

71 Individua l’altezza e la base relativa nei seguenti triangoli. Completa come nell’esempio.

a) b) c) d)

CN è l’altezza relativa alla base AB

72 Quali di questi segmenti è l’altezza di un triangolo? Giustifica la risposta.

ESEMPIO

COME COSTRUIRE L’ALTEZZA RELATIVA A UN LATO

CON RIGA E COMPASSO

1) Punta il compasso in C e con un’apertura a piacere trova nel lato AB due punti X e Y (un punto potresti trovarlo prolungando il lato AB ).

2) Punta con il compasso in X e poi in Y con apertura maggiore della metà di XY: traccia due archi sopra AB Chiama H il punto di intersezione dei due archi.

3) Con il righello traccia la retta passante per H e C, troverai sul lato AB il punto D: CD è l’altezza relativa al lato AC

73 MATH In the following triangles, draw the height CH relative to the base AB. a)

74 Riporta ciascuno dei seguenti triangoli sul quaderno, traccia le tre altezze relative ai tre lati e individua l’ortocentro. a)

75 MATEMATICA IN AZIONE Con l’aiuto del disegno e tenendo conto che LH è l’altezza relativa al lato JK , completa la tabella.

BISETTRICI E INCENTRO

76 Completa le seguenti affermazioni.

a) Bisecare significa

b) La bisettrice di un angolo è una uscente dal dell’angolo che divide a l’angolo stesso.

c) Le .............. bisettrici degli ................................... di un triangolo si incontrano in un punto detto ........................................................... del triangolo.

77 Completa lo schema.

incentro punto in comune delle

sempre

78 Riconosci le bisettrici e i relativi angoli.

a) bisettrice dell’angolo

b) bisettrice dell’angolo

c)

bisettrice dell’angolo

ESEMPIO

COME COSTRUIRE LA BISETTRICE DI UN ANGOLO CON RIGA E COMPASSO

1) Con apertura <AC punta il compasso in A e disegna due archi nei lati AB e AC: indica con J e K i punti trovati.

2) Punta ora il compasso prima in J e poi in K con la stessa apertura e chiama L il punto di intersezione dei due archi.

3) Unisci il vetrice A con L : AL è la bisettrice dell’angolo A .

79 Traccia le tre bisettrici di ciascuno dei seguenti triangoli e individua l’incentro. a) b) c) d)

80 STEM Ogni faccia della piramide di Cheope è un triangolo. All’interno della piramide si trova la Camera funeraria del Faraone posta all’altezza dell’incentro di ogni faccia. Traccia le bisettrici del triangolo evidenziato per trovare la posizione della Camera funeraria. 81 In base alle indicazioni fornite, calcola le ampiezze degli angoli evidenziati in colore. La lettera O indica l’incentro.

5

MEDIANE E BARICENTRO

82 Completa le seguenti affermazioni.

a) In ogni triangolo ci sono mediane, una per ogni ; le mediane si incontrano in un che si chiama del triangolo.

b) Il baricentro di un triangolo è sempre ................................................. al triangolo.

c) Il baricentro divide ogni mediana in due parti, tali che una è il dell’altra.

83 Completa lo schema.

punto in comune delle

84 Individua le mediane e i relativi lati. a) c) b)

mediana di RT

85 Esiste un triangolo con due mediane tra loro congruenti: quale?

E un triangolo con tre mediane congruenti? Disegnali sul quaderno con misure a tua scelta ed evidenzia le mediane congruenti.

ESEMPIO

COME COSTRUIRE LA MEDIANA CON RIGA E COMPASSO

1) Punta il compasso in C e in B con l’apertura maggiore della metà di BC e traccia gli archi sopra e sotto il lato BC.

2) Unisci con il righello i punti R e S per trovare M, punto medio di BC

3) Congiungi A con M: AM è la mediana del lato BC

86 Traccia le tre mediane e individua, in ogni triangolo, il baricentro.

Risolvi i seguenti problemi.

87 Dati E, F, G punti medi dei lati BA , AC , CB:

• BF è

• AG è

• la mediana che parte da C è il segmento

• se BG = 10 m, allora il lato = 20 m

• se AC = 16 m, allora FC =

• se AB = 12 m, allora EA =

88 MATEMATICA IN AZIONE In questa vetrata a forma di triangolo isoscele le saldature corrispondono alle mediane del triangolo.

Se LM misura 20 cm, quanto misura AL? E AM ?

ASSI E CIRCOCENTRO

89 Osserva il disegno e completa le affermazioni.

a) M è il punto del segmento AB

b) La retta a è .............................................................. al segmento AB.

c) La retta a e il segmento AB hanno in comune il punto

d) La retta a è l’....................... di .......................

90 Completa le seguenti affermazioni.

a) In ogni triangolo ci sono assi, ciascuno perpendicolare ad un lato.

b) Gli si incontrano in un punto detto

91 Completa lo schema.

circocentro punto in comune degli punto medio dell’ipotenusa nel triangolo interno nel triangolo esterno nel triangolo

92 Il tipografo ha commesso un errore nell’abbinare termini e definizioni. Prova tu a rimettere a posto il testo collegando ogni termine con la definizione corretta.

a) Altezza 1) Segmento che congiunge un vertice con il punto medio del lato opposto.

b) Mediana 2) Semiretta che ha origine nel vertice e divide l’angolo in due parti cogruenti.

c) Bisettrice 3) Retta perpendicolare a un lato e passante per il suo punto medio.

d) Asse 4) Segmento perpendicolare che congiunge un vertice con il lato opposto.

Classifica i seguenti segmenti tracciati in rosso: mediana, bisettrice, altezza, asse (simboli uguali indicano elementi congruenti).

93 a) b) c)

Riconosci quale punto notevole è rappresentato in ciascun triangolo (simboli uguali indicano elementi uguali).

= baricentro

ESEMPIO

COME COSTRUIRE L’ASSE DI UN LATO CON RIGA E COMPASSO

1) Punta il compasso in A con un’apertura maggiore della metà di AB; traccia due archi sopra e sotto il lato AB.

2) Punta il compasso in B e, con la stessa apertura, traccia due archi uno sopra e uno sotto AB. Si individuano due punti P e Q

3) Unisci P con Q: PQ è l’asse di AB e M il suo punto medio.

99 In ogni triangolo traccia l’asse relativo al lato AC . Esegui l'esercizio sul tuo quaderno.

100 Classifica i triangoli seguenti rispetto agli angoli; per ciascuno di essi individua il circocentro e indicalo con O. a) b) c)

101 EDUCAZIONE CIVICA I proprietari di tre aziende agricole compartecipano alla costruzione di un laghetto artificiale per l’irrigazione dei campi. Decidono che l’invaso deve essere fatto in una posizione equidistante dalle tre fattorie. In quale posizione andrà il laghetto? Motiva la tua risposta.

TRIANGOLI ISOSCELE ED EQUILATERO E LORO PROPRIETÀ

102 Osserva la figura e completa in modo opportuno.

• RS e TS sono i e sono

• RT è la

• T e R sono gli ....................................... alla e sono tra loro

• S è l’angolo al

103 Osserva il seguente triangolo equilatero e completa utilizzando i termini corretti.

• M , N , P sono ampi

• MN, NP, PM, sono i

• L’altezza relativa alla base MN è anche

Triangolo isoscele

104 MATH In the following triangles, calculate the sizes of the unknown angles. a) b) c)

Segna la risposta esatta.

105 In un triangolo isoscele la base misura 10,6 cm e i lati obliqui 13,4 cm ciascuno.

Il perimetro è:

a) 84 cm

b) 36 cm

c) 37,4 cm

d) 36,4 cm

106 In un triangolo isoscele la base misura 23,2 cm e i lati obliqui 32,3 cm ciascuno.

Il perimetro è:

a) 78 cm

b) 89 cm

c) 87,8 cm

d) 87,8 m

107 In un triangolo isoscele il perimetro misura 92 dm e la base 44 dm. Ciascun lato obliquo misura:

a) 34 dm

b) 21 dm

c) 36 dm

d) 24 dm

108 In un triangolo isoscele la base misura 84 cm e ciascun lato obliquo è i 3 4 della base.

Il perimetro è:

a) 210 cm

b) 230 cm

c) 76 cm

d) 120 cm

109 In un triangolo isoscele la base misura 45 cm e ciascun lato obliquo è i 4 5 della base.

Il perimetro è:

a) 110 cm

b) 130 cm

c) 117 cm

d) 220 cm

110 In un triangolo isoscele il perimetro misura 51 dm e la base è i 3 7 di ciascun lato obliquo.

Il lato obliquo misura:

a) 21 dm

b) 23 dm

c) 16 dm

d) 12 dm

111 L’angolo al vertice di un triangolo isoscele misura 118°. L’ampiezza di ciascuno dei due angoli alla base è:

a) 13°

b) 29°

c) 31°

d) 62°

112 Un angolo alla base di un triangolo isoscele misura 63°. L’ampiezza dell’angolo al vertice è:

a) 52°

b) 54°

c) 63°

d) 117°

113 Un triangolo isoscele ha gli angoli esterni che misurano 40°, 160° e 160°. Il triangolo è:

a) rettangolo

b) acutangolo

c) ottusangolo

d) nessuna delle precedenti

Risolvi i seguenti problemi riferiti anche a situazioni presenti nella realtà.

114 Il perimetro di un triangolo isoscele è di 96 dm. Sapendo che la base è lunga 27 dm, calcola la misura dei lati obliqui. [34,5 dm]

115 In un triangolo isoscele la base è la metà di ciascun lato obliquo. Calcola il perimetro, sapendo che il lato obliquo è lungo 12,4 cm. [31 cm]

116 Un angolo alla base di un triangolo isoscele è ampio 48°. Calcola l’ampiezza dell’angolo al vertice. [84°]

117 STEM La foto a lato mostra la piramide di Caio Cestio a Roma.

Tenendo conto delle misure indicate calcola le ampiezze degli altri due angoli di una faccia della piramide.

118 L’angolo al vertice di un triangolo isoscele è 1 2 di ciascuno degli angoli alla base. Calcola le ampiezze dei tre angoli interni. [36°; 72°; 72°]

119 Ciascun lato obliquo di un triangolo isoscele è il triplo della base. Calcola la lunghezza dei lati, sapendo che il perimetro è lungo 84 dm. [12 dm; 36 dm; 36 dm]

120 Un manifesto pubblicitario ha la forma di un triangolo isoscele. Sapendo che l’angolo al vertice è ampio 80°, calcola le misure dei due angoli alla base. [50°; 50°]

121 EDUCAZIONE CIVICA Immagina un nuovo segnale di pericolo che indichi “attraversamento di pedoni distratti dal telefonino”. Sapendo che il segnale ha la forma di un triangolo isoscele e uno dei tre angoli misura 40°, qual è l’ampiezza dell’angolo al vertice? [100°]

122 EDUCAZIONE CIVICA Le frecce tricolori durante una loro esibizione assumono una disposizione a forma di triangolo isoscele. Tenendo conto del dato riportato nella foto, calcola le ampiezze degli altri due angoli del triangolo.

Nell’eseguire i problemi sui triangoli isoscele potrebbe capitarti di dimenticare che non solo due lati sono uguali, ma anche gli angoli alla base. Perché è importante ricordarlo? Se tra i dati del problema c’è l’angolo al vertice, basta sottrarre quel valore alla somma degli angoli interni (che è sempre 180 gradi) e poi dividere il risultato per due: questo ti permetterà facilmente di trovare l’ ampiezza degli angoli alla base .

imparaerrore dall'

Nei triangoli isosceli ed equilateri, non dimenticare che l’altezza relativa alla base è anche bisettrice dell’angolo al vertice e mediana del lato opposto. Queste proprietà, se ben applicate, renderanno la soluzione dei problemi meno complessa. Disegna sempre i triangoli e riporta non soltanto i dati del problema, ma usa delle etichette, dei simboli o dei colori, per visualizzare sulla figura le sue proprietà. Per esempio, su un triangolo isoscele segna i due lati e i due angoli uguali e su un triangolo equilatero, scrivi 60° su ogni angolo.

123 Il perimetro di un triangolo isoscele è lungo 156 dm. Sapendo che la base è i 5 4 di ciascun lato obliquo, calcola le lunghezze dei lati del triangolo. [60 dm; 48 dm; 48 dm]

124 MATEMATICA IN AZIONE Un triangolo isoscele ha il perimetro di 116 cm.

Calcola le lunghezze dei suoi lati, sapendo che la base è i 2 3 di ciascun lato obliquo. [29 cm; 43,5 cm; 43,5 cm]

125 Una veranda ha una copertura a forma di triangolo isoscele il cui perimetro misura 18 m.

Se due misure della copertura sono 7 m e 4 m, quale delle due sarà quella della base? Perché?

126 Il perimetro di un triangolo isoscele è lungo 17,6 cm e la sua base è i 3 11 del perimetro. Quanto sono lunghi i lati del triangolo? [4,8 cm; 6,4 cm; ]

127 Calcola le ampiezze degli angoli di un triangolo isoscele, sapendo che la somma dell’angolo al vertice e di un angolo alla base è di 140°. [40°; ; ]

128 L’angolo al vertice di un triangolo isoscele misura 68°. Traccia la bisettrice di uno degli angoli alla base e determina le ampiezze degli angoli che la bisettrice forma con i lati obliqui. [28°; 84°; 96°]

129 L’angolo al vertice di un triangolo isoscele è maggiore di quelli alla base di 16° 3'. Calcola le misure degli angoli interni e dell’angolo esterno adiacente a uno degli angoli alla base. [54° 39'; 70° 42'; 125° 21']

Triangolo equilatero

130 MATH Calculate the perimeter of the following equilateral triangles. a) b) c)

= 12.4 cm

= 3.5 cm

= 7.3 cm

Risolvi i seguenti problemi.

131 Un triangolo equilatero ha il perimetro di 47,7 dm. Calcola le misure dei lati. [15,9 dm]

132 MATEMATICA IN AZIONE Il triangolo è uno strumento musicale a percussione con tutti i lati uguali. È una barretta di acciaio triangolare, che rimane aperta da un vertice.

Se un lato dello strumento deve essere di 15 cm, quanto sarà lunga l’intera barretta? [45 cm]

133 Trova la misura di ciascun angolo esterno di un triangolo equilatero.

134 Un triangolo equilatero ha il semiperimetro che misura 27,3 cm. Calcola la misura del suo lato. [18,2 cm]

135 Il triangolo equilatero ABC ha il perimetro lungo 540 dm. Calcola la misura del lato del triangolo DEF il cui perimetro è i 4 3 del perimetro di ABC . [240 dm]

136 Un triangolo ABC ha il lato AB che misura 72 cm, il lato BC = 5 9 di AB e il lato AC = 7 5 di BC . Un triangolo DEF equilatero è isoperimetrico al triangolo ABC. Individua la misura di un suo lato, congruente a uno dei tre di ABC . [56 cm]

137 Il lato di un triangolo equilatero misura 11 dm. Questo triangolo è isoperimetrico a un triangolo isoscele avente ciascun lato obliquo uguale ai 4 3 della base. Calcola le misure dei lati del triangolo isoscele. [ ; ; 9 dm]

138 Un triangolo equilatero ha il lato lungo 16 cm ed è isoperimetrico a un triangolo isoscele. Calcola le misure dei lati del triangolo isoscele, sapendo che la differenza tra il lato obliquo e la base misura 3 cm. [14 cm; ; 17 cm]

139 Il perimetro di un triangolo equilatero misura 120 m. Un secondo triangolo equilatero ha il perimetro corrispondente ai 3 2 di quello del primo. Calcola le lunghezze dei lati dei due triangoli. [40 m; 60 m]

TRIANGOLO RETTANGOLO E SUE PROPRIETÀ

140 Osserva i due triangoli rettangoli del disegno e completa la tabella.

Triangolo ABC Triangolo EFG

Angolo retto G

Angoli acuti B e C Ipotenusa

Cateto maggiore

Cateto minore

Altezza relativa all’ipotenusa

141 Rispondi alle seguenti domande relative a dei triangoli rettangoli.

a) Quando un triangolo è rettangolo?

b) Quanto misura la somma degli angoli acuti?

c) Quali lati sono i cateti?

d) Quale lato è l’ipotenusa?

e) Quale altezza non coincide con i lati?

f) Come lo classifichi rispetto ai lati, se ha gli angoli acuti di 45°?

g) Se ha un angolo acuto di 30°, quanto è ampio l’altro angolo acuto?

h) Se ha un angolo acuto di 30°, che cosa puoi dire dell’ipotenusa rispetto al cateto minore?

142 Nei seguenti triangoli rettangoli calcola l’ampiezza dell’angolo acuto incognito. a) b) c)

Osserva i seguenti disegni, completa quanto richiesto effettuando i calcoli sul tuo quaderno.

143 È un triangolo È la metà di un

CB = 18 cm

B = ?

AC = ?

A = 90°

B = 60°

BC = 29 cm

C = ?

AB = ?

È un triangolo | È la metà di

A = 90°

B = 30°

AC = 4,8 cm

C = ?

CB = ?

È un triangolo

È la metà di

146 MATH Determine the length of the side marked as x in each of the following right triangles.

Risolvi i seguenti problemi.

147 MATEMATICA IN AZIONE In architettura, la “leggerezza delle altezze” si traduce nelle forme triangolari, come il timpano o il frontone di chiese e templi. Il timpano di una chiesa ha la forma di un triangolo isoscele, con l’angolo al vertice retto. Determina le misure dei due angoli alla base. [45°; 45°]

148 Un triangolo rettangolo isoscele ha l’ipotenusa che misura 16,97 cm. Calcola la misura di uno dei due cateti, sapendo che il perimetro è lungo 40,97 cm. [12 cm]

149 MATEMATICA IN AZIONE Una mattonella ha la forma di un triangolo isoscele rettangolo.

Se il suo perimetro è 34,1 cm e uno dei cateti è 10 cm, quanto misura l'ipotenusa? Quanto misura il perimetro della figura formata da quattro mattonelle? [14,1 cm; 56,4 cm]

150 Un triangolo rettangolo ha i cateti lunghi rispettivamente 2,8 cm e 2,1 cm. Calcola la misura del suo perimetro, sapendo che l’ipotenusa è i 5 4 del cateto maggiore. [8,4 cm]

151 Un triangolo rettangolo ha l’angolo al vertice retto e i due angoli alla base congruenti. Sapendo che il perimetro è lungo 51,21 cm e un cateto misura 15 cm, calcola la misura della base. Classifica il triangolo rispetto ai lati. [21,21 cm; ]

CRITERI DI CONGRUENZA DEI TRIANGOLI

152 Rispondi con Vero o Falso.

a) Due triangoli sono congruenti quando hanno tre angoli congruenti. V F

b) Due triangoli sono congruenti anche se lati o angoli non combaciano perfettamente. V F

c) Un triangolo rettangolo e uno isoscele possono essere congruenti. V F

d) Un triangolo equilatero e uno ottusangolo non possono essere congruenti. V F

e) Un triangolo equilatero e uno acutangolo non possono essere congruenti. V F

153 Facendo riferimento alle coppie di triangoli congruenti disegnati sotto, completa la tabella e le frasi (simboli uguali indicano elementi congruenti).

a) ABC e MNO

b) DEF e STU

c) ILM e VWX

a) Due triangoli sono congruenti se hanno rispettivamente due e compreso.

Questo è il di congruenza

1° criterio (coppia a)

b) Due triangoli sono se hanno rispettivamente

un ………………… e i due angoli ad esso

Questo è il …………………………………………… di congruenza (coppia ……).

c) Due triangoli che hanno i tre rispettivamente sono

Questo è il criterio (coppia ).

154 Nelle seguenti coppie di triangoli congruenti stabilisci quali sono le coppie di lati e di angoli congruenti.

a) Lati Angoli

b) Lati Angoli c) Lati Angoli

155 Quale criterio di congruenza vale tra le seguenti coppie?

a) AD ≅ CD criterio c) S ≅ Q criterio

b) M ≅ O

criterio d) KP

criterio

156 MATEMATICA IN AZIONE Osserva e rispondi. Su due barche, che hanno l’albero e il boma della stessa lunghezza, sono montate due vele. Sapendo che il boma è perpendicolare all’albero possiamo stabilire che le due vele sono congruenti. In base a quale criterio?

a) 1° criterio b) 2° criterio c) 3° criterio Scrivine la definizione.

Due triangoli sono congruenti se hanno

157 Per tutte le coppie di triangoli puoi stabilire la congruenza? In caso affermativo, scrivi il criterio di congruenza (a simboli uguali corrispondono misure uguali).

158 Stabilisci quali coppie di triangoli sono congruenti e per quale criterio di congruenza (a simboli uguali corrispondono misure uguali).

159 Considera diversi triangoli ABC e MNO e stabilisci di volta in volta se sono congruenti e rispetto a quale criterio.

a)

c)

Risolvi i seguenti problemi.

160 STEM Per calcolare la larghezza (x) di un canyon nel quale c’è una diga, un ingegnere utilizza un metodo indiretto per misurare i lati e gli angoli indicati nella figura.

Quanto è largo il canyon? Motiva la risposta.

161 Il perimetro di un triangolo equilatero misura 32,16 cm. Si può affermare che è congruente a un altro triangolo equilatero il cui lato misura 16,4 cm?

162 Un triangolo ha le misure di due lati e del perimetro rispettivamente di 15 m, 23 m e 64 m. Calcola le misure dei tre lati di un triangolo congruente al primo.

163 Due triangoli scaleni PQR e STU hanno i tre angoli congruenti di 20°, 60° e 100°. Quale altra condizione devi avere, almeno, per stabilire se i due triangoli sono congruenti?

164 Considera due triangoli equilateri: del primo conosci la misura del perimetro che è 54 m, del secondo sai che il lato misura 18 m. Riesci a stabilire se i due triangoli sono congruenti? Motiva la risposta.

165 Il triangolo equilatero ABC ha il perimetro (in cm) uguale al prodotto di 24 × 48; il triangolo equilatero DEF ha il perimetro uguale al prodotto di 96 × 12; il triangolo equilatero GHI ha il perimetro uguale al prodotto di 36 × 36. Dei tre triangoli, due sono congruenti per il terzo criterio. Prova a individuarli scomponendo in fattori i prodotti dati.

166 Di due triangoli sai che sono isoperimetrici e che hanno la stessa misura della base. Sono sicuramente congruenti? Motiva la tua risposta.

167 Disegna un triangolo isoscele e traccia l’altezza relativa alla base. Dimostra che i due triangoli rettangoli in cui l’altezza divide il triangolo isoscele sono congruenti.

168 Disegna un triangolo equilatero e la mediana della base. Dimostra che i due triangoli ottenuti sono congruenti.

169 Disegna un triangolo isoscele e la bisettrice dell’angolo al vertice. Dimostra che i due triangoli ottenuti sono congruenti.

Risolvi i seguenti quesiti nel piano cartesiano.

170 In un riferimento cartesiano disegna il triangolo DEF con vertici D (9; 4), E (13; 4), F(10; 8) e il triangolo ABC con vertici A (4; 1), B (8; 1), C (5; 5). Usando righello o compasso verifica che i due triangoli sono congruenti.

171 Dati i punti A (7; 0), B (9; 9), C (4; 6) individua in un piano cartesiano il triangolo ABC . Considera, poi, il segmento EF: [E (15; 12) F (10; 9)], costruisci il triangolo DEF congruente ad ABC e verifica la congruenza.

172 Rappresenta sul piano cartesiano il triangolo LMN di vertici L(0; 4), M (3; 4), N (3; 9). Rappresenta sullo stesso piano cartesiano il segmento TS: [T (5; 6) S (8; 6)] e individua il punto R, tale che il triangolo RST sia congruente a LMN. Verifica la congruenza ed elenca tutti gli elementi congruenti dei due triangoli.

RISOLVERE PROBLEMI

LA PENDENZA

La pendenza di una salita viene espressa con una percentuale. Per calcolarla occorre

dividere le misure dei due cateti che la salita forma: pendenza = altezza : base × 100

Poiché di solito si conosce la lunghezza della salita e non la base, per angoli α minori di 45°, si suppone che la salita sia congruente con la base.

Ad esempio:

Lunghezza della salita = base = 1 600 m

Altezza dislivello = 200 m

Pendenza = altezza : base × 100 = 200 : 1 600 × 100 = 12,5%

La salita ha una pendenza del 12,5%, cioè ogni 100 m percorsi salirai di 12,5 m.

1 Il ciclista Frank percorre una salita di 10 km, partendo da un’altitudine di 500 metri e arrivando a una di 1 500 metri. Calcola la pendenza media della salita.

a) Supponendo che la base sia uguale alla lunghezza della salita, esegui l’equivalenza: base = 10 km = ……………… m

b) Calcola il dislivello.

dislivello = 1 500 – = m

c) Calcola la pendenza. pendenza = dislivello : base × 100 =

2 Nella figura sono schematizzate due strade che un ciclista può percorrere per andare dal paese di Sottoalmonte a Sopralmonte.

Le lunghezze delle strade sono 8 km una e 16 km l’altra, mentre il dislivello, indicato con h, è identico. In quale caso dovrà affrontare una pendenza maggiore?

UTILIZZARE IL LINGUAGGIO MATEMATICO

3 Scrivi il testo del problema che abbia come riferimento i disegni e i dati indicati.

AC ≅ CB

AC + CB = 72 cm

AC = 4 3 × AB

DF ≅ FE ≅ ED

2p(DEF) = 6 5 × 2p(ABC)

DF = ?

ARGOMENTARE

4 Prova a dimostrare che i due triangoli AMC e MC ’B sono congruenti, sapendo che CM è la mediana del triangolo ABC e CM = MC ’.

ANALIZZARE E INTERPRETARE DATI

5 I numeri triangolari

Sin dall’antichità sappiamo che alcuni numeri possono essere rappresentati con la forma di un triangolo, proprio come nella figura. Essi si ricavano sommando i numeri naturali: 1, 1+2, 1+2+3 ecc.

Continuando la serie, quale sarà il numero rappresentato dalla decima figura? Stabilisci se 91 è un numero triangolare E il 151?

SFIDA MATEMATICA

6 Indovina il lato Il triangolo più grande ha tre lati uguali. È diviso in sette regioni da tre segmenti paralleli ai suoi lati. Ognuno dei quattro piccoli triangoli azzurri nel disegno ha i tre lati uguali fra loro. I lati del triangolo in alto a sinistra misurano 1 cm. Quelli del triangolo in alto a destra misurano 2 cm. Quelli del triangolo in basso misurano 3 cm. Infine, quelli del triangolo al centro misurano 4 cm. Quanto misurano i lati del triangolo grande?

(Testo tratto dalla gara Finale di Parigi Campionati Internazionali del 2015, organizzata dal Centro PRISTEM dell’Università Bocconi di Milano)

ROAD MAP PER TUTTI

il triangolo

DATO UN POLIGONO

Che cos'è un triangolo?

Un triangolo è un poligono con tre lati e tre angoli

Qual è la somma degli angoli interni di un triangolo?

La somma degli angoli interni di un triangolo è sempre 180°

ESEMPIO

β = 180° – (18° + 72°) = = 180° – 90° = 90°

Qual è la proprietà dei lati di un triangolo?

Il lato di maggiore lunghezza è minore della somma degli altri due

ESEMPIO

• AB = 16 cm, BC = 8 cm, AC = 6 cm,

AB > BC + AC → 16 > 8 + 6 → non è un triangolo

• PQ = 24 cm, QR = 10 cm, PR = 16 cm

PQ < QR + PR → 24 < 10 + 16 → è un triangolo

1 Stabilisci se le seguenti terne di angoli possono appartenere a un triangolo.

2 Trova le ampiezze degli angoli segnati con β.

β = 180° – (18° + 72°) = = 180° – 90° = 90°

3 Stabilisci se con le seguenti terne è possibile costruire un triangolo. (Le misure sono espresse in metri.)

45; 26; 56 < < SÌ NO

12; 9; 7 SÌ NO

44; 11; 12 SÌ NO

67; 34; 46

SÌ NO

4 Il Signor Bruno nel suo giardino ha realizzato 10 aiuole fiorite di forma triangolare. Le misure dei lati di ogni aiuola sono: 185 cm, 135 cm e 124 cm. Basteranno 45 m di tubi per realizzare l'impianto di irrigazione goccia a goccia per le 10 aiuole?

classificazione dei triangoli

DATO UN TRIANGOLO

Come si classifica rispetto ai lati?

In base alle misure dei lati i triangoli:

• equilatero se ha tre lati congruenti;

• isoscele se ha almeno due lati congruenti;

• scaleno se non ha lati congruenti

ESEMPIO

Come si classifica rispetto agli angoli?

In base alle ampiezze degli angoli il triangolo è:

• acutangolo se ha tre angoli acuti;

• ottusangolo se ha un angolo ottuso;

• rettangolo se ha un angolo retto

ESEMPIO

80°

45° 55°

acutangolo

123°

ottusangolo

cateto maggiore

90°

cateto minore ipotenusa

rettangolo

5 Classifica i seguenti triangoli rispetto ai lati.

indicate, classifica i seguenti triangoli rispetto agli angoli e ai lati (a simboli uguali corrispondono elementi congruenti).

Congruenti vuol dire che hanno la stessa ampiezza.

Risolvi i seguenti problemi seguendo le indicazioni.

7 Uno degli angoli alla base di un triangolo isoscele è ampio 38°. Calcola l’ampiezza dell’angolo al vertice e classifica il triangolo rispetto agli angoli.

A = 180° – (B + C ) = ……………………………………………………

Essendo A = …………… …, il triangolo è isoscele ……………………………………

8 I due angoli acuti A e B di un triangolo rettangolo sono uno i 3 7 dell’altro. Determina le loro ampiezze.

B = 3 7 × A

A = ?

B = ?

A + B = 180° – 90° =

Congruenti vuol dire che hanno la stessa ampiezza.

L’angolo A è formato da 7 parti congruenti, l’angolo B da 3 parti congruenti e la loro somma è 7 + 3 = 10 parti congruenti; quindi:

A = : 10 × 7 = B = : × 3 = [63°; 27°]

9 In un triangolo rettangolo i due angoli acuti sono uno i 2 3 dell’altro. Calcola le loro ampiezze.

Che cos'è l'altezza?

L'altezza è un segmento perpendicolare che unisce un vertice con il lato opposto

ESEMPIO

PUNTI NOTEVOLI DEL TRIANGOLO

DATO UN TRIANGOLO

Che cos'è la bisettrice?

La bisettrice è una semiretta che divide l'angolo in due parti congruenti e ha l'origine in un vertice

ESEMPIO

= bisettrice dell’angolo U

Che cos'è la mediana?

La mediana è un segmento che unisce un vertice con il punto medio del lato opposto

ESEMPIO

PAGG. 246-252

Che cos'è l'asse?

L'asse di un lato è la perpendicolare al lato che passa per il suo punto medio

ESEMPIO

Dove si incontrano le altezze?

Dove si incontrano le bisettrici?

Dove si incontrano le mediane?

Dove si incontrano gli assi?

Si incontrano in un punto detto ortocentro

Si incontrano in un punto detto incentro

Si incontrano in un punto detto baricentro

Si incontrano in un punto detto circocentro

ESEMPIO

10 Nei seguenti triangoli traccia le altezze uscenti da A.

11 Calcola il valore dell’angolo in U, sapendo che i segmenti colorati sono bisettrici.

12 Nei seguenti triangoli traccia le mediane uscenti da A.

13 Nei seguenti triangoli traccia l’asse relativo al lato AB dopo aver individuato il punto medio.

14 Associa ad ogni figura il tipo di punto notevole rappresentato.

perimetro del triangolo TEORIA PAGG. 254-256

DATO UN TRIANGOLO

Come si calcola la misura del suo perimetro?

Il perimetro 2p si calcola sommando le misure dei suoi tre lati

ESEMPIO

AB = 12cm

BC = 15cm

AC = 14cm;

2p = AB + BC + AC = 12 + 15 + 14 = 41 cm

ESEMPIO

Triangolo equilatero

2p = ℓ × 3, da cui ℓ = 2p : 3

ℓ = 9 cm

2p = 9 × 3 = 27 cm

Ci sono casi particolari?

ESEMPIO

Triangolo rettangolo

2p = C + c + i

C = 12 cm

c = 5 cm

i = 13 cm

2p = 12 + 13 + 5 = 30 cm

ESEMPIO

Triangolo isoscele

2p = b + ℓ × 2, da cui b = 2p – ℓ × 2

b = 10 cm

ℓ = 8 cm,

2p = 10 + 8 × 2 = 26cm

Risolvi i seguenti problemi.

Triangolo scaleno

15 Nel triangolo ABC la somma dei lati BC e AC è 102 cm e il secondo è 1 2 del primo. Calcola il perimetro del triangolo, sapendo che il lato AB misura 85 cm.

AB = 85 cm

AC + BC = 102 cm

AC = 1 2 × BC

2p(ABC) = ?

AC + BC è formato da 1 + 2 = segmentini congruenti, quindi:

AC = 102 : …… = …………

BC = × =

2p(ABC) =

16 La base di un triangolo misura 42 dm; un lato è la metà della base e l’altro lato misura 28 dm.

Calcola il perimetro del triangolo.

17 MATEMATICA IN AZIONE Un’imbarcazione che percorre il tragitto

[91 cm]

Gela-Gozo-Pantelleria-Gela, seguendole linee tracciate in rosso, descrive un triangolo il cui perimetro è lungo circa 517 km.

Il tratto Gela-Gozo è lungo circa 110 km e il tratto Gozo-Pantelleria è di circa 211 km.

Quanto è lungo all’incirca il tratto Pantelleria-Gela?

a) 176 km

b) 216 km

c) 196 km

d) 165 km

18 Completa le seguenti tabelle relative a dei triangoli rettangoli come quello del disegno.

Cateto minore AC Cateto maggiore CB Ipotenusa AB 2p

Triangolo isoscele ed equilatero

19 La base e il lato obliquo di un triangolo isoscele misurano rispettivamente 24 cm e 18 cm. Calcola la misura del perimetro.

AB = 24 cm 2p(ABC) = ?

BC ≅ CA = 18 cm

Trova il perimetro sommando la base AB con il doppio del lato obliquo BC (nel triangolo isoscele i lati obliqui sono congruenti):

2p(ABC) = AB + BC × 2 =

20 In un t riangolo isoscele ABC il lato obliquo è i 4 7 della base. Sapendo che il perimetro misura 165 dm, determina le misure dei tre lati.

BC ≅ AC = 4 7 × AB AB = ?

2p(ABC) = 165 dm AC ≅ BC = ?

Nel perimetro ci sono ……… segmentini, quindi: u = 165 : ........................................................

AB = u × ......................................................

BC = u × .......................................................

= u × .......................................................

[60 cm]

21 MATEMATICA IN AZIONE La sorella minore di Emma, utilizzando 9 tessere a forma di triangolo equilatero, ha composto un triangolo equilatero più grande.

Se una tessera piccola ha il lato lungo 3 cm, quanto misura il perimetro del triangolo equilatero grande?

Triangolo rettangolo

22 Un triangolo rettangolo ha l’ipotenusa che misura 15 cm, il cateto maggiore che misura 12 cm e il cateto minore è uguale al cateto maggiore diminuito di 3 cm.

Calcola il perimetro.

AB = CA – 3 cm =

[36 cm]

23 Calcola il perimetro di un triangolo rettangolo, sapendo che l’ipotenusa misura 45 cm, il cateto minore 27 cm e il cateto maggiore è i 4 5 dell’ipotenusa.

CA = 45 : 5 × 4 =

[108 cm]

24 L’ipotenusa di un triangolo rettangolo misura 117 m, un cateto è i 5 12 dell’altro e il perimetro misura 270 m.

Determina le misure dei due cateti.

C + c = 270 – 117 = [45 m; 108 m]

SIMULAZIONE DI VERIFICA

1 Rispondi con Vero o Falso ed effettua la correzione di ogni falso.

a) In un triangolo un angolo esterno è sempre congruente alla somma degli angoli interni non adiacenti. V F

b) In un triangolo la somma degli angoli interni misura 360°. V F

c) In un triangolo la somma di due lati è sempre minore del terzo lato.

d) In un triangolo la mediana è una retta perpendicolare passante per il punto medio di un lato.

e) In un triangolo la bisettrice è una semiretta uscente da un vertice che divide l’angolo in due parti congruenti.

f) In un triangolo l’asse è il segmento che unisce il vertice con il punto medio del lato opposto

g) Due triangoli sono congruenti se h anno tutti gli angoli ordinatamente congruenti.

2 Segna con Ѵ l’abbinamento possibile e con X quello impossibile.

Equilatero Isoscele Scaleno

h) Acutangolo

i) Rettangolo

j) Ottusangolo

3 Scrivi il nome dei segmenti indicati (simboli uguali indicano elementi congruenti).

a) AF = b) HG = c) MO = d) PN =

4 Trova per ogni termine la definizione corretta.

a) Ortocentro b) Baricentro c) Incentro d) Circocentro

1) Intersezione delle bisettrici 3) Intersezione degli assi

2) Intersezione delle mediane 4) Intersezione delle altezze

F

F

F

5 Calcola le ampiezze degli angoli incogniti e classifica i triangoli rispetto ai lati. a) b) c)

6 Con quali terne di segmenti, espresse in metri, si può costruire un triangolo. a) 22; 17; 39 b) 16; 32; 20

7 La finestra in figura è un triangolo isoscele, in cui la base (AG) misura 6 m e il lato obliquo è i suoi 2 3 .

Determina il perimetro.

8 In un triangolo la differenza delle ampiezze di due angoli è 36° e un angolo è i 4 7 dell’altro. Calcola le ampiezze dei tre angoli e classifica il triangolo.

9 Osserva le figure e scrivi il criterio di congruenza che rappresentano. ?

criterio di congruenza criterio di congruenza criterio di congruenza

10 MATEMATICA IN AZIONE Una nave viaggia parallelamente alla riva lungo la retta RT; quando è nel punto indicato con R l’angolo che la nave forma con il faro è ampio 35°. Dopo aver navigato per circa 4 km, nel punto indicato con S, il capitano misura ancora l’angolo che la nave forma con il faro, scoprendo che è di 70°.

a) Quanto misura l’angolo RLS ?

b) Quanto misura il lato SL? Motiva la risposta.

c) Quale deve essere l’ampiezza dell’angolo LST affinché il segmento SL sia uguale alla distanza della nave dal faro?

I QUADRILATERI UNITÀ 7

Chi ha della

paura matematica?

Che forma ha un campo da pallavolo? E le finestre della tua scuola? Un aquilone, invece? Se hai risposto a queste domande senza esitazione, sei già in grado di capire come molti oggetti che ti circondano possano essere identificati in base alla loro forma e alle loro proprietà. Non è la prima volta che senti parlare di trapezi, rombi, rettangoli, ma in questa unità esplorerai a fondo la famiglia dei quadrilateri e scoprirai come queste figure siano tutte imparentate tra di loro. Arriverai a proclamare il quadrato il membro più potente della famiglia,ilquadrilatero cheriunisceinsétutteleproprietàdeglialtri elementidelclan! Non devi temere questo argomento: ogni quadrilatero nasconde dei segreti, che si rivelano osservando i suoi lati, i suoi angoli e le sue diagonali. Sì, le diagonali! Spesso sono trascurate, ma possono dirci molto su una figura, per esempio, se si tagliano a metà o se, oltre a questo, si incrociano in modo perfetto e sono tra di loro perpendicolari. Dai, la sfida è superabile!

ROAD MAP la nostra

DEFINIAMO I QUADRILATERI E LE LORO PROPRIETÀ

SCOPRIAMO LE CARATTERISTICHE DEI TRAPEZI E DEI PARALLELOGRAMMI

3

CONOSCIAMO LE CARATTERISTICHE DEI RETTANGOLI

2

5

SCOPRIAMO LE CARATTERISTICHE DEI ROMBI E DEI QUADRATI

INTRODUCIAMO I DELTOIDI

4

MATERIALE INTEGRATIVO MULTIMEDIALE

Focus

I quadrilateri: definizioni e proprietà 1

SUCCEDE CHE...

Il giardino dei nonni di Pietro ha la forma di un quadrilatero concavo. In tre vertici del giardino ci sono degli irrigatori le cui ampiezze d’azione sono uguali alle ampiezze degli angoli (vedi immagine a lato). Per irrigare tutto il giardino, il nonno di Pietro vuole mettere nel vertice A un altro irrigatore. Quale ampiezza d’azione deve avere?

Per rispondere alla domanda occorre conoscere la proprietà degli angoli interni dei quadrilateri.

Un quadrilatero è un poligono che ha quattro lati e quattro angoli.

Il quadrilatero ABCD della figura ha:

• 4 lati: AB; BC; CD; DA

• 4 angoli interni: A ; B ; C ; D

• 4 vertici: A; B; C; D

• 2 diagonali: AC; BD

Il perimetro di un quadrilatero (2p) è la somma delle misure dei suoi lati.

Un quadrilatero è convesso quando tutti gli angoli interni sono convessi.

Un quadrilatero è concavo quando ha un angolo interno concavo (contiene il prolungamento dei suoi lati).

I quadrilateri possiedono le seguenti proprietà:

• ogni lato è minore della somma degli altri tre (condizione di esistenza di un quadrilatero);

• la somma degli angoli interni è uguale a 360°;

• la somma degli angoli esterni è uguale a 360°.

OS LUZIONE

Primi

Poiché la somma delle ampiezze degli angoli interni di un quadrilatero è di 360°, l’irrigatore A dovrà avere un’ampiezza di azione di 360° – (75° + 40° + 40°) = 205°.

ESERCIZI

1 Scrivi la definizione di quadrilatero.

2 Dato il quadrilatero ABCD, indica e, se necessario, disegna:

a) i lati:

b) i vertici:

c) le diagonali:

d) gli angoli interni:

e) gli angoli esterni:

3 Indica la risposta corretta.

a) Se le misure a, b, c di tre lati di un quadrilatero ABCD sono a = 22 cm, b = 25 cm, c = 30 cm, allora la misura del quarto lato può essere:

1) d = 98 cm 2) d = 78 cm 3) d = 37 cm

Spiega il perché:

Calcola il perimetro del quadrilatero:

b) Se tre angoli di un quadrilatero ABCD sono A = 43°, B = 140°, C =110°, il quarto angolo deve misurare:

1) D = 35°

Spiega il perché:

2) D = 46°

3) D = 67°

4 MATEMATICA IN AZIONE Il quadrilatero che unisce Peschiera, Verona, Legnago e Mantova (o Mantua) ha un’importanza storica.

Nel periodo della seconda guerra d’Indipendenza italiana (1859) fu infatti utilizzato dall’Austria come sistema difensivo.

Distanze in linea d’aria:

• Peschiera-Verona = 23,38 km

• Legnago-Mantova = 40,38 km

a) Quali sono le città ai vertici?

• Verona-Legnago = 37 km

• Mantova-Peschiera = 32,11 km

b) Il quadrilatero che unisce i quattro vertici di che tipo è?

c) Calcola il contorno del quadrilatero in linea d’aria:

LEZIONE I trapezi 2

SUCCEDE CHE...

Pietro si accorge che in un locale le pareti sono rivestite con piastrelle tutte uguali a forma di trapezio isoscele e che due di queste accostate formano un esagono regolare.

Senza altri dati, è possibile stabilire le ampiezze degli angoli interni del trapezio?

Per rispondere occorre conoscere le proprietà dei trapezi rispetto agli angoli.

Congiungendo nell’ordine i punti A, B, C, D, segnati sulle rette parallele s e r, si ottiene un trapezio.

Il trapezio è un quadrilatero con una coppia di lati paralleli.

Nel trapezio ABCD si hanno:

AB base maggiore: è il lato parallelo maggiore;

CD base minore: è il lato parallelo minore;

AD e CB lati obliqui: sono i due lati non paralleli;

DH o CK altezza: è la distanza tra le due basi;

AH è la proiezione del lato obliquo AD sulla base maggiore;

KB è la proiezione del lato obliquo CB sulla base maggiore.

Osserviamo gli angoli interni di un trapezio:

A, B , C , D . Essendo ottenuti da due rette parallele r e s tagliate da due trasversali t e z, gli angoli A e D , B e C sono coniugati interni, e quindi supplementari.

In un trapezio gli angoli adiacenti a uno stesso lato obliquo sono supplementari.

Un trapezio può essere:

• scaleno: non ha i lati obliqui congruenti;

• rettangolo: ha un lato obliquo perpendicolare alle basi, possiede quindi due angoli retti;

• isoscele: ha i lati obliqui congruenti. Inoltre:

– ha gli angoli adiacenti a ciascuna base congruenti;

– ha le diagonali congruenti;

– ha le proiezioni dei lati obliqui sulla base maggiore congruenti.

Sì, Pietro può stabilire le ampiezze degli angoli; infatti gli angoli adiacenti alla base minore di un trapezio isoscele sono congruenti e hanno l’ampiezza uguale a quella dell’angolo dell’esagono regolare, cioè 120°. Poiché nei trapezi gli angoli adiacenti a ogni lato obliquo sono supplementari, ciascuno degli altri due angoli misura 180° – 120° = 60°.

Primi

ESERCIZI

1 Scrivi la definizione di trapezio.

2 Perché EFGH è un trapezio?

a) La base maggiore è

b) La base minore è

c) Le altezze sono e

d) I lati obliqui sono e

e) Gli angoli adiacenti alla base maggiore sono e

f) Gli angoli adiacenti alla base minore sono e

3 Nei seguenti trapezi isosceli calcola l’ampiezza degli a ngoli 1 , 2 , 3 .

4 MATEMATICA IN AZIONE Identifica i trapezi ripassando il loro contorno come nella prima immagine e poi classificali.

LEZIONE I parallelogrammi 3

SUCCEDE CHE...

Pietro osserva lo specchio appeso in bagno. Quando lo sposta, nota che il quadrilatero LMNO si allarga e si stringe ma i lati opposti, NM e OL, ON e LM, rimangono paralleli e congruenti. Che tipo di quadrilatero è LMNO?

Per rispondere alla domanda occorre conoscere la definizione di parallelogramma. Date due coppie di rette parallele r e s, t e v che si intersecano, congiungendo i quattro punti individuati, A, B, C e D, si ottiene un parallelogramma

Un parallelogramma è un quadrilatero con due coppie di lati paralleli e conguenti.

Indicando con ,1 e ,2 i due lati consecutivi del parallelogramma e con 2p il perimetro, si ha: 2p = (,1 + ,2) × 2 da cui: ,1 = 2p : 2 – ,2 e ,2 = 2p : 2 – ,1

Dato il lato AB, l’altezza ad esso relativa (DH) è la distanza tra questo lato e il suo opposto.

Poiché ogni lato può considerarsi base, ogni parallelogramma ha due altezze (DH e DK). A H B K C D

Se consideriamo singolarmente le due diagonali di un parallelogramma, si può provare che: ogni diagonale divide il parallelogramma in due triangoli congruenti.

Gli angoli opposti di un parallelogramma sono congruenti. Gli angoli adiacenti a un lato sono supplementari

Le diagonali formano quattro triangoli, a due a due congruenti e si tagliano scambievolmente a metà.

triangolo AOB ≅ triangolo COD

triangolo AOD ≅ triangolo BOC

OS LUZIONE

Primi

Il quadrilatero LMNO, sia aperto sia chiuso, è sempre un parallelogramma perché i lati opposti rimangono paralleli e congruenti.

ESERCIZI

1 Osserva il seguente parallelogramma e completa.

a) Il lato AB è opposto al lato

b) Il lato AD è opposto al lato

c) L’altezza è il segmento

d) La diagonale è il segmento

e) L’angolo A è congruente all’angolo

f) L’angolo B è congruente all’angolo

g) Gli angoli A e D , B e C sono

2 Calcola ciò che è richiesto (a simboli uguali corrispondono elementi congruenti).

3 MATEMATICA IN AZIONE Il pantografo da disegno è uno strumento utilizzato per riprodurre immagini. È costituito da quattro listelli uniti tramite cerniere a formare un parallelogramma articolato (ABCD in figura).

Calcola il perimetro e le ampiezze degli angoli del parallelogramma articolato ABCD in entrambe le situazioni disegnate. a) b)

SUCCEDE CHE...

Nella libreria di Emma sono stati aggiunti dei supporti metallici ( MP, NO, PR, OS nella figura a lato ). I supporti sono tutti di uguale lunghezza e a due a due si tagliano a metà. I quadrilateri OPNM e RSPO sono rettangoli?

Per rispondere alla domanda occorre conoscere i rettangoli e le proprietà delle loro diagonali.

Se intersechiamo una coppia di rette parallele r e s con un’altra coppia di rette t e v perpendicolari ad esse, il quadrilatero ottenuto è un rettangolo.

Un rettangolo è un parallelogramma con i lati consecutivi perpendicolari.

Puoi osservare che il rettangolo ha quattro angoli congruenti e retti, per questo è equiangolo Inoltre, scegliendo come base uno dei suoi lati, il lato consecutivo, essendo perpendicolare alla base, è l’altezza del rettangolo.

I lati consecutivi perpendicolari vengono detti base e altezza o anche dimensioni del rettangolo.

Inoltre, le diagonali del rettangolo sono congruenti e si dimezzano nel punto di intersezione.

Il perimetro del rettangolo è la somma dei suoi lati, che sono uguali a due a due. Quindi, indicando con b la misura della base, con h la misura dell’altezza e con 2p la misura del perimetro, si ha:

2p = (b + h) × 2 da cui si ottengono:

b = 2p : 2 – h e h = 2p : 2 – b

OPNM e RSPO sono rettangoli perché MP, NO, PR, OS sono le loro diagonali e hanno le stesse proprietà di quelle dei rettangoli.

1 Osserva il rettangolo ABCD e completa.

a) AB e DC sono e congruenti.

b) AD e sono lati opposti.

c) AB è la

d) AD è l’

e) Gli angoli interni sono perché sono ampi

f) AC e DB sono le e sono

2 Considera i seguenti rettangoli e calcola ciò che è richiesto.

ESEMPIO

Un rettangolo ha la base lunga 14 cm e il perimetro di 68 cm; calcola la misura dell’altezza.

Dati Richiesta

AB (b) = 14 cm BC (h) = ?

2p = 68 cm

Risoluzione 14 cm

2p = ?

2p = ?

MN = ?

3 MATEMATICA IN AZIONE Di seguito, sono riportate le dimensioni delle porte utilizzate in alcuni sport.

Calcola il perimetro di ogni porta.

a) Pallamano 3 m × 2 m

b) Hockey su ghiaccio 183 cm × 122 cm

c) Pallanuoto 3 m × 90 cm

I ROMBI 5

SUCCEDE CHE...

Emma osserva suo padre usare un cric meccanico a manovella per sollevare l’auto. Si accorge che, durante il sollevamento, il cric ha sempre forma di un quadrilatero con i lati uguali e man mano che si solleva la diagonale AB è sempre bisettrice degli angoli A e B. Che parallelogramma è?

Per rispondere alla domanda occorre introdurre un nuovo tipo di parallelogramma.

Un rombo è un parallelogramma con i lati congruenti.

Le proprietà più importanti del rombo riguardano le sue diagonali.

Dato il rombo ABCD, le sue diagonali sono di diversa lunghezza e per distinguerle chiameremo

AC la diagonale maggiore, in simboli D, e BD la diagonale minore, in simboli d

In un rombo:

• le diagonali sono perpendicolari; in simboli: D 9 d;

• ogni diagonale è bisettrice degli angoli interni;

• le diagonali dividono il rombo in quattro triangoli rettangoli congruenti

diagonale minore diagonale maggiore lato (,)

Anche nel rombo, essendo un parallelogramma, possiamo tracciare l’altezza. Nel disegno, h è l’altezza relativa al lato AB.

Il perimetro del rombo si ottiene sommando le misure dei suoi lati. Poiché essi sono tutti uguali, indicando con , la misura di un suo lato e con 2p la misura del perimetro, si ha:

2p = , × 4

Conoscendo il perimetro, la misura del lato del rombo si calcola nel seguente modo: , = 2p : 4

Il cric è un bell’esempio di rombo: infatti, anche quando si solleva o si abbassa, i lati rimangono sempre uguali e le diagonali, perpendicolari, sono bisettrici degli angoli.

1 Completa le formule relative a un rombo.

2p = , =

2 Calcola quanto richiesto.

ESEMPIO

Un rombo ha il perimetro di 50 cm; calcola la misura del lato.

Dati Richiesta

3 Nei seguenti rombi, calcola l’ampiezza degli angoli

4 MATEMATICA IN AZIONE Per realizzare questo anello a forma rombica occorre mettere su ogni lato 12 piccoli smeraldi.

Quanti ne servono in tutto? (In ogni vertice c’è uno smeraldo.)

SUCCEDE CHE...

Sopra la scrivania di Pietro c’è una lampada a pantografo attaccata al muro. Il pantografo è formato da 4 quadrilateri uguali. Pietro osserva che, nella posizione raffigurata, le diagonali sono perpendicolari e congruenti. Quindi sono dei rombi particolari; come si chiamano?

Per rispondere alla domanda occorre introdurre un nuovo tipo di quadrilatero.

Un quadrato è un parallelogramma che ha i lati e gli angoli congruenti.

Il quadrato è un parallelogramma che ha le stesse caratteristiche del rettangolo e le stesse caratteristiche del rombo.

Come il rettangolo ha:

• i quattro angoli retti;

• le diagonali congruenti.

Come il rombo ha:

• i lati congruenti;

• le diagonali perpendicolari e bisettrici degli angoli interni.

Il quadrato è un poligono regolare essendo equiangolo (le ampiezze degli angoli sono uguali) ed equilatero (le misure dei lati sono uguali).

Indicando con , la misura di un lato e con 2p il perimetro di un quadrato, si ha:

2p = , × 4 da cui , = 2p : 4

In base a quanto detto finora si ha il seguente schema riassuntivo.

PARALLELOGRAMMI

(due coppie di lati paralleli)

RETTANGOLI

(parallelogrammi con i quattro angoli congruenti)

QUADRATI

(parallelogrammi con i quattro lati congruenti)

(parallelogrammi con i quattro angoli congruenti e i quattro lati congruenti)

Il pantografo della lampada forma dei quadrati, avendo i lati e le diagonali congruenti.

1 Completa la tabella segnando Sì o No per indicare se il quadrilatero possiede o meno la caratteristica considerata.

una coppia di lati paralleli

due coppie di lati paralleli

lati congruenti a coppie

quattro lati congruenti

2 Dei seguenti quadrati calcola quanto richiesto.

ESEMPIO

Dati Richiesta

2p(ABCD) = 156 cm , = ?

Risoluzione , = 156 : 4 = 39 cm

p = 144 cm , = ? , = 25 cm 2p = ?

3 MATEMATICA IN AZIONE Emma si allena per completare il cubo di Rubik nel minor tempo possibile. Mentre gioca, osserva che ogni faccia è divisa in 9 piccoli quadrati colorati, ma quanti altri quadrati di lato diverso si possono riconoscere in una faccia? Disegnali.

Il lato del quadratino più piccolo misura 2 cm; calcola le misure dei perimetri dei quadrati che sei riuscito a individuare.

, = 0,4 cm 2p = ?

LEZIONE I deltoidi 7

SUCCEDE CHE...

Emma osserva l’immagine che mostra il Centro per le Tecnologie Innovative a Herndon, in Virginia (USA). Non riesce a capire a quale forma può collegare la facciata dell’edificio. Vede che ha due coppie di lati uguali ma non sono quelli opposti, ha le diagonali perpendicolari ma non sono congruenti né si dividono scambievolmente a metà. Di che quadrilatero si tratta?

Per rispondere bisogna conoscere le caratteristiche del deltoide.

Il deltoide è un quadrilatero che ha due coppie di lati consecutivi congruenti.

Le proprietà dei deltoidi sono le seguenti:

• possono essere concavi o convessi; concavo

• due angoli opposti sono congruenti e due non lo sono;

• le due diagonali sono perpendicolari;

• una diagonale (DB) è bisettrice dei due angoli opposti (D e B ) non congruenti e divide a metà l’altra diagonale (AC).

Indicando con ,1 e ,2 le misure dei lati consecutivi di un deltoide, per il calcolo del perimetro si usa la formula:

2p = (,1 + ,2) × 2

Le formule per calcolare la misura di un lato conoscendo il perimetro e l’altro lato, sono: ,1 = 2p : 2 – ,2 oppure ,2 = 2p : 2 – ,1

La facciata del Centro per le Tecnologie Innovative di Herndon ha le caratteristiche di un deltoide.

1 Osserva il deltoide della figura e completa.

a) AB e BC sono lati

e

b) AD e DC sono lati

e

c) AC e DB sono e sono

d) Gli angoli D e B sono ma non sono congruenti.

e) Gli angoli A e C sono e

2 Calcola il perimetro dei seguenti deltoidi.

ESEMPIO

Un deltoide ha due lati consecutivi non congruenti di 14 cm e 9 cm. Calcola la misura del perimetro.

Dati Richiesta

AB ≅ BC = 14 cm 2p = ?

DA ≅ DC = 9 cm

Risoluzione

2p = (,1 + ,2) × 2 = (14 + 9) × 2 = 46 cm

EH ≅ HG = 10 cm

≅ GF = 16 cm

2p = ?

p = ?

3 MATEMATICA IN AZIONE Un aquilone ha la forma di un deltoide.

Calcola le ampiezze degli angoli D e F

(La somma degli angoli interni misura )

p = ?

MAPPA

TRAPEZI

QUADRILATERI

convesso concavo E F H G somma angoli interni = 360°

perimetro (2p) = somma delle misure dei lati

DELTOIDI

Trapezi isosceli

Trapezi rettangoli

Trapezi scaleni

AD ≅ BC

A ≅ B e ≅ D

AC ≅ BD

PARALLELOGRAMMI

AB ≅ CD e BC ≅ AD

B ≅ D e A ≅ C

B + C = 180°

A + D = 180°

e BD si tagliano scambievolmente a metà

RETTANGOLI

ROMBI

AC è bisettrice di A e C

BD è bisettrice di B e D

AC ⊥ BD

QUADRATI

LEZIONE

1 ESERCIZI E PROBLEMI

I QUADRILATERI: DEFINIZIONI E PROPRIETÀ

1 Contrassegna i quadrilateri.

2 Rispondi con Vero o Falso.

a) I quadrilateri hanno quattro lati, quattro angoli e quattro diagonali.

b) In ogni quadrilatero la somma degli angoli interni è un angolo giro.

c) Nei quadrilateri ogni lato è maggiore della somma degli altri tre.

d) I quadrilateri possono essere concavi o convessi.

e) In un quadrilatero concavo la somma degli angoli esterni è un angolo piatto.

3 Osserva il quadrilatero LMNO e completa.

a) I lati sono , , ,

b) Gli angoli interni sono , , ,

c) Le diagonali sono ,

d) Il lato LM è opposto al lato

e) Gli angoli adiacenti al lato NO sono e

f) L’angolo M è opposto all’angolo

4 MATH Which of the following quadrilaterals are concave? Highlight the concave angles using a colour.

F

F

F

F

F

5 MATEMATICA IN AZIONE Individua un quadrilatero concavo e uno convesso nella piantina della metropolitana di Milano.

6 Sul quaderno disegna un quadrilatero convesso ed evidenzia con colori diversi i lati, gli angoli e le diagonali.

7 Sul quaderno disegna un quadrilatero concavo e uno convesso.

8 Con quali delle seguenti quaterne è possibile costruire un quadrilatero? (Le misure sono espresse in centimetri.)

ESEMPIO 12 7 < 23 21 ∙ 23 è la misura maggiore 7 + 12 + 21 è la somma delle altre misure

SÌ 23 < 40 la disuguaglianza è vera si può costruire il quadrilatero

9 Stabilisci se le seguenti quaterne possono essere le ampiezze degli angoli interni di un quadrilatero. Se NO, spiega perché.

a) 27°; 167°; 160°; 90° SÌ NO

b) 82°; 151°; 45°; 62° SÌ NO

c) 58°; 89°; 106°; 107° SÌ NO

d) 100°; 30°; 70°; 160° SÌ NO

10 Completa le seguenti quaterne in modo che rappresentino le ampiezze degli angoli interni di un quadrilatero.

11 Osserva le illustrazioni e, in base alle indicazioni, calcola le ampiezze degli angoli incogniti.

Risolvi i seguenti problemi.

12 Un quadrilatero ha due angoli congruenti di 135° e un terzo angolo ampio 52°; quanto è ampio il quarto angolo? [38°]

13 Un quadrilatero RSTV ha l’angolo S retto, l’angolo T è 3 2 di S e l’angolo V di 110°. Quanto misura l’angolo R ? [25°]

14 Calcola il perimetro dei seguenti quadrilateri. a) b) c) d)

AB = 23 cm

BC = 26 cm

CD = 17 cm

DA = 19 cm

EF = 30 cm

FG = 1 2 EH

GH = 2 × EH

EH = 14 cm

15 EDUCAZIONE CIVICA Nella mappa a lato il quadrilatero tracciato racchiude all’incirca la zona che anticamente era il castrum della città romana Augusta Taurinorum, oggi Torino. I lati AB e CD del quadrilatero misurano circa 600 metri e i lati BC e AD circa 850 metri. Quanto è lungo il perimetro di ABCD ?

LM = 23 cm

MN = 21 cm

NO = 2 3 × MN

OL = 18 cm

TU = 35 cm

UV = 20 cm

VW = 4 5 × TU

WT = 16 cm

16 Un quadrilatero ha un lato di 54,3 cm e due lati congruenti che misurano 65,2 cm ciascuno. Sapendo che il suo perimetro misura 240 cm, calcola la misura del quarto lato. [55,3 cm]

17 Considera un quadrilatero ABCD in cui AB = 14 m, BC = 3 2 di AB, DA = 4 × AB e il perimetro è di 136 m. Quanto misura il lato CD ? [45 m]

18 Un quadrilatero ha il perimetro di 430 cm e un lato di 112 cm. Sapendo che gli altri tre lati sono congruenti, calcola la loro misura. [106 cm]

Risolvi i seguenti quesiti nel piano cartesiano.

19 In un piano cartesiano individua i punti A (2; 2), B (8; 4), C (7; 9), D (2; 8). Congiungili nell’ordine dato per ottenere una figura chiusa. Che tipo di quadrilatero ottieni? Indica le coordinate di un punto E tale che il quadrilatero ABCE sia concavo.

20 Rappresenta in un piano cartesiano il segmento AB: A (2; 1,5), B (5; 2). Costruisci, a tuo piacere, un quadrilatero concavo ABCD

I TRAPEZI

21 Rispondi con Vero o Falso.

a) Il trapezio ha due lati paralleli.

b) La base maggiore di un trapezio è sempre perpendicolare alla minore.

c) Gli angoli opposti di un trapezio sono complementari.

d) Il trapezio rettangolo ha due diagonali congruenti.

e) Gli angoli adiacenti al lato obliquo di un trapezio sono supplementari.

f) Esistono trapezi isosceli, scaleni, rettangoli e regolari.

22 Stabilisci il nome esatto dei seguenti trapezi; indica con una crocetta la base minore e con un cerchietto quella maggiore.

a) c) b) d)

23 Osserva il seguente trapezio e completa le affermazioni.

a) LM è la base

b) è la base minore.

c) OL e sono i lati

d) e sono le altezze.

e) OM e LN sono le

f) LK e sono le dei lati obliqui sulla

g) O e N sono gli angoli adiacenti alla

24 Nei seguenti triangoli traccia la parallela al lato UV passante per A e classifica il trapezio ottenuto. a) b) c)

25 Classifica i seguenti trapezi e completa la tabella. a) b) c)

b)

Base maggiore AB

Base minore Altezze

Proiezione/i HB Diagonali Lati obliqui

26 Classifica i seguenti trapezi e determina la misura del loro perimetro. a) b) c)

c)

27 Calcola il perimetro dei seguenti trapezi, dove B = base maggiore, b = base minore, ,1 e ,2 = lati obliqui.

B = 56 cm b = 36 cm ,1 = 34 cm ,2 = 24 cm 2p = b)

c) B = 3 × b b = 12 m ,1 = 26 m ,2 = 19 m 2p = e) B = 20 cm b = 12 cm ,1 = 3 × ,2 ,2 = 6 cm 2p = a)

B = 74 cm b = 25 cm ,1 = ,2 ,2 = 31 cm 2p = d) B = 42 cm b = 1 3 × B ,1 = ,2 ,2 = 15 cm 2p = f) B = 4 3 × b b = 18 m ,1 = 14 m ,2 = 2 × ,1 2p =

28 MATH Given a trapezoid, determine the required measurements.

a) LM = 64 m LO ≅ NM = NO = 53 m

2p = 143 m

b) LM = 86 dm LO ≅ NM = NO = 45 dm

2p = 179 dm

Segna la risposta esatta.

29 In un trapezio isoscele la base maggiore misura 34 cm e i lati obliqui 23 cm ciascuno. Se la base minore è la metà della base maggiore, il perimetro misura: a) 94 cm b) 59 cm c) 97 cm d) 74 cm

30 Un trapezio scaleno ha la base minore che misura 36 cm, la base maggiore è i suoi 5 4 e i lati obliqui misurano 26 cm e 28 cm. Il perimetro misura: a) 135 cm b) 124 cm c) 111 cm d) 168 cm

31 In un trapezio rettangolo la base minore misura 68 cm e il lato obliquo è i suoi 3 4 Sapendo che la base maggiore supera la minore di 10 cm e che l’altezza misura 48 cm, il perimetro è: a) 251 cm b) 241 cm c) 245 cm d) 231 cm

32 Un trapezio scaleno ha la base maggiore di 45 cm e la minore che è i suoi 3 5 Sapendo che i due lati obliqui misurano 27 cm e 31 cm, il perimetro è: a) 100 cm b) 115 cm c) 125 cm d) 130 cm

Risolvi i seguenti problemi riferiti anche a situazioni presenti nella realtà.

33 I lati di un terreno a forma di trapezio misurano 38 m, 20 m, 25 m e 17 m. Per recintarlo completamente basterà un rotolo di rete da 100 m? Perché? [Sì; ]

34 La finestrella di un abbaino a forma di trapezio ha i lati obliqui che misurano 24 cm e 46 cm. Calcola il suo perimetro sapendo che la somma delle basi è 156 cm. Che trapezio è? [226 cm; ]

35 In un trapezio le basi misurano rispettivamente 68 cm e 45 cm, un lato obliquo misura 34 cm. Classifica il trapezio, sapendo che ha il perimetro di 179 cm.

36 Un terreno che ha la forma di trapezio con i lati che misurano 34 m, 25 m, 54 m e 37 m deve essere recintato lungo i suoi tre lati maggiori con una costruzione che costa 5,40 € al metro lineare. Quanto si spenderà per questo lavoro?

[675 €]

37 Lo specchietto laterale di un’automobile a forma di trapezio rettangolo ha i lati con queste misure: 17 cm, 12 cm, 14 cm e 18,5 cm. Quanto misura il suo perimetro? [61,5 cm]

38 In un trapezio isoscele il perimetro misura 79 cm e il lato obliquo 19 cm. Calcola la misura di ognuna delle basi, sapendo che la loro differenza è 17 cm. [12 cm; 29 cm]

39 STEM Marco, in mansarda, ha due finestre a forma di trapezio rettangolo. Calcola il perimetro di ciascuna di esse conoscendo le seguenti misure:

• prima finestra: lati paralleli 0,83 m e 0,59 m; altri lati 1,10 m e 1,18 m;

• seconda finestra: lati paralleli 56 cm e 32 cm; altri lati 113 cm e 115 cm.

[3,70 m; 316 cm]

ESEMPIO

In un trapezio isoscele la base maggiore misura 90 cm, ciascuna proiezione del lato obliquo sulla base maggiore misura 11 cm e il perimetro è di 242 cm. Calcola le misure della base minore e dei lati obliqui.

Dati

AB = 90 cm

AH ≅ KB = 11 cm

2p(ABCD) = 242 cm

Richieste

CD = ?

AD ≅ CB = ?

Risoluzione

La base maggiore è la somma di tre segmenti: le due proiezioni e un segmento congruente alla base minore.

Per calcolare la base minore si sottraggono dalla base maggiore le due proiezioni:

CD = AB − ( AH + KB ) = 90 − (11 + 11) = 90 − 22 = 68 cm

I lati obliqui, che sono congruenti, si trovano sottraendo dalla misura del perimetro le due basi e poi dividendo per due:

AD = CB = [2p − ( AB + CD )] : 2 = [242 − (90 + 68)] : 2 = 42 cm

40 Il lato obliquo di un trapezio isoscele e la sua proiezione sulla base maggiore misurano 25 mm e 22 mm. Calcola le misure delle basi, sapendo che il perimetro è 138 mm. [22 mm; 66 mm]

41 In un trapezio isoscele la base maggiore è 230 cm, ciascuna proiezione del lato obliquo sulla base maggiore è 35 cm e il perimetro è 582 cm. Calcola le misure della base minore e dei lati obliqui. [160 cm; 96 cm]

42 Una faccia laterale di un vaso ha la forma di trapezio isoscele. Se le due basi del trapezio misurano 56 cm e 30 cm e il suo perimetro è lungo 152 cm, quanto misura ciascun lato obliquo?

43 In un trapezio isoscele il perimetro misura 142 dm e ciascun lato obliquo è lungo 29 dm. Sapendo che la base maggiore è il triplo della minore, calcola le misure delle basi del trapezio.

[21 dm; 63 dm]

44 Le proiezioni dei lati obliqui sulla base maggiore di un trapezio isoscele misurano 30 dm; il perimetro del trapezio è 375 dm e ciascun lato obliquo è la decima parte del perimetro. Determina la misura di ciascuna delle basi. [120 dm; ]

45 In un trapezio isoscele le proiezioni dei lati obliqui sulla base maggiore misurano 58 cm ciascuna e la base maggiore è lunga 174 cm. Calcola la misura del perimetro, sapendo che i lati obliqui sono il doppio della base minore. [464 cm]

46 In un trapezio isoscele il perimetro misura 114 dm e la proiezione del lato obliquo sulla base maggiore è lunga 12 dm. Sapendo che la base minore è il doppio del lato obliquo, calcola le misure dei lati del trapezio. [15 dm; 15 dm; 54 dm; 30 dm]

ESEMPIO

In un trapezio rettangolo il perimetro misura 618 cm, l’altezza 84,2 cm, il lato obliquo 104,7 cm e la sua proiezione sulla base maggiore 62,2 cm. Calcola le misure delle basi.

Dati

Richieste

2p(ABCD) = 618 cm CB = 104,7 cm DC = ?

DA = 84,2 cm HB = 62,2 cm AB = ?

Risoluzione

Se sottraiamo dal perimetro le misure di DA e CB otteniamo la somma delle basi:

AB + DC = 2p − (DA + CB ) = 618 − (84,2 + 104,7) = 618 − 188,9 = 429,1 cm

La base maggiore è formata da un segmento congruente alla base minore e dalla proiezione del lato obliquo su di essa. Quindi:

DC = ( AB + DC ) − HB 2 = 429,1 − 62,2 2 = 366,9 2 = 183,45 cm

AB = DC + HB = 183,45 + 62,2 = 245,65 cm

47 In un trapezio rettangolo la base maggiore è 38 cm e la proiezione del lato obliquo sulla base maggiore è di 12 cm. Determina la misura della base minore. [26 cm]

48 La base minore di un trapezio rettangolo misura 56 dm e la proiezione del lato obliquo sulla base maggiore è 27 dm. Quanto misura la base maggiore del trapezio? [83 dm]

49 In un trapezio rettangolo il perimetro è di 107 cm e l’altezza misura 20 cm. Determina le misure della base maggiore e del lato obliquo, sapendo che la base minore è lunga 26 cm e la proiezione del lato obliquo sulla base maggiore è di 10 cm. [................ ; 25 cm]

50 Un trapezio scaleno ha la base minore che misura 45 cm e la base maggiore che la supera di 17 cm. Calcola il perimetro del trapezio, sapendo che i lati obliqui sono rispettivamente i 3 5 e i 4 5 della base minore. [170 cm]

51 Individua e contrassegna le coppie di angoli adiacenti a ciascun lato obliquo. Qual è la loro caratteristica?

52 Determina le ampiezze degli angoli incogniti dei seguenti trapezi. a) b) c)

Risolvi i seguenti problemi.

53 MATEMATICA IN AZIONE Una falda del tetto di una casa ha la forma di trapezio isoscele. Se un angolo adiacente alla base maggiore è ampio 40°, quanto sono ampi gli altri angoli di questa parte di tetto?

54 In un trapezio scaleno gli angoli adiacenti alla base maggiore misurano 35° e 49°. Determina le misure degli altri due angoli. [145°; 131°]

55 In un trapezio isoscele un angolo adiacente alla base maggiore misura 78°. Calcola le misure degli altri tre angoli. [102°; .....]

56 Dato un trapezio isoscele LMNO, determina le ampiezze dei suoi angoli secondo le indicazioni date.

a) O = 2 × L O = L = b) O = 3 × L O = L =

57 Se in un trapezio rettangolo l’angolo acuto misura 31° 40', quali sono le ampiezze degli altri angoli? [148° 20’; ..........]

58 In un trapezio isoscele un angolo è 2 3 del suo supplementare. Calcola le ampiezze degli angoli del trapezio.

59 Dato un trapezio rettangolo ABCD retto in A , sapendo che la base maggiore misura 48 cm e la base minore è i suoi 5 6 , calcola:

a) il perimetro, sapendo che il lato obliquo misura 34 cm e l’altezza è di 25 cm;

b) le misure degli angoli adiacenti al lato obliquo BC , sapendo che uno è i 2 3 dell’altro. [147 cm; 72°; 108°]

60 Individua in un piano cartesiano i punti A(4; 2), B (16; 2), C(15; 6), D (5; 6).

a) Uniscili nell’ordine e classifica il quadrilatero ABCD

b) Calcola le misure dei lati paralleli assumendo u = 1 cm.

I PARALLELOGRAMMI

61 Rispondi con Vero o Falso.

a) Un quadrilatero con due coppie di lati paralleli è un parallelogramma.

b) Gli angoli opposti di un parallelogramma sono supplementari.

c) Ogni parallelogramma ha tre altezze di misure diverse.

d) Le diagonali di un parallelogramma sono sempre congruenti.

e) 2p = (,1 + ,2) si usa per calcolare il perimetro di un parallelogramma.

f) Un parallelogramma è un poligono concavo.

g) Ogni diagonale divide un parallelogramma in due triangoli congruenti.

62 Osserva i seguenti quadrilateri e contrassegna i parallelogrammi. a) b) c) d)

F

F

F

F

F

F

F

63 Osserva il seguente parallelogramma e completa.

a) I lati paralleli sono e , e

b) DH è relativa al lato

c) è relativa al lato

d) AC e sono le

e) Gli angoli A e D sono adiacenti al lato ………

f) L’angolo A è opposto all’angolo ………

g) L’angolo B è congruente all’angolo ………

h) Gli angoli B e C sono ……….……………, cioè la loro somma è uguale a ………

64 Nei seguenti parallelogrammi traccia l’altezza relativa al lato AB.

65 Senza usare il goniometro, determina le ampiezze degli angoli dei seguenti parallelogrammi.

a)

b)

1) Traccia un segmento orizzontale AB lungo ad esempio 7 quadretti.

2) Spostati a destra di 3 quadretti, in alto di 4, segna un punto e indicalo con C.

3) Spostati a sinistra di 7 quadretti, segna il punto D e congiungilo con C e A

4) Congiungi C con B

Ecco il parallelogramma

Risolvi i seguenti problemi.

66 In un parallelogramma l’ampiezza di un angolo acuto è 49°. Calcola le ampiezze degli altri angoli. [131°; ] ] ]

67 MATEMATICA IN AZIONE La fotografia mostra l’edificio Kristallen (Cristallo in italiano) a Copenaghen. Supponi che la facciata ABCD, il cui contorno è evidenziato in colore, sia un parallelogramma inclinato di circa 20° rispetto al piano stradale. Calcola le ampiezze degli angoli interni del parallelogramma ABCD, sapendo che il lato AD è perpendicolare alla strada.

68 In un parallelogramma i due angoli adiacenti allo stesso lato sono uno i 2 3 dell’altro. Quali sono le ampiezze degli angoli del parallelogramma? [72°; ; ; ]

69 L'angolo ottuso di un parallelogramma supera l’ampiezza di quello acuto di 55°. Calcola le ampiezze dei quattro angoli del trapezio. [ .............. ; 117° 30'; ............... ; ...................]

70 MATH Find the required measurements for the following trapezoids (<1 and <2 are consecutive sides).

a) ,1 = 14 cm ,2 = 2 × ,1 2p = .............. c) ,

71 Determina il perimetro dei seguenti parallelogrammi. a) b) c)

Segna la risposta esatta.

72 In un parallelogramma due lati consecutivi misurano 23 cm e 54 cm. Il perimetro misura: a) 154 cm b) 243 cm c) 153 cm d) 135 cm

73 In un parallelogramma il perimetro misura 116 cm e il lato maggiore misura 31 cm; l’altro lato è lungo: a) 21 cm b) 34 cm c) 27 cm d) 47 cm

Risolvi i seguenti problemi.

ESEMPIO

Un parallelogramma ha il perimetro che misura 160 cm e i lati consecutivi sono uno i 3 5 dell’altro. Determina le misure dei lati.

Dati

2p = 160 cm

AB = 3 5 × BC

Richieste

AB = ?

BC = ?

Risoluzione

Il semiperimetro (p) corrisponde alla somma dei lati consecutivi, quindi:

p = AB + BC = 160 : 2 = 80 cm

Il semiperimetro comprende 8 parti congruenti: u = 80 : 8 = 10 cm

AB = 10 × 3 = 30 cm e BC = 10 × 5 = 50 cm

74 MATEMATICA IN AZIONE La ringhiera di una scala è a forma di parallelogramma e il suo perimetro misura 42 m.

Se un lato è i 3 4 del suo consecutivo, calcola la misura del lato più lungo della ringhiera. [12 m]

75 MATEMATICA IN AZIONE La finestrella di un sottoscala ha la forma di un parallelogramma.

I due lati sono uno i 2 3 dell’altro e il perimetro della finestra è 230 cm; qual è la misura di ciascuno dei lati?

[46 cm; ]

76 Un parallelogramma ha il perimetro di 130 cm e un lato supera il consecutivo di 20 cm.

Determina la misura dei due lati.

[22,5 cm; 42,5 cm]

77 MATEMATICA IN AZIONE La ringhiera di una rampa di scale è formata da 8 moduli congruenti che hanno la forma di parallelogramma.

Il lato più corto del modulo (CD ) è 2 5 di quello più lungo (DE ). Se il perimetro del modulo (CDEF ) è lungo 280 cm, quanto è lunga, in metri, tutta la ringhiera ( AB )?

78 Un parallelogramma ha il perimetro di 54 cm e un lato il doppio dell’altro.

Determina le misure dei suoi lati e quelle dei lati di un rettangolo isoperimetrico al parallelogramma avente un lato multiplo dell’altro secondo il numero 8.

[9 cm; 18 cm; 3 cm; 24 cm]

79 Un parallelogramma avente il perimetro di 52 dm ha il lato maggiore che supera di 5 dm il minore. Determina le misure dei suoi lati, le misure dei lati del triangolo isoscele isoperimetrico al parallelogramma e avente i lati obliqui doppi della base.

[15,5 dm; 10,5 dm; 10,4 dm; 20,8 cm]

80 Un parallelogramma MNOP ha il perimetro di 160 dm e l’angolo M che è il doppio del suo consecutivo N . Calcola:

a) le misure dei suoi lati, che sono uno i 3 5 dell’altro; b) le misure degli angoli interni.

81 MATEMATICA IN AZIONE Il pannello di una recinzione a forma di parallelogramma ha il perimetro di 192 cm. Calcola:

a) Ie misure dei lati, sapendo che uno è il triplo dell’altro;

b) le ampiezze degli angoli, sapendo che l’angolo acuto è i 2 3 di quello ottuso. [24 cm; 72 cm; 72°; ..............]

82 Considera un parallelogramma nel quale la differenza tra i due lati consecutivi è 18 dm e due angoli adiacenti sono uno i 2 3 dell’altro. Calcola:

a) le misure dei due lati, sapendo che il perimetro è 654 dm; b) le misure degli angoli interni. [154,5 dm; ; ; 108°]

83 Osserva il piano cartesiano sottostante e determina le coordinate dei vertici dei quadrilateri disegnati, dopo averli riconosciuti.

84 Individua in un sistema di riferimento cartesiano i punti A(3; 3), B (9; 3), C(8; 7) e determina le coordinate di un punto D in modo che il quadrilatero ABCD sia un parallelogramma.

I RETTANGOLI

85 Elimina il termine errato tra le due opzioni in corsivo.

Un rettangolo:

a) è un quadrilatero con i lati consecutivi paralleli / perpendicolari

b) ha i lati opposti paralleli e congruenti / non congruenti.

c) gli angoli sono retti / acuti e sono ampi 90° / più di 90°

d) ha due dimensioni che sono la base e l’altezza / la diagonale

e) le due diagonali sono congruenti / perpendicolari.

86 Osserva il rettangolo LMNO e completa.

a) I lati paralleli sono LM e , e

b) Le basi sono ,

c) Le altezze relative al lato MN sono ………, ………

d) Le diagonali sono ,

e) Le coppie di angoli opposti sono ………,

87 Completa.

Le dimensioni del rettangolo sono la e l’ ; per calcolare il perimetro occorre sommare

e moltiplicare per ……………

88 Completa le seguenti formule relative al perimetro del rettangolo.

2p = da cui b = 2p : e h =

89 Determina il perimetro dei seguenti rettangoli.

90 Consider some rectangles and calculate what is required.

a) b = 12 cm h = 3 × b 2p =

b) b + h = 42 cm h = 2 × b b = h = .............. 2p = ..............

91 Completa i seguenti schemi.

a) b = 11 dm h = 21 dm p = 2p =

b) b = dm h = 24 dm p = 59 dm 2p =

Segna la risposta esatta.

c) h = 35 cm b = 2 5 × h 2p = ..............

d) b + h = 28 cm

b − h = 14 cm b = h = 2p =

c) b = …… dm h = 56 dm p = 2p = 268 dm

d) b = 33 dm h = dm p = 86 dm 2p =

92 In un rettangolo le dimensioni misurano 21,4 cm e 33,5 cm. Il perimetro è: a) 100 cm b) 108,8 cm c) 109,8 cm d) 106,8 cm

93 In un rettangolo l’altezza è il doppio della base che misura 12,5 m. Il perimetro è: a) 50 m b) 37,5 m c) 62,5 m d) 75 m

94 In un rettangolo il perimetro è 560 dm e la base è i 2 3 dell’altezza. L’altezza è: a) 186 dm b) 168 dm c) 112 dm d) 120 dm

95 In un rettangolo il perimetro è 918 dm e l’altezza è i 5 4 della base. La base è: a) 510 dm b) 408 dm c) 255 dm d) 204 dm

96 In un rettangolo il semiperimetro misura 192 m e l’altezza è il quadruplo della base. La base è: a) 48 m b) 38,4 m c) 24 m d) 37,4 m

Risolvi i seguenti problemi riferiti anche a situazioni presenti nella realtà.

97 MATEMATICA IN AZIONE Un contadino vuole recintare un orto di forma rettangolare avente le dimensioni di 31,7 m e 15,8 m; la rete per la recinzione costa 4,20 € al metro.

Quanto spenderà il contadino?

98 MATEMATICA IN AZIONE Un maratoneta si allena in una pista di forma rettangolare lunga 58 m e larga 27 m.

Quanti metri percorre ogni giro? Se il suo passo misura mediamente 85 cm, quanti passi fa al giro?

ESEMPIO

In un rettangolo la base supera l’altezza di 21 cm e il perimetro è di 256 cm.

Quanto misurano le sue dimensioni?

Dati

AB − BC = 21 cm

2p = 256 cm

Richieste

AB = ?

BC = ?

Risoluzione

Sottraendo dal perimetro i due segmenti di cui si conosce la misura (21 cm), si ottengono 4 segmenti uguali all’altezza, quindi:

BC = [2p − (21 × 2)] : 4 = [256 − (21 × 2)] : 4 = = 53,5 cm

AB = BC + 21 = 53,5 + 21 = 74,5 cm

99 Un rettangolo ha la base che supera l’altezza di 35 cm e il perimetro è di 320 cm. Determina le misure delle sue dimensioni. [62,5 cm; 97,5 cm]

100 In un rettangolo l’altezza supera la base di 28 cm. Sapendo che il semiperimetro è di 64 cm, determina le misure delle sue dimensioni. [18 cm; 46 cm]

101 Un orto rettangolare ha la base che supera di 12 m il triplo dell’altezza.

Determina le misure delle sue dimensioni, sapendo che il perimetro è lungo 96 m. [9 m; 39 m]

102 In un rettangolo la base supera l’altezza di 40 cm. Sapendo che l’altezza è 3 8 della base, calcola le misure delle due dimensioni e il perimetro. [64 cm; 24 cm; 176 cm]

103 Un terreno di forma rettangolare viene lottizzato e diviso, lungo la dimensione maggiore, in tre lotti rettangolari uguali. Sapendo che le dimensioni del terreno sono 36 m × 96 m, quale sarà il perimetro di ciascuno dei tre lotti? [136 m]

104 In un rettangolo la somma delle due dimensioni è 56,4 cm e la loro differenza è 23,6 cm. Determina le misure della base e dell’altezza. [16,4 cm; 40 cm]

105 Il perimetro di un campo rettangolare è 109,2 m e la larghezza è i 3 4 della sua lunghezza. Calcola le misure delle due dimensioni del campo. [23,4 m; 31,2 m]

106 Un grande cartellone pubblicitario ha il perimetro di 40 m.

Determina le sue dimensioni sapendo che una è il quadruplo dell’altra. [4 m; 16 m]

107 Un triangolo equilatero ha il perimetro di 45 m. Calcola il perimetro di un rettangolo avente la base congruente al lato del triangolo e l’altezza di 34 m. [98 m]

108 Un rettangolo ha il perimetro di 190 cm e l’altezza di 56 cm. Determina il perimetro di un triangolo isoscele avente la base congruente con la base del rettangolo e il lato obliquo lungo 23 cm. [85 cm]

109 Un rettangolo ha le dimensioni che misurano rispettivamente 45 dm e 56 dm. In un parallelogramma isoperimetrico al rettangolo un lato è il triplo dell’altro.

Calcola le misure dei lati del parallelogramma. [25,25 dm; 75,75 dm]

110 Un rettangolo e un parallelogramma sono isoperimetrici. La base del rettangolo misura 12 m ed è la metà del triplo dell’altezza; i lati consecutivi del parallelogramma sono uno il triplo dell’altro. Calcola le misure dei lati del parallelogramma. [5 m; .............]

111 Un rettangolo ha la base di 2,4 cm e l’altezza uguale al triplo della metà della base. Determina le misure dei lati del parallelogramma isoperimetrico al rettangolo e avente il lato maggiore che supera il doppio del lato minore di 1,2 cm. [1,6 cm; 4,4 cm]

112 ABCD è un rettangolo e M, N, O, P sono i punti medi dei suoi lati. Sapendo che le dimensioni del rettangolo misurano 68 cm e 42 cm, calcola: a) il perimetro del rettangolo ABCD ; b) il perimetro del rettangolo AMSP [220 cm; ..............]

113 Un parallelogramma con la base lunga 76 cm è formato da un rettangolo e da due triangoli rettangoli congruenti che hanno un cateto congruente con l’altezza del parallelogramma e l’altro di 24 cm. Calcola: a) il perimetro del rettangolo, sapendo che l’altezza misura 32 cm; b) l’ipotenusa di uno dei due triangoli, sapendo che il suo perimetro è di 96 cm; c) il perimetro del parallelogramma. [168 cm; 40 cm; 232 cm]

114 In un riferimento cartesiano individua i punti D (8; 8), E (19; 8), F (11; 13).

Determina poi le coordinate di un quarto punto in modo che il quadrilatero individuato congiungendo i quattro vertici sia: un trapezio isoscele; A (………; ………) un trapezio rettangolo; B (………; ………) o C (………; ………) un parallelogramma; G (………; ………) un trapezio scaleno. L (………; ………)

I ROMBI LEZIONE 5

115 Rispondi con Vero o Falso.

a) Il rombo è un parallelogramma equilatero.

b) I lati opposti del rombo sono congruenti e perpendicolari.

c) In un rombo gli angoli opposti sono congruenti.

d) Le diagonali del rombo sono incidenti e perpendicolari.

e) Il rombo ha due angoli acuti e due ottusi.

f) Le diagonali di un rombo lo dividono in quattro triangoli isosceli congruenti.

116 Osserva il rombo ABCD e completa.

a) Le coppie di lati paralleli sono e , e

b) Le diagonali sono ………, ………

c) L’altezza relativa al lato AB è

d) Gli angoli adiacenti al lato CB sono e

e) Le coppie di angoli opposti sono , e ,

117 Completa le seguenti formule relative al perimetro del rombo.

2p = ………………………… da cui , = 2p : ………… ……

118 Traccia nei seguenti rombi le altezze relative al lato AB.

119 Nel seguente rettangolo evidenzia i punti medi dei lati e congiungili.

Che figura ottieni? Sapendo che la base del rettangolo misura 24 cm e l’altezza 15 cm, quanto misurano le diagonali della figura trovata?

F

F

F

F

F

F

120 Considera il seguente rombo e traccia la diagonale minore. a) In quanti poligoni la diagonale divide il rombo? .................. b) Classifica i poligoni ottenuti. ......................................................

121 Determina le ampiezze degli angoli interni dei seguenti rombi. a) c)

122 Osserva il rombo e calcola ciò che è richiesto.

a) α = 148° β = α + β =

b) α = β = 37° α + β =

c) α = 110° 26' β = α + β =

d) α = β = 135° 49' α + β =

Risolvi i seguenti problemi.

123 In un rombo gli angoli adiacenti a uno stesso lato sono uno i 2 3 dell’altro. Quanto misurano le loro ampiezze? [72°; 108°]

124 La diagonale maggiore di un rombo divide l’angolo interno di un rombo in due angoli di 42°. Determina le ampiezze degli angoli interni del rombo. [84°; ............]

125 In un rombo l’angolo ottuso supera quello acuto di 24° 52'. Calcola le ampiezze degli angoli interni. [77° 34'; 102° 26']

126 In un rombo due angoli consecutivi sono uno i 3 7 dell’altro. Quanto misurano i suoi angoli interni? [54°; 126°]

127 MATH Find the measures of the numbered angles in each rhombus. a) b) c)

128 Determina la misura del perimetro dei seguenti rombi. a) b) c)

129 Completa i seguenti schemi. a) , = 46 cm 2p = c) , = 7,24 cm 2p = b) , = ……...…… 2p = 9,6 mm d) , = ………...… 2p = 340 dm

Segna la risposta esatta.

130 In un rombo la somma delle due diagonali è 85 cm. Sapendo che sono una i 2 3 dell’altra, quanto misura la diagonale maggiore? a) 51 cm b) 34 cm c) 17 cm d) 25 cm

131 In un rombo la differenza delle diagonali è 24 cm. Sapendo che sono una i 5 3 dell’altra, quanto misura la diagonale minore? a) 48 cm b) 12 cm c) 60 cm d) 36 cm

132 La diagonale maggiore di un rombo supera quella minore di 21 m. Se la loro somma è 114 m, quanto misura la diagonale maggiore? a) 93 m b) 46,5 m c) 67,5 m d) 46,5 dm

ESEMPIO

COME SI DISEGNA UN ROMBO SU UN FOGLIO A QUADRETTI

1) Disegna, in verticale, un segmento AC ad esempio di 6 quadretti e segna il suo punto medio.

2) Disegna un segmento orizzontale BD di 4 quadretti, che passi per il punto medio di AC (si forma una croce).

3) Congiungi A con B, B con C, C con D e D con A Ecco il rombo ABCD

Risolvi i seguenti problemi.

133 MATEMATICA IN AZIONE Il perimetro di un rombo che decora un tappeto misura 348 mm. Determina la misura del lato. [87 mm]

134 MATEMATICA IN AZIONE Un maglione ha sul davanti dei disegni a forma di rombo il cui lato è lungo 3,5 cm. Quanto misura il perimetro di ogni decoro? [14 cm]

135 Le diagonali di un rombo sono una i 5 7 dell’altra. Sapendo che la loro somma misura 360 mm, determina le loro misure. [150 m; 210 m]

136 MATEMATICA IN AZIONE La somma delle diagonali di un orecchino a forma di rombo è 103,2 mm. Se la minore è i 3 5 della maggiore, quanto misura ciascuna diagonale?

[38,7 mm; 64,5 mm]

137 In un rombo la differenza delle sue diagonali è di 45 cm e la loro somma è di 68 cm. Quali sono le misure delle diagonali? [11,5 cm; 56,5 cm]

138 Un rombo è isoperimetrico a un rettangolo che ha le dimensioni di 34 cm e 28 cm. Determina la misura del lato del rombo. [31 cm]

139 Un rombo e un trapezio isoscele sono isoperimetrici. Il trapezio ha il lato obliquo che è i 3 7 della somma delle sue basi. Sapendo che tale somma è di 56 cm, determina la misura del lato del rombo. [26 cm]

140 STEM Laura vuole far realizzare una ringhiera in ferro battuto con una struttura a rombi tutti uguali per la finestra della sua casa di campagna.

Calcola:

a) quanti metri lineari di ferro battuto serviranno in totale per realizzare la struttura a rombi, se il lato di ogni rombo misura 48 cm;

b) quale sarà la spesa della struttura, se il ferro battuto costa 180 € al metro lineare.

141 Un rombo ha il lato di 73,5 cm ed è isoperimetrico a un parallelogramma che ha i lati consecutivi uno i 2 5 dell’altro. Determina le misure dei lati del parallelogramma. [42 cm; 105 cm]

142 Un rombo è isoperimetrico a un rettangolo che ha la base il triplo dell’altezza. Sapendo che il lato del rombo misura 56 cm, determina le misure della base e dell’altezza del rettangolo. [28 cm; 84 cm]

143 MATEMATICA IN AZIONE Il perimetro di un campo rettangolare è 840 dm e la base misura 270 dm. Calcola le lunghezze delle diagonali del rombo ottenuto congiungendo i punti medi dei lati del rettangolo. [150 dm; .................]

144 Un trapezio rettangolo ha le basi che misurano rispettivamente 34 cm e 45 cm, l’altezza è i 3 2 della base minore e il lato obliquo è i 3 5 della base maggiore. Determina il lato di un rombo isoperimetrico al trapezio. [39,25 cm]

145 Individua in un piano cartesiano i punti di coordinate A (4; 1), B (7; 6), C (4; 11). Indica le coordinate del punto D in modo che il quadrilatero ABCD sia un rombo.

146 Il punto M (5; 4) è il punto di incontro delle diagonali di un rombo ABCD Individualo nel piano cartesiano, determina le coordinate dei vertici del rombo e disegnalo, sapendo che due suoi vertici appartengono agli assi.

I QUADRATI LEZIONE

147 Rispondi con Vero o Falso.

a) Il quadrato è un parallelogramma equilatero ed equiangolo.

b) Gli angoli interni del quadrato sono quattro e sono tutti piatti.

c) Il quadrato è un rettangolo particolare.

d) I quadrati, come i rettangoli, hanno due diagonali congruenti e perpendicolari.

e) Le diagonali del quadrato sono congruenti e sono bisettrici degli angoli interni.

f) La formula per calcolare il perimetro di un quadrato è uguale a quella per il rombo.

g) Il quadrato è un poligono regolare con quattro diagonali.

h) La somma degli angoli interni di un quadrato è uguale alla somma degli angoli esterni.

148 Completa.

a) Un quadrato è un rettangolo perché ha quattro angoli e le diagonali

b) Un quadrato è un rombo perché ha quattro

congruenti e le diagonali

c) Per calcolare il perimetro di un quadrato occorre moltiplicare la misura del

149 Completa la seguente tabella riassuntiva dei quadrilateri.

Lati

Angoli Nome del quadrilatero

Lati opposti congruenti e paralleli Angoli opposti congruenti

Lati paralleli e congruenti a coppie Quattro angoli retti

Trapezio

F

F

Quadrato

F

F

150 Nei seguenti quadrati traccia una diagonale e verifica che la lunghezza di ogni diagonale è maggiore del corrispondente lato.

151 MATH Draw four different squares with sides of different lenghts by connecting the dots.

152 Nel seguente quadrato individua i punti medi dei lati e congiungili. Classifica il quadrilatero ottenuto.

153 Completa i seguenti schemi.

a) , = 4,7 cm 2p = d) , = 5,4 cm 2p = b) , = 2p = 344 m e) , = 2,8 cm 2p = c) , = 2p = 3,6 mm f) , = 2p = 648 dm

Segna la risposta esatta (fai attenzione alle unità di misura).

154 Il lato di un quadrato misura 7,2 dm; il suo perimetro in centimetri è: a) 28,8 b) 2 808 c) 288 d) 2,88

155 Il perimetro di un quadrato è 224 dm; il suo lato in centimetri è: a) 5,6 b) 56 c) 560 d) 5 600

156 Il lato di un quadrato misura 13 m; il suo perimetro in decimetri è: a) 520 b) 52 c) 5,2 d) 0,52

In base alle illustrazioni e alle indicazioni che ti sono date, risolvi i seguenti problemi.

≅ BC ≅ CD 2p ( ACDF ) = 2p ( ABEF ) = 280 cm

159 Osserva la figura e calcola quanto richiesto.

456 cm

Il poligono è formato da cinque quadrati congruenti. Il lato AB misura 18 dm.

Risolvi i seguenti problemi.

c) Aggiungi 3 quadrati in modo da formare un rettangolo e calcola il suo perimetro.

d) Confronta la misura del perimetro del rettangolo con quella del perimetro di AEFHILMN ; che cosa osservi?

160 MATEMATICA IN AZIONE Un cartello segnaletico a forma quadrata, posto all’ingresso dell’autostrada, ha il perimetro di 12 m. Calcola la misura del suo lato in centimetri. [300 cm]

161 Un quadrato ha il perimetro di 784 cm; calcola la misura del lato. [196 cm]

162 MATEMATICA IN AZIONE Il comune di Bellolampo vuole illuminare una piazza di forma quadrata con il lato di 20 m. Si posizioneranno dei lampioni lungo il contorno, a distanza di 5 m l’uno dall’altro. In ogni vertice della piazza ce ne sarà uno. Quanti lampioni si dovranno comperare?

163 Un quadrato è isoperimetrico a un rettangolo che ha la base di 42 cm e l’altezza di 36 cm. Calcola la misura del lato del quadrato. [39 cm]

164 MATEMATICA IN AZIONE Due terreni, uno a forma quadrata e l’altro a forma rettangolare, sono isoperimetrici.

Se le dimensioni del rettangolo sono 54 m e 42 m, quanto misura il lato del terreno quadrato? [48 m]

165 Un quadrato ha il perimetro di 320 cm. Determina il perimetro di un rombo, sapendo che il suo lato è il triplo del lato del quadrato. [960 cm]

166 Un triangolo equilatero ha il lato di 68 dm; calcola il lato del quadrato isoperimetrico al triangolo. [51 dm]

167 Considera un quadrato il cui perimetro è 636 mm e un triangolo equilatero il cui lato supera di 32 mm il lato del quadrato. Il perimetro del triangolo equilatero sarà maggiore o minore di quello del quadrato? Di quanto? [................... ; 63 mm]

168 Un rettangolo ha il perimetro di 320 cm e l’altezza di 21 cm. Calcola il perimetro di un quadrato con il lato congruente alla base del rettangolo. [556 cm]

169 MATEMATICA IN AZIONE In taverna Francesco ha due tavoli, uno rettangolare e uno quadrato, che hanno lo stesso perimetro di 4,8 m. Ciascuno dei due tavoli può aprirsi a metà per accogliere una prolunga di mezzo metro. Qual è il perimetro di ogni tavolo dopo l’inserimento della prolunga?

170 Un rettangolo ha la base che supera l’altezza di 14 cm e il perimetro di 350 cm.

Determina il perimetro di un quadrato avente il lato congruente alla base del rettangolo. [378 cm]

171 Un parallelogramma ha la somma dei lati consecutivi di 84 cm e il lato maggiore supera il minore di 12 cm. Calcola il perimetro del quadrato avente il lato congruente al lato minore del parallelogramma. [144 cm]

172 MATEMATICA IN AZIONE Una pavimentazione è stata ottenuta alternando quadrati di pietra e di erba isoperimetrici. Se il contorno di ogni quadrato è di 92 cm qual è il perimetro della parte, evidenziata in figura, composta da 12 quadrati? [322 cm]

173 Un quadrato ha il perimetro di 540 cm. Determina il perimetro di un rombo, sapendo che il suo lato è i 3 5 di quello del quadrato. [324 cm]

174 Un rombo ha il lato che misura 46 cm, un quadrato ha il perimetro che è il doppio di quello del rombo. Calcola la misura del lato del quadrato. [92 cm]

175 Un trapezio isoscele ha il perimetro di 598 cm, la base maggiore lunga 136 cm e la minore 114 cm. Determina la misura del perimetro di un quadrato avente il lato congruente al lato obliquo del trapezio. [696 cm]

176 La somma delle diagonali di un rombo è di 574 cm e una è i 5 2 dell’altra. Calcola il perimetro del quadrato avente il lato congruente alla diagonale maggiore del rombo. [1 640 cm]

177 Disegna un quadrato con il lato di 6 cm e un rettangolo isoperimetrico al quadrato avente l’altezza il triplo della base. Quanto misurano le dimensioni del rettangolo? E il perimetro? [3 cm; ; ]

178 Un trapezio è formato da un quadrato e due triangoli rettangoli isosceli. Sapendo che il perimetro del quadrato misura 64 cm e l’ipotenusa dei triangoli è di 22,6 cm, calcola il perimetro del trapezio. [109,2 cm]

179 MATEMATICA IN AZIONE Una finestra è formata da sei vetri di forma quadrata. Se la somma dei perimetri dei 6 vetri è 960 cm, qual è il perimetro di un quadrato di vetro? [160 cm]

180 Un parallelogramma è formato da due triangoli rettangoli congruenti e un quadrato. Determina il perimetro del parallelogramma basandoti sui dati e il disegno.

[360 cm]

181 Nel piano cartesiano sono rappresentati tre quadrati che hanno i punti A e C come vertici comuni. Determina le coordinate dei vertici di ciascuno dei tre quadrati.

182 Nel riferimento cartesiano individua i punti A (6; 1), B (9; 4), C (6; 7). Determina poi le coordinate del punto D in modo che il quadrilatero ABCD sia un quadrato.

I DELTOIDI LEZIONE

183 Rispondi con Vero o Falso.

a) I deltoidi hanno i lati opposti paralleli.

b) I deltoidi hanno due coppie di lati congruenti.

c) Le diagonali dei deltoidi sono congruenti.

d) Le diagonali dei deltoidi sono perpendicolari.

e) Le diagonali dei deltoidi sono bisettrici degli angoli interni.

f) I deltoidi possono essere concavi o convessi.

g) Nei deltoidi i lati congruenti sono consecutivi.

h) La somma degli angoli interni di un deltoide è 360°.

184 In ogni deltoide congiungi i punti medi dei lati; che cosa ottieni? a)

F

F

F

F

F

F

F

F

185 In ogni deltoide traccia la diagonale minore e classifica i triangoli ottenuti. Se invece tracci la diagonale maggiore che triangoli ottieni?

a)

b)

c)

186 Calcola le misure mancanti degli angoli interni dei seguenti deltoidi. a) b) c)

187 Calcola la misura del perimetro dei seguenti deltoidi. a) b) c)

188 MATEMATICA IN AZIONE I lati consecutivi non congruenti di un aquilone a forma di deltoide misurano 53 cm e 92 cm. Quanto nastro servirà per ripassare il contorno dell’aquilone?

189 MATEMATICA IN AZIONE Per costruire un aquilone a forma di deltoide occorre mettere delle bacchette lungo le diagonali (AC e DB ). Deducendo le misure dal disegno, quanto sono lunghe le bacchette di questo aquilone? [33 cm; ....................]

COMPETENZE

RISOLVERE PROBLEMI

REGOLA DEL PARALLELOGRAMMA

Se su un oggetto agiscono due forze che hanno direzione diversa, la forza risultante è la diagonale del parallelogramma che si costruisce con le due forze.

Perché, quando camminiamo sotto la pioggia, dobbiamo tenere l’ombrello inclinato in avanti per non bagnarci?

La pioggia cade verso il basso verticalmente, mentre la bambina si muove orizzontalmente.

Per la regola del parallelogramma, come si può notare dal disegno, la pioggia rispetto alla bambina segue la diagonale del parallelogramma (risultante); ecco perché è meglio tenere l’ombrello inclinato in avanti.

1 Osserva la figura e applica la regola del parallelogramma per rispondere alla seguente domanda: partendo dal punto A , la barca arriverà nel punto B o nel punto C ?

2 Una mongolfiera sta effettuando la discesa a terra.

Considerando la direzione del vento, dove atterrerà?

ARGOMENTARE

3 Un pezzo di carta copre una parte di alcuni quadrilateri. Disegna la parte mancante e classificali motivando le risposte. (Ci possono essere più alternative.) a) b) c) d)

4 Dato il rettangolo in figura, disegna dei rettangoli di ugual base (b1) ma con le altezze che siano il doppio, il triplo, il quadruplo dell’altezza di partenza (h1).

Calcola il loro perimetro sapendo che b1 = 2 cm e h1 = 4 cm. Come varia il loro perimetro al variare dell’altezza?

SPIEGARE PROCEDIMENTI

5 EDUCAZIONE CIVICA Utilizzando squadra, righello e goniometro riconosci se il quadrilatero dell’Unesco è un quadrilatero generico o un trapezio, spiegando come hai fatto.

CHE COS’È L’UNESCO?

L’UNESCO (acronimo, dall’inglese, di United Nations Educational, Scientific and Cultural Organization) è l’Organizzazione delle Nazioni Unite per l’Educazione, la Scienza e la Cultura. Promuove la pace e la comprensione tra le nazioni attraverso l’istruzione, la scienza, la cultura, la comunicazione e l’informazione.

SFIDA MATEMATICA

6 Le divisioni di Nando

“Quadrilatero dell’Unesco” è il nome del progetto turistico nato per rafforzare il turismo nelle zone interessate dal terremoto del maggio 2012. Coinvolge le regioni dell’Emilia-Romagna, della Lombardia e del Veneto: un ampio territorio le cui estremità formano un quadrilatero. Le aree incluse (le province di Modena, Ferrara, Reggio Emilia, Bologna, Mantova, Rovigo e Delta del Po) sono state classificate dall’Unesco come Patrimonio dell’Umanità.

Nando divide il suo prato quadrato in 5 parti rettangolari, ciascuna delle quali ha un perimetro di 150 m. Quanto misura il perimetro dell’intero prato?

(Testo tratto dalla gara Giochi di Rosi del 2014, organizzata dal Centro PRISTEM dell’Università Bocconi di Milano)

ROAD MAP PER TUTTI

i quadrilateri

Un QUADRILATERO è un poligono con quattro lati e quattro angoli

Come si chiamano gli elementi principali del quadrilatero?

Quanto misura la somma degli angoli interni di un quadrilatero?

Come si calcola il perimetro di un quadrilatero?

La somma degli angoli interni di un quadrilatero è sempre 360°

• Il lato è il segmento che unisce due vertici consecutivi

• La diagonale unisce due vertici opposti

• L’angolo interno è l’angolo formato da due lati consecutivi

angolo interno diagonale

AB = 7 cm

BC = 8 cm,

CD = 9 cm

AD = 11 cm

Il perimetro di un quadrilatero, 2p, si calcola sommando le misure dei quattro lati

ESEMPIO

2p = 7 + 11 + 9 + 8 = 35 cm

Come si chiamano gli elementi caratteristici di un trapezio?

B = base maggiore b = base minore

ℓ = lato obliquo h = altezza

i trapezi

Un TRAPEZIO è un quadrilatero con due lati paralleli

Come si classificano i trapezi in base ai loro lati? Come si calcola il perimetro?

Che proprietà hanno gli angoli dei trapezi?

In tutti i trapezi gli angoli adiacenti a uno stesso lato obliquo sono supplementari: A + D = 180° e

B + C = 180°

base minore

base maggiore lato obliquo altezza ℓ

b B h

Scaleno: i lati obliqui sono di misura diversa

2p = B + b + ℓ 1 + ℓ 2

Nel trapezio rettangolo due angoli sono retti.

Nel trapezio isoscele gli angoli adiacenti a ciascuna base sono congruenti.

Rettangolo: un lato obliquo è perpendicolare alle basi

2p = B + b + ℓ 1 + ℓ 2

Isoscele: i lati obliqui sono congruenti

2p = B + b + ℓ × 2

1 Calcola la misura degli angoli contrassegnati con la x. a) b) c)

a) x = 360° – (109° + + ) =

b) x = 360° – ( + + ) =

c) x = 360° – ( + + ) =

2 Svolgi i calcoli sul tuo quaderno e completa la tabella riferita a dei quadrilateri ABCD.

3 Per ciascuno dei trapezi in figura esegui sul quaderno le seguenti richieste.

a) Scrivi il nome del trapezio.

b) Individua e scrivi il nome della base maggiore e minore.

c) Calcola le ampiezze degli angoli.

d) Traccia le diagonali e scrivi il loro nome.

4 Completa la seguente tabella relativa a dei trapezi isosceli (2p = b + B + , × 2).

i parallelogrammi TEORIA PAG. 316

Un PARALLELOGRAMMA

è un quadrilatero con due coppie di lati paralleli. Ha quindi i lati opposti congruenti.

Come si chiamano gli elementi caratteristici di un parallelogramma?

ℓ 1 = lato

ℓ 2 = lato

h 1 = altezza relativa al lato ℓ 1 h 2 = altezza relativa al lato ℓ 2 h1 h2 l 1 l 2 altezza relativa al lato ℓ 1

Come si calcola il perimetro di un parallelogramma?

altezza relativa al lato l 2 lati consecutivi

Che proprietà hanno gli angoli dei parallelogrammi?

• Gli angoli opposti sono congruenti

• Gli angoli adiacenti a un lato sono supplementari (la somma è 180°)

2p = (ℓ1 + l2) × 2

da cui: ℓ1 = 2p : 2 – l2 e ℓ2 = 2p : 2 – ℓ1

5 Osserva i due parallelogrammi e stabilisci se le affermazioni sono vere o false.

a) AC è una diagonale V F

b) AB e BD sono le due diagonali? V F

c) AB è // a CD. V F

d) AB è ≅ a AD V F

a) DH è perpendicolare a AB. V F

b) DK è ⊥ a BC V F

c) A è congruente a B ? V F

d) D è ≅ B V F

≅ significa congruente ⊥ significa perpendicolare // significa parallelo

6 Calcola le ampiezze degli angoli incogniti dei seguenti parallelogrammi. A B D C 133° ? ? ?

a) D = 180........ A ≅ C = 180° – 80........ = 1.......80

E G F 55° ? ? ?

b) F = 18......0° E ≅ G = 180° 180

7 Completa la seguente tabella riferita a dei parallelogrammi.

5 × ℓ 2 = ℓ 2 : 5 × 4 = 100 dm

8 In un parallelogramma un lato è il triplo del suo consecutivo che misura 23,5 dm; calcola il perimetro. Completa i dati e svolgi i calcoli sul quaderno. NM = 3 × 2p = ?

9 MATEMATICA IN AZIONE Un pavimento è formato da piastrelle a forma di parallelogramma. I L M N

D B

Se la somma di due lati consecutivi AB e AD è di 20 cm:

a) completa il disegno del parallelogramma ABCD; b) calcola il perimetro di una piastrella.

i rettangoli

Un RETTANGOLO è un parallelogramma con quattro angoli retti

Come si chiamano gli elementi caratteristici di un rettangolo?

b = base

h = altezza

d = diagonale

base e altezza sono le dimensioni del rettangolo

Come si calcola il perimetro di un rettangolo?

2p = (b + h) × 2

da cui: b = 2p : 2 – h h = 2p : 2 – b

b = base h = altezza

ESEMPIO

2p = 48 cm

b = 14 cm

h = (48 : 2) – 14 = 10 cm d

10 Osserva il rettangolo e stabilisci se le affermazioni sono vere o false.

a) RS e UT sono lati paralleli e congruenti. V F

b) UT è la base e UR l’altezza. V F

c) RS e ST sono le dimensioni del rettangolo. V F

d) Gli angoli S , T , U , R sono acuti. V F

e) U ≅ R = 90° V F

f) RT e SU sono le diagonali e sono ≅ . V F

11 Completa il seguente problema.

AB = 3 × BC

AB + BC = 48 cm

AB = ?

BC = ?

AB + BC contiene (3 + 1) = 4 parti congruenti a BC, quindi:

BC = (AB + BC) : =

AB = BC × 3 = [12 cm; 36 cm]

Come sono gli angoli opposti di un rombo?

Un ROMBO è un parallelogramma con i quattro lati congruenti: AB BC CD AD

Due angoli opposti sono acuti e congruenti, gli altri due sono ottusi e congruenti:

A C, B D

A C D B

Come si chiamano gli elementi caratteristici di un rombo?

Come si calcola il perimetro di un rombo?

2p = ℓ × 4 da cui ℓ = 2p : 4

D = diagonale maggiore

d = diagonale minore

h = altezza

ℓ = lato

ESEMPIO

ℓ = 18 cm

2p = 18 × 4 = 72 cm

D h d diagonale maggiore diagonale minore altezza l

lato

i quadrati

Un QUADRATO è un parallelogramma con i lati e gli angoli congruenti

Quali sono gli elementi caratteristici di un quadrato?

ℓ = lato d = diagonale

lato d diagonale l

Come si calcola il perimetro di un quadrato?

2p = ℓ × 4 da cui: ℓ = 2p : 4

ESEMPIO

2p = 96 cm ℓ = 96 : 4 = 24 cm

12 Calcola le ampiezze degli angoli incogniti dei seguenti rombi.

13 Completa la tabella riferita a dei rombi.

14 STEM Il mosaico raffigurato è costituito da tessere rombiche con il lato di 1,5 cm.

Calcola i perimetri dei rombi colorati di rosso, di giallo e di arancione.

Rosso → (1,5 × 10) × 4 =

Giallo →

Arancione →

15 Completa la tabella riferita a dei quadrati.

cm

17 MATEMATICA IN AZIONE Calcola il perimetro di un orto quadrato avente il lato di 4,5 m. [18 m] ,

16 MATEMATICA IN AZIONE Un terreno quadrato ha il perimetro di 464 m; calcola la misura del lato. [116 m]

18 Disegna un quadrato e un rettangolo, osservali e stabilisci quali caratteristiche hanno in comune.

a) 4 lati congruenti

b) 4 angoli retti

c) Diagonali perpendicolari

d) Diagonali congruenti

e) Solo una coppia di lati paralleli

f) Formula per il calcolo del perimetro

19 Quali caratteristiche hanno in comune un quadrato e un rombo?

a) 4 lati congruenti

b) 4 angoli retti

c) Diagonali perpendicolari

d) Diagonali congruenti

e) Solo una coppia di lati paralleli

f) Formula per il calcolo del perimetro

20 Riconosci i seguenti quadrilateri (simboli uguali corrispondono a misure uguali).

21 MATEMATICA IN AZIONE Mara ha una Polaroid che stampa fotografie di forma quadrata con il lato lungo 9 cm.

Ha un portafoto anch’esso quadrato con una cornice il cui contorno è lungo 50 cm. Potrà inserire nel portafoto una delle foto scattate con la Polaroid? Perché? [Sì, perché il lato della cornice è 12,5 cm]

22 MATEMATICA IN AZIONE La figura mostra il logo di una casa automobilistica.

Individua nel logo tre tipi diversi di quadrilateri, colorali e scrivi i loro nomi.

SIMULAZIONE DI VERIFICA

1 Rispondi con Vero o Falso ed effettua la correzione di ogni falso.

a) Un rettangolo ha quattro angoli retti.

b) Un quadrato ha le diagonali non congruenti.

c) Un poligono convesso ha un solo angolo concavo.

d) Le diagonali di un quadrilatero sono quattro.

e) I lati opposti del parallelogramma sono paralleli.

f) Nel rombo gli angoli opposti sono supplementari.

g) Nei trapezi gli angoli adiacenti a ciascun lato obliquo sono complementari.

h) Le basi del trapezio sono perpendicolari.

i) I parallelogrammi hanno due altezze non necessariamenti congruenti tra loro.

F

F

F

F

F

F

Scrivi il nome del poligono e la formula per calcolare il perimetro di ciascuna figura, scegliendo tra quelle suggerite.

F

F

4 Osserva le seguenti figure e completa la tabella inserendo i termini corrispondenti.

5 Completa.

Un parallelogramma che ha:

a) gli angoli retti e i lati diversi è un

b) i lati congruenti e le diagonali diverse è un

c) i lati congruenti e gli angoli congruenti è un

d) le diagonali perpendicolari e congruenti è un

e) le diagonali congruenti ma non perpendicolari è un

Calcola il perimetro dei seguenti quadrilateri.

, = 7,5 cm

LM = 85 cm NM = 70,7 cm OL = 62 cm ON = 3 5 × LM

EF = 34 cm HG = 16 cm

HE = 26 cm GF = HE + 3 cm d) e) f)

Risolvi i seguenti problemi.

8 In un trapezio isoscele la somma delle basi misura 280 cm e ciascuna proiezione del lato obliquo sulla base maggiore è 25,8 cm.

Calcola la misura di ciascuna base.

9 Considera un rettangolo e un rombo isoperimetrici. Le dimensioni del rettangolo sono una i 2 5 dell’altra e la loro somma è 56 m. Calcola le dimensioni del rettangolo e il lato del rombo.

10 La somma dei lati consecutivi di un parallelogramma è 38,4 cm e la loro differenza è 12,8 cm. Calcola:

a) le misure dei lati del parallelogramma; b) la lunghezza del lato di un quadrato isoperimetrico al parallelogramma.

11 Gli angoli adiacenti alla base maggiore di un trapezio scaleno sono di 48° e 53°. Calcola l’ampiezza degli altri due angoli.

12 Gella finestra qui raffigurata:

FD ≅ FH ≅ HB ≅ BD; A, C, E , G sono retti;

GJ ≅ FD e CJ ≅ HB

Classifica i quadrilateri ACEG e BDFH.

Se BD = AC = 60 cm e AG = 1,10 m

calcola:

a) il perimetro di BDFH

b) il perimetro di ACEG

• TAVOLE PITAGORICHE

• FORMULE DIRETTE

E INVERSE DEI QUADRILATERI

TAVOLE PITAGORICHE

FORMULE DIRETTE E INVERSE DEI QUADRILATERI

figura formule dirette formule inverse

Trapezio B ,1 ,2 b

Parallelogramma ,1 ,2

Rettangolo

Rombo , , , , 2p = ,  4 , = 2p : 4

Quadrato , , , , 2p = ,  4 , = 2p : 4

Deltoide

Coordinamento redazionale Marco Mauri

Responsabile editoriale Martina Mirabella

Redazione Edistudio

Art director Enrica Bologni

Progetto grafico Edistudio

Impaginazione Edistudio

Ricerca iconografica Martina Mirabella

Immagini di copertina Creata con IA

Si ringrazia Federico Zanni per la collaborazione redazionale.

Referenze iconografiche

Shutterstock

Tutte le altre immagini provengono dall’Archivio Principato-Gruppo Editoriale Eli. Per le riproduzioni di testi e immagini appartenenti a terzi, inserite in quest’opera, l’editore è a disposizione degli aventi diritto non potuti reperire, nonché per eventuali non volute omissioni e/o errori di attribuzione nei riferimenti.

Contenuti digitali

Realizzazione bSmart labs, ITG Torino

Font: leggimi©Sinnos - www.sinnos.org

Prima edizione: gennaio 2026

Printed in Italy

© 2026 - Proprietà letteraria riservata. È vietata la riproduzione, anche parziale, con qualsiasi mezzo effettuata, compresa la fotocopia, anche ad uso interno o didattico, non autorizzata. Le fotocopie per uso personale del lettore possono essere effettuate nei limiti del 15% di ciascun volume dietro pagamento alla SIAE del compenso previsto dall’art. 68, commi 4 e 5, della legge 22 aprile 1941 n. 633. Le riproduzioni per finalità di carattere professionale, economico o commerciale o comunque per uso diverso da quello personale, possono essere effettuate a seguito di specifica autorizzazione rilasciata da CLEARedi (Centro licenze e autorizzazioni per le riproduzioni editoriali), corso di Porta Romana 108, 20122 Milano, e-mail autorizzazioni@clearedi.org e sito web www.clearedi.org

L’editore fornisce – per il tramite dei testi scolastici da esso pubblicati e attraverso i relativi supporti o nel sito www.gruppoeli.it – materiali e link a siti di terze parti esclusivamente per fini didattici o perché indicati e consigliati da altri siti istituzionali. Pertanto l’editore non è responsabile, neppure indirettamente, del contenuto e delle immagini riprodotte su tali siti in data successiva a quella della pubblicazione, dopo aver controllato la correttezza degli indirizzi web ai quali si rimanda.

Principato-Gruppo Editoriale El Viale E. Jenner 17 - 20159 Milano

sito web: www.gruppoeli.it e-mail: info@gruppoeli.it

La casa editrice attua procedure idonee ad assicurare la qualità nel processo di progettazione, realizzazione e distribuzione dei prodotti editoriali.

La realizzazione di un libro scolastico è infatti un’attività complessa che comporta controlli di varia natura. È pertanto possibile che, dopo la pubblicazione, siano riscontrabili errori e imprecisioni. La casa editrice ringrazia fin da ora chi vorrà segnalarli a: Servizio clienti Principato-Gruppo Editoriale Eli e-mail: info@gruppoeli.it