

Acknowledgements
Academic Authors: Muskan Panjwani, Anna Danchenko
Creative Directors: Alena Sizintseva
Book Production: Natalia Karabanova, Anastasia Voitovich
All products and brand names used in this book are trademarks, registered trademarks or trade names of their respective owners.
© Uolo EdTech Private Limited First edition 2026
This book is sold subject to the condition that it shall not by way of trade or otherwise, be lent, resold, hired out, or otherwise circulated without the publisher’s prior written consent in any form of binding or cover other than that in which it is published and without a similar condition including this condition being imposed on the subsequent purchaser and without limiting the rights under copyright reserved above, no part of this publication may be reproduced, stored in or introduced into a retrieval system, or transmitted in any form or by any means, electronic, mechanical, photocopying, recording or otherwise, without the prior written permission of both the copyright owner and the abovementioned publisher of this book.
Book Title: DinoLab Math Smartbook 6
ISBN: 978-93-89789-84-3
Published by: Uolo EdTech Private Limited
Corporate Office Address: 91Springboard, 3rd Floor 145, Sector 44, Gurugram, Haryana 122003
CIN: U74999DL2020PTC360472
Printed by: Printpro Solutions
All suggested use of the internet should be under adult supervision.
How to get access to DinoLab
Get access to animated interactive courses, Marathons, Olympiads, and much more — all in the Uolo Learn app!
1. Download the "Uolo Learn" app from Google Pay (Android) or AppStore (iPhone).
2. In the app click scanner to scan the QR code below.
Class:
Name:
School:
3. Follow the instruction in the app to access the content.
Welcome to DinoLab!
DinoLab is an AI-powered self-learning platform that helps children learn Mathematics and other subjects step by step, at their own pace. Students can practise and revise every topic digitally and through printed Smartbook.
The DinoLab Mathematics Smartbook is a companion to the digital course. Each exercise has a QR code linking to the Uolo Learn app for continued practice.
Using AI, DinoLab creates a personalised learning path: it explains the concept, gives guided practice, and adapts if mistakes occur — helping students gain clear understanding.
Digital content is presented as interactive flashcards with 50,000+ gamified exercises and animations, making learning engaging and enjoyable.
DinoLab works in Uolo apps and on multiple devices
To use DinoLab on the web, Smartboards, and in computer labs, your school will receive special access for each student and teacher.
Uolo Mobile App SmartboardComputer Lab Smartbooks Tablet and Laptop
How to Use the DinoLab Solution
Once the Uolo Learn app is installed and you are logged in, you can access DinoLab. Our Mathematics course is designed with interactive exercises that help children cover the school syllabus step by step, at their own pace.
1 2 3
Compete and win in Marathons!
• Solve problems and earn points
• Leaderboards of your class, school and all of India
• Get achievement certificates
In this Smartbook, you will find QR codes placed next to the exercises. Simply use the QR scanner inside the app to access the interactive content. QR codes in the Smartbook
1 2 3
1. LARGE NUMBERS AND OPERATIONS
UNDERSTANDING LARGE NUMBERS
1. Match the numbers with their place values.






2. Write the numbers.
Three hundred fifty six =
Eight thousand twenty five = Fourteen thousand one = 356
Nine hundred six = Four hundred eighty two = Three thousand twelve =
3. Write the expanded form of the numbers.
300 + 50 + 6 356 = 4871 = 1,00,001 =
ESTIMATE LARGE NUMBERS
4. Round the numbers to the closest tens, hundreds and thousands.
5. Which of these is rounding to hundreds? Circle the correct answer.
6. Match the numbers with their rounded values
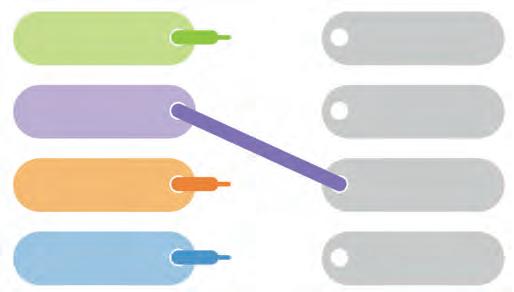


7. Round up the population of the cities to the correct values.
PopulationTo hundreds To thousands
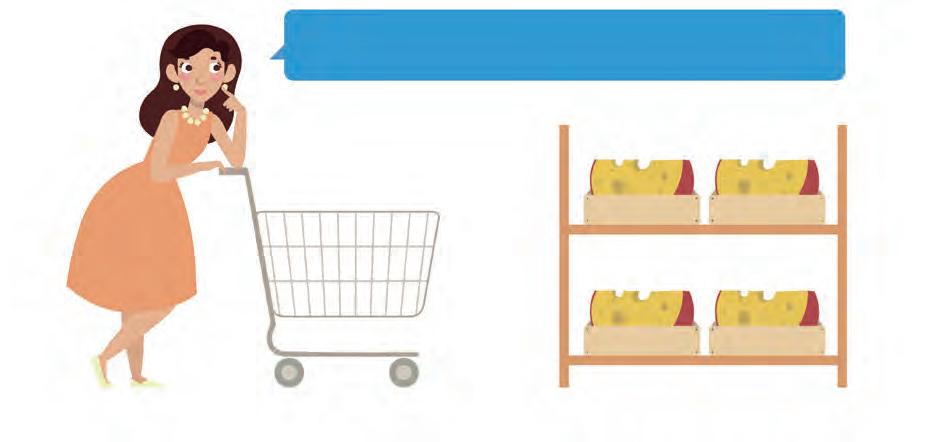
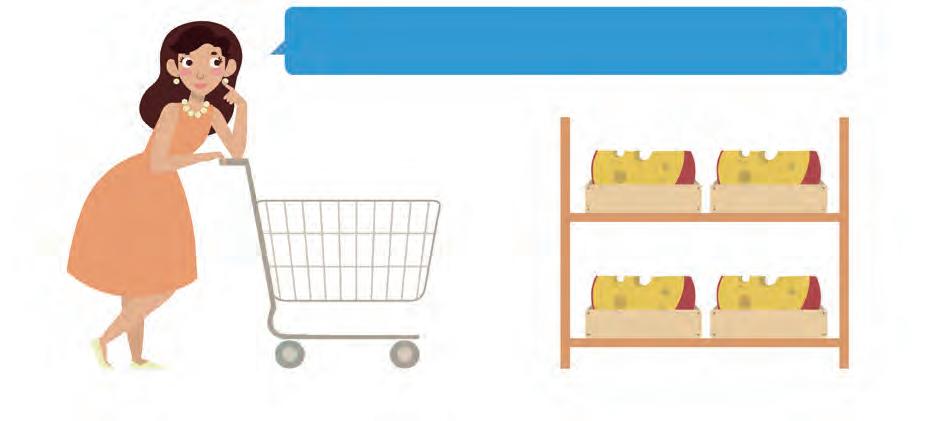
8. Circle the piece of cheese the lady wants.
I need approximately two hundred grams cheese
I need approximately four hundred grams cheese
I need approximately three hundred grams cheese

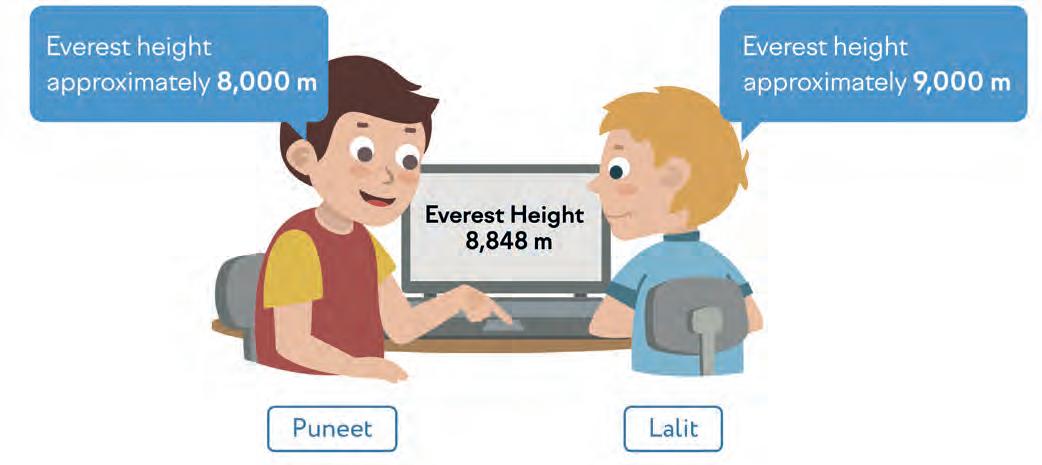
9. Who is more accurate? Circle the correct name.
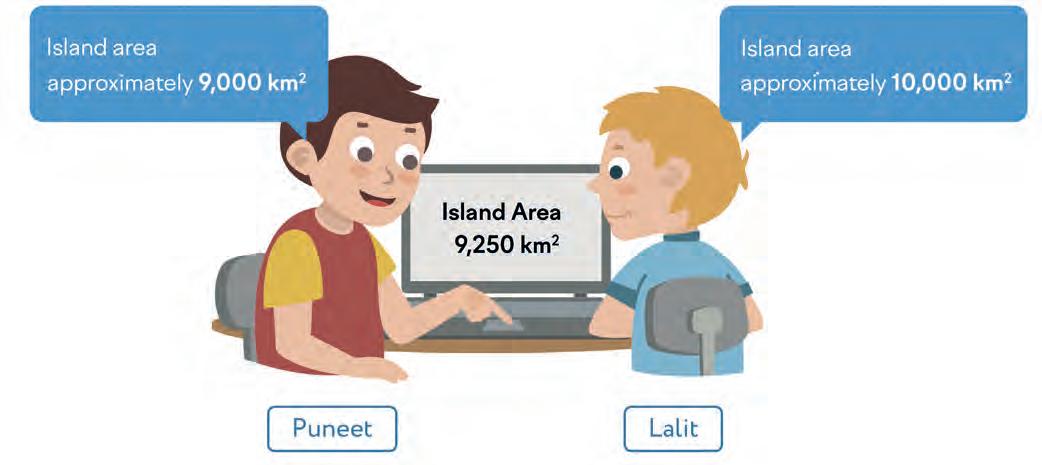
+ 10 =
OPERATIONS ON LARGE NUMBERS
10. Calculate the expressions.
−
+
−
−
+
=
−
11. Help the mouse get to the cheese by adding 10 at each step.
12. Help the mouse get to the cheese by adding 10 each step.
13. Help the mouse get to the cheese by adding 10 each step.
14. Calculate the expressions.
47,383 + 8,274 = 38,927 + 1,839 =
37,452 + 3,874 = 82,654 + 1,281 =
5,00,091 + 377 = 17,499 + 8,346 =
85,167 + 1,098 = 17,776 + 2,771 =
15. Measure the gaps and write the correct length to help the horse cross.




17. Calculate the expressions.
47,383 − 8,274 = 38,927 − 1,839 =
37,452 − 3,874 = 82,654 − 1,281 =
5,00,091 − 377 = 17,499 − 8,346 =
85,167 − 1,098 = 17,776 − 2,771 =
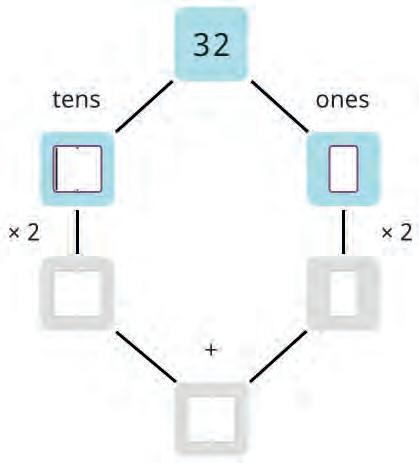
18. Fill the boxes.
Let’s learn to double a number! First split the number in tens and ones.
Then double both numbers.
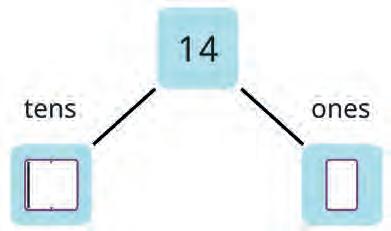


Then add both the numbers.
Now double another number in the same way. Fill in all the boxes.
19. Help the hedgehog count how many mushrooms he brought home today?
20. Calculate the expressions.
21. Calculate the expressions.
22. Calculate the expressions.
÷ 16 =
÷ 27 = 238 × 71 =
23. Calculate the expressions.
100 – (50 – 38) – (25 + 13) = 50
1) 50 – 38 = 12 2) 25 + 13 = 38
3) 100 – 12 = 88 4) 88 – 38 = 50
(49 +11 – 16) – (92 – 76) =
(51 – 17) + (85 – 46) + (43 – 24) =
(29 + 64 – 72) – (35 + 35 – 49) =
27 + (9 × 6 – 25) + 72 ÷ 8 = 24. Calculate the expressions.
100 – (63 + 27 – 58) ÷ 4 =
(31 – 30) × (63 ÷ 7 + 64 ÷ 8) =
(63 – 23) × 2 – (45 + 45) ÷ 30 – (72 + 28) ÷ 10 =
25. The smallest bird in the world, the hummingbird, beats its wings 80 times per second. How many beats will this bird make in three hours?
26. One squirrel eats 950 nuts in one winter. How many nuts will four squirrels eat in three winters?
27. The weight of fifteen sacks of flour is 2040 kg. What is the weight of one sack?
28. The book consists of 57 pages. Each page has 23 lines. Each line has 9 words. How many words are in the book?
29. Fifteen kg of bananas were sold on the first day. On the second day three times more bananas were sold than on the first day. On the third day 12 kg less bananas were sold than on the second day. How many kilograms of bananas were sold in three days?
2. PATTERNS IN WHOLE NUMBERS
WHOLE NUMBERS AND NATURAL NUMBERS
1. Fill in the blanks on the number line.



2. What is the distance between the points on the number line?
a) 4 and 9?
Answer d) 0 and 14?
Answer
b) 15 and 29?
Answer e) 13 and 21?
Answer
c) 2 and 13?
Answer f) 4 and 43?
Answer
3. Write the missing points on the number line.
c) 0510
4. Fill in the blanks.
c) 21 × (51 + ) = 21 × 51 + 21 × 42 d) ÷ 312 = 0 e) (31 × 24) × 3 = 31 × ( × 3) f ) 0 × 2829 = g) × 8472 + × 3717 = 2025 × ( + )h) 1 × = 831
Answer a) 5 × 13 = 13 × b) 382 × = 382
5. How many whole numbers between 21 and 49?
PATTERNS
6. Find the pattern and write the missing numbers.
2, 8, 32, 128, 14, 28, 56, 112, 5, 15, 45, 135, 5, 20, 80, 3, 9, 27, 81, 4, 12, 36, 108
2, 4, 12, 48, 1, 5, 10, 16, 23, 1, 4, 9, 16, 25, 2, 3, 5, 8, 13,
7. Complete the table.
8. Draw the missing term in the pattern.
3. PLAYING WITH NUMBERS: FACTORS
AND MULTIPLES
REVIEWING FACTORS AND MULTIPLES
1. Find two factors of the numbers given below.
a) 14: ;
c) 36: ;
b) 19: ;
d) 67: ;
2. Find two multiples of the numbers given below.
a) 18: ;
c) 71: ;
b) 43: ;
d) 103: ;
3. List all the factors and any three multiples of the numbers given below.
Factors: 46
Multiples: Factors: 32
Multiples: Factors: 25
Multiples: Factors: 56
Multiples:
TYPES OF NUMBERS
4. Is the number of students even or odd?

Answer:
5. Is there an even or odd number of fish?

Answer:
6. Sort the numbers into even and odd.
Numbers: 73, 14, 42, 85, 2, 51,102, 52, 37, 1, 88, 8, 67, 31 odd: even:
Numbers: Factors and Multiples
7. Define the value of an expression as odd or even.
even + odd
odd + odd
even * odd
even * even
odd * odd
even + even even even even even even even odd odd odd odd odd odd
8. Find all the factors of 14 (excluding itself) and circle the right answers.
Now, sum of factors =
14 ?
Therefore, 14 is a perfect number. a) 12 : 1, 2, 3, 4, 6.1 + 2 + 3 + 4 + 6 = 16 12 ≠ 16
9. Check whether the number is a perfect number or not, then circle only perfect numbers.
10. How many factors do prime numbers have? Circle the right answer.
11. Check whether the number is a prime number or composite.
a) 17 = 1 × 17 — prime number
12. Circle all the numbers divisible by 10.
13. True or False?
1) If a number ends with a digit 0 then it is divisible by 8
2) If a number ends with a digit 0 then it is divisible by 10
3) If a number ends with a digit 3 then it is not divisible by 10
14. Circle all the numbers divisible by 5.

15. True or False?
1) If a number ends with a digit 0 then it is divisible by 5
2) If a number ends with a digit 5 then it is divisible by 3
3) If a number ends with a digit 3 then it is not divisible by 5
16. Circle all the numbers divisible by 2.

17. True or False?
1) If a number ends with an odd digit then it is not divisible by 2
2) If a number ends with an even digit then it is divisible by 8
3) If a number ends with 5 then it is not divisible by 2
18. Choose the right answer.
1) To see if the number is divisible by 10, you need to check that the ___ is divisible by 10
Last digit
Sum of its digits
3) To see if the number is divisible by 2, you need to check that the ___ is divisible by 2
Last digit
Sum of its digits
5) To see if the number is divisible by 5, you need to check that the ___ is divisible by 5
Last digit
Sum of its digits
2) To see if the number is divisible by 3, you need to check that the ___ is divisible by 3
Last digit
Sum of its digits
4) To see if the number is divisible by 9, you need to check that the ___ is divisible by 9
Last digit
Sum of its digits
19. Make a number that is divisible by 3 and divisible by 5 using the given numbers.
You may not use all digits
20. Make a numbers that is divisible by 3 and NOT divisible by 9 using the given numbers.
You may not use all digits
21. Make an even numbers, that is divisible by 3 using the given numbers.
You may not use all digits
22. Sort the numbers into columns: divisible by 10, by 5, by 2, by 3 and by 9.
Numbers: 12, 18, 27, 10, 25, 35, 20, 30, 50, 4, 8, 14, 9, 36, 45
by 10
by 5
by 2
by 3
23. Verify the divisibility rule for sums and differences.
by 9
DivisorSum (yes/no)
Difference (yes/no)
24. Write the appropriate numbers in circles.

25. Find all the factors of the product.
Factors of 8125
Hint: 8125 = 25 × 25 × 13
Factors of 6220
Hint: 6220 = 20 × 311
26. To play, children are divided into teams with the equal number of boys and girls. Tick the correct answer.
1) Is it possible to divide 12 boys and 10 girls into 2 teams?
Yes, there can be __ boys and __ girls in the teams.
2) Is it possible to divide 22 boys and 12 girls into 3 teams?
Yes, there can be __ boys and __ girls in the teams. No. No.
27. Write the missing factors of 12 and 8.

Circle the pairs of common factors. The highest common factor of 12 and 8 is .
28. Write the missing factors of 6 and 10.

Circle the pairs of common factors. The highest common factor of 6 and 10 is .
29. Write the missing factors of 15 and 16.

Circle the pairs of common factors. The highest common factor of 15 and 16 is .
30. Write the missing multiples of 4 and 6.

Circle the pairs of common multiples. The lowest common multiple of 4 and 6 is .
31. Write the missing multiples of 3 and 2.

Circle the pairs of common multiples. The lowest common multiple of 3 and 5 is .
32. Write the missing multiples of 5 and 3.

Circle the pairs of common multiples. The lowest common multiple of 5 and 3 is .
WORKING WITH LCM AND
HCF
33. Circle the true statement.

34. Circle the true statement.

35. True or False?

a) 9 and 4 are co-prime
b) 7 and 14 are co-prime HCF = ( 4, 9 ) = HCF = ( 14, 7 ) =
36. Circle pairs of numbers that is co-primes.
a) 13 and 24
d) 27 and 58
b) 35 and 49
e) 32 and 33 c) 56 and 39 f) 46 and 69
a) 13 = 1 × 1324 = 1 × 2 × 3 × 4 × 6 × 8 × 12 × 24HCF (13, 24) = 1
37. Calculate Highest Common Factor (HCF):
a) HCF ( 5; 9 ) =
b) HCF ( 6; 12 ) =
c) HCF ( 5; 10 ) =
d) HCF ( 14; 21 ) =
e) HCF ( 35; 63 ) =
38. Calculate Lowest Common Multiple.
a) LCM ( 8; 4 ) =
b) LCM ( 9; 3 ) =
c) LCM ( 6; 5 ) =
d) LCM ( 11; 10 ) =
e) LCM ( 18; 9 ) =
4. LINES, ANGLES AND SHAPES
RAYS, LINES AND LINE SEGMENTS
1. Write the correct word.




2. A straight line or a curved line? Write correct answer.


The shortest path between the ship and the island is a
line.
These are lines. straight straight curved curved
3. Choose the correct word.
This is a . It has a starting point but has no end point. line segment ray line segment ray
This is a . It has two end points.
4. Count all possible line segments between marked points on the given line. Write down your answer.
5. Count all possible rays on the given straight line. Write down your answer.
6. Tick the name of the straight line below.

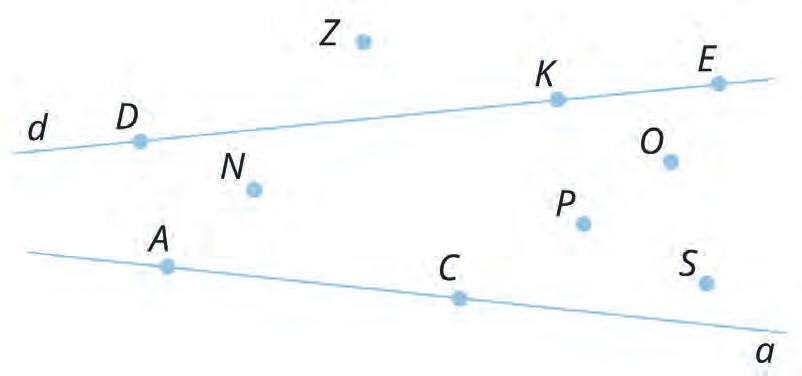
7. Circle all points on the line d.
8. Аdd the given line: then circle to make the statement true.

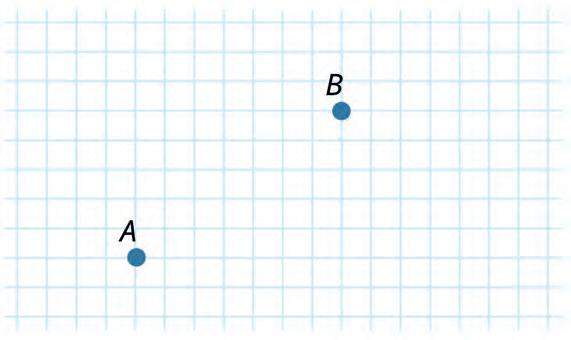
9. Draw straight lines through points A and B.

10. Circle the right answer.
How many different straight lines can be drawn through one point?
How many different curves can be drawn through one point?
How many different curves can be drawn through two point?
How many different straight lines can be drawn through two point?
11. Connect the dots.
12. Connect the dots.

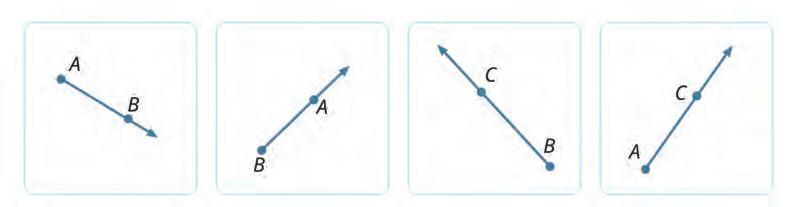
13. Tick the name of the ray.
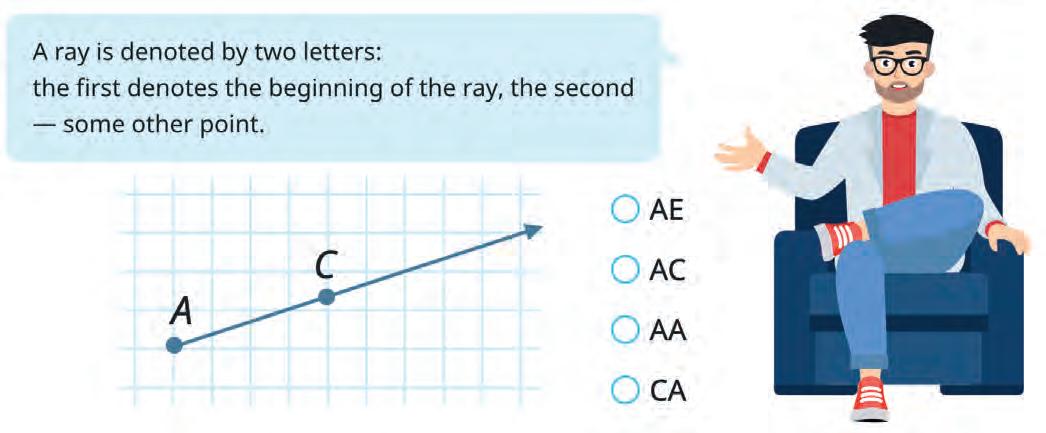
14. Circle rays AB and BC.
ANGLES
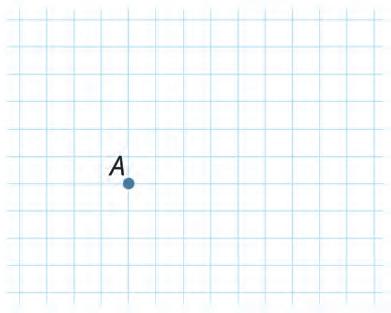
15. Draw two rays from the given point.

16. Circle a the angle that matches the given name.

a)
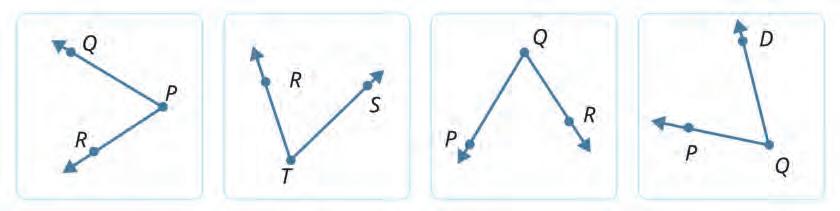
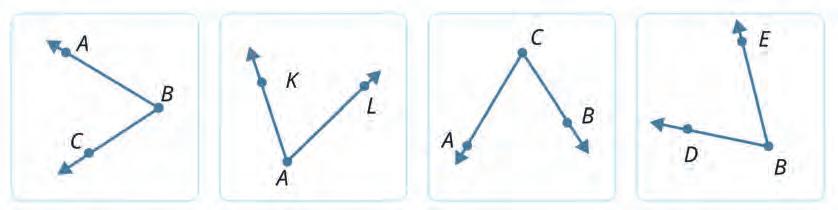
PQR
b) ABC
17. Name the elements from the given.
18. Write the correct statement.

19. Write correct angles.
Straight angles: Right angles:
UNDERSTANDING POLYGONS
20. Circle the figure with 4 vertices and 3 line segments.


21. Tick the figure with 5 vertices and 5 line segments.
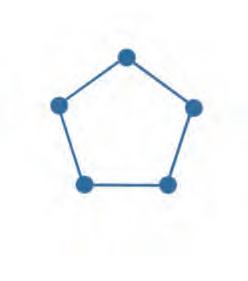
22. Tick the figure with 3 vertices and 3 line segments.
23. Count the number of vertices and sides.

vertices vertices vertices sides sides sides
24. Circle all the polygons in the picture.
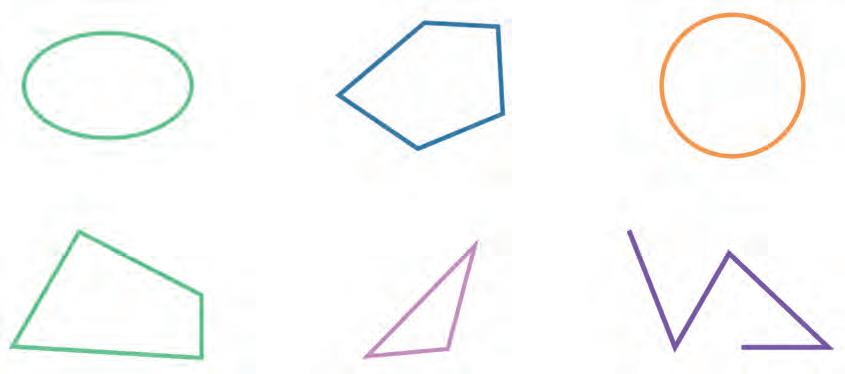
25. Draw a simple polygonal chain on the left and a closed polygonal chain on the right, marking all vertices with red dots and all segments with blue lines.
26. What are these figures called?

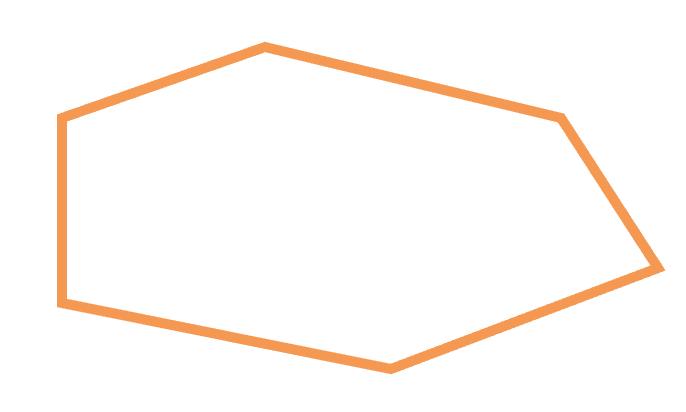

27. Make the definition.
If __________ of the angles of a triangle is _________ , then it is called right-angled triangle.
1) 2) 2) 3)
If __________ of the angles of a triangle is _________ , then it is called obtuse-angled triangle.
If __________ of the angles of a triangle are _________ , then it is called acute-angled triangle.
28. Make the definition.
If _________ sides of a triangle are _________ , then it is called isosceles.
If _________ sides of a triangle are _________ , then it is called equilateral.
all all one two obtuse equal right-angle acute one
29. Choose the correct statement.

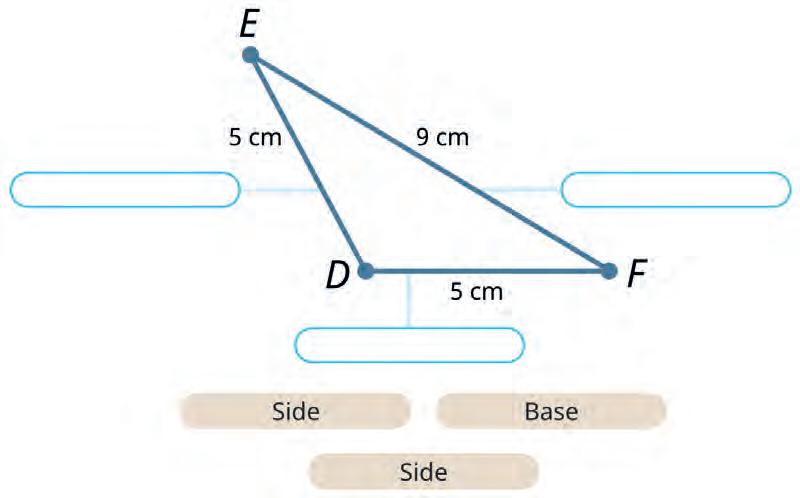
30. Name the parts of the isosceles triangle.
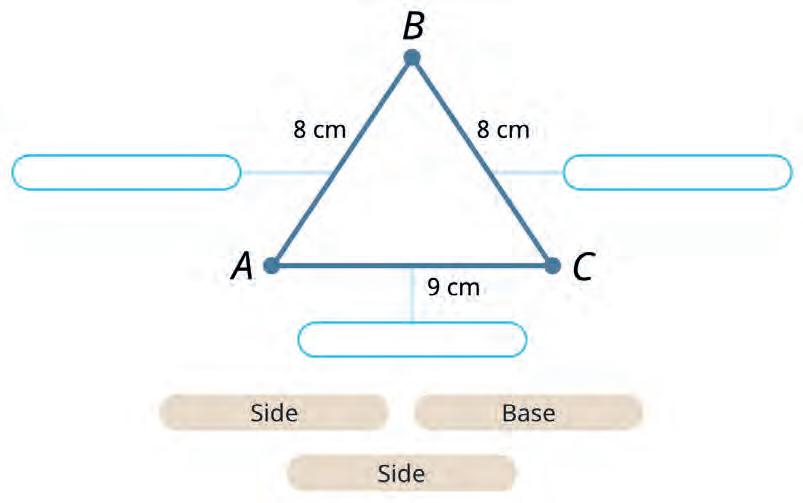
Alex
Kamal
31. Mark all isosceles triangles.
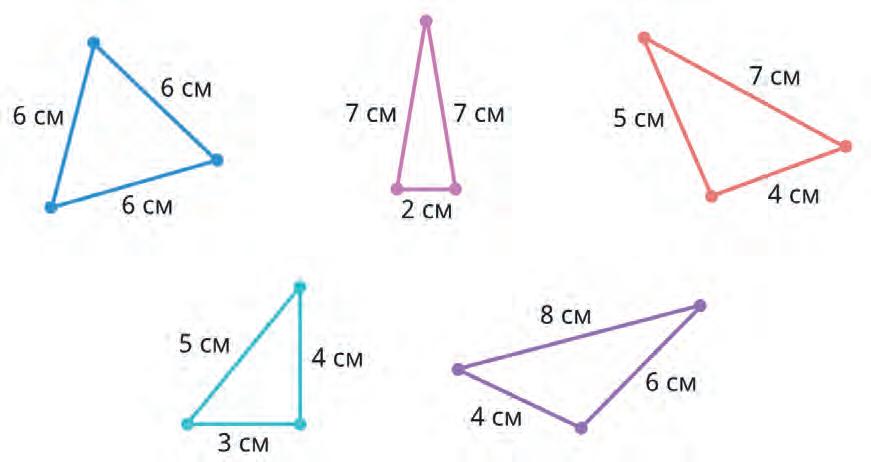
32. Tick obtuse-angled Triangles.


33. Tick right-angled Triangles.

34. Tick the equal sides.



35. Choose the correct statement.
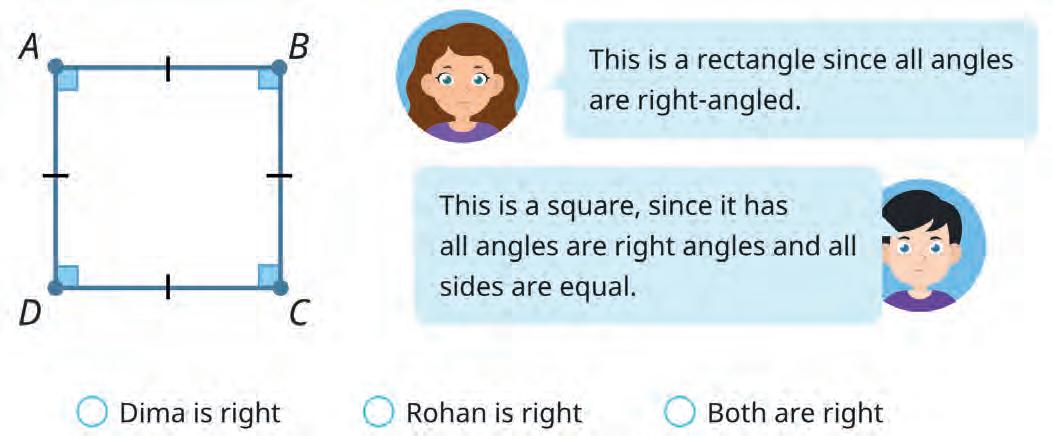
36. Tick all rectangles.

Dima
Rohan
UNDERSTANDING CIRCLES
37. Draw two of each type of curve.
Simple curve
Non-simple Curve
Open Curve
Closed Curve
38. Using a compass, construct circles with the given measures.
radius = 1 cm
radius = 2 cm
radius = 15 mm
radius = 25 mm
39. Match each element of the circle.
40. Make the statement.
1) means half of a circle.
2) circles are circles that share the same centre but have different radius.
Concentric Semicircle
41. Using a compass, construct circles with the given measures.
diameter = 2 cm
diameter = 4 cm
diameter = 30 mm
diameter = 50 mm
Vertices
5. 3-D SHAPES
UNDERSTANDING 3-D SHAPES
1. Complete the table.
2. Fill in the blanks.
1) Square pyramid has edges and vertices.
2) Rectangular pyramid has 5 and 8 .
3) Pentagonal pyramid has faces and edges.
4) Hexagonal pyramid has 7 and vertices.
3. Which of the following will make a cube when folded? Circle them.
4. Draw the net of a cylinder.
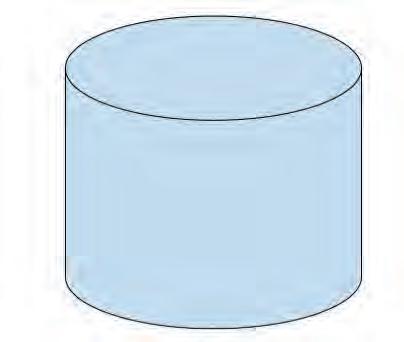
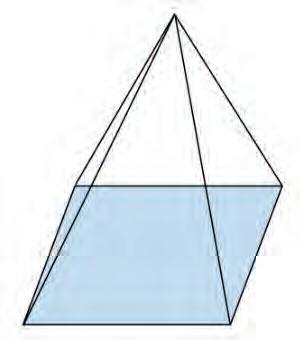
5. Draw the net of a square pyramid.
6. INTEGERS
UNDERSTANDING INTEGERS
1. What temperature does the thermometer show? Circle the right answer.



2. It was -5 °C in the morning, but it is 20 °C warmer in the evening. What is the temperature in the evening?
Answer:
3. It was 0 °C in the morning, but it is 5 °C colder in the evening. What is the temperature in the evening?
Answer:
4. How many coins are left after the payment? Circle the right answer.






5. How many coins are left after the payment?









6. Write the point on the number line.
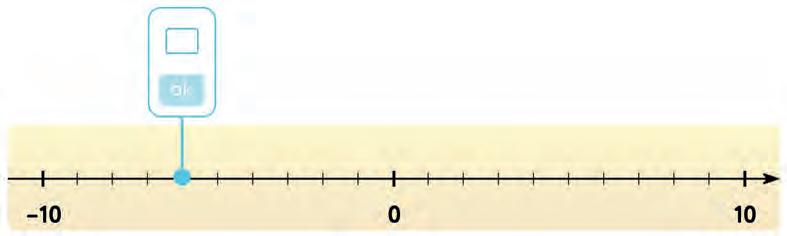
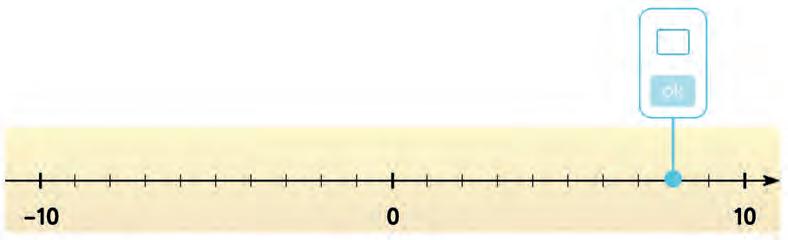
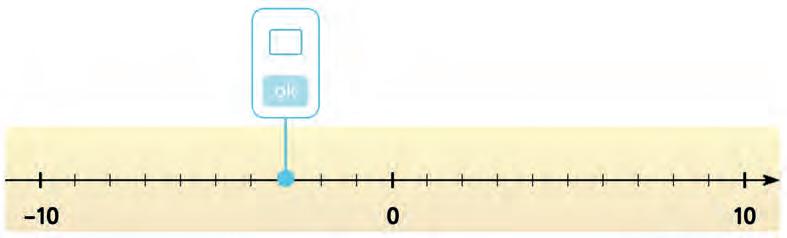
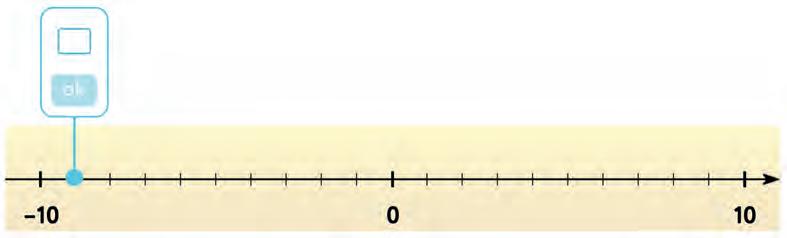
7. What’s the temperature on the thermometer? Circle the right answer.



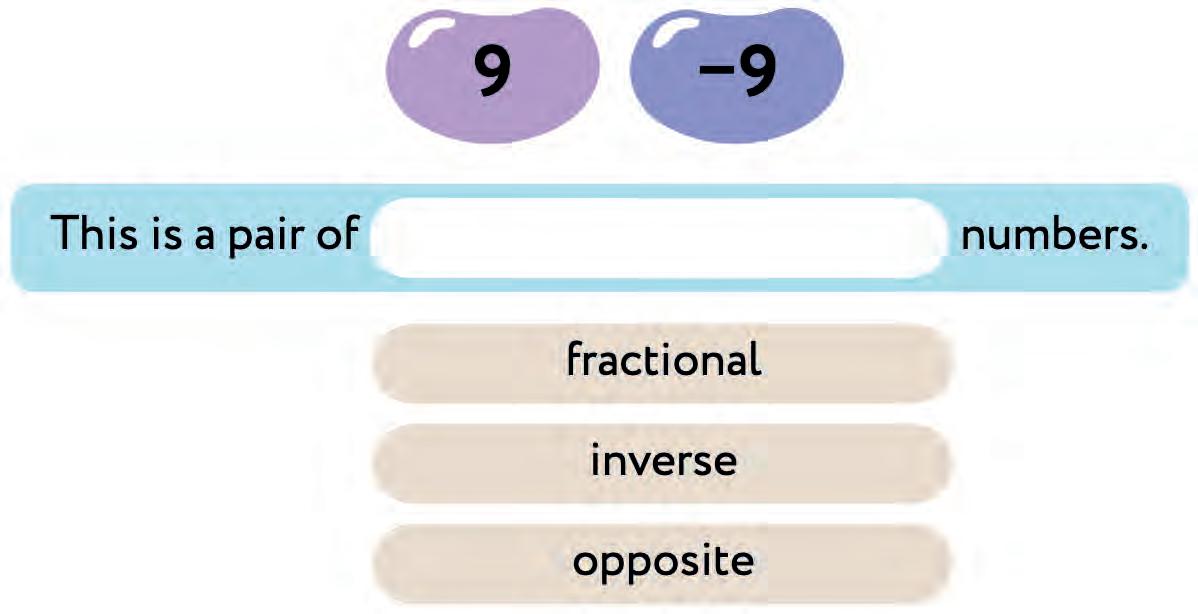
8. Circle a bean with the opposite number.
Opposite numbers differ in sign






9. Find a pair of acorns with opposite numbers. Circle the right answer in each case.
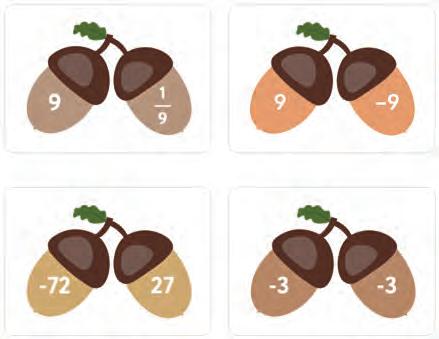

a)
b)
10. Put each book in a suitable bookcase. Match the book and its bookcase.


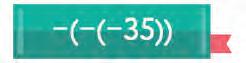


11. Fill in the blanks.
a) The number is negative if the number of minuses is ____ (odd/even).
b) The number is positive if the number of minuses is ____ (odd/even).
12. Calculate the expression.
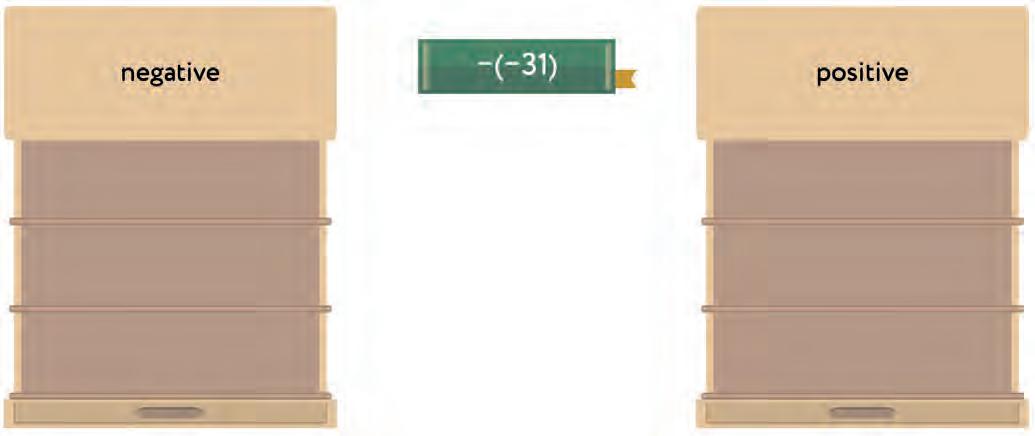
a) –(–(–3) = b) –(–12) = c) –4 = d) –(–0) = e) –(–(–(–6) = f ) –(–(–(–(–2) =
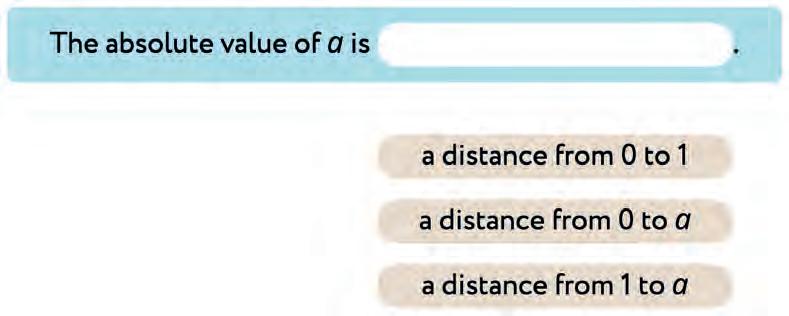
13. Complete the definition of the absolute value. Circle the right answer.
14. Find the absolute value.
a) |9| = b) |-5| = c) |0| =
d) |13| = e) |-9| = f ) |8| =
15. Circle the right answer.
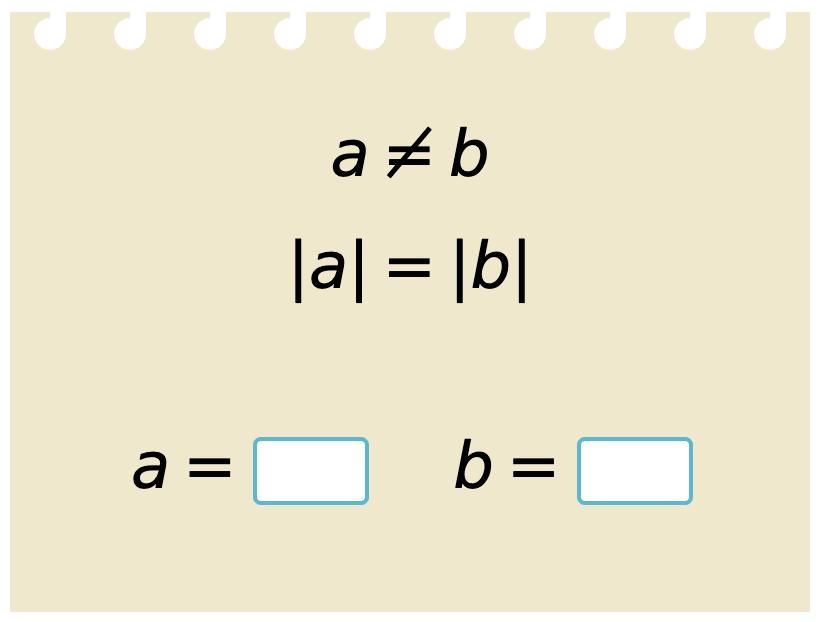
16. Give an examples.

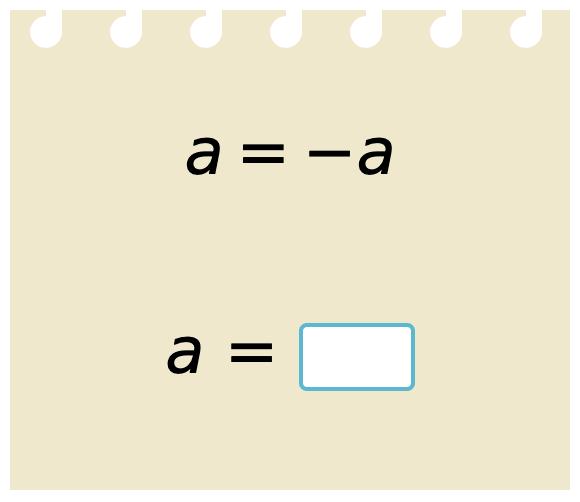
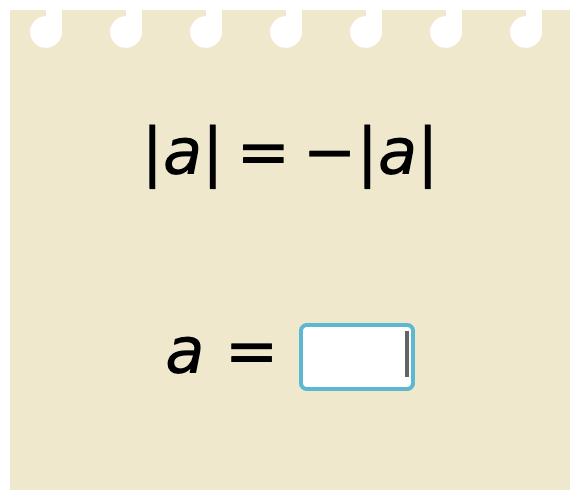
17. Solve the expressions.
18. Connect the height above/below sea level.

19. Connect the height above/below sea level.

20. Mark the numbers on the number line and compare it.


21. Guess the Sphinx Number.


22. True or False?
Any positive number is larger than any negative number.
Any negative number is larger than zero.
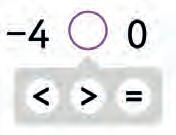
23. Compare the numbers.
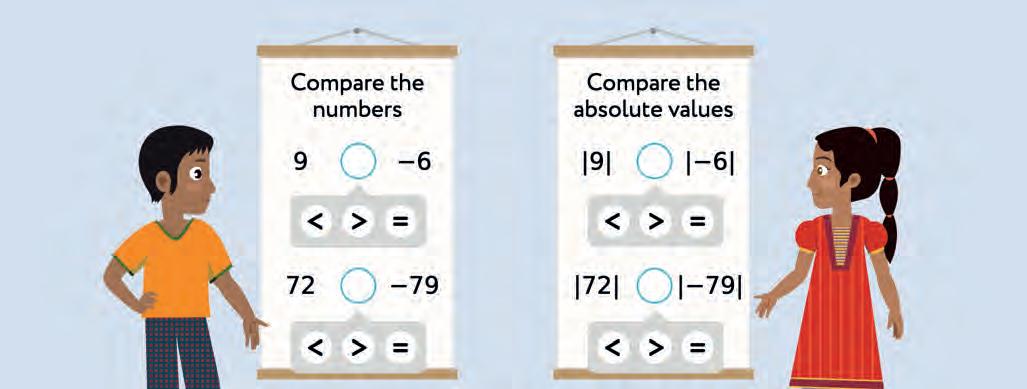
24. Use <, >, = to compare the numbers.
a)
OPERATIONS ON INTEGERS
25. Write down where the robot will go.
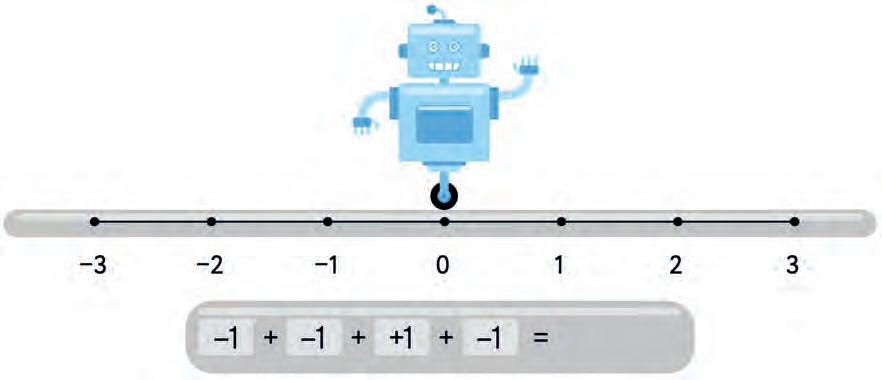
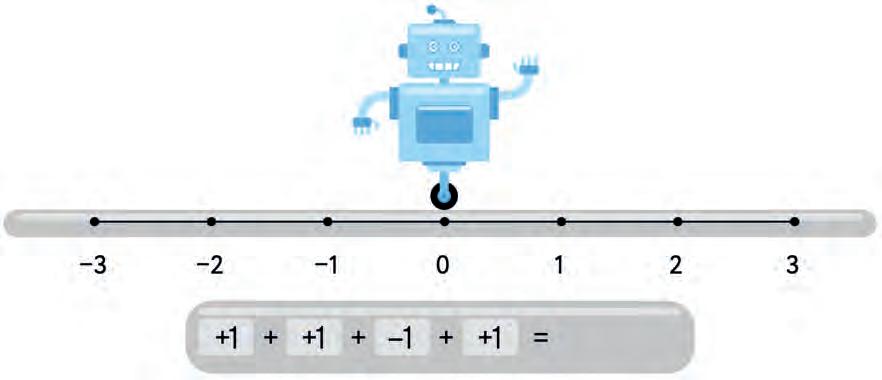

26. Use number line to solve the expression.
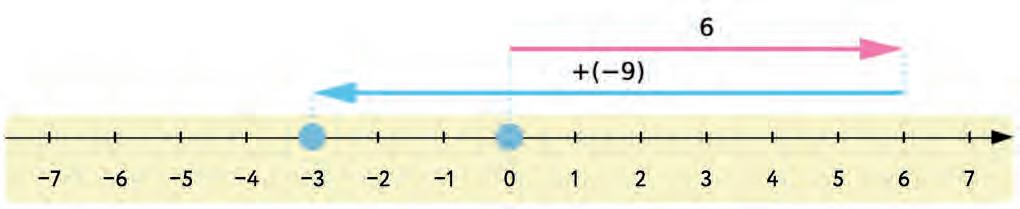
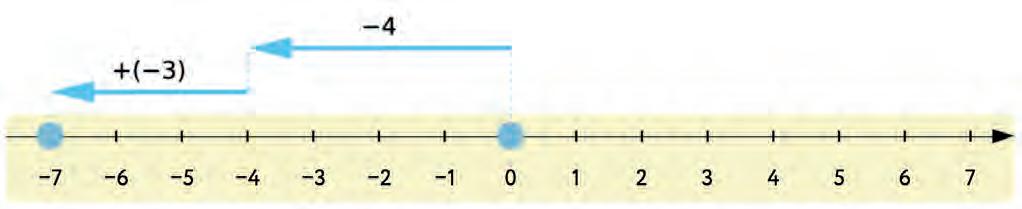
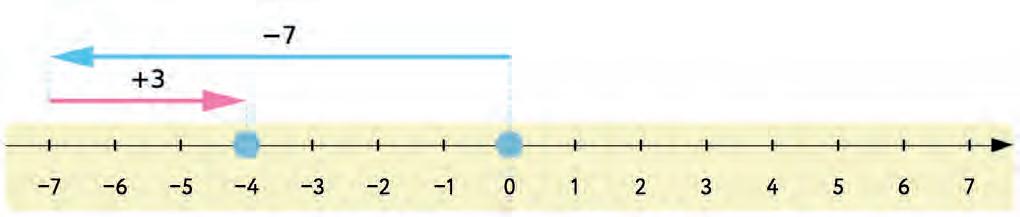
27. How to add a whole number on the number line?

a) If the number is positive, I draw an arrow to the (left/right).
b) If the number is negative, I draw an arrow to the (left/right).
Answer:
28. Mary runs up and down the stairs. She goes up 4 steps, and then goes down 8 steps. As a result, has Mary gone up or down?
Answer: Circle the right expression Circle the right expression
+ 8
+ (–8)
+ 8
+ (–8)
29. Peter takes out 20 rupees from his wallet, and then he puts back 14 rupees. Does Peter have more or less money in his wallet now?
+ 14
+ (–14)
+ 14
+ (–14)
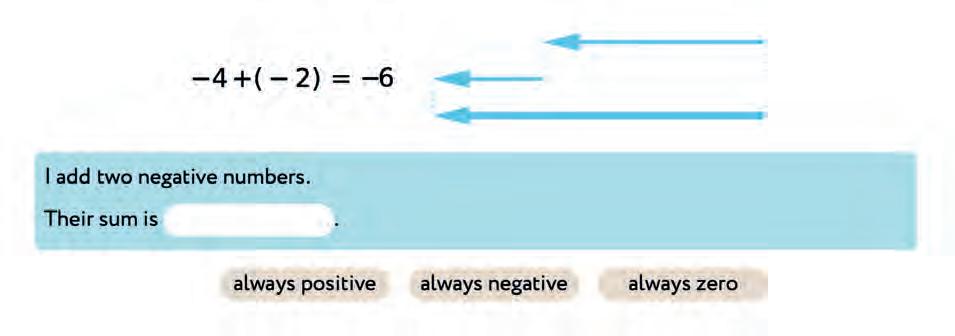
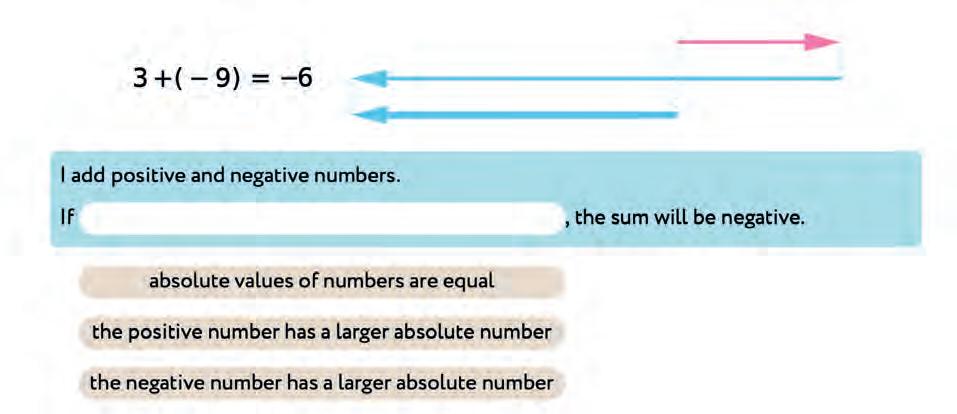
30. Make a rule.

31. What is the sum.
24 + 47 –49 + 14 –5 + 5 –29 + 18 –3 + 25 15 + (–22) 4 + (–4) –43 + (–5) 32 + (–9) 84 + 26 –74 + 21
32. Write the missing numbers.
27 + = 27
–9 + = 4
16 + = 12
33. Calculate the expressions.
a) –24 + 12 =
d) 61 + (–17) =
g) 93 + 34 =
j) –76 + (–43) =
m) 50 + (–51) = + (–8) = 17 –12 + 3 = –10 + 5 =
b) –82 + 32 =
e) –52 + 52 =
h) 51 + 72 =
–5 + (–7) = + 19 = 12
c) 45 + (–11) = f ) 73 + (–73) = i) -28 + (–34) =
l) 82 + (–49) =
k) 63 + (–23) = n) 39 + (–46) = + 14 = 0
34. Choose all the expressions that fill the graph.
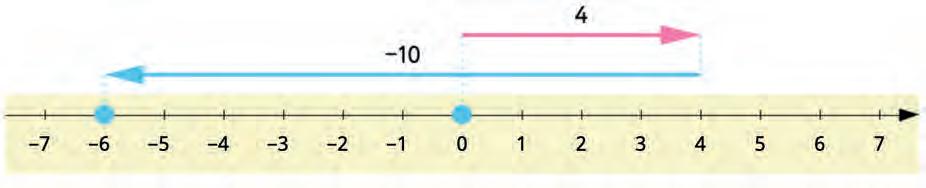
–4 – 10 4 + 10 4 + (–10) 4 – 10
35. Make a rule. Circle the right answer.

36. Connect the same actions.

37. Write the correct numbers.
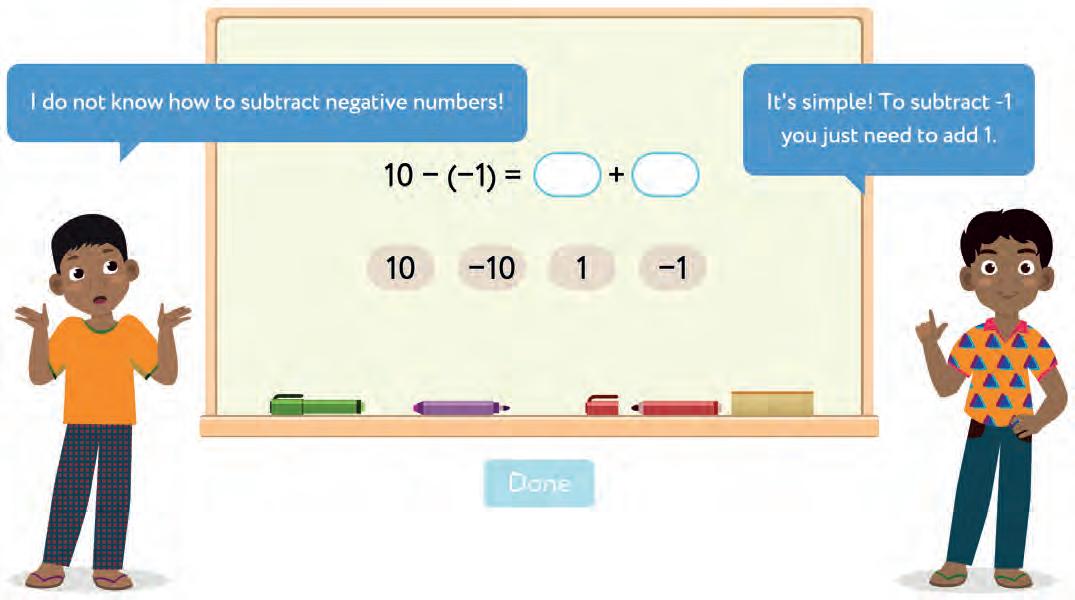
38. Choose the right answer.
a) If you add a negative number, then the number becomes (larger/smaller).
b) If you subtract a negative number, then the number becomes (larger/smaller).
39. Calculate the expressions.
a) 33 – (–2) =
c) 24 + (–5) = b) 21 – (–4) = d) 31 + (–2) =
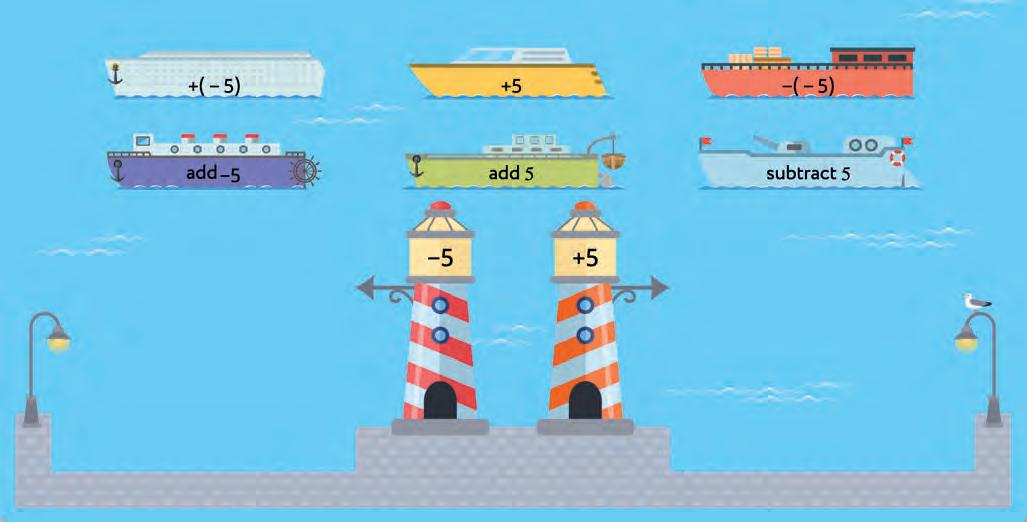
40. Connect ships with the right bays.
41. What is the result?
–40 + 4
–24 + 24
–18 + (–18)
–45 – 26 –13 + 15 –31 – (–12) –21 – (–26) 43 + (–5)
– (–68)
+ (–91)
+ (–13)
42. Write the missing numbers.
23 – = 23
–7 – = 3
18 – = 6
– (–3) = 19 –12 – 9 = –12 – 8 = – 16 = 0
–2 – (–7) = – 14 = 19
43. Calculate the expression.
a) –2 – (–3) =
–2 + 3 = 1
b) –4 – (–4) =
c) –7 – (–13) =
d) 0 – (–15) =
e) 3– (–11) =
f) 5 – 82 =
g) –24 – 26 =
h) 74 – (–34) =
i) 48 – (–24) =
j) 63 – 24 =
k) 13 – (–29) =
l) 14 – 17 =
m) 78 – 89 =
n) –19 – (–75) =
44. Find the distance between the points.


45. Find the distance between the points.


46. Circle the right number line.

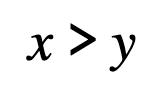

Choose the correct sign

47. Circle the right number line.

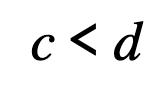

Choose the correct sign

48. Make a rule.
Distance between different points is always (negative/positive).
49. Choose the right answer.
How to find the distance between a and b, if you do not know what value is larger?
50. Fill in the table.
7. FRACTIONS
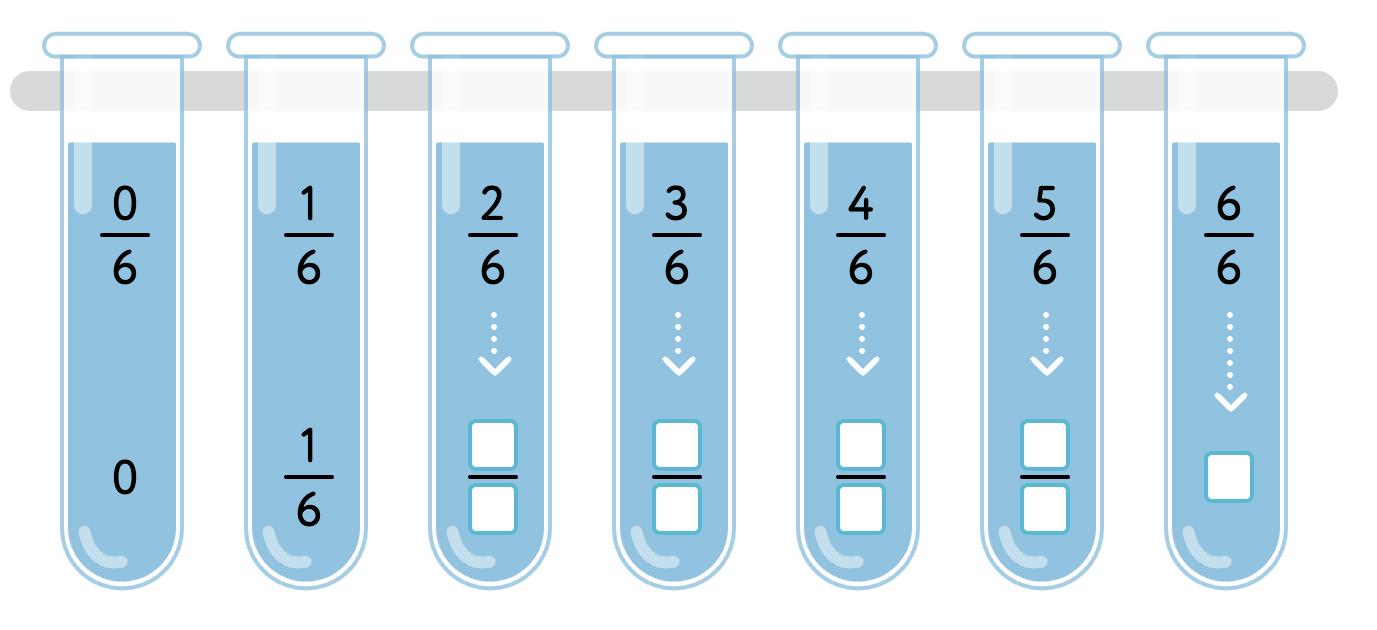
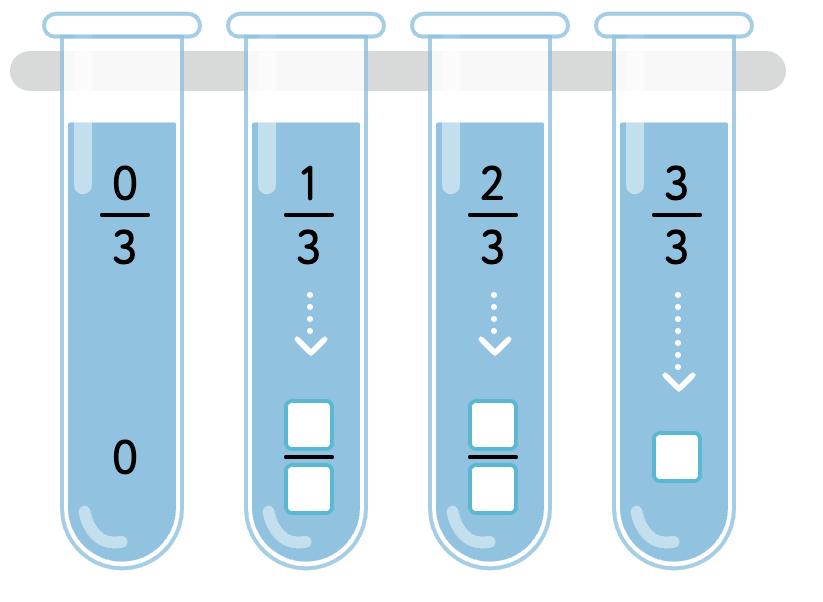
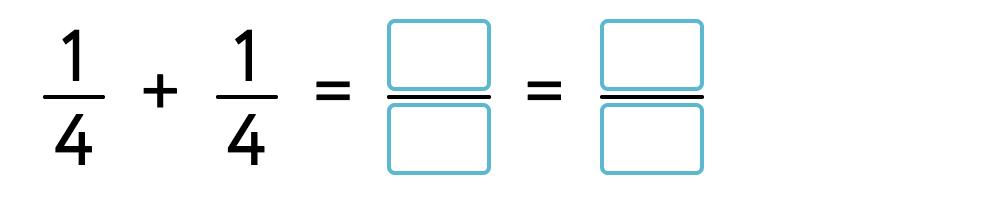
REVIEWING FRACTIONS 1
1. Shade 2 whole circles and .
6
2 . Shade 1 whole circle and 6 8 .
3. Match each element of the fraction from the given.
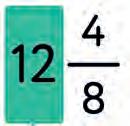
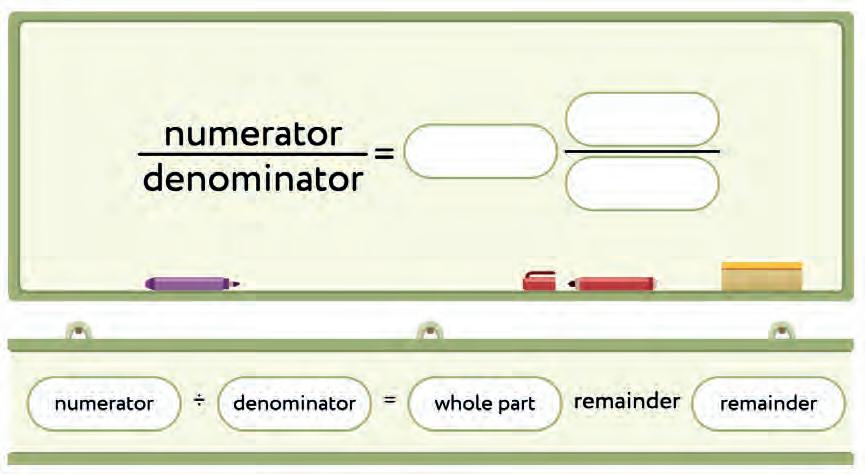
mixed fraction fraction part numerator whole part fraction bar denominator a) b) c) d) f) e)
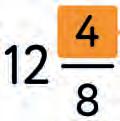

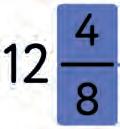
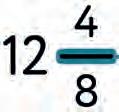
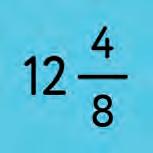
4. Write the right labels.

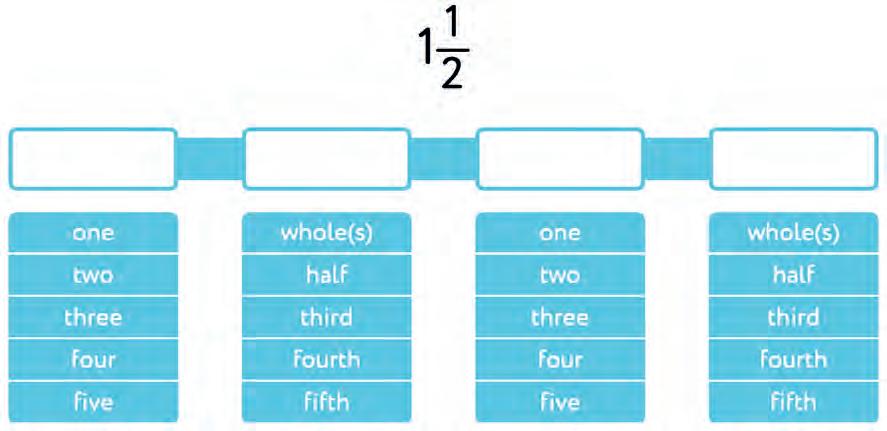
5. Write the mixed fraction on the number line.
6. Sort the fractions. Connect to the right box.








7. Think of a good way to calculate and make a rule.
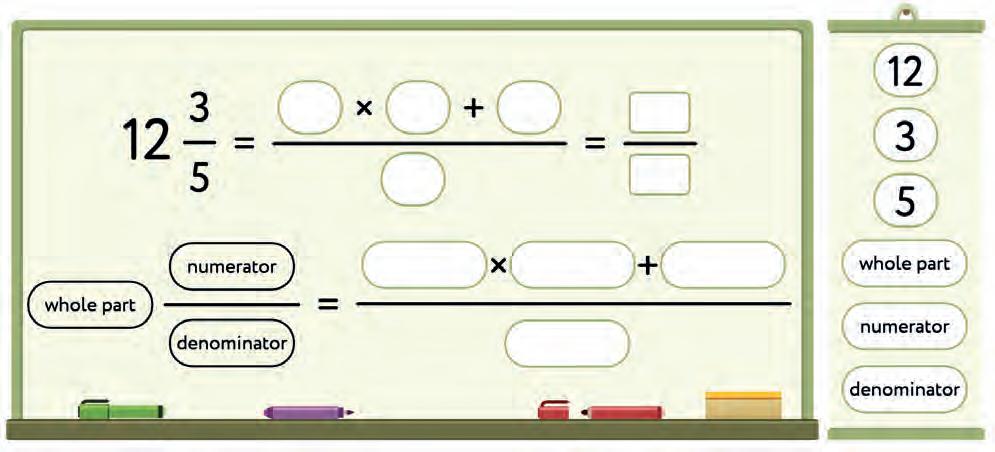
8. Change the
into an improper fractions.
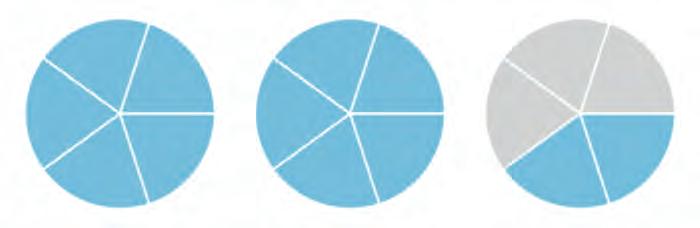
9. Write the mixed fraction on the
10. Write the mixed fraction on the number line.
11. Write the fraction on the picture in two ways.

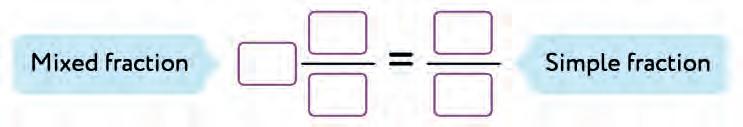

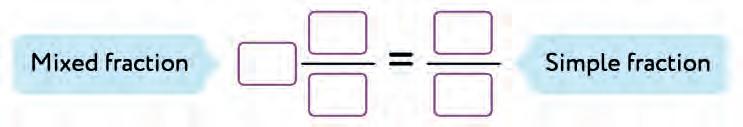
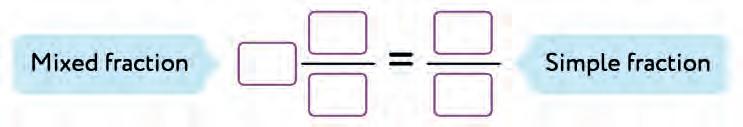
12. Write the mixed fraction as an improper fraction and improper fraction as mixed fraction.
13. Write and compare the


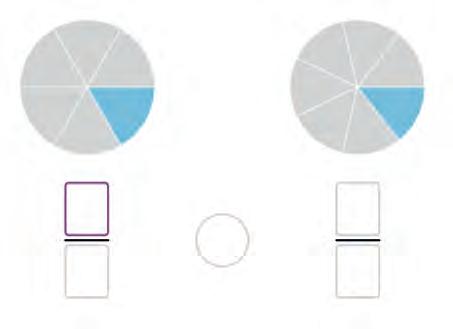
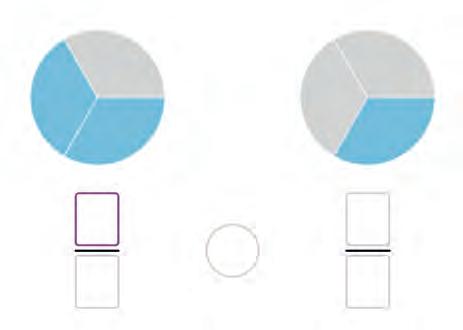
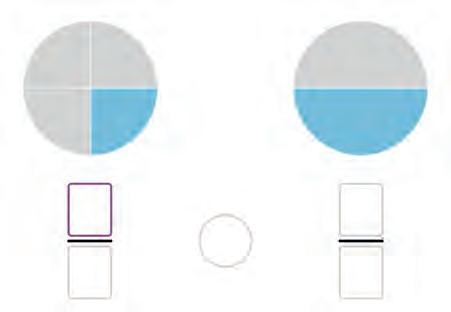
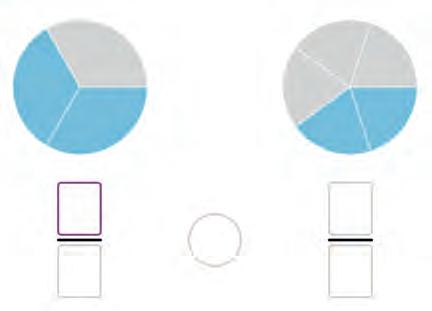
14. Arrange the fractions from the smallest to the largest.

These fractions have the same denominators.
The larger the numerator the (larger/smaller) the fraction.
15. Arrange the fractions from the smallest to the largest.
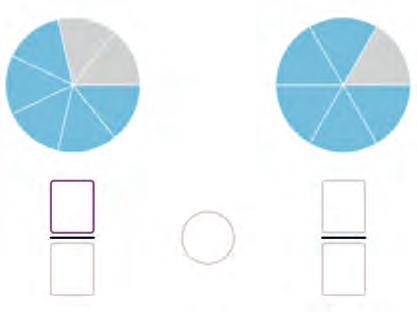
These fractions have the same numerators.
The larger the denominator the (larger/smaller) the fraction.
16. Compare the fractions.
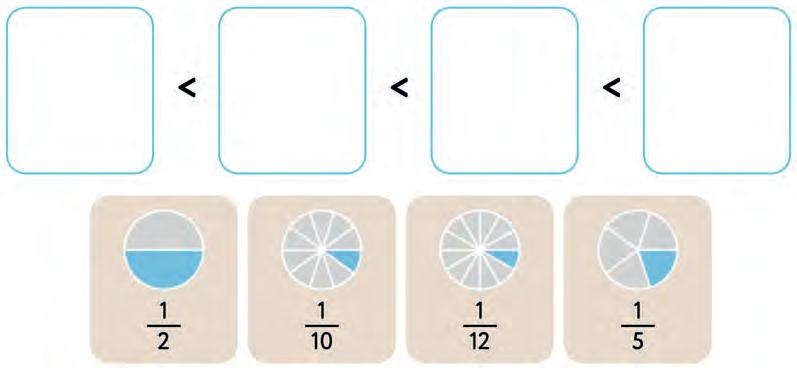
17. Look at the number line and choose the correct sign.
18. Look at the number line and choose the correct sign.
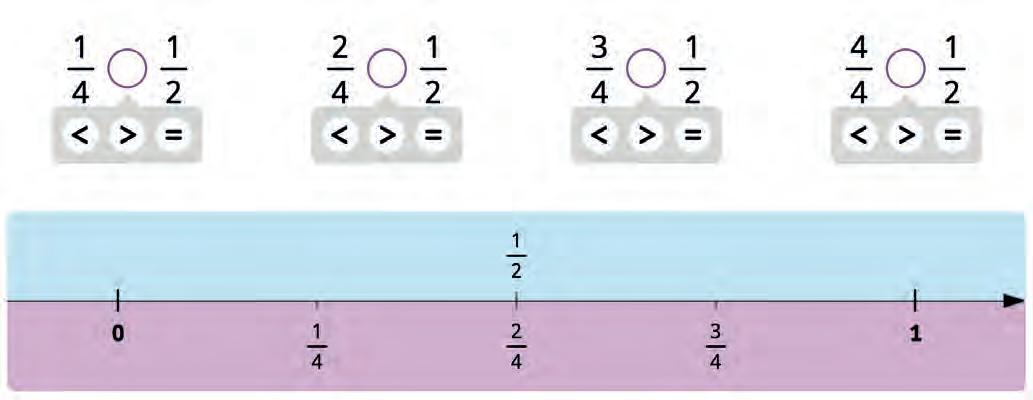
1 2
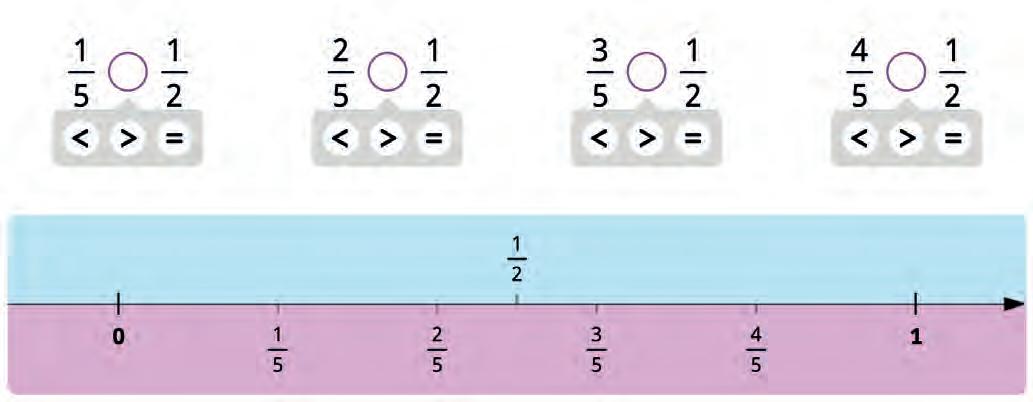
19. Compare the fractions with and with each other.
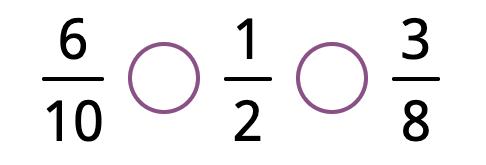
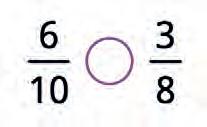
20. Find the closest whole numbers.
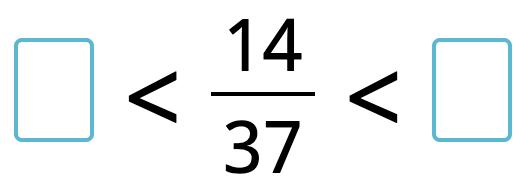
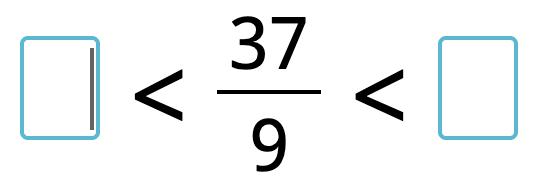
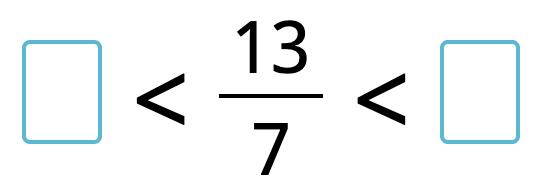
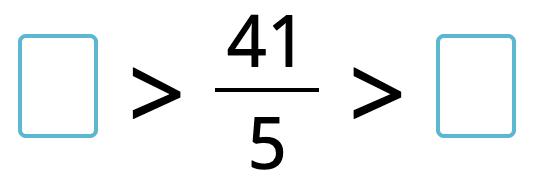
21. Circle the shapes that have equivalent part shaded. Choose two pictures.
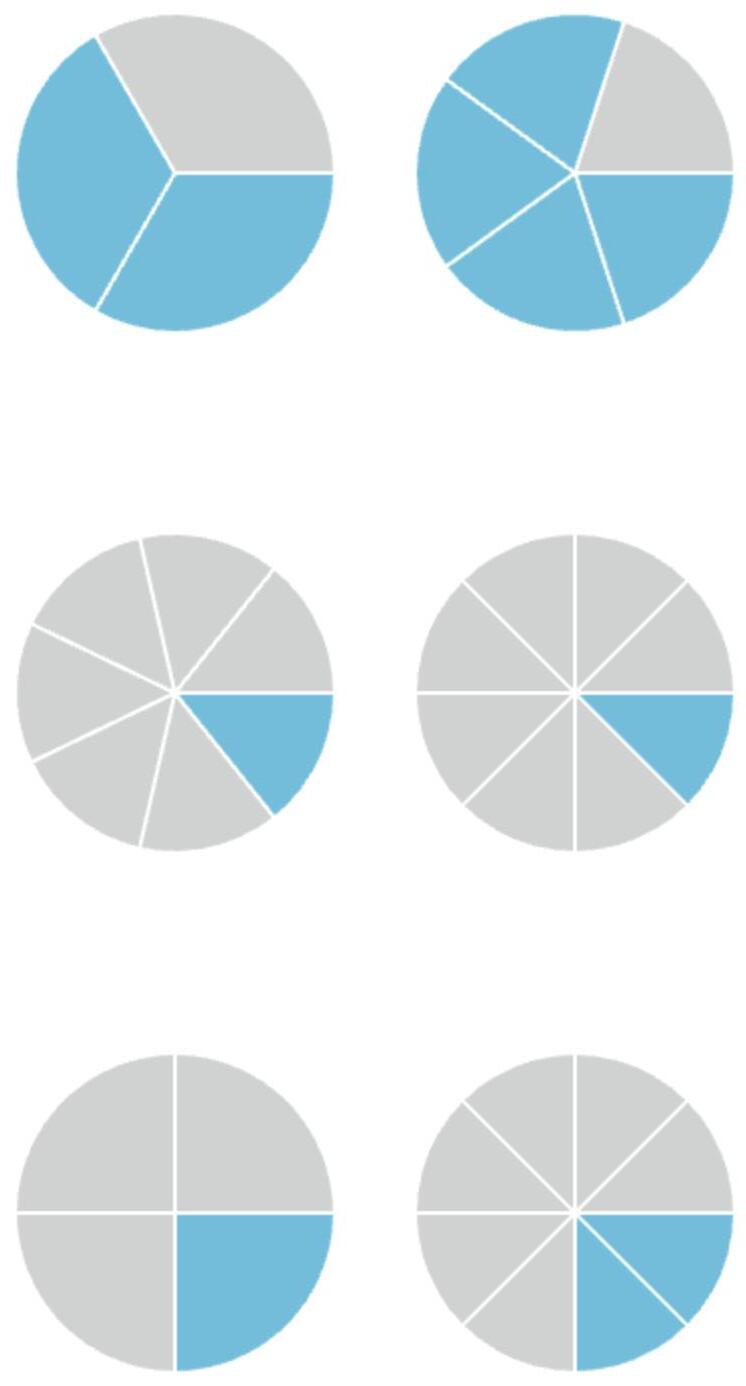
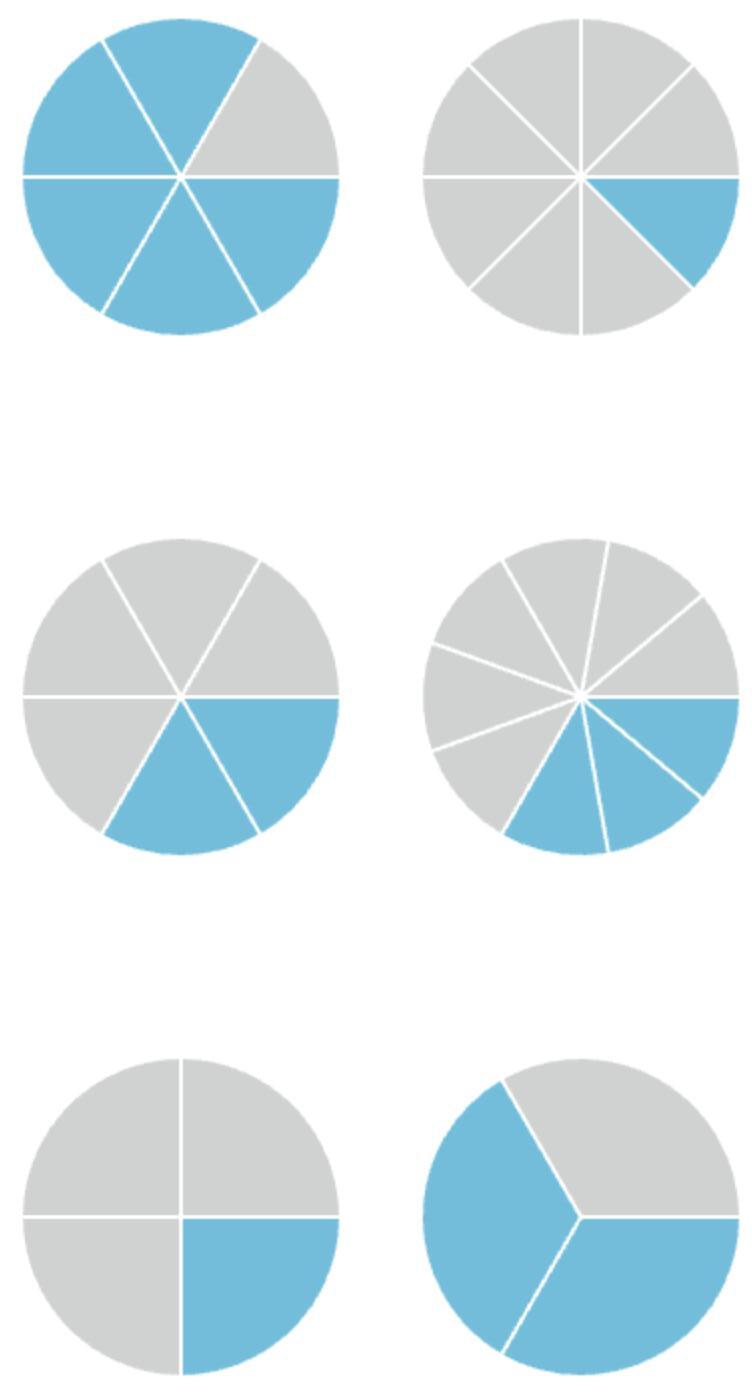
22. Fill in the blanks.

23. Fill in the gaps.
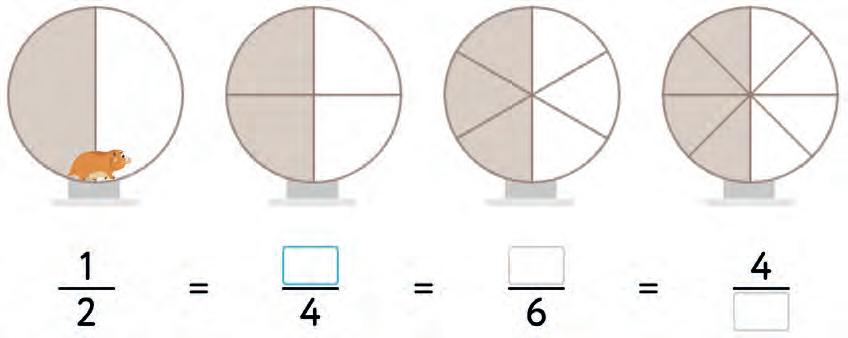
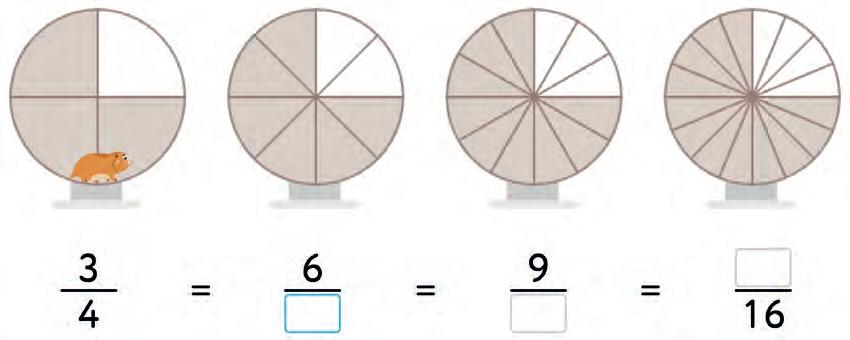
24. Fill in the gaps.

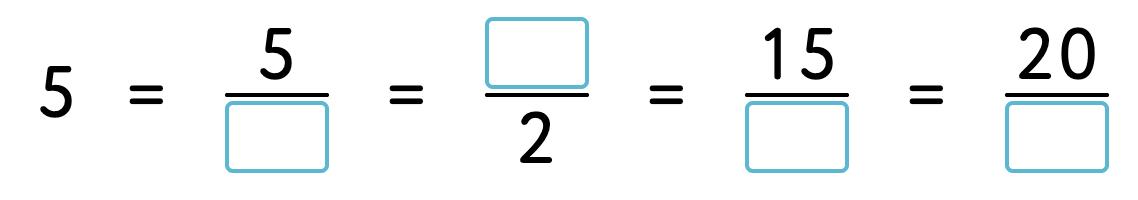
25. Compare the fractions with the number line.






26. Write all the fractions in a simplified form.
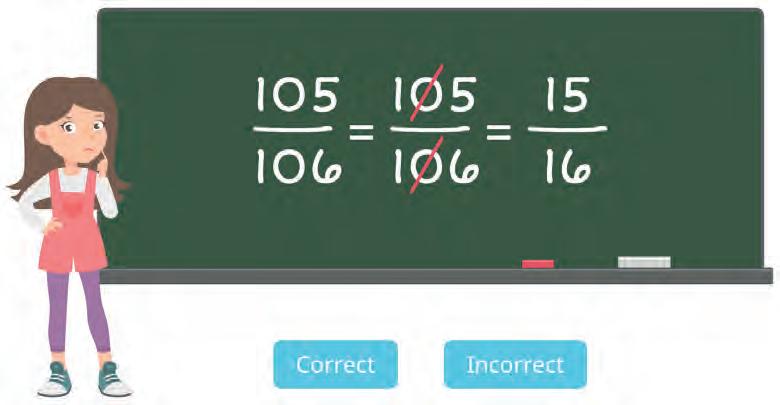
27. Did Gagan simplify the fraction correctly? Circle the correct answer.



28. Simplify the fractions.
OPERATIONS
29. How many litres of lemonade?

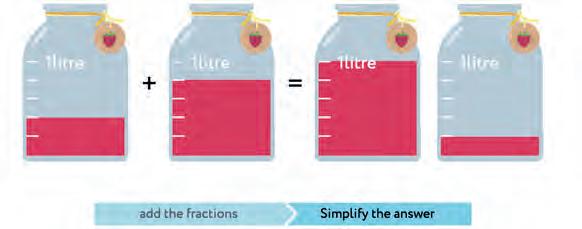
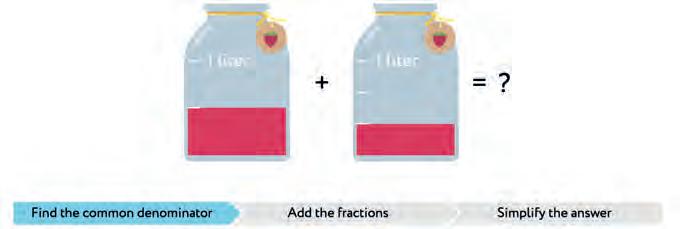
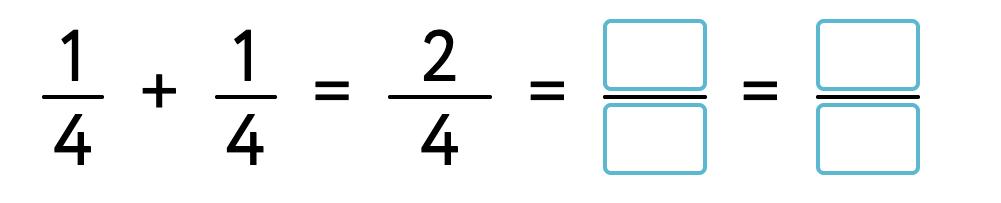
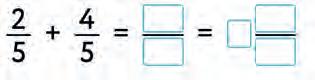
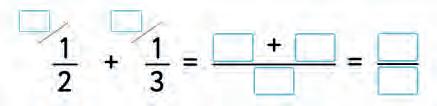
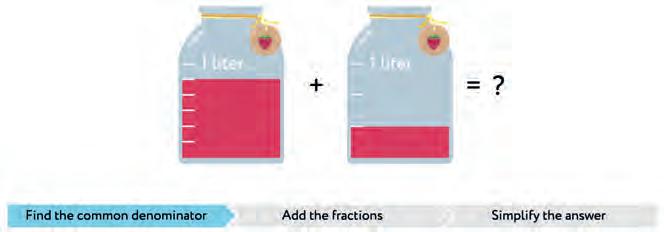
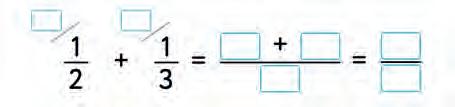
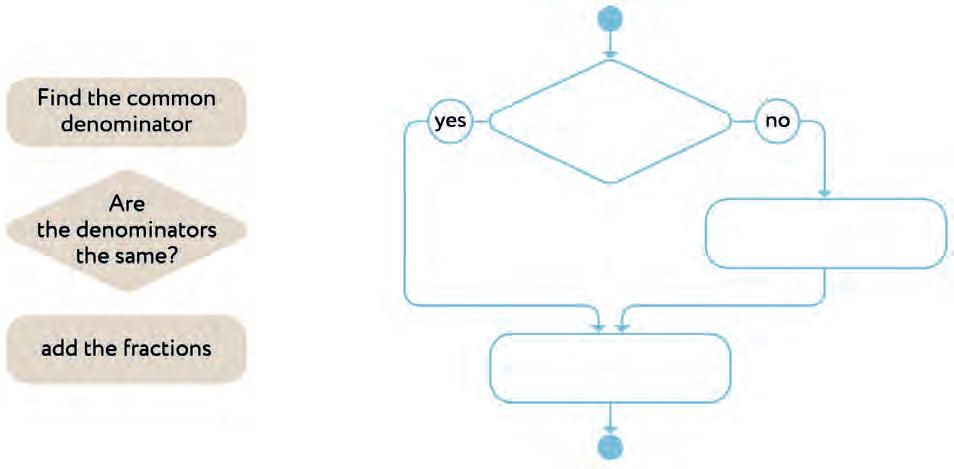
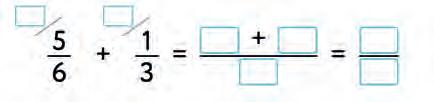
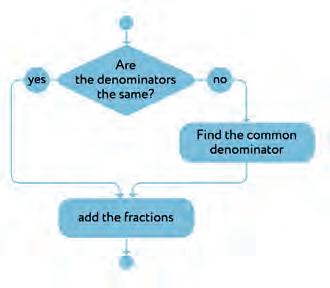
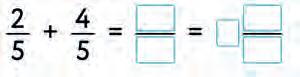
30. Make a rule “How to add/subtract fractions”. Connect with a line.

Subtract the fractions
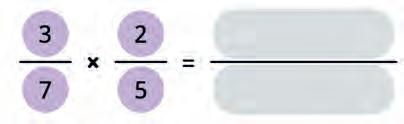
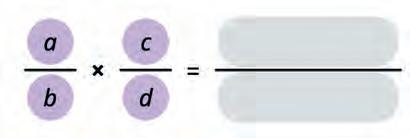
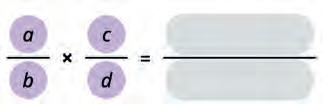
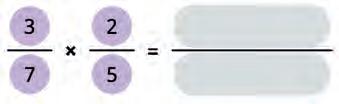
32. Make the formula for multiplication of fractions and solve the expression.
33. Fill in the blanks in the solution.
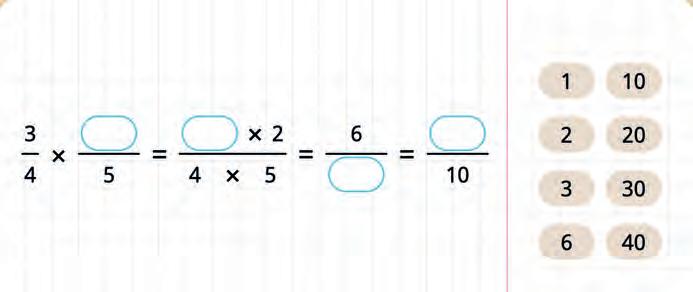
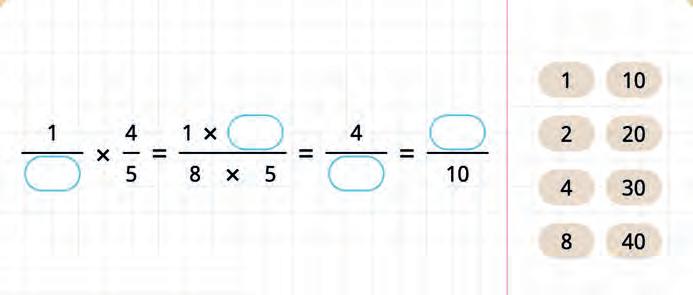
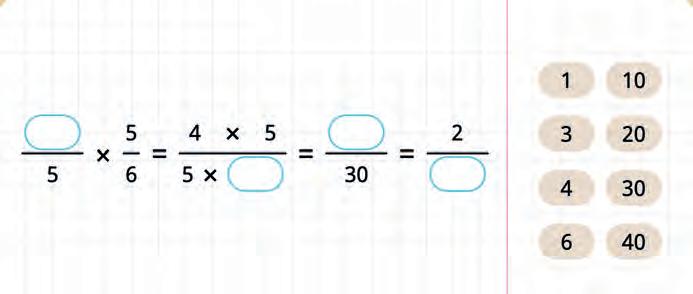
34. Count in two ways.
First multiply and then reduce:
First multiply and then reduce: a)
35. Reduce the fraction.


36. Did Ira simplify the fractions correctly?

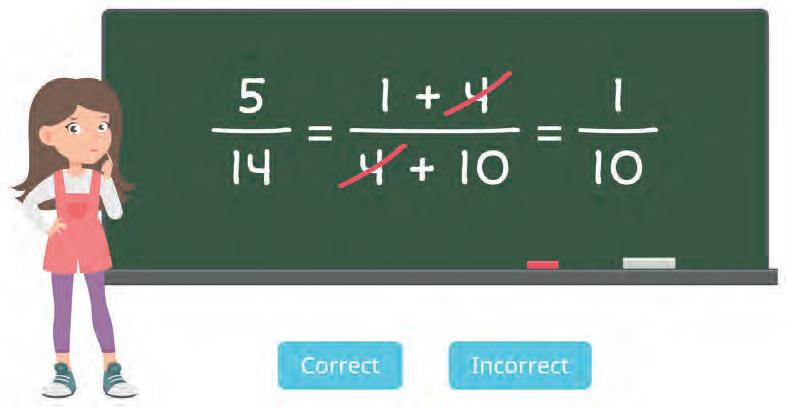
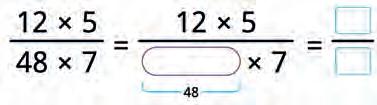
37. Count in two ways.
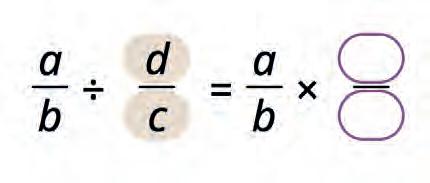
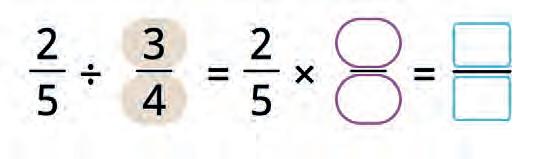
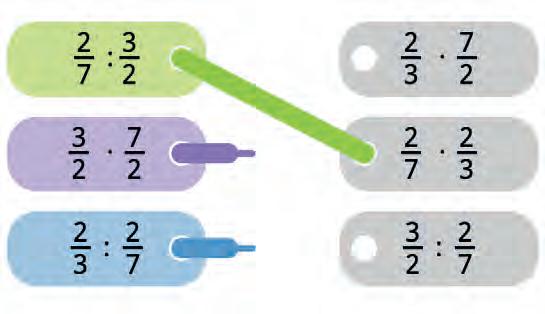
38. Match equal expressions.
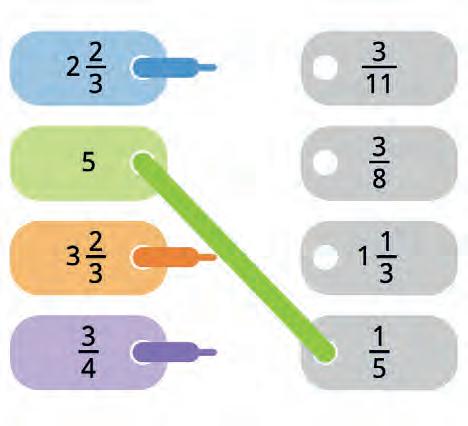
39. Match the pairs of reciprocal numbers.
40. Calculate the expressions.
41. Misha
42. Sveta paints 1 2 3 of a meter in an hour. How many meters of a fence will she paint for 1 1 2 hours?
43. Rita makes rolls. She has 2 1 2 glasses of rice, and for each roll you need 1 4 glasses of rice. How many rolls can Rita Make?
44. Grandmother cooked 4 2 4 litres of soup. Dinosaur portion is 2 1 4 litre. How many dinosaurs can grandma feed?
8. DECIMALS
UNDERSTANDING DECIMALS
1. How much water is in the bottle?
a) Write the answer as a simple fraction
a) Write the answer as a decimal fraction
2. What is the temperature in the thermometer?
a) The answer: b) The answer:
c) The answer:
3. What is the length?
4. What part of the square if shaded?
Write it as a simple fraction and then as a decimal fraction
5. Fill in the gaps in the table.
3 tenths
3 hundredths
3 thousandths
3 ten thousandths
3 hundred thousandths
6. Write the number as a decimal fraction.
five and seven hundred seventy four thousandths
two hundred and thirty four and nineteen hundredths
eighty four and sixty five thousandths
zero and eleven hundredths
twelve and twelve thousandths
7. Names of the digits.
8. Match the equal numbers.
9. Complete the table.
10. Compare the numbers.
11. Write a suitable number.
12. Convert to ordinary fractions and compare.
OPERATIONS ON DECIMALS
13. Fill in the blanks.
14. Has John done the correct calculations? Circle the correct answer.
2,543 5,329 + 7,862 6,375 2,068 + 8,443
CorrectWrong
CorrectWrong 11
15. Make a rule. Circle the correct answer.
Attaching zeros of a decimal fraction doesn’t change its value at any place in the middle to the end
16. Has John done the correct calculations? Circle the correct answer.
7,861 5,328 –2,543 8,443 2,068 6,375
CorrectWrong
17. Circle numbers equal to this one.
CorrectWrong –4.2000.424.204.02 4.2
18. Fill in the blanks.
19. Match the answers with the expressions.
20. Calculate the expressions.
49.266 + 14.42 =
– 24.718 =
6.6226 + 55.14 =
23.51 + 562.57 =
– 456.2 = 64.11 – 23.741 =
344.15 + 13.24 =
– 24.541 =
21. Did Gagan put the decimal point to the right place? Circle the right answer.
CorrectWrong
1.627 0.4 × 0.6508 0.128 8 10.24 1.236 0.7 8.652
CorrectWrong × ×
CorrectWrong
22. Fill in the blanks then put the decimal point to the right place.
23. Calculate the expressions.
24. Calculate the expressions.
25. Circle to make a true statement.
a) If 9 tenths is divided by 3 then you will get
b) If 5 hundredths is divided by 5 then you will get
c) If 3 thousandths is divided by 3 then you will get . . .
26. How to convert a divisor into a natural number without changing the quotient? Write the smallest suitable number.
You need to move the decimal point to the right digits.
27. Calculate the expressions.
645 × 6.4 =
28. Calculate the expressions.
0.0998 × 9.4 =
0.25 × 756 =
0.034 × 48 = 9 ÷ 0.12 = 900 ÷ 12 = 315 ÷ 7.2 =
153 ÷ 2.4 =
0.6912 ÷ 0.432 =
9. DATA HANDLING
1. Answer the questions.
The table contains the weight and height of savanna animals.
1) What is the weight of an elephant? _______ kg.
2) Which animal is 140 cm? ______
3) Choose the animal with the smallest height. It is ______ cm.
2. Find the answer in the table.
The table shows how many students of the 1st, 2nd, 3rd and 4th grade visited the school library this week. How many students of the 4th grade would come to the library on the 4th day, if each of the fourth graders brought one classmate?
The answer: kids.
3. Find the answer in the table.
The table shows how many and what flowers were planted in the park. How many tulips will be in the park, when 100 more are planted?
The answer: flowers
4. Find the answer in the table.
The table shows how many hours of each subject per year are in 1–4 grades. How many hours of Art will be in the 5th grade if it is half as much as in the 4th grade?
The answer: hrs.
5. Mark Anusha’s height at 5 years and complete the graph. Find the difference between the greatest and the smallest height.
At 4 years, Anusha’s height was 1 m, at 5 years — 1.1 m, in 6 years — 1.15 m, at 7 years — 1.2 m. When she was 8 years old, her height was 1.25 m.
6. Mark all the points and complete the graph.
The population of a city in 2011 was 4.9 million people, in 2012 — 4.95 million, in 2013 — 5.05 million, in 2014 — 5.1 million, in 2015 — 5.2 million.
7. Mark all the points and complete the graph.
In May the rainfall is 60 mm, in June — 50 mm, in July — 95 mm, in August — 85 mm, in September — 55 mm.
8. Mark all the points and complete the graph.
9. Answer the question using the graph.
The graph shows how the price of sandals changed for several months. How much did sandals cost in September?
The answer: rupees
10. Circle the right answer using the graph.
a) The graph shows how approximately the Earth population changed in the second half of the 20th century. How many millions of people lived on Earth in 1970?
b) The graph shows how many countries participated in the Winter Olympics in different years. What year number of participating countries was 82?
11. Circle the right answer using the graph.
a) The graph shows the change in the Aral sea area due to the negative impact of human activities. What is the smallest area of the Aral Sea?
km2 2 o’clock
km2
km2
km2
b) The graph shows how the temperature is changing in the Sahara desert during the day. At what time is the air temperature the lowest?
o’clock
o’clock
o’clock
c) The graph shows how the altitude of the helicopter varied during the flight. How many minutes after the flight began, the helicopter reached the highest altitude?
12. Is the statement true? Circle the right answer.
The graph shows what temperature the water begins to boil, depending on the altitude above sea level.
a) At an altitude of 3,000 m the water boils at a temperature of 80 °C.
b) The smallest boiling point is at an altitude of 9,000 m.
c) At an altitude of 1,000 m and 5,000 m, water boils at the same temperature.
13. Fill in the table.
Girls made paper snowflakes and wrote down in a table how many pieces they made. On the second day, every girl made snowflakes twice as many as on the first day. Write it in the table.
14. Circle the answer using the graph lines.
The graph shows how the temperature in the Sahara desert changes during the day. Select all hours when the temperature is below 34 ºC.
15. Circle the answer using the graph.
The graph shows how the population of Bhopal changed in recent years. How much has the population of Bhopal decreased from 2007 to 2015?
16. Circle the answer.
The chart shows the length in meters of a football field, basketball, badminton and tennis courts and a swimming track.
What is the length of the basketball court?
DATA H ANDLIN G 10. MENSURATION
UNDERSTANDING PERIMETER
1. Find the perimeter.
a) The perimeter of the triangle is
b) The perimeter of the quadrilateral is
с) The perimeter of the pentagon is cm. cm. cm.
2. One side of the triangle is 2 cm, the second one is 3 cm, and the third one is 2 cm larger than the first one. Find the perimeter of the triangle.
The answer:
3. One side of the triangle is 6 cm, the second one is 5 cm, and the third one is 2 cm smaller than the second one. Find the perimeter of the triangle.
The answer:
UNDERSTANDING AREA
4. Find the perimeter and area.
a) The perimeter of the square is
The area of the square is
b) The perimeter of the rectangle is
The area of the rectangle is cm. cm. cm2. cm2.
5. Find the length of the rectangle if its width is 5 cm, and perimeter equals the perimeter of the square with side 6 cm. Then find their areas.
1) The perimeter of the square is equal
2) Hence, the perimeter of the rectangle is
4) Area of the square is
3) Measure the sides of the rectangle cm. cm. cm2. cm2. + 5 ++ 5 = 24 (cm)
5) Area of the rectangle is
6. Write perimeter expression and find it. Then find area of the rectangle.
1) Perimeter = AB +
2) Area = AB
PERIMETER AND AREA PROBLEMS
7. Find the perimeter.
8. Find the perimeter and the area.
9. What is the area of shaded rectangle?
DATA H ANDLIN G 11.
INTRODUCTION TO ALGEBRA
ALGEBRA AND PATTERNS
1. What are the signs of mathematical operations? Choose all the correct answers.
2. Choose the right expression.
a) The sum of the one hundred and five and three hundred sixty.
b) The difference between one hundred and seven and eighty-five.
c) The product of one hundred forty-five and sixty-eight.
d) The quotient of three hundred five and twenty-three.
3. Match the verbal and the numerical form.
Sum of four and two
Difference of four and two
Product of four and two
Divide four by two
4. Make an expression.
a) Sachet won 14 games, and then he won 6 games 12 times. How many games did he win?
14 + 6 × 12
b) Sachet won a games, and then he won 11 games 6 times. How many games did he win?
c) Aadhan bought 7 buckets of popcorn which costed 150 coins each and one can of soda. He paid 1300 coins in total. How much did soda cost?
d) Aadhan bought a buckets of popcorn which cost 140 coins each and one can of soda that costs x coins. He paid b coins in total. How much did soda cost.
ALGEBRAIC EXPRESSIONS AND EQUATIONS
5. Circle the right answer.
Numerical expressions with letters are called algebraic
The letters of the Latin alphabet is commonly used.
Is it an algebraic expression?
75 + a + 43
34 + n $ 6 – – 7 765 × 765 – n765
Yes No Yes No Yes No
Is it an algebraic expression?
Is it an algebraic expression? Is it an algebraic expression?
6. Connect the verbal and the numerical forms.
Sum of seventy five and n
Quotient of x and seventy five
Difference of forty three and n
Product of x and forty three
7. Connect the verbal and the numerical forms.
Product of x and twenty five
Difference of eighty four and n
Quotient of x and eighty four
Sum of twenty five and n a) 42 ÷ a + 12 b)
8. Solve the algebraic expression for the different values.
For a = 1 For a = –6 For a = 42 For a = 42 For a = 8 For a = 18
÷ (a – 10)
9. Choose the right answers.
A game console costs x rupees, and a game costs y rupees
What does expression 2x + y mean?What does expression 2x = y mean?
Cost of two consoles and a game
Cost of a game and two consoles
The difference in cost of two consoles and a game
The equality of cost of two consoles and two games
The equality of cost of a console and two games
The equality of cost of two consoles and a game
10. Make the formula for the perimeter of the triangle.
Usually the perimeter is represented by the Latin letter P
11. Make an expression and solve it.
12. Solve the given equations.
a) 14 + x = 48
b) 59 – x = 38
c) x – 34 = 27
d) 6x = 108
e) x ÷ 13 = 15
f ) 196 ÷ x = 14
g) 5x + 3 = 128
h) 178 – 3x = 142
i) 19x – 13 = 6
j) 9x + 12x – 5 = 79
k) 23x – 12x + 10 = 32
l) 16x – x = 150
12. INTRODUCTION TO RATIO AND PROPORTION
DATA H ANDLIN G
UNDERSTANDING RATIO
1. Circle the right answer.
a) There is one big fish per four small fish. The ratio of the number of big fish to the number of small ones is ...
:
b) There are three small fish per one big fish. The ratio of the number of small fish to the number of big fish is ...
2. Circle the right statement.
The number of bananas refers to the number of monkeys as four to one.
The ratio of the number of monkeys to the number of bananas is 1 : 2.
The ratio of the number of monkeys to the number of bananas is 2 : 1.
There are eight bananas per one monkey.
The ratio of the number of bananas to the number of monkeys is 4 : 1.
The number of monkeys is four times larger than the number of bananas.
The ratio of the number of monkeys to the number of bananas is 3 : 2.
The number of monkeys refers to the number of bananas as two to five.
There are three bananas per one monkey.
a) … as 1 : 1
3. Colour the flag to have the ratio of blue to pink…
b) … as 5 : 3
c) … as 1 : 3
d) … as 5 : 1
4. Circle the right picture (pictures).
a) The ratio of donuts to cupcakes is four to one
b) The ratio of purses to coins is 1 : 3
c) The ratio of tomatoes to plates is 2 : 1
a) 1 : : :
5. Write the ratio of hares to carrots.
6. Solve the problems.
a) The most convenient ratio of the height of the step to its length is 1 : 2. The optimal height of one step is 150 mm. What is the length of a step?
The answer:
The answer: mm
b) Dino takes pictures on the camera. The ratio of frame height to the frame width is three to four. What is the width of all photos with height 9 cm?
UNDERSTANDING PROPORTION
7. Write the correct ratio.
The ratio of the number of floors in the blue building to the number of floors in the orange building is
8. Circle the right pictures then circle the right ratio.
There are 2.5 times more glasses with orange juice than with apple juice. The ratio of the number of glasses with orange juice to the number of glasses with apple juice is
5 : 22 : 5 5 2
9. Circle the right pictures then write the ratio.
There are 3.5 times more carrots than aubergines. The ratio of the number of carrots to the number of aubergines is
10. Circle the right picture then circle the right ratio.
Number of balloons takes of number of cacti. The ratio of number of balloons to number of cacti is
11. Circle to make a definition.
UNITARY METHOD
12. Solve the problem using unitary method.
Amrit picked 15 bananas in 20 minutes. How many bananas does he pick in 3 minutes?
The answer:
DATA H ANDLIN G 13. SYMMETRY
LINES OF SYMMETRY
1. Look at the shapes. Write whether they are symmetrical or non-symmetrical.
2. Draw and write the number of line (lines) of symmetry for each shape.
a) Lines of symmetry =
b) Lines of symmetry =
c) Lines of symmetry =
d) Lines of symmetry =
REFLECTION AND ROTATIONAL SYMMETRY
3. Circle the picture that looks the same in its mirror image.
4. Draw the reflection of the figures along the mirror line.
14. CONSTRUCTION OF LINE SEGMENTS AND ANGLES
DATA H ANDLIN G
CONSTRUCTION OF LINE SEGMENTS
1. Use a ruler to draw line segments of the given length.
a) 7.3 cm b) 2.9 cm c) 5.5 cm
Perimeter =
2. Construct a rectangle ABCD of length 6 cm and width 2 cm using a ruler, compass and protractor. Find its perimeter and area.
Area =
3. Construct a copy of a line segment.
4. Given OP = 1.7 cm and KM = 2.9 cm, construct line segments such that:
a) CM = 4KM – 2OP = 4 × 2.9 – 2 × 1.7 =
b) LH = 2OP + KM
c) DG = 3 × (OP+KM) – 4KM b) A C B D
CONSTRUCTION OF ANGLES
5. Construct the perpendicular to AB passing through point F using a ruler and a compass.
6. Construct the perpendicular to KM passing through point L using a ruler and a compass.
a) 128°
7. Construct the angle bisectors of ABC and POQ.
8. Draw the angles of given measures. Construct their angle bisectors.
b) 90°
a) 30°
9. Draw the angles of given measures using only a ruler and compass.
b) 60°
c) 90°
d) 120°
ANSWERS
1. Large Numbers and Operations
1. 2 — ten thousands, 3 — thousands, 1 — hundreds, 6 — tens, 9 — ones
2. 1st column: 8025 14,001 2nd column: 906 482 3012
3. 1st column: 4000 + 800 + 70 + 1; 10,000 + 300 + 80 + 2 2nd column: 1,00,000 + 1; 3,00,000 + 70,000 + 1000 + 900 + 30 + 8
4. 1st column: 2160 2160 2150 2nd column: 4500 4600 4500 3rd column: 4000 5000 5000
5. 5482 � 5500 8256 � 830 3078 � 3080
6. 1st column: 6687 — 6700; 687 — 690; 6187 — 6000; 68,187 — 70,000 2nd column: 4612 — 4600; 46,612 — 47,000; 41,266 — 40,000; 46,118 — 46,120
7. Chandigarh: 9,60,800 — 9,61,000 Moradabad: 8,89,800 — 8,90,000
Bhiwandi: 7,11,300 — 7,11,000
Noida: 6,42,400 — 6,42,000
Asansol: 5,64,500 — 5,64,000
Kurnool: 4,30,200 — 4,30,000
Dhule: 3,76,100 — 3,76,000
Purnia: 2,80,500 — 2,81,000
8. a) 193 g; b) 368 g; c) 285 g
9. a) Lalit; b) Puneet
10. 1st column: 579 618 404 619 232 197 2nd column: 691 831 204 816 110 866
—
—
—
—
—
—
—
—
—
—
—
(pages 1–7)
—
—
14. 1st column: 55,657 41,326
5,00,468 86,265
2nd column: 40,766 83,935 25,845 20,547
15. 70; 40; 120; 50
16. 1st spider: 208 — 215; 284 —
291; 163 — 170
2nd spider: 130 — 125; 167 — 162; 206 — 201; 118 — 113
17. 1st column: 39,109 33,578 4,99,714 84,069
2nd column: 37,088 81,373 9153 15,005
18.
19. 5040 — 1260 — 420 — 60 — 10 — 5
20. 1st column: 36 84 88 160
2nd column: 312 301 17 21
3rd column: 18 19 16 14
21. 1st column: 7052 7106 68,400 10,824
2nd column: 13,728 15,639 10,808 1338
3rd column: 25 16 253 39
22. 1st column: 26,768 49,203
10,692 16,898
2nd column: 15 439 503 56
3rd column: 18 26 27 91
23. 28; 92; 0 24. 65; 92; 17; 67
25. 8,64,000 26. 11,400
27. 136 28. 11,799 29. 93
2. Patterns in Whole Numbers (pages 8–23)
1. 1st line: 295; 305;335
2nd line: 607; 597;567
3rd line: 277; 247; 237
2. a) 5 b) 14 c) 11 d) 14 e) 8 f) 39
3. a) 100; 250 b) 15; 20; 35 c) 500; 1500; 3000
4. a) 5 b) 1 c) 42 d) 0 e) 24 f) 0 g) 2025 2025 8472 3717 h) 831
5. 27
6. 1st column: 512; 405; 243; 240; 36
2nd column: 224; 320; 324; 31; 21
7. 1st column: 16 256 1024
2nd column: 25 125 625
3rd column: 100 1000 1,00,000
3. Playing with Numbers: Factors and Multiples
1. a) 7; 2 b) 1; 19 c) 12; 3 d) 1; 67
2. a) 18; 36 b) 43; 86 c) 71; 142 d)103; 206
3. 1st column: F. 1 2 23 46
M. 46 92 138
2nd column: F. 1 2 4 8 16 32
M. 32 64 96
3rd column: F. 1 5 25
M. 25 50 75
4th column: F. 1 2 4 7 8 14 28 56
M. 56 112 168
4. Odd 5. Odd
6. Odd: 73; 85; 51; 37; 1; 67; 31
Even: 14; 42; 2; 102; 52; 88; 8
7. even + even even + odd odd + odd even * odd even * even odd* odd
8. 1 — 2 — 7; No; No
9. a) No b) Yes c) No d) No e) No f) Yes
10. 2
11. a) prime b) prime c) composite d) prime e) composite f) composite
12. 10; 20; 30; 40; 50
13. 1) False 2) True 3) True
14. 5; 10; 15; 20; 25; 30; 35; 40; 45; 50
15. 1) True 2) False 3) True
16. 22; 24; 26; 28; 30; 32; 34; 36; 38; 40; 42; 44; 46; 48; 50
17. 1) True 2) False 3) True
18. 1) last digit 2) sum of its digits
3) last digit 4) sum of its digits 5) last digit even odd even even even odd
(pages 9–33)
19. 240 420 480 840
20. 12 21 102 120 201 210
21. 24 42 54 552
and 36
and
and
24. 12 6 24 3
25. Factors of 8125: 1 8125 25 5 13 125 325 1625 625 65 Factors of 6220: 1 6220 20 311 2 3110 10 622 4 1555 5 1244
26. 1. 6 boys, 5 girls 2. No
27. 12: 3 12 8: 2
The highest common factor of 12 and 8 is 4
28. 6: 2 3 10: 5
The highest common factor of 6 and 10 is 2
29. 15: 3 16: 4 16
The highest common factor of 15 and 16 is 1
30. 4: 12 20 6: 12 24
The lowest common multiple of 4 and 6 is 12
31. 3: 6 9 2: 4 12
The lowest common multiple of 3 and 2 is 6
32. 5: 5 20 3: 3 9
The lowest common multiple of 5 and 3 is 15
33. LCM — the lowest common multiple
34. HCF — the highest common factor
35. a) True HCF 1; b) False HCF 7
36. c) 56 and 39; d) 27 and 58 e) 32 and 33
37. a) 1 b) 4 c) 6 d) 2 e) 5 f) 3 g) 7 h) 5 i) 7 j) 1
38. a) 8 b) 12 c) 9 d) 28 e) 30 f) 18 g) 110 h) 52 i) 18 j) 75
4. Lines, Angles and Shapes
1. Point; Curved; Straight
2. Curved; Straight
3. Ray; Line segment
4. 6 5. 4 6. a; CD 7. D; K; E
8. Infinitely many straight lines
9. Only one straight line
10. Infinite; Infinite; Infinite; One
11.
13. АС 14.
15. Two; Point
16. a) b)
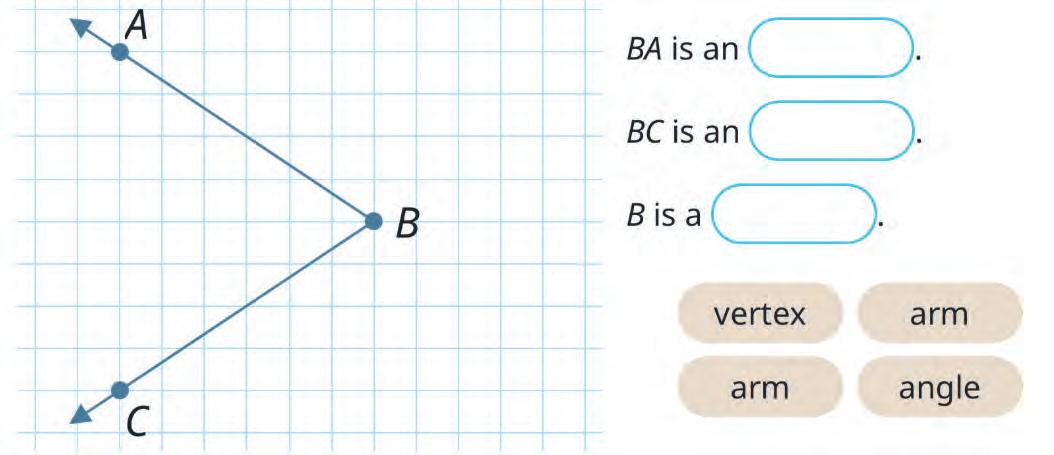
17. BA is an arm; BC is an arm; B is a vertex
18. BA; BC; ABC
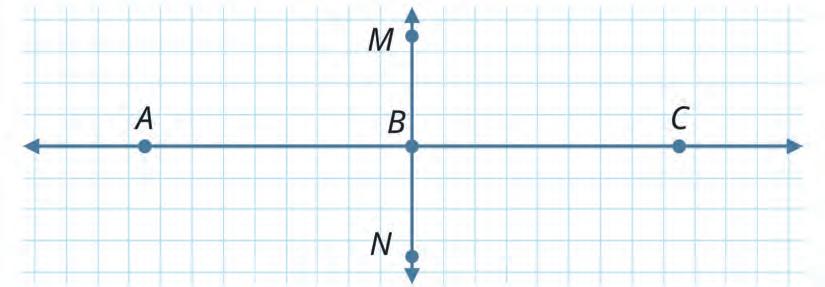
19. Straight angles: ABC; NBM Right angles: NBC; MBC; ABM; ABN
20. 21. 22.
23. The pink figure: 3; 3
The green figure: 4; 4
The blue figure: 5; 5
24.
25. 26. Pentagon; Hexagon; Quadrilateral
(pages 40–54)
27. 1) one, right-angle
2) one, obtuse 3) all, acute
28. 1) two, equal 2) all, equal
29. Both are right
30. a) AB, BC: side AC: base b) FD, DE: side FE: base
31.
32. ACD; COD 33. ESK; CBO
34. CO and CD; AB and AE
35. Both are right
40. 1) Semicircle 2) Concentric
5. 3-D Shapes
2. 1) 8; 5 2) faces; edges 3) 6; 10 4) faces; 7
Chord
a; b; c; e; f; h
6. Integers
1. a) 11 ̊C b) –18 ̊C c) 26 ̊C
2. 15 ̊C 3. –5 C 4. a) 50 b) –10
5. a) 0 b) –11 c) 90
6. a) –6 b) 8 c) –3 d) –9
7. a) minus eight b) fifteen
c) minus six
8. –4; 112
9. a) 9 — 9 b) 4 — 4
10. 1st column: –32 –(–(–35))
–(–(–(–(–4))))
2nd column: –(–31) 12
–(–(–(–12)))
11. a) odd b) even
12. a) –3 b) 12 c) –4
d) 0 e) 6 f) –2
13. a distance from 0 to a
14. a) 9 b) 5 c) 0 d) 13 e) 9 f) 8
15. Opposite
16. a) a = –5 b) 0
c) a = 5; b = –5 d) 0
17. 1st column: 50; 110; –42; 4; 0
2nd column: 21; 5; 34; 23; 15; –7
20. –3 < 2; 0 < 4; –4 < 0
–4–3 24 0
18, 19
21. a) –6 b) 0 22. 1) True 2) False
23. 1st column: 9 > –6 72 > –79
2nd column: |9| > |–6| |72| < |–79|
24. a) –7= –|–7| b) –(–7) > –7
c) –|7| > |–7| d) –|–3| > 2
e) 3 > –2 f) |–3| > |–2|
g) 0 < |–9| h) –(–5) =|–5| i) |4| > 0
25. a) –2 b) 2 c) -3 26. a) –3 b) –7 c) –4
27. a) right b) left 28. down; 4 + (–8)
29. less; (–20) + 14
30. a) the positive number has a larger absolute number b) always negative
c) the negative number has a larger absolute number
(pages 68–83)
24 + 47
–49 + 14
–5 + 5
–29 + 18
–3 + 25
15 + (–22)
4 + (–4)
–43 + (–5)
32 + (–9)
84 + 26
–74 + 21
32. 1st column: 0; 13; (–4)
2nd column: 25; –9; –5
3rd column: –14; –12; –7
33. a) –12 b) –50 c) 34 d) 44 e) 0
f) 0 g) 127 h) 123 i) –62 j) –119 k) 40 l) 33 m) –1 n) –7
34. 4 – 10; 4 + (–10)
35. opposite to b; a – b = a + (–b)
36. add –5 — subtract 5 multiply by 10 — multiply by 2... subtract 10 — add –10 add 3 and then add 2 — add 5
37. 10 + 1 = 11
38. a) smaller b) larger
39. a) 35 b) 25 c) 19 d) 29
–40 + 4 –24 + 24 –18 + (–18) –45 – 26 –13 + 15
–31 – (–12) –21 – (–26) 43 + (–5) 57 – (–68) 82 + (–91) 13 + (–13)
42. 1st column: 0; (–10); 12
2nd column: 16; –21; –20
3rd column: 16; 5; 33
43. a) 1 b) 0 c) 6 d) 15 e) 14 f) –77 g) –50 h) 108 i) 72 j) 39 k) 42 l) –3 m) –11 n) 56
44. 4 1st column: –4; 4 2nd column: 4; 4
45. 9 1st column: –9; 9 2nd column: 9; 9
46. x – y > 0; y – x < 0; |x – y| > 0; |y – x| > 0
47. c – d < 0 d – c > 0 |c – d| > 0 |d – c| > 0 yx
48. positive 49. |a – b| 50.
6. Proper fractions:
Improper fractions: Mixed fractions:
numerator denominator whole p × denom × numer. denominator whole part =
numerator denominator remainder deniminator = whole part
7. Fractions
3. a) whole part b) numerator c) denominator d) fraction part e) fraction bar f) mixed fraction
4. a) four whole three fourth b) one whole one half

27. a) Correct; b) Incorrect; c) Incorrect.


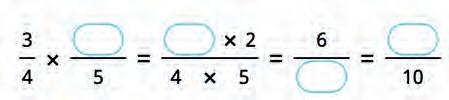
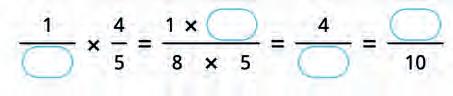
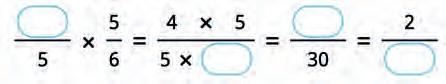
36. a) correct; b) incorrect; c) incorrect.
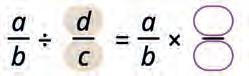
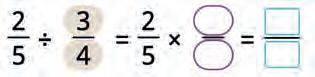

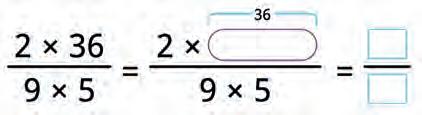
8. Decimals
10. 1) 1.463 < 2.456 2) 2.76 > 2.2933
3) 401.34 > 41.34 4) 528.2 > 52.82
5) 49.1 > 49.01
11. 1) 0.726 < 0.734 < 0.738
2) 9.21 > 9.14 > 9.11
3) 83.39 < 83.41 < 83.42
4) 57.2 < 57.3 < 57.4 5) 82.406 < 82.506 < 82.606
12.
18. a) b)
0.46 = 46 100 = 23 50
0.76 = 76 100 = 19 25
0.8 = 8 10 = 4 5 0.256 = 256 1000 = 32 125
13. a) b)
19. c) d)
21. a) correct b) incorrect c) incorrect
22. a) b)
+
14. a) wrong b) correct
15. to the end
16. a) wrong b) correct
17. 4.200 and 4.20
23. 1st line: 8.08; 9.99; 4.2 2nd line: 8.24; 6.82; 4.14
24. 1st column: 3137.1; 52510; 4243 2nd column: 921.52; 0.004781; 2.385
25. a) 3 tenths b) 1 hundredth c) 1 thousandth
26. 2
27. 1.11 3.12 2.14
28. 1st column: 4128; 0.93812; 189; 1.632
2nd column: 75; 43.75; 63.75; 1.6
9. Data Handling
1. 1) 7000 2) zebra 3) 70 2. 26 3. 320 4. 17
400 10. a) 3600 b) 2010 11. a) 8000 km² b) 6 o’clock c) 50 min 12. a) False b) True c) False
5. difference — 0.25 1. a) 16 cm b) 19 cm c) 23 cm 2. 9 cm
2 6 22
15 thous.
. 28 m
10. Mensuration
14 cm
a) 16 cm 16 cm² b) 20 cm 24 cm²
6. 1) Perimeter = AB+BC+CD+DA = = 8+11+8+11 = 38 cm
2) Area = AB×BC = 8×11 = 88 cm²
7. Perimeter = 30 m Area = 37.5 m²
8. Perimeter = 62 m Area = 165.5 m²
9. 12 m²
11. Introduction to Algebra
1.
2. a) 105+360 b) 107-85 c) 145×68 d) 305÷23
3.
of four and two
of four and two
of four and two Divide four by two
4. b) a+11×6 c) 250 d) a×140+x=b
5. Yes: 75+a+43 765×765 – n⁷⁶⁵
8. a) 54 5 13 b) 1 -16 4
9. 1st column: cost of two consoles and a game 2nd column: the equity of cost of two consoles and a game
10. P=3a
11. P = 3a = 3×3b = 9b
12. a) x = 34 b) x = 21 c) x = 61
d) x = 18 e) x = 195 f) x = 14
g) x = 25 h) x = 12 i) x = 1 j) x = 4 k) x = 2 l) x= 10
12.
Introduction to Ratio and Proportion
1. a) 1:4 b) 3:1
2. a) The ratio of the number of monkeys to the number of bananas is 1:2
No: 6 – – 7 34+n$ 6. 7.
Sum of seventy five and n
Quotient of x and seventy five
Difference of forty three and n
Product of x and forty three
Product of x and twenty five
Difference of eighty four and n
Quotient of x and eighty four
Sum of twenty five and n
b) The ratio of the number of bananas to the number of monkeys is 4:1 c) The number of monkeys refers to the number of bananas as two to five 3. a) b)
5. a) 1:4 b) 2:3 c) 1:1
6. a) 300 mm b) 12 cm
7. 2
8. 5:2 9. 7:2 10. 1:4
11. non-zero quotient
12.
15 20 = 3 4 3 4 × 3 = 9 4 = 2 1 4
13. Symmetry
1. a) symmetrical b) non-symmetrical c) symmetrical d) symmetrical
2. a) 2 b) 0 c) 0 d) an infinite number of lines of symmetry
14. Construction of Line Segments and Angles
1. a) 7.3 cm b) 2.9 cm c) 5.5 cm
2. Perimeter = 16 cm Area = 12 cm²
6
3. a) b)
4. a) CM = 8.2 cm b) LH = 6.3 cm c) DG = 2.2 cm
5.
6. C L D


