9789144196473

RIK MATEMATIK FKA LÄRARPAKET

Tryckt bok + Digital lärarlicens 36 mån

LÄS OCH PROVA

LÄRARPAKETETS

SAMTLIGA DELAR

RIK MATEMATIK FKA LÄRARPAKET

Tryckt bok + Digital lärarlicens 36 mån

Rik matematik är utvecklat för en undervisning där både elever och lärare är aktiva. Eleverna får resonera, diskutera och lösa problem, och utveckla en djupare förståelse för matematik.

LÄRARHANDLEDNING

I lärarhandledningen får du det stöd och de resurser du behöver för att planera och genomföra din undervisning. Det finns mer än 80 detaljerade lektionsförslag per läsår, som ger konkret stöd och tips på saker att betona, frågor att ställa och exempel att visa. Bildspelen, som hör till varje lektion, fungerar som ett stöd genom hela lektionen, både visuellt för att fånga elevernas uppmärksamhet och för att tydliggöra matematiken med pedagogiska animeringar och bilder.

I lärarhandledningen finns även avslutslappar, extra övningsblad m.m.

DIGITALT LÄROMEDEL

Det digitala lärarmaterialet är ett komplement till den trycka lärarhandledningen. Här finns alla digitala resurser samlade, samt kom igång-hjälp och annat stöd som du kan behöva.

Interaktiv version av lärarmaterialet, i vilken det går att söka, stryka under, anteckna och länka.

Fungerar på dator och surfplatta.

Lärarhandledning

Andreas Ryve

Manuel Tenser

Patrik Gustafsson

Hillevi Gavel

Fredrik Blomqvist

Innehållsförteckning

Välkommen till Rik matematik f-klass

Med Rik matematik f-klass får du som lärare ett bra stöd i att lära eleverna grundläggande matematik, samtidigt som du förbereder dem för matematikundervisningen i högre årskurser. Läromedlet ger dig stöd att bedriva en rik och varierad undervisning där eleverna får resonera, lösa problem, diskutera, tänka och räkna. På så sätt utvecklar de förståelse för matematiken samtidigt som de lär sig att räkna. Vi kallar det rik matematikundervisning.

Rik matematikundervisning är en förståelseorienterad undervisning där eleverna utvecklar förståelse för matematiska begrepp i samspel med dig som lärare, och i samspel med sina klasskamrater, innan de färdighetstränar i boken för att befästa det som de har lärt sig. I rik matematikundervisning håller du som lärare ihop klassen kring samma matematiska innehåll för att kunna ha ett levande matematiskt samtal i klassrummet, samtidigt som du kan utmana elever på olika nivåer vid behov.

Lärarhandledningen har därför många detaljerade lektionsförslag med bildspel till varje lektion som hjälper dig att visualisera, förklara, utmana och resonera med eleverna om den matematik ni arbetar med. Elevboken är full av uppgifter och problem, så att eleverna kan färdighetsträna, och på lärarwebben finns resurser, såsom extra färdighetsträning, avslutslappar, diagnoser och kopieringsunderlag av olika slag som du kan skriva ut vid behov.

Välkommen till Rik matematik!

Introduktion

Så här fungerar Rik matematik f-klass

Områden och lektionsserier

Rik matematik f-klass är uppdelat i områden. Varje område fokuserar på olika delar av matematiken, såsom taluppfattning, mönster eller geometri. Varje område inleds med en områdesintroduktion, där vi går igenom vad det är för matematik som området handlar om och hur undervisningen i området är upplagd. Det är alltid bra att läsa områdesintroduktionen när ni ska börja arbeta med ett nytt område.

Ett område består av ett antal lektionsserier. En lektionsserie består av fyra detaljerade lektionsförslag, och till varje lektion finns ett färdigt bildspel. Bildspelet laddar du ned från lärarwebben där du också kan ladda ner och skriva ut andra resurser, såsom material för extra färdighetsträning och ”avslutslappar”.

En lektionsseries uppbyggnad

Varje lektionsserie har ett antal lärandemål som visar vad eleverna ska lära sig under arbetet med lektionsserien. Lärandemålen hjälper dig som lärare att planera och genomföra undervisningen, baserat på lektionsförslagen.

En lektionsserie består alltså av fyra lektionsförslag med bildspel. I den första lektionen introduceras det nya matematiska innehållet som eleverna ska arbeta med och lära sig under lektionsserien. Bildspelet ger dig som lärare stöd att visualisera, förklara och diskutera den matematik som är i fokus. I den andra och tredje lektionen får eleverna öva, ofta genom lek eller spel och genom att arbeta i elevboken. I den fjärde och sista lektionen i lektionsserien sammanfattas de viktigaste lärdomarna, och eleverna repeterar och tilllämpar dem. Här får eleverna också göra avslutslappen som ger dig stöd att bedöma elevernas kunskaper.

Lektionsförslagen och undervisningen

Lektionsförslagen ger en detaljerad bild av hur du med hjälp av bildspelet skulle kunna hålla lektionen. Tänk på att det är ett förslag, inte ett manus som du ska försöka memorera och följa till punkt och pricka.

När du har en tydlig bild av lektionen använder du bildspelet som stöd för att visualisera och förklara matematiken, men också som stöd för att du själv ska komma ihåg lektionen på ett ungefär. Det räcker för att du ska lyckas med undervisningen, så länge du har fokus på lärandemålen och använder bildspelet som stöd. En lektion blir aldrig precis så som man har tänkt sig, så var därför beredd att göra anpassningar vid behov för att ge eleverna så goda förutsättningar som möjligt för att nå lärandemålen.

I lektionsförslagen får du också konkreta uppslag på hur du kan förklara saker, frågor du kan ställa, exempel du kan visa och så vidare. Du kan ha lärarhandledningen liggandes uppslagen på katedern så att du kan snegla på lektionsförslaget under lektionen.

Lektionernas struktur

Alla lektioner har samma struktur. De inleds alltid med en uppstartsfas. Här repeterar ni det viktigaste i föregående lektion innan eleverna får möta innehållet i den nya lektionen, ofta genom en lärarledd genomgång med stöd av bildspelet.

I aktivitetsfasen sker huvudparten av lektionsarbetet. Arbetet är varierande med många olika typer av aktiviteter. Ofta har de inslag av att eleverna diskuterar och resonerar, räknar och löser problem, ofta i grupp eller i par. Här har du som lärare en viktig roll i att utmana elever, ställa frågor för att stimulera tänkande och diskussion, fånga upp och bygga vidare på elevernas egna tankar och styra mot det som eleverna ska lära sig.

I avslutsfasen sammanfattar du lektionen tillsammans med eleverna och lyfter upp det mest centrala som ni har arbetat med och lärt er.

Uppmärksamma och stötta

Sista sidan i varje lektionsserie ger dig tips och råd kring vanliga missuppfattningar och fel under rubriken Uppmärksamma och stötta. Läs detta innan ni börjar arbeta med en lektionsserie, så att du är beredd att hjälpa eleverna när du märker att de har en vanlig missuppfattning, eller gör ett klassiskt fel. Här finns också tips på hur du kan förenkla uppgifter för elever som har det behovet – eller utmana mer för de elever som behöver det.

Avslutslapparna

Varje lektionsserie avslutas med att eleverna gör en avslutslapp. Den innehåller ett litet antal noggrant uttänkta uppgifter som gör att du snabbt och enkelt kan bedöma om eleverna har nått lärandemålen. Du ser också om det är något som många i klassen har svårt för och som du behöver undervisa mer om, eller om det finns elever i klassen som behöver arbeta extra med något.

Lärartaktiker

I de detaljerade lektionsförslagen använder vi vissa nyckelord för att på ett mer effektivt sätt kommunicera instruktioner till dig. Ett sådant nyckelord kan vara återge, och det ser då ut så här: ÅTERGE

Nyckelorden är namn på olika lärartaktiker. En lärartaktik är något du kan göra för att åstadkomma ett visst resultat. Om det t.ex. står att du ska låta någon återge så betyder det att en elev ska återge vad någon annan elev just sagt, fast med egna ord. Återge är en lärartaktik som du kan använda för att signalera att det som sades är viktigt.

På lärarwebben hittar du ett ramverk med förklaringar av alla lärartaktiker.

Klassrumsnormer och Professor Uggla

Rik matematikundervisning ställer höga krav på ett gott klassrumsklimat. Det är därför viktigt att du arbetar systematiskt och enträget med att skapa bra normer i klassrummet så att eleverna vågar berätta vad de tänker, är tysta och lyssnar när någon annan har ordet, och så vidare. Vi kallar detta rika klassrumsnormer

Karaktären Professor Uggla kommer att dyka upp då och då i bildspelet och hjälpa till. Uggla kommer bland annat att förklara att en matematiker är en person som arbetar med matematik, och på matematiklektionerna så är eleverna matematiker. Professor Uggla kommer att berätta om hur matematiker tänker och arbetar, vilka regler de har att följa i matematikarbetet och varför det är viktigt att följa reglerna.

Läs mer om rika klassrumsnormer i ramverket för normer som finns på lärarwebben.

Konkret material

Ni kommer ofta att arbeta med konkret material i lektionerna. På lektionsseriernas förstasidor kan du alltid se vilket material som behövs till varje lektion. Ibland är det något som du kan skriva ut ifrån lärarwebben, ibland är det konkret material som du behöver ordna med själv, som kuber eller andra typer av plockisar.

På lärarwebben hittar du en sammanställning av vilka olika typer av material som behövs.

Förstå läromedlets grundtankar

Det är viktigt att förstå grundtankarna med det läromedel man använder. Rik matematik är designat för att ge dig stöd att bedriva rik matematikundervisning. I rik matematikundervisning ligger tyngdpunkten på att eleverna lär och utvecklas i samspel med läraren och med varandra, under lärarledd undervisning. När de arbetar i boken färdighetstränar de primärt för att befästa kunskaper och förståelse som de redan har utvecklat under den lärarledda undervisningen.

Om du tidigare har arbetat med ett läromedel där tyngdpunkten ligger vid att eleverna lär sig genom att arbeta var för sig i elevboken så kommer du förmodligen uppleva att det är väldigt annorlunda att arbeta med Rik matematik. Du får vara beredd på att delar av arbetssättet kommer att kännas lite ovana, och att du måste ge dig själv tid för att komma in i det delvis nya arbetssättet. Tänk då också på att det är vanligt att man har föreställningar, normer, rutiner och vanor som ibland kan vara ett hinder för att utveckla sin undervisning. Ta dig an Rik matematik med lite tålamod och ett öppet sinne.

Lärarens viktiga roll

I rik matematikundervisning har du som lärare en central roll för elevernas kunskapsutveckling, inte minst genom lärarledd undervisning. Du planerar undervisningen, baserat på lektionsförslagen och bildspelen, och undervisar genom att visa och förklara, utmana och ställa frågor, leda matematiska samtal och diskussioner, summera och synliggöra viktiga samband, bedöma och uppmuntra, skapa struktur och normer. Allt detta är lättare sagt än gjort, men Rik matematik är utvecklat av forskare och lärare för att ge dig förutsättningar att lyckas med det.

Lektionsförslag, inte manus

Se lektionsförslagen som just förslag, inte som manus som du ska försöka memorera och följa till punkt och pricka. Det är inte tanken, och det är heller inte möjligt. Utgå istället ifrån lärandemålen, läs lektionsförslagen för att få en god bild av lektionen och använd bildspelen som stöd för minnet när du undervisar. Gör anpassningar av lektionen vid behov, både innan och under pågående lektion, utifrån just din klass och dina elever, och styr mot den matematik som de ska lära sig.

Målfokus istället för sidfokus

I arbetet med Rik matematik är det viktigt att ha fokus på vad eleverna ska lära sig istället för hur långt de har kommit i elevboken. Det är viktigt att ha målfokus istället för ”sidfokus”. Alla elever behöver inte göra alla uppgifter, och det är viktigt att eleverna inte tror

att matematik handlar om att räkna så mycket som möjligt på så kort tid som möjligt. Matematikämnet handlar om mer än så. Eleverna ska inte bara lära sig att räkna, de ska också utveckla förståelse för matematiken så att de kan använda den i olika sammanhang.

Elevboken

Det är en vanlig missuppfattning att alla elever måste göra alla uppgifter i elevboken, under eller efter lektionen. Det är inte nödvändigt. Det räcker oftast att ha som ambition att alla gör de första grundläggande uppgifterna. Om du då har elever som är snabba går de vidare till extrauppgifterna och de mer utmanande uppgifterna. Om du bedömer att en elev har nått lärandemålen med en lektionsserie så spelar det ingen roll om eleven endast gjort uppgifter på grundläggande nivå.

När snabba elever räcker upp handen och anser sig klara med alla uppgifter måste du också kontrollera om de verkligen har löst uppgifterna med tillräcklig noggrannhet. Utmana dem att vara noggranna istället för snabba genom att låta dem göra om slarvigt eller felaktigt utförda uppgifter och uppmana dem att i fortsättningen vara noggranna från början.

Ta vara på spontana tillfällen till lärande

I vardagen dyker många tillfällen till lärande upp då du kan passa på att knyta an till matematik som ni har arbetat med tidigare eller håller på med just nu. Det kan vara när ni står i kö i matsalen, och t.ex. kan arbeta med skillnaden mellan antal och ordningstal. Det kan vara när ni ser föremål eller former som ni kan resonera om utifrån ett geometriskt perspektiv.

Arbeta långsiktigt och med tålamod

Arbeta med tålamod och långsiktighet. Stressa inte upp dig om arbetet med läromedlet inte fungerar perfekt direkt. Rik matematikundervisning är mer utmanande än att låta eleverna sitta och räkna var för sig i boken större delen av tiden. I takt med att ni – du och eleverna – lär er hur Rik matematik fungerar och kommer in i arbetssättet så kommer det att gå lättare. Ta hjälp av det stöd som finns på lärarwebben och hos Rik matematik-kollegor för att snabbare komma in i arbetssättet. Skriv till oss på Rik matematik-sidan på Facebook om du behöver råd och stöd.

Digitalt stöd

Det digitala stöd som hör till lärarhandledningen finns i din digitala lärarresurs. Lärarresursen når du via licensen som du får när du köper lärarhandledningen. Inloggning sker på sidan "Min bokhylla" som finns på studentlitteratur.se.

För att visa bildspelen (ppt) som inleder varje lektion, laddar du först ner dem till din dator och öppnar sedan upp dem med Powerpoint.

Bildspelen är ofta animerade. Se till att starta bildspelen så att du får en verklig bild av hur de ser ut.

Om din skola inte har en installerad version av Powerpoint kan du använda den webbaserade gratisversionen av Powerpoint.

Om du arbetar med en Chromebook kan du se filmen nedan för att lära dig om hur du då startar upp bildspelen.

Så här fungerar bildspelen i Rik matematik

Så här fungerar de webbaserade bildspelen i Rik matematik

Så här fungerar Rik matematiks bildspel med Chromebook

Ikoner i lärarhandledningen

Förmågeikoner

Ikonerna visar vilken/vilka förmågor som lektionen direkt utvecklar.

Begreppsförmåga

Kommunikationsförmåga

Metodförmåga

Problemlösningsförmåga

Resonemangsförmåga

Konstellationsikoner

Dessa ikoner visar i vilken konstellation en aktivitet är tänkt att genomföras i.

Undervisning under lärarens ledning

Enskilt arbete

Enskilt arbete i elevboken

Arbete i par

Arbete/diskussioner i grupp

Övriga ikoner

Här kommer du direkt till bildspelet.

Ljudfil i bildspelet

Visar att det finns en särskild funktion i bildspelet och att läraren måste klicka på ett särskilt sätt för att använda funktionen.

Stanna upp innan du klickar fram svaret. Fråga hur ni kan göra.

BETÄNKETID

Film

Dokumentet kan laddas ner.

Övrigt

Referat av det som sägs av berättarrösten

Extra information

Guldkantslektion

F-klass A – översikt

Sammanfattning av F-klass A

Rik matematik f-klass A består av fyra områden. Varje område innehåller ett antal lektionsserier. En lektionsserie består av fyra lektioner.

I område 1, Mönster, kommer ni att arbeta med mönster på olika sätt. Eleverna kommer att få lära sig vad ett mönster är, hur man kan lista ut vad i ett upprepat mönster som upprepar sig och hur man då kan fortsätta mönstret. De kommer även få lära sig att man kan visa ett och samma mönster på olika sätt.

I område 2, Antal och räkning, börjar du utveckla elevernas grundläggande taluppfattning. De får träna på räkneramsan, och på att räkna ett mindre antal saker och säga hur många det är. Eleverna kommer att få öva på subitisering, dvs. att se hur många det är av något när det är ett litet antal saker som visas, och säga hur många det är utan att räkna. De får också börja jämföra antal och lära sig att beskriva antal med begrepp som fler än och färre än

I område 3, Tal som antal och ordning, börjar eleverna arbeta lite mer formellt med tal och hur man kan visa tal med siffror. De får också lära sig hur man kan använda tal för att visa hur många det är av något, dvs. antal, och hur man kan använda tal för att visa vilken plats i ordningen något har, dvs. ordningstal

I område 4, Talraden 0–10, får eleverna upptäcka talraden och lära sig hur man kan använda talraden och talgrannar för att jämföra tal. Eleverna får också lära sig hur man kan använda talen 5 och 10 som ankartal, med hjälp av 5-rutan och 10-rutan, för att säga hur mycket större eller mindre olika tal är jämfört med talen 5 och 10.

4: Talraden 0–10

Område 1 Mönster

Område 1: Mönster

Mönster är det första området som ni kommer att arbeta med i matematikundervisningen. Det är ett spännande möte med en viktig aspekt av matematik där eleverna kommer att utveckla en grundläggande förståelse för mönster och lära sig att hantera mönster på olika sätt. Både du och dina elever kommer också att börja lära er hur arbetet med Rik matematik fungerar. Karaktären Professor Uggla kommer ibland att dyka upp i bildspelen för att berätta för eleverna om viktiga regler och hur man gör på matematiklektioner.

Sammanfattning av området

I områdets första lektionsserie får eleverna lära sig vad upprepade mönster är. De kommer att få kopiera och fortsätta enkla upprepade mönster.

I den andra lektionsserien kommer eleverna att få lära sig hur de kan lista ut vilken regel ett enkelt upprepat mönster har, så att de kan visa vilken del av mönstret som upprepas eller fylla luckor i mönstret. De kommer också att få översätta upprepade mönster från en representationsform till en annan, exempelvis omvandla ett mönster som består av pärlor i två olika färger till ljud som handklapp och stamp i golvet.

Översikt

Lektionsserie

till mönster

Lektion

Visa samma mönster på olika

Introduktion

Mönster finns överallt i vår vardag och i alla matematiska områden. Mönster finns i byggnader, i naturen, i musik och konstverk. Mönster finns också i matematiken, och dessa mönster kan ibland vara till stor hjälp när man ska lära sig matematik, eller använda matematik till något.

Att lära sig leta efter mönster för att sedan beskriva och utveckla dessa är en central del av matematiken och ett viktigt steg i att utveckla ett algebraiskt tänkande. Att låta eleverna leta efter eller skapa mönster, samt tolka, beskriva och utveckla dessa på olika sätt, är därmed en bra ingång i matematiken.

Om eleverna utvecklar sin förmåga att se och arbeta med mönster har de bättre förutsättningar att lyckas med matematiken i stort. Det handlar om att se mönster inom bland annat aritmetiken, hur olika räknesätt fungerar, och kunna generalisera det så att man kan använda matematiken på ett effektivt sätt i olika sammanhang

Upprepade mönster

Det finns många olika sorters mönster i alla möjliga sammanhang, också inom olika matematiska områden. Att arbeta med mönster i olika uttrycksformer, som olika föremål, färger, rörelser och ljud, kan bygga en grund för att senare kunna upptäcka och beskriva mönster med tal.

Vi har valt att i förskoleklass arbeta mestadels med upprepade mönster, vilket är en vanligt förekommande form av mönster även i vardagen. Upprepade mönster kan bestå av olika saker, t.ex. tal, bokstäver, färger, symboler, ljud, rörelser, etc.

Ett upprepat mönster med tal kan se ut så här:

1 1 2 1 1 2 1 1 2 1 1 2

Mönstrets regel och olika representationsformer

Alla upprepade mönster har en del som upprepar sig; en kärna. I läromedlet talar vi om det som att mönstret följer en regel som beskriver vad i mönstret som upprepas och hur. Regeln i mönstret ovan skulle kunna beskrivas som först kommer talet 1 två gånger, sedan kommer talet 2 en gång, och så upprepas det om och om igen.

Samma regel kan beskrivas på olika sätt, och samma mönster, baserat på regeln, kan också visas på olika sätt. Ett och samma mönster kan visas med olika representationsformer, som med tal här ovan eller som med asterisker i olika färger som i efterföljande text.

Att träna på att identifiera vilken regel ett upprepat mönster har och beskriva regeln med sina egna ord så att andra förstår, är avgörande för elevernas utveckling av förståelse för mönster.

Utveckla elevernas förståelse för mönster

Den planerade undervisningen om mönster följer en noggrant genomtänkt progression baserad på forskning om hur barn bäst utvecklar dessa kunskaper. Eleverna kommer att få:

• Kopiera mönster

Genom att eleverna får kopiera befintliga mönster lär de sig se mönster och avbilda mönster.

• Fortsätta mönster

Nästa steg är att eleverna får fortsätta befintliga mönster. Detta börjar på enklaste sätt med att eleverna får fundera på vilken färg nästa kula borde ha i ett mönster bestående av kulor i olika färger.

• Identifiera mönstrets regel

Därefter kommer eleverna att få lära sig att ett upprepat mönster följer en viss regel, t.ex. två gröna och en blå, och så upprepas det. Ett upprepat mönster med just denna regel kommer hela tiden ha två gröna som följs av en blå, som följs av två gröna, om och om igen.

* * * * * * * * * * * *

Eleverna kommer att få arbeta med att försöka lista ut vilken regel olika mönster har. De visar detta genom att ringa in den del av mönstret som upprepas. I exemplet ovan skulle eleverna då ringa in grön-grön-blå.

* * * * * * * * * * * *

Eleverna får också öva på att beskriva upprepade mönsters regler med ord. Regeln i mönstret ovan kan t.ex. beskrivas som ”två gröna och en blå, om och om igen”.

• Komplettera mönster

I nästa steg får eleverna arbeta med upprepade mönster där det finns luckor i mönstret. Eleverna ska då komplettera mönstret genom att lägga till de delar som ska finnas i luckorna. För att kunna göra detta måste eleverna ha utvecklat tillräckliga förkunskaper i de föregående stegen 1–3: de måste kunna se vad mönstret är och identifiera mönstrets regel för att kunna avgöra vad som ska finnas i luckan för att mönstret ska bli helt.

• Skapa egna upprepade mönster

Eleverna kommer att få skapa egna upprepade mönster. Du som lärare stöttar eleverna genom att ställa frågor som riktar elevernas uppmärksamhet mot det centrala: Varför är det här ett upprepat mönster? Kan

du visa mig vad i mönstret som upprepar sig? Hur skulle mönstret fortsätta?

• Översätta till andra uttrycksformer

Slutligen får eleverna arbeta med att översätta mönster från en representationsform till en annan. Detta utvecklar en djupare förståelse för mönster.

T.ex. kan mönstret

översättas till en annan representationsform, som

A A B A A B A A B

Representationerna av mönstret är olika, men regeln som styr vad som upprepas och hur är densamma.

Eleverna kommer att få använda flera olika representationsformer, dels olika symboler men också rörelser och ljud, t.ex. klapp och stamp.

Konkret material

Det kan underlätta elevernas utveckling av förståelse för mönster om de får arbeta med konkret material som representationsform för mönster. Konkret material kan vara kuber eller pärlor i olika färger eller storlekar. Att eleverna kan arbeta taktilt med mönstret, att de kan undersöka, kopiera, skapa eller fortsätta mönster fysiskt med sina händer, kan vara gynnsamt för utvecklingen av deras förståelse.

En fördel med det konkreta materialet är att eleverna enkelt kan testa olika varianter, justera och ändra på ett sätt som inte är möjligt när man använder papper och penna. När eleven sedan är nöjd med vad hen åstadkommit med det konkreta materialet kan hen dokumentera det med papper och penna. De fysiska materialen gör det också möjligt att arbeta med mönster som inte passar ett papper eller på en sida i boken.

Uppmärksamma mönster i omgivningen

Passa på när tillfälle ges att uppmärksamma och låta eleverna studera upprepade mönster som finns i omgivningen. Det kan vara mönster i byggnader, såsom tegelfasader eller hur fönster är placerade, hur träd är planerade eller andra fenomen i naturen. I vardagliga sammanhang finns massor av upprepade mönster att undersöka, t.ex. en veckas uppbyggnad i veckodagar, ramsor, musik, dans, etc.

Områdets referenser

Blanton, M., Brizuela, B. M., Gardiner, A. M., Sawrey, K., & Newman-Owens, A. (2015). A learning trajectory in 6-year-olds’ thinking about generalizing functional relationships. Journal for Research in Mathematics Education, 46(5), 511–558.

Blanton, M., Brizuela, B. M., Stephens, A., Knuth, E., Isler, I., Gardiner, A. M., ... & Stylianou, D. (2018). Implementing a framework for early algebra. In Teaching and Learning Algebraic Thinking with 5-to 12-Year-Olds (pp. 27–49). Springer, Cham.

Carraher, D. W., Schliemann, A. D. (2007). Early algebra and algebraic reasoning. Second handbook of research on mathematics teaching and learning, 2, 669–705.

Friel, S. N., & Markworth, K. A. (2009). A framework for analyzing geometric pattern tasks. MatheMatics teaching in the Middle school, 15(1), 24–33.

Papic, M. (2007). Promoting repeating patterns with young children – More than just alternating colours! Australian Primary Mathematics Classroom, 12(3), 8.

Schifter, D., Russell, S. J., & Bastable, V. (2009). Early Algebra to Reach the Range of Learners. Teaching Children Mathematics, 16(4), 230–237.

Van de Walle, J. A., Karp, K. S., & Bay-Williams, J. M. (2019). Elementary and middle school mathematics: Teaching developmentally, global edition (uppl. 10). New York, NY: Pearson Education.

Warren, E., & Cooper, T. (2006). Using repeating patterns to explore functional thinking. Australian Primary Mathematics Classroom, 11(1), 9.

Lektionsserie 1: Introduktion till mönster

Syftet med denna första lektionsserie är att väcka elevernas intresse för matematik genom att visa att matematik är intressant, kul och användbart. Syftet är också att börja utveckla elevernas förståelse för upprepade mönster. Den kloka Professor Uggla kommer också att lära eleverna att de är matematiker när de arbetar med matematiken och vilka regler som gäller för matematiker: MATEMATIKER LYSSNAR OCH FÖRSÖKER FÖRSTÅ , GÖR SITT

BÄSTA OCH LÄR SIG AV FEL samt gör JAG MED -tecknet för att visa när de har gjort eller tänkt likadant som den som har ordet.

Lektionsseriens mål

• Eleven har en uppfattning om vad matematik är och vad matematik kan användas till, och visar det genom att kunna berätta om några tillämpningar av matematik.

• Eleven kan kopiera ett upprepat mönster.

• Eleven har en grundläggande förståelse för upprepade mönster och visar det genom att fortsätta enkla upprepande mönster i båda riktningarna.

Matematiska begrepp: matematiker, mönster, vänster, höger, uppe, nere

SvA: lyssna, förstå, upprepa, likadan, kopia, avancerad

L1: Vad är matematik?

• Du berättar vad matematik är och kan användas till.

• Professor Uggla berättar om regler i klassrummet och regeln MATEMATIKER LYSSNAR OCH FÖRSÖKER FÖRSTÅ.

• Eleverna arbetar med enkla mönster, och ni har er första diskussion om hur man kan tänka ut hur mönster ska fortsätta.

Material och förberedelser

Lektion 1: Se till så att alla par efter parindelning kan få tio orange och tio blå multilink eller centikuber.

Lektion 2: Ta fram blandade föremål i olika färg och storlek, t.ex. knappar eller logiska block.

Lektion 3: Ha tillgång till multilink eller centikuber samt färgpennor.

Lektion 4: Ta fram färgpennor och skriv ut avslutslappar.

Avslutslapp – Lektionsserie 1

Fortsätta mönster

• Du repeterar vad mönster är.

• Professor Uggla lär eleverna JAG MED -tecknet.

• Ni arbetar med mönster på samlingsmattan (eller motsvarande) där du bygger mönster, och barnen förklarar hur det ska fortsätta och varför.

L3: Elevboken

• Du gör ett upprepat mönster med ljud, t.ex. stamp-stampklapp, och eleverna funderar på hur mönstret ska fortsätta.

• Eleverna arbetar i elevboken.

Ännu mera mönster

• Du repeterar att MATEMATIKER LYSSNAR OCH FÖRSÖKER FÖRSTÅ och att eleverna ska göra JAG MED -tecknet för att visa att de tänkt eller gjort likadant, eller håller med om det som någon säger.

• Du visar ett mönster och ni diskuterar hur det borde fortsätta.

• Professor Uggla lär eleverna regeln MATEMATIKER GÖR SITT BÄSTA OCH LÄR SIG AV FEL.

• Eleverna arbetar i par med att fortsätta mönster i elevboken. Efter varje mönster leder du en kort diskussion om hur mönstret ska fortsätta och varför

• Avslutslapp

Lektion 1: Vad är matematik?

2 Genomgång: Vad är matematik? 10 min

Berätta att ni ska ha en lektion i ett ämne som heter matematik. Fråga eleverna om de har några idéer om vad matematik är. Fördela ordet och skriv upp idéerna på tavlan.

Berätta att matematiker räknar, löser problem, kommer på nya sätt att räkna och mycket mer. Säg att eleverna är matematiker när de arbetar med matematik.

3 Genomgång: Matematiska problem

Ge exempel på problem som kan lösas med matematik. Hur fort måste en rymdraket åka för att komma ut i rymden? Hur mycket medicin ska man ge för att patienten ska bli frisk? För lite hjälper inte. För mycket kan bli farligt. Hur mycket ska man ta betalt för en glass? Är den för dyr vill ingen köpa. Säljer man den för billigt förlorar man pengar på att sälja den. Om man har kommit på ett datorspel behöver man matematik för att programmera det.

4 Uggla: Trafikregler för matematiker

Hej alla matematiker. Jag är professor Uggla och jag kommer att berätta om matematik och matematiker. Idag ska jag berätta lite om hur man jobbar i matematikklassrummet. I matematiken, precis som i trafiken, måste det finnas trafikregler. Varför har vi trafikregler? Titta på det här: Bilen som ville in i rondellen stannade, och lät den som redan var där köra förbi. Annars skulle rondellen bli full med bilar. Reglerna är till för att alla ska komma fram, och för att ingen ska krocka eller bli överkörd. På samma sätt behöver vi trafikregler i klassrummet.

5 Uggla: Matematiker lyssnar och försöker förstå

Här är en viktig regel: När någon talar så är vi tysta, lyssnar, och försöker förstå. Just nu tänkte jag att ni ska få lyssna på er lärare.

6 Paraktivitet: Bygga ett likadant mönster 15 min

Berätta att en sak som matematiker brukar hålla på med är att leta efter mönster. De vill veta varför ett mönster ser ut på ett speciellt sätt då, det kan underlätta när man ska komma på saker. Det finns massvis av olika sorters mönster. Idag ska vi titta på mönster som man kan göra med kuber i olika färger.

Visa mönstret (blå, orange, blå, orange, etc.). Dela in eleverna i par. Förse dem med tio orangea och tio blå multilinkkuber eller centikuber (det fungerar också med centimeterrutat papper och färgpennor). Säg att paren ska bygga samma mönster med sina kuber. Låt dem börja när alla förstått. Bryt när alla börjar bli klara.

7 Diskussion: Är mönstret likadant?

Säg att ni ska ha en diskussion. Påminn om att Professor Uggla har sagt att MATEMATIKER LYSSNAR OCH FÖRSÖKER FÖRSTÅ . Det gäller både när läraren pratar och när andra elever pratar.

Fråga: ”Hur vet ni om ni gjort ett likadant mönster?” Låt några par berätta hur de tänker. Upprepa viktiga saker som elever säger, t.ex. ”efter en blå kommer en orange, hela tiden” eller ”varannan är blå, varannan orange”. Eleverna kan också visa och jämföra med mönstret i bildspelet eller beskriva med ord exakt hur mönstret är uppbyggt, alltså säga färgerna i tur och ordning.

8 Parövning: Hur ska mönstret fortsätta?

Klicka fram en vit kub efter den orangea.  Säg: ”Hur ska mönstret fortsätta? Vilken färg ska nästa kub till höger ha? Diskutera det med din partner.” CIRKULERA (gå runt i klassrummet och håll koll på hur det går och om du behöver stötta någonstans) när paren diskuterar. Påminn vid behov om att MATEMATIKER LYSSNAR och försöker förstå. Bryt efter en liten stund.

Fördela ordet, och när någon svarar att nästa kub ska vara blå ber du hen förklara varför hen tycker det. Ställ frågor för att hjälpa eleven att förklara. Exempel på förklaringar är att det hela tiden kommer orange efter blå och blå efter orange, eller varannan är blå och varannan orange. Förklara själv vid behov.

Klicka fram en vit kub längst till vänster.  Fråga: ”Vilken färg ska den här kuben ha?” Låt paren diskutera en stund. Fördela sedan ordet tills någon svarar ”orange” och be hen förklara hur hen tänker. Ställ frågor för att hjälpa hen att förklara: efter blå kommer orange.

Gör på samma sätt som ovan med mönstret blå, blå, orange, blå, blå, orange etc.

9 Sammanfattning: Vad har vi lärt oss? 5 min

Berätta att människor ofta måste använda matematik för att lösa olika problem eller för att kunna göra saker som man vill göra. Om man vill skicka en rymdfärja till månen, hur ska man göra då? Matematiker kan arbeta med att lösa sådana problem.

Berätta att matematiker ofta försöker hitta mönster. Det är intressant, men det kan också vara till hjälp ibland när man ska lösa problem. Idag har eleverna arbetat med två olika mönster. De har först funderat på vad mönstret är, så att de kunde kopiera det och fortsätta mönstret. Ett mönster kan fortsätta i olika riktningar; åt vänster och åt höger, uppåt eller nedåt.

Sammanfatta också vad Professor Uggla har lärt er: att man måste ha regler i klassrummet, och att en sådan är att MATEMATIKER LYSSNAR OCH FÖRSÖKER FÖRSTÅ. Lektionsserie 1 | Introduktion till mönster

Lektion 2: Fortsätta mönster

2 Repetition: Mönster 5 min

Visa mönstret (gul, röd, blå, gul, röd, blå, etc.). Klicka fram en gul till höger  (”Varningstriangeln” i nedre hörnet visar att vid nästa klick så visas svaret). Visa vad som är vänster och höger och säg: ”Vilken färg ska nästa till höger ha?” Ge BETÄNKETID. Fördela ordet tills någon svarar ”röd”. Fråga då hur hen tänker. FÖRSTÄRK om hen kan förklara varför det kommer en röd. Förklara själv vid behov. Säg: ”Det var säkert fler som tänkte precis likadant, men som inte hade ordet. Hur gör man då? Det ska Professor Uggla berätta.”

3 Uggla: JAG MED-TECKNET

Hej! Jag sa tidigare att man ska lyssna då andra talar. Men ibland vill man ju tala om att precis så där gjorde jag med. Det kan man göra genom att visa det här tecknet med handen. Det betyder jag med. Det gör att du kan vara med i diskussionen även då du inte själv talar.

Säg: ”Nu ska vi träna på JAG MED -tecknet. Jag kommer säga något och alla som håller med eller tänker likadant gör JAG MED.” Visa tecknet. Fortsätt: ”Nästa kub i mönstret skulle vara röd eftersom det alltid varit en röd efter en gul tidigare.”. Låt eleverna göra JAG MED. Öva på JAG MED ett par gånger till där du gör enkla påståenden som: glass är gott, mitt namn börjar på A etc. Låt eleverna göra JAG MED om de håller med.

4 Klassaktivitet: Fortsätta mönstret 20 min

Samla eleverna på samlingsmattan (eller motsvarande). Bygg ett enkelt mönster med plockisar. Lägg mönstret utan att berätta vad du gör. Fråga: ”Hur ska mönstret fortsätta?” Låt eleverna SURRA . Säg att alla ska göra JAG MED -tecknet när de håller med eller har tänkt likadant, och be någon visa hur hen tycker att mönstret ska fortsätta. Be hen förklara varför. Ställ frågor för att hjälpa hen att förklara. Fråga hur mönstret ska fortsätta i andra riktningen. BETÄNKETID. Låt någon svara. Visa och förklara sedan själv.

Gör ett nytt mönster och upprepa enligt ovan.

Du kan bygga mönster med plockisar på flera olika sätt. Det kan vara kuber i olika färger, kuber i olika storlekar eller olika position. Ett mönster som ABBCABBC kan t.ex. visas med blå, röd, röd, gul, blå, röd, röd, gul.

5 Sammanfattning: Vad har vi lärt oss? 5 min Sammanfatta: ni har övat på att fortsätta mönster både åt höger och åt vänster. Visa bara det översta mönstret. Påstå att nästa färg till höger är grön. Säg att de som håller med ska göra JAG MED -tecknet. Påstå att nästa färg till vänster är orange. Eleverna svarar med JAG MED

Lektion 3: Elevboken

2 Övning: Mönster med ljud 5 min

Ställ dig så att alla ser dig tydligt. Du kan också sitta på en stol. Stampa två gånger med foten och klappa händerna en gång (stamp-stamp-klapp), tre gånger i rad. Be eleverna göra mönstret tillsammans med dig. Gör så några gånger, bryt sedan.

Säg att eleverna ska titta på dig igen. Börja mönstret igen men stoppa i början av tredje gången: stamp-stamp-klapp, stamp-stamp-klapp, stamp…

Fråga: ”Hur ska jag fortsätta mönstret?” Upprepa mönstret vid behov och ge sedan BETÄNKETID. Påminn om JAG MED och fördela ordet. Om någon säger att mönstret ska fortsätta med ett stamp och sedan en klapp frågar du hur hen kom fram till det. FÖRSTÄRK om hen kan förklara, t.ex. genom att repetera mönstret eller förklara med ord.

3 – 5 Elevboken: s. 1–3 20 min

Dela ut elevboken. Säg att eleverna då och då kommer att arbeta i den. Förklara att det inte är viktigt att man hinner göra allt i boken, det viktigaste är att man gör sitt bästa. Man får bara arbeta med de sidor som läraren säger.

Läs instruktionerna på den första sidan, visa och förklara uppgiften med bildspelet. Låt eleverna sätta ord på hur de tänker när de ska lösa exemplet.

Låt dem börja arbeta enskilt i boken när alla förstått. CIRKULERA (gå runt i klassrummet och håll koll på hur det går och om du behöver stötta någonstans). Efter en stund förklarar du vid behov nästa moment i elevboken. Se till så att eleverna inte börjar på nästa lektion.

Elever som behöver kan använda centikuber eller multilink för att bygga mönstren innan de fyller i elevboken. Då kan de lättare testa vad som stämmer bäst innan de ritar i boken.

Utmaningarna kan du göra som en gruppuppgift eller i helklass. Du kan också låta endast de elever som har behov av extra utmaningar arbeta med uppgifterna. Klicka på triangeln som pekar till höger för att hoppa över den sidan i bildspelet.

6 Sammanfattning: Vad har vi lärt oss? 5 min

Visa mönstret AABBAABBAABB med pennor: A betyder att pennan ligger horisontellt och B lodrätt. Du behöver inte använda dessa ord utan kan förklara på annat sätt, till exempel genom att visa med händerna.

Berätta att mönster kan se ut på många olika sätt. Påminn om JAG MED, peka till höger om pennorna och påstå felaktigt: ”Nästa penna i mönstret ska stå upp.” Visa i bildspelet. Ge ordet till någon som inte gör JAG MED och fråga vad hen tänker. Ställ frågor för att hjälpa hen att förklara varför nästa penna ska ligga ned. Klicka fram pennan. Visa och förklara själv att pennan ska ligga om man fortsätter mönstret.

Lektion 4: Ännu mera mönster

2 Repetition: Vad matematiker gör 10 min Repetera att MATEMATIKER LYSSNAR OCH FÖRSÖKER FÖRSTÅ. Det betyder att man lyssnar noggrant på den som har ordet och försöker förstå vad hen menar. Om den som pratar har tänkt eller gjort likadant som man själv har – eller om man håller med – då gör man tecknet för JAG MED. Då är man med i diskussionen även om man inte själv pratar.

3 Repetition: Fortsätta ett mönster

Visa mönstret blå, röd, blå, röd, blå, röd. Repetera att det är ett mönster: Klicka fram en röd till höger. Påminn om JAG MED och påstå felaktigt: ”Efter röd borde det komma en röd.” Ge ordet till någon som inte gör JAG MED. Be hen förklara varför hen inte håller med. Ställ frågor för att hjälpa hen att förklara: det har alltid kommit en blå efter röd, och om man ska fortsätta mönstret måste det fortsätta så. Visa och förklara själv.

Visa en vit/tom cirkel till vänster. Fråga: ”Vad händer om vi flyttar den röda till vänster?” Låt eleverna SURRA . Visa och konstatera att mönstret då stämmer.

4 Övning: Ett svårare mönster

Visa mönstret: grön, grön, blå, röd, grön, grön, blå, röd, grön grön, blå, röd.

Säg att mönster kan vara väldigt avancerade. Avancerade betyder att de är svårare, och att det kan ta längre tid innan man kommer på vad mönstret är. Det kan då vara lätt att göra fel. Lyssna på vad Professor Uggla säger om att göra fel.

5 Uggla: Matematiker gör sitt bästa och lär sig av fel

Hej! Professor Uggla igen. När vi jobbar så gör vi vårt bästa, men ibland blir det fel. Men det gör inget. Vi lär oss aV fel Ofta förstår man något bättre när man tänkt om.

Repetera att eleverna är matematiker när de arbetar med matematik. Säg att Professor Ugglas regel, att MATEMATIKER GÖR SITT

BÄSTA OCH LÄR SIG AV FEL , är väldigt bra eftersom man kan lära sig så mycket när man gör fel. Därför ska man alltid göra sitt bästa, men inte vara rädd för att göra eller säga fel.

Berätta gärna om något fel du har gjort matematiskt eller i livet som du lärde dig något av. Om någon elev vill berätta så är det bra, men begränsa er till något enstaka exempel.

6 – 9 Parövning: Avancerade mönster 15 min

Dela in eleverna i par och förse dem med färgpennor. Be dem slå upp s. 4 i elevboken. Repetera att MATEMATIKER LYSSNAR OCH FÖRSÖKER FÖRSTÅ . Gör så här:

• Be paren titta på det första mönstret. Säg att de ska diskutera med varandra – prata och försöka komma överens – om hur mönstret ska fortsätta åt båda hållen. När de är överens gör de klart mönstret i elevboken. Repetera höger och vänster om det behövs.

• Låt dem börja när alla förstått. CIRKULERA och stötta vid behov. Bryt efter en stund när alla har kommit en bit på väg.

• Fråga och led en kort diskussion: Hur ska mönstret fortsätta åt höger och åt vänster? Varför ska det fortsätta så? Påminn om JAG MED och låt olika par förklara för hur de tänker. När någon säger något viktigt kan du antingen UPPREPA , eller låta någon annan elev ÅTERGE det sagda med sina egna ord. Påminn vid behov om att MATEMATIKER GÖR SITT BÄSTA OCH LÄR SIG AV FEL

Elever som behöver det kan använda centikuber eller multilink för att bygga mönstren innan de fyller i elevboken. Då kan de lättare testa vad som stämmer bäst.

Det sista mönstret kan man hoppa över om det är för avancerat. Klicka i så fall på triangeln som pekar till höger i det övre högra hörnet.

10 Helklass Vad finns det för mönster?

Prata i helklass om var man kan hitta olika sorters mönster. Om det behövs ger du exempel: på kläder, mattor, tapeter, tegelväggar, gatstenar, ramsor (huvud, axlar, knä och tå, t.ex.), och i mycket mer.

11 Sammanfattning: Vad har vi lärt oss? 5 min

Berätta att det finns olika sorters mönster nästan överallt, det märker man om man börjar titta efter dem: i tegelväggar, i tröjor, i tyger, i parker, i musik mm. Säg att ni har tittat på en viss sorts mönster som kallas för upprepat mönster. Det betyder att en del av mönstret upprepas; det kommer igen och igen och igen.

12 Avslutslapp

Berätta att bilden visar en avslutslapp. Säg att det är en bra lapp, för med den kan eleverna visa vad de har lärt sig. Ibland kommer ni att göra avslutslappar i slutet av lektionen.

Peka i bildspelet och förklara hur det går till med just den här avslutslappen: det första mönstret ska eleverna fortsätta åt höger på, och det andra mönstret ska de fortsätta åt både höger och vänster. När de är klara med uppgifterna ska de fundera på hur de tycker att det gick, och ringa in den gubbe som visar hur de känner: gick det inte så bra och jag behöver träna mer? Gick det ganska bra, men jag skulle kanske vilja träna mer? Gick det superbra och jag behöver inte träna mer just nu? Lektionsserie

Uppmärksamma och stötta

Uppmärksamma elever som är passiva eller inte verkar vara nyfikna. Försök aktivera och väcka deras intresse genom att fråga dem saker. Du behöver även uppmärksamma elever som inte kan kopiera ett mönster, fortsätta ett enkelt mönster eller beskriva ett mönster. Detta kan vara ett tecken på brister i rumsuppfattningen och svårigheter med att känna igen och tolka figurer. Notera detta och låt dem fortsätta att träna med mönster.

Skolverkets kartläggningsmaterial, Hitta matematiken, lyfter fram att man ska vara uppmärksam redan i det här skedet på en elev som inte visar nyfikenhet och intresse för att arbeta med mönster. Detta kan vara ett tidigt tecken på att eleven kan få svårigheter att nå kunskapskraven i åk 3. Det rekommenderas därför att du tar stöd av personal med specialpedagogisk kompetens för att avgöra om extra anpassningar behöver sättas in redan nu.

Det är vanligt att eleverna kommer från förskolan med stor variation i förkunskaper. En del elever kanske redan nu behärskar mer avancerade mönster och kan beskriva dem med antal, ordningstal eller på andra sätt. Andra kan ha mycket svårt att förklara hur ett mönster är uppbyggt på grund av att de inte har en grundläggande taluppfattning och/eller har ett outvecklat språk. Det är därför viktigt att du låter eleverna förklara mönster på ett sätt som de känner att de klarar av, och att du anpassar språket så att eleverna i klassen förstår. Här är också visualiseringarna i bildspelet till stor hjälp. Använd dem och liknande sätt för att visualisera matematiska idéer och begrepp.

De elever som kan förklara hur ett mönster är uppbyggt med antal och ordningstal, t.ex. genom att säga ”var tredje är grön och sedan är det två blå emellan”, ska självklart få uttrycka sig så. Därefter kan du förenkla hens beskrivning och återge den på ett enklare sätt för hela klassen: ”blå, blå, grön, blå, blå, grön och sedan fortsätter det”. På samma sätt kan du göra med de elever som bara vill peka och visa. Bekräfta dem, eftersom de faktiskt beskriver mönstret och hur det ska fortsätta, men sätt sedan själv ord på det så att eleverna kan utveckla sina språkförmågor.

Använd lägesord som uppe, nere, höger och vänster vid behov. Använd också jämförelseord som liten, stor, lång och kort under Lektion 2. Var då väldigt tydlig, och använd gärna kroppsspråk för att visa på innebörden av orden. Du kan t.ex. använda logiska block och göra mönster med stora och små rektanglar för att få in jämförelseorden stor och liten. Du kan också skapa mönster kopplat till föremåls läge genom att lägga samma typ av föremål

längs en tänkt linje där det som skapar mönstret är att vissa av föremålen har ett högre läge. Du kan exempelvis dra en linje, lägga två klossar på linjen och en över linjen, etc. Du kan då arbeta med lägesorden uppe respektive nere. Om ni har föremål i olika längd kan ni också arbeta med mönster för att eleverna ska förstå kort och lång.

Förenkla

Det är viktigt att hålla ihop klassen under de lärarledda lektionerna så att eleverna arbetar med samma matematiska innehåll. Men du kan behöva förenkla innehållet för vissa elever. I den här lektionsserien kan du vid behov förenkla genom att förenkla mönstren som eleverna arbetar med. Enklare mönster kan vara ABABAB, ABCABCABC eller AABAAB. I början kan ni enbart använda färg, men försök sedan att byta representationsformer, till exempelvis olika föremål, ljud, m.m.

Utmana mer

Utmana eleverna vid behov med mer avancerade mönster. De kan t.ex. skapa egna mönster och sedan låta en annan elev kopiera det och lista ut hur mönstret ska fortsätta åt båda hållen. Låt dem träna på att förklara hur mönstret är uppbyggt för dig och för varandra.

Avslutslappen

Avslutslappen visar om eleven kan identifiera ett enkelt, upprepat mönster och fortsätta mönstret. Klarar de detta har de sannolikt en grundläggande förståelse för upprepade mönster.

De elever som inte klarar uppgiften kan komma att behöva lite mer stöd i nästa lektionsserie om mönster. Se till att dessa elever får en extra förklaring innan de får fortsätta med enskilda uppgifter. Om flera elever har problem med att fortsätta mönster kan du låta dem träna mer på dessa, exempelvis genom aktiviteterna som presenteras nedan.

Arbeta vidare med mönster

Passa på att uppmärksamma mönster i omgivningen när du får chansen. Kanske finns något mönster på skolgården, i skolbyggnaden, i något golv? Har elementen på skolan något mönster? Kan ni hitta något mönster i naturen? Arbeta gärna med upprepade mönster i bildämnet och när eleverna gör pärlplattor eller annat pyssel. Glöm inte bort att uppmärksamma vad det är som gör mönstret till ett mönster: det måste gå att förstå hur mönstret ska fortsätta.

Ett bra sätt att träna på mönster är att låta eleverna skapa arm- eller halsband. Alla elever i klassen påbörjar ett halsband men knyter inte ihop det. Halsbandet skickas vidare till en kamrat som fortsätter.

Lektionsserie 2: Upprepat mönster

Lektionsseriens syfte är att utveckla elevernas förståelse för upprepade mönster genom att låta dem försöka hitta vad i mönstret som upprepar sig: vad är den regel som mönstret upprepar sig efter?

Lektionsseriens mål

• Eleven kan identifiera regeln i enkla upprepade mönster och visar det genom att ringa in det som upprepas och genom att komplettera luckor i mönster.

• Eleven kan skapa ett upprepat mönster och förklara vad i mönstret som upprepar sig.

• Eleven kan översätta ett upprepat mönster till andra uttrycksformer som rörelser/gester, ljud, ord, fysiska föremål eller bilder.

Matematiska begrepp: mönster, upprepat mönster, regel, höger, vänster, liten, uppe, nere

SvA: upprepa, hjärta, gem, ananas

Material och förberedelser

Lektion 1: Ta fram färgpennor och/eller centikuber/ multilink.

Lektion 2: Ta fram centikuber/multilink. Skriv ut kopieringsunderlaget Hemligt mönster i färg. Klipp isär så att du har en hög med mönster A och en hög med mönster B. Eleverna ska arbeta i par där den ena i paret har mönster A och den andra B. Måste du göra en trio får den tredje eleven mönster C.

Lektion 3: Ha centikuber/multilink till hands.

Lektion 4: Skriv ut avslutslappar och ta fram centikuber i färgerna grön, svart och rosa (två av varje färg till varje grupp).

Hemligt mönster

Avslutslapp – Lektionsserie 2

L1: Mönstrets regel

• Du repeterar Professor Ugglas regler för matematiker.

• Du repeterar vad mönster är.

• Eleverna arbetar i par med att försöka lista ut regeln i upprepade mönster, alltså vad i mönstret som upprepar sig och hur.

• Du visar upprepade mönster med luckor i, och eleverna försöker lista ut vad som saknas utifrån hur mönstret upprepar sig.

• Du repeterar hur en regel styr hur ett mönster upprepar sig och hur man kan lista ut vad ett upprepat mönster har för regel.

• Eleverna arbetar i par där de får varsin hemlig regel som de bygger ett mönster utifrån. De byter sedan mönster med varandra och försöker lista ut vilken regel partnerns mönster har.

L3: Elevboken

• Du repeterar upprepade mönster.

• Eleverna arbetar i elevboken.

• Du repeterar vad som menas med upprepade mönster och hur de styrs av en regel som avgör vad som upprepas.

• Du visar hur samma mönster kan visas på olika sätt: med olika färger, med olika stora gem, med olika ljud, etc.

• Paren hittar på ett mönster som de sedan översätter till ett mönster med ljud.

• Några par visar sitt mönster med ljud och övriga elever försöker översätta det till färg.

• Avslutslapp

Lektion 1: Mönstrets regel

2 Repetition: Vad matematiker gör 10 min

Repetera att MATEMATIKER LYSSNAR OCH FÖRSÖKER FÖRSTÅ: man lyssnar på den som har ordet och väntar på sin tur. Om man inte förstår ska man självklart fråga. Och ibland tänker eller gör man fel. Det gör inget, eftersom MATEMATIKER GÖR SITT BÄSTA OCH LÄR SIG AV FEL. Man ska inte vara rädd för att göra eller säga fel, för vi lär oss av fel. Påminn även om JAG MED som ett sätt att visa att man håller med eller tänkt på samma sätt.

3 Repetition: Mönster

Repetera att matematiker tycker om att leta efter mönster som hjälper dem att lösa problem. Ett sorts mönster som ni har arbetat med redan kallas upprepat mönster. När något upprepas kommer samma sak om och om igen.

Visa och säg att det här är ett exempel på ett upprepat mönster.

4 Genomgång: Mönstrets regel

Klicka fram tre vita cirklar till höger. Fråga: ”Om det här är ett upprepat mönster, vad i mönstret är det då som upprepas. Vad är det som kommer om och om igen? Vilka färger ska cirklarna till höger ha?”

Låt eleverna SURRA en stund. Fördela sedan ordet. När någon säger att det ska vara orange, blå och grön frågar du hur hen kom fram till det. FÖRSTÄRK om de på något sätt beskriver regelbundenheten i mönstret.

Säg: ”Man kan beskriva mönstret med en regel, t.ex. orange, blå och grön upprepas hela tiden.” Ringa in de tre första cirklarna, visa och förklara: ”Det är detta som upprepas hela tiden i det här upprepade mönstret. Man kan säga att mönstrets regel är orange, blå, grön, som hela tiden upprepas.”

Visa ett nytt mönster: rosa och vit som upprepas tre gånger.

Låt eleverna SURRA om vad mönstrets regel är. Fördela ordet tills någon svarar ungefär ”först en rosa, sedan en vit, och så håller det på så”. FÖRSTÄRK i så fall. Visa och förklara själv vid behov.

5 – 8 Parövning: Hitta mönstrets regel 15 min

Dela in eleverna i par eller smågrupper om det passar bättre. Låt dem ha tillgång till färgpennor, multilink eller centikuber om de behöver. Gör så här:

1. Visa ett upprepat mönster i bildspelet. Fråga: ”Vad i det här upprepade mönstret är det som upprepar sig? Vad har mönstret för regel?”

2. Låt eleverna undersöka detta i paren genom att bygga mönstret med plockisar eller genom att rita. De ska hjälpas åt och prata med varandra för att försöka komma på svaren. Bryt när de flesta börjar bli klara.

3. Låt något par visa och förklara hur de har tänkt och gjort. Låt någon annan ÅTERGE viktiga saker som sägs. Sammanfatta själv vid behov.

Lektionsserie 2 | Upprepat mönster

Gör på samma sätt med nästa mönster.

Det finns fyra mönster som ni kan arbeta med. Det sista är mer avancerat och kan hoppas över om du känner att det inte passar eller om de tre första har tagit lång tid. Klicka på triangeln i övre högra hörnet för att snabbt hoppa över det mönstret.

Påminn om att MATEMATIKER LYSSNAR OCH FÖRSÖKER FÖRSTÅ och att man kan göra JAG MED -tecknet om man har gjort eller tänkt likadant som den som har ordet.

Om någon säger fel och har missuppfattat regeln som mönstret har kan du, om det passar, påminna om att MATEMATIKER GÖR SITT BÄSTA OCH LÄR SIG AV FEL . Aktivera hela klassen i att försöka ta reda på regeln.

9 Helklassaktivitet: Täpp till luckan i mönstret

Visa ett upprepat mönster med hjärtan: litet, litet, stort, som upprepas fyra gånger. Peka och säg: ”Det är en lucka i det här mönstret. Ett hjärta saknas. Kan man ta reda på om hjärtat ska vara stort eller litet?”

Ge BETÄNKETID. Led sedan en kort diskussion med målet att eleverna ska förstå att om man kan lista ut mönstrets regel, hur mönstret upprepar sig, så kan man ta reda på vad som saknas.

Visa och sammanfatta hur man kan lista ut hur mönstret upprepar sig och därmed förstå att det är ett litet hjärta som saknas.

Visa ett nytt upprepat mönster med en lucka i. Visa vilken del av mönstret som upprepas och låt eleverna SURRA om vilken färg som ska vara i luckan. Fördela ordet. När någon svarar ”blå” ber du hen förklara varför. Visa och sammanfatta själv: det kommer hela tiden två blå efter orange.

10 Sammanfattning: Vad har vi lärt oss? 5 min

Peka och sammanfatta: ”I ett upprepat mönster är det en del av mönstret som upprepas, som kommer om och om igen. Man kan säga att hur mönstret upprepas är mönstrets regel.”

Ringa in regeln.

Fortsätt: ”Här är ett upprepat mönster. Man kan säga att mönstrets regel är grön, blå, blå, grön, och så upprepas det. Om man följer den regeln så kan man fortsätta mönstret.”

Klicka fram ytterligare en del av mönstret som har en lucka. Peka och förklara: ”Om man har listat ut att mönstrets regel är grön, blå, blå, grön, och så upprepas det, så kan man snabbt komma på att det ska vara en blå i luckan.”

Lektion 2: Bygga mönster efter en regel

2 Repetition: Mönstrets regel 5 min

Berätta: ”Det här kallas för ett upprepat mönster. Ett upprepat mönster har en del som upprepas, alltså kommer igen och igen. Man kan säga att mönstret har en regel som säger hur mönstret ska upprepas. Vad är det som upprepas i det här mönstret? Vilken regel har mönstret?”

Låt eleverna SURRA . Fördela ordet, och när någon svarar rätt ber du eleven visa och förklara hur man kan se att regeln är grön, blå, blå, orange, som upprepas. Om eleverna säger fel hjälper du dem att se vilken regel som gäller, och påminner om att MATEMATIKER GÖR MISSTAG OCH LÄR SIG AV FEL.

Klicka fram ytterligare en mönsterdel, men en som har en lucka. Låt eleverna SURRA om vilken färg som saknas. Konstatera att det ska vara en grön i luckan.

3 – 5 Pararbete: Hemliga regeln 20 min

Dela in eleverna i par. Förse dem med centikuber. Säg att alla ska få ett hemligt mönster som de inte får visa för sin partner. Ge mönster A från kopieringsunderlaget till den ena eleven i paret och mönster B till den andra (om det blir en triss får den tredje eleven mönster C). Förklara och visa hur aktiviteten går till med hjälp av bildspelet:

1. Båda eleverna i paret tittar på sitt hemliga mönster och bygger det med kuber som ett upprepat mönster. Det ska upprepas två gånger. Det är viktigt att partnern inte ser.

2. Eleverna i paret byter sina byggda mönster med varandra och ska lista ut vilken regel partnerns mönster följer – hur mönstret upprepas – och sedan fortsätta mönstret. Det räcker med att fortsätta med en mönsterdel.

3. När båda är klara beskriver de för varandra vad de tror att partnerns hemliga regel är, och hur de därför har fortsatt mönstret. De tittar på pappret med det hemliga mönstret och ser om det stämmer.

Låt dem börja när alla förstått. CIRKULERA när de arbetar och stötta vid behov.

Avsluta med att låta några elever berätta hur de listade ut regeln och fortsatte mönstret. Låt övriga delta med JAG MED. Om det finns tid kan du låta eleverna bygga egna mönster, byta med varandra och låta kamraten förklara regeln.

6 Sammanfattning: Vad har vi lärt oss? 5 min

Sammanfatta att eleverna har tränat på att lista ut vilken regel ett upprepat mönster har. Vet man regeln kan man fortsätta mönstret. Visa och förklara: ”Regeln i det här mönstret är gul, gul, blå, blå, och så upprepas det.” Visa och förklara hur mönstret då fortsätter.

Lektion 3: Elevboken

2 Repetition: Upprepat mönster 5 min

 Fråga: ”Det här mönstret består av små och stora kvadrater. Vad har det här mönstret för regel? Vad är det som upprepas i mönstret?” Låt eleverna SURRA en stund.

Fördela sedan ordet. Om någon säger ungefär ”det är en liten och sedan tre stora, hela tiden” så låter du någon annan elev ÅTERGE detta med egna ord. Vid behov ställer du frågor för att hjälpa eleverna att komma på regeln.

Visa hur den upprepande mönsterdelen ringas in. Säg: ”Regeln är en liten och tre stora, och så upprepas det.”

Visa en fjärde mönsterdel som har en lucka. Fråga: ”Vad ska vara i luckan?” Låt eleverna SURRA igen. Påminn om regeln, och konstatera att det ska vara en stor i luckan.

Om elever svarar fel kan du, om det passar, påminna om att

MATEMATIKER GÖR SITT BÄSTA OCH LÄR SIG AV FEL.

3 – 5 Elevboken: s. 5–7 20 min

Be eleverna ta fram sina elevböcker. Berätta vilken sida de ska börja på och hur långt de får jobba under den här lektionen. Säg också: ”Det är viktigt att vara noggrann, inte snabb. Ta gott om tid att tänka efter ordentligt. Koncentrera er och gör ert bästa. Det är det viktiga.”

Förklara första uppgiftstypen med exemplet i bild 3. Låt eleverna börja arbeta enskilt när alla förstått. CIRKULERA och stötta vid behov.

Med hjälp av bild 4 och 5 kan du senare vid behov förklara resten av uppgiftstyperna. De mer utmanande uppgifterna på bild 5 kan du välja att göra som en gruppuppgift eller i helklass. Du kan också låta endast de elever som har behov av extra utmaning lösa dem.

Om du tror att det underlättar för eleverna kan du låta dem SURRA och berätta hur de tänker.

Klicka på triangeln för att hoppa över den sidan i bildspelet.

6 Sammanfattning: Vad har vi lärt oss? 5 min

Visa och berätta: ”Ett upprepat mönster har en del som upprepar sig, som kommer igen och igen. Man kan säga att mönstret har en regel som det följer. Om man listar ut vad regeln är kan man fortsätta mönstret, eller laga mönstret om det finns luckor i det. Det här upprepade mönstret har två luckor på slutet. Om man undersöker vad i mönstret som upprepar sig kan man lista ut regeln.”

Peka och låt klasen säga med dig: ”Grön, blå, blå, orange, och så upprepas det: grön, blå, blå, orange…”

Fortsätt: ”Alltså saknas en blå och en orange.”

Lektion 4: Visa samma mönster på olika sätt

2 Repetition: Mönstrets regel 10 min

 Peka och säg: ”Här är ett upprepat mönster. Det betyder att det är en del av mönstret som upprepas hela tiden, som kommer igen och igen. Vad är mönstrets regel? Vi försöker ta reda på det. Säg med mig: grön, grön, svart … grön, grön, svart … grön, grön, svart. Regeln verkar vara grön, grön, svart, och så upprepas det. Vilken färg ska då vara i den tomma luckan?”

Ge BETÄNKETID. Konstatera: ”Det ska alltså vara en svart i luckan.”

3 Genomgång: Översätta mönster

Säg och visa att man kan visa samma mönster på ett helt annat sätt, t.ex. med gem. Gemen är inte i olika färg, men de är i olika storlek. Visa och säg: ”Istället för grön, grön, svart kan man visa samma mönster med liten, liten, stor. Förklara begreppen liten och stor om det behövs.

Klicka fram samma mönster med gem. Fortsätt: ”Det här mönstret har samma regel, men det visas med små och stora gem istället för med gröna och svarta kuber. Man kan säga att vi har visat samma mönster på ett annat sätt.”

Gör ett mönster med ljud: stamp-stamp-klapp, fyra gånger. Säg att eleverna ska fortsätta mönstret tillsammans med dig, och gör mönstret några gånger till så att alla hänger med. Fråga: ”Vilken regel hade mönstret? Vad i mönstret var det som upprepade sig?” Låt eleverna SURRA en stund.

Fördela sedan ordet. Ställ frågor för att hjälpa eleverna att formulera att regeln är stamp-stamp-klapp, och så upprepas det. Konstatera att mönstret har samma regel som mönstren med kuber och gem. Det är samma mönster som är visat på ett annat sätt.

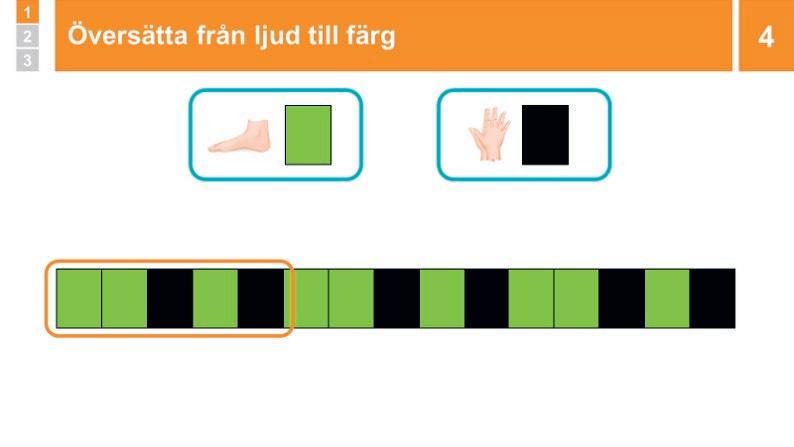
4 Genomgång: Översätta från ljud till färg

Gör mönstret stamp-stamp-klapp-stamp-klapp, några gånger. Säg att eleverna ska göra mönstret med dig och gör mönstret några gånger så att alla hänger med.

Visa en fot (stamp) tillsammans med färgen grön och två händer (klapp) tillsammans med färgen svart. Säg: ”Nu ska vi använda färg för att visa samma mönster som vi nyss gjorde med ljud. Istället för att stampa använder vi grön, och istället för att klappa använder vi svart. Hur ser mönstret ut i färg?” Låt eleverna SURRA om det en stund.

Påminn om JAG MED, och låt några elever förklara hur de tänker. Ställ frågor för att hjälpa dem att formulera att stamp-stampklapp-stamp-klapp blir grön-grön-svart-grön-svart. Avsluta med att visa och förklara själv.

Lektionsserie 2 | Upprepat mönster

5 Pararbete: Hitta på en regel 15 min

Dela in eleverna i par. Förse dem med gröna, svarta och rosa centikuber. Förklara aktiviteten: paren ska hitta på en regel, t.ex. grön-grön-svart-rosa, genom att sätta ihop den första delen av mönstret. Regeln måste ha minst två olika färger.

Låt paren börja när alla förstått. CIRKULERA och stötta. Bryt när de har bestämt och konstruerat sitt mönster.

6 Pararbete: Översätta ett mönster

Säg att paren nu ska visa samma mönster med ljud istället för med färg: grön blir stamp, svart blir klapp och rosa blir en knackning i bänken.

Låt paren börja när alla förstått. VÄLJ UT några par som får visa och förklara sin regel för klassen.

7 Övning: Från ljud till färg

Låt det första paret du valt ut göra sitt mönster med ljud. När de visat några gånger låter du hela klassen vara med och göra mönstret med ljud några gånger.

Påminn om vilka ljud och färger som hörde ihop. Fråga klassen: ”Hur ser samma mönster ut om man visar det med färger istället?” Fördela ordet och ställ frågor för att hjälpa klassen att komma fram till hur mönstret ser ut i färg, samtidigt som du bygger mönstret med färgade kuber. Avsluta med att jämföra med hur mönstret var i ljud.

Om ni hinner gör du på samma sätt med nästa par.

8 Sammanfattning: Vad har vi lärt oss? 5 min

Sammanfatta att ett upprepat mönster har en del som upprepas hela tiden. Man kan säga att mönstret har en regel som det följer, som bestämmer vad i mönstret som upprepas.

Visa mönstret blå-blå-blå-gul, som upprepas tre gånger. Berätta att man kan visa samma mönster på olika sätt. Visa och förklara hur samma mönster först visas med andra färger och sedan med getingar och nyckelpigor. Visa gärna mönstret med ljud också.

9 Avslutslapp

Dela ut avslutslappen och säg att eleverna ska ringa in mönstrets regel, den del i mönstret som upprepar sig, och fylla i den lucka som finns i mönstret.

Uppmärksamma

och stötta

Använd lägesord som uppe, nere, höger och vänster, och jämförelseord som liten, stor, lång och kort under lektion 2. Du kan t.ex. använda logiska block och göra mönster med stora och små rektanglar. Du kan också lägga exakt samma sak längs en tänkt linje, men där två är över linjen och en under för att arbeta med lägesorden uppe och nere, under och över. Om ni har föremål i olika längd kan ni också arbeta med mönster för att eleverna ska förstå orden kort och lång, kortare och längre.

När eleverna kommer från förskolan är det stora variationer i vad de kan och förstår. Vissa elever klarar redan av mer avancerade mönster och kan beskriva dem med antal, ordningstal eller på andra sätt, medan andra har mycket svårt med detta då de ännu inte har en tillräckligt utvecklad taluppfattning eller ett adekvat språk. Det är därför viktigt att du låter eleverna förklara mönster på ett sätt som de känner att de klarar av, och att du återger och anpassar språket så att eleverna i klassen förstår. Elever som kan förklara hur ett mönster är uppbyggt med antal och ordningstal (exempelvis var tredje är grön och sedan är det två blå emellan) ska självklart få uttrycka sig så, men du kan sedan förenkla hens beskrivning till resten av klassen (t.ex. grön, blå, blå, och så upprepas det hela tiden). På samma sätt kan du göra med elever som bara vill peka och visa. Bekräfta för dem att de visar mönstret rätt, men sätt ord på förklaringen så att eleven utvecklar sitt språk.

Var uppmärksam på de elever som lägger tid på att noggrant fylla i alla rutor när mönster ska ritas. Det är onödigt att eleverna lägger tid på detta under matematiklektionerna. Det viktiga är att det går att förstå, inte att det blir fint.

Elever kan ha svårt med att lämna uppgifter halvfärdiga eller att inte hinna med allt. Påminn då om att det viktiga är vad man lär sig och att man förstår, inte hur många uppgifter man hinner göra.

Förenkla

Du kan förenkla elevernas arbete med mönsteruppgifter vid behov genom att stötta med frågor som vägleder eleverna. Börja med öppna frågor för att inte ta bort utmaningen för eleverna, och ställ mer ledande frågor efter hand om det behövs. Du kan t.ex. låta eleverna säga färgerna i mönstret högt och sedan fråga vilken del av mönstret som upprepas. Om eleverna inte förstår kan du exempelvis markera mönsterdelarna med en tydlig paus.

Utmana mer

Utmana eleverna mer vid behov genom att låta dem skapa egna cirkulära mönster med ett visst antal fält. Välj ett antal fält som är delbart på fler än ett sätt så att eleven inte får en omöjlig uppgift. Om antalet fält i det cirkulära är ett primtal, t.ex. 13, så finns det inget annat sätt att lösa det på än att skapa ett mönster där en enda sak upprepas – eller att 13 likadana saker upprepas. Resultatet ser likadant ut. Du kan t.ex. rita cirkulära mönster med 12, 18, 24 eller 32 fält.

Du kan också utmana eleverna att i par skapa mer avancerade mönster med centikuber och sedan låta partnern kopiera det, lista ut vad mönstrets regel är och hur det ska fortsätta i båda riktningarna. Låt eleverna träna på att förklara för dig och för varandra.

Avslutslappen

Avslutslappen visar om eleven kan hitta mönstrets regel och därmed kunna fylla i luckan i mönstret. Om eleven inte klarar uppgiften kan du prata med hen för att se varför hen inte gjorde det. Om du ställer några öppna frågor kanske det räcker för att hen ska kunna lösa uppgiften.

Om hen trots det inte förstår kan det bero på att hen har svårt att se och förstå mönster och regler som styr upprepade mönster. Fortsätt att repetera mönster då och då så att eleverna får fortsätta att utveckla sin förmåga i att upptäcka och beskriva mönster. Testa av eleven senare under terminen igen för att se att hen utvecklats.

Arbeta vidare med mönster

Passa på att uppmärksamma mönster i omgivningen när du får chansen. Kanske finns något mönster på skolgården, i skolbyggnaden, i något golv? Har elementen på skolan något mönster? Kan ni hitta något mönster i naturen? Arbeta gärna med upprepade mönster i bildämnet och när eleverna gör pärlplattor eller annat pyssel. Glöm inte bort att uppmärksamma vad det är som gör något till ett mönster: det måste gå att förstå hur det mönstret fortsätter och varför.

Ett bra sätt att träna på mönster är att eleverna skapar arm- eller halsband. Alla elever i klassen påbörjar ett halsband men knyter inte ihop det. Halsbandet skickas sedan vidare till en kamrat som fortsätter.

Rik matematik FkA

– Lärarhandledning

Rik matematik ger lärare stöd att planera, genomföra och utvärdera rik matematikundervisning. Rik matematikundervisning kännetecknas av aktiva elever och en aktiv lärare där begrepp, resonemang och problemlösning står i fokus. Förskoleklassens lärarhandledningar innehåller tillsammans mer än 80 strukturerade lektioner med bildspel. Lektionerna har tydliga inledningar och avslutningar där central matematik betonas. Med Rik matematik får läraren stöd att varje lektion bedriva en undervisning som engagerar och utvecklar elevernas matematiska tänkande.

Rik matematik är utvecklat i ett nära samarbete mellan lärare och forskare. Varje lektion är utprovad av många lärare som undervisat heltid med Rik matematik under hela läsåret.

Rik matematik Fk A omfattar 4 områden:

Område 1 – Mönster

Område 2 – Antal och räkning

Område 3 – Tal som antal och ordningstal

Område 4 – Talraden 0–10