9789144182285

RIK MATEMATIK 2A

Lärarpaket – Tryckt + Digitalt

RIK MATEMATIK 2A

Lärarpaket – Tryckt + Digitalt

Rik matematik är utvecklat för en undervisning där både elever och lärare är aktiva. Eleverna får resonera, diskutera och lösa problem, och utveckla en djupare förståelse för matematik.

LÄRARHANDLEDNING

I lärarhandledningen får du det stöd och de resurser du behöver för att planera och genomföra din undervisning. Det finns mer än 100 detaljerade lektionsförslag per läsår, som ger konkret stöd och tips på saker att betona, frågor att ställa och exempel att visa. Bildspelen, som hör till varje lektion, fungerar som ett stöd genom hela lektionen, både visuellt för att fånga elevernas uppmärksamhet och för att tydliggöra matematiken med pedagogiska animeringar och bilder. I lärarhandledningen finns även avslutslappar, diagnoser, extra övningsblad m.m.

DIGITALT LÄROMEDEL

Det digitala lärarmaterialet är ett komplement till den trycka lärarhandledningen. Här finns alla digitala resurser samlade, samt kom igång-hjälp och annat stöd som du kan behöva.

Interaktiv version av lärarmaterialet, i vilken det går att söka, stryka under, anteckna och länka.

Fungerar på dator, surfplatta och mobiltelefon.

klicka på bilden och prova

2A

Lärarhandledning

Andreas Ryve

Manuel Tenser

Patrik Gustafsson

Jannika Lindvall

Hillevi Gavel

Fredrik Blomqvist

Välkommen till Rik matematik!

Med Rik matematik får du stöd att varje lektion bedriva en strukturerad undervisning där eleverna får resonera, lösa problem, diskutera, tänka och räkna matematik.

Rik matematikundervisning kännetecknas också av att både läraren och eleverna är aktiva – en elevaktiv och lärarledd undervisning. För att genomföra detta har lärarhandledningen mer än 100 detaljerade lektionsförslag per läsår, med bildspel till varje lektion, medan elevboken är full av forskningsbaserade uppgifter och problem. Bildspelen hjälper dig att visualisera och förklara den matematik som ni arbetar med och blir en utgångspunkt för resonemangen.

I din digitala lärarresurs finns lektionernas alla bildspel men där finns också fler resurser, såsom färdighetsträning, avslutslappar, diagnoser och kopieringsunderlag. Lärarresursen når du via licensen som du får när du köper lärarhandledningen. Inloggning sker på sidan "Min bokhylla" som du hittar på Studentlitteratur.se.

Kapitelstrukturen

Alla kapitel här i lärarhandledningen inleds med en kort matematisk och didaktisk genomgång: Vad är det för matematik, vad vet vi från forskning om hur barn lär sig den och hur har vi därför lagt upp undervisningen? Varje lektion har en översiktssida där du bland annat hittar lektionsmålen och en sammanfattning av lektionen. Är du erfaren räcker det kanske att läsa sammanfattningen och klicka igenom bildspelet innan lektionen.

Lektionerna

Vill du ha mer stöd så ger lektionsförslaget också en detaljerad bild av hur du med bildspelet kan genomföra lektionen. Här får du konkret stöd och tips på saker att betona, frågor att ställa, exempel att visa. På lektionens sista sida får du tips på vanliga missuppfattningar och fel, hur du kan agera då, och hur du kan ge elever extra stöd och mer utmaning vid behov.

Lektionerna inleds alltid med en uppstartsfas. Här repeterar ni det viktigaste i föregående lektion,

och här får eleverna möta innehållet i den nya lektionen, ofta genom en lärarledd genomgång med stöd av bildspelet. I aktivitetsfasen diskuterar, tänker, räknar och löser eleverna problem, ofta i grupp eller par. Läraren har en viktig roll under aktivitetsfasen i att utmana elever, ställa frågor för att uppmana tänkande och diskussion, samla information inför avslutningen av lektionen, etc. Naturligtvis finns det också tid för enskild färdighetsträning. I avslutsfasen sammanfattar du lektionen tillsammans med eleverna och lyfter upp den centrala matematiken. Ofta gör eleverna en avslutslapp där de får visa vad de lärt sig och samtidigt tänka igenom det mest centrala i lektionen.

Var beredd att anpassa

Se lektionsplaneringen som ett förslag, inte som ett strikt manus. Följ inte alltid lektionsplaneringen till punkt och pricka utan utgå ifrån vad eleverna säger och tänker, och styr mot den matematik som de ska lära sig. Om du inte tror att grupparbete kommer att funka, kör par eller enskilt. Förstod de inte? Förklara på ett annat sätt. Och hoppa över delar som eleverna redan förstått.

Avslutslappar och diagnoser

Många lektioner avslutas med en avslutslapp. Det är ett effektivt sätt för dig att ta reda på vad eleverna kan:

• Har eleverna nått målen?

• Är det något som många har missat?

• Finns det enskilda elever som behöver arbeta mer med något?

Nästan varje kapitel avslutas också med att eleverna gör en diagnos. Svaren matar du enkelt in i diagnosverktyget som visar en sammanställning på klass- och elevnivå. Då kan du svara på frågor som:

• Vad kan eleverna bra, vad är svårare?

• Vilka behöver extra anpassningar eller särskilt stöd?

• Vilka behöver utmanas mer?

När du har koll på det kan du fundera på hur din undervisning påverkat resultaten:

• Vad gick bra och varför?

• Vad gick mindre bra och varför?

• Vad tar du med dig?

Lärarhandledningen ger dig stöd vid analysen, inte bara av hur elevernas resultat är på individ- och klassrumsnivå utan också hur du kan planera och genomföra framtida undervisning.

Både avslutslappar och diagnoser finns att ladda ner och skriva ut från din digitala lärarresurs.

Förstå läromedlets grundtankar

Forskning visar att det kan vara lätt att missförstå grundtanken med ett läromedel – och att normer, rutiner och gamla vanor ibland kan vara ett hinder för förbättring av undervisningen. I Sverige är det t.ex. väldigt vanligt att lärare låter eleverna sitta och räkna själva i boken större delen av lektionerna, i tron att de utvecklas matematiskt på det sättet. I rik matematikundervisning ligger tyngdpunkten på att eleverna lär och utvecklas i samspel med läraren och med varandra. När de arbetar i boken färdighetstränar de oftast för att befästa kunskaper. Vi vet också att allt för få lektioner har en avslutning där den centrala matematiken och lärandet lyfts fram, diskuteras och repeteras. Vi lyfter därför här några viktiga grundtankar i den undervisning som Rik matematik stödjer.

Lärarens viktiga roll

Läraren har en central roll i klassrummet. Du planerar undervisningen, diskuterar mål, utmanar elever, förklarar matematik, ställer frågor för att få igång diskussioner, summerar och pekar ut viktiga samband, bedömer, uppmuntrar, skapar struktur, etc. Rik matematik är utvecklat för en undervisning där både elever och lärare är aktiva.

Stöd för diskussion och interaktion

Att som lärare låta eleverna komma till matematisk förståelse genom att resonera, argumentera och lyssna i matematiska diskussioner är ett arbetssätt som är utmanande för alla lärare, men det är också roligt och stimulerande.

Läromedlet tillhandahåller strukturer och resurser som ger stöd för att du ska lyckas med detta. Utöver lektionsförlag med tydliga mål och bildspel, tillhandahåller läromedlet en ”verktygslåda” med en uppsättning diskussionstyper, lärartaktiker och en repertoar av frågetyper som du kan använda för att styra diskussion och interaktion mot avsett mål.

Ramverk för diskussion och interaktion

Målfokus istället för sidfokus

Ha fokus på mål och lärande istället för ett fokus på hur långt eleverna kommit i elevboken. Alla ska inte göra alla uppgifter. När eleverna nått målen ska ni gå vidare till nästa lektion, och nästa mål. Det viktiga är elevernas lärande och större delen av lärandet sker under aktiviteter där de inte sitter själva och löser uppgifter i boken. Det är också viktigt att eleverna inte tror att matematik handlar om att räkna många uppgifter så snabbt som möjligt. Matematiker tänker, funderar och försöker förstå begrepp och samband. Matematiker löser problem.

Elevbok

Det är en vanlig missuppfattning att alla elever måste göra alla uppgifter i elevboken, under eller efter lektionen. Det är inte tanken. Det viktiga är att eleverna når lektionsmålen.

Om du har elever som är snabba eller behöver utmanas kan de arbeta med de mer utmanande uppgifterna, vilka markeras med en eller två cirklar innan instruktionen.

När snabba elever räcker upp handen och anser sig klara med alla uppgifterna, måste du kontrollera om de verkligen löst uppgifterna med tillräcklig noggrannhet och kvalité. Utmana dem i att vara noggranna istället för snabba, genom att låta dem göra om slarvigt eller felaktigt utförda uppgifter, och uppmana dem att i fortsättningen vara noggranna från början.

Korta pass med färdighetsträning

Lägg in färdighetsträningspass mellan lektionerna. Det är bra att kunna saker utantill eftersom det frigör utrymme för tänkande och problemlösning. Lägg in pass på 5–20 minuter emellanåt då eleverna får träna för att befästa delar av matematiken, exempelvis genom arbete i elevboken eller träning med winnetkakort.

Winnetkakort är små papperskort med ett räkneuttryck på ena sidan, till exempel en addition, där summan av additionen framgår av kortets baksida. Korten är lämpliga för färdighetsträning som syftar till att eleverna ska bli mer förtrogna med olika räknestrategier och automatisera grundläggande talkombinationer. Winnetkakort finns för utskrift i den digitala lärarresursen.

Tomoyo

Tomoyo är ett spelifierat, digitalt läromedel där arbetet med de matematiska momenten varvas med fantasifulla berättelser. Tomoyo ingår i elevpaketet.

Elevens motivation och engagemang höjs när hen får snabb återkoppling och samlar poäng och märken.

Svårighetsnivån regleras automatiskt. Övningarna anpassas så att eleven får dem på samma, enklare eller svårare nivå, beroende på hens tidigare svar.

I Tomoyo är all text inläst och till varje övning finns det skräddarsydd hjälp i form av filmer, tips och begreppsförklaringar.

Som lärare kan du skapa ett digitalt klassrum och på så sätt följa dina elevers arbete och skicka uppdrag. Här hittar du även förberedda uppdrag som är kopplade till lektionerna i Rik matematik

Klassrumsnormer och Professor Uggla

För att kunna bedriva en rik matematikundervisning är det viktigt med ett tillåtande och respektfullt klassrumsklimat där eleverna vågar berätta vad de tänker, vågar göra fel och är tysta och lyssnar när någon annan har ordet. Strukturer och resurser som stödjer detta arbetssätt finns inbyggt i materialet. Till din hjälp har du även karaktären Professor Uggla som dyker upp i bildspelen och hjälper till att etablera de viktigaste klassrumsnormerna.

Ramverk för Rika klassrumsnormer

Arbeta långsiktigt!

Arbeta med tålamod och långsiktighet! Rik matematikundervisning är mer utmanande än att låta eleverna sitta ensamma och räkna i boken. Stressa inte upp dig om det inte fungerar perfekt direkt. Kapitel och lektioner kan ta längre tid i början.

I takt med att ni – du och eleverna – lär er hur Rik matematik fungerar och kommer in i arbetssättet, kommer det att gå allt lättare och bättre. Låt det ta den tid det tar! Tänk på att du ska ha eleverna i tre läsår.

Ta hjälp av det stöd som finns i den digitala lärarresursen och hos Rik-matematikkollegor för att snabbare komma in i läromedlet. Skriv till oss på Rik matematik-sidan på Facebook om du behöver råd och stöd.

Digitalt stöd

Det digitala stöd som hör till lärarhandledningen finns i din digitala lärarresurs. Lärarresursen når du via licensen som du får när du köper lärarhandledningen. Inloggning sker på sidan "Min bokhylla" som finns på studentlitteratur.se.

För att visa bildspelen (ppt) som inleder varje lektion, laddar du först ner dem till din dator och öppnar sedan upp dem med Powerpoint.

Bildspelen är ofta animerade. Se till att starta bildspelen så att du får en verklig bild av hur de ser ut.

Om din skola inte har en installerad version av Powerpoint kan du använda den webbaserade gratisversionen av Powerpoint.

Om du arbetar med en Chromebook kan du se filmen nedan för att lära dig om hur du då startar upp bildspelen.

Så här fungerar bildspelen i Rik matematik

Så här fungerar de webbaserade bildspelen i Rik matematik

Så här fungerar Rik matematiks bildspel med Chromebook

Ikoner i lärarhandledningen

Förmågeikoner

Ikonerna visar vilken/vilka förmågor som lektionen direkt utvecklar.

Begreppsförmåga

Kommunikationsförmåga

Metodförmåga

Problemlösningsförmåga

Resonemangsförmåga

Konstellationsikoner

Dessa ikoner visar i vilken konstellation en aktivitet är tänkt att genomföras i.

Undervisning under lärarens ledning

Enskilt arbete

Enskilt arbete i elevboken

Arbete i par

Arbete/diskussioner i grupp

Övriga ikoner

Här kommer du direkt till bildspelet.

Ljudfil i bildspelet

Visar att det finns en särskild funktion i bildspelet och att läraren måste klicka på ett särskilt sätt för att använda funktionen.

Nästa bild

Stanna upp innan du klickar fram svaret. Fråga hur ni kan göra. BETÄNKETID

Film

Dokumentet kan laddas ner.

Övrigt

Referat av det som sägs av berättarrösten

Extra information

Guldkantslektion

Addition och subtraktion 2A

1.0 Introduktion

Syftet med kapitlet är att utveckla elevernas taluppfattning och förståelse för positionssystemet inom talområdet 0–99. Syftet är också att utveckla elevernas färdighet i att göra additions- och subtraktionsberäkningar, med särskild fokus på tiotalsövergång.

Sammanfattning

Kapitlet börjar med en lektion som repeterar talen 0–99 och samtidigt utvecklar elevernas taluppfattning kopplat till positionssystemet.

Sedan får eleverna lära sig att läsa av klockan mer noggrant, utifrån 5-minutersintervall med fokus på 5, 10, 15 över och i heltimme.

I lektion 3 repeterar och befäster vi lilla plus och minus, samt de räknestrategier som eleverna tidigare fått lära sig, för att beräkna talkombinationer i de tabellerna.

I lektion 4 får eleverna lära sig addera och subtrahera jämna tiotal med tvåsiffriga tal.

Därefter får eleverna återigen arbeta med frekvenstabellen och skapa stapeldiagram utifrån egna undersökningar. De får också träna på att göra jämförelser utifrån diagrammet.

Lektion 6 är snarlik lektion 3, med skillnaden att vi här arbetar med stora plus och minus. Eleverna får också arbeta med textuppgifter.

Sedan, i lektion 7, introducerar vi strategin Nästan 10 för beräkningar i talområdet 0–99. I lektion 8 får eleverna öva mer på detta, men också på andra strategier som är lämpliga vid tiotalsövergång.

I slutet på kapitlet får eleverna arbeta mer med egenskaperna udda och jämnt i en guldkantslektion. De får då utveckla sitt algebraiska tänkande genom att försöka förklara mönstret att ett udda antal udda termer ger udda resultat. I sista lektionen före diagnosen lär Uggla ut sin metod för problemlösning, ALP, som eleverna får träna på när de läser textproblem i två steg.

- Addition och

och mätområden

1.0.1 Klockan

I åk 1 arbetade ni med att utveckla förståelse för minutoch timvisarens samband och förhållande till varandra, kopplat till klockslagen prick, lite över/i hela och halva timmar. Nu bygger vi vidare på detta genom att fokusera på att läsa av klockan mer noggrant utifrån 5-minutersintervall i närheten av heltimme.

För att eleverna ska bli helt säkra på att läsa av klockan kan de behöva träna vid många tillfällen parallellt med att ni arbetar med det första kapitlet. Exempelvis kan du några gånger under skoldagen ta en paus och be olika elever läsa av vad klockan är och/eller ta fram en klocka under samlingen och låta eleverna läsa av tiden.

1.0.2 Räknestrategier

Alla räknestrategier (nedan endast benämnt som strategier) handlar i grunden om att använda kunskap om räknelagar, kända talfakta, samband mellan tal och tals egenskaper för att omforma ett uttryck till ett annat uttryck som har samma värde, men där värdet är enklare att bestämma. Omformar man exempelvis 1+7 till 7+1 (vilket är en tillämpning av kommutativa lagen för addition) kan man utnyttja att addition med ett ger talets granne.

Med strategier kan eleverna resonera sig fram till rätt resultat på talkombinationer som de ännu inte automatiserat. Varje gång eleverna gör detta bidrar det till automatisering av den aktuella talkombinationen. Om eleven sedan glömmer en kombination kommer hen alltid att kunna resonera sig fram till rätt resultat.

Gamla strategier

I kapitlet repeteras strategier för lilla och stora additions- och subtraktionstabellen, samt hur eleverna ska generalisera dessa strategier i ett utökat talområde. Dessa strategier går att läsa i sin helhet i kapitel 2, 3, 5 och 9 i årskurs 1. I bildspelen för lektion 3 och 6 i detta kapitel repeteras samtliga strategier som eleverna mött i årskurs 1.

Nya strategier

Vi går igenom hur eleven kan tänka vid addition och subtraktion med hela 10-tal, och från den kunskapen introduceras strategin nästan 10. Ska eleven exempelvis beräkna 56 + 9 så kan hen tänka 56 + 10 – 1 eller 56 – 1 + 10. I subtraktionen 56 – 9 kan man istället tänka 56 – 10 + 1 eller 56 + 1 – 10. Strategin nästan 10 kan också vara användbar vid addition eller subtraktion med 8.

1.0.3 Matematisk problemlösning

I det här kapitlet introducerar vi en systematisk metod för matematisk problemlösning.

Definitionen av problem

I dagligt tal brukar problem vara något som man skulle vilja lösa, men där man inte är säker på hur detta ska gå till. Vet man hur man ska göra så är det inget problem. Ofta är frasen ”detta är ett problem” en omskrivning för ”detta går faktiskt inte att göra”.

I skolämnet matematik används ordet ofta i bemärkelsen större räkneuppgift, eller benämnt tal. I matematikdidaktiken används ordet i betydelsen ”uppgift som den lösande saknar en färdig strategi för”.

Vi kommer i det här läromedlet använda beteckningen problem i betydelsen ”uppgift som kräver inledande tanke- och planeringsarbete innan man kan starta med själva räkningarna”.

Modellering

De flesta matematiska problem som startar med en problembeskrivning i ord, både sådana i läroböcker och sådana som uppstår i verkliga livet, innefattar ett moment av matematisk modellering. En modell kan beskrivas som en förenklad version av verkligheten, och en matematisk modell är en beskrivning av verkligheten i matematiska termer. ”Skriv på mattespråk” är matematisk modellering.

Vid modelleringen försöker man skala bort allt som är oväsentligt för resultatet. Ibland tar man även bort sådant som har inverkan, men där inverkan är så pass liten att man får ett tillräckligt bra svar även om man struntar i det. Poängen är att förenklingarna tar ner svårighetsgraden på matematiken, så att man får något som över huvud taget går att lösa. Ett exempel på en sådan förenkling kan vara ”vi antar att löparen håller samma hastighet hela loppet”. Alltför stora förenklingar leder dock till svar som inte har något med verkligheten att göra, så ett viktigt moment är att granska både modeller och resultat kritiskt.

Så länge man arbetar med heltalsproblem brukar förenklingarna inte påverka resultaten. Då man sammanfattar ”två äpplen och tre bananer är fem frukter” som 2 + 3 = 5 förenklar man bort informationen om vilken sorts objekt det handlade om, men svaret, 5, är helt korrekt.

Problemlösningsmetoden ALP

Vi kommer att lära ut följande process:

1. Analysera: Vad är egentligen problemet?

• Förstå problemet. Vad handlar det om? Vad frågar man efter?

• Tänk på svaret. Vad kommer svaret att säga oss? Vad kan vara ett rimligt svar?

2. Lösa: Hur kan vi lösa det?

• Tänk ut en plan. Vad vet vi? Vad vet vi inte som vi behöver veta? Hur tar vi reda på det?

• Genomför planen.

• Värdera. Verkar detta rätt?

3. Presentera: Skriv ett svar.

1.0.4 Algebra

I Rik matematik arbetar vi redan från början med att utveckla elevernas algebraiska tänkande kopplat till respektive kapitels innehåll. I aritmetik räknar man med kända tal som är representerade med siffror. I algebra representeras tal även med bokstäver (som a, n och x). Dessa kan t.ex. stå för värden som varierar, variabler, värden som man försöker ta reda på, obekanta, och ibland för alla tänkbara tal. Detta gör att man kan undersöka, formulera och representera matematiska regler, som a + b = b + a, eller teckna funktioner för samband som t.ex. y = 10x – 50 där y är vinsten i kr om jag säljer x glassar på en dag. Med hjälp av algebra kan man även lösa många problem genom att ställa upp och lösa ekvationer. Enligt forskning tjänar eleverna på att börja utveckla en grundläggande förståelse för algebra redan i lågstadiet. Genom hela åk 1–3 arbetar vi då och då med algebraiska perspektiv i lektioner där det passar.

I åk 1–3 får eleverna möta:

• Generaliserad aritmetik

Detta innefattar generalisering, representation, motivering och resonemang med aritmetiska relationer, inklusive räknelagar och tals egenskaper.

• Likheter, uttryck, ekvationer och olikheter Innefattar utveckling av relationell förståelse för likhetstecknet och generalisering, representation och resonemang med uttryck, ekvationer och olikheter samt deras symboliska former.

• Funktionstänkande

Innefattar generalisering av samband mellan samvarierande storheter och representation, motivering och resonemang kring dessa generaliseringar genom vardagligt språk, notation med variabler, teckningar, tabeller och grafer.

Likhetsrelationens egenskaper

Mycket matematiskt arbete handlar om att man ges ett uttryck och ska finna ett enklare uttryck för samma

objekt. Det är vad ”räkna ut” handlar om. Den typen av beräkning består av en kedja av likheter där uttrycken steg för steg blir allt enklare. Detta kan ge missuppfattningen att likhetstecknet betyder ”gör nästa steg i arbetet”, men också att det är obligatoriskt att gå från komplicerat till enkelt. Svårigheter med likhetstecknet visar sig ofta vid hantering av algebraiska uttryck och speciellt vid ekvationslösning då eleverna behöver kunna uppfatta likhetstecknet statiskt. Därför har vi försökt vara noggranna med att låta eleverna utveckla en statisk förståelse för likhetstecknet i åk 1, vilket innebär att = förstås som att det är lika på båda sidor, istället för en dynamisk förståelse av likhetstecknet i bemärkelsen en uppmaning att göra något. Det här kan ta tid, men det är viktigt att redan tidigt stödja den här utvecklingen, t.ex. genom att alltid uttala symbolen = som ”(är) lika med”, och inte ”blir”. Men, om man har uttrycket 1 + 1 = 2 så kan man säga att 1 + 1 blir 2, om man syftar på operationen addition ifråga om termerna på vardera sidan om additionstecknet. Om man istället avser relationen mellan det som står till vänster om likhetstecknet (1 + 1) och det på höger sida (2), så säger man är lika med. Detta är viktigt för att skapa goda förutsättningar för att utveckla algebraiskt tänkande.

Vi har tidigare i åk 1 arbetat kontinuerligt med olika sorters öppna utsagor som t.ex. 5 + 1 = ⎕ + 4. Dessa uppgifter kan dels synliggöra och utmana felaktiga uppfattningar om likhetstecknets betydelse, och bygga en grund för att förstå och kunna hantera ekvationer med obekanta.

Forskning visar att man tidigt bör byta ut luckorna i öppna utsagor mot bokstäver, och vi väljer att göra detta nu i åk 2.

Tänk på att om eleverna har svårt med algebra så beror det ofta på en svag eller felaktig förståelse för symbolerna som används. Detta är extra tydligt när det gäller symboler för likheter och bokstavssymboler vid ekvationslösning. Eleverna kan helt enkelt inte förstå ekvationer om de inte har en stark förståelse för de matematiska symbolerna. De måste kunna uppfatta likhetstecknet statiskt, och förstå att likhetstecknet beskriver att det som står till vänster om likhetstecknet är lika med det som står på höger sida.

När det gäller bokstavssymbolen för en obekant vid ekvationslösning så behöver eleverna förstå att de ska bestämma vilket tal bokstaven står för om utsagan är sann, alltså att det är lika på båda sidorna om likhetstecknet.

1.0.5 Ekvationer och andra utsagor

I det här kapitlet fortsätter vi det arbete med ekvationer som vi förra året inledde med ”öppna utsagor”.

Utsagor

En utsaga är ett uttryck som har ett sanningsvärde. Exempel på utsagor är

• 2 är ett primtal (sant)

• 3 är ett jämnt tal (falskt)

• 4 = 2 + 2 (sant)

• 5 > 6 (falskt)

• Det är onsdag idag – sanningshalten beror på vad ”idag” är.

• x + 7 = 8 – sanningshalten beror på vad ”x” är.

Öppna utsagor

De två sista exemplen är öppna utsagor Deras sanningshalt beror på vilket värde man ger den ingående variabeln. En variabel är något vars värde kan variera. I matematiken representeras variabler oftast med bokstäver; i talat språk kan det vara ord som ”idag” eller pronomen.

Öppna utsagor ska i många sammanhang tolkas som frågor: Vilket/vilka värde(n) ska vi tilldela variabeln om vi vill att utsagan ska vara sann?

Vi har tidigare arbetat med öppna utsagor där värdet som kan varieras representeras av en lucka. Uppgiften har då varit att skriva något i luckan som gör det som står sant, och detta har vi kallat att lösa utsagan

Räkneregler

Räkneregler, som kommutativa lagen för addition, är inte frågor. Ordentligt formulerad lyder den lagen

För alla tal a och b gäller att a + b = b + a

Denna utsaga är inte öppen, trots att den innehåller variabler, eftersom det framgår vilka värden variablerna ska ha. Det där med ”för alla” lämnas ofta underförstått.

Ekvationer

En utsaga som innehåller ett likhetstecken kallas en ekvation (likhet). Då man använder det namnet brukar man oftast mena en öppen utsaga med en variabel, och att lösa ekvationen innebär att man söker det eller de värden på variabeln som gör utsagan sann, men strikt formellt är även t.ex. 2 = 2 en ekvation.

Inom alla yrken och verksamheter där man arbetar med beräkningar är ekvationslösning en mycket vanlig aktivitet.

• När ska vi starta, om vi vill vara framme innan tre?

• Vilken diameter ska vi ge röret, om vi vill få ett tillräckligt flöde?

• Vad ska vi begära för pris, om vi inte vill gå med förlust?

Variabler som ingår i ekvationer brukar kallas obekanta

De är något vars värde vi från början inte känner till, och där uppgiften är att ta reda på värdet.

Lösningar

Så länge de enda räknesätt man har att tillgå är addition och subtraktion, har de flesta ekvationer antingen ingen eller precis en lösning; det är sällan de har t.ex. två olika lösningar.

Ekvationen x + 3 = 2 saknar lösning om man bara accepterar naturliga tal. Godtar man även negativa heltal så har den lösningen x = – 1, men inga andra.

Även här finns det dock ekvationer med mer än en lösning. x + 1 = 1 + x stämmer oavsett vilket tal man sätter in på x:s plats. Denna ekvation har alltså den oändliga lösningsmängden alla tal

När man introducerar fler räknesätt kommer det också att uppstå ekvationstyper med mer än ett men mindre än oändligt många lösningar. Andragradsekvationer brukar exempelvis ha två lösningar.

Variabler och bokstavsbeteckningar i övrigt Bokstäver används alltså för att beteckna tal och andra matematiska objekt vilkas värde kan variera. Typografiskt signalerar man detta genom att använda kursiv stil. Symboler vilkas innebörd är fix (fastslagen, icke varierande) skrivs med upprätt stil.

Även konstanter kan betecknas med bokstäver. Många viktiga konstanter, som π, går inte att uttrycka exakt med siffror, och i andra fall kan det förenkla att använda en bokstav istället för tio siffror. Det går fortare att skriva och är lättare att läsa.

Samband

Ordet variabel används framför allt då man studerar samband, som A = πr2, sambandet mellan arean och radien hos en cirkel.

Val av beteckning

I räkneregler, som kommutativa lagen för addition, brukar man oftast använda bokstäver från början av alfabetet.

I samband brukar man försöka ta bokstäver som är lätta att tolka, som r för radie och A för area.

I ekvationer och samband där man inte har någon speciell tolkning i tankarna brukar man i första hand ta bokstaven x (som inte är begynnelsebokstav i någonting vettigt, och därmed inte leder tankarna åt något håll). Behöver man flera obekanta kan man fortsätta med y och z. Även t är ett vanligt val, framför allt då man döper om något.

1.1.6 Övningsblad

I det här kapitlet finns övningsblad att dela ut efter lektion 1, 2, 4, 6, 8 och 11. Övningsbladen kan användas som extra färdighetsträning eller som extrauppgifter/utmaningar till elever som snabbt blir klara.

Generellt om övningsblad

Till alla kapitel finns övningsblad som du kan skriva ut och ge elever som extra färdighetsträning – under lektioner, mellan två lärarledda lektioner eller som läxa. Det finns alltid ett övningsblad på grundläggande nivå och ett mer utmanande blad, och det framgår av lektionsförslagen när det är lämpligt att dela ut dem.

Övningsbladen möjliggör extra färdighetsträning på saker som eleverna lärt sig under den lärarledda undervisningen i syfte att de ska befästa kunskaperna. Poängen med övningsbladen, oavsett hur du väljer att arbeta med dem, är att förlänga lärandet som skett i klassrummet så att eleverna befäster kunskaperna i högre grad. Om du väljer att skicka hem övningsbladet som läxa måste du därför försäkra dig om att eleven inte behöver hjälp att förstå uppgiften av en vuxen. Detta gäller särskilt de övningsblad som testar eleven på en högre nivå.

Mer generell information om hur du kan arbeta med övningsbladen finns på lärarwebben.

1.1.7 Referenser

Baroody, A. J. (2006). Why children have difficulties mastering the basic number combinations and how to help them. Teaching Children Mathematics, 13 (1): 22–31.

Carraher, D. W., Schliemann, A. D. (2007). Early algebra and algebraic reasoning. In Second handbook of research on mathematics teaching and learning, 2, 669-705. Reston, VA: National Council of Teachers of Mathematics.

Kieran, C. (2007). Learning and teaching algebra at the middle school through college levels: Building meaning for symbols and their manipulation. In Second handbook of research on mathematics teaching and learning, 2, 707-762. Reston, VA: National Council of Teachers of Mathematics.

Lesh, R., & Zawojewski, J. (2007). Problem solving and modelling. I F. K. Lester (Red.), Second handbook on research of mathematics teaching and learning, 763–804. Reston, VA: National Council of Teachers of Mathematics.

McIntosh, A. (2020). Förstå och använda tal: En handbok (uppl. 2). Göteborg: Nationellt centrum för matematikutbildning.

Stephens, A., Ellis, A., Blanton, M & Brizuela, B. (2017). Algebraic thinking in the elementary and middle grades. I C. J. (Red.), Compendium for research in mathematics education (s. 893–907). Reston, VA: National Council of Teachers of Mathematics.

Van de Walle, J. A., Karp, K. S., & Bay-Williams, J. M. (2019). Elementary and middle school mathematics: Teaching developmentally, global edition (uppl. 10). New York, NY: Pearson Education.

Verschaffel, L., Greer, B, & DeCorte, E. (2007). Whole number concepts and operations. I F.K. Lester (Red.), Second handbook on research of mathematics teaching and learning, 557–628. Reston, VA: National Council of Teachers of Mathematics.

1.1 Talen 0–99:s uppbyggnad

Syftet med lektionen är att utveckla elevernas taluppfattning i relation till positionssystemet, samt befästa elevernas kunskap om talen 0–99:s uppbyggnad. Syftet är också att motivera eleverna inför åk 2 genom att introducera det nya läsårets matematik. Detta sker bland annat genom att visa ett spännande utmaningsproblem som eleverna kommer kunna lösa i slutet av åk 2. Nästa gång vi arbetar fokuserat med positionssystemet (i kapitel 7) introducerar vi hundratal och tusental.

Lektionsmål

• Eleven förstår talen 0–99:s uppbyggnad och visar det genom att t.ex.

o läsa och skriva tvåsiffriga tal utifrån representationer med tiobasmaterial eller pengar,

o identifiera tiotal och ental samt avgöra vilket värde respektive siffra står för i ett tvåsiffrigt tal,

o skriva tvåsiffriga tal i utvecklad form.

Matematiska begrepp: Positionssystemet, utvecklad form, tiotal, ental

SvA: Mynt, tiokrona, enkrona

Material: Miniwhiteboards och pennor.

Förberedelser

• Se till att det finns miniwhiteboard och penna till varje par av elever.

• Övningsblad finns. Skriv ut vid behov.

Övningsblad grundläggande Övningsblad utmanande

Välkomna

Du hälsar alla matematiker välkomna till ett nytt läsår med matematik.

Repetition: Gruppering, ental och tiotal

Du visar med kuber i bildspelet hur man grupperar och räknar i tiotal och ental.

Repetition och övning: Tal som mynt

Kuberna byts till mynt, och du visar och förklarar hur mynt kan ses som ental och tiotal. Du visar olika mynt, och eleverna säger vilka tal de motsvarar.

Genomgång: Utvecklad form och platsvärde

Du repeterar hur man skriver tal i utvecklad form och kopplar det till platsvärde.

10 min

Parövning: Tal i utvecklad form Du visar ett tvåsiffrigt tal, t.ex. 21. Paren diskuterar och skriver talet i utvecklad form på miniwhiteboards. Du låter olika par redogöra för hur de tänkte innan du visar i bildspelet.

Elevboken s. 3−6

30 min

Sammanfattning: Vad har vi lärt oss?

Du sammanfattar hur man kan visa tal med tiobasmaterial och mynt. Du visar och förklarar hur man skriver tal i utvecklad form och hur den utvecklade formen visar vilka värden som siffrorna i det ursprungliga talet representerar.

Uggla: Matematiken i årskurs 2 Uggla berättar om årskurs 2 och om ett problem som eleverna kommer att kunna lösa i slutet av läsåret.

10 min

Uppstart

1 Välkomna

Hälsa alla matematiker välkomna till ett nytt läsår med matematik.

10 min

2 Repetition: Gruppering, ental och tiotal

Visa ett antal kuber i oordning och säg: ”Varje kub motsvarar talet 1, ett ental. Ett bra sätt om man vill räkna kuberna är att gruppera dem i grupper om tio, alltså i 10-grupper.”

Visa hur tio kuber byggs ihop till en stav och säg: ”Varje stav består av en grupp av tio ental och är ett tiotal. Ett tiotal är en grupp med tio ental.”

Visa hur resten av kuberna grupperas i tiotal och ental. Fråga: ”Hur många kuber är det? BETÄNKETID. Låt någon svara. FÖRSTÄRK , eller förklara själv om det behövs.

”Ett tiotal är en grupp med tio ental. Tre tiotal är 10, 20, 30. Tre tiotal är alltså 30!” Peka på de kuber som är kvar och berätta att det måste vara tio ental för att skapa ett tiotal. Det här är bara fyra ental, så de får istället räknas var för sig: 31, 32, 33, 34. Visa talet 34, och berätta att 3 tiotal och 4 ental är 34, treTIO-fyra.

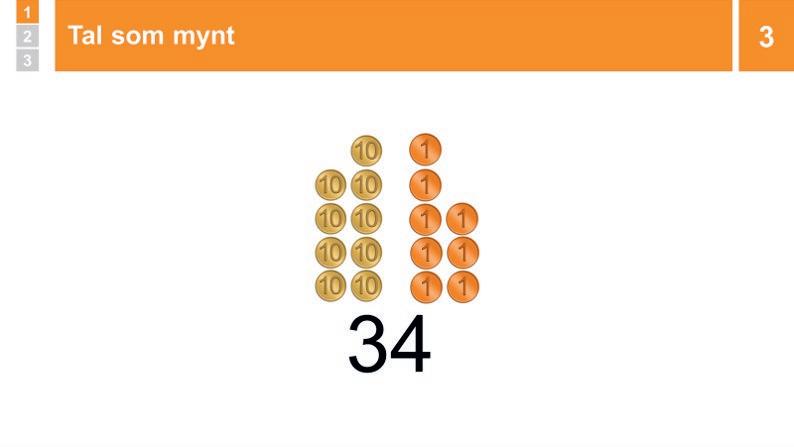
3 Repetition och övning: Tal som mynt

Visa hur tiobasmaterialet byts till tiokronor och enkronor. Berätta att man kan använda mynt för att visa tiotal och ental. En tiokrona motsvarar ett tiotal, och en enkrona motsvarar ett ental eftersom det behövs 10 enkronor för att växla till en tiokrona. Visa och säg: ”Tre tiotal och fyra ental är 34, precis som 3 tiokronor och 4 enkronor är 34 kronor”.

Byt till fem tiokronor och tre enkronor. Fråga hur mycket det är. Ge BETÄNKETID och fördela ordet. När en elev säger 53 kronor bekräftar du och följer upp med att fråga hur vi skriver talet 53 med siffror. FÖRSTÄRK om eleven ger ett korrekt svar. Visa talet i bildspelet.

 Visa talet 17 med mynt. Be eleverna tänka ut vilket tal mynten visar. Ge kort BETÄNKETID. Låt någon svara, eller låt alla ropa ut om de är tillräckligt säkra.

Gör på samma sätt med 48, 92 och 76.

4 Genomgång: Utvecklad form och platsvärde

Berätta att vi kan visa de olika positionernas värde genom att skriva ett tal i utvecklad form. Visa hur talet 28 delas upp i 20 + 8 och säg: ”I talet 28 står siffran 2 för två tiotal, vilka har värdet 20. Siffran 8 står för åtta ental, vilka har värdet 8. 28 är alltså lika med 20 + 8. 20 + 8 är talet 28 i utvecklad form.”

Visa tiokronor och enkronor ovanför uttrycket 20 + 8. Påminn om hur talet 20 motsvarar två tior och talet åtta motsvarar åtta enkronor.

Aktivitet

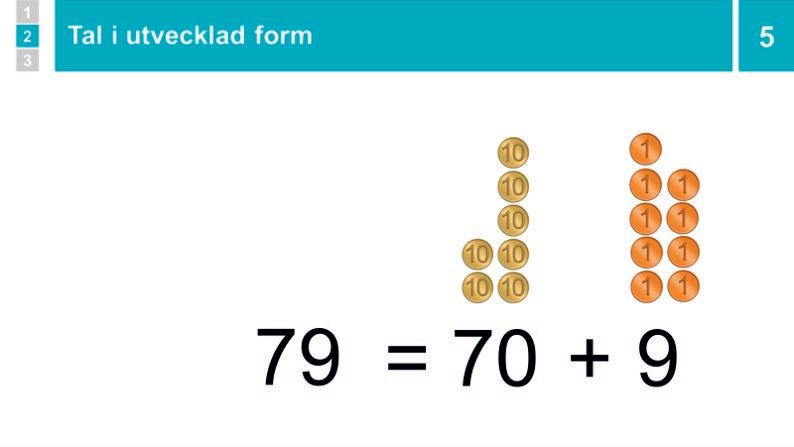
5 Parövning: Tal i utvecklad form 30 min

 Dela in i eleverna par, och förse dem med miniwhiteboards och penna. Berätta att de ska få öva på att skriva tal i utvecklad form. Gör så här:

• Visa talet 21 och säg talet.

• Be paret diskutera hur talet skrivs i utvecklad form och skriva det på sin miniwhiteboard.

• Be alla par hålla upp sina miniwhiteboards.

• Ge ordet till ett par som skrivit 20 + 1 och be dem förklara hur de tänkt. FÖRSTÄRK om de kan redogöra för platsvärde (att siffran 2 i 21 står för 20 och 1 för 1).

• Visa talet i utvecklad form i bildspelet, tillsammans med mynt som konkretisering.

Gör på samma sätt med talen 19, 46, 64, 50 och 79.

6 Elevboken s. 3−6

Avslut

7 Sammanfattning: Vad har vi lärt oss? 10 min

Man kan visa tal med tiobasmaterial. Tio ental motsvarar ett tiotal. I talet 37 är det tre tiotal och sju ental. Man kan också visa tal med hjälp av mynt. Talet 37 kan ses som tre tiokronor och sju enkronor.

När man skriver tal i utvecklad form visar vi värdet som siffrorna har utifrån deras position. Siffran längst till vänster har alltid det högsta värdet, och siffran längst till höger det lägsta. I talet 37 står siffran 3 på tiotalsplatsen, vilket gör att siffran visar tre tiotal, alltså 30. Siffran sju står på entalsplatsen och visar sju ental, alltså 7. I utvecklad form skrivs talet 37 som 30 + 7.

8 Uggla: Matematiken i årskurs 2

Låt professor Uggla berätta om innehållet i årskurs 2 och om ett problem som eleverna kommer att kunna lösa i slutet av läsåret.

1.1.1 Uppmärksamma och stötta

De elever som har svårt att göra kopplingen mellan platsvärde (i termer av talsorter) och hur siffran på en viss plats representerar ett av siffran givet antal ental eller tiotal, kan behöva använda konkret material under lektionen. Börja med att låta eleven arbeta med mynt. Vid behov kan du ha en kort genomgång med eleven om hur en tiokrona motsvarar tio enkronor, och vice versa. Om eleven fortfarande inte klarar detta kan hen istället behöva använda sig av ett proportionellt material, som exempelvis tiobasmaterialet.

Uppmärksamma de elever som kastar om positionerna när de skriver tal i utvecklad form, exempelvis skriver talet 25 som 5 + 20. Detta är förvisso inte fel, eftersom 5 + 20 är lika med 25, men när man skriver tal i utvecklad form brukar man skriva talets värde i samma ordning talet skrivs.

Förenkla

Låt elever som behöver det använda konkret material under arbetet i elevboken. Mynt eller tiobasmaterial kan fungera som stöd för att förstå talens uppbyggnad. Om eleven klarar av att använda mynt är det att föredra, då det är mer abstrakt och således ett steg närmare talens abstrakta natur.

Utmana mer

Låt eleverna skriva tal i utvecklad form i talområdet över 99. Låt dem även skriva tal som har siffran 0 på någon position. De elever som du bedömer har en tillräckligt god förståelse för positionssystemet kan skriva fyrsiffriga tal.

Använd tiobasmaterial eller läromedelspengar och lägg ett tal. Låt eleverna tolka vilket tal det är, skriva talet och sedan skriva det i utvecklad form.

1.2 Klockan 5, 10, 15 och 20 över och i heltimme

Syftet med lektionen är att fortsätta att utveckla elevernas förståelse för och färdighet i att läsa av den analoga klockan. Detta sker genom att fortsätta studera sambandet mellan visarna ifråga om rörelse och placering i förhållande till varandra, med fokus på 5, 10, 15 och 20 minuter i och över heltimme.

Lektionsmål

• Eleven vet var tim- och minutvisarna befinner sig vid 5, 10, 15 och 20 i och över hel timme och visar det genom att läsa av och ställa in en klocka med två visare.

Matematiska begrepp: lite i, lite över, kvart, medurs, moturs, fjärdedel

SvA: minutvisare, timvisare, rotera

Material: Elevklockor

Förberedelser

• Se till att det finns en elevklocka till varje elevpar.

• Skriv ut avslutslappar.

• Övningsblad finns. Skriv ut vid behov.

Avslutslapp

Övningsblad grundläggande Övningsblad utmanande

Repetition: Tim- och minutvisaren

Du repeterar tim- och minutvisaren.

Genomgång: Minuter

Du repeterar minuter och att en timme är 60 minuter.

Genomgång och övning: 5, 10, 15 och 20 över

Du går igenom klockslagen. Sedan låter du eleverna öva genom att du visar klockslag som eleverna får läsa av.

Genomgång och övning: 5, 10, 15 och 20 i

Du gör som ovan, fast med klockslag som är i.

Parövning: Var ska visarna peka?

Du säger klockslag som elevparen ställer in sina klockor på. När de är klara visar du i bildspelet och förklarar hur tim- och minutvisarna visar klockslaget. Paren korrigerar klockan om det behövs.

Elevboken s. 7−10

Låt eleverna arbeta enskilt i elevboken. Påpeka att de kan förkorta ordet minuter till ”min” om de vill.

Sammanfattning: Vad har vi lärt oss?

Du spelar den animerade genomgången med berättarröst som sammanfattar hur man ser att klockan är 5, 10 och 15 minuter över respektive i, heltimme.

Avslutslapp

Uppstart

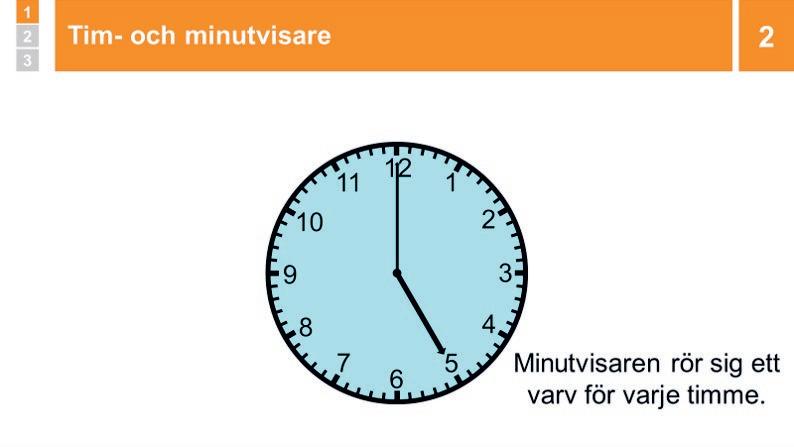
2 Repetition: Tim- och minutvisaren 10 min

Peka och berätta att timvisaren visar vilken timme det är. Just nu pekar den rakt på 5, vilket betyder att klockan visar prick 5. Peka och berätta att minutvisaren, som är lite längre, används för att läsa av klockan mer noggrant. Den rör sig snabbare än timvisaren. När den pekar rakt på 12 är klockan hel timme, just nu prick 5. Låt klockan gå (den stannar på 6), och berätta under tiden att både timvisaren och minutvisaren roterar åt samma håll. För varje timme går minutvisaren ett varv, och timvisaren visar en timme mer än innan. Här går den från 5 till 6.

Berätta att det håll som visarna roterar på en klocka kallas medurs. Ur betyder klocka. Motsatt riktning kallas moturs

Konstatera att klockan visar prick 6. En timme har gått.

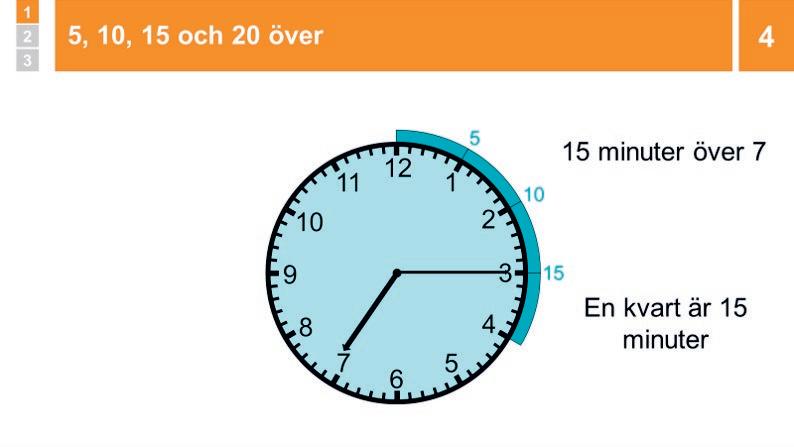
3 Genomgång: Minuter

Påminn om att en timme är 60 minuter. Visa en förstorad del av klockan där minutvisaren rör sig 1 minut i taget. Konstatera att det nu har gått 5 minuter, och att det tar 5 minuter för minutvisaren att röra sig mellan två tal. Visa även på den stora klockan hur 5 minuter går.

Klicka så att klockan går 5 minuter i taget, och visa hur minuterna ökar från 5 till 10, 15, 20 o.s.v. Påpeka att timvisaren också rör sig lite när minutvisaren går.

När minutvisaren har gått ett varv och återigen pekar på 12 säger du att det har gått 60 minuter, d.v.s. 1 timme. Klockan visar nu prick 7. Visa hur 60 ändras till 0 och säg att nu börjar en ny timme.

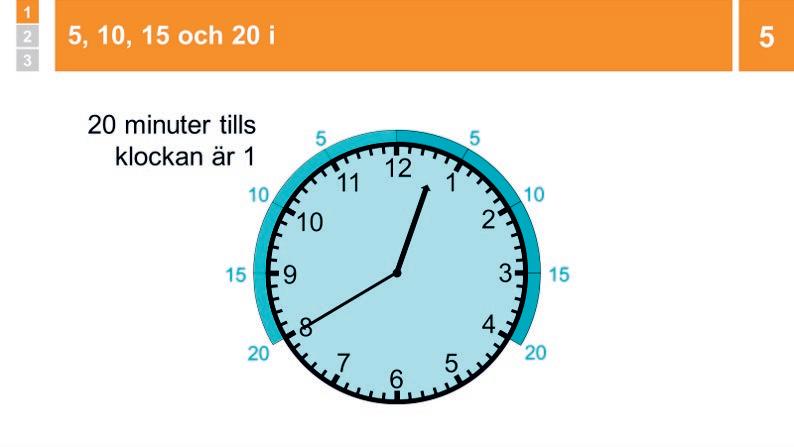
4 Genomgång och övning: 5, 10, 15 och 20 över

Låt klockan gå och konstatera att den är lite över 7. Säg att minutvisaren gör att man mer noggrant kan säga vad klockan är. Säg och visa: ”Timvisaren har gått lite förbi 7, så klockan är lite över 7. Minutvisaren pekar rakt på 1. Då har det gått 5 minuter efter att klockan var prick 7. Man kan säga att klockan är 5 minuter över 7, eller 5 över 7. Det är mer noggrant än att säga ’lite över 7’”.

Låt klockan bli 10 över 7. Fråga hur mycket klockan är. BETÄNKETID. Fördela ordet. Bekräfta om någon säger lite över 7, och be hen säga hur många minuter över 7 klockan är. FÖRSTÄRK om någon säger 10 minuter över 7.

Låt klockan bli 15 över 7. Visa att minutvisaren pekar rakt på 3, och säg att det betyder att det gått 15 minuter sedan klockan var 7; klockan är 15 minuter över 7. Säg att man också kan säga ”kvart över”. Kvart betyder fjärdedel, och 15 minuter är en fjärdedels timme. Fyra kvartar är en hel.

Visa 20 över 7 och förklara på samma sätt.

 Visa olika klockslag, ge eleverna BETÄNKETID och låt dem svara vad klockan visar, enskilt eller samtidigt.

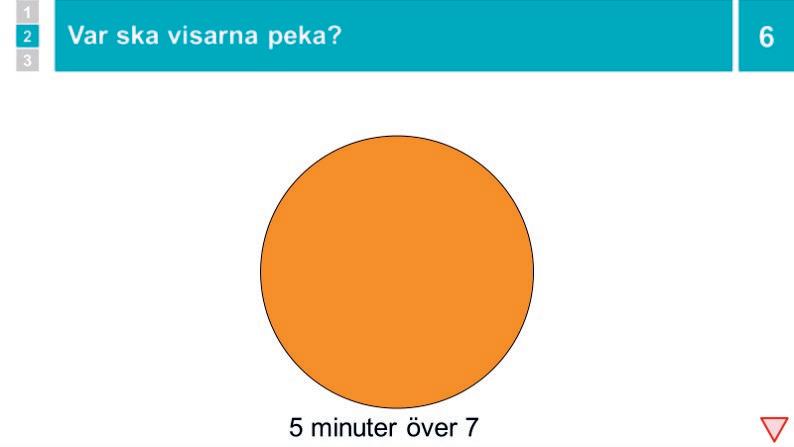
5 Genomgång och övning: 5, 10, 15 och 20 i

Låt klockan bli 20 över 12. Repetera att det har gått 20 minuter sedan klockan var prick 12. Låt klockan bli 20 i 1, och visa att det är 20 minuter kvar tills klockan är prick 1. Man brukar då säga att klockan är 20 minuter i. Just nu visar klockan 20 i 1.

Låt 5 minuter gå och säg: ”När minutvisaren pekar rakt på 9 kan man säga att klockan är kvart i. Minutvisaren har 15 minuter kvar att gå innan klockan blir prick, och 15 minuter är en kvart. Klockan är kvart i 1 eftersom timvisaren är lite i 1 och minutvisaren pekar rakt på 9.”

Visa och förklara på samma sätt med 10 i 1 och 5 i 1

 Visa olika klockslag, låt eleverna i par SURRA om vad klockan är och låt sedan ett par svara.

Aktivitet

6 Parövning: Var ska visarna peka? 30 min

Dela in i eleverna i par och förse varje par med en elevklocka. Gör så här:

 Säg ”Var ska visarna peka för att visa prick 4?”Be eleverna ställa visarna så att klockan visar prick 4

• När alla är klara visar du i bildspelet och förklarar hur tim- och minutvisarna tillsammans visar klockslaget. Be eleverna korrigera klockorna om de behöver.

Fortsätt på samma sätt resten av klockslagen.

7 Elevboken s. 7−10

Låt eleverna arbeta enskilt i elevboken. Påpeka att de kan förkorta ordet minuter till ”min” om de vill.

Avslut

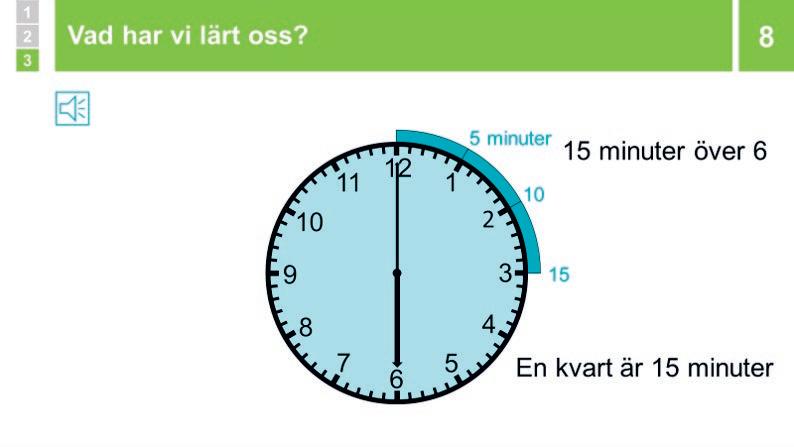
8 Sammanfattning: Vad har vi lärt oss? 10 min

Minutvisaren hjälper oss att läsa av klockan mer noggrant. Mellan varje tal på klockan är det 5 minuter. När minutvisaren pekar rakt på 1 och timvisaren lite över 6 har det alltså gått 5 minuter sedan klockan var prick 6. Nu är klockan 5 minuter över 6. När minutvisaren pekar rakt på 3 har det gått 15 minuter. Vi kan säga att klockan är 15 minuter över 6, men vi kan också säga kvart över 6. En kvart betyder 15 minuter.

När det är 15 minuter kvar tills klockan är prick 7 pekar minutvisaren rakt på 9 och timvisaren lite i 7. Vi kan säga att klockan är kvart i 7 eller 15 minuter i 7. När minutvisaren pekar rakt på 10 är det 10 minuter kvar tills klockan är prick 7. Klockan är alltså 10 minuter i 7.

1.2.1 Uppmärksamma och stötta

Om du märker att några elever enbart skriver exempelvis 5 i, 5 över och 10 över och utelämnar timmen så kan det betyda att eleven ser minutvisaren som överordnad timvisaren. Repetera hur man kan läsa av klockan med enbart timvisaren, och visa och förklara sedan hur minutvisaren kan användas för att läsa av klockan mer noggrant.

Ställ in klockan på några olika klockslag och låt eleven börja med att utifrån timvisarens position förklara om klockan är lite i eller lite över. Sedan ber du hen utifrån minutvisaren och timvisaren tillsammans förklara om klockan är 5, 10, 15 över eller i.

Det kan vara svårt att läsa av tiden när minut- och timvisare är nära varandra, t.ex. 5 över 1, 10 över 2, kvart över 3, kvart i 9, 10 i 10 och 5 i 11. Undvik dessa klockslag tills eleverna är riktigt säkra.

Förenkla

Om en elev har svårt med klockan kan du låta hen fokusera på enbart klockslag med kvart i och kvart över. När hen är helt säker på dessa så kan du utöka med 10 över och i, och så vidare.

Utmana mer

De elever som är helt säkra på avläsning av klockan kan utmanas genom att öva på vad klockan kommer att vara om en viss tid, eller vad klockan var för en viss tid sedan.

Låt dem ställa en elevklocka på en heltimme. Fråga sedan vad klockan kommer att vara om t.ex. 10 minuter, eller vad den var för 10 minuter sedan. Anpassa svårighetsgraden genom att välja om hur lång tid, eller vilken tid som förflutit.

Du kan också låta eleverna träna på att avrunda – om en klocka är 9 minuter över 4 så säger man oftast 10 minuter över 4.

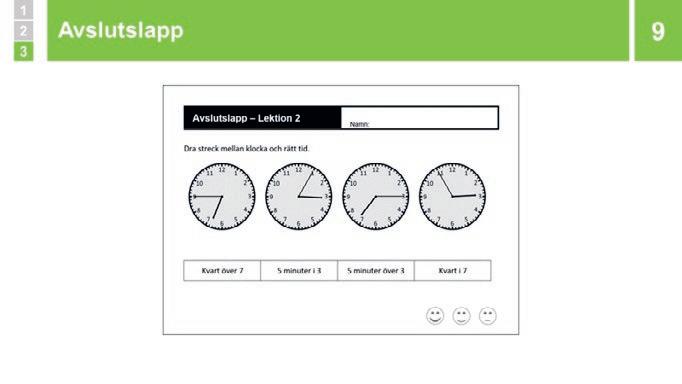
Avslutslappen

Avslutslappen visar om eleven kan läsa av klockan och koppla till rätt klockslag. Om elever blandar ihop över och i så tyder det på att eleven inte är tillräckligt säker på dessa ords betydelse i förhållande till klockan och tiden. Fortsätt att träna på klockslag, och var tydlig med när klockan är över och när den är i heltimme.

Om många elever har svårigheter behöver du överväga att göra någon av genomgångarna igen.

Träna vidare på klockan För att eleverna ska bli helt säkra på att läsa av klockan kommer de att behöva träna vid många tillfällen parallellt med att ni arbetar med det första kapitlet. Pausa gärna arbetet under skoldagen och be olika elever läsa av vad klockan är. Du kan också ta fram en klocka under samlingen eller vid liknande tillfällen och låta eleverna läsa av tiden.

1.3 Lilla additions- och subtraktionstabellen

Syftet med lektionen är att utveckla elevernas metodförmåga ifråga om att beräkna talkombinationer inom lilla additions- och subtraktionstabellen. Detta sker genom att eleverna får repetera och använda olika räknestrategier. Lektionen ger också eleverna möjlighet att öka sin förståelse för räknesätten genom att tolka och lösa enkla textuppgifter. I nästa lektion introducerar vi och övar på strategier för att addera och subtrahera tvåsiffriga tal med tiotal.

Lektionsmål

• Eleven har räknestrategier för att hantera alla talkombinationer i lilla addition och subtraktion, och visar det genom att resonera sig fram till rätt svar när hen inte direkt vet resultatet.

• Eleven har automatiserat delar eller hela lilla addition- och subtraktionstabellen, och visar det genom att direkt veta resultatet av flera talkombinationer.

Matematiska begrepp: Addition, subtraktion, term, summa, differens

SvA: spelpjäs, tärning

Material: Kopieringsunderlagen Spelplan 0–10 och Spelplan 0–99 samt spelpjäser och tärningar.

Förberedelser

• Fundera på vilka elever som behöver träna mer på lilla additions- och subtraktionstabellen, och vilka som är tillräckligt säkra för att kunna generalisera den i ett högre talområde. Fundera också över vilka strategier eleverna behöver repetera.

• Tänk igenom parindelningen till steg 5. Skriv ut till Spelplan 0–10 i A3 till de som behöver öva på lilla plus och minus, och Spelplan 0–99 till de som kan generalisera i ett högre talområde.

Spelplan 0−10

Spelplan 0−10 Färg

Spelplan 0−99

Spelplan 0−99 Färg

Repetition: Utvecklad form och platsvärde

Du repeterar utvecklad form. Utvecklad form är när man skriver två tal som visar vad siffrorna i exempelvis 25 står för.

Repetition: Strategier

Du visar animerade filmer för att repetera strategier.

Genomgång: Mönster i addition och subtraktion

Du spelar den animerade genomgången med berättarröst som går igenom mönster i addition och subtraktion.

Aktivitet: Spelet Först i mål Du delar in eleverna i par. De par som automatiserat lilla plus och minus eller är säkra på strategierna får Spelplan 10–99, övriga får Spelplan 0–10. Eleverna övar på strategier och automatiserar kombinationer när de spelar.

Elevboken s. 11−14

Sammanfattning: Huvudräkning Du berättar att bra strategier gör huvudräkningen enklare, och om man tränar tillräckligt mycket kommer man lära sig många kombinationer utantill. Att vara helt säker på alla beräkningar i lilla additions- och subtraktionstabellen är viktigt, och underlättar när talen blir större.

Uppstart

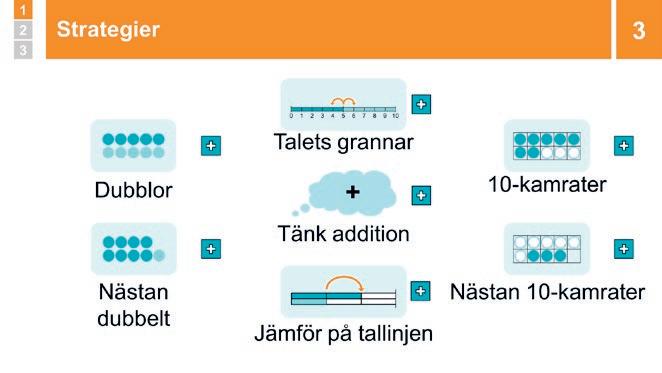
2 Repetition: Utvecklad form och platsvärde 5–15 min Repetera att när man skriver ett flersiffrigt tal i utvecklad form så skriver man två nya tal som visar vad siffrorna i det första talet står för. I talet 25 står siffran 2 på tiotalsplatsen och betyder därför två tiotal, alltså 20. Siffran 5 står på entalsplatsen och betyder fem ental, det vill säga 5. Talet 25 skrivs därför i utvecklad form som 20 + 5.

3 Repetition: Strategier Säg att ni under lektionen kommer repetera addition och subtraktion.

Klicka på de strategier du vill repetera, så spelas en animering med berättarröst upp. Klicka på returikonen när animationen är klar för att komma tillbaka till bilden med alla strategierna. Du kan i slutet av filmen klicka på playikonen för att visa hur man kan generalisera kunskapen inom lilla addition och subtraktion i ett högre talområde. Samma film kan du nå genom att direkt klicka på plustecknen vid ikonen.

4 Genomgång: Mönster i addition och subtraktion

I additionerna 4 + 3, 24 + 3 och 54 + 3 kan vi se att det är samma ental som adderas, och dessa har summan 7. Däremot skiljer sig tiotalen i den första termen i additionerna. Det innebär att 24 + 3 kommer att vara 20 mer än 4 + 3 eftersom talet 24 är 20 mer än talet 4.

54 + 3 kommer att vara 50 mer än 4 + 3 då talet 54 är 50 mer än 4.

I subtraktion ser vi samma mönster. I samtliga subtraktioner är entalet i den första termen 8, och i den andra termen är entalet 6. Vi vet att 8 − 6 är lika med 2. 18 − 6 kommer att vara 10 mer än 8 − 6 eftersom talet 18 är 10 mer än 8, medan 38 − 6 kommer att vara 30 mer då talet 38 är 30 mer än 8.

Vi kan alltså genomföra beräkningen av entalen först och sedan lägga till tiotalen.

Om vi tittar på dessa subtraktioner så ser vi att det är lika många tiotal i båda termerna. Även här kan vi bortse från tiotalen och enbart genomföra beräkning med entalen. Vi vet att 8 − 6 är lika med 2 eftersom skillnaden mellan talen 6 och 8 är 2. Samma differens är det i subtraktionen 18 − 16 och 48 − 46.

Aktivitet

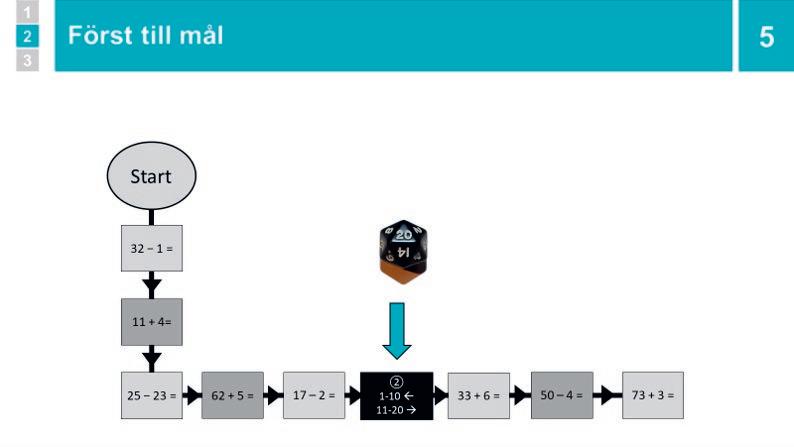
5 Aktivitet: Spelet Först i mål 30–45min Dela in eleverna i par så att de kan arbeta med samma spelplan. De elever som har automatiserat lilla additions- och subtraktionstabellen eller är säkra på strategierna ger du Spelplan 10–99, övriga får Spelplan 0–10.

Förse paren med spelplan, 20-sidig tärning och pjäser, och förklara spelet. Så här funkar spelet:

• Eleven som spelar ska slå en 20-sidig tärning och gå så många steg framåt som tärningen visar.

• Spelaren ska sedan lösa additions- eller subtraktionsuppgiften de hamnar på. Svaret säger de till medspelaren, som hjälper till att kontrollera om det är rätt. Om svaret är rätt får spelaren stå kvar, om svaret är fel får spelaren gå ett steg tillbaka.

• Om spelaren hamnar på en mörkblå ruta får hen slå tärningen igen. Om den visar 1–10 går spelaren tillbaka så många steg som cirkeln visar, om tärningen visar 11–20 går spelaren framåt.

• Turen går över till medspelaren.

Låt paren börja spela när alla förstått. CIRKULERA

De elever som blir snabbt klara kan spela igen eller arbeta i elevboken.

6 Elevboken s. 11−14 Avslut

7 Sammanfattning: Vad har vi lärt oss? 5 min

Att kunna bra strategier gör huvudräkningen enklare. Om man tränar tillräckligt mycket kommer man efter ett tag veta direkt vad exempelvis 8 − 5 är, lika lätt som 1 + 1.

Att vara helt säker på alla beräkningar i lilla additions- och subtraktionstabellen är viktigt och underlättar när man ska göra beräkningar med större tal.

1.3.1 Uppmärksamma och stötta

Lektionen ger dig möjlighet att upptäcka elever som ännu inte har automatiserat lilla additions- och subtraktionstabellen samt elever som saknar lämpliga strategier för talkombinationerna. Att eleven saknar hållbara strategier kan exempelvis upptäckas genom att eleven räknar på fingrarna, nickar rytmiskt, eller räknar upp eller ned.

Det fortsatta arbetet bör individualiseras utifrån elevernas specifika brister. Notera vilka kombinationer som eleven gör fel på och kontrollera att hen har lämpliga strategier för dessa kombinationer. Om inte, undervisar du strategin och övar specifikt i korta pass på ca 5 minuter, gärna dagligen. Exempelvis kan eleven öva med winnetkakort.

Uppmärksamma också elever som inte använder sig av kommutativa lagen för addition. Märker du att en elev räknar upp från 1 i additionen 1 + 6 påminner du om att addition är kommutativt och visar på tallinjen hur eleven istället kan utgå från talet 6 och addera 1.

Det är vanligt att elever fastnar i att tänka subtraktion som att det alltid betyder ta bort, och alltid gör det oavsett uppgift. Det är viktigt att eleverna förstår subtraktion som skillnad, och inser när det är lämpligt att tänka så.

Påminn om att en lämplig strategi för att genomföra beräkningar med subtraktion är att tänka addition.

Om du har elever som redan automatiserat lilla additions- och subtraktionstabellen bör du låta dem hoppa över de uppgifter i elevboken som rör sig inom det talområdet. Låt eleven istället arbeta med uppgifterna som gör att de måste generalisera tabellkunskaper och strategier till ett högre talområde. Eleven kan även göra utmaningsuppgifterna. Du kan också låta dessa elever spela spelet lite längre, eller återgå till detta efter att uppgifterna i elevboken är klara.

Förenkla

De elever som behöver kan använda 10-rutor, 100-rutor eller tallinjen som stöd för räknestrategierna.

Ta reda på vilka talkombinationer som eleven inte kan beräkna och vilka strategier som eventuellt används. Om eleven saknar strategier behöver hen undervisas om dessa och träna på dem.

Utmana mer

Elever som redan har automatiserat lilla additions- och subtraktionstabellen samt kan generalisera dessa i ett högre talområde kan istället träna på addition och subtraktion med växling över tiotalet. Du kan låta eleven slå två tiosidiga tärningar och skriva en utsaga av utfallet. Eleven kan därefter göra om additionen till två subtraktioner, vilket tränar elevens förståelse för räknesätten som varandras inverser. Exempelvis slår eleven 5 och 6. Eleven skriver utsagan 5 + 6 = 11 och gör sedan om den till subtraktionerna 11 – 6 = 5 och 11 – 5 = 6.

4.1 Vinkelbegreppet

Syftet med lektionen är att börja utveckla elevernas förståelse för vinkelbegreppet. Nästa lektion fortsätter vi det arbetet genom att introducera begreppen rät, spetsig och trubbig vinkel.

Lektionsmål

• Eleverna har en viss förståelse för vinkelbegreppet och visar det genom att konstruera vinklar av olika storlek.

• Eleven kan jämföra vinklars storlek och visar det genom att ange eller konstruera vinklar som är större än och mindre än givna vinklar.

Matematiska begrepp: Vinkel, vinkelben, vinkelspets, vinkelbåge, linje

SvA: Möts, gap, sax, öppen, öppnad

Material: Linjaler, styv stål- eller aluminiumtråd eller piprensare.

Förberedelser

• Klipp till metalltråden så att varje elev kan få varsin bit som är runt 10 cm lång.

• Skriv ut avslutslappar.

Avslutslapp

Elevbok s. 3

Uppstart: Kapitel 4

Genomgång: Vinkel

Du introducerar vinkelbegreppet utifrån gapet på en sax och visar att en vinkel kan vara större eller mindre, precis som saxens gap. Saxen ersätts med två vinkelben.

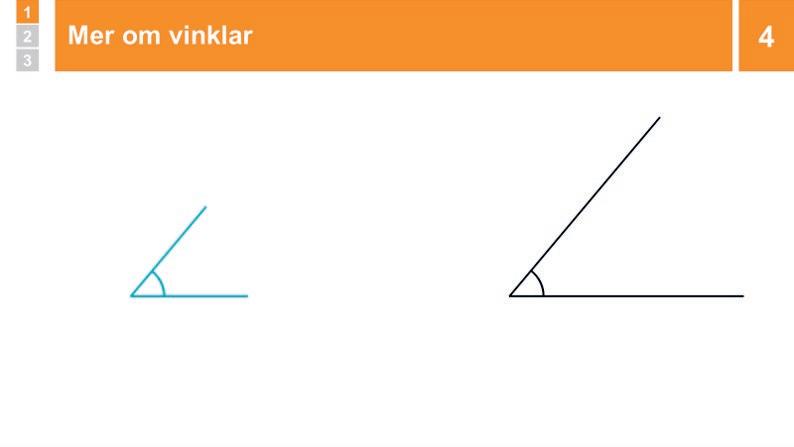
Genomgång: Mer om vinklar

Du visar att vinklar kan vara lika stora även om de har olika långa vinkelben, och/eller har sin spets åt olika håll. Du konstaterar att det är mellanrummet mellan vinkelbenen, som vinkelbågen visar, som avgör vinkelns storlek.

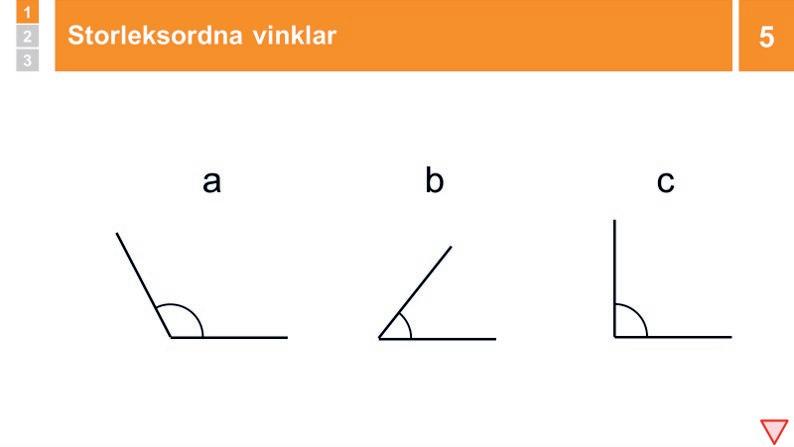
Övning: Storleksordna vinklar

Du visar tre olika vinklar, och eleverna SURRAR om vilken vinkel som är störst respektive minst.

15 min

Parövning: Rita och jämföra vinklar

Eleverna skapar varsin vinkel med en bit ståltråd och jämför i paren för att avgöra vilken vinkel som är störst. Du låter något par visa sina vinklar och förklara hur man ser vilken som är störst respektive minst. Om de lägger vinklarna på varandra, eller jämför på något annat bra sätt, så FÖRSTÄRKER du. Eleverna ritar med linjal varsin vinkel i elevboken och jämför de ritade vinklarna med hjälp av ståltråden.

Elevboken s. 4−6

25 min

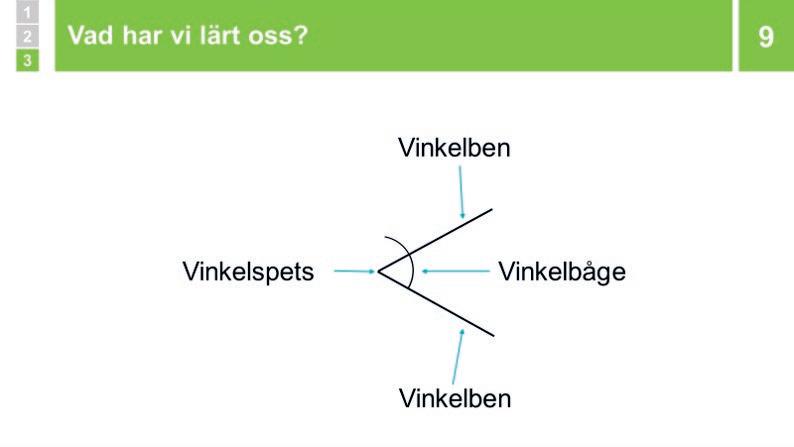
Sammanfattning: Vad har vi lärt oss?

Du visar en vinkel och repeterar begreppen vinkelben, vinkelspets och vinkelbåge. Du visar att själva vinkeln är mellanrummet mellan vinkelbenen.

Du visar tre olika vinklar och konstaterar genom att lägga dem på varandra att de är lika stora, trots att de har olika långa vinkelben och är vridna åt olika håll.

Avslutslapp

10 min

Uppstart

2 Uppstart: Kapitel 4 15 min

Välkomna alla matematiker till ett nytt kapitel. Visa några månghörningar och berätta att ni i det här kapitlet bland annat kommer att fördjupa er i trianglars och fyrhörningars egenskaper. Visa några kroppar och berätta att ni också kommer att fördjupa er i tredimensionella objekts egenskaper. Men först ska ni lära er vad vinklar är.

3 Genomgång: Vinkel

Visa hur saxen öppnar sig. Säg att eleverna ska titta på saxens gap, alltså hur mycket saxen är öppnad. Låt gapet minska och fråga om gapet är mindre eller större nu. Konstatera att gapet är mindre. Visa hur gapet ökar igen och konstatera att gapet nu är större. Klicka fram vinkelbågen och säg att den visar att man ska titta på mellanrummet. Låt saxen stängas lite och säg att gapet nu är mindre igen.

Låt saxen ersättas av två linjer. Visa att linjerna möts i en spets. Säg att mellanrummet mellan linjerna är en vinkel. Berätta att linjerna kallas för vinkelben och att spetsen där de möts kallas vinkelspets. Visa en vinkelbåge och säg att den används för att markera vinkeln.

Klicka fram en ny vinkelbåge för vinkeln på utsidan av vinkelbenen. Den mindre bågen på insidan försvinner. Säg att den nya vinkelbågen visar att ni nu ska titta på det här området mellan vinkelbenen – mellanrummet mellan vinkelbenen på utsidan.

4 Genomgång: Mer om vinklar

Visa två par linjer som öppnar sig till varsin vinkel med samma storlek. Visa hur båda vinklarna ökar i storlek lika mycket. Konstatera att båda vinklarna är lika stora, trots att den ena har längre vinkelben. Visa att så är fallet genom att lägga dem ovanpå varandra, vinkelspets mot vinkelspets.

Visa två nya vinkar och säg att även dessa vinklar är lika stora, trots att de har olika långa vinkelben. Visa att det är så genom att lägga dem på varandra. Konstatera att vinkelbenens längd inte påverkar vinkelns storlek.

Avsluta med att visa två lika stora vinklar i olika positioner. Konstatera att även dessa vinklar är lika stora, även om de är vridna åt lite olika håll. Visa att det är så genom att lägga dem på varandra.

5 Övning: Storleksordna vinklar

Visa tre olika vinklar. Låt eleverna SURRA om vinklarnas storlek och storleksordna dem från största till minsta vinkel. Fördela ordet tills någon ger en korrekt storleksordning. FÖRSTÄRK om hen utgår ifrån området mellan vinkelbenen. Konstatera att det är mellanrummet mellan vinkelbenen som avgör vinkelns storlek och inte vinkelbenens längd. När alla förstår och är säkra på storleksordningen visar du i bildspelet.

Genomför tre omgångar till på samma sätt.

Fånga upp missuppfattningar, till exempel att vinkelbenens längd skulle avgöra vinkelns storlek eller att hur vinkeln är vriden har betydelse. I sista omgången är det stora vinklar som ska jämföras. Påminn om att vinkelbågen visar vilket mellanrum man ska titta på.

Aktivitet

6 – 7 Parövning: Rita och jämföra vinklar 25 min

Förse eleverna med varsin bit ståltråd. Visa hur de ska böja ståltråden på mitten för att skapa en vinkel. När alla skapat en vinkel delar du in eleverna i par. Låt dem jämföra inom paren och avgöra vilken vinkel som är störst. Låt något par visa sina vinklar och förklara hur man ser vilken som är störst respektive minst. FÖRSTÄRK om de lägger vinklarna på varandra, eller jämför på något annat bra sätt.

Be eleverna slå upp s. 3 i elevboken. Säg att de med linjal ska rita varsin vinkel i elevboken. Därefter ska de mäta vinkeln med sin ståltrådsvinkel och använda den för att jämföra med partnerns vinkel. Visa hur det görs på tavlan eller i bildspelet.

Låt dem börja när alla förstått. CIRKULERA . När de är klara gör paren gemensamt resten av uppgifterna på s. 3.

8 Elevboken s. 4-6

När paret gjort klart s. 3 fortsätter de enskilt på s. 4−6.

Avslut

9 Sammanfattning: Vad har vi lärt oss?

10 min

Visa en vinkel och repetera begreppen vinkelben, vinkelspets och vinkelbåge. Berätta att själva vinkeln är mellanrummet mellan vinkelbenen, alltså linjerna. Visa och berätta hur vinkeln först blir större och sedan mindre.

Visa tre nya vinklar. Konstatera genom att lägga dem på varandra att vinklarna är lika stora, trots att de har olika långa vinkelben och är vridna åt olika håll.

10 Avslutslapp

Låt eleverna ha tillgång till en linjal och en bit ståltråd.

4.1.1 Uppmärksamma och stötta

En vanlig missuppfattning hos elever är att vinkelns storlek bestäms av vinkelbenens längd. En annan vanlig missuppfattning är att ett vinkelben måste vara horisontellt. För att inte dessa missuppfattningar ska befästas hos eleverna får de se många olika sorters vinklar. De får se vinklar som är lika stora, men med olika långa vinkelben och/eller vridning. När du själv ritar vinklar på tavlan behöver du variera i vinklarnas vridning och längden på vinkelbenen.

Eleverna behöver förstå att vinkelbågens funktion är att markera vinkeln, men att den inte anger vinkelns storlek. Om du märker att elever försöker mäta vinkelbågen för att avgöra vinkelns storlek behöver du hjälpa dem med förståelsen. Exempelvis kan du rita två lika stora vinklar, den ena med vinkelbågen nära vinkelspetsen och den andra med vinkelbågen längre ifrån vinkelspetsen. Visa genom att exempelvis klippa ut vinklarna och lägga dem ovanpå varandra att de är lika stora, trots att vinkelbågarna är olika.

Uppmärksamma de elever som visar tendenser till att ha dessa missuppfattningar. Låt dem använda ståltråd eller liknande för att jämföra vinklarna.

Förenkla

Om någon elev har svårt att jämföra vinklar i steg 7, Rita och jämföra vinklar, kan du skriva ut sidan från elevboken och låta hen klippa ut de olika vinklarna. Då kan eleven göra en direkt jämförelse genom att lägga dem på varandra.

Om några elever har svårt att rita vinklar kan de istället visa olika vinklar med hjälp av två glasspinnar eller liknande.

Utmana mer

Du kan låta ett elevpar rita varsin vinkel, byta vinkel med varandra och sedan försöka rita en vinkel som är lika stor som partnerns.

Avslutslappen

Avslutslappen visar om eleven kan skapa en vinkel med hjälp av penna och linjal, men också om eleven kan jämföra storleken på flera vinklar genom ögonmått eller indirekt mätning.

Om eleven skapar en vinkel med längre vinkelben där en större vinkel ska skapas, och tvärtom där en mindre ska skapas, är det ett tecken på att eleven inte förstått vad en vinkel är. Repetera då för eleven vad en vinkel är, och låt hen titta på stora vinklar med korta vinkelben och små vinklar med långa vinkelben.

4.2 Räta, spetsiga och trubbiga vinklar

Syftet med lektionen är att vidareutveckla elevernas förståelse för vinklar genom att introducera begreppen spetsig, rät och trubbig vinkel. I nästa lektion återkommer dessa begrepp då vi arbetar med spetsvinkliga, rätvinkliga och trubbvinkliga trianglar.

Lektionsmål

• Eleven kan identifiera olika typer av vinklar, och visar det genom att med hjälp av ett mätdon för räta vinklar identifiera och namnge räta, spetsiga och trubbiga vinklar.

• Eleven har en grundläggande förståelse för vinklar, och visar det genom att beskriva begreppet rät vinkel, spetsig vinkel och trubbig vinkel med ord, bilder och föremål.

Matematiska begrepp: Vinkel, vinkelben, vinkelspets, vinkelbåge, rät vinkel, trubbig vinkel, spetsig vinkel, rak vinkel, konvex vinkel, hake

SvA: Utåtbuktande, inåtbuktande, buktar utåt, buktar inåt

Material: Kopieringsunderlagen Vinkelverktyg och Tanketavla samt linjaler.

Förberedelser

• Skriv ut underlaget Vinkelverktyg, helst på ett transparent overheadpapper så att eleverna kan se vinkeln de arbetar med igenom det. Annars på ett lite tjockare papper eller ett inplastat papper. Klipp ut rutorna så att varje elev får varsitt vinkelverktyg för räta vinklar.

• Använd gamla tanketavlor, eller gör nya. Se Uppmärksamma och stötta för tips på hur du kan montera tanketavlorna.

Vinkelverktyg

Tanketavla

Elevbok s. 7

Repetition: Vinkel

Du repeterar begreppen vinkel, vinkelben, vinkelspets och vinkelbåge.

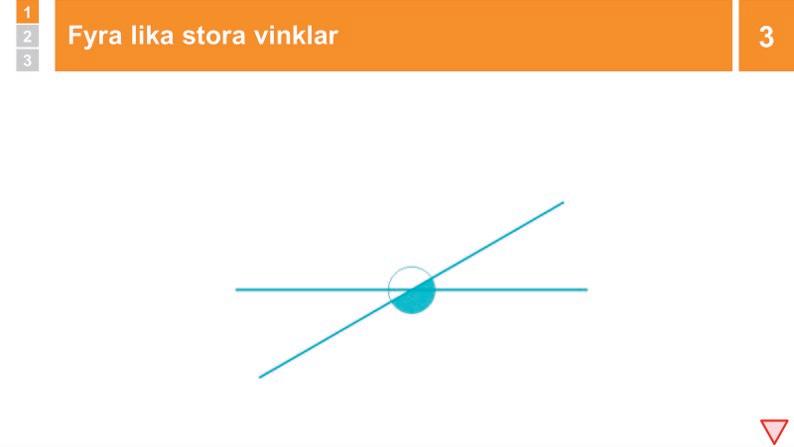
Genomgång: Fyra lika stora vinklar

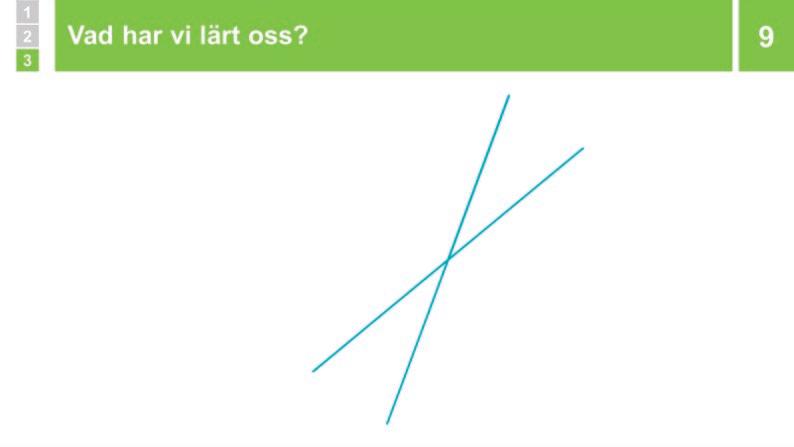
Du visar två linjer som skär varandra och bildar fyra vinklar. Eleverna identifierar vilka vinklar som är lika stora. De funderar på om linjerna kan ändras så det bildas fyra lika stora vinklar.

Genomgång: Rät vinkel

Den ena linjen vrids så att de fyra vinklarna blir lika stora. Tre av vinklarna försvinner och en rät vinkel är kvar. Du säger att en sådan vinkel kallas rät vinkel.

Eleverna letar räta vinklar i klassrummet.

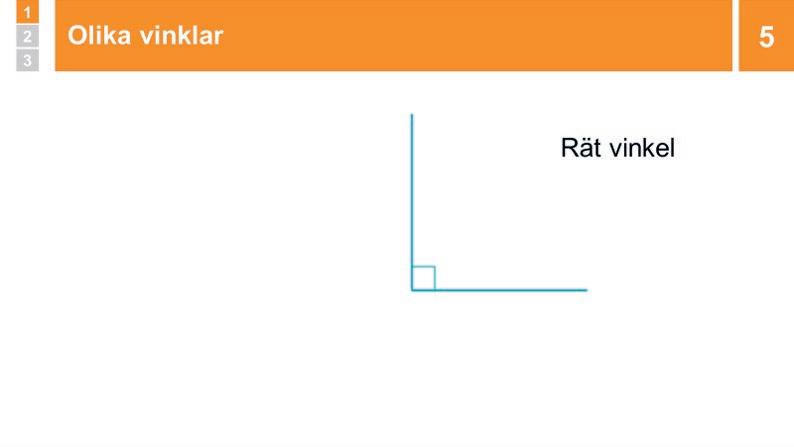
Genomgång: Olika vinklar

Du går igenom rak, konvex, trubbig och spetsig vinkel.

Elevboken s. 7−9

Du visar hur eleverna ska använda vinkelverktyget för att ta reda på om en vinkel är trubbig eller spetsig. Eleverna arbetar enskilt i elevboken med att avgöra vilken typ olika vinklar tillhör.

Paraktivitet: Rät vinkel med tanketavlan

Paren ritar en rät vinkel i tanketavlans fält Uttryck och gör sedan klart resten av fälten.

Redovisning: Rät vinkel Några par redovisar sina tanketavlor. Du ställer frågor som hjälper dem att förklara hur de olika fälten hör ihop.

Sammanfattning: Vad har vi lärt oss?

Du visar och sammanfattar: Om två linjer skär varandra och bildar fyra lika stora vinklar så är dessa vinklar räta. Du visar och repeterar hur man kan se om en vinkel är rät, rak, spetsig respektive trubbig.

Uppstart

2 Repetition: Vinkel 15 min

Repetera att hur mycket saxen är öppnad kan beskrivas med en vinkel. Visa hur den öppnar sig mer och säg att vinkeln nu är större. Låt saxen minska igen och sedan övergå till två vinkelben. Peka och repetera begreppen vinkelben, vinkelspets och vinkelbåge.

3 Genomgång: Fyra lika stora vinklar

Visa två linjer som skär varandra med en vinkelbåge runt skärningspunkten. Berätta att två linjer som skär varandra skapar fyra stycken vinklar. Låt eleverna SURRA om huruvida det finns några vinklar som är lika stora. Fördela ordet. Om någon säger att de motstående vinklarna ser lika stora ut så FÖRSTÄRK och visa i bildspelet.

 Fråga: ”Går det att ändra linjerna så att man får fyra lika stora vinklar?” Låt eleverna SURRA en stund. Eventuellt kan du tipsa om att de kan undersöka saken genom att rita med linjal på kladdpapper eller genom att korsa två pennor.

När eleverna har funderat en stund fördelar du ordet och RESONERAR kring elevernas förslag. Fånga upp om elever säger saker som att linjerna ska bilda ett kors, att en linje ska vara lodrät och en annan vågrät, eller liknande.

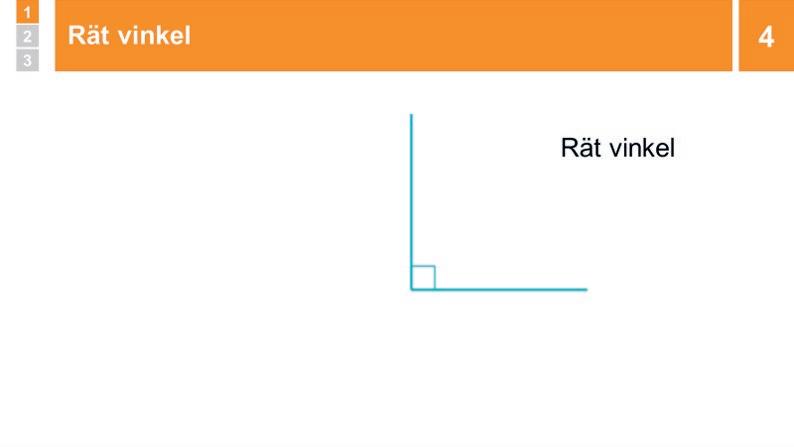
4 Genomgång: Rät vinkel

Visa hur den ena linjen vrids så att de fyra vinklarna blir lika stora. Konstatera att de är lika stora, och låt sedan tre av fyra vinklar i korset försvinna så att endast en vinkel är kvar. Berätta att en sådan vinkel kallas för en rät vinkel. Den runda vinkelbågen övergår till en kvadrat, som kallas hake. Säg att man brukar markera räta vinklar så här för att det ska vara tydligt att vinkeln är rät.

Visa hur den räta vinkeln vrids. Poängtera att vinkeln är rät hela tiden, oavsett åt vilket håll vinkelspetsen pekar.

Låt eleverna titta efter räta vinklar i klassrummet en kort stund. Låt dem komma med olika förslag. Konstatera att räta vinklar är ganska vanliga.

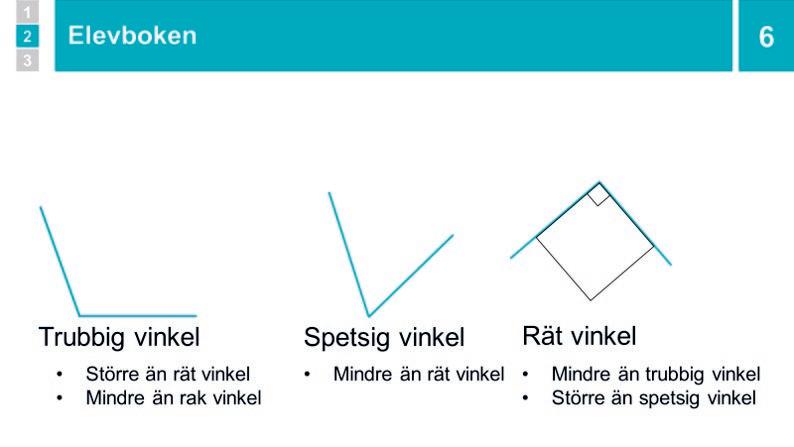
5 Genomgång: Olika vinklar

Låt den räta vinkeln bli större tills den bildar en rak vinkel. Berätta att en sådan här vinkel kallas för rak vinkel. Låt vinkeln bli ännu större, och säg att en vinkel som är större än en rak vinkel kallas för konvex vinkel. Berätta att konvex betyder att den buktar utåt medan en konkav vinkel buktar inåt..

Låt vinkeln minska igen. Peka och säg att en vinkel som är större än en rät vinkel men mindre än en rak kallas för trubbig vinkel.

Visa hur vinkeln minskar ytterligare och säg: ”En vinkel som är mindre än en rät vinkel kallas för spetsig vinkel.

Aktivitet

6 Elevboken s. 7−9 30 min

Dela ut varsitt vinkelverktyg till eleverna. Visa att det är en rät vinkel, och visa hur verktyget används för att ta reda på om en annan vinkel är trubbig: vinkeln är större än en rät vinkel, och vinkeln är inte rak, alltså är den trubbig. Visa på samma sätt hur en spetsig respektive en rät vinkel identifieras. Låt eleverna sedan arbeta enskilt i elevboken.

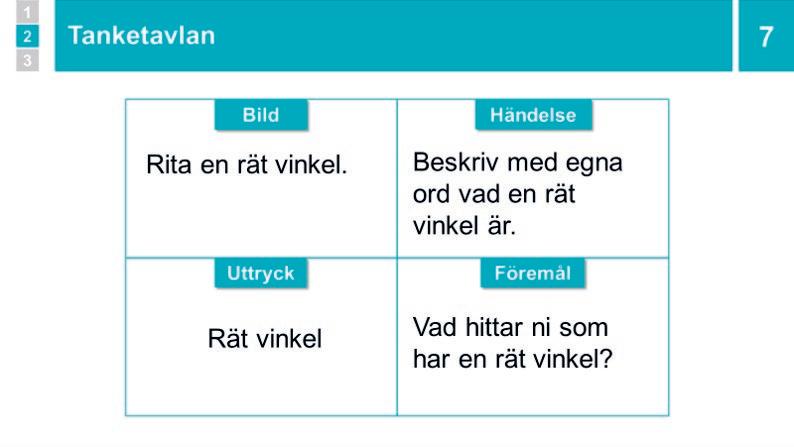
8 Paraktivitet: Rät vinkel med tanketavlan

Bryt när ca 20 minuter av lektionen återstår. Dela in eleverna i par. Förse dem med tanketavla och penna. Förklara aktiviteten. De ska:

• skriva ”Rät vinkel” i fältet Uttryck

• rita en rät vinkel i fältet Bild

• med egna ord förklara vad en rät vinkel är i fältet Händelse. En spetsig vinkel kan till exempel beskrivas som en vinkel som är mindre än en rät vinkel.

• skriva en sak i klassrummet som har en rät vinkel i fältet Föremål.

CIRKULERA . VÄLJ UT OCH ORDNA två–tre par till redovisningen. Försök hitta elever som förklarat på olika sätt vad en rät vinkel är. Deras definition av rät vinkel behöver inte vara matematiskt korrekt.

8 Redovisning: Rät vinkel

Låt de par du valt ut redovisa sina tanketavlor. Ställ frågor som hjälper dem att förklara hur de olika fälten hör ihop.

Avslut

9 Sammanfattning: Vad har vi lärt oss? 5 min Sammanfatta: Om två linjer skär varandra och bildar fyra lika stora vinklar så är dessa vinklar räta. Visa att räta vinklar markeras med en hake istället för en båge.

Visa hur vinkeln minskar. Berätta att en vinkel som är mindre än en rät vinkel kallas spetsig. Visa en rak vinkel och säg att den kallas rak vinkel. Visa en trubbig vinkel och säg att en vinkel som är större än en rät vinkel men mindre än en rak kallas för trubbig vinkel. Man kan säga att en rät vinkel är större än en spetsig vinkel, men mindre än en trubbig.

4.2.1 Uppmärksamma och stötta

En vanlig missuppfattning är att vinkelns storlek bestäms av vinkelbenens längd. En annan vanlig missuppfattning är att ett vinkelben måste vara horisontellt. För att undvika dessa missuppfattningar, får eleverna se många olika vinklar med olika långa vinkelben och vridning. När du själv ritar en vinkel på tavlan behöver du variera i vilken riktning vinkelns spets pekar åt.

En annan vanlig missuppfattning är att en vinkel alltid är rät. Det är anledningen till att vi inte introducerar den räta vinkeln först. I fortsatt arbete med vinklar är det viktigt att variera mellan spetsiga, trubbiga och räta vinklar, och senare även konvexa och raka vinklar.

Om du märker att eleverna inte använder vinkelverktyget på rätt sätt, behöver du hjälpa dem genom att förklara och visa hur det ska användas.

Förenkla

De elever som har svårt med att jämföra vinklarna i elevboken med vinkelverktyget, kan vara hjälpta av att du skriver ut sidan från elevboken och låter dem klippa ut vinklarna. Då kan eleverna göra en direkt jämförelse genom att exempelvis lägga vinklarna ovanpå varandra.

Utmana mer

Låt elever i par rita varsitt vinkelben, byta med varandra och sedan bestämma om partnern ska skapa en spetsig, rät eller trubbig vinkel. Du kan också låta dem göra konvexa eller raka vinklar.

Montera tanketavlan

Skriv ut tanketavlan på fyra A4-papper och plasta in dem. Tejpa ihop med gaffatejp på baksidan. Låt eleverna skriva och rita med ickepermanent tusch så att tavlorna kan återanvändas. Tuschen kan torkas av med en fuktig trasa.

4.3 Trianglar

I årskurs 1 började vi utveckla elevernas förståelse för grundläggande egenskaper hos månghörningar; deras antal sidor och hörn. I åk 2 utvecklar vi detta genom att dela in månghörningen triangel i ytterligare klasser utifrån vinkelbegreppet. Under nästa lektion utvecklas arbetet ytterligare genom att vi klassificerar och beskriver olika typer av fyrhörningar.

Lektionsmål

• Eleven har en grundläggande förståelse för sidor, hörn och vinkel, och visar det genom att till exempel använda termerna för att beskriva trianglar.

• Eleven kan känna igen olika trianglar, och visar det genom att skilja på och namnge spetsvinkliga, rätvinkliga, trubbvinkliga, liksidiga och likbenta trianglar.

Matematiska begrepp: Triangel, vinkel, sida, hörn, likbent, liksidig, spetsvinklig, trubbvinklig, rätvinklig

SvA: Spets

Material: Kopieringsunderlagen Sorteringstabell för trianglar, Olika trianglar och Vinkelverktyg samt linjal.

Repetition: Olika vinklar

Du repeterar rät, trubbig och spetsig vinkel.

Repetition: Triangel

Ni konstaterar att en triangels hörn är vinklar.

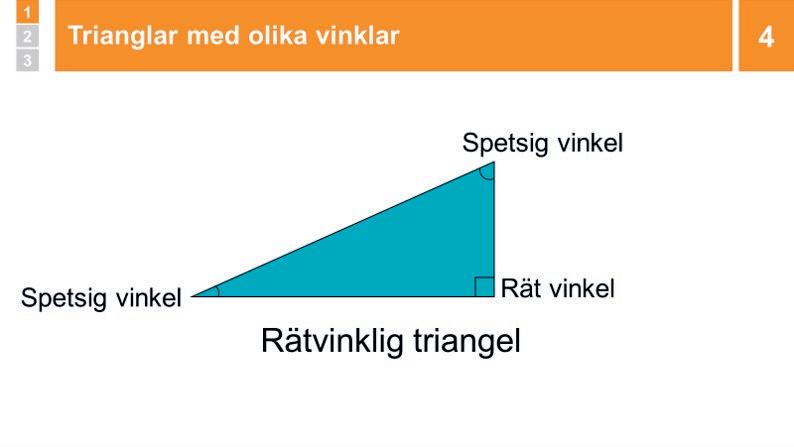
Genomgång: Trianglar med olika vinklar

Du visar en rätvinklig, trubbvinklig och spetsvinklig triangel, en i taget, och låter eleverna SURRA om vad deras olika vinklar är av för sort. Du visar vad som kännetecknar de olika trianglarna.

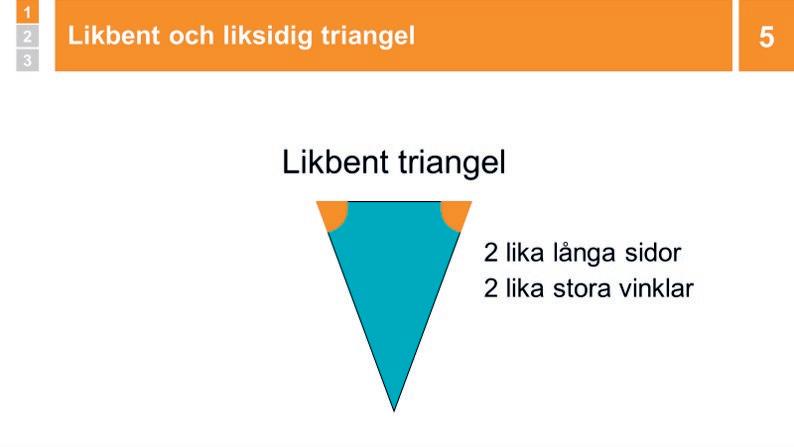
Genomgång: Likbent och liksidig triangel

Ni konstaterar att trianglar med minst två sidor som är lika långa kallas för likbenta trianglar, och att en liksidig triangel därför också är en likbent triangel.

15 min

Förberedelser

• Skriv ut kopieringsunderlaget Sorteringstabell för trianglar i storlek A3 till varje grupp.

• Skriv ut och klipp till kopieringsunderlaget Olika trianglar så att varje grupp kan få varsin uppsättning.

• Skriv ut avslutslappar.

• Övningsblad finns. Skriv ut vid behov.

Sorteringstabell för trianglar

Olika trianglar

Vinkelverktyg

Avslutslapp

Övningsblad grundläggande Övningsblad utmanande

Gruppaktivitet: Sortera trianglar efter egenskaper

Grupperna får 14 trianglar. De använder Sorteringstabell för trianglar för att sortera in trianglarna i kategorier utifrån deras egenskaper ifråga om vinklar och sidor.

Diskussion: Olika trianglar

Du leder en diskussion om olika trianglar med målet att få eleverna att bestämma vilken kategori trianglarna tillhör baserat på vilka egenskaper deras sidor, hörn och vinklar har. Ni avslutar med att diskutera varför det inte finns några liksidiga trianglar som är rät- eller trubbvinkliga.

Sammanfattning: Vad har vi lärt oss?

Du sammanfattar att trianglar kan sorteras i olika grupper och namnges efter hur deras sidor och hörnens vinklar är. Om två sidor hos en triangel är lika långa och två vinklar lika stora så är den likbent. Om en triangel har tre lika långa sidor och lika stora vinklar så är den liksidig. Har en triangel ett hörn där vinkeln är rät kan triangeln kallas rätvinklig. Är vinkeln i ett hörn trubbig kan triangeln kallas trubbvinklig.

Avslutslapp

25 min

10 min

Uppstart

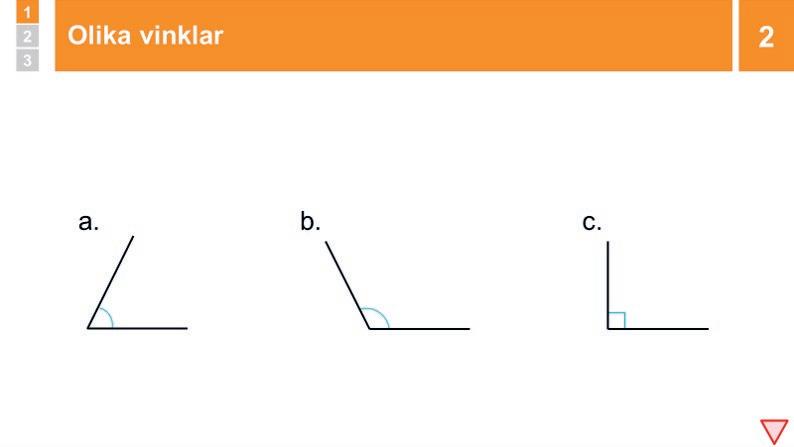
2 Repetition: Olika vinklar 15 min

 Fråga vilken av vinklarna som är en rät vinkel. BETÄNKETID. Fördela ordet. Om någon svarar vinkel c frågar du hur hen kan veta detta. FÖRSTÄRK om eleven kan ge en begriplig förklaring av vad en rät vinkel är. Gör på samma sätt med trubbig och spetsig vinkel.

3 Repetition: Triangel

Säg att ni ser en triangel. Låt någon säga hur många hörn och sidor den har. Konstatera att en triangel har tre hörn och tre sidor. Alla sidor är raka. De tar den närmaste vägen mellan två hörn, och det blir därför en rak linje.

Be eleverna titta noggrant på triangelns hörn. Fråga: ”Hur kan man beskriva hörnen?” BETÄNKETID. Fördela ordet. FÖRSTÄRK om någon säger att det är vinklar, annars visar du det själv. Konstatera att sidorna i triangelns tre hörn bildar vinklar. Ordet triangel betyder just tre vinklar

4 Genomgång: Trianglar med olika vinklar

Visa en rätvinklig triangel. Låt eleverna SURRA en kort stund om vad de olika vinklarna är av för sort. Fördela ordet. Om en elev pekar på den räta vinkeln och säger att den är rät, ber du en annan elev ÅTERGE . Berätta att en triangel som har en rät vinkel kallas rätvinklig triangel

Visa och gör på samma sätt med först en trubbvinklig triangel och sedan en spetsvinklig triangel.

5 Genomgång: Likbent och liksidig triangel

Visa en likbent triangel och be eleverna titta på dess sidor. Upptäcker de något? Ge BETÄNKETID. Fördela ordet. Om någon säger att två av sidorna är lika långa FÖRSTÄ RKER du. Säg att en triangel där minst två sidor är lika långa kallas för likbent triangel. Visa att två vinklar är lika.

Visa en ny triangel och konstatera att den också är likbent. Visa att den dessutom har tre lika långa sidor, och att alla vinklar därför är lika stora. Säg att den då är en liksidig triangel. Alla liksidiga trianglar är likbenta, men alla likbenta trianglar är inte liksidiga.

Aktivitet

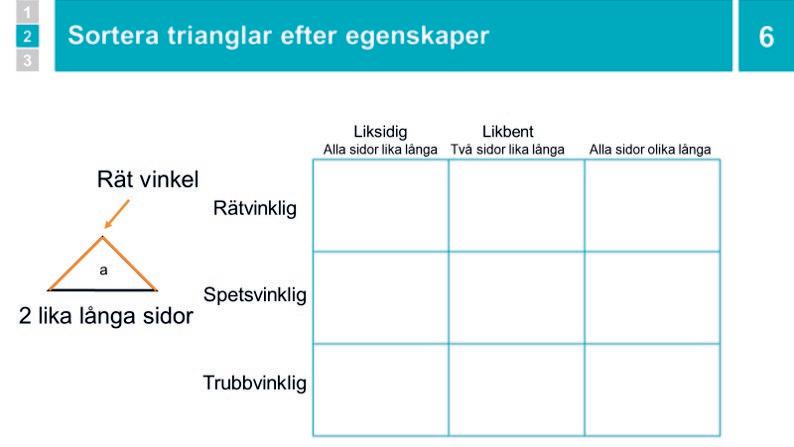
6 Gruppaktivitet: Sortera trianglar efter egenskaper Dela in eleverna i grupper om fyra. Förse dem med kopieringsunderlaget Sorteringstabell för trianglar och en uppsättning utklippta trianglar. Förklara aktiviteten med triangel A som exempel:

• Gruppen väljer en triangel och undersöker dess vinklar och sidor. Ni väljer triangel A i exemplet.

• Vilken rad hör triangel A hemma på? Konstatera att triangel A har en vinkel som är rät. Den ska alltså ligga på raden för räta vinklar. Raden markeras. Påminn om att man kan använda en rät vinkel för att avgöra om en vinkel är spetsig, trubbig eller rät.

• Vilken kolumn hör triangel A hemma i? Konstatera att triangel A har två lika långa sidor, och att den därför är likbent. Den ska alltså placeras i kolumnen för likbenta trianglar. Visa hur triangel A läggs i rätt ruta. Påminn om att de kan använda linjal för att mäta sidorna på trianglarna.

När alla har förstått kan grupperna börja arbeta med att sortera resten av trianglarna på samma sätt. CIRKULERA och stötta. Se till att de fokuserar på vinklar och sidor.

7 Diskussion: Olika trianglar

 Led en diskussion om en triangel i taget med målet att eleverna ska bestämma vilken kategori trianglarna tillhör baserat på vilka egenskaper deras sidor, hörn och vinklar har. Du kan, om det passar bättre, vända på det. Utgå ifrån en kategori i taget och diskutera vilka trianglar som hör hemma i vilken kategori.

CIRKULERA VÄLJ UT OCH ORDNA två–tre par till redovisningen. Försök hitta elever som förklarat på olika sätt vad en rät vinkel är. Deras definition av rät vinkel behöver inte vara matematiskt korrekt.

Stötta och uppmuntra eleverna i att använda geometrisk terminologi: rätvinklig, trubbvinklig, spetsvinklig, liksidig och likbent. När elever använder andra ord på ett begripligt sätt kan du förtydliga genom att upprepa det sagda med korrekt terminologi.

Poängtera att en liksidig triangel också är likbent. En likbent triangel har minst två lika långa sidor. I en liksidig triangel är dessutom den tredje sidan lika lång som de andra två.

Visa sorteringen i bildspelet. Fråga: ”Varför finns det ingen liksidig triangel som är rät- eller trubbvinklig?” Ge BETÄNKETID

Visa en liksidig triangel, och hur dess ena vinkel ändras till en rät vinkel. Den tredje sidan är nu för kort och måste förlängas. Alltså är den längre än de övriga sidorna, och triangeln är inte längre liksidig. Visa hur vinkeln istället blir trubbig, och konstatera att den tredje sidan nu måste vara ännu längre. Alltså kan inte en liksidig triangel ha en rät eller trubbig vinkel.

Kapitel 4 |

Avslut

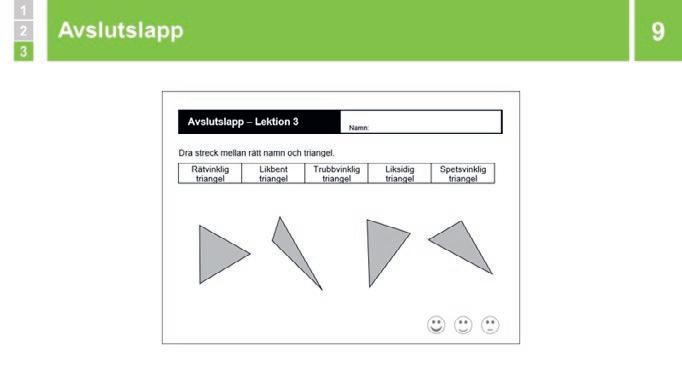
8 Sammanfattning: Vad har vi lärt oss? 10 min Sammanfatta att trianglar kan sorteras i olika grupper och namnges efter hur deras sidor och hörnens vinklar är. Om två sidor hos en triangel är lika långa och två vinklar är lika stora, är triangeln likbent. Om en triangel har tre lika långa sidor och lika stora vinklar, är den liksidig. Har en triangel ett hörn där vinkeln är rät kallas triangeln rätvinklig.

9 Avslutslapp

Påminn om att en och samma triangel kan tillhöra mer än en kategori.

4.3.1 Uppmärksamma och stötta

Uppmärksamma de elever som har svårt att analysera trianglarnas olika delar och egenskaper. Dessa elever kanske har svårt att se något annat än objektet i dess helhet. Det är då viktigt att du visar för eleven hur hen ska titta på exempelvis triangelns hörn för att avgöra storleken på hörnets vinkel. Du kan också låta elever konstruera trianglar av tre raka föremål, till exempel blompinnar av olika längd, för att de lättare ska kunna se triangeln som en sammansättning av olika delar.

Varje liksidig triangel är även en likbent triangel, men det är mer noggrant att säga liksidig triangel eftersom det ger mer information om figuren. Däremot är inte alla likbenta trianglar liksidiga. Man kan säga att liksidiga trianglar är en specialvariant av likbenta trianglar där alla sidor är lika långa. Det är viktigt att eleverna förstår att en likbent triangel har minst två sidor som är lika långa och två vinklar som är lika stora, medan alla vinklar hos en liksidig triangel har samma storlek och sidorna är lika långa.

Förenkla

Låt eleverna titta på en egenskap i taget. De kan först sortera trianglar efter sidornas längd och sedan avgöra deras vinklar. Du kan också begränsa antalet trianglar eleverna arbetar med.

Utmana mer

Låt de elever som behöver mer utmaning rita egna trianglar efter kriterier som du säger. Du kan exempelvis be dem rita en rätvinklig triangel som är likbent.

Du kan också låta eleverna ta reda på om en triangel kan ha två räta eller trubbiga vinklar och förklara varför, eller varför inte, det är möjligt.

Avslutslappen

Avslutslappen avgör om eleven kan titta på trianglars egenskaper och använda sig av dessa för att namnge trianglarna.

Om eleven har svårt att se om sidorna är lika eller olika långa kan du låta dem använda linjal. Om de har svårigheter med vinklarna kan du låta dem jämföra med en känd vinkel, exempelvis en rät.

Om eleven namnger den liksidiga triangeln som likbent kan du påtala att det är helt korrekt, men att det är mer noggrant att ange den som en liksidig triangel.

Studentlitteratur AB

Box 141

221 00 LUND

Besöksadress: Åkergränden 1

Telefon 046-31 20 00 studentlitteratur.se

Kopieringsförbud

Detta verk är skyddat av upphovsrättslagen. Kopiering, utöver lärares begränsade rätt att kopiera för undervisningsbruk enligt Bonus Copyright Access skolkopieringsavtal, är förbjuden. Kopieringsunderlag får dock kopieras under förutsättning att kopiorna delas ut endast i den egna undervisningsgruppen. För information om avtalet hänvisas till utbildningsanordnarens huvudman eller Bonus Copyright Access.

Vid utgivning av detta verk som e-bok, är e-boken kopieringsskyddad.

Användning av detta verk för text- och datautvinningsändamål medges ej.

Den som bryter mot lagen om upphovsrätt kan åtalas av allmän åklagare och dömas till böter eller fängelse i upp till två år samt bli skyldig att erlägga ersättning till upphovsman eller rättsinnehavare.

Studentlitteraturs trycksaker är miljöanpassade, både när det gäller papper och tryckprocess.

Art.nr 46135

ISBN 978-91-44-18228-5

Upplaga 3:1

© Andreas Ryve, Rik matematik AB och Studentlitteratur 2024 © Andreas Ryve, Rik matematik AB och Bonnierförlagen Lära 2021

Formgivning: Marit Messing – Go Form AB, Frangkle

Illustrationer: Jessica Svendeborn (uggla och barn), Sinnebild (alla saker och ting, förutom spargris: Andrew Rybalko/Shutterstock, alptopp: Vlasov_38RUS/Shutterstock, svampar, klubbor, piltavla, bandyklubba, minichoklad: Manuel Tenser, larv: Anka Drozd/Shutterstock, blad: Jr images/ Shutterstock)

Foto: bullar: Manuel Tenser, äggkartong: Manuel Tenser, snäckor: Manuel Tenser, choklad: paket/Shutterstock, geléhallon: Manuel Tenser, jordgubbar: Manuel Tenser, humla: Manuel Tenser, målare: Africa Studio/Shutterstock

Printed by Eurographic Group, 2024

Rik matematik

2A – Lärarhandledning

Rik matematik ger lärare stöd att planera, genomföra och utvärdera rik matematikundervisning. Rik matematikundervisning kännetecknas av aktiva elever och en aktiv lärare där begrepp, resonemang och problemlösning står i fokus. Varje årskurs innehåller mer än 100 strukturerade lektioner med bildspel. Lektionerna har tydliga inledningar och avslutningar där central matematik betonas. Med Rik matematik får läraren stöd att varje lektion bedriva en undervisning som engagerar och utvecklar elevernas matematiska tänkande.

Rik matematik är utvecklat i ett nära samarbete mellan lärare och forskare och noggrant utprovat i klass.

I Rik matematik 2A Lärarpaket ingår utöver det tryckta lärarmaterialet, även en digital lärarresurs samt tillgång till förberedda uppdrag i Tomoyo, en digital spelifierad färdighetsträning. De digitala delarna nås via Min bokhylla på Studentlitteratur.se

Rik matematik 2A omfattar 5 områden:

Kapitel 1 – Addition och subtraktion

Kapitel 2 – Multiplikation

Kapitel 3 – Division

Kapitel 4 – Mer om geometriska objekt

Kapitel 5 – Mer om klockan och bråk