9789144176697

RIK MATEMATIK 1A

Lärarpaket – Tryckt + Digitalt

LÄS OCH PROVA

LÄRARPAKETETS

SAMTLIGA DELAR

RIK MATEMATIK 1A

Lärarpaket – Tryckt + Digitalt

Rik matematik är utvecklat för en undervisning där både elever och lärare är aktiva. Eleverna får resonera, diskutera och lösa problem, och utveckla en djupare förståelse för matematik.

LÄRARHANDLEDNING

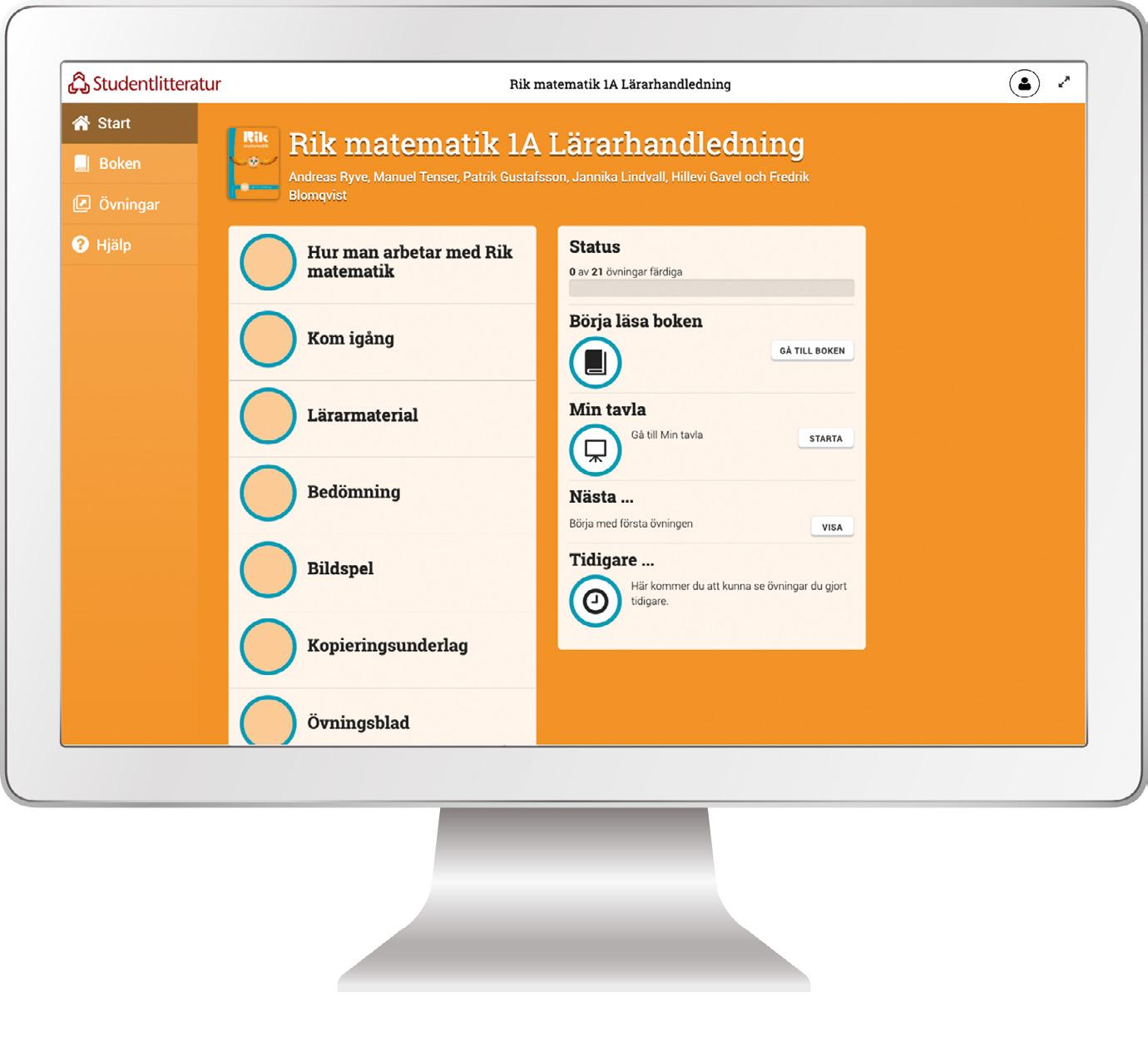
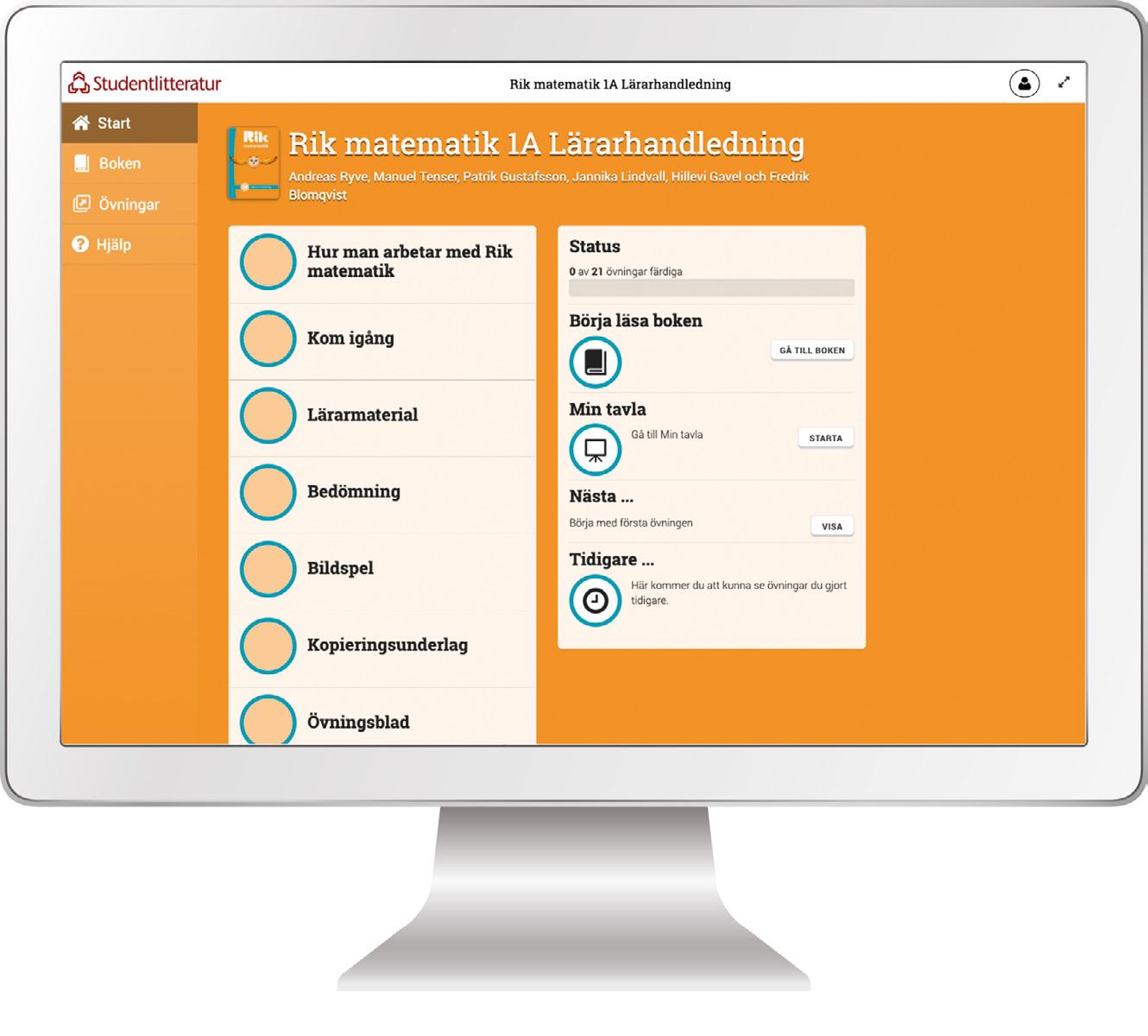
I lärarhandledningen får du det stöd och de resurser du behöver för att planera och genomföra din undervisning. Det finns mer än 100 detaljerade lektionsförslag per läsår, som ger konkret stöd och tips på saker att betona, frågor att ställa och exempel att visa. Bildspelen, som hör till varje lektion, fungerar som ett stöd genom hela lektionen, både visuellt för att fånga elevernas uppmärksamhet och för att tydliggöra matematiken med pedagogiska animeringar och bilder. I lärarhandledningen finns även avslutslappar, diagnoser, extra övningsblad m.m.

DIGITALT LÄROMEDEL

Det digitala lärarmaterialet är ett komplement till den trycka lärarhandledningen. Här finns alla digitala resurser samlade, samt kom igång-hjälp och annat stöd som du kan behöva.

Interaktiv version av lärarmaterialet, i vilken det går att söka, stryka under, anteckna och länka.

Fungerar på dator, surfplatta och mobiltelefon.

klicka på bilden och prova

1A Lärarhandledning

Lärarhandledning

Andreas Ryve

Manuel Tenser

Patrik Gustafsson

Jannika Lindvall

Hillevi Gavel

Fredrik Blomqvist

Välkommen till Rik matematik!

Med Rik matematik får du stöd att varje lektion bedriva en strukturerad undervisning där eleverna får resonera, lösa problem, diskutera, tänka och räkna matematik.

Rik matematikundervisning kännetecknas också av att både läraren och eleverna är aktiva – en elevaktiv och lärarledd undervisning. För att genomföra detta har lärarhandledningen mer än 100 detaljerade lektionsförslag per läsår, med bildspel till varje lektion, medan elevboken är full av forskningsbaserade uppgifter och problem. Bildspelen hjälper dig att visualisera och förklara den matematik som ni arbetar med och blir en utgångspunkt för resonemangen.

I din digitala lärarresurs finns lektionernas alla bildspel men där finns också fler resurser, såsom färdighetsträning, avslutslappar, diagnoser och kopieringsunderlag. Lärarresursen når du via licensen som du får när du köper lärarhandledningen.

Inloggning sker på sidan "Min bokhylla" som du hittar på Studentlitteratur.se.

Kapitelstrukturen

Alla kapitel här i lärarhandledningen inleds med en kort matematisk och didaktisk genomgång: Vad är det för matematik, vad vet vi från forskning om hur barn lär sig den och hur har vi därför lagt upp undervisningen? Varje lektion har en översiktssida där du bland annat hittar lektionsmålen och en sammanfattning av lektionen. Är du erfaren räcker det kanske att läsa sammanfattningen och klicka igenom bildspelet innan lektionen.

Lektionerna

Vill du ha mer stöd så ger lektionsförslaget också en detaljerad bild av hur du med bildspelet kan genomföra lektionen. Här får du konkret stöd och tips på saker att betona, frågor att ställa, exempel att visa. På lektionens sista sida får du tips på vanliga missuppfattningar och fel, hur du kan agera då, och hur du kan ge elever extra stöd och mer utmaning vid behov.

Lektionerna inleds alltid med en uppstartsfas. Här repeterar ni det viktigaste i föregående lektion,

och här får eleverna möta innehållet i den nya lektionen, ofta genom en lärarledd genomgång med stöd av bildspelet. I aktivitetsfasen diskuterar, tänker, räknar och löser eleverna problem, ofta i grupp eller par. Läraren har en viktig roll under aktivitetsfasen i att utmana elever, ställa frågor för att uppmana tänkande och diskussion, samla information inför avslutningen av lektionen, etc. Naturligtvis finns det också tid för enskild färdighetsträning. I avslutsfasen sammanfattar du lektionen tillsammans med eleverna och lyfter upp den centrala matematiken. Ofta gör eleverna en avslutslapp där de får visa vad de lärt sig och samtidigt tänka igenom det mest centrala i lektionen.

Var beredd att anpassa

Se lektionsplaneringen som ett förslag, inte som ett strikt manus. Följ inte alltid lektionsplaneringen till punkt och pricka utan utgå ifrån vad eleverna säger och tänker, och styr mot den matematik som de ska lära sig. Om du inte tror att grupparbete kommer att funka, kör par eller enskilt. Förstod de inte? Förklara på ett annat sätt. Och hoppa över delar som eleverna redan förstått.

Avslutslappar och diagnoser

Många lektioner avslutas med en avslutslapp. Det är ett effektivt sätt för dig att ta reda på vad eleverna kan:

• Har eleverna nått målen?

• Är det något som många har missat?

• Finns det enskilda elever som behöver arbeta mer med något?

Nästan varje kapitel avslutas också med att eleverna gör en diagnos. Svaren matar du enkelt in i diagnosverktyget som visar en sammanställning på klass- och elevnivå. Då kan du svara på frågor som:

• Vad kan eleverna bra, vad är svårare?

• Vilka behöver extra anpassningar eller särskilt stöd?

• Vilka behöver utmanas mer?

När du har koll på det kan du fundera på hur din undervisning påverkat resultaten:

• Vad gick bra och varför?

• Vad gick mindre bra och varför?

• Vad tar du med dig?

Lärarhandledningen ger dig stöd vid analysen, inte bara av hur elevernas resultat är på individ- och klassrumsnivå utan också hur du kan planera och genomföra framtida undervisning.

Både avslutslappar och diagnoser finns att ladda ner och skriva ut från din digitala lärarresurs.

Förstå läromedlets grundtankar

Forskning visar att det kan vara lätt att missförstå grundtanken med ett läromedel – och att normer, rutiner och gamla vanor ibland kan vara ett hinder för förbättring av undervisningen. I Sverige är det t.ex. väldigt vanligt att lärare låter eleverna sitta och räkna själva i boken större delen av lektionerna, i tron att de utvecklas matematiskt på det sättet. I rik matematikundervisning ligger tyngdpunkten på att eleverna lär och utvecklas i samspel med läraren och med varandra. När de arbetar i boken färdighetstränar de oftast för att befästa kunskaper. Vi vet också att allt för få lektioner har en avslutning där den centrala matematiken och lärandet lyfts fram, diskuteras och repeteras. Vi lyfter därför här några viktiga grundtankar i den undervisning som Rik matematik stödjer.

Lärarens viktiga roll

Läraren har en central roll i klassrummet. Du planerar undervisningen, diskuterar mål, utmanar elever, förklarar matematik, ställer frågor för att få igång diskussioner, summerar och pekar ut viktiga samband, bedömer, uppmuntrar, skapar struktur, etc. Rik matematik är utvecklat för en undervisning där både elever och lärare är aktiva.

Stöd för diskussion och interaktion

Att som lärare låta eleverna komma till matematisk förståelse genom att resonera, argumentera och lyssna i matematiska diskussioner är ett arbetssätt som är utmanande för alla lärare, men det är också roligt och stimulerande.

Läromedlet tillhandahåller strukturer och resurser som ger stöd för att du ska lyckas med detta. Utöver lektionsförlag med tydliga mål och bildspel, tillhandahåller läromedlet en ”verktygslåda” med en uppsättning diskussionstyper, lärartaktiker och en repertoar av frågetyper som du kan använda för att styra diskussion och interaktion mot avsett mål.

Ramverk för diskussion och interaktion

Målfokus istället för sidfokus

Ha fokus på mål och lärande istället för ett fokus på hur långt eleverna kommit i elevboken. Alla ska inte göra alla uppgifter. När eleverna nått målen ska ni gå vidare till nästa lektion, och nästa mål. Det viktiga är elevernas lärande och större delen av lärandet sker under aktiviteter där de inte sitter själva och löser uppgifter i boken. Det är också viktigt att eleverna inte tror att matematik handlar om att räkna många uppgifter så snabbt som möjligt. Matematiker tänker, funderar och försöker förstå begrepp och samband. Matematiker löser problem.

Elevbok

Det är en vanlig missuppfattning att alla elever måste göra alla uppgifter i elevboken, under eller efter lektionen. Det är inte tanken. Det viktiga är att eleverna når lektionsmålen.

Om du har elever som är snabba eller behöver utmanas kan de arbeta med de mer utmanande uppgifterna, vilka markeras med en eller två cirklar innan instruktionen.

När snabba elever räcker upp handen och anser sig klara med alla uppgifterna, måste du kontrollera om de verkligen löst uppgifterna med tillräcklig noggrannhet och kvalité. Utmana dem i att vara noggranna istället för snabba, genom att låta dem göra om slarvigt eller felaktigt utförda uppgifter, och uppmana dem att i fortsättningen vara noggranna från början.

Korta pass med färdighetsträning

Lägg in färdighetsträningspass mellan lektionerna. Det är bra att kunna saker utantill eftersom det frigör utrymme för tänkande och problemlösning. Lägg in pass på 5–20 minuter emellanåt då eleverna får träna för att befästa delar av matematiken, exempelvis genom arbete i elevboken eller träning med winnetkakort.

Winnetkakort är små papperskort med ett räkneuttryck på ena sidan, till exempel en addition, där summan av additionen framgår av kortets baksida. Korten är lämpliga för färdighetsträning som syftar till att eleverna ska bli mer förtrogna med olika räknestrategier och automatisera grundläggande talkombinationer. Winnetkakort finns för utskrift i den digitala lärarresursen.

Tomoyo

Tomoyo är ett spelifierat, digitalt läromedel där arbetet med de matematiska momenten varvas med fantasifulla berättelser. Tomoyo ingår i elevpaketet.

Elevens motivation och engagemang höjs när hen får snabb återkoppling och samlar poäng och märken.

Svårighetsnivån regleras automatiskt. Övningarna anpassas så att eleven får dem på samma, enklare eller svårare nivå, beroende på hens tidigare svar.

I Tomoyo är all text inläst och till varje övning finns det skräddarsydd hjälp i form av filmer, tips och begreppsförklaringar.

Som lärare kan du skapa ett digitalt klassrum och på så sätt följa dina elevers arbete och skicka uppdrag. Här hittar du även förberedda uppdrag som är kopplade till lektionerna i Rik matematik

Klassrumsnormer och Professor Uggla

För att kunna bedriva en rik matematikundervisning är det viktigt med ett tillåtande och respektfullt klassrumsklimat där eleverna vågar berätta vad de tänker, vågar göra fel och är tysta och lyssnar när någon annan har ordet. Strukturer och resurser som stödjer detta arbetssätt finns inbyggt i materialet. Till din hjälp har du även karaktären Professor Uggla som dyker upp i bildspelen och hjälper till att etablera de viktigaste klassrumsnormerna.

Ramverk för Rika klassrumsnormer

Arbeta långsiktigt!

Arbeta med tålamod och långsiktighet! Rik matematikundervisning är mer utmanande än att låta eleverna sitta ensamma och räkna i boken. Stressa inte upp dig om det inte fungerar perfekt direkt. Kapitel och lektioner kan ta längre tid i början.

I takt med att ni – du och eleverna – lär er hur Rik matematik fungerar och kommer in i arbetssättet, kommer det att gå allt lättare och bättre. Låt det ta den tid det tar! Tänk på att du ska ha eleverna i tre läsår.

Ta hjälp av det stöd som finns i den digitala lärarresursen och hos Rik-matematikkollegor för att snabbare komma in i läromedlet. Skriv till oss på Rik matematik-sidan på Facebook om du behöver råd och stöd.

Digitalt stöd

Det digitala stöd som hör till lärarhandledningen finns i din digitala lärarresurs. Lärarresursen når du via licensen som du får när du köper lärarhandledningen. Inloggning sker på sidan "Min bokhylla" som finns på studentlitteratur.se.

För att visa bildspelen (ppt) som inleder varje lektion, laddar du först ner dem till din dator och öppnar sedan upp dem med Powerpoint.

Bildspelen är ofta animerade. Se till att starta bildspelen så att du får en verklig bild av hur de ser ut.

Om din skola inte har en installerad version av Powerpoint kan du använda den webbaserade gratisversionen av Powerpoint.

Om du arbetar med en Chromebook kan du se filmen nedan för att lära dig om hur du då startar upp bildspelen.

Så här fungerar bildspelen i Rik matematik

Så här fungerar de webbaserade bildspelen i Rik matematik

Så här fungerar Rik matematiks bildspel med Chromebook

Ikoner i lärarhandledningen

Förmågeikoner

Ikonerna visar vilken/vilka förmågor som lektionen direkt utvecklar.

Begreppsförmåga

Kommunikationsförmåga

Metodförmåga

Problemlösningsförmåga

Resonemangsförmåga

Konstellationsikoner

Dessa ikoner visar i vilken konstellation en aktivitet är tänkt att genomföras i.

Undervisning under lärarens ledning

Enskilt arbete

Enskilt arbete i elevboken

Arbete i par

Arbete/diskussioner i grupp

Övriga ikoner

Här kommer du direkt till bildspelet.

Ljudfil i bildspelet

Visar att det finns en särskild funktion i bildspelet och att läraren måste klicka på ett särskilt sätt för att använda funktionen.

Nästa bild

Stanna upp innan du klickar fram svaret. Fråga hur ni kan göra. BETÄNKETID

Film

Dokumentet kan laddas ner.

Övrigt

Referat av det som sägs av berättarrösten

Extra information

Guldkantslektion

Kapitel 1 Tal och taluppfattning

1A Lärarhandledning

1.0 Introduktion

Syftet med kapitel 1 är att säkerställa att alla elever har en grundläggande taluppfattning inom talområdet 0–10, eftersom detta är avgörande för deras matematiska utveckling framöver. Det innebär att det för många blir repetition från förskoleklassen. Syftet är också att börja etablera klassrumsnormer och arbetssätt för en rik matematikundervisning, med mycket diskussion och problemlösning. I det arbetet får du mycket stöd, bland annat av Professor Uggla som i bildspelen kommer att förklara hur matematiker (elever) arbetar med matematik, och hur de är mot varandra i klassrummet.

Sammanfattning

I det här kapitlet får eleverna i huvudsak utveckla sin grundläggande taluppfattning genom att arbeta med räkneramsan, tal som antal, talraden, uppdelning av tal i heltalstermer samt ordningstal.

Vi vet att detta är ett innehåll som många av eleverna redan behärskar, men vi väljer ändå att repetera det, då alla elever måste behärska det för att kunna fortsätta utvecklas på bästa sätt.

Vi fokuserar samtidigt på att utveckla bra klassrumsnormer för matematikundervisningen och ett rikt arbetssätt med mycket diskussion och problemlösning. Om själva innehållet då till en början är repetition så gör det inget.

Pedagogisk planering – Tal och taluppfattning

1.0.1 Talbegreppet och barns utveckling av taluppfattning

Fokus i detta kapitel är talbegreppet i form av naturliga tal upp till 10. Naturliga tal motsvarar antal.

Antal anger hur många objekt det finns i en mängd, vilket kallas mängdens kardinalitet. En mängd är en samling objekt, exempelvis eleverna i klassen eller pennorna på bordet. Mängdens kardinalitet är en av dess egenskaper – den som vi intresserar oss för här.

Talbegreppet kommer med tiden att utvidgas, dels uppåt till allt större tal och dels med fler sorters tal: negativa tal som −2, rationella tal som ½, irrationella tal som �� och √2, vilket ger oss de reella talen, och slutligen med imaginära tal som i

Reella tal

Rationella tal

Hela tal

Naturliga tal

Räkneord och antal

Att kunna avgöra antalet föremål i en mängd genom räkning är nödvändigt för att kunna förstå tal och antal, och eleverna behöver då:

• lära sig räkneramsan

• lära sig räkna genom parbildning mellan räkneord och antal

• utveckla kardinaltalsprincipen: förståelse för att det sist nämnda räkneordet vid uppräkning anger antalet föremål i mängden. Då kan eleven även svara på frågan ”Hur många?” och ta fram eller räkna upp x stycken föremål

• utveckla antalskonservation: man är säker på hur många objekt som finns i en mängd när man räknat dem och behöver inte räkna om dem, t.ex. efter att de flyttats på

• kunna räkna bakåt genom att plocka bort ett föremål i taget eller muntligen räkna bakåt

• kunna räkna från andra tal än 1 och kunna talens grannar

• kunna räkna med 2, 3, 5 eller 10 steg i taget.

Det är viktigt att du som lärare ser till att eleverna lär sig och utvecklar alla dessa färdigheter. Om en elev fastnar på något kan du använda aktiviteter ifrån kapitlet eller skapa egna för att hjälpa eleven vidare. Prata med eleven för att förstå hur hen tänker, och använd konkret material för att förklara.

Lära sig att beteckna tal

De naturliga talen kan representeras på många sätt. Ett av dem är med siffror, och i detta kapitel introduceras det decimala talsystemet

Formellt är en siffra en symbol som representerar ett naturligt tal, som 5 i det decimala systemet eller V i det romerska. Däremot är t.ex. π inte en siffra eftersom symbolen inte representerar ett naturligt tal. 10 är inte heller en siffra utan två siffror, som när de står tillsammans på det här sättet representerar talet 10.

Eftersom tal större än 9 måste representeras med flera decimala siffror, är det viktigt att hålla isär begreppen siffra och tal.

Hur man representerar flersiffriga tal med hjälp av positionssystemet kommer eleverna att få lära sig i kapitel 6. Så småningom bygger vi på med decimaler, unärt minustecken och andra symboler som gör det möjligt att representera samtliga reella tal.

Räkneramsan

Att låta eleverna räkna högt med räkneramsan gör att de skapar viktiga minnesbilder och mönster. Genomför ofta muntlig upp- och nedräkning i kör eller i stafett tillsammans med eleverna. Anpassa talområdet till klassens nivå. Utveckla så småningom övningen genom att räkna i 2-, 5- eller 10-skutt, för att förstärka förståelsen för mönstret i vårt talsystem. Använd gärna miniräknarens kontantfunktion för att visualisera detta.

När eleven väl upptäckt det generella mönstret är det lika lätt att räkna från 21 till 32 som från 421 till 432. I det här kapitlet behandlar vi främst räkneramsan från 0 till 10.

Siffrorna

Att kunna skriva siffrorna rättvänt och läsbart är viktigt för att det ska vara tydligt vilken siffra och vilket tal som avses. Ett vanligt misstag i början är att spegelvända siffror. Var uppmärksam på om problemet kvarstår under läsåret då det kan leda till svårigheter för eleven.

I lektion 2 och 3 får eleverna börja träna på att skriva siffror. Visa tydligt hur man skriver siffror på rätt sätt, och säkerställ att eleverna vid behov får öva ofta och under korta intensiva pass. Träna i början av årskurs 1 så pass mycket att sifferskrivandet automatiseras, eftersom det gör att eleverna kan fokusera mer på matematiken.

En förutsättning för att kunna koppla siffrorna till räkneord och antal är att eleven känner igen siffrorna. Eleven behöver också förstå antal som en egenskap hos en mängd.

För de elever som är osäkra kan det i början vara bra att ha tydliga bilder i klassrummet som visar siffrorna tillsammans med räkneord och så många objekt som det antal de symboliserar.

Talraden

Talraden är en grafisk representation av räkneramsan. Med hjälp av talraden kan man visualisera relationer mellan tal och operationer, som addition och subtraktion. Talraden kommer senare att byggas ut till tallinjen, som då också visar tal mellan heltalen samt negativa tal till vänster om noll.

Att behärska talraden inom ett givet talområde innebär att eleven förstår att en position på talraden motsvarar ett tal. Det innebär också att kunna talens inbördes ordning och deras grannar, både uppåt och nedåt, oavsett var i talraden man befinner sig. Viktiga förutsättningar är att kunna räkneramsan och känna igen tal skrivna med symboler. I kapitel 1 fokuserar vi på talraden 0–10, men om dina elever redan behärskar den bör du utvidga till ett större talområde som passar din klass.

Att skriva talen är inte detsamma som att säga talen. Därför kan det vara en bra idé att, när eleverna behärskar att skriva siffror, också skriva motsvarande talföljd utifrån en muntligt uttryckt räkneramsa. Detta stödjer utvecklandet av en mental talrad.

1.0.2 Utveckla förståelse för talens egenskaper

Dela upp tal

Genom att träna på att dela upp naturliga tal i heltalstermer börjar eleverna kunna se tal som en sammansättning av två eller flera delar. Detta är en egenskap hos tal som det är väldigt viktigt att eleverna förstår, bland annat för att senare kunna utveckla olika huvudräkningsstrategier.

Ett exempel är när eleverna ska lära sig att addera med tiotalsövergång med hjälp av strategier som bygger på uppdelning av tal, t.ex. 9 + 4 = 9 + 1 + 3 = 13.

Eleverna kommer också att få lära sig talkamrater Talkamrater är två positiva heltal vars summa ger ett visst tal; i exemplet ovan har vi 10-kamraterna 9 och 1, samt 4-kamraterna 1 och 3. Det är viktigt att eleverna automatiserar talkombinationer, till att börja med inom talområdet 0–10, och talkamrater är ett sätt att arbeta mot det målet.

Vårt talsystem är uppbyggt på talet 10, och 5 två gånger

är lika med 10. Vi låter eleverna utveckla förståelse för talen 0–9 i relation till talen 5 och 10, t.ex. genom att tänka på talet 7 som 2 mer än 5, eller 3 mindre än 10. Vi konkretiserar också talen 0–10 med hjälp av 10-rutor, som består av två rader med fem rutor.

I samband med uppdelningar av tal låter vi också eleverna studera sambandet mellan antalet uppdelningar och talets storlek, som ett led i arbetet med att utveckla elevernas algebraiska tänkande.

Ordningstal

Eleverna kommer i kontakt med ordningstal vid många tillfällen i vardagen. I almanackor används siffror, och man behöver lära sig att t.ex. 3 där ska läsas som den tredje.

Många elever kan ha svårt att skilja på ordningstal, som anger placering, och tal som anger antal. Om man har en rad med tio elever så kan man välja ett antal om tre elever på många olika sätt, men den tredje eleven från vänster avser en viss elev. Var tydlig med att man måste säga om man räknar från vänster eller höger för att de ska förstå att det krävs för att ett angivet ordningstal ska avse en viss placering. Om inte alla elever kan vänster och höger så kan du peka och tillägga: ”från vänster, alltså den sidan.”

1.0.3 Algebra

I Rik matematik arbetar vi redan från första början med att utveckla elevernas algebraiska tänkande kopplat till respektive kapitels innehåll. Ordet algebra kommer från arabiskans ”al-djebr”, som betyder ungefär "återförening av delar". Ordet är en del i titeln på ett verk av den persiske 800-talsmatematikern Muhammad Al-Kwarizmi.

I aritmetik räknar man med kända tal som är representerade med siffror. I algebra representeras tal även med bokstäver (som a, n och x). Dessa kan t.ex. stå för värden som varierar, variabler, värden som man försöker ta reda på, obekanta, och ibland för alla tänkbara tal.

Detta gör att man kan undersöka, formulera och representera matematiska regler, som a + b = b + a, eller teckna funktioner för samband som till exempel " y = 10x – 50 där y är vinsten i kr om man säljer x glassar på en dag". Med hjälp av algebra kan man även lösa många problem genom att ställa upp och lösa ekvationer.

Enligt forskning tjänar eleverna på att börja utveckla en grundläggande förståelse för algebra redan i lågstadiet. Genom hela åk 1–3 lyfter vi algebran i lektioner där det passar, och vi kommer att börja redan i åk 1 med att använda bokstavssymboler för att representera variabler och obekanta tal.

I åk 1–3 får eleverna möta:

• Generaliserad aritmetik

Detta innefattar generalisering, representation, motivering och resonemang med aritmetiska relationer, inklusive räknelagar och tals egenskaper.

• Likheter, uttryck, ekvationer och olikheter

Innefattar utveckling av relationell förståelse för likhetstecknet och generalisering, representation och resonemang med uttryck, ekvationer och olikheter samt deras symboliska former.

• Funktionstänkande

Innefattar generalisering av samband mellan samvarierande storheter och representation, motivering och resonemang kring dessa generaliseringar genom vardagligt språk, notation med variabler, teckningar, tabeller och grafer.

Mönster

Eleverna får redan i lektion 10 i kapitel 1 arbeta med mönster. Eleverna kommer i åk 1–6 att få möta geometriska mönster och mönster i talföljder, vilket enligt Skolverkets kommentarmaterial till kursplanen kan bestå av t.ex. återkommande geometriska figurer (upprepade mönster) eller mönster som växer symmetriskt (växande mönster). Mönster som inte består av tal kan användas för att upptäcka och studera mönster och relationer i talföljder.

Eleverna kommer också att få leta efter mönster, och tolka, beskriva, översätta, utveckla och skapa mönster, vilket är en central del av algebra. Detta gäller specifikt utvecklandet av ett funktionstänkande då mönster möjliggör studie av olika sorters samband.

Upprepade mönster

Upprepade mönster kan se olika ut och den del som upprepas kan bestå av olika antal objekt, former, handlingar, symboler eller bokstäver.

I ett upprepat mönster kan talen bytas ut mot bokstäver, t.ex. A, B, B, A, B, B, … eller mot geometriska former då mönstret fortfarande har sin grundstruktur. Detta är något som eleverna måste upptäcka och inse.

Förståelsen för upprepade mönster kan stärkas om eleverna ges möjlighet att identifiera, motivera och översätta olika typer av mönster utifrån olika former och material.

Fysiska material kan underlätta då de kan användas för att pröva, testa och justera, och på så sätt möjliggöra studie av mönster som inte ryms på en sida i boken. Använd färgade klossar, knappar, centikuber, stickor etc. för

att skapa och fortsätta mönster som kan beskrivas och generaliseras. De konkreta mönstren kan dokumenteras med symboler. Exempelvis kan rött-blått skrivas som AB eftersom kärnan i mönstret består av två olika element. Nyckeln när man arbetar med upprepade mönster är att upptäcka själva kärnan i mönstret. Vad är det som upprepas? Att utmana eleverna till att identifiera och beskriva kärnan i mönstret samt antalet repetitioner genom att ställa frågor, är en nyckel i undervisningen. För att förstärka detta kan man lägga mönster under en dokumentkamera och högt säga vad som ligger där och vad nästa objekt som kommer läggas är. Efter ett antal objekt kan man fråga eleverna om de ser mönstret. Sedan kan man representera de olika objekten med bokstäver och beskriva mönstret som exempelvis ABC.

Uppmärksamma elever på upprepade mönster i vardagen som t.ex. veckodagar, månader, årstider och ramsor. Muntliga mönster kan sägas och repeteras, t.ex. "do mi mi, do mi mi", och sedan beskrivas med ABB. Kroppsrörelser kan också användas på samma sätt, t.ex. ett steg bakåt, två steg framåt.

Viktiga aktiviteter är att låta eleverna:

• Kopiera mönster

Visa ett mönster och låt eleverna kopiera det.

• Fortsätta mönster (åt flera håll …) Lägg ett mönster och fråga: ”Vad kommer efter den sista xx? Vad kommer före den första xx?” Be eleverna att förlänga mönstret åt båda hållen.

• Identifiera kärnan (elementet) som upprepas Visa/säg ett mönster högt. Be eleverna identifiera det som upprepas genom att ringa in det.

• Komplettera mönster (identifiera borttagna delar)

Lägg mönster och be eleverna identifiera kärnan. Plocka bort delar. Fråga vad som saknas.

• Skapa egna mönster

Ställ frågor som ”Varför är detta ett upprepat mönster? Kan ni visa mig/ringa in den upprepade delen? Hur fortsätter mönstret?”

• Översätta till andra uttrycksformer

Låt eleverna träna på att uttrycka samma mönster med en annan representationsform, t.ex. andra symboler, eller rörelser/gester, ord, ljud, fysiska föremål, bilder. Att göra på detta sätt flyttar fokus från representationen i sig till det bakomliggande mönstret.

Därefter kan eleverna få studera mönster mellan olika grupper. Då man letar mönster i en enstaka grupp kan man inte komma längre än till att föra resonemang om hurmönstretförändrasivarjesteg,medanfleragrupper möjliggörettdjuparefunktionstänkande.

1.0.4 Klassrumsnormer och lärartaktiker

Rik matematik ger stöd för att utveckla bra klassrumsnormer,förattmatematikarbetetskafungerasåbrasom möjligt. Ikapitel1dykerProfessorUgglauppibildspeletochintroducerardeförstaavdessanormer.Läsmer omklassrumsnormernaidindigitalalärarresurs,därdu ocksåhittartipspåhurdukanarbetameddem.

I lektionsförslagen återkommer vissa arbetssätt, lärartaktiker och diskussionstyper. I kapitel 1 förklarar vi dem kortfattat första gången de används i ett lektions-förslag.

Ramverk för Rika klassrumsnormer

Ramverk för diskussion och interaktion

1.0.5 Referenser

Blanton, M., Brizuela, B. M., Stephens, A., Knuth, E., Isler, I., Gardiner, A. M., ... & Stylianou, D. (2018). Implementing a framework for early algebra. I C. Kieran (Red.), Teaching and learning algebraic thinking with 5- to 12-year-olds: The global evolution of an emerging field of research and practice. (s. 27- 49). Hamburg: Springer International Publishing.

Clements, D. H., & Sarama, J. (2014). Learning and teaching early math: The learning trajectories approach. New York, NY: Routledge.

Hargreaves, M., Shorrocks–Taylor, D., & Threlfall, J. (1998). Children’s strategies with number patterns. Educational Studies, 24(3), 315–331.

Kazemi, E. & Hintz, A. (2014). Intentional talk: How to structure and lead productive mathematical discussions. Portland, ME: Stenhouse Publishers.

Smith, M.S. & Stein, M.K. (2014). 5 undervisnings – praktiker i matematik: För att planera och leda rika matematiska diskussioner. Stockholm: Natur & kultur.

Papic, M. (2007). Promoting repeating patterns with young children-More than just alternating colours!. Australian Primary Mathematics Classroom, 12(3), 8 –13.

Van de Walle, J. A., Karp, K. S., & Bay-Williams, J. M. (2015). Elementary and middle school mathematics: Teaching developmentally, global edition (uppl. 9). New York, NY: Pearson Education.

Verschaffel, L., Greer, B, & DeCorte, E. (2007). Whole number concepts and operations. I F.K. Lester (Red.), Second handbook on research of mathematics teaching and learning (s. 557–628). Charlotte, NC: Information Age Publishing.

Warren, E., & Cooper, T. (2006). Using repeating patterns to explore functional thinking. Australian Primary Mathematics Classroom, 11(1), 9–14.

1.1 Vad är matematik?

Syftet med denna första lektion är att väcka intresse för matematik genom att visa att det är intressant, kul och användbart. I den här lektionen får eleverna se exempel på vad de kommer att lära sig i åk 1. Ett av dessa exempel kommer de själva att få lösa i kapitel 9 med hjälp av det som de har lärt sig i åk 1.

Lektionsmål

• Eleven har en uppfattning om vad matematik är och vad den kan användas till, och visar det genom att kunna berätta om några tillämpningar av matematik

Matematiska begrepp: Matematik

SvA: Rymdraket, pris, karta, uppvärmning, uggla

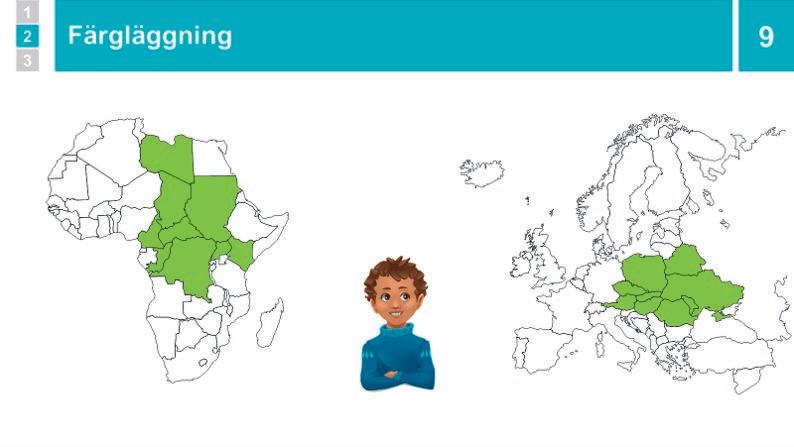
Material: Kopieringsunderlagen Afrika och Europa samt eventuellt Fyrfärgsproblemet, färgpennor i minst sex färger

Förberedelser

• Skriv ut kopieringsunderlagen Afrika och Europa som eleverna ska färglägga så att varannan elev kan få karta 1 och varannan karta 2.

• Klicka igenom bildspelet.

• Var beredd på att lektioner kan ta längre tid än planerat i början. Tänk igenom var du vill bryta om du behöver dela upp lektionen i två delar. Ta del av lärarhandledningens råd och information om hur läromedlet fungerar och hur du kan arbeta med det på bästa sätt.

Afrika

Europa

Fyrfärgsproblemet

Genomgång: Vad är matematik?

Du frågar vad matematik är och ger exempel. Du konstaterar att en matematiker arbetar med matematik. Eleverna är därför matematiker på matematiklektionerna.

Genomgång: Matematiska problem

Du ger exempel på problem som kan lösas med matematik och utbildningar där man får lära sig sådant. I bildspelet finns ett exempel på ett problem som eleverna själva ska få försöka lösa i slutet av åk 1.

Genomgång: Lektionsfaserna Du berättar att varje lektion har tre faser: uppstartsfas, aktivitetsfas och avslutsfas.

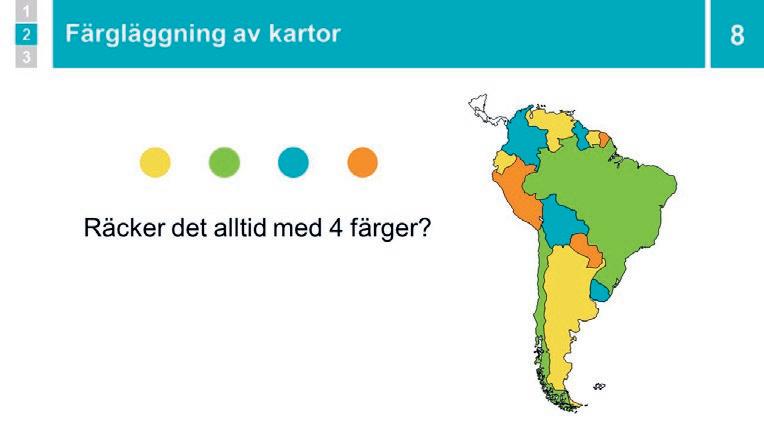
Genomgång och diskussion: Färgläggning av kartor

Eleverna SURRAR : Räcker fyra färger för att inga grannländer ska behöva ha samma färg?

Aktivitet: Färglägg och undersök Eleverna undersöker genom att färglägga varsin karta.

Professor Uggla: Om att färglägga kartor

Uggla: Historien om fyrfärgsproblemet

Sammanfattning: Vad har vi lärt oss?

Eleverna funderar på vad de har lärt sig och ger några exempel.

Avslut: Att lära sig matematik

Du konstaterar att fyrfärgsproblemet är för svårt att börja med, men om eleverna gör sitt bästa och kämpar på alla lektioner kommer de snabbt att lära sig mycket matematik och kunna lösa allt svårare problem!

Uppstart

2 Genomgång: Vad är matematik? 10 min Berätta att ni ska ha en lektion i ett ämne som heter matematik, och fråga eleverna om de har några idéer om vad matematik är. Fördela ordet (låt några svara) och skriv upp på tavlan.

Klicka fram några förslag, och säg att eleverna bland annat kommer att hålla på med liknande saker på matematiken. Säg att eleverna på matematiklektionerna är matematiker

3 – 6 Genomgång: Matematiska problem

Ge exempel på problem som kan lösas med matematik, och nämn olika utbildningar där man får lära sig lösa sådana problem.

I sista exemplet, bild 7, säger du att eleverna kommer lära sig så mycket matematik i åk 1 att de kommer att kunna lösa problemet i slutet av ettan (se Kapitel 9, lektion 12).

Aktivitet

7 Genomgång: Lektionsfaserna 30 min Berätta att lektionerna består av tre faser. Den orangea fasen som ni började med kallas uppstartsfasen. Då sätter ni igång med lektionen. Nu är ni framme vid aktivitetsfasen. Då kommer ni ofta att arbeta och träna på olika saker. Den sista fasen kallas avslutsfasen. Då sammanfattar ni vad ni lärt er.

8 Genomgång och diskussion: Färgläggning av kartor Klicka fram kartan. Säg att ni ska färglägga den, och fråga om två länder som ligger bredvid varandra bör ha samma färg. Ge eleverna en stunds BETÄNKETID

Fördela ordet (låt några svara). Om någon elev säger ungefär att länder bredvid varandra måste ha olika färg, för att det annars ser det ut som ett land, så UPPREPAR du det. Annars förklarar du själv.

Klicka för att färglägga kartan och konstatera att kartan har fyra färger. Fråga: ”Tror ni att det alltid räcker med fyra färger?” Låt eleverna fundera enskilt en stund på det.

9 Aktivitet: Färglägg och undersök

Berätta att eleverna enskilt ska få undersöka hur många färger som behövs genom att färglägga varsin bit av Afrika eller Europa så att inga grannländer har samma färg. Dela ut färgpennor (ca sex olika färger per elevpar), och kartor så att varannan elev får Europa och varannan Afrika. Låt dem börja när alla förstått uppgiften.

CIRKULERA (gå runt i klassen och överblicka arbetet, hjälp till där det behövs och bryt och förklara för alla om många verkar behöva få samma hjälp).

När de flesta är klara bryter du. Fråga om någon lyckades med bara fyra färger, och vilka som använde fler än fyra (sannolikt har några ”målat in sig i ett hörn”, se steg 10).

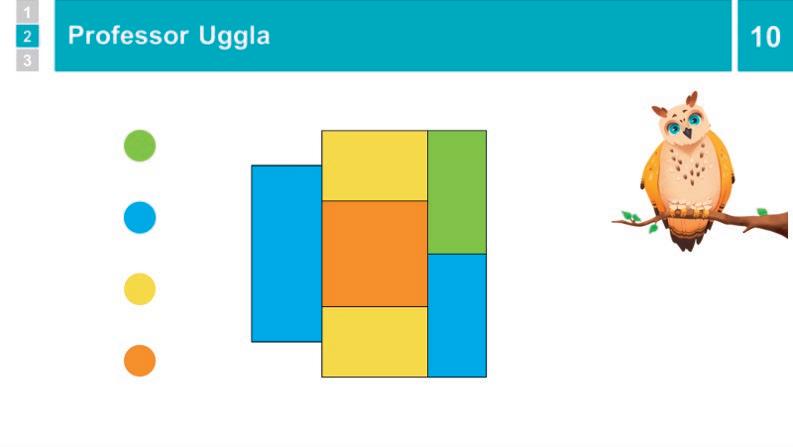
10 Professor Uggla: Om att färglägga kartor

Professor Uggla presenterar sig, och visar hur det kan bli då man färgar kartor.

Hej! Jag är professor Uggla, och jag kommer att berätta om matematik och matematiker. Jag tänkte se om jag också kan färga kartor, och jag ska försöka klara mig med bara fyra färger. Färg 1 … färg 2 … färg 3 … färg 4 … Vad gör jag nu då?

Låt eleverna komma med tips till Ugglan om du vill.

Jag använder en färg igen. Men vad ska jag ha för färg i mitten? Alla fyra färgerna finns ju på kanten!

Eleverna kan tipsa igen.

Jag provar att ändra färgen på ett ställe! Nu har jag en färg som jag kan använda! Så det gick att färga det här med bara fyra färger.

Ser ni att det faktiskt finns en likadan bit i era kartor? Ett land med fem länder runt sig. Då kan det bli så här klurigt.

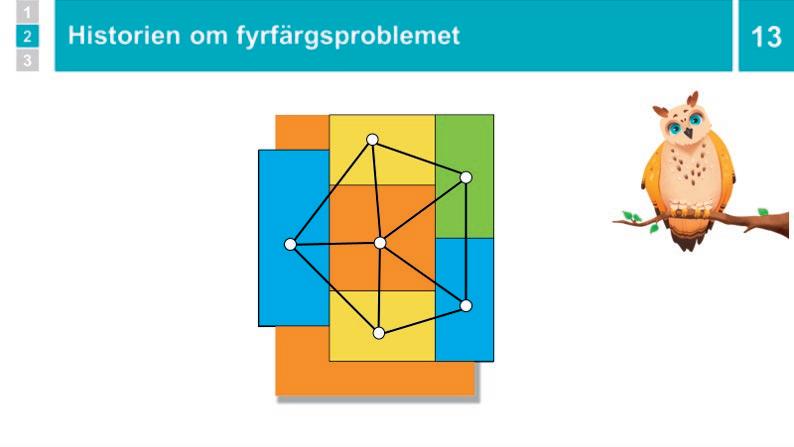
11 – 13 Uggla: Historien om fyrfärgsproblemet

Låt Uggla berätta historien, eller läs själv.

Problemet med om fyra färger räcker till alla kartor började matematiker försöka lösa för nästan 200 år sedan, år 1851, då tåg var uppfunna men inte bilar.

Det var en kille som hette Francis som satt och färgade en karta och märkte att han inte behövde mer än fyra färger. Francis frågade sin bror, som studerade matematik, om det alltid var så att fyra färger räckte.

Hans bror visste inte, men frågade sin lärare. Läraren visste inte heller, och frågade sina matematikerkompisar. De visste inte heller, men flera av dem försökte ta reda på det.

Ingen hittade någon karta där man behövde fler än fyra färger, men bara för det kunde man ju inte vara helt säker på att det inte fanns någon!

Nästan 30 år efter att Francis undrat var det en matematiker som påstod att det alltid räcker med fyra färger; och skrev en förklaring. Bra, tyckte alla, då vet vi det!

Men tio år senare var det en annan matematiker som läste förklaringen väldigt noga och såg att den bara förklarade att alla kartor som såg ut på ett visst sätt gick att färga med fyra färger. Men kartor som inte såg ut på det sättet då?

Problemet var inte alls löst!

Sedan arbetade många matematiker i nästan 100 år med att försöka lösa problemet, och hittade på en massa spännande saker. Till sist kom en av dem på att kartor inte kan se ut på hur många sätt som helst, om det bara är hur man färgar länderna som man bryr sig om. Det var fortfarande väldigt många kartor, men några år senare hade datorerna blivit uppfunna, och då gjorde två matematiker ett datorprogram som år 1976 provade att färglägga alla kartor med fyra färger, och det gick!

Så nu, 125 år efter att Francis frågade, vet vi svaret!

Vad kan man lära sig av det här? Jo:

• Matematiker vill alltid veta hur och varför saker och ting är som de är, och vet man inte så försöker matematiker ta reda på det.

• Problem som verkar enkla kan vara mycket komplicerade.

• En förklaring som låter bra och är framförd av en riktigt duktig matematiker kan ändå vara felaktig. Man måste alltid tänka kritiskt!

Avslut

14 Sammanfattning: Vad har vi lärt oss?

10 min

Berätta att nu börjar avslutsfasen. Då ska man tänka igenom vad man har gjort under lektionen och fundera på vad man har lärt sig. Be eleverna fundera en stund på det. Fördela sedan ordet (låt några elever ge exempel). Ge sedan själv några exempel.

15 Avslut: Att lära sig matematik Berätta att eleverna nu har gjort sin första lektion som matematiker. Så svåra problem som fyrfärgsproblemet kan man ju inte börja med, precis som man inte kan börja med att spela i landslaget, dansa solo på operan eller uppträda i Globen. Men, om de gör sitt bästa och kämpar på mattelektionerna, kommer de att lära sig väldigt mycket matematik snabbt och kunna lösa allt svårare problem!

1.1.1 Vad är matematik?

Ett vanligt svar på frågan är räkning. Det är förstås en del av matematiken, och den ursprungliga anledningen till att matematiken utvecklades, men matematik är mycket mer än räkning. Frågan om vad matematik är har inget enkelt svar. Är matematik något som man:

• bestämmer (som regler i ett spel)?

• uppfinner (som datorerna)?

• upptäcker (som naturlagarna)?

Delar av matematiken är helt klart något man bestämmer, som terminologi och notation. Men stora delar går inte att bestämma. Om man beslutade att 2+2 från och med nu skulle vara lika med 5 så skulle det inte påverka det verkliga antalet utan bara hur man väljer att representera det med symboler. Två äpplen och ytterligare två äpplen är fyra äpplen till antalet, oavsett hur man kommer överens om att det ska representeras med symboler eller hur det ska benämnas.

Matematiker ser det ofta som att man uppfinner något grundkoncept, t.ex. addition, och att man sedan utforskar vilka regler som gäller detta koncept, t.ex. kommutativa lagen för addition.

Matematik som vetenskap

Matematiken är förmodligen den vetenskap som har bedrivits under vetenskapliga former längst tid. Begrepp ska vara glasklart definierade, och en diskussion ”vinner” man med logiska argument. Som sanning accepteras bara sådant som logiskt har bevisats.

Utveckling och tillämpning

Matematiken är ett stort forskningsämne som växer och utvecklas. Ibland är inspirationen ett problem man vill lösa, ibland en kreativ lust att experimentera med matematiken i sig. Matematiken har också många mycket viktiga tillämpningar. I nästan alla yrken används matematik på något sätt.

1.1.2 Problem som ingång till matematiken

För att visa lite av matematikens användningsområden inleds lektionen med en presentation av några verkliga problem som människor löser med hjälp av matematik. Sedan gör vi en djupdykning i det berömda och mycket komplexa fyrfärgsproblemet

Fyrfärgsproblemet

Vi valde fyrfärgsproblemet då det är lättbegripligt och har en intressant historia. Matematiker arbetar dessutom fortfarande med att visa att satsen är sann på logisk väg, istället för att färglägga alla kartor.

Några andra intressanta problem

Om du skulle vilja läsa in dig på några fler intressanta problem så följer här några förslag. De är relativt lätta att sätta sig in i, samtidigt som de är fascinerande komplexa och svåra.

Kryptering

Det finns ett stort antal krypteringsmetoder, som i princip alla bygger på olika sorters matematik. Det här är ett område där många saker som man tidigare trodde bara var relevanta för matematiker (som primfaktorisering) visat sig ha mycket stor praktisk användning. En del enklare metoder kommer vi att ta upp lite längre fram i läromedlet.

”P = NP?”

Det finns en grupp problem som har det gemensamt att man vet hur man ska lösa dem, men att beräkningarna tar så lång tid, även med dator, att de i praktiken är olösbara. Det är möjligt att det går att komma på snabbare metoder även om man inte lyckats än, men det är också kan också vara så att det inte finns några snabbare metoder.

Då det handlar om problem som man vill lösa skulle det vara av stort kommersiellt värde att få fram snabba metoder, eller kunna slå fast att problemen inte går att lösa snabbare så att man kan sluta lägga pengar på att försöka.

Relativitetsteorin

Einsteins relativitetsteori innebar en helt ny syn på fysiken, och i det sammanhanget kom mycket matematik till ny användning. Delar var sådant som matematiker hittat på mest för att det var intressant, som andra versioner av geometri än den som står i Euklides Elementa. Den visade sig lämplig att beskriva det krökta rummet med. Viktiga delar av matematiken, som differential- och integralkalkylen, kom för övrigt till i samband med att den klassiska fysiken utvecklades på 1600-talet av bland andra Newton. Man behövde matematiska redskap för att beskriva verkligheten. Och dessa redskap har sedan fått stor användning inom annat än fysik.

Så ”vad kan man ha det här till?” är en fråga som kan visa sig få nya svar med tiden.

1.2 Tal och antal samt siffrorna 1–5

Syftet med lektionen är att säkerställa att eleverna kan räkna ett mindre antal föremål, samt att börja utveckla elevernas förståelse för kopplingen mellan tal, antal och siffror. Syftet är också att börja etablera normen MATEMATIKER LYSSNAR OCH FÖRSÖKER FÖRSTÅ . I nästa lektion får eleverna öva mer på tal, antal och siffror, då talområdet utvidgas till 0–9.

Lektionsmål

• Eleven tillämpar kardinaltalsprincipen och visar det genom att koppla ihop sista räkneordet med antalet räknade föremål i mängden.

• Eleven vet att tal kan representeras på olika sätt och visar det t.ex. genom att dra streck mellan siffror och bilder på ett antal objekt.

• Eleven skriver siffrorna 1–5 läsligt och rättvänt.

Matematiska begrepp: Antal, tal, siffror, räkneord, räkneramsa

SvA: Lyssna, föremål

Material: Inget särskilt

Förberedelser

• Inga särskilda

Uggla: Trafikregler för matematiker

Uggla berättar varför man behöver regler i klassrummet.

Uggla: Matematiker lyssnar och försöker förstå

Uggla berättar att MATEMATIKER LYSSNAR OCH FÖRSÖKER FÖRSTÅ.

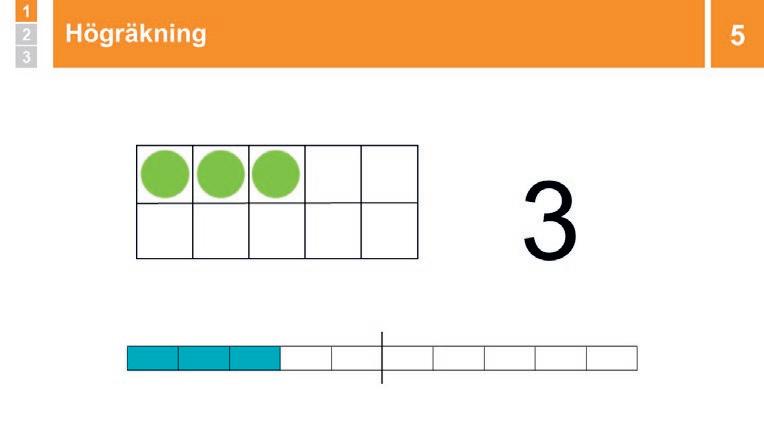
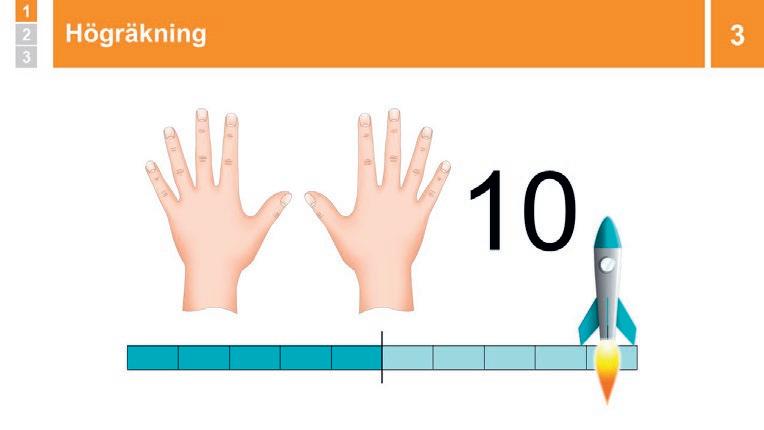
Övning: Högräkning 1–10 Ni högräknar 1–10.

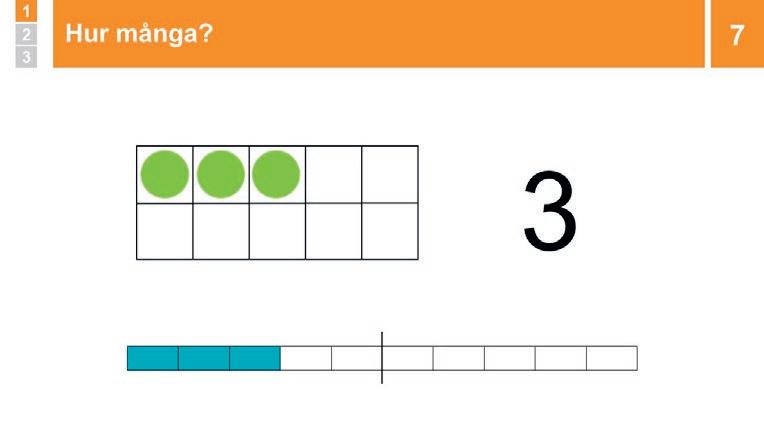
Övning: Hur många?

Eleverna får se representationer av tal, räknar och säger antalet.

Genomgång: Siffror visar tal Du går igenom skillnaden mellan siffror och tal, och att tal symboliseras med siffror.

Aktivitet: Hur siffrorna 1–5 skrivs Du visar hur siffrorna 1–5 skrivs. Eleverna spårar med fingret.

Elevboken s. 3−6

I mån av tid: eleverna räknar föremål i boken och skriver talet eller drar streck till den siffra som visar antalet.

Sammanfattning: Vad har vi lärt oss?

Sammanfatta vad ni lärt er:

• MATEMATIKER LYSSNAR OCH FÖRSÖKER FÖRSTÅ

• Räkna föremål

• Skriva siffror

• Siffror visar tal

Uppstart

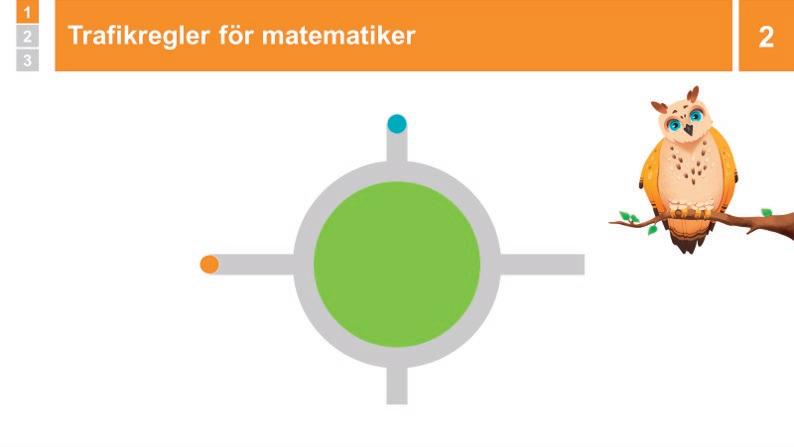
2 Uggla: Trafikregler för matematiker 15 min

Hej alla matematiker! Här är professor Uggla igen. Den här gången tänkte jag berätta lite om hur man jobbar i matematikklassrummet. I matematiken, precis som i trafiken, måste det finnas trafikregler. Varför har vi trafikregler? Titta på det här:

Bilen som ville in i rondellen stannade, och lät bilen som redan var där köra förbi. Annars skulle rondellen bli full med bilar.

Reglerna är till för att alla ska komma fram, och för att ingen ska krocka eller bli överkörd. På samma sätt behöver vi trafikregler i klassrummet.

3 Uggla: Matematiker lyssnar och försöker förstå Uggla berättar att MATEMATIKER LYSSNAR OCH FÖRSÖKER FÖRSTÅ .

Här är en viktig regel: När någon talar så är vi tysta, lyssnar, och försöker förstå. Just nu tänkte jag att ni ska få lyssna på er lärare.

4 – 6 Övning: Högräkning 1–10

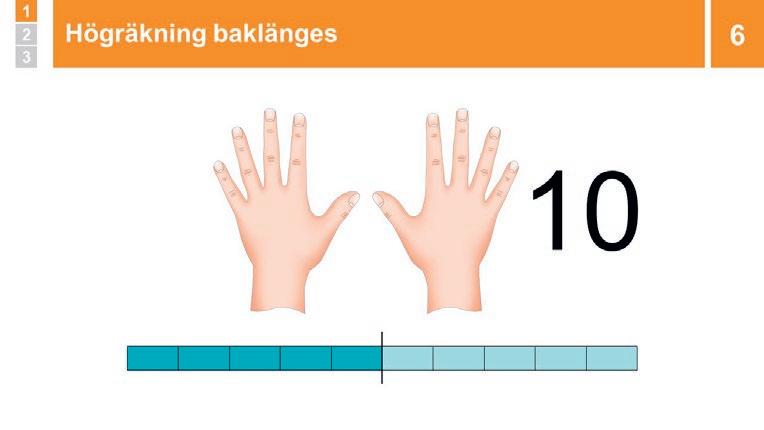
Högräkna tillsammans i kör till bildspelet, från 1 till 10. Bild 6 är räkning baklänges.

Om eleverna redan kan detta klickar du på triangeln i nedre högra hörnet för att direkt komma till nästa bild.

Lektion

7 Övning: Hur många?

När denna skylt visas avslöjar nästa klick en viktig poäng i bildspelet, så att du inte råkar klicka fram den.

Visa två bildrepresentationer av talet 3, men utan siffran 3. Fråga: ”Hur många?” Ge kort BETÄNKETID. Låt en elev svara, klicka fram siffran och säg ”tre”. Vid behov: räkna cirklarna en-och-en samtidigt som du pekar.

Gör på samma sätt med de tal som kommer: 5, 7, 9 och 8.

8 Genomgång: Siffror visar tal Klicka för att visa alla siffror. Berätta att det finns tio siffror och att de används för att visa tal. En enda siffra kan visa ett tal, t.ex. visar siffran 1 talet 1. Det är ungefär som att vissa ord bara har en bokstav, t.ex. Ö och Å. Men när det gäller många tal måste man använda flera siffror för att visa. Ett exempel är talet 10 som man behöver både siffran 1 och siffran 0 för att visa.

Visa en felvänd fyra och fråga eleverna vad det är. Konstatera att det inte är en fyra, eftersom den är felvänd. Förklara att alla siffror måste skrivas på rätt sätt för att andra ska förstå vad man menar. Visa en felvänd nia och påpeka att 9 och 6 lätt kan förväxlas.

Aktivitet

9 Aktivitet: Hur siffrorna 1–5 skrivs

30 min

Be eleverna slå upp s. 3 i elevboken. Visa hur siffrorna 1–5 skrivs och låt eleverna spåra med fingret i elevboken på samma sätt.

10 Elevboken s. 3−6

Låt eleverna träna på att skriva siffrorna från 1 till 5, till och med s. 6. CIRKULERA och stötta där det behövs.

Avslut

11 Sammanfattning: Vad har vi lärt oss? 5 min Berätta att man genom att räkna ett antal föremål kan avgöra hur många det är. Visa en räkning av fyra föremål.

Man kan visa hur många det är genom att skriva ett tal med siffror, i det här fallet siffran 4 som visar talet 4. Det är fyra cirklar!

Tal skrivs med siffror och det är viktigt att siffrorna skrivs på rätt sätt. Om siffran 9 skrivs upp och ned kan den förväxlas med siffran 6 eller bokstaven b.

1.2.1 Uppmärksamma och stötta

Subitisering och matematiksvårigheter

Att direkt se hur många föremål det finns i en mängd kallas subitisering. Notera de elever som inte direkt ser antal upp till 5. Dessa elever kan löpa större risk att hamna i matematiksvårigheter.

I kapitel 2 testas samtliga elever i subitisering. Om du misstänker att en elev har svårt med subitisering, kan du göra följande test redan nu och se om det kvarstår senare:

Täck över ett antal föremål (1–5) som eleven inte ser, visa dem och dölj dem efter någon sekund. Be eleven säga eller visa hur många föremål hen såg. Upprepa några gånger. Om eleven har svårigheter med detta indikerar det att hen kan behöva extra stöd för sin matematikutveckling. Följ i sådana fall noggrant elevens utveckling i matematik.

Förståelse för kardinalitet

Innan eleverna förstår antal är det vanligt att de ramsräknar utan att relatera det de säger till antal; de kopplar alltså inte ihop räkneorden med det antal de dittills har räknat, eller det sista räkneordet med det totala antalet i den räknade mängden. Ett tecken på att de verkligen räknar, och inte bara säger ramsan, är om eleven samtidigt pekräknar. För att säkerställa att eleven faktiskt räknar kan du fråga hur många det var i mängden. Du kan också visa pekräkning och uppmana eleverna att göra likadant, eller räkna på fingrarna samtidigt som de säger ramsan.

Elever som har svårt med detta behöver få mer strukturerade erfarenheter. Låt eleven använda laborativt material när hen räknar.

Antalskonservation

Om elever gång på gång vill räkna om samma mängd för att vara säker på antalet föremål, kan det vara ett tecken på att eleven inte förstått att antalet i en given mängd alltid är samma, oavsett hur många gånger eller från vilket håll man räknar.

Du kan göra några experiment med elever som behöver få upptäcka, och själva kunna konstatera, att så verkligen är fallet. Ta ett antal lämpliga föremål, t.ex. fem klossar, och lägg dem på rad. Be eleven räkna dem. Flytta övertydligt om klossarna så att de ligger på ett annat sätt och fråga igen hur många det är. Uppmana eleven att räkna igen. Upprepa några gånger, och fråga till slut om eleven verkligen behöver räkna igen: det är ju samma mängd föremål, så det måste ju vara lika många hela tiden oavsett hur de ligger.

Om eleven har svårt att hålla reda på vilka objekt som räknats kan du hjälpa hen med struktur, exempelvis genom att rada upp objekten på lämpligt sätt.

Felvända siffror

Elever som felvänder siffror kan få svårigheter med matematik då arbetsminnet belastas när de måste anstränga sig för att komma ihåg hur siffrorna ska skrivas. Uppmärksamma sådana tendenser och visa eleverna hur de ska göra för att siffrorna alltid ska vara rättvända. Låt dem träna ofta under korta stunder.

Förenkla

Elever som har svårt med finmotorik i steg 9 kan behöva skriva siffror på ett större papper eller på whiteboardtavlan. De kan också fortsätta att spåra siffror med fingrar eller med krita, innan de börjar skriva. Elever som har svårt med motoriken kan få träna ofta under korta stunder.

Utmana mer

Elever som redan kommit långt i sin taluppfattning måste utmanas mer. Du kan utmana dem genom att låta eleverna arbeta med tal i ett högre talområde. Du kan också låta dem räkna hur många föremål det totalt är i en samling föremål av olika sort. Det kan till exempel vara fyra kulor och två frukter vilket tillsammans är sex saker.

1.3 Tal och antal samt siffrorna 6–9 och 0

Syftet med lektionen är att fortsätta utveckla elevernas färdighet i att räkna föremål och fortsätta utveckla deras förståelse för sambandet mellan tal, antal och siffror.

Lektionsmål

• Eleven förstår talen 1–10 som antal och visar det t.ex. genom att räkna föremålen i en mängd högt och koppla ihop sista räkneordet med antalet föremål i mängden.

• Eleven förstår talet 0 som antal och visar det genom att göra kopplingar mellan representationer av 0 och talet 0.

• Eleven skriver siffrorna 0–9 läsligt och rättvänt.

Matematiska begrepp: Siffra, tal, antal

SvA: Lyssna, betänketid

Repetition: Ugglas regler

Högräkning: 1–10, upp- och nedräkning

Genomgång: Räkna från talet Ni högräknar, först från 4 och sedan från 6.

Övning: Hur många?

Du visar olika antal med bildspelet och eleverna håller upp talkort som visar antalet.

Uggla: Betänketid

Genomgång: Talet 0

Du visar representationer av talet 0 och konstaterar att 0 är lika mycket som … inget.

15 min

Material: Kopieringsunderlaget Talkort 0–10

Förberedelser

• Förbered talkort 0–10 till alla i klassen. Låt eleverna behålla dem, eller samla in dem efter lektionen, då de kommer att användas fler gånger.

• Skriv ut avslutslapp till varje elev.

• Övningsblad finns. Skriv ut vid behov.

Talkort 0−10

Avslutslapp

Övningsblad grundläggande Övningsblad utmanande

Övning: Skriva siffrorna 6–9 och 0

Du visar hur siffrorna skrivs och eleverna spårar samtidigt i elevboken. De övar sedan på att skriva dem.

Elevboken s. 7−9

Eleverna arbetar enskilt.

Grupparbete: Hämta lika många!

Du ger varje grupp ett tal och uppgiften att hämta så många föremål.

Sammanfattning: Vad har vi lärt oss?

Säg att ni lärt er:

• hur siffrorna 6–9 och 0 skrivs

• vilka tal man kan visa med varje siffra

• att räkna föremål och visa hur många det är med en siffra.

Avslutslapp

Eleverna gör en avslutslapp för att visa för dig och sig själva vad de kan.

Du säger tal och eleverna skriver den siffra som visar talet.

25 min

10 min

Uppstart

2 Repetition: Ugglas regler 15 min

Repetera professor Ugglas regel för MATEMATIKER LYSSNAR OCH FÖRSÖKER FÖRSTÅ : När någon talar så är vi tysta, lyssnar och försöker förstå.

3 Högräkning: 1–10, upp- och nedräkning

Högräkna upp till 10, och ned till 0, då raketen lyfter.

Om eleverna redan kan detta klickar du på triangeln i högra hörnet för att direkt komma till nästa steg.

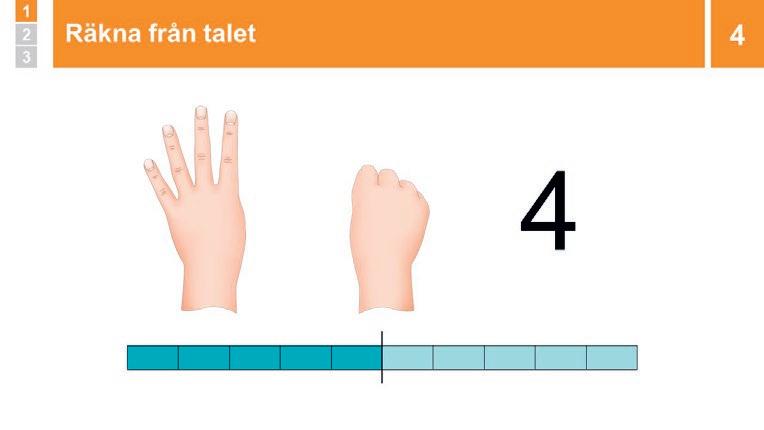
4 Genomgång: Räkna från talet

Berätta att ni ska öva på att räkna från olika tal, och att ni ska börja från 4. Säg att eleverna ska räkna med dig och betona starten: ”Fyyyyra, fem …”

Gör en omgång till där ni börjar räkna från 6.

5 Övning: Hur många?

Dela ut talkorten. Be eleverna räkna cirklarna som visas på bilden och hålla upp det talkort som visar talet. Konstatera att det är sex cirklar.

Klicka, vilket gör att cirklarna flyttar sig. Fråga: ”Hur många är det nu?” Notera de elever som visar ett annat antal eller som tar lång tid på sig och räknar om.

Gör övningen två gånger till. Konstatera att även om föremålen flyttas så är det fortfarande lika många.

6 Uggla: Betänketid

Hej! Här är professor Uggla igen. Jag tänkte berätta mer om hur matematiker arbetar. Matematiker tar ofta en stund på sig för att fundera. Det är viktigt att funderingarna får ta tid och att man inte blir störd. Det kallas för BETÄNKETID

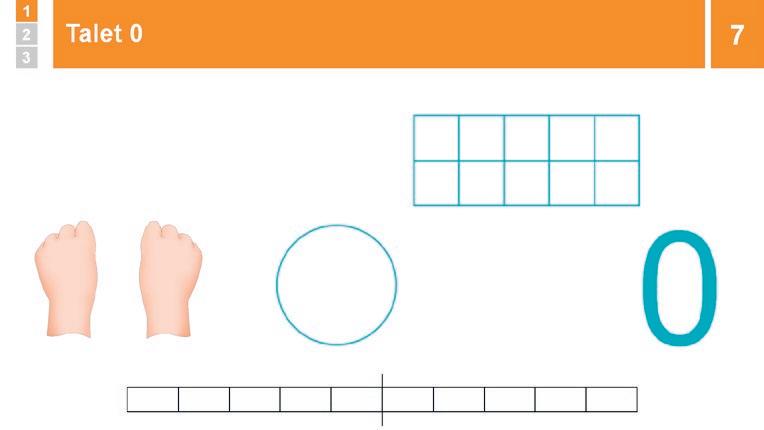
7 Genomgång: Talet 0

Visa representationer av talet 0. Fråga: ”Hur många fingrar hålls upp? Hur många prickar är det i cirkeln? Hur många brickor ligger i 10-rutan?”

Konstatera att det är noll. Berätta att 0 faktiskt är ett tal som kommer innan talet 1. 0 är ett tal som betyder lika många som … inget!

Aktivitet

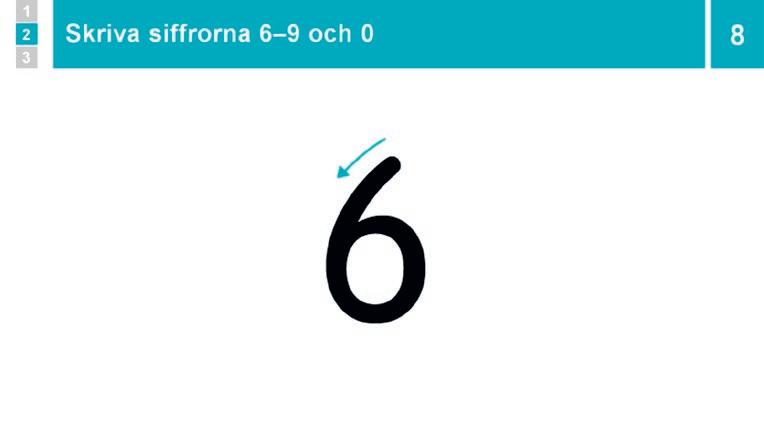
8 Övning: Skriva siffrorna 6–9 och 0 25 min Be eleverna slå upp s. 7 i elevboken. Visa hur siffrorna 6, 7, 8, 9 och 0 skrivs och låt eleverna spåra några gånger med fingret i elevboken.

9 Elevboken s. 7–9

Låt eleverna träna på att skriva siffrorna, till och med s. 9.

CIRKULERA och stötta där det behövs.

Bryt när det är ungefär 15 minuter kvar av lektionen.

10 Grupparbete: Hämta lika många!

Dela in eleverna i fyra grupper. Ge varje grupp ett tal mellan 6 och 9. Säg att gruppen ska hämta så många föremål som talet motsvarar. Dessutom ska de komma överens om hur de ska lägga föremålen så att de är lätta att räkna.

CIRKULERA . Fråga hur de kan veta att de har rätt antal föremål. Visa vid behov hur man kan gruppera föremålen så att det blir lättare att räkna. Antalet sju kan grupperas som fem och två till exempel.

När alla är klara låter du grupperna berätta hur många föremål de har och visa detta genom att räkna dem.

Avslut

11 Sammanfattning: Vad har vi lärt oss? 10 min Konstatera att man genom att räkna ett antal föremål kan avgöra hur många det är och att man kan visa antalet med siffror. Antalet sju, t.ex. sju frukter, visas med siffran 7. Att kunna skriva alla siffror läsligt och rättvänt är viktigt så att man inte blir missförstådd.

Talet 0 betyder att det inte finns något, och det visas med siffran 0. Här (i bildspelet) visas t.ex. noll äpplen, dvs. inga alls!

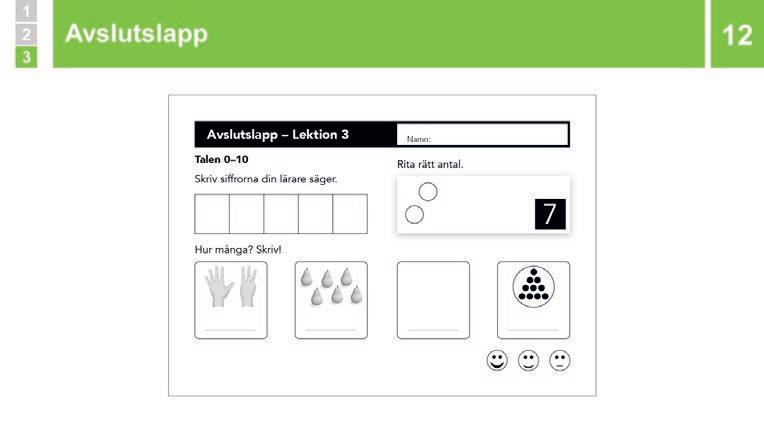
12 Avslutslapp

Berätta att ni ser en avslutslapp. I slutet av vissa lektioner kommer eleverna att få göra sådana, för att visa vad de lärt sig.

Förklara hur det går till med just den här avslutslappen. Du kommer säga ett tal och eleverna ska då skriva den siffra som visar talet i rutan från vänster till höger.

När rutorna är ifyllda ska eleverna enskilt göra resten av uppgifterna.

När de är helt klara ska de ringa in en smiley som visar hur de tycker att det gick: jätteglad betyder att man är säker på att man kan det här, ganska glad betyder att man är ganska säker men skulle vilja öva lite till. En figur som inte ler betyder att man behöver öva mer.

Låt eleverna göra avslutslappen. Säg talen i följande ordning 2, 5, 9, 3 och 4. Låt dem sedan göra resten av uppgifterna.

1.3.1 Uppmärksamma och stötta

Antalskonservation

Elever som har räknat ett antal föremål, men som måste räkna om dem om de flyttas på, har svårt för att konservera antal. Dessa elever behöver få upptäcka att antalet inte ändras bara för att föremålen t.ex. flyttas på.

Lägg ut ett mindre antal föremål, upp till fem stycken, framför eleverna och fråga: ”Hur många?” De räknar och säger antalet. Be dem räkna igen, fast från andra hållet, och fråga om det fortfarande är lika många.

Flytta om föremålen så att de tydligt ser att du inte ändrar antalet föremål, och fråga hur många det är. Om de vill räkna om kan du först fråga om de tror att antalet har ändrats. Om de inte tror det kan du uppmana dem att kontrollera genom räkning. Dra sedan slutsatsen att eftersom det är samma antal så behöver man alltid bara räkna en gång, för sedan vet man antalet. Det kan också vara värt att låta dem själva flytta om föremålen och sedan räkna igen.

Vissa elever ser frågan ”hur många” som en uppmaning att räkna. Ta reda på om de egentligen vet antalet och enbart räknar för att de uppfattat frågan som en uppmaning att räkna.

Avslutslappen

Avslutslappen ger en fingervisning om huruvida eleverna är redo att gå vidare i kapitlet. Eleverna får visa om de genom räkning kan bestämma antalet föremål i en mängd och använda rätt symbol för att representera mängden. De visar också om de kan skriva siffrorna 0–9 tydligt och rättvänt.

Felvända siffror

De elever som vänder på siffror i avslutslappen behöver träna bort detta. Det är ganska påfrestande för en elev att lära om, så använd korta pass ofta.

Ha gärna planscher i klassrummet som visar hur siffrorna skrivs. Gå igenom siffror vid samlingar och liknande tillfällen, och påminn då om hur siffrorna skrivs. Var uppmärksam på elever som trots detta fortsätter att vända siffror, då de riskerar att hamna i matematiksvårigheter.

Räkna och benämna antal

De elever som inte klarar antalsuppgifterna måste fortsätta att öva på att bestämma antalet föremål i en mängd och koppla samman detta med rätt siffra. Ta reda på vari problematiken ligger. Eleven kanske förstår antalet föremål men har svårt att visa det med siffror då det är mer abstrakt. Även i det fallet kan det vara en fördel om du i klassrummet har en plansch som visar skrivna tal med motsvarande antal föremål.

Om du har en eller flera elever som inte kan bestämma rätt antal genom pekräkning kan du försöka utnyttja tillfällen då du kan ställa frågor som uppmuntrar dem att fundera över antal. ”Hur många är vi kring bordet?”, ”Kan du hämta pennor så att det räcker åt alla?”, ”Hur många siffror har du skrivit nu?”

Det är överhuvudtaget mycket betydelsefullt att resonera med elever som har svårigheter. Tyst arbete i böcker kommer inte att ge samma utveckling av förståelse. Laborativt material är också något du ska använda dig mycket av. Lägg fram ett antal föremål framför eleven och låt eleven räkna dem högt. Fråga hur många det är. Eleven ska vara säker på att antalet motsvarar det sista räkneordet hen sa i högräkningen, och inte känna ett behov av att ramsräkna igen för att svara på frågan.

4.1 Behovet av att mäta

Syftet med lektionen är att introducera mätning genom att utifrån ett historiskt och nutida perspektiv visa på behovet av att kunna mäta. Lektionen syftar också till att ge elever na den grundläggande kunskap om längd och egenskaper av längd som behövs för att kunna förstå och utföra längdmätningar

Lektionsmål

• Eleven kan göra direkta jämförelser och visar det genom att jämföra och storleksordna föremål efter längd.

Matematiska begrepp: Mäta, längd

SvA: A4-papper, ark

Material: Sugrör eller pinnar.

Förberedelser:

• Klipp eller bryt sugrör/pinnar så att varje elev i klassen kan få ett eget med en längd som skiljer sig från alla andra. Gör skillnaden tydlig.

Repetition: Talraden och talgrannar Du repeterar talraden 0−20 och talgrannarna.

Diskussion: Hur mäta utan mätredskap?

Två barn behöver mäta, men har inget att mäta med. Du låter eleverna diskutera hur de skulle kunna mäta ändå. Ni ser en animerad film där två barn mäter med varsitt A4-papper. Den ena mäter med långsidan och den andra med kortsidan.

Diskussion: Vad blev fel?

Låt grupperna diskutera vad som blev fel i några minuter. Du visar och förklarar med ett A4.

Genomgång: Att mäta längd Du går igenom vad längd är och ger exempel på när man kan behöva mäta längd.

5 min

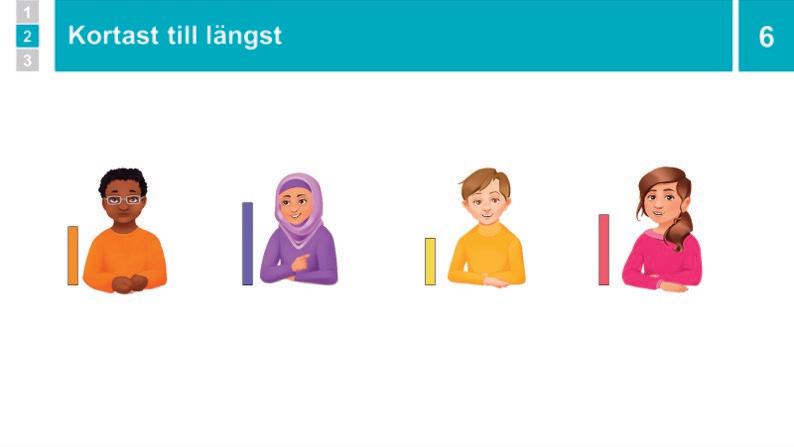
Aktivitet: Kortast till längst Eleverna får var sitt sugrör eller pinne, i olika längder, och ska ställa sig i längdordning utan att prata med varandra.

Diskussion: Jämför för att kontrollera

Eleverna står kvar, och diskuterar hur de skulle kunna kontrollera om sugrören är i längdordning.

Eleverna kontrollerar med sina närmaste grannar att de står i längdordning.

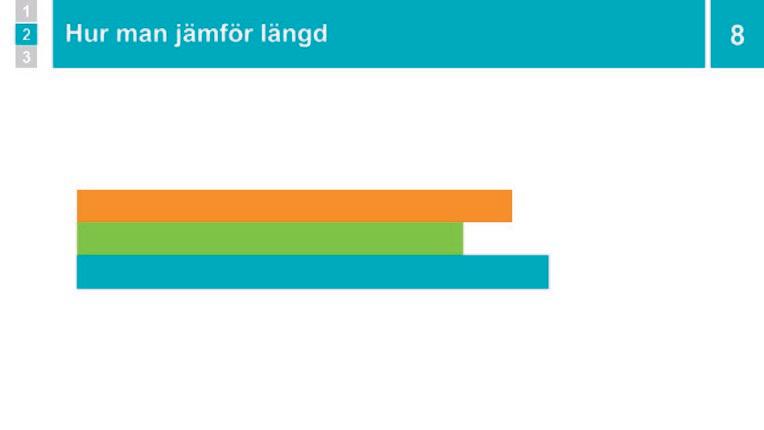
Genomgång: Hur man jämför längd

Du visar hur man jämför föremåls längd med varandra.

Uggla: Behovet av mätning

Genomgång: När behöver man kunna mäta?

Elever ger förslag på när man kan behöva mäta längd, och du skriver upp förslagen på tavlan.

Sammanfattning: Vad har vi lärt oss?

Längd beskriver hur långt något är, som bredden på en bokhylla eller avståndet från skolan och hem.

Man kan jämföra olika föremåls längd genom att lägga dem intill varandra. Det är viktigt att föremålen ligger vid samma startpunkt.

30 min

15 min

Uppstart

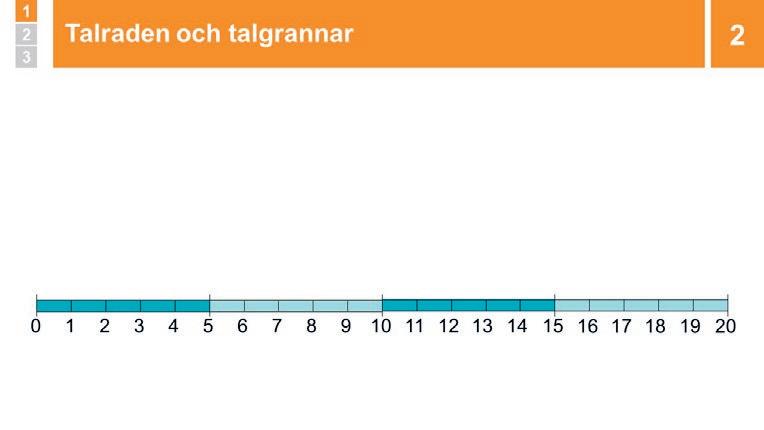
2 Repetition: Talraden och talgrannar 5 min Räkna högt tillsammans med eleverna, fram och tillbaka på tallinjen.

Högerpil = räkna upp, vänsterpil = räkna ned. Fråga om grannarna till de tal som visas ensamma. Berätta att ni idag börjar lektion 1 i ett kapitel där eleverna kommer få lära sig om vad längd är och hur man kan mäta längd.

3 Diskussion: Hur mäta utan mätredskap? 30 min

Säg: "Två barn ska mäta en bokhylla för att se om den får plats. Men de har inget mätredskap, som linjal eller måttband. Hur skulle de kunna göra?"

Dela in eleverna i grupper. Påminn om att MATEMATIKER LYSSNAR OCH FÖRSÖKER FÖRSTÅ . Låt grupperna diskutera hur barnen skulle kunna mäta, trots att de inte har något mätredskap.

CIRKULERA VÄLJ UT några grupper som har förslag på fungerande sätt att lösa behovet av mätning, t.ex. att måtta med händer eller jämföra med ett föremål. När eleverna diskuterat en stund bryter du.

Påminn om JAG MED, och låt de grupper du valt ut berätta hur de skulle lösa uppgiften. Visa gärna elevernas förslag på en bokhylla eller annat lämpligt föremål i klassrummet.

Klicka på högtalaren för att spela animeringen som visar hur barnen mäter med A4-papper, det ena barnet mäter med långsidan och det andra mäter med kortsidan.

4 Diskussion: Vad blev fel?

Låt grupperna diskutera vad som blev fel i Lucas och Hugos mätning. Bryt efter några minuter.

Låt någon grupp berätta om hur de tänker. Ta fram två A4-ark och visa hur långsidan och kortsidan förhåller sig till varandra, eller visa i bildspelet. Konstatera att de fick fel resultat när de mätte eftersom de inte mätte med samma sida på A4-pappret: den ena sidan är längre än den andra.

5 Genomgång: Att mäta längd

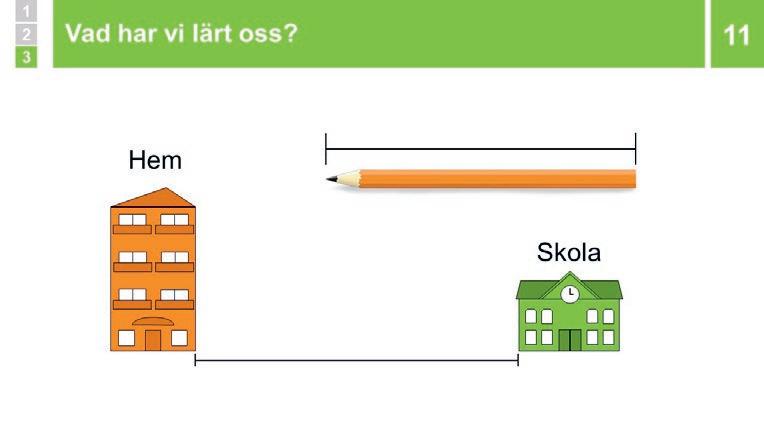
Berätta att längd beskriver hur långt någonting är. I filmen ville personerna ta reda på hur långt det var mellan fönstret och tavlan, för att se om en bokhylla fick plats där. Man kan också t.ex. vilja veta hur långt avståndet är mellan hemmet och skolan.

Aktivitet

6 Aktivitet: Kortast till längst

Ge eleverna varsitt sugrör. Säg att eleverna ska ställa sig i längdordning, från den med kortast sugrör till den med längst, utan att prata med varandra. Låt dem börja när alla förstått, och stötta vid behov så att eleverna åtminstone ordnar sig på ett ungefär efter längd.

7 Diskussion: Jämför för att kontrollera

Låt alla stå kvar och fråga: ”Hur skulle vi kunna kontrollera om sugrören är i längdordning, från kortast till längst?”

BETÄNKETID

Fördela ordet. Om någon säger att de kan jämföra längden med varandra för att ta reda på det, be då hen visa och förklara hur det skulle gå till. Visa själv om det behövs.

Låt alla kontrollera med sina närmaste grannar att de står i längdordning. För att spara tid kan du välja att inte kontrollera hela klassen. Fokus ligger på att eleverna ska göra korrekta jämförelser.

8 Genomgång: Hur man jämför längd

Låt eleverna sitta ned. Visa tre rektanglar som ligger i oordning. Säg: ”Om man ska jämföra föremåls längd måste man lägga föremålen intill varandra så att de börjar på samma ställe.”

Visa, och säg att det är tydligt att den nedersta rektangeln är längst medan den mittersta är kortast. Konstatera att det var så eleverna gjorde när de kontrollerade om de stod i längdordning eller inte.

Avslut

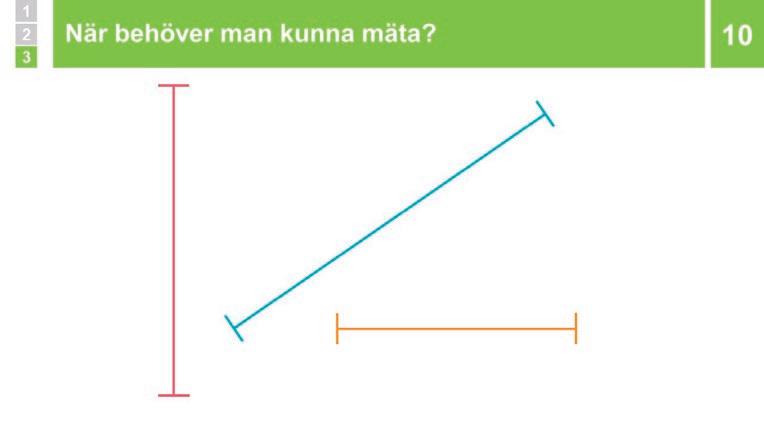
9 Uggla: Behovet av mätning 15 min

Professor Uggla berättar om behovet av längdmätning, och lite historiska fakta.

10 Genomgång: När behöver man kunna mäta?

Fråga om eleverna har fler förslag på när man kan behöva mäta längd, och be dem förklara varför längdmätningen behövs i deras förslag. Skriv upp förslagen på tavlan.

11 Sammanfattning: Vad har vi lärt oss?

Berätta att längd beskriver hur långt något är. Det kan exempelvis vara hur lång bredden på en bokhylla är, eller avståndet mellan skolan och hemmet.

Man kan jämföra olika föremåls längd genom att lägga dem intill varandra. Det är viktigt att föremålen då börjar på samma plats.

4.1.1 Uppmärksamma och stötta

I vardagligt tal är det vanligt att uttala sig om storleken på föremål i generella ordalag, istället för mer precist i termer av en specifik storhet som t.ex. längd. Det är vad som sker när folk säger saker som ”den största bananen”. Detta leder oftast inte till något problem, men det kan ju betyda längst eller störst volym – kanske till och med tyngst. Det kan förstås också avse alla storheter på samma gång.

När eleverna ska lära sig begreppen är det väldigt viktigt att uttrycka sig på ett sätt så att det inte finns utrymme för oklarheter. Det är viktigt att du stöttar eleverna i att använda ett tillräckligt precist och begreppsligt klart språk när de arbetar med längd och mätning, dels för att det utvecklar begreppsförståelsen men också för att det är en förutsättning för att kunna förstå och hantera mätning. Var alltså noggrann med att själv uttrycka dig begreppsligt klart och korrekt.

Var uppmärksam på hur eleverna jämför sina sugrör/ pinnar med varandra. Om du märker att de inte jämför längden genom att låta ändarna börja på samma nollpunkt kan du behöva avbryta för att kortfattat förklara vikten av detta, och visa vad som händer med mätresultatet om man inte gör så. Du kan som exempel jämföra din och en elevs längd genom att låta eleven ställa sig på en stol, och sedan fråga klassen vem som är längst. Alla bör förstå att ni båda måste stå på golvet för att det ska vara en fungerande jämförelse. Förklara att detta betyder att golvet blir utgångspunkten för jämförelsen av era längder, eftersom ni båda står på golvet.

Förenkla

Om du märker att aktiviteten där eleverna ska sortera sina sugrör/pinnar i längdordning inte fungerar kan du låta dem prata med varandra. Var beredd att själv styra aktiviteten så att eleverna får se hur det går till.

Utmana mer

I aktiviteten där eleverna ska ordna sugrören/pinnarna efter längd är det svårt att utmana mer, bland annat på grund av att aktiviteten sker i helklass.

4.2 Längdmätning

Syftet med lektionen är att börja utveckla elevernas förståelse för mätning, genom att visa hur man kan använda ett jämförelseobjekt för att jämföra längden på två föremål som inte direkt kan jämföras med varandra.

I senare lektioner bygger vi vidare på detta när eleverna istället för ett jämförelseobjekt, vilket som helst, använder ett standardiserat mätredskap.

Lektionsmål

• Eleven kan göra indirekta jämförelser mellan två objekt med ett jämförelseobjekt och visar det genom att mäta objekten med ett snöre/stav och sedan resonera om objektens längder i relation till varandra.

• Eleven kan jämföra längd hos objekt som inte är raka och visar det genom att mäta med hjälp av ett snöre.

• Eleven kan konservera längd och visar det genom att ange vilket föremål som är längst också efter att föremålen bytt plats.

Matematiska begrepp: Längd, mäta, kortare, längre, längst, kortast, höjd

SvA: Fågelvägen

Material: Kopieringsunderlagen Rak och krokig sträcka och Raka sträckor, pinnar i olika längd

Genomgång: Längst och högst

En elev står på en stol/kateder bredvid dig, och övriga elever säger vem som är längst. Du klargör skillnaden mellan längst och högst.

Genomgång: Vilken är längst?

Eleverna avgör vilken figur som är längst, innan och efter förflyttning. Ni konstaterar att saker inte ändrar längd när de förflyttas.

Genomgång: Uppskatta längd

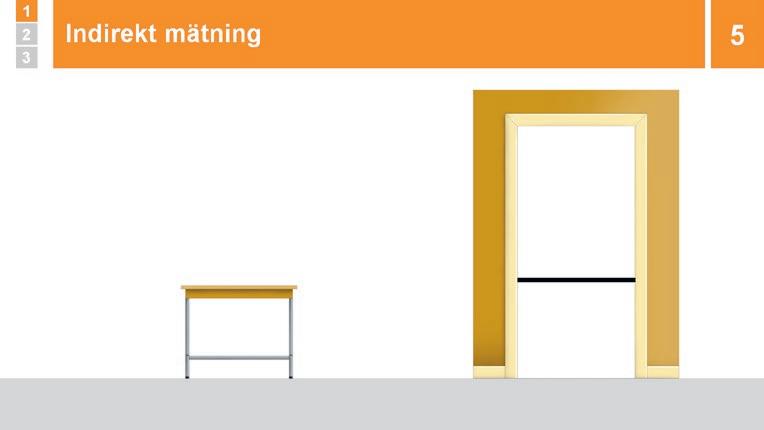
Eleverna uppskattar längd genom att uppskatta om en bänk ryms i dörröppningen eller inte.

Genomgång: Indirekt mätning

Eleverna SURRAR om hur de kan använda ett snöre för att ta reda på om bänken ryms i dörröppningen eller inte.

15 min

Förberedelser:

• Skriv ut två exemplar vardera av Rak och krokig sträcka och Raka sträckor till alla elever.

• Förbered tre stationer för mätning (se steg 6). Gör en dubblett av varje station så att det totalt finns sex platser att mäta på. Se till att det finns snören eller pinnar att mäta med.

• Skriv ut avslutslappar.

• Övningsblad finns. Skriv ut vid behov.

Station 2, Rak och krokig sträcka Station 3, Raka sträckor Avslutslapp

Övningsblad grundläggande

Övningsblad utmanande

Aktivitet: Indirekt mätning vid stationer

Eleverna arbetar i grupper och gör indirekta mätningar med snören vid tre olika stationer.

Sammanfattning: Vad har vi lärt oss?

Du konstaterar att föremål som är högre upp inte behöver vara längre. Det är längden på föremålen i sig själva som avgör, och inte hur de befinner sig i förhållande till varandra. Du repeterar hur man mäter, både genom direkta och indirekta jämförelser.

Avslutslapp

25 min

10 min

Uppstart

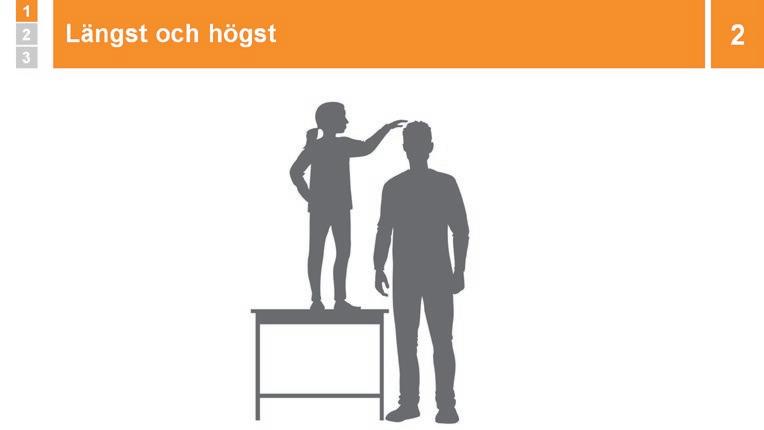
2 Genomgång: Längst och högst 15 min Be en elev ställa sig på en stol eller ett bord bredvid dig (eleven ska komma högre upp än du).

Fråga vem som är längst. BETÄNKETID. Påminn om JAG MED och låt någon svara. Oavsett vad eleven svarar följer du upp med frågan: ”Hur tänkte du?”

Om hen säger att eleven är längre kan du följa upp med frågan ”Blir hen kortare när hen hoppar ned på golvet?” eller ”Skulle jag bli längre om jag också ställde mig på en stol?”

Konstatera att ett föremål eller en person inte blir längre bara för att det befinner sig högre upp. Låt eleven hoppa ned och ställa sig bredvid dig, och konstatera vem som är längst.

3 Genomgång: Vilken är längst?

Fråga: ”Vilken av de tre kritorna är längst?” Låt någon svara och konstatera att det är den gröna kritan.

Klicka så att kritorna flyttas. Påminn om JAG MED och påstå: ”Den orangea kritan är längst.” Ge ordet till någon som inte gör JAG MED. Be hen förklara varför hen inte håller med, och låt hen berätta vilken som är längst. Konstatera att saker inte ändrar längd när man flyttar på dem; den gröna är fortfarande längst, men inte längre högst upp.

4 Genomgång: Uppskatta längd Peka på en bänk i klassrummet och säg: ”Går den här bänken att bära ut genom dörren utan att vrida på den?” BETÄNKETID. Låt några elever svara. Berätta att detta kallas för att man gör en uppskattning: man gissar inte, utan man gör en uppskattning baserat på vad man vet och kan se.

5 Genomgång: Indirekt mätning Visa ett snöre/pinne. Låt eleverna SURRA om hur de kan använda föremålet för att ta reda på om bänken ryms i dörröppningen eller inte. Lyssna efter par som talar om att jämföra bänken och dörren genom att jämföra båda med snöret, och låt dem berätta hur de tänker.

Låt paret testa sin lösning. Visa själv om det behövs. Säg: "När man vill jämföra längden på föremål som man inte kan lägga intill varandra kan man jämföra båda föremålen med ett tredje föremål, t.ex. ett snöre.”

Aktivitet

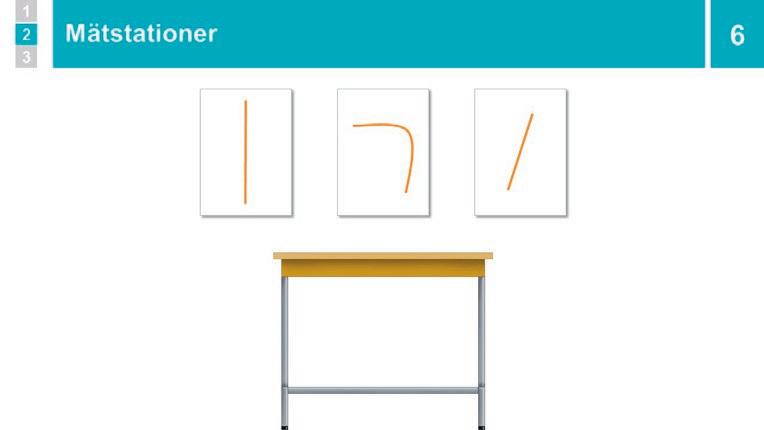
6 Aktivitet: Indirekt mätning vid stationer 25 min

Dela in eleverna i sex grupper. Berätta att de ska få mäta vid olika stationer, och att de vid varje station först ska göra en uppskattning och sedan mäta med ett snöre/pinne. Visa de olika stationerna och gå igenom vad de genom mätning ska avgöra vid respektive station:

Station 1: Är bänkens höjd längre än dess bänkskiva?

Station 2: Vilken av vägarna är längst på pappret Rak och krokig sträcka?

Station 3: Vilken av vägarna är längst på pappret Raka sträckor?

Säg att de ska arbeta tillsammans som en grupp: de ska följa Ugglas regler om hur matematiker gör, men de ska också turas om att göra mätningarna.

Låt dem börja när alla förstått. CIRKULERA och stötta vid behov. Se till att alla får göra mätningar. Bryt efter ungefär sex minuter på varje station om eleverna inte är klara.

Avslut

7 Sammanfattning: Vad har vi lärt oss? 10 min

Konstatera att ett föremål som är högre upp än ett annat inte behöver vara längre. Det är hur långa föremålen är i sig själva som avgör, inte hur de befinner sig i förhållande till varandra.

Berätta att när man jämför föremåls längd lägger man dem intill varandra, kant i kant. När man ska mäta och jämföra längden på föremål som man inte kan lägga intill varandra kan man istället använda ett tredje föremål, t.ex. ett snöre eller en trästav, och jämföra båda föremålen med snöret/ trädstaven.

8 Avslutslapp

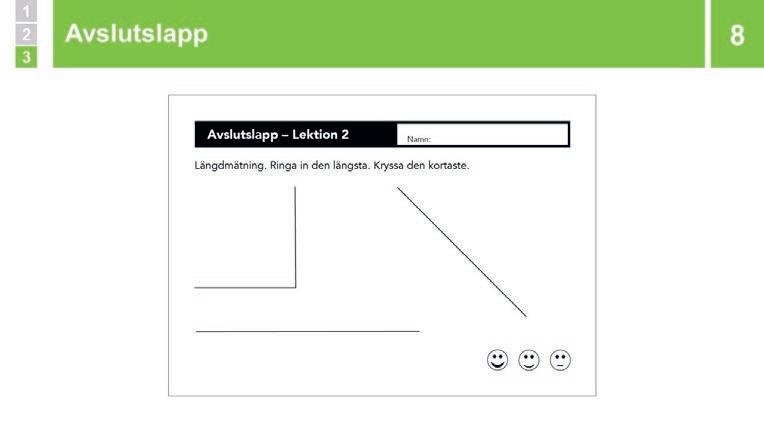
Se till att alla har var sitt snöre/pinne, och dela ut avslutslappen. Berätta att eleverna ska använda snöret för att ta reda på vilken av figurerna som är längst och ringa in den. Den figur som är kortast ska de markera med kryss. Låt eleverna börja när alla förstått uppgiften.

4.2.1 Uppmärksamma och stötta

Det är en relativt vanlig missuppfattning att elever tror att föremål som befinner sig högre upp är längre än de som är nedanför. Om eleverna har den missuppfattningen kan du visa i praktiken genom att jämföra din längd med elevens när ni står på golvet, och sedan låta eleven ställa sig på en stol eller katedern så att hen kommer högre upp. Antagligen förstår eleven då att hen inte helt plötsligt blivit längre än du, utan att hen nu är högre upp än du. Poängtera att inget föremål ändrar längd när det flyttas på.

Om du märker att eleverna inte är noggranna i sina jämförelser behöver du hjälpa dem med det. Var tydlig med att när man gör direkta jämförelser så måste föremålen utgå från samma nollpunkt, så att de jämförs kant i kant.

När eleverna ska göra uppskattningar bör du vara uppmärksam på elever som gissar vilt. Förtydliga att en uppskattning bygger på ett antagande eller en enklare undersökning, och är något man faktiskt tror stämmer på ett ungefär. T.ex. kan uppskattningen bygga på att man gjort en uppskattning med ett personligt referensmått, t.ex. bredden på sitt finger, längden av sin arm etc.

En vanlig missuppfattning är att tro att en sträckas längd är avståndet mellan ändpunkterna fågelvägen. Om du märker att eleverna mäter en sträcka som inte är rak på det sättet, visar du dem hur de ska göra för att mäta längs med hela sträckan (kurvan).

Anpassa till andra föremål, eller utomhuslektion

Om du bedömer att det finns andra föremål i klassrummet eller på skolgården som bättre lämpar sig än förslagen ovan byter du till dem.

Förenkla

Att göra en direkt jämförelse av längden på en kurva som inte är rak med hjälp av ett snöre kan vara svårt, då snöret kan röra på sig. Du kan underlätta för eleverna genom att ge tipset att de kan samarbeta för att hålla

fast snöret, och sedan flytta fingrarna och trycka fast snöret längre fram på kurvan. Då kan de släppa den del av snöret som redan är mätt. Du kan också själv hjälpa till att trycka fast snöret, så att eleven kan koncentrera sig på mätningen.

Utmana mer

Låt eleverna uppskatta omkretsen (längden av sträckan runt föremålet) på runda föremål, exempelvis burkar och bollar. Eleven kan göra detta genom att rita den uppskattade längden som en rak linje på ett papper. Sedan mäter de omkretsen med ett snöre och ritar ut den som en rät linje på samma papper, och jämför slutligen linjerna med varandra.

Avslutslappen

Avslutslappen låter eleverna visa om de kan använda sig av ett jämförelseobjekt för att göra indirekta jämförelser mellan föremål som inte läggs intill varandra. Genom att använda ett snöre kan eleven mäta en linje och sedan jämföra med övriga, och på så sätt avgöra vilken som är längst respektive kortast. Den vågräta linjen är 22 cm lång, linjen med rät vinkel är 20 cm och den sneda linjen är 18 cm.

Låt de elever som har motoriska svårigheter använda en blompinne eller liknande istället för ett snöre.

Om eleven svarar att linjen med rät vinkel är kortast så kan det bero på att hen har mätt fågelvägen mellan ändpunkterna. Om eleven svarat att den sneda linjen är längst så kan det bero på att eleven tror att den automatiskt är längst eftersom den är placerad högst upp på pappret. Det är också möjligt att elever som har fel har nöjt sig med att uppskatta längden med hjälp av ögonmått istället för att genomföra en ordentlig mätning med hjälp av snöret. Undersök vad eventuella felsvar beror på genom att låta eleven göra en liknande uppgift då du kan observera vad eleven gör och ställa frågor.

4.3 Mäta med föremål

Syftet med lektionen är att börja utveckla elevernas förståelse för enhetsiteration genom att de får lära sig mäta med enhetsobjekt, även om eleverna inte använder just de orden. I nästa lektion bygger vi vidare på detta, när standardenheterna meter och centimeter introduceras.

Lektionsmål

• Eleven kan mäta längd med enhetsobjekt och visar det genom att:

1. lägga enhetsobjekt från början till slut längs med föremålet som mäts,

2. lägga enhetsobjekten utan glipor eller överlappningar,

3. uttrycka föremålets längd som det antal enhetsobjekt som lagts ut.

• Eleven har en grundläggande förståelse för vad det innebär att mäta ut och visar det genom att med visst stöd mäta ut en T­rex.

• Eleven har insett att enhetsobjektens storlek påverkar mätetalet och visar det genom att beskriva att mätetal påverkas av enhetsobjekts storlek.

Matematiska begrepp: Enhet, enhetsobjekt, avrunda

SvA: Dinosaurie, tyrannosaurus rex (T-rex)

Material: Kopieringsunderlagen Station 1, 2 och 3, T­rex samt multilink och kaplastavar

Förberedelser:

• Skriv ut de tre kopieringsunderlagen i två exemplar var (Station 3, T­rex, består av fyra A3 som tejpas ihop). Förbered två av varje mätstation (se steg 7).

Station 1, Mäta med multilink

Station 2, Mäta med kaplastavar

Station 3, T-rex

Repetition: Indirekt mätning och mäta ut

Du repeterar indirekt mätning, och vad det innebär att mäta ut.

Genomgång: Mäta med kaplastavar

Du visar hur tre barn i bildspelet mäter bänken med kaplastav, men två av dem gör vanliga misstag och de får därför olika resultat.

Diskussion: Varför fick de olika mätresultat?

Eleverna SURRAR . Ni konstaterar att kaplastavarna måste läggas utan glipor eller överlappning.

Genomgång: Att avrunda

Du spelar den animerade genomgången med berättarröst som går igenom hur man avrundar.

Genomgång: Mätstation 1–3 Du berättar att eleverna återigen ska få mäta vid stationer, och går igenom vad de ska göra vid varje station.

Grupparbete: Mät och skriv upp Eleverna arbetar i grupper och mäter vid de olika stationerna

Diskussion: Varför olika mätetal?

Eleverna SURRAR om varför de fick olika mätetal när de mätte samma rektangel med multilink respektive kaplastavar.

Ni konstaterar att en kaplastav är längre än en multilink, och att det behövs därför fler multilink för att täcka rektangelns längd.

Sammanfattning: Vad har vi lärt oss?

Man kan mäta med föremål, t.ex. stavar, genom att undersöka hur många som får plats längs med det man mäter. Föremålen man mäter med måste vara lika långa och läggas kant i kant utan överlappningar eller glipor.

Uppstart

2 Repetition: Indirekt mätning och mäta ut 10 min Berätta att du har ordnat en rabatt där du ska ha blommor. För att skilja rabatten från gräsmattan ska du sätta dit ett litet staket. Låt eleverna SURRA om hur du ska kunna köpa tillräckligt långt staket om du inte har något måttband.

Låt eleverna komma med förslag. FÖRSTÄRK om några elever säger att du kan mäta längs kanten med ett snöre, och sedan ta med snöret till affären och mäta ut rätt längd på staketet.

3 Genomgång: Mäta med kaplastavar

Visa en kaplastav för klassen. Berätta att Oscar, Ellen och Roshan ska mäta med kaplastavar hur långa deras bänkskivor är. Klicka, så mäts det i bildspelet.

Säg att Oscar fick mätresultatet sju kaplastavar, Ellen fem kaplastavar och Roshan sex kaplastavar.

4 Diskussion: Varför fick de olika mätresultat?

Låt eleverna SURRA om varför de fick olika mätresultat.

Påminn om JAG MED och fördela ordet. FÖRSTÄRK när någon säger att kaplastavarna måste ligga kant mot kant, utan glipor eller överlappning.

Visa i bildspelet eller ännu hellre med riktiga kaplastavar.

5 Genomgång: Att avrunda

Venja mäter olika längder med kaplastavar. På den första hon mätte behövde hon lite fler än fem kaplastavar. Hon mäter ett annat föremål och den här gången räckte nästan tre kaplastavar. Lägger hon en fjärde sticker den ut väldigt långt. Venjas lärare förklarar att hon kan avrunda. Att avrunda betyder att man använder sig av närmsta hela antal. Det är inte lika noggrant som att svara exakt men det är praktiskt då det ger en uppfattning om hur långt det var. På den första mätningen kan hon avrunda upp till fem kaplastavar då det var närmre fem stavar som behövdes än fyra. På den andra mätningen får hon avrunda ned till tre. Om det är svårt att se om vi ska avrunda upp eller ned brukar man oftast avrunda uppåt.

Aktivitet

6 – 8 Genomgång: Mätstation 1–3 30 min

Dela in eleverna i sex grupper och säg att de återigen ska få mäta vid stationer. Be dem slå upp s. 4 i elevboken. Gå igenom vad de ska göra vid varje station och visa i bildspelet. Visa hur de ska fylla i mätresultaten i elevböckerna.

Station 1, multilink: De ska mäta längden på föremålen i kopieringsunderlagen med multilink. Elevboken s. 4.

Station 2, kaplastavar: Som ovan, fast här mäter de med kaplastavar och fyller i på s. 5.

Station 3, T-rex: De ska använda fotavtrycket från en T-rex för att mäta ut om en T-rex skulle få plats i klassrummet. Berätta att just den här var 17 T-rexfötter lång och åtta T-rexfötter hög.

9 Grupparbete: Mät och skriv upp

Låt grupperna börja arbeta. Ge eleverna ca åtta minuter vid varje station, och låt dem sedan rotera. CIRKULERA och stötta vid behov.

Avslut

10 Diskussion: Varför olika mätetal?

10 min

Låt eleverna sitta i grupperna. Fråga hur många multilink lång rektangel B är. Låt en elev svara och konstatera att den är 18 multilink lång. Säg att det kallas mätetal; mätetalet är 18.

Fråga hur lång rektangel B är i kaplastavar. Konstatera att den är tre kaplastavar lång – mätetalet är 3. Låt eleverna SURRA om varför mätetalet skiljer sig åt mellan mätningarna trots att det är samma rektangel.

Låt några par komma med idéer. Konstatera att en kaplastav är mycket längre än en multilink, och det behövs därför fler multilink för att täcka rektangelns längd.

Påminn om JAG MED och påstå: T-rex får inte plats i klassrummet.

11 Sammanfattning: Vad har vi lärt oss?

Sammanfatta: Man kan mäta med föremål, t.ex. stavar, genom att undersöka hur många som får plats längs med det man mäter. Föremålen man mäter med måste vara lika långa och läggas kant i kant utan överlappningar eller glipor.

Om det inte går att mäta exakt med föremålet kan man avrunda till närmaste heltal. Var det exempelvis väldigt nära fem kaplastavar som behövdes avrundar man till 5.

4.3.1 Uppmärksamma och stötta

Uppmärksamma de elever som inte mäter med tillräcklig noggrannhet, och uppmuntra dem att göra det. Eleverna måste inse att föremålen som används för att mäta med måste ha samma längd, läggas utan glipor eller överlappningar och täcka hela längden på det som ska mätas.

Förenkla

Om du märker att vissa har svårt att mäta i stationerna kan det vara bättre att dessa elever får fokusera på några få mätningar som görs väldigt noggrant. Visa för eleven hur hen ska börja lägga föremål från samma startpunkt på föremålet vars längd ska mätas. Låt eleven lägga föremål, exempelvis kaplastavar, och uppmana vid behov eleven att justera så att föremålen ligger dikt an mot varandra. Be eleven räkna högt. Visa för eleven att föremålets längd motsvarar längden av det antal enhetsobjekt eleven använt.

Utmana mer

Du kan låta eleverna göra en uppskattning av hur många föremål längden på det som ska mätas motsvarar. Påminn om att de inte ska göra en vild gissning. De kan till exempel uppskatta utifrån ett personligt referensmått som ungefär motsvarar längden på föremålet de ska använda för att mäta.

Låt eleverna mäta med andra föremål och jämföra resultaten. Exempelvis gem och post-it-lappar kan bjuda på lite mer utmaning, då de är svårare att iterera utan överlappning eller glipor.

Låt eleverna göra mätningar som ger större mätetal.

Om det finns tid över kan eleverna mäta bänkens bredd och dörrens höjd med kaplastavar och skriva mätetalet i elevboken.

Studentlitteratur AB

Box 141

221 00 LUND

Besöksadress: Åkergränden 1

Telefon 046-31 20 00 studentlitteratur.se

Kopieringsförbud

Detta verk är skyddat av upphovsrättslagen. Kopiering, utöver lärares begränsade rätt att kopiera för undervisningsbruk enligt Bonus Copyright Access skolkopieringsavtal, är förbjuden. Kopieringsunderlag får dock kopieras under förutsättning att kopiorna delas ut endast i den egna undervisningsgruppen. För information om avtalet hänvisas till utbildningsanordnarens huvudman eller Bonus Copyright Access.

Vid utgivning av detta verk som e-bok, är e-boken kopieringsskyddad.

Användning av detta verk för text- och datautvinningsändamål medges ej.

Den som bryter mot lagen om upphovsrätt kan åtalas av allmän åklagare och dömas till böter eller fängelse i upp till två år samt bli skyldig att erlägga ersättning till upphovsman eller rättsinnehavare.

Studentlitteraturs trycksaker är miljöanpassade, både när det gäller papper och tryckprocess.

Art.nr 46125

ISBN 978-91-44-17669-7

Upplaga 3:1

© Andreas Ryve, Rik matematik AB och Studentlitteratur 2024

© Andreas Ryve, Rik matematik AB och Bonnierförlagen Lära 2021

Formgivning: Marit Messing – Go Form AB, Frangkle

Illustrationer: Jessica Svendeborn (uggla och barn), Sinnebild (alla saker och ting)

Foto: rymdraket: NASA Official: images-assets.nasa.gov/image/KSC-2009-3108, sjuksköterska: Monkey Business Images/Shutterstock, glass: JeniFoto/Shutterstock, klassrum: Iryna Inshyna/Shutterstock, fotbollsstadium: Paolo Bona/Shutterstock, fotbollsspelare: barbsimages/Shutterstock, stickning: Larysa Shcherbyna/ Shutterstock, tegelvägg: Kirill Tonkikh/Shutterstock, violinister: Stokkete/ Shutterstock, tallrikar, barn med födelsedagstårta: Manuel Tenser, Nicole Oresme: ur Traité de l'espère/Wikimedia commons, pyramiderna: sculpies/Shutterstock, blomsterrabatt: nieriss/Shutterstock, T-rex: Sarjuki Aja/Shutterstock, Kajsa Bergqvist: Christian Seeling/AP Photo/SCANPIX /TT, affär: mokjc/Shutterstock

Printed by Eurographic Group, 2024

Rik matematik 1A – Lärarhandledning

Rik matematik ger lärare stöd att planera, genomföra och utvärdera rik matematikundervisning. Rik matematikundervisning kännetecknas av aktiva elever och en aktiv lärare där begrepp, resonemang och problemlösning står i fokus. Varje årskurs innehåller mer än 100 strukturerade lektioner med bildspel. Lektionerna har tydliga inledningar och avslutningar där central matematik betonas. Med Rik matematik får läraren stöd att varje lektion bedriva en undervisning som engagerar och utvecklar elevernas matematiska tänkande.

Rik matematik är utvecklat i ett nära samarbete mellan lärare och forskare och noggrant utprovat i klass.

I Rik matematik 1A Lärarpaket ingår utöver det tryckta lärarmaterialet, även en digital lärarresurs samt tillgång till förberedda uppdrag i Tomoyo, en digital spelifierad färdighetsträning. De digitala delarna nås via Min bokhylla på Studentlitteratur.se

Rik matematik 1A omfattar 5 områden:

Kapitel 1 – Tal och taluppfattning

Kapitel 2 – Addition och subtraktion 1–10

Kapitel 3 – Tal och räknestrategier

Kapitel 4 – Längdmätning

Kapitel 5 – Jämförelser och subtraktion