9789144174655

FAVORIT MATEMATIK 2A

UTÖKAT STÖD

Lärarpaket – Tryckt + Digitalt

LÄS OCH PROVA

LÄRARPAKETETS

SAMTLIGA DELAR

FAVORIT MATEMATIK 2A UTÖKAT STÖD

Lärarpaket – Tryckt + Digitalt

FAVORIT MATEMATIK UTÖKAT STÖD är en kompletterande lärarhandledning för klasslärare. I Finland finns en tydlig organisation för extra hjälp till elever som behöver det. Dessutom finns speciellt framtagna läromedel att använda i arbetet. Favorit matematik Utökat stöd kommer från Finland. Materialet har anpassats och granskats av både lärare och forskare som är verksamma i Sverige.

LÄRARHANDLEDNING

Favorit matematik Utökat stöd innehåller lektionsspecifika tips och förslag på extra hjälp framtagna med tanke på undervisning av elever som visar en lägre nivå i matematik. I de olika aktiviteterna används laborativt material. Eleven övar i sin ordinarie elevbok. Arbetet i elevboken kan också kompletteras med kopieringsunderlag för ytterligare förståelse och träning.

Kopieringsunderlagen i Favorit matematik Utökat stöd är framtagna med tanke på behoven hos de elever som behöver extra hjälp

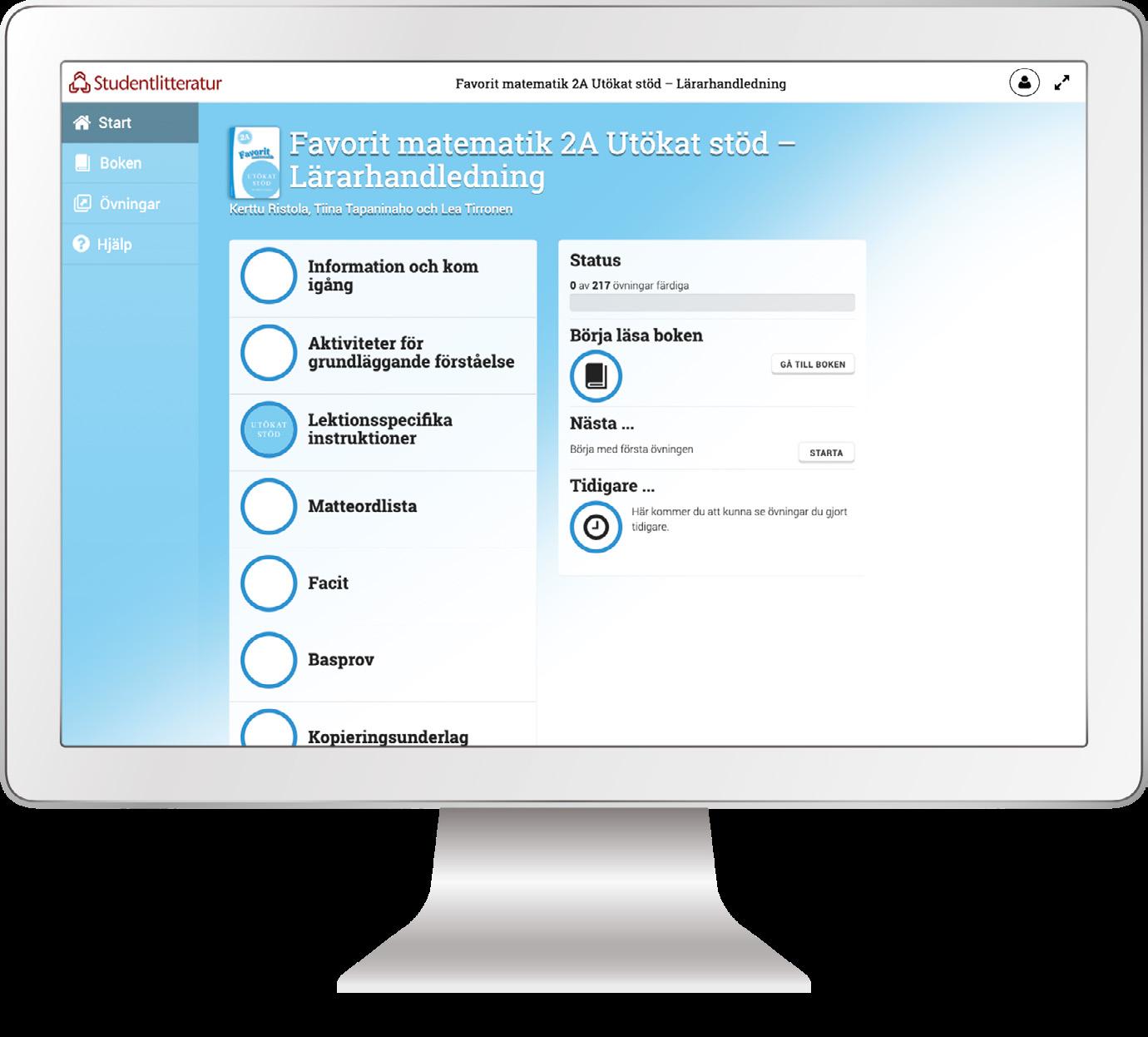
Interaktiv version av lärarmaterialet, där det går att söka, stryka under, anteckna och länka.

DIGITALA RESURSER

Med lärarhandledningens digitala resurser får du tillgång till flera praktiska verktyg för din undervisning. Introducera ett nytt moment, förklara olika begrepp, samlas kring lärorika uppgifter - tillsammans.

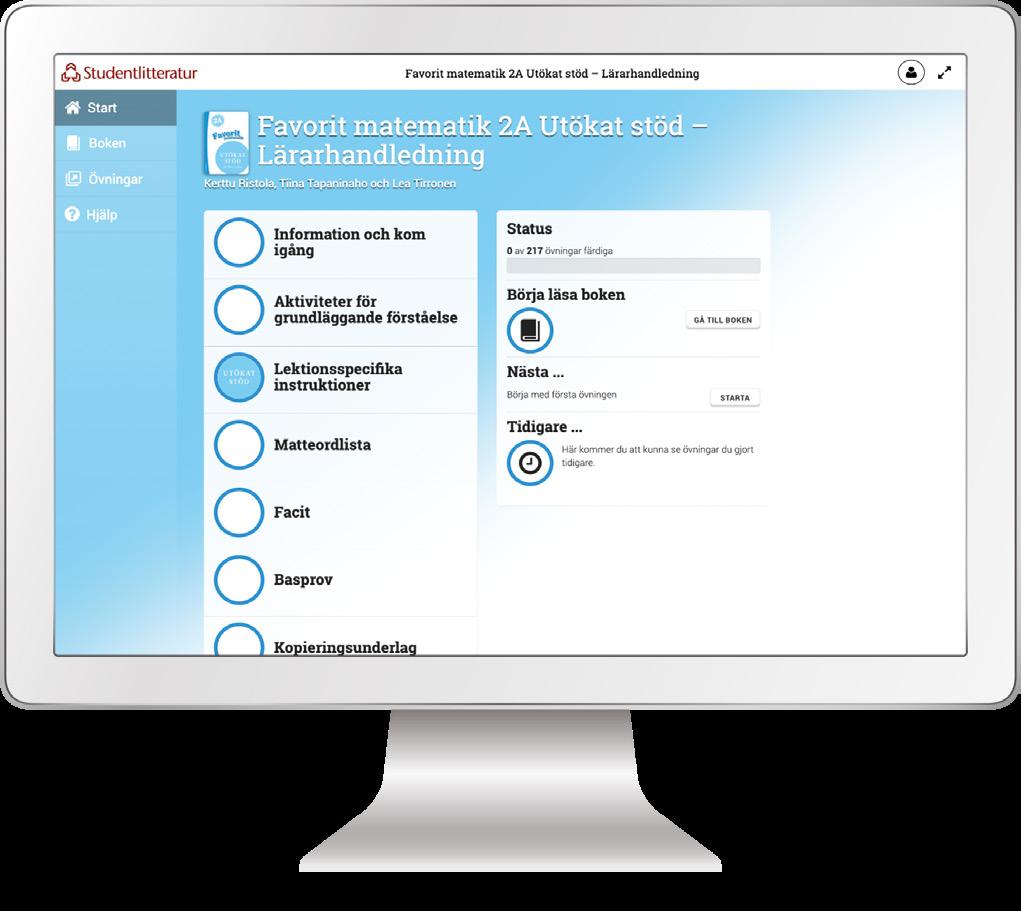
Här hittar du bland annat en matteordlista, kopieringsunderlag och facit till kopieringsunderlagen.

Favoritmatematik

UTÖKAT STÖD

Studentlitteratur AB

Box 141

221 00 Lund

Besöksadress: Åkergränden 1

Telefon 046-31 20 00

studentlitteratur.se

Kopieringsförbud

Detta verk är skyddat av upphovsrättslagen. Kopiering, utöver lärares begränsade rätt att kopiera för undervisningsbruk enligt Bonus Copyright Access skolkopieringsavtal, är förbjuden. Kopieringsunderlag får dock kopieras under förutsättning att kopiorna delas ut endast i den egna undervisningsgruppen. För information om avtalet hänvisas till utbildningsanordnarens huvudman eller Bonus Copyright Access.

Vid utgivning av detta verk som e-bok, är e-boken kopieringsskyddad.

Användning av detta verk för text- och datautvinningsändamål medges ej.

Den som bryter mot lagen om upphovsrätt kan åtalas av allmän åklagare och dömas till böter eller fängelse i upp till två år samt bli skyldig att erlägga ersättning till upphovsman eller rättsinnehavare.

Studentlitteraturs trycksaker är miljöanpassade, både när det gäller papper och tryckprocess.

Art.nr 43073

ISBN 978-91-44-17465-5

Upplaga 1:2

© Författarna och Studentlitteratur 2022

Originalets titel: Tuhattaituri 2a Opettajan opas E

© Otava Publishing Company Ltd, Helsingfors 2008

Översättning: Cilla Heinonen

Kompletterande texter: Kirsti Hemmi

Illustrationer: Maisa Rajamäki, Terhi Ekebom (kopieringsunderlagen)

Printed by Eurographic Group, 2024

Erfarenheter från undervisning i Finland

Förord

De kartläggningar vi gjort i början av olika matematikprojekt visar att det som lärare mest efterfrågar är kunskap om hur de ska kunna hjälpa elever som inte hänger med i den ordinarie undervisningen. I heterogena klasser måste en lärare kunna leda sina elever framåt till nya och mer krävande områden i matematiken och samtidigt stötta de elever som fortfarande kämpar med det mest elementära innehållet. Utan relevant material är det en svår uppgift.

Favorit matematik Utökat stöd innehåller en elevbok och lärarhandledning som underlättar lärares arbete att integrera elever med svårigheter i det dagliga arbetet i klassrummet och samtidigt möta deras specifika behov av kontinuerligt och relevant stöd. Materialet hjälper lärare både med uppföljning av elevers kunskaper och valet av lämpliga stödåtgärder.

Materialet är unikt eftersom det bidrar till ett arbete med en struktur och kontinuitet så att det inte bara blir ett ”ryck” då och då. Lärarhandledningen är ett kompletterande material som används parallellt med, och inkluderat i den ordinarie undervisningen. Den extra hjälpen i klassrummet och specialundervisningen flätas samman med den ordinarie undervisningen. Läromedlet ger förslag på framgångsrika metoder och verktyg, vilket ökar lärarens kapacitet och professionella utveckling. Elever med behov av särskilt stöd kan också vara delaktiga i arbetet med resten av klassen vilket bidrar till deras lärande och till en positiv självbild.

Lärarhandledningarna Utökat stöd 1a och 1b fokuserar bland annat på grundläggande aritmetik och taluppfattning. Grunden läggs också för användning av mer effektiva metoder för tiotalsövergången i addition och subtraktion. Det är möjligt att några elever behöver fortsatt stöd i dessa områden. Gedigna kunskaper inom grundläggande aritmetik och tiotalsövergången inom talområdet 0–20 utgör grunden för en effektiv hantering av operationer inom större talområden. Ibland behöver vi därför gå tillbaka till aktiviteter som presenteras i materialet för 1a och 1b. Under höstterminen i åk 2 utökas talområdet för elevers operationer till 0–100. Centralt är att utveckla elevers förståelse för tiosystemet. Uppställning av talen i addition och subtraktion illustreras och genomförs i början med hjälp av laborativt material. På det sättet främjas elevers förståelse för tiosystemet samtidigt som de befäster sina kunskaper gällande tiotalsövergången i addition och subtraktion. Grunden läggs även för multiplikations ­ och divisionsbegreppen samt bråkbegreppet under höstterminens andra halva.

Det är fortfarande viktigt att elever får använda flera sinnen då de bekantar sig med nya matematiska begrepp och operationer. De ska kunna lyssna, tala, känna, iaktta företeelser och samtidigt fortsätta utveckla sin finmotorik. Att kunna tänka och resonera logiskt samt att kunna koncentrera sig är grunden för all matematisk verksamhet. Det är vanligt att flera elever i åk 2 fortfarande behöver extra träning i koncentration i form av korta övningstillfällen så som den lilla huvudräkningsstunden och hemläxan (Träna ­ rutan). Dessa aktiviteter förstärker även minnet och ger tillfälle för lärare att kontinuerligt följa elevers framsteg och erbjuda snabb feedback. Detta är speciellt viktigt när det gäller yngre elevers lärande i matematik. Ytterligare idéer för övningar som förstärker koncentrationsförmågan finns i Favorit matematik Utökat stöd 1a

Den lektionsspecifika strukturen i boken är densamma som i den ordinarie lärarhandledningen, vilket underlättar planeringen. Introduktion till nya områden och huvudräkning kan med fördel genomföras samtidigt med hela klassen. Lektionerna kan planeras olika beroende på hur man vill introducera elever till nya områden. Det går alldeles utmärkt att starta med ett problem som elever i heterogena grupper diskuterar. Flera aktiviteter i denna bok lämpar sig också för hela klassen; svårighetsgraden kan lätt varieras och anpassas till olika elevers för utsättningar. Från elevboken kan läraren välja lämpliga uppgifter utifrån elevers olika behov. Det är dock viktigt att även elever med svårigheter i matematik, någon gång får ta del i problemlösning som förekommer på PRÖVA ­ sidorna och i den ordinarie lärarhandledningen. Materialet fungerar som en inspirationskälla för lärare när de komponerar sina lektioner med aktiviteter som främjar elevers lärande och ger möjligheter till mångsidig formativ bedömning.

För att varje dag kunna ägna en stund åt elever med särskilda behov måste resten av klassen aktiveras med annat. På s. 8 har jag exemplifierat hur undervisningen med hjälp av detta material kan organiseras på ett sätt som underlättar det dagliga arbetet med heterogena klasser.

Jag hoppas att materialet kan inspirera dig och ge dig mycket glädje då alla elever gör framsteg och får aha­upplevelser.

Kirsti Hemmi

professor i de matematiska ämnenas didaktik vid Åbo Akademi

Innehåll

INLEDNING

Att utveckla elevens förståelse för tiosystemet – positionssystemet 9

Att utveckla elevens förståelse vid addition och subtraktion med uppställning 13

Att utveckla elevens förståelse för multiplikation

Att utveckla elevens förståelse för division

KAPITEL 5

39. Favoritsidor – laborativ övning 122

40. Division, delningsdivision 126

41. Division, innehållsdivision 130

42. Tal i bråkform

43. Favoritsidor – laborativ övning

44. Vi övar 140

45. Vad har jag lärt mig? 142

46. Vi repeterar 144

47. Vi repeterar uppställning 146

48. Vi repeterar multiplikation 148

BASPROV

Innehåll och instruktioner 150 Huvudräkningsuppgifter till basproven 151

INLEDNING

Favorit matematik Utökat stöd

Favorit matematik 2A Utökat stöd Lärarhandledning innehåller tips, framtagna med tanke på undervisning av elever som behöver utökat stöd. Tanken är att Favorit matematik 2A Utökat stöd ska komplettera innehållet i den ordinarie lärarhandledningen Favorit matematik 2A Lärarhandledning, eftersom den ordinarie också innehåller flera praktiska övningar, spel och lekar som passar elever i behov av extra hjälp och stöd.

Favorit matematik 2A Utökat stöd Lärarhandledning inleds med allmän information om inlärningssvårigheter i matematik och olika metoder som du kan använda för att stödja eleven. Huvuddelen av innehållet i den kompletterande lärarhandledningen Favorit matematik 2A Utökat stöd, består i att du till varje lektion hittar enklare huvudräkningsuppgifter, tips på aktiviteter eller stöd som hör till precis det matematiska moment som lektionen behandlar. Det ingår kopieringsunderlag till varje lektion. Kopierings underlagen är framtagna med tanke på behoven hos de elever som visar låg nivå i matematik.

För klassläraren

Ordinarie lärarhandledning

För klassläraren

Tillägg för elever som visar låg nivå i matematik. Stöd, lektion för lektion.

För specialläraren

Tillägg för elever som behöver ännu mer stöd eller specialundervisning. Områden med fokus på det viktigaste i varje kapitel.

Inlärningssvårigheter i matematik

Inlärningssvårigheter i matematik kan bero på många orsaker. Bakom svårigheterna ligger ofta brister inom minst ett av följande delområden:

• språkliga färdigheter

• att gestalta* och minnas det man hört

• att gestalta* och minnas det man sett

• uppmärksamhet

• motorik

En del elever kan behöva ytterligare stöd utanför skolans arbete för att stärka de ovan nämnda förutsättningarna för lärande. Som lärare kan du ändå främja även en sådan elevs inlärning med hjälp av lämpliga pedagogiska metoder. En elev med inlärningssvårigheter i matematik behöver i högre utsträckning än sina jämnåriga:

1. stöd i form av laborativt material och bilder

2. repetition och befästande av tidigare introducerat innehåll

3. individuellt stöd/instruktioner

4. uppmuntran

5. tid att lära.

Om en elev har svårigheter med att lära sig matematik ska undervisningen innehålla praktisk verksamhet med konkreta och laborativa material . Aktiviteterna ska syfta till att tydliggöra matematiskt innehåll och stötta elevens matematikinlärning. För elever med matematik svårigheter kan det vara rörigt att använda många olika laborativa material. Det viktiga är att eleven känner till det laborativa materialet och inte behöver känna sig osäker med det. Därefter och i mycket långsam takt går vi vidare till abstrakta begrepp (siffror, matematiska begrepp). Även elever som inte har särskilda svårig heter med att lära sig grund begreppen drar nytta av praktiska övningar som befäster grundläggande begrepp. Praktiska övningar vidgar elevens uppfattning om vad som är matematik, samtidigt som de knyter an de matematiska begreppen till elevens vardag. En praktisk och laborativ form av undervisning kan också minska den ångest som en del elever upplever när det kommer till matematikinlärning, och därmed förebygga att de underpresterar. Gemensamma praktiska och laborativa övningar stärker även sammanhållningen i elevgruppen och hjälper elever som behöver särskilt stöd att känna samhörighet med resten av gruppen.

En ojämn kunskapsutveckling är typiskt för elever med matematiksvårigheter. Ibland kan det kännas som om eleven fått grepp om baskunskaperna, andra gånger kan enkla räkneuppgifter kännas helt omöjliga. De här variationerna kan hänga ihop med elevens motivation, uppmärksamhet eller minne. För att främja lärandet på bästa sätt är det viktigt med mångsidig undervisning och övningar som upprepas ofta. Kontrollera regelbundet hur väl eleverna behärskar baskunskaperna (till exempel tiokompisar, uppdelning av tal i talområdet 0 till 20 och förståelse av positionssystemet), eftersom matematikinlärningen bygger på de här kunskaperna.

* Det finska ordet hahmotus/hahmottaminen är svåröversatt. Här har vi valt att använda ordet gestalta men det kunde också stå ”skapa sig en bild av, uppfatta” eller liknande (lite beroende på situation).

Att använda olika hjälpmedel och laborativt material (till exempel tiobasmaterial, hundratavla) stöder inlärningen och gör att eleven kan skapa inre bilder och uppleva mindre oro vid uppgifter som känns svåra. Tipsa eleverna och deras föräldrar om att använda hjälpmedlen och det laborativa materialet även när de löser uppgifter hemma (t.ex. Träna­uppgifterna).

I vilken grad du som klasslärare kan stödja olika typer av elever beror på flera faktorer, som du inte alltid har möjlighet att påverka (till exempel elevgruppens storlek). Med realistiska målsättningar, en uppmuntrande inställning och en varierad undervisning kan du ändå hjälpa till att ”kratta manegen” för olika elever, det vill säga ge alla de bästa förutsättningarna för inlärning. Samtidigt får du själv uppleva känslan av att lyckas!

Förslag till organisation av undervisning för elev

Introduktionen till nya områden och huvudräkning kan med fördel genomföras samtidigt med hela klassen. Även andra aktiviteter i denna bok lämpar sig för hela klassen då aktivi teterna förstärker elevens grundläggande taluppfattning. Svårighetsgraden på aktiviteterna kan lätt varieras och anpassas till olika elevers förutsättningar.

För att varje dag kunna ägna en stund åt elever med särskilda behov måste resten av klassen aktiveras av annat. Under tiden kan läraren ägna sig åt elever som behöver extra stöd. Här är tre förslag på hur elever i klassen kan arbeta medan läraren ger stöd till elever med matematiksvårigheter.

Lärarhandledningen har många olika förslag

Den ordinarie lärarhandledningen erbjuder förslag på problem och spel som kan aktivera klassen då läraren arbetar med elever som har svårigheter i matematik.

Eleverna arbetar med elevbokens uppgifter

Ett sätt kan vara att utnyttja den tid då elever arbetar med uppgifter i elevboken.

Eleverna kontrollerar och rättar sina uppgifter

I Finland är det vanligt att lära elever att själva kontrollera och rätta sina uppgifter med korta mellanrum, till exempel vid en kontrollstation någonstans i klassrummet redan från början av åk 1. Efter att eleven räknat enbart några uppgifter i ett nytt område, gör hen en kontroll för att från början se till att vara på rätt väg och inte ha missförstått något. På kontrollstationen markerar eleven de uppgifter som blivit fel. Eleven får sedan själv rätta till sina felaktiga lösningar till exempel med hjälp av laborativt material, eventuellt i samråd med en annan elev.

Kirsti Hemmi professor i de matematiska ämnenas didaktik vid Åbo Akademi

AKTIVITETER FÖR

GRUNDLÄGGANDE FÖRSTÅELSE

Att utveckla elevens förståelse för

tiosystemet – positionssystemet

Eleverna ska utveckla en förståelse för tiobassystemet som är ett positionssystem och byggs upp av ”talsorter”, så som ental, tiotal och hundratal. Tio ental bildar ett tiotal, tio tiotal ett hundratal och så vidare. Eleverna ska också bli medvetna om att varje talsort i positionssystemet har sin egen plats, som uttrycker hur många av den aktuella talsorten som ingår i talet. Om ett tal saknar till exempel tiotal skriver vi en nolla på tiotalens plats.

Innan eleverna börjar arbeta med tiobasmaterial kan de gruppera olika föremål i grupper om tio. Du kan ge eleverna till exempel knappar, stenar, pärlor och burkar. Be eleverna placera tio föremål i varje burk. Till sist ska eleverna säga hur många föremål de fick. Du kan upprepa övningen så att eleverna får räkna ett annat antal föremål. Det går också att lägga till uppskattning, genom att be eleverna uppskatta antalet föremål de fått av dig innan de räknar. Eleverna kan ange antalet muntligt, med talkort eller genom att skriva antalet på ett papper.

Praktiska tips

Spel: Tio stickor

I spelet Tio stickor övar eleverna på att bilda grupper om tio. Eleverna spelar parvis. För att kunna spela spelet behöver varje elev en äggkartong med plats för tio ägg, en tärning, gummiband och pysselstickor eller liknande. Den ena spelaren kastar tärningen. Hen får till exempel en sexa, och tar så många stickor som prickarna på tärningen visar. Därefter placerar spelaren stickorna i sin äggkartong så att det finns en sticka i varje fördjupning. Stickorna ska placeras i äggkartongen på det sätt eleverna lärt sig tidigare, från vänster till höger och den övre raden före den nedre. Efter det kastar den andra eleven tärningen och gör på samma sätt. Eleven som började säger: ”Jag har sex stickor. Jag behöver fyra till för att ha tio.” Eleven kastar tärningen, tar igen så många stickor som tärningen visar och placerar dem i äggkartongen. Om äggkartongen fylls får eleven bunta ihop 10 stickor med ett gummiband. Eleven lägger bunten till vänster om äggkartongen. Eventuella stickor som blir över placeras i var sin fördjupning i äggkartongen inför nästa omgång. Spelet tar slut när stickorna tar slut eller efter en viss tid. Eleverna säger hur många stickor de fick och ser efter vem som fick flest. Den som fick flest stickor vinner.

Öva med olika laborativa material

Tiobasmaterial

För att eleverna verkligen ska få en förståelse för tiobassystemet behöver de använda laborativt material som hjälper dem att förstå hur systemet byggs upp. Lättast är det att konkretisera systemet med hjälp av tiobasmaterial, där det i tio­, hundra­ och tusentalen går att urskilja också entalen som de större talsorterna består av. Ett tiobasmaterial består alltså av ental (klossar/kuber, pärlor eller liknande), tiotal (stavar, pärlband eller liknande), hundratal (hundrabräden eller liknande) och tusental

(tusenkuber eller liknande). Om ni inte har tillgång till färdiga tiobasmaterial kan ni tillverka egna av till exempel trä. Såga till lagom stora klossar för att få entalskuber. En tiotalsstav ska vara lika lång som tio entalskuber på rad. Märk ut små skåror i stavarna som visar de ental som vi tänker oss att talsorten byggs upp av. Ett hundrabräde är lika stor som tio tiostavar bredvid varandra. Hundrabrädena ska också ha skåror som visar entalskubernas platser. En tusenkub är lika stor som tio hundrabräden på hög. Tusenkubens sidor ska också ha skåror som visar entalskubernas konturer. Det går också att tillverka tiobasmaterial med entalskuber, tiostavar och hundraskivor av kartong.

Introducera gärna tiobasmaterialet genom att låta eleverna bekanta sig med det. Du kan hjälpa eleverna att upptäcka att en stav består av tio kuber, pärlor eller liknande. Lägg märke till att det behövs tio stavar för att få ett bräde av kuber, pärlor eller liknande. Titta på och samtala om entalen, pärlorna eller vad ni nu använder tillsammans och namnge talsorterna. Räkna entalen: ”En, två, tre, … tio!” Fundera på vad som är lika mycket som tio ental. Lägg märke till att tio ental är lika med ett tiotal. Räkna sedan tiotal tillsammans: ”Tio, tjugo, trettio, … nittio. Vilket tal kommer efter det?” Det är möjligt att någon elev säger att efter nittio kommer tio tiotal vilket i sig är en korrekt slutsats. Ni kan tillsammans fundera på hur man skriver tio tiotal. Tio tiotal är ju ett hundratal.

När eleverna blivit vana vid arbete med tiobasmaterialet kan eleverna börja bilda tal. Förutom tiobasmaterialet behöver eleverna talkort. Ni kan tillverka talkort av kartong eller använda korten från det laborativa materialet som medföljer elevboken. Om du vill kan du kopiera korten på kartong i olika färger: tiotalskort på röda papper och entalskort på blå papper. På det sättet motsvarar färgerna på korten de färger som används i elevboken. Tillverkar ni korten själva är det bra att göra dem olika breda. Hundratals korten ska vara bredast, tiotalskorten lite smalare och entalskorten allra smalast så att det går att bilda tal (till exempel 235) genom att placera de kort som behövs (200, 30 och 5) på varandra. Använd gärna de färger som används i elevboken (hundratalen tillverkas av gula papper).

Praktiska tips

Hundrapärlor

Film: Hundrapärlor

När eleverna börjar arbeta med talområdet 0 till 100 kan de använda hundrapärlor som stöd. Hundrapärlor är pärlor i två olika färger som träs på ett snöre i grupper om tio. Snöret måste vara tillräckligt långt för att det ska gå att flytta på pärlorna. I snörets ändar ska det gärna finnas två stora pärlor som skiljer sig från de andra och som eleven kan hålla i. Om du vill kunna hänga upp hundrapärlorna på tavlan fäster ni magneter i snörändarna.

Du kan be eleverna visa olika antal med hjälp av hundrapärlorna (till exempel ”Visa 45 pärlor”). Eleverna kan också visa ordningstal (”Visa den femtonde pärlan”). I det senare exemplet är svaret bara en pärla. Kontrollera gärna att eleverna kan begreppen första och sista. Ni kan räkna addition, subtraktion och multiplikation med hundrapärlorna. Hundrapärlorna är ett bra verktyg för att öva talföljder: samtidigt

som man räknar tal flyttar man pärlor på snöret. Öva talföljder fram­ och baklänges och i intervall om en, två, fem och tio.

Övningar med tiobasmaterial

Läraren eller en elev säger ett tal som består av ental och tiotal och skriver det på tavlan. Först bygger eleverna talet med talkort. Under korten bygger de talet med hjälp av tiotalsstavar och entalskuber. När eleverna förstår övningen behöver ni inte längre skriva upp talen på tavlan men det är viktigt att eleven säger vilket tal det är och att du ser till att eleven säger talen i sin helhet.

Eleverna kan öva på positionssystemet med hjälp av arbetsstationer. Bygg tal av tiostavar och entalskuber och placera dem på golvet eller på ett litet bord. Eleverna lägger ut talkort under konstruktionerna. Vid en annan station kan det finnas tal som bildats av talkort. Där ska eleverna bygga talen av tiotalsstavar och entalskuber. En del av eleverna kan bygga tal av tiotalsstavar och entalskuber och ordna en Talutställning. Utställningsobjekten kan placeras på små bord eller på elevernas platser. Eleverna bygger ett överenskommet antal tiotal på borden. Till exempel talet 46 byggs genom att man placerar fyra tiotalsstavar på bordet och sedan sex entalskuber till höger om dem. När utställningen är klar går resten av eleverna runt med papper och penna och skriver de tal de ser. Det är viktigt att eleverna kan koppla samma antal, talets namn och talets beteckning med siffror.

Positionsplatta

Tillverka en positionsplatta för tiobasmaterialen till exempel av kartong. Dela in underlaget med lodräta streck i tre (eller fyra, om ni vill ta med tusentalen) delar. Skriv bokstäverna H, T, E för hundratal, tiotal och ental högst upp. Du kan använda positionsplattan för att introducera tiosystemet, och som stöd när eleverna räknar addition och subtraktion med tiotal. Till en början är det viktigt att eleverna övar ordentligt på hur man utläser tal. Att säga tal högt hjälper eleven att förstå tiosystemet. Särskilt viktigt är det att du ser till att eleverna säger talen i sin helhet.

Övningar med positionsplatta

Du eller en elev säger tal och eleverna läger dem med hjälp av tiobasmaterialet på sina positionsplattor. De kan också bilda talet med talkort under materialet. Eleverna kan arbeta parvis så att den ena eleven lägger talet på underlaget och den andra eleven lägger talet med talkort. Det går också att göra övningen tvärtom – den ena bildar talet med talkort och den andra bygger samma tal.

Spel: Vems tal är störst?

Eleverna kan spela spelet Vems tal är störst? på underlagen. Eleverna behöver talkorten 0 till 9, två positionsplattor, tiobasmaterial och talkort för tiobassystemet. Eleverna placerar talkorten (0 till 9) på bordet med talsidan nedåt och blandar dem. Den ena eleven tar ett kort. Eleven placerar så många entalskuber, pärlor eller liknande i entalsrutan på plattan som kortet anger. Sedan lägger eleven tillbaka kortet på bordet och blandar. Efter det tar den andra eleven ett kort och placerar så

Film: Positionssystemet

i varje. Hur många påsar med bullar får han? Uttrycket är det samma, 6 /2 = 3. Svar: 3 påsar. Vid innehållsdivision löser vi alltså hur många gånger ett tal går i ett annat eller hur många gånger ett tal kan subtraheras från ett annat tal. Fastän du i det här skedet inte lär ut begreppen innehålls ­ och delningsdivision till eleverna är det ändå bra att påminna dem om att vara uppmärksamma på vilken enhet svaret på en division har.

en fjärdedel

Vid divisionerna snuddar vi också vid begreppet bråk . Vi börjar med att vi lär oss dela en figur (kvadrat, triangel, tårta, pizza eller liknande) i lika stora delar. Först delar vi figurerna i två lika stora delar, och eleven lär sig begreppet ”halv” eller ”hälften”. Eleverna övar på att känna igen och namnge bråk genom att säga hur stor del av de olika figurerna i boken som är målade. Eleven kan öva på vad vi menar med bråk inom matematiken med laborativt material, exempelvis klossar eller knappar. Bilda en rad av till exempel fyra klossar och be eleven fundera på vad som är en fjärdedel av raden. Eleverna kan klippa ut kvadrater och cirklar av färgat papper och sedan dela dem i två, fyra eller åtta lika stora delar enligt dina instruktioner. Eleverna kan börja med att vika figurerna och sedan klippa längs vecken. De utklippta bitarna hjälper eleverna att förstå att till exempel en fjärdedel är större än en åttondel, fastän talet åtta är större än talet fyra.

LEKTIONSSPECIFIKA INSTRUKTIONER

Innehåll till varje

lektion

UTÖKAT STÖD 2. Vi repeterar subtraktion

Lektionens innehåll

Att repetera subtraktion inom talområdet 0 till 20

• Begreppet ”term” vid subtraktion

Huvudräkning

Skriv gärna upp talen i huvudräkningsuppgifterna på tavlan. Eleverna kan använ-

da laborativt material som stöd när de löser huvudräkningsuppgifterna.

1. Sally ser 12 lastbilar. 5 av dem kör i väg. Hur många lastbilar är kvar? (7)

2. Kurre ser 12 bilar. 3 av dem kör i väg. Hur många bilar är kvar? (9)

3. Isa ser 12 lastbilar. Först kör 2 av dem i väg och sedan 4 till Hur många lastbilar är kvar? (6

Förslag på utökat stöd

Kopieringsunderlag 2a–c

Elevbokens uppgifter uppgift 4 kan eleverna ta hjälp av till exempel knappar, klossar eller makaroner. Eleven kan skriva svaren på uttrycken på bilden och be dig kontrollera dem innan hen börjar måla. På det sättet undviker vi att någon blir ledsen på grund av att ha målat fel. uppgift 5 ska du försäkra dig om att eleven har förstått principen för ”mirakelmaskinen”. Man ”matar in”ett tal på maskinens vänstra sida, och maskinen omvandlar talet. Maskinen visar det omvandlade talet på sin högra sida. Elevens uppgift är räkna ut vilken princip maskinen fungerar enligt, det vill säga vad maskinen gör med de tal man matar in den. Eleven skriver regeln i rutan högst upp på maskinen. Efter det kan eleven lösa resten av talen. Mirakelmaskinen bygger en grund för funktioner. (Ev. information om funktioner)

Kopieringsunderlag Kopieringsunderlag 2a: Subtraktion Kopieringsunderlag 2b: Fundera Kopieringsunderlag 2c: Mirakelmaskin Anteckningar

1. Lektionens innehåll

Visar vad lektionen handlar om och vad som är lektionens matematiska moment.

2. Huvudräkning

Till varje lektion finns det huvudräkningsuppgifter. Du använder huvudräkningsuppgifterna bäst genom att använda dem när du har introducerat lektionens matematiska innehåll. Ovanför samtals bilden i elevboken finns tre rutor där eleven kan skriva svaren.

För alla elever, men framför allt elever som visar låg nivå i matematik, är det viktigt att du använder huvudräkningsuppgifterna på ett strukturerat sätt. Uppgifterna får inte stressa eleven för då blockeras korttidsminnet. De elever som behöver, ska ha tillgång till laborativt material.

Gör så här vid varje tillfälle:

• Först kan du enbart läsa huvudräkningsuppgiften. Då kan en del av eleverna, men inte alla, skriva svar.

• Därefter läser du uppgiften lugnt en gång till, samtidigt skriver du de aktuella talen på tavlan.

Alla elever vet från början att du kommer att upprepa uppgiften och dessutom skriva talen på tavlan.

För dig som lärare ger huvudräkningsuppgifterna en bra möjlighet för en fortsatt formativ (framåtsyftande) under visning.

För eleven kan uppgifterna vara till hjälp för reflektion över sitt eget lärande. Aktiviteten hjälper dessutom eleven att koncentrera sig i ”små portioner”, något som kan vara extra svårt för vissa elever (i början).

3. Förslag på utökat stöd

Här finns tips och aktiviteter, ofta laborativa, som förtydligar och stöttar lärandet för elever som behöver extra hjälp. Film är en symbol som talar om att här finns en film som visar en lärare och elev/elever som kommunicerar det matematiska innehållet under aktiviteten.

4. Kopieringsunderlag

Arbetsmaterial på enklare nivå än kopieringsunderlagen i den ordinarie lärarhandledningen.

5. Elevbokens uppslag

Här visas de sidor i elevboken som hör till lektionen.

7. Subtrahera ental

Lektionens innehåll

• Att repetera subtraktion inom talområdet 0 till 100, i uttryck där enbart entalen minskar

Huvudräkning

Skriv gärna upp talen i huvudräkningsuppgifterna på tavlan. Eleverna kan använda laborativt material som stöd när de löser huvudräkningsuppgifter.

1. Skeppsmusen har 24 bollar. Hon får 3 bollar till. Hur många bollar har hon sammanlagt? (27)

2. Skeppsmusen har 32 bollar. Hon får 6 bollar till. Hur många bollar har hon sammanlagt? (38)

3. 12 – 2 – 4 (6)

Förslag på utökat stöd

Räkneberättelser

Du kan hitta på räkneberättelser som eleverna bygger med tiobasmaterial. Berätta till exempel: ”Skeppsmusen har 27 bollar (eleverna bygger talet 27 av två tiotalsstavar och sju entalskuber). Kurre får fyra av dem (eleverna tar bort fyra entalskuber). Hur många bollar har skeppsmusen efter det?” Eleverna kan lägga talen med talkort under det laborativa materialet.

Räkneutställning

Några elever bygger med hjälp av tiobasmaterial en utställning med uttryck där entalen minskar. Bygg enbart uttryck utan tiotalsövergång. I subtraktionsutställningen visar de tiobasmaterial som läggs fram bara den första termen i uttrycket. Bilda uttrycket med talkort under det laborativa materialet. När utställningen är klar går eleverna runt i små grupper och löser uttrycken på ett papper.

Spel: räknematch

Eleverna spelar parvis. Det är bra om eleverna sitter bredvid varandra så att bägge kan se uttrycket tydligt. Varje par behöver spelkorten från kopieringsunderlag 5c och 5d . Klipp ut korten och lägg dem i en hög med textsidan nedåt. Eleverna turas om att vända det översta kortet i högen. Den som löser uttrycket först placerar sin hand på kortet och säger svaret omedelbart. Om svaret är rätt får eleven behålla kortet. Om den andra eleven anser att svaret är fel löser eleverna problemet genom att diskutera. Du kan ställa upp en kontrollstation i klassrummet där eleverna vid behov kan kontrollera sina svar. Om svaret är fel lägger eleverna kortet underst i högen. Den som har flest kort när högen tar slut vinner.

Elevbokens uppgifter

I uppgift 2 och uppgift 3 kan eleven ta hjälp av tiobasmaterial eller så kan du lära eleven att rita talen så att en tiotalsstav (det vill säga ett tiotal) motsvaras av ett långt streck medan ental motsvaras av cirklar eller kvadrater.

I uppgift 4 visar du eleven att först skriva det tal som tiotalsstavarna och entalsbollarna anger och sedan räkna hur många bollar man dragit streck över och skriva antalet som den andra termen i subtraktionen.

Forts. s. 46

Favorit 2A s. 30–33

7. Subtrahera ental

2 4 – 3 = 2

Subtrahera entalen.

1. Dra lika många streck över entalen som den andra termen visar. Subtrahera.

och

4. Subtrahera. Ringa in differensen i rutan.

Subtrahera.

3. Subtrahera. Ringa in differensen i rutan.

1. Dra lika många streck över entalen som den andra termen visar. Subtrahera.

Subtrahera.

Metod – använder utvecklingsbara metoder för att utföra beräkning med subtraktion vid huvudräkning, förstår att beräkningar i ett talområde kan uttryckas i ett utökat talområde, t.ex. att om

5. Hur mycket pengar har du kvar när du har handlat?

c.

6. Måla båtarna.

a. Tiotalen är 4 Tiotalen är 7 b. Entalen är 5 Entalen är 8

17:43

Forts. från s. 44

I uppgift 5 instruerar du eleven att först räkna hur mycket pengar det finns, och skriva beloppet i rutan.

I uppgift 6a kan du visa eleven genom att ringa in tiotalen på skeppen i en uppgift och i uppgift 6b entalen på skeppen i en av uppgifterna.

Kopieringsunderlag

Kopieringsunderlag 7a: Entalen minskar

Kopieringsunderlag 7b: Addition och subtraktion

Anteckningar

Anteckningar

Kopieringsunderlag

8. Subtrahera ental och tiotal

Lektionens innehåll

• Att repetera subtraktion inom talområdet 0 till 100, i uttryck där både entalen och tiotalen minskar

Huvudräkning

Skriv gärna upp talen i huvudräkningsuppgifterna på tavlan. Eleverna kan använda laborativt material som stöd när de löser huvudräkningsuppgifterna.

1. Du köper två spel. Det ena spelet kostar 8 kronor och det andra 11 kronor. Hur mycket kostar spelen sammanlagt? (19 kr)

2. Isa har 27 kronor. Hon köper en båt som kostar 5 kronor. Hur mycket pengar har Isa kvar? (22 kr)

3. Charlie köper två olika nallar. Den ena nallen kostar 7 kronor och den andra är 2 kronor dyrare. Hur mycket kostar den dyrare nallen? (9 kr)

Förslag på utökat stöd

Spel: räknematch

Eleverna spelar parvis. Det är bra om eleverna sitter bredvid varandra så att bägge kan se uttrycket tydligt. Varje par behöver spelkorten från kopieringsunderlag 5c och 5d. Klipp ut korten och lägg dem i en hög med textsidan nedåt. Eleverna turas om att vända det översta kortet i högen. Den som löser uttrycket först placerar sin hand på kortet och säger svaret omedelbart. Om svaret är rätt får eleven behålla kortet. Om den andra eleven anser att svaret är fel löser eleverna problemet genom att diskutera. Du kan ställa upp en kontrollstation i klassrummet där eleverna vid behov kan kontrollera sina svar. Om svaret är fel lägger eleverna kortet underst i högen. Den som har flest kort när högen tar slut vinner.

Elevbokens uppgifter

Uttryck där både entalen och tiotalen minskar är fortfarande mycket svårt för många elever. För att hjälpa eleven finns det alltid en bild som stöd vid sådana uttryck i elevboken.

I uppgift 4 kan du visa eleven hur man kan jämföra talen genom att bygga talen med tiotalsstavar och entalskuber.

I uppgift 5a kan du som visa genom att ringa in tiotalen på lastbilarna i en av uppgifterna och i uppgift b entalen på lastbilarna i en uppgift.

I uppgift 6 kan eleven ta hjälp av de fem tiokronor och åtta enkronor som finns på sidan. Visa hur eleven kan täcka för de pengar som motsvarar priset på inköpet.

Kopieringsunderlag

Kopieringsunderlag 8a: Entalen och tiotalen minskar

Kopieringsunderlag 8b: Att rita subtraktion

Favorit 2A s. 34–37

2. Subtrahera.

på berättelsen.

Subtrahera entalen och subtrahera tiotalen.

1. Dra streck över entalen och tiotalen. Subtrahera. a. 4 2 – 2 1 = b. 5 7 – 3 2 =

a. 58 – 10 = 58 – 20 = 58 – 30 =

– 40 = 58 – 50 = b. 32 – 20 = 75 – 30 = 67 – 40 = 81 – 50 = 52 – 40 =

3. Subtrahera. Ringa in differensen i rutan.

a. 75 – 13 =

1. Dra streck över entalen och tiotalen. Subtrahera.

Taluppfattning och tals användning – centrala metoder för beräkningar med subtraktion

4. Skriv <, = eller >

2. Subtrahera. 68 – 20 = 46 – 30 = 41 – 40 = 37 – 35 = 57 – 45 = 65 – 23 = 38 – 15 = 99

Begrepp – använder och förstår begreppen tiotal och ental Metod – använder utvecklingsbara metoder med subtraktion vid huvudräkning, använder och förstår positionssystemet

978-91-44-12419-3_06_book.indb 35

6. Julia har 58 kr. Hur mycket pengar har hon kvar när hon har handlat?

5. Måla lastbilarna.

a. Tiotalen är 6 Tiotalen är 9 b.

Favoritmatematik

Utökat stöd

Lärarhand L edning

Favorit matematik är ett basläromedel i matematik med en gedigen, välfungerande och tydlig struktur. Materialet kommer från Finland där det är uppskattat för strukturen och de goda resultaten hos eleverna.

Favorit matematik 2A Utökat stöd är en kompletterande lärarhandledning för klasslärare. Här finns lektionsspecifika tips, filmer och förslag på extra hjälp till elever som har svårt att nå målen i matematik. Kopieringsunderlag som kan stötta lärandet medföljer i en bilaga men finns även som filer i den digitala lärarresursen. Den muntliga kommunikationen och det laborativa arbetet är centralt och lyfts genomgående fram i aktiviteterna.

Det beprövade och framgångsrika läromedlet har anpassats samt granskats av både lärare och forskare som är verksamma i Sverige.

studentlitteratur.se