9789127464230

HEUREKA!

Fysik nivå 2

VÄLKOMMEN TILL HEUREKA!

Arkimedes sägs ha utropat Heureka! – Jag har det! – när han kom på den princip som beskriver lyftkraften på en kropp nedsänkt i en vätska.

Arkimedes princip påstås vara den äldsta av alla vetenskapliga förklaringar som vi fortsatt använder. Under mer än två tusen år har den visat sig hålla för både experimentell prövning och teoretisk granskning – själva grunden för ett naturvetenskapligt arbetssätt. I bokens första kapitel Fysik – teori och experiment beskriver vi hur fysikaliska teorier bildas, hur de experimentellt prövas och vad som utmärker ett naturvetenskapligt arbetssätt.

Krafter och rörelse

I bokens andra kapitel, Mekanik, beskriver vi rörelser i två dimensioner, exempelvis rörelsen hos en boll du kastar snett uppåt. Kapitel 3, Harmonisk rörelse, handlar om rörelse i cirkel eller hos en svängande kropp, som till exempel en pendel. Den beskrivningen använder vi sedan för att analysera vågrörelser. Det kan vara vattenvågor som i kapitel 4, ljud i kapitel 5 eller ljus i kapitel 8.

Energi, energiresurser och elektromagnetism

Elektromagnetism – samspelet mellan elektriska och magnetiska krafter – ligger till grund för såväl generatorer, transformatorer som ljus och annan elektromagnetisk strålning. Elektriska och magnetiska krafter studerar vi kapitel 6 Magnetism och 7 Elektromagnetisk induktion. I kapitel 9, Nytt ljus över fysiken, blir ljuset en utgångspunkt för att beskriva den moderna fysiken: relativitetsteorin och kvantfysiken.

Universum, materien och strålning

Kapitel 10 Atomen handlar om just atomen och dess samverkan med elektromagnetisk strålning. I kapitel 11 Universum, lär vi oss hur vi detekterar och tolkar universums olika typer av strålning. Det ger oss kunskaper att diskutera universums tillstånd, uppkomst och utveckling. Här möter vi gränserna för vad vi faktiskt kan säga att vi vet och vad som ännu återstår att ta reda på.

Läromedelsserien Heureka! har funnits i över 40 år och är ett samarbete mellan erfarna lärare och etablerade fysiker.

Lycka till med dina fysikstudier!

Författarna

Innehåll

8.2 Ljusets

8.3

9.3

9.4

Så fungerar Heureka!

9.3 ELEKTROMAGNETISK STRÅLNING

Elektromagnetisk strålning består av energi-kvanta. Energin E hos ljuskvanta är proportionell mot strålningens frekvens f: E = hf

där h = 6,626 · 10–34 Js är Plancks konstant.

KONTROLL

8 Beskriv kortfattat begreppen: a absolut svart kropp b strålningsjämvikt c emittans.

TÄNK TILL!

2 Varför märker vi inte i vardagslivet att partiklar också är vågor? Hur stor är våglängden för en tennisboll som rör sig med hastigheten 5 m/s?

Fråga forskaren:

Vad är tid?

Ljusklockan kan synkroniseras med alla andra klockor: armbandsur, kvartsur, timglas, atomur, biologiska klockor

Varje kapitel är indelat i delkapitel.

Innehållet sammanfattas löpande i röda rutor.

Texten stöttas av Kontroll. Frågor som hjälper dig att se vad som är särskilt viktigt. Förslag på svar till frågorna hittar du i facit.

Med Tänk till! får du träna på att föra fysikaliska resonemang. Frågorna varierar från relativt enkla till riktigt svåra. De passar bra att arbeta med i grupp.

Forskning i fysik är i dag mer aktiv än någonsin tidigare. Med Fråga forskaren vill vi ge en utblick mot aktuell forskning.

SAMMANFATTNING

ÖVNINGAR

I slutet av kapitlet hittar du en sammanfattning. Den ger en överblick av hela kapitlet.

Övningarna är indelade efter delkapitel och inleds med ett grundläggande exempel. Några av övningarna är mer utmanande.

9.3 Elektromagnetisk strålning

EXEMPEL

Sett från rymden har jorden medeltemperaturen −18 ˚C.

a) Jordens yta är 5,1 ∙ 1014 m2. Med hur stor total effekt strålar jorden på grund av sin värme?

b) Vid vilken våglängd är den utstrålade effekten som störst?

LÖSNING

a) Stefan-Boltzmans lag ger emittansen M, alltså den utstrålade effekten per areaenhet. Temperaturen uttrycks i kelvin.

BLANDADE ÖVNINGAR

Allra sist i kapitlet hittar du Blandade övningar. De är indelade i tre nivåer och blandar alla delmoment i kapitlet.

LJUS

Vi är omgivna av ljus. Solen skiner, olika typer av lampor lyser, och när vi vill skapa en trevlig stämning, tänder vi stearinljus. I alla de här fallen är det förändringar i materiens inre som ger upphov till den elektromagnetiska vågrörelse vi kallar ljus.

Flertalet elektromagnetiska vågor är osynliga för oss. Det ljus vi kan uppfatta med våra ögon kallar vi för synligt ljus. Det är ljus i våglängdsområdet

400–750 nm.

8.1 EGENSKAPER HOS LJUS

Figur 1 De skarpa gränserna mellan belysta och skuggade områden förklaras av att ljus utbreder sig rätlinjigt.

Nästan dagligen lägger vi märke till brytning och reflexion av ljus i medier som vatten och glas. Vi ser hur solljuset blänker i fönstret och hur en sked i ett vattenglas ser ut att vara knäckt vid vattenytan. I det här kapitlet kommer vi att beskriva ljus som en vågrörelse. Du kommer därför att ha nytta av beskrivningen av vågor du läste om i kapitel 4. Men till skillnad från exempelvis vattenvågor behöver ljus inget medium att färdas igenom – det fortplantar sig även i absolut tomrum (vakuum).

Ljusets hastighet

Ljusets hastighet är en viktig storhet inom flera av fysikens områden. Ända sedan Galileis tid har fysiker försökt bestämma den så noggrant som möjligt. När man på 1970-talet erhöll värdet 299 792 458 m/s på ljusets hastighet i vakuum, var detta ett resultat som inte kunde förbättras. Det var osäkerheten i den då gällande definitionen av 1 m som satte gränsen (grundenheten 1 s var noggrannare definierad). År 1983 valde man att tilldela ljusets hastighet c i vakuum det exakta värdet 299792 458 m/s. Följden blev att grundenheten 1 m är den sträcka som ljuset färdas i vakuum på tiden 1/299792458 s.

Mätningar har visat att ljushastigheten i olika genomskinliga medier alltid är lägre än i vakuum. I till exempel vanligt glas är den avsevärt mindre, ungefär 200 Mm/s. Skillnaden mellan hastigheterna i luft och vakuum är däremot obetydlig. Med tre värdesiffror är den 300 Mm/s i båda medierna.

Ljusets fart i vakuum är c = 299 792 458 m/s exakt. 1 m är den sträcka ljuset färdas i vakuum på tiden 1/299 792 458 s.

Sambandet v = f ∙ λ mellan utbredningshastighet v, frekvens f och våglängd λ, som vi använt för mekaniska vågor i kapitel 4, gäller också för elektromagnetiska vågor som ljus. Vi skriver då vanligtvis c = f ∙ λ, där c är ljusets fart.

Ljusstrålar

När solen lyser genom ditt fönster blir ett skarpt avgränsat område på väggen eller golvet belyst. Det visar att ljuset utbreder sig rätlinjigt. Vi ritar därför räta linjer – strålar – för att visa vilka vägar ljuset tar. Ljusstrålen blir modell för ljusets utbredning.

En klar natt kan du se stjärnor, eftersom de skickar ut ljus som når dina ögon. Stjärnor är exempel på ljuskällor. En lampa, en tv-skärm eller en laser är andra exempel.

I dagsljus kan du se föremål omkring dig trots att de inte skickar ut något eget ljus. Det förklarar vi med att ljus från vår starkaste ljuskälla, solen, först har träffat föremålen. Sedan har delar av det ljuset studsat vidare – reflekterats – mot dig.

KONTROLL

1 Går ljuset fortare eller långsammare i glas jämfört med i luft?

2 Hur kan man se att ljuset utbreder sig rätlinjigt?

Reflexion

Låt oss undersöka hur ljus reflekteras. Vi börjar med att studera vad som händer när en ljusstråle från en laser träffar en spegel. Vi låter ljuset stryka utefter en rutad skärm och träffa en plan spegel, figur 3a.

Figur 3a Foto av en laserljusstrimma som stryker längs en skärm. Ljusstrimman reflekteras mot en spegel i skärmens nedre kant.

b Teckning av strålens väg. Infallsvinkeln αi och den lika stora reflexionsvinkeln αr har markerats. α r αi

Figuren visar hur ljusstrålen reflekteras. Där strålen träffar spegeln tänker vi oss en linje vinkelrät mot spegeln, en normal till spegelytan. Vi ser att den reflekterade strålen bildar lika stor vinkel med normalen som den infallande strålen. Vi kallar vinkeln αi för infallsvinkel och vinkeln αr för reflexionsvinkel. Sambandet αi = αr , reflexionslagen, visar sig gälla vid alla infallsvinklar.

Reflexionslagen

Reflexionsvinkeln är lika med infallsvinkeln.

Noggrann längdmätning

Det exakta värdet på ljushastigheten tillsammans med den noggranna definitionen av en sekund, gör det möjligt att mäta både långa och korta sträckor med stor precision. Avståndet från en punkt på jorden till en punkt på månen kan nu bestämmas på 2 mm när. Det gör man genom att mäta den tid det tar för en laserpuls att färdas fram och tillbaka till någon av de reflektorer som placerades där 1969. Tack vare de här mätningarna vet vi att månen avlägsnar sig från jorden med 3,8 cm/år.

Figur 4

Fotografiet visar en av de reflektorer som Neil Armstrong och Edwin Aldrin placerade på månen år 1969.

Diffus och regelbunden reflexion

Vi riktar ett ljusknippe mot en lite ojämn yta, till exempel en vägg. Träffpunkten lyser starkt och syns från alla håll. Det beror på att väggens yta är skrovlig. Var och en av strålarna i knippet följer visserligen reflexionslagen, men på grund av ojämnheterna i väggens yta blir infallsvinklarna olika. Därför reflekteras strålarna åt alla möjliga håll, bland annat i riktning mot ditt öga så att du ser ljuset, figur 6a. Reflexionen är oregelbunden eller diffus.

Figur 5 När vattenytan är blank reflekteras himlen regelbundet i sjön.

Figur 6a Diffus reflexion. Parallella strålar som träffar en skrovlig yta reflekteras åt olika håll.

b Regelbunden reflexion. Vid en plan yta reflekteras de parallella strålarna åt samma håll.

Om ljusknippet träffar en spegel, som i figur 6b, ser du däremot ingen träffpunkt. Spegelytan är så jämn att praktiskt taget alla delar av strimman reflekteras åt samma håll. Reflexionen är regelbunden, och inget av ljuset kan nå ögat i figuren. Det är tack vare diffust reflekterat ljus från solen eller lampor som vi kan se föremålen omkring oss. En perfekt speglande, plan yta är omöjlig att se.

8.2 LJUSETS BRYTNING

Du har säkert lagt märke till att ett sugrör som står i ett vattenglas ser ut att vara knäckt vid vattenytan, figur 7a. Fotot i figur 7b visar två lika långa sugrör i jämnhöjd. Det ena är nerdoppat i ett glas vatten. Tittar man snett uppifrån verkar det kortare än det andra.

b Rören är lika långa!

c Eftersom ljuset bryts vid vattenytan ser den nerdoppade delen av sugröret kortare ut.

I figur 7c betraktar ett öga det nerdoppade sugröret. Sugröret tycks sluta vid A1 i stället för vid A. Det betyder att ljus från A måste gå vägen BC i luften till ögat, så att det ser ut att komma från A1. Om ljuset utbreder sig rätlinjigt även i vatten, måste det ha gått vägen AB i vattnet. Slutsatsen är att ljuset ändrar riktning – bryts – vid vattenytan. Nu kan vi förklara varför sugröret i fotot ser ut att vara knäckt. Ljusets brytning gör att sugrörets delar nere i vattnet ser ut att ligga närmare vattenytan än de gör i verkligheten.

Reversibel strålgång

Med en laser kan vi skicka en ljusstrimma i omvänd riktning – från C mot B i figur 7c. Vi finner då att ljuset bryts på samma sätt och följer vägen BA ner i vattnet. Vi säger att strålgången är reversibel, alltså omvändbar. Det är endast om strimman träffar vattenytan rakt uppifrån som brytningen uteblir.

Brytning i en gränsyta

Ljuset uppträder på liknande sätt när det går in i andra genomskinliga ämnen än vatten, till exempel glas eller plast. Med uppställningen i figur 8a kan vi närmare undersöka vad som händer när ljus träffar en gränsyta mellan luft och glas.

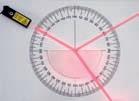
Figur 8a Foto av en ljusstrimma som kommer från luft och går in i glas.

b Teckningen visar vad som händer i figur 8a.

En halv cirkulär glaskropp är fäst vid en cirkulär gradskiva så att medelpunkterna sammanfaller. En ljusstråle stryker utefter gradskivan och träffar glaskroppens plana yta vid den gemensamma medelpunkten. Vi ser att en del av ljuset reflekteras enligt reflexionslagen och att resten bryts in i glaset. Strålens infallsvinkel αi mäts, precis som i reflexionslagen, mellan den infallande strimman och normalen, se figur 8b. Vinkeln αb mellan strålen i glaset och normalen kallas brytningsvinkel.

Om strålen skulle gå åt motsatt håll – så att brytningsvinkeln blev infallsvinkel − skulle strålen följa samma väg och den ursprungliga infallsvinkeln skulle bli brytningsvinkel. Strålgången är reversibel.

I fortsättningen betecknar vi därför vinklarna med αluft respektive αglas i stället för infallsvinkel och brytningsvinkel.

Vi ser att αglas är mindre än αluft. Om ljuset kommer från luft bryts det alltså mot normalen. Man säger att glas är optiskt tätare än luft. En motsvarande undersökning av hur ljus bryts vid en gränsyta mellan luft och vatten ger liknande resultat. Även vatten är alltså optiskt tätare än luft.

TÄNK TILL!

1 Figuren till höger visar vad som händer när en ljusstråle träffar en gränsyta mellan två genomskinliga ämnen A och B.

a Vilken av strålarna 1, 2 och 3 måste vara den infallande?

b Är ämne A eller B det optiskt tätare?

1

αluft αglas sinα luft sinα glas

00–

10,0°6,6°1,51

20,0°13,2°1,50

30,0°19,5°1,50

40,0°25,4°1,50

50,0°30,7°1,50

60,0°35,3°1,50

70,0°38,8°1,50

80,0°41,0°1,50

90,0°41,8°1,50

Brytningslagen

Vi undersöker sambandet mellan infallsvinkeln αluft och brytningsvinkeln αglas när ljus bryts i en gränsyta mellan luft och vanligt glas. Noggranna mätningar ger värden på αluft och αglas enligt tabell 1.

Finns det något matematiskt samband mellan infalls- och brytningsvinklarna? För värdeparen i tabell 1 beräknar vi värdet av kvoten

sin sin α α lu 1,50 glas Se tabellen.

Resultaten tyder på att kvoten sinsinαα lu glas är konstant. Avrundat till tre siffror är värdet 1,50. För brytning från luft till glas eller omvänt får vi

sin sin α α lu 1,50 glas

som också kan skrivas:

sin αluft = 1,50 · sin αglas (1)

En motsvarande undersökning av brytningen mellan luft och vatten ger

sin αluft = 1,33 · sin αvatten (2)

Vad händer när ljus går direkt från glas till vatten? För att söka svaret tänker vi oss ett jämntjockt luftlager mellan glaset och vattnet. Se figur 9.

Figur 9 Vinklarna αglas och αvatten ändras inte när luftskiktets tjocklek ändras. Strålens väg skulle vara densamma om den gått i motsatt riktning. αvatten är något större än αglas

De båda brytningarna beskrivs av sambanden (1) och (2). I dem är vänsterleden lika. Då måste även högerleden vara lika och vi får: 1,50 ∙ sin αglas = 1,33 ∙ sin αvatten (3)

Det sambandet innehåller ingenting om luftskiktets tjocklek. Gäller det kanske även om luftskiktet tas bort så att ljuset går direkt från glas till vatten? Experiment visar att så är fallet.

Brytningsindex

Talen 1,50 och 1,33 kallas brytningsindex för glas respektive vatten och betecknas med bokstaven n:

nglas = 1,50 och nvatten = 1,33

Olika sorters glas har något olika brytningsindex, men ofta kan vi använda värdet 1,50. En ekvation av samma slag som ekvation (3) gäller för alla par av genomskinliga ämnen. För brytning mellan ämne 1 och ämne 2 kan vi därför skriva:

n1 ∙ sin α1 = n2 ∙ sin α2

Det sambandet kallas allmänna brytningslagen. När vi jämför ekvationerna (1) och (2) på föregående sida med allmänna brytningslagen ser vi att luft har brytningsindex 1,00.

nluft = 1,00

Brytningsindex betecknas med n. Olika ämnen har olika brytningsindex. Optiskt tätare ämnen har högre brytningsindex.

EXEMPEL 1

Ljus går från glas med brytningsindex 1,50 till en vätska. Infallsvinkeln är 30,7° och brytningsvinkeln 35,2°. Beräkna vätskans brytningsindex.

Lösning

Allmänna brytningslagen ger:

nglas · sin αglas = nvätska · sin αvätska

1,50 · sin 30,7° = nvätska · sin 35,2°

n = ⋅ = 150307

35 2 1 3285 ,sin , sin, , ... o o vätska

nvätska = 1,33

Svar: Vätskans brytningsindex är 1,33. (Vätskan kan alltså vara vatten).

KONTROLL

3 Jämför de två strålarna i figur 10. Vad kan du säga om strålgången?

EXEMPEL 2

En ljusstråle i luft infaller mot en gränsyta till glas. Infallsvinkeln är 48,5°. Beräkna brytningsvinkeln. Glasets brytningsindex är 1,50.

Lösning

Allmänna brytningslagen:

nluft · sin αluft = nglas · sin αglas

1,00 sin 48,5° = 1,50 sin αglas

αglas = 29,953…°

Svar: Strålen bryts mot normalen och brytningsvinkeln är 30,0°.

Kommentar: I båda exemplen skulle beräkningen ha gjorts på samma sätt om strålgången varit den motsatta.

Ljus och vattenvågor

För ljus som passerar en gränsyta mellan medium 1 och medium 2 gäller enligt allmänna brytningslagen: n1 sin α1 = n2 sin α2

Här är α1 och α2 vinklarna mellan gränsytans normal och strålarna i respektive medier. Talen n1 och n2 är motsvarande brytningsindex.

Se figur 10.

Figur 10 En ljusstråles brytning i gränsytan mellan två medier med brytningsindex n1 respektive n2 Här är n2 större än n1.

För vakuum, där ljushastigheten är störst, har man satt brytningsindex till exakt 1. När ljus går från vakuum till ett genomskinligt ämne kan brytningslagen därmed skrivas:

1 · sin αvakuum = nämne · sin αämne eller

sin sin α α vakuum n ämne ämne (1)

där αvakuum och αämne är infallsvinkel respektive brytningsvinkel.

I kapitel 4 såg vi att när vattenvågor bryts vid övergång från ett vattendjup till ett annat gäller

sinα

sinα 1 2 1 2 v v (2)

där α1 är infallsvinkel, α2 brytningsvinkel och v1 och v2 är vågornas utbredningshastigheter vid respektive vattendjup.

Följer ljus samma brytningslag som vågor? I så fall är högerleden i ekvationerna (1) och (2) lika. Då är n c c = ämne ämne det vill säga kvoten

mellan ljusets hastighet i vakuum och i ämnet. Man kan visa att detta stämmer för såväl glas som andra genomskinliga ämnen.

För vanligt glas som har brytningsindex nglas = 1,50 får vi

c cglas

Mm/s

Mm/s == 300 200 0,15

Med tre värdesiffror är nluft = 1,00. Med samma noggrannhet är ljushastigheten i luft 300 Mm/s. (Med fem värdesiffror är brytningsindex för luft 1,0003 vid normalt tryck och 15 °C. Ljushastigheten är alltså bara en aning lägre i luft än i vakuum). Vi slår fast att ljus bryts enligt samma lag som vågor!

Sambandet

n c c = ämne ämne visar att brytningsindex för ett ämne alltid är större än 1. Ju större brytningsindex är, desto långsammare går ljuset i ämnet och desto större optisk täthet säger man att ämnet har. Känner du ett ämnes brytningsindex kan du alltså beräkna ljushastigheten i ämnet enligt

c c n = ämne ämne

KONTROLL

4 Strålen i figur 10 bryts mot normalen in i medium 2. Är ljusfarten där högre eller lägre?

5 Vatten har brytningsindex 1,33. Hur fort går ljuset genom vatten?

6 Vad får oss att förstå att ljus och vattenvågor bryts på samma sätt?

KONTROLL

7 Titta på figur 11.

a Är brytningsindex störst för det röda eller det violetta ljuset?

b Vilken slutsats kan du dra om hastigheten i glaset för ljussorter av olika färg?

Om ljus med våglängden λ går från vakuum in i ett annat ämne blir våglängden kortare, eftersom ljushastigheten där är lägre, men frekvensen är oförändrad. Sambandet

tillsammans med ekvationen c = f · λ ger

Ljusets våglängd i ett genomskinligt ämne är alltså kvoten mellan våglängden i vakuum och ämnets brytningsindex.

Dispersion – färgspridning

Ibland ser man hur prismor i en ljuskrona eller andra glasföremål skimrar i alla regnbågens färger. Vi undersöker detta.

Vitt ljus får falla in mot ett prisma och sedan stryka utefter ett papper, figur 11. Vi ser att strimman som lämnar prismat visar färgspridning eller dispersion. I övre kanten är strimman rödaktig och i den undre violett. Vitt ljus är tydligen sammansatt av ljus med olika färger. Det röda ljuset bryts minst och det violetta mest. Om vi vill beräkna brytningsvinklarna noggrant måste vi använda något olika värden på brytningsindex för olika färger.

Figur 11 I ett prisma bryts det röda ljuset minst och det violetta mest.

Det är materialets sammansättning som avgör om dispersionen är stor eller liten. Till exempel diamant har högt värde på brytningsindex och stor dispersion. Det gör att diamanter, med rätt slipning, kan gnistra i regnbågens alla färger. I olika typer av optiska instrument, som kameraobjektiv, använder man glas med så liten dispersion som möjligt.

Totalreflexion

Ibland kan det hända att ljus inte kan ta sig ut ur ett genomskinligt ämne. Figur 12a visar hur en ljusstrimma bryts från normalen när den går ut ur glas till luft, som är optiskt tunnare. Brytningsvinkeln αluft är större än infallsvinkeln αglas. Du kan också se att en del av ljuset reflekteras tillbaka in i glaset.

Textprov mager Corporate new 02_16 abc

12a En stråle som går från glas till luft bryts från normalen. sig en viss gränsvinkel αg, närmar sig brytningsvinkeln 90°. En allt större del av ljuset reflekteras.

Om infallsvinkeln är större än αg inträffar totalreflexion. Allt ljus reflekteras, inget bryts.

Vad händer om infallsvinkeln αglas ökas? Brytningsvinkeln αluft ökar också, och samtidigt reflekteras alltmer av ljuset. När infallsvinkeln närmar sig ett visst gränsvärde αg, närmar sig den större brytningsvinkeln sitt största möjliga värde, 90°, figur 12b. Låter vi infallsvinkeln bli större än αg, kan inget ljus ta sig ut från glaset. Allt ljus reflekteras, figur 12c. Vi har åstadkommit totalreflexion. Lägg märke till att detta enbart kan inträffa när ljus träffar gränsytan mot optiskt tunnare ämnen, det vill säga ämnen med lägre brytningsindex.

En beräkning av gränsvinkeln αg för ljus som går från vanligt glas med brytningsindex 1,50 till luft kan göras så här: vi sätter brytningsvinkeln till exakt 90° när infallsvinkeln är αg. Allmänna brytningslagen ger:

nglas ∙ sin αg = nluft ∙ sin αluft

1,50 sin αg = 1,00 sin 90°

sin ,sin , , , α,. g 10090 150 100 150 06666 o αg = 41,8°

För alla infallsvinklar större än ca 42° sker alltså totalreflexion när en ljusstråle går från vanligt glas till luft.

Figur 13 När solen befinner sig bakom betraktaren, kan den en regnig dag ge upphov till en vacker regnbåge.

Regnbågen

Regnbågen är resultatet av ljusets reflexion och dispersion, se figur 13. I regnbågen är det vita solljuset uppdelat i spektralfärger. De går gradvis över i varandra, från rött över orange, gult, grönt, blått och indigo till violett. Färgspridningen, dispersionen, uppkommer när ljuset bryts i regnbågens vattendroppar, figur 14. Olika färger har alltså något olika brytningsindex i vatten liksom i glas.

Vitt ljus från solen Vitt

KONTROLL

8 När inträffar totalreflexion?

9 Hur bildas en regnbåge?

Figur 14a När solljus reflekteras och bryts i vattendroppar kan en regnbåge uppkomma. Ljusstrålar som träffar droppen sprids och reflekteras. Bara när vinkeln mellan det inkommande och det spridda ljuset är ca 40° blir ljuset så starkt att man kan se det mot himlen.

b Solen måste stå lågt och befinna sig bakom dig om du ska kunna se regnbågen.

8.1 Egenskaper hos ljus

• Ljus uppvisar flera vågegenskaper och kan beskrivas som en transversell vågrörelse.

• Synligt ljus omfattar våglängdsområdet

400–750 nm.

• Ljushastigheten i vakuum har fastlagts till exakt 299 792 458 m/s. I materia är ljushastigheten lägre.

• Reflexionsvinkeln är lika stor som infallsvinkeln: αr = αi

8.2 Ljusets brytning

• När en ljusstråle går från ett genomskinligt ämne till ett annat gäller allmänna brytningslagen:

n1 ∙ sin α1 = n2 ∙ sin α2

n1 och n2 är ämnenas brytningsindex. α1 och α2 är vinklarna mellan stråle och normal i respektive ämne.

• Om strålen träffar ett optiskt tätare medium (n2 > n1) bryts den mot normalen.

• Strålgången är reversibel, omvändbar. Om strålen skulle gå åt motsatt håll skulle strålen följa samma väg.

• En stråle som passerar från ett optiskt tätare ämne till ett optiskt tunnare, totalreflekteras om infallsvinkeln är större än en viss gränsvinkel.

• Ett genomskinligt ämnes brytningsindex är

n c c = ämne ämne

där c är ljushastigheten i vakuum och cämne ljushastigheten i ämnet.

• Dispersion är färgspridning vid ljusbrytning. Den orsakas av att ljus med olika färg har något olika hastighet i andra medier än vakuum.

8.3 Diffraktion – böjning

• Ett ljusknippe som går genom en smal öppning böjer av åt sidorna. Böjningen, eller diffraktionen, blir tydlig om strålknippet passerar en öppning med en bredd av storleksordningen 0,1 mm eller mindre.

• Villkor för interferensmaximum vid vinkelrätt infallande ljus med våglängden λ mot dubbelspalt eller gitter med spaltavståndet d: nλ = d sin αn n = 0, 1, 2, ...

8.4 Polarisation och interferens i tunna skikt

• Ljus kan polariseras och beskrivs därför som en transversell vågrörelse.

• Vid tunna skikt interfererar strålar som på grund av transmission och reflexion i skiktets ytor gått olika lång väg när de träffas. Interferensen påverkar intensiteten hos både reflekterat och transmitterat ljus. Strålarna förstärker eller försvagar varandra beroende på skiktets tjocklek och eventuella fasförskjutningar vid reflexionerna.

• Vitt ljus innehåller alla spektralfärger.

• Med primärfärgerna rött, grönt och blått kan alla spektralfärger skapas. Det sker i färgskärmarna för tv, datorer och mobiltelefoner.

• Till skillnad från ljuskällor har föremål ingen egen färg utan bara förmåga att reflektera eller absorbera en eller flera av det belysande ljusets komponenter.

8.1 Egenskaper hos ljus

EXEMPEL

Rita ut den reflekterade strålen och beräkna reflexionsvinkeln.

LÖSNING:

Reflexionsvinkeln r är lika med infallsvinkeln i. Båda vinklarna mäts mot normalen.

α r = α i = 90° − 70° = 20°

1 Avståndet mellan solen och jorden är 8 ljusminuter. Det motsvarar den sträcka ljuset färdas på tiden 8 minuter. Hur långt är avståndet i kilometer?

2 Ljuset från en laser har våglängden 633 nm. Vilken frekvens har ljuset?

3 Figurerna visar vågfronter från två olika ljuskällor. Rita ut några strålar i figurerna.

4 Markera infallsvinkeln i och reflexionsvinkeln r samt ange deras storlek.

5 Anledningen till att du kan se föremål som inte är ljuskällor är att de reflekterar ljus. En slätare yta ger en skarpare reflekterad bild, tack vare en mer regelbunden reflexion. Rangordna följande ytor efter hur väl de reflekterar en bild.

A Polerad metallyta

B Badrumsspegel

C Oljad trämöbel

D Bomullströja

6 Rita strålarnas fortsättning.

7 A och B är punktformiga föremål framför en plan spegel. Om du kan se deras spegelbilder eller inte, beror på var du placerar ditt öga. Var går gränserna för det område där ögat kan uppfatta spegelbilderna?

8.2 Ljusets brytning

EXEMPEL

En ljusstråle infaller mot en glasyta enligt figur. Glasets brytningsindex är 1,5. Beräkna vinkeln mellan normalen och den brutna strålen.

LÖSNING

Brytningsindex för luft är 1,00. Vi söker vinkeln αb i figuren. Brytningslagen ger: nluft ∙ sin αi = nglas ∙ sin αb 1,00 ∙ sin 22˚ = 1,5 ∙ sin αb b sin ,sin , 1 10022 15 14 ≈ α

Svar: Vinkel αb i figuren är14˚.

8 Rita ut ungefär hur strålen fortsätter i följande figurer och markera infallsvinkeln i och brytningsvinkeln b. a b

9 Brytningsindex för glaset är 1,5.

a Markera infallsvinkeln i figuren.

b Beräkna brytningsvinkeln.

glas luft 65°

10 En ljusstråle infaller i luft mot en gränsyta till en glassort som har brytningsindex 1,56. Brytningsvinkeln är 25,1°. Beräkna infallsvinkeln. Rita figur!

11 En ljusstråle i luft infaller mot en vattenyta med infallsvinkeln 60,0°. Bestäm brytningsvinkeln, om:

a ljuset är rött, b ljuset är violett.

Vattnets brytningsindex för rött ljus är 1,33 och för violett 1,34.

12 En ljusstråle passerar en gränsyta mellan glas och en vätska, som figuren visar. Beräkna vätskans brytningsindex. Glasets brytningsindex är 1,50.

glas vätska 42,4° 39,0°

13 En kort ljuspuls sänds genom en 1,00 km lång, rak glasfiber. Glasets brytningsindex är 1,515. Hur mycket längre tid tar det för ljuspulsen att färdas genom fibern jämfört med att färdas samma sträcka i luft.

14 Från en laser sänds en kort ljuspuls lodrätt ned mot en horisontell vattenyta. Pulsens varaktighet är 1,00 ns. Beräkna längden i meter av både den reflekterade pulsen och den puls som fortsätter genom vattnet.

15 När ljus går från glas till luft kan totalreflexion inträffa. Anta att glasets brytningsindex är 1,5. Vilken blir då den minsta infallande vinkel som ger totalreflexion?

16 Dispersion innebär att brytningsindex skiljer sig lite åt för olika våglängder av ljus. För vatten är n = 1,331 för rött ljus och n = 1,342 för lila ljus. Rött och lila ljus bryts alltså olika mycket. En ljusstråle innehåller både rött och lila ljus och går från luft till vatten med infallsvinkeln 42˚. Hur stor vinkel är det mellan det röda och det lila ljuset i vattnet?

17 Pavel vill bestämma brytningsindex för en okänd vätska. Han har en laser som han riktar snett mot vätskeytan och mäter infallande vinkel och brytningsvinkel med gradskiva. Han gör mätningar för flera olika vinklar och vill konstruera ett diagram där han kan bestämma vätskans brytningsindex som lutningen för en anpassad rät linje. Vad bör han välja att ha på axlarna i sitt diagram?

8.3 Diffraktion − böjning

EXEMPEL

Ett gitter med 600 spalter/mm belyses med ljus från en laser. Våglängden för ljuset är 628 nm. Med vilken vinkel böjs ljuset av till första ordningens maximum?

LÖSNING

Vi använder gitterformeln n ∙ λ = d ∙ sin α. Gitterkonstanten d beräknas som d 1 600 110 600 3 mm m

Eftersom vi räknar på första ordningen sätter vi n = 1

9 3 162810 110600 22 n d λ

Svar: Ljuset böjs av med vinkeln 22˚.

18 En ljusstråle faller in mot ett runt hål i en metallplatta och träffar en skärm en meter bakom hålet.

a Hur ser ljuset på skärmen ut om hålet har radien 1 mm?

b Radien på hålet kan ändras. Hur ser ljuset på skärmen ut om radien minskar till några mikrometer?

19 Diffraktion påverkar hur skarpt ett fotografi kan bli. I en kamera passerar ljus ett hål med justerbar storlek, en så kallad apertur. Kommer diffraktion påverka skärpan i bilden som mest när du väljer en stor eller när du väljer en liten apertur?

20 En mobiltelefon kan ta emot radiosignaler från en sändare trots att den är skymd bakom ett hus. Synligt ljus kan vi däremot inte uppfatta om ljuskällan är skymd. Förklara vad detta säger om våglängden hos radiovågor och synligt ljus.

21 En dubbelspalt belyses med ljus från en laser. Det har våglängden 0,63 µm. På en vägg ett stycke från spalterna ser man ett interferensmönster. Figuren visar ett foto av mönstret. Från punkten M är avstånden till de båda spalterna lika stora.

BM AC

03_U_04

Hur stor är skillnaden mellan avstånden till de båda spalterna från a punkten A b punkten B c punkten C, där ljusintensiteten har minimum?

22 Enfärgat ljus passerar genom en dubbelspalt med spaltavståndet 0,10 mm. På en skärm, som placerats 1,0 m bakom spalterna, ser man då ett interferensmönster. Dess centrala del visas i figuren. Den mittersta ljusa linjen har markerats med en pil. Beräkna ljusets våglängd.

24 mm

03_U_05

23 Monokromt ljus med okänd våglängd faller in mot ett gitter som har 300 spalter per mm. Ljusets avböjning till tredje ordningens maximum är 27,0˚. Bestäm ljusets våglängd.

24 Ljus med våglängder från och med 450 nm till och med 600 nm faller vinkelrätt in mot ett gitter G med gitterkonstanten 2,0 µm. Första ordningens spektrum omfattar vinkeln v1, se figuren nedan.

a Beräkna v1.

03_U_09

b Bestäm motsvarande vinkel v2 för andra ordningens spektrum.

25 Tove ska göra ett experiment för att bestämma en okänd gitterkonstant. Hon har stativ, hållare, skärm, linjal och en laser med känd våglängd till hands. Hon vill naturligtvis bestämma gitterkonstanten så noggrant som möjligt. “Släck ned i rummet och försök hitta ljusfläckar att mäta på som ligger så långt från centralmaximum som möjligt, då bli mätnogrannheten bättre” säger Åsa . “Ställ skärmen nära så att ljusfläckarna blir skarpa och så att det blir enklare att mäta,” säger Lena. Vilka råd ska Tove ta hänsyn till?

8.4 Polarisation och interferens i tunna skikt

EXEMPEL

En glasyta med brytningsindex 1,50 har belagts med en film med tjockleken 0,80 μm och brytningsindex 1,35. Glasskivan belyses rakt ovanifrån med ljus med våglängderna 400 nm till 700 nm. Genom konstruktiv interferens kommer vissa våglängder i det reflekterade ljuset att förstärkas maximalt. Bestäm de våglängderna.

LÖSNING

Både stråle 1 och stråle 2 i figuren reflekteras mot ett tätare medium. För konstruktiv interferens måste vägskillnaden 2d mellan strålarna vara ett helt antal våglängder.

2d = kλm, där k = 1, 2, 3… och λm är

våglängden i det tunna skiktet, dvs. λm = λ/1,35. Då blir

2 135 dk , λ

Med insatt värde för d blir

1352 080102 1610 66 ,, , kk m m λ

28 Ett tunt skikt av en metalloxid ska läggas på en glasyta för att blått ljus med våglängden 450 nm ska framhävas i det transmitterade ljuset. Glaset har brytningsindex 1,5 och metalloxidens brytningsindex är 1,33. Ge exempel på hur tjockt lager som kan läggas på glasytan.

29 När ljus passerar genom en glasruta reflekteras det delvis vid båda glasytorna. Detta medför att ljuset går upprepade gånger mellan dessa. Se figuren! Vid vinkelrätt infall reflekteras 4% av ljusintensiteten varje gång ljuset träffar rutans fram- eller baksida.

12 3 4

56

Ta reda på hur många procent av den ursprungliga ljusintensiteten som finns i

03_U_14

a strålarna 1, 2 och 3

Beräknar vi våglängden λ för k = 1, 2, 3, … finner vi att i intervallet 400 nm till 700 nm kommer våglängderna 430 nm och 540 nm att bli förstärkta.

Svar: De våglängder som förstärks maximalt är 430 nm och 540 nm.

26 Kan ljudvågor ha polarisationsriktning?

27 Varför syns det inga färgskiftningar när ett tunt lager bensin spillts ut på torr asfalt? 03 _ex_02_S n =1,35 d n =1,50 glas 1 2

b strålarna 4, 5 och 6 när ljuset faller in vinkelrätt mot glasrutan. (Då ligger förstås alla dessa strålar längs samma linje.)

Bortse från absorption i glaset.

30 En glasyta med brytningsindex 1,50 har belagts med en film med tjockleken 1,0 μm och brytningsindex 1,38. Glasskivan belyses rakt ovanifrån med vitt ljus i intervallet 400 nm till 700 nm. Vilka våglängder saknas helt i det reflekterade ljuset på grund av destruktiv interferens?

31 På en horisontell glasplatta läggs en annan, mindre glasplatta ABCD. Den berör den undre plattan längs AB. BC är 10,0 cm. Längs CD skiljs plattorna åt av en tunn tråd. När plattorna belyses rakt uppifrån, ser man i det reflekterade ljuset

mörka linjer, som är parallella med AB. Mellanrummet mellan linjerna är lika stort överallt. Ljusets våglängd är 0,60 µm. På en sträcka av 4,00 cm parallellt med BC räknar man 16 linjemellanrum.

1 En ljusstråle faller in från luft mot vatten med en vinkel på 22˚ mot normalen. Rita en figur med infallande stråle och de strålar som beskriver ljuset efter att det träffat ytan. Ange vinklar i figuren. Brytningsindex för vatten är 1,3.

2 Strålen i figuren träffar väggen under rät vinkel vid A. Vilken vinkel bildar strålen med väggen, om spegeln S vrids 5°?

a Luftskiktet mellan plattorna har olika tjocklek vid början och slutet av den 4 cm långa sträckan. Hur många ljusvåglängder utgör skillnaden?

b Beräkna trådens tjocklek.

2,0 m

3 Du står i vatten upp till knäna och ser en fisk någon meter framför dig. Gör ljusets brytning att du uppfattar att fisken är på större eller mindre djup än den verkligen är?

4 Kan totalreflexion ske för ljus som går från vatten till glas? Motivera ditt svar.

5 En dubbelspalt har spaltavståndet 0,15 mm. Ljus av våglängden 0,63 µm ger upphov till ett interferensmönster, som fångas upp på en skärm, 4,0 m från spalterna. Beräkna avståndet mellan centralmaximum och ett angränsande maximum.

6 En ljusstråle i luft infaller mot en vattenyta med infallsvinkeln 60,0°. Bestäm brytningsvinkeln om a ljuset är rött b ljuset är violett.

Vattnets brytningsindex för rött ljus är 1,33 och för violett 1,34.

7 a I figuren går ljuset 4,50 cm i luft och lika långt i glas med brytningsindex 1,50. Hur lång tid tar det?

2

10 a Skissera strålens fortsatta väg. b Hur stor är brytningsvinkeln? glas 25°

luft

Att ljuset följer allmänna brytningslagen är liktydigt med att det mellan två punkter A och B går den väg som tar kortast tid.

b Mät i figuren och beräkna hur mycket längre tid det skulle tar det för ljuset att gå från A till B?

8 Ett smalt ljusknippe bryts vid övergång från luft till en vätska. Infallsvinkeln är 30,0° och brytningsvinkeln 20,0°. Ljusknippet är monokromatiskt med våglängden 0,60 µm i luft. Beräkna

a frekvensen i luft

b frekvensen i vätskan

c våglängden i vätskan

d ljusknippets fart i vätskan.

9 Ett gitter har gitterkonstanten 4,0 µm. Ljus av en viss våglängd faller vinkelrätt in mot gittret. Första ordningens avböjningsvinkel är 10,1°.

a Beräkna ljusets våglängd.

b Beräkna tredje ordningens avböjningsvinkel.

c Vilket är det högsta ordningstal som förekommer i detta fall?

11 Ljus faller in snett från luft mot vatten. Påverkar ljusets våglängd a reflexionsvinkeln, b brytningsvinkeln?

Motivera dina svar.

12 Ett smalt ljusknippe träffar en glasyta under infallsvinkeln 20°. Glasets brytningsindex är 1,50.

a Bestäm ljusknippets riktningsändring.

b Hur påverkas riktningen i glaset om glasytan täcks av ett jämntjockt skikt av vatten? Vattnets brytningsindex är 1,34.

13 Ljus får infalla vinkelrätt mot en av sidorna hos ett glasprisma enligt figuren. När ljuset passerat prismat har det en ny riktning som bildar vinkeln 19,0° med den gamla. 30,0° A 19,0°

a Bestäm infalls- och brytningsvinkel vid A.

b Bestäm glasets brytningsindex.

14 a Det ljus från området ovanför vattenytan som når dykarens ögon kommer in genom ett cirkelrunt område i vattenytan. Varför?

b Det kommer ljus även från resten av vattenytan som ser mörkare ut underifrån. Varifrån kommer det ljuset?

c Rita några strålar som visar hur ljuset passerar genom luft och vatten. Det ska synas hur ljuset når dykarens ögon från både den ljusa och den mörka delen av vattenytan.

18 På ena kortsidan av ett tunnväggigt glaskärl, med rektangulär botten och lodräta väggar, fästs ett gitter med vertikala spalter. På den andra kortsidan fästs ett stycke papper.

Avståndet från gittret till papperet är 15 cm.

Ljusknippet från en laser faller vinkelrätt in mot gittret.

papper 35 mm 15 cm

laserstråle gitter

Avståndet mellan interferensmaxima av 0:e och 2:a ordningarna är 35 mm. Våglängden är 0,63 µm. a Beräkna gitterkonstanten.

03_U_11

En vätska hälls i kärlet till sådan höjd att ljuset mellan gittret och papperet går under vätskeytan. Avståndet mellan interferensmaxima av 0:e och 2:a ordningarna är nu 26 mm.

b Beräkna vätskans brytningsindex.

15 När varm luft stiger upp ovanför ett element eller något annat varmt föremål ser det ut som om föremål bakom luften vibrerar och skakar. Vad orsaker detta fenomen?

16 Hur stor är infallsvinkeln, reflexionsvinkeln respektive brytningsvinkeln?

S1

19 Av tre spalter S1, S2 och S3 sitter S2 mitt emellan de två andra. Spalterna belyses med ljus av våglängden λ. Punkten P är belägen långt från spalterna och så att PS1 – PS3 = λ. a Uppskatta vägskillnaden PS2 – PS1.

03_U_07

En av spalterna täcks över. Blir det ljusare eller mörkare i P, om den övertäckta spalten är

b S1 c S2?

17 Ett prisma har ett tvärsnitt i form av en likbent, rätvinklig triangel. En ljusstrimma infaller vinkelrätt mot en av de två lika sidorna, se figur. Bestäm strimmans fortsatta väg genom prismat. Glasets brytningsindex är 1,50.

20 När vitt ljus faller in mot ett gitter, griper 2:a och 3:e ordningens spektra in i varandra.

Vilken våglängd i 3:e ordningens spektrum sammanfaller med våglängden 0,69 µm i spektrum av 2:a ordningen?

21 Ett reflexionsgitter uppstår när en polerad metallyta ritsas så att ett stort antal långsmala reflekterande ”band” återstår av den ursprungligen släta ytan. Deras inbördes avstånd d är reflexionsgittrets gitterkonstant. Anta att ljus av våglängden λ infaller vinkelrätt mot ett sådant gitter.

23 En oljefläck på vatten ger regnbågsskimrande speglingar. Ge exempel på två möjliga tjocklekar för oljelagret där fläcken ser grön ut, om ljuset reflekteras som på bilden.

30°

24 När vitt ljus passerar ett gitter syns spektrum på en skärm bakom gittret. Är det korrekt att påstå att andra ordningens spektrum alltid är bredare, dvs. upptar större vinkel än första ordningens?

Gitterekvationen kan alltså även i detta fall skrivas d sin αn = nλ.

22 I ett tankeexperiment belyses en dubbelspalt av två identiska monokroma ljuskällor så att ljuset från varje källa endast träffar varsin öppning i dubbelspalten. Ljuset från den ena källan är förskjutet en halv våglängd jämfört med ljuset från den andra. Beskriv hur interferensmönstret som bildas kommer att se ut. d 1 2

a Visa att vägskillnaden mellan strålarna 1 och 2 i figuren är d sin α.

b Anta att d = 1,5 µm och att λ = 0,60 µm. I hur många riktningar reflekteras ljus från gittret?

c Vilken eller vilka riktningar får det reflekterade ljuset, om de reflekterande banden ligger så tätt att d < λ? Räkna t.ex. med d = 0,50 µm och λ = 0,60 µm.

Ledning: Ta hjälp av beräkningar eller utnyttja utseendet hos kurvan y = sin x

25 En hinna av såplösning hålls uppspänd av en vertikal ring, se figuren. Hinnan belyses med monokromt ljus med våglängden 0,70 μm.

03_U_16

Hinnans brytningsindex är 1,3. Beräkna hinnans tjocklek i punkten

a A

b B

c Förklara varför det blir ett mörkt område vid hinnans överkant.

NYTT LJUS ÖVER FYSIKEN

Albert Einstein förändrade synen på rum och tid i sin relativitetsteori, där ljus spelar en central roll. Tidigare hade fysikerna förklarat ljuset som ett elektriskt och magnetiskt kraftspel som kan färdas som en våg.

Albert Einstein visade att ljus också kan ses som en ström av partiklar. Den dubbeltydigheten har givit upphov till kvantmekaniken som beskriver sambandet mellan våg och partikel och som är en viktig del av den moderna fysiken.

I dag använder vi de elektromagnetiska vågorna för olika typer av kommunikation. Kvantmekaniken är grunden för mycket av den teknik vi kallar modern – som till exempel datorer, mobiltelefoner och LED-lampor.

Rune Alphonce

Lars Bergström

Ulf Christiansson

Tobias Eriksson

Per Gunnvald

Erik Johansson

Roy Nilsson

HEUREKA!

Fysik nivå 2

Heureka! är ett komplett läromedel för gymnasieskolans fysik nivå 1 och nivå 2 samt fysik fördjupning.

I Heureka! ingår

• läroböckerna Heureka! fysik nivå 1, fysik nivå 2 och fysik fördjupning

• lärarhandledningar

• ledtrådar och lösningar till övningsuppgifterna i läroböckerna

• övningsmaterial för mer problemlösning.

Heureka! finns även som digitalt läromedel.

Läs mer om Heureka! på nok.se/heureka

Solens höga temperatur gör att stora mängder laddade partiklar slungas ut i rymden. När de partiklarna når jordens magnetfält böjs deras bana –fältet fungerar som en skyddande sköld. Vid polerna tränger ändå en liten del av partiklarna igenom magnetfältet. Där kolliderar de med atmosfärens gaser och ger upphov till det skimrande ljus som vi kallar norrsken.