Helicities
Geophysics Astrophysics and Beyond Geophysical Monograph 1st Edition Kirill Kuzanyan
Visit to download the full and correct content document: https://textbookfull.com/product/helicities-in-geophysics-astrophysics-and-beyond-geo physical-monograph-1st-edition-kirill-kuzanyan/
More products digital (pdf, epub, mobi) instant download maybe you interests ...
Shale Subsurface Science and Engineering Geophysical Monograph Series 1st Edition Thomas Dewers
https://textbookfull.com/product/shale-subsurface-science-andengineering-geophysical-monograph-series-1st-edition-thomasdewers/
Dayside Magnetosphere Interactions Geophysical Monograph Series 1st Edition Qiugang Zong (Editor)
https://textbookfull.com/product/dayside-magnetosphereinteractions-geophysical-monograph-series-1st-edition-qiugangzong-editor/
Techniques for Disaster Risk Management and Mitigation
Geophysical Monograph 1st Edition Prashant K. Srivastava (Editor)
https://textbookfull.com/product/techniques-for-disaster-riskmanagement-and-mitigation-geophysical-monograph-1st-editionprashant-k-srivastava-editor/
Geophysics realism and industry how commercial interests shaped geophysical conceptions 1900 1960 1st Edition Anduaga
https://textbookfull.com/product/geophysics-realism-and-industryhow-commercial-interests-shaped-geophysicalconceptions-1900-1960-1st-edition-anduaga/
Submarine Landslides Subaqueous Mass Transport Deposits from Outcrops to Seismic Profiles Geophysical Monograph Series 1st Edition Kei Ogata (Editor)
https://textbookfull.com/product/submarine-landslides-subaqueousmass-transport-deposits-from-outcrops-to-seismic-profilesgeophysical-monograph-series-1st-edition-kei-ogata-editor/
Spectral Methods in Geodesy and Geophysics 1st Edition
Christopher Jekeli
https://textbookfull.com/product/spectral-methods-in-geodesy-andgeophysics-1st-edition-christopher-jekeli/
Formulations of General Relativity Gravity Spinors and Differential Forms 1st Edition Kirill Krasnov
https://textbookfull.com/product/formulations-of-generalrelativity-gravity-spinors-and-differential-forms-1st-editionkirill-krasnov/
Inverse Problems: Basics, Theory and Applications in Geophysics 2nd Edition Mathias Richter
https://textbookfull.com/product/inverse-problems-basics-theoryand-applications-in-geophysics-2nd-edition-mathias-richter/
Application of Soft Computing and Intelligent Methods in Geophysics Alireza Hajian
https://textbookfull.com/product/application-of-soft-computingand-intelligent-methods-in-geophysics-alireza-hajian/
GeophysicalMonographSeries
234Pre-EarthquakeProcesses:AMultidisciplinaryApproachto EarthquakePredictionStudies DimitarOuzounov,Sergey Pulinets,KatsumiHattori,andPatrickTaylor (Eds.)
235ElectricCurrentsinGeospaceandBeyond AndreasKeiling, OctavMarghitu,andMichaelWheatland(Eds.)
236QuantifyingUncertaintyinSubsurfaceSystems Celine Scheidt,LewisLi,andJefCaers(Eds.)
237PetroleumEngineering MoshoodSanni(Ed.)
238GeologicalCarbonStorage:SubsurfaceSealsandCaprock Integrity StephanieVialle,JonathanAjo-Franklin,andJ.William Carey(Eds.)
239LithosphericDiscontinuities HuaiyuYuanandBarbara Romanowicz(Eds.)
240ChemostratigraphyAcrossMajorChronologicalEras Alcides N.Sial,ClaudioGaucher,MuthuvairavasamyRamkumar,and ValderezPintoFerreira(Eds.)
241MathematicalGeoenergy:Discovery,Depletion,andRenewal PaulPukite,DennisCoyne,andDanielChallou(Eds.)
242OreDeposits:Origin,Exploration,andExploitation Sophie DecreeandLaurenceRobb(Eds.)
243KuroshioCurrent:Physical,BiogeochemicalandEcosystem Dynamics TakeyoshiNagai,HiroakiSaito,KojiSuzuki,and MotomitsuTakahashi(Eds.)
244GeomagneticallyInducedCurrentsfromtheSuntothePower Grid JenniferL.Gannon,AndreiSwidinsky,andZhonghuaXu (Eds.)
245Shale:SubsurfaceScienceandEngineering ThomasDewers, JasonHeath,andMarceloSánchez(Eds.)
246SubmarineLandslides:SubaqueousMassTransportDeposits FromOutcropstoSeismicProfiles KeiOgata,AndreaFesta, andGianAndreaPini(Eds.)
247Iceland:Tectonics,Volcanics,andGlacialFeatures TamieJ. Jovanelly
248DaysideMagnetosphereInteractions QiugangZong,Philippe Escoubet,DavidSibeck,GuanLe,andHuiZhang(Eds.)
249CarboninEarth’sInterior CraigE.Manning,Jung-FuLin,and WendyL.Mao(Eds.)
250NitrogenOverload:EnvironmentalDegradation, Ramifications,andEconomicCosts BrianG.Katz
251BiogeochemicalCycles:EcologicalDriversandEnvironmental Impact KaterinaDontsova,ZsuzsannaBalogh-Brunstad,And GaëlLeRoux(Eds.)
252SeismoelectricExploration:Theory,Experiments,and Applications NielsGrobbe,AndréRevil,ZhenyaZhu,and EvertSlob(Eds.)
253ElNiñoSouthernOscillationinaChangingClimate MichaelJ. McPhaden,AgusSantoso,andWenjuCai(Eds.)
254DynamicMagmaEvolution FrancescoVetere(Ed.)
255LargeIgneousProvinces:ADriverofGlobalEnvironmental andBioticChanges Richard.E.Ernst,AlexanderJ.Dickson, andAndreyBekker(Eds.)
256CoastalEcosystemsinTransition:AComparativeAnalysisof theNorthernAdriaticandChesapeakeBay ThomasC. Malone,AlenkaMalej,andJadranFaganeli(Eds.)
257Hydrogeology,ChemicalWeathering,andSoilFormation AllenHunt,MarkusEgli,andBorisFaybishenko(Eds.)
258SolarPhysicsandSolarWind NourE.RaouafiandAngelos Vourlidas(Eds.)
259MagnetospheresintheSolarSystem RomainMaggiolo, NicolasAndré,HiroshiHasegawa,andDanielT.Welling(Eds.)
260IonosphereDynamicsandApplications ChaosongHuangand GangLu(Eds.)
261UpperAtmosphereDynamicsandEnergetics WenbinWang andYongliangZhang(Eds.)
262SpaceWeatherEffectsandApplications AntheaJ.Coster, PhilipJ.Erickson,andLouisJ.Lanzerotti(Eds.)
263MantleConvectionandSurfaceExpressions HaukeMarquardt, MaximBallmer,SanneCottaar,andJasperKonter(Eds.)
264CrustalMagmaticSystemEvolution:Anatomy,Architecture, andPhysico-ChemicalProcesses MatteoMasotta,Christoph Beier,andSilvioMollo(Eds.)
265GlobalDroughtandFlood:Observation,Modeling,and Prediction HuanWu,DennisP.Lettenmaier,QiuhongTang, andPhilipJ.Ward(Eds.)
266MagmaRedoxGeochemistry RobertoMorettiandDanielR. Neuville(Eds.)
267WetlandCarbonandEnvironmentalManagement KenW. Krauss,ZhiliangZhu,andCamilleL.Stagg(Eds.)
268DistributedAcousticSensinginGeophysics:Methodsand Applications YingpingLi,MartinKarrenbach,andJonathanB. Ajo-Franklin(Eds.)
269CongoBasinHydrology,Climate,andBiogeochemistry:A FoundationfortheFuture(Englishversion) RaphaelM. Tshimanga,GuyD.MoukandiN’kaya,andDouglasAlsdorf (Eds.)
269Hydrologie,climatetbiogéochimiedubassinduCongo:une basepourl’avenir(versionfrançaise) RaphaelM.Tshimanga, GuyD.MoukandiN’kaya,etDouglasAlsdorf(Éditeurs)
270Muography:ExploringEarth’sSubsurfacewithElementary Particles LászlóOláh,HiroyukiK.M.Tanaka,andDezso˝ Varga(Eds.)
271RemoteSensingofWater-RelatedHazards KeZhang,Yang Hong,andAmirAghaKouchak(Eds.)
272GeophysicalMonitoringforGeologicCarbonStorage Lianjie Huang(Ed.)
273IsotopicConstraintsonEarthSystemProcesses KennethW.W. Sims,KateMaher,andDanielP.Schrag(Eds.)
274EarthObservationApplicationsandGlobalPolicyFrameworks ArgyroKavvada,DouglasCripe,andLawrenceFriedl(Eds.)
275ThreatstoSpringsinaChangingWorld:ScienceandPolicies forProtection MatthewJ.CurrellandBrianG.Katz(Eds.)
276Core-MantleCo-Evolution:AnInterdisciplinaryApproach TakashiNakagawa,MadhusoodhanSatish-Kumar,Taku Tsuchiya,andGeorgeHelffrich(Eds.)
277CompressionalTectonics:PlateConvergencetoMountain Building(TectonicProcesses:AGlobalView,Volume1) ElizabethJ.CatlosandIbrahimÇemen(Eds.)
278ExtensionalTectonics:ContinentalBreakuptoFormationof OceanicBasins(TectonicProcesses:AGlobalView,Volume 2) IbrahimÇemenandElizabethJ.Catlos(Eds.)
279Strike-SlipTectonics:OceanicTransformFaultstoContinental PlateBoundaries(TectonicProcesses:AGlobalView,Volume 3) IbrahimÇemenandElizabethJ.Catlos(Eds.)
280LandscapeFire,Smoke,andHealth:LinkingBiomassBurning EmissionstoHumanWell-Being TatianaV.Loboda,NancyH. F.French,andRobinC.Puett(Eds.)
281CloudsandTheirClimaticImpacts:Radiation,Circulation, andPrecipitation SylviaSullivanandCorinnaHoose(Eds.)
282FastProcessesinLarge-ScaleAtmosphericModels:Progress, Challenges,andOpportunities YangangLiuandPavlos Kollias(Eds.)
283HelicitiesinGeophysics,Astrophysics,andBeyond Kirill Kuzanyan,NobumitsuYokoi,ManolisK.Georgoulis,and RodionStepanov(Eds.)
KirillKuzanyan
NobumitsuYokoi
ManolisK.Georgoulis
Thiseditionfirstpublished2024
©2024AmericanGeophysicalUnion
Allrightsreserved.Nopartofthispublicationmaybereproduced,storedinaretrievalsystem,ortransmitted,inanyformorby anymeans,electronic,mechanical,photocopying,recordingorotherwise,exceptaspermittedbylaw.Adviceonhowtoobtain permissiontoreusematerialfromthistitleisavailableathttp://www.wiley.com/go/permissions.
PublishedundertheaegisoftheAGUPublicationsCommittee
MatthewGiampoala,VicePresident,Publications
CarolFrost,Chair,PublicationsCommittee
FordetailsabouttheAmericanGeophysicalUnionvisitusatwww.agu.org.
TherightofKirillKuzanyan,NobumitsuYokoi,ManolisK.Georgoulis,andRodionStepanovtobeidentifiedastheeditorsof thisworkhasbeenassertedinaccordancewithlaw.
RegisteredOffice
JohnWiley&Sons,Inc.,111RiverStreet,Hoboken,NJ07030,USA
EditorialOffice 111RiverStreet,Hoboken,NJ07030,USA
Fordetailsofourglobaleditorialoffices,customerservices,andmoreinformationaboutWileyproductsvisitusat www.wiley.com.
Wileyalsopublishesitsbooksinavarietyofelectronicformatsandbyprint-on-demand.Somecontentthatappearsinstandard printversionsofthisbookmaynotbeavailableinotherformats.
LimitofLiability/DisclaimerofWarranty
Whilethepublisherandauthorshaveusedtheirbesteffortsinpreparingthiswork,theymakenorepresentationsorwarranties withrespecttotheaccuracyorcompletenessofthecontentsofthisworkandspecificallydisclaimallwarranties,includingwithout limitationanyimpliedwarrantiesofmerchantabilityorfitnessforaparticularpurpose.Nowarrantymaybecreatedorextended bysalesrepresentatives,writtensalesmaterialsorpromotionalstatementsforthiswork.Thefactthatanorganization,website,or productisreferredtointhisworkasacitationand/orpotentialsourceoffurtherinformationdoesnotmeanthatthepublisher andauthorsendorsetheinformationorservicestheorganization,website,orproductmayprovideorrecommendationsitmay make.Thisworkissoldwiththeunderstandingthatthepublisherisnotengagedinrenderingprofessionalservices.Theadvice andstrategiescontainedhereinmaynotbesuitableforyoursituation.Youshouldconsultwithaspecialistwhereappropriate. Further,readersshouldbeawarethatwebsiteslistedinthisworkmayhavechangedordisappearedbetweenwhenthisworkwas writtenandwhenitisread.Neitherthepublishernorauthorsshallbeliableforanylossofprofitoranyothercommercial damages,includingbutnotlimitedtospecial,incidental,consequential,orotherdamages.
LibraryofCongressCataloging-in-PublicationData
Names:Kuzanyan,Kirill,editor.|Yokoi,Nobumitsu,editor.|Georgoulis, ManolisK.,editor.|Stepanov,Rodion,editor.
Title:Helicitiesingeophysics,astrophysics,andbeyond/editorsKirill Kuzanyan,NobumitsuYokoi,ManolisK.Georgoulis,RodionStepanov.
Description:Hoboken,NJ:Wiley,2024.|Includesbibliographical referencesandindex.
Identifiers:LCCN2023035109(print)|LCCN2023035110(ebook)|ISBN 9781119841685(hardback)|ISBN9781119841692(adobepdf)|ISBN 9781119841708(epub)
Subjects:LCSH:Particles(Nuclearphysics)–Helicity.|Geophysics.| Astrophysics.
Classification:LCCQC793.3.H44H452024(print)|LCCQC793.3.H44 (ebook)|DDC521–dc23/eng/20231017
LCrecordavailableathttps://lccn.loc.gov/2023035109
LCebookrecordavailableathttps://lccn.loc.gov/2023035110
CoverDesign:Wiley
CoverImage:©AceClipart_Etsy/Pixabay;CourtesyofNobumitsuYokoi
Setin10/12ptTimesNewRomanMTStdbyStraive,Chennai,India
1IntroductiontoFieldLineHelicity .....................................................................3 AnthonyR.YeatesandMitchellA.Berger
2MagneticWinding:TheoryandApplications ...........................................................17 DavidMacTaggart
3TransportinHelicalFluidTurbulence ..................................................................25 NobumitsuYokoi
PartIIHelicityManifestationsinNatureandTheirObservations51
4ObservationsofMagneticHelicityProxiesintheSolarPhotosphere:HelicityWithSolarCycles. ........53 HongqiZhang,ShangbinYang,HaiqingXu,XiaoYang,JieChen,andJihongLiu
5ChiralityofSolarFilamentsandtheSupportingMagneticField .........................................75 Peng-FeiChen
6SolarFlaresandMagneticHelicity. ....................................................................83 ShinToriumiandSung-HongPark
7MagneticHelicityMeasurementsintheSolarWind. ...................................................105 YasuhitoNarita
8MagneticHelicityinRotatingNeutronStars ............................................................117 MaximDvornikov
9WrithingFromBiophysicstoSolarPhysicsandBack....................................................133 ChristopherPriorandArronN.Bale
10KineticHelicityintheEarth’sAtmosphere. .............................................................149 OttoChkhetianiandMichaelKurgansky
11EffectsofP-Noninvariance,Particles,andDynamos..
VictorB.SemikozandDmitryD.Sokoloff
12StabilityofPlasmasThroughMagneticHelicity .........................................................179 SimonCandelaresiandFabioDelSordo
13Helicity-ConservingRelaxationinUnstableandMergingTwistedMagneticFluxRopes. .................189 PhilippaK.Browning,MykolaGordovskyy,andAlanW.Hood
14EmergenceofMagneticStructureinSupersonicIsothermalMagnetohydrodynamicTurbulence.... ......203 Jean-MathieuTeissierandWolf-ChristianMüller
15NonlinearMean-FieldDynamosWithMagneticHelicityTransportandSolarActivity:SunspotNumber andTilt................................................................................................217 NathanKleeorin,KirillKuzanyan,IgorRogachevskii,andNikolaiSafiullin
16TheSpatialSegregationofKineticHelicityinGeodynamoSimulations.... ..............................241 AvishekRanjanandPeterDavidson
HelicityEssentials:Basicand FundamentalConcepts
IntroductiontoFieldLineHelicity
AnthonyR.Yeates 1 andMitchellA.Berger 2
ABSTRACT
Fieldlinehelicitymeasuresthenetlinkingofmagneticfluxwithasinglemagneticfieldline.Itoffersafiner topologicaldescriptionthantheusualglobalmagnetichelicityintegralwhilestillbeinginvariantinanideal evolutionunlessthereisafluxofhelicitythroughthedomainboundary.Inthischapter,weexplorehowto appropriatelydefinefieldlinehelicityindifferentvolumesinawaythatpreservesameaningfultopologicalinterpretation.Wealsoreviewthetimeevolutionoffieldlinehelicityunderbothboundarymotionsandmagnetic reconnection.
1.1.DEFINITIONSOFFIELDLINEHELICITY
Webrieflyreviewtopologicalmeasuresofmagneticfield structure.Someoftheserefertothestructureofthetotal fieldwithinavolume(the magnetichelicity),andothers totherelationshipbetweenindividualpairsoffieldlines (linkingandwinding).Fieldlinehelicityisintermediate betweentheseideas,asitmeasuresthenetlinkingorwindingofonefieldlinewiththetotalfield.Helicityintegrals dependonboththetanglingoffieldlineswitheachother andthetopologyandgeometryofthevolumeinwhichthe fieldlinesreside.Astrongrationaleforconsideringtopologicalmeasuresisthatfieldlinetopologyisconservedin anyidealevolutionofthefield(Moffatt,1969).
1.1.1.DefinitionsofFieldLineHelicityforClosed Volumes
Thesimplestsituationoccurswithtwoclosedfield linesresidingwithinavolume wherethefieldlines
1 DepartmentofMathematicalSciences,DurhamUniversity, Durham,UK
2 DepartmentofMathematics,UniversityofExeter,Exeter, UK
donotcrosstheboundaryof (orwithinaninfinite space).Historically,Gauss(1809)discoveredadouble lineintegral,whichmeasuresthelinkingoftwoclosed curves L1 and L2 .Letpositionsonthecurvesbegivenby ⃗ x(�� ) and ⃗ y(�� ).Then
where ⃗ r = ⃗ x ⃗ y.Thismaybecalculatedbycounting signedcrossings(seeFig.1.1).
Foramagneticfieldconsistingofafinitecollectionof closedmagneticfluxtubes(averyspecialcase),wecan defineanoverallinvariant
where Φi representsthemagneticfluxofeachtubeand ij isthelinkingnumberbetweenthetubes.Thisinvariantis calledthe magnetichelicity.Foramoregeneralmagnetic fieldconsistingentirelyofclosedfieldlines(stillaspecial case),wecantake N → ∞ inequation(1.2)sothatthe sumsbecomeintegrals.Accountingforthemagneticflux, thetangentvectorsinequation(1.1)becomemagnetic
HelicitiesinGeophysics,Astrophysics,andBeyond,GeophysicalMonograph283, FirstEdition. EditedbyKirillKuzanyan,NobumitsuYokoi,ManolisK.Georgoulis,andRodionStepanov. ©2024AmericanGeophysicalUnion.Published2024byJohnWiley&Sons,Inc. DOI:10.1002/9781119841715.ch01
Figure1.1 Forthislink(theWhiteheadlink),theGausslinking number, 12 ,iszero.Ingeneral,thelinkingnumberequalshalf thedifferencebetweenthenumberofpositivecrossingsandthe numberofnegativecrossings,asseeninanyplaneprojection.
fieldvectors,andthemagnetichelicitymaybewritten
theequivalentexpressionforthefieldlinehelicitywill simplybe
Heretheintegralisoverallspaceoroveravolume containingallfieldlines.Infact,inthisequation,we donotneedtoassumethatthefieldlinescloseupon themselves–somemayergodicallyfillasubvolumeor twistaroundatoroidalsurfacewithanirrationalwinding number.Suchfieldscanbeconstructedasthelimitas N → ∞ ofasequenceoffieldsconsistingof N thinclosed fluxtubes(Arnol’dandKhesin,1998).Thus,regardless ofwhetherthefieldlinescloseuponthemselves,wecan approximateanymagneticfieldasacollectionofsuch tubes.
Returningtothefinitesetof N fluxtubeswithfluxes Φi , noticethatequation(1.2)canbewrittenas
Thisisjustthenetmagneticfluxencircledby L,and since L isaclosedcurve,itismanifestlygaugeinvariant. WeremarkthatYahalom(2013)interprets (L) asa magnetohydrodynamicanalogoftheAharonov-Bohm effectfromquantummechanics:if ⃗ B =∇�� ×∇�� ,then ⃗ A = �� ∇�� +∇�� ,sothatanonzero H requiresjumpsin �� aroundclosedfieldlines,withsuchjumpsgiving (L) Supposeourvolume issimplyconnected(e.g.,a sphere,notatorus).Notethatbecause L isclosed,we cangaugetransform ⃗ A → ⃗ A +∇�� foranarbitrarygauge function �� withoutaffecting (L).Ifwehaveamultiply connectedvolume,adifficultyarises:thewrongchoiceof ⃗ A mayimplytheexistenceofmagneticfluxintheexternal regionthatthreadsthroughahole,whichmakes ∮L ⃗ A dl dependentontheunknownexternalfield.Toremedythis, onecanrestrictthegaugeof ⃗ A sothat ∮L ⃗ A ⋅ dl = 0for anyclosedcurveontheboundaryencirclingaholethe longwayaround(seealsoMacTaggartandValli,2019).
1.1.2.DefinitionsofFieldLineHelicityforOpen Volumes
Thelimitas N → ∞ of i isanothertopologicalmeasure,thistimedefinedforeveryindividualmagneticfield line–thisiswhatwecallthe fieldlinehelicity
Sincethefieldlinesdonotcrosstheboundaryofthe volume,wecannowusetheBiot-Savartformula
Wenowgotovolumeswithfluxcrossingtheboundary.Supposeafieldlineformsaloop,withbothends onthesameboundary(as,forexample,inFig.1.2b). Anearlyapproach(Antiochos,1987)involvesdrawing ageodesicbetweenthetwoendpoints,thusforminga closedcurveforwhich ∮ ⃗ A ⋅ dl canbemeasured.This schemedoesnotintegratetothefullhelicity,however. Wewishtodefinefieldlinehelicitytobeconsistentwith fullhelicitybutalsosothatgaugetransformationsof ⃗ A donotchangeourresults.Therearetwoprincipal approachestothisproblem.Oneconsistsofdefining topologicalquantitiessuchaswindingnumbersand thensummingtofindthehelicities.Iftheboundary fluxdoesnotmove,idealmotionsofthefieldlineswill notchangethewindings,sofieldlinehelicitywillbe conserved.Iftheboundaryfluxdoesmove,thetopologicalstructurecancrosstheboundary,leadingto changesinhelicitymeasures.Thiswillbediscussedin section1.2.
tofind
Historically,invarianceoftheexpressioninequation(1.6) wasknownbeforetheinterpretationintermsofGauss linkingnumberwasidentified(Moffatt,1969;Moffatt andRicca,1992).Foraclosedline L withinthefield,
Thesecondapproachistomeasurehelicity relative to apotentialfield:i.e.,afieldwithzerocurrentinthevolume.Asthepotentialfieldistheminimumenergystatefor givenboundaryconditions,itsstructuredependsonlyon theshapeoftheboundaryandthedistributionoffluxon theboundary(andformultiplyconnectedvolumes,specifiednewfluxesaroundeachhole).Forhighlysymmetric
Figure1.2 Examplesofapairofmagneticfieldlinesindifferent domains,including(a)thevolumebetweentwoparallelplanes; (b)thevolumeaboveaplane;(c)asphericalshell(thevolume betweentwoconcentricspheres);and(d)thevolumebetween twomoregeneralsurfaces.
volumessuchasthoseboundedbyplanesorspheres,the twoapproachesgiveidenticalresults.
Formorecomplicatedvolumes,theshapeoftheboundaryorboundariescanaddextratermsthatdistinguishthe twoapproaches,asdiscussedinsection1.1.2.Adefinition offieldlinehelicitycanalsobebasedonrelativehelicity (Moraitisetal.,2019),tobediscussedinsection1.1.3.
VolumesbetweenParallelPlanes
Supposethevolumeofinterest isthespacebetween parallelplanes,say z = 0and z = h,asillustratedin Fig.1.2a.Wewillfirstassumethatallfieldlinesstartat z = 0andendat z = h.Thennotwofieldlineslinkinthe Gausssense;however,theywilltwistabouteachother throughsomeangle ����ij .The windingnumber makesthis anintegerforcompletetwists:
linehelicityof Li willbe
FortheexampleinFig.1.2a,wehave ��ij =(��b ��a )∕(2�� )+ 1. Wecannowadoptformulaeforthehelicityandfield linehelicitysimilartotheclosedfieldcase,withthe windingnumberreplacingthelinkingnumber.Wedenote horizontalpositionsby x =(x, y).Also,wedistinguish positionsinthebottom x y planeby ̃ x =(x, y, 0).Let Li bethefieldlinewithfootpointat xi .Alsolet ��( ̃ xi , ̃ xj ) bethewindingnumberbetween Li and Lj .Thenthefield
Letusbuildup (Li ) oneplaneatatime–inother words,findexpressionsford(Li )∕dz.Fornow,wemake thesimplifyingassumptionthat Bz > 0everywhere.There aretwocontributionstothe z derivative:first(I),horizontalfluxintheplanecanwraparoundthefieldline Li . Second(II), Li canmovehorizontallyaboutotherfield lines.Now ̂ �� ij = ̂ z × ̂ rij istheangulardirectionat xj about xi ,with ⃗ rij = xj xi .Also,afieldlinetravelingfrom (r,��, z) to (r + dr,�� + d��, z + dz) satisfiestheequation dr Br = rd�� B�� = dz Bz . (1.10)
Thusforafieldlineat xj =(x, y, z) (writing ⃗
etc.),
Next,thefieldline Li canmovehorizontallyaroundother fieldlines.Inthiscase,
Bzj (1.12)
Summingthelasttwoequations,thetotalchangeinwindingbetweenlines Li and Lj is d��ij dz = ⃗ Bi Bzi ⋅ ⃗ rij × ⃗ Bj r2 ij Bzj (1.13)
Let Sz bethehorizontalplaneatheight z.Supposewe addupcontributionsfromallovertheplane:wemultiply thepreviousexpressionby Bzj d2 xj andintegrate.Dividing by2�� tomakecompleteturnsintointegers,
(Li ) dz = 1 2�� ⃗ Bi Bzi ⋅ ∫Sz ⃗ rij × ⃗ Bj r2 ij d2 xj (1.14)
Thisexpressionforthefieldlinehelicitycanbe expressedverysimplyusingaspecialvectorpotential–the windinggauge (PriorandYeates,2014):forapointon fieldline Li at (x, y, z), ⃗ A W (x, y, z)= 1 2�� ∫Sz ⃗ rij × ⃗ Bj r2 ij d2 xj . (1.15)
Wehave
(Li )= ∫ ⃗ A W ⋅ dl = ∫ ⃗ A W ⋅ dl dz dz, (1.16)
VolumeaboveaPlane
Intheprevioussection,weassumedthat Bz > 0everywhere.Thusthefieldlineswerebraidedabouteachother, andsimplewindingnumberssufficedtomeasurepairwiseentanglements.Ifweremovetherestrictionon Bz , fieldlinescangoupanddown.Wewillalsoremovethe restrictionofanupperplaneinthefollowingdiscussion, althoughthatisnotstrictlynecessary.Suchadomainis illustratedinFig.1.2b.
Iffieldlinescanformloopsthatgoupanddown,we canmeasuretopologicalstructureinseveralways.One methodistocutthefieldlinesatanylocalminimaormaximawhere Bz = 0andthensumthewindingnumbersas before(BergerandPrior,2006).Thewindinggaugewill stillworkinthissituation,astheformulaeforcalculating ⃗ A W donotrequire Bz > 0.
Asecondmethod,whenconsideringthewinding betweentwoloops,consistsofexaminingtheanglesof thequadrilateralformedbythefourfootpointsofthe loops(Berger,1986;Demoulinetal.,2006).Considerthe upperhalfspace {z > 0},showninFig.1.2b.Thefoot pointsofloops1and2arelabeled1+ ,1 ,2+ ,and2 , where Bz > 0at1+ and2+ .Iftheloopscrossasseenfrom above,weassumethatloop1istheupperloop.Consider thequadrilateral1+ 2+ 1 2 .Let �� and �� betheanglesat vertices1+ and1 ,respectively.Then(fromconsidering thenetchangeofhelicityfoundwhenbringingthetwo loopsinfrominfinity)Berger(1984)showedthat
Poloidal-ToroidalRepresentation
Thewindinggaugeemployedintheprevioussectionsis equivalenttothevectorpotentialfoundwhenemploying apoloidal-toroidalrepresentationforthefield(Moffatt, 1978;BergerandHornig,2018).Becausethemagneticfield ⃗ B isathree-vectorsubjecttoonecondition (∇ ⋅ ⃗ B = 0),wecanoftenexpressitintermsoftwoscalar functions.Herewelet P and T bethe poloidal and toroidal functions.LetthehorizontalsurfaceLaplacianbe Δ∥ = �� 2 ∕�� 2 x + �� 2 ∕�� 2 y .Inanyplane z = const., P isdetermined bytheverticalflux,
P =−Bz , (1.19) while T isdeterminedbytheverticalcurrent,
T =−Jz =−(∇× ⃗ B)z (1.20)
Weassume T , P, Bz ,and Jz allvanishatinfinity.Thenthe surfaceLaplacianshaveuniquesolutions,
Wecannowcreateavectorpotential
A =∇× P ̂ z + T ̂ z (1.23)
Notethatthehorizontalcomponentsof ⃗ A onlyinvolvethe poloidalfunction P.Furthermore,thehorizontaldivergenceof ⃗ A vanishes: ∇∥ ⋅ ⃗ A∥ = 0.Onecanthenemploy equations(1.21)and(1.22)toshowthatthisvectorpotentialisidenticaltothewindinggauge, ⃗ A W =∇× P ̂ z + T ̂ z, providedthatthevolumeconsideredisinfiniteinthe x and y directions.Wecanagainemploythisvectorpotentialto calculatefieldlinehelicities.Thetotalhelicitycanalsobe regardedasthenetlinkingoftoroidalandpoloidalfields (BergerandHornig,2018),
= 2
∇×(T
VolumesBoundedbyaSphere
Sphericalboundaries–suchasinFig.1.2c–can,for themostpart,betreatedthesamewayasplanarboundaries,withtheradialunitvector ̂ r replacingthevertical vector ̂ z.Inessence,windinganglesbecomeazimuthal angles.Supposeweconsiderthreepoints A, B,and C ona sphere.Rotatethesphericalcoordinatessothat B isatthe Northpoleand A isattheazimuthalcoordinate �� = 0. Thentheangle ∠ABC equalstheazimuthalcoordinate of C .
Thepoloidalandtoroidalfluxfunctionsare(Kimura andOkamoto,1987)
�� = cos �� cos �� ′ + sin �� sin �� ′ cos(�� ��′ ) (1.27) isthesphericaldistancebetween (��,��) and (�� ′ ,��′ ).With thesefunctions,
A =∇P × ̂ r + T ̂ r; ⃗ B =∇×(∇P × ̂ r)+∇T × ̂ r (1.28)
Somecaremustbetakeninsphericalgeometries.One mustensurethatnomagneticmonopolesarehidinginside thesphere–i.e.,thenetfluxthroughthespheremustvanish(similarlyforthenetcurrent).
Also,inthespecialcaseofasphericalshellgeometry wherefluxentersattheinnersphereandexitsattheouter sphere(asinFig.1.2c),theseparationofhelicityinto self helicity and mutualhelicity canbeambiguous(Campbell andBerger,2014).Selfhelicitymeasuresthetwistand writheofindividualtubes,whilemutualhelicitymeasures linkingandintertwiningbetweentubes.Thiswillnot affectthefieldlinehelicity,however.
MoreGeneralVolumes
Forvolumesboundedbyplanesorspheres,thereare naturaldefinitionsof angle and windingangle depending onlyontheEuclideanmetric.Thewindinggauge,orthe poloidal-toroidalvectorpotential,capturesthisnatural definition.Wecouldalsoconsideravolumewithboundariesconsistingofabottomplaneandsideboundaries, wherefluxonlycrossesthebottomplane.Suchavolume couldrepresentaclosedactiveregion.Wecouldchoose windingangleswithoutregardtothesideboundaries, usingthesamewindinggauge.Analternativewillbe describedlaterwhenusingrelativemeasuresofhelicity. Next,consideravolumeboundedbyoneortwosimply connectedsurfacesthatlackthesymmetryofplanes orspheres.AnexampleisshowninFig.1.2d.Here, definitionsofanglearelessobvious.However,wecan stillemployageneralizationofthepoloidal-toroidal representation(BergerandHornig,2018)todefinethe windinggauge.
Letourvolume beslicedintonestedsurfaces.Employ coordinates (u,��,��),where �� = const.labelsoneofthe nestedsurfaces.Thetoroidalfield(whichisresponsiblefor thecurrentperpendiculartosurfacesofconstant ��)can bewrittenintermsofatoroidalfunction T asbefore:
However,thepoloidalfieldismorecomplicated.Letthe normalcomponentofthecurlbegivenbytheoperator ,
Thisoperatorhasaninverse 1 .Tomaketheinverse unique,werequirethattheinversenormalcurlgivesa divergence-freevectorfieldparalleltothesurface.Thus
Let Bn bethenormalmagneticfield.Ordinarily,we wouldwritethepoloidalfieldas
However,withoutsphericalorplanarsymmetry,thismagneticfieldmayhavenonzeronormalcurrent Jn –butthe toroidalfieldhasalreadytakencareof Jn .Thus(Berger andHornig,2018)wemustadda shape term
Puttingitalltogether,thegeneralizedwindinggauge becomes
1.1.3.RelativeFieldLineHelicity
Intheprevioussections,helicityandfieldlinehelicity havebeendefinedintermsofgeometricalquantitiessuch aswindingandlinking.Thehelicityofopenfieldsina volume canalsobedefinedintermsofhowmuchthe magneticstructurewithin contributestothehelicityof allspace(BergerandField,1984).Letthefieldinside becalled ⃗ B .Alsoconsiderapotential(zerocurrent)field
P inside withthesameboundaryconditions
n|S .Apotentialfieldminimizesthemagneticenergy inthevolumesubjecttotheconstraintofthegivenboundaryfluxdistribution.Hencepotentialfieldscanbesaidto havetheminimumstructure(moreaccurately,theirstructureonlydependsontheboundaryconditions,sothey addzero additional structuretothefield).
Herewecomparethetotalhelicityofallspacewith thehelicitythatwouldbeobtainedif,inside , ⃗ B were replacedby ⃗ P .Allintegralsaregaugeinvariant,sothe differencebetweenthetwohelicitieswillalsobegauge invariant.Letspaceexternalto be ′ .Thentherelative helicity HR ( ) is
Itisimportanttonotethatthecalculationof HR ( ) does notrequireknowledgeoftheexternalfield B ′ (Bergerand Field,1984;FinnandAntonsen,1985).
Forsymmetricvolumes(i.e.,boundariesconsisting ofaplaneorparallelplanesoroneortwoconcentric spheres),thetopologicalandrelativedefinitionsgive thesameanswers(BergerandField,1984;Bergerand Hornig,2018).Formorecomplicatedgeometries,they maydiffer.Forexample,supposethevolume consists ofahelicaltuberisingbetweenparallelplanes.Suppose weplaceapotentialfieldbothinsideandoutside .Then thehelicityofallspacewillbenonzerobecauseofthe helicalstructure.Nowaddsomeaxialcurrentinside sothefieldhasanextratwist.Thentherelativehelicity inside willonlymeasurethisextratwistbecausethe helicityduetotheaxiswritheissubtractedwiththe potentialterm.
Therelativehelicityofapotentialfieldis,bydefinition,zero.Supposeagainthattheboundaryisplanar orspherical.Thenthetopologicalhelicity(summing windingnumbersasinprevioussections)willalsobe zero:thepotentialfieldispurelypoloidal,sothereis
nolinkagebetweentoroidalandpoloidalcomponents. However,forapotentialfield,thefieldlinehelicitiesof individualfieldlinesmaynotbezero,eveniftheysum tozero(Yeates,2020).Thesepotentialfieldlinehelicities reflectirregularitiesandlackofmirrorsymmetryinthe distributionofboundaryflux(BourdinandBrandenburg, 2018).Thusthefieldlinehelicityofthepotentialfieldcan helpcharacterizemagneticdistributions,forexample,in thesolarphotosphere.
Thisraisesaquestion,however:iftherearecurrents insideavolume,howdotheychangethefieldlinehelicitiesfromtheirminimal(potentialfield)values?Weneed tosubtractthepotentialfieldlinehelicitiestoremove thecontributionsfromtheboundaryfluxdistribution. Thus,wecanadopttherelativehelicityviewpointfor fieldlinehelicityaswell(YeatesandPage,2018;Moraitis etal.,2019;Moraitisetal.,2021).First,toavoidgauge ambiguity,weemploythesamegaugeconditionsasapply inthepoloidal-toroidalformulation.Letthepotential fieldbe ⃗ P,withvectorpotential ⃗ AP .Inparticular,for thecomponentsofthevectorpotentialsparalleltothe boundary,wehave
1.2.IDEALEVOLUTION
Justlikethetotalmagnetichelicity,thefieldlinehelicitieswithinagivendomain maychangeintwoways: by(i)boundarymotionsor(ii)non-idealprocessesin theinterior.Inthissection,weshowhowtoderivean evolutionequationforcase(i),whilecase(ii)isdeferredto section1.3.Wewillgivesomeexampleswherethesehave beenapplied,althoughmuchremainstobeexplored.
Aswehaveseen, isdeterminedentirelybythechoice oftangentialcomponents ⃗ A × ̂ n ontheboundary �� , alongwithanextraconditionwhentheboundaryhas twodisconnectedcomponents.Typically,wethinkof setting ⃗ A × ̂ n = ⃗ AP × ̂ n forsomereferencevectorpotential ⃗ AP .Thuswhen ⃗ B ̂ n on �� isevolving,wecannotkeep afixedreferencebutmustevolve ⃗ AP insomesuitable wayovertimethatpreservesthephysicalinterpretation. Forexample,Yeates(2020)choosestheso-calledminimal gauge.
If ⃗ B evolvesideallyinsomevolume sothat
Itcanbeshown(YeatesandPage,2018)thatthischoice ofgaugefor ⃗ AP minimizestheboundaryintegral ∮S | ⃗ AP × ̂ n|2 d2 x.Next,let ��+ bethepositiveendpointofafieldline. Thefieldlinesthrough ��+ for ⃗ B and ⃗ P willgenerallyhave differenttrajectoriesandconnecttodifferentexitpoints
�� and ��P .Wecannowtakethedifferenceinfieldline helicities
thenitiswellknownthatmagneticfieldlinesretaintheir identity:iftwofluidelementslieonthesamemagnetic fieldlineatsomeinitialtime,theywillcontinuetodosoat alllatertimes.Moreover,byAlfvén’stheorem,fieldlines cannotchangetheirmutuallinkage.Itfollowsimmediatelythat (L) ispreservedforevery closed fieldline L in .Moreover,anyfunctionalof willalsobepreserved, includingnotonlythetotalhelicity
Wecouldalsodothisforthenegativeendpoints.Starting atthesamenegativeendpoint �� ,wecouldtrackthefield linesbackwardtoeither ��+ or ��P+ .Inthiscase,wecould write
Finally,wecantaketheaverageofthetwo(fortheendpoints ��+ and �� ofthetruefieldline ⃗ B)tofind
butalsothehelicityofanysubregioncomposedofclosed fieldlines,aswellastheunsignedhelicitydefinedby
Thisisthemeasureof relativefieldlinehelicity adopted byMoraitisetal.(2019),althoughthoseauthorsusea slightlydifferentgaugeintheircomputations.
Toinjectorremovefieldlinehelicitybycontinuous idealevolutionthereforerequires open fieldlineswhere Bn
B
n | | |S ≠ 0alongwith ⃗ u ≠ ⃗ 0ontheboundary S ,as illustratedinFig.1.3(b).Inthiscase,thefundamental issueofgaugechoiceisimportant.Aphysicallymeaningfulapproachistofixsomethinglikethewindingor poloidal-toroidalgaugefor ⃗ A atalltimes.Consideran openfieldline Lt ,wherethesubscript t denotesthatthis linemoveswiththefluid.Toderivetheevolutionequation for (Lt ),notefirstthatuncurlingequation(1.42)gives
Figure1.3 Examplesofclosed(left)andopen(right)fieldlinesinadomain V withconnectedboundary �� .Foot pointsoftheopenfieldline Lt aredenoted x0 (t),where
forsomescalarfunction ��( ⃗ x, t) thatdependsonthechosengaugeof ⃗ A andwillgenerallybenonzeroforthe poloidal-toroidalgauge.
Nowlet t,�� beaninfinitesimalfluxtubesurrounding Lt andmovingwiththefluid.Let Φ(
and
⃗ B d3 x bethemagneticfluxandhelicityofthisfluxtube. Thentherateofchangeoffieldlinehelicityis
BytheReynoldstransporttheorem,since t,�� isamaterial volume,wehave d dt h(t,�� )=
Which,usingequation(1.45),reducesto d dt h(t,�� )= ∮St,�� (�� + ⃗ A ⃗ u) ⃗ B ̂ nd 2 x (1.49)
Thisisjustthestandardexpressionfortheevolutionof magnetichelicityinamaterialvolume(e.g.,Moffattand Dormy(2019)p.61).Since t,�� isamagneticfluxtube, ⃗ B ⋅ ̂ n isnonzeroonlyonthetwoportionsofthetubeboundary St,�� thatcoincidewiththeboundaryof –inother words,theendsofthetube.Sosubstitutingintoequation (1.47)andtakingthelimit,notingthat ⃗ B ⋅ ̂ n → Φ(t,�� ) at bothendsofthetube,gives
dt (Lt )= [�� + ⃗ A ⋅ ⃗ u]x1 (t) x
, (1.50)
where x0 (t) and x1 (t) denotetheendpointsof Lt onthe boundaryof . Theexpressioninequation(1.50)showsthateven thoughfieldlines Lt canbeuniquelytrackedintime
duringanidealevolution,theirfieldlinehelicities (Lt ) dependonthechosengaugeof ⃗ A ontheboundaryover time,sincethischangesboth ⃗ A ⋅ ⃗ u and ��,thelatterbeing definedforagivenchoiceof ⃗ A throughequation(1.45). Formeaningfulresults,thisgaugeshouldbechosen objectively–suchasthepoloidal-toroidalgauge–rather thanforcomputationalconvenience.Indeed,itisalways possibleto“cancel”theeffectofanidealevolutionby choosing �� =− ⃗ A ⋅ ⃗ u inequation(1.45)sothat remains invariantforallfieldlines,butthisisahighlyartificial choice;ineffect,itcorrespondstomeasuringwindingwithrespecttoaframemovingwiththeboundary motions.Ofcourse,iftherearenoboundarymotions, willbeinvariantintimeforallfieldlinesprovided that �� ontheboundaryisnotvaried.Inparticular,if theboundaryisaconnectedsurface,itissufficienttofix ⃗ A × ̂ n.Incaseslikethevolumebetweentwospheres,one mustalsofixtheintegralof ⃗ A alongalinebetweenthetwo boundaries.
Whenthereareboundarymotions,thewindinggauge makesitpossibletoexpresstheevolutionof intermsof themeanangularmotionsoffieldlineendpointsaround oneanother(Berger,1988;MacTaggartandPrior,2021). Intherestrictedcasewherethereareboundarymotions buttheypreservetheboundarydistribution B ⋅ ̂ n|S and, inaddition,themagneticfieldhasa“simpletopology” (meaningthemappingfrompositivetonegativeendpoints iscontinuous),Aly(2018)derivedthealternativeformula
Heretheboundarymotionshavebeenwrittenas ⃗ u =( ̂ n × ∇�� )∕ ⃗ B ⋅ ̂ n,andthegaugeof ⃗ A hasbeenchoseninaparticularway.Specifically,theparallelcomponentsof ⃗ A onthe boundaryaresetbyequation(1.38),butwith ⃗ AP = U ∇V , where U and V areEulerpotentialsforthereferencefield ⃗ P =∇U ×∇V .Formula(1.51)maybeshowntobeequivalenttoequation(1.50)forthisgaugechoice.
1.2.1.SimpleExamples
Thesimplestexamplesareobtainedbyconsidering amagneticfieldbetweentwoplanes z = 0and z = 1 onwhich ⃗ B ⋅ ̂ n | | |S = Bz = 1andapplyingaxisymmetric boundarymotionsontheupperplane.Inthissituation, thepotentialreferencefieldis ⃗ P = ̂ z atalltimes,with poloidal-toroidalvectorpotential ⃗ AP =(r∕2) ̂ �� .Wefixthe gaugeof bysetting ⃗ A × ̂ z = ⃗ AP × ̂ z on z = 0and z = 1 and,bytheadditionalcondition(becausetheboundary hastwodisconnectedcomponents z = 0and z = 1), that ∫L ⃗ A dl = ∫L ⃗ AP dl = 0fortheverticalline L at r = 0.Thisgivesus inthewinding,orequivalently poloidal-toroidalgauge(thetwoareequivalentinthis volume).
Supposefirstthatweapplyarigidrotationoftheupper boundarywithrespecttothelowerone,givenby ⃗ u = rz ̂ �� . Inthiscase, ⃗ u × ⃗ B = u�� Bz ̂ r = rz ̂ r,somaintainingthegauge condition ⃗ A × ̂ z = ⃗ AP × ̂ z requires,accordingtoequation (1.45),that
fieldlinehelicity:
Thusforafieldlineatradius r,equation(1.50)gives
[
Thisshowsthatarigidrotationgeneratesnofieldline helicity(asnotedbyYeatesetal.(2021)).Ineffect,allthe fieldlinesrotatetogethersothatnoneofthemacquires anytwistwithrespecttotheothers.Thisexampleis shownbythedashedlinesintheright-handpanelsof Fig.1.4.
Foranexamplewithnontrivialinjectionoffieldline helicity,wecanapplyalocalizedrotation ⃗ u = 2re r2 ̂ �� for whichasimilarcomputationleadstoalocalizedpatchof
Thisisshownbythesolidlinesintheright-handpanels ofFig.1.4.Oneobtainsthesame patterninthetopologicallyequivalentsituationofatoroidalfluxringlocalizedin z,asshownbyYeatesandHornig(2014).Indeed, theinitialconditioninFig.1.8(later)isproducedbythe superpositionofsixsuchfluxrings,offsetsothefieldlines followatangledpattern.
Afinalanalyticalexampledemonstrateshowfieldline helicitymaybeinjectedintoamagneticfielddefinedon thehalf-space z > 0throughshearingmotionsonthe lowerboundary z = 0insteadoftwisting.Thismodels theshearingofanarcadeofcoronalmagneticloopsinthe Sun’satmosphere.Wesupposethatthearcadeisinitially current-freeand(forsimplicity)invariantin x,with ⃗ B = ⃗ P = z ̂ y y ̂ z,thesolarsurfacebeingtheplane z = 0and thevolume V with z > 0representingthecorona.Asuitablepoloidal-toroidalreferencevectorpotentialis ⃗ AP = (y2 ∕2 + z2 ∕2) ̂ x.Supposeweapplytheconstantshearing velocity ⃗ u = ye y2 ̂ x,localizednearthepolarityinversion line y = 0.Here ⃗ u × ⃗ B =−ux Bz ̂ y + ux By ̂ z,sorequiring that ̂ n × ⃗ A = ̂ n × ⃗ AP ontheboundary z = 0impliesthat ���� �� y = ux Bz =−y2 e y2 ⟹
Substitutingintoequation(1.50)andevaluatingonthe fieldlinerootedat y > 0thengives
ThisprofileisshowninFig.1.5.Thefirsttermvanishes ontheunshearedfieldlinesatlarge y.Butthesecond
Figure1.4 Simpleexamplewheretheboundaryhastwoparallelcomponents,oneofwhichisrotatedwithrespect totheother.Thegraphsshowtheazimuthalvelocity(top)andrateofgenerationoffieldlinehelicity(bottom)for thetwoexamplesinthetext(dashedandsolidlines).
Figure1.5 Simpleexampleofaninitialpotential“arcade”beingshearedbyaflowonthelowerboundary. Althoughtheyarelargelyunsheared,theoverlyingfieldlinesacquirenegativefieldlinehelicity,asmaybeseen fromtheirnegativecrossingswiththeshearedfieldlinesbeneath.
termdoesnot.Thisdemonstratesthenonlocalnature ofhelicity:thefieldlinesintheoverlyingarcadegain afieldlinehelicitybecausethecoreofthearcadeis sheared.Effectively,amagneticfluxispassingthrough them.Indeed,thiswaspreciselythewayAntiochos(1987) proposedtodefinefieldlinehelicity,asmentionedearlier. Noticeherethatthesignoftheerf(y) termisnegative, consistentwithStokes’stheoremandthedirectionofthe shearedfieldrelativetotheorientationoftheoverlying arcade.Onecouldalsoinferthissignbylookingatthe arcadefromaboveandobservinganegativecrossing (Fig.1.5).
1.2.2.ApplicationtotheGlobalSolarCorona
Toafirstapproximation,themagneticfieldintheSun’s atmosphereevolvesideallyinresponsetotheemergence ofnewmagneticactiveregionsfrominsidetheSun, decayofthesestrongmagneticfieldsduetoconvective shredding,andtransportoftheresultingmagneticfluxby large-scalemotionssuchastheSun’sdifferentialrotation. Duringtheseprocesses,magnetichelicitybuildsupin thecoronaandisejectedintotheheliosphere.Fieldline helicityofferstheexcitingprospectofalocalizedmeasure forstudyingwherethishelicityislocatedwithinthe corona.
YeatesandHornig(2016)usedaglobalmagnetofrictionalmodelinasphericalshelltostudyhowfield linehelicityevolvesinthecoronainresponsetotheevolutionofthesolarsurfacemagneticfield(Fig.1.6).Inthe simulationshown,activeregionemergenceisneglected sothatthedominantinjectionofhelicityisshearingby differentialrotationoffieldlinefootpointsonthesolar surface.Thebehavioroffieldlinehelicityisfoundto bedifferentonopenandclosedmagneticfieldlines.On openfieldlines(meaninginthiscontextthatonefield
lineendpointisontheouterboundary),injectedfieldline helicityislostatasteadyratethroughtheouterboundary byrelaxationofthefieldline.Bycontrast,closedfield lines,withbothendpointsonthesolarsurface,canstore fieldlinehelicity–asinthesimplearcadeexamplein Fig.1.5.
Thisstorageofhelicityonclosedfieldlinesisimportant becauseeventually,theseformtwistedfluxropesthat loseequilibriumanderupt,leadingtoburstsofhelicity fluxoutputandbelievedtoexplaintheoriginofcoronal massejections.LowderandYeates(2017)studiedthese eruptionsinthemagneto-frictionalmodelandusedfield linehelicityasadiagnostictooltodefinefluxropesin thefirstplace.Theoverallmagneticfluxandhelicity contentofthesestructureswasfoundtobecomparabletothatestimatedinobservationsofinterplanetary magneticclouds.Recently,BhowmikandYeates(2021) haveusedfieldlinehelicitytoshowthatepisodiclosses ofhelicityinthemagneto-frictionalmodelcomenotonly fromtheeruptionoffluxropesformedalongpolarity inversionlinesinthelowcoronabutalsofromasecond typeoferuptiongeneratedintheoverlyingstreamers. Similareruptionsareknowninmagnetohydrodynamic (MHD)simulations(LinkerandMikic,1995)andhave beensuggestedasapossibleexplanationforso-called stealthcoronalmassejections(CMEs)thatlackan obviouslow-coronalsource(Lynchetal.,2016).Many unansweredquestionsremain,notleasttheroleofactive regionsintheglobalhelicitybalanceorthepossibilityof long-termstorageoftheirhelicityinthecorona.Field linehelicitywillgreatlyfacilitatetheseinvestigations.
1.2.3.ApplicationtoSolarActiveRegions
Fieldlinehelicityalsooffersthepossibilitytoidentify locationsofhelicitystorageonasmallerscale,within
Figure1.6 Evolutionoffieldlinehelicityinamagneto-frictionalmodelofthesolarcoronaasaninitialpotential field(a)isshearedbytheSun’sdifferentialrotationfor(b)25daysand(c)50days.Fieldlinesarecoloredby theirfieldlinehelicityinpoloidal-toroidalgauge,withredforpositiveandbluefornegative(fordetailsofthe simulation,see(YeatesandHornig,2016)).
individualactiveregions,providedthree-dimensional magneticfieldmodelsareavailable.Eveninapotential fieldmodel,asimplebipolaractiveregioncanhave nonzerofieldlinehelicityifitsfieldlinesarelinkedwith theoverlyingbackgroundfield(Yeates,2020).Butmuch largervaluesoffieldlinehelicityareexpectedinmore realisticcurrent-carryingmodelsofactiveregions.This hasbeenconfirmedbyMoraitisetal.(2019)bothinidealizedMHDmodelsandinextrapolations.Forexample, Moraitisetal.(2021)havecomputedfieldlinehelicityin nonlinearforce-freeextrapolationsofarealactiveregion NOAA11158(Fig.1.7).
Figure1.7showsahighlyshearedmagneticfieldin thecoreoftheactiveregion,whichhaspositivefieldline helicity.Theauthorsfoundthatduringaflare,theregion lost25%ofitsrelativemagnetichelicity.Comparingthe fieldlinehelicitybetweenthetwoextrapolationsshown at01:11UTand01:59UTrevealsthatthedecreasein helicitytookplacewithinthesameregion(thegreen box)whereemissionfromalargeX-classsolarflarewas observedinextremeultraviolet(EUV).Thissupportsthe ideathatadecreaseinhelicitywasindeedassociatedwith theflare.ItisworthnotingthatMoraitisetal.(2021) usesrelativefieldlinehelicity(section1.1.3).However, theyshowthatusingtheordinaryfieldlinehelicity(in poloidal-toroidalgauge)leadstothesamequalitative conclusionsinthisexample,albeitwithlowervalues.
1.3.NON-IDEALEVOLUTION
Supposeequation(1.42)isgeneralizedto
where ⃗ N = ⃗ E + ⃗ u × ⃗ B representssomenon-idealterm inOhm’slaw.Acommonexamplewouldbe ⃗ N = �� ⃗ J
correspondingtoresistiveMHD.Itiswell-knownthat thetotalhelicityisnolongerconservedbutcanbedissipatedwithinthevolumewhen ⃗ N ⃗ B ≠ 0.Inthissection, weshowhow–formagneticfieldsofsimpletopology withoutnullpoints–equations(1.50)and(1.51)havebeen generalizedtothisnon-idealcase.Formagneticfieldsof morecomplextopology–forexample,thesolarcoronal examplesinsections1.2.2and1.2.3–evolutionequations havenotyetbeenderivedexplicitly.Indeed,differential equationsmaynotbeappropriatesincethedistributionof isdiscontinuousacrossmagneticseparatricesbetween differentconnectivitydomains.Reconnectioncantransport acrosstheseseparatrices,butitsevolutioninsuch asituationremainstobestudiedindetail.
Thereisanimportantcaveattowhatfollows:field linehelicitycanholdphysicalsignificanceinanon-ideal evolutiononlyifthemagneticfieldlinesthemselves retainsufficientidentityovertimefortheirtopologyto playaphysicalrole.Inpractice,thismeansthemagneticReynoldsnumber(Rm)mustbesufficientlylarge or,equivalently,the(effective)resistivitymustbesufficientlysmall.Thereisnoprecisethresholdforthis,butitis alreadyaccessiblefortheparametersachievableinnumericalsimulations,aswillbeillustratedinsection1.3.2.
1.3.1.EvolutionEquationforNon-NullMagnetic Fields
Thetrickforgeneralizingequation(1.50)orequation (1.51)tonon-idealevolutioninthenon-nullcaseis todecompose ⃗ N intoparallelandperpendicularparts (YeatesandHornig,2011),writing
Whenthemagneticfieldhasasimpletopology,this decompositionexistsglobally,with ⃗ �� and �� continuous
Figure1.7 Fieldlinehelicityinanonlinearforce-freemodelofactiveregionNOAA11158,fromMoraitisetal. (2021).Panel(a)showsthefieldlinescoloredby(relative)fieldlinehelicityintheextrapolationat01:11UT,while panel(b)showsanimageofEUVemissionfromSDO/AIAduringtheX-classflareat01:47UT.Panels(c)and (d)show(relative)fieldlinehelicitybeforeandaftertheflare(blue/red),whilepanel(e)showstheirdifference. Credit:Moraitisetal.,2021/TheEuropeanSouthernObservatory(ESO).
throughout V ,althoughtheyarenotunique(asweshall discussshortly).Substitutingthisdecompositioninto equation(1.57)showsthatinanon-nullmagneticfield, wecanwrite
)
where
whichshowsthatthemagneticfieldisstillfrozen,butinto the fieldline(transport)velocity ⃗ �� ratherthantheplasma velocity ⃗ u.Thus,inanon-idealevolutionwhere ⃗ �� ≠ ⃗ 0,the fieldlinesslipatsomevelocity ⃗ �� throughtheplasma(Newcomb,1958;PriestandForbes,1992;Aulanieretal.,2006; Schindler,2010).Uncurling,wehave
Thus,ifweidentifythesamefieldline Lt atdifferenttimes bythefactthatitisfrozenintotheflowof ⃗ ��,anargument similartosection1.2showsthat
Similarly,Aly(2018)showedthatequation(1.51)becomes
Noticethat [�� ]x
E
dl ,whichispreciselythe parallelelectricfieldusedtodefinethereconnectionrate inthetheoryofgeneralmagneticreconnection(Schindler etal.,1988).Itrepresentsthechangein (Lt ) duetoa (nonlocal)changeinthemagneticfluxlinkedwith Lt Theterm ⃗ A ⃗ �� ishardertointerpretingeneralbecauseit dependsonthechoicesof ⃗ A and ⃗ ��.Withthegaugecondition ̂ n × ⃗ A = ̂ n × ⃗ AP ontheboundary,the [ ⃗ AP ⃗ ��]
(
) termeffectivelyrepresents“workdone”bymotionofthe fieldline Lt withrespecttothereferencefield(Russell etal.,2015).
Foragivennon-idealevolutionof ⃗ B,thefieldline velocity ⃗ �� isnotuniquelydefined,andconsequently,the identificationofthefieldline Lt overtimeisnotunique. Whilethecomponentof ⃗ �� parallelto ⃗ B isarbitrary–as
isclearfromequation(1.58)–itisthenon-uniquenessof theperpendicularcomponent ⃗ ��⟂ thatchangestheidentificationof Lt .Toseethatthiscomponentisnon-unique, notethatequation(1.58)implies
Oneachfieldline,wecanspecifyaninitialvalueof �� .This doesnotchange [�� ]x1 (t) x0 (t) butdoeschange ⃗ ��⟂ . Onesituationwhereanaturalchoiceof ⃗ ��⟂ arisesis thecasewhenthefield-lineendpointsareline-tiedonthe boundary,meaning ⃗ u = ⃗ N = ⃗ E = ⃗ 0there(Russelletal., 2015).Inthatcase,wecanidentify Lt overtimebyfixing oneendpoint–say, ⃗ ��⟂ (x0 )= ⃗ 0–forallfieldlines.Thisis
achievedbychoosing �� = 0throughouttheregionofthe boundarywhere ⃗ B ̂ n|S < 0.Attheoppositeendpoints x1 (t),thevaluesof �� willthenbefixedby [�� ]x1 (t) x0 (t) ,leading to ⃗ ��⟂ (x1 ) ≠ ⃗ 0ingeneralsothattheseendpointswillmove intimeinanon-idealevolution.Wecouldequallywellfix �� = 0ontheregionwith ⃗ B ⋅ ̂ n|S > 0,thusdefiningthefield linesbyfixed x1 positionssothat x0 (t) variesovertime. If ⃗ u isnonzeroontheboundarybut ⃗ N remainszero there(orcanbeneglected),thenitispossibletosubtract theidealterm [ ⃗ A ⋅ ⃗ u]x1 (t) x0 (t) fromequation(1.61)andisolate thechangeinfieldlinehelicitycomingfromnon-idealevolution.Ananalogouscalculationwasimplementedforthe magneticwindingmeasurebyGekelmanetal.(2020)in
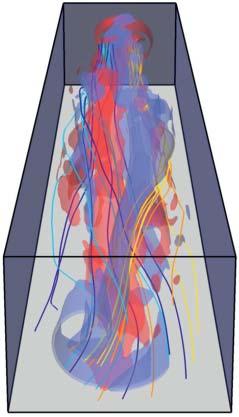
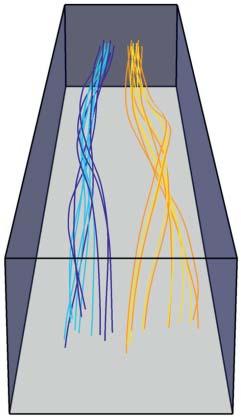
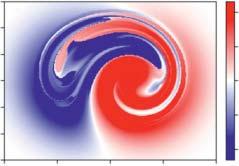
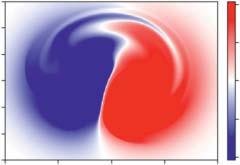
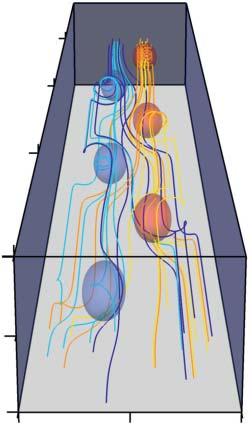
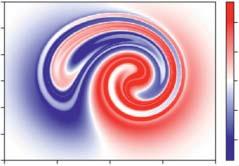
Figure1.8 Evolutionoffieldlinehelicityduringline-tiedresistiverelaxationofabraidedmagneticfield(seeYeates etal.(2021)fordetailsofthesimulation).Panelsa–cshowmagneticfieldlinesandisosurfacesofcurrentdensity (a)intheinitialcondition,(b)duringtheturbulentrelaxation,and(c)intherelaxedstate.Panelsd–fshowcross sectionsoffieldlinehelicityonthe z =−24boundaryatthesametime.Chenetal.2021/CambridgeUniversity Press/LicensedunderCCBY4.0.
datafromalaboratoryexperimentofinteractingmagnetic fluxropes.
1.3.2.ApplicationtoTurbulentMagneticRelaxation
Thenon-idealevolutionof hasbeenexploredonlyin thecontextofbraidedmagneticfields,whereallfieldlines connectbetweentwoplanarboundaries z = 0and z = 1 atwhich ⃗ u = ⃗ N = ⃗ 0.Themostsignificantfindingtodate isthatwhenthemagneticfieldlinemappingfrom z = 0to z = 1iscomplexwithsharpgradients,theevolutionof forhighRmisdominatedbyredistributionbetweenfield lines,ratherthandissipation(Russelletal.,2015;Yeates etal.,2021).
Toseethis,considertheevolutionof onthefieldline tracedfromafixedpoint x0 onthelowerboundary z = 0. Russelletal.(2015)madethenaturalchoice ⃗ �� = ⃗ 0on z = 0,inwhichcaseequation(1.61)reducesto
(x1 (t))
where Lt isthefieldlinedefinedbytracingfromthe fixedpoint x0 atsubsequenttimes.Theyarguedthat the ⃗ A ⃗ �� dominatesthe �� terminamagneticfieldwith complexmapping,because | ⃗ ��| scaleslike |∇�� |∕B from equation(1.63).Since �� (x1 (t)) isafield-lineintegrated quantity,andsincethefieldlinemappinghassharp gradients,wewouldexpect | ⃗ A ⃗ ��| ≫ |�� | forhighRm. Thiswasdemonstratedoriginallyinkinematicexamples (seealsoYeates(2019))andhasrecentlybeenconfirmed bydirectcalculationofthetermsinequation(1.64)in resistiveMHDsimulations(Yeatesetal.,2021).Onesuch simulationisillustratedinFig.1.8.
Watchingthefullevolutionof (x0 ) intheFig.1.8simulationsuggeststhatthe patternevolvespredominantly byrearrangementwithsomefictitiousflow.Toseethis fromtheevolutionequation,wecanemploytheseemingly unhelpfultrickoflabelingfieldlinesbyfixingtheirendpoint x1 on z = 1sothat �� = 0and ⃗ ��⟂ = ⃗ 0on z = 1.Then insteadofequation(1.64),equation(1.50)becomes
term ⃗ �� ∇ iseffectivelyaproductoftwogradientsof field-lineintegratedquantities,soonemightexpectthisto bethelargest.Itisthereforenosurprisethatthedominant behaviorobservedisarearrangementofthe patternby advection.
Chenetal.(2021)tookthisideaanddevelopeda variationalmodelforturbulentmagneticrelaxationthat predictstherelaxedstatetohavethe“simplest”pattern offieldlinehelicityachievablebypureadvection.This alreadypredictsthetwooppositelytwistedmagnetic “fluxtubes”inFig.1.8(f).However,closerinspectionof thenumericalsimulationsbyYeatesetal.(2021)shows thattheothertermsinequation(1.66)playarolein establishingthesubstructureofthefinalstate.
REFERENCES
Aly,J.J.(2018).Newformulaeformagneticrelativehelicity andfieldlinehelicity. FluidDynamicsResearch, 50(1),011408. https://doi.org/10.1088/1873-7005/aa737a
Antiochos,S.K.(1987).Thetopologyofforce-freemagnetic fieldsanditsimplicationsforcoronalactivity. TheAstrophysicalJournal , 312,886.
Arnold,V.I.,&Khesin,B.A.(1998). Topologicalmagnetohydrodynamics.Springer.
Aulanier,G.,Pariat,E.,Démoulin,P.,&DeVore,C.R.(2006). Slip-runningreconnectioninquasi-separatrixlayers. Solar Physics, 238(2),347–376.https://doi.org/10.1007/s11207-0060230-2
Berger,M.A.(1984).Rigorousnewlimitsonmagnetichelicitydissipationinthesolarcorona. Geophysical&AstrophysicalFluidDynamics, 30(1–2),79–104.https://doi.org/10.1080/ 03091928408210078
Berger,M.A.(1986).Topologicalinvariantsoffieldlinesrooted toplanes. JournalofPhysicsA:MathematicalandGeneral , 34, 265–281.
Berger,M.A.(1988).Anenergyformulafornonlinearforce-free magneticfields. AstronomyandAstrophysics, 201,355–361. Berger,M.A.,&Field,G.B.(1984).Thetopologicalproperties ofmagnetichelicity. JournalofFluidMechanics, 147 ,133–148. Berger,M.A.,&Hornig,G.(2018).Ageneralizedpoloidal–toroidaldecompositionandanabsolutemeasureofhelicity. JournalofPhysicsA:MathematicalandTheoretical , 51(49), 495501.
Tocomputetheevolutionof atafixedposition x0 ,we mustnowaccountforthefactthatthefieldlinesaremovingpastthispointwiththelocalfieldlinevelocity ⃗ ��(x0 ) Thusthetimederivativeinequation(1.65)isaLagrangian one,soatthefixedposition x0 ,wehave
Noticethatallthetermshereare“local,”although �� and arestillfield-lineintegratedquantities.Theadvection
Berger,M.A.,&Prior,C.(2006).Thewritheofopenandclosed curves. JournalofPhysicsA:MathematicalandGeneral , 39, 8321–8348.
Bhowmik,P.,&Yeates,A.R.(2021).Twoclassesoferuptiveeventsduringsolarminimum. SolarPhysics, 296(7),109. https://doi.org/10.1007/s11207-021-01845-x
Bourdin,P.A.,&Brandenburg,A.(2018).Magnetichelicity frommultipolarregionsonthesolarsurface. TheAstrophysicalJournal , 869,3.
Campbell,J.,&Berger,M.A.(2014).Helicity,linking,and writheinasphericalgeometry. JournalofPhysics:Conference Series, 544,012001.https://doi.org/10.1088/1742-6596/544/1/ 012001
Chen,L.,Yeates,A.R.,&Russell,A.J.B.(2021).Optimal unstirredstateofapassivescalar. JournalofFluidMechanics, 911,A30.https://doi.org/10.1017/jfm.2020.1154
Demoulin,P.,Pariat,E.,&Berger,M.A.(2006).Basicpropertiesofmutualmagnetichelicity. SolarPhysics, 233,3–27. Finn,J.M.,&Antonsen,T.M.Jr.(1985).Magnetichelicity: Whatisitandwhatisitgoodfor? CommentsonPlasma PhysicsandControlledFusion, 9,11.
Gekelman,W.,DeHaas,T.,Prior,C.B.,&Yeates,A.R. (2020).Usingtopologytolocatethepositionwherefully three-dimensionalreconnectionoccurs. SNAppliedSciences, 2(12),2187.https://doi.org/10.1007/s42452-020-03896-4
Kimura,Y.,&Okamoto,H.(1987).Vortexmotiononasphere. JournalofthePhysicalSocietyofJapan, 56,2024.
Linker,J.A.,&Mikic,Z.(1995).Disruptionofahelmet streamerbyphotosphericshear. TheAstrophysicalJournal Letters, 438,L45.https://doi.org/10.1086/187711
Lowder,C.,&Yeates,A.(2017).Magneticfluxropeidentificationandcharacterizationfromobservationallydrivensolar coronalmodels. TheAstrophysicalJournal , 846,106.https:// doi.org/10.3847/1538-4357/aa86b1
Lynch,B.J.,Masson,S.,Li,Y.,DeVore,C.R.,Luhmann, J.G.,Antiochos,S.K.,&Fisher,G.H.(2016).Amodel forstealthcoronalmassejections. JournalofGeophysical Research:SpacePhysics, 121(11),10,677–10,697.https://doi .org/10.1002/2016JA023432
MacTaggart,D.,&Prior,C.(2021).Helicityandwindingfluxes asindicatorsoftwistedfluxemergence. GeophysicalandAstrophysicalFluidDynamics, 115(1),85–124.https://doi.org/10 .1080/03091929.2020.1740925
MacTaggart,D.,&Valli,A.(2019).Magnetichelicityinmultiplyconnecteddomains. JournalofPlasmaPhysics, 85(5), 775850501.https://doi.org/10.1017/S0022377819000576
Moffatt,H.K.(1969).Thedegreeofknottednessoftangled vortexlines. JournalofFluidMechanics, 35,117–129. Moffatt,H.K.,&Ricca,R.L.(1992).Helicityandthe Calugareanuinvariant. ProceedingsoftheRoyalSocietyof LondonSeriesA:Mathematical,PhysicalandEngineeringSciences, 439(1906),411–429.https://doi.org/10.1098/rspa.1992 .0159
Moffatt,H.K.(1978). Magneticfieldgenerationinelectrically conductingfluids.CambridgeUniversityPress.
Moffatt,H.K.,&Dormy,E.(2019). Self-excitingfluiddynamos CambridgeTextsinAppliedMathematics.CambridgeUniversityPress.https://doi.org/10.1017/9781108766508
Moraitis,K.,Pariat,E.,Valori,G.,&Dalmasse,K.(2019).Relativemagneticfieldlinehelicity. AstronomyandAstrophysics, 624,A51.https://doi.org/10.1051/0004-6361/201834668
Moraitis,K.,Patsourakos,S.,&Nindos,A.(2021).Relativefield linehelicityofalargeeruptivesolaractiveregion. Astronomy andAstrophysics, 649,A107. Newcomb,W.A.(1958).Motionofmagneticlinesofforce. AnnalsofPhysics, 3(4),347–385.https://doi.org/10.1016/ 0003-4916(58)90024-1
Priest,E.R.,&Forbes,T.G.(1992).Magneticflipping:reconnectioninthreedimensionswithoutnullpoints. Journalof GeophysicalResearch, 97 (A2),1521–1531.https://doi.org/10 .1029/91JA02435
Prior,C.,&Yeates,A.R.(2014).Onthehelicityofopenmagneticfields. TheAstrophysicalJournal , 787 ,100.
Russell,A.J.B.,Yeates,A.R.,Hornig,G.,&Wilmot-Smith, A.L.(2015).Evolutionoffieldlinehelicityduringmagnetic reconnection. PhysicsofPlasmas, 22(3),032106.https://doi .org/10.1063/1.4913489
Schindler,K.,Hesse,M.,&Birn,J.(1988).Generalmagnetic reconnection,parallelelectricfields,andhelicity. Journalof GeophysicalResearch, 93(A6),5547–5557.https://doi.org/10 .1029/JA093iA06p05547
Schindler,K.(2010). Physicsofspaceplasmaactivity.CambridgeUniversityPress. Yahalom,A.(2013).Aharonov-Bohmeffectsinmagnetohydrodynamics. PhysicsLettersA, 377 (31–33),1898–1904.https:// doi.org/10.1016/j.physleta.2013.05.037
Yeates,A.R.(2019). Magnetohydrodynamicrelaxationtheory CISMInternationalCentreforMechanicalSciences.Springer InternationalPublishing.https://doi.org/10.1007/978-3-03016344-0
Yeates,A.R.(2020).Theminimalhelicityofsolarcoronalmagneticfields. TheAstrophysicalJournalLetters, 898,L49. Yeates,A.R.,&Hornig,G.(2011).Ageneralizedfluxfunction forthree-dimensionalmagneticreconnection. PhysicsofPlasmas, 18(10),102118.https://doi.org/10.1063/1.3657424
Yeates,A.R.,&Hornig,G.(2014).Acompletetopologicalinvariantforbraidedmagneticfields. JournalofPhysics ConferenceSeries, 544,012002.https://doi.org/10.1088/17426596/544/1/012002
Yeates,A.R.,&Hornig,G.(2016).Theglobaldistribution ofmagnetichelicityinthesolarcorona. Astronomyand Astrophysics, 594,A98.https://doi.org/10.1051/0004-6361/ 201629122
Yeates,A.R.,&Page,M.H.(2018).Theminimalhelicity ofsolarcoronalmagneticfields. JournalofPlasmaPhysics, 84(775840602).
Yeates,A.R.,Russell,A.J.B.,&Hornig,G.(2021).Evolution offieldlinehelicityinmagneticrelaxation.https://arxiv.org/ abs/2108.01346
MagneticWinding:TheoryandApplications
DavidMacTaggart
ABSTRACT
Magneticwindingisarenormalizationofmagnetichelicitythatprovidesadirectmeasureoffieldlinetopology. Despiteitscloseconnectiontomagnetichelicity,magneticwindingcanprovidedifferentandimportantinformationaboutfieldlinetopologythatisnotclearfromananalysisofmagnetichelicityalone.Inthischapter,we introducemagneticwindingfromatheoreticalperspective,withakeeneyeonitsroleinunderstandingmagnetic helicityandfieldlinetopology.Wealsoprovidepracticalapplicationsofmagneticwinding,highlightingthatit canbeusedasanimportantmeasureforunderstandingtheevolutionofactiveregionsinsolarobservations.
2.1.INTRODUCTION
Magnetichelicityisaconservedquantityofidealmagnetohydrodynamics(MHD).Whatitconservesrelatesto thetopologyofmagneticfieldlines.Tounderstandthis concept,wewillconsidermagnetichelicitywrittenina usefulgauge.Inaboundeddomain Ω ⊂ ℝ3 withgenus g thatismagneticallyclosed(B ⋅ n = 0on �� Ω,forsurface unitnormalvector n),thegaugeinvariantformofmagnetichelicitycanbewrittenas
Althoughequation(2.1)holdsforanyvectorpotential A indomainsofarbitrarytopologicalcomplexity,itis toogeneraltoyieldusefulinformationaboutmagnetic fieldlinetopology,which,asmentionedatthestart,is relatedtowhat H conserves.If,againwith B ⋅ n = 0on �� Ω,wemakethegaugechoice A = BS(B ),whereBS(B ) is theBiot-Savartoperator
where B isthemagneticfield, A isamagneticvectorpotential, ��i areclosedpathsaround“holes”inthedomain(e.g., theholeofatorus)andhaveunittangentvectors ti ,and the Σi arethesurfacesofcutsthroughthedomainwith unitnormalvectors nΣi .Equation(2.1)isderivedinMacTaggartandValli(2019),whichdescribesmoredetailsof thegeometricalsetup(seealsoFaracoetal.(2022)foran applicationtoarigorousproofofTaylor’sconjecture).
SchoolofMathematicsandStatistics,UniversityofGlasgow, Glasgow,UK
where x and y arepositionvectorsin ℝ3 ,thenequation (2.1)reducestotheclassicalformofmagnetichelicity,
Equation(2.3)holdsthekeytounderstandinghowhelicityincludesfieldlinetopology.Indeed,itwasthisformof helicitythatMoffattconsideredinhisseminalworkonthe subject(Moffatt,1969).
Letusnowtakeasidestepandconsiderafundamental topologicaldescriptionoflinkedloops.Let C1 and C2 be twoclosedanddistinctloopswithassigneddirections,as showninFig.2.1.
HelicitiesinGeophysics,Astrophysics,andBeyond,GeophysicalMonograph283, FirstEdition. EditedbyKirillKuzanyan,NobumitsuYokoi,ManolisK.Georgoulis,andRodionStepanov. ©2024AmericanGeophysicalUnion.Published2024byJohnWiley&Sons,Inc. DOI:10.1002/9781119841715.ch02
Figure2.1 Twoclosedandlinkedloops, C1 and C2 ,withspecifieddirections.
Anydeformationthatdoesnotbreaktheloopspreservesthelinkage.Therefore,linkage,inthisscenario,is atopologicalquantity.Ifpositionvectorsofpointson C1 aredenotedby x andthoseon C2 by y,theGauss linkingnumber,whichmeasuresthenetalgebraiclinkage, isgivenby
= 1 4
where s1 and s2 areparameterizationsof C1 and C2 , respectively.Thelinkage Lk isanintegeriftheloopsin thelinkareclosed.Theclosureofthelinksisalsonecessaryfor Lk tobeatopologicalinvariant:i.e.,indifferent todeformationsthatdonotbreakclosedloops.Fora historicalaccountofthedevelopmentofequation(2.4), thereaderisdirectedtoRiccaandNipoti(2011).
FortheexampleinFig.2.1,thetwoloopsareclearly linkedonce.Duetothedirectionsofthearrows, Lk = 1. Wecanalsoperformthecalculationinequation(2.4)in reverse:i.e.,assign x topointson C2 and y topointson C1 andreachthesameresult.Anotherwaytowritethis is Lk12 = Lk21 = 1.
InFig.2.1,wenowtransformtheclosedloopsinto magneticfluxtubes.Thatis,eachloopbecomestheaxis ofathinfluxtubewithflux Φi , i = 1, 2 Allfieldlinesare paralleltothetubeaxis:i.e.,forthemoment,wedonot considerinternaltwist.Withthisconstructionoftheflux tubes,wehavethat
Φi ti dx = B d3 x, whichconnectsfluxandlineelementstomagneticfield andvolumeelements.Thismeansbyrescalingdx of C1 anddy of C2 inequation(2.4)bythemagneticflux Φi associatedwitheachloop,wefindthehelicityin equation(2.3).Inotherwords,themagnetichelicityin equation(2.3)ofclosedmagneticfieldsmeasuresthe (pairwise)Gausslinkingnumberoffieldlinesweighted bymagneticflux.FortheexampleinFig.2.1,the valueis H = Lk12 Φ1 Φ2 + Lk21 Φ2 Φ1 = 2Φ1 Φ2 .Although magnetichelicitycanbeextendedtoincorporatemore complexmagneticfieldsthathaveinternaltwist(Moffatt andRicca,1992)andergodicfieldlines(Laurenceand Avellaneda,1993),thebasicpicturewehavepresented hereholds.Thatis,magnetichelicityisameasureoffield linetopologyweightedbymagneticflux.Thisconceptual
definitionofhelicitywillbeusefulfortherestofthis chapter.
2.2.RELATIVEHELICITY
Sofar,wehaveconsideredmagnetichelicityinamagneticallycloseddomain.However,therearemanyapplications,particularlyinsolarphysics,forwhich,atsome boundary,nonzeronormalcomponentsofthemagnetic fieldmustbeincluded.Inthissituation,equation(2.1) nolongerrepresentsagaugeinvariantquantity.Instead, arelativemeasureofmagnetichelicity,whichcompares twomagneticfieldswiththesamenormalboundary conditions,isrequired.Fromthismomentonwardinthis chapter,althoughnotstrictlynecessaryforeverything weintroduce,ourdomain Ω willbesimplyconnected. Thischoicenotonlysimplifiesmanydescriptionsbutalso relatestopracticalapplications–thedomainsofmost solarsimulationsandobservationsaresimplyconnected.
FollowingBergerandField(1984)andFinnandAntonsen(1985),relativemagnetichelicityhastheform
(B , B ′ )= ∫Ω (A + A′ ) (B B ′ )
Where B ′ isareferencemagneticfieldwith B ′ ⋅ n = B ⋅ n on �� Ω and A′ isareferencevectorpotential.Similarto equation(2.1),equation(2.5)istoogeneraltorevealclear informationaboutthefieldlinetopology.Wecannotjust substituteinequation(2.2)asbefore,sincefieldlines arenotnecessarilyclosed,sotheGausslinkingnumber isnolongeratopologicalinvariant.Instead,wemust findanotherdescriptionoffieldlinetopology,thistime startingfromequation(2.5).Toachievethis,wewill furtherrestrictourattentionto“tubular”domains,as illustratedinFig.2.2.
By“tubular,”wemeanthefollowing:thedomain Ω is boundedaboveandbelowbyhorizontalplanes.Themagneticfieldin Ω mustbetangenttosideboundaries.Field linescanconnecttoboth,one,orneitheroftheupper andlowerboundaries.Althoughthisrestrictswhatkind
Figure2.2 A“tubular”domain Ω betweentwohorizontal planesat z = 0and z = h.Ateachheightin Ω,thehorizontal sliceisdenoted Sz
HR
Another random document with no related content on Scribd:
nevezi, mióta csak él. A csapást nem háríthatja el, testvéreire lesújt a fenyegető végzet keze: közös halállal vesztik egymás életét. Antigone minden érzése innen kezdve az egyikhez, a boldogtalanabbikhoz, a meggyalázott bűnöshöz fordúl. Már előbb, Kolonosban, a vakmerő fiú ellen fölgerjedt atyját engedékenységre intette iránta. Úgy tartja, hogy a családi köteléket nem szakíthatja el semmi a világon:
Te adtad éltét, oh atyám, s ha ellened A rosszaságok rosszaságát tette bár, Mégsem szabad hasonló rosszal sújtanod Hagyd őt! gonosz szülöttet s bosszus haragot Ismernek mások is; de a baráti szó Szelíd intése csillapítja lelköket.
Így eseng atyja előtt Polyneikesért; majd meg ehhez fordúl s kérten kéri, hagyja abba Théba ellen szándékolt merényét. Hiába; a bűnös áldozatúl esett balsorsának. Antigone szíve ettől fogva egészen az ő gyászos emlékével telik meg. Nem ismeri, nem említi többé vétkét; csupán azt tudja, hogy neki testvére. Kegyeletének iránta csak életével áldozhat: habozás nélkül szánja rá magát s eltemeti bátyját. Tudja is, mondja is, hogy megsértette vele a törvényt, de nem tehetett másként. Keserve, szerencsétlen helyzetének kínja egész lelkét betölti s elfogúlttá teszi mindenki iránt. Kreon elé vitetve, előbb daczosan hallgat, azután daczos feleleteket ad, mint a ki szinte büszke rá, hogy meghal, de előbb megmondja az igazat. Lázadását a törvény ellen oly érdemnek tekinti, melyért dicséretet mond rá a bölcs. Egyoldalúságát érezteti a kar is, melynek egyetlen szava sincs mentségére. Ő maga azonban oly szentül meg van győződve igazságáról s egyszersmind halálának kikerűlhetetlenségéről, hogy a megindítást, engesztelést, kérlelést meg sem kisérli. Családjának élt, családjáért fog meghalni. Kegyeletének egyoldalúsága mind szűkebb és szűkebb körre szorúl. Elein általában családi érzésének élt: apját sírjához vezette s házának végső romlását meggátolni sietett vissza. Most már Polyneikes lett egyetlen gondolatává, mely minden szeretetét, lelkének egész tartalmát magába olvasztotta. Még a tágabb értelemben vett családi érzés is e további
egyoldalúságába vész. Megfeledkezik mindenről, a mi rajta kívül van: vőlegényéről, Hæmonról, is. Kreon előtt nem ő, hanem Isméne említi. Sőt a holt testvérért igaztalan lesz az élő testvérhez. A mint Isméne habozását észreveszi, ki aggódik vakmerő tervének következésein, méltatlan gúnynyal utasítja el magától. Mintha csak érzéke is elveszett volna ugyanannak az indulatnak másnemű nyilatkozásai iránt, mely a saját lelkét hevíti. Isménéből is a testvérszeretet beszél: nem a hősi és föláldozó, hanem a ragaszkodó és aggodalmas testvérszeretet. Antigone már ezt sem érti; visszautasítja. Egészen elfeledte, hogy egykor, Kolonosban, ő is ép úgy beszélt Polyneikeshez, mint most Isméne hozzá. Mennyit változott azóta! Igaz, hogy végső panaszában megint bizonyos teljességre emelkedik szeretete: emlegeti, hogy szülei tetemét is ő mosta meg s ő fektette sírba; sajnálja a soha nem hallott nászdalt, a soha nem ölelt férjet és gyermekeket. A hitvesi és anyai boldogság vágya! De e keserű búcsú általában ellentétes hősi szilárdságával; a költő, hódolva kora izlésének, inkább kiejti szerepéből, semmint siratatlan küldje halálába. Az élet sajnálatába helyezte az élénkítőt és szívszaggatót, mint S����-M���-G������� megjegyzi. Az élet sajnálata idézi eléje az élet szépségének képeit, ezek között a családi élet különböző mozzanatait.
Ime Antigone szenvedélyének egyoldalúsága, melyet helyzete egész a végletig hajt. Alakját, épen tragikai oldaláról, megvilágíthatja az összehasonlítás egy rokon tárgyú magyar legendával, Bosnyák Zsófiával, melyet T���� dolgozott föl. Sztrecsén ura, a kegyes Zsófia férje, vadúl zugolódik az isten ellen, hogy a dühöngő dögvész sorra ragadja el jobbágyait. Nem marad már sem szántóvető, sem harczos. Im most is a mezőn hét szálas testvér hullott el. A bősz várúr, daczolva a haragos éggel, így kiált:
Gyilkolni a ki tud,
A temetést se bízza másra!
S legyen bár a halott kisérete, Hollók s farkasok éhes serege: Mit bánom én!
De embernek, ki a holtakhoz ér, Halál fején!
Felesége hasztalan kérleli, hogy a hét testvérfiú hadd nyugodjék; hasztalan könyörög neki, hogy inkább fordúljon isten irgalmához. A zord ember haragja csak új átokban tör ki. Őt átkozzák, ha tíz-húsz szolgája harczban elesik mellette, s most annak, a ki ezrivel öldösi a népet, még hálát mondjon? De Zsófia éjnek idején fölkel s eltemeti a halottakat. A jótettek angyala följegyzi áldozatát, férje pedig halálra keresi a parancstörőt. Földúlatja a sírt s kihányatja az eltemetetteket. Egy gonosz szolgája elárúlja neki a titkot s a következő éjjel maga lesbe áll. Zsófia újra megjelenik ásójával; de az ég csodája látatlanná teszi. Harmadszor is hiába kér, hogy hadd porladjon, a mi porladandó. A testeket harmadszor is kivetik s az úrnő megint eltemeti őket. Keresztet is farag nekik s kezén mély sebet ejt. Míg kegyeletes munkáját végzi, az alatt a szolga által bújtogatott várúr, új istencsodájából, ágyában látja sértetlen kézzel feleségét. Hiába ad ki több parancsot; a kereszttel megszentelt föld érczkeménynyé lesz, s kapa, csákány többé nem dúlhatja föl. A kegyes asszony pedig álmot lát: saját ravatalát s százados időközökben sírboltját, koporsóját. Holtteste épen marad a messze jövendőben; a késő nemzedék, virággal hintve be, buzgó éneket mond fölötte:
Az Úr ím a kegyessel Mi nagy csodát teszen: Romlatlan víve által Időn s enyészeten
Látni való, hogy a két monda között sok a rokon vonás. Amott a király, itt a várúr ad oly parancsot, mely az istenfélelembe s a természet törvényébe ütközik. Két nő, Antigone és Zsófia, ellenkezésbe jönnek vele. Az is, ez is holtakat temet, kiket a hatalom arra kárhoztatott, hogy temetetlen maradjanak, s halálos büntetést szabott a kegyetlen parancs áthágóira. Az éj fátyla alatt végzik a temetést. Azonban a görög szűz nem menekűl meg a fölfedezéstől s életével lakol, míg Sztrecsén asszonya nemcsak büntetlen marad, hanem megdicsőűl. Hol van köztük s tetteik közt az a különbség, mely különböző sorsuknak okát adja? Az eltérés igen világos. Zsófia, kegyeletes munkájában, csak fenségesnek mutatkozik, míg
Antigone fenségében egyszersmind gyarlónak. Mert miféle parancsot hág át amaz? Olyat, melynek semmi köze az egyetemeshez, sőt a mely vadúl szembeszáll vele; az önző dühnek esztelen parancsát, a durva önkény szeszélyét, mely istenkáromló és embergyalázó egyaránt. Majdnem alacsony érdekből fakad, mely felbőszűl pusztulásán a neki szolgáló s érte harczoló jobbágyoknak. Csak sért a nélkül, hogy bármit is védelmezne. A balvégzet mindenható forrása ellen nincs ereje, nyomorúlt áldozatain akarja kitölteni dühét. Kreon itélete más természetű. Az árulók ellen védelmezi a haza és istenei érdekét, s egy nagy bűnöst kiván példásan sújtani. Ősi szokásban gyökerezik, s a ki áthágja, nemcsak a merő anyagi hatalommal daczol, hanem megsérti a haza eszméjét is, a melynek megtámadása megtorlást kiván. Sztrecsén urának rendelete bősz fölgerjedésből fakad, melylyel szemben az ellenszegülés inkább szolgálat az egyetemes iránt. E szolgálatot végzi Zsófia: az isteni félelem és emberszeretet öszhangjának áldoz. Fenséges elszánása nem kisebb, mint az Antigonéé, mert az ég megmentő beavatkozásáról, csodájáról mitsem sejthetett; de fölfogása tisztább, érzése öszhangosabb. Nincs benne semmi egyoldalúság, semmi túlzás; még hitvesi szeretetlenség sincs. Férjével szemben, kit gyöngéden óv az istenkisértéstől, nem kihívó, nem daczos; titkon kiengeszteli még az ő bűnét is. Antigone egy eszmének áldozza magát, mely egész valóját elfoglalva tartja. Az ő természeti s Kreon állami törvénye közt megvan az ellentét; de ezt jórészben az ő elfogúlt egyoldalúsága mérgesíti kibékíthetetlenné. Az egyetemesben foglalt két eszmét elszakítva egymástól, egy ép oly örök törvényt sért meg, a milyennek hódol. S������� és S����� glóriával övezve látják csak meghalni, s régi eszthetikájában G������ is e nézet felé hajlik; de a legkitünőbb és legbehatóbb Antigone-magyarázatok egyikének írója, B�����, nagy, majdnem kizáró súlyt fektet tévedésére, tragikai vétségére. Ezek már az okai annak, hogy míg Antigone kínhalállal vesz, Bosnyák Zsófia megdicsőűl. Amaz tragikai alak, ez meg, mint Szent Erzsébet, legendai, tisztán fenséges.
A romlás magva már Antigonénak egyoldalúságában megvan, mely Thébába vezeti vissza; az elszánt makacsság, mely itt hozzá
társúl, csak végletre fejleszti, s menekűlését lehetetlenné teszi. A dacz azonban a gyarlóságnak ugyane formájába tartozó jelenségeknél olykor egészen elenyészőnek látszik. Így magát az egyoldalúságot tünteti föl teljes végzetességében s a romlás közvetetlen okáúl: Arden Enoch, Tennyson tragikai idilljének hőse is. A halász Enoch s felesége, Annie, boldogan élnek egy kis tengerparti révfaluban. Jóllét, egészség, viszontszerelem, gyermekek és tisztes munka: minden áldás házukon nyugszik. De egyszerre csapás köszönt be hozzájok: a férj eltöri lábát s míg tétlenűl fekszik, lelkét sötét bú szállja meg. A szegény ember sorsának bizonytalansága, övéinek védtelensége baj, szerencsétlenség, pusztulás ellen. Képzeletét rémképek izgatják és segítségen töri fejét. Bizonytalan vakmerőséggel akar nekik biztos jövőt szerezni, a maga veszélyével venni elejét az őket fenyegető veszedelemnek. Alkalom kinálkozván rá, elhatározza, hogy távol világrészbe indúló hajóra száll, hogy onnan gazdagon térjen haza. A szegény Annie ellenzi a tervet, nem daczczal csak kéréssel és szomorú csókokkal.
Eseng, könyörg, ha ő és gyermeki Szivén feküsznek, el ne hagyja őt. De mert nem önmagára, csak reá S kicsinyjeire gondol, hjába esd, S Enoch borongva, készülődni kezd.
El is megy; de épen ellenkezőjét éri el annak, a mit akart. Családját hosszú nyomornak, nagy szenvedéseknek teszi ki, a maga boldogságát pedig mindörökre eltemeti. A hajótörésből egy puszta szigetre vetődve, ott hosszú és kínos évekig várva szabadúlását, csak sokára kerűl haza. Annie már új család anyja lett, nagy küzdés után, de nemes elhatározásból. A visszatért nem ismerteti meg magát: dolgozva, imádkozva, szent szándékából erőt merítve, küzdi végig az élet harczát. Nemes, hű léleknek nevezi a költő s meséje minden mozzanatában annak is festi. Mi volt forrása boldogtalanságának, miben rejlik életének tragikuma? Minden áldozatra készen szerette övéit; de bús tépelődései, komor képzelgése, a sors csapása az életnek egyoldalú fölfogására,
szeretetének egyoldalú törekvésére vezették. Csak a jövő biztosságára, a vagyon áldására gondolva, elfeledkezett róla, hogy a jelenlevő szeretet is támasz és védelem. A gyámoltalanoknak nemcsak reményre, de gyámolra is szükségök van. Egyoldalú fölfogással kereste boldogságukat, s míg értök fáradott, minden bajnak, veszélynek, nyomornak kitéve hagyta őket. A minek maga oly bátran eléje ment, nem lett volna szabad védtelen övéit is kitennie. Mikor a szeretteiért küzdő egyik kar kötelességét teljesítette, elmulasztotta a gyámoltalanok védelmére, ápolására hivatott másik kar kötelességét. Ezen bukott meg, nem mértéktelenség, dacz vagy makacsság okából, hanem tisztán az egyoldalúság gyarlósága miatt.
Némileg ellentétes képet nyújt G����� Tassojának egyoldalúsága. Azok közé a jelenségek közé tartozik, a hol az ellenállás által ingerelt egyoldalúság kiválóan a dacznak, makacsságnak, heves elragadtatásnak képét mutatja. Összeütközései is inkább ezekből látszanak származni, mint magából az egyoldalúságból, jóllehet csak erre vezethetők vissza. Alfonz herczeg ferrarai udvarának kényeztetett kegyencze a költő, ki azonban csak félig él a földön, félig álomvilágában. S�������, a dráma bírálatában, szépen csoportosítja a történeti Tassonak azokat a jellemvonásait, melyekből képét G����� megalkotta: «Könnyen lobot vető enthuziazmusa az életben rendkívül izgatható érzékenységnek mutatkozott; stíljének csöndes, szűzi méltósága félénk szerénységűl, művészi büszkeséggel vegyűlve; költeményei hangjában a magasztos komolyság pedig mint magányosságra és elmélkedésre való hajlam. Ezekhez járúlt még az emberek iránt szeszélyes és sötét bizalmatlanság, mely örökké gyötörte őt s nyugtalan menekvőként üldözte át az életen.» E vonásokat mind fölhaszhasználta G����� s belőlök alkotta költőjét, e képzelődő és érzékeny, nemes és ideges, hiú és büszke alakot. Csupa képzelet és álmodozás, s finom izgékonyságában nincs semmi ereje uralkodni magán. Csak költői szeszélye, féltékeny önérzete s heves vérmérséklete vezeti. Az életfelfogás egyoldalúságát képviseli; de a ferrarai udvar, mely büszke lángeszére, még így is dédelgeti és rontja. A kényeztetés, melyben hiúsága és gyöngéi részesűltek, még
jobban megzavarja fölfogását az életről, a lángész jogáról és hatalmáról. Az életnek ez egyoldalú, ideális fölfogása, a lángész korlátlan szabadságával, természetesen összeütközik a valóság rendjével. Tasso teljesen elveszti mérsékletét, mikor Antonióban saját ellentétével tűz össze, a gyakorlati érdemekre támaszkodó, komoly és megfontolt államférfival. A világfi lenéző gúnynyal ingerli őt, s a költő, mindenről megfeledkezve, kardot ránt ellene. G����� drámája ellen sok kifogást lehet tenni, talán még azt is, hogy: nem dráma. A küzdő ellentétek hatása egymásra, a világ és élet befolyása rájok, Tasso kedélyének átalakúlása: mindez nem igazi cselekvényben, hanem csak dialogokban jut kifejezésre. Egyebet is vethetni ellene; de nem tarthatjuk találónak B�������� megjegyzését, hogy a költő, drámája második felében, Tasso jellemét mind jobban elaprózza rá fordított túlságos gondjával, s gyönge oldalát nagyon is rikító színbe öltöztetvén, új Tassot vezet elénk. E beteg képzeletű, álmaiba merűlt, bizalmatlan és meghasonlott ember nem új Tasso, csak az, a kivé a régi, a szenvedély fejlődésének törvénye szerint s a viszonyok hatása alatt, szükségkép átalakúlt. Lelkének minden tartalékját elvesztvén, szemei végkép elhomályosodván a valóság iránt: egyoldalúsága végletessé lett. A Leonórának tett vallomással félszegsége elérte tetőpontját, s a fájdalom tisztító sajgása közt, Antonio barátságával, kiengesztelődik. A herczegné így jellemzi viszonyukat:
Két férfi ők, már régen érezém, Kik ellenek, csupán mert kettejökből A természet nem egyet alkotott. Ha észre térhetnének önjavukból, Barátul állva egymás oldalán, Együtt mennének át az életen, Erő, szerencse s jókedvtől kisérve.
Végűl észre térnek. Tasso alapjában nem lesz mássá, a darab végén ép oly kevéssé, mint annak második felében. De barátsága, Antonio iránt, egyoldalúságának legalább elismerését s ezzel eszmei föladását jelenti. E reflexióban keresett megoldás drámai értéke természetesen kérdéses. Gondoljunk arra, a mit G����� Z�����hez
írt: «Nem születtem tragédia-költőnek, mert természetem engesztelékeny. Azért nem is érdekel a a tisztán tragikus bukás, mely már eredetileg kiengesztelhetetlen».
Cordelia is egyoldalúságának, egyoldalú igazsága makacs védelmének áldozata. Szavakban fukar, kimért igazságszeretét mereven állítja atyja elé, ki az aggkornak követelő szeszélyével, támogatásra és teljes szeretetre szorúló gyöngeségével föltétlen odaadást, meleg ragaszkodást kiván. Öreg már: tetteket várni a szeretet bizonyságaúl, ki tudja, van-e ideje; hallani akarja legalább, a mi jól esik szívének. Meglepi az öregkor hangulata, mely a szeretetet többre becsűli a hatalomnál; midőn erről lemond, legalább cserében akarja adni amazért. Országát elosztja, hogy osztatlanúl bírja gyermekei szívét. Ő legyen az egyetlen előttök, csupán csak őt szeressék; nem kivánhatja-e, mikor atyjok s koronát ad nekik érte? E hangulata nem állandó; mikor csalódik a szeretetben s a durva önzés elveti előtte álarczát, lelke természetesen visszacsap az elfecsérelt hatalom vágyába. Királysága legalább az övé volt, s most ime, semmije sincsen. A lovaggal való beszélgetése közben a hálátlanság izgatja föl s juttatja eszébe újra fölvenni tisztét, melyet gonosz leányai örökre letettnek gondolnak. Háza romlásában jó leányának, Cordeliának, is van része. Szereti atyját; de iránta való szeretete kedveért sem tudja megtagadni tartózkodását, nemesen alárendelni igazságát egy szeszélynek. Lear dúsabb harmadot kinál neki testvéreinél; csak szavát vegye. Neki azonban csupán egy rövid szava van, hogy: semmit nem mond. Szeret tiszte szerint, sem többé, sem kevésbbé; ha csupán őt szeretné, nem menne férjhez. Midőn atyja szívtelennek nevezi, akkor sem ragadja el a gyermeki szívnek oly természetes fölindulása; majdnem hideg daczczal igazítja meg Leart:
Őszinte csak, mylord.
Nemcsak hizelegni nem tud, midőn ez a hizelgés szinte kötelesség és okosság is lenne, hanem igazán gyöngéd szava sincs. Nem veti magát atyja keblére, hogy visszatartsa őrűlt tettétől, bármint vágynék jobb helyre tenni őt testvéreinek megdicsért szívénél. A mily
mereven ragaszkodik a szigorú igazsághoz, oly rendületlenül bízik is benne. Búcsúja hideg és szilárd:
Mit a csel rejt, kifejti az idő A képmutató kudarczot vall utóbb Szerencse véletek
Gondoljuk meg, mily izgató hatások között ejti e nyugodt szavakat: atyjának megrendítő átka s romlásának félelmes sejtése a gonosz leányok között; másfelől a frank király megható nagylelkűsége, ki koldúsan, kitagadva emeli trónjára. Elmegy választottjával. Még melegebb szó gyanánt is átallja ajkaira venni azt, a miről, meggyőződése szerint, egy egész életnek kell beszélni. Ez életet éli is; nem késik megjelenni, midőn a szeretet tettet kiván; de már nem engesztelheti ki vele a végzetet, melyet egykor egy szavával elháríthatott volna. Gyermeki kötelességének egyoldalú fölfogása gátolja benne, hogy e kötelességet, bármily mélyen érzi, egész teljességében, szívvel és szóval, gyakorolja is. Makacsságával megsérti az eszmét, melyet szolgálnia kellene s romlásba dönti általa nemcsak magát, hanem szeretteit is.
Az egyoldalúság körébe tartoznak legnagyobb részt azok a törekvések, melyeket V������ az erkölcsi összeütközés neve alá foglal. Érti alatta egyenlően jogosúlt elvek küzdelmét, melyeknek azonban az eszme egységébe, az egyetemesbe, kellene foglaltatniok. Ide sorozza különösen a forradalmak jelenségeit, melyeket kiváló mértékben tragikusoknak tart. Hőseik nagyobbára az ifjúság hevével, a gondolat és tett erejével, a külső és belső erő fenséges szövetségében állanak előttünk. Új rend alapítására törekedvén, az emberi haladás szellemét képviselvén, nem tisztelik a létezőnek, fennállónak tekintélyét, mely szintén szent és szükségszerű. Ilyenek Sokrates, Bresciai Arnold, Danton és a többiek. Ide tartoznék Dózsa is, ha a vele szemben álló rendet nem tünteti föl J���� oly egészen nyomorúltnak, a pusztulásra oly teljesen megértnek, melynek a fenmaradásra többé semmi joga nincs. Ez a rend nem rend többé; az összesség érdekét semmi szempontból nem védi, meggyőződését nem fejezi ki; az egyetemesnek már
semmi köze hozzá. Valóban a történet Dózsája, a milyennek e népvezért az újabb kutatások fölmutatják, sokkal tragikusabb, mint a költőé. «Általában tévedés, írja V������, a forradalmat bukásában, mint teljesen vétlent gyászolni; a fennállónak is megvan a maga joga. Középen fekszik az igazság. De a közvetítők épen nem tragikusok. Cselekedni nem lehet fölforgatás nélkül; a közvetítő által azonban egyszerűen semmi sem történik. Mikor a határozott akarat vétkessé lett, csak a távol jövő hozza meg a hatásos közvetítést.
Antigonénak nem lehet testvérét el is temetnie, meg nem is; Kreonnak sem: kiadnia egy törvényt s aztán nem hajtania végre. De kilátás lehet rá, hogy a véres tanúlság jövendő esetekben meghozza gyümölcsét; az összeütközést eleve kerűlő mérsékletet s az állam humanitását».
A szenvedély következetlensége.
A mint a kiválóság mutatkozhatik gyarlónak makacsságában, úgy mutatkozhatik az ellenkező véglet, a következetlenség, által is. A szenvedélyes törekvés sikerének egyik fő biztosítéka következetessége, mely, magát soha meg nem tagadva, magával ellenkezésbe nem kerűlve, egyenesen tör kitűzött czélja felé. Magában a következetességben rendkívül ható erő rejlik. Ha ellenben a szenvedély nem marad meg ingadozás nélkül, rendületlenül, választott útján; ha ellenkezésbe jut magával, s a világ ellen folytatott küzdelmében egy belső harcz nyomai is nyilvánosságra jönnek: a következetlenség gyarlósága előtt állunk. Az ilyen szenvedély már csak megosztott erővel viaskodhatik, vagy önmaga segít megrontani a saját munkáját. Mikép? A lelkesedéssel képviselt eszme ellen, melynek szolgálatára szánta magát, bénítólag támad fel a természeti, az érzéki ember; vagy az érzékibb szenvedély erőkifejtését teszi kétkedővé, akadozóvá a későn ébredező megfontolás. Amott magában a következetlenségben fekszik a gyarlóság; emitt pedig rendesen ennél fogva buktatja meg az egyént a mértéktelensége vagy egyoldalúsága által megsértett egyetemes. Ez az Achilles-sarok, melyen a sebet kapja s a melynél fogva a végzet martalékává lesz. Nem kell bővebben magyaráznunk, hogy e következetlenség a jellem teljességének, egészének szempontjából már nem az: a következetlenséget képviselő indulatnak, tettnek csirája, lehetősége eleitől fogva megvolt a lélekben. E�����nek a parasztlázadásról írt regényéből való e tanúlságos idézet: «A szenvedély ott, hol állandóság kivántatik, nem elégséges soha. Mint a golyó, melyet az ágyú magasra vetett, végre,
önsúlyától levonva, földre esik: úgy, ha az indulat valakit pillanatokra elragadott is, nem maradhat senki következetes természete ellen.»
A���� J���� Eteléje a jóslat által kijelölt hős, kinek a hármas hét szám betöltével átadatik Isten kardja, hogy megbírja vele mind az egész földet. Testi, lelki tulajdonainál fogva méltónak mutatkozik rá. Akarata erős, karja győzhetetlen, szive fejedelmi, szeretete mély, szava szent és becsvágya végtelen. Az egész hún nép benne látja azt, ki az idők teljességében megigértetett, s ő is magában érzi a megigértet. De nagy lelkéhez méltón, gondolni sem gondol rá, hogy ne igaz úton jusson méltó helyére. Mikor bátyja megosztja vele a királyságot, hogy legyen Etele a kard, míg ő a pálcza marad, lelke tele van nemes eltökéléssel, hogy az egyezséget megállja. Buda esküjére ő is esküvel felel:
Hadak ura, Isten, az enyém is halljad! Soha te ne segélj, ha cselekszem ollyat, Hogy e mai szertől valaha elállok, Jó Buda bátyámmal visszát ha csinálok.
Az áldozó oltár tüzéből felcsapó «vérharagos lángok» rosszat jelentenek: a végzet kerekét nem lehet megállítani. A két hős nehezen állhat egymás oldalán. Buda maga is érzi, hogy nem született uralkodónak, kénytelen támaszt keresni s mégis király akar maradni; vele szemben a főnek termett Etele, ki tudja, hogy csak bátyjának köszöni fejedelemségét, de érzi azt is, hogy igazi hatalmának épen ő áll útjában. Mindegyikök érzi, hogy ereje részben a másikon alapszik, s ez féltékenyekké teszi őket egymásra. Nem férhetnek össze. G����� röviden és találóan jellemzi viszonyukat: «Detre bizalmas suttogásai, a két királyné versengése, a politikai viszonyok, a görög követség, a nép hangulata mind arra szolgálnak, hogy egymás ellen ingereljék a két hőst, s ha egyik erőt vesz magán, a másikat épen akkor ragadja el indulata. Budát alázza Etele növekvő népszerűsége s őszinte férfiassága. Etelét sérti Buda gyanakodása s tettvágya szenved a türelem fékén.» Minden arra látszik munkálni, hogy Etelét mértéktelenségre ragadja. A harczos húnok őt tekintik valódi fejedelmöknek, s a keleti császár követei is,
az ő kezében tudván a kard hatalmát, csupán vele kivánnak egyezkedni, föl sem véve bátyját. Buda haragra lobban s szemrehányásain Etele is fölháborodik. De legyőzi magát s másnap jó szóval és a görög ajándék megosztásával kiengeszteli testvérét. Buda gyanakvó szivét azonban a tövis újra meg újra sérti: a hadgyakorlaton Etele ereje, a vezetése alatt álló sereg, megfélemlítő alakban mutatkozik előtte. Öcscse lelkét pedig meg-meglepi a hatalom teljességének kisértése. A mátrai vadászaton már a bölényhad martalékául látja a lova alá kerűlt Budát, ha egy perczig is késik szabadításával. Csak tétlenül kellene maradnia: s az egész hún birodalomnak ő az ura. Feltűnik előtte a kísértő Ármány Budának csonka fejével: nem volna-e jobb bátyját halálra hagynia? De csak mint a nap előtt elmenő holló, úgy röppent el az árnyék Etele igaz lelkén. Egy kopjadöféssel leszúrja a bikát s örves buzogányával visszaveri az egész csordát: Budát megmenti. Sorsának e jelenet képezi fordulóját, mely a nagylelkű igaz hősiség magaslatán mutatja. Az öreg Isten látván, hogy győztes akarattal győzi magát s megharczol a riadó haraggal: méltónak tartja rá, hogy mindeneket meggyőzzön. A Világfáján meg van írva:
Úr az egész földön, ha ez egy hibáján.
Íme úrnak mutatja magát ezen is: az Isten felövezi kardjával. E kard tehát vad indulatán vett győzelmének jutalma, a lelke nemesebb felébe vetett bizodalom jele. Hozzá van kötve a világbírás; de azzal a feltétellel, hogy Etele mindig meg tudja bírni magát és következetes lesz a saját nagyságához. Megőrizve önuralmát, biztos kézzel fogja tartani szenvedélyeinek fékét. De Etele nem marad fenségében következetes. A mint a csoda-kard birtokába jut, elragadja szerencséje és indulata. Az asszonyok új czivódását elég oknak tartja, hogy elszakadjon testvérétől. Buda királylyal ezután nincsen köze semmi, ő majd otthon ura lesz jó hadának, s Buda is parancsol annak, a kinek tud. Íme már megtörte a kötést, megszegte a fogadást. Rálépett a tragikai tévedés lejtőjére, melyen nem állhat meg többé. Nem is áll meg egészen a végzetnek vakmerő kihivásáig. A Szávamenti harczból győztesen térve vissza, az
áskálódó, pártot szerző, várat építő Budát meggyilkolja. Az Isten kardját, melylyel ez ellene áll, kiüti kezéből s a magáét hátúl mellig mártja a megfutamodóba. Igaztalanság, ármány, ingerlő kihivás s a harcz heve ragadták gyilkosságra; de csak elragadták. Megsérti vele saját fenségét, mely következetlenségében gyarló oldaláról áll előttünk. Kihívja Gyöngyvér átkát s a végzetet a maga, családja és nemzete jövője ellen, mert megsérti az Istent, ki csak önlegyőzése jutalmául ajándékozta meg kardjával. Jól látva egéből a gyilkosságot, szeme könnyet ejtett a húnokért:
Jaj! betelik, mondá, már íme betelnek –Népe jövendői számlálva Etelnek. Isten, alant földjén, ő lehetett volna; De nagy ily kisértés földi halandóra –Szólt; és megnyugodott, könnyét letörölvén: Hogy örök állandó amaz erős törvény.
A nagy epikai trilogia, mely Buda halálával tragédiának indúlt, befejezetlen maradt. Csak az összeütközést látjuk, a lakolást, befejezést magában a mondában kell keresnünk. Meg is találhatjuk. A szörnyű katasztrófa nem Etelének önérzetes kijelentésére utal vissza, hogy: Budát szigorúan, de igazán büntette; hanem Gyöngyvér kétségbeesett átkozódására: veszszen ki Etele magostul Krimhilda fiában. Nem a hatalmas király föllengő lelkesűlése válik be: hogy a világ végeig kimenjen a húnok birodalma, neve, dicsősége; hanem az Isten szava, mely megszámláltnak mondja jövendőjét. A következetlenségbe esett szenvedély játszotta el, s be kell telnie rajta az örök törvénynek, mely az egyetemes ellen támadók sorsát megszabja. A költő is ebben az irányban kivánta meséjét tovább fejleszteni. A második rész elejéről maradt töredék a jóslaton kezdődik, «mely szerint Buda haláláért megjósoltatik Etelének, hogy nagy birodalma az ő halála után elenyészik.»
Etele kiválósága egy isteni küldetés betöltésére hivatott. Testi és lelki alkotása megfelel neki. De egy végzetes órában megzavarodik valójának öszhangja, következetlenné lesz saját fenségéhez s elköveti a tragikai tévedést. S������� Orleansi Szűzének már
hivatása is következetlenség magához. A természet arra alkotta, hogy kebelén maradjon s kebelét megnyissa. Élnie kellene nyájai között, a mezők csendjében, tisztelve atyját, meghallgatva derék kérője szavát, enyhet és boldogságot árasztva maga körül. De a vészes idők forgatagja magával ragadja. Szivét meghatja hazájának nyomora, melyet az angol hódító jármába vert. Senki sem reméli többé szabadulását; csak ő hisz még csodában, hogy: egy fehér galamb sasként fog a keselyűkre csapni, kik a haza testét szaggatják. A dicsőség hazájáét, a legszebbet a nap alatt, az országok paradicsomát, melyet isten szemefénye gyanánt szeret. Bertrandtól sisakját kéri; a fehér galamb ő maga. Lelkének, mely mindig az istennel, az isteni segítség szükségével foglalkozott, látása volt. Az Úr, ki mindig szerette a pásztorokat, megjelent neki s őt választotta ki csodatevő hatalma eszközévé: ragadjon fegyvert, harczoljon irgalom nélkül és meg fogja menteni királyát. A csodák lelkével ihleti, föléje emeli a természetnek; de viszont azt kivánja tőle, hogy ő is emelkedjék föléje s tagadja meg. Szivét ne érje férfi szerelme, hiú gyönyörnek bűnös lángja. Johanna felmagasztosúlva útnak indúl. Hősisége lelket önt a franczia seregbe s betölti hivatását. Fogadásához nem lesz hűtelen. A mint visszautasította otthon falusi kérőjének kezét, úgy válaszol a táborban Dunois és Lahire ajánlatára is. Hiába inti az érsek, hogy: a nő a férfi szerető társául született; ő egy más világ küldötte, melyen nem uralkodnak a természet törvényei. A király is hasztalan veti magát közbe:
Ti kis hitűk, ti elvakúlt szivűek!
Imé az ég fensége vesz körűl, Feltárva néktek csodatitkait:
S ti asszonyt láttok bennem, semmi mást Szabad-e nőnek harczi mezt felöltni S fegyverrel törni férfiak közé?
Jaj énnekem, ha isten bosszuló Kardját kezembe’ hordozván, szivem Egy földi emberért dobbanna meg Jobb lett vón akkor soha sem születnem!
Hát szót se többé, hogyha szellemem Fölingerelve, sértni nem kivánod.
A férfi-szem, ha vágyva rám esik, már Iszony nekem s szentségtelen merény.
Nemcsak a szerelmet, az érzés virágát, nem engedi meggyökerezni szivében, hanem megtagadja a női lélek egész gyöngéd valóját. Nem is ismeri nőnek magát; pánczélja szívet nem takar. Mint a halál angyala, irgalmatlanul, kardján pusztulást hordva, szágúldja be a csatamezőket. Nem könyörűl senkin, a kit britt anya szűlt. A wallisi Montgomery is csak egy pillanatra állítja meg; nem tartóztatja föl a pokol küldötte, a fekete lovag sem. A fenséges erőnek oly magas és hideg körébe emelkedett nő, hogy már szinte nem is tetszik annak: kiválóságában fekszik gyarlósága. Mert e rajongó és kegyetlen hősiség mily következetlennek mutatkozik egyszersmind, midőn nemcsak a nőt, a női hivatást általában, állíthatjuk vele szembe, hanem ha a természet gyermekére gondolunk, kinek egy kis családi tűzhelyet kellett volna édessé tennie. Melegítenie a szikrával, melytől most egy ország lángba borúlt. A vallás szava is, az érsek ajakán, ilyennek mutatja őt. De ő nem azt hiszi hivatásának, a mit az emberek általán; közvetetlen kijelentésnek lett részesévé, mely megszabadította a természet korlátaitól. Azonban valósággal megszabadította-e? Ha szíve csak egy perczre is gyönge lenne, mily szörnyű boszút fog rajta állani a megtagadott és megsértett természet. Igen; ne tekintsük megszegett fogadásának miszticizmusát, csak az egyetemest, mely a természeti szükségszerűséggel ellene fordúl. Hős ellensége, az angol Lionel, kit meg kellene ölnie, a csata hevében megigézi. Végzetes szerelmében a természet érvényesűl, mely azonban ránézve egy új következetlenség. Rajongása az volt a természet irányában, a természetnek elemi erővel ébredt hatalma pedig újra az rajongása irányában. Amabban női hivatását, ebben isteni küldetését tagadja meg. Egyetlen pillantással talál szivébe útat a földi érzelem, elejti kardját, zászlaját. Lionel megél, de neki vége.
B���� és mindazok a műbírálók, kik e regényes színmű epikai machináját drámai motivumokra kivánják visszavinni, Johanna szerelmében nem a tragikai vétséget látják, hanem kezdetét bünhődésének. Mintegy véres álomból ébred a természet valóságára. Egyszerre közönséges asszonynyá lett; kimondhatatlan kínja, hogy nem lehet többé igazán az. Pestises közelségétől,
érintése szennyétől még Sorel Ágnest, a király szeretőjét, is félti. Kettőnek érzi magát; de egyik lénye lehetetlenné teszi a másikat. A mint előbb szivében nem hitt, most látásában kétkedik. Az-e a bűne, hogy ölt, vagy az, hogy megszünt ölni? Nem tudja, csak a bűntudat gyötrelmét érzi. Ez zárja le ajakát atyjának, az öreg Thibautnak, rettentő vádjára, hogy lelkét az ördögnek adta el. Mért nem utasítja vissza? S������ J����� így felel e kérdésre: «Johanna állítólag azért hallgat, mert atyja vádló szavát büntetésnek tekinti, a mért érzésével áthágta a szentek parancsát; valósággal azonban azért, mert magába kezd szállani, kétkedés férkezik lelkébe. A váratlan, de előre érzett vád ez okból sújtja le, a nélkül, hogy egészen értené. Felmagasztosúlt hangulatának egységét elvesztette. Iszonyodás fogja el a vértől, melyet kiontott, s a melyet nem lett volna szabad ontania, mert asszony volt; és hogy csakugyan asszony, most tudja. Mint isten választott szentje a szűz egészen kötelességébe veszett; nem érezte lényének belső ellenmondását, melyet atyja helyesen felismert. Mint szerető nő, elijedve jut tudatára démoni kettős természetének, s az atyaátok csak külső kifejezése a magától való iszonyodásnak, melyet érez.» Egyik következetlensége, midőn kardot övezett, kiragadta valójából; a másik visszautasítaná hozzá, de akkor, midőn nem nyughatik meg többé benne. Belső öszhangja felbomlott, készen van a romlásra. Még egyszer diadalra vezeti végzete; de e diadalban aztán el is gázolja.
Brutust forradalomba sodorja sorsa. Eszményi álmai behálózzák borongó lelkét: sokféle szenvedély üldi egy kor óta, melyeknek nevet, hangot adni nem akar. Cassius fondor heve s zaklató szenvedélye tettre ragadják bús tépelődését. Elhatározza, hogy Cæsarnak meg kell halnia, mert nagyravágyó s a közszabadság ellene. Az ő döntő szava teszi lehetővé a merény sikerét; az ő részvéte önt reményt az elégületlenekbe, mert nevéhez Róma nagy véleménynyel van. Tiszta és őszinte, hős és gyöngéd, emberszerető és kíméletes, az igazság barátja mindenekfölött, a Stoa bölcs tanítványa. Szenvedély emészti hazája szabadságának hanyatlásán; de nem látja egyfelől e közt s az erkölcsök sülyedése közt a szükségszerű összefüggést, más felől szenvedélye épen nem forradalmi természetű. Nincs meg benne sem a kíméletlen
határozottság, sem a minden eszközzel czélra törekvés, a közjóért az egyesek érdekének kész feláldozása. Sem a katona kérlelhetetlensége, sem az államférfi mélyebb felfogása. Nemcsak Cæsar szárnyalja messze túl ezekre, hanem Cassius is maga mögött hagyja. Mikor Brutus, az emberszerető és makacsul az igazság nyomához tartó bölcselkedő, élére áll a véres mozgalomnak, következetlenségbe kerűl magával. Cassius is jól tudja s ki is fejezi:
Nemes szívű vagy Brutus Ám hiszem, Természeted más útra foghatom, Mint merre hajlik.
Maga Brutus szintén érzi ezt, s mikor a lelkében vívott sötét harczok után, melyekben lényének uralkodó eszméje szenvedett vereséget, a hasadó hajnallal várja az összeesküdteket, így beszél:
Oh összeesküvés! szégyenled-e, Éjjel mutatni vészes arczodat, Hol legszabadabb a rossz? Úgy hol találsz Barlangra nappal, mely elég sötét Szörnyarczodat befödni?
A kézfogás, melylyel szövetségöket megerősítik, Brutus részéről egy végzetes következetlenség megpecsétlése. Cæsart szereti és megöli: az egyetemes nem ismeri összeegyeztethetőnek az ellentéteket, melyeket az ő bölcselkedése kibékít. Az út, melyre lép, szükségképen bukásra vezet. Nemcsak szeretetét tagadja meg Cæsar iránt, hanem saját valóját is. De mégsem tudja annyira legyőzni, hogy újra meg újra elő ne törjön, új meg új következetlenségekbe keverve őt. Olyan pályát, minőnek Brutus a magáét képzeli és akarja, csak elvont gondolkodás konczipiálhat; az élet nem ismeri, nem tűrheti. A következetlenségek e lánczolatából folyik minden csapás, mely vállalatukat éri. A forradalmak élén csak olyan vezető van helyén, ki elhatározásából minden következtetést megvonni kész. Brutus mindig a maga eszményi felfogásával akar uralkodni a realitás fölött. A forradalmi szellem logikája Cassiusban
nyilatkozik következetesen; de Brutus ideális elvein s életnézetén folyvást megtörik. Tragikaibb s tragikumában meghatóbb viszony nem képzelhető, mint az övék. Cassius ösztönszerűleg érzi mindig a helyesebbet, mert lelke természetes útján halad; de Brutus folyvást a nemesebbet s oktalanabbat állítja vele szemben. A hevesebb Cassius fogékony a nemesség iránt, mindig enged Brutus tekintélyének s egymás után követik el a balfogásokat. Cassius szeretné Antoniust, Cæsar veszedelmes barátját is eltenni láb alól; de Brutus ádázatnak mondja a tervet s élni marad az, a ki utóbb nyakukra hág. Sőt megfoghatatlan vaksággal engedi át Antoniusnak Cæsar véres testét s a rostrumot. «Te nem tudod, mit tészsz!» mondja Cassius; Brutus azonban azt gondolja, nagylelkűségök meg fogja hatni s egészen részökre nyeri a népet. Antonius beszédének hatása a romlás útjára kergeti az összeesküdteket. Brutus eszményi emelkedettsége ezen is csak sietteti veszedelmöket. Sardesnél halljuk, hogy inkább a sereg érdekét hanyagolja el, mintsem a föld népét zsarolná. De előtte most a seregnek kellene legelsőnek lennie a világon: ebben van utolsó reményök, ügyök sikerének záloga. Újra nem követi Cassius tanácsát, hogy várják be az ellenséget s ők válaszszák a csatatért; elvonúl Philippihez, hol tragédiájuk véget ér. Brutus utolsó szavai, melyekkel kardjába dül:
Caesar, most légy nyugodt, Nem öltelek meg fél ily örömest!
mily éles világításban mutatják életének nagy következetlenségét. Ennyit S�������� hőséről. Brutusnak két nevezetes mellszobra is van. Az egyik, a római Capitoliumban, antik: egy gondolkodó elmélyedt tekintetével s erőteljessége mellett is kissé méla tartással ábrázolja az utolsó rómait. Egészen az angol költő végzetes alakja. A másik M����� A�����é, a firenzei Bargelloban. E daczosan kiszögellő csontozat, marczona alak, vakmerően hátravetett fej, büszke arczél, sastekintet: ilyen lehetett volna a győztes Brutus.
A következetlenségnek van más szerepe is a tragikumban, mint hogy a gyarlóságnak képezze külön formáját, melyből az összeütközés keletkezik. Társúlhat az a gyarlóságnak egyéb
alakjaihoz, a fejletlenséghez, mértéktelenséghez és egyoldalúsághoz, mint ezeknek visszahatása. Ilyenkor nem a tragikai kitámadásnak és ütközésnek, hanem a lakolásnak, a katasztrófának oka és alkalma. Az egyén nem következetlensége által hívja ki maga ellen az egyetemest, hanem inkább hatalmának tudatára jut benne maga felett. Az érvényesűlésre, a féktelen törekvés elnyomására irányúló egyetemesnek belső nyilatkozása. Az egyén magába száll, emberi rendeltetésének és tévedésének tudatára emelkedik, hogy emberi sorsa is teljesedésbe menjen. Megtisztúlni, megváltatni kiván e magával való következetlenségben, olykor menekvését is remélve, legtöbbször reménytelenül. Mert már tovább ment, hogysem általa a végzetet kiengesztelhetné. Inkább csak eszközévé lesz az lakolásának, melylyel tartozik. Az erejét aczélozó belső öszhang felbomlik általa, szivóssága megajzik, törekvése ingadozik, hite és bizalma megrendűl: ellenének prédájává lesz. Bünhődésének első csapása az, melylyel a szilárd alapot veszti el lábai alól. A bősz Coriolán ellágyúl Volumnia szavaira; de következetlenségében, melylyel az egyetemes felé fordúlva megtagadja rettentő magát, azonnal érzi bukása kikerűlhetetlenségét. A számüzött hős, ki daczos gőggel fordított hátat a városnak, még bízott jövőjében; a megtérő csak a sírt látja már maga előtt. Borgia Lukréczia anyai szeretetében, Gauthier Margit odaadó szerelmében megtisztulásukat keresik; mindketten csak veszedelmöket találják. Mikor Bodban fölébred a testvéri érzés s vele sötét múltjának szégyene, ezzel együtt szállja meg lelkét közel vesztének sejtése is; egy gyöngéd szót kér Maróttól, mert a harcz végével fülébe már nem hat tán semmi hang. A ki látná, hogy Danton, kit a sors viharnak rendelt, tisztítni a világot, megáll a vérpadon szeretni egy kis leánynál, s hogy könny ég szemében: megjósolhatná bukását. E jelenség, az egyetemes irányában érvényesülő következetlenség az, melyre Kemény Zsigmond megjegyzése vonatkozik: Nehéz, de a következetes szörnyalakok festésénél mégis «könnyebben kezelhető eszközlője a drámai érdeknek, midőn egy szörnyeteg vagy nyomorúlt egyén, kit különben gyülöletünk vagy megvetésünk kisérne, valami emberi érzés, valami mozgásba hozott szenvedély által tisztúlni, javúlni, emelkedni kezd; de mikor már részvétünkre igényt tart, föltámad a múlt a






























