https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html

















































































https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
а) m + n сума m і n; б) m − x різниця m і x;
в) 1 : c частка одиниці на c;
г) 2ax добуток 2, a і x;
ґ) 1 2 (x + y)
д) 2 3 (x − 2) добуток
2. Які із записів є виразами?
А. 2аx – х2 .
3. Який з виразів є виразом зі змінною?
А. 37а − 2,4.
4. Знайди значення
2х − 2 = 4;
2х = 4 + 2;
2х = 6;
х = 3.
5. Довжини
картини;
2(a + b) − периметр рамки картини; a + b − напівпериметр.
6.
a) 5 + 7 = 12;
б) 8 – (–3) : 2 = –11 : 2 = –5,5;
в) 15 · (–4) = –60;
г) 12 : 4 = 3.
8. Запиши
0,5; б) різницю чисел 38 і 7,6;
a) 7,4 • 0,5 • 2 = 74; б) 3,8 – 7,6 = 31,4; в) (38 + 12) • (38 – 12) = 50 • 26 = 130.
9. Запиши суму, різницю,

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
г) (x + y) : 2; ґ) (а − х) : 2;
д) 2 · (а · х).
11. Знайдіть значення виразу:
а) 0,5х − 3, якщо х = 10, то 0,5 · 10 − 3 = 5 − 3 = 2;
б) х + 97, якщо х = −10, то −10 + 9,7 = 0,3;
в) х(x + 2,4), якщо х = 0,6, то 0,6 · (0,6 + 2,4) = 0,6 · 3 = 1,8;
г) 3х(5 − x), якщо х = −2,5, то 3 · (−2,5) · (5 + 2,5) = −7,5 · 7,5 = 56,25.
12. Знайдіть значення виразу: а) а + с − 3, якщо а = 2 і с = 7,5, то 2 + 7,5 − 3 = 6,5; б) 2х − 3z + 1, якщо х = 1 і z = 1 3, то 2 ·
2ху(х − у), якщо х = 2 і у = 5, то 2 ·
а) а · 10 + 6;
б) 5 · 10 + b;
в) m · 10 + n;
г) с · 100 + b · 10 + a.

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
г) (0,02 · 0,5 + 7,904 : 0,38 − 21 : 101 2) ·2,9 = (0,010 + 20,8 − 21 1 · 2 21) · 2,9 = = (20,81 − 2) · 2,9 = 18,81 · 2,9 = 54,549.
19. Знайдіть значення виразу: а) 3,18 − (0,13 + 4,27 : 1,4) = 3,18 − (0,13 + 3,05) = 3,18 − 3,18 = 0; б) 5,9 − (6,3 : 3,5 5,6) = 5,9 − (1,8 − 5,6) = 5,9 + 3,8 = 9,7; в) (1 5 + 1 10 + 12 2 15) : 1 15 = ( 3 10 + 12 2 15) : 1 15 = (12 + 9 + 4 30 ) : 1 15 = 1213 30 : 1 15 = 373 · 15 30 1 = 186,5; г) (7,344 : 0,36 + 161 4 : 5 – 0,5 · 0,2) · 0,08 = (20,4 + 65 1 4 · 5 − 0,1) · 0,08 = = (20,4 + 13 5 0,1) · 0,08 = (20,4 + 3,25 − 0,1) · 0,08 = (23,65 − 0,1) · 0,08 = 1,884. 20. Для яких значень х
а) 3(х + 1) − 7 = 2х − 9;
3х + 3 − 7 = 2х − 9;
3х − 4 = 2х − 9;
3х − 2х = −9 + 4;
х = −5;
б) 2x + 5x = 2(x + 5);
7x = 2x + 10;
7x – 2x = 10;
5x = 10; x = 2.
в) 0,5х + 2(7 − х) = 1,5х − 5(х + 2);
0,5х + 14 − 2х = 1,5х − 5х − 10;
−1,5х + 14 = −3,5х − 10;
3,5х − 1,5х = −14 − 10;
2х = −24; х = −12.
21. Для
а) 8 − 2(3 − х) = 5 − 3(3 − 2х);
8 − 6 + 2х = 5 − 9 + 6х; 2 + 2х = −4 + 6x; 2x – 6x = −4 – 2; −4x = −6; x = 1,5;
б) 1 + 3(x – 5) = (1 + 3x) – 5x; 1 + 3x – 15 = 1 + 3x – 5x;
3x – 14 = 3x + 1;
3x – 14 = 1 – 2x; 3x + 2x = 15;
5x = 15; x = 3.
в) 2 3 х − 7 9 + 5 = х − 1 6 (2 − 6х);

2 3 х − 7 9 + 5 = х; 2 3 х – 2x + = 7 9 х – 5 –1 3; 4 3 x = 41 9 ; x = − 41 9 : ( 4 3); x = 41
гривнях;
а) 1000x; б) 100p; в) 1000v.
24.
а) 5k + 900x.
б) (a + (a – 10)) · 2 = (2a – 10) · 2 = 4a –
б)
а) a · S (грн);
б) (n + k) · 0,95a; в) p – 9,5a.
26. Напишіть
а) а + 0,1п + 0,01т; б) 10с + а + 0,1п + 0,01т.
+ (100с + 10b + а) = 101а + 20b + 101с = 101(а + с) + 20b.
якщо a = −5, b − c = 4, то а) 3а + 2b − 2c = 3а + 2(b − c) = 3 · (−5) + 2 · 4 = −15 + 8 = −7; б) ac ab 10 = a(���� c) 10 = 5 4 10 = 2;

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
30.
непарного;
а) 5n, n натуральне число; б) 5 · 2n = 10n; в) 5(2n + 1); г) 15n.
31. Визначте периметри многокутників,
1) P = 2(a + b − c);
2) P = 2a + 2b = 2(a + b); 3) P = 2(a + b).
32. Розв’яжіть рівняння:
а) (2х + 3) + (4х − 8) = 37;
2х + 3 + 4х − 8 = 37;
6х − 5 = 37;
6х = 37 + 5;
6х = 42;
х = 42 : 6;
х = 7;
в) 0,7 + х − (−0,7 + 4х) = −37;
0,7 + х + 0,7 − 4х = −37;
−3х = −37 − 1,4;
−3х = −38,4;
х = −38,4 : (−3);
х = 12,8;
x + 2x = 120
3x = 120
x = 40 (н.)
2 · 40 = 80 (н.)
1 + 2 + 4 + 8 = 15;
1 + 2 + 6 + 3 + 9 + 18 = 39;
1 + 2 + 4 + 7 + 14 + 28 = 56;
1 + 2 + 19 + 38 = 60.

б) 5 − 3z − (3 − 4z) = 42; 5 − 3z − 3 + 4z = 42; z + 2 = 42; z = 42 − 2; z = 40;
г) −7,2 − (3,6 − 4,5х) = 2,7х; −7,2 − 3,6 + 4,5х = 2,7х;
−10,8 + 4,5х = 2,7х; 4,5х − 2,7х = 10,8; 1,8х = 10,8;
х = 6.
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
35. Чи тотожні вирази:
а) 2a + a і 3a так, тотожні;
б) х + 2x − 3x і 0 так, тотожні;
в) 8с − 3с і 5с так, тотожні;
г) aх + ах + ах і 3ах так, тотожні;
ґ) 7xy − 2x і 5y ні, не тотожні;
д) −3с + 9 і 9 − 3с так, тотожні;
е) p2p і p3 ні, не тотожні;
є) x + x2 + x3 + x4 і x5 ні, не тотожні;
ж) а − с і с − а ні, не тотожні;
з) а2 і (−a)2 ні, не тотожні;
и) 4а + p і 5ар ні, не тотожні;
і) x − 2а і 2а + х так, тотожні.
36. Який із виразів не тотожний виразу 2x − y?
Б. 4(y − 2x) + 10x − 5y
37. Якому з виразів тотожно дорівнює вираз 3(2a + c) − 3с?
Б. 6a
38. Чи є рівність (m + 2) − (m − 2) = 0 тотожністю?
(m + 2) (m – 2) = m + 2 – m + 2 = 4.
4 = 0.
Отже, дана рівність не є тотожністю.
39. Наведи контрприклад, щоб довести, що рівність (c − 2)3 = c3 − 8 не є тотожністю.
при c = 1, (c − 2)3 = (1 − 2)3 = (−1)3 = −1, але c3 − 8 = 13 − 8 = 1 − 8 = −7.
Оскільки −1 ≠ −7, рівність не є тотожністю.
40. Спрости вираз, замінивши його тотожно рівним виразом:
а) 2с + 3с − 5 = 5с − 5;
б) 3х − 4х + х = 0х = 0;
в) 12n − 17 − 2n = 10n − 17;
г) 19с − 3с + 8 = 16с + 8;
ґ) 63 − 23р + 32р = 63 + 9р;
д) 4х + 65 − 10х = 65 − 6х.
41. Спрости вираз, замінивши
а) −4а + 3а − 7а = −4ac − 4а;
б) 9 − 23х + 40х = 9 + 17х;
в) −4 − 12 + 8ас = −16 + 8ас.
42. ГРА
43. Чи є тотожністю рівність:
а) 19x − 4(x + 5) + 20 = 15x;
19x − 4(x + 5) + 20 = 19x − 4x − 20 + 20 = 15x 15x = 15x
Отже, 19x − 4(x + 5) + 20 = 15x є тотожністю.
б) 7(2 − 3x) + 21 = 14;
7(2 − 3x) + 21 = 14 − 21x + 21 = 35 – 21x
35 − 21x ≠ 14, тому
в) 2,5 + 5(a − 1,5) a = 4a – 5; 2,5 + 5(a − 1,5) − a = 2,5 + 5a − 7,5 – a = 4a − 5
Отже, 2,5 + 5(a − 1,5) − a = 4a – 5 є тотожністю.

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
г) −2(x + 5) + 3(x − 7) = x + 11.
−2(x + 5) + 3(x − 7) = 2x − 10 + 3x − 21 = x – 31
x − 31 ≠ x + 11, тому ця рівність не є тотожністю.
44. Чи є тотожністю рівність:
а) 35 + 7(x − 1) − 28 = 7x;
35 + 7(x − 1) − 28 = 35 + 7x − 7 − 28 = 7x
Отже, 35 + 7(x − 1) − 28 = 7x є тотожністю.
б) −3(2y + 1) + 6 = −3
−3(2y + 1) + 6 = 6y − 3 + 6 = −6y + 3
−6y + 3 ≠ −3, nому ця рівність не є тотожністю.
в) −13 − 3(5 − 6x) + 6x = 12x − 28
−13 − 3(5 − 6x) + 6x = 13 − 15 + 18x + 6x = 24x – 28
24x – 28 ≠ 12x – 28, тому ця рівність не є тотожністю.
г) 1,5(5 – 2x) + 5(1,1 + x) = 13 + 2x
1,5(5 – 2x) + 5(1,1 + x) = 7,5x 3x + 5,5 + 5x = 2x + 13
Отже, 1,5(5 – 2x) + 5(1,1 + x) = 13 + 2x є тотожністю.
45. Доведіть тотожність:
а) 3с − 3(с − 1) = 3; 3с − 3с + 3 = 3; 3 = 3. Доведено;
в) 15х = 9 − 3(3 − 5х);
15х = 9 − 9 + 15х;
15х = 15х. Доведено;
46. Доведіть тотожність:
а) 8х = 6 + 2(4х − 3);
8х = 6 + 8х − 6; 8х = 8х. Доведено;
б) 5(2х + у) = 10(х + у) − 5у;
10х + 5у = 10х + 10у − 5у;
10х + 5у = 10х + 5у;
в) 7 = 12х − (−7 + 12х); 7 = 12х + 7 − 12х; 7 = 7. Доведено;
г) 3с − 3(1 + с − х) = 3х − 3; 3с – 3 − 3с + 3х = 3х − 3;
3х − 3 = 3х – 3
47. 1) Що
а) 35t

б) 2ху + 2(3 − ху) = 6; 2ху + 6 − 2ху = 6; 6 = 6. Доведено;
г) 1 − 2х = 5 − 2(х + 2); 1 − 2х = 5 − 2х − 4; 1 − 2х = 1 − 2х. Доведено.
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
Спрости
а) 2х + 4 + 2(х + 4) + 4(х − 8) = 2х + 4 + 2х + 8 + 4х − 32 = 8х − 20; б) −(5а − с + 2) + 3а − с + 2 = −5а + с − 2 + 3а − с + 2 = −2а;
в) 5(12а − 23х) − 8(6х − 13а) = 60а − 115х − 48х + 104а = 164а − 163х;
г) −6(ас − 4) + 3(7 − 2ас) = −6ас + 24 + 21 − 6ас = −12ас + 45.
52. Спрости вираз, замінивши його тотожно рівним
а) 2(х2 − 3) − 4(17 − 4х2) = 2х2 − 6 − 68 + 16х2 = 18х2 − 74;
б) 4(х2 − 3) − х(4х − 5) = 4х2 − 12 − 4х2 + 5х = 5х − 12;
в) с(3 − 2с) + 3(с − 2с2) = 3с − 2с2 + 3с − 6с2 = 6с − 8с2;
г) 2у − 3 − 2(а + у − 1) = 2у − 3 − 2а − 2у + 2 = −1 − 2а.
53. Доведи тотожність
а) 2(х − 3) − 5(х − 4) = 14 − 3х;
2х − 6 − 5х + 20 = 14 − 3х; 3х + 14 = 14 − 3х; Доведено.
б) 3(2а − 1) − 2(3а − 1) = −1; 6а − 3 − 6а + 2 = −1; 1 = −1. Доведено.
в) 5(0,5 + 2х) − 5(1,1 − х) = 15х − 3; 2,5 + 10х − 5,5 + 5х = 15х − 3; 15х − 3 = 15х – 3. Доведено.
г) 9(х − 1) − 3(2х − 3) = 3х;
9х − 9 − 6х + 9 = 3х; 3х = 3х. Доведено.
54. Доведи тотожність
а) 9х − 4(х + 5) – 1 = 7(х − 3) − 2х;
9х − 4х − 20 − 1 = 7х − 21 − 2х;
5х − 21 = 5х – 21. Доведено.
б) −2(2а + 5) = 5(2а − 9) − 7(2а − 5);
4а − 10 = 10а − 45 − 14а + 35; 4а − 10 = −4а – 10. Доведено.
в) 0,5(а + b + c) − 0,5(а − b + c) (а + b − c) = с – а;

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
0,5(a + b + c) − 0,5(a − b + c) − (a + b − c)=
= 0,5a + 0,5b + 0,5c − 0,5a + 0,5b − 0,5c − a − b + c =
= (0,5a − 0,5a − a) + (0,5b + 0,5b − b) + (0,5c − 0,5c + c)= = −a + b + c =
= c – a Доведено.
55. Доведи тотожність:
а) 3(а + с + х) − 2(а + с − х) − (а − с + х) = 2(с + 2х);
3а + 3с + 3х − 2а − 2с + 2х − а + с х = 2с + 4х;
2с + 4х = 2с + 4х. Доведено.
б) 2х + 2 = 2(х2 + х + 1) − (х2 − х + 1) (х2 + х 1);
2х + 2 = 2х2 + 2х + 2 − х2 + х − 1 − х2 − х + 1;
2х + 2 = 2х + 2. Доведено.
56. Чи тотожні вирази:
а) 1 – (1 − (1 − с)) = 1 − 1 + (1 – с) = 1 − с; 1 − с = 1 – с. Так.
б) а − b + 1 − 2(b + 1) = а − b + 1 − 2b − 2 = а − 3b − 1; 2(а − b – 1) – (a + b – 1) = 2a – 2b – 2 – a – b + 1 = a – 3b – 1;
а − 3b − 1 = а − 3b – 1. Так.
57. Чи тотожні вирази: а) 0,5(х + у) − 0,5(х − у) − у = 0,5х + 0,5у − 0,5х + 0,5у − у = 0; 0 = 0. Так.
б) n − (1 − (n − (1 − n))) = 3n − 2; n – 1 + (n − (1 − n)) = 3n − 2; n − 1 + n − (1 − n) = 3n − 2; 2n − 1 − 1 + n = 3n − 2; 3n − 2 = 3n – 2. Так.
58. Замініть у тотожності 3x – 2 = 2(x 1) + x змінну x виразом: а) c + 3; б) ac 1; в) m + 5. Чи є тотожністю одержана рівність?
Спочатку розкриємо дужки у вихідній тотожності:
3x 2 = 2x 2 + x 3x 2 = 3x 2
Отже, початкова рівність є тотожністю (ліва частина = права частина при будь-якому (x)).
а) Заміна x на c + 3
Ліва частина:
3(c + 3) 2 = 3c + 9 2 = 3c + 7
Права частина:
2((c + 3) 1) + (c + 3) = 2(c + 2) + (c + 3) = 2c + 4 + c + 3 = 3c + 7
Обидві частини однакові: 3c + 7 = 3c + 7 тотожність.
б) Заміна x на ac 1
Ліва частина:
3(ac 1) 2 = 3ac 3 2 = 3ac 5
Права частина:
2((ac 1) 1) + (ac 1) = 2(ac 2) + (ac 1) = 2ac 4 + ac 1 = 3ac 5
Обидві частини однакові: 3ac 5 = 3ac 5 тотожність.
в) Заміна x на m + 5
Ліва частина:

3(m + 5) 2 = 3m + 15 2 = 3m + 13
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
периметр прямокутника. P = 2(а + а − с) = 2(2а − с) (см).
61. Основа рівнобедреного трикутника
периметр трикутника?
Нехай бічна сторона: (а + 2) см,
P = 2а + 4 + а; P = 3а + 4.
62.
а) a + (−a) = 0;
б) a 1 ���� = 1;
в) ab = ( a) ·

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
в) |а − b| · |b − а| = (а − b)2. Так. 67. Чи є
20% у
випускників ще не працевлаштовано?
1) 150 : 100 · 10 = 15
2) 150 : 100 · 20 = 30
3)
4) 150 − (15 + 30 + 45) = 150 − 90 = 60
Відповідь: 60 випускників.
72. Укажіть координати точок,
перетину сторін трикутника ABC з
A(−1; 4); B(3; 0); C(−4; −2).
AB: (0; 3); BC: (0; −1); AC: (−3; 0).
73. За якої умови правильна пропорція: а) 3 : x = x : 27; x2 = 81; x = 9 або x = −9; б) y : 4 = 16 : y2; y3 = 64; y = 4.
зі степенями 74. Назви основу та показник степеня. а) Основа: 3,5. Показник степеня: 4.
б) Основа: −0,1. Показник степеня: 3.
в) Основа: −100. Показник степеня: 4.
г) Основа: −a. Показник степеня: 6.
ґ) Основа: 1 2 x. Показник степеня: 5.
75. Знайди квадрати чисел.
1) 12 = 1;

2) (−3)2 = 9;
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
3) 72 = 49;
4) 82 = 64;
5) (−9)2 = 81; 6) 102 = 100;
7) 202 = 900;
8) 302 = 900;
9) (−40)2 = 1600; 10) (0,2)2 = 0,04; 11) (0,03)2 = 0,0009.
76. Знайди куби чисел. 1) 13 = 1;
2) (−2)3 = −8; 3) 33 = 27;
4) 43 = 64;
5) (−5)3 = −125;
6) 103 = 1000;
7) (0,1)3 = 0,001;
8) (−1 3)3 = 1 27;
9) (−11 2)3 = (−3 2)3 = − 27 8 ;
10) (2 3)3 = 8 27;
11) (1 4)3 = 1 64
77. Чи правильно, що:
а) 51 = 1 5 (неправильно);
б) 71 = 7 (правильно);
в) (−2)4 = 16 (правильно);
г) (−7)2 = 49 (правильно);
ґ) Число 0,16 є квадратом числа 0,4 (правильно, бо 0,42 = 0,16);
д) (2 3) в п’ятому степені записують так: 25 3 ; (неправильно);
е) Добуток 5 · 5 · 5 можна записати як 53 (правильно); є) Значення виразу 23 дорівнює 2 · 3 = 6; Ні, дорівнює 8, а не 6 (правильно).
78. Істинною чи хибною є нерівність?
а) (−15)10 < 0 хибно, (−15)10 > 0 (парний степінь);
б) (−3,2)13 > 0 хибно, (−3,2)13 < 0 (непарний степінь);
в) −4,112 < 0 істинно;
г) −(−2)62 > 0 хибно, (−2)62 < 0 (парний степінь);
ґ) (−3,4)2 > −3,42 істинно;
д) x122 < 0 хибно (парний степінь);
е) ( 15)⁴ 15⁴ < 0 істинно;
8) (−6,5)4 > (−8,4)3 істинно, (−6,5)4 > 0 і (−8,4)3 < 0.
79. Прочитай вираз, використовуючи терміни «квадрат суми та різниці», «сума та різниця квадратів».
а) a² + b² – «сума квадратів»
б) (a + b)² – «квадрат суми»
в) a² – b² – «різниця квадратів»

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
г) (a – b)² – «квадрат різниці»
80. Розв’яжи рівняння.
а) x7 = 0, x = 0;
б) x8 = −1,
Немає дійсних розв'язків;
в) 15x6 = 0, x = 0;
г) x8 = 1, x = 1 або x = −1; ґ) x3 = 1, x = 1.
81. Запиши добуток у
а) 0,3 · 0,3 · 0,3 · 0,3 · 0,3 = (0,3)5;
б) c · c · c · c · c · c · c = c7;
в) (−16) · (−16) · (−16) · (−16) = (−16)4;
г) (−b) · (−b) · (−b) · (−b) · (−b) = (−b)5.
82. Запиши
a) (a − b) · (a − b) · (a − b) = (a − b)3; b) k · k · k · k = k4; c) 5 · 5 · ... · 5 (18 разів) = 518.
83. Запиши добуток
а) (−y) · (−y) · (−y) · (−y) = (−y)4;
б) (ab) · (ab) · (ab) · (ab) · (ab) · (ab) = (ab)6; в) m · m · m · ... · m (20 разів) = m20; г) (p − a) · (p − a) · (p − a) · (p − a) · (p − a) = (p − a)5.
84. ГРА
85. Стародавня єгипетська задача.
1) 7 · 7 = 49
2) 49 · 7 = 343
3) 343 · 7 = 2401
4) 2401 · 7 = 16 807 може вирости ячменю;
5) 7 + 49 + 343 + 2401 + 16 807 = 19 607.
Відповідь: 19 607.
86. Подай числа, якщо це
а) З основою 2:
1. 4 = 22;
2. 8 = 23;
3. 64 = 26; 4. 16 = 24;
5. 144 не можна; 6. 256 = 28;
7. −8 = −23;

8. −32 = −25; 9. −64 = −26;
б) З основою 5: 1. 5 = 51; 2. 25 = 52; 3. 125 = 53; 4. 225 не можна; 5. −25 = −52; 6. −125 = −53 .
а) З основою 3:
1. 27 = 33; 2. 81 = 34;
3. −9 = −32; 4. −27 = −33;
88. Обчисли:
а) 52 = 25; 25 = 32; 103 = 1000; 1003 = 1 000 000; 252 = 625;
г) (−0,5)2 = 0,25; −0,52 = −0,25; (−1)160 = 1; (−1)105 = −1.
89. Обчисли
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
1. 100 = 102 або 100 = (2 · 5)2; 2. 49 = 72;
3. 121 = 112; 4. −144 = (12)2 або −144 = −(24 · 32); 5. 169 = 132; 6. 196 = 142 .
б) (0,2)3 = 0,008; (0,3)2 = 0,09; (0,04)3 = 0,000064;
в) (3)4 = 81; (−34) = −81; (34) = −81; 34 = −81;
а) 82 = 64, 102 = 100, 33 = 27, 53 = 125, 63 = 216; б) (0,1)2 = 0,01, (0,3)3 = 0,027, (0,5)3 = 0,125;
в) 1,12 = 1,21, 1,62 = 2,56, 2,72 = 7,29, 3,52 = 12,25; г) (−1)5 = −1, (−2)6 = 64, (−9)3 = −729, (−12)2 = 144.
90. Обчисли а) 12 + 22 + 32 + 42 + 52 + 62 = 1 + 4 + 9 + 16 + 25 + 36 = 91; б) 32 − 42 + 52 − 62 + 72 = 9 − 16 + 25 − 36 + 49 = 31.
91. Обчисли
а) (−2)2 + (−2)3 + (−2)4 + (−2)5 = 4 − 8 + 16 − 32 = -20; б) 92 – 82 + 72 – 62 = 81 – 64 + 49 – 36 = 30.
92. Чи правильна рівність: а) 32 + 42 = 52; 9 + 16 = 25; 25 = 25; так; б) 152 + 162 =172; 225 + 256 ≠ 289; 481 ≠ 289; ні; в) 352 + 362 = 372; 1225 + 1296 ≠ 1369; ні;
г) 32 + 32 = 62; 9 + 9 ≠ 36; 18 ≠ 36; ні; ґ) 43 + 62 = 102; 64 + 36 = 100; 100 = 100; так; д) 972 − 962 = 97 + 96; 9409 − 9216 = 193; 193 = 193; так.

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
93. Доведи, що:
а) 102 + 112 + 122 = 132 + 142;
100 + 121 + 144 = 169 + 196; 365 = 365. Доведено.
б) 13 + 23 + 33 + ... + 93 = 452; 1 + 8 + 27 + 64 + 125 + 216 + 343 + 512 + 729 = 2025; 2025 = 2025. Доведено.
94. Обчисли площу квадратної серветки,
S = a2
а) Якщо a = 3 дм, то S = 32 = 9 (дм2); б) Якщо a = 10 см, то S = 102 = 100 (см2).
95. Обчисли об’єм
V = a3
а) Якщо a = 2 м, то V = 23 = 2 · 2 · 2 = 8 м3; б) Якщо a = 5 дм, то V = 53 = 5 · 5 · 5 = 125 дм3
96.
а) (−7)2 − (−1)9 · 34 = 49 + 1 · 81 = 130;
б) (0,02 + 0,28)4 · 105 = 0,34 · 105 = 0,0081 · 100 000 = 810; в) 63 − (4 · 2 5)2 · 61 4 = 216 – (8
г) (−1)24 : (1 2)6 + (−3)5 = 1 · 64 − 243 = 64 − 243 = −179;
ґ) (5,6 − 5,5)3 : 0,1 = (0,1)3 : 0,1 = 0,001 : 0,1 = 0,01; д) (0,32 + 0,42) − 0,52 = (0,09 + 0,16) − 0,25 = 0,25 − 0,25 = 0.
97. Знайдіть значення виразу:
а) 102 − (−1)12 · 62 = 100 − 36 = 64; б) (0,44 + 0,46)3 · (−10)4 = 0,93 · 10 000 = 0,729 · 10 000 = 7290; в) (7,8 − 7,7)4 : (0,1)5 = 0,14 : 0,15 = 0,0001 : 0,00001 = 10;
г) 32 · (2,7 − 2,8)2 = 9 · (−0,1)2 = 9 · 0,01 = 0,09.
98. Знайдіть значення виразу: а) Якщо a = −3, то 3a4 – 2a2 = 3 · (−3)4 − 2 · (−3)2 = 3 · 81 − 2 · 9 = 243 − 18 = 225; б) Якщо m = 2, то (2m − 1)2 : m3 = (2 · 2 – 1)2 : 23 = (4 – 1)2 : 8 = 32 : 8 = 9 : 8 = 1,125.
99. Знайдіть значення виразу: а) Якщо n = −2, то n3 + (n – 3)2 = (−2)3 + (−2 − 3)2 = −8 + 25 = 17; б) Якщо c = 0,5, то 5c3 – 2c2 + c = 5 · (0,5)3 − 2 · (0,5)2 + 0,5 =
·
− 2 · 0,25 + 0,5 = 0,625 − 0,5 + 0,5 = 0,625.
100. Не виконуючи обчислень, порівняй значення виразів: а) (−7)10 > 0; б) (−10)7 < 0; в) (−2)6 > (−3)5; г) −56 < (−5)6
101. Не виконуючи обчислень, порівняй значення виразів: а) (−21)7 < 0; б) (−3)6 > 0; в) (−5)5 < (−4)4; г) −78 < (−7)8.
102. Розв’яжи рівняння: а) 5x4 = 5; x4 = 1; x = 1 або x = −1; б) 4x2 = x2; 3x2 = 0; x = 0;

в) x2 + 5 = 0; x2 = −5;
103. Розв’яжи рівняння:
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
г) −2x3 = 2; x3 = −1; x = −1.
а) x2 + 1 = 0; x2 = −1; x = −1; б) x8 − 1 = 0; x2 = 1; x1 = 1; x2 = −1;
в) 2x7 = 2; x7 = 1; x = 1; г) x3 − 6 = 2; x3 = 8; x = 2.
104. Запиши у
3 · 105 км/с;
6 · 1021 т;
7,35 · 1019 т;
1,083 · 1012 км³.
000 000; ґ) 33 000; д) 105; е) 1000 000 000; є) 7004.
а) 2 · 104;
б) 7,53 · 106;
в) 1,05 · 107;
г) 9,099 · 108; ґ) 3,3 · 104; д) 1,05 · 102; е) 1 · 109; є) 7,004 · 103 .
106. Запиши у вигляді натуральних чисел: а) 9 · 104 = 9000;
б) 1,31 · 103 = 1310; в) 7,1 · 105 = 710000; г) 4,3 · 102 = 430; ґ) 2,05 · 104 = 20500; д) 3,125 · 106 = 3125000.
107. Чи правильна рівність:
а) 22 + 22 + 62 + 102 = 122; 4 + 4 + 36 + 100 = 144; 144 = 144. Так.
б) 22 + 42 + 62 + 132 = 152; 4 + 16 + 36 + 169 = 225; 225 = 225. Так.
108. Чи правильна рівність:
а) 22 + 62 + 82 + 252 = 272; 4 + 36 + 64 + 625 = 729; 729 = 729. Так.

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
б) 13 + 23 + 33 + 43 = (1 + 2 + 3 + 4)2;
1 + 8 + 27 + 64 = 100;
100 = 100. Так.
109. Обчисліть значення виразу:
а) (36 − 42)3 = (36 − 16)3 = 203 = 8000;
б) (34 + 19)5 = (81 + 19)5 = 1005 = 10 000 000 000;
в) (0,875 + 0,53)10 = (0,875 + 0,125)10 = 110 = 1;
г) (−0,3)4 · 103 = 0,081 · 1000 = 81;
ґ) (2 3)3 · (3 4)2 = 8 9 27 16 = 1 6;
д) (44 − 35 − 13)12 = (256 − 243 − 13)12 = 012 = 0.
110. Установи відповідність
1) (35 − 25)4 = (35 − 32)4 = 34 = 81; (Г).
2) 104 · (0,2)3 = 10000 · 0,008 = 80; (В).
3) (0,33 − 0,017)2 = (0,027 − 0,017)6 = 0,016 = 0,000001; (Д).
4) (27 − 53 − 4)15 = (128 − 125 − 4)15 = (−1)15 = −1; (А).
111. Знайдіть значення виразу:
a) (4x2 – y2) 2 : (2x – y) 2 , якщо x = 0,6, y = −0,2, то:
(4 · 0,62 − (−0,2)2)2 : (2 · 0,6 − (−0,2)2)2 = 12 = 1; б) (1 + b)2 – (a – 1)2 – (a + b)2 , якщо a = 1,1, b = 0,1, то: = (1 + ( 0,1))2 (1,1 1)2 (1,1 + ( 0,1))2 = (0,9)2 (0,1)2 (1)2 =
– 1 = - 0,2
112. Знайдіть значення виразу: a) 2xy + (x + 2y)3 + y2 , якщо x = −2, y = 3, то: 2 · (−2)5 + (−2 + 2 · 3)3 +
114. Обчисли, користуючись калькулятором: a) 3,45 = 454,35424; б) 5,754 + 57 = 1093,1288 + 57 = 1150,1288; в) 47,2 · 2,843 = 47,2 · 22,9215 = 1081,96; г) 3,7 + 2,74 = 3,7 + 53,1441 = 56,8441.
115.
32 + 52 = 9 + 25 = 34; (3 + 5)2 = 82 = 64; 32 + 52 < (3 + 5)2; б)
102 − 62 = 100 − 36 = 64;

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
(10 − 6)2 = 42 = 16; 102 − 62 > (10 − 6)2 .
116. Обчисли і порівняй:
a)
33 + 23 = 27 + 8 = 35; (3 + 2)3 = 53 = 125;
33 + 23 < (3 + 2)3 .
53 − 23 = 125 − 8 = 117; (5 − 2)3 = 33 = 27;
53 − 23 > (5 − 2)3 .
117. Якщо твердження
спростовує)
а)
a) Неправильне.
Контрприклад: 22 = (−2)2, але 2 ≠ −2.
б) якщо куби
б) Правильне.
в) якщо
в) Неправильне.
Контрприклад: −1 + (−1) 2 = −1 + 1 = 0 (не додатне число).
г) якщо від від’ємного
число. г) Правильне.
118. Значення якого з виразів є: 1) найбільше, 2) найменшим? a) 7² + 3² 2 = 49 + 9 2 = 58 2 = 29; найбільше значення;
(7 + 3
2 ) = 5; найменше значення;
(7 2)2 + (3 2)2 = 49 4 + 9 4 = 58 4 = 14,5; б) 7² 5²
2 = 49 25 2 = 12; найбільше значення;
(7 5 2 )2 = 12 = 1; найменше значення;
(7 2)2 + (5 2)2 = 49 4 25 4 = 24 4 = 6.
119. Значення якого з виразів найменше?
5³ + 3³
2 = 125 + 8 2 = 66,5; найбільше значення; (5 + 3
2 )3 = 43 = 64; середнє значення;
(5 2)3 + (3 2)3 = 125 8 + 27 8 = 19; найменше значення.
120. Доведіть, що рівняння не має розв'язків: а) x4 + 3 = 0; x4 = −3;
Розв’язків немає. б) 3x2 + 8 = 0; 3x2 = −8; Розв’язків немає.
121. Яке найменше значення
а) x2 + 9
Найменше значення: 9 при x = 0. б) 4 + (2 − a)2
Найменше значення: 4 при a = 2.

в) (y − 3)2 + 1 = 0; (y − 3)2 = −1; Розв’язків немає.
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
в) (x2 + 2)4 − 10
Найменше значення: −9 при x = 0.
122. Яке
а) 3 − x2
Найбільше значення: 3 при x = 0. б) 6 − (x − 4)8
Найбільше значення: 6 при x = 4.
123. Запиши у стандартному
числа: a) 2,87287 · 108; 1,753 · 107; 2,205 · 105; 9,099 · 10. б) 3 · 10 4; 2,35 · 10 1; 5 · 10 2; 4,1 · 10 9 . в) 1 2 = 0,5 = 5 · 10 1; 1 20 = 0,05 = 5 · 10 2; 1 200 = 0,005 = 5 · 10 3; 3 500 = 0,006 = 6 · 10 3; 73 500000 = 0,000146 = 1,46 · 10 4; 999 1000000000 = 9,99 · 10 7
124. Запишіть у звичайному
числа: a) 1,2 · 103 = 1200; 3,47 · 105 = 347 000; 7,3 · 104 = 73 000; 14,23 · 106 = 1 423 000; 6) 2 · 10 4 = 0,0002; 1,1 · 10 3 = 0,0011; 9 · 10 5 = 0,00009; 6,75 · 10 6 = 0,00000675.
125. Доведи, що: a) 1012 + 2 ділиться на 3; 1012 + 2, сума цифр отриманого числа дорівнює 3, тобто число буде ділитися на 3 (1 + 2 = 3; 3 : 3); б) 691 – 1191 ділиться на 5; 1015 + 8, сума цифр отриманого числа дорівнює 9, тобто ділиться на 9 (так як 1015 = 100...0; 1 + 8 = 9; 9 : 9 = 1). в) 1015 + 8 ділиться на 9; 1015 = 1000000000000000
Сума цифр: 1 + 8 = 91 + 8 = 9
А 9 ділиться на 9 → ділиться на 9. 126. Доведи, що: a) а) 1 + 1010 + 10100 ділиться на 3; 1 + 1010 + 10100, сума цифр
3, тобто ділиться на 3 (1 + 1 + 1 = 3; 3 : 3); б) б) 2613 + 1013 ділиться на 2; 1010 − 1 = 1 000 000 000 − 1 = 999 999 999
в) 1010 – 1 ділиться на 9. 1010 – 1 = 9999999999 Це число складається з 10 дев’яток → сума цифр = 9 · 10 = 90

9.
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
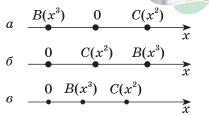
1) На графіку а: ліворуч від точки B(x3), оскільки x < 0.
2) На графіку б: між точками C(x2) і B(x3).
3) На графіку в: праворуч від точки C(x2).
128. Заміни букви цифрами так, щоб була правильною рівність: а) куб = eе; б) степінь = еее.
а) 33;
б) 2 · 22 .
129. Чи тотожні вирази:
а) 2a + a + a = 4a; 4a = 4a. Так.
б) 2b – 2a = −2(a − b) = −2a + 2b. Так.
в) x + x + x = 3x;
3x ≠ x3. Ні.
г) 5 + 5 + 5x = 10 + 5x ≠ 15x. Ні.
ґ) 3y + 2y + y − 6 = 6y – 6 ≠ у. Ні.
д) a3 – a ≠ a2. Ні.
130. Площа Києва
Нехай бічна сторона рівнобедреного трикутника (x + 3) см, основа: (x) см.
а) Якщо P = 54 см, то 2(x + 3) + x = 54; 2x + 6 + x = 54;
3x = 54 − 6;
3x = 48; x = 16.
Основа 16 см, бічна сторона 19 см.
б) Якщо P = 36 см, то 2(x + 3) + x = 6; 2x + 6 + x = 6;
3x = 0; x = 0.
Немає розв'язків.
в) Якщо P = а см, то 3x + 6 = а;
3x = a – 6; x = a – 6
3 .
Основа: a – 6 3 ;

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
Відповідь: а) 16; 19; 19; б) немає розв'язків;
в) a – 6 3 ; a + 3 3 ; a + 3 3 .
132. Спрости b30 : b5
b30 : b⁵ = b30–5 = b²⁵
133. Обчисли (22)3 (2²)³ = 2²·³ = 2⁶ = 64
134. Спрости вираз
а) 3⁵ · 3⁷ = 3⁵⁺⁷ = 3¹²
б) 12⁴ : 12³ = 12⁴⁻³ = 12¹ = 12
в) (1 2)⁴ · (1 2)³ = (1 2)⁴⁺³ = (1 2)⁷ = 1 128
г) (–4)² · (–4)³ = (–4)²⁺³ = (–4)⁵ = –1024
135. Спрости вираз
а) x⁵ · x⁸ = x⁵⁺⁸ = x¹³
б) m³ · m⁷ = m³⁺⁷ = m¹⁰
в) f⁴ : f = f⁴⁻¹ = f³
г) c³ · c⁴ · c⁵ = c³⁺⁴⁺⁵ = c¹²
ґ) z² · z⁵ · z = z²⁺⁵⁺¹ = z⁸
136. Подай вираз у вигляді степеня.
а) 625 = 5⁴;
б) (x³)⁵ = x¹⁵;
в) x² · y² = (xy)²;
г) 8 · 3³ = 2³ · 3³ = (2 · 3)³ = 6³;
д) 64 · 49 = (2⁶ · 7²);
е) x⁴ · y6 = (xy)4 ⋅ y2
137. Розв’яжи рівняння.
а) z³z = 0
z³⁺¹ = 0
z⁴ = 0 z = 0
б) 4x⁵x⁶ = 0
4x⁵⁺⁶ = 0 4x¹¹ = 0 x = 0
в) у⁵y² = 1 у⁵⁺² = 1 y7 = 1 y = 1
г) xx³ = 1 x¹⁺³ = 1 x⁴ = 1 x = 1 138.
а) 3¹³ · 3⁶ = 3¹³⁺⁶ = 3¹⁹
б) 18 · 18¹⁴ = 18¹⁺¹⁴ = 18¹⁵
в) (–11)⁵ · (–11)⁴ = (–11)⁵⁺⁴ = (–11)⁹
г) (1 6)² · (1 6)7 = (1 6)²⁺⁷ = (1 6)⁹
ґ) (12 3)¹⁰ · (12 3)⁹ = (12 3)¹⁰⁺⁹ = (12 3)¹⁹
д) (–2 5)⁹ · (–2 5)¹⁶ = (–2 5)⁹⁺¹⁶ = (–2 5)²⁵
55 · 5⁷ = 55⁺7 = 5¹²

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
а) a⁵ · a³ = a⁵⁺³ = a⁸
б) x4 · x⁴ = x4⁺⁴ = x⁸
в) m · m⁸ = m¹⁺⁸ = m⁹
г) y⁷ · y · y⁷ · y = y⁷⁺¹⁺⁷ = y¹⁶
ґ) z · z² · z³ · z5 = z¹⁺²⁺³⁺⁵ = z¹¹
д) (a + b)² · (a + b)⁵ = (a + b)²⁺⁵ = (a + b)⁷
141. Подай
а) c⁷ · c⁵ = c⁷⁺⁵ = c¹²
б) a⁷ · a⁷ = a⁷⁺⁷ = a¹⁴
в) p · p¹² = p¹⁺¹² = p¹³
г) x · x² · x³ = x¹⁺²⁺³ = x⁶
ґ) m · m⁷ · m³ · m¹⁰ = m¹⁺⁷⁺³⁺¹⁰ = m²¹
д) (x – y)³ · (x – y) = (x – y)³⁺¹ = (x – y)⁴
142.
а) 5⁸ · 25 = 5⁸ · 5² = 5⁸⁺² = 5¹⁰
б) 3¹² · 27 = 3¹² · 3³ = 3¹²⁺³ = 3¹⁵
в) 6¹⁵ · 36 = 6¹⁵ · 6² = 6¹⁵⁺² = 6¹⁷
2⁹ · 32 = 2⁹ · 2⁵ = 2⁹⁺⁵ = 2¹⁴ ґ) 0.4⁵ · 0.16 = 0.4⁵ · 0.4² = 0.4⁵⁺² = 0.4⁷
д) 0.001 · 0.14 = 0.1-⁷
3⁶ · 9 = 3⁶ · 3² = 3⁶⁺² = 3⁸ б) 5¹⁷ · 125 = 5¹⁷ · 5³ = 5¹⁷⁺³ = 5²⁰
в) 2¹¹ · 16 = 2¹¹ · 2⁴ = 2¹¹⁺⁴ = 2¹⁵
г) 4²² · 64 = 4²² · 2⁶ = 4²² · 2⁴⁺⁶ = 2⁵⁰
ґ) 0.3⁹ · 0.027 = 0.3⁹ · (0.3³) = 0.3⁹⁺³ = 0.3¹²
д) 0.01 · 0.1¹⁸ = (0.1²) · 0.1¹⁸ = 0.1²⁺¹⁸ = 0.1²⁰
144. Подай у вигляді степеня частку
а) x¹² : x⁵ = x¹²⁻⁵ = x⁷
б) a7 : a6 = a7⁺⁶ = a¹3
в) m²³ : m = m²³⁻¹ = m²²
г) c¹⁷ : c¹⁶ = c¹⁷⁻¹⁶ = c¹ = c
ґ) y¹⁹ : y⁵ = y¹⁹⁻⁵ = y¹⁴
д) (m + n)⁵ : (m + n)³ = (m + n)⁵⁻³ = (m + n)²
145. Подай у вигляді степеня частку
а) p8 : p³ = p8 ³ = p⁵
б) n¹¹ : n⁸ = n¹¹⁻⁸ = n³
в) a²³ : a = a²³⁻¹ = a²²
г) x¹² : x⁷ = x¹²⁻⁷ = x⁵
ґ) y¹⁷ : y¹⁵ = y¹⁷⁻¹⁵ = y²
д) (a + c)¹⁶ : (a + c)¹² = (a + c)¹⁶⁻¹² = (a + c)⁴
146. Знайди значення виразу
а) 7⁶ : 7⁵ = 7⁶⁻⁵ = 7¹ = 7
б) 12¹³ : 12¹¹ = 12¹³⁻¹¹ = 12² = 144
в) 1.8⁶ : 1.8⁴ = 1.8⁶⁻⁴ = 1.8²
г) 2¹⁰ : 2⁶ = 2¹⁰⁻⁶ = 2⁴ = 16

ґ) 3¹²
3¹⁰ = 3¹²⁻¹⁰ = 3² = 9
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
д) 5¹⁰ 25⁵ = 5¹⁰ (5²)⁵ = 5¹⁰ : 5¹⁰ = 1
147. Знайди значення виразу
а) 2,7¹³ : 2,7¹² = 7¹³⁻¹² = 7¹ = 7
б) 65 : 6³ = 65 ³ = 6² = 36
в) 0.58 : 0.56 = 0.5⁸⁻⁶ = 0.5² = 0.25
г) ( 0,8)5 ( 0,8)3 = (−0.8)5–3= (−0.8)² = 0.64
ґ) (11 3)8 : (11 3)6 = (11 3)⁸⁻⁶ = (11 3)² = 16 9
д) 224 4 10 = 224 20 = 24 = 16.
148. Виконай піднесення до степеня
а) (a²)³ = a²⋅³ = a⁶
б) (x³)² = x³⋅² = x⁶
в) (y⁷)² = y⁷⋅² = y¹⁴
г) ((x⁵)⁶)³ = x⁵·⁶·³ = x⁹⁰
ґ) ((2 – a)³)⁴ = (2 – a)³⋅⁴ = (2 – a)¹²
д) (((x – y)⁵)⁴)³ = (x – y)⁵ · ⁴ · ³ = (x – y)⁶⁰
149. Виконай піднесення до степеня
а) (m8)³ = m⁸⋅³ = m²⁴
б) (x¹⁰)³ = x¹⁰ ³ = x³⁰
в) (a⁵)ⁿ = a⁵ⁿ
г) ((z²)⁸)³ = z²⋅⁸⋅³ = z⁴0
ґ) ((3 – b)³)⁷ = (3 – b)³ ⁷ = (3 – b)²¹
д) ((m + n)³)⁵)² = (m + n)³⋅⁵⋅² = (m + n)³⁰
150. Гра
151. Подай вирази (c⁴)²
1) (c⁴)² = c⁴
2) (c²)⁴ = c²⋅⁴ = c⁸
не впливає на кінцевий результат.
152 Виконай піднесення до степеня
а) (xy)⁴ = x⁴y⁴
б) (3a)² = 3²a² = 9a²
в) (5x)³ = 5³x³ = 125x³
г) (–10ab)² = (–10)²a²b² = 100a²b²
ґ) (–2xy)⁵ = (–2)⁵x⁵y⁵ = –32x⁵y⁵
д) (–0.3b²d)³ = (–0.3)³(b²)³d³ = –0.027b⁶d³
153. Виконай піднесення до степеня
а) (ac)⁹ = a⁹c⁹
б) (5x)3 = 53x3 = 125x3
в) (2y)⁶ = 2⁶y⁶ = 64y⁶
г) (–8mn)² = (–8)²m²n² = 64m²n²
ґ) (–3pk)³ = (–3)³p³k³ = –27p³k³

д) (–0.5c⁴d)³ = (–0.5)³(c⁴)³d³ = –0.125c¹²d³
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
154. Додатне чи
а) (–5)²¹ : (–5)¹³ = (–5)²¹–¹³ = (–5)⁸
Оскільки показник парний (8), значення буде додатним.
б) (–8)⁸ · (–8)¹¹ = (–8)⁸+¹¹ = (–8)¹⁹
Оскільки показник непарний (19), значення буде від'ємним.
в) (–3)⁵ · (–3)⁷ · (–3)4 = (–3)5+7+4 = (–3)¹⁶
Оскільки показник парний (16), значення буде додатним.
155. Порівняй значення виразів
а) (–2)³ · (–2)¹⁰ і (–2)⁸
(–2)³ · (–2)¹⁰ = (–2)³⁺¹⁰ = (–2)¹³
(–2)¹³ < (–2)⁸
б) (–3)⁷ : (–3)⁵ і (–3)⁷⁵
(–3)⁷ : (–3)⁵ = (–3)⁷⁻⁵ = (–3)²
(–3)² > (–3)⁷⁵
в) (–10)⁵ · (–10)³⁵ і (–100)⁹¹
(–10)⁵ · (–10)³⁵ = (–10)⁵⁺³⁵ = (–10)⁴⁰
(–100)⁹¹ = (10²)⁹¹ = 10¹⁸²
(–10)⁴⁰ < 10¹⁸²
г) (–7)³² : (–7)³¹ і (–7) : (–7)
(–7)³² : (–7)³¹ = (–7)³²⁻³¹ = (–7)¹
(–7) : (–7) = (–7)¹⁻¹ = (–7)⁰ = 1
(–7)¹ = –7, 1 = 1
156. Порівняй значення виразів
1) (–6)²¹ · (–6)² < (–6)³⁰
(–6)²¹ · (–6)² = (–6)²¹⁺² = (–6)²³
(–6)²³ < (–6)³⁰
2) (–4)¹² : (–4)⁷ < (–4)¹⁶
(–4)¹² : (–4)⁷ = (–4)¹²⁻⁷ = (–4)⁵
(–4)⁵ < (–4)¹⁶
3) (–2)⁹ · (–2)¹⁵ > (–2)²⁵
(–2)⁹ · (–2)¹⁵ = (–2)⁹⁺¹⁵ = (–2)²⁴
(–2)²⁴ > (–2)²⁵
4) (–5)⁶ · (–5)⁵ < (–5) : (–5)
(–5)⁶ · (–5)⁵ = (–5)⁶⁺⁵ = (–5)¹¹ (–5) : (–2) > (–5)¹¹
157. Обчисли значення виразу
а) 2¹³ · 0.5¹³ = (2 · 0.5)¹³ = 1¹³ = 1
б) 0.5¹⁸ · 2¹⁸ = (0.5 · 2)¹⁸ = 1¹⁸ = 1
в) 2⁷ · 0.04⁷ = (25 · 0.04)⁷ = 1⁷ = 1
г) 5³³ · 0.2³³ = (5 · 0.2)³³ = 1³³ = 1
ґ) 8⁵ · (1 4)⁵ = (8 · 1 4)⁵ = 2⁵ = 32
д) (21 3)¹² · (3 7)¹² = (7 3 · 3 7)¹² = 1¹² = 1
а) 2⁷ · 5⁷ = (2 · 5)⁷ = 10⁷ = 10000000
б) 0.25¹⁰ · 4¹⁰ = (0.25 · 4)¹⁰ = 1¹⁰ = 1
в) (–8)¹¹ · 0.125¹¹ = (–8 · 0.125)¹¹ = (–1)¹¹ = –1
г) 0.2⁸ · 0.5⁸ = (0.2 · 0.5)⁸ = 0.1⁸

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
ґ) 6⁶ · (1 3)⁶ = (6 · 1 3)⁶ = 2⁶ = 64
д) (13 5)¹⁶ · (5 8)¹⁶ = (8 5)¹⁶ · (5 8)¹⁶ = 1¹⁶ = 1
159. Чи має розв’язки рівняння?
а) x² · x4 = -1
x²⁺4 = x6 = -1
Рівняння не має розв'язків
в) (x7)³ = 0
x⁷ ³ = x²¹ = 0
x = 0
160. Розв’яжи рівняння.
а) x⁸ · x⁷ = 1
x⁸⁺⁷ = x¹⁵ = 1
x = 1
в) x2 · x² = 1
x2+2 = x4 = 1
x = 1 або x = –1
161. Знайдіть суму, різницю, добуток
б) x³ · x⁶ = –1
x³⁺⁶ = x⁹ = –1
x = –1
г) (x⁸)² = 1 x¹⁶ = 1 x = 1 або x = –1
б) y4 · y5 = –1 y4+5 = y⁹ = –1 y = –1
г) z³ · z² · z⁸ = –1 z³⁺²⁺⁸ = z¹³ = –1 z = –1
a + b = 2.4 · 10⁵ + 3 · 10⁵ = (2.4 + 3) · 10⁵ = 5.4 · 10⁵ a – b = 2.4 · 10⁵ – 3 · 10⁵ = (2.4 – 3) · 10⁵ = –0.6 · 10⁵ = –6 · 10⁴ a · b = 2.4 · 10⁵ · 3 · 10⁵ = (2.4 · 3) · 10⁵⁺⁵ = 7.2 · 10¹⁰
a : b = (2.4 · 10⁵) : (3 · 10⁵) = (2.4 : 3) · (10⁵ : 10⁵) = 0.8 б)
a + b = 1.5 · 10⁷ + 5 · 10⁷ = (1.5 + 5) · 10⁷ = 6.5 · 10⁷
a – b = 1.5 · 10⁷ – 5 · 10⁷ = (1.5 – 5) · 10⁷ = –3.5 · 10⁷
a · b = 1.5 · 10⁷ · 5 · 10⁷ = (1.5 · 5) · 10⁷⁺⁷ = 7.5 · 10¹⁴
a : b = (1.5 · 10⁷) : (5 · 10⁷) = (1.5 : 5) · (10⁷ : 10⁷) = 0.3
в)
a + b = 6.4 · 10⁴ + 3.2 · 10⁴ = (6.4 + 3.2) · 10⁴ = 9.6 · 10⁴
a – b = 6.4 · 10⁴ – 3.2 · 10⁴ = (6.4 – 3.2) · 10⁴ = 3.2 · 10⁴
a · b = 6.4 · 10⁴ · 3.2 · 10⁴ = (6.4 · 3.2) · 10⁴⁺⁴ = 20.48 · 10⁸ = 2.048 · 10⁹
a : b = (6.4 · 10⁴) : (3.2 · 10⁴) = (6.4 : 3.2) · (10⁴ : 10⁴) = 2
162. Виконай дії.
а) 2.5 · 10⁵ + 3.3 · 10⁵ = (2.5 + 3.3) · 10⁵ = 5.8 · 10⁵
б) 7.7 · 10⁷ – 5 · 10⁷ = (7.7 – 5) · 10⁷ = 2.7 · 10⁷
в) (6.4 · 10⁶) : (1.6 · 10⁶) = (6.4 : 1.6) · (10⁶ : 10⁶) = 4 · 1 = 4
г) (6.4 · 10³) · (2 · 10³) = (6.4 · 2) · (10³ · 10³) = 12.8 · 10⁶
163. Заміни зірочку
а) x⁶ · * = x¹⁵
= x¹⁵ ⇒ * = 9 x⁶ · x9 = x¹⁵
m8 · * = m¹³ m8⁺* = m¹³ ⇒ * = 5 m8 · m⁵ = m¹³
a¹⁰ · * · a = a¹⁷
= a¹⁷ ⇒ * = 6
· a⁶ · a = a¹⁷
x³ · x · * = x⁹
= x⁹ ⇒ * = 5
· x · x⁵ = x⁹
(*)⁵ = x²⁰ *⁵ = x²⁰ ⇒ * = x⁴ (x4)⁵ = x²⁰
(*)⁷ = a²¹ *⁷ = a²¹ ⇒ * = a³ (a³)⁷ = a²¹

а) 0.5¹² · 2¹³ = (0.5 · 2)¹² · 2 = 1¹² · 2 = 2
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
б) 0.1²¹ · 10²⁰ = (0.1 · 10)²⁰ · 0.1 = 1²⁰ · 0.1 = 0.1
в) 0.125⁴¹ · (–8)⁴⁰ = (0.125 · –8)⁴⁰ · 0.125 = (–1)⁴⁰ · 0.125 · 0.125 = 0.125
г) 5²⁷ · 0.2³⁰ = (5 · 0.2)²⁷ · 0.2³ = 1²⁷ · 0.008 = 0.008
ґ) (–0.25)¹⁵ · 4¹⁶ = (–0.25 · 4)¹⁵ · 4 = (–1)¹⁵ · 4 = –1 · 4 = –4 д) 4³¹ · 2.5³⁰ = (4 · 2.5)³⁰ · 4 = 10³⁰ · 4
166. Обчисли
а) 5²⁰ · 0.2¹⁸ = (5 · 0.2)¹⁸ · 5² = 1¹⁸ · 25 = 25
б) 0.04¹² · 25¹¹ = (0.04 · 25)¹¹ · 0.04 = 1¹¹ · 0.04 = 0.04
в) (–2.5)¹⁷ · (0.4)¹⁹ = (–2.5 · 0.4)¹⁷ · 0.4² = (–1)¹⁷ · 0.16 = –1 · 0.16 = –0.16
г) 10²⁶ · 0.1²⁸ = (10 · 0.1)²⁶ · 0.1² = 1²⁶ · 0.01 = 0.01 ґ) 2²² · 0.5²⁰ = (2 · 0.5)²⁰ · 2² = 1²⁰ · 4 = 4 д) 1.25²² · (–0.8)²³ = (–1.25 · –0.8)²² · (–0.8) = 1²² · (–0.8) = –0.8
167. Обчисли а) (–5 7)¹²
7¹⁵ · (–1 7)¹⁶ = (7 · (–1 7))¹⁵ · (–1 7) = (–1)¹⁵ · (–1 7) = 1 7 в) (2 3)¹⁰ · (11 2)¹¹ = ((2 3)¹⁰ · (3 2))¹1 =
· 2⁸
6¹² · (1 6)¹⁴ = 6¹² · (1 6)¹² · (1 6)² = 1¹²⁻¹² · (1 6)² = 1 · (1 6)² = 1 36 в) ( 5 9 )¹³ · (–1
2.5⁹ · 0.7³ · 0.4⁹ = (2.5 · 0.4)⁹ · 0.7³ = 1⁹ · 0.7³ = 0.343
д) 0.25¹² · 54 · 4¹² = (0.25 · 4)¹² · 54 = 1¹² ·
а) a⁵ · (a²)⁷ = a⁵ · a¹⁴ = a⁵⁺¹⁴ = a¹⁹
б) (x²)³ · (x³)⁴ = x⁶ · x¹² = x⁶⁺¹² = x¹⁸
в) y · (y5)² · y⁶ = y · y¹⁰ · y⁶ = y1+¹0⁺⁶ = y¹⁷
г) (b³ · b⁵)² = (b3+5)² = b¹⁶
ґ) (x · x⁸)³ · x³ = (x¹⁺⁸)³ · x³ = x⁹ · 3 · x³ = x27 · x³ = x³⁰
д) (−a2)³ · (а3)⁵ = −a6 · а15 = −a6⁺¹⁵ = −a²¹
е) (−y)⁶ · (−y4)⁵ = y⁶ · y²⁰ = y⁶⁺²⁰ = y²⁶
є) ((–x)³)² · (–x)⁴ = x⁶ · x⁴ = x¹⁰
ж) (–a⁴)³ · ((–a)³)⁵ = –a¹² · –a¹⁵ = а12+15 = a²⁷
170. Подай у вигляді степеня добуток
а) c⁶ · (c³)⁹ = c⁶⁺²⁷ = c³³
б) (a⁴)³ · (a³)⁶ = a¹² · a¹⁸ = a¹²⁺¹⁸ = a³⁰
в) x · (x⁵)⁴ · (x⁶)³

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
б) 2¹⁰ · 64 = 2¹⁰ · 2⁶ = 2¹⁰⁺⁶ = 2¹⁶
в) 0.001 · 0.1⁵ = 0.1³ · 0.1⁵ = 0.1³⁺⁵ = 0.1⁸
г) 27 64 · 9 16 = (3 4)³ · (3 4)² = (3 4)³⁺² = (3 4)⁵
ґ) 0.4 · 0.16 = (0.2²) · (0.2⁴) = 0.2²⁺⁴ = 0.2⁶
д) (–0.3)⁵ · (–0.027)² = (–0.3)⁵ · (–0.3)⁶ = (–0.3)⁵⁺⁶ = (–0.3)¹¹
172. Подай у вигляді степеня добуток
а) 36 · 6⁸ = (6²) · 6⁸ = 6²⁺⁸ = 6¹⁰
б) 128 · 2⁵ = 2⁷ · 2⁵ = 2⁷⁺⁵ = 2¹²
в) 0.25 · 0.125 = (0.5²) · (0.52) = 0.5²⁺³ = 0.5⁵
г) 16 625 · (–8 125) = –(2 5)⁴ · (2 5)³ = –(2 5)7
ґ) 0.6 · 0.216 = (0.6) · (0.6³) = 0.6¹⁺³ = 0.6⁴
д) (–0.4)⁶ · (–0.064)⁴ = (–0.4)⁶ · (–0.4)⁹ = (–0.4)⁶⁺⁹ = (–0.4)¹⁵
173. Знайди значення виразу а) ((11⁶)⁴ 11²³ ) = 11²⁴ 11²³ = 11; б) (6⁵)³ · (6²)⁵ 6¹⁷ · (6²)³ = 6¹⁵ · 6¹⁰ (6¹⁷ · 6⁶) = 6²⁵ 6²³ = 36;
в) 5⁶ · 25⁴
25 · 125⁴ = 5⁶ · 5⁸ 5² · 5¹² = 5¹⁴ 5¹⁴ = 1;
6⁹
2⁹ 3¹⁰ = 6⁹ 6⁹ 3 = 1 3;
ґ)
5⁷ 3⁸ 15⁶ = (5 3² 15) 15⁶ = 45;
д) 12⁹ 3⁸ · 8⁶ = (3 · 3⁸ · 4⁹) (3⁸ · (2³)⁶) = 3 · 2¹⁸ 2¹⁸ = 3¹ = 3. 174. Знайди значення виразу
а) (13⁵)⁶
13²⁹ = 13³⁰ 13²⁹ = 13;
б) (8⁴)³ (8³)⁴ 8¹⁰ (8²)⁶ = 8¹² 8¹² 8¹⁰ 8¹⁶ = 8²⁴ 8²⁶ = 1 64;
в)
г)
ґ)
д)
9⁴ 27⁵
3⁵ · 81⁴ = (3²)⁴ (3³)⁵ 3⁵ · (3⁴)⁴ = 3⁸ 3¹⁵ 3⁵ · 3¹² = 3²³ 3¹⁷ = 3⁶ = 729;
3⁹ 4⁸
12⁸ = 3 12⁸ 12⁸ = 3;
7⁹ · 3⁸
21⁷ = 7² · 3 · 21¹⁷ 21⁷ = 147;
16⁹ · 5²⁰
20¹⁸ = 4¹⁸ · 5¹⁸ · 5² 20¹⁸ = 5² = 25
175. Розв’яжи рівняння.
а) 3x² · x⁵ + 3 = 0
3x⁷ + 3 = 0
3x⁷ = –3
x⁷ = –1
x = –1;
в) (2x)⁵ = –32
32x⁵ = –32
x⁵ = –1
x = 1;
176. Знайди таке
а) 53 · 54 = 55 + z; 5 + z = 7; z = 2;

3x · 35 = (32)x; 2x =
б) –2y⁴ · y⁷ = 2 y¹¹ = –1 y = –1;
г) (x⁹ · x⁴)³ = –1 (x¹³)³ = –1
x³⁹ = –1
x = –1.
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
в) ((43)x)4 = 4x · 422; 12x = x + 22; 11x = 22; x = 2. ((43)2)4 = (46)4 = 424; 42 ⋅ 422 = 42+22 = 424
а) 6ˣ · 6⁴ = (6³)ˣ
6ˣ⁺⁴ = 6³ˣ
x + 4 = 3x
2x = 4
x = 2
6² · 6⁴ = 6⁶ = (6³)² · (6³)⁶ = 7¹²⁻⁴ = 7⁴⁸
178. Знайди
б) (7⁶)⁸ = 7¹²ˣ 7⁴⁸ = 7¹²ˣ 48 = 12x x = 4
7⁸ = 7⁴⁸ = 7¹²⁻⁴
в) (2⁵)ˣ · 2² = (2³)ˣ · (2ˣ)⁴
2⁵ˣ · 2² = 2³ˣ · 2⁴
2⁵ˣ⁺² = 2⁷ˣ
5x + 2 = 7x
2x = 2 x = 1 (2⁵)¹ · 2² = 2⁵ · 2² = 2⁷ = 2³⁺¹ · 2¹⁺¹ = 2⁷
3 · 10⁻7 + 2 · 10⁻⁷ = 5 · 10⁻7;
3 · 10⁻7 – 2 · 10⁻⁷ = 1 · 10⁻7 ;
(3 · 10⁻7) · (2 · 10⁻⁷) = 6 · 10⁻¹⁴;
(3 · 10⁻7) : (2 · 10⁻⁷) = 1,5;
б)
4,5 · 10¹⁰ + 3 · 10⁹ = 4,5 · 10¹⁰ + 3 · 10⁹ = 48 · 10⁹ = 4,8 · 10¹⁰;
4,5 · 10¹⁰ – 3 · 10⁹ = 45 · 10⁹ – 3 · 10⁹ = 42 · 10⁹ = 4,2 · 10¹⁰;
(4,5 · 10¹⁰) · (3 · 10⁹) = 13,5 · 10⁹ = 1,35 · 10¹⁰;
(4,5 · 10¹⁰) : (3 · 10⁹) = 1,5 · 10 = 15 = 1,5 · 10; в) –6 · 10¹³ + 1,2 · 10¹² = –60 · 10¹² + 1,2 · 10¹² = –58,8 · 10¹² = –5,88 · 10¹³; –6 · 10¹³ – 1,2 · 10¹² = –60 · 10¹² – 1,2 · 10¹² = –61,2 · 10¹² = –6,12 · 10¹³; (–6 · 10¹³) · (1,2 · 10¹²) = –7,2 · 1025;
(–6 · 10¹³) : (1,2 · 10¹²) = –5 · 10 = –50 = –5 · 10. 179. Знайди суму, різницю,
а)
1,4 · 10⁻⁶ + 7 · 10⁻⁶ = 8,4 · 10⁻⁶;
1,4 · 10⁻⁶ – 7 · 10⁻⁶ = –5,6 · 10⁻⁶;
(1,4 · 10⁻⁶) · (7 · 10⁻⁶) = 9,8 · 10⁻¹²;
(1,4 · 10⁻⁶) : (7 · 10⁻⁶) = 0,2 = 2 · 10⁻¹;
б)
3,5 · 10⁻⁴ + 5 · 10⁻⁴ = 8,5 · 10⁻⁴;
3,5 · 10⁻⁴ – 5 · 10⁻⁴ = –1,5 · 10⁻⁴;
(3,5 · 10⁻⁴) · (5 · 10⁻⁴) = 17,5 · 10⁻⁶ = 1,75 · 10⁻⁷;
(3,5 · 10⁻⁴) : (5 · 10⁻⁴) = 0,7 = 7 · 10⁻¹.
в)
2,8 · 1021 + 7 · 10²⁰ = 2,8 · 1021 + 7 · 1020 = 3,5 · 1021
2,8 · 1021 – 7 · 10²⁰ = 2,8 · 1021 - 7 · 1020 = 2,1 · 1021
(2,8 · 1021) · (7 · 10²⁰) = 2,8 · 1021 · 7 · 1020 = 1,96 ·1042
(2,8 · 1021) : (7 · 10²⁰) = 2,8 · 1021 / 7 · 1020 = 4.
180. Виконай дії.
а)
2,5 · 10⁴ + 3,3 · 10⁵ = 2,5 · 10⁴ + 3,3 · 10 · 10⁴ = 35,5 · 10⁴ = 3,55 · 10⁵; б) 5,5 · 10⁷ + 8,3 · 10⁶ = 55 · 10⁶ + 8,3 · 10⁶ = 63,3 · 10⁶ = 6,33 · 10⁷; в) 7,7 · 10⁷ – 7,1 · 10⁶ = 7,7 · 107 – 7,1 · 106 = 6,99 · 107 г) 6,4 · 10⁻³ · 2 · 10⁴ = 6,4 · 20 = 128. 181. Користуючись
4.1,
чисел. 1²; 3²; 5², тобто (2n + 1)², де n = 0, 1, 2.

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
а) 1, 4, 9, 16, 25, 36, ...;
б) 1, 8, 27, 64, 125, ...
183. Чи є тотожністю рівність?
а) 3x + 5 = 3(x + 5); 3x + 5 ≠ 8x + 15. Ні.
б) 3(x – 4) = 3x – 12; 3x – 12 = 3x – 12. Так.
в) (2a – b)² = (b – 2a)²; 4a² – 4ab + b² = b² – 4ab + 4a². Так.
г) (2x – 3y)3 = (3y – 2x) 3; (2x – 3y)³ ≠ –((2x + 3y)³). Ні. ґ) (a + b) · 0 = a + b. Ні.
д) y · (x – x) = 0. Так.
184. Добова потреба
Нехай вага семикласника 60 кг.
Отже, 60 • 52 = 3120 (ккал) треба як мінімум.
3120 + 3120 · 1 6 = 3120 + 520 = 3640 (ккал)
щоденно потрібно 3640 калорій
185. Розклади числа 400 та 6561 на
400 = 2 · 2 · 2 · 2 · 5 · 5 = 2⁴ · 5² 6561 = 3 · 3 · 3 · 3 · 3 · 3 · 3 · 3 = 3⁸ 186. Чи є вирази одночленами?
а) 2 3 abc3 так, це

Вартість покупки: 3а. Так, це одночлен.
б) Кількість печива: 6а ∙ 20 = 120а. Так, це одночлен.
в) Площа новоутвореної ділянки: 2а ∙ а = 2а². Так, це одночлен.
193. Запиши одночлен у стандартному вигляді
а) 6аb;
б) 12а³х;
в) –5с²z²;
г) 0,6а²b²;
ґ) 6аb;
д) 1,0ах³;
е) 1 2 x⁶;
є) –4x³y²z;
ж) 5аb²c.
194. Запиши
а) 30xy;
б) –6m³n;
в) 3k⁶p³; г) –1,2a³c⁴; ґ) –2k²c³;
д) 10,5mn;
е) –8,1kc; є) 16x²y⁷.
195. Обчисли значення одночлена
а) 2 · (–1)⁴ · 5 = 10; б) –0,2² · (–3)² = 0,04 · 27 = 1,08; в) 2 3 · 36 1 · 1 2 = 12;
г) –5 · 0,2 · 1 8 = –1 8
196. Обчисли значення одночлена а) –3 · 8 · 1 = –24; б) –20 · 0,01 · 8 = –1,6.
197. Перемнож одночлени а) 2ab · 3a²c = 6a³bc; б) 0, 2xy · (–5xy) = –1x²y² = –x²y²; в) –am² · 3m³p = –3am⁵p; г) 3a³ · 2a²z · 6az³ = 36a⁶z⁴;

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
ґ) 3xy² · 1 3 x²y = x³у³;
д) 1 2 3 ax · 3 5 z = 5 3 ax · 3 5 z = axz.
198. Перемнож одночлени
а) 3m²n · mn² = 3m³n³;
б) 3xy · 1,5x³y² = 4,5x⁴y³;
в) –a⁵c³ · 9ac³ = –9a⁶c⁶; г) abcd · (–ab²c³) = –a²b³c⁴d;
ґ) 2y · (–3y)² · y³ = –6y⁶; д) 2 5 x⁵y⁴ · (–5 7 xy³) = –2 5 · 5 7 x⁶y⁷ = –2 7 x⁶y⁷.
199.Гра
200. Піднеси до квадрата і до куба одночлен
а) (2аx)² = 4a²x²; (2аx)³ = 80a³x³;
б) (5bc²)² = 25b²c⁴; (5bc²)³ = 125b³c⁶;
в) (– 1 2 x⁵c²)² = 1 4 x¹⁰c⁴; (–1 2 x⁵c²)³ = –1 8 x¹⁵c⁶; г) (0, 2x²у⁵)² = 0,04x4у10; (0, 2x²у⁵)3 = 0,008x6у15
201. Піднеси
а) (–3a²)² = 9a⁴; (–3a²)³ = –27a⁶;
б) (0, 2x³m)² = 0,04x⁶m²; (0, 2x³m)³ = 0,008x⁹m³;
в) (0,3a³c⁴)² = (0,3a³c⁴)² = 0,09a⁶c⁸; (0,3a³c⁴)³ = 0,027a⁹c¹²;
г) (– 2 3a²x³)² = 4 9 a⁴x⁶; (–2 3 a²x³)³ = –8 27 a⁶x⁹
202. Спрости вираз
а) (3аx²)³ = 27a³x⁶;
б) (x³y³)² = x⁶y⁶;
в) (–2ab)³ = –8a³b³;
г) (–3xy³)² · 2xy² = –6x²y⁵;
ґ) 2 3 a³(–3ax)⁴ = 2 3 · 81a³a⁴x⁴ = 54a⁷x⁴;
Д) –0,7y³(–1 7 y³)² = –0,7 · 1 49 y⁶ = –1 70 y⁹
203. Спрости вираз
а) (3m³c)² = 9m⁶c²;
б) (k⁵p³)⁷ = k³⁵ · p²¹;
в) (–2a²b)⁴ = 16a⁸b⁴;
г) (–2a²c)³ · a³c² = –8a⁶c³ · a³ · c² = –8a⁹c⁵;
ґ) 1 8 c²(–2xc)³ = 1 8 · (–8)c²x³c³ = –c⁵x³;
д) (1 3 pq²)⁴ · p³ · p³ = 1 81 p⁴q8· p³ · p³ = 1 81 p10q8
204. Подай вираз у вигляді
а) 16a⁴b² = (4a²b)²;
б) 0,36x⁸y¹² = (0,6x⁴y⁶)²;
в) 0,01a¹⁸c¹⁰ = (0,1a⁹c⁵)²;
г) 361m⁶n³⁰ = (19m³n¹⁵)²;
ґ) 9 25 a²⁶b¹⁴ = (3 5 a¹³b⁷)²;
д) 16 49 x¹⁶y¹²z⁴ = (4 7 x⁸y⁶z²)².
205. Подайте вираз у вигляді куба одночлена.
а) –8a⁶ = (–3a²)³;

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
б) 27x⁹y¹⁵ = (3x³y⁵)³;
в) –0,001a³b¹² = (–0,1ab⁴)³;
г) 0,064x¹⁸y²⁷ = (0,4x⁶y⁹)³;
ґ) –1 125 a⁹b⁶c³ = (–1 5 a³b²c)³;
д) 1000000y²¹x³⁰ = (100y⁷x¹⁰)³.
206. Перемножте одночлени, щоб
таблицю. x 5x –0,1x 2x²
a Ax 5ax –0,1ax 2a x²
2a 2ax 10ax –0,2ax 4a x²
–3ax –3a x² –15a x² 0,3a x² –6a x³ 4a² 4a²x 20a³x –0,4a²x 8a²x²
207. Запиши у стандартному вигляді одночлен
а) 2a · 5x · (–1 2 5 a) = 2 · (–7 5) · 5a²x = –14a²x;
б) c³ · (–2 7)cx = –2 7 c⁴x;
в) –5a²z³ · (–3 5 z) = 3a²z⁴;
г) –3ax² · 2a · (–6x³) = 36a²x⁵;
ґ) 2 3 ac² (–c²) = –2 3 ac4;
д) –4a · 3axy (–3 4 x²y) = 9a²x³y².
208. Запиши у стандартному вигляді
а) 0, 8xyz • (–5y)³ = 100xу⁴z;
б) 3a³ • (–2 3ab⁵c²) = –2a³b⁵c²;
в) 5 7xy • (–7 10xy) = –1 2x²y²;
г) –2cz³ • 3z • (–5cz) = 30z⁵c²; ґ) (– 3 4acx) • (–4 5ax³) = 3 5 a²cx4; е) –1 2cz² • 4cx • (–c) = 2c³xz³.
209. Обчисли значення одночлена а) –2 3 a2c4, Якщо a = 1 2, c = –3, то –2 3 • (1 2)² • (–3)⁴ = –2 3 • 1 4 • 81 = –27 2 = –13,5; б) 0,5a5b, якщо a = 2, b = –0,1 то 0,5 • (2)5 • (–0,1) = –1,6.
210. Обчисли значення одночлена а) 2c2x3 , якщо c = 1,5 і x = –10, то 2 • (1,5)² • (–10)³ = 2 • 2,25 • (–1000)

–axyz · 2az² · (–3x) = 6a²x²yz³;
6x²y · 0,2x²z · 10y²z = 10x⁴y³z²;
5a² · 3xy³ · (–2 3 axy³) = –10a³x²y⁶;
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
г) (–2 1 3 ab²) · (–3 7 ab²) · 3b² = –7 3 · (–3 7) · 3a²b⁶ = 3a²b⁶.
212. Знайди добуток одночленів
а) 0,5mnk³ · m²n² · 4nk² = 2m³n⁴k⁵;
б) –1 2 3 an² m · (–3an²) · (–0,2a) = –a³ · n⁴ · m.
213. Піднеси до куба одночлен
а) (3cx)³ = 27c³x³;
б) (2a²m)³ = 8a³m³;
в) (–2 3 ab²c³)³ = –8 27 c³b⁶c⁹;
г) (–1 1 2 c²n²p)³ = –8 3 c⁶n⁶p³;
ґ) (–1 2 3 an²c³)³ = –125 27 a³n⁶c⁹.
214. Піднеси до четвертого степеня одночлен
а) (3x²)⁴ = 81x⁸;
б) (–0,1ac²)⁴ = 0,0001a⁴c⁸;
в) (–2 3 x²y)⁴ = 16 81 x⁸y⁴;
г) (–1 1 2 ab²c)⁴ = 81 16 a⁴b⁸c⁴ = 5 1 16 a⁴b⁸c⁴.
215. Спрости вираз
а) –x² · (3x²y)³ = –x² · 27x⁹y³ = –27x¹¹y³;
б) c³ · (3cx²)² = c³ · 9c²x⁴ = 9c⁵x⁴;
в) 0,5mn⁴ · (–2m)⁵ = 0,5mn⁴ · (–32)m⁵ = –16m⁶n⁴;
г) (–a⁶b³)⁷ · 6a³b⁴ = –a⁴²b²¹ · 6a³b⁴ = –6a⁴⁵b²⁵;
ґ) (2a²x)² · 1 2 a = 4a⁴x² · 1 2 a = 2a⁵x²;
д) (3nz³)² · (1 3 nzx)³ = 9n²z⁶ · 1 27 n³z³x³ = 1 3 n⁵z⁹x³.
216. Установи відповідність
(А–Д) 1) – Г; 2) – В; 3) – Б.
217. Покажи, що рівняння не має розв’язків
а) x¹² + 3 = 0; x¹² = –3; б) 2x¹² = –31; x¹² = –15,5; в) –8y¹² = 64; y¹² = –8. Парна степінь числа не може дорівнювати
числу, тому дані рівняння коренів не мають.
218. Розв’яжи рівняння.
а) (x³)⁴ • x • x2 = –1 x¹² • x³ = –1 x¹⁵ = –1 x = –1;

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
б) 5x²y³ = 5 3 · 3x²y³ = 5 3 · 7 = 35 3 = 11 2 3;
в) –9x⁴y⁶ = –(3x²y³)² = –7² = –49;
г) 7 5 7 x⁶y⁹ = 54 7 x⁶y⁹ = 6 7 · (3y²y³)² = 6 7 · 7² = 42.
221. Відомо, що 2b²c = 5, (a²b)² = 2. Знайди значення виразу.
а) a⁴b²с = a⁴b² · b²c = 2 · 5 2 = 5
б) a8b6с = 4 · b² · c = 4 · 5 2 = 10
в) a⁴b6с² = a⁴b² · b⁴ · c² = 2 · b⁴ · ( 25 4b⁴
(–0,5a²b⁴)² · (2a²bc)³ · a²b = 2a12b12 ⋅
грані куба (грань – квадрат) Р = 4х (см).
Так як сума
12х – 4х = 16
8х = 16
х = 2
Сума довжин ребер куба 12 • 2 = 24 (см).
Відповідь: 24 см
б) Ребро куба 2 см.
Sп = 6x² = 6 • 2² = 24 (см²);
V = x³ = 2³ = 8 (см³).
Відповідь: 24 см²; 8 см³
225. У саду
0,4х + 0,4х + 64 = х;
0,8х + 64 = х;
0,8х – х = –64; –0,2х = –64;
х = 64 : 0,2;
х = 320.

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
Яблунь було: 320 • 0,4 = 128;
Вишень було: 128 + 64 = 192.
Відповідь: 320, 128, 192 дерева.
226. Розв’яжи рівняння.
а) 2х – 3(х + 1) = 0;
2х – 3х – 3 = 0; –х = 3; х = –3;
б) 2х + 3 = 3(х + 1) – х;
2х + 3 = 3х + 3 – х; 2х + 3 = 2х + 3; х – будь–яке число;
в) 7(2х – 5) + 3 = 45;
14х – 35 + 3 = 45; 14х = 45 + 32; 14х = 77; х = 77 : 14; х = 5,5;
г) 9(х + 2) – 3х = 6(х + 2);
9х + 18 – 3х = 6х + 12; 6х + 18 = 6х + 12; 6х – 6х + 18 = 12; 18 ≠ 12. Не має розв’язків.
227. Які з виразів є многочленами?
a) 2x – 3 – многочлен б) 37а����² – многочлен в) x² 3x + 5 x – не многочлен
г) у(x – y) – многочлен д) –21 – многочлен
228. Сумою яких
229. Обери многочлен
) 2x + 3a – 5 – не стандартний б) a⁴ – a + 5a + b – не стандартний
в) –x + 3xa – ax + a² – не стандартний
г) –0,5a – 4a² + 3a – 1 –
а) 2ax – 3a + 5 – степінь 1
б) x³ – x8 + 4x – степінь 8 в) 2x³y – 3x²y² – 1 – степінь 3 г) 0,7ax + 8a²x + 5 – степінь 1 ґ) 3x – x³ – 27px – степінь 3
д) y5x – a³y – степінь 1
8m + 4n
–6ab + 2a² + а² + 6ab = 3a²
8a – 10ab + 3a + 10ab = 11a
–0,5x² – y² + 2,2x² + 0,8y² = 1,7x² – 0,2y²;
2a²b – b²a + 7ab² = 2a²b + b²а + 7аb²;
(2 3)xy³ –3 5x³y + 1 1 3 xy³ –2 5x³y = 2xу³ – x³у. 235.

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
а) 4x² + 2x – 7x² – 9x³ – 2x = –3x² – 9x³; Степінь 3.
б) 3a⁴ – 12a² + 13a² + 5 – a² + a⁴ = 4a⁴ + 5; Степінь 4.
в) 27m⁵ – 17m³ + 3m⁵ + 10m³ – 30m⁵ = – 7m³; Степінь 3.
г) y⁴ – 2y³ + 2у + 5y³ – 2y³ – 14 + 7y⁴ = 8y⁴ + y³ + 2y – 14. Степінь 4.
236. Спрости вираз. Знайди степінь многочлена
а) a – b + 3a + 2b² = 4a + 2b² – b; Степінь 2
б) 7x – y² + 5xy – 2x • 3y = 7x – y² + 5xy – 6xy = 7x – y² – xy; Степінь 2.
в) 37 – z³ + 3t – 35z³ = –36z³ + 3t + 37; Степінь 3.
г) –105p + 15q + 10p • 10,5 = –105p + 15q + 105p = 15q; Степінь 1.
237. Спрости вираз. Знайди степінь многочлена
а) x + x² + x³ – 2x² – x = x³ – x²; Степінь 3.
б) (1 2)a + (1 3)a • 3c – ac = (1 2)a + ac – ac = (1 2)a; Степінь 1.
238. Обчисли значення многочлена.
а) x2 – 5x + 6, якщо x = 2, то (2)² – 5 • 2 + 6 = 4 – 10 + 6 = 0; б) 0,7x2 + 0,3x2 , якщо x = 0,5, то
0,7 • (0,5)² + 0,3 • (0,5)² = 0,5² = 0,25; в) 2,8a2 – 1,8a2 , якщо a = –0,2, то 2,8 • (–0,2) – 1,8 • (–0,2)² = –0,56 – 1,8 • 0,04 = –0,632; г) 3а2b + 2аb2 – 2,5а2b + аb2 – 0,5а2b, якщо a = 0,4, b = –0,5, то 3ab² = 3 • 0,4 • (–0,5)² = 1,2 • 0,25 = 0,3.
239. Обчисли значення многочлена. а) m3 – n2 , якщо m = 2; n = –3, то 2³ – (–8)² = 8 – 64 = –56; б) s + 2t2 – 2,8, якщо s = 2,3; t = 0,5, то 2,3 + 2 • (0,5)² – 2,8 = 2,3 + 2 • 0,25 – 2,8 = 0.
240. Визнач
25k + 35p + 40 (км)

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
= 0,48 + 0,8 · 1,2 – 1,44 = 1,44 – 1,44 = 0
245. Обчисли значення
а) 9x2 – 4x2 + 15х5 – 7x5 + 6х – 7x2 – 8x5, якщо х = –7, то –2x² + 6x = –2 · (–7)² – 6 · 7 = –98 – 42 = –140; б) –6a3b2 + a2b3 – 10ab + 5a3b2 – a2b3 , якщо а = 10, b = 0,9, то –a³b² – 10ab = –10³ · 0,9² – 10 · 10 · 0,9 = –810 – 90 = –900.
246. Установіть відповідність між значеннями числових виразів (1–4) і значеннями многочленів (А–Г), якщо x = 0,1. 1) – В; 2) – Г; 3) – А; 4) – Б.
247. Спрости вираз та знайди степінь многочлена а) (2a²)³ + 4 · 3a⁶ – 5a – 9 – 13a⁶ + a = = 8a⁶ + 12a⁶ – 5a – 9 – 13a⁶ + a = 7a⁶ – 4a – 9; степінь: 6; б) x² + 2x³ – (3x)² – 4x² · x³ + 7x⁵ – 2x³ = –8x² + 3x⁵; степінь: 5.
248. Спрости вираз та знайди степінь многочлена а) (3a³)³ + 4 · 3a⁶ – 14a⁹ – 9 – 13a⁶ – 3a⁴ · 4a⁵ = = 27a⁹ + 12a⁶ – 14a⁹ – 9 – 13a⁶ – 12a⁹ = a⁹ – a⁶ – 9; степінь: 9;
б) (–5x) · 2x – (x⁴)² + 6x² + 10 + x³ · 3x⁵ – 3x² = = –10x² – x⁸ + 6x² + 10 + 3x⁸ – 3x² = 2x⁸ – 7x² + 10;
степінь: 8.
249. Запиши у вигляді многочлена число, яке має: а) a тисяч, b сотень, 0 десятків і c одиниць; б) a десятків тисяч, b сотень, c десятків і 0 одиниць. а) 1000a + 100b + 10 · 0 + c · 1 = 1000a + 100b + c; б) 10000a + 100b + 10c.
250. Запиши у
а)
кілометрів вони наблизяться за пів години, рухаючись

На скільки
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
S₆ = 6a² + 9a² + 6a² + 6a² + 9a² + a² + 2a² + 2a² + a² + a² + 2a² + 2a² + 4a² + a² = 52a² см². Степінь 2.
V = 3a · 2a · 3a + a · a · 2a = 18a³ + 2a³ + 2a³ = 22a³ см³. Степінь 3. 255.
Відповідь:
257.
1) P = (2a + a) · 2 + (2a + a) · 2 + 4a = 6a + 6a + 4a = 16a. 2) P = 2(a + c) + 2(c + c – a) + 2(a + a) = 2a + 2c + 4c – 2a + 2a = 2a + 6c.
258. Обчисли.
а) 2² = 4; 2³ = 8; 2⁴ = 16; 2⁵ = 32; 2⁶ = 64; 2⁷ = 128; 2⁸ = 256; 2⁹ = 512; 2¹⁰ = 1024; б) (–1)² = 1; (–1)³ = –1; (–1)⁴ = 1; (–1)²ⁿ = 1; (–1)²ⁿ⁺¹ = –1;
в) 10² = 100; 10³ = 1000; 10⁴ = 10000; 10⁵ = 100000; 10⁶ = 1000000; 10⁷ = 10000000; 10⁸ = 100000000;
г) 0,1² = 0,01; 0,1³ = 0,001; 0,1⁴ = 0,0001; 0,1⁵ = 0,00001; 0,2² = 0,04; 0,3³ = 0,027; 0,4⁴ = 0,0256.
259. Дано вирази 3x
їх квадратів; г) квадрат
a) (3x)² – (5y)² = 9x² – 25y²; б) (3x – 5y)²; в) (3x)² + (5y)² = 9x² + 25y²; г) (3x + 5y)².
260. Пенсіонер одержав
Яка вартість путівки?
5600 : 10 • 100 = 56000 (грн)
Відповідь: вартість путівки дорівнює 56000 гривень
261. Знайди суму і різницю многочленів.
а) 2x³ - c і 3c:
Сума: (2x³ - c) + 3c = 2x³ - c + 3c = 2x³ + 2c Різниця: (2x³ - c) - 3c = 2x³ - c - 3c = 2x³ - 4c
б) 5ax - 4 і -4ax + 4:
Сума: (5ax - 4) + (-4ax + 4) = 5ax - 4 - 4ax + 4 = ax + 0 = ax
Різниця: (5ax - 4) - (-4ax + 4) = 5ax - 4 + 4ax - 4 = 9ax - 8
в) 0,5n - p² і p²:
Сума: (0,5n - p²) + p² = 0,5n - p² + p² = 0,5n
Різниця: (0,5n - p²) - p² = 0,5n - p² - p² = 0,5n - 2p²

г) -2y + c² і c² + 2y:
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
Сума: (-2y + c²) + (c² + 2y) = -2y + c² + c² + 2y = 2c² + 0 = 2c²
Різниця: (-2y + c²) - (c² + 2y) = -2y + c² - c² - 2y = -4y
262.
2
Отже, відповідь: Г -x² + 3x + 2
263. Різниця многочленів x + y і x - y дорівнює:
Різниця: (x + y) - (x - y) = x + y - x + y = 2y
Отже, відповідь: В 2y
264. Обчисли значення виразу.
а) (2a - 3c + 5) + (a + 3c - 2), якщо a = 3, c = -0,5:
Спочатку підставимо значення:
(2·3 - 3·(-0,5) + 5) + (3 + 3·(-0,5) - 2)
(6 + 1,5 + 5) + (3 - 1,5 - 2)
12,5 + (-0,5) = 12
б) (2a - 3c + 5) - (2a + 3c + 2), якщо a = -0,3, c = 2:
Спочатку підставимо значення:
(2·(-0,3) - 3·2 + 5) - (2·(-0,3) + 3·2 + 2)
(-0,6 - 6 + 5) - (-0,6 + 6 + 2)
(-1,6) - (7,4) = -9
265. Додай многочлени
x² - 3x - 2,
a) (3a² + 8a – 5) + (–5a² + 2a + 4) = 3a² + 8a – 5 – 5a² + 2a + 4 = –2a² + 10a – 1;
б) (7a² + 15) + (3a² + 2a – 15) = 10a² + 2a;
в) (12x² – 7x) + (4x² + 3x – 2) = 16x² – 4x – 2;
г) (–7a³b + 5ab² – ab) + (3ab² – 4ab + 7a²b) = –7a³b + 5ab² – ab + 3a²b – 4ab + 2a³b = = –5a³b + 3a²b + 5ab² – 5ab; ґ) (6a² – 4b² + c² + 2ab – 3bc) + (–10b² – 6a² – c² – ac) = = 6a² – 4b² + c² + 2ab – 3bc – 10b² – 6a² – c² – ac = –4b² – 9c² + 2ab – 3bc – ac.
266. Додай многочлени a) (–3n³ + 3p²) + (3n³ + 3p² – 5) = 6p² – 5; б) (3x²y³ + 5xy² – x²y²) + (–3x²y² + 5xy² – 3x²y³) = = 3x²y³ + 5xy² – x²y² – 3x²y² + 5xy⁸ – 3x²y³ = 10xy² – 4x²y².
267. Знайдіть різницю многочленів. a) (2x³ – x² – 3x + 7) – (x³ – 3x + 17) = 2x³ – x² – 3x + 7 – x² + 3x – 17 = x³ – x² – 10; б) (4x⁵ + x – 2x³ – 7) – (x⁵ + 3x – 2х³) = 4x⁵ + x – 2x³ – 7 – x⁵ + x² – 3x + 2 = 3x⁵ – 2x³ – 2x –5.
268. Знайди різницю многочленів a) (8a²c – 7ac² – a + c) – (7ac² – a + 4) = 8a²c – 7ac² – a + c = = – 7ac² + а – 4; б) (–3x²y – 2xy² – 9) – (3x²y – 2xy² – 4) = –3x²y – 2xy² – 9 – 3x²y – 2xy² + 4 = –5.
269.
a) (5a³ – 3a² + 9a) – (3a³ – 3a² + 11) = 5a³ – 3a² + 9a – 3a³ + 3a² – 11 = 2a³ + 9a – 11; б) (12c⁵ + 2c³ – 3c + 6) – (2c⁵ – 3c – 2c³) = 12c⁵ + 2c³ – 3c + 6 – 2c⁵ + 3c + 2c = 10c⁵ + 4c³ + 6.
271. Спрости вираз a) (7x³ – 2x) + (5 + 11x – 6x³) = x² + 9x + 5; б) (8ab + 7b) – (4ab + 7b – 3) = 8ab + 7b – 4ab – 7b + 3 = 4ab + 3; в) (1 – n + n²) – (3n² – 2n + 5) – 7n = 1 – n + n² – 3n² + 2n – 5 – 7n = –2n² – 6n – 4;

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
г) (x²y + xy²) – (3x²y – 2xy² – 7) + 2x²y = x²y + xy² – 3x²y + 2xy² + 7 + 2x²y = 3xy² + 7; ґ) 8ac – (3a² – 2c² + 2ac) – (4a² + 2c²) = 8ac – 3a² + 2c² – 2ac – 4a² – 2c² = –7a² + 6ac.
272. Спрости вираз a) (2a² + 3a – 4) + (5a² – a + 7) = 2a² + 3a – 4 + 5a² – a + 7 = 7a² + 2a + 3; б) (6x³ + 8x – 5) – (4x² + 8x – 5) = 6x³ + 8x – 5 – 4x² – 8x + 5 = 6x³ – 4x²; в) (3z⁴ – 2z³ + 12z – 5) – (3z⁴ – 2z – 5) = 3z⁴ – 2z³ + 12z – 5 – 3z⁴ + 2z + 5 = –2z³ + 14z;
г) (–5c³ – 2c + 3c²) – (1 – c – 2c² – 5c³) = –5c³ – 2c + 3c² – 1 + c + 2c² + 5c³ = 5c² – c – 1.
273. Обчисли значення виразу a) (c³ – 2c² + 3c – 4) – (c³ – 3c² – 5), якщо c = 2, то
c³ – 2c² + 3c + 4 – c³ + 3c² + 5 = c² + 3c + 1 = 2² + 3 • 2 + 1 = 11;
б) 4x² – (–2x³ + 4x² – 5), якщо x = –3, то 4x² + 2x³ – 4x² + 5 = 2x³ + 5 = 2 • (–3)³ + 5 = –54 + 5 = –49;
в) 2p – (1 – p² – p³) – (2p + p² – p³), якщо p = –4, то
2p – 1 + p² + p³ – 2p – p² + p³ = 2p³ – 1 = 2 • (–4)³ – 1 = –128 – 1 = –129.
274. Обчисли значення виразу
a) (x³ – 3x² + 3x – 1) – (3x – 3x²), якщо x = 3, то
x³ – 3x² + 3x – 1 – 3x + 3x² = x³ – 1 = 3³ – 1 = 27 – 1 = 26;
б) (5a⁴ – 2a³) – (4a⁴ – 2a³ + 1), якщо a = –2, то
5a⁴ – 2a³ – 4a⁴ + 2a³ – 1 = a⁴ – 1 = 16 – 1 = 15; в) a² – 2ab + b² – (a² – b² – 3), якщо a = 5, b = 4, то a² – 2ab + b² – a² + b² + 3 = 2b² – 2ab + 3 = 2 • 4² – 2 • 5 • 4 + 3 = 32 – 40 + 3 = –5.
275. При якому
один одному?
x² + 8x + 9 = x² + 6x + 4
8x – 6x = 4 – 9
2x = –5
х = –5 : 2
x = –2,5 276. При якому
один одному?
2x² + 10x + 12 = 2x² – 4x – 2
2x² – 2x² + 10x + 4x = –2 – 12
14x = –14
х = –14 : 14
x = –1
+ 5?
7t² – 2t + 1 – (7t² + 5) = 2
7t² – 2t + 1 – 7t² – 5 = 2
–2t = 2 + 4
–2t = 6
t = 6 : (–2)
t = –3
278.
3y² + 11?
3y² + 11 – 3y² – 5y + 3 = 4
–5y = 4 – 14
–5y = –10

y = –10 : (–5) y = 2
279. Розв’яжи рівняння a) (4x – 5) – (7x + 8) = 2
4x – 5 – 7x – 8 = 2
–3x = 2 + 13
x = 15 : (–3)
x = –5;
в) (5x + x³ – 7) – (2x³ + 3x) = –(1 + x³)
5x + x³ – 7 – 2x – 3x = –
1 – x³
2x = –1 + 7
x = 6 : 2
x = 3;
280. Розв’яжи рівняння a) (2x – 8) – (5x + 6) = 4
2x – 8 – 5x – 6 = 4
–3x = 4 + 14
x = 18 : (–3)
x = –6;
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
б) 9z + 17 – (4z – 6) = 38 9z + 17 – 4z + 6 = 38
5z = 38 – 23
z = 15 : 5 z = 3;
г) 19 – (3x² – 2x) – (6x –x²) = 7 – 2x² 19 – 3x² + 2x – 6x + x² = 7 – 2x² –4x = 7 – 19
x = –12 : (–4)
x = 3.
в) 24 – (x² + 8x – 17) = 5 – 5x – x²
24 – x² – 8x + 17 = 5 – 5x – x²
–8x + 5x = 5 – 24 – 17
–3x = –36
x = –36 : (–3)
x = 12;
281. Знайди суму многочленів.
б) 16y – (3 – 2y) + (7y + 1) = 48 16y – 3 + 2y + 7y + 1 = 48
25y = 48 + 2
y = 50 : 25
y = 2;
г) (x – 2x⁴ + 7) – (3x + 3 – 5x⁴) = 6 + 3x⁴
x – 2x⁴ + 7 – 3x – 3 + 5x⁴ = 6 + 3x⁴
–2x = 6 – 7 + 3
x = 2 : (–2)
x = –1.
а) ( 5xy − 4x² + y²) + (y³ − 3x² + 5xy − y² − 2) = y³ − 7y² − 2;
б) (2a⁴ − 12a² + 15a – 8) + (-3a⁴ + 12a² − 5a + 8) = a⁴ + 10a;
в) ((3 5)m³ − (5 8)m² + 6) + ((2 5)m³ + (3 8)m² − 6) = m³ − (1 4)m².
282. Знайди різницю многочленів
а) ( 2xc² − 2,5x² + 7,2x) – ( 2,8x + 0,25x² 2x²) = −2xс² − 0,75x² + 10x
б) ( 4a³ − b³ + 4a³b² + 3a²b²) – (3a³ b³ + 3a²b² 4a³b²) = −7a³ + 8a³b²
в) ( 2 3xy − 3 5x²y) – (2(1 3)xy – x²y + 21 2y²) = −3xy + (2 5)x²y (2 5)y²
283. Спрости вираз
а) (2az − 3z²) + (−az − z²) + (4z² − 5az) = 2az − 3z² + az + z² − 4z² + 5az = −4az; б) (0,7a − 0,7a² − 0,7) − (5,7a² − 4,7a − 1,7) =
−
+
+
=
+ 5,4a + 1; в) −4m² − (m − n²) + (3m + 4m²) − 2n² = −4m² − m + n² + 3m + 4m² − 2n² = 2m − n²; г) 21 2
284. Спрости вираз а) (2x² − x + c) − (x² + c + 5) − (3c − x² − x) = 2x² − x + c − x²

+ x = = 2x² − 3c − 5;
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
б) 3,6cx² + 1,8c²x − 1,2x + (−1,8c²x − 1,6cx² − 1,2x) = = 3,6cx² + 1,8c²x − 1,2x − 1,8c²x − 1,6cx² − 1,2x = 2cx² − 2,4x
в) 21 2 ax²c + 11 3x²c − (4 3 cx² + 5 2ax²c) = 0 г) 21 3az² − (2 3 a²z − 21 6 az² − 11 3z) − 41 2 az² = 2 3 a²z + 4 3 z
285. Периметр килима ABCDEF дорівнює 2p. AB = a, AF = c, EF = b. Знайди
BC, ED і DC (мал. 7.1). DC = a − b;
PABCDEF = AB + AF + FE + ED + DC + BC; PABCDEF = a + c + b + ED + a − b + BC; ED = BC − c; a + c + b + BC − b + a − b + BC = 2p; 2BC = 2p − 2a; BC = p − a; ED = p − a − c.
286. Доведи, що при будь-яких
а) (x3 + 3x² − 3x) + (x² + 4x3 − 7x) (5x3 10x – 5) = 4x² + 5 > 0. Доведено. б) –((2x3)2 – 7x9) – (6(x3)2 – (x3)3 – 3) + (10(x2)3 – (2x3)3) = 3 > 0. Доведено.
287. Доведи, що
-яких
значення. а) (5x5 + 3x³ − 1) – (x⁴ − 4x5 + 8x³) – (x5 − 5x⁴ − 11x³) = 8x5 − 4x⁴ + 6x3 1 = додатне при х > 0, тобто не завжди від’ємне б) (4 − (3x5)3) – ((3x5)2) – (2x3)5) + 9 + 5x15) = −54х15 + 9x¹⁰ − 13, що завжди < 0 при x ≠ 0 Доведено.
288. Установіть відповідність
(А–Д)
1) 0,5y – (4,3y + 2,7) + 0,3у = 46,3
3,5y = 49
y = 49 : (−3,5)
y = −14 Д
2) − 2,5x – (3,7 + 4,3x) = 1,7
1,8x = 5,4
x = 5,4 : 1,8
x = 3 Б
3)1 3 t + 2 5 + (3 5 + 2 3t) = 2 − 3t 4t = 1
t = 0,25 A
4)2 5 z = −(2 5 + z) + 3 5 z + 10
1(1 5)z = 9(3 5)
(6 5)z = 48 5
z = 48 5 : (6 5)
z = −8Г
Відповідь: 1 – Д; 2 – Б; 3 – А; 4 – Г
289. Заміни
а) * − (8a³ − 2a² + 7) = 3 − a²
рівняннями, заданими умовами (1–4), та їх
* = 3 − a² + (8a³ − 2a² + 7); * = 3 − a² + 8a³ − 2a² + 7; * = 10 + 8a³ − 3a²
б) * + (3x + 8) = −3x² + 2x − 15;
* = −3x² + 2x − 15 − (3x + 8); * = −3x² + 2x − 15 − 3x − 8; * = −3x² − x − 23
в) (2xy − 11x² + 10y²) − * = 5x² + 4y² − 6;

* = (2xy − 11x² + 10y²) − (5x² + 4y² − 6); * = 2xy − 11x² + 10y² − 5x² − 4y² + 6
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
* = −16x² + 6y² + 2xy + 6.
290. Який
- 6a + 13?
2a³ - a² - a + 3,
а) (2a³ – a² – a + 3) + * = 3a³ – 5a² – a + 7
* = 3a³ – 5a² – a + 7 – (2a³ – a² – a + 3);
* = 3a³ – 5a² – a + 7 – 2a³ + a² + a – 3; * = a³ – 4a² + 4;
б) (2a³ – a² – a + 3) + * = a² – 6a + 13;
* = a² – 6a + 13 – (2a³ – a² – a + 3); * = a² – 6a + 13 – 2a³ + a² + a – 3
* = –2a³ + 2a² – 5a + 10
291. Доведи тотожність
а) 2a⁴ – (6a⁴ – 5ab) + (4a⁴ – 3ab + 2) = 2ab + 2; 2a⁴ – 6a⁴ + 5ab + 4a⁴ – 3ab + 2 = 2ab + 2; Доведено.
б) (3a² + 2b² + c²) – (3c² + 2a² – b²) + (–3b² + 2c² – a²) = 0; = 3a² + 2b² + c² – 3c² – 2a² + b² – 3b² + 2c² – a² = 0; Доведено.
в) –z² – (x² + (y² – (x² + y² + z²) + z²) + y²) – x² = –x² – y² – z²; –z² – x² – y² + x² + y² + z² – z² – y² – x² = –x² – y² – z²; Доведено.
г) a³ – (b³ – (a²b – ab²)) – (–(–(a²b – ab²) + b³) – a³) = 2a³; = a³ – b³ + a²b – ab² – a²b + ab² + b³ + a³ = 2a³. Доведено.
292. Доведи тотожність
a) 3a² + (−2a² + 5a + 1) − (a² + 5a − 1) = 2; 3a² − 2a² + 5a + 1 − a² − 5a + 1 = 2; Доведено.
б) (−3a⁵ + a + 17) − (a⁵ − a + 2) − (4a⁵ + 2a + 10) = −8a⁵ + 5; 3a⁵ + a + 17 − a⁵ + a − 2 − 4a⁵ − 2a − 10 = −8a⁵ + 5; Доведено.
в) ab + bc + ac − (abc + ab − (abc − bc − (abc + ac))) = abc; = ab + bc + ac − abc − ab + abc − bc − abc − ac = −abc. Доведено.
293. Доведи, що при будь-якому
а) (7n + 21) – (10 – 4n) кратне 11. 11n + 11 = 11(n + 1). Доведено.
3a³ - 5a² - a + 7; б) a²
б) 8n² + 7n − 4 – (3n² + 12n – 19) кратне 5. 5n² − 5n + 15 = 5(n² − n + 3). Доведено. в) (12n – 5) – (5n – 9) при діленні на 7
294. Доведи, що при
-якому
4. 7n + 4. Доведено.
а) (12n + 17) − (10 + 5n) = 12n + 17 − 10 − 5n = 7n + 7 = 7(n + 1);
б) 9n² + (21n − 4) − (12n − 13) = 9n² + 21n − 4 − 12n + 13 = 9n² + 9n + 9 = 9(n² + n + 1);
в) (10n − 3) − (4n − 6) = 10n − 3 − 4n + 6 = 6n + 3.
295. Подай у
а) abc = 100a + 10b + c;
б) abc + ac = 100a + 10b + c + 10a + c = 110a + 10b + 2c;
в) xyz − zxy = 100x + 10y + z − 100z − 10x − y = 90x + 9y − 99z;
296. Подай у
а) xyz = 100x + 10y + x = 101x + 10y;
б) xyz − xy = 100x + 10y + z − 10x − y = 90x + 9y + z
в) abc + bca = 100a + 10b + c + 100b + 10c + a = 101a + 110b + 11c
297. Доведи, що: а) різниця
a0b і b0a кратна 99.
а) ab − ba = 10a + b − 10b − a = 9a − 9b = 9(a − b);
б) ab + bc + ca = 10a + b + 10b + c + 10c + a = 11a + 11b + 11c = 11(a + b + c) кратно 11.
в) a0b − b0a = 100a + b − 100b − a = 99a − 99b = 99(a − b) кратно 99. Доведено.

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
298. Доведи, що:
різниця (ab+ac+bc)−(ca+cb+ba) кратна 18.
а) ab + ba = 10a + b + 10b + a = 11a + 11b = 11(a + b); б) abc − cba = 100a + 10b + b − 100c − 10b − a = 99a − 99c = 99(a − c); в) (ab + ac − bc) − (ca + cb + ba) = 10a + b + 10a + c + 10b + c − 10c − a − 10c − b − 10b − a = = 18a − 18c = 18(a − c) кратно 18. Доведено.
299. Покажи, що числа, розташовані так, як на малюнку 7.2, утворюють
при будь-яких значеннях змінних a і c
Сума рядків квадрата:
Сума стовпців квадрата: a + 7c + a + a + 5c = 3a + 12c; a + 7c + a + 2c + a + 3c = 3a + 12c
a + 2c + a + 4c + a + 6c = 3a + 12c; a + a + 4c + a + 8c = 3a + 12c
a + 3c + a + 8c + a + c = 3a + 12c; a + 5c + a + 6c + a + c = 3a + 12c
Сума діагоналей: a + 7c + a + 4c + a + c = 3a + 12c a + 5c + a + 4c + a + 3c = 3a + 12c
300. Доведи, що:
303.
а) 2 : x = 7 : 10; x = 2 · 10 : 7 x = 2 6 7 б) 1 : 4 = 3 : (x + 2); x + 2 = 3 · 4 : 1 x = 12 − 2 x = 10 в) 6 : 5 = 0,9 : 3x; 3x = 5 · 0,9 : 6 3x = 0,75 x = 0,75 : 3 x = 0,25
304. Подай у вигляді многочлена добуток.
а) (x + y)c, (x - y)c, (2x - y)c:
(x + y)c = xc + yc
(x - y)c = xc - yc
(2x - y)c = 2xc - yc
б) (x + y)n, (x - y)n, (3x - y)n: (x + y)n = xn + yn
(x - y)n = xn - yn
(3x - y)n = 3xn - yn
в) (2 + a)c, (2 - a)c, (2 - an)c:
(2 + a)c = 2c + ac
(2 - a)c = 2c - ac
(2 - an)c = 2c - anc

305. Чи тотожні
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
а) 2(a - 5) і 2a - 10:
2(a - 5) = 2a - 10
Так, вирази тотожні.
б) (x - y)5 і 5x - 5y: (x - y)5 = 5x - 5y
Так, вирази тотожні.
в) 3c(a - x) і 3ac - x:
3c(a - x) = 3ca - 3cx
3ac - x = 3ac - x
Ні, вирази не тотожні, бо в першому
3cx, а в другому лише -x.
г) (x - 7)(-2) і 14 - 2x:
(x - 7)(-2) = -2x + 14
14 - 2x = 14 - 2x
Так, вирази тотожні.
306. Розв'яжи рівняння 2(x - 3) + 2(x + 3) = 8.
2(x - 3) + 2(x + 3) = 8
2x - 6 + 2x + 6 = 8
4x = 8
x = 2
Відповідь: В 2
307. Знайди значення виразу 3(a + 2) - 3(a - 1), якщо a = -0,07. 3(a + 2) - 3(a - 1) = 3a + 6 - 3a + 3 = 9
Перевіримо, підставивши a = -0,07: 3(-0,07 + 2) - 3(-0,07 - 1) = 3(1,93) - 3(-1,07) = 5,79 + 3,21 = 9
Відповідь: Г 9
308. Скільки доданків має утворитися після множення:
а) двочлена на одночлен; б) тричлена на одночлен?
а) При множенні двочлена на одночлен утворюються 2 доданки.
б) При множенні тричлена на одночлен утворюються 3 доданки.
309. Помнож вирази.
а) 3a + c · 2a = 6a² + 2ac;
б) (8x − y) · 3xy = 24x²y − 3xy²;
в) (x² − x) · 2x = 2x³ − 2x²;
г) (m³ + 3m) · m² = m² + 3m³;
ґ) (2a + 3) · 4a = 8a² + 12a;
д) (3x − y) · (−2xy) = −6x²y + 2xy².
310. Подай у вигляді многочлена
а) (x + 1)x² = x³ + x²;
б) a²(b – c) = a²b – a²c;
в) (n² – n)n³ = n⁵ – n⁴;
г) 3(2x – 7) = 6x – 21;
ґ) –3n(n² + 5n – 1) = –3n³ – 15n² + 3n;
д) 2ac(3a – 5ac + 2c) = 6a²c – 10a²c² + 4ac²
311. Подай у вигляді
а) (2a + 3b²)a = 2a² + 3ab²;
б) (–a + ac)c² = –ac² + ac³;
в) –2a² (a² – 1) = –2a⁴ + 2a²;

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
г) 6(2xy – 3) = 12xy – 18; ґ) 5p(2p² – 3p + 4) = 10p³ – 15p² + 20p; д) 3xy(5x + 6xy – 9y) = 15x²y + 18x²y² – 27xy².
312. Чи тотожні вирази
а) Так; б) ні; в) так; г) ні.
313. Чи тотожні вирази
а) Так
б) ні
в) так
г) ні
314. Спрости вираз а) 2a³(4a² + 3a) – 6a⁴ = 8a⁵ + 6a⁴ – 6a⁴ = 8a⁵; б) 7x² – 2x(3x – y) = 7x² – 6x² + 2xy = x² + 2xy;
в) 2x(x – 1) – x² = 2x² – 2x – x² = x² – 2x; г) (3 – a)a² – 3a² = 3a² – a³ – 3a² = –a³;
ґ) (m – n)mn + m(mn + n²) = m²n – mn² + m²n + mn² = 2m²n;
д) –3z(z – 2) – z(6 + 2z) = –3z² + 6z – 6z – 2z² = –5z².
315. Спрости вираз
а) –3c³ + c(3c² – 1) = –3c³ + 3c³ – c = –c; б) 2p – (p² + 2)p = 2p – p³ – 2p = –p³;
в) 5m(6 – 2m²) + 10(m³ – 3m) = 30m – 10m³ + 10m³ – 30m = 0; г) –2p(3p – 2q) – 4q(p + q) = –6p² + 4pq – 4pq – 4q² = –6p² – 4q².
316. Обчисли значення виразу.
а) (b² – 4)b – (b³ – 3b) = –b, якщо b = –2,7, то (–2,7² – 4)(–2,7) – (–2,7³ – 3(–2,7)) = 2,7; б) (a² – 1)a – (a – 1)a² = a³ – a – a³ + a² = a² якщо a = 0,8, то 0,8² – 0,8 = 0,64 – 0,8 = –0,16.
317. Обчисли значення виразу.
а) c(1 + c + c²) – c(1 + c) = c + c² + c³ – c – c² = c³, якщо c = –0,5, то c + c² + c³ – c – c² = c³ = (–0,5)³ = –0,125; б) (x – y)x + (x – y)y = x² – xy + xy – y² = x² – y²,
якщо x = 2 і y = 3, то 2² – 3² = 4 – 9 = –6.
318. Спрости вираз і знайди його значення.
а) a³ – 2a² + a – a³ = –2a² + a = –2 · (–0,5)² – 0,5 = –2 · 0,25 – 0,5 = –1; б) c⁴ – 3c³ – c⁴ + c² = –3c³ + c² = –3 · 8 + 4 = –20; в) 2x – x² + x³ + x² – x³ = 2x = –0,7 · 2 = –1,4; г) ac – c² – a² – ac = –c² – a² = –12 – 32 = –10.
319. Розв’яжи рівняння а) 2(x – 3) + 5(x – 2) = 12
2x – 6 + 5x – 10 = 12
7x – 16 = 12
7x = 28 x = 4; б) 3(1 – x) – 2(3 – x) = 5 3 – 3x – 6 + 2x = 5 –x – 3 = 5 –x = 8 x = –8;

в) 3z – 7(2z + 4) = 16 3z – 14z – 28 = 18 –11z = 18 + 28 –11z = 46 z = –4, (18) z = –4 2 11;
г) 2 + 3y – 7(5 – y) = 15 ґ) x² – 3x + 1 = x(x – 2) д) 0,7x + 0,5 = 2,6(x – 2)
2 + 3y – 36 + 7y = 16
10y – 33 = 16
10y = 48 y = 4,8;
320. Розв’яжи рівняння
а) 2z – 15(1 – 2z) = 7z
2z – 15 + 30z = 7z
32z – 7z = 15
25z = 15
z = 15 25
z = 3 5
z = 0,6
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
x² – 3x – x² – 2x = –1 –5x = – 1
x = –1 5;
г) 3z – (z – 5) • 4 = (2 – 5z) • 3
3z – 4z + 20 = 6 – 15z
–z + 15z = 6 – 20
14z = –14
z = –1;
321. Доведи тотожність
б) 8c – 2(3 – 7c) = 9c + 20
8c – 6 + 21c = 9c + 20
29c – 6 = 9c + 20
29c – 9c = 20 + 6
20c = 26
c = 26 20 c = 1,3
ґ) 3t – t² + 7 = t(2 – t) 3t – t² + 7 = 2t – t² 3t – 2t = –7 t = –7;
а) 5(8y – 1) – 7(4y + 1) + 2y(y – 6) = 2y² – 12; 40y – 5 – 28y – 7 + 2y² – 12y = 2y² – 12; Доведено.
б) 3(–5z – 2) + 5z(7 – 12z) + 6(1 + 10z²) = 20z; –15z – 6 + 35z – 60z² + 6 + 60z² = 20z. Доведено.
322. Доведи тотожність
а) 3x(2x – 5) + 7(3x – 4) – 2(3x² – 14) = 6x; 6x² – 15x + 21x – 28 – 6x² + 28 = 6x; Доведено. б) 8(x² + 5x) – 3x²(5x + 1) + 5x(3x² – 8) = 5x²; 8x² + 40x – 15x³ – 3x² + 15x³ – 40x = 5x². Доведено.
323. На 315
6x + 13(35 – x) = 315
6x + 455 – 13x = 315
7x = 315 – 455 –7x = –140
x = –140 : (–7) x = 20 (шт.)
35 – 20 = 15 (шт.)
0,7x + 0,5 = 2,6x – 5,2 1,9x = 5,7
x = 5,7 : 1,9 x = 3.
в) 1 – 8(3 – 2y) = 2(2 – y) 1 – 24 + 16y = 4 – 2y –23 + 16y = 4 – 2y 18y = 27 y = 27 18 y = 1 9 18;
д) 1,7(a – 3) + 0,2 = 2,3(a + 1) 1,7a – 5,1 + 0,2 = 2,3a + 2,3 2,3a – 1,7a = –5,1 + 0,2 – 2,3 0,6a = –7,2
a = –7,2 : 0,6
a = –12.

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
2. Визнач кількість
листівок.
3. Запиши виразом вартість усіх односторонніх листівок:
4. Розв’яжи рівняння.
Рішення:
Односторонніх ш. по 12 грн
Двосторонніх (30 – x) ш. по 9 грн
Усього 30 шт. за 300 грн
12x + 9(30 – x) = 300
12x + 270 – 9x = 300
3x = 30
x = 30 : 3
x = 10 (шт.) – односторонніх листівок 30 – 10 = 20 (шт.) – двосторонніх листівок
Відповідь: купили 10 односторонніх і 20 двосторонніх
План:
1. Познач меншу сторону прямокутника за х.
2. Познач більшу сторону прямокутника за 4х.
3. Розв’яжи рівняння
Рішення:
Нехай менша сторона прямокутника x см, а більша
(x + 3) • 4x = x • 4x + 24
4x² + 12x = 4x² + 24
12x = 24
x = 24 : 12
x = 2 (см) – менша сторона
4 • 2 = 8 (см) – більша сторона
Відповідь: 2 см; 8 см
326. Одна сторона прямокутника
зменшити на 5 см, то площа
прямокутника.
Нехай менша сторона прямокутника x см, а більша 3x см.
x(3x – 5) + 200 = x·3x
3x² – 5x + 200 = 4x²
5x = 200
x = 200 : 5
x = 40 (см) – менша сторона 3 · 40 = 120 (см) – більша сторона
Відповідь: 40 см; 120 см
327. Перетвори у многочлен добуток.
а) 2ac³ · (3a² – 4ac + 5c) = 6a³c³ – 8a²c⁴ + 40ac⁴; б) 0,4a²c · (5a³ – 10a²c + 7c² – 20) = 2a⁵c – 4a⁴c² + 2,8a²c³ – 8a²c; в) 15yz² · (1 3 z⁴ –2 5 z³ – 2z + 3 5) = 5yz⁶ – 6yz⁵ – 30yz³ + 9yz²; г) –2 3xy² · (6xy² – 3x²y – 9xy) = –4x²y⁴ + 2x³y³ + 6x²y³.

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
328. Подай у вигляді
а) (2ax + 3a – 5) · a²x³ = 2a³x⁴ + 3a³x³ – 5a²x³; б) (–0,7cy² – z²) · 2c³z = –1,4c⁴y²z – 2c³z³; в) 0,3nz · (1 3 n² –2 3z³) = 0,1n³z – 0,2nz4; г) –2 1 3x³y · (6xy² + 3 7x²) = –14x⁴y³ – x⁵y.
329. Розв’яжи рівняння а) 0,4(2x – 3) – 0,5(3x – 0,2) = –2,5
0,8x – 1,2 – 1,5x + 0,1 = –2,5 –0,7x = –1,4 x = 2;
б) 6(2z – 12) – 5(11 + 3z) = –3z + 5
12z – 72 – 55 – 15z = –3z + 5 –
3z + 3z = 5 + 127
0 = 132 коренів немає; в) –2 3 (y – 6) –3 4 (2y – 16) = –3 1 2 Домножимо на 12
–8(y – 6) – 9(2y – 16) = –7 2 · 12 1 –8y + 48 – 18y + 144 = –42 –26y = –234
y = –234 : (–26)
y = 9
г) 1 3 (3x + 2) –1 3 (9 – 2x) = 1 2 x Домножимо на 6
2(3x + 2) – 2(9 – 2x) = 3x
6x + 4 – 18 + 4x – 3x = 0
7x = 14
x = 2
330. Розв’яжи рівняння
а) 0,8(x – 0,4) + 0,6(x – 0,6) = 1
0,8x – 0,32 + 0,6x – 0,36 = 1
1,4x = 1,68
x = 1,68 : 1,4
x = 1,2;
б) 4(3y – 13) + 7(15 – 3y) = –9y + 47 12y – 52 + 105 – 21y = –9y + 47
0 = –5 коренів немає;
в) 4,3 – 2x – 3(1,1 + 2 3x) = x + 2 3
4,3 – 2x – 3,3 – 2x = x + 2 3
–4x + 1 = x + 2 3
–5x = –1 3
x = 1 15
г) 1 6 (8 – z) –1 3 (5 – 4z) = 1 2 z + 3
8 6 ���� 6 (5 3 4���� 3 ) = 1 2 z + 3
4 3 ���� 6 5 3 + 4���� 3 = 1 2 z + 3

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
1 3 + 7���� 6 = 1 2 z + 3
2 + 7z = 3z + 18
4z = 20
Z = 5
331. Доведи, що при
а) 9x(3x – 4) + 4(x + 2) – 8x(2x – 4) = 27x² – 36x + 4x + 8 – 16x² + 32x = 11x² + 8; Сума
невід’ємного і додатного додатна.
б) 2x(3x – 4) + 5(x + 6) – x(x – 3) = 6x² – 8x + 5x + 30 – x² + 3x = 5x² + 30. Сума
невід’ємного і додатного додатна.
332. Доведи, що при будь-яких
числом.
а) 6(–3y – 4) – 5y(y – 3) + 3(y – 11y²) = –18y – 24 – 5y² + 15y + 3y – 33y² = –38y² – 24; Cума
двох від’ємних від’ємна.
б) 5y(1 – 2y) – 2(y + 5) – y(3 + 5y) = 5y – 10y² – 2y – 10 – 3y – 5y² = –15y² – 10. Cума двох
від’ємних від’ємна 333. Доведи, що
a) 2(a3 + 6) + 5a(3a – a2) – 3a2(5 – a) = 2a³ + 12 + 15a² – 5a³ – 15a² + 3a³ = 12; Значення
залежить від a. б) 6x(2y2 – (5x + y) · 3y) + 3xy(2y + 30x) = 6x(2y² – 15xy – 3y²) + 3xy · 2y + 3xy · 30x = 0.
Значення
залежить
x і y. 334.
a) 2x3(8-5x) – 8x(2x2 + x3) + 6(3x4 – 4) = 16x³ – 10x⁴ – 16x³ – 8x⁴ + 18x⁴ – 24 = (16x³ – 16x³) + (–10x⁴ – 8x⁴ + 18x⁴) – 24 = 0 + 0 – 24 = –24
від x.
б) 3ab + 6((2a + b)a + 5) – 3a(3b + 4a) = 3ab + 6(2a² + ab + 5) – 3a = (3ab + 6ab – 9ab) + (12a² – 12a²) + 30 = (3b + 4a) = 3ab + 12a² + 6ab + 30 – 9ab – 12a² = 0 + 0 + 30 = 30. Значення не
залежить від a і b.
335.
а) –4x³ + 4x² + 12x + 4x³ + 2x² – 10x = 6x² + 2x = 6 · 9 + 2 · 3 = 60 б) 10a²b – 40a²b + 24a²b + 16a²b = 10a²b = 10 ·
a) 12a³ – 9a² – 24 – 12a³ – 10a + 25a² = 16a² – 10a – 24 = 16 · 0,25 – 10 · 0,5 – 24 = = 4 – 5 – 24 = –25 б) 9x²y + 6xy² – 4x²y – 5x²y = 6x²y
Розв’яжи рівняння a) 2x 3 3 + 6 3x 2 = –3
2(2x – 3) + 3(6 – 3x) = –18
4x – 6 + 18 – 9x = –18 – 5x = –30 x = 6;

в) x 5 2 + 3x 8 5 = –3
5(x – 5) + 2(3x – 8) = –3 · 10
5x – 25 + 6x – 16 = –30
11x = 11
= 2
=
5x – 7 = 8 x = 3;
x = 1 г) 2x –x + 2 8 = 3x 2 2 Домножимо 8 2x · 8 – (x + 2) = 4(3x – 2) 16x (x+2) = 4(3x−2) 15x 12x = 8 + 2
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
338. Розв’яжи рівняння
a) 2 3x 4 + x + 1 3 = 5
3(2 – 3x) + 4(x + 1) = 5 · 12
6 – 9x + 4x + 4 = 60 – 5x = 50 x = 50 : (–5)
x = –10 б) 3x 7 3 + 5 9x 6 = 2 2(3x – 7) + (5 – 9x) = 6 · 2 6x – 14 + 5 – 9x = 12 – 3x = 21 x = –7
339. Три роки тому
років кожному?
Нехай сину (x + 3) років, батьку (5x + 3) у
учетверо, маємо рівняння:
5x + 3 = 4(x + 3)
5x + 8 = 4x + 12 x = 9
Сину: 9 + 3 = 12 років.
Батьку: 6 · 9 + 4 = 48 років.
Відповідь: 12 років, 48 років
340. Скільки років учневі, якщо відомо,
був 10 років тому?
Нехай учневі x років, через 10 років (x + 10), як
тому, то
4x = 10 + 60
x = 60 : 4
x = 16. Відповідь: учневі
99 – 12x = 8(57 – 10x)
99 – 12x = 8(57 – 10x)
99 – 12x = 171 – 80x
30x – 12x = 171 – 99
18x = 72
x = 4.

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
3x = 60 x = 20.
Відповідь: 20 г
343.
a) –4x³ · (–0,2 – 3x) = 2x³ + 12x⁴, б) 5ac(������������ – �������� –���� ����) = 50a²c – 15ac² – ac, в) (–x² – 7x⁴)·(–6x) = 6x³ + 42x⁵.
344. Замість
a) (���� ����y + 0,25xy + 5y²)· 4x²y = 2x²y² + x³y² + 20x²y³
б) (2m³ – 9m)·5m³ = 10m⁶ – 45m⁴
в) 4x²y(3y² – xy³ + 4y⁴) = 12x²y³ – 4x³y⁴ + 16x²y⁵
345.
1) (2a + c) · b – 2cm
2) (a + b) · (a + b) + 2a²
3) b · c – 2am 346.
заповнюємо квадрат. 347. Додатне чи від’ємне значення виразу?
a) (–5)⁷ · (–8)⁵ = (–5)⁵ · (–8)⁵ · (–5)² = (–5)⁵ · (–8)⁵ · (–5)² = 40⁵ · 25 додатне;
б) (–4)⁸ · (–13)¹⁰ = (–4)⁸ · (–13)⁸ · (–13)² = (4 · 13)⁸ · 169 додатне;
в) (–61)¹² · (–7)¹⁷ = (61 · 7)¹² · (–7)⁵ від'ємне.
г) (–9)³ · (-10)²⁵ = 0.
348. Який із виразів є
a) не стандартний;
б) стандартний;
в) не стандартний; г) не стандартний; ґ) не стандартний.
349. Обчисли.
350. Подай
а) (1 + y)(1 + x):
(1 + y)(1 + x) = 1·1 + 1·x + y·1 + y·x = 1 + x + y + xy
б) (x + 1)(a + 1):
(x + 1)(a + 1) = x·a + x·1 + 1·a + 1·1 = xa + x + a + 1
в) (x - 1)(n + 1):
(x - 1)(n + 1) = x·n + x·1 - 1·n - 1·1 = xn + x - n - 1
г) (2 + a)(c + 1):
(2 + a)(c + 1) = 2·c + 2·1 + a·c + a·1 = 2c + 2 + ac + a

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
ґ)
(3 - y)(5 + c):
(3 - y)(5 + c) = 3·5 + 3·c - y·5 - y·c = 15 + 3c - 5y - yc
д) (2 - a)(c + 1):
(2 - a)(c + 1) = 2·c + 2·1 - a·c - a·1 = 2c + 2 - ac - a
351. Розкрий дужки у виразі.
а) (x + 1)(x + 1):
(x + 1)(x + 1) = x² + x + x + 1 = x² + 2x + 1
б) (1 - y)(1 - y):
(1 - y)(1 - y) = 1·1 - 1·y - y·1 + y·y = 1 - y - y + y² = 1 - 2y + y²
в) (a + c)(a - c):
(a + c)(a - c) = a·a - a·c + c·a - c·c = a² - ac + ac - c² = a² - c²
352. Якому з многочленів тотожно дорівнює добуток (a + 2)(a + 3)?
(a + 2)(a + 3) = a·a + a·3 + 2·a + 2·3 = a² + 3a + 2a + 6 = a² + 5a + 6
Відповідь: Г a² + 5a + 6
353. Яке з чисел є коренем рівняння (x - 1)(x + 2) - x² = 0?
Розкриємо дужки: (x - 1)(x + 2) - x² = x² + 2x - x - 2 - x² = 2x - x - 2 = x - 2 = 0 x = 2
Відповідь: Б 2
354. Перемнож многочлени a) (a + b)(m – n) = am – an + bm – bn;
б) (x – y)(x + y) = x² – y²; в) (2a – 1)(a – 2) = 2a² – 4a – a + 2 = 2a² – 5a + 2;
г) (c + ax)(a + x) = ac + cx + axc + ax²; ґ) (1 – c)(1 + c²) = 1 + c² – c – c³; д) (– a + 1)(2a – 3) = – 2a² + 3а + 2a – 3 = – 2a² + 5a – 3
355. Перемнож многочлени
а) (x – 2)(2x + 3) = 2x² + 3x – 4x – 6 = 2x² – x – 6;
б) (3y + 5)(2y – 6) = 6y² – 18y + 10y – 30 = 6y² – 8y – 30;
в) (7 – c)(c + 2) = 7c + 14 – c² – 2c = –c² + 5c + 14.
356. Подай у вигляді многочлена
a) (a – b)(c + d) = ac + ad – bc – bd;
б) (x – 2)(x – 3) = x² – 3x – 2x + 6 = x² – 5x + 6;
в) (2x – 3)(a – b) = 2xa – 2xb – 3a + 3b; г) (2a – 3c)(a + 5c) = 2a² + 10ac – 3ac – 15c² = 2a² + 7ac – 15c²;
ґ) (a² – b)(a – b²) = a³ – a²b² – ab + b³;
д) (1 – 2xz)(1 + 2xz) = 1 + 2xz – 2xz – 4x²z² = 1 – 4x²z²;
е) (x² – x + 1)(x + 1) = x³ + x² – x² – x + x + 1 = x³ + 1;
є) (c – q)(1 – c – q) = c – c² – cq – q + cq + q² = q² – c² + c – q.
357. Подай у вигляді многочлена
а) (2x + 3)(3x – 2) = 6x² – 4x + 9x – 6 = 6x² + 5x – 6;
б) (5a – 4)(3a – 2) = 15a² – 10a – 12a + 8 = 15a² – 22a + 8;
в) (7c – 1)(5 – 6c) = 35c – 42c² – 5 + 6c = –42c³ + 41c – 5;
г) (–2n + 3)(3n – 2) = –6n² + 4n + 9n – 6 = –6n² + 13n – 6;
ґ) (a² + b)(a² + b) = a⁴ + a²b + a²b + b² = a⁴ + 2a²b + b²;
д) (–2 + c)(–3 + c) = 6 – 2c – 3c + c² = 6 – 5c + c²;
е) (p – 1)(p² + p + 1) = p³ + p² + p – p³ – p – 1 = p³ – 1;
є) (x – 2)(x² – 5x + 2) = x³ – 5x² + 2x – 2x² + 10x – 4 = x³ – 7x² + 12x – 4.

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
.
(А–Д). 1 – Г; 2 – В; 3 – Д.
360. Спрости вираз a) (x – 1)(x + 2) – x(x + 1) = x² + 2x – x – 2 – x² – x = –2; б) (1 + a)(a² – a) + a(1 + a²) = a² – a + a³ – a² + a + a³ = 2a³; в) (a + 2)(a – 5) + 3(a – 1) = a² – 5a + 2a – 10 + 3a – 3 = a² – 13; г) (n – 2)(n – 2) + 4(n – 1) = n² – 4n + 4 + 4n – 4 = n²; ґ) (x – 4)(3x + 5) + 3x(7 – x) + 20 = 3x² + 5x – 12x – 20 + 21x – 3x² + 20 = 14x; д) (a + b)(a – b) – (a – 2b)(a + 2b) = a² – b² – a² – 2ab + 2ab + 4b² = 3b².
361. Спрости вираз
а) (a + 1)(a – 3) + 2a(1 – a) = a² – 3a + a – 3 + 2a – a² = –a² – 3; б) (3a + b)(a – b) – (3a² – b²) = 3a² – 3ab + ab – b² – 3a² + b² = –2ab; в) (3x + 1)(x – 6) + (2 – 3x)(x – 5) = 3x² – 18x + x – 6 + 2x – 10 – 3x² + 15x = –16; г) (x – y)(x + 7) – (y + x)(x + 7) + 14y = x² + 7x – xy – 7y – xy – 7y – x² – 7x + 14y = –2xy .
362. Спрости вираз і знайди його значення. a) a² – 3a + 2a – 6 + a² – 4a + 6a – 24 = 2a² + a – 30 = 2 • 6² + 6 – 30 = 48; б) 2x² – 2x + 3x – 3 – x² – 4x + 3x + 12 = x² + 9 = 9 + 9 = 18; в) a² – ab + ab – b² + b² = a² = 0,36; г) –x² + y⁴ + xy + x² + xy² – xy² – y⁴ = x • y = –7 • 5 = –35.
363. Обчисли значення виразу а) a² – 5a – 3a + 15 + a² + 7a + a + 7 = 2a² + 22 = 2 • 4 + 22 = 30; б) 2x² + 5x – 8x – 20 – x – 3 – 3x² – 6x = –10x – 23 = –10 • (–3,3) – 23 = 33 – 23 = 10.
364. Обчисли значення виразу.
а) x² + 2xy + y² – x² + y² = 2xy + 2y² = 2 • 0,2 • 5 + 2 • 5² = 2 + 50 = 52; б) a⁴ – b² – a⁴ = –b² = –0,04.
365. Подай у вигляді многочлена вираз
а) (a + b)² = (a + b)(a + b) = a² + ab + ab + b² = a² + 2ab + b²;
б) (x – y)² = (x – y)(x – y) = x² – 2xy + y²
в) (2a – x)² = (2a – x)(2a + x) = 4a² – 4ax + x²; г) (3a + 2)² = (3a + 2)(3a + 2) = 9a² + 12a + 4.
366. Подай у вигляді многочлена вираз
a) (x + y)² = x² + 2xy + y²;
б) (a – c)² = a² – 2ac + c²;
в) (3x + y)² = 9x² + 6xy + y²;
г) (2a – 3)² = 4a² – 12a + 9.
367. Розв’яжи рівняння
a) (x – 1)(x – 3) = x² – 5
x² – 3x – x + 3 – x² + 5 = 0 –4x = –8 x = 2;
в) (2x + 1)(x – 5) = 2(x² + 11)
2x² – 10x + x – 5 = 2x² + 22 –9x = 27
x = –3;

б) (y + 2)(y – 5) – y(y – 1) = 2 y² – 5y + 2y – 10 – y² + y = 2 –2y = 12 y = 12 : (–2) y = –6;
г) 3z(z – 2) – 9 = (1 – z)(1 – 3z)
3z² – 6z – 9 = 1 – 3z – z + 3z² –2z = 10
z = 10 : (–5)
z = –5.
368. Розв’яжи рівняння
a) (x – 2)(x + 5) = x² + 2
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
x² + 5x – 2x – 10 – x² = 2
3x = 12
x = 4;
в) (x – 1)(x + 5) = (x + 2)(x + 3)
x² + 5x – x – 5 = x² + 3x + 2x + 6
x² + 4x – x² – 5x = 6 + 5
–x = 11
x = –11;
(a + b)(c + d) = ac + ad + bc + bd
S = ad + bd + ac + bc
або S = (a + b)(c + d).
Алгебраїчне

б) (x – 6)(x – 2) – x(x + 2)= 2
x² – 2x – 6x + 12 – x² – 2x = 2 –10x = 2 – 12
x = 10 : (–10)
x = –1;
г) (2x + 3)(x – 7) + 6 = (x + 3)(2x + 1) 2x² – 14x + 3x – 21 + 6 = 2x² + x + 6x + 3
2x² – 11x – 2x² – 7x = 3 – 6 + 21 –18x = 18 x = –1.
+ 4a – 2; б) (4x² + 6x + 9)(2x – 3) = a³ – a² – 2a² + 2a – 2a + 1 = a³ – 3a² + 1.
372. Подай
a) (x + 1)(x³ – x² + x – 1) = x⁴ – x³ + x² – x + x³ – x² + x – 1 = x⁴ – 1; б) (4a² – 2ab + b²)(2a + b) = 8a³ + 4a²b – 4a²b – 2ab² + 2ab² + b³ = 8a³ + b³.
373. Спрости вираз
a) (a² – a + 1)(a + 1) – a³ = a³ + 1 – a³ = 1; б) (2a + 3x)(4a² – 6ax + 9x²) – 27(x³ – a³) = 8a³ + 27x³ – 27x³ + 27a³ = 35a³; в) (c – 5)(c + 2) + 3(c + 4) = c² + 2c – 5c – 10 + 3c + 12 = c² + 2;
г) (x² – y)(x – y²) + xy(1 + xy) = x³ – x²y² – xy + y³ + xy + x²y² = x³ + y³;
ґ) 4 9 – (2 3 – a³)(2 3 + a³) = 4 9 –4 9 + a⁶ = a⁶;
д) 1 8 x³ – (1 2 x – a²)(1 4 x² + 1 2 a²x + a⁴) = 1 8 x³ –1 8 x³ + a⁶ = a⁶.
374. Спрости вираз

a) (x² + ax + a²)(x – a) + a³ = x³ – a³ + a³ = x³;
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
б) (9c² + 12ac + 16a²)(4a – 3c) – 64(a³ – c³) = 64a³ – 27c³ = 64a³ + 64c³ = 37c³;
в) (m + 7)(3 – m) + 4(m – 5) = 3m – m² + 21 – 7m + 4m – 20 = –m² + 1;
г) (4n² – p)(2n – p²) + 2np(2np + 1) = 8n³ – 4n²p² – 2np + p³ + 4n²p² + 2np = 8n³ + p³.
375. Подай у
a) (2x – 3y)² = (2x – 3y)(2x – 3y) = 4x² – 12xy + 9y²; б) (3ac + b²)² = (3ac + b²)(3ac + b²) = 9a²c² + 6ab²c + b⁴;
в) (2a – 1)³ = (2a – 1)(2a – 1) = 4a² – 4a + 1.
376. Доведи тотожність
a) (2a – 3)(a + 6) – 3(3a – 6) = 2a²; 2a² + 12a – 3a – 18 – 9a + 18 = 2a²; Доведено.
б) (a – 1)(a + 1)(a² + 1) + 1 = a⁴; (a² – 1)(a² + 1) + 1 = a⁴ – 1 + 1 = a⁴; Доведено.
в) (2a – 3)² + 3(4a – 3) = 4a²; 4a² – 12a + 9 + 12a – 9 = 4a²; Доведено.
г) (a – b)³ + 3ab(a – b) = a³ – b³.
(a – b)(a² – 2ab + b²) + 3a²b – 3ab² = a³ – b³.
a³ – 2a²b + ab² – a²b + 2ab² = a³ – b³.
= b³ + 3a²b – 3ab² = a³ – b³. Доведено.
377. Доведи тотожність
a) (3x + 2)(x – 4) + 2(4 + 5x) = 3x²; 3x² – 12x + 2x + 8 + 8 + 10x = 3x²; Доведено.
б) c⁴ – (c – 1)(c + 1)(c² + 1) = 1;
c⁴ – (c² – 1)(c² + 1) = 1;
c⁴ – c⁴ + 1 = 1; Доведено.
в) (3a + 2)² – 4(3a + 1) = 9a²; 9a² + 12a + 4 – 12a – 4 = 9a²; Доведено.
г) (x + y)3 – 3xy(x + y) = x³ + y³. (x + y)(x² + 2xy + y²) – 3x²y – 3xy² = x³ + y³.
= x³ + 2x²y + y²x + yx² + 2xy² + y³ – 3x²y – 3x²y – 3xy² = x³ + y³. Доведено.
378. Доведи, що
a) (x + 5)(x² – 2x – 3) – (5x + x²)(x – 2) + 3(x + 5) = x³ – 2x² – 3x + 5x² – 10x – 15 – (5x² – 10x + x³ – 2x²) + 3x + 15 = = x³ + 3x² – 13x – 5x² + 10x – x³ + 2x² = –2x² + 2x² = 0; Отже, значення не залежить
xx
б) (2x² – 3x + 6)(x + 4) – (x² + 4x + 3)(2x – 3) = = 2x³ + 8x² – 3x² – 12x + 6x + 24 – (2x³ – 3x² + 8x² – 12x + 6x – 9) = = 2x³ + 8x² – 3x² – 6x + 24 – 2x³ + 3x² – 8x² + 12x – 6x + 9 = 33
значення не залежить від xx
33. 379. Доведи, що
a) (2x – 4)(3x + 2) – (2x – 3)(4x + 2) + 2x² = 6x² + 4x – 12x – 8 – (8x² + 4x – 12x – 6) + 2x² = = 6x² – 8x – 8 – 8x² + 8x + 6 + 2x² = –2;
–2. б) (x – 3)(x + 3)(x² + 9) – (x + 1)(x – 1)(x² + 1) = (x² – 9)(x² + 9) – (x² – 1)(x² + 1) = = x⁴ – 81 – x⁴ + 1 = –80.
xx
–80.
(n – 3)(n + 6) – (n –9)(n + 6)
6. (n + 6)(n – 3 – n – 9) = (n + 6) • 6

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
значення n.
381. Доведи, що при
(n + 12)(n + 3) – (n –3)(n + 9) кратне 9 n² + 3n + 12n + 36 – n² – 9n + 3n + 27 = 9n + 63 = 9 • (n + 7)
Отже, вираз завжди кратний 9, бо містить множник 9
382. Розв’яжи рівняння a) (3z² – 1)(z – 1) = 3z²(z – 1) + 7
3z³ – 3z² – z + 1 = 3z³ – 3z² + 7
–z = 7 – 1
z = –6;
б) (1 – 2y)² = 2(y – 2)(2y – 3)
1 – 4y + 4y² = (2y – 4)(2y – 3)
1 – 4y + 4y² = 4y² – 6y – 8y + 12
1 – 4y = –14y + 12
10y = 11
y = 1,1;
в) (x² – x + 1)(x² + x + 1) = x⁴ + x² + x
x⁴ + x³ + x² – x³ – x² – x + x² + x + 1 = x⁴ + x² + x
x = 1.
383. Розв’яжи рівняння
a) (2x² – 3)(x – 3) = 2x²(x – 3) + 6
2x³ – 6x² – 3x + 9 = 2x³ – 6x² + 6
–3x = 6 – 9 –3x = –3
x = 1;
б) (0,1 + x)(0,01 – 0,1x + x²) = 2x(0,5 + 0,5x²)
0,001 + x³ = x + x³
x = 0,001;
в) (3z – 2)² = 9(z – 2)(z + 3) – 5 9z² – 12z + 4 = 9z² + 27z – 18z – 54 – 5 –12z – 9z = –5 – 4 –21z = –9
г) (x³ + x² + x + 1)(x – 1) = x⁴ + 10x
x⁴ – x³ + x³ – x² + x² – x + x – 1 = x⁴ + 10x
10x = –1
10x = –1
x = –0,1;
ґ) 2 3 x – (2 3 x – 3)( 4 9 x2 + 2x + 9) = 4 9x(6 –2 3 x2)
2 3 x –8 27 x3 + 27 = 8 3 x –8 27 x3
8 3 x –2 3 x = 27
2x = 27
x = 27 : 2
x = 13,5

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
2 число x + 1
3 число x + 2
x² + 8 = (x + 1)(x + 2)
x² + 8 = x² + 2x + x + 2
x² – x² – 2x – x = 2 – 8
–3x = –6
x = 2
Відповідь: 2, 3, 4
385.
більший
x(x + 1) + 18 = (x + 2)(x + 3)
x² + x + 18 = x² + 3x + 2x + 6
x² + x – 5x = 6 – 18 –4x = –12
x = 3
Відповідь: 3, 4, 5, 6
386. Дано два
множників,
Нехай це число x. Маємо: (11 + x) • (44 + x) = (16 + x)(32 + x)
484 + 11x + 44x + x² = 512 + 16x + 32x + x²
55x + 484 = 48x + 512
7x = 28
x = 4.
Відповідь: 4
387. Дано
множників,
Нехай це число x. Маємо:
(25 + x)(51 + x) = (31 + x)(40 + x)
1275 + 25x + 51x + x² = 1240 + 31x + 40x + x²
76x + 1275 = 71x + 1240
5x = –35
x = –7.
Відповідь: –7
388. Знайди
якщо r = 0,8 м. S = 3r · 2r + πr² = 6r² + p², якщо r = 0,8 m, то S = 6 · 0,8² + 0,8² · π = 0,64(6 + p) = 5,8496 m²; P = 2(3r + 2r) + 2πr = 12r + 2πr, якщо r = 0,8 m, то P = 12 · 0,8 + 2 · π · 0,8 = 9,6 + 1,6π = 9,6 + 5,024 = 14,624.
389. Обчисли (1 –1 4) · 4 3 – (
36a⁸ = 9a • 4a⁷ = 18a⁴ • 2a⁴; б) 30x⁴y⁹ = 15x³ • 2xy⁹ = 3x³y⁵ • 3xy⁴; в) –18a¹⁰b⁵ = –9a³ • 2a⁷b⁵ = –6a⁵ • 3a⁵b⁵.

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
cx + cy = c(x + y)
б) a²x - a²y:
a²x - a²y = a²(x - y)
в) nx + ax:
nx + ax = x(n + a)
г) 2ax + 4ax²:
2ax + 4ax² = 2ax(1 + 2x)
ґ) 6cy - 9cy²:
6cy - 9cy² = 3cy(2 - 3y)
д) -ac² + c²: -ac² + c² = c²(1 - a)
392. Які з рівностей хибні?
А ay - 5y = y(a - 5)
Перевіримо: ay - 5y = y(a - 5) = ya - 5y
Ця рівність правильна.
Б cx + x = x(c + x)
Перевіримо: cx + x = x(c + x) = cx + x²
Ця рівність хибна, бо праворуч маємо доданок x².
В -9 + 6x = -3(3 + 2x)
Перевіримо: -9 + 6x = -3(3 - 2x) = -9 + 6x
Ця рівність правильна.
Г a⁶ - a = a(a⁵ - 1)
Перевіримо: a⁶ - a = a(a⁵ - 1) = a⁶ - a
Ця рівність правильна.
Хибною є тільки рівність Б.
393. Розклади на множники 18x⁶ - 12x³.
18x⁶ - 12x³ = 6x³(3x³ - 2)
Відповідь: Б 6x³(3x³ - 2)
394. Розклади на множники 4 - 4x. 4 - 4x = 4(1 - x)
Відповідь: Г 4(1 - x)
395. Розв'яжи рівняння x² - 3x = 0. x² - 3x = 0
x(x - 3) = 0
Звідси x = 0 або x = 3.
Відповідь: Г x = 0 або x = 3.
396. Обчисли зручним способом.
а) 6 · 19 + 6:
6 · 19 + 6 = 6(19 + 1) = 6 · 20 = 120
б) 27 · 5 + 13 · 5:
27 · 5 + 13 · 5 = 5(27 + 13) = 5 · 40 = 200
в) 17 · 6 + 17 · 4:
17 · 6 + 17 · 4 = 17(6 + 4) = 17 · 10 = 170
г) 5 · 32 + 32 · 15:
5 · 32 + 32 · 15 = 32(5 + 15) = 32 · 20 = 640
397. Обчисли. 2,74 · 1,68 + 2,74 · 8,32. 2,74 · 1,68 + 2,74 · 8,32 = 2,74(1,68 + 8,32) = 2,74 · 10 = 27,4
Відповідь: Б 27,4

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
398. Винеси за дужки спільний
а) xa + xb = x(a + b);
б) 2m + 2p = 2(m + p);
в) cp + tp = c(p + t);
г) ab + 3b² = b(a + 3b);
ґ) 4b² − 2ab = 2b(2b − a);
д) 6x² − 2x = 2x(3x − 1);
е) m²x + my = m(mx + y);
є) 3a²x − 2ax = ax(3a − 2);
ж) a³b³ − 6ab⁴ = ab³(a² − 6b);
з) 5y³z + 20az³ = 5z(y³ + 4az²);
и) −3a²b − 6ab² = −3ab(a + 2b);
і) −12x − 15x² = −3x(4 + 5x).
399. Винеси за дужки спільний множник.
a) 12a + 12b = 12(a + b);
b) 7n − 14n² = 7n(1 − 2n);
c) 5p³ − 5p = 5p(p2 − 1) = 5p(p − 1)(p + 1);
d) 2a² + 3a = a(2a + 3);
e) 13x − 26y = 13(x − 2y);
f) 15ab + 45c = 15(ab + 3c);
g) 4cy² − 2c²y = 2cy(2y − c);
h) 10a²x + 5a²x² = 5a²x(2 + x).
400. Розклади на множники многочлен
а) 2ac² − 8c³d + 4acd = 2c(ac − 4c²d + 2ad);
б) 3acx − 6a²x − 9a³c²x = 3ax(c − 2a − 3a²c²);
в) 8a⁴x + 7a²x² + ax³ = ax(8a³ + 7ax + x²);
г) 10n²c³ − 15nc² − 5nc³ = 5nc²(2nc − 3 − c);
ґ) −a²x³ − a⁵cx⁴ + 3a²cx² = a²x²(−x − a³cx² + 3c);
д) 7x³ − 14x² + 21x − 28x⁴ = 7x(x² − 2x + 3 − 4x³).
401. Розклади на множники многочлен
а) 5c + 12c² − c³ = c(5 + 12c − c²);
б) 5x + 10x² − 15x³ = 5x(1 + 2x − 3x²);
в) 6py² + 8p²y − 4p²z = 2p(3y² + 4py − 2pz);
г) 3x³ − 6x²y − 12xy⁴ = 3x(x² − 2xy − 4y⁴);
ґ) −m²x + 4mx² + 3m³ = m(−mx + 4x² − 3m);
д) a²b − 2a³b² + 3ab³ − ab² = ab(a − 2a²b + 3b² − b).
402. Розклади на множники многочлен
а) 3x(a + b) − 2y(a + b) = (a + b)(3x − 2y);
б) 3(2x + 5) + x(5 + 2x) = (2x + 5)(3 + x);
в) 5a(x − y) + 3(x − y) = (x − y)(5a + 3);
г) 2(m² − 2) − x(m² − 2) = (m² − 2)(2 − x);
ґ) 7p(3x + y) + (3x + y) = (3x + y)(7p + 1);
д) (3x − 1) − 17x(3x − 1) = (3x − 1)(1 − 17x).
403. Розклади на множники многочлен
а) 7p(a + b) + 8k(a + b) = (a + b)(7p + 8k);
б) 3y(5x + 2) + 2(5x + 2) = (5x + 2)(3y + 2);
в) 5z(m − n) − 2(m − n) = (m − n)(5z − 2);
г) 2n(a² + 2b) − 3(a² + 2b) = (a² + 2b)(2n − 3);

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
ґ) 2a(3a − b) − (3a − b) = (3a − b)(2a − 1); д) (6n + 5) − x(6n + 5) = (6n + 5)(1 − x).
404. Знайди значення
а) 12,3х + 12,3y, якщо x = 0,23; y = 0,77, то 12,3(0,23 + 0,77) = 12,3 ⋅ 1 = 12,3 б) x² − 1,3x = x(x − 1,3), якщо x = 11,3, то 11,3 • (11,3 − 1,3) = 11,3 • 10 = 113; в) 2,63х 2,63y, якщо x = 0,16; y = 0,84, то 2,63 • (0,16 + 0,84) = 2,63 • 1 = 2,63; г) 5,24x - x², якщо x = 4,24, то 4,24 • (5,24 − 4,24) = 4,24 • 1 = 4,24.
405. Знайди значення виразу, попередньо розклавши
а) 16,23(a + b) = 16,23 • (8,37 + 1,63) = 162,3; б) a(a + 3,6) = −13,6(−13,6 + 3,6) = −13,6 • (−10) = 136; в) 6,34(a − b) = 6,34(0,36 + 0,64) = 6,34; г) a(17,3 − a) = 7,3(17,3 − 7,3) = 73.
406. Обчисли зручним способом
а) 1,2 • 24,44 + 1,2 • 75,56 = 1,2(24,44 + 75,56) = 1,2 • 100 = 120; б) 17,8 • 0,13 − 0,13 • 7,8 = 0,13(17,8 − 7,8) = 0,13 • 10 = 1,3; в) 0,12² + 0,12 • 0,88 = 0,12(0,12 + 0,88) = 0,12 • 1 = 0,12.
407. Обчисли зручним способом а) 3,7 • 2,16 + 3,7 • 7,84 = 3,7(2,16 + 7,84) = 3,7 • 10 = 37; б) 36,6 • 2,34 – 2,34 • 26,6 = 2,34(36,6 – 26,6) = 2,34 • 10 = 23,4; в) 93,7² – 93,7 • 83,7 = 93,7(93,7 – 83,7) = 937.
408. Розв’яжи рівняння
а) x(x − 3) = 0
x₁ = 0; x₂ = 3;
г) x² − 12x = 0
x(x − 12) = 0
x₁ = 0; x₂ = 12;
409. Розв’яжи рівняння
a) x(x + 2) = 0
x₁ = 0; x₂ = −2;
г) x² − 6x = 0
x(x − 6) = 0
x₁ = 0; x₂ = 6;
б) y(5 − y) = 0
y₁ = 0; y₂ = 5;
ґ) 10x − 4x² = 0
2x(5 − 2x) = 0
x₁ = 0; x₂ = 2.5;
б) z(3 − z) = 0
z₁ = 0; z₂ = 3;
ґ) 10x² + x = 0
x(10x + 1) = 0
x₁ = 0; x₂ = −0,1;
410. Винеси за дужки спільний множник
a) 3a²b + 2ab – 5a = a(3ab + 2b – 5);
б) 7xy³ + 8x²y² – 9y⁴ = y²(7xy + 8x² – 9y²);
в) 5ac² – ac³ – 3a²c = ac(5c – c² – 3a);
г) 8az⁴ – 7az³ – 4az² = az²(8z² – 7z – 4);
ґ) 4a²b³c⁴ – 5ab³c² = ab³c²(4ac² – 5);
д) 9x³yz⁴ + 7x⁴y²z³ = x²yz³(9z + 7xy).
411. Винеси за дужки спільний множник
а) 4a² – 5ab + a = a(4a – 5b + 1);
б) 3x² + 8x²y – x³ = x²(3 + 8y – x);

в) –7m² – m²z + m³ = m²(–7 – z + m);
в) 3z(z + 4) = 0
z₁ = 0; z₂ = −4; д) 4x² + x = 0
x(4x + 1) = 0
x₁ = 0; x₂ = −1 4
в) 4y(y − 2) = 0
y₁ = 0; y₂ = 2;
д) 5x² − x = 0
x(5x − 1) = 0
x₁ = 0; x₂ = 0,2.
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
г) –x⁶ – 10x⁴y² – x² = –x²(x⁴ + 10x²y² + 1);
ґ) 18a³c²x – 9ac²x³ = 9ac² + (2a² – x²);
д) 15mn²y + 45m²n³ = 15mn²(y + 3mn).
412. За малюнком 10.1 з’ясуйте
am + bm + cm = (a + b + c)m для додатних
Це формула площі великого прямокутника.
413. Винеси за дужки спільний множник
a, b, c і m.
а) a³ + 3a²x – 3ax² – a⁴ + 2a = a(a² + 3ax – 3x² – a³ + 2);
б) 1,2a²b³c⁴ – 0,6a³b³c⁴ + 1,8a⁴b³c⁴ = 0,6a²b³c⁴(2 – a + 3a²);
в) 144x²⁰y¹⁸ + 36x¹⁸y¹⁰ = 36x¹⁸y¹⁰(4x²y⁸ + 1);
г) 169a²³b²⁰ – 49a²⁰b¹⁸ = a²⁰b¹⁸(169a³b² – 49).
414. Винеси за дужки спільний множник
a) 3x³ – 2ax² + 4a²x + ax – x⁴ = x(3x² – 2ax + 4a² + a – x³);
б) 10,5b²c⁴ + 1,5b³c²a² – 20b⁵c³a = 5b²c²(2,1c² + 0,3bd² – 4b³cd);
в) 92a¹⁵m³⁵ – 46a¹⁷b³⁰ = 46a¹⁵(2m³⁵ – a²b³⁰);
г) 576n²⁰x³¹ + 240n¹⁷x³² = 240n¹⁷x³¹(2,4n³ + x).
415. Винеси за дужки спільний множник
a) 3, 24a⁷c⁹ – 6, 48a¹⁰c¹⁵ = 3, 24a⁷c¹⁵ (c⁴ – 2a³);
б) 28, 9m³⁰x¹⁶ – 57,8m⁴⁵x¹³ = 28, 9m³ · x¹³ (x³ – 2m¹⁵);
в) 2 5 a²x¹⁰ –3 5 a⁴x⁷ = 1 5a²x⁷ (2x³ – 3a²);
г) 6 7x⁵y¹⁸ + 3 7x¹⁸y⁵ = 3 7x⁵y⁵ (2y¹³ + x¹³).
416. Розклади на множники вираз
а) x(a – 2) + y(a – 2) = (a – 2)(x + y);
б) (x + 1)² – 2x(x + 1) = (x + 1)(x + 1 – 2x) = (x + 1)(1 – x);
в) 2y(y – 6)³ – 3y(y – 6)² = y(y – 6)²(2y – 12 – 3y) = y(y – 6)²(–y – 12);
г) 4(x – y) – 3a(y – x) = (x – y)(4 + 3a);
ґ) 3(2x – 5) – 2x(5 – 2x) = (2x – 5)(3 + 2x);
д) 6(m – n)² – m(n – m) = (m – n)(6m – 6n + m) = (m – n)(7m – 6n);
е) (4x – 3y)(x + 2y) + 2x(x + 2y) = (x + 2y)(4x – 3y + 2x) = (x + 2y)(6x – 3y)
є) (a + b)(x – y) + (b – a)(y – x) = (x – y)(a + b – b + a) = 2a(x – y).
417. Розклади на множники вираз
а) a(a² + 1) + 5(a² + 1) = (a² + 1)(a + 5);
б) 8(a² – 3) + (a² – 3)² = (a² – 3)(8 + a² – 3);
в) 5b(3 + 2c)³ + 2b(3 + 2c)² = b(3 + 2c)(15 + 10c + 2b);
г) x(a – b) + 3y(b – a) = (a – b)(x – 3y);
ґ) 4(b – 3) + 5b(3 – b) = (b – 3)(4 – 5b);
д) 7(a – 4)² + (4 – a) = (a – 4)(7a – 28 – 1) = (a – 4)(7a – 29);
е) 5a(3a – b) + (b – 3a)(5a + 2b) = (3a – b)(5a – 5a – 2b) = –2b(3a – b);
є) (a + 7b)(a – 5b) – (b – 3a)(a – 5b) = (a – 5b)(4a + 6b) = 2(2a + 3b)(a – 5b)
418. Розклади
a) 6a(x – 2) + 8b(x – 2) + 4c(2 – x) = (x – 2)(6a + 8b – 4c); б) (x³ + 1)(2x + 3) + 3(2x⁴ + 3x³) + (x³ – 1)(3 + 2x) = (2x + 3)(x³ + 1 + 3x³ + x³ – 1) = = (2x + 3) • 5x³; в) (x³ – 1) + 5a(x³ – 1) + b(1 – x³) = (x³ – 1)(1 + 5a – b); г) (2x – 1)(x² + 1) + (x² – 1)(2x – 1) + (1 – 2x)(x² + 2) = (2x – 1)(x² + 1 + x² – 1 – x² – 2) = = (2x – 1)(x² – 2).
419. Винеси

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
a) (5x + 10)² = (5(x + 2))² = 25(x + 2)²; б) (3 – 12y)² = 9(1 – 4y)²;
в) (4a – 4b)³ = 64(a – b)³; г) (3a + 6c)⁴ = 3⁴ • (a + 2c)⁴ = 81(a + 2c)⁴; ґ) (6ab² – 3a²)³ = (3a)³(2b² – a)³ = 27a³ • (2b² – a)³; д) (–6a – 2ab)⁴ = (2a)⁴(–3 – b)⁴ = 16a⁴(–3 – b)⁴.
420. Винеси за дужки спільний множник
a) (16y + 12)² = 4²(4y + 3)² = 16(4y + 3)²;
б) (15 – 5y)² = 25(3 – y)²;
в) (6x – 8)³ = 8(3x – 4)³; г) (3x – 9)⁴ = 81(x – 3)⁴; ґ) (2x³y + 4x⁴)² = (2x³)²(y + 2x)² = 4x⁶(y + 2x)²; д) (–2x³ + 4x²)⁴ = (2x²)⁴(–x + 2)⁴ = 16x⁸(–x + 2)⁴.
421. Розв’яжи рівняння
a) 3(4x – 1)² – (1 – 4x) = 0
(4x – 1)(12x – 3 + 1) = 0 (4x – 1)(12x – 2) = 0
1) 4x – 1 = 0 2) 12x – 2 = 0 4x = 1 12x = 2
x₁ = 1 4 x₂ = 1 6
в) 2x³ – 5(x² – 2) = 10
2x³ – 5x² + 10 = 10
x²(2x – 5) = 0
x₁ = 0; x₂ = 2,5
x² + 6(x + 2) = 12 x² + 6x + 12 = 12 x(x + 6) = 0 x₁ = 0;
= –6
422. Розв’яжи рівняння a) 2(3x – 2)² – (2 – 3x) = 0
(3x – 2)(6x – 4 + 1) = 0
1) 3x – 2 = 0 2) 6x – 3 = 0
3x = 2 6x = 3
x₁ = 2 3 x₂ = 1 2
в) 2z⁴ – 7(z³ – 3) = 21
2z⁴ – 7z³ + 21 = 21
z³(2z – 7) = 0
z₁ = 0
2z = 7

б) x² – 5(x – 3) = 15 x² – 5x + 15 = 15 x₁ = 0; x₂ = 5
z₂ = 3,5 г) 2z⁴ –1 3z(6z² – 3) = z 2z⁴ – 2z³ + z = z
2z³(z – 1) = 0
z₁ = 0
z₂ = 1
423. Обчисли a) (3,72 2,41 2,41 2,72) (24,1 · 1,4 + 24,1 · 1,01 24,1 · 1,41) = (2,41(3,72 2,72)) (24,1(1,4 + 1,01 1,41)) = (2,41 1) (24,1 · 1) = 0,1;
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
= 5 · 3,6 = 18.
424. Обчисли а)
= 50 12,5 = –4.
425. Доведи, що: а) 1617 + 1616 ділиться на 17; 16¹⁶ • (16 + 1) = 17 • 16¹⁶; б) 69 – 68 + 67 ділит ься на 31; 6⁷ • (6² − 6 + 1) = 31 • 6⁷; в) 495 + 78 ділиться на 350; (7²)⁵ + 7⁸ = 7¹⁰ + 7⁸ = 7⁸(7² + 1) = 50 • 7⁸ = 350 • 7⁷; г) 7100 + 3 · 799 ділиться на 490; 7⁹⁹ • (7 + 3) = 10 • 49 • 7⁹⁷ = 490 • 7⁹⁷.
426. Доведи, що:
а) 512 + 510 ділиться на 13; 5¹⁰ • (5² + 1) = 26 • 5¹⁰ = 2 • 13 • 5¹⁰; б) 815 – 814 – 813 ділиться на 11; 8¹³ • (8² – 8 – 1) = 55 • 8¹³ = 5 • 11 • 8¹³; в) 8131 – 960 ділиться на 720; (9²)³¹ – 9⁶⁰ = 9⁶² – 9⁶⁰ = 9¹⁰(81 – 1) = 9⁹ • 720;
г) 3760 + 63 · 3759 ділиться на 100; 37⁵⁹ • (37 + 63) = 100 • 37⁵⁹.
427. Подай у вигляді добутку, якщо n, m і k натуральні числа.
а) xⁿ⁺¹ + xⁿ = xⁿ(x + 1);
б) aᵐ – aᵐ ² = aᵐ(1 –1 a²);
в) 9aᵏ⁺⁵ – 3aᵏ⁺² = 9a⁵aᵏ – 3a²aᵏ = 3a²aᵏ(3a³ – 1);
г) 8²ⁿ⁺¹ – 4³ⁿ⁺⁴ = 2³⁽²ⁿ⁺¹⁾ – 2²⁽³ⁿ⁺⁴⁾ = 2⁶ⁿ⁺³ – 2⁶ⁿ⁺⁸ = 2⁶ⁿ⁺³(1 – 32) = –31 · 2⁶ⁿ⁺³;
ґ) yᵐ⁺⁵ – yᵐ = yᵐ(y⁵ – 1);
д) xᵏ⁺¹ + xᵏ⁺³ = xᵏ⁺¹(1 + x²);
е) 4xⁿ⁺⁶ + 12xⁿ⁺¹ = 4xⁿ⁺¹(x⁵ + 3);
є) 3²ⁿ⁺¹ + 9ⁿ⁺² = 3²ⁿ⁺¹ + 3²ⁿ⁺⁴ = 3²ⁿ⁺¹(1 + 27) = 28 · 3²ⁿ⁺¹.
428. Продовж послідовність: а) 4x, 12x, 36x, 108x, 324x; б) 2a – 4x, 4a – 8x, 8a – 16x, 16a – 32x.
429. Із букв, написаних
що на ній написано букву: а) «Ц»; б)

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
б) 3 2 5 + (–3 7) = 3 14 35 –15 35 = 2 34 35; в) –4 3 4 + (–5 1 2) = –4 3 4 – 5 2 4 = –9 5 4 = –10,25;
г) 4 1 2 + (–1 1 3) = 4 3 6 – 1 2 6 = 3 1 6; ґ) 3 4 + (–0,5) = 0,75 – 0,5 = 0,25; д) –3 5 + 4,2 = –0,6 + 4,2 = 3,6.
432. Знайди суму многочленів.
а) 3a² + 2a + 7 + a³ – 2a² + a – 3 = a³ + a² + 3a + 4;
б) 1,5x – x² – x³ + 2,5x⁴ – 1,5x³ – 2x + 3 = 2,5x⁴ – 2,5x³ – x² – 0,5x + 3.
433. Розклади на множники вираз.
а) (a + 1)x + (a + 1)y:
(a + 1)x + (a + 1)y = (a + 1)(x + y)
б) x(2 - c) - y(2 - c):
x(2 - c) - y(2 - c) = (2 - c)(x - y)
в) p - n + c(p - n):
p - n + c(p - n) = (p - n)(1 + c)
г) (x + y)² + x + y: (x + y)² + x + y = (x + y)² + (x + y) = (x + y)(x + y + 1)
434. Розклади на множники вираз ax - ay + 7x - 7y.
ax - ay + 7x - 7y = a(x - y) + 7(x - y) = (x - y)(a + 7)
Відповідь: Б (x - y)(a + 7)
435. Які доданки слід згрупувати,
Розгляньте кілька варіантів.
а) 2a + 4b + ca + 2bc:
2a + 4b + ca + 2bc = 2a + ca + 4b + 2bc = a(2 + c) + 2b(2 + c) = (2 + c)(a + 2b)
б) kx + ky + 5x + 5y:
kx + ky + 5x + 5y = kx + 5x + ky + 5y = x(k + 5) + y(k + 5) = (k + 5)(x + y)
в) x³ + 3x² + x + 3:
x³ + 3x² + x + 3 = x²(x + 3) + 1(x + 3) = (x + 3)(x² + 1)
г) am + 3n + an + 3m:
am + 3n + an + 3m = am + an + 3m + 3n = a(m + n) + 3(m + n) = (m + n)(a + 3)
436. Чи правильно виконано перетворення? ax + 7x + a + 7 = (ax + a) + (7x + 7) = a(x + 1) + 7(x + 1) = (x + 1)(a + 7)
(ax + a) + (7x + 7)
спільні множники за дужки: a(x + 1) + 7(x + 1)

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
в) 3c + 3y + ac + ay = 3(c + y) + a(c + y) = (c + y)(3 + a);
г) 2ax – 2ay + 3x – 3y = 2a(x – y) + 3(x – y) = (x – y)(2a + 3);
ґ) ax – ay – bx + by = a(x – y) – b(x – y) = (x – y)(a – b);
д) ca + 2cx – na – 2nx = c(a + 2x) – n(a + 2x) = (a + 2x)(c – n);
е) 3m + 3n – am – an = 3(m + n) – a(m + n) = (m + n)(3 – a);
є) am – an – m + n = a(m – n) – 1(m – n) = (m – n)(a – 1);
ж) a(x + y + z) + b(x + y + z) = (x + y + z)(a + b).
439. Подай вираз у вигляді добутку
а) 2x + 2y + ax + ay = 2(x + y) + a(x + y) = (x + y)(2 + a);
б) xa – xb + ca – cb = x(a – b) + c(a – b) = (a – b)(x + c);
в) 2a – 2b + ca – cb = 2(a – b) + c(a – b) = (a – b)(2 + c);
г) nx + ny + mx + my = n(x + y) + m(x + y) = (x + y)(n + m);
ґ) ax – bx – ay + by = x(a – b) – y(a – b) = (a – b)(x – y);
д) mx + my – cx – cy = m(x + y) – c(x + y) = (x + y)(m – c);
е) 2x + 2y – ax – ay = 2(x + y) – a(x + y) = (x + y)(2 – a);
є) ap – ak – p + k = a(p – k) – 1(p – k) = (p – k)(a – 1).
440. Подай вираз у вигляді добутку
а) a(x + 3) + b(x + 3) + c(x + 3) = (x + 3)(a + b + c);
б) m(a – z) – n(a – z) + 2(a – z) = (a – z)(m – n + 2).
441. Розклади на множники многочлен
а) az – z² + ac – cz = z(a – z) + c(a – z) = (a – z)(z + c);
б) 5a – 10 + ac³ – 2с³ = 5(a – 2) + c³ (a – 2) = (a – 2)(5 + c³); в) 2a²b + ac – 6abc – 3c² = a(2ab + c) – 3c(2ab + c) = (2ab + c)(a – 3c);
г) 3a³ – 5a² – 3ab + 5b = a²(3a – 5) – b(3a – 5) = (3a – 5)(a² – b).
442. Розклади на множники многочлен
а) 3m² + 9mn – 2m – 6n = 3m(m + 3n) – 2(m + 3n) = (m + 3n)(3m – 2);
б) a³ – a²n – 3a + 3n = a²(a – n) – 3(a – n) = (a – n)(a² – 3);
в) y³ – 3y⁵ + 3y² – 9y⁴ = y³(1 – 3y²) + 3y²(1 – 3y²) = (1 – 3y²)(y³ + 3y²);
г) 3a³ + 12a² – a – 4 = 3a²(a + 4) – 1(a + 4) = (a + 4)(3a² – 1);
ґ) 4x²y² – 4xy – 5axy + 5a = 4xy(xy – 1) – 5a(xy – 1) = (xy – 1)(4xy – 5a);
д) a³x² + a²x³ – a – x = a²x²(a + x) – 1(a + x) = (a + x)(a²x² – 1).
443. Розклади на множники многочлен
а) ac + bc + a² + ab = c(a + b) + a(a + b) = (a + b)(c + a);
б) 7x⁴ – x² + 7ax² – a = x²(7x² – 1) + a(7x² – 1) = (7x² – 1)(x² + a);
в) m²p + 3my – mnp – 3ny = m(mp + 3y) – n(mp + 3y) = (mp + 3y)(m – n);
г) 3a² + 6ab – 2a – 4b = 3a(a + 2b) – 2(a + 2b) = (a + 2b)(3a – 2);
г) 5a³c² – 5ax – 8a²c³ + 8cx = 5a(a²c² – x) – 8c(a²c² – x) = (a²c² – x)(5a – 8c); д) 2x5y² + 2x³y – x²y – 1 = 2x³y(x²y – 1) – (x²y – 1) = (x²y – 1)(2x³y – 1).
444. Обчисли значення
a) x³ – 9x² + x – 9 = (x³ – 9x²) + (x – 9) = x²(x – 9) + (x – 9) = (x – 9)(x² + 1), якщо x = 19, то (19 – 9) · (19² + 1) = 10 · (361 + 1) = 3620; б) m² – mn – 2m + 2n = (m² – mn) – (2m – 2n) = m(m – n) – 2(m – n) = (m – n)(m – 2), якщо m = 0,35; n = 0,25; то (0,35 – 0,25) · (0,35 – 2) = 0,1 · (–1,65) = –0,165.
445. Обчисли
a) а3 – 5а2 + а – 5, якщо а = -15; a²(a – 5) + (a – 5) = (a – 5) • (a² + 1) = (–15 – 5)(225 + 1) = –20 • 226 = –4520; б) х2 + 2ху – 3х – 6у, якщо х = 0,7 і у = 0,15; x(x – 2y) – 3(x – 2y) = (x – 2y)(x – 3) = (0,7 – 2 • 0,15) • (0,7 – 3) = 0,4 • (–2,3) = –0,92.

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
446. Обчисли
а) 20,5 • 17 + 79,5 • 17 + 20,5 • 0,28 + 79,5 • 0,28 = = (20,5 • 17 + 20,5 • 0,28) + (79,5 • 17 + 79,5 • 0,28) = 20,5 • (17 + 0,28) + 79,5 • (17 + 0,28) = = (17 + 0,28) • (20,5 + 79,5) = 100 • 17,28 = 1728.
б) 42,2² – 42,2 • 41,2 + 57,8² – 57,8 • 56,8 = (42,2² – 42,2 • 41,2) + (57,8² – 57,8 • 56,8) = = 42,2 • (42,2 – 41,2) + 57,8 • (57,8 – 56,8) = 42,2 • 1 + 57,8 • 1 = 42,2 + 57,8 = 100.
447. Обчисли
а) 36,7 • 15 + 63,3 • 15 + 36,7 • 1,3 + 63,3 • 1,3 = = (36,7 • 15 + 36,7 • 1,3) + (63,3 • 15 + 63,3 • 1,3) = 36,7 • (15 + 1,3) + 63,3 • (15 + 1,3) = = (15 + 1,3) • (36,7 + 63,3) = 16,3 • 100 = 1630.
б) 76,2² – 76,2 • 73,2 + 23,8² – 23,8 • 20,8 = (76,2² – 76,2 • 73,2) + (23,8² – 23,8 • 20,8) = = 76,2 • (76,2 – 73,2) + 23,8 • (23,8 – 20,8) = 76,2 • 3 + 23,8 • 3 = = 3 • (76,2 + 23,8) = 3 • 100 = 300.
448. Розв’яжи рівняння
а) x³ – 5x² + 3x – 15 = 0
(x³ – 5x²) + (3x – 15) = 0
x²(x – 5) + 3(x – 5) = 0
(x – 5)(x² + 3) = 0,
звідси x – 5 = 0 або x² + 3 = 0.
Коренем першого рівняння є x = 5, а
друге рівняння розв'язків не має, бо x² ≠ –3.
Відповідь: x = 5.
б) x² – 2x³ + 7 – 14x = 0
(–2x³ + x²) + (–14x + 7) = 0
x²(–2x + 1) – 7(2x – 1) = 0
(–2x + 1)(x² – 7) = 0,
звідси –2x + 1 = 0 або x² – 7 = 0.
Коренем першого рівняння є x = 0,5,
а друге рівняння розв'язків не має.
Відповідь: x = 0,5
в) x³ – 3x² + x – 3 = 0
(x³ – 3x²) + (x – 3) = 0
x²(x – 3) + 1(x – 3) = 0
(x – 3)(x² + 1) = 0,
звідси x – 3 = 0 або x² + 1 = 0.
Коренем першого рівняння є x = 3, а
друге рівняння розв'язків не має, бо x² ≠ –1.
Відповідь: x = 3.
г) x³ + 4x² + 3x + 12 = 0
(x³ + 4x²) + (3x + 12) = 0
x²(x + 4) + 3(x + 4) = 0
(x + 4)(x² + 3) = 0,
звідси x + 4 = 0 або x² + 3 = 0.
Коренем першого рівняння є x = –4, а
друге рівняння розв'язків не має, бо
x² ≠ –3.

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
Відповідь: x = –4.
449. Розв’яжи рівняння
а) 2z³ – 3z² + 2z – 3 = 0
(2z³ – 3z²) + (2z – 3) = 0
z²(2z – 3) + 1(2z – 3) = 0
(2z – 3)(z² + 1) = 0,
звідси 2z – 3 = 0 або z² + 1 = 0.
Коренем першого рівняння є z = 1,5,
а друге рівняння розв'язків не має, бо z² ≠ –1.
Відповідь: z = 1,5.
б) z³ – 5z² + 2z – 10 = 0
(z³ – 5z²) + (2z – 10) = 0
z²(z – 5) + 2(z – 5) = 0
(z – 5)(z² + 2) = 0,
звідси z – 5 = 0 або z² + 2 = 0.
Коренем першого рівняння є z = 5, а
друге рівняння розв'язків не має, бо
z² ≠ –2.
Відповідь: z = 5.
в) y³ + 3y² + 5y + 15 = 0
(y³ + 3y²) + (5y + 15) = 0
y²(y + 3) + 5(y + 3) = 0
(y + 3)(y² + 5) = 0,
звідси y + 3 = 0 або y² + 5 = 0.
Коренем першого рівняння є y = –3, а
друге рівняння розв'язків не має, бо y² ≠ –5.
Відповідь: y = –3.
г) 3x³ + 9x² + x + 3 = 0
(3x³ + 9x²) + (x + 3) = 0
3x²(x + 3) + 1(x + 3) = 0 (x + 3)(3x² + 1) = 0,
звідси x + 3 = 0 або 3x² + 1 = 0.
Коренем першого рівняння є x = –3, а
друге рівняння розв'язків не має, бо 3x² ≠ –1.
Відповідь: x = –3.
450. Подай у вигляді добутку вираз
1) 4a² + 3z – 4az – 3a = (4a² – 4az) + (3z – 3a) = 4a(a – z) + 3(z – a) = (a – z)(4a + 3) 2) 3x² – 2y³ – 3x²y + 2y² = (3x² – 3x²y) + (–2y³ + 2y²) = 3x²(1 – y) + 2y²(1 – y) = = (1 – y)(3x² + 2y²)
3) a³ – 2c² – a²c + 2ac = (a³ – a²c) + (2ac – 2c²) = a²(a – c) + 2c(a – c) = (a – c)(a² + 2c)
4) a³ – 3b³ + a²b² – 3ab = (a³ + a²b²) + (–3b³ – 3ab) = a²(a + b²) – 3b(b² + a) = (a + b²)(a² – 3b)
451. Подай у
а) a + 12ab² – 3b – 4a²b = a – 3b – 4a²b + 12ab² = (a – 3b) – 4ab(a – 3b) = (a – 3b)(1 – 4ab).
б) a³ – 2x² – 2a²x + ax = (a³ – 2a²x) + (ax – 2x²) = a²(a – 2x) + x(a – 2x) = (a – 2x)(a² + x)

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
в) a²b + c³ + a²c² + bc = (a²b + a²c²) + (c³ + bc) = a²(b + c²) + c(b + c²) = (b + c²)(a² + c)
г) m²n + 2x² + 2mnx + mx = (m²n + 2mnx) + (2x² + mx) = mn(m + 2x) + x(2x + m) = = (m + 2x)(mn + x)
452. Знайдіть помилки в роботах учнів. Виконайте правильно.
1) ax + ay – az + nx + ny – nz = (a + n) (x + y + z)
Помилка: Учениця неправильно згрупувала доданки.
Правильне розв'язання: ax + ay – az + nx + ny – nz
= (ax + ay + nx + ny) – (az + nz)
= (a + n)(x + y) – (a + n)z
= (a + n)(x + y – z).
Відповідь: (a + n)(x + y – z).
2) 2ax + cx – 6ax² – 3cx² + 2ac + c² = x(2a + c) – 3x2(2a + c) + c(2a + c) = (x + 3x2 + c)(2a + c)
Помилка: Неправильне винесення спільних множників за дужки.
Правильне розв'язання: 2ax + cx – 6ax² – 3cx² + 2ac + c²
= x(2a + c) – 3x²(2a + c) + c(2a + c)
= (x – 3x² + c)(2a + c).
Відповідь: (x – 3x² + c)(2a + c).
Учень
1) a + b – 2 – ax – bx + 2x = (а + b – 2) – x(a + b – 2) = (a + b – 2)x
Помилка: Неправильно згрупував доданки та виніс спільний множник.
Правильне розв'язання: (a ax) + (b bx) + (−2 + 2x) = a(1 x) + b(1 x) + 2(x 1)
Відповідь: (1−x)(a+b−2)
2) ax² + bx² – bx – ax + cx² – cx = (ax2 + bx2 + cx2) – (bx – ax – cx) = x2(a + b+ c) – x(b – a - c)
Помилка: Неправильне винесення спільного множника x.
Правильне розв'язання:
ax² + bx² – bx – ax + cx² – cx = x²(a + b + c) – x(a + b + c) = (a + b + c)(x² – x).
Відповідь: (a + b + c)(x² – x).
453. Розклади на множники многочлен
а) ax² + bx² – cx² + am + bm – cm = x²(a + b – c) + m(a + b – c) = (a + b – c)(x² + m)
б) a + b + ax² + bx² – bx – ax = (a + b) + x²(a + b) – x(a + b) = (a + b)(x² – x + 1)
в) 2am + 3mx – 7m – 2ac – 3cx + 7c = 2a(m – c) + 3x(m – c) – 7(m – c) = (m – c)(2a + 3x – 7)
г) 4ax² – ax + 5a – 4bx² + bx – 5b = 4x²(a – b) – x(a – b) + 5(a – b) =(a – b)(4x² – x + 5)
454. Розклади на множники многочлен
а) 9c³x² + 2c³x – c³ + 9x² + 2x – 1 = (9x² + 2x – 1) + c³(9x² + 2x – 1) = (9x² + 2x – 1)(1 + c³)
б) 4abc² – 4ac + 4b + abc²x – acx + bx = (4abc² – 4ac + 4b) + (abc²x – acx + bx) = = 4(abc² – ac + b) + x(abc² – ac + b) = (abc² – ac + b)(4 + x).
в) x³ + x²y + x³y – xy³ – xy² – y³ = (x³ + x²y + x³y) – (xy³ + xy² + y³) = = x²(x + y + xy) – y²(xy + x + y) = (x + y)(x² – y²) = (x + y)(x – y)(x + y).
г) x² – x³ + y – y² – xy + xy² = x²(1 – x) + y(1 – x) – y²(1 – x) = (1 – x)(x² + y – y²).
455. Розклади на множники многочлен
а) az² – bz² – bz + az – a + b = (az² + az – a) – (bz² + bz – b) = a(z² + z – 1) – b(z² + z – 1) = = (z² + z – 1)(a – b).

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
б) x² + 2x – ca – 2c – cx + ax = (x² + 2x + ax) – (ca + 2c + cx) = x(x + 2 + a) – c(a + 2 + x) = = (x + 2 + a)(x – c).
в) x⁴ – a⁴ + a³x – a³x + c³x – ac³ = x⁴ – a⁴ + a³x – a³x + c³x – ac³ = x⁴ – a⁴ + c³x – ac³ = (x² –a²)(x² + a²) + c³(x – a)
г) a³ – a² + x³ – x² + a²x + аx² = a³ – a² + x³ – x² + a²x + ax² = a²(a – 1 + x) + x²(x – 1 + a)
ґ) x³ + y³ + xу² + х²у + x²z + y²z = x³ + y³ + xy² + x²y + x²z + y²z = x²(x + y + z) + y²(x + y + z) = (x² + y²)(x + y + z)
д) a³ + a + ab² – a²b – b – b³ = a³ + a + ab² – a²b – b – b³ = a(a² – ab + b²) + (a – b) – b³
456. Розклади многочлен
а) 15a²mx – 20am – 21ax + 28 = (15a²mx – 20am) – (21ax – 28) = 5am(3ax – 4) – 7(3ax – 4) = = (3ax – 4)(5am – 7).
Перевірка:
(3ax – 4)(5am – 7) = 15a²mx – 21ax – 20am + 28.
б) 0,9ax + 1,2x² – 1,2ac – 1,6cx = 0,3x(3a + 4x) – 0,4c(3a + 4x) = (3a + 4x)(0,3x – 0,4c).
Перевірка:
(3a + 4x)(0,3x – 0,4c) = 0,9ax + 1,2x² – 1,2ac – 1,6cx.
457. Розклади многочлен на множники і виконай перевірку
а) a²b + 10ab – 20a – 2a² – b + 2 = a²b – 2a² + 10ab – 20a – b + 2 = = a²(b – 2) + 10a(b – 2) – 1(b – 2) = (b – 2)(a² + 10a – 1).
Перевірка: (b – 2)(a² + 10a – 1) = a²b + 10ab – 20a – 2a² – b + 2
б) 3 13ax²y –1 13 x + 12 13a²xy² –4 13ay = 3 13ax²y + 12 13a²xy² –1 13 x –4 13ay = = 3axy ( 1 13 x + 4 13ay) – ( 1 13 x + 4 13ay) = ( 1 13 x + 4 13ay) · (3axy – 1).
458. Розклади на множники тричлен
а) x² + 4x + 3 = x² + 3x + x + 3 = x(x + 3) + 1(x + 3) = (x + 3)(x + 1).
б) x² + 6x + 8 = x² + 4x + 2x + 8 = x(x + 4) + 2(x + 4) = (x + 4)(x + 2).
в) x² − 4x + 3 = x² − 3x − x + 3 = x(x − 3) − 1(x − 3) = (x − 3)(x − 1).
г) x² + 3x − 10 = x² + 5x − 2x − 10 = x(x + 5) − 2(x + 5) = (x + 5)(x − 2).
459. Розклади на множники тричлен
а) x² + 6x + 5 = x² + 5x + x + 5 = x(x + 5) + 1(x + 5) = (x + 5)(x + 1).
б) x² + 7x + 6 = x² + 6x + x + 6 = x(x + 6) + 1(x + 6) = (x + 6)(x + 1).
в) x² – 10x + 21 = x² – 7x – 3x + 21 = x(x – 7) – 3(x – 7) = (x – 7)(x – 3).
г) x² + 2x – 8 = x² – 2x + 4x – 8 = x(x – 2) + 4(x – 2) = (x – 2)(x + 4).
460. Розв’яжи рівняння а) x² + 7x + 10 = 0
x² + 5x + 2x + 10 = 0
x(x + 5) + 2(x + 5) = 0
(x + 5)(x + 2) = 0
x₁ = –5; x₂ = –2.
461. Розв’яжи рівняння
а) x² + 4x + 3 = 0
x² + 3x + x + 3 = 0
x(x + 3) + 1(x + 3) = 0
(x + 3)(x + 1) = 0
x₁ = –3; x₂ = –1.
462. Доведи, що:
б) x² + 8x + 7 = 0
x² + 7x + x + 7 = 0
x(x + 7) + 1(x + 7) = 0
(x + 7)(x + 1) = 0
x₁ = –7; x₂ = –1.
б) x² + 8x + 12 = 0
x² + 6x + 2x + 12 = 0
x(x + 6) + 2(x + 6) = 0
(x + 6)(x + 2) = 0
x₁ = –6; x₂ = –2.
в) x² – 5x + 6 = 0
x² – 3x – 2x + 6 = 0
x(x – 3) – 2(x – 3) = 0
(x – 3)(x – 2) = 0
x₁ = 3; x₂ = 2.
в) x² – 9x + 18 = 0
x² – 6x – 3x + 18 = 0
x(x – 6) – 3(x – 6) = 0
(x – 6)(x – 3) = 0
x₁ = 6; x₂ = 3.

а) 2⁹ • 3⁵ + 2⁹ • 3³ – 2⁶ • 3⁵ – 2⁶ • 3³ ділиться на 420;
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
5¹⁰ • 7¹⁰ + 5¹⁰ • 7⁸ – 5⁸ • 7¹⁰ – 5⁸ • 7⁸ ділиться на 1200; 5⁸ • 7⁸ • (5² • 7² + 5² – 7² – 1) = = 5⁸ • 7⁸ • (5² • (7² + 1) – (7² + 1)) = 5⁸ • 7⁸ • (7² + 1) • (5² – 1) = (7² + 1) • (5² – 1) • 5⁸ • 7⁸ = = 50 • 24 • 5⁸ • 7⁸ = 1200 • 5⁸ • 7⁸. Доведено. Кратно 1200.
в) 2¹¹ • 3⁶ – 2⁷ • 3⁶ – 2⁷ • 3⁴ + 2¹¹ • 3⁴ ділиться на 150; (2¹¹ • 3⁶ – 2⁷ • 3⁶) – (2⁷ • 3⁴ – 2¹¹ • 3⁴) = = 2⁷ • 3⁶(2⁴ – 1) – 2⁷ • 3⁴(1 – 2⁴) = 2⁷ • 3⁶(2⁴ – 1) + 2⁷ • 3⁴(2⁴ – 1) = (2⁴ – 1)(2⁷ • 3⁶ + 2⁷ • 3⁴) = = 2⁷ • 3⁴ • (3² + 1)(16 – 1) = 150 • 2⁷ • 3⁴. Кратно 150. Доведено. 463. Доведи, що:
а) 2¹⁰ • 3¹² + 2⁸ • 3¹² + 2¹⁰ • 3¹⁰ + 2⁸ • 3¹⁰ ділиться на 300; (2¹⁰ • 3¹² + 2⁸ • 3¹²) + (2¹⁰ • 3¹⁰ + 2⁸ • 3¹⁰) = = 2⁸ • 3¹² (2² + 1) + 2⁸ • 3¹⁰ (2² + 1) = (2² + 1) (2⁸ • 3¹² + 2⁸ • 3¹⁰) = 5 • 2⁸ • 3¹⁰ (3² + 1) =
= 50 • 2 • 3 • 27 • 3³ = 300 • 2 • 3³. Кратно 300. Доведено.
б) 5¹⁰ • 3¹⁵ – 5⁸ • 3¹⁶ + 5¹¹ • 3¹² – 5⁹ • 3¹³ ділиться на 110; 5⁸ • 3¹² (5² • 3³ – 5⁰ • 3⁴ + 5³ – 5¹ • 3) = = (5² – 3) • (5⁸ • 3¹⁵ + 5⁹ • 3¹²) = 22 • 5⁸ • 3¹² = 2 • 11 • 2³ • 5⁸ • 3¹² = 11 • 2⁶ • 5⁸ • 3¹². Кратно 11. Доведено.
в) –7¹⁰ • 2¹⁰ + 7⁹ • 2¹⁴ – 7⁸ • 2¹⁰ + 7⁷ • 2¹⁴ ділиться на 450; (–7¹⁰ • 2¹⁰ + 7⁹ • 2¹⁴) + (–7⁸ • 2¹⁰ + 7⁷ • 2¹⁴) = = 7⁷ • 2¹⁰ (7³ – 7) + 7⁷ • 2¹⁰ (2⁴ – 7) = (2⁴ – 7) • (7⁷ • 2¹⁰ + 7⁷ • 2¹⁰) = = 9 • 7⁷ • 2¹⁰ • (7² + 1) = 9 • 5 • 10 • 7⁷ • 2¹⁰ = 45 • 5 • 7⁷ • 2¹⁰. Кратно 45. Доведено.
464. Розклади на множники
а) a² + 3ab + 2b² = a² + 2ab + b² + ab + b² = (a + b)² + b(a + b) = (a + b)(a + b + b) = = (a + b)(a + 2b). б) 2x² – 7xy + 3y² = 2x² – 6xy – xy + 3y² = 2x(x – 3y) – y(x – 3y) = (2x – y)(x – 3y).
465. Розв’яжи математичні кросворди. x − y = 10 x + z = 47 y − z = 5
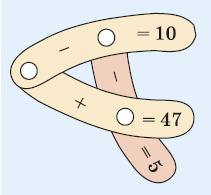
2z + 15 = 47
2z = 47 – 15
2z = 32 z = 16.
Виразимо x через y з першого рівняння: x = y + 10.
Виразимо y через z з третього рівняння: y = z + 5.
Підставимо y = z + 5 у вираз для x: x = (z + 5) + 10 = z + 15.
Підставимо x = z + 15 у друге рівняння: (z + 15) + z = 47.
Розв'яжемо рівняння для z:
Підставимо z = 16 у вираз для y: y = z + 5 = 16 + 5 = 21.
Підставимо z = 16 у вираз для x: x = z + 15 = 16 + 15 = 31.
Відповідь: x = 31; y = 21; z = 16.

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html

x + y = 80
n − m = 16
x • 20 = n y + 30 = m
З першого рівняння x + y = 80 виразимо y: y = 80 − x. З четвертого рівняння y + 30 = m підставимо y: m = (80 − x) + 30 = 110 − x. З третього рівняння x • 20 = n знаходимо n: n = 20x.
З другого рівняння n − m = 16 підставимо знайдені n і m: 20x − (110 − x) = 16.
Розв'яжемо рівняння: 20x − 110 + x = 16.
21x = 126.
x = 6.
Підставимо x = 6 у вираз для y: y = 80 − 6 = 74.
Підставимо x = 6 у вираз для n: n = 20 • 6 = 120.
Підставимо x = 6 у вираз для m: m = 110 − 6 = 104.
Відповідь: x = 6, y = 74, n = 120, m = 104.

Розв'яжемо рівняння:
2x – x = 5 + 5.
x = 10.
Знайдемо y, n і m: y = x + 8 = 10 + 8 = 18. n = x + 5 = 10 + 5 = 15. m = 2x = 2 • 10 = 20.
x + 8 = y
y – 3 = n
x • 2 = m
m – 5 = n
першого рівняння x + 8 = y виразимо y: y = x + 8. З другого рівняння y – 3 = n підставимо y: n = (x + 8) – 3 = x + 5. З третього рівняння x • 2 = m знаходимо m: m = 2x.
четвертого рівняння m – 5 = n підставимо m і n: 2x – 5 = x + 5.
Відповідь: x = 10, y = 18, n = 15, m = 20.
466. Скільки існує
координатній прямій.
|x| < 5; –5 < x < 5.

Числа: 4, −3, −2, −1, 0, 1, 2, 3, 4. Всього: 9 чисел.
467. Обчисли
а) 45 : 100 • 20 = 9;
б) 56 : 100 • 0,5 = 0,28;
в) 28 : 100 • 400 = 112.
468.
3 6 = 1 2 = 0,5 = 50%
469.

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
В (x+y)²
470. Перетвори на многочлен (х – 2у)2 . Г x² – 4xy + 4y²
471. Якому тричлену тотожно
а) (a + x)² = a² + 2ax + x² в) (a – 2)² = a² – 4a + 4
б) (x + 1)² = x² + 2x + 1 г) (x – 1)² = x² – 2x + 1
472. Піднеси до квадрата двочлен.
а) (1 + c)² = 1 + 2c + c² в) (a – n)² = a² – 2an + n² б) (1 – x)² = 1 – 2x + x² г) (x + 2)² = x² + 4x + 4
473. Якому з виразів тотожно дорівнює вираз а2 – 8а + 16?
В (a – 4)²
474. Подай у вигляді степеня.
а) 1 + 2a + a² = (a + 1)²
б) x² – 4yx + 4y² = (x – 2y)²
в) 16 – 8c + c² = (c – 4)²
г) 9z² + 12z + 4 = (3z + 2)²
ґ) 25p² + 20px + 4x² = (5p + 2x)²
д) y² – 14y + 49 = (y – 7)²
475. Вкажи вираз, що є квадратом
В 9x² – 6x + 1 = (3x – 1)²
476. Піднеси до квадрата двочлен
а) (a + c)² = a² + 2 • a • c + c² = a² + 2ac + c².
б) (x + y)² = x² + 2 • x • y + y² = x² + 2xy + y².
в) (n + 2)² = n² + 2 • n • 2 + 2² = n² + 4n + 4.
г) (m + 3)² = m² + 2 • m • 3 + 3² = m² + 6m + 9.
ґ) (1 + ab)² = 1² + 2 • 1 • ab + (ab)² = 1 + 2ab + a²b².
д) (p + 3q)² = p² + 2 • p • 3q + (3q)² = p² + 6pq + 9q².
е) (2x + 4)² = (2x)² + 2 • 2x • 4 + 4² = 4x² + 16x + 16.
є) (3a + b)² = (3a)² + 2 • 3a • b + b² = 9a² + 6ab + b².
ж) (3x + 2y)² = (3x)² + 2 • 3x • 2y + (2y)² = 9x² + 12xy + 4y².
з) (5a + 3b)² = (5a)² + 2 • 5a • 3b + (3b)² = 25a² + 30ab + 9b².
и) (2a² – 3x)² = (2a²)² – 2 • 2a² • 3x + (3x)² = 4a⁴ – 12a²x + 9x².
і) (3a² – 5c³)² = (3a²)² – 2 • 3a² • 5c³ + (5c³)² = 9a⁴ – 30a²c³ + 25c⁶. 477. Піднеси до квадрата двочлен
а) (m + 2)² = m² + 2 • m • 2 + 2² = m² + 4m + 4.
б) (2a + x)² = (2a)² + 2 • 2a • x + x² = 4a² + 4ax + x².
в) (3 + 6a)² = 3² + 2 • 3 • 6a + (6a)² = 9 + 36a + 36a².
г) (x – 1)² = x² – 2 • x • 1 + 1² = x² – 2x + 1.
ґ) (2c – 3a)² = (2c)² – 2 • 2c • 3a + (3a)² = 4c² – 12ac + 9a².
д) (5x – y)² = (5x)² – 2 • 5x • y + y² = 25x² – 10xy + y².
е) (1 – ab)² = 1² – 2 • 1 • ab + (ab)² = 1 – 2ab + a²b².
є) (cq – 2p)² = (cq)² – 2 • cq • 2p + (2p)² = c²q² – 4cqp + 4p².
ж) (ax + 5)² = (ax)² + 2 • ax • 5 + 5² = a²x² + 10ax + 25.
з) (a + c²)² = a² + 2 • a • c² + (c²)² = a² + 2ac² + c⁴.
и) (n² + 2a³)² = (n²)² + 2 • n² • 2a³ + (2a³)² = n⁴ + 4n²a³ + 4a⁶.
і) (2a² – 3cx²)² = (2a²)² – 2 • 2a² • 3cx² + (3cx²)² = 4a⁴ – 12a²cx² + 9c²x⁴.
478.
а) (m + 2)(m + 2) = m² + 2 • m • 2 + 2² = m² + 4m + 4.

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
б) (3 + p)(3 + p) = 3² + 2 • 3 • p + p² = 9 + 6p + p².
в) (3a – 5)(3a – 5) = (3a)² – 2 • 3a • 5 + 5² = 9a² – 30a + 25.
г) (2a – b²)(2a – b²) = (2a)² – 2 • 2a • b² + (b²)² = 4a² – 4ab² + b⁴.
479.
а) (5 + c)(5 + c) = 5² + 2 • 5 • c + c² = 25 + 10c + c².
б) (p – 10)(p – 10) = p² – 2 • p • 10 + 10² = p² – 20p + 100.
в) (2a³ + 1)(2a³ + 1) = (2a³)² + 2 • 2a³ • 1 + 1² = 4a⁶ + 4a³ + 1. і) (1 – xy)(1 – xy) = 1² – 2 • 1 • xy + (xy)² = 1 – 2xy + x²y².
480. Віднови записи на дошці.
а) a² – 4ab² + 4b⁴ = (a – 2b²)².
б) a²b² + 12abc + 36c² = (ab + 6c)².
481. Подай тричлен у вигляді квадрата двочлена
а) m² + 2m + 1 = (m + 1)².
б) x² – 4x + 4 = (x – 2)².
в) c² – 12c + 36 = (c – 6)².
г) a² + 14a + 49 = (a + 7)².
ґ) 9 – 6x + x² = (3 – x)².
д) 4x² + 25y² – 20xy = (2x – 5y)².
482. Подай тричлен у
а) a² + 4a + 4 = (a + 2)².
б) n² – 12n + 36 = (n – 6)².
в) x² – 10x + 25 = (x – 5)².
г) 9a² + 6ac + c² = (3a + c)².
ґ) 4m² + 4m + 1 = (2m + 1)².
д) b⁴ – 6b² + 9 = (b² – 3)².
483. Спрости вираз.
а) (x – 3)² – x(x – 6) = (x² – 6x + 9) – (x² – 6x) = x² – 6x + 9 – x² + 6x = 9
б) (m + 5)² – (m – 5)² = (m² + 10m + 25) – (m² – 10m + 25) = = m² + 10m + 25 – m² + 10m – 25 = 20m
в) 1 – (2a – 1)² = 1 – (4a² – 4a + 1) = 1 – 4a² + 4a – 1 = –4a² + 4a
г) z² + 1 – (1 + z)² = z² + 1 – (1 + 2z + z²) = z² + 1 – 1 – 2z – z² = –2z
ґ) (x – 2)(x – 4) – (x – 6)² = (x² – 6x + 8) – (x² – 12x + 36) = x² – 6x + 8 – x² + 12x – 36 = = 6x – 28
д) (2a – 3c)² – 3c(3c – 4a) = (4a² – 12ac + 9c²) – (9c² – 12ac) = = 4a² – 12ac + 9c² – 9c² + 12ac = 4a²
484. Спрости вираз.
а) (x – 2)² + (x + 5)(x – 1) = (x² – 4x + 4) + (x² + 5x – x – 5) = = x² – 4x + 4 + x² + 4x – 5 = 2x² – 1
b) (3a – 1)² + 3a(2 – 3a) = (9a² – 6a + 1) + (6a – 9a²) = 9a² – 6a + 1 + 6a – 9a² = 1
c) y(y + 2x) – (x + y)² = y² + 2xy – (x² + 2xy + y²) = y² + 2xy – x² – 2xy – y² = –x²
d) (b + 4)² – (b – 3)² = (b² + 8b + 16) – (b² – 6b + 9) = b² + 8b + 16 – b² + 6b – 9 = 14b + 7
e) 4(1 – 3a) – (3a – 2)² = 4 – 12a – (9a² – 12a + 4) = 4 – 12a – 9a² + 12a – 4 = –9a²
f) (2x + 3y)² – 3y(4x + 3y) = (4x² + 12xy + 9y²) – (12xy + 9y²) = = 4x² + 12xy + 9y² – 12xy – 9y² = 4x²
485. Розв’яжи рівняння
а) (x – 2)² = x(x – 3)
x² – 4x + 4 = x² – 3x

x² – 4x – x² + 3x = –4
б) (3y + 5)² = 9y² + 55
9y² + 30y + 25 = 9y² + 55
30y = 55 – 25
в) (c – 7)² – 2(c – 2) = c² + 21
c² – 14c + 49 – 2c + 4 = c² + 21
c² – 14c – 2c – c² = 21 – 49 – 4
x = –4
x = 4
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
30y = 30 y = 30 : 30 y = 1
г) (6 – x)² = (x + 8)(x – 4) + 4
36 – 12x + x² = x² – 4x + 8x – 32 + 4
–12x + x² – x² + 4x – 8x = –32 + 4 – 36
–16x = –64
x = –64 : (–16)
x = 4
486. Розв’яжи рівняння
а) (x – 4)² = x(x + 8)
x² – 8x + 16 = x² + 8x
x² – 8x – x² – 8x = –16 –16x = –16
x = 1
б) (5 – 2y)² = 4y² + 65 25 – 20y + 4y² = 4y² + 65 –20y + 4y² – 4y² = 65 – 25 –20y = 40 y = –2
г) (x – 3)(x – 4) – (x – 5)² = –10
x² – 4x – 3x + 12 – x² + 10x – 25 = –10
x² – 4x – 3x – x² + 10x = –10 – 12 + 25
3x = 3
x = 1
487. Розв’яжи рівняння
а) x² + 10x + 25 = 0
(x + 5)² = 0
x + 5 = 0
x = –5
в) 1 – 8x + 16x² = 0
(1 – 4x)² = 0
1 – 4x = 0
–4x = –1
x = 1 4
488. Розв’яжи рівняння
а) x² – 14x + 49 = 0
(x – 7)² = 0
x – 7 = 0
x = 7
–16c = –32
c = –32 : (–16)
c = 2

в) 4 – 12x + 9x² = 0
(2 – 3x)² = 0
2 – 3x = 0
–3x = –2
в) (x + 7)² – x² = 3(5x + 15)
x² + 14x + 49 – x² = 15x + 45 x² + 14x – x² – 15x = 45 – 49 –x = –4 x = 4
б) 25x² – 30x + 9 = 0
(5x – 3)² = 0
5x – 3 = 0
5x = 3
x = 3 5
г) 36 + 12x + x² = 0
(6 + x)² = 0
6 + x = 0
x = –6
б) 9x² + 12x + 4 = 0
(3x + 2)² = 0
3x + 2 = 0
3x = –2
x = –2 3
г) 1 + 16x + 64x² = 0
(1 + 8x)² = 0
1 + 8x = 0
8x = –1
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
x = 2 3 x = –1 8
489. Подай у вигляді многочлена вираз.
а) (0,5x² + 3y³)² = (0,5x²)² + 2(0,5x²)(3y³) + (3y³)² = 0,25x⁴ + 3x²y³ + 9y⁶.
б) (0,2m⁵ + 5ab)² = (0,2m⁵)² + 2(0,2m⁵)(5ab) + (5ab)² = 0,04m¹⁰ + 2abm⁵ + 25a²b².
в) (7a³ + 2a²)² = (7a³)² + 2(7a³)(2a²) + (2a²)² = 49a⁶ + 28a⁵ + 4a⁴.
г) (2x²y⁴ + 0,5y³)² = (2x²y⁴)² + 2(2x²y⁴)(0,5y³) + (0,5y³)² = 4x⁴y⁸ + 2x²y⁷ + 0,25y⁶.
ґ) (–3c2 + 0,8х2у3)2 = 9c⁴ – 4,8c²x²y³ + 0,64x⁴y⁶
д) (–5x² – 0,4y³)² = (–5x²)² + 2(–5x²)(–0,4y³) + (–0,4y³)² = 25x⁴ + 4x²y³ + 0,16y⁶.
490. Замініть зірочки одночленами, щоб утворилась тотожність.
а) (c + b)² = c² + 2cb + b²
б) (a + m)² = a² + 2am + m²
в) (3x – 1)² = 9x² – 6x + 1
г) (a – 3bx)² = a² – 6abx + 9b²x²
491. Спрости вираз та
а) (2a – 5)² – (2a – 3)(2a – 6), якщо a = 1,5.
4a² – 20a + 25 – (4a² – 18a + 18) = –2a + 7
якщо a = 1,5, то –2 · 1,5 + 7 = –3 + 7 = 4
б) (6x – 2)(6x + 2) – (6x – 2)², якщо x = 0,5.
36x² – 4 + (36x² – 24x + 4) = 36x² – 4 – 36x² + 24x – 4 = = 24x – 8, якщо x = 0,5, то 24 · 0,5 – 8 = 12 – 8 = 4;
в) 2(x – 1)² + 3(5 – x)² + 34x, якщо x = 2. 2x² – 4x + 2 + 3x² – 30x + 75 + 34x = 5x² + 77
якщо x = 2, то 5 4 + 77 = 20 + 77 = 97
г) 0,5(2c – 3)² + 0,75(c + 4)², якщо c = 2.
0,5(4c² – 12c + 9) + 0,75(c² + 8c + 16) = = 2c² – 6c + 4,5 + 0,75c² + 6c + 12 = 2,75c² + 16,5, якщо c = 2, то 2,75 · 2² + 16,5 = 11 + 16,5 = 27,5.
492. Спрости вираз та обчисли його значення
а) (a – 5)² – a(a + 8), якщо a = 0,5.
a² – 10a + 25 – (a² + 8a) = a² – 10a + 25 – a² – 8a = –18a + 25
якщо a = 0,5, то –18 • 0,5 + 25 = –9 + 25 = 16.
б) (3c + 0,5)² – (3c – 0,5)², якщо c = –1,2. (9c² + 3c + 0,25) – (9c² – 3c + 0,25) = = 9c² + 3c + 0,25 – 9c² + 3c – 0,25 = 6c
якщо c = –1,2, то 6 • (–1,2) = –7,2.
в) (2x – 5)² – 4(x – 2)(x – 3), якщо x = 0,125. (4x² – 20x + 25) – 4(x² – 5x + 6) = = 4x² – 20x + 25 – 4x² + 20x – 24 = 25 – 24 = 1
якщо x = 0,125. значення виразу не
493. Спрости вираз
а) (a – 5)² – (a – 3)(a + 3) + 10a = a² – 10a + 25 – (a² – 9) + 10a = = a² – 10a + 25 – a² + 9 + 10a = 25 + 9 = 34.
б) (4a² + c)² + (a² – 4c)² – 17a⁴ = (16a⁴ + 8a²c + c²) + (a⁴ – 8a²c + 16c²) – 17a⁴ = = 16a⁴ + a⁴ – 17a⁴ + 8a²c – 8a²c + c² + 16c² = 17c².
в) 10c² – (x² + 3c)² – (3x² – c)² = 10c² – (x⁴ + 6x²c + 9c²) – (9x⁴ – 6x²c + c²) = = 10c² – x⁴ – 6x²c – 9c² – 9x⁴ + 6x²c – c² = 10c² – 9c² – c² – x⁴ – 9x⁴ = –10x⁴.
г) 3a²z² – 9(2 3 az – 3)² + 4(1 2 az – 1)² = 3a²z² – 9(4 9 a²z² – 4az + 9) + 4(1 4 a²z² – az + 1)

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
= 3a²z² – (4a²z² – 36az + 81) + (a²z² – 4az + 4) = 3a²z² – 4a²z² + 36az – 81 + a²z² – 4az + 4 = = (3a²z² – 4a²z² + a²z²) + (36az – 4az) + (–81 + 4) = 0 + 32az – 77 = 32az – 77.
494. Спрости вираз
а) (3a – 2b)² – (2a – 3b)² + 5b² = (9a² – 12ab + 4b²) – (4a² – 12ab + 9b²) + 5b² = = 9a² – 12ab + 4b² – 4a² – 12ab + 9b² + 5b² = (9a² – 4a²) + (–12ab + 12ab) + (4b² – 9b² + 5b²) = = 5a² + 0 – b² = 5a² – b².
б) (2c – 1)² – (2c + 7)(2c – 7) + 5c = (4c² – 4c + 1) – (4c² – 49) + 5c = = 4c² – 4c + 1 – 4c² + 49 + 5c = (4c² – 4c²) + (–4c + 5c) + (1 + 49) = c + 50.
в) 3(2x – y)² – 2(3x – y)² + 6x² = 3(4x² – 4xy + y²) – 2(9x² – 6xy + y²) + 6x² = = (12x² – 12xy + 3y²) – (18x² – 12xy + 2y²) + 6x² = = (12x² – 18x² + 6x²) + (–12xy + 12xy) + (3y² – 2y²) = 0 + 0 + y² = y².
г) 1,5(ac – 2x²)² – 3(x² – ac)² = 1,5(a²c² – 4acx² + 4x⁴) – 3(x⁴ – 2acx² + a²c²) = = 1,5a²c² – 6acx² + 6x⁴ – 3x⁴ + 6acx² – 3a²c² = = (1,5a²c² – 3a²c²) + (–6acx² + 6acx²) + (6x⁴ – 3x⁴) = –1,5a²c² + 0 + 3x⁴ = 3x⁴ – 1,5a²c².
495. Доведи тотожність
а) (a – b)² = (b – a)²
a² – 2ab + b² = b² – 2ab + a² = (b – a)². Доведено.
б) (a + b)² + (a – b)² = 2(a² + b²)
a² + 2ab + b² + a² – 2ab + b² = 2a² + 2b² = 2(a² + b²). Доведено.
в) a² + b² = (a + b)² – 2ab
a² + b² = a² + 2ab + b² – 2ab
a² + b² = a² + b². Доведено.
г) (2a + b)² + (a – 2b)² = 5(a² + b²)
4a² + 4ab + b² + a² – 4ab + 4b² = 5(a² + b²)
5a² + 5b² = 5(a² + b²). Доведено.
496. Доведи тотожність.
а) (-a - b)² = (a + b)²:
(-a - b)² = (-a)² + 2(-a)(-b) + (-b)² = a² - 2ab + b²
(a + b)² = a² + 2ab + b²
Ця тотожність неправильна, бо a² - 2ab + b² ≠ a² + 2ab + b².
б) (a + b)² - (a - b)² = 4ab:
(a + b)² - (a - b)² = (a² + 2ab + b²) - (a² - 2ab + b²) = 4ab
Тотожність доведено.
в) (3a + b)² + (a - 3b)² = 10(a² + b²):
(3a + b)² + (a - 3b)² = (9a² + 6ab + b²) + (a² - 6ab + 9b²) = 10a² + 10b² = 10(a² + b²)
Тотожність доведено.
497. Знайди корінь рівняння
а) (x – 6)² + (2x + 3)² = 5x(x – 9)
(x – 6)² + (2x + 3)² = 5x(x – 9)
(x² – 12x + 36) + (4x² + 12x + 9) = 5x² – 45x
x² – 12x + 36 + 4x² + 12x + 9 = 5x² – 45x
5x² + 45 = 5x² – 45x
5x² – 5x² + 45x = –45
45x = –45
x = –1

б) 2(3 – x)² – x(x + 6) = (x – 4)²
2(9 – 6x + x²) – (x² + 6x) = x² – 8x + 16
18 – 12x + 2x² – x² – 6x = x² – 8x + 16
x² – 18x + 18 = x² – 8x + 16
x² – 18x – x² + 8x = 16 – 18
–10x = –2
x = 0,2
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
498. Знайди
a) (x – 5)² – 2x(x + 3) + (x – 6)² = 5
x² – 10x + 25 – 2x² – 6x + (x² – 12x + 36) = 5
x² – 10x + 25 – 2x² – 6x + x² – 12x + 36 = 5
x² – 10x – 2x² – 6x + x² – 12x = 5 – 25 – 36
–28x = –56
x = –56 : (–28)
x = 2.
499. Знайди корінь рівняння
1) (2x + 5)² + 2x(x – 6,5) = (2x – 3)(3x + 1)
4x² + 20x + 25 + 2x² – 13x = 6x² + 2x – 9x – 3
20x – 13x – 2x + 9x = –3 – 25
14x = –28
x = –28 : 14
x = –2.
2) (3x + 8)² + 11(x² + 2) – 2(3x + 4)² = 2(x – 3)²
б) (3z + 1)² – 8z(z + 1) = (z – 3)²
(9z² + 6z + 1) – 8z² – 8z = z² – 6z + 9
9z² + 6z + 1 – 8z² – 8z = z² – 6z + 9
z² – 2z + 1 = z² – 6z + 9
z² – 2z – z² + 6z = 9 – 1
4z = 8
z = 2
9x² + 48x + 64 + 11x² + 22 – 18x² – 48x – 32 = 2x² – 12x + 18
12x = –36
x = –36 : 12
x = –3.
3) (6x – 5)² – 4(2x + 1)² = 10(2x – 1)(x – 3)
36x² – 60x + 25 – 16x² – 16x – 4 = 20x² – 70x + 30
–60x – 16x + 70x = 30 – 25 + 4 –6x = 9
x = 9 : (–6)
x = –1,5.
500. Знайди
а) 1 4 x² + 1 + x = 0
(1 2x + 1)² = 0
1 2 x + 1 = 0
0,5x = –1
x = –1 : 0,5
x = –10 : 5
x = –2
а) 1 36 x² – x + 9 = 0
(1 6 x – 3)² = 0
1 6 x – 3 = 0
1 6 x = 3
x = 3 : 1 6
x = 3 • 6 1 x = 18.

б) 16 + 4x + 0,25x² = 0 (4 + 0,5x)² = 0 4 + 0,5x = 0
0,5x = –4
x = –4 : 0,5
x = –40 : 5
x = –8.
б) 2x + 25 + 0,04x² = 0 (5 + 0,2x)² = 0 5 + 0,2x = 0
0,2x = –5
x = –5 : 0,2
x = –50 : 2
x = –25.
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
502. Обчисли,
а) 11² = (10 + 1)² = 10² + 2 • 10 • 1 + 1² = 100 + 20 + 1 = 121;
б) 99² = (100 – 1)² = 100² – 2 • 100 • 1 + 1 = 10000 – 200 + 1 = 9801;
в) 101² = (100 + 1)² = 100² + 2 • 100 • 1 + 1 = 10000 + 200 + 1 = 10201; г) 202² = (200 + 2)² = 200² + 200 • 2 • 2 + 2² = 40000 + 800 + 4 = 40804.
503. Обчисли, використовуючи формулу
a) 52² = (50 + 2)² = 2500 + 2 • 50 • 2 + 4 = 2500 + 200 + 4 = 2704;
б) 61² = (60 + 1)² = 60² + 2 • 60 • 1 + 1 = 3600 + 120 + 1 = 3721;
в) 79² = (80 – 1)² = 80² – 2 • 80 • 1 + 1 = 6400 – 160 + 1 = 6241;
г) 81² = (80 + 1)² = 80² + 2 • 80 • 1 + 1 = 6400 + 160 + 1 = 6561.
504.
а) x² + 10x + 30 = (x + 5)² + 5
б) x² – 12x + 41 = (x – 6)² + 5
в) 9x² – 24x + 19 = (3x – 4)² + 3
г) x² + 22x + 130 = (x + 11)² + 9
505.
а) a² – 14a + 50 = (a – 7)² + 1
б) a² + 16a + 65 = (a + 8)² – 19
в) 25a² – 20a + 7 = (5a – 2)² + 3
г) a² + 26a + 190 = (a + 13)² + 61
506. Якого
a) a² – 4a + 10 = a² – 2 • 2a + 4 + 6 = (a – 2)² + 6
при a = 2 значення
б) a² + 8a + 180 = a² + 2 • 4a + 16 + 164 = (a + 4)² + 164
при a = −4
6;
164. 507.
a) n² – 14n + 50 = n² – 2 • 7n + 49 + 1 = (n – 7)² + 1
при n = 7
б) m² + 6m + 38 = m² + 2 • 3m + 9 + 29 = (m + 3)² + 29
при m = –3 значення
508. Для яких значень х і у
a) x² + 2 • 5x + 25 + y² + 2y + 1 = 0
(x + 5)² + (y + 1)² = 0
x = –5; y = –1;
б) x² – 2 • 6x + 36 + y² + 2 • 2y + 4 = 0
(x – 6)² + (y + 2)² = 0
x = 6; y = –2.
509.
a) x2 + у2 + 8х + 6у + 25 = 0;
x2 + y2 + 8x + 6y + 25=0
(x2 + 8x + 16) + (y2 + 6y + 9) + 25 – 16 – 9 = 0
(x + 4)2 + (y + 3)2 = 0
x = 4, y = 3
б) x2 + у2 + 14x – 2у + 50 = 0
x2 + y2 + 14x – 2у + 50 = 0
(x2 + 14x + 49) + (y2 – 2y + 1) + 50 – 49 – 1 = 0
(x + 7)2 + (y – 1)2 = 0
1;
29.

x = 7, y = 1
510.
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
(a + b + c)² = a² + b² + c² + 2ab + 2ac + 2bc
(a + b + c)² = a² + b² + c² + 2ab + 2ac + 2bc 1) ((a + b) + c)² = (a + b)² + 2 • c • (a + b) + c² = a² + 2ab + b² + 2ac + 2bc + c² = a² + b² + c² + 2ab + 2ac + 2bc; 2) (a + (b + c))² = a² + 2a(b + c) + (b + c)² = a² + 2ab + 2ac + b² + 2bc + c² = a² + b² + c² + 2ab + 2bc + 2ac.
511. Використовуючи тотожність, наведену
многочлена вираз
a) (x + y + 5)² = x² + y² + 25 + 2xy + 10x + 10y; б) (x + 2y + 3z)² = x² + 4y² + 9z² + 4xy + 6xz + 12yz; в) (x + y – 1)² = x² + y² + 1 + 2xy – 2x – 2y.
512. Використовуючи тотожність,
многочлена вираз
a) (a + b + 1)² = a² + b² + 1 + 2a + 2b + 2a; б) (a + 3b + c)² = a² + 9b² + c² + 6ab + 2ac + 6bc; в) (a + c – 3)² = a² + c² + 9 – 2ac – 6a – 6c.
513. Доведіть формули куба двочлена: 1) (a + b) ³ = (a + b)²(a + b) = (a² − 2ab + b²)(a − b) = a³ − 2a²b + ab² − a²b + 2ab² − b³ = a³ − 3a²b + 3ab² − b³
2) (a – b)³ = (a – b)²(a – b) = (a² – 2ab + b²)(a – b) = a³ – a²b – 2a²b + 2ab² + ab² – b³ = a³ – 3a²b + 3ab² – b³.
Користуючись ними, піднесіть до куба двочлен
a) x + 3 = (x + 3)³ = x³ + 9x² + 27x + 27;
б) 4a + c = (4a + c)³ = x³ – 3x²y + 3xy² – y³;
в) x – y = (x – y)³ = x³ – 3x²y + 3xy² – y;
г) m + 2a = (m + 2a)³ = m³ + 6m²a + 12ma² + 8a³.
514. Подай вираз у вигляді многочлена.
a) (x + 2)³ = x³ + 6x² + 12x + 8;
б) (y – 2)³ = y³ – 6y² + 12y – 8 ; в) (2x – 1)³ = 8x³ – 12x² + 6x – 1; г) (3x + 1)³ = 27x³ + 27x² + 9x + 1.
515. Подай многочлен у вигляді степеня
a) a³ – 3a² + 3a – 1 = (a – 1)³; б) 8у³ – 36у² + 54у – 27 = (2y – 3)³.
516. Подай многочлен у вигляді степеня
a) x³ + 9x² + 27x + 27 = (x + 3)²; б) x³ + 6x² + 12x + 8 = (x + 2)³.
517. Доведи тотожність
a) (a + b)³ = a³ + b³ + 3ab(a + b);
a³ + 3a²b + 3ab² + b³ = a³ + b³ + 3ab(a + b); Доведено. б) (a – b)³ = a³ – b³ – 3ab(a – b).
a³ – 3a²b + 3ab² – b³ = a³ – b³ – 3ab(a – b). Доведено.
518. Розв’яжи рівняння x³ + 3x² + 3x + 1 = 0
(x + 1)³ = 0
x = –1
Відповідь: В –1

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
519. Розв’яжи рівняння
a) (x – 1)³ = x²(x – 3)
x³ – 3x² + 3x – 1 = x³ – 3x²
3x – 1 = 0
x = 1 3
б) (x – 2)³ + 6x² = (x – 2)(x² + 2x + 4)
x³ – 6x² + 12x – 8 + 6x² = x³ – 8
12x = 0
x = 0
520. Розв’яжи рівняння
a) (x + 1)³ = x³ + 3x² – 2
x³ + 3x² + 3x + 1 – x³ – 3x² = –2
3x = –3
x = –1;
б) (x + 2)³ – 6x² = (x + 2)(x² – 2x + 4)
x³ + 6x² + 12x + 8 – 6x² = x³ + 8
12x = 0
x = 0.
521. Заміни * такими цифрами, щоб рівність
a) 5775 = 75 • 7 • 11;
б) 805 = 23 • 5 • 7.
522. Задача Ж. Л. Лагранжа (1736-1813). Перевір тотожність.
(A² + B² + C²)(A₁² + B₁² + C₁²) – (A A₁ + B B₁ + C C₁)² = (A B₁ – A₁B)² + (A C₁ –A₁ C)² + (B · C₁ – B₁ · C)²
Для перевірки цієї тотожності розкриємо дужки в лівій частині:
Перший множник: (A²+B²+C²)
Другий множник: (A₁²+B₁²+C₁²)
При перемноженні отримаємо:
(A²+B²+C²)(A₁²+B₁²+C₁²) = A²A₁² + A²B₁² + A²C₁² + B²A₁² + B²B₁² + B²C₁² + C²A₁² + C²B₁² + C²C₁²
Тепер розкриємо квадрат виразу:
(A·A₁+B·B₁+C·C₁)² = (A·A₁)² + (B·B₁)² + (C·C₁)² + 2(A·A₁)(B·B₁) + 2(A·A₁)(C·C₁) + 2(B·B₁)(C·C₁)
Віднімаємо другий вираз від першого, отримуємо ліву частину тотожності.
Тепер перевіримо праву частину:
(A·B₁-A₁B)² = A²B₁² + A₁²B² - 2AB₁A₁B
(A·C₁-A₁·C)² = A²C₁² + A₁²C² - 2AC₁A₁C
(B·C₁-B₁·C)² = B²C₁² + B₁²C² - 2BC₁B₁C
Додаючи ці

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
1) Так; 2) так; 3) ні.
525. ФОП,
1) 500000 : 100 • 7 = 35000 (грн) –
2) 500000 + 35000 = 535000 (грн)
Відповідь: ФОП повинен повернути
526.Подай у
а) (x + m)(x - m) = x² - m²
б) (x + z)(x - z) = x² - z²
в) (m + 4)(m - 4) = m² - 16
г) (5 + a)(5 - a) = 25 - a²
ґ) (ab + c)(ab - c) = (ab)² - c²
д) (ab - 1)(ab + 1) = (ab)² - 1
527. Подай у
(a - 2b)(a + 2b). (a - 2b)(a + 2b) = a² - (2b)² = a² - 4b²
Відповідь: Б a² - 4b²
528. На який
Якщо помножити (6x - p) на (6x + p), отримаємо: (6x - p)(6x + p) = (6x)² - p² = 36x² - p²
Відповідь: В 6x + p
529. На який
36x² - p²?
1 + 9a², щоб дістати 1 - 81a⁴?
Якщо помножити (1 + 9a²) на (1 - 9a²), отримаємо: (1 + 9a²)(1 - 9a²) = 1² - (9a²)² = 1 - 81a⁴
Відповідь: треба помножити на (1 - 9a²)
530. Якому
16 - c² = 4² - c² = (4 + c)(4 - c)
Відповідь: Г (4 + c)(4 - c)
531. Розклади на множники двочлен.
а) 25 - x² = 5² - x² = (5 + x)(5 - x)
б) a² - 1 = a² - 1² = (a + 1)(a - 1)
в) m² - 4n² = m² - (2n)² = (m + 2n)(m - 2n)
г) 100a² - 9b² = (10a)² - (3b)² = (10a + 3b)(10a - 3b)
532. Подай у
a) (4a + 1)(4a – 1) = 16a² – 1;
б) (2a – c)(2a + c) = 4a² – c²;
в) (2d + x)(2d – x) = 4d² – x²;
г) (a – c²)(a + c²) = a² – c⁴;
ґ) (8x – y²)(y² + 8x) = 64x² – y⁴;
д) (2a² + 3b)(3b – 2a²) = –4a⁴ – 9b².
533.
a) (3p – q)(3p + q) = 9p² – q²;
б) (m – 4c²)(m + 4c²) = m² – 16c⁴;
в) (4a – b)(4a + b) = 16a² – b²;
г) (5 + abc)(5 – abc) = 25 – a²b²c²;
ґ) (2y + x²)(x² – 2y) = 4y² – x⁴;
д) (m² – n²)(n² + m²) = m⁴ – n⁴.
16 - c²?

534.
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
а) (2x − c)(2x + c) − 4x² = 4x² − c² − 4x² − c²;
б) 49z² − (7z − 3x)(7z + 3x) = 49z² − 49z² + 9x² = 9x²;
в) (4a − 5b)(4a + 5b) − 8a(2a − b) = 16a² − 25b² − 16a² + 8ab = 8ab − 25b²; г) (y − 2)(y + 3) + (7c − y)(7c + y) = y² − 2y + 3y − 6 + 49c² − y² = 49c² + y − 6.
535. Спрости вираз а) (a − 2b)(a + 2b) + 4b² = a² − 4b² + 4b² = a²; б) (m² + 3y)(m² − 3y) − m⁴ = m⁴ − 9y² − m⁴ = −9y²;
в) (3a + x)(3a − x) − 9a(a − x) = 9a² − x² − 9a² + 9ax = 9ax − x²; г) (4а – 1)(а + 3) – (2a – 5y)(2a + 5y) = 4a² + 11a – 3 – (4a² – 25y²) = 11a + 25y² – 3
536. Розв’яжи рівняння а) (x − 2)(x + 2) = x² − 8x
x² − 4 = x² − 8x
8x = 4
x = 0,5;
в) x(x + 4) + (3 − x)(3 + x) = x
x² + 4x + 9 − x² = x
4x − x = −9
3x = −9
x = −3;
537. Розв’яжи рівняння
а) (9 − x)(9 + x) = 3x − x²
81 − x² = 3x − x²
3x = 81
x = 27;
в) x(x + 4) + (3 − x)(3 + x) = x
x² + 4x + 9 − x² = x
4x − x = −9
3x = 9
x = −3;
б) (3 + c)(3 − c) = 3c − c²
9 − c² = 3c − c²
3c = 9
c = 3;
г) (y + 4)(y − 4) = y² − 8y
y² − 16 = y² − 8y
8y = 16 y = 2.
б) 1 − z² = 2z − (z + 3)(z − 3)
1 − z² = 2z − z² + 9
2z = 1 − 9
z = −8 : 2
z = −4;
г) 2b − 9b² = (2 − 3b)(2 + 3b)
2b − 9b² = 4 − 9b²
2b = 4
b = 2.
538. Замініть зірочки одночленом, щоб утворилась тотожність.
а) (5m − 3a)(5m + 3a) = 25m² − 9a²;
б) (4a − 3x²)(4a + 3x²) = 16a² − 9x⁴;
в) (4m + 2p)(4m − 2p) = 16m² − 4p²;
г) (6x − 5a²)(6x + 5a²) = 36x² − 25a⁴.
539. Подай у вигляді
а) x² − m² = (x − m)(x + m);
б) a² − 9 = (a − 3)(a + 3);
в) b² − 16c² = (b − 4c)(b + 4c);
г) 1 − 16z² = (1 − 4z)(1 + 4z);
ґ) q² − p²n² = (q − pn)(q + pn);
д) 0,04 − x² = (0,2 − x)(0,2 + x);
е) c⁴ − 9a² = (c² − 3a)(c² + 3a);
є) 121x² − y⁶ = (11x − y³)(11x + y³).
540. Подай у вигляді добутку
а) n² − m² = (n − m)(n + m);
б) x² − 16 = (x − 4)(x + 4);

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
в) 4c² − 9 = (2c − 3)(2c + 3);
г) 1 − 25n² = (1 − 5n)(1 + 5n);
ґ) 9q² − p² = (3q − p)(3q + p);
д) 0,01 − a² = (0,1 − a)(0,1 + a);
е) x⁴ − 4y⁶ = (x² − 2y³)(x² + 2y³);
є) 169a² − c⁸ = (13a − c⁴)(13a + c⁴).
541. Розв’яжи рівняння
а) x² − 16 = 0
(x − 4)(x + 4) = 0
x₁ = −4; x₂ = 4;
б) 4x² − 9 = 0
(2x − 3)(2x + 3) = 0
1) 2x − 3 = 0 2) 2x + 3 = 0
2x = 3 2x = −3
x₁ = 1,5 x₂ = −1,5
в) x² + 64 = 0
коренів немає.
542. Розв’яжи рівняння
а) x² − 25 = 0
(x − 5)(x + 5) = 0
x₁ = −5; x₂ = 5;
б) 9x² − 16 = 0
(3x − 4)(3x + 4) = 0
1) 3x − 4 = 0
3x = 4
x₁ = 11 3
2) 3x + 4 = 0
3x = −4
x₂ = −11 3
в) x² + 81 = 0 коренів немає
543. Обчисли
a) 35² – 15² = 1225 – 225 = 1000;
б) 73² – 27² = 5329 – 729 = 4600;
в) 136² – 64² = 18496 – 4096 = 14400; г) 17² 8² 150 = (17 8)(17+8) 150 = 9·25 150 = 3·3·5·5 3·5·5·2 = 1,5; г) 16² 9²
13² 12² = (16 9)(16+9) (13 12)(13+12) = 7 25 1 25 = 7; д) 45² 35²
26² 24² = (45 35)(45+35) (26 24)(26+24) = 10·80 2 50 = 8.
544. Обчисли
а) 51² – 49² = 2601 – 2401 = 200; б) 27² – 23² = 729 – 529 = 200;
в) 146² – 54² = 21316 – 2916 = 18400;
г) 19² 17²
г)

144 = (19 17)(19+17) 144 = 2 36 144 = 0,5;
32² 12²
23² 21² = (32 12)(32+12) (23 21)(23+21) = 20 44 2·44 = 10;
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
д) 56² 46² 33² 18² = (56 46)(56 + 46) (33 18)(33 + 18) = 10 102 15 · 51 = 2 2 3 · 1 = 1 1 3 .
545. Обчисли без калькулятора а) 104 • 96 = 9984; б) 1007 • 993 = 999951; в) 0,95 • 1,05 = 0,9975.
546. Обчисли без калькулятора а) 102 • 98 = 9996; б) 1001 • 999 = 999999; в) 0,97 • 1,03 = 0,9991.
547. Запиши у вигляді многочлена а) (–3a + 5x²y)(3a + 5x²y) = 25x⁴y² – 9a²; б) (–2abc – 3a²)(–2abc + 3a²) = 4a²b²c² – 9a⁴; в) (–5x³ + 3y)(–5x³ – 3y) = (3y – 5x³)(3y + 5x³) • (–1) = (9y² – 25x⁶) • (–1) = 25x⁶ – 9y²; г) (–0,5ac + 1,1c²)(–0,5ac – 1,1c²) = 0,25a²c² – 1,21c⁴.
548. Запиши у вигляді многочлена
а) (–1 2 ax + 2 3 z²)(–1 2 ax –2 3 z²) = 1 4 a²x² –4 9 z⁴;
б) (–1 1 2 ac –1 3 a²)(–1 1 2 ac + 1 3 a²) = 9 4 a²c² –1 9 a⁴.
549. Запиши у
а) 2(4x – 1)(4x + 1) = 2(16x² – 1) = 32x² – 2;
б) k(m² – 2pt)(m² + 2pt) = k(m⁴ – 4p²t²) = km⁴ – 4kp²t²;
в) 9a(2 3 x – 1)( 2 3x + 1) = 9a(4 9 x² – 1) = 4ax² – 9a;
г) (2 5 m – 2n)( 2 5m + 2n) · 25m² = = ( 4 25 m² – 4n²) · 25m² = 4m⁴ – 100n²m²
550. Запиши у вигляді многочлена
а) 3(2q – cn)(2q + cn) = 3(4q² – c²n²) = 12q² – 3c²n²;
б) (0,5 + 2a)(0,5 – 2a) · 2c² = (0,25 – 4a²) · 2c² = 0,5c² – 8c²a²;
в) (1 4a + 4b)( 1 4 a – 4b) · 16a = ( 1 16 a² – 16b²) · 16a = a³ – 256ab²; г) 4c(1 2 c – p)( 1 2c + p) = 4c(1 4 c² – p²) = c³ – 4cp².
551. Запиши у вигляді многочлена
a) (x − 3)(x + 3)(x² + 9) = (x² − 9)(x² + 9) = x⁴ − 81; б) (4a² + 1)(2a + 1)(2a − 1) = (4a² + 1)(4a² − 1) = 16a⁴ − 1; в) (1 − x)(1 + x)(1 + x²)(1 + x⁴)(1 + x⁸)(1 + x¹⁶) = (1 − x²)(1 + x²)(1 + x⁴)(1 + x⁸)(1 + x¹⁶) = (1 − x⁴)(1 + x⁴)(1 + x⁸)(1 + x¹⁶) = (1 − x⁸)(1 + x⁸)(1 + x¹⁶) = (1 − x¹⁶)(1 + x¹⁶) = 1 − x³².
552. Запиши у
вигляді многочлена
a) (m + 5)(m − 5)(m² + 25) = (m² − 25)(m² + 25) = m⁴ − 625; б) (9y² + z²)(z + 3y)(3y − z) = (9y² + z²)(9y² − z²) = 81y⁴ − z⁴; в) (a − b)(a + b)(a² + b²)(a⁴ + b⁴)(a⁸ + b⁸)(a¹⁶ + b¹⁶) = (a² − b²)(a² + b²)(a⁴ + b⁴)(a⁸ + b⁸)(a¹⁶ + b¹⁶) = (a⁴ − b⁴)(a⁴ + b⁴)(a⁸ + b⁸)(a¹⁶ + b¹⁶) = (a⁸ − b⁸)(a⁸ + b⁸)(a¹⁶ + b¹⁶) = (a¹⁶ − b¹⁶)(a¹⁶ + b¹⁶) = a³² − b³².
553. Розв’яжи рівняння
a) (2x − 1)(2x + 1) = 9 + 4x(x + 5)
4x² − 1 = 9 + 4x² + 20x 20x = −1 − 9

x = −10 : 20 x = −0,5; б) 8z² − (3z + 5)(3z − 5) = z(5 − z)
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
8z² − 9z² + 25 = 5z − z²
5z = 25
z = 5;
в) (2,5y − 2)(2,5y + 2) − (1,5y + 3)(1,5y − 3) = 4y(y − 5)
6,25y² − 4 − 2,25y² + 9 = 4y² − 20y
20y = 5
y = 5 : (−20)
y = −0,25;
г) (2x + 3)(2x − 3) − 2x(x − 4) = (x + 3)(2x − 1)
4x² − 9 − 2x² + 8x = 2x² − x + 6x − 3
8x + x − 6x = −3 + 9
3x = 6
x = 2.
554. Розв’яжи рівняння
a) (3z + 2)(3z − 2) = 7z + 9(z² − 2)
9z² − 4 = 7z + 9z² − 18
7z = −4 + 18
z = 14 : 7
z = 2;
б) x² − (1,2x − 3)(3 + 1,2x) = 0,2x(1,5 − 2,2x)
x² − 1,44x² + 9 = 0,3x − 0,44x²
0,3x = 9
x = 9 : 0,3
x = 30;
в) 3x(x − 2) − (3x − 1)(3x + 1) = (3 + 2x)(1 − 3x)
3x² − 6x − 9x² + 1 = 3 − 9x + 2x − 6x²
6x + 9x − 2x = 3 − 1
x = 2.
555. Спрости вираз a) (a − 2)(a + 2) (a² + 4) − (a² − 2)² = (a² − 4) (a² + 4) − (a² − 2)² =
б) a⁴b⁴ − (ab − c)(ab + c) (a²b² + c²) = a⁴b⁴ − (a²b² − c²) (a²b² + c²) = a⁴b⁴ − a⁴b⁴ + c⁴ = c⁴
в) (3x² + y) (3x² − y) (9x⁴ + y²) − 9 (9x⁸ − y⁴) = (9x⁴ − y²) (9x⁴ + y²) − 81x⁸ + 9y⁴ = 81x⁸ − y⁴ − 81x⁸ + 9y⁴ = 8y⁴
г) 1 16 − (1 2 − 3a²b) (1 2 + 3a²b) (1 4 + 9a⁴b²) = 1 16 − (1 4 − 9a⁴b²) (1 4 + 9a⁴b²) = = 1 16 − 1 16 + 81a⁸b⁴ = 81a⁸b⁴
556. Спрости вираз a) (2x² − 1)(2x² + 1)(4x4 + 1) − (4x4 + 1)² = (4x⁴ − 1)(4x² + 1) − (4x² + 1)² = 16x8 − 1 − 16x8 − 8x⁴ − 1 = −8x⁴ − 2; б) 4(4a⁴ − c⁸) − (2a − c²)(2a + c²)(4a² + c4) = 16a⁴ − 4a⁸ − 16a⁴ + c⁸ = −3c⁸.
557. Обчисли (2 + 1) · (2² + 1) · (2⁴ + 1) · (2⁸ + 1) · (2¹⁶ + 1) – 2³² = (2 + 1) · (2 – 1) · (2² + 1) · (2⁴ + 1) · (2⁸ + 1) · (2¹⁶ + 1) – 2³² = (2² – 1) · (2² + 1) · (2⁴ + 1) · (2⁸ + 1) · (2¹⁶ + 1) – 2³² = (2⁴ – 1) · (2⁴ + 1) · (2⁸ + 1) · (2¹⁶ + 1) – 2³² = (2⁸ – 1) · (2⁸ + 1) · (2¹⁶ + 1) – 2³² = (2¹⁶ – 1) · (2¹⁶ + 1) – 2³² = 2³² – 1 – 2³² = –1.

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
558. Обчисли (3 + 2)(3² + 2²)(3⁴ + 2⁴)(3⁸ + 2⁸)(3¹⁶ + 2¹⁶) – 3³² + 2³²=
559. Розклади на множники a) (a – 3)² – 4 = (a – 3 – 4)(a – 3 + 4) = (a – 7)(a + 1);
б) (x + 5)² – 16y² = (x + 5 – 4y)(x + 5 + 4y);
+
в) (3n + 5)² – (2n – 1)² = (3n + 5 – 2n + 1)(3n + 5 + 2n – 1) = (n + 6)(5n + 4); г) (m – 6)² – (m + 7)² = (m – 6 – m – 7)(m – 6 + m + 7) = –13 • (2m + 1).
560. Розклади на множники a) (p + 6)² – 16 = (p + 6 – 4)(p + 6 + 4) = (p + 2)(p + 10);
б) (a – 7)² – 25c² = (a – 7 – 5c)(a – 7 + 5c);
в) (2x – 5y)² – (6x + y)² = (2x – 5y – 6x – y)(2x – 5y + 6x + y) = (–4x – 6y)(8x – 4y);
г) (a – 9)² – (a + 5)² = (a – 9 – a – 5)(a – 9 + a + 5) = –14 • (2a – 4).
561. Доведи, що
60² + 899² = 901²
901² – 899² = 60²
(901 – 899)(901 + 899) = 60²
2 • 1800 = 60²
3600 = 60²
60² = 60²
562. Доведи, що 10² + 11² + 12² = 13² + 14².
10² + 11² + 12² = 13² + 14²
10² = 14² – 12² + 13² – 11²
10² = (14 – 12)(14 + 12) + (13 – 11)(13 + 11)
10² = 2 • 26 + 2 • 24
10² = 2 • 50
10² = 100
10² = 10²
563. Доведи, що: a) Доведемо, що:
2113² – 2112² = 65² (2113 – 2112)(2113 + 2112) = 1 * 4225 = 65²; Доведено.
б)
доведемо, що:
25² – 22² + 26² – 23² + 27² – 24² = 21² (25 – 22)(25 + 22) + (26 – 23)(26 + 23) + (27 – 24)(27 + 24) = 3 •
= 3(47 + 49 + 51) = 3 • 147 = 441 = 21². Доведено.
564. Доведи, що при кожному натуральному значенні n:
а) число (n + 5)2 – n2 ділиться на 5; n² + 10n + 25 – n² = 5(2n + 5); Доведено.
б) число (n + 7)2 – n2 ділиться на 7; n² + 14n + 49 – n² = 7(2n + 7); Доведено.
в) число (2п + 9)2 – (2п – 5)2 ділиться на 56. 4n² + 36n + 81 – 4n² + 20n – 25 = 56n + 56 = 56(n + 1). Доведено.
565. Доведи, що
n
a) (6n + 1)2 – 1 ділиться на 12; 36n² + 12n + 1 – 1 = 12(3n² + n); б) (5п + 8)2 – (5п – 6)2 ділиться на 28. 25n² + 80n + 64 – 25n² + 60n – 36 = 140n + 28 = 28(5n + 1).
566. Площа

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
Нехай ОА – х см.
π • (r + 2)² – πr² = 18,84
π(r² + 4r + 4 – r²) = 18,84
4r + 4 = 18,84 : 3,14
4r = 6 – 4
4r = 2
r = 2 : 4
r = 0,5 (см) – внутрішній радіус
0,5 + 2 = 2,5 (см) – зовнішній радіус
Відповідь: 0,5 см і 2,5 см
567. Доведи тотожність Платона (IVст. до н. е.), (p² + 1)² - (p² - 1)² = 4p². (p² + 1)² – (p² – 1)² = 4p²
(p² + 1 + p² – 1)(p² + 1 – p² + 1) = 4p²
2 • 2p² = 4p²
4p² = 4p²
Доведено.
568. Доведи тотожність Піфагора (VI ст. до н. е.).
(2a² + 2a + 1)² - (2a² + 2a)² = (2a + 1)². (2a² + 2a + 1)² – (2a² + 2a)² = (2a² + (2a + 1))² – (2a² + 2a)² = 4a⁴ + 4a²(2a + 1) + (2a + 1)² – 4a⁴ – 8a³ – 4a² = 4a⁴ + 8a³ + 4a² + 4a² + 4a + 1 – 4a2 – 8a³ – 4a² = (2a + 1)²
569. Доведи, що
2x + 1 – непарне число (x + 1)² – x²
2x + 1 = (x + 1)² – x²
2x + 1 = x² + 2x + 1 – x²
2x + 1 = 2x + 1
570.
+ 1.
сума x + x + 1 = 2x + 1.
(x + 1)² – x² = 2x + 1
x² + 2x + 1 – x² = 2x + 1
2x + 1 = 2x + 1
571.

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html

На малюнку 13.3 зображено квадрат зі стороною c.
В цьому квадраті розміщено інший квадрат
стороною (b-a)².
Також бачимо, що в квадраті зі стороною c розміщено чотири однакові прямокутні
трикутники з катетами a і b та гіпотенузою c.
Площа великого квадрата дорівнює c².
Цей квадрат складається з площі внутрішнього квадрата (b-a)² і площі чотирьох
прямокутних трикутників.
Площа одного трикутника = (a b) 2
Площа чотирьох трикутників = 4·(a b) 2 = 2ab
Отже, маємо рівність:
c² = (b-a)² + 2ab
За формулою квадрата різниці:
(b-a)² = b² - 2ab + a²
Підставимо у попереднє рівняння:
c² = b² - 2ab + a² + 2ab
c² = a² + b²
Що й треба було довести. Це і є теорема Піфагора.
572. На основі теореми Піфагора
трикутника, катети якого дорівнюють:
а) 3 см і 4 см;
б) 5 м і 12 м;
в) 7 дм і 24 дм.
а) 3² + 4² = 9 + 16 = 25 = 5²
Відповідь: 5 см
б) 5² + 12² = 25 + 144 = 169 = 13²
Відповідь: 13 м
в) 7² + 24² = 49 + 576 = 625 = 25²
Відповідь: 25 дм
573. Обчисли.
а) 4,7 • 5,8 + (–4,7) • (–4,2) = 4,7(5,8 + 4,2) = 4,7 • 10 = 47; б) –6,3 : (–0,21) – 1,7 = 30 – 1,7 = 28,3;
в) –1,7 – 36,6 : (–6,1) = 1,7 + 6 = 7,7.
574. Автомобіль, швидкість

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
70000
35 = x 100
x = 70000 • 100 : 35 x = 200000
Відповідь: 200000 видів біоти
576. Чому дорівнює неповний квадрат: а) суми виразів a і c;
(a + c)² - 2ac = a² + 2ac + c² - 2ac = a² + c² б) різниці виразів a і c?
(a - c)² + 2ac = a² - 2ac + c² + 2ac = a² + c²
577. Як можна спростити вираз?
а) (x - 1)(x² + x + 1);
(x - 1)(x² + x + 1) = x³ + x² + x - x² - x - 1 = x³ - 1
б) (a² - a + 1)(a + 1).
(a² - a + 1)(a + 1) = a³ + a² - a² - a + a + 1 = a³ + 1
578. Спрости вираз (2m + 1)(4m² - 2m + 1) і
значення, якщо m = -1.
(2m + 1)(4m² - 2m + 1) = 8m³ - 4m² + 2m + 4m² - 2m + 1 = 8m³ + 1
При m = -1:
8m³ + 1 = 8·(-1)³ + 1 = 8·(-1) + 1 = -8 + 1 = -7
Відповідь: Г -7
579. Яка з рівностей правильна?
a³ - 27 = (a - 3)(a² + 3a + 9)
a³ - 3³ = (a - 3)(a² + 3a + 9)
Відповідь: В a³ - 27 = (a - 3)(a² + 3a + 9)
580. Розклади на множники x³ - 8. (x - 2)(x² + 4x + 4)
x³ - 8 = x³ - 2³ = (x - 2)(x² + 2x + 4)
Відповідь: В (x - 2)(x² + 4x + 4)
581. Розклади на множники двочлен.
а) n³ - 1;
n³ - 1 = n³ - 1³ = (n - 1)(n² + n + 1)
б) c³ + 27.
c³ + 27 = c³ + 3³ = (c + 3)(c² - 3c + 9)
582. Розклади на множники двочлен
а) a³ – c³ = (a – c) (a² + ac + c²);
б) x³ + 8 = (x + 2) (x² – 2x + 4);
в) 1 – p³ = (1 – p) (1 + p + p²);
г) c³ – 64x³ = (c – 4x) (c² + 4cx + 16x²);
ґ) n⁶ – 1 = (n² – 1) (n⁴ + n² + 1);
д) 27a³ + b³ = (3a + b) (9a² – 3ab + b²);
е) a³ – 8m³n³ = (a – 2mn) (a² + 2am + 4m²n²);
є) –z³ – p³ = –(z + p) (z² – zp + p³);
ж) 1 125 + y³z⁹ = (1 5 + yz³) ( 1 25 –1 5·yz³ + 6);

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
з) 1 8 + c³ = (1 2 + c) (1 4 –1 2·c + c²);
и) 8 27x³ + 1 = (2 3·x + 1) (4 9 ·x² –2 3·x + 1);
і) 27 64 + z³ = (3 4 + z) ( 9 16 –3 4·z + z²).
583. Розклади на множники двочлен
а) p³ + q³ = (p + q) (p² – pq + q²);
б) 1 – a³ = (1 – a) (1 + a + a²);
в) c³ + 8x³ = (c + 2x) (c2 – 2xc + 4x²);
г) a³ – 8 = (a – 2) (a² + 2a + 4);
ґ) 27 + m³ = (3 + m) (9 – 3m + m²);
д) 64a³ – n³ = (4a – n) (16a² + 4an + n²);
е) –125 – z³ = –(5 + z) (25 – 5z + z²);
є) 27x⁶ – a³y³ = (3x² – ay) (9x⁴ + 3x²ay + a²y²);
ж) 1 1000 – a⁶ = (0,1 – a²) (0,01 + 0,1a² + a⁴);
з) 1 8 a³x³ – c³ = (1 2 ·ax – c) (1 4 ·a²x² + 1 2·axc + c²);
и) 1 64 a³ – x³y³ = (1 4 ·a – xy) ( 1 16 ·a² + 1 4·axy + x²y²);
і) 8 27 – a³x³z³ = (2 3 – axy) (4 9 + 2 3·axy + a²x²y²).
584. Подай у вигляді многочлена
а) (a – x)(a² + ax + x²) = a³ – x³;
б) (b + 2)(b² – 2b + 4) = b³ + 8;
в) (2a – n)(4a² + 2an + n²) = 8a³ – n³;
г) (9x² – 15x + 25)(3x + 5) = 9x³ + 125.
585. Подай у вигляді многочлена
а) (a – 2)(a² + 2a + 4) = a³ – 8; б) (y + m)(y² – ym + m²) = y³ + m³;
в) (x – a²)(x² + a²x + a⁴) = x³ – a⁶;
г) (a⁴ + 1)(a⁸ – a⁴ + 1) = a¹² + 1; ґ) (2 – y)(4 + 2y + y²) = 8 – y³; д) (25 – 10m + 4m²)(5 + 2m) = 125 + 8m³.
586. Знайди значення виразу.
а) (x + 1)(x² – x + 1) – x³ , якщо x = 5,73; x³ + 1 – x³ = 1;
б) (z – 2)(z² + 2z + 4) + 8, якщо z = 0,2.
z³ – 2³ + 8 = z³ – 8 + 8, якщо z = 0,02, то 0,02³ = (2 · 10⁻²)³ = 8 · 10⁻⁶.
587. Знайди значення виразу.
а) x³ – 27 + 27 = x³ = 0,5³ = 0,125;
б) a³ + 125 – a³ = 125.
588. Розв’яжи рівняння a) (x – 1)(x² + x + 1) = 2x + x³
x³ – 1 = 2x + x³
2x = –1
x = –1 : 2
x = –0,5;
в) (1 + y)(y² – y + 1) – y³ = 5y

1 + y³ – y³ = 5y
б) (y + 2)(y² – 2y + 4) = y³ + 2y
y³ + 8 = y³ + 2y
2y = 8
y = 8 : 2
y = 4;
г) (x + 1)(x² – x + 1) = x(5 + x²)
x³ + 1 = 5x + x³
5y = 1
y = 1 : 5
y = 0,2;
589. Розв’яжи рівняння
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
5x = 1
x = 1 : 5
x = 0,2.
a) (x – 3)(x² + 3x + 9) + 3x = x³
x³ – 27 + 3x – x³ = 0
3x = 27
x = 9;
590. Знайди добуток многочленів
б) (z – 4)(16 + 4z + z²) = z(z² – 4)
z³ – 64 = z³ – 4z
4z = 64
z = 64 : 4
z = 16.
a) (0,5a² + b) • (0,25a⁴ – 0,5a²b + b²) = (0,5a² + b)(0,25a4 – 0,5a²b + b²) = 0,125a⁶ + b³; б) (4m – m²) • (m⁴ + 4m³ + 16m²) = 64m³ – m⁶.
591. Знайди добуток многочленів
a) (3a – 2b) • (9a² + 6ab + 4b²) = 27a³ – 8b³; б) (0,2a – xy) • (0,04a² + 0,2axy + x²y²) = 0,008a³ – x³y³.
592. Обчисли значення виразу a) x³ + 27 – x³ – x = 27 – x = 27 – 2,5 = 24,5; б) 8x³ – 27y³ + 27y³ = 8x³ = 8 · 1³ = 8; в) 28y³ + 125x³ – y³ – 61x³ = 27y³ + 64x³ =
г) x³ + 8 + 1 – x³ = 9.
593. Обчисли значення виразу
a) 1 + 8x³ – 3x³ = 5x³ + 1 = 5 1 · 1 125 + 1 = 1 25 + 1 = 1 1 25
б) 5x³ + 9x³ + 8y³ + 19y³ = 14y³ + 27y³ =
в) x³ – 27 – x³ – 8 = –35.
594. Розв’яжи рівняння
a) (x² + 1)(x⁴ – x² + 1) = 1
x⁶ + 1 = 1
x⁶ = 0
x = 0;
в) (x – 2)(x² + 2x + 4) – x(x + 3)(x – 3) = 1
x³ – 8 – x³ + 9x = 1
9x = 1 + 8
9x = 9
x = 9 : 9
x = 1;
595. Розв’яжи рівняння
a) (x³ + 3)(x⁶ – 3x³ + 9) – 26 = 0
x⁹ + 27 – 26 = 0
x⁹ + 1 = 0
x = –1;

·
б) (x + 3)(x² – 3x + 9) – (x – 5)(x² + 5x + 25) = 4(20 – x)
x³ + 27 – x³ + 125 = 80 – 4x
4x = 80 – 27 – 125
4x = –72
x = –18;
г) (4x² – 1)(4x² – 2x + 1) = 8x³(2x – 1)
(2x – 1)(2x + 1)(4x² – 2x + 1) = 8x³(2x – 1)
(2x – 1)(8x³ + 1) = 8x³(2x – 1)
16x⁴ + 2x – 8x³ – 1 = 16x⁴ – 8x³
2x – 1 = 0
2x = 1
x = 2.
б) (x – 2)(x² + 2x + 4) – (x + 4)(x² – 4x + 16) = 6(2x – 9)
x³ – 8 – x³ – 64 = 12x – 54
12x = –8 – 64 + 54
12x = –18
x = –18 : 12
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
x = –1,5;
в) (x + 5)(x² – 5x + 25) – x(x – 4)(x + 4) = –3
x³ + 125 – x³ + 16x = –3
16x = –3 – 125
x = –128 : 16
x = –8;
596. Доведи, що:
г) (x² – 4)(x² – 2x + 4) = x³(x – 2)
(x – 2)(x + 2)(x² – 2x + 4) = x³(x – 2)
(x – 2)(x³ + 8) = x³(x – 2)
x⁴ + 8x – 2x³ – 16 = x⁴ – 2x³
8x – 16 = 0
8x = 16 x = 2.
а) (327 − 227)(327³ + 327 • 227 + 227³) = 100 • (327³ + 327 • 227 + 227³);
б) (737 + 263)(737³ − 737 • 263 + 263³) = 1000 • (737³ − 737 • 263 + 263³);
в) (128 − 2)(128² + 128 • 2 + 4) = 126 • (128² + 260);
г) (9² − 1)(9⁴ + 81 • 1 + 1) = 80 • (9⁴ + 82).
597. Доведи, що:
а) (723 − 223)(723² + 723 • 223 + 223²) = 500 • (723² + 723 • 223 + 223²);
б) (352 + 648)(352² + 352 • 648 + 648²) = 1000 • (352² + 352 • 648 + 648²);
в) (726 − 4)(726² + 726 • 4 + 16) = 722 • (726² + 726 • 4 + 16);
г) 7⁶ + 1 = (7²)³ + 1 = (49 + 1)(49² − 49 • 1 + 1) = 50 • (49² − 50).
598. Розклади на множники вираз
а) (a + 2)³ − 8 = (a + 2 − 2)((a + 2)² + 2 • (a + 2) + 4) = a • (a² + 4a + 4 + 2a + 4 + 4) = a(a² + 6a + 12);
б) (z − 1)³ + z³ = (z − 1 + z)((z − 1)² −z(8 − 1) + z²) = (2z − 1)(z² − 2z + 1 − z² + z + z²) = (2z − 1)(z² − z + 1).
599. Розклади на множники вираз
а) 8 −(a − 2)³ = 2³ − (a − 2)² = (2 − a + 2)(4 + 2(a − 2) + (a − 2)²) = = (4 − a)(4 + 2a − 4 + a² − 4a + 4) = (4 − a)(a² − 2a + 4);
б) (x + y)³ − y³ = (x + y − y)((x + y)² + (x + y)y + y²) = x(x² + 2xy + y² + xy + y² + y²) = x(x² + 3xy + 3y²);
в) (3 − 2x)³ + 8x³ = (3 − 2x + 2x)((3 − 2x)² − 2x(3 − 2x) + 4x²) = 3 • (12x² − 18x + 9);
г) (3 − a)³ − (a − 2)³ = (3 − a − a + 2)((3 − a)² + (3 − a)(a − 2) + (a − 2))² = (5 − 2a)(9 − 6a + a² + 3a − 6 − a² + 2a + a² − 4a + 4) = (5 − 2a)(a² − 5a + 7).
600. Розклади на множники вираз
а) x³ − y³ − x + y = (x − y)(x² + xy + y²) − (x − y) = (x − y)(x² + xy + y² − 1); б) x³ + y³ −x² + xy − y² = (x + y)(x² − xy + y²) − (x² − xy + y²) = (x² − xy + y²)(x + y − 1); в) x³ − 5x² + 5x − 1 = x³ − 1 − 5x(x − 1) = (x − 1)(x² + x + 1) − 5x(x − 1) = (x − 1)(x² + x + 1 − 5x) = (x − 1)(x² − 4x + 1);
г) x³ − 8y³ + x²y + 2xy² + 4y³ = (x − 2y)(x² + 2xy + 4y²) + y(x² + 2xy + 4y²) = (x² + 2xy + 4y²)(x − 2y + y) = (x² + 2xy + 4y²)(x − y).
601. Розклади на множники вираз
а) a³ + b³ − a − b = (a + b)(a² + ab + b²) − (a + b) = (a + b)(a² + ab + b² − 1);
б) a³ − b³ − a² − ab − b² = (a − b)(a² + ab + b2) − (a² + ab + b²) = (a² + ab + b²)(a − b − 1);
в) a³ − 3a² − 3a + 1 = (a + 1)(a² − a + 1) − 3a(a + 1) = (a + 1)(a² − a + 1 − 3a) = (a + 1)(a² − 4a + 1);
г) a³ − 27c³ − a²c − 3ac² − 9c³ = (a − 3c)(a² + 3ac + 9c²) − c(a² + 3ac + 9c²) = (a² + 3ac + 9c²)(a − 3c − c) = (a² + 3ac + 9c²)(a − 4c).
602. Подай у вигляді добутку
а) x⁹ − y³ⁿ = (x³ − yⁿ)(x⁶ + x³yⁿ + y²ⁿ);
б) a³ᵐ ³ + b²¹ = (aᵐ ¹ + b⁷)(a²ᵐ ² − aᵐ ¹ • b⁷ + b¹⁴);

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
+ 64y²⁷⁺³ⁿ = (x⁴ⁿ⁻¹ + 4y⁹⁺ⁿ)(x⁸ⁿ⁻² − x⁴ⁿ⁻¹ • 4y⁹⁺ⁿ + 16y¹⁸⁺²ⁿ).
603.
а) a⁶ + b³ᵖ = (a²)³ + (bᵖ)³ = (a² + bᵖ)(a⁴ + a²bᵖ + b²ᵖ);
б) a³ᵐ⁺⁶ − b¹² = (aᵐ⁺²)³ − (b⁴)³ = (aᵐ⁺² − b⁴)(a²ᵐ⁺⁴ + aᵐ⁺² • b⁴ + b⁸);
в) a¹⁵ᵐ⁺³ + b³³⁻³ᵐ = (a⁵ᵐ⁺¹)³ + (b¹¹⁻ᵐ)³ = (a⁵ᵐ⁺¹ + b¹¹⁻ᵐ)(a²²⁻²ᵐ − a⁵ᵐ⁺¹ • b¹¹⁻ᵐ + b²²⁻²ᵐ);
г) a⁹ⁿ⁻⁶ − 27b⁶⁻¹²ⁿ = (a³ⁿ⁻²)³ − (3b²⁻⁴ⁿ)³ = (a³ⁿ⁻² − 3b²⁻⁴ⁿ)(a⁶ⁿ⁻⁴ + a³ⁿ⁻² • 3b²⁻⁴ⁿ + 9b⁴⁻⁸ⁿ).
604. Доведи тотожність.
а) a³ − b³ − (a − b)(a² + b²) = ab(a − b)
a³ − b³ − a³ − ab² + a²b + b³ = ab(a − b). Доведено.
б) a6 – b6 = (a2 – b2)(a2 – ab + b2)(a2 + ab + b2) = a6 b6 = (a2 b2)(a2 – ab + b2)(a2 +ab + b2)
Доведено.
605. Доведи, що три останні цифри числа 1993³ + 7³ нулі. 1993³ + 7³ закінчується трьома нулями, бо воно ділиться
1000.
606. У Діани і Матвія є певна кількість яблук. Доведи, що коли
x³ + y³ = (x + y)(x² + xy + y²).
607. Доведи,
1)³

610.
611. Знайди
612. Скільки кілограмів
води?
1) 200 75 = х 60 x = 200 • 60 : 75 x = 160(кг) – сухофруктів містять 60%
2) 200 – 160 = 40 (кг)
Відповідь: треба випарити 40 кг води
613. Розклади на множники многочлен
а) 5a – 10c
б) 4x² – 4x
в) a²c² – ac
Розв'язання:
а) 5a – 10c = 5(a – 2c)
б) 4x² – 4x = 4x(x – 1)
в) a²c² – ac = ac(ac – 1)
Відповідь:
а) 5(a – 2c)
б) 4x(x – 1)
в) ac(ac – 1)
614. Розклади на множники многочлен
а) a² – n²
б) 1 – c²x²
в) 9 – a⁴
Розв'язання:
а) a² – n² = (a – n)(a + n)
б) 1 – c²x² = (1 – cx)(1 + cx)
в) 9 – a⁴ = (3 – a²) (3 + a²)
Відповідь:
а) (a – n)(a + n)
б) (1 – cx)(1 + cx)
в) (3 – a²) (3 + a²)
615. Розклади на множники многочлен
а) 1 – 2n + n²
б) x² – 2xy + y²
в) 1 + 2c² + c⁴
Розв'язання:
а) 1 – 2n + n² = (1 – n)²
б) x² – 2xy + y² = (x – y)²

в) 1 + 2c² + c⁴ = (1 + c²)²
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
Відповідь:
а) (1 – n)²
б) (x – y)²
в) (1 + c²)²
616. Розклади на множники многочлен
а) x³ – y³
б) a³ + 8
в) 27 – c³
Розв'язання:
а) x³ – y³ = (x – y) (x² + xy + y²)
б) a³ + 8 = a³ + 2³ = (a + 2) (a² – 2a + 4)
в) 27 – c³ = 3³ – c³ = (3 – c) (9 + 3c + c²)
Відповідь:
а) (x – y) (x² + xy + y²)
б) (a + 2) (a² – 2a + 4)
в) (3 – c) (9 + 3c + c²)
617. Розклади на множники многочлени, наведені
1) a² – 1 = (a – 1)(a + 1)
a² + 2a + 1 = (a + 1)²
1 + x³ = (1 + x)(1 – x + x²)
3) 4c² – 1 = (2c – 1)(2c + 1)
1 – 2m + m² = (1 – m)² x³ + y³ = (x + y)(x² – xy + y²)
2) x² – 4 = (x – 2)(x + 2) x2 – 4 = (x 2)(x + 2) a2 b2 = (a b)(a + b)
4) 9x² – c² = (3x – c)(3x + c) a² – 2am + m² = (a – m)² 8x³ + 1 = (2x + 1)(4x² – 2x + 1)
618. Розклади на множники вираз a³ + a² + a + 1.
a³ + a² + a + 1 = a²(a + 1) + (a + 1) = (a + 1)(a² + 1), тому A (a² +1)(a + 1)
619. Розклади на множники многочлен
а) ap² – ax² = a(p² – x²) = a(p – x)(p + x);
б) c³ – cp² = c(c² – p²) = c(c – p)(c + p);
в) 2 – 8a² = 2(1 – 4a²) = 2(1 – 2a)(1 + 2a);
г) 27x² – 75 = 3(9x² – 25) = 3(3x – 5)(3x + 5);
ґ) 18c²x – 2x = 2x(9c² – 1) = 2x(3c – 1)(3c + 1);
д) 100a⁴ – a² = a²(100a² – 1) = a²(10a – 1)(10a + 1).
620. Розклади на множники многочлен
а) xa² – xc² = x(a² – c²) = x(a – c)(a + c);
б) a³ – an² = a(a² – n²) = a(a – n)(a + n);
в) 20x² – 5 = 5(4x² – 1) = 5(2x – 1)(2x + 1);
г) 100am² – 25ax² = a(100m² – 25x²) = a(10m – 5x)(10m + 5x);
ґ) 3x³ – 27x = 3x(x² – 9) = 3x(x2 – 9) = 3х(х – 3 ) (х + 3);
д) 45a – 5a³ = 5a(3 – a)(3 + a).
621. Розв’яжи рівняння 1. а) x⁵ – x³ = 0
x³(x² – 1) = 0
x³(x – 1)(x + 1) = 0
x₁ = 0; x₂ = 1; x₃ = –1; б) x⁴ – 36x² = 0
г) 2x³ – 8x = 0

2x(x – 2)(x + 2) = 0
x²(x² – 36) = 0
x²(x – 6)(x + 6) = 0
x₁ = 0; x₂ = 6; x₃ = –6; в) 12x⁷ – 3x⁵ = 0
ґ) 4x4 – 9x² = 0
x²(4x² – 9) = 0
3 • x⁵(4x² – 1) = 0
3x⁵(2x – 1)(2x + 1) = 0
x₁ = 0; x₂ = 0,5; x₃ = –0,5;
д) x⁵ = 4x³
x⁵ – 4x³ = 0
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
x₁ = 0; x₂ = 2; x₃ = –2; x²(2x – 3)(2x + 3) = 0
x₁ = 0; x₂ = 1,5; x₃ = –1,5; x³(x² – 4) = 0 x³(x – 2)(x + 2) = 0
x¹ = 0; x² = 2; x³ = –2.
622. Розв’яжи рівняння
a) x⁴ – x² = 0
x²(x² – 1) = 0
x²(x – 1)(x + 1) = 0
x² = 0 або x – 1 = 0 або x + 1 = 0
x = 0 x = 1 x = –1
b) x³ – 25x = 0
x(x² – 25) = 0
x(x – 5)(x + 5) = 0
x = 0 або x – 5 = 0 або x + 5 = 0
x = 0 x = 5 x = –5
c)
x⁴ – 0,04x² = 0
x²(x² – 0,04) = 0
x²(x – 0,2)(x + 0,2) = 0
x² = 0 або x – 0,2 = 0 або x + 0,2 = 0
x = 0 x = 0,2 x = –0,2
623. Розклади на множники многочлен
а) ax² – 2ax + a = a(x² – 2x + 1) = a(x – 1)²;
б) 20a³ – 20a² + 5a = 5a(4a² – 4a + 1) = 5a(2a – 1)²;
в) 27a⁶ + 3a² – 18a⁴ = 3a²(9a⁴ – 6a² + 1) = 3a²(3a² – 1)²;
г) 45x³ + 20x – 60x² = 5x(9x² + 4 – 12x) = 5x(3x – 2)²;
ґ) mx² + 4mx + 4m = m(x² + 4x + 4) = m(x + 2)²;
д) p² + 6xp² + 9x²p² = p²(1 + 6x + 9x²) = p²(1 + 3x)².
624. Розклади на множники многочлен
а) 4am² + 4am + a = a(2m + 1)²;
б) 3 – 6a + 3a² = 3(1 – 2a + a²) = 3(1 – a)²;
в) 7a² – 28a⁴ + 28a⁶ = 7a²(1 – 2а)²;
г) 6x² – 15x³ – 24x⁴ = 3x²(2 – 5x – 8x²) = –3x²(8x – 3)(x + 1).
625. Розклади на множники многочлен
а) ax⁴ – x⁴ + ax³ – x³ = x⁴(a – a) + x³(a – 1) = (a – 1)(x⁴ + x³);
б) x³ – x²y + x² – xy = x²(x – y) + x(x – y) = (x – y)(x² + x);
в) a²b – 6a² – bc² + 6c² = a²(b – 6) – c²(b – 6) = (b – 6)(a² – c²) = = (b – 6)(a – c)(a + c);
г) ap² – b + bp² – a = p²(a + b) – (a + b) = (a + b)(p² – 1) = = (a + b)(p – 1)(p + 1).
626. Розклади на множники многочлен
а) 4ab + 12b – 4a – 12 = (4ab – 4a) + (12b – 12) = 4a(b – 1) + 12(b – 1) = (b – 1)(4a + 12) = 4(b – 1)(a + 3);
б) 10y² – 6xy² – 5y + 3xy = 2y²(5 – 3x) – y(5 – 3x) = (5 – 3x)(2y² – y) = (5 – 3x) • y • (2y – 1);
в) n²a + n²b – 4a – 4b = n²(a + b) – 4(a + b) = (a + b)(n² – 4) = (a + b)(n – 2)(n + 2);
г) 9a – 9 – c²a + c² = 9(a – 1) – c²(a – 1) = (a – 1)(9 – c²) = (a – 1)(3 – c)(3 + c).
627. Розклади на множники многочлен
а) m² – 2mn + n² – 25 = (m – n)² – 5² = (m – n – 5)(m – n + 5);

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
б) a² – 6a + 9 – b² = (a – 3)² – b² = (a – 3 – b)(a – 3 + b);
в) 64 – x² + 4xy – 4y² = 8² – (x² – 4xy + 4y²) = 8² – (x – 2y)² = (8 – x + 2y)(8 + x – 2y);
г) 16 – b² – 8a + a² = 16 – 8a + a² – b² = (4 – a)² – b² = (4 – a – b)(4 – a + b).
628. Розклади на множники многочлен
a) x² – 2ax + a² – 16 = (x – a)² – 4² = (x – a – 4)(x – a + 4);
б) x² + 2x + 1 – a² = (x + 1)² – a² = (x + 1 – a)(x + 1 + a);
в) m² – x² – 4x – 4 = m² – (x + 2)² = (m – x – 2)(m + x + 2);
г) x² – y² – 6x + 9 = y² – (x – 3)² = (y² – x + 3)(y² + x – 3).
629. Розклади на множники многочлен
a) x – a + x² – a² = x – a + (x – a)(x + a) = (x – a)(1 + x + a);
б) a² – b² + a – b = (a – b)(a + b) + (a – b) = (a – b)(a + b + 1);
в) 2k + 3p + 4k² – 9p² = 2k + 3p + (2k + 3p)(2k – 3p) = (2k + 3p)(1 + 2k + 3p);
г) c² – c – m² – m = c² – m² – c – m = (c – m)(c + m) – (c + m) = (c + m)(c – m – 1);
ґ) a³ + b³ – a – b = (a + b)(a² – ab + b²) – (a + b) = (a + b)(a² – ab + b² – 1);
д) x – y – x³ + y³ = (y – x)(y² + xy + x²) – (y – x) = (y – x)(y² + xy + x² – 1).
a) a² – b² – a – b = (a – b)(a + b) – (a + b) = (a + b)(a – b – 1);
б) 3c – 3d + c² – d² = 4c² – 25a² + 5a – 2c = (2c – 5a)(2c + 5a) – (2c – 5a) = (2c – 5a)(2c + 5a –1);
в) 5a – 2c – 25a² + 4c² = 3(c – d) + (c – d)(c + d) = (c – d)(3 + c + d);
г) x² + y – y² + x = x² – y² + x + y = (x – y)(x + y) + (x + y) = (x + y)(x – y + 1);
ґ) x³ – a³ + x – a = (x – a)(x² + xa + a²) + (x – a) = (x – a)(x² + xa + a² + 1);
д) a + b – a³ – b³ = a + b – (a + b)(a² – ab + b²) = (a + b)(1 – a² + ab – b²).
631. Розклади на множники многочлен
а) ac² + bc – bc² – ac = ac² – bc² + bc – ac = c²(a – b) – c(a – b) = (a – b)(c² – c);
б) a²b + 3a + 3ab + a² = a(x – a) + a(x² – a²) = a(x – a + x² – a²) = a(x – a + (x – a)(x + a)) = a(x – a)(1 + x + a);
в) ax – a² + ax² – a³ = a²b + a² + 3a + 3ab = a²(b + 1) + 3a(1 + b) = (b + 1)(a² + 3a);
г) 9a² + 6ab + b² + 3a + b = (3a + b)² + 3a + b = (3a + b)(3a + b + 1).
632. Розклади на множники многочлен a) 2ax – axy + 2ay – ay² = ax(2 – y) + ay(2 – y) = (2 – y)(ax + ay) = (2 – y)(x + y) • a; б) nx + cx + c3x + c²nx = x(n + c) + c²x(c + n) = (c + n)(x + c²x); в) a³ – ab² – a² – ab = a(a² – b²) – a(a + b) = a((a + b)(a – b)) – a(a + b) = a(a + b)(a – b – 1); г) x² – 2xy + y² + x – y = (x – y)² + x – y = (x – y)(x – y + 1).
633. Наведіть приклад двочлена,
його на множники. a⁶ – b⁶ = (a³)2 – (b³)² = (a³ – b³)(a³ + b³)
634. Розклади на множники многочлен а) 1 8 x – 2x³
635.

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
636. Розклади на множники многочлен a) a⁴ – 6a³ + 54a – 81 = a⁴ – 81 – 6a³ + 54a = (a² – 9)(a² + 9) – 6a(a² – 9) = (a² – 9)(a² + 9 – 6a); б) x⁴ – 10x³ + 250x – 625 = x⁴ – 625 – 10x³ + 250x = (x² – 25)(x² + 25) – 10x(x² – 25) = (x² –25)(x² + 25 – 10x).
637. Розклади на множники многочлен a) m⁴ + 4m³ – 16m – 16 = m⁴ – 16 + 4m³ – 16m = (m² – 4)(m² + 4) + 4m(m² – 4) = (m² – 4)(m² + 4 + 4m) = (m + 2)(m – 2) · (m + 2)² = (m – 2)(m + 2)³; б) a⁴ – 8a³ + 128a – 256 = a⁴ – 256 – 8a(a² – 16) = (a² – 16)(a² + 16) – 8a(a² – 16) = (a² – 16)(a² + 16 – 8a) = (a – 4)(a + 4)(a – 4)² = (a + 4)(a – 4)³.
638. Розклади на множники многочлен a) ac + bc – 2c – acx – bcx + 2cx = ac – acx + bc – acx – 2c + 2cx = ac(1 – x) + bc(1 – x) –2c(1 – x) = (1 – x)(ac + bc – 2c) = c(1 – x)(a + b – 2); б) a²x² + a²y² + 2ax² + 2ay² + x² + y² = (a+1)2(x2+y2)
639. Розклади на множники многочлен a) x³ + 2x² – acx – 2cx – cx² + ax² = x³ – cx² + 2x² – 2cx – acx + ax² = x²(x – c) + 2x(x – c) + ax(x – c) = (x – c)(x² + 2x + ax); б) a²x² + a²y² – 2ax² – 2ay² + x² + y² = a²(x² + y²) – 2a(x² + y²) + x² + y² = (x² + y²) · (a² – 2a + 1) = (x² + y²)(a – 1)².
640. Розклади на множники многочлен a) (2n + 3)² – (n – 1)² = (2n + 3 – n + 1)(2n + 3 + n – 1) = (n + 4)(3n + 2);
б) 4(x – y)² – (x + y)² = (2x – 2y – x – y)(2x – 2y + x + y) = (x – 3y)(3x – y);
в) a² – 2ac + c² – x² – 2x – 1 = (a – c)² – (x + 1)² = (a – c + x + 1)(a – c – x – 1);
г) c² + 4ac + 4a² – m² + 2mn – n² = (c + 2a)² – (m – n)² = (c + 2a + m – n)(c + 2a – m + n).
641. Розклади на множники многочлен
a) (3a + 2p)² – (a + p)² = (3a + 2p – a – p)(3a + 2p + a + p) = (2a + p)(4a + 3p);
б) 9(p + q)² – (p – q)² = (3p + 3q – p + q)(3p + 3q + p – q) = (2p + 4q)(4p + 2q);
в) a⁴ – 2a² + 1 – p² + 2pc – c² = (a² – 1)² – (p – c)² = (a² – 1 + p – c)(х² – 1 – p + c);
г) p² + 6pq + 9q² – a² + 4a – 4 = (p + 3q)² – (a – 2)² = (p + 3q + a – 2)(p + 3q – a + 2).
642.
a) 3x⁵ – x⁴ – 3x + 1 = x⁴(3x – 1) – (3x – 1) = (3x – 1)(x⁴ – 1) = (3x – 1)(x² – 1)(x² + 1) = (3x + 1)(x² + 1)(x – 1)(x + 1); б) 2a² + a³ – 18a⁴ – 9a⁵ = a²(2 + a) – 9a⁴(2 + a) = (2 + a)(a² – 9a⁴) = (2 + a)(a – 3a²)(a + 3a²) = (2 + a)(1 – 3a)(1 + 3a) · a²; в) x⁴ – 37x² + 36 = x⁴ – 36x² – x² + 36 = (x² – 6x)(x² + 6x) – (x – 6)(x + 6) = x²(x – 6)(x + 6) –(x – 6)(x + 6) = (x – 6)(x + 6)(x² – 1) = (x – 6)(x + 6)(x – 1)(x + 1).
643. Подай вираз у вигляді добутку чотирьох множників a) c⁵ – 16c – c⁴ + 16 = c(c⁴ – 16) – (c⁴ – 16) = (c⁴ – 16)(c – 1) = (c² + 4)(c² – 4)(c – 1) = (c² + 4)(c – 1)(c – 2)(c + 2); б) 2x² – x³ – 2x⁴ + x⁵ = x²(2 – x) – x⁴(2 – x) = (2 – x)(x² – x⁴) = = (2 – x)(x – x2)(x + x²) = (2 – x)(1 – x)(1 + x)x²;
в) x⁴ 26x² + 25 = x⁴ x² 25x² + 25 = x²(x² 1) 25(x² 1) = (x² 1)(x² 25) = (x 1)(x + 1)(x 5)(x + 5)
644. Розв’яжи рівняння a) x³ + 2x² – x = 2
x²(x + 2) – (x + 2) = 0
(x + 2)(x² – 1) = 0
(x + 2)(x – 1)(x + 1) = 0

x₁ = –2; x₂ = 1; x₃ = –1; б) y³ – 3y² + 4y = 12
y²(y – 3) – 4(y – 3) = 0
(y – 3)(y² – 4) = 0
(y – 3)(y – 2)(y + 2) = 0
y₁ = 3; y₂ = 2; y₃ = –2;
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
в) x²(x – 3) + 2x(x – 3) + x – 3 = 0
(x – 3)(x² + 2x + 1) = 0
(x – 3)(x + 1)² = 0
x₁ = 3; x₂ = –1;
645. Розв’яжи рівняння
a) y³ – 2y² – y + 2 = 0
y²(y – 2) – (y – 2) = 0
(y – 2)(y² – 1) = 0
(y – 2)(y – 1)(y + 1) = 0
y₁ = 2; y₂ = 1; y₃ = –1;
в) x²(2x + 1) – 4x(2x + 1) + 8x + 4 = 0
x²(2x + 1) – 4x(2x + 1) + 4(2x + 1) = 0
(2x + 1)(x² – 4x + 4) = 0
(2x + 1)(x – 2)² = 0
x₁ = –0,5; x₂ = 2;
646. При яких
а) 8a³ – 4a² + 2a – 1 = 0
a
4a²(2a – 1) + (2a – 1) = 0; (2a – 1)(4a² + 1) = 0
2a – 1 = 0
4a² + 1 = 0
a = 0,5; a² ≠ –1 4
г) x²(x² – 4x + 4) – 9(x² – 4x + 4) = 0
(x² – 4x + 4)(x² – 9) = 0
(x – 2)²(x – 3)(x + 3) = 0
x₁ = 2; x₂ = 3; x₃ = –3.
б) 2x³ – 3x² + 8x = 12
x²(2x – 3) – 4(2x – 3) = 0
(2x – 3)(x² – 4) = 0
(2x – 3)(x – 2)(x + 2) = 0
x₁ = 1,5; x₂ = 2; x₃ = –2;
г) x³(x² – 6x + 9) – 4x(x² – 6x + 9) = 0
x(x² – 6x + 9)(x² – 4) = 0
x(x – 3)²(x – 2)(x + 2) = 0
x₁ = 0; x₂ = 3; x₃ = 2; x₄ = –2.
8a³ - 4a² + 2a - 1:
4a² + 1?
Відповідь: 0,5; б) 8a³ – 4a² + 2a – 1 = 0
8a³ – 4a² + 2a – 1 – 4a² – 1 = 0
8a³ – 8a² + 2a – 2 = 0
(8a³ – 8a²) + (2a – 2) = 0
8a²(a – 1) + 2(a – 1) = 0 (a – 1)(8a² + 2) = 0
a – 1 = 0
8a² + 2 = 0
a = 1; a² ≠ –1 4
Відповідь: 1
647. При яких значеннях x сума квадратів виразів x + 1 і x – 1:
9. a) (x + 1)² + (x – 1)² – 6 = ((x + 1 + x – 1) ÷ 2)²
x² + 2x + 1 + x² – 2x + 1 – 6х = x²
x² = 4
x₁ = –2; x₂ = 2; б) (x + 1)² + (x – 1)² – 84 = (x + 1)(x – 1)
x² + 2x + 1 + x² – 2x + 1 – 84 = x² – 1
x² = 81
x₁ = –9; x₂ = 9.
648.
a³ + 3a² – a = 3
a³ + 3a² – a – 3 = 0
a²(a + 3) – (a + 3) = 0
(a + 3)(a² – 1) = 0
(a + 3)(a – 1)(a + 1) = 0
649.

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
2x + 1; 2x + 3 (2x + 3)² – (2x + 1)² = 4x² + 12x +
ділиться на 8 без остачі.
Твердження доведено. 650. Квадрат непарного числа
Нехай непарне число має вигляд 2k+1, де k - ціле число.
Знайдемо квадрат цього числа:
(2k+1)² = 4k² + 4k + 1 = 4k(k+1) + 1
Розглянемо вираз 4k(k+1):
Якщо k парне, то k+1 непарне
Якщо k непарне, то k+1 парне
В обох випадках добуток k(k+1) завжди парне число, тобто k(k+1) = 2m для деякого
цілого m.
Підставляючи, отримуємо:
4k(k+1) + 1 = 4(2m) + 1 = 8m + 1
Отже, (2k+1)² = 8m + 1, де m - ціле число.
Це означає, що при
Твердження доведено.
651. Знайди корені рівняння
a) x²(x² + 4x + 4) = (5x)² + 100x + 100
x⁴ + 4x³ + 4x² = 25x² + 100x + 100
x³(x + 4) – 25x(x + 4) + 4x² – 100 = 0
(x + 4)(x³ – 25x) + 4(x² – 25) = 0
(x + 4) • x(x² – 25) + 4(x² – 25) = 0
(x² – 25)((x + 4) • x + 4) = 0
(x² + 25)(x² + 4x + 4) = 0
(x² – 25)(x + 2)² = 0
x₁ = –5; x₂ = 5; x₃ = –2; б) 4x⁴ – 12x³ + 9x² = 36x² – 108x + 81
x²(4x² – 12x + 9) = 36x² – 108x + 81
x² • (2x – 3)² = (6x – 9)²
x² • (2x – 3)² – 9(2x – 3)² = 0
(2x – 3)² • (x² – 9) = 0
x₁ = 1,5; x₂ = –3; x₃ = 3.
652. Знайди корені рівняння
a) x²(9x² – 6x + 1) = (6x)² – 24x + 4
x²(3x – 1)² = 36x² – 24x + 4
x²(3x – 1)² = 4(9x² – 6x + 1)
x²(3x – 1)² – 4(3x – 1)² = 0
(x² – 4)(3x – 1)² = 0
(x – 2)(x + 2)(3x – 1)² = 0

x – 2 = 0
або x + 2 = 0 або 3x – 1 = 0
що
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
x = 2 x = –2 x = 1 3
б) 4x⁴ + 56x³ + 196x² = x² + 14x + 49
4x²(x² + 14x + 49) = x² + 14x + 49
4x²(x + 7)² – (x + 7)² = 0
(4x² – 1)(x + 7)² = 0
(2x – 1)(2x + 1)(x + 7)² = 0
2x – 1 = 0 або 2x + 1 = 0 або x + 7 = 0
2x = 1 2x = –1 x = –7
x = 0,5 x = –0,5
653. Розклади на множники вираз.
a) x⁴ – 10x² + 9 = x⁴ – x² – 9x² + 9 = x²(x² – 1) – 9(x² – 1) = (x² – 1)(x² – 9) = = (x – 1)(x + 1)(x – 3)(x + 3)
б) a⁴ + 4b⁴ = a⁴ + 4b⁴ + 4a²b² – 4a²b² = a⁴ + 4a²b² + 4b⁴ – 4a²b² = (a² + 2b²)² – 4a²b² = (a² + 2b²
2ab)(a² + 2b² + 2ab) в) x⁴ + x² + 1 = x⁴ + 2x² – x² + 1 = x⁴ + 2x² + 1 – x² = (x² + 1)² – x² = (x² – x + 1)(x² + x + 1)
654. Доведи тотожність. (a − b)³ + (b − c)³ − (a − c)³ = (a − b + b − c)(a² − 2ab + b² − (a − b)(b − c) + b² − 2bc + c²) − (a − c)³ = (a − c)(a² − 2ab + b² − ab + ac + b² − bc + b² − 2bc + c²) − (a − c)³ = (a − c)(a² − 2ab + 3b² + ac − 3bc + c² − a² + 2ac − c²) = (a − c)(−3ab + 3b² + 2ac − 2bc) = 3(a − c)(ab − b² − ac + bc) = 3(a − c)(b(a − b) − c(a − b)) = −3(a − c)(b − c)(b − c). Тотожність доведено.
655. Розв’яжи рівняння Р. Декарта (1596–1650)
a) y³ – 8y² – y + 8 = 0
y²(y – 8) – (y – 8) = 0
(y – 8)(y² – 1) = 0
(y – 8)(y – 1)(y + 1) = 0 y = 8; y = 1; y = –1;
б) x⁴ – 4x³ – 19x² + 106x – 120 = 0
x⁴ – 3x³ – x³ + 3x² – 22x² + 66x + 40x – 120 = 0
(x⁴ – 3x³) – (x³ – 3x²) – (22x² – 66x) + 40(x – 3) = 0
x³(x – 3) – x²(x – 3) – 22x(x – 3) + 40(x – 3) = 0
(x – 3)(x³ – x² – 22x + 40) = 0
(x – 3)(x³ – 4x² + 3x² – 12x – 10x + 40) = 0
(x – 3)(x²(x – 4) + 3x(x – 4) – 10(x – 4)) = 0
(x – 3)(x – 4)(x² + 3x – 10) = 0
(x – 3)(x – 4)(x² + 5x – 2x – 10) = 0
(x – 3)(x – 4)(x(x + 5) – 2(x + 5)) = 0
(x – 3)(x – 4)(x + 5)(x – 2) = 0
x – 3 = 0
x – 4 = 0
x + 5 = 0
x – 2 = 0
x = 3; x = 4; x = –5; x = 2.
656.
а) 21, 311, 4111, 51111;
б) 21, 321, 4321, 5421;
в) 21, 321, 4331.

657.
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
а) (0,875 + 0,5³)¹⁰ = (0,875 + 0,125)¹⁰ = 1¹⁰ = 1;
б) (3⁴ + 19)⁸ = (81 + 19)⁸ = 10⁸;
в) (4⁴ – 3⁵ – 13)¹² = (256 – 243 – 13)¹² = 0¹² = 0.
658. Розв’яжи рівняння.
а) (x – 3)² – x(x + 4) = –1 x² – 6x + 9 – x² – 4x + 1 = 0 –10x = –10 x = 1;
б) (4x + 5)(x – 2) – (2x – 1)² = –9 4x² – 8x + 5x – 10 – 4x² + 4x – 1 + 9 = 0 x = 2.
659. Знайди помилку в записі.
26 7 + 48 9 = 2 6·9 7 9 + 48·7 9 7 = 254 63 + 4 8 63 = 662 63
Розглянемо цей запис крок за
26 7 + 48 9 початковий вираз
2 (6 9) (7 9) + 4 (8 7) (9 7)
254 63 + 4 8 63 = 662 63

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
f(x) = x².
Область визначення: 1, 2, 3, 4, 5, 6.
Область значень: 1, 4, 9, 16, 25, 36.
673. На
1, 2, 3, 4 та
область визначення; б) область
значень
Так, є.
f(x) = 1 х
Область визначення: 1; 2; 3; 4. Область значень: 1; 1 2; 1 3; 1 4 .
674. Функцію задано формулою y = 6
таблицю. y = 6
–6 –3 –2
675. Функцію задано формулою y = 0,3x. Заповни
676. Функцію
6x + y = 50 y = 50 – 6x

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
гривнях.
Знайдемо
Знайдемо
125 = 250m
m = 125 ÷ 250 = 0,5 кг
Відповіді:
Залежність вартості від маси: y = 250m
Вартість товару масою 18 кг: 4500 грн
Товар масою 0,5 кг коштує 125 грн
681. Нафта проходить трубою зі швидкістю 12 т/год. Скільки
нафти проходить такою трубою за 3 год; за t год? Напиши
відповідну формулу.
1) 12 • 3 = 36 т;
2) m = 12t, t – години, m – маса у тоннах.
682.
f(x) = 5x.
684. Функцію
0; -3; 7; 1000.
y = 2x + 5
y(1) = 2 • 1 + 5 = 7
y(0) = 2 • 0 + 5 = 5
y( 3) = −3 • 2 + 5 = −1
y(7) = 2 • 7 + 5 = 19
y(1000) = 2 • 1000 + 5 = 2005
685.

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
x –2 0 1,5 12 25 y –21 –5 7 91 195
Якщо x = –2, y = 8 · (–2) – 5 = –16 – 5 = –21.
Якщо x = 0, y = 8 ⋅ 0 5 = 0 – 5 = 5
Якщо x = 1,5, y = 8 ⋅ 1,5 – 5 = 12 – 5 = 7
Якщо x = 12, y = 8 ⋅ 12 – 5 = 96 – 5 = 91
Якщо x = 25, y = 8 ⋅ 25 – 5 = 200 – 5 = 195
б) y = − х 2 + 1, яке відповідає значенню аргументу, що дорівнює –8; –1; 0; 1; 20. x –8 –1 0 1 20 y 5 1,5 1 1 2 –9
Якщо x = –8, то y = 8 2 + 1 = 5;
Якщо x = –1, то y = 1 2 + 1 = 1,5.
Якщо x = 0, то y = 0 2 + 1 = 1.
Якщо x = 1, то y = 1 2 + 1 = 1 2 .
Якщо x = 20, то y = 20 2 + 1 = -9.
686. Функцію задано формулою y = 2 3 x.
дорівнює 20?
20 = 2 3 x| · 3
60 = 2x x = 30
Відповідь: 30
687. Знайди значення аргументу, при якому:
а) значення функції y = 3x + 2 дорівнює 8; 2; 8 = 3x + 2 2 = 3x + 2 3x = 6 3x = 0 x = 2 x = 0
–2 = 4 (x 3) 2 = 4 (x 3) x – 3 = 4 : (–2) x – 3 = 4 : 2 x – 3 = –2 x – 3 = 2 x = 1 x = 5
688. Напиши формулу,

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
2a + b = 180°.
Звідси можемо виразити кут a через b :
a = (180° b)
2
Область визначення: b ∈ (0°; 180°)
689. Швидкість автомобіля 70 км/год. Вирази
цим автомобілем, від часу t.
Заповни таблицю.
s = vt = 70t км
t, год 1 2 3 4 5 6 7 8 9 10
км
нього зі швидкістю 4 км/год.

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
r = 1 (2π)
695. З формули I = U R вирази: а) U; б) R.
I = U R
а) U = I · R; б) R = U I .
696. Периметр квадрата P = 4a, де a довжина його сторони. Вирази a через P. a = P 4
697. Знайди область визначення функції. а) Область визначення і область значень функції: будь–яке число. б) Область визначення: всі значення x, крім x ≠ 0.
Область значень: будь–яке число, крім y ≠ 0. в) Область визначення: будь–яке число, крім x ≠ –4. г) Область визначення: будь–яке число, крім x ≠ 0, x ≠ 3.
Область значень: будь–яке число, крім y ≠ 0. ґ)
Область визначення: будь–яке число.
Область значень: від [0; +ꝏ)
698. Знайди область визначення функції,
формулою. a) R; б) R;
в) (−∞; −5) ∪ (−5; +∞);
г) 8x − 1 = 0
8x = 1
x = 1 8
(−∞; 1 8) ∪ (1 8; +∞);
ґ) x ∈ R; x ≠ −6; x ≠ 6;
д) 1 − 25x2 = 0
−25x2 = −1
x2 = 1 25
x ∈ R; x ≠ −1 5; x ≠ 1 5 .
699. Із
S = 100 − px²; S = 100 − 3,14x².
= 64π − πx² > 0. 701.

а) y = �
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
2x + 5, якщо x ≤ 0
2x + 5, якщо x > 0 ,
x –3 –2 –1 0 1 2 3
y –1 1 3 5 3 1 –1
Якщо x = –3, то y = 2 · (–3) + 5 = –1; якщо x = –2, то y = 2 · (–2) + 5 = 1;
якщо x = –1, то y = 2 · 1 + 5 = –2 + 5 = 3; якщо x = 0, то y = 5;
якщо x = 1, y = –2 · 1 + 5 = 3; якщо x = 2, то y = –2 · 2 + 5 = 1;
якщо x = 3, то y = –2 · 3 + 5 = –1.
б) y = �x² + 3, якщо x ≤ 0 х 2 + 3 якщо x > 0 ,
x –3 –2 –1 0 1 2 3
y 12 7 4 3 3,5 4 4,5
702. З'ясуй числові

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
S = v • t
S = S
v₁ • t₁ = v₂ • t₂
Нехай x (год) це
10 • (x + 1) = 12 • x
10x + 10 = 12x
12x – 10x = 10
2x = 10
x = 5 (год)
12 • 5 = 60 (км) – відстань
Відповідь: відстань між селами дорівнює 60
706.Познач на координатній
точки A(5; 2), B(3; 2), C(0; 2), M(–1; 2), H(–3; 2), P(2; 2). Чи
відрізків AB, AC, AM, AH і AP?
Так.
AB: (4; 2); AC: (2,5; 2); AM: (2; 2); AH: (1; 2); AP: (3,5; 2).

707. Розв’яжи рівняння. а) 4(x – 3) + 2(5 – x) = 8
4x – 12 + 10 – 2x = 8
2x – 2 = 8
2x = 10 x = 5; б) 7(5 – y) + 8(y – 3) = 18 35 – 7y + 8y – 24 = 18 y = 18 – 11 y = 7.
708.

711.
x² − 9 = 0
(x − 3)(x + 3) = 0 x = 3 або x = −3
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
якщо при x = 0, y = 0. Перевіримо
кожну функцію:
а) у = 0,5x – 1: при x = 0, y = –1. Не проходить.
б) у = –25x²: при x = 0, y = 0. Проходить.
в) у = 3x: при x = 0, y = 0. Проходить.
г) у = 6x + 2: при x = 0, y = 2. Не проходить.
ґ) у = 3 – 3x: при x = 0, y = 3. Не проходить.
д) у = x – 3x²: при x = 0, y = 0. Проходить.
Відповідь: графіки функцій б), в), д) проходять через
713. Яка з точок належить графіку функції у = 7х – 2?
7 • 1 – 2 = 5
Відповідь: В (1; 5)
714. На малюнку 17.9 зображено
добу (по годинах). Установи:
Температура була:
• додатною: з 11 до 23
8
11
і о 23 год; • 2°: о 13 год і о 21 год.
• о 6 год: −4°;
о 14 год: 3°;

о 21 год: 2°.
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
715. Установи відповідність між графіками функцій (1–2) та їх областями значень (А-Г): 1) В –4 ≤ y ≤ 4. Область визначення: –4 < x ≤ 5; функція зростаюча. 2) А –2 ≤ y ≤ 4. Область визначення: –6 ≤ x ≤ 6; функція спадаюча 716. Познач на координатній площині точки A(5; 4), B(3; 3), C(1; 0), D(7; 3), E(-2; 5), F(-2; -2). Побудуй прямі AC, BD, EF. Знайди координати точок, у

17.10 зображено
Знайди: а) значення цієї функції, які відповідають таким значенням аргументу: –1; 0; 3; 4; б) значення аргументу, які відповідають таким значенням функції: –1; 0; 3; 5. а) (–1; 3), (0; 5), (3; 1,5), (4; 1); б) y = –1 → x = –2,8; y = 0 → x = –2; y = 3 → x₁ = –1, x₂ = 1,3; y = 4 → x₁ = –0,7, x₂ = 0,8. 718.
функції (мал. 17.11) заповни таблицю. x –3 –2 –1 0 1 2 3 4 5 y –1,8 –1 0 2 2 0 –1 0 1,2 719.
функції (мал. 17.12) заповни таблицю.
x –1 –0,5 0 1 1,5 2 2,5 3 3,5 y –5 –4 –3 –1 0 1 2 3 4 720.

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
17.13 знайди: а) значення y, для яких x = -3; -1; 0; 1; 4;
б)
значення x, для яких y = -2; -1; 0; 1; 3;
в) значення x, для яких значення y додатні;
г) значення x, для яких значення y від'ємні.
а) Якщо x = −3, то y = 3;
якщо x = −1, то y = −1,5; якщо x = 0, то y = −2; якщо x = 1, то y = −2; якщо x = 4, то y = 2.
б) y = −2, якщо x = 0 і x = 1; y = −1, якщо x = −1,5 і x = 2; y = 0, якщо x = −2 і x = 3; y = 1, якщо x = −2,5 і x = 3,5; y = 3, якщо x = −3 і x = 4,5.
в) у додатне, якщо −4 < x < 2 і 3 < x < 6. г) у від'ємне, якщо −2 < x < 3. 721.На малюнку 17.14 зображено графік деякої функції.
1.Знайди: а) область визначення функції; б) значення функції, яке відповідає значенню аргументу, що дорівнює -4; -3; 0; 2; 3; 4; 6.
2.При яких значеннях аргументу: а) значення функції дорівнює -1; 0; 2; 3; б) функція набуває додатних значень;
X –4 –3 0 2 3 4 6 Y –3 0 3 2 1 0 –1,2 2.

A(5; 1); б) B(-1; 3); в) C(-1; -3); г) D(3; -7).
f(5) = –2 • 5 – 1 = –11

належить;
f(–1) = –2 • (–1) – 1 = 2 – 1 = 1 не належить;
f(–1) = –2 • (–1) – 1 = 1 не належить;
f(3) = –2 • 3 – 1 = –7 належить.
724.
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
точок A(5; –4), B(3; 3), C(1; 0), D(1; 7), E(–2; 5)
а) y = 5x + 2
не
належить: A, B, C, D, E; б) y = –x + 1
не
належить: B, D, E
належать: A, C;
в) y = x² + 1
не
належать: A, B, C, D
належать: E;
г) y = 10x – 3
не
належать: A, B, C, E
належать: D.
725. Побудуй графік функції
а) y = –x, якщо –5 ≤ x ≤ 4 x –5 –4 –3 –2 –1 0 1 2 3 4 y 5 4 3 2 1 0 –1 –2 –3 –4
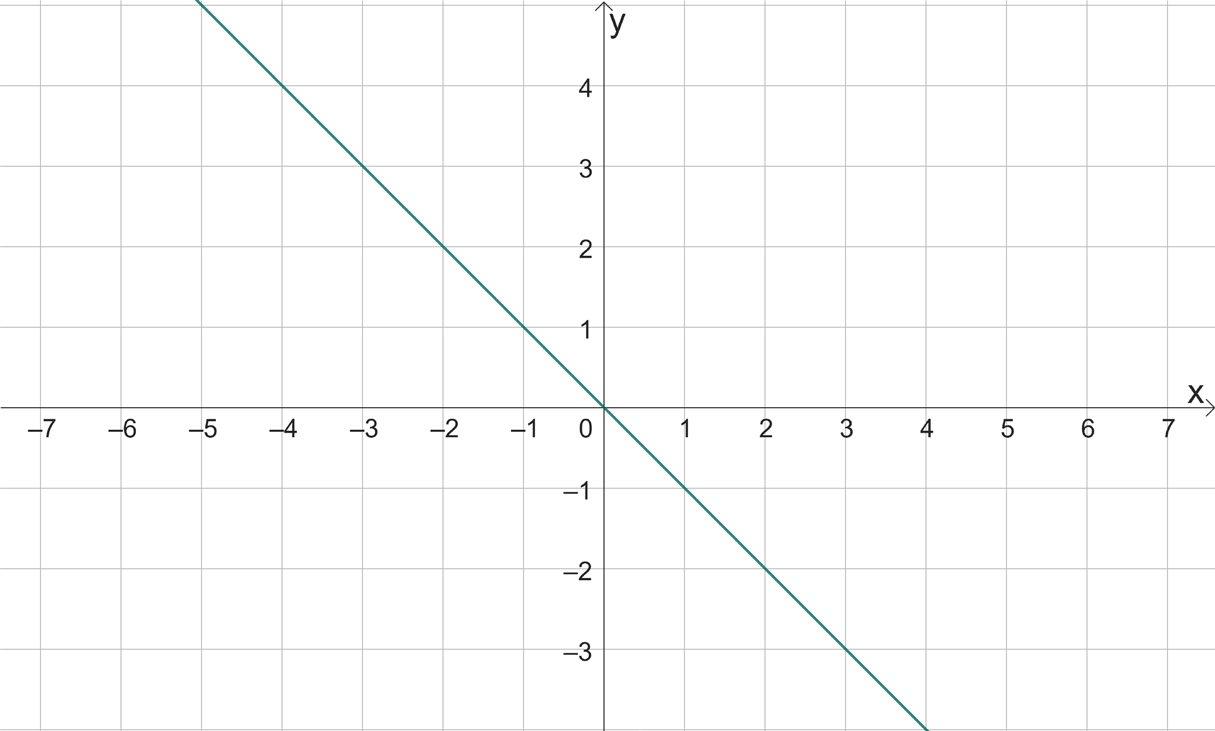
б) y = 0,5x + 3, якщо –6 ≤ x ≤ 6 x –6 –5
Якщо x = –6, то y = 0,5 · (–6) + 3 = 0.
Якщо x = –5, то y = 0,5 · (–5) + 3 = 0,5.
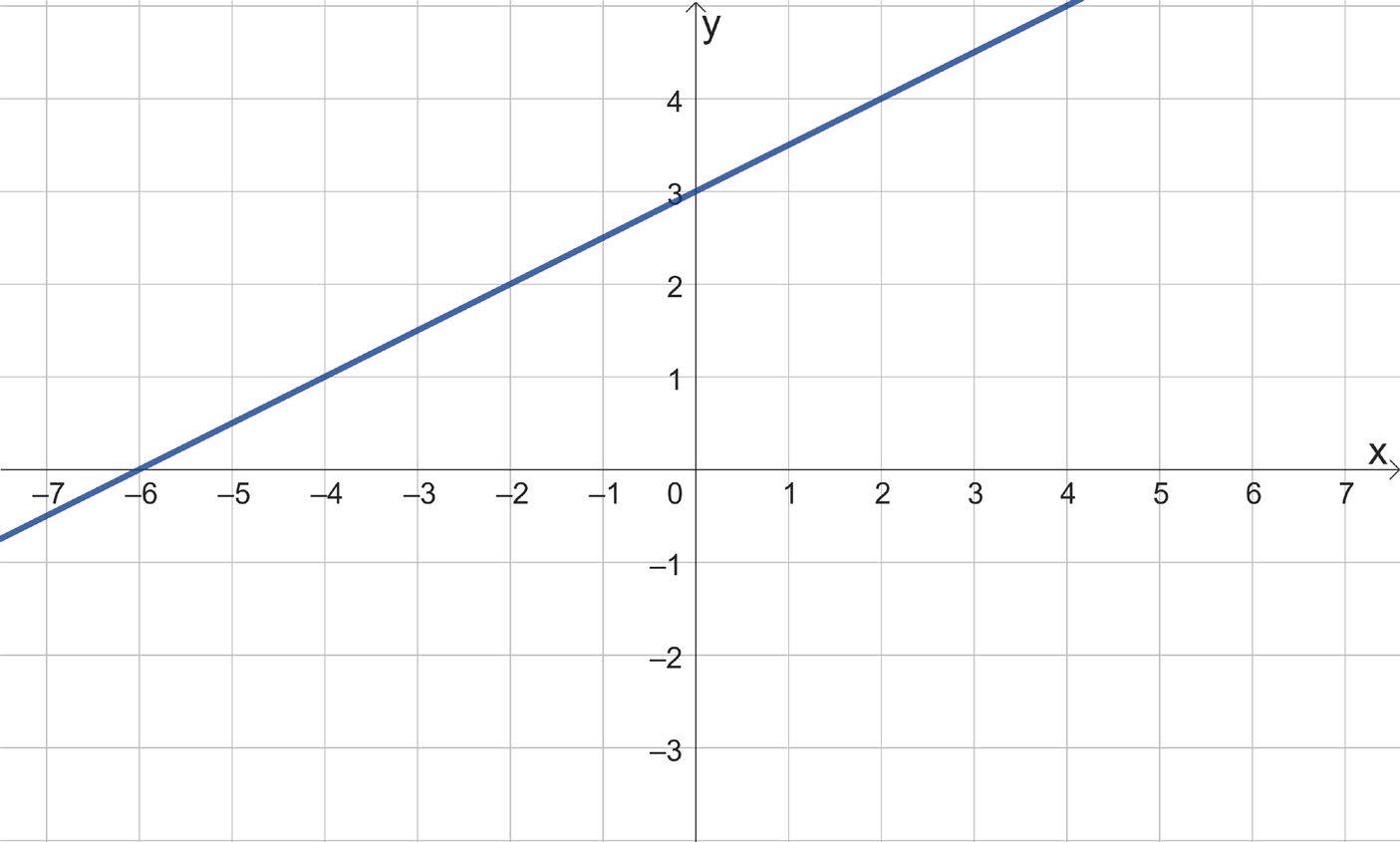
726. Побудуй графік функції
а) y = 2x, якщо –3 ≤ x ≤ 6 x –3 –2 –1 0 1 2 3 4 5 6

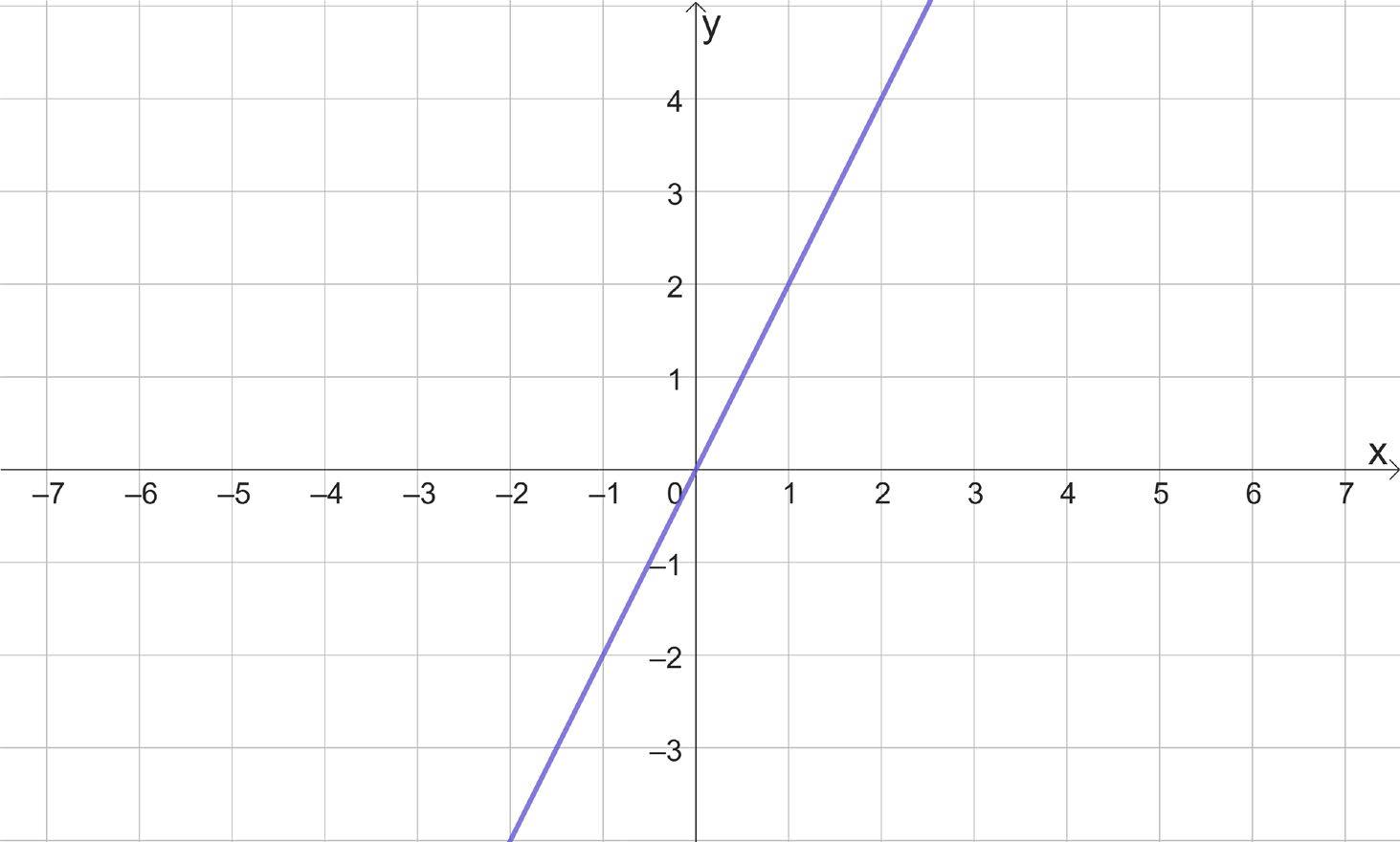
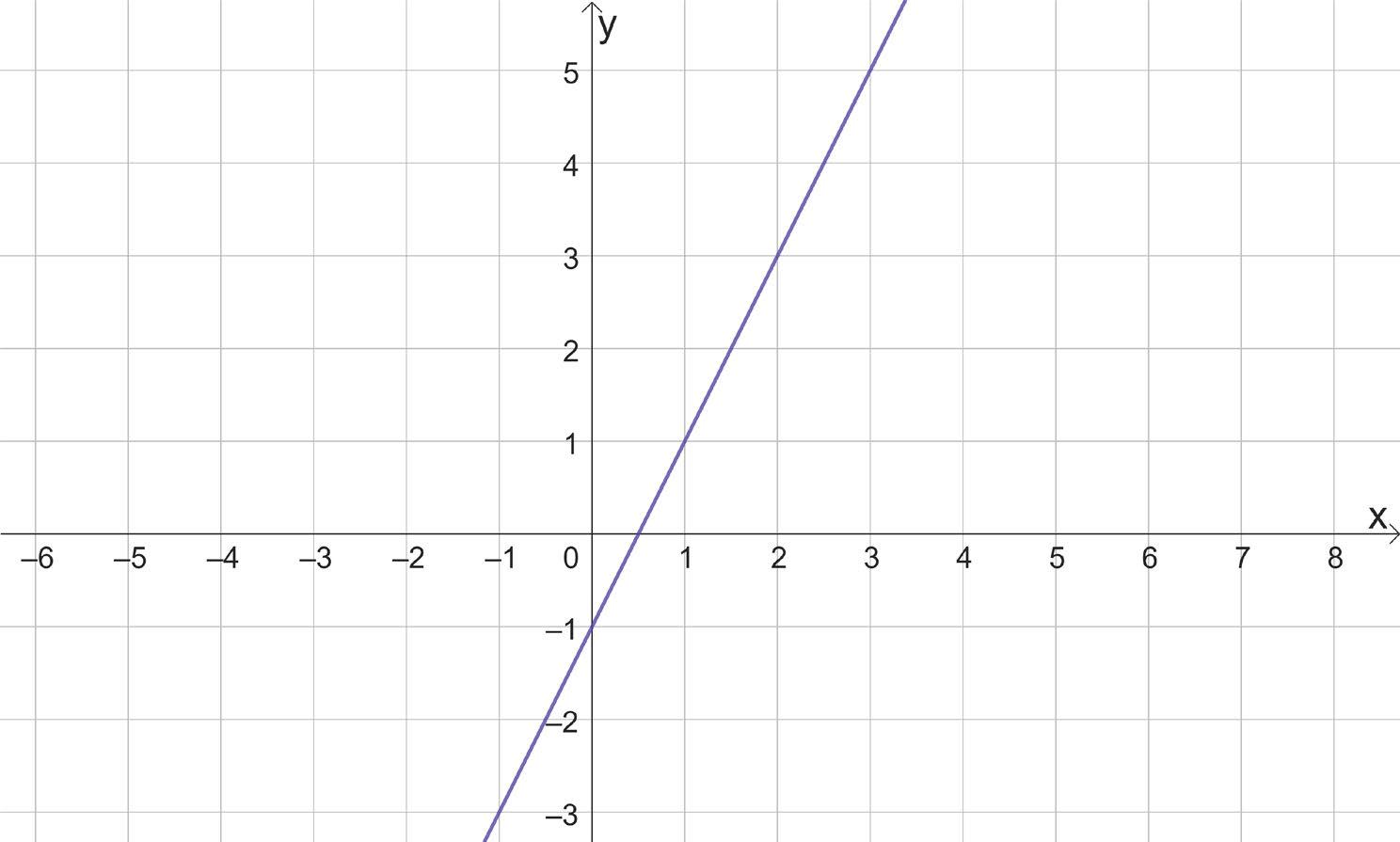


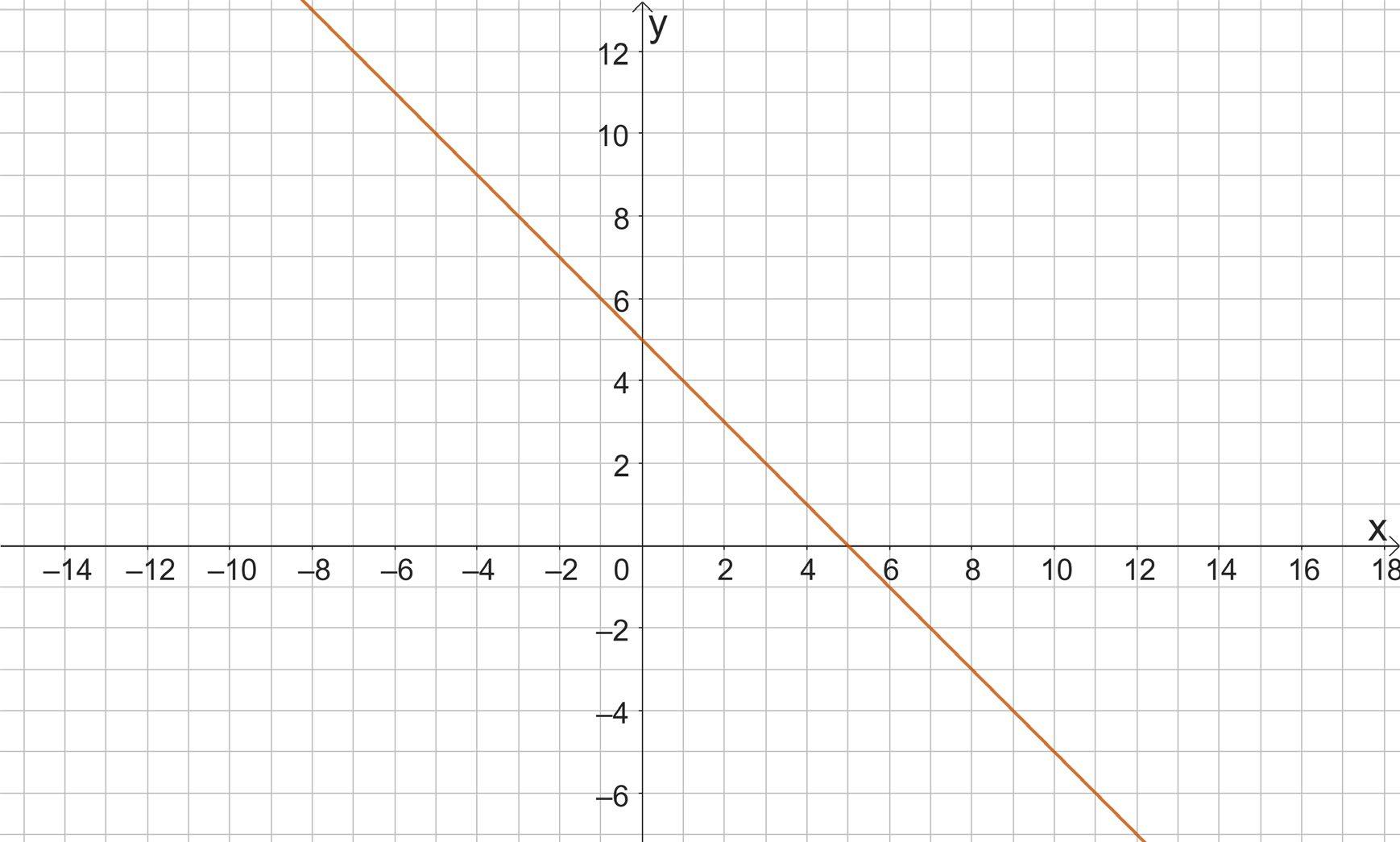
x
–1 0 1 2 3 4 5 6 y 8 6 4 2 0 –2 –4 –6 –8 а) якщо x = 0, то y = 4; якщо x = 1, то y = 2; якщо x = –1, то y = 6; якщо x = 2, то y = 0; якщо x = –2, то y = 8; якщо x = 2,5, то y = –1. б) y = –6, якщо x = 5; y = –2, якщо x = 3; y = 0, якщо x = 2; y = 4, якщо x = 0 в) x < 2, y додатні г) x > 2, y від'ємні


а)
значення x, для яких y = –3; –2; –1; 0; 1; 2; 3; y = −3, якщо x = −2; y = −2, якщо x = 0; y = −1, якщо x = 2; y = 0, якщо x = 4; y = 1, якщо x = 6; y = 2, якщо x = 8; y = 3, якщо x = 10
б)
значення y, для яких x = –2; 0; 2; 4; 6; 8; якщо x = –2, то y = –3; якщо x = 0, то y = –2; якщо x = 2, то y = –1; якщо x = 4, то y = 0; якщо x = 6, то y = 1; якщо x = 8, то y = 2
в) значення x, для яких значення y додатні; x ≥ 4, y додатні
x, для яких значення y
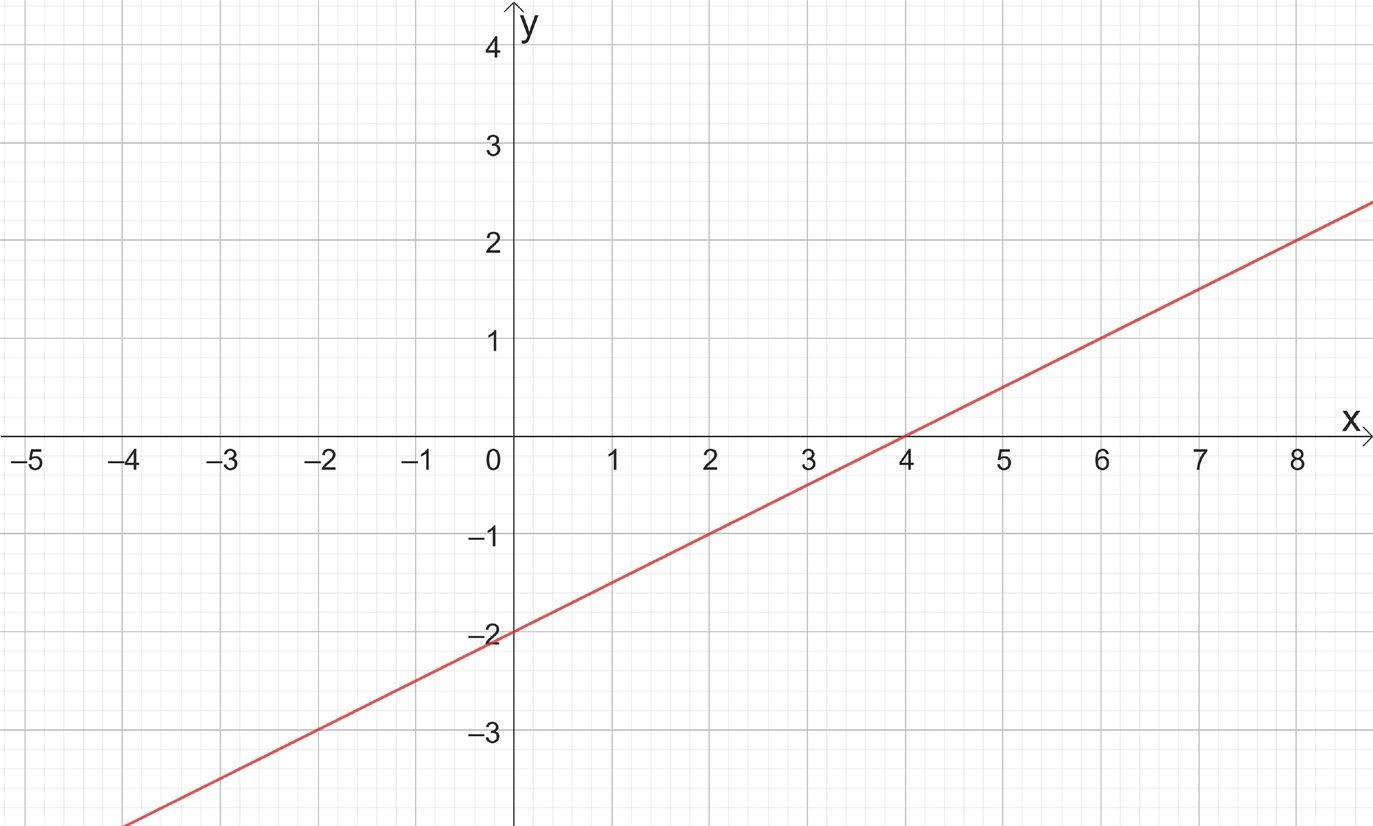

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
б) y = 2(х – 4) = 2(3 – 4) = 2 · (–1) = –2;
г) y = 3х – 2 = 7 3 · 3 – 9 = 7 – 9 = –2;
г) y = 21 3 х 9 = 1 7 · (1 – 5 · 3) = 1 7 – (–14) = –2.
734. Визнач, чи належать графіку
а) y = 0,5x + 4; A(4; 6), B(–8; 0), C(2; 5);
Якщо x = 4, то y = 0,5 • 4 + 4 = 2 + 4 = 6. Так. –
Якщо x = −8, то y = 0,5 • (−8) + 4 = −4 + 4 = 0. Так.
Якщо x = 2, то y = 0,5 • 2 + 4 = 1 + 4 = 5. Так.
б) y = −12x + 17; A(1; 5), В( 1 3;11), C(0,5; 11).
Якщо x = 1, то y = −12 • 1 + 17 = −12 + 17 = 5. Так.
Якщо x = −1 3, то y = −12 • (−1 3) + 17 = 4 + 17 = 21. Так.
Якщо x = 0,5, то y = −12 • 0,5 + 17 = −6 + 17 = 11. Так.
735. Визнач, чи
а) y = x(x – 5); A(0; –5), B(5; 0), C(0; 0);
точки.
Якщо x = 0, то y = 0 • (0 – 5) = 0. Точка A(0; –5) не належить графіку функції.
Якщо x = 5, то y = 5 • (5 – 5) = 0. Точка B(5; 0) належить графіку функції.
Якщо x = 0, то y = 0 • (0 – 5) = 0. Точка C(0; 0) належить графіку функції.
б) y = 4 –8 х ; A(1; –4), В(1 2; 0), C(4; –2). –
Якщо x = 1, то y = 4 –8 1 = –4. Точка A(1; –4) належить графіку функції.
Якщо x = 1 2, то y = 4 – 8 : 1 2 = –12. Точка B(1 2; 0) не належить графіку функції.
Якщо x = 4, то y = 4 –8 4 = 2. Точка C(4; –2) не належить графіку функції.
736. Визнач, чи належать
а) A(7; 1)
y = 1 ���� 6
1 (7 6) = 1 1 = 1; так;
B(2; 0)
1 (2 6) = –1 4; ні;
C(3; 1 3)
1
(3 6) = 1 ( 3); ні; б) y = (6 – x)²
A(7; –1)
(6 – 7)² = 1; ні; B(8; 4)
(6 – 8)² = 4; так; C(4; 4)
(6 – 4)² = 4; так.
737.Функцію
а) y = x; ( 2, 2), (0,−1), (2,0), (4,1)
б) y = –x – 1; (0,2), (1,1), (2,0), (3, 1)

в) y = 1 – x²; (0,0), (1,1), (2,0), (3,−3)
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
г) y = x². (0,0), (1,−1), (2,0), (3,3) 738.
y = 1,5x + 2, якщо −3 < x < 4; X –3 –2 –1 0 1 2 3 4 Y –2,5 –1 0,5 2 3,5 5 6,5 8 б) y = 4 − 2t, якщо −2 ≤ t ≤ 5. X –2 –1 0 1 2 3 4 5 Y 8 6 4 2
y = x+6 2 , якщо –8 ≤ x ≤ 14; б) = 1 5 x, якщо –5 ≤ x ≤ 5.

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html


3 0

0 1 741.

= 2x

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
тотожність (n² + 1)² - (n² - 1)² = 4n².
(n² + 1)² – (n² – 1)² = 4n²; (n² + 1 – n² + 1)(n² + 1 + n² – 1) = 4n²; 2 · 2n² = 4n²; 4n² = 4n². Доведено.
748. Розв’яжи рівняння.
а) (х + 3)² = х² + 9х
x2 + 6x + 9 = x2 + 9x
9 = 3х
х = 3
в) (1 – z)2 = 3 + z2
z + z = 1 – 3
2z = –2
z = –1
749. Підприємиця
б) (у – 5)² = у(у + 2)
у² – 10у + 25 = у² + 2у
2у + 10у = 25
12у = 25
у = 25 12 = 2 1 12
г) (7 – х)2 – х2 = 35
49 – 14х + х² – х² = 35
14х = 49 – 35
14х = 14 х = 1
122,2; 122,2 % – 100 % = 22,2 %.
750. Спрости вираз.
а)10x²y(0.2x + 2y)(–0.2x + 2y) = 10x²y(4y² – 0.04x²) = 40x²y³ – 0.4x⁴y
б)(1 3 x –2 3y)( 1 3 x + 2 3y) · (–9xy) = (1 9 x² –4 9y²) · (–9xy) = –x³y + 4xy³
751. Чи є лінійною функція, задана формулою?
а) y = 5x + 0,2y = 5x + 0,2y = 5x + 0,2 → так, це лінійна функція.
б) y = −3,5x + 2,8y = -3,5x + 2,8y = −3,5x + 2,8 → так, це лінійна функція.
в) y= 3 2x = −2x + 3y = 3 - 2x = -2x + 3y = 3 2x = −2x + 3 → так, це лінійна функція. г) y = x + 5y = x + 5y = x + 5 → так, це лінійна функція.
ґ) y = 2х 5 3 = 2 3 х − 5 3 → так, це лінійна

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
3
0
х = 0.
Відповідь:
755.
підставимо
1. А(1; –0,4):
у = 1,6 • 1 – 2 = 1,6 – 2 = –0,4.
Точка А лежить на графіку.
2. В(2; 0,6):
у = 1,6 • 2 – 2 = 3,2 – 2 = 1,2.
Точка В не лежить на графіку.
3. С(5; 6):
у = 1,6 • 5 – 2 = 8 – 2 = 6.
Точка С лежить на графіку.
4. Г(–0,5; –3):
у = 1,6 • (–0,5) – 2 = –0,8 – 2 = –2,8.
Точка Г не лежить на графіку.
Відповідь: через точки В і Г графік не проходить.
756. Установіть
(А-Г).
1 – А; 2 – Г.
757.

функції;
так, якщо k < 0;
в) y = –2x
–2 2
4 –4
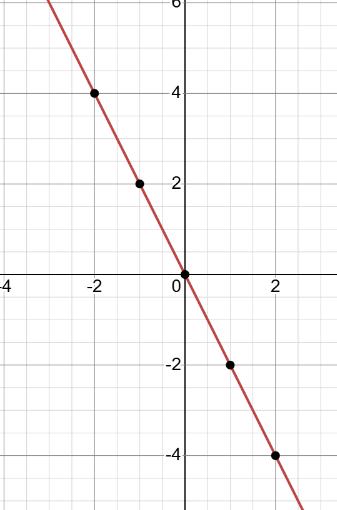
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
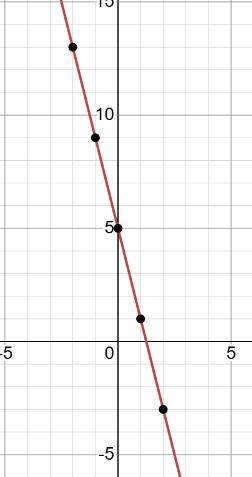
y = 3,5x

759. Побудуй графік функції.
а) y = 5x – 3 X 0 1 Y –3 2 б) y = 4 – 2x x 0 4 y 4 –4


https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html

в) y = 2,5x X –2 2 Y –5 5 г) y = –4x x –1 1 y 4 –4
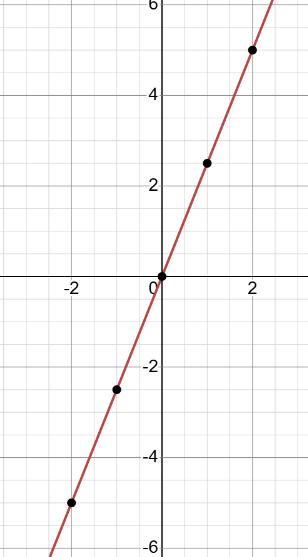
760. Plot the graph of the function
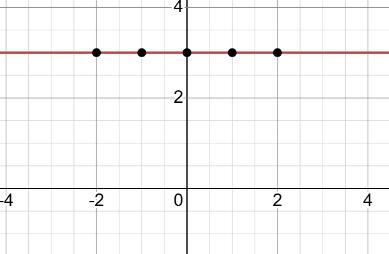




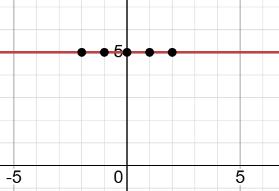


762.
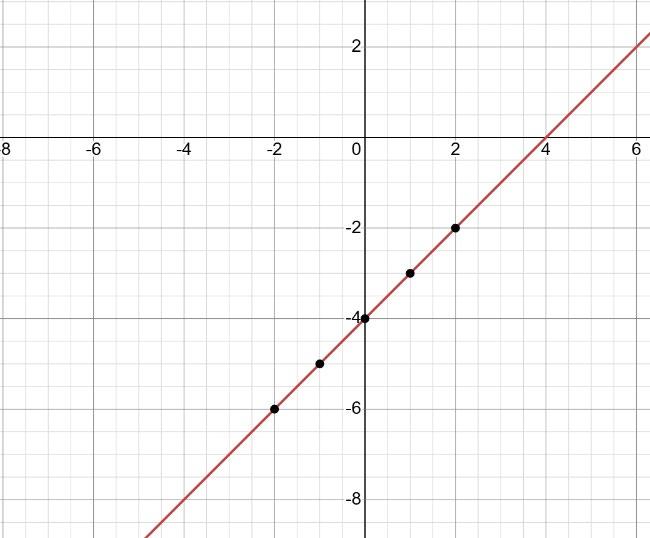
якщо
аргументу дорівнює –1; 0; 2; 5; б)
–5; –3; 1; 2. y = 3 – 2x x 0 3 y 3 –3 а) якщо x = –1, тоді y = 5; якщо x = 0, тоді y = 3; якщо x = 2, тоді y = –1; якщо x = 5, тоді y = –7;
б) y = –5, якщо x = 4; y = –3, якщо x = 3; y = 1, якщо x = 1; y = 2, якщо x = 0,5.

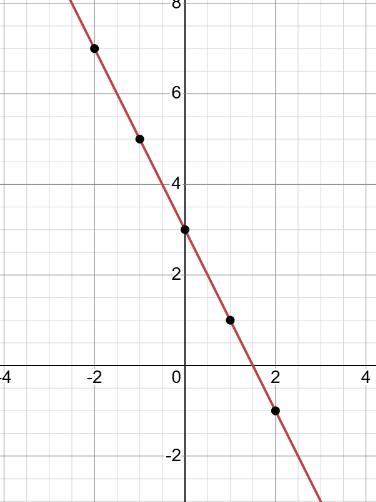
x


x


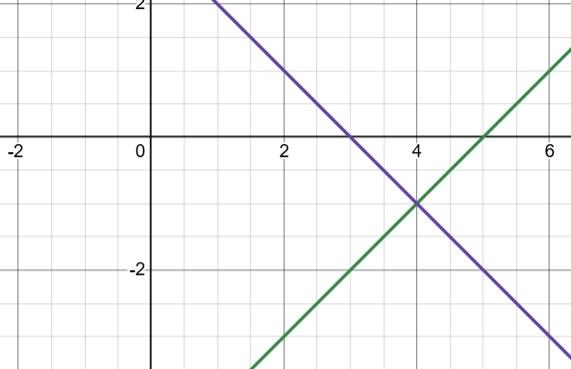




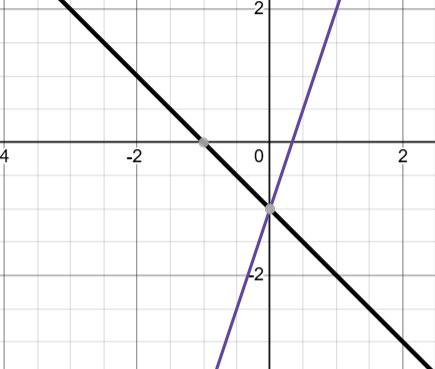
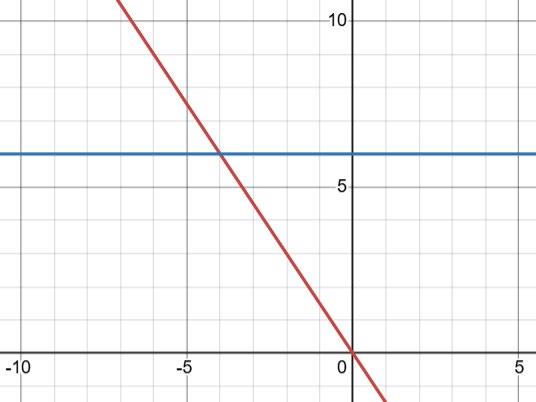
5 = 6 – 1
5 = 5
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
проходить через цю точку. –5 = –20 – 1
через точку B(–10; –5).
199 = 200 – 1 199 = 199
769. Чи проходить графік функції y = 5 – 3x через точку:
Перевіримо, чи проходить графік функції у = 5 – 3х через задані точки, підставивши координати кожної точки у рівняння функції:
а) Точка A(–1; 2):
у = 5 – 3х
2 = 5 – 3•(–1)
2 = 5 + 3
2 = 8 графік не
проходить через цю точку.
точку A(–1; 2). 770. Для функції
б) Точка B(2; –1): у = 5 – 3х –1 = 5 – 3•2 –1 = 5 – 6 –1 = –1
через цю точку.
= 7x - 12,
в) Точка C(10; –25): у = 5 – 3х –25 = 5 – 3•10 –25 = 5 – 30 –25 = –25 графік проходить через цю точку.
точки B(2; –1) і C(10; –25),
2; 6; 0; −1; −4;
2; 30; −5; −26.
Функція: у = 7х – 12.
Якщо х = 2: у = 7•2 – 12 = 14 – 12 = 2.
Якщо х = 6: у = 7•6 – 12 = 42 – 12 = 30.
Якщо х = 0: у = 7•0 – 12 = 0 – 12 = –12.
Якщо х = –1: у = 7•(–1) – 12 = –7 – 12 = –19.
Якщо х = –4: у = 7•(–4) – 12 = –28 – 12 = –40.
б) Знайдемо значення аргументу, якщо значення функції дорівнює:
Якщо у = 2: 2 = 7х – 12; 7х = 2 + 12; 7х = 14; х = 14 ÷ 7; х = 2.
Якщо у = 30: 30 = 7х – 12; 7х = 30 + 12; 7х = 42; х = 42 ÷ 7; х = 6.
Якщо у = –5: –5 = 7х – 12; 7х = –5 + 12; 7х = 7; х = 7 ÷ 7; х = 1.
Якщо у = –26: –26 = 7х – 12; 7х = –26 + 12; 7х = –14; х = –14 ÷ 7; х = –2.
Відповідь:
а) Для х = 2, у = 2; для х = 6, у = 30; для х = 0, у = –12; для х = –1, у = –19; для х = –4, у = –40.
б) Для у = 2, х = 2; для у = 30, х = 6; для у = –5, х = 1; для у = –26, х = –2. 771. Для функції y = 8 - 5x, не виконуючи побудови, знайди: а) значення
аргументу дорівнює -2; -4; 0; 1; 6; б)
3; 18; -12; 38.
у = 8 – 5x.
x = –2: у = 8 – 5•(–2) = 8 + 10 = 18. Якщо x = –4: у = 8 – 5•(–4) = 8 + 20 = 28.
Якщо x = 0: у = 8 – 5•0 = 8. Якщо x = 1: у = 8 – 5•1 = 8 – 5 = 3. Якщо x = 6: у = 8 – 5•6 = 8 – 30 = –22.

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
Якщо у = 3: 3 = 8 – 5x; 5x = 8 – 3; 5x = 5; x = 5 : 5; x = 1.
Якщо у = 18: 18 = 8 – 5x; 5x = 8 – 18; 5x = –10; x = –10 : 5; x = –2.
Якщо у = –12: –12 = 8 – 5x; 5x = 8 + 12; 5x = 20; x = 20 : 5; x = 4.
Якщо у = 38: 38 = 8 – 5x; 5x = 8 – 38; 5x = –30; x = –30 : 5; x = –6.
Відповідь:
а) Для x = –2, у = 18; для x = –4, у = 28; для x = 0, у = 8; для x = 1, у = 3; для x = 6, у = –22.
б) Для у = 3, x = 1; для у = 18, x = –2; для у = –12, x = 4; для у = 38, x = –6.
772. Побудуй графік функції а) у = 2(х + 1) = 2х + 2 х 0 1 у 1 3 б) y = 1 2 x – 5 = 0,5x – 5 x 0 2 y –5 –4

y = 3 –1 3 x x 0 3 y 3 2

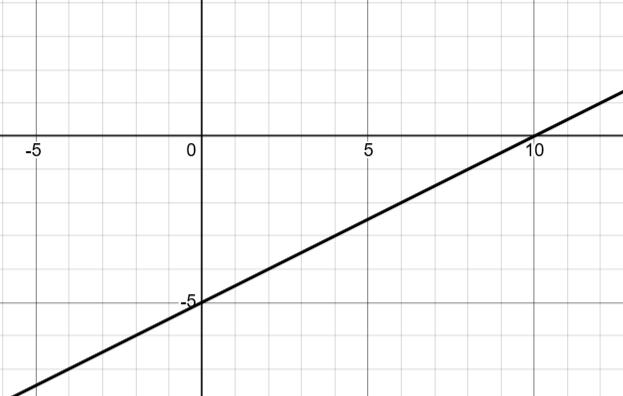
y = 3 2x 3 = 1 –2 3 x x –3 3 y 3 –1

773. Побудуй графік функції а) y = 3(2 – x) x 0 3 y 6 –3 б) y = 1 2(7x – 4) X 0 2 Y –2 5 в) y = 4x 6 6 x 0 3 y –1 1

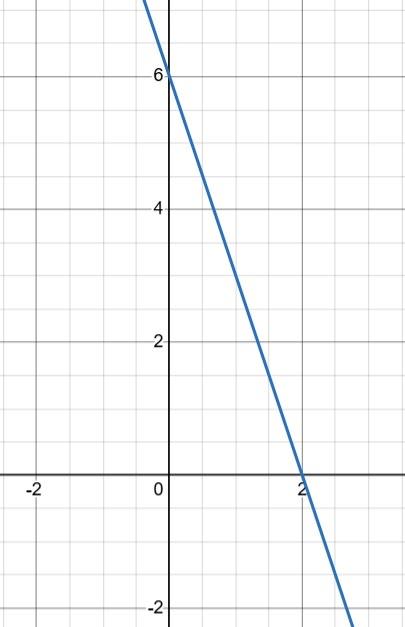
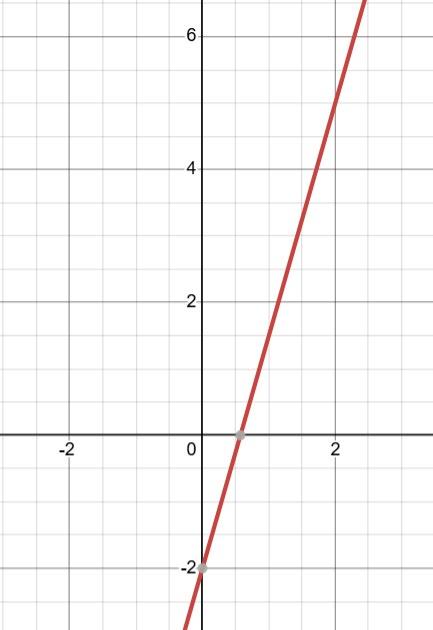




x 0 3
y –4 2
•
• Значення функції додатні, якщо: 2x – 4 > 0 → 2x
значення функції додатні.
–4) і (2; 0).
• Значення функції від'ємні, якщо: 2x – 4 < 0 → 2x < 4 → x < 2. Тобто, при x
• Функція зростаюча,
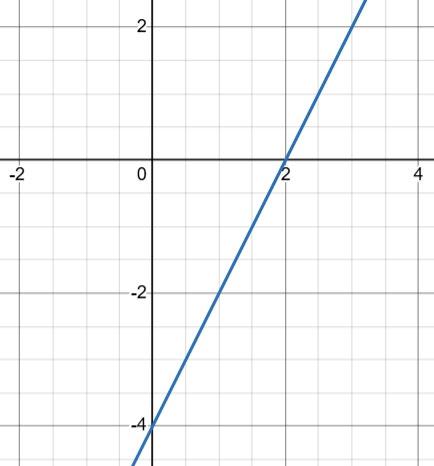

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
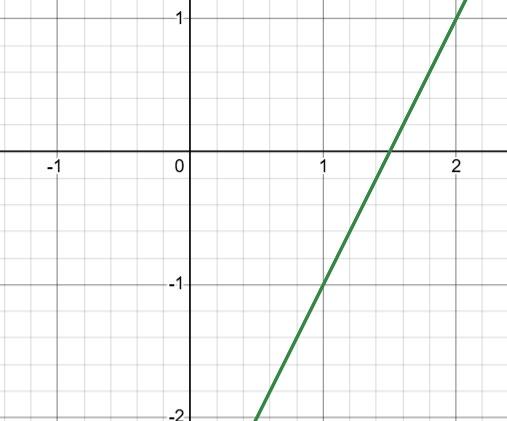
b = 0

b = 4


https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html

k = 0,5 k = 2
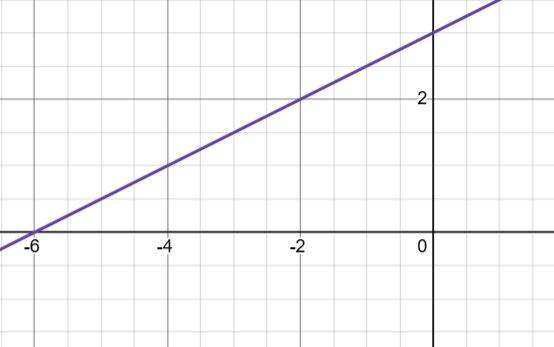

779. Дано функцію y = 2 3 x - 1, де -3 ≤ x ≤ 6.
A(0;1), B(3; 1), C(9; 5)?
Формула функції: y = 2 3 x – 1, де –3 < x < 6.
1. Перевіримо точку A(0; –1):
Підставляємо x = 0: y = 2 3 ·0 – 1 = –1.
Точка A(0; –1) належить графіку.
2. Перевіримо точку B(3; 1):

Підставляємо x = 3: y = (2 3)·3 – 1 = 2 – 1 = 1.
Точка B(3; 1) належить графіку.
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
3. Перевіримо точку C(9; 5): Оскільки x = 9 не задовольняє умову –3 < x < 6, точка C(9; 5) не належить графіку.
Відповідь: Точки A(0; –1) і B(3; 1) належать графіку, точка C(9; 5) не належить.
780. Не виконуючи побудови, знайди координати точок перетину з осями координат
графіка функції
а) Функція у = 4х + 28:
Для перетину з віссю Оу (х = 0):
у = 4•0 + 28 = 28. Точка (0; 28).
Для перетину з віссю Ох (у = 0):
0 = 4х + 28 → 4х = –28 → х = –7.
Точка (–7; 0).
б) Функція у = –9х + 27:
Для перетину з віссю Оу (х = 0):
у = –9•0 + 27 = 27. Точка (0; 27).
Для перетину з віссю Ох (у = 0):
0 = –9х + 27 → –9х = –27 → х = 3.
Точка (3; 0).
в) Функція у = 0,5 – 2х:
Для перетину з віссю Оу (х = 0):
у = 0,5 – 2•0 = 0,5. Точка (0; 0,5).
Для перетину з віссю Ох (у = 0):
0 = 0,5 – 2х → –2х = –0,5 → х = 0,25.
Точка (0,25; 0).
Відповідь: а) Точки (0; 28) і (–7; 0).
б) (0; 27) і (3; 0). в) (0; 0,5) і (0,25; 0).
781. Не виконуючи
а) Функція у = 35х – 70:
у = 35 • 0 – 70 = –70;
0 = 35х – 70; х = 2;
(0; –70) і (2; 0)
б) Функція у = 1,7х – 3,4:

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
у = 1,7 • 0 – 3,4 = –3,4; 0 = 1,7х – 3,4; х = 2; (0;–3,4) і (2;0)
в) Функція у = 2,5х + 5:
у = 2,5 • 0 + 5 = 5;
0 = 2,5х + 5; х = –2; (0;5) і (–2;0)
Відповідь:
а) Точки перетину: (0; –70) і (2; 0).
б) Точки перетину: (0; –3,4) і (2; 0).
в) Точки перетину: (0; 5) і (–2; 0).
782. Не виконуючи побудови,
а) у = 4х + 5 і у = –2х + 17;
4х + 5 = –2х + 17
6х = 12 х = 2
у = 8 + 5 = 13 (2;13)
783. Не виконуючи побудови,
а) у = –3х + 8 і у = 4х – 13; –3х + 8 = 4х – 13
7х = 21
х = 3
у = –1,2х + 3 і у = 3,4х – 6,2. –1,2х + 3 = 3,4х – 6,2 4,6х = –9,2 х = –2
у = 2,4 + 3 = 5,4 (–2;5,4)
у = –9 + 8 = –1 (3;–1) б) у = 2,3х + 4,2 і у = 4,5х – 6,8.
2,3х + 4,2 = 4,5х – 6,8
2,2х = 11
х = 5
у = 11,5 + 4,2 = 15,7 (5; 15,7) 784.
4 = –3k – 2; –3k = 6; k = –2
–3 = 2 • 5 – b; b = 2 • 5 + 3; b = 13

функції: 3 = 4k – 1
4k = 4; k = 1;
2. Для другої функції: 3 = 4p + 5.
4p = –2; p = –0,5
Функції мають вигляд: 1) у = х – 1; 2) у = –0,5х + 5.
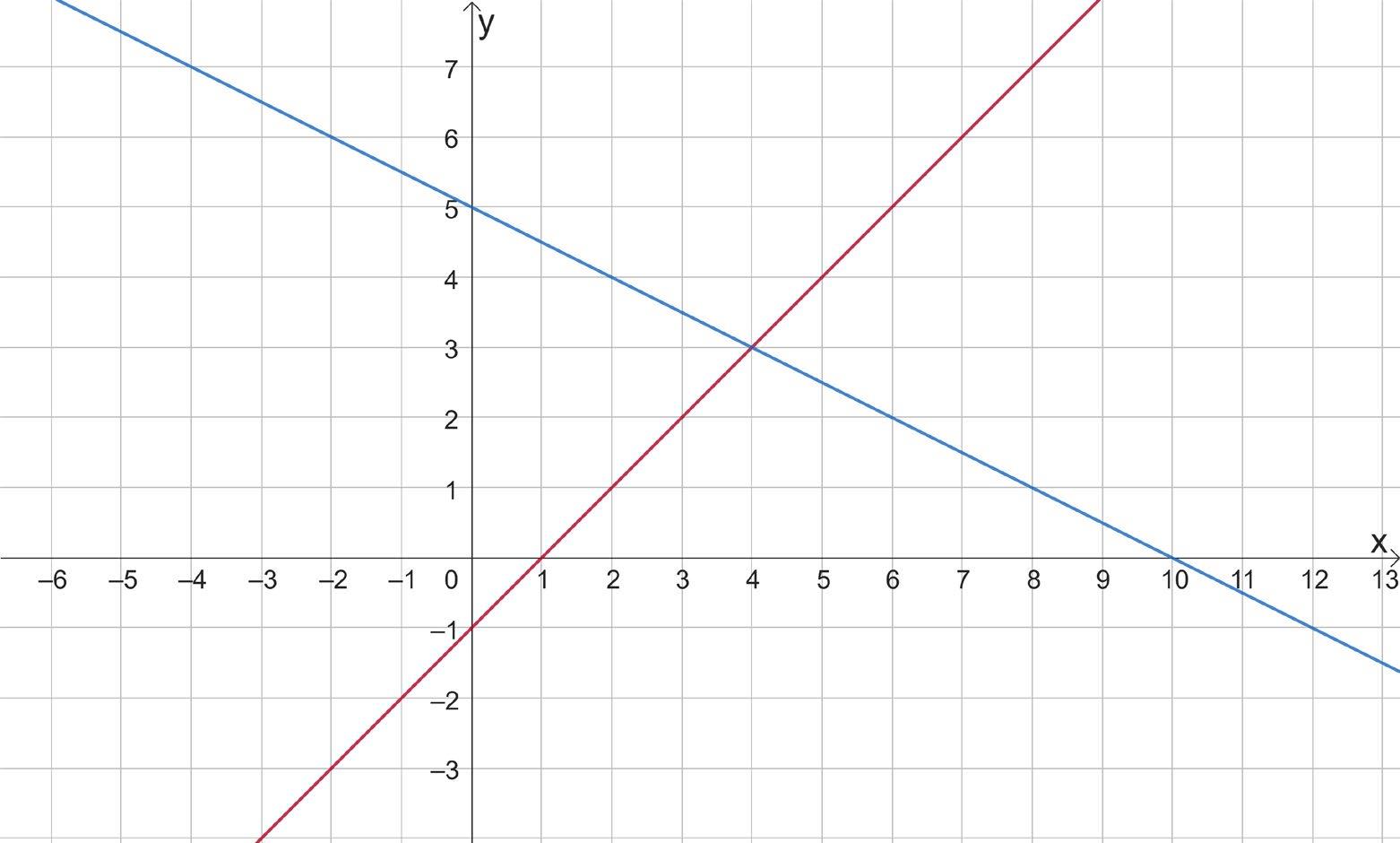
787. За якої
Якщо x = 3, y = 4, то:
1. Для першої функції: 4 = 3a + 3
3a = 4 – 3
3a = 1
a = 1 3 .
2. Для другої функції: 4 = 3c – 2
3c = 4 + 2
3c = 6 c = 2.
Тобто, функції мають
1) y = 1 3 x + 3
2) y = 2x – 2.


788. Задай формулою
Обчислимо k: k = (y₂ – y₁) : (x₂ – x₁) = (2 – 1) : (2 – 0) = 1 : 2 = 0,5.
Знайдемо p:
Підставимо
1 = 0,5 • 0 + p, p = 1.
Формула функції: y = 0,5x + 1.
1)
А(0; 1) і В(2; 2).
y = kx + p:
б) Знайдемо формулу функції, графік якої проходить через точки
Обчислимо k: k = (y₂ – y₁) : (x₂ – x₁) = (5 – (–1)) : (0 – 1) = 6 : (–1) = –6.
Знайдемо p:
Підставимо координати точки Р(0; 5) у рівняння y = kx + p:
5 = –6 • 0 + p, p = 5.
Формула функції: y = –6x + 5.
789. Задай формулою функцію
y = kx + p,
а) М(0; 3) і С(–4; 1); б) K(–3; 1) і Т(0; –2).
а) М(0; 3) і С(–4; 1);
Обчислимо k:
k = (y₂ – y₁) : (x₂ – x₁) = (1 – 3) : (–4 – 0) = (–2) : (–4) = 0,5.
Знайдемо p:
Підставимо координати точки М(0; 3) у рівняння y = kx + p: 3 = 0,5 • 0 + p, p = 3.
Формула функції: y = 0,5x + 3. б) K(–3; 1) і Т(0; –2).
Знаходимо кутовий коефіцієнт: k= -1.
Підставляємо точку T(0; –2) у формулу y = kx + p: −2 = −1 ⋅ 0 + p ⇒ p= −2
Отже, функція має вигляд: y = −x −2.

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
1. Для графіка a:
Графік зростає, k > 0. – Формула: y = x + 2.
3. Для графіка c: – Графік спадає, k < 0. – Формула: y = –0,5x.
791. Напиши формули функцій,
малюнку 18.13.
2. Для графіка b:
Графік зростає, k > 0.
Формула: y = 2x – 1.
4. Для графіка d: – Графік спадає, k < 0. – Формула: y = –x – 1.
а) малюнку 18.12; б)
а) Для графіка а: – Графік зростає, проходить через точки (0; 3) і (–3; 0).
– Формула: y = x + 3.
2. Для графіка b:
– Графік зростає, проходить через точки (0; –3) і (3; 0).
– Формула: y = x – 3.
б)
Для графіка б:
– Графік спадає, проходить через точки (–4; 0) і (0; –2).
– Формула: y = –0,5x – 2.
2. Для графіка b:
– Графік зростає, проходить через точки (0; 4) і (–4; 0).
– Формула: y = x + 4.
792. На фарбування

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html

794.
y = x + 4; y = –x + 4;
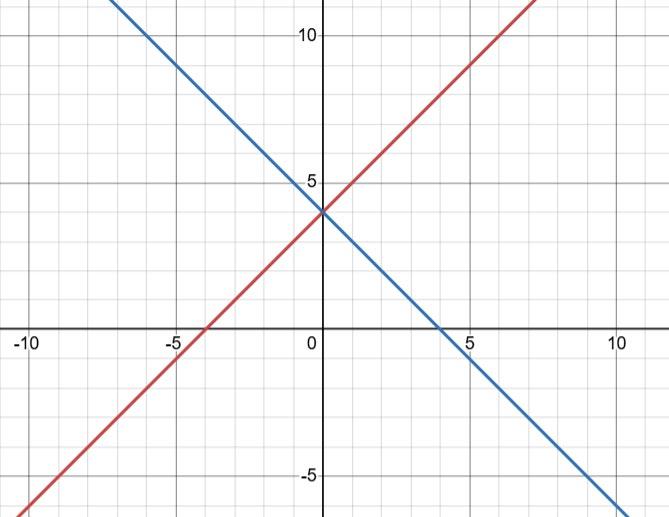
в) y = 3x; y = –3x.

795.

y = 1 – 2x; y = 1 + 2x;

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
= x + 2;
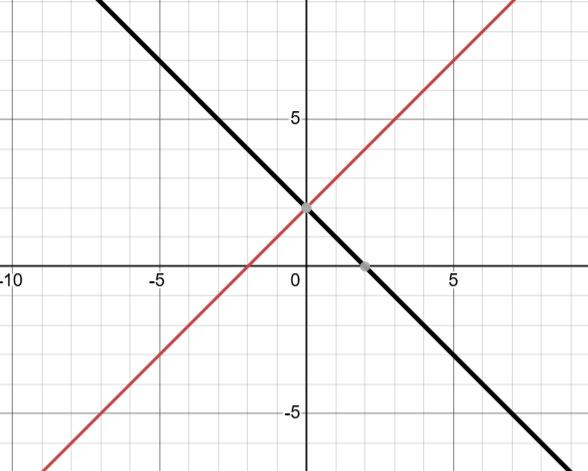
б) y = 2x + 4; y = –2x + 4;

в) y = 2,5x; y = –2,5x.

796. Побудуй графік функції
а) y = �2x + 3,x ≤ 0, x + 3,x > 0


https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
y = �−3x + 3,x ≤ 1 x 1,x > 1.

функції а) y = � 3x − 2,x ≤ 0, x 2,x > 0.
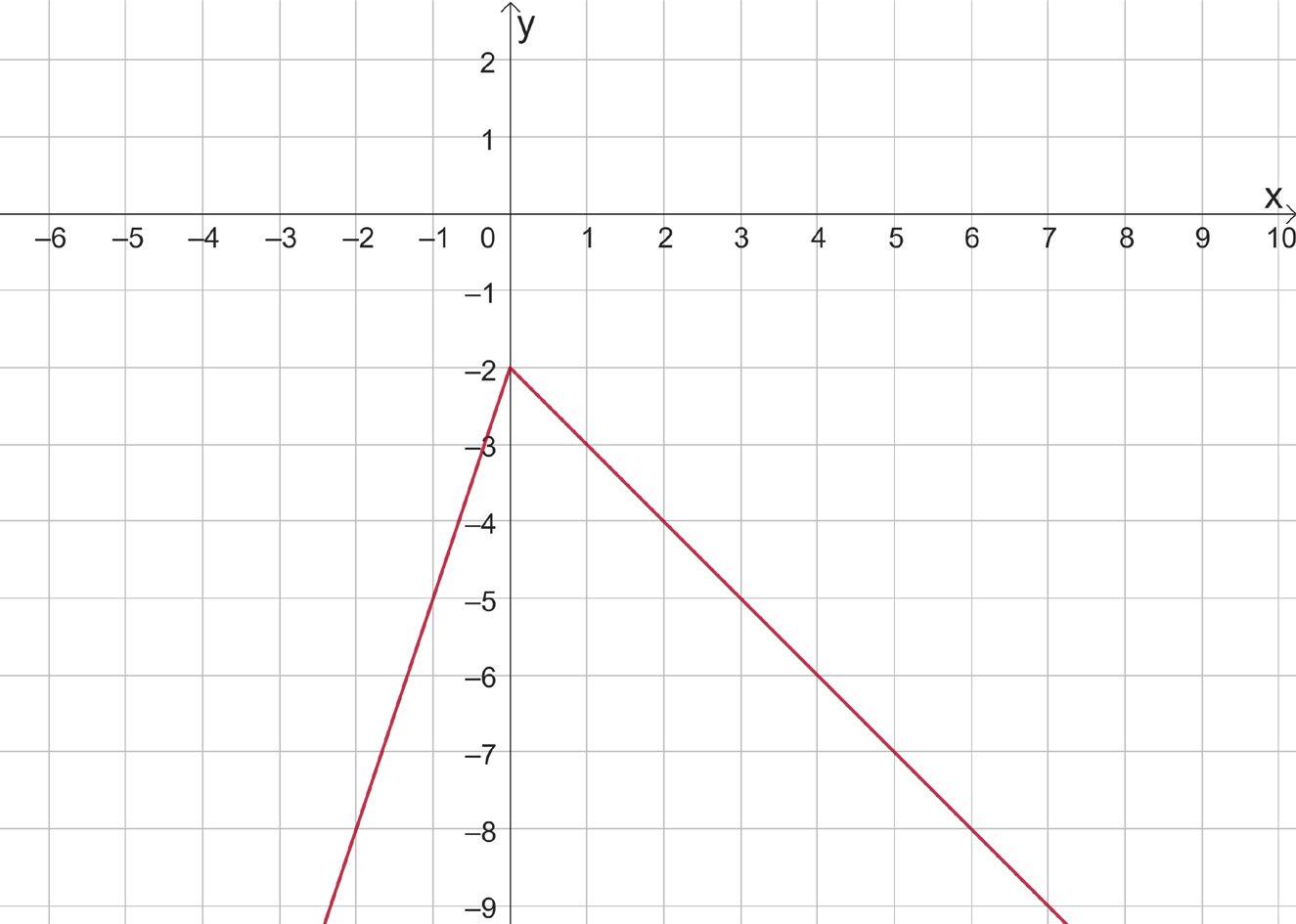
б) y = � 2x 2,x ≤ 1 x + 1,x > −1

а) y = |x|;

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html

б) y = |x + 3|;
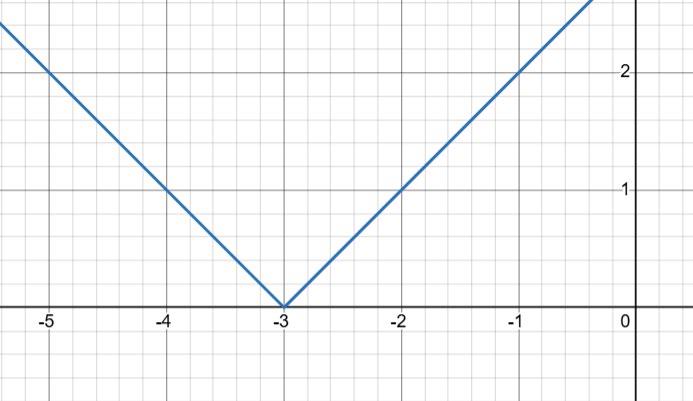
в) y = |x| + 3x.


б) y = 2x + |x|;


в) y = 2|x| – 1.

y₁ = 100 + 30x, y₂ = 150 + 20x,
краще перевозити вантаж.
Формули витрат:
у1 = 100 + 30х (перший вид транспорту),
у2 = 150 + 20х (другий вид транспорту).
Розв'яжемо рівняння у1 = у2, щоб
100 + 30х = 150 + 20х.
30х – 20х = 150 – 100.
10х = 50.
х = 5.

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
y = 2x + 50.
2. Якщо x ≥ 40, то зарплата дорівнює:
y = (2x + 50) + 0,2(2x + 50).
Спростимо формулу для x ≥ 40: y = (2x + 50) + 0,4x + 10 = 2,4x + 60.
Отже, залежність має вигляд: y = 2x + 50, якщо x < 40; y = 2,4x + 60, якщо x ≥ 40.

802. Розклади на множники многочлен.
а) ab + bc + a + c = (ab + a) + (bc + c)= a(b + 1) + c(b + 1)=(a + c)(b + 1).
б) 2x – yx + 2y – y² = (2x + 2y) – (yx + y²) = 2(x + y) – y(x + y) = (2 – y)(x + y).
в) 3 – 6a + z – 2az = (3 – 6a) + (z – 2az) = 3(1 – 2a) + z(1 – 2a) = (1 – 2a)(3 + z).
г) 10ax – 5bx + 2ay – by = (10ax – 5bx) + (2ay – by) = 5x(2a – b) + y(2a – b) = (2a – b)(5x + y).
803. Розв’яжи рівняння.
a) (2x + 3)2 = 4x2 + 3
4х2 + 12х + 9 = 4х2 + 3
12х = –6
х = –6 : 12
х = –0,5;
б) (5 – 3y)2 – 9y2 = 55
25 – 30у + 9у2 – 9у2 = 55 –
30у = 30
у = –1;
в) (4z + 2)² = 2(8z² + 13)
16z² + 16z + 4 = 16z² + 26
16z = 22
z = 22 16
z = 11 8
z = 1 3
8
г) (4 – 5x)² = (3 + 5x)²

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
16 – 40x + 25x² = 9 + 30x + 25x²
–70x = 9 – 16 –70x = –7
x = 0,1
804.Мотоцикліст
одночасно?
Швидкість
хвилин.
805. Розв’яжи рівняння.
а) x + 10 = 23
x = 23 – 10
x = 13
г) 2x + 10 = 30
2x = 30 – 10
2x = 20
x = 20 : 2
x = 10
б) x – 10 = 15 x = 15 + 10 x = 25
ґ) 3x – 5 = 40
3x = 40 + 5
3x = 45 x = 45 : 3 x = 15
е) 10y = 70 y = 70 : 10 y = 7
з) x(x – 3) = 0
x = 0 або x – 3 = 0
x = 0 x = 3
є) 10y = –3 y = –3 : 10 y = –0,3
и) (x + 5)x = 0 x = 0 або x + 5 = 0 x = 0 x = –5
806. Чи рівносильні рівняння?
а) 4x + 5x = 18 і 9x = 18 Так
б) 7x – x = 24 і 6x = 24 Так
в) 2(x + 3) = 16 і 2x + 3 = 16 Ні
г) 0,4 · (y – 2) = 1 і 0,4y – 0,8 = 1 Так
807. Поясніть, чому
а) x² + 1 = 0;
x² = –1
б) x² + 8 = 7;
x² = –1
в) 2x² + 3 = –7;

2x² = –10;
в) x + 7 = 13 x = 13 – 7 x = 6
д) 4x – 8 = 0
4x = 8
x = 8 : 4
x = 2
ж) –y = 15 y = –15
і) –3,5x² = 0
x² = 0 : (–3,5)
x² = 0
x = 0
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
x² = –5
(x + 2)² = –4
А) x – 5 = 7 12 – 5 = 7, 7 = 7. Б) 7 – 2x = 17 7 – 2 • 12 = 17, 7 – 24 = 17, –17 ≠ 17. В) 3x + 4 = 40 3 • 12 + 4 = 40, 36 + 4 = 40, 40 = 40. В) 0,5x + 5 = 11 0,5 • 12 + 5 = 11 6 + 5 = 11, 11 = 11.
є розв'язком
809.
а) x² = 16
7 – 2x = 17.
(x – 4)(x + 4)=0 x = 4 або x = –4 б) x³ = 8 x³ – 8 = 0 (x – 2)(x² + 2x + 4) = 0 x = 2 в) x² = 0,01 (x – 0,1)(x + 0,1) = 0 x = 0,1 або x = –0,1
810. Розв’яжи
а) x² = 4
(x – 2)(x + 2)=0 x = 2 або x = –2
б) x³ = 27 x³ – 27 = 0 (x – 3)(x² + 3x + 9) = 0 x = 3
811. Розв’яжи рівняння
а)
25 + x = 37
x = 37 – 25 x = 12 б) x – 12 = 23 x = 23 + 12 x = 35
812. Розв’яжи
2x + 3 = 19
2x = 19 – 3
2x = 16
x = 16 : 2
x = 8

б) 3y – 4 = –1
3y = –1 + 4 3y = 3 y = 3 : 3 y = 1
в) (x – 2)(x +2)=0 x = 2 або x = –2
г) 2x² = 18 x² = 18 : 2 x² = 9 (x – 3)(x + 3) = 0 x = 3 або x = –3
г) x(x – 2) = 0 x = 0 або x – 2 = 0 x = 0 або x = 2
в) 24 – 10x = 18 –10x = 18 – 24 –10x = –6
x = –6 : (–10) x = 0,6 г) 13x + 6 = 32 13x = 32 – 6 13x = 26 x = 26 : 13 x = 2
1 – 3x = 25 –3x = 25 – 1 –3x = 24 x = 24 : (–3) x = –8 г) 4z – 12 = –8 4z = –8 + 12
4z = 4
z = 4 : 4 z = 1
5,7y = 57
y = 57 : 5,7
y = 570 : 57 y = 10 б) 7x = 4,2 x = 4,2 : 7 x = 42 : 70 x = 0,6 в) 0,6x = 0,3 x = 0,3 : 0,6 x = 3 : 6 x = 0,5 г) 3,7x = 11,1
2 3 x = 5
x = 5 • 3 2
x = 15 : 2
б) –5 7y = 1 y = 1 • (–7 5) y = –7 : 5
1 –3 4 x = 5 8
x = 11,1 : 3,7
x = 111 : 37 x = 3
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
x = 7,5 y = –1,4 –3 4 x = –3 8 x = –3 8 • –4 3 x = 1 2
816. Покажи, що рівняння:
а) x – 2 = 3x має розв’язок x = –1;
x – 2 = 3x
2x = –2
x = –1
817. Покажи, що рівняння:
а) 8z – 5 = 5z має розв’язок z = 5 3
8z – 5 = 5z –
3z = –5
z = 5 3
б) z(z – 2)(z + 3) = 0 має розв’язки z = 0, z = 2 і z = –3. z(z – 2)(z + 3) = 0
z = 0 або z – 2 = 0 або z + 3 = 0 z = 0 або z = 2 або z = –3
б) x(x – 3) = 0 має розв’язки x = 0 і x = 3.
x(x – 3) = 0
x = 0 або x – 3 = 0 x = 0 x = 3
818. Які з чисел –2, –1, 0, 1, 2 задовольняють рівняння?
а) x(3x – 6) = 0
x = 0 або 3x – 6 = 0
x = 0 x = 2
б) (2n + 2)n = 0
2n + 2 = 0 або n = 0
n = –1 n = 0
819. Розв’яжи рівняння і зроби перевірку.
а) x – (3 – 2x) = 9
x – 3 + 2x = 9
3x – 3 = 9
3x = 9 + 3
3x = 12
x = 12 : 3
x = 4
Перевірка:
4 – (3 – 8) = 4 + 5 = 9
820. Розв’яжи рівняння і
a) x – (3x – 5) = 9
x – 3x + 5 = 9
–2x + 5 = 9
–2x = 9 – 5
–2x = 4
x = 4 : (–2)
x = –2
Перевірка:
–2 – (3 • (–2) – 5) = = –2 + 11 = 9

б) 8 – (3x – 2) = 13 8 – 3x + 2 = 13 10 – 3x = 13 –3x = 13 – 10 –3x = 3
x = 3 : (–3)
x = –1
Перевірка:
8 – (–3 – 2) = 8 + 5 = 13
в) 3(x – 2) = 27 3x – 6 = 27
3x = 27 + 6
3x = 33
x = 33 : 3
x = 11
Перевірка: 3(11 – 2) = 3 · 9 = 27
b) 12 – (5x + 4) = 13
12 – 5x – 4 = 13
8 – 5x = 13
–5x = 13 – 8 –5x = 5
x = 5 : (–5)
x = –1
Перевірка: 12 – (5 • (–1) + 4) = = 12 + 1 = 13
c) 6(2x – 1) = 18
12x – 6 = 18
12x = 18 + 6
12x = 24
x = 24 : 12
x = 2
Перевірка: 6(2 • 2 – 1) = 6 • 3 = 18
а) 2(x – 3) = 36
2x – 6 = 36
2x = 36 + 6
2x = 42
x = 42 : 2
x = 21
г) 36 – (y – 3) = 12y
36 – y + 3 = 12y
39 – y = 12y
39 = 12y + y
39 = 13y
y = 39 : 13
y = 3
822. Розв’яжи рівняння
а) 3(x + 5) = 27
3x + 15 = 27
3x = 27 – 15
3x = 12
x = 12 : 3
x = 4
г) 17 + 2(x + 4) = 7x
17 + 2x + 8 = 7x
25 + 2x = 7x
2x – 7x = –25
–5x = –25
x = –25 : (–5)
x = 5
823. Розв’яжи рівняння
а)
8(4 – 7z) = 5(4 – 11z)
32 – 56z = 20 – 55z
32 – 20 = –55z + 56z
z = 12
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
б) 4(5 – x) = 12
20 – 4x = 12
–4x = 12 – 20
–4x = –8
x = –8 : (–4)
x = 2
ґ) 2x – (3 – x) = 18 – 4x
2x – 3 + x = 18 – 4x
3x – 3 = 18 – 4x
3x + 4x = 18 + 3
7x = 21
x = 21 : 7
x = 3
б) 5(x – 3) = 15
5x – 15 = 15
5x = 15 + 15
5x = 30
x = 30 : 5
x = 6
ґ) 12x – (x – 9) = 20x
12x – x + 9 = 20x
11x + 9 = 20x
9 = 20x – 11x
9 = 9x
x = 9 : 9
x = 1
б) 4(x + 1) = 3(3x – 17)
4x + 4 = 9x – 51
4 = 9x – 4x – 51
4 + 51 = 5x
55 = 5x
x = 55 : 5
x = 11
в) 3x + (8 – x) = 10x
3x + 8 – x = 10x
2x + 8 = 10x
8 = 10x – 2x
8 = 8x
x = 8 : 8
x = 1
д) 8z – 3(5 – 4z) = 25
8z – 15 + 12z = 25
8z + 12z = 25 + 15
20z = 40
z = 40 : 20 z = 2

в) 8(3 – x) + 4x = 40
24 – 8x + 4x = 40
24 – 4x = 40 –4x = 40 – 24 –4x = 16
x = 16 : (–4)
x = –4
д) 5 – (4y – 7) = –10y
5 – 4y + 7 = –10y
12 – 4y = –10y
12 = –10y + 4y
12 = –6y
y = 12 : (–6) y = –2
в) 0,2(3 – 8x) = 0,5(–2x + 6)
0,6 – 1,6x = –x + 3
0,6 – 3 = 1,6x – x –2,4 = 0,6x
x = –2,4 : 0,6
x = –24 : 6
x = –4
г) 17 + 3(z – 2)=5(z –1)
17 + 3z – 6 = 5z – 5
11 + 3z = 5z – 5
11 + 5 = 5z – 3z
16 = 2z
z = 16 : 2
z = 8
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
ґ) 0,4z – 0,3(7 + 3z)=1,4
0,4z – 2,1 – 0,9z = 1,4 –0,5z – 2,1 = 1,4 –0,5z = 1,4 + 2,1 –0,5z = 3,5
z = 3,5 : (–0,5)
z = 35 : (–5) z = –7
д) 1,7(y + 1) + 0,2(8 –15y)=3
1,7y + 1,7 + 1,6 – 3y = 3 –1,3y + 3,3 = 3 –1,3y = 3 – 3,3 –1,3y = –0,3
y = –0,3 : (–1,3) y = 3 : 13 y = 3 13
824. Складіть і розв’яжіть задачу за малюнком 19.1. Нехай зошит коштував x грн, тоді книга 3x грн. Складаємо рівняння:
3x – x = 120
2x = 120
x = 60 (грн) – ціна зошита;
3 • 60 = 180 (грн) – ціна книги.
Відповідь: 60 грн і 180 грн.
825. Розв’яжи рівняння а) 16 – x² = 0
x² = 16
(x – 4)(x + 4) = 0
x = 4 або x = –4
826. Розв’яжи рівняння а) 4x² – 1 = 0
(2x – 1)(2x + 1) = 0
2x = 1 або 2x = –1
x = 1 2 x = –1 2
827. Знайди корінь рівняння а) x² – 16x + 64 = 0
(x – 8)² = 0
x – 8 = 0
x = 8
828. Знайди корінь рівняння а) x² – 18x + 81 = 0
(x – 9)² = 0
x – 9 = 0 x = 9
829.

б) 36x² = 1,44 x² = 1,44 36 x² = 0,04 (x – 0,2)(x + 0,2) = 0 x = 0,2 або x = –0,2
б) 0,09x² = 36 x² = 36 0,09
x² = 400 (x – 20)(x + 20) = 0 x = 20 або x = –20
б) 0,25x² + 3x + 9 = 0
(0,5x + 3)² = 0
0,5x + 3 = 0
0,5x = –3
x = –6
б) 0,25x² + 5x + 25 = 0
(0,5x + 5)² = 0
0,5x + 5 = 0
0,5x = –5
x = –10
830. Розв’яжи рівняння
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
а) 2(11 6x) 3(7 4x) = 1
22 12x 21 + 12x = 1
22 21 = 1
1 = 1
будь яке значення x
в) 0,4(6x 1) = 0,1(12x+5)
2,4x 0,4 = 1,2x + 0,5
2,4x 1,2x = 0,5 + 0,4
1,2x = 0,9
б) 2,5(y + 6) = y + 1,5(y 10)
2,5y + 15 = y + 1,5y 15 2,5y y 1,5y = 15 15
0y = 30
Немає розв'язків
x = 0,9 : 1,2 x = 0,75 г) 5(0,6m 2) = 2(m 3,6) 3m 10 = 2m 7,2
ґ) 2 3(6 9x) = 15
4 6x = 15
6x = 15 4
6x = 11 x = 11 6 = 1 5 6
831. Розв’яжи рівняння
а) 3(5 8x) 2(7 12x) = 1
15 24x 14 + 24x = 1
15 14 = 1
1 = 1
будь яке значення x
в) 7(y + 6) = 4(3y 5) 3
7y + 42 = 12y 20 3
7y + 42 = 12y 23
42 + 23 = 12y 7y
65 = 5y y = 65 : 5
y = 13
ґ) 2 5(8 5x) = 1 5 16
10х 5 = 1 5 16 10x = 1
10x = 1 16
10x = 15
x = 15 : ( 10)
x = 15 10 = 3 2 = 1 1 2
3m 2m = 7,2 + 10 m = 2,8
д) 3 4 (12 x) =
= 30 : ( 3)
б) 1,2(x + 3) = 2x 4(0,2x 5) 1,2x + 3,6 = 2x 0,8x + 20 1,2x + 3,6 = 1,2x + 20 3,6 ≠ 20 Немає розв'язків
7,5(4 x) 5x = 5(0,5x+3)
30 7,5x 5x = 2,5x + 15
30 15 = 7,5x + 5x + 2,5x 15 = 15x x = 15 : 15 x = 1
1 3 (6 + x) = 2 3 (2x 15)
= 12 832.

2x + 26 = 5x + 2 26 – 2 = 5x 2x 24 = 3x
= 30 x = 3
833. Розв’яжи рівняння
а)8 3y 5 1 2y 2 = 6y + 17 10 | · 10
2 · (8 3y) 5 · (1 2y) = 6y + 17
16 6y 5 + 10y = 6y + 17
11 + 4y = 6y + 17
11 17 = 6y 4y
6 = 2y y = 6 2 y = 3
834. Яке
135 − x = 3(83 − x)
135 − x = 249 − 3x
2x = 114 x = 57

4 · (2 4x) = 10 · (1 2x) + 5 · (x + 3)
8 16x = 10 20x + 5x + 15
8 16x = 25 15x 16x + 15x = 25 8 x = 17 x = 17
а)6x : 8 = 3 : 2
6x
8 = 3 2
6x · 2 = 8 · 3
12x = 24
x = 24 : 12
x = 2
г)7 : 2 = 5(x 1) : 3
7 2 = 5(x 1)
3
7 · 3 = 2 · 5(x 1)
21 = 10(x 1)
21 = 10x 10
10x = 31
x = 31 : 10
x = 3,1
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
б)5 : (2x) = 3 : 18
5 2х = 3 18
5 · 18 = 2x · 3
90 = 6x
x = 90 : 6
x = 15
ґ)2 : m = m : 8
2 m = m 8
2 · 8 = m · m
16 = m²
m = 4 або m = 4
837. За властивістю пропорції,
а)1 : (3x) = 4 : 12
1 3х = 4 12
1 · 12 = 3x · 4
12 = 12x
x = 12 : 12
x = 1
838. Розв’яжи рівняння
б)5 : (c 3) = 2 : 3 5 (c 3) = 2 3
5 · 3 = 2 · (c 3) 15 = 2(c 3) 15 = 2c 6
2c = 21
c = 21 : 2
c = 10,5
а) (x + 4)(x 4) = x² 5x + 9
x² 16 = x² 5x + 9
x² x² 16 = 5x + 9
16 = 5x + 9
16 9 = 5x
25 = 5x x = 5
839. Розв’яжи рівняння а) (6 y)(y + 6) = y² 2y(y 3)
36 y² = y² 2y² + 6y
36 y² = y² + 6y
36 = 6y
y = 36 : 6
y = 6
840. Знайди корені рівняння
в)(x 5) : 2 = 5 : 4
(x 5) 2 = 5 4
4(x 5) = 10 4x 20 = 10 4x = 30
x = 30 : 4
x = 7,5
д)2n : 9 = 2 : n 2n 9 = 2 ����
2n · n = 9 · 2
2n² = 18
n² = 18 : 2 n² = 9 n = 3 або n = 3

в)x : 10 = 0,1 : x
x 10 = 0,1 х
x · x = 10 · 0,1
x² = 1
x = 1 або x = 1
б) 8 + 9x(x + 4) = (3x 2)(3x + 2)
8 + 9x² + 36x = 9x² 4
9x² + 36x + 8 = 9x² 4
36x + 8 = 4
36x = 12
x = 12 36 x = 1 3
б) 2x(2x 4) 17 = (5 + 2x)(2x 5)
4x² 8x 17 = 10x 25 + 4x² 10x
4x² 8x 17 = 4x² 25
8x 17 = 25
8x = 8
x = 8 : ( 8)
x = 1
а) (x + 1)² 9 = 0
x² + 2x + 1 9 = 0
x² + 2x 8 = 0
(x 2)(x + 4) = 0
x = 2 або x = 4
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
б) (3x 2)² = 121
(3x 2)² 11² = 0
(3x 2 11)(3x 2 + 11) = 0
(3x 13)(3x + 9) = 0
3x 13 = 0 або 3x + 9 = 0
3x = 13 або 3x = 9
x = 41 3 або x = 3
в) (x 1)² (3 x)² = 0
(x 1 3 + x)(x 1 + 3 x) = 0
2(2x 4) = 0
4(x 2) = 0
x 2 = 0
x = 2
ґ) (x² + x + 1)(x 1) = x(x² + 1)
x³ 1 = x³ + x
x = 1
841. Знайди корені рівняння
а) 4 (x 3)² = 0
(2 x + 3)(2 + x 3) = 0
(5 x)(x 1) = 0
5 x = 0 або x 1 = 0
x = 5 або x = 1

г) (4x 10)² = (3x 4)² (4x 10)² (3x 4)² = 0
(4x 10 3x + 4)(4x 10 + 3x 4) = 0
(x 6)(7x 14) = 0
x 6 = 0 або 7x 14 = 0
x = 6 або x = 2
д) (9x² + 4) · 3x = (3x + 2)(9x² 6x + 4)
27x³ + 12x = 27x³ + 8
12x = 8 x = 8 12 = 2 3
в) (3x 2)² (x + 6)² = 0
(3x 2 x 6)(3x 2 + x + 6) = 0
(2x 8)(4x + 4) = 0
2x 8 = 0 або 4x + 4 = 0
x = 4 або x = 1
ґ) (2x + 1)(4x² 2x + 1) = 4x(2x² 5)
8x³ + 1 = 8x³ 20x
1 = 20x
x = 1
б) (5x + 4)² = 196
(5x + 4)² 14² = 0
(5x + 4 14)(5x + 4 + 14) = 0
(5x 10)(5x + 18) = 0 5x 10 = 0 або 5x + 18 = 0
x = 2 або x = 33 5
г) (2x 1)² = (4 5x)²
(2x 1)² (4 5x)² = 0
(2x 1 4 + 5x)(2x 1 + 4 5x) = 0
(7x 5)(3 3x) = 0
7x 5 = 0 або 3 3x = 0
x = 5 7 або x = 1
д) x(8x² 5) = (4x² 10x + 25)(2x + 5)
8x³ 5x = 8x³ + 125 5x = 125
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
x = 25
842.
а) 3ax + 96 = 0
Якщо х = 8, то
24a + 96 = 0;
24a = 96;
a = 4
843. При якому
а) 5ax + 120 = 0
Якщо х = 3, то
15a + 120 = 0;
15a = 120;
a = 8
844. При яких
а) 2(x 1) = 4 x і ax = x + a
2(x 1) = 4 x
2x 2 = 4 x
3x = 6
x = 2
ax = x + a
a·2 = 2 + a
2a = 2 + a
a = 2
845. При яких
a
а) 3(x 2) + 5 = 2x і ax + a = x
3(x 2) + 5 = 2x
3x 6 + 5 = 2x
3x 1 = 2x
x = 1
ax + a = x
a·1 + a = 1
a + a = 1
a = 1 2
846.
а) 4(х + 3) = 36 і 3х + 2m = 19
4(х + 3) = 36
4х + 12 = 36
4х = 24
х = 6
3х + 2m = 19
18 + 2m = 19
2m = 1
m = 1 2
847.
2m(x + 8) = 44 і 2(3x − 2) = 11 + x
б) 1а 4 х =1 2
Якщо х = 2, то 1 а 4 · 2 = 1 2; 1 1 2 a = 1 2; a = 3
б) 4(a – 3)x = 48
Якщо х = 6, то
24(a 3) = 48;
a 3 = 2;
a = 5
б) (1 a)x = x і x² = 0
x² = 0
x = 0
(1 a)x = x
(1 a) · 0 = 0
При
якому
a

2(3x − 2) = 11 + x
б) (1 + 2a)x = x і x 1 = 0
x 1 = 0
x = 1
(1 + 2a)x = x
(1 + 2a)·1 = 1
1 + 2a = 1
2a = 0
a = 0
б) (8 − х) − 7 = 28 і 5(2х − 3m) = 0
(8 − х) − 7 = 28
8 − х = 35
х = −27
5(2х − 3m) = 0
5(−54 − 3m) = 0
270 − 15m = 0
15m = −270
m = −18
2m(x + 8) = 44
6x − 4 = 11 + x
5x = 15 x = 3
848. При
а) x² = k; при k < 0
б) |x| + k = 0; при k > 0
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
2m(3 + 8) = 44 22m = 44 m = 2
в) k + 2x = 2(x − 3), k ≠ −6
849. Запиши

Лінійне
Рівнянням
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
856.
Безліч коренів
857. Знайди корінь рівняння. а) 0x = 35 0 ≠ 35
Коренів немає б) 0y = 13 13 0 = 0
в) 2x = 3 + 2x
немає г) 2x + 5 = 3(x + 5) 2x + 5 = 3x + 15 х = 10 x = 10
858. Поясни, чому не має розв’язків рівняння.
а) x + 15 = x 15 = 0 б) 3x 7 = 3x 7 = 0 в) 17 x = 5 x 17 = 5
Це неможливо, тому рівняння не мають розв'язків.
859. Поясни, чому має безліч розв’язків рівняння. а) 3x = 2x + x; 3x = 3x, x будь яке число б) 6y = 7y y; 6y = 6y, x будь яке число
860. Чи правильна схема, зображена
861. Зведи рівняння до
а) 2 – 3x = 5 – 7x
2 + 7x = 5 + 3x
4x = 3 x = 3 4 б) 15 – 3x = 7x – 5 15 + 5 = 7x + 3x
= 10x x = 2

в) 8z + 2 = 3z + 2 + 5z. 8z + 2 = 8z + 2, x будь яке число
3x + 2(x + 7) = 2x 3x + 2x + 14 = 2x 5x + 14 = 2x 3x = 14 x = 14 3 = 42 3 г) 4(2 + x) – x = 3x + 9
8 + 4x – x = 3x + 9
8 + 3x = 3x + 9
8 = 9
2x + x 7x + 3=8
4x + 3 = 8
4x = 8 3
4x = 5
ґ) 1 3 x = 6 − 1 2 x 1 3 x + 1 2 x = 6 (2x+3x) 6 = 6 5х 6 = 6 5x = 36 x = 36 5 = 71 5 д) x 4 2 = 1 x−4 = 2 x = 6
б) y 5y=8 y y + y 5y = 8 3y = 8 y = 8 3 = 22 3
x = 5 4 = 11 4
в) c + 31(2 c)=32c
c + 62 31c = 32c
62 c 31c = 32c
62 = 32c + 32c
62 = 64c
c = 62 64 = 31 35
863. Розв’яжи рівняння а) 32x = 16
x = 16 : 32
x = 0,5
г) 2(5 8x) = 4(4x + 3)
10 16x = 16x 12
16x 16x = 12 10
0x = 22
Розв'язків
864. Розв’яжи рівняння
а) 0,5y = 0,5
y = 0,5 : ( 0,5) y = 1
г) 2 5y = 5(1 2y)
2 5y = 5 10y
10y 5y = 5 2
5y = 3
y = 3 5
865. Марк
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html

б) x + 4x = 5x 5x = 5x
г) 0,7=2(x + 3,5) 2x
0,7 = 2x + 7 2x
0,7 = 7 Розв'язків
ґ) 2(x 3) = 3(2x 1) 2x 6 = 6x 3
2x 6x = 6 3 4x = 3 x = 3 4
б) 6x = 8 + 6x
6x 6x = 8
0x = 8
в) x = 3(x + 1) 2x x = 3x + 3 2x
x x = 3 0x = 3
Розв'язків не має
д) 4(5 x) = 5x + 2
20 4x = 5x + 2
5x 4x = 2 20
x = 18
Розв'язків не має в) 4 3x = 8(1 x) 4 3x = 8 8x 8x 3x = 8 4
5x = 4 x = 4 5
ґ) 8(9 2x) = 5(2 3x) 72 16x = 10 15x 15x 16x = 10 72 x = 62 x = 62
д) 5(z + 3) = 8(10 z)
5z + 15 = 80 8z
5z + 8z = 80 15
13z = 65
z = 65 : 13 z = 5
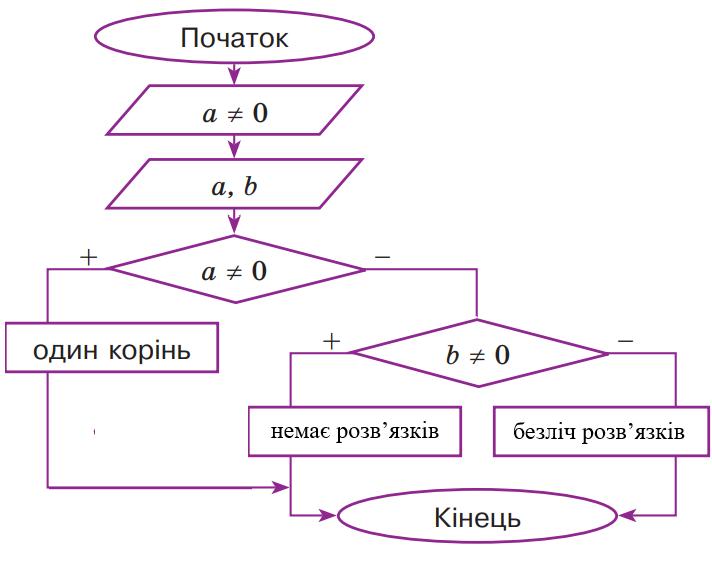
866. Установіть
1 – Б один; 2 – А жодного; 3 – Г безліч.
867. Розв’яжи рівняння
a) 3(x + 4) + 6(11 x) = 9
3x + 12 + 66 − 6x = 9
78 − 3x = 9
3x = 9 − 78
3x = 69
x = 23
в) 7(x 5) 3(2x 6) = 10
7x − 35 − 6x + 18 = 10
x − 17 = 10
x = 27
868. Розв’яжи рівняння
a) 7(4 t) + 3(t 5) = 9t
28 − 7t + 3t − 15 = 9t
13 − 4t = 9t
4t − 9t = 13
13t = 13
t = 1

в) 5(3 2x) (12 7x) = 0
15 − 10x − 12 + 7x = 0
3 − 3x = 0
3x = 3
x = 1
б) 8(1 x) + 5(x 2) = 2
8 − 8x + 5x − 10 = 2
3x − 2 = 2 3x = 4 x = 4 3 = −11 3
г) 18 + 3(x 5) + 8x = 2(5 + 2x)
18 + 3x − 15 + 8x = 10 + 4x
11x + 3 = 10 + 4x
11x − 4x = 10 − 3
7x = 7 x = 1
б) 3(x + 1,5) + 2(3 + x) = 5
3x + 4,5 + 6 + 2x = −5
5x + 10,5 = −5
5x = 5 − 10,5
5x = 15,5
x = 15,5 : 5
x = 155 : 50
x = 3,1
г) 5z + 2(4 + z) = 3z + 28
5z + 8 + 2z = 3z + 28
7z + 8 = 3z + 28
7z − 3z = 28 − 8
4z = 20
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
869. Розв’яжи рівняння a) 3(2x + 3) 5(7 4x) 2(5x + 4) = 2
6x + 9 35 + 20x 10x 8 = 2
16x 34 = 2
16x = 34 2
16x = 32
x = 2
870. Розв’яжи рівняння a) 6(x + 2) + 3(3x + 7) = 4(5 + 4x) 7
6x + 12 + 9x + 21 = 20 + 16x 7
15x + 33 = 16x + 13
15x 16x = 13 33
x = 20
б) 8(4 3x) + 7(x 3) + 3(9 + 7x) = 10
32 24x + 7x 21 + 27 + 21x = 10
4x + 38 = 10
4x = 28 x = 7
x = 20 б) 5(12 x) 11(4x 5) = 9(9 5x) 26
871. Розв’яжи рівняння
a) 1 2 x + 1 4 (x 2) = x | · 4
2x + x 2 = 4x
2x + x 4x = 2
x = 2
60 5x 44x + 55 = 81 45x 26
49x = 55 45x
49x = 55 115 4x = 60 x = 15
x = 2 б) 1 2 (4x 5) + 3 2 (2x + 1) = x + 3 | · 2 4x 5 + 6x + 3 = 2x + 6 4x + 6x 2x = 6 + 5 3
в) 2 3(5 3x) + 1 3 (2 + 9x) = 2x 1 | · 3
2(5 3x) + 1(2 + 9x) = 3(2x 1)
10 6x + 2 + 9x = 6x 3
6x + 9x 6x = 3 10 2
8x = 8
x = 1
3x = 15 x = 5 г) 2 + 1 4 (8x + 1) = 5x + 3 4 (4x 1) | · 4 4 · 2 + (8x + 1) = 4 · 5x + 4(4x 1)
872. Розв’яжи рівняння
a) 1 2 + 2(1 3n + 1) = 3n
1 2 + 2 3n + 2 = 3n | · 6
3 + 4n + 12 = 18n
3 + 12 = 18n 4n
15 = 14n
8 + 8x + 1 = 20x + 12x 3 9 + 8x = 32x 3 8x 32x = 3 9 24x = 12 x = 1 2
n = 15 14 = 1 1 4 б) 3 5 (6 + 7x) 2x = 2 5 (4 + 3x) + 3 | · 5 5 · 3 5 (6 + 7x) 5·2x = 5 · 2 5 (4 + 3x) + 5·3
3(6 + 7x) 10x = 2(4 + 3x) + 15
18 + 21x 10x = 8 + 6x + 15
18 + 11x = 23 + 6x
11x 6x = 23 – 18 5x = 5 x = 1
873. Розв’яжи рівняння a) (2x 3) 3 + (x 1) 2 = (5x 3) 6 | · 6
2(2x 3) + 3(x 1) = 5x 3

4x 6 + 3x 3 = 5x 3
б) (3x + 1) 4 (2x 4) 3 = 3 (7 x) 2 | · 12
3(3x + 1) 4(2x 4) = 36 6(7 x) 9x + 3 8x + 16 = 36 42 + 6x
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
7x 9 = 5x 3
7x 5x = 3 + 9
2x = 6
x = 6 2 x = 3
в)
(2 3x)
2 + (6x + 1) 5 = (x 4) 4 | · 20
10(2 3x) + 4(6x + 1) = 5(x 4)
20 30x + 24x + 4 5x 20
24 6x 5x 20
24 + 20 = 5x + 6x
44 = 11x
x + 19 = 6x 6 x 6x = 6 19 5x = 25 x = 25 5 x = 5
x = 44 11 x = 4 г)
(x + 6) 5 (5 2x) 3 = 2x (3x 2) 9 | · 30 6(x + 6) 10(5 2x) = 60x + 15(3x 2)
6x + 36 50 + 20x = 60x 45x + 30 26x 14 = 15x + 30 26x 15x = 30 + 14 11x = 44 x = 44 11 x = 4
874. Розв’яжи рівняння а)
(x + 1)
2 + (3x 5) 6 = (5x 6) 4 | · 12
6(x + 1) + 2(3x 5) = 3(5x 6)
6x + 6 + 6x 10 = 15x 18
12x 4 = 15x 18
12x 15x = 18 + 4 3x = 14
3x + 1) 5 (6 x) 4 = 3x + (5x + 16) 2 | · 20 4(3x + 1) 5(6 x) = 60x + 10(5x + 16)
12x + 4 30 + 5x = 60x + 50x + 160 12x + 5x 60x 50x = 160 + 30 4 93x = 186 x = 186 93 x = 2 875.
1) 5x 4(x 6) = 40
5x 4x + 24 = 40
x = 16
2) 16 6 = 10
10

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
x 1 3 x = 1 3
2 3 x = 1 3
2x = 1
x = 1 2
невідоме число.
Відповідь: 1 2 .
878. Розв’яжи рівняння і зроби перевірку
а) |x| + 5 = 12
|x| = 12 5
|x| = 7
x = 7 або x = 7
Перевірка:
|7| + 5 = 7 + 5 = 12
| 7| + 5 = 7 + 5 = 12
в) |x 2| = 12
x 2 = 12 або x 2 = 12
x = 14 або x = 10
Перевірка:
|14 2| = |12| = 12
| 10 2| = | 12| = 12
б) 2|x| + 3 = 25
2|x| = 25 3
2|x| = 22
|x| = 22 : 2
|x| = 11
x = 11 або x = 11
Перевірка:
2|11| + 3 = 2 • 11 + 3 = 22 + 3 = 25
2| 11| + 3 = 2 • 11 + 3 = 22 + 3 = 25
г) |2x 3| + 8 = 5 |2x 3| = 5 8 |2x 3| = 3
Розв'язків не має
879. Розв’яжи рівняння і зроби перевірку
а) |x| 8 = 3
|x| = 3 + 8
|x| = 5
x = 5 або x = 5
Перевірка:
|5| 8 = 5 8 = 3
| 5| 8 = 5 8 = 3
в) |x + 4| = 0
x + 4 = 0 або x + 4 = 0
x = 4
Перевірка:
| 4 + 4| = |0| = 0
880. Розв’яжи тільки
а) (x² 2)² x⁴ = 0
(x² 2)² = x⁴
(x² 2)(x² 2) = x⁴
x⁴ 4x² + 4 = x⁴
4x² + 4 = 0
4x² = 4
x² = 1

x = 1 або x = 1
б) |2x| 3 = 5
|2x| = 5 + 3
|2x| = 8
2x = 8 або 2x = 8 x = 4 або x = 4
Перевірка:
|2(4)| 3 = |8| 3 = 8 3 = 5
|2( 4)| 3 = |8| 3 = 8 3 = 5
г) |x 1| + 7 = 3 |x 1| = 3 7 |x 1| = 4
Розв'язків не має
рівнянь.
б) (x + 2)² (x + 1)² = 0
(x + 2 + x + 1)(x + 2 x 1) = 0
(2x + 3) · 1 = 0
2x + 3 = 0
2x = 3
x = 3 2
881. Розв’яжи тільки
a) (x² 4)² x⁴ = 8
(x² 4)² = x⁴ + 8
x⁴ 8x² + 16 = x⁴ + 8
8x² + 16 = 8
8x² = 8 16
8x² = 8
x² = 1
x = 1 або x = 1
882. Розв’яжи рівняння а) (a + 3)x = 12
x = 12
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
b) (x + 3)² (x 3)² = 12
(x + 3 + x 3)(x + 3 x + 3) = 12
2x • 6 = 12
12x = 12 x = 1
(a + 3) a ≠ 3 б) (a 6)x = a 6 x = (a + 6) (a 6) = 1 a ≠ 6
883. Розв’яжи рівняння а) (a 4)x = 15
x = 15
(a 4) a ≠ 4 б) (a + 7)x = a + 7 x = (a 7) (a + 7) a ≠ 7
884. Доведи,
а) (a² + 3)x = 5; x = 5 (a²+3)
(a² + 1)x =
в) 4 5x = a²x;
значень a.
Отже, рівняння
а) (a² + 6)x = 5; x = 5 (a²+6), де a² + 6 ≠ 0.
Оскільки a² ≥ 0, то a² + 6 > 0
єдиний корінь.
б) (a² + 8)x = a; x = a (a²+8), де a² + 8 ≠ 0.
в) a²x = 2x + 3; x(a² + 2) = 3; x = 3 (a²+2), де a² + 2

в) (a² + 5)x = 2 x = 2 (a² + 5) a ≠ 0
в) (a² + 2)x = 4 x = 4 (a² + 2) a ≠ 0
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
Єдиний корінь при k ≠ 3.
Не має коренів при k = 3.
Безліч коренів немає. в) kx = k:
Єдиний корінь при k ≠ 0.
Не має коренів немає.
Безліч коренів при k = 0. г) (2 k)x = (2 k):
Єдиний корінь при k ≠ 2.
Не має коренів немає.
Безліч коренів при k = 2.
887. Для кожного з пунктів
має єдиний корінь; 2)
а) mx = 12
1) m ≠ 0; 2) m = 0;
3) неможливо.
б) (m – 5)x = 15; 1) m ≠ 5; 2) m = 5;
3) неможливо.
в) mx = 2т;
1) m ≠ 0;
2) неможливо;
3) m = 0;
г) (7 + m)x = (7 + m)
1) m ≠ 7;
2) неможливо; 3) m = 7.
888. Для
щоб утворилось рівняння,
коренів. а)
1) 5x 4 + 2x = 0;
2) 5x 4 + 2x = 7x 4; 3) 5x 4 + 2x = 7x; б)
1) 2(1, 5x 7) 3x = x; 2) 2(1, 5x 7) 3x = 14; 3) 2(1, 5x 7) 3x = 0; в)
1) 3x+2 5 = 1;
2) 3x+2 5 = (3x+2)

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
(150 + x) + 150 = (x +
Складемо рівняння:
2x = 300 + x
2x x = 300 x = 300
150 + 300 = 450 (г) важить голова; 300 • 2 = 600 (г) важить тулуб;
450 + 600 + 150 = 1200 (г) = 1 кг 200
Відповідь: 1 кг 200 г. 890. Значення виразу 3(x+a) 2 +0,5x+3
виразу, якщо x = 5?
3(x + a)
2 + 0,5x + 3 = 4, при x = 1
3( 1 + a)
2 + 0,5( 1) + 3 = 4
( 3 + 3a)
2 1 2 + 3 = 4
( 3 + 3a)
2 + 5 2 = 4| · 2
3 + 3a + 5 = 8
3a = 6 a = 2
3(5 + 2)
2 + 0,5 · 5 + 3 = 21 2 + 5 2 + 3 = 26 2 + 3 = 13 + 3 = 16 891. Перебуваючи
Оператор 1:
1 хв → 10 грн
t хв (���� ≥ 1) → 10 + 2 ∙ (t - 1)
C1(t) = 10 + 2(t - 1) = 2t + 8
Оператор 2:
1 хв → 7 грн
t хв (���� ≥ 1) → 7 + 3 ∙ (t - 1)
C2(t) = 7 + 3(t - 1) = 3t + 4
2.

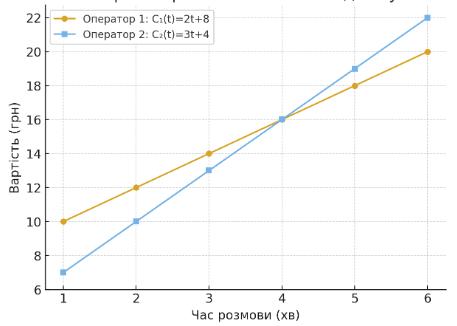
У точці t = 4 обидва оператори дають однакову ціну (16 грн).
4. Висновок
Якщо розмова коротка (1–3 хв) вигідніше користуватися другим оператором.
Якщо розмова 4 хв різниці немає.
Якщо розмова довша за 4 хв вигідніше користуватися першим оператором.
892. Знайди значення виразу.
а) 5a³ . Якщо а = 0,2, то
5 • 0,2³ = 5 • 0,008 = 0,04;
б) 2x2 – x4 – 5. якщо х = 2, то
2 • ( 2)² − ( 2)⁴ − 5 = 8 − 16 − 5 = 13;
в) a³ + 3a2 якщо а = 0,2, то
0,2³ + 3 • 0,2² = 0,008 + 3 • 0,04 = 0,008 + 0,12 = 0,128;
г) 3a4 – a2. якщо а = 1,2, то
3 • ( 1,2)⁴ − ( 1,2)² = ( 1,2)² • (3 • ( 1,2)²) − 1) = 1,44 • 3,32 = 4,7808.
893. Знайди:
а) 20 % від 350; 350 : 100 • 20 = 350 • 0,2 = 70; б) 30 % від 56 000; 5600 : 100 • 30 = 1680; в) 12 % від 0,75; 0,75 : 100 • 12 = 0,09; г) 125 % від 1,4.1,4 • 1,25 = 1,75.
894. Наведи приклад: а) Абстрактна задача:
895.

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
рівняння:
x + (1 + x) = 3
2x = 3 − 1
2x = 2
x = 1 − перше число; 1 + 1 = 2 − друге число.
Відповідь: 1 і 2. 897.Знайди два числа, якщо
Нехай перше число дорівнює x,
друге число 4x. Маємо
рівняння:
x + 4x = 10
5x = 10
x = 2 − перше число; 4 • 2 = 8 − друге число.
Відповідь: 2 і 8.
898. Знайди числа x і y, якщо x + y = 25 і
Підставимо
у + у = 25
2у = 25
у = 25 : 2
у = 12,5
x = y = 12,5
Відповідь: 12,5 і 12,5.
899. Учень
(x − 7) : 3 = 5
x − 7 = 5 • 3
x − 7 = 15
x = 15 + 7

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
абстрактна
число
х. Його
половина – це 1 2х, а
третя частина –1 3 х.
Маємо рівняння:
1 2 х − 1 3х = 0,5 | • 6
3х − 2х = 3
х = 3
Відповідь: число 3.
Перевірка:
1 2 • 3 − 1 3 • 3 = 3 2 − 1 = 1 2
б) абстрактна
Нехай перше число
дорівнює х, тоді
друге число (х – 1,6).
Маємо рівняння:
х + (х – 1,6) = 13,6
х + х – 1,6 = 13,6
2х = 15,2
х = 7,6 – перше
число;
7,6 – 1,6 = 6 – друге
число.
Відповідь: 7,6 і 6.
Перевірка:
7,6 + 6 = 13,6 і
7,6 – 6 = 1,6
в) прикладна Нехай на одну
частину припадає х, тоді перше число
становить х, а друге – 2х. Маємо
рівняння:
х + 2х = 105
3х = 105
х = 35 – перше
число; 2 • 35 = 70 – друге
число.
Відповідь: 35 і 70.
Перевірка: 35 + 70 = 105 901.
частин, тобто: x + (x + 130) = 430.
Спрощуємо рівняння: 2x + 130 = 430.
Віднімаємо 130 з обох частин рівняння: 2x = 300.
Ділимо обидві частини на 2: x = 150.
Отже,
x + 130 = 150 + 130 = 280 га. Таким

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
4. Розв'язуємо рівняння для знаходження х.
1. Спрощуємо рівняння: 4х = 84.
2. Ділимо обидві частини на 4:
х = 84 : 4
х = 21
Отже, довжина коротшої частини мотузки х = 21 метрів.
3. Довжина більшої частини: 3х = 3 • 21 = 63 метри.
Відповідь:
Довжина коротшої частини мотузки – 21 метр.
Довжина більшої частини мотузки – 63 метри.
903. Периметр прямокутника дорівнює 118 см, одна його сторона на 12 см довша за іншу. Знайдіть довжини сторін прямокутника. Запишіть план для складання рівняння та розв’яжіть задачу.
План для складання рівняння:
1.
2. Позначимо довжину довшої частини мотузки через х + 12 метрів.
3. Розв'язуємо рівняння для знаходження х.
Нехай коротша сторона прямокутника
Маємо рівняння:
2(х + х + 12) = 118
2(2х + 12) = 118
4х + 24 = 118
4х = 118 – 24
4х = 94
х = 94 : 4
х = 23,5 – коротша сторона.
х + 12 = 23,5 + 12 = 35,5 – довша сторона.
Відповідь: коротша сторона
х + 15 = 2х – 15
15 + 15 = 2х
30 = х.
2х = 2 • 30 = 60.

16 = 2х
х = 8.
3х = 3 • 8 = 24. Відповідь: у
Маємо рівняння:
х + (х + 10) = 50
х + х + 10 = 50
2х + 10 = 50
2х = 50 – 10
2х = 40
х = 20
х + 10 = 20 + 10 = 30
Відповідь: довжина
(х – 87) грн. Маємо рівняння:
х – 48 = 4(х – 87)
х – 48 = 4х – 348
х – 4х = 348 + 48
3х = 300
х = 100 (грн) – було грошей в
кожного спочатку.
Відповідь: 100 грн.

+ 24 = 72
Перевірка: У Оксани залишилося: 100 – 48 = 52 грн.
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
3x = 72 24
3x = 48
x = 16 (га) зорав третій трактор;
x + 9 = 16 + 9 = 25 (га) зорав другий трактор;
x + 15 = 16 + 15 = 31 (га) зорав перший трактор.
Відповідь: 31 га, 25 га, 16 га. 910. У трьох класах 79 учениць.
класі?
Нехай в першому класі х учениць, тоді в другому (x + 3) учениці, а в третьому (x 2) га. Маємо рівняння:
x + (x + 3) + (x 2) = 79
x + x + 3 + x 2 = 79
3x + 1 = 79
3x = 79 1
3x = 78
x = 26 (уч.) в першому класі;
x + 3 = 26 + 3 = 29 (уч.) в другому класі; x 2 = 26 2 = 24 (уч.) в третьому класі.
Відповідь: 26 учнів, 29 учнів, 24 учні. 911. За 3 дні
2(х 12) = 2х 24 доставок. Маємо рівняння:
х 12 + х + 2х 24 = 56
4х 36 = 56
4х = 56 + 36
4х = 92
х = 92 : 4
х = 23 (д.) здійснено
23 12 = 11 (д.) здійснено
2х 24 = 2 • 23 24 = 22 (д.)
Відповідь: 11 доставок, 23 доставки, 22 доставки.
912. Поле площею
х + 1,5 х + 2,5х = 860
5х = 860
х = 860 : 5 х = 172 (га)

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
5х х = 32
4х = 32
х = 8 (років) синові;
8 • 5 = 40 (років) батькові.
Відповідь: 8 років, 40 років
914. Матері 38 років, а доньці 12. Коли донька
матері? А вдвічі?
Нехай через х років донька буде
втричі молодшою за матір. Тоді, тоді
матері зараз (38 + x) років, а доньці (12 + x) років. Маємо рівняння.
38 + x = 3 • (12 + x)
38 + x = 36 + 3x
x 3x = 36 38 2x = 2 x = 1
Відповідь: через 1 рік донька буде
втричі молодшою за матір.
40 + х = 3 • (10 + х)
40 + х = 30 + 3х
2х = 10
х = 5
Відповідь:
була утричі?
а Сороці (2х 2) років.
2х 2 = 3(х 2)
2х 2 = 3х 6
2х 3х = 6 + 2
х = 4
х = 4 (р.) років Галці;
4 • 2 = 8 (р.) років Сороці.
8
5х + 3 = 4(х + 3) 5х + 3 = 4х + 12

+ 2 = 11
Нехай мати вдвічі старшою від
дочки стане через x років, тоді
матері зараз (38 + x) років, а доньці (12 + x) років. Маємо рівняння.
38 + x = 2 • (12 + x)
38 + x = 24 + 2x x 2x = 24 38 x = 14 x = 14
Відповідь: через 14 років донька буде вдвічі молодшою
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
45 + 2 = 47 (років) –
будинку
8n. Маємо рівняння: 8n = 5n + 12.
8n 5n = 12
3n = 12
n = 4.
5 • 4 = 20 (п.)
8 • 4 = 32 (п.) поверхів у першому будинку;
Відповідь: 32 поверхи і 20 поверхів.
919. Мати на 20 років старша за сина, а їх роки відносяться, як 7 : 2. Скільки років
матері?
Нехай коефіцієнт пропорційності
рівняння:
7n – 2n = 20
5n = 20 n = 4
7 • 4 = 28 (років) – вік матері;
2 • 4 = 8 (років) – вік синові.
Відповідь: 28 років і 8 років. 920. Поїзд
3x = 2,5(x + 10)
3x = 2,5x + 25
0,5x = 25
x = 25 : 0,5
x = 250 : 5
x = 50 (км/год)

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
– 3(х + 10) км. Маємо рівняння:
3х + 3(х + 10) = 450
3х + 3х + 30 = 450
6х + 30 = 450
6х = 450 – 30
6х = 420
х = 420 : 6
х = 70 (км/год) – швидкість першого автомобіля;
70 • 3 = 210 (км) – проїхав перший поїзд;
3 • (70 + 10) = 3 • 80 = 240 (км) – проїхав другий поїзд.
Перевірка: 210 + 240 = 450 км.
Відповідь: 210 км і 240 км.
923. Із міст A і
рівняння:
х – (210 – х) = 30
х – 210 + х = 30
2х = 240
х = 120 (км) – проїхав перший автомобіль
210 – 120 = 90 (км) –
120 : 1,5 = 80 (км/год) – швидкість першого автомобіля; 90 : 1,5 = 60 (км/год) – швидкість
Відповідь: 80 км/год і 60 км/год. 924. Велосипедист
2х + х + 4 = 28
3х + 4 = 28
3х = 28 – 4
3х = 24

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
х = 24 : 3
х = 8 (км/год) – швидкість
8 + 4 = 12 (км/год)
s, км v, км/год t, год
За течією 22x 22 x
Проти течії 18(5 x) 18 5 x
22x = 18(5 x)
22x = 90 18x
40x = 90
x = 2,25 (год) – час руху за течією річки; 2,25 • 22 = 49,5 (км) – відстань між пристанями.
Відповідь: 49,5 км.
926. Катер у стоячій воді
18x = 14(x + 0,5)
18x = 14x + 7
4x = 7
x = 1,75 (год) – час руху за течією річки; 1,75 • 18 = 31,5 (км) – відстань між пристанями.
Відповідь: 31,5 км.
927. До якого числа слід додати 4 і 19, щоб утворені суми відносились, як 8 : 11?
Нехай число, до якого потрібно
Маємо рівняння:
х + 4
х +19 = 8 11
11(x + 4) = 8(x + 19)
11x + 44 = 8x + 152
11x 8x = 152 44
3x = 108 x = 36
Відповідь:

18x + 72 = 18; 18x = 54; x = 3.
Цифри 3 і 5, число 35.
Відповідь: 35. 929.
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
Маємо рівняння:
8000 + x + 619 = 40x
8619 + x = 40x
x 40x = 8619
39x = 8619
x = 221
Перевірка: (8000 + 221) + 619 = 8840; 8840 = 40 • 221
Відповідь: трицифрове
4000 + 10x + 4 = 54x
4004 + 10x = 54x
44x = 4004
x = 91
Відповідь:
10x + 9 + 2x = 633
12x + 9 = 633
12x = 633 9
12x = 624
x = 624 : 12
x = 52
Відповідь:

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
x = 3,5.
Відстань: 60 • 3,5 = 210 км.
Відповідь: 210 км
933. Пасажирський
Знайди ці швидкості.
Потяг s, км v, км/год t, год
Пасажирський 3x x 3
Товарний 4(x 20) x 20 4
3x 4(x 20) = 10 3x 4x + 80 = 10 x = 70 (км/год) швидкість пасажирського потяга;
70 20 = 50 (км/год) швидкість товарного
Відповідь: 70 км/год і 50 км/год. 934. Від станції
6,75 + (32x 216) 27 = x + 5 12
729 + 4(32x 216) = 108x + 9 • 5
729 + 128x 864 = 108x + 45
128x 108x = 864 729 + 45
20x = 180 x = 9 (год)

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
За планом X 5 5x
Фактично x + 12 4 4(x + 12)
5x = 4(x + 12)
5x = 4x + 48
x = 48
Отже, за 5 днів майстри мали скласти 5x = 5 • 48 = 240 шаф.
Відповідь: 240 шаф.
937. Мотузку
Знайди
Нехай довжина коротшої частини мотузки
частини буде x + 0,5x = 1,5x (м).
складаємо рівняння: x + 1,5x = 25,
2,5x = 25, x = 10 (м) довжина коротшої частини.
1,5x = 1,5 • 10 = 15 (м) довжина довшої частини.
Перевірка. Сума довжин частин мотузки: 10 + 15 = 25 м. Умова задачі виконується. Відповідь: 10 м і 15 м. 938. Кількість уболівальників та уболівальниць команди A відноситься до кількості уболівальників та уболівальниць команди B, як 3 : 2. Якщо 8 уболівальників та уболівальниць перейдуть з команди A до
залишиться 3x 8, а в команді В стане 2x + 8.
(3x 8) : (2x + 8) = 5 : 6
6(3x 8) = 5(2x + 8)
18x 48 = 10x + 40
8x = 88
x = 11 (ос.)
11 • 3 8 = 33 8 = 25 (ос.) в команді А; 11 • 2 + 8 = 22 + 8 = 30 (ос.) в команді В.
Відповідь: 25 осіб і 30 осіб. 939. За моделлю складіть умову задачі та розв’яжіть
x + 5x + x 5 =
7x 5 = 555
7x = 555 + 5
7x = 560 x = 80 (г)
• 5 = 400

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
швидкістю долають шлях 24 • 1,25 = 30 км. Маємо рівняння:
0,5x + 30 = 36
0,5x = 6
x = 12 (км/год) швидкість першої велосипедистки; 24 12 = 12 (км/год) швидкість другої велосипедистки.
Відповідь: 12 км/год.
941. О 5 год 30 хв з міста A в місто B
місті B посадку на 30 хв і зі швидкістю 200 км/год
Знайди відстань між містами A і B.
Час старту: 5 год 30 хв
Час посадки: 12 год 45 хв
Швидкість v₁: 250 км/год
v₂: 200 км/год
зупинки: 30 хв = 0,5 год
Знайти відстань S.
Знайдемо загальний час події:
Час зворотного шляху:
Складаємо рівняння:
S 250 + 0,5 + S 250 = 7,25
S 250 + S 250 = 7,25 0,5
4S 1000 + 5S 1000 = 6,75 · 1000
4S + 5S = 6750
9S = 6750
S = 750 (км) –
20x + 12x + 10x + 15x + 360 = 60x
20x + 12x + 10x + 15x 60x = 360
3x = 360
x = 120 (шт.)

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
2 + х 4 + х 7 + 3 = x |·28
14x + 7x + 4x + 84 = 28x
14x + 7x + 4x 28x = 84
3x = 84
x = 28
Відповідь: 28 учнів.
944. Розв’яжи математичні кросворди (мал. 21.14 і 21.15).
Нехай число ліворуч дорівнює х. Тоді праворуч х + 36. Маємо рівняння:
3х = х + 36
2х = 36
х = 18 – число ліворуч; 18 + 36 = 54 – число праворуч.
Відповідь: 18 і 54.
2) Нехай число
Маємо рівняння:
х + 5х = 100
6х = 100
х = 100 6 = 50 3 = 162 3 – число праворуч; 50 3 • 5 = 250 3 = 831 3 – число ліворуч.
Відповідь: 831 3 і 162 3 .
буде 4 і в остачі 5. Знайди ці числа. Нехай більше число
х = (100 х) • 4 + 5
х = 400 4х + 5
5х = 405
х = 81 більше число; 100 81 = 19 менше число.
Відповідь: 81 і 19.
946. Обчисли
| 2,7| + 2,4 = 2,7 + 2,4 = 5,1
б) 2,4 + | 2,3| = 2,4 + 2,3 = 0,1
в) | 10,5| : 7 3,2 = 10,5 : 7 3,2 = 1,5 3,2 = 1,7
г)

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
а) (2с 1) (3с 2) = 2с 1 3с + 2 = с + 1
б) (1 2а) + 3(1 а) = 1 + 2а + 3 3а = 2 а
в) х² 2(8 + х) + 16 = х² 16 2х + 16 = х² 2х г) х² 2х + 2(2 х) = х² 2х + 4 2х = х² 4х + 4
949. Назви рівняння з двома змінними.
Рівняння з двома змінними:
а) 3x – y = 5 б) x3 + 4z = 9 в) xy – 28 = 3 д) x 2(3 y) = 5
Не підходять:
г) три змінні; ґ) змінних немає.
Які з цих рівнянь лінійні?
а), д)
950. Знайдіть кілька розв’язків рівняння.
а) x + y = 5; (0; 5), (1; 4), (2; 3).
б) x − y = 2; (2; 0), (3; 1), (4; 2).
в) xy = 30. (5; 6), (6; 5), (3; 10).
951. Чи має розв’язки рівняння?
а) x² + y² = −3; Рівняння не має розв'язків, оскільки x² + y² ≥ 0
б) |x| + |y| = 0; Рівняння має безліч розв'язків, наприклад: (1; −1), (2; −2), (0; 0).
в) x⁴ + |y| = −8. Рівняння не має розв'язків, оскільки x⁴ + |y| ≥ 0
952. Чи задовольняють значення x = 5 і y = –2 рівняння 5x – 2y = 10?
Якщо x = 5, y = 2, то 5 • 5 2 • ( 2) = 25 + 4 = 29
29 ≠ 10. Ні.
953. Яка з пар чисел є розв’язком рівняння 2х – 5у = 9?
А) Якщо x = 1, y = 2, то 2 • 1 5 • 2 = 2 10 = 8, 8 ≠ 9. Ні.
Б) Якщо x = 1, y = 2, то 2 • ( 1) 5 • 2 = 2 10 = 12, 12 ≠ 9. Ні.
В) Якщо x = 2, y = 1, то 2 • ( 2) 5 • 1 = 4 5 = 9, 9 ≠ 9. Ні.
Г) Якщо x = 2, y = 1, то 2 • 2 5 • ( 1) = 4 + 5 = 9, 9 = 9. Так.
Відповідь: Г (2; 1).
954. Які з пар (3; 2), (4; –3), (1; 4) є розв’язками рівняння?
а) 2x + 7у = 20:
(3; 2): 2•3 + 7•2 = 6 + 14 = 20. Так.
(4; 3): 2•4 + 7•( 3) = 8 21 = 13. Ні.
(1; 4): 2•1 + 7•4 = 2 + 28 = 30. Ні.
б) 2t + 3z = 10:
(3; 2): 2•3 + 3•2 = 6 + 6 = 0. Ні.
(4; 3): 2•4 + 3•( 3) = 8 9 = 17. Ні.
(1; 4): 2•1 + 3•4 = 2 + 12 = 10. Так.
в) x 4y = 16:
(3; 2): 3 4•2 = 3 8 = 5. Ні.
(4; 3): 4 4•( 3) = 4 + 12 = 16. Так.
(1; 4): 1 4•4 = 1 16 = 15. Ні.
Відповіді: а) (3; 2). б) (1; 4). в) (4; 3).
955. Які з пар (1; 2), (2; 7), (–1; 1) є розв’язками рівняння?
а) x + y = 0:
(1; 2): 1 + 2 = 3. Ні.

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
(2; 7): 2 + 7 = 9. Ні.
( 1; 1): 1 + 1 = 0. Так.
б) 5x y = 3:
(1; 2): 5•1 2 = 5 2 = 3. Так.
(2; 7): 5•2 7 = 10 7 = 3. Так.
( 1; 1): 5•( 1) 1 = 5 1 = 6. Ні.
в) 2x + 3y = 1:
(1; 2): 2•1 + 3•2 = 2 + 6 = 8. Ні.
(2; 7): 2•2 + 3•7 = 4 + 21 = 25. Ні.
( 1; 1): 2•( 1) + 3•1 = 2 + 3 = 1. Так.
Відповідь: а) ( 1; 1). б) (1; 2), (2; 7). в) ( 1; 1).
956. Знайди три будь-які розв’язки рівняння
а) x y = 16: (16; 0), (17; 1), (18; 2).
б) 2x + y = 3,5: (0; 3,5), (1; 1,5), ( 1; 5,5).
957. Знайди два будь-які розв’язки рівняння
а) 2x + y = 7; x = 2; y = 3; (2; 3); x = 0; y = 7; (0; 7).
958.Гра
b) 2x 3z = 10; x = 5; z = 0; (5; 0); x = 2; z = -2; (2; -2).
в) 4a + 5b = 20: (0; 4), (5; 0), ( 5; 8).
c) 4x + 5n = 21; x = 0; n = 4,2; (0; 4,2); x = 5; n = 0,2; (5; 0,2).
959. Заміни зірочки числами так, щоб пари (1; *), (4; *), (–2; *), (*; 2), (*; 0), (*; –5)
задовольняли рівняння x + 3y = 10.
x + 3y = 10
1. Якщо x = 1, то 1 + 3y = 10; 3y = 9; y = 3. Пара: (1; 3).
2. Якщо x = 4, то 4 + 3y = 10; 3y = 6; y = 2. Пара: (4; 2).
3. Якщо x = 2, то 2 + 3y = 10; 3y = 12; y = 4. Пара: ( 2; 4).
4. Якщо y = 2, то x + 3 · 2 = 10; x + 6 = 10; x = 4. Пара: (4; 2).
5. Якщо y = 0, то x + 3 · 0 = 10; x = 10. Пара: (10; 0).
6. Якщо y = 5, то x + 3 · ( 5) = 10; x 15 = 10; x = 25. Пара: (25; 5).
Відповідь: (1;3), (4;2), ( 2;4), (4;2), (10;0), (25; 5)
960. Заміни зірочки числами так, щоб пари (1; *), (3; *), (–4; *), (*; 2), (*; –3), (*; 0)
задовольняли рівняння 5x + y = 12. 5x + y = 12
1. Якщо x = 1, то 5 · 1 + y = 12; 5 + y = 12; y = 7. Пара: (1; 7).
2. Якщо x = 3, то 5 · 3 + y = 12; 15 + y = 12; y = 3. Пара: (3; 3).
3. Якщо x = 4, то 5 · ( 4) + y = 12; 20 + y = 12; y = 32. Пара: ( 4; 32).
4. Якщо y = 2, то 5x + 2 = 12; 5x = 10; x = 2. Пара: (2; 2).
5. Якщо y = 3, то 5x 3 = 12; 5x = 15; x = 3. Пара: (3; 3).
6. Якщо y = 0, то 5x + 0 = 12; 5x = 12; x = 2,4. Пара: (2,4; 0).
Відповідь: (1;7), (3; 3), ( 4;32), (2;2), (3; 3), (2,4;0)
961. Склади
a) (3;2); 2x + y = 8
2·3+2=6+2=8 б) ( 2;5); 3x y = 11 3·( 2) 5= 6 5= 11. в) (1 2; 2 5). 6x + 2y = 4
962.

a) (1;4);
( 2;3); в) ( 4,2; 1,5).
= 4.
3x + y = 7.
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
3·1 + 4 = 3 + 4 = 7 2x + y = 1 2·( 2) + 3 = 4 + 3 = 1
963.
a) x y = 2
1) x = 2 + y
2) y = x – 2
964.
a) x y = 7
1) x = 7 + y
б) 5x + y = 15
1) x = (15 y) 5 2) y = 15 5x
2) y = x – 7 б) x + 3y = 12 1) x = 12 3y
2) y = (12 x) 3
в) x 2y = 6
1) x = 6 + 2y 2) y = (x 6) 2
x.
в) 3x y = 6 1) x = 6 + 2y
2) y = (x 6) 2
965. Знайдіть таке число c, щоб пара (c; –c) задовольняла рівняння.
a) 2x + 3y = 20
2c 3c = 20
c = 20
c = 20 ( 20; 20). б) 5x y = 12
5c + c = 12
6c = 12
c = 2 (2; 2). в) x 8y = 9
c + 8c = 9
9c = 9
c = 1 (1; 1).
7x 3y = 20
7c + 3c = 20
10c = 20
c = 2 (2; 2).
966. Знайди таке число n, щоб пара (n; –n) задовольняла рівняння.
a) 5x + 4y = 3
5n 4n = 3
n = 3 б) 9x² y = 70
9n² + n – 70 = 0
n = 2,85 в) x² + 4y = 0 n² 4n = 0
n(n 4) = 0 n = 0 або n = 4 г) x + |y| = 4
n + | n| = 4
n + n = 4
2n = 4 n = 2
967. Знайди значення коефіцієнта a в рівнянні ax + 5y = 1, якщо відомо, що пара x = 3, y = –4 є розв’язком цього рівняння.
3a + 5 • ( 4) = 1
3a 20 = 1
3a = 21
a = 7
968. Знайди
3 • (−2) + 5k = 14
6 + 5k = 14
5k = 20
k = 4 969.
a) 5 • 2 a = 2
10 a = 2 a = 8

5 • 1 2a = 2 5 2a = 2 2a = 3 a = 1,5
5 • 4 3a = 2 20 3a = 2
3a = 18 a = 6
5 • ( 5) 9a =2
25 9a = 2
9a = 27 a = 3
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
дорівнювати
971. Чи має розв’язки рівняння
а) x² + y² = 1;
Розв'язків немає, оскільки x² ≥ 0 та y² ≥ 0, x² + y² ≥ 0. б) x² y² = 3;
Рівняння має розв'язок при y > x. в) x² + 3y² = 0.
Рівняння має розв'язок при x = 0 та y = 0.
972. Доведи, що рівняння не має розв’язків
а) x² + (y 1)² = 3;
x² ≥ 0 та (y 1)² ≥ 0, сума x² + (y 1)² ≥ 0. Отже, ліва частина рівняння не може
дорівнювати від'ємному числу. Розв'язків немає.
б) x² + y² + 2 = 2y;
x² + y² 2y + 1 + 1 = 0; x² + (y 1)² = 1. Оскільки x² ≥ 0 та (y 1)² ≥ 0, сума x² + (y 1)² ≥ 0, тому не може
рівняння дорівнювати 1
в) |x| + y² + 1 = 0. |x| ≥ 0 та y² ≥ 0, а отже |x| + y² + 1 ≥ 1, тому не може рівняння дорівнювати 0
Відповідь: Усі рівняння не мають розв'язків.
973. Розв’яжи рівняння
а) x² + (y 1)² = 0
x² = 0 і (y 1)² = 0
x = 0 y = 1
(0;1)
974. Розв’яжи рівняння
a) x² + (y 2)² = 0
x² = 0 i (y 2)² = 0
x = 0 y = 2
(0;2)
975. Розв’яжи рівняння
а) x² + y² + 1 = 2x
x² 2x + 1 + y² = 0
(x 1)² + y² = 0
(x 1)² = 0 i y² = 0
x = 1 y = 0
(1;0)
б) x² + y² + 9 = 6x
x² 6x + 9 + y² = 0
(x 3)² + y² = 0
(x 3)² = 0 i y² = 0
x = 3 y = 0
(3;0)

б) (x + 3)² + y² = 0 (x + 3)² = 0 і y² = 0 x = 3 y = 0
( 3;0)
б) (x 3)² + (y + 1)⁴ = 0
(x 3)² = 0 i (y + 1)⁴ = 0
x = 3 y = 1
(3; 1)
в) (2x + 3)⁴ + y² = 0
(2x + 3)⁴ = 0, y² = 0
2x + 3 = 0 і y = 0
x = 3 2 y = 0
( 3 2;0)
в) |x| + y² = 0
|x| = 0 i y² = 0
x = 0 y = 0
(0;0)
в) x² + 4y² + 1 = 4y
x² + 4y² 4y + 1 = 0
x² + (2y 1)² = 0
x² = 0 i (2y 1)² = 0
x = 0 y = 1 2
(0; 1 2)
г) 4x² + y² + 2 = 2(2x y)
4x² + y² + 2 = 4x 2y
4x² 4x + 1 + y² + 2y + 1 = 0
(2x 1)² + (y + 1)² = 0
(2x 1)² = 0 i (y + 1)² = 0
x = 1 2 y = 1
976. Розв’яжи рівняння
а)
x² + y² + 4 = 4x
x² + y² + 4 + 4x = 0
x² + 4x + 4 + y² = 0
(x + 2)² + y² = 0
(x + 2)² = 0 i y² = 0
x = 2 y = 0
( 2;0)
б) x² + y² + 16 = 8y
x² + y² 8y + 16 = 0
x² + (y 4)² = 0
x² = 0 i (y 4)² = 0
x = 0 y = 4
(0;4)
977. При яких
x² + y² = n
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
(1 2; 1)
в) x² + 2x + y² + 5 = 4y
x² + 2x + y² 4y + 4 = 0
(x + 1)² + (y 2)² = 0
(x + 1)² = 0 i (y 2)² = 0
x = 1 y = 2
( 1;2)
г) x² + y² + 8 = 4(y x)
x² + y² + 8 4y + 4x = 0
x² + 4x + 4 + y² 4y + 4 = 0
(x + 2)² + (y 2)² = 0
(x + 2)² = 0 i (y 2)² = 0
x = 2 y = 2 ( 2;2)
виконується лише за умови x = 0 і y = 0.
Відповідь: а) n = 0. б) n = 1.
978. При яких значеннях n рівняння
розв’язок а) |x| + |y| = n + 2
рівняння має тільки один розв'язок (0;0), якщо n = 2 б) (x 3)⁴ + y⁴ = n⁴,
рівняння має тільки один розв'язок (3;0), якщо n = 0
Відповідь: а) n = 2. б) n = 0.
979. Установи відповідність
1) А; 2) В; 3) Г.
980. Знайди натуральні значення x і y,
а) x + 4y = 13; (9;1), (5;2), (1;3)
б) 5x + y = 14; (1;9), (2;4)
в) 3x + 2y = 22. (2;8), (4;5), (6;2)
981.
а) x + 12y = 37; (25;1), (13;2), (1;3)
б) 3x + y = 16; (1;13), (2;10), (3;7), (4;4), (5;1)
в) 4x + 5y = 29. (1;5), (6;1)
982.
а) x² + y² = 2
x = 1, y = 1 → 1² + 1² = 2; (1; 1).
б) 2x² + y² = 9;

x = 2, y = 1 → 2•2² + 1² = 9; x = 0, y = 3 → 2•0² + 3² = 9; (2; 1), (0; 3).
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
983. Знайди цілі розв’язки рівняння
а) x² + y² = 5; (2;1), (1;2)
x = 2, y = 1 → 2² + 1² = 5; x = 1, y = 2 → 1² + 2² = 5;
б) x² + 3y² = 31. (2;3)
x = 2, y = 3 → 2² + 3 • 3² = 31;
984. Знайди таке значення a, щоб рівняння 3x – 2y2 = 6 мало розв’язок.
а) 3a 2 • 3² = 6
3a 18 = 6
3a = 24
a = 8 б) 3 • 2 2a² = 6 6 2a² = 6
2a² = 0 a = 0 в) 3a 2 • 0² = 6
3a = 6 a = 2 г) 3 • 8 2a² = 6
24 2a² = 6
2a² = 18 a² = 9 a = 3 або a = 3
985. Знайдіть двоцифрове число,
а) 2 рази:
10a + b = 2(a + b)
10a + b = 2a + 2b
10a 2a = 2b b
8a = b
a = b 8
b = 0 i a = 0;
b = 8 i a = 1.
(0;0) не підходить.
Невідоме число: 18
б) 6 разів:
10a + b = 6(a + b)
10a + b = 6a + 6b
4a = 5b
a = 5b 4
b = 4, тоді a = 5;
b = 8, тоді a = 10.
(10;8) не підходить.
Невідоме число: 54
986. Знайди двоцифрове число,
а) 3 рази;
10a + b = 3(a + b)
10a + b = 3a + 3b
7a = 2b
a = 2b
7
b = 7 і a = 2.
Невідоме число: 27
б) 5 разів;
10a + b = 5(a + b)
10a + b = 5a + 5b
5a = 4b
a = 4b 5
b = 5 і a = 4.
Невідоме число: 45
в) 4 рази:
10a + b = 4(a + b)
10a + b = 4a + 4b
6a = 3b
a = 3b 6
b = 8 i a = 4;
b = 6 i a = 3;
b = 4 i a = 2;
b = 2 i a = 1.
Невідомі числа: 12; 24; 36; 48
в) 8 разів.
10a + b = 8(a + b)
10a + b = 8a + 8b
2a = 7b
a = 7b 2
b = 2 і a = 7;
b = 4 і a = 14;
b = 6 і a = 21; b = 8 і a = 28.
(7:2) підходить.
Невідоме число: 72
(від 0 до 9).
10a + b = 2,5ab | • 2
20a + 2b = 5ab Оскільки 5ab і 20a діляться
10a + 5 = 2,5 • 5a;
10a + 5 = 12,5a; 2,5a = 5; a = 2.

Відповідь: 25.
988. Знайди
Позначимо
10a + b = 2ab;
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
10a +
9),
Оскільки 2ab і 10a діляться на 2, отже b повинно ділитися на 2, тоді b може
натуральні значення 2; 4; 6; 8.
Якщо b = 2, 4, 6, 8, то а набуває відповідно значення −1 3, −2, 3, 12 3 .
Єдиний розв'язок а = 3, b = 6.
Відповідь: 36.
989. Є труби завдовжки 7 м і 8 м. Скільки треба
трубопровід завдовжки 67 м?
Нехай труб довжиною 7 м було x штук, а
7x + 8y = 67
Значення у
990.
2x + 5y = 37
5y = 37 − 2x
y = (37 2x) 5 ,
Щоб у було цілим числом, вираз 37 − 2x
Отже, 37 − 2x = 5; 10; 15; 20; 25; 30; 35.
Розв'яжемо для кожного значення:
Якщо 37 − 2x = 5, тоді x = 16, у = 1.
Якщо 37 − 2x = 15, тоді x = 11, у = 3.
Якщо 37 − 2x = 25, тоді x = 6, у = 5.
Якщо 37 − 2x = 35, тоді x = 1, у = 7.
Отже, хлопчик може заплатити без решти так: 16 монет

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
x = (30 3y) 2 , Щоб х було цілим числом,
Перебираємо значення у:
Якщо у = 2, тоді x = (30 3 • 2) 2 = 12.
Якщо у = 4, тоді x = (30 4 • 2) 2 = 9.
Якщо у = 6, тоді x = (30 3 • 6) 2 = 6.
Якщо у = 8, тоді x = (30 3 • 8) 2 = 3.
Отже, хлопець може взяти: 12 коробок по 200 г і 2 коробки по 300 г.
9 коробок по 200 г і 4 коробки по 300 г.
6 коробок по 200 г і 6 коробок по 300 г.
3 коробки по 200 г і 8 коробок по 300 г. 992.
число.
десятки
a + b. За умовою:
(10a + b)(a + b) = 370. 370 = 37 • 2 • 5. Оскільки 37
Якщо 10a + b = 37, то a = 3, b = 7.
Отже, число 37.
Відповідь: 37.
993. Склади таке рівняння зі змінними x і y, щоб
а) ( 2;6) і (0;0); 3x + y = 0
б) (5;0) і ( 1; 3); x + 2y = 5
в) ( 3;2) і (0; 4); 2x + y + 4 = 0
г) (2;1) і (1;−1); 2x + y = 3
994. Побудуй графік функції y = –1,5x + 2. y = 1,5x + 2
Х 0 2
У 2 1

995. Доведи тотожність двома способами:
а) 4a⁴ + 1 = (2a² − 2a + 1)(2a² + 2a + 1);
1 спосіб: 4a⁴ + 1 =

= 4a⁴ + 4a² + 1 − 4a² = = (1 + 2a²)² − (2a)² = = (1 + 2a² 2a)(1 + 2a² + 2a) =
2 спосіб: (2a² − 2a + 1)(2a² + 2a + 1) = = (2a² + 1)² − (2a)² = = 4a⁴ + 4a² + 1 − 4a² = = 4a⁴ + 1
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
= (2a² 2a + 1)(2a² + 2a + 1)
Тотожність доведено
б) a⁴ + a² + 1 = (a² a + 1)(a² + a + 1)
1 спосіб:
a⁴ + a² + 1 = = a⁴ + 2a² + 1 a² = = (a² + 1)² a² = = (a⁴ + 1 a)(a² + 1 + a)
Тотожність доведено
2 спосіб:
(a² a + 1)(a² + a + 1) = = (a² + 1)² a² = = a⁴ + 2a² + 1 a² = = a⁴ + a² + 1.
Тотожність доведено
996. За якої умови рівняння (a – 1)x = 3a – 3 має безліч розв’язків? (а 1)х = 3(а 1)
а 1 = 0
а = 1.
Відповідь: рівняння має безліч розв'язків, якщо а = 1. 997. Скільки розв’язків має рівняння?
а) 0x + 0y = 20; жодного
б) 0x + 0y = 0; безліч
в) 0x + 2y = 0; безліч
г) 9x + 0y = 18; безліч
ґ) x + y = 0; безліч
д) x y = 1. безліч
998. Графіком якої функції є
Б) y = 2x + 8.
999. Чи відрізняється графік функції
графіки
а) 3x − 2y = 0;
б) 2x − 3y = 7;
в) 3(x − 4) = 4(y − 3).
Розв'язання:
- це точка з координатами (0; 0).
Щоб перевірити, чи проходить
підставити x = 0 та y = 0 у рівняння. Якщо рівняння виконується (тобто
а) 3x − 2y = 0
Підставимо x = 0 та y = 0:
3·0
0
2
0

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
в) 3(x − 4) = 4(y − 3)
Підставимо x = 0 та y = 0:
3(0 − 4) = 4(0 − 3)
3(−4) = 4(−3)
12 = −12
Рівність
координат.
Відповідь:
б) не проходить через початок координат.
1001.
Точка А(5;0) належить графіку. 5 3 • 0 = 5
Точка Б (8;1) належить графіку. 8 3 • 1 = 5
Точка В ( 1; 2) належить графіку. 1 3 • ( 2) = 5
Точка Г (4; 3) не належить графіку. 4 3 • ( 3) = 13
1002. Точка з абсцисою 2 належить
графіку рівняння 7x – 2y = 12.
Знайди ординату цієї точки.
Якщо х = 2, то 7 • 2 2у = 12; 14 2у = 12;
2у = 12 14;
2у = 2;
у = 1
1003.Точка з ординатою 1,5
належить графіку рівняння 5x + 4y = 16. Знайди абсцису цієї точки.
Якщо у = 1,5, то 5х + 4 • 1,5 = 16;
5х + 6 = 16;
5х = 16 − 6;
5х = 10;
х = 2
1004. Чи належить точка A(–3; 2) графіку рівняння?
а) 5x + 12y = 9; Так 5 • ( 3) + 12 • 2 = 15 + 24 = 9
б) 2x + 3y = x; Ні 2 • ( 3) + 3 • 2 = 6 + 6 = 0; 0 ≠ 3 в) 5(x + 3) = 4(y 2). Так 5 • ( 3 + 3) = 4 • (2 2), 0 = 0
1005. Чи належить точка М(2; –1) графіку рівняння?
а) 3x + 5y = 1; Так 3 • 2 + 5 • ( 1) = 6 5 = 1 б) 3x + 7y = y; Так 3 • 2 + 7 • ( 1) = 6 7 = 1; в) 2(x 2) = 4(y 1). Ні 2 • (2 2) = 4 • ( 1 1), 0 ≠ 8
1006. Виразіть з
a) x + y = 7 y = 7 x Якщо x = 0, то y = 7
Якщо x = 1, то y = 6 (0;7) і (1;6)

б) 2x + y = 5 y = 5 2x
Якщо x = 0, то y = 5
Якщо x = 1, то y = 3 (0;5) і (2;1)
в) 4x + 3y = 12 y = (12 4x) 3 y = 4 4 3 x
Якщо x = 0, то y = 4
Якщо x = 3, то y = 0 (0;4) і (3;0)
1007.
a) x y = 4 x = y + 4
Якщо y = 0, то x = 4
Якщо y = 1, то x = 5 (4;0) і (5;1)
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
б) x + 3y = 6 x = 6 3y
Якщо y = 0, то x = 6
Якщо y = 1, то x = 3 (6;0) і (3;1)
в) 2x + 5y = 10 x = (10 5y) 2 x = 5 5 2y
Якщо y = 0, то x = 5
Якщо y = 2, то x = 0 (5;0) і (0;2)
1008.
3x + 4y = 8 y = (8 3x) 4 y = 2 3 4 x
Якщо x = 0, то y = 2 (3 4) • 0 = 2;
Якщо x = 4, то y = 2 (3 4) • 4 = 2 3 = 1;
Якщо x = 8, то y = 2 (3 4) • 8 = 2 6 = 4;
Якщо x = 4, то y = 2 (3 4) • ( 4) = 2 + 3 = 5;
Якщо x = 8, то y = 2 (3 4) • ( 8) = 2 + 6 = 8;
Відповідь: (0;2), (4; 1), (8; 4), ( 4;5), ( 8;8).
Точки на графіку розміщені
1009.
3y = 6 2x y = (2x 6) 3 y = (2 3)x 2
Якщо x = 0, то y = (2 3) • 0 2 = 2;
Якщо x = 3, то y = (2 3) • 3 2 = 0;
Якщо x = 6, то y = (2 3) • 6 2 = 4 2 = 2;
Якщо x = 3, то y = (2 3) • ( 3) 2 = 2 2 = 4.
Відповідь: (0; 2), (3;0), (6;2), ( 3; 4).
Точки на графіку розміщені
рівняння a) x + y = 4
Х 0 4
У 4 0 б) 2x + y = 6 х 0 3 у 6 0 в) 3x + 2y = 0 х 0 2 у 0 3


1011. Graph the equation.
а) 2x + y = 5 Х 0 2,5
5 0
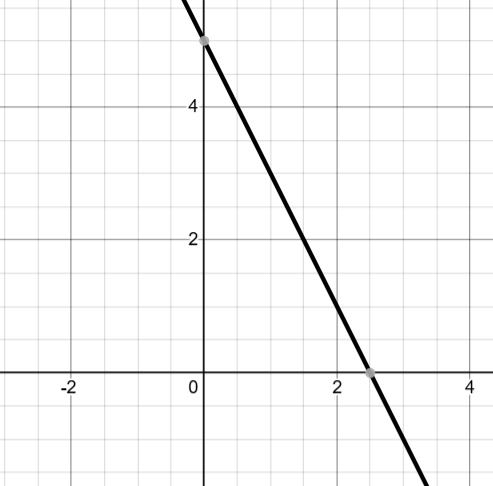
1012. На
абсциса дорівнює:
0,6x + y = 2,2:
а) Якщо абсциса x = 8:
0,6•( 8) + y = 2,2
4,8 + y = 2,2 y = 2,2 + 4,8 y = 7.
Ордината дорівнює 7.
в) Якщо абсциса x = 2:
0,6•2 + y = 2,2
1,2 + y = 2,2 y = 2,2 − 1,2 y = 1.
Ордината дорівнює 1.
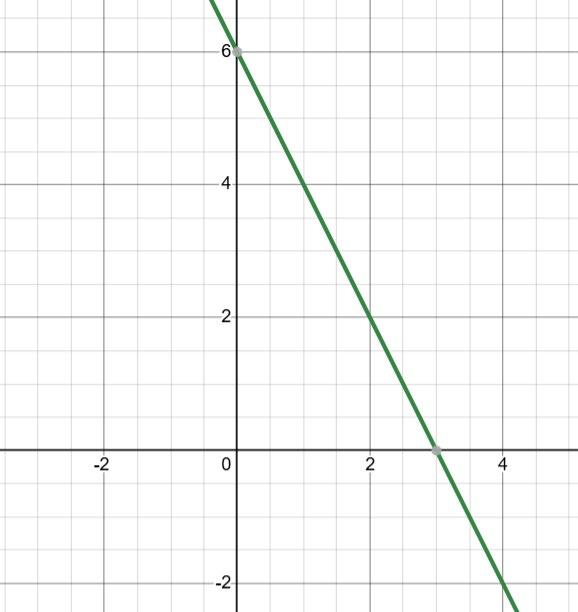
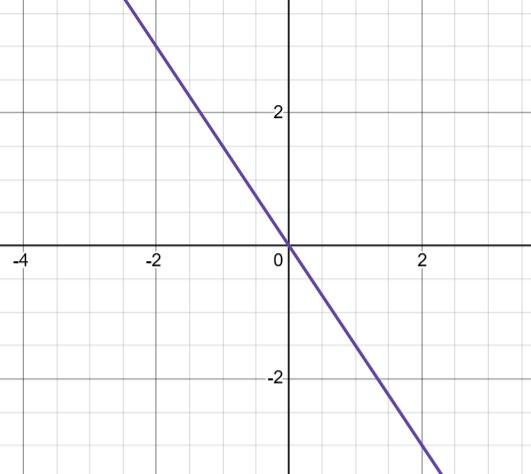


б) Якщо абсциса x = 3:
0,6•( 3) + y = 2,2 1,8 + y = 2,2 y = 2,2 + 1,8 y = 4.
Ордината дорівнює 4.
г) Якщо абсциса x = 7:
0,6•7 + y = 2,2
4,2 + y = 2,2
y = 2,2 − 4,2 y = 2.
Ордината дорівнює 2.
рівняння 11x – 4y = 80,
11x – 4y = 80:
а) Якщо ордината у = 31:
11х – 4•(−31) = 80
11х + 124 = 80
11х = 80 − 124
11х = 44

х = 44 : 11
б) Якщо ордината у = 20:
11х – 4•(−20) = 80
11х + 80 = 80
11х = 80 − 80
11х = 0
х = 0 : 11
х = 4.
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
х = 0.
4.
в) Якщо ордината у = 3,5:
11х – 4•( 3,5) = 80
11х + 14 = 80
11х = 80 14
11х = 66
х = 66 : 11
х = 6.
Абсциса дорівнює 6.
г) Якщо ордината у = 2:
11х – 4•2 = 80
11х 8 = 80
11х = 80 + 8
11х = 88
х = 88 : 11
х = 8.
Абсциса дорівнює 8.
1014. Графік рівняння 2x + 5y = c проходить
між точками, заданими умовами (1–4), та значенням с (А–Д), яке
1. Точка A(3; 1):
2•3 + 5•1 = c
6 + 5 = c
c = 11.
Відповідь: Г.
3. Точка C( 3; 4):
2 • ( 3) + 5•4 = c
6 + 20 = c
c = 14.
Відповідь: Д.
Відповідність: 1 – Г, 2 – В, 3 – Д, 4 – Б.
2. Точка B( 5; 2):
2 • ( 5) + 5•2 = c 10 + 10 = c
c = 0.
Відповідь: В.
4. Точка D( 2; 1):
2 • ( 2) + 5 • ( 1) = c 4 5 = c
c = 9.
Відповідь: Б.
1015. Яким має бути коефіцієнт a рівняння ax – 4y = 12, щоб графік цього рівняння
проходив через точку: а) Точка М(10; 2)
ax – 4y = 12
a • 10 – 4 • 2 = 12
10a – 8 = 12
10a = 12 + 8
10a = 20
a = 20 : 10
a = 2
в) Точка P(2; –3)
ax – 4y = 12
a • 2 – 4 • (–3) = 12
2a + 12 = 12
2a = 12 – 12
2a = 0
a = 0
б) Точка N(–1; –1)
ax – 4y = 12
a • (–1) – 4 • (–1) = 12 –a + 4 = 12
–a = 12 – 4 –a = 8 a = –8
Точка Q(6; 6)
ax – 4y = 12
a • 6 – 4 • 6 = 12
6a – 24 = 12
6a = 12 + 24
6a = 36
a = 36 : 6
a = 6
Відповідь: а) a = 2 б) a = –8 в) a = 0 г) a = 6 1016.
Точка N(2; 3)
6x + by = 0
6 • 2 + b • 3 = 0

12 + 3b = 0
Точка O(0; 0)
6x + by = 0
6 • 0 + b • 0 = 0
0 + 0 = 0
3b = 12
b = 12 : 3
b = 4
в) Точка P( 4; 8)
6x + by = 0
6 • ( 4) + b • 8 = 0
24 + 8b = 0
8b = 24
b = 24 : 8
b = 3
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
г) Точка R( 3; 2)
6x + by = 0
6 • ( 3) + b • ( 2) = 0
18 2b = 0
2b = 18
b = 18 : ( 2)
b = 9
Відповідь: а) b = 4; б) b будь яке; в) b = 3; г) b = 9. 1017.
3x 2y = 4
2y = 3x + 4
y = ( 3x + 4)
2 y = 1,5x 2
1,5x + c = 1,5x 2
c = 2
Відповідь: c = 2..
1018. Не
графіка рівняння
а) 3x + 2y = 6;
б) x + 5y = 10;
в) 3x + 4y = 24.
3x – 2y = 4?
а) Ось абсцис: y = 0; 3x = в; x = 2; (2; 0); ось ординат: x = 0; 2y = 6; y = 3; (0; 3);
б) якщо y = 0, то x = 10; (10; 0); якщо x = 0, то 5y = 10; y = 2; (0; 2);
в) вісь Ox: якщо y = 0
3x + 4 • 0 = 24
3x = 24
x = 8 (8; 0);
вісь Oy: якщо x = 0
3 • 0 + 4y = 24
4y = 24
y = 6 (0; 6).
1019. Не виконуючи побудови,
графіка рівняння
а) 2x − 7y = 14
Перетин з віссю Ox (y = 0):
2x − 7 • 0 = 14
2x = 14
x = 14 : 2
x = 7
Точка: (7; 0)
Перетин з віссю Oy (x = 0):
2 • 0 − 7y = 14
7y = 14

y = 14 : (−7)
y = −2
б) −x + 2y = 4
Перетин з віссю Ox (y = 0):
x + 2 • 0 = 4
x = 4
x = −4
Точка: (−4; 0)
Перетин з віссю Oy (x = 0):
0 + 2y = 4
2y = 4
y = 4 : 2
y = 2
Точка: (0; 2)
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
Точка: (0; −2)
в) 5x − 6y = 30
Перетин з віссю Ox (y = 0):
5x − 6 • 0 = 30
5x = 30
x = 30 : 5
x = 6
Точка: (6; 0)
Перетин з віссю Oy (x = 0):
5 • 0 − 6y = 30
6y = 30 y = 30 : (−6)
y = −5
Точка: (0; −5)
Відповідь: а) (7; 0) і (0; −2); б) (−4; 0) і (0; 2); в) (6; 0) і (0; −5).
1020.
2x + 3y = 5
Х 1 2.5
У 1 0
2x + 3y = 10
Х 2 5 У 2 0

1021.
5x − y = 7
Х 0 2
У 7 3
10x − 2y = 14
Х 0 2
У 7 3


2x − 9y = 18 і 3x − 5y = 15
графіків рівнянь
а) 3x + 2y = 6 і 2x + 4y = 11
3 2 ≠ 2 4 Прямі перетинаються.
б) 3x + 2y = 6 і 6x + 4y = 12
3 6 = 2 4 = 6 12 Прямі збігаються.
в) 2x − 7y = 1 і 6x − 21y = 5
2 6 = −7 −21 ≠ 1 5 Прямі паралельні.
1024. Побудуй
точки їх перетину
а) x + y = 5 і x − y = −1 y = 5 − x x 0 5
y 5 0
y = x + 1
x 0 2 y 1 3 Координати точки

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html

б) 2x − y = 6 і 4x − 3y = 12 y = 2x − 6 x 0 3
y 6 0
y = 4 3 x − 4 x 0 3
y 4 0 Координати точки
(3;0)

а) 2x + 3y = −9 і x + 3y = −6 y = −2 3 x −3
X 0 6
Y 3 0
y = − 1 3 x −2
X 0 4.5
Y 2 0

(−3;−1)

x − 5y = 0 і 2x − 5y = −10 y = 1 5 x x 0 5

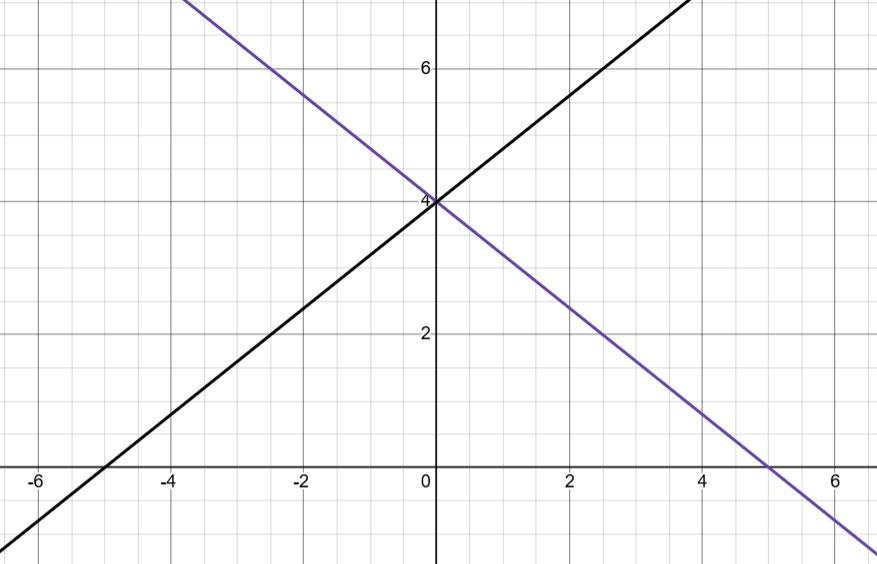




https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html



x = 4


0 • x + 3y = 6
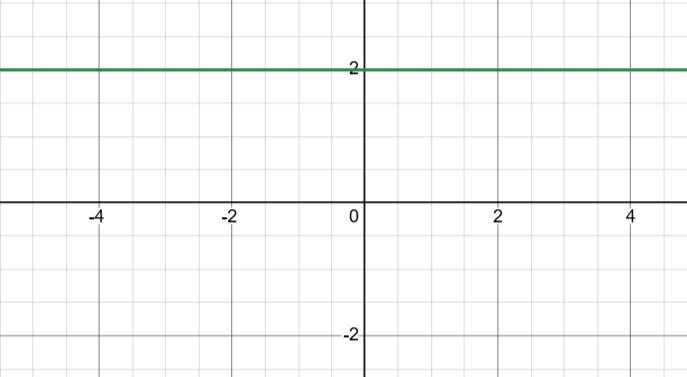
3y = 15



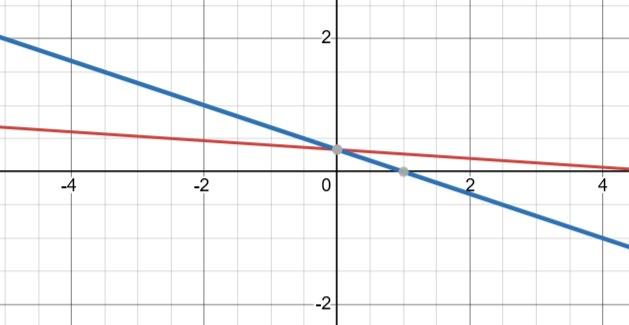
а) Точка А(4; 3)
y = 2x − 5
Перевірка: 3 = 2 • 4 − 5
y = 0,5x + 5
Перевірка: 3 = 0,5 • 4 + 5
y = x − 1
Перевірка: 3 = 4 – 1
в) Точка К( 2; 4)
y = x + 2
Перевірка: 4 = ( 2) + 2
y = 2x + 8
Перевірка: 4 = 2 • ( 2) + 8
y = 0,5x + 3
Перевірка: 4 = 0,5 • ( 2) + 3
Відповідь:
а) y = 2x − 5, y = 0,5x + 5, y = x − 1
б) y = 2x − 3, y = x − 3, y = 4x − 3
в) y = x + 2, y = 2x + 8, y = 0,5x + 3
г) y = x − 1, y = 3x − 3, y = 2x + 2
1032. Гра 1033.
Точка Х(2; 2)
y = kx
2 = 2k
k = 1
Рівняння: y = x
б) Точка С(0; 3)
y = 2x − 3
Перевірка: 3 = 2 • 0 − 3
y = x − 3
Перевірка: 3 = 0 − 3
y = 4x − 3
Перевірка: 3 = 4 • 0 3
г) Точка М(1; 0)
y = x − 1
Перевірка: 0 = 1 − 1
y = 3x − 3
Перевірка: 0 = 3 • 1 − 3
y = 2x + 2
Перевірка: 0 = 2 • 1 + 2
Точка Y( 5; 2) y = kx
2 = 5k; k = 2 5
Рівняння: y = 2 5 x Відповідь: а) y = x; б) y = 2 5 x 1034. Склади
Точка Р( 4; 6)
y = kx
6 = 4k
k = 6 4 = 3 2
1) y = kx 1 = 3k
k = 1 3
y = 3 2 x
y = 1 3 x Відповідь: а) y = 3 2x; б) y = 1 3 x.

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
y = kx + b, де: k
а) А( 3;0) і В(0;1)
Точка В(0;1) лежить на прямій.
1 = 0 • k + b
b = 1
y = kx + 1
Точка А( 3;0) лежить на прямій.
0 = 3k + 1
3k = 1
k = 1 3
Рівняння прямої: y = 1 3 x + 1
1036. Склади рівняння,
а) Точки Р(0; 3) і Q(3; 0)
y = kx + b
Точка Р(0; 3) лежить на прямій.
3 = 0 • k + b
b = 3
y = kx 3
Точка Q(3;0) лежить на прямій.
0 = 3k 3
3k = 3
k = 1
б) М(4; 0) і N(0; 5)
Точка М(4;0) лежить на прямій.
0 = 4k + b
b = 4k
y = kx + 5
Точка N(0;5) лежить на прямій.
5 = 0 • k + b
b = 5
0 = 4k + 5 4k = 5
k = 5 4
Рівняння: y = 5 4 x + 5
Рівняння: y = x 3 б) Точки С(0; 4) і D( 2; 0) y = kx + b
Відповідь: а) y = x 3, б) y = 2x – 4
Точка С(0; 4) лежить на прямій.
4 = 0 • k + b
b = 4
y = kx 4
Точка D( 2;0) лежить на прямій.
0 = 2k 4
2k = 4
k = 2
Рівняння: y = 2x – 4
1037. Запиши рівняння, графіки яких зображено на малюнку 23.6.
а) (0;2) і ( 1;0)
y = kx + b
Точка (0;2) лежить на прямій.
2 = 0 • k + b
b = 2
y = kx + 2
Точка ( 1;0) лежить на прямій.
0 = k + 2
k = 2
Рівняння: y = 2x + 2
с) (0;2) і (2;0)
y = kx + b
Точка (0;2) лежить на прямій.
2 = 0 • k + b
b = 2

y = kk + 2
б) (0; 4) і (4;0)
Точка (0; 4) лежить на прямій.
4 = 0 • k + b
b = 4
y = kx 4
Точка (4;0) лежить на прямій.
0 = 4k 4
4k = 4
k = 1
Рівняння: y = x – 4
d) (0; 2) і ( 4;0)
y = kx + b
Точка (0; 2) лежить на прямій.
2 = 0 • k + b
b = 2
y = kx 2
Точка (0;2) лежить
0 = 2k + 2
2k = 2
k = 1
Рівняння: y = x + 2
1038. Склади рівняння,
через точку
Прямі, які проходять
а) Точка К(4; 2)
2x − y = b
2 • 4 − 2 = b
8 − 2 = b
b = 6
Рівняння: 2x y = 6
1039. Склади рівняння,
через точку:
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
0 = 4k − 2
4k = 2
k = 1 2
Рівняння: y = 1 2 x − 2
б) Точка L(0; 5)
2x − y = b
2 • 0 − 5 = b
0 − 5 = b b = −5
Рівняння: 2x y = 5
Прямі, які проходять паралельно, матимуть вигляд 3x – y = c, де b ≠ 0.
а) Точка М(–3; 0)
3x – y = b
3 • (–3) – 0 = b
b = –9
Рівняння: 3x – y = –9
б) Точка А(2; –1)
3x – y = b
3 • 2 – (–1) = b
b = 7
Рівняння: 3x – y = 7
1040. Чи правильно, що графіком рівняння |x – 2| + |y – 3| = 0 є одна точка K(2; 3)?
А рівняння |x – 2| = |y – 3|?
|x – 2| + |y – 3| = 0
x – 2 = 0 і y – 3 = 0
x = 2 y = 3
Висновок: Графіком рівняння є точка К(2; 3).
|x – 2| = |y – 3|
x – 2 = y – 3 або x – 2 = −(y – 3)
x – y = 3 + 2 x – 2 = y + 3
x – y = 1 x + y = 3 + 2
x + y = 5
Висновок: Графіком рівняння є дві прямі x – y = 1 та x + y = 5.
1041. Побудуй графік рівняння.
а) x² − 9y² = 0
(x − 3y)(x + 3y) = 0
x − 3y = 0 або x + 3y = 0
y = 1 3 x y = 1 3 x
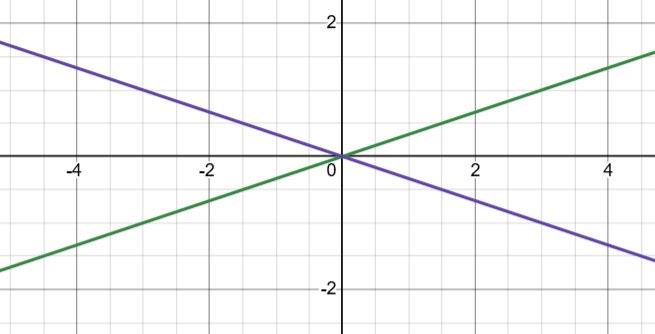


днів: 2000 + 2500 + 1500 + 3000 + 2500 =
а) x² = 64
x = 8 або x = −8
б) (x − 2)² = 25
x − 2 = 5 або x − 2 = −5
x = 5 + 2 x = 5 + 2
x = 7 x = 3

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
1046.
а) Прямі перетинаються один розв'язок.
б) Прямі паралельні жодного розв'язку.
в) Прямі збігаються
1047.
1049. Чи є пара чисел (2; –1) розв’язком системи рівнянь?
а) � x + y = 1 ���� − 2���� = 6, ⇒ � 2 + ( 1) = 1 2 2 • ( 1) = 4, Не є розв'язком
б) � x + y = 1, 4x 3y = 11, ⇒ � 2 + ( 1) = 1, 4 • 2 3 • ( 1) = 11, Є розв'язком
в) � x y = 3 2���� + ���� = 3, ⇒ � 2 ( 1) = 3 2 • 2 + ( 1) = 3, Є розв'язком
1050. Чи є пара чисел (–1; 3) розв’язком системи рівнянь?
а) � x + y = 2, 3x y = 6, ⇒ � 1 + 3 = 2 3 • ( 1) 3 = 6, Є розв'язком б) �3x + y = 0 x + 2y = 5, ⇒ �3 • ( 1) + 3 = 3 + 3 = 0 1 + 2 • 3 = 1 + 6 = 5 , Є розв'язком
в) � 3x 2y = 9 3x + 2y = 3 ⇒ �3 • ( 1) 2 • 3 = 9 3 • ( 1) + 2 • 3 = 3 , Не є розв'язком
1051. Склади систему рівнянь, що має розв’язок а) (3;4) � x y = 1, 2x + y = 10
x + y = 3 2x y = 3 ,
( 2;0) � x y = 2, 3x + 2y = 6 1052.
(0;−4) � x y = 4 x + 2y = 8 1053.
x + y = 3 2x y = 3

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
а) �x + y = 6
����−���� = 2
x + y = 6 ⇒ y = −x + 6
x−y = 2 ⇒ y = x−2
y = −x + 6
Х 0 6
У 6 0
y = x – 2
Х 0 1
У 2 1
Відповідь: (4;2)

в)
2x + y = 4
3����−���� = 1 ;
2x + y = 4 ⇒ y = −2x + 4
3x−y = 1 ⇒ y = 3x−1
y = −2x + 4
Х 0 1
У 4 2
y = 3x – 1
Х 0 1
У 1 2
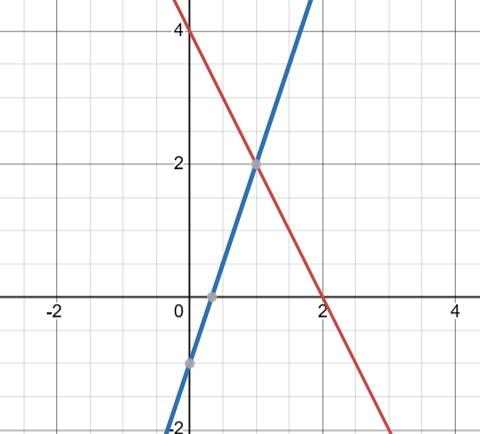
Відповідь: (1;2)
y = 0 4����−���� = 6 x−y = 0 ⇒ y = x 4x−y = 6 ⇒ y = 4x−6 y = x Х 1 1
1 1 y = 4x – 6 Х 0 1
6 2
Відповідь: (2;2)
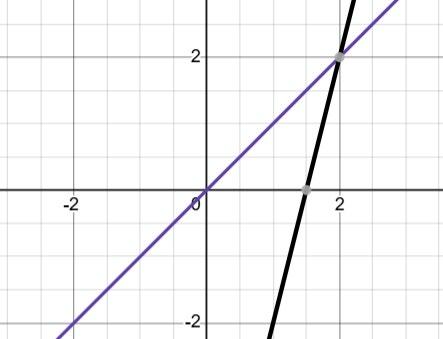
x − y = −2 ���� + 3���� = 10 x−y = −2 ⇒ y = x + 2 x + 3y = −10

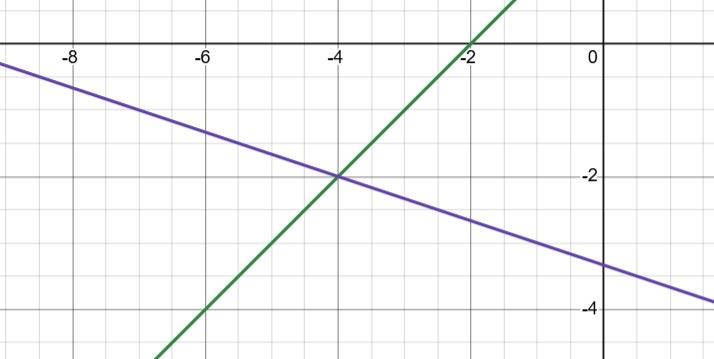
Відповідь: (−4;−2)
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
x y = 0
3����−���� = 4
x−y = 0 ⇒ y = x
3x−y = 4 ⇒ y = 3x−4
y = x
Х 1 1
У 1 1
y = 3x – 4
Х 0 1
У 4 1

Відповідь: (2;2)
в)
2x y = 2
3x y = 5
2x−y = 2 ⇒ y = 2x−2
3x−y = 5 ⇒ y = 3x−5
y = 2x – 2
Х 0 1
У 2 0
y = 3x – 5
Х 0 1
У 5 2
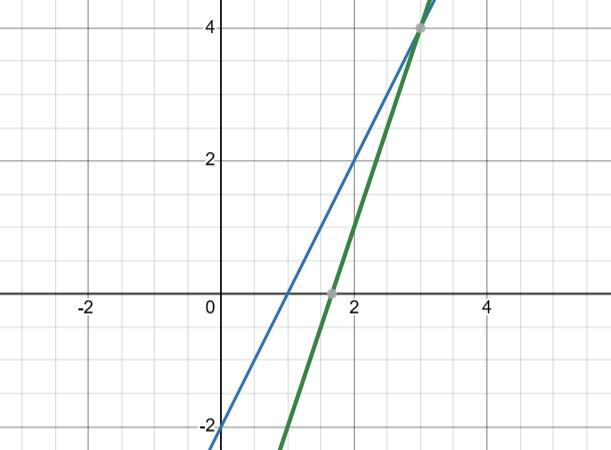
Відповідь: (3;4)
x + y = 7 ����−���� = 3
x + y = 7 ⇒ y = −x + 7
x−y = 3 ⇒ y = x−3
y = −x + 7 х 0 1 у 7 6
y = x – 3 х 0 1
3 2

Відповідь: (5;2)

x + y = 4, ����−���� = 2
x + y = 4 ⇒ y = −x + 4
x−y = 2 ⇒ y = x−2 y = −x + 4
Х 0 1 у 4 3
y = x – 2 Х 0 2 у 2 0
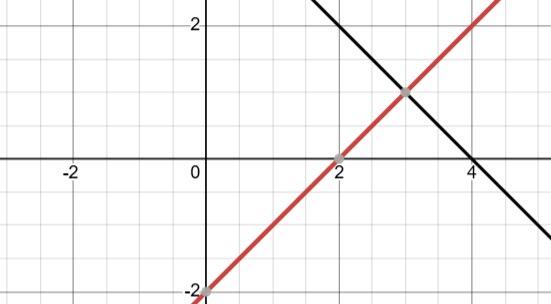
Відповідь: (3;1)
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
� 4x y = 5 3���� + 2���� = 12;

Відповідь: (2;3)
�5x + 4y = 13 3x + 5y = 13
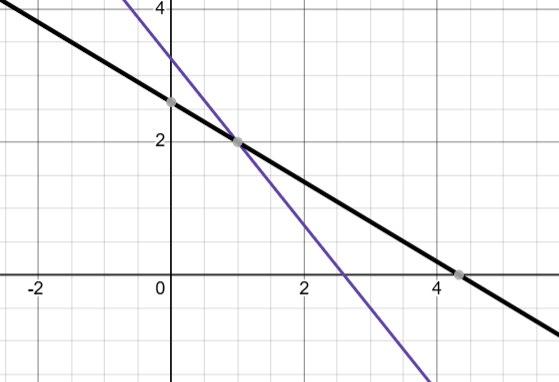
Відповідь: (1;2) в)
x + 3y = 5 3x + 9y = 21
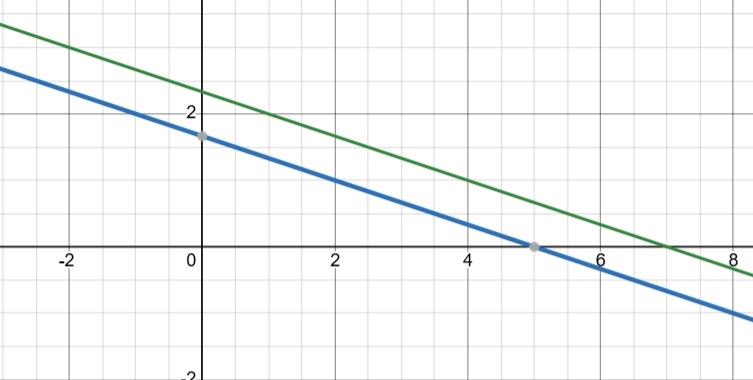
�5x 2y = 3 2x 3y = 1

( 1; 1)
�2x + 1 2 y = 6 4x + y = 12

� x + y = 1 2x 2y = 2

� 3x + 5y = 1 4x y = 10 Відповідь: (3; 2)

� x y = 2 3x 3y = 6
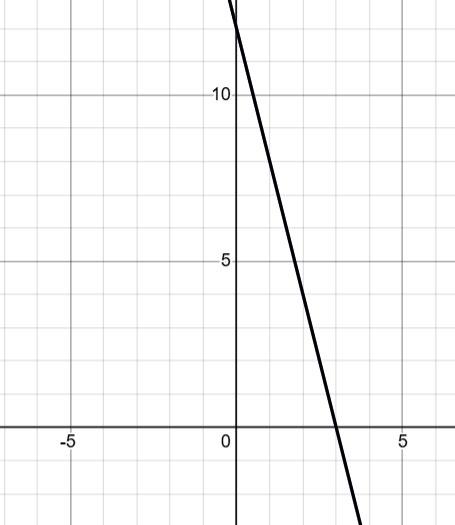

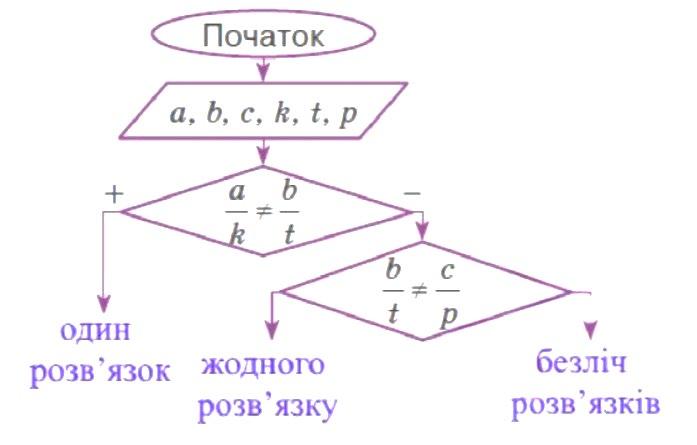

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
а) a₁
a₂ = b₁ b₂ ≠ c₁ c₂
Прямі паралельні. Немає розв'язків.
б) a₁
a₂ = b₁ b₂
Прямі паралельні. Немає розв'язків.
1062. Не будуючи графіків, доведи, що має безліч розв’язків система рівнянь. Знайди три
будь-які її розв’язка
6���� + 10���� = 36
3���� + 5���� = 18
2(3x + 5y = 18)
6x + 10y = 36
Це те саме, що й перше рівняння.
Приклади: (1; 3), (6; 0), (4; 5 6).
1063. Розв’яжи
� 0,5x + y = 2 0,4x + y = 2


Відповідь: (0;2)
Відповідь: (1; 1,5) 1064. Розв’яжи

а) �0,2x + 0,6y = 1,8 x 0,5y = 2 Відповідь: (3;2) б) �1,1x + y = 0,1 1,2x y = 2,2
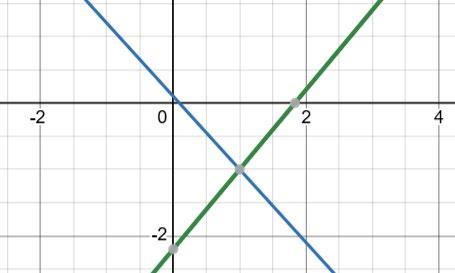
Відповідь: (1; 1) 1065
a) 3x − 2y = −6
0 2
3 0
A( 2; 0)

x + 2y = 2
2 0 у 0 1
5x + 2y = 22
4,4 0
0 11
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
розв'язок системи �3x − 2y = −6 x + 2y = −2 ,.
B(2; 6)
розв'язок системи �3x 2y = 6, 5x + 2y = 22
C(6; −4)
розв'язок системи � x + 2y = 2, 5x + 2y = 22
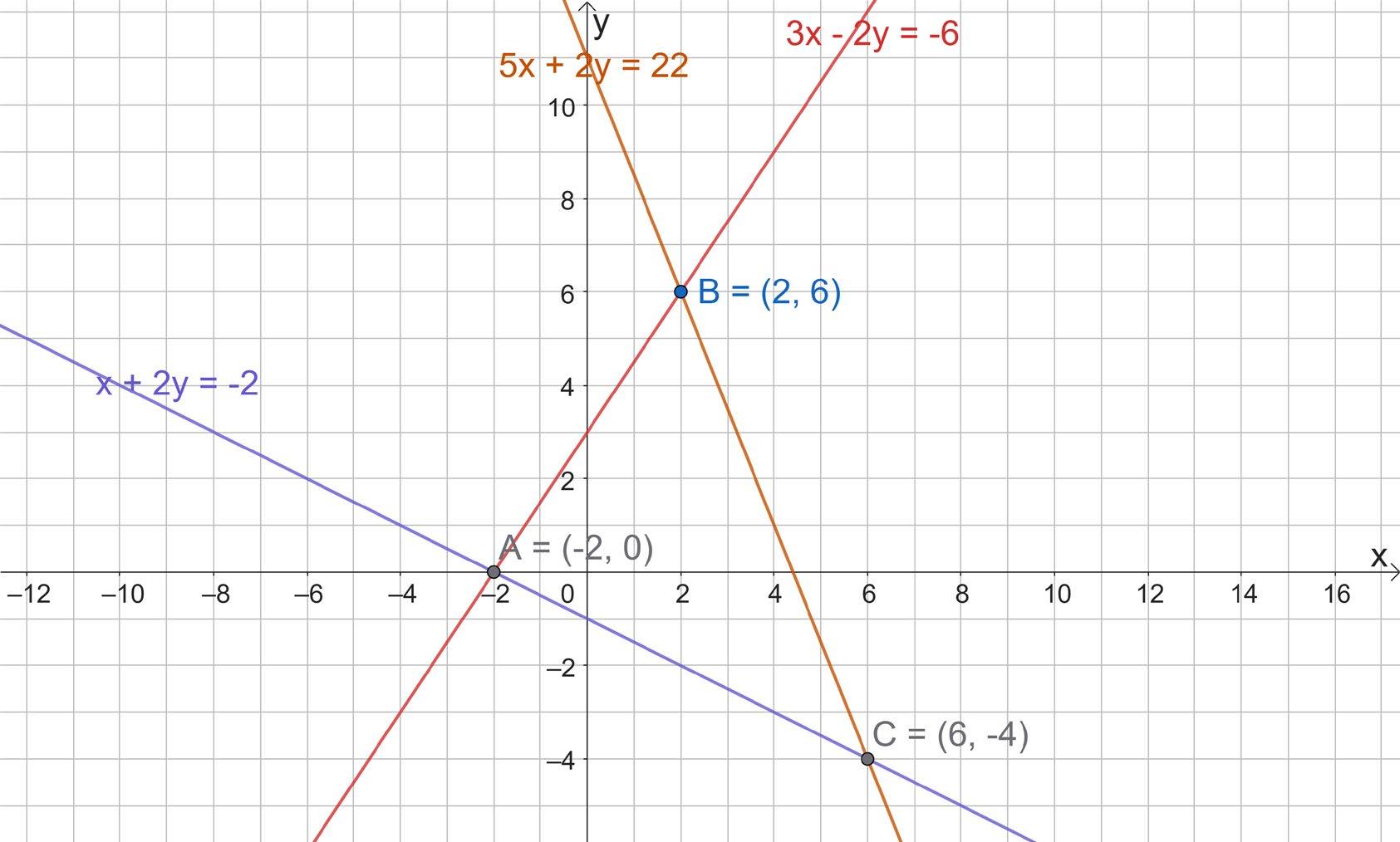


3
а) � 3x y = 3, ���� �������� = 1; Системи мають один розв'язок, якщо
3 1 ≠ 1 a ; 3 1 ≠ 1 1; a ≠ 1 3; б) �7x + 2y = 11, ax + 4y = 22
Системи мають один розв'язок, якщо
7 a ≠ 2 4; 11 22 ≠ 1 2; a ≠ 14.
: 3 1 = 1 a ; a = 1 3; Тобто � 3x y = 3 x 1 3 y = 1;
7 a = 1 2; a = 14.
Тобто � 7x + 2y = 11, 14x + 4y = 22
1071.

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
а)�bx + 2y = 7 3x y = 5 ;
Система має єдиний розв'язок, якщо
b 3 ≠ 2 1
b 3 ≠ 2
b ≠ 6
Система не має розв'язків, якщо
b 3 = 2 1
b = 6
Тобто:� bx + 2y = 7 6���� + 2���� = 10
б)� 4x + 8y = 5, 2x + by = 1
Система має єдиний розв'язок, якщо
4 2 ≠ 8 b
2 ≠ 8 b b ≠ 4
Система не має розв'язків, якщо
4 2 = 8 b = 5 1 b = 4
Тобто: � 4x + 8y = 5,
4���� + 2�������� = 2 1072. Чи має розв’язок система рівнянь?
а) �x − y = 1, x + y = 3, 2x = 6.
Розв'яжемо систему:
З третього рівняння: 2x = 6, ⇒ x = 3.
Підставимо x = 3 у перше рівняння: 3 y = 1, ⇒ y = 2.
Перевіряємо друге рівняння: 3 + 2 = 5, 5 ≠ 3.
Оскільки одне з рівнянь не
виконується, система не має розв'язку.
в) � 3x + y = 13, 5x 4y = 1, 7x − 5y = 1.
Розв'яжемо систему:

Візьмемо перше рівняння: 3x + y = 13, y = 13 3x.
б) �3x − y = 1 x + y = 3 4y = 8.
Розв'яжемо систему:
З третього рівняння: 4y = 8, y = 2.
Підставимо y = 2 у друге рівняння: x + 2 = 3, x = 1.
Перевіряємо перше рівняння: 3 · 1 2 = 3 2 = 1.
Усі рівняння виконуються, отже, система має розв'язок: (1; 2).
г) �2x + 7y = 16, 3x y = 1, ���� + 4���� = 1.
З другого рівняння: 3x y = 1, y = 3x 1
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
Підставимо y = 13 3x у друге
рівняння:
5x − 4(13 − 3x) = 1
5x − 52 + 12x = 1
17x = 51 x = 3.
Підставимо x = 3 у y = 13 − 3x: y = 13 − 3 · 3 = 13 − 9 = 4.
Перевіримо в третьому рівнянні:
7·3 − 5·4 = 21 − 20 = 1.
Усі рівняння виконуються, отже, система має розв'язок: (3; 4). Підставляємо
рівняння 2x + 7y = 16:
2x + 7(3x − 1) = 16
2x + 21x − 7 = 16
23x = 23 x = 1
Підставляємо x в друге рівняння: y = 3 · 1 − 1 = 2
Підставляємо x і y в третє рівняння: 1 + 4 · 2 = 9, 9 ≠ 1. Не задовільняє рівняння, тому система не має розв'язку.
1073. При якому значенні k система рівнянь
а)
3x 2y = 1
5x 3y = 2
2x + ky = 25
3x 2y = 1
5���� 3���� = 2
Розв'язок (7;11), тому
2x + ky = 25
2 · 7 + k · 11 = 25
14 + 11k = 25
11k = 11
k = 1
Відповідь: при k = 1
розв’язок?
б) �k(x + y) + 5x = 2, 9���� + 11���� = 7, 4x 3y = 11 �9���� + 11���� = 7 4���� 3���� = 11
Розв'язок (2; 1), тому k(x + y) + 5x = 2
k(2 − 1) + 5 · 2 = 2
k + 10 = 2
k = −8
Відповідь: при k = −8
1074. Розв’яжи графічно систему рівнянь.
а) �x² y² = 0
2x y = 6
�(x y)(x + y) = 0
2���� ���� = 6
�x y = 0 або x + y = 0
2���� ���� = 6 (6;6); (2; 2)


https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
�x² + 2xy + y² = 9, 2x + y = 5
(x + y)² = 3²
2���� + ���� = 5
+ ���� = 3 або ���� + ���� = 3 2���� + ���� = 5 (2;1), (8; 11) в)

|x − y| = 2
|x + y| = 2
���� = 2 x + y = 2 або � x y = 2 x + y = −2
���� = 2 x + y = 2 або �x y = 2 x + y = 2 (2;0), ( 2;0), (0;2), (0; 2)

1075.
1 + 2 = 3
4 + 5 + 6 = 7 + 8
9 + 10 + 11 + 12 = 13 + 14 + 15 16 + 17 + 18 + 19 + 20 = 21 + 22 + 23 + 24 1076.

х = 5, то 4 • 5² + 5 • 5 = 4 • 25 + 25 = 100 + 25 = 75
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
б) (8a² a³)a + (a² 8a + 5)a² = 8a³ a⁴ + a⁴ 8a³ + 5a² = 5a²
Якщо a = 0,2, то 5 • 0,2² = 5 • 0,04 = 0,2
1077. Перемнож двочлени.
а) (x + 3)(x 2) = x² 2x + 3x 6 = x² + x 6
б) (a 5)(a + 4) = a² + 4a 5a 20 = a² a 20 в) (m + n)(m n) = m² mn + mn n² = m² n²
г) (3 z)(5 + z) = 15 + 3z 5z z² = 15 2z z²
1078. Щоб
олова. Скільки кілограмів міді, цинку
Нехай міді 17k, цинку 2k, олова k. Маємо рівняння: 17k + 2k + k = 200; 20k = 200; k = 10.
17 • 10 = 170 (кг) – узяли міді; 2 • 10 = 20 (кг) – узяли цинку; 1 • 10 = 10 (кг) – узяли олова.
Відповідь: 170 кг; 20 кг; 10 кг.
1079. Вирази із
y через x.
a) 2x + y = 3; y = 3 2x б) 5x y = 0; y = 5x в) x 2y = 0. 2y = x y = х 2
1080. Вирази із рівняння
a) x y = 2;
x = 2 + y
x через y.
у = х – 2 б) x + 3y = 5; x = 5 3y у = 5 х 3
1081. Розв’яжи систему рівнянь.
а) �x = y + 2
x + y = 4,
x = y + 2
(y + 2) + y = 4
(y + 2) + y = 4
2y + 2 = 4
2y = 2
y = 1
x = y + 2 = 1 + 2 = 3
Відповідь: (3;1)
в) 2x + 5y = 0. 2x = 5y, x = 5 2y y = 2,5х
б) �y = 2x 1 x + y = 5 , � y = 2x − 1
���� + (2���� 1) = 5
x + 2x 1 = 5
3x = 6
x = 2
y = 2x 1 = 2 • 2 1 = 4 1 = 3
Відповідь: (2;3)
1082. Розв’яжи способом підстановки систему рівнянь
а) � x 2y = 5,
3x + 5y = 26
� x = 5 + 2y
3(5 + 2����) + 5���� = 26
3(5 + 2y) + 5y = 26
15 + 6y + 5y = 26
11y = 11
y = 1

x = 5 + 2y = 5 + 2 • 1
x = 5 + 2
б) �3x + 4y = 10
7x y = 13 , �3x + 4(7x 13) = 10
���� = 7���� 13
3x + 4(7x 13) = 10
3x + 28x 52 = 10
31x = 62
x = 2
y = 7 • 2 13
y = 14 13
в) � y 2z = 6, y + 2z = 10; � y = 6 + 2z
(6 + 2����) + 2���� = 10
(6 + 2z) + 2z = 10
6 + 4z = 10
4z = 4
z = 1
y = 6 + 2z = 6 + 2 • 1
y = 6 + 2
x = 7
Відповідь: (7;1)
г) �
2z + 3y = 3, ���� + ���� = 2; �2(2 − y) + 3y = 3 ���� = 2 ����
2(2 y) + 3y = 3
4 2y + 3y = 3
y = 1
z = 2 y = 2 ( 1)
z = 3
Відповідь: (3; 1)
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
y = 1 Відповідь: (2;1)
ґ) �9x + 2y 4 = 0
8x + y 2 = 0 , �9x + 2(2 8x) 4 = 0 y = 2 8x
9x + 2(2 8x) 4 = 0
9x + 4 16x 4 = 0 7x = 0
x = 0 y = 2 8x = 2 8 • 0 y = 2
Відповідь: (0;2)
y = 8
Відповідь: (8;1)
д)
�5u + 7v + 33 = 0
10u v + 6 = 0 , �5u + 7(10u + 6) + 33 = 0
���� = 10���� + 6
5u + 7(10u + 6) + 33 = 0
5u + 70u + 42 + 33 = 0
75u = 75
u = 1
v = 10 • ( 1) + 6
v = 4
Відповідь: ( 1; 4)
1083. Розв’яжи
а) � 3x y = 1
3x + 8y = 19;, � y = 3x − 1
3x + 8(3x 1) = 19,
3x + 24x 8 = 19; 27x = 27; x = 1; y = 3 · 1 1 = 2; Відповідь: (1; 2).
б) �
3x + 2y = 27
x + 5y = 35; , �
3(35 5y) + 2y = 27
x = 35 5y ,
105 15y + 2y = 27; 13y = 78; y = 6; x = 35 5 · 6 = 5. Відповідь: (5; 6).
в) � 2p + q = 11
5p 2q = 41,
� q = 11 2p
5p 2q = 41
5p 2q = 41
5p 2(11 2p) = 41
5p 22 + 4p = 41
9p = 63
p = 7
q = 11 2 • 7 = 3
Відповідь: (7; 3)
ґ) �

3x + z 1 = 0,
5x + 4z 11 = 0; � z = 1 3x
5x + 4z 11 = 0
5x + 4z 11 = 0
5x + 4(1 3x) 11 = 0
5x + 4 12x 11 = 0
7x 7 = 0
x = 1
z = 1 3 • ( 1) = 4
г) �6a 3b = 9
2a + b = 5 , � q = 11 2p
5p 2q = 41
5p 2q = 41
5p 2(11 2p) = 41
5p 22 + 4p = 41
9p = 63
p = 7
q = 11 2 • 7 = 3
Відповідь: (7; 3)
д) �5x + 7z 45 = 0, 7x − z − 9 = 0; � z = 1 − 3x
5x + 4z 11 = 0
5x + 4z 11 = 0
5x + 4(1 3x) 11 = 0
5x + 4 12x 11 = 0
7x 7 = 0
x = 1
z = 1 3 • ( 1) = 4
Відповідь: ( 1; 4)
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
Відповідь: ( 1; 4)
1084. Розв’яжи способом
а) �15y 8z = 29, 3y + 2z = 13;
z = (13 3y) 2
15y 8 (13 3y) 2 ) = 29
15y 4(13 3y) = 29
15y 52 + 12y = 29
27y = 81
y = 3
z = (13 3 • 3) 2
z = (13 9) 2
z = 4 2
z = 2
Відповідь: (3; 2)
б) � 3x + 8t = 30
6x + 5t = 27;,
t = (30 3x) 8
6x + 5 (30 3x) 8 = 27
6x + 5(30 3x) 8 = 27 | • 8
48x + 5(30 3x) = 216
48x + 150 15x = 216
33x = 66
x = 2
t = (30 3 • 2) 8 t = (30 6) 8
t = 24 8 t = 3
Відповідь: (2; 3)
в) �14u 9v = 24
7u − 2v = 17
�2 · 7u 9v = 24
7u = 17 + 2v; 2 · (17 + 2v) 9v = 24
34 + 4v 9v = 24
34 5v = 24
5v = 10
v = 2;
7u = 17 + 2 · 2;
7u = 21;

u = 3
Відповідь: u = 3; v = 2
г) �5x + 4y = 13 3x + 2y = 7
�5x = 13 4y
3x + 5y = 13
x = 13 5 4 5 y
3( 13 5 4 5 y) + 5y = 13 39
5 12 5 y + 5y = 13 13
5 y = 13 39 5 13
5 y = 26 5 y = 2; x = 13 5 8 5 = 1
Відповідь: (1; 2)
1085. Розв’яжи способом
а) � 6a − 5b = 13, 2a + 7b = 13; З другого рівняння:
2a + 7b = 13, 2a = 13 7b, a = (13 7b)
2 .
Підставимо у перше рівняння:
6(13 7b)
2 5b = 13,
3(13 7b) 5b = 13,
39 21b 5b = 13, 39 26b = 13, 26b = 13 39, 26b = 26, b = 1.
Знаходимо a:
a = (13 7•1) 2 = (13 7) 2 = 6 2 = 3.
Відповідь: (3; 1)
в) � 6x − 4y = −2, 3x 5y = 7;
З другого рівняння:
3x 5y = 7,
3x = 7 + 5y,
x = ( 7 + 5y) 3 .
Підставимо у перше рівняння:
6( 7 + 5y)
3 4y = 2,

2( 7 + 5y) 4y = 2, 14 + 10y 4y = 2,
б) � 2a − 7b = 5, 4a 9b = 15; З першого рівняння:
2a 7b = 5, 2a = 5 + 7b,
a = (5 + 7b)
2
Підставимо у друге рівняння:
4(5 + 7b)
2 9b = 15,
2(5 + 7b) 9b = 15, 10 + 14b 9b = 15, 10 + 5b = 15, 5b = 15 10, 5b = 5, b = 1.
Знаходимо a:
a = (5 + 7•1) 2 = (5 + 7) 2 = 12 2 = 6.
Відповідь: a = 6; b = 1.
г) �7x + 4y = 3, 9x + 16y = 7.
З першого рівняння: 7x + 4y = 3, 7x = 3 4y,
x = ( 3 4y)
7 .
Підставимо у друге рівняння:
9( 3 4y)
7 + 16y = 7, ( 27 36y)
7 + 16y = 7, | • 7
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
14 + 6y = 2
6y = 2 + 14
6y = 12
y = 2.
Знаходимо x:
x = ( 7 + 5•2)
3 = ( 7 + 10) 3 = 3 3 = 1.
Відповідь: x = 1; y = 2.
1086. Не виконуючи
а) �x + y = 37
x y = 5
x = 5 + y
(5 + y) + y = 37
(5 + y) + y = 37
5 + 2y = 37
2y = 32 y = 16
x = 5 + 16 = 21
Координати точки (21; 16)
а) � x + 2y = 8 ���� 2���� = 2
x = 2 + 2y
(2 + 2����) + 2���� = 8
(2 + 2y) + 2y = 8
2 + 4y = 8
4y = 6
y = 1,5
x = 2 + 2 • 1,5 = 2 + 3 = 5
27 36y + 112y = 49
27 + 76y = 49
76y = 49 + 27
76y = 76, y = 1.
Знаходимо x: x = ( 3 4•1) 7 = ( 3 4) 7 = 7 7 = 1.
Відповідь: x = 1; y = 1.
2(1 2y) 3y = 16
2(1 2y) 3y = 16
2 4y 3y = 16
2 7y = 16 7y = 14
точки (5; 2)
Координати точки (5;1,5) б) �4x 7y = 15 3
25x = 50 x = 2
y = 5 3 • 2 = 5 6 = 1
Координати точки (2; 1) 1088. Розв’яжи способом підстановки
�3x + 0,5y = 1 x + 0,25y = 1,
3(1 0,25y) + 0,5y = 1 ���� = 1 0,25����
3(1 0,25y) + 0,5y = 1
3 0,75y + 0,5y = 1
3 0,25y = 1
0,25y = 2 y = 8
x = 1 0,25 • 8 = 1 2 = 1
Відповідь: ( 1;8)

� 0,2x + y = 7 1,5x + y = 13,5,
y = 7 − 0,2x 1,5���� + (7 0,2����) = 13,5 1,5x + (7 0,2x) = 13,5 1,5x + 7 0,2x = 13,5 1,3x + 7 = 13,5 1,3x = 6,5 x = 5 y = 7 0,2 • 5 = 7 1 = 6
а) �0,6x + 0,8y = 1, x + 4y = 3 b) � 0,5x y = 1,5, 0,3x 0,4y = 1
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
0,6(3 4y) + 0,8y = 1
���� = 3 4����
0,6(3 4y) + 0,8y = 1
1,8 2,4y + 0,8y = 1
1,8 1,6y = 1
1,6y = 0,8
y = 0,5
x = 3 4 • 0,5 = 3 2 = 1
Відповідь: (1;0,5)
� y = 0,5x 1,5
0,3���� 0,4(0,5���� 1,5) = 1
0,3x 0,4(0,5x 1,5) = 1
0,3x 0,2x + 0,6 = 1
0,1x + 0,6 = 1
0,1x = 0,4 x = 4
y = 0,5 • 4 1,5 = 2 1,5 = 0,5
Відповідь: (4;0,5)
1090. За малюнком 25.1 запиши систему рівнянь
2x + y = 5
0,5x + 2y = 3
y = 5 2x
0,5x + 2(5 2x) = 3
0,5x + 10 4x = 3
3,5x = 7
x = 2
y = 5 2 • 2 = 5 4 = 1
Відповідь: розв'язки співпадають.
1091. Розв’яжи систему
a)
4(x + 2y) = 5x + 6
3(2x y) = 24y + 6
4x + 8y = 5x + 6
6x 3y = 24y + 6
x = 8y 6
6 · (8y 6) = 27y + 6
48y 36 27y = 6
21y = 6 + 36
21y = 42
y = 2
x = 8 · 2 6
x = 16 6
x = 10
Відповідь: (10; 2)
б) �
5(x − 3y) = 2x + 7
3(x + 6y) = 9y + 15;
5x 15y = 2x + 7,
3x + 18y = 9y + 15;
5x 2x 15y = 7;
3x + 18y − 9y = 15;
3x 15y = 7
3x + 9y = 15;
3x 15y = 7
3x = 15 9y;
x = 5 3y
3 · (5 3y) 15y = 7; 15 9y 15y = 7

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
24y = 7 15
y = 8 : ( 24)
y = 1 3
x = 5 3 · 1 3
x = 5 1
x = 4
Відповідь: (4; 1 3)
1092. Розв’яжи систему рівнянь
а) � 5x 2 = 4(x + 2y) 8, 3(2x y) + 6 = 24y + 12;
5x 2 = 4x + 8y 8
6x 3y + 6 = 24y + 12 � x − 8y = −6
6x 27y = 6 � x = 8y 6
6(8y 6) 27y = 6
6(8y 6) 27y = 6
48y 36 27y = 6
21y = 42
y = 2
x = 8 • 2 6 = 16 6 = 10
Відповідь: (10;2)
1093. Знайди розв’язок системи рівнянь
а) �
7 + x 2 = y + 13 3 · 6
5x − 3y = 8
3(7 + x) 2(y + 3)
5x 3y = 8 �
21 + 3x 2y + 6
5x 3y = 8
3x 2y = 27
5x 3y = 8
2y = 5 − 3x
5x 3y = 8
y = 2,5 + 1,5x
5x 3( 2,5 + 1,5x) = 8
5x 3( 2,5 + 1,5x) = 8
5x + 7,5 4,5x = 8
0,5x = 0,5
x = 1
y = 2,5 + 1,5 · 1 = 2,5 + 1,5 = 1
Відповідь: (1; 1)
б) � 2x 3 = 5(x y), 2(3x 1) = y 35. �2x 3 = 5x 5y 6x 2 = y 35 � 3x + 5y = 3 6x y = 33 � 3x + 5(6x + 33) = 3 y = 6x + 33 3x + 30x + 165 = 3 27x = 162 x = 6 y = 6 • ( 6) + 33 = 36 + 33 = 3
Відповідь: ( 6; 3)
б) �5x 3y 4 = x 5y 3 | · 12
7x + y = 12
3(5x 3y) = 4(x 5y)
7x + y = 12
15x 9y = 4x 20y
7x + y = 12
11x + 11y = 0
y = 12 7x �11x + 11(12 7x) = 0
y = 12 7x
11x + 132 77x = 0 66x = 132
x = 2
y = 12 7 · 2 = 12 14 = 2
Відповідь: (2; 2)
в) � 1 3 (x + y) 1 4 (x y) = 5, | · 12 1 12 (���� + ����) + 1 3 (���� ����) = 6; | · 12

4(x + y) − 3(x − y) = 60, (x + y) + 4(x y) = 72;
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
4x + 4y − 3x + 3y = 60, x + y + 4x − 4y = 72;
x + 7y = 60, → x = 60 7y, 5x 3y = 72;
5(60 7y) 3y = 72;
300 35y 3y = 72; 38y = 228; y = 6;
→ x = 60 7 · 6 = 60 42 = 18
Відповідь: (18; 6).
г)
1
x + 2y 4 = 3 + 3x 5y 2
3 · x + 1 2 · y = 7 1 4 (x 2y) · 12
x + 2y = 12 + 2(3x − 5y)
4x + 6y = 84 3(x 2y)
x + 2y = 12 + 6x 10y
4x + 6y = 84 3x + 6y
5x + 12y = 12 7x = 84
5 · 12 + 12y = 12 x = 12
5 · 12 + 12y = 12
60 + 12y = 12
12y = 72 y = 6
Відповідь: (12;6)
1094. Знайди розв’язок системи
a) �
4(x − 3z) + 33z = 50
5(x + 2z) 3x = 18
4x 12z + 33z = 50
5x + 10z 3x = 18
4x + 21z = 50
2x + 10z = 18
2x = 18 10z
4x + 21z = 50
x = 9 − 5z
4 · (9 5z) + 21z = 50
36 20z + 21z = 50
z = 50 36
z = 14
x = 9 5 · 14
x = 9 70
x = 61
Відповідь: x = 61; z = 14
б) � 4x + 7 = 5(x + t)
3(x + 5t) − 6t = 15
4x + 7 = 5x + 5t
3x + 15t 6t = 15
x = 7 5t

3x + 9t = 15
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
3 · (7 5t) + 9t = 15
21 15t + 9t = 15
6t = 15 21
6t = 6
t = 1
x = 7 5 · 1
x = 7 5
x = 2
Відповідь: x = 2; t = 1
1095. Знайди розв’язок системи рівнянь
a) � 3x + 1 = 5(3 2y)
4(x 1) = 2(8,5 5y)
3x + 1 = 15 10y
4x 4 = 17 10y
3x + 10y = 14
4x = 21 10y
x = 5,25 − 2,5y
3 · (5,25 2,5y) + 10y = 14 15,75 7,5y + 10y = 14
2,5y = 14 15,75
y = 1,75 : 2,5
y = 0,7
x = 5,25 2,5 · ( 0,7)
x = 5,25 + 1,75
x = 7
Відповідь: (7; 0,7)
б) � 6(x 2y) = 7 9y
8x + 3y = 5(2x + 1)
6x 12y = 7 9y
8x + 3y = 10x + 5
6x 3y = 7
3y 2x = 5;
2x = 3y 5
6x 3y = 7;
� x = 1,5y 2,5
6 · (1,5y 2,5) 3y = 7 9y 15 3y = 7
6y = 22
y = 22 : 6
y = 32
3
x = 3
2 · 11 3 2,5
x = 5,5 2,5
x = 3
Відповідь: (3; 32 3)
1096. Знайди

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
5
5 = y 3 4 x 2y = 2
2(2 + 2y) 5 5 = (y 3) 4 x = 2 + 2y
Розв'язуємо рівняння:
2(2 + 2y) 5 5 = (y 3) 4 · 20
4(2(2 + 2y) 5) = 5(y 3)
4(4 + 4y 5) = 5y 15
4 + 16y = 5y 15
11y = 11 y = 1
Підставляємо y у рівняння x = 2 + 2y: x = 2 + 2 · ( 1) = 2 2 = 0
Відповідь: (0; 1)
б)
4x 1 3 = 3y 11 2 4x y = 9
(4���� 1) 3 = (3(4���� 9) 11) 2 ���� = 4���� 9
Розв'язуємо рівняння: (4x 1)
3 = (3(4x 9) 11) 2 · 6
2(4x 1) = 3(3(4x 9) 11)
8x 2 = 3(12x 27 11)
8x 2 = 3(12x 38)
8x 2 = 36x 114
28x = 112 x = 4
Підставляємо x у рівняння y = 4x 9: y = 4 · 4 9 = 16 9 = 7
Відповідь: (4; 7)
в)
1 4 (y 1) 1 3 (x + 1) = 2 | · 12 1 4 (���� + 3) 1 3 (���� + 1) = 4 | · 12
3(y 1) 4(x + 1) = 24
3(x + 3) 4(y + 1) = 48
3y 3 4x 4 = 24
3x + 9 4y 4 = 48
3y 4x = 31
3x 4y = 53

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
3y 4 (( 53 + 4y) 3 ) = 31 x = ( 53 + 4y) 3
Розв'язуємо рівняння: 3y 4(( 53 + 4y) 3 = 31 | · 3
9y + 212 16y = 93
7y = 119 y = 17
Підставляємо y у рівняння x = ( 53 + 4y) 3 : x = ( 53 + 4 · 17) 3 = ( 53 + 68) 3 = 15 3 = 5
Відповідь: (5; 17) г)
(x + y) 4 (x y) 3 = 5 | · 12 (���� + ����) 8 + (���� ����) 6 = 1,5 | · 24
3(x + y) − 4(x − y) = 60
3(���� + ����) + 4(���� ����) = 36
3x + 3y − 4x + 4y = 60
3x + 3y + 4x 4y = 36
x + 7y = 60
7x y = 36
x = 7y 60
7(7y 60) y = 36
Розв'язуємо рівняння:
7(7y 60) y = 36
49y 420 y = 36
48y = 456 y = 9,5
Підставляємо y у рівняння x = 7y 60: x = 7 · 9,5 60 = 66,5 60 = 6,5
Відповідь: (6,5; 9,5)
1097. При яких
С(–1; –1)?
� a + 3b = 1 a b = 1
a = 1 3b
1 + 3b b = 1
1 + 3b − b = 1
2b = 2
b = 1

a = −2, b = 1
1098.
K(3; –2)
� a + 4b = 7
3a 2b = 7
a = 7 4b
3(7 4b) 2b = 7
3(7 − 4b) − 2b = 7
21 − 12b − 2b = 7
21 − 14b = 7
14b = 14 b = 1 a = 7 − 4 · 1 = 7 − 4 = 3
Відповідь: a = 3, b = 1 1099.
(А–Д).
1) � 7(2x + y) 5(3x + y) = 6 3(x + 2y) 2(x + 3y) = 6 → Г ( 6; 0)
2) �u + 1 3 (u + v 3) = 14 1 3 v 1 6 (u + v) = 5 6 → В (8; 13) 3) �0,2a + 4b = 5 0,8a 2,5a + 0,5b = 1 1 2 b → A (1; 1,5) 1100.
⎧x + 1 3 y + 1 3 z = 14 | · 3 y + 1 4 x + 1 4 z = 8 | · 4 z + 1 5 x + 1 5 y = 8 | · 5
3x + y + z = 42
4y + x + z = 32
5z + x + y = 40
3x + y + (32 4y x) = 42 z = 32 4y x
5(32 − 4y − x) + x + y = 40
2x 3y = 10
− 20y − 5x + x + y = 40

4(5 + 1,5y) 19y = 120 20 6y 19y = 120 25y = 100
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
2x − 10 = 3y −4x − 19y = −120 � x = 5 + 1,5y 4(5 + 1,5y) 19y = 120 y = 4
Підставляємо знайдене значення y у рівняння x = 5 + 1,5y: x = 5 + 1,5 · 4 = 5 + 6 = 11
Підставляємо знайдені значення x і y у рівняння z = 32 4y x: z = 32 4 · 4 11 = 32 16 11 = 5
Відповідь: x = 11, y = 4, z = 5. 1101. Задача Е. Безу (1730–1783). Розв’яжи систему �5x + 3y = 65 2y z = 11
3x + 4z = 57
Крок 1: Виразимо z із другого рівняння.
З другого рівняння: 2y z = 11
Виразимо z : z = 2y 11
Крок 2: Підставимо z = 2y 11 у третє рівняння.
Третє рівняння:
3x + 4z = 57
Підставимо значення z :
3x + 4(2y 11) = 57
Розкриємо дужки:
3x + 8y 44 = 57
3x + 8y = 101
Крок 3: Розв'яжемо систему рівнянь (1) і (2).
� 5���� + 3���� = 65
3���� + 8���� = 101
Розв'яжемо її далі.
Розрахунки для x і y: x = 7, y = 10
Крок 4: Знайдемо z.
Підставимо y = 10 у рівняння для z:
z = 2(10) 11.
z = 20 11 = 9.
1102. Який многочлен треба додати до 3y⁴-2y²+5, щоб одержати
5y⁴+y³-2y²+8? (3y⁴ 2y² + 5) + P = 5y⁴ + y³ 2y² + 8; P = 5y⁴ + y³ 2y² + 8 (3y⁴ 2y² + 5); P = 5y⁴ + y³ 2y² + 8 3y⁴ + 2y² 5; P = 2y⁴ + y³ + 3.
1103. Знайди добуток многочленів.
а) (2a – n)(4a² + 2an + n²) = (2a)³ – n³ = 8a³ – n³; б) (1 + c + c²)(1 – c) = 1 – c³.
1104. Обчисли значення виразу.
а) 2¹³ • 0,5¹³ = (2 • 0,5)¹³ = 1¹³ = 1; б) 0,5¹⁸ • 2¹⁸ = (0,5 • 2)¹⁸ = 1¹⁸ = 1;

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
в) 25⁷ • 0,04⁷ = (25 • 0,04)⁷ = 1⁷ = 1; г) 5³³ • 0,2³³ = (5 • 0,2)³³ = 1³³ = 1.
1105. Додай
а) �3���� + 2���� = 7
5���� ���� = 12
3x + 2y + 5x y = 7 + 12
8x + y = 19 б) ����� 8���� = 15 4���� 3���� = 2 x 8y + 4x 3y = 15 + 2 5x 11y = 17
1106. Розв’яжи систему
а) � x + y = 5, 2x y = 1
3x = 6
x = 2
x + y = 5
2 + y = 5
y = 3
Відповідь: (2;3) б) � x 2y = 2, 3x + 2y = 6 4x = 8 x = 2 x 2y = 2 2 2y = 2 2y = 0 y = 0
1107. Скільки розв’язків
8 2 + у 3 = 6 4 + у 3 = 6
3 = 2 y = 6 Відповідь: (8;6) 1109. Розв’яжи способом
а) �x + y = 7, x y = 3
2x = 10
x = 5
x + y = 7
5 + y = 7 y = 2
Відповідь: (5;2)
1110. Розв’яжи

5x y = 16 x + y = 14 , 6x = 30 x = 5 x + y = 14
5 + y = 14 y = 9
Відповідь: (5;9)
(2;0) в) � a c = 3, 2a + c = 6
3a = 9
a = 3
a c = 3
3 c = 3
c = 0
Відповідь: (3;0)
3x + 2y = 18 7x − 2y = 2 , 10x = 20 x = 2
3x + 2y = 18
3 · 2 + 2y = 18
6 + 2y = 18
2y = 12 y = 6
Відповідь: (2;6)
4x 3y = 2
3x + 3y = 5, 7x = 7 x = 1
3x + 3y = 5
3 · 1 + 3y = 5
3 + 3y = 5
3y = 2 y = 2 3
Відповідь: (1; 2 3)
2x + y = 17
2x y = 3 ,
4x = 20
x = 5
2x + y = 17
2 · 5 + y = 17
10 + y = 17
y = 7
Відповідь: (5;7)
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
3u − v = 26,
5u + v = 38; 8u = 64
u = 8
3u v = 26
3 · 8 v = 26
24 v = 26
v = 2
Відповідь: (8; 2) в)
� x 2y = 5
3x + 2y = 7,
4x = 12
x = 3
3x + 2y = 7
3 · 3 + 2y = 7
9 + 2y = 7
2y = 2
y = 1
Відповідь: (3; 1)
3���� + 4���� = 25, 7x 4y = 5
10x = 30
x = 3
3x + 4y = 25
3 · 3 + 4y = 25
9 + 4y = 25
4y = 16
y = 4
Відповідь: (3;4)
а) � x 4y = 5
���� 3���� = 12 | · ( 1)
x − 4y = 5
−x + 3y = −12
y = 7
y = 7
x 4y = 5
x 4 · 7 = 5
x 28 = 5
x = 33
Відповідь: (33;7)
в)
15y 8z = 29
3���� + 2���� = 13 | · 4
15y 8z = 29
12y + 8z = 52
27y = 81
y = 3
3y + 2z = 13
3 · 3 + 2z = 13
9 + 2z = 13
2z = 4
z = 2
3x + y = −1 3x + 8y = 19
9y = 18
y = 2
3x y = 1
3x 2 = 1
3x = 3
x = 1
Відповідь: (1;2)
г) � 3x + 8t = 29 | · 2
Відповідь: (3;2) б) �3x y = 1 | · ( 1) 3���� + 8���� = 19
6���� + 5���� = 47 | · ( 1)
� 6x + 16t = 58 6x 5t = 47
11t = 11
t = 1
3x + 8t = 29
3x + 8 · 1 = 29
3x + 8 = 29
3x = 21
x = 7
Відповідь: (7;1)
1112. Розв’яжи способом додавання систему рівнянь
а) � x + 7z = 26
���� + 4���� = 17 | · ( 1)
� x + 7z = 26 ���� 4���� = 17
z = 9
z = 3
x + 7z = 26
x + 7 · 3 = 26
x + 21 = 26
x = 5
Відповідь: (5;3)

в) � 14u 9v = 24
7���� 2���� = 17 | · ( 2)
б) � 5x + 7z = 29 5���� 2���� = 34 | · ( 1)
� 5x + 7z = 29
5x + 2z = 34
9z = 63
z = 7
5x + 7z = 29
5x + 7 · 7 = 29
5x + 49 = 29
5x = 20
x = 4
Відповідь: ( 4;7)
14u − 9v = 24
14u + 4v = 34
5v = 10
v = 2
7u 2v = 17
7u 2 · 2 = 17
7u 4 = 17
7u = 21
u = 3
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
Відповідь: (3;2) г) �5x + 4y = 13 | · ( 3)
1113.
а)
3a − 5b = 13 | · (−2)
2a + 7b = 81 | · 3
6a + 10b = 26
6a + 21b = 243
31b = 217
b = 7
3a 5b = 13
3a 5 · 7 = 13
3a 35 = 13
3a = 48
a = 16
Відповідь: (16;7)
в)
3x + 2y = 27 | · 5
4x + 5y = 50 | · ( 2) �
15x + 10y = 135
8x 10y = 100
7x = 35
x = 5
3x + 2y = 27
3 · 5 + 2y = 27
15 + 2y = 27
2y = 12
y = 6
Відповідь: (5;6)
1114. Розв’яжи способом
а)
�
8z + 3t = 7 | · 5
−3z − 5t = 9 | · 3
�
40z + 15t = 35
9���� 15���� = 27
31z = 62
z = 2
8z + 3t = 7

8 · 2 + 3t = 7
3���� + 2���� = 13 | · 5
15x 12y = 39 15x + 10y = 65
5v = 10
v = 2
7u 9v = 24
7u 2·2 = 17
7u 4 = 17
7u = 21
u = 3
Відповідь: (3;2)
б) � 2a − 7b = 8 | · 5 5���� 9���� = 3 | · ( 2)
10a 35b = 40 10a + 18b = 6
17b = 34
b = 2
2a 7b = 8
2a 7 · ( 2) = 8
2a + 14 = 8
2a = 6
a = 3
Відповідь: ( 3; 2) Г)
� 4x + 5y = 11 | · 3
3x + 8y = 4 | · ( 4)
�12x + 15y = 33 12x 32y = 16
17y = 17
y = 1
4x + 5y = 11
4x + 5 · 1 = 11
4x + 5 = 11
4x = 16
x = 4
Відповідь: ( 4;1)
b)
� 3m 7n = 8 | · 5
5m + 8n = 26 | · ( 3)
� 15m 35n = 40 15m 24n = 78
59n = 118
n = 2
3m 7n = 8
3m 7 · 2 = 8
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
16 + 3t = 7
3t = −9
t = 3
Відповідь: (2; 3)
c)
3x + 5y = 7 | · 5
5x + 6y = 26 | · 3
15x + 25y = 35
15x + 18y = 78
43y = 43
y = 1
3x + 5y = 7
3x + 5 · 1 = 7
3x + 5 = 7
3x = 12
x = 4
Відповідь: (4;1)
3m 14 = 8
3m = 6
m = 2
Відповідь: (2;2)
d)
4x + 3y = 22 | · 3
3x 7y = 2 | · ( 4)
12x + 9y = 66
12���� + 28���� = 8
37y = 74
y = 2
4x + 3y = 22
4x + 3 · 2 = 22
4x + 6 = 22
4x = 16 x = 4
Відповідь: (4;2) 1115.
x − 2y = 1
2x + y = 7 | · 2
� x 2y = 1
4x + 2y = 14
5x = 15
x = 3
x − 2y = 1
3 − 2y = 1
2y = 2
y = 1
Точка перетину: (3;1)


5x + 2y = 1 | · 7 4x 7y = 18 | · 2
35x + 14y = 7
8x 14y = 36
43x = 43
x = 1
5x + 2y = 1
5 · 1 + 2y = 1
5 + 2y = 1
2y = −4
y = 2
Точка перетину: (1; 2)
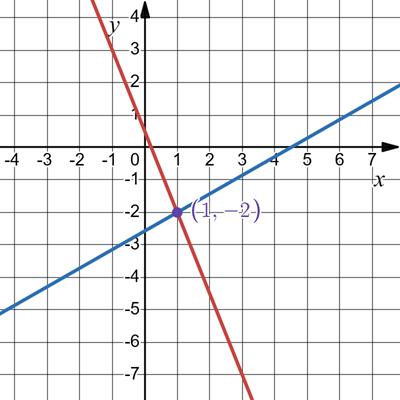
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
2x y = 3
x 3y = 4 | · ( 2)
2x y = 3
2x + 6y = 8
5y = −5
y = 1
x − 3y = 4
x − 3 · ( 1) = 4
x + 3 = 4
x = 1
Точка перетину: (1; 1)

б)
3x + 2y = 8 | · 3
5x 3y = 7 | · 2
9x + 6y = 24
10x 6y = 14
19x = 38
x = 2
3x + 2y = −8
3 · ( 2) + 2y = −8
6 + 2y = −8
2y = 2
y = 1
Точка перетину: ( 2; 1)
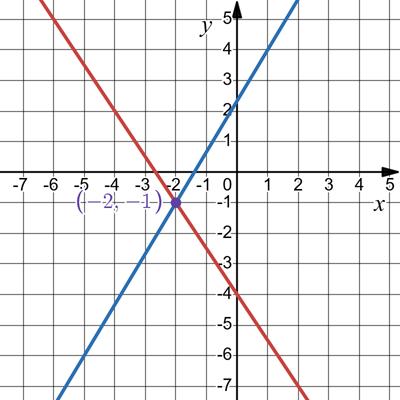
1117. Розв’яжи різними способами систему рівнянь а) Метод додавання
3x + y = 7
4x y = 7
7x = 14
x = 2
3x + y = 7
6 + y = 7
y = 1
Відповідь: (2;1)

Метод підстановки �3x + y = 7
4x y = 7 � y = 7 3x
4x (7 3x) = 7
4x − (7 − 3x) = 7
4x − 7 + 3x = 7
7x = 14
x = 2
y = 7 − 3x
y = 7 − 3 • 2 = 1
Відповідь: (2;1)
додавання
3x − 2y = 2
5x + 4y = 18
12x 8y = 8
10x + 8y = 36
22x = 44
x = 2
11x = 22
3x − 2y = 2
3 · 2 − 2y = 2
6 − 2y = 2
−2y = −4
y = 2
Відповідь: (2;2)
Метод додавання
3x y = 11
5x + y = 13
8x = 24
x = 3
3x y = 11
3 • 3 y = 11
9 y = 11
y = 2
Відповідь: (3; 2)
б) Метод додавання
4���� + 3���� = 10
−
2���� + 7���� = 12
4x + 3y = 10
4���� + 14���� = 24
17y = 34
y = 2
4x + 3y = 10
4x + 3 · 2 = 10
4x + 6 = 10
4x = 4
x = 1
Відповідь: (1;2)
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
3x − 2y = 2
5x + 4y = 18
y = 1.5x 1
5x + 4(1.5x 1) = 18
5x + 4(1,5x − 1) = 18
5x + 6x − 4 = 18
11х = 22
x = 2
y = 1.5x − 1
y = 1,5 · 2 − 1 = 2
Відповідь: (2;2)

3x y = 11 5x + y = 13
y = 3x − 11 5x + (3x 11) = 13
5x + (3x 11)=13
5x + 3x 11 = 13
8x = 24
x = 3
y = 3x 11
y = 3 • 3 11
y = 9 11
y = 2
Відповідь: (3; 2)
Метод підстановки
4���� + 3���� = 10 2���� + 7���� = 12
���� = 2.5 0.75���� 2(2.5 0.75����) + 7���� = 12
2(2.5 0.75y) + 7y = 12
5 + 1.5y + 7y = 12
8.5y = 17 y = 2
x = 2.5 0.75y
x = 2.5 0.75 • 2
x = 2.5 1.5
x = 1
Відповідь: (1;2)
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
10���� 21���� = 9
5���� + 14���� = 29 | · ( 2)
10x − 21y = 9
10���� 28���� = 58
49y = 49
y = 1
10x 21y = 9
10x 21 · 1 = 9
10x 21 = 9
10x = 30
x = 3
Відповідь: (3; 1)
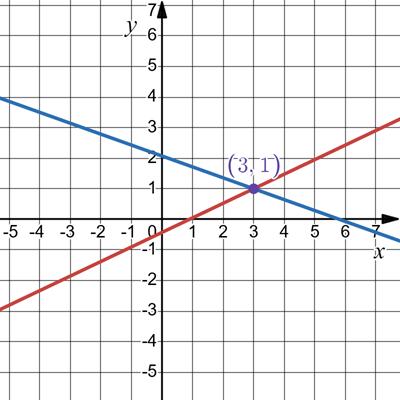
8���� 3���� = 2 2���� + 5���� = 12 | · ( 4)
8���� 3���� =
23y = 46 y = 2
8x 3y = 2 8x 3 • 2 = 2
8x 6 = 2
8x = 8
x = 1
Відповідь: (1; 2) 1122.
0.1���� + 0.2
0.3p = 0.3 p = 1
0.1p + 0.2q = 0.3
0.1 · 1 + 0.2q = 0.3
0.2q = 0.2 q = 1

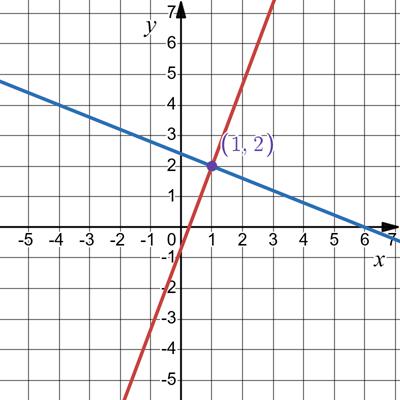
1.2���� 3.4���� = 12 | · 7 2.5���� + 1.4���� = 25 | · 17
8.4���� 23.8���� = 84
+ 23.8y = 425 50.9x = 509 x = 10 1.2x 3.4y = 12 1.2 · 10 3.4y = 12 12 3.4y = 12 y = 0
(10;0)
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
5���� 2 = 4���� + 8���� 8
6���� 3���� + 6 = 24���� + 12
8���� = 6 | · ( 6)
6���� 27���� = 6
6���� + 48���� = 36
6���� 27���� = 6
21y = 42
y = 2
x 8y = 6
x 8 · 2 = 6
x 16 = 6
x = 10
Відповідь: (10;2)
1124. Розв’яжи способом
5���� 6 = 5(���� ����)
2(3���� 1) = 4���� 5
5���� 6 = 5���� 5����
6���� 2 = 4���� 5
0 − 5���� = −6 | · (−4)
6���� 4���� = 3 | · 5
0 + 20���� = 24
30���� 20���� = 15
30x = 9
x = 0,3
6x 4y = 3
6 · 0,3 4y = 3
1,8 4y = 3
4y = 4,8 y = 1,2
Відповідь: (0,3;1,2) В)
6(x 1) (5y 2x) 2 = 0 | · 2 12x
5 − y = 2 | · 5
12(x 1) (5y 2x) = 0
12x 5y = 10
12x 12 5y + 2x = 0
12x − 5y = 10 | · (−1)
14x 5y = 12
12x + 5y = 10
2x = 2
x = 1
14x 5y = 12
14 · 1 5y = 12
� 10���� + 7���� = 51
10���� + 2���� = 24

14 5y = 12
9v = 27 v = 3
10u + 7v = 51
10u + 7 · 3 = 51
10u + 21 = 51
10u = 30 u = 3
Відповідь: (3;3)
| ·
5x 4y = 0 15x + 8y = 200
10x 8y = 0
15x + 8y = 200
25x = 200 x = 8
25x = 200 x = 8
5x 4y = 0 5 • 8 4y = 0 40 4y = 0 4y = 40 y = 10
Відповідь: (8;10) Г)
x − 6 ( 2 3 y − x) = 24 2x 6 ( 1 2 x y) = 2
x 4y + 6x = 24 2x 3x + 6y = 2
7x 4y = 24 x + 6y = 2
7x 4y = 24
7x + 42y = 14
38y = 38
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
5y = 2
y = 0,4
Відповідь: (1;0,4)
1125. Розв’яжи способом
а) �
1,5���� − 2,2���� = 0,1
4,2���� 2,5���� = 7,6
·2,5: 3,75x - 5,5y = 0,25
·2,2: 9,24x - 5,5y = 16,72
3,75x - 9,24x = 0,25 - 16,72 -5,49x = -16,47
x = 3
y = 2
6(���� 1) 5���� 2���� 2 = 0 12���� 5 ���� = 2
7x - 2,5y = 6
y = 12x 5 - 2
7x - 2,5(12x 5 - 2) = 6
x = 1
y = 0,4
1126. Розв’яжи способом додавання
2.5u 0.2(u v) = 2.3
3.7u 1.5(v u) = 5.2
�2.5u 0.2u + 0.2v = 2.3
3.7u 1.5v + 1.5u = 5.2 �
2.3u + 0.2v = 2.3
5.2u 1.5v = 5.2
y = 1 x + 6y = 2
x + 6 · 1 = 2
x = 4
x = 4
Відповідь: (4;1)
б) � 2,7���� 3(���� + ����) = 2,1 3,2���� − 2(���� − ���� ) = 17,6 -0,3x - 3y = 2,1 5,2x - 2y = 17,6
·(-2 3): 0,2x + 2y = -1,4
5,2x - 2y = 17,6 5,4x = 16,2
x = 3
y = -1

3,5x - 2y = 121 3 ·x + 2y = 2 3
·3: -x + 6y = 2
3,5x - 2y = 12
2,5x = 14 x = 5,6 y = 1,27
�3.5y 0.2(2y z) = 31.2 5.2z + 0.7(y 2z) = 10.8
� 35y 4y + 2z = 312
52z + 7y 14z = 108 �31y + 2z = 312 | · ( 19)
�23u + 2v = 23 | · 15
52u − 15v = 52 | · 2
�345u + 30v = 345
104u − 30v = 104
449u = 449
u = 1
23u + 2v = 23
23 + 2v = 23
v = 0
Відповідь: (1;0) в) б)
7y + 38z = 108
� 589y 38z = 5928
7y + 38z = 108
582y = 5820 y = 10
7y + 38z = 108
70 + 38z = 108
38z = 38
z = 1
Відповідь: (10;1) г)
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
2x + 7(x y) 2 = 5 | · 2
5(x 1) + 3x 7y 2 = 0 | · 2
4x + 7x − 7y = 10
10x 10 + 3x 7y = 0
11x 7y = 10
13x 7y = 10 | · ( 1)
11x 7y = 10
13x + 7y = 10
2x = 0
x = 0
11x 7y = 10
7y = 10
y = 10 7
y = 13 7
Відповідь: (0; 13 7)
3 + ���� 4 = 5
= 45 a = 9 Підставимо a = 9 у рівняння a
= 5
2 = 9 5
2 = 4 b = 8
a = 9, b = 8.
2 5 x 3 4 y = y 8 | · 20 1 3 (x 3y) = 3x 10 | · 3
8x 15y = 20y 160 x 3y = 9x 30
8x − 35y = −160 8x 3y = 30 38y = 190 y = 5 8x 15y = 30 8x 15·5 = 30 8x 75 = 30
8x = 45 x = 1,875
Відповідь: (1,875;5)

= 0.4���� 0.3���� | · 10
3(1 − 3���� ) − 4(4 − 2����) = 0 4y 3x = 7
3 9x 16 + 8y = 0 4y 3x = 7
9x + 8y = 13 3x + 4y = 7 | · ( 3) � 9x + 8y = 13 9x 12y = 21 4y = 8 y = 2 4y 3x = 7
8 3x = 7 3x = 1 x = 1 3 Відповідь: (1 3;2) г)
2���� = 12
6���� + 6���� ���� + ���� = 42
x + 5y = 12 | · ( 5) 5���� + 7���� = 42
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
2 ���� 3 = 1 | · 6
2���� 1 2 = 3���� 1 3 + 5 6 | · 6
3���� 2���� = 6
3(2���� 1) = 2(3���� 1) + 5
3���� 2���� = 6 | · ( 2)
6���� − 3 = 6���� − 2 + 5
6x + 4y = 12
6x 6y = 6
2y = 6 y = 3
3x 2y = 6
3x 6 = 6
3x = 12 x = 4
Відповідь: (4;3) � 5x 25y = 60 5���� + 7���� = 42 18y = 18 y = 1
1128. Розв’яжи способом
���� 3 ���� 3 = 0
3 = 0, m 3 + 7 6 n = 2 3
n 3 + 7 6 n = 2 3
2n
6 + 7n 6 = 2 3
5n
6 = 2 3
5n = 4 n = 4 5
Підставимо n = 4 5 у рівняння:
m 7 2 · ( 4 5) = 2
m + 28 10 = 2
m + 14 5 = 2
m = 2 –14 5
m = 10 5 14 5
m = 4 5
Відповідь: m = 0.8, n = 0.8 в)
5x + 7y = 42
5x + 7 = 42
5x = 35 x = 7
Відповідь: (7;1)

=
| ·
2���� = 1.5���� + 2.5 | · 10
4(2���� 1) 3(9 5����) = 0 20���� = 15���� + 25 �8x 4 27 + 15y = 0 20���� 15���� = 25 � 8���� + 15���� = 31 20���� − 15���� = 25 28x = 56 x = 2
8x + 15y = 31 16 + 15y = 31 15y = 15 y = 1
Відповідь: (2;1) г)
5х 3 7 + ���� = 9 | · 7 ���� + ���� 4 ���� 5 9 = 2 | · 36
5���� 3 + 7���� = 66 9���� + 9���� 4���� + 20 = 72
5x + 7y = 66 5���� + 9���� = 52 | · ( 1)
5���� + 7���� = 66 5���� 9���� = 52 2y = 14
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
+ ���� 2 ���� ���� 3 = 8 | · 6 ���� + ���� 3 + ���� ���� 4 = 11 | · 12
3(x + y) 2(x y) = 48
4(���� + ����) + 3(���� ����) = 132
3���� + 3���� 2���� + 2���� = 48
4���� + 4���� + 3���� 3���� = 132
x + 5y = 48
7x + y = 132 | · (−5) � ���� + 5���� = 48
35���� 5���� = 660
34x = 612
x = 18
x + 5y = 48
18 + 5y = 48
5y = 30
y = 6
Відповідь: (18;6)
1129.
Точки: (0; 4), (4; 0)
y = 7
5x + 7y = 66
5x + 7( 7) = 66
5x 49 = 66
5x = 115
x = 23
Відповідь: (23; 7)
26.2
Точки: (0; 2), (2; 0)

�4 = k · 0 + b
0 = k · 4 + b
� b = 4
0 = 4k + 4
4k = 4
k = 1
y = x + 4
a) � 3���� 8���� = ����
4x + 8y = 20a
7x = 21a
x = 21a ÷ 7
x = 3a
4 · 3a + 8y = 20a
8y = 20a 12a
8y = 8a
y = a
Точки: (0; 3), ( 5; 0) � 3 = k · 0 + b
0 = k · ( 5) + b
b = 3
0 = 5k + 3
5k = 3
k = 3 5 = 0.6
y = 0.6x + 3
2 = k · 0 + b 0 = k · 2 + b � b = 2 0 = 2k 2 2k = 2 k = 1 y = x – 2
Відповідь: (3a; a) б) �3x + 7y = m, | · (−1) 8x + 7y = n
3x 7y = m 8���� + 7���� = ����; + 5x = n m
x = (n m)
3 · (n m) 5 + 7y = m
0,6(n m) + 7y = m
7y = m 0,6n + 0,6m
7y = 1,6m 0,6n y = (1,6m 0,6n)
1131.
a) � 5x + y = 10c
5���� − 2���� = 10����; +
y = 20c
y = 20c
5x – 2у = 10c
5x + 40c = 10c
б) �3x 4y = k, | · ( 1) 5x 4y = p � 3x + 4y = k 5x 4y = p
2x = p k
x = 0,5(p k)
5x = 10c 40c
5x = 30c
x = 6c
Відповідь: ( 6c; 20c)
1132. Знайди
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
3 · 0,5 · (p k) 4y = k 4y = 1,5p 1,5k k 4y = 1,5p 2,5k y = 0,375p 0,625k
Відповідь: (0,5(p k); 0,375p 0,625k)
a) � (���� + 3)² − 2���� = ����² + 13
6���� + (���� 1)² = ����(���� 5)
����² + 6���� + 9 2���� = ����² + 13
6���� + ����² 2���� + 1 = ����² 5����
6���� 2���� = 4
6���� + 3���� = 1 | · ( 1)
6���� 2���� = 4 −6���� − 3���� = 1
5y = 5
y = 1
6x 2y = 4
6x + 2 = 4
6x = 2
x = 1 3
Відповідь: (1 3; 1)
б) � 10x + (y + 4)² = y² + 18
(2x − 1)² + 7y = 2x(2x + 3)
10x + y² + 8y + 16 = y² + 18
4x² 4x + 1 + 7y = 4x² + 6x
10x + 8y = 2
10���� 7���� = 1
y = 3
10x 7y = 1
10x 21 = 1
10x = 22
x = 22 10 = 2,2
Відповідь: (2,2; 3)
1133. Знайди
a) �x(x + 3) + 9 = (x y)(x + y) + y(y 3)
26 + 3(2x − y) = 9x − 5(3x + 2y)
+ 3x + 9 = x² y² + y² 3y
26 + 6x − 3y = 9x − 15x − 10y
�3���� + 3���� = 9 | · ( 4)
12���� + 7���� = −26
12���� − 12���� = 36
12���� + 7���� = 26
5y = 10
y = 2
3x 3y = 9

3x 6 = 9
3x = 3
x = 1
Відповідь: ( 1; 2)
б) �(���� + 3)² 5 + ����(���� 1) = ���� (���� + 3) + (���� + 1)² 7(2���� + 3) 6���� = 9 4(2���� 7)
+ 6���� + 9 5 + ����² ���� = ����² + 3���� + ����² + 2���� + 1 14���� + 21 6���� = 9 8���� + 28
3���� 3���� = 3 | ∶ 3
8���� + 8���� = 16 | ∶ 8
x y = 1 ���� + ���� = 2
2x = 1 x = 1 2 x + y = 2 1 2 + y = 2 y = 1 1 2
Відповідь: (1 2, 11 2) 1134. Розв’яжи систему рівнянь a) �x + y = 3, x + z = 4 y + z = 5 · ( 1) ⟺ � x + y = 3, x z = 4 y + z = 5 ⟺ � x + y = 3, y z = 1 y + z = 5
⟺ �x + y = 3 2y = 4, y + z = 5 ⟺�x = 3 y y = 2 z = 5 y �x = 1 y = 2 z = 3
Відповідь: (1; 2; 3).
б) �x + y = 5, x z = 2 y z = 1 · ( 1) ⟹ � x + y = 5 x + z = 2 y z = 1 ⟺
x + y = 5 x + y = 1 y z = 1 , ⟺ �x + y = 5, 2y = 4 y z = 1 ⟺ �x = 5 y, y = 2 z = y 1 ⟺ �x = 3 y = 2 z = 1 ,
Відповідь: (3; 2; 1).
в)
7x + 6y + 7z = 100, x 2y + z = 0,• ( 7)
3x + y 2z = 0
7x + 6y + 7z = 100,
7x + 14y 7z = 0
3x + y 2z = 0.
Додаємо перше і друге рівняння 20y = 100.
y = 5.
Підставимо y = 5 у друге рівняння x 2(5) + z = 0.

x 10 + z = 0. Підставимо y = 5 у третє рівняння 3x + 5 2z = 0.
Підставимо z = 10 x.
x + z = 10.
z = 10 x.
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
3x + 5 2(10 x) = 0.
3x + 5 20 + 2x = 0.
5x 15 = 0.
5x = 15.
x = 3.
Знайдемо z
z = 10 3 = 7.
Відповідь: (3; 5; 7).
1135. Розв’яжи систему рівнянь
3x + 2z = 13
3���� + 4���� = 29
а) � 2x + 3y = 11
З
першого: 2x = 11 - 3y
x = (11 3y)
2
Підставляю в друге:
3(11 3y)
2 + 2z = 13
(33 9y)
2 + 2z = 13
33 - 9y + 4z = 26
-9y + 4z = -7
З третього: 4z = 29 - 3y
z = (29 3y)
4
Підставляю в рівняння -9y + 4z = -7: -9y + 4(29 3y) 4 = -7 -9y + 29 - 3y = -7
-12y = -36 y = 3
Знаходжу z: z =(29 3·3) 4 = (29 9) 4 = 20 4 = 5
Знаходжу x: x =(11 3·3) 2 = (11 9) 2 = 2 2 = 1
Відповідь: x = 1, y = 3, z = 5
б) �x + y z = 11 x y + z = 1 ���� + ���� − ���� = 5
Додаю перше і друге: 2x = 12
x = 6
Додаю друге і третє: 2z = 6 z = 3
Підставляю в перше: 6 + y - 3 = 11
y = 8
Відповідь: x = 6, y = 8, z = 3

в) �2x 2z 3t = 1 x + 4z + 2t = 7
3x z + t = 0
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
третього: t = z - 3x
Підставляю в перше:
2x - 2z - 3(z - 3x) = 1
2x - 2z - 3z + 9x = 1
11x - 5z = 1
Підставляю t у друге:
x + 4z + 2(z - 3x) = 7 x + 4z + 2z - 6x = 7
-5x + 6z = 7
Розв'язую систему з двох рівнянь:
11x - 5z = 1 -5x + 6z = 7
Множу перше на 5: 55x - 25z = 5
Множу друге на 11: -55x + 66z = 77
Додаю: 41z = 82 z = 2
Підставляю в 11x - 5z = 1:
11x - 5·2 = 1
11x - 10 = 1
11x = 11 x = 1
Знаходжу t: t = z - 3x = 2 - 3·1 = -1
Відповідь: x = 1, y = 2, z = -1 1136. Проаналізуй послідовність.
її два члени.
1, 3, 6, 10, 15, 21, 28 1137. Задача
x + y + z = 12
2x + y + 1 2 z = 12
x + y + z = 12
4x + 2y + z = 24
x + y + z = 12
3x + y + (x + y + z) = 24
x + y + z = 12
3x + y + 12 = 24
x + y = 12 z
2x + 12 z + 12 = 24
x + y = 12 z
2x z = 0
x + y = 12 2x
z = 2x
y = 12 3x

z = 2x
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
Якщо x=1, то y = 12 3 = 9, z = 2
Якщо x=2, то y = 12 6 = 6, z = 4
Якщо x=3, то y = 12 9 = 3, z = 6
Якщо x=4, то y = 12 12 = 0, z = 8
Якщо x > 4, тоді y < 0, не підходить.
Відповідь: (1;9;2), (2;6;4), (3;3;6).
б)
x + y + z = 12
8x + 5y + 3z = 60
x + y + z = 12
3x + (5x + 5y + 5z) − 2z = 60
x + y + z = 12
3x + 60 2z = 60
x + y + z = 12
3x = 2z
x + y + 1,5x = 12
z = 1,5x
y = 12 2,5x
z = 1,5x
Якщо x = 2, y = 12 2,5 • 2 = 7, z = 1,5 • 2 = 3
Якщо x = 4, y = 12 2,5 • 4 = 2,
z = 1,5 • 4 = 6
Якщо x = 6, y = 12 2,5 • 6 = 3, z = 1,5 • 6 = 9
Якщо x > 6, тоді y < 0, не
підходить.
Відповідь: (2;7;3), (4;2;6).
в)
x + y + z = 12
4x + 3y + 2z = 36
x + y + z = 12
x + 3(x + y + z) z = 36
x + y + z = 12
x + 36 z = 36 �x + y + z = 12 z = x �y = 12 2x
z = x
Якщо x = 1, то y = 12 2 • 1 = 10, z = 1
Якщо x = 2, то y = 12 2 • 2 = 8, z = 2
Якщо x = 3, то y = 12 2 • 3 = 6, z = 3
Якщо x = 4, то y = 12 2 • 4 = 4, z = 4
Якщо x = 5, то y = 12 2 • 5 = 2, z = 5
Якщо x = 6, то y = 12 2 • 6 = 0, z = 6
Якщо x > 6, тоді y < 0, не підходить.
Відповідь: (1;10;1), (2;8;2), (3;6;3), (4;4;4), (5;2;5).
1138. Обчисли значення многочлена.
а) 2y² + 8,6y – 6,5, якщо y = –4,3, то

2 • (–4,3)2 + 8,6 • (–4,3) – 6,5 = 2 • 4,32 + 2 • 4,3 • (–4,3) – 6,5 = –6,5;
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
б) 19,7a + 19,7c + 10, якщо a = 3,8 і c = 6,2, то 19,7 • 3,8 + 19,7 • 6,2 + 10 = 19,7 • (3,8 + 6,2) + 10 = 19,7 • 10 + 10 = 197 + 10 = 207. 1139.
це числа n; n + 1; n + 2; n + 3; n + 4.
Знайдемо суму цих чисел: n + (n + 1) + (n + 2) + (n + 3) + (n + 4) = 5n + 10 = 5(n + 2). Кратно 5.
Доведено.
Знайдемо суму чотирьох послідовних
n + (n + 1) + (n + 2) + (n + 3) = 4n + 6 не ділиться на 4.
1140.
дорівнює: a) 12; б) -12?
Якщо y = 12, то 6 x = 12;
12x = 6; x = 1 2
Якщо y = 12, то 6 x = 12;
12x = 6; x = 1 2
1141.
40,
�x + y = 40 y = 3x �x + 3x = 40 y = 3x
x + 3x = 40
4x = 40
x = 10
y = 3 • 10
y = 30
Відповідь: 10 і 30
20;
3;
x + y = 40 y x = 20
x + y = 40 x + y = 20 2y = 60 y = 30 30 x = 20 x = 10
Відповідь: 10 і 20.
y − x = 10 y = 3x
3x x = 10 y = 3x 3x x = 10
2x = 10 x = 5
y = 3 • 5
y = 15
Відповідь: 5 і 15 1142. Якій системі рівнянь відповідає кожна схема (мал. 27.1)? �x + y = 37
���� − ���� = 7
Додаємо рівняння: 2y = 44
y = 22
Підставляємо y = 22 у рівняння x + y = 37: x + 22 = 37 x = 15
Відповідь: x = 15, y = 22.
�x + y = 80
y = 3x
Підставляємо y = 3x у перше рівняння: x + 3x = 80
4x = 80

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
x = 20
Підставляємо x = 20 у рівняння y = 3x:
y = 3 · 20 = 60
Відповідь: x = 20, y = 60.
1143. Знайди
Нехай перше число x, друге y, так як їх сума, то
x + y = 35, 5; різниця x y = 12, 5. ����� + ���� = 35, 5
���� ���� = 12, 5
2x = 48
x = 24
24 + y = 35, 5
y = 35, 5 24 = 11, 5
Відповідь: 24; 11,5
1144.
Нехай перше число x, а друге число y.
(x + y)
2 = 37,9 | · 2 (x y)
2 = 7,5 | · 2
�x + y = 75,8 x y = 15
Додаємо рівняння:
2x = 90,8
x = 45,4
Підставляємо x = 45,4 у рівняння x + y = 75,8: 45,4 + y = 75,8 y = 30,4
Відповідь: 45,4 і 30,4. 1145. Купили
x + y = 9
1200x + 900y = 9900
y = 9 x
1200���� + 900(9 − ���� ) = 9900
1200x + 900(9 x) = 9900
1200x + 8100 900x = 9900
300x + 8100 = 9900
300x = 1800
x = 6
y = 9 6
y = 3

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
їх всіх стало 130.
Нехай мулярів працювало x, теслярів y, разом x + y = 50; так як
збільшилось у 2 рази, а теслярів у 3 рази, то 2x + 3y = 130.
Маємо систему: �x + y = 50, | · ( 2)
2x + 3y = 130
2x − 2y = −100
2x + 3y = 130 y = 30
Теслярів 30 , мулярів 50 30 = 20.
Відповідь: 30 теслярів; 20 мулярів 1147. Швидкість
її.
для складання рівняння:
1. Позначимо власну швидкість човна через х км/год.
2. Позначимо швидкість течії через y км/год.
3. Розв'язуємо рівняння для знаходження х та у
Нехай власна швидкість човна x км/год, а швидкість течії y км/год.
2
20 + y = 23 y = 3 Відповідь: Власна

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
x y = 1,6
0,5x + 0,5y = 9
x = 1,6 + y
0,5(1,6 + y) + 0,5y = 9
0,5(1,6 + y) + 0,5y = 9
0,8 + 0,5y + 0,5y = 9
y = 8,2
x = 1,6 + 8,2
x = 9,8
Відповідь:
6x 6y = 3
6x + 6y = 57
12x = 60
x = 5
6 • 5 6y = 3
30 6y = 3
6y = 27
y = 4,5
Відповідь:
+ 3y =
6x + 3y =
x y = 5
6(y + 5) + 3y =
x = y + 5
6(y + 5) + 3y = 570
6y + 30 + 3y = 570
9y = 540

y = 60
x = 60 + 5
x = 65
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
3x + 5y = 212 | · 5
5x + 3y = 268 | · ( 3)
15x + 25y = 1060
15���� − 9���� = −804
16y = 256
y = 16
3x + 5 · 16 = 212
3x + 80 = 212
3x = 132
x = 44
Відповідь:
10x + 16y = 160.
Так як 5
10x + 16y = 160
5x 7y = 5; | · ( 2)
10x + 16y = 160
10x + 14y = 10
30y = 150
y = 5
10x + 16 · 5 = 160
10x + 80 = 160
10x = 80
x = 8 Відповідь:
x y = 8
x + y = 84
x y = 8
2x = 92

x = 46
y = 84 46 = 38 Відповідь: 38 см; 46 см 1155.
x y = 24
x = 3y
3y y = 24
x = 3y
3y y = 24
2y = 24
y = 12
x = 3 • 12
x = 36
Відповідь:
y x = 10
2x + y = 82
y = x + 10
2x + (x + 10) = 82
2x + x + 10 = 82
3x = 72
x = 24
y = 24 + 10
y = 34
Відповідь: Бічні
x + y = 17
2(x 8) = y
x + y =
2x y = 16
3x = 33 x = 11
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
x y = 7
x + y = 65
2x = 72
x = 36

36 + y = 65
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
y = 29
x + y = 65
x − y = 7
2x = 60
x = 30
30 + y = 78
y = 48
Відповідь: 30 книжок і 48
�x + y = 72
x y = 4
2x = 76 x = 38
38 + y = 72 y = 34 Відповідь:
x² y² = 44
= ���� + 4
(���� + 4)² ����² = 44
(y + 4)² y² = 44
y² + 8y + 16 y² = 44
8y = 28
y = 3,5
x = 3,5 + 4
x = 7,5
Відповідь: 7,5 і 3,5.
y² = 60
x = 12 y
(12 y)² y² = 60
(12 y)² y² = 60

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
144 24y + y² y² = 60
144 24y = 60
24y = 84
y = 3,5
x = 12 3,5
x = 8,5
Відповідь: 8,5 і 3,5.
Порівняння
1162. Сформулюйте задачі, що відповідають
Розв’яжіть задачі.
Два види болтів коштують разом 250
грн за певну кількість. Якщо від
вартості першого виду відняти
вартість другого, різниця становить
130 грн. Скільки коштує кожен вид
болтів?
Розв'язання:
Нехай x вартість першого виду
болтів (грн); y вартість другого
виду болтів (грн).
Складаємо систему рівнянь:
�x + 2y = 250 x y = 130
�
130 + y + 2y = 250 x = 130 + y
130 + y + 2y = 250
130 + 3y = 250
3y = 120
y = 40
x = 130 + 40
x = 170
Відповідь: Перший вид болтів
коштує 170 грн, другий 40 грн.
голів і 94 ноги? Нехай фазанів x, кролів y. так як у
4x + 2y = 94.
Маємо систему: �x + y = 35, | · (−2)
4x + 2y = 94; � 2x 2y = 70
4x + 2y = 94
2x = 24 x = 12
Якщо x = 12, то y = 35 12 = 23.
Відповідь: фазанів 12, кролів 23

Маса груші на 50 г більша за масу яблук. Маса трьох яблук дорівнює
масі двох груш. Знайдіть масу
одного яблука та однієї груші.
Розв'язання:
Нехай x маса одного яблука (г); y
маса однієї груші (г)
Складаємо систему рівнянь: �y x = 50 3x = 2y �1,5x x = 50 y = 1,5x 1,5x x = 50
0,5x = 50 x = 100 y = 1,5 • 100 y = 150
Відповідь: Маса одного яблука 100 г, маса однієї
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
5x + 2y = 11 | · ( 2)
2x + 8y = 8 | ∶ 2
10x 4y = 22
x + 4y = 4
9x = 18
x = 2
2 + 4y = 4
4y = 2
y = 0,5
5x = 5 · 2 = 10 (таслів)
10 : 0,5 = 20 (б.)
�
y + 1 = 2(x 1)
x + 1 = y 1
y + 1 = 2((y − 2) − 1)
x = y 2
y + 1 = 2((y 2) 1)
y + 1 = 2(y 3)
y + 1 = 2y 6
2y y = 1 + 6
y = 7
x = 7 2
x = 5
Відповідь:
числа.
Нехай
(x + y)
2 y = 5 | · 2
(x + y) 2 (x y) 2 = 1 | · 2
x + y 2y = 10
x + y (x y) = 2
x y = 10
2y = 2
x 1 = 10
y = 1
x 1 = 10
x = 11

Відповідь: 11 і 1.
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
2x (x y) = 26
2(x y) (x y) = 24
2x x + y = 26
2x 2y x + y = 24
x + y = 26
x y = 24
2x = 50 x = 25
25 + y = 26 y = 1
Відповідь: 25 і 1.
ці числа.
Нехай ці числа x і y. Так як
різниці (x y)² = 121, то маємо систему:
x² y² = 275
(x − y)² = 121;
(x − y)(x + y) = 275 x − y = 11;
або �(x − y)(x + y) = 275 x − y = −11
Розв'яжемо системи:
(x − y)(x + y) = 275 x − y = 11;
або �(x y)(x + y) = 275 x − y = −11; �11(���� + ����) = 275, x y = 11 � 11(x + y) = 275 x y = 11; �x + y = 25 x y = 11
2x = 36 x = 18
Якщо x = 18, y = 7.
Відповідь: 18; 7 або 18; 7 1169. Відстань

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
Відстань
8(x + y) = 320
Проти течії за 10 годин: 10(x y) = 320, то маємо:
8(x + y) = 320
10(x − y) = 320
x + y = 40
x y = 32
2x = 72
x = 36
36 + y = 40 y = 4
Відповідь: 36 км/год; 4 км/год
Знайди швидкість течії
швидкість катера
5 · (x + y) = 210
6 · (x y) = 210
x + y = 42
x y = 35
2x = 77
x = 38,5(км/год) швидкість катера
38,5 + y = 42 y = 42 38,5
y = 3,5(км/год)
3(x + y) = 174
x y = 7
x + y = 58
2x = 65
x = 32,5
32,5 y = 7

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
xy = (x + 3)(y 1)
xy = (x 2)(y + 1)
xy = xy x + 3y 3
xy = xy + x 2y 2
xy xy + x 3y + 3 = 0
xy xy x + 2y + 2 = 0
x − 3y + 3 = 0
x + 2y + 2 = 0
y = 5
y = 5
x 3·5 = 3
x 15 = 3
x = 12
xy = 12 · 5 = 60
км.
швидкість
= (���� + 24)(���� 1) �������� = (���� − 12)(���� + 1)
= �������� ���� + 24���� 24
�������� = �������� + ���� 12���� 12
�������� �������� + ���� 24���� = 24
�������� �������� ���� + 12���� = 12 � ���� 24���� = 24
���� + 12���� = 12
12y = 36
y = 3
x 24 · 3 = 24
x 72 = 24
x = 48
xy = 48 · 3 = 144

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
���� + ���� = 10000
���� + 0,5���� = 4(���� 0,5���� )
���� = 10000 ����
10000 ���� + 0,5���� = 4(���� 0,5����)
10000 x + 0,5x = 4x 0,5x
x + 0,5x 4x + 0,5x = 10000
4x = 10000
x = 2500
2500 + y = 10000
y = 7500
Відповідь: 2500 грн і 7500 грн. 1175. На
3x + y = 6y
x = 80 − y
3(80 y) = 5y
3(80 y) = 5y
240 3y = 5y
3y 5y = 240
8y = 240
y = 30
x = 80 30
x = 50
x + y = 100
0,35x + 0,4y = 38 � x = 100 − y
0,35(100 y) + 0,4y = 38
0,35(100 y) + 0,4y = 38
35 0,35y + 0,4y = 38
0,35y + 0,4y = 38 35
0,05y = 3
y = 60
x = 100 60
x = 40

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
59
x + y = 760
0,4y 0,3x = 59
y = 760 x
0,4(760 x) 0,3x = 59
0,4(760 x) 0,3x = 59
304 0,4x 0,3x = 59
0,4x 0,3x = 59 304
0,7x = 245 x = 350
y = 760 350 y = 410
= y + 3 x 3 = y 1;
x = 2y + 6, x = 3y 3; 2y + 6 = 3y 3 y = 9 x = 24. Відповідь: 24

x 2 = y x 2 = y 2 | · 2
x 2 = y x = 2y 4
x
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
x = 2x 4 4
x = 8
x = 8
y = 8 2
y = 6
Відповідь: 8 горобців і 6 стовпців. 1180. По
x y = 12
x + y = 30
2x = 42
x = 21
21 y = 12 y = 9
Відповідь:
�6x 6y = 90 x = 4y
�6 · 4y − 6y = 90 x = 4y
6 · 4y 6y = 90
24y 6y = 90
18y = 90
y = 5
x = 4 · 5
x = 20
+ y = 35 x = 1,5y
1,5y + y = 35 x = 1,5y
1,5y + y = 35
2,5y = 35 y = 14

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
x = 1,5 • 14
x = 21
Відповідь: 21 кВт і 14 кВт. 1183.
2 1 3 x = 35
7 3 x = 35
x = 35 : 7 · 3
35 15 = 20(м )
15 м і 20 м 1184. Найбільшими
� x + y = 79
y = x + 26,5
79 x y = x + y + 7
y = x + 26,5
Підставимо у = х + 26,5 у перше рівняння:
79 x (x + 26,5) = x + (x + 26,5) + 7
79 2x 26,5 = 2x + 33,5
52,5 2x = 2x + 33,5
52,5 33,5 = 4x
19 = 4x
x = 4,75
y = x + 26,5 = 4,75 + 26,5 = 31,25
79 x y = 79 4,75 31,25 = 43
Відповідь: На
2x + 3y + 7z = 131
2x + 3y + 8z = 140
2x + 3y + 7z = 131 | · ( 1)
2x + 3y + 8z = 140
2x 3y 7z = 131
2x + 3y + 8z = 140
z = 9 Підставимо
2x + 3y + 63 = 131
2x + 3y + 72 = 140
2x + 3y = 68

2x + 3y = 68
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
x = 34 (3 2)y
Якщо y = 2, x = 34 (3 2)·2 = 34 3 = 31, z = 9
Якщо y = 4, x = 34 (3 2)·4 = 34 6 = 28, z = 9
Якщо y = 6, x = 34 (3 2)·6 = 34 9 = 25, z = 9
Якщо y = 8, x = 34 (3 2)·8 = 34 12 = 22, z = 9
Відповідь: (2; 31; 9), (4; 28; 9), (6; 25; 9), (8; 22; 9).
1186.Знайти число, яке при діленні на 4,7 і 11 дає остачі відповідно 2,1 і 6, причому
часток на 2 менша від половини шуканого числа.
Розв'язання:
Позначимо шукане число як x.
Складаємо систему рівнянь для остач:
x ≡ 2( mod 4)
x ≡ 1( mod 7)
x ≡ 6( mod 11)
З
першого рівняння:
x = 4k + 2, k ∈ ℤ
Підставимо у друге рівняння:
4k + 2 ≡ 1( mod 7)
4k ≡ 1( mod 7)
4k ≡ 6( mod 7)
Знайдемо обернене до 4 за модулем 7.
Множимо 4 на 2:
4 · 2 = 8 ≡ 1( mod 7)
Обернене 2.
k ≡ 6 · 2( mod 7)
k ≡ 12 ≡ 5( mod 7)
k = 7m + 5
З
першого рівняння:
x = 4(7m + 5) + 2
x = 28m + 20 + 2
x = 28m + 22
Підставимо в третє рівняння:
28m + 22 ≡ 6( mod 11)
28m ≡ 16 ≡ 5 ≡ 6( mod 11)
6m ≡ 6( mod 11)
Поділимо на 6 (обернене до 6 це 2 за модулем 11): m ≡ 1
Перевірка:
50 mod 4 = 2
50 mod 7 = 1
50 mod 11 = 6
Умова на частки: Частки:
50 : 4 = 12, 50 : 7 = 7, 50 : 11 = 4
Сума часток: 12 + 7 + 4 = 23
Половина числа:

2 = 25
3x + y = 1
y = x 3 y = 3x + 1
x 0 3
y 3 0

+ 2y = 0
x y = 6
2y y = 6
2y y = 6
3y = 6 y = 2
x = 2 · 2
x = 4

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
Відповідь: В 20 г
1192.
12 • 100 : 20 = 60
Відповідь: В 60 г
1193.
3 • 100 300 = 1%
Відповідь: Г 1%
1194. Який
100% – 18% = 82% – води в напої; Концентрація цукру – це масова
3 12 × 100% = 25%
Б 25%; (2 1) 1
1196. Скільки грамів солі в 125 грамах 8 % розчину?
125 • 8 100 = 10 (г) – маса солі.
Відповідь: 10 г.
1197. У скількох грамах 16 %-го розчину є 24 г солі?
24 : 16 100 = 150 (г) – маса розчину.
Відповідь: 150 г.
1198. How many grams of the 15 % solution contain 30 g of salt?
30 : 15 100 = 200 (г) – маса розчину.
Відповідь: 200 г.
1199. У 750 г розчину є 15 г солі. Яка
концентрація? 15 750 • 100% = 2% – концентрація розчину. Відповідь: 2%.
1200. Шляхом

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
6840 • 20 100 = 1368 (грн)
6840 • 27 100 = 1846,8 (форінтів)
6840 • 25 100 = 1710 (євро) –
Відповідь: 1) 1368 грн; 2) 1846,8 форінтів; 3) 1710 євро. 1204. За деяку роботу робітникові
42650 грн. Із них 13 % прибутковий податок, 2 % відрахування у пенсійний фонд, 1 % відрахування у фонд зайнятості, 1 %
1) 13 + 2 + 1 + 1 = 17 %
2) 42650 • (1 – 0,17) = 35399,5 (грн)
Відповідь: після всі відрахувань працівник одержить 35399,5 гривень 1205. Розглянь діаграму, що ілюструє
(мал. 28.4). Дай
1) 100 – (45 + 30 + 15) = 10 % – на сорок
2) 2 : 10 • 100 = 20 (пташок) – усього
1) 10 %; 2) 20 пташок 1206. Першого
32 %, а третього
у пункті?
І д. – ? кг, 20 %
ІІ д. – ? кг, 32 %
ІІІ д. – 240 кг, ? % Усього – ? кг
1) 100 – (20 + 32) = 48 %
2) 240 : 48 • 100 = 500 (кг) –
туристи
– ? км, 15 %
– ? км, 25 %
д. – 24 км, ? %
1) 100 – 55 = 45 %
2) 45 : 100 • 70 = 31,5 %

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
1209.
І п. – 25 %
30 %
Залишилося – ? %
1) 100 – 25 = 75 %
2) 75 : 100 * 70 = 52,5 %
Відповідь: 52,5 %
3,2 – 2,5 = 0,7
2,5
100 = 0,7 x x = 0,7 • 100 : 2,5 x = 28%
Відповідь: на 28 %
1211.
скільки
Розв'язання
Число 40 більше за число 32.
Для обчислення відсотків використовуємо формулу:
Відсотки = (Різниця чисел) (Базове число) · 100
Базове число: 32 .
Обчислюємо різницю чисел: 40 − 32 = 8
Підставляємо в формулу:
Відсотки = 8 32 · 100 = 0,25 · 100 = 25%
Отже, число 40 більше за число 32 на 25%.
2. Число 32 менше від числа 40
У цьому випадку базове число 40.
Формула залишається такою ж:
Відсотки = (Різниця чисел) (Базове число) · 100
Обчислюємо різницю чисел: 40 − 32 = 8
Підставляємо в формулу:
Відсотки = 8 40 · 100 = 0,2 · 100 = 20
Отже, число 32 менше від числа 40 на 20%.

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
m₍речовини₎ = 15 100 · 80 = 12г.
Знайдемо масу нового розчину після додавання води.
До 80 г додали 20 г води:
m₍нового розчину₎ = 80 + 20 = 100г.
Обчислимо нову концентрацію розчину.
Нова концентрація обчислюється за формулою:
Концентрація = m₍речовини₎ m₍розчину₎ · 100
Підставимо знайдені значення:
Концентрація = 12 100 · 100 = 12
Відповідь: після додавання 20 г води концентрація розчину становить 12.
1213. До 40 г 20% го розчину додали 60 г води. Якої концентрації став розчин?
Розв'язання
Визначимо масу розчиненої речовини в початковому розчині.
Маса розчину 40 г. Концентрація 20.
Обчислимо масу розчиненої речовини:
m₍речовини₎ = 20 100 · 40 = 8г
Знайдемо масу нового
m₍нового розчину₎ = 40 + 60 = 100г.
Обчислимо нову концентрацію розчину.
Нова концентрація обчислюється за формулою:
Концентрація = m₍речовини₎ m₍розчину₎ · 100
Підставимо значення:
Концентрація = 8 100 · 100 = 8
Відповідь: після додавання 60 г води концентрація розчину становить 8%.
1214. Зливок міді зі сріблом загальною масою
Скільки чистого срібла потрібно додати до нього, щоб утворений сплав містив 30%
Маса зливка 15 кг, концентрація міді 45%.
m₍міді₎ = 45 100 · 15 = 6,75 кг.
Позначимо масу доданого срібла.
Позначимо масу чистого срібла, яке потрібно додати, як x кг.
Після додавання срібла
сплаву₎ = 15 + x

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
6,75 = 0,3 · (15 + x)
Розкриємо дужки:
6,75 = 4,5 + 0,3x
Віднімемо 4,5 від обох частин:
2,25 = 0,3x
Поділимо на 0,3: x = 2,25 0,3 = 7,5
Перевіримо розрахунок.
Якщо додати 7,5 кг срібла, маса нового сплаву буде:
m₍нового сплаву₎ = 15 + 7,5 = 22,5 кг.
Маса міді залишиться 6,75 кг.
Концентрація:
6,75 22,5 · 100 = 30
Відповідь: потрібно додати 7,5 кг чистого
1215. Розчин містить 5 %
40
100 = x 5
x = 40 · 5 : 100
x = 2(кг) солі
2
2 = x 100
x = 2 · 100 : 2
x = 100(кг)
100 40 = 60 (кг) треба додати
Відповідь:
масу солі: m₍солі₎ = 40 100 · 300 = 120 г. Позначимо масу нового розчину. Нехай маса нового розчину дорівнює x г.
новому розчині
· 100 = 6 Розв'яжемо рівняння
m₍солі₎ = 120 г: 120
· 100 = 6
рівняння: 120 х = 0,06
обидві частини на x: 120 = 0,06x
Поділимо на 0,06: x = 120 0,06 = 2000

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
1217. Змішали 100 г 20% го і 50 г 32%
Визначимо масу речовини в кожному розчині
Маса речовини в 100 г 20% го розчину:
m₁ = 20 100 · 100 = 20г.
Маса речовини в 50 г 32% го розчину:
m₂ = 32 100 · 50 = 16г.
Знайдемо загальну масу речовини в новому розчині.
Загальна маса речовини:
mречовини = m₁ + m₂ = 20 + 16 = 36 г.
Обчислимо масу нового розчину.
Загальна маса нового розчину:
mрозчину = 100 + 50 = 150 г.
Обчислимо концентрацію нового розчину.
Концентрація обчислюється за формулою:
Концентрація = mречовини/mрозчину · 100.
Підставимо значення:
Концентрація = 36 150 · 100 = 24
Відповідь: отримали розчин концентрації 24%.
1218. Є два водно-сольові розчини:
Перший розчин містить 15%, а другий
містить 18% солі?
Розв'язання
Позначимо:
x г маса першого розчину, 800 − x г маса другого розчину.
Запишемо рівняння для концентрації солі.
Маса солі в першому розчині:
0,15x
Маса солі в другому розчині: 0,30(800 − x)
Маса солі в отриманому розчині:
0,18 · 800 = 144 г
Рівняння:
0,15x + 0,30(800 − x) = 144
Розв'яжемо рівняння
Розкриємо дужки:
0,15x + 240 − 0,30x = 144
Зведемо подібні доданки: 0,15x + 240 = 144
Віднімемо 240 від обох частин: 0,15x = −96
Поділимо на −0,15 :
x = 96 0,15 = 640
Знайдемо

другого розчину
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
800 − x = 800 − 640 = 160 г.
Відповідь:
1219.
Перший сплав містить 80 міді (тобто 20 олова).
Другий сплав містить 70 міді (тобто 30 олова).
Скільки кілограмів кожного сплаву потрібно взяти, щоб
який містить 24 олова?
Розв'язання
Позначимо:
x кг маса першого сплаву (20% олова),
200 x кг маса другого сплаву (30 олова).
Запишемо рівняння для вмісту олова.
Маса олова в першому сплаві:
0,2x
Маса олова в другому сплаві:
0,3(200 − x)
Загальна маса олова в новому сплаві (24 від 200 кг):
0,24 · 200 = 48 кг.
Складаємо рівняння:
0,2x + 0,3(200 − x) = 48
Розв'яжемо рівняння.
Розкриваємо дужки:
0,2x + 60 − 0,3x = 48
Зводимо подібні доданки:
0,1x + 60 = 48
Віднімаємо 60 від обох частин:
0,1x = −12
Ділимо на −0,1: x = 12 0,1 = 120
Знайдемо масу другого сплаву
200 − x = 200 − 120 = 80 кг.
Відповідь: потрібно

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
Розв'яжемо рівняння для x: x = 24 0 9375 .
Обчислимо значення x: x = 25.6.
Отже, початкова ціна батону становила 25,6 грн.
Відповідь: початкова ціна батону була 25,6 грн. 1221. Зарплату спочатку
змінилась?
Розв'язання:
Позначимо початкову зарплату через x.
Після збільшення на 20 нова зарплата стала: x + 0.2x = 1.2x
Потім зарплату зменшили на 20.
Знижка обчислюється від нової зарплати 1.2x, тому зарплата стала: 1.2x − 0.2 · 1.2x = 1.2x · (1 − 0.2) = 1.2x · 0.8 = 0.96x
Отже, остаточна зарплата становить 0.96x, що на 0.04x менше за початкову.
У відсотках зміна становить:
0 04x
х · 100 = 4
Відповідь: зарплата зменшилась на 4%. 1222. Розгляньте
скількох музикантів складається
Скрипалі – 27 людей, 45 %
Струнно–смичкові інструменти – ?
1)
2) 60 : 15 • 100 = 400 (людей)
міді?
Цинк – ? г, 50 %
Мідь – ? г, 40 %
Алюміній – ? г, на 600 г менше,
1) 40 – 10 = 30 %
2) 60 : 30 • 100 = 200 (г) –
3) 200 • 0,1 = 20 (г) алюмінію
4) 200 • 0,5 = 100 (г) – цинку
5) 200 • 0,4 = 80 (г) – міді
Відповідь: 100 г; 80 г; 20 г 1224.

Після
Залишилось 600 кг руди Заліза
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
z − 48 кг Вміст заліза зріс на 20 %: (z − 48)/600 = 1.2 • (z/1000)
Розв’язуємо рівняння: 1000(z − 48) = 600 × 1.2z
1000z − 48000 = 720z
280z = 48000
z = 171.43 кг початкова кількість
171.43 − 48 = 123.43 кг
123.43
0.25x = 1.25x
Друга партія принесла
y + 0.5y = 1.5y
Сума доходів від обох партій дорівнює загальному
1.25x + 1.5y = 35000
Розв'яжемо систему рівнянь (1) та (2): З рівняння (1) виразимо y: y = 25000 – x
Підставимо y = 25000 − x у рівняння (2):
1.25x + 1.5(25000 − x) = 35000
Розкриємо дужки:
1.25x + 1.5 · 25000 − 1.5x = 35000
1.25x + 37500 − 1.5x = 35000
0.25x + 37500 = 35000
0.25x = 35000 − 37500
0.25x = −2500
x = 2500
0 25 = 10000
Знайдемо y: y = 25000 − x = 25000 − 10000 = 15000

Позначимо:
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
x = z + 80 У другому ящику на 10
1.1x.
У другому ящику на 30 більше, ніж у третьому, тобто: 1.3z.
Оскільки кількість горіхів у другому ящику однакова, маємо рівняння: 1.1x = 1.3z
Підставимо x = z + 80 із рівняння (1) у рівняння (2):
1.1(z + 80) = 1.3z
Підставимо x = z + 80 із рівняння (1) у рівняння (2):
1.1(z + 80) = 1.3z
Розкриємо дужки:
1.1z + 88 = 1.3z
1.3z − 1.1z = 88
0.2z = 88 z = 88 0,2 = 440
Знайдемо x:
x = z + 80 = 440 + 80 = 520
Знайдемо кількість горіхів у другому ящику:
1.1x = 1.1 · 520 = 572
Відповідь:
1227. За 2 столи і
стіл і скільки стілець?
Нехай стіл коштував
2x + 8y = 8800, | · ( 0,5)
1,1 · ���� + 0,8 · 5���� = 4520; � x 4y = 4400
1,1x + 4y = 4520 ,
0,1х = 120
х = 120 : 0,1
х = 1200(грн) – стіл
2 • 1200 + 8у = 8800
8у = 8800 – 2400
у = 6400 : 8
у = 800(грн) стілець

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
5���� + 3���� = 4650
3(���� + 0,2���� ) + 2(���� 0,1����) = 3222
Спрощую друге рівняння:
5���� + 3���� = 4650
3(1,2���� ) + 2(0,9����) = 3222
5���� + 3���� = 4650
3,6���� + 1,8���� = 3222
Щоб розв'язати систему, помножу перше рівняння на 0,6:
3���� + 1,8���� = 2790
3,6���� + 1,8���� = 3222
Віднімаю перше від другого:
0,6x = 432 x = 720
Підставляю x у перше рівняння:
5·720 + 3y = 4650
3600 + 3y = 4650
3y = 1050 y = 350
Відповідь: футбольний
100000.
0.12x + 0.15y = 13800
З рівняння (1) виразимо y: y = 100000 x
Підставимо y = 100000 x у рівняння (2):
0.12x + 0.15(100000 x) = 13800
Розкриємо дужки:
0.12x + 0.15 · 100000 0.15x = 13800
0.12x + 15000 0.15x = 13800.
0.03x + 15000 = 13800
0.03x = 13800 15000.
0.03x = 1200. x = 1200 0 03 = 40000

Знайдемо y: y = 100000 x = 100000 40000 = 60000
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
першого банку: 0.12x
Відсоткові гроші, отримані з другого банку: 0.14y
0.14y 0.12x = 3400
Розв'яжемо систему рівнянь (1) і (2):
рівняння (1) виразимо y: y = 80000 x
Підставимо y = 80000 x у рівняння (2):
0.14(80000 x) 0.12x = 3400
Розкриємо дужки:
0.14 · 80000 0.14x 0.12x = 3400
11200 0.14x 0.12x = 3400
11200 3400 = 0.26x
7800 = 0.26x x = 7800 0 26 = 30000
Знайдемо y: y = 80000 x = 80000 30000 = 50000
Відповідь:

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
x · (1 + p 100) + x · (1 + k 100) 2x = m
x + p
100 · x + x + k 100 · x 2x = m
p
100 · x + k 100 · x = m
Винесемо x за дужки:
x · ( p 100 + k 100) = m
Спрощуємо:
x · (p+k)
100 = m
Звідси знайдемо x:
x = m · 100 (p+k)
Відповідь:

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
Після всіх роздач у Марини залишилось 1 яблуко: x 8 17 4 = 1
Розв'яжемо рівняння: x 8 17 4 = 1
Приведемо до спільного знаменника: x 8 34 8 = 1 (x 34) 8 = 1
Помножимо обидві частини на 8: x 34 = 8 x = 42
Перевірка:
Спочатку у Марини було 42 яблука.
Першому другу: 42 2 1 = 21 1 = 20 яблук залишилось.
Другому другу: 20 2 2 = 10 2 = 8 яблук залишилось.
Третьому другу: 8 2 3 = 4 3 = 1 яблуко залишилось.
Усі умови виконуються.
Відповідь: спочатку у Марини було 42 яблука.
1234. Запиши наступні члени числової послідовності.
а) 11, 33, 99, 297, 891.
б) 45, 23, 69, 47, 141, 119.
1235. Знайди добуток многочленів.
а) (a³ 1)(a³ + 1)(a⁶ + 1) = (a⁶ 1)(a⁶ + 1) = a¹² 1; б) (m 2)(m + 2)(m² + 4) = (m² 4)(m² + 4) = m⁴ 16.
1236. Склади рівняння
а) A(1; 3) і B(3; 7);
б) K(3; 2) і P( 1; 2);
в) C(2; 4) і D(5; 2);
г) E(1; 2) і F(3; 3).
Розв'язання:
а) Точки A(1; 3) і B(3; 7):
Знайдемо k:
k = (7 3) (3 1) = 4 2 = 2.
y = kx + p,
Підставимо A(1; 3) у рівняння y = kx + p: 3 = 2(1) + p ⇒ p = 3 2 = 1.
Рівняння: y = 2x + 1
б) Точки K(3; 2) і P( 1; 2):
Знайдемо k:
k = ( 2 2) ( 1 3) = 4 4 = 1.

Підставимо K(3; 2) у рівняння y = kx + p: 2 = 1(3) + p ⇒ p = 2 3 = 1
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
Рівняння:
y = x 1
в) Точки C(2; 4) і D(5; 2):
Знайдемо k:
k = ( 2 4) (5 2) = 6 3 = 2.
Підставимо C(2; 4) у рівняння y = kx + p:
4 = 2(2) + p ⇒ p = 4 + 4 = 8
Рівняння:
y = 2x + 8
г) Точки E(1; 2) і F(3; 3):
Знайдемо k:
k = (3 2) (3 1) = 1 2 .
Підставимо E(1; 2) у рівняння y = kx + p:
2 = 1 2 (1) + p ⇒ p = 2 1 2 = 4 2 1 2 = 3 2
Рівняння:
y = (1 2)x + 3 2
Відповідь:
а) y = 2x + 1,
б) y = x 1,
в) y = 2x + 8,
г) y = (1 2)x + (3 2).
1237. В якій квартирі живе Орися, якщо її
збільшується на 30?
Розв'язання:
Позначу номер квартири Орисі як x.
За умовою: 7x + 30 = номер квартири
Але номер квартири - це і є x.
Тому маємо рівняння: 7x + 30 = x
Віднімаю x від обох частин: 6x + 30 = 0
6x = -30
x =30 6 = -5
Отримали від'ємне число, що неможливо для номера квартири.
Перевірю, чи правильно я зрозумів умову.
Альтернативне розуміння: якщо номер
на 30
Тоді: 7x = x + 30
6x

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
(2 + 10 + 7 + 10 + 5 + 5 + 20) ÷ 7 =
3 + 2 + 20 + 0 = 25
таблиці видно, що найбільше учнів (20) обрали літо. У скількох учнів
Весну обрали 2 учні, осінь - 0 учнів.
Разом: 2 + 0 = 2 учні.
Відповідь: 1) 25 дітей; 2) літо; 3) 2 учні. 1242. В таблиці наведено
середній місячний дохід підприємця? (56 + 46 + 30 + 35 + 38 + 26) : 6 = 231 : 6 = 38,5 (т. грн)
Відповідь: середній
Отже, змінна e = 3.5
1244. Три мішки картоплі
4 мішків 59 кг?
четвертого мішка: 236 - 162 = 74 кг

+ 200 + 300 + 400 =
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
1246.
(мал. 29.7).
писали тест? Знайди середнє
вибірки. На всі запитання тесту відповіли 2 учня.
Писали тест 9 учнів. (5 + 7 + 2 · 8 + 3 · 9 + 2 · 10) ÷ 9 = 75 ÷ 9 = 81 3 – середнє арифметичне 1247. Знайди найбільше,
а) Вибірка: 2; 5; 4; 5; 3; 2; 2; 2; 4; 5; 5; 6; 5; 6; 5
Найменше значення:
Найменше число в вибірці 2. Найбільше значення: Найбільше число в вибірці 6.
Середнє значення:
Середнє значення обчислюється за формулою:
Середнє = Сума всіх значень / Кількість значень
Сума всіх значень:
2 + 5 + 4 + 5 + 3 + 2 +
Кількість значень: 15.
Середнє значення:
Середнє = 61 15 ≈ 4,07.
б) Вибірка: 1, 5; 1, 6; 1, 2; 2, 1; 2, 4; 2, 7; 2, 8; 3, 0; 3, 0; 3, 0; 3, 1; 3, 1; 3, 1; 3, 4
Найменше значення:
Найменше число в вибірці 1, 2.
Найбільше значення:
Найбільше число в вибірці 3,4.
Середнє значення:
Сума всіх значень: 1, 5 + 1, 6 + 1, 2 + 2, 1 + 2, 4 + 2, 7 + 2, 8 + 3, 0 + 3, 0 + 3, 0 + 3
Кількість значень: 14.
Середнє значення:
Середнє = 36,0 14 ≈ 2,57.

Відповідь: а) найменше: 2, найбільше: 6, середнє: 4,07; б) найменше: 1,2, найбільше: 3,4, середнє: 2,57
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
a) 12; 17; 11; 13; 14; 15; 16; 13; 13.
b) 0,95 ; 0,99 ; 1,03 ; 1,06 ; 0,97 ; 0,97 ; 1,0 ; 1,01 ; 0,98 ; 0,97 ; 0,99; 0,96; 1,02; 0,97; 1,0. a) Вибірка:
12, 17, 11, 13, 14, 15, 16, 13, 13
Найбільше значення:
Найбільше число у вибірці 17.
Найменше значення:
Найменше число у вибірці 11.
Середнє значення вибірки:
Середнє значення вибірки обчислюється за формулою:
Середнє = Сума всіх значень / Кількість значень
Сума всіх значень:
12 + 17 + 11 + 13 + 14 + 15 + 16 + 13 + 13 = 124
Кількість значень: 9.
Середнє значення:
Середнє значення = 124 9 ≈ 13.78
b) Вибірка: 0.95, 0.99, 1.03, 1.06, 0.97, 0.97, 1.00, 1.01, 0.98, 0.97, 0.99, 0.96, 1.02, 0.97, 1.00
Найбільше значення:
Найбільше число у вибірці 1.06
Найменше значення:
Найменше число у вибірці 0.95.
Середнє значення вибірки:
Середнє значення вибірки
Середнє = Сума всіх значень / Кількість значень Сума всіх значень: 0.95 + 0.99 + 1.03 + 1.06
+ 1.00 = 14.78
Кількість значень: 15
Середнє значення:
Середнє значення = 14.78 15 ≈ 0.985
Відповідь:
Найбільше: 1,06,
Найменше: 0,95,
Середнє: 0,985.
1249.

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
Середнє
× Частота) = (10 · 2) + (9 · 2) + (8 · 1) + (7 ·
+ (3 · 5) + (2 · 4) + (1 · 5)
= 20 + 18 + 8 + 28 + 24 + 20 + 24 + 15 + 8 + 5 = 170 Сума частот: ∑ Частота = 2 + 2 + 1 + 4 + 4 + 4 + 6 + 5 + 4 + 5 = 37
Середнє значення:
Середнє значення = 170/37 ≈ 4,59.
Відповідь: 4,59°С.
4)На твою думку, про який місяць йде мова?
Середня температура близько +4,59°С характерна
регіону.
Відповідь:
а) 4 дні, б) 4 дні, в) 5 днів. а) +10°С, б) +1°С. 4,59°С.
Березень або листопад. 1250. Чому дорівнює
одиниць (мал. 29.8).
а) (39 + 41 + 43) : 3 = 123 : 3 = 41
б) (39 + 40 + 42) : 3 = 121 : 3 ≈ 40
в) (41 + 42 + 43) : 3 = 42
1251. За діаграмою (мал. 29.9)

1253.
Найбільше 5 (кг); найменше 0 (кг); середнє значення 21 9 = 2,1(кг).

Найбільше 90 (балів);
найменше 45 (балів);
середнє значення:Д
(90 + 65 + 55 + 90 + 90 + 65 + 55 + 45 + 90 + 75) : 10 = = 72 (бала).
1255. Перед вами
Математика: 6, 10, 4, 7, 8, 4, 9, 10, 6, 8, 5, 9, 10
Англійська мова:
1) Знайдіть середню оцінку
(мал. 29.10).
(9 + 10 + 4 + 7 + 8 + 4 + 9 + 10 + 6 + 8 + 5 + 9 + 10) : 13 ≈
: 16 = 7,75
: 8 = 7,875
2) Математика:
найменше: 4;
найбільше: 10.
Англійська мова:
найбільше: 10;
найменша: 4.
Географія:
найбільше: 10;
найменша 5.
3)

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html

0 до 3 5 від 4 до 6 10
від 7 до 9 30
від 10 до 12 4
від 13 до 15 16
від 16 до 18 10
від 19 до 21 2 від 22 до 24 3
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
Місяць Число пожеж
червень 5
липень 7
серпень 3
вересень 4
жовтень 2
листопад 3
грудень 3
січень 4
лютий 1
березень 6
квітень 6
травень 7
Найбільше 7; найменше 1. 1258. Опитавши
(см) Частота
2. Найменше і найбільше значення: Найменше значення: 25 см; найбільше значення:

x = Сума всіх значень Кількість значень
де:
x середнє значення, Сума всіх значень сума всіх
Кількість значень кількість опитаних осіб (60). Крок 1. Обчислимо суму

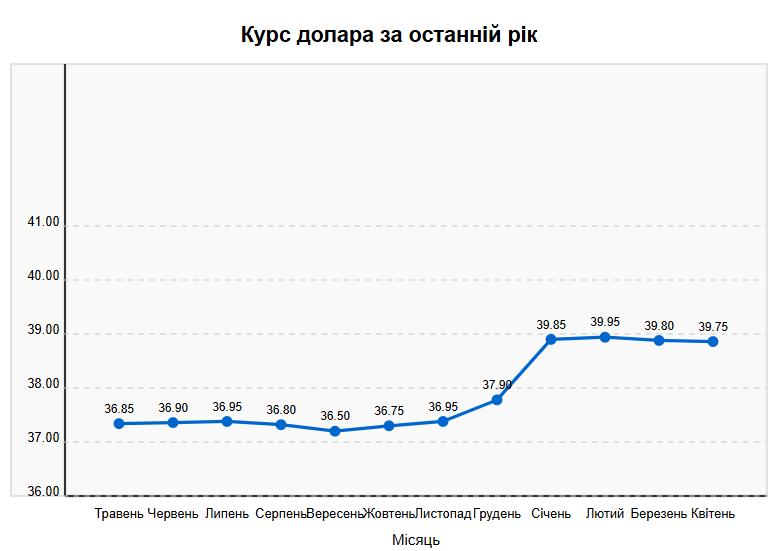
1)
3)
4)
1262.
Виходить, що 60 грн. це дві третини від ціни.
Отже 60 : 2 • 3 = 90 грн.
Відповідь: 90 грн
1263. Склади рівняння прямих,
Пряма а y = 3,
пряма b y = –0,5x + 2,
пряма c x = –4.
1264. Доведи тотожність a) a² + 3a + 2 = (a + 1)(a + 2)
a² + 3a + 2 = a² + 2a + a + 2
a² + 3a + 2 = a² + 3a + 2
б) 7x³ + 5x² 6x + 3 = ((7x + 5)x 6)x + 3
7x³ + 5x² 6x + 3 = (7x² + 5x 6)x + 3
7x³ + 5x² 6x + 3 = 7x³ + 5x² 6x + 3
1265. Після
Розв'язання:

29.11
Скільки
Оскільки
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
Відповідь:
капітана?
Розв'язок:
Капітаном
Розв'язок:
вибираємо заступника з 4 гравців, що залишились (4 способи).
Загальна кількість способів за правилом множення: 5 × 4 = 20 способів.
Відповідь: Б 20 1270. Скількома способами можна

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
1.
номер.
2. Підрахунок вільних номерів:
Тримісні номери:
Загальна кількість тримісних номерів: 10
Зайнято тримісних номерів: 3
Вільних тримісних номерів: 10 − 3 = 7.
Чотиримісні номери:
Загальна кількість чотиримісних номерів: 3
Зайнято чотиримісних номерів: 1
Вільних чотиримісних номерів: 3 − 1 = 2
3. Загальна кількість варіантів поселення:
Сім'я може заселитися або в тримісний, або в чотиримісний номер.
Тому підсумуємо кількість вільних номерів: 7 + 2 = 9 Відповідь:
1. Перша страва: 3 варіанти.
2. Друга страва: 6 варіантів.
3. Салат: 4 варіанти.
Оскільки ми

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
3. Толя, Олег, Ігор
4. Толя, Ігор, Олег
5. Ігор, Олег, Толя
6. Ігор, Толя, Олег
2. Варіанти, в яких Ігор на першому місці
Якщо Ігор на першому місці, то залишаються 2 місця для Олега і Толі.
Вони можуть помінятися місцями, і отже є 2 варіанти розташування:
1. Ігор, Олег, Толя
2. Ігор, Толя, Олег
Тобто, є 2 варіанти, в яких Ігор на першому місці.
3. Варіанти, в яких Олег не на останньому місці
Щоб знайти варіанти, де Олег не на останньому місці, потрібно подивитись на всі
можливі варіанти черги (всього 6 варіантів), а потім виключити ті, де Олег на
останньому місці.
Варіанти, де Олег на останньому місці:
1. Толя, Ігор, Олег
2. Ігор, Толя, Олег Є 2 варіанти, де Олег на останньому місці.
Отже, кількість варіантів, де Олег не на останньому місці: 6 − 2 = 4.
Тобто, є 4 варіанти, в яких Олег не на останньому місці.
Відповіді:
а) кількість варіантів,
Кількість
3! = 3 • 2 • 1 = 6
Тобто, існує 6 варіантів маршруту, які
1. Варшава, Краків, Гданськ
2. Варшава, Гданськ, Краків
3. Краків, Варшава, Гданськ
4. Краків, Гданськ, Варшава
5. Гданськ, Варшава, Краків
6. Гданськ, Краків, Варшава
Відповідь: існує 6 варіантів

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
5!
Отже, існує
Відповідь:
1. кількість варіантів
2. кількість послідовностей
1276. Скількома способами можна розставити на полиці 5 різних книжок?
Потрібно знайти, скількома
Кількість
5!=5
4! = 4 • 3 • 2 • 1 = 24.
Отже, існує 24 способи
Відповідь: існує 24 способи розставити 4 різні книжки
полиці. 1278. Скільки парних п’ятицифрових
цифри 3, 4, 5, 7 і 1?
Потрібно знайти, скільки парних п'ятицифрових
цифри 3, 4, 5, 7 і 1, за умови, що всі цифри різні.
1. Умови:
• Число повинно бути п'ятицифровим.
• Число повинно бути парним.
• Цифри числа повинні бути різними.
• Для запису числа доступні цифри: 3, 4, 5, 7, 1.
2. Визначимо, які числа є парними: • Для того, щоб число було парним, його остання

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
використовуючи цифри 3, 4, 6, 8?
Потрібно визначити, скільки непарних чотирицифрових чисел, усі цифри яких різні, можна записати, використовуючи цифри 3, 4, 6, 8.
1. Умови:
• Число повинно бути чотирицифровим.
• Число повинно бути непарним.
• Цифри числа мають бути різними.
• Для запису числа доступні цифри: 3, 4, 6, 8.
2. Умови для непарності:
• Для того, щоб число було непарним, його остання цифра
• У нашому наборі цифр є тільки 3 (непарна).
Отже, остання цифра нашого числа повинна бути 3.
3. Вибір перших трьох цифр:
• Після того, як ми вибрали 3 для останньої цифри, залишаються цифри 4, 6, 8.
• Для першої цифри є 3 варіанти (можна вибрати одну з цифр 4, 6, 8).
• Для другої цифри, після того, як вибрана перша, залишиться 2 варіанти.
• Для третьої цифри залишиться 1 варіант.
Отже, кількість способів вибрати і розставити
3 • 2 • 1 = 6.
4. Загальна кількість варіантів:
• Оскільки остання цифра вже визначена

2 • 2 • 2 = 8.
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
(0 або 1).
Загальна кількість можливих варіантів коду визначається як:
24 = 16. Тобто, всього є 16 можливих варіантів коду.
У найгіршому випадку, щоб відчинити двері, потрібно перебрати всі 16 варіантів, якщо правильний код знаходиться на останньому місці.
Відповідь: у найгіршому випадку потрібно перебрати 16 варіантів коду 1283. У групі 13 учнів/учениць. Скількома способами можна скласти список учнів/учениць?
Це задача на перестановки 13 елементів.
Кількість перестановок 13 учнів/учениць обчислюється
13: 13! = 13 • 12 • 11 • 10 • ⋯ • 1.
Враховуючи великий розмір числа, точне значення 13! дорівнює: 13! = 6,227,020,80013! = 6,227,020,80013! = 6,227,020,800
Отже, існує 6,227,020,800 способів скласти список учнів/учениць.
Відповідь: існує 13! = 6,227,020,800 способів скласти список учнів/учениць.
1284. Зустрілися семеро
потискає руку А), потрібно
руки.
Кількість таких пар можна знайти
C(n,2) = n(n 1) 2 де n = 7 це кількість друзів.
C(7,2) = (7(7 1)) 2 = (7×6) 2 = 21

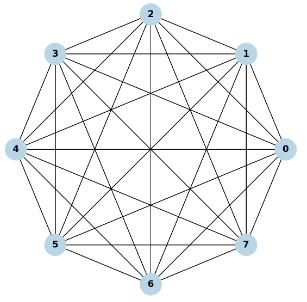
Отже,
C(14,2) = 14(14 1) 2 =
91×2 = 182
1.
2.

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
10 • 10 • 10 = 1000.
Отже, існує 1000
Відповідь: можна придумати 1000 різних
1289. З цифр 1, 3, 5, 7 і 9 склали різні
різні. Скільки чисел було складено?
Ми маємо 5 доступних цифр: 1, 3, 5, 7, 9, і потрібно створити трицифрові
цифри різні.
1. Перша цифра (сотні): Для першої цифри ми можемо вибрати будь–яку з
цифр (1, 3, 5, 7, 9).
Отже, для першої цифри є 5 варіантів.
2. Друга цифра (десятки): Друга цифра повинна
другої цифри залишиться 4 варіанти.
3. Третя цифра (одиниці): Третя цифра
для неї залишиться 3 варіанти.

1.
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
1, 3, 5, 7, 9.
першої цифри є 5 варіантів (1, 3, 5, 7, 9).
2. Друга цифра (десятки): Друга цифра повинна
другої цифри залишиться 4 варіанти.
3. Третя цифра (одиниці): Третя цифра
для неї залишиться 3 варіанти.
Отже, загальна кількість трицифрових чисел,
обчислюється як:
5 • 4 • 3 = 60.
Відповідь: існує 60 трицифрових
чисел?
1. Чисельник:
4 варіанти.
2. Знаменник:

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
Отже, кількість двоцифрових чисел, що діляться на 5, дорівнює: 9 • 2 = 18.
Відповідь: Г
2. Число, що ділиться на 10
Число ділиться на 10, якщо його остання цифра дорівнює 0. • Перша цифра може бути будь–якою від 1 до 9 (9 варіантів).
• Остання цифра повинна бути 0 (1 варіант).
Отже, кількість двоцифрових чисел, що діляться на 10, дорівнює: 9 • 1 = 9.
Відповідь: А
3. Число, що ділиться на 2
Число ділиться на 2, якщо його остання цифра є парною (0, 2, 4, 6, 8).
• Перша цифра може бути будь–якою від 1 до 9 (9 варіантів).
• Остання цифра повинна бути парною (5 варіантів: 0, 2, 4, 6, 8).
Отже, кількість двоцифрових чисел, що діляться на 2, дорівнює: 9 • 5 = 45.
Відповідь: Б
Остаточні відповідності:
1. Число, що ділиться на 5 – Г (18 способів)
2. Число, що ділиться на 10 – А (9 способів)
3. Число, що ділиться на 2 – Б (45 способів) 1295. Комплексний
• 2 перші страви,
• 3 гарніри,
• 2 м'ясні страви,
• напій (кількість варіантів не вказана, але припустимо, що є один напій на вибір).
Потрібно визначити, скільки існує варіантів різних
1. Перша страва: Є 2 варіанти.
2. Гарнір: Є 3 варіанти.
3. М'ясна страва: Є 2 варіанти.
4. Напій: Є 1 варіант (як припускаємо з умови).

страв.
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
k₅ = 2: 5×2 = 10 грн 1 варіант (2 монети по 5 грн)
k₅ = 1: 5×1 = 5 грн, залишилось заплатити 5 грн
Для решти 5 грн можливі варіанти:
k₂ = 2, k₁ = 1: (5 грн, 2 грн, 2 грн, 1 грн)
k₂ = 1, k₁ = 3: (5 грн, 2 грн, 1 грн, 1 грн, 1 грн)
k₂ = 0, k₁ = 5: (5 грн, 1 грн, 1 грн, 1 грн, 1 грн, 1 грн)
Всього 3 варіанти
k₅ = 0: залишилось заплатити 10 грн
Можливі варіанти:
k₂ = 5, k₁ = 0: (2 грн, 2 грн, 2 грн, 2 грн, 2 грн)
k₂ = 4, k₁ = 2: (2 грн, 2 грн, 2 грн, 2 грн, 1 грн, 1 грн)
k₂ = 3, k₁ = 4: (2 грн, 2 грн, 2 грн, 1 грн, 1 грн, 1 грн, 1 грн)
k₂ = 2, k₁ = 6: (2 грн, 2 грн, 1 грн, 1 грн, 1 грн, 1 грн, 1 грн, 1 грн)
k₂ = 1, k₁ = 8: (2 грн, 1 грн, 1 грн, 1 грн, 1 грн, 1 грн, 1 грн, 1 грн, 1 грн)
k₂ = 0, k₁ = 10: (1 грн, 1 грн, 1 грн, 1 грн, 1 грн, 1 грн, 1 грн, 1 грн, 1 грн, 1 грн)
Всього 6 варіантів
Загалом: 1 + 3 + 6 = 10 варіантів заплатити 10 грн
1297.Скільки існує варіантів
Розв'язок:
z - кількість монет по 5 грн
За умовою маємо рівняння:
1·x + 2·y + 5·z = 10
Треба знайти
це рівняння.
Розглянемо можливі значення для z:
z = 0: 1·x + 2·y = 10
y = 0: x = 10 (10 монет по 1 грн)
y = 1: x = 8 (8 монет по 1 грн та 1 монета по 2 грн)
y = 2: x = 6 (6 монет по 1 грн та 2 монети по 2 грн)
y = 3: x = 4 (4 монети по 1 грн та 3 монети по 2 грн)
y = 4: x = 2 (2 монети по 1 грн та 4 монети по 2 грн)
y = 5: x = 0 (5 монет по 2 грн)
z = 1: 1·x + 2·y = 5
y = 0: x = 5 (5 монет по 1 грн
y = 1: x = 3 (3 монети по 1
y = 2: x = 1 (1 монета по 1
z = 2: 1·x + 2·y = 0
y = 0: x = 0 (2 монети по 5 грн)
Отже, всього маємо 10 різних
Відповідь: 10 варіантів 1298. Розв’яжи рівняння.
а) z² + 14z + 49 = 0 (z + 7)² = 0
z = 4;

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
б) x² x + 0,25 = 0
(x 0,5)² = 0
x = 0,5
1299. В
а) танцювальних номерів;
б) музичних номерів.
а) Тaнцювальні номери
Розв'язання:
Дані: 180, 220, 260, 300, 360
Найменше значення: 180.
Найбільше значення: 360.
Середнє значення:
Середнє значення обчислюємо за формулою:
Середнє = сума
Сума = 180 + 220 + 260 + 300 + 360 = 1320
Середнє = 1320 5 = 264
Середнє: 264
б) Музичні номери Дані: 540, 680, 620, 760, 660.
Найменше значення: 540.
Найбільше значення: 760.
Середнє значення:
Сума = 540 + 680 + 620 + 760 + 660 = 3260
Середнє = 3260 / 5 = 652
Відповідь для музичних номерів:
Найменше: 540.
Найбільше: 760.
Середнє: 652.
1300. Знайди суму, різницю,
а) 4 · 10⁸ і 2 · 10⁷; б) 3,6 · 10¹⁹ і 2 · 10¹⁹.
Розв'язок: а) 4 · 10⁸ і 2 · 10⁷
Сума: 4 · 10⁸ + 2 · 10⁷ = 4 · 10⁸ + 0,2 · 10⁸ = 4,2 · 10⁸
Різниця: 4 · 10⁸ - 2 · 10⁷ = 4 · 10⁸ - 0,2 · 10⁸ = 3,8 · 10⁸
Добуток: 4 · 10⁸ · 2 · 10⁷ = 8 · 10¹⁵
Частка: 4 · 10⁸ : 2 · 10⁷ = 4 : 2 · 10⁸ : 10⁷ = 2 · 10¹
б) 3,6 · 10¹⁹ і 2 · 10¹⁹
Сума: 3,6 · 10¹⁹ + 2 · 10¹⁹ = 5,6 · 10¹⁹
Різниця: 3,6 · 10¹⁹ - 2 · 10¹⁹ = 1,6 · 10¹⁹
Добуток: 3,6 · 10¹⁹ · 2 · 10¹⁹ = 7,2 · 10³⁸
Частка: 3,6 · 10¹⁹ : 2 · 10¹⁹ = 3,6 : 2 = 1,8

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
ймовірність того, що воно червоне?
2. Кількість днів тижня:

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
(тобто, 7 подарунків).
Отже, ймовірність
Відповідь: ймовірність того, що
або приблизно 0,1429 (14,29%).
1307. Яка ймовірність того, що при
очок, що дорівнює парному числу?
Розв'язання: Гральний кубик
числа на гральному кубику це 2, 4 і 6.
Тобто, є 3 сприятливі
Ймовірність того, що випаде парне число, обчислюється як відношення
1. Усього учасників
2.
відношення кількості призерів
P = Кількість призерів

обчислюється як
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
кількість карт 36. Ймовірність того, що
P(чорний король) = 2 36 = 1 18
королем:
г) Туз: У колоді є 4 туза (по одному на кожну масть), отже, є 4 туза.
Загальна кількість карт 36.
Ймовірність того, що вибрана карта є тузом:
P(туз) = 4 36 = 1 9
1310. З усіх натуральних чисел, більших за 9 і
число. Установіть
1 – Г, 2 – Д, 3 – Б, 4 – В 1311. Яка ймовірність того,
3; б) не менше 2? а) 2 6 = 1 3; б) 5 6 . 1312. Яка ймовірність того, що
Розв'язання: а) Є кратним числа 13:
Двоцифрові числа, кратні 13, це числа від 13 до 99, які діляться на 13.
Перелік двоцифрових чисел, кратних 13: 13, 26, 39, 52, 65, 78, 91. Це 7 чисел.
Загальна кількість двоцифрових чисел це числа від 10 до 99, тобто: 99 10 + 1 = 90.
Ймовірність того, що навмання вибране число є кратним 13:
P(кратне 13) = 7 90
б) Є дільником числа 80:
Щоб число було дільником 80, воно повинно ділити 80 без остання.
Дільники числа 80: 1, 2, 4, 5, 8, 10, 16, 20, 40, 80.
Тільки двоцифрові числа серед цих дільників це: 10, 20, 40. Це 3 числа.
Загальна кількість двоцифрових чисел 90. Ймовірність того, що навмання вибране число є
P(дільник 80) = 3 90 = 1 30
в) Має суму цифр 9:
числа 80:
Перелічимо всі двоцифрові числа, сума цифр яких дорівнює 9:
18(1 + 8)
27(2 + 7)
36(3 + 6)
45(4 + 5)
54(5 + 4)
63(6 + 3)
72(7 + 2)
81(8 + 1)

90(9 + 0) Це 9 чисел.
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
цифра однакові: 11, 22, 33, 44, 55, 66, 77, 88, 99 Це 9 чисел.
Загальна кількість двоцифрових чисел 90.
Ймовірність того, що
P(однакові цифри) = 9 90 = 1 10
1313. З натуральних чисел від 1 до 30 включно учень навмання називає одне. Яка
ймовірність того, що це число є дільником числа 28?
Розв'язання:
Дільники числа 28:
Для початку знайдемо дільники числа 28.
Вони обчислюються так: 28 = 2² × 7
Дільниками числа 28 є: 1, 2, 4, 7, 14, 28.
Числа від 1 до 30:
Ми працюємо з числами від 1 до 30.
Тобто, з усіх натуральних чисел від 1 до 30
вибране число є одним із дільників числа 28.
Кількість сприятливих варіантів: Дільники числа 28, які знаходяться
Ймовірність

P(червона ручка) = 8 27 Відповідь:
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
квіток у букеті:
У букеті є 13 білих троянд і 18 червоних троянд.
Загальна кількість квіток: 13 + 18 = 31.
Кількість червоних квіток:
Червоних троянд 18.
2. Ймовірність того, що квітка буде червоною:
Ймовірність того, що навмання
P(червона) = 18 31
троянд 13.
Розв'язання: 1. Загальна кількість

карток, що не є синіми:
ми шукаємо ймовірність
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
Розв'язання:
1. Загальна кількість карток:
У коробці є:
5 синіх карток,
2 червоних картки,
4 зелених картки.
Загальна кількість карток: 5 + 2 + 4 = 11.
Кількість карток, що не є синіми:
Нам потрібно знайти кількість карток, які не є синіми.
Це сума червоних і зелених карток:
2 (червоні) +4 (зелені) = 6.
Ймовірність того, що картка не буде синьою:
Ймовірність того, що вибрана картка не буде синьою, обчислюється
кількості карток, що не є синіми,
P(не синя) = 6 11
1319. У шухляді
3. Кількість сприятливих варіантів: Тільки одна
4. Ймовірність

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
P(A або B) = P(A) + P(B)
Ймовірність вибору
P(A) = 28 100
Ймовірність
P(B) = 36 100
Тому загальна ймовірність:
P(A або B) = 28 100 + 36 100 = 64 100 = 16 25
A:
1321. У коробці лежать 42 олівці, з
Розв'язання:
1. Загальна кількість олівців: Загальна кількість олівців у коробці 42.
2. Кількість червоних і синіх олівців: • Червоних олівців: 14,
• Синих олівців: 16.
3. Кількість зелених олівців: Оскільки всього 42 олівці, то кількість зелених олівців обчислюється як:
Зелені олівці = 42 14 16 = 12.
4. Ймовірність того, що олівець
Загальна кількість лотерейних квитків – 1800.
2. Кількість призів:
16
призів, 20 речових призів. Загальна кількість призів: 16 + 20 = 36.

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
P(не виграє) = 1764 1800
Спростимо дроб: 1764
1800 = 441 450
Тому ймовірність
P(не виграє) = 441 450
Відповідь: ймовірність
або 0,98 (приблизно 98%).
1323. Двічі підкидають
Розв'язання:
a) Хоча б один раз:
1. Можливі результати підкидання монети:
При кожному підкиданні монети є два можливі результати: герб (Г) або решка (Р).
Тому всі можливі результати двічі підкинутих
Г,Г, Г,Р, Р,Г, Р,Р
Тобто, є 4 можливих варіанти.
2. Ймовірність того, що
шукаємо
Для цього
(це варіант "Р, Р").
Залишаються такі
Г,Г, Г,Р, Р,Г
Це 3 сприятливі варіанти з 4 можливих.
Тому
P(хоча б один раз герб) = 3 4
б) Двічі:
Ймовірність того, що

3.
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
треба вийняти навмання, щоб
кулька, дорівнювала 1?
Розв'язання:
1. Загальна кількість кульок: У коробці є: • 12 чорних кульок, • 9 червоних кульок.
Отже, всього кульок у коробці: 12 + 9 = 21.
Що означає ймовірність 1?
Ймовірність 1 означає, що подія обов'язково відбудеться.
Тому нам потрібно вийняти таку кількість кульок, щоб серед них обов'язково
одна червона кулька.
2. Кількість кульок, які не можуть бути червоними: Всього є 12 чорних кульок.
3. Що відбудеться, якщо виймемо 12 кульок? Якщо ми виймемо
4. Що відбудеться, якщо виймемо 13 кульок?

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
Таким чином, ми маємо 15 × 24 = 360
2.
способів
кількість таких варіантів:
C(6, 3) = 6! (3!(6 3)!) = 20
Для кожної вибраної групи 4 букв ми можемо
4! = 24
Таким чином, маємо 20 × 24 = 480 можливих слів.
4. Загальна кількість можливих слів
360 + 480 + 120 = 960
Ймовірність
річки.
Пароплав рухається швидше при русі з течією і
Пліт також рухатиметься під
• Vпліт – швидкість плота відносно води.
• Vтечія – швидкість течії річки.
• Vпароплав−1v– швидкість
В.
• Vпароплав−2v – швидкість пароплава

можливих (У, К, Р, Ї, Н, А), то
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
S 5 = vпліт + vтечія
S 5 + S 7 = 2vпліт
7S
35 + 5S 35 = 2vпліт
12S 35 = 2vпліт
v
= 6S
Час = S vпліт = S (6S 35) = 35 6 ≈ 5.83 діб
Відповідь:
1328. Розклади на множники.
а) 1 (a b)² = (1 a + b)(1 + a b);
б) (x + c)² 9x²c⁴ = (x + c 3xc²)(x + c + 3xc²).
1329. Розв’яжи рівняння.
а) 9x² + 6x + 1 = 0
(3x + 1)² = 0
3x + 1 = 0
3x = 1
x = 1 3
б) 48x³ + 12x = 0
12x(4x² + 1) = 0
4x² + 1 = 0
x² = 1 4
коренів немає.
1330. Мама і донька йдуть на прогулянку. У
Скільки є
маємо 2
– маму та доньку. Мама має 5 кишень, а донька – 4 кишені.

(5 9 25 2,36) : (3 4 5 + 0,2)
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
0,75
Вираз: (3 3 4 : 11 4 0,75) : 1 1 2 + 0,75 Розв'язання:
9x⁴ 4x², якщо x = 1 3
Розв'язання: 9(1 3)⁴ 4(1 3)² = 9( 1 81) 4(1 9) = 9
Б) Вираз:
10a² + 125a³, якщо a = 0,2.
Розв'язання:
10a² + 125a³ = 5a²(2 + 25a)
Підставимо a = 0,2: 5( 0,2)²(2 + 25( 0,2)) = 5(0,04)(2 5) = 5(0,04)( 3) = 5( 0,12) = 0,6
Відповідь: 0,6
1334. Перемнож одночлени а) 5a²b · 3 5 ab³ · 3ac⁴
Множимо коефіцієнти: 5 · 3 5 · 3 = 3 · 3 = 9
Множимо змінні:
a² · a · a = a²⁺¹⁺¹ = a⁴
b · b³ = b¹⁺³ = b⁴
c⁴
Відповідь:
9a⁴b⁴c⁴
б) 8xy · ( 2,5)b² · 0,1ax

Множимо коефіцієнти:
8 · ( 2,5) · 0,1 = 20 · 0,1 = 2
Множимо змінні: x · x = x² y a b²
Відповідь: 2ax²yb²
1335. Перемнож одночлени а) 4pq² · 0,15pz² · 5pqz
Множимо коефіцієнти: 4 · 0,15 · 5 = 3
Множимо змінні: p · p · p = p³ q² · q = q³ z² · z = z³
Відповідь: 3p³q³z³
б) 1 5 7 ax² · 1 3 ax²y · 2 5 8 xy
Приведемо коефіцієнти:
Множимо змінні:
a·a = a²
x²·x²·x = x⁵
y·y = y²
Відповідь:
5 8 a²x⁵y²
1336. Піднеси до степеня одночлен.
Зведемо одночлени до степеня: а)
(2x³)⁵ = 2⁵ · x³·⁵ = 32x¹⁵ б)
( xy)⁷ = ( 1)⁷ · x⁷ · y⁷ = x⁷y⁷ в)
( 3a)⁴ = ( 3)⁴ · a⁴ = 81a⁴ г)
(0,5m²)³ = 0,5³ · m²·³ = 0,125m⁶
Відповіді: а) 32x¹⁵
б) x⁷y⁷ в) 81a⁴
г) 0,125 m⁶
1337. Спрости вираз.
Спрощуємо вирази: а)

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
3x² · 4x²ym = (3 · 4) · x²⁺² · y · m = 12x⁴ym
3 aⁿ⁺¹ · 6aⁿ⁻² = (2 3 · 6) ·
3 · a²ⁿ⁻¹ = 4a²ⁿ⁻¹
Відповіді: а) 12x⁴ym б) 4a²ⁿ⁻¹
1338. Знайди різницю многочленів.
а) (6x³ 2x⁵ + x) (8x³ + 3x⁵ 4x²)
Розкриваємо дужки:
6x³ 2x⁵ + x 8x³ 3x⁵ + 4x²
Групуємо подібні члени:
( 2x⁵ 3x⁵) + (6x³ 8x³) + 4x² + x
5x⁵ 2x³ + 4x² + x
Відповідь:
5x⁵ 2x³ + 4x² + x
б) (3a² + 2ab b²) (2b² 2a²)
Розкриваємо дужки: 3a² + 2ab b² 2b² + 2a²
Групуємо подібні члени: (3a² + 2a²) + 2ab + ( b² 2b²) 5a² + 2ab 3b²
Відповідь: 5a² + 2ab 3b²
1339. Перетвори вираз у многочлен стандартного вигляду. а)
12x² − (−3x⁶ + 8 − 10x²)
Розкриваємо дужки:
12x² + 3x⁶ − 8 + 10x²
Групуємо подібні члени:
3x⁶ + (−12x² + 10x²) − 8
3x⁶ − 2x² − 8
Відповідь:
3x⁶ − 2x² − 8
б)
9m³ − 5m + (m − 6m³ − 2m⁴)
Розкриваємо дужки:
9m³ − 5m + m − 6m³ − 2m⁴
Групуємо подібні члени:
2m⁴ + (9m³ − 6m³) + (−5m + m)
2m⁴ + 3m³ − 4m
Відповідь:
2m⁴ + 3m³ − 4m
в)
(−4xy + 7y²) − (−8x²) + (6xy − 10x² − 5)
Розкриваємо дужки:
4xy + 7y² + 8x² + 6xy − 10x² − 5
Групуємо подібні члени:
(8x² − 10x²) + (−4xy + 6xy) + 7y² − 5
2x² + 2xy + 7y² − 5
Відповідь:
2x² + 2xy + 7y² − 5
г)
(3b² + 4b²c) + (6b² − c²b + b²c) − (2b² + 5b²c)
Розкриваємо дужки:

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
3b² − 4b²c + 6b² − c²b + b²c − 2b² − 5b²c
Групуємо подібні члени:
(−3b² + 6b² − 2b²) + (−4b²c + b²c − 5b²c) − c²b
b² − 8b²c − c²b
Відповідь: b² − 8b²c − c²b
1340. Виконай множення: а)
3x (2x⁴ − 5x + 1) = 3x · 2x⁴ − 3x · 5x + 3x · 1 = 6x⁵ − 15x² + 3x
Відповідь:
6x⁵ − 15x² + 3x б)
5a² (3a² + 4a − 2) = −5a² · 3a² + (−5a² · 4a) + (−5a² · (−2)) = −15a⁴ − 20a³ + 10a²
Відповідь:
15a⁴ − 20a³ + 10a² в)
(−ab + 2a² − 3b²) (−a²b) = (−ab · −a²b) + (2a² · −a²b) + (−3b² · −a²b) = a³b² − 2a⁴b + 3a²b³
Відповідь:
a³b² − 2a⁴b + 3a²b³ г)
(4x²y − 3xy² + 5) · 2xy = (4x²y · 2xy) + (−3xy² · 2xy) + (5 · 2xy) = 8x³y² − 6x²y³ + 10xy
Відповідь:
8x³y² − 6x²y³ + 10xy ґ)
0,25 (2m² − 4m + 6) = −0,25 · 2m² + (−0,25 · (−4m)) + (−0,25 · 6) = −0,5m² + m − 1,5
Відповідь:
0,5m² + m − 1,5 д)
(−10n⁵ − 6n³ + 2)(−1,5m) = (−10n⁵ · −1,5m) + (−6n³ · −1,5m) + (2 · −1,5m) = 15n⁵m + 9n³m − 3m
Відповідь:
15n⁵m + 9n³m − 3m
1341. Перемнож вирази: а)
12x³ · (1 6 x + 2 3 x² − 3 4)
Розподіляємо множник:
12x³ · 1 6 x + (−12x³ · 2 3x²) + (−12x³ · (−3 4))
Обчислюємо:
2x⁴ − 8x⁵ + 9x³
Відповідь:
8x⁵ − 2x⁴ + 9x³
б)
10xy · ( 0,7x³ + 3,2y² x²y²)
7x4y+32xy3 10x3y3
в)
(−3 5 ax²) · (5ax² − 5 8 a²x + 1 2 a)

Розподіляємо множник:
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
3 5 ax² · 5ax² + (−3 5 ax² · −5 8a²x) + (−3 5 ax² · 1 2a)
Обчислюємо:
3a²x⁴ + 15 40 a³x³ − 3 10 a²x²
3a²x⁴ + 3 8 a³x³ − 3 10 a²x²
Відповідь:
3a²x⁴ + 3 8 a³x³ − 3 10 a²x²
г)
0,5y⁶ · (−0,8xy + 1,2x³ + 7x²y)
Або, якщо зберігати порядок
0,5y⁶ · (−0,8xy) + 0,5y⁶ · 1,2x³ + 0,5y⁶ · 7x²y
Обчислюємо:
0,4xy⁷ + 0,6x³y⁶ + 3,5x²y⁷
Відповідь:
0,4xy⁷ + 0,6x³y⁶ + 3,5x²y⁷ 1342.
а)
5x(x + 4) − x (6 − 2x²)
Розкриваємо дужки:
5x² + 20x − 6x + 2x³
Групуємо подібні члени:
2x³ + 5x² + 14x
Відповідь:
2x³ + 5x² + 14x
б)
y²(2y − 6) + 4y (y² − y)
Розкриваємо дужки:
2y³ + 6y² + 4y³ − 4y²
Групуємо подібні члени:
(−2y³ + 4y³) + (6y² − 4y²)
2y³ + 2y²
Відповідь:
2y³ + 2y²
в)
6a²b³ b²(5a²b + b² 1)
Розкриваємо дужки:
6a²b³ 5a²b³ b⁴ + b²
Групуємо подібні члени:
(6a²b³ 5a²b³) + b² b⁴
a²b³ + b² b⁴
Відповідь:
a²b³ + b² b⁴
г)
3xy(2 4x²y + xy²) 7xy
Розкриваємо дужки: (3xy · 2) + (3xy · 4x²y) + (3xy · xy²) 7xy
6xy 12x³y² + 3x²y³ 7xy

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
Групуємо подібні члени: (6xy 7xy) 12x³y² + 3x²y³
xy 12x³y² + 3x²y³
Відповідь:
xy 12x³y² + 3x²y³
1343. Доведи тотожності:
а)
x(y z) + y(z x) = z(y x)
Розкриваємо дужки:
xy xz + yz yx
Групуємо подібні члени: (xy yx) + (yz xz)
0 + z(y x)
Отримали рівність z(y x) = z(y x)
Доведено.
б)
x(y + z yz) y(x + z xz) = z(x y)
Розкриваємо дужки: xy + xz xyz yx yz + yxz
Групуємо подібні члени: (xy yx) + (xz yz) + ( xyz + yxz)
0 + z(x y) + 0
Доведено.
в)
ab(a + b + c) b²(a c) = bc(a + b + c) b(c² a²)
Розкриваємо дужки:
a²b + ab² + abc ab² + b²c
Групуємо подібні члени:
a²b + (ab² ab²) + (abc + b²c)
a²b + bc(a + b)
З іншого боку:
bc(a + b + c) b(c² a²)
Розкриваємо дужки:
abc + b²c + bc² bc² + ba²
a²b + bc(a + b)
Доведено.
г)
ab(b + c) bc(a + b) + ac(a + c) = a(b² + c²) + c(a² b²)
Розкриваємо дужки:
abb + abc abc bca + aca + acc
ab² + ac² abc + abc
ab² + ac²
Розкриваємо іншу частину рівності:
a(b² + c²) + c(a² b²)
ab² + ac² + ca² cb²
ab² + ac² + ca² cb²
Видно, що обидві сторони рівні.

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
1344. Знайди добуток: а)
( 2a b) · ( 2a + b)
Використовуємо формулу різниці
(A B)(A + B) = A² B²
( 2a)² b² = 4a² b²
Відповідь:
4a² b²
б)
( x² + y³) · ( x² y³)
Знову використовуємо формулу
(A B)(A + B) = A² B²
( x²)² (y³)² = x⁴ y⁶
Відповідь:
x⁴ y⁶
в)
( abc + 1) · (abc + 1)
Формула різниці квадратів:
A² B²
( abc)² 1² = a²b²c² 1
Відповідь:
a²b²c² 1
г)
(–0,2x4 – x) · (x – 0,2x4)
(−0,2x4) ⋅ x + (−0,2x4) ⋅ (−0,2x4) + (−x) ⋅ x + (−x) ⋅ (−0,2x4)
0,2x5 + 0,04x8 x2 + 0,2x5
0,04x8 x2
ґ)
(a + b + c) · (a b c)
Розкриваємо дужки: a² ab ac + ab b² bc + ac bc c²
Групуємо подібні члени: a² b² c² 2bc
Відповідь: a² b² c² 2bc д)
(x + y z) · (x y + 2)
Розкриваємо дужки: x² xy + 2x + xy y² + 2y xz + yz 2z
Групуємо подібні члени: x² y² xz + yz + 2x + 2y 2z
Відповідь: x² y² xz + yz + 2x + 2y 2z 1345. Спрости вирази: а)
(2x 3)(2x + 3)(4x² + 9) + 81
Використовуємо

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
(A B)(A + B) = A² B²
(2x 3)(2x + 3) = 4x² 9
Підставляємо у вираз: (4x² 9)(4x² + 9) + 81
Знову застосовуємо формулу різниці квадратів: (4x²)² 9² + 81
16x⁴ 81 + 81
16x⁴
Відповідь: 16x⁴ б)
(5 + x⁵)(5 x⁵)(x¹⁰ + 25) + x²⁰
Застосовуємо формулу різниці квадратів:
(5 + x⁵)(5 x⁵) = 25 x¹⁰
Підставляємо у вираз: (25 x¹⁰)(x¹⁰ + 25) + x²⁰
Знову застосовуємо формулу різниці квадратів: 25² x¹⁰·x¹⁰ + x²⁰
625 x²⁰ + x²⁰
625
Відповідь:
625
в)
256a⁴ (4a b³)(4a + b³)(16a² + b⁶)
Крок 1: Використаємо формулу різниці квадратів (4a b³)(4a + b³) = 16a² b⁶
Підставляємо у вираз:
256a⁴ (16a² b⁶)(16a² + b⁶)
Крок 2: Знову застосовуємо формулу різниці квадратів (16a² b⁶)(16a² + b⁶) = (16a²)² (b⁶)² = 256a⁴ b¹²
Підставимо у вираз:
256a⁴ (256a⁴ b¹²)
Крок 3: Розкриваємо дужки
256a⁴ 256a⁴ + b¹² = b¹²
Відповідь: b¹² г) (0,1y²)⁴ + ( x 0,1y²)(0,1y² x)(0,01y⁴ + x²)
Обчислюємо перший доданок: (0,1y²)⁴ = 0,0001y⁸
Другий доданок має вигляд
( x 0,1y²)(0,1y² x) = x² (0,1y²)² = x² 0,01y⁴
Помножимо на останній множник: (x² 0,01y⁴)(0,01y⁴ + x²)
Знову застосовуємо формулу
x⁴ (0,01y⁴)²
=x⁴ 0,0001y⁸

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
Підставимо у вираз: 0,0001y⁸ + (x⁴ 0,0001y⁸)
0,0001y⁸ + x⁴ 0,0001y⁸ x⁴
Відповідь: x⁴
1346. Подай двочлен у вигляді добутку: а)
p² q²
Застосовуємо формулу різниці квадратів: p² q² = (p q)(p + q)
Відповідь: (p q)(p + q)
б)
25 0,25m²
Перетворюємо в квадрат: (5)² (0,5m)²
Застосовуємо формулу
(5 0,5m)(5 + 0,5m)
Відповідь: (5 0,5m)(5 + 0,5m)
в)
9x² a⁴
Перетворюємо в квадрат: (3x)² (a²)²
Застосовуємо формулу
(3x a²)(3x + a²)
Відповідь: (3x a²)(3x + a²) г)
0,04x⁶ 1
Перетворюємо в квадрат: (0,2x³)² 1²
Застосовуємо формулу різниці квадратів: (0,2x³ 1)(0,2x³ + 1)
Відповідь: (0,2x³ 1)(0,2x³ + 1) ґ)
x²y⁴ + a⁶b⁸
Перетворюємо в квадрат: a⁶b⁸ (xy²)²
Застосовуємо формулу
(a³b⁴ xy²)(a³b⁴ + xy²)
Відповідь:
(a³b⁴ xy²)(a³b⁴ + xy²)
д)
a²b²c² 121x⁶
Перетворюємо в квадрат:

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
(abc)² (11x³)² Застосовуємо
(abc 11x³)(abc + 11x³)
Відповідь:
(abc 11x³)(abc + 11x³)
е)
4
81 z10 – x16
4
81 z10 – x16 = (2 9 ����5 ����8) (2 9 ���� + ����8)
є)
64 + 36m4n²
36m4n2 64
4(9m4n2 16)
9m4n2 – 16 = (3m2n 4)(3m2n + 4)
64 + 36m4n2 = 4(3m2n 4)(3m2n + 4)
ж)
a² (b + c)²
Застосовуємо формулу різниці квадратів:
(a (b + c))(a + (b + c))
Відповідь:
(a b c)(a + b + c)
1347. Обчисли.
а) 24² 14² = (24 14)(24 + 14) = 10 · 38 = 380
б) 62² 38² = (62 38)(62 + 38) = 24 · 100 = 2400
в) 98² 97² = (98 97)(98 + 97) = 1 · 195 = 195
г) 52,5² 48,5² = (52,5 48,5)(52,5 + 48,5) = 4 · 101 = 404
ґ) 14,3² 4,3² = (14,3 4,3)(14,3 + 4,3) = 10 · 18,6 = 186 д) 5,92 – 5,12 = (5,9 − 5,1)(5,9 + 5,1) = 0,8 ⋅ 11 = 8,8
є) (72 3)² (21 3)² = (23 3 )² (
1348. Подай вираз у вигляді многочлена Розкриємо квадрати виразів.
а) (0, 4a² 5ab)² = 0, 16a⁴ 2 (0, 4a² · 5ab) + 25a²b² = 0, 16a⁴ 4a³b + 25a²b²
б) (6, 5xy + 8y²)² = 42, 25x²y² + 2 (6, 5xy · 8y²) + 64y⁴ = 42, 25x²y² + 104xy³ + 64y⁴
в) (xy 1)² = x²y² 2xy + 1
г) (2 + a⁶b⁴)² = 4 + 4a⁶b⁴ + a¹²b⁸
1349. Подай вираз у вигляді многочлена
Розкриємо квадрати виразів.
а) ( x + y²)² = x² 2xy² + y⁴
б) ( 2a² + 3y³)² = 4a⁴ 12a²y³ + 9y⁶
в) ( 1 3 3x²)² = ( 1 3 3x²)² = 1 9 + 2 · 1 3 · 3x² + 9x⁴ = 1 9 + 2x² + 9x⁴
г) ( 1 2 m³ 0,2n)² = 1 4 m⁶ + 2 · 1 2m³ · 0,2n + 0,04n² = 1 4m⁶ + 0,2m³n + 0,04n²
ґ) ( 0,1xy + 5)² = 0,01x²y² 2(0,1xy · 5) + 25 = 0,01x²y² xy + 25
д) ( 6x²y 0,5y)² = 36x⁴y² + 2(6x²y · 0,5y) + 0,25y² = 36x⁴y² + 6x²y² + 0,25y² 1350. Спрости вирази.
а)

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
(3x 5y)² 3x(3x 10y) = x² 30xy + 25y² (9x² 30xy) = 9x² 30xy + 25y² 9x² + 30xy = 25y²
б)
8a(b 2a) + (4a + b)² = 8ab 16a² + 16a² + 8ab + b² = 16ab + b² в)
(4x + y)(3x + 4y) (2y + 3x)² = 12x² + 16xy + 3xy + 4y² (4y² + 12xy + 9x²) = 12x² + 19xy + 4y² 4y² 12xy 9x² = 3x² + 7xy г)
(3a + 6b)² (2a + 9b)(3a + 4b) = 9a² + 36ab + 36b² (6a² + 12ab + 27ab + 36b²) = 9a² + 36ab + 36b² 6a² 39ab 36b² = 3a² 3ab 1351. Доведи, що
x а)
(2x − 5y)² + 4x(5y − x) = 4x² − 20xy + 25y² + 20xy − 4x² = 4x² − 20xy + 25y² + 20xy − 4x² = 25y²
Залежить лише від y. б)
3x(12x − 4y) − (6x − y)² = 36x² − 12xy − (36x² − 12xy + y²) = 36x² − 12xy − 36x² + 12xy − y² = −y²
Залежить лише від y. 1352. Доведи, що
від x а)
(4x + 5y)² − 8(2x − y)(x + 3y) = 16x² + 40xy + 25y² − 8 (2x² + 6xy − yx − 3y²) = 16x² + 40xy + 25y² − (16x² + 48xy − 8yx − 24y²) = 16x² + 40xy + 25y² − 16x² − 40xy + 24y² = 25y² + 24y² = 49y²
Залежить лише від y. б)
4(x − 6y)(x − 3y) − (2x − 9y)² = 4 (x² − 3xy − 6xy + 18y²) − (4x² − 36xy + 81y²) = 4x² − 12xy − 24xy + 72y² − 4x² + 36xy − 81y² = 4x² − 36xy + 72y² − 4x² + 36xy − 81y² = −9y²
Залежить лише від y. 1353.Подай вираз у вигляді многочлена.
Розкриємо куби виразів.
Використовуємо формулу куба суми та куба різниці:
(a + b)³ = a³ + 3a²b + 3ab² + b³
(a − b)³ = a³ − 3a²b + 3ab² − b³
а) (x + 3)³ = x³ + 3x²(3) + 3x(9) + 27 = x³ + 9x² + 27x + 27
б) (y − 2)³ = y³ − 3y²(2) + 3y(4) − 8 = y³ − 6y² + 12y − 8
в) (2x − 1)³ = (2x)³ − 3(2x)²(1) + 3(2x) (1²) − 1³ = 8x³ − 12x² + 6x − 1
г) (3x + 1)³ = (3x)³ + 3(3x)²(1) + 3(3x) (1²) + 1³ = 27x³ + 27x² + 9x + 1
ґ) (m − 2n)³ = m³ − 3m²(2n) + 3m (4n²) − 8n³ = m³ − 6m²n + 12mn² − 8n³
д) (2a + 3)³ = (2a)³ + 3(2a)²(3) + 3(2a)(9) + 27 = 8a³ + 36a² + 54a + 27
1354. Розклади
а) x³ + x²y + 2x² + 2xy = x²(x + y) + 2x(x + y) = (x² + 2x)(x + y) = x(x + 2)(x + y)
б) a³c² − a²c² + a³ − a² = a²c²(a − 1) + a²(a − 1) = a²(a − 1) (c² + 1)
в) 4xy + 12x²y − 4x − 12x² = 4x(y − 1) + 12x²(y − 1) = (4x + 12x²)(y − 1) = 4x(1 + 3x)(y − 1)
г) 6a²b − 18a² − 3ab + 9a = 6a²(b − 3) − 3a(b − 3) = (6a² − 3a)(b − 3) = 3a(2a − 1)(b − 3)
ґ) xyz − 4xz − 5xy + 20x = x(yz − 4z − 5y + 20) = x[(yz − 5y) − (4z − 20)] = x[y(z − 5) − 4(z − 5)] = x(y − 4)(z − 5)
д) 4ab + 3ac − abc − 12a = 4ab − 12a + 3ac − abc = 4a(b − 3) + 3c(a − b) =

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
4a(b − 3) − 3(a − b) = (b − 3)(4a − 3c)
1355. Розклади
а) a² − b² − a + b = (a − b)(a + b) − (a − b) = (a − b)(a + b − 1)
б) x + y + x² − y² = x² − y² + x + y = (x − y)(x + y) + (x + y) = (x + y)(x − y + 1)
в) 4a² − 9 − 2a − 3 = 4a² − 2a − 12 = (2a − 4)(2a + 3)
г) 5 − 3x + 25 − 9x² = 30 − 3x − 9x² = −3 (x² + x − 10) = −3(x − 2)(x + 5)
1356. Подай у вигляді добутку.
а) x² − 2xy + y² − z² = (x − y)² − z²
(x − y − z)(x − y + z)
б) a² + 2a + 1 − b² = (a + 1)² − b²
(a + 1 − b)(a + 1 + b)
в) x² − y² + 8y − 16 = x² (y² − 8y + 16)
x² − (y − 4)² = (x − (y − 4))(x + (y − 4))
(x − y + 4)(x + y − 4)
г) a² − b² − 14b − 49 = a² − (b² + 14b + 49)
a² − (b + 7)² = (a − (b + 7))(a + (b + 7))
(a − b − 7)(a + b + 7)
1357. Подай у вигляді
а) ab² − 4a − b³ + 4b = a (b² − 4) − b³ + 4b
a(b − 2)(b + 2) − b (b² − 4)
a(b − 2)(b + 2) − b(b − 2)(b + 2) = (a − b)(b − 2)(b + 2)
б) x³ + x²y − 9x − 9y = x²(x + y) − 9(x + y)
(x² − 9)(x + y) = (x − 3)(x + 3)(x + y)
в) x²a + 3a² − a³ − 3x² = x²(a − 3) + 3a² − a³
x²(a − 3) − a³ + 3a² = x²(a − 3) − a²(a − 3)
(a − 3) (x² − a²) = (a − 3)(x − a)(x + a)
г) x³ − 5b² + 5x² − xb² = x³ + 5x² − xb² − 5b²
x²(x + 5) − b²(x + 5) = (x² − b²)(x + 5) =
(x − b)(x + b)(x + 5)
1358. Розклади на множники а) Розкладемо вираз на множники:
a²x² − 2abx² + 2ab + b²x² − a² − b²
Групуємо члени: (a²x² − 2abx² + b²x²) + (2ab − a² − b²)
Першу групу можна подати як повний квадрат: (ax − bx)² + (2ab − a² − b²)
Перетворимо другу групу: 2ab − a² − b² = − (a² − 2ab + b²) = −(a − b)²
Отже, маємо: (ax − bx)² − (a − b)²
Це різниця квадратів, тож розкладемо за формулою: (ax − bx − (a − b))(ax − bx + (a − b))
Піднесемо до спрощеного вигляду: (x(a − b) − (a − b))(x(a − b) + (a − b))
Винесемо (a − b) за дужки: (a − b)(x − 1)(x + 1)
Отже, остаточний розклад: (a − b)(x − 1)(x + 1)

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
a²x² − 4b²x + 4b² + 4a² − 4a²x + b²x²
(a2 + b2)x2 4(a2 + b2)x + 4(a2 + b2)
(a2 + b2)(x2 4x + 4)
x2 4x + 4 = (x 2)2
(a² + b²)(x − 2)²
Відповідь:
а) (a − b)(x − 1)(x + 1)
б) (a² + b²)(x − 2)²
1359. Розклади на множники
а) a² − b² + x² − y² + 2ax + 2by
Розглянемо вираз: a² − b² + x² − y² + 2ax + 2by
Групуємо доданки:
(a² − b²) + (x² − y²) + (2ax + 2by)
Тут перші дві групи це різниці
множник.
2. Застосовуємо формулу різниці квадратів:
(a − b)(a + b) + (x − y)(x + y) + 2(ax + by)
Об'єднуємо в повний квадрат:
a² + x² − b² − y² + 2ax + 2by = (a + x)² − (b + y)²
Застосовуємо формулу різниці квадратів:
(a + x − (b + y))(a + x + (b + y))
Спрощуємо:
(a − b + x − y)(a + b + x + y)
Відповідь:
(a − b + x − y)(a + b + x + y)
б). Розкладемо на множники.
Розглянемо вираз:
x⁴ + y⁴ x² y² + 2x²y² 2xy
Групуємо доданки Звернемо увагу, що
утворюють
три це (x + y)². Отже, весь вираз можна записати як різницю квадратів: (x² + y²)² (x + y)²
Застосовуємо формулу різниці
a² b² = (a b)(a + b)
де a = x² + y², b = x + y
Виконуємо розкладення (x² + y²)² (x + y)² = ((x² + y²) (x + y)) ((x² + y²) + (x + y))
Остаточна відповідь (x² + y² x y) (x² + y² + x + y) 1360. Доведи, що: а) 145² 144² = 17²
Застосуємо формулу: 145² 144² = (145 144)(145 + 144) = 1 · 289 = 289
Оскільки 17² = 289, рівність доведена. б) 221² 220² = 21²
Застосуємо формулу:

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
221² 220² = (221 220)(221 + 220) = 1 · 441 = 441 Оскільки 21² = 441, рівність також
1361. Обчисли вирази.
a² b² = (a b)(a + b)
47² 41² 28² 16² = (47 41)(47 + 41) (28 16)(28 + 16) = 6 88 12 44 = 528 528 = 1
57² 42² 29² 26² = (57 42)(57 + 42) (29 26)(29 + 26) = 15 99 3 55 = 1485 165 = 9 в) 51² 12² 30² 9² = (51 12)(51 + 12) (30 9)(30 + 9) = 39 63 21 · 39 = 2457 819 = 3
61² 11² 36² 24² = (61 11)(61 + 11) (36 24)(36 + 24) = 50 72 12 · 60 = 3600 720 = 5
1362. Обчисли вирази. а)
6³² · 4³² (24¹⁶ 5) (24¹⁶ + 5) Запишемо степені по іншому:
(6 · 4)³² (24¹⁶)² + 5²
Оскільки 6 · 4 = 24, то маємо:
24³² 24³² + 5² = 25
б)
(56¹⁰ 7) (56¹⁰ + 7) 7²⁰ · 8²⁰
Застосуємо формулу різниці квадратів:
56²⁰ 7² 7²⁰ · 8²⁰
Перепишемо 8²⁰ як (2³)²⁰ = 2⁶⁰, тому:
56²⁰ 49 7²⁰ · 2⁶⁰
Знаючи, що 56 = 7 · 8, отримуємо: (7 · 8)²⁰ 49 7²⁰ · 8²⁰
Розписуємо:
7²⁰ · 8²⁰ 7²⁰ · 8²⁰ 49 = 49
в) Обчислимо вираз:
4¹⁸ · 9¹⁸ + (4 36⁹) (36⁹ + 4)
Обчислимо перший множник:
4¹⁸ · 9¹⁸
Оскільки 4 = 2², а 9 = 3², то:
4¹⁸ = (2²)¹⁸ = 2³⁶, 9¹⁸ = (3²)¹⁸ = 3³⁶
Тому:
4¹⁸ · 9¹⁸ = 2³⁶ · 3³⁶ = (2 · 3)³⁶ = 6³⁶
Обчислимо другий множник: (4 36⁹) (36⁹ + 4)
Це також різниця квадратів: (2² 36⁹) (36⁹ + 2²)
Розписуємо правильно: 16 36¹⁸
Підставимо у вираз:

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
6³⁶ + (16 36¹⁸)
Враховуємо, що 6³⁶ = 36¹⁸:
36¹⁸ + 16 36¹⁸
Розписуємо правильно: 16 36¹⁸
Підставимо у вираз:
6³⁶ + (16 36¹⁸)
Враховуємо, що 6³⁶ = 36¹⁸:
36¹⁸ + 16 36¹⁸
Спрощуємо:
36¹⁸ 36¹⁸ + 16 = 16
Відповідь: 16
1363. Розв'яжи рівняння. а) 5x⁵ x⁴ = 0
Винесемо x⁴ за дужки:
x⁴(5x 1) = 0.
Добуток дорівнює нулю, якщо
x⁴ = 0 ⇒ x = 0.
5x 1 = 0 ⇒ x = 1 5
Відповідь: x = 0 або x = 1 5 .
б) 3x³ 12x = 0
Винесемо 3x за дужки:
3x (x² 4) = 0
Розв'яжемо:
3x = 0 ⇒ x = 0.
x² 4 = 0 ⇒ x² = 4 ⇒ x = ±2.
Відповідь: x = 0, 2, 2.
в) 10x⁶ = 3x⁵
Перенесемо все в одну сторону:
10x⁶ 3x⁵ = 0
Винесемо x⁵ за дужки:
x⁵(10x 3) = 0
Розв'яжемо:
x⁵ = 0 ⇒ x = 0.
10x 3 = 0 ⇒ x = 3 10 .
Відповідь: x = 0 або x = 3 10 .
1364. Розв'яжи рівняння.
а) x³ + 4x² x = 4
Перенесемо все в одну сторону: x³ + 4x² x 4 = 0.
Групуємо доданки:
(x³ x) + (4x² 4) = 0
Винесемо спільний множник: x(x² 1) + 4(x² 1) = 0
Винесемо (x² 1):

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
(x + 4)(x² 1) = 0
Розпишемо різницю квадратів:
(x + 4)(x 1)(x + 1) = 0
Розв'язки:
x = 4, 1, 1
Відповідь: x = 4, 1, 1.
б) x³ 3x² + 2x = 6
Перенесемо все в одну сторону:
x³ 3x² + 2x 6 = 0.
Групуємо:
(x³ 3x²) + (2x 6) = 0.
Винесемо спільний множник:
x²(x 3) + 2(x 3) = 0
Винесемо (x 3):
(x 3)(x² + 2) = 0
Розв'язки:
x 3 = 0 ⇒ x = 3
Рівняння x² + 2 = 0 дійсних коренів не має.
Відповідь: x = 3.
в) 2x³ + x² 8x = 4
Перенесемо все в одну сторону:
2x³ + x² 8x 4 = 0
Групуємо:
(2x³ 8x) + (x² 4) = 0
Винесемо спільний множник: 2x(x² 4) + 1(x² 4) = 0
Винесемо (x² 4): (x² 4)(2x + 1) = 0
Розпишемо різницю квадратів: (x 2)(x + 2)(2x + 1) = 0
Розв'язки: x = 2, 2, 1 2 .
Відповідь: x = 2, 2, 1 2 .
г) 12x³ 8x² 3x = 2
Перенесемо все в одну сторону: 12x³ 8x² 3x + 2 = 0
Групуємо: (12x³ 8x²) + ( 3x + 2) = 0
Винесемо спільний множник: 4x²(3x 2) 1(3x 2) = 0
Винесемо (3x 2): (3x 2)(4x² 1) = 0
Розпишемо різницю квадратів: (3x 2)(2x 1)(2x + 1) = 0
Розв'язки:
x = 2 3, 1 2, 1 2 .

Відповідь: x = 2 3, 1 2, 1 2 . 1365.
f(x) = x + 4
f(x) = x 9
f(x) = 3x г) Значення
f(x) = x ґ)
f(x) = 1 x , x ≠ 0
Відповіді:
а) f(x) = x + 4
б) f(x) = x 9
в) f(x) = 3x
г) f(x) = x
ґ) f(x) = 1 x , x ≠ 0.
1366. Прямокутний
що
умовою:
a · b · 6
b = 12 а , a ≠ 0
рівняння: 3α + x = 180°
Виразимо x:
x = 180° 3α
Відповідь: x = 180° 3α.
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html

b від a.
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
x? Знайдемо
тканини. Запишемо формулу для залишку тканини
Кількість тканини, яка є спочатку: 200 м.
Кількість тканини, необхідна для пошиття x сорочок: 2.5xм.
Формула для залишку тканини: S = 200 2.5x.
Визначимо можливі значення x Оскільки тканина не може стати від'ємною, виконаємо умову:
200 2.5x ≥ 0.
Розв'яжемо нерівність: 2.5x ≤ 200 x ≤ 200 2 5 = 80
Оскільки кількість сорочок
x ∈ {0, 1, 2, . . . , 80}
Відповідь:
Формула залишку тканини: S = 200 2.5x
Можливі значення x:
x ∈ {0, 1, 2, . . . , 80}
1369. Знайди область визначення функції,
функції.
Область визначення функції це всі допустимі
має зміст.
а) y = x(x 5)
Функція є многочленом, а область визначення
D(y) = ( ∞; +∞)
б) y = x² + 6x + 8
Це також многочлен, тому
D(y) = ( ∞; +∞)
в) y = 16 x² x+5 x + 5 = 0 x = 5
Функція не визначена при x=−5x = -5, бо
(−∞;−5)∪(−5;+∞)
г) y = x²+9 3x 1
Знаменник не повинен дорівнювати нулю: 3x 1 ≠ 0.
x ≠ 1 3
Отже, область визначення: D(y) = ( ∞; 1 3) ∪ (1 3; +∞)

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
ґ) y = 1 х 1 x 2
x ≠ 0, x 2 ≠ 0
x ≠ 0, x ≠ 2
Отже, область визначення:
D(y) = ( ∞; 0) ∪ (0; 2) ∪ (2; +∞)
д) y = 3 x(x+1)
Знаменник не повинен
x(x + 1) ≠ 0 x ≠ 0, x ≠ 1 Отже,
визначення: D(y) = ( ∞; 1) ∪ ( 1; 0) ∪ (0; +∞)
1370.

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
Якщо y = −7:
3x + 2 = −7 ⇒ x = 3
Якщо y = 0:
3x + 2 = 0 ⇒ x = 2 3
Якщо y = 5:
3x + 2 = 5 ⇒ x = −1
б) y = x(x − 3), шукаємо x при заданих значеннях y:
Якщо y = −2:
x(x − 3) = −2
Розв'язки: x = 1 або x = 2.
Якщо y = 0:
x(x − 3) = 0
Розв'язки: x = 0 або x = 3.
Якщо y = 10:
x(x − 3) = 10
Розв'язки: x = −2 або x = 5.
1373.
x 4 1 0 2 3 5
y 12 3 0 6 9 15
Припустимо, що функція
y = kx + b
Знайдемо коефіцієнти k та b.
Відомо, що при x = 0, y = 0.
0 = k · 0 + b ⇒ b = 0
Тобто функція має вигляд: y = kx
Тепер підставимо іншу
12 = k · ( 4)
Звідси: k = 12 4 = 3
Отже, рівняння функції: y = 3x

наприклад, ( 4,
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
y = 5x
б)y = 5x 1
в)y = 5x
г)y = 5x + 3

1376.
в)y = 3x
y = х 3

1377.

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
Загальне рівняння лінійної функції: y = kx + b
Запишемо систему рівнянь для двох точок: � 3k + b = 2
5k + b = 4
Розв'яжемо систему:
Віднімемо друге рівняння від першого:
(3k + b) − (−5k + b) = 2 − 4.
3k + b + 5k − b = −2.
8k = −2.
k = −1 4
Підставимо k = −1 4 у перше рівняння:
3 · (−1 4) + b = 2.
3 4 + b = 2.
b = 2 + 3 4 = 8 4 + 3 4 = 11 4 .
Записуємо рівняння функції:
y = 1 4 x + 11 4 .
Відповідь:
y = 1 4 x + 11 4
1378. Розв'яжи рівняння.
а) 7x + 15 + 15x + 8 10 = 9x
Спрощуємо:
(7x + 15x) + (15 + 8 10) = 9x
22x + 13 = 9x
Переносимо 9x вліво:
22x 9x = 13.
13x = 13. x = 1
Відповідь: x = 1.
б) 25 + 5y 17 + 7y = 150 130y
Спрощуємо:
(5y + 7y) + (25 17) = 150 130y
12y + 8 = 150 130y
Переносимо 130y вліво та 8 вправо: 12y + 130y = 150 8
142y = 142 y = 1
1379. Розв'яжи рівняння. а) 7x − 39 = 2(x + 3) + 11 − 2x
Розкриваємо дужки:
7x − 39 = 2x + 6 + 11 − 2x
Спрощуємо:
7x − 39 = 6 + 11
7x − 39 = 17
Переносимо 39 вправо:

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
7x = 17 + 39.
7x = 56
x = 8
Відповідь: x = 8.
б) 3(x − 5) = 5(x − 3) − 4(7 − 3x)
Розкриваємо дужки:
3x − 15 = 5x − 15 − 4 · 7 + 4 · 3x
3x − 15 = 5x − 15 − 28 + 12x
Спрощуємо:
3x − 15 = 17x − 43
Переносимо 17x вліво, а 15 вправо:
3x − 17x = −43 + 15
14x = −28
x = 2
1380. Розв'яжи рівняння.
а) 1 2(2x − 4) + 1 2 (4x − 2) = x + 5
Розкриваємо дужки:
1
2 · (2x−4) + 1 2 · (4x−2) = x + 5.
(x−2) + (2x−1) = x + 5
Спрощуємо:
x−2 + 2x−1 = x + 5.
3x−3 = x + 5.
Переносимо x вліво, а 3 вправо:
3x−x = 5 + 3.
2x = 8.
x = 4.
Відповідь: x = 4.
б) 2 3(3x + 1) + 1 3 (6x − 2) = x + 6
Розкриваємо дужки:
2
3 · (3x + 1) + 1 3 · (6x − 2) = x + 6. (2x + 2 3) + (2x − 2 3) = x + 6.
Спрощуємо:
2x + 2 3 + 2x − 2 3 = x + 6.
4x = x + 6
Переносимо x вліво:
4x − x = 6.
3x = 6.
x = 2.
1381. Розв'яжи рівняння.
а) 5(x − 3) + 7(3x + 6) = 2(x − 2) + 103
Розкриваємо дужки:
5x − 15 + 21x + 42 = 2x − 4 + 103.
Спрощуємо:
26x + 27 = 2x + 99.
Переносимо 2x вліво та 27 вправо:

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
26x − 2x = 99 − 27.
24x = 72.
x = 3.
б) 8(y − 2) + 5(3y − 2) = 3(y − 5) + 69
Розкриваємо дужки:
8y − 16 + 15y − 10 = 3y − 15 + 69
Спрощуємо: 23y − 26 = 3y + 54
Переносимо 3y вліво та 26 вправо: 23y − 3y = 54 + 26. 20y = 80. y = 4.
1382. Розв'яжи рівняння.
а) 1 4(x − 3) + 1 8 (x − 4) = 1 2 (x − 5) + 1 8 (x − 1)
Розкриваємо дужки: x 4 − 3 4 + x 8 − 4 8 = x 2 − 5 2 + x 8 − 1 8
Приводимо до спільного знаменника (8):
2x 8 − 6 8 + x 8 − 4 8 = 4x 8 − 20 8 + x 8 − 1 8
Спрощуємо: 3x 8 10 8 = 5x 8 21 8
Переносимо всі члени
3x 8 5x 8 = − 21 8 + 10 8 2x 8 = − 11 8 x 4 = − 11 8 x = 11 2 = 5.5
Відповідь: x = 5.5. б) 1 6(8 − x) − 1 3(5 − 4x) = 1 2(x + 6)
Розкриваємо дужки:
8
6 − x 6 − 5 3 + 4x 3 = x 2 + 3
до спільного знаменника (6):
8 6 − х 6 − 10 6 + 8x 6 = 3x 6 + 18 6
Спрощуємо: (8 10 + 8x x) 6 = (3x + 18) 6 .
2 6 + 7x 6 = 3x 6 + 18 6
6 3x 6 = 18 6 + 2 6
4x
6 = 20 6
2x
3 = 10 3
2x = 10 x = 5

Відповідь: x = 5.
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
1383.
(a + 2)x − (a + 3)x = 5
Перевіримо, чи
Винесемо x за дужки:
x · [(a + 2) − (a + 3)] = 5
Спрощуємо:
x · [a + 2 − a − 3] = 5
x · (−1) = 5
x = −5
Отримали, що x = −5 незалежно від
воно стає тотожно рівним 0 або
1384. Чи може рівняння мати (a² + 1)x = 7 при якому-небудь значенні a мати безліч
коренів? Чому?
(a² + 1)x = 7
Дослідимо випадок безлічі коренів
Рівняння має безліч коренів, якщо воно єтотожністю, тобто
Це можливо, якщо коефіцієнт перед x
a² + 1 = 0
Але рівняння a² + 1 = 0
додавання 1 робить його завжди додатним: a² + 1 ≥ 1 > 0
Отже, вираз a² + 1 ніколи не
безлічі коренів.
2. Висновок
Рівняння
x = 7 (a² + 1)
1385.За якої умови рівняння ax =
Розглянемо рівняння: ax = 12.
Щоб рівняння не мало
знайти x.
Рівняння немає розв'язку, якщо ділити неможливо.
Розв'яжемо рівняння для x : x = 12

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
a − 3 = 0 a = 3
При цьому
Відповідь: a = 3.
1387. Побудуй графік рівняння.
а) x + y = 4;
б) 2x + y = 6;
в) –3x + 2y = 5;
г) –x – 7y = 7.

1388. Яким має бути коефіцієнт b рівняння 4x + by = 0
щоб графік цього рівняння
Розв'язання:
Оскільки точка B(10; 8) належить
4(10) + b(8) = 0
40 + 8b = 0
Розв'яжемо відносно b : 8b = −40 b = −5
Відповідь: b = −5.
2x + 3y = c
2(6) + 3(−1) = c
12 − 3 = c c = 9

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
Відповідь: c = 9.
1390.
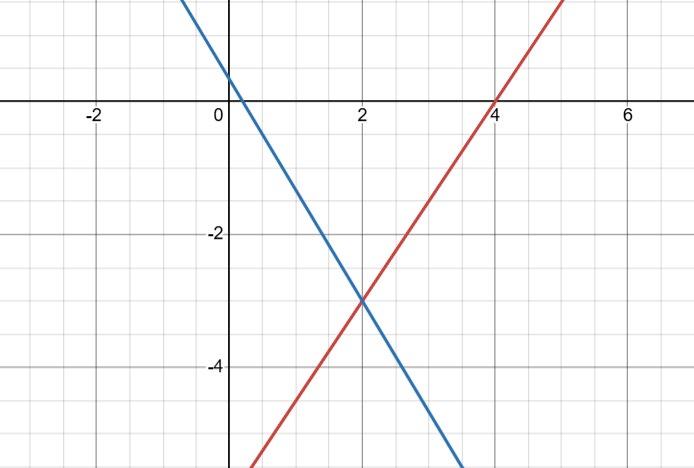
Перевірка:
1. 3x 2y = 12 ⇒ 3 ⋅ 2 2 ⋅ (−3) = 6 + 6 = 12
2. 5x + 3y = 1 ⇒ 10 – 9 =1 Отже, точка (2; −3) справді є розв’язком системи.
1391. Розв’яжи систему рівнянь а) Розв'яжемо систему рівнянь: �2x + y = 12
3x 5y = 5
Розв'язання:
Виразимо y з першого рівняння: y = 12 − 2x
Підставимо у друге рівняння:
3x − 5(12 − 2x) = 5
3x − 60 + 10x = 5
13x = 65 x = 5
Знайдемо y : y = 12 − 2(5) = 12 − 10 = 2
Відповідь: x = 5, y = 2.
б) Розв'яжемо систему рівнянь: �x − 4y = 11
3x + 2y = 5
Розв'язання:
Виразимо x з першого рівняння: x = 11 + 4y
Підставимо у друге рівняння:
3(11 + 4y) + 2y = 5
33 + 12y + 2y = 5
14y = −28
y = −2
Знайдемо x :
x = 11 + 4(−2) = 11 − 8 = 3

Відповідь: x = 3, y = −2.
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
в) Розв'яжемо систему рівнянь: �2x − 3y = −3
x + 3y = 21
Розв'язання:
Виразимо x з другого рівняння: x = 21 - 3y.
Підставимо у перше рівняння: 2(21 - 3y) - 3y = -3
42 - 6y - 3y = -3 -9y = -45 y = 5
Знайдемо x: x = 21 - 3(5) = 21 - 15 = 6
Відповідь: x = 6, y = 5.
1392. Розв’яжи систему рівнянь а) Розв'яжемо систему рівнянь: � 2x 3(x y) = 7
5y 2(x 2y) = 23
Розв'язання:
Розкриємо дужки в першому рівнянні:
2x - 3x + 3y = 7
-x + 3y = 7 x = 3y - 7
Розкриємо дужки в другому рівнянні:
5y - 2x + 4y = 23
-2x + 9y = 23
Підставимо x = 3y - 7 у друге рівняння:
-2(3y - 7) + 9y = 23
-6y + 14 + 9y = 23 3y = 9 y = 3
Знайдемо x: x = 3(3) - 7 = 9 - 7 = 2
Відповідь: x = 2, y = 3.
б) Розв'яжемо систему рівнянь: � 4y 5(y x) = 8
2(3x y) + 7y = 9
Розв'язання:
Розкриємо дужки в першому рівнянні:
4y - 5y + 5x = 8
-y + 5x = 8 y = 5x - 8
Розкриємо дужки в другому рівнянні:
6x - 2y + 7y = -9
6x + 5y = -9
Підставимо y = 5x - 8 у друге рівняння:
6x + 5(5x - 8) = -9
6x + 25x - 40 = -9

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
31x = 31
x = 1
Знайдемо y:
y = 5(1) - 8 = 5 - 8 = -3
Відповідь: x = 1, y = -3.
в) Розв'яжемо систему рівнянь:
�0.5���� + 0.3���� = 8 1.2���� 0.5���� = 7
Розв'язання:
Помножимо перше рівняння на 10 для зручності:
5x + 3y = 80
Помножимо друге рівняння на 10:
12x - 5y = 70
Розв'яжемо методом підстановки або додавання.
Помножимо перше рівняння на 5, а друге на 3, щоб позбутися y:
25x + 15y = 400
36x - 15y = 210
Додаємо рівняння:
61x = 610 x = 10
Знайдемо y:
5(10) + 3y = 80
50 + 3y = 80
3y = 30 y = 10
Відповідь: x = 10, y = 10.
г) Розв'яжемо систему рівнянь: �
1.4x 2.5y = 39
0.8x 1.3y = 21
Розв'язання:
Помножимо перше рівняння на 10:
14x - 25y = 390
Помножимо друге рівняння на 10: 8x - 13y = 210
Розв'яжемо методом підстановки або додавання.
Помножимо перше рівняння на 8, а друге на 14: 112x - 200y = 3120
112x - 182y = 2940
Віднімемо друге рівняння від першого: -18y = 180
y = -10
Знайдемо x:
8x - 13(-10) = 210.
8x + 130 = 210
8x = 80
x = 10
Відповідь: x = 10, y = -10. 1393. Розв’яжи систему рівнянь

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
Розв'яжемо систему рівнянь: � 4
2
5 ���� ���� = 7
3 ���� + 1 5 ���� = 11
Розв'язання:
Помножимо перше рівняння на 5, щоб позбутися дробу: 4x - 5y = 35
Помножимо друге рівняння на 15 (спільний знаменник 3 і 5):
10x + 3y = 165
Розв'яжемо систему: � 4���� 5���� = 35
10���� + 3���� = 165
Помножимо перше рівняння на 3, а друге на 5, щоб
коефіцієнти при x: 12x - 15y = 105
50x + 15y = 825
Додаємо рівняння:
62x = 930 x = 15
Підставимо x = 15 у перше рівняння:
4(15) - 5y = 35
60 - 5y = 35 -5y = -25 y = 5
Відповідь: x = 15, y = 5.
б) Розв'яжемо систему рівнянь:
3
7 x z = 15
2 5 x + 3 7 z = 14
Розв'язання:
Помножимо перше рівняння на 7, щоб позбутися дробу: 3x - 7z = 105
Помножимо друге рівняння на 35 (спільний знаменник 5 і 7): 14x + 15z = 490
Розв'яжемо систему: � 3x − 7z = 105
14x + 15z = 490
Помножимо перше рівняння на 14, а друге на 3:
42x - 98z = 1470
42x + 45z = 1470
Віднімемо друге рівняння від першого: -143z = 0
z = 0
Підставимо z = 0 у перше рівняння: 3x - 0 = 105
x = 35
Відповідь: x = 35, z = 0.

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
Розв'яжемо систему рівнянь: �x + y 3 + x = 15
у (y x) 5 = 6
Розв'язання:
Перше рівняння домножимо на 3: (x + y) + 3x = 45 4x + y = 45
Друге рівняння домножимо на 5: y - x = 30
Розв'яжемо систему: �4x + y = 45 y x = 30
Домножимо друге рівняння на 4: 4x + 16y = 120
Віднімемо перше: (4x + 16y) - (4x + y) = 120 - 45 → 15y = 75 → y = 5
Підставимо y = 5 у перше рівняння: 4x + 5 = 45 → 4x = 40 → x = 10
Відповідь: x = 10, y = 5
1394. Розв’яжи систему рівнянь
а) Розв'яжемо систему рівнянь: � 7 + x 5 2x y 4 = 3y 5
5y 7 6 + 4x 3 2 = 20 5x
Розв'язання:
Помножимо перше рівняння на 20 (спільний знаменник 5 і 4):
4(7 + x) - 5(2x - y) = 60y - 100
28 + 4x - 10x + 5y = 60y - 100
-6x + 5y = 60y - 128 -6x - 55y = -128
Помножимо друге рівняння на 6
(5y - 7) + 3(4x - 3) = 120 - 30x
5y - 7 + 12x - 9 = 120 - 30x
12x + 5y - 16 = 120 - 30x
42x + 5y = 136
Маємо систему: � 6���� 55���� = 128
42���� + 5���� = 136 Помножимо
(-6x - 55y) × 7 = -128 × 7
-42x - 385y = -896 Помножимо
(-6x - 55y) × 7 = -128 × 7
-42x - 385y = -896

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
(-42x - 385y) + (42x + 5y) = -896 + 136.
-380y = -760 y = 2
Підставимо y = 2 у рівняння -6x - 55y = -128:
-6x - 55(2) = -128
-6x - 110 = -128
-6x = -18 x = 3
Відповідь: x = 3, y = 2.
б) Розв'яжемо систему рівнянь: �x² y² = 80 x + y = 10
Розв'язання:
Виразимо y з другого рівняння: y = 10 - x
Підставимо у перше рівняння:
x² - (10 - x)² = 80
Розкриємо дужки:
x² - (100 - 20x + x²) = 80 x² - 100 + 20x - x² = 80
20x - 100 = 80
20x = 180 x = 9
Знайдемо y: y = 10 - 9 = 1
Відповідь: x = 9, y = 1. 1395. Розв’яжи систему рівнянь
а) Розв'яжемо систему рівнянь: � 5 + y 3 3x + 4y 4 = 3x + 1
7x + 2 3 + 4x 3 2 + 11 6 = 1 3x
Розв'язання:
Помножимо перше рівняння на 12 (спільний знаменник 3 і 4):
4(5 + y) - 3(3x + 4y) = 36x + 12
20 + 4y - 9x - 12y = 36x + 12
-9x - 8y + 20 = 36x + 12
-9x - 8y = -8
9x + 8y = 8
Помножимо друге рівняння на 6 (спільний знаменник 3,2 і 6):
2(7x + 2) + 3(4x - 3) + 11 = 6(1 - 3x)
14x + 4 + 12x - 9 + 11 = 6 - 18x
26x + 6 = 6 - 18x
26x + 18x = 6 - 6
44x = 0
x = 0
Знайдемо y:
9(0) + 8y = 8.

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
8y = 8. y = 1.
Відповідь: x = 0, y = 1.
б) Розв'яжемо систему рівнянь:
7 + x 5 − 2x y 4 − 3y = −5 5y 7 2 3 4x 6 18 = 5x
Розв'язання:
Помножимо перше рівняння на 20 (спільний знаменник 5 і 4):
4(7 + x) - 5(2x - y) - 60y = -100
28 + 4x - 10x + 5y - 60y = -100 -6x - 55y = -128
Помножимо друге рівняння на 6 (спільний знаменник 2 і 6):
3(5y - 7) - (3 - 4x) - 108 = -30x
15y - 21 - 3 + 4x - 108 = -30x
15y + 4x - 132 = -30x
34x + 15y = 132
Маємо систему рівнянь:
6x 55y = 128
34x + 15y = 132
Помножимо
(-6x - 55y) × 3 = (-128) × 3
-18x - 165y = -384
(34x + 15y) × 11 = (132) × 11
374x + 165y = 1452
Додаємо рівняння:
(-18x - 165y) + (374x + 165y) = -384 + 1452.
356x = 1068
x = 3
Знайдемо y:
-6(3) - 55y = -128
-18 - 55y = -128
-55y = -110
y = 2
Відповідь: x = 3, y = 2. 1396. Установи
x = 1.
Розв'язок: Спочатку знайдемо корені рівнянь: 2x + 3 = -7
2x = -10
x = -5
Корінь: x = -5
(x - 7)² = 0
x - 7 = 0
x = 7
Корінь: x = 7

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
3x² + 2x = 3x(x - 1)
3x² + 2x = 3x² - 3x
2x + 3x = 0
5x = 0
x = 0
Корінь: x = 0
(5 + x) : 7 = 1
5 + x = 7
x = 2
Корінь: x = 2
Тепер знайдемо значення функцій при x = 1:
А) y = 6x - 1 = 6·1 - 1 = 5
Б) y = x - 1 = 1 - 1 = 0
В) y = 10x + 3 = 10·1 + 3 = 13
Г) y = 1 + 6x = 1 + 6·1 = 7
Д) y = x² + x = 1² + 1 = 2
Встановлюємо відповідність:
1 → x = -5 → не
2 → x = 7 → Г (y = 7)
3 → x = 0 → Б (y = 0)
4 → x = 2 → Д (y = 2)
Відповідь: 1 - відповідність не встановлена, 2
1397.
Позначимо:
5x + 45 = y
Якщо кожен внесе по
7x + 3 = y
Отримуємо систему рівнянь: �5x + 45 = y
7x + 3 = y
Розв'яжемо систему
Прирівняємо праві частини рівнянь: 5x + 45 = 7x + 3.
45 - 3 = 7x - 5x.
42 = 2x. x = 21.
Знайдемо y: y = 5(21) + 45 y = 105 + 45 = 150.
Відповідь:

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
Після смерті сина Діофант прожив ще 4 роки.
Складаємо рівняння:
Спільний знаменник для 6, 12, 7, 2 - це 84: 14x 84 + 7x 84 + 12x 84 + 5 + 42x 84 + 4 = x.
(14x + 7x + 12x + 42x) 84 + 9 = x.
75x 84 + 9 = x
Розв'яжемо рівняння
75x + 756 = 84x.
756 = 9x. x = 84.
Відповідь: Діофант жив 84 роки. 1399. П’ята частина

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
Спільний знаменник для 5 і 3 - це 15:
3x
15 + 5x 15 + 3(5x 153x 15) + 1 = x
3x
15 + 5x 15 + 3 × 2x 15 + 1 = x
(3x + 5x + 6x) 15 + 1 = x
14x
15 + 1 = x
14x + 15 = 15x
15 = x - 14x x = 15
Відповідь: всього 15 бджіл
1400. Поділи число 10 на дві частини, різниця яких дорівнювала б 5.
Розв'язання
Позначимо дві частини як x і y, де x ≥ y.
Складаємо систему рівнянь: x + y = 10 x - y = 5
Розв'яжемо систему методом додавання:
Додаємо рівняння:
(x + y) + (x - y) = 10 + 5
2x = 15 x = 7.5
Знайдемо y: y = 10 - 7.5 = 2.5
Відповідь: число 10 можна поділити на
одержаного результату на
Розв'язання
Позначимо дві частини числа
x + y = 10
За умовою задачі: 5x у = 10 3
Розв'яжемо систему рівнянь
Виразимо y з першого рівняння: y = 10 - x
Підставимо у друге рівняння: 5x (10 x) = 10 3
Розв'яжемо відносно x: 5x · 3 = 10(10 - x)
15x = 100 - 10x.
15x + 10x = 100.
25x = 100 x = 4
Знайдемо y: y = 10 - 4 = 6

Відповідь: число
https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
флорини: x + 2
Пропорція зарплати за 7
до річної зарплати: 7 12 × (x + 10) = x + 2
Розв'яжемо рівняння
Розкриємо дужки: 7 12 x + 70 12 = x + 2
Помножимо на 12, щоб позбутися дробів: 7x + 70 = 12x + 24
Перенесемо всі доданки з x в один бік: 7x - 12x = 24 - 70. -5x = -46. x = 9.2.
Відповідь: одяг оцінили в 9.2 флорина. 1403. Селянин хвалився
Розв'язання
Позначимо кількість овець як x.
Спочатку овець було x, вони народили стільки
x + x = 2x
Додав одну молоду вівцю: 2x + 1
Купив три рази по стільки, скільки стало: 3(2x + 1)
Всього стало 100: 2x + 1 + 3(2x + 1) = 100
Розв'яжемо рівняння
Розкриємо дужки: 2x + 1 + 6x + 3 = 100.
Спростимо: 8x + 4 = 100
Віднімаємо 4: 8x = 96.
Ділимо на 8: x = 12

https://shkola.in.ua/3317-hdz-alhebra-7-klas-bevz.html
Розв'язання
Позначимо:
Вік молодшого сина ����.
Вік середнього ���� + 2.
Вік старшого (���� + ���� + 2) + 6.
Записуємо рівняння:
���� + (���� + 2) + ((���� + ���� + 2) + 6) = 58
Розкриваємо дужки:
���� + ���� + 2 + ���� + ���� + 2 + 6 = 58
Спрощуємо:
4���� + 10 = 58
Розв'язуємо рівняння:
4���� = 48
���� = 12
Знайдемо вік інших братів:
Середній: ���� + 2 = 12 + 2 = 14.
Старший: (12 + 12 + 2) + 6 = 32.
Відповідь:
Молодший син - 12 років,
Середній син - 14 років,
Старший син - 32 роки.

