

УДК 514*кл8(075.3)
2.



3.
4.
5.
6.
7.
8.
23.
24.
25.
29.
30.
трикутники
31. Чи можна утворити трикутник із відрізків завдовжки: 1) 3 см, 5 см, 9 см; 2) 5 см, 4 см, 2 см?
32. Чи існує трикутник зі сторонами: 1) 2 см, 2 см, 4 см; 2) 5 см, 12 см, 13 см?
33. Як зміниться периметр трикутника, якщо всі його сторони: 1) збільшити на 3 см; 2) збільшити у 3 рази; 3) зменшити в 1,5 раза; 4) зменшити на 1,5 см?
34. Як зміниться
1) зменшити на 12 см; 2) збільшити в 6 разів?
49.
50.
51.
52.
39.
40.
41.
55.
58.


62.
63.
64.
65.











іншої. Знайдіть невідомі сторо
чотирикутника.
ABCD — даний чотирикутник, у якого CD = 3 см, AD = 9 см, РABCD = 24 см (мал. 9). Нехай AB = х. Тоді, за умовою, BC = 2х.
Оскільки Р = 24 см, то х + 2х + 3 + 9 = 24. Звідси х = 4. Отже, AB = 4 см, BC = 8 см.
Відповідь: 4 см, 8 см.

5. Властивість сторін чотирикутника Чи може чотирикутник мати такі сторони: 1 см, 2 см, 3 см, 6 см?

Дано: чотирикутник ABCD (мал. 10). Довести: ∠A + ∠B + ∠C + ∠D = 360° . Доведення. У даному чотирикутнику ABCD проведемо діагональ AC (мал. 11). Одер
жали два трикутники — DABC і DACD. Тоді ∠A = ∠BAC + ∠CAD, ∠С =∠BCA + ∠ACD. Звідси: ∠A + ∠





3.

75'.
b
c
91°.
92°.
93°.
100.
101.
102.
103. У чотирикутнику ABCD діагональ BD ділить кути B і D навпіл (мал. 24).
Доведіть, що AB = CB і DA = DC.
104.
що в чотирикутнику ABCD (мал. 24) діагоналі AC і BD — перпендикулярні, якщо AB = CB і DA = DC.
105.
кути чотирикутника,
1) 1, 2, 3 і 4; 2) 4, 6, 12 і 14.
106.
утворюють чотирикутник MNKP (мал. 28). Доведіть, що сума протилежних кутів чоти
рикутника MNKP дорівнює 180° .
122. На малюнку 29 зображено земельну ділянку в масштабі 1 : 2000. Межі
124.




2.




qr.orioncentr.com.ua/Uq1Ln
1.
2.
125'.
1)
3)
126'.
127'.
1)
2)
3)
148°.
155.
156.
157.
(мал. 46).
і ОD;
3) сторони АD і DС.
149°. Основа піраміди — паралелограм АВСD (мал. 47). Знайдіть кути паралелограма, якщо ∠А = 35° .
150°. Основа піраміди — паралелограм
158.
159.
160.
151.



Дано: ABCD — чотирикутник (мал. 55),
AB = DC, BC = AD.
Довести: ABCD — паралелограм.
Доведення. У даному чотирикутнику
ABCD проведемо діагональ BD (мал. 56).
Розглянемо DBCD і DDAB. У них BD — спільна сторона, DC = AB і BC = AD за умовою.
Отже, DBCD = DDAB за трьома сторонами. Із рівності трикутників випливає: ∠CBD = ∠ADB
CDB = ∠ABD. Кути CBD і ADB — внутріш
Дано: ABCD — чотирикутник (мал. 58),
AB = DC, AB || DC. Довести: ABCD — паралелограм.
ABCD проведемо

кути при пара
лельних прямих AB і DC та січній



178'. Чи є
179'. Чому чотирикутник
180'.
181'.

184°.
185°.
= 3
=
см; 2) ВС = 2,5 см, СD = 3,7 см.
інших сторін цього чотирикутника, щоб був правильним висновок: АВСD — паралелограм?
186°. Доведіть, що чотирикутник АВСD — паралелограм, якщо:
1) АВ = 3 см, ВС = 0,4 дм, СD = 30 мм, АD = 40 мм;
2) АВ + ВС = 7 см, ВС – СD = 3 см, АD = ВС = 5 см; 3) АВ : ВС : СD : АD = 2 : 1 : 2 : 1.
187°.
Доведіть, що чотирикутник АВСD — паралелограм, якщо:
1) АВ = 0,5 дм, ВС = 2,7 см, СD = 5 см, АD = 27 мм;
2) АВ – АD = 3 см, СD = 2ВС, АВ = СD = 6 см.
188°.
чотирикутнику АВСD АВ = СD, ВС = АD. Знайдіть:
1) AB, якщо CD = 4 см;
2) BC, якщо AD = 2 см;
3) ∠В, якщо ∠D = 120°;
4) ∠А, якщо ∠С = 60° .
Щоб довести рівність (паралельність) двох відрізків:
1) виділіть на малюнку
192°.
1) AD || BC, АD = 0,5 дм, ВС = 50 мм;
2) AB || CD, АВ = 2 см, СD = 0,02 м;
3) AB = CD, ∠ВАD = 45° , ∠
193°.
1) AB || CD, АВ = 3 см, СD = 30 мм;
2) AD = BC, ∠АВС = 120° , ∠ВАD = 60
якщо:
199°. На сторонах ВС і АD паралелограма АВСD
позначено точки Е і F так, що ЕС = АF
(мал. 67). Доведіть, що чотирикутник
АЕСF — паралелограм.
200°. У піраміді SАВСD (мал. 68) АВ = 4 см,
ВС = 0,7 дм, DС = 40 мм, АD = 70 мм. Дове
діть, що основа піраміди — паралелограм.
201°. Доведіть, що основою піраміди SАВСD (мал. 68) є паралелограм, якщо АВ || DС, АВ = 65 мм, DС = 6,5 см.
202. На сторонах АВ, ВС, СD і АD паралелограма АВСD позначено точки E, M, K і N відповідно і так, що BM = DN, BE = DK (мал. 69). Доведіть, що EMKN — паралелограм.
203. На сторонах паралелограма АВСD
паралелограм.
70. Доведіть, що MNPK —
204. У паралелограмі АВСD точка М — середина сторони АD, а N — середина сторони ВС. Доведіть, що ВNDМ — паралелограм.
205.
— паралелограм (мал. 71), AE = CF. Доведіть, що відрізки CE
206.
(мал. 72), ОМ = ОN.
210.
Доведіть.
211. АВСD — паралелограм (мал. 73), АМ = KС, BN = РD. Доведіть, що MР = NK і МР || NK.
212. Діагоналі паралелограма АВСD перетинаються в точці О. Доведіть, що чотирикутник MNPK, вершинами якого є середини відрізків ОА, ОВ, ОС і ОD, — паралелограм.
213. У чотирикутнику ABCD відомо, що
214.
215*.













1.
2.
qr.orioncentr.com.ua/11bYy
2)
(мал. 84),

1) 5,86 + 4,14; 0,79 + 9,21; 8,62 + 1,38; 2) 3,56 + 6,44; 4,25 + 5,75; 1,13 + 8,87.
(n)rectangle
226'.
227°.
230°.
242°.
243°.
244°.
245°.
247.
1) d = 4 см;
2) d = 14 мм;
3) d = 0,44 дм.
248.
254.
255.
256.
257.
258.
259.
260.
261.
262*.
250.
269*.








розв’язання Нехай ABCD — даний паралелограм, у якому AC ⊥ BD (мал. 102). Доведемо, що
ABCD — ромб. Розглянемо DAOB і DAOD. У них
AO — спільна сторона, OB = OD за властивістю діагоналей паралелограма, ∠AOB = ∠AOD = 90°
DAOB = DAOD за двома сторо
AB = AD. Тоді





285'.
ромбrhombusRhombus (m) losange
квадратsquareQuadrat (n)carré
qr.orioncentr.com.ua/bNAbg
286'.
1) рівні;
2) взаємно перпендикулярні;
289°.
290°.
291°.
295°.
305°.
306°.
307°.
308°.
ділять сторони трикутника.
324. У рівнобедрений прямокутний
325.
326.
334*.

343.
344.















352°.
353°.
1)
поясніть.
357°. DE i EF — середні лінії трикутника АВС, які відповідно
1)
FC, якщо DE = 4 см; 2) відрізок BD, якщо EF = 7 см.
358°. Знайдіть середні
374.
375.
,
1) 18 см; 2) 2,4 дм; 3) 300 мм.
376. Середня лінія рівнобедреного
377.
378.
394*.
397*.










(мал. 162), EF — серед
Довести: 1) EF || AD, EF || BC, 2) . 2 ADBC EF + =
Оскільки EF — середня
ABCD, то AE = BE, DF = CF.
точки B i F проведемо пряму, яка перетне продовження основи AD в точці Q (мал. 163). Розгля
немо DBCF і DQDF. У них CF = DF за умовою, ∠BFC = ∠QFD як вертикальні, ∠BCF = ∠QDF
як внутрішні різносторонні кути при пара
лельних прямих BC i AQ та січній CD. Отже, DBCF = DQDF за стороною та прилеглими до неї кутами. З рівності трикутників випливає: BF = QF, тобто середня лінія





1.
2.
3.
4.
5.
6.
7.
8.
qr.orioncentr.com.ua/KZpew
407'.
Чи правильно, що в рівнобічній трапеції (мал. 166):
1) основи рівні;
2) усі сторони рівні;
3) бічні сторони рівні?
408'. Які з наведених тверджень правильні?
У прямокутній трапеції (мал. 167):
1) основи перпендикулярні;
2) один із кутів — прямий;
3) бічна сторона перпендикулярна до основи.
409'. Чи правильно,
2)
415°.
171–173
412°.
2.
малюнку 168 зображено трапецію ABCD, у якій AD || BC.
Назвіть:
1) основи трапеції; 3) кути, прилеглі
2) бічні сторони трапеції; 4) кути,
413°. За малюнками 169, 170 знайдіть:
1) сторону CD рівнобічної трапеції ABCD (мал. 169);
2) кут N трапеції MNKL (мал. 170).
416°. ABCD
417°.
423°. MNKL — трапеція з основами ML і NK, NF || KL (мал. 176). Знайдіть:
1) основу ML, якщо MF = 5 см, NK = 2 см; 2) основу NK, якщо ML = 10 см, MF = 7 см. Мал. 177 Мал. 176
424°. BM і CK —
рівнобічної трапеції ABCD з основами AD і BC (мал. 177). Доведіть, що DABM = DDCK.
425°.
427°. Основою піраміди SАВСD є трапеція із середньою лінією МK (мал. 182). Знайдіть сторону АD основи піраміди, якщо:
1) МK = 3 см, ВС = 2 см; 2) МK = 11 см, ВС = 7 см;
3) МK = 14,5 см, ВС = 12 см.
428°. Трапеція АВСD (АD || BC) — основа піраміди (мал. 182). Точки М і K — середини сторін
і СD основи
429°.
430°.
431°.
432°.
433°.
434.
435.
437.
Мал. 181
447.
452.
453.
454.
460*.
461*.
462*.
466.
195, 196).




467.










474°.
479°.
494.
495.
496.
497.
498.
499.
500.
501.
515*.
507.
516*.
517*.
510.
518*.
511.
519.







Довести: AB + CD = BC + AD.


AE = AP, BE = BF, CK = CF, DK = DP.
AE + BE + CK + DK = AP + BF + CF + DP,
AB + CD = BC + AD

522'.

circumscribed circle umschriebene Kreis (m) cercle circonscrit
inscribed circle einbeschriebener Kreis (m) cercle inscrit
523'.
524'.
534°.
см?
535°.
1) 20 см; 2) 3,2 дм.
536°.
1) 12 см, 16 см, 28 см; 2) 10 см, 14 см, 16 см.
537°. Доведіть, що центром
(мал. 269).
538°. Чи можна вписати коло в довільний: 1) прямокутник; 2) квадрат; 3) ромб? Відповідь поясніть.
539. Знайдіть
540.
532°.
541.
542.
555*.
543.
544.
556*.
545. Чи можна вписати
557*.
546.
558*.
559.
560.
561.
562.
= 8 см. А. 20 см. Б. 40 см. В. 44 см.
Г. 64 см.
А. 8 см.
Б. 12 см.
В. 2 см.
Г. 6 см.
3°.
Б. 20 см.
30 см. Г. 40 см.
4.







100 : 25; 25 : 100; 63 : 7; 7 : 63; 36 : 18; 18 : 36; 72 : 9; 9 : 72.
563'.
трикутниках: 1) усі кути рівні; 2) відповідні кути рівні; 3) усі
564'.
565'.
1) D
DKLM; 2) DАВС DLKM; 3) DАВС DMLK?
566'.
1) ; ABBCAC KMKLLM == 2) ? ABBCAC KLLMKM ==
567'.
1) –2; 2) 0; 3) 3; 4) 1; 5) 1 ; 5 6) 6 ? 5
568°.
569°.
1)
50 см, 50 см і 5 см, 50 мм, 50
(мал. 283).
575°.
3 дм, 4 дм, 5 дм і 9 м, 12 м, 15 м?
576°. D
В1С1, якщо:
1) АВ = 8 см, ВС = 10 см, А1В1 = 56 мм, А1С1 = 42 мм;
2) АВ = 40 мм,
579°.
1) k = 2; 2) 2 . 3 k =
582°.
583°.
584°.
587.
599*.
589.
600*.
590.
601*.
591.
602*.
592.
593.
603*.
604*.
595.
605*.
596.
606.
597.
607.








. BCBA NCKA
AMBN MCNC
ACBC MCNC
= BCBA NCNM

qr.orioncentr.com.ua/0YY23
1)
2)
3)
4)
613°.
614°.
615°.
621°.
622°.
623°.
624°.
626°.
627°.
628°.
629°.
633°.
1) 1, 2, 3; 2) 6, 3, 4; 3) 3, 5, 7.
1)
2)
639.
1) d = 5 см, m = 3, n = 2; 2) d = 16 см, m = 5, n = 1.
640. На малюнку 300 AB || DC || KL, AD : DK : : KF = 2 : 3 : 2. Знайдіть довжини відрізків
BC, СL, LF, DС і KL, якщо:
1) AB = 70 мм, FС = 40 мм; 2) AB = 21 см, FС = 15 см.
641. На малюнку 301 AМ || BN || CK || DP. Знайдіть довжини відрізків MN, NK і KP, якщо:
1) a = 2,5 см, b = 4 см, c = 2 см, MP = 12,5 см; 2) a = 10 см, b = 16 см, c = 8 см, MP = 50 см.
642. Сторони кута А перетинають
1) АН, якщо АВ = 8 см, АО = 12 см, АС = 10 см; 2) АО, якщо 3 ::0,6, 11 ACAH = ВО = 12 дм.
643.
644.
645.
646.
647.
649.
653*.
2) а = 10 см.
302
654*. На малюнку 303 AB || CD.
1. Застосувавши теорему про пропорційні відрізки, доведіть, що AO : OD = OB : OC.
2. Знайдіть АО і ОD, якщо АD = 10 см, ОВ = 5 см, ОС = 3 см.
655*. Відрізок MN має кінці на сторонах AB і AC трикутника
661.
662.




2)
664'.
3)
665°.

signs of similarity of triangles Zeichen der Ähnlichkeit von Dreiecken conditions de similitudes des triangles
679°.
680°.
681°.
682°.
683°.
684°.
685°.
689°.
690°.
грані трапецію BKPC (мал. 319).
подібність трикутників BSС і KSP.
691°.
ребро піраміди SАВС дорівнює m. Відрізок KP грані BSС відтинає від неї трапецію BKPC (мал. 319). Знайдіть:
1) сторону KP трикутника KSP, якщо
692.
693.
699.
701.
702.
703.
704.
708.
709.
710.
722*.
723*.
724*.
725.


== ABACBC ABACBC 121222 111111
== ACBC c kckbka 1222 ,
== ACBC ba 1222
= 9, AK = KС = 7,5; RT = 6, RM = MT = 5.
AK RT RM 937,53 ,. 6252
R, ==== ACABAKAK RTRSRMRM 323 ,. 222





732°.
Euler line ['s] Eulersche Gerade (f) la droite d’Euler
qr.orioncentr.com.ua/IfC08
733°.
734°.
735°.
736°.
1) 1, 2, 3; 2, 3, 4; 3, 4, 5; 4, 5, 10; 2) 4,56, 5,44 і 10; 2,39, 3,61 і 5; 7,65, 1,35 і 6,3?
1)
2)
739°.
1) АВ = 12 см, АС = 15 см, ВD = 2 см, СЕ = 7 см;
2) АВ = 15 см, АС = 18 см, ВD = 3 см, СЕ = 8 см;
3) АВ = 20 см, АС = 21 см, ВD = 10 см, СЕ = 10,5 см?
740°.
1) ВА = 10 см, ВС = 12 см, АМ = 5 см, СР = 6 см;
2) ВА = 22 см, ВС = 16 см, АМ = 11 см,
2) а = 17 см, b = 8 см, с = 15 см, d = 56 см.
746°.
748°.
749°.
750°.
751°.
752°.
753°.
754°.
759.
760.
761.
771*.
772*.
762.
773*.
763.
775*.
776*.
780.

781.
782.
783.
784.

AOB
∠AOB = ∠A1OB1 як

Дано: DАВС (мал. 341), CL — бісектриса. Довести: AL : BL = АC : ВC.
прямої СL (мал. 342).
Розглянемо DАMC і DBNC.
У них: ∠АMC = ∠ВNС = 90° , ∠АCM = ∠ВСN, оскільки СL — бісектриса кута C.
Отже, DАMC DBNC за двома кутами.
Звідси = ACAM BCBN . (1)
Розглянемо DАLM і DВLN. У них: ∠АML =
=
DАML DBNL за двома кутами.
Звідси = AMAL BNBL . (2) Із рівностей (1)
785'.

співвідношення для трикутника АСВ (мал. 348): 1) CH = АС · ВС; 6) АC2 = АH · АВ; 2) CH2 = АВ · ВH; 7) ВC = ВА · АH; 3) CH2 = АH · ВH; 8) ВC2 = АС · ВА; 4) АC = АH · ВH; 9) ВC2 = ВH · ВА?
5) АC2 = ВС · АВ;
788°. Медіани трикутника дорівнюють: 1) 9 см, 12 см і 15 см; 2) 6 см, 6 см і 3 см; 3) 45 см, 45 см і 45 см.
789°.
791°.
798°.
800.
801.
795°.
2) катети; 3) висоту,
803.
804.
805.
806.
816*.
817*.
818*.
810.
1) D
і DDВM (мал. 355); 2) DADM і DСВM (мал.
819*.
821.














А. 2 см.
Б. 15 см.
В. 25 см.
Г. 50 см.
3°.
сторону?
А. 1,5 см і 2 см.
Б. 3,5 см і 3,5 см.
В. 2 см і 5 см. Г. 3 см і 4 см.
4.
10 см і 15 см.
6 см і 9,5 см.
12 см і 18 см.
18 см і 12 см.
5*.
5,4 см.
7,2 см.
9,6 см.
12 см.













1.
2.
3.
qr.orioncentr.com.ua/fPUx0
825'.
826'.
AB — 16 см.
838°. Знайдіть сторону ромба, якщо його діагоналі
839°. Доведіть, що коли a — сторона ромба, d1 і d2 — його діагоналі, то =+ add 222 12 4.
840°. Доведіть, що
ного паралелепіпеда дорівнює сумі квадратів трьох його
d2 =
2 + b2 + с2 (мал. 381).
841°. Діагональ прямокутного паралелепіпеда дорівнює 13 см, а його довжина
842°. Основою піраміди SАВСD
16 см (мал. 382). Знайдіть бічне ребро піраміди, якщо висота SМ її грані дорівнює 15 см.
843°. Кожне ребро трикутної піраміди дорівнює m. Знайдіть висоту грані піраміди.
844°. Із точки A до прямої проведено перпендикуляр AB і похилу
854.
855.
856.
857.
858.
859.
1) а = 2 см, b = 18 см, r = 3 см;
860.
1) b = 6 см, с = 4 см; 2) b = 5 см, с = 8 см.
861.
1) r = 25 см, а = 40 см, b = 48 см; 2) r = 65 см,
= 120 см, b = 32 см.
862.
863.
864.
877*.
865.
866.
878.
879.
870*.
й інший
якщо: 1) b = 60, n = 12; 2) b = 35, n = 14.
якщо: 1) с = 60 см, h = 12 см, m = 13 см; 2) с = 42 см, h = 12 см, m = 13 см.
871*.
880.
881.
















1.
2.
6.
синусsineSinus (m)sinus
косинусcosineKosinus (m)cosinus
тангенсtangentTangens (m)tangente
qr.orioncentr.com.ua/7af0l
884'.
1) tg b дорівнює: а) 5 ; 15 б) 12 ; 5 в) 5 ; 13
2) cos b дорівнює: а) 12 ; 13 б) 13 ; 5 в) 5 ; 13
3) sin b дорівнює: а) 5 ; 12 б) 12 ; 13 в) 13 . 5
885'. За малюнком 404 назвіть
(мал. 403).
1) для кута a відношення a c є: а) sin a; б) cos a; в) tg a; 2) для кута b відношення a c є: а) sin b; б) cos b; в) tg b;
3) для кута b відношення b a є: а) sin b; б) cos b; в) tg b.
886'. Чи правильно, що
(мал. 405):
1) синус кута зменшується; 2) синус кута збільшується; 3) косинус кута зменшується; 4) косинус кута збільшується; 5) тангенс кута зменшується; 6) тангенс кута збільшується?
887'. Чи є правильною рівність: 1) 3 sin30; 2 °= 4) 2 sin45; 2 °= 7) 1 sin60; 2 °= 2) 3 cos30; 2 °= 5) 2 cos45; 2 °= 8) 1 cos60; 2 °=
3) 3 tg30; 2 °= 6) 2 tg45; 2 °= 9) 1 tg60? 2 °=
1) 2 sin 30°; 3) 3tg30; ° 5) 2 cos 30°; 2) 4 cos 60°; 4) 6 sin 45°; 6) 8 tg 45° .
1) 4 sin 60°; 2) 2 cos 45°; 3) 3tg60. °
1) tg 30° · tg 60°; 2) 2cos45tg45; °⋅° 3) 2sin303cos30; °+° 4) 6cos603tg30. °−°
895°.
1) 8 sin 30° · cos 60°; 2) 2cos452sin30. °−° Мал. 406
896°. Яка градусна міра кута a, якщо: 1) a= 1 sin; 2 3) tg3; a= 5) a= 1 cos; 2 2) a= 2 cos; 2 4) a= 3 sin; 2 6) tg a = 1?
897°. Яка градусна міра кута a, якщо: 1) a= 2 sin; 2 2) a= 3 cos; 2 3) 3 tg? 3 a=
898°. Запишіть у порядку збільшення: 1) sin 15°, sin 46°, sin 75°, sin 10°, sin 11°; 2) tg 37°, tg 87°, tg 66°, tg 17°, tg 48°
899°.
900°.
903°.
1) MN, якщо MK = 3 см; 3) MK, якщо = NK 73 см.
2) NK, якщо = MK 23 см; 904°. Кут А
1) АВ, якщо = AC 2 см; 3) АС, якщо ВС = 9 см.
2) ВС, якщо = AB 52 см;
1) косинуси даних кутів на синуси: cos 20°, cos 35°, cos 50°;
2) синуси даних
формулами cos a = sin (90° – a), sin a = cos (90° – a), замініть:
1) косинуси даних кутів
1) 2 cos (90° – a) – sin a; 3) 3 cos a – 2 sin (90° – a); 2) sin a + cos (90° – a); 4) 3 sin (90° – a) – 4 cos a.
1) sin (90° – a) – cos a; 2) cos a – 2 sin (90° – a).
дорівнює: а) 3 ; 5 б) 0,3; 2)
якого дорівнює: а) 2; б) 4 . 7
0,5;
2) косинус якого дорівнює 5 12 ; 3) тангенс якого
912°.
2
3
3 sin. 4 A = 914°.
1) с = 6 см, = A 1 cos; 3 2)
1) ВС = 16 см, = B 1 cos; 8 3) ВС = 5 см, cos В = 0,5; 2) ВС = 12 см, = B 3 cos; 4 4) ВС = 7 см, cos A = 0,7.
916°.
якщо: 1) ВС = 24 см, = A 3 sin; 8 2) ВС = 10 см, 1 sin. 5 A = 917°.
1) АС = 8 см, tg A = 0,6; 3) AC = 11 см, tg A = 1,5. 2) AC = 12 см, tg A = 4; 918°.
= 90°), якщо: 1) AB = c, ∠B = b; 2) BC = a, ∠A = a; 3) AC = b, ∠B = b.
919°.
1) sin a, cos a, tg a, якщо a дорівнює: 43°; 22°; 35
; 58
20′; 64°13′; 2) кут a, якщо: sin a дорівнює: 0,642; 0,771; 0,910; 0,640; 0,712; cos a дорівнює: 0,342; 0,962; 0,087; 0,914; 0,809; tg a дорівнює: 0,178; 0,269; 0,035; 0,447; 0,532.
920°.
Скориставшись калькулятором, знайдіть:
1) sin a, cos a, tg a,
якщо a дорівнює: 39°; 54°12′;
2) кут a, якщо:
sin a дорівнює: 0,750; 0,515; cos a дорівнює: 0,602; 0,915; tg a дорівнює: 0,934; 0,781.
921°.
За таблицями (додатки 1, 2) знайдіть: 1) sin 20°, sin 75°, sin 33°, sin 85°;
2) cos 6°, cos 67°, cos 51°, cos 24°; 3) tg 65°, tg 1°, tg 73°, tg 19° .
922°. За таблицями (додатки 1, 2) знайдіть: 1) sin 53°, sin 2°; 2) cos 62°, cos 13°; 3) tg 10°, tg 16° .
923°. За таблицями (додатки 1, 2) знайдіть кут a, якщо:
1) sin a = 0,999; sin a = 0,017; sin a = 0,574; 2) cos a = 0,766; cos a = 0,966; cos a = 0,225; 3) tg a = 0,900; tg a = 0,344; tg a = 0,781.
924°. За таблицями (додатки 1, 2) знайдіть кут a, якщо: 1) sin a = 0,588; 2) cos a = 0,731; 3) tg a = 0,839.
925.
трикутнику ABC (∠C = 90°) AC = 18 мм, BC = 24 мм. Знайдіть: 1) sin A, cos A, tg A; 2) sin B, cos B, tg B.
932.
933.
934.
935.
936.
938.
939.
940.
954.
955.
956.
957.
958.
959.
960.
962.
963*.
964*.
966*.
967*.











АС = b,
= а.
AB, ∠A,
AB = c, BC = a.
=+ ABab22 ,
AC, ∠A, ∠B 1) =− ACca22 , 2) = a A c sin, 3) ∠B = 90° – ∠A
Дано: AB = c, ∠A = a.
Знайти: AC, BC, ∠B 1) ∠B = 90° – a, 2) AC = c · cos a, 3) BC = c · sin a
Дано: BC = a, ∠A = a.
Знайти: AB, AC, ∠B 1) ∠B = 90° – a,
a = 76° (мал. 431).
2) = a a AB , sin
3) tg a AC = a
c = 16
1) ∠B = 90° – a = 90° – 76° = 14°; 2) AC = c · cos a = 16 · cos 76°≈ 16 ·









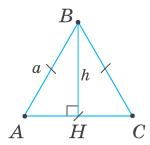
tgtg DCDC ACBC−=− ab , tgtg tgtg ABDC b−a = a⋅b , ⋅a⋅b = b−a a DC tgtg . tgtg
⋅a⋅b =+ b−a a DK h tgtg . tgtg
Тоді ⋅°⋅°⋅⋅ =+≈+≈ °−° DK 10tg35tg40100,7000,839 1,5 1,543,8 tg40tg350,8390,700 (м). 4.
975°.

979°.
980°.
994.
986°.
йдіть кут, утворений дотичними, якщо
ВМ = 30 см.
987. Знайдіть невідомі сторони й гострі кути прямокутного трикутника за такими да
ними:
1) за двома катетами:
а) а = 20, b = 21; в) а = 24, b = 18;
б) а = 9, b = 12; г) а = 23,5, b = 40,2;
2) за гіпотенузою та катетом:
а) с = 17, а = 15; в) с = 65, а = 56; б) с = 20, а = 16; г) с = 2,93, b = 2,85.
988. Знайдіть невідомі сторони й гострі кути
прямокутного трикутника за такими
ними:
1) за гіпотенузою та гострим кутом:
с = 8,
= 70°; в) с = 18,2, ∠А = 32°;
с = 82, ∠А = 42°; г) с = 4,67,
= 12,
995.
996.
997.
998*.
999*.
1003.
1005.
1006.
1007.
1008.

1012.





3.
1°.




2°.
3°.
Відрізки,
яких складається многокутник, називають його сторонами, кути, утворені суміжними сторонами, — його кутами



AC, AD, AE



(1980).

English
коло circumscribed circle umschriebene Kreis (m) cercle circonscrit вписане
inscribed circle einbeschriebene Kreis (m) cercle inscrit
2.
3.
4.
5.
6.
qr.orioncentr.com.ua/Q2oYD
1026°.
1027°.
1) 90°;
1030°.
1031°.
1033°.
1020'.
1035°.
1041.
1054*.
1055*.
1056*.




= 22 = 4 (см2), SKLMN = 2,52 = 6,25 (см2).

qr.orioncentr.com.ua/1Oo5x
(2 + 3)2; (4 + 6)2; (2 + 3)2 : (4 + 6)2; (4 + 6)2 : (2 + 3)2.
1060'.
1061'.
3) S = а : 2; 4) S = а2?
1062'.
1) S = 2(а + b); 3) S = а2b2; 2) S = 2аb; 4) S = аb?
1) S = а + b; 3) = Sab22 1 ; 2
2) S = аb; 4) 1 ? 2 Sab =
1065°.
1066°.
1067°. Доведіть, що діагональ прямокутника
1068°. Точку всередині трикутника сполучено
з його вершинами. Знайдіть
трикутника, якщо утворені частини мають площу 12 см2, 39 см2 і 45 см2.
1069°. Точку всередині трикутника сполучено
трикутника
площу 90 см2, 25 см2 і 45 см2. Знайдіть площу
1070°.
1071°.
1072°.
1087.
1088.
1089.
1090.
1091.
1092.
1093.
1094.
1) а = 3 см, b = 4 см, d = 1 см; 2) а = 6 см, b = 8 см, d =
1095*.
1096*.
1102.
1103.
1104.
1105.
1106.


2) SАМСD = SНМСD + SDАНD.
Тому SАВСD + SDВМC = SНМСD + SDАНD. Розглянемо DВМС і DAНD. У них: СМ = DН як
грама, AD = ВС як
DВМС = DAНD за катетом і гіпотенузою.
Тому, за властивостями площі, SDВМC = SDАНD.
Отже, SАВСD = SНМСD.
Для прямокутника НМCD маємо: SНМСD = CD · DН = AВ · DН = аh а .
Оскільки, за доведеним, площа даного паралелограма ABCD
площі прямокутника НМCD, то: SАВСD = аh а .
задача У паралелограмі сторони дорівнюють 8 см і 6,4 см,
сторони,
SАВСD = ВС · DМ = 8 · 6 = 48 (см2), (1)
SАВСD = АВ · DН. (2) Із рівностей (1) і (2) одержуємо:







1117°.
1127°.
1118°.
1) S = 60 см2, a = 15 см; 3) S = 75 см2, a = 25 см; 2) S = 175 см2, a = 35 см; 4) S = 96 см2, a = 12 см. 1122°.
1128°.
1129°.
1132°.
1140.
1141.
1142.
1155*.
якщо:
1) S = 56 см2, m = 4 см, n = 3,5 см; 2) S = 36 см2, m = 2 см, n = 3 см.
1143.
1)
1156*.
1159.
1160.





Мал. 523 Мал. 524 Мал. 525
1165°. У трикутнику ABC проведено висоту
(мал. 526). Знайдіть
якщо:
1) АC = 6 см, ВН = 5 cм;
2) АC = 25 см, ВН = 100 см.
1166°. У трикутнику ABC
якщо
1) a = 10 см, h а = 0,8a; 2) h а = 12 мм, a
1174°.
2) 1,2 дм; 3) 2 м; 4) 23 см; 5) 6 дм.
1175°.
1) 10 см; 2) 3 дм.
1176°. Знайдіть площу рівнобедреного трикутника, якщо
1) 26 см і 20 см; 2) 17 см і 16 см.
1177°. Знайдіть площу рівнобедреного
1178°.
1179°.
1190.
1191.
1192.
1193.
1) 25 см, 3 : 4; 3) 25,5 см, 8 : 15; 2) 5 см, 7 : 24; 4) 82 см, 9 : 40.
1194. Катети
1) 39 см; 2) 26 см.
1195. Площа
1) S = 720 см2, m = 9, n = 40; 2) S = 1320 см2, m = 11, n = 9,6.
1196.
1197.
1198.
1199.
1200.
1209*.
1201.
1210*.
1202.
1211*.
1212*.
SbcAacB 11 sinsin 22 (мал. 534).
SbcAacBabC 111 sinsinsin 222 (мал. 535).
1213.
1214.
1217.
AB

а висоти, проведені до цієї сторони, дорівнюють


ABD складений

qr.orioncentr.com.ua/v71c7
1) =⋅ ABCD SABDH 1 2 (мал. 546);
2) ()=+ ABCD SABDH 1 2 (мал. 546);
3) () =+⋅ KLMN SKLNMTL 1 2 (мал. 547);
4) () =+⋅ KLMN MH SKLLM 2 (мал. 547);
5) SPQНT = PQ · PT (мал. 548);
6) + =⋅ PQHT HTPQ S PT 2 (мал. 548)?
1222°.
1)
= 60 см, CD = 36 см, СН = 50 см; 2)
= 25 см, CD = 55 см, СН
1224°.
1) a = 10 см, b = 0,8a, h = a;
2) a = 2 дм, b = 0,75a, h = 0,5
1232°.
1233°.
1234°.
1235°.
1236.
1) S = 60 см2, h = 12 см;
2) S = 150 см2, h = 25 см.
1237.
1238.
1) S = 60 см2, q = 15 см;
2) S = 175 см2, q = 35 см. 1229°.
1240.
1253*.
1254*.
1241.
1255*.
1242.
1243.
1257*.
1258*.
1244.
1259*.
1245.
1260*.
1246.
1261.
1262.
2°.







А. 6 см.
Б. 9 см.






















В. 20 см.




3°.
Г. 36 см.




АВ = 100 см. А. 24 см і 48 см.
Б. 48 см і 48 см.





В. 48 см і 96 см.
Г. 96 см і 96 см.
4. У трапеції АВСD
А. 45 см2.
Б. 56 см2.
В. 75 см2.
Г. 88 см2.
5*.
А. 90 см2.
Б. 135 см2.
В. 180 см2.
Г. 54 см2.


= ВС = CD = DA
Дано: a, с
Знайти: b, A, B
Дано: c, a
Дано: a, a
1295.
1283.
1296.
1297.
1298.
1299.
1287.
1288.
1289.
1314.
1315.
1304.
1309.
1310.


1322.
1323.
1324.
1326.
∆ABC так, щоб
AB = BC = b, AD = mb , (D — середина BC)
1333.
1334.
1335.
(мал. 558); 2) за стороною а та діагоналями d1 і d2 (мал. 559).
побудуйте допоміжний трикутник (DАDС на мал. 558 або DАОD на мал. 559). Потім добудуйте цей трикутник до паралелограма (ромба), спираючись на властивості паралелограма
1336.
1337.
1338.
1339.
1340.
1342.
1353.
1354.
1355.
1362.


1
0,01721° 0,38441° 0,86961° 1,8081° 6,31
2° 0,03522° 0,40442° 0,90062° 1,8882° 7,12
3
4
5
6
0,08725° 0,46645° 1,00065° 2,1485° 11,4
0,10526° 0,48846° 1,0466° 2,2586° 14,3
7° 0,12327° 0,51047°
10
12
0,21332° 0,62553° 1,2872° 3,08
§ 2. Паралелограм та
125. 1) Ні; 2) ні; 3) так. 126. 1) Ні; 2) ні; 3) так. 127. 1) Ні; 2) так; 3) ні; 4) так. 128. Ні (мал. 37); ні (мал. 38). 129. 1,2 дм, 0,4 дм. 130. 10 см, 5 см. 132. 1) 3 см, 21 см, 3 см, 21 см; 2) 15,5 см, 8,5 см, 15,5 см, 8,5 см. 133. 6,5 см, 9,5 см, 6,5 см, 9,5 см. 134. AB = CD = 4 см, AD = BC = 6 см (мал. 39); AB = CD = 10 см, AD = BC = = 10 см (мал. 40). 135. AB = CD = 6 см, AD = BC = 6,8 см. 136. Вказівка: скористайтеся
72. 1) Ні; 2) так. 73. Мал. 16. 74. 1) Ні; 2) так; 3) ні. 75. 2). 76. Ні (мал. 18); так (мал. 19). 77. 1) ∠ENM, ∠FNP; 2) ∠AMN, ∠CMK; 3) ∠DKM, ∠BKP.
79. 5 см, 45 см, 45 см, 45 см. 80. 30 см, 60 см, 60 см, 60 см. 81. 1) Так; 2) ні. 82. Ні. 83. 100°, 100°, 100° (мал. 21); 100°, 100° (мал. 22). 84. 60° . 85. 1) 60°; 2) 70° . 86. 150° . 87. 1) Ні; 2) ні. 88. Так. 90. Ні. 91. 90°, 90°, 90°, 90° . 92. 180° .
93. Вказівка: знайдіть градусну міру четвертого кута. 94. 1) 105°; 2) 90° . 95. 1) 100°; 2) 60° . 96. Чотирикутником. 97. 5 граней і 8 ребер. 98. 15 см, 7 см, 23 см, 21 см. 99. 64 см. 100. 1) Ні; 2) так; 3) ні. 101. Вказівка: скористайтеся нерівністю трикутника. 102. Вказівка: скористайтеся нерівністю трикутника. 103. Вказівка: скористайтеся ознакою рівності
леглими кутами. 104. Вказівка: скористайтеся
108
, 144°; 2) 40
, 135
. 169. 9,6 см, 14,4 см, 9,6 см, 14,4 см. 170.
см. 171. 1) 45°; 2) 135° . 172. 2 см або 4 см. 173. 10 см, 15 см, 10 см, 15 см. 174. Сторони відносяться як 1 : 2. 175. 7 см, 14 см, 7 см, 14 см. 176. 1) АВ || CD. § 3. Ознаки паралелограма 178. 1) Ні; 2) ні; 3) так. 180. За ознакою паралелограма. 181. На мал. 64. 184. 1) MN = 4 см, LM = 6 см; 2) KL = 5,3 дм, NK = 3 дм; 3) MN = 1,5 см, NK = = 25 мм; 4) KL = 0,3 дм, LM = 5 см. 185. 1) СD = 3 см, ВС = 2 см; 2) АD = 2,5 см, АВ = 3,7 см. 186. Вказівка: скористайтесь ознакою паралелограма. 187. Вказівка: скористайтесь ознакою паралелограма. 188. 1) 4 см; 2) 2 см; 3) 120°; 4) 60° . 189. 1) 35°; 2) 5 см. 190. 1) KL || MN; 2) LM || NK; 3) KL || MN;
5.
277. 1) Ні; 2) так. 278. Так. 279. Наприклад,
280. 1) Ні; 2) так; 3) так. 281. 1) Ні; 2) так. 282. 1) Ні; 2) так. 283. Так. 284. Так. 285. 1) Так; 2) так; 3) так; 4)
ралелограма. 207. Вказівка: скористайтесь ознакою паралелограма.
а потім — властивістю паралелограма. 214. Вказівка: доведіть, що чотирикутник — паралелограм та скористайтеся властивістю сторін паралелограма. 216. Вказівка: спочатку доведіть рівність трикутників, а потім скористайтесь ознакою паралелограма. 217. Вказівка: скористайтеся властивістю
діагоналей паралелограма. 218. Вказівка: скористайтесь ознакою паралельності прямих, а потім — ознакою паралелограма. 219. Вказівка: скористайтесь
ознакою паралелограма. § 4. Прямокутник
222. 1) Ні; 2) так. 223. Так. 224. Властивість діагоналей паралелограма.
225. 1) Ні; 2) так. 226. 1) Ні; 2) так. 227. 1) АD = 16 см, DС = 12 см; 2) ВD = 20 см;
3) АО = ОС = ВО = ОD = 10 см. 228. 54°, 36°, 54° . 229. 1) по 6 см; 2) по 3 см;
3) по 9 мм. 230. 1) 14 см і 14 см; 2) 28 см. 231. Вказівка: скористайтеся влас
тивостями діагоналей прямокутника. 232. 35°, 125°, 55° (мал. 88); 30°, 60° , 30° (мал. 89). 233. 65°, 130°, 25° . 234. 30° (мал. 91); 60°(мал. 92). 235. 90° . 237. 1) 32 см; 2) 30 см. 238. 56 см. 239. 1) LN = 4 см; 2) KM = 3 дм; 3) LN = 1,5 дм; 4) KL = 2,7 см. 240. 1) ВD = 2 см; 2) АС = 7 см. 241. Вказівка: доведіть рівність діагоналей KM і LN. 242. Вказівка: доведіть рівність діагоналей АС і ВD.
243. Вказівка: доведіть, що всі кути даного паралелограма — прямі.
244. Вказівка: доведіть, що паралелограм є прямокутником. 245. 4 см і 20 см.
246. 6 см і 24 см. 247. 1) 2 см; 2) 7 мм; 3) 0,22 дм. 248. 1) 20 см; 2) 0,5 дм; 3) 14 мм. 249. Вказівка: скористайтеся тим, що кути рівностороннього трикут
ника дорівнюють по 60° . 250. 1) 54°, 36°; 2) 18° . 251. 1) 9,6 см, 14,4 см; 2) 10 см, 14 см; 3) 8 см, 16 см. 252. 1) 6 см; 2) 4,3 см. 253. 1) 26 см або 22 см; 2) 14 см або 16 см. 254. 1) 90 см; 2) 22,8 дм. 258. Вказівка: обчисліть кути чотирикутника. 259. Вказівка: нехай a — кут між діагоналлю та стороною паралелограма; знайдіть кути паралелограма. 260. Вказівка: врахуйте, що сума
дорівнює 360° . 261.
3 = ∠4 = 45° , ∠2 = 90° . 306. 1) 64 см; 2) 2,4 дм. 307. 168
308. 1) KL ⊥ LM; 2) LM ⊥ MN; 3) MN ⊥ NK; 4) KL ⊥ NK. 309. Вказівка: обчисліть кути чотирикутника.
§ 6. Теорема Фалеса. Середня лінія трикутника
345. 1) Ні; 2) так; 3) ні; 4) ні; 5) так. 346. 1) Ні; 2) так. 347. 1) Ні; 2) так; 3) ні; 4) так. 348. 4 см (мал. 133); 3 см (мал. 134). 349. Ні. 350. 1) 6 см; 2) 4 см.
351. 15 см. 355. 4 см (мал. 138); 12 см (мал. 139). 356. Ні. 357. 1) 4 см; 2) 7 см.
358. 1) 4 см, 2,5 см, 3,5 см; 2) 15 мм, 20 мм, 25 мм. 359. 4,5 см; 5 см; 7 см.
360. Вказівка: виразіть середні лінії трикутника через його сторони.
361. 1) По 4 дм; 2) по 8 мм. 362. По 2 см. 363. 1) 4,8 дм; 2) 600 мм. 364. 24 см.
365. 1) 28 см; 2) 56 см; 3) 60 см. 366. 1) Рівносторонній; 2) рівнобедрений.
367. 1) 1,2 дм і 1,8 дм; 2) 200 мм і 28 см. 368. 10 см і 22 см. 369. 96 см. 370. 36 см.
373. 1) 9 см; 2) 12 см; 3) 20 см. 374. 1) 4 см, 5 см, 6 см; 2) 0,25 дм, 6 см, 6,5 см.
375. 1) 36 см; 2) 4,8 дм; 3) 600 мм. 376. 10 см; 10 см; 5 см. 377. 15 см; 15 см; 10 см.
378. 2 см. Вказівка: продовжте відрізок АМ на 4 см за точку М, одержите точку Р; продовжте відрізок ОK за точку K на 4 см, одержите точку D; розгляньте трикутник ВАР. 379. 1) 7,5 см, 10 см, 12,5 см; 2) 6 см, 8 см, 10 см. 380. 1) 28 см, 32 см, 36 см; 2) 1,4 дм, 1,6 дм, 1,8 дм. 381. Вказівка: виразіть периметри
трикутників через сторони одного з них. 382. 2) 12 см, 24 см, 30 см; 3) 24 см.
383. 1) По 4 см і по 6 см; 2) 6 см і 12 см; 4 см і 8 см. 384. Вказівка: виразіть сторони кожного з чотирьох трикутників через сторони даного трикутника.
385. Вказівка: скористайтеся теоремою Фалеса для кутів
і DВС та прямих
дана трапеція з основами BC і AD (BC
(мал. 185); ∠A = ∠D = 60° , ∠B = ∠C = 120° (мал.
і АN. 386. 1) 25 см; 2) 3,5 дм. 387. 1) 10 см; 2) 49 см. 388. 1) 16 см; 2) 2,6 дм. 391. Вказівка:
лініям трикутника. 392. Вказівка: через
се
п’ятій лінії. 401. Вказівка: MN — середня
трикутника АВС. 404. 2) Таких доріг є три. Вони є середніми лініями трикутника ABC. § 7. Трапеція 405. 1) Ні; 2) так. 406. 1) Ні; 2) так. 407. 1) Ні; 2) ні; 3) так. 408. 1) Ні; 2) так; 3) так. 409. 1) Ні; 2) ні; 3) так. 410. 1) Ні; 2) ні; 3) так; 4) ні; 5) так. 411. 1) Ні; 2) так; 3) ні. 412. 1) BC і AD; 2) AB і CD; 3) ∠A і ∠D — прилеглі до основи AD,
∠B і ∠C — прилеглі до основи BC; 4) ∠A і ∠B — прилеглі до бічної сторони AB, ∠C і ∠D — прилеглі до бічної сторони CD. 413. 1) 3 см (мал. 169); 2) 90° (мал. 170). 414. Вказівка: скористайтеся властивістю паралельних прямих. 415. ∠B = 130° , ∠D = 40° (мал. 171); ∠B = 90° , ∠C = 134° (мал. 172); ∠B = 140° , ∠C = 144° (мал. 173). 416. 1) ∠A = 70° , ∠C = 150°; 2) ∠A = 55° , ∠D = 35° . 417. 1) 20°; 2) 45°; 3) 85° . 418. 1) ∠A = 140° , ∠C = 60°; 420. KCDМ — трапеція. 421. ABCD — трапеція. 422. Вказівка: 1) скористайтесь
423. 1) 7 см; 2) 3 см. 424. Вказівка: скористайтесь ознакою рівності прямокутних трикутників за гіпотенузою та гострим кутом. 425. 4 см (мал. 178); 7 см (мал. 179); 15 см (мал. 180). 426. Ні. 427. 1) 4 см; 2) 15 см; 3) 17 см; 428. 7 см. 429. 1) 8 см; 2) 9 см; 3) 13 см; 4) 9 см; 5) 12 см. 430. 8 см, 16 см, 12 см. 431. 4 см, 11 см, 7,5 см. 432. 1) 40 см; 2) 62 см. 433. 62 см. 434. 1) 134° і 36°; 2) 145° і 25° . 435. 128° і 56° . 436. 1) 2 см; 2) 38 мм. 437. Вказівка: нехай ABCD —
Ні; 2) так. 475. 90° (мал. 221); 180° (мал. 222). 476. 60° . 477. 1) 180°; 2) 120°; 3) 240° . 478. 1) 30° і 330°; 2) 62° і 298°; 3) 100° і 260° . 479. 1) 70°; 2) 210° . 480. 1) 12 см; 2) 0,2 дм; 3) 39 мм. 481. Вказівка: доведіть рівність дуг АC і ВD. 482. Вказівка: скористайтеся тим, що дуга BC є спільною. 483. 60° (мал. 227); 25° (мал. 228); 90
(мал. 229). 484. 70
(мал. 230); 20° (мал. 231). 485. 1) 26°; 2) 63°; 3) 100
(мал. 232); 140° (мал. 233); 190° (мал. 234). 488. 1) 60°, 60
, 60
; 2) 36
, 72
, 72° . 489. 30°, 60°, 90° . 490. 1) 120°, 60°, 180°; 2) 56°, 84°, 220° . 491. 70
. 492.
§ 9.
чотирикутники
521. Мал. 255. 522. Мал. 258. 523. Ні. 524. Ні. 525. 1) 9 см; 2) 180° . 526. ∠B = 100° , ∠C = 85° (мал. 262); ∠M = 75° , ∠N = 120° , ∠K = 105° (мал. 263); ∠F = 90° , ∠E = 60° , ∠Q = 90° , ∠P = 120° (мал. 264). 527. а) Ні; б) так. 528. а) Так; б) ні. 529. 1) 125°; 2) 108°; 3) 120° . 530. 1) Так; 2) так; 3) ні. 531. Вказівка: скористайтеся наслідком 2 з теореми про вписаний кут. 532. 1) Вказівка: скорис
тайтеся наслідком 2 з теореми про вписаний кут; 2) за умови, що AD ⊥ BC.
533. 10 см (мал. 266); 3 см і 7 см (мал. 267); 1 3 3 см і 2 6 3 см (мал. 268).
534. 1) Так; 2) ні. 635. 1) 40 см; 2) 6,4 дм. 636. 1) 80 см; 2) 52 см. 538. 1) Ні; 2) так; 3) так. 539. 1) 90°; 2) 60° . 540. 1) 10 см; 2) 2,3 дм. 541. 1) Так; 2) ні. 545. 1) Так; 2) ні. 546. Так. 547. Вказівка: в утвореному чотирикутнику сусідні сторони мають бути рівними. 548. 1) 3 мм, 10,5 мм, 18 мм, 10,5 мм; 2) 4 см, 14 см, 24 см, 14 см. 549. Середня
550. 20 см. 552. 1) Вказівка:
557. Так.
591. 1) Так; 2) так. 592. Так, 2 . 3 k = 593. Так, k = 2. 594. 6 см. 595. 37,5 см. 596. 112 см, 64 см. 597. 30 см, 45 см. 598. 1) 12 см; 2) 10 см. 599. Так. 600. Так. 601. Так, k = 1. 602. 1 . 2 k = 603. 1) 15 см, 30 см, 30 см; 2) 3,75 см, 11,25 см, 11,25 см. 604. Вказівка: скористайтеся
трикутників. 605. Вказівка: скористайтеся
608. 1)
1 : 250 000; 2) 10 км; 3) 12,5 км. 609. 45 см, 50 см, 25 см. 610. 1) Так.
1 4 P , тому: 1) 4 см; 2) 50
розДіл 3. поДібніСть трикутників § 10. Подібні трикутники
563. 1) Ні; 2) так; 3) ні; 4) ні; 5) так. 564. 1) Ні; 2) так; 3) так; 4) ні; 5) так. 565. 1) Ні; 2) ні; 3) так. 566. 1) Ні; 2) так. 567. 1) Ні; 2) ні; 3) так; 4) так; 5) так; 6) так. 568. DАВС і DLMK (мал. 280): 1) ∠А і ∠L, ∠В і ∠М, ∠С і ∠K; 2) АВ і LM, ВС і МK, АС і LK; DАВС і DPTQ (мал. 281): 1) ∠А і ∠P, ∠
T, ∠
Q;
2) АВ і PT, ВС і TQ, АС і PQ. 569. 1) 1 1; 3 2) 2. 570. 1) KC AC і ; DC BC 2) AB KD і ; BC DC 3) AB KD і . AC KC 571. 1) Ні; 2) ні; 3) ні. 572. 1) ∠A1 = 30
теорема Фалеса 611. 1) Ні; 2) так; 3) ні; 4) ні; 5) так. 612. 1) Ні; 2) ні; 3) ні; 4) так. 613. 3 : 5 (мал. 292); 4 : 2 (мал. 293). 614. 4 : 3. 615. 1) PM; 2) MH. 616. РH. 617. 1) Ні; 2) ні. 618. 1) 2 : 3; 2) 5 : 1. 619. 2 : 1. 620. 4. 621. Так. 622. Так. 623. 1) 4 см, 6 см; 2) 12 см, 4 см. 624. 6 см, 8 см. 630. 1) Ні; 2) ні. 631. Так. 632. 1) 6 або 1,5; 2) 8 або 4,5; 3) 2 11 3 або 4,2. 633. 1) Так; 2) так; 3) ні; 4) ні. 634. Так. 635. Вказівка: скористайтеся наслідком з узагальненої теореми Фалеса. 637. ; am AC mn = + . an CB mn = + 638. 1) 16 см, 32 см, 30 см; 2) 10 см, 24 см, 16 см. 639. 1) 15 см, 10 см; 2) 20 см, 4 см. 640. 1) BC = 16 мм, CL = 24 мм, LF = 16 мм, DC = 50 мм, KL = 20 мм; 2) BC = 6 см, CL = 9 см, LF = 6 см, DC = 15 см, KL = 6 см. 641. 1) 125 34 см, 100 17 см, 50 17 см, 2) 250 17 см, 400 17 см, 200 17 см. 642. 1) 15 см; 2) 22 см. 643. 1) 3 см, 6 см; 2) 5,6 см, 8,4 см. 644. 1) 12 см; 2) 1,2 дм. 645. 1) 1 , 3 2 ; 3
2) 2 , 5 3 ; 5 3) 4 , 9 5 . 9 646. 1) 4 см, 8 см, 12 см; 2) 3,1 см, 6,2 см, 9,3 см. 647. Вказів
скористайтеся
648. 1) 10 ; 3
2) 4,5. 651. ; a abc ++ ; b abc ++ ; c abc ++ ; ab abc + ++ . bc abc + ++ 652. 1) 21,6 см;
2) 36 см. 653. Вказівка: скористайтесь узагальненою
654. 1) Вказівка: спочатку
що DAOB DDOC; 2) 6,25 і 3,75.
655. Вказівка: нехай AA1 перетинає MN в точці O; доведіть, що DAMO DABA1 і DANO DACA1. 656. 1) Так; 2) лише для рівнобічної трапеції. 657. 1) 8 см, 9 см; 2) 1 11 3 см, 2 12 3 см. 658. 1) 12 , 33 ab + 21 ; 33 ab + 2) 13 , 44 ab + 11 , 22 ab + 31 . 44 ab + 660. 10 хв. 661. 28 м. 662. 36 м.
§ 12. Перша ознака подібності трикутників
663. 1) Ні; 2) ні; 3) ні; 4) ні; 5) так. 664. 1) Ні; 2) так. 666. Так. 669. DABС DPBQ, DABС DRQC, DPBQ DRQC. 670. DABС і DМNС. 672. 1) Так; 2) так; 3) так; 4) ні. 673. Так. 674. Тому, що з рівності даних відношень не випливає рівність відповідних кутів трикутників. 675. 1) ∠A = ∠B = ∠C = 60° , AB = BC = AC = 2 см, ∠A1 = ∠B1 = ∠C1 = 60° , AB1 = BC1 = AC1 = 6 см; 2) ∠A = = ∠B = ∠C = 60° , AB = BC = AC = 4 см, ∠A1 = ∠B1 = ∠C1 = 60° , AB1 = BC1 = AC1 = = 2 см. 676. ∠A
AB1= BC1= AC1= 3 см. 677. Вказівка: скористайтесь ознакою рівнобедреного трикутника та ознакою подібності трикутників за
кутами. 678. 1) Так; 2) ні. 679. Так. 680. Вказівка: скористайтесь ознакою
681.
кутами. 683. 1) Так; 2) так. 684. Ні. 685. Вказівка:
кутами. 686. a : b або b : a. 687. 1) 66 мм, 132 мм; 2) 0,9 дм, 1,5 дм. 688. 9 6 11 см, 2 18 11 см. 689.
690.
694. Вказівка: скористайтесь
695. 1) 5 см, 7 см, 3 см; 15 см, 21 см, 9 см; 2) 6 см, 8 см, 4 см; 4,5 см, 6 см, 3 см. 696. 8 см, 10 см, 6 см; 16 см, 20 см, 12 см. 697. 10 см, 8 см. 698. Вказівка: скористайтеся тим, що медіани трикутника точкою їх перетину діляться у відношенні 2 : 1,
3) ні; 4) так. 732. DABС DKLМ. 733. Ні. 734. Наприклад, 10 см і 16
50° між ними. 736. DABС і DМNС. 738. Перший і третій. 739. 1) Ні; 2) ні; 3) так. 740. 1) Так; 2) ні. 741. Так. 742. Ні. 743. Наприклад, 10 см, 12 см, 18 см. 744. Перший і другий. 745. 1) 27 см, 36 см; 2) 119 см, 105 см. 746. 30 см, 45 см. 747. Так. 748. Перший і третій. 749. Другий і третій. 750. 1) 24 см; 2) 128 см. 751. 27 см. 752. 1) 36 мм; 2) 0,9 дм. 753. 16 см. 754. 1) 144 см, 96 см, 48 см; 2) 56 см, 1 37 3 см, 2 18 3 см. 755. 40 см, 2 26 3 см, 1 13 3 см. 756. 1) 6,4 мм, 10,4 мм,
38,4 мм, 62,4 мм; 2) 6 см, 10 см, 12 см, 20 см. 757. 2 2 3 см, 2 6 3 см, 2 6 3 см, 2 16 3 см. 758. Вказівка: перетворіть дану рівність добутків у
759. 1) AB = 5 см, BC = 7 см, AC = 3 см, KL = 15 см, LM = 21 см, KM = 9 см; 2) AB = 6 см, BC = 8 см, AC = 4 см, KL = 4,5 см, LM = 6 см, KM = 3 см. 760. TO = 8 см, OM = 10 см, TM = 6 см, BC = 16 см, CE = 20 см, BE = 12 см. 761. Вказівка: скористайтесь ознакою
подібності трикутників
785. 1) Так; 2) ні; 3) так. 787. 1) Ні; 2) ні; 3) так; 4) ні; 5) ні; 6) так; 7) ні; 8) ні; 9) так. 788. 1) 6 см і 3 см, 8 см і 4 см, 10 см і 5 см; 2) 4 см і 2 см, 4 см і 2 см, 2 см і 1 см; 3) 30 см і 15 см, 30 см і 15 см, 30 см і 15 см. 789. 12 см і 6 см, 12 см і 6 см, 18 см і 9 см. 790. 1) 18 см, 24 см, 36 см; 2) 6 см, 6 см, 9 см; 3) 12 см, 12 см, 12 см. 791. 9 см, 15 см, 21 см. 792. 1) АD = 8 см, DС = 12 см; 2) AC = 26 см, DC = 12 см; 3) АD = 1,5 см, BC = 5 см; 4) АC = 12 см, DС = 9 см. 793. L. Вказівка: скористайтеся властивістю бісектриси і властивістю медіани трикутника. 794. Н. 795. Мал. 338: 1) 25 од.; 2) 15 од. і 20 од.; 3) 12 од.; мал. 339: 1) 169 од.; 2) 65 од. і 156 од.; 3) 60 од. 796. 1) 289 од.; 2) 136 од. і 255 од.; 3) 120 од. 797. 2 од. (мал. 341); 2 од. (мал. 342); 6 од. (мал. 343). 798. 1) 4 см; 2) 2 см. 799. 6 см. 801. 8 см, 12 см, 16 см. 802. 1 : 2. 803. 1)Так; 2) Ні. 804. 6 см, 9 см. 805. 22,5 см, 37,5 см. 806. 62 см, 32 см. 807. 1) 3 4 ; 2) 1 6 . 808. 4,8 см. 809. 6,72 см.
810. 1) 24 см; 2) 120 мм. 811. Вказівка: скористайтесь ознакою
сторонами та
між ними. 812. Вказівка: див. задачу 811 (1). 813. Вказівка: див. задачу 811 (2). 814. Вказівка: див. задачу 811 (3). 817. Вказівка:
824. 3). 825. Так (мал. 366); ні (мал. 367). 826. 3). 827. 1) 13 см; 2) 15 м; 3) 16 см. 828. 1) 5 см; 2) 8 м; 3) 12a. 829. 1) a = 12 см; 2) b = 16 см; 3) c = 10a. 830. 1) d = 25 см; 2) b = 24 см; 3) b = 9a. 831. Вказівка: у
трикутнику. 832. 4 см. 833. 1) 2 см; 2) 8 см; 3) 2. a 834. 1) 1 см; 2) 42 см; 3) 2 . 2 m 835. 1) 1,5 см; 2) 53 см; 3) 3 . 2 a 836. 1) 24 см; 2) 15 см; 3) 12 см. 837. 1) 15 см; 2) 20 см.
842. 17 см. 843. 3 2 m . 844. 1) 26 см; 2) 8 см; 3) 15 см. 845. 1) 5 см; 2) 5 см; 3) 24 см. 846. 19 см (мал. 382); 62 см (мал. 383). 847. 13 см. 848. 1) 5 см, 12 см, 13 см; 2) 7 см, 24 см, 25 см. 849. 1) 15 см, 20 см; 2) 12 см, 16 см. 850. 9 см, 12 см, 15 см. 851. 30 см, 16 см, 34 см. 852. 1) 15 см, 18 см; 2) 16 см, 17 см. 853. 1) 12 см, 211721,6 ≈ см; 2) 24 см, 219327,8 ≈ см. 854. 1) 10 см; 2) 29 см. 855. Вказівка: розгляньте два прямокутні трикутники, одним із катетів яких є менша бічна сторона трапеції. 856. 8 см (мал. 385); 5 см (мал. 386). 857. 14 см. 858. 1) 20 см; 2) 13 см. 859. 1) 10 см; 2) 25 см. 860. 1) 4 см; 2) 6 см. 861. 1) 8 см або 22 см; 2) 38 см або 88 см. 862. 8 см. 863. 1) 10 см; 2) 52 см. 864. 21 см або 11 см. 865. 1) 6 см, 15 см; 2) 8 см. 866. Вказівка: скористайтесь ознакою рівності
трикутників
867.
скористайтеся
Піфагора. 868. 1) 120 см; 2) ≈ 80,7 см. 869. 1) 61 см, 11 см; 2) 37 см, 12 см. 870. 1) 37 см, 76927,7 ≈ см; 2) 20 см, 220528,6 ≈ см. 871. 1) 8 см, 9,6 см, 9,6 см; 2) 12 см, 5,6 см, 4,2 см. 872. Вказівка:
24115,5 ≈ м. 880. 328 м. 881. 1) 6,5 м; 2) ≈ 6,7 м. 882. 12 футів. § 16. Співвідношення між сторонами і кутами прямокутного трикутника 884. 1) б; 2) в; 3) б. 885. 1) а; 2) б; 3) в. 886. 1) Ні; 2) так; 3) так; 4) ні; 5) ні; 6) так. 887. 1) Ні; 2) так; 3) ні; 4) так; 5) так; 6) ні. 889. sin, BD AB a= cos, AD AB a= () tg , BD BDA AD a=D sin, BC AC a= cos, AB AC a=() tg . BC ABC AB a=D 890. 1) Ні; 2) так; 3) ні. 891. 1) Так; 2) так; 3) так. 892. 1) 1; 2) 2; 3) 1; 4) 32; 5) 3; 6) 8. 893. 1) 23; 2) 2; 3) 3. 894. 1) 1; 2) 1; 3) 2,5; 4) 2. 895. 1) 2; 2) 0. 896. 1) 30°; 2) 45°; 3) 60°; 4) 60°; 5) 60°; 6) 45° . 897. 1) 45°; 2) 30°; 3) 30° . 898. 1) sin 10° , sin 11°, sin 15°, sin 46°, sin 75°; 2) tg 17°, tg 37°, tg 48°, tg 66°, tg 87° . 899. cos 72° , cos 50°, cos 34°, cos 25°, cos 20° . 900. 2 см (мал. 407); 4 см (мал. 408); 10 см (мал. 409). 901. 12 см (мал. 410); 10 см (мал. 411); 7 см (мал. 412). 902. 1) 2 см; 2) 6 см; 3) 8 см. 903. 1) 6 см; 2) 6 см; 3) 7 см. 904. 1) 2 см; 2) 5 см; 3) 9 см. 905. 1) sin 70°; sin 55°; sin 40°; 2) cos 80°; cos 25°; cos 5° . 906. 1) sin 50°, sin 16°; 2) cos 35°, cos 65° . 907. 1) sina; 2) 2 sina; 3) cosa; 4) –cosa. 908. 1) 0; 2) –cosa.
911. c · cos a (мал. 413); c · sin a (мал. 414); b · tg a (мал. 415). 912. tg a a (мал. 416); sin a a (мал. 417); cos b a (мал. 418). 913. 1) 3 см; 2) 8 см; 3) 12 см; 4) 6 см. 914. 1) 2 см; 2) 4 см. 915. 1) 128 см; 2) 16 см; 3) 10 см; 4) 10 см. 916. 1) 64 см; 2) 50 см. 917. 1) 4,8 см; 2) 48 см; 3) 16,5 см. 918. 1) BC = c · cosb, AC = c · sinb; 2) , sin a AB = a ; tg a AC = a 3) , sin b AB = b . tg b AC = b 919. 1) ≈ 0,682; ≈ 0,731; ≈ 0,933. 920. 1) a = 39°: 0,629; 0,777; 0,809; a = 54°12′ : 0,811; 0,585; 1,387; 2) 48°35′; 31°; 52°59′; 23°48′; 43°3′; 37°59′ . 921. 1) 0,342; 0,966; 0,545; 0,996; 2) 0,994; 0,391; 0,629; 0,913; 3) 2,14; 0,017; 3,27; 0,344. 922. 1) 0, 799; 0,035; 2) 0,469; 0,974; 3) 0,176; 0,287. 923. 1) 88°, 1°, 35°; 2) 40°, 15°, 77°; 3) 42°, 19°, 38° . 924. 1) 36°; 2) 43°; 3) 40° . 925. 1) sin A = 0,8; cos A = 0,6; 4 tg; 3 A = 2) sin B = 0,6; cos B = 0,8; 3 tg. 4 B = 926. 1) sin A = 0,8; cos A = 0,6; 2) sin B = 0,6; cos B = 0,8.
927. 1) 0,96; 2) 0,96; 3) 24 . 7 928. 1) 3; 2) 6. 929. 2. 930. 4 см. 931. 18 см.
932. 1) 103 см; 2) 5 см; 3) 53 см. 933. 1) 8 см і 83 см; 2) 82 см і 82 см. 934. 23 см і 6 см (мал. 420); 33 см і 9 см (мал. 421). 935. 4 см і 23 см.
936. 4 см, 43 см. 937. 12 см і 12 см. 938. 1) 123 см і 24 см; 2) 12 см і 123 см.
939. 3 , 6 a r = 3 . 3 a R = 940. 1) 4 см; 2) 43 см. 941. 1:2. 942. 1) 52 см і 10 см;
2) 5 см і 53 см. 943. 53 см. 944. 1) sin A = 0,8; cos A = 0,6; 4 tg; 3 A =
2) sin B = 0,6; cos B = 0,8; 3 tg. 4 B = 947. b · sina. 948. cos. 2 l a 949. 1) 2b · cosa;
2) b · sina. 950. 1) ; sin h a 2) 2 . tg h a 951. 1) ; 2tg 2 a a 2) . 2sin 2 a a 952. tg sin a a b і tg tg a a b
(мал. 423); cos sin a b a і sin sin a b a (мал. 424). 953. a · sina і a · sina · tga. 954. 2m · cosa,
2m · sina. 955. . 2cos b a 956. 1) 2 ; tg 2 r a 2) . costg 2 r a a 957. tg 2 . tg h a a 958. . 2cos a a
959. 1) ; tg 2 a a 2) . sin 2 a a 960. 1) ; 2sin 2 d a 2) tg. 2 d a 962. «–». 963. 24 см і 36 см. 964. 10 см і 24 см. 965. 11 , tgtg22
973. 1) Ні; 2) так; 3) ні; 4) ні; 5) так. 974. 1) Ні; 2) так; 3) ні; 4) так; 5) ні; 6) так; 7) ні; 8) так. 975. y ≈ 4,5 см і x ≈ 5,36 см (мал. 439); x ≈ 13,37 см і y ≈ 16, 09 см (мал. 440). 976. a≈ 51° і b≈ 38° (мал. 441); a≈ 53° і b≈ 36° (мал. 442). 977. 1) ≈ 4,1 см; 2) ≈ 10,67 см; 3) ≈ 4,69 см. 978. 1) ≈ 11,52 см і ≈ 14,62 см; 2) ≈ 13,76 см і ≈ 17,01 см. 979. 1) ≈ 5,92 см; 2) ≈
983.
52′ , b≈ 53
8′; в) c = 30, a≈ 36°56′ , b≈ 53°4′; г) c ≈ 46,56; a≈ 30°19′; b≈ 59°41′; 2) а) b = 8, a≈ 61°56′ , b≈ 28°4′; б) b = 12, a≈ 53°8′ , b≈ 36°52′; в) b = 33, a≈ 59°29′ , b≈ 30°31′; г) a ≈ 0,68; a≈ 13°25′; b≈ 76°35′ . 988. 1) а) a ≈ 7,52; b ≈ 2,74; ∠B = 20°; б) a ≈ 54,87; b ≈ 60,94; ∠B = 48°; в) a ≈ 9,64; b ≈ 15,43; ∠B = 58°; г) a ≈ 4,23; b ≈ 1,97; ∠B = 25°; 2) а) b ≈ 7,5, c ≈ 14,15, ∠B = 58°; б) b ≈ 5,5, c ≈ 18,82, ∠B = 73°; в) b ≈ 15,92, c ≈ 19,4, ∠B = 37°; г) b ≈ 1,71, c ≈ 3,92, ∠B = 71° . 989. ≈ 14,69 см і ≈ 20,22 см. 990. 1) ≈ 6,21 см; 2) ≈ 11,59 см. 991. 1) ≈ 6,71 см; 2) ≈ 8,19 см. 992. 1) ≈ 23,04 см; 2) ≈ 65°44′ . 993. 1) ≈ 41,22 см; 2) ≈ 46,26 см; 3) ≈ 36,72 см і ≈ 9,53 см. 994. 1) ≈ 17,15 см і ≈ 36,88 см; 2) ≈ 8,31 см і ≈ 33,69 см. 995. 2,81 см. 996. ≈ 2,94 см і ≈ 4,70 см. 997. ≈ 31,25 см і ≈ 125,16 см. 998. ≈ 119,14 см. 999. ≈ 7,43 см. 1000. ≈ 3,4 см. 1001. ≈ 73,1 см. 1002. ≈ 61° . 1003. ≈ 0°57′
1013. ≈ 129,1 м.
5. многокутники. площі
§ 18. Многокутник та його властивості 1015. Ні. 1016. 1) Ні; 2) так. 1017. 1) Ні; 2) так. 1018. 1) Ні; 2) ні; 3) так. 1020. 1) Ні; 2) так. 1021. 1) Ні; 2) так. 1022. 1) 14 см; 2) 20 см; 3) 18 см. 1024. 1) 5; 2) 5. 1025. 1) 540°; 2) 1260° . 1026. 2700° . 1027. 1) 10; 2) 8. 1028. 11. 1029. 1) 4; 2) 10. 1030. 15. 1031. 1) 30°, 60°, 120°, 150°, 180°; 2) 80° , 100°, 110°, 110°, 140°; 3) 100°, 110
,
,
,
;
,
,
, 180
, 100° . 1032. 1) 90°; 2) 24° . 1033. 36° . 1034. Восьмикутник. 1035. Семикутник. 1036. Семикутник. 1039. 8,4 см. 1040. Вказівка: скористайтеся
кутника. 1041. () 3 . 2 nn 1042. 1) 35; 2) 119. 1043. 1) Ні; 2) ні. 1044. Ні. 1045. 1) 5; 2) 6. 1046. 5. 1047. 1) 6 :
1049. 1) 6; 2) 9. 1050. 360 . n ° 1051. 23. 1052.
1053. 1) 3 і 6; 2) 6
1055. 1) 4; 2) 6; 3) 7. 1056.
доведіть, що DВОD — прямокутний. § 19. Поняття площі. Площа прямокутника 1059. 1) Ні; так. 1060. 1) Ні; 2) ні. 1061. 1) Ні; 2) ні; 3) ні; 4) так. 1062. 1) Ні; 2) ні; 3) ні; 4) так. 1063. 1) Ні; 2) ні; 3) ні; 4) так. 1064. 1) S1 ≈ 6 кв. од. 1065. SKLM ≈ 22,5 кв. од. 1068. 96 см2. 1069. 160 см2. 1070. 1) 4 см; 2) 3 см; 3) 11 см. 1071. 1) 5 см; 2) 7 см. 1072. 4 см2 (мал. 491); 8 см2 (мал. 492). 1073. 2 см2. 1074. 1) Збільшиться у 3 рази; 2) зменшиться в 4 рази; 3) збільшиться на 50 %. 1075. 1) Збільшиться в 9 разів; 2) зменшиться в 16 разів; 3) збільшиться на 125 %. 1076. 1) b = 1,5 см; S = 6 см2; 2) a = 0,5 см; P = 25 см; 3) a = 3,5 см; S = 24,5 см2; 4) b = 0,5 см; P = 17 см. 1077. 1) 20 і 30; 2) 15 і 40; 3) 610 і 1010. 1078. 3 см і 6 см. 1079. 1) 7,5 см2; 2) 5 см2; 3) 22,5 см2. 1080. 18 см2. 1081. 1) 2 см2;
2) 4,5 см2; 3) 25 2 см2. 1082. 18 см2. 1083. 1) 24 см, 26 см; 2) 24 см, 40 см. Квадрат.
1084. 40 см, 50 см. Квадрат. 1085. 1) 192 см2; 2) () 248705 + см2. 1086. 1) 162 см2; 2) 72 см2. 1087. 2 7 . 9 a 1088. 2 5 . 9 a 1089. 1) 81 см2, 25 см2; 2) 19 см2, 16 см2.
1090. 1) 56 см, 40 см; 2) 200 см, 176 см. 1091.) ; mS n . nS m 1092. () ; 2 nP mn + () . 2 nP mn + 1093. 1) Площа
1094. 1) 1 см; 2) 2 см. 1095.
1104. 600 м2, 0,06 га. 1105. 250 м2. 1106. Так. § 20. Площа паралелограма 1112. Ні (мал. 504); так (мал. 505). 1113. 1) Ні; 2) ні; 3) ні; 4) так. 1114. 1) Ні; 2) ні; 3) ні; 4) так. 1115. 45 кв. од. 1116. 42 кв. од. 1117. 1) 3000 см2; 2) 1000 см2. 1118. 2500 см2. 1119. 1) 80 см2; 2) 300 см2. 1120. 30 см2. 1121. 1) 4 см; 2) 5 см; 3) 3 см; 4) 8 см. 1122. 12 см. 1123. 1) h a = 8,2 см; hb = 4,1 см; 2) h a = 4 см; hb = 2 см; 3) h a = 4,5 см; hb = 3 см; 4) h a = 4 см; hb = 6,4 см. 1124. 1) 8 см; 2) 5 см. 1125. 4 см. 1126. 1) 4 см; 2) 12 мм. 1127. 15 см. 1128. Вказівка:
1139. 1) 753
трикутника 1162. 1) Ні; 2) так; 3) ні; 4) ні; 5) ні; 6) ні. 1163. 10 кв. од. (мал. 523); 210 кв. од. (мал. 524). 1164. 42,5 кв. од. 1165. 1) 15 см2; 2) 1250 см2. 1166. 5 дм2. 1167. 1) 40 см2; 2) 108 мм2. 1168. 1,5 дм2. 1169. 1) 12 см; 2) 31 см; 3) 20 см. 1170. 12 см. 1171. 1) 168 13 a h = см, 12 hb = см, 168 15 c h = см; 2) 252 13 a h = см, hb = 12,6 см, h c = 12 см; 3) h а = 12 см, 42 15 hb = см, h c = 2,1 см; 4) h а = 8 см, hb = 7,2 см, 72 17 c h = см. 1172. 1)
1185. 1) р = 42 см, S = 210 см2; 2) р = 27 см, S = 126 см2; 3) р = 21 см, S = 42 см2; 4) р = 45 см, S = 240 см2. 1186. 1 см. 1187. 432 см2; 756 см2. 1188. 3 см2; 144 3 см2. 1189. 1) 108 см2; 2) 136 см2. 1190. 260 см2. 1191. 1) 39 см2; 2) 60 см2. 1192. Вказівка: скористайтеся
1193. 1) 150 см2; 2) 3,36 см2; 3) 135 см2; 4) 720 см2. 1194. 1) 270 см2; 2) 120 см2. 1195. 1) 18 см, 80 см; 2) 48 см, 55 см. 1196. 1) 39 см2; 2) 34 см2. 1197. 1) 83 см2;
2) 183 см2. 1198. 1) 24 см2; 2) 120 см2.
1202. 1) 16 3 см; 2)
1206.
складених фігур. 1208. Вказівка:
кутника. 1209. 7S, де S — площа даного трикутника. 1210. ()() 1:21:32.
1211. 4. m mn + 1214. Вказівка: трикутники АВС
трикутника
ширину лінійки. 1217. 0,927 кг. § 22. Площа трапеції
1219. 1) Ні; 2) так; 3) так; 4) ні; 5) ні; 6) так. 1220. 300 кв. од. (мал. 549); 150 кв. од. (мал. 550). 1221. 44 кв. од. 1222. 1) 2400 см2; 2) 4000 см2. 1223. 1400 см2. 1224. 1) 90 см2; 2) 1,75 дм2. 1225. 33 см2. 1226. 1) 10 см; 2) 12 см. 1227. 12 см. 1228. 1) 4 см; 2) 5 см. 1229. 3 см. 1230. 1) q = 12 см, S = 84 см2; 2) b = 27 см, h = 5 см; 3) a = 20 см, q = 21 см; 4) a = 23 см, h = 11 см. 1231. 1) Не зміниться; 2) збільшиться у 2 рази. 1232. Не зміниться. 1233. 1) 20 см, 16 см;
2) 36 см, 24 см. 1234. 20 см, 10 см. 1235. 2 . a b 1236. 1) 144 см2; 2) 44 см2. 1237. 276 см2. 1238. 1) 645 см2; 2) 180 см2. 1239. ()1833 + см2. 1240. 1) 10,5 см2;
2) 8 см2. 1241. 1) 6 см2; 2) 13,5 см2. 1242. 45° . 1243. 1) 5,6 см2; 2) 96 см2. 1244. Роз
гляньте два випадки: 8 см і 12 см або 2 см і 6 см. 1245. 12 см. 1246. Вказівка: якщо трапеція є описаною навколо кола, то сума її основ дорівнює сумі бічних
сторін. 1247. 2 . S P 1248. 10 см. 1249. ≈ 130,03 см2. 1250. 963 см2. 1251. Вказів
1253. 2 . ab ab + 1254.


Властивість бісектриси трикутника 150
діагоналей паралелограма 24 — кутів вписаного чотирикутника 97
рівнобічної трапеції 74
сторін описаного чотирикутника 98
діагоналей прямокутника 41
Властивості діагоналей ромба 50
— медіан трикутника 149
— середніх пропорційних у прямокутному трикутнику 151
— середньої лінії трапеції 75 — трикутника 64
— площі 212
— похилих 162
Дельтоїд 53
Діагональ nкутника 204
чотирикутника 12
кола 85 Квадрат 52
трикутника 172
74
74
подібні 109
достатня 34
34
проста 206
206
212
212


214
222
214
240
231
11
у коло 96
13
навколо кола 96
13
12
вершини 11
12
11
12
13
12
14
11
12
12
12
Головна редакторка І. В. Красуцька Редакторка І. В. Луценко
художниця І. П. Медведовська Художня редакторка К. В. Берсенєва Технічний редактор Е. А. Авраменко Коректорка Ю. О. Твердохліб Комп’ютерна графіка О. І. Дядика Презентації та інтерактивні вправи Л. М. Шабанової В оформленні підручника використано фото з вільних джерел мережі «Інтернет», фотобанку Shatterstock
Бренди та ресурси зображуються лише

