International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 09 Issue: 08 | Aug 2022 www.irjet.net p-ISSN: 2395-0072
A REVERSE CONVERTER FOR THE FIVE COPRIME MODULI SET { }
School of Computing and Information Sciences, CKT-University of Technology and Applied Sciences P.O. Box 24, Navrongo. ***
Abstract
Residue to binary conversion is presented for the five moduli set { } in this paper. A novel converter for the moduli set usingmodularadders,multipliers,andcarrysaveadders is proposed using a cyclic jump method. The binary representation, hardware implementation and comparison with a state-of- the- art scheme put the proposed converter ahead. The moduli set is carefully selected to provide for larger dynamic range needed for digitalsignalprocessing.
Keywords: Residue Number system; Moduli set; Dynamic Range; Cyclic Jump Technique
i. Introduction
Residue Number System (RNS) is an emerging area of research. This is because of its suitability for the implementation of high-speed digital signal processing devices and its inherent parallelism, modularity, fault tolerance and carry free propagation properties [7] Arithmetic operations such as addition and multiplication are performed more easily and efficiently in RNS than conventional two’s complement number systems[6]
Thetraditionalmoduliset{ },hasbeen oneofthemostpopularlystudiedinRNS.
The moduli set{ } which shares a common factor of 2 between the third, fourth and fifth moduli has been applied. This moduli set offers consecutiveness and allows for equal width adders and multipliers in hardware design. This gives it high study significance thanthetraditionalmodulisets[5].
ii. Fundamentals of Residue Number System(RNS)
RNS is presented using relatively prime moduli set { } such that, the greatest common divisor ( ) for , while
∏ , is the dynamic range. The residues of a decimal number is obtained as | | .A decimal number X can therefore be represented in RNS as , . This representation is unique for any integer [ ] | | is the modulooperationof withrespectto [1],[4]
Two standard conversion techniques exist for performing reversion conversions in RNS. They are The Chinese Remainder Theorem and the Mixed Radix ConversionMethod.However,otherderivedversionsfor performingbackwardconversionalsoexist.
iii. Mixed Radix Conversion
The Mixed Radix Conversion (MRC) approach is an alternative method to the CRT for performing reverse conversion. This method does not involve the use of the large modulo-M computation as is required by the CRT. This method is used to perform `residue to binary conversion of based on the moduli set { }asfollows; = (2) Where (MRDs) which canbecomputedbelowasshownin[2],[3],[8];
iv. The Cyclic Jump Technique
A cyclic jump approach to reverse conversion is presented in this paper. The technique uses the first residue as an initial position and then jumps to new locations until a final point is reached. The various jumps are then summed when all residues turn to zero, to arrive at the decimal number This technique is an MRCbasedapproach.
© 2022, IRJET | Impact Factor value: 7.529 | ISO 9001:2008 Certified Journal | Page185
Prof. Mohammed I Daabo, Valentine Aveyom, Gabriel Kofi Armah (PhD)International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 09 Issue: 08 | Aug 2022 www.irjet.net p-ISSN: 2395-0072
v. Jump Technique for the 5- Moduli Set { }
General algorithm for a five moduli set
1. The first jump is defined by the number which normallycorresponds to the first residue in X i.e.
The first location L1 after the jump is defined by = Thus [
| | | | | | | | | | ]
2. The second jump is defined by the number , such that: and | | | | | |
Thesecondlocation isgivenby Thus [
| | | | | | | | | | ]
3. Thethirdjumpisdefinedby ,suchthat and | | | | | |
Thethirdlocationisgivenby Thus [
| | | | | | | | | | ]
4. Thefourthjumpisdefinedby ,suchthat: and| | | | | |
Thefourthlocationisgivenby Thus [
| | | | | | | | | | ]
5. Thefifthjumpisdefinedby suchthat: and| | | | | | The fourth location is given by Thus [
| | | | | | | | | | ]
Where
Therefore,thedecimalnumberisgivenby: vi. Numerical illustrations
For example, given the moduli set { } andassumingwearegiven aresiduenumber
Thereforewehave, , , , and When n = 3 , , , , , , , , , , and
International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 09 Issue: 08 | Aug 2022 www.irjet.net p-ISSN: 2395-0072
1. The first jump is defined by the number which normallycorrespondstothefirstresidueinX. Thus
Thefirstlocationisdefinedby: Therefore: [
| | | | | | | | | | ]
2. Thesecondjumpisdefinedbythenumber ,suchthat: and | | 0 | | =0 | | =5 Thus
Thesecondlocationisdefinedby: Therefore: [
| | | | | | | | | | ]
3. The third jump is defined by the number , suchthat: =7 and | | | | =0 = | | =2 Thus
Thethirdlocationisdefinedby: Therefore: [
| | | | | | | | | | ]
4. The fourth jump is defined by the number , suchthat: =7*8* and | | | | =0 =1 Thus
Thefourthlocationisdefinedby: Therefore: [
| | | | | | | | | | ]
5. Thefifthjumpisdefinedbythenumber ,suchthat: =7*8*9*3 and | | | | =0 = | | =2 Thus
Thefifthlocationisdefined by: Therefore: [
| | | | | | | | | | ]
Therefore the corresponding decimal number is: =3677 i.e. 3677
vii Binary Representation for the Moduli Set { } Given the moduli set { }, its binary representation is given as follows;
Step 1: Firstjump( ,whichisequaltofirstresidue . i.e
Firstlocation isdefindas =( =( =( =( =(
International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

| | | | | | | | | | ] [
[
|( ) | |( ) | |( ) | |( ) ( )| |( ) ( )| ] [
|( ) | |( ) | |( ) ( )| |( ) ( )| ] [ ]
Step 2: Secondjump( )isdefinedby: and| | | | | | theexpression(*)iscontinuouslyiteratedbyrepeatedly adding the modulus until such a time that | | = Location isgivenas: [
| | | | | | | | | | ] [
|( ) | |( ) | |( ) ( )| |( ) ( )| ]
[
|( ) | |( ) ( )| |( ) ( )| ] [ ]
Step 3:Thirdjumpisdefinedby andthisisgivenby; and | | | | | |
ThirdLocation afterthejump isgivenby: [
| | | | | | | | | | ] [
|( ) | |( ) | |( ) ( )| |( ) ( )| ] [ |( ) ( )| |( ) ( )| ] [ ]
Volume: 09 Issue: 08 | Aug 2022 www.irjet.net p-ISSN: 2395-0072 © 2022, IRJET | Impact Factor value: 7.529 | ISO 9001:2008 Certified Journal | Page188
International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 09 Issue: 08 | Aug 2022 www.irjet.net p-ISSN: 2395-0072
Step 4: Fourthjump isgivenby: and| | | | | | | | FourthLocation afterthejump isgivenby: Also, [
| | | | | | | | ] [|( ) ( )| ] [ ]
Step 5: Firthjump isgivenby: and| | | | | | | | | | | | =0
FirthLocation afterthejump isgivenby: And,
[
| | | | | | | | | | ] [
|( ) ( )| |( ) ( )| |( ) ( )| |( ) ( )| ] [|( ) ( )| ] [ ] where
Thebinarynumberiscomputedasfollows; + + +
v. Proposed Hardware Implementation Scheme
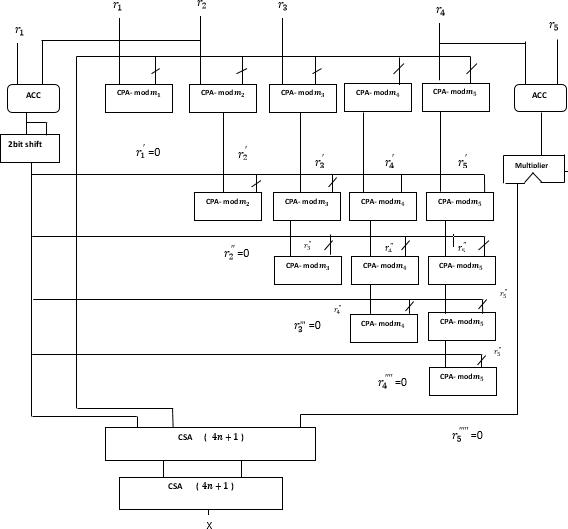
Thehardwareimplementationforthenew5-moduliset reverse converter is as shown in figure 1; In the implementation,theresiduesarepassedthroughvarious adderchannelstoyieldtherespectivenewresidues.The full conversion takes place in just 5 steps making the speedverygood.
International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 09 Issue: 08 | Aug 2022 www.irjet.net p-ISSN: 2395-0072
[3] K. A. Gbolagade, and S.D. Cotofana, Residue-toDecimal Converters for Moduli Sets with Common Factors.IEEE,Pp.624-627,2009a.
[4] K.A.Gbolagade,“EffectiveReverseConversionin Residue Number System Processors”.PhD Thesis, Delft UniversityofTechnologyTheNetherlands,2010,PP.15.
[5] A. Omondi & B Premkumar, Residue Number System: Theory and Implementation Imperial College Press,2007 ISBN978-1-86094-866-4.
[6] A.B Premkumar,“AnRNStoBinaryconverterin 2n+l,2n,2n-1moduliset”,IEEETransactionsonCircuits andSystems,1992-I1Vol.39,No.7,pp.480-482.
[7] A.B.Premkumar,“AnRNStoBinaryconverterin a three moduli set with common factors”, IEEE Transactions on Circuits and Systems, 1995-11, Vol. 42, No.4,pp.298-301.
[8] V. Aveyom, M.I. Daabo & A.B. Alhassan, Efficient Reverse Converter for Three Moduli Set {2n − 2, 2n − 3, 2n − 4} Sharing a Common Factor, International Journal of Electrical Engineering. ISSN 0974-2158 Volume 12, Number1(2019),pp.21-35
Figure 1: Hardware Architecture for the proposed cyclic jump method
viii. Conclusion
Thepaperproposedanovelconverterfortheselected5moduliset
{ }. The proposed converter is very fast and efficient in performing reverse conversions compared with a stateof-the-art converter presented in [7]. This is because, it uses fewer steps to generate the decimal value for any given conversion The converter is best suited for applicationsrequiringverylargedynamicrangessuchas DSPoperations
References
[1] R. Chaves, and L. Sousa, "Improving residue number system multiplication with more Circuits & Communication,2007.
[2] K. A. Gbolagade, and S.D. Cotofana, MRC Techniques for RNS to Decimal Conversion Using the Moduliset{ } Proceedingsofthe16th Annual Workshop on Circuits, Systems and Signal processing,Veldhoven,theNetherlands,2008
