Inventory Model for Perishable Items with Deterioration and Time Dependent Demand Rate by IRJET Journal

Inventory Model for Perishable Items with Deterioration and Time Dependent Demand Rate

Shakib Ali1, R.B. Singh2

1PG student, Department of Mathematics, Monad University, Hapur 2Professor, Department of Mathematics, Monad University, Hapur ***

Abstract - In this paper, an inventory management of the perishable items is needed in order to avoid therelevantlosses due to their deterioration. This research work develops an inventory model for perishable items, constrained by both physical and freshness condition degradations. By working with perishable items that eventually deteriorates, this inventory model also takes into consideration the expiration date, a salvage value, and the costofdeterioration. Inaddition, the holding cost is modelled as a quadratic function of time. The proposed inventory model jointly determines the optimal price, the replenishment cycle time, and the order quantity, which together result in maximum total profitperunitoftime. The inventory model has a wide application since it can be implemented in several fields such as food goods (milk, vegetables, and meat), organisms, and ornamental flowers, among others. Some numerical examples are presented to illustrate the use of the inventory model. The resultsshowthat increasing the value of the shelf-life results in an increment in price, inventory cycle time, quantity ordered, and profits that are generated for all price demand functions. Finally, a sensitivity analysis is performed, and several managerial insights are provided.

Key Words: Inventory, Perishable Items, Deterioration, Salvagevalue,Optimalprice,Replenishmentcycletime.

1.INTRODUCTION

Deterioration of physical goods is one of the important factorsinanyinventoryandproductionsystem.Iftherateof deterioration is very low its effect can be ignored. But in manypracticalsituationsdeteriorationplaysanimportant role.Itisimportanttocontrolandmaintaintheinventories of decaying items for the model corporation. Most of the physical goods undergo decay or deterioration over time. Commoditiessuchasfruits,vegetables-andfoodstuffssuffer fromdepletionbydirectspoilagewhilekeptinstore.Highly volatile liquids such as alcohol, gasolines etc. undergo physical depletion over time through the process of evaporation. Electronic goods, photographic film, grain, chemicals, pharmaceuticals etc. deteriorate through a graduallossofpotentialorutilitywiththepassageoftime. Thusdeteriorationofphysicalgoodsinstockisveryrealistic feature.Deteriorationrateofanyitemiseitherconstantor timedependent.Whendeteriorationistimedependent,time is accompanied by proportional loss in the value of the

product. Realization of this factor motivated modelers to consider the deterioration factor as one of the modeling aspects.

Mashud et al. [1] determined the optimal replenishment policy of deteriorating goods for the classical newsboy inventory problem by considering multiple just-in-time deliveries. Additionally, Mashud et al. [2] derived an inventorymodelfordeterioratingproductsthatcalculates theoptimalvalesforreplenishmenttime,price,andgreen investmentcost.

Giventhattheinherentperishabilitycanoccurimmediately, Pal et al. [3] addressed a production-inventory model for deterioratingproductswhentheproductioncostdependson bothproductionorderquantityandproductionrate.Bhunia A.KandM.Maiti,[4]werethefirstproponentfordeveloping adeterministicinventorymodelfordeterioratingitemswith finiterateofreplenishment dependentoninventorylevel. ChengTCE[5]discussedaneconomicorderquantitymodel withdemand-dependentunitproductioncostandimperfect production processes. In most of the inventory models, authorshavetakenconstantrateofdeterioration.Inpractice itcanbeobservedthatconstantrateofdeteriorationoccurs rarely. Most of the items deteriorate as fast as the time passes.Itcanbenoticedthatdeteriorationdoesnotdepends upontimeonly:itcanbeaffectedduetoweatherconditions, humidity,andstorageconditionsetc.Thereforeitismuch morerealistictoconsiderdeteriorationrateastwoorthree parameterWeibulldistributionfunction.Manyresearchers considered the constant demand rate in their inventory models, but the assumption of constant demand is not alwaysapplicableinrealsituations.

Tirkolaee et al. [8] noted that the inherent perishability widely occurs in food goods (e.g., milk, vegetables, and meat), organisms, and ornamental flowers. These authors alsostatedthatthetimewindowbetweenpreparationand sales of perishable items is very significant for producers andpurchasers.Girietal.[9]notedsuchdemandpatternfor fashionableproductswhichinitiallyincreasesexponentially withtimeforaperiodoftimeafterthatitbecomessteady ratherthanincreasingexponentially.Theramp-typedemand demonstrates a time period classified demand pattern. In differenttimeperiodsthedemandiseitherconstantorits rateofchangeisdifferent.

Page1058

2022, IRJET | Impact Factor value: 7.529 | ISO 9001:2008 Certified Journal |

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 09 Issue: 08 | Aug 2022 www.irjet.net p-ISSN: 2395-0072

AccordingtoYavarietal.[13],oneofthechallengeswhen managinginventoriesistheinherentperishabilityofmany items, which means their freshness and quality decrease over time, and these cannot be sold after their expiration date.Manyresearchershavemodifiedinventorypoliciesby consideringthe"timeproportionalpartialbackloggingrate".

Thepresentsectiondealswithamathematicalmodeloftie economic order quantity for finite time horizon. This inventory model has been developed for a single deterioratingitembyconsideringtheconstant-deterioration rate. In this model, a new demand pattern has been introducedinwhichthedemandfollowsquadraticpatternin theinitial periodoftimeandbecomeslinearlateron.It is believedthatsuchtypeofdemandisquiterealisticfornewly launchedproductinthemarket.Shortagesareallowedand thebackloggingrateisdependentonthedurationonwaiting timeandtakenasexponentialdecreasingfunctionoftime. Theeffectduetochangeofdeteriorationparameterhasbeen consideredfordifferentparametersnumerically.

2. ASSUMPTIONS AND NOTATIONS

To develop inventory models for perishable items with variable demand and partial back logging. The following notationsandassumptionareused.

(i) I(t)betheinventorylevelattimet, t0 

(ii) 1t is the time at which shortage starts and T is the lengthofreplenishmentcycle 1 0tT 

(iii) Replenishmentrateisinfiniteandleadtimeiszero.

(iv) There is no repair OR replenishment of deteriorated unitsduringtheperiod.

(v) Asingleitemisconsideredovertheprescribedperiod Tunitsoftime.

(vi) S be the initial inventory level after fulfilling backorders.

(vii) Inthismodel  betheconstantrateofdefectiveunits outofonhandinventoryatanytime, 0  (viii) DemandrateD(t)isassumedtobeafunctionoftime suchthat

and‘a’istheinitialrateofdemand,bistheratewith whichthedemandrateincrease.Therateofchangein demandrateitselfincreaseatarate‘c’. a, b and c are positiveconstant.

(ix) Unsatisfied demand is back logged at a rate exp  x ,wherexisthetimeuptonextreplenishment. Thebackloggingparameters  isapositiveconstant.

(x) 123C,C,C and 4C aretheholdingcostperunittime, unitpurchasecostperunit,shortagecostperunitper unittimeandtheunitcostoflostsalesrespectively.C’ istheinventoryorderingcostperorder.

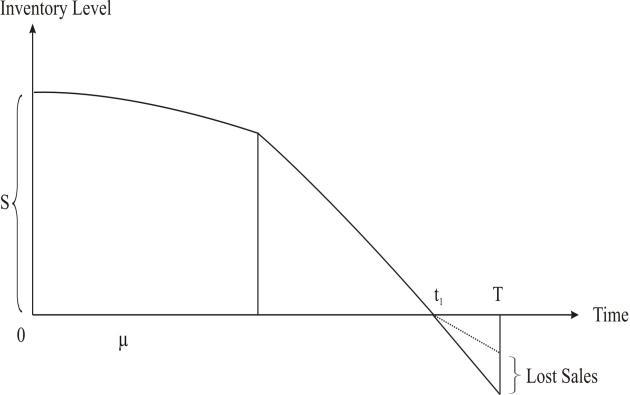
3. FORMULATION AND SOLUTION OF THE MODEL

Figure 1

Thedepletionofinventoryduringtheinterval  10,t isdue tojointeffectofdemandanddeterioratingofitemsandthe demandispartiallybackloggedintheinterval  1 t,T .The depletionofinventoryisgiveninthe(figure1). The governing deferential equations of the proposed inventorysystemintheinterval(0,T)are

(2.4) Solutionoftheequation(2.1)

Certified Journal | Page1059

IRJET

Impact Factor value: 7.529 | ISO 9001:2008

        DtabtcttHtt  where   Ht 

  1ift Ht 0ift      

is the Heaviside’s functions defined as follows.

     2ItItabtct   ,0t

     ItItakt   , 1tt …

    t Itakte   , 1 ttT  …

where kbc

   1 I0SandIt0  …

…(2.1)

(2.2)

(2.3)

withtheconditions

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056 Volume: 09 Issue: 08 | Aug 2022 www.irjet.net p-ISSN: 2395-0072

© 2022, IRJET | Impact Factor value: 7.529 | ISO 9001:2008 Certified Journal | Page1060       2 dIt Itabtct dt  dt t IFee     Now     ttt ttt 000 deItdtaedttedt     t 2tt 0 CtedteItS   ttt ttt 2 000 abb etee     ttt 2ttt 2 000 CC2b tetete      ttt t2tt 22000 bCC2 etete      t t 3 0 2C e       ttt ab eItSe1te    t 2 b e1     2t C te     t 2 2C te    t 3 2C e1     2 t 223 abtbct2ct2c e      23 ab2c    t 2222 3 e abtbct2ct2c     2 3 1 ab2c    t 2222 3 e abtbct2ct2c     2 3 1 ab2c        2t 3 1 ItSab2ce         2 3 1 abt1     22 ct2t2  , 0t …(2.5) Nowthesolutionoftheequation(2.2)       dIt Itakt dt        11 tt tt tt deItdtaktedt     11 tt ttt tt eIt0aedtktedt    111 ttt ttt 2 ttt akk etee     1t t 1 22 aktkatkk ee           t t 2 e eItaktk       1t 1 2 e aktk            1 tt 1 2 1 Itakt1e       2 1 akt1  ,  1tt …(2.6) Bytheequations(2.5)and(2.6)wegetinitialinventorylevel afterfulfillingbackorders(S)

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056 Volume: 09 Issue: 08 | Aug 2022 www.irjet.net p-ISSN: 2395-0072

© 2022, IRJET | Impact Factor value: 7.529 | ISO 9001:2008 Certified Journal | Page1061       1 tt 1 2 1 akt1e       2 1 akt1    3 2t 1 Sab2ce           2 3 1 abt1     22 ct2t2  Multiplyingonbothsidesby t e    2 3 1 Sab2c         t 222 3 e abt1ct2t2    1t 2 e        1 akt1      t 2 1 akt1e     2 3 1 ab2c      1t 1 2 1 akt1e      t 2 3 e abt1       2222 ct2t2aktk    2 3 1 ab2c      1t 1 2 1 akt1e   t 222 3 e btbct      22 2ct2ctbtcbc   Putting t    2 3 1 Sab2c       1t 1 2 1 akt1e    t 222 3 e bbct    222 2c2cbcbc     2 3 1 Sab2c       1t 1 2 1 akt1e     3 e 2cc      2 3 1 Sab2c       1t 1 2 1 akt1e     3 c 2e   …(2.7) Using(2.7)in(2.5),weget     2t 3 1 Itab2ce         1 t1 1 2 1 akt1e      t 3 c 2e     2t 3 1 ab2ce         222 3 1 abt1ct2t2           1 tt 1 2 1 Itakt1e          t 2 33 c12eabt1      22 ct2t2 ,  0t …(2.8) Nowthesolutionoftheequation(2.4)

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 09 Issue: 08 | Aug 2022 www.irjet.net p-ISSN: 2395-0072

© 2022, IRJET | Impact Factor value: 7.529 | ISO 9001:2008 Certified Journal | Page1062     t dIt akte dt       t dItaktedt       111 ttt tt ttt dItdtaedtktedt     1 t t t a It0e     11 tttt 2 tt kk tee     11 tttt 1 ak eetete     1t t 2 k ee      t 2 atkk e       1t 1 2 atkk e             t 2 1 Itakt1e         1t 1

 

 , 1

1 2

        1 1 t

  





 

     1t t 1 1 2 0 C akt1eedt           1t 1 1 2 Ceakt11e             1 1 t t 1 1 3 C Iakt1ee     …(p) Nowsecondintegrationterm    t 1 3 0 CC II2edt        t 1 3 0 CC 2eedt        t 1 3 0 CCe 2e           1 4 CC II21e   …(q) Nowthirdintegrationterm     C abt1Ct2t2dt 0 222 1 3         CC 2edt 0 1 3  t       C Cakt1edt 2 0 1 H1 tt    1         CCItdtItdt H1 0 t1  c duringtheperiod H Hencetheinventoryholdingcost  Ct2t2dt  22       C IIIabt1 0 1 3 2  

akt1e



ttT  …(2.9) (0,T)becomes

akt1edt

     1t 1 2 C akt1dt

   Solvingallintegrationintheaboveequationseparatelynow firstintegrationterm

  

1 tt 1 1 2 0 C Iakt1edt    

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056 Volume: 09 Issue: 08 | Aug 2022 www.irjet.net p-ISSN: 2395-0072

© 2022, IRJET | Impact Factor value: 7.529 | ISO 9001:2008 Certified Journal | Page1063 2 22 1 3 Ctatbbt 2      32 2 0 tt C2C2Ct 32     23 222 1 3 C abbC 23      22 22 2C2Cabb 22   32 2 C2C2C 32     2 1 2 abb IIIC 2          32 23 CC2C 3          …(r) Nowthefourthintegrationterm       1 1 t tt 11 2 1 IVCakt1edt             1t 2 1 akt1dt         1 1 t t t 1 1 2 C akt1eedt         11 tt 11 2 CCkakdtdt          1 1 t t 1 1 2 C e akt1ee           1 1 2 C akt   22 1 1 Ck t 2            1t 1 1 3 C akt1e1       1 1 2 C akt     22 1 1 Ck t 2           1t 1 1 3 C akt1e1      1 1 2 C akt  1 2 C    2 abc    22 1 1 Ck t 2           1t 1 1 3 C IVakt1e1      111 1 22 CacCb akt      2 22 11 1 2 CCCk t 2     …(s) Afteraddingp,q,rands,weget HC as         1 1 t t 1 H1 3 C Cakt1ee       1 4 CC 21e   232 1 223 abbcc2c C 23          1 1 3 C akt1      1t e1    11 1 2 Cca akt    

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 09 Issue: 08 | Aug 2022 www.irjet.net p-ISSN: 2395-0072

Certified Journal | Page1064   2 22 111 1 22 cbccck t 2          1t 1 1 3 C akt1e1       23 111 4 cccbcc 21e 23         22 111 11 32 2cccckaktt 2          1t 1 1 3 C akt1e1       2 11 4 cccb 21e 2      1 3 c 3     32 1 1 2 c c6cakt     22 1 1 ck t 2        1t 1 1 3 C akt1e1       2 11 4 cccb 21e 2      1 3 cc 3       22 1 1 2 c 6akt    22 1 1 ck t 2      H1 4 c CC21e          1t 1 3 1 akt1e1    2 b 2     22 3 c 6 3        22 11 2 1k aktt 2       …(2.10) The cost due to deterioration of units   DC during the period(0,T)     1t D2 0 CCItdtItdt            1t 2 0 CItdtItdt           D2 4 c CC21e          1t 1 3 1 akt1e1    2 b 2     22 3 c 6 3        22 11 2 1k aktt 2       …(2.11) The cost due to shortage of units   sC during the given periodisgivenby   1 T s3 t CCItdt       1 T t 3 s 2 t C Cakt1e          1t 1 akt1edt         3 1 2 C akt1  11 TT 33tt 22 tt CCkaedttedt     1 T t 3 2 t Ck edt        3 1 2 C akt1  1 1 T t t edt       11 TT 33tt tt CaCkedttedt    1 T t 3 2 t Ck edt   

9001:2008

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056 Volume: 09 Issue: 08

Aug 2022 www.irjet.net p-ISSN: 2395-0072

© 2022, IRJET | Impact Factor value: 7.529 | ISO 9001:2008 Certified Journal | Page1065     3 1 2 C akt1  1 1 T t t edt       11 TT tt 3 3 2 tt Ck ak Cedttedt              1t 3 11 2 C akt1eTt      1t T 3 2 C ak ee          1t T 3 1 2 Ck Tete      1t T 3 3 Ck ee           1t 3 11 2 C akt1eTt      T 333 3 e Ca2CkCTk      1t 3331 3 e Ca2CkCtk    3 2 C         1t 11 akt1eTt       T 3 s 3 C Ceak2T          1t 1eak2t         1t 2 11 akt1eTt   …(2.12) Theopportunitycostduetolostsales   0C isgivenby    1 T t 04 t CC1eaktdt        11 TT t 44 tt CaktdtCeaktdt      11 TT t 44 tt CaktdtCaedt   1 T t 4 t Cktedt      1 11 TT T 442t 4 t tt CkCa Catte 2     11 44ttTT 2 tt CkCk tee         22 4 411 Ck CaTtTt 2  T 444 2 CaTCkCk e       1t e  4144 2 CatCkCk           22 4 411 Ck CaTtTt 2      T 4 2 Ce ak1T    1t 4 2 Ce      1ak1t      22 0411 k CCaTtTt 2         T 2 e ak1T    1t 2 e       1ak1t    …(2.13) The total average cost (k) of the inventory system permit timeisgivenby

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056 Volume: 09 Issue: 08 | Aug 2022 www.irjet.net p-ISSN: 2395-0072

© 2022, IRJET | Impact Factor value: 7.529 | ISO 9001:2008 Certified Journal | Page1066   HDs0 CCCCC R K TT    whereRisthetotalcostofhtinventorycycle    1 4 1CC KC21e T             1 2 t 11 1 3 Ccb akt1e1 2          22 11 1 32 CCC6akt 3         22 12 1 3 CkCC t21e 2          1 2 t 22 1 2 CCb akt1e1 2         22 22 1 2 CCC6akt 3            22T 3 2 1 3 C Ck teak2T 2        1t 1eak2t         1t 2 11 akt1eTt       22 411 k CaTtTt 2         T 2 1 akT1e       1t 1 2 e akt1         To minimize (k), the optimal values of 1t & T can be obtainedbysolving 1 k 0 t    and k 0 T    simultaneously. Now   1 1 t t 1 11 2 1 Cake kCkte t        1t 111111 222 CkeCkCaCkCkt    1t 2 Cae  11 1 tt t 22 21 CkeCke Ckte     22 221 CkCkCaCkt     11 tt 331 2 CeCtke a2k       1 1 t t 2 33 22 CkeCT ake     11 tt 3 31 C CTkteeTk       11 33tt 1 2 CCteakeak     11 tt 2 3 311 C Cktee.2tk     1t 4 441 Ce CaCktak    11 tt 4 41 C Cektke    1 1 t t 111 2 CCkte ake      11 1111tt 2 2 CCaCktkeCae    1t 2 Cke  1 1 t t 2 212 Cke CkteCa    

2395-0056

2395-0072

Issue:

© 2022, IRJET | Impact Factor value: 7.529 | ISO 9001:2008 Certified Journal | Page1067 111 ttt 3331 21 2 Cae2kCeCtke Ckt     1 11 t tt 33 3 2 CCTke keCTae     111 ttt 3 3131 C CTkteeTkCtae   111 333ttt 1 2 CCaCtkeeke    11 tt 2 3 311 C Ckte2tke      11 tt 441 Ca1eckt1e 111 111ttt 1 22 CCkCk aeete    1 1 t t 1111 2 2 CkeCaCkt Cae      1t 2 Ck e   11 tt 2 21 Ck Cktee   1 1 t t 33 221 2 CaCkteCa2kCe     1t 31 Ctke   1 1 t t 3 3 2 Cke CTae    1 1 t t t 33 31 CTkeCCTkteTke      1t 31 Ctae  1 1 t t 313 CtkCea e     1 11 t tt 2 33 311 2 CkeCCkte2tke      1t 4 Ca1e   1t 41 Ckt1e.  11 tt 111111 CaeCkteCaCkt    11 tt 2212 CaeCkteCa   21Ckt 1t 3 CTae 11 tt 3131 CTkteCtae    11 tt 2 3141 CkteCaeakt       11 111tt CaCkt e1e1       11 tt 2131 Ckte1TCeakt        11 tt 31141 CteaktC1eakt    1t 111 221 CaCkt e1CaCkt         1t 311 CetTakt      1t 41 Cakt1e        1t 1 121 C e1aktCakt         1t 311 CetTakt      1t 41 Cakt1e      11 tt 1 231 C eCCetT            1t 441 CeCakt     Nowputting 1 k 0 t    ,weget   1t 1 2 1 kC 0e1C t             114 ttC 3141 CetTCeakt       1t 1 2 C e1C     

International Research Journal of Engineering and Technology (IRJET) e-ISSN:

Volume: 09

Aug 2022 www.irjet.net p-ISSN:

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056 Volume: 09 Issue: 08 | Aug 2022 www.irjet.net p-ISSN: 2395-0072

arehighlynonlinearequations. Thereforenumericalsolutionoftheseequationobtainedby usingthesoftwareMATLAB7.0.1.

4. CONCLUSIONS

Thisresearchworkdevelopsaninventorymodelwithprice, stock, and time-dependent demand. The physical deteriorationandconditionoffreshnessdegradationover time are both considered, and zero-ending inventory is assumed. When working with perishable products, a salvagedvalueandadeteriorationcostareconsideredinthe entire cycle. A nonlinear time-dependent holding cost is included,specificallywithaquadratic-typefunction.

© 2022, IRJET | Impact Factor value: 7.529 | ISO 9001:2008 Certified Journal | Page1068     1t 3144 eCtTCC0   …(2.14) Nowfor k 0 T    Since R k T   2 kRR1R TTTTT T      T 3 22 Ce kR1 a2k TT T           1t TT 333 22 CkTCCekeake     1t 3 144 C tkeCaCkT    T 4C e     TT 4 4 C akCkTeek       T 3 222 R1a2kkTk Ce T T        1t 1 3 2 aktk Ce        T 44 kk CakTCeakT      T 3 22 R1akkT Ce T T          1t 1 34 2 aktk CeC          T 4 CeakT          1t 3 1 22 C R1 eak1t T T           T eak1T      T 4 CakT1e    Putting k 0 T    ,weget      1t 3 1 22 C kR1 eak1t TT T             T eak1T   4C    T akT1c0         1t 3 1 2 C akt1e           T 4 akT1eCakT       T R 1e0 T   …(2.15) Theaboveequations 1 k 0 t    and k 0 T    provided,

satisfythefollowingconditions: 22 22 1 2 222 22 1 1 kk 0,0 tT kkk 0 tT tT                 …(2.1

Equation

they

(2.14)and(2.15)

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 09 Issue: 08 | Aug 2022 www.irjet.net p-ISSN: 2395-0072

Throughanalgorithm,theinventorymodeldeterminesthe optimal valuesforprice, the inventorycycletime,and the orderquantity.Somenumericalexamplesareprovided,and a sensitivity analysis is presented for all the input parameters. By observing the behavior of the decision variablesandtotalprofits,itwasfoundthatanincreasein theorderingcost,purchasingcost,andshelf-life resultsina similarpatterninthesellingprice,theinventorycycletime, thequantitytoorder,andthetotalprofit.Furthermore,an increaseinthevalueoftheshelf-liferesultsinanincrement inprice,inventorycycletime,quantityordered,andprofits generatedforallfunctions.Inaddition,astheorderingcost increases,price, the inventory cycle time and quantity ordered also increase for all functions. Nonetheless, the profits show a decreasing trend. Finally, by escalating the purchasingcostforallfunctions,thereisanincreaseinboth thepriceandtheinventorycycletime;however,thequantity toorderandtotalprofitstendtodecrease.

Thisresearchwork extends andwidelycontributestothe state-of-the-art on the inventory field, with focus on perishableitemswithprice-stock-time-dependentdemand. Theinventorymodelstudiedherehassomelimitationsfrom whereseveraldirectionsforextensionandfurtherresearch arehighlighted.First,aninventorymodelcanbebuiltwith thesamecharacteristicsanddemandpattern,butincluding thesustainabilityelements,sotheeffectsofthecarbon-tax andcap-and-trademechanismscanbeassessed.Second,a modelthatallowsshortageswithfullorpartialbacklogging should be explored. Third, the trade-off and benefits of investingonpreservationtechnologyshouldbealsostudied. Fourth,thenoninstantaneousitem’sfreshnessdegradation canbeintegratedintotheproposedinventorymodel.Finally, othercomponentssuchasincorporatingdiscountpoliciesor advertisingeffortscanalsobeinvestigated.

5. REFERENCES

[1] A. H. M. Mashud, H.M. Wee, C. V. Huang, and J. Z. Wu, “Optimal replenishment policy for deteriorating products in a newsboy problem with multiple just-intimedeliveries,” Mathematics,vol.8,no.11,pp.1–18, 2020.

[2] A.H.M.Mashud,D.Roy,Y. Daryanto,andM.H.Ali,“A sustainableinventory model with imperfect products, deterioration,andcontrollableemissions,” Mathematics, vol.8,no.11,pp.1–21,2020.

[3] B. Pal, S. S. Sana, and K. Chaudhuri, “A stochastic productioninventorymodelfordeterioratingitemswith productsʼfinitelife-cycle,” RAIRO-Operations Research, vol.51,no.3,pp.669–684,2017.

[4] BhuniaA.KandM.Maiti,Deterministicinventorymodel fordeterioratingitemswithfiniterateofreplenishment dependent on inventory level. Computers and OperationsResearch25(11),997-1006,1998.

[5] Cheng TCE., An economic order quantity model with demand-dependentunitproductioncostandimperfect productionprocesses,IIETransactions23,23-28,1991.

[6] Chu. P and Patrick S.H., A note on inventory replenishment policies for deteriorating items in an exponentially declining market. Computers and OperationsResearch29(13),1827-1842,2002.

[7] Covert,R.PandG.C.Philip,AnEOQmodelforitemswith Weibulldistributeddeterioration.AIIETransactions5, 323-326,1973.

[8] E. B. Tirkolaee, A. Goli, M. Bakhsi, and I. Mahdavi, “A robustmulti-tripvehicleroutingproblemofperishable products with intermediate depots and time windows,”NumericalAlgebra,Control&Optimization, vol.7,no.4,pp.417–433,2017.

[9] Giri,B.C.andChaudhariK.S.,“Deterministicmodelsof perishableinventorywithstockdependentdemandrate and nonlinear holding cost”, European Journal of OperationalResearch,105,3,pp467-474,1998.

[10] YanH.andTCECheng,Optimalproductionstoppingand restarting times for an EOQ model with deteriorating items.JournalofOperationalResearchSociety,49,12881295,1998

[11] Kuo-Lung Hou, An inventory model for deteriorating items with stock-dependent consumption rate and shortages under inflation and time discounting. EuropeanJournalofOperationsResearch168,463-474, 2006.

[12] ChandraM.G.,AnEPQinventorymodelforexponentially deterioratingitemsunderretailpartialtradepolicyin supply chain, Expert Systems and applications. 39(3), 3537-3550,2012.

[13] M. Yavari, H. Enjavi, and M. Geraeli, “Demand management to cope with routes disruptions in location-inventory-routing problem for perishable products,”Research in Transportation Business & Management,vol.37,ArticleID100552,pp.1–14,2020.

[14] TengJ.T.andChangC.T.,Economicproductionquantity models for deteriorating items with price- and stockdependent demand. Computers and Operations Research32,297-308,2005.

[15] Zaid T. Balkhi & Lakdere Benkherouf, An inventory model for deteriorating items with stock dependent demandandtime-varyingdemandrates.Computersand pertainsResearch31,223-240,2004.

Certified Journal | Page1069

2022, IRJET | Impact Factor value: 7.529 | ISO 9001:2008