Multi-Objective Trip Planning With Tourist Attractions, Restaurant Selection And Public Transportati

International Research Journal of Engineering and Technology (IRJET) e ISSN: 2395 0056

Volume: 09 Issue: 07 | July 2022 www.irjet.net p ISSN: 2395 0072

Multi-Objective Trip Planning With Tourist Attractions, Restaurant Selection And Public Transportation Facility Details

Student, Dept. Of Computer Science and Engineering, Indira Gandhi Institute Of Engineering And Technology, APJ Abdul Kalam Technological University, Kerala, India ***

Abstract - The Trip Planner web application helps the trip planners, such as tourists, tour companies, and government agencies, to plan their trip with user priorities. Trip planner applicationsequences anoptimalsetofpointofinterest(POIs) and then generates a planned route that maximizes their pleasure. However, the traditional Tourist Trip Design Problems (TTDP) does not include the break period at a local restaurant, which causes the rest of the itinerary in the afternoon to shift. Moreover, as tourism contributes to high greenhouse gas emissions, especially from its transportation, minimizing the itinerary's total distance is also considered. Unfortunately, this objectiveconflicts withtheprofitscores,So I includedthe publictransportationfacilitiesintheregion.The tourists can choose their medium of transportation and if possible they can select some of the public transportation facilities in the area. To address the real world issues in the itinerary selection, I formulate a new variant of the well known orienteering problem with time windows (OPTW) called the multi objective orienteering problem with TimeWindows, Restaurant Selection, and Compulsory POIs (MOPTW RSCP). The proposed problem is provided with a mathematical formulation and two exact algorithms for solving them, i.e., greedy and branch and cut Pareto based techniques.

Key Words: (Size10&Bold)Keyword1,Keyword2,Key word3,etc(Minimum5to8keywords)…

1.INTRODUCTION

Travellers visit tourist destinations for a limited timeperiod,anditisnotpossibletovisitalltheattractions inanarea.Therefore,theyneedanitinerarywithoptionto selectPOIs basedontheirpreferencesandconstraints, So tourists can make an itinerary with required POIs for a convenienttimeperiod.

Thetouristtripdesignproblem(TTDP)isproposed to describe the issue. It takes a list of POIs, a POI to POI distancetable,andatourperiodastheinputs.EachPOIhas a profit score and a visiting period, these profit score describesasatisfyinglevelinthePOI.Therefore,thesolution ofTTDPisaplannedroutehavingasubsetofPOIstogether with the highest total profit that satisfies the tour period. Many TTDPs also consider the time window of each POI (Operationalhours)asaconstrainttoreflecttherealworld.

However,makingamostprofitabletravelrouteisacomplex, toolong,andtime consumingprocess.

TTDP is a very complex problem, and the requirementsmay bevarying. Several modified modelsof TTDPhavebeenproposedinthepastdecadetoachievereal world requirements. During the literature review, I found variants of TTDP models that attempted to meet the real world scenarios, but there were some limitations. Firstly, mostofthemareavoidingthelunchperiod.Theignoranceof this time period may cause the whole POIs to visit in the afternoon to be forced to shift. In addition, the user preference of restaurant selection is not considered. Moreover,SomePOIsareusuallyputintheitinerarybythe tourist’spersonalpreferencesortherecommendationfrom other sources. Unfortunately, most of the existing TTDP models do not support these compulsory POIs in the itinerary.

Awalkingtour hasitscharacteristic thatthelong totaldistancetobecoveredinawalkingtourmaycausethe tourists to betired. Soa trade off betweenthetotal profit and distance is needed. However, the suitable amount of distancevariesfrompersontopersonandfromtimetotime. Inotherwords,inanysituationthereisnosinglesuitable total distance that suits for a tourist. Hence, the total distance should be considered as important as the total profit. Therefore, the multi objective optimization model shouldabletoconsiderbothaspectsequally.

Multi objective optimization model is not only providingasinglebestitinerarybutasetofnon dominated itineraries that let the trip planners choose the most appropriate one. However, If there are no preferences available, a solution ranking technique can support the decision.

My idea proposes a multi objective orienteering problem with time windows, restaurant selection, and compulsory POIs (MO OPTW RSCP) based on user preferencestosolvetheproblemsabove.Followingarethe maincontributionsofthispaper.

1. Areal worldMO OPTW RSCPmodelisformulated and introduced for the first time. The model supports the real world issues by including

International Research Journal of Engineering and Technology (IRJET) e ISSN: 2395 0056

lunchtime with restaurant selection and compulsoryPOIs.

2. Two Pareto based multi objective algorithms, branchand cutandgreedy based,areproposedfor solvingthemodel.

3. Asolutionrankingtechniquetohelptripplanners chooseoutstandingitinerariesfromtheParetofront containingasetofPareto optimalsolutions.

2. METHODOLOGY

2.1 Background And Related Works

2.1.1 Orienteering Problem

Orienteering problem is a combination of node selectionanddeterminingthemosteffectivepathbetween theselectednodes.Thetouristtripdesignproblem(TTDP) canbeviewedasanapplicationoftheorienteeringproblem (OP). The OP was originated from a sport in which competitorscanchoosetovisittheplaceswithvariousprofit scoresintheforest.Theonewhocancollectthehighesttotal profitfromasubsetoflocationswithinalimitedperiodwill win.In1984,Tsiligiridesdidthemathematicalformulation oftheproblem.TheproblemisanNP hardproblem.Several well known variants of the problem have been modelled, including OP with time window (OPTW), team OP (TOP), time dependent OP (TDOP), team OPTW (TOPTW), TDOP with time window (TDOPTW), and team TDOPTW (TD TOPTW).

2.1.2 OP for TTDP

TTDPcanbemappedtotheOPbyreplacingvisiting places with POIs and competitors with tourists. Furthermore,tomaketheplannedroutemorepractical,each POIhasitsownopenandclosetimeastimewindow.Hence, themost popular modelsof TTDPare basedonOPTWfor single dayitinerariesandTOPTWormulti dayitineraries.In thisproject,IwillfocusonlyontheOPTWforasingleday travel.TTDPitselfhasseveralspecifiedmodelswhichhave beenproposedtocapturesomeuniquereal worldaspects. For example, Divsalar, presented OP with hotel selection (OPHS)tochoosethehotelthatmakesthecostoftraveling lowest.Havinglunchfortouristsisalsovitalformanytrip plannerstospecifyarestaurantintheitineraryexplicitlyfor reasonssuchasthepreferencesofthetourists,beliefsand religions,andlimitationssuchasfoodallergy.Theoriginal basepaperofTTDPbyVansteenwagenandOudheusdenhas also considered having lunch break in a restaurant. Then, Vansteenwegen formalized the concept by designing the lunch break by enabling virtual POIs without locations. Tenemaza assigned the lunch break at the current POI, assumedthateveryPOIhasaplacetoeat,andallowedthe currentPOItooverlapthelunchbreak,thenoptimizedfor minimizingthatoverlapperiod.Finally,Expositoproposed

themodelTTDPwithclusteredPOIs(TTDP clustered)that separatePOIsintoseveralcategories,includingarestaurant. Themodelsupportsrestaurantselectionandlunchbreakby specifyingtheconstraintsoftherestaurantcategory.Some POIsarepreferablecomparedtotheremaining.Forexample, somepointofinterestshighlightthateveryoneshouldvisit first time tourists, or some POIs match the trip planner’s preferences.Consequently,somePOIsarecompulsoryPOIs sotheymustbeincludedintheplannedroute.Theconcept was introduced into OP by Gendreau. Palomo Martínez modeltheOPwithmandatoryvisitsandconflict(OPMVC). ThemodelsupportsbothcompulsoryandconflictedPOIs.If conflicted POIs are there only one can be selected. For example,onlyonepalacecanbeaddedtotheitinerary.Inthe same year, Palomo Martínez solved the orienteering problem by using VNS and GRASP. Li and merged OPTW withcompulsoryPOIsand modelleditastheorienteering problem with compulsory POIs and time windows (OPCNTW).LinandYu introducedthecompulsoryPOIsto the TOPTW model and named it TOPTW with mandatory visits(TOPTW MV).

2.1.3 Multi Objective OPTW

Theorienteeringproblemwithtimewindows(OPTW)deals withtheproblemaboutselectingasetofpointsofinterest and then finding the route to visit the POIs under the particulartimewindow.Butsomemodelshavingmorethan one objective to be optimized. Then, they are classified as multi objective optimization models with more than one goal. Popular techniques to address this problem are to merge multiple objectives and create a single objective, hierarchical ordering of the objectives, or using a Pareto based method. The first two techniques may lead in to a single best solution, whereas the last technique may give multiple non dominated solutions. In my approach, I only considerthePareto basedmodel.ThePareto basedmulti objectiveoptimizationisbasedonParetodominancewhich workslikeIfwehavetwoitinerariesitineraryAandB,then ifitineraryAhasatleastoneobjectivesuperiortoitineraryB with no worse objective, then I can say that itinerary A dominatesitineraryB,anditineraryBmayeliminated.When I did pair wise tournament comparisons, only the non dominateditinerariesareleft.Theyarethesolutionstothe problem,whichcanbeconsideredasaParetofront.Pareto fronttheplotwiththeaxesareobjectives.Fig.2.1represent theconceptof Pareto front for a specific TTDP, whichhas two objectives:first oneis thetotal profit (the higher, the better)andthesecondoneisthetotaldistance(thelower, thebetter).TheParetodominance'sconceptofanitinerary isdemonstratedinthefigureasthedominanceareaformed byanitineraryandthemostunsuccesfullpointatthetop leftcornerofthegraph.Eliminateallitinerarieswithinthe region. Hence, only two solutions, non dominated itineraries,areleftanditformsaParetofront.Srinivasand Deb comeupwiththeconceptoftheParetofront.Sincethat time, it has become a research focus. Nowadays, so many

Volume: 09 Issue: 07 | July 2022 www.irjet.net p ISSN: 2395 0072 © 2022, IRJET | Impact Factor value: 7.529 | ISO 9001:2008 Certified Journal |

International Research Journal of Engineering and Technology (IRJET) e ISSN: 2395 0056

Volume: 09 Issue: 07 | July 2022 www.irjet.net p ISSN: 2395 0072

state of the art algorithms have been proposed including VEGA,MOEA/D,andNSGA II.Objectivesfor TTDP maybe varied in these. One of the most well known objectives is havingmultiplescoresforeachPOI,suchaslevelofinterest, entrancefees,relaxation,readiness,etc.Schildeproposeda generic bi objective POI scores model for orienteering problem with the result as a Pareto front. The papers contributedonthistypeofproblemareMartí,Purevsuren, RezkiandAghezzaf,Aghezzaf,andRezki,Martín Morenoand Vega RodríguezRezkiandAghezzaf.ChenandHuproposed the[T]OPTWvariantofthistypeofproblem.Byusingalocal search, minimizing the total distance of the trip may be implicitly achieved. However, bringing the trade off itinerarieswithvaryingsatisfactiontotalprofit(maximizing) andtotaldistance(minimizing)willhelpthetripplannerto balance. Unfortunately, there are only a few papers that addresstheproblem.TheyareKarimiandBashiri,Hapsari and Falco applied TOPTW with five objectives: maximize profit score, time of the tour, minimize the total distance number of preferred POIs of the tourists, and number of recommendedPOIs.Ontheotherhand,Mirzaeiattemptedto balancethesatisfactionlevelforeachday.HenceforaTOP model,theobjectivesaretomaximizethescore,minimize thedifferencebetweenthehighestandlowestscores.Table 2.1 presents the summary of the related works and the proposed model. I am focused on these four points: restaurantselection,compulsoryPOIs,lunchperiod,andbi objectiveoftotalprofitanddistances.Thetablerevealsthat none of the existing multi objective models address the compulsory POIs, restaurant selection, or lunch period. Hence, the proposed model is proposed to fill in these researchgaps

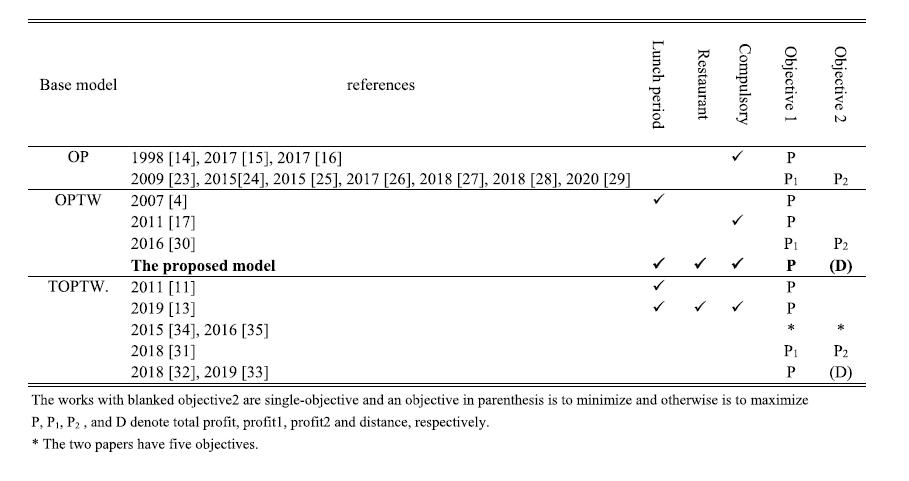
Table2.1 Summaryofrelatedworksandtheproposed model.

2.1.4 Itinerary Selection From Pareto Front

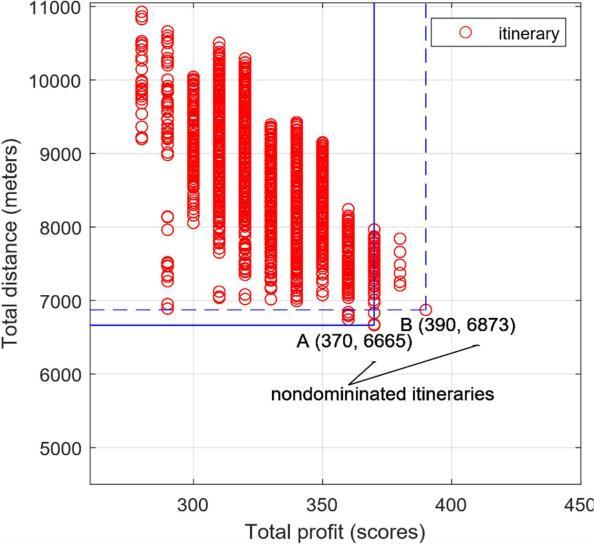
FromthegivenParetofront,thetripplannersmay selectonlyoneoutstanding itinerarytoimplement,which depends on the trip planners route preference. The two obvious preferences available in route planning are the itinerarywithminimumdistanceandmaximumprofit.The firstoneisthe itinerarythathavingmaximumtotalprofit whichisoftenselectedwhenthetouristsfocusonexploring as many as possible highlighted POIs, near to the target destination, especially when visiting for the first time. Moreover, If the tourists travel with travel agents they sometimes organize familiarization trips on almost all possible highlighted POIs. Then, the travel partners can designanitinerarythatmatchesthecustomerexpectations. The second one is when the tourists consist of elders or youngchildrenintourstheshortesttotaldistanceisoften selected.

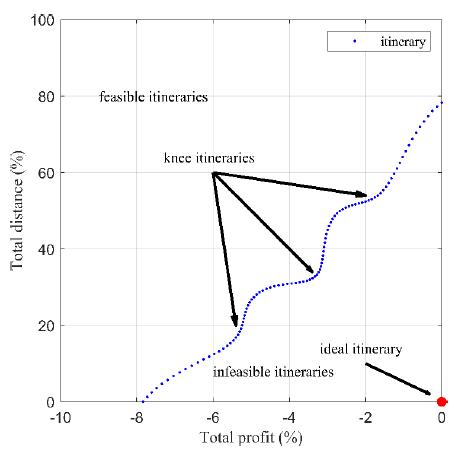
VirtuallyallitinerariesontheParetofrontdominate the inferior itineraries, i.e., they are non dominated itineraries, so Selecting an outstanding itinerary from a Pareto front when no preference is available is not an important task. Sanyapong Petchrompo did a clustering technique by a cut off technique and discovered an outstanding solution for each cluster. However, many researchersagreeonkneesolutionwhichisanoutstanding, well balanced trade offs and diversity solution. The knee solutions concept can be depicted for a convex shape of a Paretofrontofbothobjectives:distanceandtotalprofitFig. 2.2. The figure illustrates Pareto front with three knee itineraries.

2.1TheconceptoftheParetofront.

Thethreemostpopulartechniquesforfindingknee solutions are the maximum distance from the hyperplane focus, utility based focus, and angle based focus. The maximum distance from the hyperplane focus was firstly described by Das. First, Das defined a hyperplane that connectstheextremesolutions.Then,thekneesolutionis the solution with the most extended length from itself perpendiculartothehyperplane.Thistechniqueisthebasic forseveralkneesearchingalgorithms.

International Research Journal of Engineering and Technology (IRJET) e ISSN: 2395 0056

Volume: 09 Issue: 07 | July 2022 www.irjet.net p ISSN: 2395 0072

EBrankeintroducedtheutility basedfocusbased on the trade off of objective functions in his research "ParallelProblemSolvingFromNature".Thekneesolution hasasmallgainofanobjectthatcausesthehighestlossof theotherobjective.

E Branke also seeded the angle based focus. The typicalParetodominancecanbegeographicallyviewedas theareaofdominationtoberectangularshaped,soitisthe rightangleatthesolution.However,Scopeofdominationis extended if the angle is more expansive. Therefore, some non dominated solutions are eliminated, and the rest are considered as knee solutions. The knee solution acts as decisionsupport,notamandatoryitinerarytoselectinthe real world Choachaicharoenkul and Wattanapongsakorn providetheangle basedfocussolutionrankingthatwillrank thesolutionsonaParetofronttoempowerthetripplanners.

focusesontheshorterdistance,theprofittendstobehigher andviceversa.ThesolutionsetcanbevisualizedasaPareto front, which an objective is represented by each axis. Typically,thetripplannersneedonlyasingleplannedroute fromthesolutionaccordingtotheirrequirements.

Secondly,themodelincludesanexplicitlunchbreak and a small set of restaurants in the area. The list of restaurantsisfilteredaccordingtothePOIsselected.

Thirdly, the model create itineraries based on the compulsoryPOIs.ThecompulsoryPOIsarethehighlighted POIs that need to be traversed in between source and destination.

Finally, the model included public transportation facilitydetailsintheareaaspartofCO2emissioncontrol.

2.2.1 Mathematical Model

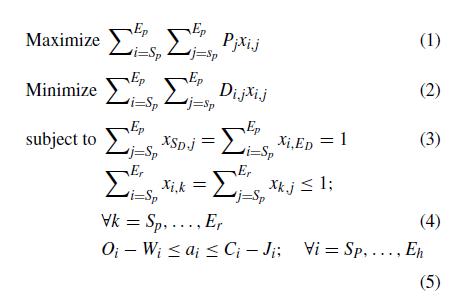
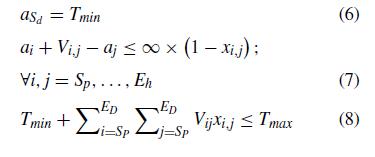
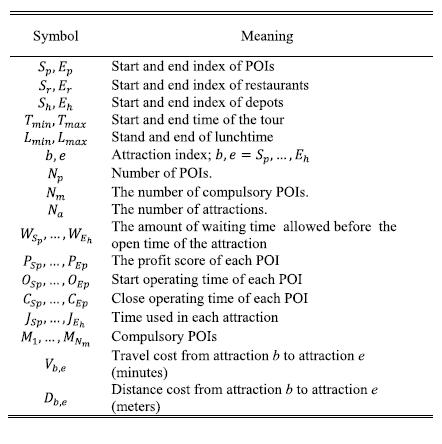
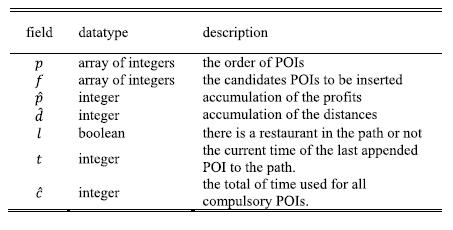
Assumingthatnattractionsarethereinbetweenthe sourceand destination,theseattractionsareseparatedinto threetypes:pointofinterest(POI),restaurant,andstartand end locations. Then, the attractions are encoded into an arraythatcanberepresentedinFig.2.4. Sp and Ep, Sr and Er ,and Sh and Eh keeptrackofthestartandstopindexesof POIs,restaurants,andstartandendlocations,respectively. The meaning of symbols are mentioned in the two tables, table2.2forthelistofparametersandtable2.3forthelistof decision variables. There are two objectives in MOPTW RSCP, one for maximizing total profit and the other for minimizing the total distance that can be represented as follows

Figure2.2 Kneeitineraryconcept

2.2 Problem Description And Formulation

This section proposes the extension of the Orienteering ProblemwithTimeWindows(OPTW)calledMulti objective Orienteering Problem with TimeWindows, Restaurant Selection, and Compulsory POIs (MOPTW RSCP). I focus OPTW on the TTDP application for a one day trip with restaurant selection. MOPTW RSCP extends the OPTW in belowaspects.

Firstly,themodelhastwoobjectives:minimizingthe totaldistanceandmaximizingthetotalprofitoftheselected POIs in the itineraries. So, the model becomes a multi objective. However, the objectives conflict, as the usual characteristicofthemultiobjectivemodel.Inthisparticular case, the total profit conflicts with the total distance; therefore,bothobjectivescan'tsatisfysimultaneouslyinany single itinerary. Set of trade offs between non dominated itinerarieswill bethesolutionto thisproblem.Ifa tourist

Factor value:

International Research Journal of Engineering and Technology (IRJET) e ISSN: 2395 0056

Volume: 09 Issue: 07 | July 2022 www.irjet.net p ISSN: 2395 0072

Constraint (3) makes sure that the itinerary starts at the startlocationandendsattheendlocation.Eachplacemust visitonlyonce,constraint(4)forcesthechancetoincludea POI at most once into the itinerary. Each POI has a time windowandopentime,Constraint(5)statesthatthearrival time to eachPOIinthe itinerarymust be withinthattime window or within z1 minutes before the open time of the POI.Constraints(6)setsthestarttimeofthetourat Tmin. Constraint (7) ensures the validity of path between two attractionsifthepathisincludedintheitinerary.Constraint (8)providesthattheitineraryiswithinthetimebudget,we need itineraries for a single day . Constraint (9) and (10) have the scope to modify in the set of equations it ensure that the itinerary must include exactly one restaurant. Constraint(11)providesthattheitinerarycomprisesofall compulsoryPOIs.Finally,constraint(12)makesurethatno POIisconnectedtoitself.

Table2.3Decisionvariables

2.2.2 Case Study Area And Dataset

The research is intended to match as much as possiblereal worldproblems.So,Iselectedcertainregions ofKerala,India.Keralaisoneofthemost magnificenttourist destinationsintheworld.

Icollected10datasetswithnearly30POIs.Then,I seekthehelpofatourcompanytofillupthetimesusedin minutesandprofitscoresintherangeof1to100basedon popularity among tourists for each selected POI. I also collected most preferable restaurants in the 10 selected areasbylocalsaswellastourists.Finally,Icollectdetailed descriptionofthePOIsandavailablepublictransportation details inthe areatogivethetouristsmorepossibilitiesin travel.

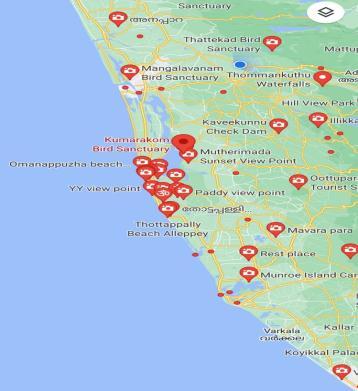
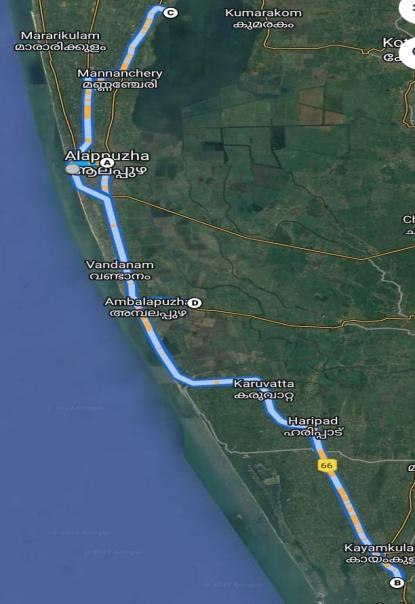
As a result, the map with POIs in the districts Ernakulam,Kottayam,Alappuzha,andKollam isshownin Fig.2.3.Fromthefigure,theredlocationsymboldenotesa POI,wherethecameraiconwithbiglocationsymboldenotes POIshavingmoreprofitscore:Kumarakambirdsanctuary, ThottappallybeachAlappuzha,Munroeislandetc.

The idea in the project is to plan a single day itinerary; the region proposed having POIs to cover for a week, so I created 10 different datasets with 2 or 3 combinations of POIs So the user can select whichever sourceanddestinationsfromthe10sourceanddestination combinationsfromtheregionandthese10datasets have differentcombinationsofPOIs.

Figure2.3 ThePOImapofacertainregionof Kerala.

Table2.2 Parameters

International Research Journal of Engineering and Technology (IRJET) e ISSN: 2395 0056

Volume: 09 Issue: 07 | July 2022 www.irjet.net p ISSN: 2395 0072

Figure2.4Thestructureofattractions.

3. PROPOSED ALGORITHMS

I proposed two algorithms for this work: branchand cutandagreedyalgorithm.Thebranch and cut algorithm guarantees the optimal itineraries, but computational complexity is high. At the same time, the greedyalgorithmcanproducehigh qualityitineraries,not alwaystheoptimalsolutions,though,butthecomputational complexityismuchlower.

3.1 Branch-And-Cut Optimization Algorithm

The branch and cut algorithm have a straightforwardconcept;itisatree based,recursive,and branch and cut algorithm that enhances performance using increment searching and tree pruning. The incrementsearchingstartsatthestartlocationandthen appends all possible attractions to fulfil the itineraries. Duetothecharacteristicoftheincrementalprocess,the need for re calculation from the start location is eliminated. The pruning technique will stop traversing down the tree's deeper levels if any of the following conditionsaremet.

 Thelunchperiodisover,butnorestaurant isincludedintheitinerary.

 APOIwiththeclosingtimeisoverdue

 There is not enough time to append the compulsoryPOIstotheitinerary.

 Arestaurantifthelunchperiodisfulfilled

Whena validitineraryisfound,thealgorithm willperformthePareto dominancetestingforthenewly found itinerary against the current solution set of itinerariestoguaranteethatthesolutionsetalwayskeeps the non dominated itineraries. Algorithm 3.1.1 implements the above concept by eliminating the itinerariesinthecurrentsolutionset;ifthenewitinerary dominates them, the new itinerary will be appended to thesolutionset..However,thealgorithmwillnotinsert theitineraryinto the solutionsetifany itinerary in the solutionsetcandominateit.Theeliminateformulaisat line 4 which each relational operator results in one for trueandzeroforfalse.Thus,thenewitinerarydominates in the solution set if r is positive and the reverse is negative,butbotharenon dominatedsolutionsif r iszero.

Table3.1Thedatastructureofanitineraryusedin algorithms.

Algorithm3.1.1 ParetoDominance

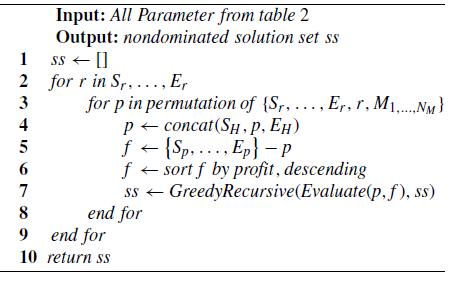
Algorithms3.1.2and3.1.3depictthemainandthe corerecursivealgorithmofthebranch and cutalgorithm, respectively. The main algorithm prepares an empty solutionsetandinitializesanitinerarytohaveonlythe start depot in the path. The itinerary structure is presented in Table 3.1. The core recursive algorithm, Algorithm3.1.2,isarecursivebranch and cutalgorithm thatattemptsto trial all possibilitiesofthesequenceof POIstosearchforallvaliditineraries.Lines1 4checkfor a valid itinerary; if the algorithm can append the end depot, the itinerary is a valid itinerary. The Pareto dominancealgorithmisperformedtoincludetheitinerary tothesolutionset.Line5isthetreepruningthatexecutes whenlunchtimeisoverdue,butnorestaurantisincluded, orthetimeleftforthetourislessthanthetimetovisitthe rest compulsory POIs. Lines 6 17 append each of the candidate POIs into the current itinerary if the current timeplus thetimecosttothecandidatePOIisbetween theoperationaltimeofthePOI.IfthecandidatePOIcanbe appended,thencreateanewitinerarywiththePOIand the new candidate POIs excluding the POI and all restaurants, if the POI is a restaurant. Finally, the algorithmwill call itselfinline16totraversedownthe wholetree.

International Research Journal of Engineering and Technology (IRJET) e ISSN: 2395 0056

Volume: 09 Issue: 07 | July 2022 www.irjet.net p ISSN: 2395 0072

Algorithm3.2.2depictsthecorerecursivealgorithm thatinjectseachPOIfromfintothegivenitinerary.Line1,if the current itinerary is completed, no deeper level is traversed,theParetoDominancefunctioniscalledtoattempt toinsertitintothesolutionset.Afterthat,thepositionofthe restaurant(r)isdeterminedinline3,andattemptstofind thebestorderstobeinsertedandtraverseddown for the before noon period (Lines 4 and 5) and afternoon period (Lines6and7).Line8and9,Thealgorithmalsoignoresthe currentbestunassignedPOIforgivingthechancetoproduce theitinerarieswithoutthatPOI.

Algorithm3.1.2 BranchAndCutMain

Algorithm3.1.3 BranchAndCutRecursive

3.2 Greedy Algorithm

The greedy algorithm builds up the itineraries by filling them with higher profit POIs into all starter paths segments made from each restaurant's permutation and compulsoryPOIs.Therecursive techniqueisemployedtofill up a POI per level of calling, and the algorithm will stop traversing down if a valid itinerary is found. Thus, the algorithmisfastandcanobtainhigh qualityitineraries; it cannotguaranteeoptimaltanneries.

ThemainalgorithmisshowninAlgorithm3.2.1.It buildsthepermuteditinerariesthatcontain onlyessential POIs:arestaurantandcompulsoryPOIs.Theprocessisdone inlines3 5.Consequently,foreachsequenceofPOIs(p);the correspondingunassignedPOIs(f)areassignedandsorted by high to low profits for being injected into p. Line 7, Evaluatefunctionconvertspintoanitineraryandthenfeed tothecorerecursivealgorithm.

Algorithm3.2.1 GreedyMain

Algorithm3.2.2GreedyRecursive

Algorithm 3.2.3 computes the variables from the structure of an itinerary (Table 3.1) from a given POI list. ThealgorithmalsodeterminesthePOIlistthatisvalid,semi valid, or invalid. A valid itinerary is a usable itinerary, whereastheinvaliditineraryviolatestheconstraints:reach aPOIafteritsclosetime(line6),morethanonerestaurant (line10).Moreover,thenumberofcompulsoryPOIsisnot fulfilled (line 15), but no semi valid POI is found, also consideredaninvaliditinerary.Thesemi validiswhenthe constraintoftheopentimeofaPOIisnotsatisfied;thePOIis reached too early. For this case, it is possible to insert anotherPOIbeforethisone(line7).Themainloopinlines5 14 considers each POI in the POI list and gathers nc the numberofcompulsoryPOIs,nrthenumberofrestaurants, andthevariablesintheitinerarystructure.

International Research Journal of Engineering and Technology (IRJET) e ISSN: 2395 0056

Volume: 09 Issue: 07 | July 2022 www.irjet.net p ISSN: 2395 0072

Algorithm3.2.3 Evaluate

Algorithm3.2.4convertsasequenceofPOIsintoan itinerary. Loop in lines 5 14 will try to insert the current highestprofit(f1)intoeachsegmentandthevaliditinerary withtheshortesttotaldistancewillbereturnedtothecaller.

Algorithm3.2.5 LocalSearch

3.3 Solution Ranking

AParetofrontconsistofmultipleitinerariessothe tripplannershavemorechoicestochoosefrom.Basedon their preferences they can choose the most suitable itinerary.Forexample,iftheywanttoenjoythetripasmuch as possible, they may select the itinerary with the highest totalprofitorchoosethelowesttotaldistanceiftheydonot wanttospendmuchtimewalking.Unfortunately,choosing the most suitable itinerary might not be a very important task whentheydonotprovideapreference.

Algorithm3.2.4 FindBestInterpolate

Algorithm 3.2.5 is used for the local search. It attemptstoreplaceaPOIineachitineraryofthesolutionset withaPOIintheunassignedPOIsthatminimizesthetotal distance.Lines1 3areforloopingallPOIsineachitinerary in the solution set. The POIs in the loop must not be the compulsory POIs nor the restaurant, the for loop is implementedwiththischeckinline4.Then,thealgorithm will check if any POIs having equal profit scores with the unassigned POIs, if do, a POI that makes the lowest total distancewillbereplacedwiththeoriginalone.Finally,the algorithmwillreturnthelocalsearchsolutionsetinline15.

Iembracetheconceptofkneesolutionstosolvethis problem,thewidelyacceptedtechniquewhennopreference is provided. Moreover, knee based solution ranking is employedtohighlightoutstandingitinerariesandoffertrip plannersmorechoices.Forthisreason,Iranktheitineraries fromtheParetofrontsthatgeneratedfromtheprevioussub sectionsbyusinganangle dominanceknee basedsolution ranking algorithm called RADA. However, I have post processed the result from RADA not to index the extreme solutions as they are always good choices for the trip plannerstobeconsidered.

Table3.3Parameterssetting.

International Research Journal of Engineering and Technology (IRJET) e ISSN: 2395 0056

Volume: 09 Issue: 07 | July 2022 www.irjet.net p ISSN: 2395 0072

I’mabletogetasmanyneededcombinationsfrom theregion.Figure4.1 showstheparetofrontsoftheregion. Whichincludethebestitinerariescanbefoundforasingle daytripwiththecompulsoryPOIs.

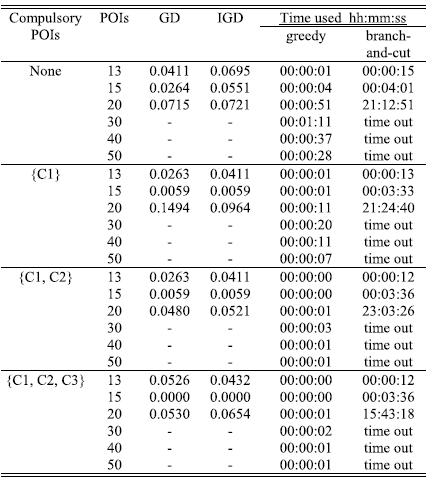
Table3.2Timeusedforgreedyandbranch and cut algorithmsagainstthedataset.

4. EXPERIMENTS AND RESULTS

4.1 Parameter Setting

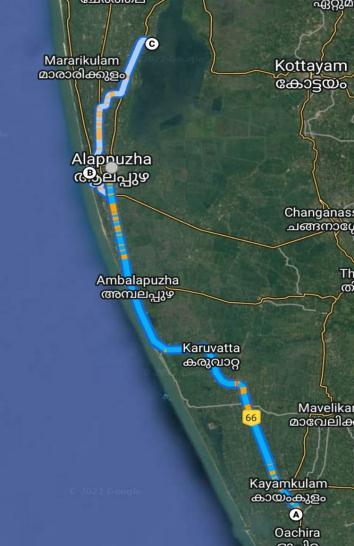
In the experiments, I produce 5 subsets from Alappuzhdistrictinthetheproposedregion,asmentioned inSection2.2.2,eachsubsethavingacombinationofPOIs. The route having 3 compulsory POIs, they are mentioned below..

• AlappuzhaBeach{A}

• KrishnapuramPalace{B}

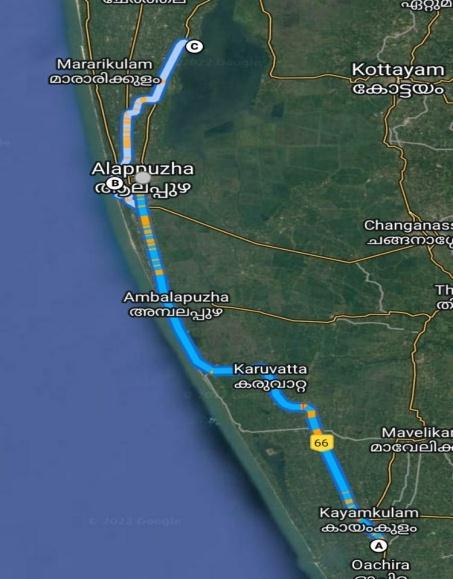
• Pathiramanal{C}

The compulsory POIs are found by the reference of more thanonereliabletouristwebsitesoftheregion.Thereare othermajorattractionsintheareaincluding,

• Kuttanadu

• Karumadi

• AmbalappuzhaTemple

• ArthunkalChurch

• Mannarsalatemple

International Research Journal of Engineering and Technology (IRJET) e ISSN: 2395 0056

Volume: 09 Issue: 07 | July 2022 www.irjet.net p ISSN: 2395 0072

4.2 Evaluation Metrics

This research chooses the top three indicators to evaluate the greedy algorithm against the benchmarked branch and cutalgorithmfromthestandardindicatorsfor multi objectiveoptimization.Theseindicatorsareprobably themostacceptedindicatorsforPareto basedmultiobjective optimization.First,Ipre processedtheresultsbynegating the total profit to minimize both objectives. Then the two objectiveswerenormalizedtothevaluesbetweenzeroand one.TheGandEdenotethesetofgreedyandbranchand cut solutionsets,respectively.

4.2.1 Generational Distance (Gd.)

Generational distanceisdefinedastheaverageof thedistanceofeachitineraryinthegreedysolutionsettoits closestitineraryinthebranch and cutsolutionset.Zerois the ideal solution that implies that two Pareto fronts are preciselythesame.ThedefinitionofGDisshownasEq.V B3.

5.2.2 Inverted Generational Distance (IGD)

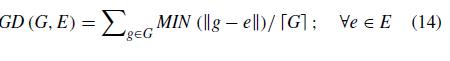
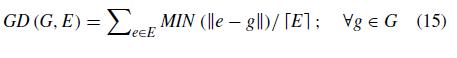
The inverted generational distance (IGD) is the inverse version of GD, defined as the average of the total distanceofeachitineraryinthebranch and cutsolutionset toitsclosestitineraryintheGreedysolutionset.Theconcept ofthevaluesisthesameasGD;Zeroistheidealvalue.The definitionofIGDisshownasEq.(15).

4.3 Itinerary Selection

The above set of POIs are generated on the basis of researchdoneonalmostallthe availabletouristwebsitesof the region. The POIs listed above have the largest profit scores. All of the itineraries generated on the basis of compulsory POIs. The web application is able to list the restaurantsoftheregionalso,soeachitinerarywillhaveits oncorrespondingsetofrestaurants.Atouristhavesomany prioritiestochooseanitinerary,foodisoneofthehighest priority.

Inthisparticularexperiment,Iconsidered Ambalappuzha willhavethelunchbreakandlisted3famousrestaurantsin thePOI.

4.3.1 Itinerary Analysis

We can analyze itineraries from the pareto front, followingistheitineraryconsistsofonlycompulsoryPOIs.

Fig

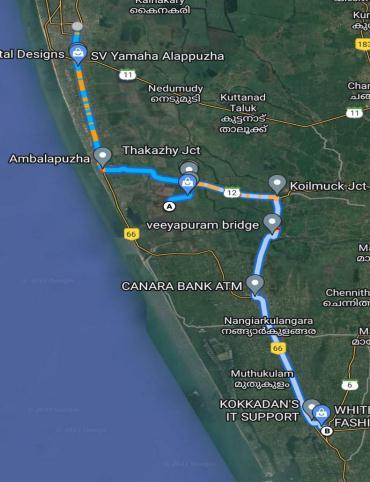
4.2

ItineraryonlyhavingcompulsoryPOIs

Kuttanadu is one of the famous attractions of the area,ItriedtoaddthePOItoourrecommendedroute,and belowisthecorrespondingitinerary.

Fig4.3Unreliableitinerary

SoItisclearfromtheitinerarythatKuttanaduwill givehigherprofittothetrip,butitisnotfitintheitinerary withtheother3compulsoryPOIsandiswillmakethetripto missotherPOIs.

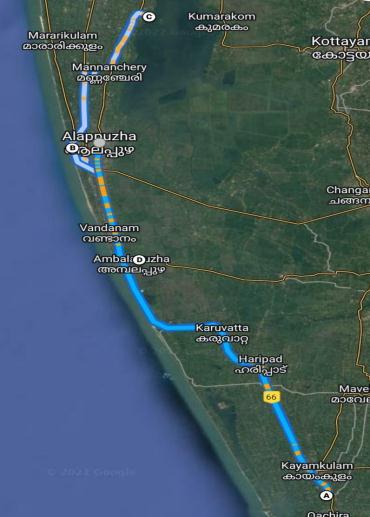
The itinerary only having compulsory POIs is enoughtoplanaonedaytrip,butwearetryingtoincludeall the possible POIs that will satisfy all the requirements. So from the above combination of POIs, below is the one itinerary that include the compulsory POIs and by adding onePOI(D)alongthepathisnotaffectingthetotaldistance butitsgivingmoreprofitinthetravel.

International Research Journal of Engineering and Technology (IRJET) e ISSN: 2395 0056

Volume: 09 Issue: 07 | July 2022 www.irjet.net p ISSN: 2395 0072

complexityofthebranch and cutalgorithmmeasuredina timelimitof48hoursandfounditcaneasilysearchforthe optimalParetofrontsfor13and15POIs,butfor20POIs,it took 15 23 hours runtime. Hence, the branch and cut algorithm failed to find the solutions when the number of POIsismorethan20.Conversely,thegreedyalgorithmcould efficientlyfindsolutionswithinthetimelimit.

I used reactJS and css to develop the UI, The ui having option to enter source and destination then it will populate the well known attractions in the area. After selection of the POIs user have the option for restaurant selectionnearbythePOIs.Thewebapplicationincludethe description of the area and as part of the CO2 emission control,Ihaveincludedtheavailablepublictransportation details,Sothetravelercanrelyonthepublictransportation facilitiesinsteadoftheprivatevehiclewheneverpossible.

Fig4.4Mostsuitableitinerary

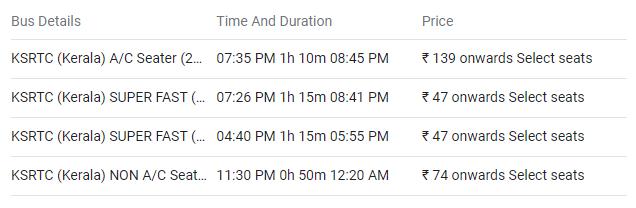
OncethePOIsarefixedbytheuser,thewebsitewill giveasuitabledescriptionabouttheitineraryarea.Fig4.5is thedescriptionusergetforthecurrentitinerary.

Fig4.5 Itinerarydescription

The applicationalsoincluded the public transportation detailsoftheareainadescriptionboxasinFig4.6.

REFERENCES

[1] G.LiandW. Y.Chung,``CombinedEEG gyroscope tDCS brainmachineinterfacesystemforearlymanagementof driverdrowsiness,''IEEETrans.Human Mach.Syst.,vol. 48,no.1,pp.50_62,Feb.2014

[2] Tourism United Behind the Glasgow Declaration on Climate Action at COP26, UNWTO, Glasgow, U.K., 2021.M.Young,TheTechnicalWriter’sHandbook.Mill Valley,CA:UniversityScience,1989.

[3] S. Sohrabi, K. Ziarati, and M. Keshtkaran, ``A greedy randomized adaptive search procedure for the orienteeringproblemwithhotelselection,''Eur.J.Oper. Res.,vol.283,no.2,pp.426440,Jun.2020.

[4] P.Vansteenwegen,W.Souffriau,G.V.Berghe,andD.Van Oudheusden,``Thecitytripplanner:Anexpertsystem for tourists,'' Expert Syst. Appl., vol. 38, no. 6, pp. 65406546,2011.

Fig4.6 Publictransportationdetails

3. CONCLUSIONS

Introducedthenewreal worldtouristtripdesign problem called the multi objective orienteering problem with restaurant selection and compulsory POIs (MOPTW RSCP).Iproposedtwoexactmulti objectivealgorithmsfor solvingtheproblemanddevelopedthewebapplicationin reactJSbyinspiringfromthealgorithms.

Bytheoreticalbasis,thebranch and cutalgorithm can search for all optimized solutions. But, the time complexityofthealgorithmisexponentiallyhigh.Thetime