A Settled Framework for Perishable Component with Lead Time and Price Dependent Condition

International Research Journal of Engineering and Technology (IRJET) e ISSN: 2395 0056

Volume: 09 Issue: 06 | Jun 2022 www.irjet.net p ISSN: 2395 0072

A Settled Framework for Perishable Component with Lead Time and Price Dependent Condition

Lovekush1, Lokendra Kumar2

1M.Sc Student, Monad University, Hapur

2Associate Professor, Department of Mathematics, Monad University ,Hapur ***

Abstract: In the enable paper, an effort has been created to develop a settled inventory model for biodegradable things with time interval and value dependent demand. Shortages area unit allowed and utterly backlogged. The matter of unsatisfactoriness or deterioration plays a crucial role within the field of internal control and management. The aim of our study is to reduce the whole variable inventory value throughout a given amount of your time. A numericalexample is given to demonstrate the developed model.

Key Words: Inventory, Deterioration, Lead Time and Price DependentDemand

1. INTRODUCTION

Academicians likewise as industrialists have nice interest withinthedevelopmentofinternalcontrolandtheiruses. Thereareaunitseveralmerchandisethateitherdeteriorate or become obsolete with passage of your time. For such destructible merchandise totally different modeling techniquesareaunitapplied.Destructibleinventoryforms atiny low a part of total inventory and includes trendy clothes, electronic things, digital merchandise and periodicals. The destructible merchandise is classified supported two categories: (1) deterioration (2) degeneration. Deterioration is outlined as harm, decay or spoilageofthethingsthatareaunitkeepforfutureuseand thatperpetuallylooseapartoftheirworthwithpassageof your time. Degeneration happens thanks to the arrival of latestandhighermerchandisewithinthemarket.

Intheexistingliterature,someinventorymodelsthatwere developedbymodernresearchersconsideringsomeorallof the parameters associated with constant demand rate, increasing/decreasingoperateofyourtime,valueandstock dependent are quoted. The demand of fresh arrived merchandise in market is influenced by their costs, as a result of the enticing costs or offers on the merchandise inspiretheshopperstoshopforalotof.Thisexamplewill increasetheorderamountoftheretailersorcustomers.In recent years some researchers additionally gave their attentiontowardsatimedependentrate,asaresultofthe demandoffreshlaunchedmerchandiseliketrendyclothes, electronicthings,motorcars,mobilesetc.willincreasewith timeandlateritbecomesconstant.

But within the real world there area unit several things within which these assumptions aren't valid like seasonal merchandise, work merchandise, electronic things and medicines.Someresearcheswithinthespaceareaunitvalue mentioning.GoswamiandChaudhuri[1]developedanEOQ modelfordeterioratingthingswithlineartrendindemand andshortages.PadmanabhanandVrat[2]thought aboutan EOQ model for destructible things with stock dependent commerce rate. Giri et al. [3] projected a list model for deteriorating things with stock dependent demand rate. Hargia[4]gaveanEOQmodelfordeterioratingthingswith timevariabledemand.GiriandChaudhuri[5]developeda settledinventorymodelfordeterioratingthingswithnon linear holding value and stock dependent demand rate. ChangandDyeprojectedtwoinventorymodels[6]and[11]. Themodel[6]isanEOQmodelfordeterioratingthingswith timevariabledemandandpartialbacklogging.andalsothe model [11] is a list model for destructible things with permissibledelayinpaymentsandshortages.Chungetal.[7] gave a note on EOQ models for deteriorating things with stockdependentcommercerate.Linetal.[8]projectedAN EOQ model for deteriorating things with time variable demandandpermittingshortages.PapachristosandSkouri developedtwoinventorymodels[9]and[12].Inmodel[9] they gave an optimum refilling policy for deteriorating things with exponential kind backlogging rate and time variable demand. The model [12] may be a continuous reviewinventorymodelfordeterioratingthingswithtime dependentdemandandpermittingshortages.GoyalandGiri developed two inventory models [10] and [15]. In model [10] they thought about recent trends in modeling of deterioratinginventory.andalsothemodel[15]maybea production inventory model with time variable demand, production and deterioration rate. Chinese [13] projected AN EOQ model for Weibull deteriorating things with time variabledemandandpermittingshortages.Wang[16]gavea noteonEOQmodelfordestructiblethingswithexponential distribution,deteriorationandtimedependentdemandrate. Theyadditionallythought aboutshortagesintheirinventory model.DyeandOuyang [17]developedanEOQ model for destructiblemerchandisewithstockdependentcommerce rateandpermittingshortages.Sovereign[18]projectedalist modelfordeterioratingthingswithcontinuanceofcashand permissible delay in payments. She thought about a finite comingupwithhorizon in herinventory model.HouANd sculptor [19] developed an EOQ model for deteriorating thingswithvalueandstockdependentcommercerate.They

International Research Journal of Engineering and Technology (IRJET) e ISSN: 2395 0056

Volume: 09 Issue: 06 | Jun 2022 www.irjet.net p ISSN: 2395 0072

thought about the impact of inflation and continuance of cashintheirinventorymodel.Dyepresentedajointrating and ordering policy for deteriorating things with partial backlogging. Roy et al. [21] given a list model for deterioratingthingswithstockdependentdemandrateand fuzzy kind inflation. They additionallythought about time discountingoverarandomcomingupwithhorizon.Minand Chowdynasty[22]developedalistmodelfordeteriorating thingswithstockdependentcommercerateandpermitting shortages. Jain et al. [23] projected a list model for deteriorating things with fuzzy kind inflation and money discountingoverrandomcomingupwithhorizon.Pandaet al. [24] developed a two warehouse inventory model for deteriorating things with fuzzy kind demand rate and interval. Roy [25] projected a fuzzy inventory model for deteriorating things with value dependent demand rate. ChaudharyandSharma[26]givenalistmodelforWeibull deteriorating things with value dependent demand rate beneathinflation.MaragathamandPalani[27]developeda list model for destructible things with interval, value dependentdemandandpermittingshortages

2. ASSUMPTIONS NOTATIONS

Weconsiderthefollowingassumptionsandnotations

Thedemandrateis R(p) a p b , a,b 0

Here p isthesellingprice.

Thedeteriorationrateistakenas (t) t

Oc istheorderingcostperorder.

hc istheholdingcostperunittime.

sc istheshortagecostperunittime.

pc isthepurchasecostperunittime.

T isthereplenishmentcyclelength.

I(t) istheinventorylevelatanytimetin 0,T .

T1 isthetimeatwhichinventorylevelbecomeszero

TC(L,T1,T)isthetotalvariableinventorycostpercycle.

Thereplenishmentrateisinfinite.

TheleadtimeisL.

There is no repair or replacement of the deteriorated items

3. MATHEMATICAL FORMULATION

Suppose a list system contains the utmost inventory level letterR(p)withinthestartingofeverycycle,whereverR(p)is thattheworthdependentdemand.Throughouttheinterval L,T1,theinventoryleveldecreasesbecauseofeachdemand

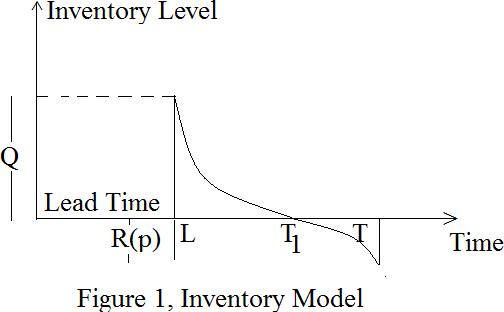
anddeteriorationanditbecomeszeroatt,T1.Throughout the shortage interval [T1,T ] the demand is unhappy. The instant inventorylevel atany time tinL, Tis given by the subsequentdifferentialequations:

Boundarycondition I(T1) 0 istakeninbothequations.

The solutions of the above equations are given by the followingequations.Byconsideringthefirstdegreetermsin θ,wehave

Themaximuminventorylevelisobtainedbyputting t Lin equation(3),so

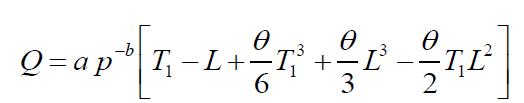
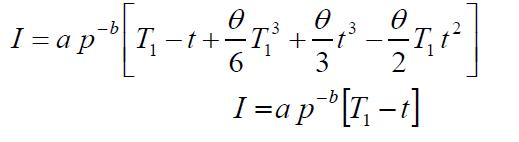
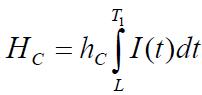
Thequantity Q LD(p)is ordered in the beginning ofeach cycle. The maximum backorderedquantity IB is obtainedbyputting t T inequation(4).Therefore

TheorderingcostpercycleisOc=Oc

Theholdingcostpercycleis

2022, IRJET | Impact Factor value: 7.529 | ISO 9001:2008 Certified Journal

International Research Journal of Engineering and Technology (IRJET) e ISSN: 2395 0056

or Putting the values of OC , HC , DC , SC and PC in above equation,weobtain

Thenecessaryconditionsfor TC(L,T1,T)tobeminimumare

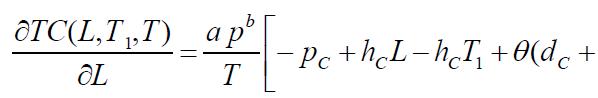
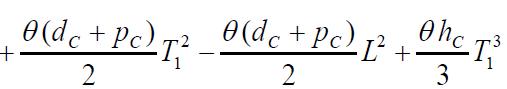
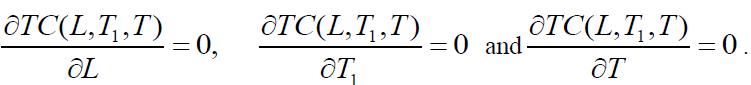
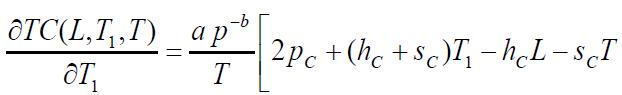
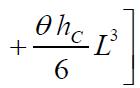
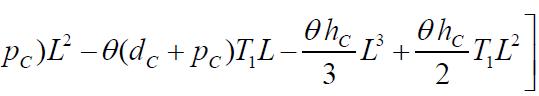
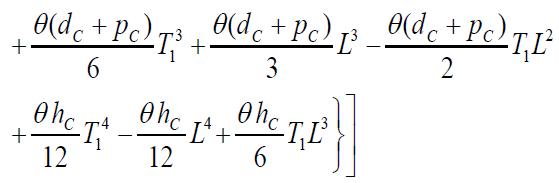
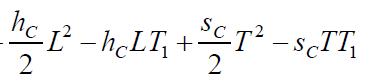
Onsolvingtheseequations,wefindtheoptimumvaluesofL, T1 and T for which the total variable inventory cost is minimum The sufficient conditions for TC(L,T1,T ) to be minimumarethattheprincipalminorsofHessianmatrixor Hmatrixarepositivedefinite.TheHessianmatrixisdefined asfollows:

Partiallydifferentiatingequation(13),wehave

Volume: 09 Issue: 06 | Jun 2022 www.irjet.net p ISSN: 2395 0072 © 2022, IRJET | Impact Factor value: 7.529 | ISO 9001:2008 Certified Journal

International Research Journal of Engineering and Technology (IRJET) e ISSN: 2395 0056

Volume: 09 Issue: 06 | Jun 2022 www.irjet.net p ISSN: 2395 0072

Numerically,theHessianmatrixorHmatrixisgivenby

4. NUMERICAL EXAMPLE

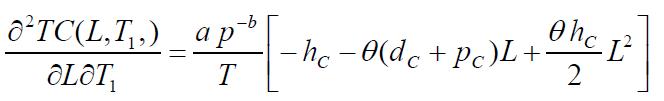
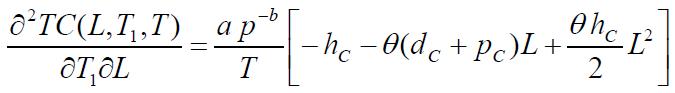
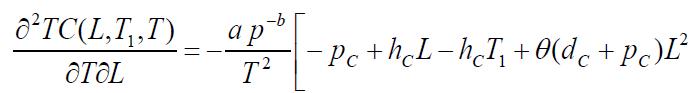
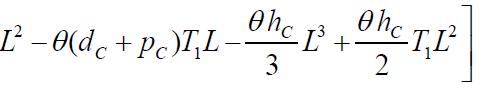
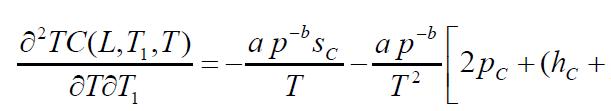
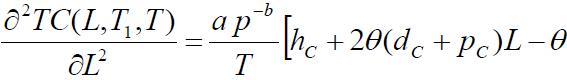
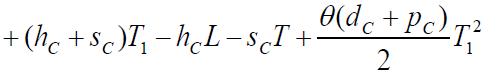
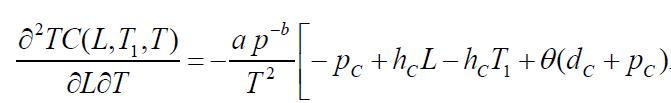
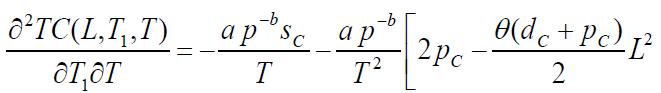
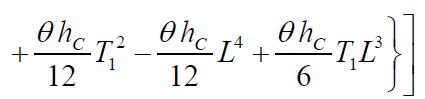
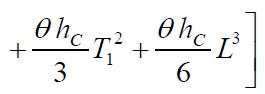
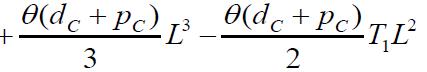
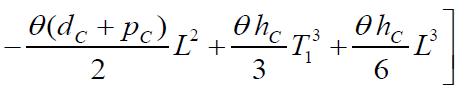
Let us consider the following data for parameters in the appropriateunitsasfollows

L T1 T TC(L,T1,T)

0.05 15.2579 6.0163 10.4284 303.5640 0.10 12.4212 4.4046 8.8553 307.2574 0.15 11.2630 3.7017 8.4324 334.1419 0.20 10.6132 3.2903 8.3558 366.2981 0.25 10.1905 3.0164 8.4296 399.6628

Table 1, variation in total inventory cost with respect to a

Fromthetable1,weseethatifweincreasethedeterioration parameter thenthevaluesof L, T1 and T aredecreased, butthevaluesof TC(L,T1,T)getincreased.

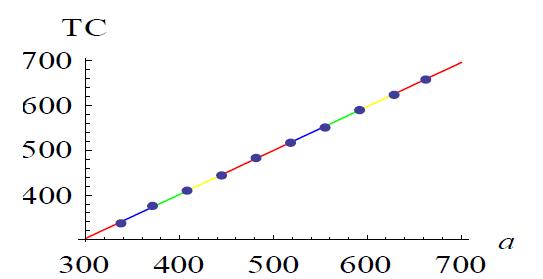
a L T1 T TC(L,T1,T)

300 15.2579 6.0163 10.4284 303.5640 400 15.2507 6.0088 10.3936 401.0250 500 15.2449 6.0028 10.3660 498.3465 600 15.2423 6.0000 10.3531 595.7901 700 15.2404 5.9981 10.3439 693.2439

Table 2, variation in total inventory cost with respect to a

2022, IRJET | Impact Factor value: 7.529 | ISO 9001:2008 Certified Journal | Page2022

International Research Journal of Engineering and Technology (IRJET) e ISSN: 2395 0056

From this table, we see that if we increase the demand parameter a, then the values of values of TC(L, T1, T ) get increased.L,T1andTaredecreased,butthevaluesof TC(L, T1, T)getincreased.

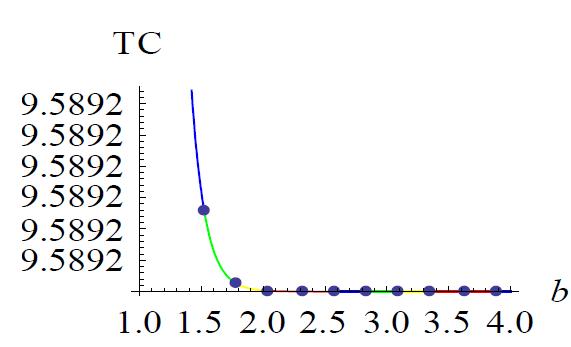
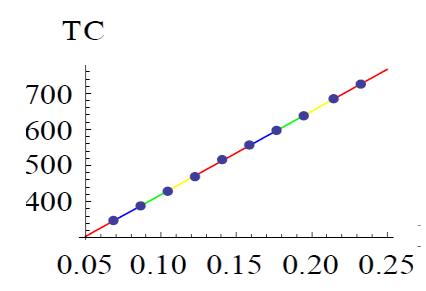
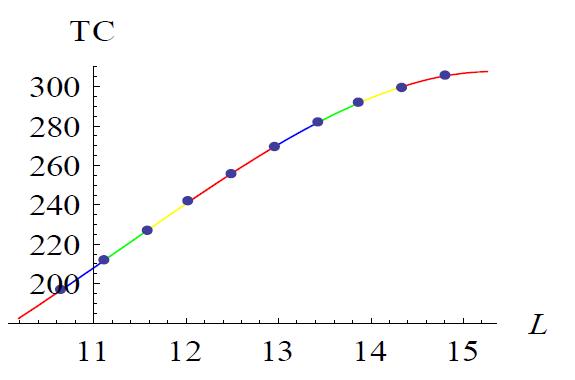
Figure 2, variation in TC with respect to θ ,

Figure 5, variation in TC with respect to L

5. CONCLUSION

The results of the proposed model show that the total variableinventorycostisdeeplyimpactedbytheparameters aandbincomparisonwitht the reason that the newly arrived goods/products in the supermarketincreasethedemand.Thecyclelengthandlead timearemaincomponentsforoptimizingthecost/profitof an organization. The products such as vegetables, milk, bakeryproductsandnewspapersarenecessarilytobesold inthemarketasthecyclelengthdecreases.

REFERENCES

Figure 3, variation in TC with respect to a

b L T1 T TC(L,T1,T)

1 15.2579 6.0163 10.4284 303.5640

2 3 4

15.8578 19.9962 30.4007

6.6203 10.1909 17.8134

13.4213 40.6606 183.5960

21.3155 4.5005 1.0255

Table 3, variation in total inventory cost with respect to b

From this table, we see that if we increase the demand parameterb,thenthevaluesofL,T1andTareincreased,but thevaluesofTC(L,T1,T)getdecreased.

[1] A. Goswami and K. S. Chaudhuri, “An EOQ model for deteriorating items with linear trend in demand and allowing shortages”, Journal of Operational Research Society,Vol.42,pp.1105 1110,1991.

[2] G. Padmanabhan and P. Vrat, “An EOQ model for perishable items with stock dependent selling rate”, European Journal of Operational Research, Vol. 86, pp.281 292,1995.

[3] B. C. Giri, S. Pal, A. Goswami and K. S. Chaudhuri, “An inventory model for deteriorating items with stock dependent demand rate”, European Journal of OperationalResearch,Vol.95,pp.604 610,1996.

[4] M.Hargia,“AnEOQmodelfordeterioratingitemswith timevaryingdemand”,JournalofOperationalResearch Society,Vol.47,pp.205 213,1996.

[5] B.C.GiriandK.S.Chaudhuri,“Adeterministicinventory model for deteriorating items with stock dependent demand rate and non linear holding cost”, European Journal of Operational Research, Vol.105, pp.464 467,1998.

[6] H.J.ChangandC.Y.Dye,“AnEOQ model for deteriorating items with time varying demand and partial backlogging”, Journal of Operational Research Society,Vol.50,pp.1176 1182,1999.

Figure 4, variation in TC with respect to b

[7] K.J.Chung,P.ChuandS.P.Lan,“AnoteonEOQmodels for deteriorating items with stock dependent selling

Volume: 09 Issue: 06 | Jun 2022 www.irjet.net p ISSN: 2395 0072 © 2022, IRJET | Impact Factor value: 7.529 | ISO 9001:2008 Certified Journal | Page

International Research Journal of Engineering and Technology (IRJET) e ISSN: 2395 0056

rate”, European Journal of Operational Research, Vol.124,pp.550 559,2000.

[8] B. Lin, B. Tan and W. C. Lee, “An EOQ model for deteriorating items with time varying demand and shortages”, International Journal of Systems Science, Vol.31,pp.391 400,2000.

[9] S. Papachristos and K. Skouri, “An optimal replenish policy for an inventory model of deteriorating items with time varying demand and exponential type backloggingrate”,OperationsResearch Letters, Vol.27,pp.175 184,2000.

[10] S.K.GoyalandB.C.Giri,“Recenttrendsinmodelingof deteriorating inventory”, European Journal of OperationalResearch,Vol.134,pp.1 16,2001.

[11] H. J. Chang and C.Y. Dye, “An inventory model for deterioratingitems withpermissibledelayinpayments andallowing shortages”, International Journal of SystemScience,Vol.32pp.345 352,2001.

[12] K. Skouri and S. Papachristos, “A continuous review inventorymodelfor perishable items with time dependent demand and partial backlogging”, Applied MathematicalModeling,Vol.26,pp.603 617,2002.

[13] K.S.Wu,“AnEOQmodelforweibull deteriorating items with time varying demand and partial backlogging”InternationalJournalofSystemsScience, Vol.33,pp.323 329,2002.

[14] S. P. Wang, “An optimal lot sizing policy for an inventory model of deteriorating items with time varying demand and shortages”, Journal of Chinese InstituteofIndustrialEngineering,Vol.20,pp.449 456, 2003.

[15] S.K.GoyalandB.C.Giri,“Aproductioninventorymodel for deterioratingitemswithtimevaryingdemandrate”, EuropeanJournalofOperationalResearch,Vol.147,pp. 549 557,2003.

[16] W. H. Lee and J. W. Wu, “A note on EOQ model for deteriorating items with exponential distribution deterioration and time dependent demand and shortages” International Journal of Systems Science, Vol.31,pp.677 683,2004.

[17] Y.DyeandL.Y.Ouyang,“AnEOQmodelforperishable items with stock dependent selling rate and time dependent artial backlogging”, European Journal of OperationalResearch,Vol.163,pp.776 783,2005.

[18] N.H.Shah,“Aninventorymodelfordeterioratingitems together with time value of money for a finite time horizon under permissible delay in payments”,

InternationalJournalofSystemsScience,Vol.37,pp.9 15, 2006.

[19] K.L.HouandL.C.Lin,“AnEOQmodelfordeteriorating itemswithpriceandstockdependentsellingrateunder inflationandtimevalueofmoney”,InternationalJournal ofSystemsScience,Vol.37,pp.1131 1139,2006.

[20] C. Y. Dye, “A joint pricing and ordering policy for deteriorating items with partial backlogging”, Omega TheInternationalJournalManagementScience,Vol.35, pp.184 189,2007.

[21] A.Roy,M.MaitiandM.K.Kar,“Aninventorymodelfor deterioratingitemswithstockdependentrateandtime discounting over a random planning horizon under fuzzyinflation”,AppliedMathematicalModeling,Vol.33, pp.744 759,2009.

[22] J.MinandY.W.Zhou,“Aperishableinventorymodelfor deterioratingitems with stock dependentselling rate, shortages together with capacity constraints”, InternationalJournalofSystemsScience,Vol.40,pp.33 44,2009.

[23] D.K.Jain,B.DasandT.K.Roy,“Aninventorymodelfor perishable items with fuzzy type inflation and cash discountingoverrandomplanninghorizon”,Advances inOperationsResearch,Vol.2013,pp.1 15,2013.

[24] D. Panda, M. Rong and M. Maiti, “A two warehouse inventorymodelfordeterioratingitemswithfuzzytype demand rate and lead time”, European Journal of OperationsResearch,Vol.22,pp.187 209,2014.

[25] A.Roy,“Fuzzy inventory model of deterioratingitems with price dependent demand rate”, International Journal of Management Science and Engineering Management,Vol.10,Issue.4,pp.237 241,2015.

[26] R. R. Chaudhari and V. Sharma, “A model for weibull deterioratingitemswithpricedependentdemandrate andinflation”,IndianJournalofScienceandTechnology, Vol.8,Issue.10,pp.975 981,2015.

[27] M.MaragathamandR. Palani,“An inventorymodelfor deteriorating items with lead time, price dependent demand and shortages”, Advances in Computational ScienceandTechnology,Vol.10,Issue.6,pp.1839 1847, 2017.

Volume: 09 Issue: 06 | Jun 2022 www.irjet.net p ISSN: 2395 0072 © 2022, IRJET | Impact Factor value: 7.529 | ISO 9001:2008 Certified Journal |