TWO WAREHOUSE INVENTORY MODEL FOR DETERIORATING THINGS WITH SHORTAGES BELOW THE CONDITIONS OF PERMIS by IRJET Journal

TWO WAREHOUSE INVENTORY MODEL FOR DETERIORATING THINGS WITH SHORTAGES BELOW THE CONDITIONS OF PERMISSIBLE DELAY IN PAYMENTS

Jatin1, Lokendra Kumar2

1M.Sc Student, Monad University, Hapur 2Associate Professor, Department of Mathematics Monad University, Hapur ***

Abstract: In this paper, a deterministic inventory model for deteriorating items with two warehouses and shortages is developed. The conditions of permissible delay in payments are also taken into consideration. A rented warehouse is used when the ordering quantity exceeds the limited capacity of the owned warehouse, and it is assumed the deterioration rates of items in the two warehouses may be different. In addition, shortages are neither completely backlogged nor completely lost assuming the backlogging rate to the inversely proportional to the waiting time for the next replenishment. We obtain the condition when to rent the warehouse and provide simple solution procedures for finding the minimum total cost per unit time. We presented special cases of this model. In one of the case we considered that the capacity of OW is infinite so there is no need of rented warehouse. In other case we consider that deterioration is not allowed and shortage are allowed and completely backlogged.

Key-Words : Two warehouseinventorymodel,shortage, time dependent demand rate, time dependent partial backlogging rate, time dependent deterioration rate, permissibledelayinpayments.

1. INTRODUCTION

In today's business transactions, it's oftentimes ascertained that a client is allowed some grace amount before subsiding the account with the provider or the producer. The client doesn't need to pay any interest throughout this fastened amount however if the payment gets on the far side the amount interest are going to be charged by the provider. This arrangement comes intent onbeterriblyadvantageoustotheclientashemightdelay thepaymentuntilthetipofthepermissibledelayamount. throughout the amount he might sell the products, accumulate revenues on the sales and earn interest on it revenue. Thus, it makes economic sense for the client to delay the payment of the renewal account upto the Judgment Day of the settlement amount allowed by the provider or the producer. Goyal (1985) 1st developed associate degree economic order amount (EOQ) model below the condition of permissible delay in payments. Chung (1989) given the discounted income approach for

the analysis of the best inventory police within the presence of trade credit. Later, Shinn et al. (1996) extended Goyal's (1985) model and thought of amount discountsforfreightprice.Recently,toaccommodatealot of sensible options of the $64000 inventory systems, Aggarwal and Jaggi (1995) and Hwang and Shinn (1997) extended Goyal's (1985). afterward Jamal et al (1997) extended Aggarwal and Jaggi (1995) model to permit for shortagesandcreateitalotofapplicableinuniverse.

Inclassicalinventorymodelsisthattheorganizationowns one warehouse while not capability limitation. In follow, whereasan oversized stock is to becommand, becauseof the restricted capability of the in hand warehouse (OW), one extra warehouse is needed. this extra warehouse is also a rented warehouse (RW), that is assumed to be accessible with luxuriant capability. There exist some sensible reasons specified the organizations area unit impelledtoorderalotofthingsthenthecapabilityofOW. for instance, the worth discount for bulk purchase is also advantageoustothemanagement;thedemandofthingsis also high enough specified a substantial increase in profit is predicted, and so on. In these things, it's usually assumedthattheholdingpriceinRWisabovethatinOW. to scale back the inventory prices, it'll be economical to consumetheproductsofRWattheearliest.

Anearlydiscussionontheimpactoftwo warehouseswas thought of by David Hartley (1976). Recently different authors have thought of this kind of inventory model. Sarma (1983) developed a settled inventory model with finite renewal rate. Dave (1988) any mentioned the cases of bulk unharness pattern for each finite and infinite renewalrates.HecorrectedtheerrorsinMurdeshwarand Sathe(1985)offer|andprovides}anentireanswerforthe model give by Sarma (1983). within the higher than literature, deterioration development wasn't taken into consideration. Presumptuous the deterioration in each warehouses,Sarma(1987)extendedthemodeltothecase of infinite renewal rate with shortages. Pakkala and Achary (1992) extended the two warehouse inventory modelfordeterioratingthingswithfiniterenewalrateand shortages, taking time as separate and continuous variable,severally.Inthesemodelsmentionedhigherthan

International Research Journal of Engineering and Technology (IRJET) e ISSN: 2395 0056

Volume: 09 Issue: 06 | Jun 2022 www.irjet.net p ISSN: 2395 0072

thedemandratewasassumedtobeconstant.lateron,the concepts of your time variable demand and stock dependent demand thought of by some authors, like Goswami and Chaudhuri (1998) Bhunia and Maiti (1998) Bankherouf (1997), kar et al. (2001) et al.. Dye, Ouyang andHsich(2006)developedasettledinventorymodelfor deteriorating things with capability constraint and time proportionalbackworkrate.

Furthermore, the characteristics of all higher than papers area unit that shortages don't seem to be allowed or assumed to be fully backlogged. Zhou (2003) given a multi warehouse inventory model for non perishable things with time varyingdemandand partial backlogging. In his model, the backlogging operate was assumed to be addicted to the number of demand backlogged. In several casescustomersareaunitconditionedtoashippingdelay, and will be willing toattendfor a brief timeso as tourge their 1st selection. usually speaking, the length of the waitingtimeforsucceedingrenewalisthatthemainissue for deciding whether or not the backlogging are going to beacceptedornot.Thetemperamentofa clienttoattend for backlogging throughout a shortage amount declines with the length of the waiting time. Abad (1996, 2001) mentioned a valuation and lot sizing downside for a productwithavariablerateofdecay,permittingshortages andpartialbacklogging.

In this paper, we have a tendency to develop a settled inventory model for deteriorating things with two warehouses. We have a tendency to assume that the inventory prices (including holding price and deterioration price in RW area unit above those in OW). additionally shortages area unit allowed within the in hand warehouse and therefore the backlogging rate of unhappydemandisassumedtobeadecreasingoperateof the waiting time. Shortages area unit of nice importance particularly in a very model that considers a delay in payment because of the very fact that shortages will impact the amount ordered to learn from the delay in payment. Currently there arises a natural question whether or not the amount of the amount ordered influences the length of the permissible delay amount. Intuition results in the very fact that {the volume/the amount/the amount/the degree} of the ordered quantity ought to have an on the spot impact on the length of this era. The current paper incorporates this reality in a list model permittingshortagesandobtainsthebestordering policy.

2. NOTATIONS AND ASSUMPTIONS

To develop the planned inventory model with two warehouses, the subsequent notations and assumptions squaremeasureutilizedinthispaper:

I1(t) theamountofinventorypositiveinRWofyourtime t.

I2(t) thelevelofpositiveinventoryinOWofyourtimet.

I3(t) thelevelofnegativeinventoryattimet.

D thedemandrateperunittime

A therefillingpriceperorder

C thebuyingpriceperunit

S thepriceperunit,whereS≥C

W thecapabilityoftheinhandwarehouse

H theholdingpriceperunitperunittimeinOW

F theholdingpriceperunitperunittimeinRW,where F>H

C2 theshortagepriceperunitperunittime

π theopportunitycostperunit

α thedeteriorationrateinOW,wherever 1 0   

β thedeteriorationrateinRW,wherever 1 0   

Tw thetimeatthattheinventorylevelreacheszeroinRW

t1 thetimeatthattheinventorylevelreacheszeroinOW

t2 thelengthofamountthroughoutthatshortagessquare measureallowed

T thelengthoftheinventorycycle,henceT=t1 +t2

Ie interestwhichmightbeattained

Ir interestchargesthatendowedininventory,Ir >Ie M permissibledelayinsubsidingtheaccounts,0<M<T

CM(t1,T) Average total inventory price per unit time, once permissibledelayamountinpaymentisM Let

Thefollowingassumptionsareused: (i) Replenishment rate is infinite, and lead time is zero. (ii) The time horizon of the inventory system is infinite.

  M1 1 Ct,T for MtMCt,T11 2 Ct,T for MtM 11              

uswrite:

International Research Journal of Engineering and Technology (IRJET) e ISSN: 2395 0056

Volume: 09 Issue: 06 | Jun 2022 www.irjet.net p ISSN: 2395 0072

(iii) The closely held warehouse (OW) contains a fastened capability of W units, the rented warehouse(RW)hasunlimitedcapability.

(iv) The product of OW square measure consumed solelyonceintensetheproductsunbrokeninRW.

(v) The unit inventory costs (including holding cost and deterioration cost) per unit time in RW are higherthanthoseinOW,thatis,F+C>H+C.

(vi) To guarantee the optimal solution exists, we assume that the maximum deteriorating quantity fortimesinOW, W,islessthanthedemanddate D,that, W<D

(vii) Shortages are allowed. Unsatisfied demand is backlogged, and the fraction of shortages back ordered is 1 1x  , where x is the waiting time up to the next replenishment and  is a positive constant.

No payment to the supplier is outstanding at the time of placinganorderi.e.M<T.

3. MATHEMATICAL FORMULATION

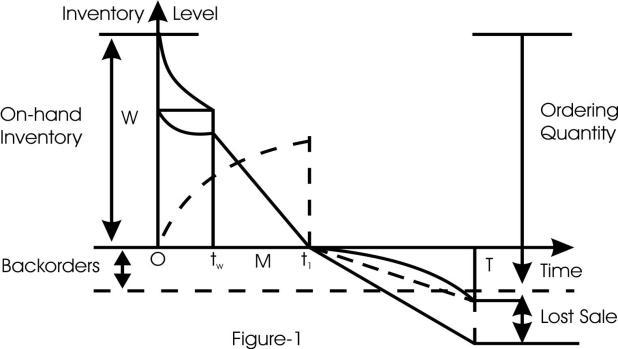
with the initial condition I2(0) = W, respectively. Solving equations (1) and (2), we get the inventory level as follows:     w tt 1 D Ite1     , 0<t<tw ...(3) and I2(t)= –tWe  , 0<t<tw ...(4)

Duringtheinterval[tw,t1],theinventoryinOWis depleted due to the combined effects of demand and deterioration. Hence, the inventory level at OW is governedbythefollowingdifferentialequation:     2 2 dIt DIt dt  , tw <t<t1 ...(5)

with the boundary condition I2(t1) = 0. Solving the differentialequation(5),Wegettheinventorylevelas:     1 tt 2 D Ite1     , tw <t<t1 ...(6)

Due to continuity of I2(t) of point t = tw, from equation(4)and(6),wehave   1w w tt –t D Wee1      ...(7)

Thisimpliesthat w–t 1w 1We ttIn1 D

      ...(8)

AsshowninFig.1,weconsiderthefollowingtime intervals separately, [0, tw], [tw, t1] and [t1, T]. During the interval[0,tw],theinventorylevelsarepositiveatRWand OW.AtRW,theinventoryisdepletedduetothecombined effectsofdemandanddeterioration.AtOW,theinventory is only depleted by the effect of deterioration. Hence the inventory level at RW and OW are governed by the followingdifferentialequations;

whichshowsthatt1 isafunctionoftw Furthermore, at time t1, the inventory level reaches zero in OW and lack happens. During [t1, T], the inventory level solely depend upon demand, and a few demand is lost whereas a fraction   1 1Tt  of the demand is backlogged, where t  [t1, T]. The inventory levelisgovernedbythefollowingdifferentialequation:

T …(9)

with the boundary condition I3(t1) = 0. Solving the differentialequation(10),wegettheinventorylevelas:

boundarycondition

  

 1 1 dIt dtDIT,  0<t<tw ...(1) withthe

w)=0and     2 2 dIt It dt  , 0<t<tw …(2)

    3 dIt D dt1Tt,   t1<t<

    





  31 D ItIn1TtIn1Tt,  

t1 <t<T ...(10)

International Research Journal of Engineering and Technology (IRJET) e ISSN: 2395 0056 Volume: 09 Issue: 06 | Jun 2022 www.irjet.net p ISSN: 2395 0072

ISO

Basedonequations(3),(4),(6)and(11),thetotal costpercycleconsistsofthefollowingelements: 1. Orderingcostpercycle=A 2. HoldingcostpercycleinRW   wt RW1 0 HCFItdt    wt 2 w FDet1/   3. HoldingcostpercycleinOW     w 1 w t t OW22 0t HCHItdtItdt        1w HWDtt/    4. Shortagecostpercycle:         1 T 2 23211 t SCCItdtCDTtIn1Tt/     5. Opportunitycostduetolostsalespercycle:   1 T t 1 OCD1dt 1Tt                11 DTt–In1Tt/    ThenumberofdeteriorateditemsinRWin[0,tw]is I(0) wt 0 Ddt  wt w D e1Dt      andthenumberofdeteriorateditemsinOWin[0,t1]is     1t 2 0 I0Dt    1wWDtt  6. Deteriorationcostpercycle: DC  wt 1 D Pe1DtW        Case

M < t1

credit

1) TheinterestearnedIE1 is IE1=CIe   1t 2 1 1e1e 0 t IECIDttdtDCI 2   ...(11)

    1t 2 r r11 M DCI IPCIDttdttM 2   ...(12) Thereforethetotalaveragecostperunittimeis:   1 RWOW1 M1 OCHCHOSCOCDCIPIE Ct,T T       wt w1w 2 1FDH Aet1WDtt T             2 2222 2 CD D tIn1ttIn1t           w 2 2 t r1 11e DCIt D Pe1DtWtMDCI 22          (13) Optimal values of t1 and T, which minimize   1 M1 CtT areobtainedbysolvingtheequations.     11 M1M1 1 Ct,TCt,T and 0 dtdT   Whichgive Providedtheysatisfythesufficientconditions         ** 1 ** 1 2121 M1M1 22 t,T 1 t,T Ct,TCt,T0,0 tT    and         ** 1 212121 M1M1M1 22 1 1 t,T Ct,TCt,TCt,T0 tTtT        ...(14) Case 2: M > t1: SinceM>T1,thebuyerpaysnointerestbutearns interestatanannualrateIe duringtheperiod(0,M) interestearnedinthiscase,denotedbyIE2,isgivenby:     11 tt 2e11 00 IECIttDdtMtDdt      1 e1 t CIDtM 2    ...(15) Thenthetotalaveragecostperunittimeis     2 M1RWOW2 1 Ct,TOCHCHCSCOCDCIE T      wt 2 w1w 22 CD 1FDH Aet1WDtt T         

value: 7.529 |

9001:2008 Certified Journal | Page2010

In this state of affairs, since the length of amount with positive stock is larger than the

amount, the client willusethesalerevenuetoearninterestatanannualrate Iethatisin(0,t

Howeverbeyondcreditperiod,theunsoldstockis supposed to be financial with an annual rate I

and the interestpayableIPisgivenby:

International Research Journal of Engineering and Technology (IRJET) e ISSN: 2395 0056 Volume: 09 Issue: 06 | Jun 2022 www.irjet.net p ISSN: 2395 0072

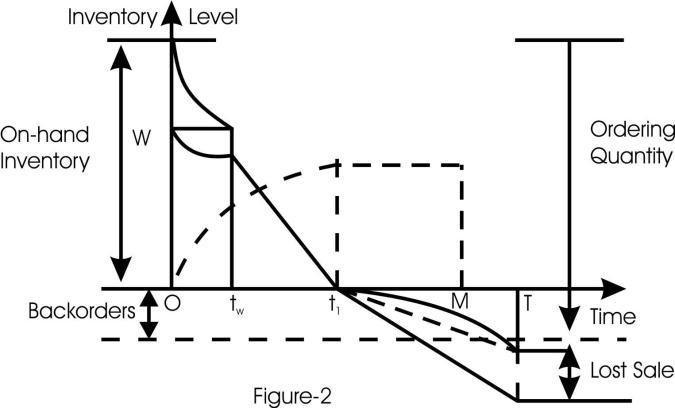
problem without capacity constraint in OW:WhenthespaceofOWissoabundantthenthereisno need to use RW; In this situation the previous model reduces to the single warehouse inventory problem. We removethecapacityconstraintoftheOW

These results are same as those obtain by Chung Yuan Dye (2002).

3.2. Particular Case B Now we consider the deterioration rate is zero and shortages are allowed and completely backlogged. Case 1: M ≤ t1 :Inthisthetotalaveragecostperunittime

…(20) Case 2: M > t1: Inthisthetotalaveragecostperunittime

Theseresultsaresameasthoseobtainby M. Pal and S. K. Ghosh (Online).

Journal

Page2011           1111 D TtIn1(TtTtIn1Tt         wt 1 1e1 t D Pe1DtWCIDtM 2           ..(16) Optimalvaluesoft1 andTwhichminimize   2 M1 Ct,T are obtainedbysolvingtheequations:   2 M1 1 Ct,T0 dt   and   2 M1 Ct,T0 dT   whichgive providedtheysatisfythesufficientconditions:         ** 1 ** 1 2222 M1M1 22 t,T 1 t,T Ct,TCt,T0,0 tT           ** 1 222222 M1M1M1 22 1 1 tT Ct,TCt,TCt,T0 tTtT        ..(17) 3.1.

Inventory

Case 1: M ≤ t1: Inthisthetotalaveragecostperunittime   1 1 M1 OCHCSCOCDCIPIE Ct,T T     1t 1 2 1HD Aet1 T           2 2222 2 CD D tIn1ttIn1t         1t 1 D Ce1t       2 2 r1 1e DCIt tMDCI 22     ...(18) Case 2: M > t1: Inthisthetotalaveragecostperunittime     2 M12 1 Ct,TOCHCSCOCDCIE T    1t 2 1 22 CD 1HD Aet1 T       \           1111 D TtIn1(TtTtIn1Tt         1t 1 1e1 t D Ce1tCIDtM 2           ...(19)

9001:2008 Certified

Particular Case A

  1 1 M1 OCHCSCIPIE

T       2 2 2 12r 11

    2 1 e t

  

    2 M12 1

  2 2 21 11r1 1HDDCt AtTtDCIt(M)

   

Ct,T

DHtDCDCI 1 ATttM T222

DCI 2

Ct,TOCHCSCIE T

T222

...(21)

International Research Journal of Engineering and Technology (IRJET) e ISSN: 2395 0056

Volume: 09 Issue: 06 | Jun 2022 www.irjet.net p ISSN: 2395 0072

4. CONCLUSION

In this paper, a list model is developed for deteriorating things with two warehouses, allowing shortage and time proportional backlogging rate below the conditions of permissible delay in payments. Holding prices and deterioration prices area unit totally {different/ completely different} in OW and RW because of different preservation environments. The inventory prices (including holding price and deterioration cost) in RW areaunitassumedtobeabovethoseinOW.tocutbackthe inventory prices, it'll be economical for corporations to productinOWbeforeRW,howeverclearthestocksinRW before OW. Particularly, the backlogging rate thought abouttobeadecreasingoperation ofthewaitingtimefor ensuingfillingisalotofrealistic.Infollow,wewillobserve sporadicallytheproportionofdemand,whichmightsettle for backlogging, and therefore the corresponding waiting timeforensuingfilling.wehaveatendencytoadditionally noticethattheoptimumaverageinventoryprice.

REFERENCES

[1] Chung K.H. (1989). Inventory Control and Trade Credit Revisited. Journal of the Operational Research Society,40,495 498.

[2] ShinnS.W.,HwangH.P.andSungS.(1996).JointPrice and Lot Size Determination under Conditions of Permissible Delay in Payments and Quantity Discounts for Freight Cost. European Journal of OperationalResearch,91,528 542.

[3] Aggarwal S.P. and Jaggi C.K. (1995). Ordering Policies of Deteriorating Items Under Permissible Delay in Payments. Journal of the Operational Research Society,46,658 662.

[4] Hwang H. and Shinn S.W. (1997). Retailer's Pricing and Lot Sizing Policy for Exponentially Deteriorating Product Under the Condition of Permissible Delay in Payments. Computers & Operations Research, 24, (1997)539 547.

[5] Jamal A.M., Sarker, B.R. and Wang S. (1997). An Ordering Policy for Deteriorating Items with AllowableShortageandPermissibleDelayinPayment. Journal of the Operational Research Society, 48, 826 833.

[6] Hartley R.V. (1976). Operations Research A ManagerialEmphasis,GoodYearPublishingCompany, California,pp.315 317.

[7] Sarma K.V.S. (1983). A deterministic inventory model withtwolevelofstorageandanoptimumreleaserule. Opsearch,20, 175 180.

[8] MurdeshwarT.A.and Sathe Y.S.(1985).Some aspects of lot size model with two levels of storage. Opsearch 22,255 262.

[9] DaveU.(1988).OntheEOQmodelswithtwolevelsof storage.Opsearch,25,190 196.

[10] Sarma K.V.S. (1987). A deterministic order level inventory model for deteriorating items with two storage facilities. European Journal of Operational Research,29,70 73.

[11] Pakkala T.P.M. and Achary K.K. (1992). Discrete time inventory model for deteriorating items with two warehouses.Opsearch,29,90 103.

[12] Pakkala T.P.M. and Achary K.K. (1992). A deterministicinventory model fordeteriorating items with two warehouses and finite replenishment rate. European Journal of Operational Research, 57, 157 167.

[13] Goswami A. and Chaudhuri K.S. (1998). On an inventorymodelwithtwolevelsofstorageandstock dependent demand rate. International Journal of SystemsSciences,29,249 254.

[14] Bhunia A.K. and Maiti M. (1998). A two warehouse inventory model for deteriorating items with a linear trend in demand and shortages, Journal of the OperationalResearchSociety,49,287 292.

[15] KarS.,Bhunia A.K.andMaitiM.(2001).Deterministic inventory model with two levels of storage, a linear trendindemandanda fixedtimehorizon.Computers &OperationsResearch,28,1315 1331.

[16] Zhou Y.W. (2003). A multi warehouse inventory model for items with time varying demand and shortages. Computers & Operations Research, 30, 2115 2134.

[17] Abad P.L. (2001). Optimal price and order size for a reseller under partial backordering. Computers & OperationsResearch,28,53 65.

[18] Brigham, E. F., & Houston, J. F. (2015). Fundamentals of Financial Management, concise 8th edition, Mason, OH:South Western,CengageLearning

[19] Porteus, E.L. Optimal lot sizing, process quality improvement and setup cost reduction", Oper. Res., 34(1),pp.137 144(1986).

[20] Rosenblatt,M.andLee,H.Economicproductioncycles with imperfect production processes", IIE. Trans., 18(1),pp.48 55(1986).

International Research Journal of Engineering and Technology (IRJET) e ISSN: 2395 0056

[21] Lee, H.L. and Rosenblatt, M.J. Simultaneous determination of production cycles and inspection schedulesinaproductionsystem",Manage.Sci.,33(9), pp.1125 1137(1987).

[22] Salameh, M.K. and Jaber, M.Y. \Economic production quantitymodelforitemswithimperfectquality",Int.J. Prod.Econ.,64(3),pp.59 64(2000)

[23] Crdenas Barr on, L.E. Observation on : Economic production quantity model for items with imperfect quality",Int.J.Prod.Econ.,64,pp.59 64(2000),Int.J. Prod.Econ.,67(2),p.201(2000).

[24] Goyal, S.K. and C ardenas Barr on, L.E Note on: Economic production quantity model for items with imperfect quality a practical approach", Int. J. Prod. Econ.,77(1),pp.85 87(2002).

[25] Papachristos, S. and Konstantaras, I. Economic ordering quantity models for items with imperfect quality", Int. J. Prod. Econ., 100(1), pp. 148 154 (2006).

[26] Moussawi Haidar, L., Salameh, M. and Nasr, W. Effect of deterioration on the instantaneous replenishment model with imperfect quality items", Appl. Math. Model.,38(24),pp.5956 5966(2014).

[27] Goyal, S.K. and Giri, B.C. Recent trends in modeling of deterioratinginventory",Eur.J.Oper.Res.,134(1),pp. 1 16 (2001). C.K. Jaggi et al./Scientia Iranica, Transactions E: Industrial Engineering 24 (2017) 390{412411

[28] Bakker, M., Riezebos, J. and Teunter, R.H. Review of inventory systems with deterioration since 2001", Eur.J.Oper.Res.,221(2),pp.275 284(2012).

[29] Hartley, V.R., Operations Research A Managerial Emphasis, Good Year Publishing Company, California, pp.315 317(1976).

[30] Das, B., Maity, K. and Maiti, M. A two warehouse supply chain model under possibility/ necessity/ credibilitymeasures",Math.Comput.Model,46(3),pp. 398 409(2007).

[31] Hsieh, T.P., Dye, C.Y. and Ouyang, L.Y. Determining optimal lot size for a two warehouse system with deterioration and shortages using net present value", Eur.J.Oper.Res.,191(1),pp.182 192(2008).

[32] Lee, C.C. Two warehouse inventory model with deterioration under FIFO dispatching policy", Eur. J. Oper.Res.,174(2),pp.861 873(2006).

[33] Bhunia,A.K.andMaiti,M.Atwowarehousesinventory model for deteriorating items with a linear trend in

demandandshortages",J.Oper.Res.Soc.,49,pp.287 292(1998).

[34] Niu,B.andXie, J. A noteon two warehouseinventory modelwithdeteriorationunderFIFOdispatchpolicy", Eur.J.Oper.Res.,190(2),pp.571 577(2008).

[35] Bhunia, A.K., Jaggi, C.K., Sharma, A. and Sharma, R. A two warehouse inventory model for deteriorating itemsunderpermissibledelayinpaymentwithpartial backlogging", Appl. Math. Comput., 232, pp. 1125 1137(2014).

[36] Chung, K.J., Her, C.C. and Lin, S.D. A two warehouse inventory model with imperfect quality production process", Comput. Ind. Eng., 56(1), pp. 193 197 (2009).

[37] Jaggi, C.K., Tiwari, S. and Sharma Effect of deterioration on two warehouse inventory model with imperfect quality", Comput. Ind. Eng., 88, pp. 378 385(2015).