W-O-C model on Solid Transportation Problem over Fermatean Fuzzy Environment

Volume: 09 Issue: 06 | June 2022 www.irjet.net p-ISSN:2395-0072

W-O-C model on Solid Transportation Problem over Fermatean Fuzzy Environment

2

1Research Scholar, Department of Mathematics, Dr. N. G. P. Arts and Science College,Coimbatore, India 641 048 2Professor, Department of Mathematics, Dr. N. G. P. Arts and Science College, Coimbatore, India 641 048

Abstract:

2021-22 BAS007 -------------***------ --------------------------------------------------------------

Inthisarticle,Manufacturingindustryconsiderwarehouses,outletsandconveyanceinSolidTransportationProblemon Fermatean Fuzzy Environment. Three type of warehouses, three type of outlets and three type of transference are taken in Fermatean Fuzzy Environment. Fermatean Fuzzy numbers are taken as livestock to transmit warehouses to outlets through transference. Ferematean Fuzzy values are changes as crisp values to get an optimal solution for the W O C model using Fermateangradefunction.NewalgorithmisusedinZeroPointmethodtogetanoptimalsolutionfortheW O Cmodel.

Key

Words:

FermateanFuzzySet,q RungOrthopairFuzzySet,Warehouse Outlets Conveyance,FuzzySet,SolidTransportationProblem.

1. Introduction

Operation research abides the discipline of coherent decision making, the investigation, plan and consolidation of convoluted circumstances and methodology with the aim of system actions and enhancing or evaluating system representation. Operation researchhas three necessary features. Theanswer processofSTP isa development ofthe revised allocationmethod,familiarizedbyhaley.m+n+l 2significancesofthedeterminationvariablesarenecessaryfordiscoveringan optimal answer to begin with a primary feasible answer. A mathematically ideal technique for solid transportation problem withvariedrestrictionsisdesignedbyTripathyandPatel.ProgrammingmodelunderfuzzyforaMOSTPwasdesignedbyBit. Theoptimumanswerofastablestaticcontrollineartransportationissue,analgorithmisfurnishedbyBasu.Antechniquefor solvingaBCSTPwithfuzzynumberswasgivenbyGen. In2020,YagerandSenapatifixedq=3anduntriedq ROFSisnamedas Fermateanfuzzy sets (FFS). Underthisspecial idea,the decisiontakers possessmoreadditional spacesincetheyreveal their opinionsaboutbelongingnessandnon belongingnessconcerningtheconditionofatopic.

2.Preliminaries

2.1 Mapping of a Fuzzy set

LetEbefilled inelementsandFbeanon emptyfuzzysetwhichcontainelementsandthataremappedtounitinterval[0,1] andthemembershipfunctionofFisalsomappedtounitinterval[0,1]i.e,( ( ) , -)

2.2 q Rung Orthopair Fuzzy set

Qisaq RunginalimiteduniverseofdiscourseEisdefinedbyYager * ( ) ( ) +

where DMF is betoken $\mu_{Q}: E \to [0,1] $and DNMF is betoken , -( ), direct towards to q ROF set Q, withthestatusthat ( ( ) ( ) ) ( )

2.3 Grade function of Fermatean Fuzzy set

Let ̃ beanyFS,thegradefunctionisdenotedby ( ) andisdefinedas

International Research Journal of Engineering and Technology (IRJET) e ISSN:2395 0056

Volume: 09 Issue: 06 | June 2022 www.irjet.net p ISSN:2395 0072

Thegradefunctiondefinedsenapatiandyager[13],[14],thegradevalueliesintheinterval[ 1,1].i.e ( ) , -.Itistobe noted that the function is positive when ( ) , - and negative when ( ) , ). In the purpose of grade of FNs/FSs (eitherIFSorPFS)mostoftheresearchershaveconsideredgradefunctionswhosegradevaluesareliesintheinterval0and1. SotomaintainthesamewehaveproposedsomegradefunctionsfortherankingofFFSs. ( ) ( )

2.4 Algorithm of W O C on Solid Tansportation Problem over Fermatean Fuzzy

LetswebeginwithnewmethodofW O ConSolidTransportationProblemoverFermateanFuzzy

Step1:ToverifytheappropriateFermateanfuzzySTPisbalancedornot.IfnotthenchangeasbalancedSTP.

Step2:ToconvertthecrispvalueofthegivenFermateanfuzzySTPusingthegradefunction.

Step3:ChangetheFermateanfuzzySTPtabletoarowandcolumnreductiontable.

Step 4: Change W O C table to Warehouses Outlets table and to check the Warehouses Outlets satisfy the allocation of the Fermateanfuzzysupplyandnecessity.Ifyes,gotonextstep6;otherwise,gotostep5.

Step 5: Use row and column reduced method to cross out the row and column, then take the smallest value in unmarked places. Add the smallest value in the intersection place and subtract the smallest value in the unmarked place of an appropriatetable.

Step6:TochecktheOutlets ConveyancestabletosatisfytheallocationofFermateanfuzzynecessityandtransference.Ifyes, gotothenextstep7;otherwise,gotostep5.

Step 7: To check the Conveyances Warehouses table to satisfy transference and supply. If yes, then go to next step 8; otherwise,gotostep5.

Step8:TochecktheWarehouses Outletstabletosatisfysupplyandnecessity.Ifyes,thengotostep9;otherwise,gotostep5.

Step9:TocheckWarehouses Outlets ConveyancetablesatisfyFermateanFuzzysupply,necessityandtransference.Ifyesthen gotostep10;otherwise,gotostep5.

Step10: To find theSolid TransportationProblem onFermateanFuzzy Environmentambiance on optimal solution fromthe appropriatetable.

3. W O C model on Solid Transportation Problem using Fermatean Fuzzy

ManufacturingIndustrycanhandle with Warehouses, OutletsandConveyancetotransmit goods. Solidtransportationdeals withthreetypeofWarehouses,threetypeofOutletsandthreetypeofConveyanceonFermateanfuzzyenvironment.

Fuzzysolidtransportationproblemstructureisdefinedgivenbelow,

International Research Journal of Engineering and Technology (IRJET) e ISSN:2395 0056

Volume: 09 Issue: 06 | June 2022 www.irjet.net p ISSN:2395 0072

∑∑

∑ istotalstockofthewarehouses.∑ istotalorderoftheOutlets.∑ istotalconveyance. isamount of livestock transmit from warehouses to Outlets by virtue of Conveyance which deals with ( ) represents numberofproductsexportedfrom warehousesto Outletsbyvirtueof Conveyanceand ( )representsnumberof productnotexported.Fermateanfuzzysubset ̃ satisfy ( ) ( ) andalsothereondegreeofindeterminacy ( ) , - which is of the form ( ) ( ( )) ( ( )) ,If degree of indeterminacy ( ) ( ( )) ( ( )) 1

UsingFermateanfuzzycondition tomakeproperFermateanFuzzySTP.

Table1:SolidTransportationProblemonFermateanFuzzyEnvironment

Conveyance K1 K1 K1 0.16 K2 K2 K2 0.36 K3 K3 K3 0.49 Warehouses/Ou tlets O1 O2 O3 Warehou ses supply

W1 <0.6,0.9 2> <0.8,0.7 8> <0.3,0.9 9> <0.9,0.6 4> <0.7,0.8 6> <0.6,0.9 2> <0.5,0.9 5> <0.4,0.9 7> <0.9,0.6 4> 0.27 W2 <0.4,0.9 7> <0.7,0.8 6> <0.4,0.9 7> <0.2,0.9 9> <0.8.0.7 8> <0.5,0.9 5> <0.4,0.9 7> <0.7,0.8 6> <0.6,0.9 2> 0.49 W3 <0.7,0.8 6> <0.5,0.9 5> <0.6,0.9 2> <0.7,0.8 6> <0.4,0.9 7> <0.7,0.8 6> <0.6,0.9 2> <0.5,0.9 5> <0.8,0.7 8> 0.25 Outletsorder 0.81 0.04 1.01 Fromstep2useFermateangradefunctionforthetable1thenthevaluesarechangedascrispvalue. Table2:CrispValueSolidTransportationProblemonFermateanFuzzyEnvironment Conveyance K1 K1 K1 0.16 K2 K2 K2 0.36 K3 K3 K3 0.49 Warehouses/Outlets O1 O2 O3 Warehouses supply W1 0.216 0.512 0.027 0.729 0.343 0.216 0.125 0.064 0.729 0.27 W2 0.064 0.343 0.064 0.008 0.512 0.125 0.064 0.343 0.216 0.49 W3 0.343 0.125 0.216 0.343 0.064 0.343 0.216 0.125 0.512 0.25 Outletsorder 0.81 0.0 4 0.16 1.01 Toreduceallstockedvaluebyitslowestlevelofstockedvalueineachrow.

International Research Journal of Engineering and Technology (IRJET)

e ISSN:2395 0056

Volume: 09 Issue: 06 | June 2022 www.irjet.net p ISSN:2395 0072

Table3:ReducedSolidTransportationProblemonFermateanFuzzyEnvironment

Conveyance K1 K1 K1 0.16 K2 K2 K2 0.36 K3 K3 K3 0.49

Warehouses/Outlets O1 O2 O3 Warehousessupply

W1 0.189 0.485 0 0.702 0.316 0.189 0.098 0.037 0.702 0.27 W2 0.056 0.335 0.056 0 0.504 0.117 0.056 0.335 0.208 0.49 W3 0.279 0.061 0.152 0.279 0 0.279 0.152 0.061 0.448 0.25 Outletsorder 0.81 0.04 0.16 1.01

ToverifyW Otablesatisfy4ifnotthengotostep5untilW Otablesatisfysupplyanddemandvalueinzeropoint.

Table4:Warehouses OutletsofSolidTransportationProblemonFermateanFuzzyEnvironment

Warehouses/Outlets O1 O2 O3 Warehousessupply W1 0.245 0.485 0 0.758 0.316 0.189 0.117 0 0.665 0.27 W2 0.056 0.279 0 0 0.448 0.061 0.019 0.242 0.115 0.49 W3 0.335 0.061 0.152 0.335 0 0.279 0.171 0.024 0.411 0.25 Outletsorder 0.81 0.04 0.16 1.01

Changelivestock warehousesto Outletsbyvirtueof conveyanceofWarehouses OutletstoOutlets Conveyancewith correspondingOutletsorderandconveyance.

Table5:Outlets ConveyanceofSolidTransportationProblemonFermateanFuzzyEnvironment

Outlets/Conveyance K1 K2 K3 Outletsorder

O1 0.245 0.056 0.335 0.485 0.279 0.061 0 0 0.152 0.81

O2 0.758 0 0.335 0.316 0.448 0 0.189 0.061 0.279 0.04 O3 0.117 0.019 0.171 0 0.242 0.024 0.665 0.115 0.411 0.16 Conveyance 0.16 0.36 0.49 1.01

ToverifyO Ctablesatisfy6ifnotthengotostep5untilO Ctablesatisfyoutletorderandconveyancevalueinzeropoint.

Table6:Outlets ConveyanceofSolidTransportationProblemonFermateanFuzzyEnvironment

Outlets/Conveyance K1 K2 K3 Outletsorder

O1 0.306 0.117 0.396 0.546 0.34 0.122 0 0 0.152 0.81

O2 0.758 0 0.335 0.316 0.448 0 0.128 0 0.218 0.04

O3 0.117 0.019 0.171 0 0.242 0.024 0.604 0.054 0.35 0.16 Conveyance 0.16 0.36 0.49 1.01

International Research Journal of Engineering and Technology (IRJET)

e ISSN:2395 0056

Volume: 09 Issue: 06 | June 2022 www.irjet.net p ISSN:2395 0072

Changelivestock warehousesto outletsbyvirtueof conveyanceofOutlets ConveyancetoConveyance Warehouses withconveyanceandwarehousesstock.

Table7:Conveyance WarehousesofSolidTransportationProblemonFermateanFuzzyEnvironment

Conveyance/Warehouses W1 W2 W3 Conveyance

K1 0.306 0.758 0.117 0.117 0 0.019 0.396 0.335 0.171 0.16 K2 0.546 0.316 0 0.34 0.448 0.242 0.122 0 0.024 0.36 K3 0 0.128 0.604 0 0 0.054 0.152 0.218 0.35 0.25 Warehousessupply 0.27 0.49 0.25 1.01

Change livestock warehouses to outlets by virtue of conveyance of Conveyance Warehouses to Warehouses Outletsandincludedwiththeconveyance,warehousesstockandoutletsorder.

Table8:Warehouses Outlets ConveyanceofSolidTransportationProblemonFermateanFuzzyEnvironment

Conveyance K1 K1 K1 0.16 K2 K2 K2 0.36 K3 K3 K3 0.49 Warehouses/Outlets O1 O2 O3 Warehouses supply

W1 0.306 0.546 0(0.11) 0.758 0.316 0.128 0.117 0(0.16) 0.604 0.27 W2 0.117(0.11) 0.34 0(0.38) 0 0.448 0 0.019 0.242 0.054 0.49 W3 0.396(0.05) 0.122(0.16) 0.152 0.335 0(0.04) 0.218 0.171 0.024 0.35 0.25 Outletsorder 0.81 0.04 0.16 1.01 OptimalsolutionofSolidTransportationonFermateanFuzzyenvironmentis , , , , , , .TotalminimumSolidTransportationProblemonFermatean FuzzyEnvironmentcostis0.05996.

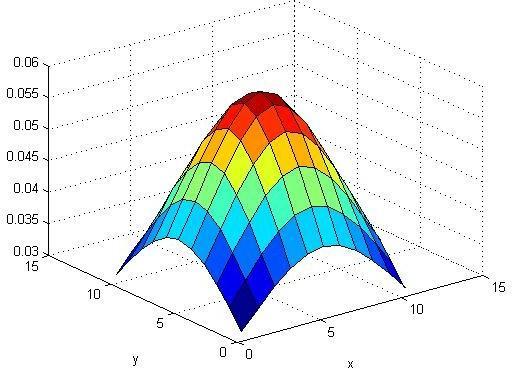
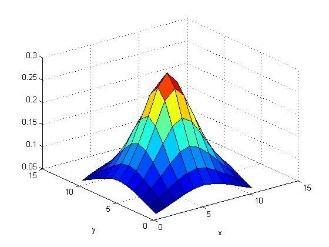
4. Result

International Research Journal of Engineering and Technology (IRJET) e ISSN:2395 0056

Volume: 09 Issue: 06 | June 2022 www.irjet.net p ISSN:2395 0072

MATLABApproachforSTPoutcomeunderFermateanfuzzyenvironment

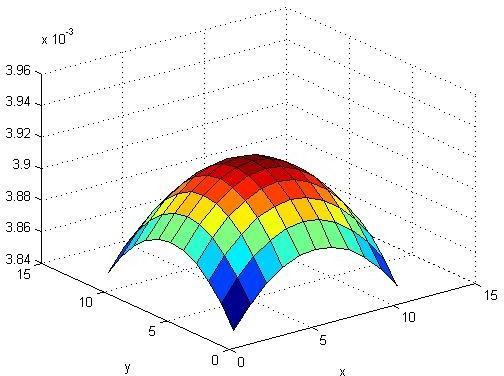
Matlab approach on Zero Point method based algorithm on the Fermatean Fuzzy used in Solid transportation problem withthreewarehouses,threeoutletsandthreemodeofconveyancesaresolvedusinggradefunctionthentheresultisgivenin differentdimensional.

5. Conclusion

We considered three type of warehouses, three type of outlets and three type of transference in the Manufacturing industry is evaluated using Solid transportation problem with Fermatean Fuzzy numerals. Fermatean fuzzy numerals are changedascrispvaluesusingFermateangradefunctiontoappraisetheW O Cmodel.NewalgorithmisproposedusingZero Point method on W O C model. Optimal solution is obtained with the support of Zero Point method which is used on crisp valuetoevaluatetheW O CmodeloverFermateanFuzzyenvironment.

Reference

[1]P.Pandian,andD.Anuradha,"ANewApproachforSolvingSolidTransportationProblems",AppliedMathematicalSciences, vol.4,no.72,2010,PP 3603 3610.

[2] K. B. Haley, "The Solid Transportation Problem Method for Solving Transportation Problem", New Methods in MathematicalProgramming,11,1960,PP 446 448.

[3]A.K.Bit,M.P.BiswalandS.S.Alam"FuzzyprogrammingapproachtomultiobjectiveSolidTransportation Problem",Fuzzy SetsandSystems,no.57,1993,PP 183 194.

[4]M.Basu,B.B.Pal,A.Kundu"AnalgorithmforfindingtheoptimumsolutionofsolidfixedchargeTransportationproblem", AJournalofMathematicalProgrammingandOperationsResearch,vol.31,no.3,1994,PP 283 291.

[5]A.Zadeh,"FuzzySets",InformationandControl,vol.,no.,1965,PP 338 353.

[6] Ronald A. Yager, "Generalized Orthopair Fuzzy Sets", IEEE Transactions on Fuzzy Systems, vol.25, no.5, 2017, PP 1222 1230.

[7] Peide Liu, Peng Wang "Some q Rung orthopair fuzzy aggregation operators and their applications to multiple attribute decisionmaking",InternationalJournalofIntelligentSystems,vol.33,no.2,2017,PP 259 280.

[8]KrassimirT.Atanassov,"IntuitionisticFuzzySets",FuzzySetsandSystems,vol.20,no.1,1986,PP 87 96.

[9]RonaldR.Yager,"PythagoreanFuzzySubsets",JointIFSAworldcongressandNAFIPSannualmeeting(IFSA/NAFIPS,2013, PP 1379 9608.

International Research Journal of Engineering and Technology (IRJET) e ISSN:2395 0056 Volume: 09 Issue: 06 | June 2022 www.irjet.net p ISSN:2395 0072

[10] Ronald R. Yager, "Pythagorean Membership Grades in Multicriteria Decision Making", IEEE TRANSSACTIONS ON FUZZY SYSTEMS,vol 22,no.4,2014,PP 1063 6706.

[11]TapanSenapati,RonaldR.Yager,"Fermateanfuzzysets",JournalofAmbientIntelligenceandHumanizedComputing,.

[12] Laxminarayan Sahoo "A new score function based Fermatean fuzzy transportation problem", Results in Control and Optimization,2021,PP 2666 7207.

[13]TapanSenapati,RonaldR.Yager,"Fermateanfuzzyweightedaveraging/geometricoperatorsanditsapplicationinmulti criteriadecision makingmethods",EngineeringApplicationsofArtificialIntelligence,85,2019,PP 112 121.

[14] Sudipta Midya, Sankar Kumar, Vincent F. Yu, "Intuitionistic fuzzy multi stage multi objective fixed charge solid transportation problem in green supply chain", International Journal of Machine Learning and Cybemetics, vol.13, 2021, PP 699 717.

[15]PeterVassilev,"OntheintuitionisticFuzzysetswithmetrictyperelationbetweenthemembershipandnonmembership functions",NotesonIntuitionisticFuzzySets,vol.18,no.3,2012,PP 30 38.

[16]ShashiAggarval,ChaviGupta,"SolvingIntuitionisticFuzzySolidTransportationProblemViaNewRankingMethodBased onsignedDistance",InternationalJournalofUncertainty,vol.24,no.4,2016,PP 483 501.

[17] Yinzhen Li, Kenichi Ida, Mitsuo Gen, Reiko Kobuchi, "Neural Network Approach for Multicriteria Solid Transportation Problem",Computers&industrialEngineering,vol.33,no.3 4,1997,PP 465 468.

[18] Y. Li, K. Ida, M. Gen, "Improved genetic algorithm for solving multiobjective Solid Transportation Problem with fuzzy numbers",Computers&industrialEngineering,vol.9,no.2,1997,PP 239 250.

[19]F.Jimenez,J.L.Verdegay,"UncertainSolidTransportationProblems",FuzzySetsandSystems,vol.100,no.1 3,1998,PP 45 57.

[20]F.Jimenez,J.L.Verdegay,"SolvingBicriteriaSolidTransportationProblemswith Fuzzynumbersbyageneticalgorithm", Computers&industrialEngineering,vol.29,no.1 4,1995,PP 537 541.