COMPUTATION OF FRICTION FACTOR AND ITS EFFECT ON DESIGN OF WATER PIPE LINE

International Research Journal of Engineering and Technology (IRJET)

www.irjet.net pISSN:23950072

COMPUTATION OF FRICTION FACTOR AND ITS EFFECT ON DESIGN OF WATER PIPE LINE

Department

Abstract - The title of our Major Project is ‘calculation of friction factor in different and its effect on design of water Pipe line ’. Form friction factor we can calculate friction loss and friction loss is the energy loss of fluid inflow in Pipe. When a fluid flows through a pipe it came across lot of resistance like be bends, turns, change in pitch, roughness, friction and other factors like diameter, velocity, viscosity and density of fluid causes fluid inflow to decelerate down which affect in loss of energy or simply further energy is needed for the fluid inflow. This loss of energy is known as energy loss. The significance of friction factor in pipe design is that we can be suitable to find out the pressure loss in the pipe by knowing the values of friction factor. Consequently, One can calculate the pumping power needed or demanded to carry the fluid in the pipe and thereby we can elect the pump of needed power and capacity. In this Project, by using various empirical equations, friction factor for various pipe diameter, different pipe material and by considering smooth and rough pipe is determined. The result obtained by empirical equations is validated by actual performing the test and for friction factor in the laboratory. By using various friction factor the most economic diameter is obtained. It is recommended that Darcy Wiesbach equation is more reliable and gives the optimum diameter of the pipe network.

Key Words: Calculating Friction Factor by different equation.

1. INTRODUCTION

Friction loss is a measure of the quantum of energy your pipeline system loses because your fluids are meeting resistance.Asfluidoverflowsthroughyourpipes,itcarries energywithit.Unfortunately,wheneverthere’sresistanceto inflow rate, it diverts fluids and energy escapes. These opposing forces beget friction loss in pipes. It may not be egregious,butfrictionlosscanbringyoutime,plutocrat,and effectiveness. Then are a many ways friction loss strips plutocratoutofyourpipelinesystem.

1.1WhatCausesFrictionLoss:

Allkindsofthingscancausefrictionloss,buttherearea fewfriction factorsthat tend to affect your pipe flow the

most.Here’sacloserlookatthecommoncausesoffriction loss:

1)Viscosity: The density of the fluid you ’re transporting cancontributetofrictionloss.Putsimply,densitydescribes the consistence of the fluid your pipes are transporting. Fluids with advanced density will be more likely to meet resistancethanthosewithalowdensity.Forcase,wateris more likely to rush un defied through pipes than thicker fluids,similarasoilpainting.

2)Internalpipediameter: Basically,thelowerfaceyour fluidshavetorunover,thelowerthechanceoffrictionloss. That’s why pipes with a lower periphery generally have furtherfrictionloss.

3)Internalpiperoughness: Theroughertheinternalshells of your pipes are, the harder fluids need to work to slide around or over them. That’s why internal erosion and buildupcanbegetresistanceandfrictionloss.

4)Changesinpipeslope: Ifyourpipeschangeinelevation, itcanforceliquidstoworkagainstgraveness,andyoucan lose energy along the way. That’s why uneven or sagging piperunscanstinkenergyoutofyoursystem.

5)Pipelength: Thefartherfluidshavetotravel,theharder they've to work. Longer pipe runs will naturally have advancedeventualityforfrictionlossthanshorterruns.

6)Valvesandfittings Internalpipewallsarenottheonly effectsthatcontributetofrictionloss.faucetsandfittingscan alsoinhibitinflowandbegetfurtherfriction.

1.2HowtoreducefrictionLossinPipe:

By precluding friction loss at every pass, you’ll boost the effectiveness of your pipeline system, ameliorate product, and save plutocrat. Then are a many ways to cut down frictionlossandencouragesteadypipeinflow:

1)ReduceInteriorRoughness: Bysmoothingoutinterior pipeshells,you’llpaveaclearerpathforliquidstoflow.That means drawing pipes completely and keeping them free fromdebris.Italsorequiresavisionaryapproachtofighting

International Research Journal of Engineering and Technology (IRJET) eISSN:23950056 Volume:09Issue:06|Jun2022 www.irjet.net pISSN:23950072

pipeerosion.Whenpipeserode,itcausesexpensivedipsand blockages. That’s why it’s important to keep erosion from creepingintopipeshellsandeatingdownessence.

2)IncreasePipeDiameter: Diameter By widening pipe compasses,youinsurethatliquidsdonothavetoworkas hardtosqueezethroughpipes.Inturn,you’llreduceinflow resistance and friction loss in pipes. Just be sure you’re supportinglargerpipeswithstrong,effectivepipesupports.

3)ReduceTurns: Byuncurlingoutpiperunsandclearing yourpipe’spath,youcanavoidfrictionloss.Negotiatethis byremovingtees,fittings,andothersharpturnswhenever it’spossible.

2. LITERATURE REVIEW

1] Analysis of Friction Losses in Pipe with Analytical Method Divyesh A. PatelVimal N. ChaudhariDeep R. Patel Corresponding Author: Divyesh A. PatelDate of Submission:04 04 2019Dateofacceptance:19 04 2019

2] Aresearchondeterminingthefrictionlossesformedin the small diameter floppy polythene pipe line Abdullah KadayifciGokhan Ismail TuyluUlas SenyigitHasan OzUniversity of Süleyman Demirel, College of Agriculture, Isparta Turkey.University of Ege, College of Agriculture, zmir Turkey.University of Süleyman Demirel, College of Agriculture,Isparta Turkey.Accepted26November,2009

3] FrictionLossesinLargeDiameterPipesJ.Berlamont1DOI: 10.1061/(ASCE)PS.1949 1204.0000174.©2014American SocietyofCivilEngineers

4] Evaluation of Friction Losses In Pipes And Fittings Of Process Engineering Plants F. W. NtengweM. ChikwaL. K. Witika INTERNATIONAL JOURNAL OF SCIENTIFIC & TECHNOLOGYRESEARCHVOLUME4,ISSUE10,OCTOBER 2015

5] A Study on Laminar Pipe flow & losses, Prabir Chakraborty (B.E)Devender SinghHimanshu KumbhareAnkur SinghAll Final Year, Mechanical Engg. Department (B.E)RSRRCET, Bhilai, Chhattisgarh, IndiaVOLUME4,ISSUE3,Jan2016

6] Variation of Coefficient of Friction and Friction Head LossesAlongaPipewithMultipleOutletWissamH.Alawee YousefA.AlmolhemBadronnisaYusufhamerA.Mohammad HayderA.DhahadReceived:26December2019;Accepted: 14March2020;Published:17March2020

7] StudyofPressureLossesinPipingSystemSeroorAtalah KhaleefaAliDr.HudaT.HamadVolume8Issue6,June2019

8] Effect of Unsteady Friction Models and Friction Loss IntegrationonTransientPipeFlowA.VakilB.FiroozabadVol. 13,No.3,pp245SharifUniversityofTechnology,July2006

9] HydraulicExperimentforFrictionLossCoefficientinNon circularPipe JungHwanKimaSoonHoKwonaKwangSeok YoonbDuHanLeebGunhuiChungDateofSubmission:04 04 2016Dateofacceptance:19 04 2016

3. EMPIRICAL FORMULAS:

EquationName Equation

RelativeRoughness: k= Newton Raphson Equation: Gregory Forgarasi Equation: Where,A= Colebrook& WhiteEquation: Blasius Equation: 0.184 NikuradseEquation: Jain Equation: Von Karman equation: +1.74

Table1:DifferentFrictionFactorFormulaswithout Roughness Table2:DifferentFrictionFactorFormulaswith

EquationName Equation

Bernoulli’sEquation: hf=( + +z1) ( + +z2)

Hazen Williams formula: V=0.849Chw & hf= Manning’sFormula: V= & hf= Darcy Weisbach equation: hf= Hagen Poiseuille equation: hf= BlasiusEquation: f= Prandtlequation: Nikuradseequation:

© 2022, IRJET | Impact Factor value: 7.529 | ISO 9001:2008 Certified Journal | Page1145

International Research Journal of Engineering and Technology (IRJET)

Roughness

1] Bernoulli’s Equation: Bernoulli’s principlestatesthat: Thetotalmechanicalenergyofthemovingfluidcomprising the gravitational potential energy of elevation, the energy associatedwiththefluidpressureandthekineticenergyof thefluidmotion,remainsconstant.

2] HazenWilliams formula: Itis anempirical relationshipwhichrelatestheflowofwaterinapipewith the physical properties of the pipe and the pressure drop causedbyfriction.

3] Manning’s Formula: Itisanempiricalformulaestimating theaveragevelocityofaliquidflowinginaconduitthatdoes not completely enclose the liquid, i.e.,open channel flow. However,thisequationisalsousedforcalculationofflow variablesincaseofflowinpartiallyfullconduits,astheyalso possessafreesurfacelikethatofopenchannelflow.

4]DarcyWeisbachequation: Influiddynamics,theDarcy Weisbachequationisaphenomenologicalequation,which relates themajor head loss, or pressure loss, due tofluid frictionalongagivenlengthofpipetotheaveragevelocity. This equation is valid forfully developed, steady, incompressiblesingle phaseflow.

5]HagenPoiseuilleequation: Itisaphysicallawthatgives thepressuredropinanincompressibleandNewtonianfluid in laminar flow flowing through a long cylindrical pipe of constantcrosssection.

6]BlasiusEquation: Blasiusdeterminedanequationfrom experiments on smooth pipes. The Blasius equation is the most simple equation for solving the Darcy friction factor becausetheBlasiusequationhasnotermforpiperoughness, isvalidonlytosmoothpipe.

7]PrandtlEquation: Prandtl derived a formula from the logarithmic velocity profiles and experimental data on smoothpipes.

8]NikuradseEquation: Thedevelopmentofapproximate equations for the calculation of friction factor began with Nikuradse'sturbulentpipeflowinvestigationsin1932and 1933. Nikuradse had verified the Prandtl‟s mixing length theory and proposed the following universal resistance equationforfullydevelopedturbulentflowinsmoothpipe.

9] Von Karman Equation: The following form of the equationisfirstderivedbyVonKarman(Schlichting,1979) and later supported by Nikuradse‟s experiments. Von Karman'srelationwaswidelyusedforturbulentregimein roughpipes.

10]Colebrook&WhiteEquation: Colebrook and White (1937)proposedtheequationfortransitionregimeinwhich thefrictionfactorvarieswithbothRand€/D.Theequation universallyadoptedforcalculatingthefrictionfactor.

3.2MOODYCHART

TheMoodyCharteventuallyhandedasystemofchancingan accuratefrictionfactorandthisencourageduseoftheDarcy Weisbach equation, which snappily came the system of choice for hydraulic engineers. The introduction of the personnelcomputerFromthe1980'sonwardsreducedthe time needed to calculate the friction factor and pipe head loss.ThisitselfhaswidenedtheuseoftheDarcy Weisbach formula to the point that utmost other equations are no longerused.

4. PROBLEM STATEMENT:

Frictionfactorplaysanimportantroleindesignofpipeline. Thecomputationofpressuredropinpipelinedependson frictionfactor.A numberof correlationsforfrictionfactor determinations in smooth and rough pipes have been availableintheliterature.Itistheneedoftimetocheckthe more suitable and reliable equation for determination of frictionfactoranditseffectondesignofwaterpipe,whenit isrunningfullcondition.

5. METHODOLOGY:

In our Major Project, beside finding research Papers, differentformulastocalculatefrictionfactor,studymaterials whatwedidwetooktwoproblemswithdifferentdiameter of pipe with same data and same fluid i.e. water. We calculated/solvedeachexamplebydifferentfrictionfactor formulas for different Pipes for calculation friction factor. Thedifferentfrictionfactorformulaswefoundoutonsome researchpapersandsomeonstudymaterials.Theproblems, we calculated them by both analytically, practically and experimentallytofindoutfrictionfactor.Aftercalculating friction factor, we compare the result to find out which analytical and experimental method gives more accurate resultandhowmuchdeviationhappensineachresult.

eISSN:23950056 Volume:09Issue:06|Jun2022 www.irjet.net pISSN:23950072 © 2022, IRJET | Impact Factor value: 7.529 | ISO 9001:2008 Certified Journal | Page1146

International Research Journal of Engineering and Technology (IRJET) eISSN:23950056

www.irjet.net

Afterthat,wetookPipedistributionnetworkproblem, wecalculatedthediameterofpipefornetworkbydifferent friction factor we obtained by different formulas, experimentationandMoody'schart.Thenwecomparethe diameter to find out which friction Factor gives more economical and accurate result for the design of water pipelinedistributionNetwork.

5.1PROBLEMS:

5.2PIPE1: FindtheHeadlossandfrictionfactorvalueof different pipes in which water is flowing. TheHeadLoss&FrictionFactoriscalculatedbyfollowing Formulas (without Considering the Roughness)

1) Darcy Weisbach equation: 2) Hagen Poiseuille equation: 3) Blasius Equation: 4) Prandtl equation: 5) Nikuradse equation: The Friction Factor is calculated by following Formulas ( With Considering the Roughness )

1) Newton Raphson Equation: 2) Gregory Forgarasi Equation: 3) Colebrook & White Equation: 4) Nikuradse Equation: 5)JainEquation:

Inside diameter, D= 0.022 m Density of water, �� = 1000 Kg/m3 Velocity, V= 0.8 m/s Viscosity of water, �� = 0.001003 Ns/m3 LengthofPipe,L=1.25m

5.3PIPE2: FindtheHeadlossandfrictionfactorvalueof different pipes in which water is flowing. TheHeadLoss&FrictionFactoriscalculatedbyfollowing Formulas (without Considering the Roughness)

1) Darcy Weisbach equation: 2) Hagen Poiseuille equation: 3) Blasius Equation: 4) Prandtl equation: 5) Nikuradse equation: The Friction Factor is calculated by following Formulas ( With Considering the Roughness )

1) Newton Raphson Equation: 2) Gregory Forgarasi Equation: 3) Colebrook & White Equation: 4) Nikuradse Equation: 5) Jain Equation:

Inside diameter, D= 0.016 m Density of water, �� = 1000 Kg/m3 Velocity, V= 1.4 m/s Viscosity of water, �� = 0.001003 Ns/m3 LengthofPipe,L=1m

5.4PYTHONCOADING:

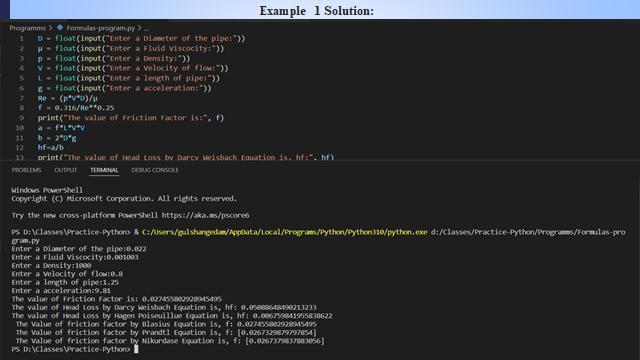
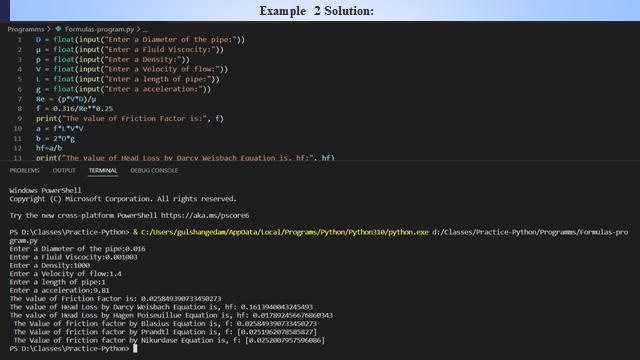
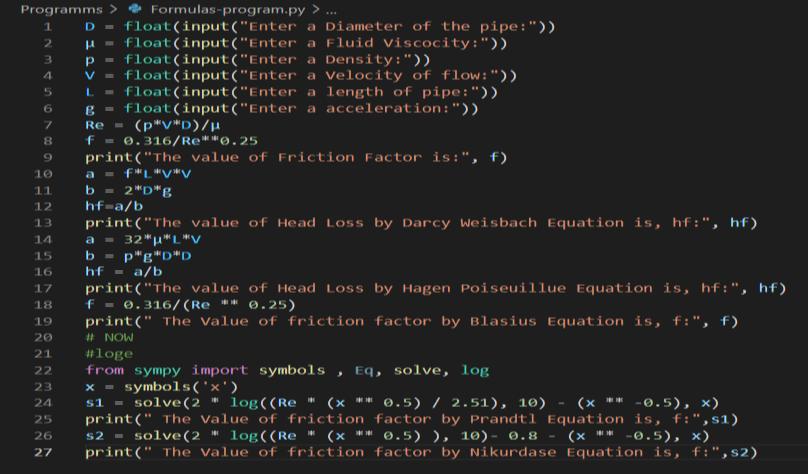
For calculation of friction factor by different formulas we usedpythonprogramminglanguage.

5.5OUTPUT:

International Research Journal of Engineering and Technology (IRJET)

eISSN:23950056

Volume:09Issue:06|Jun2022 www.irjet.net pISSN:23950072

6. EXPERMENTATION:

COMPUTATION OF FRICTION FACTOR BY EXPERIMENTATION:

PIPE 1: 1) Diameter of Pipe: 0.022 m

2) Length of Pipe: 1.25 m

3)AreaofMeasuringTank:0.077sq.m

Averagefrictionfactor=0.0368

PIPE 2: 1) Diameter of Pipe: 0.016 m 2) Length of Pipe: 1 m

3)AreaofMeasuringTank:0.077sq.m

Averagefrictionfactor=0.0239

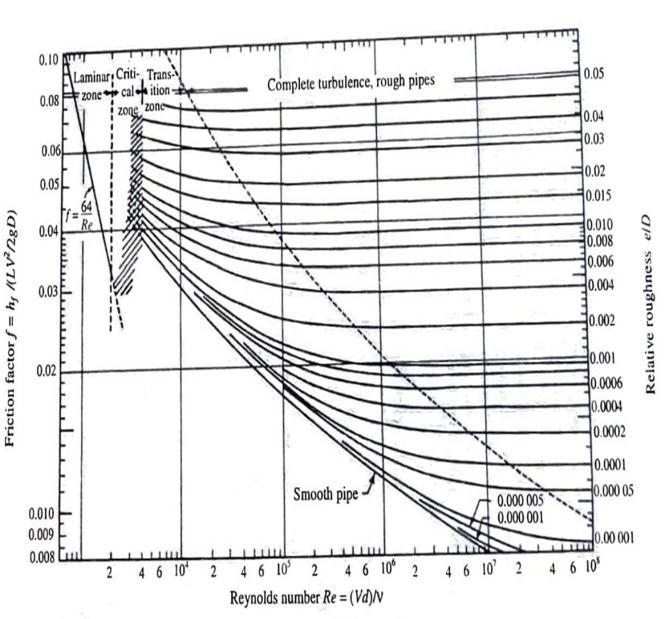
7. MOODY’S CHART:

FromFig.1(p.g 4)

For Pipe 1:

1) Reynold’s Number = 18000 i.e 2) Relative Roughness = Roughness/ Diameter = 0.000045 / 0.022 = 2.045 x 10^ 3 = 0.002045

By Comparing Relative roughness with Reynold’s Number we get Friction Factor = 0.0350

For Pipe 2:

1) Reynold’s Number = 23000 i.e 2) Relative Roughness = Roughness/ Diameter = 0.000045 / 0.016 = 2.812 x 10^ 3 = 0.00281

By Comparing Relative roughness with Reynold’s Number we get Friction Factor =0.0270

8. DESIGN OF PIPE NETWORK:

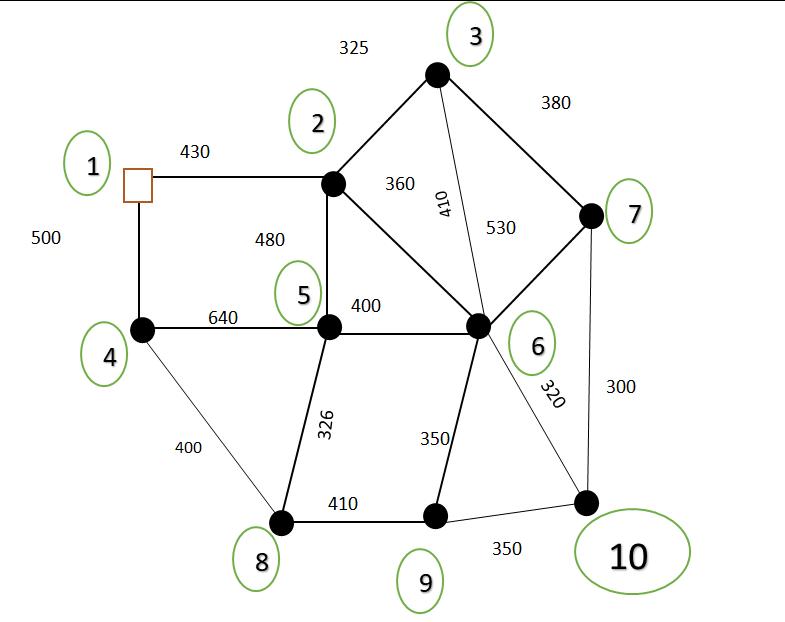
Forthenetworkshownbelowfindthetreehavingminimum path(byPathconcept).DeterminePrimaryandsecondary pipe,ifavailableHGLatsourceis100m&HGLatdemand nodesare2 96,3 93,4 96,5 93,6 94,7 90,8 93,9 92,10 89.findthenodalHGLvalues.

© 2022, IRJET | Impact Factor value: 7.529 | ISO 9001:2008 Certified Journal | Page1148

International Research Journal of Engineering and Technology (IRJET)

eISSN:23950056

Volume:09Issue:06|Jun2022 www.irjet.net pISSN:23950072

ForPipe1:Diameterobtainedbydifferentfrictionfactor

SR. No. Path Length (m) Discharge Q (m3/min)

Head Loss HL(m)

Forf=0.0350[From Moody’sChart]

Friction Factorf Diameter D(m)

For f = 0.0305 [From Newton Raphson, Gregory Forgarasi & Colebrook & White Equation]

For f = 0.0368 [ From Experimental Readings]

Friction Factorf Diameter D(m) Friction Factorf Diameter D(m)

1 1 2 430 16.5 2.97 0.0350 0.501 0.0305 0.487 0.0368 0.506

2 2 3 325 3.5 3.18 0.0350 0.251 0.0305 0.244 0.0368 0.254

3 2 6 360 7 2.49 0.0350 0.355 0.0305 0.346 0.0368 0.359

4 2 5 490 2 4.03 0.0350 0.208 0.0305 0.202 0.0368 0.210

5 3 7 390 2 3.58 0.0350 0.200 0.0305 0.195 0.0368 0.202

6 6 10 320 2.5 5.54 0.0350 0.196 0.0305 0.190 0.0368 0.198

7 6 9 380 3 2.54 0.0350 0.255 0.0305 0.248 0.0368 0.257

8 1 4 500 4.5 3.85 0.0350 0.291 0.0305 0.283 0.0368 0.294

9 4 8 400 2.5 7.00 0.0350 0.195 0.0305 0.190 0.0368 0.197

ForPipe2:Diameterobtainedbydifferentfrictionfactor

SR. No. Path Length (m) DischargeQ (m3/min)

HeadLoss HL(m)

Forf=0.0270[From Moody’sChart]

For f = 0.0306[From Newton Raphson, Gregory Forgarasi & Colebrook & White Equation]

Forf=0.0239[From Experimental Readings]

Friction Factorf Diameter D(m)

Friction Factorf Diameter D(m)

Friction Factorf Diameter D(m) 1 1 2 430 16.5 2.97 0.0270 0.475 0.0306 0.488 0.0239 0.464 2 2 3 325 3.5 3.18 0.0270 0.238 0.0306 0.244 0.0239 0.233 3 2 6 360 7 2.49 0.0270 0.337 0.0306 0.346 0.0239 0.329 4 2 5 490 2 4.03 0.0270 0.197 0.0306 0.202 0.0239 0.192 5 3 7 390 2 3.58 0.0270 0.193 0.0306 0.198 0.0239 0.188 6 6 10 320 2.5 5.54 0.0270 0.186 0.0306 0.191 0.0239 0.181 7 6 9 380 3 2.54 0.0270 0.242 0.0306 0.248 0.0239 0.236 8 1 4 500 4.5 3.85 0.0270 0.276 0.0306 0.284 0.0239 0.270 9 4 8 400 2.5 7.00 0.0270 0.185 0.0306 0.190 0.0239 0.181

International Research Journal of Engineering and Technology (IRJET) eISSN:23950056

Volume:09Issue:06|Jun2022 www.irjet.net pISSN:23950072

9. RESULT AND DISCUSSION:

9.1ComparisonofFrictionFactorWithoutRoughness:

SR. NO EQUATIO N NAME

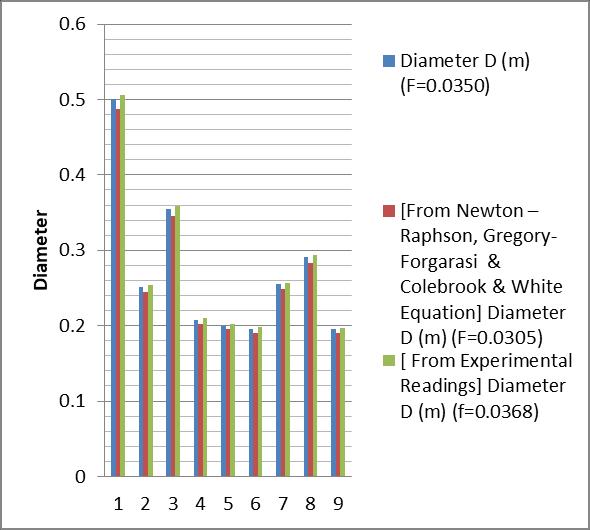
9.3ComparisonofDiameterObtainedDifferentFriction Factor:

ForPipe1:

1 Darcy Weisbach equation:

2 Hagen Poiseuille equation:

For Pipe 1 [ Diameter = 0.022 m ]

Percent age Deviati on

For Pipe 2 [ Diameter = 0.016 m ]

Perce ntage Devia tion FRICTIPO N FACTOR, “f”

FRICTIPO N FACTOR, “f”

0.02744 0% 0.0258 0%

0.02744 0% 0.0258 0%

3 Blasius Equation: 0.02744 0% 0.0258 0%

4 Prandtl equation: 0.02670 2.6% 0.0251 2.7%

5 Nikuradse equation: 0.02673 2.5% 0.0252 2.3%

From following result it shows that the friction factor obtained by empirical equations without roughness are approximatelysameonly2% 3% deviationhappensinthe resultforbothPipe1andPipe2.

9.2.ComparisonOfFrictionFactorWithRoughness:

Sr No Equations Name For Pipe 1 [Diamete r = 0.022 m ]

1. Newton Raphson Equation:

2. Gregory Forgarasi Equation:

3. Colebrook &White Equation:

[ From Moody’s Chart] [From Empirical Equation]

Diameter D(m) (f=0.0270)

Diameter D(m) (f=0.0306)

[From Experimental Readings]

Diameter D(m) (f=0.0239)

0.475 0.488 0.464 0.238 0.244 0.233 0.337 0.346 0.329 0.197 0.202 0.192 0.193 0.198 0.188 0.186 0.191 0.181 0.242 0.248 0.236 0.276 0.284 0.270 0.185 0.190 0.181

Percen tage Deviati on

For Pipe 1 [ Diameter = 0.016 m ]

Percenta ge Deviatio n Stainless SteelPipe Stainless SteelPipe

0.0305 0% 0.0307 0%

0.0305 0% 0.0306 0.3%

0.0304 0.3% 0.0307 0%

From following result it shows that the friction factor obtained by empirical equations with roughness are approximately same only 0. 3% deviation happens in the result for Newton Raphson Equation, Gregory Forgarasi Equation, Colebrook& WhiteEquation in bothPipe1 and Pipe2.ForNikuradaseandJainequationthedeviationinthe resultistoomuchsotheywillbeavoidedforthecalculation ofdiameterinfurthernetwork.

International Research Journal of Engineering and Technology (IRJET)

eISSN:23950056

ForPipe2:

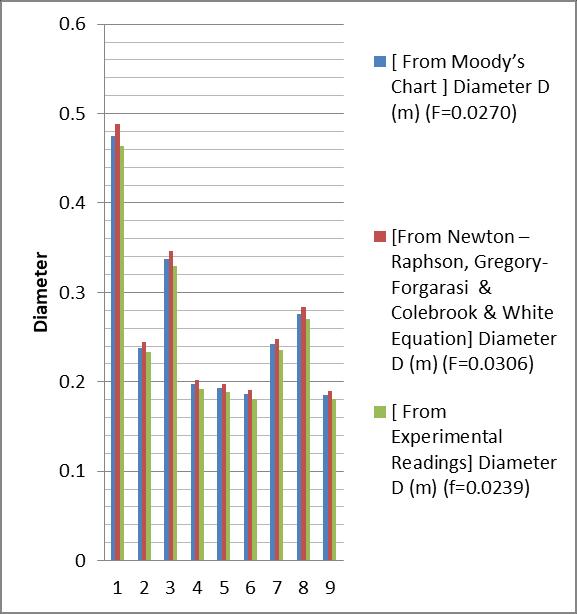
[ From Moody’s Chart]

Diameter D(m) (f=0.0270)

[From Empirical Equation]

Diameter D(m) (f=0.0306)

[From Experimental Readings]

Diameter D(m) (f=0.0239)

0.475 0.488 0.464

0.238 0.244 0.233

0.337 0.346 0.329

0.197 0.202 0.192

0.193 0.198 0.188

0.186 0.191 0.181

0.242 0.248 0.236

0.276 0.284 0.270

0.185 0.190 0.181

2. The deviation in friction factor is for smooth pipes observed in the range of 2 to 3 % by considering various empiricalequations.

3.Thedeviationinfrictionfactorisforroughpipesobserved in the range of 0.2 to 0.3 % considering various empirical equations.

4. If the diameter of pipe increases the friction factor increase.

5. The friction factor obtained by various empirical equationsisveryclosetotheexperimentalresult.

6.TheFrictionfactorobtainedbyallempiricalequationis almostsame.

7.Astheroughnessofthepipematerialincreasesthefriction factorofthepipeisalsoincreases.

8.ThefrictionfactorobtainedforRustedpipeandCastIron Pipeismoreascomparedtothestainlesssteelpipe.

9. Plastic Pipe has lowest friction factor and relative roughnessascomparedtotheotherpipesconsidered.

10. CONCLUSION:

Bystudyingall the empirical equationsitisobservedthat thefrictionfactorobtainedbyusingallequationisveryclose to each other, therefore any equation can be used for the determinationoffrictionfactor.

However the friction factor calculated by using Moody's Chart and Darcy Wiesbach equation is match with the Experimentation.

The diameter obtained by Darcy Wiesbach equation is optimalandhenceitisrecommendedthatDarcy Wiesbach equation must be used for the determination of friction factor.

11.

REFERENCE:

https://www.iosrjournals.org/iosr jmce/papers/vol16 issue2/Series 4/H1602046368.pdf

https://www.mdpi.com/2073 4441/12/3/844/pdf

https://www.researchgate.net/publication/237433 625_A_research_on_determining_the_friction_losses _formed_in_the_small_diameter_floppy_polythene_pi pe_lines

DISCUSSION:

1. It is observed that friction factor increases as the roughnessofpipeisconsidered.

https://www.researchgate.net/publication/273311 775_Friction_Losses_in_Large Diameter_Pipes

https://www.ijstr.org/final

Volume:09Issue:06|Jun2022 www.irjet.net pISSN:23950072 © 2022, IRJET | Impact Factor value: 7.529 | ISO 9001:2008 Certified Journal | Page1151

International Research Journal of Engineering and Technology (IRJET)

eISSN:23950056

Volume:09Issue:06|Jun2022 www.irjet.net pISSN:23950072

print/oct2015/Evaluation Of Friction Losses In Pipes And Fittings Of Process Engineering Plants.pdf 

https://www.researchgate.net/publication/273311 775_Friction_Losses_in_Large Diameter_Pipes  https://www.ijsr.net/archive/v8i6/ART20198900. pdf  http://scientiairanica.sharif.edu/article_2582_3366 444960992fa738c55d6e2118a7a4.pdf  https://www.sciencedirect.com/science/article/pii /S1877705816319713 

https://www.ijert.org/research/investigations on energy losses in pipelines IJERTV2IS90208.pdf  https://reader.elsevier.com/reader/sd/pii/S11100 16818302278?token=6F9363F2DFB0C43217D25F 170F9DE103905DE2C0012AB473E716C7C5FB43C D1FF6F7B054F0CD6209927ED521246234D7&orig inRegion=eu west 1&originCreation=20220223031055 

https://www.researchgate.net/publication/333936 052_Fracture_pressure_analysis_and_perforation_de sign  http://https://www.researchgate.net/publication/ 229533770_Fluid_Flow_through_90_Degree_Bends 

https://www.ukessays.com/essays/engineering/fri ctional pressure losses in pipes.php 

https://www.researchgate.net/publication/263690 27_Friction_losses_in_valves_and_fittings_for_power law_fluids 

https://www.ijstr.org/final print/oct2015/Evaluation Of Friction Losses In Pipes And Fittings Of Process Engineering Plants.pdf 

http://downloads.hindawi.com/journals/tswj/201 9/8640893.pdf 

https://journalijcar.org/issues/theoretical and experimental comparison losses piping systems using similar more complex 

https://www.e3s conferences.org/articles/e3sconf/pdf/2021/56/e3 sconf_icsf2021_10009.pdf 

r

https://www.researchgate.net/publication/228806 746_Evaluation_of_energy_losses_in_pipes#:~:text= Energy%20losses%20in%20pipes%20used,the%2 0direction%20of%20the%20flow









https://www.sciencedirect.com/science/article/pii /S2352854016300754





https://www.trp.org.in/wp content/uploads/2019/04/TARCE Vol.8 No.1 January June 2019 pp. 1 8.pdf