Latent Factor Model For Collaborative Filtering

International Research Journal of Engineering and Technology (IRJET) e ISSN:2395 0056

Volume: 09 Issue: 05 | May 2022 www.irjet.net p ISSN:2395 0072

Latent Factor Model For Collaborative Filtering

Naveen Kumar Kateghar1

1B.Tech,Computer Science and Engineering, TKR college of Engineering and Technology, Telangana, India ***

Abstract - The restrictions of neighborhood based Collaborative Filtering (CF) methods including scalability and inadequate information present impediments to efficient recommendation systems. These strategies result in less precision, accuracy and consume a huge amount of time in recommending items. Model based matrix factorization is an effective approach used to overcome the previously mentioned limitations of CF. In this paper, we are going to discuss a matrix factorization technique called singular value decomposition, which would help us model our recommendationsystemandresultingoodperformance.

Key Words: Recommendation systems, Collaborative Filtering, Matrix factorization, Latent Factors, Singular valuedecomposition

1. INTRODUCTION

Arecommendersystem,alsoknownasarecommendation engine or platform, is a type of information filtering system that attempts to forecast a user's "rating" or "preference" for an item.These algorithms are used to recommend products to online customers in online advertising,ottande commerceplatforms.Whenyoulook at a product on an e commerce site, the recommender system may offer additional products that are similar to theoneyou'relookingat.Ingeneral,therearetwosortsof recommendation system approaches, content based and collaborativefilteringbasedsystems.

1.1 Content Based Recommendation

The content filtering approach creates a profile for each user or product to characterize its nature. For example, a movie profilecould include attributes regardingits genre, the participating actors, its box office popularity, and so forth.Userprofilesmightincludedemographicinformation or answers provided on a suitable questionnaire. The profile allows us to associate users with matching products. Of course, content based strategies require gatheringexternalinformationthatmightnotbeavailable oreasytocollect.

1.2 Collaborative Filtering

The limitation of content based recommendation systems incollectingvariousattributesandcharacteristicsofusers and items is addressed by collaborative filtering. This method attempts to account for interactions between

users and items. There are two different kinds of collaborativefilteringsystems.

(i) Neighborhood/Memory Based: This method takes into account a user item matrix including user ratings on items and calculates the similarity between user user or item item. To suggest items to a user using a user user similarity based strategy, the system detects users who are similar to the target user and recommends items that are rated highly by those users. Because user interests vary over time, this strategy does not work in real world circumstances. An item item based system tries to recommendanitemtoauserbasedonpreviousitemsthat theuserliked.Sparsityisoneoftheprimaryconcernswith this technique. Because the user item matrix is sparse, computingsimilaritieswouldbeinaccurate.

(ii) Model Based: The model based approach intends to build a recommender system using machine learning techniques and poses the recommendation system as an optimization problem , where the algorithm learns the parameters to best predict the ratings . This way, wecan overcome the problems faced by memory based techniques.

Fig -1:User UservsItem ItemModel

2. LATENT FACTOR MODEL

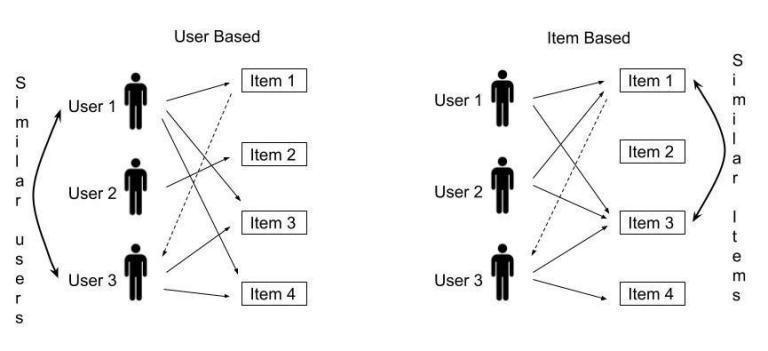
The Latent Factor model explains the ratings by characterizing both items and users according to many factors inferred from the rating pattern. This method representstheuseranditemprofilesink dimensionspace .This is known as the k rank approximation of a matrix. Although this method is highly inspired by Singular Value Decomposition (SVD) , we approach it by formulating a minimization problem because SVD is not defined when thematrixhasmissingvalues.

International Research Journal of Engineering and Technology (IRJET) e ISSN:2395 0056

Volume: 09 Issue: 05 | May 2022 www.irjet.net p ISSN:2395 0072

2.1 Eigenvalue Decomposition

Eigenvaluedecomposition(EVD)isamethodofbreakinga square matrix into its components. factorization of a matrix. Itcan be thought of asananalogyfor factoring an integer.

EVD states that every square matrix Anxn can be decomposedasproductofthreematricesnamely U Λ U 1 where U is a matrix containing eigenvectors of A as its columns and Λ is diagonal matrix containing eigenvalues ofAasitselements.

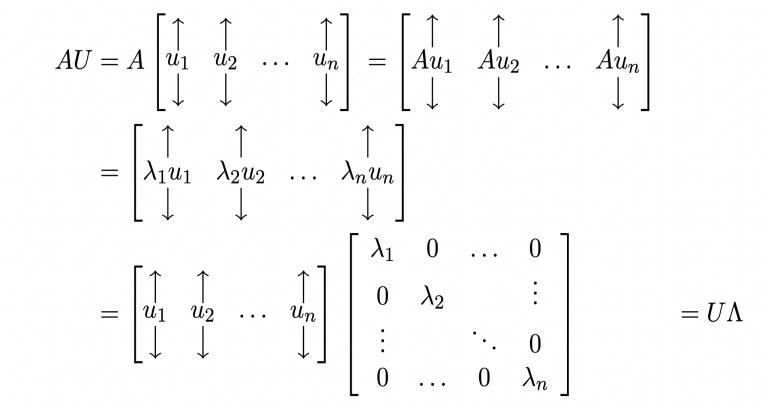
Letu1,u2,...,unbetheeigenvectorsofamatrixAandlet λ1,λ2,...,λnbethecorrespondingeigenvalues.Consider amatrixUwhosecolumnsareu1,u2,...,un.

BydefinitionofEigenvectorswecanwrite, Aui =λiui ∀1≤i≤n AU=UΛ

Now,If U 1 exists,thenwecanwrite, AUU 1 = UΛU 1

A = UΛU 1 (∵ U 1U = I) [eigenvalue decomposition] and

U 1AU = U 1UΛ U 1AU=Λ(∵U 1U=I)[diagonalizationofA]

Note that U 1 only exists if the columns of U are linearly independent and since the U contains eigenvectors corresponding to different eigenvalues of A, they are linearlyindependent.

Furthermore,ifthematrix A issymmetricandthecolumns ofUarenormalizedtounitlengthwecaneasilyprovethat , U TU=I ( I isanidentitymatrix) thismeansthat UT=U 1 andtheEVDofAcanberewritten as,

A = U Λ UT

2.2 Singular Value Decomposition

One of the major limitations of Eigenvalue decomposition includes that EVD exists only for a square matrix because eigenvalues aren't defined for rectangular matrices, so EVDforanon squareorrectangularmatrixdoesnotexist. Singular Value Decomposition(SVD) overcomes this problem and provides a decomposition ofanymatrixinto itscomponents.

Notethatwewereabletodecomposeamatrix becauseof this equation, Aui = λiui. This gave us an Eigenvalue decompositionforasquarematrix.Intheearlierscenario, while we were dealing with square matrices we selected u1, u2, . . . ,un to be eigenvectors and also note that they also form a basis for the space Rn . Since we are dealing with rectangular matrices , they perform linear transformations betweentwodifferent spaces.

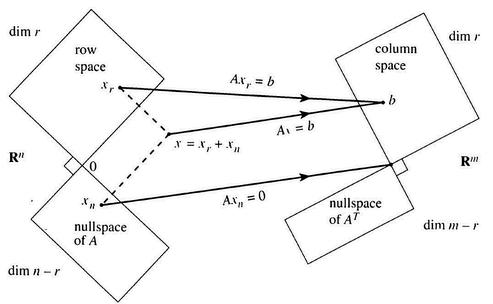
Let Amxn isamatrixwhichperformstransformationsfrom n dimensionspacetom dimensionspaceandletv1,v2,.,vr ,.,vn bethebasisofinputspacei.e., Rn and u1,u2,.,ur ,., um bethe basisofoutput spacei.e., Rm.Now our goal is to findthesebasissuchthat,

Avi = σiui

We have to select first r vi’s such that it spans the row space of A and is also orthogonal (where r is the rank of matrix A). We then have to select the remaining n r vi’s suchthattheyspanthenullspaceofA.Sincethenullspace of A is orthogonal to the row space of A, the vi’s we selectedwouldactasabasisforthe Rn Nowfor1≤i≤k defineui tobeaunitvectorparalleltoAvi andextendthis basissuchthatitspanstheleftnullspacei.e.,nullspaceof AT.SincenullspaceofAT isorthogonaltothecolumnspace of A,theui’sweselectedwouldactasabasisforthe Rm .

Fig 2:Strangdiagramoffourfundamentalsubspaces

2022, IRJET | Impact Factor value: 7.529 | ISO 9001:2008 Certified Journal

International Research Journal of Engineering and Technology (IRJET) e ISSN:2395 0056

Volume: 09 Issue: 05 | May 2022 www.irjet.net p ISSN:2395 0072

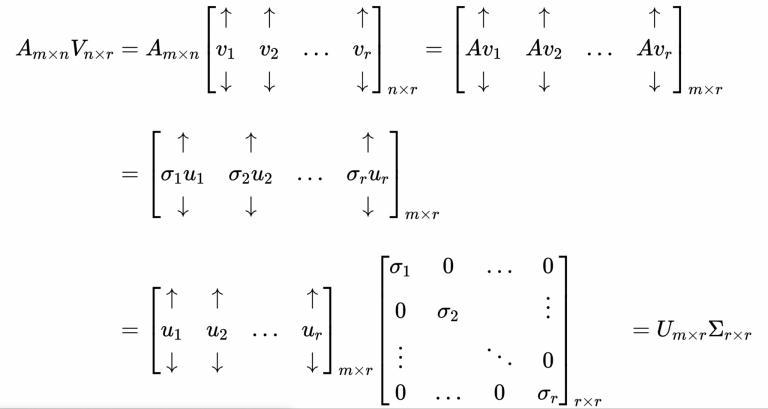
Now let's see what would be our matrix decomposition after selecting such a basis . Let Umxr be a matrix containing u1,u2,...,ur asitscolumnswhereui isthebasis vectorin Rm and Vnxr isamatrixcontaining v1,v2,...,vr as its columns where vi is the basis vector in Rn Σ is a diagonalmatrixwiththesingularvalues. weknowthat Avi = σiui so, AmxnVnxr = Umxr Σ rxr

WecanextendthematricesUandVfromnxrandmxr tonxnandmxmrespectivelybyputtingintheremaining n randm rbasisvectors.

Hence,theequationbecomes, AmxnVnxn = Umxm Σ mxn

ObservethatthematrixΣdimensionsnowwouldbemxn wherein the last m r rows and n r columns would be zeros.

Now, AmxnVnxn V 1 nxn= Umxm Σ mxn V 1 nxn

Let's assume matrix V’s columns are normalized to unit lengthand,sinceweknowUandVareorthogonal(bythe waywe haveconstructedUandV).

Amxn = Umxm Σ mxn V 1 nxn ( ∵VV 1 =I) Amxn = Umxm Σ mxn VT nxn ( ∵V 1 =VT)

Hence,theSVDdecompositionof anymatrixA=UΣ VT Till now, we have discussed how to select a basis so that Avi =σiui ,andwhatdecompositionwouldweget ifsucha

basiswereselected.Nowlet'sseehowtoactuallycompute U,VandΣ.

weknowthat A=UΣ VT .so,

ATA = (UΣ VT)T UΣ VT = V ΣT UT U Σ VT ∵ (AB)T = BT AT = VΣ2VT ∵ UTU=I

ThisistheeigenvaluedecompositionofATA.Thus,matrix V contains the eigenvectors of ATA. Similarly, AAT= UΣ2UT , thus matrix U contains the eigenvectors of AAT . We know that AAT is a square symmetric matrix hence, ATAandAAT havethe sameeigenvalues.Therefore,Σis a diagonalmatrixwithitselementsas √λi whereeach λi istheeigenvalueofATA/AAT .

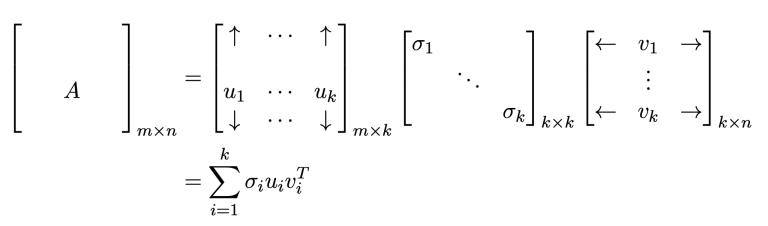
We can formulate the singular value decomposition of a matrixAinbelowmanner,

We order decomposition in such a way that σ1 ≥ σ2 ≥ …≥ σk. we can prove that σ1u1v1T is a rank 1 matrix and σ1u1v1T will be the best rank 1 approximation of the original matrix A because σ1 is the largest σ and it correspondstothelargestσiuiviT term.Hence,bestrank 1 approximation. Similarly, ∑ σiuiviT is the best rank k approximationofmatrixA.

3. IMPLEMENTATION

The way we have defined the SVD of a matrix, we realize that the SVD is not defined if the matrix does not contain any value. In real world scenarios, the user item matrix, wherein the rows represent the ratings of a user on various items and the columns represent the ratings of various users on an item, is largely sparse. Hence, we cannot perform SVD on the user item matrix. Hence, we change our approach and try to formulate a minimization problemandfindtheoptimalsolutiontoit.

3.1 Formulating Optimization Problem

Let Am x n be the user item rating matrix . We know that this matrix can be decomposed into Umxk VTnxk (∵Σ can be interpreted as a scalar on the U matrix i.e, UΣ = U) where U contains the basis for rows of the user item matrixi.eTheusers(rows)canbeformedbythematrix U

© 2022, IRJET | Impact Factor value: 7.529 | ISO 9001:2008 Certified Journal | Page 3160

International Research Journal of Engineering and Technology (IRJET) e ISSN:2395 0056

andsimilarlyVcontainsthebasisforcolumnsoftheuser item matrix i.e., the items(columns) can be formed by the matrixV. ∴A≈UmxkVTnxk

Now,eachrating rij ofmatrixAcanbecomputedas, rij ≈ ∑ uikvTjk

bias)comparedtoothermovies,andtheaveragedeviation ofauser'srating(userbias)comparedtootherusers.This part allows us to capture various aspects of the data, whichimprovestheperformanceofourmodel.

The predicted rating of a user i on movie j can be computedas, rij ≈μ+bi+cj+ ∑ uikvTjk

Where K is the dimension of latent factors in which we wantourdecompositiontoberepresented.

Our objective is to minimize the sum of squared errors between known ratings in the matrix and computed ratingsfortheseratings.i.e.,

where, μ=averageratingofallusersonallitems. bi =standarddeviationofui cj = standarddeviationofvjT

Wecancalculateμdirectlyfromthematrixandinclude bi ,cj into the optimization equation and learn from the data.Themodifiedequationwouldbe,

where rij is the actual rating of the user i on item j and uikvTjk isthecomputedorpredictedratingfortheuserion itemj.IntheaboveequationX,isthesetofknownratings. This means we only perform the summation over the known ratings.We want to find such ui ‘s and vj ‘s that minimizetheabovefunction.

We have overcome the problem of sparsity with this approach as we are iterating only through the known ratings of the user item matrix. Now since we know that there would be only a few such cells in the matrix where ratings are present, this leads to overfitting, i.e., if we optimize for the above equation, we won’t be able to generalize the predicted ratings for unknown data. To solve this limitation, we introduce regularization. This allowsusnottomaketheparametersoftheminimization equationcomplex,whichleadstooverfitting.

Themodifiedoptimizationequationwouldbe, Here, λistheregularizationstrength,whichcontrolsthe trade off between underfitting and overfitting , we can estimate this variable using techniques like cross validationetc.,

Finally, we can also account for global effects. This includes the average rating of the entire user item rating matrix, the average deviation of a movie’s rating (movie

This is the final problem formulation. In the next section, we’llseehowtosolvefortheequationparameters.

3.2 Solving Optimization Problem

To solve the optimization problem in the above section, wecanchooseanyvariantofgradientdescentalgorithms. In our case, we are going to implement the Stochastic GradientDescentversionasitperforms betterandisalso time efficient. I am going to demonstrate implementation inpython.

ThealgorithmforSGDisgivenas:

Fig 3:SGDAlgorithm

Volume: 09 Issue: 05 | May 2022 www.irjet.net p ISSN:2395 0072 © 2022, IRJET | Impact Factor value: 7.529 | ISO 9001:2008 Certified Journal |

The dataset is being collected here . It contains a large numberofdatapointsof26millionusersandratings(ona scale of 5) of each user on movies. Only 100K data points are being considered for demonstration purposes. Here is asampleofthedataset.

International Research Journal of Engineering and Technology (IRJET) e ISSN:2395 0056

Volume: 09 Issue: 05 | May 2022 www.irjet.net p ISSN:2395 0072

Fig 4:SampleData

We would split the complete dataset into train and test sets so as to measure the goodness of our recommendationsystem.

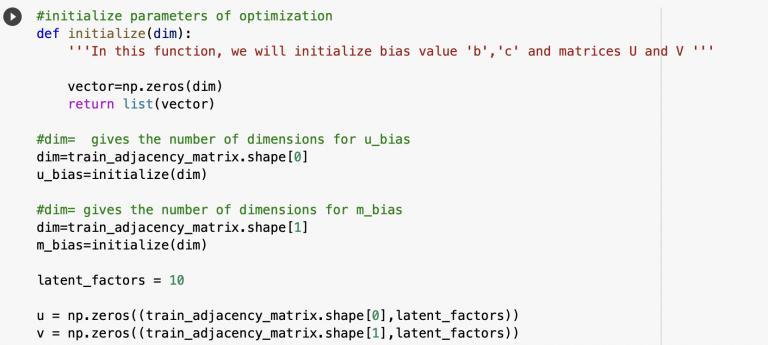
The first step is to initialize the parameters of the minimization equation and decide on the dimension of latentfactors.

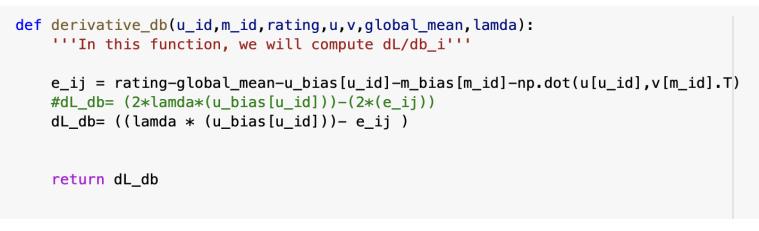
Fig 7: Derivativeofmininizationeqnw.r.tuservector

Fig 5:Codeforinitializingparameters

In the above piece of code, train_adjacency_matrix is the user moviematrixformedfromthetraindataset.

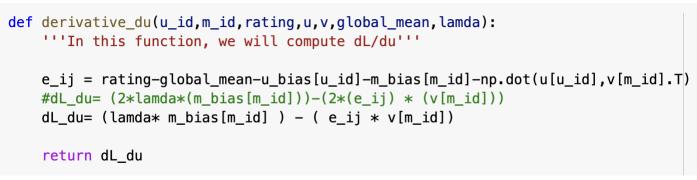
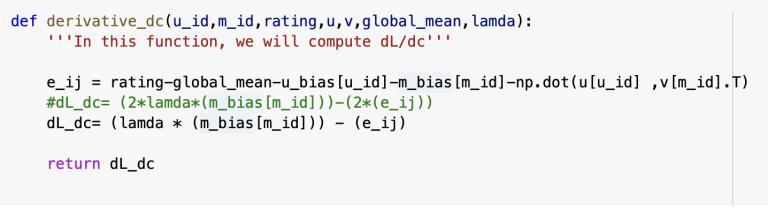
Next, we will calculate the derivative of the minimization equation w.r.t u_bias (user bias), m_bias (movie bias), ui (user i’s row in matrix U) and vj (movie j’s row in matrix VT).

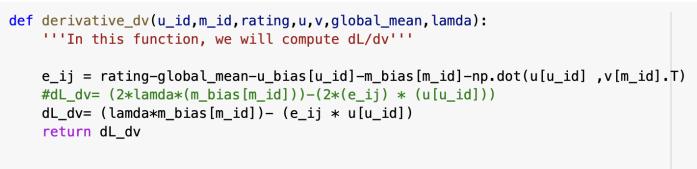
Fig 8: Derivativeofmininizationeqnw.r.t

movievector

Following that, we define values for alpha (learning rate), reg_strength (regularization strength), and the number of epochs for converging the minimization equation, and we run stochastic gradient descent training on our train dataset, calculating the test and train MSE (mean squared error),whichistheevaluationcriterionforgoodnessoffit.

After iterating for all the epochs, we get the final best parametersoftheequation,whichareb,c,U,andV.

Fig 5:Derivativeofmininizationeqnw.r.tuserbias

Fig 6:Derivativeofmininizationeqnw.r.tmoviebias

Fig 9:TrainingSGDonourdata

International Research Journal of Engineering and Technology (IRJET) e ISSN:2395 0056

Volume: 09 Issue: 05 | May 2022 www.irjet.net p ISSN:2395 0072

4. RESULT ANALYSIS

Resultsforeachepochare:

Fig 10:Resultsoneachepoch

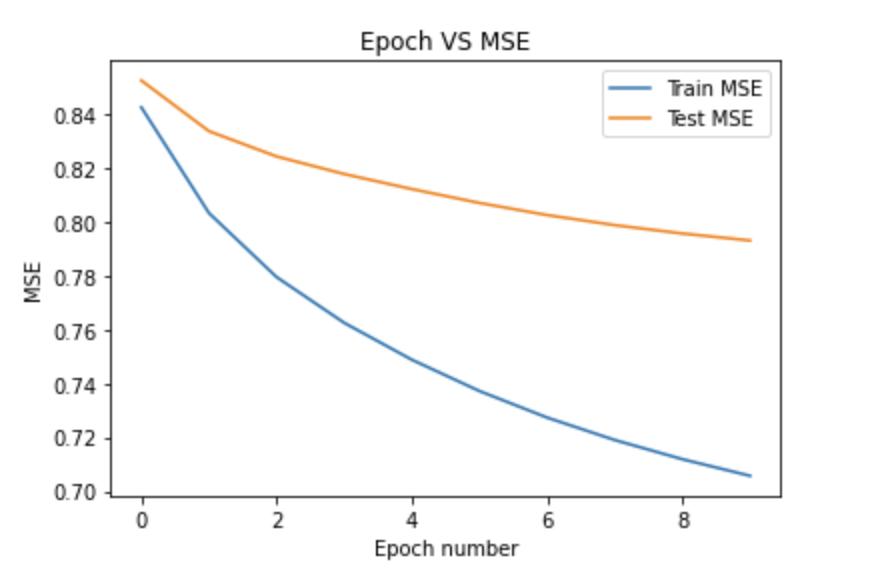
Observe that the MSE for the last epoch is 0.74, which means, on an average, we are mistaken by 0.74 in predictingratingsforunknownuser itempairs.

We were still able to achieve a good MSE for random selections of various parameters. We can use more techniqueslikecross validationtoselectthebestlearning rate, regularization parameter, and also the number of latentfactors.Therearealsomanyadvancedconvergence algorithms like AdaGrad, Adam Optimizer, etc. Since we have initialized all the parameters of the equation with zeros, we could be more mindful and use better initializationstrategies.

GivenbelowisthegraphwhichdepictsthechangeinMSE withanincreaseinthenumberofepochs.Thisgivesusan ideaofwhetherourmodelisoverfittingorunderfitting.If the train error is decreasing while the test error is increasingwithanincrease inthenumberofepochs,then themodelissaidtobeoverfitted.Ifboththetrainandtest errorsincreasewithanincreaseinthe numberofepochs, then the model is said to be underfitted. In our case, both theabovescenariosdonotseemtooccur,soourmodel is abletogeneralizethepredictionsmadeonratings.

Fig -11:TrainandTestErrorVSNumberofepochs

5. CONCLUSION

In this paper , we have discussed the theory of latent factor models which uses matrix factorization techniques and also practically implemented the truncated svd method for matrix factorization. We have also briefly discussed various types of recommender systems present and the limitations faced by them. Latent factor model is matrix factorization technique in which the model finds the relationships between the user and an item by representing the user and item vectors in latent dimensions. This technique employed recommendation system overcomes many limitations such as sparsity, scalability,computationtime,memoryetc,.

REFERENCES

[1] SandeepKumarRaghuwanshi,RajeshKumarPateriya, Accelerated Singular Value Decomposition (ASVD) using momentum based Gradient Descent Optimization, https://doi.org/10.1016/j.jksuci.2018.03.012 (https://www.sciencedirect.com/science/article/pii/ S1319157818300636)

[2] DanKalman.TheAmericanUniversityWashington,DC 20016,”ASingularlyValuableDecomposition:TheSVD of Matrix” (https://www users.cse.umn.edu/~lerman/math5467/svd.pdf)

[3] Nicolas Hug , “Understanding matrix factorization for recommendation” (http://nicolas hug.com/blog/matrix_facto_1)

[4] Yehuda Koren, Yahoo Research“ MATRIX FACTORIZATION TECHNIQUES FOR RECOMMENDER SYSTEMS”

[5] (https://datajobs.com/data science repo/Recommender Systems %5BNetflix%5D.pdf)

International Research Journal of Engineering and Technology (IRJET) e ISSN:2395 0056

Volume: 09 Issue: 05 | May 2022 www.irjet.net p ISSN:2395 0072

[6] https://en.wikipedia.org/wiki/Stochastic_gradient_de scent

[7] https://en.wikipedia.org/wiki/Recommender_system

[8] Aggarwal, C.C., 2016. Model based collaborative filtering. In: Recommender Systems, Springer International Publishing, Cham, pp. 71 138. https://doi.org/10.1007/978 3 319 29659 3_3.

[9] Bell, R., Koren, Y., Volinsky, C., 2007. Modeling relationshipsatmultiplescalestoimproveaccuracyof large recommender systems. In: Proc. 13th ACM SIGKDD Int. Conf. Knowl. Discov. data Min. KDD ’07 95.https://doi.org/10.1145/1281192.1281206.

[10] Koren, Y., Bell, R., Volinsky, C., 2009. Matrix factorization techniques for recommender systems. Computer (Long. Beach. Calif). 42, 30 37. https://doi.org/10.1109/MC.2009.263.

[11] Gilbert Strang, Linear Algebra and its Applications, 2ndedition,AcademicPress,NewYork,1980.

BIOGRAPHIES

K.NaveenKumar B.Tech,CSE TKR College Of Engineering and Technology